Title: Istitutioni harmoniche
Author: Gioseffo Zarlino
Publication: Francesco de' Franceschi (Venezia, 1589)
Principal editor: Frans Wiering
Funder: Utrecht University Netherlands Organization for Scientific Research (NWO)
Edition: 2000
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht NetherlandsΚαὶ καμάτῳ ἀκαματῳ ἅμα εὔξησα,
Εὐνόῳ νῆν νόῳ, καὶ ὁδῳ εὐόδῳ ἐδιδαξα.

Καὶ μὴ διδόντος, ὀυδὲν ἰσχύι πόνος.IN VENETIA, MDLXXXIX. Appresso Francesco de' Franceschi Senese.page ii
Tauola del contenente de tutte l'Opere diuise in Quattro volumi,
| IL PRIMO DE I QVALI CONTIENE, | L'Istitutioni Harmoniche diuise in Quattro parti, |
| IL SECONDO, | Le Dimostrationi Harmoniche, contenute da Cinque Dialoghi, |
| IL TERZO, | I Sopplimenti Musicali, partiti in Otto Libri; & |
| IL QVARTO, |
|

ALL'ILLVSTRISSIMO ET REVER.MO SIG. VINCENZO DIEDO PATRIARCA DI VENETIA.
Di V.S. Illustrissima & Reuerendissima Seruitore affettionatissimo Gioseffo Zarlino.
page v
TAVOLA PRIMA DI TVTTE LE MATERIE PRINCIPALI, CHE SONO CONTENVTE NELL'OPERA.
| IL Proemio, nel quale si dimostra, in qual maniera la Musica habbia hauuto principio, & come sia stata accresciuta; & si ragiona della diuisione dell'Ope-ra. | Facciata 1. | |
| Dell'origine, & certezza della Musica. | cap. 1. | fac. 5 |
| Delle laudi della Musica. | cap. 2. | fac. 7 |
| A che fine la Musica si debba imparare. | cap. 3. | 11 |
| Dell'vtile, che si hà della Musica, & dello studio, che vi dobbiamo porre, & in qual modo vsarla. | cap. 4. | 12 |
| Quello che sia Musica in vniuersale, & della sua diuisione. | cap. 5. | 14 |
| Della Musica mondana. | cap. 6. | 16 |
| Della Musica humana. | cap. 7. | 21 |
| Della Musica piana, & misurata, ò vogliamo dir Canto fermo, & figurato. | cap. 8. | 24 |
| Della Musica Rhythmica, & della Metrica. | cap. 9. | 24 |
| Quello che sia Musica in particolare, & perche sia cosi detta. | cap. 10. | 25 |
| Diuisione della Musica in Speculatina, ò Contemplatiua, & in Prattica; per la quale si pone la dif-ferenza tra 'l Musico, & il Cantore. | cap. 11. | 26 |
| Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità è Nume-ro. | cap. 12. | 27 |
| Delle varie specie de' Numeri; & che nel Senario si trouano le Forme de tutte le Consonanze semplici. | cap. 13. | 29 |
| Che dal numero Senario si comprendono molte cose della Natura, & dell'Arte. | cap. 14. | 30 |
| Delle Proprietà del numero Senario, & delle sue parti; & come tra loro si ritroua la Forma d'ogni Consonanza musicale. | cap. 15. | 32 |
| Quel che sia Consonanza semplice, ò Composta; & che nel Senario in potenza si ritrouano le forme di tutte le Consonanze; & onde habbia origine l'Hexachordo minore. | cap. 16. | 34 |
| Della Quantità continoua, & della discreta. | cap. 17. | 35 |
| Del Soggetto della Musica. | cap. 18. | 36 |
| Quel che sia Numero sonoro. | cap. 19. | 37 |
| Per qual cagione la Musica sia detta Subalternata all'Arithmetica, & mezana tra la Mathematica, & la Naturale. | cap. 20. | 39 |
| Quel che sia Proportione: & della sua diuisione. | cap. 21. | 39 |
| In quanti modi si compara l'vna quantità all'altra. | cap. 22. | 41 |
| Quel che sia Parte aliquota, & Nonaliquota. | cap. 23. | 41 |
| Della produttione del genere Molteplice. | cap. 24. | 42 |
| Quel che sia Denominatore; & in qual modo si troui; & come di due proposte proportioni si possa conoscere qual sia la maggiore, ò la minore. | cap. 25. | 43 |
| Come nasca il genere Superparticolare. | cap. 26. | 45 |
| Della produttione del genere Superpa tiente [sic: Superpatiente]. | cap. 27. | 45 |
| Del genere Molteplice Superparticolare. | cap. 28. | 46 |
| Della produttione del Quinto & vltimo genere, detto Molteplice superpatiente. | cap. 29. | 47 |
| Della Natura, & proprietà de i sopranominati Generi. | cap. 30. | 48 |
| Del primo modo di moltiplicar le Proportioni. | cap. 31. | 51 |
| Il Secondo modo di moltiplicar le Proportioni. | cap. 32. | 53 |
| Del Sommare le Proportioni. | cap. 33. | 54 |
| Del Sottrar le Proportioni. | cap. 34. | 54 |
| Del Partire, ò Diuidere le Proportioni, & quello che sia Proportionalità. | cap. 35. | 56 |
| Della Proportionalità, ò diuisione Arithmetica. | cap. 36. | 57page vi |
| Della Diuisione, ò Proportionalità Geometrica. | cap. 37. | 58 |
| In qual modo si possa cauare la Radice quadrata da vn proposto numero. | cap. 38. | 60 |
| Della diuisione, ouero Proportionalità harmonica. | cap. 39. | 61 |
| Consideratione sopra quello, che si è detto intorno alle Proportioni, & proportionalità. | c. 40. | 62 |
| Che il Numero non è cagione propinqua, & intrinseca delle Proportioni musicali, nè meno delle Consonanze; & quali siano le quattro cagioni, Finale, Efficiente, Materiale, & Formale nella Musica. | cap. 41. | 66 |
| Della inuentione delle Radici delle proportioni. | cap. 42. | 68 |
| In che modo si possa ritrouar la Radice di più proportioni moltiplicate insieme | cap. 43. | 68 |
| Della proua di ciascheduna delle sopramostrate operationi. | cap. 44. | 69 |
| QVANTO la Musica sia stata da principio semplice, roza, & pouera di Consonan-ze. | cap. 1. | fac. 71 |
| Per qual cagione gli Antichi nelle loro Harmonie non vsassero le Consonanze imper-fette; & Pitagora vietaua il passare oltra la Quadrupla. | cap. 2. | 73 |
| Dubbio sopra la inuentione di Pitagora. | cap. 3. | 75 |
| Della Musica antica. | cap. 4. | 75 |
| Delle materie che recitauano gli Antichi nelle lor Canzoni, & di alcune Leggi musicali. | c. 5. | 79 |
| Quali siano stati gli Antichi Musici. | cap. 6. | 82 |
| Quali cose nella Musica habbiano possanza da indur l'Huomo in diuerse passioni. | cap. 7. | 86 |
| In qual modo l'Harmonia, & la Melodia, & il Numero possino muouer l'Animo, & disporlo à va-rij affetti; & indur nell'Huomo variati costumi. | cap. 8. | 89 |
| In qual genere di Melodia siano stati operati li narrati effetti. | cap. 9. | 92 |
| De i Suoni, & delle Voci, & in qual modo naschino. | cap. 10. | 94 |
| Da che nascono i suoni graui, & da che gli acuti. | cap. 11. | 96 |
| Quel che sia Consonanza, Dissonanza, Harmonia, & Melodia. | cap. 12. | 97 |
| Diuisione delle Voci. | cap. 13. | 99 |
| Quel che sia Canto, & Modulatione, & in quanti modi si possa cantare. | cap. 14. | 99 |
| Quel che sia Interuallo, & delle sue specie. | cap. 15. | 100 |
| Quel che sia Genere; & di tre generi di Melodia, ò Cantilena appresso gli Antichi; & delle loro specie. | cap. 16. | 101 |
| Per qual cagione ciascun de gli Interualli contenuto ne i mostrati Tetrachordi sia detto Incom-posto. | ca. 17. | 106 |
| In qual modo si possa accommodare alla sua proportione qual si voglia Consonanza, ouero Inter-uallo. | cap. 18. | 107 |
| Vn'altro modo di accommodar le Consonanze alla loro proportione. | cap. 19. | 109 |
| In qual modo si possa vdir qual si voglia Consonanza accommodata alla sua proportione. | c. 20. | 110 |
| Del primo modo di Moltiplicar le Consonanze. | cap. 21. | 111 |
| Del Secondo modo di moltiplicar le Consonanze. | cap. 22. | 112 |
| Come si possa diuidere rationalmente qual si voglia Consonanza, ò Interuallo. | cap. 23. | 114 |
| In qual modo si possa diuidere qual si voglia Interuallo musicale in due parti equali. | cap. 24. | 115 |
| Altro modo di diuider qual si voglia Consonanza, ouero Interuallo musicale in due, ouero in più parti equali. | cap. 25. | 116 |
| In qual modo la Consonanza si faccia diuisibile. | cap.26. | 118 |
| Quel che sia Monochordo; & perche sia cosi chiamato. | cap. 27. | 119 |
| Della Diuisione, ouero Ordinatione del Monochordo della prima specie del genere diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi fu l'Inuentore di questo Gene-re. & del suo ordine. | cap. 28. | 119 |
| Che gli Antichi attribuirono alcune chorde de i loro istrumenti alle Sphere celesti. | cap. 29. | 123 |
| In che modo le predette Sedici chorde siano state da i Latini denominate. | cap. 30. | 126 |
| Consideratione sopra la mostrata Diuisione, ouer ordinatione; & sopra l'altre specie del genere Diatonico ritrouate da Tolomeo. | cap. 31. | 128 |
| Del genere Chromatico; & chi sia stato il suo Inuentore; & in qual maniera lo potesse trouare; & delle chorde, che aggiunse Timotheo nel solito Istrumento. | cap. 32. | 132 |
| Diuisione del Monochordo Chromatico. | cap. 33. | 136 |
| Consideratione sopra la mostrata diuisione, & sopra alcune altre specie di questo genere, ritrouapage viite da Tolomeo. | cap. 34. | 138 |
| Chi sia stato l'Inuentore del genere Enharmonico, & in qual maniera l'habbia ritroua-to. | cap. 35. | 140 |
| Della Diuisione, ò Compositione del monochordo Enharmonico. | cap. 36. | 140 |
| Consideratione sopra la mostrata Partitione, ouero Compositione; & sopra quella specie di En-harmonico, che ritrouò Tolomeo. | cap. 37. | 142 |
| Della Compositione del Monochordo Diatonico diatono, inspessato dalle chorde Chromatiche & dalle Enharmoniche. | cap. 38. | 143 |
| Che 'l Diatonico Naturale, ò syntono di Tolomeo sia quello, che dalla Natura è prodotto, & che naturalmente habbia la sua forma da i Numeri harmonici. | cap. 39. | 146 |
| Della diuisione del Monochordo Naturale, ouer syntono Diatonico, fatta secondo la natura, & & [sic: &] proprietà de i Numeri sonori. | cap. 40. | 149. |
| Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle mostrate specie Diatoniche. | cap. 41. | 150 |
| Quel, che si dee osseruare nel temperamento de gli Instrumenti artificiali, di modo che nel numero delle chorde, & nella equalità de i Tuoni s'assimigli al Diatonico ditonico: ma ne gli Interualli consonanti; quantunque accidentali, al Naturale o Syntono di Tolomeo. | cap. 42. | 153 |
| Dimostratione, dalla quale si può comprendere, che la mostrata Partecipatione, ò Distributione sia ragioneuolmente fatta; & che per altro modo non si possa fare, che stia bene. | cap. 43. | 155 |
| Della compositione del Monochordo diatonico equalmente temperato nel primo modo. | c. 44. | 159 |
| Se nelle Canzoni seguitiamo cantando gli Interualli prodotti da i veri Numeri sonori numeri, ouero i temperati; & della risolutione d'alcuni dubbij. | cap. 45. | 164 |
| Della inspessatione del Monochordo Diatonico dalle chorde del genere Chromatico. | cap. 46. | 167 |
| In che maniera possiamo inspessare il detto Monochordo con le chorde Enharmoniche. | cap. 47. | 170 |
| Che più ragioneuole è dire, che gli Interualli minori nascano da i maggiori; che dire, che i mag-giori si compongano de i minori; & che meglio è ordinato l'Hexachordo moderno, che il Te-trachordo antico. | cap. 48. | 173 |
| Che ciascuno de i tre Generi nominati, si può dire Genere & Specie; & che ogn'altra Diuisione, ouer'Ordinatione de Suoni sia vana & inutile. | cap. 49. | 174 |
| Per qual cagione le Consonanze hanno maggiormente origine dalle Proportioni di maggio-re inequalità, che da quelle di minore. | cap. 50. | 176 |
| Dubbio sopra quello, che si è detto. | cap. 51. | 178 |
| QVEL che sia Contrapunto, & perche sia cosi nominato. | cap. 1. | fac. 180 |
| Dell'inuentione delle Chiaui & delle Figure cantabili. | cap. 2. | 181 |
| De gli Elementi, che compongono il Contrapunto. | cap. 3. | 183 |
| Diuisione delle mostrate specie. | cap. 4. | 185 |
| Se la Quarta è consonanza; & donde auiene, che i Musici non l'habbiano vsata, se non nelle com-positioni de più voci. | cap. 5. | 186 |
| Diuisione delle Consonanze nelle Perfette & Imperfette. | cap. 6. | 188 |
| Che la Quinta & la Quarta sono mezane tra le Consonanze perfette & l'imperfette. | cap. 7. | 189 |
| Quali Consonanze siano più piene, & quali più vaghe. | cap. 8. | 190 |
| Della differenza che si troua tra le consonanze Imperfette. | cap. 9. | 191 |
| Della propietà, ò natura delle consonanze Imperfette. | cap. 10. | 191 |
| Ragionamento particolare intorno all'Vnisono. | cap. 11. | 192 |
| Della Prima consonanza, detta Diapason, ouero Ottaua. | cap. 12. | 194 |
| Della Diapente, ouer Quinta. | cap. 13. | 195 |
| Della Diatessaron, ouer Quarta. | cap. 14. | 197 |
| Del Ditono, ouer Terza maggiore. | cap. 15. | 198 |
| Del Semiditono, ouer Terza minore. | cap. 16. | 198 |
| Dell'utile; che apportano nella Musica gli Interualli dissonanti. | cap. 17. | 199 |
| Del Tuono maggiore & del minore. | cap. 18. | 201 |
| Del Semituono maggiore & del minore. | cap. 19. | 201 |
| Dell'Hexachordo maggiore, ouero Sesta maggiore. | cap. 20. | 202 |
| Dell'Hexachordo minore, ouer Sesta minore. | cap. 21. | 203 |
| Della Diapente col Ditono, ouero della Settima maggiore. | cap. 22. | 204page viii |
| Della Diapente col Semiditono, ouero della Settima minore. | cap. 23. | 205 |
| In qual maniera naturalmente, ò per accidente, tali Interualli da i Prattici alle volte si pongano superflui, ò diminuti. | cap. 24. | 206 |
De gli effetti che fanno questi segni  . b. & . b. &  . .
|
cap. 25. | 209 |
| Quel che si ricerca in ogni Compositione; & prima del Soggetto. | cap. 26. | 210 |
| Che le Compositioni si debbono essentialmente comporre prima di Consonanze, & dopoi per accidente di Dissonanze. | cap. 27. | 212 |
| Che si debbe dar principio alle compositioni per vna delle consonanze perfette. | cap. 28. | 213 |
| Che non si debbe porre due Consonanze, contenute sotto vna istessa proportione, l'una dopo l'altra ascendendo, ouero discendendo, senza alcun mezo. | cap. 29. | 216 |
| Quando le parti della Cantilena hanno tra loro Harmonica relatione; & in qual modo potiamo vsare la Semidiapente & il Tritono nelle compositioni. | cap. 30. | 219 |
| Che rispetto si dè hauere à gli Interualli relati nelle compositioni di più voci. | cap. 31. | 222 |
| In qual maniera due, ò più Consonanze perfette, ouero imperfette, contenute sotto vna istessa forma, si possino porre immediatamente l'vna dopò l'altra. | cap. 32. | 224 |
| Che due, ò più Consonanze perfette, ouero imperfette, contenute sotto diuerse forme, poste l'vna immediatamente dopò l'altra, si concedono. | cap. 33. | 224 |
| Che dopò la Consonanza perfetta stà bene il porre la imperfetta; ouero per il contrario. | c. 34. | 225 |
| Che le parti della Cantilena debbono procedere per mouimenti contrarij. | cap. 35. | 226 |
| In qual maniera le parti della Cantilena possino insieme ascendere, ò discendere. | cap. 36. | 226 |
| Che si debbe schiuare, più che si può, i Mouimenti fatti per salto; & similmente le Distanze, che possono accascare tra le Parti della cantilena. | cap. 37. | 229 |
| In qual maniera si debba procedere da vna Consonanza ad vn'altra. | cap. 38. | 230 |
| In qual maniera si debba terminare ciascuna cantilena. | cap. 39. | 233 |
| Il modo, che si dè tenere nel far li Contrapunti semplici à due voci, chiamati di Nota contra nota. | cap. 40. | 234 |
| Che ne i Contrapunti si debbono schiuare gli Vnisoni, più che si puote, & che non si dè molto di lungo frequentare le Ottaue. | cap. 41. | 237 |
| De i Contrapunti diminuiti à due voci; & in qual modo si possino vsar le Dissonanze; & de molte Regole, che si deono osseruare in essi. | cap. 42. | 238 |
| Il modo, che hà da tenere il Compositore nel fare i Contrapunti sopra vna Parte, ò Soggetto di-minuito. | cap. 43. | 244 |
| Quando è lecito vsare in vna parte della Cantilena due, ò più volte vn passaggio, & quando non. | cap. 44. | 247 |
| Che non è necessario, che la parte del Soggetto, & quella del Contrapunto incomincino insieme; & di quattro differenze, che si trouano delle Figure cantabili. | cap. 45. | 250 |
| Che le Modulationi debbono essere ben regolate, & quel che dè osseruare il Cantore nel can-tare. | cap. 46. | 251 |
| Che non si dè continuar molto di lungo nel graue, ò nell'acuto nelle modulationi. | cap. 47. | 253 |
| Che 'l porre vna Dissonanza, ouer vna Pausa di minima tra due Consonanze perfette d'vna istes-sa specie, che ascendino insieme, ò discendino, non fà, che tali consonanze non siano senza alcun mezo. | cap. 48. | 254 |
| Della Battuta. | cap. 49. | 256 |
| Della Sincopa. | cap. 50. | 259 |
| Della Cadenza; quello che ella sia; delle sue specie; & dell'vso suo. | cap. 51 | 260 |
| Il modo di fuggir le Cadenze; & quello, che si haurà da osseruare, quando il Soggetto farà il mo-uimento di salto. | cap. 52 | 266 |
| Delle Pause. | cap. 53. | 267 |
| Delle Consequenze. | cap. 54. | 269 |
| Delle Imitationi; & quello che elle siano. | cap. 55. | 275 |
| De i Contrapunti doppij, & quello che siano. | cap. 56. | 279 |
| Quel che dè osseruare il Contrapuntista oltra le Regole date; & d'alcune licenze, che potrà pigliare, quando li torneranno commode. | cap. 57. | 289 |
| Il modo, che si hà da tenere nel comporre le Cantilene à più di due voci; & del nome delle Parti. | cap. 58. | 293 |
| Delle Cantilene, che si compongono à Tre voci; & di quello, che si dè osseruar nel com-porle. | cap. 59. | 298 |
| In Qual maniera la Quarta si possa porre nelle compositioni. | cap. 60. | 302 |
| Di alcune Regole poste in commune. | cap. 61. | 304page ix |
| Delle uarie sorti de Contrapunti arteficiosi; & prima di quelli, che si chiamano Doppij. | c. 62. | 310 |
| Delle uarie sorti de Contrapunti à Tre uoci, che si fanno à mente in Consequenza sopra un Sog-getto; & di alcune Consequenze, che si fanno di fantasia; & quello che in ciascheduna si hà da da [sic: da] osseruare. | cap. 63. | 316 |
| Quel che si dè osseruare, quando si uolesse fare una Terza parte alla sproueduta sopra due altre proposte. | cap. 64. | 331 |
| Quel che bisogna osseruare intorno le Compositioni di quattro, ò di più uoci. | cap. 65. | 336 |
| Alcuni auertimenti intorno le compositioni, che si fanno à più di Tre uoci. | cap. 66. | 340 |
| Del Tempo, del Modo, & della Prolatione; & in che quantità si debbino finire, ò numerare le Cantilene. | cap. 67. | 347 |
| Della perfettione delle Figure cantabili. | cap. 68. | 350 |
| Della Imperfettione delle Figure cantabili. | cap. 69. | 353 |
| Del Punto, delle sue specie; & de i suoi effetti. | cap. 70. | 355 |
| Dell'Vtile, che apportano i mostrati Accidenti nelle buone Harmonie. | cap. 71. | 359 |
| Delle Chorde communi, & delle Particolari delle cantilene Diatoniche, Chromatiche, & En-harmoniche. | cap. 72. | 362 |
| Se l'uno de i due ultimi Generi si possa usar semplice nelle sue chorde naturali, senza adoperar le Chorde particolari de gli altri. | cap. 73. | 364 |
| Che la Musica si può usare in due maniere; & che le Cantilene, che compongono alcuni Moder-ni, non sono sottoposte ad alcuno de i due nominati Generi. | cap. 74. | 365 |
| Che 'l Diatonico può procedere nelle sue modulationi per gli Interualli di Terza maggiore, & di minore; & che ciò non faccia uariatione alcuna di Genere. | cap. 75. | 365 |
| Che doue non si ode nelle compositioni alcuna uarietà di Harmonia, iui non può essere uarietà alcuna di Genere. | cap. 76. | 368 |
| Dell'utile, che apportano i predetti due Generi; & in qual maniera si possino usare, che faccino buoni effetti. | cap. 77. | 368 |
| Per qual cagione le Compositioni, che compongono alcuni Moderni per Chromatiche, facciano tristi effetti. | cap. 78. | 370 |
| Delle cose, che concorreuano nella compositione de i Generi. | cap. 79. | 372 |
| Opinioni delli Chromatisti ributtate. | cap. 80. | 375 |
| QVELLO, che sia Modo, ò Tuono; & delle sue Specie. | cap. 1. | fac. 377 |
| Che i Modi sono stati nominati da molti diuersamente; & per qual cagione. | c. 2. | 383 |
| Del Nome, & del Numero de i Modi. | cap. 3. | 385 |
| De gli Inuentori de i Modi. | cap. 4. | 387 |
| Della Natura, ò Proprietà de i Modi. | cap. 5. | 388 |
| Dell'Ordine de i Modi. | cap. 6. | 392 |
| Che l'Hypermistolydio di Tolomeo non è quello, che noi chiamiamo Decimo modo. | c. 7. | 394 |
| In qual maniera gli Antichi segnauano le Chorde de i loro Modi. | cap. 8. | 395 |
| In qual maniera s'intenda la Diapason essere harmonicamente, ouero arithmeticamente me-diata. | cap. 9. | 397 |
| Che i Modi moderni sono necessariamente Dodici; & in qual maniera si dimostri. | cap. 10. | 398 |
| Altro modo da dimostrare il numero delli Dodici Modi. | cap. 11. | 399 |
| Diuisione de i Modi in Autentichi, & Plagali. | cap. 12. | 402 |
| Delle Chorde finali di ciascun Modo; & quanto possa ascendere, ò discendere di sopra, & di sotto le nominate chorde. | cap. 13. | 403 |
| De i Modi communi, & de i Misti. | cap. 14. | 404 |
| Altra diuisione de i Modi; & di quello, che si hà da osseruare in ciascuno, nel comporre le canti-lene; & in qual maniera le Otto sorti di Salmodie con essi si accompagnino. | cap. 15. | 405 |
| Se co 'l leuare da alcuna cantilena il Tetrachordo Diezeugmenon; ponendo il Synemennon in suo luogo, restando gli altri immobili; un Modo si possa mutare nell'altro. | cap. 16. | 408 |
| Della Trasportatione de i Modi. | cap. 17. | 410 |
| Ragionamento particolare intorno al Primo modo; della sua Natura; de i suoi Principij; & del-le sue Cadenze. | cap. 18. | 411 |
| Del Secondo Modo. | cap. 19. | 414 |
| Del Terzo modo. | cap. 20. | 415page x |
| Del Quarto modo. | cap. 21. | 418 |
| Del Quinto modo. | cap. 22. | 420 |
| Del Sesto Modo. | cap. 23. | 421 |
| Del Settimo modo. | cap. 24. | 423 |
| Dell'Ottauo modo. | cap. 25. | 425 |
| Del Nono modo. | cap. 26. | 427 |
| Del Decimo modo. | cap. 27. | 428 |
| Dell'Vndecimo modo. | cap. 28. | 430 |
| Del Duodecimo, & vltimo modo. | cap. 29. | 433 |
| In qual maniera si debbe far giudicio de i Modi; & quello, che si dee osseruare nelle Composi-tioni. | cap. 30. | 434 |
| Del modo, che si hà da tenere, nell'accommodar le Parti della Cantilena; & delle estremità loro. | cap. 31. | 436 |
| In qual maniera le Harmonie si accommodino alle soggette Parole. | cap. 32. | 438 |
| Il modo che si hà da tenere; nel por le Figure cantabili sotto le Parole. | cap. 33. | 440 |
| Delle Legature. | cap. 34. | 441 |
| Quel che dè hauer ciascuno, che desidera di venire à qualche perfettione nella Musica. | c. 35. | 444 |
| Della fallacia de i Sentimenti; & che 'l giudicio non si dè fare solamente col loro mezo: ma se li debbe accompagnar la Ragione. | cap. 36. | 445 |
 page xi
page xi
A I STVDIOSI LETTORI.
| Facciata. | Linea. | |
| 21 | nel margine. | Musicae libro. |
| 27 | 15 | Voce, ò co 'l mezo. |
| 35 | 3 | quale. |
| 4 | Diapason. | |
| 5 | de. | |
| 51 | 32 | Il perche venendo al proposito |
| 52 | 6 | termini, ò numeri. |
| 9 | che vorremo. | |
| 64 | 30 | volessimo accommodare alla |
| 77 | 47 | alcuna, che si |
| 80 | 43 | Percussioni |
| 83 | 38 | Sacada |
| 93 | 37 | habbiamo detto; visse |
| 138 | 35 | Superparticolare. |
| 147 | 22 | la Sesquiquinta. |
| 153 | 8 | nella Sesquisesta proportione |
| Facciata. | Linea. | |
| 160 | 15 | violentemente. |
| 169 | 16 | questa X. tanto. |
| 238 | 3 | Fortunatam. |
| 255 | 1 | Particella. |
| 261 | 29 | Cadenze di due. |
| 266 | 10 | ò Periodo. |
| 285 | 19 | habbia le sincope. |
| 304 | nel margine. | Vide Def. Demonst. |
| 353 | 28 | l'essere Imperfetto |
| 360 | 47 | Chordae, & Chorda. |
| 434 | 5 | le quali non sono. |
| 440 | 8 | tener. |
| 448 | 4 | prima furono giudicati. |
| 9 | allora fu riputato. | |
| 28 | costui. |
| 220 | Nel Primo essempio de i Tritoni; la prima nota della parte graue vuol essere nel secondo spacio tra la prima, & la seconda riga. |
| 245 | Nell'vltima riga della parte graue, la sesta Fi-gura vuol stare sopra la prima riga. |
| 248 | La chiaue nel principio della parte del Sog-getto, vuol essere sopra la riga di mezo. Et la 31. nota vuol stare sopra la seconda riga. |
| 278 | L'ultima nota del secondo ordine del Canto del primo essempio, vuol essere nella seconda riga. |
| 287 | Nel primo ordine della parte acuta, bisogna leuare la Semiminima posta auanti la mi-nima col punto nel fine. |
| 300 | Nell'vltimo ordine la seconda nota delle due che si trouano nella prima riga, vuol stare nella seconda. |
| 304 | Il luogo proprio dell'vltimo essempio è tra la line 29. & la 30. |
| 315 | La prima Figura del primo ordine nella par-te più acuta, uuol essere una Breue: & nel Secondo, manca dopò la terza nota una Semiminima nel secondo spacio. |
| 321 & 322 | L'vno de due essempij è superfluo, ma ciò importa poco. |
| 322 | Nell'antepenultima dell'essempio ui uà una coronata [[mus.ferm]]. |
| 323 | L'ultima nota del quarto ordine, uuol essere una Chroma. |
| 325 | Nel terzo ordine dell'essempio ui è di più il Segno del Tempo nel principio.page xii |
| 332 | La Figura, ò nota posta delle parte più acuta nel fine nel quarto ordine, vuol essere so-pra la riga del mezo. Et nella parte graue, nel quarto ordine, la Vndecima Figura, vuol essere Semiminima. |
| 339 | Nel principio del primo ordine nella parte acuta, il Segno del Tempo, vuol esser ta-gliato. |
| 341 | Nel principio del primo essempio, & primo ordine, che è nella parte più acuta; prima se porrà la chiaue nella prima riga; dopoi s'accommoderà la prima nota co 'l punto, & l'altra nota seguente sopra il Secondo Spacio; perche sono poste al riuersa. |
| 345 | Sopra la quarta nota della parte nell'Alto, nel principio manca il Segno della Presa. |
| 355 | Nel primo ordine tra le due prime Semibre-ui vi manca il punto di diuisione. |
| 357 | Nel primo ordine l'vna delle tre Breui dopò e 'l punto è superflua. |
| 363 | Nell'ordine Chromatico la Cifera  và po-sta nel secondo spacio. và po-sta nel secondo spacio.
|
| 401 | Nel primo essempio manca nel quarto spacio vna Breue nera. |
| 416 | Nel terz'ordine auanti le due Chrome man-ca il punto nel secondo spacio; & nel se-sto il primo punto è superfluo. |
| 425 | Nel quarto ordine l'vltima delle quattro Semiminime, vuol essere vna Minima. |
SECONDA TAVOLA DELLE COSE PIV' NOTABILI CONTENVTE NEL PRIMO VOLVME.
A
B
 lettera quadrata, perche sia stata ritrouata da
Guidone. 126. f
lettera quadrata, perche sia stata ritrouata da
Guidone. 126. f
C
D
E
F
G
H
I
L
M
N
O
P
Q
R
S
T
V

L'ISTITVTIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Capella della Serenissima Signoria DI VENETIA:
PROEMIO: Nel quale si dimostra, in qual maniera la Musica habbia hauuto principio, & come sia stata accresciuta; & si ragiona della diuisione dell'Opera.
 page 5
page 5
LA PRIMA PARTE DELLE ISTITVTIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Capella della Serenissima Signoria DI VENETIA:
Della Origine & certezza della Musica.Cap. 1.
Pronàque cum spectent animalia caetera terras,& questo perche ei non fermasse l'amor suo nelle cose basse & terrene; ma leuasse l'intel-letto à contemplar le superiori & celesti; & penetrasse alle occulte & diuine col mezo delle cose, che sono & si comprendono per via de i Cinque sentimenti. Et benche, in quan-to all'Essere, due soli fussero sufficienti; nondimeno per il Ben'essere, tre di più vene ag-giunse: imperoche se per il Tatto si conoscono le cose dure & aspre, dalle tenere & po-lite; & per il Gusto si fà la differenza tra i cibi dolci & amari, & d'altri sapori; per questo & per quello si sente la diuersità del freddo & del caldo, del duro & del tenero, del gre-ue & del leggiero; cose che veramente all'Esser nostro bastarebbono; non resta però, ch'al Ben'essere il Vedere, l'Vdire, & l'Odorare necessarij non siano; per i quali l'Huo-mo viene à rifiutare ciò che è cattiuo, & eleggere il buono. De questi chi vorrà ben essaminare la lor virtù, senza dubbio ritrouerà il Vedere, considerato da per sè, essere à i corpi di maggior vtilità; & consequentemente più necessario, che gli altri; ma ben si conoscerà poi, l'Vdito esser molto più necessario & migliore; considerandolo per acci-dente, nelle cose che appartengono all'Intelletto; conciosia che se bene per il senso del page 6Vedere si conoscono più differenze di cose; essendo che più si estende, che l'Vdito, non-dimeno questo nell'acquisto delle Scienze & giudicio intellettuale più si estende, & mol-to maggior vtile ne apporta. Onde ne segue, che l'Vdito veramente sia & più necessa-rio & megliore de gli altri Sentimenti; auenga che tutti Cinque si chiamino Istrumenti dell'Intelletto: percioche ogni cosa che vediamo, vdimo, tocchiamo, gustiamo, & odoriamo,1. metaph. c. 1. si offerisce à lui per il mezo de i Sensi & del Senso commune; ne di cosa al-cuna può hauer cognitione, saluo che per il mezo di vno de questi cinque: essendo ve-ro, ch'Ogni nostra cognitione da essi habbia l'origine. Dall'Vdito adunque, come dal più necessario de gli altri Sentimenti, la scienza della Musica hà hauuto la sua origine; la cui nobiltà facilmente si può per l'antichità dimostrare; percioche (come dicono Mo-sè,Gene. 4. Gioseffo,Antiq. 1. c.4. & Beroso CaldeoAntiq. lib. 1.) auanti che fusse il Diluuio vniuersale, fù al suono de martelli trouata da Iubale della stirpe di Caino; ma perduta poscia per lo soprauenuto diluuio, di nuouo fu da Mercurio ritrouata: conciosia che (come vuole DiodoroHist. lib. 1. Nym. Mercu.) egli fù il primo, che osseruò il Corso delle stelle, l'Harmonia del Canto, & le Proportioni de i Numeri; & dice ancora, lui essere stato l'Inuentore della Lira con tre Chorde; del cui pa-rere è stato anco Homero & Luciano;Dial. Deorum. quantunque Lattantio, in quello che fà della Fal-sa religione,Lib. 1. c. 10. attribuisca l'inuentione della Lira ad Apollo; & PlinioNat. histo. lib. 7. c. 56. voglia, che l'In-uentore della Musica sia stato Anfione, Ma sia à qual modo si voglia; BoetioMusicae li. 1. cap. 10. (accostan-dosi all'opinione di Macrobio,De Som. lib. 2. cap. 1. & allontanandosi da Diodoro) vuole, che Pitagora, & non Platone, come vuol Guidone Aretino;Microlo. lib. 1.c. 20. sia stato colui, che ritrouò la Ragione delle musicali proportioni al suono de martelli: Percioche passando egli appresso vna botte-ga di fabri, i quali con diuersi martelli batteuano vn ferro acceso sopra l'incundine, gli peruenne all'orecchie un certo ordine de suoni, che gli mouea l'udito con dilettatione; & fermatosi alquanto, cominciò ad inuestigare, onde procedesse cotale effetto; & paren-dogli primieramente, che dalle forze diseguali de gli huomini potesse procedere; fece che coloro, iquali batteuano, cambiassero i martelli: ma non vdendo suono diuerso da quello di prima; giudicò (com'era il vero) che la diuersità del peso de martelli fusse la ca-gione. Per la qual cosa hauendo fatto pesare ciascun di loro separatamente, ritrouò tra i Numeri de i pesi le ragioni delle Consonanze & dell'Harmonie; lequali egli poi in-dustriosamente accrebbe in questo modo; c'hauendo fatto chorde di budella di pecore di grossezza vguale; attaccando ad esse i medesimi pesi de martelli; ritrouò le medesime consonanze; tanto più sonore, quanto che le chorde per sua natura rendono il Suono all'vdito più grato. Continuossi quest'Harmonia per alquanto spatio di tempo; & dopoi i successori, i quali sapeuano già i suoi fondamenti esser posti in certi & determinati Nu-meri, più sottilmente facendone proua, à poco à poco la ridussero à tale; che le diede-ro nome di perfetta & certa Scienza. Et rimouendo i falsi & dimostrando i veri con-centi, con euidentissime ragioni de Numeri & infallibili, ne diedero in iscritto chiarissi-me Regole; come apertamente in tutte l'altre Scienze vediamo esser auenuto; che i Pri-mi inuentori di esse, come chiaramente lo dimostra Aristotele,2. Elen. c. 1 2. Metaph. cap. 1. non n'hebbero mai per-fetta cognitione; anzi con quel poco di lume erano mescolate molte tenebre di errori; i quali rimossi da chi li conosceua, in vece loro succedeua la verità; come fece egli in-torno à i Principij della Filosofia naturale; che adducendo diuerse opinioni de gli An-tichi filosofi, approuò le buone & vere, rifiutò le false, dichiarò le oscure & male intese, & aggiungendoui la sua opinione & autorità, dimostrò & insegnò la vera scienza della Filosofia naturale. Cosi della nostra scienza della Musica i posteri mostrando gli errori de passati, & aggiungendoui la loro autorità, la fecero talmente chiara & certa, che la 2. Metaph. com. 16. connumerarono, & fecero parte delle scienze Mathematiche; & questo non per altro, saluo che per la sua certezza: percioche questa con l'altre insieme auanza di certezza l'al-tre Scienze, & tiene il primo grado di verità; il che dal suo nome si conosce; poi che Ma-thematica è detta da Μάθημα parola greca, che in latino significa Disciplina; & nella no-In prooe-mio Arith. stra lingua importa Scienza, ò Sapienza; la quale (come dice Boetio) altro non è che page 7vna Intelligenza; o per dirla piu chiaro, capacità di verità delle cose che sono & di loro natura non sono mutabili; della qual Verità queste Scienze fanno particolar professio-ne; essendo che considerano le cose, che di lor natura hanno il vero essere. Et sono in tanto differenti d'alcune altre Scienze; che queste essendo fondate sopra le opinioni de diuersi huomini, non hanno in se fermezza alcuna; & quelle hauendo i Sentimenti per loro proua, uengono ad hauere ogni certezza. Percioche i Mathematici nelle cose es-sentiali sono d'un'istesso parere; ne ad altro consentono, che à quel, che si può sensata-mente capire. Et è tanta la certezza di dette Scienze; che col mezo de' Numeri si sà infallibilmente il Riuolgimento de cieli, gli Aspetti uarij de i pianeti, l'Eclisse della Lu-na, & quello del Sole, & infiniti altri bellissimi secreti, senza esser tra loro punto di discor-dia. Ilperche da questo si può conoscere, che la Musica sia & nobile & certissima; es-sendo parte delle Scienze mathematiche.
Os Homini sublime dedit coelumque videre
Iussit; & erectos ad sydera tollere vultus.
Delle Laudi della Musica.Cap. II.
Et longum formose vale, vale (inquit) Iola;Facendo dal pianto & da sospiri quasi interrompere il Verso, fà proferir lunga quella Sillaba, che prima hauea posta breue. Dopoi uolendo mostrare, quanto sia ueloce il Tempo, lo dimostra col uerso composto de molti Datili, che sono Piedi atti alla uelocità & à mostrar un tale effetto, dicendo;Georg. 3.
Sed fugit interea fugit irreparabile tempus.Et uolendo dimostrar, con quanto silentio la città de Ilio fusse da Greci assalita, lo mostra con un Verso composto di molti Spondei, i quali sono Piedi per loro natura at-ti alla tardità & alle cose deboli & ociose, dicendo; Aeneid. 2.
Inuadunt vrbem somno, vinoque sepultam.Lascierò hora di dire, come uolendo mostrare i Cartaginesi essere stati sempre nemici & contrarij à Romani; nel descriuere il sito di Cartagine, pospose à bello studio quella parola, che andaua preposta, & disse;
Italiam contra.Aeneid. 1. Et infiniti altri, che troppo lungo sarebbe il raccontargli in questo luogo, de i quali l'Opera è piena. Basterà hora per ultima conclusione dire; che la Poesia sarebbe senza leggiadria alcuna, se dalle pa-role harmonicamente poste non gli fusse data. Oltra di ciò lascierò da parte il dire, quanta simiglianza & vnione con essa habbiano l'Arithmetica & la Geometria, per-cioche si conosce nel trattar la Scienza; & dirò solamente, che se l'Architettore non hauesse cognitione della Musica; come ben lo dimostra Vitruuio;De Archi. lib. 1. cap. 1. non saprebbe con ra-gion fare il temperamento delle machine, & ne i Theatri collocare i vasi, & dispor bene & musicalmente gli edificij. L'Astronomia medesimamente, se non fusse aiutata da i fon-damenti harmonici, non saprebbe gl'influssi buoni & rei. Anzi dirò più; se l'Astrono-mo non sapesse la concordanza de i Sette pianeti, & quando l'uno con l'altro si congiun-ga, ouero l'uno all'altro si opponga, non predirebbe mai le cose future. La Filosofia ancora, laquale hà per suo proprio il discorrer con ragione le cose produtte dalla natura & possibili à prodursi, non confessa ella dal Primo motore dependere ogni cosa, & esser ordinata con si mirabil ordine, che ne risulta nell'Vniuerso una tacita harmonia? Ecco, che primieramente le cose graui tengono il luogo basso, le leggieri il soprano, & quelle di men peso, secondo la loro natura, posseggono il luogo di mezo. Et più oltra proce-dendo, i Filosofi affermano, che i Cieli riuolgendosi fanno harmonia; la quale se bene non udimo, questo può auenire, ò per la loro ueloce reuolutione, ò per la troppo di-stanza, ouero per altra cagione à noi occulta. La Medicina da questa non può star lon-tana; imperoche se 'l Medico non hà cognitione della Musica, come saprà egli ne i suoi medicamenti proportionar le cose calide con le frigide, secondo i loro gradi? & come potrà hauere ottima cognitione de i Polsi? i quali il dottissimo Herofilo dispose secon-do l'ordine de i Numeri musicali. Et per salire più alto, la Theologia nostra ponendo nel page 9cielo i Spiriti angelici, diuide quelli in noue Chori contenuti in tre Hierarchie; come scriue Dionisio Areopagita.De caelest. hierar. c. 6. Queste sono di continuo presenti alla Diuina maestà, & non cessano di cantare Santo, Santo, Santo, Signore Iddio de gli esserciti; come è scrit-to in Isaia.Isa. cap. 6. Et non solo questi, ma i quattro Animali ancora, i quali nel Libro delle Reuelationi sono descritti da San Giouanni,Apoca. ca. 4. 5. 14. 15. & 19. stanno auanti il trono di Dio, & cantano l'istesso canto. Stanno oltra ciò i vintiquattro Vecchi inanzi all'Agnello immaculato, & con suono di Cetere & altissime uoci cantano all'Altissimo Iddio vn nuouo canto; il-quale è cantato anco dalle vocide [sic: voci de] Citaristi citarizanti nelle cetere loro auanti i quattro Animali & vintiquattro Vecchi. Di queste & altre quasi infinite cose al proposito nostro n'è piena la diuina Scrittura, lequali per breuità trapasseremo; bastando sola-mente dire, per suprema laude della Musica; senza far mentione alcuna d'altra Scienza; che ella, secondo la testimonianza de Sacri libri, sola si troua nel Paradiso, & è quiui nobilissimamente essercitata. Et si come nella Celeste corte, che Chiesa trionfante vien detta; cosi nella nostra terrena, che Militante si chiama, non con altro, che con la Musi-ca, si lauda & ringratia il Creatore. Ma lasciamo hormai da parte le cose superiori, & ritorniamo à quelle, che sono dalla Natura produtte per ornamento del Mondo, che uederemo ogni cosa esser piena de musici concenti. Il mare primamente hà le Sirene, le quali (s'è lecito dar fede à i Scrittori) à nauiganti vdir si fanno di tal sorte, che vinti molte uolte dall'Harmonia loro, & soprapresi dal sonno, perdono quello, che sopra ogn' altra cosa è carissimo à tutti gli animali. Nell'Aria & nella Terra insieme sono gli Vc-celli, che ancor'essi co i loro concenti dilettano & ricreano, non pur gli animi lassi & pie-ni di noiosi pensieri; ma i corpi ancora: percioche il Viandante molte uolte stanco per il lungo viaggio, ricrea l'animo, riposa il corpo, & si dimentica le passate fatiche, per la soaue harmonia de boscarecci canti de vccelli de tante varie sorti, che sarebbe impossi-bile il uolerle raccontare. I Fiumi & li Fonti medesimamente dalla natura fabricati so-glion dare grato piacere à chiunque ad essi uicino si ritroua; & l'inuitano ben spesso per ricrearsi ad accompagnare il suo rustico canto co i loro strepitosi concenti. Tutte que-ste cose il Dottissimo Virgilio espresse con poche parole: quando disse;In Sileno.
Tum uerò in numerum Faunosque, ferasque uideresDinotandoci ch'al canto di Sileno, non solo i Fauni & l'altre fiere; ma le dure Quercie ancora ballauano; saltando quelli & queste spesso mouendosi con numerosi mouimenti; per dimostrarci, che non pur le cose sensibili; ma ancora quelle, che mancano del senso, sono quasi prese & vinte da i concenti musicali; & fansi di dure & aspre, mansuete & piaceuoli. Ma se tanta Harmonia si troua nelle cose celesti & terrestri; oue-ro, per dir meglio, se 'l Mondo dal Creatore fu composto pieno di tanta harmonia; perche dobbiamo credere l'Huomo esserne priuo di essa? Et se l'Anima del Mondo (come uogliono alcuni) non è altro che Harmonia, potrà esser che l'Anima nostra non sia in noi cagione d'ogni Harmonia, & che col Corpo non sia harmonicamente congiunta? massimamente hauendo Iddio creato l'Huomo alla similitudine del Mondo maggiore, detto da Greci Κόσμος; cioè, Ornamento, ouer'Ornato, & essendo fatto à quella simili-tudine di minor quantità, à differenza del quale uien chiamato Μικρόκοσμος; cioè, Pic-ciol mondo; certo che non è cosa ragioneuole. Onde Aristotele2. De anima. c. 3. volendo mostrar il mu-sicale componimento dell'Huomo molto ben disse; La parte Vegetatiua alla Sensitiua, & questa alla Intellettiua hauer la medesima conuenienza, che hà la Figura di tre lati à quella di quattro. Certa cosa è adunque, che non si ritroua cosa alcuna buona, che non habbia musicale dispositione; & la Musica ueramente, oltra che rallegra l'ani-mo, riduce anche l'Huomo alla contemplatione delle cose celesti; & hà tal proprietà, page 10ch'ogni cosa à cui si aggiunge fà perfetta; & quegli Huomini sono veramente felici & beati, che sono dotati di essa; come afferma il Santo Profeta, dicendo;Psal. 88. Beato è quel populo, che sà la Giubilatione. Per la quale autorità, Hilario Vescouo Pittauiense dot-tore catholico, esponendo il Salmo 65. si mosse à dire; che la Musica è necessaria all'huo-mo Christiano; conciosia che nella scienza di essa si ritroua la beatitudine. Onde per questo hò ardimento di dire; che quelli, che non hanno cognitione di questa Scienza, so-no da esser connumerati tra gl'ignoranti. Anticamente (come dice IsidoroLib. 3. Ety-mol. c. 15.) non era men uergogna il non sapere la Musica, che le Lettere; però non è marauiglia, se Hesio-do poeta famosissimo & antichissimo (come narra Pausania Lib. 10. Descript. veteris Graeciae) fù escluso dal certame; co-me colui, che non hauea mai imparato à sonar la Cetera, ne col suono di quella accom-pagnare il canto. Cosi ancora Temistocle (come narra TullioTusculan. Quaest. li. 1.) rifiutando di sonar la Lira nel conuito, fu men dotto & men sauio riputato. Il contrario leggiamo, che furono in gran pregio appresso gli Antichi Lino & Orfeo, amendue figliuoli de i loro Dei; per-cioche col soaue canto (come si dice) non solamente addolciuano gli Animi humani; ma le fiere, & gli uccelli ancora; & quello, che è più marauiglioso da dire, moueano le pietre da i proprii luoghi, & à i fiumi riteneuano il corso. Et questo istesso Horatio attribuisce ad Anfione, dicendo.De Arte poetica.
Ludere: tum rigidas motare cacumina quercus.
Nec tantum Phoebo gaudet Parnasia rupes,
Nec tantum Rhodope miratur, & Ismarus Orphea:
Quantum omnis mundus gaudet cantante Sileno.
Dictus & Amphion Thebanae conditor arcisDa i quali per auentura impararono gli antichi Pitagorici, che con musici suoni in-teneriuano gli animi feroci; & Asclepiade medesimamente, che molte uolte per que-sta via racchetò la discordia nata nel populo, & col suono della Tromba restitui l'Vdi-to à i sordi. Parimente Damone pitagorico ridusse col Canto alcuni gioueni dediti al ui-no & alla lussuria à temperata & honesta uita. La onde dissero bene coloro, che affer-mauano la Musica esser una certa legge & regola di modestia; essendoche Theophrasto ritrouo alcuni Modi musicali da racchetare i spiriti perturbati. Però meritamente & sapientemente Diogene Cinico beffaua i Musici de suoi tempi, i quali hauendo le chor-de delle loro cetere concordi, haueano l'animo incomposto & discorde; essendo abban-donato dall'harmonia de costumi. Et se dobbiamo prestar fede alla Historia; ci debbe parer quasi nulla quello, che habbiamo detto: percioche molto maggior cosa è l'hauere uirtù di sanar gl'infermi, che di corregger la uita de sfrenati giouani; come ancora leggiamo di Senocrate, ilquale col suono de gli organi ridusse i pazzi alla pristina sa-nità, & Talete di Candia, col suono della Cetera scacciò la pestilenza.Alexan. ab Alex. li. 2. c. 16. Ge-ni. Die. Et noi vedia-mo hoggidì, che per uia della Musica s'oprano cose marauigliose; imperoche tanta è la forza de i Suoni & de i Balli contra il veleno delle Tarantole, che in breuissimo tempo risana coloro, che da esse sono stati morsi; come si vede ogni giorno per esperienza nella Puglia, paese abondantissimo de cotali animali. Ma senza più testimonii profani, non habbiamo noi nelle Sacre lettere1. Reg. c. 6., che 'l profeta Dauid racchetaua lo Spirito maligno di Saul col suono della sua Cetera? Et per questo credo io, che esso regio Profeta ordi-nasse, che nel Tempio d'Iddio si usassero i canti & gli harmonici suoni;1. Paral. c. 25. conoscendo ch'erano atti à rallegrare i spiriti, & à ridur gli huomini alla contemplatione delle cose celesti. I Profeti ancora (come dice Ambrosio sopra 'l Salmo 118. volendo profetizare, dimandauano, ch'un perito del Suono si ponesse à sonare; accioche inuitati da quella 4. Reg. c. 3. dolcezza gli fusse infusa la gratia spirituale. Però Eliseo non uolse profetizare al Re d'Israele quel, che douesse fare per l'acquisto delle acque; accioche gli esserciti non morissero di sete; se prima non gli fù menato al suo conspetto un Musico, il quale can-tasse; & cantando egli fu dello Spirito diuino inspirato, & predisse il tutto. Ma passia-mo più oltra; percioche non mancano gli essempij. Timotheo (si come insieme con mol-ti altri narra il Gran BasilioHomil. 54. Ad adolescentes.) con la Musica incitaua il Re Alessandro al combattere; & quello medesimo essendo incitato riuocaua. Narra Aristotele nel Libro della Natura page 11de gli Animali, che i Cerui per il canto de cacciatori sono presi; & che della Sampogna pastorale & del canto ancora molto si dilettano; il che conferma Plinio nella sua Natu-Lib. 9. c. 5. Lib. 8. c. 32 rale Historia. Et per non mi distendere più sopra di questo, solamente dirò di conosce-re alcuni, i quali hanno veduto de i Cerui, che fermando il lor corso, se ne stauano at-tenti ad ascoltare il Suono della Lira & del Leuto; & medesimamente si uede ogni gior-no gli Vccelli vinti & ingannati dall'Harmonia, il più delle uolte restare presi dall'Vc-cellatore. Narra etiandio Herodoto & Plinio,Vrania lib. 1. Nat. hist. lib. cap. 8. che la Musica campò Arione dalla mor-te, che precipitandosi nel mare, fu portato dal Delfino nel lito di Teniaro isola. Ma la-sciamo stare hormai molti altri essempi, che potremmo addurre, & diciamo vn poco del buon Socrate maestro di Platone, che già uecchio & pieno di sapienza volse impa-rare à sonar la Cetera: & il vecchio Chirone tra le prime arti, che insegnasse ad Achil-le nella tenera età, fu la Musica; & uolse, che le sanguinolenti sue mani, prima che s'imbrattassero del sangue Troiano, sonassero la Cetera. PlatoneDe legi-bus. 3. & Aristotele8. Politi. c. 3. non com-portano, che l'Huomo bene istituito sia senza Musica; anzi persuadono con molte ra-gioni tale Scienza douersi imparare; & mostrano la forza della Musica esser in noi gran-dissima; & perciò vogliono, che dalla fanciullezza vi si dia opera; conciosia che è soffi-ciente à indurre in noi un nuouo habito & buono, & un costume tale, che ne guida & conduce alla virtù, & rende l'animo più capace di felicità: & il Seuerissimo Licurgo Re de Lacedemonij tra le sue seuerissime Leggi lodò & sommamente approuò la Musica; per-cioche molto ben conosceua, ch'all'Huomo era necessaria molto, & di giouamento grandissimo nelle cose della guerra; di modo che i loro Esserciti (come narra ValerioDict. Fact. lib. 2. ca. 1.) non usauano di andar mai a combattere, se prima non erano ben riscaldati & inanima-ti dal Suono de Pifferi. Osseruasi ancora tal costume à i tempi nostri; percioche di due esserciti l'uno non assalirebbe l'inimico, se non inuitato dal suono delle Trombe & de Tamburi, ouero da alcun'altra sorte de musicali istrumenti. Et benche, oltra i narrati, non manchino infiniti altri essempi, da i quali si potrebbe maggiormente conoscere la digni-tà & eccellenza della Musica; nondimeno, per non andar più in lungo, li lasciaremo; essendo à bastanza quello, che fin'hora si è ragionato.
Saxa mouere sono testudinis, & prece blanda
Ducere quo vellet;
A che fine la Musica si debba imparare.Cap. III.
Dell'Vtile che si hà della Musica, & dello Studio che vi dobbiamo porre, & in qual modo usarla.Cap. IIII.
Eneruant animos citharae, cantusque lyraeque,Ne d'altro sanno ragionare, che di tali cose; ne altro che dishoneste parole dal-la loro sporca bocca si sentono uscire. Per il contrario poi, sono alcuni, i quali per cotale studio non solo molli & effeminati; ma importuni, dispiaceuoli, superbi, perti-naci & inhumani diuentano; di modo che uedendosi ad un certo termine arriuati, sti-mandosi sopra d'ogn'altro eccellenti (il che è proprio d'una gran parte de quelli, ch'esser-citano la Musica ne i nostri tempi) si gloriano, si essaltano & si lodano; & vituperando gli altri, per parere d'esser pieni di sapienza & di giudicio; se ben sono ignoranti, & goffi; stanno con la maggior riputatione & superbia del mondo; ne mai se non con grande istantia de prieghi, & con laudi molto maggiori, che à loro conuengono, si possono ridurre à mostrare un poco del loro sapere. Per la qual cosa de tutti questi Tigelii si verifica il detto di Horatio.Ser. lib. 1. Ser. 3
Et uox, & numeris brachia mota suis.
Omnibus hoc uitium est Cantatoribus, inter amicos,A' tali faceua dibisogno, che i padri loro più presto hauessero fatto imparare qualch'al-tro mestiero, quantunque vile; che forse non sarebbono caduti in tali errori, & hauerebbono acquistate megliori creanze. Tutto questo hò uoluto dire, accioche quelli, che dell'arte della Musica vogliono fare professione, s'innamorino della Scienza, & diano opera allo studio della Speculatiua; percioche non dubito, che congiungendo questa insieme con la Prattica non habbiano da diuentar virtuosi, honesti & costumati; & in tal modo uerranno ad imitare gli Antichi, i quali (come si è detto) accompagnauano la Musica con la Ginnastica: percioche cosi accompagnata ella sarà potente di ridur cia-scun suiato nella diritta via de buoni costumi. Ne alcun debbe credere, che quello c'hò detto in questo proposito dell'arte della Musica, l'habbia detto per uituperarlo; ne an-che per dir male di coloro, che in tal maniera si essercitano; cosa che giamai non mi è caduto nell'animo; ma più tosto l'hò detto, accioche congiungendola in tal modo con altre honoreuoli Scienze piene di seuerità , la difendiamo da i uagabondi & ottiosi ruf-fianesmi de bagatellieri; & la riponiamo nel suo uero luogo; si ch'ella non habbia da seruir più à coloro, che sono dediti solamente alle uoluttà; ma sia per uso de i Studiosi delle buone Scienze, & di coloro che seguitano le uirtù, costumatamente & ciuilmen-te viuono.
Vt nunquàm inducant animum cantare rogati,
Iniussi nunquàm desistant.
Quello che sia Musica in vniuersale, & della sua Diuisione.Cap. V.
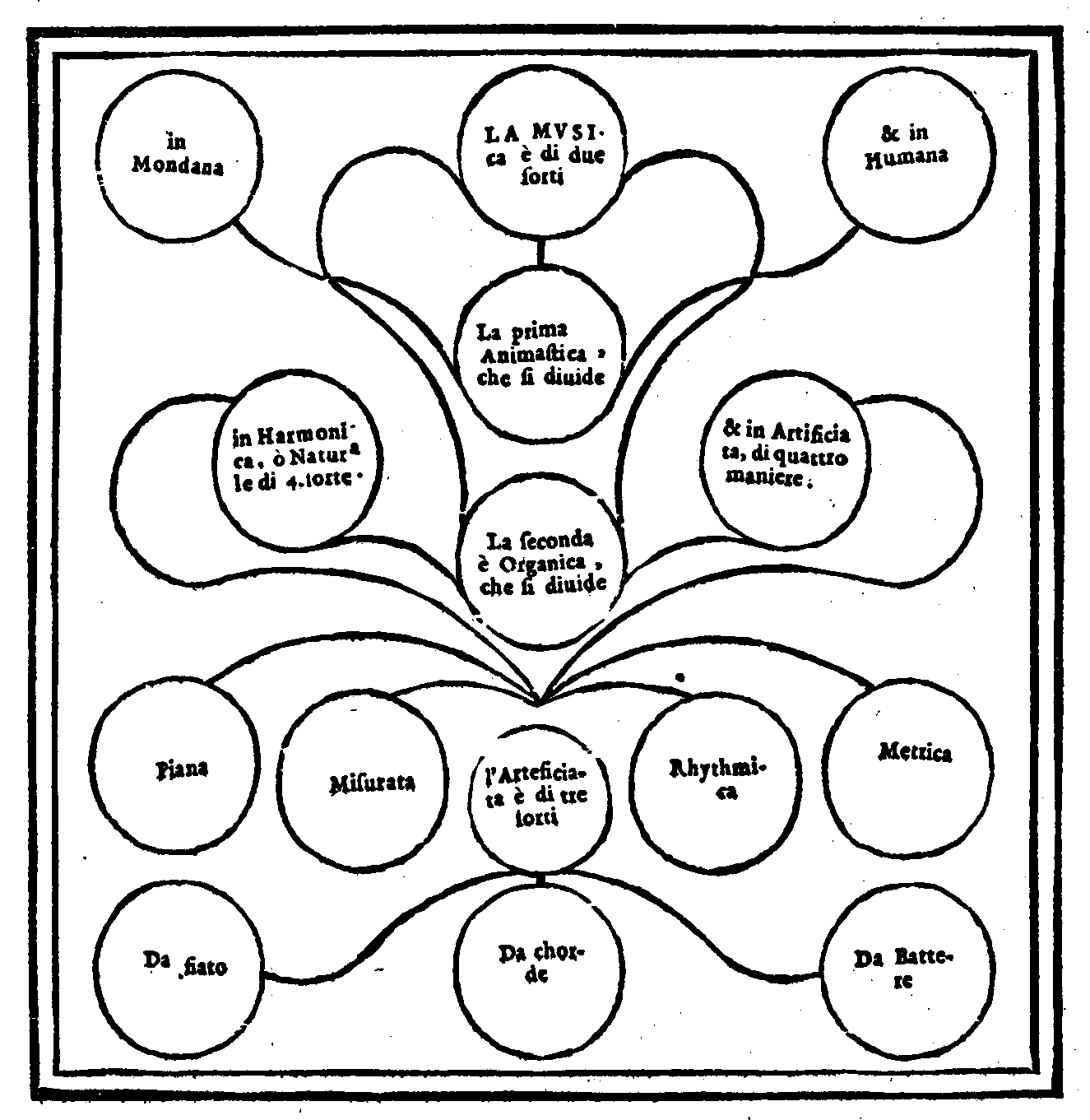
Della Musica mondana.Cap.VI.
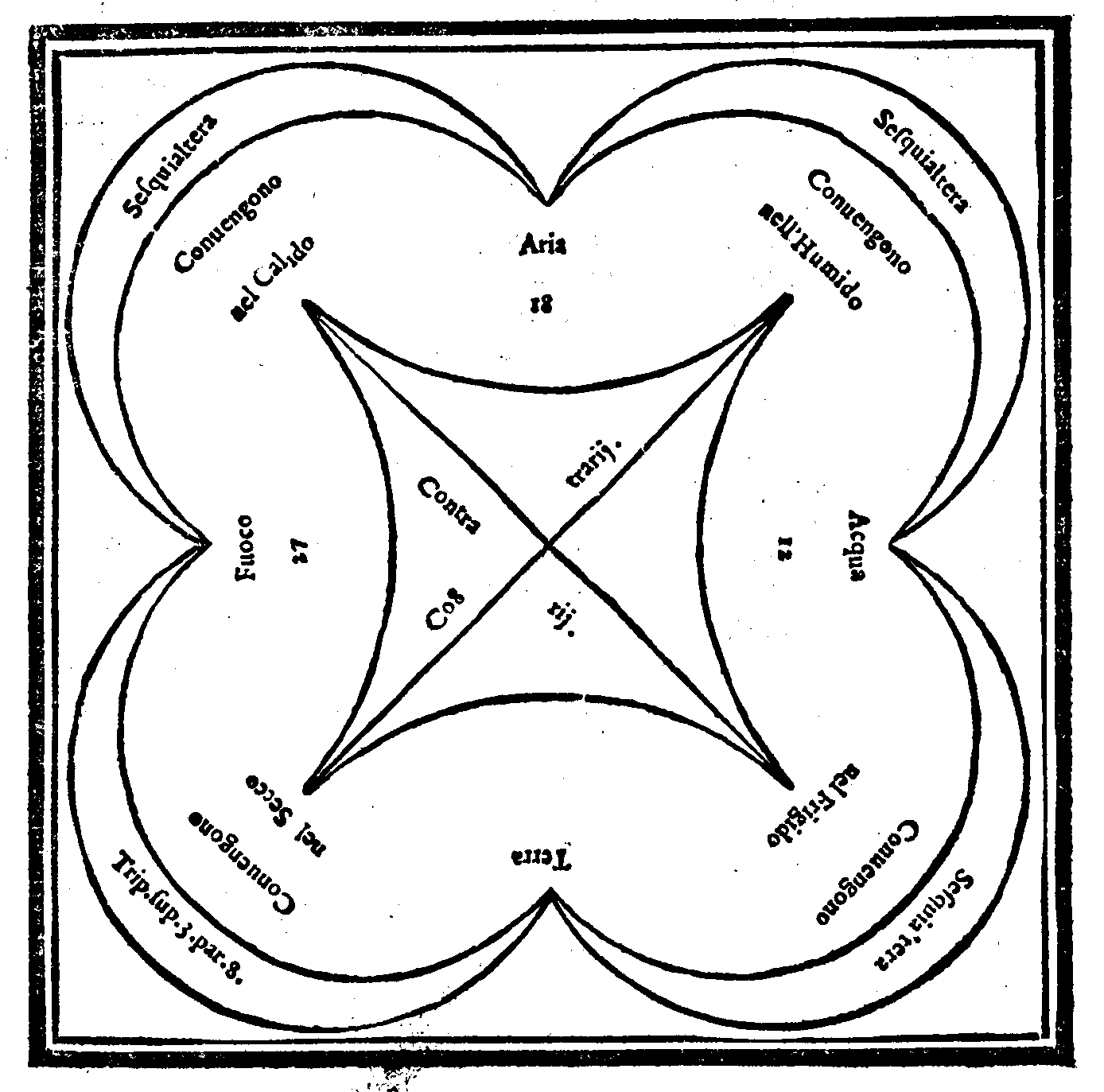
Vos o Calliope precor aspirate canenti;Inuocando particolarmente Calliope nel numero del più, come principale, & come quella, al cui uolere si muouono & si girano tutte l'altre. Et tanto hebbero gli Antichi page 17questa opinione per uera, che ne i sacrificij loro usauano musicali istrumenti, & can-tauano alcuni Hinni composti di sonori versi; i quali conteneuano due parti, l'una dellequali nominauano Στροφὴ & l'altra Α'ντιστροφὴ. per mostrare i diuersi giri fatti dal-le sphere celesti: percioche per l'una intendeuano il moto, che fà la sphera delle stelle fisse dall'Oriente in Occidente; & per l'altra i mouimenti diuersi, che fanno l'altre sphe-re de pianeti procedendo al contrario; secondo l'opinione di alcuni; dall'Occiden-ta in Oriente. Et con tali Istrumenti ancora accompagnauano i corpi de i lor Morti alla sepoltura: essendoche erano di parere, che dopo la morte l'Anime ritornassero all'origine della dolcezza della Musica; cioè, al cielo. Tal costume osseruarono gli He-brei anticamente nella morte de loro parenti; di che ne habbiamo chiarissima testimo-nianza nell'Euangelio,Matth. c. 9 nel quale è descritta la Resuscitatione della figliuola del prenci-pe della Sinagoga, doue erano musicali istrumenti; à sonatori de i quali commandò il Signor nostro, che più non sonassero. Et faceano questo (come dice AmbrosioSuper Lu-cam ca. 8. lib. 6:) per osseruar l'usanza de i loro Antichi; i quali in cotal modo inuitauano i circostanti à pian-gere con esso loro. Molti ancora haueano opinione, ch'in questa vita ogn'Anima fusse vinta per la Musica; & se bene era nel carcere corporeo rinchiusa, ricordandosi & essendo consapeuole della Musica del cielo, si domenticasse ogni dura & noiosa fa-tica. Ma se ciò ne paresse strano, habbiamo dell'Harmonia del cielo il testimonio delle Sacre lettere, doue il Signor parla à Giobbe dicendo:Iob. c. 38. chi narrerà le ragioni, ò voci de Cieli? Et chi farà dormire il loro concento? Et se mi fusse dimandato; onde proceda, che tanto grande & si dolce suono non sia udito da noi; altro non saprei ri-spondere, che quello, che dice Cicerone nel luogo di sopra allegato; che gli orecchi nostri ripieni di tanta Harmonia sono sordi; come per essempio auiene à gli habitato-ri de quei luoghi doue il Nilo da monti altissimi precipita, detti Catadupa; i quali per la grandezza del rimbombo mancano del senso dell'vdito: ouer che, si come l'occhio nostro non può fissar lo sguardo nella luce del sole, restando da i suoi rag-gi uinta la nostra luce; cosi gli orecchi nostri non possono capire la dolcezza dell' harmonia celeste, per l'eccellenza & grandezza sua. Ma ogni ragione ne persuade à credere almeno, che 'l Mondo sia composto con harmonia; si perche (come uuol PlatoneIn Timeo.) l'Anima di esso è Harmonia; si anche perche i Cieli sono girati intorno dal-le loro Intelligenze con harmonia; come si comprende da i loro riuolgimenti, i quali sono l'uno dall'altro proportionatamente più tardi, ò più veloci. Si conosce ancora tale Harmonia dalle distanze delle sphere celesti, percioche sono distanti tra loro (co-me piace à molti) in harmonica proportione; laquale, benche non uenga misurata dal senso, è nondimeno misurata dalla ragione: imperoche i Pitagorici (come dimostra PlinioNatu. hist. li. 2. c. 22.) misurando la distanza de cieli & i loro interualli, poneuano innanzi ogni al-tra cosa dalla Terra alla prima Sphera lunare essere lo spatio di 12600. stadij; & que-sto diceuano essere l'Interuallo del Tuono; auegna che questo (secondo 'l mio pare-re) sia detto fuori d'ogni ragione, quando alla Terra attribuissero suono: concio-sia che non può essere, che quelle cose, le quali per loro natura sono immobili, co-m'è questo Elemento, siano atte à generare l'Harmonia; hauendo i Suoni (come uuol BoetioMusicae li-bro. 4. c. 1.) il loro principio dal mouimento. Dopoi andauano ponendo dalla sphe-ra della Luna à quella di Mercurio l'interuallo d'un Semituono maggiore; & da Mer-curio à Venere, quello del minore; e da Venere al Sole il Tuono & il minore Se-mituono; & questa diceuano esser distante dalla terra per tre Tuoni & uno Semituo-no; il qual spatio è nominato Diapente. Et dalla Luna al Sole poneuano la distan-za di due Tuoni & uno Semituono; iquali costituiscono lo spatio della Diatessaron. Ritornando poi al principiato ordine, dissero; il Sole esser lontano da Marte per la medesima distanza, ch'è la Luna dalla terra; & da Marte à Gioue esser l'interual-lo del Semituono minore; & da questo à Saturno lo spatio del Semituono maggio-re; dal quale per fino all'ultimo cielo,oue sono i segni celesti posero lo spatio del minor page 18Semituono. Per la qual cosa dall'ultimo Cielo alla sphera del Sole si comprende esser lo spatio, ò interuallo della Diatessaron; & dalla terra all ultimo cielo lo statio de cinque Tuoni & due minori Semituoni; cioè, la Diapason. Ma chi uorrà esserminar i Cieli nel-le loro parti, secondo che con gran diligenza hà fatto Tolomeo,Harmo. libro 3. c. 9. ritrouera (comparate insieme le dodici parti del Zodiaco, nelle quali sono i dodici segni celesti) le consonan-ze musicali; cioè, la Diatessaron, la Diapente, la Diapason & l'altre per ordine; & ne i motti fatti verso l'Oriente & l'Occidente potrà conoscere esser collocati i suoni grauissimi; & in quelli, che si fanno nel mezo del cielo gli acutissimi. Nelle altezze poi ritrouerà il Diatonico, il Chomatico [sic: Chromatico] & l'Enharmonico genere. Simigliantemente nelle larghez-ze i Tropi, ò Modi, che uogliamo nominarli; & nelle faccie della Luna, secondo i uarij aspetti col Sole, esser le congiuntioni de i Tetrachordi. Ne solamente dalle predette cose si può conoscere cotale Harmonia; ma da i uarii aspetti de i sette Pianeti ancora, dalla natura, & dalla positione, ò sito loro. Da gli aspetti prima, come dal Trino, dal Qua-dratto, dal Sestile, dalle Congiuntioni & dalle Oppositioni; i quali fanno nelle cose inferiori, secondo i loro influssi buoni & rei, una tale & tanta diuersita d'harmonia de co-se, ch'è impossibile di poterla esplicare. Dalla natura poi, conciosiache essendone al-cuno (come uogliono gli Astrologi) di natura trista & maligna; da quelli, che buoni & benigni sono, in tal modo uengono ad esser temperati; che ne risulta poi tale Har-monia, ch'apporta gran commodo & utile à mortali. Et questa si comprende anco dal Si-to, ouer dalla Positione loro; conciosiache sono tra loro in tal modo collocati, quasi nel modo che sono collocate le Virtù tra i Vitii. Onde, si come questi, che sono estremi, si riducono ad un'habito uirtuoso, per uia d'uno mezo conueniente; cosi quel-li Pianeti, che sono di natura maligni, si riducono alla temperanza per uia d'un'altro Pianeta posto nel mezo loro, che sia di natura benigna. Però si uede, che essendo Sa-turno & Marte posti nel luogo soprano di natura maligna, cotal malignità da Gioue po-sto tra l'uno & l'altro, & dal & Sole posto sotto di Marte con una certa harmonia è tempe-rata, si che non lasciano operare à i loro influssi cattiui nelle cose inferiori quel mali-gno effetto, che potrebbono operare, non vi essendo tale interpositione. Hanno etian-dio i loro influssi tale possanza sopra i corpi inferiori, che mentre i due primi nominati pianeti si ritrouano hauere il dominio dell'anno; allora si discioglie l'harmonia de i quat-tro Elementi; percioche si altera l'aria de tal maniera, che genera nel mondo pestilen-za uniuersale. Vogliono ancora gli Astrologi, che i due Luminari maggiori, che sono il Sole & la Luna, faccino corrispondente harmonia di beniuolenza tra gli huomini; quando nel nascimento dell'uno, quello si ritrona essere nel Saggittario, & questa nel Montone; & nel nascimento dell'altro, il Sole sia nel Montone, & la Luna nel Sa-gittario. Simile harmonia dicono ancora farsi, quando nel loro nascimento hanno hauuto un medesimo segno, ouero di simile natura, ouero un medesimo pianeta, ò di natura simile in ascendente; ouero che due benigni pianeti col medesimo aspet-to habbiano riguardato l'angolo dell'oriente. Questo istesso dicono auenire, quando Venere si ritroua nella medesima casa della loro natiuità, ò nel medesimo grado. Ha-uendo adunque hauuto riguardo à tutte le sopradette opinioni, & essendo (come affer-ma Mercurio TrismegistoPimandro Ser. 10.) il mondo istrumento, ouero Organo d'Iddio, nella dichiaratione della Musica mondana hò detto, ch'è Harmonia, laquale si scorge tra quelle cose, che si veggono & conoscono nel cielo. Et soggiunsi, che anco nel legamento de gli Ele-menti si comprende; conciosiache essendo stati creati dal grande Architettore Iddio (si come creò ancora tutte l'altre cose) in Numero, in Peso & in Misura;Sap. 11. da ciascuna di queste tre cose si può comprendere tale harmonia; & prima dal Numero, medianti le qualità passibili, che sono quattro & non piu; cioè, Siccittà, Frigidità, Humidità, & Calidità, che si ritrouano in essi; imperoche à ciascuno di loro principalmente vna di esse qualità è appropriata; come la siccità alla terra, la frigidità all'acqua, l'humidità all'aria; & la calidità al fuoco; ancora che la siccità secondariamente si attribuisca page 19al fuoco, la calidità all'aria, l'humidità all'acqua, & la frigidità alla terra; per le qua-li non ostante, che tra loro essi Elementi siano contrarii; restano nondimeno in un me-zano elemento secondo una qualità concordi & uniti; essendo che ad ogn'un di loro (com'habbiamo ueduto) due ne sono appropriate, per mezo delle quali mirabilmente insieme si congiungono, & in tal modo; che si come due numeri Quadrati conuengono in un mezano numero proportionato: così due di essi Elementi in un mezano si congiungono: conciosia che al modo, che 'l Quaternario & Nouenario numeri Quadrati si con-uengono nel Senario, ilqual supera il Quaternario di quella quantità, ch'esso è supera-to dal Nouenario; in tal modo il Fuoco & l'Acqua, che sono in due qualità contrarii, in vn mezano elemento si congiungono. Imperoche essendo il Fuoco per sua natura cal-do & secco; & l'Acqua fredda & humida; nell'Aria calda & humida mirabilmente con grande proportione s'accompagnano; il quale se bene dall'Acqua per il calido si scompagna, seco poi per l'humido si unisce. Et se l'humido dell'Acqua ripugna al secco della Terra, il frigido non resta però d'unirli insieme. Di modo che sono con tanto maraui-glioso ordine insieme uniti, che tra essi non si ritroua più disparità, che si ritroui tra due mezani Numeri proportionali, collocati nel mezo di due numeri Cubi; come nell'es-sempio si può uedere.
Tu numeris Elementa ligas, ut frigora flammisEt in un'altro luogo,Lib. 4. met. 6.
Arida conueniant liquidis, ne purior Ignis
Euolet, aut mersas deducant pondera Terras. page 20
Tu triplicis mediam naturae cuncta mouentem
Connectens animam, per consona membra resoluis.
Haec concordia temperat aequisMa chi vorrà dal Peso loro comprendere anco la Mondana harmonia, la potra cono-scere; percioche essendo l'uno dell'altro più graue, ò più leggiero; sono in tal modo insie- me concatenati & legati; che con una certa harmonia la circonferenza di ciascuno pro-portionatamente è lontana dal centro del Mondo, secondo i luoghi ò siti loro. Noi uediamo che quelli, che sono per loro natura graui, sono tirati all'insù da quelli, che sono per loro natura leggieri; & li graui tirano all'ingiù i leggieri in tal maniera, che niun di loro uà fuori del suo proprio luogo. Et in tal guisa stanno insieme sempre uniti & serrati, che tra loro non si troua per alcun tempo, quantunque breue, in alcuna parte il Vacuo; il quale la Natura grandemente abhorrisce. Et sono poi in tal modo collocati, che la Terra, la quale per sua natura è semplicemente graue; & il Fuoco ch'è semplicemente leggiero, sono quelli, che posseggono gli ultimi luoghi. La Terra tien l'infimo; percioche Ogni graue tende al basso, & il Fuoco stà nel supremo; essendo che Ogni cosa leggiera tende à tal luogo. Ma perche i mezi ritengono la natura de i loro estremi; però hà ordinato bene il Creatore, che essendo l'Acqua & l'Aria, secondo un certo rispetto graui & leggieri, douessero tenere il luogo mezano; l'Acqua accompagnandosi alla Terra, come più graue; & l'Aria al Fuoco, come pi ù [sic: più] leggiero; accioche ciascuno s'accompagnasse à quello, ch'era di natura à lui più simile. Il qual ordine & legamento leggiadramente Ouidio espresse con queste parole.Metamor. lib. 1
Elementa modis, vt pugnantia
Vicibus cedant humida siccis
Iungantque fidem frigora flammis.
Pendulus ignis surgat in altum,
Terraeque graues pondere sidant.
Ignea conuexi vis, & sine pondere coeliMa se più sotilmente ancora uorremo essaminar la cosa, ritrouaremo l'Harmonia mondana nella loro misura & quantità, mediante la trammutatione delle parti, che si fà dell'uno nell'altro; come mostra il Filosofo:De Gene-rat. lib. 2. conciosiache cosi si trammuta una parte di terra in acqua, & una parte d'acqua in aria; come si trammuta una parte d'aria in fuoco: Et si come si trammuta una parte di fuoco in aria & una parte d[unclear: ']aria in acqua; cosi si trammuta una parte d'acqua in terra: essendo che trammutandosi la terra in acqua, si uiene à far tale trammutatione in proportione Decupla. Di modo che quando si trammuta un pugno di terra (dirò cosi) in acqua, si generano (come dicono alcuni Peripatetici) dieci pugni d'acqua; & quando si trammuta tale acqua in aria, uiene à far cento pugni d'aria: onde trammutandosi ultimamente tutto questo nel supremo elemento, viene a multipli-care in mille pugni di fuoco. Cosi per il contrario, mille pugni di fuoco si conuertono in cento d'aria, & questi in dieci di acqua, & dieci d'acqua in uno di terra; & ciò auiene dal-la loro rarità & spessezza, che più in uno, che in un'altro si ritroua: percioche quanto più s'auicinano al cielo, & sono lontani dal centro del mondo; tanto più sono rari; & quan-to più s'auicinano à questo, & si allontanano da quello, tanto più sono spessi.Onde quando da questo si uolesse giudicar la loro misura, si potrebbe dire, che la quantità del fuoco fusse in proportione Decupla con quella dell'aria; & quella dell'aria, con quella dell'acqua medesimamente in proportione Decupla; & cosi la quantità dell'acqua con tutta la quantità della terra, nella medesima proportione. Et si potrebbe anco dire (poi page 21che gli Elementi sono corpi d'un'istesso genere, & il tutto con le parti conuiene in una istessa natura & in una ragione istessa) che la Proportione, che si ritrouatra la quantità della sphera del fuoco & tutta la massa della terra, sia quella, che si ritroua tra il numero Millenario & l'Vnitade. A questo modo adunque, dal mouimento, dalle distanze & dalle parti del cielo; & similmente da gli aspetti; dalla natura & dal sito de i Sette piane-ti; & dal Numero etiandio, dal Peso & dalla Misura de i quattro elementi, uenimo al-la cognitione dell'harmonia Mondana: essendo che la concordanza & l'harmonia loro partorisce l'harmonia de i tempi, che si conosce prima ne gli Anni, per la mutatione della primauera nella State; & di questa nell'Autunno; similmente dell'Autunno nel Verno; & del Verno nella Primauera: dopoi si conosce ne i Mesi, per il crescere & sciemare re-golatamente, che fà la Luna; & finalmente ne i Giorni, per il cambieuole apparir della luce & delle tenebre; dalla quale Harmonia nasce la diuersità de fiori & de frutti: Il per-che Ouidio in questo proposito disse:De Re-med. 1.
Emicuit, summaque locum sibi legit in arce.
Proximus est Aer illi leuitate locoque.
Densior his Tellus elementaque grandia traxit,
Et praessa est grauitate sui. circumfluus humor
Vltima possedit, solidumque coercuit orbem.
Poma dat Autumnus; formosa est mensibus Aestas;Onde come afferma Platone,In Sympo-sio: quando 'l caldo col freddo, & il secco con l'humido pro-portionatamente s'uniscono; dall'Harmonia di queste qualità ne risulta l'Anno à cia-scun uiuente utilissimo, pieno di varie sorti de fiori odoriferi & de frutti ottimi; ne alcun' altra sorte di piante, ò d'animali uiene à patire offesa: come all'opposito auiene; che dalla discordanza & distemperamento loro si generano pestilenza, sterilità, infirmità & ogni cosa à gli Huomini, alle Bestie & alle Piante nociua. Et ueramente la Natura hà seguito un bello & ottimo ordine, facendo, che quel che il Verno ristringe & rinchiu-de, Primauera lo apra & mandi fuori; & quel che la State secca, l'Autunno final-mente maturi. Di maniera che si uede l'un tempo all'altro porgere aiuto; & de quattro tempi harmonicamente disposti farsi un corpo solo. Questa tale Harmonia troppo bene conobbero Mercurio & Terpandro; conciosia che l'uno hauendo ritrouata la Lira, oue-ramente la Cetera; pose in essa Quattro chorde ad imitatione della Musica mondana (come dice BoetioMae liusic bro [sic: Musicae libro] 1. cap. 20. & MacrobioSatur. lib. 1. cap. 19.) la quale si scorge ne i quattro Elementi, ouer nel- la uarietà de i quattro tempi dell'Anno; & l'altro la ordinò con Sette chorde al-la similitudine de i sette Pianeti. Fu poi il numero delle Quattro chorde nominato Qua-drichordo, ouer Tetrachordo; che tanto uuol dire, quanto Di quattro chorde; & quello di sette, Heptachordo, che uuol dire Di sette chorde. Ma il primo fù da i Musici di maniera riceuuto & abbracciato; che le Quindeci chorde comprese nel Systema massimo, furono accresciute secondo il Numero delle chorde del predetto Tetrachordo; come uederemo; ancora che si ritrouino distanti l'una dall'altra sot-to diuerse Proportioni. Et questo basti quanto alla dichiaratione della Musica mondana.
Ver praebet flores; igne leuatur Hyems.
Della Musica humana.Cap. VII.
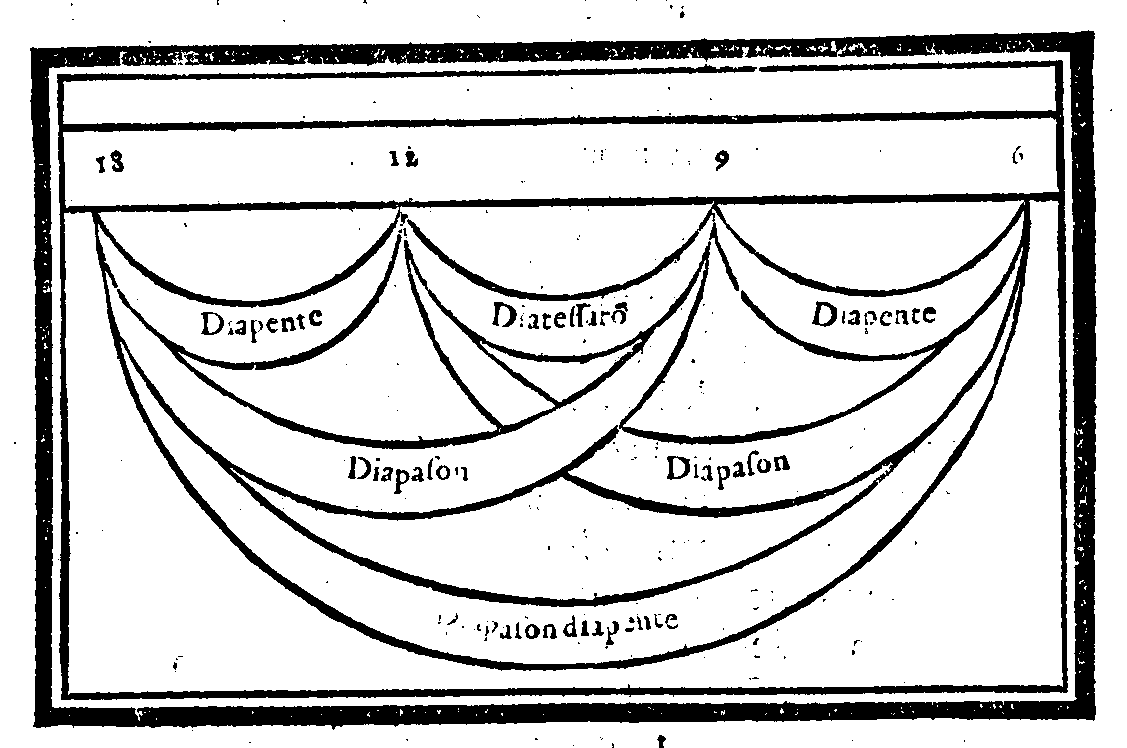
Sex in lacte dies, tres sunt in sanguine terni,Et veramente questo mirabilissimo ordine hà in se concento & harmonia, considera-ta la distanza d'un Numero all'altro, come è chiaro da uedere; che dal primo al secon-do si ritroua la forma della Consonanza Diapente; & da questo al terzo quella della Diatessaron; & dal terzo all'ultimo quella della medesima Diapente. Et di nuouo dal primo al terzo & dal secondo all'ultimo la forma della Diapason; & dal primo all'ultimo chia-ramente si scorge quella della Diapasondiapente; come più facilmente nella figura si ve-
Bis seni carnem, ter seni membra figurant.
Explebo numerum, reddarque tenebris.Ma perche queste cose s'appartengono più à i ragionamenti della Filosofia, ch'à quel-li della Musica; lascierò di parlarne più oltra; contentandomi d'hauerne detto queste poche, & dimostrato la varietà della Musica animastica; della quale, come di quella, che nulla, ò poco fà al proposito, non ne farò più mentione. page 24
Della musica Piana, & Misurata; ò vogliamo dire canto Fermo, & Figurato.Cap. VIII.
Della Musica Rhythmica & della Metrica.Cap. IX.
Quel che sia Musica in particolare, & perche sia cosi detta.Cap. X.
Pan primus calamos cera coniungere pluresEt quantunque queste opinioni siano buone; tuttauia quello, ch'à me par più ra-gioneuole, & più mi piace, è l'opinione di Platone;In Alcibia-de. 1. ch'ella sia nominata dalle Muse; alle quali (come dice AgostinoMusicae li-bro 1. c. 1.) è conceduto vna certa onnipotenza di cantare; & vo-gliono i Poeti, che siano figliuole di Gioue & di Memoria; & dicono bene: percioche se l'Huomo non ritiene i Suoni, & gli Interualli delle voci Musicali nella memoria, non fà profitto alcuno; & questo auiene; perche non si possono à via alcuna scriuere; tanto più, ch'ogni Scienza & ogni Disciplina (come uuole QuintilianoInstitu. o-rat. lib. 11: cap. 2.) consiste nella me-moria; conciosia che in vano ci è insegnato; quando quello, che noi ascoltiamo, dal-le menti nostre si parte. Et perche habbiamo detto la Musica essere Scienza Speculati-ua; però auanti che più oltra passiamo, vederemo (hauendo consideratione del fine) com'anche la possiamo dimandare Prattica.
Instituit.
Diuisione della Musica in Speculatiua ò Contemplatiua & in Prattica; per la qua-le si pone la differenza tra 'l Musico, & il Cantore.Cap. XI.
Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità é NumeroCap. XII.
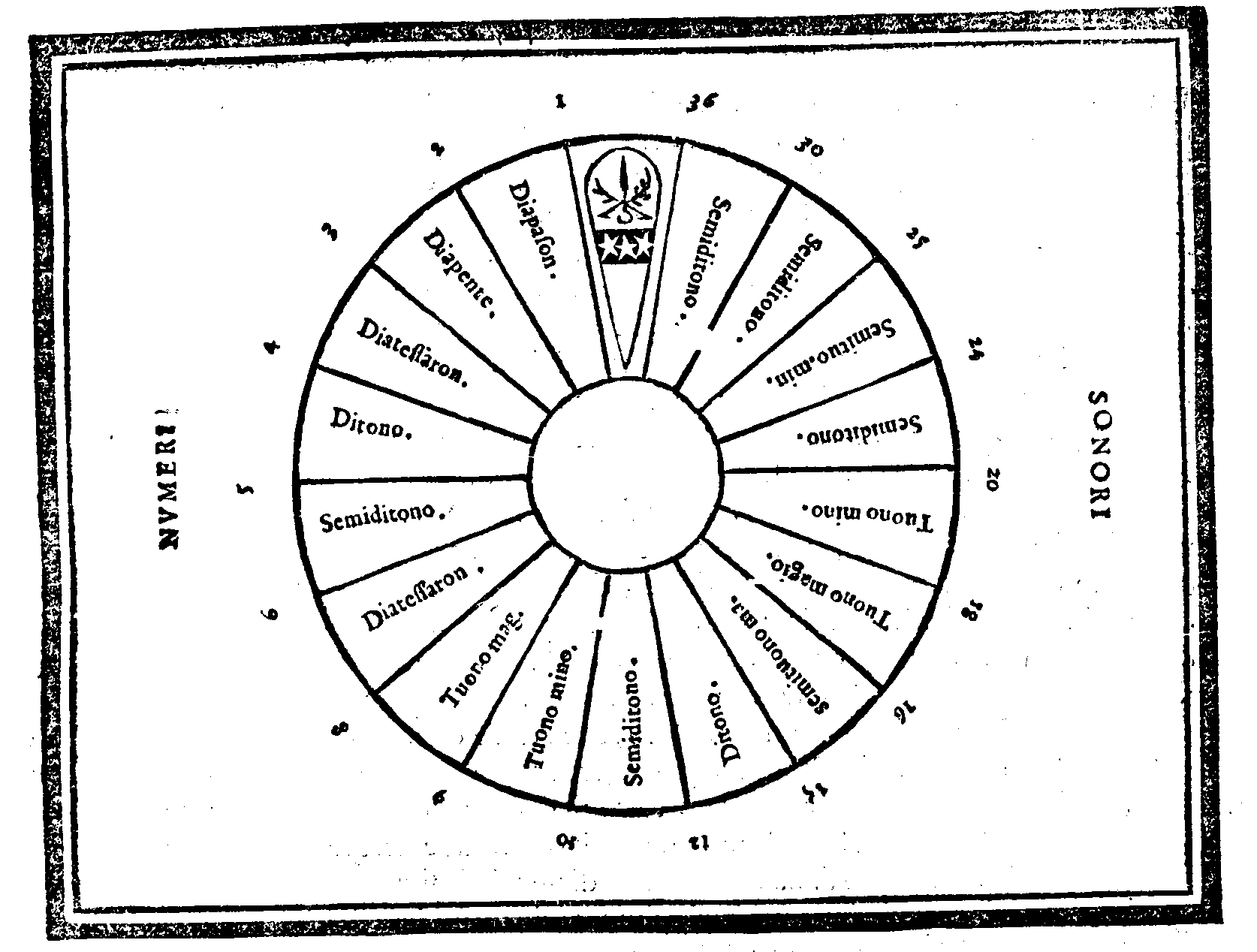
Delle Varie specie de Numeri; & che nel Senario si trouano le Forme de tutte le Consonanze semplici.Cap. 13.
Che dal numero Senario si comprendo molte cose della Natura & dell'Arte.Cap. 14.
Delle Proprietà del numero Senario & delle sue parti; & come tra loro si ritroua la forma d'ogni Consonanza musicale. Cap. XV.
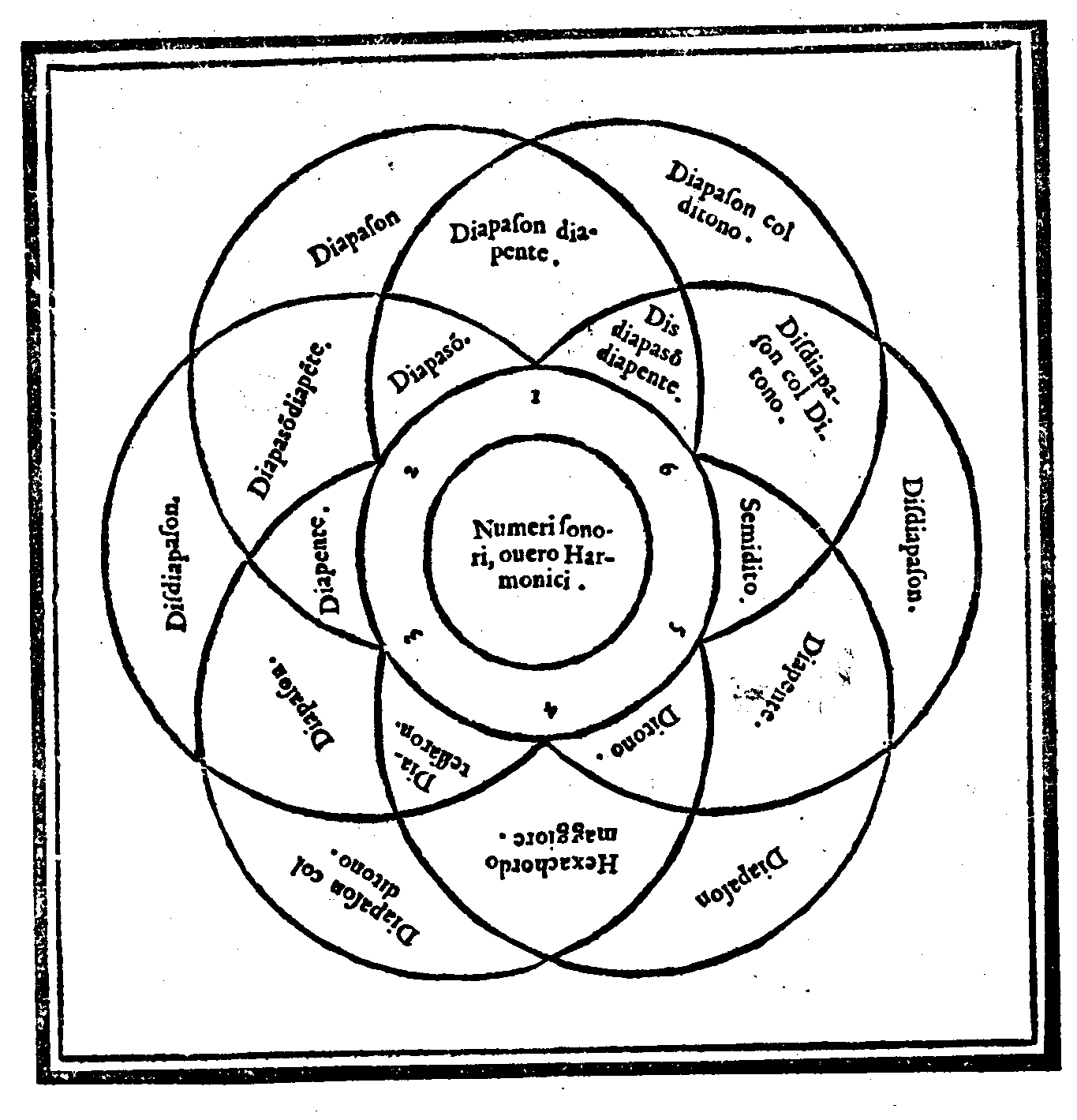
Quel sia Consonanza semplice ò Composta; & che nel Senario in potenza si ri-trouano le Forme de tutte le Consonanze; & onde habbia origine l'Hexachordo minoreCap. XVI.
Della Quantità continua & della discreta.Cap. XVII.
Del Soggetto della Musica.Cap. XVIII.
Quel che sia Numero sonoro.Cap. XIX.
Per qual cagione la Musica sia detta subalternata all'Arithmetica, & mezana tra la Mathematica & la Naturale.Cap. XX.
Quel che sia Proportione; & della sua diuisione.Cap. XXI.
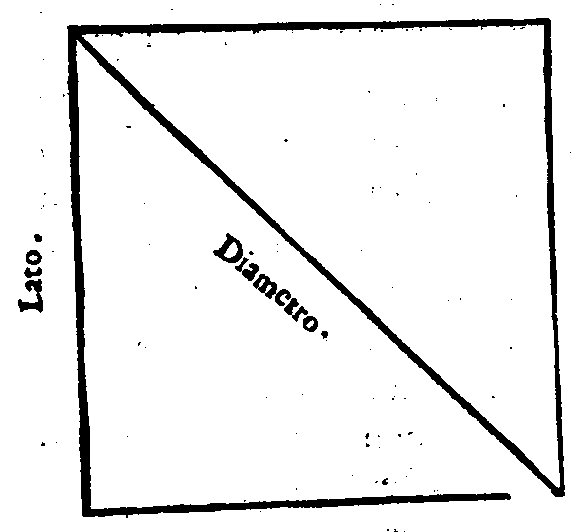
In quanti modi si compara l'una Quantità all'altra.Cap. XXII.
Quel che sia parte Aliquota, & Nonaliquota.Cap. XXIII.
Della produttione del genere Moltiplice.Cap. XXIIII.
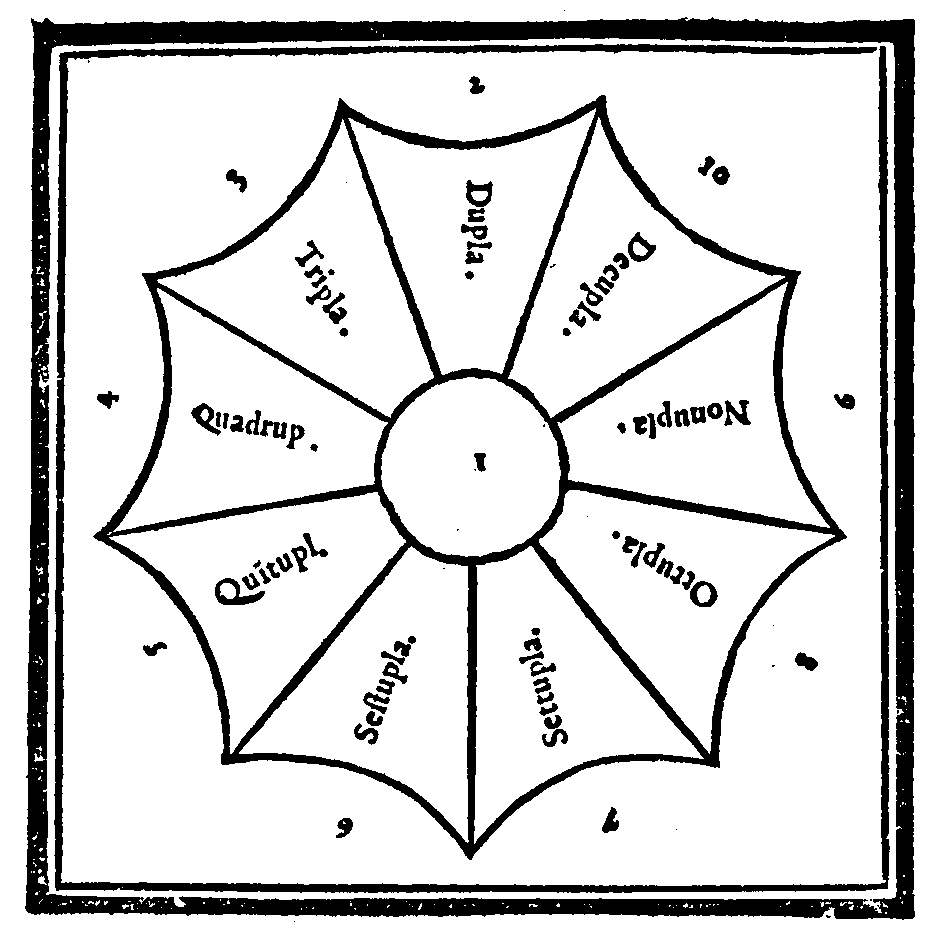
Quel che sia Denominatore, & in qual modo si troui; & come di due proposte Proportioni si possa conoscere qual sia la maggiore, ò la minore.Cap. XXV.
Come nasca il genere Superparticolare.Cap. XXVI.
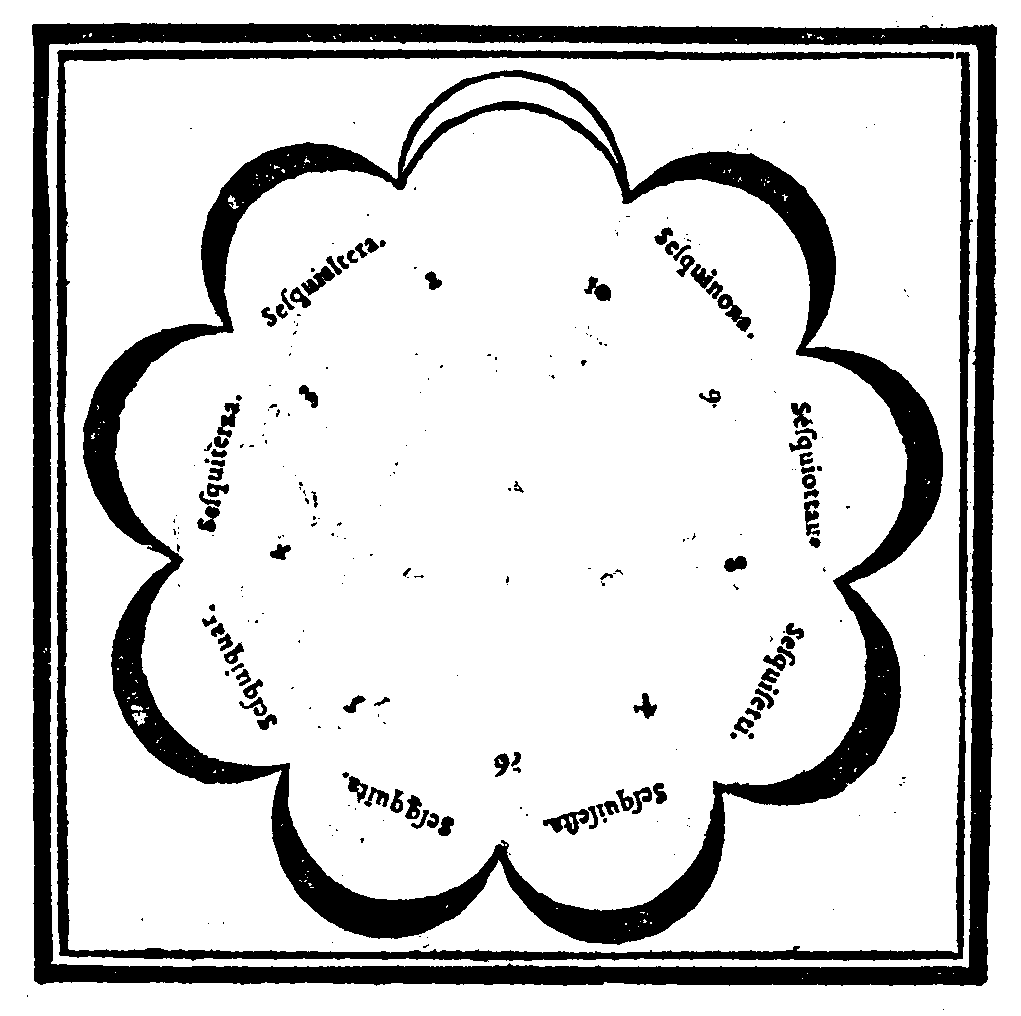
della prodottione del gener Superpartiente.Cap. XXVII.
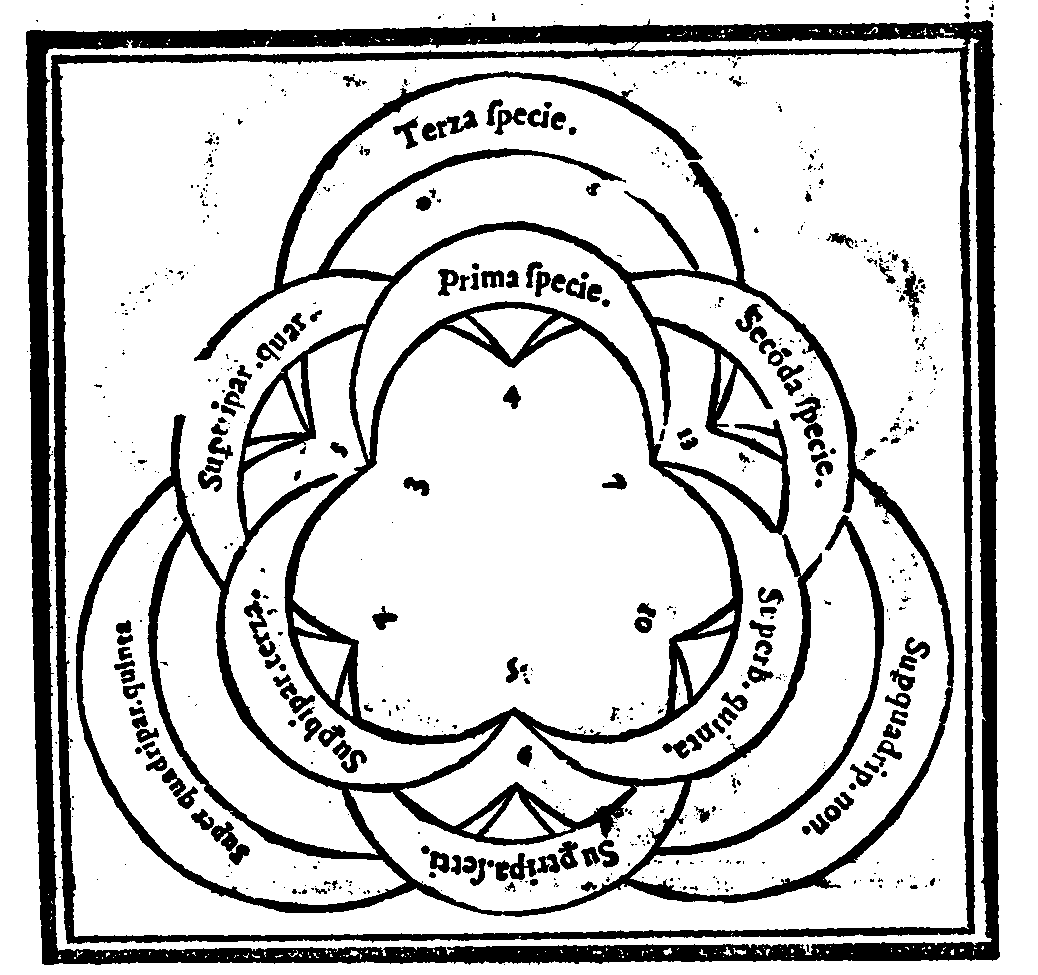
Del Genere molteplice superparticolare.Cap. XXVIII.
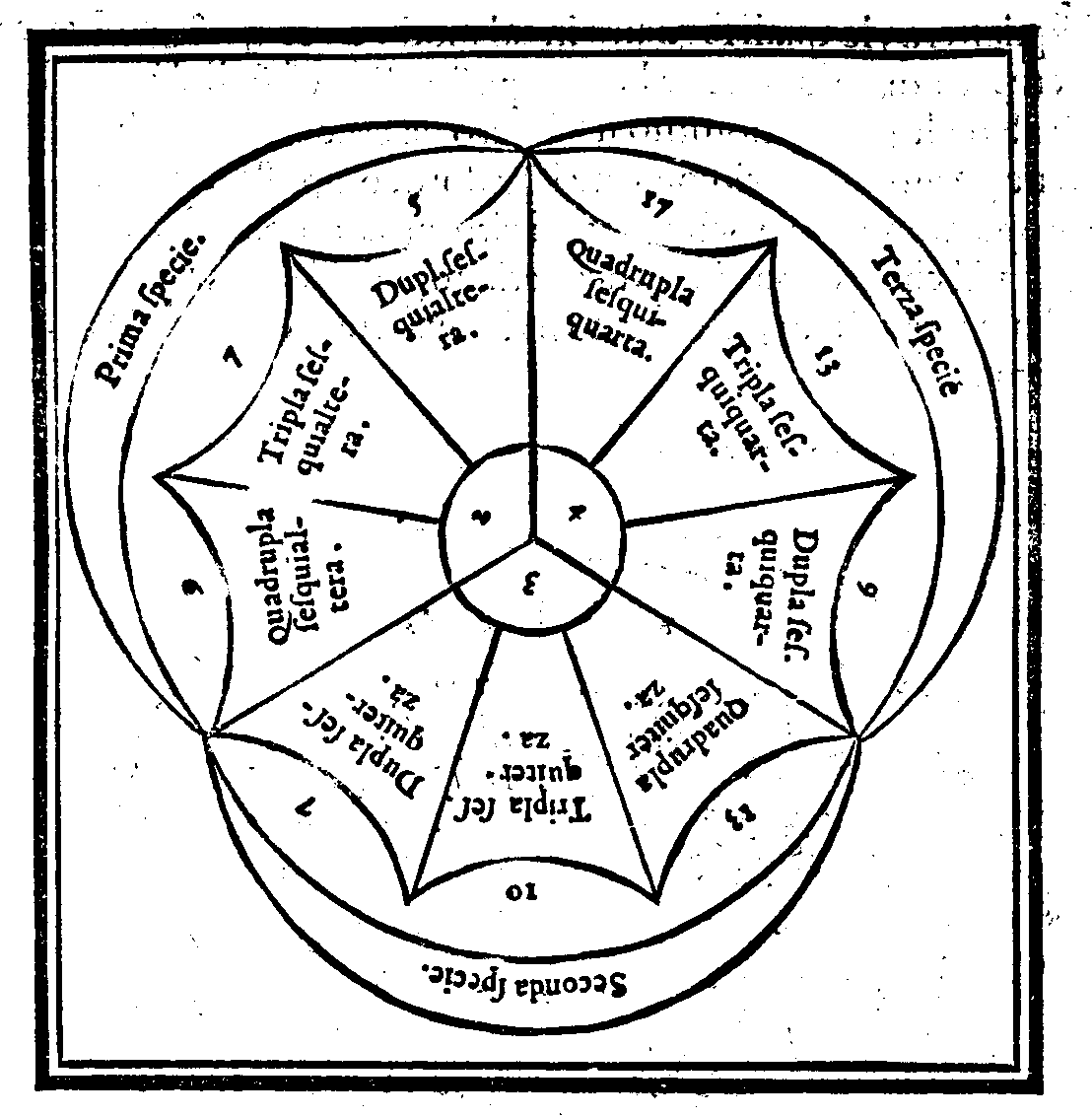
Della prodottione del Quinto & vltimo Genere, detto Molteplice-superpartiente.Cap. XXIX.
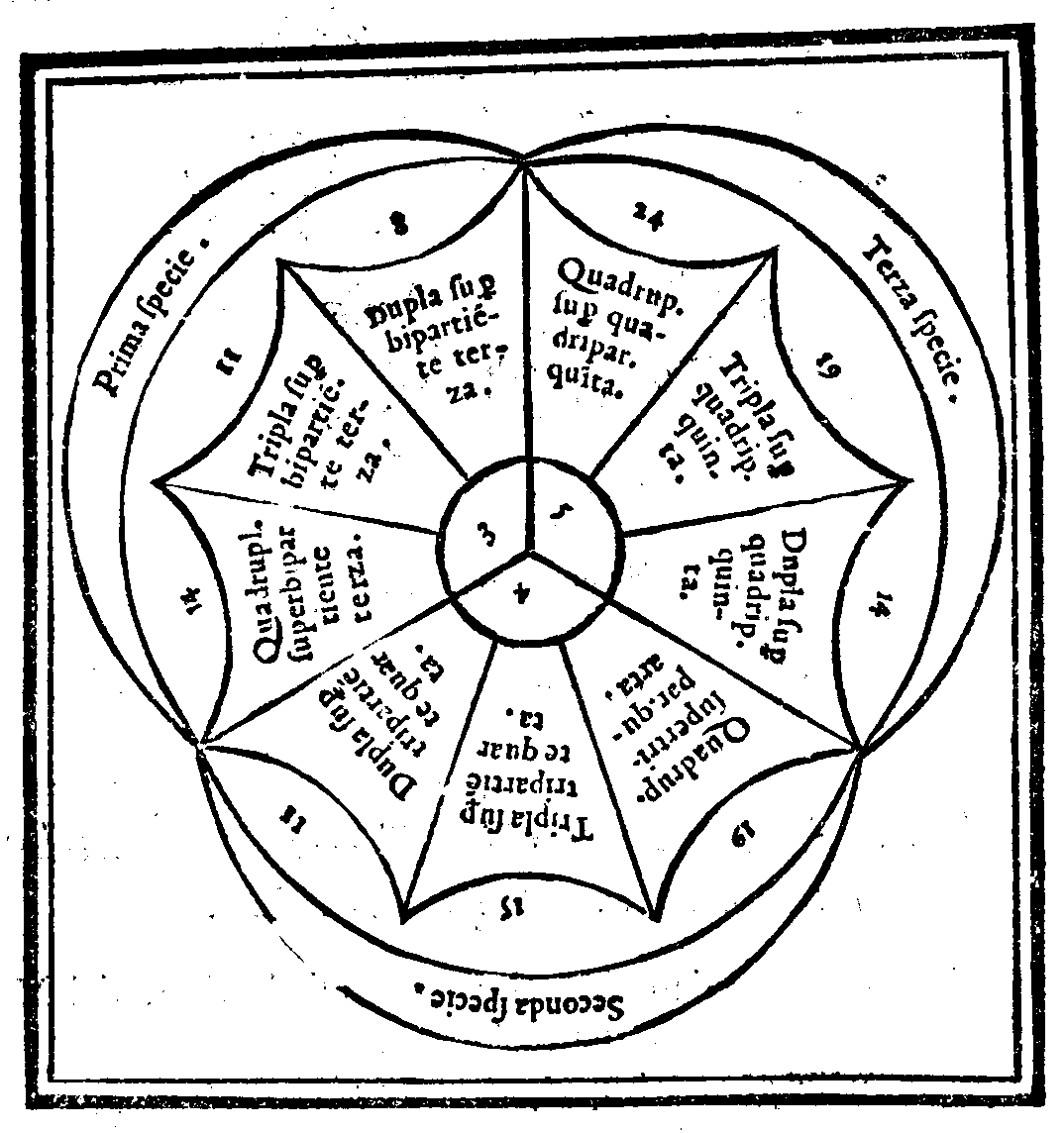
Della Natura & proprietà de i nominati Generi.Cap. XXX.

Del primo modo di Moltiplicar le Proportioni.Cap. XXXI.

Il Secondo modo di moltiplicar le Proportioni.Cap. XXXII.

Del Sommar le Proportioni.Cap. XXXIII.

Del Sottrar le Proportioni.Cap. XXXIIII.
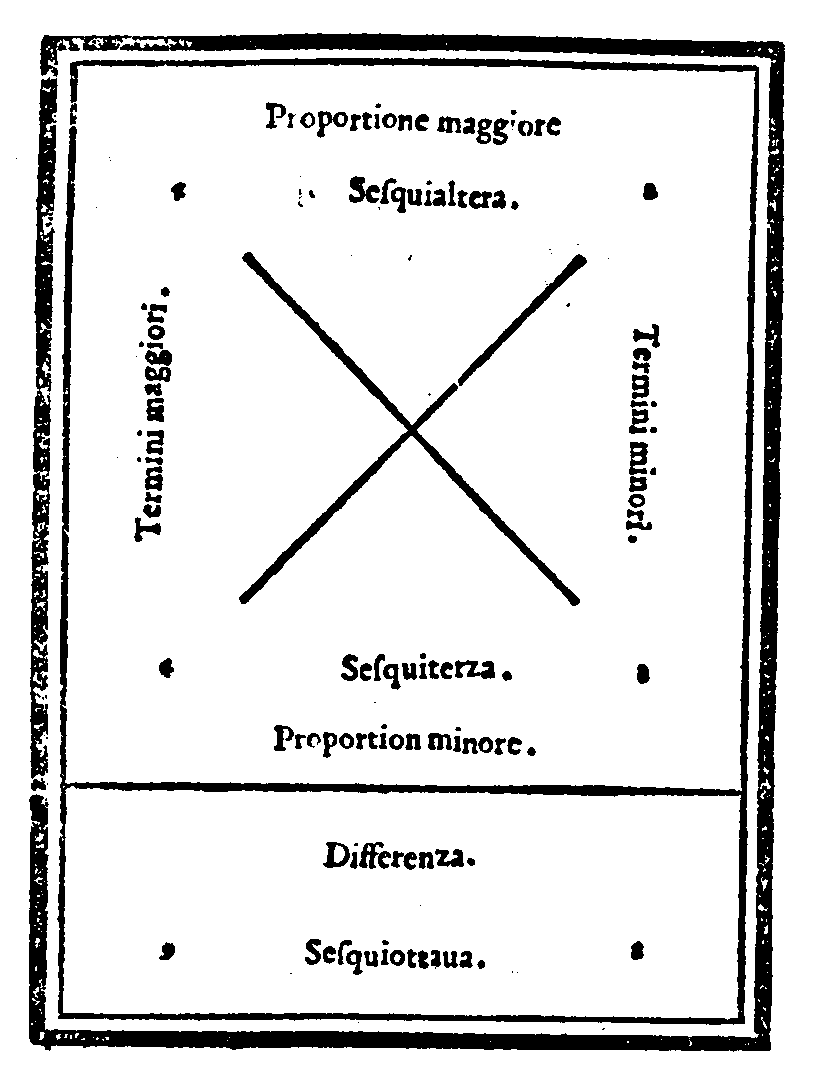
Del Partire, ò Diuidere le proportioni; & quello che sia Proportio-nalità.Cap. XXXV.
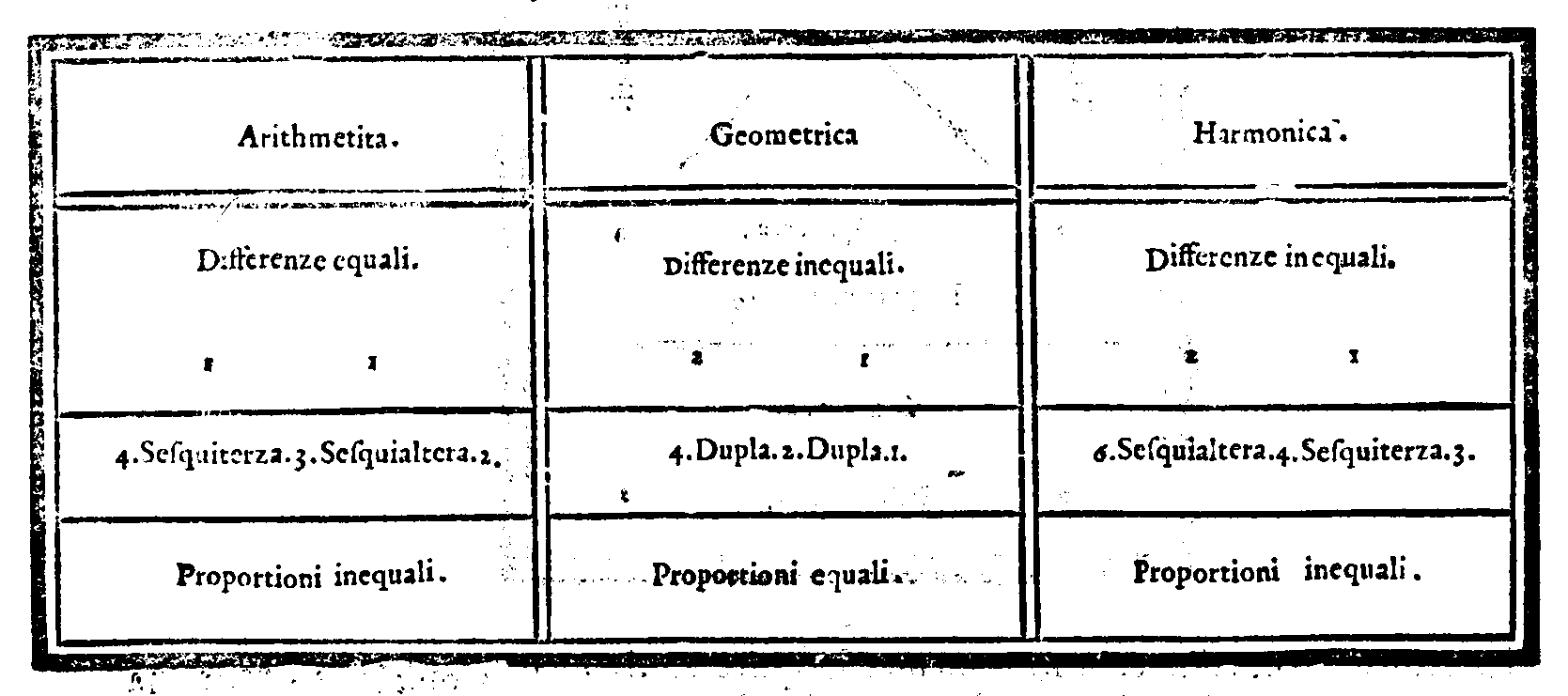
Della proportionalità, ò Diuisione arithmetica.Cap. XXXVI.

Della Diuisione, ò Proportionalità Geometrica.Cap. XXXVII.

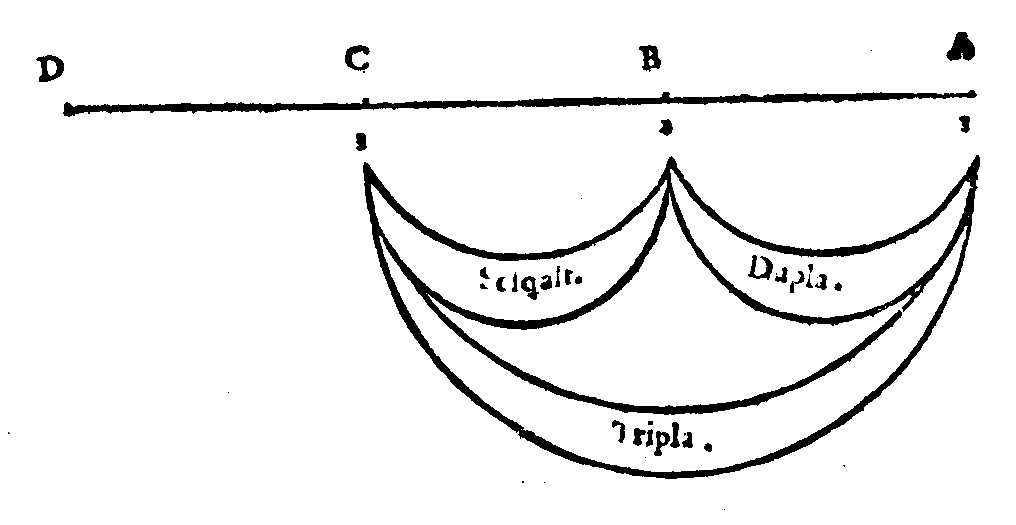
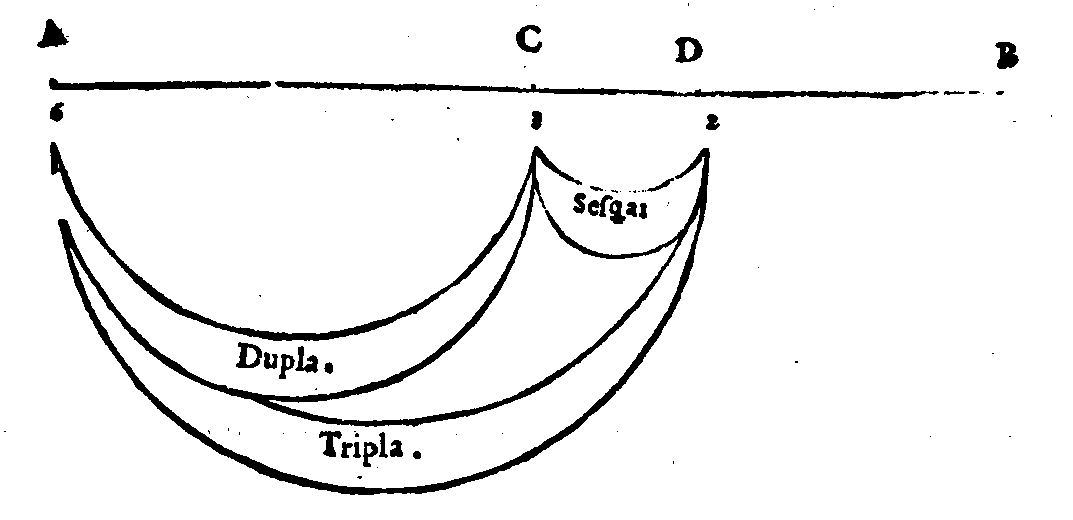
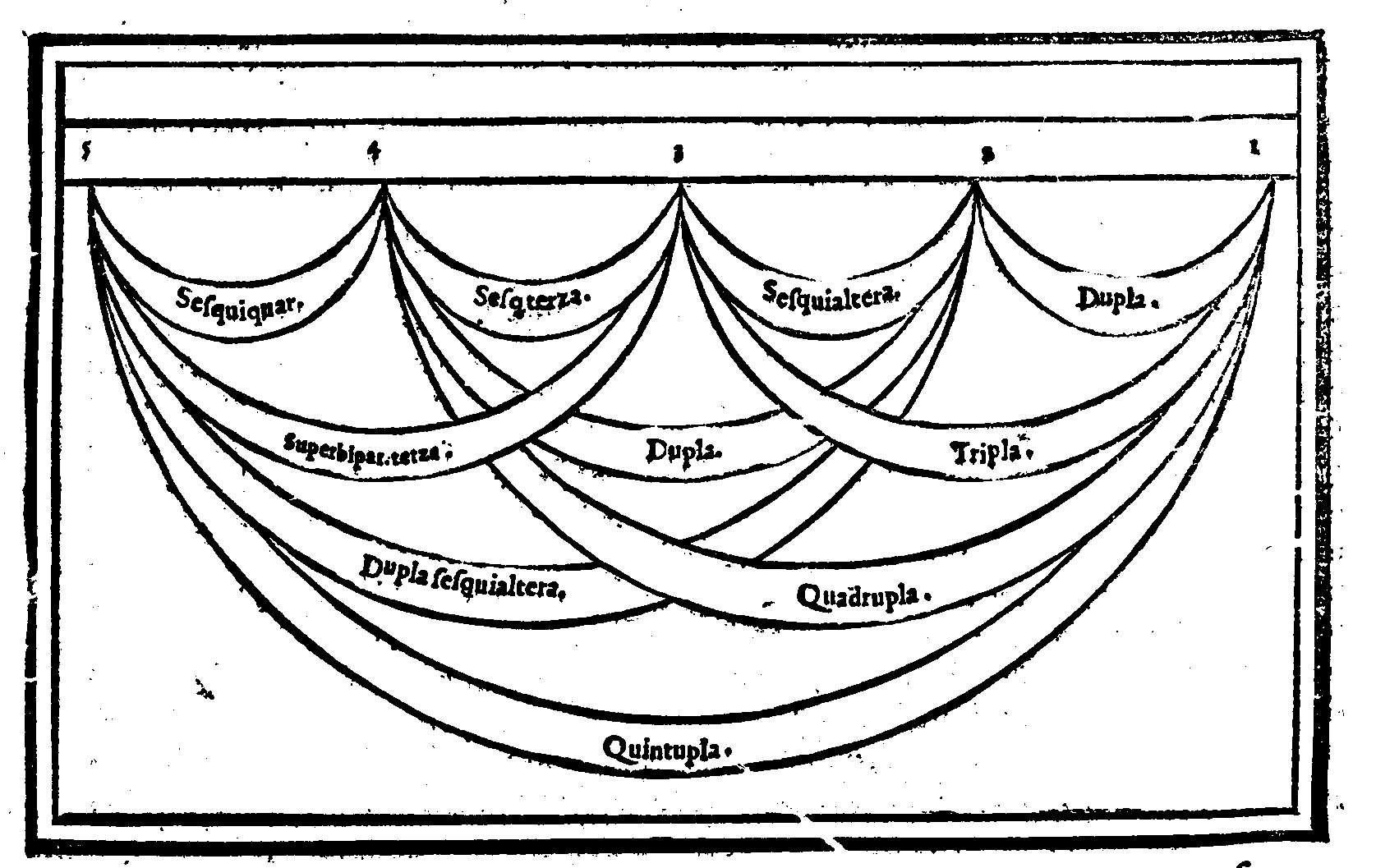
![Proportioni da diuidere secondo la
Geometrica proportionalita.
3Sesquialtera2
Proportione diuisa irrationalmen-
te in due parti equali.
Sesquialtera.
Diuisore.
3[[mus.Resp]]. 6.2](../../zarins89/ill/137_2.gif)
In qual modo si possa cauar la Radice quadrata da un proposto numero.Cap. XXXVIII.

Della Diuisione, ouer Proportionalità harmonica.Cap. XXXIX.

Consideratione sopra quello, che si è detto intorno alle Proportioni & Proportionalità.Cap. XL.
Che 'l Numero non è Cagione propinqua & intrinseca delle Proprtioni musicali, ne meno delle Consonanze; & quali siano le quattro Cagioni, Finale, Efficiente, Materiale & Formale nella Musica.Cap. XLI.
Dell'Inuentione delle Radici delle proportioni.Cap. XLII.
In che modo si possa ritrouar la Radice de più Proportioni moltiplicate insiemeCap. XLIII.

Della Proua di ciascuna delle mostrate Operationi. Cap. XLIIII

LA SECONDA PARTE DELLE ISTITVTIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Capella della Serenissima Signoria DI VENETIA;
Quanto la Musica sia stata da principio semplice, roza, & pouera di Consonanze.Cap. I.
Tibia, non ut nunc, oricalcho uincta, tubaequepage 72Alquale dopoi Hiagne Frigio à quei tempi dotto nella Musica, che fù padre & Mae-stro di Marsia, u'aggiunse i fori, & incominciò à sonar quello con uariati suoni; & fu il primo che fece sonar due Pifferi con un sol fiato; & che sonò tale Istrumento con la destra & con la sinistra mano; cioè, mescolò il suono graue con l'acuto, con destri fori & sinistri. Vsarono etiandio gli Antichi da principio la Cetera, ò la Lira con tre chor-de, ouer con quattro solamente; della quale fù inuentore Mercurio; come uuol Boe-tio;Music li-bro 1. c. 20 & erano in quella ordinate di modo, che la prima con la seconda, & la terza con la quarta conteneuano la Diatessaron; la prima con la terza, & la seconda con la quarta, la Diapente; & di nuouo la seconda con la terza il Tuono; & la prima con la quarta la Diapason, & insino al tempo di Orfeo fu seruato cotale ordine; ilquale fu dopoi ac-cresciuto in uarii Istrumenti; & prima Chorebo di Lidia u'aggiunse la Quinta chorda; dopoi dal sopranominato Hiagne ui fù aggiunta la Sesta; ma la Settima aggiunse Ter-pandro Lesbio. Et questo Numero de chorde (come dice Clemente AlessandrinoStromat. lib. 6.) era prima contenuto nell'antica Lira, ò Cetera; dopoi da Licaone da Samo fù aggiunta la Ottaua; ancorache PlinioNat. hist. libro 7. ca-pit. 56. attribuisca l'Inuentione di tal chorda à Simonide, & della Nona à Timotheo; & BoetioIbidem, ut supra. uoglia, che questa chorda sia stata aggiunta da Profrasto Pe-riota, la Decima da Estiacho Colofonio, & la Vndecima da esso Timotheo. Ma sia co-me si uoglia; Suida attribuisce l'aggiuntione della Decima & della Vndecima chorda à Timotheo Lirico. Et certo è, che da molti altri ue ne furono aggiunte tante, che crebbe-ro al numero de Quindeci. Aggiunsero dopoi à queste la Sestadecima chorda; ne più oltra passarono & si contentarono di tal numero, & le collocarono nell'ordine, che più oltra dimostraremo; diuidendole per Tuoni & Semituoni in cinque Tetrachordi, osser-uando le Ragioni delle proportioni Pitagoriche; ritrouate ne i martelli da Pitagora; nel modo che nella Prima parte hò mostrato; le quali conteneuano quelle istesse, che si ritrouauano tra le chorde della sopradetta Cetera, ò Lira ritrouata da Mercurio: & che nel sottoposto essempio si ueggono. Imperoche il maggiore (come dicono) pesaua li-
Aemula; sed tenuis, simplexque foramine pauco
Adspirare, & adesse choris erat utilis:

Per qual cagione gli Antichi nelle loro Harmonie non vsassero le Consonanze im-perfette, & Pitagora vietaua il passare oltra la Quadrupla.Cap. II.
Dubbio sopra l'Inuentione di Pitagora.Cap. III.
Della musica antica.Cap. IIII.
Si plausoris eges aulaea manentis, & usqueEt era usanza (come afferma il Filosofo3. Reth. c.) che i Poeti istessi recitauano le Tragedie, & le Comedie, che haueano composte. Onde (come narrra Tito LiuioHist. Dec. 1. lib. 7.) uno chiamato Li-uio , hauendo fatto una Fauola in uersi, ordinata col suo argomento, egli stesso la recitaua; dopoi non potendo più dire; percioche la uoce gli era mancata, pregò che li fusse perdonato; & pose un Fanciullo à cantarla; il quale hauendosi portato bene, fu introdotta una usanza; che cotali cose fussero cantate da gli Istrioni. Et di questo ne tocca una parola Horatio, dicendo nella sua dell'Arte Poetica;
Sessuri, donec Cantor, Vos plaudite, dicat.
Ignotum Tragicae genus inuenisse camoenaeCredo anco, che gli Oratori orassero al popolo al suono di qualche Istrumento: ancora ch'al parer mio tale usanza durasse poco tempo; imperoche Cicerone nella Oratione, che fece in fauor di P. Sestio, ne tocca una parola; & anche nel fine del Libro terzo dell' Oratore, parlando di Gaio Gracco, lo dimostra; benche questo paia alquanto strano ad Aulo GellioAtti. noct. lib. 1. c. 11.; ma PlutarchoIn Vitis. T. & C. Graccorum. modestamente recita cotal cosa, & dice; Essendo Gaio Gracco huomo uehemente nel dire, spesse uolte era trasportato dall'ira; di modo che ueniua alle uillanie & uituperii; & cosi egli soleua turbare la sua Oratione; onde cono-scendo tal cosa, s'imaginò di rimediarui, col fare, ch'un Seruo dotto nella Musica, nomi-nato Licino li stesse dopo le spalle nel pulpito; & che mentre lo udiua inasperire, & riti-rarsi fuori della sua uoce, con un'Istrumento lo auertiua, & gli faceua achettare cotal vehementia. Et di ciò non ci dobbiamo marauigliare; poi che l'arte Oratoria hà hauu-to principio (come vuole StraboneDe Situ orbis. lib. 1.) dalla Poesia; & i Poeti orauano al popolo cantan-do Versi al suono della Cetera, ò Lira; & io tirauano à fare il loro uolere; il che ben lo dimostra anco l'Ariosto, dicendo:Satyra 6.
Dicitur, & plaustris uexisse poemata Thespis,
Quae canerent, agerentque peruncti fecibus ora.
Catauano [sic: Cantauano] anco gli Antichi al suono del Piffero, recitando diuerse Canzoni compo-ste in uersi; & questo faceuano alle uolte, quando erano due insieme; l'un de i quali sapesse Cantare & l'altro Sonare; come accennò il Poeta, quando introdusse Menalca dire à Mopso pastore queste parole. In DaphniLi Scrittori indi fer l'indotta plebe
Creder, che al suon delle soaui cetre
L'un Troia, & l'altro edificasse Thebe.E hauesson fatto scendere le pietre
Da gli alti monti, & Orpheo tratto al canto
Tigri, e Leon, dalle spelunche tetre.
Tu calamos inflare leueis ego dicere uersus:Percioche l'uno era perito sonatore di Piffero, & l'altro era ottimo cantore. Era anco appresso gli Antichi usanza di Saltare & di Ballare, mentre che 'l Musico al suono della Lira, ò Cetera, ouer d'alcuno altro Istrumento recitaua alcuna cosa; come si troua ap-presso di Homero nella Odissea;Odiss li-bro 8. che cantando Demodoco al suono della Cetera, i Greci saltauano & ballauano. Et simigliantemente Virgilio, nel Libro 1. dell'Eneida, imitandolo, dice; che cantando Ioppa al suono della Cetera;
Ingeminant plausu Tyrii, Troesque sequuntur:Et in un'altro luogo più chiaramente manifesta tal cosa, dicendo:Aeneid. 6.
Pars pedibus plaudunt Choreas, & carmina dicunt.Similmente Horatio, nel luogo citato di sopra (auegna che non faccia mentione alcuna, che si cantasse) dice;
Sic priscae motumque & luxuriam addidit arti Tlbicen [sic: Tibicen].Di questo si potrebbono hauere infiniti essempii, iquali hora per breuità la-scio; poiche le Ode di Pindaro di ciò fanno indubitata fede; conciosia ch'essendo diuise page 78i tre parti dellequali; la prima è chiamata Στροφὴ; Αντιστροφὴ la seconda; & la terza. Ε'πωδὸς; & sono comprese ne i uersi Lirici; gli Antichi le cantauano al suono della Lira, ò della Cetera, & ballauano, ò saltauano in tal maniera; che quando i Saltatori si uolgeuano dalla parte destra, uerso la sinistra, cantauano la prima parte; & quando andauano dalla sinistra, alla destra, cantauano la seconda; & ueniuano à riposarsi, quando cantauano la terza; la qual maniera di ballare, ò saltare dura fino al di d'hoggi appresso i Candioti, & quel-li, che habitano nell'Isola di Cipro. Gli Antichi adunque usauano la Musica nella ma-niera c'habbiamo detto; accompagnando la uoce ad un solo Istrumento; & s'alle uolte ne usauano de piu sorti, ui accompagnauano la uoce; come tra genti barbare al presente ancora si costustuma in alcune parti, & massimamente del Leuante; come da huomini de-gni di fede più uolte hò udito dire; ma i due primi modi (come fanno fede l'historie) erano grandemente in uso. Vsarono anco gli Antichi ne i loro Esserciti uarie sorti d'istru-menti; imperoche i Toscani usarono la Tromba; della quale (come uogliono alcuni) essi furono gli inuentori; gli Arcadi la Sampogna; i Siciliani alcuni istrumenti, i quali no-minauano Πύκτιδας; i Candioti la Lira; i Lacedemonii il Piffero, ouer la Lira (come uuole PausaniaLaconic. li-bro 1.) al canto d'alcune canzoni; quelli di Thracia il Corno; gli Egittii il Timpano; & gli Arabi il Cembalo. I Romani si seruirono nelle lor Comedie d'alcune sorti de Pifferi, de i quali alcuni chiamauano Destri & alcuni Sinistri; & alcuni nominauano Sa-ranni; da i quali i Spettatori poteuano comprender sotto qual Genere si contenessero le Comedie, che doueuano recitare. Imperoche quando la Comedia conteneua in se ma-teria, ò soggetto seuero & graue, si udiua il concento graue de i Pifferi sinistri; & quando era giocoso & festeuole, il concento era fatto co i Pifferi destri, & era acuto; ma s'era mi-sta, le Cantilene musicali erano temperate dell'una & dell'altra sorte di concento. Et tali Cantilene non erano fatte dal Poeta, c'hauea composto la Comedia; ma da un perito nell'arte della Musica; come nel principio di ciascuna Comedia di Terentio si può aper-tamente uedere; oue dice;
Modos fecit Flaccus Claudii filius.Nominando le sorti de gli Istrumenti detti di sopra; co i quali eran fatte le Musiche: lequali erano uariate di Modo, ò. Tuono, che lo uogliamo dire; & le faceuano udire auanti che cominciassero à rappresentar la Comedia; accioche la materia compresa in essa (com'hò detto) si potesse sapere auanti da gli Spettatori. Nondimeno à i nostri tempi sono incognite cotali sorti de Piffe-ri; ancora che Seruio nel Lib. 9. dell'Eneide di Virgilio, sopra quel uerso;
O uere Phry-giae,mostri ch'eran di due sorti; delle quali l'una nomina Seranni & l'altra Frigii. I primi erano Pari; & cosi si chiamauano; percioche haueano le loro cauerne pari & equali; i secondi Impari; conciosia che le cauerne loro erano inequali. Adduce dopoi Seruio l'autorità di Marco Varrone, uolendo dichiarar quali fussero Pifferi destri & sinistri, dicendo; che la Tibia Frigia destra hà un solo foro, & la sinistra ne hà due; de quali l'uno hà il suono acuto, & l'altro graue. Ma queste parole son molto differenti da quelle, che sono poste nel Lib. 1 al Cap. 2. delle cose della Villa; doue egli dice, che l'una sorte de Pifferi sonaua i Modi d'un'istesso Verso in uoce acuta, & l'altra in uoce graue; onde seguendo più à basso, dalle sue parole si può comprendere, che 'l sinistro mandaua fuori il suono graue, & il destro lo acuto. Et questo si può confermare con l'autorità di Plinio,Nat. hist. Lib. 16. capit. 36. ilquale parlando de i Calami acquatici, dice; Che si soleuano tagliare in tempo conueniente circa la stella Arturo, fino all'età di Antigene sonator di Piffero; usandosi ancora la Mu-sica semplice à quei tempi; & cosi preparati dopo alcuni anni incomiciauano ad esser buoni; & anche allora bisognaua adoperarli molto spesso, & quasi insegnar loro sonare; percioche le linguelle si ueniuano à toccare l'una con l'altra; ilche era molto più utile per mostrare i costumi ne i Theatri; ma dopoi che soprauenne la uarietà & la lasciuia de i canti, incominciarono à tagliarli auanti il Solsticio, & il terzo anno erano buoni; con-ciosia c'haueano le linguelle loro più aperte, & più atte à uariare i suoni; lequali hoggidi ancora cosi sono. Ma allora era opinione, che s'accordassero insieme quelli, ch'erano d'una medesima canna; & quella parte, ch'era uicina alla radica, conuenirsi al Piffero page 79sinistro, & quella ch'era uicina alla cima al destro. Questo dice Plinio seguendo quello, che dice Teofrasto nella Historia delle pianteCap. 12. li-bro 4. con maggior copia di parole; & parmi es-ser ben detto; imperoche quelli, che sono uicini alla radice, sono necessariamente più grossi de quelli, che sono più uerso la cima; onde ogni giorno si comprende dalla esperienza, ch'essendo il corpo loro più grande & più largo, rende anco il suono più graue; come il contrario si scorge in quelli, che sono più minuti, & più ristretti; ilche ancora si uede & ode ne gli Istrumenti, che chiamiamo Organi; le canne de i quali quanto sono più lar-ghe, tanto rendono i suoni piu graui; & le piu ristrette i piu acuti. Ma à quello che si è detto par che sia contrario un'Autore incerto di quello Epigramma Greco, ch'incomincia; Τὸν σοφὸν ἐν κιθάρη; percioche chiama la chorda graue Δεξιτερὴν ὑπάτην; cioè, destra Hy-pate; & l'acuta Λαιὴν νήτην; cioè sinistra Nete. Ma questo importa poco; conciosia che considerata ben la cosa, torna commodo all'uno & all'altro modo; essendo che le parti d'ogni Istrumento si posso considerare & denominare in due modi; prima, in quanto à noi; dopoi, in quanto ad esso Istrumento. In quanto à noi, la parte dell'Istrumento posta dalla man destra è detta Destra, et rende i suoni acuti; come ne gli Organi, Monochor-di, & altri Istrumenti simili si uede; & quella, ch'è posta alla sinistra è detta Sinistra, & rende i suoni graui. Ma in quanto all'Istrumento, quella ch'è destra à noi, adesso è sini-stra; & per il contrario, quella ch'è à lui destra, à noi è sinistra; come si potrebbe uedere in due, i quali insieme giuocassero alla lotta; che la parte destra dell'uno sarebbe la sini-stra all'altro, & la sinistra la destra. Non è adunque inconueniente, se l'uno nomina quella parte destra, la quale l'altro chiama sinistra; essendo tali parti diuersamente, secondo al-cune loro opinioni, considerate.Infra. Cap. 29. In questo modo adunque da gli Antichi era posta in uso la Musica; il qual modo quanto sia differente dall'uso moderno, ciascuno da se lo potrà sempre uedere; come etiandio potrà uedere altroue, quanto era differente il loro con-cento dal moderno. Ma quali materie recitassero nelle lor cantilene, quel che contiene il seguente Capitolo lo farà manifesto.
Delle materie, che recitauano gli Antichi nelle lor Canzoni: & d'al-cune Leggi musicali.Cap. V.
Musa dedit fidibus diuos, puerosque deorum,Et come dimostra Platone nel Protagora, gli Antichi insegnauano tutte queste mate-rie à i loro Giouani; accioche le hauessero à cantare al suono della Lira, ouer della Cete-ra, onde Homero scriue d'Achille.
Et pugilem uictorem, & equum certamine primum
Et iuuenum curas, & libera uina referre.
Α῎ειδε δ´ἁρακλέα ἀνδρων.cioè;
Ma le lodi de gli huomini uirili Cantaua.Et di Demodoco dice che Cantaua le gloriose imprese de gli Huomini, la contentione d'Vlisse con Achille, la fauola di Venere & di Marte, & il Cauallo Troiano. Femio anco nella OdisseaOdys. 22 si escusa con Vlisse, dicendo; che Cantaua à i Dei & à gli Huomini. Onde è da pensare, che non cantaua se non cose graui & seuere; hauendo già cantato il lugubre & funebre ri-torno de i Greci nella loro patria. Et se ben cantò l'adulterio di Marte & di Venere: non lo fece perche lodasse tal sceleratezza; ma per rimouere (come dice AtheneoDipnos. li-bro 1. c. 7.) i Pheaci dalle dishoneste loro uoluttà & piaceri. In cotal modo ancora appresso di Virgilio.Aeneid. 1.
Cithara crinitus IopasEt Creteo amico alle Muse medesimamente:Aeneid. 9.
Personat aurata, docuit quae maximus Atlas.
Hic canit erratem Lunam, Solisque labores:
Vnde hominum genus & pecudes, unde imber & ignes:
Arcturum; pluuiasque hyadas, geminosque Triones:
Quid tantum Oceano properent se tingere Soles
Hyberni, uel quae tardis mora noctibus obstet.
Semper equos, atque arma uirum, pugnasque canebat.Nerone etiandio, appresso di Suetonio nella Vita di questo sceleratissimo Imperato-re,Cap. 21. canta al suono della Cetera la fauola di Niobe, & molt'altre Tragedie, maschera-to; come Canace parturiente, Oreste ucciditor della madre, Edippo fatto cieco, & Her-cole furioso. Et LucianoDe Salta-tione. dice, che gli Argomenti & le Materie delle cantilene appresso gli Antichi erano quelle cose; cominciando da principio del mondo; ch'erano successe fi-no à i tempi di Cleopatra regina d'Egitto; le quali, mi pare (secondo che lui racconta) che siano quasi tutte quelle, che descriue & canta Ouidio nelle sue Trasformationi; & à cotal canto ballauano. Tutte queste cose recitauano sotto una determinata Harmonia, con determinati Rhythmi Versi & Precussioni [sic: Percussioni]; ancora che fussero uariati in ogni manie-ra di cantilena; & cosi con numeri, percussioni, modi & concenti; & con la uoce huma-na, esprimeuano materie conueneuoli & buoni costumi. Nominarono poi tali deter-minationi Leggi; imperoche altro non è Legge nella Musica, che un modo di cantare, il qual contiene in se un determinato concento, & un determinato Rhythmo & Metro. Et furono cosi chiamate; percioche non era lecito ad alcuno di mutare, ouero innoua-re in esse alcuna cosa; si nell'Harmonie, come etiandio ne i Rhythmi & Metri; ancora che siano alcuni, che dicano, che si chiamauano Leggi; imperoche auanti che si scriuessero le Leggi ciuili, si cantauano: onde Aristotele afferma,prob. 28. secr. 19. che nella sua etade erano anco page 81solite à cantarsi da i popoli Agathirsi. Erano però, cotali Leggi scritte in uersi, & le cantauano al suono della Lira, ò Cetera; accioche i popoli più facilmente le ritenesse-ro nella memoria & sapessero quello, che douessero osseruare; come scriue Eliano diDe Varia hist. lib. 2. quello, che faceuano i Candioti intorno le Discipline. Ma sia come si uoglia, erano cotal Leggi di tre sorti; imperoche alcune eran dette Citharistiche, che si cantauano al-la Cetera, ò Lira; & alcune Tibiarie, le quali si cantauano al suono de i Pifferi; ma quelle della terza specie si chiamauano Communi; & si cantauano al suono dell'una & del-l'altra sorte de gli Istrumenti nominati. Et benche cotal Leggi fussero molte; nondi-meno ciascuna hauea il suo nome acquistato, ò da i popoli, che le usauano; ò da i Rhy-thmi & Metri, che conteneuano; ouero da i Modi; ò da gli Inuentori; ò da i loro Amatori; oueramente da gli Argomenti. Da i popoli fù nominata l'Eolia & la Boetia; da i Rhy-thmi & Metri, la Orthia & la Trochea; da i Modi, l'Acuta & la Tetraedia; da gli A-matori & inuentori, la Terpandria & la Hieracia; & da gli Argomenti, il Certame Pi-thico & il Corrule. Queste leggi (come uuol PlutarchoIn Musica.) furono publicate da Terpan-dro; il quale hauendo prima diuiso le Citharistiche, pose nome alle lor parti. Le leggi Tibiarie hebbero molti nomi, che si lasciano per non andare in longo; i quali (secondo che si dice) ritrouò Cleone ad imitatione di Terpandro. La legge Orthia apparteneua à Pallade, & conteneua in se materie di guerra, & era una specie di modulatione nella Musica, la quale Aulo GellioNoct. At-tica. libro 16. c. 19. nomina Verso orthio, forse detto in tal modo da suoi Nu-meri, i quali sono veloci & sonori; conciosia che i Greci nominan Ο῎ρθιος quello, che noi chiamiamo Sonoro, ancora che molti lo interpretano per il Canto appartenente ad uno Essercito d'huomini d'arme. Era la Trochea un segno, che dauano gli Antichi à i sol-dati col canto, ò suono della Tromba; & i Lacedemonij usauano ne i loro Esserciti il canto della legge Castoria, per accender l'animo de i soldati à prender l'arme contra gli inimici; & tal legge era composta sotto un Rhythmo detto Embaterio. La Currule s'ac-quistò il nome della materia, che conteneua in se; cioè, dall'argumento, nel quale si narraua il modo, ch'Hettore figliuolo del Re Priamo fù strascinato con le carrette intor-no le mura Troiane. Di queste Leggi hò voluto far un poco di memoria; accioche si pos-sa uedere, ch'erano composte di Verso numeroso, accommodate à commuouere & ge-nerare ne gli animi diuerse passioni. Non sarà etiandio fuori di proposito, che ueggia-mo in qual maniera i Musici anticamente recitassero alcune delle predette Leggi al suo-no del Piffero cantando; accioche da una si possa comprendere, in qual modo potesse-ro recitar l'altre; & questa sarà il Certame Pithico, del quale fà mentione Horatio, di-mostrando le qualità del Musico, c'hauea da recitarlo, dicendo;De Arte poetica.
Abstinuit Venere & Vino, qui Pithia cantatLequali troppo ben conobbe il uanissimo Imperatore Nerone (come si legge in Sue-tonioIn uita Neronis. cap. 20.) che si asteneua da i pomi, usaua il vomito & li Cristeri, per purgarsi bene il petto; accioche hauesse recitando nella Scena la uoce chiara & netta. L'Argomento adunque di tal legge era la Battaglia d'Apolline col serpente Pithone, ilquale dà il nome alla Fauola; & il nome di tutta la cantilena era Delona; & forse fù cosi nominata; percioche Apollo nacque nell'Isola di Delo. Era questa legge (come mostra Giulio PolluceOnomast. lib. 4. c. 10.) diuisa come sono le nostre Comedie; in cinque parti; delle quali la prima nominauano Rudimento, ouero Esploratione, la seconda Prouocatione; Iambico la terza; la quarta Spondeo; & la quinta & vltima Ouatione, ò Saltatione. La Rapresentatione (com'hò detto) era il modo della pugna d'Apollo col Dragone; & nella prima parte si recitaua, in qual modo Apollo inuestigaua & contemplaua il luogo, s'era atto alla pugna, ouer non; nella seconda si dichiaraua il modo che teneua à prouocare il Serpente alla battaglia; nella terza il combattimento; & questa parte conteneua un modo di cantare al suono del Piffero chiamato Ο'δοντισμὸς; dal battere de i denti che faceua il Serpente quando era saettato: nella quarta si raccontaua la vittoria d'Apollo; & nell'ultima si dichiaraua com'egli faceua festa con balli & salti, per page 82la riceuuta uittoria del Serpente. Non sarebbe gran marauiglia, se gli Antichi hauesse-ro anco saltato & ballato, quando si recitaua cotal Legge; percioche usauano questo an-co nelle loro Tragedie & Comedie; & à ciascuna Saltatione haueano accommodato il Diphno. libro. 1. c. 16. suo proprio modo; conciosiache (come mostra Atheneo) haueano una specie di Salta-tione detta Emmelia, & accommodarono alla Comedia quella, ch'era detta Cordace. Era anche appresso di loro una specie di Saltatione satirica, la quale chiamarono Σίκιννις; & fù istituita da Bacco, dopo che hebbe domata l'India. Questa era una delle Leggi ti-biarie, nella quale i Rhythmi, i Modi, i Costumi, & le Harmonie si mutauano, secondo che la materia ricercaua. Haueano etiandio la Saltatione detta Carpea, la quale lascia-rò di raccontare; percioche è recitata da AtheneoVt supra. lib. 1. c. 8. tanto chiaramente, ch'ogn'uno leg-gendo la potrà conoscere, quello che ella fusse, & in qual maniera la usassero; & da que-ste due; cioè dal Certame pithico, & dalla Saltatione carpea, si potrà scorgere, in qual modo gli Antichi recitassero l'altre Leggi. Potiamo hora uedere da quello, che si è det-to, che la Musica hauea piu parti; l'Harmonia, il Rhythmo, il Metro, & l'Istrumento; dal quale questa parte si diceua Organica, & ui era etiandio la Poesia & la Saltatione: Ma queste parti alle uolte concorreuano tutte in una compositione; & tallora non tutte, ma la maggior parte loro. Ne era lecito (come altre uolte si è detto) di mutare, ouero innouare alcuna cosa, che di tal mutatione l'Inuentore non ne hauesse à riportare la pu-nitione; onde durò lungo tempo tal costume, percioche conseruandosi la Musica in co-tale essere, si conseruò anche la sua riputatione; ridotta dopoi à poco à poco nello sta-to, nel quale hoggidi la ueggiamo; hauendosi dato i popoli alla crapula & alla lussuria, poco curandosi di tal cosa, presero i Musici maggior licenza; & con molte altre cose in-sieme, perdettero eglino & la Musica la sua antica grauità & riputatione; il che si uede detto da Horatio, quando dice;De Arte poetica.
Tibicen, didicit prius extimuitque magistrum.
Postquàm coepit agros extendere victor, & urbemEt piu oltra seguita, dicendo quello, che di sopra hò commemorato; cioè,
Latior amplecti muros, vinoque diurno
Placari genius festis impune diebus,
Accessit numerisque, modisque licentia maior;
Sic priscae motumque & luxuriam addidit artiEt dopoi segue etiandio, dicendo;
Tibicem.
Sic etiam fidibus uoces creuere seueris.Onde è da notare, che Horatio nomina l'Antiche chorde Seuere, & bene; percioche gli Antichi al suono di quelle recitauano se non cose seuere & graui. In tal modo adun-que i Musici antichi, nella età che la Musica piu fioriua & era in maggior prezzo & ri-putatione, recitauano le narrate materie nelle lor cantilene. Ma quali cose, & in qual modo da i Moderni siano recitate; & quali siano state lasciate da un canto, ogn'uno, che hà cognitione della Musica, da quello, che leggerà, & haurà accuratamente letto, lo potrà giudicare & conoscere.
Quali siano stati gli antichi Musici.Cap. VI.
Ne forte pudoriPercioche dice prima Sonatore della Lira; come quello (come uogliono alcuni) che fù l'Inuentore di essa; dopoi lo chiama Poeta col nome di Cantore. Lascierò di raccontare, quali fussero Orfeo & Arione; percioche è manifesto, che costoro non solo furono Musici; ma celebratissimi Poeti ancora. Hesiodo etiandio fù posto tra i Musici; ancora che non usasse mai d'accompagnare il Canto col suono della Lira; percioche usaua una Verga di lauro, con la quale percotendo l'aria (come narra PausaniaIn De-script. ueteris Graeciae lib. 9.) faceua un certo suo-no, al quale era solito cantare i suoi Poemi; la onde gli Antichi li fecero una statua con la Cetera sopra le ginocchia, & la posero tra quelle di Thamira, Arione, Sacaba [sic: Sacada], & d'al-tri nobilissimi & eccellentissimi Musici; per non priuarlo di cotale honore. Pindaro si-migliantemente fù Musico & Poeta; come dalle sue opere si può comprendere; & da quello etiandio che fece il magno Alessandro; imperoche quando fece ispianare & ruinare Thebe, fece scriuere (come dicono Dione Chrisostomo,De Regno Oratio. 2. Arriano De Gestis Alexand. lib. 1. & Pli-nioNat. hist. lib. 7. c. 29) sopra la sua casa questo Verso;
Sit tibi musa lyrae solers, & cantor Apollo;
Πινδάρου τοῦ μουσοποιοῦ τὴν στέγαν μή καίετε;che uogliono dire;
Non abbrusciate la casa di Pindaro Musico.Et per non andare più in lungo, il Santissimo Dauid Re di Hierusalem & gran Pro-feta, da Basilio magnoHomil. 54 Ad adole-scentes. è chiamato non solamente Musico, ma Poeta anco de Sacre can-tilene; & dal santo & dottissimo Hieronimo Ad Paulinum. uien chiamato Simonide, Pindaro, Alceo, Flacco, Catulo & Sereno; percioche scrisse con stile elegante i sacri Salmi in Verso liri-co, alla guisa di Horatio & de i nominati; & si può credere, che più uolte li cantasse al suono della Cetera, nel modo che cantaua, quando iscacciaua il maligno spirito da Saul. Onde non è dubbio, ch'essendo stato Poeta, non si debba anco nominar Musico; con-ciosiache la Scrittura santa lo chiama in più luoghi Psaltes; che vuol dire Cantore ò So-natore; & il suo diuino Poema nomina Psalterium. Et di questo è testimonio Origene,Homil. 18. c. 24. lib. Nume. dicendo; Che diremo noi della Musica? della quale il sapientissimo Dauid ne hauea ogni scienza, & hauea raccolto la Disciplina di tutta la Melodia & de i Rhythmi; accioche da tutte queste cose potesse ritrouar suoni, con i quali potesse mitigar sonando il Re turbato & molestato dallo spirito maligno. Il simile dice AgostinoDe ciuit. Dei cap. 4. lib. 17. ancora. La onde ogni ragion ne persuade à credere, che i Poeti antichi cantassero da se stessi i loro Poemi; & c'hauessero congiunto la Musica con la Poesia; percioche se fusse stato altramente, non hauerebbono usato tanto spesso nelle loro compositioni questa uoce Cantare; co-me fece Homero; il quale diede principio all'Iliade in cotal modo, page 84
Μῆνιν ἄειδε θεὰ.cioè;
Canta Dea l'ira;& Hesiodo, che incominciò la Teogonia in questa maniera.
Μουσάων ἑλικωνιάδων ἀρχῶμεθ´ἀέιδειν;che uuol dire;
Le Muse d'Elicona incominciamo Cantare;A i quali aggiungeremo il prencipe de i Poeti latini Virgilio, il quale incominciò in cotal modo la sua Georgica;
Quid faciat laetas segetes, quo sydere terramEt alla sua Eneide pose un tal principio;
Vertere Mecoenas, vlmisque adiungere uites
Conueniat; qua cura boum, qui cultus habendo
Sit pecori, atque apibus quanta experientia parcis,
Hinc canere incipiam;
Arma, uirumque cano.Cosi anche Ouidio incomincia i Fasti con questi versi;
Tempora cum causis Latium digesta per annum,Onde il Petrarcha, imitando tutti costoro, diede principio ad una sua canzone in questa maniera;1. Part. can. 4.
Lapsaque sub terras, ortaque signa canam.
Nel doce [sic: dolce] tempo della prima etade,Et il moderno Ariosto per seguir tal costume, incominciò anco lui il suo elegante poema in questo modo;
Che nascer vide, & ancor quasi in herba,
La fera uoglia, che per mio mal crebbe.
Perche cantando il duol si disacerba,
Canterò, com'io vissi in libertade.
Le donne, i caualier, l'arme, gli amori,Ma doue vò io più uagando, se TerentioIn Prolo-gis Heau-tont. Hecyrae: et Phormionis. poeta comico dimostrandoci la Poesia & la Musica esser congiunte & quasi una istessa cosa, la nominò Studio musicale. Non è adunque marauiglia, se i Musici & li Poeti erano anticamente riputati essere una cosa istessa. Et se bene il Poeta è chiamato alle uolte con questa uoce latina Vates; che con-uiene etiandio all'Indouino; non è fuor di proposito; conciosia che l'uno & l'altro (seconIn Ione. do il parer di Platone) sono mossi & agitati da un'istessa diuinità, ò diuina alienatione di mente, & da un'istesso furore. Onde HomeroOdys. 22. nomina il Musico Αὐτοδίδακτος; per-cioche canta non per humana istitutione; ma inspirato da i Dei; il che si scorge dalle parole, che soggiunge, le quali dicono;
Le cortesie, l'audaci imprese io canto.
Θεὸς δέμοι ἐνφρεσὶν οἶμας.cioè,
Παντοίας ἐνέφυσεν;
Percioche Dio mi produsse in la mentePerò adunque molti Poeti gentili hanno alcuna uolta predetto le cose, c'haueano da uenire; come si uede, che Virgilio, secondo l'opinione di Agostino Dottor Santo,De Ciuit. Dei. lib. 10 cap. 27. & Lib. 1. E-pist. 3. Ad Volusia-num. non conoscendo il nostro Redentore, ne per lume naturale, ne per uiua fede, cantò sotto 'l nome d'un'altro il suo nascimento, quando disse; In Pollio-ne.
Ogni mia cantilena.
Vltima cumaei uenit iam carminis aetas:Ancorache il Diuino Hieronimo, scriuendo à Paulino, sia d'altro parere; conciosiache Virgilio si mosse à cantar queste cose, inuitato da gli Oracoli della Sibilla Cumana; co-me cantò poco più oltra la liberatione del peccato originale, in cotal modo. page 85
Magnus ab integrò, seclorum nascitur ordo.
Iam redit & virgo, redunt Saturnia regna:
Iam noua progenies coelo demittitur alto.
Te duce, si qua manent sceleris vestigia nostri.Et, che colui, c'hauea da nascere sarebbe Dio & Huomo, seguendo più à basso;
Irrita, perpetuo soluent formidine terrras.
Ille Deûm uitam accipiet, diuisque videbisEt che il Serpente nimico della humana natura douea perdere il regno, & che douea rimanere in noi alcuna cosa, per rispetto del peccato originale, dicendo;
Permixtos heroas, & ipse videbitur illis.
Occidet & Serpens, & fallax herba veneni.Et più oltra ancora;
Pauca tamen suberunt priscae vestigia fraudis.Ouidio ancora lui nelle sue TrasformationiLib. 1. Metamor. chiaramente mostrò la uenuta del Figliuolo di Dio in carne, con queste parole:
Summo delabor Olympo,Et de i miracoli che fece, poco più abasso disse;
Et Deus humana lustro sub imagine terras.
Signa dedi venisse Deum.Pose etiandio le parole, che dissero quelli, che lo crucifissero; cioè, Se era figliuol di Dio, che si liberasse dalla croce, & disse,
Experiar Deus hic discrimine aperto,Lucano ancora cantò quello, che auerrebbe auanti il futuro vniuersale & finale giu-dicio con tali parole;De Bello ciuili. lib 1
An sit mortalis, nec erit dubitabile uerum.
Sic cùm compage solutaHauendo medesimamente Ouidio cantato tal cose con queste parole;Metamor. lib. 1.
Saecula tot mundi suprema coegerit hora,
Antiquum repetens iterum Chaos, omnia mistis
Sidera sideribus concurrent, ignea pontum
Astra petent, tellus extendere littora nolet,
Excutietque fretum; fratri contraria Phoebe
Ibit, & obliquum bigas agitare per orbem
Indignata, diem poscet sibi; totaque discors
Machina diuulsi turbabit foedera mundi.
In se magna ruunt.
Esse quoque in fatis reminiscitur, affore tempusDi coteste cose sono molti essempii; ma lasciandoli da un canto, uerremo à quelli de Sacri libri, & ritroueremo l'autorità del Santissimo Apostolo Paolo; il quale scriuendo à Tito;Capit. 1. adducendo una sentenza di Epimenide Poeta candioto; lo chiama Profeta, di-cendo; Ι῎διος τῶν αὐτῶν προφήτης: che uuol dire; propio Profeta di costoro; cioè, de i Candioti. Douendosi adunque allora chiamare il Musico & il Poeta, ò l'Indouino per vn nome commune, era conueniente ancora, che 'l nome di Sapiente li conuenisse; percioche (come ne fà auertiti PlatoneDe Leg. 1.) al uero Musico appartiene sapere & hauer cognitione de tutte le Scienze; & cosi al Poeta, secondo il parere di Strabone;De Situ orbis. lib. 1. la onde meritò da gli Antichi esser chiamato solo Sapiente; conciosia che à quei tempi le città della Grecia faceuano imparare à lor figliuoli la Poesia, non solo per cagione di piacere; ma per ca-gione di casta moderatione. La onde i Musici, ch'insegnauano la Poesia, il Canto & li Modi, che si sonauano con la Lira, ò Cetera & col Piffero, fecero professione, & si attribuirono tal uirtù, d'esser non solo Correttori & emendatori de costumi; ma si fecero etiandio chiamare Maestri; la qual cosa conferma Homero con queste parole;Odys. 3.
Quo mare, quo tellus, correptaque regia coeli
Ardeat, & mundi moles operosa loboret.
Πὰρ γὰρ ἔην καὶ ἀειδὸς ἀνὴρ, ὧ πόλλ´ἐπετελλενpage 86Che uogliono dire;
Ατρείδης τροίην δὲ κιὼν εἴρησθαι ἄκοιτιν;
Hauea presso di se un Cantore, al qualeMeritamente adunque gli Antichi riputauano i Musici, i Poeti, ouero Indouini & li Sapienti essere una cosa medesima.
Atride andando à Troia impose molte,
Che douessi seruar casta la moglie.
Quali cose nella Musica habbiano possanza da indur l'Huomo in diuerse passioni.Cap. VII.
Giunto Alessandro alla famosa tombaSi ricerca adunque un Soggetto tale, che sia ben disposto; conciosia che senza esso (come ancora hò detto) nulla ò poco si uederebbe. Et benche in simili mouimenti fatti per la Musica, ui concorrino le nominate cose; nondimeno il preggio & l'honore si dà al Composto delle tre prime, che si chiama Melodia; percioche se ben l'Harmonia sola hà una certa possanza di dispor l'animo & di farlo allegro, ò mesto; & che dal Numero posto in atto le siano raddoppiate le forze; non sono però potenti queste due cose poste insieme di generare alcuna passione estrinseca in alcun soggetto, al modo detto; essendoche tal possanza acquistano dalla Oratione, che esprime alcun costume. Et che questo sia uero, lo potiamo uedere; percioche Alessandro non fù mosso dall'Harmonia solamente; ne meno dall'Harmonia accompagnata col Numero; ma si bene (come uuole Suida, Eu-thimio & altri ancora In Proe-mio lib. Psalmorum.) dalla legge Orthia, di sopra commemorata, & dal Modo Fri-gio; dal qual, & forse anco da tal Legge, il sudetto giouane Taurominitano ebbrio (co-me narra BoetioMusicae li-bro 1. ca. 1.) fù sospinto, quando uolse abbrusciar la casa d'un suo riuale, nella quale era nascosta una meretrice; la onde Pitagora ò Damone Musico, che ei fusseAttic. no-cti. lib. 16. cap. 19.; co-me scriue Galeno;De placi-tis lib. 5. conoscendo tal cosa, commandò al Musico, che mutasse il Modo & cantasse lo Spondeo, col quale placò l'ira del Giouane & lo ridusse al primo stato. Arione etiandio Musico & inuentore del Dityrambo (secondo l'opinione di Herodoto,Hist. lib. 1. & di Dion Chrisostomola Orat. corinthia-ca. 37. ) prese ardire di precipitarsi nel mare, hauendo (per mio pare-re) cercato di comporsi prima col mezo di cotal Legge (come recita GellioAttic. no-cti. lib. 16. cap. 19. ) un'animo intrepido & uirile; per poter fare cotal cosa senz'alcun timore. Hora potiamo uedere, che tali & cosi fatti mouimenti sono stati fatti, non per uirtù delle prime parti della Me-lodia; ma si bene dal tutto; cioè, dalla Melodia istessa, la quale ha gran forza in noi, per uirtù della terza parte; cioè, delle Parole, che concorrono alla sua compositione, sen-za le quali sempre si haurebbe fatto, ò farà nulla ò poco; percioche il Parlare da sè sen-za l'Harmonia & senza il Numero hà gran forza di commouer l'Animo; conciosia che se noi haueremo riguardo à cotal cosa, uederemo ch'alcune fiate, quando udimo leg-gere, ò raccontare alcuna Fauola, ouero Historia, siamo costretti ridere, ò piangere; & alcune uolte c'induce all'ira & alla colera; & alle fiate di mesti ne fà diuentare allegri; & cosi per il contrario; secondo il soggetto che in essa si contiene. Ne dobbiamo di ciò marauigliarsi: percioche il Parlare ne induce alla furia & ne placa; ne fà esser crudeli & anco ne addolcisce. Quante uolte è accaduto, che leggendosi semplicemente una pietosa Historia, ò Nouella, gli ascoltanti non siano stati presi da compassione in tal modo, che al loro dispetto dopo alcuni sospiri, li sia stato dibisogno accompagnarli le lagri-me? Dall'altra parte, quante fiate è auenuto, che leggendosi, ò narrandosi alcuna Fa-cetia, ò Burla, alcuni non siano quasi scoppiati dalle risa? Et non è marauiglia; percio-che il più delle uolte se 'l si rappresenta à noi alcuna cosa degna di commiseratione, l'animo è commosso da lei & è indutto à piangere; & se udimo cosa, la quale habbia del feroce & del crudele, l'animo declina & si piega in quella parte. Et di ciò (oltra ch'è manife-sto) n'è testimonio Platone,De Rep. 10 quando dice; che Qualunque uolta udimo Homero, ouer alcun altro Poeta tragico, che imiti alcuno de gli Heroi afflitto per il dolore gridar for-temente & pianger la sua fortuna con modi flebili, percuotendosi il petto con pugni; ad un certo modo si dilettiamo; & hauendo una certa inclinatione à coteste cose, seguitia-mo quelle & insieme siamo presi da tal passioni, & lodiamo quello, come buon Poeta, il qual grandemente commuoua l'animo nostro. Questo ancora più espressamente con-ferma Aristotile,Politi. lib. 8. cap. 5. dicendo; Ancora si uede, che gli Huomini udendo l'Imitationi, han-no compassione à quei casi, quantunque siano senza Numero & senz'Harmonia. Ma se 'l Parlare hà possanza di muouer gli animi & di piegargli in diuerse parti, & ciò senza page 89l'Harmonia, & senza il Numero; maggiorimente haurà forza quando sarà congiunto co i Numeri, & co i Suoni musicali, & con le Voci. Et tal possanza si fà chiaramente manifesta per il suo contrario; percioche si uede, che quelle Parole muouono men l'animo, le quali sono proferite senza Melodia & senza Proportione, che quelle, che sono profe-rite con i debiti modi[unclear: .] Però gran forza hà da se stesso il Parlare; ma molto più hà forza quando è congiunto all'Harmonia; per la simiglianza che hà questa con noi & alla po-tenza dell'Vdito; conciosiache niuna cosa è tanto congiunta con le nostre menti; come dice Tullio;De Orato-re. lib. 3. Pro Arc. che i Numeri & le Voci, per le quali si commouiamo, infiammiamo, pla-chiamo & rendiamo languidi. Non è questo gran marauiglia; dice egli ancora; che i sassi, le solitudini, le spelunche, & gli antri rispondono alle uoci? & le bestie crudeli & feroci spesse uolte sono dal canto fatte mansuete, & da esse sono fermate? Nè ci dobbia-mo di ciò marauigliare; conciosia che se 'l uedere una Historia, ò Fauola dipinta sola-mente, ne muoue à compassione tallora, tallora ne induce à ridere; & tallora ne sospin-ge alla colera; maggiormente questo può fare il Parlare, il qual meglio esprime le cose, che non fà alcun Pittore, quantunque eccellente sia, col suo pennello. Onde si legge di uno, ilquale riguardò una imagine dipinta, & fù sospinto à piangere;Aristot. in Poetica. & di Enea, Aeneid. libro. 1. che entrato nel tempio fabricato da Didone nella nuoua Carthagine;
Del fero Achile, sospirando disse: Franc. Pe-trarca. o-de. 115.
O fortunato, che si chiara tromba
Hauesti, che di te si alto scrisse.
Videt Iliacas ex ordine pugnas,Et di Porcia figliuola di Catone Vticense si legge ancora,Plutar. in Vita M. Bruti. che hauendo ueduto una certa Tauola di pittura, pianse amaramente. Et benche la Pittura habbia forza di com-mouer l'animo; nondimeno maggior forza hebbe la uiua uoce di Demodoco Musico & sonatore di Cetera, il quale riducendo in memoria Vlisse, dipingendoli le cose passate, come se li fussero state presenti, lo costrinse à piangere; dal qual effetto; come dice Ho-mero Odis. 8. & Aristotele;In Poetica fu subito conosciuto dal Re Alcinoo. Ma non pure allora accascarono coteste cose; ma etiandio à i nostri tempi si uede accascare il medesimo tra molte genti Barbare; imperoche raccontandosi da i lor Musici con certi uersi al suono d'uno Istru-mento i fatti di alcuno loro capitano; secondo le materie, che recitano, quelli ch'ascol-tano cambiano il uolto, facendolo per il riso sereno, & tallora per le lagrime oscuro; & per tal modo sono presi da diuerse passioni. Si può adunque concludere, che dalla Me-lodia; & principalmente dalla Oratione, nella quale si contenga alcuna Historia, ò Fa-uola, ouero altra cosa simile, che esprima imitationi & costumi, siano stati & ancora si possino porre in atto cotali effetti; & l'Harmonia & il Numero esser cose, le quali dispon-gono l'animo; purche 'l Soggetto sia sempre preparato & disposto; senza il quale in uano ogni Musico sempre si affaticarebbe.
Bellaque iam fama totum vulgata per orbem,
Atridas, Priamumque & saeuum ambobus Achillem.
Constitit; & lachrymans: Quis iam locus (inquit) Achate,
Quae regio in terris nostri non plena laboris?
En Priamus: sunt hîc etiam sua premia laudi:
Sunt lachrymae rerum, & mentem mortalia tangunt.
Solue metus; feret haec aliquam tibi fama salutem.
Sic ait: atque animum pictura pascit inani.
Multa gemens, largoque humectat flumine uultum.
In qual modo l'Harmonia, la Melodia & il Numero possino muouer l'animo & disporlo à varij effetti; & indur nell'Huomo variati costumi.Cap. VIII.
Proprio rabies armauit Iambo.Dalle quali cose si può comprendere, in qual modo l'Harmonia & il Numero con una certa dispositione possino diuersamente mutar le passioni & costumi dell'animo. Ma perche hò detto; che Ogn'uno naturalmente più si diletta di quella Harmonia, la quale è più simile, conueniente & proportionata alla sua natura, ò complessione, & secondo ch'è disposto; però è da notare; che essendo l'Harmonia & li Numeri parti del-la Melodia; & hauendo l'Harmonia & li numeri facoltà di mouer l'Huomo interiormente, come si è dimostrato: non è dubio che la Melodia non habbia maggiormente forza di mutar di dentro le Passioni & i costumi dell'Animo di quello, che hà ciascuna di esse parti separatamente. Auertisca però qui ogn'uno, che (secondo la dottrina de 'l Filoso-fo 2. Ethi. c. 1) le Virtù morali & li Vitij non nascono con esso noi; ma si generano per molti habiti buoni, ò tristi frequentati, nel modo che uno per sonare, ò scriuere spesse fiate male, diuenta tristo Sonatore, ò Scrittore; ouer per il contrario, essercitandosi spesse uolte bene, diuenta buono & eccellente. La onde colui che spesso essercita la Iniustitia, per tal cosa diuenta Iniusto; & colui ch'essercita la Iustitia, diuenta Iusto; nel modo che colui, che si usa à temere i pericoli diuenta timido, & non li stimando diuiene audace. Di maniera che, quali sono le Operationi, tali sono gli Habiti; & dalle buone sono i buoni, & dalle triste i tristi Habiti. Essendo adunque l'Harmonie & i Numeri simili alle Passioni dell'animo; come afferma Aristotele;Probl. 29. parti. 19. potiamo dire, che l'assuefarsi alle Harmonie & à i Numeri, non sia altro, che uno assuefarsi & disporsi à diuerse Passioni, & à diuersi Habiti morali & costumi dell'animo; percioche quelli, che odono le Harmonie & li Numeri, si sentono tramutare secondo la dispositione dell'animo, alcuna uolta nell' amore, alcuna uolta nell'ira, & alcuna uolta nell'audacia; il che da altro non auiene come hò detto; che dalla simiglianza, che si troua tra le sopradette Passioni con le Har-monie. Et questo si uede; conciosia che uno, il quale hauerà più uolte udito una sorte d' Harmonia, ò de Numeri, si dilettarà maggiormente, per hauersi già assuefatto in quel-la. Dobbiamo però sapere (per maggiore intelligenza di quello, che si è detto) che il Numero quantunque si piglia (come nella Prima parte uedemmoCap. 12.) per la Moltitudine. composta de più unità, & per l'Aria (dirò così) d'alcuna Canzone; come intese ilIn Moeri. Poeta, quando disse;
Numeros minimi, si uerba tenerem;Et in molti altri modi; nondimeno in questoluogo non è altro, che una certa misura di tempo breue, ò lungo, nel quale si scorge la proportione, ò misura di due mouimen-ti, ò più, insieme comparati, secondo una cambieuole ragione di tempo di essi moui-menti; il quale è detto Rhythmo; & si scorge ne i piedi del Metro & del Verso, che si compongono di piu Rhythmi ò Numeri, con un certo ordine, ò spacio determinato. Ma il Metro & il uerso è una certa Compositione & ordine de piedi, ritrouata per dilet-tar l'vdito; oueramente è un'Ordine & Compositione de più uoci, finita con Numero & modo. Potrei hora dire la differenza, che si ritroua tra il Metro & il Verso; ma per breuità la uoglio passare; imperoche coloro, che desiderassero di saperla, leggendo il Cap. 2. del Terzo lib. della Musica del P. S. Agostino, potranno d'ogni suo desiderio esser satisfatti. Solamente si haurà da auertire, che il Rhythmo è differente dal Metro & del Verso in questo; che il Metro & il Verso contengono in se un certo spacio determi-nato; & il Rhythmo è piu uniuersale, & ha i suoi spacij liberi & non determinati; onde è come il Genere; ma il Metro & il Verso sono meno uniuersali, & sono come la Specie; percioche da quello si hà la quantità, ò la materia, & da questi la qualità, ò la forma. Alcuni altri dicono, che 'l Metro & il Verso è Ragione con modulatione; & il Rhy-thmo modulatione senza ragione. Ma sia quello, che si uoglia, questo sia detto à ba-stanza intorno à cotal cosa. page 92
In qual genere di Melodia siano stati operati i narrati effettiCap. IX.
De i Suoni & delle Voci, & in qual modo naschino.Cap. X.
Da che nascono i Suoni graui, & da che gli acuti.Cap. XI.
Quel che sia Consonanza, Dissonanza, Harmonia & Melodia. Cap. XII.
Diuisioni delle Voci.Cap. XIII.
Quel che sia Canto, & Modulatione; & in quanti modi si possa cantare. Cap. XIIII.
Vt reduces illis ludunt stridentibus alis,Et questo ultimo modo non fà al nostro proposito, ma i due primi; percioche in essi si comprende ogni Harmonia & ogni Melodia. E' però la Modulatione un Mouimento fatto da un suono all'altro per diuersi interualli, il quale si ritroua in ogni sorte d'Harmo-nia; & di Melodia; & la vsiamo in due modi; prima quando si muouiamo da un suono all'altro senza uarietà di tempo, con diuersi interualli, non facendo alcuna Propria har-monia; procedendo equalmente da un'Interuallo all'altro per il medesimo tempo; co-me si fà ne i Canti fermi; & questa è detta Modulatione impropriamente; perche contiene solamente un proceder semplice, senz'alcuna Consonanza; dal quale effetto si uede, che tal Modulatione hà ragion de imperfettione; essendo che manca à se stessa del debito fine. Dopoi quando per il suo mezo peruenimo all'uso dell'Harmonia & Melodia, come al suo proprio fine; come faciamo nel Canto figurato, nel qual cantiamo non solo con semplici suoni & semplici eleuationi & abbassamenti de voci; ma si muouiamo anco da un'interuallo all'altro con ueloci & tardi mouimenti; secondo il tempo mostrato nelle sue figure cantabili; & questa è detta Modulatione propriamente. Laonde toccando allora varie consonan-ze, dal nostro cantare è formata ogni sorte d'Harmonia & di Melodia; laquale non può napage 100scere se non con l'aiuto delle Consonanze; ancorache possiamo hauer la Modulatione senza la Harmonia propria, & senz'alcuna Consonanza, & senza Melodia.Vide cap. 17. lib. 2. Supple. Potiamo nondimeno hauer la Modulatione in tre modi; prima quando noi Cantiamo nominata-mente ciascuna chorda, ò suono col nome di una di queste sei sillabe, Vt, Re, Mi, Fa, Sol, La, secondo il modo ritrouato da Guidone Aretino; come uederemo al suo luogo; il qual modo i Prattici chiamano Solfizare, ò Solmizare; & non si può far se non con la uoce. Dopoi quando noi proferimo solamente il suono, ò la uoce & gli interualli de-scritti; come fanno gli Istrumenti arteficiali. Ma l'ultimo modo è, quando noi appli-chiamo le Parole alle figure cantabili, il quale è proprio del Cantore; percioche da que-sta maniera di cantare nasce la Melodia; come habbiamo detto.
Et coetu cinxére polum, Cantusque dedére.
Quel che sia Interuallo, & delle sue Specie.Cap. XV.
Quel che sia Genere; & di tre generi di Melodia, ò Cantilena appresso gli An-tichi; & delle loro Specie.Cap. XVI.








Per qual cagione ciascun de gli Interualli contenuto ne i mostrati Tetrachordi sia detto Incomposto.Cap. XVII.
In qual modo si possa accommodare alla sua proportione qual si voglia Consonanza, ouero Interuallo.Cap. XVIII.
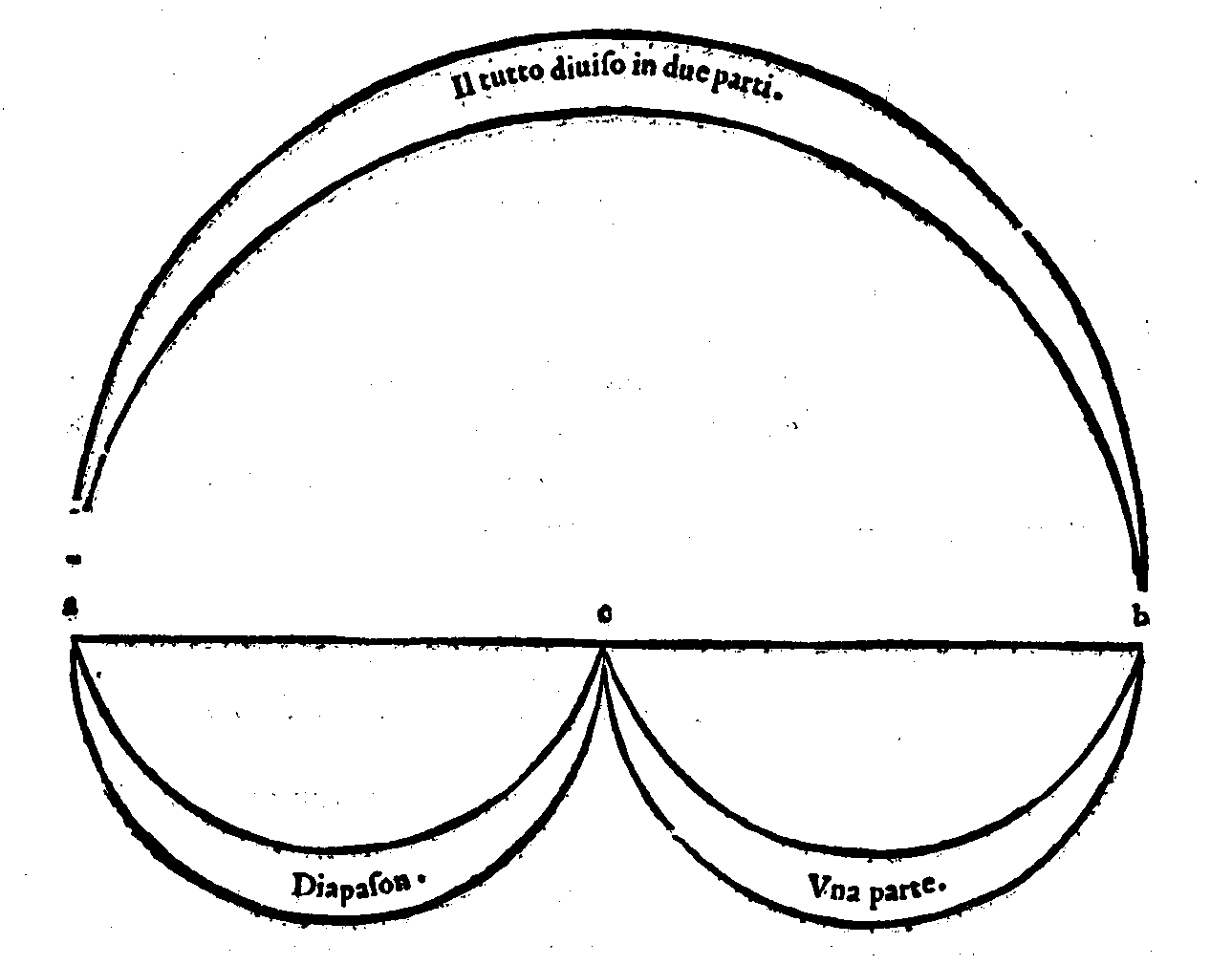
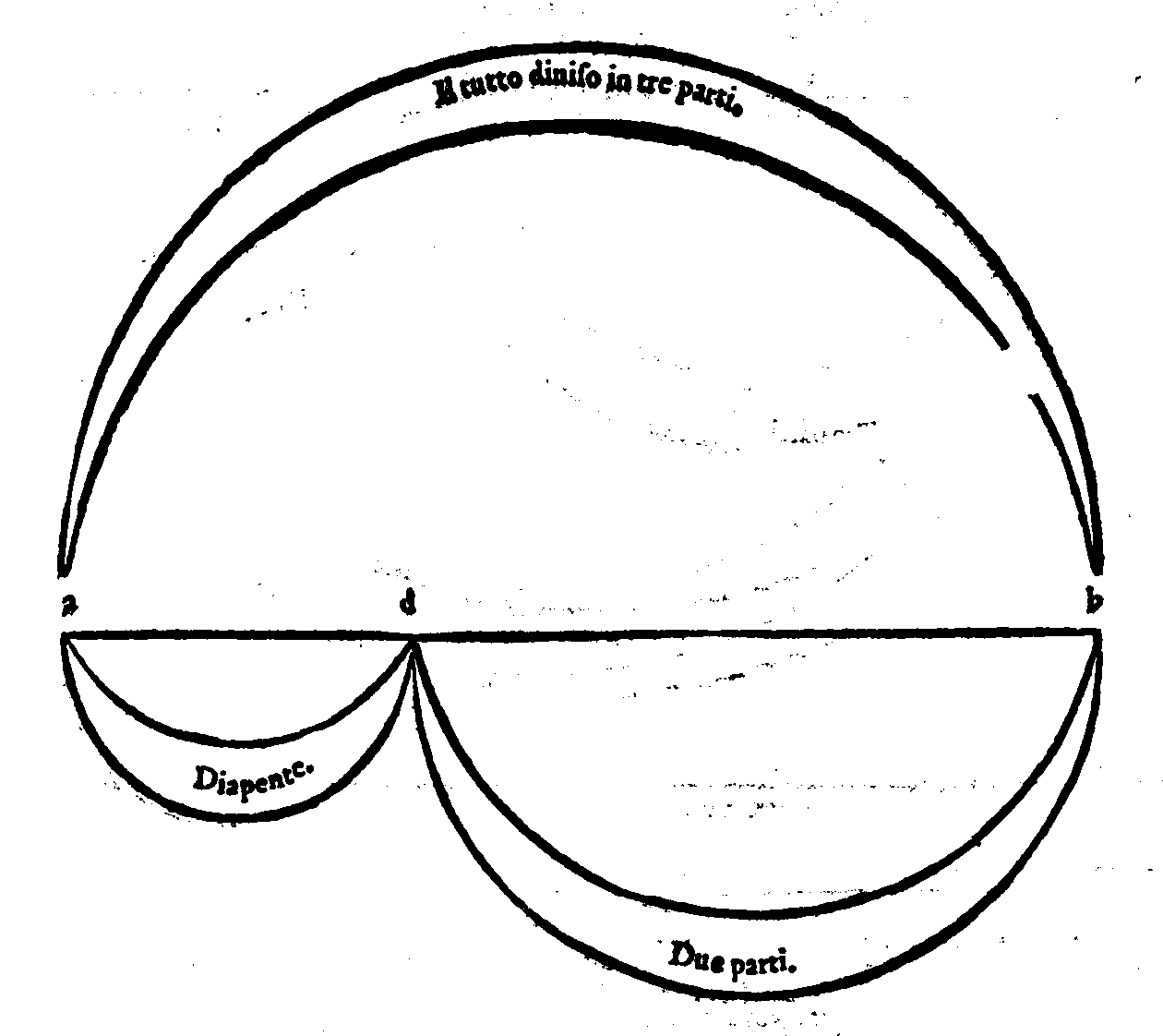
Vn'altro modo di accommodar le Consonanze alla loro proportione. Cap. XIX.
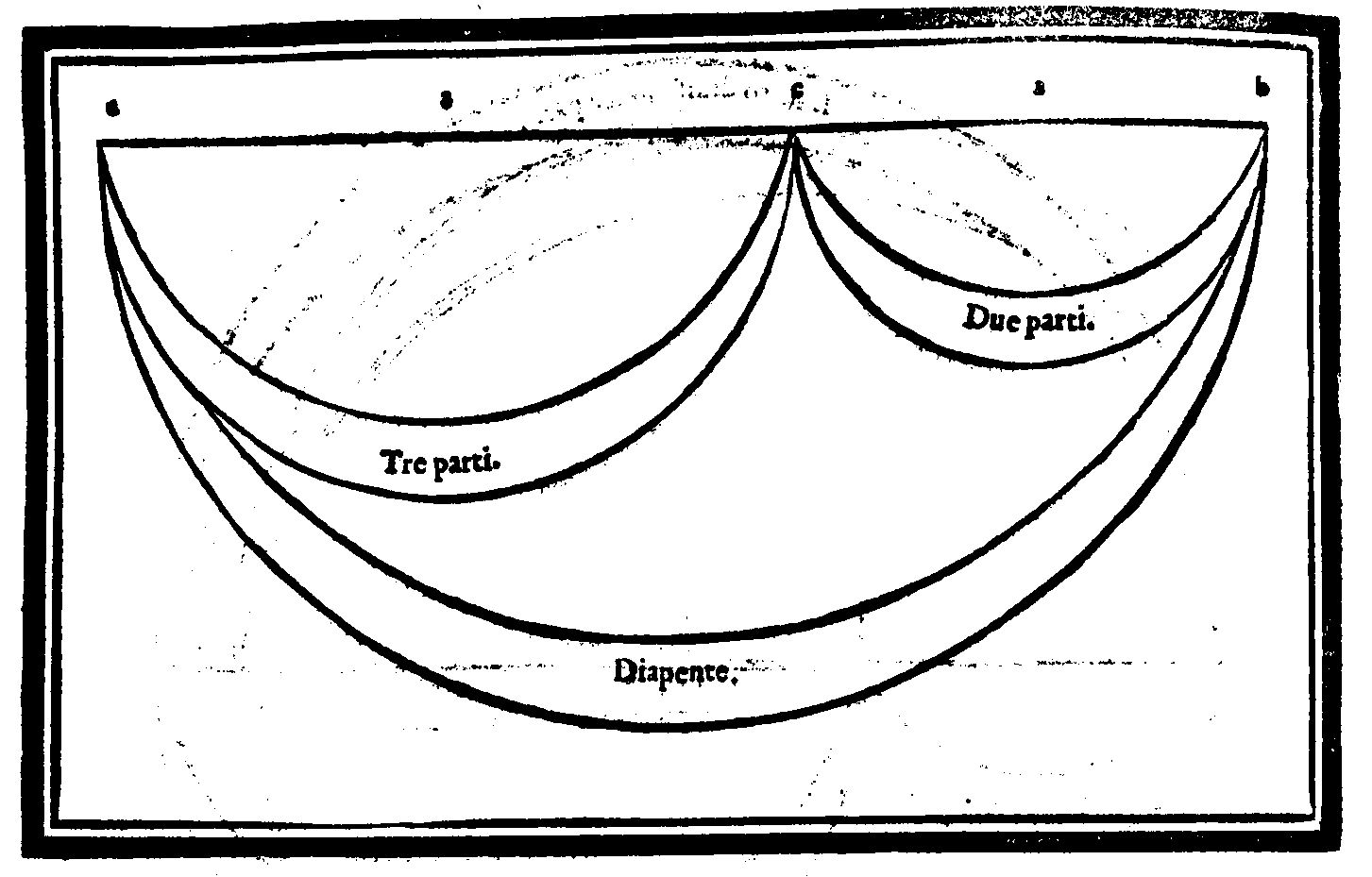
In qual modo si possa Vdire qual si voglia Consonanza accomodata alla sua proportione.Cap. XX.
 do fabricati, ouero in altra maniera; purche siano secondo le qualità,
che hò descritto. Ordinate poi le cose in tal guisa; se noi pigliaremo uno
de questi Scannelli, & lo porremo sotto qual si uogliadelle tirate chorde, di
maniera che tal chorda si posi sopra lo Scannello in punto C. posto nello essempio del
Cap. 18. se 'l si percuoterrà la chorda C B. posta dalla parte destra con qualche altra chor-da senza Scannello; percioche in tal parte sempre porrò i Suoni acuti; si per rispetto de
i termini delle sue proportioni; come etiandio perche ne gli Istrumenti si ritrouano da
questa parte; tra 'l Suono di questa, che sarà A B. & il Suono della C B. si udirà la Diapa-son consonanza. Ma se noi segnaremo con uno de i Scannelli mobili vna terza chorda in
punto D. come si uede nel secondo essempio nel luogo nominato; percuotendo questa
insieme con una delle non segnate; cioè, D B. con A B. da i Suoni nati da queste due chorde si farà la consonanza Diapente. Similmente se noi percuoteremo insieme le chorde page 111A B. & C B. con la D B. vdiremo la Diapason tramezata dalla D B. & diuisa in Proportionalità harmonica in vna Diapente A B. & D B. & in una Diatesseron D B. & C B. le quali in-sieme aggiunte fanno la consonanza Diapason. Oltra di questo, se uorremo vdire la
già accommodata Diapente nel Capitolo precedente, bastarà solamente porre uno de i
Scannelli mobili in punto C. percioche percuotendo dalla parte destra & dalla sinistra le
chorde A C. & C B. si potrà vdire senza dubbio tal Consonanza; conciosia che in questa
diuisione è sofficiente una sola chorda. E' ben vero, che questo modo è piu difficile,
che il primo; & nel primo fanno dibisogno più d'una chorda; come habbiamo ueduto;
& è modo più facile; & si può vdire non solo ogni Consonanza semplice, contenuta da
due Suoni solamente; ma qualunque altra etiandio, che fusse tramezata da più Suoni;
ilche sarebbe molto difficile da vdire, quando il Musico si uolesse seruire d'una chorda so-la, seguendo il secondo modo. Essendo adunque il Secondo modo meno vtile & piu fa-ticoso del primo, lasciarò quello da un canto, & seguirò questo in ogni Diuisione; come
quello che hà da condurre ogni mia fatica à quella perfettione, ch'io desidero.
do fabricati, ouero in altra maniera; purche siano secondo le qualità,
che hò descritto. Ordinate poi le cose in tal guisa; se noi pigliaremo uno
de questi Scannelli, & lo porremo sotto qual si uogliadelle tirate chorde, di
maniera che tal chorda si posi sopra lo Scannello in punto C. posto nello essempio del
Cap. 18. se 'l si percuoterrà la chorda C B. posta dalla parte destra con qualche altra chor-da senza Scannello; percioche in tal parte sempre porrò i Suoni acuti; si per rispetto de
i termini delle sue proportioni; come etiandio perche ne gli Istrumenti si ritrouano da
questa parte; tra 'l Suono di questa, che sarà A B. & il Suono della C B. si udirà la Diapa-son consonanza. Ma se noi segnaremo con uno de i Scannelli mobili vna terza chorda in
punto D. come si uede nel secondo essempio nel luogo nominato; percuotendo questa
insieme con una delle non segnate; cioè, D B. con A B. da i Suoni nati da queste due chorde si farà la consonanza Diapente. Similmente se noi percuoteremo insieme le chorde page 111A B. & C B. con la D B. vdiremo la Diapason tramezata dalla D B. & diuisa in Proportionalità harmonica in vna Diapente A B. & D B. & in una Diatesseron D B. & C B. le quali in-sieme aggiunte fanno la consonanza Diapason. Oltra di questo, se uorremo vdire la
già accommodata Diapente nel Capitolo precedente, bastarà solamente porre uno de i
Scannelli mobili in punto C. percioche percuotendo dalla parte destra & dalla sinistra le
chorde A C. & C B. si potrà vdire senza dubbio tal Consonanza; conciosia che in questa
diuisione è sofficiente una sola chorda. E' ben vero, che questo modo è piu difficile,
che il primo; & nel primo fanno dibisogno più d'una chorda; come habbiamo ueduto;
& è modo più facile; & si può vdire non solo ogni Consonanza semplice, contenuta da
due Suoni solamente; ma qualunque altra etiandio, che fusse tramezata da più Suoni;
ilche sarebbe molto difficile da vdire, quando il Musico si uolesse seruire d'una chorda so-la, seguendo il secondo modo. Essendo adunque il Secondo modo meno vtile & piu fa-ticoso del primo, lasciarò quello da un canto, & seguirò questo in ogni Diuisione; come
quello che hà da condurre ogni mia fatica à quella perfettione, ch'io desidero.
Del Moltiplicar le Consonanze.Cap. XXI.
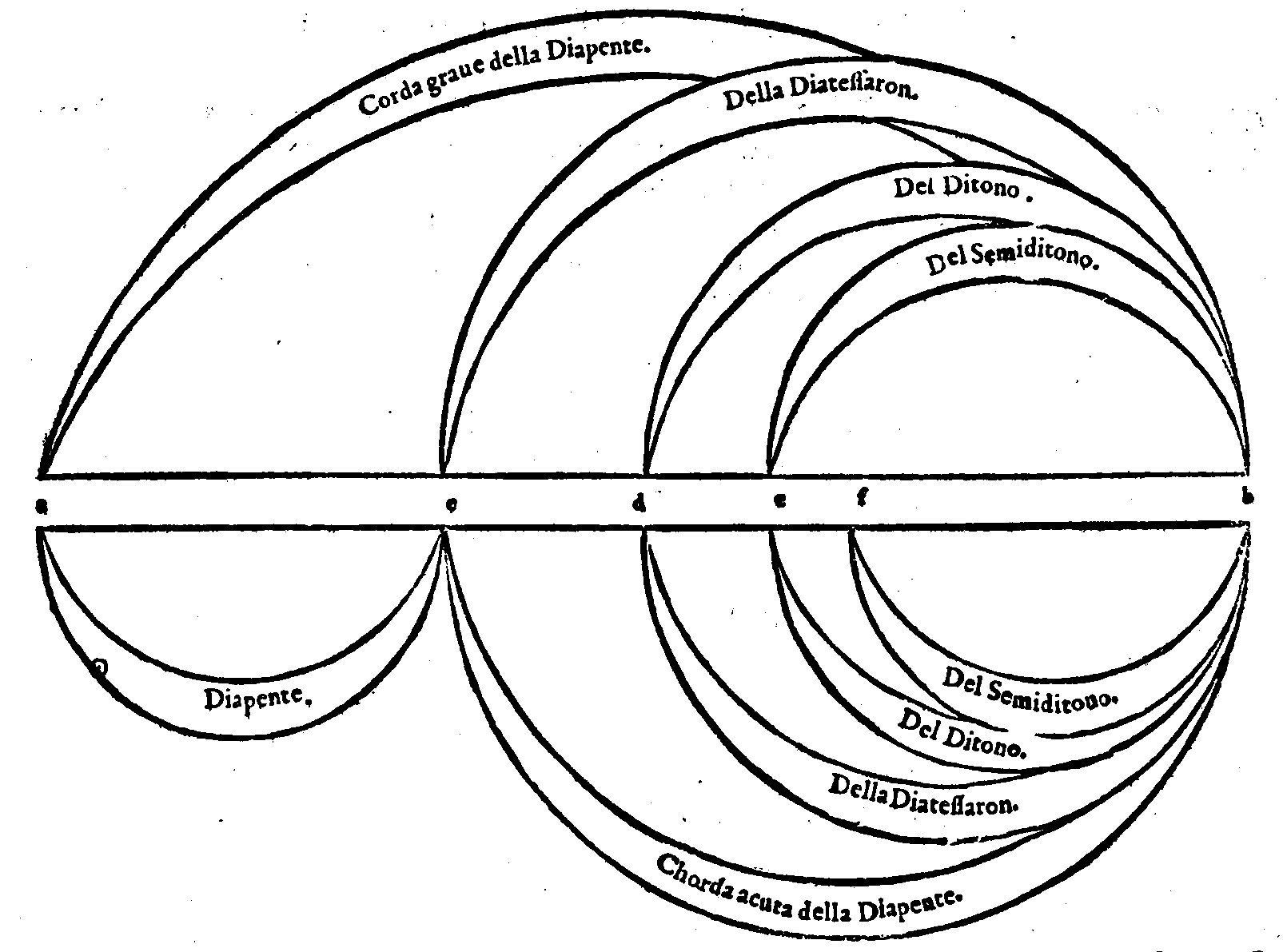
Del Secondo modo di moltiplicar le Consonanze.Cap. XXII.
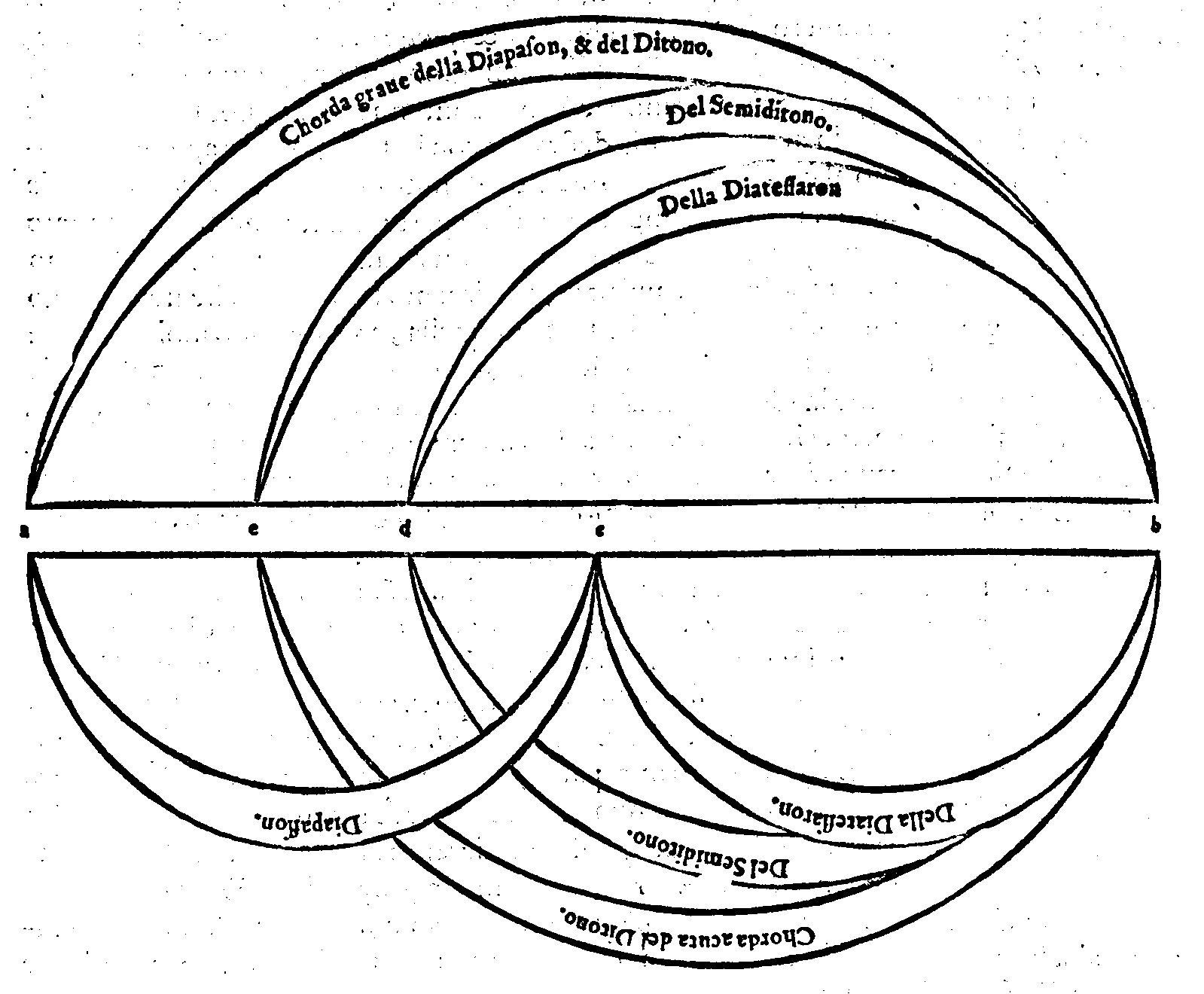
Come si possa diuidere rationalmente qual si voglia Consonanza ò Interuallo.Cap. XXIII.
In qual modo si possa Diuidere qual si voglia Interuallo Musicale in due parti equali.Cap. XXIIII.
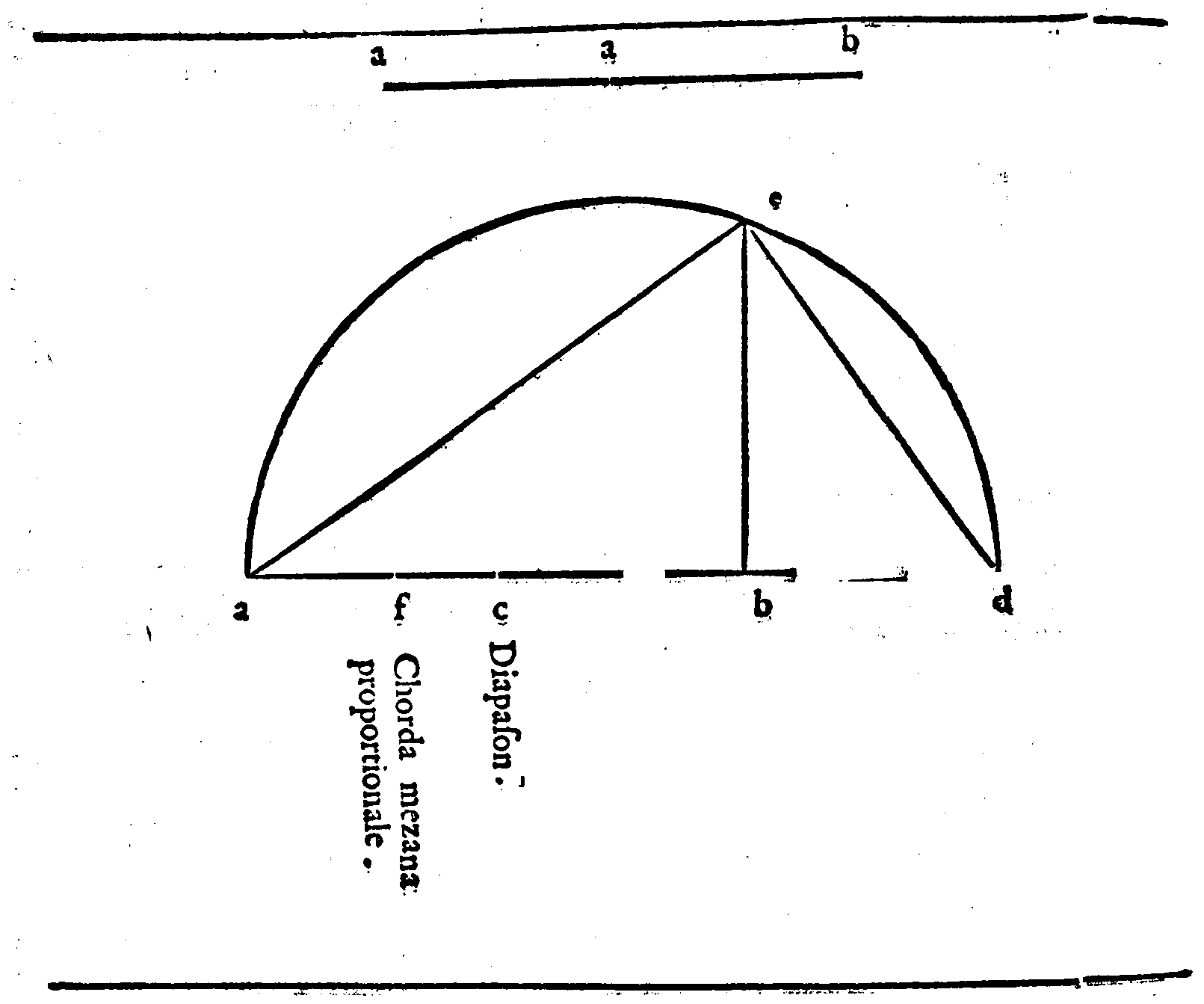
Altro modo di diuider qual si voglia Consonanza, ouero Interuallo in due, ò in più parti equali.Cap. XXV.
 equidistanti, le sponde del canale, uenghino ad esser alte quan
to è una costa di coltello, & non piu. Fatto questo, faremo
prima Tre figure quadrate di Metallo, ò di Legno sottilissime;
le quali i Geometri chiamano Paralellogrammi, che habbia-no quattro angoli retti, & che siano lunghe quanto è largo il
canale, & larghe quanto si vuole; purche siano fabricate in
tal maniera, che l'una sia equale all'altra; cioè, che i lati dell'
una siano equali à i lati dell'altra. Dopoi tiraremo à due di esse una linea diametrale dall'angolo superiore sinistro all'angolo destro inferiore di ciascuno in tal maniera, che le superficie
siano diuise in due triangoli Orthogonij equali; come nell'essempio si uede. Porremo hora primieramente i Quadrati nel detto
canale l'un dopo l'altro in tal modo; che 'l primo senza diametro sia nella parte sinistra, & resti immobile; dopoi gli altri, che
hanno i diametri; cioè, il secondo & il terzo per ordine à banda
destra; di maniera che il lato destro dell'uno sia posto sopra il
sinistro dell'altro; & cosi haueremo fatto & ordinato il detto
Istrumento; ilquale sarà D E F G. & sia H I K L. il primo quadra-to immobile senza diametro; il secondo N O P Q. il cui diametro sia N Q. & il terzo sia R S
T V. del quale R V. sia il diametro. Poniamo hora che si habbia da ritrouare una Chor-da mezana proportionale, laqual diuida in due parti equali la Diapason, contenuta dalla proportion Dupla, tra le due sottoposte chorde, ò linee A E. & C B. & siano equali alla
A B. & alla C B. poste nel Capitolo precedente. Faremo primieramente il lato destro del
primo quadrato; cioè, L K. equale alla A B. in punto M. & sarà L M. dopoi pigliaremo il secondo quadrato, & lo spingeremo sotto il primo tanto, che 'l suo diametro N Q. seghi il lato K L. del primo quadrato nel punto M. & cosi il primo, & il secondo quadrato resteran-no immobili. Faremo dopoi il lato destro del terzo quadrato, che è V T. equale alla C B. in
punto X. & fermato che si haurà un filo sottilissimo, che sarà M G. nel punto M. lo distenderemo tanto, che passi per il punto X. Spingeremo hora il terzo quadrato tanto sotto 'l secondo, che [unclear: ']l lato P Q. uenghi ad esser segato dal diametro R Vv. & dal detto filo in un punto
che sarà Y. & quella parte del lato destro del secondo quadrato, laqual resterà sotto 'l filo,
che è la Q Y. sarà la ricercata Linea, ò Chorda proportionale; come nella figura si uede.
Et questo è manifesto; imperoche la Linea mezana proportionale Q Y. ritrouata nel Me-solabio tra la A B. & la C B. è equale alla B E. ritrouata nel Capitolo precedente. Questo si
potrebbe prouare, se 'l si descriuesse in una superficie piana tutte le linee fatte nel Mesolabio; allungando primieramente, per la Seconda dimanda del Primo d'Euclide, la linea
M X. nel punto Z. percioche allhora haueressimo tre Triangoli contenenti un'angolo ret-to; cioè, L M Z. Q Y Z. & V X Z. da i quali si dimostrarebbe per i Principij & Demostra-tioni di esso Euclide, il tutto esser uero; come per il Secondo parer commune, &
per il Nono; per la 28. & per la Seconda parte della 32. del Primo; per la Seconda, per la
Quarta, & per la Sesta del Sesto; & per la Vndecima del Quinto, lequali lascio; percioche
nella Vndecima del Terzo delle nostre Dimostrationi harmoniche hò cotal cosa diffusa-mente trattato. Bastami solamente hora dire, che uolendo ritrouar piu linee mezane, ò
chorde proportionali; cioè, uolendo diuidere in piu parti qual si uoglia Interuallo mu-sicale, si potrà usare il mostrato modo. Bisogna però auertire, che per ogni linea, ò chorda, che si uorrà aggiungere oltra la ritrouata, sarà dibisogno di aggiungere etian-dio un'altro Paralellogrammo, ò Quadrato col suo diametro, fatto di maniera &
di grandezza, come sono i primi; facendo, che i lati destri d'ogni Quadrato uen-ghino ad esser segati in un punto istesso da i diametri & dal filo al mostrato modo. page 118Auertendo etiandio di por sempre il primo quadrato senza diametro, che sia immobile;
& che 'l suo lato destro sia segato dal diametro del seguente in quel punto, che si porrà per
la lunghezza della linea, ò chorda proposta maggiore; & che 'l lato destro dell'vltimo sia
segato dal filo in quella parte, che si piglia la lungezza della linea minore proposta, se-condo 'l modo dato. Et se la maggior linea proposta fusse piu lunga, che 'l Quadrato posto nel Mesolabio, non si potrebbe far cosa alcuna. E' ben uero, che pigliando la metà
di Ciascuna delle due proposte, si potrà hauere il proposito; perche dopo fatto il tutto, le
mezane ritrouate si potranno allungar secondo la ragione della parte presa delle proposte linee, & cosi ogni cosa tornerà bene.
equidistanti, le sponde del canale, uenghino ad esser alte quan
to è una costa di coltello, & non piu. Fatto questo, faremo
prima Tre figure quadrate di Metallo, ò di Legno sottilissime;
le quali i Geometri chiamano Paralellogrammi, che habbia-no quattro angoli retti, & che siano lunghe quanto è largo il
canale, & larghe quanto si vuole; purche siano fabricate in
tal maniera, che l'una sia equale all'altra; cioè, che i lati dell'
una siano equali à i lati dell'altra. Dopoi tiraremo à due di esse una linea diametrale dall'angolo superiore sinistro all'angolo destro inferiore di ciascuno in tal maniera, che le superficie
siano diuise in due triangoli Orthogonij equali; come nell'essempio si uede. Porremo hora primieramente i Quadrati nel detto
canale l'un dopo l'altro in tal modo; che 'l primo senza diametro sia nella parte sinistra, & resti immobile; dopoi gli altri, che
hanno i diametri; cioè, il secondo & il terzo per ordine à banda
destra; di maniera che il lato destro dell'uno sia posto sopra il
sinistro dell'altro; & cosi haueremo fatto & ordinato il detto
Istrumento; ilquale sarà D E F G. & sia H I K L. il primo quadra-to immobile senza diametro; il secondo N O P Q. il cui diametro sia N Q. & il terzo sia R S
T V. del quale R V. sia il diametro. Poniamo hora che si habbia da ritrouare una Chor-da mezana proportionale, laqual diuida in due parti equali la Diapason, contenuta dalla proportion Dupla, tra le due sottoposte chorde, ò linee A E. & C B. & siano equali alla
A B. & alla C B. poste nel Capitolo precedente. Faremo primieramente il lato destro del
primo quadrato; cioè, L K. equale alla A B. in punto M. & sarà L M. dopoi pigliaremo il secondo quadrato, & lo spingeremo sotto il primo tanto, che 'l suo diametro N Q. seghi il lato K L. del primo quadrato nel punto M. & cosi il primo, & il secondo quadrato resteran-no immobili. Faremo dopoi il lato destro del terzo quadrato, che è V T. equale alla C B. in
punto X. & fermato che si haurà un filo sottilissimo, che sarà M G. nel punto M. lo distenderemo tanto, che passi per il punto X. Spingeremo hora il terzo quadrato tanto sotto 'l secondo, che [unclear: ']l lato P Q. uenghi ad esser segato dal diametro R Vv. & dal detto filo in un punto
che sarà Y. & quella parte del lato destro del secondo quadrato, laqual resterà sotto 'l filo,
che è la Q Y. sarà la ricercata Linea, ò Chorda proportionale; come nella figura si uede.
Et questo è manifesto; imperoche la Linea mezana proportionale Q Y. ritrouata nel Me-solabio tra la A B. & la C B. è equale alla B E. ritrouata nel Capitolo precedente. Questo si
potrebbe prouare, se 'l si descriuesse in una superficie piana tutte le linee fatte nel Mesolabio; allungando primieramente, per la Seconda dimanda del Primo d'Euclide, la linea
M X. nel punto Z. percioche allhora haueressimo tre Triangoli contenenti un'angolo ret-to; cioè, L M Z. Q Y Z. & V X Z. da i quali si dimostrarebbe per i Principij & Demostra-tioni di esso Euclide, il tutto esser uero; come per il Secondo parer commune, &
per il Nono; per la 28. & per la Seconda parte della 32. del Primo; per la Seconda, per la
Quarta, & per la Sesta del Sesto; & per la Vndecima del Quinto, lequali lascio; percioche
nella Vndecima del Terzo delle nostre Dimostrationi harmoniche hò cotal cosa diffusa-mente trattato. Bastami solamente hora dire, che uolendo ritrouar piu linee mezane, ò
chorde proportionali; cioè, uolendo diuidere in piu parti qual si uoglia Interuallo mu-sicale, si potrà usare il mostrato modo. Bisogna però auertire, che per ogni linea, ò chorda, che si uorrà aggiungere oltra la ritrouata, sarà dibisogno di aggiungere etian-dio un'altro Paralellogrammo, ò Quadrato col suo diametro, fatto di maniera &
di grandezza, come sono i primi; facendo, che i lati destri d'ogni Quadrato uen-ghino ad esser segati in un punto istesso da i diametri & dal filo al mostrato modo. page 118Auertendo etiandio di por sempre il primo quadrato senza diametro, che sia immobile;
& che 'l suo lato destro sia segato dal diametro del seguente in quel punto, che si porrà per
la lunghezza della linea, ò chorda proposta maggiore; & che 'l lato destro dell'vltimo sia
segato dal filo in quella parte, che si piglia la lungezza della linea minore proposta, se-condo 'l modo dato. Et se la maggior linea proposta fusse piu lunga, che 'l Quadrato posto nel Mesolabio, non si potrebbe far cosa alcuna. E' ben uero, che pigliando la metà
di Ciascuna delle due proposte, si potrà hauere il proposito; perche dopo fatto il tutto, le
mezane ritrouate si potranno allungar secondo la ragione della parte presa delle proposte linee, & cosi ogni cosa tornerà bene.
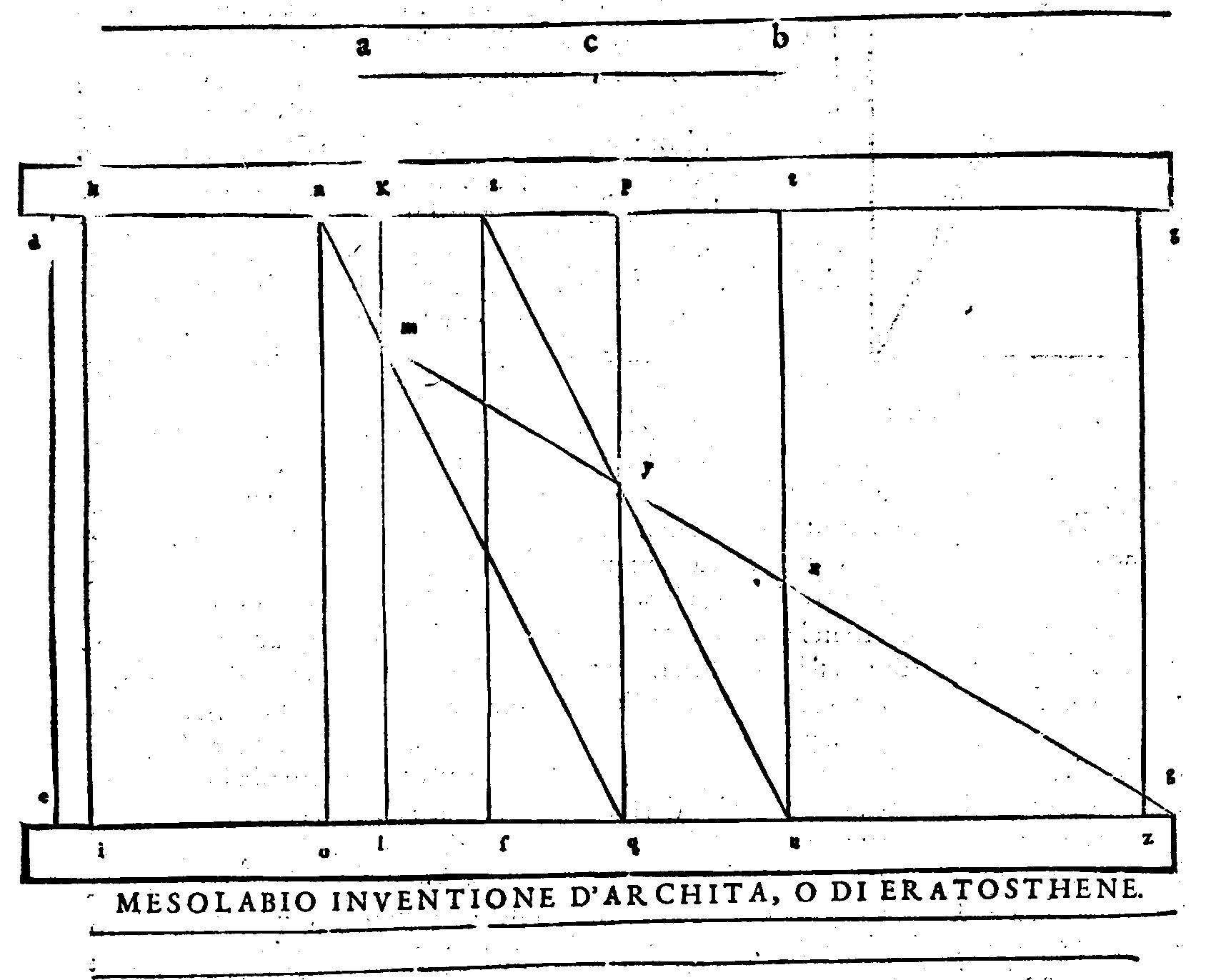
In qual modo la Consonanza si faccia diuisibile.Cap. XXVI.
Quel che sia Monochordo, & perche sia cosi chiamato.Cap. XXVII.
Della Diuisione, ouero Ordinatione del Monochordo della Prima specie del genere Diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi fu l'Inuentore di questo Genere & del suo ordine. Cap. XXVIII.
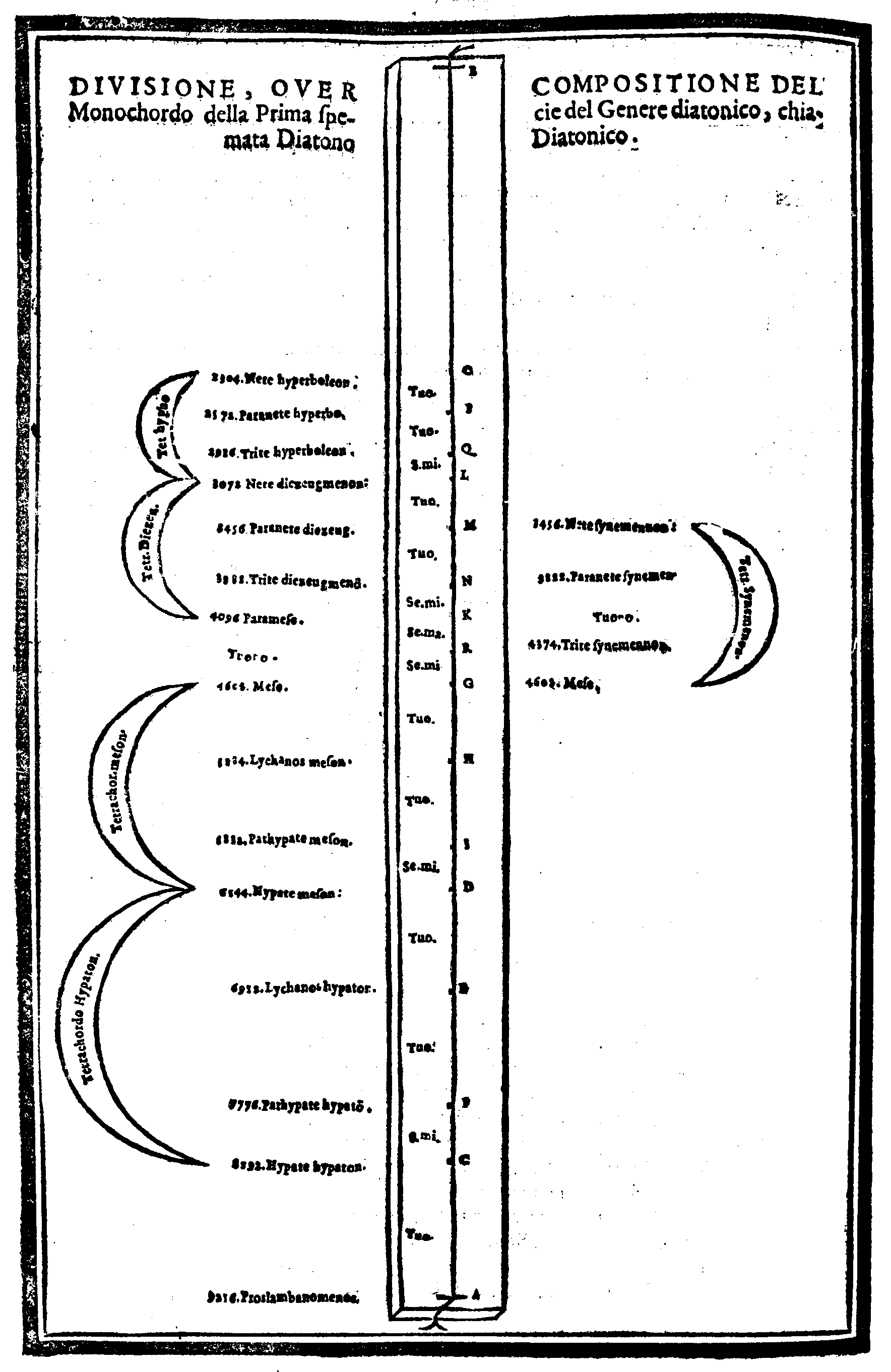
Che gli Antichi attribuirono alcune chorde de i loro Istrumenti alle Sphere celesti.Cap. XXIX.
Insonuere poli, longeque auditus ab alto.< lb>E' ben uero, che quello, che dice, si può accommodare à qual si uoglia delle due nar-rate opinioni; percioche se noi uorremo attribuire la Tardità del mouimento annuale alla Sphera di Saturno; ueramente il suo mouimento è più tardo d'ogn'altra Sphera in-teriore; come mostra Platone nell'Epinomide; conciosia che fà la sua reuolutione in trenta anni; & questo sarà in fauor de quelli, che tengono, che i Corpi maggiori fanno il Suono più graue. Ma se la tardanza s'attribuirà al mouimento diurno sarà in fauor de quel-li, che fauoriscono la prima opinione; & bisognerà intendere il contrario: poiche non è dubbio alcuno; come si uede col senso; che 'l mouimento della Sphera della Luna sia più tardo d'ogn'altro, quando dall'Oriente si muoue all'Occidente. Ma sia pure più tardo, ò piu veloce, quanto si uoglia; come cosa che importa poco à noi, lasciaremo della loro tardità, ò velocità la cura à gli Astronomi. Dell'altra fattione si ritrouano molti; impe-roche Dione historicoHistori. li-bro 37. raccontando la cagione, perche i Giorni siano stati denominati dal nome delle Sphere celesti, & non siano numerati secondo l'ordine loro; incomincia render tal ragione, secondo l'opinione de gli Egitij, dalla Sphera di Saturno uenendo à quella del Sole; ponendo l'una & l'altra per gli estremi della consonanza Diatessaron; lasciando le due mezane; cioè, quella di Gioue & quella di Marte; dopoi da quella del-la Luna, & forma un'altra Diatessaron; similmente da questa à quella di Marte, & da Marte à Mercurio ne fà due altre; di modo che lasciando sempre le due mezane Sphere, rende la ragion di tal Problema; ritornando sempre circolarmente alla prima Sphera; la onde si uede, che incominciando dalla Sphera di Saturno, & uenendo à quella del So-le, & da questa, à quella della Luna; pone la prima come quella, che fà il suono graue; & venendo uerso l'altre Sphere, le pone come quelle, che fanno i suoni acuti; impero-che è costume della maggior parte di coloro, che trattano della Musica, di por prima il Graue nelle loro ragioni; come cosa piu ragioneuole; & dopoi l'Acuto. Ne debbe parer strano, se Dione ritorna dalla Sphera della Luna à quella di Marte, facendo un'ordine riuerso, procedendo dall'acuto al graue, contrario di quello che hauea mostrato prima; percioche à lui bastaua solamente con tal mezo di mostrar la ragione di cotal cosa; anco-ra che questa ragione non sia molto sufficiente à fauorir tale opinione. Euui etiandio l'o-Lib. 2. cap. 3. & 22. pinione de gli Antichi, che pone Plinio nella sua Historia naturale; primieramente dell'Harmonia celeste, dopoi dell'ordine; onde dice, che la Sphera di Saturno fà il tuo-no Dorio, quella Gioue il Frigio, & l'altre per ordine gli altri Tuoni. Onde non è dub-bio, essendo il Dorio tenuto dalla maggior parte de i Musici piu graue del Frigio, che la Sphera di Saturno sia quella, che faccia il suono graue. Oltra di questo (lasciandone molt' altri da parte) ui è Boetio;Musicae li-br. 1. c. 27. il quale, quasi recitando l'altrui opinione, attribuisce la chorda Hypate à Saturno, ch'è d'ogn'altra grauissima; dopoi piu abbasso attribuisce alla me-desima sphera (secondo la prima opinione medesimamente da lui recitata) il suono acu-to, & i graui per ordine; attribuendo il grauissimo al globo lunare. Da queste differenze nacque, che i Filosofi, per uoler mostrare in atto quella Harmonia, che per ragioni co-nosceuano esser nelle sphere celesti; attribuirono à ciascuna (come erano de diuersi pareri del Sito de i suoni graui & acuti) diuerse chorde de i loro Istrumenti variatamente ordi-nate; imperoche quelli che fauoriuano la prima opinione, attribuirono alla Sphera della Luna, Pianeta à noi più uicino, la chorda Proslambanomenos; perche fà il suono più graue di qualunque altra Sphera; à quella di Mercurio la Hypate hypaton; & all'altre page 125sphere altre chorde per ordine; secondo che sono poste nella figura. PlutarchoDe Ani-mae procr. ex Timeo. dice, ch'alcuni attribuirno la chorda Proslambanomenos alla Terra, & a la Luna la Hypate, & al So-le (lasciando di nominar gli altri pianeti) alla Mese. Ma quelli, c'haueano contraria opinione, attribuirono la chorda Hypate meson alla sphera di Saturno; perche si pensa-uano, che facesse il suono più graue d'ogn'altra sphera; la Parhypate, à Gioue; Lycha-nos, à Marte; Mese, al Sole; & cosi all'altre attribuirono altre chorde, secondo il mo-strato ordine. Et si come furono di uario parere intorno à quello, c'hò detto; cosi anco furono differenti nel porre le chorde à i loro Istrumenti; essendo che quelli, c'hebbero opinione, che Saturno facesse il suono acuto & la Luna il graue, posero le Chorde acute nel soprano luogo, ouer nella parte destra; & le graui nel luogo più basso, ouer nella par-te sinistra; & quelli, ch'erano di contrario parere, faceuano al contrario; conciosiache poneuano le graui nella parte superiore, ouer nella banda destra & le acute nella inferiore, ouer nella sinistra. Ilche dimostra esso Plutarcho nella Questione 8. delle Pla-
Concentus, mixtumque melos, pars ocyus acta
Clarius, & cantu longè resonabat acute,
Tarda ibat grauiore sone.
![Diapa-son.
diapte. Diapt.
Diatessa.
Diatessa.
Mese. Vrania. [Heaven]
tuo. Lychanos meson. . [Saturn]
tuo. Parhypate mes. . [Jupiter]
sem. Hypate meson. . [Mars]
tuo. Lychanos hypa. . [Sun]
tuo. Parhypate hypa. . [Venus]
sem. Hypate hypat. . [Mercury]
tuo. Proslbanomenos . [Moon]
Diapa-son.
Diapte. Diapte.
Diatessa.
Diatess.
Netesynemnon. .
tuo. Paranete syne.
tuo. Tritesynemn.
sem. Mese.
tuo. Lychanos mes.
tuo. Parhypate. mes.
sem. Hypate meson.
tuo. Lychanos hypa.](../../zarins89/ill/229_1.gif)
In che modo le predette Sedeci chorde siano state da i Latini denominate. Cap. XXX.
Vt queant laxis Resonare fibris Mira getorum Famuli tuo- rum; Solue polluti Labij reatum sancte Iohannes;& li concatennò con tale arteficio & in tal maniera; che ciascuno contiene tutte le Specie della Diatessaron, le quali sono tre; co-me vederemo nella terza parte; accommodando il Semituono, circoscritto da queste due sillabe mezane Mi & Fa, nel mezo di ciascuno. La onde aggiunse primieramente al-la Proslambanomenos di questo suo ordine nella parte graue una chorda, distante per un Tuono, segnata con lettera Greca maiuscola ritrouata forse per inanti, ouero aggiun-ta da altri Musici de suoi tempi all'ordine delle chorde Greche in questo modo Γ; & l'al-tre poi con lettere Latine; che dinota, la Musica (come uogliono alcuni) essere stata ri-trouata primamente da i Greci, & posta in uso; & al presente da i Latini essere honore-uolmente posseduta, abbracciata & accresciuta. Et alla predetta Lettera aggiunse la prima delle Sei sillabe; cioè, Vt; in questo modo Γ, vt; che uuol dire Gamma ut; & cosi nominò la chorda aggiunta di tal nome; & è la prima chorda della sua ordinatione. Chia-mò poi Proslambanomenos de i Greci A re; ponendo insieme la prima lettera latina & la seconda sillaba delle mostrate; & fù la seconda chorda del suo Introdottorio. La ter-za poi; cioè, la seconda Greca, detta Hypate hypaton, nominò
 mi; ponendo insie-me la seconda lettera latina, & la terza sillaba seguente; & pose tal lettera quadrata, dif-ferente da la b rotonda; per dinotarci la differenza de i Semituoni, che fanno queste due
chorde; conciosiache non sono in un'istesso luogo; quantunque siano alle fiate congiunte
quasi in una istessa lettera sopra una istessa riga, ouero spacio; come altroue vederemo.
Nominò dopoi la quarta C fa ut, & il resto per ordine, fino à Netehyperboleon, applicandoli vna delle prime lettere latine, A,
mi; ponendo insie-me la seconda lettera latina, & la terza sillaba seguente; & pose tal lettera quadrata, dif-ferente da la b rotonda; per dinotarci la differenza de i Semituoni, che fanno queste due
chorde; conciosiache non sono in un'istesso luogo; quantunque siano alle fiate congiunte
quasi in una istessa lettera sopra una istessa riga, ouero spacio; come altroue vederemo.
Nominò dopoi la quarta C fa ut, & il resto per ordine, fino à Netehyperboleon, applicandoli vna delle prime lettere latine, A,  , ouer B, C, D, E, F, G; descriuendole nel primo
ordine maiuscole, nel secondo picciole, & nel terzo raddoppiate; come nell'Introdot-page 127
, ouer B, C, D, E, F, G; descriuendole nel primo
ordine maiuscole, nel secondo picciole, & nel terzo raddoppiate; come nell'Introdot-page 127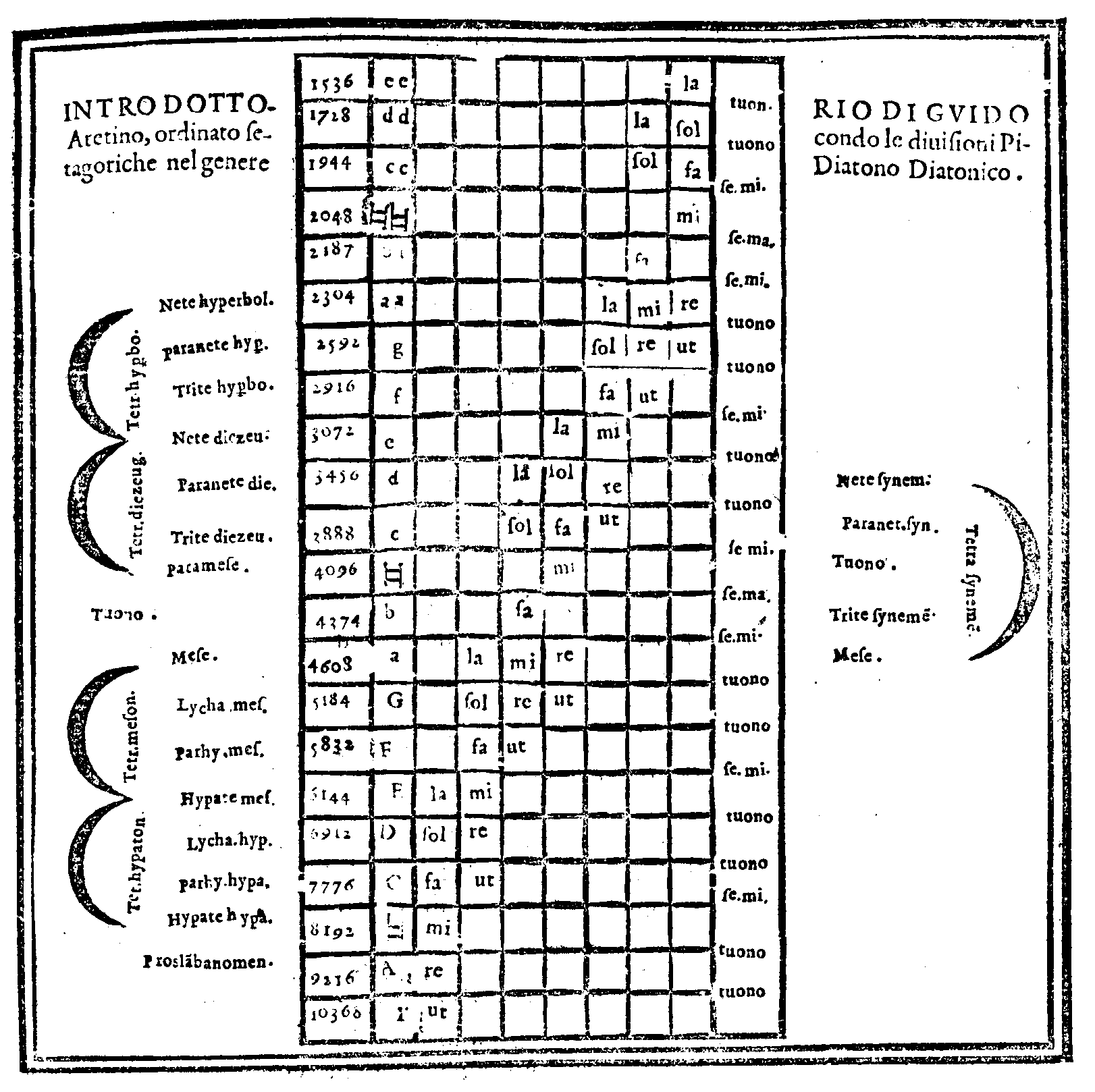

 mi; cc sol fa; dd la sol; & ee la; & fece questo per finire
gli ultimi due Hexachordi, de i quali l'uno hà principio in f; & l'altro in g: & per tal
modo le chorde Greche acquistarono altra denominatione. Fù tenuto tale ordine da
Guido (com'io credo) forse non senza consideratione, applicando cotali Sil-labe alle chorde sonore, moltiplicate per il numero Settenario; perche comprese, che
nel Senario si conteneua la diuersità de i Tetrachordi; & che nel Settenario erano Sette
suoni, ò uoci, l'una dall'altra per natural diuisione al tutto uariate & differenti; come si
può vedere, & udire nelle prime Sette chorde, le quali sono essentiali, & niuna di lo-ro s'assimiglia all'altra di suono; ma sono molto diuerse. Questa diuersità conobbe il
dottissimo Homero, quando nell'Hinno fatto à Mercurio disse;
mi; cc sol fa; dd la sol; & ee la; & fece questo per finire
gli ultimi due Hexachordi, de i quali l'uno hà principio in f; & l'altro in g: & per tal
modo le chorde Greche acquistarono altra denominatione. Fù tenuto tale ordine da
Guido (com'io credo) forse non senza consideratione, applicando cotali Sil-labe alle chorde sonore, moltiplicate per il numero Settenario; perche comprese, che
nel Senario si conteneua la diuersità de i Tetrachordi; & che nel Settenario erano Sette
suoni, ò uoci, l'una dall'altra per natural diuisione al tutto uariate & differenti; come si
può vedere, & udire nelle prime Sette chorde, le quali sono essentiali, & niuna di lo-ro s'assimiglia all'altra di suono; ma sono molto diuerse. Questa diuersità conobbe il
dottissimo Homero, quando nell'Hinno fatto à Mercurio disse;
Ε῾πτὰ δὲ συμφώνους ὀΐον ἐτανύσσατο ΧορδὰςChe uuol dire.
Ma Sette chorde fatte di budellaCosi Horatio parlando all'istesso Mercurio, commemorò tali chorde con queste parole;Carmi. li-bro 3. ode. 11.
Di pecore distese, che tra loro
Erano consonanti.
Tuque testudo resonare septempage 128Et se ben Theocrito Idyllium. 8. pone, che la Sampogna di Menalcha pastore facesse Noue suo-ni differenti, quando disse:
Callida neruis.
Σύριγγ' ἅν ἐπόησα καλὰν ἐγὼ ἐννεάφωνον.
Questa bella Sampogna, la qual feciCredo, che questo habbia fatto; perche (com'è manifesto & lo afferma Giouanni GrammaticoDe Diale-stis.) Theocrito scrisse nella lingua Doricale sue poesie, le quali cantandosi alla Cetera, ouer Lira, si cantauano nel Modo Dorio; che procedeua (secondo che uede-remo nella Quarta parte) dal graue all'acuto, ò per il contrario, per un tal numero di chorde. Ma Virgilio suo imitatore, accordandosi con Homero, nella Bucolica Cap. 8. In Cory-done. espresse il numero di sette chorde solamente, dicendo:
De Noue suoni.
Est mihi disparibus septem compacta cicutisEt nel libro Sesto dell'Eneida toccò tal numero; quando disse,
Fistula.
Necnon Threicius longa cum veste sacerdos,Similmente Ouidio nel Secondo libro delle Trasformationi disse:
Obloquitur numeris septem dicrimina uocum.
Dispar septenis fistula cannis.Et però con giudicio (com'hò detto) esse Lettere da Guido furono replicate, & non variate; perche conobbe, che l'Ottaua chorda era simile di uoce alla prima; la Nona, alla seconda; la Decima, alla terza, & l'altre per ordine. E' vero, che non mancano quelli, che per le autorità addotte de i Poeti uogliono intendere le Sette consonanze di-uerse, contenute nella Diapason; che sono l'Vnisono, il Semiditono, il Ditono, la Diapente, l'Hexachordo minore, il maggiore, & essa Diapason; & altri anco, che inten-dono il simigliante; lasciando fuori l'Vnisono; perche non è Consonanza propriamen-te detta; come vederemo al suo luogo; ponendoui la Diatessaron; le quali opinioni non sarebbono da sprezzare, quando fussero secondo la mente de tali autori, & non fussero lontane dalla verità; imperoche seguendo i Poeti indubitatamente l'opinione di Pitagora, di Platone, di Aristotele, & d'altri eccellentissimi Musici & Filosofi più antichi; non si può dire, che mai hauessero alcuna opinione, di porre il Semiditono, il Ditono, & li due Hexachordi nel numero delle Consonanze; per le ragioni dette di sopra.Cap. 1. Ma s'al-cun dicesse, che nella Diapason si ritrouano non solo Sette suoni, ò voci differenti; ma di più ancora; come si può uedere ne gli Istrumenti artificiali; il che arguisce contra quello, che di sopra hò detto; Si risponderebbe, ch'è uero, che tra la Diapason si ritrouano molti Suoni differenti, oltra i Sette nominati; ma tali Suoni non sono ordinati secondo la natura del genere Diatonico; ne meno sono acquistati per alcuna diuisione della Proportionalità harmonica.
Consideratione sopra la mostrata Diuisione, ouer Ordinatione, & sopra l'altre specie del genere Diatonica ritrouate da Tolomeo.Cap. XXXI.
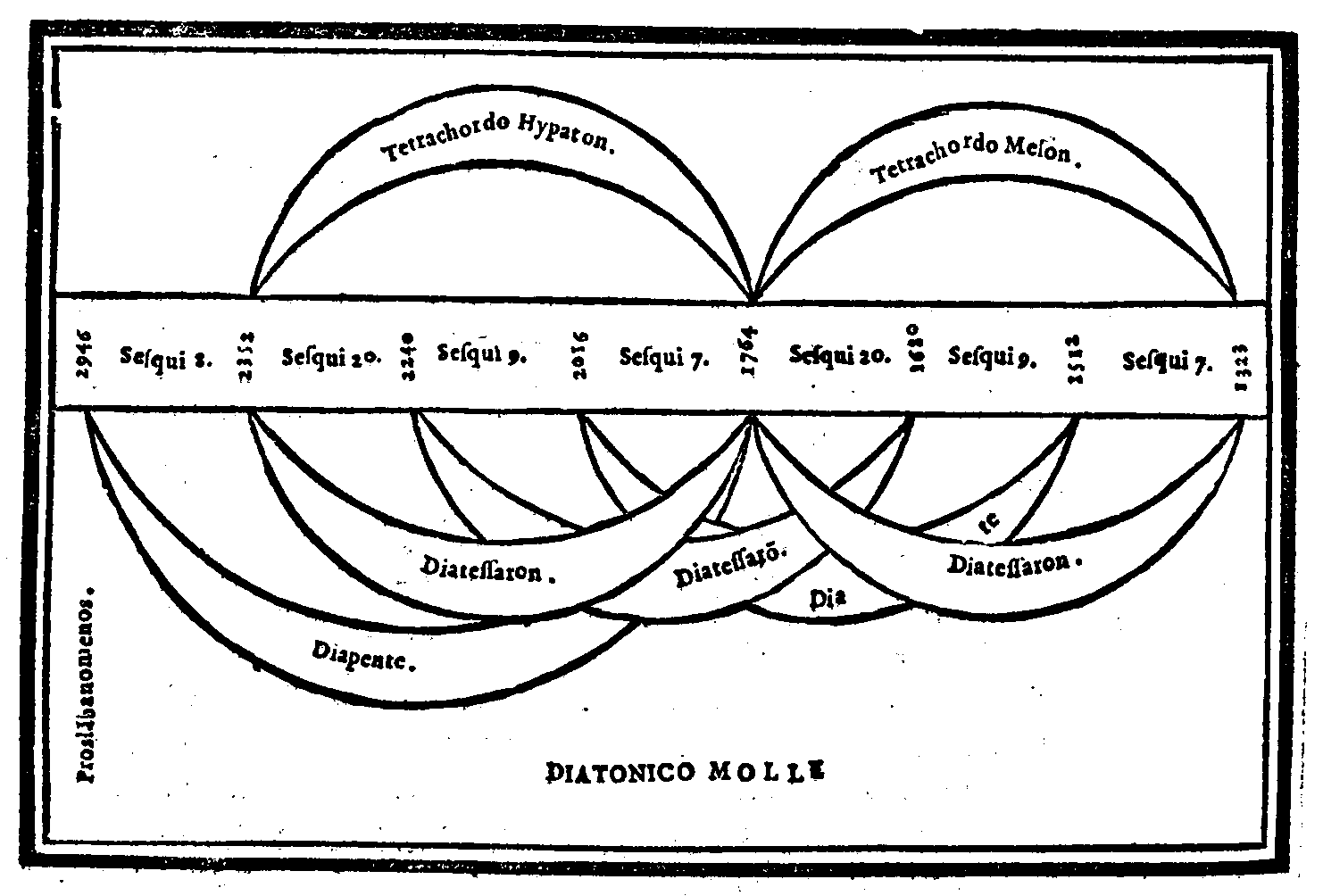
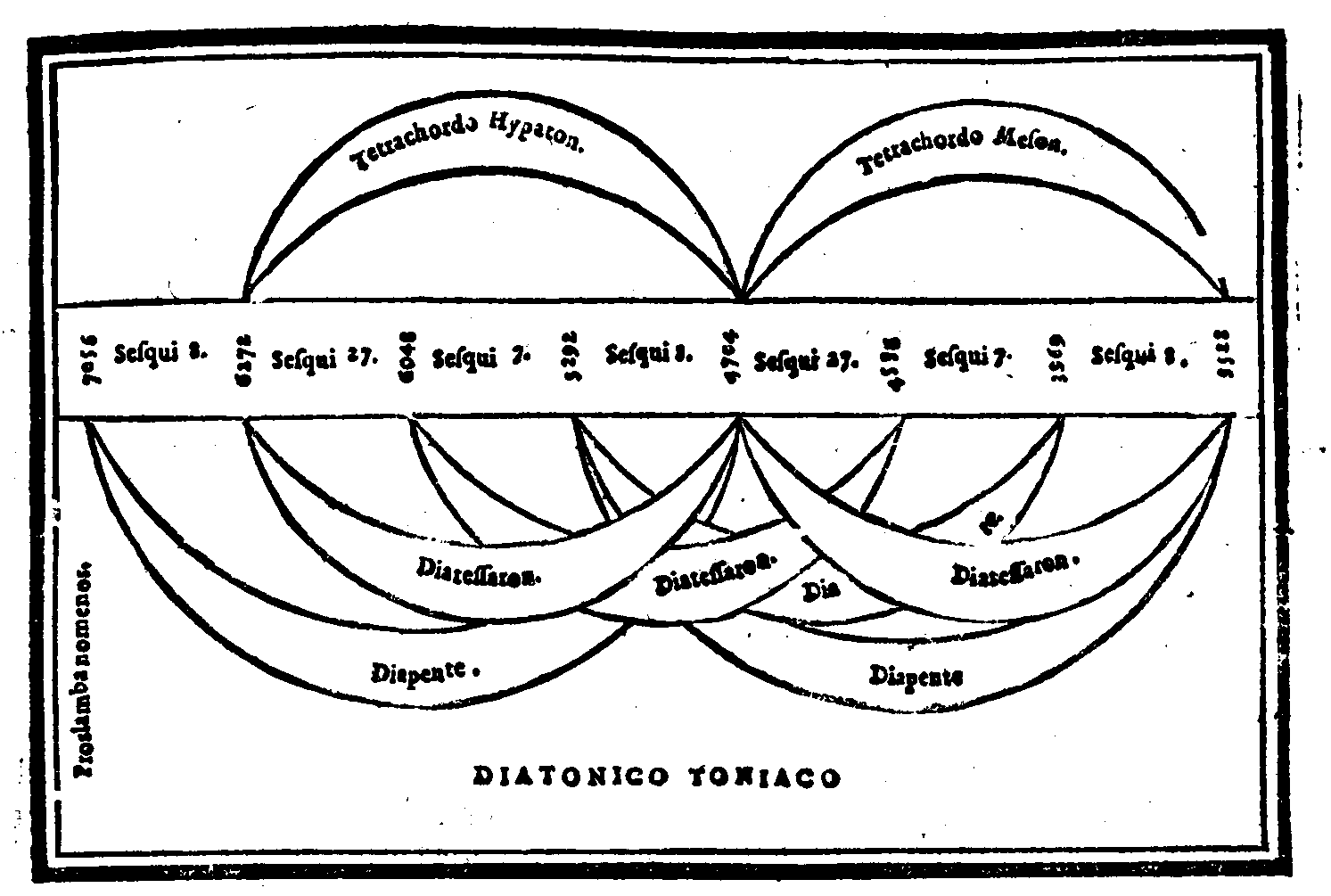
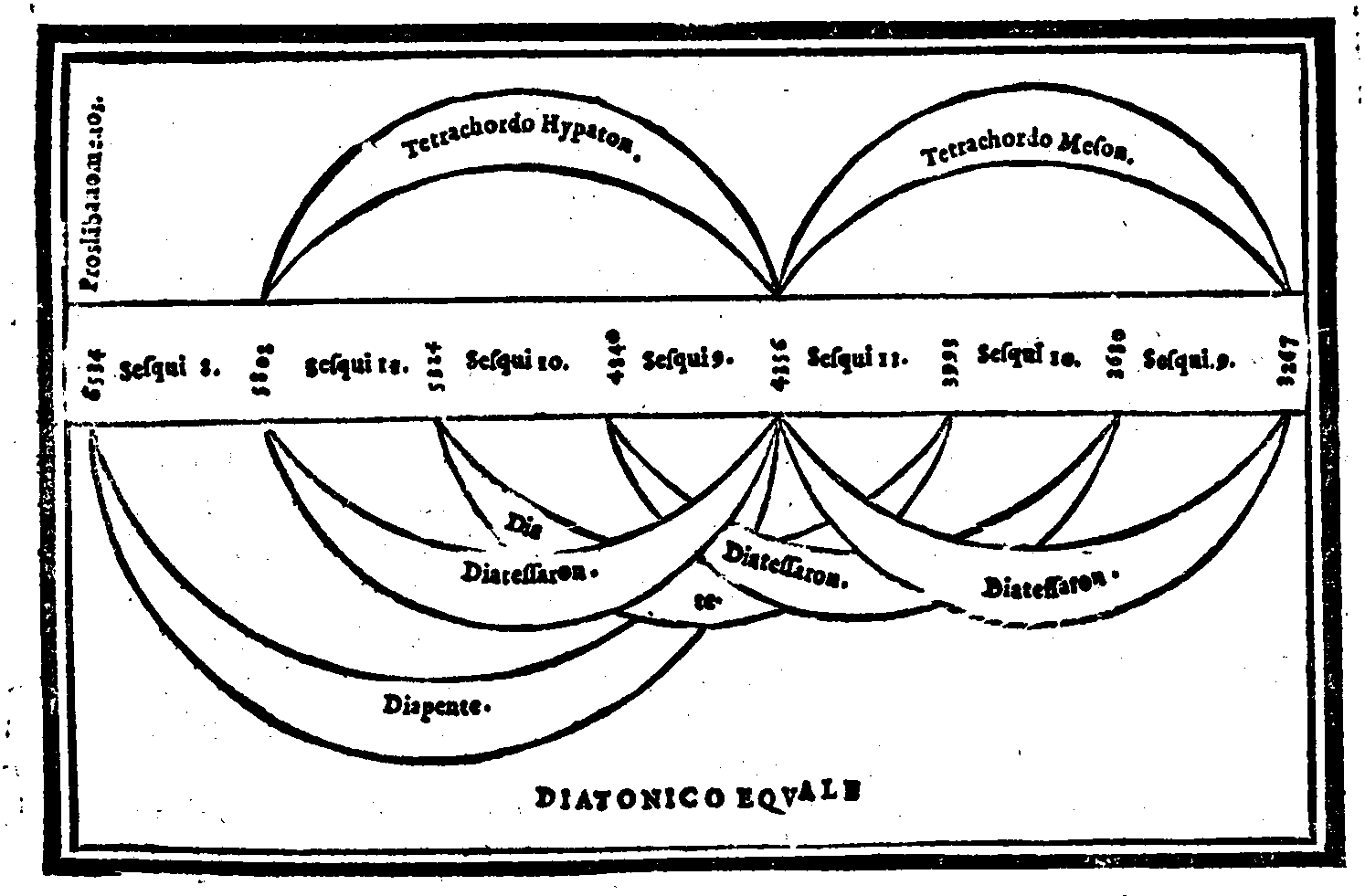
Del genere Chromatico, & chi sia stato il suo Inuentore; & in qual maniera lo potesse trouare: & delle Chorde, che aggiunse Timotheo nel solito Istrumento.Cap. XXXII.



Diuisione del Monochordo Chromatico.Cap. XXXIII.
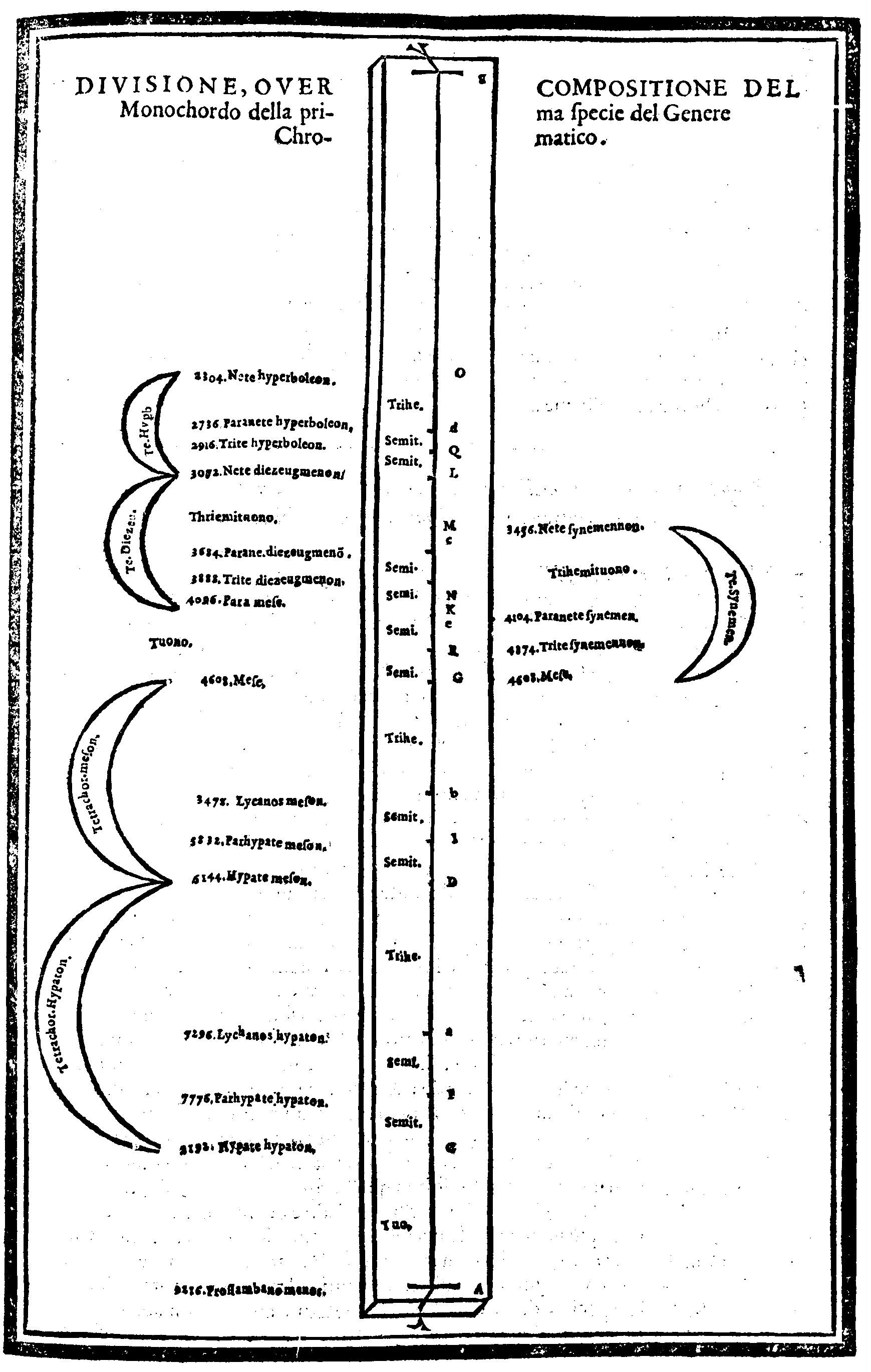
Consideratione sopra la mostrata Diuisione, & sopra alcun'altre Specie di questo Genere, ritrouate da Tolomeo.Cap. XXXIIII.
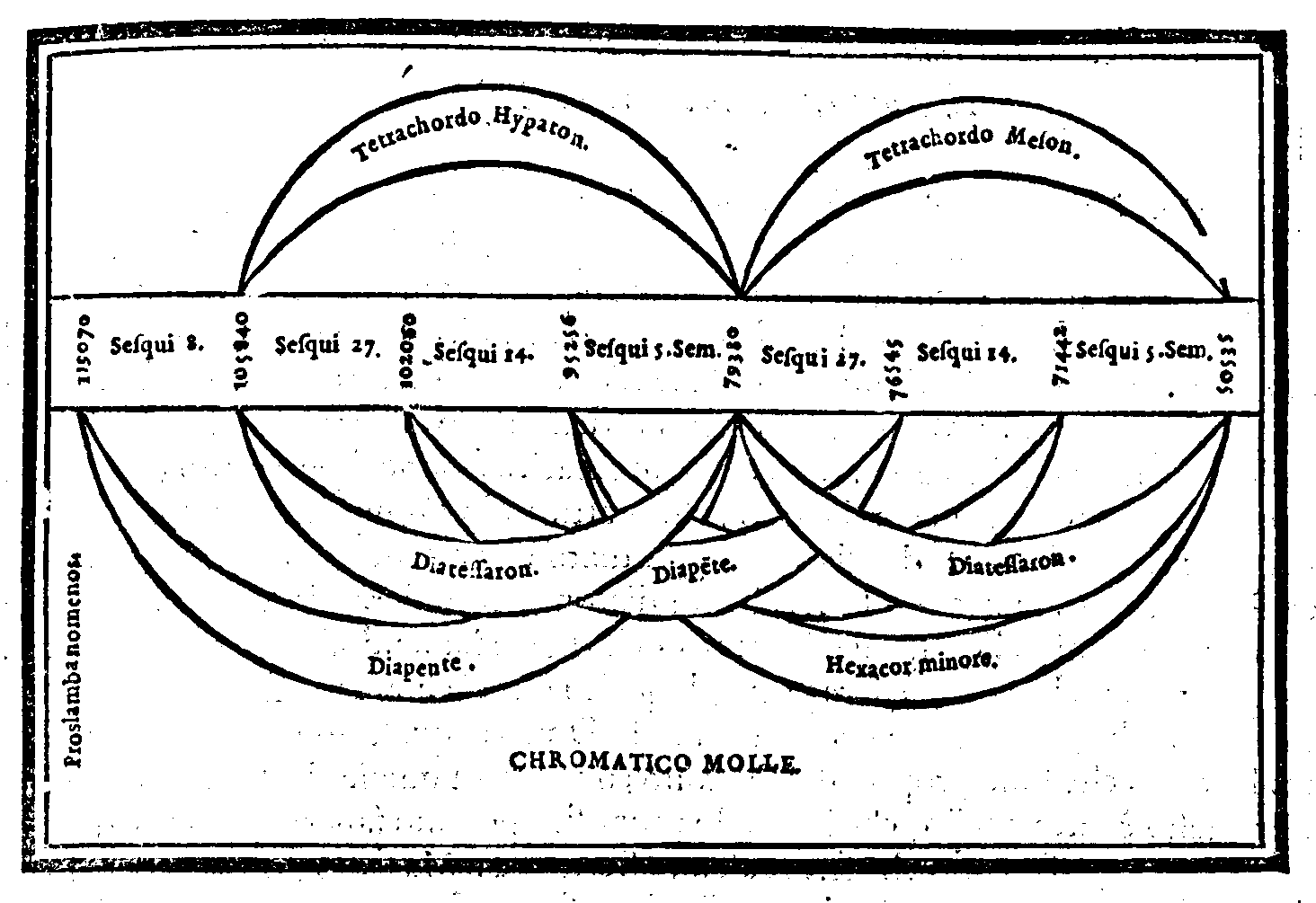
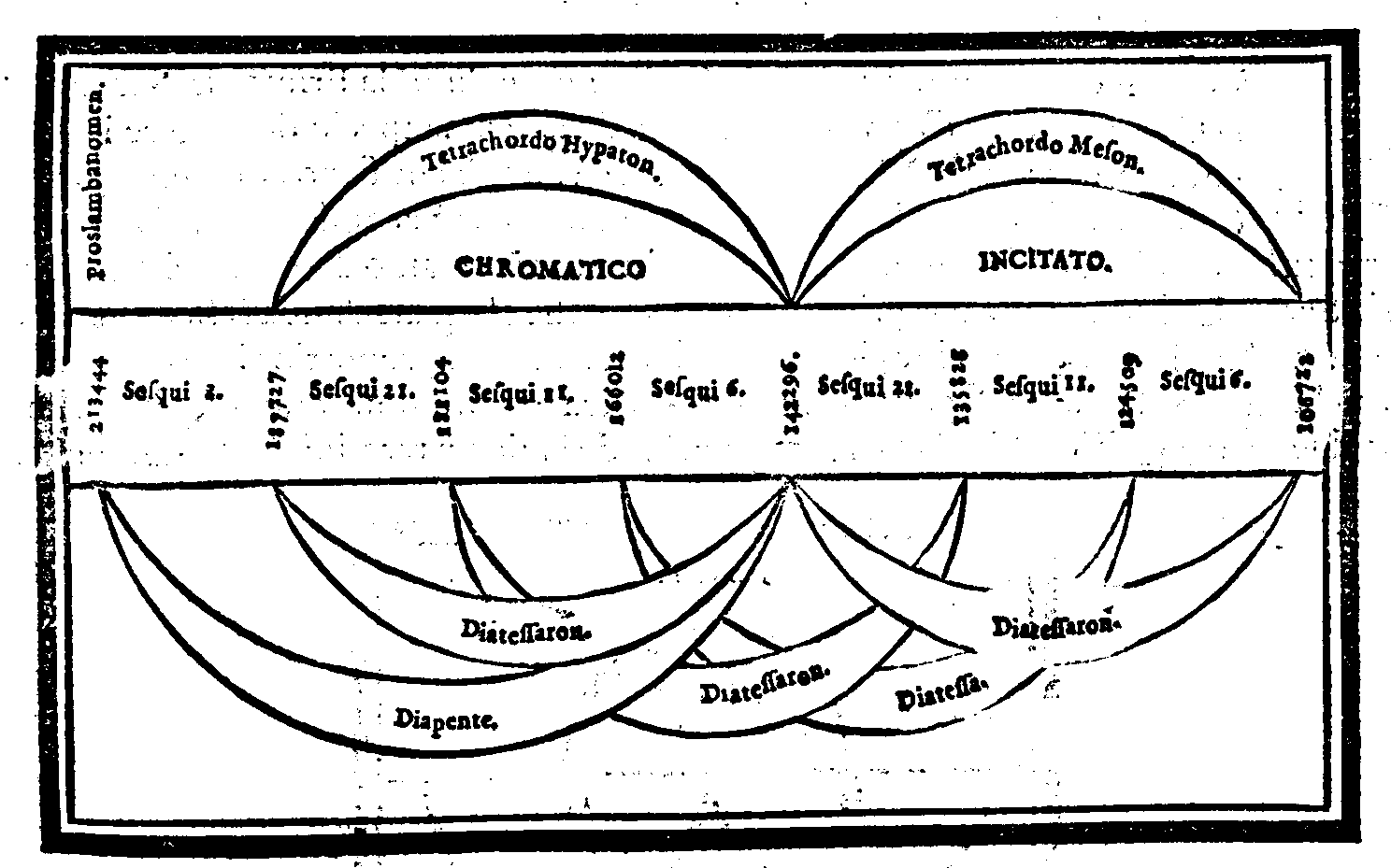
Chi sia stato l'Inuentore del genere Enharmonico, & in qual maniera l'habbia ritrouato.Cap. XXXV.
Della Diuisione, ò Compositione del Monochordo Enharmonico. Cap. XXXVI.
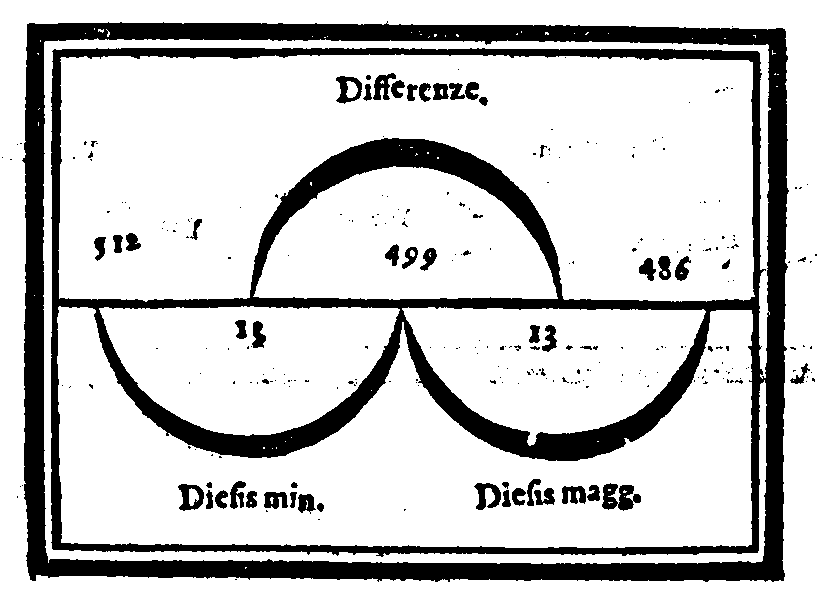
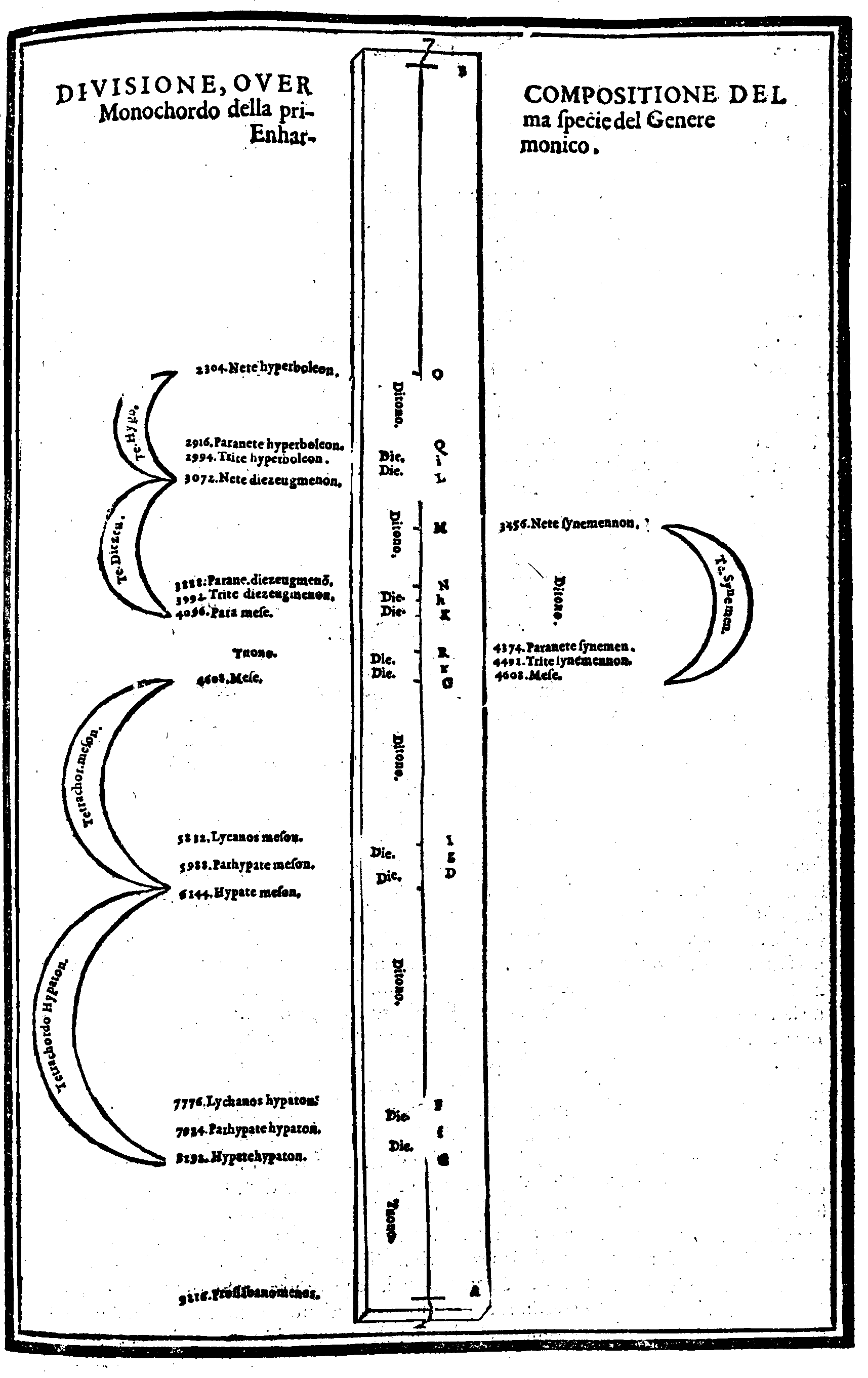
Consideratione sopra la mostrata Particione, ouer Compositione; & sopra quella specie d'Enharmonico, che ritrouò Tolomeo. Cap. XXXVII.
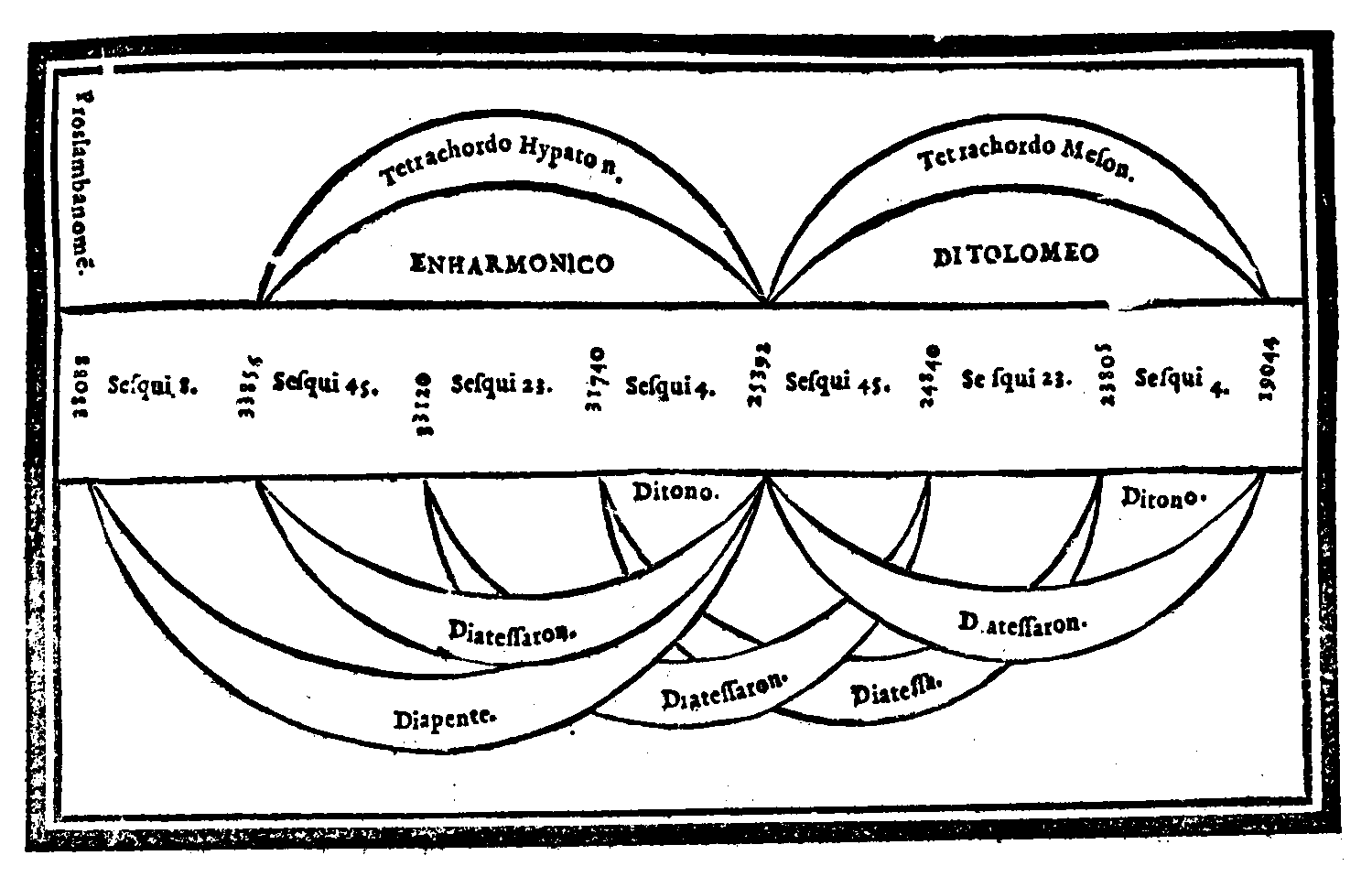
Della Compositione del Monochordo Diatono diatonico, inspessato dalle chorde Chromatiche, & dalle Enharmoniche. Cap. XXXVIII.
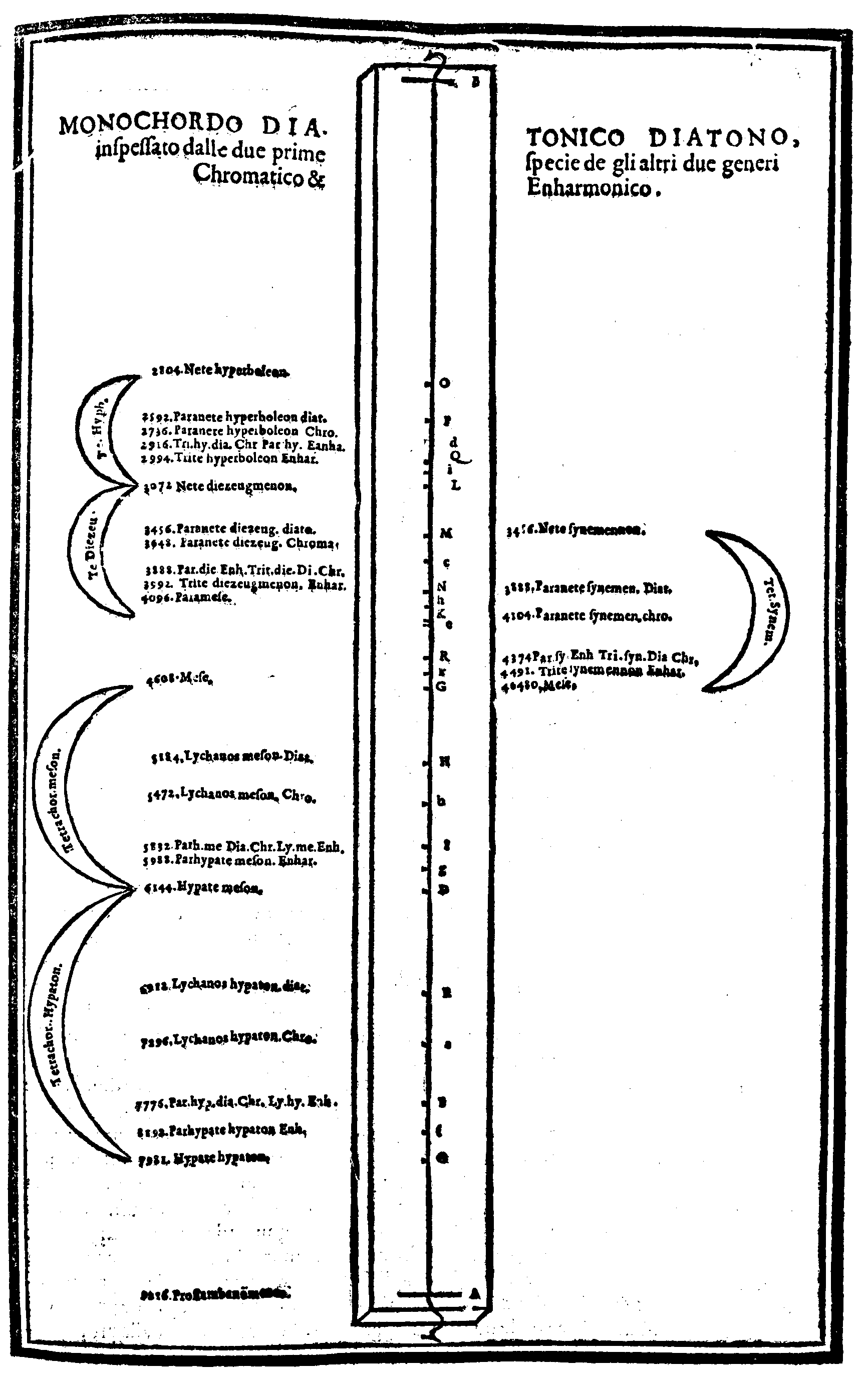
Che 'l Diatonico Naturale, ò syntono di Tolomeo sia quello, che dalla natura è prodotto, & che naturalmente habbia la sua forma da i Numeri harmonici.Cap. XXXIX.
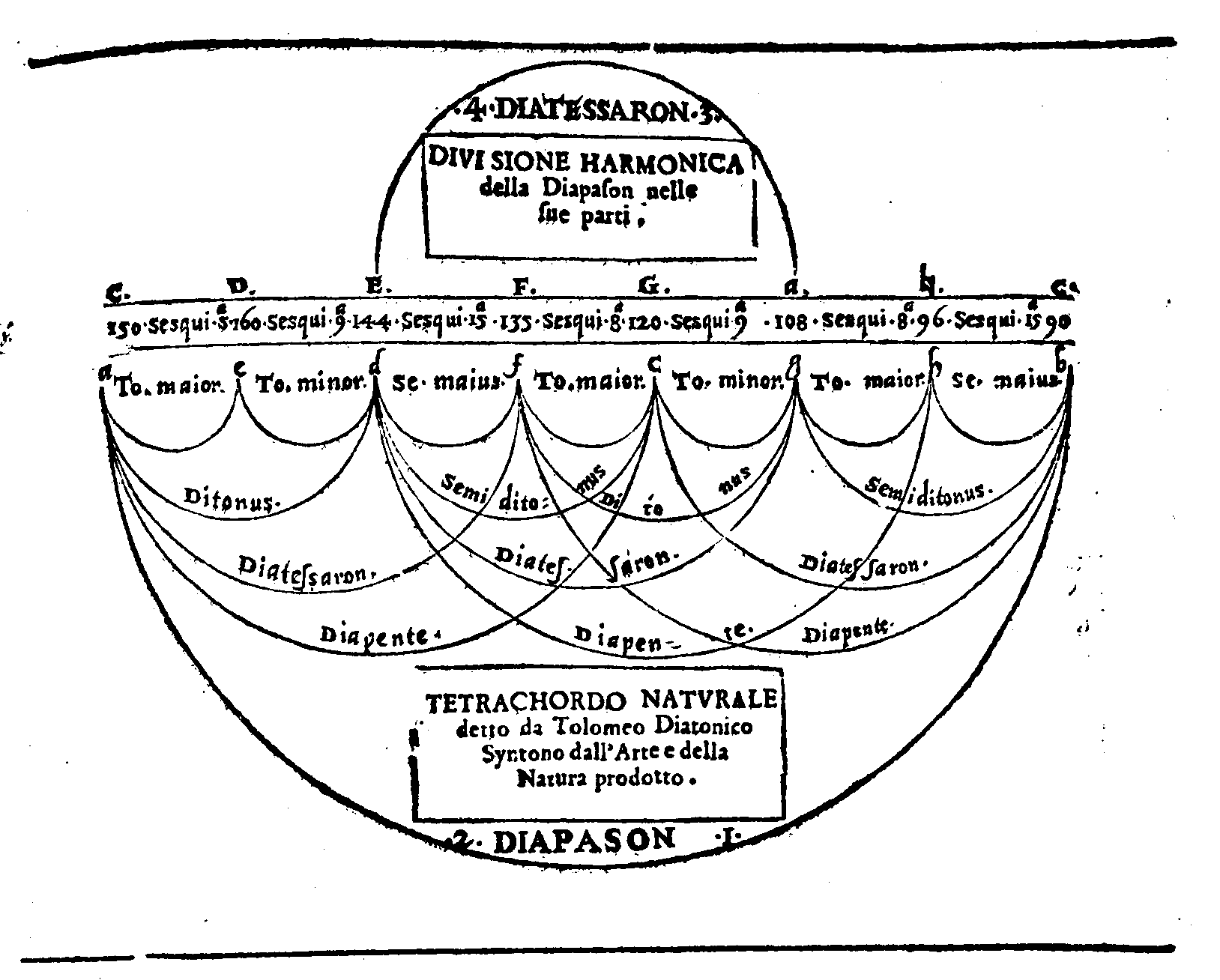
 . c. & fanno la Prima specie della Diapason, come al
suo luogo uederemo; come nella 14. Def. del Quinto delle Dimostrationi hò dichiarato.
Et quantunque si ueda che naturalmente il Tuono maggiore a e. tenga il luogo graue, &
dopo esso immediatamente seguita il minore e d. uerso l'acuto, & il Semituono d f. ten-ga il più acuto luogo nella Diaressaron C. D. E. F. & che Tolomeo habbia prima colloca-to il Semituono d f. nel graue, & dopoi di mano in mano i duo Tuoni f c. & c g. per l'ordine mostrato uerso l'acuto, contra la natura de i Numeri harmonici; tuttauia si debbe scusare; percioche lo fece per seguir nelle sue Dimostrationi il costume de i primi Inuentori
de i Generi mostrati; i quali poneuano primieramente nella parte graue de i loro Tetra-chordi l'Interuallo minore; & dopoi li maggiori per ordine; percioche credettero che 'l
primo Interuallo nella Musica fusse il Minimo rationale, che si potesse ritrouar, dal quale
hauessero origine & si componessero gli altri Interualli; come si uede, che Aristotele1. post. c.
17. & 10.
Metaphy.
cap. 2. pone il
Diesis per il Principio di questo genere Melodia, non potendo far di manco. Ma non è dub-bio, che tal Semituono sempre tiene il suo luogo (come si può uedere) procedendo dal graue all'acuto, dopo il Tuono minore, & auanti il maggiore; anzi più tosto dopo il maggiore
& lo minore, nella Compositione & congiuntione de i Tetrachordi; come ricerca la na-tura de i Numeri harmonici; i quali ne danno primieramente i maggiori, & dopoi i mi-nori Interualli per ordine. Et è tanta la necessità di questo Interuallo, che senza il suo me-zo non si può procedere dal Ditono alla Diatessaron, ne dalla Diapente all'Hexachordo
minore; come uederemo. Ond'è chiamato Semituono maggiore, à differenza di quella page 149quantità contenuta dalla Sesquiuentesimaquarta proportione, detta Semituono mino-re, per la quale il Semiditono è superato dal Ditono. Il perche aggiunti questi due Se-mituoni insieme, arriuano alla perfettione del Tuono minore, contenuto dalla propor-tione Sesquinona; come dimostra la Decimanona proposta del libro Secondo delle Dimostrationi. Concluderemo adunque di nuouo, c'hauendo origine tutti gli Interualli
del Tetrachordo Diatonico naturale, ò syntono di Tolomeo dalla diuisione della Dia-pason, fatta harmonicamente nelle sue parti; che esso Tetrachordo sia etiandio diuiso,
& ordinato secondo la natura & passione de i numeri harmonici; come hò detto. Ma ueniamo hormai alla Diuisione, ò Compositione del Monochordo.
. c. & fanno la Prima specie della Diapason, come al
suo luogo uederemo; come nella 14. Def. del Quinto delle Dimostrationi hò dichiarato.
Et quantunque si ueda che naturalmente il Tuono maggiore a e. tenga il luogo graue, &
dopo esso immediatamente seguita il minore e d. uerso l'acuto, & il Semituono d f. ten-ga il più acuto luogo nella Diaressaron C. D. E. F. & che Tolomeo habbia prima colloca-to il Semituono d f. nel graue, & dopoi di mano in mano i duo Tuoni f c. & c g. per l'ordine mostrato uerso l'acuto, contra la natura de i Numeri harmonici; tuttauia si debbe scusare; percioche lo fece per seguir nelle sue Dimostrationi il costume de i primi Inuentori
de i Generi mostrati; i quali poneuano primieramente nella parte graue de i loro Tetra-chordi l'Interuallo minore; & dopoi li maggiori per ordine; percioche credettero che 'l
primo Interuallo nella Musica fusse il Minimo rationale, che si potesse ritrouar, dal quale
hauessero origine & si componessero gli altri Interualli; come si uede, che Aristotele1. post. c.
17. & 10.
Metaphy.
cap. 2. pone il
Diesis per il Principio di questo genere Melodia, non potendo far di manco. Ma non è dub-bio, che tal Semituono sempre tiene il suo luogo (come si può uedere) procedendo dal graue all'acuto, dopo il Tuono minore, & auanti il maggiore; anzi più tosto dopo il maggiore
& lo minore, nella Compositione & congiuntione de i Tetrachordi; come ricerca la na-tura de i Numeri harmonici; i quali ne danno primieramente i maggiori, & dopoi i mi-nori Interualli per ordine. Et è tanta la necessità di questo Interuallo, che senza il suo me-zo non si può procedere dal Ditono alla Diatessaron, ne dalla Diapente all'Hexachordo
minore; come uederemo. Ond'è chiamato Semituono maggiore, à differenza di quella page 149quantità contenuta dalla Sesquiuentesimaquarta proportione, detta Semituono mino-re, per la quale il Semiditono è superato dal Ditono. Il perche aggiunti questi due Se-mituoni insieme, arriuano alla perfettione del Tuono minore, contenuto dalla propor-tione Sesquinona; come dimostra la Decimanona proposta del libro Secondo delle Dimostrationi. Concluderemo adunque di nuouo, c'hauendo origine tutti gli Interualli
del Tetrachordo Diatonico naturale, ò syntono di Tolomeo dalla diuisione della Dia-pason, fatta harmonicamente nelle sue parti; che esso Tetrachordo sia etiandio diuiso,
& ordinato secondo la natura & passione de i numeri harmonici; come hò detto. Ma ueniamo hormai alla Diuisione, ò Compositione del Monochordo.
Della Diuisione del Monochordo naturale, ouer syntono Diatonico; fatta secondo la natura & propietà de i Numeri sonori.Cap. XL.
Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle mostrate specie Diatoniche.Cap. XLI.
 che sia compreso nella sua uera & natural forma, ouer propor-tione; percioche il numero delle lor chorde non può dare gli Interualli, che si ritroua-no nel Diatonico syntono; ne meno comprendono quelli del Diatonico diatono mo-page 151
che sia compreso nella sua uera & natural forma, ouer propor-tione; percioche il numero delle lor chorde non può dare gli Interualli, che si ritroua-no nel Diatonico syntono; ne meno comprendono quelli del Diatonico diatono mo-page 151
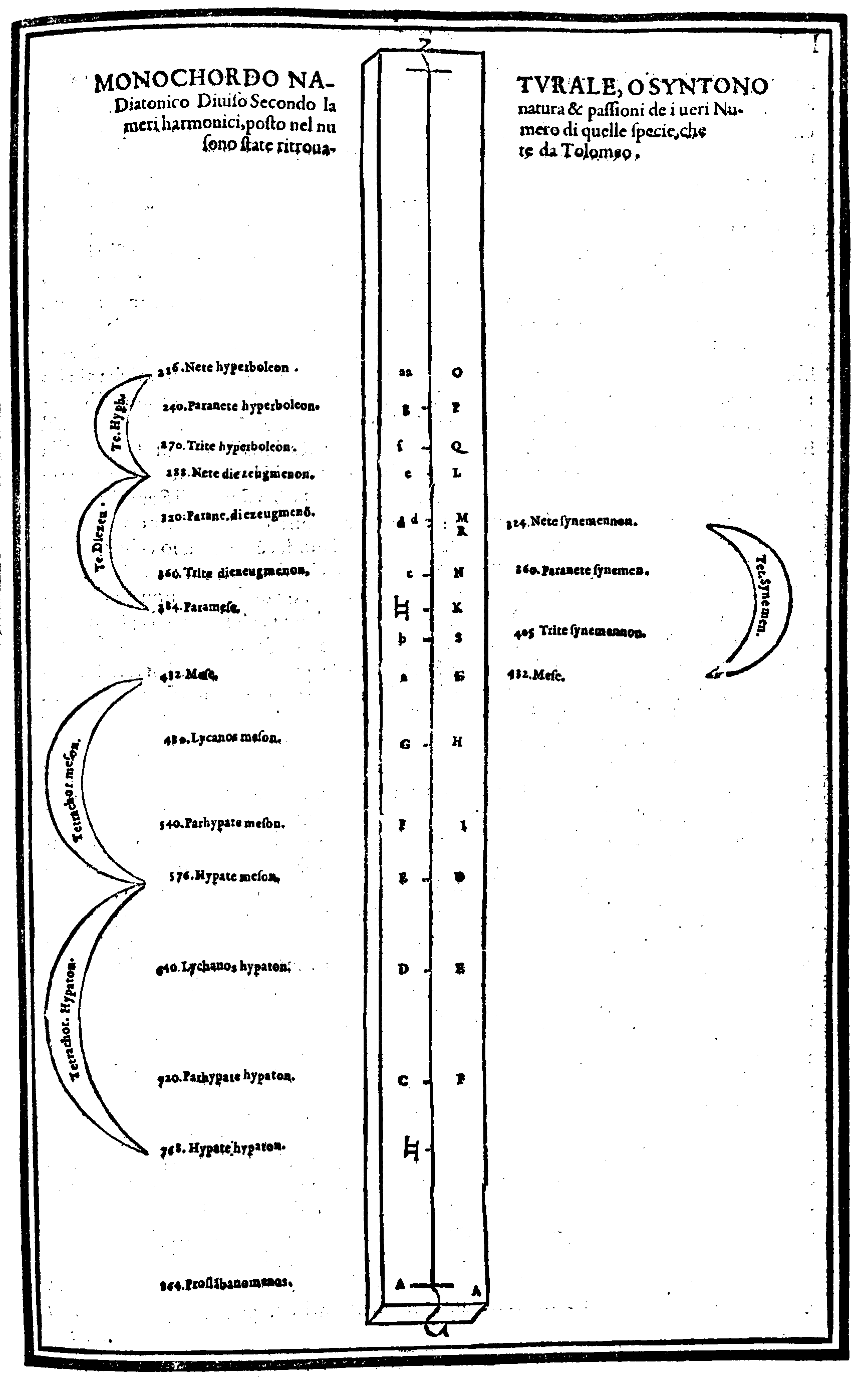
Vnde sit, vt & si Sesquitonus iucundè, suauiterque auditum feriat; nondum tamen Consonantia ponendus sit.Et nella Seconda,
Itidem Ditonus inter Sesquiter-tiam atque Sesquiquartam medius, minimè Musicam complet atque perficit harmoniam:percioche quando dice, che 'l Sesquituono ferisce giocondamente & soauemente l'Vdito; lo dice, perche lo ode in atto nella proportione Sesquiquinta; ma quando dice,
Nondum tamen Consonantia ponendus sit;lo considera nella Sesquiquinta & la Sesquisesta proportione; & l'istesso fà del Ditono; ma non è marauiglia, se non ne hauendo fatto altra esperienza; ei credesse, che l'uno & l'altro fusse contenuto nelle lor forme uere; in cotali proportio-mi. E' credibile adunque, che alcun perito nella Musica, dopo un certo spacio di tem-po, à caso prima, & dopoi l'hauerne fatto molte esperienze, nell'istesso Istrumento le riducesse à tal temperamento & sotto quelle proportioni, ò forme, le quali hora usiamo; non però sotto alcuna de quelle, che di sopra in molte Diuisioni hò mostrato; percioche sarebbe stato impossibile d'osseruare il Numero delle chorde, l'Ordine de gli Interualli, & le Forme, ò Proportioni mostrate; ma si bene sotto quelle, ch'io sono per mostrare.
Quel che si dee osseruare nel Temperamento de gli Istrumenti Arteficiali, di mo-do che nel numero delle Chorde & nella equalità de i Tuoni s'assimigli al Dia-tono diatonico: ma ne gli Interualli consonanti; quantumque acciden-tali, al Naturale ò Syntono di Tolomeo.Cap. XLII.
Dimostratione, dalla quale si pùo comprendere, che la mostrata Participatione, ò Distributione sia ragioneuolmente fatta; & che per altro modo non si possa fare, che stia bene.Cap. XLIII.
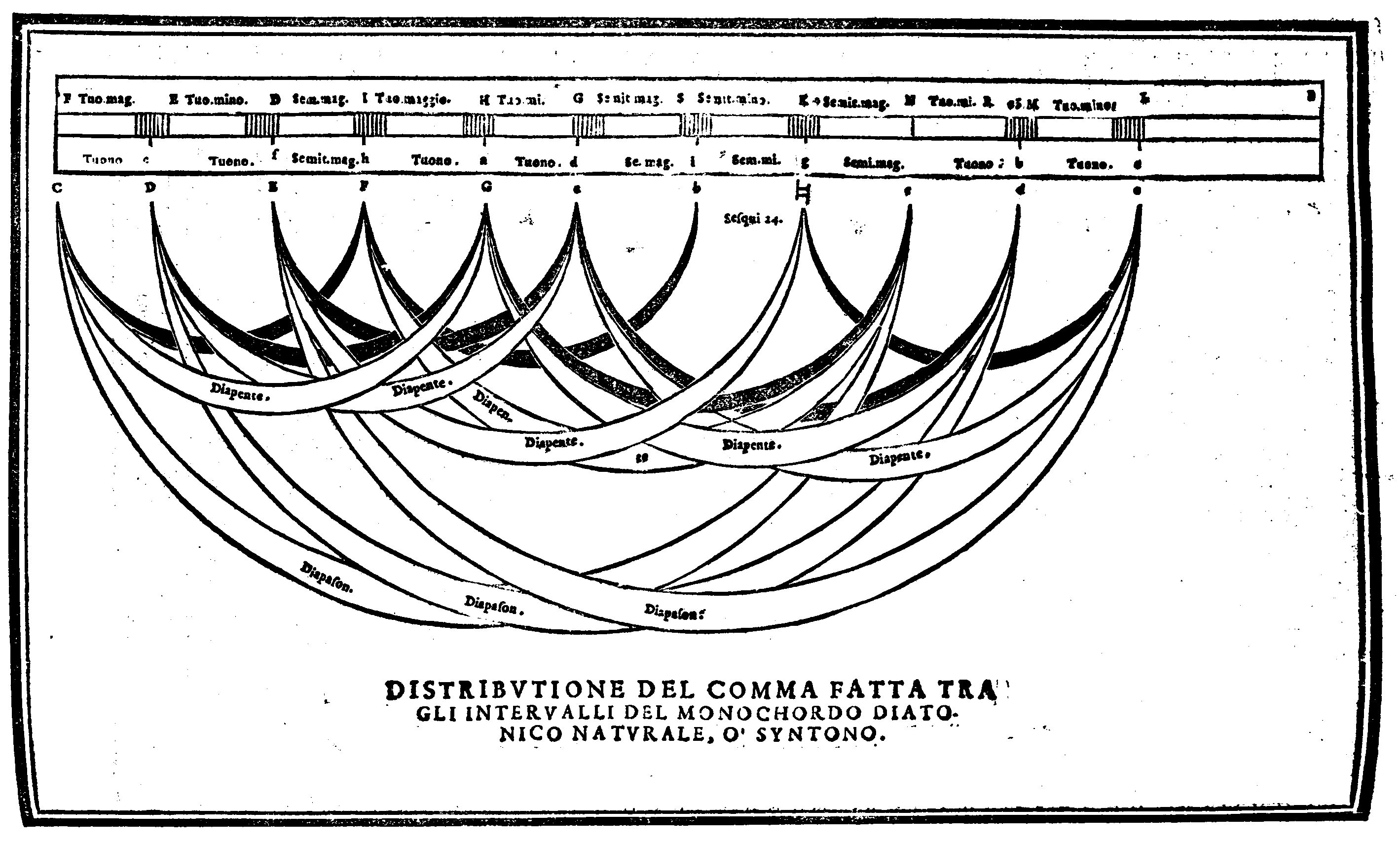
Della Compositione del Monochordo diatonico equalmente temperato nel pri-mo modo.Cap. XLIIII.
 , minore di quattro parte
d'un Comma. Soggiungeremo immediatamente à questo il Semituono maggiore,
contenuto dalla proportione Sesquiquintadecima; il quale aggiunto al Tuono mag-giore, fà il Semiditono, contenuto dalla proportione Sesquiquinta. Et perche il Se-mituono piglia aumento di tre settime parti del Coma, & il Tuono discresce quattro;
però cauando le tre dalle quattro, ne resterà una, che sarà quella parte, della quale il page 161Semiditono si uiene à minuire; secondo che di sopra si è detto. Pigliaremo adunque so-lamente una parte del Comma a b, & c b, che sarà la più uicina alla c, & la metteremo
insiemecon la c b, diuidendo questo Tutto in sei parti equali; & pigliandole cinque,
che sarà in punto f, tra la diuisa, & la f b, haueremo collocato il Semiditono alla sua na-turale proportione; & tra la c b, & la f b haueremo; per le ragioni già dette; il diminu-to di una settima parte del Comma, nella sua forma accidentale. In tal maniera adun-que haueremo una terza chorda, la quale segnaremo con la lettera C, & sarà la secon-da del primo Tetrachordo, che con la
, minore di quattro parte
d'un Comma. Soggiungeremo immediatamente à questo il Semituono maggiore,
contenuto dalla proportione Sesquiquintadecima; il quale aggiunto al Tuono mag-giore, fà il Semiditono, contenuto dalla proportione Sesquiquinta. Et perche il Se-mituono piglia aumento di tre settime parti del Coma, & il Tuono discresce quattro;
però cauando le tre dalle quattro, ne resterà una, che sarà quella parte, della quale il page 161Semiditono si uiene à minuire; secondo che di sopra si è detto. Pigliaremo adunque so-lamente una parte del Comma a b, & c b, che sarà la più uicina alla c, & la metteremo
insiemecon la c b, diuidendo questo Tutto in sei parti equali; & pigliandole cinque,
che sarà in punto f, tra la diuisa, & la f b, haueremo collocato il Semiditono alla sua na-turale proportione; & tra la c b, & la f b haueremo; per le ragioni già dette; il diminu-to di una settima parte del Comma, nella sua forma accidentale. In tal maniera adun-que haueremo una terza chorda, la quale segnaremo con la lettera C, & sarà la secon-da del primo Tetrachordo, che con la  contenerà il Semituono maggiore, accresciu-to di tre settime parti. Aggiungeremo à questo immediatamente il Tuono; accioche
la prima chorda con la quarta habbiano la consonanza Diatessaron; & tal Tuono sarà
il primo del primo Tetrachordo posto nel graue. Ma perche tal Consonanza con-tiene il Tuono maggiore, il minore, & il maggior Semituono; hauendo collocato per
auanti il Tuono maggiore tra la prima & la seconda chorda; fà dibisogno, che noi
habbiamo il minore; & però procederemo in tal modo; accommodando prima la det-ta Consonanza alla sua proportione, lasciando da un canto le due prime parti del Comma c b, & d b poste appresso la c; & dopoi pigliando solamente le cinque, diuideremo
tutta la linea fina in punto b, in quattro parti equali, per il maggior termine della Ses-quiterza proportione, ch'è la uera forma di essa Diatessaron; & pigliando tre parti in
punto g, haueremo prima tra la diuisa, & la g b. la Diatessaron nella sua uera forma, &
dopoi l'accresciuta de due parti del Comma tra la c b, & la g b; conciosiache se le
aggiunge quelle due parti, che prima che si diuidesse tal linea, furono lasciate da un canto. Et perche tra 'l Tutto diuiso, & la g b, si ritroua la proportione Sesquiterza; se per
l'aggiuntione d'alcuna parte si uiene à crescere alcuna proportione di quella quantità,
che se le aggiunge; è manifesto (per quello che si è detto di sopra) che hauendosi ag-giunto due settime parti delle mostrate alla chorda graue della proportione Sesquiter-za, & rimanendo l'acuta nel suo primo essere, tal proportione sia fatta maggiore di
tanta quantità quanta era quella, ch'è stato aggiunta. Ma perche tra la chorda c b, &
la e b habbiamo il Tuono maggiore diminuto; & tra la e b, & la f b il Semituono mag-giore accresciuto; però tra la f b, & la g b haueremo il. Tuono minore, il quale uer-rà per la integratione della Diatessaron accresciuta de due parti del Comma; come la ragione sempre ce lo sarà uedere. Haueremo adunque la chorda D; che con la C con-tiene il Tuono minore, accresciuto di tre parti del Comma; il qual Tuono in questo
luogo solamente, & nelle sue chorde corrispondenti in proportione Dupla, segue im-mediatamente dopo il Semituono maggiore, procedendo dal graue all'acuto. Onde
mi penso, che da altro non possa nascer la difficultà, che si troua nell'accordare, ò tem-perar bene i moderni Istrumenti la chorda G con la d, & questa con la aa, se non per-che le chorde D & d de i detti Istrumenti pigliano il luogo del Comma; onde ne seguo-no due Tuoni minori immediatamente l'un dopo l'altro, tra le chorde C & D, & tra
le D & E; & cosi tra quelle, che corrispondono con queste in Dupla proportione. Et per
seguitar quello, c'habbiamo incominciato, aggiungeremo alla chorda D. un'altra chorda, la quale con essa lei dalla parte acuta contenga il Tuono minore, ilquale uiene ad es-sere il Secondo del primo Tetrachordo; & faremo, che questa chorda aggiunta con la
A. contenerà la Diapente; ma prima è dibisogno, che sappiamo la sua proportione, la
quale è la diminutione di due settime parti d'un Comma. Pigliaremo adunque, le
due parti più propinque alla c, poste tra a & c, & le accompagneremo con tutta la c b,
& cosi diuideremo questo Tutto in tre parti equali, secondo 'l maggior termine conti-nente la proportione della Diapente, & pigliate le due per il minore, che sarà la h b,
tra questa & la diuisa haueremo collocato alla sua uera Proportione la Diapen-te; & la diminuta, secondo le ragioni altre uolte addotte, sara tra la c b, & la h b;
& per tal uia haueremo la chorda E, che con la D contenerà il sopradetto Tuo-no, accresciuto de quelle parti, che fanno dibisogno; & sarà l'ultima chorda page 162
contenerà il Semituono maggiore, accresciu-to di tre settime parti. Aggiungeremo à questo immediatamente il Tuono; accioche
la prima chorda con la quarta habbiano la consonanza Diatessaron; & tal Tuono sarà
il primo del primo Tetrachordo posto nel graue. Ma perche tal Consonanza con-tiene il Tuono maggiore, il minore, & il maggior Semituono; hauendo collocato per
auanti il Tuono maggiore tra la prima & la seconda chorda; fà dibisogno, che noi
habbiamo il minore; & però procederemo in tal modo; accommodando prima la det-ta Consonanza alla sua proportione, lasciando da un canto le due prime parti del Comma c b, & d b poste appresso la c; & dopoi pigliando solamente le cinque, diuideremo
tutta la linea fina in punto b, in quattro parti equali, per il maggior termine della Ses-quiterza proportione, ch'è la uera forma di essa Diatessaron; & pigliando tre parti in
punto g, haueremo prima tra la diuisa, & la g b. la Diatessaron nella sua uera forma, &
dopoi l'accresciuta de due parti del Comma tra la c b, & la g b; conciosiache se le
aggiunge quelle due parti, che prima che si diuidesse tal linea, furono lasciate da un canto. Et perche tra 'l Tutto diuiso, & la g b, si ritroua la proportione Sesquiterza; se per
l'aggiuntione d'alcuna parte si uiene à crescere alcuna proportione di quella quantità,
che se le aggiunge; è manifesto (per quello che si è detto di sopra) che hauendosi ag-giunto due settime parti delle mostrate alla chorda graue della proportione Sesquiter-za, & rimanendo l'acuta nel suo primo essere, tal proportione sia fatta maggiore di
tanta quantità quanta era quella, ch'è stato aggiunta. Ma perche tra la chorda c b, &
la e b habbiamo il Tuono maggiore diminuto; & tra la e b, & la f b il Semituono mag-giore accresciuto; però tra la f b, & la g b haueremo il. Tuono minore, il quale uer-rà per la integratione della Diatessaron accresciuta de due parti del Comma; come la ragione sempre ce lo sarà uedere. Haueremo adunque la chorda D; che con la C con-tiene il Tuono minore, accresciuto di tre parti del Comma; il qual Tuono in questo
luogo solamente, & nelle sue chorde corrispondenti in proportione Dupla, segue im-mediatamente dopo il Semituono maggiore, procedendo dal graue all'acuto. Onde
mi penso, che da altro non possa nascer la difficultà, che si troua nell'accordare, ò tem-perar bene i moderni Istrumenti la chorda G con la d, & questa con la aa, se non per-che le chorde D & d de i detti Istrumenti pigliano il luogo del Comma; onde ne seguo-no due Tuoni minori immediatamente l'un dopo l'altro, tra le chorde C & D, & tra
le D & E; & cosi tra quelle, che corrispondono con queste in Dupla proportione. Et per
seguitar quello, c'habbiamo incominciato, aggiungeremo alla chorda D. un'altra chorda, la quale con essa lei dalla parte acuta contenga il Tuono minore, ilquale uiene ad es-sere il Secondo del primo Tetrachordo; & faremo, che questa chorda aggiunta con la
A. contenerà la Diapente; ma prima è dibisogno, che sappiamo la sua proportione, la
quale è la diminutione di due settime parti d'un Comma. Pigliaremo adunque, le
due parti più propinque alla c, poste tra a & c, & le accompagneremo con tutta la c b,
& cosi diuideremo questo Tutto in tre parti equali, secondo 'l maggior termine conti-nente la proportione della Diapente, & pigliate le due per il minore, che sarà la h b,
tra questa & la diuisa haueremo collocato alla sua uera Proportione la Diapen-te; & la diminuta, secondo le ragioni altre uolte addotte, sara tra la c b, & la h b;
& per tal uia haueremo la chorda E, che con la D contenerà il sopradetto Tuo-no, accresciuto de quelle parti, che fanno dibisogno; & sarà l'ultima chorda page 162
 . C. D. E. F. G. & a, haueremola Diapason tra-mezata da Sei chorde, & diuisa in sette Interualli; ciascun de i quali è accresciuto,
ouer diminuto secondo la proportione, che se gli appartiene, nel modo che si è mo-strato. Et perche diuidendo in due parti equali qualunque chorda si uuole, se le può
ritrouarla corrispondente per una Diapason; come hò mostrato; perche dalla metà
della chorda haueremo sempre il proposito; però se noi diuideremo le chorde meza-ne della Diapason in due parti equali, haueremo le chorde m b, n b, o b, p b, q b,
r b; & similmente la s b, diuidendo la estrema acuta della Diapason, che corrispon-deranno alle chorde e b, f b, g b, h b, i b, K b & l b in Dupla proportione, & in
tal maniera haueremo la compositione del Monochordo temperato ne i suoi Interual-li secondo le loro proportioni, & ridotte le sue chorde al numero de Quindeci, con-tenute ne i quattro primi Tetrachordi; à i quali uolendo aggiungere il quinto, bastarà
d'aggiungere in esso solamente la chorda Tritesynemennon; cioè, accommodare il Se-mituono maggiore, & il minore alle loro proportioni. Et perche il minore (come
ho detto) resta nella proportione Sesquiuentesimaquarta, la quale è rationale; pe-rò diuideremo la linea, ò chorda m b in Ventiquattro parti equali; pigliandone uen-ticinque dalla parte destra in punto t, haueremola chorda t b, la quale ne darà il no-stro proposito; percioche le chorde l b, t b, n b, & o b saranno quelle del Te-trachordo synemennon, che noi cerchiamo; ancora che le chorde l b, n b & o b sia-no à gli altri Tetrachordi communi. Ma quando uorremo ritrouar nel graue alcuna
chorda, che corrispondi con una acuta in proportione Dupla, & faccia udire la Dia-pason; raddoppiaremo la chorda acuta, & haueremo quello, che desideriamo. Se
noi adunque uorremo ritrouar la corrispondente chorda graue alla chorda t b, rad-doppiaremo solamente la detta chorda t b, & in punto u haueremo il tutto; percio-che la chorda u b, con la t b, saranno in proportione Dupla, & faranno essa Dia-pason. Per tal modo adunque haueremo il Monochordo diuiso in cinque Tetrachor-di, nel quale per l'aggiuntione della chorda u b; contenerà il numero di Dicisette chor-de; A. B.
. C. D. E. F. G. & a, haueremola Diapason tra-mezata da Sei chorde, & diuisa in sette Interualli; ciascun de i quali è accresciuto,
ouer diminuto secondo la proportione, che se gli appartiene, nel modo che si è mo-strato. Et perche diuidendo in due parti equali qualunque chorda si uuole, se le può
ritrouarla corrispondente per una Diapason; come hò mostrato; perche dalla metà
della chorda haueremo sempre il proposito; però se noi diuideremo le chorde meza-ne della Diapason in due parti equali, haueremo le chorde m b, n b, o b, p b, q b,
r b; & similmente la s b, diuidendo la estrema acuta della Diapason, che corrispon-deranno alle chorde e b, f b, g b, h b, i b, K b & l b in Dupla proportione, & in
tal maniera haueremo la compositione del Monochordo temperato ne i suoi Interual-li secondo le loro proportioni, & ridotte le sue chorde al numero de Quindeci, con-tenute ne i quattro primi Tetrachordi; à i quali uolendo aggiungere il quinto, bastarà
d'aggiungere in esso solamente la chorda Tritesynemennon; cioè, accommodare il Se-mituono maggiore, & il minore alle loro proportioni. Et perche il minore (come
ho detto) resta nella proportione Sesquiuentesimaquarta, la quale è rationale; pe-rò diuideremo la linea, ò chorda m b in Ventiquattro parti equali; pigliandone uen-ticinque dalla parte destra in punto t, haueremola chorda t b, la quale ne darà il no-stro proposito; percioche le chorde l b, t b, n b, & o b saranno quelle del Te-trachordo synemennon, che noi cerchiamo; ancora che le chorde l b, n b & o b sia-no à gli altri Tetrachordi communi. Ma quando uorremo ritrouar nel graue alcuna
chorda, che corrispondi con una acuta in proportione Dupla, & faccia udire la Dia-pason; raddoppiaremo la chorda acuta, & haueremo quello, che desideriamo. Se
noi adunque uorremo ritrouar la corrispondente chorda graue alla chorda t b, rad-doppiaremo solamente la detta chorda t b, & in punto u haueremo il tutto; percio-che la chorda u b, con la t b, saranno in proportione Dupla, & faranno essa Dia-pason. Per tal modo adunque haueremo il Monochordo diuiso in cinque Tetrachor-di, nel quale per l'aggiuntione della chorda u b; contenerà il numero di Dicisette chor-de; A. B.  . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f. g. & aa. come nella figura si può uedere.
La onde con questo mezo potremo hauer senza molta fatica, & senz'alcun'errore la
via & il modo di comporre il Monochordo temperato ne i suoi Interualli, & accom-modato al numero delle chorde pitagoriche nel primo modo; nel quale potremo ac-commodar quante chorde uorremo, accrescendo, ò diminuendo i suoi Interualli, con
la proportione di ciascuno, secondo 'l modo che si è mostrato di sopra. Ma in qual mo-do si uenga à comporre cotal Monochordo nella seconda maniera; da quello, che si è
dimostrato nella Prima proposta del Quinto delle Dimostrationi; si potrà con facilità
comprendere. page 164
. c. d. e. f. g. & aa. come nella figura si può uedere.
La onde con questo mezo potremo hauer senza molta fatica, & senz'alcun'errore la
via & il modo di comporre il Monochordo temperato ne i suoi Interualli, & accom-modato al numero delle chorde pitagoriche nel primo modo; nel quale potremo ac-commodar quante chorde uorremo, accrescendo, ò diminuendo i suoi Interualli, con
la proportione di ciascuno, secondo 'l modo che si è mostrato di sopra. Ma in qual mo-do si uenga à comporre cotal Monochordo nella seconda maniera; da quello, che si è
dimostrato nella Prima proposta del Quinto delle Dimostrationi; si potrà con facilità
comprendere. page 164Se nelle Canzoni seguitiamo cantando gli Interualli prodotti da i ueri Numeri sonori; ouero i Temperati; & della Risolutione d'alcuni dubij.Cap. XLV.
Della inspessiatione del Monochordo diatonico dalle chorde del genere Chromatico.Cap. XLVI.
 .
uiene ad esser diuiso dalla chorda b, in due parti; cioè, in un Semituono maggiore, &
in uno minore; per il che à caso & necessariamente nasce un nuouo Tetrachordo, tra
le chorde a. b.
.
uiene ad esser diuiso dalla chorda b, in due parti; cioè, in un Semituono maggiore, &
in uno minore; per il che à caso & necessariamente nasce un nuouo Tetrachordo, tra
le chorde a. b.  . & d; imperoche tra la a & la b. si ritroua il Semituono maggiore, tra la b. &
la
. & d; imperoche tra la a & la b. si ritroua il Semituono maggiore, tra la b. &
la  . il Semituono minore, & tra la
. il Semituono minore, & tra la  . & la d. il Trihemituono; come nell'essempio si può
Vedere. Et perche tale Tetrachordo non s'assimiglia per alcun modo ad alcuno de i
Tetrachordi diatonici, posti nel Cap. 16. non si può con uerità dire, che sia Diatonico;
ma si può dire, che sia Chromatico; accostandosi molto al Chromatico molle di Tolo-meo; & in tutto & per tutto esser quello di Didimo; come si uede appresso di esso Tolo-meo, nel Cap. 13. del 2. lib. de gli Harmonici. Essendo che procede dal graue all'acuto
per un Semituono nel primo Interuallo, nel secondo similmente per un'altro Semituo-no, & nel terzo per uno Trihemituono, secondo la forma de i Tetrachordi chromatici
già mostrati. Si che potiamo ueramente dire, che questo sia il uero Tetrachordo chro-matico ricercato, utile & necessario molto alla inspessatione del mostrato Monochordo
. & la d. il Trihemituono; come nell'essempio si può
Vedere. Et perche tale Tetrachordo non s'assimiglia per alcun modo ad alcuno de i
Tetrachordi diatonici, posti nel Cap. 16. non si può con uerità dire, che sia Diatonico;
ma si può dire, che sia Chromatico; accostandosi molto al Chromatico molle di Tolo-meo; & in tutto & per tutto esser quello di Didimo; come si uede appresso di esso Tolo-meo, nel Cap. 13. del 2. lib. de gli Harmonici. Essendo che procede dal graue all'acuto
per un Semituono nel primo Interuallo, nel secondo similmente per un'altro Semituo-no, & nel terzo per uno Trihemituono, secondo la forma de i Tetrachordi chromatici
già mostrati. Si che potiamo ueramente dire, che questo sia il uero Tetrachordo chro-matico ricercato, utile & necessario molto alla inspessatione del mostrato Monochordo

 . il Semituono minore, che non si usa nelle modulationi diatoniche, ne anco nelle En-harmoniche; & tra la chorda
. il Semituono minore, che non si usa nelle modulationi diatoniche, ne anco nelle En-harmoniche; & tra la chorda  , & la d. hà il Trihemituono incomposto che nel diatonco [sic: diatonico]
è composto; il qual'è contenuto dalla proportione Sesquiquinta, com'è contenuto quell'Interuallo, ch'è posto nella parte acuta del Chromatico molle di Tolomeo, e di quello di Didimo; come si può conoscer riducendo le quattro mostrate chorde nelle lor proprie forme,
che sono tra gli harmonici Numeri, nelle chorde del primo Tetrachordo detto Hypaton,
le quali in questa figura si possono chiaramente vedere. Et ancora ch'ei sia ne i due primi
, & la d. hà il Trihemituono incomposto che nel diatonco [sic: diatonico]
è composto; il qual'è contenuto dalla proportione Sesquiquinta, com'è contenuto quell'Interuallo, ch'è posto nella parte acuta del Chromatico molle di Tolomeo, e di quello di Didimo; come si può conoscer riducendo le quattro mostrate chorde nelle lor proprie forme,
che sono tra gli harmonici Numeri, nelle chorde del primo Tetrachordo detto Hypaton,
le quali in questa figura si possono chiaramente vedere. Et ancora ch'ei sia ne i due primi

 , ilquale nominarono Diesis; seguitando forse l'opinione di
Filolao, ilquale (come recita BoetioMusicae libro 3. c. 8.) diceua, che quello Spacio, per il quale la Sesqui-terza è maggiore di due Tuoni, si chiamaua Diesis; ilquale spatio alcuni Moderni chiamano Semituono minore; perche il più delle uolte si pone, per dinotare, che si debba
far l 'lnteruallo del Semituono; com'altroue uederemo. Et quando uoleuano, che tal
Semituono si cantasse in alcun luogo delle lor cantilene, & saliuano dal graue all'acuto,
poneuano il b. ma quando discendeuano dall'acuto nel graue, poneuano il
, ilquale nominarono Diesis; seguitando forse l'opinione di
Filolao, ilquale (come recita BoetioMusicae libro 3. c. 8.) diceua, che quello Spacio, per il quale la Sesqui-terza è maggiore di due Tuoni, si chiamaua Diesis; ilquale spatio alcuni Moderni chiamano Semituono minore; perche il più delle uolte si pone, per dinotare, che si debba
far l 'lnteruallo del Semituono; com'altroue uederemo. Et quando uoleuano, che tal
Semituono si cantasse in alcun luogo delle lor cantilene, & saliuano dal graue all'acuto,
poneuano il b. ma quando discendeuano dall'acuto nel graue, poneuano il  ; il che fan-no anco i più Moderni, quando salendo & discendendo, col mezo de tali segni, ò chorde, uogliono porre in essere il Tuono. Credo che la forma di questo segno
; il che fan-no anco i più Moderni, quando salendo & discendendo, col mezo de tali segni, ò chorde, uogliono porre in essere il Tuono. Credo che la forma di questo segno  fusse intro-dotta da alcuni, che si sognarono, che 'l Tuono fusse, ò si componesse di noue Comma;
ouer, che si potesse diuidere almeno in tante parti; percioche uoleuano, che 'l Semituono maggiore fusse de cinque, & il minore de quattro; & per questo, quando procedeua-no dalle chorde Diatoniche alle Chromatiche, nel modo c'hò detto, per lo spatio d'un
Semituono poneuano tal segno, per dinotarci questo Interuallo; perc'hebbero opinio-ne; come hanno anche molti de i Moderni; che tale Interuallo fusse il Semituono mi-nore, & fusse de quattro Comma; onde segnauano lo spacio con quattro uirgolette in-crociate, che sono le quattro poste in tal segno; conciosia che seguiuano l'ordine delle
chorde, il numero & le proportioni Pitagoriche, mostrate di sopra. Ma quanto co-storo s'ingannino, facilmente si può comprender da quello, che detto & ueduto hab-biamo, & da quello che si è dimostrato nella Ventesimaprima Proposta del Secondo
delle Dimostrationi, & nelle tre sequenti; simigliantemente da quello, che dice Boe-tio nel Cap. 15. del terzo libro della Musica; mostrando che 'l Tuono di proportione Sesquiottaua è maggiore di otto, & minore di noue de i suoi Comma. Et nel Cap. 14. dice,
che 'l Semituono minore è maggiore di tre Comma, & minore di quattro. Però adun-que se 'l Tuono è maggior di otto, & minor di noue Comma, & non si può hauer certez-z'alcuna della sua quantità, per essere irrationale; parmi certamente grande arroganza
il uolere affermare determinatamente una cosa, che la Scienza pone in dubbio & indeterminata. Onde se quest'Interuallo non si può denominar con una quantità determinata,
minormente si potranno denominar quelli che sono minori; come sono il Semituono maggiore, & il minore & gli altri simili. page 170
fusse intro-dotta da alcuni, che si sognarono, che 'l Tuono fusse, ò si componesse di noue Comma;
ouer, che si potesse diuidere almeno in tante parti; percioche uoleuano, che 'l Semituono maggiore fusse de cinque, & il minore de quattro; & per questo, quando procedeua-no dalle chorde Diatoniche alle Chromatiche, nel modo c'hò detto, per lo spatio d'un
Semituono poneuano tal segno, per dinotarci questo Interuallo; perc'hebbero opinio-ne; come hanno anche molti de i Moderni; che tale Interuallo fusse il Semituono mi-nore, & fusse de quattro Comma; onde segnauano lo spacio con quattro uirgolette in-crociate, che sono le quattro poste in tal segno; conciosia che seguiuano l'ordine delle
chorde, il numero & le proportioni Pitagoriche, mostrate di sopra. Ma quanto co-storo s'ingannino, facilmente si può comprender da quello, che detto & ueduto hab-biamo, & da quello che si è dimostrato nella Ventesimaprima Proposta del Secondo
delle Dimostrationi, & nelle tre sequenti; simigliantemente da quello, che dice Boe-tio nel Cap. 15. del terzo libro della Musica; mostrando che 'l Tuono di proportione Sesquiottaua è maggiore di otto, & minore di noue de i suoi Comma. Et nel Cap. 14. dice,
che 'l Semituono minore è maggiore di tre Comma, & minore di quattro. Però adun-que se 'l Tuono è maggior di otto, & minor di noue Comma, & non si può hauer certez-z'alcuna della sua quantità, per essere irrationale; parmi certamente grande arroganza
il uolere affermare determinatamente una cosa, che la Scienza pone in dubbio & indeterminata. Onde se quest'Interuallo non si può denominar con una quantità determinata,
minormente si potranno denominar quelli che sono minori; come sono il Semituono maggiore, & il minore & gli altri simili. page 170In che maniera possiamo inspessare il detto Monochordo con le chorde Enharmoniche.Cap. XLVII.
![Diatessaron.
Semit. maggiore.
Diesis.
Diesis.
Ditono.
300. a. Mese.
Sesquiquarta.
375. F. Lychanos meson.
Supertripartiente 125.
384. [[mus.hsharp]]. Parhypate meson.
Sesquiuentesimaquarta.
400. E. Hypate meson.](../../zarins89/ill/247_1.gif)
Ch'è più ragioneuole dire, che gli Interualli minori nascono da i mag-giori; che dire, che i maggiori si compongano de i minori; & che meglio è ordinato l'Hexachordo moderno, che il Tetrachordo antico.Cap. XLVIII.
Che ciascun del i tre Generi nominati si può dire Genere, & Specie; & che ogn'altra Diuisione, ouer'Ordinatione de Suoni sia vana, & inutile.Cap. 49.
Per qual cagione le Consonanze hanno maggiormente l'orgine loro dalle Proportioni di maggiore inequalità, che da quel-le di minore.Cap. L.
Dubbio sopra quel che si è detto.Cap. LI.
LA TERZA PARTE DELLE ISTITVTIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA:
Quel che sia Contrapunto; & perche sia cosi nominato.Cap. I.
Dell'Inuentione delle Chiaui, & delle Figure cantabili.Cap. II.
 . quadrato, ouer du-ro; & disse che la proprietà era una Deriuatione de più Voci, ò Suoni da un'istesso principio; ouer ch'era una Deduttione singulare, ò particolare di ciascun'ordinato Hexa-chordo. La onde bisogna sapere, che Guido congiunse ogni Deduttione con uno de i
Tetrachordi Greci, aggiungendo à ciascun di loro due chorde di più dalla parte graue;
com'è quella dell'Vt, & quella del Re; percioche ogni Tetrachordo hauea principio nella
chorda del Mi; come nella Seconda parte fu commemorato, di maniera ch'ogni Hexa-chordo contiene ciascuna specie della Diatessaron, che sono Tre; come uederemo al suo
luogo; & la sede ouero il luogo delle Voci, ò Suoni, il quale Musici nominano Chorde,
nominò Chiaui; le quali sono distante l'una dall'altra per linee equidistanti; intendendo-ui però i Spacii di mezo; abenche le Voci, ò Suoni non siano equalmente distanti l'una
dall'altra. Onde collocò la prima chiaue, laquale nominò Gamma ut, nella linea, ouer
riga; & A re, che è la seconda nello spacio. Similmente collocò
. quadrato, ouer du-ro; & disse che la proprietà era una Deriuatione de più Voci, ò Suoni da un'istesso principio; ouer ch'era una Deduttione singulare, ò particolare di ciascun'ordinato Hexa-chordo. La onde bisogna sapere, che Guido congiunse ogni Deduttione con uno de i
Tetrachordi Greci, aggiungendo à ciascun di loro due chorde di più dalla parte graue;
com'è quella dell'Vt, & quella del Re; percioche ogni Tetrachordo hauea principio nella
chorda del Mi; come nella Seconda parte fu commemorato, di maniera ch'ogni Hexa-chordo contiene ciascuna specie della Diatessaron, che sono Tre; come uederemo al suo
luogo; & la sede ouero il luogo delle Voci, ò Suoni, il quale Musici nominano Chorde,
nominò Chiaui; le quali sono distante l'una dall'altra per linee equidistanti; intendendo-ui però i Spacii di mezo; abenche le Voci, ò Suoni non siano equalmente distanti l'una
dall'altra. Onde collocò la prima chiaue, laquale nominò Gamma ut, nella linea, ouer
riga; & A re, che è la seconda nello spacio. Similmente collocò  mi in riga, & C fa
ut in spacio, & di mano in mano collocò etiandio in tal maniera l'altre; come si uedono
per ordine nell'Introdottorio nominato, segnando ciascuna con la sua propria lettera.
Ma perche alle uolte tal cosa poteua generar confusione, i piu Moderni; forse ricordan-dosi, che in uano si fà alcuna cosa col mezo de più cose, che si può fare con poche & be-ne; ritrouarono prima alcune Cifere, per lequali i Cantori s'hauessero à reggere; accioche hauendone lasciate alcun'altre, per quelle solamente hauessero cognitione d'ogni
modulatione, & d'ogni cantilena, & da quelle hauessero notitia de i Spacij, ouero In-terualli di Tuono, di Semituono, & de gli altri ancora. Le quali Cifere chiamarono
poi Chiaui; stando in questa similitudine, che si come per la Chiaue s'apre l'Vscio & si
entra in casa, & iui si uede quello, che ui è entro; cosi per tali Cifere s'apre la modula-tione, & si conosce ciascuno de i nominati Interualli. Ma intrauerrebbe allora il contrario, quando fussero rimosse; percioche ogni cosa si empirebbe di confusione; come ogn'
uno si può imaginare. Nominarono poi le sudette Chiaui co i nomi, con i quali sono
notate nel sottoposto essempio. Di queste; se ben tallora alcune sono poste sopra una
mi in riga, & C fa
ut in spacio, & di mano in mano collocò etiandio in tal maniera l'altre; come si uedono
per ordine nell'Introdottorio nominato, segnando ciascuna con la sua propria lettera.
Ma perche alle uolte tal cosa poteua generar confusione, i piu Moderni; forse ricordan-dosi, che in uano si fà alcuna cosa col mezo de più cose, che si può fare con poche & be-ne; ritrouarono prima alcune Cifere, per lequali i Cantori s'hauessero à reggere; accioche hauendone lasciate alcun'altre, per quelle solamente hauessero cognitione d'ogni
modulatione, & d'ogni cantilena, & da quelle hauessero notitia de i Spacij, ouero In-terualli di Tuono, di Semituono, & de gli altri ancora. Le quali Cifere chiamarono
poi Chiaui; stando in questa similitudine, che si come per la Chiaue s'apre l'Vscio & si
entra in casa, & iui si uede quello, che ui è entro; cosi per tali Cifere s'apre la modula-tione, & si conosce ciascuno de i nominati Interualli. Ma intrauerrebbe allora il contrario, quando fussero rimosse; percioche ogni cosa si empirebbe di confusione; come ogn'
uno si può imaginare. Nominarono poi le sudette Chiaui co i nomi, con i quali sono
notate nel sottoposto essempio. Di queste; se ben tallora alcune sono poste sopra una
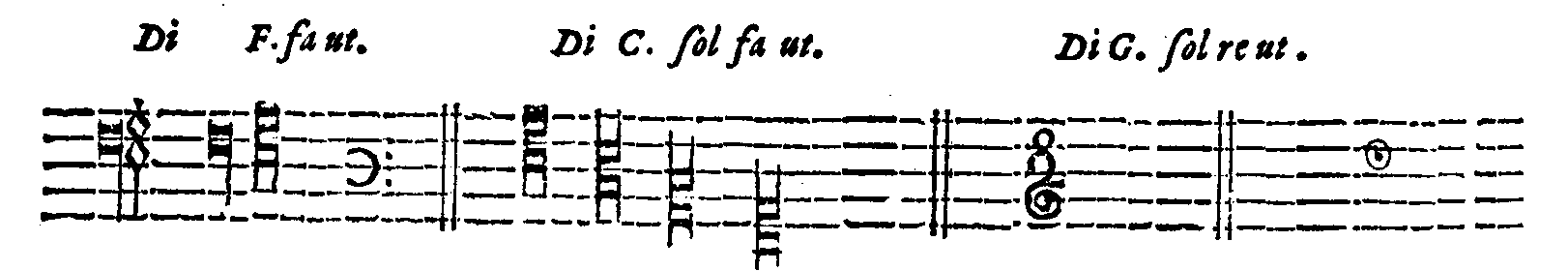

 quadrati, b rotondi, Diesis, Legature, Prese, Coronate, Ritornelli, & altri, che possono accascare; de i quali una buona parte ne adoperano anco i Moderni; nondimeno
non intendo parlare, se non de quelli, che faranno al proposito, & secondo che tor-neranno commodi; imperoche principalmente intendo di trattar quelle cose, che sono
necessarie alle buone harmonie; & cadono sotto 'l sentimento dell'Vdito; il cui Sogetto
è ueramente il Suono; lasciando (per quanto potrò) da parte quelle, ch'à tal Sentimento
sono stranie & forastiere.
quadrati, b rotondi, Diesis, Legature, Prese, Coronate, Ritornelli, & altri, che possono accascare; de i quali una buona parte ne adoperano anco i Moderni; nondimeno
non intendo parlare, se non de quelli, che faranno al proposito, & secondo che tor-neranno commodi; imperoche principalmente intendo di trattar quelle cose, che sono
necessarie alle buone harmonie; & cadono sotto 'l sentimento dell'Vdito; il cui Sogetto
è ueramente il Suono; lasciando (per quanto potrò) da parte quelle, ch'à tal Sentimento
sono stranie & forastiere.
De gli Elementi, che compongono il Contrapunto.Cap. III.

Diuisione delle mostrate Specie.Cap. IIII.
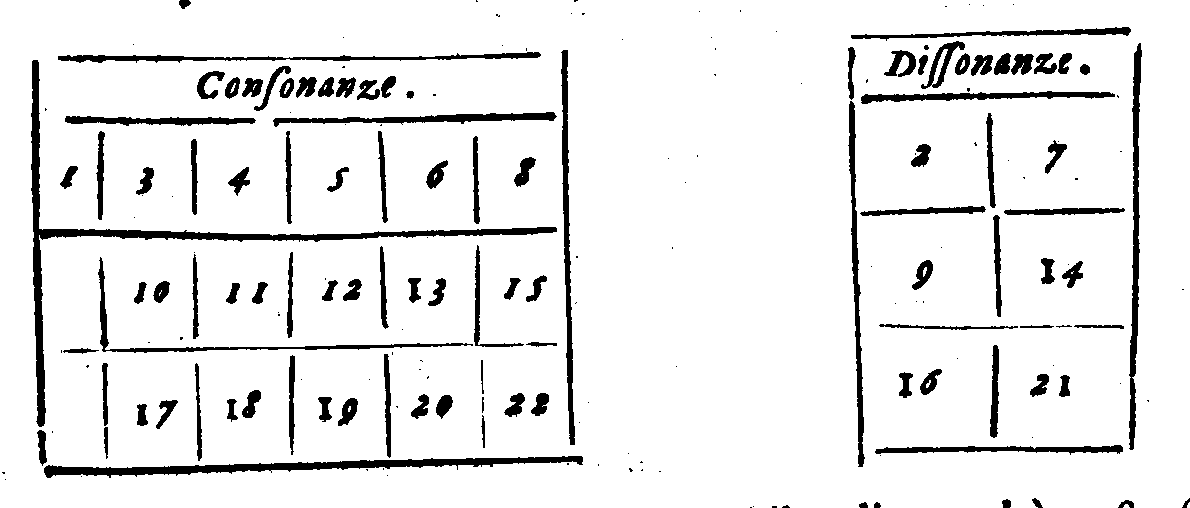
Se la Quarta è Consonanza; & donde auiene, che i Musici non l'hab-biano usata, se non nelle Compositioni de più uoci. Cap. V.
Diuisione della Consonanze nelle Perfette, & nelle Imperfette.Cap. VI.
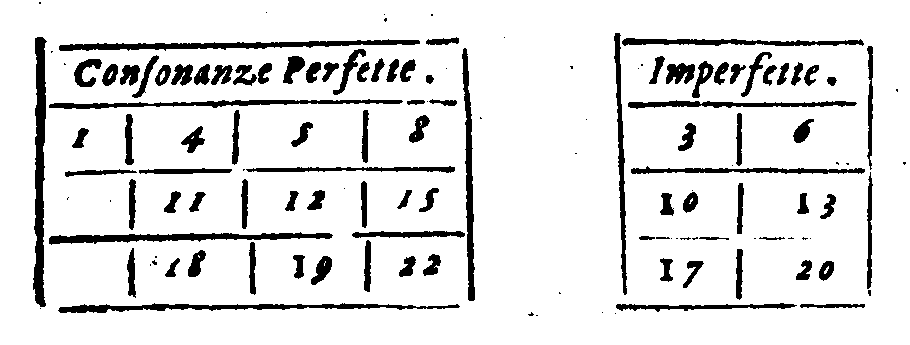
Che la Quinta & la Quarta sono mezane tra le Consonanze perfette & l'Im-perfette.Cap. VII.
Quali Consonanze sino più piene, & quali più uaghe.Cap. VIII.
Della Differenza, che si troua tra le Consonanze Imperfette. Cap. IX.
| Consonanze imperfette Maggiori. | Consonanze imperfette Minori. |
| Ditono, ò Terza maggiore. | Semiditono, ò Terza minore. |
| Hexachordo, ò Sesta maggiore. | Hexachordo, ò Sesta minore. |
| Et le Replicate. | Et le replicate. |
Della Propietà, ò Natura delle consonanze Imperfette.Cap. X.
Ragionamento particolare intorno all'Vnisono.Cap. XI.
 Il medesimo potremo anco dire, quando due ò più parti di tal Canzone si ritroueranno
essere in una medesima chorda; come sono le due sottoposte.
Il medesimo potremo anco dire, quando due ò più parti di tal Canzone si ritroueranno
essere in una medesima chorda; come sono le due sottoposte.
 page 194
page 194Della Prima consonanza detta Diapason, ouer'Ottaua. Cap. XII. >
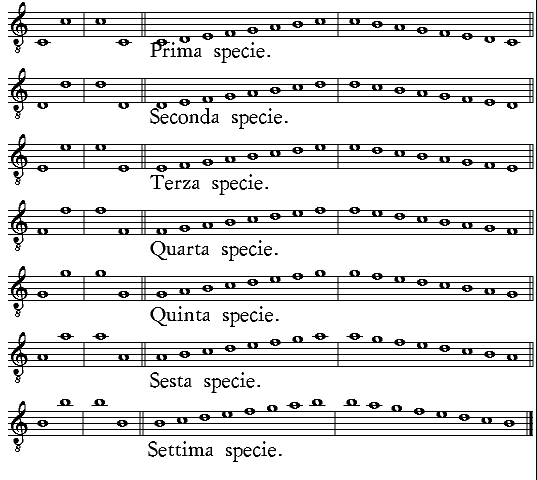 Quando adunque nelle compositioni ritrouaremo due parti, l'una distante dall'altra
per un simile Interuallo, di modo che la graue occupi il luogo graue, & l'acuta, il luogo
acuto di qual si uoglia dell'una delle Specie de i mostrati essempi; allora diremo, che cota-li parti saranno distanti tra loro per una Ottaua; come in questo essempio si uedono.
Quando adunque nelle compositioni ritrouaremo due parti, l'una distante dall'altra
per un simile Interuallo, di modo che la graue occupi il luogo graue, & l'acuta, il luogo
acuto di qual si uoglia dell'una delle Specie de i mostrati essempi; allora diremo, che cota-li parti saranno distanti tra loro per una Ottaua; come in questo essempio si uedono.
 Ilperche quando alcuno uorrà porre in una sua cantilena l'Ottaua, potrà porre la par-te graue lontana dall'acuta per uno de mostrati Interualli, sopra le notate chorde, &
ottenerà il suo proposito.
Ilperche quando alcuno uorrà porre in una sua cantilena l'Ottaua, potrà porre la par-te graue lontana dall'acuta per uno de mostrati Interualli, sopra le notate chorde, &
ottenerà il suo proposito.
Della Diapente, ouer Quinta.Cap. XIII.
 Et ciascuna de loro contiene in se cinque Voci, ò Suoni & quattro Interualli, c'han-no tra loro due Tuoni maggiori, un minore, & un Semituono maggiore; & per questa
cagione, dal numero delle chorde, che contiene, è detta Quinta da i Prattici; ma i
Greci la chiamano Diapente, con queste due parole; Διὰ, che significa Per; & Πέντε,
che uuol dir Cinque; quasi uolendo dire, Consonanza, che procede Per cinque voci,
ò Suoni. Quando adunque saranno due parti lontane l'una dall'altra di maniera, che l'una
tenga la parte graue di ciascuna delle dette specie, & l'altra l'acuta; allora diremo, che sa-
Et ciascuna de loro contiene in se cinque Voci, ò Suoni & quattro Interualli, c'han-no tra loro due Tuoni maggiori, un minore, & un Semituono maggiore; & per questa
cagione, dal numero delle chorde, che contiene, è detta Quinta da i Prattici; ma i
Greci la chiamano Diapente, con queste due parole; Διὰ, che significa Per; & Πέντε,
che uuol dir Cinque; quasi uolendo dire, Consonanza, che procede Per cinque voci,
ò Suoni. Quando adunque saranno due parti lontane l'una dall'altra di maniera, che l'una
tenga la parte graue di ciascuna delle dette specie, & l'altra l'acuta; allora diremo, che sa-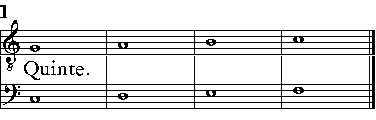 ranno lontane l'una dall'altra per una Diapente, ò per vna Quinta;
come qui si uede. Boetio nel Cap. 13. del Quarto Libro della Mu-sica, pose la specie di questa consonanza tra le chorde Hypate hy-paton & Parhypate meson, che è una Quinta diminuta; essen-do che contiene due Tuoni & due Semituoni; ma credo, che
forse s'ingannasse nel porre l'essempio; oueramente che non
curasse di porre essattamente il uero della cosa, pur che mostrasse page 197col numero delle chorde quello, che uolea intendere. Sia però stato quel che si uo-glia, basta sapere almeno, che cotale essempio sia falso; acciò alcuno non piglias-se errore.
ranno lontane l'una dall'altra per una Diapente, ò per vna Quinta;
come qui si uede. Boetio nel Cap. 13. del Quarto Libro della Mu-sica, pose la specie di questa consonanza tra le chorde Hypate hy-paton & Parhypate meson, che è una Quinta diminuta; essen-do che contiene due Tuoni & due Semituoni; ma credo, che
forse s'ingannasse nel porre l'essempio; oueramente che non
curasse di porre essattamente il uero della cosa, pur che mostrasse page 197col numero delle chorde quello, che uolea intendere. Sia però stato quel che si uo-glia, basta sapere almeno, che cotale essempio sia falso; acciò alcuno non piglias-se errore.
Della iatessaron [sic: Diatessaron], ouer Quarta.Cap. XIIII.
 Questa da i Greci è chiamata prima Sinfonia, ouer (come la nomina Filon GiudeoDe Opifi-
cio Mundi.)
prima Harmonia, & BoetioMusicae li.
1. c. 10. la dimanda Minima consonanza; la onde si uede, che non
hebbero il Ditono, ne il Semiditono per consonanze, come nel principio del Primo li-bro delle nominate Dimostrationi hò anco dichiarato. La chiamarono etiandio Dia-tessaron dal numero delle chorde, ò uoci, che in se contiene; percioche ogni Diates-saron procede al modo mostrato per quattro uoci; imperoche è detta da Διὰ, ò Per, &
da Τέσσαρα, ò Quattro; cioè, Consonanzadi quattro uoci, ò suoni; dal qual nume-
Questa da i Greci è chiamata prima Sinfonia, ouer (come la nomina Filon GiudeoDe Opifi-
cio Mundi.)
prima Harmonia, & BoetioMusicae li.
1. c. 10. la dimanda Minima consonanza; la onde si uede, che non
hebbero il Ditono, ne il Semiditono per consonanze, come nel principio del Primo li-bro delle nominate Dimostrationi hò anco dichiarato. La chiamarono etiandio Dia-tessaron dal numero delle chorde, ò uoci, che in se contiene; percioche ogni Diates-saron procede al modo mostrato per quattro uoci; imperoche è detta da Διὰ, ò Per, &
da Τέσσαρα, ò Quattro; cioè, Consonanzadi quattro uoci, ò suoni; dal qual nume- ro i nostri Moderni la chiamarono Quarta. Quando adunque
uorremo far due parti nelle nostre compositioni, lequali siano tra
loro distanti per una Diatessaron; porremo in una delle chor-de estreme di uno de i sopraposti essempi la uoce graue, & nell'al-tro l'acuta; come si uede nell'essempio. Il perche ritrouandosi an-co nelle Cantilene due parti accommodate l'una con l'altra in cotal
modo; potremo dire, che l'una sia distante dall'altra per una Dia-tessaron, oueramente per unaQuarta. page 198
ro i nostri Moderni la chiamarono Quarta. Quando adunque
uorremo far due parti nelle nostre compositioni, lequali siano tra
loro distanti per una Diatessaron; porremo in una delle chor-de estreme di uno de i sopraposti essempi la uoce graue, & nell'al-tro l'acuta; come si uede nell'essempio. Il perche ritrouandosi an-co nelle Cantilene due parti accommodate l'una con l'altra in cotal
modo; potremo dire, che l'una sia distante dall'altra per una Dia-tessaron, oueramente per unaQuarta. page 198Del Ditono, ouer Terza maggiore.Cap. XV.
 Et tal differenza nasce dalla uarietà de i suoi Interualli; conciosia che nel primo Inter-uallo della prima specie si ritroua il Tuono maggiore, & nel secondo il minore, ascen-dendo dal graue all'acuto, & cosi discendendo; & nella Seconda specie si ritroua il con-trario; cioè, il Minore nel primo, & nel secondo il Maggiore: Differentia c'haurebbe
accresciuto maggior copia nella Diapente, ò Quinta; come accennai, parlando di essa.
Et tal differenza nasce dalla uarietà de i suoi Interualli; conciosia che nel primo Inter-uallo della prima specie si ritroua il Tuono maggiore, & nel secondo il minore, ascen-dendo dal graue all'acuto, & cosi discendendo; & nella Seconda specie si ritroua il con-trario; cioè, il Minore nel primo, & nel secondo il Maggiore: Differentia c'haurebbe
accresciuto maggior copia nella Diapente, ò Quinta; come accennai, parlando di essa.
 Diremo adunque, che allora le parti de i Contrapunti sono distanti l'una dall'altra per un Ditono, quando l'una di esse si ritroua in
alcuna delle chorde estreme graui de i mostrati essempi & l'altra
nell'estreme acute; come nell'essempio si uede. Questa Consonan-za è detta Ditono, perche contiene in sè due Tuoni; quantun-que i Prattici la dimandano Terza maggiore; perch'è diuisa in due
Interualli contenuti da tre chorde; delle quali l'estreme sono più
distanti di quello, che sono l'estreme del Semiditono per un Se-mituono minore; come à mano à mano uederemo.
Diremo adunque, che allora le parti de i Contrapunti sono distanti l'una dall'altra per un Ditono, quando l'una di esse si ritroua in
alcuna delle chorde estreme graui de i mostrati essempi & l'altra
nell'estreme acute; come nell'essempio si uede. Questa Consonan-za è detta Ditono, perche contiene in sè due Tuoni; quantun-que i Prattici la dimandano Terza maggiore; perch'è diuisa in due
Interualli contenuti da tre chorde; delle quali l'estreme sono più
distanti di quello, che sono l'estreme del Semiditono per un Se-mituono minore; come à mano à mano uederemo.
Del Semiditono, ouer Terza minore.cap. XVI.
 Ma considerandola senz'alcun mezano suono; cioè, ne i suoi estremi solamente, è di
una sola specie; conciosiache le chorde estreme d'uno posto nel graue, & quelle d'un'al-tro posto nell'acuto, sono contenute da un'istessa proportione. Dicono i Prattici, che
quando le Parti delle lor Compositioni sono distanti l'una dall'altra di maniera,
che l'una parte occupi qual chorda si uoglia graue, & l'altra occupi qual si uoglia
acuta d'uno de gli essempi mostrati di sopra; sono lontane per un Semiditono, ouer
Terza minore; come sono le due sottoposte. Questo Interuallo è chiamato Semidito-no; non già da Semis parola latina, che uuol dir Mezo; come fusse mezo Ditono à pun-
Ma considerandola senz'alcun mezano suono; cioè, ne i suoi estremi solamente, è di
una sola specie; conciosiache le chorde estreme d'uno posto nel graue, & quelle d'un'al-tro posto nell'acuto, sono contenute da un'istessa proportione. Dicono i Prattici, che
quando le Parti delle lor Compositioni sono distanti l'una dall'altra di maniera,
che l'una parte occupi qual chorda si uoglia graue, & l'altra occupi qual si uoglia
acuta d'uno de gli essempi mostrati di sopra; sono lontane per un Semiditono, ouer
Terza minore; come sono le due sottoposte. Questo Interuallo è chiamato Semidito-no; non già da Semis parola latina, che uuol dir Mezo; come fusse mezo Ditono à pun- to; ma si bene da Semus, che significa Sciemo; percioche (co-me uuole Boetio1. Music.
Cap. 16.) in tal maniera si chiama quella cosa, che non è
l'intero mezo del suo Tutto; onde si dice Semituono quell'Inter-<
uallo, che non arriua all'intiero del Tuono; ma è Tuono imper-fetto. Si dice adunque il Semiditono, Ditono imperfetto; con-ciosiache è diminuto di un Semituono minore, contenuto dalla
proportione Sesquiuentesima quarta. Lo nominano anco Terza,
dal numero delle chorde; & le aggiungono, Minore; percioche
i suoi estremi sono più ristretti, & di minor proportione, che
non sono quelli del Ditono. Ma questo sia detto à bastanza intorno à quelli Interual-li, che sono ueramente consonanti.
to; ma si bene da Semus, che significa Sciemo; percioche (co-me uuole Boetio1. Music.
Cap. 16.) in tal maniera si chiama quella cosa, che non è
l'intero mezo del suo Tutto; onde si dice Semituono quell'Inter-<
uallo, che non arriua all'intiero del Tuono; ma è Tuono imper-fetto. Si dice adunque il Semiditono, Ditono imperfetto; con-ciosiache è diminuto di un Semituono minore, contenuto dalla
proportione Sesquiuentesima quarta. Lo nominano anco Terza,
dal numero delle chorde; & le aggiungono, Minore; percioche
i suoi estremi sono più ristretti, & di minor proportione, che
non sono quelli del Ditono. Ma questo sia detto à bastanza intorno à quelli Interual-li, che sono ueramente consonanti.
Dell'vtile che apportano nella Musica gli Interualli dissonanti.Cap. XVII.
Del Tuono maggiore, & del minore.Cap. XVIII.
 , & a
, & a  . senz'alcun mezo; Mà il Minore segue sempre il maggiore uerso l'acuto; & tiene sempre l'Interuallo,
che è il terzo di ciascun Tetrachordo nella parte acuta; come nell'essempio si uede.
. senz'alcun mezo; Mà il Minore segue sempre il maggiore uerso l'acuto; & tiene sempre l'Interuallo,
che è il terzo di ciascun Tetrachordo nella parte acuta; come nell'essempio si uede.
 Habbiamo adunque nel genere Diatonico due specie di Tuono; cioè, il Maggiore, &
il Minore; però quando ritrouaremo due parti ne i Contrapunti, che saranno di-stanti l'una dall'altra per uno de questi Interualli; diremo, che quelle sono lonta-ne per un Tuono maggiore, ouer minore; oueramente diremo, che siano distanti
per una Seconda maggiore; conciosia ch'è cosi nominato da Prattici tale Interuallo,
per differenza della minore, ch'è il Semituono maggiore; & è cosi chiamata dal numero delle sue chorde, lequali contengono questi Interualli, che sono diatonici; come
nell'essempio si ueggono.
Habbiamo adunque nel genere Diatonico due specie di Tuono; cioè, il Maggiore, &
il Minore; però quando ritrouaremo due parti ne i Contrapunti, che saranno di-stanti l'una dall'altra per uno de questi Interualli; diremo, che quelle sono lonta-ne per un Tuono maggiore, ouer minore; oueramente diremo, che siano distanti
per una Seconda maggiore; conciosia ch'è cosi nominato da Prattici tale Interuallo,
per differenza della minore, ch'è il Semituono maggiore; & è cosi chiamata dal numero delle sue chorde, lequali contengono questi Interualli, che sono diatonici; come
nell'essempio si ueggono.
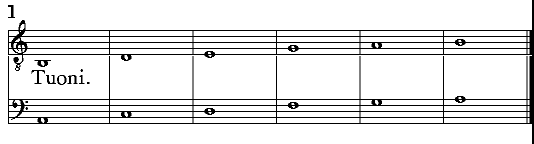
Del Semituono maggiore, & del minore.Cap. XIX.
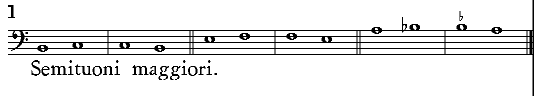 & è collocato naturalmente
tra le chorde poste in questo
essempio. Guidone pose il Semituono nel mezo di ciascun
Hexachordo, come in luogo
più degno, & più honorato,
nel quale (come si dice) consiste la Virtù; conciosia che l'eccellenza & nobilità sua è ta-le, che senza lui ogni Cantilena sarebbe aspra & insopportabile da udire; ne si potrebbe
hauere alcuna Harmonia, che fusse perfetta, senza il suo mezo. Questo è detto Maggiore, à differenza del Minore, che si ritroua in acuto ascendendo tra le chorde b. &
& è collocato naturalmente
tra le chorde poste in questo
essempio. Guidone pose il Semituono nel mezo di ciascun
Hexachordo, come in luogo
più degno, & più honorato,
nel quale (come si dice) consiste la Virtù; conciosia che l'eccellenza & nobilità sua è ta-le, che senza lui ogni Cantilena sarebbe aspra & insopportabile da udire; ne si potrebbe
hauere alcuna Harmonia, che fusse perfetta, senza il suo mezo. Questo è detto Maggiore, à differenza del Minore, che si ritroua in acuto ascendendo tra le chorde b. &  . ò
per il contrario; ilquale non si adopera nel genere Diatonico, & è il sottoposto.
. ò
per il contrario; ilquale non si adopera nel genere Diatonico, & è il sottoposto.
 na dall'altra per uno de i gradi acuti de i mostrati essempi, & l'altra
per uno de i graui, allora diremo, che quelle sono distanti per un Semituono maggiore, ouer per una Seconda minore; come nell'essempio seguente si uede. Fu chiamato Semituono, per le ragioui, che
io dissi parlando nel Cap. 16. del Semiditono, da questa uoce Semus,
che uuol dir Sciemo, & Imperfetto; percioche il Tuono non è mai
diminuto, ouer fatto imperfetto della sua meza parte intera; come
l'esperienza lo dimostra; essendo che niuna proportione Superparticolare (come hò detto più uolte) si può diuidere in due parti equali.
Et Guido monaco Aretino nel Primo libro detto Micrologo chia-ma il Semituono, Non pieno Tuono. Ma questo sia detto à bastan-za intorno queste due specie de Semituoni; che si ritrouano di Cin-que specie; come si è mostrato nel Cap. 11. del Libro de i Soppli-menti: & circa gli Interualli diatonici contenuti dalle proportioni Molteplice, &
dalle Superparticolari.
na dall'altra per uno de i gradi acuti de i mostrati essempi, & l'altra
per uno de i graui, allora diremo, che quelle sono distanti per un Semituono maggiore, ouer per una Seconda minore; come nell'essempio seguente si uede. Fu chiamato Semituono, per le ragioui, che
io dissi parlando nel Cap. 16. del Semiditono, da questa uoce Semus,
che uuol dir Sciemo, & Imperfetto; percioche il Tuono non è mai
diminuto, ouer fatto imperfetto della sua meza parte intera; come
l'esperienza lo dimostra; essendo che niuna proportione Superparticolare (come hò detto più uolte) si può diuidere in due parti equali.
Et Guido monaco Aretino nel Primo libro detto Micrologo chia-ma il Semituono, Non pieno Tuono. Ma questo sia detto à bastan-za intorno queste due specie de Semituoni; che si ritrouano di Cin-que specie; come si è mostrato nel Cap. 11. del Libro de i Soppli-menti: & circa gli Interualli diatonici contenuti dalle proportioni Molteplice, &
dalle Superparticolari.
Dell'Hexachordo maggiore, ouero Sesta maggiore.Cap. XX.
 I Musici chiamano questo Interuallo Hexachordo, per il numero delle chorde, che
contiene, che sono Sei; Percioche appresso de i Greci tanto uuol dire Ε῞ξ, quanto Sei
appresso de noi; & similmente tanto uuol dire Χορδή, quanto Chorda. Onde è detto In-teruallo, che contiene Sei chorde, ouer Consonanza de sei Voci; percioche è com-
I Musici chiamano questo Interuallo Hexachordo, per il numero delle chorde, che
contiene, che sono Sei; Percioche appresso de i Greci tanto uuol dire Ε῞ξ, quanto Sei
appresso de noi; & similmente tanto uuol dire Χορδή, quanto Chorda. Onde è detto In-teruallo, che contiene Sei chorde, ouer Consonanza de sei Voci; percioche è com-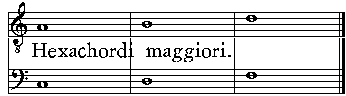 preso da tal numero de chorde. La onde i Prattici lo chiamano
Sesta maggiore, à differenza della minore, la quale è compresa
da minor proportione; & dicono, che la Sesta maggiore, oue-ro il maggiore Hexachordo è una compositione de sei uoci, ò
suoni, che contiene quattro Tuoni, & un Semituono maggiore.
Quando adunque saranno due parti ne i nostri Contrapunti di-stanti l'una dall'altra per il graue & per l'acuto, secondo la ra-gione de gli estremi d'alcuno de i sopraposti essempi; allora di-remo, che tali parti seranno distanti l'una dall'altra per un'He-xachordo, ouer Sesta maggiore; come nel essempio si uede.
preso da tal numero de chorde. La onde i Prattici lo chiamano
Sesta maggiore, à differenza della minore, la quale è compresa
da minor proportione; & dicono, che la Sesta maggiore, oue-ro il maggiore Hexachordo è una compositione de sei uoci, ò
suoni, che contiene quattro Tuoni, & un Semituono maggiore.
Quando adunque saranno due parti ne i nostri Contrapunti di-stanti l'una dall'altra per il graue & per l'acuto, secondo la ra-gione de gli estremi d'alcuno de i sopraposti essempi; allora di-remo, che tali parti seranno distanti l'una dall'altra per un'He-xachordo, ouer Sesta maggiore; come nel essempio si uede.
Dell'Hexachordo minore, ouer Sesta minore. Cap. XXI.
 Ma quando fusse considerato ne i suoi estremi solamente, senza esser tramezato d'alcu-na chorda mezana; si trouerebbe di lui una sola specie per le ragioni dette de gli altri
Interualli. Et ancora che non si possa chiamare assolutamente Semplice; percioche i suoi
termini radicali sono tramezati dal numero Senario in cotal modo 5. 6. 8. come si può
uedere tra i Numeri harmonici posti nel Cap. 15. della Prima parte; onde lo potiamo
chiamar composto della Diatessaron, & del Semiditono; tuttauia per le ragioni dette
dell'Hexachordo maggiore, lo chiamaremo anco lui Semplice ad un certo modo. Quando adunque due parti de i nostri Contrapunti saranno distanti l'una dall'altra per il gra-
Ma quando fusse considerato ne i suoi estremi solamente, senza esser tramezato d'alcu-na chorda mezana; si trouerebbe di lui una sola specie per le ragioni dette de gli altri
Interualli. Et ancora che non si possa chiamare assolutamente Semplice; percioche i suoi
termini radicali sono tramezati dal numero Senario in cotal modo 5. 6. 8. come si può
uedere tra i Numeri harmonici posti nel Cap. 15. della Prima parte; onde lo potiamo
chiamar composto della Diatessaron, & del Semiditono; tuttauia per le ragioni dette
dell'Hexachordo maggiore, lo chiamaremo anco lui Semplice ad un certo modo. Quando adunque due parti de i nostri Contrapunti saranno distanti l'una dall'altra per il gra- ue & per l'acuto, secondo la ragione delle chorde estreme d'al-cuno de i mostrati essempij; allora potremo dire, che saran-no distanti per uno Hexacordo, ò Sesta minore; come nell'
essempio si ritroua. Questo etiandio si chiama Hexachordo per
le ragioni dette dell'Hexachordo maggiore; la onde à sua
differenza gli aggiunsero Minore; & tanto l'uno, quanto
l'altro non erano connumerati da gli antichi tra le consonan-ze; conciosiache le loro estreme chorde sono tirate sotto le
ragioni delle proportioni predette, lequali si ritrouano esser
connumerate tra quelle del genere Superpartiente. Ma perche i Musici moderni le
pongono in cotale ordine; & perche sono composte (se cosi le uoglian considerare)
della Diatessaron & del Ditono, ouer del Semiditono; che poste insieme, non pos-sono esser se non consonanti, quando sono collocati à i loro luoghi proprij; però hò
uoluto far di loro particolar mentione, & mostrar le loro Specie. Onde facendo fine
di ragionar più de quelli Interualli, le cui proportioni, sono comprese nel genere Mol-teplice & nel Superparticolare, & de quelli, c'hanno le lor forme nel genere Superpar-tiente, & sono accettati da ciascun Musico per consonanti; verrò à ragionar de quelli,
c'hanno le lor forme in questo genere istesso, & sono al tutto Dissonanti.
ue & per l'acuto, secondo la ragione delle chorde estreme d'al-cuno de i mostrati essempij; allora potremo dire, che saran-no distanti per uno Hexacordo, ò Sesta minore; come nell'
essempio si ritroua. Questo etiandio si chiama Hexachordo per
le ragioni dette dell'Hexachordo maggiore; la onde à sua
differenza gli aggiunsero Minore; & tanto l'uno, quanto
l'altro non erano connumerati da gli antichi tra le consonan-ze; conciosiache le loro estreme chorde sono tirate sotto le
ragioni delle proportioni predette, lequali si ritrouano esser
connumerate tra quelle del genere Superpartiente. Ma perche i Musici moderni le
pongono in cotale ordine; & perche sono composte (se cosi le uoglian considerare)
della Diatessaron & del Ditono, ouer del Semiditono; che poste insieme, non pos-sono esser se non consonanti, quando sono collocati à i loro luoghi proprij; però hò
uoluto far di loro particolar mentione, & mostrar le loro Specie. Onde facendo fine
di ragionar più de quelli Interualli, le cui proportioni, sono comprese nel genere Mol-teplice & nel Superparticolare, & de quelli, c'hanno le lor forme nel genere Superpar-tiente, & sono accettati da ciascun Musico per consonanti; verrò à ragionar de quelli,
c'hanno le lor forme in questo genere istesso, & sono al tutto Dissonanti.
Della Diapente co 'l Ditono, ouer Settima maggiore. Cap. XXII.
 I Prattici lo nominano Settima dal numero delle uoci, ò de i suoni, che sono contenuti
I Prattici lo nominano Settima dal numero delle uoci, ò de i suoni, che sono contenuti
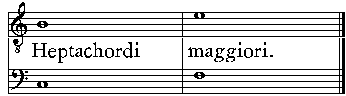 in esso; & lo chiamano anco Heptachordo, de Ε'πτὰ, Sette, & da
Χορδή, Chorda; & à differenza del minore gli aggiungono questa
parola, Maggiore. Diremo etiandio di esso quello, che si è det-to de gli altri Interualli; che tutte le uolte, che si ritrouerà in
alcuna cantilena due parti, che siano poste l'una nelle chorde
graui de i mostrati essempi, & l'altra nell'acuta; che tali Parti
saranno distanti l'una dall'altra per una Settima maggiore, ouera-mente per un'Heptachordo maggiore; come sono le due poste
nell'essempio.
in esso; & lo chiamano anco Heptachordo, de Ε'πτὰ, Sette, & da
Χορδή, Chorda; & à differenza del minore gli aggiungono questa
parola, Maggiore. Diremo etiandio di esso quello, che si è det-to de gli altri Interualli; che tutte le uolte, che si ritrouerà in
alcuna cantilena due parti, che siano poste l'una nelle chorde
graui de i mostrati essempi, & l'altra nell'acuta; che tali Parti
saranno distanti l'una dall'altra per una Settima maggiore, ouera-mente per un'Heptachordo maggiore; come sono le due poste
nell'essempio.
Della Diapente co 'l Semiditono, ouer Settima minore.Cap. XXIII.
 Dal numero delle chorde i Prattici lo chiamarono Settima; è ben uero che u'aggiunse-ro questa parola, Minore, per farlo differente dal Maggiore. Lo nominarono etiandio
Heptachordo da quelle due parole greche poste nel Capitolo precedente. Quando adunque saranno due parti distanti l'una dall'altra, come sono le chorde estreme de i sopra-posti essempi, allora diremo, che sono lontani per una Settima minore; come sono le sot-
Dal numero delle chorde i Prattici lo chiamarono Settima; è ben uero che u'aggiunse-ro questa parola, Minore, per farlo differente dal Maggiore. Lo nominarono etiandio
Heptachordo da quelle due parole greche poste nel Capitolo precedente. Quando adunque saranno due parti distanti l'una dall'altra, come sono le chorde estreme de i sopra-posti essempi, allora diremo, che sono lontani per una Settima minore; come sono le sot- toposte. Qui porrò fine al ragionar delle Consonanze, &
de gli Interualli semplici; lasciando etiandio, per più breuità, di ragionar de i Composti; conciosiache ogn'altro, qual
si uoglia, che sia maggior della Diapason, si considera composto di lei, & di una sua parte, & non sarà molto difficile il
uoler sapere la loro ragione; laquale sempre si potrà hauere,
quando aggiungeremo sopra la proportione della Diapason
quella dell'Interuallo, che le uorremo porre appresso, som-mando insieme i termini radicali, che contengono tali pro-portioni. Dirò ben questo, che gli estremi suoni della Diapasondiapente, ouer Duode-cima sono contenuti dalla proportione Tripla; quelli della Disdiapason, ouer Quinta-decima dalla Quadrupla; quelli della Disdiapason co 'l Ditono, ouer Decimasettima
dalla Quintupla; & quelli della Disdiapasondiapente, ouer Decimanona dalla Sestu-pla: come si è detto altroue ma gli altri si potranno inuestigar facilmente con la ra-gione al modo detto.
toposte. Qui porrò fine al ragionar delle Consonanze, &
de gli Interualli semplici; lasciando etiandio, per più breuità, di ragionar de i Composti; conciosiache ogn'altro, qual
si uoglia, che sia maggior della Diapason, si considera composto di lei, & di una sua parte, & non sarà molto difficile il
uoler sapere la loro ragione; laquale sempre si potrà hauere,
quando aggiungeremo sopra la proportione della Diapason
quella dell'Interuallo, che le uorremo porre appresso, som-mando insieme i termini radicali, che contengono tali pro-portioni. Dirò ben questo, che gli estremi suoni della Diapasondiapente, ouer Duode-cima sono contenuti dalla proportione Tripla; quelli della Disdiapason, ouer Quinta-decima dalla Quadrupla; quelli della Disdiapason co 'l Ditono, ouer Decimasettima
dalla Quintupla; & quelli della Disdiapasondiapente, ouer Decimanona dalla Sestu-pla: come si è detto altroue ma gli altri si potranno inuestigar facilmente con la ra-gione al modo detto.
In qual maniera naturalmente, ò per accidente tali Interualli da i Prat-tici alle volte si ponghino superflui, ò diminuti. Cap. XXIIII.
 ad F. collocata tra cinque chorde, è senza dubbio alcuno diminuta d'un Semituono minore; percioche in luogo di tre Tuoni, & di un Semituono maggiore, con-tiene due Tuoni, & due Semituoni; & è ne i suoi estremi dissonante; perche è contenu-ta dalla proportione Super 19. partiente 45. che non hà luogo tra i Numeri harmonici;
& però la chiamano Semidiapente, & Quinta imperfetta, ouer diminuta. Il medesimo
potiamo dire della Quarta contenuta nel Numero de quattro chorde tra F. &
ad F. collocata tra cinque chorde, è senza dubbio alcuno diminuta d'un Semituono minore; percioche in luogo di tre Tuoni, & di un Semituono maggiore, con-tiene due Tuoni, & due Semituoni; & è ne i suoi estremi dissonante; perche è contenu-ta dalla proportione Super 19. partiente 45. che non hà luogo tra i Numeri harmonici;
& però la chiamano Semidiapente, & Quinta imperfetta, ouer diminuta. Il medesimo
potiamo dire della Quarta contenuta nel Numero de quattro chorde tra F. &  , che per
ritrouarsi in lei tre Tuoni, è chiamata Tritono; & è superflua d'un Semituono minore.
La onde non essendo le sue chorde estreme contenute sotto le proportioni de gli harmo-nici Numeri; percioche la sua forma è contenuta dalla Super 13. partiente 32. è sopra-modo dissonante; come qui in essempio si uede.
, che per
ritrouarsi in lei tre Tuoni, è chiamata Tritono; & è superflua d'un Semituono minore.
La onde non essendo le sue chorde estreme contenute sotto le proportioni de gli harmo-nici Numeri; percioche la sua forma è contenuta dalla Super 13. partiente 32. è sopra-modo dissonante; come qui in essempio si uede.
 Questo errore non solamente può accascare nella Quinta, & nella Quarta tra le chorde
pure diatoniche; ma etiandio nell'Ottaua tra le chorde naturali de i modi, & le accidentali chromatiche; percioche se 'l si hauerà riguardo al Numero delle chorde solamente,
che si ritrouano tra la chorda
Questo errore non solamente può accascare nella Quinta, & nella Quarta tra le chorde
pure diatoniche; ma etiandio nell'Ottaua tra le chorde naturali de i modi, & le accidentali chromatiche; percioche se 'l si hauerà riguardo al Numero delle chorde solamente,
che si ritrouano tra la chorda  . & la b. diremo che tale Ottaua sia senz'alcun dubbio di-minuta d'un Semituono minore; essendo ch'è contenuta nelle sue estreme chorde dal-la proportione Super 21. partiente 135. onde è dissonante, quanto dir si possa; & si uede
posta tra le chorde diatoniche del sottoposto essempio, & si può anco nominare Semidia-
. & la b. diremo che tale Ottaua sia senz'alcun dubbio di-minuta d'un Semituono minore; essendo ch'è contenuta nelle sue estreme chorde dal-la proportione Super 21. partiente 135. onde è dissonante, quanto dir si possa; & si uede
posta tra le chorde diatoniche del sottoposto essempio, & si può anco nominare Semidia-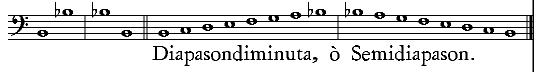 pason. Simili errori si possono ancora commettere tra la chorda b. che si pone alcune uolte nel graue, tra A. & la
pason. Simili errori si possono ancora commettere tra la chorda b. che si pone alcune uolte nel graue, tra A. & la  . la quale corrisponde alla
. la quale corrisponde alla  . & alla E. poste nel acuto & tra essa
b. & la
. & alla E. poste nel acuto & tra essa
b. & la  . Si trouerà la Diapason superflua, di proportione Dupla super 7. partiente 64.
& tra l'istessa b & la E. il Tritono, di proportione Super 13. partiente 32. ilche hauerà
simigliantemente tra le chorde diatoniche, & le chromatiche; percioche se noi porre-mo la chorda
. Si trouerà la Diapason superflua, di proportione Dupla super 7. partiente 64.
& tra l'istessa b & la E. il Tritono, di proportione Super 13. partiente 32. ilche hauerà
simigliantemente tra le chorde diatoniche, & le chromatiche; percioche se noi porre-mo la chorda  . posta in acuto tra la c. & la d. per l'uno de gli estremi della Ottaua;
& la chorda C. posta nel graue per l'altro estremo; haueremo una Ottaua Dissonantissi-ma, contenuta dalla proportione Dupla sesquiduodecima; & sarà una Diapason superflua
d'un Semituono minore. Onde se di nouo pigliaremo la detta chorda
. posta in acuto tra la c. & la d. per l'uno de gli estremi della Ottaua;
& la chorda C. posta nel graue per l'altro estremo; haueremo una Ottaua Dissonantissi-ma, contenuta dalla proportione Dupla sesquiduodecima; & sarà una Diapason superflua
d'un Semituono minore. Onde se di nouo pigliaremo la detta chorda  con la F. ha-ueremo una Quinta dissonante, contenuta dalla proportione Super 9. partiente 16. detta
Diapente superflua. La medesima chorda ancora accompagnata alla G. ne darà il
Tritono, che contiene tre Tuoni; & la proportione Super 7. partiente 18. comene i
sottoposti essempi si uede. page 208
con la F. ha-ueremo una Quinta dissonante, contenuta dalla proportione Super 9. partiente 16. detta
Diapente superflua. La medesima chorda ancora accompagnata alla G. ne darà il
Tritono, che contiene tre Tuoni; & la proportione Super 7. partiente 18. comene i
sottoposti essempi si uede. page 208 Tutti questi Interuali si potranno etiandio diminuire dell'istessa quantità, quando pi-gliaremo la chorda chromatica
Tutti questi Interuali si potranno etiandio diminuire dell'istessa quantità, quando pi-gliaremo la chorda chromatica  posta nel graue tra la C. & la D. in luogo della C. & fa-remo la Ottaua
posta nel graue tra la C. & la D. in luogo della C. & fa-remo la Ottaua  & c; percioche allora tale Ottaua sarà diminuta d'un Semituono minore, & contenuta dalla proportione Super 23. partiente 25. ch'è minor della Dupla; la onde si chiama Semidiapason. Similmente tal chorda accompagnata con la G. ne darà vna
Semidiapente, contenuta dalla Super 11. partiente 25. & accompagnata con la F. ne darà
la Semidiatessaron, compresa sotto la forma della proportione Super 21. partiente 75. laquale insieme con l'altre sono contenute nel sottoposto essempio, & sono al tutto dissonanti.
& c; percioche allora tale Ottaua sarà diminuta d'un Semituono minore, & contenuta dalla proportione Super 23. partiente 25. ch'è minor della Dupla; la onde si chiama Semidiapason. Similmente tal chorda accompagnata con la G. ne darà vna
Semidiapente, contenuta dalla Super 11. partiente 25. & accompagnata con la F. ne darà
la Semidiatessaron, compresa sotto la forma della proportione Super 21. partiente 75. laquale insieme con l'altre sono contenute nel sottoposto essempio, & sono al tutto dissonanti.
 Questi, & tutti gli altri Interualli mostrati di sopra sono disonantissimi, & non si debbo-no porre ne i Contrapunti; perche generano fastidio all'Vdito. Onde non senza giudicio,
i Musici prattici più periti diedero una Regola, per schiuar questi errori; Che non si douesse mai porre la uoce del Mi, contra quella del Fa, nelle Consonanze perfette. Si debbe però auertire, ch'alle uolte si pone la Semidiapente ne i Contrapunti in luogo della
Diapente; similmente il Tritono in luogo della Diatessaron, che fanno buoni effetti; ma
in qual maniera s'habbiano à porre lo dimostrerò più oltra. Quando adunque ritrouaremo due parti, l'una delle quali nell'acuto tenga il luogo d'alcuna delle chorde estreme d'
alcuno de i mostrati essempi, & l'altra tenga il luogo d'alcuna posta nel graue; allora di-remo, che saranno distanti l'una dall'altra per uno de i detti Interualli; come si uede.
Questi, & tutti gli altri Interualli mostrati di sopra sono disonantissimi, & non si debbo-no porre ne i Contrapunti; perche generano fastidio all'Vdito. Onde non senza giudicio,
i Musici prattici più periti diedero una Regola, per schiuar questi errori; Che non si douesse mai porre la uoce del Mi, contra quella del Fa, nelle Consonanze perfette. Si debbe però auertire, ch'alle uolte si pone la Semidiapente ne i Contrapunti in luogo della
Diapente; similmente il Tritono in luogo della Diatessaron, che fanno buoni effetti; ma
in qual maniera s'habbiano à porre lo dimostrerò più oltra. Quando adunque ritrouaremo due parti, l'una delle quali nell'acuto tenga il luogo d'alcuna delle chorde estreme d'
alcuno de i mostrati essempi, & l'altra tenga il luogo d'alcuna posta nel graue; allora di-remo, che saranno distanti l'una dall'altra per uno de i detti Interualli; come si uede.
 Qui si haurebbe potuto porre
molti altri essempi, & mostrar
più in lungo in quante maniere
cotali Interualli si accrescono,
& minuiscono col mezo delle
chorde chromatiche; ma per non
andare in lungo hò uoluto la-sciarli. Similmente si hauerebbe page 209potuto mostrare, in qual modo, per uia dell'istesse chorde chromatiche, il Ditono diuen-ti Semiditono; & il Semiditono Ditono. Ma perche cambiandosi in tal maniera, non
fanno alcun'Interuallo dissonante; però hò uoluto etiandio lasciar da parte tal ragiona-mento; accioche io possa dichiarare, & mostrar gli effetti, che fanno questi tre segni
Qui si haurebbe potuto porre
molti altri essempi, & mostrar
più in lungo in quante maniere
cotali Interualli si accrescono,
& minuiscono col mezo delle
chorde chromatiche; ma per non
andare in lungo hò uoluto la-sciarli. Similmente si hauerebbe page 209potuto mostrare, in qual modo, per uia dell'istesse chorde chromatiche, il Ditono diuen-ti Semiditono; & il Semiditono Ditono. Ma perche cambiandosi in tal maniera, non
fanno alcun'Interuallo dissonante; però hò uoluto etiandio lasciar da parte tal ragiona-mento; accioche io possa dichiarare, & mostrar gli effetti, che fanno questi tre segni  .
quadrato, b molle, &
.
quadrato, b molle, &  Diesis.
Diesis.
De gli Effetti che fanno questi segni.  . b. &
. b. &  .Cap. 25.
.Cap. 25.
 . & tra queste
due uoci, ò sillabe Fa & Mi, stando il Mi sopra il Fa; le quali cifere sono differenti di forma; come si ueggono descritte nel sottoposto essempio; percioche la uoce, ò chorda se-gnata col
. & tra queste
due uoci, ò sillabe Fa & Mi, stando il Mi sopra il Fa; le quali cifere sono differenti di forma; come si ueggono descritte nel sottoposto essempio; percioche la uoce, ò chorda se-gnata col  è più acuta di quella, ch'è segnata col b. La onde Guido Aretino, per non
è più acuta di quella, ch'è segnata col b. La onde Guido Aretino, per non
 confondere i Cantori, pose nel suo Introduttorio queste due Lettere, ò Cifere differenti, in un'istesso luogo; & uolse, che per l'una
di esse s'intendesse la chorda Tritesynemennon, & per l'altra la
Paramese. Vedendo dopoi i Musici questa differenza, ordinaro-no due sorti di cantilena, l'una delle quali chiamarono di Natura
& di
confondere i Cantori, pose nel suo Introduttorio queste due Lettere, ò Cifere differenti, in un'istesso luogo; & uolse, che per l'una
di esse s'intendesse la chorda Tritesynemennon, & per l'altra la
Paramese. Vedendo dopoi i Musici questa differenza, ordinaro-no due sorti di cantilena, l'una delle quali chiamarono di Natura
& di  . quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, &
per quelle del Diezeugmenon; & non poneuano nel principio delle parti della can-tilena alcuna delle mostrate cifere. L'altra nominarono di Natura, & di b molle;
& questo quando le parti procedeuano per le chorde del Tetrachordo Synemen-non & quelle del Meson; lasciando da un canto quelle, che sono del Tetrachordo
Diezeugmenon; & in questa sorte di canzone poneuano nel principio delle Parti
della cantilena la cifera, ouer segno del b molle, auanti i segni del Tempo. Et
se ben nelle Cantilene, che procedeno per il Tetrachordo Meson, & per il Die-zeugmenon, non si costuma di porre la cifera del
. quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, &
per quelle del Diezeugmenon; & non poneuano nel principio delle parti della can-tilena alcuna delle mostrate cifere. L'altra nominarono di Natura, & di b molle;
& questo quando le parti procedeuano per le chorde del Tetrachordo Synemen-non & quelle del Meson; lasciando da un canto quelle, che sono del Tetrachordo
Diezeugmenon; & in questa sorte di canzone poneuano nel principio delle Parti
della cantilena la cifera, ouer segno del b molle, auanti i segni del Tempo. Et
se ben nelle Cantilene, che procedeno per il Tetrachordo Meson, & per il Die-zeugmenon, non si costuma di porre la cifera del  . nondimeno i Moderni ue la in-tendono; & tal Cifera si ritroua ne i Libri ecclesiastici; cioè ne i Canti fermi molto spesso, se ben ne i Canti figurati sia stata & è anco poco usata; percioche quando uogliono porre alle uolte la chorda Paramese in luogo della Tritesynemennon, pongono la cifera
. nondimeno i Moderni ue la in-tendono; & tal Cifera si ritroua ne i Libri ecclesiastici; cioè ne i Canti fermi molto spesso, se ben ne i Canti figurati sia stata & è anco poco usata; percioche quando uogliono porre alle uolte la chorda Paramese in luogo della Tritesynemennon, pongono la cifera  . in
luogo del
. in
luogo del  . ancora che tal cosa si faccia impropriamente; conciosia che si douerebbe u-sar la propria cifera della cosa, che uogliono intendere, & non un'altro segno forestiero;
quantunque questo importi poco; percioche hormai ogn'uno conosce, qual chorda si hà
da usare in luogo della Tritesynemennon, quando pongono la cifera del
. ancora che tal cosa si faccia impropriamente; conciosia che si douerebbe u-sar la propria cifera della cosa, che uogliono intendere, & non un'altro segno forestiero;
quantunque questo importi poco; percioche hormai ogn'uno conosce, qual chorda si hà
da usare in luogo della Tritesynemennon, quando pongono la cifera del  . Ma in uero
io lodarei molto, che si usasse il segno propio. Per tornare adunque a gli Effetti, che fanno cotali Cifere, dico; che dinotano che si leua, ouer aggiunge il sudetto Semituono
minore nel cantare; Imperoche se noi uorremo essaminare con diligenza il Primo de
i due sequenti essempi; ritrouaremo, che dalla prima figura alla Seconda, ui è l'Inter-page 210uallo del Tuono, onde se tra loro porremo il segno del b, come si uede nel secondo; non
è dubbio, che uorremo à leuare della parte acuta del detto Tuono il Semituon minore,
& tra le sue figure si ritrouerà il maggiore; perche dalla diuisione del Tuono, fatta per la
chorda Tritesynemennon, nasce il Semituono maggiore & il minore; com'altroue si è
detto. Similmente il
. Ma in uero
io lodarei molto, che si usasse il segno propio. Per tornare adunque a gli Effetti, che fanno cotali Cifere, dico; che dinotano che si leua, ouer aggiunge il sudetto Semituono
minore nel cantare; Imperoche se noi uorremo essaminare con diligenza il Primo de
i due sequenti essempi; ritrouaremo, che dalla prima figura alla Seconda, ui è l'Inter-page 210uallo del Tuono, onde se tra loro porremo il segno del b, come si uede nel secondo; non
è dubbio, che uorremo à leuare della parte acuta del detto Tuono il Semituon minore,
& tra le sue figure si ritrouerà il maggiore; perche dalla diuisione del Tuono, fatta per la
chorda Tritesynemennon, nasce il Semituono maggiore & il minore; com'altroue si è
detto. Similmente il  . fà un tale effetto nel Quarto essempio; perche, si come tra le fi-gure del Terzo si ritroua il Tuono; cosi posta la Chorda
. fà un tale effetto nel Quarto essempio; perche, si come tra le fi-gure del Terzo si ritroua il Tuono; cosi posta la Chorda  . in luogo della b. è rimosso dalla parte graue il minore, & resta il maggior Semituono. Tal'effetto fà anco il
. in luogo della b. è rimosso dalla parte graue il minore, & resta il maggior Semituono. Tal'effetto fà anco il  . percio-che, si come tra le figure del Quinto essempio si scorge il Tuono, cosi tra quello del Sesto
è posto il Semituono maggiore. Et tutto questo si è detto per la diminutione dell'Inter-uallo del Tuono, col mezo delle mostrate cifere, ò chorde, leuandoli il Semituono minore. Ma se noi uorremo accrescere l'Interuallo del Semituon maggiore, per passare al Tuo
. percio-che, si come tra le figure del Quinto essempio si scorge il Tuono, cosi tra quello del Sesto
è posto il Semituono maggiore. Et tutto questo si è detto per la diminutione dell'Inter-uallo del Tuono, col mezo delle mostrate cifere, ò chorde, leuandoli il Semituono minore. Ma se noi uorremo accrescere l'Interuallo del Semituon maggiore, per passare al Tuo no, con l'aggiungerli il Minore, si potrà far l'istesso con le predette cifere, ò chorde; co-me ne i sottoposti essempi si uede.
no, con l'aggiungerli il Minore, si potrà far l'istesso con le predette cifere, ò chorde; co-me ne i sottoposti essempi si uede.
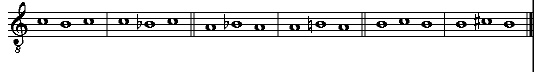 Dobbiamo però auertire, accioche le parti della Cantilena riuscischino più facili, & più
ageuoli da cantare; & gli Interualli siano piu facili da proferire; che quando si uorrà porre la chorda del b. che la Figura cantabile, laquale è posta auanti quella, che si uuol se-gnare con tal segno, proceda dal graue all'acuto; & quando si uorrà porre il
Dobbiamo però auertire, accioche le parti della Cantilena riuscischino più facili, & più
ageuoli da cantare; & gli Interualli siano piu facili da proferire; che quando si uorrà porre la chorda del b. che la Figura cantabile, laquale è posta auanti quella, che si uuol se-gnare con tal segno, proceda dal graue all'acuto; & quando si uorrà porre il  . ouero il
. ouero il
 . fare, che procedino al contrario; cioè, dall'acuto al graue; ancora che non sarebbe
grande errore, & di molta importanza, quando si facesse altramente.
. fare, che procedino al contrario; cioè, dall'acuto al graue; ancora che non sarebbe
grande errore, & di molta importanza, quando si facesse altramente.
Quel che si ricerca in ogni Compositione, & prima del Sogetto. Cap. XXVI.
Aut prodesse volunt, aut delectare Poeta:page 211Hà nel suo Poema per soggetto l'Historia, ouer la Fauola; la quale, ò sia stata ritrouata da lui, ouer se l'habbia pigliata d'altrui; adorna & polisse in tal maniera con uarij costu-mi, come piu gli aggrada; non lasciando da parte alcuna cosa, che sia degna & lodeuo-le, per dilettar l'animo de gli uditori; onde hà poi del magnifico & marauiglioso; cosi il Musico, oltra che è mosso dall'istesso fine di giouare & dilettare gli animi de gli ascoltan-ti con gli accenti harmonici; hà il Soggetto, sopra il quale è fondata la sua Cantilena; la quale adorna con uarie modulationi & uarie harmonie, di modo che porge grato piacere à gli Ascoltanti. La Seconda è, che sia composta principalmente de Consonan-ze; dopoi habbia in sè per accidente molte Dissonanze collocate in essa con debiti mo-di; secondo le Regole, le quali piu abbasso uoglio mostrare. La terza è, che le parti del-la Cantilena procedino bene; cioè, che le Modulationi procedino per ueri & legitimi Interualli, che nascono da i Numeri sonori; accioche per il mezo loro s'acquisti l'uso delle buone Harmonie. La Quarta conditione, che si ricerca, è; che le Modulationi, & il Concento sia uariato; percioche da altro non nasce l'Harmonia, che dalla diuersi-tà delle modulationi, & dalla diuersità delle Consonanze messe insieme con uarietà. La Quinta è, che la Cantilena sia ordinata sotto una prescritta & determinata Harmonia, ò Modo, ò Tuono, che uogliamo dire; & che non sia disordinata. Et la Sesta & ultima (oltra l'altre, che si potrebbono aggiungere) è; che l'Harmonia, che in essa si contie-ne, sia talmente accommodata all'Oratione; cioè, alle Parole; che nelle materie alle-gre l'Harmonia non sia flebile; & per il contrario, nelle flebili, l'Harmonia non sia alle-gra. Onde accioche del tutto si habbia perfetta cognitione, uerrò à ragionar de tutte queste cose separatamente, secondo che mi uerranno al proposito, & secondo 'l bisogno. Incominciando adunque dalla Prima, dico. Il Soggetto d'ogni compositione musica-le chiamarsi quella Parte, sopra la quale il Compositore caua l'Inuentione di far l'altre Parti della cantilena, siano quante si uogliano; & tal Soggetto può essere in molti modi: prima può essere inuentione propria; cioè, che 'l Compositore hauerà ritrouato da sè; dopoi può essere, che l'haurà pigliata dall'altrui compositioni, accommodandolo al-la sua cantilena, & adornandolo con uarie parti, & uarie modulationi; come piu gli aggrada, secondo la grandezza del suo ingegno. Et tal Soggetto si può ritrouare de piu sorte; percioche può essere un Tenore, ouero altra Parte di qual si uoglia cantilena di Canto fermo, ouer di Canto figurato; ouer potrà esser due, o piu Parti, che l'una seguiti l'altra in Consequenza, ouero à qualunque altro modo; essendo che i uarij mo-di de tali Soggetti sono infiniti. Ritrouato adunque che hauerà il Compositore il Sog-getto; farà l'altre Parti, nel modo che piu oltra uederemo; ilche fatto, cotal maniera di comporre si chiamerà, secondo i nostri Prattici, Far contrapunto. Ma quando non hauerà ritrouato prima il Soggetto; quella parte, che sarà primieramente messa in atto; ouer quella, con la quale il Compositore darà principio alla sua cantilena; sia qual si uo-glia, & incomincia à qual modo piu li piace; ò sia graue, oueramente acuta, ò mezana; sempre sarà il Soggetto, sopra 'l quale poi accommodarà l'altre in Consequenza, oue-ro ad altro modo; come piu li piacerà di fare; accommodando l'Harmonie alle Parole, secondo che ricerca la materia contenuta in esse. Ma se 'l Compositore andrà cauando il Soggetto dalle Parti della cantilena; cioè, quando cauerà una parte dall'altra; & an-drà facendo insieme la Compositione; come uederemo altroue; quella Particella, che lui cauerà fuori dell'altre, sopra la quale dopoi componerà le parti della sua composi-tione, si chiamerà sempre Soggetto. Et tal modo di comporre i Prattici dimandano Comporre di fantasia; ancora che si possa etiandio nominare Contrapuntizare, ò Far contrapunto; come dicono. page 212
Aut simul & iucunda, & idonea dicere vitae.
Che le Compositioni si debbono comporre primieramente di Consonan-ze, & dopoi per accidente di Dissonanze. Cap. XXVII.
Che si debbe dar principio alle Compositioni per una delle Consonanze perfette.Cap. XXVIII.
 Il medesimo dobbiamo osseruar ne i Principij de i Contrapunti, ò Compositioni, quando nella parte del Soggetto si ponesse alcuna Pausa; com'intrauiene, quando si piglia un
Tenore di qualche Canzone, ò di qual si uoglia Cantilena, per comporli sopra l'altre Parti; percioche allora le Parti, che s'aggiungono, si debbono incominciare al modo mo-strato; osseruando quello, ch'intorno ciò è stato detto; come si uede ne i sottoposti es-sempi, de i quali il Soggetto è composto nel Sesto modo.
Il medesimo dobbiamo osseruar ne i Principij de i Contrapunti, ò Compositioni, quando nella parte del Soggetto si ponesse alcuna Pausa; com'intrauiene, quando si piglia un
Tenore di qualche Canzone, ò di qual si uoglia Cantilena, per comporli sopra l'altre Parti; percioche allora le Parti, che s'aggiungono, si debbono incominciare al modo mo-strato; osseruando quello, ch'intorno ciò è stato detto; come si uede ne i sottoposti es-sempi, de i quali il Soggetto è composto nel Sesto modo.
 Si debbe etiandio auertire (ilche è cosa di non poca importanza) & corrisponde quasi à
quello c'habbiamo detto disopra) di ordinar nelle Compositioni & ne i Contrapunti a più
uoci in tal maniera le Parti, che i loro principij corrispondino tra lo ro [sic: loro] & habbiano rela-tione per una delle Consonanze perfette, ouero imperfette; di modo che uolendole can-page 215tare nel pigliar le uoci delle parti, non si oda alcuna dissonanza; essendo che que-sto non solo porge fastidio à i Cantori; ma alle uolte è cagione di farli errare più
facilmente, pigliando una uoce per un'altra; massimamente quando non sono molto sicuri nel cantare. E' ben uero, ch'è lecito porre nel graue il principio de
due parti, che siano distanti l'una dall'altra per una Quarta, senza esserui alcun'al-tra parte piu graue, alle quali l'altre corrispondino per Ottaua; massimamente ne i
Modi Placali, ouero Impari, che li uogliamo dire; quando le Parti della cantile-na incominciano à cantar sopra le chorde principali de i loro Modi, ne i quali è
composta; conciosiache uolendo torre la libertà al Compositore di poter porre due
parti in tal maniera, non è cosa honesta; massimamente potendolo fare à due uo-ci; & sarebbe farlo Soggetto & obligato ad una cosa fuori d'ogni proposito; essen-doche l'Incominciare in tal modo è stato posto in uso da molti Prattici periti; co-me da Giosquin de Pris, da Motone, & da altri antichi & moderni Composito-ri; & di ciò potiamo hauer l'essempio nel Canto, che fece Adriano à cinque uo-ci. Laus tibi sacra rubens; lasciandone infiniti altri. Tal licenza presi anch'io in quel-li tre Canti; Osculetur me osculis oris sui; Ego rosa Saron; & Capite nobis vulpes paruu-las; i quali già composi à Cinque uoci; come ogn'un potrà uedere; & saranno es-sempio alle cose che di sopra sono state dette. Questo adunque si concede à tutti
li Compositori; ma non è però anco da lodare, che due parti siano distanti ne i
loro principij dalla parte del Soggetto, ò nel graue, ò nell'acuto, l'una per una
Quarta, & l'altra per una Quinta; percioche allora queste parti uerrebbono ad es-ser distanti l'una dall'altra per una Seconda; & nel pigliar le uoci farebbono dissonan-za; & potrebbe essere, che l'una di esse parti facesse il suo principio sopra una chor-da, che non fusse del Modo, sopra 'l quale è fondata la compositione, ò cantile-na. Et quantunque tale auertimento sia buono; tuttauia non è anco necessario,
quando 'l Soggetto principale della compositione fusse composto con tale arteficio,
che l'una parte cantasse sopra l'altra in Consequenza, di modo che due di loro can-tassero sopra la principale di cotal Soggetto nell'acuto, ouer nel graue, l'una di-stante dall'altra per una Quinta, ouer per una Quarta; oueramente che l'una fus-se distante dal Soggetto per una Quarta, & l'altra per una Quinta, ò per altro In-teruallo; come si può uedere nel Canto fatto à sei uoci; Pater de coelis Deus: che
fece P. della Rue, & nel Canto Virgo prudentissima; ch'io composi simigliantemen-te à Sei uoci; nel quale tre parti cantano in Consequenza, due uerso l'acuto, &
una uerso il graue per gli istessi Interualli; & nel pigliar le uoci si ode un tal incommo-do. Ma si debbe auertire, ch'io chiamo la Parte del Soggetto, quella sopra la quale sono accommodate l'altre Parti in consequenza; & è la Principale & la Guida de tutte l'altre. Io non dico quella, che prima d'ogn'altra incomincia à cantare; ma quella, che
osserua & mantiene il Modo, sopra laquale sono accommodate l'altre distanti l'una
dall'altra per qual si uoglia interuallo; Come si potrà uedere nella Oratione domini-cale, Pater noster; & nella Salutatione angelica, Aue Maria; ch'io composi à Sette uo-ci; doue il principale Soggetto di quelle tre parti, che cantano in Consequenza, non
è quella parte, che prima incomincia à cantare, ma la seconda. In simili casi adunque
sarà lecito porre in una compositione molte Parti tra loro discordanti ne i loro princi-pij; massimamente non uolendo, ne potendo ueramente discommodar l'arteficioso Soggetto; che facendolo sarebbe pazzia; ma ne gli altri non si debbe (per mio consiglio)
dar tal incommodità à i Cantanti. page 216
Si debbe etiandio auertire (ilche è cosa di non poca importanza) & corrisponde quasi à
quello c'habbiamo detto disopra) di ordinar nelle Compositioni & ne i Contrapunti a più
uoci in tal maniera le Parti, che i loro principij corrispondino tra lo ro [sic: loro] & habbiano rela-tione per una delle Consonanze perfette, ouero imperfette; di modo che uolendole can-page 215tare nel pigliar le uoci delle parti, non si oda alcuna dissonanza; essendo che que-sto non solo porge fastidio à i Cantori; ma alle uolte è cagione di farli errare più
facilmente, pigliando una uoce per un'altra; massimamente quando non sono molto sicuri nel cantare. E' ben uero, ch'è lecito porre nel graue il principio de
due parti, che siano distanti l'una dall'altra per una Quarta, senza esserui alcun'al-tra parte piu graue, alle quali l'altre corrispondino per Ottaua; massimamente ne i
Modi Placali, ouero Impari, che li uogliamo dire; quando le Parti della cantile-na incominciano à cantar sopra le chorde principali de i loro Modi, ne i quali è
composta; conciosiache uolendo torre la libertà al Compositore di poter porre due
parti in tal maniera, non è cosa honesta; massimamente potendolo fare à due uo-ci; & sarebbe farlo Soggetto & obligato ad una cosa fuori d'ogni proposito; essen-doche l'Incominciare in tal modo è stato posto in uso da molti Prattici periti; co-me da Giosquin de Pris, da Motone, & da altri antichi & moderni Composito-ri; & di ciò potiamo hauer l'essempio nel Canto, che fece Adriano à cinque uo-ci. Laus tibi sacra rubens; lasciandone infiniti altri. Tal licenza presi anch'io in quel-li tre Canti; Osculetur me osculis oris sui; Ego rosa Saron; & Capite nobis vulpes paruu-las; i quali già composi à Cinque uoci; come ogn'un potrà uedere; & saranno es-sempio alle cose che di sopra sono state dette. Questo adunque si concede à tutti
li Compositori; ma non è però anco da lodare, che due parti siano distanti ne i
loro principij dalla parte del Soggetto, ò nel graue, ò nell'acuto, l'una per una
Quarta, & l'altra per una Quinta; percioche allora queste parti uerrebbono ad es-ser distanti l'una dall'altra per una Seconda; & nel pigliar le uoci farebbono dissonan-za; & potrebbe essere, che l'una di esse parti facesse il suo principio sopra una chor-da, che non fusse del Modo, sopra 'l quale è fondata la compositione, ò cantile-na. Et quantunque tale auertimento sia buono; tuttauia non è anco necessario,
quando 'l Soggetto principale della compositione fusse composto con tale arteficio,
che l'una parte cantasse sopra l'altra in Consequenza, di modo che due di loro can-tassero sopra la principale di cotal Soggetto nell'acuto, ouer nel graue, l'una di-stante dall'altra per una Quinta, ouer per una Quarta; oueramente che l'una fus-se distante dal Soggetto per una Quarta, & l'altra per una Quinta, ò per altro In-teruallo; come si può uedere nel Canto fatto à sei uoci; Pater de coelis Deus: che
fece P. della Rue, & nel Canto Virgo prudentissima; ch'io composi simigliantemen-te à Sei uoci; nel quale tre parti cantano in Consequenza, due uerso l'acuto, &
una uerso il graue per gli istessi Interualli; & nel pigliar le uoci si ode un tal incommo-do. Ma si debbe auertire, ch'io chiamo la Parte del Soggetto, quella sopra la quale sono accommodate l'altre Parti in consequenza; & è la Principale & la Guida de tutte l'altre. Io non dico quella, che prima d'ogn'altra incomincia à cantare; ma quella, che
osserua & mantiene il Modo, sopra laquale sono accommodate l'altre distanti l'una
dall'altra per qual si uoglia interuallo; Come si potrà uedere nella Oratione domini-cale, Pater noster; & nella Salutatione angelica, Aue Maria; ch'io composi à Sette uo-ci; doue il principale Soggetto di quelle tre parti, che cantano in Consequenza, non
è quella parte, che prima incomincia à cantare, ma la seconda. In simili casi adunque
sarà lecito porre in una compositione molte Parti tra loro discordanti ne i loro princi-pij; massimamente non uolendo, ne potendo ueramente discommodar l'arteficioso Soggetto; che facendolo sarebbe pazzia; ma ne gli altri non si debbe (per mio consiglio)
dar tal incommodità à i Cantanti. page 216Che non si debbe porre due Consonanze contenute sotto un'istessa proportio-ne l'una dopo l'altra ascendendo, ouer discendendo senz'alcun mezo.Cap. XXIX.
 Conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra
loro diuerse, discordanti, & contrarie; & non da quelle, ch'in ogni cosa conuengono.
La onde se da tal uarietà nasce l'Harmonia; sarà dibisogno, che nella Musica, non solo
le Parti della cantilena siano distanti l[unclear: ']una dall'altra per il graue & per l'acuto; ma
etiandio che le lor modulationi siano differenti ne i mouimenti; & che contenghino
uarie Consonanze, contenute da diuerse proportioni. Et tanto più potremo allora giu-dicar, che quella cantilena sia harmoniosa, quanto più si ritrouerà nella compositione
delle sue parti, diuerse distanze tra l'una & l'altra per il graue & per l'acuto; diuersi moui-menti, & diuerse proportioni. Videro forse gli Antichi, che le Consonanze poste in-sieme in altra maniera, di quella, ch'io hò detto; ancorache fussero alle uolte uarie ne i
loro estremi per il graue & per l'acuto; erano simili nel procedere, & simili di forma
nelle loro proportioni; però conoscendo, che tale simiglianza non generaua alcuna
uarietà di concento, & giudicando (com'era uero) che la perfetta Harmonia consi-stesse nella uarietà, non tanto de i Siti, ò Distanze delle parti della cantilena, quan-to nella varietà de i Mouimenti, delle Modulationi, & delle Proportioni; giudica-rono, che 'l por due Consonanze l'una dopo l'altra simili di proportioni, uariauano se
non il luogo di graue in acuto, ò per il contrario; senza fare alcuna buona Harmonia;
ancorache i loro estremi fussero uariati l'uno dall'altro. Però non uolsero, che due, ò
più Consonanze perfette contenute da un'istessa proportione, ascendenti insieme, ò di-scendenti le parti, si potessero porre nelle compositioni l'una dopo l'altra, senz'alcun'altro mezano interuallo. Et massimamente uietarono gli Vnisoni, i quali non hanno
alcuno estremo ne i suoni, ne sono differenti di sito, ne sono distanti tra loro, ne fan-no uariatione alcuna nel procedere, & sono simili in tutto & per tutto; ne si ritroua in loro cantando differenza alcuna di graue, ò di acuto; non cadendo tra l'uno, & l'altro
suono alcun'Interuallo; percioche le uoci di una parte si ritrouano in quell[unclear: ']istesso luogo,
che si ritrouano le uoci dell'altra; come nell'essempio posto di sopra, & nella definitio-ne posta al Cap. 11. dell'Vnisono, si può uedere; ne anco si ritroua diuersità alcuna di
modulatione; percioche quell'istessi Interualli canta una parte, per i quali procede
l'altra. Il medesimo si potrebbe etiandio dire di due, ò più Ottaue; se non fusse, che page 217i loro estremi sono differenti l'un dall'altro per lo graue, & per lo acuto; cosa che porge
all'Vdito alquanto più diletto, di quello, che non fanno gli Vnisoni; per esser l'Ottaua
ne i suoi estremi alquanto uaria. L'istesso si può dire di due, ò più Quinte; che per il pro. [sic: delete]
ceder che fanno per gradi & per proportioni simili, alcuni de gli Antichi hebbero
opinione, che più presto ne uscisse ad un certo modo Dissonanza, che Harmonia, ò
Consonanza. Onde hebbero per uero, che qualunque uolta si perueniua ad una Con-sonanza perfetta, se fusse uenuto al fine & alla perfettione, alla quale tende la Musi-ca; la qual perfettione non uolsero che si replicasse molte uolte, per non generare sa-cietà all'Vdito. Questo bello & utile auertimento conferma esser uero & buono l'ope-rationi della Natura, la quale nel produrre in essere gli Indiuidui di ciascuna specie,
mai li produce di maniera, che s'assimiglino in tutto l'uno all'altro; ma uariati per qual-che differenza, la qual differenza, ò uarietà molto piacere porge à i nostri Sentimenti. Debbe adunque ogni Compositore imitare un tale & tanto bell'ordine; percioche sarà riputato tanto migliore, quanto le sue operationi s'assimiglieranno à quelle di una si gran Ma-dre. A tale osseruanza ne inuitano i Numeri & le Proportioni, percioche nell'ordine
loro naturale non si troua due Proportioni l'una immediatamente dopo l'altra, che sia-no simili; come è un simil progresso, 1. 1. 1. oueramente 2. 2. 2. & altri simiglianti,
che sarebbono le forme di due Vnisoni; ne meno un tal progresso 1. 2. 4. 8. il qual non
è Harmonico; ma Geometrico, nel quale si contengono le forme di tre Ottaue conti-nue, ne meno si ritroua un tal'ordine 4. 6. 9. che contiene le forme di due Quinte con-tinuate. Non dobbiamo adunque per alcun modo porre due Vnisoni l'uno dopo l'altro
immediatamente, ne due Ottaue, ne due Quinte; poiche naturalmente la cagione del-le Consonanze, che è il Numero harmonico, non contiene nel suo progresso, ouer'ordine naturale due proportioni simili l'una dopo l'altra, senz'alcun mezo; come nel Cap. 15.
della Prima parte si può uedere; percioche se ben queste Consonanze; quando fussero
poste in tal maniera; non facessero euidentemente alcuna Dissonanza tra le parti; tutta-uia farebbono udire un non so chè di tristo, che dispiacerebbe. Per tante ragioni adun-que non dobbiamo à patto alcuno far contra questa Regola; cioè, non dobbiamo por-re le Consonanze l'una dopo l'altra al modo mostrato di sopra; ma dobbiamo cercare
di uariar sempre i Suoni, le Consonanze, i Mouimenti, & gli Interualli; & per tal mo-do, dalla uarietà di queste cose uerremo à fare una buona & perfetta harmonia.
Conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra
loro diuerse, discordanti, & contrarie; & non da quelle, ch'in ogni cosa conuengono.
La onde se da tal uarietà nasce l'Harmonia; sarà dibisogno, che nella Musica, non solo
le Parti della cantilena siano distanti l[unclear: ']una dall'altra per il graue & per l'acuto; ma
etiandio che le lor modulationi siano differenti ne i mouimenti; & che contenghino
uarie Consonanze, contenute da diuerse proportioni. Et tanto più potremo allora giu-dicar, che quella cantilena sia harmoniosa, quanto più si ritrouerà nella compositione
delle sue parti, diuerse distanze tra l'una & l'altra per il graue & per l'acuto; diuersi moui-menti, & diuerse proportioni. Videro forse gli Antichi, che le Consonanze poste in-sieme in altra maniera, di quella, ch'io hò detto; ancorache fussero alle uolte uarie ne i
loro estremi per il graue & per l'acuto; erano simili nel procedere, & simili di forma
nelle loro proportioni; però conoscendo, che tale simiglianza non generaua alcuna
uarietà di concento, & giudicando (com'era uero) che la perfetta Harmonia consi-stesse nella uarietà, non tanto de i Siti, ò Distanze delle parti della cantilena, quan-to nella varietà de i Mouimenti, delle Modulationi, & delle Proportioni; giudica-rono, che 'l por due Consonanze l'una dopo l'altra simili di proportioni, uariauano se
non il luogo di graue in acuto, ò per il contrario; senza fare alcuna buona Harmonia;
ancorache i loro estremi fussero uariati l'uno dall'altro. Però non uolsero, che due, ò
più Consonanze perfette contenute da un'istessa proportione, ascendenti insieme, ò di-scendenti le parti, si potessero porre nelle compositioni l'una dopo l'altra, senz'alcun'altro mezano interuallo. Et massimamente uietarono gli Vnisoni, i quali non hanno
alcuno estremo ne i suoni, ne sono differenti di sito, ne sono distanti tra loro, ne fan-no uariatione alcuna nel procedere, & sono simili in tutto & per tutto; ne si ritroua in loro cantando differenza alcuna di graue, ò di acuto; non cadendo tra l'uno, & l'altro
suono alcun'Interuallo; percioche le uoci di una parte si ritrouano in quell[unclear: ']istesso luogo,
che si ritrouano le uoci dell'altra; come nell'essempio posto di sopra, & nella definitio-ne posta al Cap. 11. dell'Vnisono, si può uedere; ne anco si ritroua diuersità alcuna di
modulatione; percioche quell'istessi Interualli canta una parte, per i quali procede
l'altra. Il medesimo si potrebbe etiandio dire di due, ò più Ottaue; se non fusse, che page 217i loro estremi sono differenti l'un dall'altro per lo graue, & per lo acuto; cosa che porge
all'Vdito alquanto più diletto, di quello, che non fanno gli Vnisoni; per esser l'Ottaua
ne i suoi estremi alquanto uaria. L'istesso si può dire di due, ò più Quinte; che per il pro. [sic: delete]
ceder che fanno per gradi & per proportioni simili, alcuni de gli Antichi hebbero
opinione, che più presto ne uscisse ad un certo modo Dissonanza, che Harmonia, ò
Consonanza. Onde hebbero per uero, che qualunque uolta si perueniua ad una Con-sonanza perfetta, se fusse uenuto al fine & alla perfettione, alla quale tende la Musi-ca; la qual perfettione non uolsero che si replicasse molte uolte, per non generare sa-cietà all'Vdito. Questo bello & utile auertimento conferma esser uero & buono l'ope-rationi della Natura, la quale nel produrre in essere gli Indiuidui di ciascuna specie,
mai li produce di maniera, che s'assimiglino in tutto l'uno all'altro; ma uariati per qual-che differenza, la qual differenza, ò uarietà molto piacere porge à i nostri Sentimenti. Debbe adunque ogni Compositore imitare un tale & tanto bell'ordine; percioche sarà riputato tanto migliore, quanto le sue operationi s'assimiglieranno à quelle di una si gran Ma-dre. A tale osseruanza ne inuitano i Numeri & le Proportioni, percioche nell'ordine
loro naturale non si troua due Proportioni l'una immediatamente dopo l'altra, che sia-no simili; come è un simil progresso, 1. 1. 1. oueramente 2. 2. 2. & altri simiglianti,
che sarebbono le forme di due Vnisoni; ne meno un tal progresso 1. 2. 4. 8. il qual non
è Harmonico; ma Geometrico, nel quale si contengono le forme di tre Ottaue conti-nue, ne meno si ritroua un tal'ordine 4. 6. 9. che contiene le forme di due Quinte con-tinuate. Non dobbiamo adunque per alcun modo porre due Vnisoni l'uno dopo l'altro
immediatamente, ne due Ottaue, ne due Quinte; poiche naturalmente la cagione del-le Consonanze, che è il Numero harmonico, non contiene nel suo progresso, ouer'ordine naturale due proportioni simili l'una dopo l'altra, senz'alcun mezo; come nel Cap. 15.
della Prima parte si può uedere; percioche se ben queste Consonanze; quando fussero
poste in tal maniera; non facessero euidentemente alcuna Dissonanza tra le parti; tutta-uia farebbono udire un non so chè di tristo, che dispiacerebbe. Per tante ragioni adun-que non dobbiamo à patto alcuno far contra questa Regola; cioè, non dobbiamo por-re le Consonanze l'una dopo l'altra al modo mostrato di sopra; ma dobbiamo cercare
di uariar sempre i Suoni, le Consonanze, i Mouimenti, & gli Interualli; & per tal mo-do, dalla uarietà di queste cose uerremo à fare una buona & perfetta harmonia.
 co, conciosiache tra le parti, ouer tra le uoci delle due Terze maggiori & delle due Seste minori non si troua la Relatione harmonica; ilche fa, che siano alquanto più triste dell'altre; come più oltra uederemo. Laonde dobbiamo sommamente auertire, ch'in ogni progresso,
ouer modulatione, che fanno le parti cantando insieme, almeno una di quelle si muoua,
ò faccia l'interuallo del Semituono maggiore, potendolo fare; accioche la modulatio-ne & l'harmonia, che nasce da i mouimenti, che fanno insieme le parti della cantilena,
siano più diletteuoli, & più soaui. La qual cosa si hauerà facilmente, quando le Conso-nanze si porranno l'una dopo l'altra, che siano diuerse di specie; come dopo la Terza, ò
la Sesta maggiore si porrà la Minore, ò per il contrario; & dopo la Terza maggiore si
porrà la Sesta minore, ouer dopo questa si porrà quella; & dopo la Terza minore la Se-sta maggiore, similmente dopo la Sesta maggiore la Terza minore. Ne ui è maggior ra-gione, che più ne uieti il porre due Perfette, che due Imperfette consonanze immedia-tamente l'una dopo l'altra; percioche se ben le prime sono consonanze Perfette; tutta-uia ciascuna dell'Imperfette si ritroua esser perfetta nella sua proportione. Et si come non
si può dire con uerità, ch'un'Huomo sia più Huomo d'un'altro; non si può dire, ch'una
Terza maggiore, ouero una minore; & cosi l'una, ò l'altra delle due Seste posta nel gra-ue, sia maggiore, ò minore di un'altra posta nell'acuto, ò per il contrario; di modo che
si come è uietato il porre due Consonanze perfette d'una istessa specie l'una dopo l'altra;
cosi maggiormente non dobbiamo porre due Imperfette d'una istessa proportione; con-ciosiache non sono tanto consonanti, quanto sono le Perfette. E' ben uero, che due Terze minori poste l'una dopo l'altra ascendenti insieme, ouer discendenti per grado; Simil-mente due Seste maggiori si potranno sopportare; percioche se ben nelle lor modulatio-ni non si ode cantare il Semituono maggiore, & le Terze siano per loro natura alquanto
meste, & le Seste alquanto dure; quella poca differenza, che si troua ne i mouimenti,
che fanno le parti, uiene, à fare alquanto di uarietà; conciosiache la parte graue sem-pre ascende, ò discende per un Tuono minore, & l'acuta per un maggiore, ò per il con-trario, & fà un non sò che di buono all'Vdlto [sic: Vdito]; tanto più quanto che le Voci delle parti sono lontane tra loro in harmonica relatione. Ma quando le parti si mouessero per salto;
allora per niun modo porremo due, ò piu simili ascendenti, ò discendenti l'una dopo
l'altra; percioche, oltra il non osseruar le conditioni toccate di sopra, le Voci delle
parti non sarebbono distanti l'una dall'altra in harmonica relatione; come qui sot-to si ueggono.
co, conciosiache tra le parti, ouer tra le uoci delle due Terze maggiori & delle due Seste minori non si troua la Relatione harmonica; ilche fa, che siano alquanto più triste dell'altre; come più oltra uederemo. Laonde dobbiamo sommamente auertire, ch'in ogni progresso,
ouer modulatione, che fanno le parti cantando insieme, almeno una di quelle si muoua,
ò faccia l'interuallo del Semituono maggiore, potendolo fare; accioche la modulatio-ne & l'harmonia, che nasce da i mouimenti, che fanno insieme le parti della cantilena,
siano più diletteuoli, & più soaui. La qual cosa si hauerà facilmente, quando le Conso-nanze si porranno l'una dopo l'altra, che siano diuerse di specie; come dopo la Terza, ò
la Sesta maggiore si porrà la Minore, ò per il contrario; & dopo la Terza maggiore si
porrà la Sesta minore, ouer dopo questa si porrà quella; & dopo la Terza minore la Se-sta maggiore, similmente dopo la Sesta maggiore la Terza minore. Ne ui è maggior ra-gione, che più ne uieti il porre due Perfette, che due Imperfette consonanze immedia-tamente l'una dopo l'altra; percioche se ben le prime sono consonanze Perfette; tutta-uia ciascuna dell'Imperfette si ritroua esser perfetta nella sua proportione. Et si come non
si può dire con uerità, ch'un'Huomo sia più Huomo d'un'altro; non si può dire, ch'una
Terza maggiore, ouero una minore; & cosi l'una, ò l'altra delle due Seste posta nel gra-ue, sia maggiore, ò minore di un'altra posta nell'acuto, ò per il contrario; di modo che
si come è uietato il porre due Consonanze perfette d'una istessa specie l'una dopo l'altra;
cosi maggiormente non dobbiamo porre due Imperfette d'una istessa proportione; con-ciosiache non sono tanto consonanti, quanto sono le Perfette. E' ben uero, che due Terze minori poste l'una dopo l'altra ascendenti insieme, ouer discendenti per grado; Simil-mente due Seste maggiori si potranno sopportare; percioche se ben nelle lor modulatio-ni non si ode cantare il Semituono maggiore, & le Terze siano per loro natura alquanto
meste, & le Seste alquanto dure; quella poca differenza, che si troua ne i mouimenti,
che fanno le parti, uiene, à fare alquanto di uarietà; conciosiache la parte graue sem-pre ascende, ò discende per un Tuono minore, & l'acuta per un maggiore, ò per il con-trario, & fà un non sò che di buono all'Vdlto [sic: Vdito]; tanto più quanto che le Voci delle parti sono lontane tra loro in harmonica relatione. Ma quando le parti si mouessero per salto;
allora per niun modo porremo due, ò piu simili ascendenti, ò discendenti l'una dopo
l'altra; percioche, oltra il non osseruar le conditioni toccate di sopra, le Voci delle
parti non sarebbono distanti l'una dall'altra in harmonica relatione; come qui sot-to si ueggono.
 page 219Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre
due Terze, ò due Seste l'una dopo l'altra; osseruaremo di porre primieramente la mag-giore, & dopoi la minore; ò per il contrario; pongansi poi in qual maniera si uoglino, ò
con mouimenti di grado, ouer di salto; percioche ogni cosa tornerà bene. Ma si debbe auertire, che quando si porrà la Terza dopo la Sesta; oueramente la Sesta dopo la Terza, di
fare, che l'una sia maggiore & l'altra minore; & ciò faremo quando ciascuna delle parti
farà il mouimento nel graue, ouer nell'acuto. Ma quando l'una di esse non facesse al-cun mouimento; allora tal Regola non si potrà osseruare, senza partirsi dalle Regole,
che più oltra daremo; che saranno per il ben'essere della cantilena; conciosiache allora
dopo la Terza maggiore sarà dibisogno darli la Sesta maggiore, & dopo la minore, la Sesta minore; ouer per il contrario; come nel sottoposto essempio si uede.
page 219Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre
due Terze, ò due Seste l'una dopo l'altra; osseruaremo di porre primieramente la mag-giore, & dopoi la minore; ò per il contrario; pongansi poi in qual maniera si uoglino, ò
con mouimenti di grado, ouer di salto; percioche ogni cosa tornerà bene. Ma si debbe auertire, che quando si porrà la Terza dopo la Sesta; oueramente la Sesta dopo la Terza, di
fare, che l'una sia maggiore & l'altra minore; & ciò faremo quando ciascuna delle parti
farà il mouimento nel graue, ouer nell'acuto. Ma quando l'una di esse non facesse al-cun mouimento; allora tal Regola non si potrà osseruare, senza partirsi dalle Regole,
che più oltra daremo; che saranno per il ben'essere della cantilena; conciosiache allora
dopo la Terza maggiore sarà dibisogno darli la Sesta maggiore, & dopo la minore, la Sesta minore; ouer per il contrario; come nel sottoposto essempio si uede.
 Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette,
nel modo ch'io hò mostrato; che non si douerebbe anco porre due Quarte, in qual si uo-glia compositione, come fanno alcuni in alcune particelle delle loro Canzoni, che chia-mano Falso bordone; conciosia che, senza dubbio alcuno, la Quarta è consonanza perfetta: ma di questo ne ragionerò, quando mostrerò il modo di comporre à più uoci.
Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette,
nel modo ch'io hò mostrato; che non si douerebbe anco porre due Quarte, in qual si uo-glia compositione, come fanno alcuni in alcune particelle delle loro Canzoni, che chia-mano Falso bordone; conciosia che, senza dubbio alcuno, la Quarta è consonanza perfetta: ma di questo ne ragionerò, quando mostrerò il modo di comporre à più uoci.
Quando le Parti della Cantilena hanno tra loro Harmonica relatione; & in qual modo potiamo usare la Semidiapente & il Tritono nelle com-positioni.Cap. XXX.
 E' ben uero che due parti, ch'insieme ascendono, & habbiano un mouimento, che contenga il Semituono, tanto in una quanto nell'altra; par che sian tollerate dall'Vdito; per ca-gione de i mouimenti fatti per cotali Semituoni; come sono quelli del primo luogo, della
Diapason superflua, & della Semidiapente, posti nel primo & nel terzo luogo dell'essempio. Onde accioche le nostre compositioni siano purgate d'ogni errore, & siano corrette,
cercaremo di fuggir tali relationi, quanto più potremo; massimamente quando componeremo à Due uoci; percioche genera alle purgate orecchie alquanto di fastidio; essendo
che simili Interualli non si ritrouano esser collocati tra i Numeri sonori, & non si canta-no in alcun genere di Cantilena; ancora ch'alcuni habbiano hauuto contraria opinione;
ma sia come si uoglia, sono molto difficili da cantare, & fanno tristo effetto. Et molto
mi merauiglio di coloro, che non si hanno punto schiuato di far cantare ò modulare in
alcuna delle parti delle lor cantilene alcuno de questi Interualli; ne mi sò imaginare, per
qual ragione l'habbiano fatto. Et ancorache sia minor male il ritrouarlo per relatione
tra due modulationi, che udirlo nella modulatione di una parte; tuttauia quel male istes-so, che si ode in una parte sola, si ritroua diuiso tra due; & è quella istessa offesa dell'Vdi-to; percioche nulla, ò poco rileua l'essere offeso d'uno istesso colpo, più da uno, che da
molti; quando il male non è minore. Questi Interualli adunque, che nel modulare non
si ammettono, si debbono schiuare nelle cantilene di maniera, che non si odino per
relationi tra le parti; laqual cosa uerrà fatta, quando le parti si potranno mutar fra loro
con interualli Harmonici proportionati, contenuti nel genere Diatonico; cioè, quan-do da una voce della parte graue, potrà ascender alla seguente della parte acuta per un
spatio legittimo & cantabile, & cosi per il contrario; ma non già quando tra le parti di
qual si uoglia Compositione, tra quattro uoci, al detto modo, non si vdirà la relatione
de i detti Interualli; perche non si potranno, se non con gran discommodo, mutare; co-me ne i sottoposti essempi tutti gli Interualli dell'altro essempio mutati si ueggono.
E' ben uero che due parti, ch'insieme ascendono, & habbiano un mouimento, che contenga il Semituono, tanto in una quanto nell'altra; par che sian tollerate dall'Vdito; per ca-gione de i mouimenti fatti per cotali Semituoni; come sono quelli del primo luogo, della
Diapason superflua, & della Semidiapente, posti nel primo & nel terzo luogo dell'essempio. Onde accioche le nostre compositioni siano purgate d'ogni errore, & siano corrette,
cercaremo di fuggir tali relationi, quanto più potremo; massimamente quando componeremo à Due uoci; percioche genera alle purgate orecchie alquanto di fastidio; essendo
che simili Interualli non si ritrouano esser collocati tra i Numeri sonori, & non si canta-no in alcun genere di Cantilena; ancora ch'alcuni habbiano hauuto contraria opinione;
ma sia come si uoglia, sono molto difficili da cantare, & fanno tristo effetto. Et molto
mi merauiglio di coloro, che non si hanno punto schiuato di far cantare ò modulare in
alcuna delle parti delle lor cantilene alcuno de questi Interualli; ne mi sò imaginare, per
qual ragione l'habbiano fatto. Et ancorache sia minor male il ritrouarlo per relatione
tra due modulationi, che udirlo nella modulatione di una parte; tuttauia quel male istes-so, che si ode in una parte sola, si ritroua diuiso tra due; & è quella istessa offesa dell'Vdi-to; percioche nulla, ò poco rileua l'essere offeso d'uno istesso colpo, più da uno, che da
molti; quando il male non è minore. Questi Interualli adunque, che nel modulare non
si ammettono, si debbono schiuare nelle cantilene di maniera, che non si odino per
relationi tra le parti; laqual cosa uerrà fatta, quando le parti si potranno mutar fra loro
con interualli Harmonici proportionati, contenuti nel genere Diatonico; cioè, quan-do da una voce della parte graue, potrà ascender alla seguente della parte acuta per un
spatio legittimo & cantabile, & cosi per il contrario; ma non già quando tra le parti di
qual si uoglia Compositione, tra quattro uoci, al detto modo, non si vdirà la relatione
de i detti Interualli; perche non si potranno, se non con gran discommodo, mutare; co-me ne i sottoposti essempi tutti gli Interualli dell'altro essempio mutati si ueggono.
 Tutte le volte adunque che le Parti della compositione, ò cantilena non si potranno mu-tar l'una nell'altra, dalla qual mutatione ne nasca il procedere per ueri & legittimi in-terualli cantabili, tal compositione si debbe fuggire; massimamente se noi desideriamo
d'hauere una corretta compositione, & purgata da ogni errore. E' ben uero, che nelle page 221compositioni de più uoci molte volte è impossibile di poterli schiuare, & di non incorre-re in simili intrichi; percioche accade alle volte, che 'l Compositore componerà sopra al-cun Soggetto, che lo inuiterà spesse uolte à far contra questo precetto; onde astretto dal-la necessità lo lascierà scorrere; come quando lui uedesse, che le parti della compositio-ne non potessero cantare commodamente; ouero quando uolesse accommodare una
Consequenza; che si potesse cantare commodamente; come altroue uederemo; ma
quando la necessità l'astringesse, debbe almeno hauer riguardo, che tal diffetto si com-metta nelle chorde diatoniche, & in quelle, che sono proprie & naturali del Modo, &
non tra quelle, che sono accidentali, che nel mezo delle Cantilene si segnano con que-sti segni
Tutte le volte adunque che le Parti della compositione, ò cantilena non si potranno mu-tar l'una nell'altra, dalla qual mutatione ne nasca il procedere per ueri & legittimi in-terualli cantabili, tal compositione si debbe fuggire; massimamente se noi desideriamo
d'hauere una corretta compositione, & purgata da ogni errore. E' ben uero, che nelle page 221compositioni de più uoci molte volte è impossibile di poterli schiuare, & di non incorre-re in simili intrichi; percioche accade alle volte, che 'l Compositore componerà sopra al-cun Soggetto, che lo inuiterà spesse uolte à far contra questo precetto; onde astretto dal-la necessità lo lascierà scorrere; come quando lui uedesse, che le parti della compositio-ne non potessero cantare commodamente; ouero quando uolesse accommodare una
Consequenza; che si potesse cantare commodamente; come altroue uederemo; ma
quando la necessità l'astringesse, debbe almeno hauer riguardo, che tal diffetto si com-metta nelle chorde diatoniche, & in quelle, che sono proprie & naturali del Modo, &
non tra quelle, che sono accidentali, che nel mezo delle Cantilene si segnano con que-sti segni  .
.  . & b; percioche allora non generano tanto tristo effetto. Si debbe però
notare, ch'io chiamo Errori naturali quelli, che nascono nel modo mostrato di sopra nel
primo essempio; & quelli dico nascere per accidente, quando tra le uere chorde d'alcun
Modo se ne pone un'altra, che non è di quell'ordine, & da tal chorda nasce un tale in-commodo; come può accascare nel Quinto Modo, del quale molte fiate la mezana chorda, che è la
. & b; percioche allora non generano tanto tristo effetto. Si debbe però
notare, ch'io chiamo Errori naturali quelli, che nascono nel modo mostrato di sopra nel
primo essempio; & quelli dico nascere per accidente, quando tra le uere chorde d'alcun
Modo se ne pone un'altra, che non è di quell'ordine, & da tal chorda nasce un tale in-commodo; come può accascare nel Quinto Modo, del quale molte fiate la mezana chorda, che è la  , è lasciata da un canto, & in suo luogo si pone la b. per accidente. Onde
tra questa & la precedente, ò la seguente nasce uno de i mostrati disordini; come nel primo
essempio seguente si uede. Et tanto più è senza soauità, quanto che la chorda
, è lasciata da un canto, & in suo luogo si pone la b. per accidente. Onde
tra questa & la precedente, ò la seguente nasce uno de i mostrati disordini; come nel primo
essempio seguente si uede. Et tanto più è senza soauità, quanto che la chorda  . che è la principale del Quinto modo, è rimossa dal suo proprio luogo, & posto la chorda b, laquale è
accidentale. Et benche per le ragioni dette non si possa usar tali Interualli accommoda-ti in cotal maniera nelle cantilene; nondimeno potremo usare alle uolte la Semidiapen-te in una istessa percussione; & ciò faremo, quando immediatamente da essa uerremo al
Ditono; come nel secondo essempio uediamo; percioche le parti si possono mutar tra
loro senz'alcun discommodo; come nel terzo essempio si può uedere. Et questo si osser-ua da i migliori Musici moderni; com'è stato etiandio osseruato per il passato d'alcuni de
i più Antichi. Ne solamente sarà lecito usar la Semidiapente, ma il Tritono anco alle
uolte; come uederemo al suo luogo. E' ben uero, che tornerà meglio vsar la Semidia-pente, che 'l Tritono; percioche allora le Consonanze saranno poste à i lor propri luo-ghi; il che non sarà quando si porrà il Tritono. Si debbe però auertire, che quelle parti,
c'haueranno la Semidiapente, ouero il Tritono, debbono hauere primieramente auan-ti essa Semidiapente ò Tritono senz'alcun mezo una Consonanza, sia poi perfetta ouer'
imperfetta, che questo non fà cosa alcuna; percioche dalla Consonanza precedente, &
dalla seguente, la detta Semidiapente uiene à temperarsi di maniera, che non fà tristo ef-fetto, anzi buono; come si proua con la esperienza, & si ode ne i seguenti essempij.
. che è la principale del Quinto modo, è rimossa dal suo proprio luogo, & posto la chorda b, laquale è
accidentale. Et benche per le ragioni dette non si possa usar tali Interualli accommoda-ti in cotal maniera nelle cantilene; nondimeno potremo usare alle uolte la Semidiapen-te in una istessa percussione; & ciò faremo, quando immediatamente da essa uerremo al
Ditono; come nel secondo essempio uediamo; percioche le parti si possono mutar tra
loro senz'alcun discommodo; come nel terzo essempio si può uedere. Et questo si osser-ua da i migliori Musici moderni; com'è stato etiandio osseruato per il passato d'alcuni de
i più Antichi. Ne solamente sarà lecito usar la Semidiapente, ma il Tritono anco alle
uolte; come uederemo al suo luogo. E' ben uero, che tornerà meglio vsar la Semidia-pente, che 'l Tritono; percioche allora le Consonanze saranno poste à i lor propri luo-ghi; il che non sarà quando si porrà il Tritono. Si debbe però auertire, che quelle parti,
c'haueranno la Semidiapente, ouero il Tritono, debbono hauere primieramente auan-ti essa Semidiapente ò Tritono senz'alcun mezo una Consonanza, sia poi perfetta ouer'
imperfetta, che questo non fà cosa alcuna; percioche dalla Consonanza precedente, &
dalla seguente, la detta Semidiapente uiene à temperarsi di maniera, che non fà tristo ef-fetto, anzi buono; come si proua con la esperienza, & si ode ne i seguenti essempij.
 page 222
page 222Che rispetto si de hauere à gli Interualli relati nelle Compositioni di più voci.Cap. XXXI.
 rietà dipende tutta la diuersita, & la perfettione dell'Harmonie; conciosiache è neces-sario (come dirò altroue) che nella Compositione perfetta si ritrouino sempre in atto la page 223Quinta & la Terza, ouer le sue Replicate; essendo che oltra queste due consonanze l'Vdi-to non può desiderar suono, che caschi nel mezo, ouer fuori de i loro estremi, che sia in
tutto differente & uariato da quelli, che sono ne gli estremi di queste consonanze poste
insieme; ritrouandosi iui tutti quelli Suoni differenti, che possono far l'Harmonie diuerse. Ma perche gli estremi della Quinta sono inuariabili, & sempre si pongono contenuti
sott'vna istessa proportione; lasciando certi casi, ne i quali si pone imperfetta; però gli
estremi delle Terze si pongono differenti tra essa Quinta. Non dico però differenti di
proportione, ma dico differenti di luogo; percioche (come hò detto altroueSupra.
cap. 10.) quando
si pone la Terza maggiore nella parte graue, l'Harmonia si fà allegra; & quando si pone
nell'acuto si fà mesta. Di modo che dalla positione diuersa delle Terze, che si pongono
nel Contrapunto tra gli estremi della Quinta, ouer si pongono sopra l'Ottaua, nasce la
uarietà dell'harmonia. Se adunque noi uorremo uariar l'harmonia, & osseruare più che
si può la Regola posta di sopra nel Cap. 29. (ancora che nelle compositioni di piu uoci
non sia tanto necessaria, quanto è in quelle di due uoci) è dibisogno, che noi poniamo
le Terze differenti in questa maniera; c'hauendo prima posto la Terza maggiore, che
faccia la mediatione Harmonica; poniamo dopoi la minore, che farà la diuisione Ari-thmetica; la qual cosa non si potrebbe osseruar cosi di leggieri, quando s'hauesse rispet-to à queste relationi; conciosiache mentre si cercasse di fuggirle, si uerrebbe à continua-re il concento per alquanto spatio di tempo in una delle sopradette diuisioni, senz'alcun
mezo; & far che la cantilena alle uolte si udirebbe mesta nelle parole, che portano seco
allegrezza, ouer si udirebbe allegra in quelle, che trattano materie meste, senz'alcun
proposito. Io non dico già, che 'l Compositore non possa porre due diuisioni Arithme-tiche l'una dopo l'altra; ma dico, che non dee continuare in tal diuisione lungo tempo;
perche farebbe il concento molto maninconico. Ma il porre molte diuisioni Harmoni-che l'una dopo l'altra, non potrà mai dar noia; purche siano fatte nelle chorde na-turali, & con qualche iudicio, & proposito nell'accidentali; percioche allora l'Harmo-nia hà le sue parti collocate secondo i lor gradi, & tocca il suo ultimo fine, & fà ottimo ef-fetto. E' ben uero, che quando due parti ascendessero, ò discendessero per un grado,
ouer per due, la mediatione si debbe porre diuersa; massimamente quando tra le due
parti, che fanno tali ascese & discese, può cascare il Tritono, ò la Semidiapente per re-latione; che è quando si pone nel primo modo due Terze maggiori l'una dopo l'altra, &
nel secondo due minori; ma quando la relatione fusse d'una Semidiatessaron; & fusse
tra i segni accidentali; come sarebbe il b. & il
rietà dipende tutta la diuersita, & la perfettione dell'Harmonie; conciosiache è neces-sario (come dirò altroue) che nella Compositione perfetta si ritrouino sempre in atto la page 223Quinta & la Terza, ouer le sue Replicate; essendo che oltra queste due consonanze l'Vdi-to non può desiderar suono, che caschi nel mezo, ouer fuori de i loro estremi, che sia in
tutto differente & uariato da quelli, che sono ne gli estremi di queste consonanze poste
insieme; ritrouandosi iui tutti quelli Suoni differenti, che possono far l'Harmonie diuerse. Ma perche gli estremi della Quinta sono inuariabili, & sempre si pongono contenuti
sott'vna istessa proportione; lasciando certi casi, ne i quali si pone imperfetta; però gli
estremi delle Terze si pongono differenti tra essa Quinta. Non dico però differenti di
proportione, ma dico differenti di luogo; percioche (come hò detto altroueSupra.
cap. 10.) quando
si pone la Terza maggiore nella parte graue, l'Harmonia si fà allegra; & quando si pone
nell'acuto si fà mesta. Di modo che dalla positione diuersa delle Terze, che si pongono
nel Contrapunto tra gli estremi della Quinta, ouer si pongono sopra l'Ottaua, nasce la
uarietà dell'harmonia. Se adunque noi uorremo uariar l'harmonia, & osseruare più che
si può la Regola posta di sopra nel Cap. 29. (ancora che nelle compositioni di piu uoci
non sia tanto necessaria, quanto è in quelle di due uoci) è dibisogno, che noi poniamo
le Terze differenti in questa maniera; c'hauendo prima posto la Terza maggiore, che
faccia la mediatione Harmonica; poniamo dopoi la minore, che farà la diuisione Ari-thmetica; la qual cosa non si potrebbe osseruar cosi di leggieri, quando s'hauesse rispet-to à queste relationi; conciosiache mentre si cercasse di fuggirle, si uerrebbe à continua-re il concento per alquanto spatio di tempo in una delle sopradette diuisioni, senz'alcun
mezo; & far che la cantilena alle uolte si udirebbe mesta nelle parole, che portano seco
allegrezza, ouer si udirebbe allegra in quelle, che trattano materie meste, senz'alcun
proposito. Io non dico già, che 'l Compositore non possa porre due diuisioni Arithme-tiche l'una dopo l'altra; ma dico, che non dee continuare in tal diuisione lungo tempo;
perche farebbe il concento molto maninconico. Ma il porre molte diuisioni Harmoni-che l'una dopo l'altra, non potrà mai dar noia; purche siano fatte nelle chorde na-turali, & con qualche iudicio, & proposito nell'accidentali; percioche allora l'Harmo-nia hà le sue parti collocate secondo i lor gradi, & tocca il suo ultimo fine, & fà ottimo ef-fetto. E' ben uero, che quando due parti ascendessero, ò discendessero per un grado,
ouer per due, la mediatione si debbe porre diuersa; massimamente quando tra le due
parti, che fanno tali ascese & discese, può cascare il Tritono, ò la Semidiapente per re-latione; che è quando si pone nel primo modo due Terze maggiori l'una dopo l'altra, &
nel secondo due minori; ma quando la relatione fusse d'una Semidiatessaron; & fusse
tra i segni accidentali; come sarebbe il b. & il  ; oueramente quando concorresse un so-lo de questi segni solamente, non ci dobbiamo per niente schiuare; perche essendo due
mediationi harmoniche, fanno buono effetto; com'è manifesto; ancora che non sia-no uariate. Et di ciò alcun non si debbe marauigliare; percioche quando uorrà con di-ligenza essaminar le Consonanze poste in cotali ordini; ritrouerà, che quell'ordine,
ch'è Aritametico, ouer s'assimiglia alla proportionalità Arithmetica, si lontana un po-co dalla perfettione dell'harmonia; conciosia che le sue parti vengono ad esser colloca-te fuori de i lor luoghi naturali. Per il contrario ritrouerà, che l'Harmonia, che nasce
dalla diuisione Harmonica, ouero à quella si s'assimiglia, consonerà perfettamente; per-che le parti di tal diuisione saranno collocate & ordinate secondo i proprii gradi di tal
proportionalità; & secondo l'ordine, che tengono i Numeri sonori nel loro ordine
naturale; come si può uedere nel Cap. 15. della Prima parte. Et questo sia detto à ba-stanza per hora; percioche forse un'altra fiata, per maggiore intelligenza di questo, ch'io
hò detto, ne toccherò una parola. page 224
; oueramente quando concorresse un so-lo de questi segni solamente, non ci dobbiamo per niente schiuare; perche essendo due
mediationi harmoniche, fanno buono effetto; com'è manifesto; ancora che non sia-no uariate. Et di ciò alcun non si debbe marauigliare; percioche quando uorrà con di-ligenza essaminar le Consonanze poste in cotali ordini; ritrouerà, che quell'ordine,
ch'è Aritametico, ouer s'assimiglia alla proportionalità Arithmetica, si lontana un po-co dalla perfettione dell'harmonia; conciosia che le sue parti vengono ad esser colloca-te fuori de i lor luoghi naturali. Per il contrario ritrouerà, che l'Harmonia, che nasce
dalla diuisione Harmonica, ouero à quella si s'assimiglia, consonerà perfettamente; per-che le parti di tal diuisione saranno collocate & ordinate secondo i proprii gradi di tal
proportionalità; & secondo l'ordine, che tengono i Numeri sonori nel loro ordine
naturale; come si può uedere nel Cap. 15. della Prima parte. Et questo sia detto à ba-stanza per hora; percioche forse un'altra fiata, per maggiore intelligenza di questo, ch'io
hò detto, ne toccherò una parola. page 224In qual Maniera due, ò più Consonanze perfette, ouero imperfette contenute sotto vna istessa forma, si possino porre immediatamente l'una dopo l'altra.Cap. XXXII.
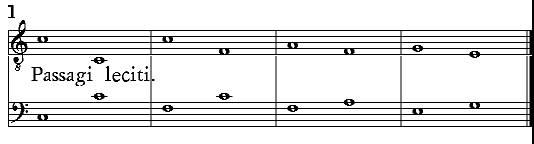 graue d'una parte della cantilena si pone nel luo-go della uoce acuta dell'altra, & per il contrario;
come qui si uede. Percioche nel mutare, ò cam-biare tali chorde tra loro la Consonanza non si
trasporta dall'acuto al graue, ouer dal graue
all'acuto; ma resta nelle sue prime chorde, non
mutando ne luogo, ne suoni; la onde non si ode
alcuna uarietà di graue, ò di acuto. Non si udendo adunque tal uariatione; non si può dire, che
siano due Consonanze contenute da un' istessa
forma, poste l'una dopo l'altra, nel modo che s'intende di sopra; ma si bene una sola
consonanza replicata nell'istesse chorde; com'è manifesto al senso. Et quantunque le
parti si mutino tra loro ascendendo & discendendo, & che l'una piglia il luogo dell'al-tra, & le lor modulationi siano uariate per i mouimenti contrarii, che fanno; non sono
però uariati i lor suoni; ancora che si potesse udire qualche uarietà, quando la parte, che
era nel graue, s'udisse più nell'acuto, & quella ch'era nell'acuto, più si udisse quando
fusse nel graue. Ma tal cosa non farebbe assolutamente uarietà alcuna secondo [unclear: ']l propo-sito; ma si bene ad un certo modo; come si può comprendere dal sottoposto essempio;
che quando le parti non mutassero luogo, necessariamente le modulationi di ciascuna
uerrebbono ad essere unisone.
graue d'una parte della cantilena si pone nel luo-go della uoce acuta dell'altra, & per il contrario;
come qui si uede. Percioche nel mutare, ò cam-biare tali chorde tra loro la Consonanza non si
trasporta dall'acuto al graue, ouer dal graue
all'acuto; ma resta nelle sue prime chorde, non
mutando ne luogo, ne suoni; la onde non si ode
alcuna uarietà di graue, ò di acuto. Non si udendo adunque tal uariatione; non si può dire, che
siano due Consonanze contenute da un' istessa
forma, poste l'una dopo l'altra, nel modo che s'intende di sopra; ma si bene una sola
consonanza replicata nell'istesse chorde; com'è manifesto al senso. Et quantunque le
parti si mutino tra loro ascendendo & discendendo, & che l'una piglia il luogo dell'al-tra, & le lor modulationi siano uariate per i mouimenti contrarii, che fanno; non sono
però uariati i lor suoni; ancora che si potesse udire qualche uarietà, quando la parte, che
era nel graue, s'udisse più nell'acuto, & quella ch'era nell'acuto, più si udisse quando
fusse nel graue. Ma tal cosa non farebbe assolutamente uarietà alcuna secondo [unclear: ']l propo-sito; ma si bene ad un certo modo; come si può comprendere dal sottoposto essempio;
che quando le parti non mutassero luogo, necessariamente le modulationi di ciascuna
uerrebbono ad essere unisone.

Come due, ò più Consonanze perfette, ouero imperfette, contenute sotto diuer-se forme, poste l'una immediatamente dopo l'altra si concedono. Cap. XXXIII.
 Osseruando però, che le Parti procedino nelle lor modulationi per Interualli cantabili,
& con bel procedere, accioche ne risulti buona & diletteuole harmonia.
Osseruando però, che le Parti procedino nelle lor modulationi per Interualli cantabili,
& con bel procedere, accioche ne risulti buona & diletteuole harmonia.
Che dopo la Consonanza perfetta stà bene il porre l'Imperfetta: ouero per il contrario.Cap. XXXIIII.
 Imperoche da tal uarietà non potrà nascere se non buona, uaga, diletteuole, & perfetta
Harmonia. Osseruando sempre (com'hò detto ancora) che le Parti della cantilena siapage 226no cantabili; cioè, che cantino bene, accioche dalla compositione de tante cose ben poste insieme, habbiamo l'uso delle perfette harmonie.
Imperoche da tal uarietà non potrà nascere se non buona, uaga, diletteuole, & perfetta
Harmonia. Osseruando sempre (com'hò detto ancora) che le Parti della cantilena siapage 226no cantabili; cioè, che cantino bene, accioche dalla compositione de tante cose ben poste insieme, habbiamo l'uso delle perfette harmonie.
Che le parti della Cantilena debbono procedere per mouimenti contrarij. Cap. XXXV.

In qual maniera le Parti della Cantilena possino insieme ascendere, ò di-scendere.Cap. XXXVI.
 E' ben uero, ch'è molto più lodeuole, quando le parti discendono insieme nel graue;
percioche allora necessariamente i Mouimenti loro si fanno tardi; & tanto più è lode-uole, quanto più sono graui; perche per la tardità si comprende facilmente la diuersità
delle specie; Il che non cosi facilmente si comprende ne i suoni acuti nati dalla uelocità
de i mouimenti; conciosiache tendono quasi ad una simiglianza; massimamente quan-do le parti ascendono insieme dalla Perfetta minore alla Perfetta maggiore. Ma per-che queste cose non sono hoggidi considerate da i Prattici; essendoche pongono tali
passaggi ne i lor Contrapunti senz'alcuno auertimento; però dico solamente, che non si
debbono vsare spesse fiate ne i Contrapunti à due uoci; conciosia che dal Senso sono
maggiormente compresi, di quello che sarebbono, se tali mouimenti si ritrouassero in
una cantilena à più voci; percioche allora la diuersità de mouimenti, che farebbono
le parti tra loro, & la loro moltitudine non lasciarebbono udire ne questi, ne altri simili.
Ne anco è cosa lodeuole che si oda ne i Contrapunti due parti, che ascendino insieme da
una consonanza maggiore, che sia di specie Imperfetta, ad una minore, che sia Perfet-ta, & facino i loro mouimenti per salto; cioè, per più d'un grado; oueramente due par-ti, che ascendino, ò discendino insieme per detti mouimenti da una consonanza conte-nuta da una proportione maggiore, sia perfetta, ouero imperfetra, ad una che segue, che
sia perfetta; come dalla Terza all'Vnisono, & dalla Decima all'Ottaua; percioche sem-pre darà qualche noia alle purgate orecchie. Ne anco torna bene il por la Sesta auanti
la Quinta, quando le parti ascendono, ò discendono insieme; ancora che l'una si muoui
per grado, & l'altra per salto; come nel sotto posto essempio si può comprendere.
E' ben uero, ch'è molto più lodeuole, quando le parti discendono insieme nel graue;
percioche allora necessariamente i Mouimenti loro si fanno tardi; & tanto più è lode-uole, quanto più sono graui; perche per la tardità si comprende facilmente la diuersità
delle specie; Il che non cosi facilmente si comprende ne i suoni acuti nati dalla uelocità
de i mouimenti; conciosiache tendono quasi ad una simiglianza; massimamente quan-do le parti ascendono insieme dalla Perfetta minore alla Perfetta maggiore. Ma per-che queste cose non sono hoggidi considerate da i Prattici; essendoche pongono tali
passaggi ne i lor Contrapunti senz'alcuno auertimento; però dico solamente, che non si
debbono vsare spesse fiate ne i Contrapunti à due uoci; conciosia che dal Senso sono
maggiormente compresi, di quello che sarebbono, se tali mouimenti si ritrouassero in
una cantilena à più voci; percioche allora la diuersità de mouimenti, che farebbono
le parti tra loro, & la loro moltitudine non lasciarebbono udire ne questi, ne altri simili.
Ne anco è cosa lodeuole che si oda ne i Contrapunti due parti, che ascendino insieme da
una consonanza maggiore, che sia di specie Imperfetta, ad una minore, che sia Perfet-ta, & facino i loro mouimenti per salto; cioè, per più d'un grado; oueramente due par-ti, che ascendino, ò discendino insieme per detti mouimenti da una consonanza conte-nuta da una proportione maggiore, sia perfetta, ouero imperfetra, ad una che segue, che
sia perfetta; come dalla Terza all'Vnisono, & dalla Decima all'Ottaua; percioche sem-pre darà qualche noia alle purgate orecchie. Ne anco torna bene il por la Sesta auanti
la Quinta, quando le parti ascendono, ò discendono insieme; ancora che l'una si muoui
per grado, & l'altra per salto; come nel sotto posto essempio si può comprendere.
 Quanto poi siano grati questi mouimenti all'Vdito, l'Esperienza maestra delle cose,
per uia del senso, ce lo manifesta; essendo che la Natura hà in odio le cose senza pro-portione & senza misura, & si diletta di quelle, c'hanno tra loro conuenienza. Per il-contrario adunque sarà lecito il porre una Consonanza maggiore, che sia imperfetta,
auanti una minore, che sia perfetta; quando le parti ascenderanno, delle quali l'una,
cioè, l'acuta ascendi per grado, & la graue per salto. Starà anche bene, che da una Con-sonanza imperfetta minore si uada ad una perfetta maggiore, ascendendo la parte gra-ue per grado, & l'acuta per salto; ouero ascendendo l'acuta per grado, & la graue per
salto. Si concede etiandio che dalla Consonanza imperfetta, che sia minore di proporpage 228tione della seguente, si uadi all'Ottaua; quando insieme ascendono, ouer discendono
le parti; pur che una di esse faccia il Mouimento di grado, & tal Mouimento sia d'un
Semituono maggiore; come nell'essempio seguente si uede.
Quanto poi siano grati questi mouimenti all'Vdito, l'Esperienza maestra delle cose,
per uia del senso, ce lo manifesta; essendo che la Natura hà in odio le cose senza pro-portione & senza misura, & si diletta di quelle, c'hanno tra loro conuenienza. Per il-contrario adunque sarà lecito il porre una Consonanza maggiore, che sia imperfetta,
auanti una minore, che sia perfetta; quando le parti ascenderanno, delle quali l'una,
cioè, l'acuta ascendi per grado, & la graue per salto. Starà anche bene, che da una Con-sonanza imperfetta minore si uada ad una perfetta maggiore, ascendendo la parte gra-ue per grado, & l'acuta per salto; ouero ascendendo l'acuta per grado, & la graue per
salto. Si concede etiandio che dalla Consonanza imperfetta, che sia minore di proporpage 228tione della seguente, si uadi all'Ottaua; quando insieme ascendono, ouer discendono
le parti; pur che una di esse faccia il Mouimento di grado, & tal Mouimento sia d'un
Semituono maggiore; come nell'essempio seguente si uede.
 E' concesso etiandio il venire dalla Consonanza perfetta all'imperfetta; quando le parti
ascendono, ouer discendono insieme; pur che l'una di esse si muoua per grado, & la Consonanza imperfetta sia di maggior proportione della perfetta. E' lecito etiandio por due
Consonanze l'una dopo l'altra, che faccino tra due parti il mouimento di salto; pur che
l'una di esse si muoua per un Semiditono; come qui si uede.
E' concesso etiandio il venire dalla Consonanza perfetta all'imperfetta; quando le parti
ascendono, ouer discendono insieme; pur che l'una di esse si muoua per grado, & la Consonanza imperfetta sia di maggior proportione della perfetta. E' lecito etiandio por due
Consonanze l'una dopo l'altra, che faccino tra due parti il mouimento di salto; pur che
l'una di esse si muoua per un Semiditono; come qui si uede.
 Si può ancora con mouimenti di salto por due parti ne i Contrapunti, che insieme
ascendino ò discendino, quando la parte acuta discende per una Terza, & la graue per
una Quinta, & si uiene dalla Terza alla Quinta; ouer per il contrario, si ascende dalla
Quinta alla Terza, & l'una delle parti; cioè, la graue ascende per una Quinta, & l'acuta
per una Terza. E' ben uero, che quando una de loro facesse il moto per un Ditono; mas-simamente discendendo, che tali mouimenti si potranno schiuare; percioche 'l procedere
in cotal modo è alquanto aspro; come l'esperienza ce lo manifesta. Ma l'ascendere dalla
Si può ancora con mouimenti di salto por due parti ne i Contrapunti, che insieme
ascendino ò discendino, quando la parte acuta discende per una Terza, & la graue per
una Quinta, & si uiene dalla Terza alla Quinta; ouer per il contrario, si ascende dalla
Quinta alla Terza, & l'una delle parti; cioè, la graue ascende per una Quinta, & l'acuta
per una Terza. E' ben uero, che quando una de loro facesse il moto per un Ditono; mas-simamente discendendo, che tali mouimenti si potranno schiuare; percioche 'l procedere
in cotal modo è alquanto aspro; come l'esperienza ce lo manifesta. Ma l'ascendere dalla
 Quinta al Ditono si concede; percioche le parti procedono per alcuni mouimenti, i quali non solamente sono sopportabili; ma anco molto dilettano; essendo che sono molto sonori; & questo percioche procedono uerso l'acuto, onde si generano i Mouimenti ueloci,
da i quali sono ascose le durezze, che per la tardità de mouimenti si manifestano, quando uanno uerso 'l graue. Lungo sarebbe il voler porre d'uno in uno tutti i Mouimenti & passaggi, che page 229possono far le parti de i Contrapunti; & di uno uolerne assignare la ragione paticola-re; ma di ciò sia detto à sufficienza, poi che da quello, che si è detto, si può hauere un
modo, ò Regola generale di conoscere i buoni passaggi da i tristi; laqual cognitione
non sarà molto difficile d'acquistare à tutti coloro, che si uorranno essercitare nell'osser-uanza delle nostre Regole.
Quinta al Ditono si concede; percioche le parti procedono per alcuni mouimenti, i quali non solamente sono sopportabili; ma anco molto dilettano; essendo che sono molto sonori; & questo percioche procedono uerso l'acuto, onde si generano i Mouimenti ueloci,
da i quali sono ascose le durezze, che per la tardità de mouimenti si manifestano, quando uanno uerso 'l graue. Lungo sarebbe il voler porre d'uno in uno tutti i Mouimenti & passaggi, che page 229possono far le parti de i Contrapunti; & di uno uolerne assignare la ragione paticola-re; ma di ciò sia detto à sufficienza, poi che da quello, che si è detto, si può hauere un
modo, ò Regola generale di conoscere i buoni passaggi da i tristi; laqual cognitione
non sarà molto difficile d'acquistare à tutti coloro, che si uorranno essercitare nell'osser-uanza delle nostre Regole.
Che si debbe schiuare più che si può, i Mouimenti fatti per salto; & similmen-te le Distanze, che possono accascare tra le Parti della cantilena. Cap. XXXVII.
 Conciosia che tali distanze, oltra che sono difficili da cantarsi; percioche non cosi fa-cilmente si possono formar le Voci & proportionare gli Interualli, & le Consonanze in
quelle modulationi, che procedono in cotal modo; come quelle, che si cantano l'una
per grado & l'altra per salto; generano etiandio alcuni effetti, ch'alle uolte all'Vdito
non sono molto grati. Onde è da notare, che i Mouimenti quanto più sono uniti; cioè,
non molto lontani, come sono quelli, che si muouono per grado, sono senza dubbio più
cantabili, & con maggior diletto fanno udire l'Harmonia, che nasce da loro tra le parti;
che quelli, che sono lontani; & ciò nasce; perche quanto più sono congiunti, tanto più
sono naturali; essendo che allora si procede naturalmente, quando si uà dall'uno estre-mo all'altro d'alcuna cosa per i debiti mezi. Di maniera che molto è da lodare & da
commendare tale uicinità; come quella, che s'accosta più alla natura. Il che molto lo-dò anco Agostino il Santo nel Cap. 10. del 2. lib. della Musica, dicendo; La uicinità
delle parti, tanto è più degna d'essere approuata, quanto è più uicina all'equalità; an-cora che iui ragionasse in altro proposito. Et quantunque queste distanze da sè non sia-no dissonanti, generano nondimeno un non sò chè di tristo all'Vdito, che non si può
udir con diletto. Schiuaremo adunque queste distanze, accioche i nostri Contrapunti
siano grati, dolci, sonori, & pieni di buona harmonia. page 230
Conciosia che tali distanze, oltra che sono difficili da cantarsi; percioche non cosi fa-cilmente si possono formar le Voci & proportionare gli Interualli, & le Consonanze in
quelle modulationi, che procedono in cotal modo; come quelle, che si cantano l'una
per grado & l'altra per salto; generano etiandio alcuni effetti, ch'alle uolte all'Vdito
non sono molto grati. Onde è da notare, che i Mouimenti quanto più sono uniti; cioè,
non molto lontani, come sono quelli, che si muouono per grado, sono senza dubbio più
cantabili, & con maggior diletto fanno udire l'Harmonia, che nasce da loro tra le parti;
che quelli, che sono lontani; & ciò nasce; perche quanto più sono congiunti, tanto più
sono naturali; essendo che allora si procede naturalmente, quando si uà dall'uno estre-mo all'altro d'alcuna cosa per i debiti mezi. Di maniera che molto è da lodare & da
commendare tale uicinità; come quella, che s'accosta più alla natura. Il che molto lo-dò anco Agostino il Santo nel Cap. 10. del 2. lib. della Musica, dicendo; La uicinità
delle parti, tanto è più degna d'essere approuata, quanto è più uicina all'equalità; an-cora che iui ragionasse in altro proposito. Et quantunque queste distanze da sè non sia-no dissonanti, generano nondimeno un non sò chè di tristo all'Vdito, che non si può
udir con diletto. Schiuaremo adunque queste distanze, accioche i nostri Contrapunti
siano grati, dolci, sonori, & pieni di buona harmonia. page 230In qual maniera si debba procedere da vna Consonanza ad vn'altra. Cap. XXXVIII.
 Quando poi si porr[unclear: à] la consonanza Imperfetta dopo la Perfetta, allora non è neces-sario hauere questa consideratione; pur che si osserui che i mouimenti, che fanno
le parti, siano regolati, secondo 'l modo mostrato di sopra. Io dico dalla Perfetta
all'Imperfetta, per questa ragione; percioche Ciascuna cosa desidera naturalmente
la sua perfettione, alla quale desidera di peruenire più presto, & col migliore & più
breue modo, che puote; la qual perfettione in questo genere s'attribuisce alle Con-sonanze perfette. La onde ciascuna cosa facilmente (come ad ogn'uno è manifesto)
dalla perfettione può passare all'imperfettione, ma non per il contrario; percioche
è cosa più difficile fare una cosa, che non è il distrugger la & roinarla. Di modo che
quando si operasse altramente di quel che hò detto, sarebbe un'operare contra l'or-dine & contra la natura delle cose; conciosia che le Imperfette tanto più parteci-pano della perfettione, quanto più s'accostano alla lor uicina Perfetta, & si ren-dono etiandio all'Vdito tanto più dolci & più soaui. Mi potrebbe alcun dire; Se
la Sesta maggiore è più uicina alla Quinta, che non è all'Ottaua, com'è manifesto;
per qual cagione la dobbiamo maggiormente porre auanti la Ottaua, che la Quin-ta; poi c'habbiamo d'andare dalla consonanza Imperfetta alla Perfetta con la più
uicina? Dico, che quantunque la Sesta maggiore sia più uicina alla Quinta, che
all'Ottaua; per questo non è uero, che la Minore non sia più uicina alla Quinta
della Maggiore. Onde dobbiamo sapere, che essendo tra le Consonanze perfette
l'Ottaua maggior della Quinta; & tra le Seste, la maggiore di maggior quantità,
che non è la minore; dobbiamo accompagnar la maggiore delle Perfette con la mag-giore dell'Imperfette; per la simiglianza (dirò cosi) ò consenso, che è tra loro;
percioche facil cosa è di passar da una cosa ad un'altra & senza molta fatica, quan-do tra loro si ritroua qualche simiglianza. Onde dobbiamo andare alla Quinta
con la Sesta minore; percioche hà tal consentimento con lei, & à lei è più uicina.
Quando poi si porr[unclear: à] la consonanza Imperfetta dopo la Perfetta, allora non è neces-sario hauere questa consideratione; pur che si osserui che i mouimenti, che fanno
le parti, siano regolati, secondo 'l modo mostrato di sopra. Io dico dalla Perfetta
all'Imperfetta, per questa ragione; percioche Ciascuna cosa desidera naturalmente
la sua perfettione, alla quale desidera di peruenire più presto, & col migliore & più
breue modo, che puote; la qual perfettione in questo genere s'attribuisce alle Con-sonanze perfette. La onde ciascuna cosa facilmente (come ad ogn'uno è manifesto)
dalla perfettione può passare all'imperfettione, ma non per il contrario; percioche
è cosa più difficile fare una cosa, che non è il distrugger la & roinarla. Di modo che
quando si operasse altramente di quel che hò detto, sarebbe un'operare contra l'or-dine & contra la natura delle cose; conciosia che le Imperfette tanto più parteci-pano della perfettione, quanto più s'accostano alla lor uicina Perfetta, & si ren-dono etiandio all'Vdito tanto più dolci & più soaui. Mi potrebbe alcun dire; Se
la Sesta maggiore è più uicina alla Quinta, che non è all'Ottaua, com'è manifesto;
per qual cagione la dobbiamo maggiormente porre auanti la Ottaua, che la Quin-ta; poi c'habbiamo d'andare dalla consonanza Imperfetta alla Perfetta con la più
uicina? Dico, che quantunque la Sesta maggiore sia più uicina alla Quinta, che
all'Ottaua; per questo non è uero, che la Minore non sia più uicina alla Quinta
della Maggiore. Onde dobbiamo sapere, che essendo tra le Consonanze perfette
l'Ottaua maggior della Quinta; & tra le Seste, la maggiore di maggior quantità,
che non è la minore; dobbiamo accompagnar la maggiore delle Perfette con la mag-giore dell'Imperfette; per la simiglianza (dirò cosi) ò consenso, che è tra loro;
percioche facil cosa è di passar da una cosa ad un'altra & senza molta fatica, quan-do tra loro si ritroua qualche simiglianza. Onde dobbiamo andare alla Quinta
con la Sesta minore; percioche hà tal consentimento con lei, & à lei è più uicina.
 Questo è ultimamente da notare; che quello, che si è detto delle Consonanze semplici,
si dee anco intender delle Replicate. Similmente si debbe auertire; che quando due
Questo è ultimamente da notare; che quello, che si è detto delle Consonanze semplici,
si dee anco intender delle Replicate. Similmente si debbe auertire; che quando due
 parti della cantilena discenderanno insieme, &
dalla Sesta maggiore uerranno alla Terza, che sia
Maggiore; allora la parte acuta cascherà meglio,
& farà megliore effetto, che se cascasse sopra la
Minore; ancora che l'uno & l'altro modo sia buo-no; percioche cascherà senza dubbio alcuno so-pra una Consonanza, che più si auicina alla per-fettione, che non fà la Terza minore; come si
potrà udire & essaminare in questi due essempi, po-sti qui da canto.
parti della cantilena discenderanno insieme, &
dalla Sesta maggiore uerranno alla Terza, che sia
Maggiore; allora la parte acuta cascherà meglio,
& farà megliore effetto, che se cascasse sopra la
Minore; ancora che l'uno & l'altro modo sia buo-no; percioche cascherà senza dubbio alcuno so-pra una Consonanza, che più si auicina alla per-fettione, che non fà la Terza minore; come si
potrà udire & essaminare in questi due essempi, po-sti qui da canto.
In qual maniera si debba terminare ciascuna Cantilena.Cap. XXXIX.
Il modo che si dee tenere nel far i Contrapunti semplici à due voci, chiamati di Nota contra nota.Cap. XL.
Ordinis haec virtus erit, & Venus, aut ego fallor.La qual Regola molto ben sapea il dottissimo Virgilio, come si può comprendere; c' hauendo preso un Soggetto determinato, ch'era di scriuere la Roina, & l'Incedio [sic: Incendio] di Troia, & la Nauigatione di Enea; incominciò primieramente dalla Nauigatione, interrompendo l'ordine; nondimeno la Nauigatione fù dopo; ma comprese, che con mag-giore arteficio, & con maggior maestà sarebbe riuscito il suo Poema,2. Aenei. se hauesse fatto re-citar l'Historia per ordine da Enea alla presentia di Didone, come fece; prendendo l'occasione dalla fortuna ch'ei hebbe riducendolo in Cartagine. Cosi sogliono fare i Poeti, & non solo i Poeti; ma anco i Pittori; i quali accommodano le historie, ò fauole, come meglio li tornano in proposito; percioche la Pittura non è altro, che una Poesia muta. Onde il Pittore hauendosi proposto alcuna uolta di dipingere un'historia, ò fauola, accommoda le figure & le accompagna insieme, secondo ch'à lui pare, che stiano meglio, & che faccino me-gliori effetti; ne fà caso alcuno di porne una più in un modo, che in un'altro; cioè, che più stia in piedi, ouer'à sedere in una maniera, che in un'altra; pur che osserui l'ordine della Historia, ò fauola, che vuol dipingere; ilche si uede, ch'infiniti Pittori haueranno dipinto una cosa istessa in infinite maniere; come più uolte hò ueduto l'historia di Lucretia Romana moglie di Collatino; quella d'Horatio Cocle, & molte altre; nondimeno [unclear: t]utti haueranno hauuto un'istesso fine, di rappresentar le dette historie. Et non solamente questo si uede fatto da diuersi Pittori d'un'istesso soggetto; ma etiandio da un solo, il-quale haurà dipinto una cosa istessa in diuersi modi. Debbe adunque il Musico etiandio cercare di uariar sempre il suo Contrapunto sopra un Soggetto; & potendo far molti passaggi, eleggerà quello, che sarà il migliore, che li tornerà più in proposito, & che farà il suo Contrapunto più sonoro & meglio ordinato, & lascierà da un canto gli altri. Però adunque quando gli occorrerà di poter fare un passaggio; come sarebbe dire una Cadenza, & non tornerà bene secondo 'l proposito, la debbe riseruare ad un'altro luogo piò commodo; & ciò farà, quando la Clausula, ouer il Periodo nelle Parole, ouer'Oratione non sarà terminato; conciosia che debbe sempre aspettare, che ciascun de questi sia finito; & similmente auertir debba, che sia il luogo proprio, & che [unclear: ']l Modo, sopra il quale è fondata la cantilena, lo ricerchi. Tutte queste cose debbe osseruar colui, ilquale desidera di introdursi bene nell'arte del Contrapunto; ma sopr'ogn'altra cosa dee con ogni studio essercitarsi primieramente molti giorni in tal sorte di compositione; accioche con più fa-cilità possa uenire dopoi all'uso del Contrapunto diminuito, nel quale potrà usar molt'altre cose; come uederemo à i loro luoghi. Ma accioche si habbia qualche intelligenza di tutto quello, c'hò detto, porrò qui sotto alcuni Contrapunti di Nota contra nota uaria-ti, composti sopra 'l Soggetto nominato, hora nell'acuto & hora nel graue; i quali prima essaminati, si potranno dopoi facilmente intender quelle cose, che mostrerò altroue; & si potrà operare con minor fatica. Ciascun però debbe esser'auertito, che 'l fare del Contrapunto di Nota contra nota, par che sia & è ueramente alquanto più difficile di quello, che non è, il farlo diminuito; & questo procede, perche in questo non gli è quella libertà che si ritroua in quello; essendo che nel primo è dibisogno, ch'ogni Nota, ò Figura cantabile habbia una Consonanza solamente; & nel secondo se ne pongano molte mescola-te con Dissonanze, secondo l'arbitrio & il buon giudicio del Compositore. Onde nel primo modo non si può cosi bene, & à suo uolere ordinar le parti, che siano senza salti; mas-simamente quando sopra un'istesso Soggetto si uolesse comporre molti Contrapunti, che fussero in ogni parte uariati. Ne per questo alcuno si debbe attristare; conciosiache quantunque da questa radice si gusti alquanto di amaritudine; dopo non molto tempo si godono i frutti, che da essa nascono, che sono dolci soaui & saporiti; essendo che la Virtù (come affermano i Sauij) consiste intorno al difficile, & non intorno alla cosa facile. page 237
Vt iam nunc dicat: iam nunc debentia dici
Pleraque differat, & praesens in tempus omittat.

Che ne i Contrapunti si debbono schiuar gli Vnisoni, più che si puo-te; & che non si dè molto di lungo frequentare le Ottaue.Cap. XLI.
O fortunatam natam me consule Romam;per il raddoppiamen-to delle due insieme aggiunte sillabe, Natam, & per la terminatione del uerso nella sil-laba Mam; & nel principio di quella Epistola, che scriue Cicerone à Lentulo Procon-suleEpist. fam. lib. 1. epist. 1.,
Ego omni officio; che in tre parole si legge quattro uolte la lettera O, & in altri luoghi quasi infiniti; onde si ode un non so chè di tristo, che le orecchie purgate non possono udire; sarebbe ueramente il Musico degno di reprensione, quando comportasse un simi-le disordine ne i suoi componimenti; conciosiache se tutti costoro di commun parere hanno con leggi uniuersali concluso, che non è lecito, ne in Prosa, ne in Verso (saluo se non fusse posto cotal cosa arteficiosamente, per mostrar qualche effetto) porre questi modi strani di parlare; maggiormente il Musico debbe bandire dalle sue compositioni ogni tristo suono, & qualunque altra cosa, che potesse offendere il senso. Debbe adunque il Compositore auertire, di non commetter simil cose nelle sue cantilene; & di regolare in tal maniera i suoi concenti, che in loro si odi ogni cosa buona. Non debbe adunque fa-re udire ne i suoi Contrapunti (come hò detto) molti Vnisoni, ò molte Ottaue l'una dopo l'altra, che siano tramezate solamente da un'altra Consonanza; massimamente quando sono poste sopra una chorda istessa, ancora che procedessero le parti per salti; im-peroche quando fussero collocate in cotal maniera, dal sequente essempio si potrà conoscere quanto sarebbono grate à ciascun di sano giudicio.
 Io non dico però che non si debbino adoperare; ma dico, che non si debbono usare troppo spesso; percioche quando occorresse, che 'l Compositore non potesse accommodare
una buona & commoda modulatione, & un bello & elegante procedere, con un bello
& leggiadro cantare; le debbe per ogni modo usare, tramezate però d'alcun'altre Con-sonanze; & debbe più presto porre sempre l'Ottaua, che l'Vnisono quando li tornerà
commodo.
Io non dico però che non si debbino adoperare; ma dico, che non si debbono usare troppo spesso; percioche quando occorresse, che 'l Compositore non potesse accommodare
una buona & commoda modulatione, & un bello & elegante procedere, con un bello
& leggiadro cantare; le debbe per ogni modo usare, tramezate però d'alcun'altre Con-sonanze; & debbe più presto porre sempre l'Ottaua, che l'Vnisono quando li tornerà
commodo.
De i Contrapunti diminuiti à due voci; & in qual modo si possino vsar le Dissonanze; & de molte Regole che si deono osseruare in essi.Cap. XLII.
 page 240to; però è da auertire di porre il Punto, che sia consonante; percioche se 'l si ponesse altra-mente, ciascun potrebbe da se stesso conoscere, quanto fusse grato da udire. Et benche la
Minima legata in cotal modo si possa porre in due modi ne i Contrapunti; prima nel battere, ò nel principio della Battuta; dopoi nel leuare; però il primo modo si debbe porre
solamente nel principio de i Contrapunti & non nel mezo; & questo dico ne i Contra-punti di due uoci; ma il secondo modo si può porre non solo nel principio, ma etiandio
nel mezo, come nel sopraposto essempio si è ueduto. Potrà anco alle uolte il Contrapuntista porre scambieuolmente due minime, delle quali l'una sia consonante, & l'altra dis-sonante; pur che la consonante caschi nel battere, & la dissonante nel leuar la battuta;
ma debbono procedere uerso il graue, ò uerso l'acuto per molti gradi continuati senz'alcun salto. Et quando un simil procedere incominciasse nel principio del Contrapunto;
allora potrà auanti ogn'altra cosa usar la Semibreue col punto; purche torni bene, ma
non già nel mezo; conciosia che anco non si usa in simil luogo la Semibreue semplice, ne
la Minima puntata, se non sincopata; anzi (fuori di tal caso) ogni figura del Soggetto,
che sia Canto fermo, debbe hauere almeno sopra di se due consonanze, l'una nel batte-re, & l'altra nel leuare della battuta nel Contrapunto diminuito; percioche poste in tal
maniera hanno molta gratia; come l'esperienza ce lo manifesta. Ma quando 'l Soggetto
fusse diminuito; cioè, una parte di Canto figurato, allora le figure del Contrapunto si possono fare equali alle sue figure; pur che procedino in tal modo insieme; che se ben è di-minuito, il Contrapunto habbia in se qualche leggiadria; & tal uolta procedi con figure
d'alquanto più ualore, che quelle, che sono contenute nel Soggetto; percioche fà dibisogno, che si oda almeno una parte, che faccia mouimento, si nel battere, come anco nel
leuar della Battuta. Quando adunque tra molte Minime se ne ritrouasse alcuna, che non
procedesse per grado; non sarà mai lecito, ch' ella sia disonante, anzi l'una & l'altra de
due figure, che faranno tal Grado, si debbono porre consonanti; Conciosia che se ben
la Dissonanza è posta nella seconda minima nel mouimento di grado; tal mouimento &
quel poco di uelocità, che si ritroua nel proferir simili figure, non lasciano udir cosa ue-runa, che dispiaccia. Ma non è già cosi ne i Mouimenti di salto; percioche per tal sepa-ratione la Dissonanza si fà tanto manifesta, ch'apena si può tolerare; com'è manifesto à
tutti quelli, c'hanno giudicio di cotal cosa. Si potrà nondimeno porre la Prima parte della battuta, che sia dissonante, quando sarà la seconda minima d'una Semibreue sincopa-ta del Contrapunto; percioche la prima parte di tal figura sarà posta, senza dubbio, nel
leuar la battuta, & la seconda nel battere, & tal Dissonanza si potrà sopportare; percio-che nel cantar la Semibreue sincopata si tiene salda la uoce, & si ode quasi una sospensio-ne, ò taciturnità, che si troua nel mezo della percussione, dalla quale nascono i suoni;
& per essa si discernono l'un dall'altro, & consiste nel tempo; onde l'Vdito quasi non la
sente; perche da lei non è mosso di maniera, che la possa comprendere pienamene [sic: pienamente], per
non esser da lei percosso, & anco per la debolezza del mouimento, che si scorge in essa;
perche manca della percussione, che lo muoue; la onde la Voce allora nel perseuerar
della Sincopa perde quella uiuacità, c'hauea nella prima percussione, di modo che fatta debole, & essendo percossa da un mouimento più gagliardo d'un'altra uoce forte, che si muoue da un luogo all'altro con più gagliardo mouimento, nella quale è nascosta la Disso-nanza sopra la sua seconda parte, tal Dissonanza à pena si ode; essendo anco che
prestamente se ne passa. Et se pure il Senso è da qualche parte offeso; è dopoi ragguagliato per tal maniera dalla Consonanza che succede senz'alcun mezo, che non solamente tal
Dissonanza non li dispiace; ma grandemente in lei si compiace; perche con maggior
dolcezza & maggior soauità fà udire tal Consonanza. Et questo forse auiene; perche
Ogni contrario maggiormente si scopre & si fà al sentimento più noto per la comparatione del suo Opposto. Ma non si debbe giamai por la Prima parte della Semibreue, che
sia dissonante; sia poi sincopata, ò non sincopata; & si dee auuertire pero gni modo due
cose; la prima, che Dopo la Dissonanza segua una Consonanza à lei più uicina; la seconpage 224
page 240to; però è da auertire di porre il Punto, che sia consonante; percioche se 'l si ponesse altra-mente, ciascun potrebbe da se stesso conoscere, quanto fusse grato da udire. Et benche la
Minima legata in cotal modo si possa porre in due modi ne i Contrapunti; prima nel battere, ò nel principio della Battuta; dopoi nel leuare; però il primo modo si debbe porre
solamente nel principio de i Contrapunti & non nel mezo; & questo dico ne i Contra-punti di due uoci; ma il secondo modo si può porre non solo nel principio, ma etiandio
nel mezo, come nel sopraposto essempio si è ueduto. Potrà anco alle uolte il Contrapuntista porre scambieuolmente due minime, delle quali l'una sia consonante, & l'altra dis-sonante; pur che la consonante caschi nel battere, & la dissonante nel leuar la battuta;
ma debbono procedere uerso il graue, ò uerso l'acuto per molti gradi continuati senz'alcun salto. Et quando un simil procedere incominciasse nel principio del Contrapunto;
allora potrà auanti ogn'altra cosa usar la Semibreue col punto; purche torni bene, ma
non già nel mezo; conciosia che anco non si usa in simil luogo la Semibreue semplice, ne
la Minima puntata, se non sincopata; anzi (fuori di tal caso) ogni figura del Soggetto,
che sia Canto fermo, debbe hauere almeno sopra di se due consonanze, l'una nel batte-re, & l'altra nel leuare della battuta nel Contrapunto diminuito; percioche poste in tal
maniera hanno molta gratia; come l'esperienza ce lo manifesta. Ma quando 'l Soggetto
fusse diminuito; cioè, una parte di Canto figurato, allora le figure del Contrapunto si possono fare equali alle sue figure; pur che procedino in tal modo insieme; che se ben è di-minuito, il Contrapunto habbia in se qualche leggiadria; & tal uolta procedi con figure
d'alquanto più ualore, che quelle, che sono contenute nel Soggetto; percioche fà dibisogno, che si oda almeno una parte, che faccia mouimento, si nel battere, come anco nel
leuar della Battuta. Quando adunque tra molte Minime se ne ritrouasse alcuna, che non
procedesse per grado; non sarà mai lecito, ch' ella sia disonante, anzi l'una & l'altra de
due figure, che faranno tal Grado, si debbono porre consonanti; Conciosia che se ben
la Dissonanza è posta nella seconda minima nel mouimento di grado; tal mouimento &
quel poco di uelocità, che si ritroua nel proferir simili figure, non lasciano udir cosa ue-runa, che dispiaccia. Ma non è già cosi ne i Mouimenti di salto; percioche per tal sepa-ratione la Dissonanza si fà tanto manifesta, ch'apena si può tolerare; com'è manifesto à
tutti quelli, c'hanno giudicio di cotal cosa. Si potrà nondimeno porre la Prima parte della battuta, che sia dissonante, quando sarà la seconda minima d'una Semibreue sincopa-ta del Contrapunto; percioche la prima parte di tal figura sarà posta, senza dubbio, nel
leuar la battuta, & la seconda nel battere, & tal Dissonanza si potrà sopportare; percio-che nel cantar la Semibreue sincopata si tiene salda la uoce, & si ode quasi una sospensio-ne, ò taciturnità, che si troua nel mezo della percussione, dalla quale nascono i suoni;
& per essa si discernono l'un dall'altro, & consiste nel tempo; onde l'Vdito quasi non la
sente; perche da lei non è mosso di maniera, che la possa comprendere pienamene [sic: pienamente], per
non esser da lei percosso, & anco per la debolezza del mouimento, che si scorge in essa;
perche manca della percussione, che lo muoue; la onde la Voce allora nel perseuerar
della Sincopa perde quella uiuacità, c'hauea nella prima percussione, di modo che fatta debole, & essendo percossa da un mouimento più gagliardo d'un'altra uoce forte, che si muoue da un luogo all'altro con più gagliardo mouimento, nella quale è nascosta la Disso-nanza sopra la sua seconda parte, tal Dissonanza à pena si ode; essendo anco che
prestamente se ne passa. Et se pure il Senso è da qualche parte offeso; è dopoi ragguagliato per tal maniera dalla Consonanza che succede senz'alcun mezo, che non solamente tal
Dissonanza non li dispiace; ma grandemente in lei si compiace; perche con maggior
dolcezza & maggior soauità fà udire tal Consonanza. Et questo forse auiene; perche
Ogni contrario maggiormente si scopre & si fà al sentimento più noto per la comparatione del suo Opposto. Ma non si debbe giamai por la Prima parte della Semibreue, che
sia dissonante; sia poi sincopata, ò non sincopata; & si dee auuertire pero gni modo due
cose; la prima, che Dopo la Dissonanza segua una Consonanza à lei più uicina; la seconpage 224 da, che 'l Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, &
esser di grado, & non ascendere. Onde potrà esser utile questa Regola: Quando la Disso-nanza sarà posta nella seconda parte della Semibreue sincopata, la quale sarà una Se-conda; allora dopo lei accommodaremo ottimamente la Terza, che le è più uicina.
da, che 'l Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, &
esser di grado, & non ascendere. Onde potrà esser utile questa Regola: Quando la Disso-nanza sarà posta nella seconda parte della Semibreue sincopata, la quale sarà una Se-conda; allora dopo lei accommodaremo ottimamente la Terza, che le è più uicina.
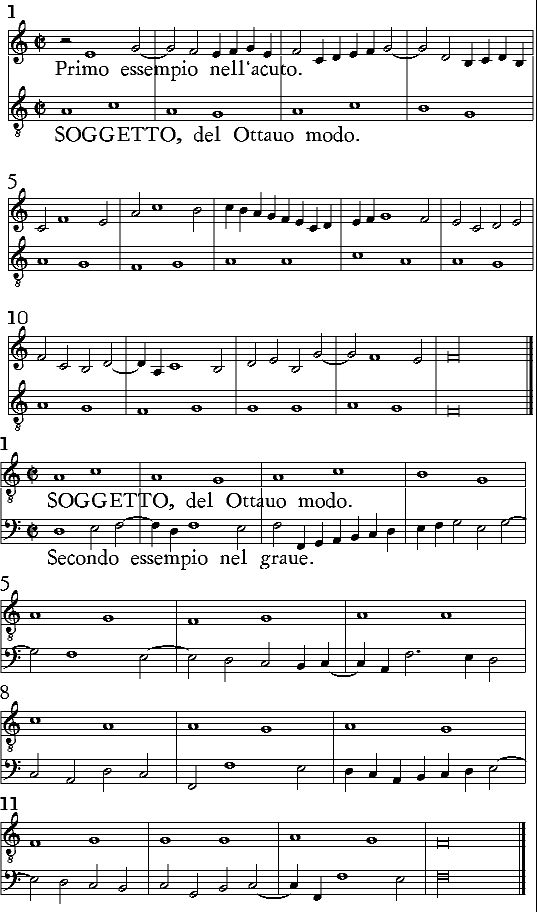 page 242Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Setti-ma poi se le accompagnerà la Sesta; percioche le è più uicina. Smilmente [sic: Similmente] si potrebbe dir
delle Replicate; come della Nona, dopo la quale si accompagna la Decima; & della
Vndecima, che riceue la Decima; come si può uedere nell'essempio: Ma basterà quel
che detto habbiamo, & mostraremo più oltra, dicendo; che Si potrà anco alle uolte (come costumano fare i buoni Musici, non senza suo gran commodo) dalla Seconda sinco-pata uenire all'Vnisono, & ciò quando le parti sarano ordinate in tal maniera, che l'una
faccia il mouimento di Tuono & l[unclear: ']altra di Semituono. Vsaremo etiandio la Quarta sin-
page 242Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Setti-ma poi se le accompagnerà la Sesta; percioche le è più uicina. Smilmente [sic: Similmente] si potrebbe dir
delle Replicate; come della Nona, dopo la quale si accompagna la Decima; & della
Vndecima, che riceue la Decima; come si può uedere nell'essempio: Ma basterà quel
che detto habbiamo, & mostraremo più oltra, dicendo; che Si potrà anco alle uolte (come costumano fare i buoni Musici, non senza suo gran commodo) dalla Seconda sinco-pata uenire all'Vnisono, & ciò quando le parti sarano ordinate in tal maniera, che l'una
faccia il mouimento di Tuono & l[unclear: ']altra di Semituono. Vsaremo etiandio la Quarta sin- copata, dopo la quale segua senz'alcun mezo la Semidiapente, & dopo questa immediatamente succeda la Terza maggiore; percioche la Semidiapente è posta in tal maniera, che fà buono effetto; essendoche tra
le parti non si ode alcuna trista relatione.
copata, dopo la quale segua senz'alcun mezo la Semidiapente, & dopo questa immediatamente succeda la Terza maggiore; percioche la Semidiapente è posta in tal maniera, che fà buono effetto; essendoche tra
le parti non si ode alcuna trista relatione.
 uimenti, & l'una delle parti ascenda per Quarta,
ò discenda per Quinta, & l'altra discenda per
grado; come più oltra nell'essempio si uede.
uimenti, & l'una delle parti ascenda per Quarta,
ò discenda per Quinta, & l'altra discenda per
grado; come più oltra nell'essempio si uede.
 Hò detto legata ad un'altra figura; percioche quando si risolue la sincopa di Semibreue, nellaquale sia la dissonanza, allora seguita la Minima senz'alcuna figura mezana; laquale dico
allora esser legata, quando dopo la Dissonanza segue non la Minima, ma un'altra Semibreue sincopata, ouero una Minima col punto; della qual Semibreue la seconda parte battuta
sia consonante, ò dissonante; & cosi ancora dico del Punto, che stà appresso la nominata Minima. La onde dico, che al primo modo la Minima è legata ad un'altra Minima; & al secondo modo la Minima è legata alla Semiminima, ch'è il Punto. Quelle adunque, che nelle cantilene si concedono sono le sottoposte; perche hanno molta gratia; ma quelle ueramente
che i boni Compositori non vsano, sono quelle, che seguitano; imperoche quando non si osserua in page 243
Hò detto legata ad un'altra figura; percioche quando si risolue la sincopa di Semibreue, nellaquale sia la dissonanza, allora seguita la Minima senz'alcuna figura mezana; laquale dico
allora esser legata, quando dopo la Dissonanza segue non la Minima, ma un'altra Semibreue sincopata, ouero una Minima col punto; della qual Semibreue la seconda parte battuta
sia consonante, ò dissonante; & cosi ancora dico del Punto, che stà appresso la nominata Minima. La onde dico, che al primo modo la Minima è legata ad un'altra Minima; & al secondo modo la Minima è legata alla Semiminima, ch'è il Punto. Quelle adunque, che nelle cantilene si concedono sono le sottoposte; perche hanno molta gratia; ma quelle ueramente
che i boni Compositori non vsano, sono quelle, che seguitano; imperoche quando non si osserua in page 243 loro la sopradetta Regola' [sic: delete], la figura, che segue la Dissonanza, non fà bene il suo officio, &
quel che debitamente à lei appartiene. Onde non hà in se quella gratia, c'hà la prima;
percioche la Dissonanza si risolue con un modo freddo (dirò cosi) essendo che non rag-guaglia pienamente l'Vdito di quello; che forse per auanti in qualche modo fu offeso dalla Dissonanza; come nel seguente essempio si potrà udire. Et perche g[gap — ] Antichi Prat-
loro la sopradetta Regola' [sic: delete], la figura, che segue la Dissonanza, non fà bene il suo officio, &
quel che debitamente à lei appartiene. Onde non hà in se quella gratia, c'hà la prima;
percioche la Dissonanza si risolue con un modo freddo (dirò cosi) essendo che non rag-guaglia pienamente l'Vdito di quello; che forse per auanti in qualche modo fu offeso dalla Dissonanza; come nel seguente essempio si potrà udire. Et perche g[gap — ] Antichi Prat- tici hanno usatto [sic: usato], & i Moderni ancora usano, di porre alle uolte confusamente ne i loro
Contrapunti hora la prima, & hora la seconda Semiminima, che seguono la Minima
battuta, ouer la Semibreue col punto, ò pur la detta Semibreue senza 'l punto sincopata
consonante; massimamente quando il loro procedere è per Mouimenti di grado uerso la
parte graue; però accioche non si generi confusione nell'animo del Compositore, determinaremo hora, quale delle due Semiminime si habbia da porre, che sia consonante.
tici hanno usatto [sic: usato], & i Moderni ancora usano, di porre alle uolte confusamente ne i loro
Contrapunti hora la prima, & hora la seconda Semiminima, che seguono la Minima
battuta, ouer la Semibreue col punto, ò pur la detta Semibreue senza 'l punto sincopata
consonante; massimamente quando il loro procedere è per Mouimenti di grado uerso la
parte graue; però accioche non si generi confusione nell'animo del Compositore, determinaremo hora, quale delle due Semiminime si habbia da porre, che sia consonante.
 Ma quando per Soggetto si piglierà una parte di Canto figurato; allora si osseruarà di porre cotali Semiminime consonanti; secondo la dispositione, si della parte del Contrapun-to; come ancora del Soggetto; come à i luoghi proprij son per dimostrare.
Ma quando per Soggetto si piglierà una parte di Canto figurato; allora si osseruarà di porre cotali Semiminime consonanti; secondo la dispositione, si della parte del Contrapun-to; come ancora del Soggetto; come à i luoghi proprij son per dimostrare.
Il modo che hà da tenere il Compositore nel fare i Contrapunti sopra vna Parte, ò Soggetto diminuito.Cap. XLIII.
 page 246che li tornerà più al proposito, & se ciò non vorrà fare, potrà comporre tal Parte da se
stesso; & secondo il suo ingegno comporne vn'altra nel graue; ouer, secondo che li verrà
meglio fatto, nell'acuto. E' ben uero, che uolendo comporre il Soggetto da se stesso, potrà
aiutato da vna Parte della sua compositione comporre l'altra, di modo che tutto in vn
tempo uerrà à comporre il Soggetto, & à dar fine alla Cantilena. La onde tanto più age-uolmente lo potrà fare; quanto più vorrà osseruar quelle Regole, lequali hauera osser-uato nel fare i Contrapunti sopra il Canto fermo. Ben'è uero, che questo modo di com-porre gli sarà più libero & più espedito; percioche potr[unclear: à], diminuire qual si uoglia par-te, sia graue, ouero acuta; lasciando vna di esse parti con le Figure di alquanto maggior valore; ouero ponendo le Figure tra tutte due, che siano simili, ò diuerse l'vna contra l'altra,
ilche non poteua fare nel primo modo. Potrà adunque il Compositore far quello che li
tornerà più commodo; auertendo però di accommodar sempre in tal maniera le Parti
della cantilena, che cantino bene, & habbiano bello & elegante procedere, con un non
page 246che li tornerà più al proposito, & se ciò non vorrà fare, potrà comporre tal Parte da se
stesso; & secondo il suo ingegno comporne vn'altra nel graue; ouer, secondo che li verrà
meglio fatto, nell'acuto. E' ben uero, che uolendo comporre il Soggetto da se stesso, potrà
aiutato da vna Parte della sua compositione comporre l'altra, di modo che tutto in vn
tempo uerrà à comporre il Soggetto, & à dar fine alla Cantilena. La onde tanto più age-uolmente lo potrà fare; quanto più vorrà osseruar quelle Regole, lequali hauera osser-uato nel fare i Contrapunti sopra il Canto fermo. Ben'è uero, che questo modo di com-porre gli sarà più libero & più espedito; percioche potr[unclear: à], diminuire qual si uoglia par-te, sia graue, ouero acuta; lasciando vna di esse parti con le Figure di alquanto maggior valore; ouero ponendo le Figure tra tutte due, che siano simili, ò diuerse l'vna contra l'altra,
ilche non poteua fare nel primo modo. Potrà adunque il Compositore far quello che li
tornerà più commodo; auertendo però di accommodar sempre in tal maniera le Parti
della cantilena, che cantino bene, & habbiano bello & elegante procedere, con un non
 page 247sò che misto di grauità. Et accioche si vegga il modo, che hà da tenere nel comporre si-mili Contrapunti, ò Compositioni (poiche non si può dar Regola particolare d'ogni co-sa, per essere infiniti gli indiuidui) hò posto due essempi, l'uno de i quali è fondato sopra
il Soggetto, ch'incomincia; Scimus hoc nostrum meruisse crimen: ilquale è una Parte d'u-na leggiadra compositione à due voci d'Adriano, composta del Primo modo. L'al-tro poi è tutto composto di fantasia. Di maniera che vedendo & essaminando queste
due, & altre simili compositioni, potrà venire all'uso di comporre à cotesto modo facil-mente & bene.
page 247sò che misto di grauità. Et accioche si vegga il modo, che hà da tenere nel comporre si-mili Contrapunti, ò Compositioni (poiche non si può dar Regola particolare d'ogni co-sa, per essere infiniti gli indiuidui) hò posto due essempi, l'uno de i quali è fondato sopra
il Soggetto, ch'incomincia; Scimus hoc nostrum meruisse crimen: ilquale è una Parte d'u-na leggiadra compositione à due voci d'Adriano, composta del Primo modo. L'al-tro poi è tutto composto di fantasia. Di maniera che vedendo & essaminando queste
due, & altre simili compositioni, potrà venire all'uso di comporre à cotesto modo facil-mente & bene.
Quando è lecito vsare in vna parte della Cantilena due, ò più volte vn passaggio, & quando non.Cap. XLIIII.
 Hò detto, che non si debbe usar molte uolte un passaggio, intendendo del Contrapunto
replicato nelle istesse consonanze, ne gli istessi mouimenti, & nelle istesse chorde; percio-che non solo è lecito, ma è molto lodeuole il Replicar quante uolte si vuole, ò puote una
modulatione istessa, & un'istesso passaggio; pur che 'l Contrapunto sia sempre differente
& uariato; essendo che tali Repliche hanno un non so chè d'ingegnoso; la onde ogn'uno
si dee sforzare di far tali Repliche, qualunque uolta gli occorrerà di poterle fare, che stia-no bene, senza esserli alcuno errore; percioche sarà riputato da gli Intelligenti huomo di page 248pellegrino ingegno, & abondante d'inuentione. Hò detto, che si dee sforzare; percioche
à far questo il Contrapuntista non è obligato di maniera, che non possa mutare & cambiar
simili passaggi secondo 'l suo uolere; essendo che replicati in cotal modo, non si potreb-beno vsar troppo di lungo, se non con gran discommodo delle Parti; cioè, con sini-stre modulationi. Ma quando non accaderanno cotali inconuenienti; si potranno repli-care; percioche fanno buono effetto; come ne i sottoposti essempi si puo vdire.
Hò detto, che non si debbe usar molte uolte un passaggio, intendendo del Contrapunto
replicato nelle istesse consonanze, ne gli istessi mouimenti, & nelle istesse chorde; percio-che non solo è lecito, ma è molto lodeuole il Replicar quante uolte si vuole, ò puote una
modulatione istessa, & un'istesso passaggio; pur che 'l Contrapunto sia sempre differente
& uariato; essendo che tali Repliche hanno un non so chè d'ingegnoso; la onde ogn'uno
si dee sforzare di far tali Repliche, qualunque uolta gli occorrerà di poterle fare, che stia-no bene, senza esserli alcuno errore; percioche sarà riputato da gli Intelligenti huomo di page 248pellegrino ingegno, & abondante d'inuentione. Hò detto, che si dee sforzare; percioche
à far questo il Contrapuntista non è obligato di maniera, che non possa mutare & cambiar
simili passaggi secondo 'l suo uolere; essendo che replicati in cotal modo, non si potreb-beno vsar troppo di lungo, se non con gran discommodo delle Parti; cioè, con sini-stre modulationi. Ma quando non accaderanno cotali inconuenienti; si potranno repli-care; percioche fanno buono effetto; come ne i sottoposti essempi si puo vdire.

 page 249Et perche alle uolte i Musici si sogliono obligar di fare il Contrapunto, vsando sempre
vn passaggio, & replicarlo; uariando però il concento; il qual modo dicono Far con-trapunto con obligo; onde tali Repliche, ò passaggi chiamano Pertinacie; però quando
alcun uorrà obligarsi ad una cosa simile, piglierà un Thema, ò Passaggio, & incomincie-rà à fare il Contrapunto sopra il proposto Soggetto. Ma perche questa maniera di far
Contrapunto è molto difficile; però il Contrapuntista potrà prendere alcune licenze; co-me sarebbe dire, usare alle uolte alcune modulationi, che non fussero cosi ageuoli al can-tare; come portarebbe il douere, quando il Contrapunto si ponesse in iscritto, & fusse
senza obligo alcuno. Et potrà usar quelle Figure, che piu gli torneranno commode,
uariando il concento, usando hora le Breui, hora le Semibreui, hora le Minime, & altre
Figure; le quali potrà porre hora sincopate, & hora senza la sincopa; acciò possa satisfa-re all'obligo. Debbe nondimeno sempre hauer l'occhio all'osseruanza di quello, ch'è
stato detto di sopra & mostrato; & di schiuar quanto potrà gli errori; accioche il Con-
page 249Et perche alle uolte i Musici si sogliono obligar di fare il Contrapunto, vsando sempre
vn passaggio, & replicarlo; uariando però il concento; il qual modo dicono Far con-trapunto con obligo; onde tali Repliche, ò passaggi chiamano Pertinacie; però quando
alcun uorrà obligarsi ad una cosa simile, piglierà un Thema, ò Passaggio, & incomincie-rà à fare il Contrapunto sopra il proposto Soggetto. Ma perche questa maniera di far
Contrapunto è molto difficile; però il Contrapuntista potrà prendere alcune licenze; co-me sarebbe dire, usare alle uolte alcune modulationi, che non fussero cosi ageuoli al can-tare; come portarebbe il douere, quando il Contrapunto si ponesse in iscritto, & fusse
senza obligo alcuno. Et potrà usar quelle Figure, che piu gli torneranno commode,
uariando il concento, usando hora le Breui, hora le Semibreui, hora le Minime, & altre
Figure; le quali potrà porre hora sincopate, & hora senza la sincopa; acciò possa satisfa-re all'obligo. Debbe nondimeno sempre hauer l'occhio all'osseruanza di quello, ch'è
stato detto di sopra & mostrato; & di schiuar quanto potrà gli errori; accioche il Con-
 page 250trapunto non sia più tosto biasimato, che lodato; percioche Quella cosa, che si fà ben nel
difficile, è molto più da lodare, che non è quella, ch'è fatta bene senz'alcuna difficultà.
Adunque accioche si habbia di cotal cosa piena cognitione, hò posto due essempi, da i
quali si potrà conoscer quello, che si potrà far ne gli altri simili.
page 250trapunto non sia più tosto biasimato, che lodato; percioche Quella cosa, che si fà ben nel
difficile, è molto più da lodare, che non è quella, ch'è fatta bene senz'alcuna difficultà.
Adunque accioche si habbia di cotal cosa piena cognitione, hò posto due essempi, da i
quali si potrà conoscer quello, che si potrà far ne gli altri simili.
Che non è necessario, che la patre [sic: parte] del Soggetto & quella del Contrapunto incomincino insieme; & di quattro differenze che si trouano delle Figure cantabili.Cap. XLV.
Che le Modulationi debbono essere ben regolate; & quel che dee osseruare il Can-tore nel cantare.Cap. XLVI.
Che non si dè continuar molto di lungo nel graue ò nell'acuto nelle modulatio-ni.Cap. XLVII.
Che 'l porre vna Dissonanza, ouer vna Pausa di minima tra due Consonanze perfette d'una istessa specie, che insieme ascendino, ò discendino; non fà, che tali Consonanze non siano senz'alcun mezo.Cap. XLVIII.
 page 255Sogliono anco alle uolte i Compositori in una particella della compositione, dopo l'Ot-taua posta sopra una figura di Semibreue, che discenda, & habbia sopra, ò sotto di se una
Minima, porre immediatamente due Semiminime, lequali descendino per gradi & senz'
altro mezo; & dopoi la figura seguente ascendi & uenghi all'Ottaua. Simigliantemente
sogliono, dopo una figura di Semiminima posta in Ottaua sopra una Minima, che discendi,
porre un'altra Semiminima, laquale si muoua per salto, & uenghi medesimamente all'
Ottaua; & non solo ciò fanno, ma etiandio pongono in luogo delle Semiminime la Minima col punto, con due chrome seguenti, & altre cose simili; come qui si uedono.
page 255Sogliono anco alle uolte i Compositori in una particella della compositione, dopo l'Ot-taua posta sopra una figura di Semibreue, che discenda, & habbia sopra, ò sotto di se una
Minima, porre immediatamente due Semiminime, lequali descendino per gradi & senz'
altro mezo; & dopoi la figura seguente ascendi & uenghi all'Ottaua. Simigliantemente
sogliono, dopo una figura di Semiminima posta in Ottaua sopra una Minima, che discendi,
porre un'altra Semiminima, laquale si muoua per salto, & uenghi medesimamente all'
Ottaua; & non solo ciò fanno, ma etiandio pongono in luogo delle Semiminime la Minima col punto, con due chrome seguenti, & altre cose simili; come qui si uedono.
 Le quali, auenga che non si possa dire con uerità, che facciano due Ottaue poste l'una dopo l'altra, senz'alcun mezo; percioche si ritroua un'altra Consonanza posta tra loro, ch'è
la Sesta, ouer la Decima; nondimeno non si debbono usar di lungo per due ragioni. La
prima delle quali fù detta nel Cap. 4. & la seconda è, che per la mutatione ueloce, che fà
la Sesta, ò la Decima poste tra loro; ouero per il ueloce mouimento, che fanno, quasi non si
ode; tanto più, che nelle due Semiminime, che seguono la minima, ouer la semibreue sin-copata, la prima è posta nel numero delle dissonanze. Onde maggiormente tali Ottaue
si odono, & si uiene à far contra quello, che si è detto nel sudetto Capitolo, che non si
douessero usar molto spesso accommodate nel Contrapunto in cotal maniera. Et per di-re il uero, i passaggi, che fanno le due Semiminime con la Minima inanti, ouer la Mi-nima col punto, & le due Chrome sequenti; non sono altro, che la diminutione del
mouimento di grado, che fanno insieme due Semibreui. A cotesti anco s'aggiunge, che
non si dè usar quel passaggio, che fanno due parti ascendendo, ò discendendo insieme,
l'una per i gradi della Quinta, procedendo per quattro semiminime, & l'altra per il salto di Quinta, ascendendo per semibreui senz'alcuna diminutione; & le Consonanze,
che cascano nel battere sono due Quinte; come nell'essempio si uede; percioche se ben
Le quali, auenga che non si possa dire con uerità, che facciano due Ottaue poste l'una dopo l'altra, senz'alcun mezo; percioche si ritroua un'altra Consonanza posta tra loro, ch'è
la Sesta, ouer la Decima; nondimeno non si debbono usar di lungo per due ragioni. La
prima delle quali fù detta nel Cap. 4. & la seconda è, che per la mutatione ueloce, che fà
la Sesta, ò la Decima poste tra loro; ouero per il ueloce mouimento, che fanno, quasi non si
ode; tanto più, che nelle due Semiminime, che seguono la minima, ouer la semibreue sin-copata, la prima è posta nel numero delle dissonanze. Onde maggiormente tali Ottaue
si odono, & si uiene à far contra quello, che si è detto nel sudetto Capitolo, che non si
douessero usar molto spesso accommodate nel Contrapunto in cotal maniera. Et per di-re il uero, i passaggi, che fanno le due Semiminime con la Minima inanti, ouer la Mi-nima col punto, & le due Chrome sequenti; non sono altro, che la diminutione del
mouimento di grado, che fanno insieme due Semibreui. A cotesti anco s'aggiunge, che
non si dè usar quel passaggio, che fanno due parti ascendendo, ò discendendo insieme,
l'una per i gradi della Quinta, procedendo per quattro semiminime, & l'altra per il salto di Quinta, ascendendo per semibreui senz'alcuna diminutione; & le Consonanze,
che cascano nel battere sono due Quinte; come nell'essempio si uede; percioche se ben
 sono tramezate dalla Terza, hanno però poca gratia.
E' ben uero, che 'l secondo passaggio è più sopporta-bile del primo; ma non è però lodeuole; percioche
nel cantar la parte diminuita, si ode la Terza posta
tra due Quinte nella terza semiminima, laquale è consonante, & è percossa nella seconda parte della Battuta. Et tanto più si possono sopportare, quanto che le
Quinte tramezate in cotal maniera, non sono cosi
facilmente comprese dall'Vdito; perche non sono semplici, com'è l'Ottaua; & i moui-menti, che fanno le parti, che contengono le Semibreui, non sono di grado, come sono
quegli altri, c'hò mostrato. Ma perche alcuni cantano tali passaggi per diminuire il sal-to di Quinta, che fanno alle uolte le parti; però dico, che si debbono fuggire per ogni
modo. Et se pure ad alcun paresse d'usare non solamente questi, ma gli altri ancora mo-strati di sopra, non debbe però usarli molto spesso, percioche quando non ui fussero al-tre ragioni, ui sono almeno queste, che si uiene à far contra quella Regola, che dice;
Che dobbiamo procedere da una Consonanza all'altra per mouimenti contrarii; & contra quella, che ne auertisce, Che facciamo muouere le parti insieme, quando ascendo-no, ò discendono, l'una di esse almeno per grado, che dourebbono ritrouarsi in quelle page 256parti, che si muouono per salto, & contengono le Semibreui; & nondimeno non lo fan-no; come si può chiaramente uedere. Ma questo basti intorno à i mouimenti, che fan-no due parti cantando insieme.
sono tramezate dalla Terza, hanno però poca gratia.
E' ben uero, che 'l secondo passaggio è più sopporta-bile del primo; ma non è però lodeuole; percioche
nel cantar la parte diminuita, si ode la Terza posta
tra due Quinte nella terza semiminima, laquale è consonante, & è percossa nella seconda parte della Battuta. Et tanto più si possono sopportare, quanto che le
Quinte tramezate in cotal maniera, non sono cosi
facilmente comprese dall'Vdito; perche non sono semplici, com'è l'Ottaua; & i moui-menti, che fanno le parti, che contengono le Semibreui, non sono di grado, come sono
quegli altri, c'hò mostrato. Ma perche alcuni cantano tali passaggi per diminuire il sal-to di Quinta, che fanno alle uolte le parti; però dico, che si debbono fuggire per ogni
modo. Et se pure ad alcun paresse d'usare non solamente questi, ma gli altri ancora mo-strati di sopra, non debbe però usarli molto spesso, percioche quando non ui fussero al-tre ragioni, ui sono almeno queste, che si uiene à far contra quella Regola, che dice;
Che dobbiamo procedere da una Consonanza all'altra per mouimenti contrarii; & contra quella, che ne auertisce, Che facciamo muouere le parti insieme, quando ascendo-no, ò discendono, l'una di esse almeno per grado, che dourebbono ritrouarsi in quelle page 256parti, che si muouono per salto, & contengono le Semibreui; & nondimeno non lo fan-no; come si può chiaramente uedere. Ma questo basti intorno à i mouimenti, che fan-no due parti cantando insieme.
Della Battuta.Cap. XLIX.

 Imperoche il Pyrrhichio si troua tra questi due tempi, ò sillabe breui ˘˘, uane; lo Spon-deo tra queste due tempi lunghi, ò sillabe ¯¯, sù co; il Dattilo ¯˘˘, Giouane; l'Ana-pesto ˘˘¯, cominciò; lo Procelesmatico ˘˘˘˘, uane comin; lo Ionico maggiore ¯¯˘˘,
sù come fan; lo minore ˘˘¯¯, so la sù co; il Coriambo ¯˘˘¯, noi salirem'; l'Antispasto
˘¯¯˘, la sù come; lo Iambo ˘¯, gridan; & lo Tribracho ˘˘˘, bile ca; i quali piedi
(com'hò detto) tutti si possono ridurre anco sotto la Battuta equale. Ma di questo leggasi
il Cap. 13. del Lib. 8. De i Sopplimenti, acciò non si prenda errore. Et perch'è costume de
i Musici, di porre il più delle uolte nella Battuta equale una Breue imperfetta, la quale
contenga due Tempi lunghi, & nella inequale una Breue perfetta, che ne contenga tre;
però ci contentaremo al presente di queste due; percioche ciascun'altra Battuta, che
l'Huomo si potesse imaginare, si potrà sempre ridurre à queste; la prima delle quali si
potrà veramente chiamar battuta Spondaica, & la seconda Trochaica. Et s'alcuno
prendesse di ciò marauiglia, com'io introducessi cosa nuoua, legga Boetio nel proemio della Musica, oue ritrouerà, che Pitagora volendo ritrahere un giouine Taurominita-no dalla furia alla quiete, commandò che 'l Musico douesse cantar lo Spondeo; il quale
ueramente s'vdiua, come etiandio si ode à i nostri giorni ne i Balli, che dimandano page 259Passo è mezo, & Padoane; & in quelli, che nominano Balletti, udimo la Battuta del
Trocheo. Dobbiamo oltra di ciò auertire, accioche alcuno non si marauigli, che essen-do necessario, ch'ogni Compositione incomincia & finisca ancora nella Positione della
mano; cioè, nel principio della Battuta; di sopra hò detto, che lo Iambo si può accom-modare sotto la Battuta inequale, pur che la Cantilena uenghi à terminar sccondo 'l co-stume de i Musici moderni. Ma questo sia detto à bastanza intorno alla Battuta.
Imperoche il Pyrrhichio si troua tra questi due tempi, ò sillabe breui ˘˘, uane; lo Spon-deo tra queste due tempi lunghi, ò sillabe ¯¯, sù co; il Dattilo ¯˘˘, Giouane; l'Ana-pesto ˘˘¯, cominciò; lo Procelesmatico ˘˘˘˘, uane comin; lo Ionico maggiore ¯¯˘˘,
sù come fan; lo minore ˘˘¯¯, so la sù co; il Coriambo ¯˘˘¯, noi salirem'; l'Antispasto
˘¯¯˘, la sù come; lo Iambo ˘¯, gridan; & lo Tribracho ˘˘˘, bile ca; i quali piedi
(com'hò detto) tutti si possono ridurre anco sotto la Battuta equale. Ma di questo leggasi
il Cap. 13. del Lib. 8. De i Sopplimenti, acciò non si prenda errore. Et perch'è costume de
i Musici, di porre il più delle uolte nella Battuta equale una Breue imperfetta, la quale
contenga due Tempi lunghi, & nella inequale una Breue perfetta, che ne contenga tre;
però ci contentaremo al presente di queste due; percioche ciascun'altra Battuta, che
l'Huomo si potesse imaginare, si potrà sempre ridurre à queste; la prima delle quali si
potrà veramente chiamar battuta Spondaica, & la seconda Trochaica. Et s'alcuno
prendesse di ciò marauiglia, com'io introducessi cosa nuoua, legga Boetio nel proemio della Musica, oue ritrouerà, che Pitagora volendo ritrahere un giouine Taurominita-no dalla furia alla quiete, commandò che 'l Musico douesse cantar lo Spondeo; il quale
ueramente s'vdiua, come etiandio si ode à i nostri giorni ne i Balli, che dimandano page 259Passo è mezo, & Padoane; & in quelli, che nominano Balletti, udimo la Battuta del
Trocheo. Dobbiamo oltra di ciò auertire, accioche alcuno non si marauigli, che essen-do necessario, ch'ogni Compositione incomincia & finisca ancora nella Positione della
mano; cioè, nel principio della Battuta; di sopra hò detto, che lo Iambo si può accom-modare sotto la Battuta inequale, pur che la Cantilena uenghi à terminar sccondo 'l co-stume de i Musici moderni. Ma questo sia detto à bastanza intorno alla Battuta.
Della Sincopa.Cap. L.
 Si può etiandio chiamar Sincopata quella Minima, c'hà appresso di sè il Punto, ne
i primi segni, quando è posta nel leuar della battuta; & cosi la Semibreue col punto, sotto l'altro segno; come qui sotto si uedono; ancora che si possa veramente dire, che non siano
Si può etiandio chiamar Sincopata quella Minima, c'hà appresso di sè il Punto, ne
i primi segni, quando è posta nel leuar della battuta; & cosi la Semibreue col punto, sotto l'altro segno; come qui sotto si uedono; ancora che si possa veramente dire, che non siano
 Sincope, se non impropriamente. E' ben uero, che la Semibreue si chiama sincopata, sotto qual segno si uoglia, che dimostri il Tempo perfetto, ò imperfetto; quando uien posta page 260da i Compositori ne i loro contrapunti al detto modo. La Sincopa adunque si fà da una
figura, ò nota, che le uadi auanti, la qual sia di ualore della metà della figura sincopa-ta; oueramente si fà, quando se le pone auanti due, ò più figure, che siano equiualenti à tal
metà. Sono anco tali figure sincopate alle uolte dalle Pause, che si pongono à loro inan-ti; & tali Pause sono di ualore della meza parte delle figure sincopate; come qui si
ueggono.
Sincope, se non impropriamente. E' ben uero, che la Semibreue si chiama sincopata, sotto qual segno si uoglia, che dimostri il Tempo perfetto, ò imperfetto; quando uien posta page 260da i Compositori ne i loro contrapunti al detto modo. La Sincopa adunque si fà da una
figura, ò nota, che le uadi auanti, la qual sia di ualore della metà della figura sincopa-ta; oueramente si fà, quando se le pone auanti due, ò più figure, che siano equiualenti à tal
metà. Sono anco tali figure sincopate alle uolte dalle Pause, che si pongono à loro inan-ti; & tali Pause sono di ualore della meza parte delle figure sincopate; come qui si
ueggono.
 Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne stà bene il sin-copar le Pause; siano poste sotto qual segno si uoglia, ò perfetto, ouer'imperfetto che
sia il Tempo; come sono le sequenti:
Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne stà bene il sin-copar le Pause; siano poste sotto qual segno si uoglia, ò perfetto, ouer'imperfetto che
sia il Tempo; come sono le sequenti:
 Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il prin-cipio di ciascuna, sotto i lor Segni proprii; come mostrerò altroue; & genera anco in-commodo à i Cantori, i quali confidandosi spesse uolte nella loro integrità, non pensan-do che 'l Tempo sia in loro uariato, senza tenerne memoria & conto alcuno, pongono la
Battuta nel loro principio; & per tal maniera ingannati, uengono necessariamente ad
errar cantando. Questi incommodi adunque si debbono per ogni modo schiuare; percioche non furono mai sopportati da i buoni & discreti Musici; come si può ueder nelle
compositioni d'Ocheghen, di Giosquino, di Motone, & d'altri più Antichi di loro; pur
che non siano state guaste d'alcuno ignorante Scrittore. Per la qual cosa, quando oc-correrà di por le Pause di breue ò di semibreue, & non caschera nno [sic: cascheranno] nel principio della
Battuta, & del loro Tempo, allora si debbono ridurre sotto l'uno & l'altro; come nel
seguente essempio si uede.
Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il prin-cipio di ciascuna, sotto i lor Segni proprii; come mostrerò altroue; & genera anco in-commodo à i Cantori, i quali confidandosi spesse uolte nella loro integrità, non pensan-do che 'l Tempo sia in loro uariato, senza tenerne memoria & conto alcuno, pongono la
Battuta nel loro principio; & per tal maniera ingannati, uengono necessariamente ad
errar cantando. Questi incommodi adunque si debbono per ogni modo schiuare; percioche non furono mai sopportati da i buoni & discreti Musici; come si può ueder nelle
compositioni d'Ocheghen, di Giosquino, di Motone, & d'altri più Antichi di loro; pur
che non siano state guaste d'alcuno ignorante Scrittore. Per la qual cosa, quando oc-correrà di por le Pause di breue ò di semibreue, & non caschera nno [sic: cascheranno] nel principio della
Battuta, & del loro Tempo, allora si debbono ridurre sotto l'uno & l'altro; come nel
seguente essempio si uede.
Della Cadenza, quello ch'ella sia, delle sue Specie, & del suo uso.Cap. LI.
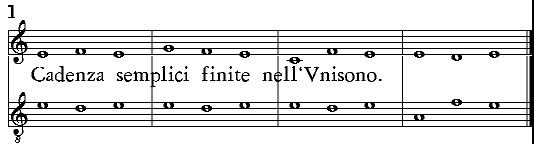 page 262Le Diminuite terminate per l'Vnisono sono quelle, che contengono un simil procedere;
ma si fanno con diuerse figure, tra le quali si ritroua la Sincopa, della quale la sua secon-da patte, ch'è quella, ch'è percossa dalla Battuta, si troua dissonante; cioè, una Se-conda. Onde dopo essa immediatamente seguendo la Terza minore, si uiene à fini-re all'Vnisono.
page 262Le Diminuite terminate per l'Vnisono sono quelle, che contengono un simil procedere;
ma si fanno con diuerse figure, tra le quali si ritroua la Sincopa, della quale la sua secon-da patte, ch'è quella, ch'è percossa dalla Battuta, si troua dissonante; cioè, una Se-conda. Onde dopo essa immediatamente seguendo la Terza minore, si uiene à fini-re all'Vnisono.
 Et perche i Prattici sogliono il più delle uolte diminuire quella parte della Cadenza,
che contiene la Sincopa, per potere, secondo che li torna commodo, accommodar le
Harmonie alle Parole; però auanti ch'io uada più oltra, uoglio porre tali Diminutioni,
che si ueggano; & saranno le seguenti, le quali potranno apportar molto utile nell'accommodar le Figure cantabili alle Parole soggette; come uederemo nella Quarta parte.
Et perche i Prattici sogliono il più delle uolte diminuire quella parte della Cadenza,
che contiene la Sincopa, per potere, secondo che li torna commodo, accommodar le
Harmonie alle Parole; però auanti ch'io uada più oltra, uoglio porre tali Diminutioni,
che si ueggano; & saranno le seguenti, le quali potranno apportar molto utile nell'accommodar le Figure cantabili alle Parole soggette; come uederemo nella Quarta parte.
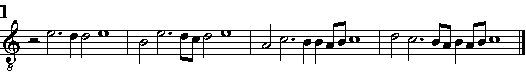 Qui debbe ciascun Compositore auertire, che quantunque le Cadenze siano poste so-lamente ne i mostrati luoghi; nondimeno si possono fare anco in qualunque altro luogo,
oue torna più commodo, pur che si osserui la Regola data di sopra nel Cap. 38. di andare dalla Consonanza imperfetta alla Perfetta con la più uicina. La onde fà dibisogno,
che nelle penultime figure di queste Cadenze sia la Terza minore, la qual sempre si udi-rà, quando faranno il mouimento all'Vnisono di maniera, che l'una discenda per grado
di Tuono, & l'altra con un simile mouimento di Semituono maggiore ascenda, ò per il
contrario. Et ciò si potrà sempre fare in ciascun luogo, senza porre il segno
Qui debbe ciascun Compositore auertire, che quantunque le Cadenze siano poste so-lamente ne i mostrati luoghi; nondimeno si possono fare anco in qualunque altro luogo,
oue torna più commodo, pur che si osserui la Regola data di sopra nel Cap. 38. di andare dalla Consonanza imperfetta alla Perfetta con la più uicina. La onde fà dibisogno,
che nelle penultime figure di queste Cadenze sia la Terza minore, la qual sempre si udi-rà, quando faranno il mouimento all'Vnisono di maniera, che l'una discenda per grado
di Tuono, & l'altra con un simile mouimento di Semituono maggiore ascenda, ò per il
contrario. Et ciò si potrà sempre fare in ciascun luogo, senza porre il segno  della chor-da chromatica, per far dell'interuallo del Tuono un Semituono; imperoche in quel-la parte, che la penultima Figura & l'ultima si troua il mouimento, che ascende, sempre
s'intende esser collocato il Semituono; pur che l'altra parte non discenda per simile In-teruallo; conciosiache allora il Semituono non si potrebbe porre da due parti; cioè, nel-la parte graue, & nell'acuta; perche s'vdirebbe un'Interuallo minore d'un Semiditono,
che sarebbe dissonante. Ma la Natura hà prouisto in simil cosa; percioche non solamen-te i periti della Musica, ma anco i Contadini, che cantano senz'alcuna arte, procedo-no cantando à questo modo per l'interuallo del Semituono. Queste sono dette
Cadenze propriamente; ancora che quando le lor prime Figure si ritrouassero distanti page 263l'vna dall'altra per Quinta, & le seconde per un Semiditono, & le ultime finissero per
l'Vnisono; come sono le sequenti non farebbono, che non si potessero anco chiamare Ca-denze; quantunque si potesse dire, che si chiamassero impropriamente. La Cadenza ter-
della chor-da chromatica, per far dell'interuallo del Tuono un Semituono; imperoche in quel-la parte, che la penultima Figura & l'ultima si troua il mouimento, che ascende, sempre
s'intende esser collocato il Semituono; pur che l'altra parte non discenda per simile In-teruallo; conciosiache allora il Semituono non si potrebbe porre da due parti; cioè, nel-la parte graue, & nell'acuta; perche s'vdirebbe un'Interuallo minore d'un Semiditono,
che sarebbe dissonante. Ma la Natura hà prouisto in simil cosa; percioche non solamen-te i periti della Musica, ma anco i Contadini, che cantano senz'alcuna arte, procedo-no cantando à questo modo per l'interuallo del Semituono. Queste sono dette
Cadenze propriamente; ancora che quando le lor prime Figure si ritrouassero distanti page 263l'vna dall'altra per Quinta, & le seconde per un Semiditono, & le ultime finissero per
l'Vnisono; come sono le sequenti non farebbono, che non si potessero anco chiamare Ca-denze; quantunque si potesse dire, che si chiamassero impropriamente. La Cadenza ter- minata per Ottaua è di tal sorte, che le sue Figure vo-gliono esser ordinate di modo; che la prima, la seconda,
& la terza della parte acuta; & la prima, la seconda, &
la terza della parte graue, si muouino con mouimen-ti contrarij di grado l'una parte contra l'altra; & le se-conde Figure delle parti siano distanti l'una dall'altra
per una Sesta maggiore, & le ultime per una Ottaua. Et
quantunque potesse essere alcuna differenza de moui-menti tra le prime & le seconde Figure; percioche fa-cendo le Figure della parte acuta i loro mouimenti sem-pre di grado, quelle della parte graue alcune uolte potranno procedere per mouimenti
di salto, discendendo alcuna uolta insieme; tuttauia siano accommodate in qual manie-ra si uogliano, le seconde Figure della Cadenza si porranno sempre distanti l'una dall'al-tra per l'interuallo di Sesta maggiore, & le ultime finiranno in Ottaua. Et ciò sempre tor-nerà bene, quando una parte farà il mouimento de grado de Semituono, ò nel graue,
oueramente nell'acuto; & l'altra quello del Tuono, cosi in queste come in ogn'altra sorte
di Cadenza, sia semplice, ò diminuita. E' ben uero che le Cadenze diminuite hanno la
Sincopa, nella quale si ode la Settima sopra la sua seconda parte; cioè, nel battere; ma la
Cadenza semplice è tutta consonante; percioche le sue figure sono tra loro equali; come
ne i sequenti essempi si può uedere.
minata per Ottaua è di tal sorte, che le sue Figure vo-gliono esser ordinate di modo; che la prima, la seconda,
& la terza della parte acuta; & la prima, la seconda, &
la terza della parte graue, si muouino con mouimen-ti contrarij di grado l'una parte contra l'altra; & le se-conde Figure delle parti siano distanti l'una dall'altra
per una Sesta maggiore, & le ultime per una Ottaua. Et
quantunque potesse essere alcuna differenza de moui-menti tra le prime & le seconde Figure; percioche fa-cendo le Figure della parte acuta i loro mouimenti sem-pre di grado, quelle della parte graue alcune uolte potranno procedere per mouimenti
di salto, discendendo alcuna uolta insieme; tuttauia siano accommodate in qual manie-ra si uogliano, le seconde Figure della Cadenza si porranno sempre distanti l'una dall'al-tra per l'interuallo di Sesta maggiore, & le ultime finiranno in Ottaua. Et ciò sempre tor-nerà bene, quando una parte farà il mouimento de grado de Semituono, ò nel graue,
oueramente nell'acuto; & l'altra quello del Tuono, cosi in queste come in ogn'altra sorte
di Cadenza, sia semplice, ò diminuita. E' ben uero che le Cadenze diminuite hanno la
Sincopa, nella quale si ode la Settima sopra la sua seconda parte; cioè, nel battere; ma la
Cadenza semplice è tutta consonante; percioche le sue figure sono tra loro equali; come
ne i sequenti essempi si può uedere.
 Si può etiandio uedere, in qual maniera spesse uolte si potrà
cambiar le parti della Cadenza tra loro, & porre quel passag-gio, che fà la parte posta nel graue, nella parte acuta; & per
il contrario, quel che fà la parte acuta, nella parte graue, che
corrispondino per una Ottaua, percioche tali mutationi sono
molto commode à i Compositori. Oltra queste due sorti di
Cadenza, ue n'è un'altra terminata per Ottaua, ouer per Vni-sono; laqual si fà, quando si pone le seconde Figure della par-te graue & quelle della parte acuta distanti tra loro per un Ditono; facendo discende-re la parte graue per un salto di Quinta, ouero ascendere per quello di Quarta; & ascen-dere la parte acuta per grado; come si uede.
Si può etiandio uedere, in qual maniera spesse uolte si potrà
cambiar le parti della Cadenza tra loro, & porre quel passag-gio, che fà la parte posta nel graue, nella parte acuta; & per
il contrario, quel che fà la parte acuta, nella parte graue, che
corrispondino per una Ottaua, percioche tali mutationi sono
molto commode à i Compositori. Oltra queste due sorti di
Cadenza, ue n'è un'altra terminata per Ottaua, ouer per Vni-sono; laqual si fà, quando si pone le seconde Figure della par-te graue & quelle della parte acuta distanti tra loro per un Ditono; facendo discende-re la parte graue per un salto di Quinta, ouero ascendere per quello di Quarta; & ascen-dere la parte acuta per grado; come si uede.
 Et sono queste Cadenze di due sorti medesimamente; Semplice & Diminuite; come si
può vedere. Quelle che sono Semplici, hanno le Figure simili; & le Diminuite hanno
le Figure diuerse; & tra loro si ritroua la Sincopa, che hà nella sua seconda parte la Quar-ta, dopo la quale segue immediatamente la Terza maggiore; come hò mostrato. Ma per-che queste Cadenze non si vsano molto nelle Compositioni de due voci; conciosia che
l'ascendere per i mostrati salti, & lo discendere anco è proprio della parte grauissima di al-cuna compositione composta à più voci; però si guardaremo di porle spesso; & quando
le vorremo porre, sempre le porremo nel mezo, & non nel fine della Cantilena; & quan-do la necessità ciò fare ne astringesse; cioè, quando volessimo porre le Parti della compo-sitione in Consequenza, ouero nella Imitatione; Secondo i modi che si mostrerà più oltra;
& quando non si potesse hauere per altra via vn passaggio commodo al cantare, & vna
grata m odulatione [sic: modulatione]. E' ben uero, che questo voglio che più tosto sia conseglio, che pre-cetto; percioche quando si ponessero anco nel principio & nel fine, non sarebbe errore.
Oltra di questo si troua la Cadenza terminata per Quinta, ouero, per Terza, ò per altra
Consonanza; la quale è detta Cadenza impropriamente; & è contenuta similmente da
vn numero simile de Figure; & è ordinata in tal modo, che essendo le Seconde figure dell'una & dell'altra parte distanti per vna Terza, le vltime vengono à cascare in vna delle
nominate Consonanze; & questo quando la parte acuta fà il mouimento di grado ascen-dendo; & è di due sorti, Semplice & Diminuita; ciascuna delle quali hormai per tanti es-sempi dati di sopra, credo che sia da ogn'vno conosciuta; la onde bastarà dire solamente,
che nella Diminuita si ode la Quarta nella seconda parte della Sincopa & non altra disso-nanza; come si può udire in ciascuna, che si troua ne i sottoposti essempi. page 265
Et sono queste Cadenze di due sorti medesimamente; Semplice & Diminuite; come si
può vedere. Quelle che sono Semplici, hanno le Figure simili; & le Diminuite hanno
le Figure diuerse; & tra loro si ritroua la Sincopa, che hà nella sua seconda parte la Quar-ta, dopo la quale segue immediatamente la Terza maggiore; come hò mostrato. Ma per-che queste Cadenze non si vsano molto nelle Compositioni de due voci; conciosia che
l'ascendere per i mostrati salti, & lo discendere anco è proprio della parte grauissima di al-cuna compositione composta à più voci; però si guardaremo di porle spesso; & quando
le vorremo porre, sempre le porremo nel mezo, & non nel fine della Cantilena; & quan-do la necessità ciò fare ne astringesse; cioè, quando volessimo porre le Parti della compo-sitione in Consequenza, ouero nella Imitatione; Secondo i modi che si mostrerà più oltra;
& quando non si potesse hauere per altra via vn passaggio commodo al cantare, & vna
grata m odulatione [sic: modulatione]. E' ben uero, che questo voglio che più tosto sia conseglio, che pre-cetto; percioche quando si ponessero anco nel principio & nel fine, non sarebbe errore.
Oltra di questo si troua la Cadenza terminata per Quinta, ouero, per Terza, ò per altra
Consonanza; la quale è detta Cadenza impropriamente; & è contenuta similmente da
vn numero simile de Figure; & è ordinata in tal modo, che essendo le Seconde figure dell'una & dell'altra parte distanti per vna Terza, le vltime vengono à cascare in vna delle
nominate Consonanze; & questo quando la parte acuta fà il mouimento di grado ascen-dendo; & è di due sorti, Semplice & Diminuita; ciascuna delle quali hormai per tanti es-sempi dati di sopra, credo che sia da ogn'vno conosciuta; la onde bastarà dire solamente,
che nella Diminuita si ode la Quarta nella seconda parte della Sincopa & non altra disso-nanza; come si può udire in ciascuna, che si troua ne i sottoposti essempi. page 265 Ne in queste (quando si fanno à due uoci) è necessario, che sempre si odi in vna parte il
grado del Semituono maggiore, ò graue, ouero acuta ch'ella sia; percioche si vdirebbe al-le volte tra le Parti la relatione, che non sarebbe harmonica; come nel Cap. 30 hò dichia-rato. Sarebbe cosa molto tediosa, s'io volesse dare essempio particolare d'ogni Ca-denza propria & non propria; conciosia che sono quasi infinite; onde è dibisogno, che 'l
Contrapuntista s'ingegni di ritrouarne sempre di nuoue, inuestigando di continuo nuo-ue maniere; & guardandosi di non commettere errore. Et accioche ei possa vedere in
qual modo le Cadenze si possono per diuersi modi ordinare, & in qual maniera si possono
usare; per non andare in lungo; porrò molti essempi, da i quali potrà scorger quello, che
hauerà da fare nella inuentione delle altre.
Ne in queste (quando si fanno à due uoci) è necessario, che sempre si odi in vna parte il
grado del Semituono maggiore, ò graue, ouero acuta ch'ella sia; percioche si vdirebbe al-le volte tra le Parti la relatione, che non sarebbe harmonica; come nel Cap. 30 hò dichia-rato. Sarebbe cosa molto tediosa, s'io volesse dare essempio particolare d'ogni Ca-denza propria & non propria; conciosia che sono quasi infinite; onde è dibisogno, che 'l
Contrapuntista s'ingegni di ritrouarne sempre di nuoue, inuestigando di continuo nuo-ue maniere; & guardandosi di non commettere errore. Et accioche ei possa vedere in
qual modo le Cadenze si possono per diuersi modi ordinare, & in qual maniera si possono
usare; per non andare in lungo; porrò molti essempi, da i quali potrà scorger quello, che
hauerà da fare nella inuentione delle altre.
 Non voglio etiandio restar di dire, che i Prattici sogliono vsare alle uolte nelle Cadenze,
& in altri luoghi ancora, in vece della Semibreue sincopata la Semibreue col punto, che
sia dissonante; vsando poi quelle circonstanze, che conuengono alla Cadenza & alla Sin-copa posta in cotal modo. Et benche cotal cosa sia tollerata, nondimeno non sodisfà à
pieno il sentimento. La onde essortarei il Compositore à non far simil passaggi molto spes-so ne[unclear: l]le sue compositioni, se non sforzato da necessità; percioche (secondo 'l mio giudi-cio) parmi, che non siano da esser poste nel numero delle Cadenze; massimamente non page 266osseruando tutto quello, che ricerca la Cadenza; come ogn'vno potrà giudicare, dopo
c'haurà vditi & essaminati i sequenti essempi.
Non voglio etiandio restar di dire, che i Prattici sogliono vsare alle uolte nelle Cadenze,
& in altri luoghi ancora, in vece della Semibreue sincopata la Semibreue col punto, che
sia dissonante; vsando poi quelle circonstanze, che conuengono alla Cadenza & alla Sin-copa posta in cotal modo. Et benche cotal cosa sia tollerata, nondimeno non sodisfà à
pieno il sentimento. La onde essortarei il Compositore à non far simil passaggi molto spes-so ne[unclear: l]le sue compositioni, se non sforzato da necessità; percioche (secondo 'l mio giudi-cio) parmi, che non siano da esser poste nel numero delle Cadenze; massimamente non page 266osseruando tutto quello, che ricerca la Cadenza; come ogn'vno potrà giudicare, dopo
c'haurà vditi & essaminati i sequenti essempi.
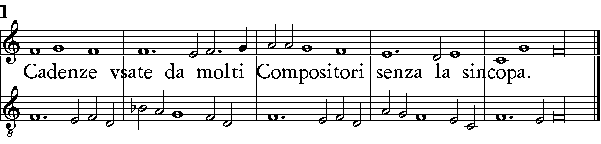 Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfet-tione delle parti di tutto il concento; come anco, accioche per il loro mezo si hauesse à fi-nire la Sentenza perfetta delle parole; è honesto, che volendola terminare per esse, che si
finisca per una delle consonanze perfettissime; cioè per la Ottaua, ò almeno per l'Vniso-no; accioche il Perfetto proportionatamente si uenga à finire col Perfetto. Ma quando
si vorrà fare alcuna distintione mezana dell'Harmonia & delle Parole insieme, le quali
non habbiano finita perfettamente la loro sentenza, ò pericolo; potremo vsar quelle Cadenze, che finiscono per Terza, per Quinta, per Sesta, ò per altre simili consonanze; per-che il finire à cotesto modo, non è fine di Cadenza perfetta; ma si chiama fuggir la Ca-denza, come hora la chiamano i Musici. Et fù buono il ritrouar; che le Cadenze finisse-ro anco in tal maniera; conciosia che alle uolte accasca al Compositore, che venendoli
alle mani un bel passaggio, nel quale si accommodarebbe ottimamente la Cadenza, &
non hauendo fatto fine al Periodo nelle parole; non essendo honesto, c'habbiano à finire
in essa; cerca di fuggirla, non solamente al modo mostrato; ma nella maniera ch'io mo-strerò nel seguente Capitolo. Et se ben da quello c'hò detto, si possa concludere, che
qualunque uolta alcuna Cadenza non finirà nella Ottaua, ouer nell'Vnisono, si potrà
chiamare Imperfetta; perche si fugge il fine perfetto; tuttauia perche il fuggir la Ca-denza si fà in molti altri modi, voglio che uediamo hora in qual guisa la si possa fuggire,
& il modo che si potrà tenere, quando vna parte del Contrapunto farà il mouimen-to di salto; cioè, quand o [sic: quando] si mouerà di due, ò più gradi; come accade molte volte nel-le Compositioni.
Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfet-tione delle parti di tutto il concento; come anco, accioche per il loro mezo si hauesse à fi-nire la Sentenza perfetta delle parole; è honesto, che volendola terminare per esse, che si
finisca per una delle consonanze perfettissime; cioè per la Ottaua, ò almeno per l'Vniso-no; accioche il Perfetto proportionatamente si uenga à finire col Perfetto. Ma quando
si vorrà fare alcuna distintione mezana dell'Harmonia & delle Parole insieme, le quali
non habbiano finita perfettamente la loro sentenza, ò pericolo; potremo vsar quelle Cadenze, che finiscono per Terza, per Quinta, per Sesta, ò per altre simili consonanze; per-che il finire à cotesto modo, non è fine di Cadenza perfetta; ma si chiama fuggir la Ca-denza, come hora la chiamano i Musici. Et fù buono il ritrouar; che le Cadenze finisse-ro anco in tal maniera; conciosia che alle uolte accasca al Compositore, che venendoli
alle mani un bel passaggio, nel quale si accommodarebbe ottimamente la Cadenza, &
non hauendo fatto fine al Periodo nelle parole; non essendo honesto, c'habbiano à finire
in essa; cerca di fuggirla, non solamente al modo mostrato; ma nella maniera ch'io mo-strerò nel seguente Capitolo. Et se ben da quello c'hò detto, si possa concludere, che
qualunque uolta alcuna Cadenza non finirà nella Ottaua, ouer nell'Vnisono, si potrà
chiamare Imperfetta; perche si fugge il fine perfetto; tuttauia perche il fuggir la Ca-denza si fà in molti altri modi, voglio che uediamo hora in qual guisa la si possa fuggire,
& il modo che si potrà tenere, quando vna parte del Contrapunto farà il mouimen-to di salto; cioè, quand o [sic: quando] si mouerà di due, ò più gradi; come accade molte volte nel-le Compositioni.
Il modo di fuggir le Cadenze; & quello che si haurà da osseruare, quando il Soggetto fa-rà il mouimento di salto.Cap. LII.

Delle Pause.Cap. LIII.
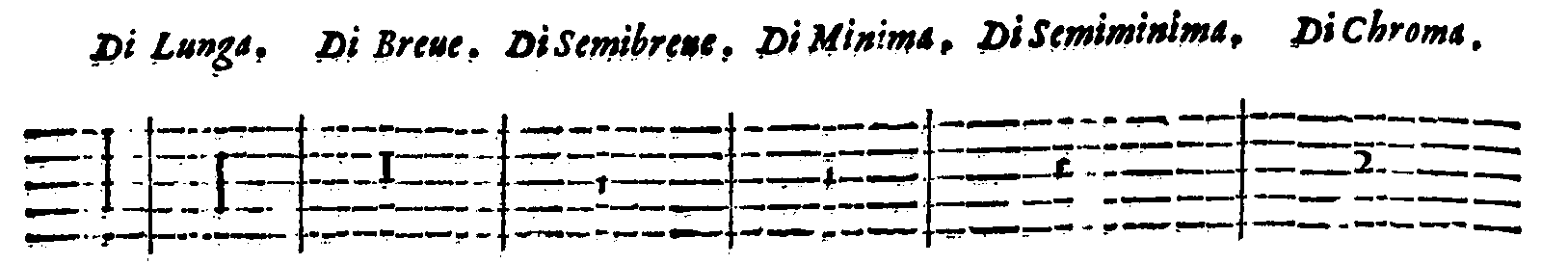
Quod caret alterna requie, durabile non est.Ritrouarono questo opportuno rimedio. La onde si può dir con uerità della Pausa quello che segue.
Haec reparat vires, fessaque membra leuat.Furono poi ritrouate le Pause per ornamento della cantilena; percioche per mezo lo-ro, le Parti si possono porre l'una dopo l'altra in Consequenza; come uederemo; il qual modo fà la cantilena non solo arteficiosa, ma etiandio diletteuole; conciosia che 'l cantare di continuo, che fanno cotali parti insieme genera noia non solamente à i Cantori, ma anche à gli Ascoltanti induce sacietà; & il farle tacere alcune uolte con qualche proposi-to, facendone can[unclear: t]are hora due, hora tre, hora quatro, & tallora (essendo la compositione à più voci) tutte insieme, massimamente nel fine, conciosia ch'è necessario, che tutte le par-ti insieme cantino & insieme finiscano; fà, che le compositioni per tal uarietà riusci-scono più uaghe, & più diletteuoli. Onde ritrouarono un segno, che rappresentas-se questa taciturnità, ò silentio; & l'usarono per la cosa significata, & lo nominarono Pausa; la quale, dal suo officio dissero esser'un' certo Intralasciamento arteficioso di uo-ce. Et ben dissero Arteficioso intralasciamento; uolendoci auertire, che non douessi-mo por le Pause nelle cantilene fuor di proposito, & senz'arteficio, ma collocarle di ma-niera che si ueda, che la necessità, & l'arteficio lo richieda. Imperoche si come è ui-tiosa cosa ad alcuno, che parli sempre, & non sappia por fine, ò meta al suo parla-re; cosi è cosa uitiosa al Musico, che non sappia à tempo & luogo dar riposo alle parti della sua compositione. Di modo che; si come non è senza uirtù il saper ragionare, & tace-re con proposito; cosi ancora non è senza uirtù, che 'l Musico sappia far tacere, & can-tare le parti della sua cantilena à tempo & luogo. Ma si debbe auertire, che doue ac-cascasse di porre più Pause, le quali eccedessero il ualore di quella della Lunga, al-lora questa si debbe raddoppiare; come auerebbe, quando si uolesse segnar la Pausa della Massima; ma quando si uolesse raddoppiar le Pause, che rappresentano essa Massima, ouer porle appresso altre pause minori, allora si potrà por quelle, che si aggiungono sopra l'altre linee; percioche non si costuma tra i Musici di porre insieme tante Pause sopra quelle righe istesse, che sopr'auanzino il ualore di essa Massima; come in questo es-sempio si ueggono.
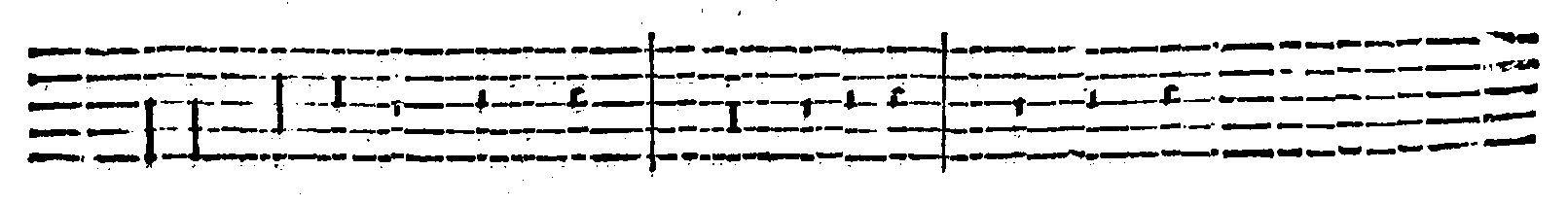 page 269Sono state uarie opinioni di questo nome Pausa; percioche alcuni hanno hauuto pare-re, che sia stata detta da Παύομαι parola Greca, che significa Cessare, Posare, ò Lasciare.
Altri hanno uoluto, che sia cosi chiamata dal Batter delle mani, che da i Latini è detto
Plausus; conciosia ch'è misurata dalla Positione & dalla Leuatione della Battuta, la quale
si conosce dal segno formato dalla mano, come di sopra habbiamo ueduto.Supra
cap. 49. Et forse, che
non fù detta da principio ne all'uno, ne all'altro modo de i due nominati; ma piò presto
(come pare ad alcuni) da Posa parola Francese, che significa Posata. Onde si suol dire
Vna pausa, due pause, & l'altre; cioè, una posata, due posate, & cosi il resto. Ma sia
detta da che si uoglia, questo importa poco; purche si sappia, che quando [unclear: ']l Compositore pone le Pause nella cantilena, uuole, che iui il Cantore taccia per tanto spacio di tempo, quanto significa il ualor delle Pause. Gli Ecclesiastici etiandio pongono le Pause ne
i lor canti, non già per ornamento, ma per necessità; perche è impossibile di poter peruenire al fine di cotali cantilene, senza pigliare alcun riposo. La onde di ciò aueduti, ritrouarono un segno, dal quale ciascuno Cantore è auertito, che arriuando à quello, s'hab-bia da fermare, & pigliare Spirito, ò fiato. Perilche da un tale effetto lo chiamarono
Πνεῦμα, che uuol dire Spirito. Posero etiandio cotal segno, accioche ogn'uno de i Cantori concordeuolmente si hauesse da fermare; onde lo dimandarono Νεῦμα; che uuol dir
Cenno & Consenso. E' ben uero, che non pongono tali Pause nel modo, che si pon-gono l'altre mostrate di sopra; percioche le pongono di maniera, che cingono & abbracciano tutte le linee della cantilena; tallora ponendole semplici, & tallora raddoppiate;
come qui si ueggono. Et si debbe per ogni modo osseruar quello, che già molti de gli
page 269Sono state uarie opinioni di questo nome Pausa; percioche alcuni hanno hauuto pare-re, che sia stata detta da Παύομαι parola Greca, che significa Cessare, Posare, ò Lasciare.
Altri hanno uoluto, che sia cosi chiamata dal Batter delle mani, che da i Latini è detto
Plausus; conciosia ch'è misurata dalla Positione & dalla Leuatione della Battuta, la quale
si conosce dal segno formato dalla mano, come di sopra habbiamo ueduto.Supra
cap. 49. Et forse, che
non fù detta da principio ne all'uno, ne all'altro modo de i due nominati; ma piò presto
(come pare ad alcuni) da Posa parola Francese, che significa Posata. Onde si suol dire
Vna pausa, due pause, & l'altre; cioè, una posata, due posate, & cosi il resto. Ma sia
detta da che si uoglia, questo importa poco; purche si sappia, che quando [unclear: ']l Compositore pone le Pause nella cantilena, uuole, che iui il Cantore taccia per tanto spacio di tempo, quanto significa il ualor delle Pause. Gli Ecclesiastici etiandio pongono le Pause ne
i lor canti, non già per ornamento, ma per necessità; perche è impossibile di poter peruenire al fine di cotali cantilene, senza pigliare alcun riposo. La onde di ciò aueduti, ritrouarono un segno, dal quale ciascuno Cantore è auertito, che arriuando à quello, s'hab-bia da fermare, & pigliare Spirito, ò fiato. Perilche da un tale effetto lo chiamarono
Πνεῦμα, che uuol dire Spirito. Posero etiandio cotal segno, accioche ogn'uno de i Cantori concordeuolmente si hauesse da fermare; onde lo dimandarono Νεῦμα; che uuol dir
Cenno & Consenso. E' ben uero, che non pongono tali Pause nel modo, che si pon-gono l'altre mostrate di sopra; percioche le pongono di maniera, che cingono & abbracciano tutte le linee della cantilena; tallora ponendole semplici, & tallora raddoppiate;
come qui si ueggono. Et si debbe per ogni modo osseruar quello, che già molti de gli
 Antichi hanno osseruato; di non porre tali Pause, se non nel fine
delle Clausule, ò punti della Oratione, sopra la quale è composta la
cantilena; & simigliantemente nel fine d'ogni Periodo. Ilche fà dibisogno, che i Compositoti [sic: Compositori] etiandio auertiscano; accioche i Membri
dell'Oratione siano diuisi, & la Sentenza delle parole si oda & intenda interamente; percioche facendo in cotal modo, allora si potrà dire, che le Pause siano state poste nelle Parti della cantilena con qualche proposito, & non à caso. Ne si debbono per l'auenire porre per alcun modo, auanti che sia finita la Sentenza nel mezo della Clausula, conciosia
che colui, che le ponesse à cotal modo, dimostrarebbe ueramente essere un pecora campi, un goffo & un'ignorante. Però adunque il Musico si sforzerà di non cascare in simili
errori; accioche non dia à i dotti di sè mala opinione.
Antichi hanno osseruato; di non porre tali Pause, se non nel fine
delle Clausule, ò punti della Oratione, sopra la quale è composta la
cantilena; & simigliantemente nel fine d'ogni Periodo. Ilche fà dibisogno, che i Compositoti [sic: Compositori] etiandio auertiscano; accioche i Membri
dell'Oratione siano diuisi, & la Sentenza delle parole si oda & intenda interamente; percioche facendo in cotal modo, allora si potrà dire, che le Pause siano state poste nelle Parti della cantilena con qualche proposito, & non à caso. Ne si debbono per l'auenire porre per alcun modo, auanti che sia finita la Sentenza nel mezo della Clausula, conciosia
che colui, che le ponesse à cotal modo, dimostrarebbe ueramente essere un pecora campi, un goffo & un'ignorante. Però adunque il Musico si sforzerà di non cascare in simili
errori; accioche non dia à i dotti di sè mala opinione.
Delle Consequenze.Cap. 54.
 si uicine & unite; & si allontanarono alquanto da quelle, che sono tanto communi; & cercaranno con ogni lor potere di farle, che fussero più noue; conciosiache quando si faranno la Guida & il Consequente alquanto distanti l'uno dall'altro per tre Pause di Mini-ma, ouer per cinque, ò per altre simili; uerranno senza dubbio, à far qualche noua uariatione. Io non dico già che le Consequenze distanti per l'una Pausa di Minima, ò di
Semibreue non si debbino usare; ma dico, che non si debbono usar molto spesso; per non
cascare in quello, ch'è tanto commune; n [sic: &] che non si ritroua libro, nel quale non sia molte
& molte uolte replicato; il qual lascio di mostrare, per non esser tedioso, & per non of-fender alcuno. Ma accioche si caui qualche frutto da quello, ch'io hò detto; porrò pri-ma l'essempio delle Consequenze sciolte, le quali si fanno sopra i Canti fermi à loro
imitatione; percioche di quelle che si trouano tra due parti diminuite, se ne potrà
hauere due accommodati essempi, posti di sopra nel Cap. 43. Ma delle legate, che
si fanno in molte maniere, ne porrò qui alcune solamente: essendo ch'è impossi-bile di poterle por tutte, & dimostrarle con breuità in poche carte; nelle quali s'hauerà
da osseruar questo nella prima maniera, che siano poste l'una con l'altra in Con-sequenza all'Vnisono, ouero alla Quarta, oueramente alla Quinta, ò pure all'Ot-taua incominciando da qual parte si uoglia, sia la graue, ouer l'acuta, che que-sto importa poco. La onde finito che sarà il tutto; come qui si uede; si piglierà la par-page 272
si uicine & unite; & si allontanarono alquanto da quelle, che sono tanto communi; & cercaranno con ogni lor potere di farle, che fussero più noue; conciosiache quando si faranno la Guida & il Consequente alquanto distanti l'uno dall'altro per tre Pause di Mini-ma, ouer per cinque, ò per altre simili; uerranno senza dubbio, à far qualche noua uariatione. Io non dico già che le Consequenze distanti per l'una Pausa di Minima, ò di
Semibreue non si debbino usare; ma dico, che non si debbono usar molto spesso; per non
cascare in quello, ch'è tanto commune; n [sic: &] che non si ritroua libro, nel quale non sia molte
& molte uolte replicato; il qual lascio di mostrare, per non esser tedioso, & per non of-fender alcuno. Ma accioche si caui qualche frutto da quello, ch'io hò detto; porrò pri-ma l'essempio delle Consequenze sciolte, le quali si fanno sopra i Canti fermi à loro
imitatione; percioche di quelle che si trouano tra due parti diminuite, se ne potrà
hauere due accommodati essempi, posti di sopra nel Cap. 43. Ma delle legate, che
si fanno in molte maniere, ne porrò qui alcune solamente: essendo ch'è impossi-bile di poterle por tutte, & dimostrarle con breuità in poche carte; nelle quali s'hauerà
da osseruar questo nella prima maniera, che siano poste l'una con l'altra in Con-sequenza all'Vnisono, ouero alla Quarta, oueramente alla Quinta, ò pure all'Ot-taua incominciando da qual parte si uoglia, sia la graue, ouer l'acuta, che que-sto importa poco. La onde finito che sarà il tutto; come qui si uede; si piglierà la par-page 272 te, che incomincia à cantare; cioè, la Guida, & si scriuerà di lungo & doue 'l Con-sequente hà da incominciare à cantare; cioè, sopra la figura posta nella Guida, si porrà
un segno tale, [[mus.sigcon]] il qual da i Musici uien detto Presa; Et nel fine, ou'hà da fermarsi, si
segnarà la parte della Guida col detto segno, ouer con questo [[mus.ferm]] ponendolo sopra la fi-gura finale, oue si hà da fermare il Consequente; & cotal segno chiamano Coronata.
te, che incomincia à cantare; cioè, la Guida, & si scriuerà di lungo & doue 'l Con-sequente hà da incominciare à cantare; cioè, sopra la figura posta nella Guida, si porrà
un segno tale, [[mus.sigcon]] il qual da i Musici uien detto Presa; Et nel fine, ou'hà da fermarsi, si
segnarà la parte della Guida col detto segno, ouer con questo [[mus.ferm]] ponendolo sopra la fi-gura finale, oue si hà da fermare il Consequente; & cotal segno chiamano Coronata.
 Oltra di ciò se 'l Consequente cantasse nel graue in luogo di dire, Acuta; si porrebbe,
Graue. Et se la Consequenza fusse fatta per una Quarta, allora si direbbe; In Diatessa-ron; & se cantasse per una Quimta, si direbbe; In Diapente; & se per l'Vniso-no, si direbbe; All'Vnisono, oueramente, Nell'istesso suono, ò uoce istessa. Lungo sarebbe il uoler raccontare tutte le specie delle Consequenze d'una in una; & il uoler dar'
un'essempio particolare; ma perche de queste ne sono i Libri pieni; però lasciarò di ra-gionarne più oltra, rimettendo 'l resto al buon giudicio del Compositore; che uedendo page 273& essaminando gli essempi sopra detti, li saranno guida & lume di ritrouar cose assai maggiori. Non voglio però restar di dire, che si troua etiandio vn'altra sorte di Consequen-za, la quale si fà per gli istessi Interualli, per mouimenti contrarij, detta Consequenza
per Α῎ρσιν, & Θέσιν; cioè, per Leuatione & Abbassamento di voce; il qual modo è vsa-to da i buoni Prattici; & nel comporla si procede à quell'istesso modo, col quale si pro-cede nell'altre. Sono nondimeno due le sue Specie; Legate, & Sciolte. Le Legate po-tremo conoscere, quando haueremo piena cognitione delle precedenti; il simile anco
auerrà delle Sciolte. Ma perche, considerato quello, che di sopra hò detto, con facili-tà si può fare, ò compor le Sciolte; lasciandole da vn canto, verrò à mostrar le Legate,
che sono alquanto più difficili, & porrò solamente alcuni essempi, da i quali si potrà co-noscere & comprender quello, che si dè osseruare, quando si vorrà comporre in tal
maniera. Se noi adunque ordinaremo la Guida col Consequente, che procedino l'vno
contra l'altro per contrarij mouimenti, osseruando di porre quelli istessi Interualli de Tuoni, de Semituoni & gli altri in vna parte, che si pone nell'altra; non è dubbio, che que-ste Parti si potranno ordinare in diuerse maniere; percioche si potrà porre il Conse-quente sopra la Guida distante per lo spatio del Semiditono, aspettando due Tempi in-teri di Breue imperfetta; cioè, dimorando all'incominciare per lo spatio di vna Pausa
di Lunga, & cosi haueremo il seguente essempio: Ouero si potrà porre l'vna delle par-
Oltra di ciò se 'l Consequente cantasse nel graue in luogo di dire, Acuta; si porrebbe,
Graue. Et se la Consequenza fusse fatta per una Quarta, allora si direbbe; In Diatessa-ron; & se cantasse per una Quimta, si direbbe; In Diapente; & se per l'Vniso-no, si direbbe; All'Vnisono, oueramente, Nell'istesso suono, ò uoce istessa. Lungo sarebbe il uoler raccontare tutte le specie delle Consequenze d'una in una; & il uoler dar'
un'essempio particolare; ma perche de queste ne sono i Libri pieni; però lasciarò di ra-gionarne più oltra, rimettendo 'l resto al buon giudicio del Compositore; che uedendo page 273& essaminando gli essempi sopra detti, li saranno guida & lume di ritrouar cose assai maggiori. Non voglio però restar di dire, che si troua etiandio vn'altra sorte di Consequen-za, la quale si fà per gli istessi Interualli, per mouimenti contrarij, detta Consequenza
per Α῎ρσιν, & Θέσιν; cioè, per Leuatione & Abbassamento di voce; il qual modo è vsa-to da i buoni Prattici; & nel comporla si procede à quell'istesso modo, col quale si pro-cede nell'altre. Sono nondimeno due le sue Specie; Legate, & Sciolte. Le Legate po-tremo conoscere, quando haueremo piena cognitione delle precedenti; il simile anco
auerrà delle Sciolte. Ma perche, considerato quello, che di sopra hò detto, con facili-tà si può fare, ò compor le Sciolte; lasciandole da vn canto, verrò à mostrar le Legate,
che sono alquanto più difficili, & porrò solamente alcuni essempi, da i quali si potrà co-noscere & comprender quello, che si dè osseruare, quando si vorrà comporre in tal
maniera. Se noi adunque ordinaremo la Guida col Consequente, che procedino l'vno
contra l'altro per contrarij mouimenti, osseruando di porre quelli istessi Interualli de Tuoni, de Semituoni & gli altri in vna parte, che si pone nell'altra; non è dubbio, che que-ste Parti si potranno ordinare in diuerse maniere; percioche si potrà porre il Conse-quente sopra la Guida distante per lo spatio del Semiditono, aspettando due Tempi in-teri di Breue imperfetta; cioè, dimorando all'incominciare per lo spatio di vna Pausa
di Lunga, & cosi haueremo il seguente essempio: Ouero si potrà porre l'vna delle par- ti; cioè, il Consequente lontano dalla Guida per vna Settima, & haueremo la seguente
cantilena; nella quale il Consequente seguirà la Guida per due tempi di Breue imperfet-ta; cioè, dopo vna Pausa di Lunga. page 274
ti; cioè, il Consequente lontano dalla Guida per vna Settima, & haueremo la seguente
cantilena; nella quale il Consequente seguirà la Guida per due tempi di Breue imperfet-ta; cioè, dopo vna Pausa di Lunga. page 274 Volendo poi scriuere in lungo cotali essempi, ò cantilene, si potranno ordinare di maniera, che i Consequenti potranno hauer le loro chiaui, che dimostreranno, per quali chor-de haueranno à procedere nel cantare, come hà la Guida. Lequali Chiaui si porranno
sempre auanti quella, che serue ad essa Guida; & tra queste & quelle si porranno le Pau-se, che 'l Consequente haurà da fare, auanti che incominci à cantare; ancora che la Re-gola posta sopra di loro gli insegni, in qual maniera si habbia da procedere; come ne i
due sottoposti essempi si uede.
Volendo poi scriuere in lungo cotali essempi, ò cantilene, si potranno ordinare di maniera, che i Consequenti potranno hauer le loro chiaui, che dimostreranno, per quali chor-de haueranno à procedere nel cantare, come hà la Guida. Lequali Chiaui si porranno
sempre auanti quella, che serue ad essa Guida; & tra queste & quelle si porranno le Pau-se, che 'l Consequente haurà da fare, auanti che incominci à cantare; ancora che la Re-gola posta sopra di loro gli insegni, in qual maniera si habbia da procedere; come ne i
due sottoposti essempi si uede.

 page 275Vedremo poi al suo luogo, quel ch'importi vn tempo, due tempi, & più ancora; concio-siache allora mostrarò etiandio, quante Figure in esso si pongano, & à qual figura il Tempo s'attribuisca. Si debbe oltra di ciò auertire, che queste maniere di Consequenza non
sono per alcun modo da sprezzare; anzi si debbono abbracciare; percioche oltra che so-no belle, eleganti & ingegniose; hanno anco un certo non sò che di grandezza, essendo
che un tal modo di comporre non è cosi commune, come sono gli altri modi. Però adun-que, chi si uorrà essercitare nel comporre simili maniere, non è dubbio, che in breue tem-po diuenterà buon Musico. Et quello c'hò detto nelle Consequenze legate, uoglio che
s'intenda anco delle Slegate, ò Sciolte, che si compongono senza obligo alcuno. Ne si
debbe alcuno imaginare; hauendo io solamente posto i mostrati essempi; che queste sola-mente siano tutte le maniere delle Consequenze, & che non se ne possa fare alcun'altra,
per altra maniera; come il porre più, ò meno tempi; & che la Guida non si possa porre
nell'acuto, & il Consequente nel graue; conciosia che sono quasi infiniti li modi, & lungo
sarebbe il raccontarli di uno in uno; ma hò posto solamente questi pochi, accioche siano
vn lume & una guida à ciascuno, che uorrà sotto en trare [sic: entrare] à questa bella, ingegnosa, & ho-noreuol fatica.
page 275Vedremo poi al suo luogo, quel ch'importi vn tempo, due tempi, & più ancora; concio-siache allora mostrarò etiandio, quante Figure in esso si pongano, & à qual figura il Tempo s'attribuisca. Si debbe oltra di ciò auertire, che queste maniere di Consequenza non
sono per alcun modo da sprezzare; anzi si debbono abbracciare; percioche oltra che so-no belle, eleganti & ingegniose; hanno anco un certo non sò che di grandezza, essendo
che un tal modo di comporre non è cosi commune, come sono gli altri modi. Però adun-que, chi si uorrà essercitare nel comporre simili maniere, non è dubbio, che in breue tem-po diuenterà buon Musico. Et quello c'hò detto nelle Consequenze legate, uoglio che
s'intenda anco delle Slegate, ò Sciolte, che si compongono senza obligo alcuno. Ne si
debbe alcuno imaginare; hauendo io solamente posto i mostrati essempi; che queste sola-mente siano tutte le maniere delle Consequenze, & che non se ne possa fare alcun'altra,
per altra maniera; come il porre più, ò meno tempi; & che la Guida non si possa porre
nell'acuto, & il Consequente nel graue; conciosia che sono quasi infiniti li modi, & lungo
sarebbe il raccontarli di uno in uno; ma hò posto solamente questi pochi, accioche siano
vn lume & una guida à ciascuno, che uorrà sotto en trare [sic: entrare] à questa bella, ingegnosa, & ho-noreuol fatica.
Delle Imitationi, & quello che elle siano.Cap. LV.
 page 276fuori. Il perche, si potrà porre alla Seconda, alla Terza, alla Sesta, alla Settima & ad altri
Interualli simili. Diremo adunque che la Imitatione è quella, che si troua tra due, ò più
parti; delle quali il Consequente imitando i mouimenti della Guida, procede solamente
per quell'istessi Gradi, senz'hauer'altra consideratione de gli Interualli. Et la cognitio-ne tanto della Legata, quanto della Sciolta si potrà hauer facilmente, quando s'hauerà
conosciuto quello, che uoglia dire Consequenza legata & Consequenza sciolta. Ma per
maggior chiarezza uerrò ad uno essempio particolare, dal quale si potrà conoscer quel-lo, c'hò voluto dire in vniuersale. Le Imitationi adunque, che si fanno per contrarij mo-uimenti, hanno al medesimo modo, che hanno le Consequenze, la Guida & il Con-sequente; onde si usa anco nel scriuere la Guida in lungo gli istessi modi, che furono usati
nelle Consequenze; cioè, porre le lor Prese & le Coronate, come hò mostrato. Ma il Ca-none, ò Regola de queste si scriue in cotal Guisa. Si canta alla Seconda, ouero alla terza, ò
pur ad altre simili; acuta, ouer graue, pausando due tempi, ò più, ò meno. Et se le Parti procedono
per mouimenti contrarij, s'aggiunge queste parole; Per mouimenti contrarij. Si debbe do-poi auertire, che nelle Sciolte si può cauare il Consequente dalla Guida, parte per imita-tione & parte in consequenza. Cosi parte in mouimenti simili & parte in mouimenti
contrarij; onde sarebbe cosa troppo lunga, se 'l si uolesse dar notitia particolare d'ogni co-sa minima. Ciascuno però sarà auertito per sempre, di ordinare in tal maniera le Parti
della sua compositione, massimamente nelle Fughe & Imitationi legate, che procedono
per mouimenti contrarij; che si possino cantar senza discommodo. Et per dare di ciò
qualche lume, hò posto di sopra lo essempio particolare delle Imitationi sciolte; accioche
da esso si possa trar frutto di quello, c'hò detto di sopra; & hora uerrò à mostrare gli es-sempi delle Imitationi legate. La Imitatione legata si potrà conoscer da questo, che ha-uerà la Guida & il Consequente, che l'uno seguiterà l'altro; non per gli istessi Interualli;
page 276fuori. Il perche, si potrà porre alla Seconda, alla Terza, alla Sesta, alla Settima & ad altri
Interualli simili. Diremo adunque che la Imitatione è quella, che si troua tra due, ò più
parti; delle quali il Consequente imitando i mouimenti della Guida, procede solamente
per quell'istessi Gradi, senz'hauer'altra consideratione de gli Interualli. Et la cognitio-ne tanto della Legata, quanto della Sciolta si potrà hauer facilmente, quando s'hauerà
conosciuto quello, che uoglia dire Consequenza legata & Consequenza sciolta. Ma per
maggior chiarezza uerrò ad uno essempio particolare, dal quale si potrà conoscer quel-lo, c'hò voluto dire in vniuersale. Le Imitationi adunque, che si fanno per contrarij mo-uimenti, hanno al medesimo modo, che hanno le Consequenze, la Guida & il Con-sequente; onde si usa anco nel scriuere la Guida in lungo gli istessi modi, che furono usati
nelle Consequenze; cioè, porre le lor Prese & le Coronate, come hò mostrato. Ma il Ca-none, ò Regola de queste si scriue in cotal Guisa. Si canta alla Seconda, ouero alla terza, ò
pur ad altre simili; acuta, ouer graue, pausando due tempi, ò più, ò meno. Et se le Parti procedono
per mouimenti contrarij, s'aggiunge queste parole; Per mouimenti contrarij. Si debbe do-poi auertire, che nelle Sciolte si può cauare il Consequente dalla Guida, parte per imita-tione & parte in consequenza. Cosi parte in mouimenti simili & parte in mouimenti
contrarij; onde sarebbe cosa troppo lunga, se 'l si uolesse dar notitia particolare d'ogni co-sa minima. Ciascuno però sarà auertito per sempre, di ordinare in tal maniera le Parti
della sua compositione, massimamente nelle Fughe & Imitationi legate, che procedono
per mouimenti contrarij; che si possino cantar senza discommodo. Et per dare di ciò
qualche lume, hò posto di sopra lo essempio particolare delle Imitationi sciolte; accioche
da esso si possa trar frutto di quello, c'hò detto di sopra; & hora uerrò à mostrare gli es-sempi delle Imitationi legate. La Imitatione legata si potrà conoscer da questo, che ha-uerà la Guida & il Consequente, che l'uno seguiterà l'altro; non per gli istessi Interualli;
 page 277ma per quelli istessi Mouimenti, ouer Gradi; come nell'essempio seguente si uede. Et
questa si conosce esser manifestamente Imitatione, & non Fuga; percioche il Consequente canta per un Ditono più acuto della Guida. Et ancora che l'uno, & l'altro procedino
per gli istessi Gradi; non procedono però per gli istessi Interualli; come hò detto. Vo-lendo adunque ridurre tale Imitatione in vna parte sola, la disponeremo à questo modo;
ponendole di sopra la Regola, ch'insegnerà quello, che si hauerà da tenere nel cantarla,
in questa maniera.
page 277ma per quelli istessi Mouimenti, ouer Gradi; come nell'essempio seguente si uede. Et
questa si conosce esser manifestamente Imitatione, & non Fuga; percioche il Consequente canta per un Ditono più acuto della Guida. Et ancora che l'uno, & l'altro procedino
per gli istessi Gradi; non procedono però per gli istessi Interualli; come hò detto. Vo-lendo adunque ridurre tale Imitatione in vna parte sola, la disponeremo à questo modo;
ponendole di sopra la Regola, ch'insegnerà quello, che si hauerà da tenere nel cantarla,
in questa maniera.
 Ma in quelle Imitationi, che procedono per Mouimenti contrarij, si tiene altro modo;
come nell'essempio seguente si può vedere.
Ma in quelle Imitationi, che procedono per Mouimenti contrarij, si tiene altro modo;
come nell'essempio seguente si può vedere.
 page 278Et acciò si uegga in qual maniera per l'auenire s'habbia da procedere, quando si vor[gap — ]
porre insieme la Guida & il Consequente; scriuerò tale Imitatione in lungo, col suo Ca-none, ò Regola in cotal modo.
page 278Et acciò si uegga in qual maniera per l'auenire s'habbia da procedere, quando si vor[gap — ]
porre insieme la Guida & il Consequente; scriuerò tale Imitatione in lungo, col suo Ca-none, ò Regola in cotal modo.
 Si troua etiandio una sorte di Compositione simile, laqual contiene la Guida & il Conse-quente, parte in Consequenza & parte in Imitatione; come quì si uede.
Si troua etiandio una sorte di Compositione simile, laqual contiene la Guida & il Conse-quente, parte in Consequenza & parte in Imitatione; come quì si uede.
 page 279La quale si suol ridurre sopra vna parte sola, col suo Canone, ò Regola in questo modo.
page 279La quale si suol ridurre sopra vna parte sola, col suo Canone, ò Regola in questo modo.
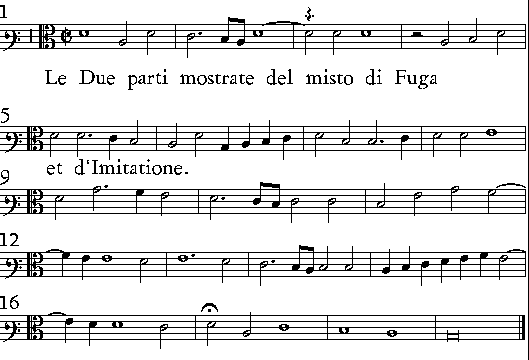 Questa communemente da i Prattici è detta Fuga; & si usa molto spesso nelle Composi-tioni à più voci; come si può uedere in molte cantilene. Et in uero non è da sprezzare,
anzi da porla spesse volte in uso; percioche fà la compositione ingegnosa, & fà anco buo-nissimo effetto. Ma si dee sapere, che nelle Consequenze & nelle Imitationi, che si troua-no nelle compositioni à più voci, Legate, ò Sciolte che siano, si possono por le Quarte, &
far molti passaggi, che ritornano bene; percioche l'altre parti sono di grande aiuto al
compositore; ancora che nelle compositioni de due voci le Quarte non si ponghino; per
che non fanno quel buono effetto, che fanno l'altre Consonanze. Però sarà bisogno, che 'l
Compositore stia auertito, acciò non cada in qualche errore. Ma questo sia detto à suffi-cienza intorno alle Consequenze & alle Imitationi; percioche d'alcune di quelle, che si
pongono nelle compositioni à più uoci, ragionaremo altroue.
Questa communemente da i Prattici è detta Fuga; & si usa molto spesso nelle Composi-tioni à più voci; come si può uedere in molte cantilene. Et in uero non è da sprezzare,
anzi da porla spesse volte in uso; percioche fà la compositione ingegnosa, & fà anco buo-nissimo effetto. Ma si dee sapere, che nelle Consequenze & nelle Imitationi, che si troua-no nelle compositioni à più voci, Legate, ò Sciolte che siano, si possono por le Quarte, &
far molti passaggi, che ritornano bene; percioche l'altre parti sono di grande aiuto al
compositore; ancora che nelle compositioni de due voci le Quarte non si ponghino; per
che non fanno quel buono effetto, che fanno l'altre Consonanze. Però sarà bisogno, che 'l
Compositore stia auertito, acciò non cada in qualche errore. Ma questo sia detto à suffi-cienza intorno alle Consequenze & alle Imitationi; percioche d'alcune di quelle, che si
pongono nelle compositioni à più uoci, ragionaremo altroue.
De i Contrapunti doppij, & quello che siano.Cap. LVI.
 decima. Ma uolendo comporre quello, che tiene il Secondo luogo nella Prima manie-ra; cioè, quello, che nella Replica procede per gli istessi mouimenti; ma per Interualli
differenti da quelli, che sono nel Principale; osseruaremo di non porre per alcun modo
nel Principale due Consonanze simili; come sono due Terze, ò due Seste, l'vna dopo l'al-tra, senz'alcun mezo; ancora che l'una fusse maggiore, & l'altra minore; & di porre le Sin-cope, che siano in tutte le lor parti consonanti. Io dissi, che non si pone due Seste; per-cioche in questi & in altri simili Contrapunti la Sesta si può vsare, che fà buono effetto; &
si può far che la Parte graue piglia il luogo dell'acuta, & questa quella del graue; come tor-na più commodo; con questa conditione però, che quando saranno poste in tal maniera;
l'una non sia lontana dall'altra per più d'vna Terza; essendo che restando ciascuna ne i
suoi termini, allora si potranno porre distanti l'una dall'altra per vna Duodecima. E' ben
uero, che se ben passasse più oltra, non bisognarebbe porre per alcun modo la Terzade-cima; perche non tornarebbe molto commoda. Non passaremo adunque la Duodeci-ma, & osseruaremo le Regole date, & faremo, che le Parti della cantilena cantino commodamente, con mouimenti di grado, più che sia possibile; percioche quelli di Quarta & di
Quinta possono in alcuni luoghi della Replica generar qualche discommodo; Il che osser-uato, potremo hauere un Contrapunto purgato da ogni errore simile à quel che seguita.
Dal quale potremo hauere non solo vna; ma due Repliche; l'una quando prima fare-mo la sua parte graue più acuta per vna Ottaua, & l'acuta più graue per una Decima;
Et l'altra, quando si farà graue la Parte acuta per una Ottaua, & la graue si cantarà acuta
per vna Decima; & più piacerà, perche si udirà il Modo mantenuto maggiormente ne i
suoi termini, con altr'harmonia. Et queste sorte de Contrapunti si potranno cantare
etiandio à Tre voci; facendo prima cantare sotto la parte acuta del Principale un'altra
parte distante nel graue per una Decima; & dopoi nella prima Replica l'acuta, si cantarà
più graue, per una Diapason; & restando la graue nel suo essere; si farà cantare una Ter-za parte nel graue, distante per una Decima da quella che si canta più graue nella Repli-ca per una Diapason. Fatto questo, nella Seconda replica si fara cantare una parte più
acuta per una Terza, sopra la parte graue della Replica, & si haurà il proposito; cioè,
Tre maniere di contrapunto à Tre uoci, che saranno l'una dall'altra differenti. E' ben
uero che 'l Contrapunto non verria ad esser cosi bene espurgato da errori; come sarebbe
il douere. Ma perche il fare questa sorte di Contrapunto è molto difficile, uolendolo
far, che uenghi nella Replica senza errore; però voglio porre alcune regole generali, page 282
decima. Ma uolendo comporre quello, che tiene il Secondo luogo nella Prima manie-ra; cioè, quello, che nella Replica procede per gli istessi mouimenti; ma per Interualli
differenti da quelli, che sono nel Principale; osseruaremo di non porre per alcun modo
nel Principale due Consonanze simili; come sono due Terze, ò due Seste, l'vna dopo l'al-tra, senz'alcun mezo; ancora che l'una fusse maggiore, & l'altra minore; & di porre le Sin-cope, che siano in tutte le lor parti consonanti. Io dissi, che non si pone due Seste; per-cioche in questi & in altri simili Contrapunti la Sesta si può vsare, che fà buono effetto; &
si può far che la Parte graue piglia il luogo dell'acuta, & questa quella del graue; come tor-na più commodo; con questa conditione però, che quando saranno poste in tal maniera;
l'una non sia lontana dall'altra per più d'vna Terza; essendo che restando ciascuna ne i
suoi termini, allora si potranno porre distanti l'una dall'altra per vna Duodecima. E' ben
uero, che se ben passasse più oltra, non bisognarebbe porre per alcun modo la Terzade-cima; perche non tornarebbe molto commoda. Non passaremo adunque la Duodeci-ma, & osseruaremo le Regole date, & faremo, che le Parti della cantilena cantino commodamente, con mouimenti di grado, più che sia possibile; percioche quelli di Quarta & di
Quinta possono in alcuni luoghi della Replica generar qualche discommodo; Il che osser-uato, potremo hauere un Contrapunto purgato da ogni errore simile à quel che seguita.
Dal quale potremo hauere non solo vna; ma due Repliche; l'una quando prima fare-mo la sua parte graue più acuta per vna Ottaua, & l'acuta più graue per una Decima;
Et l'altra, quando si farà graue la Parte acuta per una Ottaua, & la graue si cantarà acuta
per vna Decima; & più piacerà, perche si udirà il Modo mantenuto maggiormente ne i
suoi termini, con altr'harmonia. Et queste sorte de Contrapunti si potranno cantare
etiandio à Tre voci; facendo prima cantare sotto la parte acuta del Principale un'altra
parte distante nel graue per una Decima; & dopoi nella prima Replica l'acuta, si cantarà
più graue, per una Diapason; & restando la graue nel suo essere; si farà cantare una Ter-za parte nel graue, distante per una Decima da quella che si canta più graue nella Repli-ca per una Diapason. Fatto questo, nella Seconda replica si fara cantare una parte più
acuta per una Terza, sopra la parte graue della Replica, & si haurà il proposito; cioè,
Tre maniere di contrapunto à Tre uoci, che saranno l'una dall'altra differenti. E' ben
uero che 'l Contrapunto non verria ad esser cosi bene espurgato da errori; come sarebbe
il douere. Ma perche il fare questa sorte di Contrapunto è molto difficile, uolendolo
far, che uenghi nella Replica senza errore; però voglio porre alcune regole generali, page 282 page 283delle quali la prima sarà (lasciando molt'altre cose alla discretione & al buon giudi-cio del Compositore) che non si dè por mai la Terza dopo l'Vnisono, ne la Terza me-desimamente, ouer la Decima dopo la Ottaua, quando le parti della cantilena discen-deranno insieme. Osseruaremo, anco che quando le parti ascenderanno, di non por
dopo la Quinta la Sesta, ne meno la Decima dopo la Duodecima; massimamente
quando la parte acuta non procederà per grado, il quale è alquanto più tolerabile del
mouimento per salto. Similmente si auertirà, di non procedere dalla Ottaua alla De-cima minore, se non quando la parte acuta farà il mouimento di Tuono, & la graue
quello del Semituono; ne meno dalla Terza, ò dalla Quinta alla Decima minore, per
contrarij mouimenti. Schiuaremo il porre la parte acuta, che si muoua dalla Quinta
alla Terza maggiore, quando la graue non farà mouimento alcuno. Cosi quando la
parte acuta non farà mouimento, & la graue si muouerà, procedendo dalla Quinta al-la Terza minore, ouer dalla Duodecima alla Decima minore; Imperoche la Replica
non uerrebbe secondo le Regole date. In questa maniera di Contrapunto ogni Deci-ma, che si pone nel Principale, diuenta Ottaua nella Replica; & ogni Terza ritorna
Quintadecima. Ma debbe il Contrapuntista comporre insieme il Principale & la Replica;
& cosi il tutto verrà ad esser senza errore. Quanto al Secondo modo, oue la Replica và
modulando per mouimenti contrarij à quelli, che sono contenuti nel Principale, osser-uando pero nelle sue parti gli istessi Interualli; fà dibisogno, ch'esso Principale habbia
Sincope (se ne hauerà alcuna) che siano tutte consonanti; siano poste poi à qual mo-do si uoglia; percioche se hauesse alcuna dissonanza, non verrebbono à far buoni ef-fetti nella replica. Qui si potrà vsare (facendo bisogno) la Sesta nel principale; ma
bisogna auertire, di non porre la Decima, dopo la quale seguiti la Ottaua; ne la Ter-za auanti l'Vnisono, quando le parti ascendono insieme; come nel sottoposto essem-pio si è osseruato.
page 283delle quali la prima sarà (lasciando molt'altre cose alla discretione & al buon giudi-cio del Compositore) che non si dè por mai la Terza dopo l'Vnisono, ne la Terza me-desimamente, ouer la Decima dopo la Ottaua, quando le parti della cantilena discen-deranno insieme. Osseruaremo, anco che quando le parti ascenderanno, di non por
dopo la Quinta la Sesta, ne meno la Decima dopo la Duodecima; massimamente
quando la parte acuta non procederà per grado, il quale è alquanto più tolerabile del
mouimento per salto. Similmente si auertirà, di non procedere dalla Ottaua alla De-cima minore, se non quando la parte acuta farà il mouimento di Tuono, & la graue
quello del Semituono; ne meno dalla Terza, ò dalla Quinta alla Decima minore, per
contrarij mouimenti. Schiuaremo il porre la parte acuta, che si muoua dalla Quinta
alla Terza maggiore, quando la graue non farà mouimento alcuno. Cosi quando la
parte acuta non farà mouimento, & la graue si muouerà, procedendo dalla Quinta al-la Terza minore, ouer dalla Duodecima alla Decima minore; Imperoche la Replica
non uerrebbe secondo le Regole date. In questa maniera di Contrapunto ogni Deci-ma, che si pone nel Principale, diuenta Ottaua nella Replica; & ogni Terza ritorna
Quintadecima. Ma debbe il Contrapuntista comporre insieme il Principale & la Replica;
& cosi il tutto verrà ad esser senza errore. Quanto al Secondo modo, oue la Replica và
modulando per mouimenti contrarij à quelli, che sono contenuti nel Principale, osser-uando pero nelle sue parti gli istessi Interualli; fà dibisogno, ch'esso Principale habbia
Sincope (se ne hauerà alcuna) che siano tutte consonanti; siano poste poi à qual mo-do si uoglia; percioche se hauesse alcuna dissonanza, non verrebbono à far buoni ef-fetti nella replica. Qui si potrà vsare (facendo bisogno) la Sesta nel principale; ma
bisogna auertire, di non porre la Decima, dopo la quale seguiti la Ottaua; ne la Ter-za auanti l'Vnisono, quando le parti ascendono insieme; come nel sottoposto essem-pio si è osseruato.
 Haueremo la Replica, ponendo graue la parte acuta, & l'acuta graue; questa distante
dalle parti principali per una Settima, & quella per vna Nona; come quì si vede. page 284
Haueremo la Replica, ponendo graue la parte acuta, & l'acuta graue; questa distante
dalle parti principali per una Settima, & quella per vna Nona; come quì si vede. page 284 Componendo in cotal maniera, le Parti della compositione si possono porre nel Principa-le distanti l'vna dall'altra per qual si uoglia Interuallo; se bene ariuassero alla Quintade-cima; perche nella Replica tornano bene; ma non si debbe porre le Parti molto lontane
Componendo in cotal maniera, le Parti della compositione si possono porre nel Principa-le distanti l'vna dall'altra per qual si uoglia Interuallo; se bene ariuassero alla Quintade-cima; perche nella Replica tornano bene; ma non si debbe porre le Parti molto lontane


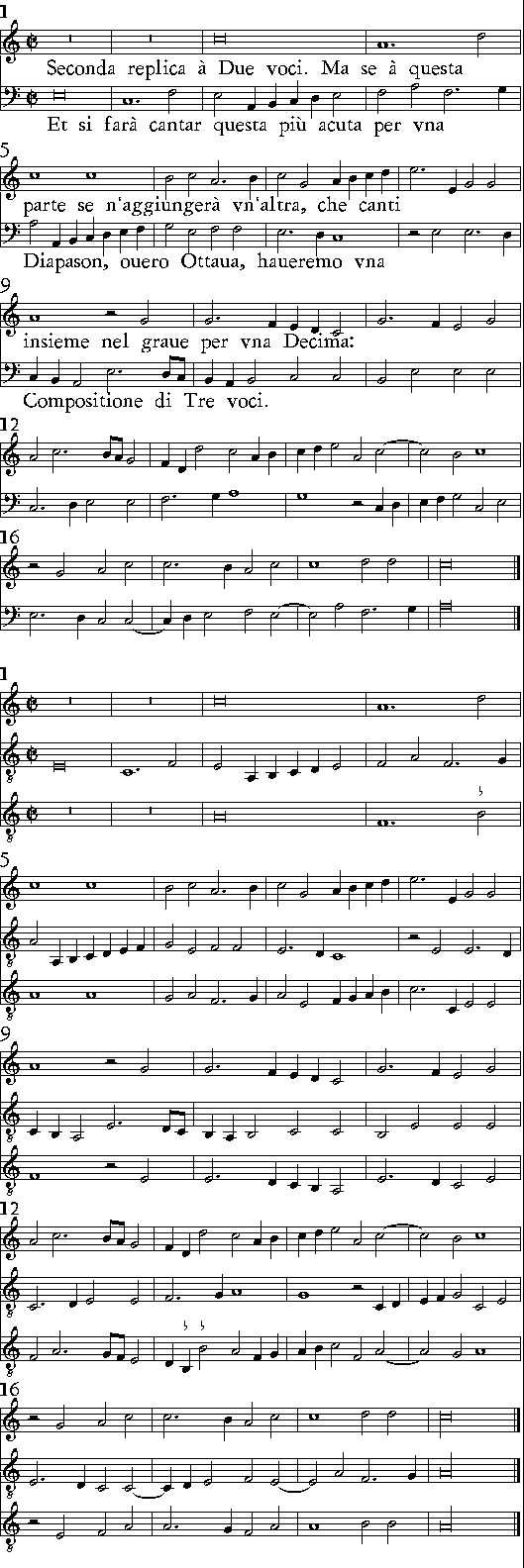
 page 286l'vna dall'altra. Hò uoluto dar questi pochi essempi; accioche essaminati, il diligente
Compositore possa ritrouare col suo intelletto altre noue, & belle inuentioni. La onde
voglio etiandio auertire vna cosa; che se 'l si osseruarà tutto quello che le Regole ne to-glie, di potere vsare alcuna cosa ne i Contrapunti mostrati di sopra; potremo comporre
vn Contrapunto di tal sorte, che si potrà cantare à ciascuno de i modi mostrati, con gran-de uarietà d'harmonia; come ne i poco fà mostrati si potrà conoscere. Non voglio ta-cere anco questo, acciò si ueda l'arteficio di questa sorte di Contrapunto; che se noi ag-giungeremo à qual si uoglia parte delle Cantilene, che si cantano à Due voci, un'altra
nel graue, ò nell'acuto; secondo c'hò notato in esse particolarmente; ciascuna da per sè
si potrà cantare à tre uoci. E' ben vero, che le parti aggiunte non ueranno fatte con l'os-seruanza delle Regole date di sopra: Ma questo basti. Si debbe etiandio sapere; che ol-tra le mostrate maniere di Contrapunto doppio, se ne ritrouano molt'altre; le quali uo-lendole raccogliere insieme sarebbe cosa lunga & difficile; ma per hora basterà di mo-strarne alcune, che si fanno in Consequenza; le quali sono marauigliose. La onde (per
venire al fatto) dico; che se nella Consequenza fatta per mouimenti contrarij osserua-remo di non por mai alcuna Dissonanza; verrà una Compositione di tal maniera, c'ha-urà una Replica, nella quale, quella parte, ch'era nel Principale Consequente, potrà esser
Guida; come nel sequente essempio, il quale corrisponde alla Seconda maniera di Con-sequenza legata, posta nel Cap. 54. si può comprendere.
page 286l'vna dall'altra. Hò uoluto dar questi pochi essempi; accioche essaminati, il diligente
Compositore possa ritrouare col suo intelletto altre noue, & belle inuentioni. La onde
voglio etiandio auertire vna cosa; che se 'l si osseruarà tutto quello che le Regole ne to-glie, di potere vsare alcuna cosa ne i Contrapunti mostrati di sopra; potremo comporre
vn Contrapunto di tal sorte, che si potrà cantare à ciascuno de i modi mostrati, con gran-de uarietà d'harmonia; come ne i poco fà mostrati si potrà conoscere. Non voglio ta-cere anco questo, acciò si ueda l'arteficio di questa sorte di Contrapunto; che se noi ag-giungeremo à qual si uoglia parte delle Cantilene, che si cantano à Due voci, un'altra
nel graue, ò nell'acuto; secondo c'hò notato in esse particolarmente; ciascuna da per sè
si potrà cantare à tre uoci. E' ben vero, che le parti aggiunte non ueranno fatte con l'os-seruanza delle Regole date di sopra: Ma questo basti. Si debbe etiandio sapere; che ol-tra le mostrate maniere di Contrapunto doppio, se ne ritrouano molt'altre; le quali uo-lendole raccogliere insieme sarebbe cosa lunga & difficile; ma per hora basterà di mo-strarne alcune, che si fanno in Consequenza; le quali sono marauigliose. La onde (per
venire al fatto) dico; che se nella Consequenza fatta per mouimenti contrarij osserua-remo di non por mai alcuna Dissonanza; verrà una Compositione di tal maniera, c'ha-urà una Replica, nella quale, quella parte, ch'era nel Principale Consequente, potrà esser
Guida; come nel sequente essempio, il quale corrisponde alla Seconda maniera di Con-sequenza legata, posta nel Cap. 54. si può comprendere.
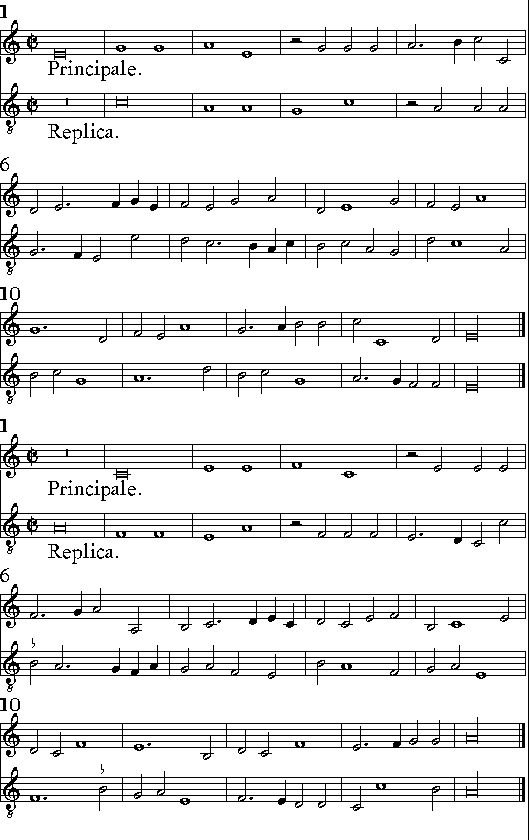 Percioche essendo la parte acuta Guida nel principale, & la graue il Consequente; nella
Replica viene il contrario; cioè, la graue Guida, & l'acuta Consequente. Questo istesso
ne verrà fatto nelle Imitationi per contrarij mouimenti; quando osseruaremo medesi-mamente di non far mai alcuna Dissonanza. Onde nascerà una compositione simile alla
sequente; corrispondente al Secondo modo d'Imitatione legata posta nel Cap. 55. La
quale hauerà la sua Replica.
Percioche essendo la parte acuta Guida nel principale, & la graue il Consequente; nella
Replica viene il contrario; cioè, la graue Guida, & l'acuta Consequente. Questo istesso
ne verrà fatto nelle Imitationi per contrarij mouimenti; quando osseruaremo medesi-mamente di non far mai alcuna Dissonanza. Onde nascerà una compositione simile alla
sequente; corrispondente al Secondo modo d'Imitatione legata posta nel Cap. 55. La
quale hauerà la sua Replica.
 Ma al misto di Consequenza, & d'Imitatione posto nel nominato Cap. 55. corrispon-de il sequente essempio; nel quale se 'l si osseruerà, sopra ogn'altra cosa, di non fare
Sesta; onde ne uiene, che non si può fare la Sincopa, nella quale sia nascosta la Settima;
& haueremo una Replica; nella quale il Consequente del principale diuenterà Guida,
& la Guida ritornerà Consequente; come nel sequente essempio si può vedere.
Ma al misto di Consequenza, & d'Imitatione posto nel nominato Cap. 55. corrispon-de il sequente essempio; nel quale se 'l si osseruerà, sopra ogn'altra cosa, di non fare
Sesta; onde ne uiene, che non si può fare la Sincopa, nella quale sia nascosta la Settima;
& haueremo una Replica; nella quale il Consequente del principale diuenterà Guida,
& la Guida ritornerà Consequente; come nel sequente essempio si può vedere.
 discendendo; & haueremo una Cantilena, com'è la sequente, con due Repliche; nella
Prima delle quali, quello ch'era Consequente nel Principale, & cantaua dopo la Gui-da per l'Interuallo de due Tempi, per vna Terza più graue; potrà cantar per lo spacio di
essi due Tempi per vna Diapente simigliantemente più graue; Ma nella Replica, l'uno
& l'altro de i due Consequenti; cioè, quello del Principale, il quale cantò dopo la Gui-da per vna Terza più graue; & anco questo che cantò per vna Diapente, potranno can-tare insieme con la Guida, facendo prima ciascheduno due Tempi, come haueano fat-to prima; & cosi si potrà hauere vna cantilena à tre Voci; come nel sequente essempio
si potrà vdire. Ma bisogna auertire, di non procedere molto per salti di Quarta & di
discendendo; & haueremo una Cantilena, com'è la sequente, con due Repliche; nella
Prima delle quali, quello ch'era Consequente nel Principale, & cantaua dopo la Gui-da per l'Interuallo de due Tempi, per vna Terza più graue; potrà cantar per lo spacio di
essi due Tempi per vna Diapente simigliantemente più graue; Ma nella Replica, l'uno
& l'altro de i due Consequenti; cioè, quello del Principale, il quale cantò dopo la Gui-da per vna Terza più graue; & anco questo che cantò per vna Diapente, potranno can-tare insieme con la Guida, facendo prima ciascheduno due Tempi, come haueano fat-to prima; & cosi si potrà hauere vna cantilena à tre Voci; come nel sequente essempio
si potrà vdire. Ma bisogna auertire, di non procedere molto per salti di Quarta & di
 Quinta; essendo che ne i Consequenti alle fiate vengono discommodi, per li salti di Tritono & Semidiapente. Poniamo hormai fine à coteste cose; essendo che (per quello ch'io
m'aueggio) fin'hora ne hò insegnate tante, che ogn'uno di eleuato ingegno da se stesso
potrà non solamente accommodarle nelle sue Compositioni; ma etiandio ritrouarne
dell'altre; con nuoue & belle inuentioni; percioche seguitando i modi, c'hò insegnato
di sopra, non li sarà difficile. Ma di questo sia detto à sufficienza. page 289
Quinta; essendo che ne i Consequenti alle fiate vengono discommodi, per li salti di Tritono & Semidiapente. Poniamo hormai fine à coteste cose; essendo che (per quello ch'io
m'aueggio) fin'hora ne hò insegnate tante, che ogn'uno di eleuato ingegno da se stesso
potrà non solamente accommodarle nelle sue Compositioni; ma etiandio ritrouarne
dell'altre; con nuoue & belle inuentioni; percioche seguitando i modi, c'hò insegnato
di sopra, non li sarà difficile. Ma di questo sia detto à sufficienza. page 289Quel che dè osseruare il Contra puntista [sic: Contrapuntista] oltra le Regole date, & d'alcune licenze, che potrà pigliare, quando li tornaranno commodo.Cap. LVII.
 mente si dè tollerar la Sesta, che
non solamente non è dissonante,
ma appresio d'ogn'uno è riceuuta
per consonante? Potrebbe forse
alcun dire, che con questa licen-za, & con l'istesso modo si potreb-be anco peruenire dalla Sesta mi-nore all'Ottaua: Rispondo, che
questo si farebbe contra ogni do-uere; imperoche quantunque la
Maggiore habbia natura di per-uenire all'Ottaua, come alla sua
propinqua, è nondimeno più uicina alla Quinta, che non è la Minore all'Ottaua. La
mente si dè tollerar la Sesta, che
non solamente non è dissonante,
ma appresio d'ogn'uno è riceuuta
per consonante? Potrebbe forse
alcun dire, che con questa licen-za, & con l'istesso modo si potreb-be anco peruenire dalla Sesta mi-nore all'Ottaua: Rispondo, che
questo si farebbe contra ogni do-uere; imperoche quantunque la
Maggiore habbia natura di per-uenire all'Ottaua, come alla sua
propinqua, è nondimeno più uicina alla Quinta, che non è la Minore all'Ottaua. La
 onde si uede, che douendosi (co-m'è il douere) andar dalla Con-sonanza imperfetta alla perfetta
con la più uicina; stando in que-sta licenza, la Sesta maggiore con-uiene più alla Quinta, che la mi-nore all'Ottaua. Non gli è adun-que ragione alcuna, che scusi, ò
diffendi, quando si uolesse com-mettere un tal disordine. E' ben
uero che dalla Sesta minore potrà alle fiate andare all'Ottaua con una figura di Semimi-nima; perche la Quarta semiminima, che si parte dalla Terza co 'l mouimento di grado,
si può sempre pigliar per non buona; come nel Cap. 42. fu detto. Onde se una Secon-da, ouer'una Settima, ò qualunque altra dissonanza posta in cotal modo si sopporta,
quanto maggiormente si può tollerare una Sesta? Et tanto più è da tollerare, quanto
spesse fiate da i Cantori periti, non potendo il lor'udito sentire alcun discommodo in al-cuna cosa, quantunque minima, è fatta maggiore. Ma ueramente questi passaggi non
onde si uede, che douendosi (co-m'è il douere) andar dalla Con-sonanza imperfetta alla perfetta
con la più uicina; stando in que-sta licenza, la Sesta maggiore con-uiene più alla Quinta, che la mi-nore all'Ottaua. Non gli è adun-que ragione alcuna, che scusi, ò
diffendi, quando si uolesse com-mettere un tal disordine. E' ben
uero che dalla Sesta minore potrà alle fiate andare all'Ottaua con una figura di Semimi-nima; perche la Quarta semiminima, che si parte dalla Terza co 'l mouimento di grado,
si può sempre pigliar per non buona; come nel Cap. 42. fu detto. Onde se una Secon-da, ouer'una Settima, ò qualunque altra dissonanza posta in cotal modo si sopporta,
quanto maggiormente si può tollerare una Sesta? Et tanto più è da tollerare, quanto
spesse fiate da i Cantori periti, non potendo il lor'udito sentire alcun discommodo in al-cuna cosa, quantunque minima, è fatta maggiore. Ma ueramente questi passaggi non
 sono altro, che la diminutione de quelli,
che sono posti qui da canto; per iquali non
si toglie ad alcuno, che non possa aggiungere à suo bel piacere à tal Semiminima po-sta ne i primi essempi, il segno
sono altro, che la diminutione de quelli,
che sono posti qui da canto; per iquali non
si toglie ad alcuno, che non possa aggiungere à suo bel piacere à tal Semiminima po-sta ne i primi essempi, il segno  , & far la Sesta di minore maggiore per virtù della chorda Chromatica; & cosi quella del b, secondo che occorrer puote nel fare i Con-trapunti; & se ben tali chorde non si segnassero, non si debbe attribuire al Compositore,
che l[unclear: ']habbia fatte per errore; massimamente in cotali cose che sono minime. Potrà simil-
, & far la Sesta di minore maggiore per virtù della chorda Chromatica; & cosi quella del b, secondo che occorrer puote nel fare i Con-trapunti; & se ben tali chorde non si segnassero, non si debbe attribuire al Compositore,
che l[unclear: ']habbia fatte per errore; massimamente in cotali cose che sono minime. Potrà simil- mente usar'alle volte; ma non spesso; una
modulatione d'una Semidiapente, quando tornarà commodo nell'accommodar la
modulatione alle parole, e procederà per
le chorde diatoniche naturali del Modo,
sopra 'l quale è fondata la cantilena; co-me qui si uede. Ma quando ui entrasse
alcuna delle chorde chromatiche (quantunque si ponesse per l'acquisto d'alcuna page 291consonanza) non si debbe usare; conciosia che tali chorde non furono ritrouate à de-struttione delle buone harmonie, & de i buoni costumi Musicali, ma si bene alla loro edi-ficatione, & al lor bene essere. Non sarà adunque lecito di usare alcun passaggio, che sia
mente usar'alle volte; ma non spesso; una
modulatione d'una Semidiapente, quando tornarà commodo nell'accommodar la
modulatione alle parole, e procederà per
le chorde diatoniche naturali del Modo,
sopra 'l quale è fondata la cantilena; co-me qui si uede. Ma quando ui entrasse
alcuna delle chorde chromatiche (quantunque si ponesse per l'acquisto d'alcuna page 291consonanza) non si debbe usare; conciosia che tali chorde non furono ritrouate à de-struttione delle buone harmonie, & de i buoni costumi Musicali, ma si bene alla loro edi-ficatione, & al lor bene essere. Non sarà adunque lecito di usare alcun passaggio, che sia
 simile ad uno de questi qui in essempio; percioche le chorde chroma-tiche haueranno sempre nella mo-dulatione una chorda diatonica corrispondente per vna Semidiapente,
ouer per un Tritono, ò Semitrito-no, secondo l'ordine della compo-sitione; i quali sono Interualli, ò Modulationi senz'harmonia. Gli sarà
anco permesso di potere usare alle
uolte le chorde chromatiche, quan-do uorrà procedere da una Sesta
fatta maggiore per uirtù de tali chorde alla Decima; ò Terza maggiore, col mouimen-to di Quarta, ò di Quinta; per poter da quelle peruenire all'Ottaua, oueramente all'
Vnisono; come qui si uede; & ciò per due ragioni, l'una delle quali è; perche il proce-dere è Diatonico nelle chorde chromatiche; l'altra perche i mouimenti, che fanno le
parti, procedono per Interualli harmonici, & sono anco regolati secondo i precetti mo-strati di sopra. Queste chorde si debbono segnar col segno
simile ad uno de questi qui in essempio; percioche le chorde chroma-tiche haueranno sempre nella mo-dulatione una chorda diatonica corrispondente per vna Semidiapente,
ouer per un Tritono, ò Semitrito-no, secondo l'ordine della compo-sitione; i quali sono Interualli, ò Modulationi senz'harmonia. Gli sarà
anco permesso di potere usare alle
uolte le chorde chromatiche, quan-do uorrà procedere da una Sesta
fatta maggiore per uirtù de tali chorde alla Decima; ò Terza maggiore, col mouimen-to di Quarta, ò di Quinta; per poter da quelle peruenire all'Ottaua, oueramente all'
Vnisono; come qui si uede; & ciò per due ragioni, l'una delle quali è; perche il proce-dere è Diatonico nelle chorde chromatiche; l'altra perche i mouimenti, che fanno le
parti, procedono per Interualli harmonici, & sono anco regolati secondo i precetti mo-strati di sopra. Queste chorde si debbono segnar col segno  per molti rispetti; & mas-
per molti rispetti; & mas- simamente per i poco accorti Can-tori; acciò non commettessero alle
uolte qualche errore, ponendo una
chorda in luogo d'un'altra; cioè, la
Diatonica in luogo della Chroma-tica, & ne segua la dissonanza. E' ben
uero, che nelle modulationi si trouano alcun'Interualli, come sono quelli di Quarta, di Quinta, & di Otta-ua; ne i quali il Cantore dè porre la
chorda chromatica, ancora che non
sia stata segnata dal Compositore;
accioche la modulatione delle parti sia drittamente ordinata. Ne il Compositore la debbe porre, perche è superfluo; essendo che ueramente non si dè cantare se non quelli In-terualli, che sono harmonici; come qui si uede. Ne debbe far, come fanno alcuni, iqua
simamente per i poco accorti Can-tori; acciò non commettessero alle
uolte qualche errore, ponendo una
chorda in luogo d'un'altra; cioè, la
Diatonica in luogo della Chroma-tica, & ne segua la dissonanza. E' ben
uero, che nelle modulationi si trouano alcun'Interualli, come sono quelli di Quarta, di Quinta, & di Otta-ua; ne i quali il Cantore dè porre la
chorda chromatica, ancora che non
sia stata segnata dal Compositore;
accioche la modulatione delle parti sia drittamente ordinata. Ne il Compositore la debbe porre, perche è superfluo; essendo che ueramente non si dè cantare se non quelli In-terualli, che sono harmonici; come qui si uede. Ne debbe far, come fanno alcuni, iqua li fuori d'ogni proposito, & senz'alcuna utilità, ò necessità danno principio alle lor can-tilene sopr'alcune chorde, che non sono naturali de i Modi, & mescolano le chorde
chromatiche con le diatoniche di maniera, che non solamente nel principio; ma nel
mezo, & nel fine anco non si uede altro che
li fuori d'ogni proposito, & senz'alcuna utilità, ò necessità danno principio alle lor can-tilene sopr'alcune chorde, che non sono naturali de i Modi, & mescolano le chorde
chromatiche con le diatoniche di maniera, che non solamente nel principio; ma nel
mezo, & nel fine anco non si uede altro che Diesis & b molli; la qual cosa; quando la
compositione la ricercasse, sarebbe da sopportare. Però sarà auertito ciascuno d'aste-nerse più che potrà da simil cosa, se non fusse costretto dalle parole, ouer d'altra cosa,
che accade nella cantilena; conciosia che per il lungo continuare in essi, la cantilena page 292viene à mutare il Modo, entrando d'uno nell'altro; com'è uitio particolare di qualche
Compositor moderno. Et sopra 'l tutto si dè guardare, da porre tali chorde nel princi-pio senza proposito; come fanno alcuni, che non solamente segnano la Seconda figura
della modulatione col segno
Diesis & b molli; la qual cosa; quando la
compositione la ricercasse, sarebbe da sopportare. Però sarà auertito ciascuno d'aste-nerse più che potrà da simil cosa, se non fusse costretto dalle parole, ouer d'altra cosa,
che accade nella cantilena; conciosia che per il lungo continuare in essi, la cantilena page 292viene à mutare il Modo, entrando d'uno nell'altro; com'è uitio particolare di qualche
Compositor moderno. Et sopra 'l tutto si dè guardare, da porre tali chorde nel princi-pio senza proposito; come fanno alcuni, che non solamente segnano la Seconda figura
della modulatione col segno  Chromatico, ma etiandio la prima; & fanno, che spesse volte, credendosi dar principio ad una modulatione del terzo Modo (per dar un'essempio)
non si accorgendo, incominciano una cantilena del Nono; come si può uedere nel prin
Chromatico, ma etiandio la prima; & fanno, che spesse volte, credendosi dar principio ad una modulatione del terzo Modo (per dar un'essempio)
non si accorgendo, incominciano una cantilena del Nono; come si può uedere nel prin cipio dell'essempio posto qui da canto. A-uertisca etiandio ogni Compositore, che si
pone alle uolte tra la chorda g. & la aa. un'al-tra chorda, segnata col segno commune
chromatico
cipio dell'essempio posto qui da canto. A-uertisca etiandio ogni Compositore, che si
pone alle uolte tra la chorda g. & la aa. un'al-tra chorda, segnata col segno commune
chromatico  ; onde nascono alcune modu-lationi, che non si possono chiamar Diato-niche semplicemente, ne Chromatiche;
percioche tanto nell'acuto quanto nel gra-ue, non si possono accommodar tra le chor-de naturali Diatoniche ad una modulatio-ne, che sia diatonica; come sono le sequen-ti conciosia; che essendo 'l primo Interuallo, che fanno le tre prime figure il Semituo-no maggiore, & quello che fanno la terza & la quarta il Ditono, & medesimamente è
il Semituono maggiore quello, che è contenuto tra le due ultime; se noi discorreremo
; onde nascono alcune modu-lationi, che non si possono chiamar Diato-niche semplicemente, ne Chromatiche;
percioche tanto nell'acuto quanto nel gra-ue, non si possono accommodar tra le chor-de naturali Diatoniche ad una modulatio-ne, che sia diatonica; come sono le sequen-ti conciosia; che essendo 'l primo Interuallo, che fanno le tre prime figure il Semituo-no maggiore, & quello che fanno la terza & la quarta il Ditono, & medesimamente è
il Semituono maggiore quello, che è contenuto tra le due ultime; se noi discorreremo
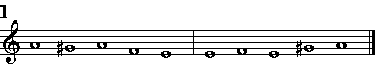 tutte le chorde diatoniche, & anche le Chromatiche insieme, non ritrouaremo, ne uer-so 'l graue, ne uerso l'acuto, di poter accom-modar questi Interualli, senza l'aiuto d'un'
altra chorda forastiera, la qual segnaremo con questo segno X, col quale si segna
ogni seconda chorda d'ogni Tetrachordo Enharmonico; Et questa chorda non si po-trà chiamar Diatonica; perche non hà luogo tra le chorde diatoniche; ne anco
Chromatica; conciosia che per il suo mezo da parte alcuna non si può hauere il Trihemituono; ne meno la potremo nominare Enharmonica, essendo che non diuide il Se-mituono maggiore in due Diesis; il che è ufficio della uera chorda Enharmonica; come
si può uedere in ciascuna diuisione fatta nella Seconda parte. Et bench'ella si possa chiamar Diatonica, perche si troua in una compositione diatonica, & fà il Semituono, ch'è
diatonico; tuttauia è nominata impropriamente; essendo che allora sarà detta Diato-nica, ò Chromatica, oueramente Enharmonica, quando sarà posta in luogo, oue po-trà in uno de i detti Generi fare 'l suo ufficio; ma non giamai altramente; com'auiene
di quella, ch'è posta nel quarto luogo del Quarto essempio qui di sotto.
tutte le chorde diatoniche, & anche le Chromatiche insieme, non ritrouaremo, ne uer-so 'l graue, ne uerso l'acuto, di poter accom-modar questi Interualli, senza l'aiuto d'un'
altra chorda forastiera, la qual segnaremo con questo segno X, col quale si segna
ogni seconda chorda d'ogni Tetrachordo Enharmonico; Et questa chorda non si po-trà chiamar Diatonica; perche non hà luogo tra le chorde diatoniche; ne anco
Chromatica; conciosia che per il suo mezo da parte alcuna non si può hauere il Trihemituono; ne meno la potremo nominare Enharmonica, essendo che non diuide il Se-mituono maggiore in due Diesis; il che è ufficio della uera chorda Enharmonica; come
si può uedere in ciascuna diuisione fatta nella Seconda parte. Et bench'ella si possa chiamar Diatonica, perche si troua in una compositione diatonica, & fà il Semituono, ch'è
diatonico; tuttauia è nominata impropriamente; essendo che allora sarà detta Diato-nica, ò Chromatica, oueramente Enharmonica, quando sarà posta in luogo, oue po-trà in uno de i detti Generi fare 'l suo ufficio; ma non giamai altramente; com'auiene
di quella, ch'è posta nel quarto luogo del Quarto essempio qui di sotto.
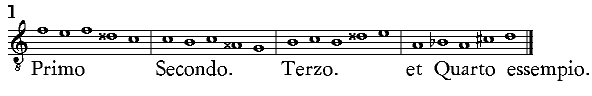 Et se ben tal chorda posta in cotal maniera non è Diatonica, non si debbe restar di usarla, poi che in questi, & altri simili passaggi, non fà alcun tristo effetto, & torna mol-to al proposito alle uolte al Compositore. Et perche si ritrouano infinite cantilene Diatoniche, le quali sono piene di questi, & d'altri simili passaggi, & non sono considera-ti da i Prattici; però ne hò uoluto far qui mentione, & rimettere cotal cosa al sa-no giudicio de i buoni & eccellenti Compositori, acciò uedino, in qual maniera si
debbino usare. Rimetto etiandio molt'altre cose, dellequali non uoglio tacere que-sta; che non è il douere, che si ponga la Semibreue sincopata, in modo, che dopo le
seguiti immediatamente la Minima dissonante col mouimento di grado; conciosia che si page 293farebbe contra quello, che si conuiene alla natura della Sincopa tutta consonante, la quale non riceue dopo se alcuna dissonanza, ma si bene la Consonanza. Però quando uorremo porre tal Minima dissonante, porremo sempre la battuta sopra la Semibreue; po-nendo appresso il punto, il qual dè esser sempre consonante; uenga poi la Minima à
qual modo si uoglia, ò consonante, ò dissonante, pur che procedi per grado; come qui
si uede. Debbe oltra di questo auertire, che tutte le uolte, che uorrà fare il Contrapun-
Et se ben tal chorda posta in cotal maniera non è Diatonica, non si debbe restar di usarla, poi che in questi, & altri simili passaggi, non fà alcun tristo effetto, & torna mol-to al proposito alle uolte al Compositore. Et perche si ritrouano infinite cantilene Diatoniche, le quali sono piene di questi, & d'altri simili passaggi, & non sono considera-ti da i Prattici; però ne hò uoluto far qui mentione, & rimettere cotal cosa al sa-no giudicio de i buoni & eccellenti Compositori, acciò uedino, in qual maniera si
debbino usare. Rimetto etiandio molt'altre cose, dellequali non uoglio tacere que-sta; che non è il douere, che si ponga la Semibreue sincopata, in modo, che dopo le
seguiti immediatamente la Minima dissonante col mouimento di grado; conciosia che si page 293farebbe contra quello, che si conuiene alla natura della Sincopa tutta consonante, la quale non riceue dopo se alcuna dissonanza, ma si bene la Consonanza. Però quando uorremo porre tal Minima dissonante, porremo sempre la battuta sopra la Semibreue; po-nendo appresso il punto, il qual dè esser sempre consonante; uenga poi la Minima à
qual modo si uoglia, ò consonante, ò dissonante, pur che procedi per grado; come qui
si uede. Debbe oltra di questo auertire, che tutte le uolte, che uorrà fare il Contrapun-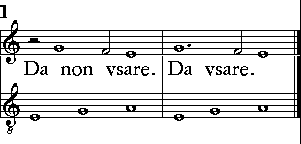 to alquanto languido ò mesto; simigliantemente dolce, ò
soaue, debbe procedere anco per mouimenti dolci & soa-ui; come sono quelli, che procedono per il Semituono,
per il Semiditono, & altri simili; usando le Consonanze
imperfette minori, che sono il Semiditono, l'Exachordo
minore, & l'altre Replicate; le quali Consonanze per sua
natura sono (come hò detto nel Cap. 10.) atte à tali cose.
Per il contrario uolendolo fare allegro, usarà il mouimento
del Tuono, quello del Ditono; & d'altri simili, con i suoi
Interualli. Et uolendolo far, che qualche uolta habbia dell'aspro, potrà usar le Maggiori,
che sono il Ditono, l'Hexachordo maggiore, & le Replicate nelle parti graui della can-tilena. Et tanto più sarà aspro, quanto maggiormente hauerà in sè il detto Hexachor-do, nelle figure di alquanto ualore, nella parte graue del concento. E' cosa difficile uera-mente il uolere insegnare particolarmente, in qual maniera, & à che tempo s'habbiano
da usar cotal cose; ma perche questo c'hò detto potrà molto giouare, quando si uor-rà alle uolte usar cotali maniere; però bastarà questo per hora; percioche forse un'al-tra uolta ne dirò più diffusamente.
to alquanto languido ò mesto; simigliantemente dolce, ò
soaue, debbe procedere anco per mouimenti dolci & soa-ui; come sono quelli, che procedono per il Semituono,
per il Semiditono, & altri simili; usando le Consonanze
imperfette minori, che sono il Semiditono, l'Exachordo
minore, & l'altre Replicate; le quali Consonanze per sua
natura sono (come hò detto nel Cap. 10.) atte à tali cose.
Per il contrario uolendolo fare allegro, usarà il mouimento
del Tuono, quello del Ditono; & d'altri simili, con i suoi
Interualli. Et uolendolo far, che qualche uolta habbia dell'aspro, potrà usar le Maggiori,
che sono il Ditono, l'Hexachordo maggiore, & le Replicate nelle parti graui della can-tilena. Et tanto più sarà aspro, quanto maggiormente hauerà in sè il detto Hexachor-do, nelle figure di alquanto ualore, nella parte graue del concento. E' cosa difficile uera-mente il uolere insegnare particolarmente, in qual maniera, & à che tempo s'habbiano
da usar cotal cose; ma perche questo c'hò detto potrà molto giouare, quando si uor-rà alle uolte usar cotali maniere; però bastarà questo per hora; percioche forse un'al-tra uolta ne dirò più diffusamente.
Il modo che si hà da tenere nel comporre le Cantilene à più di due voci; & del nome delle parti.Cap. LVIII.
Plus ascoltantum Sopranus captat orecchias.I quali hò uoluto porre, accioche 'l Compositore ricordandoseli, possa saper quello, c'haurà da fare, componendo coteste parti. Queste sono adunque le Parti principali, & Elementali d'ogni compositione perfetta; delle quali, ancora che l'Alto sia l'ultimo à comporsi; percioche composte l'altre parti, uiene a supplire, & à far perfetta l'Harmonia, che tra loro non si potea (doue mancauano) hauere; nondimeno non è legge fatale, che 'l si habbia da porre sempre ultimo nel comporre; come etiandio non è cosa alcuna, che ne astringa, à compor prima l'una, che l'altra Parte della compositione. Si debbe però auer-tire, che quando i Musici uogliono comporre alcuna cantilena à Tre uoci, il più delle uolte lasciano fuori il Contralto, ouer il Soprano, & pigliano l'altre parti; Et se uoglio-no procedere oltra le Quattro nominate, non ui aggiungono alcuna parte nuoua; ma le uengono à raddoppiare, facendo due Soprani, ò due Alti, ò due Tenori, & cosi due Bassi; & hanno il loro proposito. Qualunque uolta adunque che si uorrà compor-re alcun concento sopra un Soggetto ritrouato, sia Canto fermo, ò figurato; ouer se 'l si uorrà comporre alcuna Canzone, Madrigale, ouer altra cosa, & faccia dibisogno, che 'l Compositore sia l'Inuentore di tal Soggetto; debbe prima auertire di qual Modo ella sia; oueramente sopra qual modo uorrà comporre la cantilena, accio conosca le chorde, sopra le quali si haueranno da far le Cadenze, per poter comporre il concento in tal maniera, che 'l fine non sia dissonante dal mezo, & dal principio. La onde considera-te queste cose, potrà incominciare, da qual parte li tornarà più commodo; incomin-ciando però sempre in una chorda, la quale sia regolare del Modo, sopra 'l quale ha-urà da fondar la cantilena; osseruando quello, ch'in molte Regole poste di sopra si con-tiene. Ma perche i Musici costumano di dar principio alle lor Compositioni il più del-le uolte per il Tenore; & dopoi pongono il Soprano, alquale Aggiungono il Basso, & ultimamente l'Alto; hauendo di sopra mostrato molti essempi, contenuti tra queste due parti, Soprano, & Tenore; però non accade, se non porre la se-guente Tauola, nella quale si potrà comprender senza molta fatica tutti gli accor-di, che potranno far le Parti aggiunte insieme alle due nominate, siano quante si uogliono. Et hò tenuto tal'ordine, di porre primieramente gli accordi, che dan-no insieme il Soprano col Tenore; dopoi quanto potrà essere il Basso lontano dal Te-nore nella parte graue; accioche il tutto s'accordi; & cosi stante le nominate parti, quel che fà dibisogno, che sia l'Alto sopra 'l Basso; accioche l'Harmonia uenghi ad esser perfetta. Ma si dè auertire, che si trouarà alle uolte nell'Alto più d'uno accordo; onde tali accordi potranno seruire non solamente ad esso Alto; ma etiandio all'altre Parti, che si aggiungessero alla cantilena, oltra le Quattro nominate. Ne si troua-rà il Contralto posto con l'altre parti in Vnisono, ne in Ottaua, se non in quattro luoghi; percioche quando l'altre Parti haueranno tra loro la Quinta, & la Terza, ouer una delle Replicate; allora le aggiunte à queste, siano quante si uogliano, ne-cessariamente uerranno ad esser con una delle tre nominate in Ottaua, ouero in Vniso-no. Ma accioche si habbia piena intelligenza di quello, che si è detto, porrò un'essem-pio primieramente delle Compositioni, che si uorranno fare à Tre uoci; le quali si com-pongono senza la parte dell'Alto; dopoi ne porrò un'altro di quelle, che si fanno à Quat-tro. Sia adunque che noi uogliamo comporre una Cantilena à tre uoci; & che 'l page 296s'habbia posto il Soprano Vnisono col Tenore; dico, ch'allora bisognerà porre la parte del Basso, Terza, ò Quinta, ò Sesta; ouer Ottaua, ò Decima, ò Duodecima, ò Terza-decima, oueramente Quintadecima, sotto 'l Tenore. Simigliantemente quando si ha-uesse posto il Soprano in Terza col Tenore; bisogno sara di porre il Basso Terza, ò Se-sta, ouer'Ottaua, ò Decima sotto 'l detto Tenore. Si potrebbe anco dire, che quan-do le dette due parti si ponessero lontane l'una dall'altra per una Quarta, che 'l Basso si potrebbe porre Quinta, ò Duodecima sotto 'l Tenore, & cosi dell'altre; ma perche tut-ti questi & altri accordi si possono ueder nella Tauola seguente; però passarò più oltra, & dirò, che nelle Compositioni de Quattro uoci bisogna tener quest'ordine; che quan-do nella compositione il Soprano sarà posto Vnisono col tenore; cioè, quando l'uno & l'altro staranno sopra una chorda istessa; uolendo aggiunger la Terza parte à queste due, sarà dibisogno di porre il Basso distante per una di queste consonanze; Terza, ò Quin-ta, ò Sesta, ouer'Ottaua, ò per qualunque altra (come si uede nella Tauola) sotto 'l Te-nore; onde essendo il Basso lontano per una Terza; l'Alto potrà esser distante dal Basso nell'acuto per vna Quinta, ò per una Sesta, & l'altre parti (se fussero più di Quattro) potranno esser Vnisone, ouer distanti per una Ottaua dall'una di queste quattro. Ma se 'l Basso fusse distante dal Tenore nel graue per una Quinta, & l'Alto si potrà porre sopra 'l Basso distante per una Terza, ouer per una Decima; & l'altre parti, che s'aggiungessero sarebbono Vnisone, ouer lontane dall'una di queste quattro per una Ottaua. Et se 'l Basso fusse anco distante per una Sesta, riguardando nel Terzo essempio della Tauola, si trouerà quello, che potrà essere il Contralto; il che si potrà etiandio uedere dell'altre qui di sotto, chiaramente & distintamente per ordine. SEGVITA LA TAVOLA DE GLI ACCORDI, CHE POSSONO FARE CANTANDO INSIEME LE PARTI DELLE CANTILENE. page 298ONDE da questi accordi ciascun da se stesso potrà uedere, quando 'l Soprano fusse lontano dal Tenore per un'altra Consonanza, & il Basso fusse per alcun'altro Interuallo sotto 'l Tenore, quello che necessariamente sarebbe dibisogno, che 'l Contralto fusse di-stante nell'acuto dal Basso; ilche si lascia al giudicio del discreto Compositore, per non andare in lungo. Debbe però auertire, ch'alle uolte (secondo 'l uolere de chi compone) la parte del Basso si pone nel luogo del Tenore; ancora che ciò intrauenga di raro, & per il contrario, quella del Tenore nel luogo del Basso; cosi ancora il Soprano alle fiate si pone nel luogo dell'Alto, & questo in quello del Soprano; ouer si pone il Tenore nel luogo del Contralto, & cosi per il contrario; Però ciascuno sarà auertito, che in questa Tauola sempre si piglia il Soprano per la parte più acuta, & il Basso per quella, che è più graue; quantunque alle uolte le Parti nominate con questi nomi cambiano per accidente i loro assignati & proprij luoghi. Debbe etiandio intendere per il Tenore quella parte, che segue immediatamente il Basso uerso l'acuto; & per il Contralto quella, che si com-pone dopo le tre nominate; Imperoche intesa la cosa per tal maniera, ciascun po-trà commutar le parti l'una nell'altra; secondo che li tornerà commodo, senz'alcu-no errore.
Sed Tenor est, vocum rector, uel Guida canentum.
Altus Apollineum carmen depingit, & ornat.
Bassus alit voces, ingrassat, fundat, & auget.
Delle Cantilene che si compongono à Tre voci; & di quello, che si dè osseruar nel comporle.Cap. LIX.
 comprendere; ne i quali hò uoluto porre una parte sola per due cagioni; prima, perche
non mancano le dotte compositioni de molti eccellenti Musici, che sono piene di
queste cose; dalle quali si potrà comprendere il modo, che si haurà da tenere nella compositione dell'altre cantilene; dopoi per non accrescere il uolume con tanti essempi;
essendo che da questa sola parte si potrà comprender quello c'hò uoluto dire, & in qual
maniera si potrà procedere, cauando l'Inuentione d'una parte dal proceder dell'altra,
per potere impire il Contrapunto di belle fantasie & leggiadre inuentioni. Ma si
debbe anco auertire, che quantunque il basso possa alle uolte tenere il luogo del
Tenore, & cosi l'una dell'altre parti, quel dell'altra; nondimeno si dè fare, che 'l Bas-so finisca sempre sopra la Chorda regolare & finale del Modo, sopra 'l quale è compo-sta la cantilena, & cosi l'altre parti à i lor luoghi proprij; percioche da tal chorda ha-ueremo à giudicare il Modo. Et se bene il Tenore uenisse à finire in altra chorda, che
nella finale, questo non sarebbe di molta importanza; pur che si habbia proceduto nel-la sua modulatione secondo la natura del Modo della cantilena; Ilche si debbe anche in-tendere di ciascuna dell'altre parti. Oltra di questo è da auertire, che quella Composi-tione si può chiamar Perfetta, nella quale in ogni mutatione di chorda, tanto uerso 'l
graue, quanto uerso l'acuto, sempre si odono tutte quelle Consonanze, che fanno
uarietà di suono ne i loro estremi. Et quella è ueramente Harmonia perfetta; ch'in es-sa si ode tal consonanze; ma i Suoni ò Consonanze, che possono far diuersità al senti-page 300
comprendere; ne i quali hò uoluto porre una parte sola per due cagioni; prima, perche
non mancano le dotte compositioni de molti eccellenti Musici, che sono piene di
queste cose; dalle quali si potrà comprendere il modo, che si haurà da tenere nella compositione dell'altre cantilene; dopoi per non accrescere il uolume con tanti essempi;
essendo che da questa sola parte si potrà comprender quello c'hò uoluto dire, & in qual
maniera si potrà procedere, cauando l'Inuentione d'una parte dal proceder dell'altra,
per potere impire il Contrapunto di belle fantasie & leggiadre inuentioni. Ma si
debbe anco auertire, che quantunque il basso possa alle uolte tenere il luogo del
Tenore, & cosi l'una dell'altre parti, quel dell'altra; nondimeno si dè fare, che 'l Bas-so finisca sempre sopra la Chorda regolare & finale del Modo, sopra 'l quale è compo-sta la cantilena, & cosi l'altre parti à i lor luoghi proprij; percioche da tal chorda ha-ueremo à giudicare il Modo. Et se bene il Tenore uenisse à finire in altra chorda, che
nella finale, questo non sarebbe di molta importanza; pur che si habbia proceduto nel-la sua modulatione secondo la natura del Modo della cantilena; Ilche si debbe anche in-tendere di ciascuna dell'altre parti. Oltra di questo è da auertire, che quella Composi-tione si può chiamar Perfetta, nella quale in ogni mutatione di chorda, tanto uerso 'l
graue, quanto uerso l'acuto, sempre si odono tutte quelle Consonanze, che fanno
uarietà di suono ne i loro estremi. Et quella è ueramente Harmonia perfetta; ch'in es-sa si ode tal consonanze; ma i Suoni ò Consonanze, che possono far diuersità al senti-page 300 mento sono due, la Quinta & la Terza, ouer le Replicate dell'una & dell'altra; percio-che i loro estremi non hanno tra loro alcuna simiglianza, come hanno quelli dell'Ottaua;
essendo che gli estremi della Quinta non mouono l'Vdito nella maniera, che fanno quel-li della Terza, ne per il contrario; onde aggiunto il Ditono al Semiditono, generano la
Quinta, la quale è ne i suoi estremi contenuta da suoni molto uariati da quelli, che si odono ne gli estremi del Ditono, ò del Semiditono; perche gli estremi del Ditono sono an-co molto differenti da quelli del Semiditono. Et ciò non si ritroua nell'Ottaua; impero-che i suoi estremi hanno tal simiglianza, che paiono un solo suono, & s'assimigliano di maniera all'Vnisono, che aggiungendole qual Consonanza si uoglia; par che sia congiunto
(come etiandio hò detto altroue) quasi ad un solo suono. Ritrouandosi adunque la uarietà solamente tra gli estremi della Quinta & quelli della Terza; & componendosi l'Harmonia
di cose, che tra loro sono diuerse; dobbiamo per ogni modo (accioche habbiamo perfetta
cotale harmonia) cercare con ogni nostro potere, di fare udir nelle nostre Compositioni queste due consonanze, più che sia possibile, ouer le loro Replicate. E' ben uero, che molte uolte i Prattici pongono la Sesta in luogo della Quinta, & è ben fatto. Ma si de auertire, che
quando si porrà in una delle parti la detta Sesta sopra 'l Basso, di non porre alcun'altra
parte; che sia distante per una Quinta sopra di esso; percioche queste due parti uerrebbono ad esser distanti tra loro per un Tuono, ouer per un Semituono; di maniera che si
udirebbe la dissonanza. Hò detto però, che dobbiamo far ogni nostro potere, di por sem-pre queste due Consonanze nelle compositioni; conciosia che sempre non si possono porre; massimamente nelle compositioni di Tre uoci; perche in luogo d'una di loro si pone
spesso l'Ottaua, per non guastar il bello, elegante & facile cantare, che fanno le parti; la
onde uolendo osseruare di por sempre cotali Consonanze in simili compositioni, sareb-be quasi impossibile; massimamente uolendo far cantare cotali parti, & uoler'acquistar le
sudette Consonanze; percioche si potrebbe procedere per alcuni mouimenti tanto discommodi, che sarebbono cagione di roinare in parte la compositione; ma nelle Compositio-ni de Quattro ò più uoci, sarebbe più errore lasciarne una delle due nominate, che in quelle, che si compongono di Tre; conciosia che oue non si può osseruar cotal Regola con tre
parti, la quarta parte ce lo permette; & tanto maggiormente siamo obligati all'osseruan-za di cotal Legge, quanto più cresce 'l numero delle parti: la onde non osseruando quel-lo che si è detto, si uerrebbe à mostrar quanto si fusse stato buoni Imitatori della Natura;
la quale, quando non è deprauata, riduce tutte le cose alla loro perfettione. Ma ueramente è gran uergogna d'alcuni, che non solo fanno pouere le lor compositioni de Quattro
uoci d'una delle dette consonanze; ma fanno anco peggio, che pongono le parti in tal page 301maniera, che sono tra loro Vnisone, ouer lontane l'una dall'altra, per un'Ottaua sola-mente; onde simili Ottaue, si chiamano Raddoppiate, & fanno l'harmonia molto smembrata & pouera. Et questo sarebbe anco di poco momento, quando non si ritrouasse l'
istesso errore nelle compositioni de Cinque, de Sei, de Sette, & de più uoci; nelle qua-li sono alcuni luoghi smembrati & poueri in tal maniera; che s'odono con poca satisfat-tione dell'vdito. Però il Contrapuntista si debbe guardare da commettere tali mancamenti, degni ueramente di correttione; & debbe sapere, che tali errori si commettono non
solamente nelle figure, che si proferiscono nel battere, ò leuare della battuta; ma anche
in ogni figura cantabile, che si pone nel numero delle Consonanze. Osseruarà adunque
il Compositore questo, c'hò detto nelle sue compositioni; cioè, di far più ch'ello po-trà, che si ritroui la Terza, & la Quinta, & qualche fiate la Sesta in luogo di questa, ò
le Replicate; accioche la sua cantilena uenghi ad esser sonora & piena; & accioche
contenga in sè ogni perfettione d'harmonia. Ma non per questo dè intendere, ch'
ei debba osseruar cotal legge dal principio della compositione infin'al fine; impe-roche dè anco auertire in ogni cantilena, di dar qualche riposo alle parti; & di non
farle cantare sempre insieme; ma far che se ne odi hora due, hora tre, hora quattro,
mento sono due, la Quinta & la Terza, ouer le Replicate dell'una & dell'altra; percio-che i loro estremi non hanno tra loro alcuna simiglianza, come hanno quelli dell'Ottaua;
essendo che gli estremi della Quinta non mouono l'Vdito nella maniera, che fanno quel-li della Terza, ne per il contrario; onde aggiunto il Ditono al Semiditono, generano la
Quinta, la quale è ne i suoi estremi contenuta da suoni molto uariati da quelli, che si odono ne gli estremi del Ditono, ò del Semiditono; perche gli estremi del Ditono sono an-co molto differenti da quelli del Semiditono. Et ciò non si ritroua nell'Ottaua; impero-che i suoi estremi hanno tal simiglianza, che paiono un solo suono, & s'assimigliano di maniera all'Vnisono, che aggiungendole qual Consonanza si uoglia; par che sia congiunto
(come etiandio hò detto altroue) quasi ad un solo suono. Ritrouandosi adunque la uarietà solamente tra gli estremi della Quinta & quelli della Terza; & componendosi l'Harmonia
di cose, che tra loro sono diuerse; dobbiamo per ogni modo (accioche habbiamo perfetta
cotale harmonia) cercare con ogni nostro potere, di fare udir nelle nostre Compositioni queste due consonanze, più che sia possibile, ouer le loro Replicate. E' ben uero, che molte uolte i Prattici pongono la Sesta in luogo della Quinta, & è ben fatto. Ma si de auertire, che
quando si porrà in una delle parti la detta Sesta sopra 'l Basso, di non porre alcun'altra
parte; che sia distante per una Quinta sopra di esso; percioche queste due parti uerrebbono ad esser distanti tra loro per un Tuono, ouer per un Semituono; di maniera che si
udirebbe la dissonanza. Hò detto però, che dobbiamo far ogni nostro potere, di por sem-pre queste due Consonanze nelle compositioni; conciosia che sempre non si possono porre; massimamente nelle compositioni di Tre uoci; perche in luogo d'una di loro si pone
spesso l'Ottaua, per non guastar il bello, elegante & facile cantare, che fanno le parti; la
onde uolendo osseruare di por sempre cotali Consonanze in simili compositioni, sareb-be quasi impossibile; massimamente uolendo far cantare cotali parti, & uoler'acquistar le
sudette Consonanze; percioche si potrebbe procedere per alcuni mouimenti tanto discommodi, che sarebbono cagione di roinare in parte la compositione; ma nelle Compositio-ni de Quattro ò più uoci, sarebbe più errore lasciarne una delle due nominate, che in quelle, che si compongono di Tre; conciosia che oue non si può osseruar cotal Regola con tre
parti, la quarta parte ce lo permette; & tanto maggiormente siamo obligati all'osseruan-za di cotal Legge, quanto più cresce 'l numero delle parti: la onde non osseruando quel-lo che si è detto, si uerrebbe à mostrar quanto si fusse stato buoni Imitatori della Natura;
la quale, quando non è deprauata, riduce tutte le cose alla loro perfettione. Ma ueramente è gran uergogna d'alcuni, che non solo fanno pouere le lor compositioni de Quattro
uoci d'una delle dette consonanze; ma fanno anco peggio, che pongono le parti in tal page 301maniera, che sono tra loro Vnisone, ouer lontane l'una dall'altra, per un'Ottaua sola-mente; onde simili Ottaue, si chiamano Raddoppiate, & fanno l'harmonia molto smembrata & pouera. Et questo sarebbe anco di poco momento, quando non si ritrouasse l'
istesso errore nelle compositioni de Cinque, de Sei, de Sette, & de più uoci; nelle qua-li sono alcuni luoghi smembrati & poueri in tal maniera; che s'odono con poca satisfat-tione dell'vdito. Però il Contrapuntista si debbe guardare da commettere tali mancamenti, degni ueramente di correttione; & debbe sapere, che tali errori si commettono non
solamente nelle figure, che si proferiscono nel battere, ò leuare della battuta; ma anche
in ogni figura cantabile, che si pone nel numero delle Consonanze. Osseruarà adunque
il Compositore questo, c'hò detto nelle sue compositioni; cioè, di far più ch'ello po-trà, che si ritroui la Terza, & la Quinta, & qualche fiate la Sesta in luogo di questa, ò
le Replicate; accioche la sua cantilena uenghi ad esser sonora & piena; & accioche
contenga in sè ogni perfettione d'harmonia. Ma non per questo dè intendere, ch'
ei debba osseruar cotal legge dal principio della compositione infin'al fine; impe-roche dè anco auertire in ogni cantilena, di dar qualche riposo alle parti; & di non
farle cantare sempre insieme; ma far che se ne odi hora due, hora tre, hora quattro,
 page 302secondo 'l numero che saranno, & tallora tutt'insieme, & massimamente nel fine; percio-che tal uariatione uerrà à portar seco commodo al Compositore & al Cantore; bellezza
alla cantilena, & diletto & piacere all'udito. Oltra di questo si debbe sapere, ch'accom-modato che si haurà tre parti di qualunque compositione, le quali tra loro contenghino
le già dette Consonanze, ouer la Sesta in luogo della Quinta; l'altre parti, che s'aggiungessero à queste, uerrebbono ad esser necessariamente Vnisone, ouer in Ottaua con una
delle tre nominate; siano poi quante si uoglino le Aggiunte; come di sopra nell'essem-pio in molti luoghi si può comprendere. Però il Compositore potrà accommodarle alla
Cantilena, come meglio li tornerà commodo; E' ben uero, che più tosto debbe porre
nella sua Compositione l'Ottaua, che l'Vnisono; percioche (come dicemmo altre uolte)
non è consonanza.
page 302secondo 'l numero che saranno, & tallora tutt'insieme, & massimamente nel fine; percio-che tal uariatione uerrà à portar seco commodo al Compositore & al Cantore; bellezza
alla cantilena, & diletto & piacere all'udito. Oltra di questo si debbe sapere, ch'accom-modato che si haurà tre parti di qualunque compositione, le quali tra loro contenghino
le già dette Consonanze, ouer la Sesta in luogo della Quinta; l'altre parti, che s'aggiungessero à queste, uerrebbono ad esser necessariamente Vnisone, ouer in Ottaua con una
delle tre nominate; siano poi quante si uoglino le Aggiunte; come di sopra nell'essem-pio in molti luoghi si può comprendere. Però il Compositore potrà accommodarle alla
Cantilena, come meglio li tornerà commodo; E' ben uero, che più tosto debbe porre
nella sua Compositione l'Ottaua, che l'Vnisono; percioche (come dicemmo altre uolte)
non è consonanza.
In qual maniera la Quarta si possa porre nelle Compositioni. Cap. LX.
 perche non sono poste insieme secondo l'ordine naturale de cotali consonanze; anzi sono aggiunte insieme in un'ordine accide ntale [sic: accidentale]; perche non si troua nell'ordine nominato, che 'l Ditono sia posto senz'al-cun mezo auanti la Diatessaron; la Onde essendo queste due consonanze accommodate l'una dopo l'altra contra la loro natura; essendo posta
nell'acuto quella, che douerebbe esser collocata nel graue, & nel graue quella, che douerebbe tener l'acuto; de qui uiene, che i Suoni, che
nascono dalle chorde ordinate in tal maniera, sono men grati all'udi-to, de quelli, che nascono dalle chorde tese secondo i lor gradi natu-rali; Il perche ciascuno da se stesso con l'esperienza potrà conoscer da
i seguenti essempi sensatamente, & euidentemente comprender delli
due accompagnamenti qual sia ueramente il Buono. Quando poi s'ac-page 303compagna la Quarta con la Terza posta in acuto; ciò si può fare simigliantemente in due
modi; percioche, ouer se le aggiunge la Terza maggiore, ouer se le accompagna la minore. Quando è accompagnata con la maggiore fà buon effetto; ma quando è accompagnata con la minore, fà quasi dissonanza. Et ciò non è senza cagione; percioche oltra che si
potrà comprendere da i due essempi seguenti, quando le uoci, ò i suoni saranno ridotti
in atto; l'ordine naturale de i Numeri harmonici ce lo dimostra; nel quale ritrouandosi la
proportione della Diatessaron tra questi termini 4 & 3. come si può uedere nel detto luogo; segue senz'alcun mezo la proportione del Ditono posta tra 5 & 4. Ma in cotal'ordine
non si troua, che dopò la proportione, ò forma della Quarta segua immediatamente quella della Terza minore, come ogn'un può uedere. Per questo adunque auiene, che quel
perche non sono poste insieme secondo l'ordine naturale de cotali consonanze; anzi sono aggiunte insieme in un'ordine accide ntale [sic: accidentale]; perche non si troua nell'ordine nominato, che 'l Ditono sia posto senz'al-cun mezo auanti la Diatessaron; la Onde essendo queste due consonanze accommodate l'una dopo l'altra contra la loro natura; essendo posta
nell'acuto quella, che douerebbe esser collocata nel graue, & nel graue quella, che douerebbe tener l'acuto; de qui uiene, che i Suoni, che
nascono dalle chorde ordinate in tal maniera, sono men grati all'udi-to, de quelli, che nascono dalle chorde tese secondo i lor gradi natu-rali; Il perche ciascuno da se stesso con l'esperienza potrà conoscer da
i seguenti essempi sensatamente, & euidentemente comprender delli
due accompagnamenti qual sia ueramente il Buono. Quando poi s'ac-page 303compagna la Quarta con la Terza posta in acuto; ciò si può fare simigliantemente in due
modi; percioche, ouer se le aggiunge la Terza maggiore, ouer se le accompagna la minore. Quando è accompagnata con la maggiore fà buon effetto; ma quando è accompagnata con la minore, fà quasi dissonanza. Et ciò non è senza cagione; percioche oltra che si
potrà comprendere da i due essempi seguenti, quando le uoci, ò i suoni saranno ridotti
in atto; l'ordine naturale de i Numeri harmonici ce lo dimostra; nel quale ritrouandosi la
proportione della Diatessaron tra questi termini 4 & 3. come si può uedere nel detto luogo; segue senz'alcun mezo la proportione del Ditono posta tra 5 & 4. Ma in cotal'ordine
non si troua, che dopò la proportione, ò forma della Quarta segua immediatamente quella della Terza minore, come ogn'un può uedere. Per questo adunque auiene, che quel le Consonanze, che sono fuori de i loro luoghi naturali, & non sono ordinate, secondo c'hanno le forme tra i Numeri harmonici,
senz[unclear: ']alcun dubbio fanno qualche rumore. Onde dico, che la Quarta accompagnata con la Terza minore posta nel graue, si potrà sempre usare, & quella etiandio, che haurà la Terza maggiore nell'a-cuto; percioche non potranno far se non buoni effetti; ma quando
hauerà la Terza maggiore nel graue, ouer la minore nell'acuto, sem-pre s'udirà qualche effetto tristo. Ne ciò debbe parer strano ad alcuno; conciosiache quello ch'intrauiene al Vedere intorno la cosa Visibile, intrauiene anco all'Vdito intorno l'Vdibile. Onde si come sarebbe strana cosa da uedere in un'edificio una parte posta nel luogo d'
un'altra; come sarebbe; se i Fondamenti fussero posti nel luogo del
Tetto, & nel luogo delle Porte le Finestre, & tutte le cose fussero
poste al contrario fuori de i loro luoghi, & senz'alcuna propor-tione; cosi sarebbe cosa strana da udire una massa de Suoni, ò Consonanze poste in-sieme senza proportione, & fuori de i lor luoghi naturali; i quali parmi che d'alcuni mo-derni Scrittori, fin hora siano stati male intesi; tra i quali è uno Andrea Papio nel Cap.
20. del Lib. 2. del suo Trattato De Diatessaron. Si ritrouerà etiandio, uolendo inuesti-gar più oltra, che la Quarta, laquale hà nell'acuto il Ditono, è più grata all'Vdito di quella, che 'l hà nel graue; come etiandio è più grata quella, c'hà il Semiditono nella parte
graue, di quella che 'l hà nell'acuta; & che di queste due compositioni, quella Quarta,
che sarà accompagnata con la Terza minore nel graue, farà miglior'effetto di ciascun'altro accompagnamento; come si potrà comprendere da i seguenti essempi.
le Consonanze, che sono fuori de i loro luoghi naturali, & non sono ordinate, secondo c'hanno le forme tra i Numeri harmonici,
senz[unclear: ']alcun dubbio fanno qualche rumore. Onde dico, che la Quarta accompagnata con la Terza minore posta nel graue, si potrà sempre usare, & quella etiandio, che haurà la Terza maggiore nell'a-cuto; percioche non potranno far se non buoni effetti; ma quando
hauerà la Terza maggiore nel graue, ouer la minore nell'acuto, sem-pre s'udirà qualche effetto tristo. Ne ciò debbe parer strano ad alcuno; conciosiache quello ch'intrauiene al Vedere intorno la cosa Visibile, intrauiene anco all'Vdito intorno l'Vdibile. Onde si come sarebbe strana cosa da uedere in un'edificio una parte posta nel luogo d'
un'altra; come sarebbe; se i Fondamenti fussero posti nel luogo del
Tetto, & nel luogo delle Porte le Finestre, & tutte le cose fussero
poste al contrario fuori de i loro luoghi, & senz'alcuna propor-tione; cosi sarebbe cosa strana da udire una massa de Suoni, ò Consonanze poste in-sieme senza proportione, & fuori de i lor luoghi naturali; i quali parmi che d'alcuni mo-derni Scrittori, fin hora siano stati male intesi; tra i quali è uno Andrea Papio nel Cap.
20. del Lib. 2. del suo Trattato De Diatessaron. Si ritrouerà etiandio, uolendo inuesti-gar più oltra, che la Quarta, laquale hà nell'acuto il Ditono, è più grata all'Vdito di quella, che 'l hà nel graue; come etiandio è più grata quella, c'hà il Semiditono nella parte
graue, di quella che 'l hà nell'acuta; & che di queste due compositioni, quella Quarta,
che sarà accompagnata con la Terza minore nel graue, farà miglior'effetto di ciascun'altro accompagnamento; come si potrà comprendere da i seguenti essempi.
 Percioche quantunque le Seste, che contengono gli estremi de
queste parti poste insieme, non siano l'un dall'altro differenti nella
proportione, & non faccino variatione de suoni & di consonan-ze; nondimeno la uarietà delle chorde, che riceuono nel loro mezo, è cagione, che l'accompagnamento s'udirà esser migliore del-l'altro, & di far la differenza tra due accompagnamenti, che siano
buoni, dal buono al migliore. Tanta è la possanza delle Consonanze quando sono poste ne i lor proprij luoghi & naturali, che non solamente quelle, che sono tramezate in cotal maniera secondo la
natura de gli Harmonici numeri, sono più grate all'udito di quelle,
che sono poste al contrario; ma anche fanno più allegra & più so-nora ogni compositione, nellaquale sono poste. Questo adunque
raccoglieremo da quel che si è detto; che le Quarte si potranno porre ottimamente nelle compositioni, quando saranno collocate in
tal maniera, che sotto di loro nel graue habbiano la Quinta, ouer la Terza; come hò
mostrato di sopra; & etiandio si potrà porre alle uolte con la Terza nell'acuto; massima-mente quando sarà la maggiore; ancora che questo dall'uniuersità de i Musici Prattici
fin'hora sia stata poco considerata; percioche se l[unclear: ']accompagnamento della Quarta con la page 304Terza maggiore posta nel graue, che non è ueramente molto consonante è sopportata;
non sò ueder ragione perche non si dè sopportare l'accompagnamento della Terza maggiore posta nell'acuto; essendo che questo ueramente è migliore, come la esperien-za ce lo farà sempre uedere. Non bisogna pero fermarsi molto sopra tale Composi-tione; come anco non si dimora per molto tempo sopra la Sesta, ò maggiore, ò mino-re che ella sia.
Percioche quantunque le Seste, che contengono gli estremi de
queste parti poste insieme, non siano l'un dall'altro differenti nella
proportione, & non faccino variatione de suoni & di consonan-ze; nondimeno la uarietà delle chorde, che riceuono nel loro mezo, è cagione, che l'accompagnamento s'udirà esser migliore del-l'altro, & di far la differenza tra due accompagnamenti, che siano
buoni, dal buono al migliore. Tanta è la possanza delle Consonanze quando sono poste ne i lor proprij luoghi & naturali, che non solamente quelle, che sono tramezate in cotal maniera secondo la
natura de gli Harmonici numeri, sono più grate all'udito di quelle,
che sono poste al contrario; ma anche fanno più allegra & più so-nora ogni compositione, nellaquale sono poste. Questo adunque
raccoglieremo da quel che si è detto; che le Quarte si potranno porre ottimamente nelle compositioni, quando saranno collocate in
tal maniera, che sotto di loro nel graue habbiano la Quinta, ouer la Terza; come hò
mostrato di sopra; & etiandio si potrà porre alle uolte con la Terza nell'acuto; massima-mente quando sarà la maggiore; ancora che questo dall'uniuersità de i Musici Prattici
fin'hora sia stata poco considerata; percioche se l[unclear: ']accompagnamento della Quarta con la page 304Terza maggiore posta nel graue, che non è ueramente molto consonante è sopportata;
non sò ueder ragione perche non si dè sopportare l'accompagnamento della Terza maggiore posta nell'acuto; essendo che questo ueramente è migliore, come la esperien-za ce lo farà sempre uedere. Non bisogna pero fermarsi molto sopra tale Composi-tione; come anco non si dimora per molto tempo sopra la Sesta, ò maggiore, ò mino-re che ella sia.
D'alcune Regole poste in commune.Cap. LXI.
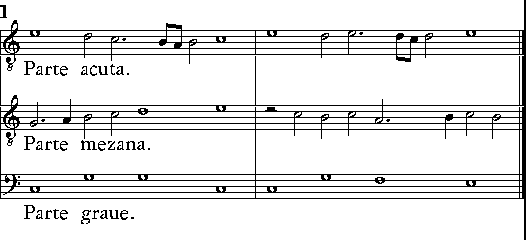 comprendere. Potrà ancora usar la Vndecima; come più à basso si uederà; la qual
si compone dell'Ottaua & della Quarta;
poi che Tolomeo nel Cap. 5. del Primo libro de gli Harmonici, & Boetio nel Cap.
10. del Libro primo della Musica, la pon-gono tra le Consonanze;Vide Def.
Demonst. di modo che da
questi essempi si potrà conoscere la loro
natura, & quanto possano esser grate all[unclear: ']V-dito; ancora che ne potrebbe bastar l'uso
de i Moderni, & de gli Antichi Composi-tori, i quali molte uolte l'hanno accompagnata in tal maniera. Vsano alcuni di por-re la parte acuta con la mezana distante
per una Quarta, & questa con la graue per
una Terza di maniera che 'l Basso uiene ad
esser lontano dal Soprano per una Sesta, tramezata dalla Terza, ò maggiore, ò minore:
comprendere. Potrà ancora usar la Vndecima; come più à basso si uederà; la qual
si compone dell'Ottaua & della Quarta;
poi che Tolomeo nel Cap. 5. del Primo libro de gli Harmonici, & Boetio nel Cap.
10. del Libro primo della Musica, la pon-gono tra le Consonanze;Vide Def.
Demonst. di modo che da
questi essempi si potrà conoscere la loro
natura, & quanto possano esser grate all[unclear: ']V-dito; ancora che ne potrebbe bastar l'uso
de i Moderni, & de gli Antichi Composi-tori, i quali molte uolte l'hanno accompagnata in tal maniera. Vsano alcuni di por-re la parte acuta con la mezana distante
per una Quarta, & questa con la graue per
una Terza di maniera che 'l Basso uiene ad
esser lontano dal Soprano per una Sesta, tramezata dalla Terza, ò maggiore, ò minore:
 Onde essendo le parti composte in tal maniera, sogliono farle ascendere, ò discendere insieme più gradi, & tal modo di procedere chiamano Falso bordone. Ma in uerità, anco-ra che tal maniera sia molto in uso, & che con difficultà grande si potesse leuare, non è pe-rò molto lodeuole: imperoche, oltra che la Quarta è consonanza perfetta; com'altroue hò
mostrato;Supra
Cap. 5. & che non dobbiamo far contra la Regola data nel Cap. 29. genera alle uolte
tra le parti alcune relationi, che non sono harmoniche; la onde poco diletto apportano
all'Vdito; come ciascuno col mezo dell'essempio posto qui di sotto potrà conoscere.
Onde essendo le parti composte in tal maniera, sogliono farle ascendere, ò discendere insieme più gradi, & tal modo di procedere chiamano Falso bordone. Ma in uerità, anco-ra che tal maniera sia molto in uso, & che con difficultà grande si potesse leuare, non è pe-rò molto lodeuole: imperoche, oltra che la Quarta è consonanza perfetta; com'altroue hò
mostrato;Supra
Cap. 5. & che non dobbiamo far contra la Regola data nel Cap. 29. genera alle uolte
tra le parti alcune relationi, che non sono harmoniche; la onde poco diletto apportano
all'Vdito; come ciascuno col mezo dell'essempio posto qui di sotto potrà conoscere.
 L'errore di cotesto abuso si manifesta da questo; percioche se noi uorremo porre le Terze
à i lor luoghi naturali, oue si debbono ragioneuolmente porre; ouer sopra l'Ottaua alme-no; si potrà conoscere con quanta ragione si possa fare una cosa simile; conciosia che si come nel mostrato essempio si udiuano molte Quarte, cosi nel sottoposto potremo udire al-tretante Quinte.
L'errore di cotesto abuso si manifesta da questo; percioche se noi uorremo porre le Terze
à i lor luoghi naturali, oue si debbono ragioneuolmente porre; ouer sopra l'Ottaua alme-no; si potrà conoscere con quanta ragione si possa fare una cosa simile; conciosia che si come nel mostrato essempio si udiuano molte Quarte, cosi nel sottoposto potremo udire al-tretante Quinte.
 Io sò ben ch'appresso de molti più uarranno le autorità d'alcuni, che si habbiano usurpata cotal licenza, che le ragioni addotte di sopra; ma faccino pur'il peggio, che sanno, con
dire questa cosa è stata usata da molti, che poco mi curo; poi che non sono, ne uogliono
esser capaci di ragione. Et benche la Terza sia consonanza, & si possa porre in qual luogo
torna commodo; tuttauia il suo uero luogo non è nel graue, ma nell'acuto, sopra la Disdiapason, ouer Quintadecima: Imperoche naturalmente l'Ottaua posta nel graue, non può
esser tramezata d[unclear: ']altro suono; ma uuol'esser posta semplice, senz'alcuna mediatione;
come hò raccontato nel principio del Primo libro delle Dimostrationi; & come etian-dio ci mostrano i Numeri harmonici, posti nel Cap. 15. della Prima parte; tra i quali,
si uede la prima Dupla contenuta nel Senario tra 2 & 1. ch'è la sua forma, la quale
non è mediata d'alcun termine mezano, ma si bene la seconda posta tra 4. & 2. la-quale è diuisa dal 3. in una Sesquialtera, che si troua tra 3 & 2. & in una Sesqui-terza, che si troua tra 4 & 3. che sono le forme della Diapente, & della Diates-saron consonanze. Onde la Sesquialtera nella detta seconda Diapason resta non diui-sa & intera; ma oltra la Quadrupla, ch'è la forma della Disdiapason, si troua diuisa in due
parti; cioè, in una Sesquiquarta, ch'è la forma uera del Ditono, & in una Sesquiquin-ta, ch'è quella del Semiditono; delle quali, l'una è collocata tra 5 & 4. & l'al-tra 6 & 5. Si uede adunque, che la prima Ottaua è collocata naturalmente tra i
Numeri sonori senz'alcun altro numero mezano; & che la Quinta le succede senz'
alcun mezo; dopoi segue la Quarta, & da queste due parti maggiori si compone la
seconda Diapason, onde nasce la Disdiapason; ò Quintadecima. Dopo queste uie-ne il Ditono, & immediatamente dopo lui segue il Semiditono; di maniera che, se
tali consonanze fussero poste ne i Contrapunti (se ciò si potesse far sempre commoda-mente) à i lor luoghi proprij & naturali; non è dubbio, che nascerebbe un concento
tanto harmonioso, quanto l'Huomo si potesse imaginare. Et di ciò potiamo ueder l'esperienza sempre ne gli Istrumenti arteficiali; massimamente nell'Organo, oue poste le consonanze nominate per ordine l'una dopo l'altra, secondo c'hò mostrato; non si può dire
il buono effetto che fanno. Ma se per caso la prima Ottaua si pone tramezata nel graue,
dalla Quinta; allora il concento si fà alquanto tristo; & se tal Quinta si diuidesse in
due Terze, non si potrebbe à pena udire tal composto, massimamente se la Terza mino-re tenesse il luogo della maggiore; cioè, s'ella fusse posta nel graue. E' nondimeno sop-portabile la prima Ottaua tramezata in proportionalità harmonica per la Quinta; & quando sopra di essa si pone la Terza, non fà tristo effetto; ancora che cotali Consonanze
non siano poste à i lor luoghi proprij; & ciò intrauiene; percioche tengono il luogo
mezano nell'istrumento, oue si contiene tale ordine. Si debbe adunque porre la page 306Terza immediatamente dopo la Quintadecima, ò almeno dopo l'Ottaua in ordine; &
debbe esser la maggiore, acciò che 'l concento sia più allegro & più pieno; ma se 'l si ab-batterà, ch'ella sia la minore; come infinite uolte suole accascare, allora il concento sa-rà più mesto. Queste cose ueramente sono poco considerate da i Prattici; percioche sen-z'alcun riguardo pongono la Quinta tra le chorde graui, & anco la Terza, come torna à loro più commodo; la qual cosa quanto diletto apporti all'Vdito lasciarò considerare à
coloro c'hanno giudicio. Onde uoglio dir questo solamente, che douendosi porre la Ter-za nella compositione, è meglio porla sempre sopra l'Ottaua, che tra essa; Voglio inferi-re, che migliore effetto farà sempre la Decima, che la Terza. Et quantunque si potreb-be dire, che meglio sarebbe anco, porre la Quinta sopra l'Ottaua posta nel graue della
cantilena; come cosa più propinqua, secondo la natura de i Numeri harmonici; che la
Terza, come più lontana; tuttauia pongansi à qual modo si uoglia, tornarà sempre bene.
Ma quanto miglior'effetto faccia la Decima, che la Terza, da questi due essempi, ciascuno, che hà giudicio, lo potrà conoscere. Si debbe però auertire, ch'in uno essempio; cioè,
Io sò ben ch'appresso de molti più uarranno le autorità d'alcuni, che si habbiano usurpata cotal licenza, che le ragioni addotte di sopra; ma faccino pur'il peggio, che sanno, con
dire questa cosa è stata usata da molti, che poco mi curo; poi che non sono, ne uogliono
esser capaci di ragione. Et benche la Terza sia consonanza, & si possa porre in qual luogo
torna commodo; tuttauia il suo uero luogo non è nel graue, ma nell'acuto, sopra la Disdiapason, ouer Quintadecima: Imperoche naturalmente l'Ottaua posta nel graue, non può
esser tramezata d[unclear: ']altro suono; ma uuol'esser posta semplice, senz'alcuna mediatione;
come hò raccontato nel principio del Primo libro delle Dimostrationi; & come etian-dio ci mostrano i Numeri harmonici, posti nel Cap. 15. della Prima parte; tra i quali,
si uede la prima Dupla contenuta nel Senario tra 2 & 1. ch'è la sua forma, la quale
non è mediata d'alcun termine mezano, ma si bene la seconda posta tra 4. & 2. la-quale è diuisa dal 3. in una Sesquialtera, che si troua tra 3 & 2. & in una Sesqui-terza, che si troua tra 4 & 3. che sono le forme della Diapente, & della Diates-saron consonanze. Onde la Sesquialtera nella detta seconda Diapason resta non diui-sa & intera; ma oltra la Quadrupla, ch'è la forma della Disdiapason, si troua diuisa in due
parti; cioè, in una Sesquiquarta, ch'è la forma uera del Ditono, & in una Sesquiquin-ta, ch'è quella del Semiditono; delle quali, l'una è collocata tra 5 & 4. & l'al-tra 6 & 5. Si uede adunque, che la prima Ottaua è collocata naturalmente tra i
Numeri sonori senz'alcun altro numero mezano; & che la Quinta le succede senz'
alcun mezo; dopoi segue la Quarta, & da queste due parti maggiori si compone la
seconda Diapason, onde nasce la Disdiapason; ò Quintadecima. Dopo queste uie-ne il Ditono, & immediatamente dopo lui segue il Semiditono; di maniera che, se
tali consonanze fussero poste ne i Contrapunti (se ciò si potesse far sempre commoda-mente) à i lor luoghi proprij & naturali; non è dubbio, che nascerebbe un concento
tanto harmonioso, quanto l'Huomo si potesse imaginare. Et di ciò potiamo ueder l'esperienza sempre ne gli Istrumenti arteficiali; massimamente nell'Organo, oue poste le consonanze nominate per ordine l'una dopo l'altra, secondo c'hò mostrato; non si può dire
il buono effetto che fanno. Ma se per caso la prima Ottaua si pone tramezata nel graue,
dalla Quinta; allora il concento si fà alquanto tristo; & se tal Quinta si diuidesse in
due Terze, non si potrebbe à pena udire tal composto, massimamente se la Terza mino-re tenesse il luogo della maggiore; cioè, s'ella fusse posta nel graue. E' nondimeno sop-portabile la prima Ottaua tramezata in proportionalità harmonica per la Quinta; & quando sopra di essa si pone la Terza, non fà tristo effetto; ancora che cotali Consonanze
non siano poste à i lor luoghi proprij; & ciò intrauiene; percioche tengono il luogo
mezano nell'istrumento, oue si contiene tale ordine. Si debbe adunque porre la page 306Terza immediatamente dopo la Quintadecima, ò almeno dopo l'Ottaua in ordine; &
debbe esser la maggiore, acciò che 'l concento sia più allegro & più pieno; ma se 'l si ab-batterà, ch'ella sia la minore; come infinite uolte suole accascare, allora il concento sa-rà più mesto. Queste cose ueramente sono poco considerate da i Prattici; percioche sen-z'alcun riguardo pongono la Quinta tra le chorde graui, & anco la Terza, come torna à loro più commodo; la qual cosa quanto diletto apporti all'Vdito lasciarò considerare à
coloro c'hanno giudicio. Onde uoglio dir questo solamente, che douendosi porre la Ter-za nella compositione, è meglio porla sempre sopra l'Ottaua, che tra essa; Voglio inferi-re, che migliore effetto farà sempre la Decima, che la Terza. Et quantunque si potreb-be dire, che meglio sarebbe anco, porre la Quinta sopra l'Ottaua posta nel graue della
cantilena; come cosa più propinqua, secondo la natura de i Numeri harmonici; che la
Terza, come più lontana; tuttauia pongansi à qual modo si uoglia, tornarà sempre bene.
Ma quanto miglior'effetto faccia la Decima, che la Terza, da questi due essempi, ciascuno, che hà giudicio, lo potrà conoscere. Si debbe però auertire, ch'in uno essempio; cioè,
 nel primo si contiene il Tritono, & nel secondo la Semidiapente; i quali tanto più sono
sopportabili, quanto che dopo sè l'uno hà la Terza, & l'altro la Decima maggiori, che
fanno relatione harmonica con le uoci, che contengono il Tritono, ouer la Semidiapente. Et se bene gli Interualli, che sono nelle seconde figure de i mostrati essempi, sono ueramente dissonanti; tuttauia sono in tal maniera collocati, che per il procedere, secondo
l'ordine mostrato nelle Regole, se ne passano, che l'Vdito se ne contenta. Si debbe oltra
di ciò auertire, che quando dissi, che La prima Ottaua si pone senz'alcun mezo, potiamo
intendere tale Ottaua esser quella, la quale incomincia nella chorda più graue del Basso
della cantilena, salendo di mano in mano all'acuto fin'all'Ottaua chorda; & per la seconda si può intender quella, ch'incomincia dalla chorda estrema acuta di tale Ottaua, & uà
fino alla Quintadecima. Pongono i Prattici alle uolte il Tritono tra due parti, il quale casca sopra la seconda parte d'alcuna Semibreue sincopata posta nel graue in cotal manie-ra; il quale si ode nella loro relatione; ma non è percossa l'una delle parti acute con la par
nel primo si contiene il Tritono, & nel secondo la Semidiapente; i quali tanto più sono
sopportabili, quanto che dopo sè l'uno hà la Terza, & l'altro la Decima maggiori, che
fanno relatione harmonica con le uoci, che contengono il Tritono, ouer la Semidiapente. Et se bene gli Interualli, che sono nelle seconde figure de i mostrati essempi, sono ueramente dissonanti; tuttauia sono in tal maniera collocati, che per il procedere, secondo
l'ordine mostrato nelle Regole, se ne passano, che l'Vdito se ne contenta. Si debbe oltra
di ciò auertire, che quando dissi, che La prima Ottaua si pone senz'alcun mezo, potiamo
intendere tale Ottaua esser quella, la quale incomincia nella chorda più graue del Basso
della cantilena, salendo di mano in mano all'acuto fin'all'Ottaua chorda; & per la seconda si può intender quella, ch'incomincia dalla chorda estrema acuta di tale Ottaua, & uà
fino alla Quintadecima. Pongono i Prattici alle uolte il Tritono tra due parti, il quale casca sopra la seconda parte d'alcuna Semibreue sincopata posta nel graue in cotal manie-ra; il quale si ode nella loro relatione; ma non è percossa l'una delle parti acute con la par te graue di tale Interuallo. Et perche le parti procedono in cotal modo, & sono concate-nate tra loro di maniera, che senza partirsi dall'osseruanza delle Regole date, fanno buo-page 307no effetto; però queste parti porgono all'Vdito & grato & soaue piacere; perche quel poco di dissonanza, che si ode nel Tritono & nella Semidiapente, se ne passa presto, & aggiunge soauità alla consonanza seguente, più di quello, che si udirebbe, se non ui fusse; essendo
te graue di tale Interuallo. Et perche le parti procedono in cotal modo, & sono concate-nate tra loro di maniera, che senza partirsi dall'osseruanza delle Regole date, fanno buo-page 307no effetto; però queste parti porgono all'Vdito & grato & soaue piacere; perche quel poco di dissonanza, che si ode nel Tritono & nella Semidiapente, se ne passa presto, & aggiunge soauità alla consonanza seguente, più di quello, che si udirebbe, se non ui fusse; essendo
 che Di due opposti l'uno si conosce maggiormente per la comparatione, che si fà con l'altro. Frequentano i Moderni molto spesso tali passaggi; onde parendoli la cosa riuscibile
pongono alle uolte la parte graue sincopata
in tal maniera, che la seconda parte della Sin-copa contiene col Tenore la Seconda, & il
Tenore col Soprano hora la Terza, hora la
Quarta, & tallora la Quinta; come si uede
nell'essempio. Ma quello, che contiene la
Quarta, senza dubio è men buono de gli al-tri; percioche si ode tale Interuallo senz'al-cun'accompagnamento. Oltra di questo si
dè auertire, che alle uolte si potrà passare
dalla Sesta minore all'Ottaua, quando le parti saranno collocate in tal maniera, che 'l Basso col Tenore procedino ordinatamente secondo l'ordine & modo dato nelle Regole u-niuersali; & il Soprano procedi per Decima sopra 'l Basso; come qui si uede.
che Di due opposti l'uno si conosce maggiormente per la comparatione, che si fà con l'altro. Frequentano i Moderni molto spesso tali passaggi; onde parendoli la cosa riuscibile
pongono alle uolte la parte graue sincopata
in tal maniera, che la seconda parte della Sin-copa contiene col Tenore la Seconda, & il
Tenore col Soprano hora la Terza, hora la
Quarta, & tallora la Quinta; come si uede
nell'essempio. Ma quello, che contiene la
Quarta, senza dubio è men buono de gli al-tri; percioche si ode tale Interuallo senz'al-cun'accompagnamento. Oltra di questo si
dè auertire, che alle uolte si potrà passare
dalla Sesta minore all'Ottaua, quando le parti saranno collocate in tal maniera, che 'l Basso col Tenore procedino ordinatamente secondo l'ordine & modo dato nelle Regole u-niuersali; & il Soprano procedi per Decima sopra 'l Basso; come qui si uede.
 Si potrà anche dalla Terza maggiore passare all'Vnisono, quando 'l Soprano pro-cederà dall[unclear: ']acuto al graue col mouimento del Ditono; & il Basso col Soprano sarà ordinato secondo i precetti dati di sopra, stando il Tenore, senza mutar luogo; come si uede; percioche essendo le parti estreme, che sono più dell'altre comprese dal senso, ben regolate; s'alle uolte uerrà qualche cosa nell'altre, che non sia cosi ben regolata, si potrà soppor-
Si potrà anche dalla Terza maggiore passare all'Vnisono, quando 'l Soprano pro-cederà dall[unclear: ']acuto al graue col mouimento del Ditono; & il Basso col Soprano sarà ordinato secondo i precetti dati di sopra, stando il Tenore, senza mutar luogo; come si uede; percioche essendo le parti estreme, che sono più dell'altre comprese dal senso, ben regolate; s'alle uolte uerrà qualche cosa nell'altre, che non sia cosi ben regolata, si potrà soppor- tare. La onde si concede al compositore, che possa pigliare alle fiate qualche licenza fuo-ri della Regola data di sopra nel Cap. 38. Gli sarà etiandio lecito di passar dalla Terza minore, per contrarij mouimenti, all'Ottaua; quando le parti saranno ordinate in tal maniera, che quella, che si trouerà lontana per simile consonanza, & dopoi passarà all'Ot-taua, habbia nel graue la Terza maggiore, di maniera che la parte acuta sia lontana dalla
graue per una Quinta; come nell'essempio seguente si uede. Anzi dirò di più; che
tare. La onde si concede al compositore, che possa pigliare alle fiate qualche licenza fuo-ri della Regola data di sopra nel Cap. 38. Gli sarà etiandio lecito di passar dalla Terza minore, per contrarij mouimenti, all'Ottaua; quando le parti saranno ordinate in tal maniera, che quella, che si trouerà lontana per simile consonanza, & dopoi passarà all'Ot-taua, habbia nel graue la Terza maggiore, di maniera che la parte acuta sia lontana dalla
graue per una Quinta; come nell'essempio seguente si uede. Anzi dirò di più; che
 sarà necessario, che le Parti stiano in cotal mo-do; perche se si ponessero altramente, facen-do maggiore quella Terza, ch'è minore, col se-gno
sarà necessario, che le Parti stiano in cotal mo-do; perche se si ponessero altramente, facen-do maggiore quella Terza, ch'è minore, col se-gno  . accioche (secondo le date Regole) dal-la Imperfetta più propinqua si peruenghi alla page 308Perfetta; non si potrebbe far tal cosa per alcun modo, senza grande offesa dell'Vdito; conciosia che si uerrebbe à fare una Quinta, che hauerebbe due Terze maggiori. Ma ciò sia
detto per sempre, che l'obligo stà nelle cose possibili, & non nelle impossibili; al quale
niuno è obligato. Dobbiamo oltra di questo osseruare, che nelle Cadenze principali della cantilena, le parti siano ordinate & accommodate in tal maniera, che la seconda parte
della figura sincopata, la qual si pone dissonante, sia sempre con la parte graue distante
per una Quarta, oueramente per una Vndecima; & con l'altra sempre lontana per una
Seconda, ò per una Settima; ilche si debbe osseruare etiandio in ogni figura sincopata,
nella quale sia la dissonanza; come si uede ne i seguenti essempi; da i quali si potrà com-prender il modo, che si haurà da tenere in altre simili; quando accascheranno. Ma se uorremo aggiunger la Quarta parte à queste, sempre ella si porrà in Ottaua dell'una delle due,
che sono distanti tra loro per Quinta, ò per Duodecima; accommodando la hora in un
luogo & hora in un'altro secondo che tornerà meglio.
. accioche (secondo le date Regole) dal-la Imperfetta più propinqua si peruenghi alla page 308Perfetta; non si potrebbe far tal cosa per alcun modo, senza grande offesa dell'Vdito; conciosia che si uerrebbe à fare una Quinta, che hauerebbe due Terze maggiori. Ma ciò sia
detto per sempre, che l'obligo stà nelle cose possibili, & non nelle impossibili; al quale
niuno è obligato. Dobbiamo oltra di questo osseruare, che nelle Cadenze principali della cantilena, le parti siano ordinate & accommodate in tal maniera, che la seconda parte
della figura sincopata, la qual si pone dissonante, sia sempre con la parte graue distante
per una Quarta, oueramente per una Vndecima; & con l'altra sempre lontana per una
Seconda, ò per una Settima; ilche si debbe osseruare etiandio in ogni figura sincopata,
nella quale sia la dissonanza; come si uede ne i seguenti essempi; da i quali si potrà com-prender il modo, che si haurà da tenere in altre simili; quando accascheranno. Ma se uorremo aggiunger la Quarta parte à queste, sempre ella si porrà in Ottaua dell'una delle due,
che sono distanti tra loro per Quinta, ò per Duodecima; accommodando la hora in un
luogo & hora in un'altro secondo che tornerà meglio.
 Et perche la Cadenza si può fare in molte maniere con uarietà delle parti; però uoglio
por qui molti essenpi accommodati sopra Quattro parti; i quali potranno etiandio ser
Et perche la Cadenza si può fare in molte maniere con uarietà delle parti; però uoglio
por qui molti essenpi accommodati sopra Quattro parti; i quali potranno etiandio ser uire alle compositioni di Tre uoci; ouer se li potrà aggiunger nell'altre, quando fusse bi-sogno; accioche io non habbia da replicar più cosa alcuna in questa materia. Ma non uoglio restar di dire, che si conosce per esperienza, che quella Cadenza non hà gratia alcuna
ò leggiadria in sè, la qual sia senza la Dissonanza, che si troua nelle mostrate; mas-simamente quando le parti procedono insieme per l'istesse figure; ancora che siano
sincopate, ouer non sincopate, che si proferiscono nel leuare, ò nel battere della bat-tuta; come sono queste.
uire alle compositioni di Tre uoci; ouer se li potrà aggiunger nell'altre, quando fusse bi-sogno; accioche io non habbia da replicar più cosa alcuna in questa materia. Ma non uoglio restar di dire, che si conosce per esperienza, che quella Cadenza non hà gratia alcuna
ò leggiadria in sè, la qual sia senza la Dissonanza, che si troua nelle mostrate; mas-simamente quando le parti procedono insieme per l'istesse figure; ancora che siano
sincopate, ouer non sincopate, che si proferiscono nel leuare, ò nel battere della bat-tuta; come sono queste.
 Però il Contrapuntista si guardarà di usarle, & debbe schiuare al tutto, di fare ch'alcu-na parte della cantilena non faccia la Cadenza, quando l'altre parti fussero ordina-te in un modo, che qualunque altra delle più graui facesse la Quinta con la figura meza-na della cadenza posta nell'acuto, mouendosi per l'interuallo del Semituono, quando tal
figura si potrà segnare con la cifra
Però il Contrapuntista si guardarà di usarle, & debbe schiuare al tutto, di fare ch'alcu-na parte della cantilena non faccia la Cadenza, quando l'altre parti fussero ordina-te in un modo, che qualunque altra delle più graui facesse la Quinta con la figura meza-na della cadenza posta nell'acuto, mouendosi per l'interuallo del Semituono, quando tal
figura si potrà segnare con la cifra  . Chromatica; percioche (com'hò detto altroue) proferendosi tal parte della Cadenza naturalmente col Semituono, sarebbe cosa difficile,
che 'l Cantore potesse hauer'in tal caso riguardo, di non proferirla, con quel modo che si
proferisce naturalmente. Onde uerrebbe poi à commettere errore, & à porre una dis-sonanza in luogo della consonanza; cioè, uerrebbe à porre la Diapente superflua in
luogo della uera; come qui si uede. page 310
. Chromatica; percioche (com'hò detto altroue) proferendosi tal parte della Cadenza naturalmente col Semituono, sarebbe cosa difficile,
che 'l Cantore potesse hauer'in tal caso riguardo, di non proferirla, con quel modo che si
proferisce naturalmente. Onde uerrebbe poi à commettere errore, & à porre una dis-sonanza in luogo della consonanza; cioè, uerrebbe à porre la Diapente superflua in
luogo della uera; come qui si uede. page 310 Accascherà anco un simile errore, quando le parti à Tre uoci saranno ordinate in tal maniera, che essendo 'l Tenore sopra 'l Basso lontano per una Terza, discendendo per salto
di Quarta sotto 'l Basso una Terza, ascendendo il Basso per grado di Tuono; & ritornando dopoi ciascun'à i suoi primi luoghi; il Soprano farà la Cadenza distante dalla parte
graue per una Quinta uerso l'acuto; come in questo essempio si uede.
Accascherà anco un simile errore, quando le parti à Tre uoci saranno ordinate in tal maniera, che essendo 'l Tenore sopra 'l Basso lontano per una Terza, discendendo per salto
di Quarta sotto 'l Basso una Terza, ascendendo il Basso per grado di Tuono; & ritornando dopoi ciascun'à i suoi primi luoghi; il Soprano farà la Cadenza distante dalla parte
graue per una Quinta uerso l'acuto; come in questo essempio si uede.
 Seguirebbe anco un'altro errore, che qualunque uolta si uolesse sonar queste tre parti so-pra un'Istrumento, si udirebbe senz'alcun' dubio tre Quinte. La onde i Compositori debbono auertire cotal cosa, & non far che le parti mutino luogo tra loro in questa maniera;
percioche tale inconueniente apportarebbe all'Vdito cosa, che non molto li piacerebbe;
ancora che nel cantar le parti non si potessino udire tali Quinte. Et perche da molti Prat-tici questo non è molto auertitò; per[unclear: ò] hò uoluto toccarne una parola. Hora hauendo à
bastanza ragionato intorno alle cose necessarie à simili compositioni; lasciarò l'altre co-se, che possono accascare & non sono di molto momento, al giudicio del Compositore;
imperoche col mezo delle Regole date, potrà quando gli occorrerà alcun dubio, quan-tunque fusse di molta importanza, darne perfetta risolutione. Lasciando adunque di parlare più intorno à cotal materia, uerrò à ragionar de i Contrapunti, che arteficiosamente si compongono à tre uoci, i quali si chiamano Doppij, & de quelli che si fanno con
qualche obligo. Ma perche i primi con maggior libertà da i Compositori, & più correttamente secondo i nostri precetti possono esser composti, ma non già i secondi; percio-che 'l Compositore non può cosi ben purgare il suo Contrapunto, per esser li leuato il po-tere dalla natura della cosa in sè; la quale ricerca (come uederemo) alcune osseruanze,
che non si possono lasciare, uolendo condur l'opera sua al desiderato fine; però ragione-rò prima de i primi; dopoi dimostrerò gli altri; scoprendo quelle Regole & precetti, che
concorrono alla lor compositione; accioche ogn'uno possa restar (per quanto si potrà da
me fare) satisfatto.
Seguirebbe anco un'altro errore, che qualunque uolta si uolesse sonar queste tre parti so-pra un'Istrumento, si udirebbe senz'alcun' dubio tre Quinte. La onde i Compositori debbono auertire cotal cosa, & non far che le parti mutino luogo tra loro in questa maniera;
percioche tale inconueniente apportarebbe all'Vdito cosa, che non molto li piacerebbe;
ancora che nel cantar le parti non si potessino udire tali Quinte. Et perche da molti Prat-tici questo non è molto auertitò; per[unclear: ò] hò uoluto toccarne una parola. Hora hauendo à
bastanza ragionato intorno alle cose necessarie à simili compositioni; lasciarò l'altre co-se, che possono accascare & non sono di molto momento, al giudicio del Compositore;
imperoche col mezo delle Regole date, potrà quando gli occorrerà alcun dubio, quan-tunque fusse di molta importanza, darne perfetta risolutione. Lasciando adunque di parlare più intorno à cotal materia, uerrò à ragionar de i Contrapunti, che arteficiosamente si compongono à tre uoci, i quali si chiamano Doppij, & de quelli che si fanno con
qualche obligo. Ma perche i primi con maggior libertà da i Compositori, & più correttamente secondo i nostri precetti possono esser composti, ma non già i secondi; percio-che 'l Compositore non può cosi ben purgare il suo Contrapunto, per esser li leuato il po-tere dalla natura della cosa in sè; la quale ricerca (come uederemo) alcune osseruanze,
che non si possono lasciare, uolendo condur l'opera sua al desiderato fine; però ragione-rò prima de i primi; dopoi dimostrerò gli altri; scoprendo quelle Regole & precetti, che
concorrono alla lor compositione; accioche ogn'uno possa restar (per quanto si potrà da
me fare) satisfatto.
Delle varie sorti de i Contrapunti arteficiosi; & prima de quelli, che si chiamano Doppij.Cap. LXII.
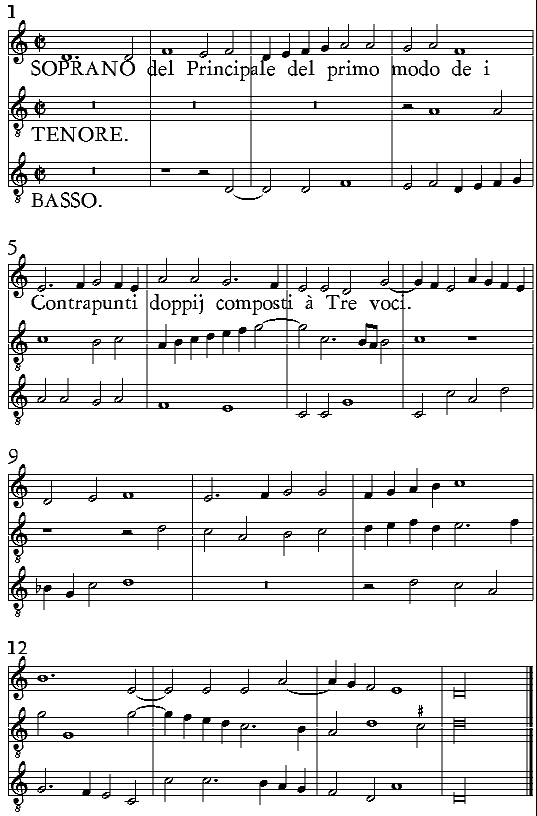
 page 312Replica, & molto differente da quella, che si ode nel principale. Però adunque ricordan-dosi quello, ch'è Contrapunto doppio à due uoci; è superfluo il uoler replicare, & dir quello, che sia Contrapunto doppio à tre uoci; percioche sapendo quel ch'importa il primo, facilmente si può hauer notitia di quel ch'importa il secondo. Volendo adunque ragionar
de quei Contrapunti doppij, che si compongono à tre Voci, dico; che le Specie loro son
molte; imperoche si possono comporre in uarie maniere, con l'osseruanza d'alcune Re-gole; che cantandosi prima ad un modo nel Principale, & udendosi una sorte d'harmo-nia, nella Replica poi diuersamente si cantano le Parti con quelle figure & interuall'istessi, & si ode gran diuersità di concento. Ma ancora che molti siano i modi di comporre tali Contrapunti; come hò detto; porrò solamente quelli, che mi sono paruti più difficili &
più eleganti; acciò non sia tedioso à i Lettori; da i quali ciascuno ingegnoso potrà com-prendere, come si haurà da reggere in qualunque altra maniera de simili compositioni. Il
primo modo adunque sarà, che composto che si haueranno prima Tre parti principali, con
l'aiuto d'alcune auertenze molto necessarie ad un tal negotio; haueremo la prima Specie;
percioche Quando uorremo la Replica, porremo poi il Basso del Principale nel luogo del
Soprano più acuto per una Quinta; & il Soprano in quello del Tenore; & il Tenore nel luogo del Basso, l'uno & l'altro più graue per una Ottaua; come nell'essempio si uede. Ma sarebbe ueramente impossibile, che potesse riuscir bene, quando non si osseruasse, di non por
mai il Basso nel Principale con l'altre parti distante per una Sesta; ancora che l'altre due tra
loro si possino porre; ne di porre la Quarta tra le due parti piu acute. Similmente bisogna osseruare, di non por mai il Basso co 'l Tenore in Terza, dopo la quale seguiti la Quinta; ne il
Basso col Soprano in Decima, dopo la quale uenghi la Duodecima, quando le parti insieme discendono; percioche la Duodecima, che si pone nel Principale tra 'l Basso, & il So-prano; nella Replica uiene Vnisono tra 'l Tenore & il Soprano; & la Quinta simigliante-mente uiene Ottaua, & l'Vnisono del Basso co 'l Tenore diuenta Duodecima. Potiamo
hora uedere, che in simil sorte di Contrapunto, ò Compositione, nel Principale non si
può far la Sincopa di Settima; conciosiache non si può risoluere con la Sesta. In questa
sorte di Contrapunto, il Tenore potrà discendere sotto 'l Basso per Terza & Sesta; ma
non per Quinta: ma bisogna auertire, che non passi la Sesta; percioche le parti uengono
ad esser distanti l'una dall'altra per lungo spacio. Molt'altre cose sarebbe da mostrare, per
hauer'il modo facile da comporre; ma per non andare in lungo, & per non esser molto necessarie, si lasciano. Et ueramente questa cagione mi muoue à lasciarle; perche desiderando alcuno di uoler far cosa ottima, è dibisogno che faccia insieme il Principale & la Replica; & cosi potrà uedere tutti gli incommodi, che potranno occorrere. Vltimamente è dibisogno sapere, che se 'l si componerà il Principale secondo l'osseruanza delle Regole no-stre mostrate di sopra, la Replica similmente uerrà ad esser'osseruata; & se 'l si farà altramente, ne seguirà il contrario. Et ciò sia detto à bastanza intorno la Prima sorte di Contra-punto doppio à Tre uoci, la cui Replica procede per gli istessi mouimenti, che sono con-tenuti nel Principale; perciò la seconda è quella, della quale la Replica procede per mouimenti contrarij a quelli, che si trouano nelle parti del suo Principale; come ne i seguenti
essempi si può uedere. Ma la Replica non potrebbe mai tornar bene, se non si osseruasse alcune cose; come sarebbe dire; far che tutte le parti delle Sincope, che si pongono
nel Principale siano consonanti; & non por mai il Tenore distante dal Soprano per una
Quarta. Queste cose si debbono principalmente per ogni modo osseruare; l'altre poi,
che potrebbono accascare non saranno difficili; quando si componerà la Replica insie-me col Principale. In simil sorte di Contrapunto si potranno usar le Seste, & por-re le parti lontane l'una dall'altra per qual'Interuallo si uorrà. Il Tenore potrà
pigliare il luogo del Basso; & il Soprano quello del Tenore, & quello del Basso
anco. Et per hauer la Replica, si porra il Basso del Princi pale [sic: Principale] nel luogo del Soprano
più acuto per una Sesta; il Soprano nel luogo del Basso più graue per una Decima; & il
Tenore più graue per un Tuono; facendo, che le Parti procedino per contrarij mouimenti page 313
page 312Replica, & molto differente da quella, che si ode nel principale. Però adunque ricordan-dosi quello, ch'è Contrapunto doppio à due uoci; è superfluo il uoler replicare, & dir quello, che sia Contrapunto doppio à tre uoci; percioche sapendo quel ch'importa il primo, facilmente si può hauer notitia di quel ch'importa il secondo. Volendo adunque ragionar
de quei Contrapunti doppij, che si compongono à tre Voci, dico; che le Specie loro son
molte; imperoche si possono comporre in uarie maniere, con l'osseruanza d'alcune Re-gole; che cantandosi prima ad un modo nel Principale, & udendosi una sorte d'harmo-nia, nella Replica poi diuersamente si cantano le Parti con quelle figure & interuall'istessi, & si ode gran diuersità di concento. Ma ancora che molti siano i modi di comporre tali Contrapunti; come hò detto; porrò solamente quelli, che mi sono paruti più difficili &
più eleganti; acciò non sia tedioso à i Lettori; da i quali ciascuno ingegnoso potrà com-prendere, come si haurà da reggere in qualunque altra maniera de simili compositioni. Il
primo modo adunque sarà, che composto che si haueranno prima Tre parti principali, con
l'aiuto d'alcune auertenze molto necessarie ad un tal negotio; haueremo la prima Specie;
percioche Quando uorremo la Replica, porremo poi il Basso del Principale nel luogo del
Soprano più acuto per una Quinta; & il Soprano in quello del Tenore; & il Tenore nel luogo del Basso, l'uno & l'altro più graue per una Ottaua; come nell'essempio si uede. Ma sarebbe ueramente impossibile, che potesse riuscir bene, quando non si osseruasse, di non por
mai il Basso nel Principale con l'altre parti distante per una Sesta; ancora che l'altre due tra
loro si possino porre; ne di porre la Quarta tra le due parti piu acute. Similmente bisogna osseruare, di non por mai il Basso co 'l Tenore in Terza, dopo la quale seguiti la Quinta; ne il
Basso col Soprano in Decima, dopo la quale uenghi la Duodecima, quando le parti insieme discendono; percioche la Duodecima, che si pone nel Principale tra 'l Basso, & il So-prano; nella Replica uiene Vnisono tra 'l Tenore & il Soprano; & la Quinta simigliante-mente uiene Ottaua, & l'Vnisono del Basso co 'l Tenore diuenta Duodecima. Potiamo
hora uedere, che in simil sorte di Contrapunto, ò Compositione, nel Principale non si
può far la Sincopa di Settima; conciosiache non si può risoluere con la Sesta. In questa
sorte di Contrapunto, il Tenore potrà discendere sotto 'l Basso per Terza & Sesta; ma
non per Quinta: ma bisogna auertire, che non passi la Sesta; percioche le parti uengono
ad esser distanti l'una dall'altra per lungo spacio. Molt'altre cose sarebbe da mostrare, per
hauer'il modo facile da comporre; ma per non andare in lungo, & per non esser molto necessarie, si lasciano. Et ueramente questa cagione mi muoue à lasciarle; perche desiderando alcuno di uoler far cosa ottima, è dibisogno che faccia insieme il Principale & la Replica; & cosi potrà uedere tutti gli incommodi, che potranno occorrere. Vltimamente è dibisogno sapere, che se 'l si componerà il Principale secondo l'osseruanza delle Regole no-stre mostrate di sopra, la Replica similmente uerrà ad esser'osseruata; & se 'l si farà altramente, ne seguirà il contrario. Et ciò sia detto à bastanza intorno la Prima sorte di Contra-punto doppio à Tre uoci, la cui Replica procede per gli istessi mouimenti, che sono con-tenuti nel Principale; perciò la seconda è quella, della quale la Replica procede per mouimenti contrarij a quelli, che si trouano nelle parti del suo Principale; come ne i seguenti
essempi si può uedere. Ma la Replica non potrebbe mai tornar bene, se non si osseruasse alcune cose; come sarebbe dire; far che tutte le parti delle Sincope, che si pongono
nel Principale siano consonanti; & non por mai il Tenore distante dal Soprano per una
Quarta. Queste cose si debbono principalmente per ogni modo osseruare; l'altre poi,
che potrebbono accascare non saranno difficili; quando si componerà la Replica insie-me col Principale. In simil sorte di Contrapunto si potranno usar le Seste, & por-re le parti lontane l'una dall'altra per qual'Interuallo si uorrà. Il Tenore potrà
pigliare il luogo del Basso; & il Soprano quello del Tenore, & quello del Basso
anco. Et per hauer la Replica, si porra il Basso del Princi pale [sic: Principale] nel luogo del Soprano
più acuto per una Sesta; il Soprano nel luogo del Basso più graue per una Decima; & il
Tenore più graue per un Tuono; facendo, che le Parti procedino per contrarij mouimenti page 313 di quelli, che si trouano nel Principale; & cosi haueremo l'harmonia differente; come uarii & differenti sono i siti & li mouimenti dell'uno & dell'altro. Et se noi osseruaremo
di quelli, che si trouano nel Principale; & cosi haueremo l'harmonia differente; come uarii & differenti sono i siti & li mouimenti dell'uno & dell'altro. Et se noi osseruaremo
 page 314nella compositione del Principale le Regole, che di sopra nel far le sudette due sorti de
Contrapunti sono state dichiarate; non è dubbio che la Replica (se non in tutto, almeno
in molte parti) uerrà ad esser osseruata. Si potrà anco comporre una Terza specie di Contrapunto doppio, che participarà dell'una & dell'altra sorte de questi Contrapunti: quando si osseruarà tutte quelle Regole, che s'osseruano nelle compositioni; delle due mo-strate specie; le quali Regole sono negatiue; cioè, uietano il far'alcuna cosa; Il che
fatto haueremo poi un Contrapunto, che potrà hauer la Replica simile à quella del
Primo & del Secondo modo mostrati; come qui si può uedere.
page 314nella compositione del Principale le Regole, che di sopra nel far le sudette due sorti de
Contrapunti sono state dichiarate; non è dubbio che la Replica (se non in tutto, almeno
in molte parti) uerrà ad esser osseruata. Si potrà anco comporre una Terza specie di Contrapunto doppio, che participarà dell'una & dell'altra sorte de questi Contrapunti: quando si osseruarà tutte quelle Regole, che s'osseruano nelle compositioni; delle due mo-strate specie; le quali Regole sono negatiue; cioè, uietano il far'alcuna cosa; Il che
fatto haueremo poi un Contrapunto, che potrà hauer la Replica simile à quella del
Primo & del Secondo modo mostrati; come qui si può uedere.


 Ma quando prima si componerà il Principale di maniera, che dopoi il Basso resterà nel-le sue chorde principali senz'alcuna mutatione; & il Soprano diuenterà nella Replica il
Basso, trasportato per una Duodecima più graue; & il Tenore si trasportarà per una Quinta; si haurà una Quarta specie di Contrapunto doppio; nel modo che qui di sotto si uede.
E' ben uero, che questo modo è più difficile di ciascuno de i mostrati; onde uolendolo fa-re, acciò la Replica torni bene; bisogna osseruar molte cose, & prima. Quando 'l Tenore
si farà cantare col Basso à due voci; non bisogna, che le parti siano distanti l'una dall'al-tra per Ottaua, ne per Sesta; massimamente quando 'l Tenore si porrà sopra 'l Basso; ma
quando si porrà di sotto, non si dè porre distante da esso Basso, ne per Terza, ne per
Quinta; ma si ben per Sesta, ò per Ottaua, & per Quinta ancora; con questa condi-tione, che tal Quinta si troui nella seconda parte della sincopa, dopo la quale senz'al-cun mezo ne uenga la Sesta; percioche quando queste due parti si pongono à i loro
luoghi proprij, non possono esser distanti l'una dall'altra per maggiore spacio, che di page 315
Ma quando prima si componerà il Principale di maniera, che dopoi il Basso resterà nel-le sue chorde principali senz'alcuna mutatione; & il Soprano diuenterà nella Replica il
Basso, trasportato per una Duodecima più graue; & il Tenore si trasportarà per una Quinta; si haurà una Quarta specie di Contrapunto doppio; nel modo che qui di sotto si uede.
E' ben uero, che questo modo è più difficile di ciascuno de i mostrati; onde uolendolo fa-re, acciò la Replica torni bene; bisogna osseruar molte cose, & prima. Quando 'l Tenore
si farà cantare col Basso à due voci; non bisogna, che le parti siano distanti l'una dall'al-tra per Ottaua, ne per Sesta; massimamente quando 'l Tenore si porrà sopra 'l Basso; ma
quando si porrà di sotto, non si dè porre distante da esso Basso, ne per Terza, ne per
Quinta; ma si ben per Sesta, ò per Ottaua, & per Quinta ancora; con questa condi-tione, che tal Quinta si troui nella seconda parte della sincopa, dopo la quale senz'al-cun mezo ne uenga la Sesta; percioche quando queste due parti si pongono à i loro
luoghi proprij, non possono esser distanti l'una dall'altra per maggiore spacio, che di page 315 quello della Quinta; & tal Quinta nella Replica uiene à far l'Vnisono. Simigliante-mente, quando il Soprano & il Basso canteranno soli, bisogna auertir di non fare, che 'l
Soprano passi sotto 'l Basso; ne si debbe porre la sincopa di Settima; benche quella di Se-conda & di Quarta si possa vsar'ottimamente nel Soprano; ne si debbe por queste par-ti lontane l'una dall'altra per una Sesta, ne uogliono esser più distanti d'una Duodeci-ma. Non si fà laTerza & dopoi la Quinta; ouer non si fà la Decima & dopoi la Duo-decima, quando le parti discendono. Quando poi il Tenore & il Soprano cante-ranno insieme, non si dè far la Quinta, se non quando il Tenore sarà la sincopa, nella se-conda parte della quale tal Quinta sia contenuta; & dopo lei bisogna che seguiti, senz'
alcun mezo, la Sesta; & dopo questa la Terza, ouer un'altra Sesta. Non si fà Sesta &
dopoi Ottaua, quando le parti discendono; ma si pone la Sesta ad un'altro modo, che
uenga bene. Il Soprano può discendere sotto 'l Tenore fin'alla Ottaua uoce, quando
torna commodo, & quando si porrà la sincopa di Quarta nell'una & nell'altra di que-ste due parti, tornerà molto bene. Bisogna auertire di non dimorar lungo tempo so-pra la Terza, percioche nella Replica uiene Sesta col Basso; ne dobbiamo anco fer-mar le parti sopra l'Ottaua, conciosia che torna Vnisono. Tutte queste cose si debbo-no osseruare, accioche si possa peruenire con qualche facilità al fine desiderato. Et per-che osseruando queste Regole, sarà facile il comporre questi contrapunti à Tre uoci; page 316tanto più, componendo in un tempo il Principale & la Replica, accioche il Com-positore possa ueder gli incommodi, che possono occorrere in tali compositioni.
Pero si dè auertire per ultima conclusione, che quantunque il Principale si purgasse da
ogni errore, che si potesse commettere contra le date Regole uniuersali, è impossibile
che la Replica in tutti possa venire osseruata. Questi pochi essempi hò uoluto porre,
da i quali ciascun potrà uedere il modo, che haurà da tenere uolendone comporre
de gli altri.
quello della Quinta; & tal Quinta nella Replica uiene à far l'Vnisono. Simigliante-mente, quando il Soprano & il Basso canteranno soli, bisogna auertir di non fare, che 'l
Soprano passi sotto 'l Basso; ne si debbe porre la sincopa di Settima; benche quella di Se-conda & di Quarta si possa vsar'ottimamente nel Soprano; ne si debbe por queste par-ti lontane l'una dall'altra per una Sesta, ne uogliono esser più distanti d'una Duodeci-ma. Non si fà laTerza & dopoi la Quinta; ouer non si fà la Decima & dopoi la Duo-decima, quando le parti discendono. Quando poi il Tenore & il Soprano cante-ranno insieme, non si dè far la Quinta, se non quando il Tenore sarà la sincopa, nella se-conda parte della quale tal Quinta sia contenuta; & dopo lei bisogna che seguiti, senz'
alcun mezo, la Sesta; & dopo questa la Terza, ouer un'altra Sesta. Non si fà Sesta &
dopoi Ottaua, quando le parti discendono; ma si pone la Sesta ad un'altro modo, che
uenga bene. Il Soprano può discendere sotto 'l Tenore fin'alla Ottaua uoce, quando
torna commodo, & quando si porrà la sincopa di Quarta nell'una & nell'altra di que-ste due parti, tornerà molto bene. Bisogna auertire di non dimorar lungo tempo so-pra la Terza, percioche nella Replica uiene Sesta col Basso; ne dobbiamo anco fer-mar le parti sopra l'Ottaua, conciosia che torna Vnisono. Tutte queste cose si debbo-no osseruare, accioche si possa peruenire con qualche facilità al fine desiderato. Et per-che osseruando queste Regole, sarà facile il comporre questi contrapunti à Tre uoci; page 316tanto più, componendo in un tempo il Principale & la Replica, accioche il Com-positore possa ueder gli incommodi, che possono occorrere in tali compositioni.
Pero si dè auertire per ultima conclusione, che quantunque il Principale si purgasse da
ogni errore, che si potesse commettere contra le date Regole uniuersali, è impossibile
che la Replica in tutti possa venire osseruata. Questi pochi essempi hò uoluto porre,
da i quali ciascun potrà uedere il modo, che haurà da tenere uolendone comporre
de gli altri.
Delle varie sorti de Contrapunti à Tre uoci, che si fanno à mente in Consequenza so-pra un Soggetto; & d'alcune Consequenze, che si fanno di fantasia; & quel che in ciascheduna si hà da osseruare.Cap. LXIII.
 page 319L'altra sorte de Contrapunto all'Vnisono si fà sotto la parte del Soggetto, con l'istess'os-seruanze de gradi & salti; nel quale si dè anco sommamente auertire; come ho detto della mostrata di sopra; di non far alcun mouimento di grado da una Minima all'altra, ne
uerso 'l graue, ne uerso l'acuto; & in questa particolarmente non si farà alcun salto di
Quarta. Et quando le due nominate Semibreui saranno unisone, la detta Seconda minima
della prima potrà esser'Vnisono, ò Terza, ouer Quinta. Ma quando conteneranno il
mouimento di grado ascendente, tal minima si porrà Terza, ò Quarta, oueramente
Quinta; & uorrà esser Quinta, ò Sesta quando tal grado sarà discendente. Il salto di Terza ascendente uorrà Vnisono, ò Terza; & quel di Terza discendente, uorrà Vnisono,
ò Terza, oueramente Quinta. Quel di Quarta ascendente, uorrà Vnisono, ò Terza,
ò Quinta, & Sesta; oueramente Ottaua dourà essere quello di Quarta, discendente.
Quando tal salto sarà di Quinta, ascendente, tal Minima dourà essere Vnisona, ò quar-ta, ouer Sesta, & anco Terza sopra 'l Soggetto. Ma quando sarà discendente, potrà es-ser Decima, ouer Duodecima. In quello di Sesta ascendente potrà esser Terza, ouera-mente Quinta; & in quello che sarà di Sesta discendente, sarà dibisogno che sia Quar-ta, ò Sesta, ouer'Ottaua, & anco Decima. Ma in quelli d'Ottaua, s'accommoderà l'Vni-sono, ò la Terza, oueramente alla Quinta; come nel sequente essempio si uede osseruato.
page 319L'altra sorte de Contrapunto all'Vnisono si fà sotto la parte del Soggetto, con l'istess'os-seruanze de gradi & salti; nel quale si dè anco sommamente auertire; come ho detto della mostrata di sopra; di non far alcun mouimento di grado da una Minima all'altra, ne
uerso 'l graue, ne uerso l'acuto; & in questa particolarmente non si farà alcun salto di
Quarta. Et quando le due nominate Semibreui saranno unisone, la detta Seconda minima
della prima potrà esser'Vnisono, ò Terza, ouer Quinta. Ma quando conteneranno il
mouimento di grado ascendente, tal minima si porrà Terza, ò Quarta, oueramente
Quinta; & uorrà esser Quinta, ò Sesta quando tal grado sarà discendente. Il salto di Terza ascendente uorrà Vnisono, ò Terza; & quel di Terza discendente, uorrà Vnisono,
ò Terza, oueramente Quinta. Quel di Quarta ascendente, uorrà Vnisono, ò Terza,
ò Quinta, & Sesta; oueramente Ottaua dourà essere quello di Quarta, discendente.
Quando tal salto sarà di Quinta, ascendente, tal Minima dourà essere Vnisona, ò quar-ta, ouer Sesta, & anco Terza sopra 'l Soggetto. Ma quando sarà discendente, potrà es-ser Decima, ouer Duodecima. In quello di Sesta ascendente potrà esser Terza, ouera-mente Quinta; & in quello che sarà di Sesta discendente, sarà dibisogno che sia Quar-ta, ò Sesta, ouer'Ottaua, & anco Decima. Ma in quelli d'Ottaua, s'accommoderà l'Vni-sono, ò la Terza, oueramente alla Quinta; come nel sequente essempio si uede osseruato.
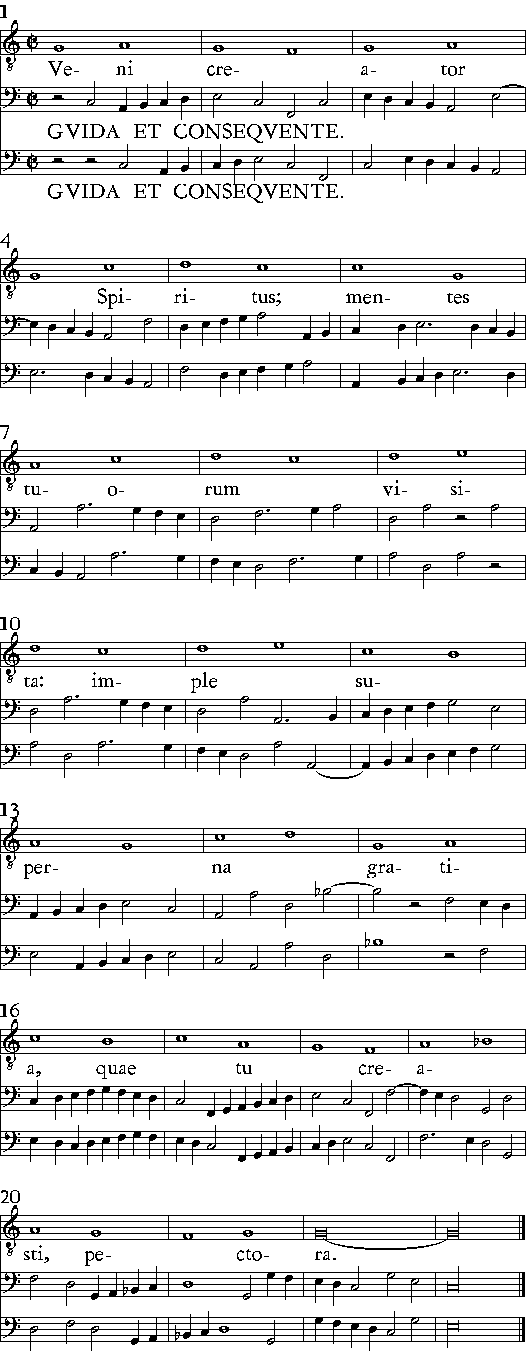 page 320Et questo è quanto à i due primi modi, ne i quali il consequente canta all'Vnisono con
la Guida dopo 'l tempo d'una Minima; tanto di sopra, quanto di sotto la parte del Sog-getto. Ma se 'l Consequente si uorrà far cantare in Diapason nell'acuto con la Guida, do-po il tempo, che importa una Minima, facendo ch'essa Guida canti sotto la parte del
Soggetto; si potrà ottimamente fare, quando si osseruarà, sopra ogn'altra cosa, alcune
Regole molto necessarie; come è di non far mai mouimento nel Contrapunto per gra-do; ne mai salto di Quarta all'ingiù. Ancora di non fare la Sesta, dopo la quale ne uen-ga l'Ottaua, quando 'l Soggetto discende per grado; ne anche Ottaua, quand'è salto di
Quarta. Il Grado etiandio non uuole Ottaua; ne il Salto di Terza ascendente vuol
Quinta. Il mouimento del Soggetto fatto di Vnisono vuole hauer la Seconda minima
Vnisona, ò Terza, ouer Quinta sopra, ouer sotto la parte del Soggetto; ma 'l grado
ascendente uuol Terza, ouer Quinta; & il descendente Quinta, ò Sesta. Quel salto, che
si fà per Terza ascendente uuole Vnisono, oueramente Terza, ò Quinta, ouer'Ottaua
sopra 'l Soggetto; & lo discendente vuole Vnisono, ò Terza, ò Quinta, & anche Otta-ua sotto esso Soggetto, oueramente Terza di sopra. Il salto di Quarta ascendente uuol
Terza ò Quinta, oueramente Sesta sopra la parte del Soggetto; & quel di Quar-ta discendente uuol Sesta, ouer'Ottaua nel graue. Salto di Quinta all'insù uuol Sesta,
ouer Ottaua, ò pur Quinta sopra 'l Soggetto; & quello all'ingiù uuol Terza, pur di sopra,
page 320Et questo è quanto à i due primi modi, ne i quali il consequente canta all'Vnisono con
la Guida dopo 'l tempo d'una Minima; tanto di sopra, quanto di sotto la parte del Sog-getto. Ma se 'l Consequente si uorrà far cantare in Diapason nell'acuto con la Guida, do-po il tempo, che importa una Minima, facendo ch'essa Guida canti sotto la parte del
Soggetto; si potrà ottimamente fare, quando si osseruarà, sopra ogn'altra cosa, alcune
Regole molto necessarie; come è di non far mai mouimento nel Contrapunto per gra-do; ne mai salto di Quarta all'ingiù. Ancora di non fare la Sesta, dopo la quale ne uen-ga l'Ottaua, quando 'l Soggetto discende per grado; ne anche Ottaua, quand'è salto di
Quarta. Il Grado etiandio non uuole Ottaua; ne il Salto di Terza ascendente vuol
Quinta. Il mouimento del Soggetto fatto di Vnisono vuole hauer la Seconda minima
Vnisona, ò Terza, ouer Quinta sopra, ouer sotto la parte del Soggetto; ma 'l grado
ascendente uuol Terza, ouer Quinta; & il descendente Quinta, ò Sesta. Quel salto, che
si fà per Terza ascendente uuole Vnisono, oueramente Terza, ò Quinta, ouer'Ottaua
sopra 'l Soggetto; & lo discendente vuole Vnisono, ò Terza, ò Quinta, & anche Otta-ua sotto esso Soggetto, oueramente Terza di sopra. Il salto di Quarta ascendente uuol
Terza ò Quinta, oueramente Sesta sopra la parte del Soggetto; & quel di Quar-ta discendente uuol Sesta, ouer'Ottaua nel graue. Salto di Quinta all'insù uuol Sesta,
ouer Ottaua, ò pur Quinta sopra 'l Soggetto; & quello all'ingiù uuol Terza, pur di sopra,
 page 321oueramente Ottaua, ò Decima, ò Duodecima di sotto. Quel di Sesta, ch'ascende; uuo-le Vnisono, ò Terza, ò Quinta, ouer la medesima Terza sopra cotal Soggetto; come
quello che discende uuole Ottaua, ò Sesta, ouer Decima. Et si come il salto d'Ottaua
ascendente uuole Vnisono, ò Terza, ò Quinta; cosi quel della discendente uuole
Ottaua, ouer Decima; come si può considerare nel sequente essempio.
page 321oueramente Ottaua, ò Decima, ò Duodecima di sotto. Quel di Sesta, ch'ascende; uuo-le Vnisono, ò Terza, ò Quinta, ouer la medesima Terza sopra cotal Soggetto; come
quello che discende uuole Ottaua, ò Sesta, ouer Decima. Et si come il salto d'Ottaua
ascendente uuole Vnisono, ò Terza, ò Quinta; cosi quel della discendente uuole
Ottaua, ouer Decima; come si può considerare nel sequente essempio.
 Et questo sia detto intorno à i Consequenti d'Vnisono & di Ottaua. Ma per uenire à quelli, che seguono la Guida per una Diapente acuta, ouer graue; incominciaremo da quel-li, che si fanno sopra la parte del Soggetto, & hanno il Consequente in acuto. Onde tra l'
altre cose, che sono d'importanza in questa sorte de Consequenti, si dè osseruar di fare,
che la Guida non faccia mai salto ne di Quarta, ne di Sesta all'insù; ne anche salto di Terza,
ne di Quinta all'ingiù. Et quando le due nominate Semibreui saranno l'una dall'altra lontane per Vnisono; sarà dibisogno, che la Seconda minima, che casca sopra la prima di
esse, sia Ottaua sopra, ouer Terza sotto 'l Soggetto. Ma quando conteneranno il mouimento di grado all'insù, tal minima sarà Terza, ouer Quinta sopra di esso; oueramente si por-rà tutta la prima Semibreue, che sarà Ottaua; onde nel Consequente nascerà la Sinco-pa di Vndecima, che si haurà da risoluere; come di sopra si è mostrato, con la Decima; perpage 322cioche allora necessariamente bisognerà che la Guida faccia la prima Minima della se-conda Semibreue Sesta, & la seconda Quinta; similmente si potrà porre la prima semibreue, che nella prima minima siano due semiminime, l'una Terza & l'altra Seconda; & che
la seconda minima sia tutta Terza. Ma quando le due Semibreui conteneranno il gra-do ascendente; allora la detta seconda minima sarà Terza, ouer Quinta. Quando poi il
salto sarà di Terza ascendente, la detta Minima sarà Vnisona ò Terza; & se 'l sarà di-scendente, si farà Terza sotto la parte del Soggetto. Salto di Quarta ascendente uuol
Terza; & discendente uuol simigliantemente Terza, ouer Quinta. Il salto di Quinta
ascendente uuol Quinta, & quel che discende uuol medesimamente Quinta; ma sotto
esso soggetto. Quel di Sesta ascendente uuol Sesta, & quello che discende uuol Terza.
Salto d'Ottaua ascendente uuol Sesta; & quando è discendente uuol Quinta, ò pure Ottaua, l'una & l'altra sotto la parte del Soggetto. La onde osseruando queste cose primieramente, che sono necessarie, & continuamente essercitandosi; potrà nascere un tal
Contrapunto con la sua Guida & Consequente; come è quello, che segue.
Et questo sia detto intorno à i Consequenti d'Vnisono & di Ottaua. Ma per uenire à quelli, che seguono la Guida per una Diapente acuta, ouer graue; incominciaremo da quel-li, che si fanno sopra la parte del Soggetto, & hanno il Consequente in acuto. Onde tra l'
altre cose, che sono d'importanza in questa sorte de Consequenti, si dè osseruar di fare,
che la Guida non faccia mai salto ne di Quarta, ne di Sesta all'insù; ne anche salto di Terza,
ne di Quinta all'ingiù. Et quando le due nominate Semibreui saranno l'una dall'altra lontane per Vnisono; sarà dibisogno, che la Seconda minima, che casca sopra la prima di
esse, sia Ottaua sopra, ouer Terza sotto 'l Soggetto. Ma quando conteneranno il mouimento di grado all'insù, tal minima sarà Terza, ouer Quinta sopra di esso; oueramente si por-rà tutta la prima Semibreue, che sarà Ottaua; onde nel Consequente nascerà la Sinco-pa di Vndecima, che si haurà da risoluere; come di sopra si è mostrato, con la Decima; perpage 322cioche allora necessariamente bisognerà che la Guida faccia la prima Minima della se-conda Semibreue Sesta, & la seconda Quinta; similmente si potrà porre la prima semibreue, che nella prima minima siano due semiminime, l'una Terza & l'altra Seconda; & che
la seconda minima sia tutta Terza. Ma quando le due Semibreui conteneranno il gra-do ascendente; allora la detta seconda minima sarà Terza, ouer Quinta. Quando poi il
salto sarà di Terza ascendente, la detta Minima sarà Vnisona ò Terza; & se 'l sarà di-scendente, si farà Terza sotto la parte del Soggetto. Salto di Quarta ascendente uuol
Terza; & discendente uuol simigliantemente Terza, ouer Quinta. Il salto di Quinta
ascendente uuol Quinta, & quel che discende uuol medesimamente Quinta; ma sotto
esso soggetto. Quel di Sesta ascendente uuol Sesta, & quello che discende uuol Terza.
Salto d'Ottaua ascendente uuol Sesta; & quando è discendente uuol Quinta, ò pure Ottaua, l'una & l'altra sotto la parte del Soggetto. La onde osseruando queste cose primieramente, che sono necessarie, & continuamente essercitandosi; potrà nascere un tal
Contrapunto con la sua Guida & Consequente; come è quello, che segue.
 Dopo questo seguita il Quinto modo, doue 'l Consequente segue la Guida, la quale can-ta sotto la parte del Soggetto nel graue per una Diapente acuta; nel qual modo si dè os-seruar sopra ogn'altra cosa, che la Guida non faccia salto di Terza, ne di quinta all'in-giù; ne di Quarta ne di Sesta all'insù. Et quando 'l Soggetto canterà le due nominate
Semibreui, che saranno Vnisone, la Guida sarà la detta seconda minima della prima
Semibreue, Vnisono, ò Terza; ò Quinta, ouer'Ottaua, come li tornerà piu commo-page 323do; & quando farà il mouimento di grado all'insù, porrà tutta la detta minima Sesta; ouer'
Ottaua, oueramente porrà tutta la prima Semibreue Vnisona, ouer Terza; onde nascerà la
Sincopa nel Consequente. Et quando tal mouimento sarà fatto all'ingiù, la detta Minima
sarà Terza, ò Sesta, oueramente Ottaua. Al salto di Terza ascendente si darà l'Vnisono,
ò Terza, ò Quinta, ò Sesta, ouer'Ottaua, secondo che si ritrouerà ordinata la parte del
Soggetto; ma à quello di Terza discendente si darà la Quinta, ouer Decima. Quello di
Quarta ascendente vuole la detta seconda minima, che sia Sesta; & la discendente, quel-la che sia Ottaua, ò Decima. Salto di Quinta ascendente ricerca la Terza, ò Sesta, ouer
l'Ottaua; & quella della descendente ricerca la Sesta, ò la Duodecima. A quello di Se-sta ascendente s'accommoda la Terza, ò la Quinta; & à quello di Sesta discendente se
li dà l'Ottaua, ò la Decima. Quel di Ottaua ascendente uuole Vnisono, ò Terza, ò
Quinta, ouer'Ottaua; & quello di discendente ricerca Ottaua, ò Decima, ò Duodeci-ma: come nel sequente essempio in gran parte si può uedere.
Dopo questo seguita il Quinto modo, doue 'l Consequente segue la Guida, la quale can-ta sotto la parte del Soggetto nel graue per una Diapente acuta; nel qual modo si dè os-seruar sopra ogn'altra cosa, che la Guida non faccia salto di Terza, ne di quinta all'in-giù; ne di Quarta ne di Sesta all'insù. Et quando 'l Soggetto canterà le due nominate
Semibreui, che saranno Vnisone, la Guida sarà la detta seconda minima della prima
Semibreue, Vnisono, ò Terza; ò Quinta, ouer'Ottaua, come li tornerà piu commo-page 323do; & quando farà il mouimento di grado all'insù, porrà tutta la detta minima Sesta; ouer'
Ottaua, oueramente porrà tutta la prima Semibreue Vnisona, ouer Terza; onde nascerà la
Sincopa nel Consequente. Et quando tal mouimento sarà fatto all'ingiù, la detta Minima
sarà Terza, ò Sesta, oueramente Ottaua. Al salto di Terza ascendente si darà l'Vnisono,
ò Terza, ò Quinta, ò Sesta, ouer'Ottaua, secondo che si ritrouerà ordinata la parte del
Soggetto; ma à quello di Terza discendente si darà la Quinta, ouer Decima. Quello di
Quarta ascendente vuole la detta seconda minima, che sia Sesta; & la discendente, quel-la che sia Ottaua, ò Decima. Salto di Quinta ascendente ricerca la Terza, ò Sesta, ouer
l'Ottaua; & quella della descendente ricerca la Sesta, ò la Duodecima. A quello di Se-sta ascendente s'accommoda la Terza, ò la Quinta; & à quello di Sesta discendente se
li dà l'Ottaua, ò la Decima. Quel di Ottaua ascendente uuole Vnisono, ò Terza, ò
Quinta, ouer'Ottaua; & quello di discendente ricerca Ottaua, ò Decima, ò Duodeci-ma: come nel sequente essempio in gran parte si può uedere.
 Et questo sia detto intorno à quelle Consequenze, che si cantano alla Diapente acuta.
Ma quando uorremo far quelle, che si cantano alla Diapente graue, sopra la parte
del Soggetto; bisognerà osseruar sopra ogn'altra cosa, di non far che la Guida canti
per salti di Quarta all'ingiù; se non quando si porrà la prima Minima della prima page 324delle due nominate Semibreui, & due Semiminime sequenti, che uadino per gradi uerso 'l graue; percioche torna alle fiate commodo. Ne debbe far due salti di Quarta l'una
dopo l'altra. Ma quando la parte del Soggetto si muouerà da una figura all'altra per
Vnisono; la seconda minima, già tante fiate nominata, si porrà Vnisona, ò Terza,
ouer Quinta sopra la prima delle due nominate Semibreui. Facendo poi il passag-gio di grado uerso l'acuto, potrà porsi Ottaua, ouer Decima. Et non solamente si po-trà far questo, ma etiandio si potrà far la detta prima Semibreue, che sia tutta Duode-cima; percioche nel Consequente uerrà la Sincopa. Ma quando tal passaggio sarà
uerso 'l graue, cotal Minima potrà esser Quarta, ò Sesta, oueramente Ottaua. E'
ben uero, che la detta prima Semibreue potrà anco esser tutta Decima; percioche me-desimamente 'l Consequente contenerà la Sincopa. Quando 'l salto sarà di Terza,
all'insù, allora si porrà la seconda minima Duodecima; & anco si potrà far la pri-ma, che sia Decima, con due Semiminime sequenti, che discendino per grado;
delle quali l'una sia Nona & l'altra Ottaua; che saranno (come di sopra hò detto) di
gran commodo. Il salto etiandio di Terza all'ingiù ricerca, che tale Minima si pon-ga Terza, ò Quinta, ouer Decima; ma 'l mouimento di Quarta all'insù uuole Otta-
Et questo sia detto intorno à quelle Consequenze, che si cantano alla Diapente acuta.
Ma quando uorremo far quelle, che si cantano alla Diapente graue, sopra la parte
del Soggetto; bisognerà osseruar sopra ogn'altra cosa, di non far che la Guida canti
per salti di Quarta all'ingiù; se non quando si porrà la prima Minima della prima page 324delle due nominate Semibreui, & due Semiminime sequenti, che uadino per gradi uerso 'l graue; percioche torna alle fiate commodo. Ne debbe far due salti di Quarta l'una
dopo l'altra. Ma quando la parte del Soggetto si muouerà da una figura all'altra per
Vnisono; la seconda minima, già tante fiate nominata, si porrà Vnisona, ò Terza,
ouer Quinta sopra la prima delle due nominate Semibreui. Facendo poi il passag-gio di grado uerso l'acuto, potrà porsi Ottaua, ouer Decima. Et non solamente si po-trà far questo, ma etiandio si potrà far la detta prima Semibreue, che sia tutta Duode-cima; percioche nel Consequente uerrà la Sincopa. Ma quando tal passaggio sarà
uerso 'l graue, cotal Minima potrà esser Quarta, ò Sesta, oueramente Ottaua. E'
ben uero, che la detta prima Semibreue potrà anco esser tutta Decima; percioche me-desimamente 'l Consequente contenerà la Sincopa. Quando 'l salto sarà di Terza,
all'insù, allora si porrà la seconda minima Duodecima; & anco si potrà far la pri-ma, che sia Decima, con due Semiminime sequenti, che discendino per grado;
delle quali l'una sia Nona & l'altra Ottaua; che saranno (come di sopra hò detto) di
gran commodo. Il salto etiandio di Terza all'ingiù ricerca, che tale Minima si pon-ga Terza, ò Quinta, ouer Decima; ma 'l mouimento di Quarta all'insù uuole Otta- page 325ua, ò Decima; come quell'all'ingiù uuol Sesta. Quel di Quinta uerso l'acuto uuol la
Prima minima della prima semibreue Duodecima, & la Seconda diuisa in due Semi-minime, delle quali la prima sia Vndecima & Decima l'altra. Ma all'ingiù uuol Ter-za, ouer Quinta. Il mouimento di Sesta uerso l'acuto uuole Ottaua, ò Decima, ouera-mente Duodecima; & quello uerso il graue uuol la prima Minima, che sia Terza, & Quarta la seconda. Ma i mouimenti d'Ottaua all'insù uogliono la Duodecima; & quelli
all'ingiù uogliono Quinta; come nell'essempio una buona parte delle nominate co-se si possono ottimamente uedere osseruate. Se uorremo dopo questa far quella ma-niera di Consequenza alla Quinta graue, sotto la parte del Soggetto; sopra tutte l'altre
cose osseruaremo di non far salto di Quarta all'ingiù. Però quando il Canto fermo pro-cederà da una figura all'altra per Vnisono, osseruaremo di far, che la Guida faccia
la sudetta seconda Minima della prima Semibreue, che sia Vnisono, ouer'Otta-ua. Ma quando si muouerà di grado uerso l'acuto, la detta minima farà Terza,
ouer Quinta; imperoche 'l grado discendente uuol Quinta, ouer Decima; ò pur
la prima Minima della prima Semibreue, si farà Sesta, & la seconda sarà di-uisa in due Semiminime, delle quali l'una sarà Settima & l'altra Ottaua con
page 325ua, ò Decima; come quell'all'ingiù uuol Sesta. Quel di Quinta uerso l'acuto uuol la
Prima minima della prima semibreue Duodecima, & la Seconda diuisa in due Semi-minime, delle quali la prima sia Vndecima & Decima l'altra. Ma all'ingiù uuol Ter-za, ouer Quinta. Il mouimento di Sesta uerso l'acuto uuole Ottaua, ò Decima, ouera-mente Duodecima; & quello uerso il graue uuol la prima Minima, che sia Terza, & Quarta la seconda. Ma i mouimenti d'Ottaua all'insù uogliono la Duodecima; & quelli
all'ingiù uogliono Quinta; come nell'essempio una buona parte delle nominate co-se si possono ottimamente uedere osseruate. Se uorremo dopo questa far quella ma-niera di Consequenza alla Quinta graue, sotto la parte del Soggetto; sopra tutte l'altre
cose osseruaremo di non far salto di Quarta all'ingiù. Però quando il Canto fermo pro-cederà da una figura all'altra per Vnisono, osseruaremo di far, che la Guida faccia
la sudetta seconda Minima della prima Semibreue, che sia Vnisono, ouer'Otta-ua. Ma quando si muouerà di grado uerso l'acuto, la detta minima farà Terza,
ouer Quinta; imperoche 'l grado discendente uuol Quinta, ouer Decima; ò pur
la prima Minima della prima Semibreue, si farà Sesta, & la seconda sarà di-uisa in due Semiminime, delle quali l'una sarà Settima & l'altra Ottaua con
 page 326la parte del Soggetto. Il salto di Terza all'insù uuol Sesta, ouer che la prima minima
sia Vnisono, & delle due sequenti Semiminime l'una sia Seconda & l'altra Terza, & quel
di Terza all'ingiù uuol Sesta, ouer'Ottaua. Salto di Quarta all'insù vuol Terza, ò
Quinta; & quello all'in giù vuol Quinta, ouer che la prima minima sia Ottaua, & la se-conda sia diuisa in due Semiminime, delle quali la prima faccia Nona, & l'altra Decima.
Quel di Quinta uerso l'acuto uuol Quarta, oueramente Quinta; & uerso 'l graue uuol Se-sta, ouer Ottaua, ò Decima. Quando la parte del Soggetto fà il salto di Sesta in sù, tal minima uorrà esser Sesta, ouer'Ottaua, ò Decima; & quando in giù, si sarà la prima minima
Ottaua, & la seconda due Semiminime Nona & Decima; oueramente si farà la prima minima Sesta, & le Seminime Settima & Ottaua. Ma 'l mouimento di Ottaua tanto all'insù
quanto all'ingiù uuol Sesta. La onde osseruando cotali Regole, nasce la compositione,
che si uede nello essempio, & altre simili. Et tutte queste sono Consequenze fatte al-la Diapente hor'acuta, & hora graue, si di sopra, come anco di sotto la parte del Sog-getto. Ma per uenire all'Ottaua maniera di Consequenza, nella quale il Consequente seguita per una Diapente acuta la Guida dopo una pausa di Semibreue; bisogna
auertire, che questo modo è alquanto più difficile de gli altri; percioche, si come in
quelle, che fin qui habbiamo mostrato, il Consequente seguitaua la Guida dopo una
pausa di Minima, & si hauea à considerar due Semibreui l'una sequente l'altra, per ca-gione de i Mouimenti, che conteneuano; cosi in questa fà dibisogno considerarne, &
hauer l'occhio à tre; però bisogna osseruar nelle due prime (secondo i gradi & salti, che
faranno insieme) la seconda Minima della prima, & la prima della seconda Semi-breue; & saper la consonanza, che si ritroua nella seconda, quel ch'ella potrà fare,
ò ritorni nella Terza; acciò il Consequente con la Guida non faccino dissonanza, nel
muouersi la parte del Canto fermo, ouer Soggetto da un luogo all'altro, cosi uerso l'acu-to, come etiandio uerso 'l graue. Bisogna adunque auertire, che nelle due prime Se-mibreui, quando si trouerà la modulatione fatta per Vnisono, allora la Seconda mini-ma della prima Semibreue sarà Quinta graue sotto la parte del Soggetto, & la pri-ma della Seconda sarà simigliantemente Terza graue; oueramente l'una Terza gra-ue & l'altra Vnisona, ouer Terza graue: simigliantemente l'una & l'altra si porrà
Vnisona, oueramente l'una Vnisona & l'altra Terza; ouer che nella prima si farà la
Pausa & l'altra farà la Quinta; ancora la Seconda si porrà Sesta & la prima nominata
si farà Quinta. Ma nel grado ascendente la Seconda & la Prima saranno Terze;
ouer la seconda sarà Quinta & la prima Terza; oueramente l'una sarà Quinta & l'al-tra Quarta acuta; ò pur l'una Terza & l'altra simigliantemente Terza; graue però, &
sotto la parte del Soggetto; & si potrà far anco, che la Semibreue haurà la prima
Minima unisona, la seconda due Semiminime, che faranno Seconda & Terza;
& la prima minima della seconda Semibreue farà Terza graue; ancora la prima
Semibreue potrà hauer la prima minima Terza, & la seconda due semiminime Se-conda & Vnisono; & cosi la prima minima della sequente Semibreue potrà esser Ter-za graue. Ma nel grado discendente la detta seconda minima sarà Terza, & la prima
della seguente simigliantemente Terza; oueramente l'vna sarà Terza & l'altra Quin-ta; ouer'Vnisona la seconda & Terza la prima; ancora la seconda potrà esser Ter-za, & la prima Quarta; ouer la seconda Quinta, & la prima Sesta; etiandio l'una
farà Terza nel graue, & l'altra farà la Seconda sincopata. Il salto di Terza all'
insù uuol la seconda Vnisona, & la prima Terza graue, ouer l'una & l'altra di
queste Terza; oueramente che la seconda sia Terza & la prima Vnisona; co-m'anco à tutta la prima Semibreue si dà la prima minima, che sia Quarta sin-copata dopo la quale ne seguino due Semiminime, che l'una sia Terza & Secon-da l'altra; ò pur la seconda minima Terza, & Terza nel graue la prima mini-ma della seguente Semibreue. Il salto ueramente di Terza all'in giù uuole la det-ta seconda minima, che sia Terza graue, & la prima Vnisona, ouer Terza; & page 327anco la detta seconda, che faccia Quinta, & Terza la prima. Ma 'l salto di Quar-ta verso l'acuto uuol Terza nella seconda, & Terza, ò Quinta nella prima; oueramente
che vuol nella seconda la Quinta, & nella prima l'Vnisono, ò Terza; come il salto di
Quarta verso 'l graue vuol la seconda, che sia Terza, & la prima che sia Quinta, ò Sesta,
ouer'Ottaua. Simigliantemente il salto di Quinta all'insù vuol la seconda, che sia Quin-ta, & la prima Vnisono; come quando uà all'in giù, vuole la seconda, che faccia una
Pausa, ouer che sia Quinta graue, & che la prima sia Quinta, ouer Vnisono; ò pur che
la seconda habbia la Pausa, & la prima sia Ottaua. Quanto al salto di Sesta uerso l'acu-to, la seconda minima della prima semibreue vuol esser Quinta, & la prima della secon-da Terza graue; & quel che uà uerso 'l graue, vuol la seconda, che sia Terza graue, &
la prima, che sia Terza acuta. Il salto d'Ottaua all'insù uuol la detta seconda Vnisona,
& la prima che sia Quinta; & quella che uiene all'in giù, vuol la seconda che sia Quin-ta, & la prima che sia Terza, ouer Quinta. Et queste sono una parte de quelli auer-timenti, che si debbono hauer nel passare dalla prima alla seconda Semibreue delle tre
nominate di sopra. Ma bisogna di nuouo auertire; accioche la Terza semibreue ac-cordi nel Consequente; di porre sopra la Seconda tal Consonanza nella Guida, che ac-cordi nella Terza col Consequente; però è da auertire, che nella modulatione, che fà il
Soggetto per Vnisono; l'Vnisono che fà la Guida nella seconda semibreue delle tre già
nominate, torna al Consequente Quinta sopra la detta terza Semibreue. Nel gra-do ascendente primieramente la Quinta torna Ottaua, & la Terza torna Sesta; ma di-poi nel grado discendente l'Vnisono torna Sesta, la Terza uiene Ottaua; & la Quinta
torna Decima. Nel salto di Terza verso l'acuto, l'Vnisono uien Terza, la Terza gra-ue Vnisona, & la Sesta Ottaua, & la Ottaua torna Duodecima; ma à quello di Terza
verso 'l graue la Sesta torna Duodecima, & la Terza graue uiene Quinta. Nel salto di
Quarta all'insù la Sesta torna Settima, & la Terza uien Quarta; & in quello, ch'è al-l'in giù, l'Vnisono torna Ottaua, la Terza Decima, & la Quinta Duodecima. Et si
come nel salto di Quinta all'insù l'Ottaua torna Ottaua, la Quinta uiene Quinta, &
la Terza uiene Terza graue; cosi all'in giù la Quinta graue ritorna Quinta acuta. Il
salto di Sesta ascendente fà, che la Sesta venga Quinta, & quel di Sesta discenden-te fà che l'Vnisono torna Decima. Hauendo adunque il Contrapuntista riguardo à tut-te queste cose, potrà compor la Guida sopra 'l suo Soggetto di maniera, che 'l Consequente la seguiterà senz'alcuno discommodo, come nel sequente essempio si può uedere.
Ma queste Consequenze siano per una parte di quelle, che si possono dimostrar, per
fare à mente sopra un Soggetto qual si uoglia, poi che le maniere sono quasi infinite;
le quali giudico essere à bastanza à i Studiosi di pronto & viuace ingegno; essendo
che da queste maniere ne potranno cauar dell'altre con lo studio, che ui porranno.
Debbe però auertire ciascheduno, che in queste sorti de Contrapunti, ò Compo-sitioni, con simili osseruanze & oblighi, il Compositore non può à suo piacere li-mare (dirò cosi) & correggere 'l suo Contrapunto, secondo quelle Regole, che di so-pra habbiamo mostrato; percioche non è libero; ma è sforzato di por le Consonan-ze l'una dopo l'altra, secondo che richiede la natura del Soggetto; La onde tali Con-trapunti, ò Compositioni si possono chiamar veramente Sforzati; & chi non lo
uorrà credere, facendone la proua da se stesso potrà esser chiaro; che in queste co-se è gran pazzia il volere ostinarsi, & cercar quello, che per uia alcuna mai si potrà
ritrouare. E' ben uero, che colui il quale si esserciterà in simili Contrapunti, po-trà correggerli con qualche facilità. Hora lasciando da un canto queste maniere de
compositioni, voglio che veniamo à dimostrare alcune sorti de Consequenze dop-pie, che si fanno à mente senza Soggetto; le quali dico esser de molte maniere; Et
porrò questa per la prima, laquale primamente dà un Contrapunto doppio à Due voci; doue 'l Consequente nel Principale canta dopo la Guida per una Diapente graue,
hauendo fatto una Pausa di lunga, & nella Replica, quel ch'era Consequente diuen-page 328
page 326la parte del Soggetto. Il salto di Terza all'insù uuol Sesta, ouer che la prima minima
sia Vnisono, & delle due sequenti Semiminime l'una sia Seconda & l'altra Terza, & quel
di Terza all'ingiù uuol Sesta, ouer'Ottaua. Salto di Quarta all'insù vuol Terza, ò
Quinta; & quello all'in giù vuol Quinta, ouer che la prima minima sia Ottaua, & la se-conda sia diuisa in due Semiminime, delle quali la prima faccia Nona, & l'altra Decima.
Quel di Quinta uerso l'acuto uuol Quarta, oueramente Quinta; & uerso 'l graue uuol Se-sta, ouer Ottaua, ò Decima. Quando la parte del Soggetto fà il salto di Sesta in sù, tal minima uorrà esser Sesta, ouer'Ottaua, ò Decima; & quando in giù, si sarà la prima minima
Ottaua, & la seconda due Semiminime Nona & Decima; oueramente si farà la prima minima Sesta, & le Seminime Settima & Ottaua. Ma 'l mouimento di Ottaua tanto all'insù
quanto all'ingiù uuol Sesta. La onde osseruando cotali Regole, nasce la compositione,
che si uede nello essempio, & altre simili. Et tutte queste sono Consequenze fatte al-la Diapente hor'acuta, & hora graue, si di sopra, come anco di sotto la parte del Sog-getto. Ma per uenire all'Ottaua maniera di Consequenza, nella quale il Consequente seguita per una Diapente acuta la Guida dopo una pausa di Semibreue; bisogna
auertire, che questo modo è alquanto più difficile de gli altri; percioche, si come in
quelle, che fin qui habbiamo mostrato, il Consequente seguitaua la Guida dopo una
pausa di Minima, & si hauea à considerar due Semibreui l'una sequente l'altra, per ca-gione de i Mouimenti, che conteneuano; cosi in questa fà dibisogno considerarne, &
hauer l'occhio à tre; però bisogna osseruar nelle due prime (secondo i gradi & salti, che
faranno insieme) la seconda Minima della prima, & la prima della seconda Semi-breue; & saper la consonanza, che si ritroua nella seconda, quel ch'ella potrà fare,
ò ritorni nella Terza; acciò il Consequente con la Guida non faccino dissonanza, nel
muouersi la parte del Canto fermo, ouer Soggetto da un luogo all'altro, cosi uerso l'acu-to, come etiandio uerso 'l graue. Bisogna adunque auertire, che nelle due prime Se-mibreui, quando si trouerà la modulatione fatta per Vnisono, allora la Seconda mini-ma della prima Semibreue sarà Quinta graue sotto la parte del Soggetto, & la pri-ma della Seconda sarà simigliantemente Terza graue; oueramente l'una Terza gra-ue & l'altra Vnisona, ouer Terza graue: simigliantemente l'una & l'altra si porrà
Vnisona, oueramente l'una Vnisona & l'altra Terza; ouer che nella prima si farà la
Pausa & l'altra farà la Quinta; ancora la Seconda si porrà Sesta & la prima nominata
si farà Quinta. Ma nel grado ascendente la Seconda & la Prima saranno Terze;
ouer la seconda sarà Quinta & la prima Terza; oueramente l'una sarà Quinta & l'al-tra Quarta acuta; ò pur l'una Terza & l'altra simigliantemente Terza; graue però, &
sotto la parte del Soggetto; & si potrà far anco, che la Semibreue haurà la prima
Minima unisona, la seconda due Semiminime, che faranno Seconda & Terza;
& la prima minima della seconda Semibreue farà Terza graue; ancora la prima
Semibreue potrà hauer la prima minima Terza, & la seconda due semiminime Se-conda & Vnisono; & cosi la prima minima della sequente Semibreue potrà esser Ter-za graue. Ma nel grado discendente la detta seconda minima sarà Terza, & la prima
della seguente simigliantemente Terza; oueramente l'vna sarà Terza & l'altra Quin-ta; ouer'Vnisona la seconda & Terza la prima; ancora la seconda potrà esser Ter-za, & la prima Quarta; ouer la seconda Quinta, & la prima Sesta; etiandio l'una
farà Terza nel graue, & l'altra farà la Seconda sincopata. Il salto di Terza all'
insù uuol la seconda Vnisona, & la prima Terza graue, ouer l'una & l'altra di
queste Terza; oueramente che la seconda sia Terza & la prima Vnisona; co-m'anco à tutta la prima Semibreue si dà la prima minima, che sia Quarta sin-copata dopo la quale ne seguino due Semiminime, che l'una sia Terza & Secon-da l'altra; ò pur la seconda minima Terza, & Terza nel graue la prima mini-ma della seguente Semibreue. Il salto ueramente di Terza all'in giù uuole la det-ta seconda minima, che sia Terza graue, & la prima Vnisona, ouer Terza; & page 327anco la detta seconda, che faccia Quinta, & Terza la prima. Ma 'l salto di Quar-ta verso l'acuto uuol Terza nella seconda, & Terza, ò Quinta nella prima; oueramente
che vuol nella seconda la Quinta, & nella prima l'Vnisono, ò Terza; come il salto di
Quarta verso 'l graue vuol la seconda, che sia Terza, & la prima che sia Quinta, ò Sesta,
ouer'Ottaua. Simigliantemente il salto di Quinta all'insù vuol la seconda, che sia Quin-ta, & la prima Vnisono; come quando uà all'in giù, vuole la seconda, che faccia una
Pausa, ouer che sia Quinta graue, & che la prima sia Quinta, ouer Vnisono; ò pur che
la seconda habbia la Pausa, & la prima sia Ottaua. Quanto al salto di Sesta uerso l'acu-to, la seconda minima della prima semibreue vuol esser Quinta, & la prima della secon-da Terza graue; & quel che uà uerso 'l graue, vuol la seconda, che sia Terza graue, &
la prima, che sia Terza acuta. Il salto d'Ottaua all'insù uuol la detta seconda Vnisona,
& la prima che sia Quinta; & quella che uiene all'in giù, vuol la seconda che sia Quin-ta, & la prima che sia Terza, ouer Quinta. Et queste sono una parte de quelli auer-timenti, che si debbono hauer nel passare dalla prima alla seconda Semibreue delle tre
nominate di sopra. Ma bisogna di nuouo auertire; accioche la Terza semibreue ac-cordi nel Consequente; di porre sopra la Seconda tal Consonanza nella Guida, che ac-cordi nella Terza col Consequente; però è da auertire, che nella modulatione, che fà il
Soggetto per Vnisono; l'Vnisono che fà la Guida nella seconda semibreue delle tre già
nominate, torna al Consequente Quinta sopra la detta terza Semibreue. Nel gra-do ascendente primieramente la Quinta torna Ottaua, & la Terza torna Sesta; ma di-poi nel grado discendente l'Vnisono torna Sesta, la Terza uiene Ottaua; & la Quinta
torna Decima. Nel salto di Terza verso l'acuto, l'Vnisono uien Terza, la Terza gra-ue Vnisona, & la Sesta Ottaua, & la Ottaua torna Duodecima; ma à quello di Terza
verso 'l graue la Sesta torna Duodecima, & la Terza graue uiene Quinta. Nel salto di
Quarta all'insù la Sesta torna Settima, & la Terza uien Quarta; & in quello, ch'è al-l'in giù, l'Vnisono torna Ottaua, la Terza Decima, & la Quinta Duodecima. Et si
come nel salto di Quinta all'insù l'Ottaua torna Ottaua, la Quinta uiene Quinta, &
la Terza uiene Terza graue; cosi all'in giù la Quinta graue ritorna Quinta acuta. Il
salto di Sesta ascendente fà, che la Sesta venga Quinta, & quel di Sesta discenden-te fà che l'Vnisono torna Decima. Hauendo adunque il Contrapuntista riguardo à tut-te queste cose, potrà compor la Guida sopra 'l suo Soggetto di maniera, che 'l Consequente la seguiterà senz'alcuno discommodo, come nel sequente essempio si può uedere.
Ma queste Consequenze siano per una parte di quelle, che si possono dimostrar, per
fare à mente sopra un Soggetto qual si uoglia, poi che le maniere sono quasi infinite;
le quali giudico essere à bastanza à i Studiosi di pronto & viuace ingegno; essendo
che da queste maniere ne potranno cauar dell'altre con lo studio, che ui porranno.
Debbe però auertire ciascheduno, che in queste sorti de Contrapunti, ò Compo-sitioni, con simili osseruanze & oblighi, il Compositore non può à suo piacere li-mare (dirò cosi) & correggere 'l suo Contrapunto, secondo quelle Regole, che di so-pra habbiamo mostrato; percioche non è libero; ma è sforzato di por le Consonan-ze l'una dopo l'altra, secondo che richiede la natura del Soggetto; La onde tali Con-trapunti, ò Compositioni si possono chiamar veramente Sforzati; & chi non lo
uorrà credere, facendone la proua da se stesso potrà esser chiaro; che in queste co-se è gran pazzia il volere ostinarsi, & cercar quello, che per uia alcuna mai si potrà
ritrouare. E' ben uero, che colui il quale si esserciterà in simili Contrapunti, po-trà correggerli con qualche facilità. Hora lasciando da un canto queste maniere de
compositioni, voglio che veniamo à dimostrare alcune sorti de Consequenze dop-pie, che si fanno à mente senza Soggetto; le quali dico esser de molte maniere; Et
porrò questa per la prima, laquale primamente dà un Contrapunto doppio à Due voci; doue 'l Consequente nel Principale canta dopo la Guida per una Diapente graue,
hauendo fatto una Pausa di lunga, & nella Replica, quel ch'era Consequente diuen-page 328 ta Guida, & la Guida consequente, ilquale canta dopo essa Guida per una Diapason
acuta, dopo lo spacio di tanto tempo, quanto cantarono prima; cioè, della pausa di
Lunga. La onde si ode un Contrapunto molto diuerso dal primo. Dopoi se 'l si ritor-nerà à far cantare il Principale, & la Replica con i loro Consequenti dopo le lor Gui-de per ordine, come prima si fece; haueremo una Doppia consequenza, che si po-trà cantare à tre uoci insieme; come nel sequente essempio si può udire & uedere.
Ma in questa sorte di doppia Consequenza sopr'ogn'altra cosa si dè osseruare, che
nel Principale non ui sia Sesta per niun modo; ne si dè far, che la Guida passi sot-to 'l Consequente; ne si dè por mai Terza, & poi Quinta descendendo l'una & l'al-tro; ne si passa dall'Ottaua alla Quinta per contrarii mouimenti; percioche nella
Replica il Contrapunto non ritornarebbe bene. Et perche in tal sorte de Contra-punti la Quinta, che si pone nel Principale, ritorna Ottaua nella Replica; però
cotal Quinta non si haurà da continuare molto di lungo. Si debbe etiandio sa-pere, che quando questa sorte di Consequenza si ristringe à far che 'l Consequente page 329
ta Guida, & la Guida consequente, ilquale canta dopo essa Guida per una Diapason
acuta, dopo lo spacio di tanto tempo, quanto cantarono prima; cioè, della pausa di
Lunga. La onde si ode un Contrapunto molto diuerso dal primo. Dopoi se 'l si ritor-nerà à far cantare il Principale, & la Replica con i loro Consequenti dopo le lor Gui-de per ordine, come prima si fece; haueremo una Doppia consequenza, che si po-trà cantare à tre uoci insieme; come nel sequente essempio si può udire & uedere.
Ma in questa sorte di doppia Consequenza sopr'ogn'altra cosa si dè osseruare, che
nel Principale non ui sia Sesta per niun modo; ne si dè far, che la Guida passi sot-to 'l Consequente; ne si dè por mai Terza, & poi Quinta descendendo l'una & l'al-tro; ne si passa dall'Ottaua alla Quinta per contrarii mouimenti; percioche nella
Replica il Contrapunto non ritornarebbe bene. Et perche in tal sorte de Contra-punti la Quinta, che si pone nel Principale, ritorna Ottaua nella Replica; però
cotal Quinta non si haurà da continuare molto di lungo. Si debbe etiandio sa-pere, che quando questa sorte di Consequenza si ristringe à far che 'l Consequente page 329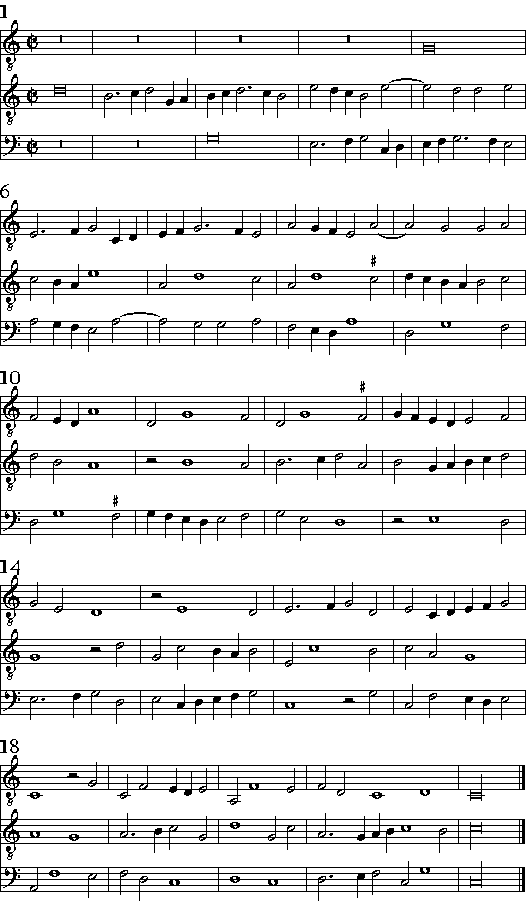 seguiti la Guida per poco spacio di tempo; come sarebbe dire, d'una pausa di Semibre-ue come nel seguente essempio si uede oltra quello, che si hà osseruato di sopra, bisogna
seguiti la Guida per poco spacio di tempo; come sarebbe dire, d'una pausa di Semibre-ue come nel seguente essempio si uede oltra quello, che si hà osseruato di sopra, bisogna
 anco auertire, non solamente di non continuare quattro Terze l'una dopo l'altra ascen-dendo, ouer discendenti le parti; percioche non tornarebbono bene, quando cantassero le Guide & li Consequenti insieme; ma che i mouimenti nel discendere siano di Terza,
ò di Quinta; & nell'ascendere non siano minori de quelli di Quarta. Non si farà Terza
& poi Decima per contrarij mouimenti; & sopra ogn'altra cosa bisogna auertire di non
replicare immediatamente alcun passaggio in Quarta più acuta, il qual passaggio contenga tante figure, che siano equiualenti ad un Tempo; cioè, à due Semibreui; & questo
perche nel secondo Consequente ritornano tante Ottaue. Vltimamente, quando si porrà il Soprano, che sia Guida del Tenore & questo dell'Alto, & siano l'uno all'altro Con-sequenti; & che l'uno canti dopo l'altro per una Pausa di Semibreue; cioè, il Tenore dopo il Soprano, per una Diapason graue, & l'Alto sopra esso Tenore per una pausa simigliantemente di Semibreue per una Diapente acuta; oueramente sotto esso Soprano dopo
un Tempo, ò pausa di breue, per una Diatessaron graue; ne uerrà una Cantilena co-me è la sequente. page 330
anco auertire, non solamente di non continuare quattro Terze l'una dopo l'altra ascen-dendo, ouer discendenti le parti; percioche non tornarebbono bene, quando cantassero le Guide & li Consequenti insieme; ma che i mouimenti nel discendere siano di Terza,
ò di Quinta; & nell'ascendere non siano minori de quelli di Quarta. Non si farà Terza
& poi Decima per contrarij mouimenti; & sopra ogn'altra cosa bisogna auertire di non
replicare immediatamente alcun passaggio in Quarta più acuta, il qual passaggio contenga tante figure, che siano equiualenti ad un Tempo; cioè, à due Semibreui; & questo
perche nel secondo Consequente ritornano tante Ottaue. Vltimamente, quando si porrà il Soprano, che sia Guida del Tenore & questo dell'Alto, & siano l'uno all'altro Con-sequenti; & che l'uno canti dopo l'altro per una Pausa di Semibreue; cioè, il Tenore dopo il Soprano, per una Diapason graue, & l'Alto sopra esso Tenore per una pausa simigliantemente di Semibreue per una Diapente acuta; oueramente sotto esso Soprano dopo
un Tempo, ò pausa di breue, per una Diatessaron graue; ne uerrà una Cantilena co-me è la sequente. page 330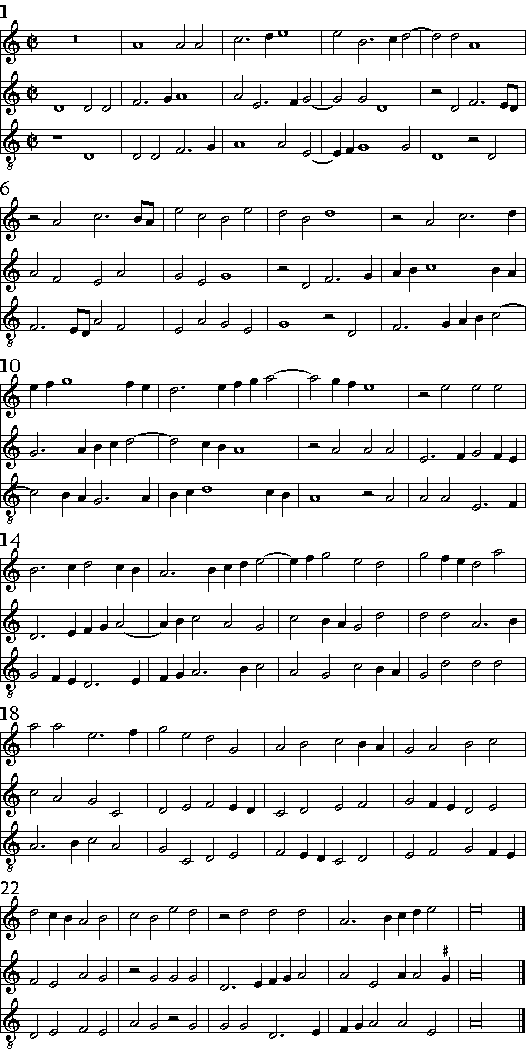 Quando però si osseruarà di non far mai Sesta; ne due Terze, che ascendino, ò discen-dino l'una dopo l'altra; ne di far Sincopa alcuna, nella quale sia alcuna dissonanza. Quelli gradi, che si osseruano nel modulare, ò Cantare, sono, che si ascende per Terza, ouer
per altro salto maggiore; ma non si discende per minore di quello di Quarta. Et questo
basti intorno à quelli Contrapunti & Consequenze, che si fanno à mente. Non creda
però alcuno, ch'io habbia posto in ciascheduna sorte di esse tutte quelle Regole, che osseruar si debbono, percioche sarebbe in errore; essendo che solamente hò posto quelle, che mi
è paruto esser di maggior'importanza, & essentialmente fanno alla natura del Contrapunto; però colui, il quale si uorrà essercitare in simili maniere di Consequenze & Contra-punti; dando opera allo studio, potrà ritrouar quello, da che si haura da guardare, &
quel che douerà osseruare, accioche il suo Contrapunto uenga netto, & purgato da mol-ti errori, i quali possono occorrere, facendo dette sorti di Contrapunto. Si dè però sa-pere, ch[unclear: ']è impossibile in tutte queste sorti de Contrapunti Doppij, quando sono fatti con
simili oblighi, di potere osseruar pienamente le Regole date di sopra, come hò detto ancora; massimamente quando cotali oblighi crescono; essendo che non si può osseruar in
essi la bellezza & il decoro, si quanto alla Modulatione, quanto ancora intorno all'in-uentione, & il modo di por le Consonanze; percioche è leuata la libertà al Composito-re, c'hauea nel comporre gli altri senz'alcun obligo; & questo dico, accioche 'l diligen-te Osseruatore de i nostri Precetti, uedendo alcune cose, che non uengono cosi ben corrette, non si marauigli; perche non hò posto qui cotali Compositioni, accioche lunga-mente, & per sempre s[unclear: ']habbiano da usare; ma si bene alle uolte, quando li tornerà in
proposito, per mostrar la uiuacità del suo ingegno, & la prontezza del suo intelletto
con alcuni, che ad altro non attendono, che à simil cose, & poi nel resto si ritrouano es-sere nudi, come una pietra. Sono queste maniere ueramente molto ingegnose; percio-che scoprono, quanto possa fare il Musico, il qual sappia adoperare gli Harmonici nu-meri; ancora che si oda alle uolte qualche cosa, che sia strana da udire; ma è buono
saper tutte le cose (se fusse possibile) massimamente le necessarie & le utili in ciascun'Ar-page 331te & in ciascuna Scienza; & non solo queste, che sono buone; ma l'altre ancora quan-tunque siano triste; l'une per mettere in opera, l'altre poi per sapersi guardare, & seruir-sene di esse à tempo & luogo conueniente. Et s'alle uolte hò mostrato delle cose, che non
sono molto buone; hò uoluto in ciò imitare il Filosofo, il quale, hauendo mostrato il buono della Logica & della Filosofia; & mostrato il uero modo d'argumentare; dopo l'hauer
scritto molte cose nell'una & nell'altra facultà; scrisse etiandio i Libri de i Sillogismi fallaci, ò Soffistici, i quali chiamò Elenchi; non perche s'hauessero da usare; ma accioche
(accadendo) ogn'uno si sapesse guardare da gli intrichi de i Sofisti, che uogliono esser tenuti dotti, ancora che non siano. Buona cosa è ueramente & ottima il sapere cotali Contrapunti, & usarli quando torna commodo; ma il frequentarli nelle compositioni non lo-do molto; conciosia che non si può far, ch'essendo 'l Contrapuntista obligato all'osser-uanza de tante cose, il Contrapunto uenga ad essere in tal maniera elegante & sonoro,
che porga in tutto & per tutto grato piacere all'Vdito.
Quando però si osseruarà di non far mai Sesta; ne due Terze, che ascendino, ò discen-dino l'una dopo l'altra; ne di far Sincopa alcuna, nella quale sia alcuna dissonanza. Quelli gradi, che si osseruano nel modulare, ò Cantare, sono, che si ascende per Terza, ouer
per altro salto maggiore; ma non si discende per minore di quello di Quarta. Et questo
basti intorno à quelli Contrapunti & Consequenze, che si fanno à mente. Non creda
però alcuno, ch'io habbia posto in ciascheduna sorte di esse tutte quelle Regole, che osseruar si debbono, percioche sarebbe in errore; essendo che solamente hò posto quelle, che mi
è paruto esser di maggior'importanza, & essentialmente fanno alla natura del Contrapunto; però colui, il quale si uorrà essercitare in simili maniere di Consequenze & Contra-punti; dando opera allo studio, potrà ritrouar quello, da che si haura da guardare, &
quel che douerà osseruare, accioche il suo Contrapunto uenga netto, & purgato da mol-ti errori, i quali possono occorrere, facendo dette sorti di Contrapunto. Si dè però sa-pere, ch[unclear: ']è impossibile in tutte queste sorti de Contrapunti Doppij, quando sono fatti con
simili oblighi, di potere osseruar pienamente le Regole date di sopra, come hò detto ancora; massimamente quando cotali oblighi crescono; essendo che non si può osseruar in
essi la bellezza & il decoro, si quanto alla Modulatione, quanto ancora intorno all'in-uentione, & il modo di por le Consonanze; percioche è leuata la libertà al Composito-re, c'hauea nel comporre gli altri senz'alcun obligo; & questo dico, accioche 'l diligen-te Osseruatore de i nostri Precetti, uedendo alcune cose, che non uengono cosi ben corrette, non si marauigli; perche non hò posto qui cotali Compositioni, accioche lunga-mente, & per sempre s[unclear: ']habbiano da usare; ma si bene alle uolte, quando li tornerà in
proposito, per mostrar la uiuacità del suo ingegno, & la prontezza del suo intelletto
con alcuni, che ad altro non attendono, che à simil cose, & poi nel resto si ritrouano es-sere nudi, come una pietra. Sono queste maniere ueramente molto ingegnose; percio-che scoprono, quanto possa fare il Musico, il qual sappia adoperare gli Harmonici nu-meri; ancora che si oda alle uolte qualche cosa, che sia strana da udire; ma è buono
saper tutte le cose (se fusse possibile) massimamente le necessarie & le utili in ciascun'Ar-page 331te & in ciascuna Scienza; & non solo queste, che sono buone; ma l'altre ancora quan-tunque siano triste; l'une per mettere in opera, l'altre poi per sapersi guardare, & seruir-sene di esse à tempo & luogo conueniente. Et s'alle uolte hò mostrato delle cose, che non
sono molto buone; hò uoluto in ciò imitare il Filosofo, il quale, hauendo mostrato il buono della Logica & della Filosofia; & mostrato il uero modo d'argumentare; dopo l'hauer
scritto molte cose nell'una & nell'altra facultà; scrisse etiandio i Libri de i Sillogismi fallaci, ò Soffistici, i quali chiamò Elenchi; non perche s'hauessero da usare; ma accioche
(accadendo) ogn'uno si sapesse guardare da gli intrichi de i Sofisti, che uogliono esser tenuti dotti, ancora che non siano. Buona cosa è ueramente & ottima il sapere cotali Contrapunti, & usarli quando torna commodo; ma il frequentarli nelle compositioni non lo-do molto; conciosia che non si può far, ch'essendo 'l Contrapuntista obligato all'osser-uanza de tante cose, il Contrapunto uenga ad essere in tal maniera elegante & sonoro,
che porga in tutto & per tutto grato piacere all'Vdito.
Quel che si dè osseruare, quando si volesse fare vna Terza parte alla sproueduta sopra Due altre proposte.Cap. LXIIII.
 page 333
page 333 Contrapuntista tal riguardo, potrà ottimamente accommodare 'l suo Contrapunto, in
quella maniera, che li parerà meglio, & li tornerà più commodo; tanto uolendo aggiungere una parte acuta sopra la parte graue delle due proposte; quanto uolendo far sotto di
esse una parte graue. E' ben uero, che 'l porre alle uolte la parte, che si aggiunge distante
per una Decima, ouer per una Terza dall'una delle due, torna molto commodo; ma bi-sogna auertire, che quando le parte proposte fussero per una Terza lontane l'una dall'al-tra, & quella che s'aggiunge cantasse per una Decima, tra l[unclear: ']aggiunta & l'una delle due, che
sarebbe la graue; quando la parte s'aggiungesse nell'acuto; ouer sarebbe l'acuta, quando
l'aggiunta fusse più graue; sempre si udirebbe l'Ottaua; & cosi dico, quando fussero di-stanti per una Decima, & l'aggiunta cantasse per una Terza; onde se le Due proposte
hauessero molte Terze, ò Decime l'una dopo l'altra; come si sogliono porre alle uolte, s'
udirebbono con l'aggiunto tante Ottaue senza mezo alcuno, quante erano le Terze, ò
le Decime contenute tra le parti; & per tal maniera si uerrebbe a far errore. Però è cosa
buona, anzi necessaria il uedere il Contrapunto delle Due proposte, per potere schiuare
gli errori, che potessero occorrere; percioche; quando si facesse altramente, sarebbe im-possibile di far cosa buona, s'almen non s'hauesse alla memoria ciascuna delle due par-ti della Cantilena proposta. Et perche può occorrere d'accommodare, ouero aggiunge-re tal parte in due maniere; Prima ad alcune cantilene, che non saranno composte secondo gli auertimenti, ò Regole date; dopoi ad alcune, che saranno ordinate secondo i mo-di mostrati; però il Contrapuntista non sarà obligato cosi strettamente d'osseruare i Pre-cetti dati di sopra, nel fare la Terza parte sopra quelle, che saranno composte senza i dati auertimenti; ancora che sarà sempre lodeuole, quando potrà fare, che tal parte aggiunta sia posta con quelle conditioni, che si ricerca in ciascuna buona compositione. Ma quan-do la Cantilena sarà composta regolatamente, debbe per ogni modo star nell'osseruan-za de i mostrati precetti, più che puote; percioche è il douere. Ma accioche si possa comprendere il modo, che si dè tenere in un tal negotio, hò uoluto prima aggiungere due page 334
Contrapuntista tal riguardo, potrà ottimamente accommodare 'l suo Contrapunto, in
quella maniera, che li parerà meglio, & li tornerà più commodo; tanto uolendo aggiungere una parte acuta sopra la parte graue delle due proposte; quanto uolendo far sotto di
esse una parte graue. E' ben uero, che 'l porre alle uolte la parte, che si aggiunge distante
per una Decima, ouer per una Terza dall'una delle due, torna molto commodo; ma bi-sogna auertire, che quando le parte proposte fussero per una Terza lontane l'una dall'al-tra, & quella che s'aggiunge cantasse per una Decima, tra l[unclear: ']aggiunta & l'una delle due, che
sarebbe la graue; quando la parte s'aggiungesse nell'acuto; ouer sarebbe l'acuta, quando
l'aggiunta fusse più graue; sempre si udirebbe l'Ottaua; & cosi dico, quando fussero di-stanti per una Decima, & l'aggiunta cantasse per una Terza; onde se le Due proposte
hauessero molte Terze, ò Decime l'una dopo l'altra; come si sogliono porre alle uolte, s'
udirebbono con l'aggiunto tante Ottaue senza mezo alcuno, quante erano le Terze, ò
le Decime contenute tra le parti; & per tal maniera si uerrebbe a far errore. Però è cosa
buona, anzi necessaria il uedere il Contrapunto delle Due proposte, per potere schiuare
gli errori, che potessero occorrere; percioche; quando si facesse altramente, sarebbe im-possibile di far cosa buona, s'almen non s'hauesse alla memoria ciascuna delle due par-ti della Cantilena proposta. Et perche può occorrere d'accommodare, ouero aggiunge-re tal parte in due maniere; Prima ad alcune cantilene, che non saranno composte secondo gli auertimenti, ò Regole date; dopoi ad alcune, che saranno ordinate secondo i mo-di mostrati; però il Contrapuntista non sarà obligato cosi strettamente d'osseruare i Pre-cetti dati di sopra, nel fare la Terza parte sopra quelle, che saranno composte senza i dati auertimenti; ancora che sarà sempre lodeuole, quando potrà fare, che tal parte aggiunta sia posta con quelle conditioni, che si ricerca in ciascuna buona compositione. Ma quan-do la Cantilena sarà composta regolatamente, debbe per ogni modo star nell'osseruan-za de i mostrati precetti, più che puote; percioche è il douere. Ma accioche si possa comprendere il modo, che si dè tenere in un tal negotio, hò uoluto prima aggiungere due page 334 page 335
page 335 Terze parti uariate l'una dall'altra; ad una compositione de due uoci di Giosquino, che
si troua nel Canto Benedicta es coelorum Regina; à sei uoci; & dopoi n'hò aggiunto due al-tre ad una leggiadra compositione d'Adriano, fatta pure à due uoci; le quali, dopoi che
saranno state uedute & essaminate, si potrà uedere il modo, che si haurà à tenere uolen-do aggiungere tal parte in alcun'altra compositione, composta pure à Due uoci. Si deb-page 336be però auertire, che se le parti aggiunte alcune uolte procedessero per alcuni mouimenti alquanto lontani; questo sarà soppportabile, per la difficultà, che si troua nell'accommodar
tal parte alla modulatione continua della cantilena; essendo che, altro è il Comporre insie-me tutte le parti; & altro è aggiungere à Due parti la Terza, ch'è cosa molto difficile, & da
Huomo consumato nella Musica; & è cosa molto lodeuole, quando s'aggiunge, che stia
bene. Et quello, c'hò detto dell'aggiungere una parte à Due, si può anco intendere, quando se ne uolesse aggiungere una a Tre, & anco à Quattro; percioche non è cosa impos-sibile, se ben è difficile. E' ben uero, che quanto più sarà il numero delle Parti, tanto
più difficultà apporterà à colui, che uorrà aggiungere cotale Parte. Ma bisogna sopra il
tutto tre cose; Buona memoria, & Lunga essercitatione; & Buon occhio per potere raccogliere con prestezza le parti della Cantilena, sopra le quali s'haurà da aggiungere co-tal Parte: Senza le quali cose nulla, ò poco almeno si farebbe.
Terze parti uariate l'una dall'altra; ad una compositione de due uoci di Giosquino, che
si troua nel Canto Benedicta es coelorum Regina; à sei uoci; & dopoi n'hò aggiunto due al-tre ad una leggiadra compositione d'Adriano, fatta pure à due uoci; le quali, dopoi che
saranno state uedute & essaminate, si potrà uedere il modo, che si haurà à tenere uolen-do aggiungere tal parte in alcun'altra compositione, composta pure à Due uoci. Si deb-page 336be però auertire, che se le parti aggiunte alcune uolte procedessero per alcuni mouimenti alquanto lontani; questo sarà soppportabile, per la difficultà, che si troua nell'accommodar
tal parte alla modulatione continua della cantilena; essendo che, altro è il Comporre insie-me tutte le parti; & altro è aggiungere à Due parti la Terza, ch'è cosa molto difficile, & da
Huomo consumato nella Musica; & è cosa molto lodeuole, quando s'aggiunge, che stia
bene. Et quello, c'hò detto dell'aggiungere una parte à Due, si può anco intendere, quando se ne uolesse aggiungere una a Tre, & anco à Quattro; percioche non è cosa impos-sibile, se ben è difficile. E' ben uero, che quanto più sarà il numero delle Parti, tanto
più difficultà apporterà à colui, che uorrà aggiungere cotale Parte. Ma bisogna sopra il
tutto tre cose; Buona memoria, & Lunga essercitatione; & Buon occhio per potere raccogliere con prestezza le parti della Cantilena, sopra le quali s'haurà da aggiungere co-tal Parte: Senza le quali cose nulla, ò poco almeno si farebbe.
Quel che bisogna osseruare intorno le Compositioni de Quattro, ò de più uoci. Cap. LXV.
Quo Semel est imbuta recens, seruabit odoremEt se la Speculatiua senza la Prattica (com'altre uolte hò detto) ual poco; atteso che la Musica non consiste solamente nella Speculatiua; cosi questa senza la prima è ueramente imperfetta. Et questo è manifesto; conciosia c'hauendo uoluto alcuni Theorici trattar le cose della Musica; per non hauer'hauuto buona cognitione della Prattica, hanno detto mille chiachiere, & commesso mille errori. Simigliantemente alcuni, che si hanno uoluto gouernare con la sola Prattica, senza conoscere alcuna ragione; hanno fatto nelle loro compositioni mille & mille pazzie, senza punto auedersene di cosa alcuna. Ma per ritornare al nostro proposito, dico; che uolendo dar principio alle Compositioni nominate di sopra; primieramente si ritrouerà il Soggetto; dopoi ritrouato, si potra incomincia-re 'l Contrapunto da quella parte, che tornarà più commodo. La onde poniamo, che si uolesse dar principio alla Cantilena con la parte del Basso, subito il Compositore potrà page 337conoscere il luogo del Contralto, del Soprano, & quello del Tenore. Cosi ancora uo-lendo dar principio per il mezo di qualunque altra parte; come per il Tenore, ò per il Contr'alto; saprà i luoghi dell'altre parti per ordine, reggendosi secondo 'l modo mostrato nella Tauola; osseruando anche quelle Regole, che di sopra in molti luoghi hò dichiarato, quando fù ragionato intorno il modo di comporre à Due & à Tre uoci. Per la qual cosa osseruando il tutto, potrà hauere il desiderato fine, & acquistarsi honore; al quale spesse fiate ne conseguita grande utile ancora. Ma accioche si uegga 'l modo, che si ha-urà da tenere, & il procedere in simili compositioni; ancora che siano infiniti gli es-sempi à Quattro uoci, composti da molti compositori eccellenti; porrò solamente due Compositioni sopra 'l Canto fermo, dalle quali (poi che si haueranno essaminate) si potrà hauer qualche lume, per poter seguire più oltra di bene in meglio, & porsi à maggiori imprese, & comporre altre cantilene di fantasia; preparandosi il Sogget-to, ò pigliando alcun'altro Canto fermo, ouer qualunque altra parte, come pare-rà meglio al Compositore. Et benche in ogni compositione perfetta Quattro parti sola-mente siano basteuoli; come il Soprano, l'Alto, il Tenore, & il Basso; tuttauia quando si uorrà passar più oltra & hauer maggior numero de Parti, bastarà solamente raddoppiare (com'hò detto altroueSupr. c. 58.) una delle Quattro nominate; & cotal parte aggiunta si chia-mera medesimamente Soprano, ò Tenore, ouer Alto, ò Basso; secondo la parte, che si hauerà doppiata; aggiungendoli questa parola Secondo, ò Terzo, secondo 'l numero de quelle parti, che si troueranno aggiunte. Et le chorde estreme della Parte aggiun-ta, si fanno equali à quelle della Parte, che uiene raddoppiata; ancora che non sarebbe errore, quando non fussero equali, & le chorde della parte aggiunta si estendessero più uerso 'l graue, ò uerso l'acuto, che quelle della raddoppiata; cioè, della parte principa-le. Si debbe però auertire, ch'alle uolte si costuma di compor la cantilena senza 'l Soprano, nel luogo del quale si pone un Contr'alto, alquanto più acuto del principale per una Terza più, ò meno, che importa poco. Il medesimo si fà, lasciando il Soprano & l'Alto, componendo con tre Tenori, & un Basso; oueramente con tre Bassi & un Tenore; & alle uolte con quattro Bassi, & ad altro modo anco, come torna più commodo; ilqual mo-do di comporre si chiama à Voci mutate, ouer'à Voci pari. Si compone anche con due Soprani & un Contr'alto, ouer'un Tenore & il Basso; alle uolte con tre Soprani & un Basso; & tal fiata con quattro Soprani, tanto à quattro uoci, quanto à cinque, & piu oltra; sempre aggiungendo quelle parti, che fanno dibisogno; come si uede ogni giorno nelle moderne compositioni. Ma questa maniera di comporre; ancora che le parti si uenghino à molteplicare & accommodare altramente di quello, che si fà nell'altre; non fà però uarietà alcuna di concento; cioè, non partorisce uariatione d'accordi, oltra quelli che nel Cap. 58. di sopra hò mostrato. E' ben uero, che si troua tal differenza tra le prime & queste seconde compositioni; che essendo in quelle il campo piu largo; cioè, piu lontana la parte graue dalla parte acuta di tutto il concento, in questo luogo è piu ristretto; per-cioche gli estremi delle parti graui & dell'acute insieme si conchiudono commodamente tra Quindeci Chorde al più, & meno anco, secondo che fà dibisogno; & in quelle si conchiudono in Venti; come nella Quarta parte uederemo.Cap. 31. page 338
Testa diu.
 page 339
page 339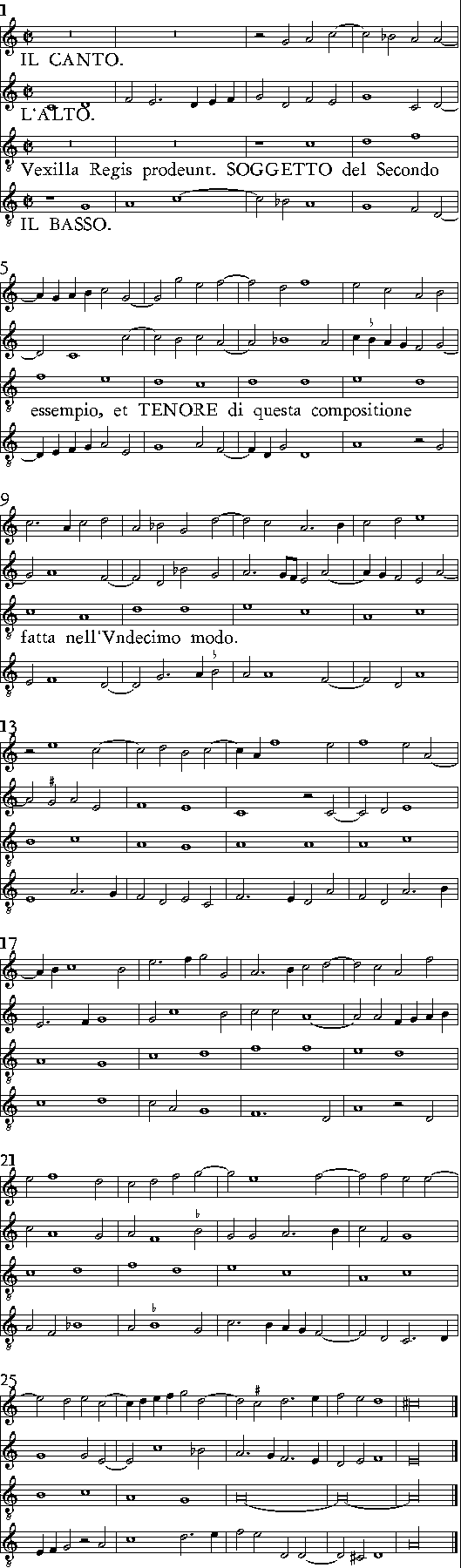 page 340
page 340Alcuni auertimenti intorno le Compositioni, che si fanno à più di Tre voci.Cap. LXVI.
 Et perche accaderà alle uolte di compor sopra alcune Parole, le quali ricercano l'Harmonia alquanto dura & aspera; acciò si uenga con gli effetti (quanto può fare il Musico)
ad imitar'il Soggetto contenuto nell'Orattione; però, quando bisognarà usar simi-li durezze, allora si potranno porre le Seste, nelle quali siano le figure d'alquan-to ualore; come de Breui & de Semibreui mescolate; oueramente si porranno le
Dissonanze tra loro, che siano ordinate secondo le Regole & modi mostrati di so-pra; & si hauerà il proposito; come auerrebbe ponendo la Quarta, ouer l'Vnde-cima nella Sincopa; come ne i sottoposti essempi si può uedere. Accascherà alle
uolte, che nella prima, ò nella seconda parte della Battuta si troueranno due Parti so-pra una medesima chorda Vnisone; ouero si troueranno in un'istesso tempo esser lontane
l'una dall'altra, per una Diapason; dico, se bene tali Parti ascendessero, ò discendes-sero dopoi per un sol grado, & per più gradi ancora, & toccassero un'istessa chorda: page 341
Et perche accaderà alle uolte di compor sopra alcune Parole, le quali ricercano l'Harmonia alquanto dura & aspera; acciò si uenga con gli effetti (quanto può fare il Musico)
ad imitar'il Soggetto contenuto nell'Orattione; però, quando bisognarà usar simi-li durezze, allora si potranno porre le Seste, nelle quali siano le figure d'alquan-to ualore; come de Breui & de Semibreui mescolate; oueramente si porranno le
Dissonanze tra loro, che siano ordinate secondo le Regole & modi mostrati di so-pra; & si hauerà il proposito; come auerrebbe ponendo la Quarta, ouer l'Vnde-cima nella Sincopa; come ne i sottoposti essempi si può uedere. Accascherà alle
uolte, che nella prima, ò nella seconda parte della Battuta si troueranno due Parti so-pra una medesima chorda Vnisone; ouero si troueranno in un'istesso tempo esser lontane
l'una dall'altra, per una Diapason; dico, se bene tali Parti ascendessero, ò discendes-sero dopoi per un sol grado, & per più gradi ancora, & toccassero un'istessa chorda: page 341 pur che ascendessero, ò discendessero una dopo l'altra; & che quella, che sarà la prima
à toccar la seconda chorda, non aspetti l'altra parte; ma subito muti luogo; hauendo la
seconda primieramente una Pausa, che sia di ualore della figura posta sopra la seconda
chorda; se ben l'una & l'altra di queste due parti toccassero cotal chorda; che mai si potrà
con uerità dire, che tra loro siano fatti due Vnisoni, ouer due Ottaue. Et se ben hò già
detto nel Cap. 48. che la Pausa, ò la Dissonanza posta tra due Consonanze perfette di
un'istessa Specie, che ascendino, ò discendino, non è atta à far uarietà alcuna di concento; & non fà, che elle siano senz'alcun mezo; dico hora, che iui mostrai le Figure, che
fanno il Contrapunto, esser poste in altra maniera, di quello, che sono poste in simili
Contrapunti; percioche ueramente allora si fanno due Vnisoni, ò due Ottaue, quando
le parti ascendono, ò discendino, insieme senza esser tramezate d'alcuna Pausa; ouer quan-do dopo la Pausa, l'una delle Parti casca sopra l'altra, senz'alcun mezo. Quando adun-que s'interpongono le Pause, & l'una Parte fugge, auanti che l'altra arriui alla già toccata
chorda, non s'intendono, ne sono, ne si potrà mai dire per alcun modo, che siano poste
contr'alcune delle date Regole; come qui sotto in essempio si uede.
pur che ascendessero, ò discendessero una dopo l'altra; & che quella, che sarà la prima
à toccar la seconda chorda, non aspetti l'altra parte; ma subito muti luogo; hauendo la
seconda primieramente una Pausa, che sia di ualore della figura posta sopra la seconda
chorda; se ben l'una & l'altra di queste due parti toccassero cotal chorda; che mai si potrà
con uerità dire, che tra loro siano fatti due Vnisoni, ouer due Ottaue. Et se ben hò già
detto nel Cap. 48. che la Pausa, ò la Dissonanza posta tra due Consonanze perfette di
un'istessa Specie, che ascendino, ò discendino, non è atta à far uarietà alcuna di concento; & non fà, che elle siano senz'alcun mezo; dico hora, che iui mostrai le Figure, che
fanno il Contrapunto, esser poste in altra maniera, di quello, che sono poste in simili
Contrapunti; percioche ueramente allora si fanno due Vnisoni, ò due Ottaue, quando
le parti ascendono, ò discendino, insieme senza esser tramezate d'alcuna Pausa; ouer quan-do dopo la Pausa, l'una delle Parti casca sopra l'altra, senz'alcun mezo. Quando adun-que s'interpongono le Pause, & l'una Parte fugge, auanti che l'altra arriui alla già toccata
chorda, non s'intendono, ne sono, ne si potrà mai dire per alcun modo, che siano poste
contr'alcune delle date Regole; come qui sotto in essempio si uede.
 Il perche quando si porranno in tal maniera, si potranno sempre usare in ciascuna com-positione di Quattro, di Cinque, ò di qual'altro numero si uoglia de uoci. Ne si potrà
anco dire; se ben quello, c'hò detto nel Cap. 48. pare che sia contrario à questo; che due
parti distanti l'una dall'altra per una Diapente ascendendo, ouer discendendo insieme per
grado, faccino due Quinte; quando l'una di esse haurà la Pausa inanti la seconda figu-ra; & un'altra parte del Contrapunto farà Sesta nel luogo della Pausa, sopra la se-conda figura di quella parte, che si muouerà senza pausa; come qui si uede tra la
Il perche quando si porranno in tal maniera, si potranno sempre usare in ciascuna com-positione di Quattro, di Cinque, ò di qual'altro numero si uoglia de uoci. Ne si potrà
anco dire; se ben quello, c'hò detto nel Cap. 48. pare che sia contrario à questo; che due
parti distanti l'una dall'altra per una Diapente ascendendo, ouer discendendo insieme per
grado, faccino due Quinte; quando l'una di esse haurà la Pausa inanti la seconda figu-ra; & un'altra parte del Contrapunto farà Sesta nel luogo della Pausa, sopra la se-conda figura di quella parte, che si muouerà senza pausa; come qui si uede tra la
 page 342Quarta & la Quinta figura posta nel Basso, con la parte del Tenore, & quella dell'Alto.
Et questo ch'io dico in questo essempio, uoglio che s'intenda in altri simili; che potran-no occorrere; percioche allora ciascun potrà hauer da quello, che si è detto, piena resolutione; La onde non mi estenderò più oltra, per non perder tempo. Qualunque uolta
etiandio occorrerà di uoler comporre alcuna cantilena à Cinque, ouer'à Sei, oueramente à più uoci; si potrà osseruar quello, che da molti Musici celebratissimi è osseruato; conciosia che prima pigliano alle uolte per Soggetto un Tenore di Canto fermo, & dopoi l'
accommodano con uarie figure, come li tornaua più commodo; & fondano la Compositione sopra tal Tenore, & fanno cantar le Parti à quel modo, che li tornano meglio, di
maniera, che facciano buona Harmonia; usando di porle in Consequenza l'una con l'altra; ouer di fare, che l'una imita l'altra, nel modo, c'hò mostrato di sopraSupra cap.
54. & 55.. Il che si può
uedere, uolendo di ciò qualche essempio, in più Canti già composti d'Adriano; come
in quello, che incomincia; Nil postquam sacrum, à Sei uoci; & in quelli; Victor, io salue; &
Inclyte sforciadum; composti à Cinque uoci; & in molt'altri fatti d'altri Compositori.
page 342Quarta & la Quinta figura posta nel Basso, con la parte del Tenore, & quella dell'Alto.
Et questo ch'io dico in questo essempio, uoglio che s'intenda in altri simili; che potran-no occorrere; percioche allora ciascun potrà hauer da quello, che si è detto, piena resolutione; La onde non mi estenderò più oltra, per non perder tempo. Qualunque uolta
etiandio occorrerà di uoler comporre alcuna cantilena à Cinque, ouer'à Sei, oueramente à più uoci; si potrà osseruar quello, che da molti Musici celebratissimi è osseruato; conciosia che prima pigliano alle uolte per Soggetto un Tenore di Canto fermo, & dopoi l'
accommodano con uarie figure, come li tornaua più commodo; & fondano la Compositione sopra tal Tenore, & fanno cantar le Parti à quel modo, che li tornano meglio, di
maniera, che facciano buona Harmonia; usando di porle in Consequenza l'una con l'altra; ouer di fare, che l'una imita l'altra, nel modo, c'hò mostrato di sopraSupra cap.
54. & 55.. Il che si può
uedere, uolendo di ciò qualche essempio, in più Canti già composti d'Adriano; come
in quello, che incomincia; Nil postquam sacrum, à Sei uoci; & in quelli; Victor, io salue; &
Inclyte sforciadum; composti à Cinque uoci; & in molt'altri fatti d'altri Compositori.
 Et comporre etiandio Quattro parti in tal maniera, che 'l Soprano co 'l Basso, & il Con-tralto co 'l Tenore cantino in Consequenza per contrarij mouimenti; come nell'essem-pio posto qui di sotto si uede.
Et comporre etiandio Quattro parti in tal maniera, che 'l Soprano co 'l Basso, & il Con-tralto co 'l Tenore cantino in Consequenza per contrarij mouimenti; come nell'essem-pio posto qui di sotto si uede.
 Ma si debbe auertire, di non por mai l'Alto col Soprano, che facino Quarta; percio-che l'altre parti non tornarebbono bene. Quattro parri [sic: parti] simili compose etiandio l'Eccel-lentissimo Adriano di maniera, che quando si è arriuato al fine, di nuouo si può incominciare dal principio, & ritornar quante fiate si uuole; come dimostrano i Ritornelli posti
nel fine di ciascuna di esse; & nell'essempio dal quale si potrà comprendere, come elle
si componghino.
Ma si debbe auertire, di non por mai l'Alto col Soprano, che facino Quarta; percio-che l'altre parti non tornarebbono bene. Quattro parri [sic: parti] simili compose etiandio l'Eccel-lentissimo Adriano di maniera, che quando si è arriuato al fine, di nuouo si può incominciare dal principio, & ritornar quante fiate si uuole; come dimostrano i Ritornelli posti
nel fine di ciascuna di esse; & nell'essempio dal quale si potrà comprendere, come elle
si componghino.
 Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osser-ua, di non comporre il Canto di alcuna Messa, se non sopra qualche Soggetto; il medesimo si farà etiandio per l'auenire. Ma bisogna sapere, che tal Soggetto può essere fat-to dal Compositore; come fece Giosquino i Tenori La, sol, fa, re mi; & Her-page 346cules Dux Ferrariae, cauati dalle uocali de cotali parole; sopra i quali Tenori ei compose
il canto de due Messe à Quattro uoci, che sono degne d'essere udite; Oueramente tal Soggetto lo piglia da altri; percioche si piglia alcun Tenore di Canto fermo; come fece il medesimo Giosquino, quando compose il canto delle Messe Pange lingua, Gaudeamus, & Aue
maris stella, & Brumello in quello de i Defunti, tutte à Quattro uoci; percioche molto si
dilettauano di comporre sopra i Canti fermi, sopra i quali se ne uedono infinite altre, che
sarebbe impossibile à numerarle. Quando adunque uorremo comporre il canto di alcu-na Messa, ritrouaremo prima il Soggetto, sia di Canto fermo, ò qualche altro canto di
Musica figurata, come si usa, oueramente altro simile; & dopoi cercaremo d'accommo-darlo à diuersi modi; ritrouando noue inuentioni & belle fantasie, imitando gli Antichi;
pigliando l'essempio da quella Messa, che fece P. Molù; Alma redemptoris, la quale com-pose in tal maniera, che si può cantar con le Pause & senza, & torna molto bene; & da
quella, che fece Giouanni Occheghen, maestro del sudetto Giosquino, la qual compose
di maniera, che si poteua cantare sotto diuersi tempi & diuerse Prolationi, che faceua buon
effetto. Accaderà di comporre alle uolte alcuni Salmi in una maniera, che si chiama Choro
spezzato, i quali spesse uolte si sogliono cantare in Venetia ne i Vesperi & altre hore delle
feste solenni; & sono ordinati & diuisi in due, ò più Chori, ne i quali cantano Quattro
ò più uoci; & li chori si cantano hora uno hora l'altro à uicenda; & alcune uolte (secon-do 'l proposito) tutti insieme; massimamente nel fine; il che stà molto bene. Et perche
cotali Chori si pongono alquanto lontani l'un dall'altro; però auertirà il Compositore
(acciò non si odi dissonanza in alcun di loro tra le parti) di fare in tal maniera la compo-sitione, che ogni Choro sia consonante; cioè, che le parti d'un Choro siano ordinate in
tal modo, quanto fussero composte à Quattro uoci semplici, senza considerar gli altri
Chori; hauendo però riguardo nel por le parti, che tra loro insiememente accordino, &
non ui sia alcuna dissonanza; percioche composti i Chori in cotal maniera, ciascun da per
sè si potrà cantare, che non si udirà cosa alcuna, che offendi l'Vdito. Questo auertimen-to non è da sprezzare; percioche è di gran commodo; & fù ritrouato dall'Eccellentissi-mo Adriano. Et benche si rendi alquanto difficile, non si debbe però schiuar la fatica;
percioche è cosa molto lodeuole & virtuosa; & tal difficultà si sarà alquanto più facile,
quando si hauerà essaminato le dotte compositioni di esso Adriano; come sono questi Salmi: Confitebor tibi domine in toto corde meo in consilio iustorum. Laudate pueri dominum: Lauda Ierusalem dominum: Deprofundis: Memento domine Dauid, & molti altri; tra i quali sono i
Salmi; Dixit Dominus Domino meo: Laudate pueri dominum: Laudate Dominum omnes gen-tes: Lauda anima mea Dominum; Laudate Dominum quoniam bonus est Psalmus. Lauda Ierusa-lem Dominum; & il Cantico della Beata Vergine; Magnificat anima mea Dominum, ilquale
composi già molt'anni fà à tre Chori, per uso della Cappella del Famosissimo Tempio di
S. Marco; della quale da questi Sig. Illustriss. già uentiquattro anni sono, mi fù dato il go-uerno. Queste compositioni vedute & essaminate saranno di gran giouamento à tutti coloro, che si dilettaranno di comporre in tal maniera; conciosiache ritroueranno, che i Bassi de i
Chori si pongono tra loro sempre distanti; per Vnisoni, ouer per Ottaua; ancora ch'alcu-ne uolte si pongano in Terza; ma non si pongono però in Quinta; se non sopra la parte del
Tenore; percioche altramente torna molto incommodo; & oltra la difficultà che nasce;
è impossibile di far cosa, che torni bene secondo il proposito; essendo che si ode sempre
nel cantare qualche asprezza. Et questa osseruanza uien'ad essere molto commoda à i
Compositori; percioche lieua à loro la difficultà di far cantar le parti de i Chori, che
tra loro non si ritroua dissonanza. Lodarei però, ne haurei per inconueniente quello, che
molte fiate hò fatto anch'io; che quando si passasse 'l numero de due chori, & anco
nell'istessi due chori, che i Bassi d'un Choro cantasse anco la parte dell'altro; percioche
ne seguitarebbe, che 'l Canto tutto & l'Harmonia tutta, hauerebbe una base, & un fondamento, dirò cosi, che la sustentarebbe di maniera, che la farebbe comparere altra
tanto; essendoche quella parte che è raddoppiata si uiene più à udire, che se la si cantas-page 347se semplicemente da una uoce; come ben lo dimostra Aristotele nel Problema 2. della
19. Settione. Oltra di questo il Compositore potrebbe uariare l'Harmonia, piu che non si
fà; percioche ponendo i Bassi differenti di modulatione, non si può far molta uarietà d'
Harmonia nelle Compositioni. Et chiunque prouerà cotesta cosa, potrà conoscer l'uti-le, ch'ella potrà apportare. Nè però alcuno si dee conturbar di questo; percioche se 'l bisognasse hauere cotal rispetto; per dire che canteranno quest'istesso l'una parte che can-teranno l'altre parti; non bisognerebbe anco che nelle capelle, ne i chori, non ui fusse al-tro che una uoce per parte, nel cantar le compositioni che iui si cantano. Hora per concluder questo ragionamento, dico; che hauendo il Compositore intese tutte queste cose, dè
auertire anco à quello ch'è obligato; poi ch'è legge osseruata da gli Antichi; di terminare
il numero delle Figure di ciascuna sua compositione, secondo che ricercano il Tempo, il
Modo, & la Prolatione, sotto i quali Accidenti componer[unclear: à] la cantilena. Er perche simili accidenti erano già in grande consideratione, & anco appresso d'alcuni sono in uso;
però accioche ciascun habbia cognitione di simil cose, uerrò à ragionar di quelle;
che sono più bisognose; lasciando quelle, che sono superstitiose, & fanno poco al pro-posito; & incomincierò dal Tempo, come da quello, ch'è (secondo 'l mio parere)
più uniuersale, & primo d'ogn'altro accidente.
Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osser-ua, di non comporre il Canto di alcuna Messa, se non sopra qualche Soggetto; il medesimo si farà etiandio per l'auenire. Ma bisogna sapere, che tal Soggetto può essere fat-to dal Compositore; come fece Giosquino i Tenori La, sol, fa, re mi; & Her-page 346cules Dux Ferrariae, cauati dalle uocali de cotali parole; sopra i quali Tenori ei compose
il canto de due Messe à Quattro uoci, che sono degne d'essere udite; Oueramente tal Soggetto lo piglia da altri; percioche si piglia alcun Tenore di Canto fermo; come fece il medesimo Giosquino, quando compose il canto delle Messe Pange lingua, Gaudeamus, & Aue
maris stella, & Brumello in quello de i Defunti, tutte à Quattro uoci; percioche molto si
dilettauano di comporre sopra i Canti fermi, sopra i quali se ne uedono infinite altre, che
sarebbe impossibile à numerarle. Quando adunque uorremo comporre il canto di alcu-na Messa, ritrouaremo prima il Soggetto, sia di Canto fermo, ò qualche altro canto di
Musica figurata, come si usa, oueramente altro simile; & dopoi cercaremo d'accommo-darlo à diuersi modi; ritrouando noue inuentioni & belle fantasie, imitando gli Antichi;
pigliando l'essempio da quella Messa, che fece P. Molù; Alma redemptoris, la quale com-pose in tal maniera, che si può cantar con le Pause & senza, & torna molto bene; & da
quella, che fece Giouanni Occheghen, maestro del sudetto Giosquino, la qual compose
di maniera, che si poteua cantare sotto diuersi tempi & diuerse Prolationi, che faceua buon
effetto. Accaderà di comporre alle uolte alcuni Salmi in una maniera, che si chiama Choro
spezzato, i quali spesse uolte si sogliono cantare in Venetia ne i Vesperi & altre hore delle
feste solenni; & sono ordinati & diuisi in due, ò più Chori, ne i quali cantano Quattro
ò più uoci; & li chori si cantano hora uno hora l'altro à uicenda; & alcune uolte (secon-do 'l proposito) tutti insieme; massimamente nel fine; il che stà molto bene. Et perche
cotali Chori si pongono alquanto lontani l'un dall'altro; però auertirà il Compositore
(acciò non si odi dissonanza in alcun di loro tra le parti) di fare in tal maniera la compo-sitione, che ogni Choro sia consonante; cioè, che le parti d'un Choro siano ordinate in
tal modo, quanto fussero composte à Quattro uoci semplici, senza considerar gli altri
Chori; hauendo però riguardo nel por le parti, che tra loro insiememente accordino, &
non ui sia alcuna dissonanza; percioche composti i Chori in cotal maniera, ciascun da per
sè si potrà cantare, che non si udirà cosa alcuna, che offendi l'Vdito. Questo auertimen-to non è da sprezzare; percioche è di gran commodo; & fù ritrouato dall'Eccellentissi-mo Adriano. Et benche si rendi alquanto difficile, non si debbe però schiuar la fatica;
percioche è cosa molto lodeuole & virtuosa; & tal difficultà si sarà alquanto più facile,
quando si hauerà essaminato le dotte compositioni di esso Adriano; come sono questi Salmi: Confitebor tibi domine in toto corde meo in consilio iustorum. Laudate pueri dominum: Lauda Ierusalem dominum: Deprofundis: Memento domine Dauid, & molti altri; tra i quali sono i
Salmi; Dixit Dominus Domino meo: Laudate pueri dominum: Laudate Dominum omnes gen-tes: Lauda anima mea Dominum; Laudate Dominum quoniam bonus est Psalmus. Lauda Ierusa-lem Dominum; & il Cantico della Beata Vergine; Magnificat anima mea Dominum, ilquale
composi già molt'anni fà à tre Chori, per uso della Cappella del Famosissimo Tempio di
S. Marco; della quale da questi Sig. Illustriss. già uentiquattro anni sono, mi fù dato il go-uerno. Queste compositioni vedute & essaminate saranno di gran giouamento à tutti coloro, che si dilettaranno di comporre in tal maniera; conciosiache ritroueranno, che i Bassi de i
Chori si pongono tra loro sempre distanti; per Vnisoni, ouer per Ottaua; ancora ch'alcu-ne uolte si pongano in Terza; ma non si pongono però in Quinta; se non sopra la parte del
Tenore; percioche altramente torna molto incommodo; & oltra la difficultà che nasce;
è impossibile di far cosa, che torni bene secondo il proposito; essendo che si ode sempre
nel cantare qualche asprezza. Et questa osseruanza uien'ad essere molto commoda à i
Compositori; percioche lieua à loro la difficultà di far cantar le parti de i Chori, che
tra loro non si ritroua dissonanza. Lodarei però, ne haurei per inconueniente quello, che
molte fiate hò fatto anch'io; che quando si passasse 'l numero de due chori, & anco
nell'istessi due chori, che i Bassi d'un Choro cantasse anco la parte dell'altro; percioche
ne seguitarebbe, che 'l Canto tutto & l'Harmonia tutta, hauerebbe una base, & un fondamento, dirò cosi, che la sustentarebbe di maniera, che la farebbe comparere altra
tanto; essendoche quella parte che è raddoppiata si uiene più à udire, che se la si cantas-page 347se semplicemente da una uoce; come ben lo dimostra Aristotele nel Problema 2. della
19. Settione. Oltra di questo il Compositore potrebbe uariare l'Harmonia, piu che non si
fà; percioche ponendo i Bassi differenti di modulatione, non si può far molta uarietà d'
Harmonia nelle Compositioni. Et chiunque prouerà cotesta cosa, potrà conoscer l'uti-le, ch'ella potrà apportare. Nè però alcuno si dee conturbar di questo; percioche se 'l bisognasse hauere cotal rispetto; per dire che canteranno quest'istesso l'una parte che can-teranno l'altre parti; non bisognerebbe anco che nelle capelle, ne i chori, non ui fusse al-tro che una uoce per parte, nel cantar le compositioni che iui si cantano. Hora per concluder questo ragionamento, dico; che hauendo il Compositore intese tutte queste cose, dè
auertire anco à quello ch'è obligato; poi ch'è legge osseruata da gli Antichi; di terminare
il numero delle Figure di ciascuna sua compositione, secondo che ricercano il Tempo, il
Modo, & la Prolatione, sotto i quali Accidenti componer[unclear: à] la cantilena. Er perche simili accidenti erano già in grande consideratione, & anco appresso d'alcuni sono in uso;
però accioche ciascun habbia cognitione di simil cose, uerrò à ragionar di quelle;
che sono più bisognose; lasciando quelle, che sono superstitiose, & fanno poco al pro-posito; & incomincierò dal Tempo, come da quello, ch'è (secondo 'l mio parere)
più uniuersale, & primo d'ogn'altro accidente.
Del Tempo, del Modo, & della Prolatione; & in che Quantità si debbino fini-re, ò numerare le Cantilene.Cap. LXVII.
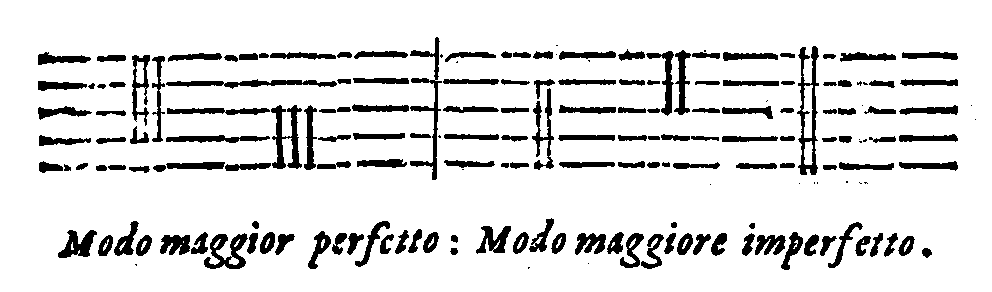



 ; & l'Imperfetta quando erano posti senza i punti
; & l'Imperfetta quando erano posti senza i punti 
 & face-uano ualere la Semibreue tre Minime sotto i due primi; & sotto quelli che non erano
puntati due; il perche nelle cantilene numerauano in questa maniera; che quelle ch'era-no poste sotto la Prolation perfetta procedeuano & erano numerate di tre in tre mi-nime; & quelle ch'erano composte sotto la Imperfetta, di due in due. Et perche ne i Mo-di spesse uolte s'aggiungeuano insieme questi gradi, cioè, Maggiore & Minore; & an-co il Perfetto & l'Imperfetto, de i quali, il maggiore include, ouero in sè contie-ne il minore; il che fà etiandio il Perfetto, che in sè contiene l'Imperfetto, ma
non per il contrario; però auertiuano in tale congiuntione; che se 'l Modo mag-giore era congiunto col minore; & l'uno & l'altro fussero stati Perfetti; allora nu-merauano la cantilena di tre Lunghe, in tre perfette; ma se 'l Modo fusse stato mag-giore perfetto, & minore imperfetto; la numerauano di tre Lunghe, in tre Lun-ghe, lequali fussero imperfette. Oltra di questo, quando 'l Modo maggior imperfet-to era posto insieme col minor perfetto, numerauano le lor compositioni di due in due
Lunghe perfette; & se l'uno & l[unclear: ']altro modo erano imperfetti, numerauano quelle di due
Lunghe in due, l'una & l'altra imperfette. Ancora quando 'l Modo era solamente Mi-nor perfetto, le numerauano con due lunghe perfette; & quando era imperfetto, nume-rauano quella à Lunghe imperfette; cioè, d'una in una. Et con simile consideratione
procedeuano ne gli altri gradi; come nel Tempo, & nella Prolatione, perfetti & imperfetti; percioche ne i Perfetti numerauano di tre, in tre; & ne gli Imperfetti numeraua-no di due, in due. Potiamo hora uedere, che per i Segni; cioè, per il Circolo, & per lo
Semicircolo dauano la cognitione del Tempo perfetto, ouer'imperfetto; per le Pause,
quella del Modo maggiore, ò minore perfetto, ouer imperfetto che 'l si fusse; & per i se-gni del Tempo puntati, ò non puntati, intendeuano la Prolatione perfetta, ouer imperfetta. Di maniera che potiamo etiandio comprendere, che attribuirono il Modo maggior
perfetto alla Massima di ualore di tre Lunghe, & à quella di ualor di due il Modo mag-giore imperetto [sic: imperfetto]; similmente alla Lunga di ualor di tre Breui attribuirono il Modo mi-nor perfetto, & à quella di ualor di due il Modo minore imperfetto. Il Tempo perfetto
attribuirono alla Breue di ualor di tre Semibreui, & l'Imperfetto à quella, che ual due;
& la Prolatione perfetta alla Semibreue di ualor di tre Minime; ma la imperfetta diede-ro à quella di due. Soleuano anco gli Antichi tagliare i segni del Tempo in tal maniera;
& face-uano ualere la Semibreue tre Minime sotto i due primi; & sotto quelli che non erano
puntati due; il perche nelle cantilene numerauano in questa maniera; che quelle ch'era-no poste sotto la Prolation perfetta procedeuano & erano numerate di tre in tre mi-nime; & quelle ch'erano composte sotto la Imperfetta, di due in due. Et perche ne i Mo-di spesse uolte s'aggiungeuano insieme questi gradi, cioè, Maggiore & Minore; & an-co il Perfetto & l'Imperfetto, de i quali, il maggiore include, ouero in sè contie-ne il minore; il che fà etiandio il Perfetto, che in sè contiene l'Imperfetto, ma
non per il contrario; però auertiuano in tale congiuntione; che se 'l Modo mag-giore era congiunto col minore; & l'uno & l'altro fussero stati Perfetti; allora nu-merauano la cantilena di tre Lunghe, in tre perfette; ma se 'l Modo fusse stato mag-giore perfetto, & minore imperfetto; la numerauano di tre Lunghe, in tre Lun-ghe, lequali fussero imperfette. Oltra di questo, quando 'l Modo maggior imperfet-to era posto insieme col minor perfetto, numerauano le lor compositioni di due in due
Lunghe perfette; & se l'uno & l[unclear: ']altro modo erano imperfetti, numerauano quelle di due
Lunghe in due, l'una & l'altra imperfette. Ancora quando 'l Modo era solamente Mi-nor perfetto, le numerauano con due lunghe perfette; & quando era imperfetto, nume-rauano quella à Lunghe imperfette; cioè, d'una in una. Et con simile consideratione
procedeuano ne gli altri gradi; come nel Tempo, & nella Prolatione, perfetti & imperfetti; percioche ne i Perfetti numerauano di tre, in tre; & ne gli Imperfetti numeraua-no di due, in due. Potiamo hora uedere, che per i Segni; cioè, per il Circolo, & per lo
Semicircolo dauano la cognitione del Tempo perfetto, ouer'imperfetto; per le Pause,
quella del Modo maggiore, ò minore perfetto, ouer imperfetto che 'l si fusse; & per i se-gni del Tempo puntati, ò non puntati, intendeuano la Prolatione perfetta, ouer imperfetta. Di maniera che potiamo etiandio comprendere, che attribuirono il Modo maggior
perfetto alla Massima di ualore di tre Lunghe, & à quella di ualor di due il Modo mag-giore imperetto [sic: imperfetto]; similmente alla Lunga di ualor di tre Breui attribuirono il Modo mi-nor perfetto, & à quella di ualor di due il Modo minore imperfetto. Il Tempo perfetto
attribuirono alla Breue di ualor di tre Semibreui, & l'Imperfetto à quella, che ual due;
& la Prolatione perfetta alla Semibreue di ualor di tre Minime; ma la imperfetta diede-ro à quella di due. Soleuano anco gli Antichi tagliare i segni del Tempo in tal maniera;
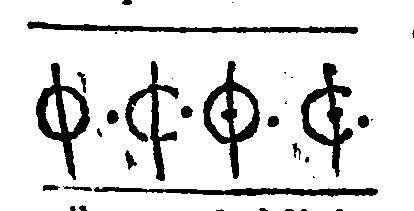 & questo faceuano, quando uoleuano, che le Figure sottoposte
alla perfettione & all'imperfettione, & anche all'Alteratione nel
Tempo perfetto & nell'imperfetto, fussero più ueloci; lequali figu-re (come uederemo) sono cinque; Massima, Lunga, Breue, Se-mibreue, & Minima. E ben uero, che ne per il tagliare i Segni, ne per il far nere le det-te Figure; come molte fiate accade, & più oltra uederemo; leuauano à loro il nome,
ma lo riteneuano tanto, quanto che tali Segni fussero stati intieri, & le Figure senza co-lore. Ne per il tagliare de i detti segni si leuaua la perfettione, ò l'Imperfettione, ne page 350meno l'Alteratione; ma tanto erano sottoposte à tali accidenti & passioni; quanto s'essi
Segni fussero stati intieri. Bisogna però sapere, che nella Prolatione perfetta gli Anti-chi vsarono la figura della Chroma bianca in luogo di quella, che è di ualore della metà
della Minima; la quale noi chiamiamo Semiminima; come son per dimostrare;Infra cap.
70. & questo
fecero, accioche se per caso bisognasse fare tal Minima nera, per rispetto di leuar l'Altera
ratione [sic: Alteratione] à cotale figura; il che può intrauenire molte fiate; rispetto à diuersi accidenti,
che occorrer possono; ch'ella non fusse riputata esser cotale Semiminima; la qual (com'
altroue hò mostratoSupra c. 2.) si diuide in due Chrome, & la Chroma in due Semichrome. Ha-ueano etiandio gli Antichi sotto 'l segno del Tempo perfetto tagliato doppia considera-tione nel numerar componendo le Cantilene; percioche numerauano à tre à tre, & an-co à due à due; cioè, di due Breue perfette in due, oueramente di tre Semibreui in tre;
di maniera che 'l numerar delle Semibreui finiua nel numero Senario; conciosia che se misurauano altramente non ritrouauano nelle lor cantilene la misura della Breue. Il che parimente cercaremo anche noi di osseruare, non solo nel Tempo perfetto; ma anco nell'
Imperfetto tagliato, procedendo in questo de due Breui imperfette in due; acciò la cantilena finisca nel numero Quaternario. Ma che diremo hora d'alcuni compositori moderni, i quali non solamente non osseruano la misura del numero Senario, ò Quaternario
nelle lor Cantilene; ma di più non osseruano il numero Ternario nel Tempo perfetto,
ne meno nell'Imperfetto il Binario, siano pur tagliati, ò non tagliati; ilche ueramente
è gran uergogna; conciosiache uengono a rompere il Tempo & la misura, delle quali cose gli Antichi furono osseruatori molto diligenti; & per tal maniera guastano & confon-dono ogni cosa di buono; dimostrandosi essere poco intelligenti delle cose della Musica.
& questo faceuano, quando uoleuano, che le Figure sottoposte
alla perfettione & all'imperfettione, & anche all'Alteratione nel
Tempo perfetto & nell'imperfetto, fussero più ueloci; lequali figu-re (come uederemo) sono cinque; Massima, Lunga, Breue, Se-mibreue, & Minima. E ben uero, che ne per il tagliare i Segni, ne per il far nere le det-te Figure; come molte fiate accade, & più oltra uederemo; leuauano à loro il nome,
ma lo riteneuano tanto, quanto che tali Segni fussero stati intieri, & le Figure senza co-lore. Ne per il tagliare de i detti segni si leuaua la perfettione, ò l'Imperfettione, ne page 350meno l'Alteratione; ma tanto erano sottoposte à tali accidenti & passioni; quanto s'essi
Segni fussero stati intieri. Bisogna però sapere, che nella Prolatione perfetta gli Anti-chi vsarono la figura della Chroma bianca in luogo di quella, che è di ualore della metà
della Minima; la quale noi chiamiamo Semiminima; come son per dimostrare;Infra cap.
70. & questo
fecero, accioche se per caso bisognasse fare tal Minima nera, per rispetto di leuar l'Altera
ratione [sic: Alteratione] à cotale figura; il che può intrauenire molte fiate; rispetto à diuersi accidenti,
che occorrer possono; ch'ella non fusse riputata esser cotale Semiminima; la qual (com'
altroue hò mostratoSupra c. 2.) si diuide in due Chrome, & la Chroma in due Semichrome. Ha-ueano etiandio gli Antichi sotto 'l segno del Tempo perfetto tagliato doppia considera-tione nel numerar componendo le Cantilene; percioche numerauano à tre à tre, & an-co à due à due; cioè, di due Breue perfette in due, oueramente di tre Semibreui in tre;
di maniera che 'l numerar delle Semibreui finiua nel numero Senario; conciosia che se misurauano altramente non ritrouauano nelle lor cantilene la misura della Breue. Il che parimente cercaremo anche noi di osseruare, non solo nel Tempo perfetto; ma anco nell'
Imperfetto tagliato, procedendo in questo de due Breui imperfette in due; acciò la cantilena finisca nel numero Quaternario. Ma che diremo hora d'alcuni compositori moderni, i quali non solamente non osseruano la misura del numero Senario, ò Quaternario
nelle lor Cantilene; ma di più non osseruano il numero Ternario nel Tempo perfetto,
ne meno nell'Imperfetto il Binario, siano pur tagliati, ò non tagliati; ilche ueramente
è gran uergogna; conciosiache uengono a rompere il Tempo & la misura, delle quali cose gli Antichi furono osseruatori molto diligenti; & per tal maniera guastano & confon-dono ogni cosa di buono; dimostrandosi essere poco intelligenti delle cose della Musica.
Della Perfettione delle Figure cantabili.Cap. LXVIII.




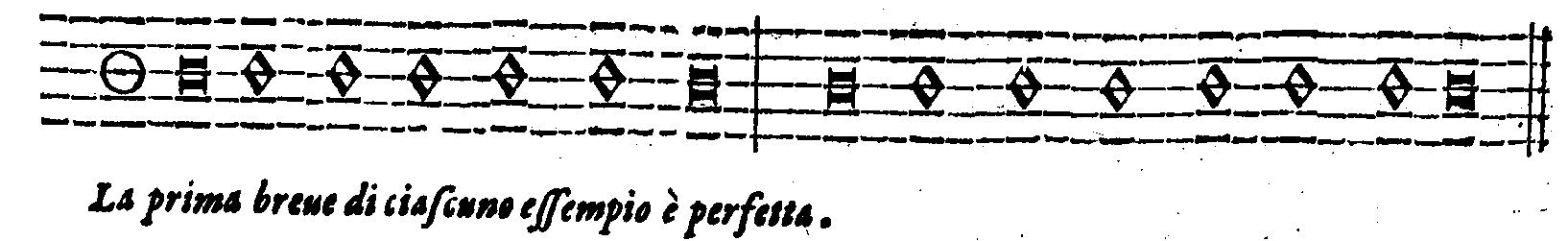
Dell'Imperfettione delle Figure cantabili.Cap. LXIX.




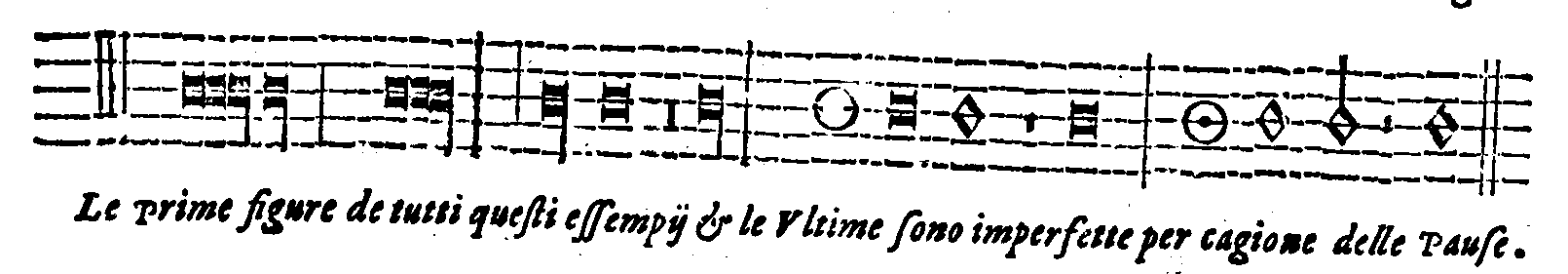
Del Punto, delle sue specie; & de i suoi effetti.Cap. LXX.
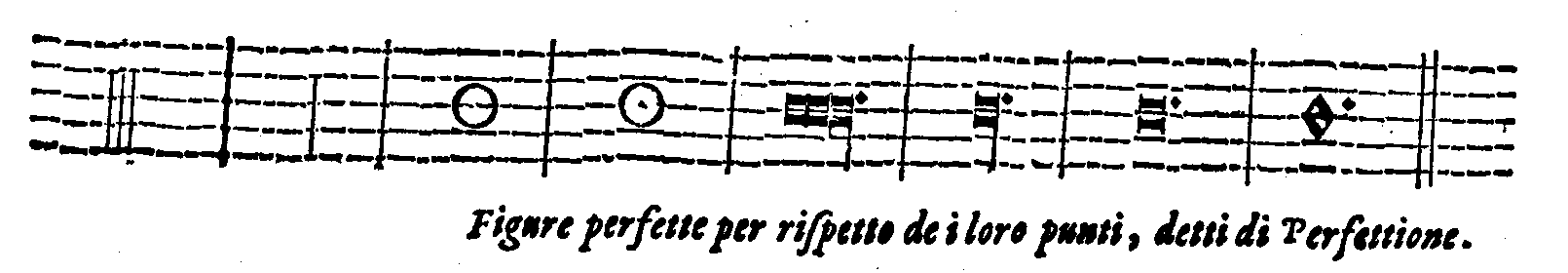




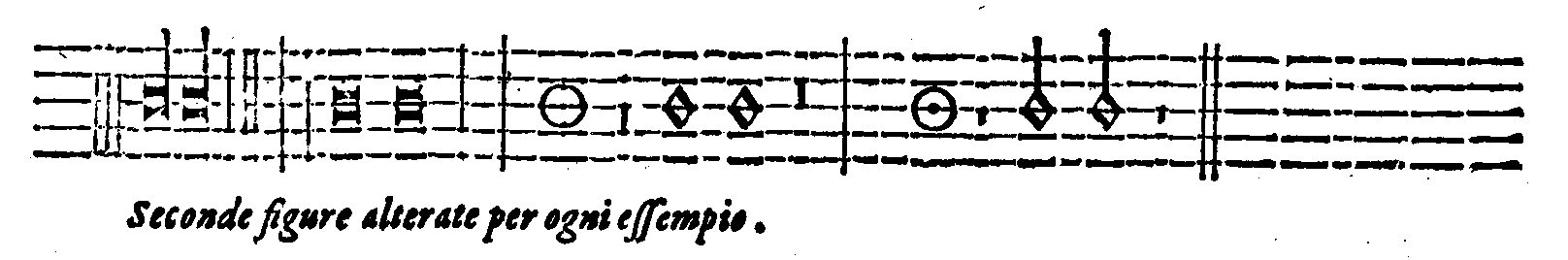
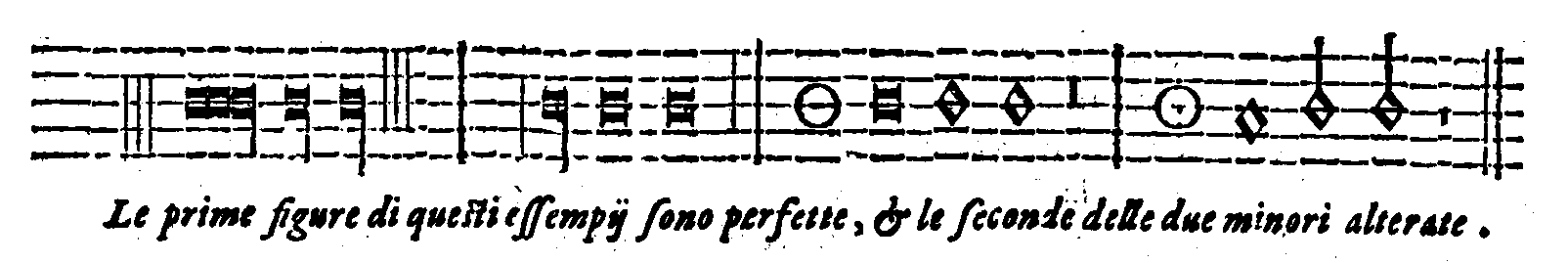

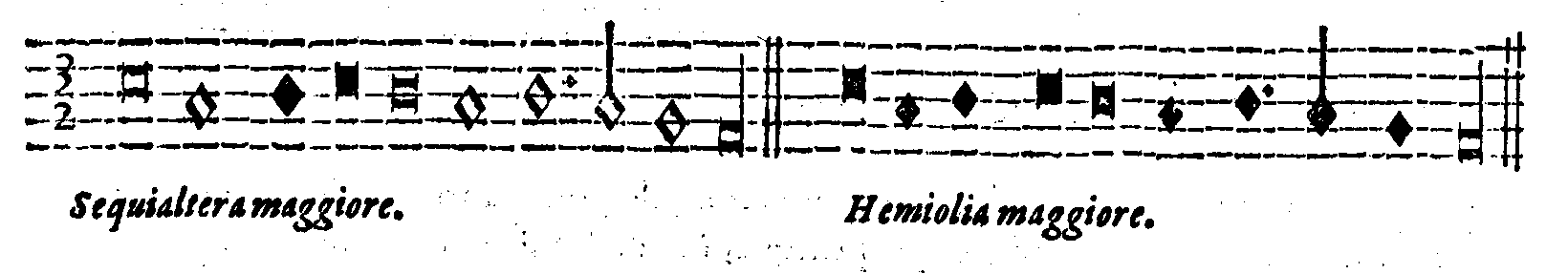

 Haueano oltra di questo gli Antichi nelle loro compositioni molti altri Accidenti, & Ci-fere di più maniere: ma perche poco più s'vsano, & non sono d'vtile alcuno alle buone, &
sonore harmonie; però lasciaremo il ragionar più in lungo di simil cose à coloro che sono
otiosi, & che si dilettano di simili Cifere più di quello, che facciamo noi.
Haueano oltra di questo gli Antichi nelle loro compositioni molti altri Accidenti, & Ci-fere di più maniere: ma perche poco più s'vsano, & non sono d'vtile alcuno alle buone, &
sonore harmonie; però lasciaremo il ragionar più in lungo di simil cose à coloro che sono
otiosi, & che si dilettano di simili Cifere più di quello, che facciamo noi.
Dell'vtile, che apportano i mostrati Accidenti nelle buone Harmonie.Cap. LXXI.
Delle Chorde Communi, & delle Particolari delle cantilene Diatoniche, Chromatiche, & Enharmoniche.Cap. LXXII.
 , & le communi saranno senza. Et
se bene le chorde b &
, & le communi saranno senza. Et
se bene le chorde b &  . fanno in questo genere il Tetrachordo Synemennon, non saran-no però particolari; ma communi à ciascun genere; perche tal Tetrachordo si congiunge
à i quattro primi per accidente; com'hò detto. Il Terzo ordine poi contenerà quelle
chorde, che seruono all'Enharmonico, nel quale ritrouaremo le chorde particolari di
questo Genere, che saranno segnate con questo segno [[mus.hsharp]]. à differenza di quelle, che so-no particolari & anco communi de gli altri due generi; come si può vedere ne i seguenti
ordini.
. fanno in questo genere il Tetrachordo Synemennon, non saran-no però particolari; ma communi à ciascun genere; perche tal Tetrachordo si congiunge
à i quattro primi per accidente; com'hò detto. Il Terzo ordine poi contenerà quelle
chorde, che seruono all'Enharmonico, nel quale ritrouaremo le chorde particolari di
questo Genere, che saranno segnate con questo segno [[mus.hsharp]]. à differenza di quelle, che so-no particolari & anco communi de gli altri due generi; come si può vedere ne i seguenti
ordini.
 Onde le chorde particolari de questi Generi saranno queste. Primieramente la Terza
chorda d'ogni Tetrachordo del primo ordine, procedendo dal graue all'acuto, sarà par-ticolare Diatonica; dopoi la Terza d'ogni Tetrachordo posto nel secondo ordine segna-ta con questo segno
Onde le chorde particolari de questi Generi saranno queste. Primieramente la Terza
chorda d'ogni Tetrachordo del primo ordine, procedendo dal graue all'acuto, sarà par-ticolare Diatonica; dopoi la Terza d'ogni Tetrachordo posto nel secondo ordine segna-ta con questo segno  . sarà particolare Chromaticha; ma ogni Seconda chorda d'ogni
Tetrachordo del Terzo ordine segnata con tale cifera [[mus.hsharp]]. sarà particolare Enharmonica;
l'altre poi, che non saranno segnate con alcuni de questi caratteri, saranno communi à
ciascun de i nominati Generi. Et se ben tali ordini sono ristretti in poche chorde; tutta-uia si potranno far maggiori, secondo che tornarà commodo; come fin'hora nelle cose
della Prattica è stato fatto da i Compositori; il che si può veder nelle loro cantilene. Ne
alcun dè prender marauiglia, ch'io habbia posto in uso cotal segno [[mus.hsharp]]. forse non più vsato
per auanti; percioche non hò ritrouato segno più commodo, che sia stato posto in vso
d'alcuno, col mezo del quale potessi mostrar la chorda Enharmonica, & l'Interuallo, fuori
che questo. Ma s'è lecito à i Filosofi (come vuole Aristotele ne i PredicamentiCap. De
Relatione.) fingere,
ò comporre nuoui Nomi, ò Vocabuli, per manifestare i lor concetti; perche non è anco page 364lecito al Musico di ritrouar nuoui Segni, per manifestar quelle cose, che fanno al propo-sito dell'Harmonie? tanto più, che (com'è noto ad ogni studio) la Musica è parte della
Filosofia.
. sarà particolare Chromaticha; ma ogni Seconda chorda d'ogni
Tetrachordo del Terzo ordine segnata con tale cifera [[mus.hsharp]]. sarà particolare Enharmonica;
l'altre poi, che non saranno segnate con alcuni de questi caratteri, saranno communi à
ciascun de i nominati Generi. Et se ben tali ordini sono ristretti in poche chorde; tutta-uia si potranno far maggiori, secondo che tornarà commodo; come fin'hora nelle cose
della Prattica è stato fatto da i Compositori; il che si può veder nelle loro cantilene. Ne
alcun dè prender marauiglia, ch'io habbia posto in uso cotal segno [[mus.hsharp]]. forse non più vsato
per auanti; percioche non hò ritrouato segno più commodo, che sia stato posto in vso
d'alcuno, col mezo del quale potessi mostrar la chorda Enharmonica, & l'Interuallo, fuori
che questo. Ma s'è lecito à i Filosofi (come vuole Aristotele ne i PredicamentiCap. De
Relatione.) fingere,
ò comporre nuoui Nomi, ò Vocabuli, per manifestare i lor concetti; perche non è anco page 364lecito al Musico di ritrouar nuoui Segni, per manifestar quelle cose, che fanno al propo-sito dell'Harmonie? tanto più, che (com'è noto ad ogni studio) la Musica è parte della
Filosofia.
Se l'uno de i due vltimi Generi si possa vsar semplice nelle sue chorde naturali, senz'adope-rar le Chorde particolari de gli altri.Cap. LXXIII.
 tenuto tra le chorde naturali del genere Diatonico; non è dubbio alcuno, che se lo vor-remo accommodare ad vna cantilene de Quattro & de più voci, noi potremmo proce-dere dal principio al fine per le Chorde naturali di questo Genere per ogni uerso, senza
toccare alcuna chorda particolare de gli altri Generi; come ciascuno potrà uedere. Ma
se lo uorremo ridurre nelle chorde Chromatiche, che saranno le contenute nel sequente
Tenore; ogn'uno, c'hauerà giudicio, potrà conoscere, ciò essere impossibile; conciosia-che quando non si vorremo partire dalle sue chorde essentiali, contenute nel Secondo
tenuto tra le chorde naturali del genere Diatonico; non è dubbio alcuno, che se lo vor-remo accommodare ad vna cantilene de Quattro & de più voci, noi potremmo proce-dere dal principio al fine per le Chorde naturali di questo Genere per ogni uerso, senza
toccare alcuna chorda particolare de gli altri Generi; come ciascuno potrà uedere. Ma
se lo uorremo ridurre nelle chorde Chromatiche, che saranno le contenute nel sequente
Tenore; ogn'uno, c'hauerà giudicio, potrà conoscere, ciò essere impossibile; conciosia-che quando non si vorremo partire dalle sue chorde essentiali, contenute nel Secondo
 ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri Generi; ri-trouaremo, che molte chorde di questo Tenore, non potranno hauer quelli accompa-gnamenti perfetti, che ricerca ogni perfetta compositione. La onde senz'alcun dubbio
potremo comprendere, che in tal Genere non si potrà comporre perfettamente alcuna
cantilena; com'alcuni s'hanno sognato; oltra che ritrouaremo etiandio alcune modula-tioni molto strane, i cui Interualli saranno molto lontani dalle forme, che sono contenu-te nel Numero sonoro. Ma lasciamo questo; percioche credo che sia manifesto à tutti
quelli, c'hanno intelligenza dell'Arte; & passiamo all'Enharmonico, che noi vedremo
quanto poco sapienti siano stati quelli, che hanno detto, che si può comporre in questo
Genere qual si voglia cantilena, non si partendo dalle sue chorde propie & naturali, sen-z'hauer'aiuto alcuno dalle chorde particolari de gli altri Generi; percioche riducendo il
mostrato Tenore nelle chorde Enharmoniche nella maniera che si uedono; se non si vorrà
passar fuori delle chorde mostrate in questo Terzo ordine; ritrouaremo molte figure, che
non si potranno accompagnare in modo, che dapoi accompagnate s'odi l'Harmonia perfetta; page 365
ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri Generi; ri-trouaremo, che molte chorde di questo Tenore, non potranno hauer quelli accompa-gnamenti perfetti, che ricerca ogni perfetta compositione. La onde senz'alcun dubbio
potremo comprendere, che in tal Genere non si potrà comporre perfettamente alcuna
cantilena; com'alcuni s'hanno sognato; oltra che ritrouaremo etiandio alcune modula-tioni molto strane, i cui Interualli saranno molto lontani dalle forme, che sono contenu-te nel Numero sonoro. Ma lasciamo questo; percioche credo che sia manifesto à tutti
quelli, c'hanno intelligenza dell'Arte; & passiamo all'Enharmonico, che noi vedremo
quanto poco sapienti siano stati quelli, che hanno detto, che si può comporre in questo
Genere qual si voglia cantilena, non si partendo dalle sue chorde propie & naturali, sen-z'hauer'aiuto alcuno dalle chorde particolari de gli altri Generi; percioche riducendo il
mostrato Tenore nelle chorde Enharmoniche nella maniera che si uedono; se non si vorrà
passar fuori delle chorde mostrate in questo Terzo ordine; ritrouaremo molte figure, che
non si potranno accompagnare in modo, che dapoi accompagnate s'odi l'Harmonia perfetta; page 365 come ricercano le buone, sonore & perfette compositioni; anzi ritrouaremo molte chorde,
che non potranno hauer quelle Consonanze, che si desiderano; & se pur l'haueranno in
alcuni luogni, sarà necessario, che le parti cantino in tal maniera, che rendino ingrato &
insoaue suono all'orecchie de gli ascoltanti; come l'esperienza sempre ce lo farà vedere.
Potiamo adunque concludere, ch'è impossibile di potere, vsar semplicemente, & da per
sè questi due Generi ultimi, di maniera che vi sia l'Harmonia perfetta, senza l'uso delle
chorde particolari d'alcun'altro Genere.
come ricercano le buone, sonore & perfette compositioni; anzi ritrouaremo molte chorde,
che non potranno hauer quelle Consonanze, che si desiderano; & se pur l'haueranno in
alcuni luogni, sarà necessario, che le parti cantino in tal maniera, che rendino ingrato &
insoaue suono all'orecchie de gli ascoltanti; come l'esperienza sempre ce lo farà vedere.
Potiamo adunque concludere, ch'è impossibile di potere, vsar semplicemente, & da per
sè questi due Generi ultimi, di maniera che vi sia l'Harmonia perfetta, senza l'uso delle
chorde particolari d'alcun'altro Genere.
Che la Musica si può vsare in due maniere; & che le Cantilene, che compongono alcuni de i Moderni, non sono d'alcuno de i due nominati Generi.Cap. LXXIIII.
Che 'l Diatonico può procedere nelle sue modulationi per gli Interualli di Terza maggiore, & di minore; & che ciò non faccia variatione alcuna di Genere.Cap. LXXV.
Che doue non si ode nelle Compositioni alcuna varietà d'Harmonia, iui non può esser varietà alcuna di Genere.Cap. LXXVI.
Dell'vtile ch'apportano i predetti due Generi; & in qual maniera si possino vsare, che faccino buoni effetti.Cap. LXXVII.
CitharoedusEt non si marauiglia alcuno, ch'io habbia detto, che s'vsino le Chorde de i Generi, & si proceda secondo i modi mostrati di sopra; imperoche vsiamo veramente le Chorde; ma non essi Generi, cioè, vsiamo le Parti, ma non il Tutto; essendo che (come più oltra vederemo) l'uso intiero del Genere non può far buon'efferto, ma si bene l'vso delle Par-ti; cioè, delle Chorde segnate con questi segni accidentali
Ridetur, chorda qui semper oberrat eadem.
 . b. &
. b. &  . & anche con que-sto [[mus.hsharp]]. vsandole nel modo, che di sopra ho mostrato. Et s'alle uolte ritrouaremo al-cuna cantilena libera al tutto da queste cifere, potremo dir (com'è uero) che proce-da per le Chorde diatoniche solamente; ma quando ne ritrouaremo alcuna, ch'hab-bia in se simili caratteri b &
. & anche con que-sto [[mus.hsharp]]. vsandole nel modo, che di sopra ho mostrato. Et s'alle uolte ritrouaremo al-cuna cantilena libera al tutto da queste cifere, potremo dir (com'è uero) che proce-da per le Chorde diatoniche solamente; ma quando ne ritrouaremo alcuna, ch'hab-bia in se simili caratteri b &  . allora diremo, che procede per le chorde Chromati-che, mescolate con le Diatoniche. Et se ne ritrouaremo alcuna, la quale hauesse al-cuna chorda, che non si ritrouasse connumerata tra le Diatoniche, ne tra le Chromati-che, la potremo nominar'Enharmonica; pur che tal chorda si possa segnare con questo
segno [[mus.hsharp]]; & possa diuidere il Semituono maggiore in due Parti; imperoche tal chorda
verrà ad essere vna di quelle, che si ritrouano nel Terzo ordine mostrato di sopra; & po-tremo dire, che tal Cantilena proceda per le chorde di ciascun de i tre nominati
Generi. Ma si debbe auertire, che tal mistione si può fare in più maniere, secondo 'l
voler de i Compositori, & de i Sonatori, trasportando i Modi più nel graue, ouer nell'a-cuto fuori delle lor chorde naturali, contenuti nelle chorde del Genere Diatonico; & la compositione (come dicono impropriamente) si canta per Musica finta. La Prima delle qua-li è (lasciando da parte quelli, che non sono cosi in vso) quando le cantilene procedono
per le chorde segnate col b. rotondo dal loro principio; trasportate verso 'l graue per vn page 370Tuono; come è il canto, Verbum iniquum & dolosum; di Morale Spagnolo à cinque; & il bel-lissimo & arteficioso Aspice Domine; d'Adriano à sei uoci. La Seconda maniera è quella,
nella quale si procede per le chorde segnate dal principio della cantilena col segno
. allora diremo, che procede per le chorde Chromati-che, mescolate con le Diatoniche. Et se ne ritrouaremo alcuna, la quale hauesse al-cuna chorda, che non si ritrouasse connumerata tra le Diatoniche, ne tra le Chromati-che, la potremo nominar'Enharmonica; pur che tal chorda si possa segnare con questo
segno [[mus.hsharp]]; & possa diuidere il Semituono maggiore in due Parti; imperoche tal chorda
verrà ad essere vna di quelle, che si ritrouano nel Terzo ordine mostrato di sopra; & po-tremo dire, che tal Cantilena proceda per le chorde di ciascun de i tre nominati
Generi. Ma si debbe auertire, che tal mistione si può fare in più maniere, secondo 'l
voler de i Compositori, & de i Sonatori, trasportando i Modi più nel graue, ouer nell'a-cuto fuori delle lor chorde naturali, contenuti nelle chorde del Genere Diatonico; & la compositione (come dicono impropriamente) si canta per Musica finta. La Prima delle qua-li è (lasciando da parte quelli, che non sono cosi in vso) quando le cantilene procedono
per le chorde segnate col b. rotondo dal loro principio; trasportate verso 'l graue per vn page 370Tuono; come è il canto, Verbum iniquum & dolosum; di Morale Spagnolo à cinque; & il bel-lissimo & arteficioso Aspice Domine; d'Adriano à sei uoci. La Seconda maniera è quella,
nella quale si procede per le chorde segnate dal principio della cantilena col segno  . &
si trasporta il Modo per un Tuono uerso l'acuto. Et nell'vna & l'altra sorte di queste can-tilene alle uolte si tocca le chorde Enharmoniche, per poter'hauer le consonanze Imper-fette maggiori & le minori secondo 'l proposito; à benche si tocchino di raro; di modo
che per tal maniera venimo ad usare i due Generi detti; che fanno mirabilissimi effet-ti. Non dico già (come anc'hò detto) che usiamo tutto 'l Genere; ma si bene alcuna parte
del Genere; cioè, alcune chorde; accommodandole al Genere Diatonico, & proceden-do secondo la sua natura per Tuoni & Semituoni maggiori; com'a ciascuno è manifesto.
. &
si trasporta il Modo per un Tuono uerso l'acuto. Et nell'vna & l'altra sorte di queste can-tilene alle uolte si tocca le chorde Enharmoniche, per poter'hauer le consonanze Imper-fette maggiori & le minori secondo 'l proposito; à benche si tocchino di raro; di modo
che per tal maniera venimo ad usare i due Generi detti; che fanno mirabilissimi effet-ti. Non dico già (come anc'hò detto) che usiamo tutto 'l Genere; ma si bene alcuna parte
del Genere; cioè, alcune chorde; accommodandole al Genere Diatonico, & proceden-do secondo la sua natura per Tuoni & Semituoni maggiori; com'a ciascuno è manifesto.
Per qual cagione le Compositioni, che compongono alcuni Moderni per Chromatiche, facciano tristi effetti.Cap. LXXVIII.
Delle cose che concorreuano nella compositione de i Generi.Cap. LXXIX.
Vt gratas inter mensas Symphonia discors,Si ritroua etiandio vn'altra sorte d'Istrumento lungo intorno vn braccio, il cui nome si chiama in Vinegia Altobasso, & è quadrato & uacuo; sopra 'l quale sono tese alquante chorde accordate tra loro per una delle nominate consonanze, & s'vsa in questa manie-ra; che mentre 'l Sonatore di questo Istrumento sott'un certo numero, ò tempo percuote con una mano le sue chorde con vna bachetta, con l'altra sona un Flauto, & fà vdir'vn'a-ria di cantilena, fatto à suo modo. Et non solamente si trouano cotali Istrumenti da chorde; ma etiandio se ne troua tra quelli da fiato vno ch'in Thoscana si chiama Corna-musa; nel quale già si soleua vdire, due ò tre suoni continui accordati insieme consonan-ti, che nasceuano da due, ò tre Pifferi graui, accordati al sudetto modo; ancora ch'al pre-sente se ne odi solamente uno, & dapoi si ode vn'aria di cantilena, che si fà da un Piffero acuto; che se ben non accorda col concento de tali Pifferi in ogni parte, almeno s'ac-corda nel fine & in alcune cadenze; come si fà etiandio in ciascuno de i nominati Istru-menti; al suono de iquali cantano i Rustici le lor Canzoni; simile à quella ch'io hò po-sto nel Cap. 2. del Lib. 8. De i Sopplimenti. L'uso di quest'Istrumento & l'istrumento an-cora è descritto da Battista Mantoano; ilquale parlando d'un suo Tonio sonatore di co-tale Istrumento, nella sua Bucolica dice;
Et cum multifori Tonius cui tibia buxo.Quest'istesso si ritroua etiandio nelle Trombe, che s'usano ne gli Esserciti & nelle Ar-mate di mare; percioche mentre molte di loro sonano con un suono continuo, fuora di quelle se ne ode una, che chiamano Chiareto; che fà udire nell'acuto un aria di Can-zone; nel modo di quella ch'io hò nominato poco fà, che rende mirabile effetto ne gli au-ditori; oltra che dà segno all'Essercito di combattere, ò di dar'all'arme, come dicono; & finalmente il raccoglierlo in uno. La onde mi penso, che quei Pifferi, che gli Antichi chiamauano Destri & Sinistri, iquali usauano (com'altre uolte hò detto2. Par. c. 4.) nelle Comedie, fus-sero accordati in tal maniera. Gli Organi Antichi etiandio à tal maniera s'accostauano; percioche non erano fatti, come moderni; & di ciò me n'hà fatto fede il rarissimo Fabri-catore de simili Istrumenti Maestro Vincenzo Colombi da Casal Sanuas; ilquale ritro-uandosi già molt'anni nel Piemonte appresso Turino, ne ritrouò un molto antico, ch'era senza canne, & tutto marcio; & hauea un Tastame di tal maniera, che dalla parte sinistra; cioè, nel graue, hauea i Tasti tanto larghi, che per man grande che fusse stata, apena pote-ua arriuare il Quinto tasto; & cotale Tastame, tanto più che si andaua uerso la banda de-stra; cioè, nell'acuto, tanto più si faceua minore. Vn Tastame quasi simile anco taccato al Somiero, mi trouo hauer nelle mani; che mi diede M. Vincenzo Colonna nella sudetta Arte à niuno inferiore de nostri tempi; ritrouato in un'Organo antichissimo; i fori del qual Somiero, & dalla lontananza d'uno d'all'altro si comprende, che le canne dell'Organo, di cui era, & dal Tastame, erano d'una istessa grossezza; onde nella lunghezza di necessità, doueano proportionatamente esser differenti; la cui forma si può vedere nel Cap. 3. del suddetto lib. De i Sopplementi & fù d'una Chiesa di Grado. Et (per quel che l'uno & l'altro uidero) tengono per fermo, che si doueano anco accordare in altra maniera di quel, che s'accorda-page 375no i nostri moderni. Si ritrouano etiandio à i nostri tempi molti altri Istrumenti, si da chor-de, come da fiato, che si sonano in tal modo; i quali (per non esser lungo) lasciò de nomina-re. Erano adunque composti i Generi d'Harmonia, di Numero, & d'Oratione: ne intrauano nelle Compositioni loro tutte le sorti de Versi, ò piedi; ma questo, ò quello; cioè, un terminato Numero; & per tal maniera i Musici Antichi essercitauano la Musica ne i lo-ro Generi; ne ciò era à loro difficile, ne anco impossibile; perche poteuano, vsandola in cotal modo, far vdire quale Interuallo voleuano nelle lor canzoni; che non poteua ge-nerar fastidio di maniera, che non si potesse tollerare; conciosia che non vsauano i Con-trapunti, che usiamo nelle nostre Compositioni; anzi vsauano vn semplice modo d'Har-monia, come si è potuto vedere.
Tandem post epulas & pocula multicolorem
Ventriculum sumpsit, buccasque inflare rubentes
Incipiens, oculos aperit, cilijsque leuatis
Multotiesque altis flatu à pulmonibus hausto
Vtrem implet, cubito vocem dat Tibia presso.
Nunc huc, nunc illuc digito saliente vocauit
Pinguibus à mensis iuuenes ad compita cantu,
Saltidico, dulcique diem certamine clausit.
Opinioni de i Chromatisti ributtate.Cap. LXXX.
LA QVARTA ET VLTIMA PARTE DELLE ISTITVTIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA:
Quel che sia Modo ò Tuono; & delle sue specie.Cap. I.
In ciascuna cosa è Modo, ò Misura.page 378il che dice anco Horatio dopo lui.Ser. lib. 1. Saty. 1.
Est modus in rebus, sunt certi denique fines:Imperoche tal mediocrità, ò moderatione non è altro, che una certa maniera, ouer ordine terminato & fermo nel procedere, per il quale la cosa si conserua nel suo essere, per uirtù della proportione, ch'in essa si ritroua; che non solo diletta; ma etiandio mol-to giouamento apporta. De qui uiene, che se per caso, ouer'à bello studio tal'ordine da essa si allontana, non si può dire, quant'offendi; & quanto il sentimento abhorrisca. Hauendo adunque i Musici & i Poeti Antichi considerato tal cosa; perche gli uni & gl'altri erano una cosa istessa (come hò detto altroueIn Proe-mio et c. 6. Secun. par.) chiamarono le loro compositioni Modi; nelle quali sotto uarie materie per uia del Parlare accompagnate l'una all'altra con proportione esprimeuano diuersi Numeri, ò Metri, & diuerse Harmonie. Onde nac-que, che posero tre Generi de Modi, non hauendo consideratione al Suono, ouer all' Harmonia che nasceua, ma solamente all'altre parti aggiunte insieme; l'uno de i quali chiamarono Dithyrambico, l'altro Tragico, & il Terzo Nomico; de i quali le lor specie furono molte; come Epithalamij, Encomij, Hinni, Peani, & altri simili; come si è dichiarato ne i Sopplimenti.Cap. 2 del 7. lib. & nel Cap. 1. del lib. 8. Considerando dopoi l'Harmonie da per sè, che usciuano da tali congiungimenti, perche riteneuano in loro una certa, propria, & terminata forma, le nominarono simigliantemente Modi; aggiungendoli Dorio; ò Frigio; ouer'altro no-me secondo 'l nome de i Popoli, che furono Inuentori di quell'Harmonia; ouer da quel-li, che più si dilettauano di una specie, che d'un'altra; imperoche l'Harmonia Do-ria fù denominata da i Doriensi, che furono i suoi inuentori; la Frigia da i popoli, che habitauano la Frigia; & la Lidia da quelli di Lidia, & cosi l'altre per ordine. E' ben uero, c'hauendo ciascuna di esse in sè alcuna cosa propria nel suo canto, & essendo ac-compagnata con diuersi Numeri, chiamarono alcune di esse graui & seuere, alcune baccanti & furiose, alcune honeste & religiose, & alcun'altre nominarono lasciue & bellicose. Onde per questo rispetto hebbero grand'auertimento nell'accompagnar co-tali Harmonie à i Numeri, & questi insieme con proposito à materie conuenienti, lequali esprimeuano nell'Oratione, ò Parlare, secondo la lor natura. Il perche hauendo con-sideratione à tutte queste cose, nominarono le lor Compositioni secondo la natura del composto; come sarebbe dire, Modi flebili, i quali sono le Elegie; imperoche conten-gono materie meste & flebili; come si può ueder espressamente in quelli due uolumi;De Tristi-bus: & De Ponto. ol-tra gli altri quasi infiniti, che sono d'altri autori; iquali scrisse Ouidio, dopo che fù man- dato in essilio in Ponto da Augusto; & da quell'anco, che scriue nella Epistola di Saffo à Faone; uolendo mostrar, che le cose amatorie sono materie flebili, & che conuengo-no alla Elegia, dicendo.
Quos vltra citraque nequit consistere rectum.
Forsitan & quare mea sint alterna requirisFece anche Horatio mentione de questi Modi, dicendo;1. Carmi. ode. 9.
Carmina, cùm lyricis sim magis apta modis:
Flendus amor meus est. Elegëia flebile carmen
Non facit ad lacrymas barbitos vlla meos.
Tu semper vrges flebilibus modisEt anco Boetio nel lib. 3. della Consolatione Filosofica;Metro 12.
Mysten ademptum.
Quondam funera coniugisCome li commemorò etiandio Cicerone nelle Tuscolane,Tus. lib. 1. quando (facendo insieme mentione de gli humili & depressi) disse;
Vates threicius gemens,
Postquàm flebilibus modis,
Syluas currere, mobiles
Amnes stare coegerat;
Hac cum pressis & flebilibus modis, qui totis thea-page 379tris moestitiam inferant, concinuntur.Et in un'altro luogo, facendo mentioni de i tardi;De Orat. lib. 1.
Solet idem Roscius dicere, se quo plus aetatis sibi accederet, eo tardiores tibicinis modos, & can-tus remissiores esse facturum.Altre nominarono Modi lamenteuoli; come si può uedere appresso Apuleio, quando dice;
Et sonus tibiae Zigiae mutatur in quaerulum Lydij modum.Alcune poi chiamarono Modi dolci; come ne mostra l'istesso Horatio in un'altro luo-go, quando dice;Car. lib. 3. ode. 9.
Me nunc Tressa Chlöe regit,Et Seneca anco:In agamem.
Dulces docta modos, &
Citharae sciens.
Sacrifica dulces tibia effundat modos.Nominarono etiandio alcun'altri Modi mesti; come si può uedere dall'autorità di Boetio;
Carmina qui quondam studio florente peregi.1. De Consi. met. 1.Et alcune Modi impudici, i quali commemora Quintiliano, dicendo:Institu. o-rat. lib. 1. cap. 10.
Flebilis heu moestos cogor inire modos:
Apertius ta-men profitendum puto, non hanc à me praecipi, quae nunc in scenis effoeminata, & impudicis mo-dis fracta.Altre chiamarono Modi rudi, ò grossi; ilche dimostra Ouidio;1. De Ar-te amandi.
Dumque, rudem praebente modum tibicine Tusco,Et altre Modi discordanti; & de questi ne fa mentione Statio.Sylua. lib. 5. Epicedii in filium.
Lydius aequatam ter pede pulsat humum:
Discordesque modos, & singultantia verbaVltimamente (lasciandone molt'altri per breuità) chiamarono in uniuersale alcune compositioni Modi lirici; come dall'autorità d'Ouidio commemorata di sopra si può comprendere. Et le loro materie non si esprimeuano con la Voce solamente; ma se le ac-compagnaua l'Harmonia, che nasceua d'alcuno Istrumento, fusse stato poi Cetera, ò Lira oueramente Piffero, ò di qualunque altra sorte. Si trouaua nondimeno gran differenza tra questi Modi; essendo che i popoli di questa prouincia usauano una maniera de Versi & un Istrumento, & quelli di quella ne usauano un'altro & un'altra maniera de Versi. Et non erano differenti solamente in questi, ma nelle Harmonie ancora; imperoche una sorte d'Harmonia usaua un popolo, & un'altro un'altra; di maniera ch'erano anco differenti ne i Numeri; i quali si ritrouauano ne i Versi. De qui nacque dopoi, che i Mo-di erano denominati da quei popoli (come di sopra hò detto) che più si dilettauano di quella maniera, ouer erano stati gl'Inuentori. La onde da questo si può comprendere, che se un popolo; come quello di Frigia, udiua alcuna maniera forestiera, diceua, quel-lo essere Modo di quella proui n ia [sic: prouincia], oue più si usaua, oueramente ou'era stato ritrouato; di maniera, che chiamauano il Modo Eolio da i popoli della Eolia suoi inuentori, ch'era contenuto in un certo Hinno, composto nel Modo lirico sott'alcuni Numeri; concio-siache questi popoli si dilettarono molto della Lira, ò Cetera; che secondo l'opinione d'alcuni (la qual reputo falsa) à quei tempi erano una cosa istessa; al suono della quale cantauano il sudetto Hinno; ma di questo si legga il Cap. 16. del lib. 1. De i Sopplimenti, che si potrà conoscere il uero di cotal cosa. Tal'Istrumento usauano similmente i Doriesi, ancora che forse cantassero altra maniera de Versi, & usassero l'Harmonia molto differen-te; del che ne fà fede Pindaro,Olymp. o-de. 1. quando nomina simili Istrumento Δορίαμ φόρμιγγα; cioè, Dorica cetera; & Horatio,In Epodo. ode. 7.
Molior.
Sonantem mistum tibijs carmen lyra,Onde si può uedere dalla parola Barbarum, la quale s'intende per il modo Fri-gio, ch'anco i popoli della Frigia usassero i Pifferi. Et cotal Modo ueramente sole-uano sonare con simili Istrumenti; come potrei mostrar con molti essempi, i quali lascio per breuità; bastando solamente uno di Virgilio, il quale dice in tal ma-niera. page 380Aeneid. 9.
Hac Dorium, illis Barbarum.
O vere phrigiae (neque enim phryges) ite per alta.Et uno d'Ouidio.Fast. lib. 4.
Dyndima, ubi assuetis biforem dat tibia cantum:
Tibia dat phrygios, ut dedit ante modos;Da i quali si può comprendere, esser uero quel, c'hò detto. Con questo Istrumento similmente quei popoli, c'habitauano la Lidia, faceuano le lor Harmonie; & di ciò n'è testimonio Horatio dicendo;Car. lib. 4. ode. 15.
Virtute functos more patrum ducesEt Pindaro,Olimpi. ode. 5. ilquale, auanti di lui, supplicando Gioue per Psaumido Camarineo vin-citore ne i giuochi Olimpici, dice;
Lydis remisto carmine tibijs,
Troiamque, & Anchisen, & alma
Progeniem Veneris canemus;
Io uengo à te supplicheuole ò Gioue sonando Λυδίοις ἀυλο͂ις: con Pifferi Lidij.Non manca per dimostrar questo etiandio il testimonio d'Apuleio, con l'Autorità addutta di sopra, & de molti altri; ma questi bastino. Da questo adun-que potiamo comprendere, che i Modi anticamente consisteuano nell'Harmonie & ne i Numeri espressi da una sorte d'Istrumento; & che la diuersità loro era posta nella uaria-tione dell'Harmonie, nella diuersità de i Numeri, & nella maniera dell'esprimere; cioè, dell'Istrumento. Et se bene alcuni popoli conueniuano con alcun'altri nelle Har-monie, ouer ne gli Istrumenti; erano poi differenti ne i Numeri; & se in questi erano concordi, discordauano poi nelle Harmonie & ne gli Istrumenti; di maniera che se in una cosa, ouer in due erano conformi, variauano poi nel resto. Questo istesso uedia-mo etiandio hoggidi in diuerse nationi; imperoche l'Italiano usa 'l Numero, ò Verso de piedi, ò sillabe commune col Francese & col Spagnolo; com'è quello d'Vndici sillabe; nondimeno quando s'odono cantar l'uno & l'altro, si scorge un'Harmonia differente, & altra maniera nel procedere; conciosia che altramente canta l'Italiano, di quello che fà il Francese; & in altra maniera canta lo Spagnuolo, di quel che fa 'l Tedesco; lascian-do di dire delle nationi barbare & infideli; com'è manifesto. Vsa l'Italiano & anco il Francese grandemente 'l Leuto, & lo Spagnolo usa il Ceterone; ancora che questo uaria poco da quello, & altri popoli usano il Piffero. Ne i Numeri, ò Versi, quanta differenza sia tra i popoli, & quanto un popolo habbia differente maniera dell'altro, si può conosce-re; incominciando da questo capo; che se ben fuori dell'Italia in alcuna parte non si usa 'l Verso legato, ò sciolto d'Vndeci sillabe, fatto alla simiglianza dell'Endecasillabo latino; tuttauia nella Italia, nella Franza, & nella Spagna molto si usa. Et quel, che in Italia si chiama Rima, credo che sia detto da questa parola greca Ρυθμὸς, che significa (com'altroue hò detto) Numero, ò Consonanza;2. Partis cap. 8. percioche da quelle corrisponden-ze & legature, che si trouano nel fine de i Versi, le quali chiamano Cadenze, nasce la Consonanza, ouer Harmonia, che si troua in essi.Vedasi il cap. 13. del lib. 8. De i Sopplim. Vsano gli Italiani cotali Cadenze, non tanto in quella maniera de Versi, che si trouano nell'Ottaue rime, ò Stanze, ne i Sonetti, ne i Capitoli, & altri simili, che dimandano Intieri; quanto nelle Canzoni ancora & Madrigali; oue si pone molte sorti de Versi; come sono quelli di Sette sillabe & altri simili, che chiamano Versi rotti; com'è manifesto; imperoche nell'Italia madre de i buoni & rari intelletti s'usa uarie maniere di comporre; come si può comprendere dal-le nominate Ottaue rime, ò Stanze; che dir le vogliamo, da i Terzetti, dalle Sestine, da i Sonetti, & da i Capitoli, ne i quali s'adoperano una sola maniera de Versi, che so-no gli Intieri & nelle Canzoni & ne i Madrigali con altri simili, ne i quali si pongono uarie sorti de Numeri ad imitatione dell'Ode d'Oratio; à benche i Numeri Horatiani siano senza le commemorate Cadenze, & gli Italiani siano per esse Cadenze al det-to modo legati; come nelle dotte & leggiadre Canzoni del Petrarca & de molt'altri eccellentissimi huomini si può uedere; delle quali tengo per certo, che i dotti spiriti Ita-liani siano stati Inuentori; conciosiache non mi ricordo hauer mai trouato appresso d'alcun'altro Poeta, ne Greco, ne Latino un simil modo di comporre, con tali Ca-page 381denze; con tutto che 'l Dottissimo Horatio habbia cantato assaissime Ode in molte ma-niere. E' ben uero, ch'altri Poeti latini (ancora che non molto spesso) hanno usato simili Cadenze, ò Corrispondenze nelle mezane sillabe, & nell'ultime d'alcuni lo-ro Versi, i quali chiamano Leonini, ò Canini; come in ciascun de questi hà fat-to il Poeta;
Ad terram misêre, aut ignibus aegra dedére. Aeneid. 2.Ibidem 12. Et Ouidio anche in questo hà osseruato cotal legge.In Epistola Helenae ad Paridem. 8.
Cornua vellatarum obuertimus antennarum.Ibidem 3.
Illum indignanti similem, similemque minanti.Ibidem 8.
Tum caput orantis nequicquàm, & multa precantis.Ibidem 10.
Ora citatorum dextra contorsit equorum:
Vim licet appelles, & culpam nomine veles;& in molt'altri, che non si mettono, per non crescere 'l volume. Onde 'l Petrarca (com' io credo) imitando tal maniera di comporre, le pose in un'altro modo, accordando 'l fine del Verso precedente, col mezo del seguente in cotal guisa:Canz. 22.
Mai non uò più cantar com'io soleua:Et cosi il restante di tal Canzone. Ilche osseruò etiandio nella Canzone, Vergine bella.Canz. 49. Quest'istesso fece il Sanazaro nel principio dell'Arcadia in quella parte, quando parlan-do Ergasto con Seluaggio pastore, dice:
Ch'altri non m'intendeua: onde hebbi scorno.
E puossi in bel soggiorno esser molesto;
Menando un giorno li agni appresso un fiume.& il resto, che segue. Ma quando ben si ritrouasse tra i Greci, ò tra i Latini poeti una tal maniera di comporre, con simili Cadenze, questo poco importarebbe; essendo che tanto si potrebbe gloriare il primo Inuentore d'una tal maniera di comporre Ita-liano, se bene hauesse pigliato l'Inuentione d'alcun poeta Greco, ò Latino; quanto si gloriaua Horatio d'esser stato il primo, che ritrouato hauesse il modo di comporre in Latino i Versi lirici alla guisa de i Greci; ilche si può comprender dalle sue parole; quando dice;Carmi. lib. 3. Ode. 31.
Vidi un bel lume in mezo di quell'onde.
Che con due bionde treccie allor mi strinse,
Et mi dipinse un uolto in mezo 'l cuore.
Dicar, quà violens obstrepit Aufidus,Delche si può etiandio gloriare Claudio Tolomei Sanese d'essere stato il primo, che habbia espresso 'l Verso Heroico & l'Essametro & lo Pentametro nelle Italiane muse; ancora che da pochi, fin'hora, cotal cosa sia stata abbracciata. Vogliono alcuni, che 'l Dottissimo Dante Aliglieri poeta Fiorentino fusse 'l primo inuentore de i Terzetti, & il Boccaccio dell'Ottaua rima; per ilche quando à cotali maniere di comporre si uolesse dare un nome particolare; uolendole denominar dalla ragione, nella quale furono ritrouate; l'una & l'altra maniera si chiamarebbe (come ne inuita Horatio con l'autorità posta di sopra) Modi Italiani; ò uolendole denominar dalla Patria, si chiamarebbono Modi thoscani. Ma se si uolessero denominar da i Proprii inuentori, la prima maniera si nominarebbe (dirò cosi) modo Dantesco, & la seconda maniera modo Boccacciano; come le legge Citaristice & le Tibiali (il che habbiamo ueduto nella Seconda parteCap. 5.) furono denominate parte de i Popoli, & parte da gli Inuentori. Et se ben nell'Italia si troua non solo una maniera de Versi, ma anco più maniere particolari; come hò mo-strato; tuttauia i Greci à i nostri giorni, oltra l'altre loro maniere hanno il Ver-page 382so de Quindeci sillabe; come sono questi, che sono di Constantino Mannasì loro Filosofo.
Et qua pauper aquae Daunus agrestium
Regnator populorum, ex humili potens
Princeps Aeolium carmen ad Italos
Deduxisse modos.
Ο῾ τοῦ θεοῦ παντέλειος, καὶ παντοκτίστωρ λόγος,& uogliono dire; La parola di Dio in tutto è perfetta; & colui, che fabricò tutte le cose del Mondo, da principio fabricò il Cielo senza stelle; de i quali Versi tutto 'l suo Hexameron è pieno; & li cantano sotto un Modo particolare, secondo 'l costume loro; il che non si usa nella Italia. Perilche (lasciando di dir de gli altri Popoli) da questi due potiamo ueder la differenza, che poteua esser de i Numeri, & delle Harmonie ne i Modi de quei popoli, nel tempo che nella Grecia la Musica era in fiore. Percioche come uediamo questi due popoli à nostri tempi hauere una maniera particolare di Verso, & una ma-niera particolare di cantare; il simil douemo creder, che fusse anticamente tra quei popoli. Et ancora che à i nostri giorni alcuni popoli di natione diuersa conuenghino insieme nel Numero, ò ne i Piedi del Verso, & nella maniera della compositione delle lor Canzoni; tuttauia sono differenti intorno la maniera del Cantare. Et non solamente si troua tra diuerse nationi tal differenze; ma anco in un'istessa patria; come si può ueder nell'Ita-lia; percioche in una maniera si cantano le Canzoni, che si chiamano Villotte nella pro-uincia di Venetia, & in un'altra maniera nella Toscana, & nel Reame di Napoli; com' era anco appresso gli Antichi; percioche se bene i Popoli della Doria, & quelli dell'Eo-lia vsauano un'istessa qualità ò sorte di Verso, & un'istesso Istrumento; le Harmonie loro poi erano in qualche parte differenti. De qui si può comprendere adunque la diuersità de i nomi ne i Modi; che si come in alcun Modo si trouaua il Numero, l'Istrumento, & l'Harmonia differente da un'altro Modo; cosi anco nacque la diuersità de i nomi. La onde credo, che 'l Modo Dorio fusse differente dall'Eolio, come il Frigio era diuerso dal Lidio; & ciò non solamente nell'Harmonie; ma etiandio ne i Numeri; come si può comprendere da i uarii effetti, che nasceuano dall'uno & dall'altro, i quali uederemo al suo luogo. Però adunque quando leggiamo di Filosseno 8. Politic. cap. 7., hauendo ei tentato di fare il Poema Dithyrambico nel modo Dorico, che non lo puote mai condurre al desiderato fine; percioche dalla natura del Modo fu tirato di nuouo nell'Harmonia Fr igia, conue-neuole à tal Poema; non dobbiamo prendere ammiratione; essendo che i suoi Piedi, & il suo Numero è più ueloce d'ogn'altro Poema; & per il contrario, i Numeri del modo Dorico più tardi & più rimessi. Perilche essend'altri Numeri nella Dorica, & altri nella Frigia Harmonia (come si è detto) era impossibile, che Filosseno potesse far cosa alcu-na, che fusse buona; come anco sarebbe impossibile, quando sotto i Numeri d'un Verso Saffico, che si compone del Trocheo, dello Spondeo, del Dattilo, & nel fine di due Trochei, ouer d'un Trocheo & uno Spondeo; come sono questi due Horatiani.1. Carm. Ode. 10. & 38.
Τὸν ὀυρανὸν τὸν ἄναστρον παρήγαγεν ἀρχῆθεν
Mercuri facunde nepos Atlantis:&
Persicos odi puer apparatus;si uolesse cantare, ò tirare in uerso Heroico, che si compone di Sei Piedi diuersamen-te con Dattili & Spondei; come si può comprendere in ciascun de i due Virgilia-ni sequenti: Georgic. 3.
Sed fugit interea, fugit irreparabile tempus.& Aeneid. 6.
Parcere subiectis, & debellare superbos.Tutto questo discorso hò uoluto fare, non ad altro fine; se non accioche più facilmen-te si potesse comprendere, quel ch'era il Modo nella Musica. Onde potiamo ueramen-te dire, che 'l Modo anticamente era una certa & determinata forma di Melodia, fatta con ragione & con arteficio, contenuta sotto un determinato & proportionato ordine de Numeri & d'Harmonia, accommodati alla materia contenuta nell'Oratione. Et benche i Musici moderni non considerino nelle lor cantilene se non un certo ordine di cantare & una certa specie d'Harmonia; lasciando da parte il considerare il Numero, ò Metro determinato; percioche dicono, che questo appartiene à i Poeti; massimamente page 383essendo la Musica à i nostri tempi separata dalla Poesia; tuttauia considerano cotal ordi-ne in quanto è contenuto tra una delle Sette già mostrate specie della Diapason harmo-nicamente, ouero arithmeticamente mediata; come più oltra vederemo; tra le quali si troua una certa maniera di cantare in una, che in un'altra è uariata. Et tal'ordine di cantare con diuersa maniera, ouero Aria dimandano Modo, & alcuni lo chiamano Tropo, & altri Tuono. Nè di ciò dobbiamo render marauiglia, poi che Τρόπος è Parola greca, che significa Modo, ò Ragione, dalla quale uogliono, che siano cosi detti. Et se fusser'anco nominati da Τροπὴ, che uuol dire, Conuersione, ò Mutatione, staria medesimamente bene; essendo che l'uno si conuerte & muta nell'altro; come uederemo; & i Grammatici alle uolte chiamano Tropi quelle conuersioni, che si fanno d'una parola ò uoce, dal proprio significato, in un'altro. Lo nominano etiandio Tuono, & ciò non è maldetto; percioche per il Tuono (come mostra Euclide nel suo Introdottorio) si può intendere Quattro cose; Primieramente, quel, che i Greci chiamano φθόγγος, che signi-fica ogni Suono, ò Voce inarticolata, la quale non si estende ne uerso il graue, ne uer-so l'acuto; secondariamente, quelli due Interualli mostrati nel Cap. 18. della Terza par-te; dopoi una forte & sonora Voce; come quando diciamo, Francesco hà un buon tuo-no, sonoro, & gagliardo; cioè, una buona; sonora, & gagliarda Voce. Vltimamente s'intende per quello c'habbiamo nominato di sopra; come quando si dice; il Tuono Do-rio, il Frigio, & gli altri; cioè, il Modo Dorio, il Frigio, & li seguenti per ordine. Et perche questo nome Tuono si estende in più cose, come uedemmo; però per schiuar la Equiuocatione, più c'hò potuto, hò uoluto nominarli Modi, & non Tuoni. Volendo adunque dichiarar quello, che sia Modo, diremo con Boetio,Musicae lib. 4. c. 4. il quale parla de i Modi ò Tuoni antichi; che Modo è una certa Costitutione in tutti gli ordini de uoci, differente per il graue & per l'acuto; & tale Costitutione è come un corpo pieno di modulatione, la quale hà l'essere della congiuntione delle Consonanze; come è la Diapason, la Dia-pasondiapente, ouer la Disdiapason. Di maniera che da Proslambanomenos à Mese uiene ad essere una Costitutione, connumerando le Chorde, ò uoci mezane; cosi ancora da Mese à Netehyperboleon, intendendoui sempre i suoni mezani. Ma perche queste Co-stitutioni sono ueramente le uarie specie della Diapason, che si trouano dall'una lettera all'altra; come nel Cap. 12. della Terza parte habbiamo ueduto; numerando le lor Chorde mezane; però diremo; come dicemmo etiandio nell'Vndecima definitione del Quinto delle Dimostrationi, & anco habbiamo detto di sopra; che 'l Modo secondo i Moderni è una certa forma, ò qualità d'Harmonia, che si troua in ciascuna delle nominate Sette specie della Diapason, le quali tramezate harmonicamente, secondo che si con-siderano hora, ne danno Sei Modi principali & autentichi; da i quali poi nascono i suoi collaterali per la diuisione arithmetica, che si chiamano (come uederemo) Plagali, ouer Placali.
Che i Modi sono stati nominati da molti diuersamente, & per qual cagione.Cap. II.
Del Nome & del Numero de i Modi.Cap. III.
De gli Inuentori De i Modi.Cap. IIII.
Antiphonas dedit ad Psalmos Ignatius aptas.Tutto questo è stato detto intorno al Canto ecclesiastico; ancora che di esso non si possa ritrouare il Primo inuentore; se bene alcuni l'attribuiscano al Dottore di S. Chiesa Gregorio primo sudetto; ma inquanto all'Inuentione de quei Modi, che sono nel Can-to figurato, & l'Inuentione di comporre nella maniera, che faciamo al presente; non è dubio, che di ciò non ne potiamo hauer'alcuna certezza; ancora che (per quello, che si può uedere) non è molto tempo, rispetto al Canto ecclesiastico; che un tal modo di comporre, fù ritrouato. Et benche intorno gli Inuentori de i Modi antichi nasca qua-si l[unclear: ']istessa difficultà; tuttauia potiamo hauer'alcuna cognitione de gli Inuentori de molti de loro; imperoche PlinioNatur. his. lib. 7. cap. 56. vuole, che Anfione figliuolo di Gioue, ò come alcuni vo-gliono di Mercurio & di Antipa, fusse inuentor dell'Harmonia Lydia, con la quale (se-condo che riferisce Plutarcho di Aristosseno nel Libro della Musica) Olimpo fù quello, che sonò col Piffero i funerali nella sepoltura del Serpente Pithone; la qual Har-monia s'adoperò anco nella pompa funebre della vergine Psiche; come di sopra fù com-memorato. E' ben uero, che Clemente AlessandrinoStromat. lib. 1. attribuisce l'Inuentione dell'Har-monie Lydie ad Olimpo di Misia, ilquale fu forse il disopra nominato; & altri uoglio-no, che la melodia Lydia fusse ritrouata non ad altro effetto, che per usarla ad un tale ufficio; come è detto di sopra. Dicono ancora, che tal Melodia usauano i Rustici ne i triuij & ne i quadriuij in honore di Diana, ad imitatione di Cerere, che con grande gridi cer-caua la rapita Proserpina; come accenna il Poeta, quando dice; In Palae-mone.
Monte prout quodam desuper audierat.
Non tu in triuijs indocte solebasOue si uede, che non faceuano vn tale vfficio con molti Istrumenti; ma con un Piffe-ro solo, del quale (come vuole ApuleioFloridorum lib. 1.) Iagne Frigio, che fù padre di quel Marsia, che fù punito grauemente da Apollo della sua arroganza, fù l'inuentore. Questo istesso fa-ceuano etiandio col Zuffolo, del quale (come vogliono alcuni, & massimamente Virgi-lio) Pan dio de pastori fù l'inuentore; perche, com'egli dice. In Alexide.
Stridenti miserum stipula disperdere carmen?
Pan primus calamos caera coniungere pluresMa le melodie Dorie, secondo l'istesso Clemente; del qual parere fù anche Plinio, furono ritrouate da Thamira di Thracia. Le Frigie, la Mistalydia, & la Mistafrigia (come vuole il detto Clemente) furono ritrouate da Marsia, che fù di Frigia; quan-page 388t[unclear: unq]ue alcuni uogliano, che Saffo Lesbia poetessa antica fusse l'Inuentrice delle Mistely-[unclear: die] & altri attribuiscano tale inuentione à Thersandro; & altri ad un Trombetta chiama-t[unclear: o] Pithoclide; ma Plutarco, pigliando 'l testimonio d'un Lisia, vuole, che Lamprocla d'A-thene fusse l'inuentore de tali Melodie. Alcuni anco vogliono, che Damone Pitagorico fusse inuentor dell'Hypofrigio, & Polimnestre dell'Hypolydio. De gli altri Modi non hò ritrouato gli Inuentori; ma quando l'autorità d'Aristotele posta nel lib. 2. della MetafisicaCapit. 1. ualesse in questo proposito, si potrebbe dire, che Timotheo fusse stato l'Inuentore del re-sto; ancora che Frinide musico perfetto de quei tempi fusse auanti lui; percioche (com ei dice) se non fusse stato Timotheo non haueressimo molte Melopeie, & non molti Modi. Ma inuerità parmi che siano più antiche di Timotheo; come legendo molti autori & es-saminandoli intorno al tempo, si può uedere. Qual di loro fusse il primo ritrouato; questo è non dirò difficilissimo, anzi impossibile da sapere; ancora ch'alcuni uoglino, che 'l Ly-dio fusse 'l primo; alla quale opinione si potressimo accostare, quando l'ordine de i Modi posti da Platone, da Plinio, da Martiano, & da molt'altri, fusse posto, secondo che l'un fù ritrouato prima dell'altro; ma ueramente è debile argomento; percioche potressi modir [sic: potressimo dir] l'istesso di qualunque altro Modo, che fusse posto primo in qualunque altro ordine; come del Frigio, ch'è posto da Luciano primo, & dell'Eolio, che è posto in cotal luogo da Apuleio. Lasciaremo hora di ragionar più di cotali cose, & uerremo à dir della loro Natura; percioche della Proprietà de i Modi moderni vn'altra fiata ne parlaremo.
Instituit.
Della Natura, ò Proprietà de i Modi.Cap. V.
Inter quas curam Clymene narrabat inanemPer tali effetti adunque gli Antichi attribuirono le narrate proprietà al modo Dorico; & ad esso applicauano materie seuere, graui, & piene di sapienza. Et quando da queste si partiuano & passauano à cose piace-uoli, liete, & leggieri, vsauano 'l Modo Frigio; essendo che i suoi Numeri erano più ue-loci de i numeri di qualunque altro Modo, & la sua Harmonia più acuta di quella del Dorio; onde da questo, credo io, che sia uenuto quel Prouerbio, che si dice; Dal Do-rio al Frigio; che si può accommodar, quando da vn ragionamento di cose altissime & graui, si passa ad uno, che contenga cose leggieri, basse, non molto ingegnose, & simi-gliantemente cose liete & festeuoli, & anche non molto honeste. Clemente Alessandri-no,Stromat. lib. 6. seguitando l'opinione d'Aristosseno, vuole; che 'l genere Enharmonico conuenghi grandemente all'Harmonie doriche, come genere ornato & elegante; & alle Frigie il Diatonico, come più uehemente & acuto. Fù già tanto in ueneratione il Dorio, che niun'altro, da lui & il Frigio in fuori, fù approuato, & admesso da i due sapientissimi Filosofi Platone & Aristotele; percioche conosceuano l'utile grande, che apportauano ad una ben'istituita Republica; istimando gli altri di poco utile & di poco ualore. Onde uolsero, che i Fanciuli [sic: Fanciulli] dalla lor tenera età fussero istrutti nella Musica. Voleuano etian-dio gli Antichi, che l[unclear: ']Hypodorio hauesse natura in tutto diuersa da quella del Dorio; im-peroche si come il Dorio disponeua ad una certa costanza uirile, & alla modestia; cosi l'Hypodorio per la grauità de i suoi mouimenti inducesse una certa pigritia & quiete.
Vulcani, Martisque dolos, & dulcia furta.
Attonitusque seces, vt quos Cybeleia materpage 390Aristotele8. Polit. Cap. 5. l'accenna Bacchico; cioè, furioso, & Baccante; & LucianoIn Harmonide. lo chiama furio-so, ò impetuoso; ancora ch'Apuleio1. Flori-dorum. lo nomini Religioso. Questo Modo (come hab-biamo veduto) si sonaua anticamente col Piffero, il quale è Istrumento molto incitati-uo; per ilche (come dicono alcuni) col mezo del suono de i Pifferi i Spartani inuitaua-no i soldati à pigliar l'arme; & (come narra ValerioDictor. & Fact. lib. 2. cap. 1.) costretti dalle seuerissime leggi di Li-curgo, osseruauano di non andar mai con l'essercito à combattere, se prima non erano be-ne inanemiti & riscaldati dal suono de i detti Istrumenti, con la misura del piede Ana-pesto; il qual si compone di tre tempi; due breui, & uno lungo. La onde da i due primi, i quali fanno la battuta più spessa & più ueloce, comprendeuano, d'hauer'assalire l'ini-mico con grand'empito; & dal lungo, d'hauere à fermarsi & resistere animosamente, quando non l'haueano rotto nel primo assalto. Il che faceuano anco i Romani; come narra Tullio;Tuscul. lib. 1. i quali non pur col suono della Tromba; ma col canto accompagnato à co-tal suono, soleuano incitare gli animi de i Soldati à combattere virilmente; & ciò ne mostra anco Virgilio,Aeneid. 6. parlando di Miseno.
Incitat, ad Phrygios uilia membra modos.
Quo non praestantior alter,Et Horatio parlando di Tirteo, dice;De Arte poetica.
Aere ciere viros, Martemque accen dere [sic: accendere] cantu.
Tyrtheusque mares animos in martia bellaImperoche gli Italiani usarono la Tromba, che fù inuentione de i popoli Tirrheni, come vuol Diodoro;Hist. li. 6. & PlinioHisto. na-tu. lib. 7. c. 56. vuole, che l'Inuentore fusse un nominato Piseo, pur Tir-rheno. Di questa inuentione Virgilio ne tocca una Parola, quando dice;Aeneid. 8.
Versibus exacuit.
Tyrrhenusque tubae mugire per aethera clangor.Ma Gioseffo nel Primo libro delle Antichità giudaiche vuole, che l'Inuentore sia sta-to Mosè, & Homero dice, che fù Dirceo, alcun'altri Tirteo, & alcuni Maleto; col suono della quale, ch'era aspro, ueloce, gagliardo, & forte (come si può comprende-re dalle Parole di Ennio poeta antico, in quale esprimendo la natura di questo istru-mento disse;
At Tuba terribili sonitu taratantara dixit.) Proferiuano il modo Frigio. Inuitati i Lacedemoni, ò Spartani adunque al combattere con grande vehementia dal suono del detto Istrumento, erano dalla tardità del suono; cioè, dalla tardità del mouimento, & dalla grauità del Modo inuitati à lasciar di combat-tere. Il grande Alessandro anco col mezo d'un Piffero come narra Suida) fù inuitato da Timotheo à pigliar l'arme, recitando la legge Orthia nel modo Frigio. Similmente vn giouine Taurominitano (come recita Ammonio In predi-cabilibus. & Boethio,Musicae lib. 1. cap. 1. & come molte volte hò commemorato) fù da questo Modo riscaldato. Per il che uoleuano gli Antichi; che le materie, che trattauano di guerra, & fussero minaccieuoli & spauentose, si accommodasse-ro à cotale Modo; & che l'Hypofrigio moderasse & sottrahesse la natura terribile & con-citata del Frigio. Onde dicono alcuni, si come i Spartani, & li Candioti inanemiuano i soldati al Combattere col modo Frigio; cosi li riuocauano dalla pugna con l'Hypofri-gio al suono de i Pifferi. Vogliono anco, che Alessandro fusse riuocato dalla battaglia da Timotheo col mezo di questo Modo, recitato al suono della Cetera; & che 'l gio-uine Taurominitano commemorato col mezo di questo Modo, & col canto dello Spon-deo fusse placato. Vuol CassiodoroVariarum. lib. 1. Boethum., che 'l Frigio habbia natura di eccitare al combatte-re, & d'infiammare gli huomini al furore, & che 'l Lydio sia rimedio contra le fatiche del-l'animo, & similmente contra quelle del corpo. Ma alcuni uogliono, che 'l Lydio sia atto alle cose lamenteuoli & piene di pianto, per partirsi dalla modestia del Dorio, in quanto è più acuto, & dalla seuerità del Frigio. Sotto questo Modo, Olimpo (come nar-ra PlutarcoIn Musi-ca.) al suono del Piffero nella Sepoltura di Pithone cantò gli Epicedij; che sono alcuni versi, che si cantauano auanti 'l Sepolchro d'alcun morto; imperoche antica-mente era usanza di far cantare al suono del Piffero, ò d'altro Istrumento nella morte de page 391i parenti, ò de gli amici più cari; dal qual canto erano indotti à piangere i circostanti la lor morte; & ciò faceuano fare ad una femina vestita in habito lugubre; come anco si osserua al presente in alcune città, massimamente nella Dalmatia, nella morte d'al-cun'Huomo honorato. Tale vsanza commemorò Statio Papinio, dicendo;Theb. lib. 6.
Cum signum luctus cornu graue mugit aduncoOnde si uede, che tali Harmonie erano fatte nel modo Frigio, ouer nel Lydio; co-me dall'autorità d'Apuleio addotta di sopra si può uedere. Alcuni hanno chiamato il Lydio da gli effetti, horribile, tristo & lamenteuole; & LucianoIn Harmonide. lo nomina furioso, ouero impetuoso; è ben uero, che Platone pone tre sorti d'Harmonie Lydie; cioè, Mi-ste, Acute, & Semplici, senza porui alcun'aggiunto. Hanno hauuto opinione alcuni, che l'Hypolydio habbia natura differente & contraria à quella del Lydio; & che conten-ga in se una certa soauità naturale & abondante dolcezza, che riempia gli animi de gli ascoltanti d'allegrezza & di giocondità, mista con soauità, & che sia lontano al tutto dalla lasciuia & da ogni uitio; perciò l'accommodarono à materie mansuete, accostu-mate, graui, & continenti in se cose profunde, speculatiue, & diuine; come sono quel-le, che trattano della gloria di Dio, della felicità eterna; & quelle, che sono atte ad im-petrare la Diuina gratia. Et uolsero similmente, che 'l Mistolydio hauesse natura d'in-citar l'animo, & di rimetterlo. Apuleio dimanda l'Eolio semplice; & Cassiodoro vuole, che habbia possanza di far tranquillo & sereno l'animo oppresso da diuerse passioni; & che dopo scacciate tali passioni, habbia possanza d'indurre il sonno; natura & proprie-tà veramente molto conforme à quella dell'Hypodorio. Onde non è da marauigliarsi, s'Atheneo, adducendo l'autorità d'Eraclide di Ponto, fù di parer, che l'Eolio fusse l'Hypodorio; ò per il contrario. Vogliono alcuni, che all'Eolio si possino accommodar materie allegre, dolci, soaui, & seuere; essendo che (come dicono) hà in se vna grata seuerità mescolata con vna certa allegrezza & soauità oltra modo; & sono di parer, che sia molto atto alle modulationi de i Versi lirici, come Modo aperto & terso. Ma s'è ue-ro quel, che si pensò Eraclide, sarebbe à tutte queste cose contrario molto; percioche hauerebbe diuersa natura; come di sopra hò mostrato. Apuleio chiama lo Iastio, oue-ro Ionico (che tanto vale) vario; & Luciano lo nomina allegro; per essere (secondo 'l parere d'alcuni) molto atto alle danze & à i balli. La onde nacque, che lo dimandaro-no lasciuo; & i popoli Inuentori di tal Modo, che furono gli Atheniesi, popoli della Io-nia, amatori de cose allegre & gioconde; & molto studiosi della eloquenza, chiamaro-no Vani & leggieri. Cassiodoro vuole, che habbia natura d'acuire l'intelletto à quelli, che non sono molto eleuati; & d'indurre vn certo desiderio delle cose celesti in coloro, i quali sono grauati da un certo desiderio terrestre & humano. Queste cose dicono in-torno la natura de i Modi; la onde si scorge vna gran varietà ne i Scrittori, volendo alcuni una cosa, & alcuni vn'altra. Il perche mi penso, che tal varietà poteua nascere dalla uarietà de i costumi d'una Prouincia, ch'essendo dopo molto tempo uariati, va-riassero ancora i Modi; & che una parte de i Scrittori parlasse di quei, che perseueraua-no d'esser nella lor prima & pura semplicità; & l'altra parte parlasse di quelli, che già haueano perso la loro prima natura; come per cagione d'essempio diremo del Dorio, ch'essendo prima honesto, graue, & seuero; per la uariatione de i costumi fusse ua-riato anche lui; & dopoi applicato alle cose della guerra. Et per questo non ci dob-biamo marauigliare; percioche se dalla varietà dell'Harmonie nasce la uariatione de i costumi; com'altroue si è detto; non è inconueniente anco, che dalla variatione de i costumi si uenga alla uarietà dell'Harmonie & de i Modi. Poteua anco nascere dal-la poca intelligenza, ch'haueano i Scrittori di quei tempi intorno à cotal cosa; co-me suole accascare etiandio à i tempi nostri, ch'alcuni si porranno scriuere alcune cose, che non intendono; ma si rimettono al giudicio & alla opinione d'vn altro, page 392il quale alle uolte ne sà men di lui; & cosi molte uolte pigliano una cosa per un'altra, & attribuiscono à tal cosa alcune proprietà, che considerandola per il dritto, è da tal pro-prietà tanto lontana & diuersa, quanto è lontano & diuerso il Cielo dalla Terra. Et mol-te volte vediamo, che pigliano una cosa per un'altra; come si può uedere in quello, che scriue Dion Chrisostomo d'Alessandro Magno ne i Commentarij del Regno,Orat. 1. essempio addutto da molti; oue dice, che fù costretto da Timotheo a pigliar l'arme col mezo del Modo Dorio; tuttauia è solo di questo parere, per quello c'hò potuto comprendere; imperoche il Magno Basilio (com'altre fiate hò detto) & molt'altri auanti lui, uuole, che fusse costretto a fare un simile atto dal Frigio. Ma di questo sia detto à bastanza; impero-che è dibisogno, che si uenghi à ragionare intorno all'Ordine.
Tibia, cui teneros suetum producere manes,
Lege Phrygum mesta.
Dell'Ordine de i Modi.Cap. VI.
 &
&  . che è la
Settima specie porremo il Sesto modo; come più à basso vederemo. Et sono al numero
de Dodici, non solamente appresso i Compositori prattici, ma etiandio appresso gli Ec-clesiastici; ancora che da molti non siano considerati in tanto numero; de i quali intendo
ragionar particolarmente, & mostrare in qual maniera al presente si vsi ciascuno di loro.
. che è la
Settima specie porremo il Sesto modo; come più à basso vederemo. Et sono al numero
de Dodici, non solamente appresso i Compositori prattici, ma etiandio appresso gli Ec-clesiastici; ancora che da molti non siano considerati in tanto numero; de i quali intendo
ragionar particolarmente, & mostrare in qual maniera al presente si vsi ciascuno di loro.
Che l'Hypermistolidio di Tolomeo non è quello, che noi chiamiamo Decimo modo.Cap. VII.
In qual maniera gli Antichi segnauano le Chorde de i loro Modi.Cap. VIII.
Verùm opere in longo fas est obrepere somnum.Percioche potrà essere ottima iscusatione à questo grauissimo autore, & etiandio à cia-scun'altro, che scriue molto di lungo.
In qual maniera s'intenda la Diapason esser'Harmonicamente, ouer'Arithme-ticamente mediata.Cap. IX.

Che i Modi moderni sono necessariamente Dodici; & in qual maniera si dimostri.Cap. X.
 . & le aggiungeremo nell'acuto la Terza
della Diatessaron, posta tra
. & le aggiungeremo nell'acuto la Terza
della Diatessaron, posta tra  & e. & haueremo tra la Terza specie della Diapason E & e.
quel che noi dimandiamo Quinto modo. Se pigliaremo hora l'istessa Diapente, & le ag-giungeremo nel graue la Diatessaron E &
& e. & haueremo tra la Terza specie della Diapason E & e.
quel che noi dimandiamo Quinto modo. Se pigliaremo hora l'istessa Diapente, & le ag-giungeremo nel graue la Diatessaron E &  . haueremo la Settima specie della Diapason
. haueremo la Settima specie della Diapason
 &
&  . & insieme quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei
unioni, ò congiuntioni; cioè, quelle della Prima specie della Diapente con la Prima della
Diatessaron, tanto nel graue, quanto nell'acuto; & quelle della Seconda di ciascuna si-milmente nel graue, & nell'acuto; cosi quelle della Terza specie fatte hora nel graue, hora
nell'acuto; & per tal uia haueremo Sei modi. Resta hora d'accompagnar la Quarta specie della Diapente con la Prima della Diatessaron, che si può accompagnar commoda-mente. Onde è d'auertire, che tutte le specie della Diatessaron si possono di nuouo ac-commodare & accompagnar con la Diapente in tre maniere; percioche la Prima specie si
può accompagnar con la Quarta specie della Diapente, la Seconda con la Prima, & la page 399Terza con la Seconda specie di essa Diapente; ne tali specie si possono congiungere insie-me commodamente in altra maniera; come è manifesto. Pigliando adunque la Quarta
specie della Diapente posta tra F & c. le accompagnaremo la prima della Diatessaron c &
f. & tra le chorde F & f. estreme dalla Quarta specie della Diapason con le sue mezane,
haueremo il Modo, che chiamiamo Settimo. Il perche se di nuouo pigliaremo la Dia-tessaron, posta tra F & C. & l'accompagnaremo nel graue con la nominata Diapente, ha-ueremo tra la Diapason c & C. Prima specie, il modo chiamato Ottauo. Aggiungeremo
hora la Seconda specie della Diatessaron posta tra d & g. alla Prima della Diapente, col-locata tra G & d. dalla parte acuta; ilche fatto tra la Quinta specie della Diapason G &
g. haueremo un'altro Modo; il quale per esser da gli otto Modi mostrati differente, lo no-minaremo Nono modo. Dalla parte graue poi di tal Diapente congiungeremo l'istessa
Diatessaron g & D. & haueremo tra la Seconda specie della Diapason d & D. quel, che
drittamente chiamiamo Decimo modo. Vltimamente se noi accompagneremo la Ter-za specie della Diatessaron postatra e & aa. dalla parte acuta, con la Seconda della Dia-pente posta tra a & e. nella Sesta specie della Diapason a & aa. haueremo il Modo, che si
chiama Vndecimo; imperoche s'accompagnaremo le dette specie per il contrario, ponendo la Diatessaron nella parte graue tra le chorde a & E. haueremo l'Vltimo Modo, detto
Duodecimo; contenuto nella Terza specie della Diapason e & E; come quì in essempio
si vede.
. & insieme quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei
unioni, ò congiuntioni; cioè, quelle della Prima specie della Diapente con la Prima della
Diatessaron, tanto nel graue, quanto nell'acuto; & quelle della Seconda di ciascuna si-milmente nel graue, & nell'acuto; cosi quelle della Terza specie fatte hora nel graue, hora
nell'acuto; & per tal uia haueremo Sei modi. Resta hora d'accompagnar la Quarta specie della Diapente con la Prima della Diatessaron, che si può accompagnar commoda-mente. Onde è d'auertire, che tutte le specie della Diatessaron si possono di nuouo ac-commodare & accompagnar con la Diapente in tre maniere; percioche la Prima specie si
può accompagnar con la Quarta specie della Diapente, la Seconda con la Prima, & la page 399Terza con la Seconda specie di essa Diapente; ne tali specie si possono congiungere insie-me commodamente in altra maniera; come è manifesto. Pigliando adunque la Quarta
specie della Diapente posta tra F & c. le accompagnaremo la prima della Diatessaron c &
f. & tra le chorde F & f. estreme dalla Quarta specie della Diapason con le sue mezane,
haueremo il Modo, che chiamiamo Settimo. Il perche se di nuouo pigliaremo la Dia-tessaron, posta tra F & C. & l'accompagnaremo nel graue con la nominata Diapente, ha-ueremo tra la Diapason c & C. Prima specie, il modo chiamato Ottauo. Aggiungeremo
hora la Seconda specie della Diatessaron posta tra d & g. alla Prima della Diapente, col-locata tra G & d. dalla parte acuta; ilche fatto tra la Quinta specie della Diapason G &
g. haueremo un'altro Modo; il quale per esser da gli otto Modi mostrati differente, lo no-minaremo Nono modo. Dalla parte graue poi di tal Diapente congiungeremo l'istessa
Diatessaron g & D. & haueremo tra la Seconda specie della Diapason d & D. quel, che
drittamente chiamiamo Decimo modo. Vltimamente se noi accompagneremo la Ter-za specie della Diatessaron postatra e & aa. dalla parte acuta, con la Seconda della Dia-pente posta tra a & e. nella Sesta specie della Diapason a & aa. haueremo il Modo, che si
chiama Vndecimo; imperoche s'accompagnaremo le dette specie per il contrario, ponendo la Diatessaron nella parte graue tra le chorde a & E. haueremo l'Vltimo Modo, detto
Duodecimo; contenuto nella Terza specie della Diapason e & E; come quì in essempio
si vede.
 Et per tal maniera non haueremo più, ne anco meno de Dodici Modi, imperoche cotali
Specie non si possono accompagnar'in altro modo l'una con l'altra, se non con grande in-commodo; come è manifesto à ciascheduno perito nella Musica.
Et per tal maniera non haueremo più, ne anco meno de Dodici Modi, imperoche cotali
Specie non si possono accompagnar'in altro modo l'una con l'altra, se non con grande in-commodo; come è manifesto à ciascheduno perito nella Musica.
Altro modo da dimostrar'il Numero de i Dodici Modi.Cap. XI.
 . haueremo il Quinto, ilquale medesimamente nasce dal-la congiuntione della Terza specie della Diapente, & della Terza della Diatessaron, che
sono E &
. haueremo il Quinto, ilquale medesimamente nasce dal-la congiuntione della Terza specie della Diapente, & della Terza della Diatessaron, che
sono E &  . &
. &  & e. come s'è detto. Presa dopoi la Quarta specie della Diapason, con-tenuta tra F & f. & diuisa harmonicamente con la chorda c. haueremo la Quarta specie
della Diapente F & c. aggiunta alla Prima specie della Diatessaron c & f. & il Settimo mo-do. Dopoi pigliata la Quinta specie della Diapason collocata tra G & g. diuisa harmoni-camente dalla Chorda d. haueremo la Prima specie della Diapente G & d. & la Seconda
della Diatessaron d & g. ch'insieme aggiunte ne danno il Nono. Pigliaremo hora la Se-sta a & aa. & la diuideremo al sopradetto modo con la chorda e. & da tal diuisione na-scerà la Seconda specie della Diapente a & e. & la Terza della Diatessaron e & aa. &
l'Vndecimo modo; come qui si vede. Et perche; per la Decima proposta del Quinto
& e. come s'è detto. Presa dopoi la Quarta specie della Diapason, con-tenuta tra F & f. & diuisa harmonicamente con la chorda c. haueremo la Quarta specie
della Diapente F & c. aggiunta alla Prima specie della Diatessaron c & f. & il Settimo mo-do. Dopoi pigliata la Quinta specie della Diapason collocata tra G & g. diuisa harmoni-camente dalla Chorda d. haueremo la Prima specie della Diapente G & d. & la Seconda
della Diatessaron d & g. ch'insieme aggiunte ne danno il Nono. Pigliaremo hora la Se-sta a & aa. & la diuideremo al sopradetto modo con la chorda e. & da tal diuisione na-scerà la Seconda specie della Diapente a & e. & la Terza della Diatessaron e & aa. &
l'Vndecimo modo; come qui si vede. Et perche; per la Decima proposta del Quinto

 &
&  . diuisa per la chorda E. ne darà il Sesto;
percioche la Terza specie della Diatessaron E &
. diuisa per la chorda E. ne darà il Sesto;
percioche la Terza specie della Diatessaron E &  . posta nel graue, s'vnisce con la Ter-za della Diapente
. posta nel graue, s'vnisce con la Ter-za della Diapente  & E. posta in acuto. Ma se pigliaremo la Diapason C & c. Prima spe-cie, diuisa dalla chorda F. arithmeticamente, haueremo l'Ottauo modo; percioche F &
C Prima specie della Diatessaron, si congiunge con la Quarta della Diapente c & F nel
graue. Hora prenderemo la Seconda specie della Diapason D & d. & la diuideremo al page 401modo mostrato con la Chorda G, & haueremo la Seconda della Diatessaron G, & D,
& la prima della Diapente d & G, che costituiscono il Decimo modo. Pigliando ultima-mente la Diapason E & e, Terza specie (lasciando la F & f Quarta specie; percioche,
per la Duodecima proposta del Quinto delle Dimostrationi non si può diuidere in tal maniera) se noi la diuideremo con la Chorda a, haueremo il Duodecimo modo, percioche
per tal diuisione nascerà la Terza specie della Diatessaron a & E. nella parte graue, uni-ta alla Seconda della Diapente e & a; come qui sotto si può uedere.
& E. posta in acuto. Ma se pigliaremo la Diapason C & c. Prima spe-cie, diuisa dalla chorda F. arithmeticamente, haueremo l'Ottauo modo; percioche F &
C Prima specie della Diatessaron, si congiunge con la Quarta della Diapente c & F nel
graue. Hora prenderemo la Seconda specie della Diapason D & d. & la diuideremo al page 401modo mostrato con la Chorda G, & haueremo la Seconda della Diatessaron G, & D,
& la prima della Diapente d & G, che costituiscono il Decimo modo. Pigliando ultima-mente la Diapason E & e, Terza specie (lasciando la F & f Quarta specie; percioche,
per la Duodecima proposta del Quinto delle Dimostrationi non si può diuidere in tal maniera) se noi la diuideremo con la Chorda a, haueremo il Duodecimo modo, percioche
per tal diuisione nascerà la Terza specie della Diatessaron a & E. nella parte graue, uni-ta alla Seconda della Diapente e & a; come qui sotto si può uedere.

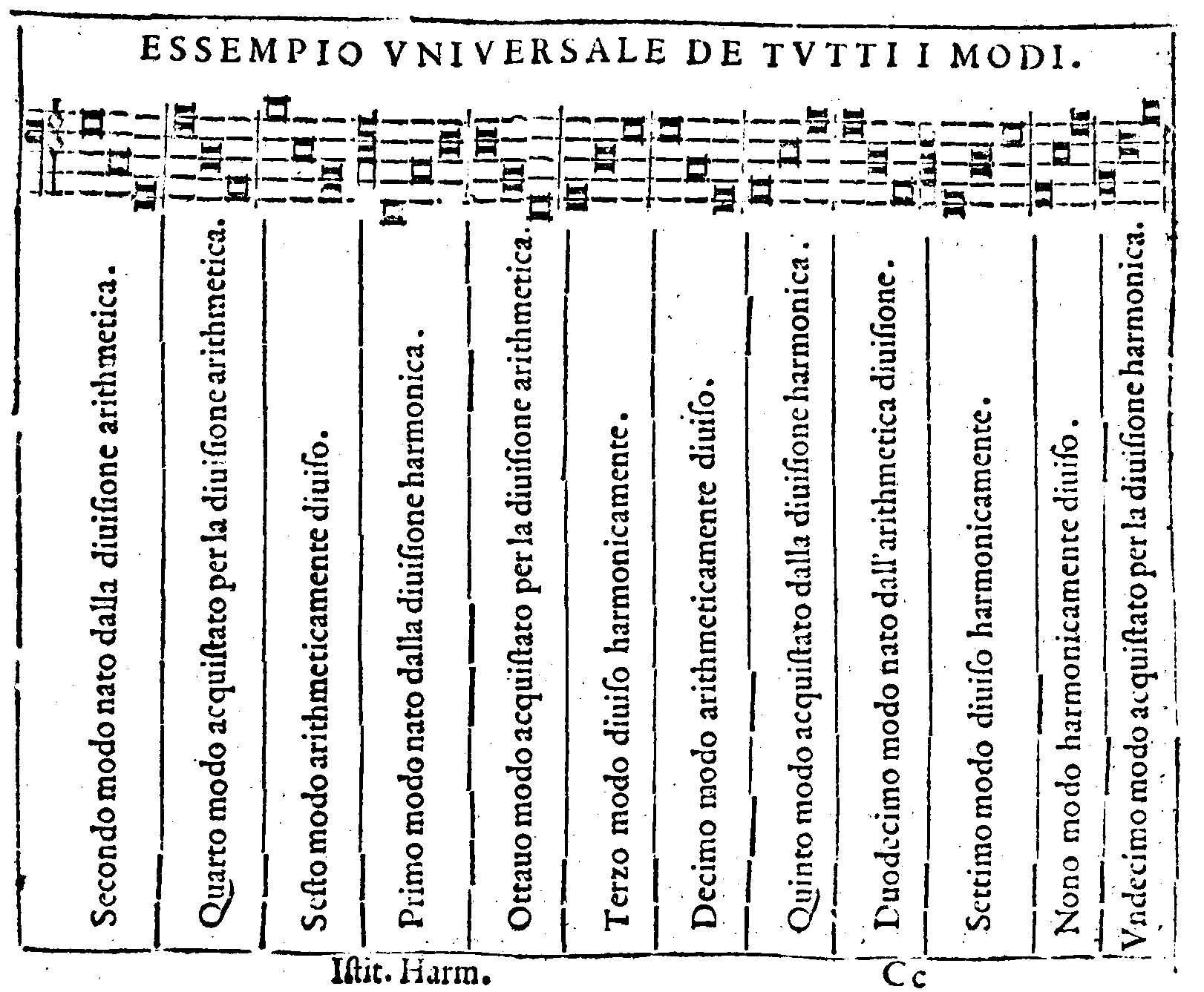
 &
&  non si possa diuidere harmonicamente; com'hò detto; percioche dalla parte gra-ue uerrebbe la Semidiapente
non si possa diuidere harmonicamente; com'hò detto; percioche dalla parte gra-ue uerrebbe la Semidiapente  & F, & il Tritono F &
& F, & il Tritono F &  nella parte acuta, quando fusse
tramezata dalla chorda F; ne meno la Quarta specie F & f arithmeticamente, essendo
che si udirebbe nel graue tra la Chorda
nella parte acuta, quando fusse
tramezata dalla chorda F; ne meno la Quarta specie F & f arithmeticamente, essendo
che si udirebbe nel graue tra la Chorda  & F il Tritono, quando fusse diuisa dalla
& F il Tritono, quando fusse diuisa dalla  , &
dalla parte acuta la Semidiapente f &
, &
dalla parte acuta la Semidiapente f &  ; tuttauia sono stati alcuni, che oltra i Dodici mostrati, le hanno attribuito altri Modi; come alla prima diuisione il Terzodecimo, & alla
seconda il Quartodecimo; ma ueramente non possono esser più de Dodeci, i quali sono notati per ordine nell'essempio di sopra, come habbiamo anco dimostrato nella Quartadecima proposta del Quinto & ultimo ragionamento delle Dimostrationi. Et nel Cap. 3.
del Lib. 6. de i nostri Sopplimenti.
; tuttauia sono stati alcuni, che oltra i Dodici mostrati, le hanno attribuito altri Modi; come alla prima diuisione il Terzodecimo, & alla
seconda il Quartodecimo; ma ueramente non possono esser più de Dodeci, i quali sono notati per ordine nell'essempio di sopra, come habbiamo anco dimostrato nella Quartadecima proposta del Quinto & ultimo ragionamento delle Dimostrationi. Et nel Cap. 3.
del Lib. 6. de i nostri Sopplimenti.
Diuisione de i Modi in Autentichi & Plagali.Cap. XII.
Delle chorde finali di ciascun Modo; & quanto si possa ascendere, ò discendere di sopra & di sotto le nominate chorde.Cap. XIII.
 adunque i Modi di sopra & di sotto il loro fine à cotal modo, si possono chiamare Per-fetti. Perilche l'Introito, che si canta nella Messa della quarta Dominica dell'Aduen-to; Rorate coeli desuper; si chiamerà Terzo modo secondo 'l nostro ordine naturale, &
quello, che si canta nella Messa dell'Ottaua della Natiuità del Signore; Vultum tuum
deprecabuntur; si potrà dimandar Quarto modo l'uno & l'altro perfetto. Ma quando i
Plagali nel graue passassero più oltra, ouer gli Autentichi nell'acuto; cotali Modi si
potranno nominare (come li nomina Franchino GaffuroPract. lib.
1. Cap. 8.) Superflui; com'anco si chia-marebbono Imperfetti, ò Diminuti, quando non arriuassero alla loro Ottaua chorda
acuta, ouer'alla Prima graue delle loro Diapason. De i primi habbiamo un'essempio
nell'Introito; Iustus es Domine del Terzo modo, che si canta nella Messa della Domi-nica Decimasettima dopo la solennità delle Pentecoste; Ma de i secondi sono quasi in-finiti gli essempi, tra i quali si ritroua l'Introito; Puer natus est nobis del Nono modo;
che si canta alla Terza Messa il Sacrosanto giorno della Natiuità del Figliuolo di Dio.
Si debbe hora auertire per sempre, che quel c'hò ragionato intorno à i Modi del
Canto fermo, intendo anco, che sia detto intorno le parti de i Modi del Canto figu-rato; se ben io non pongo di loro gli essempi; percioche uoglio, che cotal ragionamen-to sia commune all'vno & l'altro. Ma perche hò detto di sopra, ch'Ogni cosa si debbe
denominare dal fine, come da cosa più nobile; però da ogni Chorda finale haueremo da
giudicar ciascun Modo, di maniera che quello, che terminerà nella Chorda C. & sa-lirà alla Chorda c. dimandaremo Primo modo perfetto; & quando non arriuarà (come
hò detto) lo nominaremo Imperfetto; & quel che finirà nell'istessa C. & ascenderà
alla Chorda G. discendendo anco alla Γ. chiamaremo medesimamente Secondo mo-do perfetto; & simigliantemente Imperfetto, quando non ui arriuasse. Cosi anco l'uno
& l'altro si addimandarebbe Superfluo, ò Abondante, quando 'l Primo passasse la Otta-ua Chorda sopra il suo fine, & il Secondo la Quarta sotto di esso. Et ciò dico, quando fi-nissero nelle lor Chorde proprie finali, & tenessero la lor forma propria; percioche se fi-nissero nelle lor Chorde, che si chiamano Confinali, ouer'in altre Chorde, & tal forma
non si comprendesse esser in loro; allora haueremo da far'altro giudicio; come altroue
son per dimostrare.
adunque i Modi di sopra & di sotto il loro fine à cotal modo, si possono chiamare Per-fetti. Perilche l'Introito, che si canta nella Messa della quarta Dominica dell'Aduen-to; Rorate coeli desuper; si chiamerà Terzo modo secondo 'l nostro ordine naturale, &
quello, che si canta nella Messa dell'Ottaua della Natiuità del Signore; Vultum tuum
deprecabuntur; si potrà dimandar Quarto modo l'uno & l'altro perfetto. Ma quando i
Plagali nel graue passassero più oltra, ouer gli Autentichi nell'acuto; cotali Modi si
potranno nominare (come li nomina Franchino GaffuroPract. lib.
1. Cap. 8.) Superflui; com'anco si chia-marebbono Imperfetti, ò Diminuti, quando non arriuassero alla loro Ottaua chorda
acuta, ouer'alla Prima graue delle loro Diapason. De i primi habbiamo un'essempio
nell'Introito; Iustus es Domine del Terzo modo, che si canta nella Messa della Domi-nica Decimasettima dopo la solennità delle Pentecoste; Ma de i secondi sono quasi in-finiti gli essempi, tra i quali si ritroua l'Introito; Puer natus est nobis del Nono modo;
che si canta alla Terza Messa il Sacrosanto giorno della Natiuità del Figliuolo di Dio.
Si debbe hora auertire per sempre, che quel c'hò ragionato intorno à i Modi del
Canto fermo, intendo anco, che sia detto intorno le parti de i Modi del Canto figu-rato; se ben io non pongo di loro gli essempi; percioche uoglio, che cotal ragionamen-to sia commune all'vno & l'altro. Ma perche hò detto di sopra, ch'Ogni cosa si debbe
denominare dal fine, come da cosa più nobile; però da ogni Chorda finale haueremo da
giudicar ciascun Modo, di maniera che quello, che terminerà nella Chorda C. & sa-lirà alla Chorda c. dimandaremo Primo modo perfetto; & quando non arriuarà (come
hò detto) lo nominaremo Imperfetto; & quel che finirà nell'istessa C. & ascenderà
alla Chorda G. discendendo anco alla Γ. chiamaremo medesimamente Secondo mo-do perfetto; & simigliantemente Imperfetto, quando non ui arriuasse. Cosi anco l'uno
& l'altro si addimandarebbe Superfluo, ò Abondante, quando 'l Primo passasse la Otta-ua Chorda sopra il suo fine, & il Secondo la Quarta sotto di esso. Et ciò dico, quando fi-nissero nelle lor Chorde proprie finali, & tenessero la lor forma propria; percioche se fi-nissero nelle lor Chorde, che si chiamano Confinali, ouer'in altre Chorde, & tal forma
non si comprendesse esser in loro; allora haueremo da far'altro giudicio; come altroue
son per dimostrare.
De i Modi Communi, & de i Misti.Cap. XIIII.
Altra diuisione de i Modi; & di quello, che si hà da osseruare in ciascuno, nel com-porre le cantilene; & in qual maniera le Otto sorti di Salmodie con essi s'accompagnino.Cap. XV.
Deus venerunt gentes, alternandoEt alcuni sotto i quali si cantano le Antifone, Responsorij, Introiti, Graduali, & simi-li altre cose. Questi si possono chiamare Modi varij; essendo che non gli è di loro un so-lo canto, ouer'una sola & determinata forma di cantare per tutti i Modi, nella qua-le si habbiano da cantar tutte le Antifone, Responsorij, & altre cose simili nel Pri-mo modo (dirò per essempio) sotto un Tenore, ò aria, nella maniera che cantano i Salmi & li Cantici; & sotto un'altro tutte quelle del Secondo; & cosi tutte quelle de gli altri Modi, ma si bene è uariato; come si può vedere in molte cantilene; percioche can-tano sotto un Tenore, ouer modulatione l'Introito Gaudete in Domino; che si canta la Dominica terza dell'Aduento del Signore; & sotto un'altro Suscepimus Deus misericor-diam tuam, che si canta la Domenica ottaua dopo la solennità delle Pentecoste, l'uno & l'altro de i quali è composto nel Terzo modo. Ma non auiene cosi de i primi, iquali page 406potiamo chiamar Stabili; percioche sempre si cantano tutti i Salmi con i suoi Versi di qual si voglia Salmodia sotto un Tenore, ò modulatione determinata, senz'alcuna mu-tatione, & non è lecito uariar cotal Tenore; essendo che ne seguirebbe confusione. Et benche si trouino molte Forme uariate de tali Salmodie, ò Modi di cantare, che le uoglia-mo dire; come sono alcune, che chiamano Patriarchine, & alcune Monastiche; tutta-uia in ciascuna Chiesa non se ne vsa communemente più che Otto, lequali dimandano Regolari; & li Cantori le riducono sotto l'Antifone contenute ne gli Otto Modi mezani de i Dodici mostrati, lasciandone i Quattro estremi; cioè, il Primo, il Secondo, & l'Vnde-cimo, col Duodecimo in questa maniera; percioche la Prima sempre cantano dopo tut-te quelle Antifone, che sono contenute nel Terzo modo; la Seconda dopo quelle, che so-no comprese nel Quarto; & la Terza intonano dopo ciascheduna, che sia del Quinto mo-do; & il medesimo fanno dell'altre, per ordine; di maniera che l'Ottaua delle Salmodie uiene à finire quelle Antifone, che sono composte nel Decimo modo. Il perche hanno questa Regola, per sapere applicar bene cotali Salmodie alle dette Antifone; che ri-guardando il loro Fine, & il Principio del SEVOVAE, il qual segue subito dopò loro; che contiene le Lettere vocali de queste parole Seculorum Amen; hanno cognitione del tutto. Percioche à quella cantilena, che finisce in D. & il Principio del suo SEVOVAE sia in a. applicano la prima Salmodia; & quando tal fine medesimamente è posto in D. & il nominato Principio sia in F. gli applicano la Seconda. La onde applicando la Terza à quella che è terminata in E. & il detto Principio sia posto in c. & la Quarta, à quella il cui fine si troua etiandio essere in E. & il Principio sia in a. le uanno applican-do all'altre Antifone per ordine. Ma perche ne i sequenti Versi; acciò più ageuol-mente ogn'uno ricordar si possa quello, che detto habbiamo; sono contenute cotali Re-gole; essendo che mostrano qual Fine, & qual Principio de i nominati ricerca l'un de i Tenori, ò Forme delle otto Salmodie commemorate; però contentandomi di por solamente cotali Versi; i quali saranno i seguenti; non ne farò d'essi più altro ragio-namento.
Hor tre hor quattro dolce Salmodia
Le Donne incominciaro lagrimando.
Psalmodiam Primum Re La, Re Faque Secundam,Ma i Principij delle Forme, ouero Intonationi delle dette Salmodie, acciò più facil-mente ricordar si possino, saranno etiandio ridotti in questi altri quattro Versi se-quenti.
Per Sextam Mi Fa ternam praebent, & Mi La Quartam.
Fa Fa dant Quintam, Fa La ostendunt tibi Sextam,
Vt Sol Septenam, Vt Fa demonstrantque Octauam.
Psalmodiam retinent Primam, Sextamque Fa Sol La,La onde da cotali mezi aiutati, facilmente possono conoscere, qual Salmodia hanno da intonare, & sotto qual Tenore, ò Forma l'habbiano da cantare. Otto adunque sono le Salmodie, ouero Intonationi, che usano communemente gli Ecclesiastici (com'è ma-nifesto) ne i loro Diuini officij; & se alle fiate accascherà di cantarne alcuna sotto un'al-tro Tenore, che sia oltra le Otto forme nominate, le quali chiamano Principali; come è quella posta nel Cap 28. più a basso, che serue all'Vndecimo modo, & al Salmo In exitu Israel de Aegypto; come uederemo al suo luogo; cotali Salmodie dicono Irregolari; ancora che impropriamente; ma in questo proposito fà dibisogno uedere & leggere i Cap. 2. 3. 11. 12. & 13. del 24. Lib. De Re Musica; acciò si habbia maggior lume di questa cosa; & si leui ogni confusione, che potrebbe accadere. Tali Intonationi sono anco uaria-te per ogni Modo, quantunque non sia uariato il Tenore della Prima maniera, col quale cantano hora un Salmo, da quello che cantano dopoi l'istesso Primo modo un'altro. Et benche queste uarietà nel cantar diuersi Salmi sotto un'istesso Tenore non si odono; tut-page 407tauia si troua un'altra differenza; percioche gli Ecclesiastici hanno due sorti di Salmo-die; Festiue, & Feriali; & ciò auiene, perche altra maniera & più breue tengono nel cantare i Salmi feriali, di quel che fanno i festiui; ancora che si troua poca differenza tra l'una & l'altra. Ne si troua differenza alcuna tra le Salmodie tanto festiue, quanto fe-riali, con i quali cantano i Cantici euangelici, da quelle, che cantano i Salmi; se non, che nelle festiue del Cantico euangelico Magnificat anima mea Dominum; sogliono uaria-re alquanto i principij solamente di quelle, che seruono al Quarto, al Nono, & al De-cimo Modo; come si può veder nel Primo libro della Prattica di Fanchino Gaffuro dal Cap. 8. insino al fine di tal Libro; & nel Recanetto di Musica nel Cap. 59. & nel 60. del Primo libro; oue si può etiandio vedere, in quante maniere vsino gli Ecclesiastici di fi-nir cotali loro Salmodie. Et benche ne i Tenori, con i quali cantano i Versi de i Salmi ne gli Introiti delle Messe & il loro Gloria patri; si trouino alcune forme alquanto varia-te da quelle che si cantano ne i Salmi del Vespero & dell'altre Hore canoniche; come si può vedere nel Cap. 62. del nominato Recanetto; tuttauia anche loro si cantano sempre sotto un Tenore terminato senz'alcuna varietà; il che etiandio si osserua ne i Versetti de i Responsorij; che si cantano nel Matutino; imperoche vanno cantati sott'una Modula-tione non uariata, se non in alcuni luoghi, che si allungano, ò si accorciano per cagione della breuità, ò lunghezza delle Parole, che in essi si canto. Ma il loro Gloria patri, cauati de i predetti Versetti; sempre si canta secondo un Tenore prescritto; come nel Cap. 64. del nominato Recanetto si può vedere. Tutto questo hò uoluto dire, accioche se accade-rà al Compositore di comporre alcuna cantilena, uolendo seguitar l'ordine de cotali Modi habbia da saper quello, che haurà da fare; Percioche quando vorrà comporre sopra le Parole del Cantico euangelico nominato, che si canta nel Vespero, fà dibisogno, che se-guiti la Salmodia & l'Intonatione, che si canta ne i Canti fermi cantandosi il detto Can-tico; il che leggiadramente (per dare un'essempio) è stato osseruato oltra molti altri da Morale Spagnolo. Quel medesimo debbe anco osseruare, quando componerà sopra le Parole d'alcun Salmo, che si canta nel Vespero, ouero in altre hore canoniche; sia poi tal Salmo composto in maniera, che i suoi Versi si possino cantare con un'altro choro scam-bieuolmente; come hà composto Giachetto & molti altri; ò pur siano tutti intieri, come compose Lupo i Salmi In conuertendo Dominus captiuitatem Sion, & Beati omnes qui timent Dominum, à Quattro voci sotto 'l Modo ottauo delle Salmodie; oueramente siano com-posti à due chori; come i Salmi d'Adriano Laudate pueri Dominum, Lauda Ierusalem Domi-num, & molti altri: che si chiamano à choro spezzato. Ma quando haurà da compor'al-tre cantilene, non debbe seguitare 'l canto, ò Tenore de tali Salmodie; percioche non è obligato à questo; anzi quando ciò facesse, se li potrebbe attribuire à vitio, & che non hauesse inuentione. Ne dè per cosa alcuna far quello, che fanno alcuni Compositori, i quali componendo (per modo di essempio) alcuna cantilena sotto 'l Decimo modo, non sanno partirsi dal fine dell'Ottaua Salmodia; ilche fanno ancho ne gli altri Modi; di maniera che par, che vogliono, che sempre si canti 'l SEVOVAE posto ne gli Antifonarij nel fine di ciascuna Antifona. Quando adunque uorrà comporre alcuna cantilena fuo-ri delle Salmodie, allora sarà libero, & potrà ritrouare quella inuentione, che li tor-nerà più commoda. Ma ne i Modi sudetti debbe spesso far cantare i proprij membri della Diapason, che contiene il Modo sopra il quale si comporrà la cantilena; che so-no la Diapente & la Diatessaron. Dico i proprij, & non quelli d'un'altro Modo, co-me fanno alcuni; percioche dal principio al fine fanno vdire un procedere d'un Modo, toccando spesso le sue Diapente, & le Diatessaron in ogni parte; ma quando arriuano à tal fine, entrano fuori di proposito in un altro; ilche fà tristissimo effetto. Et perche io veggio, ch'alcuni fanno poca differenza nel procedere che si fà in un Modo Principale, dal procedere che si usa nel suo Collaterale; essendo che quelli istessi mouimenti & pas-saggi, che usano in uno, usano anco nell'altro; oue poi non si ode alcuna uariatio-ne di concento, & poco di uario si troua tra loro; però auertirà etiandio il Composi-page 408tore, che desidera di fare il tutto con ragione, di usare i mouimenti & passaggi Princi-pali, che uadino (più che si potrà fare) uerso l'acuto; massimamente quelli della Diapen-te & quelli della Diatessaron; ripigliando sempre (quando tornarà commodo) nel graue; & li mouimenti de i Collaterali, per il contrario; cioè, nel graue; massimamente quel-li, che procedono per le due nominate specie; percioche è il douere, essendo ueramen-te situate ne i Modi al contrario l'una dell'altra; cioè, la Diapente nel graue, & proce-dendo più oltra, & la Diatessaron nell'acuto nel Principale; & nel suo Collaterale la Dia-pente collocata nell'acuto, & la Diatessaron nel graue. Veramente è cosa giusta, hauen-do il Collaterale (come hò detto) natura contraria à quella del suo Principale; di ma-niera ch'essendo per natura differenti, debbono esser anche differenti ne i mouimenti; conciosia che da tali membri uien tal differenza, & anche da i mouimenti ueloci, ò tardi. Onde s'al Principale uorremo attribuire i mouimenti uerso l'acuto, & al suo Collaterale uerso 'l graue, il tutto sarà fatto con ragione; prima, perche 'l Modo principale si ritroua più acuto del suo Collaterale per una Diatessaron; la onde à questo conuiene i mouimen-ti tardi; i quali (com'altre uolte si è detto2. Partis cap. 11.) fanno la grauità, & à quello i ueloci, da i quali è generata l'acutezza; dopoi, perche usando i mouimenti tardi nel Collaterale, & li veloci nel Principale, uerremo à commodare il tutto al suo propio luogo. Però parmi, che fuo-ri d'ogni proposito alcuni habbiano usato alle uolte le parti graui delle loro com positio ni [sic: compositioni] con mouimenti troppo ueloci, & molto diminuite; & le acute con troppo tardi; cioè, con mouimenti molto rari; ancora che non biasimo, che alle fiate non si possa porre nel-l'acuto il mouimento tardo, & nel graue il ueloce, quando la materia lo ricerca; ma in ogni cosa bisogna adoperare 'l giudicio, senza 'l quale poco si può far di buono. Et questo sia detto à bastanza intorno tali materie; imperoche auanti ch'io passi più oltra, uoglio che ueggiamo vn'errore, che si troua tra alcuni poco periti delle cose della Mu-sica; il quale mostrato, seguiremo al particolare ragionamento di ciascuno de i nomi-nati Dodici modi.
Vt Re Fa Octauam, sic Ternam, sicque Secundam:
La Sol La Quartam, Fa Re Fa dant tibi Quintam,
Septenam vero Fa Mi Fa Sol tibi monstrant.
Se col leuare da alcuna cantilena il Tetrachordo Diezeugmenon, ponendo il Synemen-non in suo luogo, restando gli altri immobili, vn Modo si possa m u tare [sic: mutare] nell'altro.Cap. XVI.
 ; cioè,
in Paramese, & il porre il Synemennon, che hà il suo principio nella Chorda a. ch'è il page 409porre la b. sopradetta, non hà forza di trasmutare un Modo nell'altro; & che tal Tetra-chordo posto nella cantilena non sia naturale, ma accidentale; & in questo caso dicono
bene. Ma la Seconda maniera si fà, quando per tutta la cantilena; cioè, in ciascuna parte,
in luogo del Tetrachordo Diezeugmenon, vsiamo il Synemennon; & in luogo di cantar
la detta cantilena per la proprietà del
; cioè,
in Paramese, & il porre il Synemennon, che hà il suo principio nella Chorda a. ch'è il page 409porre la b. sopradetta, non hà forza di trasmutare un Modo nell'altro; & che tal Tetra-chordo posto nella cantilena non sia naturale, ma accidentale; & in questo caso dicono
bene. Ma la Seconda maniera si fà, quando per tutta la cantilena; cioè, in ciascuna parte,
in luogo del Tetrachordo Diezeugmenon, vsiamo il Synemennon; & in luogo di cantar
la detta cantilena per la proprietà del  . quadrato, la cantiamo per quella del b, molle; la
onde essendo posto in cotal maniera, non dicono bene; percioche questo Tetrachordo
non è posto accidentalmente nella cantilena; ma è in essa naturale, & il Modo si chiama
Ttasportato [sic: Trasportato]; come più à basso uederemo, & cotale Tetrachordo hà possanza di trasmu-tare un Modo nell'altro. Et che ciò sia uero, facilmente potremo conoscere con un'ac-commodato essempio, Poniamo il sottoposto Tenore del Nono modo, contenuto nel-le sue chorde naturali; cioè, ne i suoi proprij & naturali luoghi, tra la Quinta specie della
. quadrato, la cantiamo per quella del b, molle; la
onde essendo posto in cotal maniera, non dicono bene; percioche questo Tetrachordo
non è posto accidentalmente nella cantilena; ma è in essa naturale, & il Modo si chiama
Ttasportato [sic: Trasportato]; come più à basso uederemo, & cotale Tetrachordo hà possanza di trasmu-tare un Modo nell'altro. Et che ciò sia uero, facilmente potremo conoscere con un'ac-commodato essempio, Poniamo il sottoposto Tenore del Nono modo, contenuto nel-le sue chorde naturali; cioè, ne i suoi proprij & naturali luoghi, tra la Quinta specie della
 Diapason. Dico, che se in tal Tenore, ouer'in un'altro simile si mutasse lachorda
Diapason. Dico, che se in tal Tenore, ouer'in un'altro simile si mutasse lachorda  . so-lamente vna ò due uolte nella b. questa non farebbe, che tal Modo si trasmutasse, se non
in quella parte oue fusse posto; & non hauerebbe possanza di far, che tal Modo non fusse
anche Nono; imperoche se bene tal chorda posta in cotal maniera è necessaria per po-ter regolare la modulatione; tuttauia essendo accidentale, non muta la forma del Mo-do di sorte, che non si habbia da conoscere per Nono; come da questo essempio si può
uedere.
. so-lamente vna ò due uolte nella b. questa non farebbe, che tal Modo si trasmutasse, se non
in quella parte oue fusse posto; & non hauerebbe possanza di far, che tal Modo non fusse
anche Nono; imperoche se bene tal chorda posta in cotal maniera è necessaria per po-ter regolare la modulatione; tuttauia essendo accidentale, non muta la forma del Mo-do di sorte, che non si habbia da conoscere per Nono; come da questo essempio si può
uedere.
 Ma se noi porremo nel principio de tali Tenori il segno b. ilquale dimostra, che per tut-ta la Cantilena dobbiamo procedere per le chorde del Tetrachordo synemennon; di-co, che allora tal chorda sarà naturale, & non accidentale; & hauerà possanza di
mutare il Nono modo nel Terzo; percioche uaria la specie della Diapente, ch'era
Prima per inanti tra G & d. & pone in essere la Seconda tra le istesse chorde; come qui
si uede.
Ma se noi porremo nel principio de tali Tenori il segno b. ilquale dimostra, che per tut-ta la Cantilena dobbiamo procedere per le chorde del Tetrachordo synemennon; di-co, che allora tal chorda sarà naturale, & non accidentale; & hauerà possanza di
mutare il Nono modo nel Terzo; percioche uaria la specie della Diapente, ch'era
Prima per inanti tra G & d. & pone in essere la Seconda tra le istesse chorde; come qui
si uede.
 E' ben uero, che 'l Modo non si troua nelle sue chorde naturali; percioche è trasportato,
per una Diatessaron più acuta; il perche quando si uolesse porre al suo luogo, si ritroua-rebbe collocato in cotal maniera tra le chorde della Diapason D & d.
E' ben uero, che 'l Modo non si troua nelle sue chorde naturali; percioche è trasportato,
per una Diatessaron più acuta; il perche quando si uolesse porre al suo luogo, si ritroua-rebbe collocato in cotal maniera tra le chorde della Diapason D & d.
 page 410Non è adunque uero assolutamente, che 'l porre il Tetrachordo Synemennon in una
cantilena in luogo del Diezeugmenon, non habbia forza di mutar quel Modo, in cui
si pone, in un'altro; ma è ben uero, quando è posto secondo 'l modo mostrato. Diremo
adunque, se per la varieta del Tetrachordo, segue la uariatione della Diapason; & dal-la uarietà della Diapason la uarietà del Modo; procedendo dal primo all'vltimo; che tal
Tetrachordo posto al secondo modo, habbia possanza di mutare vn Modo nell'altro.
page 410Non è adunque uero assolutamente, che 'l porre il Tetrachordo Synemennon in una
cantilena in luogo del Diezeugmenon, non habbia forza di mutar quel Modo, in cui
si pone, in un'altro; ma è ben uero, quando è posto secondo 'l modo mostrato. Diremo
adunque, se per la varieta del Tetrachordo, segue la uariatione della Diapason; & dal-la uarietà della Diapason la uarietà del Modo; procedendo dal primo all'vltimo; che tal
Tetrachordo posto al secondo modo, habbia possanza di mutare vn Modo nell'altro.
 , che tal Chorda farà sempre uariare il Modo; & cosi per
il contrario, ponendo la
, che tal Chorda farà sempre uariare il Modo; & cosi per
il contrario, ponendo la  . in luogo della b. come ne mostra l'esperienza.
. in luogo della b. come ne mostra l'esperienza.
Della Trasportatione de i Modi.Cap. XVII.
 ; ouero per dir meglio, per la trasportatione del Semituono, si possa
variare vn Modo nell'altro; & di Terzo farlo diuentar Nono, & di No-no Terzo; non è dubio, che qualunque Modo sia Primo, Secondo, Terzo, Quar-to, ouero alcuno de gli altri, col fauore d'alcuna Chorda, che muti vna Diapason nel-l'altra, si potrà trasportare uerso l'acuto, ò uerso 'l graue, à nostro bel piacere. Il che
quanto alle uolte possa tornar commodo, lasciarò giudicare à ciascuno, che habbia giu-dicio; percioche tali Trasportationi non sono utili solamente, ma sommamente necessa-rie anco ad ogni perito Organista, che serue alle Musiche choriste; non solo nelle Messe,
& ne i Vesperi; ma anco nell'altre Hore canoniche & ad altri Sonatori similmente, che
sonano altre sorti d'Istrumenti, & che non sono cosi bene istrutti, come douerebbo-no essere; per accommodare il suono de quelli alle Voci, lequali alle uolte non possono
ascendere, ò discendere tanto, quanto ricercano i luoghi proprij de i Modi accommo-dati sopra i detti Istrumenti. Et tali Trasportationi sono hora in uso appresso i Mu-sici moderni; come furono anche appresso gli Antichi, Ocheghen, & il suo discepolo
Giosquino, & infiniti altri; come nelle loro compositioni si può uedere; & furono anco
in uso appresso gli antichi Greci; come si può uedere nel Cap. 3. del Lib. 7. De i nostri
Sopplimenti; percioche chiamarono cotale Trasportatione Μεταβολὴ; la quale è di
più maniere, come si potrà uedere. Quando adunque accascarà, che per necessità, ò
per qualunque altr'accidente farà dibisogno di trasportare il Modo contenuto in alcuna
cantilena; sopra ogn'altra cosa bisognarà auertire d'accommodarlo in tal maniera &
in tal luogo, che si possa ascendendo & discendendo hauer tutte quelle chorde, che so-no necessarie alla costitutione di tal Modo; cioè, che diano gli interualli e i Tuoni, &
i Semituoni necessarij al suo esser'essentiale. Et ciò debbono sommamente osseruare i
Compositori, quando uorranno compor tali cantilene, per sonare sopra qualche Istru-mento; Imperoche quando le uorranno comporre per cantare solamente, non sarebbe
grande errore, quando segnassero alcune Chorde con alcun segno accidentale, che non
si ritrouassero sopra l'Istrumento; massimamente sopra il Grauocembalo; come sono le
Enharmoniche, le quali si trouano in pochi Istrumenti arteficiali. Et questo hò detto;
percioche la Voce si può fare acuta & graue; ouer si può vsare in qualunque altra ma-niera, secondo 'l uoler del Cantore, che non si può far cosi liberamente con tali Istrumen-ti. Hora per mostrare in qual maniera commodamente si possa trasportare qual si uoglia
cantilena fuori delle sue Chorde naturali, non pigliaremo altro essempio, che 'l Terzo,
& il Quarto, posto nel Capitolo precedente; percioche ne potranno ottimamente mo-page 411strare in qual maniera ogni cantilena, che procede per la Chorda
; ouero per dir meglio, per la trasportatione del Semituono, si possa
variare vn Modo nell'altro; & di Terzo farlo diuentar Nono, & di No-no Terzo; non è dubio, che qualunque Modo sia Primo, Secondo, Terzo, Quar-to, ouero alcuno de gli altri, col fauore d'alcuna Chorda, che muti vna Diapason nel-l'altra, si potrà trasportare uerso l'acuto, ò uerso 'l graue, à nostro bel piacere. Il che
quanto alle uolte possa tornar commodo, lasciarò giudicare à ciascuno, che habbia giu-dicio; percioche tali Trasportationi non sono utili solamente, ma sommamente necessa-rie anco ad ogni perito Organista, che serue alle Musiche choriste; non solo nelle Messe,
& ne i Vesperi; ma anco nell'altre Hore canoniche & ad altri Sonatori similmente, che
sonano altre sorti d'Istrumenti, & che non sono cosi bene istrutti, come douerebbo-no essere; per accommodare il suono de quelli alle Voci, lequali alle uolte non possono
ascendere, ò discendere tanto, quanto ricercano i luoghi proprij de i Modi accommo-dati sopra i detti Istrumenti. Et tali Trasportationi sono hora in uso appresso i Mu-sici moderni; come furono anche appresso gli Antichi, Ocheghen, & il suo discepolo
Giosquino, & infiniti altri; come nelle loro compositioni si può uedere; & furono anco
in uso appresso gli antichi Greci; come si può uedere nel Cap. 3. del Lib. 7. De i nostri
Sopplimenti; percioche chiamarono cotale Trasportatione Μεταβολὴ; la quale è di
più maniere, come si potrà uedere. Quando adunque accascarà, che per necessità, ò
per qualunque altr'accidente farà dibisogno di trasportare il Modo contenuto in alcuna
cantilena; sopra ogn'altra cosa bisognarà auertire d'accommodarlo in tal maniera &
in tal luogo, che si possa ascendendo & discendendo hauer tutte quelle chorde, che so-no necessarie alla costitutione di tal Modo; cioè, che diano gli interualli e i Tuoni, &
i Semituoni necessarij al suo esser'essentiale. Et ciò debbono sommamente osseruare i
Compositori, quando uorranno compor tali cantilene, per sonare sopra qualche Istru-mento; Imperoche quando le uorranno comporre per cantare solamente, non sarebbe
grande errore, quando segnassero alcune Chorde con alcun segno accidentale, che non
si ritrouassero sopra l'Istrumento; massimamente sopra il Grauocembalo; come sono le
Enharmoniche, le quali si trouano in pochi Istrumenti arteficiali. Et questo hò detto;
percioche la Voce si può fare acuta & graue; ouer si può vsare in qualunque altra ma-niera, secondo 'l uoler del Cantore, che non si può far cosi liberamente con tali Istrumen-ti. Hora per mostrare in qual maniera commodamente si possa trasportare qual si uoglia
cantilena fuori delle sue Chorde naturali, non pigliaremo altro essempio, che 'l Terzo,
& il Quarto, posto nel Capitolo precedente; percioche ne potranno ottimamente mo-page 411strare in qual maniera ogni cantilena, che procede per la Chorda  . si possa trasportare
per una Diatessaron in acuto, con l'aiuto della Chorda b. ouer per il contrario, quan-do il canto procedesse per la Chorda b. in qual maniera si potesse trasporre nel graue
commodamente per un simile Interuallo, con l'aiuto della
. si possa trasportare
per una Diatessaron in acuto, con l'aiuto della Chorda b. ouer per il contrario, quan-do il canto procedesse per la Chorda b. in qual maniera si potesse trasporre nel graue
commodamente per un simile Interuallo, con l'aiuto della  . Ma perche alle uolte i Mu-sici, non già per necessità, ma più presto per burla & per capriccio; ò forse per uolere
intricare il ceruello (dirò cosi) à i Cantanti, sogliono trasportare i Modi uerso l'acuto,
ouero uerso il graue per un Tuono, ò per altro lnteruallo, adoperando non solamente
le Chorde chromatiche, ma anco l'Enharmoniche, per poter commodamente, quando
li fà dibisogno, trasportare à i loro luoghi i Tuoni & li Semituoni, secondo la propria for-ma del Modo; però mostraremo il modo, & come si potranno trasportare. Et benche so-gliono usar di trasportarli in più maniere; tuttauia ne porrò qui due solamente più vsate,
fatte nel Terzo modo; dalle quali potrà ogn'vno comprendere il modo, che hauerà da
tenere nell'altre; & saranno le sottoposte; l'una delle quali si fà con l'aiuto delle Chorde
segnate col b. & l'altra con l'aiuto di quelle, che sono segnate col
. Ma perche alle uolte i Mu-sici, non già per necessità, ma più presto per burla & per capriccio; ò forse per uolere
intricare il ceruello (dirò cosi) à i Cantanti, sogliono trasportare i Modi uerso l'acuto,
ouero uerso il graue per un Tuono, ò per altro lnteruallo, adoperando non solamente
le Chorde chromatiche, ma anco l'Enharmoniche, per poter commodamente, quando
li fà dibisogno, trasportare à i loro luoghi i Tuoni & li Semituoni, secondo la propria for-ma del Modo; però mostraremo il modo, & come si potranno trasportare. Et benche so-gliono usar di trasportarli in più maniere; tuttauia ne porrò qui due solamente più vsate,
fatte nel Terzo modo; dalle quali potrà ogn'vno comprendere il modo, che hauerà da
tenere nell'altre; & saranno le sottoposte; l'una delle quali si fà con l'aiuto delle Chorde
segnate col b. & l'altra con l'aiuto di quelle, che sono segnate col  . Bisogna auertire, che
i Moderni chiamano queste Trasportationi Modi trasposti per Musica finta, laquale (se-
. Bisogna auertire, che
i Moderni chiamano queste Trasportationi Modi trasposti per Musica finta, laquale (se-
 condo che la dichiarano) dicono essere una Trasportatione de Figure (intendendo però
di tutto l'ordine, che si troua in ciascun Modo) dalla lor propria sede in un'altra. Ma
questo si dè saper sopr'ogn'altra cosa; che quantunque habbia posto gli essempi solamen-te del Terzo modo, che tali Trasportationi si possono far nell'altre cantilene de g li [sic: gli] al-tri Modi; il che nella Ventesimaquinta del Quinto delle Dimostrationi hò chiaramen-te dimostrato, & nel Cap. 3. De i Sopplimenti hò simigliantemente dichiarato.
condo che la dichiarano) dicono essere una Trasportatione de Figure (intendendo però
di tutto l'ordine, che si troua in ciascun Modo) dalla lor propria sede in un'altra. Ma
questo si dè saper sopr'ogn'altra cosa; che quantunque habbia posto gli essempi solamen-te del Terzo modo, che tali Trasportationi si possono far nell'altre cantilene de g li [sic: gli] al-tri Modi; il che nella Ventesimaquinta del Quinto delle Dimostrationi hò chiaramen-te dimostrato, & nel Cap. 3. De i Sopplimenti hò simigliantemente dichiarato.
Ragionamento particolare intorno al Primo modo, & nella sua Natura, de i suoi Prin-cipij, & delle sue Cadenze.Cap. XVIII.
 . I moderni Compositori hanno etiandio composto in questo
Modo un numero quasi infinito d'ogni maniera di Cantilena; come sono Messe; Hinni, &
altre sorte de Canzoni; tra le quali si ritrouano Stabat mater dolorosa di Giosquino à cinque
uoci. O salutaris hostia; Alma redemptoris mater; Pien d'un vago pensier; d'Adriano; Descen-di in ortum meum di Giacchetto; tutti composti à Sei uoci. Cosi anco il canto Audi filia
& vide di Gomberto; con Ego ueni in ortum meum, il quale composi à cinque voci; & in-finiti altri; che 'l uoler riferirli d'uno in uno sarebbe impossibile. Et benche i ueri & natu-rali Principij non solamente di questo, ma etiandio di qual si uoglia altro Modo, siano nelle Chorde estreme della loro Diapente & Diatessaron, & nella Chorda mezana, la qual
diuide la Diapente in un Ditono & in un Semiditono; tuttauia si trouano molte cantilene,
c'hanno i lor principii sopra l'altre Chorde, lequali non starò hora à commemorare. Ma dirò solamente, ch'osseruarono gli Ecclesiastici ne i lor Canti alcuni fini mezani, nel fine d'o-gni Clausula, ò Periodo & d'ogni Oratione perfetta, i quali chiamarono Cadenze, che sono molto necessarie per la distintione delle Parole, che generano il senso perfetto; le quali
s'alcun uorrà saper quello, ch'elle siano, potrà leggere il Cap. 51. della Terza parte, percioche iui di tal materia hò à sufficienza ragionato; & potrà hauer di loro piena cognitione.
La onde basterà in questo luogo dir hora per sempre; che le Cadenze si trouano esser di
due sorti; Regolari, & Irregolari. Le Regolari sono quelle, che sempre si fanno ne gli
estremi suoni, ò Chorde de i Modi, & doue la Diapason in ciaschedun Modo harmo-nicamente, ouer'arithmeticamente è mediata, ò diuisa dalla Chorda mezana; le
quali Chorde sono l'estreme della Diapente & della Diatessaron, nelle quali è diuisa
simigliantemente doue la Diapente è diuisa da una Chorda mezana in un Ditono & in
un Semidiiono [sic: Semiditono]; & per dirla meglio, oue sono i ueri Principii & naturali di ciaschedun
Modo; l'altre poi facciansi doue si uogliano, si chiamano Irregolari. Sono adunque le
Cadenze regolari di questo Modo quelle, che si fanno in queste Chorde C, E. G & c.
& le Irregolari sono quelle, che si pongono nell'altre. Ma accioche più facilmente si co-nosca quello, che si è detto, porrò un'essempio composto à Due uoci; dal quale si potrà
conoscere i proprij luoghi delle Regolari, & uedere il modo, che si haurà da tenere nel
compor le sue modulationi; il che non solamente osseruarò in questo Primo modo, ma
ne gli altri Modi ancora; & sarà quel, che segue.
. I moderni Compositori hanno etiandio composto in questo
Modo un numero quasi infinito d'ogni maniera di Cantilena; come sono Messe; Hinni, &
altre sorte de Canzoni; tra le quali si ritrouano Stabat mater dolorosa di Giosquino à cinque
uoci. O salutaris hostia; Alma redemptoris mater; Pien d'un vago pensier; d'Adriano; Descen-di in ortum meum di Giacchetto; tutti composti à Sei uoci. Cosi anco il canto Audi filia
& vide di Gomberto; con Ego ueni in ortum meum, il quale composi à cinque voci; & in-finiti altri; che 'l uoler riferirli d'uno in uno sarebbe impossibile. Et benche i ueri & natu-rali Principij non solamente di questo, ma etiandio di qual si uoglia altro Modo, siano nelle Chorde estreme della loro Diapente & Diatessaron, & nella Chorda mezana, la qual
diuide la Diapente in un Ditono & in un Semiditono; tuttauia si trouano molte cantilene,
c'hanno i lor principii sopra l'altre Chorde, lequali non starò hora à commemorare. Ma dirò solamente, ch'osseruarono gli Ecclesiastici ne i lor Canti alcuni fini mezani, nel fine d'o-gni Clausula, ò Periodo & d'ogni Oratione perfetta, i quali chiamarono Cadenze, che sono molto necessarie per la distintione delle Parole, che generano il senso perfetto; le quali
s'alcun uorrà saper quello, ch'elle siano, potrà leggere il Cap. 51. della Terza parte, percioche iui di tal materia hò à sufficienza ragionato; & potrà hauer di loro piena cognitione.
La onde basterà in questo luogo dir hora per sempre; che le Cadenze si trouano esser di
due sorti; Regolari, & Irregolari. Le Regolari sono quelle, che sempre si fanno ne gli
estremi suoni, ò Chorde de i Modi, & doue la Diapason in ciaschedun Modo harmo-nicamente, ouer'arithmeticamente è mediata, ò diuisa dalla Chorda mezana; le
quali Chorde sono l'estreme della Diapente & della Diatessaron, nelle quali è diuisa
simigliantemente doue la Diapente è diuisa da una Chorda mezana in un Ditono & in
un Semidiiono [sic: Semiditono]; & per dirla meglio, oue sono i ueri Principii & naturali di ciaschedun
Modo; l'altre poi facciansi doue si uogliano, si chiamano Irregolari. Sono adunque le
Cadenze regolari di questo Modo quelle, che si fanno in queste Chorde C, E. G & c.
& le Irregolari sono quelle, che si pongono nell'altre. Ma accioche più facilmente si co-nosca quello, che si è detto, porrò un'essempio composto à Due uoci; dal quale si potrà
conoscere i proprij luoghi delle Regolari, & uedere il modo, che si haurà da tenere nel
compor le sue modulationi; il che non solamente osseruarò in questo Primo modo, ma
ne gli altri Modi ancora; & sarà quel, che segue.
 Si debbe però auertire, che le Cadenze delle Salmodie si debbono sempre far doue
casca 'l termine della mediatione delle loro Intonationi. La onde le Cadenze della me-diatione, ò mezano punto della Prima, della Quarta, & della Sesta si faranno in a; quella della Seconda in F; quella della Terza, della Quinta & dell'Ottaua in c; & quella
della Settima in e; essendo che tali mezi, ò punti mezani finiscono iui; come si può ue-dere nel sopranominato libro Recanetto, & in molti altri, i quali contengono simili Salmodie, ouero Intonationi, che dir le uogliamo. Le Finali poi si fanno sempre nel luogo,
che ciaschedun verso di tali Salmodie, ouer di ciaschedun Salmo si fanno finire. Dobbia-mo etiandio sempre osseruar, di far le Cadenze principalmente nel Tenore; essendo questa parte la Guida principale di caschedum Modo, sopra il quale si compone la Cantile-na; & da esso debbe il Compositore pigliar l'Inuentione dell'altre parti; è ben uero che
tali Cadenze si fanno anco nell'altre parti; & questo secondo che tornano più commo-de. Questo Modo si trasporta fuori delle sue Chorde naturali per vna Diatessaron uer-so l'acu[unclear: t]o, tra la Diapason F. & f, passando per le Chorde del Hexachordo Synemen-non, nelle quali si troua la Chorda b; come si può uedere in tutte quelle Compositioni
che di sopra hò nominato. page 414
Si debbe però auertire, che le Cadenze delle Salmodie si debbono sempre far doue
casca 'l termine della mediatione delle loro Intonationi. La onde le Cadenze della me-diatione, ò mezano punto della Prima, della Quarta, & della Sesta si faranno in a; quella della Seconda in F; quella della Terza, della Quinta & dell'Ottaua in c; & quella
della Settima in e; essendo che tali mezi, ò punti mezani finiscono iui; come si può ue-dere nel sopranominato libro Recanetto, & in molti altri, i quali contengono simili Salmodie, ouero Intonationi, che dir le uogliamo. Le Finali poi si fanno sempre nel luogo,
che ciaschedun verso di tali Salmodie, ouer di ciaschedun Salmo si fanno finire. Dobbia-mo etiandio sempre osseruar, di far le Cadenze principalmente nel Tenore; essendo questa parte la Guida principale di caschedum Modo, sopra il quale si compone la Cantile-na; & da esso debbe il Compositore pigliar l'Inuentione dell'altre parti; è ben uero che
tali Cadenze si fanno anco nell'altre parti; & questo secondo che tornano più commo-de. Questo Modo si trasporta fuori delle sue Chorde naturali per vna Diatessaron uer-so l'acu[unclear: t]o, tra la Diapason F. & f, passando per le Chorde del Hexachordo Synemen-non, nelle quali si troua la Chorda b; come si può uedere in tutte quelle Compositioni
che di sopra hò nominato. page 414Del Secondo modo.Cap. XIX.
 Si trouano composte sotto questo Modo innumerabili Compositioni da molti Musici
prattici; tra le quali è il Canto Mittit ad Virginem, à Sei uoci; & Quando nascesti Amor?
à Sette uoci; I vidi in terra angelici costumi, à Sei: & Quando fra l'altre donne, à Cinque uoci, tutti composti d'Adriano; oltra il canto Inuiolata, integra, & casta es Maria, di Giosqui-no à cinque uoci, & d'Adriano à Sette, à i quali s'aggiunge il canto à cinque uoci di Giachetto Decantabat populus; & Litigabant Iudaei; & O quàm gloriosum est regnum, i quali hò
composto da cantar con Sei uoci. Et se ben le chorde naturali di questo Modo sono le
mostrate di sopra, tuttauia i Musici con l'aiuto della chorda b. dell'Hexachordo synemen-non lo trasportano nell'acuto per una Diatessaron, tra le chorde della Diapason c. & C;
come nella maggior parte delle Compositioni nominate si può chiaramente uedere.
Si trouano composte sotto questo Modo innumerabili Compositioni da molti Musici
prattici; tra le quali è il Canto Mittit ad Virginem, à Sei uoci; & Quando nascesti Amor?
à Sette uoci; I vidi in terra angelici costumi, à Sei: & Quando fra l'altre donne, à Cinque uoci, tutti composti d'Adriano; oltra il canto Inuiolata, integra, & casta es Maria, di Giosqui-no à cinque uoci, & d'Adriano à Sette, à i quali s'aggiunge il canto à cinque uoci di Giachetto Decantabat populus; & Litigabant Iudaei; & O quàm gloriosum est regnum, i quali hò
composto da cantar con Sei uoci. Et se ben le chorde naturali di questo Modo sono le
mostrate di sopra, tuttauia i Musici con l'aiuto della chorda b. dell'Hexachordo synemen-non lo trasportano nell'acuto per una Diatessaron, tra le chorde della Diapason c. & C;
come nella maggior parte delle Compositioni nominate si può chiaramente uedere.
Del Terzo modo.Cap. XX.
 Et non solamente i Principij irregolari; ma anco le irregolari Cadenze si ritrouano esser
fatte nell'altre Chorde; come si uede in molte Cantilene, non solamente Ecclesiastiche,
ma etiandio nell'altre. Questo Modo hà strettissima parentella (dirò cosi) con l'Vndecimo, il quale è contenuto tra le Chorde a. & aa, percioche i Musici compongono nelle
sue Chorde le lor Canzoni del Modo Vndecimo, trasportandolo nell'acuto per una Diatessaron; lasciando da un canto la chorda
Et non solamente i Principij irregolari; ma anco le irregolari Cadenze si ritrouano esser
fatte nell'altre Chorde; come si uede in molte Cantilene, non solamente Ecclesiastiche,
ma etiandio nell'altre. Questo Modo hà strettissima parentella (dirò cosi) con l'Vndecimo, il quale è contenuto tra le Chorde a. & aa, percioche i Musici compongono nelle
sue Chorde le lor Canzoni del Modo Vndecimo, trasportandolo nell'acuto per una Diatessaron; lasciando da un canto la chorda  , & ponendoui la b, la qual serue all'Hexa-chordo synemennon, come fece Morale Spagnuolo nel Canto Sancta & immaculata virgi-nitas; & Giachetto nel Spem in alium; l'uno & l'altro composto per cantare à quattro uoci. Et perche il Terzo modo hà un certo mezano effetto tra 'l mesto & l'allegro, per cagione del Semiditono, che s'ode nel concento sopra le Chorde estreme della Diapente &
della Diatessaron; non hauendo altramente il Ditono dalla parte graue; però per sua natura è riputato dolce & alquanto mesto. Onde potremo ad esso accommodare ottimamente quelle parole, le quali saranno piene di grauità, & che tratteranno di cose alte & sen-tentiose; accioche l'Harmonia si conuenghi con la materia, che in esse si contiene. page 418
, & ponendoui la b, la qual serue all'Hexa-chordo synemennon, come fece Morale Spagnuolo nel Canto Sancta & immaculata virgi-nitas; & Giachetto nel Spem in alium; l'uno & l'altro composto per cantare à quattro uoci. Et perche il Terzo modo hà un certo mezano effetto tra 'l mesto & l'allegro, per cagione del Semiditono, che s'ode nel concento sopra le Chorde estreme della Diapente &
della Diatessaron; non hauendo altramente il Ditono dalla parte graue; però per sua natura è riputato dolce & alquanto mesto. Onde potremo ad esso accommodare ottimamente quelle parole, le quali saranno piene di grauità, & che tratteranno di cose alte & sen-tentiose; accioche l'Harmonia si conuenghi con la materia, che in esse si contiene. page 418Del Quarto Modo.Cap. XXII.
 & dicono, ch'è Modo atto alle Parole che rappresentano pianto, mestitia, sollicitu-dine, cattiuità, calamità, & ogni generatione di miseria; & si troua molto in uso ne i
loro canti; & le sue Cadenze principali & regolari (per esser questo dal Terzo Modo
poco differente; percioche l'uno & l'altro si compongono dell'istesse specie) si pongono
nelle Chorde a, F, D, & A; che si uedono nell'essempio; l'altre poi, che si pongono ne gli
altri luoghi sono tutte Irregolari. Imperoche i Prattici dicono, questo Modo compor-si della Seconda specie della Diapente a. & D. posta nell'acuto, & della Seconda della
Diatessaron D. & A. posta nel graue; & lo chiamano Collaterale, ouer Plagale del Ter-zo. Si trouano molte compositioni del Quarto modo, composte da molti Antichi & da
moderni Musici; tra le quali è il canto Praeter rerum seriem, composto à sei uoci da
Giosquino, & da Adriano à Sette uoci; & Che fai alma, simigliantemente à sette; con
Auertatur obsecro Domine, & Oue ch'i posi gli occhi; l'uno & l'altro à sei uoci dal detto
Adriano, con molt'altri composti. Composi anch'io in tal Modo l'Oratione Domi-nicale Pater noster; con la Salutatione angelica; Aue Maria, à sette uoci; & li canti.
Ego rosa Saron, & Capite nobis vulpes paruulas; à cinque uoci. Si trouano etiandio
molte altre compositioni fatte da diuersi compositori, le quali per esser quasi infinite
si lasciano. Questo Modo rare uolte si troua ne i Canti figurati nelle sue Chorde
proprie; ma il più delle uolte si ritroua trasportato per una Quarta; come si può
ueder ne i Canti nominati; & questo, percioche si può trasporre; come anco si
può trasporre il Terzo con l'aiuto della Chorda Tritesynemennon, uerso l'acuto.
Et si come il Terzo col Vndecimo hà molta conuenienza, cosi questo l'hà ueramen-te col Duodecimo. page 420
& dicono, ch'è Modo atto alle Parole che rappresentano pianto, mestitia, sollicitu-dine, cattiuità, calamità, & ogni generatione di miseria; & si troua molto in uso ne i
loro canti; & le sue Cadenze principali & regolari (per esser questo dal Terzo Modo
poco differente; percioche l'uno & l'altro si compongono dell'istesse specie) si pongono
nelle Chorde a, F, D, & A; che si uedono nell'essempio; l'altre poi, che si pongono ne gli
altri luoghi sono tutte Irregolari. Imperoche i Prattici dicono, questo Modo compor-si della Seconda specie della Diapente a. & D. posta nell'acuto, & della Seconda della
Diatessaron D. & A. posta nel graue; & lo chiamano Collaterale, ouer Plagale del Ter-zo. Si trouano molte compositioni del Quarto modo, composte da molti Antichi & da
moderni Musici; tra le quali è il canto Praeter rerum seriem, composto à sei uoci da
Giosquino, & da Adriano à Sette uoci; & Che fai alma, simigliantemente à sette; con
Auertatur obsecro Domine, & Oue ch'i posi gli occhi; l'uno & l'altro à sei uoci dal detto
Adriano, con molt'altri composti. Composi anch'io in tal Modo l'Oratione Domi-nicale Pater noster; con la Salutatione angelica; Aue Maria, à sette uoci; & li canti.
Ego rosa Saron, & Capite nobis vulpes paruulas; à cinque uoci. Si trouano etiandio
molte altre compositioni fatte da diuersi compositori, le quali per esser quasi infinite
si lasciano. Questo Modo rare uolte si troua ne i Canti figurati nelle sue Chorde
proprie; ma il più delle uolte si ritroua trasportato per una Quarta; come si può
ueder ne i Canti nominati; & questo, percioche si può trasporre; come anco si
può trasporre il Terzo con l'aiuto della Chorda Tritesynemennon, uerso l'acuto.
Et si come il Terzo col Vndecimo hà molta conuenienza, cosi questo l'hà ueramen-te col Duodecimo. page 420Del Quinto Modo.Cap. XXII.
 ; ouer dall'unione della Terza specie della Diapente E, &
; ouer dall'unione della Terza specie della Diapente E, &  , posta nel graue, con la Terza della Diatessaron
, posta nel graue, con la Terza della Diatessaron  . & e, posta nell'acuto. Questo Modo hà la sua Chorda finale E. commune col Sesto; & gli Ecclesiastici hanno infinite cantilene; come ne i loro libri si può uedere. Le sue Cadenze principali si fanno nelle Chorde de i
suoi principii regolari, iquali, sono le chorde mostrate E, G,
. & e, posta nell'acuto. Questo Modo hà la sua Chorda finale E. commune col Sesto; & gli Ecclesiastici hanno infinite cantilene; come ne i loro libri si può uedere. Le sue Cadenze principali si fanno nelle Chorde de i
suoi principii regolari, iquali, sono le chorde mostrate E, G,  , & e; che sono l'estreme della
sua Diapente & della sua Diatessaron, & la mezana della Diapente; l'altre poi, che sono Irrego
, & e; che sono l'estreme della
sua Diapente & della sua Diatessaron, & la mezana della Diapente; l'altre poi, che sono Irrego lari, si possono far sopra l'altre chorde. Ma perche conosciuto le Regolari, facilmente si
può conoscer le Irregolari; però hò dato l'essempio delle prime; acciò ueniamo in co-gnitione delle seconde. Si debbe però auertire, che tanto in questo, quanto nel Sesto,
nel Nono, & nel Decimo modo, regolarmente si fanno le Cadenze nella Chorda
lari, si possono far sopra l'altre chorde. Ma perche conosciuto le Regolari, facilmente si
può conoscer le Irregolari; però hò dato l'essempio delle prime; acciò ueniamo in co-gnitione delle seconde. Si debbe però auertire, che tanto in questo, quanto nel Sesto,
nel Nono, & nel Decimo modo, regolarmente si fanno le Cadenze nella Chorda  ma
perche tal Chorda non hà corrispondenza alcuna per Quinta nell'acuto, ne per Quarta
nel graue; però è chorda alquanto dura, ma tal durezza si sopporta nelle cantilene composte à piu di due uoci; percioche si tiene tal'ordine, che fanno buono effetto; come si
può ueder tra le Cadenze poste nel Cap. 51. della Terza parte. Molte compositioni si
trouano composte sotto questo modo, tra le quali è questa O Maria mater Christi, à quat-tro uoci di Izac; & d'Adriano i canti Te Deum patrem, Huc me sydereo; & Hac est domus
domini, composti à sette uoci, & I mi riuolgo indietro, composto da lui medesimamente
à cinque uoci; à i quali aggiungeremo Ferculum fecit sibi rex Salomon, il quale composi
simigliantemente à cinque uoci. Se questo Modo non si mescolasse col Nono, & si
udisse semplice, hauerebbe la sua Harmonia alquanto dura; ma perche è temperata dal-la Diapente dell'Vndecimo, & dalla Cadenza, che si fa in a, che in esso grandemente si
usa; però alcuni hanno hauuto parere, c'habbia natura di commouere al pianto; la on-de gli accommodarono uolontieri quelle parole, che sono lagrimeuoli & piene di lamenti. Ha grande conuenienza col detto Vndecimo; percioche hanno la Terza specie della
Diaressaron commune tra loro, & spesse uolte i Musici moderni lo trasportano fuori del-le sue Chorde naturali per una Diatessaron più acuta, con l'aiuto della Chorda b; ancora che 'l più delle uolte si ritroui collocato nel suo proprio & natural luogo.
ma
perche tal Chorda non hà corrispondenza alcuna per Quinta nell'acuto, ne per Quarta
nel graue; però è chorda alquanto dura, ma tal durezza si sopporta nelle cantilene composte à piu di due uoci; percioche si tiene tal'ordine, che fanno buono effetto; come si
può ueder tra le Cadenze poste nel Cap. 51. della Terza parte. Molte compositioni si
trouano composte sotto questo modo, tra le quali è questa O Maria mater Christi, à quat-tro uoci di Izac; & d'Adriano i canti Te Deum patrem, Huc me sydereo; & Hac est domus
domini, composti à sette uoci, & I mi riuolgo indietro, composto da lui medesimamente
à cinque uoci; à i quali aggiungeremo Ferculum fecit sibi rex Salomon, il quale composi
simigliantemente à cinque uoci. Se questo Modo non si mescolasse col Nono, & si
udisse semplice, hauerebbe la sua Harmonia alquanto dura; ma perche è temperata dal-la Diapente dell'Vndecimo, & dalla Cadenza, che si fa in a, che in esso grandemente si
usa; però alcuni hanno hauuto parere, c'habbia natura di commouere al pianto; la on-de gli accommodarono uolontieri quelle parole, che sono lagrimeuoli & piene di lamenti. Ha grande conuenienza col detto Vndecimo; percioche hanno la Terza specie della
Diaressaron commune tra loro, & spesse uolte i Musici moderni lo trasportano fuori del-le sue Chorde naturali per una Diatessaron più acuta, con l'aiuto della Chorda b; ancora che 'l più delle uolte si ritroui collocato nel suo proprio & natural luogo.
Del Sesto Modo.Cap. XXIII.
 . &
. &  , mediata dalla sua Chorda finale E. arithmeticamente. Que-sto (come dicono i Prattici; si compone della Terza specie della Diapente
, mediata dalla sua Chorda finale E. arithmeticamente. Que-sto (come dicono i Prattici; si compone della Terza specie della Diapente
 & E, posta in acuto, & della Terza della Diatessaron E &
& E, posta in acuto, & della Terza della Diatessaron E &  , congiunta al-la Diapente dalla parte graue. Questo medesimamente, secondo la loro opinione,
s'accommoda marauigliosamente à parole, ò materie lamenteuoli, che contengono tri-stezza, ouer lamentatione supplicheuole; come sono materie amorose, & quelle che
significano otio, quiete, tranquillità, adulatione, fraude, & detrattione; il perche
dall'effetto alcuni lo chiamarono Modo adulatorio. Questo è alquanto piu mesto del
suo Principale, massimamente quando procede dall'acuto al graue per mouimenti
tardi & contrarij. Credo io che se 'l si usasse semplicemente, senza mescolarui
la Diapente, & la Cadenza posta in a, che serue al Duodecimo; che hauereb-be alquanto più del uirile, di quello, che non hà cosi mescolato; ma accompagna-page 422to in tal maniera, s'usa grandemente, di modo, che si trouano molte cantilene compo-ste sotto questo Modo, tra le quali si troua Deprofundis clamaui ad te Domine, à quattro uoci di Giosquino; & Peccata mea Domine, con Rompi dell'empio cor'il duro scoglio, & In quel
parte del ciel; composti da Adriano, l'uno & l'altro à sei uoci. Composi anch'io molte
cantilene, tra le quali si troua à sei uoci il canto Miserere mei Deus, miserere mei; & anco
Misereris omnium Domine; & una Messa, senza usar in essa le osseruanze mostrate nella Terza parte; & ciò feci, non per altro se non per mostrare, che ciascuno il quale uorrà compor senza partirsi dalle date Regole, potrà etiandio comporre facilmente senza queste osseruanze,
& assai meglio di quello, che fanno alcuni, che non le fanno. Si trouano di questo Modo
quasi infinite Cantilene ecclesiastiche, nelle quali rarissime uolte (anzi s'io dicesse mai,
non errarei) si uede toccar la Chorda
, congiunta al-la Diapente dalla parte graue. Questo medesimamente, secondo la loro opinione,
s'accommoda marauigliosamente à parole, ò materie lamenteuoli, che contengono tri-stezza, ouer lamentatione supplicheuole; come sono materie amorose, & quelle che
significano otio, quiete, tranquillità, adulatione, fraude, & detrattione; il perche
dall'effetto alcuni lo chiamarono Modo adulatorio. Questo è alquanto piu mesto del
suo Principale, massimamente quando procede dall'acuto al graue per mouimenti
tardi & contrarij. Credo io che se 'l si usasse semplicemente, senza mescolarui
la Diapente, & la Cadenza posta in a, che serue al Duodecimo; che hauereb-be alquanto più del uirile, di quello, che non hà cosi mescolato; ma accompagna-page 422to in tal maniera, s'usa grandemente, di modo, che si trouano molte cantilene compo-ste sotto questo Modo, tra le quali si troua Deprofundis clamaui ad te Domine, à quattro uoci di Giosquino; & Peccata mea Domine, con Rompi dell'empio cor'il duro scoglio, & In quel
parte del ciel; composti da Adriano, l'uno & l'altro à sei uoci. Composi anch'io molte
cantilene, tra le quali si troua à sei uoci il canto Miserere mei Deus, miserere mei; & anco
Misereris omnium Domine; & una Messa, senza usar in essa le osseruanze mostrate nella Terza parte; & ciò feci, non per altro se non per mostrare, che ciascuno il quale uorrà compor senza partirsi dalle date Regole, potrà etiandio comporre facilmente senza queste osseruanze,
& assai meglio di quello, che fanno alcuni, che non le fanno. Si trouano di questo Modo
quasi infinite Cantilene ecclesiastiche, nelle quali rarissime uolte (anzi s'io dicesse mai,
non errarei) si uede toccar la Chorda  . Ben è uero, che passa nell'acuto alla chorda c,
di maniera che quando 'l Semituono douerebbe udirsi nel graue, si ode nell'acuto; & cosi
gli estremi di cotal Modo uengono ad esser le chorde c. & C. I suoi Principii Irregolari appresso gli Ecclesiastici si trouano in molti luoghi; ma li Regolari sono nelle Chorde
. Ben è uero, che passa nell'acuto alla chorda c,
di maniera che quando 'l Semituono douerebbe udirsi nel graue, si ode nell'acuto; & cosi
gli estremi di cotal Modo uengono ad esser le chorde c. & C. I suoi Principii Irregolari appresso gli Ecclesiastici si trouano in molti luoghi; ma li Regolari sono nelle Chorde  , E
G. &
, E
G. &  solamente che si trouano anco le sue Cadenze regolari, che sono le sottoposte;
ancora che molte siano le Irregolari. Il più delle uolte i Prattici lo trasportano per una
Diatessaron nell'acuto, ponendo la Chorda b, in luogo della
solamente che si trouano anco le sue Cadenze regolari, che sono le sottoposte;
ancora che molte siano le Irregolari. Il più delle uolte i Prattici lo trasportano per una
Diatessaron nell'acuto, ponendo la Chorda b, in luogo della  ; come si può ueder'in in-finite cantilene; il che fanno etiandio (come hò detto) ne gli altri Modi.
; come si può ueder'in in-finite cantilene; il che fanno etiandio (come hò detto) ne gli altri Modi.
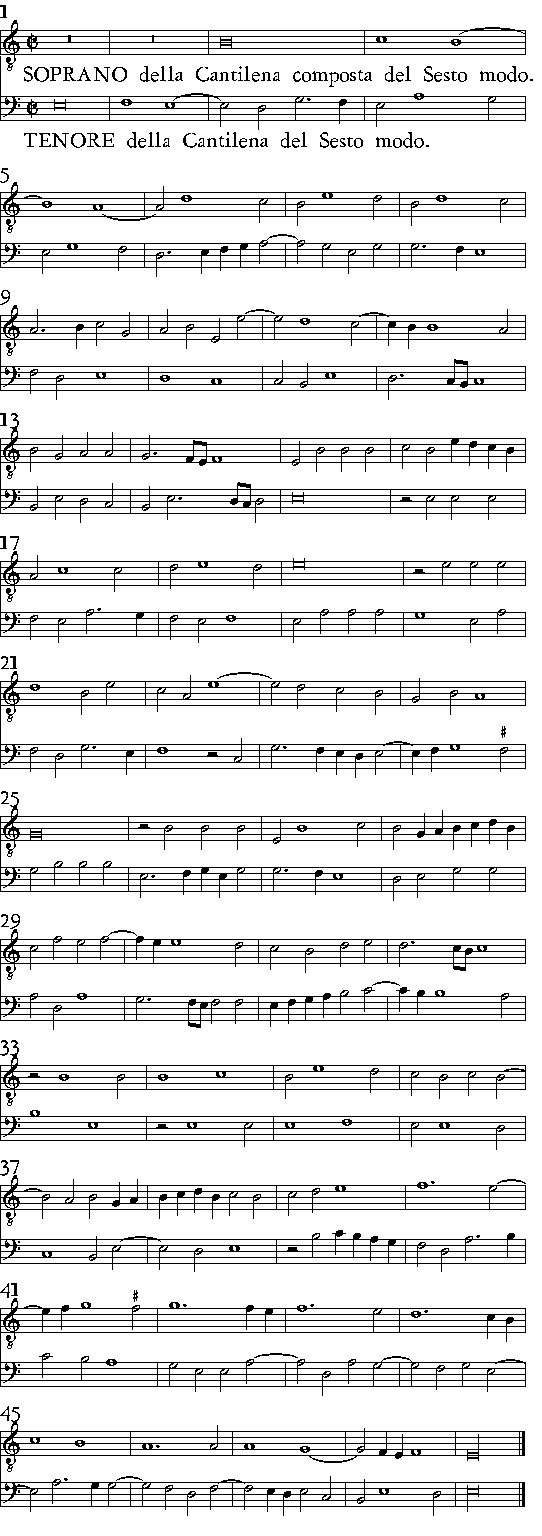
Del Settimo Modo.Cap. XXIIII
 ; come de gli altri si è fatto, nell'acuto & la sua chorda finale uerrà ad essere la b; ilche ciascun potrà uedere. page 424
; come de gli altri si è fatto, nell'acuto & la sua chorda finale uerrà ad essere la b; ilche ciascun potrà uedere. page 424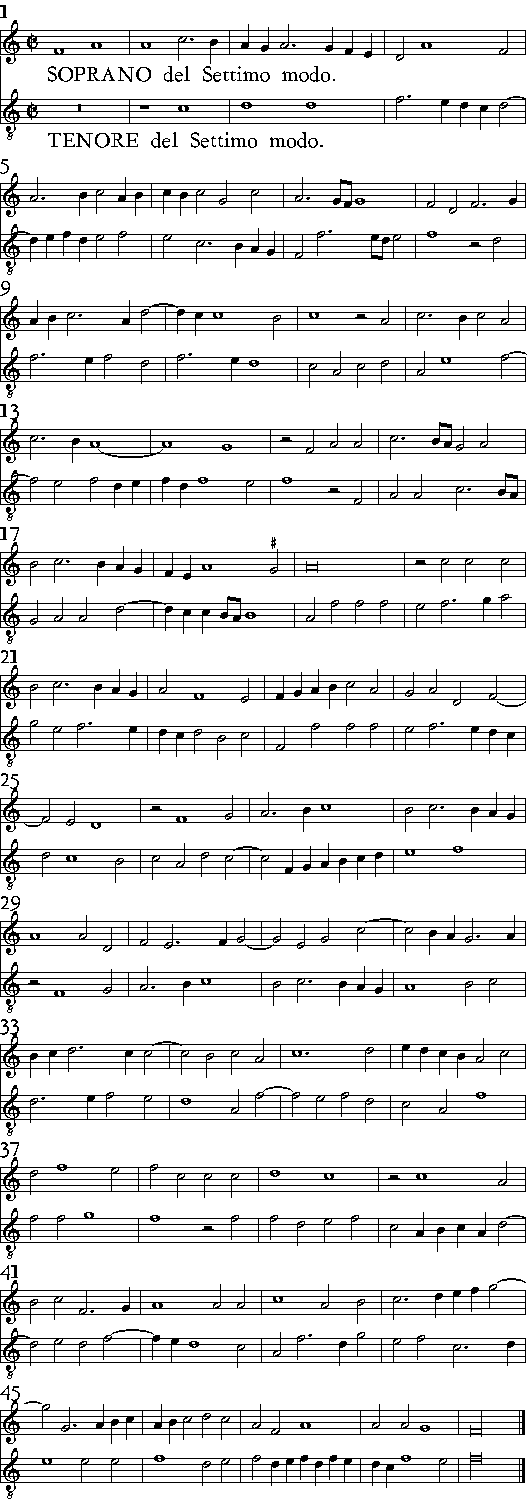
Dell[unclear: ']Ottauo Modo.Cap. XXV.
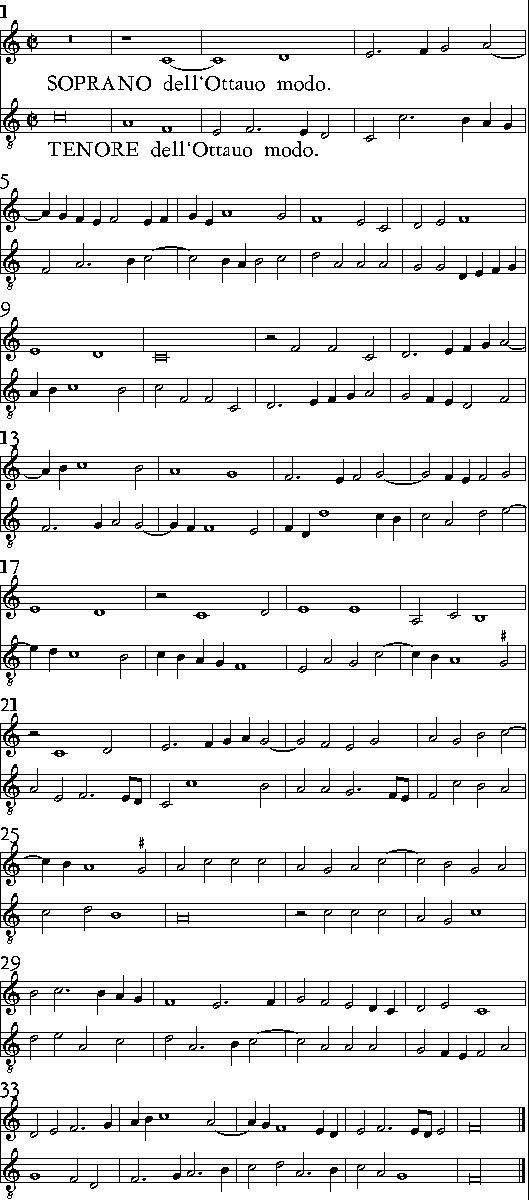 page 427
page 427Del Nono Modo.Cap. XXVI.
 (secondo che dicono) si conuiene Parole, ò materie, che siano lasciue, ò che trattino
di lasciuia, lequali siano allegre, dette però con modestia, & quelle, che significano mi-naccie, perturbationi, & ira. I suoi Principii regolari & le sue Cadenze principali & re-golari si pongono nelle Chorde G,
(secondo che dicono) si conuiene Parole, ò materie, che siano lasciue, ò che trattino
di lasciuia, lequali siano allegre, dette però con modestia, & quelle, che significano mi-naccie, perturbationi, & ira. I suoi Principii regolari & le sue Cadenze principali & re-golari si pongono nelle Chorde G,  , d, & g; come qui sotto si ueggono; ma le Irregola-ri si pongono sopra l'altre. Molte cantilene si trouano composte da i Musici sotto questo
Modo, tra le quali sono, Pater peccaui, & I piansi, hor canto, d'Adriano à sei uoci. Questo Modo è molto in uso appresso gli Ecclesiastici, & nelle cantilene de gli altri Musici si
troua il più delle uolte nelle sue Chorde naturali; ma molte uolte con l'aiuto della Chorda b, cioè, col mezo dell'Hexachordo synemennon, è trasportato nel graue per una Diapente, senz'alcun'incommodo.
, d, & g; come qui sotto si ueggono; ma le Irregola-ri si pongono sopra l'altre. Molte cantilene si trouano composte da i Musici sotto questo
Modo, tra le quali sono, Pater peccaui, & I piansi, hor canto, d'Adriano à sei uoci. Questo Modo è molto in uso appresso gli Ecclesiastici, & nelle cantilene de gli altri Musici si
troua il più delle uolte nelle sue Chorde naturali; ma molte uolte con l'aiuto della Chorda b, cioè, col mezo dell'Hexachordo synemennon, è trasportato nel graue per una Diapente, senz'alcun'incommodo.
Del Decimo Modo.Cap. XXVII.
 , G. & D; ma gli Irregolari si trouano nell'altre; & le sue Ca-denze regolari si pongono simigliantemente nelle mostrate quattro chorde; come nel seguente essempio si può uedere; ma le Irregolari si pongono sopra l'altre ancora. Ap-presso gli altri Musici si trouano molte compositioni, tra le quali si trouano Benedicta es coe-lorum regina, di Giosquino, à sei Voci; & Audite insulae, pur à sei uoci; con il canto Ver-bum supernum prodiens, & Liete & pensose, accompagnate & sole Donne, tutti d'Adriano à
sette uoci, & molt'altri. Questo modo si può trasportar come gli altri, fuori delle sue
chorde naturali, ponendolo in acuto per una Diatessaron, con l'aiuto della chorda b, ò
dell'Hexachordo synemennon; imperoch'altramente sarebbe impossibile. Gli Eccle-siastici sogliono à tutte quelle Antifone che incominciano nella chorda C. ouer D,
& finiscono nella sua finale G; le quali sono (considerata la loro forma) del Terzo modo;
quantunque finiscano nella sopra detta chorda G, applicare la Salmodia, che è posta nel
cap. sequente del Salmo In exitu Israel de Aegypto: come sono le Nos qui uiuimus, & Mar-tyres Domini, con molt'altre simili, che si trouano ne gli Antifonarii uecchi; il che dimo-stra il loro SEVOVAE. La onde per non lasciare indietro cosa, che al Musico ap-partenga, ne hò uoluto far mentione, accioche occorrendoli ueder cotal cosa, non si marauigli; percioche si può ueramente dire, che tale Salmodia sia più al proposito di quel-lo che non è l'Ottaua, laquale applicano all'altre Antifone di questo Modo; essendo
che la sua Modulatione è molto conforme alle modulationi delle già commemorate Antifone. Ma ueniamo à ragionare dell'Vndecimo. page 429
, G. & D; ma gli Irregolari si trouano nell'altre; & le sue Ca-denze regolari si pongono simigliantemente nelle mostrate quattro chorde; come nel seguente essempio si può uedere; ma le Irregolari si pongono sopra l'altre ancora. Ap-presso gli altri Musici si trouano molte compositioni, tra le quali si trouano Benedicta es coe-lorum regina, di Giosquino, à sei Voci; & Audite insulae, pur à sei uoci; con il canto Ver-bum supernum prodiens, & Liete & pensose, accompagnate & sole Donne, tutti d'Adriano à
sette uoci, & molt'altri. Questo modo si può trasportar come gli altri, fuori delle sue
chorde naturali, ponendolo in acuto per una Diatessaron, con l'aiuto della chorda b, ò
dell'Hexachordo synemennon; imperoch'altramente sarebbe impossibile. Gli Eccle-siastici sogliono à tutte quelle Antifone che incominciano nella chorda C. ouer D,
& finiscono nella sua finale G; le quali sono (considerata la loro forma) del Terzo modo;
quantunque finiscano nella sopra detta chorda G, applicare la Salmodia, che è posta nel
cap. sequente del Salmo In exitu Israel de Aegypto: come sono le Nos qui uiuimus, & Mar-tyres Domini, con molt'altre simili, che si trouano ne gli Antifonarii uecchi; il che dimo-stra il loro SEVOVAE. La onde per non lasciare indietro cosa, che al Musico ap-partenga, ne hò uoluto far mentione, accioche occorrendoli ueder cotal cosa, non si marauigli; percioche si può ueramente dire, che tale Salmodia sia più al proposito di quel-lo che non è l'Ottaua, laquale applicano all'altre Antifone di questo Modo; essendo
che la sua Modulatione è molto conforme alle modulationi delle già commemorate Antifone. Ma ueniamo à ragionare dell'Vndecimo. page 429
Dell'Vndecimo Modo.Cap. XXVIII.
 Modo il canto del Symbolo Niceno, Credo in unum
Deum; il quale hà principio per la sua Intonatione
nella chorda D, & uiene à terminare (come si uede
ne i detti corretti essemplari) nella chorda A. mede-simamente, & non nella
Modo il canto del Symbolo Niceno, Credo in unum
Deum; il quale hà principio per la sua Intonatione
nella chorda D, & uiene à terminare (come si uede
ne i detti corretti essemplari) nella chorda A. mede-simamente, & non nella  , ouer nella E. trasporta-to per una Diatessaron nell'acuto con l'aiuto della
chorda b; come ne i moderni Libri si uede; il qual
canto trasportato douerebbe per il douere finir nella chorda D. ma è stato guasto & scor-retto per l'ignoranza de i Scrittori; & per la presuntione & temerità d'alcun'altri; co-
, ouer nella E. trasporta-to per una Diatessaron nell'acuto con l'aiuto della
chorda b; come ne i moderni Libri si uede; il qual
canto trasportato douerebbe per il douere finir nella chorda D. ma è stato guasto & scor-retto per l'ignoranza de i Scrittori; & per la presuntione & temerità d'alcun'altri; co- page 431m'intrauiene anco nell'altre cose di maggiore importanza. Et non solamente i fini de i
mostrati canti si ritrouano fuori della lor propria & natural chorda; ma de gli altri anco-ra, che si trouano in tal maniera guasti & corrotti, che sarebbe cosa troppo lunga da mo-strare, quando si uolesse dar di ciascuno uno essempio particolare. Ma quanto sia facile
il trasmutare ne i Canti ecclesiastici un Modo nell'altro, variando solamente la chorda
finale, ouer trasportandolo dall'acuto al graue, ouer dal graue all'acuto, senz'alcun'aiu-to dalla chorda b, questo sarebbe facil da uedere, quando si uorrà essaminar minuta-mente le modulationi loro & il lor procedere. In questo modo si ritroua composta l'An-tifona Aue Maria gratia plena. la quale ne i libri antichi si troua terminata tra le sue chor-de naturali; come qui si uede; che ne i moderni si troua scritta più graue per vna Dia-pente, & la sua Salmodia è la Prima; la quale incomincia nella chorda c. Et che ciò sia
page 431m'intrauiene anco nell'altre cose di maggiore importanza. Et non solamente i fini de i
mostrati canti si ritrouano fuori della lor propria & natural chorda; ma de gli altri anco-ra, che si trouano in tal maniera guasti & corrotti, che sarebbe cosa troppo lunga da mo-strare, quando si uolesse dar di ciascuno uno essempio particolare. Ma quanto sia facile
il trasmutare ne i Canti ecclesiastici un Modo nell'altro, variando solamente la chorda
finale, ouer trasportandolo dall'acuto al graue, ouer dal graue all'acuto, senz'alcun'aiu-to dalla chorda b, questo sarebbe facil da uedere, quando si uorrà essaminar minuta-mente le modulationi loro & il lor procedere. In questo modo si ritroua composta l'An-tifona Aue Maria gratia plena. la quale ne i libri antichi si troua terminata tra le sue chor-de naturali; come qui si uede; che ne i moderni si troua scritta più graue per vna Dia-pente, & la sua Salmodia è la Prima; la quale incomincia nella chorda c. Et che ciò sia
 uero, da questo lo potiamo comprendere, che P. della Rue compose una Messa à quat-
tro uoci sopra questa Antifona nelle chorde uere & essentiali di cotal Modo; nel quale si
troua etiandio composto l'Introito, Gaudeamus omnes in Domino. Ne alcuno prenda di
questo marauiglia; massimamente uedendo, che la Salmodia, che segue sia la Prima,
percioche (com'hò detto ancora) non è inconueniente, che ciascun de i Quattro ultimi
Modi poco fà nominati, si pòssa [sic: possa] ridurre all'Intonatione d'alcuna delle Otto nominate. Et
se la chorda b. posta in luogo della
uero, da questo lo potiamo comprendere, che P. della Rue compose una Messa à quat-
tro uoci sopra questa Antifona nelle chorde uere & essentiali di cotal Modo; nel quale si
troua etiandio composto l'Introito, Gaudeamus omnes in Domino. Ne alcuno prenda di
questo marauiglia; massimamente uedendo, che la Salmodia, che segue sia la Prima,
percioche (com'hò detto ancora) non è inconueniente, che ciascun de i Quattro ultimi
Modi poco fà nominati, si pòssa [sic: possa] ridurre all'Intonatione d'alcuna delle Otto nominate. Et
se la chorda b. posta in luogo della  . hà possanza di mutare un Modo nell'altro; non è
dubbio, che ritrouandosi 'l detto Introito collocato nella Seconda specie della Diapason,
& cantandosi per la proprietà di b. molle, non sia anco dell'Vndecimo modo; come essa-minando il tutto, & quello ch'hò detto di sopra nel Cap. 16. manifestamente si può uede-re. Ma quando si uolesse ridur nelle sue uere chorde naturali, trasportandolo nell'acuto
per vna Diapente, si trouerebbe collocato tra la Sesta specie della Diapason a. & aa; come
fece Giosquino, che compose à quattro uoci la Messa sopra il sudetto Introito, & la ritirò
nelle sue chorde naturali; come si può uedere. Mi souiene hora, ch'alcuni non hanno
detto male, quando giudicarono, che l'Intonatione ò Salmodia del Salmo. In exitu Is-
. hà possanza di mutare un Modo nell'altro; non è
dubbio, che ritrouandosi 'l detto Introito collocato nella Seconda specie della Diapason,
& cantandosi per la proprietà di b. molle, non sia anco dell'Vndecimo modo; come essa-minando il tutto, & quello ch'hò detto di sopra nel Cap. 16. manifestamente si può uede-re. Ma quando si uolesse ridur nelle sue uere chorde naturali, trasportandolo nell'acuto
per vna Diapente, si trouerebbe collocato tra la Sesta specie della Diapason a. & aa; come
fece Giosquino, che compose à quattro uoci la Messa sopra il sudetto Introito, & la ritirò
nelle sue chorde naturali; come si può uedere. Mi souiene hora, ch'alcuni non hanno
detto male, quando giudicarono, che l'Intonatione ò Salmodia del Salmo. In exitu Is- rael de Aegypto, fusse la Nona; percioche uogliono, che la Antifona Nos qui viuimus sia sta-ta guasta & trasportata fuori del suo luogo da alcun Scrittore, che habbia uoluto mostrar-si più sauio de gli altri; com'han fatto molti anco dell'altre; ma di questo si è detto à ba-stanza nel Capitolo precedente. Questo Modo hà, com'hanno gli altri, i suoi Principij &
le sue Cadenze regolari & irregolari. I Regolari sono quelli, che si pongono nelle chor-de A, C, E, & a, come etiandio le Cadenze, che si uedono in questo essempio. ma i page 432
rael de Aegypto, fusse la Nona; percioche uogliono, che la Antifona Nos qui viuimus sia sta-ta guasta & trasportata fuori del suo luogo da alcun Scrittore, che habbia uoluto mostrar-si più sauio de gli altri; com'han fatto molti anco dell'altre; ma di questo si è detto à ba-stanza nel Capitolo precedente. Questo Modo hà, com'hanno gli altri, i suoi Principij &
le sue Cadenze regolari & irregolari. I Regolari sono quelli, che si pongono nelle chor-de A, C, E, & a, come etiandio le Cadenze, che si uedono in questo essempio. ma i page 432 Principii & similmente le Cadenze irregolari si pongono nell'altre Chorde. Trouansi in
questo Modo composte uarie cantilene, tra le quali è il canto Spem in alium numquàm ha-bui di Giachetto, & Sancta & immaculata virginitas, di Morale Spagnuolo, l'uno & l'altro
composto à quattro uoci, & le due nominate Messe. Composi anch'io sotto questo Modo il canto. Si bona suscepimus de manu Domini, I uò piangendo il mio passato tempo, à cinque
uoci, la Messa sopra il canto Benedicam Dominum in omni tempore di Gian Motone à Sei uoci; & altre cose, lequali non nomino. Ma questo Modo si può trasportar per una Dia-pente nel graue, con l'aiuto della Chorda b; come si trasporta etiandio gli altri.
Principii & similmente le Cadenze irregolari si pongono nell'altre Chorde. Trouansi in
questo Modo composte uarie cantilene, tra le quali è il canto Spem in alium numquàm ha-bui di Giachetto, & Sancta & immaculata virginitas, di Morale Spagnuolo, l'uno & l'altro
composto à quattro uoci, & le due nominate Messe. Composi anch'io sotto questo Modo il canto. Si bona suscepimus de manu Domini, I uò piangendo il mio passato tempo, à cinque
uoci, la Messa sopra il canto Benedicam Dominum in omni tempore di Gian Motone à Sei uoci; & altre cose, lequali non nomino. Ma questo Modo si può trasportar per una Dia-pente nel graue, con l'aiuto della Chorda b; come si trasporta etiandio gli altri.
Del Duodecimo & vltimo modo.Cap. XXIX.

In qual maniera si debba far giudicio de i Modi; & quelche si dè osser-uare nelle Compositioni.Cap. XXX.
 . posta nel graue, hanno la Terza della Diatessaron E.
& a; & in luogo della Terza della Diatessaron
. posta nel graue, hanno la Terza della Diatessaron E.
& a; & in luogo della Terza della Diatessaron  , & e, si troua la Seconda specie del-la Diapente a, & e, posta nell'acuto; di maniera che se ben le dette specie sono contenu-te sott'un'istessa Diapason, che è la E & e; nondimeno si troua in uno de i Modi trame-zata harmonicamente, & tiene la forma del Quinto modo; & nell'altro arithmetica-mente, & tiene la forma del Duodecimo; la onde udendosi tali specie tante & tan-page 435te uolte replicate, non solamente la maggior parte della compositione uiene à non ha-uer parte alcuna del Quinto, ma tutta la cantilena uiene ad esser composta sotto 'l Duodecimo modo. Et che ciò sia uero, da questo si può comprendere, che se noi aggiungere-mo queste due specie insieme, la Diatessaron E. & a, con la Diapente a. & e, collocan-do questa nell'acuto, & quella nel graue; non è dubbio, c'haueremo la forma di cotal
Modo, contenuto tra la Terza specie della Diapason arithmeticamente mediata. Di maniera che quella compositione, che noi giudichiamo esser del Quinto modo, non uiene
ad hauer cosa alcuna, per la quale possiamo far giudicio, che sia tale, se non il fine; percioche finisce nella Chorda E, il che è cosa molto fallace. Però adunque; se ben la Chorda
finale del Modo è quella; dalla quale (come dal fine & non auanti) dobbiamo far giu-dicio della cantilena, com'alcuni uogliono; essendo ch'Ogni cosa da esso ò in esso dritta-mente si giudica; non dobbiamo però intender, che per tal Chorda semplicemente noi
possiamo uenire in cognitione del Modo, sopra il quale è fondata la cantilena; percio-che non si dè credere, che semplicemente da lei si debba far giudicio; ma che debbia-mo aspettar tanto, che la cantilena sia condotta al fine, & iui giudicare, secondo il drit-to; cioè secondo la sua forma; conciosia che allora la cantilena è perfetta, & hà la sua forma, dalla quale si prende la occasione di far tal giudicio. Ma si dè notare, che da due cose si può pigliar simile occasione; prima dalla forma di tutta la cantilena; dopoi dal suo
fine; che è la sua Chorda finale. La onde essendo la Forma quella, che dà l'essere alla cosa, giudicarei, che fusse ragioneuole, che non dalla Chorda finale semplicemente, come
hanno uoluto molti; ma dalla Forma contenuta nella cantilena, s'hauesse da far tal giu-dicio. Onde hauendosi da giudicar la cantilena da tal forma; cioè, dal procedere, com'è
il douere; non è inconueniente, che 'l Modo principale possa finir nella Chorda mezana
della sua Diapason harmonicamente tramezata; & cosi 'l Modo collarerale nell'estreme
della sua Diapason arithmeticamente diuisa; lasciando da un canto la Chorda finale. Il
che quanto gentilmente si possa fare, si può comprendere dal canto. Si bona suscepimus de
manu Domini, composto da Verdeloto à cinque uoci, & dal canto. O Inuidia nemica di vir-tute, composto medesimamente da cantare con cinque uoci da Adriano; i quali da un
capo all'altro l'uno hà il procedere dell'Vndecimo, & l'altro del Quarto modo; tuttauia
non finiscono nella loro uera Chorda finale, ma nella mezana. Et questo ch'io dico del
Quinto & del Duodecimo, si può anche mostrar ne gli altri modi, i quali per breuità
lascio da un canto. Per la qual cosa non è da marauigliarsi, se molte uolte non si ode al-cuna differenza tra un Modo, che finisca nella Chorda E, & tra un'altro, che termini
nella a, poi che nella maniera, che s'è detto, si compongono misti; ma se si compones-sero semplici; non è dubio, che si udirebbe tra l'uno & l'altro gran uarietà d'Harmonia.
Quando adunque haueremo da far giudicio, di qual si uoglia cantilena, haueremo da
considerarla molto bene dal principio al fine, & ueder sotto qual forma ella si troua esser
composta; se sotto la forma del Primo, ò del Secondo, ò di qualunque altro Modo; ha-uendo riguardo alle Cadenze, le quali danno gran lume in tale cosa; & dopoi far giudicio;
ancora che non hauesse il suo fine nella sua propria Chorda finale, ma nella mezana, ouer'
in qualunque altra, che tornasse al proposito. Et se noi usaremo nelle Compositioni
una tal maniera di finire, non sarà fatto fuori di proposito; essendo che gli Eccle-siastici anco hanno usato un tal modo nelle lor cantilene; come si può uedere nell'ul-timo de i Κύριε ἐλέησον, i quali chiamano il Doppio minore, ouer de gli Apostoli; la
cui forma (com'è manifesto) è del Terzo modo; nondimeno finisce nella chorda a. laquale chiamano Confinale, & è la mezana delle Diapason D. & d, continente la forma
di cotal Modo; oltra che si troua l'Offertorio, che si canta nella Messa della Quarta feria
della Dominica terza di Quadragesima, Domine fac mecum, contenuto tra le sue Chorde
estreme F. & e. Et due cantilene, la prima delle quali è, Tollite hostias, contenuta tra le no-minate Chorde estreme, che si canta fatta la Communione della Messa della Dominica Decima ottaua dopo la Pentecoste; la seconda è, Per signum Crucis, che si canta ne i giorni solenpage 436ni dell'Inuentione & Essaltatione di Santa Croce; & è contenuta tra le Chorde estre-me F. & g. le quali cantilene tengono in se la Forma del Nono modo; percioche in esse si
troua la modulatione della sua Diapente G. & d. & della sua Diatessaron d. & g, & finiscono nella Chorda
, & e, si troua la Seconda specie del-la Diapente a, & e, posta nell'acuto; di maniera che se ben le dette specie sono contenu-te sott'un'istessa Diapason, che è la E & e; nondimeno si troua in uno de i Modi trame-zata harmonicamente, & tiene la forma del Quinto modo; & nell'altro arithmetica-mente, & tiene la forma del Duodecimo; la onde udendosi tali specie tante & tan-page 435te uolte replicate, non solamente la maggior parte della compositione uiene à non ha-uer parte alcuna del Quinto, ma tutta la cantilena uiene ad esser composta sotto 'l Duodecimo modo. Et che ciò sia uero, da questo si può comprendere, che se noi aggiungere-mo queste due specie insieme, la Diatessaron E. & a, con la Diapente a. & e, collocan-do questa nell'acuto, & quella nel graue; non è dubbio, c'haueremo la forma di cotal
Modo, contenuto tra la Terza specie della Diapason arithmeticamente mediata. Di maniera che quella compositione, che noi giudichiamo esser del Quinto modo, non uiene
ad hauer cosa alcuna, per la quale possiamo far giudicio, che sia tale, se non il fine; percioche finisce nella Chorda E, il che è cosa molto fallace. Però adunque; se ben la Chorda
finale del Modo è quella; dalla quale (come dal fine & non auanti) dobbiamo far giu-dicio della cantilena, com'alcuni uogliono; essendo ch'Ogni cosa da esso ò in esso dritta-mente si giudica; non dobbiamo però intender, che per tal Chorda semplicemente noi
possiamo uenire in cognitione del Modo, sopra il quale è fondata la cantilena; percio-che non si dè credere, che semplicemente da lei si debba far giudicio; ma che debbia-mo aspettar tanto, che la cantilena sia condotta al fine, & iui giudicare, secondo il drit-to; cioè secondo la sua forma; conciosia che allora la cantilena è perfetta, & hà la sua forma, dalla quale si prende la occasione di far tal giudicio. Ma si dè notare, che da due cose si può pigliar simile occasione; prima dalla forma di tutta la cantilena; dopoi dal suo
fine; che è la sua Chorda finale. La onde essendo la Forma quella, che dà l'essere alla cosa, giudicarei, che fusse ragioneuole, che non dalla Chorda finale semplicemente, come
hanno uoluto molti; ma dalla Forma contenuta nella cantilena, s'hauesse da far tal giu-dicio. Onde hauendosi da giudicar la cantilena da tal forma; cioè, dal procedere, com'è
il douere; non è inconueniente, che 'l Modo principale possa finir nella Chorda mezana
della sua Diapason harmonicamente tramezata; & cosi 'l Modo collarerale nell'estreme
della sua Diapason arithmeticamente diuisa; lasciando da un canto la Chorda finale. Il
che quanto gentilmente si possa fare, si può comprendere dal canto. Si bona suscepimus de
manu Domini, composto da Verdeloto à cinque uoci, & dal canto. O Inuidia nemica di vir-tute, composto medesimamente da cantare con cinque uoci da Adriano; i quali da un
capo all'altro l'uno hà il procedere dell'Vndecimo, & l'altro del Quarto modo; tuttauia
non finiscono nella loro uera Chorda finale, ma nella mezana. Et questo ch'io dico del
Quinto & del Duodecimo, si può anche mostrar ne gli altri modi, i quali per breuità
lascio da un canto. Per la qual cosa non è da marauigliarsi, se molte uolte non si ode al-cuna differenza tra un Modo, che finisca nella Chorda E, & tra un'altro, che termini
nella a, poi che nella maniera, che s'è detto, si compongono misti; ma se si compones-sero semplici; non è dubio, che si udirebbe tra l'uno & l'altro gran uarietà d'Harmonia.
Quando adunque haueremo da far giudicio, di qual si uoglia cantilena, haueremo da
considerarla molto bene dal principio al fine, & ueder sotto qual forma ella si troua esser
composta; se sotto la forma del Primo, ò del Secondo, ò di qualunque altro Modo; ha-uendo riguardo alle Cadenze, le quali danno gran lume in tale cosa; & dopoi far giudicio;
ancora che non hauesse il suo fine nella sua propria Chorda finale, ma nella mezana, ouer'
in qualunque altra, che tornasse al proposito. Et se noi usaremo nelle Compositioni
una tal maniera di finire, non sarà fatto fuori di proposito; essendo che gli Eccle-siastici anco hanno usato un tal modo nelle lor cantilene; come si può uedere nell'ul-timo de i Κύριε ἐλέησον, i quali chiamano il Doppio minore, ouer de gli Apostoli; la
cui forma (com'è manifesto) è del Terzo modo; nondimeno finisce nella chorda a. laquale chiamano Confinale, & è la mezana delle Diapason D. & d, continente la forma
di cotal Modo; oltra che si troua l'Offertorio, che si canta nella Messa della Quarta feria
della Dominica terza di Quadragesima, Domine fac mecum, contenuto tra le sue Chorde
estreme F. & e. Et due cantilene, la prima delle quali è, Tollite hostias, contenuta tra le no-minate Chorde estreme, che si canta fatta la Communione della Messa della Dominica Decima ottaua dopo la Pentecoste; la seconda è, Per signum Crucis, che si canta ne i giorni solenpage 436ni dell'Inuentione & Essaltatione di Santa Croce; & è contenuta tra le Chorde estre-me F. & g. le quali cantilene tengono in se la Forma del Nono modo; percioche in esse si
troua la modulatione della sua Diapente G. & d. & della sua Diatessaron d. & g, & finiscono nella Chorda  , la quale è la mezana della detta Diapente. E' ben uero, ch'alcuni
Moderni secondo il lor parere) attribuiscono tali canti al Quartodecimo modo; ma di que-sto lascierò far giudicio ad ogn'uno, c'habbia intelletto. Tali canti, in alcuni de i libri
moderni, si trouano trasportati nel graue per una Diapente senza l'aiuto della chorda b.
fuora delle loro chorde naturali; sia stata lor'ignoranza, ouer dapocagigne de i scrittori, ò
pur la presuntione d'alcuni poco intendenti; ma ne i buoni & corretti essemplari, de i
quali ne hò un appresso di me antico & scritto à mano, che si può ancora uedere & essa-minare; si trouano tra le chorde nominate di sopra. Si dè però auertire, ch'io nomino la
forma del Modo, la Ottaua diuisa nella sua Quinta & nella sua Quarta, & anco queste due
parti, che nascono dalla diuisione harmonica & arithmetica, che si odono replicate molte fiate ne i proprii Modi. Quando adunque haueremo da comporre, potremo saper da
quel, che si è detto, il modo, c'haueremo da tenere nel far cantar le parti della cantile-na; & nel por le Cadenze à i luoghi conuenienti per la distintione delle parole. Et simi-gliantemente potremo saper quello, c'haueremo da fare nel giudicar'ogn'altra Compo-sitione, sia poi in qual maniera si uoglia composta, tanto nel Canto fermo, quanto nel
Canto figurato.
, la quale è la mezana della detta Diapente. E' ben uero, ch'alcuni
Moderni secondo il lor parere) attribuiscono tali canti al Quartodecimo modo; ma di que-sto lascierò far giudicio ad ogn'uno, c'habbia intelletto. Tali canti, in alcuni de i libri
moderni, si trouano trasportati nel graue per una Diapente senza l'aiuto della chorda b.
fuora delle loro chorde naturali; sia stata lor'ignoranza, ouer dapocagigne de i scrittori, ò
pur la presuntione d'alcuni poco intendenti; ma ne i buoni & corretti essemplari, de i
quali ne hò un appresso di me antico & scritto à mano, che si può ancora uedere & essa-minare; si trouano tra le chorde nominate di sopra. Si dè però auertire, ch'io nomino la
forma del Modo, la Ottaua diuisa nella sua Quinta & nella sua Quarta, & anco queste due
parti, che nascono dalla diuisione harmonica & arithmetica, che si odono replicate molte fiate ne i proprii Modi. Quando adunque haueremo da comporre, potremo saper da
quel, che si è detto, il modo, c'haueremo da tenere nel far cantar le parti della cantile-na; & nel por le Cadenze à i luoghi conuenienti per la distintione delle parole. Et simi-gliantemente potremo saper quello, c'haueremo da fare nel giudicar'ogn'altra Compo-sitione, sia poi in qual maniera si uoglia composta, tanto nel Canto fermo, quanto nel
Canto figurato.
Del modo che si hà da tenere, nell'accomodar le Parti della cantilena; & del-l'estremità loro.Cap. XXXI.
 ; & nella Seconda parte
dia principio sopra la Chorda b; ò per il contrario. Sarà adunque auertito il Compositore di tal cosa, accioche la sua compositione sia purgata da ogni errore & da ogni discommodo; & lui sia riputato buono & perfetto Musico.
; & nella Seconda parte
dia principio sopra la Chorda b; ò per il contrario. Sarà adunque auertito il Compositore di tal cosa, accioche la sua compositione sia purgata da ogni errore & da ogni discommodo; & lui sia riputato buono & perfetto Musico.
In qual maniera l'Harmonie s'accommodino alle soggette Parole. Cap. XXXII.
Versibus exponi Tragicis res Comica non uult:Et anco Ouidio in questo proposito dice.Lib. 1. de rem. Am.
Callimachi numeris non est dicendus Achilles,Percioche se non è lecito tra i Poeti comporre una Comedia con uersi Tragici; non sarà anco lecito al Musico d'accompagnar queste due cose; cioè, l'Harmonia & le Parole insieme, fuor di proposito. Non sarà adunque conueniente, ch'in una materia allegra usiamo l'Ha[unclear: r]monia mesta & i Numeri graui; ne doue si tratta materie funebri & piene di lagrime, è lecito usar'un'Harmonia allegra & Numeri leggieri, ò ueloci, che li uoglia-mo dire. Per il contrario bisogna usar l'Harmonie allegre, & i Numeri ueloci nelle ma-terie allegre, & nelle materie meste l'Harmonie meste, & i Numeri graui; accioch'ogni cosa sia fatta con proportione. Il che penso, che ciascun saprà fare ottimamente, quando haurà riguardo à quel, c'hò scritto nella Terza parte, & considerato la natura del Modo, sopra 'l quale uorrà comporre la cantilena. Et debbe auertire d'accom-pagnare, quanto potrà, in tal maniera ogni parola, che doue ella dinoti asprezza, durezza, crudeltà, amaritudine, & altre cose simili, l'Harmonia sia simile à lei; cioè, alquanto dura, & aspra; di maniera però che non offendi. Simigliantemente quando alcuna delle parole dimostrerà pianto, dolore, cordoglio, sospiri, lagrime, & altre cose si-mili; che l'Harmonia sia piena di mestitia; ancora che questo d'alcuni moderni Aristarchi sia biasimato: ma di questo si ueda il cap. 11. del lib. 8. de i Sopplimenti. Il che farà ottimamente, uolendo esprimere i primi effetti, quando usarà di por le parti della cantilena, che page 439procedino per alcuni mouimenti senza 'l Semituono; come sono quelli del Tuono, & quelli del Ditono; facendo udire la Sesta, ouer la Terzadecima maggiori, che per loro natura sono alquanto aspre, sopra la chorda più graue del concento; accompagnandole anco con la Sincopa di Quarta, ò di Vndecima sopra tal parte, con mouimenti alquanto tardi, tra i quali si potrà usar'etiandio la sincopa della Settima. Ma quando uorrà espri-mere i secondi effetti, allora usarà (secondo l'osseruanza delle Regole date) i mouimenti, che procedono per Semituono, & per quelli del Semiditono, & altri simili; usando spes-so le Seste, ouer le Terzedecime minori, sopra la chorda più graue della cantilena, che sono per natura loro dolci & soaui; massimamente quando sono accompagnate con i debiti modi, & con discretione & giudicio. Ma si debbe auertire, che la cagione d'espri-mere simili effetti non s'attribuisce solamente alle predette consonanze poste in tal ma-niera; ma etiandio à i mouimenti, che fanno cantando le parti; i quali mouimenti sono di due sorti, Naturali & Accidentali. I Naturali sono quelli, che si fanno tra le chorde naturali della cantilena, oue non intrauiene alcun segno, ò chorda accidentale, & que-sti mouimenti hanno più del uirile, che quelli, che si fanno col mezo delle chorde acci-dentali segnate con tali segni
Cydippe non est oris Homere tui.
 . & b; i quali sono ueramente accidentali, & hanno alquanto del languido, da i quali nasce similmente una sorte d'Interualli, chiamati Acciden-tali; ma da i primi nascono quelli Interualli, che si chiamano Naturali. La onde dob-biamo notare, che i primi mouimenti fà la cantilena alquanto più sonora, & uirile; & li
secondi più dolce, & alquanto più languida. Per il che i primi potranno seruire ad
esprimere i primi effetti; & li secondi mouimenti potranno seruire à gli altri; di maniera
che accompagnando gli Interualli delle maggiori & delle minori consonanze, con li
mouimenti naturali & accidentali, che fanno le parti con qualche giudicio; si uerrà ad
imitare le parole con la ben'intesa harmonia. Quanto poi all'osseruanza de i Numeri,
considerata primieramente la materia contenuta nell'Oratione; se sarà allegra, si dè
procedere con mouimenti gagliardi & ueloci; cioè, con Figure, che portano seco uelo-cità di tempo; come sono le Minime & le Semiminime; ma quando la materia sarà
flebile, si dè procedere con mouimenti tardi & lenti; come n'hà insegnato Adriano ad
esprimere l'uno & l'altro modo in più cantilene, tra le quali si troua queste: I vidi in ter-ra angelici costumi: Aspro core e seluaggio: Oue ch'i posi gli occhi; tutte composte à sei uoci;
& Quando fra l'altre donne: & Giunto m'ha Amor, à cinque uoci; & infiniti altri. Et
questo non solamente si dè osseruare intorno i Numeri, ancora che gli Antichi inten-dessero tal cosa in un'altra maniera, di quello, che fanno i Moderni; come si uede chia-ramente in molti luoghi appresso di Platone; ma etiandio dobbiamo osseruar, di accommodare in tal maniera le parole dell'Oratione alle figure cantabili, con tali Numeri,
che non si oda alcun Barbarismo; come quando si fà proferire nel canto una sillaba longa, che si douerebbe far proferir breue; ò per il contrario una breue, che si douerebbe far
proferir longa; come in infinite cantilene si ode ogni giorno; ilche ueramente è cosa uer-gognosa. Ma di questa cosa si dee ad ogni modo molto ben considerate quello che si è
detto nel cap. 13. dell'Ottauo libro de i Sopplimenti: acciò le cose passimo bene; & non
si commetta errore ueruno. Ne si ritroua questo uitio solamente ne i Canti figurati, ma
anco ne i Canti fermi; com'è manifesto à tutti coloro, che hanno giudicio, conciosia
che pochi sono quelli, che non siano pieni di simili barbarismi, & che in essi infinite
uolte non si odi proferire le penultime sillabe di queste parole Domìnus, Angèlus,
Filìus, Miracùlum, Glorìa, & molt'altre, che sono breui, & passano presto, con lon-ghezza di tempo; ilche sarebbe cosa molto lodeuole, & tanto facile da correggere,
che mutandoli poco poco, si accommodarebbe ottimamente la cantilena, ne per
questo mutarebbe la sua prima forma; essendo che consiste solamente nella Legatu-ra di molte figure, ò note, che si pongono sotto le dette sillabe breui, senz'alcun pro-posito fatto lunghe; quando sarebbe sofficiente una sola figura. Si debbe similmen-te auertire, di non separare le parti della Oratione l'una dall'altra con Pause; co-page 440me fanno alcuni poco intelligenti; fino à tanto, che non sia finita la sua Clausula, ouer
alcuna sua parte, di maniera che 'l sentimento delle parole sia perfetto; & di non far la
Cadenza, massimamente l'una delle principali; ò di non porre le Pause maggiori di
quelle della Minima, se non è finito 'l Periodo, ò la sentenza perfetta dell'Oratione;
& di non por quella di Minima ne i punti mezani; percioche ueramente è cosa uitiosa;
la quale quanto sia osseruata d'alcuni Prattici poco aueduti de nostri tempi, ciascuno che
uorrà por mente à tal cosa, lo potrà con facilità uedere & conoscere. Debbe adunque
il compositore in cose simili aprir gli occhi, & non li tenir chiusi; percioche è di molta
importanza; accioche non sia riputato ignorante d'una cosa tanto necessaria; & deb-be auertire di porre la Pausa di Minima, ò di Semiminima (come li torna commodo)
in capo de i mezani punti dell'Oratione; percioche seruiranno in essa per i Comma; ma
in capo de i Periodi potrà porre quanta quantità de pause, ch'ei uorrà; percioche
mi pare, che poste in cotal maniera, si potrà ottimamente discernere i membri del
Periodo l'un dall'altro; & udir senz'incommodo alcuno il sentimento perfetto del-le Parole.
. & b; i quali sono ueramente accidentali, & hanno alquanto del languido, da i quali nasce similmente una sorte d'Interualli, chiamati Acciden-tali; ma da i primi nascono quelli Interualli, che si chiamano Naturali. La onde dob-biamo notare, che i primi mouimenti fà la cantilena alquanto più sonora, & uirile; & li
secondi più dolce, & alquanto più languida. Per il che i primi potranno seruire ad
esprimere i primi effetti; & li secondi mouimenti potranno seruire à gli altri; di maniera
che accompagnando gli Interualli delle maggiori & delle minori consonanze, con li
mouimenti naturali & accidentali, che fanno le parti con qualche giudicio; si uerrà ad
imitare le parole con la ben'intesa harmonia. Quanto poi all'osseruanza de i Numeri,
considerata primieramente la materia contenuta nell'Oratione; se sarà allegra, si dè
procedere con mouimenti gagliardi & ueloci; cioè, con Figure, che portano seco uelo-cità di tempo; come sono le Minime & le Semiminime; ma quando la materia sarà
flebile, si dè procedere con mouimenti tardi & lenti; come n'hà insegnato Adriano ad
esprimere l'uno & l'altro modo in più cantilene, tra le quali si troua queste: I vidi in ter-ra angelici costumi: Aspro core e seluaggio: Oue ch'i posi gli occhi; tutte composte à sei uoci;
& Quando fra l'altre donne: & Giunto m'ha Amor, à cinque uoci; & infiniti altri. Et
questo non solamente si dè osseruare intorno i Numeri, ancora che gli Antichi inten-dessero tal cosa in un'altra maniera, di quello, che fanno i Moderni; come si uede chia-ramente in molti luoghi appresso di Platone; ma etiandio dobbiamo osseruar, di accommodare in tal maniera le parole dell'Oratione alle figure cantabili, con tali Numeri,
che non si oda alcun Barbarismo; come quando si fà proferire nel canto una sillaba longa, che si douerebbe far proferir breue; ò per il contrario una breue, che si douerebbe far
proferir longa; come in infinite cantilene si ode ogni giorno; ilche ueramente è cosa uer-gognosa. Ma di questa cosa si dee ad ogni modo molto ben considerate quello che si è
detto nel cap. 13. dell'Ottauo libro de i Sopplimenti: acciò le cose passimo bene; & non
si commetta errore ueruno. Ne si ritroua questo uitio solamente ne i Canti figurati, ma
anco ne i Canti fermi; com'è manifesto à tutti coloro, che hanno giudicio, conciosia
che pochi sono quelli, che non siano pieni di simili barbarismi, & che in essi infinite
uolte non si odi proferire le penultime sillabe di queste parole Domìnus, Angèlus,
Filìus, Miracùlum, Glorìa, & molt'altre, che sono breui, & passano presto, con lon-ghezza di tempo; ilche sarebbe cosa molto lodeuole, & tanto facile da correggere,
che mutandoli poco poco, si accommodarebbe ottimamente la cantilena, ne per
questo mutarebbe la sua prima forma; essendo che consiste solamente nella Legatu-ra di molte figure, ò note, che si pongono sotto le dette sillabe breui, senz'alcun pro-posito fatto lunghe; quando sarebbe sofficiente una sola figura. Si debbe similmen-te auertire, di non separare le parti della Oratione l'una dall'altra con Pause; co-page 440me fanno alcuni poco intelligenti; fino à tanto, che non sia finita la sua Clausula, ouer
alcuna sua parte, di maniera che 'l sentimento delle parole sia perfetto; & di non far la
Cadenza, massimamente l'una delle principali; ò di non porre le Pause maggiori di
quelle della Minima, se non è finito 'l Periodo, ò la sentenza perfetta dell'Oratione;
& di non por quella di Minima ne i punti mezani; percioche ueramente è cosa uitiosa;
la quale quanto sia osseruata d'alcuni Prattici poco aueduti de nostri tempi, ciascuno che
uorrà por mente à tal cosa, lo potrà con facilità uedere & conoscere. Debbe adunque
il compositore in cose simili aprir gli occhi, & non li tenir chiusi; percioche è di molta
importanza; accioche non sia riputato ignorante d'una cosa tanto necessaria; & deb-be auertire di porre la Pausa di Minima, ò di Semiminima (come li torna commodo)
in capo de i mezani punti dell'Oratione; percioche seruiranno in essa per i Comma; ma
in capo de i Periodi potrà porre quanta quantità de pause, ch'ei uorrà; percioche
mi pare, che poste in cotal maniera, si potrà ottimamente discernere i membri del
Periodo l'un dall'altro; & udir senz'incommodo alcuno il sentimento perfetto del-le Parole.
Il modo, che si hà da tenere, nel por le Figure cantabili sotto le Parole. Cap. XXXIII.
Delle Legature.Cap. XXXIIII.
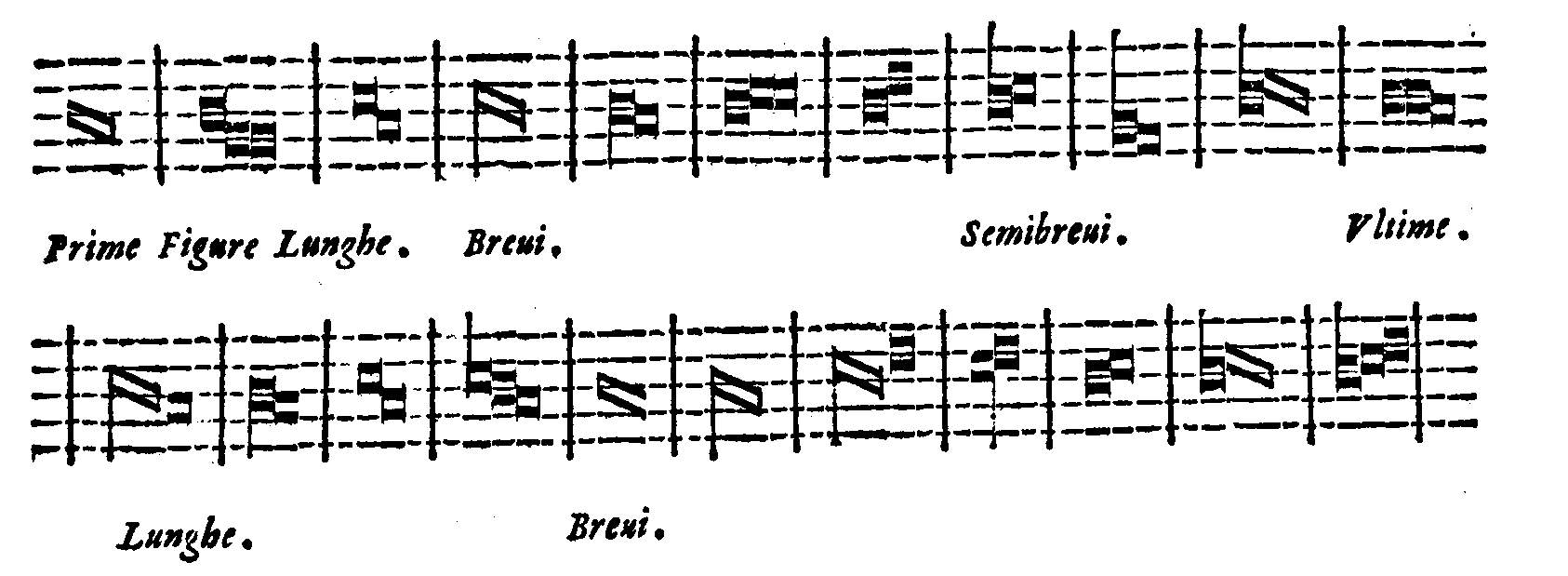
Quel che dè hauer ciascuno, che desidera di venire à qualche perfettione nel-la Musica.Cap. XXXV.
Della fallacia de i Sentimenti; & che 'l Giudicio non si dè far solamente con loro mezo; ma se li debbe accompagnar la Ragione.Cap. XXXVI.