Title: Istitutioni harmoniche
Author: Gioseffo Zarlino
Publication: Francesco de' Franceschi (Venezia, 1589)
Principal editor: Frans Wiering
Funder: Utrecht University Netherlands Organization for Scientific Research (NWO)
Edition: 2000
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht NetherlandsDA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria di Venetia,
già separatamente poste in luce; hora di nuouo corrette, accresciute,
& migliorate, insieme ristampate.
IL PRIMO VOLUME.
Contenente
L'ISTITVTIONI HARMONICHE
DIVISE IN QVATTRO PARTI;
NELLE QVALI, OLTRA LE MATERIE DELLA
Musica, si trouano molti luogi de Famosissimi Scrittori dichiarati.
CON DVE TAVOLE, L'VNA DELLE COSE PRINCIPALI;
& l'altra delle più notabili, che nellOpera si ritrouano.
Καὶ καμάτῳ ἀκαματῳ ἅμα εὔξησα,
Εὐνόῳ νῆν νόῳ, καὶ ὁδῳ εὐόδῳ ἐδιδαξα.

Καὶ μὴ διδόντος, ὀυδὲν ἰσχύι πόνος.IN VENETIA, MDLXXXIX.
Appresso Francesco de' Franceschi Senese.page ii
Tauola del contenente de tutte l'Opere diuise
in Quattro volumi,
| IL PRIMO DE I QVALI CONTIENE, |
L'Istitutioni Harmoniche diuise in Quattro parti, |
| IL SECONDO, |
Le Dimostrationi Harmoniche, contenute da Cinque Dialoghi, |
| IL TERZO, |
I Sopplimenti Musicali, partiti in Otto Libri; & |
| IL QVARTO, |
|

ALL'ILLVSTRISSIMO ET REVER.MO
SIG. VINCENZO DIEDO
PATRIARCA DI VENETIA.
Illustrissimo, & Reuerendissimo, che tutte le cose; per il desi-
derio che hanno di arriuare al loro principio; siano natural-
mente inchinate alla Propia operatione, & à conseguir la
perfettione loro: la onde essendo la Scienza la perfettione
dell'Intelletto; & l'Intendere, & il Sapere la Propia operatio-
ne dell'Huomo; mediante la quale viene à congiungersi al suo Principio: de
qui nasce, che ogn'vno naturalmente è tirato alla cognitione delle cose: nè mai
si stanca, nè satia, di andare inuestigando le loro cagioni; & di volere intendere
gli alti secreti della Natura. Nè penso, che à questo lo spinga la spe-
ranza dell'acquistar la cognitione di molte cose: ma etiandio di vna cosa sola;
percioche per conoscerla comprende, che và caminando verso la perfettione;
& giudica, che in ciò auanzando tutti gli altri, sia cosa degna di molta lode, &
honoreuole. Però stimo io, che amando gli Huomini per natura di tenere il
primo luogo in alcuna facultà: di giorno in giorno, hora aggiungendouisi vna
cosa, & hora vn'altra: per si fatto modo le Scienze, & le Arti siano cresciute; che
non è possibile quasi vedere, da qual parte se le possa aggiungere alcuna cosa di
nuouo. Et benche si potrebbe dire, che ciascuna di esse in ciò habbia hauuto
questa felicità: forse per il guadagno, che gli Huomini ne ritiranno; tuttauia fin
qui mi par di vedere, s'io non m'inganno, che la Musica sia stata poca auentu-
rata: percioche quantunque si ritrouino molti Autori, che hanno scritto molte
cose della Scienza, & dell'Arte; nondimeno l'Huomo leggendole, non ne può
acquistar quella cognitione, che egli desidera; perche veramente non hanno
tocco il uero fine, nè à sufficienza mostrato cosa alcuna di quelle, che sono di
maggiore importanza. La onde io, che fino da i teneri anni hò sempre hauu-
to naturale inchinatione alla Musica; hauendo già vna buona parte della mia
età intorno la cognitione di lei consumato; auedutomi di cotal cosa: volsi pro-
uare, s'io poteua in qualche maniera, le cose, che appartengono alla Theorica,
ò Contemplatiua, & alla Prattica, ritirar uerso la loro perfettione; & fare cono-
scere il lor Vero fine; per far cosa grata à tutti coloro, che di tal facultà si diletta-
no. Et auenga che io conoscessi, che questo era à me troppo graue carico; tutta-
uia pensai, che se bene non era per ridurle al loro vltimo grado di perfettio-
ne; almeno hauerei forse potuto incaminare la cosa di maniera, che sarei stato
page iv cagione di dar animo ad alcuno Spirito nobile di passare anco più oltra. Il per-
che hauendomi proposto cotal fine; & hauendo questi anni passati scritto le
presenti ISTITVTIONI, lequali insegnano le cose appartenenti all'vna, & al-
l'altra delle nominate parti; stimolato da gli Amici miei, che giudicarono que-
sto potere essere vtili à i Studiosi; mi è paruto di douerle mandare in luce; dedi-
candole alla Illustriss. & Reuerendiss. Sig.V. Et à ciò fare mi sono mosso primie-
ramente; per mostrare in qualche parte, quanto io resti obligato alle amore-
uolezze mostratemi da lei: dapoi; perche se perauentua fusse alcuno di animo
tanto maligno; che non hauendo rispetto, ch'io lo faccia con proponimento di
giouare altrui: si mouesse à biasimar queste mie fatiche; almeno fusse astretto
ad hauer riguardo all'Illustriss. nome di quel Signore, al quale sono state dedi-
cate. Si aggiunge oltra di ciò; che hauendo la singular Prudenza, la Giustitia, la
Religione & la Benignità; cose in lei da tutti conosciute, & lodate; parturito in
me vna incredibile riuerenza & deuotione; io non haueua altra via, nè modo da
poterla dimostrare. Nè si può veramente hauer dubbio delle singolari virtù di
vostra Sig. Illustriss. & Reuerendiss. poi che n'è stato fatto chiara testimonian-
za da questo sapientissimo Senato; il quale, per molte esperienze, hauendo cono
sciuto quanto ella era prudente ne i gouerni publici; si nella Città, come di fuo-
ri, ne i reggimenti di Bergamo, di Verona, & di Vdine; vltimamente ritrouan-
dosi in Padoa di magistrato, essendo seguita la morte del Reuerendissimo Con-
tarino; giudicandola degna di tanto honore, la elesse Patriarca di Venetia. Et
quantunque gli honori conseguiti, il più delle volte sogliono mutare gli animi,
& li costumi de gli huomini; tuttauia se bene ella è peruenuta à si honorato gra-
do, non è però mutato, ò sciemato in lei punto della bontà dell'animo suo; anzi
di gran lunga è accresciuto; come si può chiaramente vedere: che incontinente;
che ella hebbe conseguito cotal dignità, si risolue primieramente con le facultà
propie ad adornare la Chiesa, & dipoi, con grandissima spesa à riparare il Palaz
zo, che già incominciaua andare in rouina. Ma si come di continuo ella non
cessa di rinouare, & adornar la materiale; cosi di giorno in giorno (il che è segno
euidentissimo di Religione, & di Charità) non resta di souenire, & di solleuar la
spirituale; porgendo continuamente aiuto à i Poueri, non tanto à quelli del-
la sua città, quanto anche à i forestieri; & à quelli, che, partendosi dalla infe-
deltà vengono al Christianesimo: & come vigilante Pastore, & diligente Agri-
coltore & custode della Vigna del Signore, attende à prouedere, che 'l suo Greg
ge non sia da i Lupi offeso: & che da questa Vigna siano leuati li rami non buo-
ni; oueramente gouernati di maniera, che diuengano fruttuosi. Tutte queste
cose veramente fanno chiarissima fede al Mondo delle sue rare virtù: lequali mi
hanno mosso à dedicarle queste mie fatiche; quali elle si siano. Et se bene il do-
no è picciolo, riguardi almeno la osseruanza dell'animo mio verso lei, la quale
è infinitamente grande.
Di V.S. Illustrissima & Reuerendissima
Seruitore affettionatissimo
Gioseffo Zarlino.

TAVOLA PRIMA DI TVTTE
LE MATERIE PRINCIPALI, CHE SONO
CONTENVTE NELL'OPERA.
| IL Proemio, nel quale si dimostra, in qual maniera la Musica habbia hauuto prin cipio, & come sia stata accresciuta; & si ragiona della diuisione dell'Ope- ra. |
Facciata 1. | |
| Dell'origine, & certezza della Musica. | cap. 1. | fac. 5 |
| Delle laudi della Musica. | cap. 2. | fac. 7 |
| A che fine la Musica si debba imparare. | cap. 3. | 11 |
| Dell'vtile, che si hà della Musica, & dello studio, che vi dobbiamo porre, & in qual modo vsarla. |
cap. 4. | 12 |
| Quello che sia Musica in vniuersale, & della sua diuisione. | cap. 5. | 14 |
| Della Musica mondana. | cap. 6. | 16 |
| Della Musica humana. | cap. 7. | 21 |
| Della Musica piana, & misurata, ò vogliamo dir Canto fermo, & figurato. | cap. 8. | 24 |
| Della Musica Rhythmica, & della Metrica. | cap. 9. | 24 |
| Quello che sia Musica in particolare, & perche sia cosi detta. | cap. 10. | 25 |
| Diuisione della Musica in Speculatina, ò Contemplatiua, & in Prattica; per la quale si pone la dif- ferenza tra 'l Musico, & il Cantore. |
cap. 11. | 26 |
| Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità è Nume- ro. |
cap. 12. | 27 |
| Delle varie specie de' Numeri; & che nel Senario si trouano le Forme de tutte le Consonanze semplici. |
cap. 13. | 29 |
| Che dal numero Senario si comprendono molte cose della Natura, & dell'Arte. | cap. 14. | 30 |
| Delle Proprietà del numero Senario, & delle sue parti; & come tra loro si ritroua la Forma d'ogni Consonanza musicale. |
cap. 15. | 32 |
| Quel che sia Consonanza semplice, ò Composta; & che nel Senario in potenza si ritrouano le forme di tutte le Consonanze; & onde habbia origine l'Hexachordo minore. |
cap. 16. | 34 |
| Della Quantità continoua, & della discreta. | cap. 17. | 35 |
| Del Soggetto della Musica. | cap. 18. | 36 |
| Quel che sia Numero sonoro. | cap. 19. | 37 |
| Per qual cagione la Musica sia detta Subalternata all'Arithmetica, & mezana tra la Mathematica, & la Naturale. |
cap. 20. | 39 |
| Quel che sia Proportione: & della sua diuisione. | cap. 21. | 39 |
| In quanti modi si compara l'vna quantità all'altra. | cap. 22. | 41 |
| Quel che sia Parte aliquota, & Nonaliquota. | cap. 23. | 41 |
| Della produttione del genere Molteplice. | cap. 24. | 42 |
| Quel che sia Denominatore; & in qual modo si troui; & come di due proposte proportioni si possa conoscere qual sia la maggiore, ò la minore. |
cap. 25. | 43 |
| Come nasca il genere Superparticolare. | cap. 26. | 45 |
| Della produttione del genere . | cap. 27. | 45 |
| Del genere Molteplice Superparticolare. | cap. 28. | 46 |
| Della produttione del Quinto & vltimo genere, detto Molteplice superpatiente. | cap. 29. | 47 |
| Della Natura, & proprietà de i sopranominati Generi. | cap. 30. | 48 |
| Del primo modo di moltiplicar le Proportioni. | cap. 31. | 51 |
| Il Secondo modo di moltiplicar le Proportioni. | cap. 32. | 53 |
| Del Sommare le Proportioni. | cap. 33. | 54 |
| Del Sottrar le Proportioni. | cap. 34. | 54 |
| Del Partire, ò Diuidere le Proportioni, & quello che sia Proportionalità. | cap. 35. | 56 |
| Della Proportionalità, ò diuisione Arithmetica. | cap. 36. | 57page vi |
| Della Diuisione, ò Proportionalità Geometrica. | cap. 37. | 58 |
| In qual modo si possa cauare la Radice quadrata da vn proposto numero. | cap. 38. | 60 |
| Della diuisione, ouero Proportionalità harmonica. | cap. 39. | 61 |
| Consideratione sopra quello, che si è detto intorno alle Proportioni, & proportionalità. | c. 40. | 62 |
| Che il Numero non è cagione propinqua, & intrinseca delle Proportioni musicali, nè meno delle Consonanze; & quali siano le quattro cagioni, Finale, Efficiente, Materiale, & Formale nella Musica. |
cap. 41. | 66 |
| Della inuentione delle Radici delle proportioni. | cap. 42. | 68 |
| In che modo si possa ritrouar la Radice di più proportioni moltiplicate insieme | cap. 43. | 68 |
| Della proua di ciascheduna delle sopramostrate operationi. | cap. 44. | 69 |
| QVANTO la Musica sia stata da principio semplice, roza, & pouera di Consonan- ze. |
cap. 1. | fac. 71 |
| Per qual cagione gli Antichi nelle loro Harmonie non vsassero le Consonanze imper- fette; & Pitagora vietaua il passare oltra la Quadrupla. |
cap. 2. | 73 |
| Dubbio sopra la inuentione di Pitagora. | cap. 3. | 75 |
| Della Musica antica. | cap. 4. | 75 |
| Delle materie che recitauano gli Antichi nelle lor Canzoni, & di alcune Leggi musicali. | c. 5. | 79 |
| Quali siano stati gli Antichi Musici. | cap. 6. | 82 |
| Quali cose nella Musica habbiano possanza da indur l'Huomo in diuerse passioni. | cap. 7. | 86 |
| In qual modo l'Harmonia, & la Melodia, & il Numero possino muouer l'Animo, & disporlo à va- rij affetti; & indur nell'Huomo variati costumi. |
cap. 8. | 89 |
| In qual genere di Melodia siano stati operati li narrati effetti. | cap. 9. | 92 |
| De i Suoni, & delle Voci, & in qual modo naschino. | cap. 10. | 94 |
| Da che nascono i suoni graui, & da che gli acuti. | cap. 11. | 96 |
| Quel che sia Consonanza, Dissonanza, Harmonia, & Melodia. | cap. 12. | 97 |
| Diuisione delle Voci. | cap. 13. | 99 |
| Quel che sia Canto, & Modulatione, & in quanti modi si possa cantare. | cap. 14. | 99 |
| Quel che sia Interuallo, & delle sue specie. | cap. 15. | 100 |
| Quel che sia Genere; & di tre generi di Melodia, ò Cantilena appresso gli Antichi; & delle loro specie. |
cap. 16. | 101 |
| Per qual cagione ciascun de gli Interualli contenuto ne i mostrati Tetrachordi sia detto Incom- posto. |
ca. 17. | 106 |
| In qual modo si possa accommodare alla sua proportione qual si voglia Consonanza, ouero Inter- uallo. |
cap. 18. | 107 |
| Vn'altro modo di accommodar le Consonanze alla loro proportione. | cap. 19. | 109 |
| In qual modo si possa vdir qual si voglia Consonanza accōmodata alla sua proportione. | c. 20. | 110 |
| Del primo modo di Moltiplicar le Consonanze. | cap. 21. | 111 |
| Del Secondo modo di moltiplicar le Consonanze. | cap. 22. | 112 |
| Come si possa diuidere rationalmente qual si voglia Consonanza, ò Interuallo. | cap. 23. | 114 |
| In qual modo si possa diuidere qual si voglia Interuallo musicale in due parti equali. | cap. 24. | 115 |
| Altro modo di diuider qual si voglia Consonanza, ouero Interuallo musicale in due, ouero in più parti equali. |
cap. 25. | 116 |
| In qual modo la Consonanza si faccia diuisibile. | cap.26. | 118 |
| Quel che sia Monochordo; & perche sia cosi chiamato. | cap. 27. | 119 |
| Della Diuisione, ouero Ordinatione del Monochordo della prima specie del genere diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi fu l'Inuentore di questo Gene- re. & del suo ordine. |
cap. 28. | 119 |
| Che gli Antichi attribuirono alcune chorde de i loro istrumenti alle Sphere celesti. | cap. 29. | 123 |
| In che modo le predette Sedici chorde siano state da i Latini denominate. | cap. 30. | 126 |
| Consideratione sopra la mostrata Diuisione, ouer ordinatione; & sopra l'altre specie del genere Diatonico ritrouate da Tolomeo. |
cap. 31. | 128 |
| Del genere Chromatico; & chi sia stato il suo Inuentore; & in qual maniera lo potesse trouare; & delle chorde, che aggiunse Timotheo nel solito Istrumento. |
cap. 32. | 132 |
| Diuisione del Monochordo Chromatico. | cap. 33. | 136 |
| Consideratione sopra la mostrata diuisione, & sopra alcune altre specie di questo genere, ritroua page viite da Tolomeo. |
cap. 34. | 138 |
| Chi sia stato l'Inuentore del genere Enharmonico, & in qual maniera l'habbia ritroua- to. |
cap. 35. | 140 |
| Della Diuisione, ò Compositione del monochordo Enharmonico. | cap. 36. | 140 |
| Consideratione sopra la mostrata Partitione, ouero Compositione; & sopra quella specie di En- harmonico, che ritrouò Tolomeo. |
cap. 37. | 142 |
| Della Compositione del Monochordo Diatonico diatono, inspessato dalle chorde Chromatiche & dalle Enharmoniche. |
cap. 38. | 143 |
| Che 'l Diatonico Naturale, ò syntono di Tolomeo sia quello, che dalla Natura è prodotto, & che na turalmente habbia la sua forma da i Numeri harmonici. |
cap. 39. | 146 |
| Della diuisione del Monochordo Naturale, ouer syntono Diatonico, fatta secondo la natura, proprietà de i Numeri sonori. | cap. 40. | 149. |
| Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle mostrate specie Diatoni che. |
cap. 41. | 150 |
| Quel, che si dee osseruare nel temperamento de gli Instrumenti artificiali, di modo che nel nume ro delle chorde, & nella equalità de i Tuoni s'assimigli al Diatonico ditonico: ma ne gli Interual li consonanti; quantunque accidentali, al Naturale o Syntono di Tolomeo. |
cap. 42. | 153 |
| Dimostratione, dalla quale si può comprendere, che la mostrata Partecipatione, ò Distributione sia ragioneuolmente fatta; & che per altro modo non si possa fare, che stia bene. |
cap. 43. | 155 |
| Della compositione del Monochordo diatonico equalmente tēperato nel primo modo. | c. 44. | 159 |
| Se nelle Canzoni seguitiamo cantando gli Interualli prodotti da i veri Numeri sonori numeri, ouero i temperati; & della risolutione d'alcuni dubbij. |
cap. 45. | 164 |
| Della inspessatione del Monochordo Diatonico dalle chorde del genere Chromatico. | cap. 46. | 167 |
| In che maniera possiamo inspessare il detto Monochordo con le chorde Enharmoniche. | cap. 47. | 170 |
| Che più ragioneuole è dire, che gli Interualli minori nascano da i maggiori; che dire, che i mag- giori si compongano de i minori; & che meglio è ordinato l'Hexachordo moderno, che il Te- trachordo antico. |
cap. 48. | 173 |
| Che ciascuno de i tre Generi nominati, si può dire Genere & Specie; & che ogn'altra Diuisione, ouer'Ordinatione de Suoni sia vana & inutile. |
cap. 49. | 174 |
| Per qual cagione le Consonanze hanno maggiormente origine dalle Proportioni di maggio- re inequalità, che da quelle di minore. |
cap. 50. | 176 |
| Dubbio sopra quello, che si è detto. | cap. 51. | 178 |
| QVEL che sia Contrapunto, & perche sia cosi nominato. | cap. 1. | fac. 180 |
| Dell'inuentione delle Chiaui & delle Figure cantabili. | cap. 2. | 181 |
| De gli Elementi, che compongono il Contrapunto. | cap. 3. | 183 |
| Diuisione delle mostrate specie. | cap. 4. | 185 |
| Se la Quarta è consonanza; & donde auiene, che i Musici non l'habbiano vsata, se non nelle com- positioni de più voci. |
cap. 5. | 186 |
| Diuisione delle Consonanze nelle Perfette & Imperfette. | cap. 6. | 188 |
| Che la Quinta & la Quarta sono mezane tra le Consonanze perfette & l'imperfette. | cap. 7. | 189 |
| Quali Consonanze siano più piene, & quali più vaghe. | cap. 8. | 190 |
| Della differenza che si troua tra le consonanze Imperfette. | cap. 9. | 191 |
| Della propietà, ò natura delle consonanze Imperfette. | cap. 10. | 191 |
| Ragionamento particolare intorno all'Vnisono. | cap. 11. | 192 |
| Della Prima consonanza, detta Diapason, ouero Ottaua. | cap. 12. | 194 |
| Della Diapente, ouer Quinta. | cap. 13. | 195 |
| Della Diatessaron, ouer Quarta. | cap. 14. | 197 |
| Del Ditono, ouer Terza maggiore. | cap. 15. | 198 |
| Del Semiditono, ouer Terza minore. | cap. 16. | 198 |
| Dell'utile; che apportano nella Musica gli Interualli dissonanti. | cap. 17. | 199 |
| Del Tuono maggiore & del minore. | cap. 18. | 201 |
| Del Semituono maggiore & del minore. | cap. 19. | 201 |
| Dell'Hexachordo maggiore, ouero Sesta maggiore. | cap. 20. | 202 |
| Dell'Hexachordo minore, ouer Sesta minore. | cap. 21. | 203 |
| Della Diapente col Ditono, ouero della Settima maggiore. | cap. 22. | 204page viii |
| Della Diapente col Semiditono, ouero della Settima minore. | cap. 23. | 205 |
| In qual maniera naturalmente, ò per accidente, tali Interualli da i Prattici alle volte si pongano superflui, ò diminuti. |
cap. 24. | 206 |
De gli effetti che fanno questi segni  . b. & . b. &  . .
|
cap. 25. | 209 |
| Quel che si ricerca in ogni Compositione; & prima del Soggetto. | cap. 26. | 210 |
| Che le Compositioni si debbono essentialmente comporre prima di Consonanze, & dopoi per accidente di Dissonanze. |
cap. 27. | 212 |
| Che si debbe dar principio alle compositioni per vna delle consonanze perfette. | cap. 28. | 213 |
| Che non si debbe porre due Consonanze, contenute sotto vna istessa proportione, l'una dopo l'altra ascendendo, ouero discendendo, senza alcun mezo. |
cap. 29. | 216 |
| Quando le parti della Cantilena hanno tra loro Harmonica relatione; & in qual modo potiamo vsare la Semidiapente & il Tritono nelle compositioni. |
cap. 30. | 219 |
| Che rispetto si dè hauere à gli Interualli relati nelle compositioni di più voci. | cap. 31. | 222 |
| In qual maniera due, ò più Consonanze perfette, ouero imperfette, contenute sotto vna istessa forma, si possino porre immediatamente l'vna dopò l'altra. |
cap. 32. | 224 |
| Che due, ò più Consonanze perfette, ouero imperfette, contenute sotto diuerse forme, poste l'vna immediatamente dopò l'altra, si concedono. |
cap. 33. | 224 |
| Che dopò la Consonanza perfetta stà bene il porre la imperfetta; ouero per il contrario. | c. 34. | 225 |
| Che le parti della Cantilena debbono procedere per mouimenti contrarij. | cap. 35. | 226 |
| In qual maniera le parti della Cantilena possino insieme ascendere, ò discendere. | cap. 36. | 226 |
| Che si debbe schiuare, più che si può, i Mouimenti fatti per salto; & similmente le Distanze, che possono accascare tra le Parti della cantilena. |
cap. 37. | 229 |
| In qual maniera si debba procedere da vna Consonanza ad vn'altra. | cap. 38. | 230 |
| In qual maniera si debba terminare ciascuna cantilena. | cap. 39. | 233 |
| Il modo, che si dè tenere nel far li Contrapunti semplici à due voci, chiamati di Nota contra nota. |
cap. 40. | 234 |
| Che ne i Contrapunti si debbono schiuare gli Vnisoni, più che si puote, & che non si dè molto di lungo frequentare le Ottaue. |
cap. 41. | 237 |
| De i Contrapunti diminuiti à due voci; & in qual modo si possino vsar le Dissonanze; & de mol te Regole, che si deono osseruare in essi. |
cap. 42. | 238 |
| Il modo, che hà da tenere il Compositore nel fare i Contrapunti sopra vna Parte, ò Soggetto di- minuito. |
cap. 43. | 244 |
| Quando è lecito vsare in vna parte della Cantilena due, ò più volte vn passaggio, & quando non. |
cap. 44. | 247 |
| Che non è necessario, che la parte del Soggetto, & quella del Contrapunto incomincino insieme; & di quattro differenze, che si trouano delle Figure cantabili. |
cap. 45. | 250 |
| Che le Modulationi debbono essere ben regolate, & quel che dè osseruare il Cantore nel can- tare. |
cap. 46. | 251 |
| Che non si dè continuar molto di lungo nel graue, ò nell'acuto nelle modulationi. | cap. 47. | 253 |
| Che 'l porre vna Dissonanza, ouer vna Pausa di minima tra due Consonanze perfette d'vna istes- sa specie, che ascendino insieme, ò discendino, non fà, che tali consonanze non siano senza alcun mezo. |
cap. 48. | 254 |
| Della Battuta. | cap. 49. | 256 |
| Della Sincopa. | cap. 50. | 259 |
| Della Cadenza; quello che ella sia; delle sue specie; & dell'vso suo. | cap. 51 | 260 |
| Il modo di fuggir le Cadenze; & quello, che si haurà da osseruare, quando il Soggetto farà il mo- uimento di salto. |
cap. 52 | 266 |
| Delle Pause. | cap. 53. | 267 |
| Delle Consequenze. | cap. 54. | 269 |
| Delle Imitationi; & quello che elle siano. | cap. 55. | 275 |
| De i Contrapunti doppij, & quello che siano. | cap. 56. | 279 |
| Quel che dè osseruare il Contrapuntista oltra le Regole date; & d'alcune licenze, che potrà piglia re, quando li torneranno commode. |
cap. 57. | 289 |
| Il modo, che si hà da tenere nel comporre le Cantilene à più di due voci; & del nome delle Parti. |
cap. 58. | 293 |
| Delle Cantilene, che si compongono à Tre voci; & di quello, che si dè osseruar nel com- porle. |
cap. 59. | 298 |
| In Qual maniera la Quarta si possa porre nelle compositioni. | cap. 60. | 302 |
| Di alcune Regole poste in commune. | cap. 61. | 304page ix |
| Delle uarie sorti de Cōtrapunti arteficiosi; & prima di quelli, che si chiamano Doppij. | c. 62. | 310 |
| Delle uarie sorti de Contrapunti à Tre uoci, che si fanno à mente in Consequenza sopra un Sog- getto; & di alcune Consequenze, che si fanno di fantasia; & quello che in ciascheduna si hà osseruare. |
cap. 63. | 316 |
| Quel che si dè osseruare, quando si uolesse fare una Terza parte alla sproueduta sopra due altre proposte. |
cap. 64. | 331 |
| Quel che bisogna osseruare intorno le Compositioni di quattro, ò di più uoci. | cap. 65. | 336 |
| Alcuni auertimenti intorno le compositioni, che si fanno à più di Tre uoci. | cap. 66. | 340 |
| Del Tempo, del Modo, & della Prolatione; & in che quantità si debbino finire, ò numerare le Cantilene. |
cap. 67. | 347 |
| Della perfettione delle Figure cantabili. | cap. 68. | 350 |
| Della Imperfettione delle Figure cantabili. | cap. 69. | 353 |
| Del Punto, delle sue specie; & de i suoi effetti. | cap. 70. | 355 |
| Dell'Vtile, che apportano i mostrati Accidenti nelle buone Harmonie. | cap. 71. | 359 |
| Delle Chorde communi, & delle Particolari delle cantilene Diatoniche, Chromatiche, & En- harmoniche. |
cap. 72. | 362 |
| Se l'uno de i due ultimi Generi si possa usar semplice nelle sue chorde naturali, senza adoperar le Chorde particolari de gli altri. |
cap. 73. | 364 |
| Che la Musica si può usare in due maniere; & che le Cantilene, che compongono alcuni Moder- ni, non sono sottoposte ad alcuno de i due nominati Generi. |
cap. 74. | 365 |
| Che 'l Diatonico può procedere nelle sue modulationi per gli Interualli di Terza maggiore, & di minore; & che ciò non faccia uariatione alcuna di Genere. |
cap. 75. | 365 |
| Che doue non si ode nelle compositioni alcuna uarietà di Harmonia, iui non può essere uarietà alcuna di Genere. | cap. 76. | 368 |
| Dell'utile, che apportano i predetti due Generi; & in qual maniera si possino usare, che faccino buoni effetti. |
cap. 77. | 368 |
| Per qual cagione le Compositioni, che compongono alcuni Moderni per Chromatiche, facciano tristi effetti. |
cap. 78. | 370 |
| Delle cose, che concorreuano nella compositione de i Generi. | cap. 79. | 372 |
| Opinioni delli Chromatisti ributtate. | cap. 80. | 375 |
| QVELLO, che sia Modo, ò Tuono; & delle sue Specie. | cap. 1. | fac. 377 |
| Che i Modi sono stati nominati da molti diuersamente; & per qual cagione. | c. 2. | 383 |
| Del Nome, & del Numero de i Modi. | cap. 3. | 385 |
| De gli Inuentori de i Modi. | cap. 4. | 387 |
| Della Natura, ò Proprietà de i Modi. | cap. 5. | 388 |
| Dell'Ordine de i Modi. | cap. 6. | 392 |
| Che l'Hypermistolydio di Tolomeo non è quello, che noi chiamiamo Decimo modo. | c. 7. | 394 |
| In qual maniera gli Antichi segnauano le Chorde de i loro Modi. | cap. 8. | 395 |
| In qual maniera s'intenda la Diapason essere harmonicamente, ouero arithmeticamente me- diata. |
cap. 9. | 397 |
| Che i Modi moderni sono necessariamente Dodici; & in qual maniera si dimostri. | cap. 10. | 398 |
| Altro modo da dimostrare il numero delli Dodici Modi. | cap. 11. | 399 |
| Diuisione de i Modi in Autentichi, & Plagali. | cap. 12. | 402 |
| Delle Chorde finali di ciascun Modo; & quanto possa ascendere, ò discendere di sopra, & di sotto le nominate chorde. |
cap. 13. | 403 |
| De i Modi communi, & de i Misti. | cap. 14. | 404 |
| Altra diuisione de i Modi; & di quello, che si hà da osseruare in ciascuno, nel comporre le canti- lene; & in qual maniera le Otto sorti di Salmodie con essi si accompagnino. |
cap. 15. | 405 |
| Se co 'l leuare da alcuna cantilena il Tetrachordo Diezeugmenon; ponendo il Synemennon in suo luogo, restando gli altri immobili; un Modo si possa mutare nell'altro. |
cap. 16. | 408 |
| Della Trasportatione de i Modi. | cap. 17. | 410 |
| Ragionamento particolare intorno al Primo modo; della sua Natura; de i suoi Principij; & del- le sue Cadenze. |
cap. 18. | 411 |
| Del Secondo Modo. | cap. 19. | 414 |
| Del Terzo modo. | cap. 20. | 415page x |
| Del Quarto modo. | cap. 21. | 418 |
| Del Quinto modo. | cap. 22. | 420 |
| Del Sesto Modo. | cap. 23. | 421 |
| Del Settimo modo. | cap. 24. | 423 |
| Dell'Ottauo modo. | cap. 25. | 425 |
| Del Nono modo. | cap. 26. | 427 |
| Del Decimo modo. | cap. 27. | 428 |
| Dell'Vndecimo modo. | cap. 28. | 430 |
| Del Duodecimo, & vltimo modo. | cap. 29. | 433 |
| In qual maniera si debbe far giudicio de i Modi; & quello, che si dee osseruare nelle Composi- tioni. |
cap. 30. | 434 |
| Del modo, che si hà da tenere, nell'accommodar le Parti della Cantilena; & delle estremità loro. |
cap. 31. | 436 |
| In qual maniera le Harmonie si accommodino alle soggette Parole. | cap. 32. | 438 |
| Il modo che si hà da tenere; nel por le Figure cantabili sotto le Parole. | cap. 33. | 440 |
| Delle Legature. | cap. 34. | 441 |
| Quel che dè hauer ciascuno, che desidera di venire à qualche perfettione nella Musica. | c. 35. | 444 |
| Della fallacia de i Sentimenti; & che 'l giudicio non si dè fare solamente col loro mezo: ma se li debbe accompagnar la Ragione. |
cap. 36. | 445 |
 page xi
page xi
A I STVDIOSI LETTORI.
hanno, di non stampar mai Opera, che non contenga qual-
che errore; sia poi fatto, ò per la difficultà, ò per altra ca-
gione; ne hanno lasciato incorrere alcuni, tanto nel conte-
nente dell'Opera, quanto ne i essempij del Canto. Però,
Lettori humanissimi, sopportando con la vostra buona Pa-
< tienza questo diffetto; li correggerete per ordine, secondo che ui mostraranno
i numeri segnati delle facciate, à questo modo.
| Facciata. | Linea. | |
| 21 | nel margine. | Musicae libro. |
| 27 | 15 | Voce, ò co 'l mezo. |
| 35 | 3 | quale. |
| 4 | Diapason. | |
| 5 | de. | |
| 51 | 32 | Il [[per]]che venēdo al proposito |
| 52 | 6 | termini, ò numeri. |
| 9 | che vorremo. | |
| 64 | 30 | volessimo accōmodare alla |
| 77 | 47 | alcuna, che si |
| 80 | 43 | Percussioni |
| 83 | 38 | Sacada |
| 93 | 37 | habbiamo detto; visse |
| 138 | 35 | Superparticolare. |
| 147 | 22 | la Sesquiquinta. |
| 153 | 8 | nella Sesquisesta [[pro]]portione |
| Facciata. | Linea. | |
| 160 | 15 | violentemente. |
| 169 | 16 | questa X. tanto. |
| 238 | 3 | Fortunatam. |
| 255 | 1 | Particella. |
| 261 | 29 | Cadenze di due. |
| 266 | 10 | ò Periodo. |
| 285 | 19 | habbia le sincope. |
| 304 | nel margine. | Vide Def. Demonst. |
| 353 | 28 | l'essere Imperfetto |
| 360 | 47 | Chordae, & Chorda. |
| 434 | 5 | le quali non sono. |
| 440 | 8 | tener. |
| 448 | 4 | prima furono giudicati. |
| 9 | allora fu riputato. | |
| 28 | costui. |
| 220 | Nel Primo essempio de i Tritoni; la prima nota della parte graue vuol essere nel secō do spacio tra la prima, & la seconda riga. |
| 245 | Nell'vltima riga della parte graue, la sesta Fi- gura vuol stare sopra la prima riga. |
| 248 | La chiaue nel principio della parte del Sog- getto, vuol essere sopra la riga di mezo. Et la 31. nota vuol stare sopra la seconda riga. |
| 278 | L'ultima nota del secondo ordine del Canto del primo essempio, vuol essere nella secō da riga. |
| 287 | Nel primo ordine della parte acuta, bisogna leuare la Semiminima posta auanti la mi- nima col punto nel fine. |
| 300 | Nell'vltimo ordine la seconda nota delle due
che si trouano nella prima riga, vuol stare nella seconda. |
| 304 | Il luogo proprio dell'vltimo essempio è tra la line 29. & la 30. |
| 315 | La prima Figura del primo ordine nella par- te più acuta, uuol essere una Breue: & nel Secondo, manca dopò la terza nota una Semiminima nel secondo spacio. |
| 321 & 322 | L'vno de due essempij è superfluo, ma ciò importa poco. |
| 322 | Nell'antepenultima dell'essempio ui uà una coronata [[mus.ferm]]. |
| 323 | L'ultima nota del quarto ordine, uuol essere una Chroma. |
| 325 | Nel terzo ordine dell'essempio ui è di più il Segno del Tempo nel principio.page xii |
| 332 | La Figura, ò nota posta delle parte più acuta nel fine nel quarto ordine, vuol essere so- pra la riga del mezo. Et nella parte graue, nel quarto ordine, la Vndecima Figura, vuol essere Semiminima. |
| 339 | Nel principio del primo ordine nella parte acuta, il Segno del Tempo, vuol esser ta- gliato. |
| 341 | Nel principio del primo essempio, & primo ordine, che è nella parte più acuta; prima se porrà la chiaue nella prima riga; dopoi s'accommoderà la prima nota co 'l punto, & l'altra nota seguente sopra il Secondo Spacio; perche sono poste al riuersa. |
| 345 | Sopra la quarta nota della parte nell'Alto, nel principio manca il Segno della Presa. |
| 355 | Nel primo ordine tra le due prime Semibre- ui vi manca il punto di diuisione. |
| 357 | Nel primo ordine l'vna delle tre Breui dopò e 'l punto è superflua. |
| 363 | Nell'ordine Chromatico la Cifera  và po- và po-sta nel secondo spacio. |
| 401 | Nel primo essempio manca nel quarto spacio vna Breue nera. |
| 416 | Nel terz'ordine auanti le due Chrome man- ca il punto nel secondo spacio; & nel se- sto il primo punto è superfluo. |
| 425 | Nel quarto ordine l'vltima delle quattro Semiminime, vuol essere vna Minima. |
 page xiii
page xiiiSECONDA TAVOLA DELLE COSE
PIV' NOTABILI CONTENVTE
NEL PRIMO VOLVME.
A
2. f. Ritrouò il comporre i Salmmi à due chori,
che ciaschedun da se stesso accordasse. 346. m
di Pindaro. 83. f. Fù sospinto da Timotheo à
pigliar l'arme. 86. m 87. f. Fù mosso dalla leg-
ge Orthia à pigliar l'arme. 88. p. Quando re-
gnò. 93. m. Incitato dal suono di vn Piffe-
ro. 390. f
porti. 356. f. Considerata da gli Antichi in più
maniere. Doue cada. 357. f
10. m. Ritrouò il canto della Cetera, & la
sua poesia. 83. p. Musico, & poeta. 83. p. Inuen-
tore della cetera. 83. p. Inuentore dell'Harmo-
nia Lidia. 387. m
crificij. Cantauano Hinni composti di Versi
sonori: & quello che per essi intendeuano. Et
accompagnauano alla sepoltura i loro morti
con Istrumenti Musicali. 17. p. Erano poueri di
Consonanze. 71. m. prestauano gran fede alla
dottrina di Pitagora. 73. m. In qual maniera
rappresentauano le lor Comedie, & Tragedie.
Cantando le recitauano. Cantauano al suono
del Piffero, recitando le lor canzoni compo-
ste in versi. Saltauano, ò ballauano mentre
il Musico recitaua alla lira. 77. f. Vsarono va-
rij istrumenti ne i loro esserciti. 78. p Quello
che recitauano ne i loro canti. 79. f. Quali co-
se cantauano al suono de i Pifferi nella mor-
te de i loro parenti. 80. p. Et quali insegnaua-
no à i loro giouani. 80. p. Ballauano al canto de
i Musici. 80. p. In qual modo recitauano le lo-
ro Leggi musicali al suono del piffero. 81. p.
Saltauano, & ballauano, quando si recitauano
le Comedie & Tragedie. 82. p. Per qual cagio
ne diuidessero il loro Systema massimo per
Tetrachordi, & non per Pentachordi. 120. m.
Attrbuirono varie chorde de i loro Istrumen-
ti alle Sphere celesti, secondo il vario loro pa-
rere. 129. f. Diuersamente posero le chorde de
i loro Istrumēti, secondo i pareri diuersi. 124. f
Per qual cagione ritrouassero tante specie di
Melodia in ciaschedun genere. 144. m. Nelle
compositioni de i loro generi hauaeano non so
lo le Harmonie differenti; ma i Numeri.ò Me
tri determinati. 373. p. Non faceuano modu-
lare molte parti insieme. 373. f. Cantauano al
suono di vno Istrumento. 373. f
11. p. Fù Musico, & Poeta. 83. m. Inuentore del
Dithyrābico. Et in qual maniera volēdosi preci
pitare nel Mare si componesse l'animo. 88. m
ra il Numero semplice. 36. m. Attēde alla mol-
tiplicatione della Vnità. 63. f. Proportionalità,
[[per]]che habbia tra i numeri minori le Proportio
ni maggiori, & tra i maggiori le minori. 64. p.
l'imitare fa ogni cosa imperfetta. 155. p. Orato
ria hà auuto principio dalla Poesia. 77. m
ca. 385. f. Pone le Distanze, ò Interualli di cia
scheduno Modo. 303. f
ò Diapason solamente. 188. p. Et Platone qua-
li Harmonie approuassero. 329. m
farsi & disporsi à diuerse passioni dell'ani-
mo. 91. m
sica. 8. f. Fa prosessione di quelle cose che sono
in continuo mouimento. 36. f
B
tioni, nelle Parole. 439. f. Come si possino ac-
conciare ne i Canti fermi. 439. f
me sia diuersamente detta da molti, & ha due
parti. 256. m. Equale & Inequale come è se-
gnata da i Musici. 256. f. Trochaica & Spon-
daica quale sia. 258. f
C
dè vsare. 261. p. E di tanto ualore, quanto
è il punto nella Oratione. E il punto della can
tilena. 261. p. Di due sorti. 268. m. 412. m. Dee
terminare in Consonanza perfetta. 266. m
Canti fermi. Doue & quando far si debbo-
no. 412. m. 413. f
quali siano. 66. f. Sono parti essentiali della
cosa. 66. f. Non appartengono alla natura del-
la cosa. 66. f. Di due sorti. 66. f. Alcune pri-
me & alcune seconde. 66. f. Delle Cantilene
allegre & meste. 192.
pre è prima, ouero insieme cō lo effetto. 93. m
Di esprimere diuersi effettti nelle compositio-
ni, non si atribuisce solamente alle consonan-
ze. 439. p
Spartani quello che faceuano nella guerra. 390. f
rato, o misurato quello che sia. 24. p. Ouer can
tilena da che nasca. 99. m. Si piglia in molti mo
di. 99 m. Parte acuta della Cantilena è attri-
buita al fuoco. 294. p
ria & forma. 4. p. Senza il Soprano, ò Canto co
me si accompagnano. 295. m. 337. f.
Come numerino. 348. f. 350. p. Del primo
modo. 412. p. Del secondo modo. 414. p.315. f
Del Terzo modo. 416. p. Del Quarto modo
419. f. Del Quinto modo. 421. m. Del Sesto
modo. 422. p. Del Settimo modo. 423. f. Dell-
l'Ottauo modo. 425. f. Del Nono modo. 428. p
Del Decimo modo. 428. p. Dell'Vndecimo
modo. 430. f. 431. p. m. f. Del Duodecimo mo-
do. 433. f. Che nō finiscono nella propria loro
chorda finale. 435. m. Ecclesiastiche di piu ma
niere. 416. p
te chorde. 21. f. Come era da principio. 72. p.
Di Timotheo milesio appesa in altro; & perche
132. m. Di Mercurio com'era accordata. 132. f
cordate. 72. m. Perche siano dette da Horatio
seuere. 82. f. Piu lasse debolmente percuotono
l'aria & piu durano i loro suoni. 96. m. Piu te-
se piu gagliardamēte [[per]]cuotono l'aria mē du
rano i loro suoni. 36. m. Quādo tremono fanno
molti suoni differenti. 96. f. De gli Istrumenti
come fussero nominate da gli Antichi. 123. m.
Aggiunte da Timotheo nello istrumento an-
tico, fv vna secondo Boetio, & quattro secon-
page xvdo 'l parere di Pausania. 132. m Della Lira di
Mercurio contenenti la Arithmetica, Geome
trica, & Harmonica proportionalità. 132. f. E-
streme del Tetrachordo Diatonico immuta-
bili. Et à gli altri generi communi. 132. f. Me-
zane del tetrachordo diatonico sono variate
per il sito. 132. f. Del Diatonico quali siano cō
muni à gli altri generi. 127. f 136. m. 140. f. In
tutto stabili quali siano. 133. m. In tutto mobi
li. 144. p. Nè in tutto mobili, nè in tutto stabili.
143. p. Colorate ne gli istrumenti in qual ma-
niera si segnano nelle cantilene. 169. m. Enhar
moniche come si conoscono ne gli istrumēti.
171. m. Vtili quali siano in vno istrumēto. 170.
m. Denominate da i Musici in qual maniera.
181. f. 362. m. Naturali, & accidentali quali sia-
no. 219. m. Perche siano cosi chiamate. 360. f.
Naturali. & essentiali sono Quindeci. Acci-
dentali sono tre. 362. f. Particolari di ciascuno
de i tre Generi. Particolari chromatiche co-
me si conoscono. Particolari enharmoniche
come si conoscono. 363. f
Systema massimo. 121. f. Hypate attribuita à
Saturno. Proslambanomenos attribuita alla
Sphera della Luna. 124. f. Proslambanome-
nos da Latini chiamata A. re. 126. f. Terza,
Sesta, & Settima de gli Istrumenti antichi
non facceuano consonāza alcuna con la prima.
129. f. Prima della partecipatione fà bisogno
che sia stabile. 156. f. Trite synemennon se-
gnata col b rotondo. 169. f. Mese è fine del Te-
trachordo meson, & principio del Synemen-
non. 362. f. Gruissima di ciascheduna Diapen
te è come finale à due Modi. 403. p
namento del Diatonico. 93. m. Che natura
habbia. 93. m. Ritrouato da Timotheo Mile-
sio Lirico. 93. m. 132. m. Hà tre specie. Anti-
co qual sia. Molle qual sia. 104. f. Incitato qual
sia. Non durò molto tempo. Assimigliato
da Tolomeo al genere Mathematico, & allo
Economico. Doue sia cosi detto. 105. m.
Perche è detto lasciuo, & molle. 371. p. molle
di Tolomeo contiene il Semiditono & lo
Hexachordo minore consonanti.138. f. Co-
me nasca. 168. m
tempo due cose significano. 257. m. Che gli
Antichi vsauano ne i loro Modi, erano raddop
piate. 295. m
Circolo contiene Sei triangoli equilaterali equali,
& maggiori. 31. p
fiate per il dritto da quella misura, che misura
il cerchio dal centro alla circonferenza. 31. p
casta col mezo della Musica. 86. m. Data in
guardia ad vn Musico dorico. 388. f
354. p. 358. p. Non lieua all'Ethiope l'essere
Huomo, & Rationale. 351. p
Monochordo Diatonico syntono si troui. 49. f
Da qual proportione sia contenuto. Come na-
sca. 149. f. E la differenza che si troua tra il
Tuono maggiore, & il minore. 149. f. Non è
adorabile in alcun genere. 150. p
qualche harmonia, ouero hà con l'harmonia
qualche conuenienza. Perfetta qual sia. 293. f.
Ouer vnione della Diapente con la Diatessa-
ron in quanti modi fare si possa. 398. p. Di Gio
squino poco lodata. 448. p
Diuerse appresso li Musici. 412. p. De Poeti. &
de Musici chiamate Modi. 378. p
Come si caua dalla Guida nelle Imitationi
sciolte. 276. p
cantilene. 348. f. 350. p. Sopra alcune parole di
Boetio. 396. p
numeri ci fa scoprire molti secreti nelle sacre
Scritture 28. p
97. m. f. 176. f. 193. m In qual modo nasca. E
contenuta da vna sola proportione. 97. f. Har-
moniosa. 98. m. Può nascere da suoni, & da vo-
ci. 98. f. Come si accommodo alla sua propor-
tione nella quantità sonora. 107. m. & 108. m.
Come si diuida in più parte equali. 115. m. 116
f. Come si faccia diuisibile. E qualità passibile.
Da se indiuisibile. 118. f Si troua tra due suoni
distanti per il graue, & per l'acuto. 193. f
page xvi
delle Cantilene. 4. p. Sono cose della Natura.
3. m. Si dice esser composti in tre maniere.
34. m. Come si numerino, ò replichino. 35. f.
Della Musica quante erano appresso gli Anti-
chi. 74. f Perfette quali siano. 25. p. Imperfette
nō riceuute per cōsonanze, ne erano appresso
gli antichi. Imperfette perche non erano ri-
ceuute da gli antichi. 75. p. Diuerse contenute
tra la Diapason sono sette. 128. m Si aggiun
gono insieme ad vn termine commune. 173. f
Et interualli ordinari per la perfettione del-
l'Harmonia. 164. p Perche non hanno ori-
gine da i Generi di minore inequalità. 177. p.
Perfette, & imperfette quali siano. 198. p. Per
fette, & imperfette, perche siano cosi chiama
te. 188. m. In qual modo si chiamino maggior
mente perfette l'una dell'altra. 189. m. Quali
animo il graue, & quali l'acuto. 190. m. Imper
fette maggiori. Imperfette minori 191. f.
Meste, ò languide. Allegre, & sonore. 191. f.
Qual luogo tengono particolarmente nel loro
ordine. 305. m
za parte di questa opera. Quello che sia. Per-
che sia cosi detto.180. f. Di due sorti. Sempli
ce. Diminuito. Buono, & diletteuole. 181.
p. Principalmente si compone di consonan-
ze, & per accidente di dissonanze. 192. f.
Doppio di due sorti. 279. f. Quando si chiama
legato. 289. m
punti. 180. f. Doppij à più di due voci sono di
più sorti. 279. f
vna Terza parte sopra due all'improuiso quel
lo che osseruano. 331. m
Proportionato vero soggetto della Musica.
38. m. Sottoposto alla quantità continua. 63.
m. E Vnità nella Musica. 63. m. Oggetto del
Senso. Considerato diuersamente viene à por
nel Senso diuerse possanze. 359. m
teria, & di forma. 3. m. Più lontana dalla sua
origine è men pura, men semplice, men
compresa dal Senso, & meno intesa dall'In-
telletto. 41. p
71. m. Che si attribuiscano alla Natura nel-
la Musica.100. p. Che si attribuiscono all'Ar-
te. 100. p. Che considera lo Speculatiuo. 100. m.
Che appartengano al Prattico. 100. m. Che ap
partengano al Compositore. Che appartenga-
no al Cantore. 252. m
ca. 124. m. Nel comporre le Messe. 345. f. Dei
Pitagorici. 389. f De Spartani. 390. p. De gli
Antichi nel sepelire i morti. 17. p. 391. p
D
Salmi, come al presente si cantano nelle
Chiese. Ordinò che se gli aggiungesse il Ver
so Gloria Patri. 387. p
uani à vita honesta, & temperata 10. m. Inuen
tore del modo Hypofrigio. 388. p
Come si segna, & si accommodi alle figure
cantabili. 258. f
co 'l suono. Ordinò che nel Tempio di Dio si
vsassero canti, & suoni. 10. f. Musico, & Poe-
ta Santo. Posto nel numero de i poeti. Scris-
se elegantemente i Salmi in Verso Lirico.
Chiamato Cantore, ò Sonatore. Hauea
ogni Scienza nella Musica. 83. f. Quando re-
gnò. 94. p
Corfù, & compose la rouina di Troia, & le noz
ze di Venere, & Vulcano. Fù Musico, & Poe
ta. 83. p. Muoue al pianto Vlisse. 89. f
ne di gli istrumenti arteficiali. 154. p. Nō pati-
sce alteratione nella sua proportione Dupla.
156. m. Cagione delle cōsonanze, & altri inter
ualli. 183. f. Perche sia cosi detta. 173. f. Posta
tra i semplici elemēti del cōtrapunto per qual
cagione. 183. m. Non è consonanza composta.
page xviiCome nasca. 183. f. Hà principio dall'vnisono.
185. f. Da che sia detta. 194. m. Cōsiderata i due
Modi. 194. f. Hà Sette specie. 194. f. Come si pōga
ne i Cōtrapunti. 196. f. In quanti modi possa es
ser da vna chorda mezana diuisa in vna diapē
te, & in vna diatessaron. 399. f
me parti di vn Comma. 153. f. Hà quattro
specie.196. p. Cōsiderata in due modi. 196. p.
Donde sia detta. 196. f. In quante maniere
si possa vnire, ò comporre con la Diatessa-
ron. 398. p. Et diatessaron sono i lati ò mem
bri della diapason. 402. m. 384. m. Co 'l ditono
si può chiamare composto. E interuallo dis-
sonante. Si considera in due modi. Hà due
specie 204. f. Quello che sia secondo i pratti-
ci. e detto Settima. E detto Heptachordo,
& perche. come si ponga ne i Contrapunti.
205. p. Col Semiditono si può chiamare in-
teruallo composto. Si può considerare in due
modi. Hà cinque specie. 205. m. Quello che
sia secondo i prattici. E detto Settima. E det
to Heptachordo. Come si ponga ne i Contra
punti. 206. p
chi. 120. p. Accresciuta di due settime parti
di vn Comma. 153. p. Quello che sia. Con-
siderata in due modi. Hà tre specie. 197. p.
Perche sia cosi detta. Diuersamente chiama-
ta. Come si accommodi ne i Contrapunti.
197. f. In quante maniere accompagnar si pos-
sa nelle compositioni. 302. m
d'ogni altro duro, & naturale. D'ogn'altro an
tichissimo. 93. m. Hà cinque specie. Per-
che sia cosi detto. Molte fauorito da gli Anti
chi filosofi. Molto conforme alla compo-
tione del mondo. Molle quello che fusse.
302. p. Syntono quale sia. 102. m. Vsato da
Moderni. 102. m. Toniaco qual sia. Equale
qual sia stato. Perche sia cosi chiamato. 102. f.
Comparato da Tolomeo al genere Theologi-
co, & Politico. 193. f. Contiene il Chromati-
co, & lo Enharmonico. 103. f. Molle di Tolo
meo contiene il Trihemituono consonante.
138. p. Perche da gli antichi è detto più duro,
& più naturale de gli altri due generi. 378. p.
Conuiene alle Harmonie Frigie. 389. m
Meta de Semituono minore appresso gli An-
tichi. 105. f. Posto dal Filosofo per principio di
questo genere Melodia. 148. f. E il Semituono
minore secondo la opinione di Filolao. 169.
m. Appresso gli antichi posto per indiuisibi-
le, & minimo interuallo. Posto da Aristo-
tele per misura commune d'ogni consonan-
za. 173. p
suoni graui, & acuti in vna sol chorda non
sono vdibili. De Suoni in van sol chorda
perche non sono vdibili. 96. f. de i Mo-
di. 378. p. 379. m
Specifica costituisce la Specie. 366. f. di Giu-
lio Polluce tra l'Harmonia, & il Modo. 383. f.
Che si troua tra i Modi autentichi, & li pla-
gali. 402. m
ne gli Istrumenti moderni, da quello che
nasca. 161. f
do la ragione,ò la forma; ma si bene secondo
la materia, & il soggetto. 176. p
re in due modi composta. 30. p. E contenuta
dalla proportione Quadrupla. Col ditono,
ò Decimasettima contenuta dalla propor-
tione Quintupla. à 206. m. Diapente, ouer De-
cimanona contenuta dalla proportione Sestu
pla. 206. p
f. Può nascere da i Suoni, & dalle voci. 98. f.
Da che si genera nelle Cantilene uocali. 165. f.
Nella Sincopa perche è soportabile. 240. f
& come si accompagnino. 240. m. Come si ri-
soluino. 242.
page xviii
nale, ne meno descritta con numeri determi-
nati. 156. m
meo. 16. p 142. f. Imperfetto di una settima
parte si vno Comma. 153. f. Enharmonico
qual sia. 170. m. In due maniere considerato.
Ha due specie. 198. p. Come si ponga ne i Con
trapunti. 198. m
Geometrica 38. m. Harmonica. 61. f. Delle con
sonanze nella quantità continua è di due sorti.
Rationale delle consonanze fatta nella quanti-
tà continua è di tre sorti. Arithmetica delle
consonanze. Delle Consonanze harmonica.
114. f. Geometrica delle consonanze. 115. p.
Del Comma in sette parti equali è irrationale
156. m. Delle Consonanze imperfette. 188. p.
chordo. 101. m. Varie de i Tetrachordi appes
so gli antichi, più tosto appateneuano alla par
te speculatiua, che alla prattica. 131. m
56. p. Arithmetico come si troua. 57. p. Geo-
metrico come si ritroui. 58. m. Harmonico co-
me si possa hauere. 61. f
giunte insieme fanno ne gli estremi dissonan-
za, dalla Diapason in fuori, & per qual cagione
184. m. Proportioni simili non si trouano l'u-
na dopo l'altra nell'ordine naturale de Nu-
meri. 217. m
E
quanto al soggetto & la materia; ma diuer-
se inquanto alla ragione & la forma. 179. p
plice. 87. p. Narrati da Historici causati per la
Musica furono fatti nel genere Diatonico. 86.
Diuersi significati nelle parole, come si accom
pagnino con la Musica. 438. f
Elemento ha due qualità passibili. 18. f. Quello
che sia nella Musica. 16. f
siano l'uno all'altro contrarij. In qual modo
tra loro si trasmutino. Quando più sono uici-
ni al Cielo, tanto più sono rari; & quanto più
vicini alla terra tanto più densi. 20. f. Hanno le
parti loro di una istessa natura. Graui tirati in
fuso da i più leggieri; & per il contrario i leg-
gieri tirati in giù da i più graui. 20. p. Delle
lettere quali siano. 24. f. Della Musica 196. f
del Contrapunto in due sorti. Semplici del cō
trapunto quali siano. Replicati del quali sia. 183. m. Semplici del contrapunto
sono Sette. 184. f. Del contrapunto sono Do-
dici. 192. f
arteficiale Systema diatonico & Chromatico.
93. m. Di due specie. Antico quale era. 105. f.
Di Tolomeo quale sia. 106. p. Molto tempo
non durò appresso gli antichi. Comparato da
Tolomeo al genere naturale & al morale 105.
m. Di doue sia detto. 101. f.354. Come fusse
ritrouato da Olimpo. Quanto sia imperfetto.
Di Tolomeo imperfetto. 122. m. Perche è det-
to difficile da gli Antichi. 372. m. Meno har-
monioso ne cōtrapūto de gli altri due generi.
372. f. Cōuiene all'harmonie doriche. 389. m
za. 41. p. E come elemento delle proportioni
& principio della Inequalità. 49. m. Tiene il
luogo mezano tra il Genere di maggiore &
quello di minore inequalità. 51. p. E di sua na
tura semplice . 48. f. E come soggetto dell'ha-
bito & della priuatione. 50. p
torno al Diesis. 169. f. Intorno al Diesis enhar
monico. 185. f. De prattici. 206. f
page xix
nascano. 34. m. 204. p. Cosi detto dal numero
delle chorde che contiene. 203. m. Vt. re. mi.
fa. sol. la. Di doue è cauato. contiene tutte le
specie della Diatessaron. 126. m. 182. p. Con-
tiene le chorde. & gli interualli di ciascuno
genere di cantilena. 133. m. Minore consonan
te tra le chorde del Chromatico molle di To-
lomeo. 138. f. Maggiore consonate tra le
chorde dell'Enharmonico di Tolomeo. 142.
f. Maggiore, & minore l'vno & l'altro accre-
ciuto di vna settima parte divn Comma.
154. p. Maggiore non si può chiamare assolu-
tamente interuallo semplice. & perche. Consi
derato in due modi. 202. f. Maggiore ha tre
specie. 202. f. Maggiore da che sia detto. Mag-
giore quello che sia secondo i prattici. Mag-
giore come si troua nelle cantilene. 203. m.
Minore quello che sia secondo i prattici. Mi-
nore ha tre specie. Minore in due modi consi
derato. 203. f. Minore non si può assolautamēte
chiamare semplice. 204. p. Minore come si pō
ga i Contrapunti. Non era posto da gli An
tichi nel numero selle consonanze. 204. m
rato solamente nel numero delle chorde, si
possono considerarer, ò ritrouare in tre mo-
di. 206. f
F
bili posta auanti vna legatura quando è per-
fetta. 351. f
bili poste da gli Antichi in quattro differen
ze. Minori considerate come parti delle mag
giori. 251. p. 364. f. Sono Segni positiui. 267. f.
Sottoposte alla alteratione. 357. f. Delle canti
leni come si numerino. 348. f. 350. p. Alcune
agenti, alcune patienti, & quali siano. 350. m.
Perfette. & imperfette quali siano. 350. f Che
si possino fare imperfette sono quattro 353.
m. Alterabili quante siano 357. f. che fanno
la imperfettione si pongono in tre maniere.
353. f. Attiue, ò passiue, ouero Agenti, ò pa-
tienti quali siano. 250. m. 442. m. Poste nelle
Lagature sono sottoposte à gli accidenti, che
sono sottoposte esse Legature. 443. f
Filosseno tentò in vano di fare il poema Dithy
rambico nel modo Dorio. 381. m
Symbolo Apostolico, che si canta la Dome-
nica corretto. Del Canto della Oratione Do
minicale. 430. f. Del Musico, & quello del
Poeta è l'istesso. 66. m
ce. 4. p. Quello che sia 66. f. 351. p. Della Dia
pason qual sia. 29. f. Della diapente 30. p Del
la Diatessaron. 30. p Del Ditono. De Semidi
tono. Della Diapason diapente. dell'Essachor
do maggiore 30. m. Estrinseca. 66. f. E più no
bile della materia. 176. m. Della Diapason con
tiene due principij. 184. p. Del Modo quello
che sia. 436. p
G
Superparticolare come nasca. 41. m. 45. p. Su
perpartiente come è prodotto. 45. f. Moltepli
ce superpatiente come si faccia. 46. f. Moltepli
ce superparticolare come si faccia. 46. f. Molte
plice superpatiente come nasca. 47. f Diatoni
co naturale. 93. m. Quello che sia. 101. f.174.
m. Diatonico più antico d'ogn'altro, &
prodotto dalla natura. 132. m. Chromatico
come nasca. 167. m. Quantitatiuo nella Musi-
ca. 361. f
page xxComposti. quali si intendino. 41. m. Di
maggiore,& minore inequalità come naschi-
no. 41. f. Di minore inequalità nascono come
quelli di maggiore ne i numeri. 49. m. Di mag
giore, & minore inequalità si considerano
come sue oppositi corrispondenti al loro me
zo. 50. p. Delle canzoni sono tre. 110. p. Di me
lodia sono tre appresso gli Antichi. 92. p.
Chromatico, & Enharmonico sono inspessa-
tione del Diatonico. 133. f. Di possono consi-
derare in due maniere. 174. m. De i modi so-
no tre. 378. p
Tratta di quelle cose, che sono di perpetua
quiete. 36. f. Può far quante parti vuole pro-
portionali di vna linea. Può porre tra due li-
nee date quante mezane proportionali vuo-
le. 66. p
trouò noui caratteri nel canto Ecclesiastico.
395. f. Occhenghen Maestro di Giosquino.
346. p
& il Modo. 385. f. Del numero de i Modi,
che opinione habbia. 385. f
debbe. 434. f. Si dè fondare sopra due cose
435. m. Non si dè fare nella Musica co 'l Senso
solamente; ma accompagnato con la ragio
ne. 445. f
cantasse gli Introiti nella Messa, & il Kyrielei
son, & lo Haleluiah. 387. p
per sette Hexachordi. 126. m. Compose il
suo Introduttorio di sette lettere, & di sei
sillabe. 126. f. Per qual cagione si accom-
modò del numero Senario, & Settenario
nella fabrica del suo Introduttorio. Per qual
cagione replicò, & non variò il numero
delle Lettere del suo Introduttorio. 127. f.
H
conosce dal riuolgimento delle sphere 16. m.
Si conosce dalle distanze delle sphere. 17. f.
Si conosce dalle parti delle Sphere. Si co-
nosce da gli aspetti de i Pianetti. Si cono
sce dalla natura de i Pianetti. Si conosce dal
Sito, ò Positione loro. 18. m. Si conosce dal
legamento de gli Elementi. Si conosce dalla
qualità de i quattro Elementi. 18. f. Si conosce
dal peso de i quattro Elementi. Si conosce
dalla misura, & quantità de i quattro Elemen
ti. 20. f. De i tempi in che si conosca. 21. p.
Humana si conosce nelle cose, che crescono.
Si conosce da gli humori nel Corpo huma-
no. Si conosce dalle humane operationi. si
conosce dalle parti dell'Anima: 22. f. Si co
nosce dal congiungimento dell'Anima col
Corpo 23. m. Come si faccia. 61. f. Quello che
sia. 365. Semplice quello,che faccia. 87. p
Frigia, & sua natura. Mistolidia, & sua natu
ra. Doria & sua natura .90. p. Parte della Me
lodia. 91. p. Di due sorti. Propria quello che
sia. Propria di due sorti. 98. p. nasce dalle conso
nāze, & dissonanze poste insieme. Perfetta
quello che sia. Imperfetta quello che sia.
Non propria quello che sia. Propria si com-
pone di molte harmonie non propie. Pro-
pia piglia la sua forza di mutar l'anomo dal
numero, & dal parlare. 98. m. Può nascere
da i suoni, & dalle voci. 98. f. Ouer melodia
sono Generi generalissimi nella Musica.174.
f. Da che nasca. 166. f 182. p 216. m Perfetta
in che consista. 216. p. 222. f. Allegra. & mesta
in che consite. 217. f. Doria detta da i Dorien
si. Frigia detta da quelli di Frigia. 378. m. Li
dia detta da i popoli di Lidia. 378. m. Vsata da
i Doriensi qual fusse. 388. f. Et il numero deb-
bono seguitare la Oratione. 438. m
13. m. Contengono la natura delle quattro
qualità. Inqual modo possino muouer l'ani
mo. 90. p. Quanto erano imperfette appresso
gli Antichi. 73. f.
ne dellVnità. 63. f. Perche habbia tra i numer
ri maggiori le proportioni maggiori; & tra
le minori le minori. 65. m.
page xxi
de loro morti alla sepoltura con istrumenti
musicali. 17. p.
cagione nomina la Ottaua Sphera Caliope. 16.
f. fù posto tra i Musici: ancora che non cantas-
se alla lira. Vsaua vna verga di lauro, & con
quella percuoteua l'aria, & à quel suono can-
taua. Gli fu fatto vna statua conla cetera so-
pra le ginocchia, & perche. 83. m
piffero. Sono due pifferi in vna fiata. 72. m. Ag-
giunse la Sesta chorda alla lira, ò cetera. 72.n
Si gloria di esser stato l'inuentore de i Versi li-
rici appresso i Latini, alla guisa de i Gre-
ci. 381. f
che creato con la faccia verso il cielo. 5. f. Crea-
to alla simiglianza del modo. Perche è detto
Microcosmo. 9. f. Bene istituito non dee essere
senza Musica. 12. f. Composto di Anima, Spirito. &
Corpo, secondo i Platonici. 13. p
I
sia nella cantilena. Legata quello che importi.
Legato si può dire Consequenza. 270. m. A
quali Interualli si aplicano. 275. m
specie del Genere diatonico mostrate da To-
lomeo. 130. p Del Genere chromatico. 138. m
Della specie di Enharmonico di Tolomeo.
141. m. del Monochordo diatonico inspessato
dalle chorde de gli altri due Generi. 143. m
Delle Figure cantabili quello che sia. 353. p.
Nelle Figure come si faccia. 353. m
son, nasce per la diuisione di essa Diapason.30.
p. O consonanza composta, ò semplice, quel-
lo che s'intenda. 34. p. Si chiama in due modi
Commune, quello che sia. Propio quello che
se intenda. 100. m. Di dodici sorti. Maggiore
& minore. Equale. Consonante, & disso-
nante. Semplice, & composto, Diatonico,
Chromatico, & Enharmonico quello che sia.
Rationale, & irrationale. 100. f. Musicale co-
me si accōmodi alla sua proportione ne i Cor
pi sonori. 107. m. 109. f. Nella Modulatione
quello che sia. 181. m. Del Comma non è ne-
cessario nell'vso delle buone cātilene. 200. m.
Della terza minore posto quattro volte da
Boetio nel modo Lidio 368. f
dissonanti appresso gli Antichi. 129. m. & Cō
sonanze ordinate per la perfettione dell'Har-
monia. 164. p. Vtili quali siano. 170. m. Veri
del Tetrachordo chromatico.167. m. Veri del
Tetrachordo Enharmonico. 170. f. Non sono
tutti al Musico necessarij. 199. f. Dissonanti ne-
cessarij al Musico sono tre. Dissonati legitti-
mi del genere diatonico. 200. p. Falsi di due
sorti. 207. p. Diatonici considerati in due mo-
di. 366. f
ficiali quali siano. 15. p. Musicali contengono
il numero delle chorde Pitagoriche. 159. p.
Moderni non contengono tra le loro chorde
le vere, & naturali proportioni de gli Interual-
li Musicali. 150. f. Arteficiali terminati, & inua
riabili ne i loro interualli. 166. f
L
serciti, & à che modo. 11. m. vsarono i pifferi
ne i loro esserciti. 78. m. per qual cagione ban-
dirono Timotheo dalla loro città. 132. m.
Lamprocle inuentore delle Mistelidie harmo-
nie. 388. p.
maniere. 442. m. Ascendēte & discēdēte. 442.
m. Dinota positione di Voce. 351. f.
Legature si fanno cō tre sorti di Figure. 442. p. si
considerano in quanto alla figura del corpo, &
non ad altra cosa. 424
era cosi detta. 90. f. Di tre sorti. 81. p. Orthia
quello che sia. Orthia doue sia detta. Tro-
chea quello che sia. 81. m. Castoria vsata da i
Lacedemonij ne i loro esserciti. Curule quello
che sia; & perche cosi detta. 81. m.
Communi, nella Musica tutte nominate con
varij nomi: & perche. 81. p. Musicali publica-
te da Terpandro. 81. p
ne un'altro: si può fare in due modi. 408. m.
Libro vtile à i Compositori. 343. f
Cetera, ò Lira. 72. m. ordinò le Otto chorde an
tiche i due Tetrachordi separati. 120. m 134. f.
Licurgo Re de i Lacedemonij lodò sommamen
te la Musica nelle sue leggi. 11. m
Diritta, & obliqua prima materia al Prospetti
uo. 316. m
Fu Musico & Poeta compose in verso Lamen
tationi & Hinni. 83. p
21. m. come era fatta da principio. 72. f. quel-
lo, che conteneua. 132. f
M
di verità. 6. f. consistono nella dimostratio-
ne. 181. m.
Mathematico puro considera le Quantità lonta-
ne dalla materia; & in che modo. 63. p
mo. 91. p. In qual modo possa mutare i costu-
mi dell'animo. 91. p. Di tre sorti. 92. p. Di che
è composta. 91. p 98. f. Non nasce da altro, che
dalle Voci. 98. f. ouero Harmonia sono Generi
generalissimi nella Musica. 174. f
Cubo. 116. f. che tiene la Natura nella genera-
tione dell'Vomo. 22. p
per noue chorde. 128. p. Lidio da Boetio chia-
mato non solo Semplice; ma anco Prencipe
de tutti gli altri modi. 368. f Anticamēte quel
lo che fusse. 378. p. Quello che sia. 383. m. Da
che sia detto. 384. Mistolidio detto Locrico,
ò Locrense. 386. p. Trasportato. 410. m
maggiore contiene in se il minore, ma non
per il contrario. 349. m
Di cātare nominarono gli Antichi Leggi. 80. f.
Principali detti Autentici sono sei. non princi
pali detti placali sono sei. 31. f. Sono tre secon-
do Plutarco. 386. p. Trasportati. 368. f. Diuer-
page xxiiisi di harmonie. 375. m. Di tre Generi poetici
appresso gli antichi. 178. m chiamati diuersa-
mente. 383. f. Principali sei, & sei Collaterali.
401. m. varij non solo ne gli interualli, ma an-
co nel numero delle chorde. 394. p. Principali
ò Autentici, & di numero Impari: Laterali, ò
Plagali, ò pur Placali, & di numero Pari, qua-
li siano . 402. m. Autentici & plagali hanno le
Chorde finali & i luoghi delle cadenze cō-
muni. 403. p. Superflui, Imperfetti, & diminuiti.
404. m. Perfetti, & imperfetti. 404. p. Commu-
ni & misti. 404. f. si considerano in due manie-
re. 405. m. Stabili.406. p. Varij. 405. f.
di. 99. p Impropia.99. f propia 99. f. Si può
hauere senza l'harmonia propia; & senza con
sonanza & melodia. di tre maniere. 100. p
due modi. 51. f. Le proportioni nella quantità
continua detto Soggiungere; come si faccia.
111. f. Detto Preporre. 112. f
nel descriuere la fabrica del mōdo. 30. m. Inuē
tore della Tromba. 390. m
no due cose, cioè il mouente & il mosso. Lo-
cale sempre si fa in alcuno mezo & non mai
nel Vacuo. 95. p. Quando è più tardo, tanto è
più vicino al suo fine. Di qualunque chorda
nel principio veloce, & nel fine tardo. 96. f
uersità delle harmonie; come anco da i Nu-
meri, ò Rhythmi soli.90. f. alcuni equali & al
cuni inequali. in quali alcuni tardi & rari; & al
cuni veloci, & spessi. 96. p Violenti veloci nel
principio & tardi nel fine. 96. f. 258. m. che nō
si comportano tra le parti de i contrapunti.
227. f 229. m. Approuati [[per]] buoni.228. m. 231.
p. Nelle modulationi di due sorti. Naturali nel
cantare. Accidentali nel cantare. 439. p. Natu
rali fanno la cantilena più sonora & più virile.
419. m. Accidentali fanno la cantilena più dol
ce; & alquanto più languida. 439. f
& singolar dottrina. 2. p. Riputata al presente
vile & abietta; & perche. 2. m. Ha hauuto ori-
gine dal Senso dell Vdito. 6. p Come sia stata ri
trouata. 6. p. E scienza mathematica. 6. f. Quan-
to sia stato celebrata Detto Circolo delle scien
ze. Abbraccia tutte le discipline. 7. m. Nel Pa-
radiso essercitata. 9. p. E necessaria all'Huomo
Christiano. 10. p. quello che ella sia. 10. m. Gua
risce quelli, che sono morsi dalle Tarantolo
10. f. A qual fine si dee imparare. Collocata
tra quei trattimenti, che seruono à gli Huo-
mini liberi. 11. f. Perche diletti. 12. f. Si dè im-
parare cō la speculatua. & perche. 14. m. Quel
lo che ella sia in vniuersale. 14. f.E di più ma-
niere Animastica quello che sia. Organica
quello che sia. Organica di più sorti. Harmo-
nica, ò naturale come si faccia. 15. p. Artefi-
ciata come si faccia. Arteficiata si fa in tre mo
di. 15. f 16. p. Naturale di quattro sorti. Ani-
mastica di due sorti. 16. p. Mundana quello
che ella sia. 16. m. Humana quello che sia. 21.
f. Humana si conosce da tre cose. 22. m. Piana
quello che sia. Misurata quello che sia. 24. p.
Rhythmitica quello che sia. Metrica qual sia.
24. f. Rhythmitica & metrica può nascere da
instrumēti arteficiali. 24. m. Istrumentale quel-
lo che sia. In particolare quello che sia. 25. f.
34. 31. E scienza speculatiua. E scienza ma
thematica. Di doue è cosi detta. 25. f. Nasce
in tre modi. E detta dalle Muse. 26. p. Si diui
de in prattica, & speculatiua. 25. m. Non hà
maggior fermezza de quella de i Numeri. Nel
la Scrittura sacra è honereuolmente posta.
28. p. non riceue l'infinito. 35. f. Piglia impresti
do dall'Arithmetica i Numeri, & dalla Geo
metria le quantità misurabili. 38. f. E scienza
subalternata all'Arithmetica, & alla Geome
tria. Più tosto subalternata alla Geometria, che
all'Arithmetica. 38. m. Subalternata alla scien
za naturale. Quando è perfetta non è sempli
ce naturale, nè semplice mathematica. 39. m.
Da principio semplicemente trattata. 71. f.
76. m 120. m. Al presente non è priua delli
suoi effetti. 76. p. A qual fine ci sia stato data,
80. p. Hauea anticamente più parti. 82. p. Quā
do era in riputatione. 82. f. Perche hora è senza
riputatione. 82. m. Gli Abtichi intesero per lo
studio delle humane lettere. 82. f. Quanto ope
ri in vn Soggetto ben disposto. 87. m. Non ces-
sa di operar sempre varij effetti. 92. p. Come à
i nostri tempi è recitata. 92. m. Quando più di
letta. 92. f. Moderatrice delle Arti, & Scienze.
237. f. Và speculando solamente il concento,
che nasce dalle chorde, & dalle Voci. A che
fino ritrouata. 360. f. A i nostri tempi separata
dalla Poesia. 383. p.
nanze solamente. 3. p. Quello che sia. 27. p. Si
serue del Numero relato. Si serue de i Corpi
sonori, & del Numero relato nel trouar le
ragioni delle consonanze. 36. f. Dalla scienza
naturale hà la ragione de i Suoni, & delle Vo
ci. 39. m. Dalla Mathematica hà la ragione
delle Proportioni della consonanza. 39. f. Pi
glia i Numeri dall'Arithmetico; & l'altra quā
tità dalla Geometrica. 63. p. Considerea la ma-
teria, & forma delle Consonanze. In qual modo
page xxivmodo uenga a far Soggetto la sua scienza al-
l'Arithmetica & alla Geometria. 63. m. Non ri-
troua diuisore, che diuida alcuna proportione
indue parti equali. Ancora che diuida la Qua-
drupla in due parti equali, non lo fà come mu
sico; ma come Geometra. 66. p. In qual modo
sia nominato da Homero. 84. f. Conuiene haue
re notitia de tutte le Sciēze. ò Poeta solo chia
mato da gli Antichi Sapiente. 85. f. Quello che
principalmente considera. Debbe conoscere
gli Interualli dissonanti, & a che fine. 199. f.
E ad vna istessa conditione col Medico. 336. m
Può fingere, ò comporre nuoui Vocaboli &
noui Segni, per manifestare il suo concetto.
363. f. Dorico conseruatore della pudicitia di
Clitennestra. 388. f
N
tione delle cose. 155. m In tutte le cose
sempre inchinata al bene. 164. p
cantaua. 80. f. Quello che facea, quando uolea
cantare. 81. f
essempio nella mente di Dio. 27. f. Quello che
sia. Ternario perche è detto perfetto. 28. m.
Harmonico, ò sonoro è il proprio Soggetto
della Musica. 29. f. 38. m. Senario contiene tut-
te le forme delle consonanze semplici, che si
possono ritrouare. 29. f. Senario perche sia det
to Segnacolo del mondo. Senario perche è
perfetto. Senario perche è detto imitatore
della virtù. Senario perche è chiamato Ana-
logo, ò proportionato. 31. m. Senario perche
è detto Circolare. 31. f. Semplice qual sia.
Relato qual sia. 36. f. Sonoro quello che sia in
generale & in particolare. 36. f. 47. p. Maggiore
al minore; & questo à quello ciascheduno da
per se si può comparare in cinque modi. Mag-
giore contiene il minore; & cosi il minore è
contenuto dal maggiore in cinque maniere.
41. m. Non è causa propinqua & intrinsica
delle proportioni, ne delle consonanze. 66. m
E causa vniuersale, estrinseca & remota; & co-
me il Modello della proportione. 67. m. Sola
cagione di far conoscere & ritrouare artefi-
ciosamente le proportioni delle consonanze.
In qual modo sia necessario nella Musica. 67. f.
Sonoro ò harmonico è la cagione delle Conso
nanze & si ritroua nelle quantità sonore. 165. p
quanta forza le aggiunga. 87. m. Parte della Me
lodia. 91. p. Inquanti modi si piglia. Quello
che sia. 91. f. Et l'Harmonia debbono seguita-
re la Oratione. 438. m
consonanze. 3. f. Che fanno dibisogno al Mu-
sico quali siano. Pari quali siano. Impari. Pa-
rimente pari. 29. p. Primi & incomposti. Com-
posti. Contraseprimi. 29. m. Contraseprimi
di tre maniere. 29. m. Tra loro composti, ò
communicāti. 26. f. Non sono termini radicali
delle proportioni. 48. p Tra loro composti di
tre sorti. 29. m. Quadrati quali siano. Cubi,
Perfetti, Perfetti sempre finiscono nel Sena-
rio, ouero Ottonario. 29. f. Quanto piu sono
lontani dall'Vnità, tanto sono men semplici,
men puri, meno dal senso compresi, & meno
intesi dall'intelletto. 42. m. Sesquati quali sia
no. Complicati. 44. p. Contraseprimi sono
radicali termini delle proportioni. 45. f.47. f.
Quali siano chiamati Radice, ò Termini radi-
cali delle proportioni. 47. f. Della proportio-
nalità arithmetica sono Vnità poste insieme;&
quelli dell'Harmonica sono le parti fatte della
quantità sonora. 65. p. Semplici secondo la
mente di Pitagora sono quelli, che sono conte-
nuti nel Quaternario. 73. f. Harmonici sono
parti delle quantità sonore. 174. p. Del Modo
Frigio piu veloci nel suo poema d'ogn'altro
numero. 382. m. Del Modo Dorio piu tardi &
piu rimessi. 382. m
O
di perfettione. 355. m. Del punto di Accresci-
mento. 356. p. Del punto di Diuisione. 356. m
f. 140. p. Sonò con piffero nell'harmonia Li-
dia i funerali della sepoltura di Pithone. 387.
m. Di Misia ritrouatore delle Harmonie Li-
die 387. f
mondo. 7. m. De Pitagorici non accettata dal-
l'autore. 17. f. Strana de gli Antichi. 23. f. Di
Pitagora nella inuestigatione delle cose. 73. f.
Di San Hieronimo in torno alle cose di Virgi-
lio. 84. f. Falsa di alcuni intorno la Participa-
tione nella distributione del Comma. 155. f.
Di Filolao. Falsa de' moderni compositori.
169. m. De gli Antichi Musici. 17. p. Dello
Autore. 178. m
quanta forza habbia. 87. m. Tiene il luogo
principale nella Melodia. In essa si trattano
materie allegre, ò meste, & d'ogn'altra quali-
tà. 438. m
nell'opera. 3. p. Tenuto dalla Natura nel pro-
durre le consonanze l'vna dopò l'altra. 217.
p. Tenuto da Vergilio nella sua Eneida.
236. p
10. p. Volea che gli Hinni si hauessero à fini-
re nella Sesta genertione. 30. m. Fu musico, &
poeta. 83. m
sopra la parte del Soggetto. 318. m. 319. p. nel
le dette Consequenze sopra il detto Sogget-
to. 317. m. 318. p. Nelle Consequenze fatte al-
la Diapason acuta. 320. p. Nelle Consequenze
alla Diapente acuta sopra esso soggetto. 321.
f. Alla Diapente acuta sotto la parte del Sog-
getto. 323. p. Alla Diapente grue sopra la par
te detta. 324. p. Alla Diapente graue sotto la
parte detta. 325. p. Nelle Consequenze alla
Diapente acuta dopò la pausa di Semibreue.
326. m. Nel comporre Salmi à due chori spez
zati. 346. m. Vtile al compositore nel compor
re le Salmodie, ò Salmi. 407. m. Intorno il
comporre le cantilene à pari. 437. f
188. p. Perche sia più d'ogn'altra consonanza
semplice, & perfetta. 189. p. Con le sue repli-
cate non si può accresscere, ò minuire: senza
offesa dell'Vdito. 189. f
P
za habbia da commouer l'animo. 89. p. Come
si faccia. In esso Quali istrumenti concorri-
no. 95. f
biano da intendere. 65. f Di Martilio Fici-
no essaminate. 74. p. Di Psello nel Gene-
re Enharmonico. 373. m. Come si debbo-
no accompagnere che stian bene, con le Har
monie. 438. m
& contiene in se sette cose. Sensitiua corri-
sponde alla Diapente, & contiene quattro co-
se. 22. f Habituale corrisponde alla Diatessa-
ron, contiene tre cose. 23. p. Aliquota, & non
Aliquota quali siano. Aliquota detta Molti-
plicatiua. 41. f. Non Aliquota detta Aggrega-
tiua. 42. p. Non aliquota detta parte impro-
piamente. 42. f. Propinqua, Remota, & Più re-
mota, & remotissima di vna Figura cantabi-
le quali siano. 251. p. 350. f
modo corrispondino alle ragioni di tre conso
nanze. 22. f. Maggiori della Diapason, quali
siano. Della Diapason, che nascono dalla di-
uisione harmonica. Semplici, & Elementali
della Diapason. 30. p. Di vana chorda fà il
suono più acuto, che non fa il tutto, che lo fa
graue. 38. p. Del Senario come s'intendino
essser collocate in harmonia diuisione. 65. f
De gli Istrumenti considerati in due manie-
page xxvire. 79. p. Elementali delle cantilene sono quat
tro.251. f. Della cantilena à quali Elementi si
attribuiscano. 251. p Della cantilena come in
essa si accommodino. 294. p. Della cantilena
come si moltiplichino. 295. m. Della cantile-
na come ordinare si debbino. 436. m
che ella sia. 152. p. A che fine fu ritrouata. 152.
m. A che modo ritrouata. 152. f
stono in certa quantità di vna delle quattro
qualitadi. Che predominano nell'Huomo so-
no simili alle complessioni delle harmonie.
90. p. In qual maniera pigliano augumento,
ò diminuiscano. 90. f
detta. 169. p. Di Minima, ò Semiminima
quando si possa commodamente porre nel
canto. 440. p
250. p. Sono Figure priuatiue. Sono di molte
specie. 267. f Ritrouate per due ragioni. Non
abbracciano mai più di Quattro righe. 268. p.
Vsate da gli Ecclesiastici, come si chiamino.
Appresso il Musico di tanto valore quanto i
punti appresso l'Oratore. 269. m De i Modi
si pongono in due maniere. 348. m. Essentia-
li, & Indiciali de i Modi. 369. f Dinotano
Priuatione di Voce. 368. f. Quādo si habbiano
à porre ne i Canti. 439. f Sono segni priuati-
ui. Quel che significano. 267. f. Non sono
sottoposte alla imperfettione. 353. f
gure cantabili, si considerano in tre manie-
re. 358. p
come accommodar si possano alle Figure can-
tabili. 257. f. Sono di due fino à Sei silla-
be. Arriuano al numero de Centouentiquat-
tre. 258. m. O Numeri del Modo Frigio sono
veloci; & del Dorio più tardi, & più rimessi,
382. m. Che entrauano nelle compositioni
de i Generi. 373. p
te fatto di gambe di Grù. 76. f. istrumento
incitatiuo. 390. p
Destri & sinistri quali siano. 78. m. Satani qua-
li siano. Frigij. 78. m
le Consonanze Musicali. 6. m. Volle che il
Cielo nel riuolgimento facesse Harmonia
7. m. 16. m. Diligentissimo inuestigatore del-
la Natura. 73. m. Perche non pose il Ditono,
& lo Semiditono nel numero delle Conso-
nanze. 73. f. Perche non volea, che si passase
oltra la Quadupla nelle Consonanze. 74. p.
Come ritrouò le Ragioni delle Consonanze.
75. m. Placò con la Musica vn giouane Tau-
rominitano furioso. 86. m. Quando ridusse
il giouane temperato commando, che si mu-
tasse il Modo; & si cantasse lo Spondeo.
88. m. 258. m. Quando visse. 93. f. Inuentore
del Monochordo. 119. f. Inuentore del Syste-
ma . 120. f
animi feroci. 19. m. Stimauano ne i Nume-
ri esser non sò che di diuino. 28. p. In quan-
ta veneratione hebbero il numero Quaterna-
rio. 74. p
del Cielo. 16. f.126. p. Pone sei Modi sola-
mente di Harmonie nella Musica. 385. p.
Et Aristotele quali Harmonie approuasse-
ro. 389. m
nella Musica. 82. f. perche è detta da Terentio
Studio musicale. 84. m
Scienze. 85. f. O Musico era chiamato Sapien
te da gli Antichi. 85. f
accommodare i Numeri, & le Parole nelle
loro poesie. 7. p. Anticamente, come cantaua-
no i loro Versi. 25. p. Lirici perche cosi detti.
25. p. Volsero che 'l Verso heroico fusse ter-
minato nel sesto piede. . 31. m. Orauano al po-
polo cantando. 77. p. Lirici, che modo tene-
uano ne i loro certami. Lirici quello che can
tauano. Lirici quando vinceuano ne i certa-
mi quello che guadagnauano. 76. f. Antichi
recitatori delle loro Comedie, & Tragedie.
77. p. Perche vsauano spesso questa parolo
Cantare. 83. f. Et Indouini sono mossi, & agi-
tati da vna istessa cosa. Gentili hanno alle fia-
te predetto quello , che venir douea. 84. f
bia per suo fine. 16. f. E sotto posto alla Specu-
latiua. 26. f. Consiste nella compositione delle
Canzoni, ò Cantilene. 180. m. Senza la Specu
latiua nella Musica è imperfetta. 338. m
esse perfetta cognitione. 6. f. Elementi de i Ge-
neri di melodia quali siano. 106. f
consonante è sono tre. 129. p. Delle cantilene co
me habbiano da essere. 213. p. 250. m
no con numeri da Musici nelle loro Canzo-
ni. 47. f. Quello che sia. Di due maniere. 349.
p. Buone, & delle parole consiste nelle
figure cantabili, bene & male accommoda-
te. 440. m
troua nella diuisione di alcune chorda, & in
qual modo. 142. p
32. p. Della proportionalità Arithmetica. 63. f.
Della diuisione harmonica. 63. f. Della Dupla
proportione, & della Diapason Consonanza.
373. m Nel cāto è di tre maniere. 181. f. Quel-
lo che sia. 182. p. Della Ottaua, & della Quin
ta. 232. m. Di ciascuna delle parti della canti-
lena. 294. m
proportionalità Geometrica. 59. p. Del Cōtra-
punto. 181. m. Oggetto pigliato in due ma-
niere. 259. f
sonanze. 37. f. 38. p. Come è intesa dal Musico.
40. p. Propia. 40. m. Commune. 40. m. Ratio-
nale. 40. m. Irrationale. 40. m Del lato del Qua
drato col diametro è irrationale. 40. m. Che si
troua nella quantità discreta si troua anco nel
la continua. 40. f. Di equalità. 40. f. Di inequali-
tà. 41. p. Di equalità non fa per il Musico. 41. p.
Di maggiore inequalità. 41. p. Di minore ine-
qualità. 41. p. E magiore d'vn'altra per il suo
Denominatore.44. f. Si considera in due mo-
di. 62. f. E causa formale intrinseca, & propin-
qua delle consonanze.67. m. E cagione de gli
effetti che fanno le quattro qualità, & le har-
monie. 90. m. Di suono à suono è tanta, quanta
quella che è ciascuna parte di chorda al suo
tutto. 159. f. E Relatione. 177. p. Del Semituo-
no maggiore quanta sia. 201. f
40. f. Geometriche parte rationali, & parte ir-
rationali. 40. f. Irrationali non considerate dal
Musico. 40. f. Di maggiore inequalità assimi
gliate all'Habito. 50. p. 176. f. Di maggiore ine-
qualità Positiue, & Reali. Di minor inequalità
assimigliate alla Priuatione. 168. Di minore
inequalità dette Priuatiue, & Rationali. 49. f.
176. f. Della quantità discreta non sono tutte
diuisibili in due parti equali. 66. p. Della quan
tità continua tutte diuisibili in due parti equa
li. 63. f. Del genere superparticolare non si pos
sono diuidere rationalmente in due parti equa
li. 59. m. Del genere moltiplice, che nella
quantità discreta si possono diuidere in due
parti equali, quali siano. 59. m. Et proportiona
litadi Arithmetiche da che nascono. 63. p. Et
proportionalitadi Geometriche di donde ven
gano. à63. p. Che si trouano nella proportionali
tà harmonica, si trouano anco nell'Arithmeti
ca. & perche. 64. p. Che si trouano tra le quat-
tro qualità, si trouano anco tra le Harmonie.
90. m. Del diatonico syntono, ouero Incitao
sono contenute tra le proportioni, che sono
tra i numeri sonnori, ouer harmonici. 102. p. Si
possono moltiplicare, & diuidere nella quanti
tà continua. 111. m. Del Diesis maggiore, 6
minore enharmonici. 170. f
maniere.56. m. Arithmetica.57. p. Geometri-
ca. 58. m. Harmonica. 61. f. Harmonica detta
propiamente Mediocrità. 61. f. O Diuisione
harmonica. 61. f. Harmonica dipende dalla
Arithmetica, & dalla Geometrica. 64. p. Har
monica quando necessità apporti. 65. f Harmo
nica in qual modo accordi, ò discordi conl'A-
rithmetica. 64. p. 65. p. Arithmetica, & harmo
nica sempre rationali, & perche. 65. f. Geome
trica tal volta rationale, & tal volta irrationa-
le. 65. f. Harmonica hà per suo propio l'haue-
re i suoni graui di maggiore interuallo, che
non hanno gli acuti. 65. m
Q
Elementi sono sei. 30. f. Passsibile quello che
sia. 118. f. Come si faccia diuisibile. 118. f
che sia. 35. f. Discreta quello che importi. 36. p
Continua simile al Superparticolare genere.
36. p. Discreta simile al genere molteplice. 36.
p. Del Suono è tanta, quanta è la quantità della
chorda. 37. f. Incommensurabili. 40. m. Che si
vuol cauare da vn'altra, debbe essere à quella
equale,ò maggiore. 49. f. Solamente è sotto-
posta alla diuisione, & alla moltiplicatione per
se. 188. f
nanti da i Moderni. Vsata da Giosquino sem-
plice. 187. f. In quante maniere differenti accō
pagnar si possa nelle compositioni. 302. m
nè è cagione che ella sia tale; è detta maggior-
mente esser tale; come verificar si possa in tut
ti i generi delle cagioni. 189. m
R
no. 47. f. Sorda. 59. f. Quadrata di vn nume
ro come si possa hauere. 60. f. Delle propotio
ni come si trouino. 68. p. f
si possono sapere, se non co 'l mezo de i Cor-
pi sonori. 63. m. Et il Senso sono adoperati nel
far giudicio delle cose della Musica. 110. m
De Numeri quello che sia. 186. f. Senza il Sēso
non si può fare buon giudicio nelle cose della
Musica. 446. m
state ritrouate. 6. m. Che prouano la Quarta es
sere consonanza. 186. m. De i Suoni si pos-
sono sapere, se col mezo de i Corpi sono-
ri. 444. f
quello che sia.119. m. Di accompagnare le Se
ste. 233. f. Per sapere applicare le Salmodie al-
le cātilene. 406. m. Per conoscere il valore del-
le Figure legate. 442. f
sotto diuersi generi. E doppia, quando è fatta
di due cose naturali. Fondate sopra la potenza
attiua, & passiua si considera in due modi. 177.
m. Fondata sopra due estremi, che non sono
d'vno istesso genere,ouero ordine, è di due
sorti 177. f
li. Sono di due sorti. Fatte nella quantità conti
nua, & nella discreta, sono veramente reali, &
scambieueoli. 177. p
Comedie. 78. m. Col suono & canto assaliuano
il campo, ò essercito de nemici. 390. p
S
Συκκινὶς quando,& da chi fù instituita. Et era
vna delle Leggi Tibiarie. 82. p. Carpea. 82. p.
page xxixEra contenuta tra le cose della Musica. 82. p
nella memoria. 26. p. Non è de i Particolari; ma
de gli Vniuersali. 235. f
due sorti.38. f. Subalternanti. 38. f. Subal-
ternate. 38. f. Scacciano da se le cose pra-
ue. 164. m
hemisphero; & anco sotto di esso quanti sia-
no. 30. f. Cifere ordinarie nella Musica. 183.
p. O cifere del Tempo possono significare due
cose. 257. m. Del tēpo, Modo & Prolatione.
347. f. 348. m. Del Tempo tagliati, quello che
importino. 149. f Intrinsechi & estrinsechi
nelle cantilene. 359. p
gli Antichi. 128. m. Diminuito di una setti-
ma parte di vno Comma. 153. f. Ha due spe-
cie. 198. f. Come si ponga ne i contrapunti.
Da che si dica. E il ditono imperfetto. 199. f
ò senza il punto sincopata;ouero la Mini-
ma; come si pongono ne i Contrapun-
ti. 242. f. 243. m
Λεῖμμα. 121. f. Accresciuto di tre settime parti
di vno Comma. 154. p. Non nasce dalla diui-
sione harmonica di alcuno interuallo. 201. f
μὴ. 121. f. è nella uera forma nella parteci-
patione de gli istrumenti arteficiali. 156. m.
Tra quali chorde sia posto. 167. p. 202. p Non
si usa nelle modulationi Diatoniche, ne En-
harmoniche. 168. p. E maggiore di tre &
minore di quattro Comma. 169. f. Come si
aggiunga, ò leua da vn'altro Interuallo. 209. f
ne d'ogni buona harmonia nella Musica. 217.
f. Cagione della distintione delle specie delle
consonanze. 194. f. Posto da Guidone nel me
zo del suo Hexachordo. Come si troui & col-
lochi tra due parti della cantilena. Perche sia
cosi chiamato. 202. p
& fine de i numeri perfetti. 29. f. Detto Nu-
mero harmonico. 29. f. Contiene le Forme de
tutte le consonanze. 29. f. 32. p. Perche fu elet
to da Mosè nella fabrica del Mondo: 30. m
Comprende molte cose della natura. 30. f
Contiene in potenza le forme de tutte le con
sonanze. 34. p
della Musica. 447. m. Del uedere, come alle
fiate resta ingannato. 97. p. Dipende dal sensi-
bile al proprio oggetto. 446. p. Come possa
errare intorno al proprio oggetto. 446.. p. Sen-
za la ragione non può far giudicio delle cose
della Musica. 446. m. Non può conoscer le
minime differenze. 446. f
5. f. Dati all'Huomo per il ben essere sono
tre. 5. f Necessarij al ben essere. 5. f. Istrume
ti dell'Intelletto. 6. p
minore: nondimeno da essa si và alla Ottaua
& non ad essa Quinta; & perche. 231. m
diuersi.127. f. Chorde antiche quali fussero.
134. f. 135. p. Chorde antiche da Terpandro
Lesbio ordinate. 120 f. 134. p
co consonanza. 41. p. Nelle figure consiste nel
la forma. 351. p
36. f. Della Musica è il Numero sonoro.38.
p. Il Corpo sonoro proportionato. 38. m
Dell'habito non naturale, & della priuiatione
imperfetta è atto à riceuere hor l'vno hor l'al
tro per successsione. 50. m. Del Compositore
qual sia. 210. f. Può esser di molte manie-
re. 211. f
31. p. Delle voci musicali sono sei. 31. f. Di har
monia poste in vso appresso gli antichi quante
siano. 31. f. Semplici del Cōtrapunto sono Do-
dici. 192. f. De i Generi de i Modi poetici so-
no molte. 378. m Della diapason in quāto ma
niere si possino diuidere. 386. m. 397. p
m. Quello che habbia per suo fine. 26. m. Sēza
la Prattica nella Musica val poco. 336. f. Parte
della Scienza più tosto già consisteua nella
Speculatione de stranieri accidenti che de i
propij. 361. m
feriore nel mouimento diurno. 123. m. Di Sa-
turno più tarda d'ogn'altra inferiore nel moui
mento annuale. 124. p. Di Saturno fa il suo mo
uimento in Trenta anni. 124. p. Della Luna più
tarda d'ogn'altra nel mouimento Diurno. 124
p. Di Saturno fa il tuono Dorio, quella di Gio
ue il Frigio. 124. f
i Platonici. 13. p. 23. m. Primo Organo d'ogni
virtù dell'Animo. 90 f. Humano col tempo ter
mine le Voci continue. 99. p
nominati delle proportioni de i generi
di minore inequalità. 41. f
derato dal Naturale. 39. f. Quello che sia. 94. f.
96. p Può nascere in molti modi. 95. p. Come
si faccia nell'aria. 95. p. E come il genere. 96. p.
di alcuna chorda è tanto più graue, quāto più
ella è vicina alla taciturnità. 86. m
rio. 37. m. O voci materia delle consonanze.
37. O voci, tanto più che sono l'vno dall'altro
lontani meno sono compresi dal Senso. 42. m.
95. m. Considerati dal Musico. 95. f. 99. m. Gra
ui, & acuti come, e da che nascono. 96. m. Che
non sono discordanti tra loro per l'inequali-
tà, non fanno consonanza, nè dissonanza. 97.
m. Sono nell'aria, come in propio Soggetto.
95. p. Hanno più della quantità continua, che
della discreta. 173. f. Non si possono scriuere,
nè dipingere. 181. f. Della Diapason perche pa
rino vno solo. 184. p. Vnisoni, & non vnisoni
quali. 185. m
T
ta è la proportione delle chorde tre loro doue
vsciscono. 108. p
45. f. Della equalità inuariabili. 50. m. Delle
proportioni come si habbiamo à porre. 51. m.
Di qual si voglia proportione moltiplicato per
qual si voglia numero, non danno varietà di
proportione. 52. m. Di qual si voglia propor-
tione in qual modo si facciano maggiori, ò mi
nori. 159. f
21. m. Aggiunse la setttima chorda alla Lira, ò
Cetera. 72. p. 134. p. Pubblicò le leggi Musicali
71. p. Fù Musico, & poeta. 83. m. Inuentore
del Systema massimo. 120. f. Lesbio ordinò
le sette chorde antiche. 120. f. Diuise le sette
page xxxichorde antiche in due Tetrachordi congiun-
ti. 120. f. 134. p.
cimo. Per la sua natura è riputato alquanto me-
sto. Come si trasporta. 17. f
che sia.101. p. Doue sia detto.101. p. Diatonico
perche inspessato da gli Antichi. 133. f. Chro-
matico vero.167. m. Enharmonico vero. 170.
m. De i Greci incomincia dalla voce Mi ap-
presso i Latini. 182. p
gliar l'arme; & anco lo placò. 10. f. 86. m 87. f.
94. p Aggiunse la Nona chorda alla lira, ò ce-
tera. 70.135. m. Lirico aggiunse la Decima
chorda, & la Vndecima alla Lira, ò Cetera. 72.
m. 134. f. Milesio Lirico fu trouatore del Gene-
re Chromatico. 93. m. 132. m. Come aggiunse
sette chorde alla Antiche. 134. f. Milesio quan
do visse.93. f. Sonator di piffero spinse Alessan
dro à pigliar l'arme. 94. m. Perche fù bandito
da Lacedemonij. 132. m In qual modo potesse
ritruare il genere Chromatico. 136. p. Inuen
tore di molte melodie. 388. p
del Cielo. 17. f. Pone sette Modi nella Musica:
e cōmemota l'Ionico, & l'Iastioeolico. 385. m
Chromatico molle di Tolomeo. 138. m. Incō-
posto, che nel Diatonico genere è composto
tra quali chorde si ritroui. Da che proportio-
ne è contenuto. 169. p. Chromatoco come si
accommodi ne gli Istrumenti. 168. f. Pigliato
da Boetio in due maniere. 366. m
per noue chorde. 128. p. E inteso per quattro
cose. 383. m
V
getti nasce dalla diuersità delle cose diuersa-
mente considerate. 36. f. Dell'Harmonia in che
consista. 220. f. De i Generi doue nasca. 135. f
& perche è cosi detto. 81. m. In che sia differen
te dal Rhythmo. 91. f. Tragico non conuiene
alla Comedia. 438. f
pōgono. 258. m. Canini quali siano. 381. p. Sot-
to 'l nome del Sannazaro giudicati eccellen-
page xxxiiti. 448. p. Che seruono alle Intonationi delle
Salmodie. 406. f
col Numero del più; & perche. 16. f. Predisse
molte cose. 84. f. Mosso da gli oracoli della Si-
billa Cumana [[pre]]disse quello che hà scritto. 84. f
della Consonanza; & non come Consonan-
za. 183. f. 193. m. Quello che sia. 193. p Ap-
presso il Musico è tanto, quanto il Punto ap-
presso il Geometra. 193. m. Non è consonāza,
nè interuallo; & perche. 193. m. Come si pōga
nelle compositioni. 193. f
In che non sia differente dal pūto. 28. m. Prin-
cipio, & Misura commune d'ogni numero.
28. m. Nella Musica è il Corpo sonoro. 64. p.
mortali. 96. p. Quello che sia. 96. p. E come la Spe-
cie. 96. p
ze. 3. f. 39. m. Materia di ciascuno interuallo.
38. m. Considerate dal naturale. 39. m. Cōside
rate dal Musico come Elementi della sua sciē-
za. 95. f. Si generano per la concorrentia di tre
cose insieme. 95. m. Come si generino. 95. m
Humane di due sorti. 98. f. Continue. 98. f. Di-
screte. 99. p. Considerate dal Musico. 99. m. 99.
f. Discrete fanno la modulatione, & l'Harmo-
nia. 99. f. Mezane tra le continue, & le discre-
te. 96. p. Cōtinue possono essere infinite. 96. m
Discrete non hanno termine prescritto. 96. m.
Da ogni parte piegare si possono. 165. f. Non si
possono scriuere, nè dipingere. 181. f. Vnisone,
& non Vnisone quali. Non Vnisone di quante,
sorti. 185. m. Diuise in due parti. 256. f

L'ISTITVTIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Capella della Serenissima Signoria
DI VENETIA:
Nelle quali, oltra le materie appartenenti alla Musica, si trouano
dichiarati molti luoghi de Poeti, Historici, & Filosofi.
PROEMIO:
Nel quale si dimostra, in qual maniera la Musica habbia hauuto principio, & come
sia stata accresciuta; & si ragiona della diuisione dell'Opera.
te varie cose, che 'l sommo Iddio hà per sua benignità do-
nato à mortali; hò compreso chiaramente, che tra le
più marauigliose, è l'hauer conceduto loro particolar gra-
tia di vsar la Voce articolata; col mezo dellaqual sola fusse
l'Huomo sopra gli altri animali atto, à poter mandar fuori
tutti quei pensieri, che hauesse conceputo dentro nell'ani-
mo. Et non è dubbio, che per essa apertamente si manifesta quanto egli sia dis-
simile dalle Bestie, & di quanto sia loro superiore. Et credo che si possa dir ue-
ramente cotal dono essere stato di grandissima vtilità all'humana generatione:1. Supple.
cap. 3.
percioche niun'altra cosa, se non il Parlare indusse & tirò gli Huomini, i quali da
principio erano sparsi nelle selue & ne' monti, uiuendo quasi uita da fiere, à ri-
dursi ad habitare & uiuere in compagnia, secondo che alla natura dell'Huomo
è richiesto, & à fabricar città & castella; & vniti per virtù de buoni ordini conser-
uarsi; & contrattando l'vn con l'altro, porgersi aiuto in ogni lor bisogno. Essen
dosi per questa uia à vicinanza ragunati & cōgiunti: fu dopoi conosciuto di gior
no in giorno per proua, quanta fusse la forza del Parlare, ancora che rozzo. On-
de alcuni di eleuato ingegno cominciarono in esso à mettere alcune manie
re ordinate & diletteuoli, con belle & illustri sentenze; sforzandosi di auanzar gli al
tri Huomini in quello, che gli Huomini istessi restano superiori à gli altri anima
page 2li. Nè di ciò rimanendo satisfatti, tentarono di passare anco più oltra, cercando
tuttauia d'alzarsi à più alto grado di perfettione. Et hauendo per questo effetto
aggiunto al parlare l'Harmonia, cominciarono da quella à inuestigar varij Rhy
thmi &diuersi Metri, i quali con l'Harmonia accompagnati porgono grandissi
mo diletto all'Anima nostra. Ritrouata adunque (oltra l'altre, che sono molte)
una maniera di compositione, che Hinni chiamauano, ritrouarono anco il
poema Heroico, Tragico, Comico, & Dithyrambico: & cosi col Numero, col
Parlare & con l'Harmonia poteuano con quelli cantar le laudi & render gloria à
Dio; & con questi, secondo che lor piaceua, più facilmente & con maggior
forza ritener gli animi sfrenati, & con maggior dilettatione muouere i uoleri &
appettiti de gli Huomini, riducendoli à tranquilla & costumata vita. Ilche ha-
uendo felicemente conseguito, acquistarono appresso i Popoli tale autorità, che
furono da molto più tenuti & honorati, che non erano gli altri. Et costoro, che
arriuarono à tanto sapere, senza differenza alcuna uennero nominati Musici,
Poeti & Sapienti. Ma intendendosi allora per la Musica una somma & singo-
lar Dottrina, furono i Musici tenuti in gran pregio; & era portata lora una ri-
uerenza inestimabile. Benche, ò sia stato per la malignità de tempi, ò per la ne-
gligenza de gli Huomini, che habbiano fatto poca stima non solamente della
Musica; ma de gli altri Studii ancora; da quella somma altezza, nella quale era
collocata, è caduta in infima bassezza; & doue le era fatto incredibile honore,
è stata poi riputata si uile & abietta, & si poco stimata, ch'à pena da gli Huomi-
ni dotti, per quel ch'ella è ueramente viene ad esser riconosciuta. Et ciò mi par
che sia auenuto, per non le esser rimasto ne parte, ne uestigio alcuno di quella
ueneranda grauità, ch'anticamente ella era solita di hauere. Onde ciascuno si
hà fatto lecito di lacerarla; & con molti indegni modi trattarla pessimamente.
Nondimeno l'Ottimo Iddio, à cui è grato, che la sua infinita Potenza, Sapien-
za & Bontà sia magnificata & manifestata da gli Huomini con Hinni accompa-
gnati da gratiosi & dolci accenti; non li parendo di comportar più, che sia te-
nuta à vile quell'Arte, che serue al culto suo; & che qua giù ne fà cenno di quanta
soauità possano essere i canti de gli Angioli, i quali nel cielo stanno à lodar la sua
maestà; ne hà conceduto gratia di far nascere à nostri tempi Adriano Vuillaert,
ueramente uno de più rari, che habbia essercitato la prattica della Musica: il-
quale à guisa di nuouo Pitagora essaminando minutamente quello che in essa
puote occorrere; & ritrouandoui infiniti errori, cominciò à leuargli, & à ridur-
la uerso quell'honore & dignità, che già ella riteneua, & che ragioneuolemente
doueria ritenere; & hà mostrato un'Ordine ragioneuole di componere con ele-
gante maniera ogni musical Cantilena; & nelle sue Compositioni egli ne hà da-
to chiarissimo essempio. Hora perche hò inteso, che ui sono di molti, de qua-
li parte per curiosità, & parte veramente per uolere imparare desiderano, che
alcuno si muoua à mostrar loro la uia del Componer musicalmente con ordine
bello, dotto & elegante; io hò preso fatica di scriuer le presente ISTITVTIONI,
Nota per
i maligni. raccogliendo diuerse cose da i buoni Antichi; & ritrouandone ancora io molte
di nuouo; per far proua, s'io potessi perauentura esser'atto à satisfare in qualche
page 3parte à cotal desiderio, & all'obligo, che hà l'Huomo di giouare à gli altri huo
mini. Ma vedendo, che si come à chi uuol esser buon Pittore & nella Pittura
acquisitarsi gran fama, non è abastanza l'adoprar uagamente i colori, se dell'O-
pera, ch'egli hà fatto, non sà render salda ragione: cosi à colui, che desidera
hauer nome di uero Musico, non è bastante, & non apporta molta laude l'ha-
uer'unite le Consonanze, quando egli non sappia dar conto di tale unione:
però mi son posto à trattare insiememente di quelle cose, lequali & alla Pratti-
ca, & alla Contemplatiua di questa scienza appartengono; à fin che coloro,
che ameranno d'esser nel numero de buoni Musici, possano (leggendo accu-
ratamente l'Opera nostra) render ragione de i loro componimenti. Et benche
io sappia, che 'l trattare di questa materia habbia in se molte difficultà: nondi-
meno hò buona speranza, che ragionandone con quella breuità, che mi sarà
possibile, la mostrarò chiara & facilissima aprendo tai secreti di essa, che ogn'vno
per auentura in gran parte ne potrà rimaner satisfatto. Ma à finche si habbia fa
cile intelligenza di questo nostro Trattato, & si proceda con buono & regolato
ordine; mi è paruto, che sia ben fatto diuiderlo in più parti; & di tal maniera,
che si mostrino le cose, che si hanno da presupporre, prima che si uenga ad in-
segnar la detta Scienza: però hauendosi principalmente in esso à trattar due co-
se: cioè, le Consonanze, che sono cose naturali, di che si fanno le Cantilene:
& esse Cantilene, che sono arteficiali: lo diuiderò primieramente in due parti;
& nella Prima tratterò delle Consonanze; & di quelle cose, ch'appartengono al-
la parte Contemplatiua di questa Sciēza: & nella Seconda Ragionerò delle Can
tilene, che fanno alla Parte prattica: oue intrauiene l'operare, ch'appartiene al-
l'Arte. Et perche qual si uoglia cosa, sia naturale, ouero arteficiale, è compo-
sta di Materia & di Forma; se ben nell'una si considerano cotali Cose diuersa-
mente da quello, che sono considerate nell'altra; però necessariamente tratte-
rò in ciascheduna delle Due parti nominate dell'una & dell'altra, nel modo che
sarà conueneuole. Onde diuiderò secondariamente ciascheduna di queste due
Parti in altre due; di modo che saranno al numero de Quattro. Et innanzi ogn'
altra cosa prima ragionerò de i Numeri & delle Proportioni; che sono la Forma
delle Consonanze; poi che nelle cose naturali la Materia (per non essere da se cono
scibile) non si può conoscere se non col mezo della Forma;1. Phy. tex.
79. & nella Seconda trat-
terò de i Suoni & delle Voci, che sono la lor Materia. Ma à uolere costituire
gli Ordini de i Suoni & delle Voci, che sono nella Musica contenuti, fanno di-
bisogno gli harmonici Interualli, & quanto alla inuentione, & quanto al sito;
per le differenze, che accadono tra i ritrouati Suoni; però etiandio ragionerò
de i loro Principij: percioche allora diciamo di ueramente conoscere le Cose quan
do i loro principij conosciamo.1. Phy. c. 1. Ilperche hauendo prima mostrato, in che ma-
niera tutti i loro Interualli necessarii all'Harmonia, ciascheduno da per se si ac-
commodi alla suo proportione, mostrerò dopoi la diuisione del Monochordo
fatta in ciaschedun Genere, di qualunque specie di Harmonia. Et hauendo
insegnato i ueri interualli, che si possono adoperare ne i Musicali concenti; in-
segnarò etiandio in qual modo ne gli Arteficiali instrumenti si uengano à com-
page 4modare; & di più, in qual maniera si possa fabricare un'Instrumento, il quale
contenga ogni Genere di Harmonia; ne lascierò di dar notitia di tutti quelli ac-
cidenti, che possono occorrere intorno l'una & l'altra di queste due parti. Oltra
di ciò non essendo la Prattica altro, che il ridur la Musica in atto & nel suo fine,
col mezo delle Cantilene; lequali sono cose arteficiali; percioche si fanno
col mezo dell'Arte, che è detta del Contrapunto, ò di Comporre, & hanno si-
migliantemente la Materia & la Forma; come hanno etiandio le altre cose; però
sarà cosa ragioneuole, ch'io tratti dell'una & dell'altra. Et perche ogni Artefice
volendo comporre, ò fabricare alcuna cosa, apparecchia primieramente la Ma
teria, di che la uuol fare; & dopoi le dà la Forma conueniente; ancora che co-
tal forma sia prima d'ogn'altra cosa nella mente di esso Artefice; però nella Ter-
za parte, che sarà la Prima della Seconda principale, ragionerò delle Conso-
nanze & de gli Interualli; che sono la Materia delle Cantilene; dellaquale si
compongono: & dimostrerò, come, & con qual'ordine debbiano esser col-
locate nelle Compositioni di due, & come si pongano in quelle di più uoci. Ma
nella Quarta & Vltima, che sarà la Seconda della Seconda nominata, tratterò
delle lor Forme & delle loro differenze; & dirò in che modo l'Harmonie si deb-
bino accomodare alle Parole, & come queste si addattino sotto le Figure
cantabili. Si che senza dubio alcuno colui, che hauerà bene apprese tutte que-
ste cose potrà meritamente esser posto nel numero de i Musici perfetti & ho-
norati. Ma prima che entriamo à trattar quel, che di sopra habbiamo proposto;
io stimo, che non possa essere se non di piacere & di satisfattione, andar raccon-
tando alcune cose; come saria l'Origine & certezza della Musica, le sue Laudi, A'
che fine ella si debba imparare, l'Vtile che si hà di essa, In che modo la dobbia-
mo usare, & altre cose simili; & dopoi dar principio al ragionamento proposto.
 page 5
page 5
LA PRIMA PARTE
DELLE ISTITVTIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Capella della Serenissima Signoria
DI VENETIA:
Musica) copiosamente si ragiona de i Numeri & delle Proportioni, che sono
le Forme delle Consonanze; & è la Prima della parte Contemplatiua.
Della Origine & certezza della Musica.Cap. 1.
ta bontà, habbia concesso all'Huomo l'esser con le Pietre,
il crescere con gli Arbori, & il sentire commune con gli al-
tri Animali; tutta via com'ei volesse, che dalla eccellenza
della Creatura si conoscesse l'onnipotenza sua, lo dotò
dell'Intelletto; cosa che poco lo disaguagliò da gli Angio-
li.Psal. 8. Et accioche egli sapesse il suo principio & fine esser la
sù, lo creò con la faccia drizzata al cielo, doue è la sedia
di esso Iddio;Isa. 66. del che Ouidio nel Primo delle Trasforma-
tioni canta in questo proposito:
Pronàꝗ cum spectent animalia caetera terras,
Os Homini sublime dedit coelumꝗ videre
Iussit; & erectos ad sydera tollere vultus.
& questo perche ei non fermasse l'amor suo nelle cose basse & terrene; ma leuasse l'intel-
letto à contemplar le superiori & celesti; & penetrasse alle occulte & diuine col mezo del
le cose, che sono & si comprendono per via de i Cinque sentimenti. Et benche, in quan-
to all'Essere, due soli fussero sufficienti; nondimeno per il Ben'essere, tre di più vene ag-
giunse: imperoche se per il Tatto si conoscono le cose dure & aspre, dalle tenere & po-
lite; & per il Gusto si fà la differenza tra i cibi dolci & amari, & d'altri sapori; per questo
& per quello si sente la diuersità del freddo & del caldo, del duro & del tenero, del gre-
ue & del leggiero; cose che veramente all'Esser nostro bastarebbono; non resta però,
ch'al Ben'essere il Vedere, l'Vdire, & l'Odorare necessarij non siano; per i quali l'Huo-
mo viene à rifiutare ciò che è cattiuo, & eleggere il buono. De questi chi vorrà ben
essaminare la lor virtù, senza dubbio ritrouerà il Vedere, considerato da per sè, essere à
i corpi di maggior vtilità; & consequentemente più necessario, che gli altri; ma ben si
conoscerà poi, l'Vdito esser molto più necessario & migliore; considerandolo per acci-
dente, nelle cose che appartengono all'Intelletto; conciosia che se bene per il senso del
page 6Vedere si conoscono più differenze di cose; essendo che più si estende, che l'Vdito, non-
dimeno questo nell'acquisto delle Scienze & giudicio intellettuale più si estende, & mol-
to maggior vtile ne apporta. Onde ne segue, che l'Vdito veramente sia & più necessa-
rio & megliore de gli altri Sentimenti; auenga che tutti Cinque si chiamino Istrumenti
dell'Intelletto: percioche ogni cosa che vediamo, vdimo, tocchiamo, gustiamo, &
odoriamo,1. metaph.
c. 1. si offerisce à lui per il mezo de i Sensi & del Senso commune; ne di cosa al-
cuna può hauer cognitione, saluo che per il mezo di vno de questi cinque: essendo ve-
ro, ch'Ogni nostra cognitione da essi habbia l'origine. Dall'Vdito adunque, come dal
più necessario de gli altri Sentimenti, la scienza della Musica hà hauuto la sua origine;
la cui nobiltà facilmente si può per l'antichità dimostrare; percioche (come dicono Mo-
sè,Gene. 4. Gioseffo,Antiq. 1.
c.4. & Beroso CaldeoAntiq. lib.
1.) auanti che fusse il Diluuio vniuersale, fù al suono de
martelli trouata da Iubale della stirpe di Caino; ma perduta poscia per lo soprauenuto
diluuio, di nuouo fu da Mercurio ritrouata: conciosia che (come vuole DiodoroHist. lib. 1.
Nym. Mer
cu.) egli
fù il primo, che osseruò il Corso delle stelle, l'Harmonia del Canto, & le Proportioni de i
Numeri; & dice ancora, lui essere stato l'Inuentore della Lira con tre Chorde; del cui pa-
rere è stato anco Homero & Luciano;Dial. Deo
rum. quantunque Lattantio, in quello che fà della Fal-
sa religione,Lib. 1. c. 10. attribuisca l'inuentione della Lira ad Apollo; & PlinioNat. histo.
lib. 7. c. 56. voglia, che l'In-
uentore della Musica sia stato Anfione, Ma sia à qual modo si voglia; BoetioMusicae li.
1. cap. 10. (accostan-
dosi all'opinione di Macrobio,De Sō. lib.
2. cap. 1. & allontanandosi da Diodoro) vuole, che Pitagora, &
non Platone, come vuol Guidone Aretino;Microlo.
lib. 1.c. 20. sia stato colui, che ritrouò la Ragione delle
musicali proportioni al suono de martelli: Percioche passando egli appresso vna botte-
ga di fabri, i quali con diuersi martelli batteuano vn ferro acceso sopra l'incundine, gli
peruenne all'orecchie un certo ordine de suoni, che gli mouea l'udito con dilettatione;
& fermatosi alquanto, cominciò ad inuestigare, onde procedesse cotale effetto; & paren-
dogli primieramente, che dalle forze diseguali de gli huomini potesse procedere; fece
che coloro, iquali batteuano, cambiassero i martelli: ma non vdendo suono diuerso da
quello di prima; giudicò (com'era il vero) che la diuersità del peso de martelli fusse la ca-
gione. Per la qual cosa hauendo fatto pesare ciascun di loro separatamente, ritrouò
tra i Numeri de i pesi le ragioni delle Consonanze & dell'Harmonie; lequali egli poi in-
dustriosamente accrebbe in questo modo; c'hauendo fatto chorde di budella di pecore
di grossezza vguale; attaccando ad esse i medesimi pesi de martelli; ritrouò le medesime
consonanze; tanto più sonore, quanto che le chorde per sua natura rendono il Suono
all'vdito più grato. Continuossi quest'Harmonia per alquanto spatio di tempo; & dopoi
i successori, i quali sapeuano già i suoi fondamenti esser posti in certi & determinati Nu-
meri, più sottilmente facendone proua, à poco à poco la ridussero à tale; che le diede-
ro nome di perfetta & certa Scienza. Et rimouendo i falsi & dimostrando i veri con-
centi, con euidentissime ragioni de Numeri & infallibili, ne diedero in iscritto chiarissi-
me Regole; come apertamente in tutte l'altre Scienze vediamo esser auenuto; che i Pri-
mi inuentori di esse, come chiaramente lo dimostra Aristotele,2. Elen. c. 1
2. Metaph.
cap. 1. non n'hebbero mai per-
fetta cognitione; anzi con quel poco di lume erano mescolate molte tenebre di errori;
i quali rimossi da chi li conosceua, in vece loro succedeua la verità; come fece egli in-
torno à i Principij della Filosofia naturale; che adducendo diuerse opinioni de gli An-
tichi filosofi, approuò le buone & vere, rifiutò le false, dichiarò le oscure & male intese,
& aggiungendoui la sua opinione & autorità, dimostrò & insegnò la vera scienza della
Filosofia naturale. Cosi della nostra scienza della Musica i posteri mostrando gli errori
de passati, & aggiungendoui la loro autorità, la fecero talmente chiara & certa, che la
2. Metaph.
com. 16. connumerarono, & fecero parte delle scienze Mathematiche; & questo non per altro,
saluo che per la sua certezza: percioche questa con l'altre insieme auanza di certezza l'al-
tre Scienze, & tiene il primo grado di verità; il che dal suo nome si conosce; poi che Ma-
thematica è detta da Μάθημα parola greca, che in latino significa Disciplina; & nella no-
In prooe-
mio Arith. stra lingua importa Scienza, ò Sapienza; la quale (come dice Boetio) altro non è che
page 7vna Intelligenza; o per dirla piu chiaro, capacità di verità delle cose che sono & di loro
natura non sono mutabili; della qual Verità queste Scienze fanno particolar professio-
ne; essendo che considerano le cose, che di lor natura hanno il vero essere. Et sono in
tanto differenti d'alcune altre Scienze; che queste essendo fondate sopra le opinioni de
diuersi huomini, non hanno in se fermezza alcuna; & quelle hauendo i Sentimenti per
loro proua, uengono ad hauere ogni certezza. Percioche i Mathematici nelle cose es-
sentiali sono d'un'istesso parere; ne ad altro consentono, che à quel, che si può sensata-
mente capire. Et è tanta la certezza di dette Scienze; che col mezo de' Numeri si sà
infallibilmente il Riuolgimento de cieli, gli Aspetti uarij de i pianeti, l'Eclisse della Lu-
na, & quello del Sole, & infiniti altri bellissimi secreti, senza esser tra loro punto di discor-
dia. Ilperche da questo si può conoscere, che la Musica sia & nobile & certissima; es-
sendo parte delle Scienze mathematiche.
Delle Laudi della Musica.Cap. II.
manifeste; tuttauia quando considero niuna cosa ritrouarsi, la quale con
questa non habbia grandissima conuenienza, non posso di lei in tutto tra-
passar con silentio. Et se ben douerebbe bastar quello, che di essa da tanti
Filosofi eccellenti è stato scritto; nondimeno non uoglio restare anch'io per debito mio
di ragionarne alcune cose: percioche se bene io non dirò tutte quelle Laudi, che le con-
uengono; toccarò almeno una particella delle più notabili & eccellenti; & ciò farò con
quella breuità, che mi sarà possibile. La Musica adunque quanto sia stata celebrata &
tenuta per cosa sacra, ne fanno chiarissima fede gli antichi scritti de Filosofi, & massima-
mente de Pitagorici: percioche haueano opinione, il Mondo esser composto musical-
mente, & i Cieli nel girarsi esser cagione di Harmonia, & l'Anima nostra con la medesi-
ma ragione formata, per i Canti & Suoni destarsi, & quasi uiuificar le sue uirtù. Di mo-
do che alcuni di essi tennero, che la Musica tra l'Arti liberali tenesse il principato; & al-
cuni la chiamarono Ε'γκυκλοπαιδεία, quasi Circolo delle scienze: conciosia che la Musica
(come dice PlatoneDe legib. 1.) abbraccia tutte le Discipline; come si può conoscere discorrendo;
che se cominciaremo dalla Grammatica, prima tra le Sette arti liberali, ritrouaremo
esser uero quel, c'habbiamo detto; essendo che si ode grand'Harmonia nell'adattamento
& ordine proportionato delle parole; dal quale se 'l Grammatico si parte, fà udire all'o-
recchie un dispiaceuol suono del suo contesto: poi che mal si puote ascoltare, o leggere
quella Prosa, o Verso, il quale sia priuo del polito, bello, ornato, sonoro & elegante
ordine. Nella Dialettica, chi ben considera & rimira la proportione de i Sillogismi,
uedrà egli con mirabil concento & piacere grandissimo dell'udito, mostrarsi il Vero gran-
demente dal Falso esser lontano. L'Oratore poi nella sua Oratione usando gli Accenti
musici a i tempi debiti, porge marauigliosa dilettatione à gli ascoltanti; il che ottima-
mente conobbe il grande oratore Demostene, percioche tre uolte dimandato, qual fusse
la Parte principale nell'Oratore; tre uolte rispose, che la Pronuntia sopra ogn'altra cosa
ualeua. Questo ancora conobbe (come dimostra CiceroneDe Ora. 3. & Valerio MassimoDic. et Fa.
lib. 8. c. 10.) Gaio
Gracco huomo di somma eloquenza: il quale sempre, ch'egli hauea à parlare dauanti
al popolo, teneua dietro à se un Seruo musico, che ascosamente con un Flauto d'auo-
ri sonando gli daua la misura; cioè, la uoce, ouero il tuono di pronuntiare in tal modo,
che ogni uolta che lo uedeua troppo inalzato lo ritiraua, & uedendolo troppo abbas-
sato lo incitaua. Ma poscia la Poesia ben si uede con la Musica esser tanto congiunta,
che chiunque da questa separar la uolesse, restarebbe quasi Corpo separato dall'Anima;
il che conferma Platone nel Gorgia dicendo; Se alcuno da tutta la Poesia leuasse il Con-
cento & il Numero, con la Misura insieme, niuna differenza sarebbe da essa al parlare
page 8domestico & popolare. Et però si uede, che i Poeti hanno usato grandissima diligenza &
marauiglioso artificio nell'accommodare ne i Versi le parole, & disporre in essi i Piedi se
condo la cōuenienza della materia; come per tutto il suo Poema hà osseruato Virgilio;
percioche à tutte tre le sorti del parlare accommoda la propria sonorità del Verso con
tale arteficio, che propriamente pare, che col suono delle parole ponga dauanti à gli oc-
chi le cose, delle quali egli uiene à trattare: di modo che doue parla d'Amore, si uede
arteficiosamente hauer scielto alcune Parole soaui, dolci, piaceuoli & all'udito somma-
mente grate; & doue gli sia stato dibisogno cantare un fatto d'arme, descriuere una pu-
gna nauale, una fortuna di mare, ò simil cose, ou'entrano spargimenti di sangue, ire, sde
gni, dispiaceri d'animo & ogni cosa odiosa, hà fatto scielta di parole dure, aspre & dispia
ceuoli; di modo che nell'udirle & proferirle arrecano spauento. Et per darne in parte
qualche essempio; egli, nel mostrar la pouertà della capanna di Melibeo, diminuisce
quella parola Tuguri di una lettera;In Alex. quasi mostrando con essa l'effetto presente; come
ancora fece, quando uolse manifestare il cordoglio di quella Ninfa, che la gratiosa ui-
sta del suo Pastore era costretta abbandonare; che in quel uerso In Palam.
Et longum formose vale, vale (inquit) Iola;
Facendo dal pianto & da sospiri quasi interrompere il Verso, fà proferir lunga quella
Sillaba, che prima hauea posta breue. Dopoi uolendo mostrare, quanto sia ueloce il
Tempo, lo dimostra col uerso composto de molti Datili, che sono Piedi atti alla uelocità
& à mostrar un tale effetto, dicendo;Georg. 3.
Sed fugit interea fugit irreparabile tempus.
Et uolendo dimostrar, con quanto silentio la città de Ilio fusse da Greci assalita, lo
mostra con un Verso composto di molti Spondei, i quali sono Piedi per loro natura at-
ti alla tardità & alle cose deboli & ociose, dicendo;
Aeneid. 2.
Inuadunt vrbem somno, vinoꝗ sepultam.
Lascierò hora di dire, come uolendo mostrare i Cartaginesi essere stati sempre nemici
& contrarij à Romani; nel descriuere il sito di Cartagine, pospose à bello studio quella
parola, che andaua preposta, & disse;
Italiam contra.Aeneid. 1. Et infiniti altri, che troppo
lungo sarebbe il raccontargli in questo luogo, de i quali l'Opera è piena. Basterà hora
per ultima conclusione dire; che la Poesia sarebbe senza leggiadria alcuna, se dalle pa-
role harmonicamente poste non gli fusse data. Oltra di ciò lascierò da parte il dire,
quanta simiglianza & vnione con essa habbiano l'Arithmetica & la Geometria, per-
cioche si conosce nel trattar la Scienza; & dirò solamente, che se l'Architettore non
hauesse cognitione della Musica; come ben lo dimostra Vitruuio;De Archi.
lib. 1. cap. 1. non saprebbe con ra-
gion fare il temperamento delle machine, & ne i Theatri collocare i vasi, & dispor bene
& musicalmente gli edificij. L'Astronomia medesimamente, se non fusse aiutata da i fon-
damenti harmonici, non saprebbe gl'influssi buoni & rei. Anzi dirò più; se l'Astrono-
mo non sapesse la concordanza de i Sette pianeti, & quando l'uno con l'altro si congiun-
ga, ouero l'uno all'altro si opponga, non predirebbe mai le cose future. La Filosofia
ancora, laquale hà per suo proprio il discorrer con ragione le cose produtte dalla natura
& possibili à prodursi, non confessa ella dal Primo motore dependere ogni cosa, & esser
ordinata con si mirabil ordine, che ne risulta nell'Vniuerso una tacita harmonia? Ecco,
che primieramente le cose graui tengono il luogo basso, le leggieri il soprano, & quelle di
men peso, secondo la loro natura, posseggono il luogo di mezo. Et più oltra proce-
dendo, i Filosofi affermano, che i Cieli riuolgendosi fanno harmonia; la quale se bene
non udimo, questo può auenire, ò per la loro ueloce reuolutione, ò per la troppo di-
stanza, ouero per altra cagione à noi occulta. La Medicina da questa non può star lon-
tana; imperoche se 'l Medico non hà cognitione della Musica, come saprà egli ne i suoi
medicamenti proportionar le cose calide con le frigide, secondo i loro gradi? & come
potrà hauere ottima cognitione de i Polsi? i quali il dottissimo Herofilo dispose secon-
do l'ordine de i Numeri musicali. Et per salire più alto, la Theologia nostra ponendo nel
page 9cielo i Spiriti angelici, diuide quelli in noue Chori contenuti in tre Hierarchie; come
scriue Dionisio Areopagita.De caelest.
hierar. c. 6. Queste sono di continuo presenti alla Diuina maestà, &
non cessano di cantare Santo, Santo, Santo, Signore Iddio de gli esserciti; come è scrit-
to in Isaia.Isa. cap. 6. Et non solo questi, ma i quattro Animali ancora, i quali nel Libro delle
Reuelationi sono descritti da San Giouanni,Apoca. ca.
4. 5. 14. 15.
& 19. stanno auanti il trono di Dio, & cantano
l'istesso canto. Stanno oltra ciò i vintiquattro Vecchi inanzi all'Agnello immaculato,
& con suono di Cetere & altissime uoci cantano all'Altissimo Iddio vn nuouo canto; il-
quale è cantato anco dalle Citaristi citarizanti nelle cetere loro auanti i quattro
Animali & vintiquattro Vecchi. Di queste & altre quasi infinite cose al proposito
nostro n'è piena la diuina Scrittura, lequali per breuità trapasseremo; bastando sola-
mente dire, per suprema laude della Musica; senza far mentione alcuna d'altra Scienza;
che ella, secondo la testimonianza de Sacri libri, sola si troua nel Paradiso, & è quiui
nobilissimamente essercitata. Et si come nella Celeste corte, che Chiesa trionfante vien
detta; cosi nella nostra terrena, che Militante si chiama, non con altro, che con la Musi-
ca, si lauda & ringratia il Creatore. Ma lasciamo hormai da parte le cose superiori, &
ritorniamo à quelle, che sono dalla Natura produtte per ornamento del Mondo, che
uederemo ogni cosa esser piena de musici concenti. Il mare primamente hà le Sirene, le
quali (s'è lecito dar fede à i Scrittori) à nauiganti vdir si fanno di tal sorte, che vinti
molte uolte dall'Harmonia loro, & soprapresi dal sonno, perdono quello, che sopra ogn'
altra cosa è carissimo à tutti gli animali. Nell'Aria & nella Terra insieme sono gli Vc-
celli, che ancor'essi co i loro concenti dilettano & ricreano, non pur gli animi lassi & pie-
ni di noiosi pensieri; ma i corpi ancora: percioche il Viandante molte uolte stanco per
il lungo viaggio, ricrea l'animo, riposa il corpo, & si dimentica le passate fatiche, per la
soaue harmonia de boscarecci canti de vccelli de tante varie sorti, che sarebbe impossi-
bile il uolerle raccontare. I Fiumi & li Fonti medesimamente dalla natura fabricati so-
glion dare grato piacere à chiunque ad essi uicino si ritroua; & l'inuitano ben spesso per
ricrearsi ad accompagnare il suo rustico canto co i loro strepitosi concenti. Tutte que-
ste cose il Dottissimo Virgilio espresse con poche parole: quando disse;In Sileno.
Tum uerò in numerum Faunosꝗ, ferasꝗ uideresDinotandoci ch'al canto di Sileno, non solo i Fauni & l'altre fiere; ma le dure
Ludere: tum rigidas motare cacumina quercus.
Nec tantum Phoebo gaudet Parnasia rupes,
Nec tantum Rhodope miratur, & Ismarus Orphea:
Quantum omnis mundus gaudet cantante Sileno.
Quercie ancora ballauano; saltando quelli & queste spesso mouendosi con numerosi mo
uimenti; per dimostrarci, che non pur le cose sensibili; ma ancora quelle, che mancano
del senso, sono quasi prese & vinte da i concenti musicali; & fansi di dure & aspre,
mansuete & piaceuoli. Ma se tanta Harmonia si troua nelle cose celesti & terrestri; oue-
ro, per dir meglio, se 'l Mondo dal Creatore fu composto pieno di tanta harmonia;
perche dobbiamo credere l'Huomo esserne priuo di essa? Et se l'Anima del Mondo (co
me uogliono alcuni) non è altro che Harmonia, potrà esser che l'Anima nostra non sia in
noi cagione d'ogni Harmonia, & che col Corpo non sia harmonicamente congiunta?
massimamente hauendo Iddio creato l'Huomo alla similitudine del Mondo maggiore,
detto da Greci Κόσμος; cioè, Ornamento, ouer'Ornato, & essendo fatto à quella simili-
tudine di minor quantità, à differenza del quale uien chiamato Μικρόκοσμος; cioè, Pic-
ciol mondo; certo che non è cosa ragioneuole. Onde Aristotele2. De ani
ma. c. 3. volendo mostrar il mu-
sicale componimento dell'Huomo molto ben disse; La parte Vegetatiua alla Sensitiua,
& questa alla Intellettiua hauer la medesima conuenienza, che hà la Figura di tre lati
à quella di quattro. Certa cosa è adunque, che non si ritroua cosa alcuna buona, che
non habbia musicale dispositione; & la Musica ueramente, oltra che rallegra l'ani-
mo, riduce anche l'Huomo alla contemplatione delle cose celesti; & hà tal proprietà,
page 10ch'ogni cosa à cui si aggiunge fà perfetta; & quegli Huomini sono veramente felici &
beati, che sono dotati di essa; come afferma il Santo Profeta, dicendo;Psal. 88. Beato è quel
populo, che sà la Giubilatione. Per la quale autorità, Hilario Vescouo Pittauiense dot-
tore catholico, esponendo il Salmo 65. si mosse à dire; che la Musica è necessaria all'huo-
mo Christiano; conciosia che nella scienza di essa si ritroua la beatitudine Onde per que
sto hò ardimento di dire; che quelli, che non hanno cognitione di questa Scienza, so-
no da esser connumerati tra gl'ignoranti. Anticamente (come dice IsidoroLib. 3. Ety-
mol. c. 15.) non era
men uergogna il non sapere la Musica, che le Lettere; però non è marauiglia, se Hesio-
do poeta famosissimo & antichissimo (come narra Pausania Lib. 10. De
script. vete
ris Graeciae) fù escluso dal certame; co-
me colui, che non hauea mai imparato à sonar la Cetera, ne col suono di quella accom-
pagnare il canto. Cosi ancora Temistocle (come narra TullioTusculan.
Quaest. li. 1.) rifiutando di sonar la Li
ra nel conuito, fu men dotto & men sauio riputato. Il contrario leggiamo, che furono
in gran pregio appresso gli Antichi Lino & Orfeo, amendue figliuoli de i loro Dei; per-
cioche col soaue canto (come si dice) non solamente addolciuano gli Animi humani;
ma le fiere, & gli uccelli ancora; & quello, che è più marauiglioso da dire, moueano le
pietre da i proprii luoghi, & à i fiumi riteneuano il corso. Et questo istesso Horatio
attribuisce ad Anfione, dicendo.De Arte
poetica.
Dictus & Amphion Thebanae conditor arcis
Saxa mouere sono testudinis, & prece blanda
Ducere quo vellet;
Da i quali per auentura impararono gli antichi Pitagorici, che con musici suoni in-
teneriuano gli animi feroci; & Asclepiade medesimamente, che molte uolte per que-
sta via racchetò la discordia nata nel populo, & col suono della Tromba restitui l'Vdi-
to à i sordi. Parimente Damone pitagorico ridusse col Canto alcuni gioueni dediti al ui-
no & alla lussuria à temperata & honesta uita. La onde dissero bene coloro, che affer-
mauano la Musica esser una certa legge & regola di modestia; essendoche Theophrasto
ritrouo alcuni Modi musicali da racchetare i spiriti perturbati. Però meritamente &
sapientemente Diogene Cinico beffaua i Musici de suoi tempi, i quali hauendo le chor-
de delle loro cetere concordi, haueano l'animo incomposto & discorde; essendo abban-
donato dall'harmonia de costumi. Et se dobbiamo prestar fede alla Historia; ci debbe
parer quasi nulla quello, che habbiamo detto: percioche molto maggior cosa è l'hauere
uirtù di sanar gl'infermi, che di corregger la uita de sfrenati giouani; come ancora
leggiamo di Senocrate, ilquale col suono de gli organi ridusse i pazzi alla pristina sa-
nità, & Talete di Candia, col suono della Cetera scacciò la pestilenza.Alexā. ab
Alex. li. 2.
c. 16. Ge-
ni. Die. Et noi vedia-
mo hoggidì, che per uia della Musica s'oprano cose marauigliose; imperoche tanta è la
forza de i Suoni & de i Balli contra il veleno delle Tarantole, che in breuissimo tempo
risana coloro, che da esse sono stati morsi; come si vede ogni giorno per esperienza nella
Puglia, paese abondantissimo de cotali animali. Ma senza più testimonii profani, non
habbiamo noi nelle Sacre lettere1. Reg. c. 6., che 'l profeta Dauid racchetaua lo Spirito maligno di
Saul col suono della sua Cetera? Et per questo credo io, che esso regio Profeta ordi-
nasse, che nel Tempio d'Iddio si usassero i canti & gli harmonici suoni;1. Paral. c.
25. conoscendo
ch'erano atti à rallegrare i spiriti, & à ridur gli huomini alla contemplatione delle cose
celesti. I Profeti ancora (come dice Ambrosio sopra 'l Salmo 118. volendo profetizare,
dimandauano, ch'un perito del Suono si ponesse à sonare; accioche inuitati da quella
4. Reg. c. 3. dolcezza gli fusse infusa la gratia spirituale. Però Eliseo non uolse profetizare al Re
d'Israele quel, che douesse fare per l'acquisto delle acque; accioche gli esserciti non
morissero di sete; se prima non gli fù menato al suo conspetto un Musico, il quale can-
tasse; & cantando egli fu dello Spirito diuino inspirato, & predisse il tutto. Ma passia-
mo più oltra; percioche non mancano gli essempij. Timotheo (si come insieme con mol-
ti altri narra il Gran BasilioHomil. 54.
Ad adole
scentes.) con la Musica incitaua il Re Alessandro al combattere; &
quello medesimo essendo incitato riuocaua. Narra Aristotele nel Libro della Natura
page 11de gli Animali, che i Cerui per il canto de cacciatori sono presi; & che della Sampogna
pastorale & del canto ancora molto si dilettano; il che conferma Plinio nella sua Natu-Lib. 9. c. 5.
Lib. 8. c. 32
rale Historia. Et per non mi distendere più sopra di questo, solamente dirò di conosce-
re alcuni, i quali hanno veduto de i Cerui, che fermando il lor corso, se ne stauano at-
tenti ad ascoltare il Suono della Lira & del Leuto; & medesimamente si uede ogni gior-
no gli Vccelli vinti & ingannati dall'Harmonia, il più delle uolte restare presi dall'Vc-
cellatore. Narra etiandio Herodoto & Plinio,Vrania
lib. 1.
Nat. hist.
lib. cap. 8. che la Musica campò Arione dalla mor-
te, che precipitandosi nel mare, fu portato dal Delfino nel lito di Teniaro isola. Ma la-
sciamo stare hormai molti altri essempi, che potremmo addurre, & diciamo vn poco
del buon Socrate maestro di Platone, che già uecchio & pieno di sapienza volse impa-
rare à sonar la Cetera: & il vecchio Chirone tra le prime arti, che insegnasse ad Achil-
le nella tenera età, fu la Musica; & uolse, che le sanguinolenti sue mani, prima che
s'imbrattassero del sangue Troiano, sonassero la Cetera. PlatoneDe legi-
bus. 3. & Aristotele8. Politi. c.
3. non com-
portano, che l'Huomo bene istituito sia senza Musica; anzi persuadono con molte ra-
gioni tale Scienza douersi imparare; & mostrano la forza della Musica esser in noi gran-
dissima; & perciò vogliono, che dalla fanciullezza vi si dia opera; conciosia che è soffi-
ciente à indurre in noi un nuouo habito & buono, & un costume tale, che ne guida & con
duce alla virtù, & rende l'animo più capace di felicità: & il Seuerissimo Licurgo Re de
Lacedemonij tra le sue seuerissime Leggi lodò & sommamente approuò la Musica; per-
cioche molto ben conosceua, ch'all'Huomo era necessaria molto, & di giouamento
grandissimo nelle cose della guerra; di modo che i loro Esserciti (come narra ValerioDict. Fact.
lib. 2. ca. 1.)
non usauano di andar mai a combattere, se prima non erano ben riscaldati & inanima-
ti dal Suono de Pifferi. Osseruasi ancora tal costume à i tempi nostri; percioche di due
esserciti l'uno non assalirebbe l'inimico, se non inuitato dal suono delle Trombe & de
Tamburi, ouero da alcun'altra sorte de musicali istrumenti. Et benche, oltra i narrati, non
manchino infiniti altri essempi, da i quali si potrebbe maggiormente conoscere la digni-
tà & eccellenza della Musica; nondimeno, per non andar più in lungo, li lasciaremo;
essendo à bastanza quello, che fin'hora si è ragionato.
A che fine la Musica si debba imparare.Cap. III.
za Musica; però douendola imparare, auanti che più oltra passiamo, uoglio
che ueggiamo qual fine egli si debba proporre; poi che intorno à ciò sono sta-
ti diuersi pareri; il che ueduto, uederemo anco l'utile, che della Musica ne uie-
ne; & in qual maniera la dobbiamo usare. Incominciando adunque dal primo dico, che
sono stati alcuni, i quali hanno hauuto parere, che la Musica si douesse imparare per dar
solazzo & dilettatione all'Vdito; non per altra ragione, se non per far diuenir perfetto
questo Senso, nel modo che 'l Vedere diuenta perfetto, quando con diletto & piacere
riguarda una cosa bella & proportionata, ma in uero non si debbe imparare à questo fine,
imperoche è cosa da volgari & da mecanici; essendoche queste cose non hanno in se par-
te alcuna di uirtuoso; ancora che acchetando l'animo habbiano del diletteuole; & sono
cose da Huomini grossi, i quali nō cercano di satisfare al Senso, & à questo solo fine atten
dono. Altri poi uoleuano, ch'ella s'imparasse, non ad altro fine, se non per esser posta
tra le Discipline liberali, nelle quali solamente i Nobili s'esercitauano; & perche dispone
l'animo alla uirtù, & regola le sue passioni, con auezzarlo à rallegrarsi & à dolersi uirtuosa
mente, disponēdolo à i buoni costumi, nō altramente di quello, che fà la Ginnastica il cor
po à qualche buona dispositione & habitudine; & anche à fine di poter con tal mezo per-
uenire alla speculatione de diuerse sorti d'Harmonia; poi che per essa l'Intelletto cono-
sce la natura delle musicali Consonanze. Et quantunque questo fine habbia dell'hone-
page 12sto; non è però à bastanza; imperoche colui, ilquale impara la Musica, non solo l'im-
para per acquistar la perfettione dell'Intelletto; ma per potere, quando cessa dalle cure
& negocij, si del Corpo, come dell'Animo; cioè, quando è in ocio & fuori delle cottidia-
ne occupationi, passare il tempo & trattenersi virtuosamente; accioche rettamente
& lodeuolmente viuendo lontano dalla pigritia, per tal mezo diuenti prudente, & trap-
passi poi à far cose migliori, & piu lodeuoli. Ilqual fine non solo è degno di laude, & è hone
sto; ma è il vero fine: percioche non fù ritrouata la Musica, ouer ordinata per altro, se
non per quello, c'habbiamo mostrato di sopra; come nella sua PoliticaLib. 8. c. 5. il Filosofo manife
sta; adducendo & raccontando molte autorità di Homero. Onde meritamente gli An-
tichi la collocarono nell'ordine de quelli trattenimenti, che seruono à gli Huomini libe-
ri, & tra le discipline lodeuoli, & non tra le necessarie, come è l'Arithmetica; ne anche
tra le vtili, come sono alcune, lequali sono per l'acquisto solamente de beni esteriori, che
sono i denari & l'utile della famiglia; ne tra alcune altre, lequali seruono alla sanità del
corpo & alla fortezza, come la Ginnastica, ch'è un'Arte appartenente alle cose, che gio-
uano à far sano & forte il corpo; come è fare alla lotta, lanciare il palo & altre cose, che
appartengono all'essercitio della guerra. Si debbe adunque imparar la Musica, non co-
me necessaria, ma come liberale & honesta; accioche col suo mezo possiamo peruenire ad
un'habito buono & uirtuoso, che ne conduca nella uia de buoni costumi, facendone ca-
minare ad altre Scienze più utili & più necessarie; & passare il tempo virtuosamente; &
questo debbe esser la principale, ò ultima intentione, che dire la uogliamo. Ma in qual
modo habbia possanza d'indur nuoui costumi & mouer l'animo à diuerse passioni, ne
ragionaremo in altro luogo.Infra ca. 8.
Secundae
partis.
Dell'Vtile che si hà della Musica, & dello Studio che vi dobbiamo porre,
& in qual modo usarla.Cap. IIII.
temperatamente; imperoche è cosa manifesta, che non pur l'Huomo, il quale
è capace di ragione; ma anche molti de gli altri animali, che di essa mancano,
si comprende, che pigliano dilettatione & piacere; percioche dilettandosi &
rallegrandosi ogn'Animale della proportione & temperamento delle cose, & ritrouando-
si nelle Harmonie tali qualità, ne segue immediatamente il piacere & la dilettatione à
tutti i uiuenti commune. Et è in uero cosa ragioneuole; poi che la Natura consiste in ta-
le proportione & temperamento, ch'Ogni simile si diletta del suo simile, & quello appe-
tisce. Di ciò ne danno chiarissimo indicio i Fanciulli à pena nati; che presi dalla dolcez-
za del canto delle uoci delle loro nutrici, non solo dopo il lungo pianto si racchetano; ma
si rendono allegri, facendo anche spesse uolte alcuni gesti festeuoli. Et è la Musica
tanto naturale & in tal modo à noi congiunta, che uediamo ciascuno Huomo in un cer
to modo uolerne dar qual che giudicio, ancora che imperfettamente. Per la qual cosa si
potrebbe dire, Colui non esser composto con Harmonia, ilquale non piglia diletto del-
la Musica; percioche (come habbiamo detto) se ogni dilettatione & piacere nasce
dalla similitudine, è necessario, che colui, il quale non hà piacere dell'Harmonia, in
un certo modo ella non si troui in lui, & che di essa sia ignorante. Et se ben si uorrà essa-
minar la cosa, si ritrouerà colui esser di bassissimo ingegno & senza punto di giudicio; &
si potrebbe dire, che la Natura gli hauesse mancato, non gli hauendo proportionatamēte
formato l'Organo; poiche quella parte, laquale è per mezo il ceruello, & è più uicina al-
l'orecchia, quando è proportionatamente composta, serue ad un certo modo al giudi-
cio dell'Harmonia, dalla quale l'Huomo, come da cosa simile, è preso & uinto, & in
essa molto si compiace; ma se auiene, che sia priua di tal proportione, molto meno di
page 13ciascun'altro di essa prende diletto; & è in tal modo atto alle cose speculatiue & ingegno
se, come si dice in prouerbio, come è l'Asino alla Lira. Et se uogliamo in ciò seguire l'
opinione de gli Astrologi, diremo, che nel suo nascimento Mercurio gli sia stato ini-
mico; come è fauoreuole à coloro, i quali non pur dell'Harmonia si dilettano; ma non
si sdegnano, per alleuiamento delle loro fatiche, essi medesimi cantare & sonare, ricre-
andosi lo spirito & riacquistandogli le smarrite forze. Et però bene hà ordinato la Natu-
ra, che hauendo in noi, mediante lo Spirito, congiunto insieme (come uogliono i Pla-
tonici) il Corpo & l'Anima; à ciascun di loro, essendo deboli & infermi, hà proueduto
de oportuni rimedij; imperoche essendo il Corpo languido & infermo, si uiene à risanare
co' rimedij, che li porge la Medicina; & lo Spirito afflitto & debole da i spiriti aerei, &
da i Suoni & Canti, che gli sono proportionati rimedij è recreato; ma l'Anima rinchiusa
in questo corporeo carcere, si consola per uia de gli alti & diuini misterij della sacra Theo
logia. Tale utile adunque ne apporta la Musica; & di più, che scacciando la noia, che
si piglia per le fatiche, ne rende allegri, & raddoppia l'allegrezza & la conserua:
Noi vediamo i Soldati andare ad assalire l'inimico molto più ferocemente, incitati dal
suono delle Trombe & de Tamburi; & non pur essi, ma i Caualli ancora mouersi con
grande empito. Questa eccita l'animo, muoue gli affetti, mitiga & accheta la furia, fà
passare il tempo virtuosamente, & hà possanza di generare in noi un'habito de buoni co
stumi; massimamente quando con i debiti modi & temperatamente è usata: imperoche
essendo l'vfficio proprio della Musica il dilettare; nō dishonestamente, ma honestamente
la dobbiamo vsare; accioche non c'intrauenga quello, che suole intrauenir à coloro, che
smisuratamente beuono il Vino; i quali poi riscaldati, nuocono à se stessi; & facendo
mille pazzie; muouono à riso chiunque li uede: non perche la natura del Vino sia tanto
maligna, che quando temperatamente si beua, operi nell'Huomo simil efetto; ma si
mostra tale à colui, che lo beue auidamente; conciosiache Tutte le cose sono buone,
quando temperatamente si usano à quel fine, che sono state ritrouate & ordinate; ma
quando sono intemperatamente usate, & non secondo il debito fine, nuocono, & sono
pernitiose. Di modo che potiamo tener questo per vero; che non pur le cose naturali;
ma ogni Arte & ogni Scienza possono esser buone & cattiue, secondo che sono usate:
buone dico, quando sono indrizzate à quel fine, al quale sono state ordinate; & catti-
ue, quando da quel fine si allontanano. Essendo adunque nato l'Huomo à Cose molto
più eccellenti, che non è il Cantare, ò Sonare di Lira, ò altre sorti d'Istrumenti, per sa
tisfar solamente al senso dell'Vdito; vsa male la sua natura, & deuia dal proprio fine;
poco curandosi di dare il cibo conueniente all'Intelletto; ilquale sempre desidera sape-
re, & intendere nuoue cose. Non debbe adunque l'Huomo solamente imparar l'arte
della Musica, & ritrarsi dall'altre Scienze, abbandonando il suo fine; che sarebbe gran
pazzia; ma debbe impararla à quel fine, al quale è stata ordinata. Ne debbe spendere
il tempo solamente in essa; ma debbe accompagnarla con lo Studio della speculatiua; ac
cioche aiutato da quella, possa uenire in maggior cognitione delle cose, che all'uso di
essa appartengono; & mediante quest'uso possa ridurre in atto quello, che per lungo stu-
dio speculando hà inuestigato: imperoche accompagnata in tal modo porta vtile ad o-
gni Scienza & ad ogni Arte, come altre uolte habbiamo ueduto.Supra. c. 2. Et se facesse altramente,
non gli sarebbe tal cosa di molta utilità, ne di molta gloria; anzi se gli attribuirebbe à
uitio; conciosia che l'essercitarsi continuamente in essa senz'alcun'altro studio, induce
sonnolenza & pigritia; & rende gli animi molli & effeminati; la qual cosa conoscendo
gli Antichi, uolsero, che lo studio della Musica alla Ginnastica fusse congiunto; ne uole-
uano, che si potesse dar opera all'una senza l'altra; & questo faceuano, accioche per il
darsi troppo alla Musica, l'animo non uenisse à farsi uile; & dando opera solamente al-
la Ginnastica, gli animi non diuenissero oltra modo feroci, crudeli & inhumani; ma da
questi due essercitij insieme aggiunti si rendessero humani, modesti & temperati. Et à
far ciò si mossero con ragione; che chiaramente si può uedere, che coloro i quali nella gio-
page 14uentù loro, lasciati i studij delle cose di maggiore importanza, si sono dati solamente à
conuersare co gl'Istrioni, & co Parasiti, stando sempre nelle scuole de giuochi, de balli
& de salti, sonando la Lira & il Leuto; & cantando canzoni men che honeste, sono mol
li, effeminati & senz'alcun buon costume. Imperoche la Musica in tal modo vsata, ren-
de gli animi de Giouani mal composti; come ben lo dimostrò Ouidio, dicendo.
De Remed.
lib. 2.
Eneruant animos citharae, cantusque lyraeque,
Et uox, & numeris brachia mota suis.
Ne d'altro sanno ragionare, che di tali cose; ne altro che dishoneste parole dal-
la loro sporca bocca si sentono uscire. Per il contrario poi, sono alcuni, i quali per
cotale studio non solo molli & effeminati; ma importuni, dispiaceuoli, superbi, perti-
naci & inhumani diuentano; di modo che uedendosi ad un certo termine arriuati, sti-
mandosi sopra d'ogn'altro eccellenti (il che è proprio d'una gran parte de quelli, ch'esser-
citano la Musica ne i nostri tempi) si gloriano, si essaltano & si lodano; & vituperando gli
altri, per parere d'esser pieni di sapienza & di giudicio; se ben sono ignoranti, & goffi;
stanno con la maggior riputatione & superbia del mondo; ne mai se non con grande istan
tia de prieghi, & con laudi molto maggiori, che à loro conuengono, si possono ridurre
à mostrare un poco del loro sapere. Per la qual cosa de tutti questi Tigelii si verifica il
detto di Horatio.Ser. lib. 1.
Ser. 3
Omnibus hoc uitium est Cantatoribus, inter amicos,
Vt nunquàm inducant animum cantare rogati,
Iniussi nunquàm desistant.
A' tali faceua dibisogno, che i padri loro più presto hauessero fatto imparare qualch'al-
tro mestiero, quantunque vile; che forse non sarebbono caduti in tali errori, & hauereb
bono acquistate megliori creanze. Tutto questo hò uoluto dire, accioche quelli, che
dell'arte della Musica vogliono fare professione, s'innamorino della Scienza, & diano
opera allo studio della Speculatiua; percioche non dubito, che congiungendo questa in
sieme con la Prattica non habbiano da diuentar virtuosi, honesti & costumati; & in tal
modo uerranno ad imitare gli Antichi, i quali (come si è detto) accompagnauano la
Musica con la Ginnastica: percioche cosi accompagnata ella sarà potente di ridur cia-
scun suiato nella diritta via de buoni costumi. Ne alcun debbe credere, che quello c'hò
detto in questo proposito dell'arte della Musica, l'habbia detto per uituperarlo; ne an-
che per dir male di coloro, che in tal maniera si essercitano; cosa che giamai non mi è ca
duto nell'animo; ma più tosto l'hò detto, accioche congiungendola in tal modo con
altre honoreuoli Scienze piene di seuerità , la difendiamo da i uagabondi & ottiosi ruf-
fianesmi de bagatellieri; & la riponiamo nel suo uero luogo; si ch'ella non habbia da
seruir più à coloro, che sono dediti solamente alle uoluttà; ma sia per uso de i Studiosi
delle buone Scienze, & di coloro che seguitano le uirtù, costumatamente & ciuilmen-
te viuono.
Quello che sia Musica in vniuersale, & della sua Diuisione.Cap. V.
do prima quel che sia Musica, & dopoi di quante sorti si truoua, assegnando
à ciascuna sorte la sua definitione; & questo faremo per non deuiare dal buō'
ordine, c'hanno tenuto gli Antichi;Cicero De
offi. lib. 1. i quali voleuano, ch'Ogni ragionamen-
to di qualunque cosa, che ragioneuolmente si faccia, debba incominciar dalla Defini-
tione; accioche s'intenda quello, di che si hà da disputare. Però in uniuersale parlan-
do, dico; che Musica pigliata nella sua Analogia, ò proportione, non è altro, che Har-
monia; & potemo dire, ch'ella sia quella Lite & Amicitia, che poneua Empedocle; dal
la quale uoleua, che si generassero tutte le cose; cioè, una Discordante concordia; co-
page 15me dire; Concordia de varie cose, lequali si possono congiungere insieme. Ma per
che questa parola Musica è sottoposta à diuerse significationi; & la ragion vuole, ch'ogni
cosa, che porta seco molti significati, prima debba esser diuisa, che definita; massimamen
te uolendo dichiarare ogni sua parte; però noi primamente la diuideremo, dicendo; la
Musica esser di due sorti, Animastica & Organica; L'una è Harmonia, che nasce dalla
compositione de varie cose congiunte insieme in un corpo; auenga che tra loro siano di-
screpanti; come è la mistura de i quattro Elementi, ouer de altre qualità in un corpo ani
mato; L'altra è Harmonia, che può nascere da varij Istrumenti. Et questa di nuouo par-
tiremo in due; percioche si ritrouano due sorti d'Istrumenti; Naturali & Arteficiali. I Na-
turali sono quelle parti, che concorrono alla formatione delle uoci; come sono la Gola,
il Palato, la Lingua, le Labbra, i Denti, & finalmente il Polmone, formate dalla na-
tura; le qual parti essendo mosse dalla Volontà; & dal mouimento di esse nascendone il
Suono, & dal Suono il Parlare; nasce poi la Modulatione, ouero il Cantare; & cosi per
il Mouimento del corpo, per la Ragione del suono, & per le Parole accommodate al
Canto, si fà perfetta l'Harmonia, & nasce la Musica detta Harmonica, ò Naturale. Gli
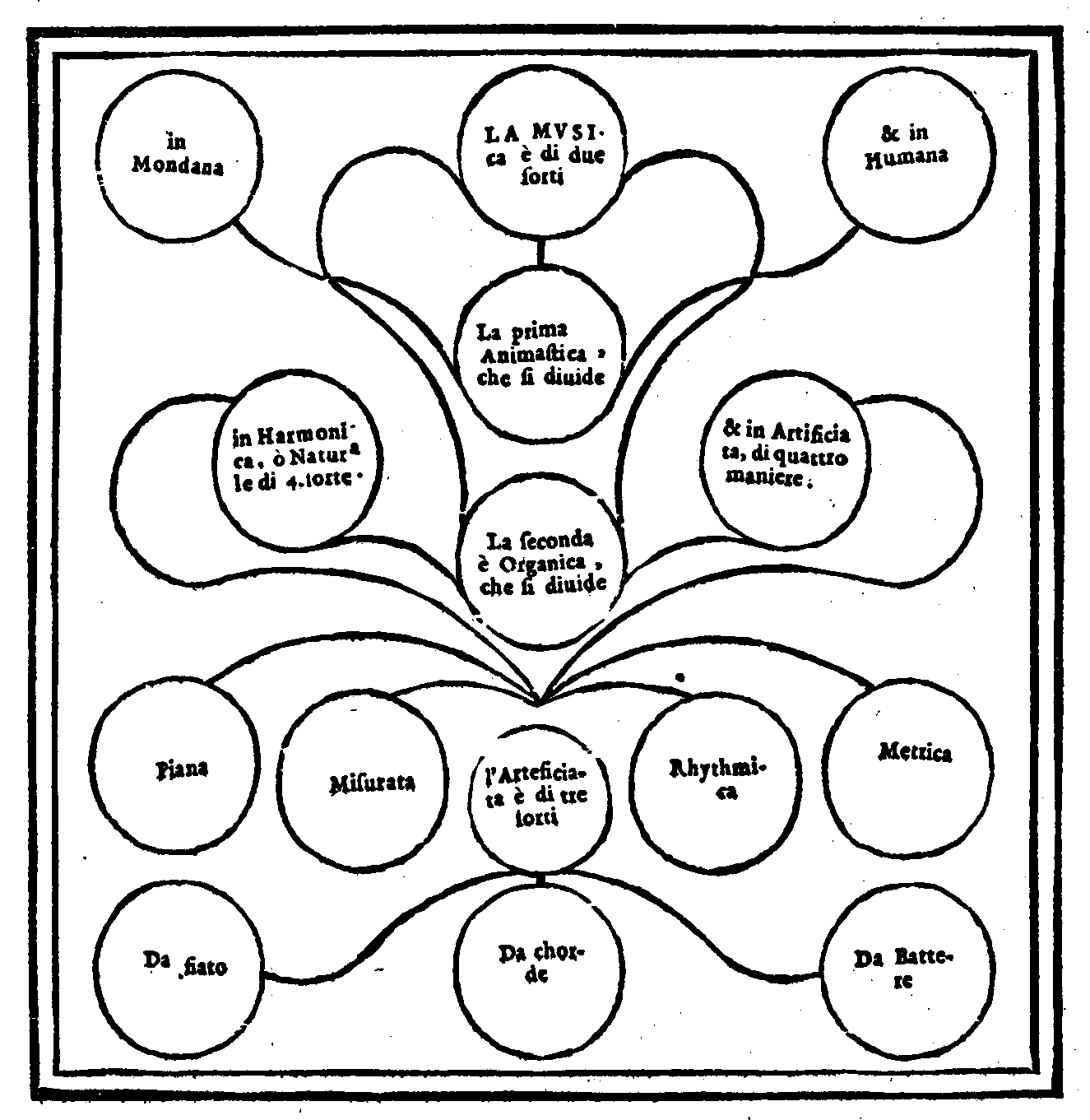
Musica arteficiata; che è quella Harmonia, che nasce da simili Istrumenti; & questa si
fà in tre modi; percioche, ò nasce da Istrumenti, che rendono Suono con fiato natura-
le, ò arteficiato; come Organi, Piferi, Trombe, & simili; ouer da Istrumenti da chor-
de, oue non fà dibisogno fiato; come Cetere, Lire, Leuti, Arpichordi, Dolcimeli, &
simili; i quali dalle dita & dalle penne & da altre cose simili sono percossi, ouer si sonano
con Archetti. Nasce ultimamente da Istrumenti da battere; come Tamburi, Cembali,
page 16Taballi, Campane & altri simili, che di legno concauo & di pelle d'animali sopra tirrate
& di metallo si fanno; quando da qual si uoglia cosa siano percossi. Di modo che l'Arte-
ficiata si troua di tre sorti; da Fiato, da Chorde & da Battere; & la Naturale di quattro,
Piana, Misurata, Rhythmica & Metrica. Benche queste quattro ancora si possano at-
tribuire all'Arteficiata, per le ragioni, ch'altroue diremo.Infra
cap. 9. Dell'Animastica poi faremo
similmente due Parti, ponendo nella prima la Mondana, & nella seconda la Humana;
come nella diuisione il tutto appare.
menti da fiato, nominandola Organica; da quella, che nasce dalle chorde & senza fiato,
chiamandola Rhythmica; nondimeno l'una & l'altra hò voluto chiamare indifferente-
mente Arteficiata; prima, percioche non è di molta importanza il nominarle più ad un
modo, che ad un'altro; dopoi per osseruare il significato della parola Organo, don-
de uien questo nome Organico, che comprende in uniuersale tutte le sorte d'Istrumenti
arteficiali; & oltra di questo per fuggir l'equiuocatione: conciosia che dicendosi Rhy-
thmica, si potrebbe intendere, non solo di quella harmonia, che nasce da gli Istrumen-
ti arteficiali da chorde; ma anco di quella che dalla Prosa ben composta risulta. Ma ue-
diamo hormai quel che sia ciascun membro della sopramostrata diuisione.
Della Musica mondana.Cap.VI.
ti, Mondana & Humana. La Mondana è quell'Harmonia, che non solo
si conosce essere tra quelle cose, che si ueggono & conoscono nel cielo; ma
nel legamento de gli Elementi & nella uarieta de i tempi ancora si compren-
de. Dico che si ueggono & conoscono nel cielo, dal Riuolgimento, dalle Distanze &
dalle Parti delle sphere celesti; & da gli Aspetti, dalla Natura & dal sito de i sette Pia-
neti; che sono la Luna, Mercurio, Venere, il Sole, Marte, Gioue & Saturno; impe-
roche è stata opinione de molti Filosofi antichi, & massimamente di Pitagora, ch'un ri-
uolgimento di si gran machina con si ueloce mouimento, non trappassi senza mandar
fuori qualche suono; la quale opinione, quantunque da Aristotele2. Cli. c. 2. sia riprobata, è non-
dimeno fauorita da Cicerone nel Lib. 6. della Rep. doue rispondendo il maggior Scipio
ne Africano al minore, che gli hauea dimandato; che Suono è questo si grande & si dol-
ze, che empie gli orecchi miei? dice; Questo è quello, che congiunto per inequali in-
terualli, nondimeno distinti per compartita proportione, è fatto dal sospingere & dal
muouere di essi circoli; ilquale temperando le cose acute con le graui, equalmente fà
diuersi concenti: perche non si possono far si grandi mouimenti con silentio; & la Na-
tura porta, che gli estremi dall'una parte grauemente & dall'altra acutamente sonino.
Per laqual cosa quel sommo corso del cielo stellato, il cui riuolgimento è più veloce, si
muoue con acuto & più forte suono; & questo lunare & infimo con grauissimo. Questo
dice Tullio,De Rep. 10 seguendo il parer di Platone, ilquale per mostrare, che da tale riuolgimen
to nasca Harmonia, finge, ch'à ciascuna sphera soprasieda una Sirena: che uuol dire
Cantatrice à Dio. Et medesimamente Hesiodo nella sua Theogonia accennando que-
sto istesso, chiamò Οὐρανία l'ottaua Musa, ch'è appropriata all'Ottaua sphera, da Οὐρανὸς,
col qual nome da i Greci uien nominato il Cielo. Et per mostrare, che la Nona sphera
fusse quella, che partorisce la grande & concordeuole unità de suoni, la nominò Καλ-
λιόπη, che uiene à significare di ottima voce; uolendo mostrar per questo l'Harmonia,
che risulta da tutte quell'altre sphere; come si uede accennato dal Poeta, quando disse.Aeneid. 9.
Vos o Calliope precor aspirate canenti;Inuocando particolarmente Calliope nel numero del più, come principale, & come
quella, al cui uolere si muouono & si girano tutte l'altre. Et tanto hebbero gli Antichi
page 17questa opinione per uera, che ne i sacrificij loro usauano musicali istrumenti, & can-
tauano alcuni Hinni composti di sonori versi; i quali conteneuano due parti, l'una
dellequali nominauano Στροφὴ & l'altra Α'ντιστροφὴ. per mostrare i diuersi giri fatti dal-
le sphere celesti: percioche per l'una intendeuano il moto, che fà la sphera delle stelle
fisse dall'Oriente in Occidente; & per l'altra i mouimenti diuersi, che fanno l'altre sphe-
re de pianeti procedendo al contrario; secondo l'opinione di alcuni; dall'Occiden-
ta in Oriente. Et con tali Istrumenti ancora accompagnauano i corpi de i lor Morti
alla sepoltura: essendoche erano di parere, che dopo la morte l'Anime ritornassero
all'origine della dolcezza della Musica; cioè, al cielo. Tal costume osseruarono gli He-
brei anticamente nella morte de loro parenti; di che ne habbiamo chiarissima testimo-
nianza nell'Euangelio,Matth. c. 9 nel quale è descritta la Resuscitatione della figliuola del prenci-
pe della Sinagoga, doue erano musicali istrumenti; à sonatori de i quali commandò il
Signor nostro, che più non sonassero. Et faceano questo (come dice AmbrosioSuper Lu-
cam ca. 8.
lib. 6:) per
osseruar l'usanza de i loro Antichi; i quali in cotal modo inuitauano i circostanti à pian-
gere con esso loro. Molti ancora haueano opinione, ch'in questa vita ogn'Anima
fusse vinta per la Musica; & se bene era nel carcere corporeo rinchiusa, ricordandosi
& essendo consapeuole della Musica del cielo, si domenticasse ogni dura & noiosa fa-
tica. Ma se ciò ne paresse strano, habbiamo dell'Harmonia del cielo il testimonio
delle Sacre lettere, doue il Signor parla à Giobbe dicendo:Iob. c. 38. chi narrerà le ragioni, ò
voci de Cieli? Et chi farà dormire il loro concento? Et se mi fusse dimandato; onde
proceda, che tanto grande & si dolce suono non sia udito da noi; altro non saprei ri-
spondere, che quello, che dice Cicerone nel luogo di sopra allegato; che gli orecchi
nostri ripieni di tanta Harmonia sono sordi; come per essempio auiene à gli habitato-
ri de quei luoghi doue il Nilo da monti altissimi precipita, detti Catadupa; i quali
per la grandezza del rimbombo mancano del senso dell'vdito: ouer che, si come
l'occhio nostro non può fissar lo sguardo nella luce del sole, restando da i suoi rag-
gi uinta la nostra luce; cosi gli orecchi nostri non possono capire la dolcezza dell'
harmonia celeste, per l'eccellenza & grandezza sua. Ma ogni ragione ne persuade
à credere almeno, che 'l Mondo sia composto con harmonia; si perche (come uuol
PlatoneIn Timeo.) l'Anima di esso è Harmonia; si anche perche i Cieli sono girati intorno dal-
le loro Intelligenze con harmonia; come si comprende da i loro riuolgimenti, i quali
sono l'uno dall'altro proportionatamente più tardi, ò più veloci. Si conosce ancora
tale Harmonia dalle distanze delle sphere celesti, percioche sono distanti tra loro (co-
me piace à molti) in harmonica proportione; laquale, benche non uenga misurata dal
senso, è nondimeno misurata dalla ragione: imperoche i Pitagorici (come dimostra
PlinioNatu. hist.
li. 2. c. 22.) misurando la distanza de cieli & i loro interualli, poneuano innanzi ogni al-
tra cosa dalla Terra alla prima Sphera lunare essere lo spatio di 12600. stadij; & que-
sto diceuano essere l'Interuallo del Tuono; auegna che questo (secondo 'l mio pare-
re) sia detto fuori d'ogni ragione, quando alla Terra attribuissero suono: concio-
sia che non può essere, che quelle cose, le quali per loro natura sono immobili, co-
m'è questo Elemento, siano atte à generare l'Harmonia; hauendo i Suoni (come
uuol BoetioMusicae li-
bro. 4. c. 1.) il loro principio dal mouimento. Dopoi andauano ponendo dalla sphe-
ra della Luna à quella di Mercurio l'interuallo d'un Semituono maggiore; & da Mer-
curio à Venere, quello del minore; e da Venere al Sole il Tuono & il minore Se-
mituono; & questa diceuano esser distante dalla terra per tre Tuoni & uno Semituo-
no; il qual spatio è nominato Diapente. Et dalla Luna al Sole poneuano la distan-
za di due Tuoni & uno Semituono; iquali costituiscono lo spatio della Diatessaron.
Ritornando poi al principiato ordine, dissero; il Sole esser lontano da Marte per la
medesima distanza, ch'è la Luna dalla terra; & da Marte à Gioue esser l'interual-
lo del Semituono minore; & da questo à Saturno lo spatio del Semituono maggio-
re; dal quale per fino all'ultimo cielo,oue sono i segni celesti posero lo spatio del minor
page 18Semituono. Per la qual cosa dall'ultimo Cielo alla sphera del Sole si comprende esser lo
spatio, ò interuallo della Diatessaron; & dalla terra all ultimo cielo lo statio de cinque
Tuoni & due minori Semituoni; cioè, la Diapason. Ma chi uorrà esserminar i Cieli nel-
le loro parti, secondo che con gran diligenza hà fatto Tolomeo,Harmo. li
bro 3. c. 9. ritrouera (comparate
insieme le dodici parti del Zodiaco, nelle quali sono i dodici segni celesti) le consonan-
ze musicali; cioè, la Diatessaron, la Diapente, la Diapason & l'altre per ordine; & ne i mot
ti fatti verso l'Oriente & l'Occidente potrà conoscere esser collocati i suoni grauissimi;
& in quelli, che si fanno nel mezo del cielo gli acutissimi. Nelle altezze poi ritrouerà il
Diatonico, il & l'Enharmonico genere. Simigliantemente nelle larghez-
ze i Tropi, ò Modi, che uogliamo nominarli; & nelle faccie della Luna, secondo i uarij
aspetti col Sole, esser le congiuntioni de i Tetrachordi. Ne solamente dalle predette cose
si può conoscere cotale Harmonia; ma da i uarii aspetti de i sette Pianeti ancora, dalla
natura, & dalla positione, ò sito loro. Da gli aspetti prima, come dal Trino, dal Qua-
dratto, dal Sestile, dalle Congiuntioni & dalle Oppositioni; i quali fanno nelle cose
inferiori, secondo i loro influssi buoni & rei, una tale & tanta diuersita d'harmonia de co-
se, ch'è impossibile di poterla esplicare. Dalla natura poi, conciosiache essendone al-
cuno (come uogliono gli Astrologi) di natura trista & maligna; da quelli, che buoni
& benigni sono, in tal modo uengono ad esser temperati; che ne risulta poi tale Har-
monia, ch'apporta gran commodo & utile à mortali. Et questa si comprende anco dal Si-
to, ouer dalla Positione loro; conciosiache sono tra loro in tal modo collocati, quasi
nel modo che sono collocate le Virtù tra i Vitii. Onde, si come questi, che sono
estremi, si riducono ad un'habito uirtuoso, per uia d'uno mezo conueniente; cosi quel-
li Pianeti, che sono di natura maligni, si riducono alla temperanza per uia d'un'altro
Pianeta posto nel mezo loro, che sia di natura benigna. Però si uede, che essendo Sa-
turno & Marte posti nel luogo soprano di natura maligna, cotal malignità da Gioue po-
sto tra l'uno & l'altro, & dal & Sole posto sotto di Marte con una certa harmonia è tempe-
rata, si che non lasciano operare à i loro influssi cattiui nelle cose inferiori quel mali-
gno effetto, che potrebbono operare, non vi essendo tale interpositione. Hanno etian-
dio i loro influssi tale possanza sopra i corpi inferiori, che mentre i due primi nominati
pianeti si ritrouano hauere il dominio dell'anno; allora si discioglie l'harmonia de i quat-
tro Elementi; percioche si altera l'aria de tal maniera, che genera nel mondo pestilen-
za uniuersale. Vogliono ancora gli Astrologi, che i due Luminari maggiori, che sono
il Sole & la Luna, faccino corrispondente harmonia di beniuolenza tra gli huomini;
quando nel nascimento dell'uno, quello si ritrona essere nel Saggittario, & questa nel
Montone; & nel nascimento dell'altro, il Sole sia nel Montone, & la Luna nel Sa-
gittario. Simile harmonia dicono ancora farsi, quando nel loro nascimento hanno
hauuto un medesimo segno, ouero di simile natura, ouero un medesimo pianeta, ò
di natura simile in ascendente; ouero che due benigni pianeti col medesimo aspet-
to habbiano riguardato l'angolo dell'oriente. Questo istesso dicono auenire, quando
Venere si ritroua nella medesima casa della loro natiuità, ò nel medesimo grado. Ha-
uendo adunque hauuto riguardo à tutte le sopradette opinioni, & essendo (come affer-
ma Mercurio TrismegistoPimandro
Ser. 10.) il mondo istrumēto, ouero Organo d'Iddio, nella dichiaratio
ne della Musica mondana hò detto, ch'è Harmonia, laquale si scorge tra quelle cose,
che si veggono & conoscono nel cielo. Et soggiunsi, che anco nel legamento de gli Ele-
menti si comprende; conciosiache essendo stati creati dal grande Architettore Iddio (si
come creò ancora tutte l'altre cose) in Numero, in Peso & in Misura;Sap. 11. da ciascuna
di queste tre cose si può comprendere tale harmonia; & prima dal Numero, medianti
le qualità passibili, che sono quattro & non piu; cioè, Siccittà, Frigidità, Humidità, &
Calidità, che si ritrouano in essi; imperoche à ciascuno di loro principalmente vna di
esse qualità è appropriata; come la siccità alla terra, la frigidità all'acqua, l'humidità
all'aria; & la calidità al fuoco; ancora che la siccità secondariamente si attribuisca
page 19al fuoco, la calidità all'aria, l'humidità all'acqua, & la frigidità alla terra; per le qua-
li non ostante, che tra loro essi Elementi siano contrarii; restano nondimeno in un me-
zano elemento secondo una qualità concordi & uniti; essendo che ad ogn'un di loro
(com'habbiamo ueduto) due ne sono appropriate, per mezo delle quali mirabilmente
insieme si congiungono, & in tal modo; che si come due numeri Quadrati conuengono
in un mezano numero proportionato: così due di essi Elementi in un mezano si congiun
gono: conciosia che al modo, che 'l Quaternario & Nouenario numeri Quadrati si con-
uengono nel Senario, ilqual supera il Quaternario di quella quantità, ch'esso è supera-
to dal Nouenario; in tal modo il Fuoco & l'Acqua, che sono in due qualità contrarii,
in vn mezano elemento si congiungono. Imperoche essendo il Fuoco per sua natura cal-
do & secco; & l'Acqua fredda & humida; nell'Aria calda & humida mirabilmente con
grande proportione s'accompagnano; il quale se bene dall'Acqua per il calido si scompa
gna, seco poi per l'humido si unisce. Et se l'humido dell'Acqua ripugna al secco della
Terra, il frigido non resta però d'unirli insieme. Di modo che sono con tanto maraui-
glioso ordine insieme uniti, che tra essi non si ritroua più disparità, che si ritroui tra due
mezani Numeri proportionali, collocati nel mezo di due numeri Cubi; come nell'es-
sempio si può uedere.
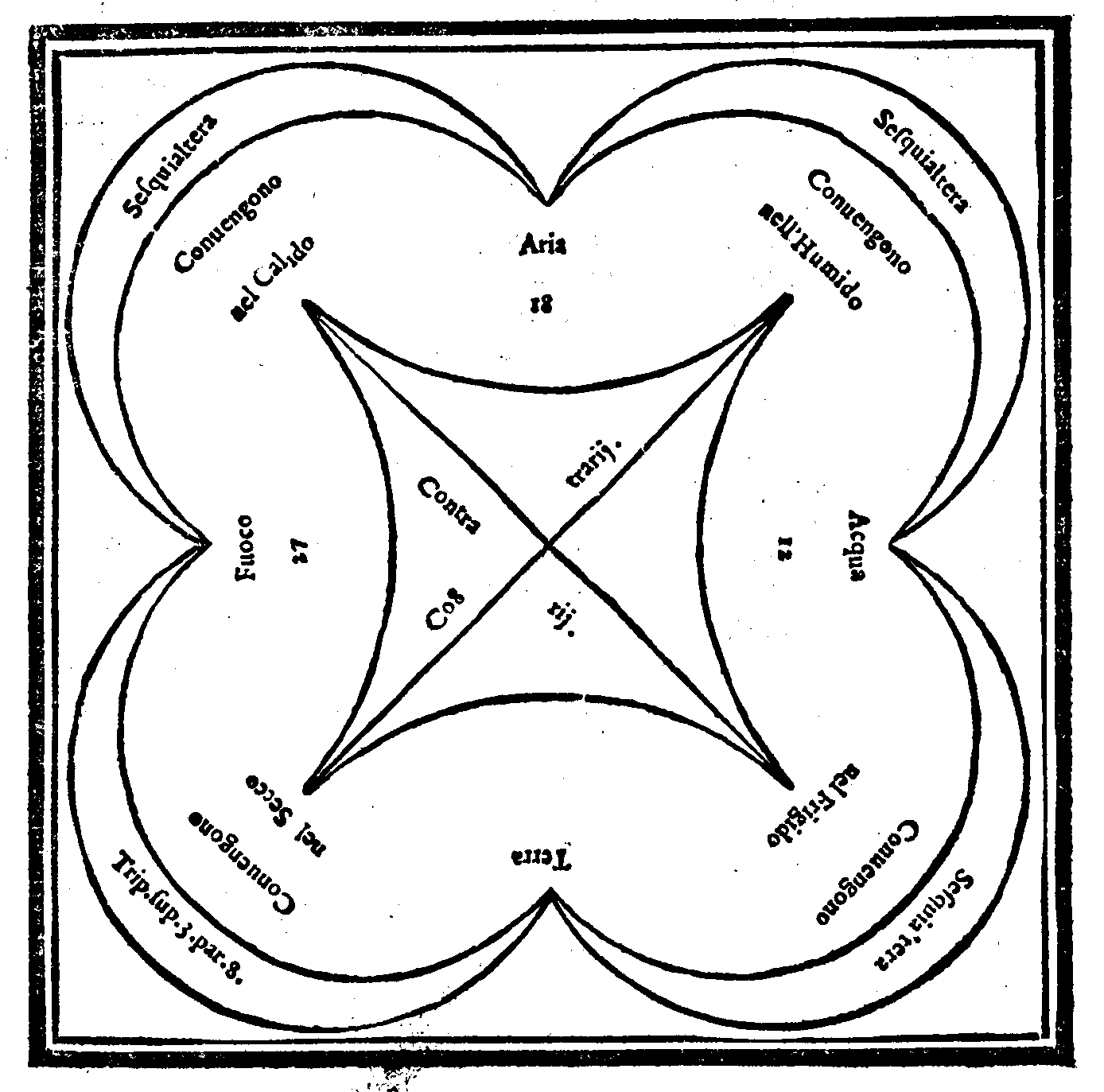
lib. 3. &
Met. 9.
Tu numeris Elementa ligas, ut frigora flammis
Arida conueniant liquidis, ne purior Ignis
Euolet, aut mersas deducant pondera Terras.
page 20
Tu triplicis mediam naturae cuncta mouentem
Connectens animam, per consona membra resoluis.
Et in un'altro luogo,Lib. 4. met.
6.
Haec concordia temperat aequis
Elementa modis, vt pugnantia
Vicibus cedant humida siccis
Iungantꝗ fidem frigora flammis.
Pendulus ignis surgat in altum,
Terraeꝗ graues pondere sidant.
Ma chi vorrà dal Peso loro comprendere anco la Mondana harmonia, la potra cono-
scere; percioche essendo l'uno dell'altro più graue, ò più leggiero; sono in tal modoinsie-
me concatenati & legati; che con una certa harmonia la circonferenza di ciascuno pro-
portionatamente è lontana dal centro del Mondo, secondo i luoghi ò siti loro. Noi uedia
mo che quelli, che sono per loro natura graui, sono tirati all'insù da quelli, che sono per lo
ro natura leggieri; & li graui tirano all'ingiù i leggieri in tal maniera, che niun di loro uà
fuori del suo proprio luogo. Et in tal guisa stanno insieme sempre uniti & serrati, che tra lo
ro nō si troua per alcun tempo, quantunque breue, in alcuna parte il Vacuo; il quale la Na
tura grandemente abhorrisce. Et sono poi in tal modo collocati, che la Terra, la quale per
sua natura è semplicemente graue; & il Fuoco ch'è semplicemente leggiero, sono quelli,
che posseggono gli ultimi luoghi. La Terra tien l'infimo; percioche Ogni graue tēde al bas
so, & il Fuoco stà nel supremo; essendo che Ogni cosa leggiera tende à tal luogo. Ma per
che i mezi ritengono la natura de i loro estremi; però hà ordinato bene il Creatore, che
essendo l'Acqua & l'Aria, secondo un certo rispetto graui & leggieri, douessero tenere il
luogo mezano; l'Acqua accōpagnandosi alla Terra, come più graue; & l'Aria al Fuoco,
come leggiero; accioche ciascuno s'accompagnasse à quello, ch'era di natura à lui
più simile. Il qual ordine & legamento leggiadramente Ouidio espresse cō queste parole.Metamor.
lib. 1
Ignea conuexi vis, & sine pondere coeliMa se più sotilmente ancora uorremo essaminar la cosa, ritrouaremo l'Harmonia
Emicuit, summaꝗ locum sibi legit in arce.
Proximus est Aer illi leuitate locoꝗ.
Densior his Tellus elementaꝗ grandia traxit,
Et praessa est grauitate sui. circumfluus humor
Vltima possedit, solidumꝗ coercuit orbem.
mondana nella loro misura & quantità, mediante la trāmutatione delle parti, che si fà
dell'uno nell'altro; come mostra il Filosofo:De Gene-
rat. lib. 2. conciosiache cosi si trammuta una parte di
terra in acqua, & una parte d'acqua in aria; come si trammuta una parte d'aria in fuoco:
Et si come si trammuta una parte di fuoco in aria & una parte d'aria in acqua; cosi si tram
muta una parte d'acqua in terra: essendo che trammutandosi la terra in acqua, si uiene
à far tale trammutatione in proportione Decupla. Di modo che quando si trammuta un
pugno di terra (dirò cosi) in acqua, si generano (come dicono alcuni Peripatetici) dieci
pugni d'acqua; & quando si trammuta tale acqua in aria, uiene à far cento pugni d'aria:
onde trammutandosi ultimamente tutto questo nel supremo elemento, viene a multipli-
care in mille pugni di fuoco. Cosi per il contrario, mille pugni di fuoco si conuertono in
cento d'aria, & questi in dieci di acqua, & dieci d'acqua in uno di terra; & ciò auiene dal-
la loro rarità & spessezza, che più in uno, che in un'altro si ritroua: percioche quanto più
s'auicinano al cielo, & sono lontani dal centro del mondo; tanto più sono rari; & quan-
to più s'auicinano à questo, & si allontanano da quello, tanto più sono spessi.Onde
quando da questo si uolesse giudicar la loro misura, si potrebbe dire, che la quantità
del fuoco fusse in proportione Decupla con quella dell'aria; & quella dell'aria, con quel
la dell'acqua medesimamente in proportione Decupla; & cosi la quantità dell'acqua cō
tutta la quantità della terra, nella medesima proportione. Et si potrebbe anco dire (poi
page 21che gli Elementi sono corpi d'un'istesso genere, & il tutto con le parti conuiene in una
istessa natura & in una ragione istessa) che la Proportione, che si ritrouatra la quantità
della sphera del fuoco & tutta la massa della terra, sia quella, che si ritroua tra il numero
Millenario & l'Vnitade. A questo modo adunque, dal mouimento, dalle distanze &
dalle parti del cielo; & similmente da gli aspetti; dalla natura & dal sito de i Sette piane-
ti; & dal Numero etiandio, dal Peso & dalla Misura de i quattro elementi, uenimo al-
la cognitione dell'harmonia Mondana: essendo che la concordanza & l'harmonia loro
partorisce l'harmonia de i tempi, che si conosce prima ne gli Anni, per la mutatione della
primauera nella State; & di questa nell'Autunno; similmente dell'Autunno nel Verno;
& del Verno nella Primauera: dopoi si conosce ne i Mesi, per il crescere & sciemare re-
golatamente, che fà la Luna; & finalmente ne i Giorni, per il cambieuole apparir della
luce & delle tenebre; dalla quale Harmonia nasce la diuersità de fiori & de frutti: Il per-
che Ouidio in questo proposito disse:De Re-
med. 1.
Poma dat Autumnus; formosa est mensibus Aestas;
Ver praebet flores; igne leuatur Hyems.
Onde come afferma Platone,In Sympo-
sio: quando 'l caldo col freddo, & il secco con l'humido pro-
portionatamente s'uniscono; dall'Harmonia di queste qualità ne risulta l'Anno à cia-
scun uiuente utilissimo, pieno di varie sorti de fiori odoriferi & de frutti ottimi; ne alcun'
altra sorte di piante, ò d'animali uiene à patire offesa: come all'opposito auiene; che
dalla discordanza & distemperamento loro si generano pestilenza, sterilità, infirmità &
ogni cosa à gli Huomini, alle Bestie & alle Piante nociua. Et ueramente la Natura hà
seguito un bello & ottimo ordine, facendo, che quel che il Verno ristringe & rinchiu-
de, Primauera lo apra & mandi fuori; & quel che la State secca, l'Autunno final-
mente maturi. Di maniera che si uede l'un tempo all'altro porgere aiuto; & de quattro
tempi harmonicamente disposti farsi un corpo solo. Questa tale Harmonia troppo bene
conobbero Mercurio & Terpandro; conciosia che l'uno hauendo ritrouata la Lira, oue-
ramente la Cetera; pose in essa Quattro chorde ad imitatione della Musica mondana
(come dice Boetio 1. cap.
20. & MacrobioSatur. lib.
1. cap. 19.) la quale si scorge ne i quattro Elementi, ouer nel-
la uarietà de i quattro tempi dell'Anno; & l'altro la ordinò con Sette chorde al-
la similitudine de i sette Pianeti. Fu poi il numero delle Quattro chorde nominato Qua-
drichordo, ouer Tetrachordo; che tanto uuol dire, quanto Di quattro chorde; &
quello di sette, Heptachordo, che uuol dire Di sette chorde. Ma il primo fù da
i Musici di maniera riceuuto & abbracciato; che le Quindeci chorde comprese nel
Systema massimo, furono accresciute secondo il Numero delle chorde del predetto
Tetrachordo; come uederemo; ancora che si ritrouino distanti l'una dall'altra sot-
to diuerse Proportioni. Et questo basti quanto alla dichiaratione della Musica
mondana.
Della Musica humana.Cap. VII.
che si riuolga alla contemplatione di se stesso: imperoche quella cosa, laqua
le mescola col corpo la viuacità incorporea della ragione, non è altro, che
un certo adattamento & temperamento, come de uoci graui & acute, il-
quale faccia quasi una consonanza. Questa è quella, che congiunge tra se le parti del-
l'Anima, & tiene unita la parte Rationale con la Irrationale; & è quella, che mesco-
la gli Elementi, ouer le qualità loro nel Corpo humano con ragioneuole Propor-
tione. Onde principalmente si deue auertire, c'hò detto, che può esser intesa da cia-
scuno, che si riuolga alla contemplatione di se stesso; accioche non si credesse, che la
Musica humana fusse, ò si chiamasse quell'ordine, che osserua la Natura nella generatio
page 22ne de i nostri corpi; la quale (come dicono i Medici; & anche lo conferma AgostinoLib. 83.
quaest. quae
stio 56.) poi
che nella matrice della donna ritroua il seme humano, corrompendolo per lo spatio di
sei giorni lo conuerte in latte; il quale in noue giorni trasforma in sangue; & in termi-
ne di dodici dì ne produce una massa di carne senza forma; ma à poco à poco in-
troducendouela, in diciotto giorni la fà diuenire humana; di modo che essendo in Qua
rantacinque giorni compita la generatione, l'Onnipotente Iddio le infonde l'Anima in
tellettiua. Onde di questo habbiamo:
Sex in lacte dies, tres sunt in sanguine terni,Et veramente questo mirabilissimo ordine hà in se concento & harmonia, considera-
Bis seni carnem, ter seni membra figurant.
ta la distanza d'un Numero all'altro, come è chiaro da uedere; che dal primo al secon-
do si ritroua la forma della Consonanza Diapente; & da questo al terzo quella della Dia
tessaron; & dal terzo all'ultimo quella della medesima Diapente. Et di nuouo dal primo
al terzo & dal secondo all'ultimo la forma della Diapason; & dal primo all'ultimo chia-
ramente si scorge quella della Diapasondiapente; come più facilmente nella figura si ve-
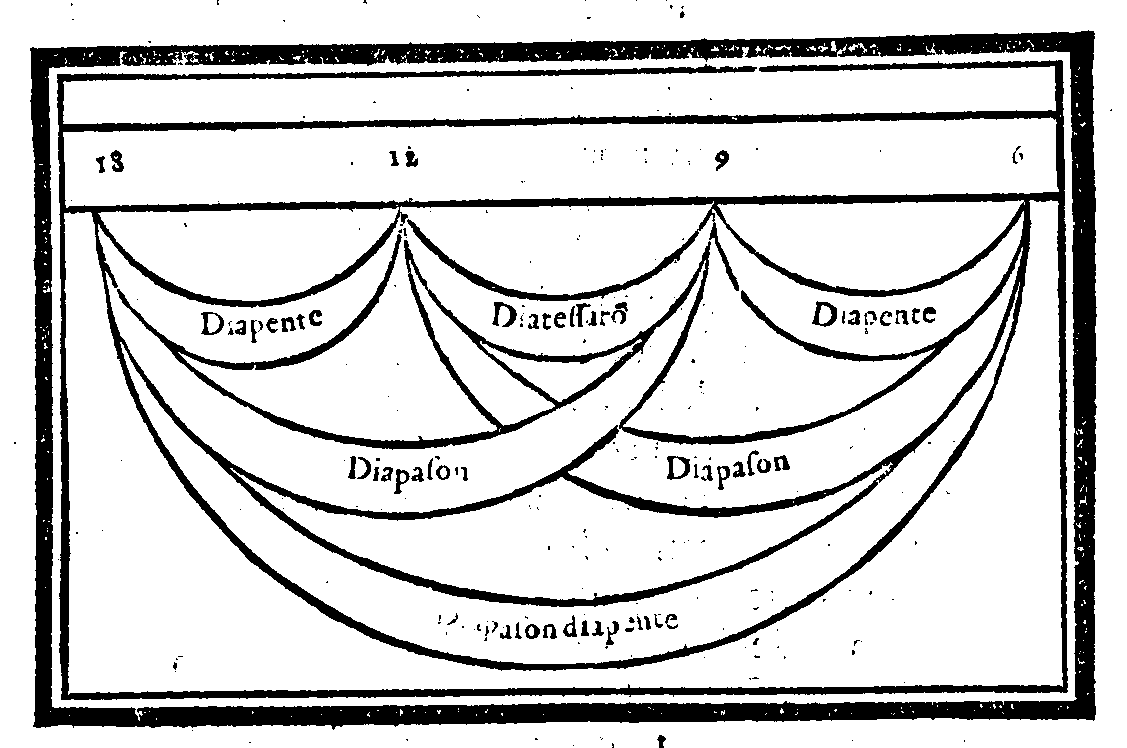
tre cose; cioè, dal Corpo, dall'Anima & dal Congiungimento dell'uno & dell'altra. Dal
Corpo, come nelle cose che crescono, ne gli humori & nelle humane operationi. Nelle
cose che crescono; noi ueggiamo ciascun uiuente quasi con vna certa harmonia cambia
re il suo stato; gli Huomini diuentano de fanciulli vecchi, & de piccioli grandi; le Pian-
te di humide, uerdi & tenere, si fanno aride secche & dure. Et benche ogni giorno si ueg-
gono, & se habbiano inanti gli occhi; nondimeno non si può ueder tal mutatione; co-
me ancora nella Musica non si può vdire lo spacio, col quale si uà dalla uoce acuta à quel
la che è graue, quando si canta; ma solamente si può intendere. Ne gli Humori; co-
me vediamo nel temperamento de tutti quattro gli Elementi nel corpo humano: Et nel-
le Humane operationi la conosciamo nell'Animal rationale; cioè, nell'Huomo: impe-
roche in tal modo è retto & gouernato dalla Ragione; che passando per i debiti mezi nel
suo operare conduce le sue cose, come una certa harmonia à perfetto fine. Conoscesi an-
cora tal harmonia dall'Anima; cioè, dalle sue parti, che sono l'Intelletto, i Sentimenti
& l'Habito. Imperoche (secondo TolomeoHarmo. li
bro. 3. c. 5.) corrispondono alle ragioni di tre conso-
nanze; cioè, della Diapason, della Diapente & della Diatessaron; conciosia che la parte
Intellettuale corrisponde alla Diapason, che hà sette Interualli; & sette sono le sue Spe-
cie; onde in essa si ritrouano sette cose; cioè, Mente, Imaginatione, Memoria, Cogita-
tione, Opinione, Ragione & Scienza. Alla Diapente, la quale hà quattro Specie & quat
tro Interualli, corrisponde la Sensitiua in quattro cose; nel Vedere, nell'Vdire, nell'O-
page 23dorare & nel Gustare; essendo che 'l Toccare è commune à ciascun de i nominati quat-
tro Sentimenti; & massimamente al Gusto. Ma alla Diatessaron, laqual si fà di tre Inter-
ualli, & contiene tre Specie, corrisponde la parte Habituale, nell'Augumento, nella
Sommità ò Stato, & nel Decrescimento. Simigliantemente se noi uorremmo che le
parti dell'Anima siano la sede della Ragione, dell'Ira & della Cupidità ; ritrouaremo nel-
la prima sette cose corrispondenti à gli Interualli & alle Specie della Diapason; cioè,
Acutezza, Ingegno, Diligenza, Conseglio, Sapienza, Prudenza & Esperienza. Nel-
la seconda ritrouaremo quattro cose, che corrisponderanno alle Specie & à gli Interual-
li della Diapente; cioè, Mansuetudine, ò Temperanza d'animo, Animosità, Fortezza
& Tolleranza: nella Terza tre cose corrispondenti à gli Interualli & alle Specie della Dia
tessaron; cioè, Sobrietà, ò Temperanza, Continenza & Rispetto. Oltra di ciò si conside
ra ancora tale Harmonia nelle potenze di essa Anima; cioè, nell'Ira, nella Ragione &
nelle Virtù; come sarebbe dire nella Iustitia & nella Fortezza; percioche queste cose
tra loro si uengono à temperare, nel modo che ne i Suoni della Consonanza si contem-
pera il Suono graue con l'acuto. Si conosce ultimamente tale Harmonia dal congiun-
gimento dell'Anima col Corpo per la naturale amicitia; mediante la quale il Corpo con
l'Anima è legato; non già con legami corporei; ma (come uogliono i Platonici) con lo
Spirito, il quale è incorporeo; come di sopra vedemmo.Cap. 4. Questo è quel leggame, dal-
quale risulta ogni humana Harmonia; & è quello, che congiunge le diuerse qualità de
gli Elementi in un composto; cioè, nel Corpo humano; seguendo l'opinione de Filoso-
fi; i quali concordeuolmente affermano, che i Corpi humani sono composti di Terra,
Acqua, Aria & Fuoco; & dicono la Carne generar si della Temperatura de tutti quat-
tro gli Elementi insieme; i Nerui di terra & di fuoco; & finalmente l'Ossa di acqua & d
terra. Ma se questo ne paresse strano, ragioneuolmente non potiamo negare, che non
siano composti almeno delle qualità elementali, mediante i quattro Humori, che in
ogni corpo si ritrouano: come è Malinconia, Flegma, Sangue & Colera; i quali benche
l'uno all'altro siano contrarij; nondimeno nel Misto, ò Composto, che uogliamo dire,
stanno harmonicamente vniti. Anzi se per patir freddi & souerchi caldi, ouer per trop-
po mangiare, ò per altra cagione facciamo uiolenza ad uno de gli Humori; in istante ne
segue il distemperamento & l'infirmità del corpo; ne egli prima si risana, se essi non sono
ridutti alla pristina proportione & concordia; la quale non potrebbe essere, quando non
ui fusse quel legamento, che di sopra hò detto, della Natura spirituale con la corporale,
& della rationale con la irrationale.Questa Cōcordia harmonica adunque della Natura
spirituale con la corporale, & della rationale con la irrationale, è quella che costituisce la
Musica humana: percioche mentre l'Anima quasi con ragion de Numeri perseuera di
stare vnita col Corpo; il Corpo ritiene col nome l'essere animato; & non essendo per al-
tro accidente impedito, hà potestà di far ciò che uuole; doue disciogliendosi l'Har-
monia, egli si corrompe; & perdendo col nome l'esser animato, resta nelle tenebre, &
l'Anima vola all'immortalità. Et ben fu detto, Quasi con ragion de Numeri; conciosia-
che gli Anrichi hebbero una strana opinione; che Quando uno si annegaua, oueramen-
te era ucciso, l'Anima sua non poteua mai andare al luogo deputato, fin che non haue-
ua finito il musical Numero; colquale dal suo nascimento era stata congiunta al corpo.
Et perche haueano per fermo, che tal Numero non si potesse trappassare; però tali acci-
denti chiamarono Fato, ouer Corso fatale. Onde il Poeta introducendo Deifobo, il-
quale fù ucciso da i Greci, à parlare, tocca questa opinione con le seguenti parole; Aeneid. 6.
Explebo numerum, reddarꝗ tenebris.
Ma perche queste cose s'appartengono più à i ragionamenti della Filosofia, ch'à quel-
li della Musica; lascierò di parlarne più oltra; contentandomi d'hauerne detto queste po
che, & dimostrato la varietà della Musica animastica; della quale, come di quella, che
nulla, ò poco fà al proposito, non ne farò più mentione.
page 24
Della musica Piana, & Misurata; ò vogliamo dire canto Fermo,
& Figurato.Cap. VIII.
facemmo della Musica; ilquale era la Organica, diuisa in Harmonica, ò Na-
turale, & in Arteficiata; ciascuna delle quali diuidemmo in Piana, Misurata,
Rhythmica & Metrica. Ripigliando adunque queste ultime parti dico, che
Musica piana si dimanda quell'Harmonia, che nasce da vna semplice & equale prola-
tione nella Cantilena, laquale si fà senza variatione alcuna di tempo, dimostrato con
alcuni Caratteri, ò Figure semplici, che Note i Musici prattici chiamano; le quali ne
si accrescono, ne si diminuiscono della loro valuta: imperoche in essa si pone il tempo
intero & indiuisibile, & da i Musici volgarmente è chiamato Canto piano, ouer Can-
to fermo; ilqual è molto usato da i Religiosi ne i Diuini loro officij. Musica misurata
dico esser l'Harmonia, che nasce da vna variata prolatione di tempo nella Cantilena,
dimostrato per alcuni Caratteri, ò Figure al modo sopradetto; lequali di Nome, Essen-
tia, Forma, Quantità & Qualità sono differenti; & non si accrescono, ne si diminuisco-
no; ma si cantano con misura di tempo, secondo che descritte si trouano. Et questo com
munemente si chiama Canto Figurato, dalle Figure ò Note, che si trouano in esso di For
ma & Quantità diuersa; le quali ne fanno crescere & minuire il tempo nella Cantilena,
secondo la loro ualuta; che Tardità, ò Velocita di tempo ne rappresentano. Ma Figura,
ò Nota, che dir uogliamo, si nel Canto fermo, come nel Figurato, dico essere un segno,
che posto sopra alcune linee, ò spatij, ci rappresenta il Suono, ò la Voce, & la Velocità
& Tardità del tempo, che bisogna vsare nella Cantilena, delle quai cose trattaremo
nella Terza parte; quando ragionaremo intorno la Materia del Contrapunto; cioè, del-
le Compositioni delle Cantilene. Et perche la Musica piana & Misurata, non solo da
Istrumenti naturali; ma da Arteficiali ancora può nascere; però nella diuisione della
Musica organica, da l'Harmonica ò Naturale, & dalla Arteficiata l'hò fatta discen-
dere.
Della Musica Rhythmica & della Metrica.Cap. IX.
ouer nella Prosa per la quantità delle Sillabe, & per il Suono delle parole,
quando insieme bene & acconciamente si compongono; la Scienza della qua
le consiste nel giudicare, se nella Prosa, ò nel Verso sia conueneuole Conso-
nanza tra parola & parola; cioè, se le Sillabe dell'una bene, ò male con le Sillabe dell'
altra si congiungono. Questo tal giudicio non si può fare, se prima in atto non si riduce
& faccia udire col mezo de Naturali strumenti; percioche non le Lettere; ma gli Ele-
menti delle lettere sono quelli; che producono tale conueneuole Consonanza; i quali
(secondo i Grammatici & secondo BoetioDe interp.
lib. 1. Edi-
ti. 2.) altro non sono, che la Pronuntia di esse Lette
re, che sono con diuerse Forme figurate; ritrouate per commodità di esprimere il concet-
to, senza parole pronunciate. Onde nella general diuisione della Musica organica; dal-
la Harmonica ò Naturale le hò fatto trar la sua origine. Potiamo adunque hora cono-
scere la differenza, che è tra questa & l'altra Specie di Musica, che Metrica si chiama; il
cui proprio è di saper giudicare ne i Versi la quantità delle Sillabe; se siano lunghe, ò
breui; mediante le quali si conoscano i Piedi & quali siano, & la loro determinata sede.
Conciosiache la diuersità de i Piedi (come di due, di tre, di quattro, ò più Sillabe) co-
stituisce la Musica metrica; la quale se medesimamente volemo dichiarare, non è altro
che l'Harmonia, che nasce dal Verso per la quantità delle Sillabe; la composition delle
page 25quali diuersi piedi; come sono il Pyrrhichio, il Iambo, lo Spondeo, il Tro-
cheo, il Tribracho, l'Anapesto, il Dattilo, il Proceleumatico, & altri, che nelle Poesie
si ritrouano; i quali secondo la loro determinata sede nel Verso, posti harmonicamente
insieme, porgono all'Vdito grandissima dilettatione. Et per le medesime ragioni, c'hab-
biamo detto della Rhythmica, la Metrica ancora dalla medesima Harmonica ò Natu-
rale discende: imperoche la lunghezza, ò breuità delle Sillabe si conosce, ò misura dal
Suono della voce; la cui Lunghezza, ò Breuità importa tempo, conosciuto per il moto.
Si che non dalle Lettere, ma dal Suono delle uoci uiene à nascer la Musica metrica; per-
che accompagnandolo col Suono de arteficiali Istrumenti, si forma il Metro, come an-
ticamente faceuano i Poeti Lirici, che al suono della Lira ò della Cetera cantauano i lo-
ro Versi; onde parimente i Poeti & i Versi loro da loro cantati vengono chiamati Lirici.
Et perche da principio essi andauano à poco à poco cercando d'accompagnar i Versi cō
Harmonia al suono de i già nominati Istrumenti; però è stata opinion de molti, che i
detti Poeti trouassero le Leggi, ò Regole de i Versi, le quali Metriche addimandauano.
Per concludere adunque dico, che la Rhythmica & la Metrica parimente discende dalla
Naturale. Ma perche (come uuole AgostinoMusices li-
bro 1. c. 1.) percuotendo noi alcuno Istrumento con
quella Velocità, ò Tardità, che noi proferimo alcuna parola, potiamo conoscere dal
mouimento gli istessi tempi Lunghi & breui; cioè, i Numeri istessi, che nelle parole si
conoscono; però non fù inconueniente dire, che queste due sorti di Musica, si possano
anco atrribuire all'Arteficiata; conciosia ch'ogni giorno vdimo farsi questo con diuersi
Istrumenti, al suono de quali ottimamente si accommodano varie sorti de Versi, se-
condo 'l Numero, che si comprende nel suono nato da loro. E' ben uero, che tra quella,
che deriua dalle Voci, & quella, che deriua da i Suoni, si ritroua tal differenza, che
l'una Rhythmica, ò Metrica naturale si potrà dire; & l'altra Rhythmica, ò Metrica ar-
teficiata. Queste due sorti di Musica (percioche al presente molto più à i Poeti & à gli
Oratori, che al Musico appartengono sapere) lasciaremo da parte, ragionando sola-
mente della Piana & della Misurata; non pretermettendo (com'è il mio principale pro-
posito) alcuna cosa, che sia degna di annotatione. Ma quanto sia differente il Rhy-
thmo dal Metro, lo uederemo altroue.Infra. c. 8.
2. partis.
Quel che sia Musica in particolare, & perche sia cosi detta.Cap. X.
& veduto quello, che sia ciascuna sua parte separatamente; resta hora (do-
uendosi ragionar solamente della Istrumentale) ueder prima quello, ch'ella
sia. Dico adunque, che la Musica istrumentale è Harmonia, laquale nasce
da i Suoni & dalle Voci; la cui cognitione in che consista facilmente dalla sua definitio-
ne potremo sapere, imperoche ella è Scienza speculatiua Mathematica, maestra de tut-
te le Cantilene, laquale col senso & con la ragione considera i Suoni, le Voci, i Nume-
meri, le Proportioni, & le loro Differenze; & ordina le uoci graui & le acute con certi
termini proportionati ne i debiti luoghi. Ne si marauigli alcuno, ch'io habbia detto,
la Musica essere Scienza speculatiua; percioche tengo, che sia possibile, che uno la pos-
sa posseder nell'Intelletto ancora che non la esserciti con i Naturali, ò Arteficiali istru-
menti. Ma perche ella sia cosi detta, & donde deriui il suo nome, non è cosa facile da
sapere; conciosia che alcuni hanno hauuto opinione, ch'ella habbia origine dal verbo
greco Μαίεσθαι; & altri (tra i quali è Platone nel Cratilo) da Μῶσθαι; cioè, dal Cerca-
e, ò Inuestigare; come di sopra si è mostrato. Et alcuni hanno hauuto parere, che
sia detta da Μωὺ, voce Egittia, ò Caldea, & da ἧχος voce Greca; che l'una uuol signifi-
care Acqua, & l'altra Suono; quasi Per il suono dell'acque ritrouata; della quale opi-
nione fu Giouanni Boccaccio ne i Libri della Genealogia de i Dei.Lib. 1. c. 2. E in uero non mi di-
page 26spiace; percioche è concorde alla opinion di Varrone, ilqual uuole, che in tre modi na-
sca la Musica; ò dal suon dell'acque; ò per ripercussione dell'aria; ò dalla voce: ancora-
che AgostinoDe Doct.
Chri. lib. 2.
c. 17. &
De Ordi.
lib. 2. c. 14.
dica altramente. Alcuni altri istimarono, che cosi fusse detta; perche ap-
presso l'acque fu ritrouata; & non per il suono dell'acque; mossi per auentura da questo;
che Pan Dio de pastori fù il primo (come narra PlinioNatu. hist.
lib. 7. c. 56) che della sua Siringa conuersa
in canna appresso Ladone fiume d'Arcadia, fece la Sampogna pastorale, onde di-
ce il Poeta;In Alexi.
Pan primus calamos cera coniungere plures
Instituit.
Et quantunque queste opinioni siano buone; tuttauia quello, ch'à me par più ra-
gioneuole, & più mi piace, è l'opinione di Platone;In Alcibia-
de. 1. ch'ella sia nominata dalle Muse;
alle quali (come dice AgostinoMusicae li-
bro 1. c. 1.) è conceduto vna certa onnipotenza di cantare; & vo-
gliono i Poeti, che siano figliuole di Gioue & di Memoria; & dicono bene: percioche
se l'Huomo non ritiene i Suoni, & gli Interualli delle voci Musicali nella memoria, non
fà profitto alcuno; & questo auiene; perche non si possono à via alcuna scriuere; tanto
più, ch'ogni Scienza & ogni Disciplina (come uuole QuintilianoInstitu. o-
rat. lib. 11:
cap. 2.) consiste nella me-
moria; conciosia che in vano ci è insegnato; quando quello, che noi ascoltiamo, dal-
le menti nostre si parte. Et perche habbiamo detto la Musica essere Scienza Speculati-
ua; però auanti che più oltra passiamo, vederemo (hauendo consideratione del fine)
com'anche la possiamo dimandare Prattica.
Diuisione della Musica in Speculatiua ò Contemplatiua & in Prattica; per la qua-
le si pone la differenza tra 'l Musico, & il Cantore.Cap. XI.
delle Scienze; conciosia che diuidendosi in due parti; l'una Theorica, ò Spe-
culatiua ò uogliamo dirla Contemplatiua, & l'altra Prattica uien detta.Quel-
la il cui fine consiste nella cognitione solamente della verità delle cose intese
dall'Intelletto; ilche è proprio di ciascuna Scienza; è detta Contemplatiua; l'altra, che
dall'essercitio solamente dipende, uien nominata Prattica. La prima (come uuol To-
lomeoAlmag. li.
1. cap. 1.) fu ritrouata per accrescimento della Scienza; imperoche per il suo mezo po-
tiamo ritrouar noue cose, & darle augumento; ma la Prattica solamente è per l'opera-
re; come dissegnare, descriuere, & fabricar con le mani le cose occorrenti. Questa al-
la prima non altramente si sottomette, di quello che fà l'Appetito alla Ragione; & è il do
uere; conciosia che Ogni Arte & ogni Scienza naturalmente hà per più nobile la Ragio
ne, con la quale si opera, che l'istesso Operare. Onde hauendo noi dall'Animo il sapere;
& dal Corpo, come suo ministro, l'opera; è cosa manifesta, che l'Animo uincendo &
superando di nobiltà il Corpo, quanto alle operationi, sia ancora più nobile; tanto più,
che se le mani non operassero quello, che dalla Ragione gli è commandato, uanamente
& senza frutto alcuno sia faticarebbono. Si che non è dubbio, che nella scienza della
Musica è più degna la Cognitione della ragione, che l'Operare. Et quantunque la spe-
culatione da per se non habbia dibisogno dell'opera; tuttauia non può lo Speculatiuo
produr cosa alcuna in atto, c'habbia ritrouato nuouamente, senza l'aiuto dell'Artefi-
ce, ouero dell'Istrumento: percioche tale speculatione, se ben'ella non fusse vana, par-
rebbe nondimeno senza frutto, quando non si riducesse all'ultimo suo fine, che consiste
nell'essercitio de Naturali & Arteficiali Istrumenti; col mezo de i quali ella viene à conse
guirlo; come ancora l'Artefice senza l'aiuto della Ragione mai potrebbe condurre l'ope
ra sua à perfettione alcuna. Et perciò nella Musica (considerandola nella sua perfettio-
ne) queste due parti sono tante insieme congiunte, che per l'assegnate ragioni non si pos-
sono separare l'una dall'altra. Et se pure si volessero separare; da questo si conosce-
page 27rebbe lo Speculatiuo ò Contemplatiuo esser differente dal Prattico; che quello sempre
piglierà il nome dalla Scienza, & uerrà detto Musico; & questo non dalla Scienza; ma
dall'Operare; come dal Comporre sarà detto Compositore; dal Cantare, Cantore; &
dal Sonare, Sonatore. Ma questo più espressamente si comprende da quelli, che esser-
citano l'opere Musicali da mano; i quali dall'Opera; cioè, dall'Istrumento, non dal-
la Scienza prendono il nome; come l'Organista dall'Organo, il Citerista, dalla Cetera,
il Lirico dalla Lira; & similmente ogn'altro, secondo la sorte dell'Istrumento, ch'ei so-
na. Et però chi uorrà essaminar bene la cosa, ritrouerà tanto esser la differenza dell'u-
no dall'altro, quanto è il loro ufficio, & il loro fine diuerso. Onde uolendo saper quello
che sia l'uno & l'altro, diremo; Musico esser colui, che nella Musica è perito & hà facultà
di giudicare non per il Suono; ma per ragione quello, che in tal scienza si contiene; Il qua
le se alle cose appartinenti alla Prattica darà opera, farà la sua scienza più perfetta; &
Musico perfetto si potrà chiamare. Ma diremo Prattico, ò Compositore, ò Cantore, ò
Sonatore, ch'egli sia, colui, che i precetti del Musico con lungo essercitio apprende
& li manda ad effetto con la Voce, col mezo d'alcuno arteficiale Istrumento. Di sor-
te ch'ogni Compositore, ilquale non per ragione, ne per scienza; ma per lungo uso
sappia comporre ogni musical Cantilena; & ogni Sonatore di qual si uoglia sorte
d'Istrumento musicale, che sappia sonare solamente per lungo uso & iudicio di orec-
chio; ancora che à tale uso l'uno & l'altro non sia peruenuto senza 'l mezo di qualche co
gnitione; Prattico si può dire. Et la Velocità delle mani, della lingua, con ogni moui-
mento & altro accidente, che si ritroua di bello nel Sonatore ò Cantore, si debbe at-
tribuire all'Vso & nō alla Scienza; conciosiache consistendo essa nella sola cognitione; se
fusse altramēte, seguirebbe che colui, ilquale hauesse maggior cognitione della Scienza,
fusse anche più atto ad essercitarla; di che in effetto si uede il contrario. Hora hauendo
ueduto la differenza, che si ritroua tra l'uno & l'altro, esser l'istessa, ch'è tra l'Artefice &
l'Istrumento; il quale essendo retto & gouernato dall'Artefice, è tanto men degno di
lui, quanto chi regge è più nobile della cosa retta; potremo quasi dire, il Musico esser
più degno del Compositore, del Cantore, ò Sonatore; quanto costui è più nobile &
degno dell'Istrumento. Ma non dico però, che 'l Compositore & alcuno, che esserciti i
naturali, ò arteficiali Istrumenti, sia ò debba esser priuo di questo nome; pur ch'egli sap-
pia & intenda quello, che operi; & del tutto renda conueneuole ragione: perche à si-
mil persona, non solo di Compositore, di Cantore, ò di Sonatore; ma di Musico anco-
ra il nome si conuiene. Anzi se con un sol nome lo doueremo chiamare, lo chiamaremo
Musico perfetto: percioche dando opera, & essercitandosi nell'una & l'altra delle nomi-
nate, ei possederà perfettamente la Musica; della quale desidero & spero, che faranno
acquisto coloro, i quali vorranno osseruare i nostri precetti.
Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità é NumeroCap. XII.
ri & le Proportioni; però parmi, che hora sia tempo di cominciare à ragionar
di cotali cose; massimamente che dalla Prima origine del mondo (come ma-
nifestamente si uede & lo affermano i Filosofi) tutte le cose create da Dio fu
rono da lui col Numero ordinate; anzi esso Numero fù il Principale essemplare nella men
te di esso Fattore. Onde è necessario, che tutte le cose, lequali sono separatamente, ouer
insieme, siano dal Numero comprese, & al Numero sottoposte; imperoche tanto è egli
necessario; che se fusse leuato uia; prima si distruggerebbe il tutto; & dopoi si leuarebbe
all'Huomo (come uuol PlatoneIn Epino-
mide.) la prudenza & il sapere; conciosiache di niuna cosa,
ch'egli hauesse nell'Intelletto, ouer nella Memoria, potrebbe render ragione, & le Ar-
page 28ti si perderebbono, ne più faria bisogno di parlare, ò scriuere alcuna cosa della Musica;
percioche del tutto la ragione di essa si annullarebbe; non hauendo ella maggior fermez-
za, che quella de i Numeri. Il Numero acuisse l'Ingegno, conferma la memoria, in-
drizza l'Intelletto alle speculationi, & conserua nel proprio esser tutte le cose. Che più?
Iddio benedetto lo donò all'Huomo, come Istrumento necessario ad ogni sua ragione
& discorso. Nelle Sacre lettere un'infinito numero de secreti mirabilissimi & diuini col
mezo de i Numeri si uengono à scoprire; della cognitione & intelligenza de i quali (co-
me piace ad AgostinoDe Doct.
Chri. lib. 2.
cap. 16.
De ciuita-
te Dei. lib.
11.) senza l'aiuto loro noi certamente saremmo priui. Il Saluator no
stro (come si uede nell'Euangelio) in molti luoghi, gli osseruò; & le ceremonie della Leg-
ge scritta tutte per numero si comprendono. Di modo che (come dice il detto Santo dot
tore) nella Scrittura in più luoghi si ritrouano i Numeri & la Musica esser posti honore-
uolmente. Onde non è da marauigliarsi, se i Pitagorici istimauano, che ne i Numeri fusse
un non sò che di diuino; poi che per quello, che detto habbiamo, & per quello, che dir
si potrebbe, discorrendo con l'intelletto, il Numero è sommamente necessario. Et ben-
che molti l'habbiano definito; nondimeno parmi, che Euclide Megarese ottimamen-
te l'habbia descritto, dicendo;Element.
libro 7.
Def. 1. il Numero esser moltitudine composto de più Vnità; Ma
la Vnità, benche non sia Numero, tuttauia è principio del Numero; & da essa ogni co-
sa, ò semplice, ò composta, ò corporale, ò spirituale che sia, uien detta Vna: Percio-
che si come non si può dir cosa alcuna bianca, se non per la bianchezza; cosi non si può
dire alcuna cosa Vna, se non per la Vnità; laquale è talmente contenuta dalla cosa, che
è, che tanto quella si conserua nell'esser proprio, quanto in se contiene essa Vnità; &
all'opposito, quando resta di essere vna, allora manca del suo essere. Et in ciò la Vnità è
niente differente dal Punto, ch'è un minimo indiuisibile nella linea; conciosia che si co-
me quando è mosso (secondo che uogliono alcuni) egli fà la Linea, & non per questo è
detto Quanto; ma si bene principio della Quantità; cosi l'Vnità non è Numero; anco-
rache di esso sia principio. Et si come il Fine non è, ne si può dire, se non rispetto del
Principio; cosi il Principio non può essere, se non hà relatione al Fine. E' perciò da no-
tare, che non uien detto Principio, se non per ragione del Fine; ne Fine, se non per ri-
spetto del Principio; di modo che non si potendo venire dal Principio al Fine, se non
per il Mezo; sarà necessario, ch'ogni cosa acciò sia intera & tutta, contenga in se prin-
cipio, mezo & fine; i quali tutti sono contenuti nel numero Ternario, detto dal Filo-
sofo 1. De Coe-
lo. cap. 1: per tal ragione Perfetto. Onde mancando l'Vnità del mezo & del fine, non si può
dire, che sia Numero; ma principio solamente di quei Numeri, che sono con ordine na
turale disposti: percioche la natural loro dispositione è tale. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. ordi-
ne che si può continuare in infinito, aggiungendoui l'Vnità; la quale, percioche da es-
sa hà principio ogni quantità, sia continua ò discreta, si chiama Genitrice; cioè, prin-
cipio, origine & misura commune d'ogni Numero: conciosia che ciascun Numero con-
tiene in sè più uolte l'Vnità; come per essempio; il Binario, che segue immediatamen-
te dopò essa, non uien formato, se non per la congiuntione de due Vnità, dalle quali
ne risulta esso Binario, Primo numero pare; & à questo aggiunta anco essa Vnità,
si forma il Ternario, Primo numero impare; dalquale con la Vnità appresso si fà il
Quaternario, detto Numero parimente pari; & da questo & dalla istessa Vnità è pro-
dutto il Quinario, detto Numero incomposto; & cosi gli altri de diuerse specie, pro-
cedendo in infinito.
page 29
Delle Varie specie de Numeri; & che nel Senario si trouano le Forme de
tutte le Consonanze semplici.Cap. 13.
uarie sorti de Numeri, & uolerne di ciascuna dir quello, che ella sia; ma per-
che dal Musico ne sono considerate alcune Specie, dirò solamente di quelle,
che fanno al proposito; lasciando da parte l'altre, come inutili. Diremo a-
dunque le specie de Numeri, le quali fà dibisogno sapere, per l'intelligenza di questo
Trattato, & sono al Musico appartinenti, esser dieci; cioè, Pari, Impari, Parimente pa-
ri, Primi & incomposti, Composti, Contrase primi, Traloro composti, ò Communican
ti, Quadrati, Cubi & Perfetti; de i quali, Pari sono quelli, che si possono diuidere in
due parti equali; come, 2. 4. 6. 8. 10. & altri simili; ma gli Impari sono, quelli, che
non possono essere in cotal modo diuisi; anzi di necessità l'una parte supera l'altra per la
Vnità; & son questi 3. 5. 7. 9. 11. & gli altri. Parimente pari sono quelli, c'hanno le
parti, che si possono diuidere in due parti equali, fino à tanto che si peruenga alla Vnità;
dalla quale incominciarono ad hauere il loro essere, continuando in doppia proportione
in infinito; come 2. 4. 8. 16. 32. 64. & gli altri. Numeri Primi & incomposti sono quelli,
i quali non possono essere numerati, ò diuisi da altro numero, che dall'Vnità; come, 2.
3. 5. 7. 11. 13. 17. 19. & altri simili; ma i Composti sono quelli, che da altri Numeri so-
no numerati & diuisi; & sono 4. 6. 8. 9. 10. 12. & gli altri procedendo in infinito. Con-
trase primi sono quelli, che non possono esser misurati, ò diuisi se non dall'Vnità, mi-
sura commune d'ogni numero; come, 9 & 10. che sono Numeri composti; ma insieme
comparati si dicono Contrase primi; essendo che non hanno altra misura commune tra
loro, che li misuri, ò diuida se non essa Vnità. Et questi si trouano di tre sorti; percio-
che, ouer sono l'uno & l'altro Composti; come i già mostrati; ouer l'uno & l'altro Pri-
mi; come, 13. & 17. ouero l' uno Composto & l' altro primo; come, 12 & 19. Tra lo-
ro composti, ò Communicanti si chiamano quelli, che sono misurati, ò diuisi da altro
numero, che dalla Vnità; & niun di loro è all'altro Primo; & si ritrouano di tre sorti;
ouer che sono tutti Pari; come, 4 & 6. ouer che sono tutti Impari; come 9 & 15.
ouer che sono Pari & Impari; come, 6 & 9. Quadrati sono quelli, che nascono
dalla moltiplicatione d'un minor numero in se stesso moltiplicato; come, 4. 9. &
16. i quali nascono dal 2. 3. & 4, che sono le Radici quadrate de tali Numeri; i qua-
li in se stessi moltiplicati, producono i primi; ma i Cubi sono quelli, che nascono
dalla moltiplicatione di qualunque numero in se stesso, & dal produtto ancora per
tal numero moltiplicato; come, 8. 27. 64. & simili; i quali uengono per la molti-
plicatione del 2. 3. & 4. in sè; che Radici Cube de tali Numeri si chiamano; & li
produtti ancora moltiplicati per essi; come sarebbe, che moltiplicando il 2. in se, pro-
duce 4. il quale moltiplicato col 2. ancora, ne nasce 8. detto numero Cubo, del qua-
le il 2. è la radice. Ma i numeri Perfetti sono quelli, che sono integrati dalle loro
parti; & sono numeri Pari & Composti, terminati sempre nel Senario, ouer nell'Otto-
nario; come, 6. 28. 496. & gli altri; conciosia che tolte le parti loro & insieme agiunte,
rendono di punto il loro tutto. Come per essempio; quelle del Senario, che sono 1. 2. &
3. le quali interamente lo diuidono; l'Vnità prima in sei parti, il Binario dopoi in
tre, & il Ternario in due; le qual parti sommate insieme rendono interamente esso
Senario. Queste sono adunque le specie de i Numeri al Musico necessarie; imperoche
la cognitione loro seruer nella Musica alla inuestigatione delle Passioni del proprio Sog-
getto, il quale è il Numero harmonico, ouer sonoro, contenuto nel primo numero Per-
fetto, che è il Senario; come uederemo; nel qual Numero sono contenute tutte le
Forme delle Semplici consonanze, possibili da ritrouarsi, atte à produr l' Harmonie &
le Melodie. Imperoche la Diapason, la quale prima nasce dalla proportione Dupla ve-
page 30ra forma di tal consonanza; è contenuta tra questi termini 2 & 1. e tal proportione il Mu-
sico piglia per il Tutto diuisibile in molte parti; dopoi la Diapente è contenuta tra questi
termini 3 & 2. nella Sesquialtera proportione; & la Diatessaron tra 4 & 3. continenti la
proportione Sesquiterza. Et queste son le due parti maggiori, & le prime, che nasco-
no dalla diuisione della Dupla, ouer della Diapason. Ma il Ditono è contenuto tra 5 &
4. nella Sesquiquarta proportione; & il Semiditono nella Sesquiquinta tra 6 & 5. & que-
ste due parti nascono dalla diuisione della Sesquialtera, ouer della Diapente. Et per-
che tutte queste sono parti della Diapason, ouer della Dupla, come etiandio uederemo
altroue;Cap. 39
2. partis. & nascono per la Diuisione harmonica; però io le chiamo Semplici & Elemen
tali: conciosia che ogni Consonanza, ouero Interuallo quantunque minimo, che sia mi
nore della , nasce non per aggiuntione de molti Interualli posti insieme; ma si
bene per la diuisione di essa Diapason; & l'altre, che sono maggiori, si compongono di
essa & di vna delle nominate parti; ouer di molte Diapason insieme aggiunte; ò pur di
due parti, come le loro Denominationi ce lo manifestano; imperoche della Diapason &
della Diapente poste insieme, si compone la Diapason diapente, contenuta dalla pro-
portione Tripla tra 3 & 1. la Disdiapason composta di due Diapason, è contenuta dalla
proportione Quadrupla tra 4 & 1. & l'Hexachordo maggiore, & anco il minore nasco-
no dalla congiuntione della Diatessaron col Ditono, ò Semiditono; come diligente-
mente habbiamo dimostrato nel Secondo Ragionamento delle Dimostrationi harmoni
che. Ma lasciando hora di dir più di queste & dell'altre; un'altra fiata più diffusamente
ne ragionaremo. Dirò ben questo, che dalle cose, c'habbiamo detto, potiamo com-
prendere per qual cagione il gran profeta Mosè,Genesis
cap.1. nel descriuer la grande & marauigliosa
fabrica del Mondo, eleggesse il numero Senario; non hauendo Iddio nelle sue operatio-
ni mai hauuto dibisogno di tempo; percioche, come colui, che d'ogni Scienza era per-
fetto maestro, conoscendo per opera dello Spirito diuino l'Harmonia, che in tal nume-
ro era rinchiusa;Roma. c. 2. & che dalle cose uisibili & apparenti conosciamo le inuisibili di Dio, la
onnipotenza & la diuinità sua; uolse col suo mezo in un tratto esprimere & insieme mo-
strar la Perfettione dell'opera, & in essa la rinchiusa Harmonia, conseruatrice dell'esser
suo; senza la quale à patto alcuno non durarebbe; ma del tutto, ò si annullarebbe, oue-
ramente ritornando le cose nel loro primo essere; se lecito è cosi dire; di nuouo si uede-
rebbe la confusione dell'antico Chaos. Volse adunque il Santo profeta marauigliosa-
mente manifestare il magisterio & la Opera perfetta del Signore, fatta senza tempo alcu-
no, col mezo del Senario; dal qual Numero quante cose, si della Natura, come ancora
dell'Arte, siano compresse, da quello che segue lo potremo conoscere.
Che dal numero Senario si comprendo molte cose della Natura
& dell'Arte.Cap. 14.
stro Intelletto à contemplar quelle, che si trouano di la sù; nel circolo detto
il Zodiaco ritrouaremo, che de Dodici segni sempre ne ueggiamo Sei alzati
sopra 'l nostro , rimanendo gli altri Sei nell'altro di sotto à noi
ascosi; & ritrouaremo, che Sei sono i Pianeti discorrenti per la Larghezza di esso Zo- diaco, hora di quà & hora di là dalla linea detta Ecclitica; come Saturno, Gioue, Mar-
te, Venere, Mercurio & la Luna; & Sei li circoli posti nel cielo; come Artico, Antartico,
due Tropici; cioè, quello del Cancro, & quello del Capricorno, l'Equinottiale, & l'Eclit-
tica. Et quà giù ritrouaremo, che sono Sei sostantiali qualità de gli Elemēti, Acuita, Ra
rità & Moto, & i loro opposti, Ottusità; Densità & Quiete. Sei gli ufficij naturali, sen-
za i quali cosa ueruna non hà l'essere; come Grandezza, Colore, Figura, Interuallo,
Stato & Moto. Sei specie ancora de i moti; Generatione, Corruttione, Accrescimen-
page 31to Diminutione, Alteratione & Mutatione di luogo. Et Sei, secondo Platone,In Timeo. le diffe-
renze de i Siti, ouer positioni, Sù Giù, Auanti, Indietro, Destro & Sinistro. Sei linee
conchiudono la Piramide triangolare; & Sei superficie la figura Quadrata solida. Sei
Triangoli equilaterali i cui lati sono al Semidiametro del loro cerchio eguali, sono
contenuti nella figura circolare; onde per dinotarci la sua perfettione, Sei uolte la
sua circonferenza di punto è misurata per il dritto da quella misura, che si misura dal
centro alla circonferenza istessa; il perche nasce, che molti chiamano Sesto quello
Istrumento geometrico, che da molt'altri è addimandato Compasso. Sei sono i gradi
dell'Huomo; Essentia, Vita, Moto, Senso, Memoria & Intelletto. Sei le sue età, Infan-
tia, Pueritia, Adolescentia, Giouenezza, Vecchiezza & Decrepità; & Sei l'Etadi del
mondo; lequali, secondo alcuni corrispondono al Senario; dal qual numero Lattantio
FirmianoDe Diui-
no premio.
lib. 7. c. 14. prese occasione di errare, dicendo; che 'l mondo non hauea da durar più de
Sei milla anni; ponendo che un giorno del Signore siano mille; adducendo per testimo-
nianza quello, che dice il Salmo,Psal. 89. Mille anni auanti gli occhi tuoi sono come il giorno
passato. Et per non commemorar tutto quello, che si potrebbe, per non andare in lun-
go; dirò solamente, che sei Sono appresso i Filosofi quelli, che chiamano Trascendenti;
come l'Ente, l'Vno, il Vero, il Buono, Alcuna cosa, ouer Qualche cosa & la Cosa; & Sei
appresso i Logici sono i Modi delle propositioni; cioè, Vero, Falso, Possibile, Impossibi
le, Necessario & Contingente. Per la perfettione di tal Numero, uolse il grande Orfeo
(come narra PlatoneIn Phile-
bo.) che gli Hinni si hauessero à terminare nella Sesta generatione;
conciosia che si pensò, che delle cose create non si potesse cantare più oltra essendo in tal
numero terminata ogni perfettione. Onde i Poeti ancora uolsero, che 'l verso del Poe-
ma heroico; come quello, che più d'ogn'altro giudicarono perfetto; terminasse nel Se-
sto piede. Non è adunque marauiglia, se questo Numero da alcuni uien detto Segnaco
lo del Mondo; poi che si come questo Mondo non hà di superfluo cosa alcuna, ne gli man
cano le cose necessarie; cosi quello hà hauuto tal temperamento, che ne per progressio-
ne si estende, ne per contratta diminutione si rimette; ma tenendo una certa mediocri-
tà, non è superfluo, ne è per sua natura diminuito; per la qual cosa egli hà ottenuto il
nome non solo di Perfetto; ma d'Imitatore della Virtù. Questo è detto numero Ana-
logo; cioè, Proportionato, dalla sua reintegratione per le sue parti; nel modo, che di
sopra hò mostrato;Cap. 13. percioche quelle generano tal numero, chè simile al suo Genitore.
Oltra di questo è detto numero Circolare; conciosia che molteplicato in se sesso, il pro-
dutto da tale molteplicatione è terminato nei Senario; & questo ancora per esso Sena-
rio moltiplicato (se bene si procedesse in infinito) genera un produtto terminato in esso
Senario. Tutto questo hò voluto dire, per dimostrare, che hauendo la Natura mirabil-
mente rinchiuso molte cose in questo Numero, hà uoluto ancora co l'istesso abbracciar-
ne la maggior parte di quelle, che si ritrouano nella Musica; conciosia che primieramen
te (come si vederà altroue) Sei sono le spetie delle Voci, tra le quali è contenuto ogni
concento musicale; cioè, Vnisone, Equisone, Consone, Emmelle, Dissone & Ecmele;
& Sei quelle, che i Prattici addimandano Consonanze; cioè, cinque semplici & ele-
mentali, che sono (come di sopra hò mostratoCap. 13.) la Diapason, la Diapente, la Diatessa-
ron, il Ditono, il Semiditono & uno Principio di esse, ilquale chiamano Vnisono; an-
cora che questo si nomini Consonanza impropriamente; come altre uolte uederemo.Infra
Cap. 4.
Tertiae
partis.
Oltra di questo si ritrouauano appresso gli Antichi musici Sei specie d'Harmonia poste in
uso; che sono Doria, Frigia, Lidia, Mistalidia, ò Locrense, Eolia & la Iastia, ouero Io
nica; & appresso i moderni Sei Modi principali, detti Autentici, & Sei non principali,
detti Plagali. Lungo sarebbe il uoler raccontare di una in una tutte quelle cose, che so
no terminate nel Senario; ma contentandoci per hora di quello, ch'è stato detto, uer-
remo alle sue proprietà; per esser necessarie al nostro proposito.
page 32
Delle Proprietà del numero Senario & delle sue parti; & come tra
loro si ritroua la forma d'ogni Consonanza musicale.
Cap. XV.
per non andar troppo in lungo, racconterò solamente quelle che fanno al pro
posito; & la prima sarà, che egli è tra i Numeri perfetti il Primo; & contie-
ne in se Parti, che sono proportionate tra loro in tal modo; che pigliandone
Due qual si uogliono, hanno tal relatione, che ne danno la ragione, ò forma di una
delle Proportioni delle musicali consonanze; ò semplice, ò composta ch'ella sia; co-
me si può uedere nella sottoposta figura.
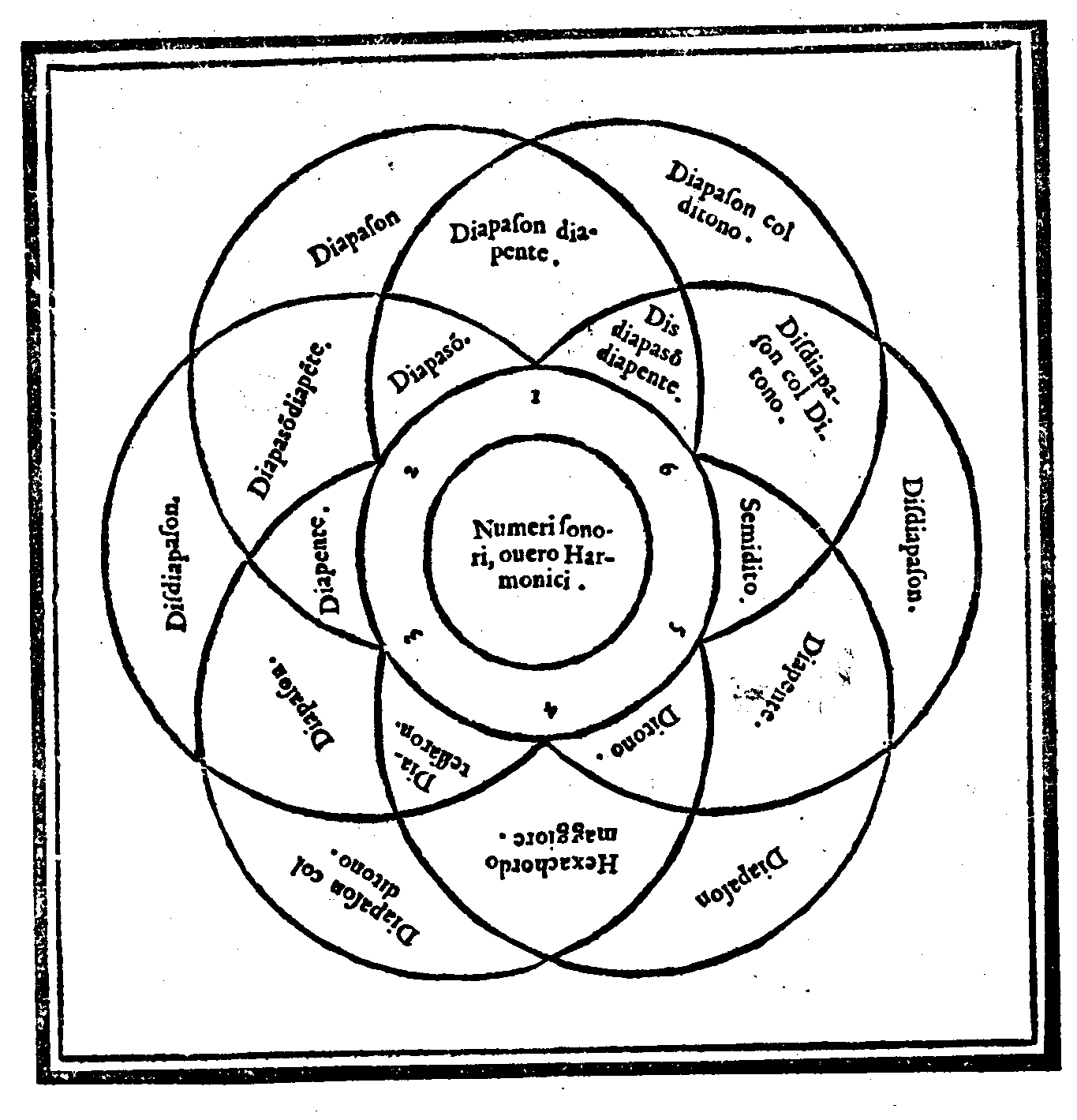
delle Due maggiori semplici consonanze, le quali da i Musici uengon chiamate Perfet-
te; essendo cōtenute tra le parti del Ternario, sono in due parti diuise in Harmonica pro
portionalità, da un termine mezano: conciosia che ritrouandosi prima la Diapason nel-
la forma & proportione, che è tra 2 & 1. senz'alcun mezo; è dopoi dal Ternario posto tra
il 4. & il 2. in due parti diuisa; cioè, in due consonanze, nella Diatessaron primamen-
te, che si ritroua tra 4. & 3. & nella Diapente collocata tra il 3. & il 2. Questa poi si ritro-
ua tra 6. & 4. diuisa dal 5. in due parti consonanti; cioè, in un Ditono contenuto tra 5.
& 4. & in un Semiditono contenuto tra 6. & 5. Ho detto, che sono diuise in Due parti
page 33in Harmonica proportionalità; non già quanto all'ordine delle Proportiomi; che ue-
ramente è Arithmetico; ma si bene quanto alla Proportione delle parti, mediante il ter-
mine mezano. Percioche sono di tanta quantità & proportione; di quanta sono quel-
le, che da un mezano termine, ò diuisore harmonico sono fatte, à ben che con ordine
contrario; come uederemo al suo luogo.Infra
cap. 40. Vedesi oltra di questo l'Hexachordo maggio-
re, contenuto in tale ordine tra questi termini 5 & 3 ilquale dico esser Consonanza com
posta della Diatessaron & del Ditono; percioche è contenuto tra termini, che sono me-
diati dal 4. come nella figura si può uedere. Et sono queste Parti in tal modo ordinate;
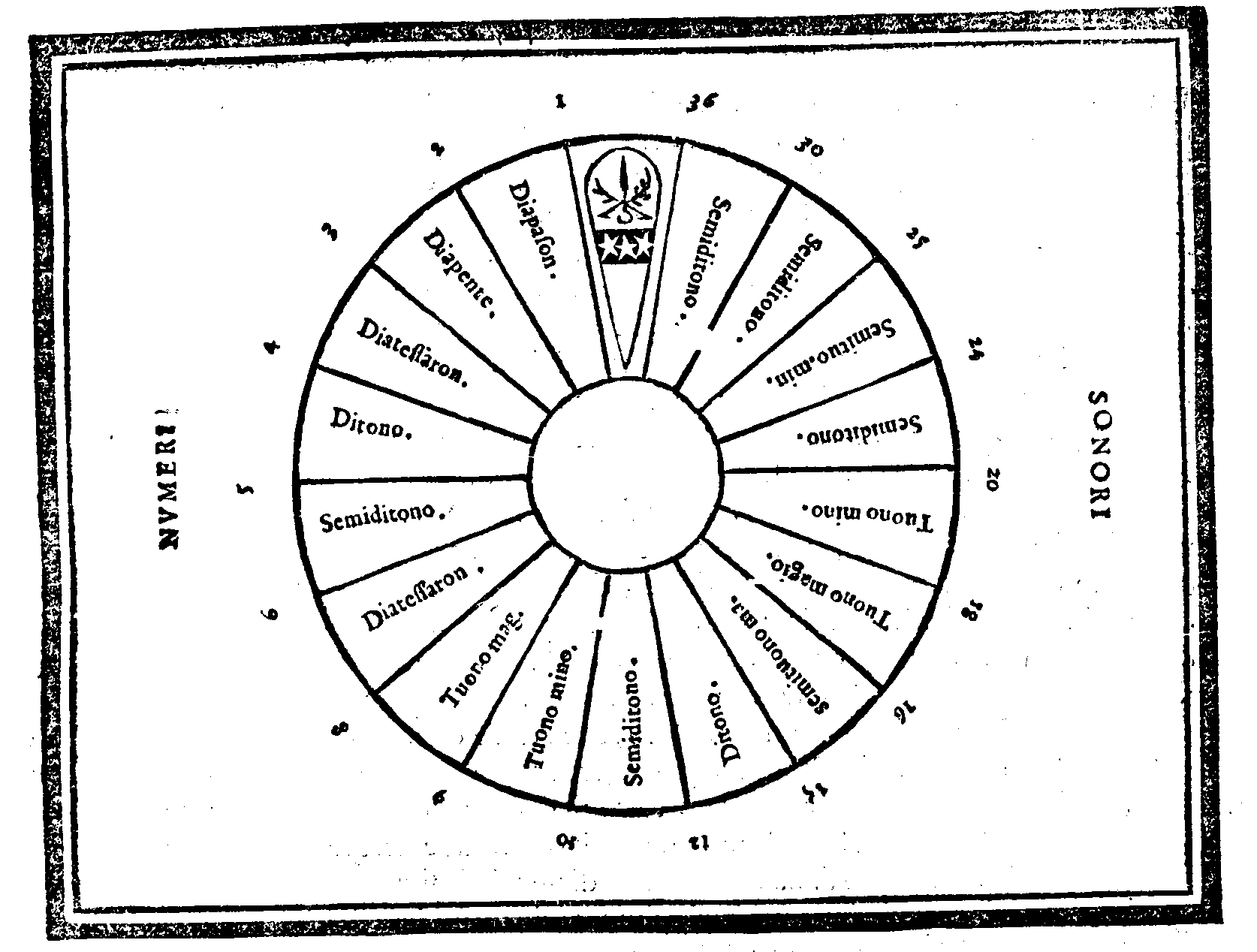
ne de i mostrati Numeri, & si percuotessero insieme; ne i Suoni, che nascerebbono
dalle predette chorde, non solo non si udirebbe alcuna discrepanza; ma da essi ne usci-
rebbe una tale Harmonia, che l'Vdito ne pigliarebbe sommo piacere; & il contrario
auerrebbe, quando tal ordine in parte alcuna fusse mutato; come etiandio hò dichiara-
to più diffusamente altroue. In princi-
pio primae
partis De-
monstra-
tionum. Hanno oltra di ciò queste Parti tal proprietà; che multipli-
cate l'una per l'altra in quanti modi è possibile, & posti li prodotti in ordine, si troua sen-
za dubbio alcuno tra loro Harmonica relatione, comparando il maggiore al minore
più propinquo. Al qual ordine s'el si aggiungerà il Quadrato di ciascuna parte; cioè,
i prodotti della sua moltiplicatione; ponendoli nel predetto ordine al loro luogo, secon-
do che sono collocati in naturale dispositione; non solo si haurà la Ragione di qualunque
consonanza, atta alle Harmonie & Melodie; ma le ragioni delle Dissonanze ancora;
ò uogliamo dire le Forme de gli interualli Dissonanti; che sono i Tuoni, & i Semituoni
maggiore & minore; differenze delle sopradette Consonanze; percioche essi dimostra-
no quanto l'una supera, ouero è superata dall'altra; come da quello, che nel Primo libro
delle Dimostrationi hò dichiarato, si può cōprendere.Infra. cap.
17. ter. par
tis. Et queste Differenze non pur sono
page 34utili; ma necessarie ancora nelle modulationi; come uederemo al suo luogo;Infra. cap.
17. ter. par
tis. Il che nelle
figura si può uedere tutto per ordine. Queste sono adunque le Proprietà del numero Se-
nario & delle sue Parti, lequali è imposibile di poter ritrouare in altro numero, che sia di
esso minore, ò maggiore.
Quel sia Consonanza semplice ò Composta; & che nel Senario in potenza si ri-
trouano le Forme de tutte le Consonanze; & onde habbia origine
l'Hexachordo minoreCap. XVI.
numero delle Consonanze; per esser la sua proportione contenuta nel genere
Superpartiente, ilquale (come dicono) non è atto à produrle: nondimeno
per essere Interuallo fin'hora approuato & riceuuto, come è ueramente, per
consonante da i Musici, l'hò posto nel numero di esse. Ma perche hò detto; che l'Hexa-
chordo è Consonanza composta; però vederemo al presente quello, che si debba inten-
dere per Interuallo semplice, ò composto. Dico adunque che Consonanza, ò Interuallo
semplice è quello, che pigliati li Minimi termini della sua proportione, in tal modo sono
ordinati, che non possono riceuere tra loro alcun termine mezano, che diuida tal propor
tione in più parti; essendo che sono sempre l'vn dall'altro distanti per l'Vnità. Cosi all'
incontro Consonanza, ouero Interuallo composto intendo, esser quello, il quale ha i mi-
nimi termini della sua proportione in tal modo l'un dall'altro distanti, che possono da
vno, ò più mezani termini esser mediati & diuisi; di modo che di una proportione, due
ò più ne potiamo hauere. Onde hò detto, che l'Hexachordo maggiore è Consonanza
composta, percioche i minimi termini della sua proportione, che sono 5 & 3. sono capaci
d'un mezano termine, che è il 4. come hò mostrato disopra; & la Diapente dico esser Con
sonanza semplice; essendo che i minimi termini della sua proportione, che sono 3 & 2.
non possono riceuere altro termine tra loro, che diuida quella in più parti, per esser distan
ti l'un dall'altro per l'Vnità. Bisogna però auertire, che in tre modi si può dire, che le Con
sonanze siano composte; come disopra anco fu detto;Cap. 13. prima quando si compongono de
due parti della Diapason, lequali insieme aggiunte, non reintegrano essa Diapason; do-
poi quando si cōpongono dalla Diapason & di una delle sue parti; ultimamente quando
più Diapason sono poste insieme. Nel primo modo si cōsidera l'Hexachordo nominato,
che si compone della Diatessaron & del Ditono; come si scorge tra i minimi termini della
sua proportione, che sono 5 & 3. iquali per il 4. sono in tal modo tramezati 5. 4. 3. Al-
quale aggiungeremo il minor Hexachordo, che nasce dalla congiuntione della Dia-
tessaron col Semiditono, i cui minimi termini contenuti nel genere Superpartiente dalla
proportione Supertripartientequinta, possono da un termine mezano esser mediati: Im-
peroche ritrouandosi tal proportione tra 8 & 5. tai termini sono capaci d'un mezano ter-
mine harmonico, ch'è il 6; il quale la diuide in questa maniera. 8. 6. 5. in due proportioni
minori; cioè, in una Sesquiterza & in una Sesquiquinta. Di modo che tal Consonanza
per questa ragione potiamo chiamar Composta; la quale fin'hora da i Musici è stata ab-
bracciata & posta nel numero dell'altre. Et benche la sua forma non si troui in atto tra
le parti del Senario; si troua nondimeno in potenza; conciosiache ueramente la piglia
dalle parti contenute tra esso; cioè, dalla Diatessaron & dal Semiditono; perche di que
ste due consonanze si compone: la onde tra 'l primo numero Cubo, il quale è 8. uiene ad
hauerla in atto. Ma nel secondo modo si considera la Diapasondiapente, la qual si com-
pone della Diapason, aggiuntoui la Diapente; percioche i minimi termini della sua pro-
portione, che sono 3 & 1. sono naturalmente diuisi in una Dupla, & in una Sesquialtera,
che sono proportioni, le quali contengono tali consonanze; come qui si uedono 3. 2.
page 351. Cosi nel terzo modo potremo porre la Disdiapason; imperoche i minimi termi-
ni della sua proportione, che sono 4 & 1. sono capaci d'un termine mezano; il-
diuide quella in due Duple, in Geometrica proportionalità; come vediamo
nel 4. 2. 1. Ancorache potiamo considerare tal Consonanza esser composta della , della Diapente & della Diatessaron; percioche tai termini sono capaci
due mezani, i quali la diuidono in tre parti, contenenti le proportioni delle no-
minate consonanze; come si uede nel 4. 3. 2. 1. Nondimeno dobbiamo auertire, che
quantunque tali Consonanze si possano considerare composte in tanti modi; io pro-
priamente & ueramente chiamo quelle esser composte, le quali si compongono della
Diapason, & d'alcuna delle sue parti, secondo l'uno de i due ultimi modi mostrati
di sopra; ma quelle, che si considerano composte nel primo modo, chiamo impropria-
mente & ad un certo modo Composte; imperoche per esser minori della Diapason, si
vedono quasi esser Simplici & Elementali; il che non intrauiene nell'altre, per la ragio-
ne che dirò altroue.Infra. c. 3.
Ter. partis. Et perche è impossibile di poter ritrouare nuoue Consonanze, lequa-
li siano semplici, dalle Cinque mostrate in fuori, che sono la Diapason, la Diapente, la
Diatessaron, il Ditono & il ; dalle quali ogn'altra Consonanza si compone;
però dico & concludo quello, che di sopra hò anco detto; che nel Senario; cioè, tra
le sue Parti, si ritroua in atto ogni Semplice musical consonanza, & anco le Com-
poste in potenza; dalle quali nasce ogni buona & perfetta Harmonia; intendendo
però delle Forme, ò Proportioni, & non de i Suoni. Ma accioche più facilmen-
te possiamo esser capaci di quello, c'hò detto, verrò à ragionar prima delle cose, che fan-
no dibisogno alla cognitione delle Proportioni; & dopoi vederemo, come si mettono
in opera; imperoche senza la loro cognitione, sarebbe impossibile di potere hauer noti-
tia alcuna dalla Musica.
Della Quantità continua & della discreta.Cap. XVII.
come si può conoscere da quello, che si è mostrato poco fà; ritengono quasi
quell'ordine, che si troua ne i Numeri posti auanti al Denario, con naturale
ordine collocati; oltra il quale non si uede, che si aggiunga nuouo Numero;
ma si bene appare, che quelli uengano ad esser replicati; conciosia che si come dopo il
Denario segue l'Vndenario, & dopo questo il Duodenario, & similmente gli altri per
ordine; nel medesimo modo ancora dopo la Diapason & la Diapente, le quali nel
loro naturale ordine si pongono senz'alcun mezo, tutte l'altre Consonanze si uan-
no replicando, secondo l'ordine mostrato, quasi in infinito; percioche posta pri-
ma la Diatessaron dopo le due nominate, immediatamente se le aggiunge il Dito-
no; dopoi il Semiditono; & à questo di nuouo s'aggiunge la Diatessaron; & con
tal ordine sempre si uanno replicando & moltiplicando. Et ancora che in tal modo si
potesse procedere in infinito, quando fusse bisogno; nondimeno la Musica non riceue l'
Infinito; percioche di esso non si hà, ne si può hauere scienza alcuna; & l'Intelletto non
è capace di esso; di modo che se gli occorre di uoler sapere la ragione d'alcuna cosa, si
serue solo d'una determinata quantità; & con tal mezo comprende & sà il uero di ciò,
che ricerca. Ma cadendo tutte le cose necessariamente sotto 'l Numero; & raccogliendo-
si (essendo una ò più) sotto questo nome di Quantità; la quale per la sua eccellenza i
Filosofi hanno giudicata pari & insieme eterna con la Sustanza; però immediatamente
la diuisero in due parti; cioè, in Continua & in Discreta. La Continua nomina-
rono quella, le cui parti sono congiunte ad un termine commune; come la Linea,
la Superficie, il Corpo; & oltra di queste il Tempo, il Luogo, & tutte quelle cose, che
page 36si attribuiscono alla Grandezza. La Discreta dissero esser quella, le cui parti non sono
congiunte ad alcun termine commune; ma restano distinte & separate; come è il Nu-
mero, il Parlare, una Greggia, un Popolo, un Monte di grano, ouer di altro; alle
quali cose conuiene il nome di Moltitudine; conciosia che molte Parti separate in-
sieme si compongono ne i loro estremi; come si uede nel Numero; che incomincian-
do dall'Vnità, sotto la quale non ui è altro Numero minore; moltiplicata in infinito,
senza ritrouare impedimento alcuno, viene à procreare gli altri Numeri; di modo che
la sua natura è molto conforme al genere Molteplice nelle proportioni; percioche con-
siderata ne i Numeri, e finita in qual si uoglia di essi; ma si rende infinita per l'ac-
crescimento; conciosia che si possa moltiplicare in infinito; come uederemo ancora
nel Molteplice, il quale è finito nelle sue Specie; ancora che cotali specie si possino
estendere in infinito. Ma la Continua, che incomincia da una finita quantità, & ri-
ceue una infinita diuisione, perdendo la quantità della misura nel crescere delle par-
ti, & moltiplicandole nel diminuire, ritiene la natura del Genere superparticolare; per-
cioche se una Linea lunga Sedici piedi si diuidesse in otto, & questi in quattro; & co-
si sempre si diuidesse il restante in due parti; si trouerebbe quella infinitamente esser di-
minuita, & molteplicata in infinito il Numero delle sue parti. Tal natura serua il nomina-
to Genere nelle proportioni; ilquale, quanto più procede à maggiori numeri conti-
nuando l'ordine naturale, tanto più si dimostra diminuito nelle sue specie, le quali
se bene sono infinite in potentia, ciascuna però da sè si ritroua esser finita in atto.
Del Soggetto della Musica.Cap. XVIII.
se stesse; come il Numero 1. 2. 3. 4. & gli altri; & alcune sono dette per rela-
tione; come il Duplo, il Triplo, il Quadruplo; & altri simili; però ogni
Numero, il quale stà da per sè; ne per l'esser suo hà dibisogno d'altro ag-
giunto, è detto Semplice; & di lui l'Arithmetica ne hà consideratione. Quello ue-
ramente, che non può esser da sè; percioche all'esser suo ha dibisogno d'un'altro,
è detto numero Relato; & di tal Numero si serue il Musico nelle sue speculationi. Ma
nella quantità Continua detta di grandezza sono alcune cose di perpetua quiete; come
la Terra, la Linea, la Superficie, il Triangolo, il Quadrato & ogni Corpo mathema-
tico; & altre continuamente sono girate, & hanno in se stesse il mouimento; come i
Corpi celesti. Delle prime se ne tratta nella Geometria; delle seconde, ne fà professio-
ne l'Astronomia; di modo che dalla diuersità delle cose diuersamente considerate na-
sce la uarietà delle Scienze, & la diuersità de i Soggetti; conciosia che si come l'Ari-
thmetico considera principalmente il Numero; cosi il Numero è il Soggetto della sua
scienza. Et perche i Musici, nel uoler ritrouar le Ragioni d'ogni musicale Interuallo,
si seruono de i Corpi sonori, & del Numero relato, per conoscer le distanze, che si
trouano tra suono & suono, & tra uoce & uoce; & per saper quanto l'una dall'altra sia
differente per il graue & per l'acuto; però mettendo insieme queste due parti; cioè, il
Numero & il Suono, & facendo un composto, dicono; che 'l Soggetto della Musica
è il Numero sonoro. Et benche AuicennaSuffic. lib.
1. cap. 8. dica, che cotal Soggetto siano i Tuoni &
li Tempi; nondimeno considerata la cosa in sè, ritrouaremo tutto esser uno; cioè, rife-
rirsi i Tempi al Numero, & li Tuoni al Suono.
page 37
Quel che sia Numero sonoro.Cap. XIX.
sto Numero, hanno detto, ch'ei non è altro, che 'l Numero delle parti d'un
Corpo sonoro; il quale, come dichiarai nella Terza definitione del Primo
delle Dimostrationi, è come sarebbe dire una chorda, laquale pigliando ra-
gione di Quantità discreta, ne fà certi della quantità del Suono da lei prodotto. Que-
sta definitione, ancora ch'ad alcuno possa parer buona; secondo 'l mio giudicio, par
che sia tronca & imperfetta; percioche le Voci, che sono principalmente considerate
dal Musico, & non sono lontane dal Numero sonoro, hauendo proportione tra lo-
ro; non caderebbono sotto tal definitione; conciosia che elle habbiano origine da i
Corpi animati & humani; cioè, dall'Huomo; & è pur ragioneuole, che tutte le cose
considerate in una Scienza; ancora che da per sè non si considerino; ma si bene in or-
dine al Soggetto; ad esso si riduchino; come è ancora ragioneuole, che la Definitio-
ne conuenga con la cosa definita. Et benche l'Huomo habbia il Corpo misurato da tre
distanze, che sono altezza, larghezza & profundità; come sono gli altri corpi; tut-
tauia questo non basta; ma si ricerca ancora, che 'l sia Sonoro. Onde bisogna c'hab-
bia tre conditioni; prima, che sia polito; dopoi, che sia duro; ultimamente, che sia
largo; le quali conditioni non sò, come in esso tutte ritrouar si possano. Ma ponia-
mo, che il corpo dell'Huomo habbia tutte queste conditioni; non per questo si po-
trà hauer col suo mezo cognitione della quantità delle Voci; percioche le parti do-
ue nascono, non sono in tal modo sottoposte al sentimento, che si possa hauer di lo-
ro alcuna determinata misura. Ma chi dicesse, che le Voci si applicano à i Suoni,
che nascono dalle chorde; & che per tal modo si uiene ad hauer la ragione delle loro pro
portioni; & che con questo mezo istesso si uengono à ridurre sotto la detta definitione;
costui direbbe ciò impropriamente; percioche i Suoni si applicano alle Voci; accio-
che di esse si habbia uera & determinata ragione; & non per il contrario. Parmi a-
dunque che meglio sia dire; che 'l Numero sonoro è Numero relato alle Voci, & à i
Suoni; il quale si ritroua arteficiosamente in un Corpo sonoro; come in una chorda,
la qual riceuendo la ragione d'alcun Numero nelle sue parti, ne fà certi della quantità
del suono produtto da essa, & della quantità delle Voci; referendo, ouero applican-
do essi Suoni ad esse Voci. Et questo dico, quando tal Numero si considerasse uni-
uersalmente in ciascuno Interuallo; ma quando si considerasse particolarmente in quel
li Interualli solamente, che sono consonanti; si potrebbe dire, che fusse la Ragione
delle proportioni, lequali sono le Forme delle Consonanze; considerate primiera-
mente nella Musica; come sono le mostrate di sopra, contenute tra le parti del nu-
mero Senario, che si ritrouano con arteficio nelle parti d'un Corpo sonoro, & rela-
to al sopradetto modo. Et perche le differenze, che si trouano tra le Voci, & i Suo-
ni graui & acuti, non si conoscono, se non co 'l mezo de i Corpi sonori; però consi-
derando i Musici tal cosa, elessero una chorda fatta di metallo, ò d'altra materia,
che rendesse Suono; la qual fusse equale da ogni parte come quella, della quale
(essendo d'ogn'altro Corpo sonoro men mutabile & meno in ogni parte uariabile)
poteuano hauer la certezza di tutto quello, che cercauano; hauendo opinione cer-
ta, che Tanto fusse la quantità del Suono della chorda, quanto era il Numero del-
le parti considerato in essa; ilperche conosciuta la sua lunghezza & quantità, secon-
do il numero delle sue parti misurate, subito faceuano giudicio delle distanze, che
si trouano esser tra i Suoni graui, & gli acuti, ò per il contrario; & conoscere la pro-
portione di ciascuno Interuallo. Et questo è quello, che dimanda il Musico innanzi
che dimostri le cose della Musica, che li sia concesso da colui, ilquale uuole imparare.
Ma se per caso cotal cosa, ch'è posta da lui per uno de i suoi Principii; come nella Prima
page 38dimanda del Terzo delle Dimostrationi dichiarai; gli fusse negata; non potrebbe à patto
alcuno far la Dimostratione. Et ciò non fecero i Musici fuor di proposito; come dalla e-
sperienza potiamo vedere; percioche se noi tirando una chorda di qual si uoglia lunghez
za sopra vna superficie piana; la diuideremo con la ragione in tre parti equali; fatta la
comparatione d'una di essa all'altre due; conosceremo manifestamente, i Suoni prodot-
ti da queste parti (hauendole insieme percosse) esser l'uno dall'altro distanti per una Dia
pason, in Dupla proportione; come nella Seconda parte uederemo.Cap. 18. Onde in cotal
modo diuisa ancora in più parti, & comparato il Tutto à due, tre, quattro, ò più di es-
se, potremo sempre conoscer variate distanze, & udire uariati Suoni, nati da quelle, se
condo la diuersità delle parti al loro Tutto; & potremo insieme conoscere, il Tutto esser
cagione del Suono graue; & le Parti, quanto più saranno minori, esser cagione de i Suo-
ni acuti. Con questo mezo, & per tal via adunque; come più sicura, secondo 'l conseglio
di Tolomeo,Harmo. li-
bro. 1. c. 8. aggiunta la Ragione al Senso, i Musici uanno primieramente inuestigan-
do le ragioni delle Consonanze, & poi di ciascun'altro Interuallo, & ogni Differenza,
che si troua tra i Suoni graui & gli acuti; & hauendo rispetto alle Voci & à i Suoni, che
sono la Materia di ciascun Interuallo musicale; & anco à i Numeri & Proportioni; le
quali (com'altre uolte hò dettoSupra ca.
13. & 15.) sono la loro Forma, aggiungendo queste due cose in-
sieme, dissero; il Numero sonoro essere il uero Soggetto della Musica; & non il Corpo
sonoro; percioche se bene tutti i Corpi sonori sono atti alla produttione de i Suoni; non
sono però tutti atti alla generatione della Consonanza; se non quelli, che sono tra loro
proportionati & contenuti sotto una terminata forma; cioè, sotto la ragione de i Nu-
meri harmonici. Ma quando, dopo l'hauer considerato bene, & ben'essaminato tutti
quelli Accidenti, & Passioni, che dimostraremo; che possono occorrere intorno à co-
tal Corpo, alcuno uorrà tenere & difendere; che più tosto il Corpo sonoro proportio-
nato, che il Numero sonoro, sia il Soggetto uero della Musica; non lo farà fuori di pro
posito, & senza gran ragione; com'ei potrà conoscere dalle Dimostrationi, che si fan-
no in questa Scienza: & potrà anco tenere, che la Musica sia più tosto Subalternata al-
la Geometria, che all'Arithmetica: se bene communemente è tenuto il contrario; co-
me da quello che segue si potrà uedere.
Per qual cagione la Musica sia detta subalternata all'Arithmetica, & mezana
tra la Mathematica & la Naturale.Cap. XX.
meri & dalla Geometria le Quantità misurabili; cioè, i Corpi sonori; pe-
rò si fà alle due nominate Scienze soggetta; & si chiama Scienza subalterna-
ta. Onde è da sapere, che di due sorti sono le Scienze; percioche sono al-
cune dette Principali, ò Subalternanti; & alcune Nonprincipali, o Subalternate.
Le prime sono quelle, lequali dependono da i Principii conosciuti per lume natura-
le & cognitione sensitiua; come l'Arithmetica & la Geometria; le quali hanno al-
cuni Principij conosciuti per la cognitione d'alcuni termini acquistati per uia de i
Sensi; come dire, che La Linea sia lunghezza senza larghezza; ch'è un principio
proprio della Geometria; & che 'l Numero sia moltitudine composta de più vnità; che
è proprio principio dell'Arithmetica; oltra i Principii communi, che sono quelli, che
dicono; Il tutto esser maggior della sua Parte; La Parte esser minore del suo Tutto; &
molti altri, de i quali l'Arithmetico & il Geometra cauano le loro conclusioni. Ma le secō
de sono quelle, che oltra i proprij Principii, acquistati per il mezo de i Sensi, ne hāno alcu
ni altri, che procedono da i principii conosciuti nell'una delle Scienze superiori & princi
page 39pali; & sono dette Subalternate alle prime; come la Prospettiua alla Geometria: con-
ciosiache, oltra i Proprii principii, ne hà alcuni altri, che sono noti & approuati nella
Scienza à lei superiore, ch'è la Geometria. Et è di tal natura la Nonprincipale & sub-
alternata, che piglia della principale l'istesso Soggetto; ma per sua differenza ui aggiun-
ge l'Accidente; percioche se fusse altramente, non ui sarebbe tra l'una & l'altra alcuna
differenza di Soggetto; come si uede della Prospettiua, che piglia per soggetto la Linea
per sè; della quale si serue anche la Geometria; & ui aggiunge per l'accidente la Visuali-
tà; & cosi la Linea visuale uiene ad esser il suo soggetto. Il medesimo intrauiene ancora
nella Musica, c'hauendo ella con l'Arithmetica per commune soggetto il Numero, ag-
giunge à questo per sua differenza la Sonorità, & si fà ad essa Arithmetica subalternata;
tenendo il Numero sonoro per soggetto. Ne solamente hà la Musica i Proprij principii;
ma ne piglia anco de gli altri dall'Arithmetica, per i mezi delle sue Demostrationi; accio
che per essi habbiamo la vera cognitione della Scienza, E' ben vero, che tali Principii
& mezi non sono tutte le conclusioni, che nell'Arithmetica si ritrouano; ma solamente
una parte, della quale il Musico ne hà dibisogno; & sono di Relatione; cioè, delle Pro
portioni; & questo per mostrar le Passioni de i numeri sonori, secondo il proposito. On-
de ancora noi pigliaremo quelle Conclusioni solamente, che ci faranno dibisogno; &
le applicaremo al Suono, ouero alla Voce, che dal Naturale (come dimostra Aristote-
le2. De Ani
ma. cap. 8.
2. Phy. ca.) sono considerate; Il perche diremo, che la Musica secondo la dottrina di questo Fi-
losofo: non solo alla Mathematica; ma etiandio alla Naturale è subalternata; non in
quanto alla Parte de i Numeri; ma si bene in quanto alla parte del Suono, ch'è natura-
le; dalquale nasce ogni Modulatione, ogni Consonanza, ogni Harmonia, & ogni Me-
lodia: la qual cosa è confermata anche da Auicenna,Suffic. lib.
1. cap. 8. il qual dice; che La Musica hà i
suoi Principij dalla Scienza naturale, & da quella de i Numeri. Et si come nelle cose
naturali, niuna cosa è perfetta mentre ch'è in potenza; ma solamente quando è ridutta
in atto; cosi la Musica non può esser perfetta, se non quando co 'l mezo de i naturali, ò
arteficiali Istrumenti si fà udire; la qual cosa non si potrà fare co 'l Numero solo, ne
con le Voci sole; ma accompagnando queste & quello insieme; massimamente essendo
il Numero inseparabile dalla Consonanza. Per questo adunque sarà manifesto, che la
Musica non si potrà dire ne semplicemente Mathematica, ne semplicemente Naturale;
ma si bene parte Naturale & parte Mathematica; & conseguentemente mezana tra
l'una & l'altra. Et perche dalla Scienza naturale il Musico hà la ragione della mate-
ria della Consonanza, che sono i Suoni & le Voci; & dalla Mathematica hà la ragio-
ne della sua forma; cioè, della sua Proportione; però douendosi denominar tutte le co-
se dalla cosa più nobile; piu ragioneuolmente diciamo la Musica esser Scienza mathema
tica, che naturale; conciosia che la Forma sia più nobile della Materia.
Quel che sia Proportione; & della sua diuisione.Cap. XXI.
bio hanno l'esser da cose naturali, & generano, & in atto fanno udire la Con-
sonanza, gouernatrice d'ogni Modulatione; per il cui mezo si peruiene al-
l'uso della Melodia; nella quale consiste tutta la perfettione della Musica.
E ben uero, ch'alla sua generatione concorrono (com'altre uolte uederemoInfra
cap. 12.
2. partis.) Due
suoni dissimili; iquali secondo la forma & la ragione de gli Harmonici numeri, pro-
portionatamente siano distanti l'un dall'altro per il graue & per l'acuto. Ma si hà
da sapere, che tutte quelle cose, dalle quali può nascer Suono; come sono Chor-
de, Nerui, Aere respirato, & altre cose simili, il Musico chiama Distanza; & la
page 40Forma, ò Ragione de Numeri, che si caua dalla misura delle chorde sonore, chiama Pro
portione; laquale immediatamente si diuide in due parti; cioè, in Commune, & in Pro-
pria. La prima è la comparatione di due cose insieme, fatta in un medesimo attributo,
ouer predicato vniuoco; come comparando Gioseffo & Francesco in bianchezza, ouero
in altra qualità, nella quale conuenghino. La seconda (come vuole Euclide)Element.
lib. 5. Def.
5. è quella cer-
ta habitudine, ò conuenienza, c'hanno due finite quantità d'un medesimo Genere pro
pinquo, siano equali, ouero inequali tra loro. Et hò detto d'un medesimo Genere pro-
pinquo, percioche non si può dir con ragione, una Linea esser maggiore, ò minore,
ouero equale ad una Superficie, ne ad un Corpo; ne il tempo esser maggiore, ò minore,
ouero equale ad un luogo; ma si bene una Linea esser maggiore, ò minore, ouero equa
le, ad un'altra; & cosi un Corpo ad un'altro corpo; & altri simili: percioche (come c'in-
segna il Filosofo7. Phy. c. 1.
summae. 4.) la comparatione si debbe far solamente nelle cose, c'hanno una sola
significatione, & che sono d'uno istesso Genere propinquo; & non in quelle, che hanno
più significati, & sono di Generi diuersi; ouero assolutamente d'un sol Genere remoto.
Ne si. ritroua solamente la Proportione nelle sopradette quantità; ma ne i Pesi, nelle
Misure; & (come uuol PlatoneIn Timeo.
Arist. cap.
De Quant.
Praedic. 2.) nelle Potenze, & ne i Suoni come uederemo; la qual
Proportione mai si ritroua in alcuna cosa, se non in quanto l'una è equale, ò maggiore, ò
minore dell'altra: conciosiache Il proprio della Quantità è, l'esser dette Equale, ouer Ine
quale; Et si ritroua tal Proportione primieramente nella Quantità; & successiuamente
dopoi nell'altre cose nominate. Lascierò di parlare della Commune; percioche non fà
punto al nostro proposito; & di nuouo diuiderò la propria nella Rationale, & nella Ir-
rationale; & diro prima, la Rationale esser quella, che da Numeri, i quali contengono,
ò sono contenuti piglia la sua denominatione; come dal 2. ch'essendo comparato all'Vni
tà, nella ragione del contenere, è denominata la Dupla proportione; onde simili quan
tità sono dette commensurabili, & communicanti; percioche l'una & l'altra sempre da
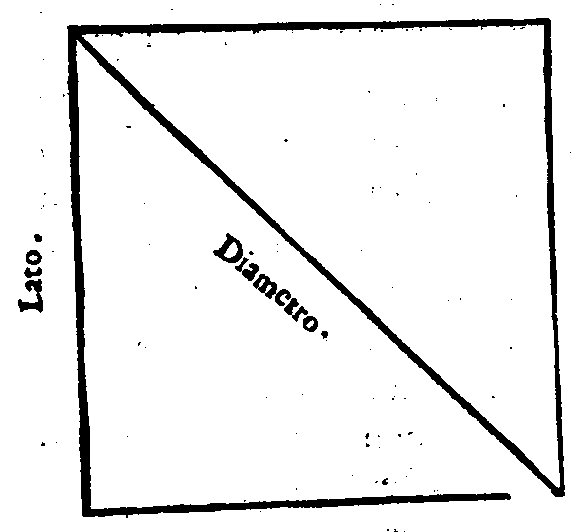
poi è quella, che per niun numero rationale si può deno-
minare, come quella del Diametro & del Lato del Qua-
drato; imperoche non si può dare alcuna misura com-
mune, che sia certa, & che misuri interamente l'uno &
l'altro; & perciò sono dette Quantità incommensurabili.
Dobbiamo però auertire, ch'ogni proportione, che si
ritroua ne i Numeri, ò Quantità discreta; si ritroua anco
nella continua; essendo che tutti i Numeri sono commen
surabili, & communicanti; essendoche almeno sono nu-
merati dall'Vnità; ilche non auiene nella continua, nel-
la quale si ritrouano infinite Ragioni, che nella discreta non si ritrouano; & questo per-
che ciascuna Proportione, la qual si ritroua in un Genere di Quantità continua, si tro-
ua anco in un'altro; laonde si come Due rette linee l'una con l'altra si conuengono; cosi
ancora si conuengono due Superficie, due Corpi, due Tempi, due Luoghi, due Suo-
ni, & altre cose simili; ma non intrauiene il medesimo nella Quantità discreta. Doue è
manifesto, che le Proportioni nella continua sono di maggiore astrattione, che quel-
le, le quali nella discreta si ritrouano; conciosia che ogni Proportione Arithmetica è
rationale; ma le Geometriche sono parte rationali, & parte irrationali. Ma perche le
Irrationali non fanno al proposito, però le lascierò da parte, & pigliarò le Rationa-
li, che si diuidono medesimamente nella Proportione di Equalità, & in quella Inequa-
lità. La proportione d'Equalità è quella, la qual si troua tra due quantità, che sono
tra loro equali; come 1 ad 1: 2 a 2: 3 a 3: & seguentemente gli altri; ò due suoni, ò due
linee, ò due superficie, ò due corpi; la qual ueramente non fà al proposito; essendo
naturalmente indiuisibile; percioche ne i suoi estremi non si ritroua differenza alcu-
na; & non si può dire, che l'una quantità sia maggior dell'altra; & questo auiene,
page 41perche la Equalità, ò simiglianza, appresso il Musico, non partorisce alcuna Con-
sonanza. La Proportione d'Inequalità, ch'è quella, della quale io intendo ragionare,
è, quando Due quantità à l'una maggior dell'altra sono poste in comparatione, di modo
che l'una contenga, ò sia contenuta dall'altra; come il Binario comparato all'Vnità, ò
per il contrario. Et questa medesimamente si diuide in due parti; cioè, in quella di
Maggiore inequalità, & in quella di Minore; percioche quando si compara il Maggior
numero al Minore; se 'l maggior contiene esso minore semplicemente, senz'hauerne al-
tra consideratione, allora nasce quella di Maggiore inequalità; ma comparando il mino-
re al maggiore; se 'l minore, senz'hauer altro riguardo, è contenuto dal maggiore, al-
lora nasce quella di Minore inequalità.
In quanti modi si compara l'una Quantità all'altra.Cap. XXII.
plicemente; ma si bene in altro modo. Onde considerata tal Comparatione
più minutamente, da ciascuno di essi Generi ne nascono altri cinque; percio-
che il maggior Numero si può comparare al minore; & cosi per il contrario,
il minore al maggiore in cinque modi, & non più; conciosia che nella Proportione di
maggiore inequalità, il maggior numero contiene in sè il minore più d'una uolta inte-
ramente; ouero vna uolta solamente, & di più una parte di esso minore, detta Aliquo-
ta; ouero contiene il minore una sola uolta, & di più una parte di esso, chiamata Non-
aliquota. Contiene anco il maggior numero il minore più d'una uolta, & di più vna
parte di esso Aliquota; oueramente lo contiene più uolte, & di più una parte Nonali-
quota. Dal primo modo hà origine quel Genere di proportione, che si dice Moltiplice;
dal secondo quello, che si chiama Superparticolare; & dal terzo quello, ch'è nomina-
to Superpartiente. Et sono detti Generi semplici; percioche nel quarto modo se ne
genera un'altro detto Moltiplice superparticolare; & nel quinto & ultimo nasce quel-
lo, che si addimanda Moltiplice ; i quali Generi del primo & de gli al-
tri due segenti si compongono; come dal nome di ciascuno da per se si comprende;
& sono detti Composti. Nella Proportione di Minore inequalità, il minor numero si-
migliantemente è contenuto dal maggiore in cinque modi, & non più; & cosi si han-
no cinque altri Generi, chiamati di minore inequalità; & sono denominati da i pro-
prij nomi de i sopradetti, aggiuntoui solamente per lor differenza questa particella
Sub, che significa Sotto; & sono nominati Submoltiplice Subsuperparticolare, Sub-
superpartiente, Submultiplice superparticolare & Submultiplice superpartiente; de i
quali i tre primi si chiamano medesimamente semplici; ma gli altri due sono detti com-
posti. Et non essendo questi cinque ultimi Generi semplicemente atti alla generatione
delle Consonanze musicali; come nella seconda parte uederemo;Cap. 5. però non ne ragio-
narò altramente più di essi.
Quel che sia parte Aliquota, & Nonaliquota.Cap. XXIII.
Parte aliquota quella quantità, laqual presa quante uolte si può in qual si uo
glia quantità maggiore, rende di punto l'intero del suo Tutto: onde il Bi-
nario è detto parte aliquota del Senario; imperoche preso tre uolte lo ren-
de di punto tutto; cioè, 6. Questa dal Campano è detta parte Moltiplicatiua; percheIn Def. 1.
lib. 5. Ele-
mēt. Eucl.
interamente numera, & misura il suo Tutto. La Parte non aliquota poi dimanda-
page 42no quella, che tolta quante uolte si può, non rende di punto il suo Tutto: ma rende
piu, ò meno; com'è il Binario, detto Parte nonaliquota del 5. percioche preso due
uolte, rende 4. & preso tre uolte, rende 6. onde tal Parte dal medesimo Campano è no
minata Aggregatiua; conciosia che aggiunta ad un'altra quantità rende il suo tutto;
come aggiunto il 4. con l'Vnità rende il 5. Et questa non propriamente; ma si bene im
propriamente, è chiamata Parte.
Della produttione del genere Moltiplice.Cap. XXIIII.
no finiti; non è però da pensare, che le loro Specie siano finite; percioche
à guisa de i Numeri (seguendo in infinito il naturale ordine loro) infinita-
mente si possono accrescere. Et quantunque tali Specie possino essere infi-
nite; nondimeno la Musica (come dissi di sopraCap. 17.) non riceue l'Infinito; ma si conten-
ta d'una particella, che sia finita, & più uicina alla semplicità; acciò possa dar buon
conto di quello, che opera: percioche troppo ben sa il Musico; che si come qualun-
que cosa, ch'è più lontana dalla sua origine, è men pura, & men semplice, & dal sen-
so è men compresa, & meno intesa dall'Intelletto; ilche auiene per il contrario, quan-
do è più uicina, perche allora non solamente la comprende il Senso; ma ancora l'Intel-
letto l'apprende; cosi sà & uede ne i Numeri, che quanto più sono lontani dall'Vnità,
la quale è semplice; tanto sono men semplici & men puri, & meno compresi dal Sen-
so, & meno dall'Intelletto intesi; & per il contrario, quanto più sono vicini, tanto più
semplici si ritrouano; & à i Sentimenti, & all'Intelletto sono più noti; percioche par-
tecipano di tal semplicità; & conosce etiandio, che 'l medesimo intrauiene de gli estre-
mi Suoni, ò Voci di qualunque Consonanza, ouero Interuallo; che quanto più so-
no l'uno all'altro vicini & uniti; tanto più sono intelligibili; & se auiene che nell'acuto,
ouer nel graue troppo si distendano; il Senso cotal cosa abhorrisce: ne può hauer cosi
presta cognitione di essi; essendo, che da gli arteficiali Istrumenti tanta distanza (se
non difficilmente) è compresa. Et quantunque uerso l'acuto, & uerso il graue molto
si potessero distendere; tuttauia non potrebbono proceder più oltra; se non tanto quan
to dalla Natura, & dall'Arte li fusse permesso. Ma perche tutti gli Harmonici suoni,
i quali sono rationali; cioè, hanno tra loro determinato & rationale interuallo, ò pro-
portione; necessariamente sono sottoposti alla ragione del Numero; percioche i lo-
ro estremi comparati l'uno all'altro necessariamente cadono sotto la ragione di una
delle Specie de i nominati Generi; però hauendo fin quì ragionato intorno di essi;
verrò hora à ragionare in che modo si generano le loro Specie. Laonde incomin-
ciando dal primo, il quale è più semplice d'ogn'altro; detto Moltiplice, dico; che po-
tremo hauer cognitione de tutte le sue Specie, co 'l dispor prima il naturale ordine de
i Numeri, incominciando dall'Vnità, & procedendo in infinito, se fusse bisogno; &
dopoi far la comparatione del Binario, Ternario, Quaternario & de gli altri Nume-
ri, per ordine, ad essa Vnità; & cosi facendo ritrouaremo in ciascuna relatione varie
Specie di proportioni; conciosiache comparando 'l Binario all'Vnità, tal proportio-
ne si chiamerà Dupla, per il suo Denominatore, ch'è il 2. Dopoi comparando il Ter-
nario, nascerà una proportione, che si nominerà Tripla medesimamente dal suo De-
nominatore, ch'è il 3. & cosi seguendo per ordine; di modo che facendo sempre la com
paratione di ciascun numero all'Vnità, haueremo in tal modo le Specie del primo ge-
nere detto Moltiplice; che sono poste nello essempio.
page 43
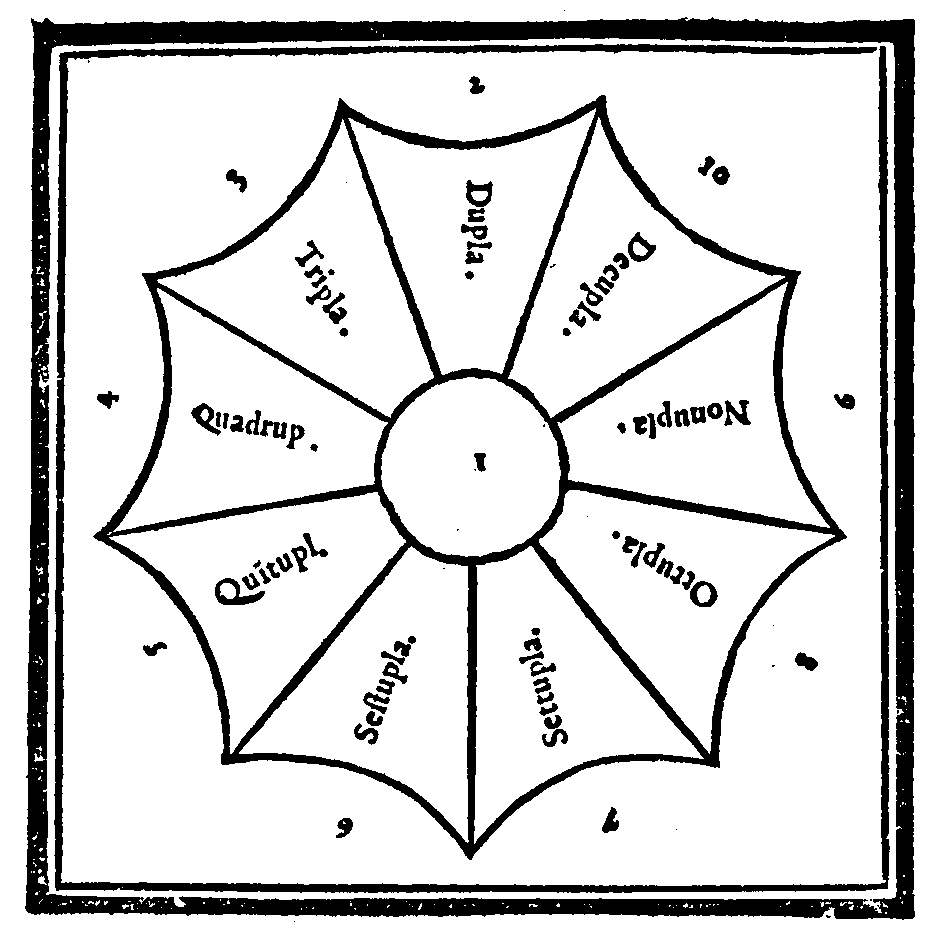
Quel che sia Denominatore, & in qual modo si troui; & come di due pro
poste Proportioni si possa conoscere qual sia la maggiore, ò la
minore.Cap. XXV.
lib. 7. Def.
13.) si chiama
quel Numero, secondo 'l quale si piglia la parte nel suo tutto; & è propriamen-
te detto da alcuni Parte aliquota, & da altri Quotiente; percioche dinota
quante uolte il maggior termine della proportione contenga il minore; & è
quello, ch è produtto dalla diuisione del maggior termine, fatta per il minore di qua-
lunque proposta proportione, di qual si uoglia genere; come per essempio, diuidendo
il magggior termine della Dupla, che si ritroua esser la prima nel genere Molteplice, il
quale è 2. per l'Vnità, che è il minore; ne nasce 2. il quale dico essere il Denominatore
di tal proportione; perche il Binario contiene due uolte essa Vnità; & questa diuide quel
lo interamente in due parti. Medesimamente diremo il 3. esser Denominatore della Tri
pla, & il 4. quello della Quadrupla; conciosia che 'l 3. contien tre uolte l'Vnità, & quat-
tro fiate il 4. & cosi de tutti gli altri seguentemente. Et tali Denominationi si chiamano
Semplici; perche sono denominate da numeri semplici; che sono 2. 3. 4. & d'altri si-
mili. Ma se nel genere Superparticolare diuideremo i termini della Sesquialtera al mo-
do detto; cioè, il maggiore per il minore; ne uerrà 1 1/2. ilquale dico esser Denominato
re della Sesquialtera; conciosia che 'l 3. termine maggiore contiene il 2. termine mi-
nore una uolta, con una meza parte; la quale secondo 'l costume de Mathematici si
descriue in tal modo 1/2. & tal denominatione si dice Composta; perche si compone dell'
Vnità, & d'una sua parte. E' ben uero, che le parti, che nascono in tal modo, tallora
si chiamano Aliquote; & tallora Nonaliquote del minor termine, che contiene la pro-
portione; ma il Numero posto sopra la linea è detto Numeratore di tal parte, & quello
posto di sotto è il suo Denominatore. Donde deriui poi questa parola Sesqui, & quello
che significhi, non è cosa facile da sapere; se non fusse quello, che uuole Agostino;Musicae, li-
bro. 1. c. 10. il-
quale (leggendo Sesque, & non & Sesqui) pensa, che sia detta quasi da Se absꝗ; cioè, da
Absꝗ se, che significa Senza se; percioche (s'io non m'inganno) piglia la denominatione
delle Proportioni dalla parte del numero maggiore, della quale sopr'auanza il minore,
page 44ne i termini, ò numeri delle proportioni del genere Superparticolare; i quali nomina
Sesquati, & quelli del Molteplice, Complicati. Et benche siano stati alcuni, i quali hab-
biano hauuto parere, che sia una aggiuntione Sillabica, & che non significhi cosa alcu-
na; ma sia stata ritrouata solamente per poter proferire con più commodità le dette spe-
cie; questo mi par esser' detto con poca consideratione; & che meglio hanno detto quel-
li, che dissero, che Sesqui uuol dir Tutto; & che Sesquialtera è detta dalle parole latine;
Sesqui, & Altera; delle quali questa si usa, quando si parla di due solamente, & significa
Altera; cioè, L'una de doi; quasi volendo dire, Proportione, il cui maggior termine
contiene tutto il minore una volta intera, con una delle due parti; & questo è ben detto:
imperoche se fusse altramente; come uogliono alcuni, che Sesqui significhi Altretanto,
& la metà; non si potrebbe addattare tal parola nell'altre; come nella Sesquiterza, nel-
la Sesquiquarta, & nelle seguenti. Nondimeno è d'auertire, che 'l Denominatore di
qualunque proportione si ritroua in due modi; cioè, ne i puri numeri, & ne i aggiunti
à questi le parti. Et potremo ritrouar questo secondo modo in quattro maniere, impe-
roche alcuna uolta ritrouaremo l'Vnita, & una parte; & alcuna uolta l'Vnita, & più
parti; ouero ritrouaremo alcun numero, & una parte; ouero alcun numero aggiunto à
più parti. Se noi ritrouaremo numeri semplici; allora denominaremo le proportioni
semplicemente, secondo che nelle specie del Molteplice si è mostrato; & se ritrouare-
mo l'Vnità aggiunta ad alcuna parte; la denominaremo, secondo che di sopra furono
denominate quelle del Superparticolare. Ma quando poi si ritrouerà l'Vnità con più
parti; allora, lasciando l'Vnità, si porrà auanti questa parola Super al Numeratore del-
le parti, & al Denominatore quest'altra Partiente; & si componerà la denominatione
della proportione delle dette due parole, & da i termini delle parti; come per essempio si
può ueder nella Prima specie del genere Superpartiente; che la proportione detta Su
perbipartienteterza è denominata da 1 & 2/3. suo Denominatore; cōciosia che diuiso il
termine maggiore di tal proportione, ch'è il 5. per il 3. il qual'è il minore; ne risulta 1 & 2/3.
La onde pigliando il Numeratore delle parti, ch'è il 2. aggiungendoui la parola Su
per, si dira Superbi; dopoi pigliando il 3. Denominatore con la seconda parola Par-
tiente, si dirà Partienteterza; & cosi aggiunte insieme si dirà, Superbipartienteterza; il
che si fà nell'altre ancora, secondo 'l suo Denominatore. Ma quando il Denominatore sa
rà cōposto d'alcun numero, & di una parte sola; si denominera prima la proportione dal
numero; come fu detto del Molteplice; dopoi s'aggiungerà la parte, nel modo che nel Su
perparticolare hò dichiarato; essēdoche tal proportione necessariamente cade nel primo
genere composto detto Molteplice superparticolare; come si può uedere nella Duplases-
quialtera, la quale si denomina da 2 & 1/2. percioche il suo termine maggiore, ch'è il 5.
contiene il 2. il quale è il minore, due uolte, & una meza parte de 'l minore; di mo
do che dal 2. piglia la della Dupla, & dalla parte, che è 1/2. piglia
quella della Sesquialtera. Quando poi il Denominatore sarà contenuto da numero
intiero, & da più parti; allora si denominerà la proportione primieramente dal nume-
ro, nel modo che si è mostrato nel Molteplice; dopoi s'aggiungeranno le parti; denomi-
nandole secondo che facemmo nel genere Superpartiente; percioche tal proportione
necessariamente caderà nel secondo Genere composto, detto Molteplicesuperpartiente.
Habbiamo l'essempio di questo nella Dupla superbipartienteterza, laquale è la prima
specie di tal Genere; come uederemo; denominata, per le ragioni dette, da 2. & 2/3.
suo Denominatore. Lungo sarebbe s'io volessi porre gli essempij di ciascuna specie; ma
perche molti di essi si potranno uedere al suo luogo; però in questo non mi estenderò
piu oltra; ma solamente dirò questo per conclusione; che ciascuna Proportione è tanto
maggior d'un'altra; come ne auertisce Euclide;Element.
lib. 7.
def. 21. quanto la fà il suo Denominatore; &
questo in ogni Genere di proportione; ilche è manifesto; essendoche la Dupla è senza
dubio alcuno maggior della Sesquialtera; conciosia che il 2. di quella è maggior di 1.
& 1/2. Denominatore di questa, & cosi si può dir ancor dell'altre, senz'alcun'errore.
page 45
Come nasca il genere Superparticolare.Cap. XXVI.
modo, che lasciata solamente nell'ordine naturale de i Numeri da un canto
l'Vnità, & incominciando dal Binario, seguendo di mano in mano tal or-
dine; da tal comparatione sarà prodotto il genere Superparticolare; del quale la pri-
ma specie è la Sesquialtera comparando il Ternario al Binario; percioche compara-
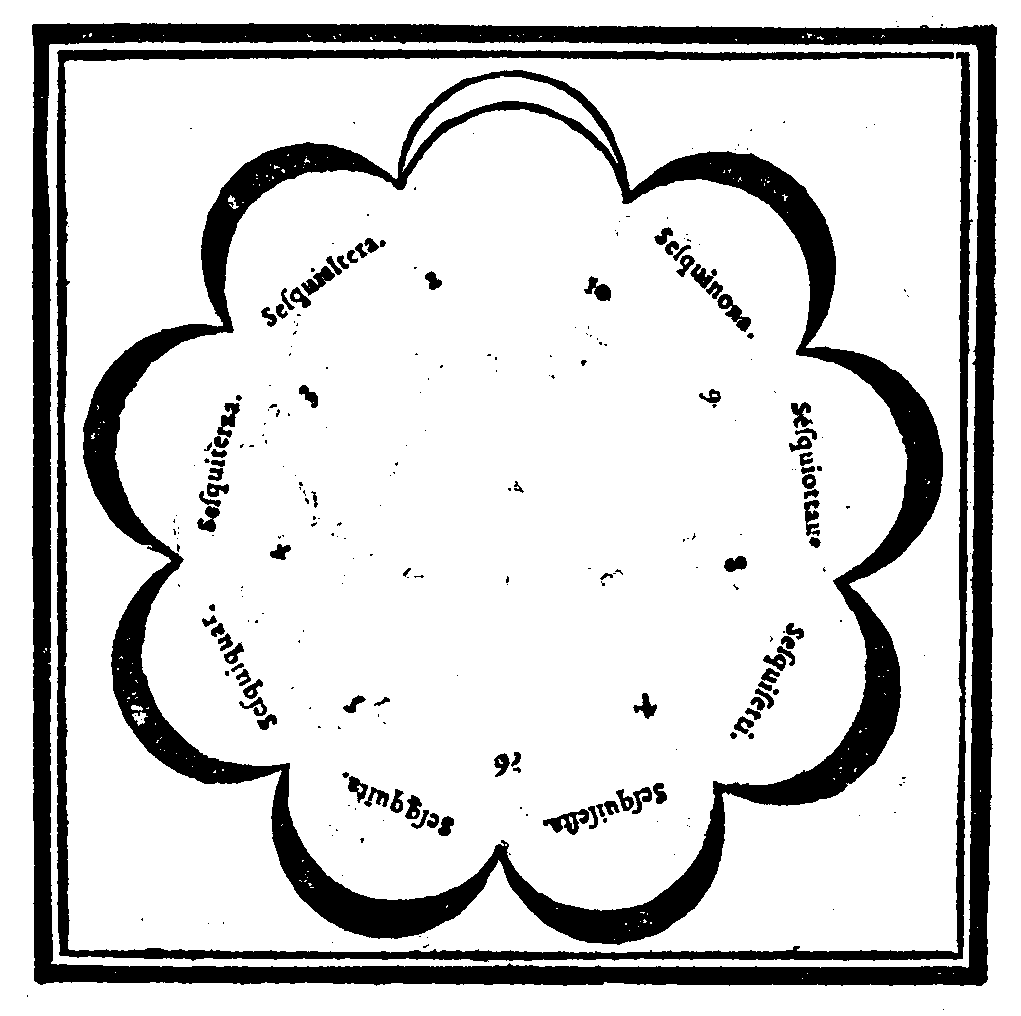
tre per ordine; ciascuna delle quali è denominata dal suo proprio Denominatore, ouer
Parte aliquota. Onde si uede, che se in alcuna proportione, la parte, per la quale il
maggior numero supera il minore, è la Metà di esso minore, quella si chiama Sesquial-
tera; & se è la Terza parte, si chiama Sesquiterza; & breuemente tutte l'altre specie,
quantunque fussero infinite, sono denominate dalle parti loro; come nell'essempio
si può uedere.
della prodottione del gener Superpartiente.Cap. XXVII.
cune sono dette Superbipartienti, alcune Supertripartienti, & alcune Su-
perquadripartienti; procedendo, secondo l'ordine naturale de i numeri.
Onde la Superbipartiente si ritroua tra due numeri differenti per il Binario,
che siano di esso maggiori, & esso non possa esser loro misura commune; & uogliono es-
ser Contraseprimi; la cui natura & proprietà è tale, che sono Termini radicali di qual
si uoglia proportione, che contengono. Lasciando adunque il Binario da parte, co-
me quello che poco fà al proposito, pigliaremo il Ternario & il Quinario, che sono
page 46nell'ordine naturale de i numeri i primi, ch'osseruano cotal legge; percioche se noi
compararemo il maggiore al minore, haueremo la proportione detta Superbipartiente-
terza; conciosia che 'l 5. contenga il 3. una uolta, & di più una sua parte Nonaliquota;
cioè, due terze parti; alla differenza della quale, tra 'l 7. & il 5. è generata la proportio-
ne Superbipartientequinta; & tra l 9. & il 7. la Superbipartientesettima, & cosi l'altre
Specie di mano in mano. Ma tra 'l 7. & il 4 nasce la Supertripartientequarta; la quale
è la prima specie tra le Supertripartienti. Onde è necessario, che si come nelle prime si
è osseruato la differenza del Binario, che cosi in queste seconde si osserui quella del Ter-
nario, & in quelle che sono dette Superquadripartienti, quella del Quaternario; per
la qual cosa osseruando tal Regola nell'altre per ordine, si potrà andare in infinito; come
si uede nell'essempio.
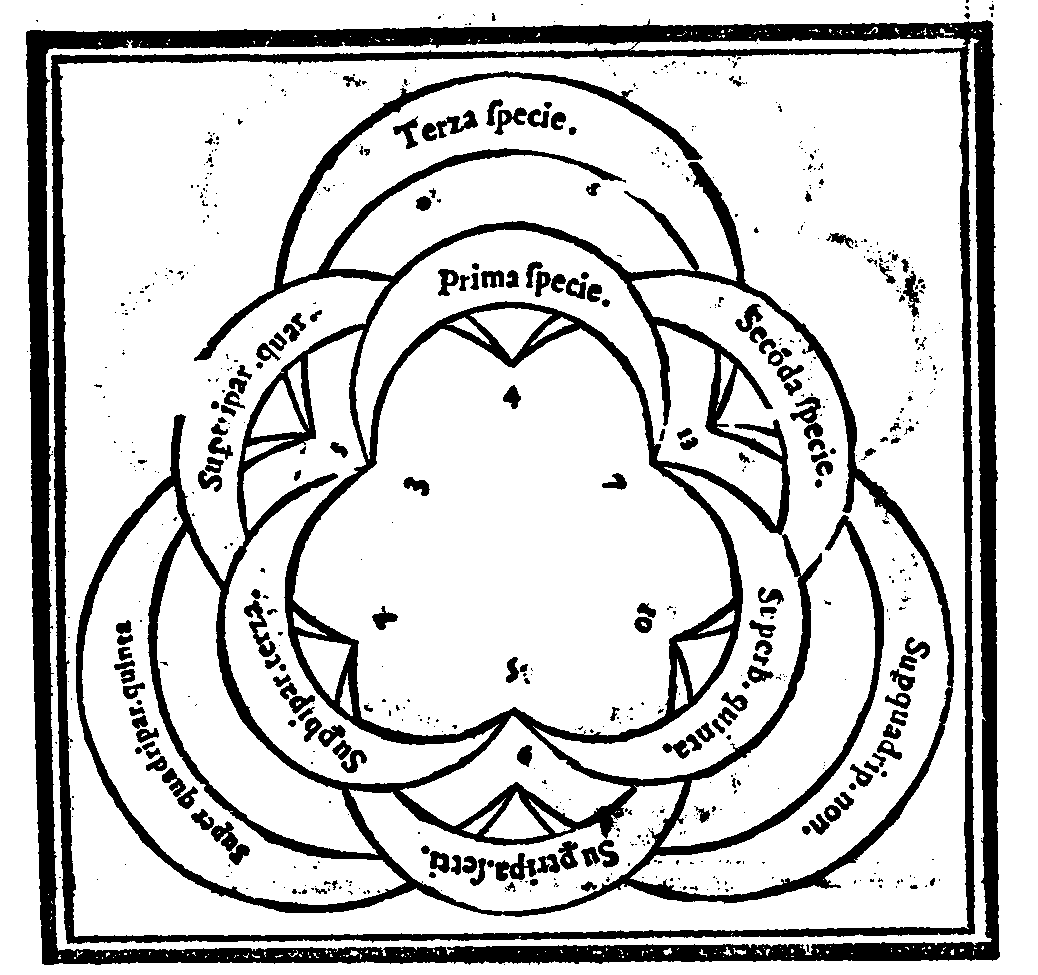
Del Genere molteplice superparticolare.Cap. XXVIII.
il minor termine di qual si uoglia proportione del genere Superparticolare
al maggiore, & aggiungendo sempre il medesimo minore al numero, che
uiene per tale aggiuntione. Onde se noi aggiungeremo il Binario minor ter-
mine della Sesquialtera al maggiore, ch'è il Ternario; ne uerrà il Quinario; al quale
medesimamente aggiunto esso Binario, nascerà il Settenario, & cosi gli altri in infinito;
di modo che osseruando l'istessa Regola nell'altre, si potranno hauere infinite Specie;
come nella figura si può comprendere.
page 47
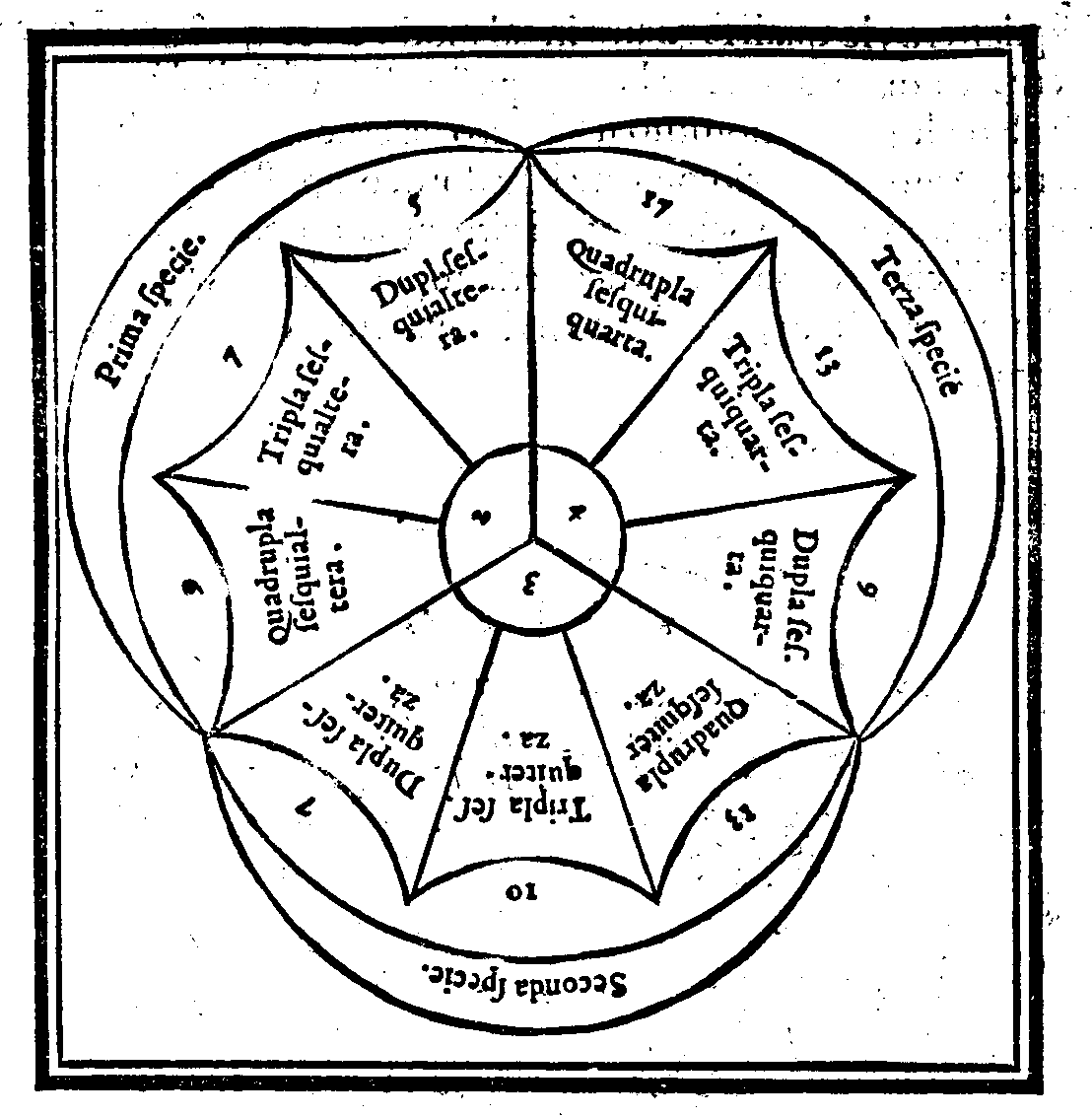
Della prodottione del Quinto & vltimo Genere, detto Molteplice-
superpartiente.Cap. XXIX.
particolare habbiamo osseruato; cioè, di aggiungere il minor termine del-
le proportioni del genere Superpartiente al termine maggiore; & al prodot-
to aggiungendo sempre esso minor termine, continuando in infinito; se far si
potesse; sarà per tale aggiuntione creato il Quinto & ultimo Genere, detto Molteplice-
superpartiente; del quale (per non esser cosa molto difficile) non mi estenderò à ragio-
nar più oltra; bastandomi solamente porre gli essempii; accioche siano guida & lume
alla intelligenza di cotal Regola; & saranno i sottoposti. Et si come ne i modi mostrati
si compone la Superbipartienteterza, la Supertripartientequarta, & la Superquadripar-
tientequinta; cosi ancora si compongono l'altre Specie; lequali (come hò detto) sono
infinite. Et quello che si è detto de i Generi & delle Specie di Maggiore inequalità; si
dice anco de quelle di Minore; le cui specie si ritroueranno collocate tra loro temini ra-
dicali; come sono le specie mostrate di sopra. Onde è da notare, che quei Numeri si di-
cono Termini radicali, ò Radici d'alcuna Proportione, de i quali è impossisibile di ritroua
re in quella istessa proportione Numeri minori; & tali Numeri sono Contraseprimi; co-
me di sopra si è mostrato, & come nel Lib. 7. de i suoi Elementi, ò Principii, che dire li
vogliamo, Euclide, & anche Boetio nel Cap. 8. del Secondo libro della Musica manifesta
no. Et li Musici nella Prolatione delle figure cantabili segnano i Numeri delle propor-
tioni di Maggiore inequalità in tal modo; che 'l maggior termine della proportione, che
uogliono mostrare, pongono sopra 'l minore; come uolendo mostrar la Prolation del
la Dupla, la segnano in questo modo 2/1. & quella della Sesquialtera cosi 3/2. Ma in quel-
li di Minore inequalità segnano al contrario; cioè, pongono il minor termine
della proportione sopra 'l maggiore; come si uede nella Prolatione della Subdupla,
page 48& della Subsesquialtera, le quali segnano in tal modo 1/2. &. 2/3. & cosi ancora nell'altre
in ciascun genere. Et quantunque io habbia posto gli essēpii de i mostrati Generi, ne
i Termini radicali delle proportioni; nō si hà però da credere, che tali proportioni non si
ritrouino anco ne gli altri numeri; come ne i Tralorocomposti, iquali non sono Termini
radicali delle proportioni; imperoche tanto si ritroua la Dupla esser tra 8 & 4. & tra 12 &
6. quanto tra 2 & 1. Il che si debbe intendere etiandio dell'altre, ne gli altri Generi; co-
me in quelli della Sesquiatera, che tanto si ritroua tra 6 & 4. quanto tra 3 & 2. come
più oltra uederemo.
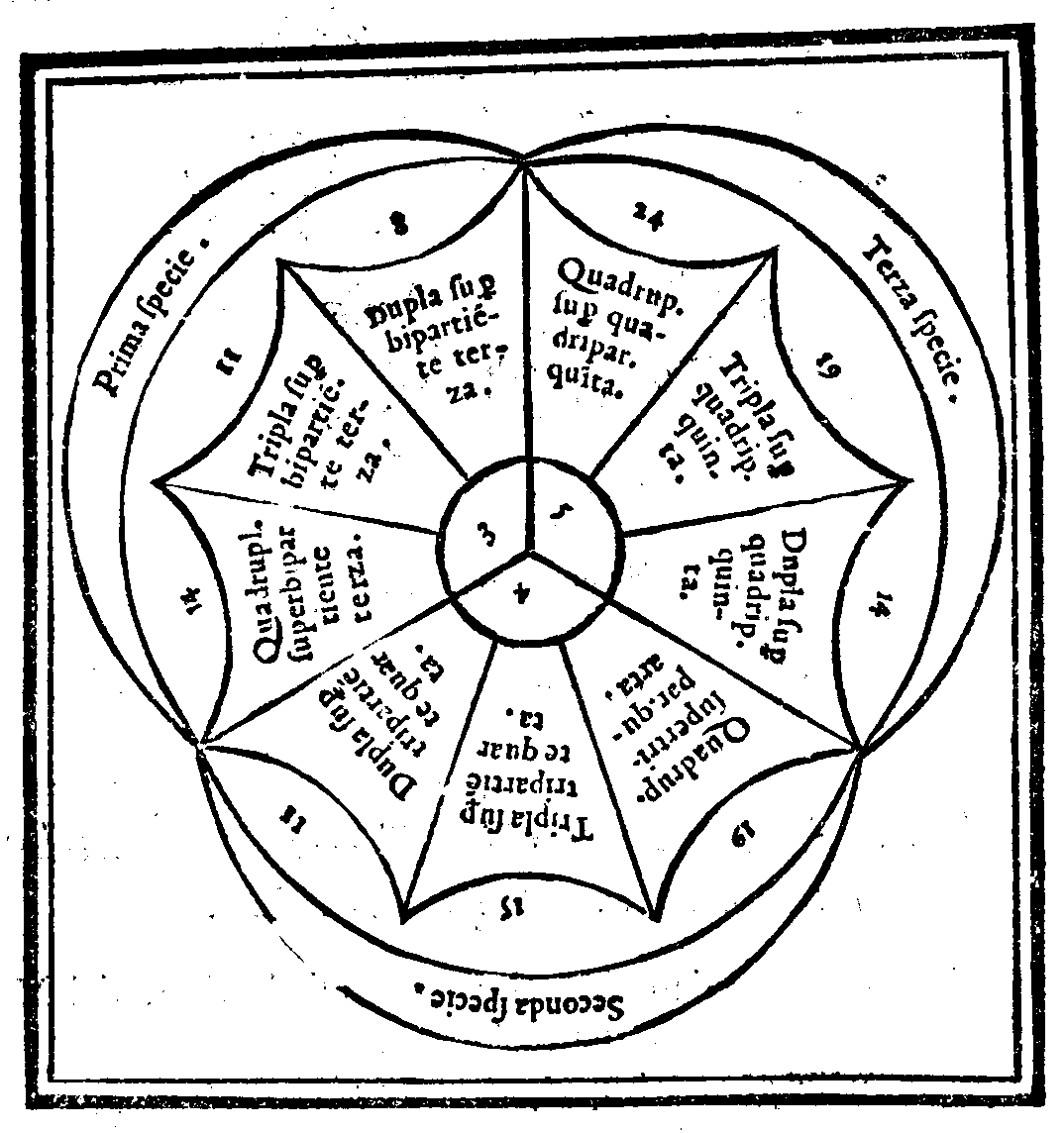
Della Natura & proprietà de i nominati Generi.Cap. XXX.
ri & le Specie delle proportioni di minore inequalità nascono tra i Nume-
ri in quel modo istesso, che nascono quelle di maggiore; ne altra differenza si
troua dall'uno all'altro, se non, che in quelle si fà la comparatione del termi-
ne minore al maggiore, in quanto l'uno è contenuto dall'altro; & in queste si fà la com-
paratione del termine maggiore al minore, in quanto l'uno contiene l'altro; & cosi tan-
to quella di maggiore, quanto quella di minore inequalità, uengono ad esser prodotte
in un tempo, & esser nell'istesso Soggetto. Ma secondo 'l mio giudicio, dirò, che le Pro-
portioni di minore inequalità si possono considerare altramente. La onde per maggiore
intelligenza di questo, & anco per conoscer la natura de questi Generi, si dè sapere; che
essendo l'Equale un certo mezo (come dice il FilosofoEthi. 2.
cap. 6.) tra lo eccesso & il difet-
to; si può dire, che tal mezo sia equalmente distante da i suoi estremi, & la Equa-
lità essere come Elemento delle Proportioni; onde ella uiene ad esser principio del-
la Inequalità; come uuol BoetioArith. lib.
2. ca. 1. &
Musicae 2.
cap. 7. & Giordano;Element.
lib. 9. & à tenere il luogo mezano tra il Gene-
re di maggiore & quello di minore inequalità; Ilperche è di sua natura semplice; con-
ciosia che (come si può uedere) essendo molteplicata, ò diuisa; quella proportione, che
page 49si ritroua nel tutto; si ritroua anche in ciascuna delle sue parti, & è sempre permanente,
& ritiene il suo essere in qualunque Genere d'Inequalità. Questo si uede manifestamen-
te esser uero: percioche in tutti i Generi di proportione ella sempre si ritroua esser co-
me loro fondamento; come si uede; che se per cagione d'essempio; dalla Proportione
di Equalità 4 & 4. si uorrà leuare la proportione 2 & 2. dell'istesso Genere; nel modo
che più abbasso dimostraremo: Simigliantemente, se 'l si uorrà moltiplicare nell'istesso
Genere la proportione 4 & 4. con la proportione 2 & 2. subito si peruenirà all'Equalità;
cioè, dall'una & l'altra parte nascerà la Proportione, che si troua tra 8 & 8. ilche non auiē
delle Proportioni d'Inequalità, che sono mutabili; lequali essendo moltiplicate, ò diui-
se; le proportioni del Tutto sono differenti da quelle delle lor Parti; & le maggiori
proportioni non hanno luogo tra i termini delle minori. Et questo primieramen-
te si uede uerificar nella Dupla 2 & 1. essendoche se nel Genere di maggiore Inequalità
ella si uorrà leuar da un'altra Dupla simile; 2 & 1. subito si uerrà all'Equalità 2. & 2. co-
me al suo proprio Elemento: Il che accascherà etiandio nel Genere di minore inequa-
lità della Subdupla 1 & 2 percioche se ella si leuarà da un'altra Subdupla 1. & 2. l'istesso
auerrà, che auenne della nominata Dupla; cioè, 2 & 1. Imperoche com'è pare-
re di Boetio2. Arith.
cap. 1.) ogni Inequalità si risolue nella Equalità, come in Elemento del pro-
prio Genere. Ma secondariamente si manifesta per la istessa Dupla, & anco per la Sesqui
altera. Percioche essendo la Dupla, maggiore della Sesquialtera, non hà luogo
tra i suoi termini; com'è manifesto; conciosia che uolendo cauar la Dupla contenuta
tra questi termini 2 & 1. dalla Sesquialtera contenuta tra questi 3 & 2. nel modo,
ch'io intendo di mostrare; nascerà la Subsesquiterza tra questi due 3 & 4. contenu-
ta nel secondo Genere di minore Inequalità, detto Subsuperparticolare; la quale
per esser di Genere diuerso dalle due prime proposte; dà segno manifesto, che la Ses-
quialtera è priua di tanta quantità, quanta è quella, per la quale la Sesquialtera è su-
perata dalla Dupla; cioè, è priua d'una Sesquiterza. Et questo è uerissimo; concio-
siache aggiungendo la Sesquialtera alla Sesquiterza, immediatamente nasce la Du-
pla; onde la Subsesquiterza uiene ad esser solamente la Ragione di quella propor-
tione, che manca tra gli estremi della Sesquialtera, per ascendere alla somma &
quantità della Dupla; il qual difetto si manifesta per la particella Sub, che se le ag-
giunge; laquale nella compositione dinota alle uolte diminutione; la onde dall'effetto
la potiamo chiamar Priuatiua. Dico Priuatina, non perche ella habbia possanza di pri-
uar'alcuna proportione della sua quantità; ma perche dichiara la proportione da cui
si aggiunge, esser priua ne i suoi termini, & diminuta di tanta quantità, quanta è la sua
denominatione sotto la proportione di equalità. Et questo non ho detto fuor di pro-
posito; percioche si come è impossibile in fatto, che da un Numero minor se ne pos-
sa cauare un maggiore, cosi ancora è impossibile, che da una proportione, che sia mino-
re, se ne possa in fatto leuar una maggiore; essendo dibisogno, che quella quantità,
dalla qual se ne caua un'altra, sia o maggiore, ouer equale à quella, ch'intendiamo le-
uare. Però operando nel modo ch'io son per mostrare, da una Dupla sempre potremo
cauare vna Sesquialtera, & ne soprauanzerà una Sesquiterza; & da vna Sesquialtera
potremo leuarne un'altra, & ne uerrà l'Equalità; ma non potremo già mai cauare una
Dupla da vna Sesquialtera, che non manchi alcuna quantità; la quale verrà sempre
nel prodotto del sottrare l'una dall'altra, come uederemo; & ne dimostrerà cotal
mancamento; essendo la Dupla maggior di essa per una Sesquiterza; & la Sesquialtera
diminuta di tal quantità; come si è potuto uedere. Laonde non si marauigliera alcu-
no, s'io assimiglierò le proportioni di Maggiore inequalità all'Habito, & le chiamerò
Positiue & Reali; conciosia che danno la ragione delle proportioni; cioè, della forma,
che dà l'esser ad un soggetto reale determinato; & quelle di Minore alla Priuatione, &
le nominerò Rationali & Priuatiue; percioche negano la proportione, che rappresen-
tano, nel nominato soggetto; & sono priue di uno de i loro termini reali; percioche non
page 50trapassano l'Equalità; ma sono di lei minori. Il perche essendo il Genere di maggiore
inequalità diuerso & opposto al Genere di minore, pigliato à questo modo; è necessa-
rio, che l'uno & l'altro si considerino sotto diuerse ragioni; cioè, il primo sotto la ragio-
ne dell'Habito, ò Positione; & il secondo sotto la ragione della Priuatione. Si debbo-
no ancora considerare come due opposti corrispondenti l'uno all'altro, nel terzo modo
di Oppositione; percioche i Generi, & le Specie sottoposte di uno, corrispondono (con
siderate sotto la ragione dell'Habito) à i Generi, & alle Specie sottoposte dell'altro,
considerate sotto la ragione della Priuatione; quasi all'istesso modo, che corrisponde
l'Ignoranza alla Scienza, le Tenebre alla Luce, & simiglianti. Si debbono considerare
anche, come due Opposti corrispondenti al loro mezo; cioè, alla Equalità, la quale è
quasi come il soggetto dell'Habito, & della Priuatione; conciosia che intorno à lei auen
gano tali cose. Ne uoglio hauer detto questo senza qualche fondamento; percioche si co
me il soggetto dell'Habito non naturale, & della Priuatione imperfetta è atto à riceue-
re hor l'uno, hor l'altro, per successione; & riceuer quello, che se gli appresenta, in si-
no à tanto ch'è priuo di esso; come uediamo dell'Aria, ch'è atta à riceuere hora la Lu-
ce, & hora le Tenebre; & tanto è lucida, quanto la luce le stà vicina, & non si separa
da essa; cosi l'Equalità è atta à riceuere hora la proportione di Maggiore, hora quella di
Minore Inequalità. Et si come 'l Soggetto mantiene la cosa, che riceue, nella sua qua-
lità, & per questo non si uaria nella sostanza; cosi l'Equalità non muta quella proportio-
ne di qual si uoglia genere, che se le accompagna; ne meno ella si uaria, quando se le
aggiunge, ò se le leua alcuna proportion di qual si uoglia genere; essendo i suoi termini
(come hò mostrato) immutabili & inuariabili. Et perche, si come nel Soggetto è sem-
pre la Priuatione, quando è rimosso l'Habito; & l'Habito, ouer l'attitudine, quando
è rimossa la Priuatione; simigliantemente rimossa dall'Equalità una proportione
qual si uoglia di maggiore inequalità, ne uiene immediatamente una quasi simi-
le contraria di quelle di minore; & ui s'introduce quella di maggiore inequalità,
quando se le leua quella di minore; come è, che leuandole una Dupla, ne uie-
ne una Subdupla; & leuandole la Subdupla, nasce la Dupla. Ma perche ogni estre-
mo hà il suo mezo, & il mezo è quello, ch'equalmente è distante da i suoi

rò hò detto, che la Equalità tiene il luogo di mezo tra l'uno & l'altro de i nominati due
generi d'Inequalità, nel modo che nella figura si può uedere. Et benche tali essempij
siano posti solamente ne i termini d'alcune Specie de i due primi generi di maggiore
& di minore Inequalità; tuttauia ui si debbono anco intender quelli dell'altre Spe-
cie; i quali hò lasciato per breuità; pensandomi, che solamente questi siano bastanti
à mostrar quanto habbiamo proposto; però ciascuno, il quale fusse desideroso di ueder
l'altre Specie de tali generi, per se stesso le potrà inuestigare, hauendo riguardo à
quello, che si è mostrato disopra. Hora per quello che si è detto potiamo comprendere,
per qual ragione le Proportioni di maggiore inequalità si possino chiamar Reali & Posi-
tiue, & quelle di minore Rationali & Priuatiue; & si possa dire anco, che siano due estre-
mi, tra i quali si ritroua collocata nel mezo l'Equalità; & similmente potiamo conoscer
la natura & proprietà di ciascuno de tali Generi; & qual sia il loro uero ufficio. Quando
adunque uorremo nominare alcuna Proportione del genere di Minore inequalità: le po-
tremo accompagnar questa particella Sub; come di sopra nel Cap. 22. si è mostrato: quelle
poi che saranno dell'altro Genere, porremo senza cotal aggiunto. Et accioche le Pro-
portioni di uno delli due opposti Generi si conoschino da quelle dell'altro, osseruaremo
quest'ordine; quando sarà dibisogno, noi porremo i termini maggiori di quelle propor-
tioni, che sono del genere di Maggiore inequalità, dal lato sinistro, & li Minori dal de-
stro; in cotal modo 3. & 2. & i termini di quelle, che sono del Genere di minore, porre-
mo al contrario in cotal maniera 2 & 3. imperoche quelli della Equalità si potranno por-
re senz'alcuna differenza di luogo; essendo per lor natura inuariabili.
Del primo modo di Moltiplicar le Proportioni.Cap. XXXI.
si trouino le lor Denominationi: daremo principio à ragionar delle loro ope-
rationi, lequali sono cinque, Moltiplicare, Sommare, Sotrrare, Partire,
& il Trouar le loro Radici. Quanto alla Prima dobbiamo sapere, che sono
stati alcuni, i quali hebbero opinione, che 'l Moltiplicare, & il Sommare fussero una
cosa istessa; & alcuni teneuano l'opposito; cioè, che fussero due Operationi separate; &
il medesimo teneuano del Sottrar & del Partire. Ma lasciando le dispute da un canto, co 'l
essempio dimostrerò tali operationi non esser'una cosa istessa; ma diuerse, & esser cosa
molto utile & necessaria al presente negocio: Il perche & esser uenendo al proposito,
dico; che 'l Moltiplicare è una dispositione de piu proportioni in un continuato ordine;
poste l'una dopo l'altra in tal modo, che 'l minor termine dell'una sia il maggior dell'altra;
& cosi per il contrario. Ma il Sommare dico esser'una adunanza de più proportioni,
adunate insieme sotto una sola denominatione. Il Moltiplicar si può fare in due modi: il
Primo è quando ad una proportione se ne moltiplica & soggiunge un'altra, ò più; inco-
minciando dalla parte sinistra, uenendo verso la destra; il qual modo nominaremo Sog-
giungere. Il Secondo è, quando procederemo al contrario; cioè, dalla destra uer-
so la sinistra; & questo modo chiamaremo Preporre, ouero aggiungere. Et per-
che questi due modi sono necessarij, & tornano bene; però mostraremo l'uno & l'altro.
Incominciando adunque dal Primo, dico; se noi hauessimo à moltiplicare insieme due,
ò piu proportioni d'un medesimo genere, ò de diuersi; il che non importa; pur che non si
ponga insieme quelle di maggiore con quelle di minore inequalità; disporremo prima
le proportioni contenute ne i loro termini radicali l'una dopo l'altra per ordine, se-
condo che le intendiamo moltiplicare; & dopoi pigliando il maggior termine
della seconda proportione in ordine da moltiplicare & soggiungere, posta à banda
sinistra, lo moltiplicaremo col maggiore & col minor termine della prima; & questo
page 52anco moltiplicaremo col minore della seconda; & haueremo Tre numeri, continenti due
continue proportioni. Hora moltiplicaremo questi per il maggior termine della pro-
portione, che si hà da moltiplicare, la qual'è terza nel sopradetto ordine; incomin-
ciando dalla sinistra, & di mano in mano uenendo uerso la parte destra; il che fatto, di
nuouo pigliando il minor termine di tal proportione, lo moltiplicaremo col minor de i
prodotti; & ne risulteranno quattro numeri; ne i quali si conteneranno le molti
plicate proportioni Et quando fusse bisogno di soggiūgerne à queste proportioni di nuo
uo alcun'altra, moltiplicaremo i prodotti numeri per il maggior termine della proportio
ne, che ne uorremo soggiungere, & il minor de i prodotti per il suo minore; & da tal mol-
tiplicatione haueremo quello, che ricerchiamo. Ma perche gli essempij maggiormen-
te muouono l'Intelletto alla intelligenza d'alcuna cosa, che non fanno le parole; massi-
mamente nel maneggio de i Numeri; però desiderando io d'esser inteso, uerrò all'essem
pio. Poniamo adunque che si habbiano da moltiplicare insieme Quattro proportioni,
contenute nel genere Superparticolare, & siano; una Sesquialtera, una Sesquiterza,
una Sesquiquarta & una Sesquiquinta; primamente le porremo l'una dopo l'altra, se-
condo l'ordine, che si uorranno moltiplicare; di modo, che sino contenute tra i loro
termini radicali, in questo modo. 3/2 | 4/3 | 5/4 | 6/5. & dopoi moltiplicaremo il maggior termi-
ne della Sesquiterza, ch'è 4. col 3. & 2. termini della Sesquialtera; & da tal mol-
tiplicatione haueremo 12 & 8. i quali medesimamente conteneranno la Sesquialtera.
Percioche i termini di qualunque proportione moltiplicati per qual si uoglia numero,
non fanno uaratione alcuna di quantità; come per la proua, & per la 18. del Lib.7. de
i Principii di Euclide, & per quello che dice Boetio nel cap. 29.del Lib. 2. della sua Mu-
sica, & per la quinta Dignità del primo delle Dimostrationi, è manifesto. Et tali Nu-
meri porremo sotto una linea retta in piano, la qual diuiderà questi dalle proposte pro-
portioni. Fatto questo, moltiplicaremo insieme i minori termini di queste due propor-
tioni; & ne uerrà 6; ilqual porremo dalla parte destra à canto l'8, & haueremo moltipli-
cato dette proportioni insieme; cioè, soggiunto alla Sesquialtera la Sesquiterza tra que
sti termini 12 8. 6. Hora per soggiungere à queste la Sesquiquarta, moltiplicaremo que-
sti termini per il suo maggior termine, ch'è il 5. incominciando dalla parte sinistra ue-
neno uerso la destra, & haueremo 60. 40. 30. Ilche fatto moltiplicaremo il minor ter-
mine de i tre primi, che è 6. per il minor termine di essa Sesquiquarta, ch'è 4. & ne nasce-
rà 24. il quale posto con gli altri, ne darà tale ordine, 60. 40. 30. 24. contenente la Se-
squialtera la Sesquiterza & la Sesquiquarta proportione. Il medesimo faremo, quando
uorremo moltiplicare à queste la Sesquiquinta; percioche moltiplicando prima i sopra-
detti Quattro termini, per il suo maggiore, ch'è 6. ne uerrà 360. 240. 180. 144. & dopoi
moltipicato il minore de i mostrati, che è 24. col minor termine di essa proportione,
che è 5. ne darà 120. ilquale posto al suo luogo, da tal moltiplicatione hauere-

come tra 360 & 240 la Sesquialtera la Sesquiterza tra 240 & 180; tra 180 & 144. la Ses
quiquarta; & tra 144 & 120. la Sesquiquinta; ancora che non si ritrouino essere ne i lor
termini radicali; come nell'essempio si uede. Quando adunque haueremo à molti-
plicare & soggiungere insieme molte proportioni; operando al modo c'habbiamo di-
mostrato, potremo hauer sempre il nostro intento.
Il Secondo modo di moltiplicar le Proportioni.Cap. XXXII.
aggiungere le Proportioni l'una all'altra, procederemo in questo modo. Mol
tiplicheremo prima per il termine minore della seconda proportione posta à
banda destra ciascun termine della prima incominciando dal minore; & do-
poi il maggior dell'una, col maggior dell'altra insieme; & da tal moltiplicatione haue-
remo Tre termini continenti tali proportioni. Dopoi moltiplicando questi Prodotti
per il minor termine della terza proportione; & il maggior di essi per il maggiore,
haueremo il nostro proposito. Se adunque noi pigliaremo il minor termine della Sesqui-
quarta, posta nel precedente Capitolo, ilquale è 4 & lo moltiplicheremo col 5. & col 6.
termini della Sesquiquinta, ne resulterà 20 & 24. i quali porremmo, come facemmo di
sopra, sotto una linea retta: onde moltiplicando anche il 5 maggior termine di detta
Sesquiquarta col 6. maggior termine della Sesquiquinta, ne uscirà 30. il quale posto ap-
presso il 24. ne darà Tre termini 30. 24. 20. che contengono le proportioni moltiplicate.
Ma per moltiplicar con queste la Sesquiterza, pigliaremo il suo termine minore, ch'è il 3.
& lo moltiplicheremo con li tre prodotti, incominciando della destra, ueuendo uerso
la sinistra parte, & haueremo 90. 72. 60. assettandoli l'altro sotto i suoi producenti; i qua-
li son 30. 24. 20. & di nuouo moltiplicando il 4. maggior termine della Sesquiterza, col
30. uscira 120. ilquale, dopo che l'haueremo aggiunto à i tre sopradetti, ne darà un tal
ordine 120. 90. 72. 60. continenti la Sesquiquinta, la Sesquiquarta & la Sesquiterza pro
portione. Ma uolendo moltiplicar con queste la Sesquialtera, pigliaremo il 2. suo minor
termine, & lo moltiplicaremo al modo detto ne i Quattro, prodotti; & haueremo 240.
180. 144. 120. Moltiplicheremo oltra di questo il 3. suo maggior termine col 120. mag-
gior termine de i prodotti; nascera 360. il quale accompagnato à i Quatttro, ne darà tut-
ta la moltiplicatione tra questi termini 360. 240. 180. 144. 120. i quali contengono le no-
minate Quattro proportioni; come nell'essempio si uede, simile à quello, che nel Capi-
tolo precedente habbiamo dimostrato.

Del Sommar le Proportioni.Cap. XXXIII.
te si uuole di uno, ò de diuersi Generi, sotto una sola denominatione; la qua-
le si ritroua anche ne gli estremi numeri, ò termini di esse proportioni, quan-
do insieme sono moltiplicate, con tal differenza, che questi estremi sono me-
diati da altre proportioni: ma quelli, che nascono dal Sommare, sono immediati: come
vederemo. Se hauessimo adunque da sommare insieme due, ò più proportioni di uno, ò
de diuersi generi, procederemo in questo modo: porremo prima i maggiori & radicali
termini delle proportioni, che si hauranno da sommare l'un sotto l'altro, ouer l'uno di-
rimpetto all'altro, similmente i minori; dopoi moltiplicaremo i maggiori l'uno nell'al-
tro, incominciando da i due primi; & il prodotto da questi nel terzo; & quello, che
nascerà, nel quarto; & cosi di mano in mano; & il prodotto da tal moltiplicatione sarà il
maggior termine continente la proportione, che hà da nascere. Il che fatto moltipliche-
remo medesimamente i minori l'uno nell'altro; & il prodotto sarà il minor termine, che in
sieme col maggiore contenerà la ricercata proportione. Come, se hauessimo da som-
mare insieme le già moltiplicate proportioni, le accommodaremo prima; come nell'
essempio si ueggono; & incominciando da i maggiori termini di quelle, moltiplicheremo
i due primi; cioe, 3 & 4. l'un con l'altro; & haueremo 12. Questo poi moltiplicato col
5. ne darà 60. il quale moltiplicato col 6. produrrà 360. & questo numero sarà il mag-
gior termine, che hauea da nascere di cotal somma. Al medesimo modo moltiplichere-
mo poi li termini minori; cioè, il 2 col 3. & ne uerrà 6. ilquale numero moltiplicato col
4. ne darà 24. Con questo si moltiplicherà poi il 5. & ne darà 120. ilquale uerrà ad esser il
minor termine, che insieme col maggiore contenerà la prodotta proportione; laquale è
la medesima, che si ritroua ne gli estremi termini delle moltiplicate di sopra Proportioni;
come si può uedere. Hauendo adunque ridotte tal proportioni sotto una sola proportio-
ne, la quale è la Tripla; & sotto un solo Denominatore, che è il 3. si può conoscere la
differenza, che si rittoua tra il Sommare & il Moltiplicare; conciosia che l'uno si ritroua
mediato almeno da una proportione: l'altro è senz'alcun mezo ne i suoi estremi termi-
ni; come ne i sottoposti essempij si può uedere.

Del Sottrar le Proportioni.Cap. XXXIIII.
una proportione; ò quantità minore da una maggiore; per saper le differenze,
ouer di quanta quantità l'una superi, oueramente sia superata dall'altra;
la quale operatione si fà in questo modo. Prima bisogna disporre i Termini
radicali delle proportioni à modo d'una figura quadrata., di maniera che i termini
della maggiore siano nelle parte superiore, & quelli della minore nella inferiore,
page 55l'un sotto l'altro, auertendo però, che i maggior termini dell'una & dell'altra tenghino
la parte sinistra, & li minori la destra. Fatto questo si moltiplicano in croce i detti termi-
ni à questo modo; il maggior posto di sopra col minore posto di sotto; & cosi il maggior
posto di sotto col minore posto di sopra; & li prodotti si pongono perpendicolarmente
sotto i termini moltiplicati posti di sopra; diuidendoli dalle Proportioni con una retta
linea in piano; & allora da tali prodotti si hà, di quanto l'una proportione supera l'altra;
& la differenza, che tra l'una & l'altra si ritroua. Volendo adunque leuare una Sesqui-
terza da una Sesquialtera, & sapere di quanto la seconda auanzi la prima, & la differen
za, che si ritroua tra loro, operaremo in questo modo. Ordinaremo prima i termini del-
le Proportioni al modo che si uedono nell'essempio; dopoi hauendo tirato di sotto una
linea retta in piano, sotto di essa portemo i termini prodotti dalla moltiplicatione, che
si farà di un termine con l'altro. Incominciando poi dal 3. maggior termine della Sesqui
altera, lo moltiplicheremo col 3. minore della Sesquiterza; & il prodotto, il quale sarà 9.
porremo perpendicolarmente sotto 'l 3 maggior termine della Sesquialtera, sotto la li-
nea à banda sinistra; & questo sarà il maggior termine della proportione, c'hà da nasce-
re; laquale contenerà la differenza, che noi cerchiamo. Il che fatto moltiplicaremo il 4.
ch'è il maggior termine della Sesquiterza, col 2. ch'è il minore della Sesquialtera & il
prodotto, che sarà 8. verrà ad essere il minore della proportione contenente la già det-
ta differenza; imperoche posto sotto la nominata linea perpendicolarmente sotto il 2.
minor termine della Sesquialtera, haueremo la proportione Sesquiottaua, contenuta
tra il 9. & l'8. la qual dico esser la Differenza di quanto l'una è maggior dell'altra; come
si uede nell'essempio.
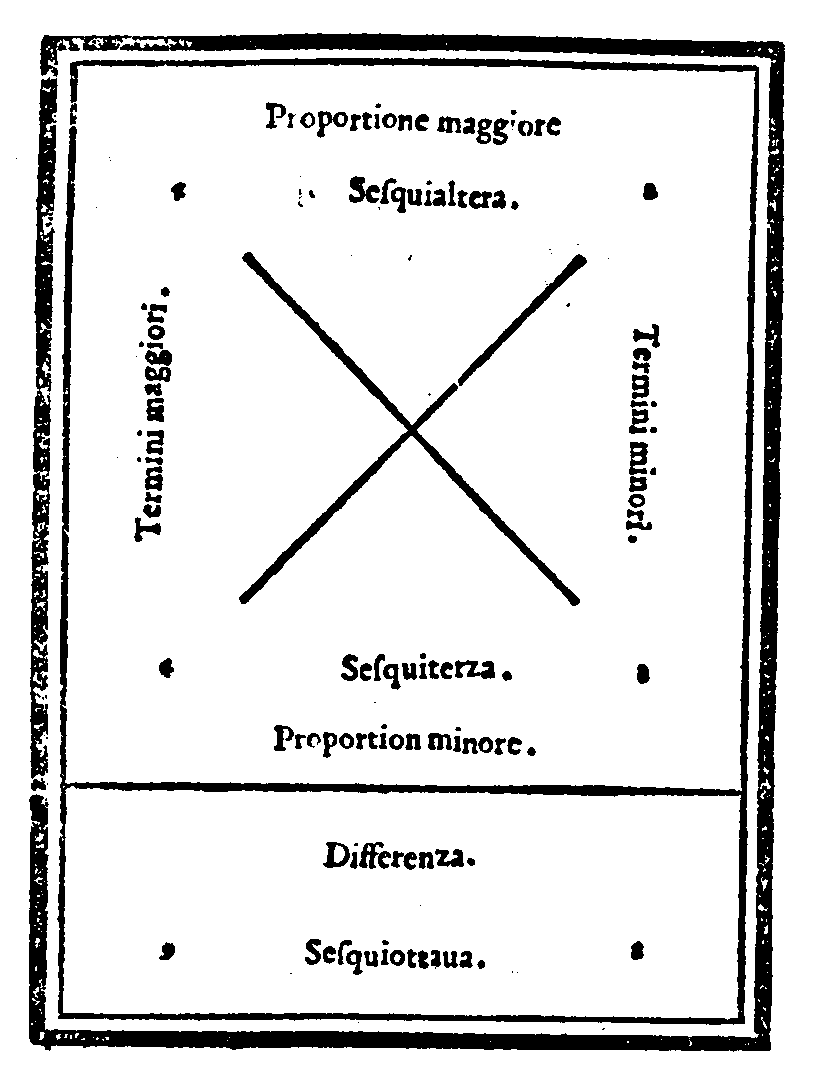
Sesquiottaua; & questa esser la Differenza, che si troua tral'una & l'altra; & esser quel-
la quantità, per la quale la maggior supera la minore, & questa da quella è superata; co-
me si può prouare: imperoche sommando insieme, nel modo mostrato, la Sesquiterza
con la Sesquiottaua, haueremo da tal somma la Sesquialtera; che fù quella proportio-
ue, che superaua la Sesquiterza di una Sesquiottaua. Et da questo si può anco vede-
page 56re, che 'l Sommar le proportioni è la proua del Sottrare; & per il contrario il Sottrare,
la proua del Sommare.
Del Partire, ò Diuidere le proportioni; & quello che sia Proportio-
nalità.Cap. XXXV.
Diuisione, ò Partimento di qualunque proportione, che si fà per la colloca-
tione di un ritrouato Numero, tra i suoi estremi; ilquale è nominato Diuisore;
che diuida quella proportionatamente in due parti; laqual Diuisione i Mathe-
matici chiamano Proportionalità, ò Progressione, & anco Mediocrità: Onde mi è
paruto esser conueniente dichiarare primieramente quello, che importi questo nome
Proportionalità, & dopoi venire alle operationi. La Proportionalità adunque secon-
do la mente d'Euclide,Element.
li .5. def. 4. è similitudine delle proportioni, che si ritroua almeno fra tre ter-
mini, che ne contengono due. Et quantunque appresso i Mathematici (come dimo-
stra BoetioArith. lib.
2. cap. 53.) le Proportionalità siano Diece, ouer (secondo la mente di GiordanoArith. li-
bro 10.) Vn-
deci; nondimeno le Tre prime, che sono le più famose, & approuate da gli antichi Fi-
losofi; Pitagora, Platone & Aristotele; sono considerate & abbracciate dal Musico,
come quelle, che fanno più al suo proposito, che l'altre. Di queste la prima è detta
Arithmetica, la seconda Geometrica, & la terza Harmonica. Et uolendo ragionare al-
cuna cosa particolarmente di esse, prima uederemo quello, che sia ciascuna separata-
mente. Incominciando adunque dalla prima dico, che la Diuisione ò Proportionali-
tà arithmetica è quella, la quale tra due termini di qualunque proportione ne hauerà un
mezano accommodato in tal modo, che essendo le differenze de i suoi termini equali,
inequali saranno le sue proportioni; per il contrario, la Diuisione, ò Proportionalità
Geometrica è quella, le cui proportioni, per uirtù del nominato termine mezano essen-
do equali; inequali saranno le sue differenze. Ma quella si chiama Harmonica, nella
quale tal termine farà inequali non solo le sue differenze, ma le sue proportioni ancora;
di maniera, che l'istessa proportione, che si troua tra esse differenze, si ritrouerà etiandio
ne i suoi estremi termini; come si uede nell'essempio.
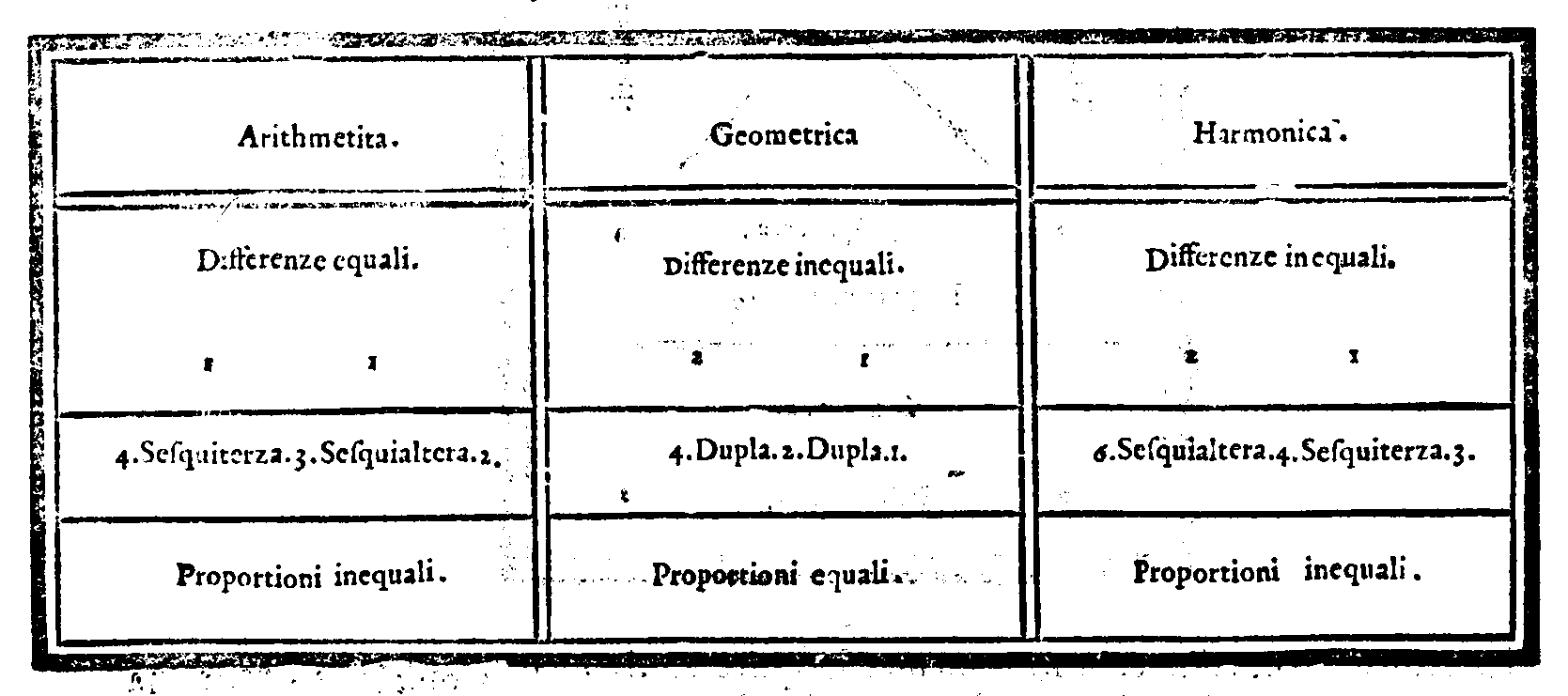
remo prima, come si possa ritrouare il Diuisore arithmetico; & in qual modo ogni pro-
portione possa da lui esser diuisa; & dopoi, in qual maniera si possano ritrouar gli altri
per ordine.
page 57
Della proportionalità, ò Diuisione arithmetica.Cap. XXXVI.
metica, quando haueremo ritrouato un Diuisore, il qual posto nel mezo de
i termini della proportion da esser diuisa diuiderà quella in tal maniera, che
essendo le differenze de i termini (come si è detto) equali, le sue proportioni sa
ranno inequali; di modo che tra i maggiori numeri si ritroueranno le proportioni mino-
ri, & tra i minori le maggiori; cosa che solo appartiene à questa Proportionalità. Que-
sto potremo ritrouar facilmente, quando sommati insieme i termini della Proportione
proposta, diuideremo il prodotto in due parti equali; percioche quel Numero, che na-
scerà da tal diuisione sarà il ricercato Diuisore, che diuiderà, secondo le sopradette con
ditioni, la detta proportione in due parti. Bisogna però auertire, che quando la proposta
proportione si ritrouerà esserne i suoi termini radicali, non si potrà osseruare il predetto
modo; percioche necessariamente sarà contenuta da numeri Contraseprimi; i quali som
mati insieme ne daranno un numero Impare, che non si può diuidere in due parti equa-
li; cioè, in due numeri intieri; la onde uolendo ritrouar tal Diuisore, & schiuare i nu-
meri rotti, che non sono riceuuti dall'Arithmetico; raddoppiaremo sempre i detti ter-
mini, & ne uerranno Due numeri pari; i quali non uarieranno la prima proportione.
Hora fatto questo, sommando questi Numeri insieme, & diuidendo il prodotto in due
parti equali; quello che ne uerrà, sarà il ricercato Diuisore. Et sia per essempio, che noi
uogliamo diuidere la proportione Sesquialtera, contenuta tra questi termini radica-
li 3 & 2. secondo la diuisione arithmetica; essendo tai numeri contraseprimi, si debbo-
no prima raddoppiare; il che fatto haueremo 6 & 4. continenti la Sesquialtera; i quali

uisore della proposta proportione; imperoche oltra che costituisce in tal proportionali-
tà le differenze equali; diuide anco la proportione (come è il proprio di tal Proportio-
nalità) in due proportioni inequali, in tal maniera; che tra i maggiori numeri si ritroua
la proportione minore; & per il contrario, tra i minori la maggiore; come tra 6 & 5. la Ses
quiquinta; & tra 5 & 4. la Sesquiquarta; come si uede nell'essempio. E' ben vero, che
questa piu tosto si chiamerà Progressione, che Proportionalità; essendoche incomin-
ciando dal minimo termine, & uenendo al mezano; & da questo al maggiore; proce-
de con equali differenze; percioche sempre si troua la Vnità, ouero il Binario, ò il Ter-
nario; oueramente altro numero, ch'è la detta differenza.
Della Diuisione, ò Proportionalità Geometrica.Cap. XXXVII.
mi d'alcuna proportione, ritiene le conditioni toccate nel Capitolo prece
dente. Onde è da sapere, che in ogn'altra Proportionalità per sua natura,
si troua diuisa la proportione proposta in due parri inequali; ma il proprio
della Geometrica è di essere diuisa in due equali; dal quale effetto è detta propriamente
Proportionalità; conciosia che tra i suoi termini maggiori & i minori; & tra le differenze
de cotali termini siano le proportioni equali; & il prodotto del Diuisore moltiplicato in
se stesso è equale al prodotto de gli estremi termini di detta Proportionalità tra lor mol-
tiplicati. Ma per ritrouare tal Diuisore osseruaremo questa Regola. Proposto c'hauere-
mo qual si voglia Proportione da diuidere, contenuta nei suoi termini radicali; per
schiuar insieme la lunghezza dell'operare, la fatica, & i molti errori, che occorrer pos-

quadrata del prodotto; la quale sarà un Numero, che moltiplicato in se stesso, ren-
derà di punto tal prodotto; & tal Radice sarà il ricercato Diuisore. Et accioche più fa-
cilmente sia inteso, verrò all'essempio. Pigliamo la Quadrupla proportione contenuta ne
i suoi Termini radicali 4 & 1. la quale uogliamo diuidere geometricamente; dobbiamo
prima moltiplicare i detti termini l'un per l'altro; & haueremo 4. dopoi pigliata la sua
Radice quadrata, che sarà 2. diremo tal Numero essere il Diuisore geometrico di tal
proportione; percioche il prodotto, che uiene dalla moltiplicatione di se stesso è equa-
le à quello, che nasce dalla moltiplicatione de i proposti termini moltiplicati tra loro:
onde tanto rende il 4. moltiplicato per la Vnità; quanto il 2. moltiplicato in se stesso. La
Quadrupla adunque è diuisa in due parti equalmente da tal Diuisore; cioè, in Due duple;
l'una delle quali si ritroua esser tra 4 & 2. & l'altra tra 2 & 1. Ma bisogna auertire; quantun
que il Proprio della proportionalità Geometrica sia il diuidere qual si uoglia proportio-
ne in due parti equali; che questo si uniuersalmente nella Quantità continua: ma non
intrauiene questo nella discreta; essendo che in essa tutte le Proportioni non sono diuisibi
li per tal modo, poiche i Numeri non patiscono la diuisione dell'Vnità. Onde si com'è im
possibile di poter diuidere rationalmente alcuna proportione, la quale sia contenuta
nel genere Superparticolare in due parti equali; come affermano Boetio nella sua Musi-
ca,Lib. 3. c. 11. & Giordano nella sua Arithmetica;Lib. 9.
prop. 61. & per quello, ch'io dimostrai nella Nona del
Primo delle Dimostrationi; per non cader tra i suoi termini altro numero, che la Vnità, la
quale non si può diuidere; cosi sarà impossibile di diuider quelle de gli altri Generi, che
sono dopo questo; essendo che quelle, le quali si possono diuidere, sono contenute nel
genere Moltiplice; & hanno (per il Corollario della Ventesimaquinta del Secondo del-
le Dimostrationi) in un de i loro estremi un numero Quadrato, & nell'altro la Vnità:
& cosi sono capaci (come etiandio afferma l'istesso Giordano) di tal diuisione. La on-
de dalla proportionalità Geometrica potiamo hauere due diuisioni; la Rationale & la
Irrationale. Prop 7.
1. Demonst. Dico prima la Rationale, che è quella che si fà per uia de i Numeri rationali;
di modo che 'l suo Diuisore sia di punto la Radice quadrata del prodotto della moltiplica-
tione de i termini d'alcuna proportione moltiplicati tra loro; & le parti di tal Diuisione
si possono denominare: come è la mostrata contenuta tra questi termini 4. 2. 1. & dopoi
la Irrationale, ch'è quella, che si fà per uia de misure, & anco de numeri; i quali si chia-
mano Sordi & Irrationali; percioche tal Diuisione à modo alcuno non si può fare, ne
meno circoscriuere con numeri ò misure rationali; & questo accade, quando dal prodot
to non potiamo hauer la sua Radice di punto; come per essempio haurebbe, quando
uolessimo diuidere in tal modo una Sesquialtera: percioche allora moltiplicati tra loro i
termini, che sono 3 & 2. & dal 6, che sarà il prodotto, non si potrà cauare tal Radice;
cioè, non si potrà hauere un numero, che moltiplicato in se stesso faccia 6. E' ben vero, che
tal Numero si potrà denominare secondo 'l costume de Mathematici, in questo modo,
dicendo; Radice 6. cioè, la Radice quadrata, che si potesse cauar di cotal numero quan-
do fusse possibile; & questo sarebbe il suo Diuisore; ma tal Radice ò numero, per la ragio-
ne detta, sempre si nominerà Sorda & Irrationale. Et perche non si può hauer la Radice
rationale di tal numero; però le parti di questa diuisione non si possono denominare, ò de
scriuere; ancora che i suoi estremi siano compresi da numeri Rationali; Onde tal Diuisio-
ne, per le ragioni dette, si chiama Sorda & Irrationale; laquale dal Musico non è conside
rata, se non per accidente; com'altroue son per dimostrare.
page 60
![Proportioni da diuidere secondo la
Geometrica proportionalita.
3Sesquialtera2
Proportione diuisa irrationalmen-
te in due parti equali.
Sesquialtera.
Diuisore.
3[[mus.Resp]]. 6.2](../../zarins89/ill/137_2.gif)
In qual modo si possa cauar la Radice quadrata da un proposto
numero.Cap. XXXVIII.
Descritto adunque il Numero, del quale uorremo la Radice, incominciare-
mo primieramente dalla prima figura posta à banda destra del predetto nu-
mero; ponendoli sotto un punto; il che fatto, lasciando quella figura, che se-
gue, ne porremo sotto la terza un'altro; & cosi sotto la quinta per ordine, lasciando sem-
pre una figura, quando fossero molte. Dopoi incomiciando dall'ultimo punto posto à ban
da sinistra, trouaremo un numero Quadrato, che sia equale à tutto il numero, che si ritroua
dal punto indietro uerso la parte sinistra, ouer li sia più uicino; pur che non lo auanzi; la
Radice del quale porremo sotto il detto punto; & cauaremo il suo Quadrato dal nume-
ro posto dall'ultimo punto indietro; & quello ch'auanzasse porremo sempre sopra questo
numero. Raddopiaremo oltra di questo la Radice, che fù posta sotto 'l punto; & quello
che nascerà, porremo sotto la figura, che segue immediatamente dopo tal punto dalla
parte destra; accommodando le figure di mano in mano uerso la sinistra. Fatto questo,
uederemo quante uolte il doppio della Radice è contenuto da quel numero, ch'è posto
sopra la Radice & il suo doppio, & il risultante, che sarà la Radice d'un'altro numero
Quadrato, porremo sotto il punto seguente; moltiplicandolo col risultante del raddop-
piato; cauandone il prodotto dal numero posto disopra. Ma bisogna auertire, che auanzi
un numero, ilquale sia equale al numero Quadrato di questa Radice; accioche sottrato
l'uno dell'altro auanzi nulla; percioche allora haueremo à punto la uera Radice quadra
page 61ta del Numero proposto; che sarà contenuta tra le radici de i Quadrati, che sono sotto-
poste à i punti. Et se auanzasse un Numero, che fusse maggior del Quadrato; allora non
si potrebbe hauere se non la Radice irrationale & sorda, nel modo detto di sopra; onde
sarebbe dibisogno ricorrere alla Quantità continua, operando nel modo, che nella Se-
conda parte son per dimostrare; & nella Decima & Vndecima del Terzo delle Dimo-
strationi hò dimostrato. Et perche è cosa molto difficile trattar questa maretia in uniuer
sale; però uerremo ad vn'essempio particolare; accioche si possa comprender quello,
che si è detto. Poniamo adunque che si uolesse cauar la Radice quadrata di 1225. dico
che primieramente dobbiamo porre un punto sotto la prima figura posta à banda destra,
ch'è il 5. dopoi, lasciando la seconda, che segue, fare un'altro punto sotto la terza; cioè,
sotto il 2. il che fatto trouaremo vn numero Quadrato, che sia equale, ò poco meno
del 12. & sarà il 9. del quale il 3. è la Radice. Questa accommodaremo primamente sot-
to il punto posto dalla parte sinistra; cioè, sotto il 2. dopoi cauaremo il 9. di 12. & re-
sterà 3. il quale porremo sopra il 2. puntato, accompagandolo col 2. non puntato; &
haueremo 32. Raddopiando hora la Radice; cioè, il 3. posto sotto il punto, haueremo
6. ilquale accommodaremo sotto il 2. non puntato; & uederemo quante uolte sia conte-
nuto dal 32. & saranno cinque fiate, & auanzerà 2. Questo dopoi accompagnato col 5.
puntato, ne darà 25. ilquale essendo pari al 25. ch'è il numero Quadrato, che nasce dal
5. ch'è la sua Radice, ne darà à punto quello, che si ricerca; cioè; la Radice di 1225,
che sarà 35. Porremo adunque questa seconda Radice, sotto il 5. puntato; & cauando
del 32. il 30. che nasce dalla moltiplicatione di tal Radice, col doppio della prima, reste
rà 2. il quale col 5 puntato dirà 25. come habbiamo detto & cosi cauando da questo il 25,
che è il secondo numero Quadrato, resterà nulla; & haueremo à punto la Radice qua-
drata del proposto numero; la quale, secondo c'hò detto, è 35. che si ritroua sotto i pun-
ti del sottoposto essempio; conciosia che moltiplicato il 35. in sè, rende à punto 1225. ch'
è il suo Quadrato; come facendone proua ad ogn'uno sara manifesto.

Della Diuisione, ouer Proportionalità harmonica.Cap. XXXIX.
ni d'alcuna proportione si hà collocato un Diuisore in tal maniera, che oltra
le conditioni toccate nel Cap.35. Tra i termini maggiori si ritrouino le maggiori, & tra i minori le minori; proprietà che solamente si ritroua
in questa proportionalità; laquale è detta propriamente Mediocrità; imperoche ne i Suo
ni prodotti da tre chorde tirate sotto la ragione de i suoi termini, la mezana partorisce
con le estreme quel soaue concento, detto Harmonia. Onde non senza ragione Pietro d'
Abano commentatore de i Problemi d'Aristotele disse,Probl. 22.
par. 19. che 'l Mezo è quello che genera l'
Harmonia. Tal Diuisore adunque potremo facilmente ritrouare; quando pigliati li
Termini radicali di quella proportione, che uorremo diuidere; li diuideremo prima-
mente nella Proportionalità Arithmetica; dopoi moltiplicati gli estremi suoi termini per
il loro termine mezano; i prodotti uerranno ad essere gli estremi dell'Harmonica: Il per
che medesimamete moltiplicato il maggiore col minimo, si uerrà à produrre il mezano
di tal Proportionalità; cioè, il Diuisore: percioche tali termini uerranno ad esse collo-
page 62cati sotto le conditioni narrate di sopra.Cap. 36. Adunque se noi uorremo diuidere harmonica-
mente una Sesquialtera, contenuta tra questi Termini radicali 3. & 2. la diuideremo pri-
ma arithmeticamente secōdo 'l modo mostrato di sopra; & haueremo cotale proportiona

6. & il 4. per il 5. & il 6. per il 4. & haueremo da i prodotti la diuisione ricercata, con-
tenuta tra questi termini 30. 24. 20. come nella figura si uede. Imperoche tanta è la pro-
portione, che si ritroua tra 6 & 4. che sono le differenze de i termini harmonici; quan-
ta è quella,che si troua tra 30 & 20. che sono gli estremi della Sesquialtera; che si hauea
da diuidere; la qual resta diuisa in una Sesquiquarta; contenuta tra 30 & 24. & in una
Sesquiquinta contenuta tra 24 & 20. Et cosi tra i termini maggiori si ritrouano le Pro
portioni maggiori, & tra i minori le minori; com'è il proprio di tal Proportionalità.
Il che etiandio con più breue modo nella Decimanona proposta del Primo delle Dimo-
strationi habbiamo dimostrato.
Consideratione sopra quello, che si è detto intorno alle Proportioni
& Proportionalità.Cap. XL.
toSupra,
Capit. 22.) Relatione d'una Quantità ad un'altra, fatta sotto un'istesso genere pro-
pinquo, ella non si possa considerare se non in due modi solamente; Prima
in quanto una quantità numera, ouero è numerata dall'altra; dopoi in quan-
to l'una misura, ò dall'altra è misurata; di maniera che da questo primo modo hanno ori-
page 63gine le proportioni & le proportionalità Arithmetiche; & dal secondo le Geometriche.
Essendo adunque due modi & non più, da i quali nascono queste due sorti di
& proportionalità; veramente ogn'altra proportione & proportionalità hà il suo essere
da loro; Onde essendo l'Harmonica (come uedemmo) molto differente dalle due nomi
nate, necessariamente uiene ad esser composta di queste due. Et benche si ueda esser di-
uersa dall'una & dall'altra; è nondimeno ad esse in tal modo congiunta, che quella di-
uersità, c'hanno insieme le due toccate di sopra, con gran marauiglia in essa è moderata;
percioche si uede tallora esser lontana dall'Arithmetica & accostarsi alla Geometrica; &
tallora per il contrario. Similmente alle uolte si uede con mirabilissimo ordine assimigliar
si all'una & all'altra; & dall'una & dall'altra tallora esser molto differente. Di modo che se
ben mancassero altre ragioni; da questo solo si può conoscere, ch'ella si habbia meritamē-
te acquistato il nome di Harmonica. Ne, per dire, ch'ella sia composta delle due nomina-
te, debbe parere strano ad alcuno; percioche il Musico piglia non solo dall'Arithmetica i
Numeri; ma dalla Geometria ancora piglia l'altre Quantità à prestanza. Et si come il pu-
ro Mathematico considera l'una & l'altra Quantità, come lontana dalla materia: se non
in quanto all'essere, almeno in quanto alla ragione; cosi il Musico, per non esser puro Ma-
thematico, considera non solo la Forma; ma la Materia ancora delle Consonanze; cioè,
le Voci & i Suoni, come materia, & i Numeri & le proportioni, come forma. Ma per-
che (com'altroue hò dettoSupra
cap. 19.) le Ragioni delle Voci & de i Suoni graui & de gli acuti non
si possono sapere, se non col mezo d'alcun Corpo sonoro, il quale è di Quantità conti-
nua; però la musica pigliando nel ritrouar tali Ragioni il mezo d'una Chorda sonora,
seruendosi dell'una & dell'altra Quantità, si uiene a' sottoporre all'Arithmetica, & alla
Geometria. La onde fu dibisogno ritrouare una Proportionalità, la quale negotiando
intorno alla Quantità discreta, non fusse lontana dalla continua; & si conuenisse alla na-
tura delle due nominate; accioche ne i Corpi sonori si scorgesse ogni Consonanza ac-
commodata secondo la forma de i Numeri harmonici. Et perche le parti delle Quantità
sonore, dalle quali nascono le Consonanze, sono ordinate, & diuise dal Musico secon-
do la ragione de i numeri, iquali sono le loro forme; & i loro progressi sono, senza dub-
bio, arithmetici; de qui nasce, che non si uede alcuna Diuisione, ouero Proportionalità
harmonica, che appartenga à i concenti musicali, che non si ritroui medesimamente nel
l'Arithmetica; percioche quelle proportioni, che ne dà l'Harmonica, l'istesse l'Arithme-
tica ne concede; ancora che in diuerso modo; imperoche l'Arithmetica; come è il suo
proprio non attende ad altro, che alla moltiplicatione dell'Vnità; ponendola nell'ordi-
ne naturale de numeri nel primo luogo, & nel secondo il Binario; dal quale nasce imme-
diatamente la Dupla proportione, il Ternario nel terzo, & cosi gli altri per ordine; ma
l'Harmonica all'incontro pare che attenda alla sua diminutione; cioè, alla Diminutione,
ò Diuisione del Corpo sonoro; nel numerare, ò molteplicar le sue parti, secondo la ragio
ne delle proportioni contenute nell'ordine naturale de i numeri; percioche diminuito
d'una meza parte, tra il Tutto & la Metà, si troua la forma della consonanza Diapason;
che tien il primo luogo nella Progressione, ouer'ordine naturale delle consonanze &
de gli altri Interualli; Et diminuito di due terze parti habbiamo la forma della Diapen-
te, nel secondo luogo, tra la metà & una terza parte; oueramente habbiamo la forma
della Diapason diapente tra il tutto & la terza parte. Similmente habbiamo la forma
della Diatessaron, ouer della Disdiapason, diminuito di tre quarte parti; cioè, l'una
tra la terza & la quarta parte di esso, & l'altra tra il tutto & la quarta parte. Si hauereb-
be anco quella del Ditono, quando fusse diminuito da quattro quinte parti; & quella del
Semiditono, quando fusse diminuito de cinque seste parti; & quella de gli altri Inter-
ualli per ordine, che sarebbe lungo il uoler discorrere particolarmente sopra di ciascuno.
Diminuendosi adunque in cotal modo; ritiene la natura della Quantità continua; & nel
diminuirsi numera & multiplica le parti, secondo le ragioni delle Proportioni contenute
nell'ordine naturale de i Numeri; & s'assimiglia alla Discreta. Et benche la Proportio-
page 64nalità harmonica habbia le istesse proportioni, che si ritrouano nell'Arithmetica; per-
cioche le forme delle Consonanze (come habbiamo ueduto) sono contenute tra le par
ti del numero Senario; che sono in Progressione arithmetica: nondimeno nell'Arithme
tica, tra i termini minori, le proportioni sono maggiori; & tra i maggiori, le minori,
& nell'Harmonica si ritroua il contrario; cioè, ne i maggiori le maggiori, & ne i minori,
le minori. Et tal diuersità nasce, perche negociando l'una intorno i numeri puri, & l'al-
tra circa le Quantità sonore; procedono al contrario; cioè, l'una per accrescimen-
to, & l'altra per diminutione del suo Principio; come hò mostrato; non si partendo qual
si uoglia di loro dalla naturale Progressione, che si ritroua nell'ordine delle proportioni
collocate ne i numeri; di modo che nell'Arithmetica i Numeri sono Vnità poste insie-
me; & nell'Harmonica sono parti delle Quantità sonore. Et accioche queste cose siano
rneglio intese, verremo ad uno essempio. Poniamo la linea A B, la quale all'Arithmetico
sia Vnità, & al Musico, Corpo sonoro; cioè, una Chorda sonora; & sia lunga cotal chorda
un piede; dico, che uolendo dare un Progresso arithmetico, sarebbe necessario; la-
sciando la intiera & indiuisibile; di procedere arithmeticamente alla molteplicatione di
cotale Vnità; raddoppiando prima (se fusse possibile) la detta linea, nel modo che ueg-
giamo l'Vnità esser raddoppiata nel Binario, il quale segue senza mezo alcuno essa Vni-
tà: il che fatto haueressimo la linea A C lunga due piedi; onde aggiungendoui anco la ter-
za Vnità, haueressimo la A D. lunga tre piedi; il perche cotale progresso; se fusse possibile;
conterrebbe tre termini in questo modo; che la proportione Tripla, che sarebbe conte-
nuta tra le due estreme unità A B & C D. & uerrebbe ad esser diuisa dalla mezana B C. po-
sta tra le sudette estreme A B. & C D. in due parti: percioche comparandosi la Vnità, ò
linea A C raddoppiata alla A B, si ritrouarebbe tra loro esserui la proportione Dupla, che
è prima nell'ordine naturale delle proportioni; come si ritroua anco l'istessa ne i numeri
tra il Binario & la Vnità; & paragonata la D A alla B A si ritrouarebbe la proportione Tri
pla; Imperoche la A D è misurata tre uolte à punto dalla A B; ouer la A D contiene tre
uolte la A B; corne ne i numeri il Ternario contiene tre uolte la Vnità. Et cosi tal propor-
tione resterebbe mediata & diuisa in due parti dalla Vnità C B in una Dupla C A & B A;
& in vna Sesquialtera D C. & C B. in proportionalità arithmetica; come tra i termini
nell'essempio manifestamente si può uedere. Ma se noi uolessimo alla sudetta Vnità
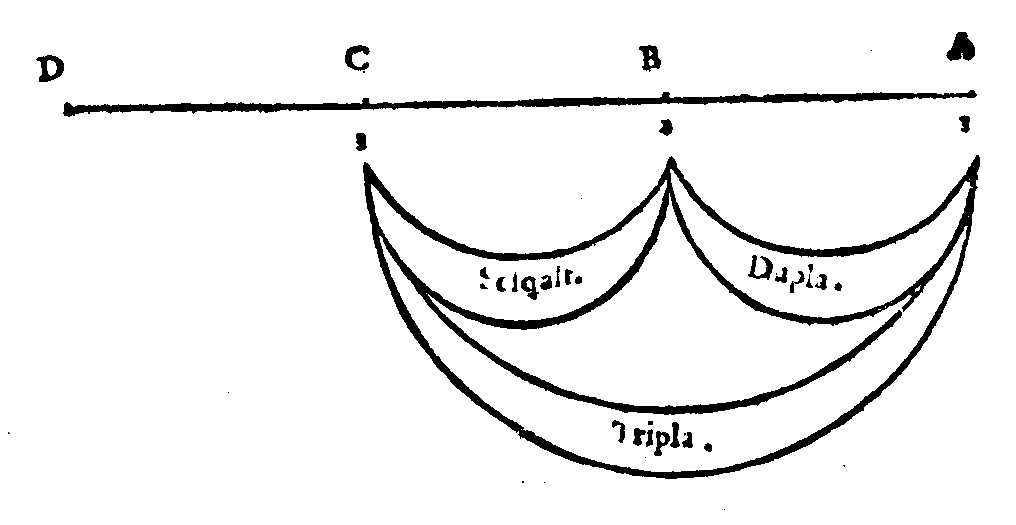
detta Vnità, ò linea A B. della sua metà in punto C; conciosiache la Metà sia prima d'ogn'
altra parte; il che fatto tra la data chorda, ò linea A B, & la sua metà, la quale è la C B
(per le ragioni, ch'altroue uederemo) si ritrouarebbe la proportione Dupla, ch'è la
prima nell'Ordine naturale delle proportioni. Diminuendo dopoi la detta A B di due
terze parti, ouero la C B di una terza parte (per seguitar l'ordine naturale) in punto D,
haueremmo la proportione Sesquialtera; laquale è nel secondo luogo nell'ordine delle
proportioni. La Sesquialtera dico tra C B & D B; & la Tripla ancora tra A B & D B; la
quale dalla C B è mediata & diuisa in due proportioni, in Harmonica ; come nell'essempio si uede. Onde è manifesto, che si come i termini della Progres-
sione arithmetica sono Vnità moltiplicate; cosi quelli dell'Harmonica sono il Numero
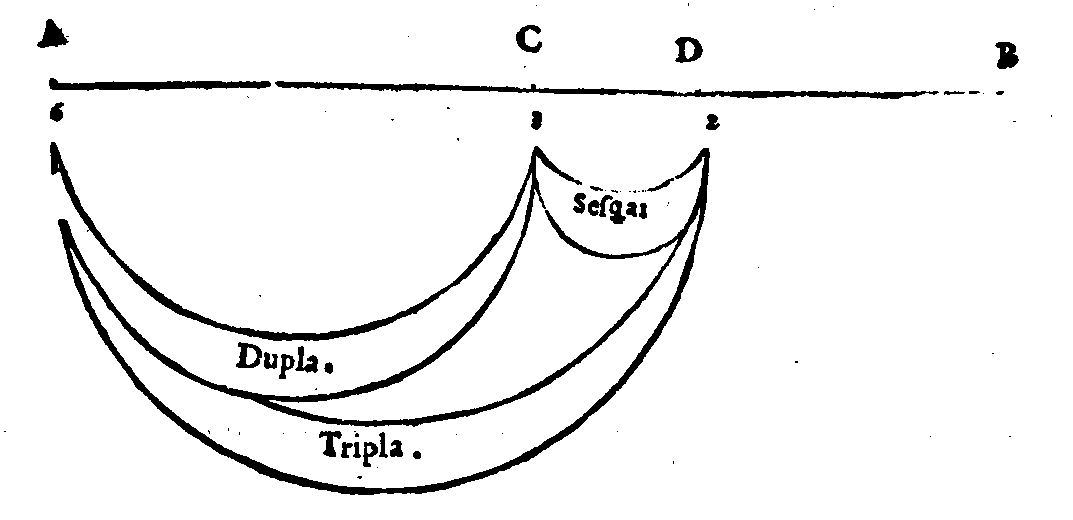
in quella si considera la moltiplicatione dell'Vnità contenuta in questo ordine 3. 2. 1. &
in questa si considera la moltiplicatione delle Parti nel soggettodiuiso, contenute tra
questi termini 6. 3. 2. Percioche se noi consideraremo il Tutto diuiso nelle parti, ritro-
uaremo, che la linea C D è la minima parte della linea A B, & misura la A B Sei uolte inte-
re; la C B tre uolte; & la D B due uolte. Hora si può uedere, per qual cagione tra i mag-
giori termini della Progressione harmonica siano contenute le proportioni maggiori &
li suoni graui; & tra i minori le minori & i suoni acuti; conciosiache questi sono prodot-
ti dalle chorde di minore estensione; & quelli da quelle di maggiore. Et potiamo anco
uedere, che si come nell'Arithmetica (dato che si potesse fare al mostrato modo) si pro-
cederebbe senza dubio dell'acuto al graue, moltiplicandosi la sudetta Vnità, ò chor-
da; cosi nell'Harmonica per il contrario si andarebbe dal graue all'acuto diminuendo-
la; & nella progressione, ò proportionalità Arithmetica gli Interualli di minor propor-
tione hauerebbono luogo nel graue, contra la natura dell'Harmonica; il cui proprio
è di hauere i Suoni graui di maggiore interuallo de gli acuti; & questi, per il contrario,
di minore. Ma perche tutte quelle Proportioni, che si ritrouano nel Progresso arithme-
tico, seguendo il loro ordine naturale, si ritrouano anco nel Progresso harmonico in
quell'ordine istesso; però potiamo uedere; acciò alcun non s'inganni; in qual modo si
habbia à pigliare il senso delle parole, poste nel Cap. 15. le quali dicono; che tra le parti
del numero Senario sono contenute tutte le Forme delle consonanze Musicali sem-
plici, possibili à prodursi; & come le Consonanze chiamate da i Prattici perfet-
ti, si trouino naturalmente in esso collocate in Harmonica diuisione; percioche
quando fussero accommodate nel Corpo sonoro tra questi termini. 60. 30. 20. 15.
12. 10. che sono le Ragioni delle sue parti, si uederebbono tramezate in quella istes-
sa maniera, che si ueggono tramezate nelle parti di esso Senario; ancora che fussero
ordinate in diuerso modo. Similmente si potrà conoscere, in qual senso si debbino
intender le parole del dottissimo Giacopo Fabro Stapulense, nella 34. del lib. 3. de
gli Elementi della Musica; & quanta sia la necessità della Proportionalità harmoni-
ca; & in qual modo, essendo concorde con l'Arithmetica, quanto alla quantità del-
le proportioni; sia discorde poi intorno al modo del procedere; & circa il sito loro. Il
che non potrà apportar marauiglia; quando si haurà considerato, ch'Ogni effetto segue
naturalmente la proprietà, & la natura della sua cagione. Et perche l'una & l'altra di
queste due Proportionalità si serue de i Numeri, i quali sono per natura Tra loro com-
municanti; ouer'hanno almeno tra loro una Misura commune, la quale è (quando al-
tro Numero non ui fusse) l'Vnità; però ogni lor Ragione è rationale; ma la Geometri
ca, il cui soggetto (assolutamente parlando) è la Quantità continua, diuisibile in poten-
za in infinite parti, considera non solo le Rationali, ma le Irrationali ancora; percioche
page 66è facil cosa al Geometra, per uirtù de i suoi Principij, far di qualunque Linea due ò tre
parti, & anco più, che siano tra loro proportionali, ouero gli è facile il porre una, ò più
Line e mezane tra due estreme, che siano proportionali con le prime; come nella Secon
da parte mostraremo;Cap. 24. &
25 ma non cosi auerrà all'Arithmetico, ne anco al Musico; percio-
che non potranno mai ritrouare un termine mezano ad ogni loro proposta proportio-
ne, che la diuida in due parti equali; conciosia che tra i termini delle loro Proportiona-
lità non cade alcun Numero mezano, che la possa diuidere secondo 'l proposito. Et ben-
che la Quadrupla si ueda alle uolte diuisa dal Musico in due parti equali; cioè, in due Du
ple; non è però tal diuisione semplicemente fatta da lui come Musico, ma si usurpa tal
diuisione, come Geometra.
Che 'l Numero non è Cagione propinqua & intrinseca delle Proprtioni musicali, ne
meno delle Consonanze; & quali siano le quattro Cagioni, Finale, Efficiente,
Materiale & Formale nella Musica.Cap. XLI.
20. che i Suoni siano la Materia delle Con-
sonanze, & i Numeri & le Proportioni la loro Forma; non si dee per questo
credere, che 'l Numero sia la cagione propinqua & intrinseca delle Propor-
tioni musicali, ne meno delle Consonanze; ma si ben la remota & estrin-
seca; come vederemo. Onde si debbe auertire, ch'essendo il proprio fine del Musico
(come uogliono i Filosofi, massimamente Eustratio 1. Ethic.
cap. 1.) il Cantare con modulatione; oue-
ramente il Sonare ogni Istrumento con harmonia, secondo i precetti dati nella Musica;
similmente il Giouare & il Dilettare; com'è quello del Poeta; hauendo ei sopra 'l tutto
riguardo à cotal cosa; piglia primieramente l'Istrumento, nel quale ritroua le Chorde,
che rendono i Suoni, apparecchiate; dopoi per poter conseguire il desiderato fine, in-
troducendo in esse la forma delle Consonanze, riducendole in una certa qualità, & in un
certo tēperamento, pone tra loro una distanza proportionata, & le tira di modo, che per
cosse da lui, rendono perfetto concento & ottima harmonia. Et quantunque in questo
concorrino quattro cose, come etiandio concorrono in ciascun'altra operatione; cioè,
il Fine dell'attione, al quale sempre si hà riguardo; ch'è il Sonare con harmona; ouero
il Giouare & Dilettare; che si dice Cagion finale; lo Agente; cioè, il Musico, che si
nomina Cagione efficiente; la Materia, che sono i Suoni mandati fuori dalle chorde; &
si chiamano Cagione materiale; & la forma, ò Proportione, che si ritroua nelle distan-
ze da un Suono all'altro; la quale si addimanda Cagione formale; nondimeno queste
due ultime sono cagioni intrinseche; & l'Agente & il Fine, estrinseche della cosa: im-
peroche queste non appartengono ne alla natura, ne all'esser suo; & quelle sono essen-
tiali di essa; conciosia che ogni cosa corruttibile è composta di materia & di forma;
& la Materia si dice quella, della quale si fà la cosa, & è permanente in essa; come i Suo-
ni, de i quali si fà la Consonanza; & la Forma è quella specie, ò similitudine, ò uo-
gliamo dire essempio, che la cosa ritiene in se; per la quale è detta tale; com'è la
Proportione nella Consonanza; & questa si chiama Cagione intrinseca, à differenza
della estrinseca; la quale è (per dir cosi) il Modello, ò uogliamo dire Essempio;
alla cui similitudine si fà alcuna cosa; come è quella della Consonanza, ch'è la Pro-
portione di numero à numero. Nondimeno è da auertire, che di queste cagioni,
alcune sono dette Prime, & alcune Seconde; & tal ordine di primo & di secondo si
può intendere in due modi; primieramente, secondo un certo ordine de numeri,
nel quale una cosa è prima & remota, & l'altra seconda & propinqua; Secondaria-
mente si può intender secondo l'ordine compreso dalla ragione in una sola cagio-
ne; il quale è posto tra l'Vniuersale & il Particolare; imperoche naturalmen-
page 67te l'Vniuersale è primo, & dopoi il Particolare. Nel primo modo diciamo propriamen-
te quella cagione esser prima, la quale dà uirtù & possanza alla seconda di operare; co-
me si dice nella cagione efficiente, che 'l Sole è prima cagione (remota però) della
generatione; l'Animal poi è cagione seconda & propinqua di tal generatione;
percioche egli dà all'Animale la uirtù & la possanza di generare. Ma nel secon-
do, il Genere è il primo, & la Specie il secondo; la onde dico, che la prima & uni-
uersal cagione della Sanità è l'Artefice; & la seconda & particolare è il Medico, ouer il tal
medico. E' ben uero, che la prima & la seconda cagione del Primo modo sono diffe-
renti dalla prima & dalla seconda del Secondo; percioche nel secondo modo non si di-
stinguono in effetto l'una dall'altra; ne la più uniuersale, dalla meno uniuersale; ne que-
sta della singolare; ma sono distinte solamente nell'intelletto: Ma nel primo modo sono
distinte; conciosia che l'una è contenuta dall'altra; & non per il contrario. Et questi due
modi (massimamente in quanto al Secondo) si ritrouano in tutti i Generi delle cagio-
ni; percioche nella materiale il Metallo è prima cagione del coltello, & il Ferro la se-
conda, come nella formale (uenendo ad uno accommodato essempio secondo 'l nostro
proposito) la prima cagione della consonanza Diapason è il numero 2 & 1. & la Secon-
da è la proportione Dupla; & cosi dell'altre per ordine. La Proportione adunque è la
cagione formale, intrinseca & propinqua delle Consonanze, & il Numero è la cagione
uniuersale, estrinseca & remota; & è come il modello della Proportione, per la quale si
hanno da regolare & proportionare i Corpi sonori, accioche rendino formalmente le
Consonanze. Et questo accennò il Filosofo,2. Post. c. 1. mentre dichiarando quel che fusse la Con-
sonanza, disse, che è Ragione de numeri nell'acuto & nel graue; intendendo della Ra-
gione, secondo la quale si uengono à regolare i detti Corpi sonori. La onde non disse,
che fusse Numero assolutamente; ma Ragion de numeri; il che si può vedere più espres
samente nelle Proportioni musicali, comprese ne i nominati corpi; imperoche non si ri-
troua in esse alcuna specie, ò forma di numero; conciosia che se noi pigliamo i loro estre
mi, misurandoli per il numero dopoi ch'è fatta cotal misura, tai corpi restano nella loro
prima integrità & continuati, come erano prima; ne si ritroua formalmente in essi Nu-
mero alcuno, il quale costituisca alcuna proportione, ma si ben la Ragione del Numero.
Percioche se ben noi prendiamo alcuna parte d'una chorda in luogo d'Vnità, & per repli
catione di quella venimo à saper la quantità di essa & la sua proportione, secondo i nume
ri determinati, & per conseguente la proportione de i Suoni prodotti dalle chorde;
come dal Tutto & dalle Parti; non potiamo però dire, se non che tali Numeri siano quel
Modello & quella Forma de i Suoni, che sono cagione essemplare & misura estrinseca di
essi Corpi sonori, che contengono le Proportioni musicali; lequali senza 'l suo aiuto dif-
ficilmente si potrebbono ri trouar nelle Quantità continue. La onde il numero è sola
cagione di far conoscere & ritrouare arteficiosamente le Proportioni delle consonanze
& di qual si uoglia Interuallo musicale; onde è necessario molto nella Musica, in quan-
to che per esso più espeditamente si uà speculando le differenze de i Suoni, secondo il
graue & l'acuto, & le loro passioni; & con piu certezza di quello, che si farebbe misu-
rando co i Compassi, ouero altre misure i Corpi sonori; hauendo prima conosciuto
con l'esperienza manifesta, come si misurino secondo la loro lunghezza con propor-
tione, & percossi insieme muouino l'Vdito secondo il graue & l'acuto; ma altramen-
te di quello, che si considerano ne i Numeri puri secondo la ragione. Il perche dirò, per
concludere, che si come il Numero non può essere à modo alcuno la cagione intrinseca
& propinqua de tali Proportioni; cosi non potrà esser la cagione intrinseca & propin-
qua delle Consonanze; come hò dichiarato.
page 68
Dell'Inuentione delle Radici delle proportioni.Cap. XLII.
Quinta & ultima Operatione, detta Inuentione delle Radici; dico, che tale
Operatione non è altro, che ridur le proportioni ne i primi loro Termini ra-
dicali, quando si ritrouano fuori di essi; percioche le Proportioni, che sono
contenute tra i termini non radicali, oltra che si rendono più difficili da conoscere; fanno
anco difficile le loro Operationi. Onde accioche si possa hauer di loro più facile cognitio
ne, & più facilmente si possino adoperare, darò hora il modo di ridurle ne i loro Termi-
ni radicali; ò ne i numeri Contraseprimi. Et perche non solo quelle Proportioni, che
sono contenute tra due termini; ma anche ogn'ordine de più proportioni moltiplicate,
può esser contenuto da altri numeri, come tra quelli, che sono Tra loro composti; pe-
rò mostrando prima, in qual modo si possino ridurre à i loro Termini radicali quel
le, che sono contenute solamente tra due termini; mostrerò dopoi in qual modo
l'altre si potranno ridurre. Incominciando adunque dalle prime, terremo questo
ordine. Essendoci proposta qual si uoglia Proportione, contenuta da numeri Tra-
lorocomposti, cercaremo di trouare un Numero maggiore, il qual numeri, ò misuri
communemente i termini della proportione proposta; per il quale diuidendo tai ter-
mini, i prodotti siano le Radici, ò Termini radicali di tal proportione. Volendo adun-
que ritrouar tal numero, diuideremo prima il maggior termine dalla proportione per il
minore; dopoi partiremo questo per quel numero, ch'auanza dopo tal diuisione; & se
di nuouo auanzasse numero alcuno, diuideremo il primo auanzato numero per il secon-
do, & questo per il terzo, & cosi di mano in mano; fino à tanto che si ritroui un Nume-
ro, che diuida à punto l'altro senz'auanzar nulla: & questo sarà il Numero ricercato; per
il quale diuidendo dopoi ciascun termine della Proportione proposta, i prodotti saran-
no i Minimi numeri & Termini radicali della proportione. Poniamo adunque che uo-
gliamo ritrouar la Radice della proportione contenuta tra questi termini, ò numeri 45.
& 40. che sono Tralorocomposti; diuideremo primieramente il 45. per il 40. & uerrà
1. auanzando 5. dopoi lasciando l'Vnità; come quella, che fà poco al proposito, si in
questa, come anco nell'altre diuisioni; pigliaremo il 5. il quale diuiderà il 40; in otto
patri a punto, senz'auanzare alcuna cosa; & questo sarà il Numero maggiore ricercato,
che numererà l'uno & l'altro de i due proposti termini. Onde diuidendo il 45. per il 5.
ne uerrà 9. & di nuouo diuidendo il 40. per esso 5. haueremo 8. i quai nurneri, 9. & 8. senza
dubbio, sono Contraseprimi & Minimi termini, ouer la Radice della proposta propor-
tione, che fù la Sesquiottaua.
In che modo si possa ritrouar la Radice de più Proportioni moltiplicate
insiemeCap. XLIII.
sono quelli, che nascono dalla Moltiplicatione de più Proportioni poste in-
sieme; ouer quelli, che uengono dalla Proportionalità harmonica; che sono
senza dubbio termini, ò numeri Tralorocomposti, procederemo in questo
modo. Ritrouaremo prima, per la Terza del Settimo d'Euclide, un Numero mag-
giore, che diuida, ò misuri communemente ciascun de i Numeri contenuti in cota-
le ordine; per il quale diuideremo poi ciascun di loro; & li prodotti, che uerranno
da tal diuisione, saranno la sua Radice. Siano adunque i sottoposti Cinque termini, ò
numeri Tralorocomposti; 360. 240. 180. 144. 120. prodotti dalle moltiplicationi fatte
nel Cap. 31. & 32. i quali uogliamo ridurre in un'ordine de numeri Contrasepri-
mi, & alla loro Radice; dico che bisogna ritrouar prima, nel modo che si è mostra-
page 69to nel Capitolo precedente, un Numero maggiore, che numeri, ò misuri communemen-
te i due maggiori termini de i proposti, che sono il 360 & 240. & tal Numero sarà il 120.
percioche diuide, ò misura il 360. tre uolte, & il 240. due uolte. Vederemo dopoi se può
misurare il 180. ma perche non lo può misurare, è dibisogno di ritrouare un'altro
numero simile, il quale diuida, ò misuri communemente il 180. & il 120. ope-
rando secondo la Regola data, che sarà il 60. Et questo; per il Corollario della Secon-
da del Settimo di Euclide; numererà communemente i tre maggiori de i proposti ter-
mini, & anco il 120, conciosia che numera il 360. sei uolte, il 240. quattro uolte, il 180.
tre uolte, & il 120 due uolte. E' ben uero, che non potrà misurare il 144 la onde sarà dibi
sogno di ritrouare un'altro rnaggior numero, che lo misuri insieme cō gli altri; onde ritro-
uatolo secōdo 'l modo mostrato; haueremo il 12, che non solo misurerà il 144. ma gli altri
ancora. Et perche tal Numero numera etiādio il minore de i proposti, ch'è il 120. però di
co, che 'l 12. è il Numero maggiore ricercato, il qual numera cōmunemente ciascuno de i
cinque proposti termini, ò numeri: cōciosia che se noi diuideremo ciascuno de questi nu-
meri per il 12. che fu l'ultimo numero maggiore ritrouato, ne uerrà 30. 20. 15. 12. 10. & tra
questi termini dico esser la Radice del proposto ordine; percioche senza dubbio sono nu
meri Contraseprimi; come nell'essempio si può essaminare. La onde osseruando tal re
gola, non solo si potranno hauere i Termini radicali di qualunque ordine, che con-
tenga quattro, cinque, & sei proportioni; ma più ancora, se ben (dirò cosi) si procedesse
all'infinito.

Della Proua di ciascuna delle mostrate Operationi.
Cap. XLIIII
mamente nel maneggio de i Numeri, ponendone per inaduertenza alle
uolte uno in luogo d'un'altro; però per non lasciare à dietro alcuna cosa,
che possa tornare utile à i Studiosi, hò uoluto aggiungere il modo, per
il quale si possa conoscere, se nelle Operationi si ritroua essere alcun'errore; accio-
che ritrouato si possa emendare. Onde incominciando dalla prima, che fù il Mol-
tiplicare, dico; Quando haueremo moltiplicato insieme molte proportioni; i termi-
ni prodotti da tal moltiplicatione saranno (come altroue si è detto) fuor de i loro
termini radicali; si che uolendo saper se le dette Proportioni saranno contenute in ta-
li termini senz'errore; pigliaremo prima due termini, tra i quali c'imaginiamo d'ha-
uer collocato alcuna proportione; & li diuideremo per i suoi termini radicali;
page 70il maggior per il maggiore, & il minor per il minore; & se i prodotti da tal diuisione sa-
ranno equali; tal proportione sarà contenuta ne i suoi termini senz'errore alcuno; & se fus
se altramente, sarebbe il contrario. Volendo adunque sapere, se la proportione Sesqui-
altera, posta tra questi Numeri 360 & 240. sia contenuta nella sua uera proportione;
pigliaremo i suoi termini radicali 3 & 2 per i quali diuideremo 360 & 240. in cotal. modo;
360 per il 3. & 240 per il 2. & ne verrà da ciascuna parte 120. il perche tale equalità di-
mostrerà, che la detta Proportione è contenuta tra i proposti numeri; quantunque non
siano radicali. Ma quando l'uno de i prodotti uenisse maggior dell'altro; sarebbe segno
manifesto, che in tal moltiplicatione si hauesse commesso errore. Il medesimo potremo
etiandio uedere, moltiplicando il maggior de i prodotti col minor termine radicale del-
la proportione, & il minor col maggiore; cioè, 360 per il 2. & 240 per il 3. percioche
allora dall'una & dall'altra parte il prodotto uerrebbe 720; che ne dimostrarebbe, che tal
proportione sarebbe contenuta tra i proposti prodotti senza errore. Et benche il Som-
mar delle proportioni possa esser la proua del Moltiplicare, & il Moltplicar, quella del
Sommare; tuttauia non potiamo uedere, se ne i loro mezani termini sia alcun'errore, se
non nel modo mostrato. Ma ueramente la uera proua del Sominare, è il Sottrare; percio
che se noi sottraremo di vna in una le sommate insieme proportioni del prodotto del Som
mare, senz'alcun fallo potremo conoscer tal somma esser fatta senza errore; quando all'
ultimo si uerrà alla Equalità. Se noi adunque dal prodotto della somma posta nel Cap.
33. ch'è la Tripla proportione leuaremo di una in una le sommate; incomin
ciando dalla maggiore, che fù la Sesquialtera; ne resterà la Dupla; dalla quale sottraen-
do la Sesquiterza, resterà la Sesquialtera; onde cauando da questa la Sesquiquarta, sen
za dubio si peruenirà all'Equalità, & ad una proportione simile alla Sesquiquinta, che
resterà da cauare; la qual ne darà à conoscere; che in tal somma non ui si troua errore al-
cuno; ma si bene sarebbe, quando alla fine restasse da cauare una proportione da un'al-
tra, che fusse di maggiore, o di minor quantità di quella, che si hauesse da cauare. Ma la
proua del Sottrare è senza dubio il Sommare. Et perche à sufficienza hò ragionato altro-
ue dico tal cosa;Supra
Cap. 36.
37. & 39. però non accade, ch'io replichi cosa alcuna. Vltimamente nel Partire,
quando nella equal diuisione delle Proportioni, i termini cōtenuti nella proportionalità
Arithmetica non si ritrouassero collocati nel modo, che di sopra hò mostrato; allora sa-
rebbe segno manifesto di errore: come sarebbe etiandio errore nella Geometrica & nell'
Harmonica, quando i loro fussero collocati altramente, che nel modo dichiarato; & che
le Proportioni, ò qualunque continuato ordine de proportioni fussero fuori de i loro ter
mini radicali, quando non si ritrouassero collocate ne i numeri Contraseprimi. Hora par
mi, che tutto cio c'ho detto di sopra sia à sufficienza, per mostrare i principij della Musica,
& tutte quelle cose, che cōcorrono intorno la cognitione delle Forme delle Cōsonanze,
le quali se noi non saperemo, non potremo hauer già mai buona cognitione delle cose
seguenti; ne mai peruenire ad un perfetto fine. La onde ogn'uno che desidera di fare ac-
quisto di questa Scienza, debbe con ogni suo potere sforzarsi di possederli perfettamen-
te; accioche possa acquistar degna laude, & honoreuole frutto delle sue fatiche.

LA SECONDA PARTE
DELLE ISTITVTIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Capella della Serenissima Signoria
DI VENETIA;
Consonanze; Et è la Seconda della Prima parte della Musica detta
Speculatiua, ò Contemplatiua.
Quanto la Musica sia stata da principio semplice, roza, & pouera
di Consonanze.Cap. I.
ri & delle Proportioni; è cosa ragioneuole, che hora si ragioni in
particolare, & secondo che tornerà à proposito, di quelle cose, che
la Musica considera in uniuersale; come de i Suoni & delle Voci de
gl'Interualli, de i Generi, de gli Ordini de Suoni, de i Modi, delle Mu
tationi, & delle Modulationi; ilche si uedrà più essattamente trattate
ne i nostri Sopplimenti. Ma prima che si uenga à tal ragionamento,
mostrerò in qual modo la Musica sia stata da principio semplice; & come da gli Antichi
era usata; dopoi, ueduto in qual modo i Suoni & le Voci naschino; & fatta la loro diui-
sione, uerrò à quello, ch'è la mia principale intentione. Dico adunque che se ben la Musi
ca ne i nostri tempi è peruenuta à tal grado & perfettione d'Harmonia, in quanto all'uso
de tutte quelle Consonanze, che si possono ritrouare; delle quali alcune appresso gli An-
tichi non erano in consideratione; & che quasi non si uegga di poterle aggiungere cosa al
cuna di nuouo; tuttauia non è dubbio, che da principio (com'è auenuto anco dell'altre
Scienze) ella non sia stata non solo semplice & roza; ma etiandio molto pouera di Conso
nanze. Ilche esser uerissimo ne dimostra quel che narra ApuleioFloridorū
lib. 1. di essa, dicendo; che Da
principio si adoperaua solamēte il Piffero; non con fori, come quelli, che si fanno al no-
stro tempo; ma senza, alla simiglianza d'una Tromba; ne si faceuano tante sorti de concē
ti, con uariati Istrumenti & variati Modi; ma gli Antichi ricreauano i loro spiriti, & si da
uano tra loro piacere & solazzo col sopra detto Piffero solamente senza uarietà alcuna
di suono. Et tal Piffero vsauano ne i loro publici spettacoli, & ne i loro Chori, quan-
do recitauano le Tragedie, & Comedie; come manifesta Horatio,De Arte
poetica. parlando in co-
tal modo;
Tibia, non ut nunc, oricalcho uincta, tubaeꝗ
Aemula; sed tenuis, simplexꝗ foramine pauco
Adspirare, & adesse choris erat utilis:
page 72Alquale dopoi Hiagne Frigio à quei tempi dotto nella Musica, che fù padre & Mae-
stro di Marsia, u'aggiunse i fori, & incominciò à sonar quello con uariati suoni; & fu
il primo che fece sonar due Pifferi con un sol fiato; & che sonò tale Istrumento con la
destra & con la sinistra mano; cioè, mescolò il suono graue con l'acuto, con destri fori
& sinistri. Vsarono etiandio gli Antichi da principio la Cetera, ò la Lira con tre chor-
de, ouer con quattro solamente; della quale fù inuentore Mercurio; come uuol Boe-
tio;Music li-
bro 1. c. 20 & erano in quella ordinate di modo, che la prima con la seconda, & la terza con la
quarta conteneuano la Diatessaron; la prima con la terza, & la seconda con la quarta,
la Diapente; & di nuouo la seconda con la terza il Tuono; & la prima con la quarta la
Diapason, & insino al tempo di Orfeo fu seruato cotale ordine; ilquale fu dopoi ac-
cresciuto in uarii Istrumenti; & prima Chorebo di Lidia u'aggiunse la Quinta chorda;
dopoi dal sopranominato Hiagne ui fù aggiunta la Sesta; ma la Settima aggiunse Ter-
pandro Lesbio. Et questo Numero de chorde (come dice Clemente AlessandrinoStromat.
lib. 6.) era
prima contenuto nell'antica Lira, ò Cetera; dopoi da Licaone da Samo fù aggiunta la
Ottaua; ancorache PlinioNat. hist. li
bro 7. ca-
pit. 56. attribuisca l'Inuentione di tal chorda à Simonide, & della No
na à Timotheo; & BoetioIbidem, ut
supra. uoglia, che questa chorda sia stata aggiunta da Profrasto Pe-
riota, la Decima da Estiacho Colofonio, & la Vndecima da esso Timotheo. Ma sia co-
me si uoglia; Suida attribuisce l'aggiuntione della Decima & della Vndecima chorda à
Timotheo Lirico. Et certo è, che da molti altri ue ne furono aggiunte tante, che crebbe-
ro al numero de Quindeci. Aggiunsero dopoi à queste la Sestadecima chorda; ne più
oltra passarono & si contentarono di tal numero, & le collocarono nell'ordine, che più
oltra dimostraremo; diuidendole per Tuoni & Semituoni in cinque Tetrachordi, osser-
uando le Ragioni delle proportioni Pitagoriche; ritrouate ne i martelli da Pitagora;
nel modo che nella Prima parte hò mostrato; le quali conteneuano quelle istesse, che si
ritrouauano tra le chorde della sopradetta Cetera, ò Lira ritrouata da Mercurio: & che
nel sottoposto essempio si ueggono. Imperoche il maggiore (come dicono) pesaua li-

da i quali numeri Pitagora cauò le Ragioni delle Consonanze musicali; che furono
appresso gli Antichi cinque; come narra Macrobio,De Som-
nio. lib. 2.
cap. 1. & nascono da Cinque numeri;
il primo de i quali chiamarono Epitrito, il secondo Hemiolio, il terzo Duplo, il
quarto Triplo, & il quinto Quadruplo; con uno Interuallo dissonante, ilquale isti-
mauano, che fusse principio d'ogni Consonanza; & lo chiamarono Epogdòo. Di
modo che dall'Epitrito era contenuta la Diatessaron, dall'Hemiolio la Diapente,
dal Duplo la Diapason, dal Triplo la Diapasondiapente, dal Quadruplo la Dis-
diapason, & dall'Epogdòo il Tuono Sesquiottauo. Alle qual Consonanze To-
page 73lomeoHarmoni.
lib. 1. c. 5. aggiunse la Diapason diatessaron, contenuta dalla proportione dupla superbi-
partienterza tra 8 & 3. laqual consonanza è posta da Vitruuio anco nel Cap 4. del Quin
to libro della Architettura; & da noi nella Vndecima del Secondo delle Dimostrationi è
dimostrata esser Consonanza communemente detta. Et ueramente gli Antichi non co-
nobbero altre Consonanze, che le sopradette; le quali tutte da i Musici moderni sono
chiamate Perfette; & non haueano per consonanti quelli Interualli, che i Moderni chia-
mano Consonanze imperfette; cioè, il Ditono, il Semiditono & li due Hexachordi, mag
giore & minore; come manifestamente dimostra Vitruuio nel nominato luogo, dicen-
do; Che nella Terza, Sesta & Settima chorda non si possono far le Consonanze; & que-
sto dice hauendo rispetto alla grauissima d'ogni Diapason; il che si può etiandio uedere
in ciascun'altro autore, si Greco, come Latino. La onde da questo potiamo comprende-
re la imperfettione, che si ritrouaua nell'antiche Harmonie, & quanto gli Antichi erano
poueri di Consonanze & di Concenti. Et se bene alcuno, mosso dall'autorità de gli Anti
chi, laquale è ueramente grande; più tosto che dalla ragione, uolesse dire, che oltra le
nominate Consonanze perfette, non si possa ritrouare alcun'altra Consonanza; non du-
bitarei affermare simile opinione esser falsa; percioche ella contradice al Senso, dal qua-
le hà origine ogni nostra cognitione. Conciosiache niuno di sano intelletto negherà,
che oltre le sopradette Consonanze perfette, non si ritrouino ancora le Imperfette, le
quali sono tanto diletteuoli, uaghe, sonore, soaui & harmoniose à quelli, che non han-
no corrotto il senso dell'Vdito; quanto dir si possa; & sono talmente in uso, che non solo
i periti Cantori & Sonatori di qualunque sorte si uoglia Istrumenti le usano nelle lor Har
monie; ma quelli ancora, che senz'hauere alcuna Scienza, cantano & sonano per
prattica solamente.
Per qual cagione gli Antichi nelle loro Harmonie non vsassero le Consonanze im-
perfette, & Pitagora vietaua il passare oltra la Quadrupla.Cap. II.
percioche essi prestarono grandissima fede alla dottrina di Pitagora; ilquale
essendo diligentissimo inuestigatore de i profondi secreti della Natura; non
le uolse accettare & porre tra i consonanti Interualli; per esser egli amatore
delle cose semplici & pure; perche si dilettaua de tutte le cose fino tanto che la materia
loro non si partiua dalla semplicità; & in essa inuestigaua le cose secrete; cioè, le loro ca
gioni; hauendo egli opinione, che ritrouandosi esser semplici; in quelle fusse fermezza
& stabilità; & essendo miste & diuerse; incostanza & uarità. Et perche istimaua, che
di queste non si postesse hauer ferma ragione; però, senza procedere più oltra, le refiu-
taua. Laonde solamente quelle Consonanze li piaceuano, le quali insieme si conueni-
uano per Ragion de Numeri, che fussero semplici, & hauessero la lor natura purissima;
come sono quelli, che nascono dal genere Moltiplice & dal Superparticolare; & sono i
Cinque mostrati, contenuti nel numero Quaternario; & rifiutò quelle, che sono com-
prese da Numeri, che si ritrouano oltra esso Quaternario, & entrano ne gli altri Generi
di proportione; da i quali nasceua il loro Ditono & il Trihemituono, lo Semiditono &
altri Interualli simili; come uederemo. Ne pose tra le Consonanze il Ditono & il Se-
miditono, contenuti nel genere Superparticolare, i quali hò mostrato nella Prima par-
te; percioche molto ben conosceua (com'io credo) la natura loro; & uedeua che dalla
mistura di tal Consonanze imperfette con le perfette, poteuano nascere i due Hexachor
di, maggiore & minore; i quali si contengono nel genere Superpartiente; come le for-
me loro ce lo manifestano. Approuò adunque solamente quelle Consonanze, come
più semplici & più nobili, c'hanno le forme loro tra le parti nel sudetto Quaternario;
page 74percioche da loro non ne può nascere alcun suono, che non sia consonante. Et forse che i
Pitagorici non per altro haueuano in somma veneratione questo Numero; se non perche
vedeuano, che da esso nasceua cotale semplicità di concento; onde hebbero opinione,
ch'appartenesse alla perfettione dell'Anima. Et tanto hebbero questo per uero, che uo-
lendo, di ciò che affermauano (il che dice PlutarcoDe Iside &
Osiride. & MacrobioDe Som-
nio libro 1.
cap. 1.) fusse loro prestata in-
dubitata fede, diceuano; Io ti giuro per colui, che dà all'Anima nostra il numero Qua
ternario. Il diuino Filosofo adunque uietaua il passare oltra la Quadrupla; percioche e-
gli oltra di essa (secondo il parere di Marsilio Ficino Filosofo platonico nel Compendio
del Timeo di Platone) non udiua Harmonia; conciosia che procedendo più oltra na-
sca la Quintupla tra 5 & 4 & la Superbipartiente tra 5 & 3 che genera dissonanza. E'
ben uero, che se le parole del Ficino si pigliassero & s'intendessero semplicemente, co-
me sonano, s'intenderebbe il falso; percioche la Quintupla non si ritroua tra 5 & 4. ma
si bene tra 5 & 1. però giudicò, che oueramente il Testo sia incorretto; & che in luogo
del 4. si debba intendere & porre la Vnità; ò che tal parole s'habbiano da intendere in
questo modo; Che procedendo oltra la Quadrupla, aggiunto il Quinario al numero Qua
ternario; come nell'essempio si vede; cioè, aggiunta la Sesquiquarta alla proportione
Quadrupla in questa forma. 5. 4. 3. 2. 1. nasca la proportione Quintupla tra 5 & 1. & simil
mente la Superbipartiente terza tra 5 & 3. laquale si parte dalla semplicità de i numeri,
& è contenuta nel terzo Genere di proportione, che si chiama Superpartiente; il qual
genere, diceua Pitagora, non essere atto alla generatione delle Consonanze musicali.
Per questa cagione adunque & non per altra, stimano alcuni, che questo Filosofo uie-
tasse il trappassar la Quadrupla; ancora ch'alcuni altri dicano, che Pitagora uoleua,
che non si hauesse à trappassar la Quadrupla nelle cantilene; cioè, il numero delle
Quindeci chorde, contenute tra la Disdiapason; percioche egli giudicò, ch'ogni ottima
uoce (hauendo la natura posto termine à tutte le cose) potesse senza suo disconcio
naturalmente ascendere dal graue all'acuto; ò per il contrario, discendere per Quin-
deci uoci; & che qualunque uolta si passasse più oltra, ò nel graue, ò nell'acuto, che ta-
li Voci non fussero più naturali, ma sforzate; & che recassero noia à gli ascoltanti; ma
di queste due ragioni la prima (secondo 'l mio giudicio) è migliore, & fà più al propo-
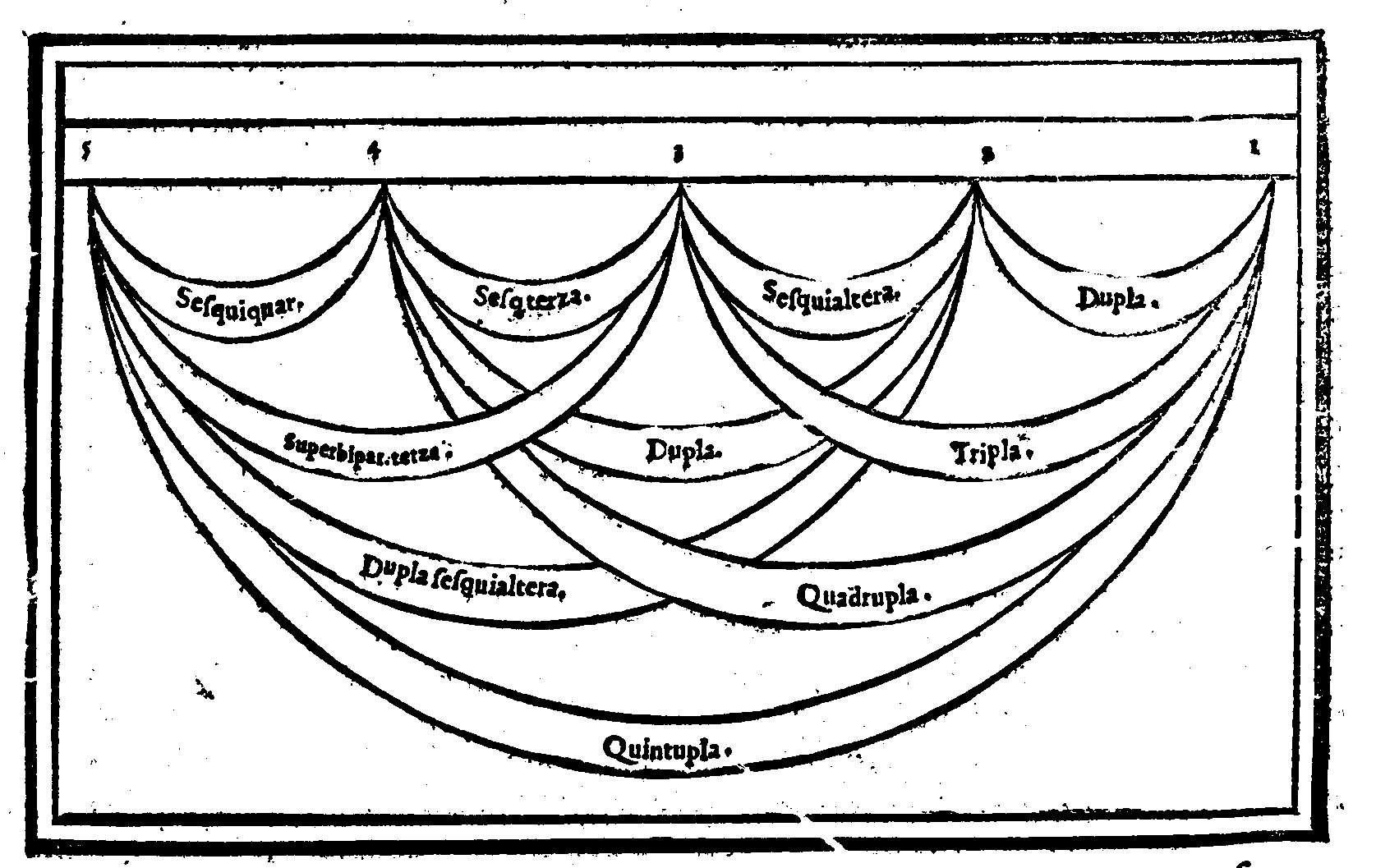
uera, ch'è posta nel principio del Primo delle Dimostrationi; la quale lascio, per cagio-
ne d'essere breue; percioche chi desiderasse saperla, leggendo il nominato luogo, sarà pie-
namente del tutto raguagliato. Non è adunque da marauigliarsi, che gli Antichi non
riceuessero cotali Consonanze; poi che dalle leggi Pitagoriche, gli era uietato il trappas-
sarla Quadrupla.
Dubbio sopra l'Inuentione di Pitagora.Cap. III.
tesse vscir Cōcento da quei due martelli, che conteneuano la proportione Ses
quiottaua; che è la forma del Tuono; ilquale senza dubbio alcuno è Inter-
uallo dissonante. A questo si può rispondere & dire; E' cosa ragioneuole, che
i Fabbri de quei tempi non percuotessero nel battere co i martelli tutti in un tempo; ma
si ben l'un dopo l'altro; come uediamo & udimo fare al di d'hoggi. Onde è credibile,
che la prima cosa, che udisse Pitagora fusse un certo ordine harmonico di suono, & che
molto li fusse grato; dal quale fusse mosso à uolere inuestigar la ragione de i Concenti har
monici. Ma perche percuotendo i Martelli l'un dopo l'altro, il Tuono non li poteua of-
fender l'udito; come gli hauerebbe offeso, quando tutti in un tratto hauessero fatto la
percossa; conciosia che la Consonanza & la Dissonanza si ode tra due suoni, ch'in un tem
po istesso percuotono l'Vdito; però nō si può dire, che Pitagora in tale atto vdisse cosa al-
cuna dissonante, di modo che lo potesse offendere; massimamente hauendo prima rimos
so il Quinto martello; come dice Boetio;Musicae li-
bro. 1. c. 10. percioche non s'accordaua con gli altri. Et
che questo sia uero; MacrobioDe Som-
nio. lib. 2.
cap. 1. lo manifesta chiaramente, dicendo; Che passando
Pitagora à caso per una uia publica, gli peruennero alle orecchie alcuni Suoni, che
si rispondeuano con un certo ordine; i quali nasceuano da i martelli d'alcuni Fabbri,
che batteuano un ferro infocato; & dice, Erano Suoni, che si rispondeuano con un certo ordi-
ne; & non dice, che fussero Suoni consonanti. Per la qual cosa, potiamo vedere, che
cotale Interuallo non li poteua dare alcuna noia; come potiamo da noi stessi vdire in
ogni nostra modulatione; che non solo nel procedere di simile Interuallo; ma di qua-
lunque altro ancora; pur che nasca da Numeri sonori & harmonici, il senso non è offe-
so. Hauendo dopoi il Filosofo ritrouato, che ciò procedeua dalla quantità del peso di
ciascun martello; incominciò da i pesi ritrouati à inuestigar le Proportioni musicali, &
i Numeri harmonici; facendo l'esperienza d'un Suono contra l'altro col peso loro; &
ritrouò la loro Ragione ne i nominati Numeri; & conobbe quelle proportioni, che
dauano le Consonanze, & quelle che faceuano le Dissonanze. Laonde Boetio uo-Vt supra.
lendo mostrare in fatto quelle Proportioni, ch'erano le uere Forme delle consonan-
ze, parlando di ciascuna di esse, le aggiunge una di queste parole Consonantia, ò Con-
cinentia; ma quando uiene alla Sesquiottaua, senz'aggiungerle alcuna cosa, dice
solamente che risonaua il Tuono; uolendo inferire, che tal Proportione non era posta
dal Filosofo nel numero di quelle, che fanno la Consonanza.
Della musica antica.Cap. IIII.
non par credibile, che i Musici potessero produrre ne gli animi humani
tanti varij effetti; come nelle Historie si raccontano; percioche si legge, che
alle uolte moueuano l'animo all'ira, alle volte dall'ira lo ritirauano alla man-
suetudine; hora induceuano al pianto, hora al riso, ouero ad altre simili passioni; &
page 76tanto meno par credibile, per esser ella hoggidi ridutta à quella perfettione dalla parte
de i Suoni & consonanze; com'hò detto altroueSupra c. 1. che quasi di meglio non può sperare; &
non si vede, che faccia alcuno de i sopradetti effetti; onde più tosto si potrebbe dire,
che la Moderna & non lAntica fusse imperfetta. Et perche tal cosa potrebbe generar
ne gli animi de i Lettori non picciol dubio; però auanti che si uada più oltra, mi è paruto
di douer sopra tal materia ragionare alcune cose; & prima dimostrare in qual maniera
da gli Antichi la Musica era posta in uso; dopoi, quali materie recitauano nelle lor can
tilene; & quali erano i Musici antichi; oltra di questo, quel ch'era potente d'indur l'
Huomo in diuerse passioni; in qual modo le Harmonie poteuano muouer l'Animo, &
produrre in esso varii costumi; & ultimamente, da qual Genere di cantilena fussero
operati simili effetti. Incominciando adunque dalla prima, dico; che se ben la Musica
anticamente hà operato molte cose marauigliose, come si legge; & si dica, c'hora non
operi più cosa alcuna delle nominate; tuttauia chi uorrà essaminar minutamente il
tutto, ritrouerà che la Musica etiandio al presente non è priua de cotali effetti; & ne po-
trebbe forse con grandissima marauiglia uedere alcuno, che sarebbe di non poca impor-
tanza. E' ben uero, che l'uso moderno è tanto vario & lontano dall'uso antico; che sarebbe
quasi impossibile crederlo; quando da molti degni & honorati Scrittori, i quali sono sta-
ti per molto tempo auanti la nostra età, non ne fusse fatta mentione alcuna di tal cosa;
percioche i Musici de quei tempi non vsarono la Musica con tante uarie sorti d'Istru-
menti; lasciando da un canto quelli, che nelle Comedie & ne gli Esserciti loro adopera-
uano, ne anco le loro cantilene erano composte de tante parti; ne con tante voci face-
uano i loro concenti; come hora facciamo; ma l'essercitauano di maniera, ch'al suono
d'un solo Istrumento; ò Piffero, ò di Cetera, ò di Lira, che fusse, il Musico semplice-
mente accompagnaua la sua uoce, & porgeua in tal maniera grato piacere à se, & à gli as
coltanti: come si legge: percioche in cotal modo Homero introduce cantare Achille,
Femio & Demodoco;Iliad. lib. 9
& 8. similmente Virgilio introduce Ioppa,Aeneid. li
bro 1. Horatio Tigellio;Ser. lib. 1.
Saty. 3. Silio
Italico Teutrate;De Bello
punico, li-
bro 11. & Suetonio scriue;In vita
Neronis.
cap. 20. che 'l simile faceua Nerone. Questo istesso faceuano
coloro che i Greci chiamauano Rapsodi, i quali erano Recitatori, Interpreti, & Canto-
ri de i uersi de i Poeti; tra i quali fu Ione; come dimostra Platone in quello del Furor
poetico; che interpretaua i uersi d'Homero al suono della Lira; & tanto gli era affettio-
nato, & tanto se lo hauea fatto famigliare; che non uoleua esporre altro Poeta, che lui.
Quando poi erano due, che cantauano; non cantauano insieme & ad un tempo, come si
fa al di d'hoggi; ma l'un dopo l'altro; & tal modo di cantare nominauano Cantare à ui-
cenda; modo ch'appresso di Theocrito cantano i pastori Dafni & Menalca; & appresso
di Virgilio Menalca & Dameta.Idylliū. 8.
Ecgloga. 3 Vsauano etiandio i Poeti lirici ne i loro Certami musica
li cantare i lor poemi & compositioni con uarii generi de Versi al suono della Lira, ouer
della Cetera; & questo faceuano adunati insieme in un cerchio al numero di Cinquanta,
in alcune lor feste; & tale ragunanza fù nominata Choro; & cantauano le Lodi de i Dei,
& di coloro, ch'erano stati uittoriosi ne' giuochi Olimpici; & riportauano per premio
del loro cantare un Bue. I Rustici anco soleuano in tal modo porgere i lor uoti à i Dei
per i frutti della terra; percioche adunati in un Choro appresso un'altare, sopra ilquale
era la Vittima del sacrificio; hora passeggiando, & hora riuolgendosi in giro cantauauo
à Bacco alcune sorti de Versi che sono hora à noi incogniti, al suono del Piffero. Et tal
Piffero non s'assimigliaua à quelli c'hora si usano; percioche in quei tempi si faceua de
ossa delle gambe di Grù; onde furono chiamati tali Istrumenti da i Latini Tibiae; essendo
cotal parte di ciascuno animale con uoce latina nominata Tibia. Ne faceua allora dibiso
gno di maggiore Istrumento; percioche il popolo, che concorreua à luoghi simili era
poco; & era maggiormente dedito alla fatica & al lauoro, che alle feste, & à i giuochi. Ha
ueuano medesimamente per costume, di rappresentar le Tragedie & le Comedie loro
cantando; & questo accenna Horatio,De Arte
poetica. dio;
page 77
Si plausoris eges aulaea manentis, & usque
Sessuri, donec Cantor, Vos plaudite, dicat.
Et era usanza (come afferma il Filosofo3. Reth. c.) che i Poeti istessi recitauano le Tragedie, &
le Comedie, che haueano composte. Onde (come narrra Tito LiuioHist. Dec.
1. lib. 7.) uno chiamato Li-
uio , hauendo fatto una Fauola in uersi, ordinata col suo argomento, egli stesso la recita
ua; dopoi non potendo più dire; percioche la uoce gli era mancata, pregò che li fusse per
donato; & pose un Fanciullo à cantarla; il quale hauendosi portato bene, fu introdotta
una usanza; che cotali cose fussero cantate da gli Istrioni. Et di questo ne tocca una parola
Horatio, dicendo nella sua dell'Arte Poetica;
Ignotum Tragicae genus inuenisse camoenae
Dicitur, & plaustris uexisse poemata Thespis,
Quae canerent, agerentꝗ peruncti fecibus ora.
Credo anco, che gli Oratori orassero al popolo al suono di qualche Istrumēto: ancora
ch'al parer mio tale usanza durasse poco tempo; imperoche Cicerone nella Oratione,
che fece in fauor di P. Sestio, ne tocca una parola; & anche nel fine del Libro terzo dell'
Oratore, parlando di Gaio Gracco, lo dimostra; benche questo paia alquanto strano
ad Aulo GellioAtti. noct.
lib. 1. c. 11.; ma PlutarchoIn Vitis. T.
& C. Grac
corum. modestamente recita cotal cosa, & dice; Essendo Gaio
Gracco huomo uehemente nel dire, spesse uolte era trasportato dall'ira; di modo che
ueniua alle uillanie & uituperii; & cosi egli soleua turbare la sua Oratione; onde cono-
scendo tal cosa, s'imaginò di rimediarui, col fare, ch'un Seruo dotto nella Musica, nomi-
nato Licino li stesse dopo le spalle nel pulpito; & che mentre lo udiua inasperire, & riti-
rarsi fuori della sua uoce, con un'Istrumento lo auertiua, & gli faceua achettare cotal
vehementia. Et di ciò non ci dobbiamo marauigliare; poi che l'arte Oratoria hà hauu-
to principio (come vuole StraboneDe Situ or
bis. lib. 1.) dalla Poesia; & i Poeti orauano al popolo cantan-
do Versi al suono della Cetera, ò Lira; & io tirauano à fare il loro uolere; il che ben lo
dimostra anco l'Ariosto, dicendo:Satyra 6.
Li Scrittori indi fer l'indotta plebe
Creder, che al suon delle soaui cetre
L'un Troia, & l'altro edificasse Thebe.E hauesson fatto scendere le pietre
Da gli alti monti, & Orpheo tratto al canto
Tigri, e Leon, dalle spelunche tetre.
anco gli Antichi al suono del Piffero, recitando diuerse Canzoni compo-
ste in uersi; & questo faceuano alle uolte, quando erano due insieme; l'un de i quali sapes
se Cantare & l'altro Sonare; come accennò il Poeta, quando introdusse Menalca dire à
Mopso pastore queste parole. In Daphni
Tu calamos inflare leueis ego dicere uersus:
Percioche l'uno era perito sonatore di Piffero, & l'altro era ottimo cantore. Era anco
appresso gli Antichi usanza di Saltare & di Ballare, mentre che 'l Musico al suono della
Lira, ò Cetera, ouer d'alcuno altro Istrumento recitaua alcuna cosa; come si troua ap-
presso di Homero nella Odissea;Odiss li-
bro 8. che cantando Demodoco al suono della Cetera, i
Greci saltauano & ballauano. Et simigliantemente Virgilio, nel Libro 1. dell'Eneida,
imitandolo, dice; che cantando Ioppa al suono della Cetera;
Ingeminant plausu Tyrii, Troesque sequuntur:
Et in un'altro luogo più chiaramente manifesta tal cosa, dicendo:Aeneid. 6.
Pars pedibus plaudunt Choreas, & carmina dicunt.
Similmente Horatio, nel luogo citato di sopra (auegna che non faccia mentione alcu
na, che si cantasse) dice;
Sic priscae motumꝗ & luxuriam addidit artiDi questo si potrebbono hauere infiniti essempii, iquali hora per breuità la-
.
scio; poiche le Ode di Pindaro di ciò fanno indubitata fede; conciosia ch'essendo diuise
page 78i tre parti dellequali; la prima è chiamata Στροφὴ; Αντιστροφὴ la secōda; & la terza. Ε'πωδὸς;
& sono comprese ne i uersi Lirici; gli Antichi le cātauano al suono della Lira, ò della Cete
ra, & ballauano, ò saltauano in tal maniera; che quando i Saltatori si uolgeuano dalla par
te destra, uerso la sinistra, cantauano la prima parte; & quando andauano dalla sinistra,
alla destra, cantauano la seconda; & ueniuano à riposarsi, quando cantauano la terza;
la qual maniera di ballare, ò saltare dura fino al di d'hoggi appresso i Candioti, & quel-
li, che habitano nell'Isola di Cipro. Gli Antichi adunque usauano la Musica nella ma-
niera c'habbiamo detto; accompagnando la uoce ad un solo Istrumento; & s'alle uolte ne
usauano de piu sorti, ui accompagnauano la uoce; come tra genti barbare al presente
ancora si costustuma in alcune parti, & massimamente del Leuante; come da huomini de-
gni di fede più uolte hò udito dire; ma i due primi modi (come fanno fede l'historie) era
no grandemente in uso. Vsarono anco gli Antichi ne i loro Esserciti uarie sorti d'istru-
menti; imperoche i Toscani usarono la Tromba; della quale (come uogliono alcuni) essi
furono gli inuentori; gli Arcadi la Sampogna; i Siciliani alcuni istrumenti, i quali no-
minauano Πύκτιδας; i Candioti la Lira; i Lacedemonii il Piffero, ouer la Lira (come
uuole PausaniaLaconic. li-
bro 1.) al canto d'alcune canzoni; quelli di Thracia il Corno; gli Egittii il Tim
pano; & gli Arabi il Cembalo. I Romani si seruirono nelle lor Comedie d'alcune sorti de
Pifferi, de i quali alcuni chiamauano Destri & alcuni Sinistri; & alcuni nominauano Sa-
ranni; da i quali i Spettatori poteuano comprender sotto qual Genere si contenessero le
Comedie, che doueuano recitare. Imperoche quando la Comedia conteneua in se ma-
teria, ò soggetto seuero & graue, si udiua il concento graue de i Pifferi sinistri; & quando
era giocoso & festeuole, il concento era fatto co i Pifferi destri, & era acuto; ma s'era mi-
sta, le Cantilene musicali erano temperate dell'una & dell'altra sorte di concento. Et tali
Cantilene non erano fatte dal Poeta, c'hauea composto la Comedia; ma da un perito
nell'arte della Musica; come nel principio di ciascuna Comedia di Terentio si può aper-
tamente uedere; oue dice;
Modos fecit Flaccus Claudii filius.Nominando le sorti de gli
Istrumenti detti di sopra; co i quali eran fatte le Musiche: lequali erano uariate di Modo,
ò. Tuono, che lo uogliamo dire; & le faceuano udire auāti che cominciassero à rappresen
tar la Comedia; accioche la materia compresa in essa (com'hò detto) si potesse sapere
auanti da gli Spettatori. Nondimeno à i nostri tempi sono incognite cotali sorti de Piffe-
ri; ancora che Seruio nel Lib. 9. dell'Eneide di Virgilio, sopra quel uerso;
O uere Phry-mostri ch'eran di due sorti; delle quali l'una nomina Seranni & l'altra Frigii. I primi
giae,
erano Pari; & cosi si chiamauano; percioche haueano le loro cauerne pari & equali; i
secondi Impari; conciosia che le cauerne loro erano inequali. Adduce dopoi Seruio
l'autorità di Marco Varrone, uolendo dichiarar quali fussero Pifferi destri & sinistri, dicen
do; che la Tibia Frigia destra hà un solo foro, & la sinistra ne hà due; de quali l'uno hà il
suono acuto, & l'altro graue. Ma queste parole son molto differenti da quelle, che sono
poste nel Lib. 1 al Cap. 2. delle cose della Villa; doue egli dice, che l'una sorte de Pifferi
sonaua i Modi d'un'istesso Verso in uoce acuta, & l'altra in uoce graue; onde seguendo
più à basso, dalle sue parole si può comprendere, che 'l sinistro mandaua fuori il suono
graue, & il destro lo acuto. Et questo si può confermare con l'autorità di Plinio,Nat. hist.
Lib. 16. ca
pit. 36. ilquale
parlando de i Calami acquatici, dice; Che si soleuano tagliare in tempo conueniente
circa la stella Arturo, fino all'età di Antigene sonator di Piffero; usandosi ancora la Mu-
sica semplice à quei tempi; & cosi preparati dopo alcuni anni incomiciauano ad esser buo
ni; & anche allora bisognaua adoperarli molto spesso, & quasi insegnar loro sonare;
percioche le linguelle si ueniuano à toccare l'una con l'altra; ilche era molto più utile
per mostrare i costumi ne i Theatri; ma dopoi che soprauenne la uarietà & la lasciuia de i
canti, incominciarono à tagliarli auanti il Solsticio, & il terzo anno erano buoni; con-
ciosia c'haueano le linguelle loro più aperte, & più atte à uariare i suoni; lequali hoggidi
ancora cosi sono. Ma allora era opinione, che s'accordassero insieme quelli, ch'erano
d'una medesima canna; & quella parte, ch'era uicina alla radica, conuenirsi al Piffero
page 79sinistro, & quella ch'era uicina alla cima al destro. Questo dice Plinio seguendo quello,
che dice Teofrasto nella Historia delle pianteCap. 12. li-
bro 4. con maggior copia di parole; & parmi es-
ser ben detto; imperoche quelli, che sono uicini alla radice, sono necessariamēte più grossi
de quelli, che sono più uerso la cima; onde ogni giorno si comprende dalla esperienza,
ch'essendo il corpo loro più grande & più largo, rende anco il suono più graue; come il
contrario si scorge in quelli, che sono più minuti, & più ristretti; ilche ancora si uede &
ode ne gli Istrumenti, che chiamiamo Organi; le canne de i quali quanto sono più lar-
ghe, tanto rendono i suoni piu graui; & le piu ristrette i piu acuti. Ma à quello che si è det
to par che sia contrario un'Autore incerto di quello Epigramma Greco, ch'incomincia;
Τὸν σοφὸν ἐν κιθάρη; percioche chiama la chorda graue Δεξιτερὴν ὑπάτην; cioè, destra Hy-
pate; & l'acuta Λαιὴν νήτην; cioè sinistra Nete. Ma questo importa poco; conciosia che
considerata ben la cosa, torna commodo all'uno & all'altro modo; essendo che le parti
d'ogni Istrumento si posso cōsiderare & denominare in due modi; prima, in quanto à noi;
dopoi, in quanto ad esso Istrumento. In quanto à noi, la parte dell'Istrumento posta
dalla man destra è detta Destra, et rende i suoni acuti; come ne gli Organi, Monochor-
di, & altri Istrumenti simili si uede; & quella, ch'è posta alla sinistra è detta Sinistra, &
rende i suoni graui. Ma in quanto all'Istrumento, quella ch'è destra à noi, adesso è sini-
stra; & per il contrario, quella ch'è à lui destra, à noi è sinistra; come si potrebbe uedere
in due, i quali insieme giuocassero alla lotta; che la parte destra dell'uno sarebbe la sini-
stra all'altro, & la sinistra la destra. Non è adunque inconueniente, se l'uno nomina quel
la parte destra, la quale l'altro chiama sinistra; essendo tali parti diuersamente, secondo al-
cune loro opinioni, considerate.Infra.
Cap. 29. In questo modo adunque da gli Antichi era posta in uso
la Musica; il qual modo quanto sia differente dall'uso moderno, ciascuno da se lo potrà
sempre uedere; come etiandio potrà uedere altroue, quanto era differente il loro con-
cento dal moderno. Ma quali materie recitassero nelle lor cantilene, quel che contiene
il seguente Capitolo lo farà manifesto.
Delle materie, che recitauano gli Antichi nelle lor Canzoni: & d'al-
cune Leggi musicali.Cap. V.
ferenti da quelli, che contengono le Canzoni moderne; imperoche erano co-
se graui, dotte & composte elegantemente in uarij uersi; come sono le Lodi
de i Dei contenutene gli Hinni di Orfeo; i Fatti illustri de gli Huomini uittorio
si ne i giuochi Olimpici, Pithij, Nemei & Istmii; che si uedono tra le Ode di Pindaro;
ouer cantauano cantilene nuttiali; simili à quelle di Catullo. S'udiuano anco Argu-
menti funebri, lamentationi, cose amatorie & appartinenti à conuiti;Cap. 2.
lib. 7. &
Cap. 1. lib.
8. Suppli. & à certe canti-
lene aggiungeuano alcuni prieghi, i quali chiamauano Epilimia, per iscacciar la pestilen
za. I Rustici etiandio haueano alcune sorti de Canzoni, lequali se ben non conteneuano
cose tanto graui & seuere, erano almeno honeste & diletteuoli; com'era quella maniera,
che chiamauano Ε'πιλήνιον ἆσμα; la quale cantauano, mentre premeuano le Vue. Canta-
uano ancora gli Antichi materie Comiche & Tragiche & altre cose simili piene di seue-
rità & di grauità; come ne dimostra chiaramente GalenoTerapeut.
lib. 1., dicendo; che Anticamente ne
i conuiti si solea portare à torno la Lira, ò Cetera, al suono della quale si cantauano le Lo
di de i Dei, de gli Huomini illustri, & altre cose simili; & duolsi, ch'à suoi tempi (come si
fà anche da molti al dì d'hoggi) si soleuano portare i bichieri pieni de bianchi uini &
uermigli; & si come gli Antichi si rallegrauano d'hauer passato il tempo uirtuosamente
con la Musica; cosi allora & al presente si gloriauano & si gloriano molti dell'hauer man
giato & beuuto assai; raccontando il numero de i bichieri da loro uuotati. Similmente
page 80CiceroneTuscul.
lib. 3. & 4.
Cap. 2. dice; Che i conuitati erano soliti cantar ne i conuiti al suono del Piffero le lo-
di & uirtù de gli Huomini illustri; adducendo l'essempio di Temistocle, commemorato
già nella prima parte. Et nel Libro de i Chiari Oratori, intitolato Bruto, dice queste
parole; Dio uolesse, che si ritrouassero quei Versi, i quali Catone per molti secoli auan-
ti la sua età lasciò scritto nel Libro delle Origini, essere stati cantati in ciascun conuito
delle Lodi de gli Huomini chiari & illustri. Tali materie si cantauano anco al suono del
Piffero nella lor morte; come l'istesso CiceroneDe Legib.
lib. 2. afferma in un'altro luogo. Et i Latini se
guitando i Greci chiamauano le Canzoni lugubri Naenia. Ne per altro ueramente ci è
stato dato la Musica, se non à questo fine; il che manifesta Horatio in questi uersi;De Arte
poetica.
Musa dedit fidibus diuos, puerosꝗ deorum,
Et pugilem uictorem, & equum certamine primum
Et iuuenum curas, & libera uina referre.
Et come dimostra Platone nel Protagora, gli Antichi insegnauano tutte queste mate-
rie à i loro Giouani; accioche le hauessero à cantare al suono della Lira, ouer della Cete-
ra, onde Homero scriue d'Achille.
Α῎ειδε δ´ἁρακλέα ἀνδρων.cioè;
Ma le lodi de gli huomini uirili Cantaua.Et di Demodoco dice
che Cantaua le gloriose imprese de gli Huomini, la contentione d'Vlisse con Achille,
la fauola di Venere & di Marte, & il Cauallo Troiano. Femio anco nella OdisseaOdys. 22 si escu
sa con Vlisse, dicendo; che Cantaua à i Dei & à gli Huomini. Onde è da pensare, che
non cantaua se non cose graui & seuere; hauendo già cantato il lugubre & funebre ri-
torno de i Greci nella loro patria. Et se ben cantò l'adulterio di Marte & di Venere:
non lo fece perche lodasse tal sceleratezza; ma per rimouere (come dice AtheneoDipnos. li-
bro 1. c. 7.) i
Pheaci dalle dishoneste loro uoluttà & piaceri. In cotal modo ancora appresso di
Virgilio.Aeneid. 1.
Cithara crinitus Iopas
Personat aurata, docuit quae maximus Atlas.
Hic canit erratem Lunam, Solisꝗ labores:
Vnde hominum genus & pecudes, unde imber & ignes:
Arcturum; pluuiasꝗ hyadas, geminosꝗ Triones:
Quid tantum Oceano properent se tingere Soles
Hyberni, uel quae tardis mora noctibus obstet.
Et Creteo amico alle Muse medesimamente:Aeneid. 9.
Semper equos, atque arma uirum, pugnasꝗ canebat.
Nerone etiandio, appresso di Suetonio nella Vita di questo sceleratissimo Imperato-
re,Cap. 21. canta al suono della Cetera la fauola di Niobe, & molt'altre Tragedie, maschera-
to; come Canace parturiente, Oreste ucciditor della madre, Edippo fatto cieco, & Her-
cole furioso. Et LucianoDe Salta-
tione. dice, che gli Argomenti & le Materie delle cantilene appresso
gli Antichi erano quelle cose; cominciando da principio del mōdo; ch'erano successe fi-
no à i tempi di Cleopatra regina d'Egitto; le quali, mi pare (secondo che lui racconta)
che siano quasi tutte quelle, che descriue & canta Ouidio nelle sue Trasformationi; & à
cotal canto ballauano. Tutte queste cose recitauano sotto una determinata Harmonia,
con determinati Rhythmi Versi & ; ancora che fussero uariati in ogni manie-
ra di cantilena; & cosi con numeri, percussioni, modi & concenti; & con la uoce huma-
na, esprimeuano materie conueneuoli & buoni costumi. Nominarono poi tali deter-
minationi Leggi; imperoche altro non è Legge nella Musica, che un modo di cantare,
il qual contiene in se un determinato concento, & un determinato Rhythmo & Metro.
Et furono cosi chiamate; percioche non era lecito ad alcuno di mutare, ouero innoua-
re in esse alcuna cosa; si nell'Harmonie, come etiandio ne i Rhythmi & Metri; ancora
che siano alcuni, che dicano, che si chiamauano Leggi; imperoche auanti che si scriues
sero le Leggi ciuili, si cantauano: onde Aristotele afferma,prob. 28.
secr. 19. che nella sua etade erano anco
page 81solite à cantarsi da i popoli Agathirsi. Erano però, cotali Leggi scritte in uersi, & le
cantauano al suono della Lira, ò Cetera; accioche i popoli più facilmente le ritenesse-
ro nella memoria & sapessero quello, che douessero osseruare; come scriue Eliano diDe Varia
hist. lib. 2.
quello, che faceuano i Candioti intorno le Discipline. Ma sia come si uoglia, erano
cotal Leggi di tre sorti; imperoche alcune eran dette Citharistiche, che si cantauano al-
la Cetera, ò Lira; & alcune Tibiarie, le quali si cantauano al suono de i Pifferi; ma quel
le della terza specie si chiamauano Communi; & si cantauano al suono dell'una & del-
l'altra sorte de gli Istrumenti nominati. Et benche cotal Leggi fussero molte; nondi-
meno ciascuna hauea il suo nome acquistato, ò da i popoli, che le usauano; ò da i Rhy-
thmi & Metri, che conteneuano; ouero da i Modi; ò da gli Inuentori; ò da i loro Amatori;
oueramente da gli Argomenti. Da i popoli fù nominata l'Eolia & la Boetia; da i Rhy-
thmi & Metri, la Orthia & la Trochea; da i Modi, l'Acuta & la Tetraedia; da gli A-
matori & inuentori, la Terpandria & la Hieracia; & da gli Argomenti, il Certame Pi-
thico & il Corrule. Queste leggi (come uuol PlutarchoIn Musica.) furono publicate da Terpan-
dro; il quale hauendo prima diuiso le Citharistiche, pose nome alle lor parti. Le leggi
Tibiarie hebbero molti nomi, che si lasciano per non andare in longo; i quali (secondo
che si dice) ritrouò Cleone ad imitatione di Terpandro. La legge Orthia apparteneua
à Pallade, & conteneua in se materie di guerra, & era una specie di modulatione nella
Musica, la quale Aulo GellioNoct. At-
tica. libro
16. c. 19. nomina Verso orthio, forse detto in tal modo da suoi Nu-
meri, i quali sono veloci & sonori; conciosia che i Greci nominan Ο῎ρθιος quello, che noi
chiamiamo Sonoro, ancora che molti lo interpretano per il Canto appartenente ad uno
Essercito d'huomini d'arme. Era la Trochea un segno, che dauano gli Antichi à i sol-
dati col canto, ò suono della Tromba; & i Lacedemonij usauano ne i loro Esserciti il
canto della legge Castoria, per accender l'animo de i soldati à prender l'arme contra gli
inimici; & tal legge era composta sotto un Rhythmo detto Embaterio. La Currule s'ac-
quistò il nome della materia, che conteneua in se; cioè, dall'argumento, nel quale si
narraua il modo, ch'Hettore figliuolo del Re Priamo fù strascinato con le carrette intor-
no le mura Troiane. Di queste Leggi hò voluto far un poco di memoria; accioche si pos-
sa uedere, ch'erano composte di Verso numeroso, accommodate à commuouere & ge-
nerare ne gli animi diuerse passioni. Non sarà etiandio fuori di proposito, che ueggia-
mo in qual maniera i Musici anticamente recitassero alcune delle predette Leggi al suo-
no del Piffero cantando; accioche da una si possa comprendere, in qual modo potesse-
ro recitar l'altre; & questa sarà il Certame Pithico, del quale fà mentione Horatio, di-
mostrando le qualità del Musico, c'hauea da recitarlo, dicendo;De Arte
poetica.
Abstinuit Venere & Vino, qui Pithia cantat
Tibicen, didicit prius extimuitꝗ magistrum.
Lequali troppo ben conobbe il uanissimo Imperatore Nerone (come si legge in Sue-
tonioIn uita
Neronis.
cap. 20.) che si asteneua da i pomi, usaua il vomito & li Cristeri, per purgarsi bene il petto; ac
cioche hauesse recitando nella Scena la uoce chiara & netta. L'Argomento adunque di
tal legge era la Battaglia d'Apolline col serpente Pithone, ilquale dà il nome alla Fauola;
& il nome di tutta la cantilena era Delona; & forse fù cosi nominata; percioche Apollo
nacque nell'Isola di Delo. Era questa legge (come mostra Giulio PolluceOnomast.
lib. 4. c. 10.) diuisa come so
no le nostre Comedie; in cinque parti; delle quali la prima nominauano Rudimēto, oue
ro Esploratione, la secōda Prouocatione; Iambico la terza; la quarta Spondeo; & la quin
ta & vltima Ouatione, ò Saltatione. La Rapresentatione (com'hò detto) era il modo della
pugna d'Apollo col Dragone; & nella prima parte si recitaua, in qual modo Apollo inue
stigaua & contēplaua il luogo, s'era atto alla pugna, ouer nō; nella seconda si dichiaraua il
modo che teneua à prouocare il Serpēte alla battaglia; nella terza il combattimento; &
questa parte cōteneua un modo di cātare al suono del Piffero chiamato Ο'δοντισμὸς; dal
battere de i dēti che faceua il Serpente quando era saettato: nella quarta si raccontaua la
vittoria d'Apollo; & nell'ultima si dichiaraua com'egli faceua festa con balli & salti, per
page 82la riceuuta uittoria del Serpente. Non sarebbe gran marauiglia, se gli Antichi hauesse-
ro anco saltato & ballato, quando si recitaua cotal Legge; percioche usauano questo an-
co nelle loro Tragedie & Comedie; & à ciascuna Saltatione haueano accommodato il
Diphno. li
bro. 1. c. 16. suo proprio modo; conciosiache (come mostra Atheneo) haueano una specie di Salta-
tione detta Emmelia, & accommodarono alla Comedia quella, ch'era detta Cordace.
Era anche appresso di loro una specie di Saltatione satirica, la quale chiamarono Σίκιννις;
& fù istituita da Bacco, dopo che hebbe domata l'India. Questa era una delle Leggi ti-
biarie, nella quale i Rhythmi, i Modi, i Costumi, & le Harmonie si mutauano, secondo
che la materia ricercaua. Haueano etiandio la Saltatione detta Carpea, la quale lascia-
rò di raccontare; percioche è recitata da AtheneoVt supra.
lib. 1. c. 8. tanto chiaramente, ch'ogn'uno leg-
gendo la potrà conoscere, quello che ella fusse, & in qual maniera la usassero; & da que-
ste due; cioè dal Certame pithico, & dalla Saltatione carpea, si potrà scorgere, in qual
modo gli Antichi recitassero l'altre Leggi. Potiamo hora uedere da quello, che si è det-
to, che la Musica hauea piu parti; l'Harmonia, il Rhythmo, il Metro, & l'Istrumento;
dal quale questa parte si diceua Organica, & ui era etiandio la Poesia & la Saltatione:
Ma queste parti alle uolte concorreuano tutte in una compositione; & tallora non tutte,
ma la maggior parte loro. Ne era lecito (come altre uolte si è detto) di mutare, ouero
innouare alcuna cosa, che di tal mutatione l'Inuentore non ne hauesse à riportare la pu-
nitione; onde durò lungo tempo tal costume, percioche conseruandosi la Musica in co-
tale essere, si conseruò anche la sua riputatione; ridotta dopoi à poco à poco nello sta-
to, nel quale hoggidi la ueggiamo; hauendosi dato i popoli alla crapula & alla lussuria,
poco curandosi di tal cosa, presero i Musici maggior licenza; & con molte altre cose in-
sieme, perdettero eglino & la Musica la sua antica grauità & riputatione; il che si uede
detto da Horatio, quando dice;De Arte
poetica.
Postquàm coepit agros extendere victor, & urbem
Latior amplecti muros, vinoꝗ diurno
Placari genius festis impune diebus,
Accessit numerisꝗ, modisꝗ licentia maior;
Et piu oltra seguita, dicendo quello, che di sopra hò commemorato; cioè,
Sic priscae motumꝗ & luxuriam addidit arti
Tibicem.
Et dopoi segue etiandio, dicendo;
Sic etiam fidibus uoces creuere seueris.
Onde è da notare, che Horatio nomina l'Antiche chorde Seuere, & bene; percioche
gli Antichi al suono di quelle recitauano se non cose seuere & graui. In tal modo adun-
que i Musici antichi, nella età che la Musica piu fioriua & era in maggior prezzo & ri-
putatione, recitauano le narrate materie nelle lor cantilene. Ma quali cose, & in qual
modo da i Moderni siano recitate; & quali siano state lasciate da un canto, ogn'uno, che
hà cognitione della Musica, da quello, che leggerà, & haurà accuratamente letto, lo
potrà giudicare & conoscere.
Quali siano stati gli antichi Musici.Cap. VI.
anticamente questi, i Poeti, ò Indouini & i Sapienti erano giudicati essere
una cosa istessa; essendo che nella Poesia era contenuta per tal modo la Mu-
sica, che gli Antichi per questa uoce Musica, non solo intesero questa Scien-
za, che principalmente tratta de i Suoni, delle Voci & de i Numeri; com'altroue
hò detto; ma intesero ancora con questa congiunto lo Studio delle humane lette-
re. La onde il Musico non era separato dal Poeta, ne il Poeta dal Musico; per-
page 83cioche essendo i Poeti de quei tempi periti nella Musica, & li musici nella Poesia; co-
me uuole Strabone; De situ or
bis. lib. 1.
l'uno & l'altro per una di queste due uoci, Musico, ò Poeta erano
chiamati. Et questo è manifesto da quello che dice Plutarco;In Musica. Che Eraclide, in quello
che raccolse gli antichi Musici & gli Inuentori di tal'Arte, uuole; che Anfione figliuolo
di Gioue & di Antipa fabricator delle mura di Thebe fusse il primo, che ritrouasse il
Canto della Cetera & la sua Poesia; & che costui non sia stato solamente Musico, ma
etiandio Poeta, & l'Inuentore del nominato Istrumento; come scriue anco Plinio;Natural.
hist. lib. 7.
cap. 56. &
ch'al suono di esso accompagnassi la uoce; & seguendo più oltra, dice; che Lino da Ne-
groponte compose in uerso Lamentationi & Hinni. Onde si può credere, che costui non
solamente fusse Poeta, ma anco Musico; conciosia che il medesimo Plinio dice, che co-
stui cantò al suono della Cetera. Segue ancora Plutarco, dicendo; che Filamone Del-
fico compose il nascimento di Latona & di Diana; & che Democodo da Corfù musico
antico compose la ruina di Troia: & che in uno poema celebrò le nozze di Venere & di
Vulcano. Non è cosa dubbiosa, che costui sia stato Musico; percioche questo è mani-
festo da quello, che si è detto. Terpandro ancora fù Musico & Poeta; come chiaramen-
te lo dimostra Plutarco dicendo; ch'ei fece in uerso Proemij al suono della Cetera.
Apollo etiandio non fù ignorante di queste due cose; come dimostra Horatio,De Arte
Poetica.
quando dice;
Ne forte pudori
Sit tibi musa lyrae solers, & cantor Apollo;
Percioche dice prima Sonatore della Lira; come quello (come uogliono alcuni) che
fù l'Inuentore di essa; dopoi lo chiama Poeta col nome di Cantore. Lascierò di racconta
re, quali fussero Orfeo & Arione; percioche è manifesto, che costoro non solo furono Mu
sici; ma celebratissimi Poeti ancora. Hesiodo etiandio fù posto tra i Musici; ancora che
non usasse mai d'accompagnare il Canto col suono della Lira; percioche usaua una Ver
ga di lauro, con la quale percotendo l'aria (come narra PausaniaIn De-
script. uete
ris Graeciae
lib. 9.) faceua un certo suo-
no, al quale era solito cantare i suoi Poemi; la onde gli Antichi li fecero una statua con
la Cetera sopra le ginocchia, & la posero tra quelle di Thamira, Arione, , & d'al-
tri nobilissimi & eccellentissimi Musici; per non priuarlo di cotale honore. Pindaro si-
migliantemente fù Musico & Poeta; come dalle sue opere si può comprendere; & da
quello etiandio che fece il magno Alessandro; imperoche quando fece ispianare &
ruinare Thebe, fece scriuere (come dicono Dione Chrisostomo,De Regno
Oratio. 2. Arriano De Gestis
Alexand.
lib. 1. & Pli-
nioNat. hist.
lib. 7. c. 29) sopra la sua casa questo Verso;
Πινδάρου τοῦ μουσοποιοῦ τὴν στέγαν μή καίετε;che uogliono dire;
Non abbrusciate la casa di Pindaro Musico.Et per non andare più in lungo, il Santissimo Dauid Re di Hierusalem & gran Pro-
feta, da Basilio magnoHomil. 54
Ad adole-
scentes. è chiamato non solamente Musico, ma Poeta anco de Sacre can-
tilene; & dal santo & dottissimo Hieronimo Ad Pauli
num. uien chiamato Simonide, Pindaro, Alceo,
Flacco, Catulo & Sereno; percioche scrisse con stile elegante i sacri Salmi in Verso liri-
co, alla guisa di Horatio & de i nominati; & si può credere, che più uolte li cantasse al
suono della Cetera, nel modo che cantaua, quando iscacciaua il maligno spirito da Saul.
Onde non è dubbio, ch'essendo stato Poeta, non si debba anco nominar Musico; con-
ciosiache la Scrittura santa lo chiama in più luoghi Psaltes; che vuol dire Cantore ò So-
natore; & il suo diuino Poema nomina Psalterium. Et di questo è testimonio Origene,Homil. 18.
c. 24. lib.
Nume.
dicendo; Che diremo noi della Musica? della quale il sapientissimo Dauid ne hauea ogni
scienza, & hauea raccolto la Disciplina di tutta la Melodia & de i Rhythmi; accioche
da tutte queste cose potesse ritrouar suoni, con i quali potesse mitigar sonando il Re
turbato & molestato dallo spirito maligno. Il simile dice AgostinoDe ciuit.
Dei
cap. 4. lib. 17. ancora. La onde ogni
ragion ne persuade à credere, che i Poeti antichi cantassero da se stessi i loro Poemi; &
c'hauessero congiunto la Musica con la Poesia; percioche se fusse stato altramente,
non hauerebbono usato tanto spesso nelle loro compositioni questa uoce Cantare; co-
me fece Homero; il quale diede principio all'Iliade in cotal modo,
page 84
Μῆνιν ἄειδε θεὰ.cioè;
Canta Dea l'ira;& Hesiodo, che incominciò la Teogonia in
questa maniera.
Μουσάων ἑλικωνιάδων ἀρχῶμεθ´ἀέιδειν;che uuol dire;
Le Muse d'Elicona incominciamo Cantare;
A i quali aggiungeremo il prencipe de i Poeti latini Virgilio, il quale incominciò in
cotal modo la sua Georgica;
Quid faciat laetas segetes, quo sydere terram
Vertere Mecoenas, vlmisꝗ adiungere uites
Conueniat; qua cura boum, qui cultus habendo
Sit pecori, atque apibus quanta experientia parcis,
Hinc canere incipiam;
Et alla sua Eneide pose un tal principio;
Arma, uirumꝗ cano.
Cosi anche Ouidio incomincia i Fasti con questi versi;
Tempora cum causis Latium digesta per annum,
Lapsaꝗ sub terras, ortaꝗ signa canam.
Onde il Petrarcha, imitando tutti costoro, diede principio ad una sua canzone in
questa maniera;1. Part.
can. 4.
Nel tempo della prima etade,
Che nascer vide, & ancor quasi in herba,
La fera uoglia, che per mio mal crebbe.
Perche cantando il duol si disacerba,
Canterò, com'io vissi in libertade.
Et il moderno Ariosto per seguir tal costume, incominciò anco lui il suo elegante
poema in questo modo;
Le donne, i caualier, l'arme, gli amori,
Le cortesie, l'audaci imprese io canto.
Ma doue vò io più uagando, se TerentioIn Prolo-
gis Heau-
tont. Hecy
rae: et Phor
mionis. poeta comico dimostrandoci la Poesia & la
Musica esser congiunte & quasi una istessa cosa, la nominò Studio musicale. Non è
adunque marauiglia, se i Musici & li Poeti erano anticamente riputati essere una cosa
istessa. Et se bene il Poeta è chiamato alle uolte con questa uoce latina Vates; che con-
uiene etiandio all'Indouino; non è fuor di proposito; conciosia che l'uno & l'altro (secon
In Ione. do il parer di Platone) sono mossi & agitati da un'istessa diuinità, ò diuina alienatione
di mente, & da un'istesso furore. Onde HomeroOdys. 22. nomina il Musico Αὐτοδίδακτος; per-
cioche canta non per humana istitutione; ma inspirato da i Dei; il che si scorge dalle
parole, che soggiunge, le quali dicono;
Θεὸς δέμοι ἐνφρεσὶν οἶμας.cioè,
Παντοίας ἐνέφυσεν;
Percioche Dio mi produsse in la mente
Ogni mia cantilena.
Però adunque molti Poeti gentili hanno alcuna uolta predetto le cose, c'haueano da
uenire; come si uede, che Virgilio, secondo l'opinione di Agostino Dottor Santo,De Ciuit.
Dei. lib. 10
cap. 27. &
Lib. 1. E-
pist. 3. Ad
Volusia-
num. non
conoscendo il nostro Redentore, ne per lume naturale, ne per uiua fede, cantò sotto 'l
nome d'un'altro il suo nascimento, quando disse;
In Pollio-
ne.
Vltima cumaei uenit iam carminis aetas:
Magnus ab integrò, seclorum nascitur ordo.
Iam redit & virgo, redunt Saturnia regna:
Iam noua progenies coelo demittitur alto.
Ancorache il Diuino Hieronimo, scriuendo à Paulino, sia d'altro parere; conciosiache
Virgilio si mosse à cantar queste cose, inuitato da gli Oracoli della Sibilla Cumana; co-
me cantò poco più oltra la liberatione del peccato originale, in cotal modo.
page 85
Te duce, si qua manent sceleris vestigia nostri.
Irrita, perpetuo soluent formidine terrras.
Et, che colui, c'hauea da nascere sarebbe Dio & Huomo, seguendo più à basso;
Ille Deûm uitam accipiet, diuisꝗ videbis
Permixtos heroas, & ipse videbitur illis.
Et che il Serpente nimico della humana natura douea perdere il regno, & che douea
rimanere in noi alcuna cosa, per rispetto del peccato originale, dicendo;
Occidet & Serpens, & fallax herba veneni.Et più oltra ancora;
Pauca tamen suberunt priscae vestigia fraudis.
Ouidio ancora lui nelle sue TrasformationiLib. 1. Me
tamor. chiaramente mostrò la uenuta del Figliuo
lo di Dio in carne, con queste parole:
Summo delabor Olympo,
Et Deus humana lustro sub imagine terras.
Et de i miracoli che fece, poco più abasso disse;
Signa dedi venisse Deum.
Pose etiandio le parole, che dissero quelli, che lo crucifissero; cioè, Se era figliuol di
Dio, che si liberasse dalla croce, & disse,
Experiar Deus hic discrimine aperto,
An sit mortalis, nec erit dubitabile uerum.
Lucano ancora cantò quello, che auerrebbe auanti il futuro vniuersale & finale giu-
dicio con tali parole;De Bello
ciuili. lib 1
Sic cùm compage soluta
Saecula tot mundi suprema coegerit hora,
Antiquum repetens iterum Chaos, omnia mistis
Sidera sideribus concurrent, ignea pontum
Astra petent, tellus extendere littora nolet,
Excutietꝗ fretum; fratri contraria Phoebe
Ibit, & obliquum bigas agitare per orbem
Indignata, diem poscet sibi; totaꝗ discors
Machina diuulsi turbabit foedera mundi.
In se magna ruunt.
Hauendo medesimamente Ouidio cantato tal cose con queste parole;Metamor.
lib. 1.
Esse quoque in fatis reminiscitur, affore tempus
Quo mare, quo tellus, correptaꝗ regia coeli
Ardeat, & mundi moles operosa loboret.
Di coteste cose sono molti essempii; ma lasciandoli da un canto, uerremo à quelli de
Sacri libri, & ritroueremo l'autorità del Santissimo Apostolo Paolo; il quale scriuendo
à Tito;Capit. 1. adducendo una sentenza di Epimenide Poeta candioto; lo chiama Profeta, di-
cendo; Ι῎διος τῶν αὐτῶν προφήτης: che uuol dire; propio Profeta di costoro; cioè, de i
Candioti. Douendosi adunque allora chiamare il Musico & il Poeta, ò l'Indouino per vn
nome commune, era conueniente ancora, che 'l nome di Sapiente li cōuenisse; percioche
(come ne fà auertiti PlatoneDe Leg. 1.) al uero Musico appartiene sapere & hauer cognitione de
tutte le Scienze; & cosi al Poeta, secondo il parere di Strabone;De Situ or
bis. lib. 1. la onde meritò da gli
Antichi esser chiamato solo Sapiente; conciosia che à quei tempi le città della Grecia
faceuano imparare à lor figliuoli la Poesia, non solo per cagione di piacere; ma per ca-
gione di casta moderatione. La onde i Musici, ch'insegnauano la Poesia, il Canto &
li Modi, che si sonauano con la Lira, ò Cetera & col Piffero, fecero professione, & si
attribuirono tal uirtù, d'esser non solo Correttori & emendatori de costumi; ma si fecero
etiandio chiamare Maestri; la qual cosa conferma Homero con queste parole;Odys. 3.
Πὰρ γὰρ ἔην καὶ ἀειδὸς ἀνὴρ, ὧ πόλλ´ἐπετελλενpage 86Che uogliono dire;
Ατρείδης τροίην δὲ κιὼν εἴρησθαι ἄκοιτιν;
Hauea presso di se un Cantore, al quale
Atride andando à Troia impose molte,
Che douessi seruar casta la moglie.
Meritamente adunque gli Antichi riputauano i Musici, i Poeti, ouero Indouini &
li Sapienti essere una cosa medesima.
Quali cose nella Musica habbiano possanza da indur l'Huomo in diuerse
passioni.Cap. VII.
in parte l'ignoranza & temerità d'alcuni sciocchi Compositori, non dirò Musi
ci, moderni; i quali, perche sanno porre insieme quattro, ouer sei Cifere mu-
sicali, predicano di loro stessi le maggiori cose del mondo; riputando nulla gli
Antichi & poco istimando alcun'altro de i Moderni; di modo che chi loro udisse, sen-
za dubbio direbbe, che ualessero più costoro nell'arte della Musica, che non ualsero
Platone & Aristotele nella Filosofia. Questi alle uolte, dopo l'hauersi lambicato il cer-
uello per molti giorni, pongono fuori alcune loro assai bene inordinate & goffe compo-
sitioni con tal riputatione & superbia, che li pare hauer composto un'altra Iliade, oue-
ro un'altra Odissea assai più dotta di quella di Homero. Meschini che sono, si douereb-
bono pur'accorgere del loro errore; percioche mai si udirà, che col mezo delle lor com-
positioni, habbiano conseruato la pudicitia & l'honestà d'alcuna femina; come già fece
uno de gli Antichi la pudicitia di Clitennestra moglie di Agamennone; come lasciarono
scritto HomeroOdys. 3. & Strabone;De Situ
orbis. li. 1. ne meno si udirà, che la Musica loro à i nostri tempi hab-
bia costretto alcuno à pigliar l'arme; come si legge appresso de molti, & spetialmen-
te appresso di Basilio Magno,Ad Ado-
lescentes.
Homil. 54 del grande Alessandro; ilquale da Timotheo musico
qual si fusse, fù col mezo della Musica sospinto ad operare un tale effetto. Non si udirà
ancora, che col canto loro habbiano fatto diuentare alcuno furioso mansueto; come
mostra Ammonio In praedi-
cab. Por-
phyrij. d'un giouane Taurominitano; che dall'accorgimento di Pitagora, &
dalla virtù del Musico, di furioso ch'era, diuentò humano & piaceuole: ma ben si ode
al presente il contrario; che le uituperose & sporche parole contenute nelle lor cantile-
ne, corrompono spesse uolte gli animi casti de gli vditori. Et se ben costoro sono degni
d'ogni biasimo & d'ogni castigo; sono nondimeno più da riprendere & castigare colo-
ro, che in luogo di ammonirli della lor pecoraggine, pigliano gran piacere & molto si
rallegrano, & lodano grandemente simili cantilene; mostrando di fuori quanto bene
siano composti nell'habito interiore; & di ciò non ci dobbiamo marauigliare; poi che
l'Animo lasciuo (come dice BoetioMusicae. li-
bro 1. c. 1.) ouer si diletta e gode de i Modi lasciui; ouer che
udendoli spesse uolte diuiene molle & effeminato; percioche Ogni simile appetisce il suo
simile. Ma lasciamo hormai costoro; poi che questi & simili altri errori lungamente si
potrebbono piangere, ma non già emendare; & ritorniamo al nostro proposito,
& diciamo, che grandemente dobbiamo lodare & riuerire i Musici antichi; con-
ciosia che per la loro virtù, col mezo della Musica, essercitata nel mostrato modo,
succedeuano tali & tanti effetti marauigliosi, che 'l uoler raccontarli, sarebbe qua-
si impossibile; & l'affermare che ciò fusse uero incredibile. Ma à fine che queste
cose non parino fauolose & strane da udire, uederemo quello, che poteua esser
la cagione de tali mouimenti. Ritrouo adunque che Quattro sono le cose, le
quali sempre hanno concorso insieme in simili effetti; delle quali mancandone
alcun, nulla, ò poco si potea uedere. Era la prima l'Harmonia, che na-
page 87sceua da i suoni, ò dalle Voci; la seconda il Numero determinato contenuto nel Verso;
il qual nominiamo Metro; la terza la Narratione d'alcuna cosa, la quale conteneua al-
cuno costume; & questa era la Oratione, ouero il Parlare; la quarta & ultima poi; sen-
za la quale nulla, ò poco si potea uedere; era un Soggetto ben disposto, atto à riceuere
alcuna passione. Et questo può esser manifesto; percioche se noi al presente poniamo
in atto la semplice Harmonia, senz'aggiungerle alcuna altra cosa; ella non hauerà pos-
sanza di fare alcuno effetto estrinseco de i sopranarrati; ancora c'haurà possan-
za ad un certo modo, di dispor l'Animo intrinsecamente ad esprimere più facilmente
alcune passioni, ouero effetti; come è ridere, ò piangere; com'è manifesto; che s'alcu-
no ode una cantilena, che non esprima altro che l'Harmonia; piglia solamente piacere
di essa, per la proportione, che si ritroua nelle distanze de i suoni, ò uoci, & si prepara
& dispone ad un certo modo intrinsecamente alla allegrezza, ouero alla tristezza; ma
non è però indotto da lei ad esprimere alcuno effetto estrinseco de i sudetti, ouer fare
alcuna altra cosa manifesta. Ma se à tale Harmonia si aggiunge il Numero determinato
& proportionato; subito ella piglia gran forza, & muoue l'Animo; come si scorge nel-
l'Harmonia, che si ode ne i Balli, la quale spesso ne inuita ad accompagnar seco alcu-
ni mouimenti estrinsechi col corpo, & à mostrare il piacere, che pigliamo di tale aggiun
to proportionato. Aggiungendo poi à queste due cose la Oratione; ò il Parlare, il
quale esprima Costumi col mezo della narratione d'alcuna Historia, ò Fauola; è impos-
sibile di poter dire quanta sia la forza di queste tre cose aggiunte insieme. E' ben uero,
che se non ui si trouasse il Soggetto disposto; cioè, l'Vditore, ilquale udissi uolentieri
queste cose, & in esse si dilettasse; non si potrebbe uedere alcun'effetto; & nulla, ò poco
farebbe il Musico. Percioche si come auiene al soldato, che per esser naturalmente in-
chinato alle cose della guerra è poco mosso da quelle, che trattano la pace & la quiete;
& alcune uolte è alterato da i ragionamenti dArme & de cose campestri, che molto li
dilettano; cosi il ragionar dell'Arme nulla, ò poco diletto porge all'Huomo, che sia per
natura pacifico, quieto & religioso; Ma si bene il ragionar delle cose di pace & della glo-
ria celeste molte uolte li muouono l'animo & lo costringono per dolcezza à piangere.
Et si come poco possono mouer i casti ragionamenti il Lussurioso; cosi gli altri, che so-
no lasciui & sporchi annogliano il Temperato & casto; imperoche ogn'uno uolontieri
ode ragionare di quella cosa, della quale maggiormente si diletta; & da simili ragiona-
menti è sommamente mosso; & per il contrario, hà in odio quelli, che non sono con-
formi alla sua natura; onde da simili ragionamenti non può esser commosso. Per la qual
cosa, se Alessandro figliuolo di Filippo Re di Macedonia fu indotto da Timotheo mu-
sico, ò da Senofanto (com'alcuni uogliono) à prender l'arme con gran furore; non
dobbiamo marauigliarsi; percioche era in tal maniera disposto, che uolontieri,
& con sommo piacere vdiua ragionamenti, che trattauano delle cose della guerra; &
da tali ragionamenti era indotto à far cose marauigliose. Onde ben lo dimostrò un cer-
to huomo ad alcuni, che si marauigliauano, che la Musica hauesse in lui tanta forza, di-
cendo; Se questo Senofante è huomo tanto ualoroso, come di lui si dice; perche non
ritroua egli alcuni modi, i quali lo riuochino dalla battaglia? Volendo inferire, che
non è gran cosa & di molta arte, spinger l'Huomo da quella parte, nella quale per sua
natura è inchinato; ma si bene è cosa marauigliosa à ritirarlo da quella; & è cosi in ue-
ro. Però se Alessandro ad altro non attendeua, che à quelle cose, le quali poteua-
no condurlo ad una gloria immortale, che erano l'Arme; non era cosa difficile di po-
terlo indurre à far li narrati effetti; della qual gloria quanto fusse ambitioso & sitibon-
do, da questo si può comprendere; che cercò d'auanzare ogn'altro; ne hebbe inuidia à
chiunque si fusse nelle arme; percioche ad alcuno mai non si riputò in cotal cosa infe-
riore; se non ad Achille, per hauere hauuto Homero, che con si sublime stile cantò
di lui; onde lo dimostrò; percioche si legge, che
page 88
Giunto Alessandro alla famosa tomba
Del fero Achile, sospirando disse: Franc. Pe-
trarca. o-
de. 115.
O fortunato, che si chiara tromba
Hauesti, che di te si alto scrisse.
Si ricerca adunque un Soggetto tale, che sia ben disposto; conciosia che senza esso (co
me ancora hò detto) nulla ò poco si uederebbe. Et benche in simili mouimenti fatti per
la Musica, ui concorrino le nominate cose; nondimeno il preggio & l'honore si dà al
Composto delle tre prime, che si chiama Melodia; percioche se ben l'Harmonia sola hà
una certa possanza di dispor l'animo & di farlo allegro, ò mesto; & che dal Numero posto
in atto le siano raddoppiate le forze; non sono però potenti queste due cose poste insieme
di generare alcuna passione estrinseca in alcun soggetto, al modo detto; essendoche tal
possanza acquistano dalla Oratione, che esprime alcun costume. Et che questo sia uero,
lo potiamo uedere; percioche Alessandro non fù mosso dall'Harmonia solamente; ne
meno dall'Harmonia accompagnata col Numero; ma si bene (come uuole Suida, Eu-
thimio & altri ancora In Proe-
mio lib.
Psalmorū.) dalla legge Orthia, di sopra commemorata, & dal Modo Fri-
gio; dal qual, & forse anco da tal Legge, il sudetto giouane Taurominitano ebbrio (co-
me narra BoetioMusicae li-
bro 1. ca. 1.) fù sospinto, quando uolse abbrusciar la casa d'un suo riuale, nella
quale era nascosta una meretrice; la onde Pitagora ò Damone Musico, che ei fusseAttic. no-
cti. lib. 16.
cap. 19.; co-
me scriue Galeno;De placi-
tis lib. 5.
conoscendo tal cosa, commandò al Musico, che mutasse il Modo
& cantasse lo Spondeo, col quale placò l'ira del Giouane & lo ridusse al primo stato.
Arione etiandio Musico & inuentore del Dityrambo (secondo l'opinione di Herodoto,Hist. lib. 1.
& di Dion Chrisostomola Orat.
corinthia-
ca. 37. ) prese ardire di precipitarsi nel mare, hauendo (per mio pare-
re) cercato di comporsi prima col mezo di cotal Legge (come recita GellioAttic. no-
cti. lib. 16.
cap. 19. ) un'animo
intrepido & uirile; per poter fare cotal cosa senz'alcun timore. Hora potiamo uedere,
che tali & cosi fatti mouimenti sono stati fatti, non per uirtù delle prime parti della Me-
lodia; ma si bene dal tutto; cioè, dalla Melodia istessa, la quale ha gran forza in noi, per
uirtù della terza parte; cioè, delle Parole, che concorrono alla sua compositione, sen-
za le quali sempre si haurebbe fatto, ò farà nulla ò poco; percioche il Parlare da sè sen-
za l'Harmonia & senza il Numero hà gran forza di commouer l'Animo; conciosia che
se noi haueremo riguardo à cotal cosa, uederemo ch'alcune fiate, quando udimo leg-
gere, ò raccontare alcuna Fauola, ouero Historia, siamo costretti ridere, ò piangere;
& alcune uolte c'induce all'ira & alla colera; & alle fiate di mesti ne fà diuentare allegri;
& cosi per il contrario; secondo il soggetto che in essa si contiene. Ne dobbiamo di ciò
marauigliarsi: percioche il Parlare ne induce alla furia & ne placa; ne fà esser crudeli &
anco ne addolcisce. Quante uolte è accaduto, che leggendosi semplicemente una pieto
sa Historia, ò Nouella, gli ascoltanti non siano stati presi da compassione in tal modo,
che al loro dispetto dopo alcuni sospiri, li sia stato dibisogno accompagnarli le lagri-
me? Dall'altra parte, quante fiate è auenuto, che leggendosi, ò narrandosi alcuna Fa-
cetia, ò Burla, alcuni non siano quasi scoppiati dalle risa? Et non è marauiglia; percio-
che il più delle uolte se 'l si rappresenta à noi alcuna cosa degna di cōmiseratione, l'animo
è commosso da lei & è indutto à piangere; & se udimo cosa, la quale habbia del feroce
& del crudele, l'animo declina & si piega in quella parte. Et di ciò (oltra ch'è manife-
sto) n'è testimonio Platone,De Rep. 10 quando dice; che Qualunque uolta udimo Homero, ouer
alcun altro Poeta tragico, che imiti alcuno de gli Heroi afflitto per il dolore gridar for-
temente & pianger la sua fortuna con modi flebili, percuotendosi il petto con pugni; ad
un certo modo si dilettiamo; & hauendo una certa inclinatione à coteste cose, seguitia-
mo quelle & insieme siamo presi da tal passioni, & lodiamo quello, come buon Poeta,
il qual grandemente commuoua l'animo nostro. Questo ancora più espressamente con-
ferma Aristotile,Politi. lib.
8. cap. 5. dicendo; Ancora si uede, che gli Huomini udendo l'Imitationi, han-
no compassione à quei casi, quantunque siano senza Numero & senz'Harmonia. Ma
se 'l Parlare hà possanza di muouer gli animi & di piegargli in diuerse parti, & ciò senza
page 89l'Harmonia, & senza il Numero; maggiorimente haurà forza quando sarà congiunto
co i Numeri, & co i Suoni musicali, & con le Voci. Et tal possanza si fà chiaramente mani
festa per il suo contrario; percioche si uede, che quelle Parole muouono men l'animo,
le quali sono proferite senza Melodia & senza Proportione, che quelle, che sono profe-
rite con i debiti modi. Però gran forza hà da se stesso il Parlare; ma molto più hà forza
quando è congiunto all'Harmonia; per la simiglianza che hà questa con noi & alla po-
tenza dell'Vdito; conciosiache niuna cosa è tanto congiunta con le nostre menti; come
dice Tullio;De Orato-
re. lib. 3.
Pro Arc. che i Numeri & le Voci, per le quali si commouiamo, infiammiamo, pla-
chiamo & rendiamo languidi. Non è questo gran marauiglia; dice egli ancora; che i
sassi, le solitudini, le spelunche, & gli antri rispondono alle uoci? & le bestie crudeli &
feroci spesse uolte sono dal canto fatte mansuete, & da esse sono fermate? Nè ci dobbia-
mo di ciò marauigliare; conciosia che se 'l uedere una Historia, ò Fauola dipinta sola-
mente, ne muoue à compassione tallora, tallora ne induce à ridere; & tallora ne sospin-
ge alla colera; maggiormente questo può fare il Parlare, il qual meglio esprime le cose,
che non fà alcun Pittore, quantunque eccellente sia, col suo pennello. Onde si legge di
uno, ilquale riguardò una imagine dipinta, & fù sospinto à piangere;Aristot. in
Poetica. & di Enea, Aeneid. li
bro. 1. che
entrato nel tempio fabricato da Didone nella nuoua Carthagine;
Videt Iliacas ex ordine pugnas,
Bellaꝗ iam fama totum vulgata per orbem,
Atridas, Priamumꝗ & saeuum ambobus Achillem.
Constitit; & lachrymans: Quis iam locus (inquit) Achate,
Quae regio in terris nostri non plena laboris?
En Priamus: sunt hîc etiam sua premia laudi:
Sunt lachrymae rerum, & mentem mortalia tangunt.
Solue metus; feret haec aliquam tibi fama salutem.
Sic ait: atque animum pictura pascit inani.
Multa gemens, largoꝗ humectat flumine uultum.
Et di Porcia figliuola di Catone Vticense si legge ancora,Plutar. in
Vita M.
Bruti. che hauendo ueduto una
certa Tauola di pittura, pianse amaramente. Et benche la Pittura habbia forza di com-
mouer l'animo; nondimeno maggior forza hebbe la uiua uoce di Demodoco Musico &
sonatore di Cetera, il quale riducendo in memoria Vlisse, dipingendoli le cose passate,
come se li fussero state presenti, lo costrinse à piangere; dal qual effetto; come dice Ho-
mero Odis. 8. & Aristotele;In Poetica fu subito conosciuto dal Re Alcinoo. Ma non pure allora accascarono
coteste cose; ma etiandio à i nostri tempi si uede accascare il medesimo tra molte genti
Barbare; imperoche raccontandosi da i lor Musici con certi uersi al suono d'uno Istru-
mento i fatti di alcuno loro capitano; secondo le materie, che recitano, quelli ch'ascol-
tano cambiano il uolto, facendolo per il riso sereno, & tallora per le lagrime oscuro; &
per tal modo sono presi da diuerse passioni. Si può adunque concludere, che dalla Me-
lodia; & principalmente dalla Oratione, nella quale si contenga alcuna Historia, ò Fa-
uola, ouero altra cosa simile, che esprima imitationi & costumi, siano stati & ancora si
possino porre in atto cotali effetti; & l'Harmonia & il Numero esser cose, le quali dispon-
gono l'animo; purche 'l Soggetto sia sempre preparato & disposto; senza il quale in uano
ogni Musico sempre si affaticarebbe.
In qual modo l'Harmonia, la Melodia & il Numero possino muouer l'animo & disporlo à
varij effetti; & indur nell'Huomo variati costumi.Cap. VIII.
lodia, & il Numero hauessero forza ciascuna da per se di dispor l'animo, & poste
tutte insieme, indurlo in diuerse passioni: essendo senz'alcun dubio cose e-
strinseche, lequali nulla, ò poco fanno alla natura dell'Huomo; ma in uero è cosa pur
page 90troppo manifesta, c'hanno cotal forza: onde è da notare, ch'essendo le Passioni dell'
Animo poste nell'Apetito sensitiuo corporeo & organico, come nel suo uero soggetto;
ciascuna di esse consiste in una certa proportione di calido & frigido, & di humido & sec
co, secondo una certa dispositione materiale; quasi di numero à numero: di maniera
che quando queste Passioni sono fatte, sempre soprabonda una delle nominate qualità in
qualunque di esse. Onde si come nell'Ira predomina il calido humido, cagione dell'in-
citamento di essa; cosi predomina nel Timore il frigido secco, il quale induce il ristrengi
mento de i spiriti. Il simile intrauiene etiandio nell'altre passioni, che dalla soprabon-
danza delle nominate qualità si generano. Et queste Passioni tutte, senza dubbio, sono
riputate uitiose nell'Huomo morale; ma quando tali soprabondanze si riducono ad una
certa mediocrità, nasce una operation mezana, che non solo si può dire uirtuosa; ma
anco lodeuole. Questa istessa natura hanno etiandio le Harmonie; onde si dice, che l'
harmonia Frigia hà natura di concitar l'Ira, & hà dell'affettuoso; che la Mistalidia fa star
l'Huomo più ramaricheuole & più raccolto in se stesso: & che la Doria è più stabile, &
molto appropriata à i costumi de Forti & Temperati; essendoche è mezana tra le due no-
minate; & questo si comprende nella diuersa mutatione dell'Animo, che si fà, quando si
ode coteste Hamonie. Per la qual cosa potiamo tener per certo, che quelle Proportio-
ni istesse, che si ritrouano nelle qualità narrate, si ritrouano anco nelle Harmonie; poi che
D'un solo effetto non gli è se non una propria cagione; la quale nelle Qualità già dette &
nelle Harmonie, è la proportione. La onde potiamo dire, che quelle istesse Proportio-
ni, che si ritrouano nella cagione dell'Ira, ò del Timore, ò d'altra passione nelle sopra-
dette qualità; quell'istesse si ritrouino anco nell'Harmonie, che sono cagioni di conci-
tare simili effetti. Queste cose adunque essendo contenute sotto simili proportioni; non
è dubbio, che si come le Passoni sono uarie, che non siano anco uarie le Proportioni del
le cagioni; perche pur troppo è uero, che Delle cose contrarie sono contrarii gli effetti. Es
sendo adunque le passioni, che predominano ne i Corpi per uirtù delle nominate quali-
tà, simili (dirò cosi) alle Complessioni, che si ritrouano nelle Harmonie; facilmente po-
tiamo conoscere, in qual modo l'Harmonie possino mouer l'Animo & disporlo à uarie
passioni; percioche s'alcuno è sottoposto ad alcuna passione con diletto, ouer con tri-
stezza, & ode un'Harmonia, la quale sia simile in proportione; tal passione piglia au-
mento; & di questo n'è cagione la Similitudine; laquale (come uuole BoetioMusicae li
bro. 1. c. 1.) ad ogn'
uno è amica & la Diuersità gli è cōtraria, & odiosa; ma se auiene, che ne oda una di pro-
portione diuersa, tal passione diminuisce; et se ne genera una contraria; & si dice, che
allora tale Harmonia purifica da tal passione colui, che la ode, per la corruttione, & per
la generatione d'un'altra cosa contraria; come si uede; che s'alcuno è molestato d'alcuna
passione, la qual uenga con tristezza, ò con lo accendersi il sangue; come la Ira; & oda
un'Harmonia di contraria proportione, laquale contenga alcuna dilettatione; allora
cessa in lui l'Ira & si corrompe; & immediatamente si genera la Mansuetudine; cosa che
suole auenire anco nell'altre passioni; poiche Ogn'uno naturalmente si diletta più di
quella Harmonia, laquale è più simile, conueniente & proportionata alla sua natura &
complessione, & secondo che è disposto; che di quella, che gli è contraria. Nascono adun
que le Dispositioni diuerse ne gli huomini, non da altro, che da i diuersi mouimenti del
lo Spirito, ilquale è il primo Organo si delle sensitiue, quanto delle motiue Virtù dell'
anima per alteratione, ò per moto locale; da i quali mouimenti alcuna uolta intrauie-
ne il raccoglimento, alcuna uolta il boglimento, & alle uolte la dilatatione de i Spiriti; i
quali Mouimenti diuersi non solamente nascono dalla diuersità delle Harmonie musica-
li; ma da i Numeri soli ancora; come è manifesto; percioche mentre noi attentamente
udimo leggere, ò recitar Versi; alcuni ci ritengono in una certa modestia, alcuni ci muo
uono à cose liberali & diietteuoli, & alcuni ci incitano à cose leggieri & uane, & altri c'in
ducono in un moto uiolento. Et di questo basta solamente lo essempio d'Archiloco: il
quale, come dice Horatio;De Arte
poetica.
page 91
Proprio rabies armauit Iambo.
Dalle quali cose si può comprendere, in qual modo l'Harmonia & il Numero con
una certa dispositione possino diuersamente mutar le passioni & costumi dell'animo.
Ma perche hò detto; che Ogn'uno naturalmente più si diletta di quella Harmonia,
la quale è più simile, conueniente & proportionata alla sua natura, ò complessione, &
secondo ch'è disposto; però è da notare; che essendo l'Harmonia & li Numeri parti del-
la Melodia; & hauendo l'Harmonia & li numeri facoltà di mouer l'Huomo interiormen
te, come si è dimostrato: non è dubio che la Melodia non habbia maggiormente forza
di mutar di dentro le Passioni & i costumi dell'Animo di quello, che hà ciascuna di esse
parti separatamente. Auertisca però qui ogn'uno, che (secondo la dottrina de 'l Filoso-
fo 2. Ethi. c. 1) le Virtù morali & li Vitij non nascono con esso noi; ma si generano per molti habiti
buoni, ò tristi frequentati, nel modo che uno per sonare, ò scriuere spesse fiate male,
diuenta tristo Sonatore, ò Scrittore; ouer per il contrario, essercitandosi spesse uolte
bene, diuenta buono & eccellente. La onde colui che spesso essercita la Iniustitia, per
tal cosa diuenta Iniusto; & colui ch'essercita la Iustitia, diuenta Iusto; nel modo che
colui, che si usa à temere i pericoli diuenta timido, & non li stimando diuiene audace.
Di maniera che, quali sono le Operationi, tali sono gli Habiti; & dalle buone sono i
buoni, & dalle triste i tristi Habiti. Essendo adunque l'Harmonie & i Numeri simili alle
Passioni dell'animo; come afferma Aristotele;Probl. 29.
parti. 19. potiamo dire, che l'assuefarsi alle Harmo
nie & à i Numeri, non sia altro, che uno assuefarsi & disporsi à diuerse Passioni, & à
diuersi Habiti morali & costumi dell'animo; percioche quelli, che odono le Harmonie
& li Numeri, si sentono tramutare secondo la dispositione dell'animo, alcuna uolta nell'
amore, alcuna uolta nell'ira, & alcuna uolta nell'audacia; il che da altro non auiene
come hò detto; che dalla simiglianza, che si troua tra le sopradette Passioni con le Har-
monie. Et questo si uede; conciosia che uno, il quale hauerà più uolte udito una sorte d'
Harmonia, ò de Numeri, si dilettarà maggiormente, per hauersi già assuefatto in quel-
la. Dobbiamo però sapere (per maggiore intelligenza di quello, che si è detto) che il
Numero quantunque si piglia (come nella Prima parte uedemmoCap. 12.) per la Moltitudine.
composta de più unità, & per l'Aria (dirò così) d'alcuna Canzone; come intese ilIn Moeri.
Poeta, quando disse;
Numeros minimi, si uerba tenerem;
Et in molti altri modi; nondimeno in questoluogo non è altro, che una certa misura
di tempo breue, ò lungo, nel quale si scorge la proportione, ò misura di due mouimen-
ti, ò più, insieme comparati, secondo una cambieuole ragione di tempo di essi moui-
menti; il quale è detto Rhythmo; & si scorge ne i piedi del Metro & del Verso, che si
compongono di piu Rhythmi ò Numeri, con un certo ordine, ò spacio determinato.
Ma il Metro & il uerso è una certa Compositione & ordine de piedi, ritrouata per dilet-
tar l'vdito; oueramente è un'Ordine & Compositione de più uoci, finita con Numero
& modo. Potrei hora dire la differenza, che si ritroua tra il Metro & il Verso; ma per
breuità la uoglio passare; imperoche coloro, che desiderassero di saperla, leggendo il
Cap. 2. del Terzo lib. della Musica del P. S. Agostino, potranno d'ogni suo desiderio esser
satisfatti. Solamente si haurà da auertire, che il Rhythmo è differente dal Metro &
del Verso in questo; che il Metro & il Verso contengono in se un certo spacio determi-
nato; & il Rhythmo è piu uniuersale, & ha i suoi spacij liberi & non determinati; onde
è come il Genere; ma il Metro & il Verso sono meno uniuersali, & sono come la Specie;
percioche da quello si hà la quantità, ò la materia, & da questi la qualità, ò la forma.
Alcuni altri dicono, che 'l Metro & il Verso è Ragione con modulatione; & il Rhy-
thmo modulatione senza ragione. Ma sia quello, che si uoglia, questo sia detto à ba-
stanza intorno à cotal cosa.
page 92
In qual genere di Melodia siano stati operati i narrati effettiCap. IX.
cap. 16.) tre sorti di
Melodia, l'una delle quali è detta Diatonica, l'altra Chromatica, & la terza
Enharmonica, sono stati alcuni, che, indotti da una lor falsa ragione, hanno
hauuto parere, che gli effetti della Musica narrati di sopra, non siano, ne pos-
sino esser stati operati nel primo de i nominati Generi; ma si bene ne i due ultimi; nel
Chromatico, ouer nell'Enharmonico; percioche dicono; se fussero stati operati nel
Diatonico, si uederebbono tali operationi anco ne i tempi nostri, essendo solamente tal
Genere, & non gli altri, essercitato da i Musici; conciosia che Ogni cagione posta in at
to non manca mai del suo effetto; quando da alcuno soprauenēte accidente non sia impe
dito. Onde non si uedendo hora tali cose, concludono, che per il passato, ne anco siano
state operate nel predetto Genere. Costoro ueramente di gran lunga s'ingannano; per-
cioche suppongono una cosa falsa per uera, & pongono due cagioni diuerse; come se fus
sero simili. La prima si dimostra esser falsa per questa ragione; che la Musica mai cessa in
diuersi modi & tempi di operare & di produr uarii effetti, secondo la natura della cagio-
ne, & secondo la natura & dispositione del Soggetto, nel quale opera cotali effetti. Laon
de uediamo etiandio à i nostri giorni, ch'ella inducein noi uarie passioni, nel modo che
anticamente faceua; imperoche alle uolte si uede, che recitandosi alcun bello, dotto & ele
gante Poema al suono d'alcuno Istrumento, gli ascoltanti sono grandemente commos-
si & incitati à far diuerse cose: come ridere, piangere, ouer'altre simili; & di ciò si è ue-
duto l'esperienza dalle belle & leggiadri compositioni dell'Ariosto; che recitandosi (ol-
tra l'altre cose) la pietosa morte di Zerbino; & il lagrimoso lamento della sua Isabella;
non meno piangeuano gli ascoltanti mossi da compassione, di quello che faceua Vlisse
udendo cantare Democodo musico & poeta eccellentissimo. Di maniera che se bene
non si ode, che la Musica al di d'hoggi operi in diuersi soggetti, nel modo che già operò
in Alessandro; questo può essere, perche le cagioni sono diuerse & non simili, come sup-
pongono costoro; percioche se per la Musica anticamente erano operati tali effetti; era
anco recitata nel modo, che di sopra hò mostrato; & non con una moltitudine de parti,
& tanti Cantori & Istrumenti, nel modo ch'ella si usa al presente, ch'alle uolte non si ode
altro che un strepito & romor de uoci mescolate con diuersi suoni, & un cantar senz'al-
cun giuditio & senza discretione, con un disconcio proferir de parole; che non si ode al
tro che confusione; onde la Musica in tal modo essercitata non può fare in noi effet-
to alcuno, che sia degno di memoria. Ma quando ella è recitata con giudicio, & più s'
accosta all'uso de gli antichi; cioè, ad un semplice modo, cantando al suono della Li-
ra, del Leuto, o d'altri simili Istrumenti alcune materie, che hanno del Comico, ouer
del Tragico, & altre cose simili con lunghe narrationi; allora si uedono i suoi effetti; per-
che ueramente possono muouer poco l'animo quelle Canzoni, nelle quali si racconta
con breue parole una materia breue; come si costuma hoggidi in alcune Canzonette,
dette Mandriali; le quali benche molto dilettino, non hanno però la sopradetta forza.
Et che sia uero che la Musica più diletti uniuersalmente quando è semplice, che quando
è recitata con tanto arteficio & cantata con molte parti; si può comprender da questo;
che con maggior dilettatione si ode cantare un solo al suono dell'Organo, della Lira, del
Leuto, ò d'un'altro simile Istrumento, che non si ode molti. Et se pur molti cantando
insieme muouono l'animo; non è dubio, che uniuersalmente con maggior piacere, s'
ascoltano quelle Canzoni, le cui Parole sono da i Cantori insieme pronunciate, che le
dotte compositioni, nelle quali si odono le Parole interrotte da molte parti. Per la qual
cosa si uede, che le cagioni sono molto diuerse de gli effetti, & differenti l'una dall'altra,
& non simili, come costoro le pongono. Onde non sarebbe marauiglia, quando bene
page 93al presente uno de i narrati effetti non si uedesse. Ma tengo & credo per certo, che quan
do i Musici moderni fussero tali, quali erano gli Antichi, & la Musica si essercitasse, come
gia si faceua; che molto più effetti l'udirebbono à i nostri tempi, che non sono quelli, che
li leggono operati per inanti; percioch'al presente è maggiore la moltitudine de i Musi
ci, che già non era. Ma lasciamo queste cose; percioche sono manifeste ad ogn'uno, che
hà giudicio; & cerchiamo di ribattere l'opinione loro con uiue & efficaci ragioni, mo-
strandogli il loro errore; il che facilmente ne uerrà fatto, per uno inconueniente, che ne
seguirebbe; oltra gli altri, che sono molti; & è questo: Che se fusse uero quel, che dico-
no; ne seguirebbe, che l'Artificiale potesse più che 'l Naturale, quando fusse soprauanza-
to nel porre in essere tali effetti; conciosia che 'l Genere diatonico è naturale, & gli altri
due sono arteficiali; come dalle parole di VitruuioArchitec.
lib. c. 4. si può comprendere, le quali dico-
no; I Generi delle Canzoni sono tre; il primo è quello, che i Greci chiamano Har-
monia, & è modulatione conceputa dall'Arte, & la sua Canzone hà molta grauità &
autorità non poca; il Chroma con sottil diligenza & spessezza de modi hà dilettatione
più soaue; & il Diatonico, per esser naturale, è più facile per la distanza de gli Interual-
li, che ei ritiene. BoetioMusicae li-
bro. 1. c. 21 ancora nomina il Diatonico più d'ogn'altro duro & naturale;
& dice Più naturale; conciosiache ciascuno d'essi Generi dalla parte de i Suoni & delle
Voci è naturale; ma non dalla parte de gli Interualli; percioche il rimettergli & lo allun
gargli appartengono all'Arte, & non alla Natura; come altroue uederemo.Infra c. 15. Franchino
Gaffuro Operis an-
gelici. cap.
10. lib. 1. etiandio mosso dall'autorità de gli Antichi dice, che 'l Chromatico è arteficiosa-
mente fatto per ornamento del Diatonico; & lo Enharmonico è detto Perfetto orna-
mēto del naturale & artificiale Systema musico Diatonico & Chromatico; & dice anco,
che 'l Tetrachordo Diatonico è naturale. Appare similmente vn'altro grande inconueniē
te; che sforzandosi costoro di diffender la loro opinione, pongono l'Effetto inanti la Ca
gione per grandissimo spacio di tempo; il che è contra ogni douere; conciosiach'ogni
cagione, ouero è prima dell'effetto, ouer si pone insieme con esso lui. Ma ueramente lun-
go tempo dopo tali effetti successero non solamente gli Inuentori, ma l'Inuentione etian
dio de tali Generi, & di questo n'è testimonio Plutarco,In Musica. ilquale dice; che 'l diatonico è
d'ogn'altro Genere antichissimo; percioche essendo per auanti ogni cosa Diatonica nella
Musica, gran tempo dopoi (s'è vero quello che scriuono alcuni) fù ritrouato il genere
Chromatico da Timotheo Milesio lirico figliuolo di Tersandro, ò di Neomiso, ouero di
Filopide, come vuole Suida & Boetio.Musicae li-
bro. 1. c. 2. Di costui come ritrouator di cose nuoue (com'io
credo) fà mentione Aristotele nella sua Metaphisica,Lib. 2. c. 2. dicendo; Se non fusse stato Timo-
theo non haueressimo la Melopeia varia, ò molteplice, che la uogliamo dire, ne costui
haurebbe acquistato cotali cose, se Frinide non fusse stato auanti di lui. Et se costui fu
quello, che operò co 'l mezo della Musica in Alessandro quel tanto marauiglioso effetto;
come di sopra habbiamo detto; & visse nella Centesima & vndecima Olimpiade; in-
torno anni 338. auanti l'Anno di nostra Salute; percioche Alessandro regnaua in quei
tempi; & pur si legge de molti altri effetti marauigliosi operati per la Musica, inanti che
costui si nominasse. Dopo costui venne Olimpo; quale egli si fusse, come di parere d'Ari-
stosseno riferisce Plutarco,In Musica. primo ritrouatore del genere Enharmonico; essendo per
auanti nella Musica ogni cosa Diatonica & Chromatica. Ragioneuolmente tali effetti
douerebbono esser successi dopo gli Inuentori, & dopo l'Inuentione; accioche (secondo
la verità) le Cagioni fussero prima de gli Effetti; ma stiamo à vedere se uogliamo scorger
la pazzia di costoro. Ritrouo nelle historie, che Pitagora, per la cui accortezza la Musi-
ca operò nel giouine Taurominitano il sopranarrato effetto; fù nel tempo, che Seruio
Tullio regnaua in Roma, & ne i tempi di Ciro Re di Persia, intorno l'anno 600. auan-
til'Auenimento del Figliuol di Dio, nel tempo di Sedechia Re de Giudei, anni intorno
260. auanti i tempi d'Alessandro. Come poteuano adunque i due sudetti generi operar
cosa alcuna; se per lungo tempo dopo, da gli Inuentori furono ritrouati? Di più; Ho-
mero Poeta famosissimo scrisse in verso Heroico gli infortuni & casi diuersi d'Vlisse; &
page 94come da Demodoco fu prouocato à piangere; & disse, che per il pianto fù conosciuto da
Alcinoo; nondimeno Homero fù per anni 490. poco più, o meno auanti Pitagora, &
auanti che Roma fusse edificata anni 160. ne i quali tempi regnaua Iosafà nella Giudea.
Più oltra: Dauid profeta, ilquale iscacciò molte uolte il maligno spirito da Saul, fù
auanti Homero intorno anni 20. per quello c'hò potuto raccorre nelle Historie; & auan
ti esso Timotheo più de anni 700. O' gran pazzia di costoro; come può essere, che non
ui essendo la cagione, che pongono; se non per tanti & tanti anni dopo; ne possa da lei
uscire alcuno effetto; Veramente se hauessero posto insieme la cagione & lo effetto, cotali
cose sarebbono almen dette con qualche ragione: ma perche Huomini sono, hanno
(come molt'altri) potuto errare; però è dibisogno d'hauerli per iscusati. Se adunque col
mezo del Chromatico, non furono operati quei effetti; i quali habbiamo raccontati di
sopra; minormente furono fatti col mezo dell'Enharmonico; percioche questo fù ritroua
to molto tempo dopo. Non essendosi adunque operati col mezo de questi due Generi, se
Nota. guita che fussero operati col mezo del Diatonico. Ma poniamo che Timotheo inuento-
re del genere Chromatico non fusse stato quello, che spingesse Alessandro à pigliar l'ar-
me; come forse alcuni potrebbono dire, seguendo l'opinione di Suida Greco dignissi-
mo scrittore; ma si bene vn altro più antico di lui; imperoche questo (come dice Dione
ChrisostomoOratione.
1. De Re-
gno. & Suida) fù veramente sonator di Piffero, & fù chiamato al seruiggio d'A-
lessandro, & fù più antico di quello;Vide cap.
3. lib. 4.
Supple. che fu sonator di Lira, ò di Cetera; ciò non farà,
che non si appiglino al falso; essendo che tanto l'uno quanto l'altro si trouarono al tem-
po di questo Re. Facciamo etiandio che le ragioni addotte di sopra da noi siano di poco
ualore per questo non conseguiranno il lor uolere; percioche se lo effeminar l'animo, ò
auilirlo, & il farlo diuenir molle; come è la natura del Chromatico; secondo che scriue
ogni Greco & Latino scrittore; è contrario effetto à farlo diuentar virile & forte; non
poteua quel Timotheo, qual'ello si fusse col mezo di questo Genere operare in Alessan-
dro vn tale effetto, che ueramente fù da virile & da forte; ma col mezo del Diatonico, il
quale è piu d'ogn'altro seuero. Tutte queste cose hò uoluto discorrere innanti ch'io inco
minci à trattar quelle cose, che appartengono à questa Seconda parte; per mostrar la dif
ferenza, che si ritroua tra la Musica antica & la moderna; accioche si vegga quello, ch'e-
ra la cagione principale, di fare operare quei mirabilissimi effetti, che si leggono, c'hà
operato la Musica; & non si attribuisca alle Harmonie (come fanno alcuni sciocchi) se nō
quello, che le conuiene; & acciò non paia strano quello, ch'io ragionerò intorno i due
vltimi generi Chromatico & Enharmonico. Ma in qual modo gli Antichi procedessero
nelle loro Harmonie, lo vederemo altroue. Ritornando adunque al nostro principale in-
tendimento, incomincierò à ragionar dell'Origine de i Suoni & delle Voci; conciosia
che sono considerate dal Musico come primi Elementi, de i quali si fanno le cose, che ei
considera nella sua Scienza.
De i Suoni & delle Voci, & in qual modo naschino.Cap. X.
tesse far uerso l'altra, ò l'una non potesse muouere, ò spinger l'altra, mancareb-
be necessariamente il Mouimento, & mancarebbono i Suoni & le Voci; & per
conseguente ogni Consonanza musicale, ogni Harmonia & ogni Melodia;
poi che da altro non nascono, che dalla repercussione violenta dell'Aria; la qual senza
dubbio alcuno non si può hauer senza il Mouimento. Onde alla loro generatione (come
vuole Aristotele2. De Ani
ma. cap. 8.) necessariamente concorrono tre cose; primieramente Quel che percuo
te, dopoi il Percosso, & ultimamente il Mezo, nel quale è riceuuto il Suono. Dico, Quel
che percuote & il Percosso; percioche dalla percussione si genera il Suono; essendo mas-
simamente il Suono (come lo dichiara BoetioMusicae li-
bro. 1. c. 3.) repercussione d'Aria non sciolta, che per-
page 95uiene infino all'Vdito; nella quale si ricerca quel che percuote, come agente; & il percos
so, come patiente; come nel Mouimento sempre si ricerca quel che muoue, & quel ch'è
mosso. Dopo queste ui concorre il Mezo, nel quale il Suono è riceuuto, come nel pro-
prio soggetto; & questo è l'Aria; conciosia che acciò si generi il Suono, fà dibisogno,
che quello, che percuote, tocchi il percosso in tal maniera, che nel toccare faccia la bot
ta; ma non senza mouimento locale, nelquale l'Aria mezana si muoue tra quel che per-
cuote & quello ch'è percosso, & peruiene alle nostre orecchie mouendo lVdito. Onde
è uero quel, che dicono i Filosofi; che l Mouimento locale sempre si fà in alcun Mezo,
& non mai nel Vacuo. E' ben uero, che 'l Suono può nascere in molti modi; primieramen
te, quando due corpi duri sono percossi l'un con l'altro: come l'Incudine & il Martello;
& questo conferma Aristotele, dicendo;De Ani-
ma, ut su-
pra. che 'l Suono nasce dalla collisione, ò confrica-
tione di due corpi solidi & duri, i quali rompino fortemente l'Aria; secondariamente na
sce, quando un corpo liquido percuote un duro & fermo come l'Aria, che percuota cō
uiolenza in vno arbore; ouer per il contrario, quando un corpo liquido è percosso da un
duro & fermo; come quando l'Aria è percossa da una uerga; simigliantemente, quando
due corpi liquidi concorrono insieme ouer s'incontrano; come fanno due Acque corren
ti; oueramente quando alcuno Vento, ouer'altro Vapore spinge uelocemente una parte
d'Aria sopra un'altra; come auiene quando si scarica un'Artigliaria, ouer'altra cosa simi
le. Et non solamente nasce il Suono in questi modi; ma etiandio quando si separa alcuna
parte d'un Corpo dall'altra; come si fà per la diuisione d'alcun Legno; ò per stracciar Ve
luto, Panno, Tella, ouer'altre cose simili, ne i quali effetti concorre sempre la uiolenta
Repercussione dell'Aria. Et si come quando si getta nell'acqua alcun sasso, subito si fà
in essa un picciol cerchio; & tanto si sà maggiore, quanto gli è permesso dal mouimento;
percioche essendo stanco, si ferma, ne procede più oltra; cosi intrauiene de i Suoni nell'
Aria & delle Voci; che tanto si diffondono i circoli fatti in esso, & si fanno maggiori, quā
to gli è permesso dal Mouimento; & in tal modo ferisce l'orecchie de i circostanti. Intra-
uien però; che si come l'Onde, che fanno i circoli, tanto maggiormente sono deboli &
di minor possanza, & dall'occhio son men comprese, quanto più sono lontane dalla lo-
ro origine; cosi ancora i Suoni, ò Voci tanto più debolmente feriscono l'Vdito, quanto
piu sono lontani dal loro principio, & si rendono all'Vdito piu oscuri, & minormente so
no intesi da esso; onde poi stanco il mouimento, non piu si odono; ma se per caso aue-
nnse, ch'alcuna cosa facesse ostacolo alle commemorate onde, ò circoli fatti nell'acqua;
ouero gli impedisce il farsi maggiori, per quanto dalla natura del mouimento li fusse con
cesso; ritornano essi circoli fin là decrescendo, oue hebbero principio, & cessa il mouimen
to. Questo istesso fà l'Aria; che s'alcuna cosa se le oppone, subito ritorna ai suo princi-
pio; cioè, alla origine del mouimento; & dalla reflessione si fà nelle nostre orecchie un
nuouo suono, ilquale chiamano Echo. Dal Mouimento adunque, come principale si fà
il Suono; alla cui similitudine nascono anco le Voci: quantunque diuersamente di quel
che fanno i Suoni; imperoche alla generatione delle Voci, non solo si ricerca le nomi-
nate cose concorrenti al nascer de i Suoni; ma di piu fà dibisogno, che ui siano due
Istromenti naturali sommamente necessarij, che sono il Polmone & la Goia. Il Polmo-
ne dico, che quasi come un Mantice tiri & mandi fuori l'Aria; & la Gola, nella quale per
cuota l'Aria. Conciosia che essendo la Voce suono; & generandosi il Suono dalla reper
cussione; è necessario, che quando la Voce si genera, che l'Aria mandata dal Polmone
percuota alla Gola; cioè alla Canna, che è detta Arteria uocale, & per tal percussione sia
generata. Et benche dal Polmone & dalla Gola naschino molti suoni; non sono però
tutti da nominare Voci; come la Tosse, & altro simil Strepito; ma quelli solamente, che
sono articolati, & significano alcuna cosa; da i quali nasce il Parlare, ch'è proprio dell'
Huomo; alla generatione de quali fanno dibisogno tutti quelli Istrumenti naturali, ch'io
commemorai nella Prima parte;Cap. 5. & questi sono considerati dal Musico; percioche fan-
page 96no al suo proposito ma non i primi, che non sono atti à fare alcuno concento. Hora po-
tiamo ueder la differenza, che si troua tra il Suono & la Voce; conciosia che il Suono è
quello, che solamente si ode; & è repercussione d'Aria non sciolta, che peruiene fino al-
l'Vdito, & non rappresenta cosa alcuna all'Intelletto; & la Voce è repercussione di Aria
respirata all'Arteria vocale, che si manda fuori con qualche significatione; lasciando da
un canto il Latrar de cani & altre come simili, che non fanno qui al proposito. Si dee pe
rò auertire, che (come dice il Filosofo nel cap. 23. della Poetica) per traslatione si chia-
mano etiandio Voci quei Suoni, che nascono dalle Tibie & dalle Fistole; de i quali anco
il Musico ne hà gran consideratione. Et si può anco dire, che 'l Suono sia come il Genere,
& la Voce come la Specie: imperoche ogni Voce è Suono; ma non per il contrario.
Da che nascono i Suoni graui, & da che gli acuti.Cap. XI.
menti alcuni sono Equali, & alcuni Inequali; & de questi alcuni sono tardi
& rari, & alcuni veloci & spessi; però è da sapere; che da i primi nascono i
Suoni graui, & da i secondi gli acuti; & questo è manifesto al Senso; percio-
che se noi pigliaremo uno Istrumento musicale, nel quale siano tese molte chorde, &
percuoteremo insieme equalmente alcune di esse, di modo che la percussione fatta all'
una, non sia più forte di quella fatta all'altra; ritrouaremo nelle chorde, che danno i Suo
ni più graui, i Mouimenti più tardi & più rari, & più lungamente durare il lor Suono; &
nelle più acute i Mouimenti più ueloci & spessi, & li Suoni più presto mancare. Con-
ciosia che le Chorde piu lasse debolmente percuotono l'Aria, & piu dura il Suono, che
nasce da loro; & questo è per la tardità de i Mouimenti; ma quelle che sono piu tirate,
percuotono l'Aria gagliardamente & con prestezza, & è men durabile il Suono, che da
esse procede; percioche per la uelocità de i Mouimenti cessa tanto piu presto & arriua al
fine. Ogni giorno vediamo per esperienza, che la chorda piu tesa rende il Suono piu acu
to; & se la tiriamo piu di quello, ch'è tirata, ritrouiamo in essa Mouimenti piu veloci;
& il Suono fatto piu acuto, di quel ch'era di prima; & se la rallentiamo, i suoi Mouimenti
sono piu tardi, & il Suono produtto da lei piu graue; conciosia che 'l Mouimento quanto
piu è tardo, tanto piu è uicino al suo fine; cioè, al fermarsi; & il Suono quanto è più gra
ue, tanto è piu uicino alla taciturnità. Si debbe però intender di quella Tardità, che si
ritroua nel fine de i Mouimenti violenti; percioche tali Mouimenti sono per loro natura
gagliardi nel principio & ueloci, nel fine poi sono deboli & tardi; essendo che à poco à
poco uanno perdendo la sua uelocità. Et questa tardità si ritroua nella chorda, quando è
vicina al fermarsi; conciosia che allora è piu debole & piu lassa. La onde il Mouimento
di qualunque chorda percossa nel principio è ueloce, & rende molto Suono; ma à poco
à poco debilitandosi il Mouimento lo và perdendo. Nascono etiandio i Suoni graui dal
le chorde grosse, & dalle sottili gli acuti; percioche 'l Suono acuto non tanto nasce dalla
velocità del Mouimento, quanto dalla sottigliezza della chorda, che è piu penetratiua
nell'Aria. Ne ci dobbiamo imaginare, che qualunqne uolta vna Chorda sia percossa,
ch'ella generi solamente un Suono; anzi bisogna esser certi, che i Suoni & le Percussio-
ni siano molte; & che tante uolte, quante da quella è l'Aria percossa, che renda tanti Suo
ni differenti, secondo la uelocità, ò tardità de i Mouimenti fatti in essa chorda; & che
percuoti l'Aria, fino à tanto che tal chorda tremi. E' ben uero, che le Differenze de i
Suoni graui & acuti, nati dalla chorda, non sono vdibili; il che può auenire non sono dal-
le percussioni, che sono ueloci, & in tal maniera congiunte, che paiono à noi una sola;
ma etiandio per i minimi Interualli, che si ritrouano da un Suono all'altro; de i quali l'
Vdito non è capace, si per la sua picciolezza; com'anco perche sono molto congiuinti;
page 97onde l'Vdito resta ingannato nella cosa vdibile, quasi all'istesso modo, che fà il Vede-
re nella cosa visibile; conciosia che sè alcuno pigliarà in mano un tizzone acceso, & lo
girerà velocemente à torno; parerà che nell'Aria sia un cerchio di fuoco; nondimeno
secondo la uerità non sarà cosi; percioche dalla uelocità del Mouimento unito, & dal-
la Forma di tal figura, la quale non hà angoli, l'occhio resta ingannato. Essendo adun-
que i Suoni graui fatti da i Mouimenti tardi & rari, & gli acuti da i ueloci & spessi; po-
tiamo dire, che dalla aggiuntione de i Mouimenti si facino i Suoni de graui acuti; & per
il contrario dalla diminutione, de acuti graui. Di modo che essendo fatti i Suoni acuti
dalla maggior parte de i Mouimenti, & i graui dalla minore; da tal differenza, che con
siste in una certa pluralità, è necessario che cadino sotto il Numero; & che comparato
il maggior numero loro al minore, si ritroui quella comparatione & proportione tra lo-
ro, che si ritroua tra i Numeri semplici nella quantità discreta. Et si come tali Mouimen
ti, comparati secondo 'l Numero, parte sono tra loro Equali, & parte Inequali; cosi an-
cora i Suoni sono tra loro parte Equali & parte distanti l'un dall'altro per l'Inequa-
lità. Onde in quelli, che non sono discordanti per alcuna Inequalità, non si può
trouare alcuna Consonanza; ne meno il suo opposto, ch'è la Dissonanza; conciosia che
la Consonanza è concordanza de più suoni tra loro differenti & inequali, redotta in uno;
& la Dissonanza è mistura di suono graue & acuto, che offende l'Vdito. Adunque si come
dalle Quantità, che sono tra loro inequali, l'una comparata all'altra (nel modo che nel-
la Prima parte vedemmoCap. 22.) nascono Cinque generi di proportione, detti di Maggiore
inequalità; de i quali le Specie sono infinite; cosi ancora dalla comparatione de i Suoni
tra loro inequali, nascono cinque generi & infinite Specie. Et benche i Suoni si ritroui-
no in atto nell'Aria, come nel loro proprio soggetto; & che di loro per uia del soggetto nō
ne possiamo hauere alcuna cognitione, ò ragione determinata; essendo che i termini lo-
ro sono incogniti à noi; tuttauia in quanto nascono da i Corpi sonori, che sono Quanti-
tà commensurabili, & si ritrouano in loro in potenza; dalla misura loro ne habbiamo
perfetta cognitione; percioche i suoi termini sono conosciuti dalla diuision delle chor-
de, come già nella Prima parte hò detto;Cap. 19. dalla quale noi cauiamo le Ragioni de i Suoni
graui & de gli acuti, & le lor differenze; & questo secondo 'l Numero delle parti, che
le misurano; dal qual Numero uenimo ad esser certi della quantità de Suoni; & non pur di
essi; ma delle Voci ancora, le quali senza dubbio sono Suoni; applicando però essi suoni,
che nascono da i corpi Sonori alle Voci; le quali sono prodotte da i Corpi humani.
Quel che sia Consonanza, Dissonanza, Harmonia & Melodia.
Cap. XII.
Consonanza, considerata principalmente dal Musico, la qual dichiarando
da nuouo dico, ch'ella è compositione di suono graue & acuto, che peruiene
alle nostre orecchie soauemente & uniformemente, & hà possanza di mutare
il senso; ouero è (secondo che la definisce Aristotele1. Post. c.[gap — reason: bad print]) Ragion de numeri nell'acuto &
nel graue. Dallequali definitioni potiamo comprendere, che la Consonanza nasce,
quando due suoni, che sono tra lor differenti senz'alcun suono mezano, si congiun-
gono concordeuolmente in un corpo; & è contenuta da una sola proportione.
Ma perche di due opposti, ritrouandosi l'uno in essere, è necessario, che si ritroui anco
l'altro, & si habbia di loro una istessa scienza; però essendo la Dissonanza contraria al-
la Consonanza, nel modo ch'io la dichiarai nel principio del Secondo delle Dimostra-
tioni; non sarà difficile saper quello, ch'ella sia; percioche ella è compositione di suo-
no graue & d'acuto, laquale aspramente peruiene alle nostre orecchie. Et nasce in tal
page 98maniera, che mentre tali Suoni non si uogliono vnire l'un con l'altro, per la dispropor-
tione, che si ritroua tra loro; & si sforzano di restar nella loro integrità; offendendosi l'un
l'altro peruengono senz'alcuna soauitade all'Vdito. Ne solamente si ritrouano due Suo
ni tra loro distanti per il graue & per l'acuto, che consonino; ma tali Suoni anco si odono
molte fiate tramezati da altri suoni, che rendono soaue concento; com'è manifesto; &
sono contenuti da più proportioni; però i Musici chiamano tal compositione Harmo-
nia. Onde si dè auertire, che l'Harmonia si ritroua di due sorti; l'una dellequali chiama
remo Propria, & l'altra non Propria. La Propria è quella, che descriue Lattantio Fir-
miano, in quello dell'Opera di Dio,Cap. 16. dicendo; i Musici nominano propriamenteHar-
monia il concento di chorde, ò di uoci consonanti ne i loro modi, senza offesa alcuna
delle orecchie; intendendo per questa il concento, che nasce dalle modulationi, che fan
no le parti di ciascuna cantilena, per fino à tanto che siano peruenute al fine. Harmonia
propria adunque è cōpositione, ò mescolanza de suoni graui & de acuti tramezati, ò non
tramezati, la qual percuote soauemente il senso; & nasce dalle parti di ciascuna canti-
lena, per il proceder che fanno accordandosi insieme, fin à tanto, che siano peruenute
al fine; & hà possanza di dispor l'Animo à diuerse passioni. Et questa Harmonia non sola-
mente nasce dalle Consonanze; ma dalle Dissonanze ancora; percioche i buoni Musi-
ci pongono ogni loro studio di fare, che nelle Harmonie le Dissonanze accordino; &
che con marauiglioso effetto consonino di maniera, che noi la potiamo considerare in
due modi; cioè, Perfetta & Imperfetta. La Perfetta quando si ritrouano molte parti
in una cantilena, che uadino cantando insieme, di modo che le estreme siano trame-
zate dall'altre; & la Imperfetta, quando solamente due uanno cantando insieme, sen-
za esser tramezate da alcun'altra parte. La non propria è quella, c'hò dichiarato di so-
pra; la quale più presto si può chiamare Harmoniosa consonanza, che Harmonia; con-
ciosia che non contiene in se alcuna modulatione; ancora c'habbia gli estremi trameza
ti da altri suoni; & non hà possanza alcuna di dispor l'Animo à diuerse passioni; come
l'Harmonia detta Propria; laquale di molte harmonie Nō proprie si compone. Et se ben
pare, che l'Harmonia Propria non habbia da se tal forza; tuttauia l'acquista col mezo del
Numero & dell'Oratione; cioè, del Parlare, ò delle Parole, che se le accompagnano; le
quali tanto più, ò meno commuouono; quanto più ò meno sono accommodate al Rhy-
thmo, oueramente al Metro cō proportione. La onde poi da tutte queste tre cose aggiun-
te insieme; cioè, dall'Harmonia propria, dal Rhythmo & dall'Oratione; nasce (come
uuol PlatoneDe Repu-
blic. 3.) la Melodia. Ma come l'Harmonia Non propria si diuida in quella, ch'è
detta Semplicemente, & nella detta Ad un certo modo; & quello che sia l'una & l'altra;
da quello, ch'io hò scritto nella Quarta & Quinta definitione del Secondo delle Dimo-
strationi, si potrà comprendere; come etiandio si potrà dalla Prima & dalla Seconda
conoscer quello che sia Consonanza Propriamente & la Communemente detta; nelle
quali essa Consonanza si uiene à diuidere.
Diuisioni delle Voci.Cap. XIII.
solo dalle Voci; ma anche da i Suoni; nondimeno la Melodia, nella qua-
le entra la Oratione non può nascere se non dalle Voci. Però ogni Voce
quantunque sia articolata, non è atta alla sua generatione; conciosia che
non sono le Voci tutte d'una specie; onde bisogna sapere, che le Voci humane (come vo
gliono Aristosseno,Harmo. e-
lement. li-
bro. 1. Tolomeo & Boetio) si diuidono in due parti, delle quali alcune sono
dette Continue & alcune Discrete, ò vogliamo dire (com'alcuni dicono) Sospese cō inter
uallo. Le Cōtinue, da i Greci sono dette Συνεχαὶ φωναὶ; & sono quelle, che usiamo ne i do-
mestici & famigliari ragionamēti cō le quali senza mutar suono, leggiamo la Prosa, ouer
page 99il Verso. Et le Discrete, che i Greci chiamano Διαστηματικαὶ φωναὶ, sono quelle, con le
quali cantiamo ogni sorte di cantilena, ordinata per interualli Musicali proportionati,
che si ritrouano nelle modulationi; & queste solamente sono quelle, che fanno al nostro
proposito; imperoche da loro hanno l'essere ogni Modulatione, dalla quale nascono
tutte le sorti d'Harmonia. Harmoni.
lib. 1. c. 4. A queste due sorti aggiunge Albino filosofo; come mostra
Boetio;Musicae li-
bro 1. c. 12
& 13. quelle, le quali partecipano della natura delle due nominate; & sono quelle,
con le quali leggiamo ogni sorte di Poesia; non come la Prosa, senza mutatione di suo-
no; ne anco distintamente con interualli determinati; come si usa nelle cantilene; ma
ad un certo modo, che piace più à noi; osseruando quelli accenti, che si danno alle pa-
role; secondo che richiede la materia contenuta in esse. Et benche le Voci continue pos-
sino essere infinite; conciosia che 'l Parlare & il Leggere si possa cont nuare per lungo tem
po, senz'alcun termine; & che le Discrete non habbiano alcun termine prescrit-
to di ascendere all'acuto, ò di descendere al graue; tuttauia la Natura dà fine all'una &
all'altra; perche lo Spirito humano col tempo insieme termina le continue; conceden-
do à ciascheduno di parlare & similmente di leggere, quanto gli è permesso dalla sua na-
tura & dal tempo; & la natura de gli Huomini dà fine alle Discrete; imperoche l'Huomo
naturalmente tanto ascende, ò discende con la uoce, quanto gli è permesso dalla dispo-
sitione de gli Istrumenti atti alla sua formatione. A quelle poi, che partecipano della na-
tura delle due prime; l'una & l'altra delle nominate cose dà fine. Sono adunque le Di-
screte quelle, che sono atte alle Modulationi, all'Harmonie, & alle Melodie; delle
quali (lasciando l'altre, come à noi poco utili) sarà il nostro ragionamento.
Quel che sia Canto, & Modulatione; & in quanti modi si possa cantare.
Cap. XIIII.
cipalmente considerate dal Musico; dopoi li Suoni applicati ad esse; percio-
che da questi & da quelle senza differenza alcuna si forma ogni nostra Canti-
lena. Questa ogn'uno la chiama Canto, dal Cantare; il quale è Modulatione,
che nasce principalmente dalla uoce humana. Dico principalmente; percioche si piglia
anco il Canto per l'Harmonia, che nasce dal Suono de gli Istrumenti arteficiali; & etian
dio per il Canto de gli animali; come si può uedere del Canto de i Cigni, del quale parla
Virgilio, dicendo;Aeneid. 1.
Vt reduces illis ludunt stridentibus alis,
Et coetu cinxére polum, Cantusꝗ dedére.
Et questo ultimo modo non fà al nostro proposito, ma i due primi; percioche in essi si
comprende ogni Harmonia & ogni Melodia. E' però la Modulatione un Mouimento fat
to da un suono all'altro per diuersi interualli, il quale si ritroua in ogni sorte d'Harmo-
nia; & di Melodia; & la vsiamo in due modi; prima quando si muouiamo da un suono
all'altro senza uarietà di tempo, con diuersi interualli, non facendo alcuna Propria har-
monia; procedendo equalmente da un'Interuallo all'altro per il medesimo tempo; co-
me si fà ne i Canti fermi; & questa è detta Modulatione impropriamente; perche contie
ne solamente un proceder semplice, senz'alcuna Consonanza; dal quale effetto si uede,
che tal Modulatione hà ragion de imperfettione; essendo che māca à se stessa del debito
fine. Dopoi quando per il suo mezo peruenimo all'uso dell'Harmonia & Melodia, come
al suo proprio fine; come faciamo nel Cāto figurato, nel qual cātiamo nō solo cō semplici
suoni & semplici eleuationi & abbassamēti de voci; ma si muouiamo anco da un'interual
lo all'altro cō ueloci & tardi mouimēti; secondo il tēpo mostrato nelle sue figure cantabi
li; & questa è detta Modulatione propriamente. Laonde toccando allora varie consonā-
ze, dal nostro cantare è formata ogni sorte d'Harmonia & di Melodia; laquale nō può na
page 100scere se non con l'aiuto delle Consonanze; ancorache possiamo hauer la Modulatione
senza la Harmonia propria, & senz'alcuna Consonanza, & senza Melodia.Vide cap.
17. lib. 2.
Supple. Potiamo
nondimeno hauer la Modulatione in tre modi; prima quando noi Cantiamo nominata-
mente ciascuna chorda, ò suono col nome di una di queste sei sillabe, Vt, Re, Mi, Fa,
Sol, La, secondo il modo ritrouato da Guidone Aretino; come uederemo al suo luogo;
il qual modo i Prattici chiamano Solfizare, ò Solmizare; & non si può far se non con la
uoce. Dopoi quando noi proferimo solamente il suono, ò la uoce & gli interualli de-
scritti; come fanno gli Istrumenti arteficiali. Ma l'ultimo modo è, quando noi appli-
chiamo le Parole alle figure cantabili, il quale è proprio del Cantore; percioche da que-
sta maniera di cantare nasce la Melodia; come habbiamo detto.
Quel che sia Interuallo, & delle sue Specie.Cap. XV.
Elementi; delle quali alcune si attribuiscono alla Natura, & alcune all'Ar-
te. Quelle che si attribuiscono alla Natura sono l'Acuto, il Graue, & l'In-
teruallo; percioch'è necessario (usando le parole di CiceroneDe Repu-
bli. lib. 6.) che gli estre-
mi di questo suonino grauemente dall'una parte, & dall'altra acutamente; onde è mani-
festo, che l'Acuto & il Graue sono gli estremi dell'Interuallo. Le cose, che si attribui-
scono all'Arte, sono la Estensione d'alcuna chorda; il farla graue, ouero acuta, la Con-
sonanza; il Concento, & ogni Compositione; sia poi nelle Voci, ouer
ne i Suoni, che non fà caso; le quali cose tutte cascano nella consideratione dello Specu-
latiuo. E' ben uero che ue ne sono alcune altre, che solamente appartengono al Pratti-
co; & queste sono il Sonare, il Cantare, & il Comporre; perche nascono dall'essercitio
& dal lungo uso; ma gli altri accidenti, che sono molti, che cascano nelle compositioni
& nelle cantilene, sono non solamente in consideratione del Prattico; ma etiandio del-
lo Speculatiuo. L'Interuallo adunque, il quale si attribuisce alla Natura, si chiama in
due modi; come uuole Aristide QuintilianoMusic li-
bro. 1., Commune & Proprio. Si dice Com-
mune; conciosia ch'Ogni grandezza terminata da certi fini, è detta Interuallo;
considerando però lo spatio, che si ritroua tra l'uno & l'altro estremo; & di questo
non intendo parlare; percioche è molto lontano dalla nostra consideratione. Si
chiama Proprio; perche la distanza, che è dal suono graue all'acuto, è detta In-
teruallo; & questo è considerato dal Musico; & si ritroua de Dodeci sorti; come
Maggiore, Minore & Equale; comparandone sempre due insieme; Consonante,
Dissonante, Semplice, Composto, Diatonico, Chromaticho; Enharmonico, Ratio-
nale & Irrationale. Il Maggiore è quello della Diapason, rispetto à quello della Dia-
pente. Minore, come quello della Diatessaron rispetto à quello della Diapente, ouer
della Diapason. Equale, come è quel di una Diatessaron, comparato à quello d'vn'
altra; & questo dico rispetto alla proportione di numero à numero; & non altra-
mente. Consonante si dice quello della Diapason, quello della Diapente, quello della
Diatessaron & gli altri tutti, c'hanno le Forme loro tra le parti del Numero senario.
Dissonante, com'è quello del Tuono, & tutti quelli, che sono minori di lui. Sempli-
ce, si chiama quello, che no nè tramezato, da un'altro suono, il quale i Greci chiama-
no Διάστημα; conciosia che i suoi estremi seguono l'un l'altro senz'alcun mezo. Compo-
sto si dice quello, che da altri suoni è tramezato, detto simigliantemente da i Greci
Σύστημα. Diatonico è quello del Tuono maggiore ò del minore; ò del maggior Semi-
tuono. Chromatico quello del Semituono minore; & Enharmonico quello del Die-
sis; come vederemo. Rationale poi si chiama quello, che si può descriuer con nume-
ri; come l'Interuallo della Diapente, che si circoscriue con questi due termini 3. & 2.
& lo Irrationale quello, che per modo alcuno non si può descriuere; come nella PrimaCap. 21.
page 101parte io mostrai. Tutte queste cose sono considerate dal Musico; come uederemo; per-
cio che alla cognitione dell'Arte & della Scienza sono molto necessarie.
Quel che sia Genere; & di tre generi di Melodia, ò Cantilena appresso gli An-
tichi; & delle loro Specie.Cap. XVI.
te Specie; nondimeno il Musico vuole anco che sia la Diuisione del Tetra-
chordo, la quale dimostra molte forme differenti, & dà un certo modo d'Har
monia, ò Melodia vniuersale. Onde Tolomeo nel Cap. 12. del Primo libro
de gli Harmonici dice, che 'l Genere nell'Harmonia non è altro, che una certa habitu-
dine, ò conuenienza de suoni, i quali tra loro compongono la Diatessaron. Ma il Tetra
chordo è un'ordine de suoni contenuto tra Quattro chorde; le cui estreme si ritrouano
l'una distante dall'altra in Sesquiterza proportione. Et è detto Tetrachordo da Τετρὰς
parola greca, che vuol dir Quattro; & da Χορδὴ, che significa Chorda; come Di quat-
tro chorde. Però è da notare, ch'appresso gli Antichi musici tre furono i Generi della
Melodia, ò Cantilena; de i quali il primo chiamarono Diatonico, il secondo Chroma-
tico, & il Terzo Enharmonico; & furon nominati Generi; perche dalle uarie diuisioni,
che fecero molti del Tetrachordo, nacquero diuerse Specie de modulationi; ciascuna
dellequali fù ridotta dopoi sotto uno de i nominati tre capi; secondo che più si accosta-
uano & riteneuano maggiormente la forma delle più antiche specie. Lasciarò hora di
por le uarie Diuisioni fatte da Aristosseno; tra le quali si troua due specie del Diatonico;
l'una delle quali nominò Molle & l'altra Incitato; & similmente tre specie del Chroma-
tico; cioè, Molle, Sesquialtero & Toniaco; & una specie dell'Enharmonico. Similmen
te lascierò da un canto le Diuisioni d'Archita; quelle di Didimo & quelle di Eratosthe-
ne, lequali per esser state riprouate con molte ragioni da Tolomeo: come appar nel Cap.
1. & 13. del Primo lib. & nel 13 & 14. del Secondo de gli Harmonici; similmente nel Cap.
15. 16. & 17. del Lib. 5. della Musica di Boetio; non fanno al nostro proposito; & porrò
solamente quelle Diuisioni, che fece Tolomeo; come quelle, che dalla maggior parte de
i Musici sono state accettate per migliori; perche sono più rationali & più consonanti al-
l'Vdito; delle quali hauendo prima mostrato le Forme contenute in diuersi Tetrachor-
di, aggiungendo ad esse le prime specie de i nominati Generi poste in uso da i più Anti-
chi; mostrerò dopoi l'Ordine di ciascuna, contenuto nel Systema massimo, diuiso in cin-
que Tetrachordi; & insieme uerrò à mostrar le Diuisioni del Monochordo per ciascuna
specie, per le quali si potrà veder l'utile, che poteuano hauere gli Antichi da ciascuna,
quando hauessero uoluto essercitar l'Harmonia in quella perfettione, che faciamo al pre
sente. Vederemo etiandio l'utile, che si potrà cauar da ciascuna specie; acciò ne possa
seruire all'uso moderno; percioche eleggendo quelli Interualli, che faranno al nostro
proposito, mostrarò la Compositione di uno Istrumento, nel quale saranno accommo-
date le sue chorde & il suo Tastame in tal maniera, che facilmente & distintamente si
potranno conoscer le chorde di ciascun genere separate da quelle di un'altro; & si po-
tranno porre in uso con facilità; quando torneranno commode. Incominciarò adunque
dal primo, del quale sono cinque le sue Specie; come si potrà comprendere dalle varie
diuisioni de cinque Tetrachordi; come dimostra Tolomeo;Harmo. li-
bro. 1. c. 15 cioè, il Diatono diatonico;
& è la Prima specie, che poneuano anco gli antichi Pitagorici; il Molle, il Syntono, oue-
ro Incitato, il Toniaco & l'Equale. Il Diatono era quello, che procedeua ne i suoi
Tetrachordi per l'Interuallo d'un minor Semituono, contenuto dalla proportione su-
per 13. partiente 243. chiamato da i Greci (come mostra BoetioMusicae. li- br. 2. c. 27) λε͂ιμμα, ouer
Δίεσις; & per due interualli di Sesquiottaua proportione, i quali nominarono Tuoni. Si-
milmente procedeuano cotali Tetrachordi dall'acuto al graue per il contrario, discen-
page 102dendo per i spacii, ouero interualli nominati; cioè, per un Tuono, & per un'altro, &
per un Semituono minore; come si uede nell'essempio. Era chiamato Diatono diato-

chi Filosofi; massimamente da Platone & da Aristotele; conciosia che lo uidero più
d'ogn'altro naturale & molto conforme alla compositione del Mondo. Ma il Diatonico
molle era quello, il cui Tetrachordo procedeua dal graue all'acuto per uno interuallo di
Sesquiuentesima proportione, per uno di Sesquinona & per uno di Sesquisettima; & si-
milmente dall'acuto al graue procedeua al contrario per gli istessi Interualli; come nell'
essempio si può uedere. Il Syntono, ouero Incitato, che lo uogliamo dire, era quello,

to tra la sua prima chorda graue & la seconda dalla Sesquiquinta decima proportione; &
per un di Sesquiottaua, posta tra la seconda & la terza, & per uno contenuto dalla Sesqui
nona, posto tra la terza & la quarta chorda acuta; & per il contrario discendendo dall'
acuto al graue, procedendo per gli istessi Interualli; come si uede. Et questo è quello,
che, come più d'ogn'altro naturale, contiene in sè tutti quelli Interualli consonanti,
che possono esser prodotti dalla Natura; ilche ne gli altri non auiene; il quale chiama-
remo Naturale; & lo vsano i Moderni nelle loro Harmonie; come uederemo; con-
ciosia che le Proportioni de i suoi termini sono quelle, che naturalmente sono conte-
nute ne i Numeri Sonori; come nel Cap. 15. della Prima parte si uede. Il Toniaco è
quello, le cui chorde erano in tal modo tese per ogni suo Tetrachordo, che la prima
graue & la seconda faceua un Interuallo di Sesquiuentesimasettima proportione; questa
& la terza uno di Sesquisettima; & la terza con l'estrema acuta uno di Sesquiottaua; &
cosi per il contrario, procedendo dall'acuto al graue, per gli istessi Interualli; come si ue-
Lo Equale era quello il cui Tetrachordo procedeua dal graue all'acuto per un'Interual-
lo contenuto dalla Sesquiundecima proportione; & per uno contenuto dalla Sesquideci-
ma; & per un'altro contenuto dalla Sesquinona, & cosi per il contrario procedendo dal-
l'acuto al graue per gli istessi Interualli; come nell'essempio si uede. Et credo ueramente
che questo fusse chiamato da Tolomeo Equale; percioche hà le Differenze de i suoi ter-
mini equali, che, senza dubbio alcuno dinotano; che le sue Proportioni sono ordina-
page 103

fin à i miei tempi si è creduto, che si usasse nel sonare, & nel cantare nella sua Prima spe-
cie; come si può vedere ne i Scritti de molti Antichi, & de Moderni, & credo che anco-
ra ne sarebbono molti, che terrebbono questo esser uero; s'io non hauesse apertamente
fatto conoscere il contrario; ma che si usa la sua Terza specie; con modi però mol-
to differenti da quelli, che gli Antichi la vsauano; & con l'uso delle Consonanze imper-
fette; com'altroue uederemo. TolomeoHarmoni.
lib. 3. c. 5. comparò questo Genere à due altri generi di-
uersi; cioè, al Theologico & al Politico, per la simiglianza & conuenienza dell'ordine,
della maestà, & della sua eccellenza, molto conforme à quelli due; percioche, si
come è cosa più honesta il preporre le cose Publiche alle Priuate, & le cose Metaphi-
sicali, ò Theologiche alle Naturali & alle Mathematiche; poiche per le prime si reggo-
no & conseruano le seconde; ne senza esse hauerebbono l'essere; cosi è cosa giusta &
honesta, che si preponga questo Genere à gli altri due, come più nobile & più eccel-
lente; hauendo gli altri l'essere da lui; essendo che 'l Diatonico virtualmente contie-
ne il Chromatico l'Enharmonico; & al fine li produce in atto; ma non per il con-
page 104trario. Fu ueramente cosa giusta, che Tolomeo dessi ogni preminenza à questo Gene-
re; poiche come Generante senza dubbio è molto più nobile del Generato; onde mi
muouono à ridere alcuni, i quali senz'assegnar ragione, ò autorità alcuna, dicono; che
questo Genere si usaua anticamente nelle feste publiche all'uso delle orecchie uolgari;
& che gli altri due eran posti in uso tra priuati Signori; ma penso, che costoro non hab-
biano mai ueduto Tolomeo; & se pur l'hanno ueduto, non l'hanno inteso. Non mi esten
derò hora à uoler dimostrar in qual modo fusse usato; percioch'io credo, che quello,
che si è detto di sopra nel Cap. 4. potrà bastare, per dimostrare, ch'era usato magnifica-
mente & con molta eccellenza da i periti Musici antichi; ma uerrò al Secondo genere
detto Chromatico, le specie del quale erano tre; cioè, l'Antica & due di Tolomeo;
l'una dellequali chiamò Molle & l'altra Incitato. Il Chromatico antico era quello, che
nella sua Modulatione in ogni Tetrachordo procedeua dal graue all'acuto per un'In-
teruallo di Semituono minore, contenuto dalla mostrata proportione della prima spe-
cie Diatonica; & per un'altro Semituono alquanto maggior di questo, di proportio-
ne Super 5. partiente 76. & un'Interuallo, che conteneua tre Semituoni, detto da
BoetioMusicae li-
bro 1. cap.
23. Trihemituono incomposto; perche in tal Genere da niun'altra chorda poteua
esser tramezato; & era contenuto dalla proportione Superpartiente 16. come nel-

che la prima grauissima, & la seconda conteneuano la proportione Sesquiuentesima-
settima; questa con la terza la Sesquiquartadecima, & la terza con l'ultima acuta la
Sesquiquinta; & questo era un'Interuallo consonante; come ne dimostrano i ter-
mini della sua proportione; i quali radicalmente si ritrouano collocati tra 6. & 5.
nelle parti del Senario; come nel Cap. 15. della Prima parte si può uedere; & tor-
nerà al nostro proposito, nella Compositione del l'ordine Chromatico nell'Istru-

dall'acuto al graue, al contrario, per gli istessi nominati Interualli; come si uede nello es-
sēpio. L'incitato era quello, le cui chorde erano ordinate in tal maniera, che ne i suoi Te-
trachordi la prima & grauissima era distante dalla seconda per una Sesquiuentesimapri-
ma proportione; questa era lontana dalla terza per una Sesquiundecima; & la terza dal-
la quarta per una Sesquisesta; come nella figura chiaramente si comprende. Questo ge-

lo rifiutarono; come narra Macrobio;De Sōnio.
lib 2. c. 4. perche effeminaua gli animi, & li rendeua molli.
Tolomeo3. Har. c. 5. l'assimiglia al genere Mathematico & all'Economico; per la commune medio-
crità, che tiene con gli altri estremi generi; conciosia che alle volte il Mathematico s'ac-
compagna col Naturale & col Sopranaturale; & l'Economico participa col Morale per
una certa ragione di cosa priuata, ò particolare, posta nellordine inferiore; & col Poli-
tico per ragione d'Imperio; percioche regge & gouerna una famiglia priuata. Questo (co
me dice Boetio) è detto Chromatico, quasi Colorato, ò Variato: da Χρῶμα parola gre-Vt supra
cap. 21.
ca, che vuol dir Colore; & prese questo nome dalla superficie d'alcuna cosa, che leuata,
le fà uariare il colore; & dice bene; percioche mutandosi solamente vna chorda mezana
del Tetrachordo diatonico, restando l'altre communi, da tal mutatione nascono differē
ti Interualli & uarie proportioni; cioè, variate forme, uariati suoni & colori. Ma in qual
modo sia trasferito à noi l'uso delle sue chorde, lo uederemo nella Terza parte. L'Enhar

quello, che ne i suoi Tetrachordi, procedendo dal graue all'acuto, si cantaua per due
Diesis & uno Ditono: chiamato da BoetioVt supra
cap. 23. ; percioche in tal genere era ac
commodato con un solo Interuallo. Et de i Diesis il graue era contenuto dalla proportio
ne Super 33. partiente 499; & l'acuto dalla Super 13. partiente 486. & erano collocati
in Proportionalità arithmetica; come si può vedere, Et uolsero gl'Antichi, che 'l Diesis
fusse la metà del Semituono minore: Se bene non era la metà intiera. Quel di Tolomeo
page 106era quello, che procedeua dal graue all'acuto; cioè, dalla prima alla seconda chorda gra
ue d'ogni suo Tetrachordo per uno interuallo di proportione Sesquiquarantesimaquin-
ta; & dalla seconda alla terza per uno di Sesquiuentesimaterza; & da questa alla quarta
per uno di Sesquiquarta; & questo ultimo Interuallo è consonante; percioche la forma
della sua proportione è contenuta tra 5. & 4. nelle parti del numero Senario; come nel
Cap. 15. della Prima parte si può uedere; & sarà il uero Ditono enharmonico nella com

terualli, faceua il contrario; come nel Tetrachordo si uede. Non durò molto tempo l'v-
so di questo Genere; percioche (come dicono alcuni) pareua à gli Antichi impossibile
di poterlo intendere per la troppo sua ascosa difficultà; ne è stato però d'alcun de i Moder
ni fin'hora inteso; ancorache alcuni presumino d'hauerlo posto in luce; se ben dal suo
uero vso, & di quello del Chromatico sono molto dalla uerità lontani. Comparò Tolo-
meoLib. 3. c. 5
Harmoni. questo Genere à due altri generi diuersi; cioè, al Naturale & al Morale; non per al
tro, se non per la commune diminutione della sua grandezza, che hà sopra gli altri; con
ciosia che si come il Naturale prattica tra quelle cose inferiori, che sono le men nobili,
che siano nel mondo; & il Morale intorno ad un solo Indiuiduo, ilquale è fuori del Nu-
mero; cosi questo Genere uà pratticando intorno à quelli Interualli, che sono men no-
bili & minimi nelle harmoniche modulationi. Questo è detto Enharmonico, quasi Otti
mamente & Attamente congiunto; ouero (come uoglion alcuni) quasi Inseparabile. Ma
in qual modo le sue chorde si ponghino in uso, lo vederemo altroue.
Per qual cagione ciascun de gli Interualli contenuto ne i mostrati Tetrachordi
sia detto Incomposto.Cap. XVII.
& il Ditono nell'Enharmonico siano chiamati Incōposti; nondimeno tutti gli
altri Interualli ancora di ciascuno de i nominati Generi, in ogni loro Specie
sono detti Incomposti; percioche (come dice BoetioMusicae li-
br. 1. c. 23.) ciascuno si pone intiero
nelle sue specie & senz'alcun mezo. Et se ben la parola Incomposto si piglia per quello,
che si suoi dire Senza ornamento, & Senz'alcuna eleganza; tuttauia Boetio la piglia
per quello, che significa Senz'alcuna compositione; volendoci mostrare, che que-
sti Interualli sono gli Elementi, de i quali si compongono ciascuna delle mostrate Specie;
conciosia che quello si dice Elemento, del quale ogni Cosa primieramente si compo-
ne, & si ritroua in essa indiuisibilmēte secondo la sua forma. Onde si come diciamo, che le
page 107Lettere sono i Primi elementi delle parole, & che quelli delle cose miste sono la Terra, l'
Acqua, l'Aria & il Fuoco; & che i Primi elementi di ciascuna Scienza sono i Primi prin
cipij, i quali sono indemostrabili in cotal Scienza; cosi ancora si dice, che i Primi elemē
ti de i Generi di melodia, ò cantilena, sono i mostrati Interualli; imperoche si compone
di essi primieramente ogni Modulatione harmonica; & ultimamente si termina & risol-
ue in essi ogni compositione di più interualli per ciascun Genere & per ciascuna Specie;
essendo ciascun nel suo genere, ò nella sua specie in ogni Tetrachordo indiuisibile; per-
cioche se fussero diuisibili, restando l'estreme chorde di ciascun Tetrachordo nella sua
qualità, non si direbbe piu Tetrachordo; ma Pentachordo, ouero Hexachordo; ò con
altro nome si chiamarebbe, secondo 'l numero delle chorde, che contenesse. Et questo
non è contrario à quello, che mostrai nella Prima parte; cioè, che Ogni Interuallo è al-
meno diuisibile in due parti; secondo l'una delle tre Proportionalità; conciosiache allo-
ra non si considerauano come Primi elementi, come si considerano al presente. Boetio
adunque non per altro hà nominato ciascun di loro Incomposto; se non per dinotarci,
che sono Primi elementi di cotali Generi; & che, quādo formano alcuno de i mostrati Te
trachordi, non riceuono alcuna diuisione; percioche di loro, come di Elementi, si com-
pone principalmente ogni sorte di Melodia & di Cantilena.
In qual modo si possa accommodare alla sua proportione qual si voglia
Consonanza, ouero Interuallo.Cap. XVIII.
nua detta Corpo sonoro, & formalmente dopoi nell'Aria suo uero sogetto;
nel modo ch'altroue hò detto1. partis.
cap. 10.; ne potendosi hauer ragione alcuna di loro, se
non col mezo de i nominati Corpi; ne meno delle Voci, se non in quanto i
Suoni si applicano ad esse; però hauendo ragionato nella Prima parte de i Numeri &
delle Proportioni, lequali sono le Forme delle Consonanze; uerrò à mostrare hormai il
modo, che si tiene nell'accommodare i Suoni, ò Consonanze & qualunque Interuallo
nelle Quantità sonore alla sua proportione; accioche dopoi possiamo uenire alla Compo
sitione, ouer Diuisione del Monochordo. Ma prima è bisogno, che si ritroui un'Asse, ò
Tauola, che la uogliamo dire, ben piana, lunga due braccia, ò piu, ò meno, che non fà
caso; laquale sia larga almen quattro dita, & grossa due, ò più; accioche da parte alcu
na non si possa piegare; & che da tutte le parti sia equale nella sua superficie, ò planitie;
laqual ritrouata, tiraremo nel mezo di essa per lungo una Linea dritta, che caschi perpē
dicolarmente da un capo all'altro della detta Asse; accioche sia più commodo il misura-
re, ò diuidere; & tal Linea seruirà in luogo di Chorda. Dai cap i di quella poi si porrà
due Scannelli immobili; sopra i quali, dopo fatta la misura, si potrà tirare una, ò piu
chorde secondo 'l bisogno. Ma si debbe auertire, che alcun di loro non sia più alto d'una
costa di coltello, & che siano equali, & che faccino nella detta superficie quattro angoli
retti. Fatto questo, si debbe pigliare prima i Termini radicali della proportione della
Consonanza, ò Interuallo, che si uorrà accommodare; i quali saranno nella quantità di
screta; cioè, ne i Numeri; & diuider tutta la Linea; incominciando dall'uno de i Scan-
nelli immobili ne i punti, sopra i quali si porranno le chorde, fino all'altro, in tante par-
ti equali, quante Vnità contenerà il maggior termine radicale di essa Consonanza, ò In
teruallo; dopoi bisogna pigliare, per il termine minore, tante parti di essa linea, quante
Vnità contenerà questo termine; incominciando sempre dalla parte destra, uenendo ver
so la sinistra; & tra il tutto della linea, laqual ne rappresenta il Suono graue, ouero il mag
gior termine della proposta Consonanza, ouero Interuallo; & la parte, ò le parti, che sa-
ranno; le quali si pigliano per il Suono acuto, ò per il minor termine; haueremo accom-
modato tal Consonanza, ò Interuallo alla sua proportione; percioche (com'altre uolte
page 108hò dettoSupra.
Cap. 19.) i Musici tengono questo per uero; che Tanta sia la proportione d'un Suono al-
l'altro di qualunque Interuallo musicale, quanta la proportione delle sue chorde, secon
do la loro lunghezza; essendo tirate sotto un'istessa qualità. Ma ueniamo all'essempio,
accioche piu facilmente s'intenda quel che si è detto. Sia la linea A B. posta in luogo di
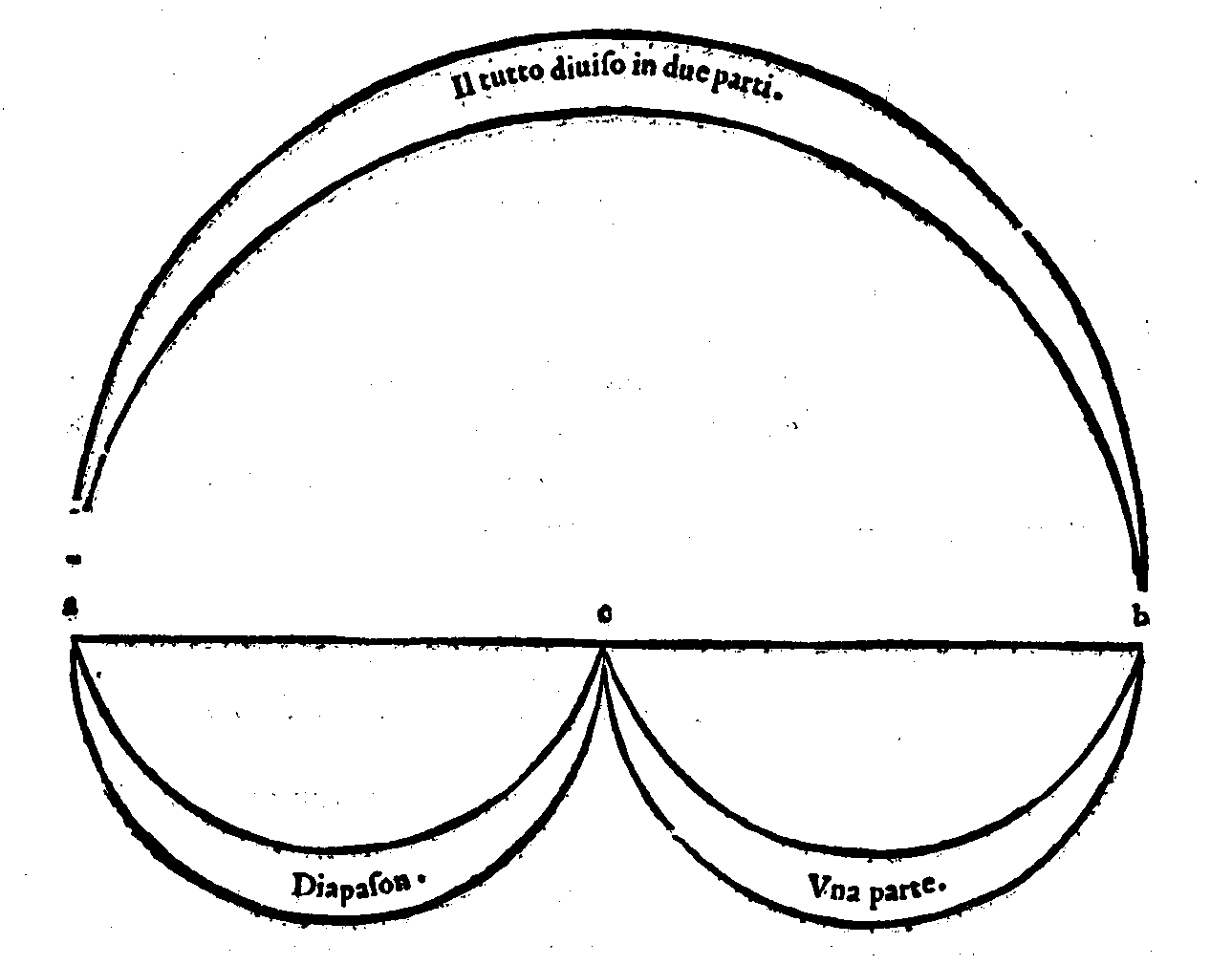
pason; bisogna prima ritrouare i Termini radicali della sua proportione, che sono 2 & 1.
dopoi diuider la linea in due parti equali, secondo 'l numero delle Vnità comprese nel
maggior termine nel punto C; ilche fatto, dico che tra la linea A B, ch è il Tutto; & la
C B, ch'è Vna parte, haueremo accommodato la consonanza Diapason alla sua propor
tione; percioche si come A B. è il tutto della linea, & C B. è la sua metà, & sono nella quā
tità continua in proportione Dupla, secondo la sua lunghezza; cosi ancora (per quel-
lo che si è detto più volte) i Suoni prodotti dalle chorde di simil lunghezza sono necessa
riamente in proportione Dupla, la quale è la prima del Genere moltiplice; conciosia
che 'l maggior termine di questa proportione contiene il minore due uolte; come si è
mostrato nel Cap. 24. della Prima parte. Similmente se 'l si volesse accommodare alla
sua proportione la Consonanza Diapente contenuta tra questi termini radicali 3 & 2.
diuideremo la linea A B. in tre parti equali, per il maggior termine della sua proportione,
il quale contiene tre Vnità; & incominciando dalla parte destra, uenendo uerso la sini-
stra, pigliaremo due parti di essa, per il termine minore, che contiene due Vnità, & ha-
ueremo la D B, che con la A B. contiene la Sesquialtera proportione, nel modo che 3 &
2. contiene quell'istessa ne i Numeri. Onde per le ragioni addotte della Diapason, i Suo
ni, che saranno mandati dalle chorde di tal lunghezza, renderanno la consonanza Dia-
pente, contenuta da tal proportione; come nella Quarantesima del Terzo delle Dimo-
strationi si è dimostrato. Il perche operando in tal modo, sempre si potranno collocare
etiandio l'altre, senza esserui punto di errore.
page 109
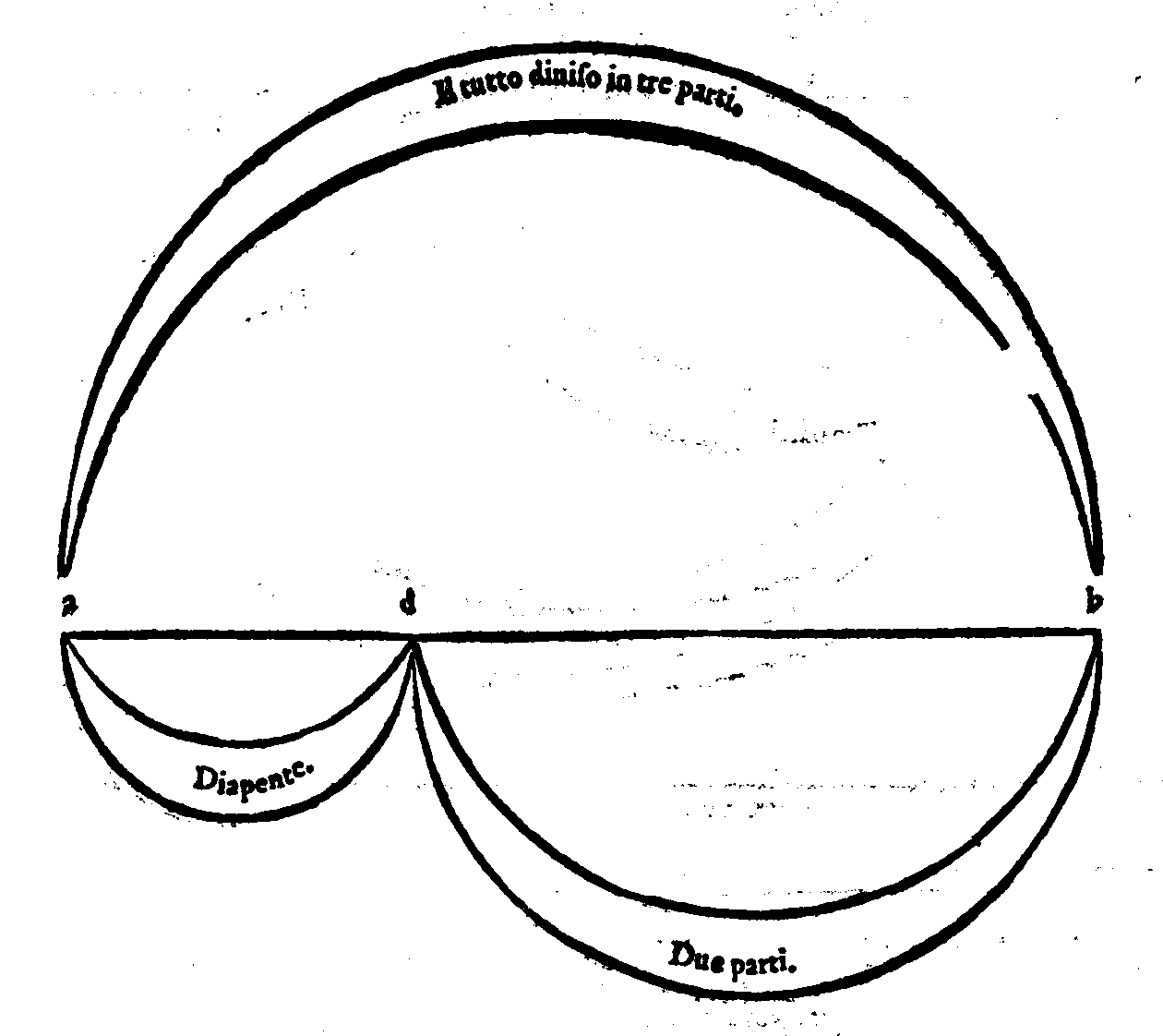
Vn'altro modo di accommodar le Consonanze alla loro proportione.
Cap. XIX.
tioMusicae.
lib. 4. c. 18.; cioè, sommando prima i Termini radicali della proportione, che contie
ne la Consonanza, che si vuole accommodare alla sua proportione; diuiden-
do dopoi tutta la linea, ò chorda in tante parti equali, quante sono le Vnità
contenute nel Numero, che uiene dalla somma; perche pigliando dalla parte sinistra uer
so la destra tante parti, quante sono le Vnità contenute nel maggior termine; quella parte
di chorda, che si piglierà, con la rimanente alla banda destra; laqual necessariamente haue
rà tante parti, quante sono le Vnità contenute nel minor termine; contenerà la propo-
sta Consonanza; come sarebbe. Se uolessimo accommodare alla sua proportione sopra
la linea A B. la consonanza Diapente; bisognerebbe prima ritrouare i Termini radicali
della sua proportione, che sono 3 & 2. dopoi sommandoli insieme haueressimo 5. per il
qual Numero sarebbe dibisogno diuider la sottoposta linea A B. in cinque parti equali; &
prender le tre poste dalla parte sinistra, secondo il numero delle Vnità cōtenute nel mag
gior termine della proportione, che sono 3. in punto C. & haueremmo la chorda A C. che
con la C B. insieme percosse ne darebbono la consonanza Diapente, secondo il proposito;
conciosia che la A C. sotto la ragione del Suono graue contenerebbe tre parti della det-
ta linea, ouer chorda A B. & la C B. sotto la ragione del Suono acuto, ne contenerebbe
due; che sono comparate l'una all'altra in proportione Sesquialtera; com'à tutti quelli,
che delle Scientie mathematiche si dilettano, è manifesto.
page 110
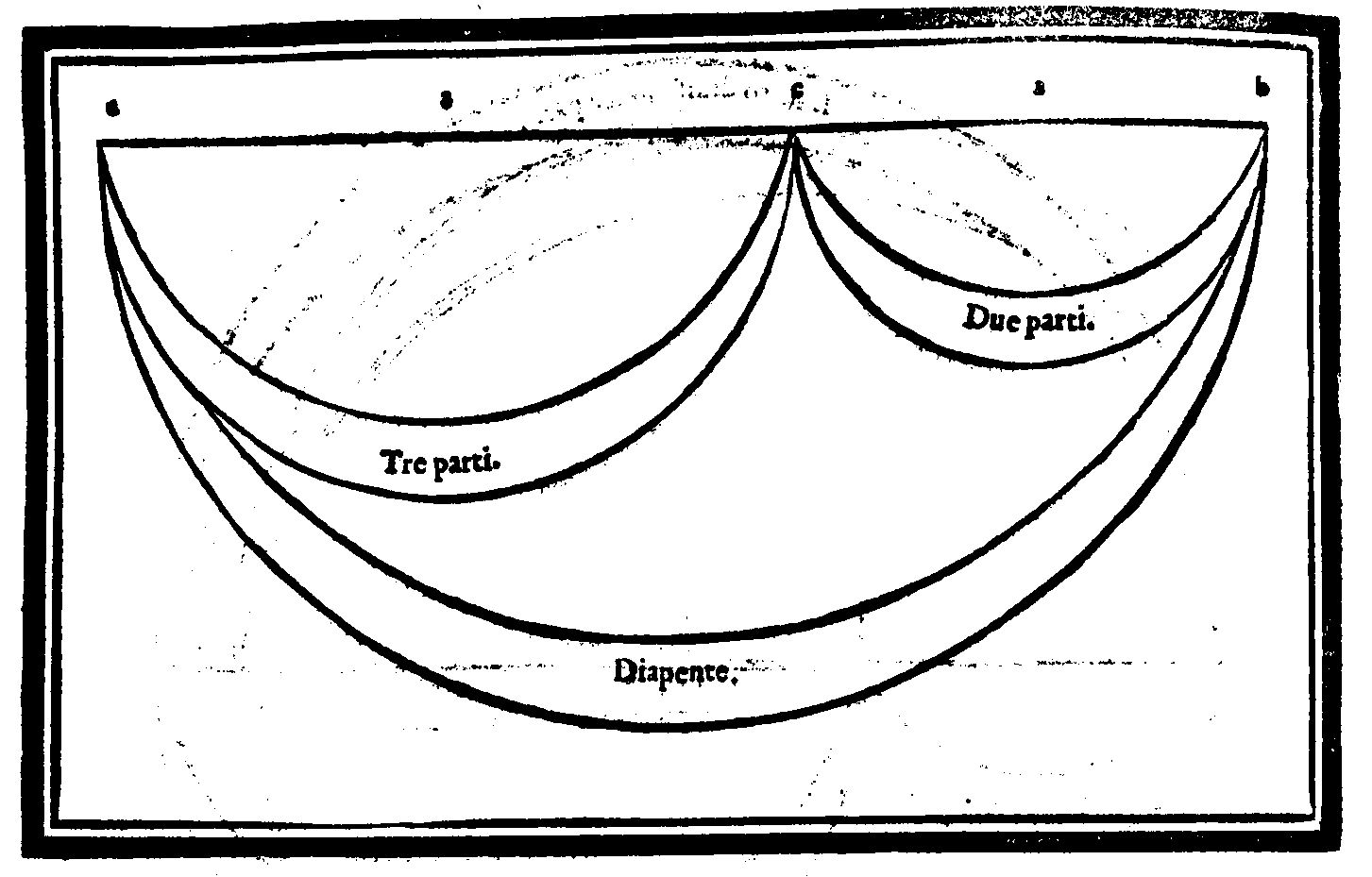
In qual modo si possa Vdire qual si voglia Consonanza accomodata alla sua
proportione.Cap. XX.
ancora, per far giudicio de i Suoni & delle Voci; perche non essendo l'uno di
scordante dall'altra, habbiamo vera & perfetta cognitione delle Consonan-
ze; però è dibisogno, che hora si dimostri il modo di rimetter tutto quello, che
fin qui si è operato con la ragione, sotto 'l giudicio del Sentimento; accioche possiamo
esser certi, che 'l Senso con la Ragione insieme sono concordi; & che le ragioni addotte
più uolte nō siano uane; però adunque, dopo che si hauerà tirato sopra la già detta super-
ficie due, ò più Chorde, le quali si posino sopra i sudetti due Scannelli immobili; fa biso-
gno che siano accordate insieme perfettamente unisone; il che fatto per la seconda Di-
manda del 3. delle Dimostrationi; si debbono pigliare in luogo d'una sola chorda. Do-
po questo ritrouaremo tanti Scannelli mobili, quante sono le chorde tirate sopra tal su-
perficie: mobili dico, acciò si possino leuar da un luogo all'altro, secondo il bisogno; fat
ti di tal lunghezza, che solamente tocchino una di esse chorde; & tanto alti, che non ec-
cedino quelli, che sono immobili; & che siano tutti d'un'istessa altezza, & à questo mo-
 do fabricati, ouero in altra maniera; purche siano secondo le qualità,
do fabricati, ouero in altra maniera; purche siano secondo le qualità, che hò descritto. Ordinate poi le cose in tal guisa; se noi pigliaremo uno
de questi Scānelli, & lo porremo sotto qual si uogliadelle tirate chorde, di
maniera che tal chorda si posi sopra lo Scannello in punto C. posto nello essempio del
Cap. 18. se 'l si percuoterrà la chorda C B. posta dalla parte destra con qualche altra chor-
da senza Scannello; percioche in tal parte sempre porrò i Suoni acuti; si per rispetto de
i termini delle sue proportioni; come etiandio perche ne gli Istrumenti si ritrouano da
questa parte; tra 'l Suono di questa, che sarà A B. & il Suono della C B. si udirà la Diapa-
son consonanza. Ma se noi segnaremo con uno de i Scānelli mobili vna terza chorda in
punto D. come si uede nel secondo essempio nel luogo nominato; percuotendo questa
insieme con una delle non segnate; cioè, D B. con A B. da i Suoni nati da queste due chor
de si farà la consonanza Diapente. Similmente se noi percuoteremo insieme le chorde
page 111A B. & C B. con la D B. vdiremo la Diapason tramezata dalla D B. & diuisa in Proportiona
lità harmonica in vna Diapente A B. & D B. & in una Diatesseron D B. & C B. le quali in-
sieme aggiunte fanno la consonanza Diapason. Oltra di questo, se uorremo vdire la
già accommodata Diapente nel Capitolo precedente, bastarà solamente porre uno de i
Scannelli mobili in punto C. percioche percuotendo dalla parte destra & dalla sinistra le
chorde A C. & C B. si potrà vdire senza dubbio tal Consonanza; conciosia che in questa
diuisione è sofficiente una sola chorda. E' ben vero, che questo modo è piu difficile,
che il primo; & nel primo fanno dibisogno più d'una chorda; come habbiamo ueduto;
& è modo più facile; & si può vdire non solo ogni Consonanza semplice, contenuta da
due Suoni solamente; ma qualunque altra etiandio, che fusse tramezata da più Suoni;
ilche sarebbe molto difficile da vdire, quādo il Musico si uolesse seruire d'una chorda so-
la, seguendo il secondo modo. Essendo adunque il Secondo modo meno vtile & piu fa-
ticoso del primo, lasciarò quello da un canto, & seguirò questo in ogni Diuisione; come
quello che hà da condurre ogni mia fatica à quella perfettione, ch'io desidero.
Del Moltiplicar le Consonanze.Cap. XXI.
tità discreta, hà luogo etiandio nella Continua; perche in questa si ritroua
ogni proportione; & di nuouo dico, che le Proportioni non solo hanno luo-
go in tal quantità, ma anco in essa si possono moltiplicare, diuidere, & far qua
lunque altra operatione; come più à basso vederemo. Hauendo io adunque mostrato,
in qual modo si possa accommodar le Consonanze alla loro proportione nella quantità
continua, & Corpi sonori; verrò à mostrare il modo, che si dee tenere volendone ac-
commodar molte l'una dopo l'altra, di maniera che l'estremo acuto dell'una posta
nel graue, sia l'estremo graue dell'altra posta in acuto; ilqual modo potremo chiamar
Moltiplicare; conciosia che l'accommodar le Consonanze in cotal maniera non è altro
che moltiplicar le loro proportioni, preponēdole, ouer soggiungendole l'una all'altra. Ma
perche io mostrai nella Prima parte,Cap. 31. &
32. che la Moltiplicatione ne i Numeri si può fare in due
modi; però uoglio anche mostrare (acciò questa operatione corrisponda à quella) due
modi di moltiplicarle, che saranno molto necessarij, & il primo corrisponderà alla molti-
plicatione posta nel Cap. 31. della Prima parte che si chiama Soggiungere, & si fà,
quando s'incomincia dalla sinistra venendo verso la parte destra. Il secondo corrispon-
derà alla moltiplicatione del Cap. 32. che procede al contrario; cioè, dalla destra parte
alla sinistra, che si nomina Aggiungere, ò Preporre. Incominciando adunque dal pri-
mo, disporremo prima i termini radicali delle proportioni de gli Interualli, che noi uor-
remo moltiplicare, l'un dopo l'altro per ordine; dopoi accommodaremo nella parte gra
ue alla sua proportione (come di sopra facemmo) la prima Consonanza posta dalla par-
te sinistra. Et per soggiungere à questa la seguente, pigliaremo sempre quella parte di
chorda, ò linea, che rappresenta il Suono acuto della Consonanza accommodata; la-
sciando quella, che si piglia per il Suono graue; & sopra tal linea accommodaremo la se
conda Consonanza, ò Interuallo; diuidendola in tanti parti, quante sono le Vnità con
tenute nel maggior termine della sua proportione, nel modo dato; & tra la diuisa, posta
per il maggior termine della detta proportione, che contiene la detta Consonanza, & le
parti poste per il minore; haueremo moltiplicato la seconda Consonanza alla prima; per
cioche pigliando sempre la minor linea, che rappresenta il Suono acuto della moltiplica-
ta Consonanza, & diuidendola secondo i termini della proportione, che contiene la
Consonanza, la qual vorremo soggiungere; lasciando da un canto quella, che si piglia
per il Suono graue; haueremo il proposito. Volendo adunque Moltiplicare, ò Soggiū-
page 112gere vna Diatessaron ad una Diapente, & alla Diatessaron il Ditono, & à questo il Semi
ditono; è necessario saper prima i Termini radicali, ò Minimi numeri delle proportioni
di queste , & collocarli l'un dopo l'altro, nel modo, che le uogliamo moltipli
care, in cotal maniera 3/2 | 4/3 | 5/4 | 6/5. Dopoi incominciando dalla Diapente, i cui termini sono
3 & 2. l'accommodaremo alla sua proportione sopra la linea A B. al modo, che nel Cap.
18. hò mostrato; & haueremo tra A B. & C B. la proportione di tal Consonanza. Hora per
soggiungerle, ò multiplicarle la Diatessaron, pigliaremo la C B. che rappresenta il Suono
acuto della Diapente; lasciando la A C. da un canto, & accommodando sopra questa li-
nea alla sua proportione la Diatessaron; tra C B. & D B. haueremo il proposito. Per sog-
giunger dopoi à queste il Ditono; lasciando da parte la A D. & pigliando la D B. la diuidere
mo in cinque parti equali; & prendendo le quattro, tra D B. & E B. haueremo congiunto
il Ditono alle due già accommodate, ò moltiplicate . Presa dopoi la E B. ac-
commodandoui alla sua proportione il Semiditono al mostrato modo; tra E B. & F B. ha
ueremo soggiunto, ò moltiplicato (secondo il proposito ) il alle tre prime
Consonanze; come nella figura si uede. Et questo è il Primo modo di moltiplicare, chia
mato Soggiungere.
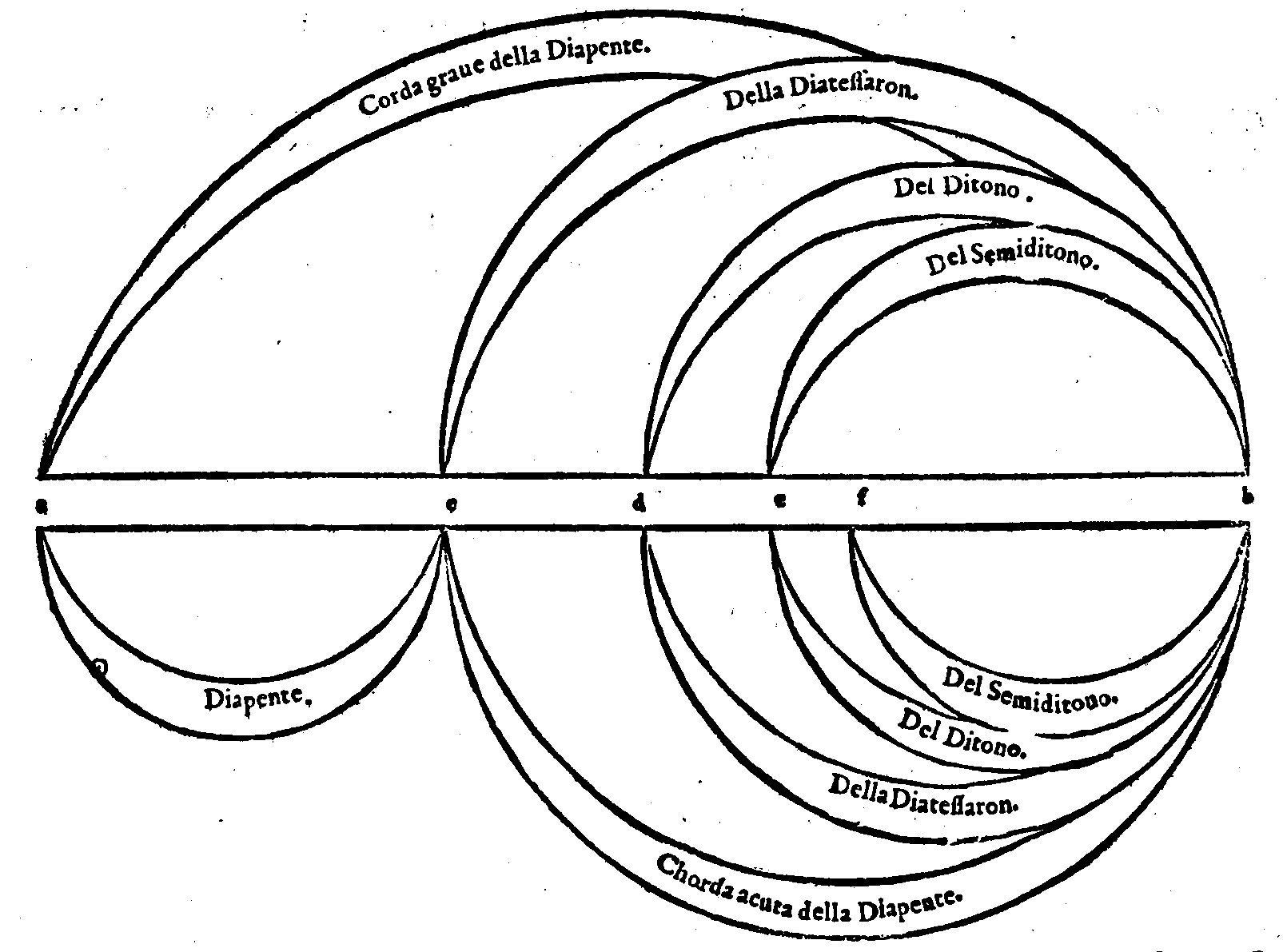
Del Secondo modo di moltiplicar le Consonanze.Cap. XXII.
tioni delle Consonanze, secondo che si uogliono moltiplicare nel modo, che
di sopra habbiamo mostrato) che si ritroui primieramēte le Chorde estreme,
che possono nascere da tal Moltiplicatione; lequali ageuolmente si potranno
trouare, quando noi sommaremo insieme le lor Proportioni, contenute ne i lor termini
radicali; & diuideremo la chorda in tante parti equali, quante saranno le Vnità contenu
te nel termine maggiore della proportione nata da tal somma; dopoi pigliandone tante
page 113dalla banda destra, quante sono le Vnità contenute nel minor termine di tal prodotto,
haueremo il proposito; Imperoche tutta la chorda, & queste parti saranno le ricercate,
che saranno al nostro bisogno. Et per Moltiplicar tali Consonanze, diuideremo l'estre-
ma acuta in tante parti equali, quāte saranno le Vnità contenute nel minor termine della
prima proportione, posta in acuto à banda destra; & con l'istessa ragione aggiungendo-
le tante parti, ch'arriuino al numero delle Vnità, contenute nel maggior termine; tra la
chorda diuisa & l'accresciuta per l'aggiungimento della parte, haueremo accommodato
nella parte acuta alla sua proportione la detta Consonanza; alla quale, se noi uorremo
aggiungere, ò preporre, e moltiplicare un'altra, pigliaremo la chorda, che ne dà il Suo
no graue della già accommodata, che sarà l'acuta di quella, che uorremo moltiplicare;
& la diuideremo in tante parti, quante sono le Vnità contenute nel minor termine della
proportione, che contiene la Consonanza, laquale uorremo moltiplicare; & più oltra,
aggiungendoui tante parti, che siano equali al suo maggior termine; tra questa chorda,
che ne darà il Suono graue, & la diuisa, che farà il Suono acuto, haueremo aggiunto la
seconda Consonanza, alla già preposta & moltiplicata; & cosi dico dell'altre; ma uenia
mo all'essempio. Poniamo che si uoglia moltiplicare insieme un Ditono, un Se-
miditono, & una Diatessaron; di maniera che la Diatessaron sia posta nella parte
acuta, il Ditono nella parte graue, & il Semiditono tenghi il luogo di mezo; di-
co, che noi dobbiamo prima porre i Termini delle proportioni di queste Conso-
nanze per ordine, nel modo che si uogliono moltiplicare; & per ritrouar le chor-
de estreme di questa moltiplicatione, sommaremo insieme le Proportioni; nel mo-
do c'hò mostrato nel Cap. 33. della Prima parte, che saranno queste. 5/4 | 6/5 | 4/3. & haue-
remo una Dupla, contenuta tra questi numeri 120. & 60. la qual ridotta ne i suoi Ter
mini radicali, si trouerà tra 2. & 1. Fatto questo diuideremo la linea A B. in due parti e-
quali in punto C. & haueremo la A B. & C B. che saranno in proportione Dupla; & uerran
no ad esser le Chorde estreme di tal moltiplicatione. Accommodaremo hora primiera-
mente alla sua proportione la Diatessaron nella parte acuta, diuidendo la linea C B. in tre
parti equali, secondo 'l numero delle Vnità contenute nel minor termine della sua pro-
portione; dopoi aggiungendole una Quarta parte in punto D. haueremo la linea D B. che
contenerà Quattro parti, secondo 'l numero delle Vnità comprese nel maggior termine
della proportione; & ne darà il Suono graue della Diatessaron. Cosi dalla C B. che con-
tiene tre parti, & da essa D B. che ne contiene quattro, sarà contenuta la Sesquiterza
proportione; & tra esse accommodata la Diatessaron nell'acuto alla sua uera proportio-
ne; come si potrebbe uedere adducendo le ragioni del modo mostrato di sopra nel Cap.
18. & 19. lequali per breuità si lasciano. Ma per moltiplicare & preporre a questa il Se-
miditono, diuideremo la D B. in Cinque parti, per il minor termine della sua proportio-
ne; & aggiungendole un'altra parte in punto E. per il maggiore tra la E B. & D B. hauere-
mo collocato il Semiditono alla sua proportione, & prepostolo alla Diatessaron; & tra
la A B. & E B. haueremo il Ditono aggiūto al Semiditono; percioche tra queste due chor
de si ritroua la proportione Sesquiquarta; essendo che la A B. contiene una uolta la E B. &
una sua Quarta parte; la qual proportione, senz'alcun dubbio, è la sua forma; come al-
troue si è ueduto. Potiamo adunque dire, che tra gli estremi della Diapason, incomin-
ciando dall'estremo acuto, habbiamo collocato alle loro proportioni le tre nominate
Consonanze, hauendole moltiplicate, preposte, & aggiunte l'una all'altra; cioè, tra la
D B. & C B. la Diatessaron, tra la E B. & D B. il Semiditono, & tra la A B. & E B. il Ditono;
come nella figura si ueggono. Lequali se uorremo udire operando al mostrato modo,
con l'aiuto de i Scannelli mobili posti sotto le chorde, potremo esser fatti chiari, non solo
di questo, ma d'ogni altro dubbio, che sopra ciò ne potesse occorrere.
page 114
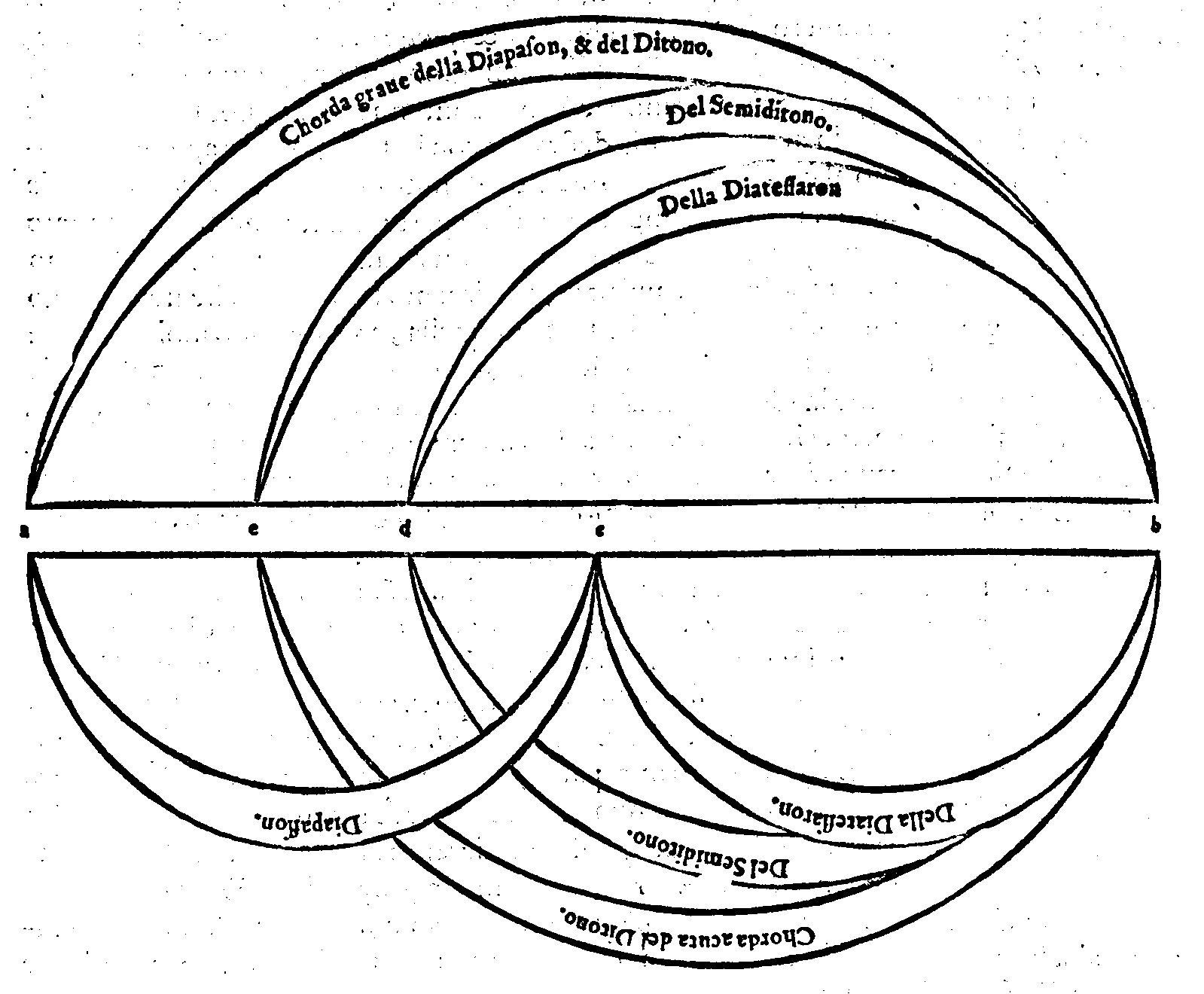
Come si possa diuidere rationalmente qual si voglia Consonanza ò
Interuallo.Cap. XXIII.
torno le Operationi delle Proportioni) seguitarebbe immediatamēte il Som-
mare & il Sottrare; ma perche non sono necessarij, uederemo solamente in
qual maniera si diuidono gl'Interualli musicali; che nō è altro, che il porre u-
na chorda tra due estreme, che diuida l'Interuallo in due parti. Et questa diuisione è di
due sorti; Rationale & Irrationale. La Irrationale non fà al proposito del Musico,
se non per accidente; ma la Rationale è di tre maniere; conciosia che, ouero è Arith-
metica, ouer Geometrica, oueramente Harmonica; & corrispondono alle Proportio-
nalità, che si fanno nella Quantità discreta; nel modo che si è mostrato nella Prima par-
te, ancora ch'ogni Consonanza & qualunque altro Interuallo à caso & senza pen-
sarui altramente si possa diuidere in due parti da una chorda mezana; la qual diui-
sione non è considerata dal Musico; perche trapassa i termini della sua Scienza. Quel-
la Consonanza adunque è diuisa in proportionalità Arithmetica, i cui estremi sono da
una chorda mezana tramezati, ò diuisi, che tra questa & la graue di tal Consonanza,
si oda la minor parte di tal diuisione, & tra essa mezana & l'acuta la maggiore; impe-
roche quella è diuisa Harmonicamente da tal chorda, quando i due membri della Di-
uisione sono situati & posti al contrario de i sopradetti in tal maniera; che la parte
maggiore occupi il luogo graue, & la minor l'acuto; come auiene nella Diuisione
page 115della Diapason; che essendo diuisa da una chorda mezana in una Diapente, & in una
Diatessaron; nell'Arithmetica la Diatessaron tiene il luogo graue, & la Diapente
l'acuto; & nella Harmonica èil contrario; che nel graue si ritroua la Diapente, & la Dia-
tessaron nell'acuto; come ne dimostra la Diuisione di ciascuna, che si fà nella Quantità
discreta. Quella Consonanza, ouer'altro Interuallo è diuiso in Geometrica proportio-
nalità, che hà li suoi estremi Suoni in tal modo da una chorda mezana tramezati; che
quelle due parti, che nascono da tal diuisione, non siano maggiori l'una dell'altra in pro-
portione; ma di tanta quantità & proportione sia quella posta in acuto, quanto quella
posta nel graue come auiene quando la Disdiapason contenuta dalla proportione Qua-
drupla, è diuisa in due Diapason da una chorda mezana; che l'una & l'altra sono compre
se, senz'alcun dubbio dalla proportione Dupla. Queste Diuisioni per maggior commodi
tà si faranno prima co i Numeri; dopoi si accōmodaranno le lor Proportioni nella Quan
tità continua sopra le chorde sonore. Ma perche ogni Diuisione arithmetica & ogni Diui
sione harmonica è solamente rationale; & la geometrica può esser rationale & irrationa
le; però essendo la Rationale facile da farsi; & tornando maggiormente in proposito alle
uolte l'Irrationale al Musico, che la Rationale; auanti ch'io uada più oltra, dimostrerò in
qual modo si possa diuidere ogni Consonanza & ogni Interuallo musicale quantunque
minimo, non solo in due parti; ma anco in più parti equali irrationali; & dimostrerò
primieramente un modo breue & espedito da diuiderlo in due parti solamente; dopoi da
rò il modo da diuiderlo in più parti, quando farà dibisogno.
In qual modo si possa Diuidere qual si voglia Interuallo Musicale in due
parti equali.Cap. XXIIII.
dere qual si uoglia Interuallo Musicale in due parti equali) la Nona proposta
del Sesto di Euclide, secondo il Campano; ouer la 13. & Problema quinto, se
condo Theone, che dice: Essendo date due rette linee, potiamo ritrouar
quella del mezo proportionale; conciosia che tanto è, come se 'l si dicesse; Essendo dati
due Suoni, potiamo ritrouare à questi un mezano suono proportionale; & questo è il
modo. Poniamo che si habbia accommodata alla sua proportione la consonanza Diapa
son, tra la chorda A B. & la C B. & sia dibisogno di ritrouare una Chorda mezana, che po
sta tra queste due, la diuida geometricamente in due parti equali. Allungaremo primie-
ramente la linea A B. incominciando dal punto B. verso la banda destra, infino al punto
D. in tal maniera, che la B D. sia equale alla C B. & haueremo la A D. Fatto questo descri-
ueremo un Semicircolo, il cui diametro sia tutta la A D. dopoi tiraremo una linea, che
partendosi dal punto B. doue la detta A B. si congiunse con la B D uada perpendicolarmen
te alla circonferenza del Semicircolo in punto E. & sarà la B E. & questa sarà la ricercata
Chorda mezana. Et per dimostrar questo tirarò la linea A E. & la E D. & verrà il Triango-
lo A E D. chiamato da i Geometri Orthogonio; ilquale (come per la 31. del Terzo d'Eucli
de è manifesto) è di tal natura; c'hà un'angolo retto, che è l'angolo E. onde essendo que-
sto Triangolo diuiso dalla linea B E. che casca perpendicolarmēte dalla circonferenza del
Semicircolo nell'angolo retto alla sua base; come si può ueder nella figura; nascono etian
dio due Triangoli minori, l'un maggior dell'altro; i quali sono A B E. & E B D. di specie &
natura in tutto simili al triangolo A E D. & sono proportionali l'uno all'altro; come per la
Ottaua del detto Sesto libro è manifesto. Et per il Corollario di tal propositione,
la Proportione della A B. alla B E. è quella istessa, ch'è dalla E B. alla B D. secondo 'l no-
stro proposito. Facendo hora la F B. equale alla B E. haueremo la Diuisione e-
quale della proposta Consonanza dalla chorda F B. come si ricercauaua. Et chi uorrà
page 116veder la proua di questa cosa, potrà diuidereia Disdiapason al mostrato modo; percioche
allora conoscerà, che quella Chorda mezana, che la diuidera in due parti, sarà equalmen
te distante, tanto dalla estrema chorda graue, quanto dalla estrema acuta di tal Conso-
nanza, per una Diapason, secondo 'l proposito; ilche è stato dimostrato etiandio nella
Decima del Terzo delle Dimostrationi con maggior diligenza; & più copiosamente.
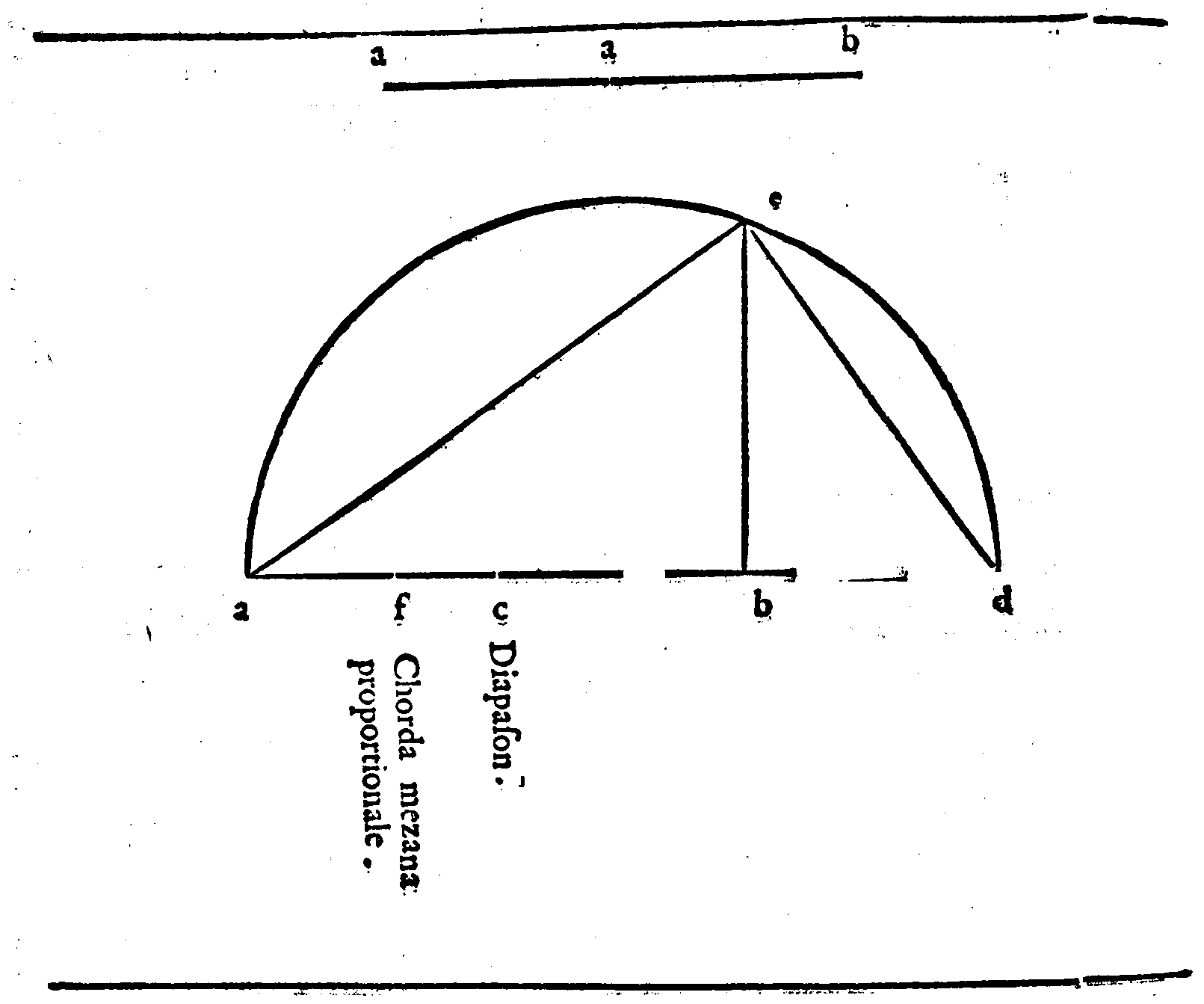
Altro modo di diuider qual si voglia Consonanza, ouero Interuallo in due,
ò in più parti equali.Cap. XXV.
uoglia, che siano equali, è non solamente bello; ma anco piu vtile del
primo; per esser piu uniuersale; & fù ritrouato (come uogliono alcuni) da
Archita, & altri da Eratosthene, quando ritrouò il Raddoppiamento del Cu-
bo, nel tempo che i Dalij (come narra Giouan Grammatico1. Poster.
com. 36.) erano molestati dalla pesti-
lenza; laquale Inuentione & molt'altre insieme raccolse Gregorio Valla Piacentino nel
Quarto libro della Geometria; insegnando di ritrouar Due mezane linee proportionali
tra due proposte. E ben vero, che senza l'aiuto d'un'Istrumento, nominato Mesolabio,
sarebbe uana & inutile ogni fatica: però auanti ch'io vada più oltra, mostrarò il modo di
fabricar l'Istrumento, & dopoi insegnerò ritrouar le Linee. Si debbe adunque primie-
ramente apparecchiare un'Asse, ouer Tauola ben piana & vguale nella sua superficie; la
qual non sia men larga d'un piede, & lunga quanto si vuole; ancorache quanto più fusse
lunga, tanto piu tornerebbe commodo. Ridotta poi in una figura quadrata lunga, la-
qale contenga ne i Capi Quattro angoli retti; per potere operar meglio & senz'alcu-
page 117no errore; faremo sopra di essa con diligenza un canale; ponendo dalle bande per lungo
della detta tauola, ò asse due righe, ò liste sottili fatte cō discretione; di modo che, essendo
 equidistanti, le sponde del canale, uenghino ad esser alte quā
equidistanti, le sponde del canale, uenghino ad esser alte quā to è una costa di coltello, & non piu. Fatto questo, faremo
prima Tre figure quadrate di Metallo, ò di Legno sottilissime;
le quali i Geometri chiamano Paralellogrammi, che habbia-
no quattro angoli retti, & che siano lunghe quanto è largo il
canale, & larghe quanto si vuole; purche siano fabricate in
tal maniera, che l'una sia equale all'altra; cioè, che i lati dell'
una siano equali à i lati dell'altra. Dopoi tiraremo à due di es
se una linea diametrale dall'angolo superiore sinistro all'ango
lo destro inferiore di ciascuno in tal maniera, che le superficie
siano diuise in due triangoli Orthogonij equali; come nell'essē
pio si uede. Porremo hora primieramēte i Quadrati nel detto
canale l'un dopo l'altro in tal modo; che 'l primo senza diame
tro sia nella parte sinistra, & resti immobile; dopoi gli altri, che
hanno i diametri; cioè, il secondo & il terzo per ordine à bāda
destra; di maniera che il lato destro dell'uno sia posto sopra il
sinistro dell'altro; & cosi haueremo fatto & ordinato il detto
Istrumento; ilquale sarà D E F G. & sia H I K L. il primo quadra-
to immobile senza diametro; il secondo N O P Q. il cui diametro sia N Q. & il terzo sia R S
T V. del quale R V. sia il diametro. Poniamo hora che si habbia da ritrouare una Chor-
da mezana proportionale, laqual diuida in due parti equali la Diapason, contenuta dal
la proportion Dupla, tra le due sottoposte chorde, ò linee A E. & C B. & siano equali alla
A B. & alla C B. poste nel Capitolo precedente. Faremo primieramente il lato destro del
primo quadrato; cioè, L K. equale alla A B. in punto M. & sarà L M. dopoi pigliaremo il se
condo quadrato, & lo spingeremo sotto il primo tanto, che 'l suo diametro N Q. seghi il la
to K L. del primo quadrato nel punto M. & cosi il primo, & il secondo quadrato resteran-
no immobili. Faremo dopoi il lato destro del terzo quadrato, che è V T. equale alla C B. in
punto X. & fermato che si haurà un filo sottilissimo, che sarà M G. nel punto M. lo disten
deremo tanto, che passi per il punto X. Spingeremo hora il terzo quadrato tanto sotto 'l se
condo, che 'l lato P Q. uenghi ad esser segato dal diametro R Vv. & dal detto filo in un punto
che sarà Y. & quella parte del lato destro del secondo quadrato, laqual resterà sotto 'l filo,
che è la Q Y. sarà la ricercata Linea, ò Chorda proportionale; come nella figura si uede.
Et questo è manifesto; imperoche la Linea mezana proportionale Q Y. ritrouata nel Me-
solabio tra la A B. & la C B. è equale alla B E. ritrouata nel Capitolo precedente. Questo si
potrebbe prouare, se 'l si descriuesse in una superficie piana tutte le linee fatte nel Mesola
bio; allungando primieramente, per la Seconda dimanda del Primo d'Euclide, la linea
M X. nel punto Z. percioche allhora haueressimo tre Triangoli contenenti un'angolo ret-
to; cioè, L M Z. Q Y Z. & V X Z. da i quali si dimostrarebbe per i Principij & Demostra-
tioni di esso Euclide, il tutto esser uero; come per il Secondo parer commune, &
per il Nono; per la 28. & per la Seconda parte della 32. del Primo; per la Seconda, per la
Quarta, & per la Sesta del Sesto; & per la Vndecima del Quinto, lequali lascio; percioche
nella Vndecima del Terzo delle nostre Dimostrationi harmoniche hò cotal cosa diffusa-
mente trattato. Bastami solamente hora dire, che uolendo ritrouar piu linee mezane, ò
chorde proportionali; cioè, uolendo diuidere in piu parti qual si uoglia Interuallo mu-
sicale, si potrà usare il mostrato modo. Bisogna però auertire, che per ogni linea, ò chor
da, che si uorrà aggiungere oltra la ritrouata, sarà dibisogno di aggiungere etian-
dio un'altro Paralellogrammo, ò Quadrato col suo diametro, fatto di maniera &
di grandezza, come sono i primi; facendo, che i lati destri d'ogni Quadrato uen-
ghino ad esser segati in un punto istesso da i diametri & dal filo al mostrato modo.
page 118Auertendo etiandio di por sempre il primo quadrato senza diametro, che sia immobile;
& che 'l suo lato destro sia segato dal diametro del seguente in quel punto, che si porrà per
la lunghezza della linea, ò chorda proposta maggiore; & che 'l lato destro dell'vltimo sia
segato dal filo in quella parte, che si piglia la lungezza della linea minore proposta, se-
condo 'l modo dato. Et se la maggior linea proposta fusse piu lunga, che 'l Quadrato po
sto nel Mesolabio, non si potrebbe far cosa alcuna. E' ben uero, che pigliando la metà
di Ciascuna delle due proposte, si potrà hauere il proposito; perche dopo fatto il tutto, le
mezane ritrouate si potranno allungar secondo la ragione della parte presa delle propo
ste linee, & cosi ogni cosa tornerà bene.
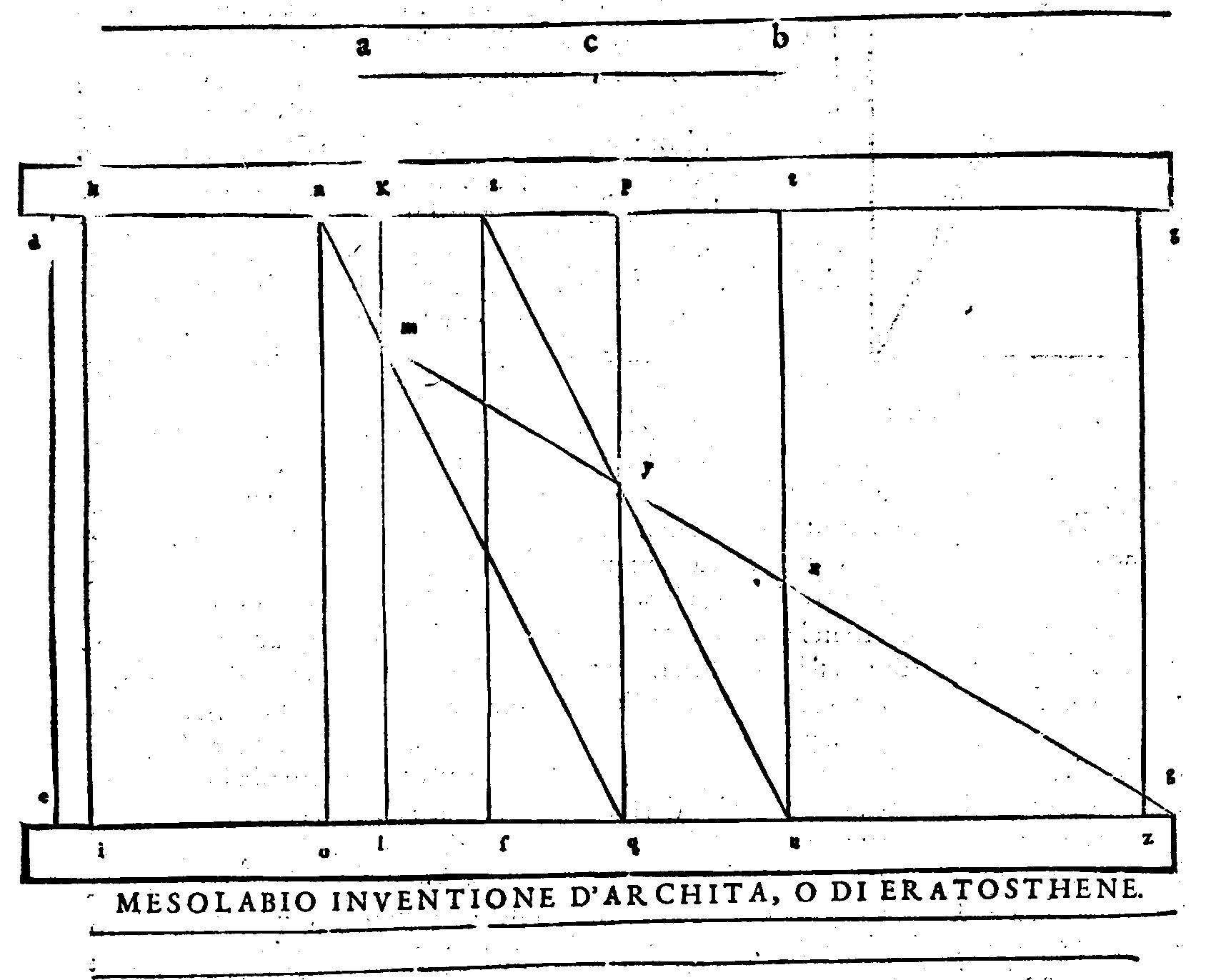
In qual modo la Consonanza si faccia diuisibile.Cap. XXVI.
è chiamato Qualità passibile; però si debbe sapere, che essendo la Consonan-
za senz'alcun dubbio Suono, & hauendo in se tal possanza; come nella sua
dichiaratione di sopra si è detto;supra
Cap 12.
può anco esser detta Qualità passibile; per-
cioche è tratta fuori della possanza del percutiente & del percosso. La onde sopra quel-
lo, c'hò detto si potrebbe meritamente dubitare;Cap. 10. In qual modo la Consonanza si pos-
sa diuidere, ò moltiplicare, non essendo ne Numero, ne Proportione; conciosia che
la Diuisione & la Moltiplicatione appartengano solamente alla Quantità, & è il
suo proprio. Al qual dubbio rispondendo, dico; quantunque la Quantità sia di-
uisibile & moltiplicabile essentialmente, & per se; non si puo però negare, che la
Qualità anche non si possa diuidere & moltiplicare per accidente; percioche è
page 119sotto posta alla Quantità; la qual diuidendosi, ò moltiplicandosi essentialmente & per se,
viene adessere insieme diuisa, ò moltiplicata la Qualità; non già propriamente; ma per
accidente. Et questo si può uedere (dando di ciò un'accommodato essempio) nella diui-Vide c. 14.
& 15. Lib.
4. Supple.
sione del graue & del leggiero; lequali cose non sono quantità; ma si bene qualità & non
conuengono alla diuisione, se non in tanto, che sono sottoposte ad un corpo diuisibile;
nella diuisione del quale, ancora che gli Accidenti siano indiuisibili, si fanno però diuisi-
bili accidentalmente; conciosia c'hanno il loro essere essentialmente nelle cose, che sono
diuisibili; come si può anco uedere del Colore posto nel legno, che diuidendosi tal legno
essentialmente; il Colore medesimamente è diuiso per accidente in molte parti. Onde
dico in proposito, che quantunque la Consonanza sia da se indiuisibile, per esser Qualità;
nondimeno diuidendosi i Corpi sonori; da i quali ella è prodotta; essentialmente in piu
parti; anche lei per accidente viene ad esser diuisibile, secondo la diuisione del Soggetto,
che sono essi Corpi sonori. Potiamo adunque dire; che quantunque la Consonanza da
se non sia diuisibile, è però diuisibile per accidente, per la diuisione del suo Soggetto; &
cosi da quello, che si è detto di sopra, & dà quello che si è detto nel Cap. 41. della Pri
ma parte, si può uedere, in qual modo si possa intendere la Definitione d'Aristote-
le della consonanza, che dice; Che è ragion de Numeri nell'acuto & nel graue; & an-
che come si potrà rispondere à coloro, che con argomenti sofistici, à cotal definitione
si uolessero opporre.
Quel che sia Monochordo, & perche sia cosi chiamato.Cap. XXVII.
alla Ordinatione, ò Compositione; ò uogliamo dire Diuisione del Monochor
do di ciascuna Specie de i tre nominati Generi; ma prima uederemo, quel che
sia Monochordo. Monochordo dico esser quell'Istrumento, ouer qualunque
altro simile, ch'io mostrai di sopra nel Cap. 18. ilquale da molti diuersamente è stato chia
mato. Imperoche TolomeoHarm. lib.
1. cap. 8. & BoetioMusicae li-
bro. 5. c. 2. lo chiamano Regola harmonica; & alcuni de i Gre
ci lo chiamano Μαγὰς; & è istrumento d'una sola chorda, col quale aggiungendoui il giu
dicio della Ragione, per virtù della Proportionalità harmonica inuestighiamo le ragioni
delle Consonanze musicali, & d'ogni lor parte; & sono piu Suoni ritrouati & accettati;
i quali collochiamo in esso secondo i gradi del graue & dell'acuto, à i loro luoghi; & li de
scriuiamo con i Nomi proprij: accioche con arteficio impariamo ad essercitar le Modu-
lationi & le Harmonie; & Pitagora (come vuol BoetioIbidem
lib. c. 11.) fu l'Inuentore di questo Istru-
mento. Deriua questo nome Monochordo da due nomi Greci aggiunti insieme; da
Μόνος, che vuol dire Solo, & da Χορδὴ, che significa Chorda; come Istrumento d'una
sola chorda; ancora che con tal nome si chiama etiandio quell'Istrumento, che si sona cō
le corde raddopiate, conosciuto hormai da ogn'uno, per esser molto in uso; ma questo
non fà al nostro proposito.
Della Diuisione, ouero Ordinatione del Monochordo della Prima specie del genere
Diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi
fu l'Inuentore di questo Genere & del suo ordine.
Cap. XXVIII.
Monochordo della prima specie dei Primo genere chiamata da TolomeoHar. lib. 2
Cap. 1.
& da altri ancora, Diatonico diatono; dobbiamo prima auertire di or-
dinarlo, ouer diuiderlo in cinque Tetrachordi; acciò seguitiamo il co-
stume de i Musici Antichi, & de Moderni; de i quali il primo chiamaremo
page 120Hypaton; cioè, Principale: percioche tiene la parte più graue; il secondo, Meson ò Me
zano; conciosia che tiene quasi il luogo di mezo, & è piu acuto del primo; il terzo, Die
zeugmenon, ò Separato; & l'ultimo de i quattro, che comprendono le Quindeci chorde
(come vederemo) nominaremo Hyperboleon, oueramente Eccellente. A questi poi ag
giungeremo il Quinto; & lo chiamaremo Synemennon, ò Congiunto; & haueremo un'
ordine de Sedici chorde, contenuto nella Disdiapason; la quale i Greci chiamano Syste
ma massimo. Ma si debbe auertire, che gli antichi diuisero, ouer'ordinarono il loro Mo-
nochordo per Tetrachordi, & non per Pentachordi, ouero Hexacordi, per due ragioni;
prima, perche haueano la Diatessaron, che si conteneua ne gli estremi, del Tetrachordo
per la prima Consonanza; essendo che appresso di loro era la minore de tutte l'altre; do-
poi perche al Tetrachordo si può sempre aggiungere dalla parte acuta quell'Interuallo
ch'è posto nel graue di esso Tetrachordo ò per il contrario; porre nel graue quello, che
si ritroua essere in acuto; che ne darà sempre la consonanza Diatessaron in ogni Specie
di harmonia per ogni genere. Et perche queste aggiuntioni non si poteuano fare commo
damente nella Diapente, ne meno nell'Hexachordo; perche togliendo un Interuallo
graue della Diatessaron, & aggiungendolo in acuto; ò per il contrario; togliendo quello
ch'è posto nell'acuto, & ponendolo nel graue; non si poteua sempre hauer la consonan-
za Diapente; quantunque si potesse hauere il numero delle chorde, dalle quali acquistò
il nome; però i Greci hauendo tale auertimento, fecero l'Ordinatione, ouer Diuisioue
del Systema massimo per Tetrachordi, & non per Pentachordi, ouero Hexachordi. Et
questa ragione stimo, che sia la uera, & è: perche nel Tetrachordo si ritrouano tutti quelli
Interualli de i quali si cōpone la Specie, come de i suoi proprij & ueri Elementi. Volendo
adūque dar principio à tal'Ordine ouer Diuisione, seguendo il costume de gl'Antichi, nō
solo in questa; ma in ciascun'altra diuisione; per suo fondamento accommodaremo pri-
mieramente nella parte piu graue il Tuono sesquiottauo alla sua proportione; accioche
la grauissima chorda detta da i Greci Proslambanomenos, con la chorda acuta del secon
do Tetrachordo chiamata Mese, contenga & faccia vdire la consonanza Diapason. Al
qual Tuono aggiungeremo il primo Tetrachordo, & à questo il secondo; & porremo ap
presso questo l'interuallo del Tuono, contenuto dalla proportione Sesquiottaua chiama
to Tuono della diuisione, come uederemo al suo luogo. Et aggiungendo à questo il ter-
zo Tetrachordo, & al terzo il quarto, nella sua parte più acuta; haueremo Quindeci chor
de contenute in tale ordine. Fatto questo, aggiungeremo sopra la chorda Mese uerso l'a-
cuto, il quinto Tetrachordo; & cosi haueremo l'Ordinatione, ouer Diuisione della pri
ma Specie diatonica, contenuta tra Sedici chorde & cinque Tetrachordi, nel modo che
uederemo. Di questo ordine, credo io che fusse l'inuentore Terpandro Lesbio, quando
ridusse le prime Sette chorde antiche in uno, congiungendole per due Tetrachordi; co-
me nel secondo essempio del Cap. 20. del Primo libro della Musica di Boetio si può uede
re; le quali furono dopoi ridotte da Licaone Samio al numero di Otto; & diuise in due
Tetrachordi separati; com'è manifesto per il terzo essempio posto da Boetio nel sopradet
to luogo. Fu dopoi da altri in tal maniera accresciuto, che arriuò al numero de Sedici
chorde; nel modo ch'io intendo di mostrare; ancora che alcuni uogliono, che Pithago
ra fusse l'Inuentore. Ma sia come si uoglia, Pitagora fu quello, che ritrouò la Ragione de
i Suoni, nel modo, c'hò mostrato nella Prima & nella Seconda Parte. Volendo adunque
mostrar l'Ordine di questa prima Specie, & la diuisione del suo Monochordo, contenuto
da cinque Tetrachordi, per poterla porre sotto 'l giudicio del sentimēto; accioche possa do
poi ragionar piu liberamēte sopra quello, ch'io hò da dire; non deuiando dal costume de
gli Antichi, preparato che si hauera un'Istrumento simile à quello, che di sopra nel Cap.
18. hò mostrato; dopo l'hauere accommodato in esso una Linea, che passi dall'un de i ca-
pi all'altro per il mezo; nel modo che si uede nell'essempio; & sarà la A B. accommodarem
mo prima alla sua proportione il Tuono sesquiottauo, che sarà tra A B. & C B. come al-
troue hò insegnato; dopoi immediatamente soggiungeremo il primo Tetrachordo
page 121detto Hypaton, in questo modo; accommodato che si hauerà i suoi estremi alla lo-
ro proportione, che saranno C B. & D B, senza esser tramezati da alcuna chorda;
moltiplicaremo nel mezo loro le mezane chorde, contenute dalle loro proportioni.
Si debbe però auertire, che non solo in questa, ma in qualunque altra Diuisione, si deb-
be accommodare & moltiplicare in tal modo gli Interualli, che sempre i maggiori con-
tenuti da Proportioni maggiori siano moltiplicati prima de gli altri; accioche si uenga
à schiuare insieme con molta fatica, infiniti errori, che potrebbono nascere; percioche
hauendo prima moltiplicato quelli, che sono maggiori, necessariamente & con poca fa
tica (come uederemo) uengono accommodarsi etiandio i minori; il che sarà manifesto
moltiplicando gli interualli de i Tetrachordi, accommodando à i loro luoghi proportiona
tamente le chorde mezane; imperoche dopo che si hauerà accōmodato alla loro propor
tione i due Tuoni Sesquiottaui, moltiplicandoli al modo, che nel Cap. 22. hò mostrato;
haueremo collocato nell'acuto il primo tra E B. & D B. & il secondo nel graue tra F B. &
E B. Et perche ogni Tetrachordo di questa specie, si compone di due Interualli Sesqui-
ottaui, & della proportione Super 13. partiente 243. la quale è la forma del Semituono
minore, essendo F B. & E B. Tuono, similmente E B, & D E; seguita che C B. & F B. sia l'in-
teruallo del Semituono; il quale è il supplimento delli due Tuoni, alla perfettione del
Tetrachordo. Et questo è manifesto; percioche se caueremo dalla Sesquiterza, ch'è la
forma del Tetrachordo, due proportioni Sesquiottaue; resterà la proportione Super 13.
partiente 243. continente il Semituono minore. Fatto questo, per aggiungere al detto
Tetrachordo il secondo nominato Meson, lo accommodaremo al modo, che si fece il
primo, sopra la linea D B & uerrà G B & D B, che saranno gli estremi; & H B. G B. sarà il
Tuono acuto; & il graue sarà I B. & H B. Ma D B. & I B, per le ragioni dette, saranno il mi
nor Semituono. A questo Tetrachordo soggiungeremo il Tuono Sesquiottauo, per il
quale separaremo il Terzo da questo; & tal separatione chiamaremo con BoetioMusicae. li
br. 2. c. 24 Διάζευξις
che uuol dire Diuisione; ilperche da questo cotal Tuono è detto il Tuono della Diuisio-
ne; & da questo nome anco il terzo Tetrachordo è anco detto Diezeugmenon, ò Sepa-
rato. Et questa separatione si ritroua solamente doue due Tetrachordi, per l'interposi-
tione del Tuono, si scompagnano l'uno dall'altro. Ma quando la chorda estrema acu-
ta di vno, è la chorda estrema graue dell'altro; allora sono l'vno all'altro congiunti; &
tal congiuntione si chiama Συναφὴ; cioè, Congiungimento; come il medesimo BoetioVt supra.
dimostra. Aggiunto adunque che si hauerà il Tuono al Tetrachordo Meson; che sarà
contenuto tra la K B. & la G B; allora senz'alcun mezo aggiungeremo nella linea K B il
terzo Tetracordo, diuidendola al modo mostrato; ilche fatto haueremo le sue chorde e-
streme K B. & L B tramezate dalle M B. & N B. che ne daranno la diuisione del Tetrachor-
do fatta in due Tuoni & in un Semituono. Hora sopra la chorda L B. collocaremo il quar
to Tetrachordo detto Hyperboleon; operando come ne gli altri si è fatto; & haueremo
L B. & O B, che sono le sue estreme chorde; P B. & Q B. che sono le mezane; lequali fanno
la diuisione in due Tuoni & in un Semituono, secondo l'ordine principiato; di modo che
haueremo un'ordine, ò diuisione de Quindici chorde; allequali aggiungeremo l'ultimo
Tetrachordo detto Synemennon; congiungendolo al secondo, in cotal modo; facen-
do sopra la chorda G B. la solita diuisione; & tra essa & la M B. haueremo l'estreme chor-
de, le cui mezane saranno N B. & R B. E' ben uero, che si aggiungerà solamente da nuouo
la chorda R B. percioche l'altre sono communi à gli altri Tetrachordi. Onde credono alcu
ni; che tal Chorda fusse stata aggiunta per due cagioni; l'una per dare ad intendere, ch'
ogni Tuono si possa deuidere in due Semituoni; l'altra per fare acquisto duna Diatessa-
ron verso l'acuto, partendosi dalla chorda Parhypatemeson: ma sia come si uoglia; se
ben per altra cagione fusse stata aggiunta, questo è di poco momento: basta che haue-
remo per tale aggiuntione etiandio un Semituono maggiore tra la R B. & K B. contenuto
dalla proportione Super 139. partiente 2187 detto da i Greci Α'ποτομὴ, ilquale aggiun
to tal minore chiamato Λε͂ιμμα, ne dà il Tuono Sesquiottauo; perciche la chorda R B.
page 122
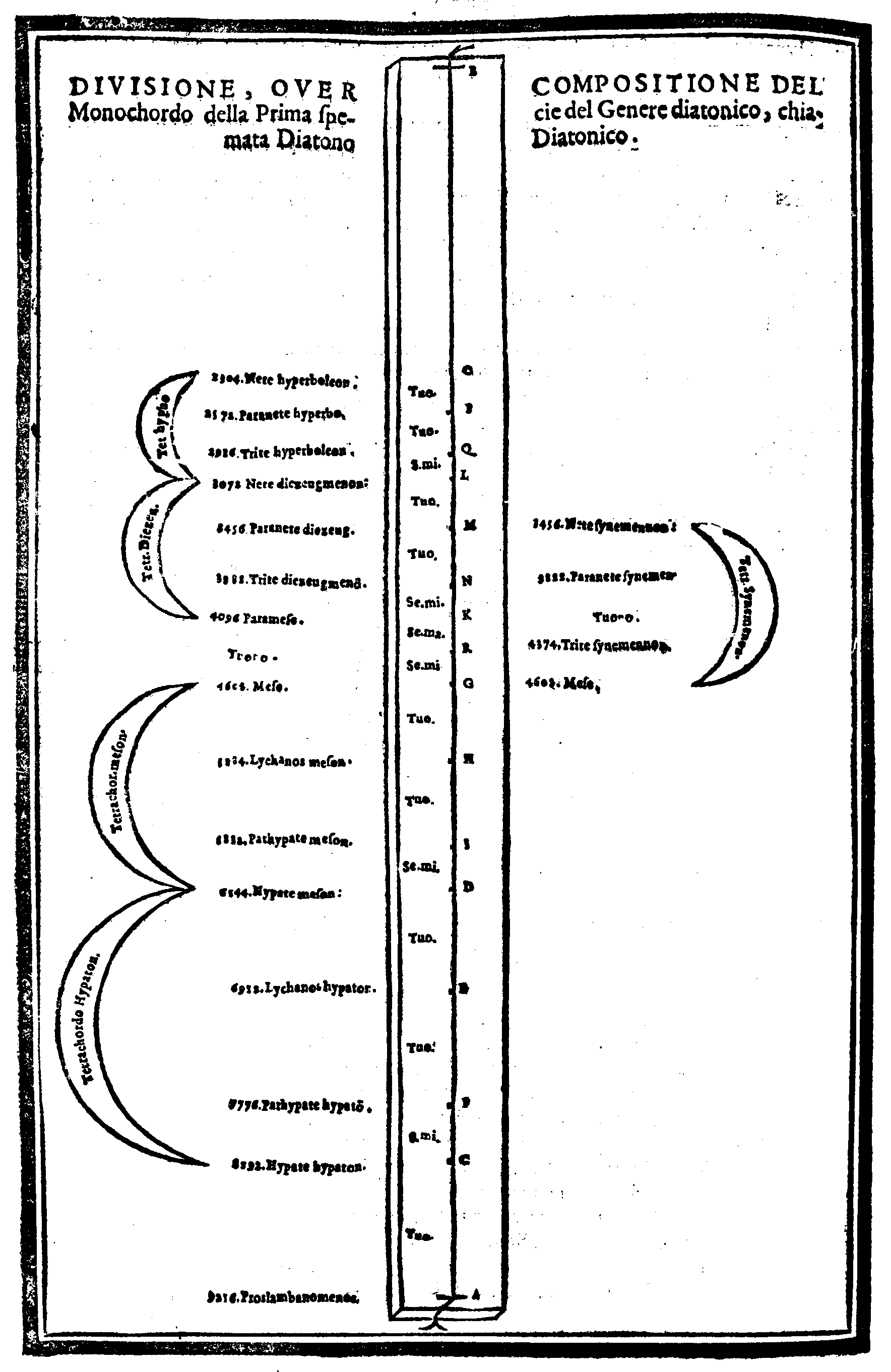
sta adunque sarà la intiera Diuisione, ò Compositione del Monochordo della prima spe
cie del Diatonico, detta Diatonico diatono; diuisa, oueramente ordinata secondo la
mente de gli antichi & moderni Pitagorici in cinque Tetrachordi; nella quale si conten-
gono Quideci interualli tra Sedeci chorde; le quali hò descritte co i Nomi antichi, &
notate con le loro Proportioni, moltiplicate secondo i modi mostrati nel Cap. 32. & 33.
della Prima parte; per maggiore intelligenza di quello, che si è detto. Et benche gli anti-
chi nominassero le chorde di questa Ordinatione co i nomi, i quali hò mostrato; che sono
molto differenti da quelli, che habbiamo al presente; questo non è di molta importanza;
imperoche è concesso à gli Inuentori delle cose, nominarle dalla cagione, ouer dall'ef-
to loro; oueramente secondo che à loro piace. Nominarono adunque gli Antichi le chor-
de delle lor Cetere con tali nomi; perche essendo la Musica (come narra BoetioMusicae li.
br. 1. c. 20. secon-
do 'l parer di Nicomaco) stata da principio in tal maniera semplice, che solamente si ado-
peraua il Quadrichordo ritrouato da Mercurio; Terpandro lo ridusse dopoi al numero di
Sette chorde. Et di queste chiamarono la più graue Hypate, ò Principale, ouer mag-
giore & più honorata; onde Senocrate appresso di Plutarcho,Plat.
quaest. 8. nomina Gioue Hypaton,
nelle cose immutabili; Onde i Consoli per la eccellenza delle lor dignità pigliaro-
no anticamente il predetto nome. La seconda fù detta Parhypate: perche era colloca-
ta appresso la Hypate; la terza chiamarono Lychanos; essendo che i Greci con tal nome
chiamano quel Dito, che nominiamo Indice, dal toccare, che si fà con lui leggiermente;
& anco perche nel sonar la detta chorda, tal Dito si poneua in opera. Mese dissero la quar
ta; conciosia che tra le Sette era collocata nel mezo; la quinta Paramese; cioè, Appresso
la Mese accōmodata; la sesta Paranete, perche era uicina alla Nete; ma la settimna chiama-
rono Nete, quasi Neate, ò Inferiore. Accresciuto poi nel modo mostrato tale ordine, le
nominarono da i Nomi sopradetti; aggiungendole il nome de i Tetrachordi, ne i quali
erano collocate; & la Chorda grauissima di tale ordine dissero Proslambanomenos, ò
Acquistata; conciosia che l'aggiunsero in ogni diuisione, per ogni genere & per ogni spe
cie; accioche con la Ottaua chorda, detta Mese; facesse vdire la consonanza Diapa-
son. Et non solamente le chorde di questa specie furono denominate da tali nomi, in
questo primo Genere; ma l'altre ancora di ciascun'altra Specie per ogni Genere; percio
che ogni Specie è diuisa, ouero ordinata in cinque Tetrachordi; come uederemo.
Che gli Antichi attribuirono alcune chorde de i loro Istrumenti alle Sphere
celesti.Cap. XXIX.
monia, ò concento del Cielo; li diede cagione di contemplare intorno à que
sto varie cose. La onde dalla diuersità de i lor pareri nacquero diuersi princi-
pii & uarie ragioni; imperoche da una parte Alcuni hebbero opinione, che 'l
Firmamento, ò uogliam dire Sphera delle stelle fisse, laquale de tutte l'altre è piu uelo-
ce nel mouimento diurno; come afferma Platone;De Repu.
10. mandasse fuori il Suono più acuto
d'ogn'altra Sphera; forse indotti da questa ragione; Che quel Corpo, il quale si muoue
più uelocemente, è cagione del Suono più acuto; onde mouendosi i Corpi superiori del
Cielo più uelocemente de gli inferiori; concludeuano, che tali Corpi facessero il Suono
più acuto. Dall'altra parte erano Alcuni, che teneuano il contrario, che la Sphe-
ra della Luna facesse il Suono più acuto, formando tal ragione; I Corpi minori rendo-
no minor Suono & più acuto di quello che fanno i maggiori; come sensatamente si com-
prende; la onde essendo che i Corpi inferiori celesti sono minori de i superiori; seguita
che gli inferiori Corpi minori mandino fuori Suoni minori & piu acuti de i superiori.
Quelli che fauorirono la prima opinione furono molti; tra i quali si troua Cicerone nel
page 124Lib. 6. della Repu. come si può cōprendere dalle parole poste nel Cap. 4. della Prima par
te; laquale opinione Ambrosio Dottore Santo recita nel suo HexameronLib. 2. c. 2.. Ma tra i mo-
derni Scrittori si troua Battista Mantoano Poeta elegantissimo, che cotal cosa ci mani-
festa à questo modo;Parth. 2. li
bro 1.
Insonuere poli, longeꝗ auditus ab alto.< lb>
Concentus, mixtumꝗ melos, pars ocyus acta
Clarius, & cantu longè resonabat acute,
Tarda ibat grauiore sone.
E' ben uero, che quello, che dice, si può accommodare à qual si uoglia delle due nar-
rate opinioni; percioche se noi uorremo attribuire la Tardità del mouimento annuale
alla Sphera di Saturno; ueramente il suo mouimento è più tardo d'ogn'altra Sphera in-
teriore; come mostra Platone nell'Epinomide; conciosia che fà la sua reuolutione in trē
ta anni; & questo sarà in fauor de quelli, che tengono, che i Corpi maggiori fanno il Suo
no più graue. Ma se la tardanza s'attribuirà al mouimento diurno sarà in fauor de quel-
li, che fauoriscono la prima opinione; & bisognerà intendere il contrario: poiche non è
dubbio alcuno; come si uede col senso; che 'l mouimento della Sphera della Luna sia più
tardo d'ogn'altro, quando dall'Oriente si muoue all'Occidente. Ma sia pure più tardo,
ò piu veloce, quanto si uoglia; come cosa che importa poco à noi, lasciaremo della loro
tardità, ò velocità la cura à gli Astronomi. Dell'altra fattione si ritrouano molti; impe-
roche Dione historicoHistori. li-
bro 37. raccontando la cagione, perche i Giorni siano stati denominati
dal nome delle Sphere celesti, & non siano numerati secondo l'ordine loro; incomincia
render tal ragione, secondo l'opinione de gli Egitij, dalla Sphera di Saturno uenendo à
quella del Sole; ponendo l'una & l'altra per gli estremi della consonanza Diatessaron;
lasciando le due mezane; cioè, quella di Gioue & quella di Marte; dopoi da quella del-
la Luna, & forma un'altra Diatessaron; similmente da questa à quella di Marte, & da
Marte à Mercurio ne fà due altre; di modo che lasciando sempre le due mezane Sphere,
rende la ragion di tal Problema; ritornando sempre circolarmente alla prima Sphera; la
onde si uede, che incominciando dalla Sphera di Saturno, & uenendo à quella del So-
le, & da questa, à quella della Luna; pone la prima come quella, che fà il suono graue;
& venendo uerso l'altre Sphere, le pone come quelle, che fanno i suoni acuti; impero-
che è costume della maggior parte di coloro, che trattano della Musica, di por prima il
Graue nelle loro ragioni; come cosa piu ragioneuole; & dopoi l'Acuto. Ne debbe parer
strano, se Dione ritorna dalla Sphera della Luna à quella di Marte, facendo un'ordine ri
uerso, procedendo dall'acuto al graue, contrario di quello che hauea mostrato prima;
percioche à lui bastaua solamente con tal mezo di mostrar la ragione di cotal cosa; anco-
ra che questa ragione non sia molto sufficiente à fauorir tale opinione. Euui etiandio l'o-
Lib. 2. cap.
3. & 22. pinione de gli Antichi, che pone Plinio nella sua Historia naturale; primieramente
dell'Harmonia celeste, dopoi dell'ordine; onde dice, che la Sphera di Saturno fà il tuo-
no Dorio, quella Gioue il Frigio, & l'altre per ordine gli altri Tuoni. Onde non è dub-
bio, essendo il Dorio tenuto dalla maggior parte de i Musici piu graue del Frigio, che la
Sphera di Saturno sia quella, che faccia il suono graue. Oltra di questo (lasciandone molt'
altri da parte) ui è Boetio;Musicae li-
br. 1. c. 27. il quale, quasi recitando l'altrui opinione, attribuisce la chor
da Hypate à Saturno, ch'è d'ogn'altra grauissima; dopoi piu abbasso attribuisce alla me-
desima sphera (secondo la prima opinione medesimamente da lui recitata) il suono acu-
to, & i graui per ordine; attribuendo il grauissimo al globo lunare. Da queste differenze
nacque, che i Filosofi, per uoler mostrare in atto quella Harmonia, che per ragioni co-
nosceuano esser nelle sphere celesti; attribuirono à ciascuna (come erano de diuersi pareri
del Sito de i suoni graui & acuti) diuerse chorde de i loro Istrumenti variatamente ordi-
nate; imperoche quelli che fauoriuano la prima opinione, attribuirono alla Sphera del
la Luna, Pianeta à noi più uicino, la chorda Proslambanomenos; perche fà il suono più
graue di qualunque altra Sphera; à quella di Mercurio la Hypate hypaton; & all'altre
page 125sphere altre chorde per ordine; secōdo che sono poste nella figura. PlutarchoDe Ani-
mae procr.
ex Timeo. dice, ch'alcu
ni attriburno la chorda Proslambanomenos alla Terra, & a la Luna la Hypate, & al So-
le (lasciando di nominar gli altri pianeti) alla Mese. Ma quelli, c'haueano contraria
opinione, attribuirono la chorda Hypate meson alla sphera di Saturno; perche si pensa-
uano, che facesse il suono più graue d'ogn'altra sphera; la Parhypate, à Gioue; Lycha-
nos, à Marte; Mese, al Sole; & cosi all'altre attribuirono altre chorde, secondo il mo-
strato ordine. Et si come furono di uario parere intorno à quello, c'hò detto; cosi anco
furono differenti nel porre le chorde à i loro Istrumenti; essendo che quelli, c'hebbero
opinione, che Saturno facesse il suono acuto & la Luna il graue, posero le Chorde acute
nel soprano luogo, ouer nella parte destra; & le graui nel luogo più basso, ouer nella par-
te sinistra; & quelli, ch'erano di contrario parere, faceuano al contrario; conciosiache
poneuano le graui nella parte superiore, ouer nella banda destra & le acute nella inferio
re, ouer nella sinistra. Ilche dimostra esso Plutarcho nella Questione 8. delle Pla-
![Diapa-son.
diapte. Diapt.
Diatessa.
Diatessa.
Mese. Vrania. [Heaven]
tuo. Lychanos meson. . [Saturn]
tuo. Parhypate mes. . [Jupiter]
sem. Hypate meson. . [Mars]
tuo. Lychanos hypa. . [Sun]
tuo. Parhypate hypa. . [Venus]
sem. Hypate hypat. . [Mercury]
tuo. Proslbanomenos . [Moon]
Diapa-son.
Diapte. Diapte.
Diatessa.
Diatess.
Netesynemnon. .
tuo. Paranete syne.
tuo. Tritesynemn.
sem. Mese.
tuo. Lychanos mes.
tuo. Parhypate. mes.
sem. Hypate meson.
tuo. Lychanos hypa.](../../zarins89/ill/229_1.gif)
buisce il nome di Hypate; & alla graue il nome di Nete. Ma PlatoneDe Repu-
bli. 10.
Cap. 6. accommodò à cia-
scuna sphera (come nella Prima parte si è detto) una Sirena; cioè, una delle noue Muse,
che manda fuori (come dice) la sua uoce, ò suono; dalquale nasce l'Harmoia del Cie-
lo. Et benche non ponga l'ordine loro; nondimeno il dottissimo Marsilio Ficino sopra
quello del Furor poetico di Platone, lo pone; & applica alla prima sphera lunare la Musa
detta Thalia, Euterpe à Mercurio, Erato à Venere, al Sole Melpomene, & cosi l'altre
per ordine; come nella figura si uede. E' ben uero, ch'attribuisce Calliope à ciascuna sphe
ra; per dinotarci il concento, che nasce dalle uoci e tutte poste insieme. Ma perche (co
me dice PlinioNat. hist.
lib. 2. cap.
32.) queste cose si uanno inuestigando più presto con sottil dilettatione, che
necessaria; pero farò fine hauendo ragionato à bastanza di tal materia; & uerrò à mo-
strare, in che modo le predette Sedeci chorde siano state nominate da i Latini.
In che modo le predette Sedeci chorde siano state da i Latini denominate.
Cap. XXX.
siderassero solamente Sedeci chorde, diuise in cinque Tetrachordi; ne ten-
tassero di passar più oltra, per la ragione detta di sopra; nondimeno i Moder-
ni non contenti di cotal numero, lo accrebbero; passando più oltra, hora nel
graue & hora nell'acuto; imperoche Guido Aretino nel suo Introdottorio, oltra le no-
minate chorde, ue n'aggiunse dell'altre alla somma de Ventidue, & le ordinò in sette
Hexachordi; & tale ordine fu & è più che mai accettato & abbracciato dalla maggior
parte de i Musici prattici; essendo che in esse sono collocate & ordinate le chorde al mo-
do delle mostrate Pitagoriche. E ben uero, ch'à ciascuno di essi, aggiunse, per commo-
dità de i cantanti, alcune di queste Sei sillabe: Vt, Re, Mi, FA, Sol, La, cauate dall'
Hinno di San Giouanni Battista;
Vt queant laxis Resonare fibris Mira getorum Famuli tuo- rum; Solue polluti Labij reatum sancte Iohannes;& li concatennò con tale arteficio & in tal
maniera; che ciascuno contiene tutte le Specie della Diatessaron, le quali sono tre; co-
me vederemo nella terza parte; accommodando il Semituono, circoscritto da queste
due sillabe mezane Mi & Fa, nel mezo di ciascuno. La onde aggiunse primieramente al-
la Proslambanomenos di questo suo ordine nella parte graue una chorda, distante per un
Tuono, segnata con lettera Greca maiuscola ritrouata forse per inanti, ouero aggiun-
ta da altri Musici de suoi tempi all'ordine delle chorde Greche in questo modo Γ; & l'al-
tre poi con lettere Latine; che dinota, la Musica (come uogliono alcuni) essere stata ri-
trouata primamente da i Greci, & posta in uso; & al presente da i Latini essere honore-
uolmente posseduta, abbracciata & accresciuta. Et alla predetta Lettera aggiunse la pri
ma delle Sei sillabe; cioè, Vt; in questo modo Γ, vt; che uuol dire Gamma ut; & cosi no
minò la chorda aggiunta di tal nome; & è la prima chorda della sua ordinatione. Chia-
mò poi Proslambanomenos de i Greci A re; ponendo insieme la prima lettera latina &
la seconda sillaba delle mostrate; & fù la seconda chorda del suo Introdottorio. La ter-
za poi; cioè, la seconda Greca, detta Hypate hypaton, nominò
 mi; ponendo insie-
mi; ponendo insie-me la seconda lettera latina, & la terza sillaba seguente; & pose tal lettera quadrata, dif-
ferente da la b rotonda; per dinotarci la differenza de i Semituoni, che fanno queste due
chorde; conciosiache non sono in un'istesso luogo; quantunque siano alle fiate congiunte
quasi in una istessa lettera sopra una istessa riga, ouero spacio; come altroue vederemo.
Nominò dopoi la quarta C fa ut, & il resto per ordine, fino à Netehyperboleon, applicā
doli vna delle prime lettere latine, A,
 , ouer B, C, D, E, F, G; descriuendole nel primo
, ouer B, C, D, E, F, G; descriuendole nel primo ordine maiuscole, nel secondo picciole, & nel terzo raddoppiate; come nell'Introdot-
page 127
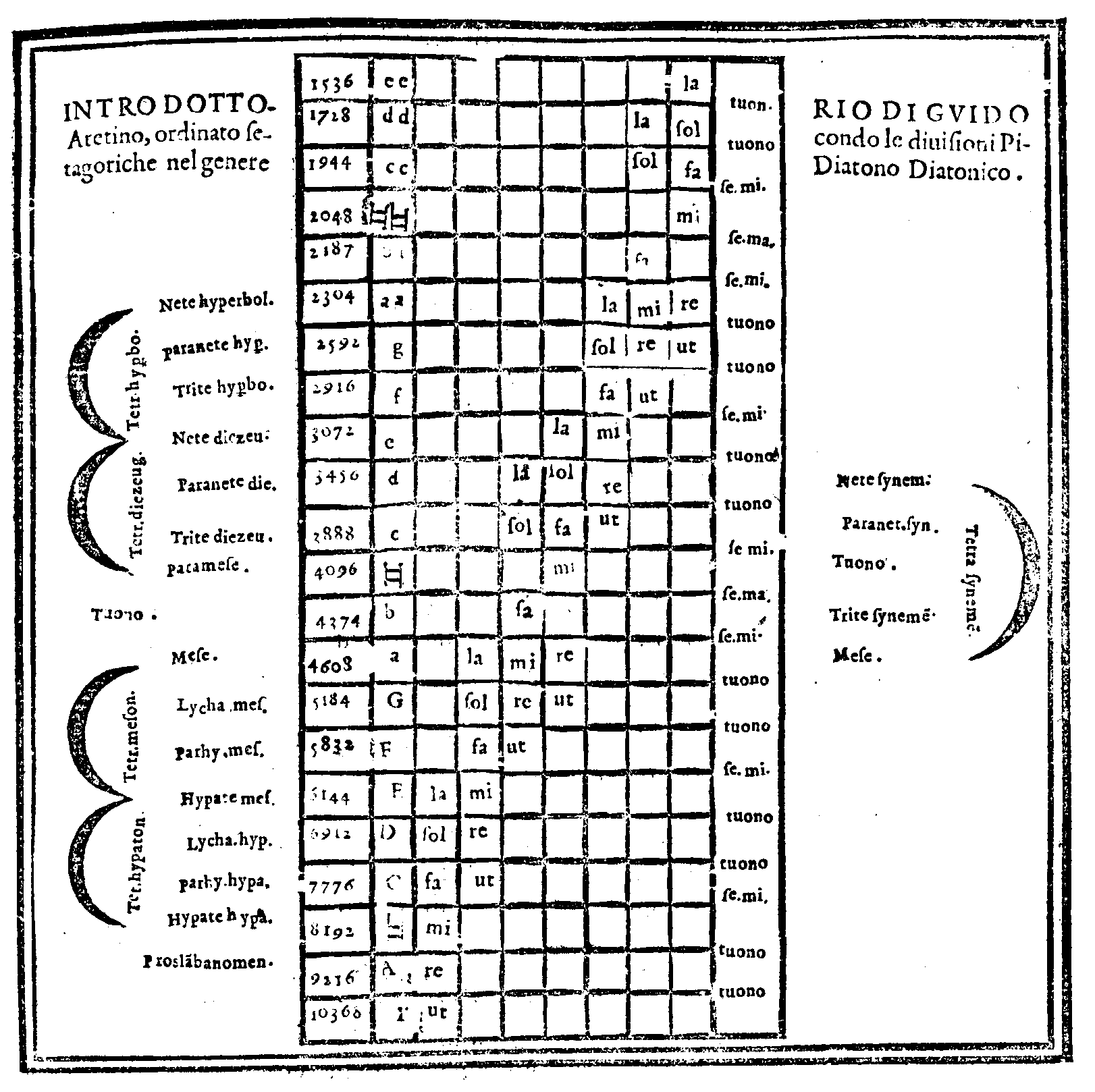
ordine; cioè, bb fa,

 mi; cc sol fa; dd la sol; & ee la; & fece questo per finire
mi; cc sol fa; dd la sol; & ee la; & fece questo per finire gli ultimi due Hexachordi, de i quali l'uno hà principio in f; & l'altro in g: & per tal
modo le chorde Greche acquistarono altra denominatione. Fù tenuto tale ordine da
Guido (com'io credo) forse non senza consideratione, applicando cotali Sil-
labe alle chorde sonore, moltiplicate per il numero Settenario; perche comprese, che
nel Senario si conteneua la diuersità de i Tetrachordi; & che nel Settenario erano Sette
suoni, ò uoci, l'una dall'altra per natural diuisione al tutto uariate & differenti; come si
può vedere, & udire nelle prime Sette chorde, le quali sono essentiali, & niuna di lo-
ro s'assimiglia all'altra di suono; ma sono molto diuerse. Questa diuersità conobbe il
dottissimo Homero, quando nell'Hinno fatto à Mercurio disse;
Ε῾πτὰ δὲ συμφώνους ὀΐον ἐτανύσσατο ΧορδὰςChe uuol dire.
Ma Sette chorde fatte di budella
Di pecore distese, che tra loro
Erano consonanti.
Cosi Horatio parlādo all'istesso Mercurio, commemorò tali chorde cō queste parole;Carmi. li-
bro 3. ode.
11.
Tuꝗ testudo resonare septem
Callida neruis.
page 128Et se ben Theocrito Idylliū. 8. pone, che la Sampogna di Menalcha pastore facesse Noue suo-
ni differenti, quando disse:
Σύριγγ' ἅν ἐπόησα καλὰν ἐγὼ ἐννεάφωνον.
Questa bella Sampogna, la qual feci
De Noue suoni.
Credo, che questo habbia fatto; perche (com'è manifesto & lo afferma Giouanni
GrammaticoDe Diale-
stis.) Theocrito scrisse nella lingua Doricale sue poesie, le quali cantandosi alla
Cetera, ouer Lira, si cantauano nel Modo Dorio; che procedeua (secondo che uede-
remo nella Quarta parte) dal graue all'acuto, ò per il contrario, per un tal numero di
chorde. Ma Virgilio suo imitatore, accordandosi con Homero, nella Bucolica Cap. 8.
In Cory-
done. espresse
il numero di sette chorde solamente, dicendo:
Est mihi disparibus septem compacta cicutis
Fistula.
Et nel libro Sesto dell'Eneida toccò tal numero; quando disse,
Necnon Threicius longa cum veste sacerdos,
Obloquitur numeris septem dicrimina uocum.
Similmente Ouidio nel Secondo libro delle Trasformationi disse:
Dispar septenis fistula cannis.
Et però con giudicio (com'hò detto) esse Lettere da Guido furono replicate, & non
variate; perche conobbe, che l'Ottaua chorda era simile di uoce alla prima; la Nona,
alla seconda; la Decima, alla terza, & l'altre per ordine. E' vero, che non mancano
quelli, che per le autorità addotte de i Poeti uogliono intendere le Sette consonanze di-
uerse, contenute nella Diapason; che sono l'Vnisono, il Semiditono, il Ditono, la Dia
pente, l'Hexachordo minore, il maggiore, & essa Diapason; & altri anco, che inten-
dono il simigliante; lasciando fuori l'Vnisono; perche non è Consonanza propriamen-
te detta; come vederemo al suo luogo; ponendoui la Diatessaron; le quali opinioni non
sarebbono da sprezzare, quando fussero secondo la mente de tali autori, & non fussero
lontane dalla verità; imperoche seguendo i Poeti indubitatamente l'opinione di Pitago
ra, di Platone, di Aristotele, & d'altri eccellentissimi Musici & Filosofi più antichi; non
si può dire, che mai hauessero alcuna opinione, di porre il Semiditono, il Ditono, & li
due Hexachordi nel numero delle Consonanze; per le ragioni dette di sopra.Cap. 1. Ma s'al-
cun dicesse, che nella Diapason si ritrouano non solo Sette suoni, ò voci differenti; ma
di più ancora; come si può uedere ne gli Istrumenti artificiali; il che arguisce contra quel
lo, che di sopra hò detto; Si risponderebbe, ch'è uero, che tra la Diapason si ritrouano
molti Suoni differenti, oltra i Sette nominati; ma tali Suoni non sono ordinati secondo
la natura del genere Diatonico; ne meno sono acquistati per alcuna diuisione della Pro
portionalità harmonica.
Consideratione sopra la mostrata Diuisione, ouer Ordinatione, & sopra l'altre
specie del genere Diatonica ritrouate da Tolomeo.Cap. XXXI.
dubbio, che ritrouaremo in lei grande imperfettione; la qual nasce per esser
priua de quelli Interualli, che da tutti i Musici, di commun parere, sono ac-
cettati al presente per Consonanti; & sono quelli del Semiditono, del Ditono,
& i composti; i quali nelle loro compositioni continuamente si odono. Et benche questi
Interualli, in quanto al nome, si ritrouino nella detta Diuisione; non sono però da i lo-
ro Inuentori stati considerati per consonanti; percioche veramente non sono. Et che
ciò sia uero, non sarà cosa difficile da mostrare, quando uorremo credere primieramen-
te questi Principii; parlando però delle Consonanze semplici; Che da niun altro Ge-
page 129nere, ò Specie di proportione, che dal Moltiplice, & Superparticolare in fuori (come
uuol la miglior parte de i Musici) potiamo hauere la Forma d'alcuno Interuallo, che sia
atto alla generatione d'alcuna Consonanza; dopoi, Che due qual si voglino Inter-
ualli semplici, contenuti da un'istessa proportione, siano di qual genere, ò specie si uo-
gliano; da quelli in fuori c'hanno la lor forma dalla Dupla; aggiunti insieme non fanno
Consonanza alcuna ne i loro estremi; come si può udire facendone la proua. Oltra di
questo, Che niuno Interuallo sia semplice, ò Composto, la cui forma si ritroua ne i suoi
termini radicali fuori delle parti del numero Senario, è consonante. Et questi tali Prin-
cipii saranno il fondamento di questo ragionamento; per i quali prouarò esser uero quel
lo c'hò detto in questo modo. Quella cosa si dice esser perfetta (secondo il Filosofo1. De Coelo
cap. 1.) oltra
la quale niuna cosa si può desiderare, che faccia alla sua perfettione; essendo adunque che
in tal Diuisione si può desiderare l'Harmonia perfetta; per esser priua de molte Conso-
nanze, che sono le già nominate; le quali fanno la perfetta Harmonia; non è dubbio al-
cuno, ch'ella non sia imperfetta; percioche se noi pigliaremo gli estremi della proportio-
ne del Ditono & del Semiditono già mostrati; che sono la Super 17. partiente 64. & la Su
per 15. partiente 81. i quali senza dubbio sono nel genere Superpartiente; per il primo
de i detti Principii potremo esser chiari, di quello c'hò detto; conciosia che essendo que
ste Due proportioni contenute nel detto genere, non sono consonanti; onde non essen-
do consonanti, sono necessariamente dissonanti. Si può anco prouare per il secondo prin
cipio, che 'l Ditono non sia consonante; percioche in esso sono aggiunte insieme due pro
portioni Sesquiottaue. Il terzo principio anco dimostra, che ne il Ditono, ne il Semi-
ditono già mostrati siano consonanti; imperoche le Proportioni, che sono la forma de
cotali Interualli, non hanno luogo tra le parti del Senario. Il medesimo etiandio si po-
trebbe dir dell'Hexachordo maggiore & del minore; perche sono composti della Diates
saron, ch'è Consonanza; & del Ditono & del Semiditono mostrati, che sono Dissonan
ti; ma per breuità lasciarò tal ragionamento da un canto. Se adunque tali Interualli
non sono Consonanti; non può esser per modo alcuno, che tale ordine sia perfetto; essen
do che in lui mancano quelle cose, che fanno alla sua perfettione. De qui facilmente si
può comprendere in quanto errore incorrino quelli, che si affaticano ostinatamente di
uoler persuadere, che i sopraposti Interualli siano Consonanti; & che siano quelli, che si
pongono in uso al presente da i Musici nelle loro Harmonie; & insieme si può uedere, in
che modo dimostrino d'hauer poco inteso Boetio,Musicae li-
bro 1. c. 5.
& 6. quādo si uogliono preualere della sua
autorità, uolendo prouare la loro falsa opinione per vera. Ma se uogliono pure l'autori-
tà de gli Antichi solamente, & non le ragioni addotte da i Moderni, bastarà solamente
quello, che dice VitruuioArchitec.
lib. 5. c. 4. in questo proposito, per mostrare il loro errore; il quale dice
chiaramente; che la Terza, la Sesta, & la Settima chorda non possono far le Consonan
ze; & tutto s'intende quando s'aggiungono alla prima; & Euclide nel suo Introdotto-
rio di Musica chiaramente dice; che gli Interualli, che son minori della Diatessaron; & so
no il Diesis, il Semituono, il Tuono, il Trihemituono, & il Ditono, sono dissonanti. Et
benche in questo Genere si ritrouino molte Specie; come hò mostrato;Supra
Cap. 16. una di esse sola-
mente è quella, che ne dà tutte le Consonanze, & la perfettione dell'Harmonia ch'è la
Naturale, ò Syntona diatonica di Tolomeo; come vederemo. Ma perche alcun po-
trebbe dire; se una sola Specie è quella, che ne dà quello, che ueramente è necessa-
rio; che bisogno adunque era dell'altre Specie? Veramente non faceuano dibiso-
gno, considerata la Musica quanto all'vso moderno; ma considerata in quanto al-
l'uso de gli Antichi non erano fuori di proposito; perche nulla, ò poca consideratio-
ne haueano de tali Consonanze; & tutta la loro Harmonia consisteua nella modula-
tione semplice di una sola parte. Onde si può dire, che à loro bastaua anco una sola
specie di modulatione per ogni Genere; cauandone i Modi de i quali parlaremo
nella Quarta parte; & che la varia diuisione de i Tetrachordi era cosa, che più
presto apparteneua alla parte Speculatiua, che alla Prattica: percioche quando
page 130hauessero uoluto porre in uso perfettamente ogni Specie di ciascun genere; ciò sarebbe
stato impossibile; come uederemo. Et accioche questo non pari strano; hauendo ueduto
di sopra la diuision della Prima specie del Diatonico, uerro alle diuisioni dell'altre Spe-
cie aggiunte da Tolomeo; lequali (come diceua) all'Vdito erano molto consentanee &
grate; & le loro proportioni (come si potrà uedere per ciascun Tetrachordo) sono sotto-
poste al genere Superparticolare; conciosiache hebbe opinione, che in questo Genere
di proportione si ritrouasse una gran forza nelle modulationi Harmoniche. Lascierò di
ragionar della sua Seconda specie; la quale hò nominato Naturale, da lui chiamata;Harmo. li-
bro 1. c. 5.
come hò detto poco fà; Diatonico syntono; percioche di essa intendo lungamente ra-
gionare; & mostrare, che in lei si ritroua la perfettione dell'Harmonia; & uerrò à ra-
gionare della Prima specie, la quale nomina Diatonico molle; & mostrarò quanto d'im
perfetto si troua in essa. Dico adunque, che dopo che noi haueremo congiunto insieme
i due primi Tetrachordi di questa specie; l'Hypaton & il Meson, aggiungendoui
nel graue la chorda Proslambanomenos, di modo che contenghino la consonanza Dia-
pason; il numero di Otto chorde, che nascerà da tal congiuntione, sarà sufficiente à mo
strar la sua imperfettione; imperoche nel primo aspetto uederemo, che in esso non solo
si ritroua la perdita del Ditono, del Semiditono, & del maggior & del minore Hexa-
chordo; ma di più uederemo, che sarà priuo de i maggiore & del minor Semituono. Si-
migliantemente lo uederemo esser priuo della Diatessaron tra la prima & la quarta
chorda, & della Diapente in molti luoghi; conciosia che le chorde estreme de tali Inter
ualli non sono sufficienti à dare tal Consonanze, per non esser tra loro proportionate per
Numeri harmonici. Per il che, si come nella diuisione del Diatonico diatono, si ritroua
da Proslambanomenos à Mese cinque uolte la Diatessaron, & la Diapente quattro uol-
te; cosi in questa, l'una si ritroua quattro uolte, & l'altra una solamente; come nell'essem
pio si può uedere. La medesima imperfettione anche si potrà ritrouare nell'altre otto
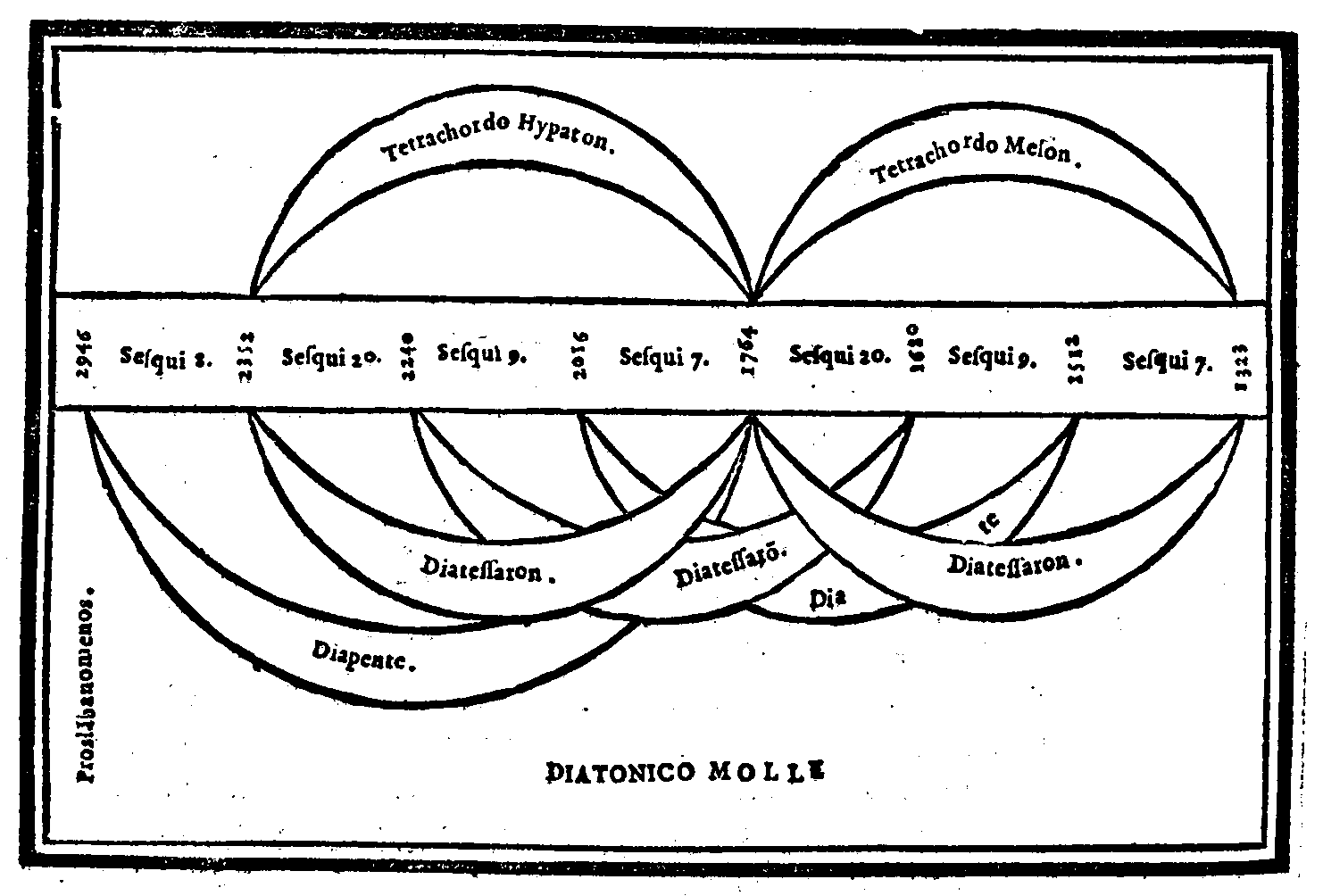
giungere à queste; ma per breuità in questa & nell'altre seguenti si lasciano; per-
cioche il discreto Lettore potrà, qualunque uolta li piacera, aggiungendole, chia-
rirsi d'ogni dubbio, che li potesse occorrere. Ma per uenire all'altra Specie, di-
page 131
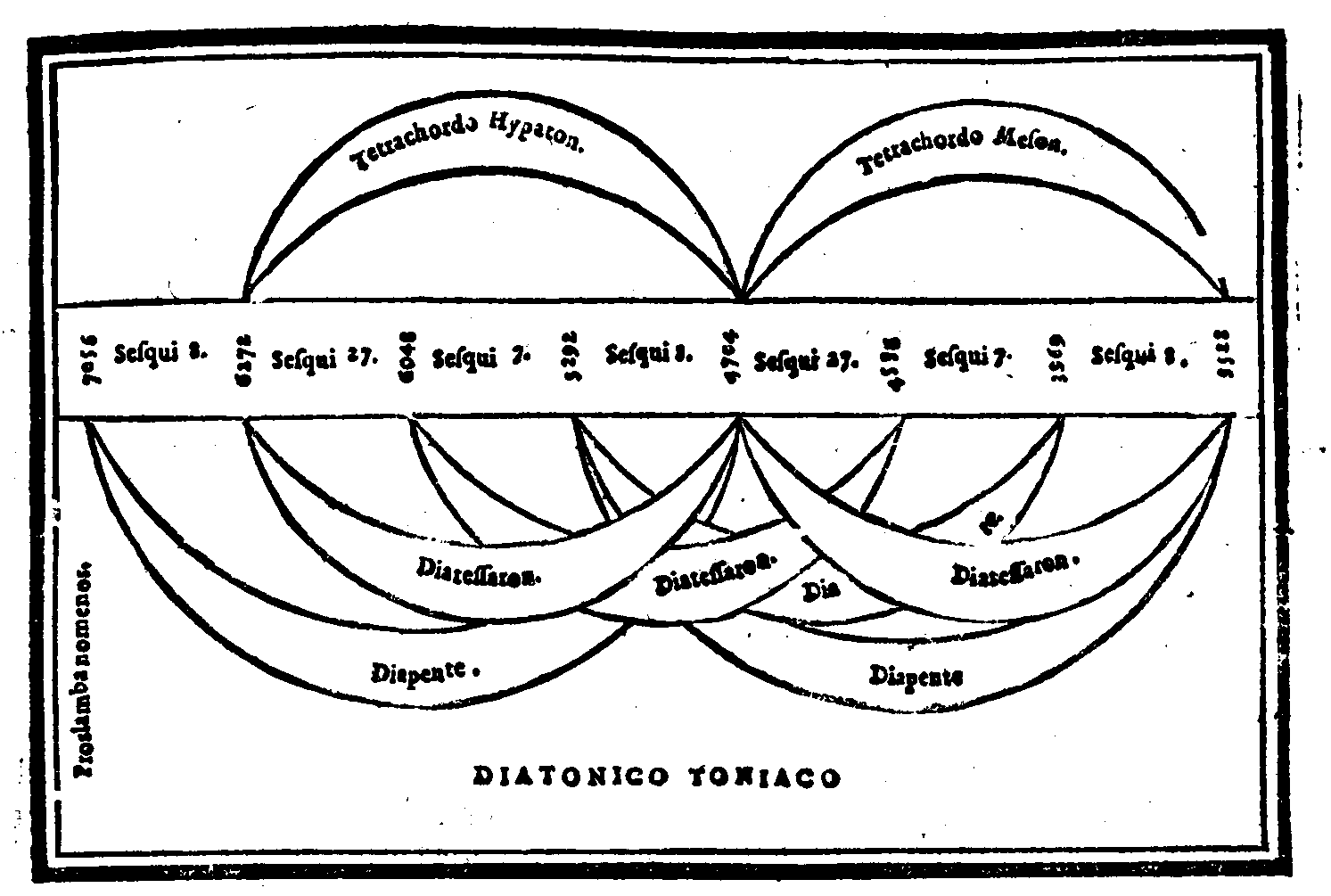
niaco, che si ritroua nel Diatonico molle; come tra i loro Interualli si uede. Non dob-
biamo però credere, che 'l Diatonico equale sia lontano dalla imperfettione; percio-
che quando questo si credesse, dalle chorde poste nell'essempio ogn'vno sarà fatto certo
di essere in errore. Onde si può tener per uero, che gli Antichi nelle loro Melodie haues-
sero maggior rispetto alla modulatione, ch'alla perfettione dell'Harmonia; & questo hor
mai è manifesto; essendo che quando ben hauessero tese le chordede i loro Istrumēti sot-
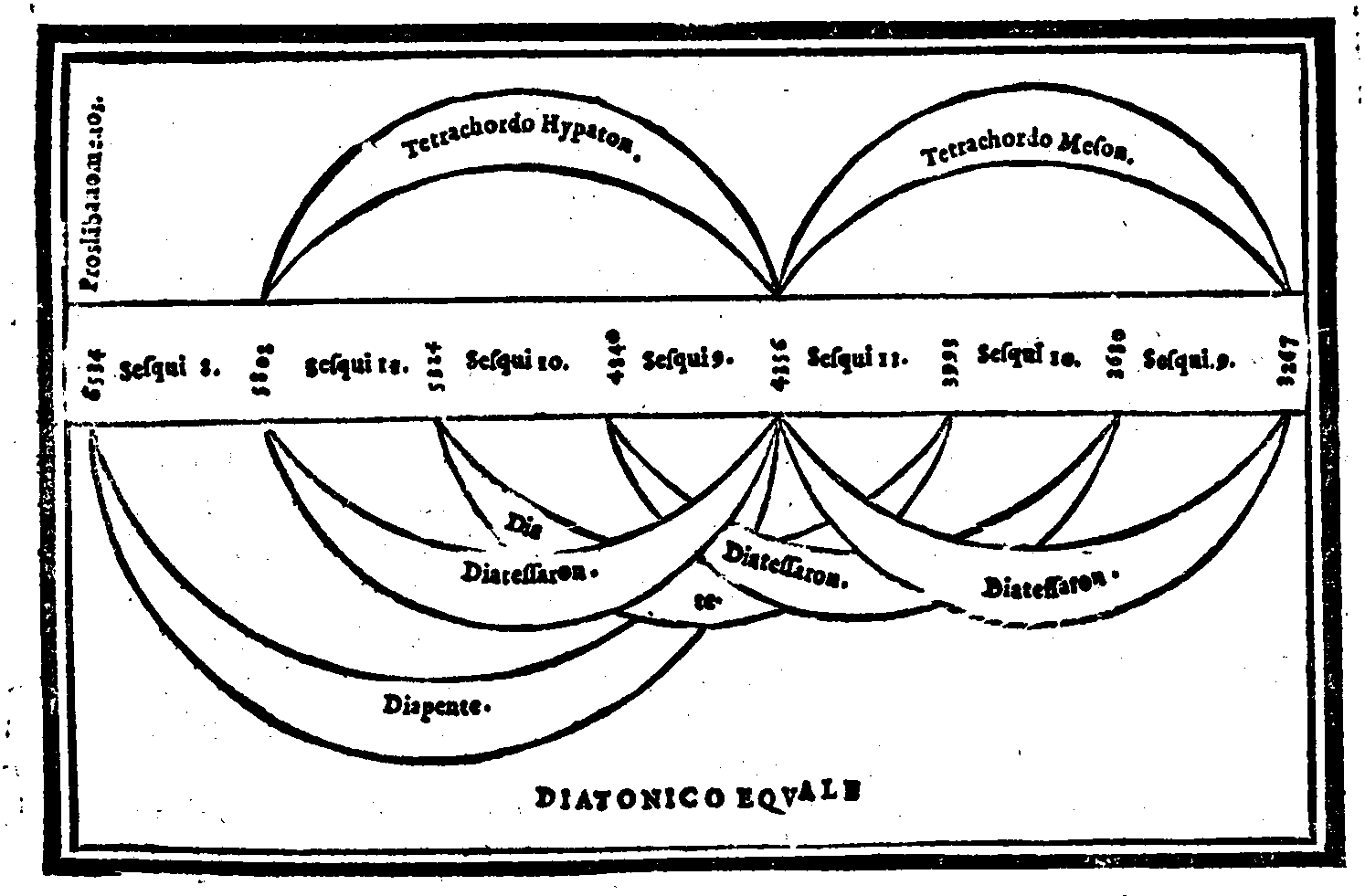
quelle ne hauessero potuto cauare l'Harmonia perfetta poi che alla sua perfettione, non
solamente vi concorrono le Consonanze perfette; come è la Diapason, la Diapente &
la Diatessaron; ma etiandio l'Imperfette; che sono il Ditono, il Semiditono & l'uno &
l'altro Hexachordo. Ne solamente si troua tal difetto nelle mostrate Specie di questo
primo Genere; ma anco in tutte l'altre Specie de gli altri Generi seguenti; come à mano
à mano, venendo alla Diuisione, ò Compositione della Prima specie del secondo ge-
nere, detto Chromatico, son per dimostrare.
Del genere Chromatico, & chi sia stato il suo Inuentore; & in qual maniera lo
potesse trouare: & delle Chorde, che aggiunse Timotheo nel solito
Istrumento.Cap. XXXII.
matico, dico che Timotheo Milesio (come uuole Suida & BoetioMusicae li-
bro 2. c. 1.) fù di esso
l'Inuentore; imperoche hauendo aggiunto una chorda sopra quelle, che ri-
trouò nell'antico Istrumento; hauendo prima riceuuto una modesta Har-
monia, moltiplicandola per tal modo, la riuoltò nel detto Genere, il quale senza dub-
bio è più molle del Diatonico. Per la qual cosa i Lacedemonii, c'hebbero sempre cura,
che non si rinouasse cosa alcuna nella loro Rep. lo bandirono di Sparta; perche haueano
opinione, che la Musica accresciuta per tal modo, offendesse grandemente l'animo de
i Giouani, à cui insegnaua; & gli impedisse, ò ritrahesse dalla modestia della uirtù. Et
per mostrar, che s'alcuno per l'auenire hauesse hauuto ardimento di aggiungere, ò ri-
nouar più alcuna cosa nella Musica, non sarebbe passato senza la debita punitione; so-
spesero (come scriue PausaniaLacon. li-
bro 3.) la sua Cetera in un luogo eminente; accioche ogn'uno
la potesse uedere. Ma perche Pausania dice, che le Chorde, ch'aggiunse Timotheo al-
le Sette antiche, furono Quattro; & Boetio dice, che fù vna; però (per non lasciar tal
cosa senza qualche consideratione) ripigliando alquanto in alto il nostro ragionamento,
diremo; Che 'l genere Diatonico, auanti ch'altro Genere fusse ritrouato; & auanti che
Pitagora ritrouasse la ragion de i Numeri, fù prodotto dalla natura nell'essere, che lo
ueggiamo nelle sue Consonanze perfette; & di ciò ne fà fede la Lira, ò Cetera di Mer-
curio, la quale fù ritrouata intorno gli anni 1655. auanti l'anno di nostra Salute; le cui
chorde (come mostra Boetio,Arith. lib.
2. c. 54. &
Music li.
1. cap. 20. & di sopra al Cap. Primo si è mostrato) erano ordinate
in tal maniera, che in esse (come nelle DimostrationiIn Propo-
sit. 12. li. 2. si è dimostrato) si scorgeua non so-
lo la proportionalità Geometrica & l'Arithmetica, ma l'Harmonica ancora; come si può
uedere tra i termini delle loro proportioni; di modo ch'alcuni hebbero opinione, che in
se contenessero una Massima & perfetta harmonia; ma gli altri Due generi furono ritro-
uati dopoi per gran spatio di tempo, & furono collocati tra 'l Diatonico. La onde es-
sendo stati per tal modo posti insieme, molti Musici antichi; tra i quali sono Tolomeo,
Briennio, & Boetio; hanno hauuto parere, ch'altro non fussero gli Due ultimi gene-
ri, che la Inspessatione del primo; conciosia che chiamauano ogni Tetrachordo in-
spessato, quando rendeua l'Interuallo acuto maggiore in quantità de gli altri due pri-
mi graui; & questo ueramente è cosa loro propria; come ne i loro Tetrachordi primi
posti di sopra al Cap. 16. si può uedere. Se adunque noi li uorremo considerare con di-
ligenza; ritrouaremo, che le Chorde estreme del Diatonico sono immutabili, & à gli al-
tri due Generi communi, non solo di proportioni, ma etiandio di sito; & ritrouaremo,
che le due mezane (ancora che siano senza uarietà de proportioni) non sono per il sito
nel loro ordine uariate. Ritrouaremo anco, che cotale Inspessatione si fà primieramen-
page 133te per l'aggiunger d'una chorda, che si pone tra la seconda & la terza del Diatonico;
la qual chorda con la ultima acuta, contiene un Trihemituono; & con la seconda & l'ul-
tima acuta costituisce da per se un Tetrachordo nuouo; il quale (per le ragioni dette
di sopraCap. 16.) si chiama Chromatico. Per l'aggiungimento poi d'un'altra chorda posta tra
la prima & la Seconda Diatonica graue, nasce il terzo genere detto Enharmonico; per-
che diuide il Semituono in due parti; cioè, in due Diesis; & per tal modo questa chorda
con la estrema graue, & la seconda diatonica, & l'uitima fà da per se un'altro Tetra-
chordo detto Enharmonico. Et quantunque la seconda Diatonica si muti nella terza
Enharmonica, quanto al sito; & che per questo uenghi à perdere il nome; nondimeno
non muta luogo, ne proportione; ma resta di quella quantità, ch'era prima. Si vede

trachordo diatonico; le quali fanno nel detto Tetrachordo gli altri due nominati; di ma-
niera che si come prima era uno, cosi si trouano hora esser tre aggiunti insieme; & di uno
Genere esserne fatti tre; & di Tetrachordo, ch'era per inanzi, esser fatto Hexachordo,
che contiene i tre nominati Generi, & i loro Tetrachordi; come nell'essempio si può ve-
dere, l'estreme chorde del quale; cioè, la graue & l'acuta sono communi & stabili, & so-
no la prima & la ultima in ogni Tetrachordo di ciascun genere; ma la seconda è la se-
conda chorda particolare del Tetrachordo Enharmonico, & non commune ad altro ge
nere, com'è la Terza; la quale è commune à ciascuno; ancora che ella sia la terza del-
l'Enharmonico, & habbia variato il nome, tenendo il proprio nome ne gli altri due, &
similmente il secondo luogo de i lor Tetrachordi. La Quarta poi è particolare, & è la
terza del Tetrachordo Chromatico; cosi anco la Quinta essendo particolare del Diato-
nico, uiene ad esser la terza chorda del suo Tetrachordo. Ne per altro il Tetrachordo
diatonico fù inspessato per cotal modo da gli altri due generi da i loro Inuentori; secon-
do il parere d'alcuni; se non accioche in un'istesso Istrumento, con quelle chorde, che
sono naturalmente ordinate & diuise nel genere Diatonico; & con le Chromatiche &
le Enharmoniche aggiunte, & ritrouate prima con arteficio, si potesse hauer nell'har-
monie maggior soauità. Per uenire adunque alla Resolutione del dubbio proposto, di-
co; quando Boetio fà mentione d'una Chorda sola, intende solamente di quella, che fà la
page 134inspessatione del Tetrachordo diatonico dalla parte acuta, la quale è la particolare & es-
sentiale del Chromatico, & è la Quarta nel mostrato ordine, che con le due estreme &
la seconda fà la uarietà del Tetrachordo chromatico. Ma quando Pausania fà mentione
de Quattro, non uuole inferire altro, se non le Quattro nominate; cioè, tutto il Tetra-
chordo intero, che sono le Chorde essentiali di tal Genere; ancora che la prima, la ter-
za, & la sesta siano etiandio diatoniche. Et che questo sia uero, lo potiamo compren-
dere dalle sue parole, che dicono; Timotheo aggiunse Quattro chorde alle Sette anti-
che ordinate da Terpandro lesbio in cotal maniera; le quali essendoui stato aggiunto

Tetrachordo Meson era già congiunto col Synemennon, cosi restarono diuisi; percio-
che li pose distanti l'un dall'altro per un Tuono, che si troua tra la chorda Mese & la Pa-
ramese; come si uede nell'essempio. Onde nacque, che l'uno de questi Tetrachordi fù
chiamato Meson, & l'altro ; & la chorda Trite del sopraposto Syne-
mennon perse il nome, ne hebbe più luogo alcuno; come ne mostra Boetio nel primo
Libro della Musica al Cap. 20. Dopoi hauēdo Profrasto aggiunto nella parte più graue di
quest'ordine una chorda, acciò facesse un'ordine di Noue chorde; lo chiamò Hyper hypa
te; percioch'era sopr'aggiunta alla chorda Hypate; & Estiacho colofonio aggiunsela De-
cima; & à queste due, senz'alcuna uariatione delle prime, Timotheo aggiunse la Vndeci-
ma (come di sopra nel Cap. 1. dicemmo) per auentura, accioche nel graue potesse haue-
re un Tetrachordo intero, & lo potesse congiungere alla chorda Hypate; onde fù no-
minato dopoi Tetrachordo Hypaton. Et di tal chorda non ne fà mentione alcuna Boe-
tio nel Cap. 1. del Libro primo della Musica; ma si bene nel Cap. 20. Essendo dopoi sta-
to accresciuto da molti il numero delle chorde nel solito Istrumento fino à Quinde-
ci, & diuise in quattro Tetrachordi; come nell'Ottauo essempio del già detto luogo di
Boetio si può vedere; Timotheo ritornò al suo luogo il Tetrachordo, il quale per auan-
ti era stato leuato da tale Istrumento da Licaone; & fù in tale ordine il Quinto; & lo
chiamò Synemennon, come era chiamato per auanti; cioè, Congiunto. Et tale ag-
giuntione fece nascere un Tetrachordo differente da gli altri; conciosiache la Trite sy-
nemennon posta tra la Mese & la Paramese, diuise il Tuono in due Semituoni; come nel
Cap. 28. di sopra si può uedere. Et queste, credo io, che siano le Quattro chorde, che di-
ce Pausania, che Timotheo aggiunse alle Sette antiche; lequali sono ueramente le Set-
te principali & essentiali del genere Diatonico; come nel Cap. 30. di sopra hò mostrato;
& sono le Sette prime contenute ne i due primi Tetrachordi della diuisione posta nel
page 135

sono disopra nel Secondo essempio; ancora che siano uariate di nome, & per altri no-
mi siano denominati i loro Tetrachordi; ilche importa poco. Per tal uia adunque fù ac-
cresciuto il Numero delle chorde dell'antico Istrumento fino al numero de Sedeci; & la
detta chorda Trite venne ad esser la Nona, & è quella, della quale parlò Boetio, quan-
do disse; che Timotheo aggiunse vna chorda à quelle, che ritrouò nell'Istrumento anti-
co; imperoche se fusse altramente, non uedo in qual modo potesse esser uero quello, che
dice Plinio nella sua Historia naturale;Lib. 7. cap.
56. che Timotheo fù quello, ch'aggiunse la
Nona chorda nel solito Istrumento. Et benche Boetio nel Lib. 1. non faccia men-
tione alcuna di questo Tetrachordo; nondimeno lo pone nelle diuisioni del Mono-
chordo, che lui fà ne gli altri Libri. Et perche forse alcuno potrebbe dire, ch'essendo il
Tetrachordo aggiunto Diatonico & non Chromatico, non poteua fare altra modula-
tione, che Diatonica, ne poteua seruire al genere Chromatico; conciosia che non ha-
uesse in sè quelle proportioni, che si ritrouano ne i Tetrachordi chromatici, mostrati da
Boetio; rispondo, che ueramente era Diatonico, & per questo non resta, che non potes-
se formare il Chromatico, procedendo dalla chorda Mese alla Tritesynemennon, & da
questa alla Paramese, & da Paramese alla Netesynemennon; lequali tutte fanno un Te-
trachordo chromatico, ancorache le sue proportioni siano molto differenti da quelle, che
ne dà Boetio; ilche importa poco; imperoche la diuersità del Genere non nasce se non
dalla mutatione & variatione de gli Interualli, che si può fare ottimamente modulando
dal graue all'acuto per un Semituono nel primo Interuallo, & per un'altro poi nel secon
do, ponendo ultimamente nel terzo vn Trihemituono, & cosi procedendo dall'acuto
al graue per il contrario. Ma la differentia delle Proportioni può nascer da questo; c'ha-
uendo Timotheo ritrouato questo Genere, & volendo ei, oueramente alcun'altro Musi-
co ridurlo sotto la Ragione delle proportioni; ritrouando la modulatione del Tetrachor
do chromatico molto differente da quella del Diatonico, uolse ancora, che le Proportio
ni de i suoi Interualli fussero differenti; perche tali differenze, per esser minime, difficil-
mente si possono capire. La onde è da credere, che dopoi le varie opinioni & diuerse ra-
gioni & principij, c'hebbero i Musici de quei tempi, li inducessero à ritrouar diuersi In-
terualli; conciosia che non contenti d'una sola Specie di modulatione & d'Harmonia per
page 136ciascun genere, fecero (diuidendo il Tetrachordo in molti modi) in ciascun Genere
molte specie; come si è mostrato. Et se bene è cosa difficile il uoler narrare in qual ma-
niera Timotheo potesse ritrouare, ò inuestigar questo Genere; essendo ch'appresso
d'alcuno Scrittore mai fin'hora non l'hò potuto ritrouare; nondimeno si può inuestigare
& mostrar qualche ragione, ch'essendo le nominate Chorde ordinate in tal maniera, &
essendo in loro la modulatione in potenza, Timotheo essercitandosi nel genere Diato-
nico, tentasse molte uolte di passar con la modulatione per l'aggiunto Tetrachordo, toc
cando dopo la Mese la Tritesynemennon; passando dopoi a questa alla Paramese; ar-
riuando etiandio alla Paranete synemennon, ouer Tritediezeugmenon, che sono
una chorda istessa; ancora che i Tetrachordi à cui serue la faccia cambiare il nome; &
dopoi considerando, che 'l passaggio fatto per queste chorde rendeua alcuna uarietà;
fatto sopra di ciò più lunga consideratione, cercasse di modulare per ogni Tetrachor-
do in cotal maniera; percioche sarebbe stato, se non impossibile, almeno troppo dif-
ficile, d'hauer hauuto alcuna consideratione sopra cotal cosa, quando non hauesse udi-
to in atto la modulatione. Ma di questo sia detto à sufficienza, acciò si uenga alla
Ordinatione di tal Genere, mostrandosi la sua diuisione.
Diuisione del Monochordo Chromatico.Cap. XXXIII.
Quarta chorda d'ogni Terrachordo diatonico, senz'alcuna uarietà, ò muta-
tione di Sito & di Proportione, communi & essentiali del Genere chroma-
tico; resta che uediamo solamente, in qual modo all'istesse tre chorde, per
ogni Tetrachordo si possa aggiunger la Terza, la quale contenga con la Quarta il Trihe-
mituono, & sia particolare & essentiale di questo genere; accioche possiamo hauere, con
quel più breue modo, che si può fare, il Tetrachordo perfetto, & la diuisione del suo Mo
nochordo. Però lasciando da parte solamente la Terza chorda d'ogni Tetrachordo del
mostrato Monochordo diatonico, per esser particolare diatonica; eccettuando le
chorde N B & M B, che uengono ad essere all'uno & all'altro genere communi; alla Se-
conda aggiungeremo la Terza, diuidendo quella parte di Linea; ch'è posta in luo-
go della Quarta & più acuta chorda d'ogni Tetrachordo in Sedeci parti, secondo la ra-
gione del minor termine della proportione, che contiene il Trihemituono, al modo che
nel Cap. 22. di sopra hò mostrato; & aggiungendole tre parti, che saranno equali al
maggior termine della proportione; quello che uerrà, sarà la lunghezza della ricercata
chorda. Et per uenire al fatto dico; se noi lasciaremo da un canto le chorde E B, H B,
& P B del Monochordo diatonico; & diuideremo la linea D B. in Sedici parti; ag-
giungeremo à queste altre tre parti; & ne haueremo 19. le quali saranno per il maggior ter
mine del Trihemituono, & la ricercata Terza chorda; & per tal modo tra a B, che con
tiene 19. parti, & D B, che contiene 16. haueremo collocato alla sua proportione il Tri
hemituono nel primo Tetrachordo detto Hypaton; & tra le chorde F B & a B. il Semi-
tuono più acuto. Et che questo sia uero lo prouo. Se dal detto Tetrachordo; cioè, dalla
Sesquiterza proportione leuaremo il Semituono minore, posto tra C B & F B. dalla par
te graue; & il Trihemituono collocato tra le mostrate chorde, contenute sotto la pro-
portione Super 3. partiente 16. necessariamente resterà il Semituono più acuto, conte-
nuto dalla proportione Super 5. partiente 76. Et cosi tra le chorde C B, F B, a B & D B,
haueremo il primo Tetrachordo chromatico, chiamato Hypaton. Et per collocare co-
tal chorda ne gli altri Tetrachordi, diuideremo al detto modo le chorde G B, M B,
L B, & O B, & haueremole chorde b B, e B, c B & d B, le quali saranno notate co i
termini continenti le loro proportioni; come nella figura si uede. Ma uolendo ritro-
uar breuemente il termine, col quale si dee notar questa chorda; si piglierà sempre la
page 137
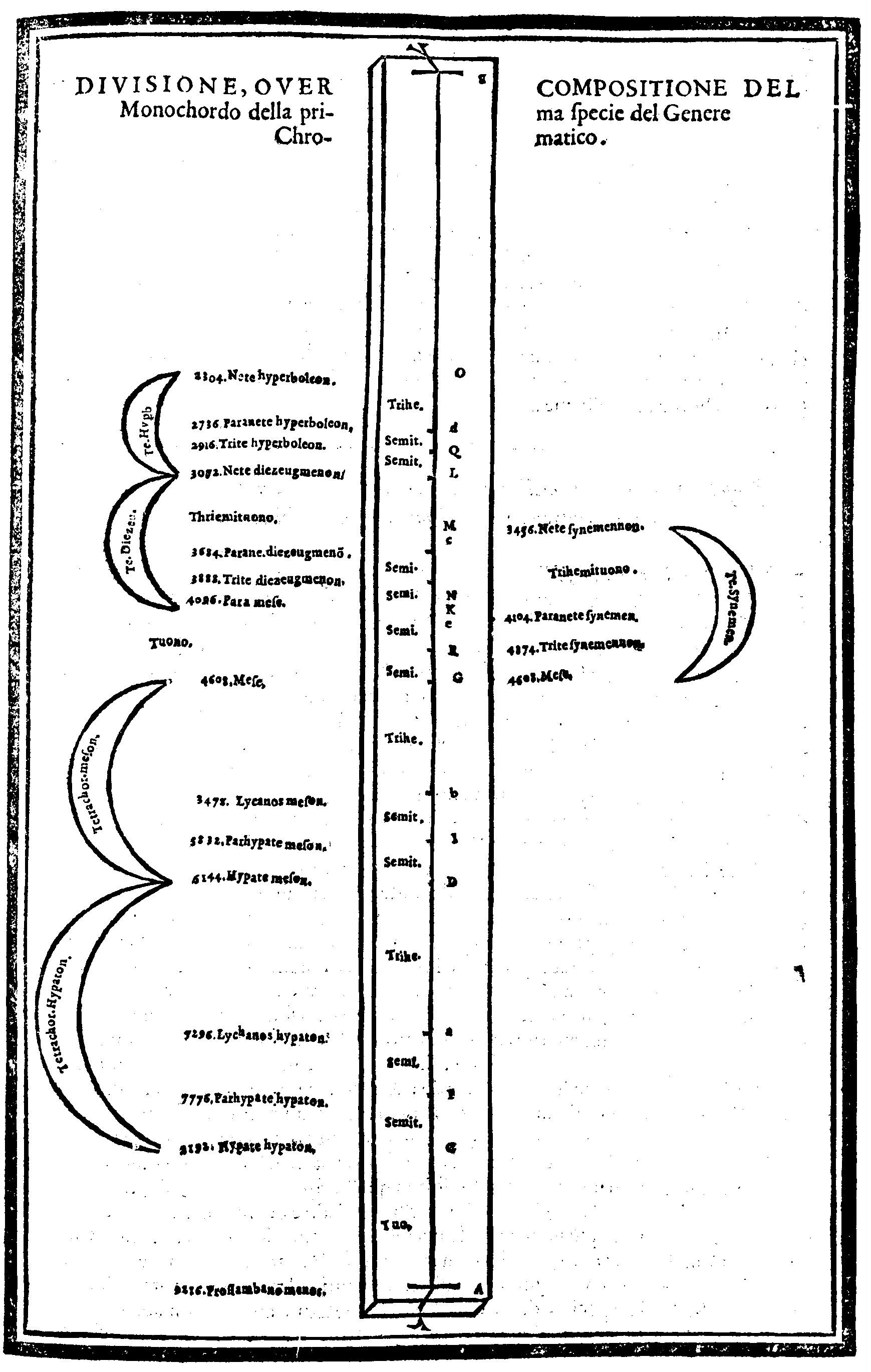
do diatonico; nelquale sarà collocato cotal chorda; come (per essempio) quelli dell'Hy
paton, che contengono il Tuono, & sono 6912. & 6144. & trattone la loro differenza, che
è 768. aggiungendo la sua metà, che è 384. al maggior delli due termini, che è 6912. ne
uerrà 7296. & questo sarà il termine, col quale si segnarà la detta terza Chorda: Il che
facendo anco ne gli altri Tetrachordi, tornerà bene. E' ancora da notare, che i Nomi
delle chorde del genere Chromatico & dell'Enharmonico, non sono uariati da quelle
del Diatonico; ancorache in questi due ultimi generi si ritrouino due chorde di più, che
non si ritrouano nel Diatonico; il che nasce dalla varietà de gli Interualli, che nascono
dalla Terza chorda di questo genere; ma non ui è altra differenza quanto al nome; se non
che nel Diatonico la chorda Lycanos si chiama Lycanos diatonica, nel Chromatico Ly
chanos chromatica, & nell'Enharmonico si nomina Lychanos enharmonica; come più
abbasso potremo uedere nell'ordine, ò compositione del Monochordo diatonico, inspes
sato dalle chorde di questi due generi.
Consideratione sopra la mostrata Diuisione, & sopra alcun'altre Specie di questo
Genere, ritrouate da Tolomeo.Cap. XXXIIII.
strato, si ritroua imperfetto, che 'l Chromatico sia di esso più perfetto; con-
ciosia che nelle sue specie, non solo è priuo di quelle Consonanze, che i Prat
tici chiamano Imperfette, ma etiandio è priuo in molti luoghi delle Perfette;
percioche se nella Prima specie del Diatonico, la qual Tolomeo chiama Diatonico dia-
tono, si ritroua la Diatessaron nelle sue Otto chorde graui, cinque uolte; & la Diapente
quattro & non più; nella poco fà mostrata diuisione la Diatessaron si ritroua solamente
quattro uolte, & una sola uolta la Diapente da Proslambanomenos ad Hypate meson.
Et s'alcuno uolesse dire, che 'l suo Trihemituono fusse consonante, & che fusse la Terza
minore, ò il Semiditono, ch'è posto à i nostri tempi da i Prattici nel numero delle Con-
sonanze; si potrà con verità rispondere, che non è uero; imperoche la sua proportione
è contenuta nel genere Superpartiente dalla Supertripartiente 16. che non è atto alla ge
neratione delle consonanze; & di questo ogn'uno si potrà certificare, quando ridurrà i
Suoni in atto, i quali nascono dalle chorde tirate sotto la ragione delle già mostrate pro
portioni; come piu uolte hò mostrato; conciosia che udirà ueramente, che non fanno
Consonanza alcuna, per non hauer la lor forma tra le Parti del numero Senario. Et
quantunque, oltra la mostrata specie di Chromatico, Tolomeo ne habbia ritrouato due
altre; l'una delle quali chiama Chromatico molle & l'altra Chromatico incitato, & siano
approuate da lui per buone; conciosiache i loro Interualli sono contenuti nel genere ; nondimeno tutti non sono atti alla generatione della Consonanza, &
dell'Harmonia perfetta; se non quello, che si troua nel Chromatico molle, tra le due
chorde piu acute di ciascun suo Tetrachordo; & si chiama Semiditono nel Diatonico;
& nel Chromatico lo nominiamo Trihemituono. Et è ueramente consonante; essendo
che la Sesquiquinta, laquale è contenuta nel genere Superparticolare, è la sua forma; &
i suoi termini sono contenuti tra i numeri, che sono le parti del Senario; come nel Cap.
15. della Prima parte si può uedere. Et se ben questa Specie è ornata di questo Inter-
uallo; hà nondimeno l'istessa imperfettione, c'hanno l'altre, contenute nel genere Dia-
tonico; come tra le Otto più graui chorde del suo Monochordo, contenute nell'essem-
pio, si può uedere; tra le quali si ritroua etiandio l'Hexachordo minore, che da i
Prattici moderni è posto tra gli Interualli consonanti. La medesima imperfettione
hà anco la Seconda Specie, detta Chromatico incitato; anzi dirò maggiore; con-
page 139
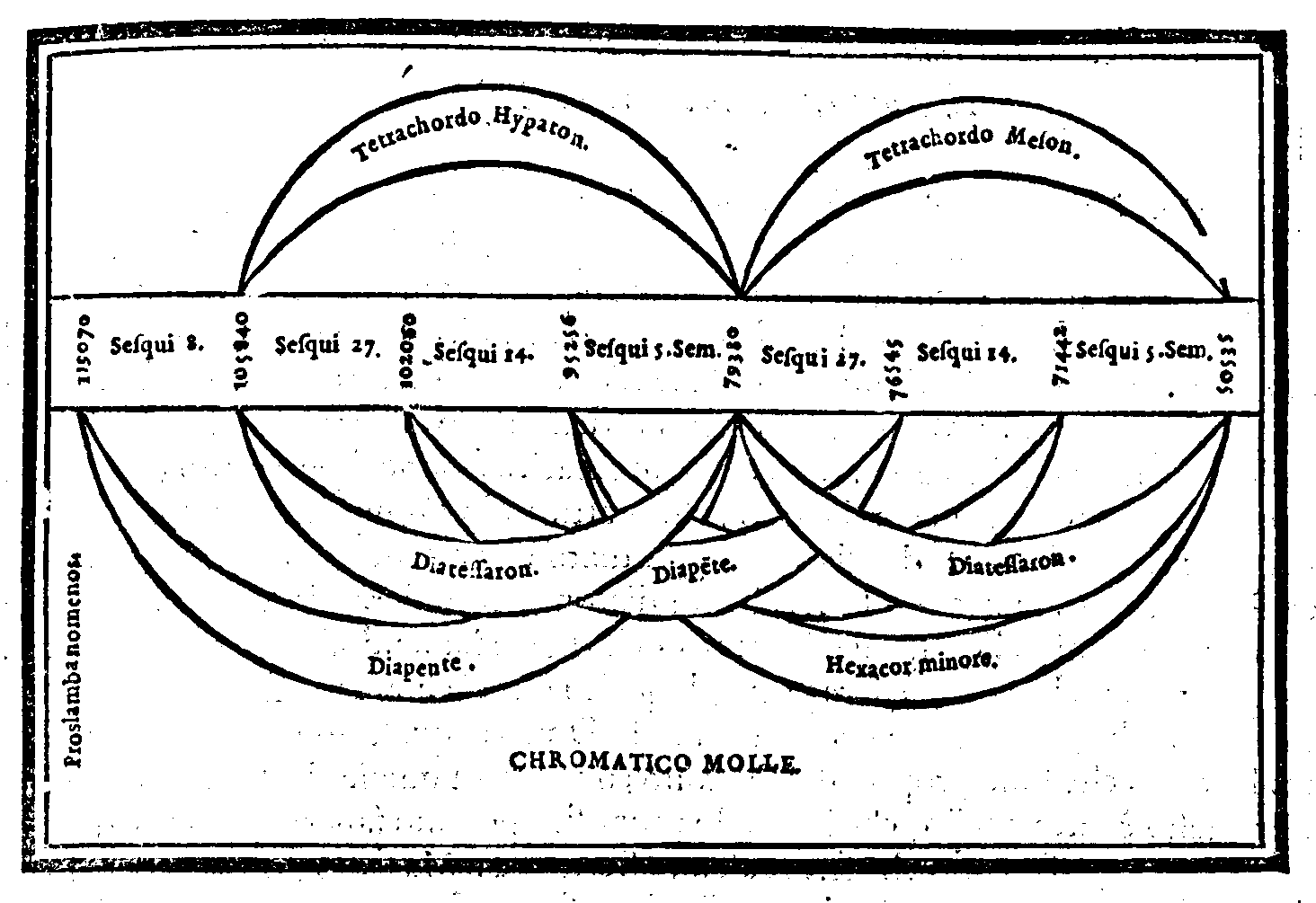
me si può uedere nel suo essempio; se non la Diapente tra la prima chorda graue & la
quinta, che si troua etiandio nell'altre.
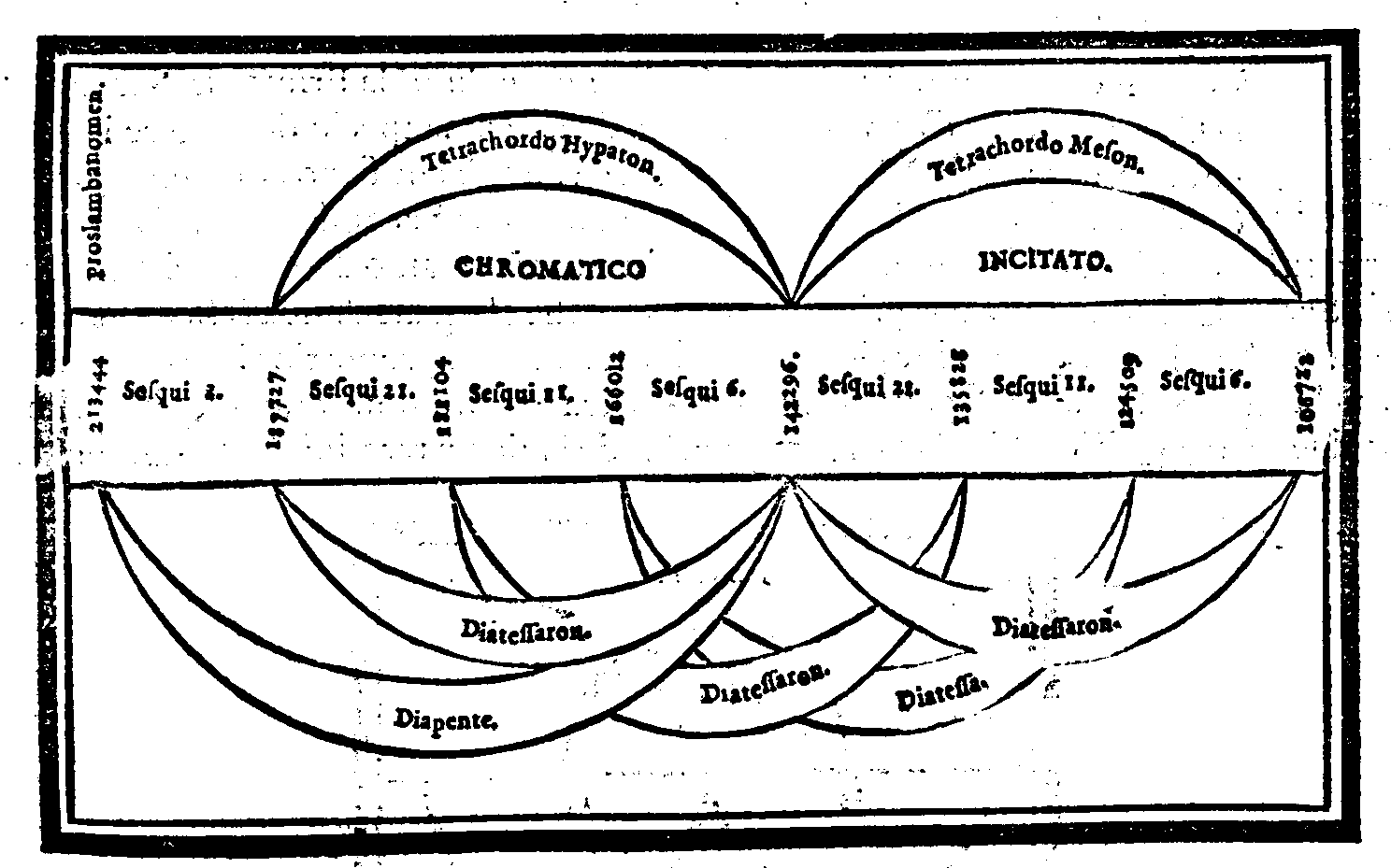
Chi sia stato l'Inuentore del genere Enharmonico, & in qual maniera
l'habbia ritrouato.Cap. XXXV.
ma si bene quanto al tempo, qual fusse quello, che fù l'Inuentore del genere En
harmonico; ancorache difficilmente si possa mostrare il modo, che lui tenne
à ritrouarlo; imperoche esso Plutarcho & molti altri ancora, con parole non
molto chiare, ne con molta fermezza adducendo l'autorita d'Aristosseno, dice: Olimpo
(secondo l'opinione de i Musici de quei tempi) fù il Primo, che ritrouò questo Genere;
essendo per auanti ogni cosa Diatonica & Chromatica; onde si pensarono, che tale In-
uentione fusse proceduta in cotal modo; che pratticando Olimpo nel Diatonico, & tra-
sportando spesse uolte il Modo alla Parhypate diatona, partendosi tallora da Mese, tallo-
ra da Paramese, trasportando la Lychanos diatona; considerando la bellezza & conue
nienza de i costumi, che nasceua dal canto delle uoci; hauendosi forte marauigliato del
la congiuntione, che costaua di ragione, laquale i Greci chiamano Σύστημα; & abbrac-
ciato che l'hebbe, fece questo genere nel modo Dorio; ilquale non si può accommoda-
re ne alle cose, che sono proprie del Diatono; ne meno à quelle che sono del Chromati
co. Et questo è tutto quello, che in questo proposito potemo sapere; non si ritrouando
altro intorno à questa cosa, che scriua alcuno Scrittore. Ma se uogliamo uedere in qual
modo questo Genere da per sè nella sua diuisione si potesse adoperare, verremo à mostrar
lo con la compositione del suo Monochordo.
Della Diuisione, ò Compositione del Monochordo Enharmonico.
Cap. XXXVI.
la Quarta chorda d'ogni Tetrachordo della Prima specie del genere Diatoni
co, chorde essentiali dell'Enharmonico; ancorache siano communi all'uno,
& all'altro de questi due Generi, & diuētando la Seconda chorda Diatonica,
Terza enharmonica; è dibisogno solamente, che noi cerchiamo di porre nel Tetrachor
do la Seconda chorda tra le due prime graui diatoniche, laquale diuida il Semituono cō
tenuto tra loro in due parti; cioè, in due Diesis, secondo le proportioni mostrate di so-
pra nel Cap. 16. Onde per seguitar la breuità, amica de i Studiosi; diuideremo solamen
te in due parti equali le Differēze de i maggiori & de i minori termini de i Semituoni; che
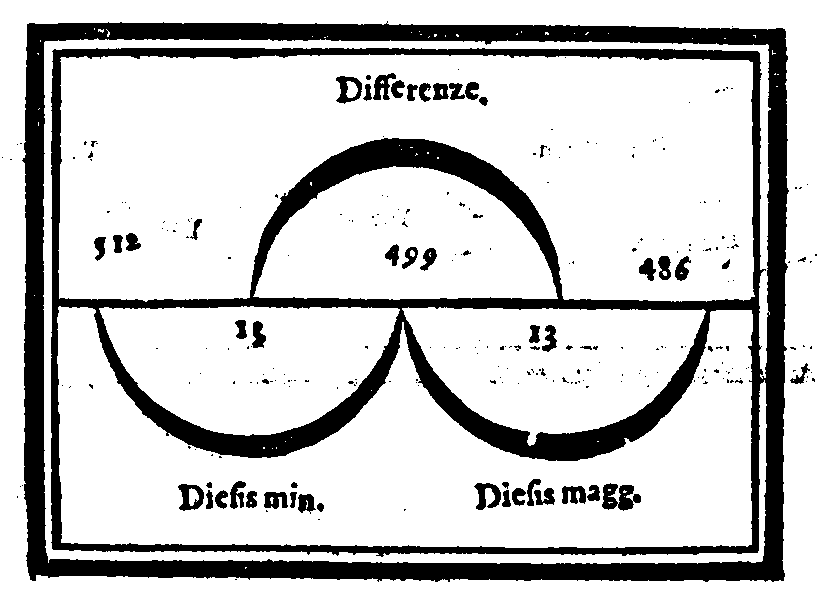
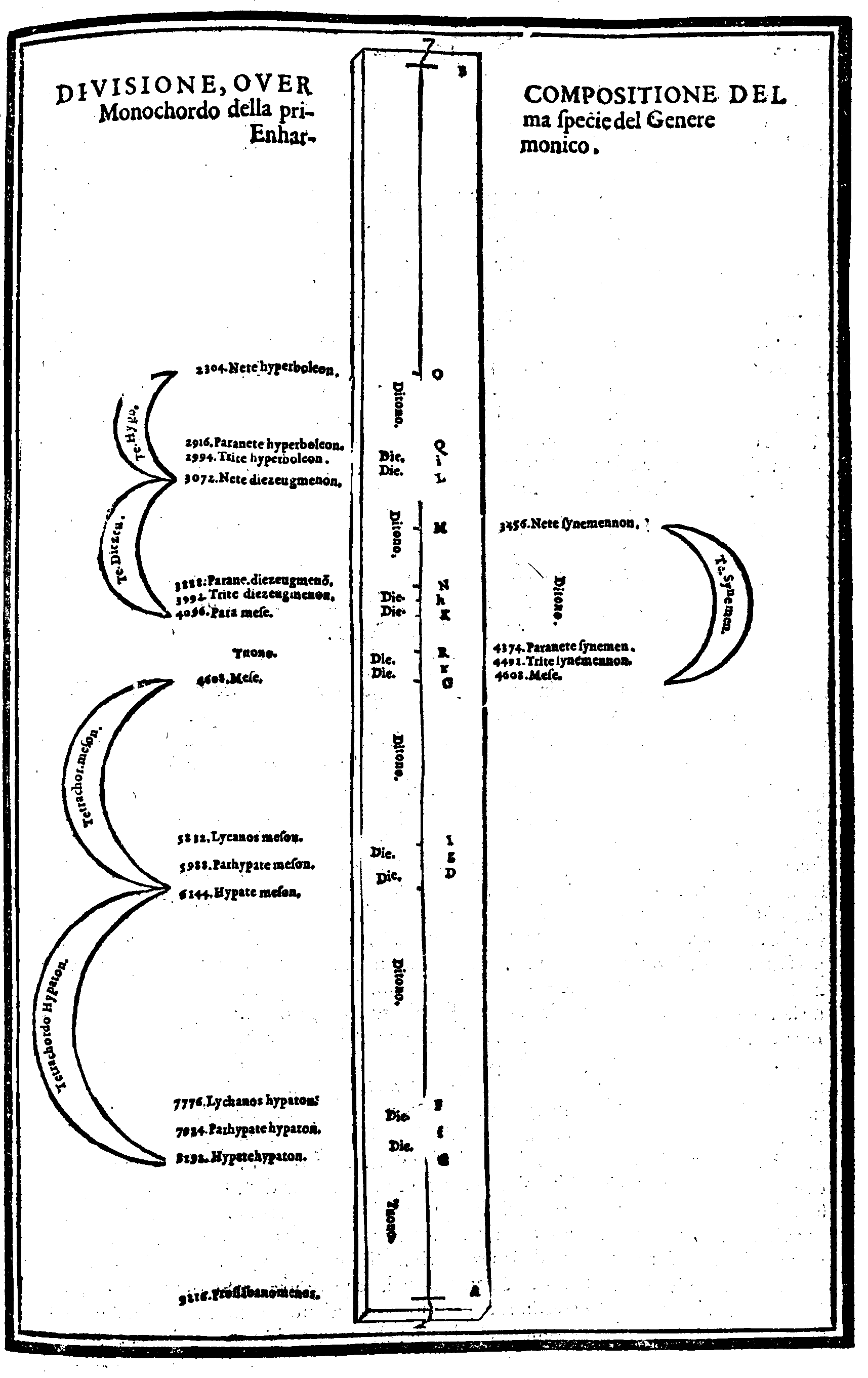
no le minori, che fanno i Suoni acuti de tali Semituoni; & porremo una Chorda meza-
na di longhezza quanto è la minore & la metà appresso della differenza; & haueremo
senz'alcun'errore il proposito. Conciosiache tra due parti equali di qualunque chorda,
che siano misurate da un'altra quantità, ò misura commune, si ritroua la Progressione
arithmetica continua, comparandole al Tutto; & le Differenze, che si ritrouano tra le
Proportioni de queste tre chorde, uengono ad essere equali; & fanno che le Proportio
ni sono ordinate in Proportionalità arithmetica; & questo torna molto commodo; impe
roche tra quelle Proportioni, che sono le forme de i due Diesis 512. 499. 486. si ritroua
la medesima proportionalità; perche le loro differenze da ogni parte sono 13. come nel-
la figura si può uedere. Pigliaremo adunque il Compasso, & diuideremo in due parti e-
quali ciascuna delle dette differenze per ogni Tetrachordo della prima specie del Diato
nico, le quali sono C F. D I. K N. L Q. & G R. ne i punti f. g. h. i. k. & haueremo insieme
le Chorde f B. í B. h B. i B. & k B. secondo 'l nostro proposito, & collocato nel graue il
Diesis di minor proportione, & nell'acuto quello di maggiore; come nella Diuisione si
può uedere; la quale etiandio contiene un'ordine di proportione, contenute ne i loro ter
mini radicali, & il nome delle chorde di tale ordine.
Consideratione sopra la mostrata Particione, ouer Compositione; & sopra
quella specie d'Enharmonico, che ritrouò Tolomeo.
Cap. XXXVII.
mini di ciascuna proportione di questa Diuisione, ò Compositione; ritrouare
mo quella īperfettione istessa, che ne gli altri due Generi in diuerse Specie hab
biamo ritrouato; massimamēte essendo priua in ogni suo Tetrachordo di quello
teruallo consonante; ilquale chiamano Ditono; percioche si ritroua in luogo di esso il
Ditono di proportione Super 17. partiente 64. ch'è ueramente dissonante. Et perche
forse alcun potrebbe credere, che quella Specie di Enharmonico, che ritrouò Tolomeo,
facesse l'Harmonia perfetta; conciosiache in ogni suo Tetrachordo habbia il Ditono con
sonante, contenuto dalla proportione Sesquiquarta, & l'Hexacordo maggiore, conte-
nuto dalla proportione Superbipartienteterza, che hanno i lor minimi termini tra le
parti del Senario; però dico, che etiandio questa Specie non può esser lontana dalla im-
perfettione; percioche si ritrouano in essa molte chorde, lequali, ne uerso il graue, ne
uerso l'acuto hanno relatione con alcun'altra chorda, che possa dare ne la Diapente,
ne la Diatessaron, ne il Semiditono; ma sono al tutto fuori d'ogni lor proportione; co-
me nelle Otto chorde ordinate secondo la natura del suo Tetrachordo si può compren-
dere. Potiamo hormai uedere, quanto di vtilità ne apporti qual si uoglia delle mostrate
Specie, nell'essercitatione dell'Harmonia perfetta; & simigliantemēte habbiamo potuto
uedere, in qual modo la Prima specie del Diatonico uenga ad essere inspessata dalla pri-
ma del Chromatico & dalla prima dell'Enh'armonico. Onde dirò per ultima conclusio-
ne, che ciascuna delle mostrate Diuisioni, sia qual si uoglia, non è atta alla generatione
dell'Harmonia perfetta; & che alla costruttione, ò fabrica d'un'Istrumento, ilquale
habbia ciascuno de i detti Tre generi, con quel modo più perfetto, che si possa hauere, si
potrà elegere per il Trihemituono chromatico, quello di Tolomeo, posto nel Chroma
tico molle, il quale è contenuto dalla proportione Sesquiquinta; & per il Ditono enhar
monico, il mostrato di sopra; che è contenuto dalla proportione Sesquiquarta; i quali
Interualli, ò Consonanze, che dir le uogliamo, sono etiandio contenuti nel Diatonico
naturale, ò Syntono di Tolomeo, che l'una si chiama Semiditono, & l'altra Ditono;
page 143come uederemo altroue. E' ben uero, che tali Interualli si considerano in ogni Te-
trachordo Diatonico composti, ouer Diuisi in due altri Interualli; ma ne gli altri due ge
neri si considerano semplici, & senz'alcuna diuisione.
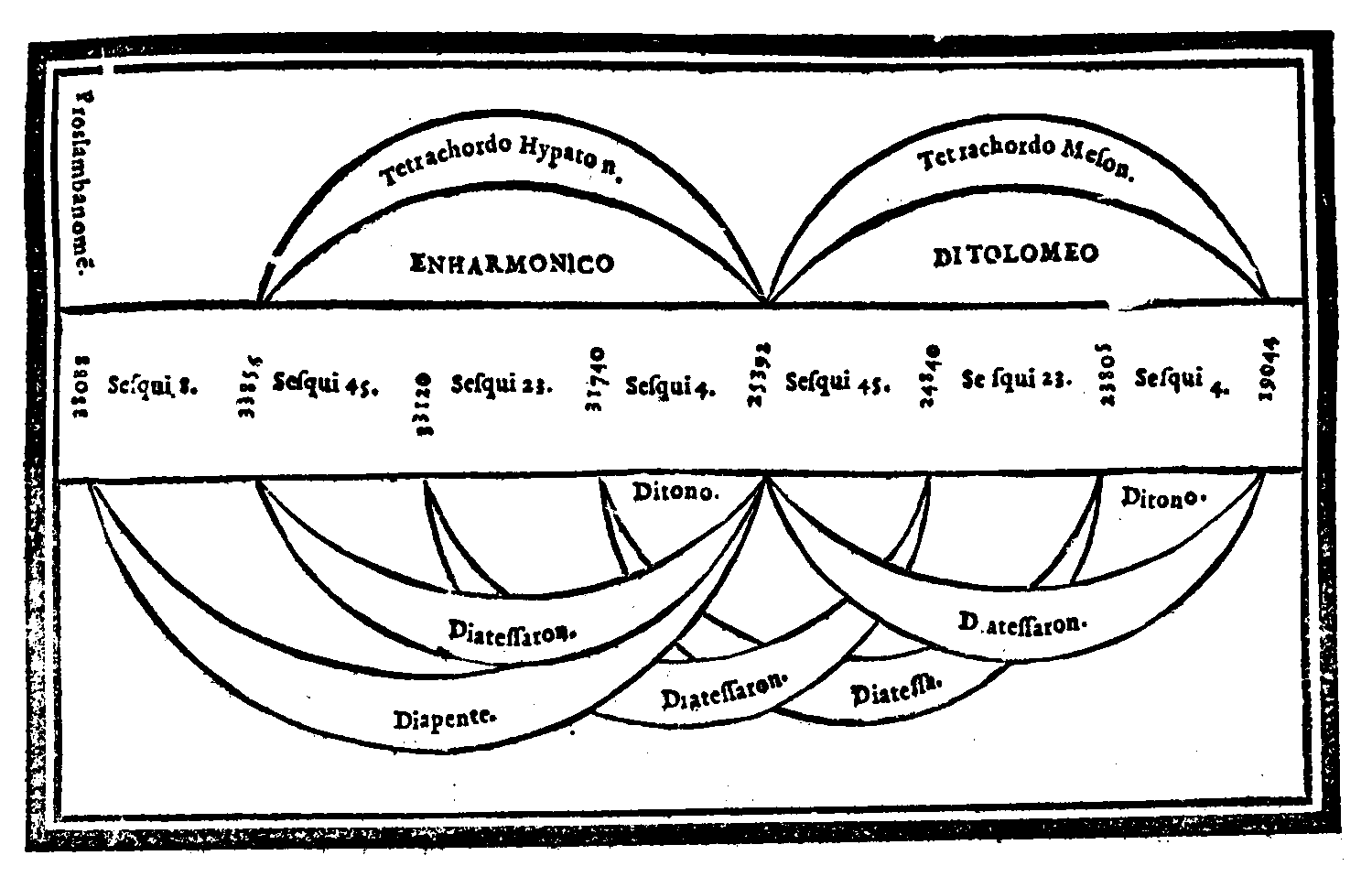
Della Compositione del Monochordo Diatono diatonico, inspessato
dalle chorde Chromatiche, & dalle Enharmoniche.
Cap. XXXVIII.
qual si uoglia Genere separatamente; non sarà fuor di proposito mostrare in
qual maniera, in un solo Istrumento le chorde della Prima specie del Diatoni
co siano inspessate dalle chorde delle Prime specie de gli altri due generi; cioè,
della prima specie del Chromatico, già mostrata; & della prima specie dell'Enharmoni-
co; accioche alcun non credesse, ch'essendo queste tre specie aggiūte insieme in un'Istru
mento, co 'l mezo di tale inspessatione, si potesse far l'Harmonia perfetta. Onde è da sa
pere, che se ben tal compositione è accresciuta per il numero delle Chorde, non fà pe-
rò il Diatonico più perfetto in cosa ueruna di quello, ch'era per auanti; conciosia che in
spessato per tal modo, tanto mancano in esso il Ditono & il Semiditono consonanti,
quanto mancauano inanzi che fusse fatta tale Inspessatione; come facendone ogni pro-
ua, si potrà uedere. Et benche tale imperfettione si ritroua in questa Inspessatione fatta
per cotal modo; si ritrouarebbe etiandio, quando il medesimo Diatonico fusse in-
spessato dalle chorde del Diatonico molle, da quelle del Toniaco, & da quelle dell'
Equale, poste di sopra nel Cap. 31. se ben se gli aggiungesse le chorde del Chroma-
tico incitato, che sono Specie ritrouate da Tolomeo. Essendo adunque il Diatonico
inspessato dal Chromatico nella parte acuta da una chorda, la quale con la vltima acu-
ta d'ogni suo Tetrachordo contiene il Trihemituono, & dall'Enharmonico nella parte
graue da un'altra, di maniera, che con la prima graue & con la seconda d'ogni Te-
trachordo Diatonico uiene à dar due Diesis; in ogni Tetrachordo accresciuto in tal
page 144modo, si ritrouano Sei chorde; dal qual numero si può nominare ueramente Hexachor
do. Onde nasce, cha tale ordine contiene in se Vintisei chorde; come nell'essempio si
può uedere; delle quali (come n'auertisce BoetioMusic
lib. 4. c. 12.) alcune si chiamano in tutto Stabili,
alcune in tutto Mobili, & alcune Ne in tutto stabili, ne in tutto mobili. Le prime sono
la Proslambanomenos, le due Hypate, la Mese, la Nete synemennon, la Paramese,
& l'altre due Nete; conciosiache in niun Genere cambiano ne il luogo loro, ne il nome;
ma lo ritengono simplicemente senz'aggiunto alcuno. Ma le seconde sono le Parane-
te & le Lycanos, alle quali, oltra i nomi proprij, s'aggiunge la denominatione del suo
genere; nominate hora Diatoniche, hora Chromatiche, & hora Enharmoniche; impero
che la Paranete diatonica è differente di luogo dalla Paranete chromatica, & dalla Para
nete enharmonica; & cosi la Paranete chromatica è diuersa dalla Paranete enharmonica;
ilche anco si può dire dell'altre; percioche si mutano in ciascun genere. Quelle poi, che so
no Ne in tutto mobili, ne in tutto stabili, sono le Parhypate, & le Trite del Diatonico, &
del Chromatico; che Lychanos & Paranete dell'Enharmonico si chiamano; percioche re
stano stabili ne i due primi generi, ma nell'Enharmonico uariano il nome, & di Seconde
diuentano Terze chorde de i Tetrachordi. Onde da quello, che si è detto, & mostrato,
facilmente si può conoscere, quanta arroganza sarebbe il uoler affermare, che tali Ge-
neri, & le loro Specie si potessro usar semplici & misti con ogni perfettione ad ogni no-
stro piacere; imperoche mai per alcun tempo, ne misti, ne semplici da gli Antichi perfet
tamente sono stati posti in uso. Resta adunque a dire, che non solo le Prime specie de i
detti Generi separate, ouer congiunte insieme, si ritrouano imperfette; ma quelle etian
dio, che furono ritrouate da Tolomeo, dal Diatonico syntono in fuori; come con la e-
sperienza si potrà uedere. Per la qual cosa non sò pensarmi, à qual fine gli Antichi ri-
trouassero tante Diuisioni in ogni genere, le quali faceuano nulla, ò poco alla perfettio
ne dell'Harmonie; se non fusse; come dissi altroue;Supra c. 31 che allora erano utili alla parte Spe-
culatiua, per dimostrare il uero di quelle cose, ch'apparteneuano alla loro Prattica;
oueramente (com'alcuni pensano) perche da cotali Diuisioni poteuano prima uenire
nella uera cognitione della Compositione d'ogni Machina, & formare con debita pro-
portione i Vasi, che riponeuano ne i loro Theatri, collocandoli dopoi in esso ne i loro
luoghi conueneuoli. Ma sia come si uoglia; basta che de qui potiamo conoscere, quan-
ta imperfettione hauerebbe la Musica, quando si uolesse adoperare solamente ne gli In
terualli mostrati; & la pazzia de quelli, che uolessero ostinatamente affermare, che cota
li Interualli fussero quelli da i quali si fanno le uere & legitime Consonanze, che hora
usiamo; & nascono da ueri & legitimi Numeri harmonici, & ci danno la perfetta Har-
monia. Ma perche niuna delle mostrate Diuisioni fà al nostro proposito; conciosia-
che tutte contradicono alla ragione, & al senso; desiderando io di mostrar quella,
che nasce da i ueri & naturali Numeri sonori, laquale usiamo al presente; & in qual
maniera si possa usare il Chromatico, & l'Enharmonico aggiunti al Diatonico; lascian-
do di parlar più cosa alcuna de loro, uerrò à dimostrare (secondo 'l mio proposito) la Di
uisione, ò Costruttione del Monochordo Diatonico natural, ò syntono; inspessando
con le chorde Chromatiche, & con l'Enharmoniche, secondo, che i sonori & ueri Nu-
meri harmonici lo concederanno.
page 145
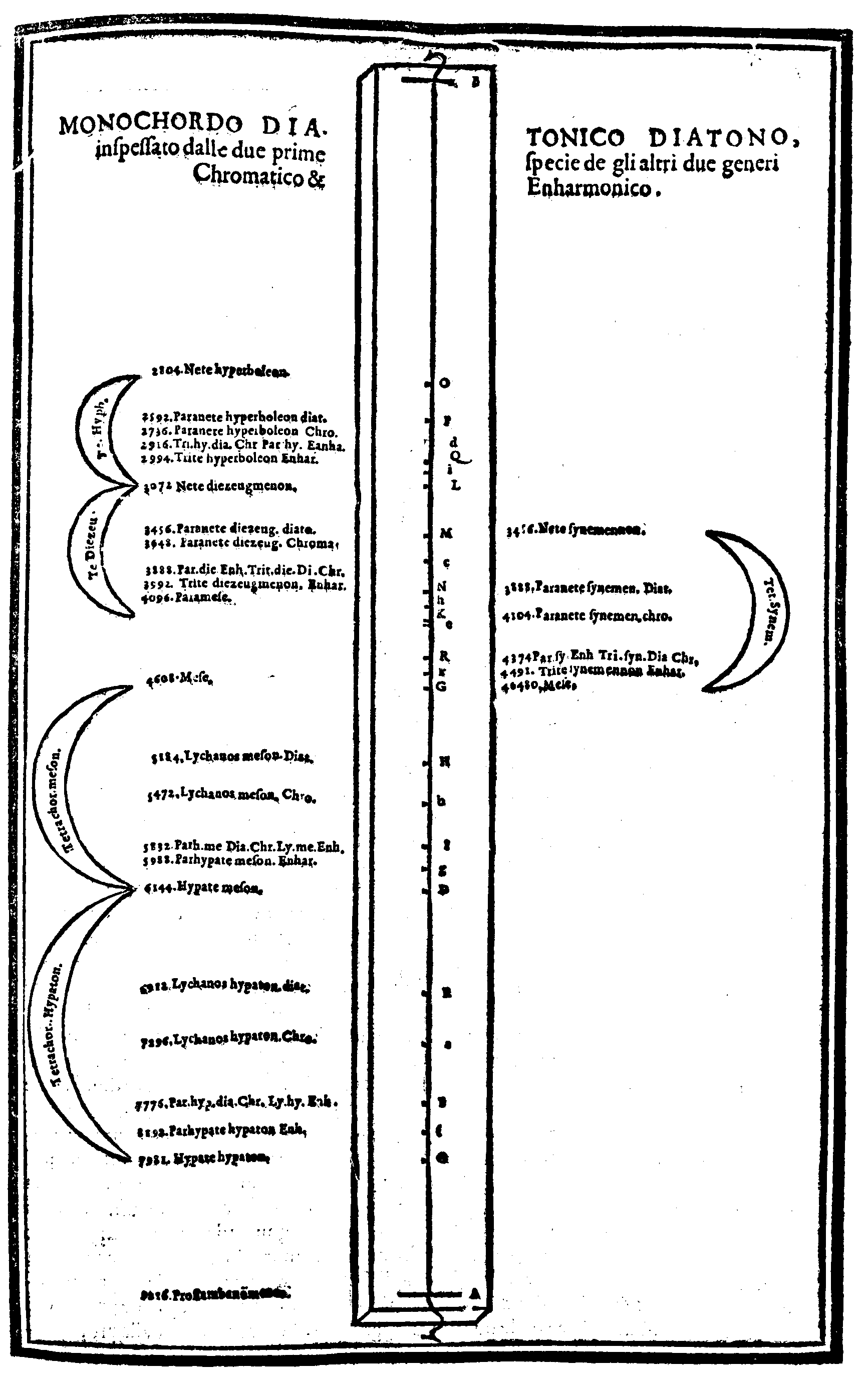
Che 'l Diatonico Naturale, ò syntono di Tolomeo sia quello, che dalla natura
è prodotto, & che naturalmente habbia la sua forma da i
Numeri harmonici.Cap. XXXIX.
mēte mostrare, per qual cagione hò detto, che 'l Diatonico naturale, ò syntono
sia prodotto dalla Natura, & nasca da i ueri Numeri harmonici; percioche do
po fatta la sua diuisione, ò compositione, verrò alla sua inspessatione; accioche (se
condo l'uso de i Moderni) possiamo usar l'Harmonie, in quel modo più perfetto, che dal
la Natura, & dall'Arte ne sarà concesso. Onde per mostrar questo, prouerò questa con-
clusione esser uera; Che 'l Tetrachordo Diatonico naturale, ò uogliamolo dire syntono,
posto nel Cap. 16. è diuiso, ouer ordinato secondo la natura & passione de i Numeri har
monici; conciosia ch'esso si ritroua in atto tra le chorde della Diapason, diuisa nelle sue
parti in Sette interualli, secondo la natura & proprietà de i detti numeri. Et accioch'io
possa dimostrarlo, aiutato dalla natura della Proportionalità harmonica, piglierò per mio
fondamento la Diuisione della Diapason nelle sue parti; la quale sarà la a b posta nella fi-
gura, la forma della quale è contenuta tra 2 & 1. nella proportione Dupla. Se adunque
vorremo diuider questa Proportione harmonicamente in due parti, secondo 'l modo da
to nel Cap. 39. della Prima parte, haueremo una Sesquialtera a c. & una Sesquiterza
c b. l'una delle quali; è la Sesquialtera, uera forma della Diapente & l'altra della Dia-
tessaron; di maniera che questa uerrà à tenere il luogo acuto, & quella il graue nel concē
to; secondo la natura loro; & saranno le Parti principali di essa Diapason. Hora piglian-
do la maggior parte di queste due, che è la Diapente a c. poi che la Diatessaron, ne alcun'
altra Parte minore di qual si uoglia Consonanza semplice diuisa harmonicamente, non
è capace di tal diuisione; essendo che le parti, che uengono sono, contenute da altre for-
me & proportioni, che da quelle, che si trouano tra le parti del Senario; diuideremo la sua
proportione, ch'è la Sesquialtera posta tra questi termini 3 & 2. al modo detto; ilche fat-
to haueremo due altre parti, l'una maggior dell'altra; cioè, a d. contenuta dalla propor-
tione Sesquiquarta, la quale chiamaremo Ditono; & d c. contenuta dalla proportione
Sesquiquinta, che nominaremo Semiditono; delle quali il Ditono (come ricerca la sua
natura) terrà la parte graue, & il Semiditono l'acuta; & queste saranno le Seconde par-
ti della Diapason, & le Prime della Diapente; nella quale esse sono collocate; & per tal
maniera haueremo fatto tre parti della Diapason, col mezo della nominata Proportiona
lità; ciascuna delle quali (oltra che ha origine dalle Proportioni contenute nel genere Su
perparticolare) hà i suoi Termini radicali collocati tra le parti del Senario; come si può
vedere. Tutte queste parti da i Moderni Musici sono chiamate Consonanze; & sono ve
ramente; come la esperienza ce lo dimostra; dalle quali potiamo incominciare à uedere
quanta simiglianza habbiano con quelli Interualli, che sono collocati tra le chorde del
sopranominato Tetrachordo naturale, ò syntono; essendo che in esso si ritrouano quelli
Interualli istessi, che sono contenuti nella Diapente a. d. c. harmonicamente diuisa; cioè
il maggiore a d. posto nel graue, tra l'ultima chorda acuta, & la seconda graue; & il mi-
nore d c. posto nell'acuto tra la prima chorda graue, & la terza posta nell'acuto del det-
to Tetrachordo. Et quantunque questi interualli siano tutti Consonanti; tuttauia quel
li, che sono le Prime parti della Diapason, chiamano Consonanze perfette; gli altri, che
sono le Seconde & le Prime della Diapente, nominano Consonanze imperfette. Volen
do hora ritrouar le Terze parti della Diapason, che uengono ad esser le Seconde della
Diapente, lequali danno le proportioni, ò forme de gli Interualli contenuti da una chor
da all'altra nel detto Tetrachordo; pigliaremo il Ditono a d. contenuto dalla proportio-
ne Sesquiquarta 5 & 4. & lo diuideremo al mostrato modo; & haueremo due parti a e. &
e d. l'una maggior dell'altra; delle quali la maggiore a e. sarà contenuta dalla proportio-
page 147
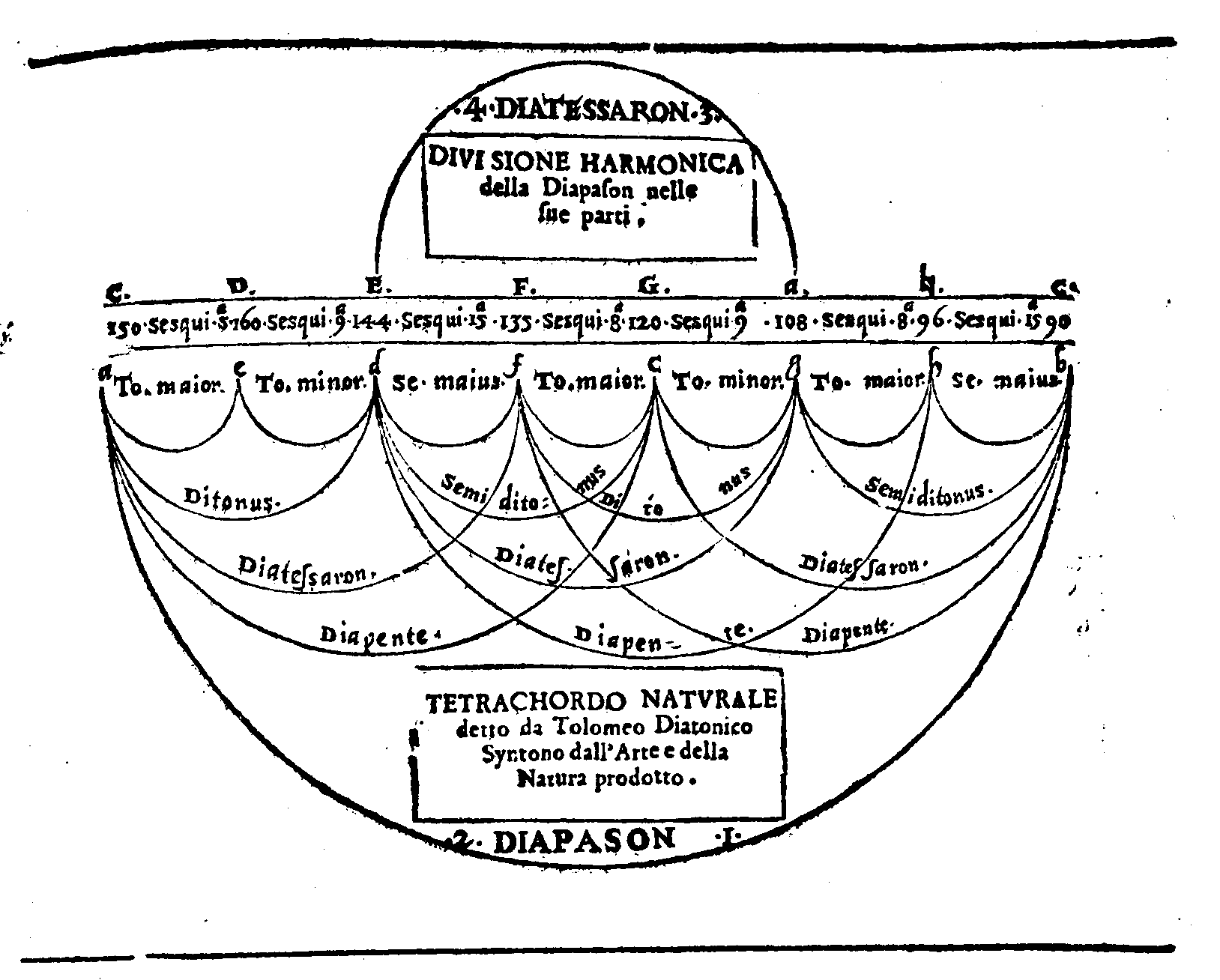
proportione Sesquinona, & la chiamaremo Tuono minore; & per tal modo haueremo
due Tuoni inequali, che si trouano tra le Quattro chorde del nominato Tetrachordo dia
tonico naturale, ò syntono di Tolomeo; come in esso si può uedere; da i quali la maggior
parte fatta della Diapente uiene chiamata & denominata Ditono, & la minore è det-
ta Semiditono; percioche non arriua alla quantità de due Tuoni; essendo che contiene
in se un Tuono maggiore, & un maggior Semituono; ilquale come s'acquisti nel detto
Tetrachordo, lo uederemo à mano à mano. Queste due parti adunque sono le maggiori
contenute nel Tetrachordo già detto; & sono le Terze parti della Diapason, le Seconde
della Diapente, & le Prime parti maggiori del Ditono; nate per la Diuisione harmonica;
come si è dimostrato; & nella lor uera forma prodotte. La onde per tal modo potremo
hauer la ragione de tutti quelli Interualli semplici, che co 'l mezo dell'Harmonica pro-
portionalità acquistar si possono. E se ben questa Diuisione è sufficiente à mostrar che 'l
sudetto Tetrachordo sia diuiso secondo la natura de i Numeri harmonici; essendo che i
suoi Interualli hanno le forme loro collocate tra essi; tuttauia per dimostrare in che
modo nasca l'Interuallo del Semituono maggiore, che non si può hauere per alcuna Di
uisione harmonica, procederemo all'intiera diuisione della Diapason in questo modo. Ac
commodaremo primamente gli estremi della Diatessaron a f. ouer quelli della Dia-
pente f b. di maniera, che tra a f. sia la proportione Sesquiterza; ouero tra f b. la Ses-
quialtera; & l'estremo acuto della Diatessaron a f. ouer l'estremo graue della Dia-
pente f b. uerrà necessariamente à cascare tra gli estremi del Semiditono d e.
nel punto f. & la f. uerrà à diuider la sua forma, ò proportione, ch'è la Sesqui-
sesta, in due parti; cioè, in una Sesquiquintadecima d f. & in una Sesquiottaua f c.
la onde dico, che tra d f. si troua il Semituono maggiore; percioche facendosi la Dia-
tessaron de due Tuoni, l'un maggiore a e. l'altro minore e d. & di un Semituono mag-
page 148giore, come vederemo; essendo a e. & e d. li due Tuoni aggiūti insieme di proportione Ses
quiquarta; non è dubbio alcuno, che uolendo arriuare alla Sesquiterza, ch'è la forma
della Diatessaron, sarà dibisogno d'aggiungerle una proportione Sesquiquintadecima,
che sara d f. percioche (per la Ventesimaseconda Definitione del Secondo delle Dimo-
strationi; & per la Quintadecima proposta del medesimo) di questa quātità il Ditono è su
perato dalla Diatessaron, & la proportione Sesquiottaua f c. è quella quantità, per laqua
le la Diatessaron è superata dalla Diapente. Percioche questa (per la Ventesima Defini-
tione del detto) è maggiore di quella, d'un'Interuallo di Tuono maggiore. Ma se accom
modaremo alla chorda d. una chorda nella parte acuta, che sia distante per una Sesqui-
terza, che caschi tra gli estremi della Diatessaron c b. la uerrà à diuidere in una Sesquino
na proportione c g. ouero in un Tuono minore; & in una Sesquiquinta g b. ò Semidito-
no & si uerrà à fare acquisto d'uno Hexachordo maggiore a g. contenuto dalla proportio
ne Superbipartienteterza; & il Tuono minore c g. verrà ad esser la differenza, che si tro-
ua tra la Diapente, & esso Hexachordo; di modo che haueremo la Diatessaron d. f. c. g.
che tra la d f. contenerà il Semituono maggiore di proportione Sesquiquintadecima tra
f c. il Tuono maggiore di proportione Sesquiottaua, & tra c g. il minore di proportione
Sesquinona; secōdo le ragioni delle proportioni mostrate nel Tetrachordo diatonico na
turale, ò syntono già nominato, ritrouato da Tolomeo secōdo 'l proposito. Onde da questo
si può concludere, che 'l Diatonico naturale, ò syntono di Tolomeo sia quello, che nasce
da i ueri Numeri harmonici; secondo ch'io proposi di prouare. Ma se uorremo procede
re piu oltra alla diuisione intiera della Diapason; ponendo la chorda d. per l'estremo gra-
ue d'una Diapente; la sua chorda acuta uerrà à cascare fuori della Diatessaron d g. nel
punto h. che diuiderà il Semiditono g b. in due parti; cioè, in un Tuono maggiore g h. di
proportione Sesquiottaua; il quale Interuallo (com'habbiamo detto di sopra) è la quan
tità per la quale essa Diatessaron è superata dalla Diapente; & in uno Semituono mag-
giore h b. di proportione Sesquiquintadecima; percioche il Semiditono (per la Ventesi-
masesta del Secondo delle dimostrationi) si uiene à comporre de questi due Interualli. Et
per tal maniera haueremo, secondo la natura de i Numeri harmonici, la Diuisione per-
fetta della Diapason in Sette interualli; come dimostra la Trentesimanona delle predet-
te; cioè, in tre Tuoni maggiori a e. f c. & g h. in due minori e d. & c g. & in due Semituoni
maggiori d f. & h b. che si trouano collocati tra Otto chorde; le quali i Moderni notano
con queste lettere, C. D. E. F. G. a.
 . c. & fanno la Prima specie della Diapason, come al
. c. & fanno la Prima specie della Diapason, come al suo luogo uederemo; come nella 14. Def. del Quinto delle Dimostrationi hò dichiarato.
Et quantunque si ueda che naturalmente il Tuono maggiore a e. tenga il luogo graue, &
dopo esso immediatamente seguita il minore e d. uerso l'acuto, & il Semituono d f. ten-
ga il più acuto luogo nella Diaressaron C. D. E. F. & che Tolomeo habbia prima colloca-
to il Semituono d f. nel graue, & dopoi di mano in mano i duo Tuoni f c. & c g. per l'ordi
ne mostrato uerso l'acuto, contra la natura de i Numeri harmonici; tuttauia si debbe scu
sare; percioche lo fece per seguir nelle sue Dimostrationi il costume de i primi Inuentori
de i Generi mostrati; i quali poneuano primieramente nella parte graue de i loro Tetra-
chordi l'Interuallo minore; & dopoi li maggiori per ordine; percioche credettero che 'l
primo Interuallo nella Musica fusse il Minimo rationale, che si potesse ritrouar, dal quale
hauessero origine & si cōponessero gli altri Interualli; come si uede, che Aristotele1. post. c.
17. & 10.
Metaphy.
cap. 2. pone il
Diesis per il Principio di questo genere Melodia, nō potēdo far di manco. Ma non è dub-
bio, che tal Semituono sempre tiene il suo luogo (come si può uedere) procedēdo dal gra
ue all'acuto, dopo il Tuono minore, & auāti il maggiore; anzi più tosto dopo il maggiore
& lo minore, nella Compositione & congiuntione de i Tetrachordi; come ricerca la na-
tura de i Numeri harmonici; i quali ne danno primieramente i maggiori, & dopoi i mi-
nori Interualli per ordine. Et è tanta la necessità di questo Interuallo, che senza il suo me-
zo nō si può procedere dal Ditono alla Diatessaron, ne dalla Diapente all'Hexachordo
minore; come uederemo. Ond'è chiamato Semituono maggiore, à differenza di quella
page 149quantità contenuta dalla Sesquiuentesimaquarta proportione, detta Semituono mino-
re, per la quale il Semiditono è superato dal Ditono. Il perche aggiunti questi due Se-
mituoni insieme, arriuano alla perfettione del Tuono minore, contenuto dalla propor-
tione Sesquinona; come dimostra la Decimanona proposta del libro Secondo delle Di
mostrationi. Concluderemo adunque di nuouo, c'hauendo origine tutti gli Interualli
del Tetrachordo Diatonico naturale, ò syntono di Tolomeo dalla diuisione della Dia-
pason, fatta harmonicamente nelle sue parti; che esso Tetrachordo sia etiandio diuiso,
& ordinato secondo la natura & passione de i numeri harmonici; come hò detto. Ma ue
niamo hormai alla Diuisione, ò Compositione del Monochordo.
Della Diuisione del Monochordo naturale, ouer syntono Diatonico; fatta secondo la
natura & propietà de i Numeri sonori.Cap. XL.
strato modo, un'Asse, ouer Tauola, nella quale la linea A B. sia la chorda, so-
pra la quale habbiamo da far tal Diuisione, per disporre & collocar per ordine
ogni suo Tetrachordo secōdo 'l modo tenuto nell'altre Diuisioni; collocaremo
prima (per la Prima del Terzo delle Dimostrationi) il Tuono maggiore alla sua propor-
tione, & haueremo la A B. & la C B. delle quali la prima contenerà noue parti, per il mag
gior termine della sua proportione; & la seconda otto, per il minore; & per tal modo tra
loro haueremo accommodato il detto Tuono. A questo soggiungeremo il primo Tetra-
chordo, detto Hypaton; diuidendo la C B. in quattro parti equali, per il termine maggio
re, che contiene la sua proportione; ilche fatto, prese le tre parti per il minore hauere-
mo collocati gli estremi tra C B. & D B. Volendolo poi diuidere in due Tuoni & in un Se
mituono, secondo la ragione de gli Interualli & Proportioni del detto Tetra chordo; ac
commodaremo prima il Tuono minore alla sua proportione diuidendo (nel modo che si
è tenuto nella Seconda del Terzo delle Dimostrationi) la D B. in noue parti equali, per il
minor termine della sua proportione; dopoi aggiungendo uerso il graue un'altra parte;
haueremo accommodato il Tuono minore tra la D B. che contiene noue parti; & la E B.
che ne cōtiene dieci. A questo immediatamente (secondo il modo che si è dimostrato nel
la 4. di esso 3.) preponeremo il magggiore, diuidendo la E B. in otto parti, aggiungendo
ui la nona parte; & tra F B. & E B. haueremo ile proposito; percioche il Semituono mag-
giore verrà ad esser collocato necessariamente tra C B. & F B. come si può prouare; concio
siache se noi aggiungeremo ad una Sesquiquarta, che contiene il Ditono, la proportione
Sesquiquintadecima, che contiene tal Semituono; per il Corollario della 20. del Primo
delle Dimostrationi; uerrà necessariamente la proportione Sesquiterza, ch'abbraccia gli
estremi del Tetrachordo. Il medesimo haueremo manifestamente da questo; che se noi le-
uaremo una Sesquiottaua, & una Sesquinona dalla Sesquiterza, ne resterà la Sesquiquin
tadecima. Il primo Tetrachordo adunque uerrà ad esser collocato al suo proprio luogo,
diuiso in due Tuoni, & in uno Semituono, secondo la natura di tal Tetrachordo. Soggiū
geremo à questo il Secondo detto Meson, & gli altri per ordine, secondo 'l modo tenuto
nell'altre Diuisioni; & haueremo il Meson tra D B. I B. H B. & G B. il Diezeugmenon tra K B.
N B. M B. & L B. lo Hyperboleō tra L B. Q E. P B. & O B. & il Synemēnon tra G B. S B. N B. & R B.
Haueremo etiandio in questa diuisione Dicesette chorde, tra le quali si ritrouerà non so
lamēte il Semituouo minore tra S B. & K B. ma un minimo Interuallo etiandio, ilquale è la
Differenza, che si troua tra 'l maggiore & il minor Tuono, che si chiama Cōma; cōtenuto
(per la Vētesima proposta del Secōdo delle Dimostrationi) nel genere Superparticolare
dalla proportione Sesquiottantesima. Et nasce questo Interuallo per la cōgiūtione del Te
trachordo Synemennon al Tetrachordo Meson nella chorda Mese; imperoche la chorda
page 150acuta del detto Synemennon diuide il mezano interuallo del Diezeugmenon in due par
ti; cioè, in un Tuono minore, che tiene la parte graue; & nel Comma, che occupa la
parte acuta di tal diuisione; de i quali l'uno è posto tra la N B. & la R B. & l'altro tra
la R B & la M B. come si uede. Questo Interuallo, quantunque sia minimo, ha dato molto da
speculare, & da dire à molti; doue che hanno inciampato in molti luoghi; ma sia come si
uoglia, la cosa ua in questo modo; che se bene l'interuallo del Comma non è adoperabile;
non è però nato in questo luogo senza utile; conciosiache quando si uolesse adoperare, in
quel modo che l'Arte ne concede, co 'l suo mezo si uerrebbe à fare acquisto di due conso-
nanze primieramente d'una Diapente posta tra R B. & O B. dopoi di un Semiditono po-
sto tra R B. & Q B. lequali senza il suo aiuto non si potrebbono hauere. Et perche quando
ueramente lo uolessero adoperare ne gli Istrumenti arteficiali; darebbe qualche noia all'
Vdito; però la Natura primieramente, & dopoi l'Arte, hanno trouato rimedio (dirò co-
si) à cotal cosa; conciosiache tra le Voci, che per loro natura in ogni parte si piegano si di-
sperde, & accommoda di maniera, che non si ode; & ne gli Istrumenti arteficiali è diui
so per la sua Distributione, che si fà in quelli Interualli, che sono contenuti tra Otto chor-
de continenti la Diapason; come altroue uederemo. Onde si dè auertire, che quantunque
le Chorde di cotal Diuisione siano denominate, secondo l'ordine tenuto nell'altre, con
nomi Greci; nondimeno, io per seguir l'uso de i Moderni, l'hò etiandio notate cō le Let
tere di Guidone; & hò segnato non solo la chorda R B. ma la M B. etiandio con la lettera d.
per non confonder tale ordinanza; di maniera, che si come nell'Istrumento mostrato,
tra queste due chorde si contiene il detto Comma; cosi ne i Moderni; come sono Orga-
ni, Clauocembali, Monochordi, Arpichordi, & altri simili, tale Interuallo non hà luogo;
percioche le chorde loro sono ridotte al numero delle chorde Pitagoriche. Ma se uor-
remo nel mostrato Monochordo ritrouar qual si uoglia Consonanza, che in esso sia pos-
sibile di ritrouare sia poi harmonicamente, ouero ad altro modo tramezata; poi che so-
pra di esso haueremo tirato tre, quattro, ò più chorde, secondo che ne saranno biso-
gno; potremo hauere il nostro proposito, & ridurla sotto 'l giudicio del sentimento, operā-
do con i Scannelli mobili in quel modo, c'habbiamo mostrato altroue; & potremo co-
noscere la differenza, che si ritroua tra questa, & l'altre mostrate Diuisioni; & l'
fatto delle Consonanze, che si chiamano Imperfette.
Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle mostrate
specie Diatoniche.Cap. XLI.
tutte quelle Consonanze, che sono possibili da ritrouarsi; per questo non dob
biamo credere, che ne i moderni Istrumenti, come sono Organi, Clauocemba
li, Arpichordi, Monochordi & altri di sorte diuerse; tanto da fiato, quanto da
chorde, i Tuoni & i Semituoni siano nella loro uera & natural forma; percioche sarebbe
errore, essendo che le Chorde & fori, & qualunque altro accidente, che sia stabile & ter-
minato, in essi sono comprese dal numero delle chorde Pitagoriche, contenute nel
Monochordo Diatonico diatono; nelle quale (seguendo l'ordine già mostrato de gli in-
terualli di Tuono & di Semituono) udendosi il Ditono, & il Semiditono consonanti;
non è possibile (se sono temperati nel modo, ch'io son per dimostrare) che si possa ri-
trouar tra loro alcun'Interuallo, sia qual si uoglia, da quello del Diapason in fuori, ilqua
le mai non patisce alteratione alcuna; & quello del Semituono minore, collocato
tra le chorde b. &
 che sia compreso nella sua uera & natural forma, ouer propor-
che sia compreso nella sua uera & natural forma, ouer propor-tione; percioche il numero delle lor chorde non può dare gli Interualli, che si ritroua-
no nel Diatonico syntono; ne meno comprendono quelli del Diatonico diatono mo-
page 151
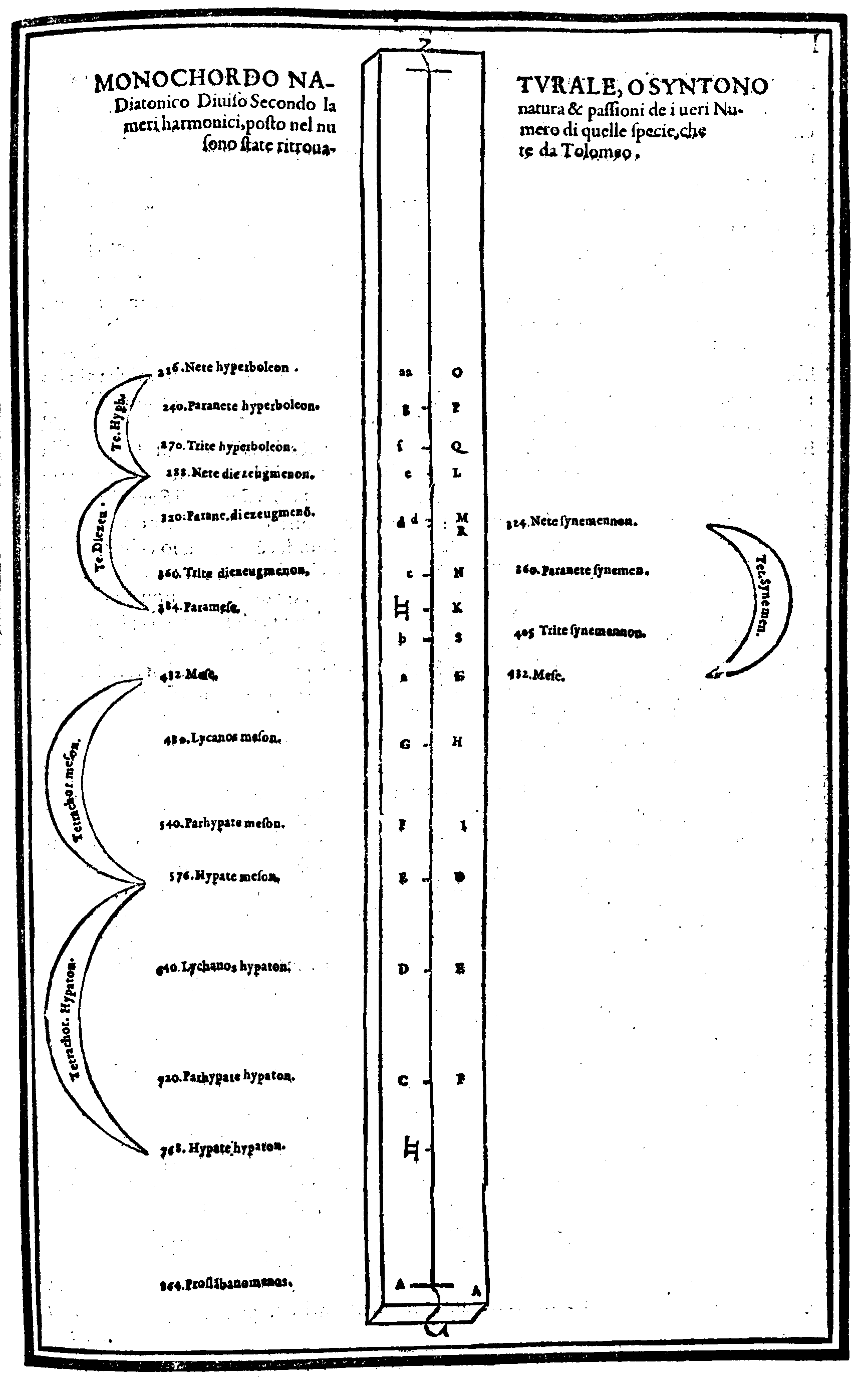
che sono Interualli dissonanti; & tra quelle de questi Istrumenti sono consonanti; come
ciascuno può udire; percioche in essi sono ridotti da i Musici nell'accordar in tal tempera
mento, con lo accrescerli, ò diminuirli secondo il proposito d'una certa quantità, nel
modo che piu oltra uederemo, che l'Vdito se ne contenta; quantunque siano fuori delle
lor uere & naturali forme. Ma perche hò detto di sopra, che udendosi ne gli Istrumen-
ti nominati gli Interualli del Ditono & del Semiditono, che sono consonanti; non è pos
sibile; se sono temperati secondo il modo, che son per dimostrare; che se ne possa ritroua
re alcun'altro, ilquale sia compreso nella sua uera & natural forma, ò proportione; però
fà dibisogno sapere, che in tre maniere (lasciando alcuni altri modi da un canto per bre
uità) si può fare il Temperamento di qual si uoglia de i nominati Istrumenti, & la Distri-
butione del nominato Cōma; come hò detto etiandio nella Prima proposta del Quarto
libro delle Dimostrationi; ciascuna delle quali, nella equalità dei Tuoni s'assimiglia al Dia
tono diatonico: ma ne gli altri Interualli s'accostano al Naturale, ò Syntono di Tolo-
meo. Trouasi però in loro questa differenza, che la Prima specie cōtiene tutti gli Interual
li, che sono Irrationali: ma nell'altre sono mescolati, i Rationali con gli Irrationali;
percioche nel Secondo Temperamento ogni Ditono, & ogni Hexacordo minore è con
tenuto da proportioni rationali nella uera forma; & nel Terzo si troua il Semiditono &
l'Hexachordo maggiore nella loro perfettione; come si potrà uedere. Essendo adunque
temperati gl'Istrumenti sudetti nell'uno de i tre sudetti modi, è necessario, che si odino
in essi l'Interuallo del Ditono & quello del Semiditono, che siano Cōsonanti. Et Questi
tali Tēperamenti i Moderni chiamano Participatione, de i quali fin'hora non sò, che da
alcun'altro ne sia stato ragionato, ò dimostrato ragione alcuna, che buona sia; se bene al
cuni, ragionando fuori di proposito, si sforzano di dar da intēder, che loro siano stati gli
Autori. Vogliono però alcuni altri, che 'l Tēperamēto de questi Istrumēti sia stato fatto, ò
ritrouato, per ridurre il numero delle chorde del Monochordo Diatonico syntono mostra
to al numero delle Pitagoriche, cōtenute nel Diatono; accioche tra loro fussero collocate
tutte le Consonanze, tanto perfette, quanto imperfette; necessarie alla generatione del-
la perfetta Harmonia; & accioche il Sonatore sonando fusse piu libero, & l'Harmonia, che
uscisse da tali Istrumenti, si potesse vdir con maggior satisfattione dell'Vdito; che non
si hauerebbe fatto, quando s'hauesse uoluto stare nel Numero delle chorde del Diatoni
co syntono; percioche sarebbe stato dibisogno di usar spesse uolte l'interuallo del Com-
ma, aggiungendolo, ò leuandolo d'alcuni Interualli, per fare acquisto di molte Conso-
nanze; massimamente volendo passare dal graue all'acuto; ò per il contrario; da una
Consonanza all'altra; il che non solamente difficultà al Sonatore, ma etiandio poco di-
letto à gli Ascoltanti hauerebbe apportato; perche in cotal caso si hauerebbe udito un
non so chè di tristo, c'hauerebbe fatto non poco fastidio. Et quantunque dichino anco
che tale Temperamento, ò Participatione, sia stata ritrouata studiosamente; accioche
per essa in cotali Istrumenti si uenisse ad imitar la Natura, la qual si dee imitare in tutte
le cose, piu che si puote; perche si come nel genere Diatonico si può procedere natural
mente con le Voci (come è manifesto) per gli suoi Interualli, dal graue all'acuto & per il
contrario, senz'incommodo alcuno; cosi anche in tale Istrumenti si potesse passar dall'
acuto al graue, ò per il contrario, senz'alcuno impedimento, & senz'alcuna offesa del
Sentimento; tuttauia credo ueramente, che tal Temperamento, ò Participatione sia
stata introdotta à caso, & non studiosamente. Et ciò mi muoue à credere; perche non è
dubbio, che ne il Ditono, ne il Semiditono, ne i due Hexachordi & altri Inter-
ualli molti, i quali hora à noi sono consonanti; non furono mai da alcuno de gli
Antichi (come da i loro Scritti si può comprendere) riceuuti nel numero delle Conso-
nanze; ne anco ueramente le usarono per consonanti, nel modo che le usiamo noi; mas-
simamente hauendo loro sempre usato il numero delle chorde Pitagoriche; come da
quelle, che sono collocate in molto antichi Istrumenti, si può comprendere; se
page 153bene il dottissimo Fabro Stapulense nella 1. & nella 2. del 3. de gli Elementi musicali,
nō si sà risoluere, se questi due Interualli siano Consonanti, ò Dissonanti; quando nel Co
rollario della Prima dice;
Vnde sit, vt & si Sesquitonus iucundè, suauiterꝗ auditum feriat;Et nella Seconda,
nondum tamen Consonantia ponendus sit.
Itidem Ditonus inter Sesquiter-percioche
tiam atque Sesquiquartam medius, minimè Musicam complet atque perficit harmoniam:
quando dice, che 'l Sesquituono ferisce giocondamente & soauemente l'Vdito; lo dice,
perche lo ode in atto nella proportione Sesquiquinta; ma quando dice,
Nondum tamenlo considera nella Sesquiquinta & la Sesquisesta proportione; &
Consonantia ponendus sit;
l'istesso fà del Ditono; ma non è marauiglia, se non ne hauendo fatto altra esperienza;
ei credesse, che l'uno & l'altro fusse contenuto nelle lor forme uere; in cotali proportio-
mi. E' credibile adunque, che alcun perito nella Musica, dopo un certo spacio di tem-
po, à caso prima, & dopoi l'hauerne fatto molte esperienze, nell'istesso Istrumento le
riducesse à tal temperamento & sotto quelle proportioni, ò forme, le quali hora usiamo;
non però sotto alcuna de quelle, che di sopra in molte Diuisioni hò mostrato; percioche
sarebbe stato impossibile d'osseruare il Numero delle chorde, l'Ordine de gli Interualli,
& le Forme, ò Proportioni mostrate; ma si bene sotto quelle, ch'io sono per mostrare.
Quel che si dee osseruare nel Temperamento de gli Istrumenti Arteficiali, di mo-
do che nel numero delle Chorde & nella equalità de i Tuoni s'assimigli al Dia-
tono diatonico: ma ne gli Interualli consonanti; quantumque acciden-
tali, al Naturale ò Syntono di Tolomeo.Cap. XLII.
tità ogni Interuallo ne i detti Istrumenti si uenga à temperare; & il modo
che haurà da tenere, uolendo far la Participatione al Primo modo; di ma-
niera che non offenda il Sentimento; pigliarò questa fatica, & mostrarò insie
me in qual modo le Dicisette chorde, poste nel Diatonico naturale syntono, si riduchi
no al numero delle Sedeci cōtenute nel Diatono. La onde si debbe auertire, che uolendo
far cotale Temperamento, ò Partecipatione con qualche ragione, & con qualche fonda
mento, fà dibisogno diuidere il Comma, contenuto tra le chorde R B, & M B, in Sette par
ti equali & distribuirle tra i Sette interualli, contenuti nelle Otto chorde della Diapason;
accioche possiamo ridurre le due mostrate chorde, che cōtengono il Comma, in una sola.
Ma si debbe fare, che l'ordine mostrato, & insieme gli Interualli restino nella lor forma, più
che sia possibile; accioche l'Vdito nō sia offeso; & che ciascuna Cōsonanza si nel graue, co
me anco nell'acuto; & quantunque altro Interuallo, quantunque minimo, sia equalmente
accresciuto, ò diminuto d'una certa & terminata quantità in tutti gli Interualli, che sono si
mili di proportione; ilche tornerà molto bene, quando si farà, ch'ogni Diapente resti dimi
nuta & imperfetta, de due Settime parti d'un Comma; & che la Diatessaron pigli uno ac-
crescimento di tanta quantità; & è il douere conciosiache restando la Diapason sempre
immutabile, & nella sua proportione uera & naturale; & essendo integrata da questi due
parti; quel che si leua da una, bisogna necessariamente dare all'altra; accioche aggiun-
gendosi insieme, ne gli estremi si oda la Diapason perfetta. Si farà anco il Ditono im-
perfetto d'una settima parte; & di tanta quantità si diminuirà etiandio il Semiditono;
percioche se queste due Consonanze concorrono all'integratione della Diapente; essen
do questa diminuta di due settime parti, è necessario, che tal diminutione si diuida tra
questi due Interualli; conciosia che facendo imperfetto il Ditono d'una settima parte, &
il Semiditono di altra tanto, che sono due settime; queste due Consonanze, che sono
parti della Diapente uengono adesser diminute di quella quantità istessa, ch'è diminu-
to il loro Tutto. Ma le parti del Ditono; che sono il Tuono maggiore & il minore, si
page 154faranno imperfette in cotal modo; si leuarà dalla prima quattro settime parti de i Com-
ma, & si farà maggiore la seconda di tre, & cosi tra loro verranno hauere quella imper
fettione istessa, che hà il loro Tutto; cioè, saranno imperfette d'una settima parte. Si da-
rà poi al Semituon maggiore l'accrescimento di tre settime parti; conciosia che essendo
questo la minor parte del Semiditono, & il Tuono maggiore la maggiore, tra queste due
parti si ritrouerà l'istesso mancamento, che si ritroua nel Semiditono; cioè, saranno di-
minute di vna settima parte. L'Hexachordo maggiore & il minore, & l'uno & l'altro uer
ranno à pigliare l'accrescimento d'una settima parte; imperoche l'uno si compone della
Diatessaron & del Ditono, & l'altro medesimamente della Diatessaron & del Semidito-
no; onde pigliando la Diatessaron accrescimento di due parti, & diminuendosi il Dito-
no, & anco il Semiditono, ciascun da per se, d'una settima parte; uengono tali Hexa-
chordi à pigliare l'accrescimento di tal quantità. Di modo che hauendo ultimamente
per tal maniera proportionato l'Istrumento, ogni Consonanza & ogni Interuallo dal
maggiore al minore cauandone la Diapason & il Semituono minore mostrato; uiene ad
esser fuori della sua uera proportione; non però molto lontano dalla sua uera forma, di
maniera che l'Vdito non se ne contenti. Vide c. 24.
Lib. 4. Sup
ple. Questo adunque bisognerà osseruare, uolendo
far la Participatione, ouer Distributione del Comma in ogni Istrumento; accioche ogni
Consonanza nella sua specie uenga ad essere equalmente accresciuta, ouer diminuta.
La onde ciascun perito del Suono debbe auertire, che uolendo temperare, ouer accor-
dare gli Istrumenti nominati, farà dibisogno di tirare, ò proportionare ciascuna Dia-
pente in tal maniera, che i suoi estremi acuti tenghino del graue, secondo la quantità
detta, com'io son per mostrare; oueramente che i graui più si auicinino all'acuto, secon-
do che nell'accordare, ò temperar detti Istrumenti tornerà più commodo. Similmente
ciascuna Diatessaron, allaquale si danno le quantità, che si tolgono alla Diapente, si
debbe accrescere in tal modo, ch'ogni suo estremo acuto sia più lontano dal graue per
tanta quantità, & il graue similmente dall'acuto. Et quantunque questi Interualli siano
per tal maniera hora cresciuti, & hora diminuti; non per questo l'Vdito (come hò det-
to) abhorrisce tale distributione; cōciosia che essendo minima & quasi insensibile la quan
tità, che à loro si leua, ò si aggiunge; & essendo non molto lontani dalle lor uere forme;
il senso si accheta. Ne di ciò dobbiamo marauigliarsi; percioche all'Vdito intrauien
quello, che suole intrauenire à gli altri Sentimenti, massimamente al Vedere; ch'alle uol-
te non s'accorge d'una quantità minima, per esser quasi insensibile; come auiene quando
si leua, ouer s'aggiunge ad un monte grande due, tre, ouer più pugni di grano; che non si
può accorgere di tal cosa; ma si bene s'accorgerebbe, quando se li leuasse, oueramente
s'aggiungesse una gran parte. Ma s'alcuno dicesse; ponendosi in uso le Consonanze, che
sono fuori delle lor uere Proportioni; le quali senza dubbio non sono senza soauità; che
i veri & legittimi Interualli consonanti fussero questi, c'ho commemorato; & non quel-
li, che già hò fatto uedere nella precedente diuisione; costui ueramente sarebbe in erro-
re; conciosia che quantunque gli Interualli già mostrati non si trouino esser ne i nomina
ti Istrumenti; non seguita però, che non siano i ueri & naturali, & che non siano quelli,
che producono perfettamente in essere ogni Consonanza, ch'è possibile da esser prodot
ta. Neanco seguita, che non si possino porre in atto & udire; percioche si possino udi-
re quando si uuole; come etiandio non seguita, che l'Huomo non sia risibile, perche non
rida sempre; perche se bene hora non ride, è almeno atto à ridere quando vuole. Et
benche ne i detti Istrumenti temperati in tal maniera, non si possino usar le Consonan-
ze nella loro perfettione; cioè, nella loro uera & naturale forma; è nondimeno possibile
di poterle vsare, quando le lor chorde si uolessero tirare sotto la ragione delle loro pro-
portioni vere & naturali. Et questo dico, perche molte uolte n'è stato fatto l'esperien-
za sopra molti Istrumenti, i quali furono fabricati à questo proposito; come già anch'io
ne feci fabricare uno; ancora che tal proua si possa anco fare sopra qualunque altro Istru
mento; & massimamente sopra Arpichordi, ò Clauocembali, che sono molto atti à tal
page 155proposito. Et s'alcuno dicesse, che quando tali Istrumenti fussero accordati perfet-
tamente, si verrebbe à perdere alquante Consonanze, che si ritrouano esser ne gli altri
Istrumenti; questo importerebbe poco; percioche basta solamente, ch'alcun non possa
contradir con uerità à quello, che si è detto di sopra, & dire che tali Consonanze non
si possano porre in atto nelle lor uere forme, ò proportioni; imperoche se bene in essi non
si potesse essercitar l'Harmonie con quel commodo & libertà, che si fà ne gli Istrumen-
ti communi; non restarebbe però, che in essi non si potesse udire ogni Consonanza &
ogni Harmonia nella sua uera forma. Ma se cotali inconuenienti (dirò cosi) si trouano
ne gli Istrumenti arteficiali; nondimeno tra le Voci (come altroue uederemo) non si
trouano tali rispetti; essendo che riducono ogni cosa nella sua perfettione; com'è il do-
uere; poiche la Natura, nel far le cose; come si è mostrato nel Cap. 4. del 1. Lib. de i Sop-
plimenti, è molto superiore all'Arte; & questa nell'imitare fà ogni cosa imperfetta; ma
quella (rimossi gli impedimenti) ogni cosa riduce à perfettione. In cotal modo adun-
que si uerrà à temperare ciascuno de i nominati Istrumenti; ne i quali si farà la Distribu-
tione del Comma in Sette interualli; come hò detto; ne altramente uerrebbe bene, uo-
lendo acquistar le Consonanze perfette & le Imperfette insieme, con quel modo meglio
re, che si può fare; accioche ogni Interuallo simile, si nel graue, come nell'acuto, uen-
ghi ad essere equalmente accresciuto, ò diminuto della sua quantità, & non si habbia
più à porre la chorda d, raddoppiata. Et se ad alcuno paresse strano, che nella Musica
occorrino simili cose; si debbe ricordare, che non solo in questa Scienza; ma in ogn'al-
tra ancora, in ogni Arte, & in ogni altra cosa creata si ritroua imperfettione. Et questo,
credo c'habbia uoluto Iddio Ottimo Massimo, accioche uedendo noi cotal cosa nelle
cose mondane inferiori, uoltiamo l'intelletto nostro alla contemplatione delle superiori;
cioè, della sua infinita Sapienza, nella quale si ritroua il tutto non solamente Perfetto,
ma etiandio Buono; & lo amiamo & adoriamo, come quello, dal quale uiene ogni co-
sa ottima & santa.
Dimostratione, dalla quale si pùo comprendere, che la mostrata Participatione,
ò Distributione sia ragioneuolmente fatta; & che per altro modo non
si possa fare, che stia bene.Cap. XLIII.
pere, che sono stati alcuni, c'hanno hauuto parere, che l'Interuallo del
Comma mostrato di sopra si douesse distribuire tra quelli due Interual-
li, che sono à lui più propinqui, posti nella parte acuta & nella graue;
facendo di esso due parti equali; accrescendo l'uno, & l'altro Interuallo di tanta
quantità, quanta è la metà di esso Comma; lasciando poi gli altri Interualli nelle
lor forme naturali; ma in uero à me pare, che molto s'ingannino per molte ra-
gioni; prima perche quelli due Interualli, che sono al Comma vicini, uerrebbono so-
li à participar delle parti del Comma, & non alcuno de gli altri; & l'Istrumento uerreb
be ad esser proportionato inequalmente; conciosia che si udirebbe in esso la Diapente &
la Diatessaron con due Interualli l'uno maggior dell'altro; dopoi, perche quelli Inter-
ualli, ne i quali si facesse questa distributione, uerrebbono ad essere dissonanti, per la
molta distanza, c'hauerebbono dalle lor forme uere; & li Tuoni, i quali sono uicini à tal
Comma, & participano di una delle sue parti, sarebbono contenuti da tale propor-
tione, che non si potrebbono aggiungere ne alla Diapente, ne alla Diatessaron, ne al
Semiditono per formare alcuna Consonanza. Et se ben dicono, che l'esperienza dimo
stra, che questi Interualli accresciuti, ò diminuti per tal modo, non si partono dalla lor
propria forma di modo, che l'Vdito ne patisca cosa alcuna, non altramente di quello
page 156che farebbe, quando tal Comma non fusse in tal maniera distribuito; questo non è ue
ro essendoui la esperientia in contrario. Onde mi penso, che questi non habbiano mai
fatto alcuna proua di questo; conciosia che 'l Sentimento istesso lo fà manifesto, che sono
dissonanti; & ciò potrà ciascun da se stesso prouare, diuidendo il detto Comma in due
parti equali; nel modo che nel Cap. 24. di sopra hò mostrato; percioche aggiunte le par
ti, che nasceranno à i due Tuoni Sesquinoni, che li sono uicini; ciascuno potra cono-
scere, che quello, ch'io hò detto, è uero; & che bisogna cercare di distribuire tal Com-
ma per altra maniera, acciò l'Vdito non sia offeso. Ma di sopra hò detto, che delle Con-
sonanze, ouero altri Interualli, alcuni si diminuiscono (facendo tale distributione) di
due, alcuni di quattro, & alcuni di una settima parte del detto Comma; similmente al-
cuni si accrescono di una settima parte, alcuni di due, & alcuni di tre parti; di maniera
che finalmente non solo ogni Diapente, ogni Diatessaron, ogni Ditono, & ogni Semi-
ditono, che sono Interualli consonanti, vengono ad essere accresciuti, ò diminuti equal
mente, & uengono à restare equali, si nella parte graue; come anco nel mezo, & nell'
acuto dell'Istrumento; ma etiandio i dissonanti, che sono il Tuono maggiore, il mino-
re, & il maggiore, & minor Semituono; Però tanto più questo tengo esser uero, & che
tal distributione sia buona, & fatta con ogni douere; quanto che 'l Semituono contenu-
to dalla proportione Super 7. partiente 128. che non si adopera nel genere Diatonico,
& è contenuto tra le chorde S B & K B, si fà minore di tutte le parti; cioè, di tutto il
Comma intiero, ch'è contenuto da la proportione Sesquiottantesima, & resta nella pro
portione Sesquiuentesimaquarta, che è rationale; l'altre poi, cauandone tutte le Diapa-
son, che contengono la proportione Dupla, sono Irrationali & incognite; conciosia
che Le parti, le quali si leuano, ò aggiungono alle quantità rationali, ch'erano le lor
prime forme naturali, sono irrationali, & questo per la diuisione fatta del Comma nel-
le sue parti, ch'è irrationale; la onde quello che uiene, è similmente irrationale. Ma
questo non intrauiene nelle Rationali; perche tutto quello che nasce, aggiungendo, ò
sottrahendo l'una quantità rationale dall'altra, è rationale. Il perche questa Distribu-
tione, che si fà aggiungendo, ò leuando tal parti, non può esser per alcuna cagione ra-
tionale si può con determinati numeri; perche non denominare, ò descriuere. Per mo-
strare adunque che tal Distributione si conuien fare necessariamente nel detto modo,
& non in altra maniera, procederemo con questo ordine. Pigliaremo prima Dodici chor
de solamente del Monochordo posto di sopra; F B, E B, D B, I B, H B, G B, S B,
K B, N B, R B, M B, & L B, le quali saranno basteuoli à dimostrare il proposito; & do
poi accommodaremo perfettamente le chorde F B & N B di maniera, che contenghino
la cōsonanza Diapason; lequali lasciaremo immutabili; & sopra di esse daremo principio
à fare tal Distributione, ancorache si potrebbe incominciar sopra qual luogo si uolesse;
ma faremo questo, per seguir la maggior parte di coloro, ch'accordano gli Istrumenti
moderni; imperoche danno principio sopra tali chorde. Si debbe però auertire, c'hò
detto Immutabili; essendo dibisogno, che la Prima chorda, sopra la quale si uiene à fon
dare la Distributione, sia stabile, & che ciascuna Diapason si riduca alla sua perfettio-
ne; cioè, nella sua uera forma, la quale è la proportione Dupla; percioche non patisce
(come ho detto ancora) mutabilità, ò uarietà alcuna. Posto adunque che noi hauere-
mo queste Chorde stabili, tra quelle, che si trouano collocate nel mezo di loro, faremo
la Distributione; seruendosi però dell'altre, che sono poste fuori di esse. Per incomincia-
re adunque pigliaremo la prima Diapente posta nel graue, che sarà la F B & H B, con-
tenuta dalla proportione Sesquialtera, & senza muouere la F B, faremo la H B, più gra
ue, secondo la quantità di due settime parti d'un Comma; come hò detto; preponen-
do primieramente & moltiplicando alla chorda H B il Comma; soggiungendo prima
alla chorda I B, il Tuono minore contenuto nella proportione Sesquinona, & diuiden-
dola in dieci parti; onde prese le noue parti di essa, tra la chorda, che contenerà tal
quantità, & la H B, laquale è la chorda acuta del Tuono maggiore I B, & H B, haue-
page 157remo il Comma; conciosia che se dal detto Tuono leuaremo il minore I B, & la quanti-
tà delle noue parti, senza dubbio resterà esso Comma, contenuto dalla proportione
Sesquiottantesima; il quale diuideremo in sette parti equali, secondo il modo mostra-
to di sopra nel Cap. 25. dopoi lasciando da un canto le due parti più acute di esso, & pi-
gliando solamente le cinque poste nel graue, haueremo in un tratto con la chorda a B,
accommodato alle loro proportioni irrationali due Consonanze; la Diapente F B, &
a B, & la Diatessaron a B, & N B. Pigliaremo hora la a B, che con la M B contiene la
Diapente più acuta di due settime parti equali del detto Comma; & diuiso che haue-
remo il Comma R B & M B. in sette parti equali, come facemmo il primo; lasciando
prima le quattro parti più acute, che sono le due parti, che si lasciano accioche habbia-
mo la Diapente nella sua uera proportione; & due altre parti dopoi per la sua diminutio
ne; la chorda b B ne darà il nostro intento. A questa chorda ritrouaremo la corrispon-
dente nel graue in proportione Dupla, accioche possiamo udire perfettamente la Dia-
pason; il che haueremo fatto, quando dopo moltiplicato & preposto il Comma alla
E B, & diuiso in sette parti equali, pigliaremo le quattro poste nell'acuto; percioche
tra c B & essa b B haueremo la ricercata Consonanza, col mezo della chorda c B, secon
do il proposito; conciosiache essendo la E B con la M B corrispondenti per suono equa-
le nella Diapason; & aggiungendosi all'una & all'altra uerso il graue quattro parti del
Comma, che sono tra loro equali, ne segue, che medesimamente gli estremi de questi
aggiunti siano equali, & che rendino essa Diapason; percioche per il Secondo & per il
Terzo Commun parere del Lib. 1. de gli Elementi di Euclide; Se à cose equali si ag-
giunge, ouer da esse si leua cose equali, quello che uiene, è similmente equale. Haue-
remo etiandio tra c B & a B vna Diatessaron accresciuta de due parti del Comma, che sa
rà equale in proportione alla a B, & N B. Faremo hora la chorda G B corrisponden-
te in proportione Sesquialtera alla c B. Preponendo alla G B il Comma diuiso secon-
do il modo dato; dopoi lasciando le quattro parti poste nell'acuto, & le due, che seguo-
no uerso il graue; tra la c B, & la d B haueremo un'altra Diapente diminuta di due par-
ti d'un Comma; & tra la d B, & la b B un'altra Diatessaron, accresciuta di tanta quan-
tità. Seguono dopoi la d B, & la L B, che contengono la Diapente diminuta di una
settima parte; onde uolendola diminuire d'un'altra parte; accioche si ritroui con l'altre
equale in proportione; preponeremo alla L B il Comma, diuiso come gli altri in sette
interualli; & lasciando il più acuto, prenderemo solamente i Sei posti nel graue; & dal-
la e B haueremo il proposito. A questa ritrouaremo primieramente la corrispondente
in proportione Dupla, diuidendo il Comma preposto alla D B in sette parti; dopoi pre-
sa la parte più acuta, haueremo la f B, che con la detta e B ne darà la consonanza Dia-
pason nella sua forma naturale, & un'altra Diatessaron equale in propoprtione con l'altre,
che sarà la f B, & d B, nella sua forma accidentale; & tra la f b, & K B uerrà una Diapen
te medesimamente nella sua forma accidentale, più acuta di una delle dette parti; per il
che volendola ridurre alla sua proportione, preponeremo alla K B il Comma diuiso al
modo dato; & lasciando la parte acuta per il superfluo, & le due parti seguenti per la
diminutione; col mezo della chorda g B, non solo haueremo la uera proportione ac-
cidentale della Diapente; ma etiandio quella della Diatessaron contenuta tra la g B, &
la e B. Resta hora à ridurre alla loro proportione la Diapente I B, & N B, & la Diatessa-
ron F B, & I B; onde soggiungeremo alla I B il Comma, il quale, dopo che sarà di-
uiso in sette parti, & prese che noi haueremo le due settime più graui, col mezo della
chorda h B, haueremo la proportione di dette Consonanze; cioè, haueremo accresciu-
ta la Diatessaron posta nel graue de tante parti, & fatta minore la Diapente posta in acu-
to di tanta quantità. Hora per dar la sua proportione alla S B, che con la h B, si ritro-
ua esser distante per vna Diatessaron, diminuta di due parti; soggiungeremo prima alla
S B il Comma, & dopoi che sarà diuiso, pigliaremo le quattro parti, più graui in pun-
to i, & tra i B, & h B haueremo fatto equale la detta Diatessaron all'altre in proportio-
page 158
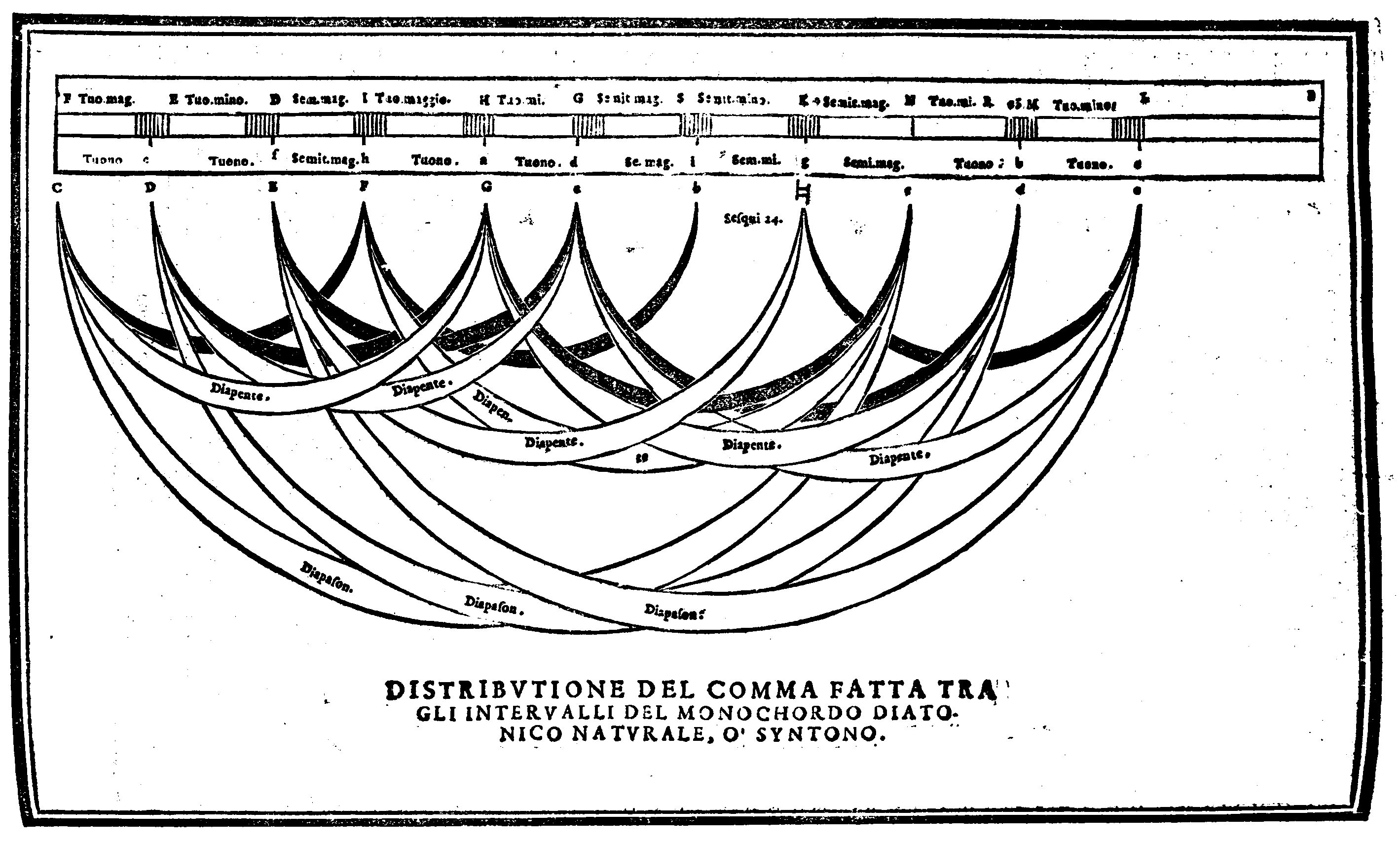
ogni Consonanza nella sua specie; ma ogn'altro Interuallo, che tra le dette chorde era
contenuto; & de Dodici chorde ch'erano prima, le haueremo ridotte al numero de Vn
deci, corrispondenti al numero delle chorde Pitagoriche, poste di sopra nel Cap. 28. le
quali potremo descriuere commodamente con le lettere di Guidone, senza raddoppia-
re altramente la d. Et quello c'hò detto di sopra intorno al Semituono S B. & K b, si ue-
de esser uerificato; conciosiache ritrouandosi nella sua proportione tra le dette chorde,
& restando diminute nel graue (come si uede nella dimostratione) delle quattro parti
del Comma, contenute tra la S B, & la i B; & nell'acuto di tre parti, contenute tra g B
& K B; se noi aggiungeremo queste tre parti alle quattro prime, non è dubbio, che ar-
riueranno al numero di Sette, & faranno tutto il Comma. Ma perche il Comma è con
tenuto dalla proportione Sesquiottantesima; però se dalla Super 7. partiente 128. ch'e-
ra la prima forma del detto Semituono, ch'è rationale, leuaremo la Sesquiottantesima,
la quale etiandio è rationale, il rimanente sarà la proportione Sesquiuentesimaquarta
rationale; la quale è la forma rationale di tal Semituono. Potiamo hora uedere in qual
maniera le parti del Comma si uengano à distribuire, con una certa equalità, in ogni
Consonanza & in ogni Interuallo; che non si troua che l'un sia maggiore, ò minor dell'al
tro in proportione. Per la qual cosa potiamo tenere per certo, che questo modo di qual
si uoglia altro in questa prima maniera di temperamento tanto più sia migliore & più ue-
ro; quanto uediamo, che ogni Consonanza & ogni Interuallo, si nel principio, come nel
mezo & nel fine, è accresciuto, ò diminuto d'una istessa quantità; secondo che ricerca la
sua proportione; ne si uede per modo alcuno, che l'un sia maggior dell'altro, ò minore;
ne si scorge, che in essa sia alcuno auanzo; quantunque minimo; d'alcuna parte del detto
Comma; imperoche quando si ritrouasse alcuna di queste cose, sarebbe segno ma-
nifesto, che tal Distributione non fusse fatta co i debiti modi. La onde concludo, che
quando si uolesse tentar di fare tal Temperamento, ò Distributione altramente; com'al-
cuni hanno tentato; che tal fatica sarebbe uana & senza frutto; come l'esperienza sem-
pre ce lo farà manifesto. Il perche non si potendo far cotal cosa in altra maniera, che tor-
ni bene, seguita; che quanto à questo primo modo tal Participatione, ò Distributione
sia fatta perfettamente, con i debiti mezi, & senz'alcuno errore.
Della Compositione del Monochordo diatonico equalmente temperato nel pri-
mo modo.Cap. XLIIII.
rore, si possa comporre il Monochordo diatonico al primo modo temperato
di maniera ne i suoi Interualli, che si ritroui esser mezano tra il Diatono &
quello, che Naturale, ò Syntono si chiama, ritrouato da Tolomeo; la qual
compositione, spero che sarà non men utile à tutti coloro, che desiderano di saper la
Temperatura, & la uera proportione de i suoi Interualli, di quello che sarà à coloro
etiandio, i quali fabricano Istrumenti musicali; & desiderano di saper la ragione &
misura di qualunque si uoglia di essi, per poter con ragione proportionare quelli de gli
Istrumenti loro. Dobbiamo adunque primieramente sapere, che cosi come ciascun ter-
mine di qualunque Interuallo collocato alla sua proportione sopra qualunque chorda,
da qual parte si uoglia; sia dalla parte graue, ouer d'acuta; si può far maggiore, ò mino-
re di tanta quantità, quanta è la proportione della parte della chorda al suo Tutto, che
si piglia, ò si lascia dall'una di queste due parti; cosi etiandio si può far di tanta quantità
più graue, ò più acuto, quanto è la proportione, che hà quella parte di chorda, che si
lascia, ò se gli aggiunge nel graue, nell'acuto, col suo Tutto; come è manifesto per la Vi-
page 160gesima sesta & Vigesimasettima definitione nel Quinto libro delle Dimostrationi; & co-
me etiandio in molti luoghi si è potuto di sopra uedere. Onde dico dopo; che si hauerà
ritrouato vn'Asse, ò Tauola ben piana & bene acconcia, come furono accommodate l'al
tre; porremo prima nel mezo di essa la Linea a b in luogo di chorda, sopra la quale fare
mo la compositione del detto Monochordo. Sopra tal linea poi accommodaremo dal-
la parte sinistra il Comma alla sua proportione, al modo più breue; & più espedito, che
sia possibile, in cotal maniera: Accommodaremo primieramente sopra la detta chorda,
nel modo che si è dimostrato nella Trentesimasesta del Terzo delle dimostrationi, il Tuo-
no maggiore alla sua proportione; dopoi il minore, di maniera, che 'l termine minore
del Tuono maggiore, sia anco il termine minore del Tuono minore. Il che fatto tra 'l
maggior termine dell'uno & l'altro de questi due Tuoni sarà collocato il Comma: percio
che uiene ad esser la differenza, che si troua tra le quantità dell'uno & dell'altro. A questo
poi ne soggiungeremo un'altro, collocandolo alla sua proportione (come habbiamo fat-
to il primo) sopra la chorda, ch'è il termine maggiore del Tuono minore; & dopoi diuide
remo ciascuno separatamente con diligenza secondo 'l modo mostrato di sopra nel Cap.
25. in sette parti equali; ritrouando tra la chorda a b, & la c b del sottoposto essempio,
che contengono il primo; & tra la c b, & la d b, che contengono il secondo, Sei li-
nee, ò chorde mezane proportionali; imperoche diuisi in tal maniera potranno
seruire ad ogn'ordine de Suoni, che si uorrà ridurre à tal Temperamento, comin-
ciando da qual chorda tornerà meglio. Ma si debbe auertire, che quelle parti, che
saranno poste tra la a c, saranno quelle delle quali si haueranno à diminuire le Con-
sonanze, ò altri Interualli di tal Monochordo; & quelle, che saranno poste tra la
c d, saranno quelle, con le quali si haueranno à far maggiori, ouero accrescere.
Et quando nominerà due, ouer più parti, sempre si intenderà di quelle, che sono più
uicine alla c, siano poste da qual canto si uoglia. Hora intese queste cose, lasciando da
un canto la a c, parte di detta linea, porremo primieramente la c b in luogo della chor-
da più graue del Monochordo, il quale si uorrà ridurre alla Participatione; & sarà se-
condo il modo de Musici moderni la Chorda A. Dopoi pigliando la c b, accommodare-
mo il Tuono maggiore alla sua proportione, nel modo, che facemmo nell'altre diuisio-
ni; & sarà il fondamento de i Tetrachordi. Ma perche questo Tuono si pone diminuto
di quattro settime parti d'un Comma; com'altroue hò detto; pigliaremo col piede del
Compasso quattro parti del Comma a c, & le aggiungeremo alla linea c b; & diuidere-
mo il Tutto in noue parti equali; & doue cascherà il fine della ottaua parte à banda sini-
stra, porremo il punto e; & haueremo la e b, che con la sopradetta diuisa contenerà il
Tuono maggiore, collocato nella sua uera proportione & con la c b, lo haueremo dimi-
nuto di quattro settime parti del detto Comma; percioche essendo tra il Tutto diuiso &
le Parti e b. collocato il Tuono nella sua uera proportione, ch'è la Sesquiottaua; se dalla
parte graue; cioè, dalla diuisa linea leuaremo tutta la proportione aggiunta alla chorda
c b, che sono le quattro parti più acute del Comma a b, & c b; non è dubbio che 'l Tut-
to diuiso non resti diminuto di tal quantità; & in suo luogo non uenghi la c b. Onde se la
proportione posta tra il Tutto diuiso, & la e b; resta diminuta di tante parti, per conse-
guēte, i Suoni che nasceranno dalle chorde tirate sotto tali proportioni, resteranno dimi-
nuti etiandio di tanta quantità; conciosia che (come nella Prima parte hò detto) li Mu-
sici giudicano tanto esser la proportione di Suono à Suono, quanto è la proportione di
ciascuna parte di chorda col suo Tutto. Haueremo adunque per tal uia fatto il Tuono
maggiore, che si troua collocato tra queste due chorde A et
 , minore di quattro parte
, minore di quattro parte d'un Comma. Soggiungeremo immediatamente à questo il Semituono maggiore,
contenuto dalla proportione Sesquiquintadecima; il quale aggiunto al Tuono mag-
giore, fà il Semiditono, contenuto dalla proportione Sesquiquinta. Et perche il Se-
mituono piglia aumento di tre settime parti del Coma, & il Tuono discresce quattro;
però cauando le tre dalle quattro, ne resterà una, che sarà quella parte, della quale il
page 161Semiditono si uiene à minuire; secondo che di sopra si è detto. Pigliaremo adunque so-
lamente una parte del Comma a b, & c b, che sarà la più uicina alla c, & la metteremo
insiemecon la c b, diuidendo questo Tutto in sei parti equali; & pigliandole cinque,
che sarà in punto f, tra la diuisa, & la f b, haueremo collocato il Semiditono alla sua na-
turale proportione; & tra la c b, & la f b haueremo; per le ragioni già dette; il diminu-
to di una settima parte del Comma, nella sua forma accidentale. In tal maniera adun-
que haueremo una terza chorda, la quale segnaremo con la lettera C, & sarà la secon-
da del primo Tetrachordo, che con la
 contenerà il Semituono maggiore, accresciu-
contenerà il Semituono maggiore, accresciu-to di tre settime parti. Aggiungeremo à questo immediatamente il Tuono; accioche
la prima chorda con la quarta habbiano la consonanza Diatessaron; & tal Tuono sarà
il primo del primo Tetrachordo posto nel graue. Ma perche tal Consonanza con-
tiene il Tuono maggiore, il minore, & il maggior Semituono; hauendo collocato per
auanti il Tuono maggiore tra la prima & la seconda chorda; fà dibisogno, che noi
habbiamo il minore; & però procederemo in tal modo; accommodando prima la det-
ta Consonanza alla sua proportione, lasciando da un canto le due prime parti del Com
ma c b, & d b poste appresso la c; & dopoi pigliando solamente le cinque, diuideremo
tutta la linea fina in punto b, in quattro parti equali, per il maggior termine della Ses-
quiterza proportione, ch'è la uera forma di essa Diatessaron; & pigliando tre parti in
punto g, haueremo prima tra la diuisa, & la g b. la Diatessaron nella sua uera forma, &
dopoi l'accresciuta de due parti del Comma tra la c b, & la g b; conciosiache se le
aggiunge quelle due parti, che prima che si diuidesse tal linea, furono lasciate da un can
to. Et perche tra 'l Tutto diuiso, & la g b, si ritroua la proportione Sesquiterza; se per
l'aggiuntione d'alcuna parte si uiene à crescere alcuna proportione di quella quantità,
che se le aggiunge; è manifesto (per quello che si è detto di sopra) che hauendosi ag-
giunto due settime parti delle mostrate alla chorda graue della proportione Sesquiter-
za, & rimanendo l'acuta nel suo primo essere, tal proportione sia fatta maggiore di
tanta quantità quanta era quella, ch'è stato aggiunta. Ma perche tra la chorda c b, &
la e b habbiamo il Tuono maggiore diminuto; & tra la e b, & la f b il Semituono mag-
giore accresciuto; però tra la f b, & la g b haueremo il. Tuono minore, il quale uer-
rà per la integratione della Diatessaron accresciuta de due parti del Comma; come la ra
gione sempre ce lo sarà uedere. Haueremo adunque la chorda D; che con la C con-
tiene il Tuono minore, accresciuto di tre parti del Comma; il qual Tuono in questo
luogo solamente, & nelle sue chorde corrispondenti in proportione Dupla, segue im-
mediatamente dopo il Semituono maggiore, procedendo dal graue all'acuto. Onde
mi penso, che da altro non possa nascer la difficultà, che si troua nell'accordare, ò tem-
perar bene i moderni Istrumenti la chorda G con la d, & questa con la aa, se non per-
che le chorde D & d de i detti Istrumenti pigliano il luogo del Comma; onde ne seguo-
no due Tuoni minori immediatamente l'un dopo l'altro, tra le chorde C & D, & tra
le D & E; & cosi tra quelle, che corrispondono con queste in Dupla proportione. Et per
seguitar quello, c'habbiamo incominciato, aggiungeremo alla chorda D. un'altra chor
da, la quale con essa lei dalla parte acuta contenga il Tuono minore, ilquale uiene ad es-
sere il Secondo del primo Tetrachordo; & faremo, che questa chorda aggiunta con la
A. contenerà la Diapente; ma prima è dibisogno, che sappiamo la sua proportione, la
quale è la diminutione di due settime parti d'un Comma. Pigliaremo adunque, le
due parti più propinque alla c, poste tra a & c, & le accompagneremo con tutta la c b,
& cosi diuideremo questo Tutto in tre parti equali, secondo 'l maggior termine conti-
nente la proportione della Diapente, & pigliate le due per il minore, che sarà la h b,
tra questa & la diuisa haueremo collocato alla sua uera Proportione la Diapen-
te; & la diminuta, secondo le ragioni altre uolte addotte, sara tra la c b, & la h b;
& per tal uia haueremo la chorda E, che con la D contenerà il sopradetto Tuo-
no, accresciuto de quelle parti, che fanno dibisogno; & sarà l'ultima chorda
page 162

ma graue del secondo. Et per ritrouar
la Seconda, la quale sia distante per
un Semituono maggiore dalla E, &
per uno Hexachordo minore dalla A;
fà dibisogno di saper primamente la
ragione dalla sua proportione, la qua-
le è; com'habbiamo ueduto; che 'l
detto Hexachordo si agumenta d'una
settima parte del Comma; come si ac-
cresce etiandio il maggiore. Per il che
prenderemo la linea c b diminuta di
cotal parte del Comma c b, & d b, &
diuideremo il restante in otto parti e-
quali; conciosia che 8. è il termine
maggiore della proportione dell'He-
xachordo; pigliando dopoi cinque
parti solamente, che saranno per il
termine minore nel punto i, hauere-
mo tra il Tutto della diuisa, & la i b,
che sarà la chorda F, il detto Hexa-
chordo, collocato nella sua uera propor
tione; & tra la c b, & la i b l'accresciu
ta di tal parte. Aggiungeremo hora
à questa sesta chorda la settima, la qua-
le sara da lei distante per un Tuono
maggiore; ma bisogna sapere primie-
ramente, che proportione habbia con
la prima, & di quanta quantità que-
sto Interuallo, che si nomina Hepta-
chordo minore, si accresca, ò dimi-
nuisca; & ritrouaremo, che la sua ue-
ra proportione è la Superquadripar-
tientequinta; & che si accresce di quat-
tro delle sopradette parti; conciosia
che de quelle parti, delle quali si di-
minuisce quell'Interuallo, che si ag-
giunge oltra la settima chorda, per
uenire all'ottaua, de quelle medesime
si accresce l'Heptachordo, che gli è
posto auanti; & per il contrario. Et per
che quell'Interuallo, che resta per fi-
nire la Diapason, è il Tuono mag-
giore, il quale si diminuisce de quat-
tro settime parti del Comma; pero si
accresce il detto Heptachordo de tan-
te parti. Il medesimo anco si osser-
ua nell'accommodar l'altre chorde,
hauendo sempre riguardo à quell'In-
teruallo, che segue immediatamente
quello, che si uuole accommodare.
page 163Pigliaremo adunque la linea c b, diminuta delle quattro parti piu uicine alla c,
che saranno quelle, che sono poste tra c & d, & cosi la diuideremo in noue par-
ti equali; & pigliandone cinque in punto K, tra la diuisa, & la K b haueremo ac-
commodato il detto Heptachordo alla sua uera proportione; & tra la c b, & la K b
lo haueremo accresciuto di quattro parti del Comma; & la chorda G uerrà ad esser
la settima di tale ordine, & la terza del secondo Tetrachordo. A' queste aggiunge-
remo l'Ottaua chorda, la quale con la prima contenerà la Diapason, diuidendo so-
lamente la c b in due parti equali, percioche tal Consonanza resta nella sua perfet-
tione, & nella proportione Dupla; & nel punto l, haueremo la chorda a, secon-
do il proposito; & tra le chorde A.
 . C. D. E. F. G. & a, haueremola Diapason tra-
. C. D. E. F. G. & a, haueremola Diapason tra-mezata da Sei chorde, & diuisa in sette Interualli; ciascun de i quali è accresciuto,
ouer diminuto secondo la proportione, che se gli appartiene, nel modo che si è mo-
strato. Et perche diuidendo in due parti equali qualunque chorda si uuole, se le può
ritrouarla corrispondente per una Diapason; come hò mostrato; perche dalla metà
della chorda haueremo sempre il proposito; però se noi diuideremo le chorde meza-
ne della Diapason in due parti equali, haueremo le chorde m b, n b, o b, p b, q b,
r b; & similmente la s b, diuidendo la estrema acuta della Diapason, che corrispon-
deranno alle chorde e b, f b, g b, h b, i b, K b & l b in Dupla proportione, & in
tal maniera haueremo la compositione del Monochordo temperato ne i suoi Interual-
li secondo le loro proportioni, & ridotte le sue chorde al numero de Quindeci, con-
tenute ne i quattro primi Tetrachordi; à i quali uolendo aggiungere il quinto, bastarà
d'aggiungere in esso solamente la chorda Tritesynemennon; cioè, accommodare il Se-
mituono maggiore, & il minore alle loro proportioni. Et perche il minore (come
ho detto) resta nella proportione Sesquiuentesimaquarta, la quale è rationale; pe-
rò diuideremo la linea, ò chorda m b in Ventiquattro parti equali; pigliandone uen-
ticinque dalla parte destra in punto t, haueremola chorda t b, la quale ne darà il no-
stro proposito; percioche le chorde l b, t b, n b, & o b saranno quelle del Te-
trachordo synemennon, che noi cerchiamo; ancora che le chorde l b, n b & o b sia-
no à gli altri Tetrachordi communi. Ma quando uorremo ritrouar nel graue alcuna
chorda, che corrispondi con una acuta in proportione Dupla, & faccia udire la Dia-
pason; raddoppiaremo la chorda acuta, & haueremo quello, che desideriamo. Se
noi adunque uorremo ritrouar la corrispondente chorda graue alla chorda t b, rad-
doppiaremo solamente la detta chorda t b, & in punto u haueremo il tutto; percio-
che la chorda u b, con la t b, saranno in proportione Dupla, & faranno essa Dia-
pason. Per tal modo adunque haueremo il Monochordo diuiso in cinque Tetrachor-
di, nel quale per l'aggiuntione della chorda u b; contenerà il numero di Dicisette chor-
de; A. B.
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f. g. & aa. come nella figura si può uedere.
. c. d. e. f. g. & aa. come nella figura si può uedere. La onde con questo mezo potremo hauer senza molta fatica, & senz'alcun'errore la
via & il modo di comporre il Monochordo temperato ne i suoi Interualli, & accom-
modato al numero delle chorde pitagoriche nel primo modo; nel quale potremo ac-
commodar quante chorde uorremo, accrescendo, ò diminuendo i suoi Interualli, con
la proportione di ciascuno, secondo 'l modo che si è mostrato di sopra. Ma in qual mo-
do si uenga à comporre cotal Monochordo nella seconda maniera; da quello, che si è
dimostrato nella Prima proposta del Quinto delle Dimostrationi; si potrà con facilità
comprendere.
page 164
Se nelle Canzoni seguitiamo cantando gli Interualli prodotti da i ueri Numeri
sonori; ouero i Temperati; & della Risolutione d'alcuni dubij.Cap. XLV.
tra le parti delle Canzoni, ò cantilene, le cui Harmonie nascono da gli Istru-
menti naturali, si odono i ueri & legitimi Interualli contenuti nelle lor uere
forme, ò pur gli accresciuti, ò diminuti ne gli Istrumenti, secondo 'l modo
mostrato. Al qual dubbio si può rispondere, & dire; che ueramente si odono quelli, che
sono contenuti nelle lor uere forme, contenute tra i Numeri sonori, & dalla Natura pro
dotti, & non gli altri conciosia ch'essa Natura (come uuole il Filosofo2. De Ge-
ne. cap. 2.) in tutte le cose è
sempre inchinata à seguire il bene, & à desiderare non solo il buono & diletteuole; ma
il migliore & quello anco, ch'è ordinato per il buono. Onde essendo ordinati cotali In-
terualli & Consonanze per la perfettione dell'Harmonia & della Melodia; i quali Inter-
ualli sono migliori & piu diletteuoli; & non solo più diletteuoli, ma appetibili maggior-
mente; però naturalmente nelle Cantilene uocali ci sforziamo di seguitar quelli, che
sono prodotti nella lor vera forma, che gli altri; i quali per loro natura non sono ne mi-
gliori, ne più atti alla perfettione dell'harmonie. Et che tale inclinatione sia in noi;
questo si conosce da molti segni euidenti; & prima: perche Ogn'un naturalmente fugge
il contrario del bene, ch'è il male & il cattiuo ò tristo che lo uogliamo dire; & non pu-
re esso, ma etiandio il men buono, & quello che è impedimento di esso buono, & eleg-
ge sempre il migliore, ouer fugge almeno il piu tristo; come si uede, ch'etiandio Ogni
Scienza (come dice PlatoneDe Regno.) con tutte le sue forze scaccia da se le cose praue, & eleg-
ge le utili & più atte. Et è pure il douere; poich'Ogni arte & ogni Dottrina; come di-
1. Ethi. ca
pi. 1. ce il Filosofo; & similmente ogni Atto & ogni Elettione, par che desiderino un certo
bene, & ogni perfettione; onde acquistata, si sforza dopoi con ogni suo potere di ri-
manere in essa, & di conseruarla. Vediamo in questo proposito, che quelli Interualli,
che sono nelle lor forme, sono maggiormente appetibili de gli altri; perche sono mi-
gliori, & ciò esperimentiamo ogni giorno; conciosia che tanto quelli, che conoscono
confusamente gli estremi d'alcuna Consonanza solamente, senza discernere il perfet-
to dallo accresciuto, ò diminuto, & non hanno la ragione della Partecipatione; quan-
to quelli, c'hanno tal giudicio & tal ragione; qualunque uolta uogliono accordare i
loro Istrumenti, riducono le Consonanze alla loro perfettione. Quelli prima; per
che non sanno la ragione dal temperare, ò proportionare; essendo che seguono quello,
che maggiormente loro diletta; & credono, che quella sia la forma uera, la quale si ri-
cerca nel volere accordare i detti Istrumenti; onde ingannati dal senso, non ottengo-
no quel, che desiderano; questi poi perche hauendo la ragione della Partecipatione,
uengono più facilmente ad accrescerle, ò minuirle; & più presto le riducono à quel-
la forma, che ricerca il numero delle chorde de tali Istrumenti; riducendo l'ope-
ra loro à perfettione. Et se fusse uero, che tanto tra le Voci, quanto tra i Suoni de
gli Istrumenti si udissero solamente le Consonanze, & gli Interualli mostrati di so-
pra fuori delle loro naturali proportioni; come alcuni poco accorti hanno detto;
ne seguitarebbe, che quelli, che sono della Natura, & nascono da i ueri Numeri
harmonici, non si ritrouassero mai posti in atto; ma fussero sempre in potenza, la qual
potenza sarebbe vana & frustatoria; conciosia che Ogni potenza naturale, quan-
do per alcun tempo non si riduce all'atto, è senza utilità alcuna nella natura.
page 165Et pure si uede, che Iddio, & essa Natura non fecero, ne fanno mai cosa alcuna in vano;
però bisogna dire, che tal potenza si riduca alcune uolte in atto; laquale se non si può
ridurre col mezo de gli Istrumenti nominati di sopra, è necessario che si riduca col me-
zo delle Voci; altramente il Numero sonoro, ò harmonico mostrato altroue, il quale è
la cagione delle Consonanze, & si ritroua nelle Quantità sonore, sarebbe al tutto uano,
& superfluo nella natura: & Iddio & la Natura istessa (il che è pazzia à pensarlo, non che
à crederlo) haurebbono prodotte queste forme in uano. Onde si può concludere, che
quelli Interualli, che si odono nelle Cantilene uocali, sono contenuti nelle lor uere for-
me, che si ritrouano tra le parti del Numero senario; ancora che potrebbe forse alcun
dire; Se la Natura è inchinata à seguire il buono, & il migliore; & se gli Interualli, che
nascono da i Numeri harmonici; sono migliori de gli altri & per conseguente più conso
nanti; da che nasce, che spesso udimo nelle cantilene uocali un non so chè, più presto
di dissonanza, che di consonanza? A questo si può dire, che può procedere da molte
cagioni; Prima, perche alcuno de i Cantori haurà l'Vdito imperfetto & impedito, il
quale sopra ogn'altra cosa debbe esser in quelli, che essercitano la Musica, senza difet-
ta alcuno; dopoi, perche potrebbe essere, che le uoci de i Cantori fussero tra loro spro
portionate; onde essendo l'una chiara & soaue, & l'altra per il contrario oscura & sgar-
bata, non può seguire concento, che sia buono. Potrà anco essere, che l'uno de Can-
tori hauerà maggior fianco, & che più si facesse udire dell'altro; ouero, che l'uno haurà
tal natura, che nel cantare crescerà più del douere la uoce nell'acuto, & l'altro la callerà
uolentieri uerso il graue; le quali cose sono sempre cagione, che non si può udir mai al-
cuno concento, che sia buono. Ma quando le Voci sono tra loro proportionate, & be-
ne unite, senz'hauere alcuno impedimento, & sono proferite da i Cantori con discre-
tione & buon giudicio; di maniera che l'una non supera l'altra; è da tener per fer-
mo, che tali Interualli si odono perfetti; onde gli Vditori pigliano non poco piacere &
contento delle Cantilene, che odono in cotal maniera concertate; percioche oltra gli
altri accidenti, che intrauengono nel cantare le parti, si odono alle uolte alcuni accenti,
& (come si dice) alcune tirate di gorgia, con alcune diminutioni molto garbate; che ne
gli Istrumenti arteficiali non si possono udire. Dirà forse qui alcuno; poniamo, che quel-
lo, che si è detto sia uero; non ne segue da questo un grande inconueniente; che si po-
trà dire, che qualunque uolta s'accompagnarà gli Istrumenti arteficiali con le Voci, mai
queste con quelli per alcun modo si potranno unire? Rispondo; chi uorrà essaminar mi-
nutamente la cosa, ritrouarà questo inconueniente accadere infinite uolte; conciosia
che mai, ò di raro auiene, che le uoci co i Suoni s'accordino tanto perfettamente, che
non si oda alcuna discrepanza tra loro, ancora che sia minima. Et benche pari à mol-
ti, che si uniscano; questo auiene per la picciola distanza, ch'è tra loro, della quale
l'Vdito de quelli, che non hanno molta prattica, & buon giudicio delle cose della Mu-
sica, non può esser capace. Non è però impossibile, che le Voci non si possino uni-
re perfettamente co i Suoni, senza intrauenire alcuno inconueniente; tanto più che
(come hò detto) la Natura desidera sempre d'accostarsi al Buono, & al Migliore,
il quale è per se desiderabile; pur che sia conosciuto; & è il suo proprio di fuggire il
Tristo, & quello ch'è ad impedimento del buono, ch'è abomineuole. Onde il Sen-
so non può soffrire la Dissonanza, che si udirebbe, quando il Cantore volesse seguita-
re naturalmente gli Interualli, che nascono secondo la natura de i Numeri sonori; &
perciò cerca di unite le Voci con i Suoni, più che puote. Et questo non gli è difficile;
perche ad esse naturalmente è concesso, che per ogni uerso si possino piegare, & far-
si di graui acute, & per il contrario, d'acute graui, con quel modo, che più torna
commodo. Ne la Natura le hà posto alcun termine, ò fine, se non nel modo, che hab-
biamo veduto nella Seconda parte.Cap 13. Ma gli Istrumenti arteficiali non possono far questo;
conciosia ch'alcuni sono stabili, & non si possono uariare, ò mutar di suono per alcun
modo, hauendogli l'Arte posto un certo termine, ò fine. Ma accordansi pure, & uniscansi
page 166perfettamente quanto si uoglino queste due cose insieme; che quando poi si separeranno
l'una dall'altra, le Voci ritornaranno alla loro perfettione, & gli Istrumnenti rimaneran-
no nella lor prima qualità. Ne questo ci debbe parer strano; poiche si ueggono mag-
giori effetti nelle cose naturali, nell'approssimarsi, ò nel mescolarsi l'una con l'altra; & ciò
non solamente nelle cose c'hanno tra loro qualche conuenienza; ma tra quelle etiandio,
che sono l'una all'altra al tutto contrarie; percioche pigliano tra loro scambieuolmente
la qualità dell'uno & dell'altro; essendo uero, che ogni Agente, il quale opera alcuna
cosa, nel farla uiene à repatire; ouero una di esse solamente pigliando la qualità del suo
contrario, separate dopoi l'una dall'altra, ritornano alla lor prima qualità, ò natura, &
nel loro primo essere. Questo potiamo uedere commodamente nell'Acqua, che per na
tura è fredda & humida, che approssimata al Fuoco suo contrario, ch'è caldo & secco,
piglia la qualità del Fuoco; cioè, diuenta calda; ma separata dopoi, ritorna nel suo pri
mo stato. Il medesimo intrauiene nell'altre cose naturali, le quali come dice il Filoso-
fo;2. Ethi.
cap. 1. per la consuetudine mai non sono uariate di natura; come si uede nelle cose graui, la
cui natura è di passare al centro; che quantunque siano gettate in alto
infinite uolte, mai pigliano natura d'ascendere; ma sempre declinano al basso; com'è
manifesto della Pietra, che per sua natura è sempre inchinata à discendere. Questo istes-
so potiamo dir della Voce humana, che quantunque molte uolte sia violentata dal
suono de gli Istrumenti arteficiali, non resta per questo, che dopo che si scompagna non
ritorni alla sua prima natura. Soggiungerà etiandio forse alcuno; Che con maggior
piacere, & diletto il più delle uolte udimo i Suoni & l'Harmonie de gli Istrumenti arte-
ficiali; come sono Organi, Grauecembali, Arpichordi, Leuti & altri simili, che non udi
mo il Concento, che nasce dalle Voci; Et questo è uero: ma ciò può nascere dalla di-
sproportione, che si troua tra le Voci, & dalla proportione & temperatura posta tra i
Suoni dell'Istrumento; percioche il buono Artefice hà cercato d'imitare in esso la Na-
tura, quanto hà potuto, & di ridurlo à quella perfettione, che dall'Arte gli è stato con-
cesso: proportionando prima con tal temperamento i suoi Interualli, di maniera che
l'uno non superi l'altro in alcuna qualità, accioche in esso non si oda alcuna discrepan-
za; la onde restando dopoi io Istrumento in tale accordo & temperamento, & in un'or-
dine de Suoni inuariabile, l'Vdito molto si diletta nell'Harmonia, che nasce da lui: essen-
do massimamente, che per natura si diletta dell'ordine proportionato. Ma se per caso ta
le ordine & temperatura muta qualità; pare che immediatamente quei Suoni; che da
lui nascono, sommamente offendino. Questo medesimo uediamo intrauenir spesso nel-
le Voci, ch'essendo disproportionate & mal vnite, non si possono udire; ma se sono
proportionate & ben unite, sommamemte dilettano al sentimento. Onde senza dub-
bio alcuno, allora con maggior diletto si ode un'Harmonia & un Concento de uoci, che
il Concento, che nasce da qual si uoglia Istrumento. Questa adunque è la cagione, per-
che alle uolte udimo con maggior dilettatione il Suono d'un'Istrumento, che l'Harmo-
nia, che nasce dalle Voci, ancora che tale Istrumento sia poco buono, ma i Suoni, che
nascono da esso, Ottimamente siano proportionati, & esse Voci siano buone & sonore,
ma tra loro disproportionate & male vnite. Et ciò non debbe parer strano, poi ch'al-
le fiate con maggior diletto, maggior contento, & con più satisfattione uediamo un bel
Cauallo, ilquale sia ben formato & proportionato, ch'un'Huomo difforme & brutto;
& pur l'Huomo è il più bello, il più leggiadro & il più nobile animale, che si ritroui tra
mortali; & una delle marauigiose cose, che Iddio benedetto habbia creato. Ma che si
può dire à questo? se non, che la Natura sommamente hà in odio quelle cose, che nella
loro specie sono imperfette, disproportionate & mostruose; & si compiace grandemente
in quelle, che sono più uicine alla loro perfettione.
page 167
Della inspessiatione del Monochordo diatonico dalle chorde del genere
Chromatico.Cap. XLVI.
Monochordo diatonico mostrato di sopra, dalle chorde del Chromatico,
& da quelle dell'Enharmonico. La onde si debbe auertire, che hauendosi
aggiunto, nella compositione mostrata il Tetrachordo synemennon col Te-
trachordo meson; per tale congiuntione, il Tuono, che è posto tra la chorda a, & la
 .
. uiene ad esser diuiso dalla chorda b, in due parti; cioè, in un Semituono maggiore, &
in uno minore; per il che à caso & necessariamente nasce un nuouo Tetrachordo, tra
le chorde a. b.
 . & d; imperoche tra la a & la b. si ritroua il Semituono maggiore, tra la b. &
. & d; imperoche tra la a & la b. si ritroua il Semituono maggiore, tra la b. & la
 . il Semituono minore, & tra la
. il Semituono minore, & tra la  . & la d. il Trihemituono; come nell'essempio si può
. & la d. il Trihemituono; come nell'essempio si può Vedere. Et perche tale Tetrachordo non s'assimiglia per alcun modo ad alcuno de i
Tetrachordi diatonici, posti nel Cap. 16. non si può con uerità dire, che sia Diatonico;
ma si può dire, che sia Chromatico; accostandosi molto al Chromatico molle di Tolo-
meo; & in tutto & per tutto esser quello di Didimo; come si uede appresso di esso Tolo-
meo, nel Cap. 13. del 2. lib. de gli Harmonici. Essendo che procede dal graue all'acuto
per un Semituono nel primo Interuallo, nel secondo similmente per un'altro Semituo-
no, & nel terzo per uno Trihemituono, secondo la forma de i Tetrachordi chromatici
già mostrati. Si che potiamo ueramente dire, che questo sia il uero Tetrachordo chro-
matico ricercato, utile & necessario molto alla inspessatione del mostrato Monochordo

nella parte più graue de i loro Tetrachordi, & gli altri di maggiore proportione poi per
ordine; & che in questo si ritroua primamente il Semituono maggiore, & dopoi il mino
re; à costui si potrebbe rispondere, che questo importa poco; poi che tal cosa non
uiene fatta fuori di proposito; essendo che tali Interualli uengono naturalmente es-
ser collocati, secondo che la natura de i Numeri harmonici lo comporta, i quali nu-
meri danno prima nella parte gruaue le Parti, ouero Interualli maggiori, & dopoi
per ordine le minori; come nel Cap. 39. di sopra habbiamo veduto. Per la qual cosa
noi dobbiamo prouedere di collocare gli Interualli in tal maniera, che possiamo acqui-
stare tutte quelle Consonanze, che sono atte alla generatione dell'Harmonia perfetta;
& non hauer riguardo, che non sia posto il maggior interuallo ne i Tetrachordi auan-
ti il minore; & dopoi ne segua la perdita de molte Consonanze. Haueano bene gli Anti
page 168chi tal riguardo; ma nō faceuano il concento loro al modo, che faciamo noi & haueuano
opinione, che i maggiori Interualli (com'altroue hò detto) si cōponessero de i minori. Se
ben'è tutto al contrario: ma qual sia più ragioneuole, che i maggiori Interualli si compon
ghino in cotal maniera, ò pur che le Cōsonanze & gli Interualli maggiori naschino da i
minori, lo uederemo più oltra. Et se l'hauer posto il maggior Semituono auanti 'l minore
non fà cosa alcuna; non farà etiandio, che cotale Tetrachordo non sia Chromatico;
poiche non è ne Diatonico, ne meno Enharmonico: se bene hà tra la chorda b, & la
 . il Semituono minore, che non si usa nelle modulationi diatoniche, ne anco nelle En-
. il Semituono minore, che non si usa nelle modulationi diatoniche, ne anco nelle En-harmoniche; & tra la chorda
 , & la d. hà il Trihemituono incomposto che nel
, & la d. hà il Trihemituono incomposto che nel è cōposto; il qual'è contenuto dalla proportione Sesquiquinta, com'è contenuto quell'In
teruallo, ch'è posto nella parte acuta del Chromatico molle di Tolomeo, e di quello di Di
dimo; come si può conoscer riducēdo le quattro mostrate chorde nelle lor proprie forme,
che sono tra gli harmonici Numeri, nelle chorde del primo Tetrachordo detto Hypaton,
le quali in questa figura si possono chiaramente vedere. Et ancora ch'ei sia ne i due primi

siderato il poco utile, che da loro si caua; essendo che non possono dare alcuna Conso-
nanza; come allora sarebbe manifesto, quando adoperar si uolessero. Questo Tetrachor
do adunque uerrà ad essere la forma de gli altri quattro, quando uorremo inspessare il
Monochordo posto di sopra nel Cap. 40. E' ben uero, che quando si ponessero in tal Mo
nochordo, che contenessero tali proportioni; più presto si uerrebbe à generar confusio-
ne, che commodo; per la moltitudine de i Tasti, & delle Chorde, che si accrescerebbo-
no, per poter ritrouar le Consonanze secondo 'l proposito, oltra le mostrate. Però ri-
durremo solamente il sopradetto Trihemituono tra le chorde diatoniche al modo mostra
to, facendolo minore in ogni Tetrachordo, una parte del Comma; come facemmo di so
pra; ouer lo faremo minore d'una quarta parte; secondo 'l modo tenuto nel Libro Quin
to delle Dimostrationi; quando si hauesse temperato gli Istrumenti in quella maniera,
ch'io dimostrai nella Prima sua proposta; & per tal modo, oltra l'incommodo, che si leua
à i Sonatori, haueremo schiuato molte cose, che sarebbono state molto strane da udire,
per i passaggi, che si farebbono dall'un'Interuallo all'altro, lequali non si odono dopo la
Participatione. Accōmodaremo adunque il Trihemituono al suo luogo proprio in que-
sta maniera; aggiungēdo prima alla chorda acuta d'ogni Tetrachordo del Monochordo
posto di sopra, una chorda nel graue, che sia da lei distante per una Sesquiquinta. Questa
poi aggiunta all'acuta detta di sopra, uerrà à contenere il ricercato Trihemituono,
& similmente uerrà à diuidere il Tuono maggiore d'ogni Tetrachordo in due parti,
secondo la ragione dell'Interuallo posto nel detto Tetrachordo; di modo che tra la
prima & la seconda diatonica, & tra l'aggiunta, & la detta chorda acuta, haueremo il
page 169Tetrachordo chromatico, secondo 'l proposito. Tal chorda dopo ridotta alla sua propor
tione col mezo della Participatione, ne darà il Monochordo diatonico inspessato dal-
le chorde chromatiche in ogni Tetrachordo, del qual Monochordo non mi estenderò
à dimostrar più cosa alcuna, per esser'il suo ordine ne gli Istrumenti moderni, già tanto
tempo usati, c'hormai da ogn'uno può esser conosciuto; nel quale, accioche le chorde
chromatiche fussero più facilmente conosciute dall'altre, colui ch'accommodò il Tasta-
me loro nel modo che si uede, fece i Tasti colorati, & forse lo fece, perche sapeua, che il
Chromatico era detto Colorato dal colore; come di sopra nel Cap. 16 fù detto. Ne fa sola
mente contento d'inspessare con tali chorde i sopradetti Tetrachordi, diuidendo i Tuoni
maggiori in due parti; ma diuise etiandio i minori in due Semituoni, l'un maggior dell'
altro; come in tal Istrumenti si può uedere; & questo, credo che facesse, per maggior
commodità de i Sonatori, accioche potessero nel graue, & nell'acuto esprimere con
maggior libertà nelle loro modulationi variati Modi & uariate Harmonie. Le chorde
colorate poi furono da i Musici prattici segnate nelle lor cantilene, & notate con due se-
gni; come la Trite synemennon con questa lettera b. rotunda, laquale chiamano b. mol-
le; & cosi tutte quelle, che sono consonāti con questa; tanto nel graue, quanto nell'acu
to, per una Diapason, oueramente per una Diapente, ò per una Diatessaron; l'altre poi
notarono con questo segno
 , ilquale nominarono Diesis; seguitando forse l'opinione di
, ilquale nominarono Diesis; seguitando forse l'opinione di Filolao, ilquale (come recita BoetioMusicae li
bro 3. c. 8.) diceua, che quello Spacio, per il quale la Sesqui-
terza è maggiore di due Tuoni, si chiamaua Diesis; ilquale spatio alcuni Moderni chia
mano Semituono minore; perche il più delle uolte si pone, per dinotare, che si debba
far l 'lnteruallo del Semituono; com'altroue uederemo. Et quando uoleuano, che tal
Semituono si cantasse in alcun luogo delle lor cantilene, & saliuano dal graue all'acuto,
poneuano il b. ma quando discendeuano dall'acuto nel graue, poneuano il
 ; il che fan-
; il che fan-no anco i più Moderni, quando salendo & discendendo, col mezo de tali segni, ò chor
de, uogliono porre in essere il Tuono. Credo che la forma di questo segno
 fusse intro-
fusse intro-dotta da alcuni, che si sognarono, che 'l Tuono fusse, ò si componesse di noue Comma;
ouer, che si potesse diuidere almeno in tante parti; percioche uoleuano, che 'l Semituo
no maggiore fusse de cinque, & il minore de quattro; & per questo, quando procedeua-
no dalle chorde Diatoniche alle Chromatiche, nel modo c'hò detto, per lo spatio d'un
Semituono poneuano tal segno, per dinotarci questo Interuallo; perc'hebbero opinio-
ne; come hanno anche molti de i Moderni; che tale Interuallo fusse il Semituono mi-
nore, & fusse de quattro Comma; onde segnauano lo spacio con quattro uirgolette in-
crociate, che sono le quattro poste in tal segno; conciosia che seguiuano l'ordine delle
chorde, il numero & le proportioni Pitagoriche, mostrate di sopra. Ma quanto co-
storo s'ingannino, facilmente si può comprender da quello, che detto & ueduto hab-
biamo, & da quello che si è dimostrato nella Ventesimaprima Proposta del Secondo
delle Dimostrationi, & nelle tre sequenti; simigliantemente da quello, che dice Boe-
tio nel Cap. 15. del terzo libro della Musica; mostrando che 'l Tuono di proportione Ses
quiottaua è maggiore di otto, & minore di noue de i suoi Comma. Et nel Cap. 14. dice,
che 'l Semituono minore è maggiore di tre Comma, & minore di quattro. Però adun-
que se 'l Tuono è maggior di otto, & minor di noue Comma, & non si può hauer certez-
z'alcuna della sua quantità, per essere irrationale; parmi certamente grande arroganza
il uolere affermare determinatamente una cosa, che la Scienza pone in dubbio & indeter
minata. Onde se quest'Interuallo non si può denominar con una quantità determinata,
minormente si potrāno denominar quelli che sono minori; come sono il Semituono mag
giore, & il minore & gli altri simili.
page 170
In che maniera possiamo inspessare il detto Monochordo con le chorde
Enharmoniche.Cap. XLVII.
de chromatiche inspessare il detto Istrumento con le Enharmoniche; accio-
che noi habbiamo in ogni Tetrachordo il Semituono maggiore, diuiso in due
Diesis; porremo solamente una Chorda in mezo di esso in tal maniera, che
con una delle nominate diatoniche, ò chromatiche, sia consonante, & haueremo il no
stro proposito. Ma auanti che più oltra si proceda; parmi di douer mostrare le Proportio
ni del Tetrachordo, accioche quando si uolesse inspessare il Monochordo diatonico
syntono, si possa saper la ragione de i suoi Interualli. Per il che bisogna auertire; che
procedendo ogni Tetrachordo enharmonico dal graue all'acuto per due Diesis, & uno
Ditono incomposto; dobbiamo elegger quello, che hà i suoi Interualli contenuti da
proportioni, che ne possono condurre all'uso dell'Harmonia perfetta; ne dobbiamo ha-
uer riguardo à quelli, che sono stati posti in molti Tetrachordi da gli Antichi; poi che
non sono atti alla generatione de i Concenti perfetti, & poco fanno al nostro proposito.
La onde eleggeremo quelli, che sono utili; accioche non si uenghi à moltiplicar le co-
se senza necessità. Et si debbe auertire, ch'io dico quelli Interualli essere utili, i qua-
li aggiunti ad alcun'altro, ne danno una Consonanza; però elegeremo primieramen-
te quello, che si può eleggere de i Tetrachordi mostrati di sopra, che sarà utile, & al pro-
posito; dopoi aggiungeremo Interualli contenuti da tali proportioni; che, dopo che sa
rà inspessato il sopradetto Monochordo, secondo le ragioni delle proportioni, ch'io
son per mostrare, ogni Chorda haurà la sua corrispondente diatonica, ò chromatica,
consonante. Il Ditono adunque che pone Tolomeo nel suo Tetrachordo enharmoni-
co, posto nel Cap. 37. farà al nostro proposito; percioche è Interuallo consonante, & la
sua uera forma si ritroua collocata tra i numeri, che contengono le proportioni, che
sono tra le parti del Senario, & non è in cosa alcuna differente dal Ditono posto nel
Monochordo diatonico syntono; ancora che si consideri composto nel Diatonico,
& nell'Enharmonico senz'alcuna compositione; conciosia che l'uno, & l'altro è con-
tenuto dalla proportione Sesquiquarta. Questo adunque sarà l'Interuallo acuto di
questo Tetrachordo, & haueremo tre chorde; cioè, le Due estreme di ciascun Tetra-
chordo diatonico, ò chromatico, che sono communi à ciascun genere, & la Se-
conda graue, la quale medesimamente à ciascun genere è commune. Questa, do-
po che si hauerà ritrouata la Quarta chorda, la quale diuiderà il Semituono di ciascun
Tetrachordo diatonico, & Chromatico in due parti, sarà la Terza acuta del Tetrachordo
enharmonico. Et la Seconda chorda Enharmonica porremo tra la prima & la seconda
diatonica in questo modo; facendola distante dalla prima per una proportione Ses-
quiuentesimaquarta, ch'è lo spacio del Semituono minore; & sarà il Diesis maggio-
re di questo Tetrachordo, & dalla Seconda, per una Supertripartiente 125. che sarà il
Diesis, minore; laquale segnaremo con questo segno [[mus.hsharp]]. & haueremo questo Tetrachor
do, nel quale potremo ueder l'utile, che da lei ne uiene; conciosia che aggiunta alla
terza chorda del Tetrachordo hypaton chromatica, che è la Perhypate hypaton, si po
trà udire il Ditono, contenuto dalla proportione Sesquiquarta. Ma perche (come hò
detto) le Due estreme, & la Terza chorda del detto Tetrachordo sono communi; però
basterà solamente aggiungere in ogni Tetrachordo la detta chorda Enharmonica, laqua
le si potrà facilmente hauere, quando s'aggiungerà alla Terza corda di ciascun Tetra-
chordo chromatico uerso l'acuto un'altra chorda, che sia distante per una pro-
portione Sesquiquarta. Questa poi, dopo che si hauerà proportionata ne i sopradet-
ti Istrumenti; quando la Participatione fusse fatta nel modo c'hò dimostrato di sopra;
page 171
![Diatessaron.
Semit. maggiore.
Diesis.
Diesis.
Ditono.
300. a. Mese.
Sesquiquarta.
375. F. Lychanos meson.
Supertripartiente 125.
384. [[mus.hsharp]]. Parhypate meson.
Sesquiuentesimaquarta.
400. E. Hypate meson.](../../zarins89/ill/247_1.gif)
ra non accaderebbe farle altro; se non lasciarla nella nominata Sesquiquarta sarà di tale
utile, & tanto; ch'ogni chorda diatonica, & ogni chromatica de i detti Istrumenti, si
uerso il graue, come etiandio uerso l'acuto, hauerà una chorda corrispondente per un
Ditono, & per un Semiditono; & ne darà un tale ordine, dal quale potremo compren-
dere, quanto uaglia l'Arte aiutata dalla Natura nel congiungere, & collocare mirabil-
mente con bello, & regolato ordine le chorde Chromatiche tra le Diatoniche, & tra l'
une & l'altre di queste le Enharmoniche; lequali si conosceranno nel Tastame de i detti
Istrumenti in questo, che à differenza delle diatoniche, & delle chromatiche, si porran
no d'un altro colore; come nel seguente Istrumento si può uedere. Ma si debbe sempre
auertire; com'altre uolte si è detto; che quelle Chorde sono poste con qualche utilità in
uno Istrumento, & in alcun ordine, le quali sono in tal maniera collocate, che uerso il
graue, ouero uerso l'acuto hanno una chorda corrispondente consonante per una Dia-
pente, ò per una Diatessaron, oueramente per un Ditono, ouero per un Semiditono; co
me sono quelle, che si ritrouano in questo Istrumento. Cosi per il contrario, quelle so-
no poste senza utile alcuno, quando non hanno tali corrispondenti; percioche niente, ò
poco tornano al proposito alla generatione d'alcuna consonanza. Potrà adunque cia
scuno per l'auenire fabricare un'Istrumento alla simiglianza di quello c'hò descritto; il-
quale sarà commodo, & atto à seruire alle modulationi & harmonie di ciascuno de i no-
minati tre Generi, & questo non sarà ad alcuno difficile; percioche uno de tali Istrumen
ti feci fare l'Anno di nostra Salute 1548. in Vinegia, per hauere nella Musica una cosa,
che fusse quasi simile alla Pietra, che si esperimenta l'oro & l'argento; acciò potesse cono
scere, & uedere, in qual maniera potessero riuscire le harmonie Chromatiche, & le En-
harmoniche, & ogni sorte di harmonia, che si potesse hauere da qual si uoglia Diuisione;
& fù un Grauecēbalo, ch'è anco appresso di me; il quale fabricò Maestro Dominico Pe
sarese , raro & eccellente fabricatore de simili Istrumenti; nel quale non solamente i Se
mituoni maggiori sono diuisi in due parti; ma anche i minori, di maniera ch'ogni Tuo-
no uiene ad essere diuiso in quattro parti. Et ancora che se ne potessero far de gli altri cō
diuerse Diuisioni, nondimeno da loro si haurebbe poca utilità; percioche in loro senz'al
cuna necessità sarebbono moltiplicate le chorde, le quali (oltra le mostrate) non sareb-
bono atte ad esprimere altri concenti più diletteuoli, de quelli, che fanno udir quelle,
che sono collocate nel nominato Istrumento, i quali ueramente sono Diatonici, ouer
Chromatici, ò pure Enharmonici. Et s'alcuni credessero, che potessino esprimere al-
tri concenti, che i tre sopradetti, di gran lunga s'ingannarebbono; perche niun'altra spe
cie di Diatonico, ne di Chromatico, ne di Enharmonico si può ridurre alla sua perfet-
page 172
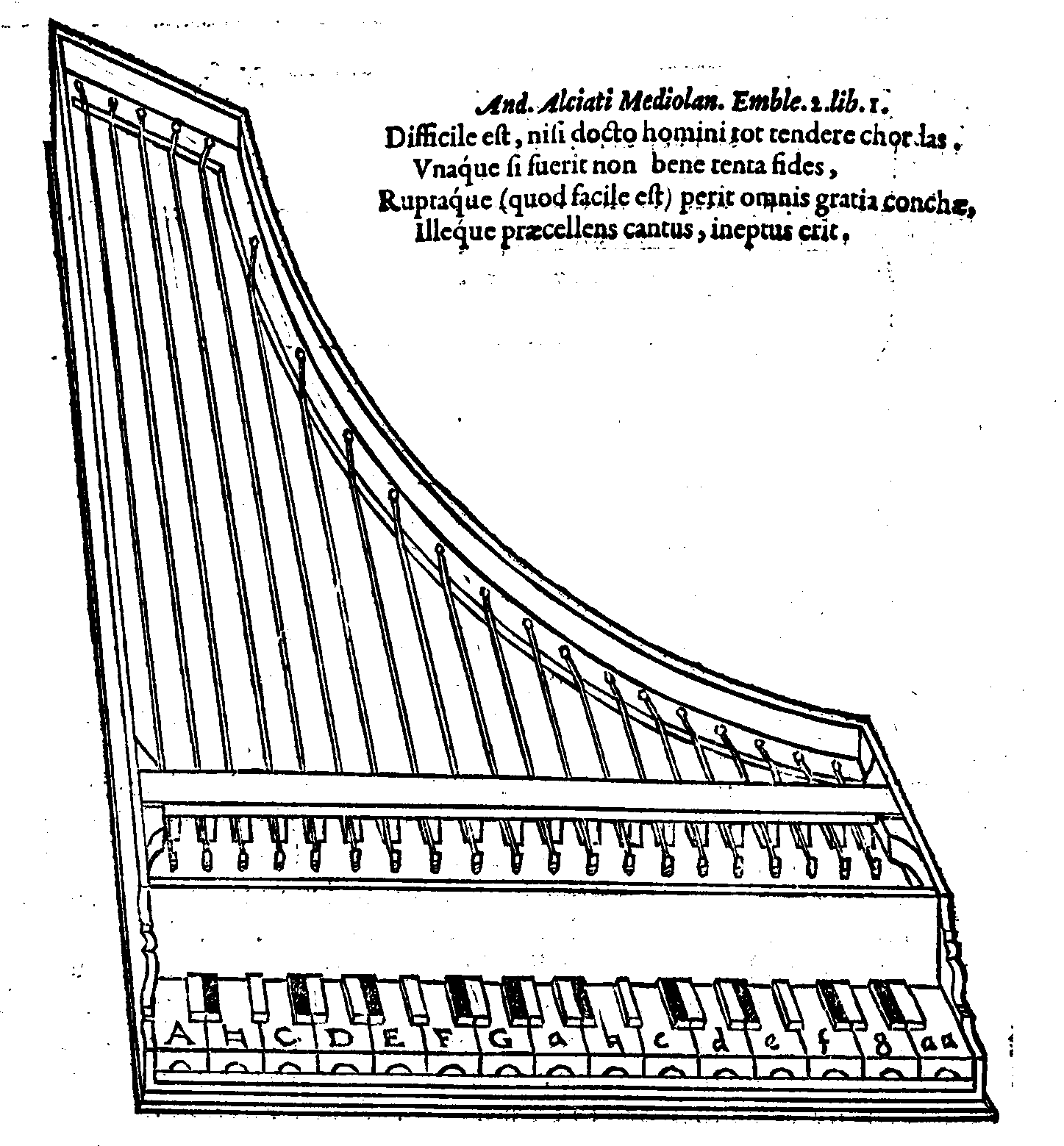
uedere. Ma perch'io credo, c'hormai la Diuisione de cotali generi, & la lor natura sia no
ta à ciascuno ingegnoso; però non mi estenderò più oltra, in uoler dar di loro alcuna al
tra ragione; conciosia che gran parte delle difficultà, che potranno occorrere, & saran
no di qualche importanza in questa Scienza, si potranno ueder dimostrate, & con ogni
diligenza esplicate nelle nostre DEMOSTRATIONI harmoniche: l'altre cose
poi lascierò al giudicio del discreto Lettore, che si hauerà nel maneggio de i Numeri
& delle Misure ottimamente essercitato. Dirò adunque per concludere, che que-
sto è un'Istrumento, sopra il quale si potrà essercitare ogni ottimo Sonatore, non so-
lamente nell'Harmonie diatoniche; ma etiandio nelle Chromatiche, & nell'Enharmo-
niche, quando potrà & saprà ridurle à i Modi antichi, oueramente quando à i nostri
tempi potranno riuscir megliori, & più soaui di quello, che si odono in alcune sgarbate
Compositioni d'alcuni Compositori moderni. Et dirò anco, che quando si uolesse ag-
giungere al numero delle mostrate Chorde alcun'altra chorda; percioche molte se ne pos
sono aggiungere; senza dubbio sarebbe cosa uana & superflua; conciosia che uanamen-
te & fuori di proposito si moltiplicano le cose; quando da quelle non si può cauare alcuna
utilità; & gli Interualli utili & necessarij, che concorrono alla costitutione d'ogni gene
re d'Harmonia, sono già accommodati à i lor proprij luoghi.
page 173
Ch'è più ragioneuole dire, che gli Interualli minori nascono da i mag-
giori; che dire, che i maggiori si compongano de i minori; &
che meglio è ordinato l'Hexachordo moderno, che
il Tetrachordo antico.Cap. XLVIII.
ler mostrare, quale è più ragioneuole; che i maggiori Interualli si compon-
ghino de i minori, ouer che le Consonanze, ò minori Interualli nasca-
no da i maggiori. Si dè adunque sapere, che gli antichi Greci hauendo
opinione, che le Consonanze & altri Interualli maggiori si componessero de più Inter-
ualli minori, haueuano un'Interuallo minimo, ilquale chiamano Diesis, & lo poneua-
no non solo indiuisibile alla guisa dell'Vnità nell'Arithmetica, ma lo chiamauano Primo
di tal genere; come si uede fatto da Aristotele nel Libro 10. della Metafisica,Cap. 2. seguendo
(secondo il mio parere) l'opinione d'Aristosseno, come etiandio fece nel Primo Libro de
i Posteriori,Cap. 17. dicendo: Ε'ν δὲ μέλει δίεσις; cioè, nel canto è il Diesis; uolendo ch'ello fusse mi
sura commune d'ogni Consonanza, come la Vnità è misura commune de tutti i Nume-
ri. Ma parmi ueramente, che ciò diceuano fuor d'ogni proposito; poiche dalla Diuisio-
ne della Diapason hanno origine tutte le Consonanze & gli altri Interualli musicali
quantunque minimi; essendo che ueramente ella è la Prima in tal genere, & è la
Cagione de tutti gli altri Interualli, & la lor Misura commune. Questo conferma
Marsilio Ficino nell'Epinomide di Platone, & nel Quarto della Republica; quando par-
la della Forma di tal consonanza & dice; che La Dupla è riputata esser proportione perfet
ta; primieramente, perche ella è la Prima tra le proportioni, generata tra l'Vnità &
il Binario; dopoi, perche mentre che par, che s'habbia partito dall'Vnità, la restui-
sce raddoppiandosi; oltra di questo, perche contiene in se ogni proportione; con-
ciosia che la Sesquialtera, la Sesquiterza, & l'altre sono in essa, come sue parti. La on-
de la Diapason nella Musica, la cui forma è essa Dupla, è la Prima, & la Più perfet-
ta d'ogn'altra Consonanza, & non patisce mutatione alcuna de i suoi estremi; & mentre
par che si parta da una certa Vnità de Suoni, restituisce tale Vnità, raddoppiandosi
nelle sue parti. Questa contiene in se ogni semplice Consonanza, & ogni minimo
Interuallo. Onde non è marauiglia, se i Greci di commun parere, dal tempo di Ter-
pandro in poi, come narra il Filosofo,Probl. 32.
Sectio. 19. la chiamarono Διὰ πασῶν; percioche hà ragione
in qual si uoglia altra Consonanza, ouero in qual si uoglia altro Interuallo; essendo che
se è semplice & minore di essa, tale Interuallo è come una delle sue parti; & se è compo
sto & maggiore, è come composto di lei & d'una di esse parti, nel modo, che nel Cap. 16.
della prima Parte hò mostrato. Et quello c'hò detto, si può comprender da questa ra
gione esser uero; che i Suoni delle Consonanze veramente hanno più tosto della quanti
tà Continua, che della Discreta; imperoche quando noi poniamo insieme la Diapente
& la Diatessaron, l'una delle quali è contenuta da Cinque, & l'altra da Quattro chor-
de, uiene la Diapason, che è contenuta tra Otto, & non tra Noue chorde; an-
cora che cinque & quattro posti insieme faccino Noue; & questo auiene, percioche l'
una & l'altra si congiungono ad un termine commune; com è il proprio della Quantità
continua; il qual termine è la Chorda più acuta della Diapente posta nella parte gra-
ue, & la più graue della Diatessaron posta nella parte acuta, congiunte insieme in Har
monica proportionalità; oueramente per il contrario nella congiuntione Arithmetica;
la chorda più acuta della Diatessaron posta nel graue, che è la più graue della Diapente
posta nell'acuto; uerrebbe ad esser questo termine commune. Ma si come si fà errore à
dire semplicemente, che 'l Tutto diuisibile si componi delle sue parti; essendo che 'l Tut-
to è prima di esse; cosi è errore il dire, che la Diapason si componi della Diapente, & del
page 174la Diatessaron, ò d'altre Consonanze, che le sono parti; percioche è prima di ciascuna
altra, & è cotale Tutto. Però meglio & con più ragione si può dire, che gli Interualli
minori nascano dalla diuisione de i maggiori, che i maggiori si componghino de i minori.
Ma come la Diapason, ch'è la maggiore de tutti gli altri Interualli consonanti sempli-
ci, ragioneuolmente nell'ordine delle Consonanze tiene il luogo più graue, & cosi gli
altri di mano in mano tengono per ordine il loro, secondo le forme loro sono
collocate ne i numeri; cosi più ragioneuolmente ordinarono i Moderni il loro He-
xachordo per Tuoni, & Semituoni, che non fecero gli Antichi il loro Tetrachor-
do; fusse poi à caso, ò studiosamente fatto; conciosia che questi posero nella par-
te graue de i loro Tetrachordi gli Interualli di minor proportione, & dopoi per or-
dine quelli di maggiore; & quelli fecero il contrario; posero i maggiori nel gra-
ue de i loro Hexachordi, & nell'acuto salendo i minori nelle prime quattro chor-
de, come è il douere, & come ne danno i Numeri harmonici; il che nel Cap. 39.
di sopra si è potuto vedere; i quali sono le parti delle Quantità sonore; come habbiamo
dimostrato altroue.
Che ciascun del i tre Generi nominati si può dire Genere, & Specie; &
che ogn'altra Diuisione, ouer'Ordinatione de Suoni sia vana,
& inutile.Cap. 49.
de i predetti Generi, secondo diuersi rispetti, Generi, & Specie; con-
ciosia che si possono considerare in due maniere; prima in quanto all'u-
so de gli Antichi, dipoi in quanto all'uso de i Moderni. Onde conside-
rati secondo luso de gli Antichi, i quali più presto cercarono di variare le lo-
ro Modulationi, che di peruenire all'uso perfetto delle Harmonie co 'l mezo dell'ac-
quisto de tutte le Consonanze; ritrouaremo uarie diuisioni & diuerse forme di Te-
trachordi; come altroue hò mostrato;Supra
2. part. c.
31. 34. &
37.
Et 4. Sup-
plem. c. 1. 2
& 3. ridutte sotto uno de questi tre capi Diato-
nico, Chromatico, & Enharmonico. Et perche quelle cose, che si sottopongo-
no ad alcuno Vniuersale sono dette Specie; & quello Vniuersale, che contiene
sotto di se tali Specie, è detto Genere; però primamente si potranno chiamar Spe-
cie, percioche ciascuno è contenuto sotto questo Genere uniuersalissimo Melodia, oue-
ro Harmonia; dipoi si potranno nominar Generi: imperoche ciascun di loro sotto
di sè hanno molte Specie. Considerati poi secondo l'uso de i Moderni, con l'ac-
quisto di tutte le Consonanze, & con la perfettione dell'Harmonia, non è dub-
bio, che non haueremo più d'una Specie di ciascuno di loro; imperoche è impossi-
bile, che da altri Numeri, & da altre Proportioni & da altro Ordine, che dal
mostrato di sopra possiamo hauere il fine desiderato: Onde non Generi, ma Spe-
cie solamente bisognerà chiamarli; percioche sotto di se non hanno se non gli
Indiuidui, che sono questa & quella cantilena. Et saranno medesimamente sotto-
posti à questo genere uniuersale Melodia, ouero Harmonia; della quale il Diato-
nico, il Chromatico, & l'Enharmonico saranno le Specie. Per il che considera-
te al primo modo si potranno chiamare Generi & Specie; ma considerati al secon-
do si solamente Specie. Et se bene le Forme de gli Interualli di ciascu-
na specie de questi tre generi, mostrate da Tolomeo nel Cap. 16. del Primo Libro
del gli Harmonici, si ritrouano collocate tra le proportioni del Genere Superparticola-
re; & gli Antichi Musici habbiano hauuto opinione ferma, massimamente esso To-
lomeo; che da altro Genere di proportione, che dal Moltiplice, & dal Superpar-
page 175ticolare in fuori, che sono generi della Proportione di maggiore inequalità, non
potesse nascere alcuno interuallo, che fusse atto alla Consonanza; dalla Duplasu-
pertripartienteterza in fuori, dalla quale nasce la consonanza Diapasondiatessaron;
nondimeno la Natura contraponendosi à tal legge, ne concede molti altri Interual-
li, i quali sono approuati dal Sentimento, & confirmati dal parer d'ogn'uno per
buoni & consonanti, molto necessarij alle modulationi & alla generatione dell'Har-
monie in ciascheduna delle nostre Specie, & hanno le lor forme contenute tra gli
altri Generi di proportione. Et benche le ragioni, che adduce Tolomeo contra leNota per i
maligni
Diuisioni fatte da Aristosseno, Archita, Didimo, & contra molti altri habbiano
hauuto forza di far credere, ch'elle siano uane & inutili, & persuadino ad alcuno,
che nelle Proportioni, & ne gli Interualli di ciascuna Specie ritrouata da lui sen-
za farne proua, consista la perfettione de i tre Generi; nondimeno (come hò mostra-
to questo non è semplicemente uero; percioche non si ritroua in loro perfettione alcuna.
Il perche desiderando io di mostrare un modo & un'ordine, co 'l mezo del quale si po-
tesse uenire alla perfetta cognitione della Scienza, & alla cognitione de i ueri In-
terualli, che fanno al proposito dell'harmonie, che si essercitano perfettamente con
le Voci, & con gli Istrumenti arteficiali, accioche il Senso non fusse discordante
dalla Ragione; deliberai necessariamente di partirmi da cotal legge, & uedere s'io
poteua ritrouare il uero di cotal cosa; ond'io mi mossi à scriuere il presente Tratta-
to; del che s'io habbia ottenuto il desiderato intento; lascio iudicare à tutti quelli,
che sono di candido animo, & della Musica hanno la uera, & non sofistica cogni-
tione. Et s'hauesse fatto altramente, haurei con molti altri errato, seguitando quel-
lo solamente, che da altri è stato lasciato scritto, senza farne esperienz'alcuna, ne
mai si hauerebbe saputo la uerità di questa cosa; percioche sarebbe intrauenuto à
me quello, che suole intrauenire à quelli ch'adoperano alcuno Istrumento per condur
qualche cosa al desiderato fine; nondimeno con tal mezo non io possono condurre
à perfettione, & resta ogni loro dissegno uano. La onde s'è uero quello che dice il
Filosofo;2. Phy.
cap. 2. che uanamente & senz'alcun'utile si pongono quelle cose in opera, col me-
zo delle quali si uuol peruenire ad alcun fine, alquale poi non si peruiene; io per mo-
do alcuno non douea seguire cotal legge, ne meno le Diuisioni, le Proportioni, &
gli Ordini ritrouati da Tolomeo, ne da altro Musico antico, ò moderno che 'l si fus-
se; da quelle del Diatonico syntono in fuori; che, come habbiamo ueduto, è dalla Na-
tura formato; ritrouato dall'Arte con mirabile arteficio; percioche s'io non hauesse uo-
luto ciò fare, & hauessi eletto tali Ordini, per dimostrar la uera proportione di ciascuno
Interuallo, & in qual modo si potesse fabricare un'Istrumento, nel quale si hauesse da es
sercitare perfettamente l'Harmonie; come è stato sempre il mio fine; & da quelli non
hauessi potuto hauer quello, che io desideraua; pazzia sarebbe stata la mia, uana la mia
fatica, & cotal legge & ordini sarebbono stati al tutto uani & senza utilità alcuna. Per la
qual cosa non mi è paruto di far'errore; se non hò uoluto sottopormi à tali oblighi; es-
sendo ch'io reputai ogn'altra Diuisione, ouer Ordinatione de Suoni uana & inutile. Ne
penso ch'alcuno mi possa con uerità & giustamente riprendere, se bene non mancano gli
inuidi & maligni reprensori; s'io hò uoluto cercare & inuestigare il uero, & non seguire
l'opinioni & le autorità de gli Huomini, le quali il più delle uolte sono uane & fallaci;
& spesse fiate difendono & pigliano alcuni principij per dimostrare alcune loro con-
clusioni, che sono ueramente lontani dal uero, & poco fanno al proposito di quello che
parlar uogliono; ma facciasi quello che si uoglia; bisogna che la Verita al fine resti uin
citrice, & gloriosa.
page 176
Per qual cagione le Consonanze hanno maggiormente l'orgine loro
dalle Proportioni di maggiore inequalità, che da quel-
le di minore.Cap. L.
tare, & insieme uoler sapere, da quello che si è detto nel Cap. 22. della Prima
parte, nel fine; onde sia, che le Proportioni di minore inequalità non siano
atte alla generatione delle Consonanze musicali; essendo che tanto si ode
la Consonanza Diapason tra due Suoni, de i quali l'uno sia contenuto sotto la ragione
dell'Vnità, & comparato all'altro, che sia contenuto sotto la ragione del Binario;
quanto si ode tra due, de i quali l'uno habbia ragione di Binario, & sia compara-
to à quello, che sotto la ragion dell'Vnità è considerato; la onde non ui essendo al-
tra differenza, che la comparatione, & restando i Suoni & termini inuariabili, non si
può dar ragione alcuna, la qual ne conuinca à dire, che tal Consonanza piu presto si fac
cia dalla proportione Dupla, contenuta in uno de i Generi di maggiore inequalità, che
dalla Subdupla, che è contenuta tra uno de quelli di minore. A questo dubbio alcuni ri
spondono, dicendo: Quantunque ogni Consonanza musicale possa nascer dall'uno &
dall'altro Genere, quanto alla prodottione semplice; nondimeno nel modo del produr-
si, tra loro è alcuna differenza; imperoche nella prodottione delle Consonanze, un Nu
mero sonoro comparato ad un'altro; si compara con più perfetto modo secondo la Pro
portione di Maggiore inequalità & più nobilmente ancora di quello che si fa, comparan
dolo secondo quella di Minore. Onde hauendo ogni cosa prodotta maggior dipenden-
za dal modo più nobile della sua prodottione, che da altro; ragioneuolmente segue, che
le predette Consonanze habbiano maggiormente origine dalle Proportioni di maggio
re inequalità, come da cosa più nobile; che da quelle di minore. Soggiungono etiandio
un'altra ragione, dicendo: Ne i Generi di maggiore inequalità, il maggior termine con
tiene il minore, & in quelli di minore si troua il contrario; il perche pigliando si il conte-
nere per la Forma, & l'esser contenuto per la Materia; essendo che la Forma è più nobile
della materia; è manifesto, chè 'l Numero sonoro comparato secondo le proportioni di
maggiore inequalità, si compari con più perfetto & più nobil modo, che secondo
quelli di minore. Et benche queste loro ragioni possino acchettar l'animo di qualchedu
no; nondimeno mi pare, che pigliando le Proportioni di minore inequalità, nel modo,
che nel Cap. 30. della Prima parte fù determinato; & come ueramente si debbono piglia
re, faccino poco al proposito; conciosiache suppongono, che ogni Consonanza musi-
cale possa nascere dall'uno & dall'altro de i nominati Generi, quanto alla prodottione
semplice, che si fà di numero à numero; ma in fatto non è cosi; percioche (come
habbiamo ueduto1. Part.
cap. 30.) le Proportioni di maggiore inequalità sono contenute sotto un ge-
nere; cioè, sotto l'Habito, & quelle di minore sotto un'altro; cioè, sotto la Priuatio
ne; & le Proportioni di maggiore inequalità sono Reali & Positiue; & quelle di mino-
re inequalità sono solamente Rationali & Priuatiue; & le prime sono maggiori del-
la Equalità; ma le seconde sono (dirò cosi) minori. Onde essendo i termini delle pri-
me reali; perche si trouano tra cose reali; & non i termini delle seconde; essendo c'han-
no al più un termine reale; è impossibile, che le Consonanze possino hauer la loro origi-
ne da queste; poi che le Voci, & li Suoni si cauano dalla potenza d'una cosa, che percuo
te, & da quella che è percossa, che sono cose reali, & hanno il loro essere nella natura;
come sono i Corpi animati, & il sonori. Et perche la Consonanza è Suono, oueramen-
te Compositione di Suono graue & acuto; & essendo il Suono cosa naturale, che nasce
da Istrumenti arteficiali, ò naturali, che si trouano in essere tra le cose naturali; non si
page 177può dire, che le Consonanze naschino dalle Proportioni di minore inequalità, pigliate
al modo detto; conciosia che non hanno se non un termine reale; onde sono dette Ra-
tionali & Priuatiue solamēte. La onde nō essendo queste Proportioni atte alla generatio
ne delle Consonanze; dico, che maggiormente hanno la loro origine da quelle di mag-
giore Inequalità, che da quelle di minore. Ma accioche non pari strano ad alcuno;
che non habbia le cose delle Scienze cosi bene alle mani; quello ch'io hò detto;
cioè, che le Proportioni di Minore inequalità habbiano solamente un termine reale;
pigliando il mio ragionamento alquanto in alto; dirò, che si debbe auertire; essendo o-
gni Proportione, Relatione; che nella Relatione reale necessariamente concorrono due
estremi reali, contenuti sotto un'istesso Genere propinquo; come appar nella sua diffini-
tione, posta nel Cap. 21. della Prima parte; ma nella Rationale non è inconueniente,
ch'un'estremo possa esser compreso sotto un Genere, & l'altro sotto un'altro; conciosia
che la Relatione (come uuole Aristotele5. Meta-
phy. c. 15.) è di due sorti; lasciando quelle, che non fanno
al nostro proposito; la Prima delle quali è, quando si fà la Relatione di due cose naturali l'
una con l'altra, secondo una certa cosa, che conuiene realmente ad ambedue; & tal Re
latione è doppia; percioche oueramente è fondata sopra la Quantità continua, ò discre
ta; ouero ch'è fondata sopra la Potenza attiua & passiua, inquanto sono principij del fa-
re, & del patire. Di questa seconda si potrebbe dire, che si può considerare in due mo-
di; cioè, inquanto che tali cose non sono congiunte all'atto, onde si dicono Attiue &
Passiue; & inquanto sono congiunte, & si chiamano Agenti & Patienti; & si potrebbe an
co dire, che tutte queste Relationi possono esser reali, pur che siano fondate sopra la potē
za Attiua, ò Passiua naturale & creata, & non sopra l'Increata; ma per breuità lasciarò
ogni cosa, & dirò solamente di quella, che si troua nella Quantità continua, comparan-
do due Linee, ouer due Quantità finite d'vn'istesso Genere l'una all'altra; ò di quella che si
troua nella Discreta, quando si compara un numero all'altro, nel modo, ch'io hò mostra
to nella Prima parte. La onde queste Relationi sono ueramente Reali & scambieuoli;
conciosiache dalla natura istessa della cosa, ogni due Quantità numerali hanno cambie-
uole ordine l'una all'altra, nella ragione della misura, fondata sopra la Quantità. Et
questo si conosce; percioche si come la Metà riguarda il Doppio, non solo per appren-
sione dell'Intelletto, ma etiandio per sua natura; cosi il Doppio hà riguardo ad essa Me-
tà. La seconda Relatione per tal ragione, è quella, ch'è fondata sopra due estremi, che
non sono di un'istesso Genere, ouer'Ordine; & questa è similmente de due maniere l'u-
na è quando l'uno de gli estremi è Naturale, & l'altro della Ragione; & è fondato sopra
la dipendentia di uno all'altro; come è il Sensibile & il Senso; & l'Intelligibile & Intel-
letto; Conciosiache quanto all'atto, il Senso dipende dal Sensibile; hauendo noi il Senso,
accioche sentiamo; similmente la Scienza speculatiua dipende dalla cosa, che si può sa-
pere; & l'Intelletto da quella, che si può intendere; le quali cose, in quanto c'hanno l'es
ser loro tra le cose naturali, sono fuori dell'ordine dell'essere Sensibile & Intelligibi-
le. Per ilche tra la Scienza & il Senso è una certa Relatione reale, secondo che sono or
dinate al Sapere, oueramente al Sentire le cose; ma considerate in se, sono fuori di
questo ordine; & in esso non è alcuna Relatione reale alla Scienza & al Senso; ma solamē
te Rationale, in quanto l'Intelletto le apprende come termini della Relatione della Sciē
za & del Senso; Percioche (come dice Aristotile) non sono ueramente dette relatiue,Vt supra.
perche si riferiscono alle cose; ma perche le cose si riferiscono à loro; come si uede,
ch'una Colonna, non hauendo ne parte destra, ne sinistra, se non inquanto si met-
te alla destra, ouero alla sinistra dell'Huomo, non fà la Relatione reale dalla sua par-
te; ma si bene l'Huomo. L'altra relatione è fondata sopra la Imitatione d'una cosa alla co
sa istessa, come è la Imagine all'Huomo; onde si dice Imagine, percioche imita, o rappre
senta l'Huomo. Ma queste Relationi sono molto differenti dalle due prime, per esser
quelle Reali & scambieuoli; essendo che l'uno de i loro estremi si riferisce all altro scambie
uolmente, & queste non sono scambieuoli; percioche la Relatione reale stà solamente in
page 178un termine, ch'è quello, che dipende, ouero imita la cosa; l'altro poi si dice solamente
per relatione; conciosiache l'altro estremo si referisce à lui, & esso è termine di tal relatio
ne; di modo che, si come la cosa, della qual si può hauere cognitione, hà la relatione al-
la Scienza, riferendosi questa à quella, la quale termina la dependenza di essa Scienza;
cosi l'Huomo hà relatione all'Imagine; perche l'Imagine si riferisce all'Huomo, & ter-
mina la sua imitatione. Dico adunque in proposito, che nel primo modo della Prima re
latione si ritrouano le Specie, ò Proportioni contenute ne i genere di Maggiore inequa-
lità, che si applicano à gli estremi di qualunque musicale Interuallo; & questo, percio-
che i termini dell'uno & dell'altro de i loro estremi sono reali, & hanno cambieuole rela
tione l'uno all'altro; ma nelle relationi della Seconda, sono quelle Proportioni, che so-
no contenute nel Genere di minore inequalità; conciosiache non ui è se non un termine
reale fondato nella Equalità, ch'è collocata tra le cose naturali, & è sempre stabile, & ri-
manente in ogni proportione; come nel Cap. 30. della Prima parte hò detto; & l'altro è
rationale solamente & imaginato. Di maniera che la Relatione è reale se non in uno estre
mo, che è quello, che dipende, ò imita la cosa naturale, & l'altro è detto per relatione; con
ciosia che l'altro estremo si riferisce à lui, & esso è il termine di tal Relatione. Non è adun
que inconueniente, che le Proportioni di Minore inequalità habbiano solamente un ter
mine reale; poi che alle uolte la Relatione si fà de due cose, che non sono comprese sot-
to un'istesso genere, ouero ordine; ma si bene sotto due generi, ouer sotto due ordini di-
uersi; come habbiamo ueduto; ancora che tali proportioni si potessero dire Reali, quan
do si considerassero solamente ne i puri numeri. Per le ragioni adunque ch'io hò detto,
le Consonanze musicali nascono da i Generi di Maggiore inequalità, & non possono
nascere da quelli, che sono di minore per alcun modo.
Dubbio sopra quel che si è detto.Cap. LI.
no solamente Rationali & non Reali; in qual modo si potrà uerificar quello,
che dicono i Filosofi, parlando delle cose, che tra loro hanno Relatione reale
& Attione scambieuole; che dal Genere di minore inequalità non prouiene
alcuna attione; conciosiache gli estremi de queste Proportioni sono ueramente colloca-
ti tra le cose naturali? La onde per satisfare à tal dimanda dico: Nascendo l'Attione (se
condo l'opinione del Commentatore4. phy. cō.
17.) dalla Vittoria della cosa che muoue, sopra la cosa
mossa; molti Filosofi considerando questa Vittoria dalla parte dell'Agente, le attribuiro
no il nome di Maggiore inequalità; conciosiache molto ben uidero, che tal cosa non po
teua esser senz'alcuna proportione tra l'uno & l'altro; & perche la considerarono etian-
dio dalla parte del Patiente, le attribuirono il nome di Minore. Ma perche tra l'Agen-
te & il Patiente si può considerar due cose; prima l'Eccesso, dopoi il Difetto; l'Ecces-
so dico dalla parte dell'Agente, rispetto al Patiente; & il difetto dalla parte del Patien-
te, rispetto all'Agente; però io son di parere, che meglio hauerebbono fatto, s'hauesse-
ro detto, che dalla Proportione dell'Eccesso ne uenisse l'Attione, & da quella del Difet-
to la Passione; essendo che la Proportione è Relatione, & tal Relatione (come uogliono
i Filosofi) si ritroua di tre maniere; cioè, di Agguaglianza, di Soprapositione, & di Sop
positione; la onde poteuano commodamente dire; che da questa ultima proportione
non uiene Attione; poi che tra due cose, che si ritrouano d'equale possanza & di uirtù
equale, di maniera che l'una nō possa superar l'altra; non uiene Attione, ne Passione alcu-
na; ma si bene nell'altre; percioche l'Agente supera il Patiente in uirtù & possanza, per
una certa ragione di soprabondanza; onde nasce l'Attione solamente; oueramente il Pa
tiente è superato dall'Agente, onde nasce la Passione, de i quali modi ne parla abondan
page 179temente i Filosofi. Et se bene le Proportioni di Soprapositione, & quelle di Sopposi-
tione in quanto al Soggetto & alla Materia, sono una cosa medesima; perche sono op-
poste per relatione solamente, & tanta è la proportione della uirtù & potenza dell'Agen
te, che fusse, poniamo 4. & quella del Patiente, che fusse 2. quanta è la proportione del
la virtù del Patiente, che fusse similmente 2. & quella dell'Agente 4. onde si ritroue-
rebbono equali in distanza, & l'Agente superarebbe il Patiente con quella proportione
con la quale il Patiente fusse superato dall'Agente; nondimeno sono differenti quanto
alla ragione & la forma; conciosiache in un modo si considera l'Attione, & in un'al-
tro la Passione, prima in quanto l'uno supera l'altro; dopoi in quanto l'uno dall'al-
tro è superato. La onde l'Agente supera il Patiente secondo l'Eccesso; & per il con-
trario il Patiente è superato dall'Agente secondo 'l Difetto. Per la qual cosa è ma-
nifesto, che l'Eccesso, & il Difetto non sono una cosa istessa secondo la Forma & la
Ragione, ancora che siano una cosa istessa secondo il Soggetto & la Materia. Con-
siderate adunque queste Proportioni in questo modo, dico che tal Propositione si ueri
fica, quando per la Proportione del genere di Minore inequalità, intendiamo la propor
tione, ò relatione di Soppositione; ma quando si uolesse intendere il genere di Minore
inequalità in altro modo, tal propositione non hauerebbe in se uerità alcuna; come
leggendo & essaminando quello, che s'è detto nel Cap. 30. della Prima parte, cia-
scuno potrà uedere. Hora per metter fine à questo nostro Ragionamento, dico,
che quello c'hò detto fin'hora, potrà esser bastante à quello, che si è ragionato in-
torno alla Prima parte della Musica, chiamata Theorica, ò Speculatiua; percioche
è dibisogno, che hormai ueggiamo quelle, cose che sono necessarie all'intelligenza
della Seconda, che si nomina Prattica; le quali saranno di molta utilità à ciascuno
Studioso; & saranno contenute nelle due parti seguenti.
 page 180
page 180
LA TERZA PARTE
DELLE ISTITVTIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
teria di che si compone le Cantilene; detto Arte del Contrapun-
to, & è la Prima della Seconda parte della Musi-
ca, che si chiama Prattica.
Quel che sia Contrapunto; & perche sia cosi nominato.Cap. I.
cienza intorno alla Prima parte della Musica, detta Teorica, ò Spe-
culatiua; & ueduto quelle cose che sono appartinenti & necessarie al
Musico; resta che in queste due seguenti, ragioni de quelle cose, che
concorrono nella Seconda, che si chiama Prattica, la qual consiste
nel modo di porre insieme le Consonanze; cioè, nella compositio-
ne delle Canzoni, ò Cantilene, che si compongono à due, ouero à
più uoci, che i Prattici nominano Arte del Contrapunto. Ma perche il Contrapunto è il
Soggetto principale di questa parte; però auanti d'ogn'altra cosa uederemo quel, ch'ello
sia, & perche sia cosi chiamato. Dico adunque che Contrapunto è quella Concordanza,
ò concēto, che nasce da un corpo, ilquale habbia in se diuerse parti & diuerse modulatio-
ni accōmodate alla cantilena, ordinate con uoci distanti l'una dall'altra per Interualli cō
mensurabili & harmonici; & è quello, che nel Cap. 12. della Seconda parte nominai Har
monia propria. Si può anche dire, che 'l Contrapunto sia un Corpo di harmonia, che
contenga in se diuerse uariationi de suoni, ò de uoci cantabili, con certa ragione di pro
portioni & misura di tempo; oueramente che 'l sia una certa unione arteficiosa de suoni
diuersi, ridotta alla concordanza. Dalle quali Definitioni potiamo raccogliere, che l'Arte
del Contrapunto non è altro, ch'una facultà, la quale insegna à ritrouar uarie parti
della cantilena, & à disporre i Suoni cantabili con ragione proportionata, & misura di
Tempo nelle modulationi. Et perche i Musici già (come uogliono alcuni) componeuano
i lor Contrapunti solamente con alcuni Punti; però lo chiamarono Contrapunto; perche
li poneuano l'uno contra l'altro; come facciamo al presente, che poniamo una Nota l'altra & pigliauano tal Punto per la Voce; conciosiache si come il Punto è princi-
pio della Linea, & è anco il suo fine, cosi il Suono, ò la Voce è principio & fine della
Modulatione; & tra essa è contenuta la Consonanza, della quale si fà poi il Contrapun-
to. Sarebbe forse stato più ragioneuole à chiamarlo Contrasuono, che Contrapunto;
percioch'un Suono si pone contra l'altro; ma per non partirmi dall'uso commune, l'
hò uoluto chiamar Contrapunto, quasi Punto contra punto, ouer Nota contra nota.
to. Il Semplice è quello, che ha le Modulationi composte solamente di Consonanze
& de Figure eguali, siano quali si uoglino, l'una contra l'altra; ma il Diminuito non
solo hà le parti composte di Consonanze, ma etiandio de Dissonanze, & in esso si
pone ogni sorte de Figure cantabili, secondo l'arbitrio del Compositore; & le sue modu
lationi sono ordinate per Interualli, ò spacii cantabili, & le Figure numerate secondo la
misura del suo Tempo. Il proprio del Contrapunto è d'ascendere & di discendere con
diuersi Suoni, ò Voci, per mouimenti contrari in un medesimo tempo, per Interualli
proportionati, che siano atti alla Consonanza; conciosiache l'Harmonia non nasce da al
tro, che dalla diuersità delle cose, che si pongono insieme, & sono tra loro opposte. E tan
to più il Contrapunto è giudicato diletteuole & buono, quanto più si usa con buona gra
tia, megliori modi, & con ornato & bel procedere; & questo secondo le Regole, che ri-
cerca l'Arte del bene & correttamente comporre. Bisogna però auertire, che l'Interual-
lo, nella modulatione, si piglia per il tacito passaggio, che si fà da un Suono, ò Voce all'
altro, ilquale è intelligibile, quantunque non si possa udire.
Dell'Inuentione delle Chiaui, & delle Figure cantabili.Cap. II.
per hauerne la verità, che in dispute & in opinioni; conciosiache concessi dall'
Auersario alcuni Principij, chiamati Premesse, si fà la Dimostratione, laquale
fà ogni cosa chiara, senza difficultà & risoluta; però uolendo uenire all'atto di
mostratiuo, fù bisogno di trouare il mezo da condur le Dimostrationi à i nostri sentimen
ti; accioche fussemo pienamēte capaci di esse. Onde si come i Mathematici, ueduto la ne-
cessità della cosa, ritrouarono alcune Cifere, nō però separate dalla materia; ancorache le
cōsiderino da essa lōtane, se nō in quāto all'esser loro, almeno secondo la ragione; ma si be
ne à lei congiūte, & furono Punti, Linee, Superficie, Corpi, Numeri, & molti altri Caratte
ri, che si depingono solamēte in carte cō alcuni colori, & le usarono in luogo della cosa si-
gnificata; cosi etiandio i Musici per poter ridurre in atto le loro speculationi & dimostra-
tioni, e porle sotto 'l giudicio del Sentimēto; poiche le Voci & li Suoni nō si possono per al
cun modo scriuere, ne depingere in carte, ne in altra materia; ritrouarono alcuni Segni,
ò Caratteri, i quali chiamarono Figure, ò Note; & li denominarono nel modo, che più
abbasso uederemo. Ma le Chorde de i loro Istrumenti, & le Voci delle cantilene denomi-
nauano con una di queste Sei syllabe poste in quest'ordine, Vt, Re, Mi, Fa, Sol, La; come
nel Cap. 30. della Seconda parte hò mostrato. Tale ordine poi chiamarono Deduttione,
ò Reduttione; laquale nō è altro, che una Trasportatione de uoci da un luogo all'altro; oue
ro (come dicono) vna Progressione naturale de Sei syllabe, che sono le nominate di sopra.
Ma perche tal Deduttione può hauere il suo principio in tre luoghi; come, nella chorda C,
nella F, & nella G; però Guido diuise il suo Introduttorio in tre parti, applicando le det-
te syllabe à tre Proprietà in tal maniera; che quando la prima delle dette syllabe (se-
guendo poi l'altre per ordine) incominciaua dalla lettera C, uoleua che tal'ordine, ò de-
duttione si cantasse per la proprietà, laquale chiama di Natura; & quando incominciaua
dalla lettera F, per quella del b. rotondo, ouer molle, che lo uogliam dire; ma quando ha-
page 182ueua principio dalla lettera G. uoleua che si cantasse per quella del
 . quadrato, ouer du-
. quadrato, ouer du-ro; & disse che la proprietà era una Deriuatione de più Voci, ò Suoni da un'istesso prin
cipio; ouer ch'era una Deduttione singulare, ò particolare di ciascun'ordinato Hexa-
chordo. La onde bisogna sapere, che Guido congiunse ogni Deduttione con uno de i
Tetrachordi Greci, aggiungendo à ciascun di loro due chorde di più dalla parte graue;
com'è quella dell'Vt, & quella del Re; percioche ogni Tetrachordo hauea principio nella
chorda del Mi; come nella Seconda parte fu commemorato, di maniera ch'ogni Hexa-
chordo contiene ciascuna specie della Diatessaron, che sono Tre; come uederemo al suo
luogo; & la sede ouero il luogo delle Voci, ò Suoni, il quale Musici nominano Chorde,
nominò Chiaui; le quali sono distante l'una dall'altra per linee equidistanti; intendendo-
ui però i Spacii di mezo; abenche le Voci, ò Suoni non siano equalmente distanti l'una
dall'altra. Onde collocò la prima chiaue, laquale nominò Gamma ut, nella linea, ouer
riga; & A re, che è la seconda nello spacio. Similmente collocò
 mi in riga, & C fa
mi in riga, & C fa ut in spacio, & di mano in mano collocò etiandio in tal maniera laltre; come si uedono
per ordine nell'Introdottorio nominato, segnando ciascuna con la sua propria lettera.
Ma perche alle uolte tal cosa poteua generar confusione, i piu Moderni; forse ricordan-
dosi, che in uano si fà alcuna cosa col mezo de più cose, che si può fare con poche & be-
ne; ritrouarono prima alcune Cifere, per lequali i Cantori s'hauessero à reggere; accio
che hauendone lasciate alcun'altre, per quelle solamente hauessero cognitione d'ogni
modulatione, & d'ogni cantilena, & da quelle hauessero notitia de i Spacij, ouero In-
terualli di Tuono, di Semituono, & de gli altri ancora. Le quali Cifere chiamarono
poi Chiaui; stando in questa similitudine, che si come per la Chiaue s'apre l'Vscio & si
entra in casa, & iui si uede quello, che ui è entro; cosi per tali Cifere s'apre la modula-
tione, & si conosce ciascuno de i nominati Interualli. Ma intrauerrebbe allora il contra
rio, quando fussero rimosse; percioche ogni cosa si empirebbe di confusione; come ogn'
uno si può imaginare. Nominarono poi le sudette Chiaui co i nomi, con i quali sono
notate nel sottoposto essempio. Di queste; se ben tallora alcune sono poste sopra una
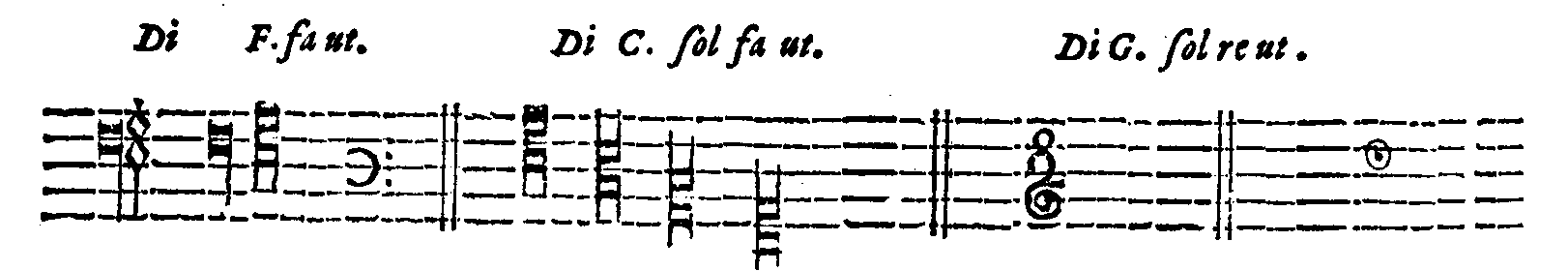
tere; cioè, per una Diapente. Ritrouarono etiandio quelle Cifere c'habbiamo com-
memorato di sopra per segnar i luoghi le Voci & de i Tempi delle loro Compositioni &
Contrapunti, & le nominarono, secondo che si uedono nominate in questo essempio.

Tempo imperfetto, la Massima ualesse due lunghe, la Lunga due breui, la Breue due se
mibreui, & cosi discorrendo; percioche nel Tempo perfetto, nel Modo, & nella Prola-
tione le considerarono in un'altra maniera; come uederemo. Ma secondo che uoglio-
no alcuni, la Breue fù madre & principio de tutte l'altre; conciosia che la Massima &
la Lunga furono ritrouate dopoi per il suo accrescimento, & la Semibreue con l'altre
page 183seguenti per la sua diminutione. Et se bene gli Antichi nelle loro Compositioni posero
altri segni & Cifere; come sono i Segni del tempo, del Modo, della Prolatione, Punti,
 quadrati, b rotondi, Diesis, Legature, Prese, Coronate, Ritornelli, & altri, che pos
quadrati, b rotondi, Diesis, Legature, Prese, Coronate, Ritornelli, & altri, che possono accascare; de i quali una buona parte ne adoperano anco i Moderni; nondimeno
non intendo parlare, se non de quelli, che faranno al proposito, & secondo che tor-
neranno commodi; imperoche principalmente intendo di trattar quelle cose, che sono
necessarie alle buone harmonie; & cadono sotto 'l sentimento dell'Vdito; il cui Sogetto
è ueramente il Suono; lasciando (per quanto potrò) da parte quelle, ch'à tal Sentimento
sono stranie & forastiere.
De gli Elementi, che compongono il Contrapunto.Cap. III.
gna auanti d'ogn'altra cosa conoscere gli Elementi, di che si compone, impe
roche Niuno saprà mai per modo alcun'ordinare, ò comporre alcuna cosa,
ne mai conoscerà la natura del composto, se primieramente non conoscerà le
cose, che si debbono ordinare, ò porre insieme, & la natura, ò ragion loro. La onde di-
co, che gli Elementi del Contrapunto sono di due sorti; Semplici & Replicati. I Sem-
plici sono tutti quelli Interualli, che sono minori della Diapason; com'è l'Vnisono (se-
guendo in ciò l'uso de i Prattici) la Seconda, la Terza, la Quarta, la Quinta, la Sesta,
la Settima, & l'Ottaua; cioè, essa Diapason. Et li Replicati sono tutti quelli, che sono
maggior di lei; come sono, la Nona, la Decima, la Vndecima, la Duodecima, & gli al
tri per ordine. Ne si debbe alcun marauigliare, c'habbia posto la Diapason tra gli Inter
ualli semplici; conciosia che non è ueramente Interuallo replicato, ne composto, come
forse alcuni pensano; imperoche è il primo tra gli altri Interualli; & (come afferma Boe-
tioMusicae li
br. 2. c. 17.) è la prima Consonanza. Er per essere il primo Interuallo non può esser composto;
essendo ch'Ogni composto è sempre dopo le parti, di che si compone; & la Diapason è
prima, & ogn'altro Interuallo è dopo lei. Et questo si uede; percioche hà la sua forma
dalla proportion Dupla, laquale è la prima della Inequalità; & l'altre Consonanze, ò In
terualli hanno le lor forme dalle proportioni, che seguono la Dupla, che sono (com'al-
troue hò dettoSecunda
part. c. 48.) le Parti della forma della Diapason, che nascon dalla sua diuisione. Es-
sendo adunque la Diapason prima; non si può dire, che ella sia composta; percioche sareb
be dibisogno, che fusse composta d'Interualli più semplici & primi, che non è il suo. Ne
anco potiamo dire, che si componi de più Vnisoni; come alcuni sciocchi hanno hauu-
to parere; percioche non sono gli Vnisoni (come uederemo) Interualli; ma sono com'è
il Punto, ch'è un minimo indiuisibile, che non si può continuare con un altro punto; co
me proua Aristotele nella Fisica.,Lib. 6. c. 2. Et à chi dimandasse in qual maniera nasce la Diapason
si potrebbe rispondere senza errore alcuno, che nasce quasi all'istesso modo, che nasce la
Linea; la è la prima Quantità diuisibile. Essendo adunque prima tra gli Interualli
musicali, & non si potendo comporre d'Vnisoni, ne d'altri Interualli quantunque
minimi; si può concludere, ch'ella sia semplice, & senza compositione; & essendo
prima, ch'ella sia Madre, genitrice, fonte, & principio, dal quale deriua ogn'altra
Consonanza, & ogn'altro Interuallo; conciosia che Quello ch'è primo, sempre è cagio-
ne di quello, che uien dopoi, & non per il contrario. Et si come diciamo, che dall'Equa
lità hà principio la Inequalità; cosi bisogna dire, che dall'Vnisono habbia principio la
Diapason; percioche dalluna hà la sua forma l'Vnisono, & nell'altra si ritroua la forma
della Diapason. Et tanta è l'amicitia, c'hanno insieme questi due, che per la lor simiglian
za & semplicità, quasi allistesso modo è mosso l'Vdito da i suoni della Diapason, co-
me è mosso da quelli dell'Vnisono. Et ciò auiene primieramente dalla simiglianza,
page 184c'hanno insieme; percioche ogni generante sempre genera il generato simile à se; &
dopoi, perche l'uno & l'altra sono Principij; cioè, l'Vnisono per la Equalità, dalla
quale hà principio l'Inequalità; & la Diapason, ch'è prima d'ogn'altra Consonan-
za, per la Dupla, dalla quale hà principio l'altre Proportioni della Inequalità. Et è in
tal maniera semplice la Diapason, che se ben è contenuta da due Suoni diuersi per il si-
to, dirò cosi; paiono nondimeno al senso un solo; percioche sono molto simili; & ciò
auiene per la uicinità del Binario all'Vnità, che sono contenuti ne gli estremi della sua
forma, che è la Dupla: Onde tal forma contiene due principij; l'Vnità, ch'è principio
de i Numeri, & è quella, che tra loro non si può diuidere; & il Binario, che è il prin-
cipio della congiuntione delle Vnità; & è il minimo numero, che diuidere si possa; &
dalla Vnità è misurato due uolte solamente; ma non si può diuidere in due numeri; per
che non contiene in se altro numero, che l'Vnità replicata. Onde, si come il Binario hà
quasi l'istessa natura, che hà l'Vnità, per esserle uicino; cosi la Diapason hà quasi la na-
tura istessa dell'Vnisono; si per esserli uicina; come si scorge ne i termini delle loro for-
me; come etiandio, perche gli estremi delle lor proportioni non sono composti d'altri
numeri, che della Vnità; di modo che imitando lo Effetto la natura della sua Cagione;
& essendo i Numeri harmonici cagione de gli Harmonici suoni; è cosa ragioneuole, che
il Suono imiti anco la natura loro, & che i detti due suoni della Diapason parino un so-
lo. Tale semplicità anco si conosce chiaramente, quando s'aggiunge dalla parte graue,
ouer dall'acuta di essa Diapason alcun'Interuallo, che sia consonante, ò dissonante, per
cioche allora pare, che sia congiunto quasi ad un solo Suono. La onde uediamo, che la
Diapasondiapente muoue l'Vdito quasi all'istesso modo, che fà la Diapente; cosi la Dia
pason col Ditono, come fà il Ditono solo. Et tanto udimo esser dissonante la Diapason
col Tuono, quanto è il Tuono, & quasi all'istesso modo l'uno & l'altro mouere il Senti-
mento; ilche si potrebbe dire dell'altre ancora; & ciò non può accascare in alcun'altra
Consonanza; com'è manifesto; conciosia che non sono tanto semplici, quanto è la Dia-
pason; ilche è chiaro da conoscere; imperoche se noi aggiungeremo il Ditono al Semi-
ditono, gli estremi di tale aggiuntione produrranno la Diapente. Simigliantemente se
noi congiungeremo due Diapente, due Diatessaron, due Ditoni, due Semiditoni, ouer
due altri simili in proportione; oltra i Suoni diuersi, che s'udiranno nelle lor chorde estre
me, l'Interuallo (come habbiamo dimostrato nella Seconda proposta del Secondo Li-
bro delle Dimostrationi) sarà etiandio dissonante; conciosia che luno & l'altro estremo
di qualunque Interuallo, non hanno alcuna ragione, ne simiglianza d'un'istesso Suo-
no; come quelli della Diapason. Et de qui nasce, che le Consonanze semplici, che so-
no poste oltra la Diapason, hāno quella simiglianza, c'haueano, quando erano simplici
& erano tra gli estremi di essa Diapason. Et hò detto semplici; percioche si uede, che
ciascun'altra, ch'è collocata oltra la Diapason, nasce in un certo modo, che pare, che
da una di quelle semplici habbia la sua origine. La onde si uede uerificar quello, ch'io
dissi nella Prima parte,Cap. 17. che le Consonanze, & le Dissonanze hanno quasi quell'istessa ra-
gione nel moltiplicarsi, di quello c'hanno i semplici Numeri oltra 'l Denario; impero-
che si come oltra esso non si uede aggiungere di nuouo altro numero, ma solamen-
te replicarsi uno de quelli, ch'è minore di lui; essendo che aggiunta la Vnità, che è pri-
ma, al Denario nasce l'Vndenario; dopoi aggiunto il Binario, nasce il Duodenario; si-
migliantemente aggiunti il Ternario & gli altri per ordine, si generano i Numeri, che so
no simili nella lor terminatione à quei semplici, che s'aggiungono; cosi anco, oltra la
detta Diapason, non s'aggiunge alcun Suono di nuouo; ma si bene quell'istessi, che
si contengono tra essa; i quali essendo finiti, si ritorna sempre circolarmente à i pri-
mi. La onde si può concludere per le ragioni addotte, che la Diapason si dee ue-
ramente chiamare Interuallo semplice, & non replicato, ò composto; atteso che è co-
me Elemento di ciascun'altra consonanza & interuallo. Seguendo adunque il costu-
me de i Prattici diremo, che gli Elementi semplici, ouer (come dicono) le Specie sempli
page 185
ci del Contrapunto sono Sette, & non più; lasciando fuori l'Vnisono; percioche non è
ne Consonanza, ne Interuallo; il che al suo luogo uederemo; come è la Seconda, la

solamente al Numero delle chorde, poste nel Monochordo del Cap. 44. della Seconda
parte, & non à gli Interualli. Da queste poi nascono le Raddopiate, che chiamano Com
poste; le quali hò posto nell'essempio, acciò si possa uedere, di che natura, & à quali
delle Semplici siano sottoposte, & s'assimigliano. De queste, dopo ch'io haurò mostra-
to la differenza, & la proprietà; uerrò à dimostrare, in qual maniera si habbiano à por-
re ne i Contrapunti. Ma si debbe auertire, che si chiamano Specie; percioche si come
la Specie è nominata da PorfirioPraedicab.
Cap. 2. quella Forma, ò Figura, che contiene in se qualunque
cosa, & è contenuta sotto alcun genere; come si suol dire; che l'Huomo è Specie dell'Ani-
male; il Bianco & il Nero del Colore, & il Triangolo & il Quadrato della Figura; cosi le
mostrate si nominano Specie, perche ciascuna de loro hà la sua propria forma, & è sot-
toposta à questo genere Interuallo.
Diuisione delle mostrate Specie.Cap. IIII.
il parer di Tolomeo, Harmoni.
lib. 1. cap.
4. chiama alcune delle Voci, ò Suoni tra se Vnisone, &
alcune Nonunisone. Quelle prima nomina Vnisone, che ciascuna da per sè,
ouero aggiunte insieme fanno un'istesso Suono. Dopoi diuide quelle, che
non sono Vnisone, & fà molte parti ponendone alcune Equisone, alcune Consone, al-
tre Emmeli, & alcune Dissone; & pone etiandio ultimamente le Ecmele molto diffe-
renti da queste. Quelle primieramente chiama Equisone, che percosse insieme, dal
temperamento & mistura loro, de due Suoni differenti, che sono, fanno ad un certo
modo un Suono semplice; com'è quello della Diapason, & quello della Disdiapason an-
cora; ma Consone nomina quelle, che quantunque facino un Suono composto, ò mi-
sto, che dir lo uogliamo, è nondimeno soaue; com'è quello della Diapente, & etiandio
quello della Diatessaron, & di quelle, che di queste due & dell'Equisone sono composte;
come quello della Diapasondiapente, & quello della Diapason diatessaron. Emmeli
poi chiama quelle, che non sono Consonanti; ma si possono accommodare ottimamen-
te alla Melodia; & sono quelle, che giungono insieme le Consonanze, & tra loro si pos-
sono porre; com'è il Tuono, ilquale è la differenza, che si troua tra la Diapente & la Dia
tessaron; per il quale di Consone che sono, si congiungono insieme Equisone in una Dia
pason. Cosi anco si possono nominare Emmeli le semplici parti de queste consonanze, le
quali se bene non sono consonanti, si possono nondimeno accommodar bene alla Melo
dia. Chiama dopoi Dissone quelle, che nō mescolano insieme alcun Suono, che sia grato;
ma feriscono amaramente & senz'alcuna soauità il nostro Sentimento. Vltimamente no
mina Ecmeli quelle, che non entrano nella cogiuntione delle Consonanze; come sareb-
be dire (per dar'uno essempio) il Diesis enharmonico, ch'alcuni poco intelligenti di quel
lo, che habbia uoluto dir Boetio, l'hanno posto nel Numero delle Emmeli; & altri Inter-
ualli simili, che non si possono aggiungere con altri, che giunghino insieme alcune Con-
nāze. Questa è la diuisione, che fà Tolomeo di cotali Specie, recitata da Boetio; ma io per
seguir l'uso commune, & per schiuar la difficultà, che potrebbe nascere, la diuidero sola-
page 186mente in due parti; in Consonanti, & in Dissonanti. Le Consonanti saranno la Terza,
La Quarta, la Quinta, la Sesta, la Ottaua, & le Replicate, ò Composte; & le Dissonanti
saranno la Seconda, la Settima, & tutte quelle, che si compongono di una di queste &
della Ottaua. Et perche nella Seconda parte habbiamo ueduto quello, ch'è Conso-
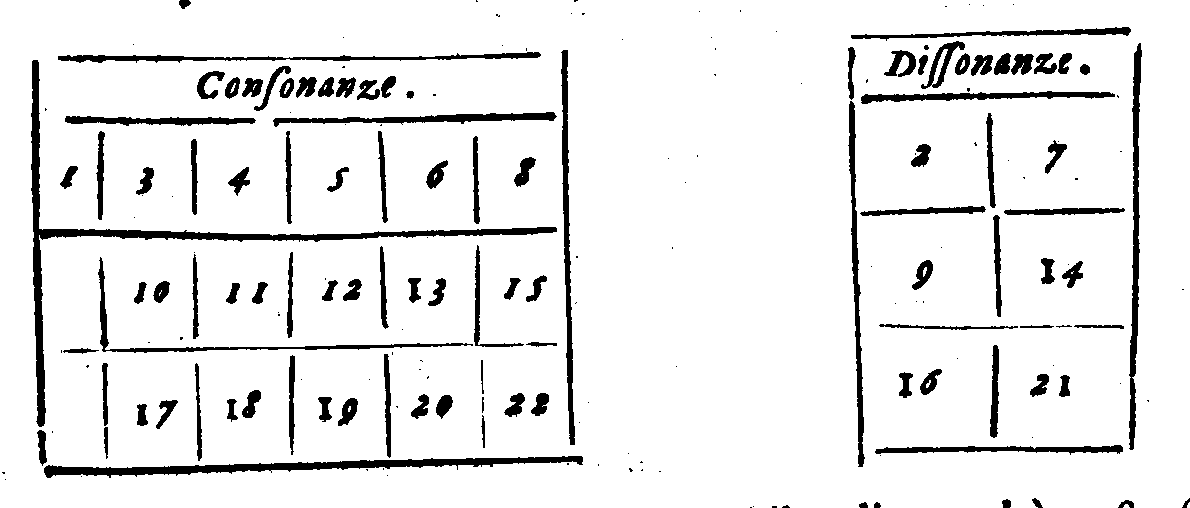
Diuisione in essempio; accioche più facilmente si scorga in esso quello, che si è detto.
Se la Quarta è Consonanza; & donde auiene, che i Musici non l'hab-
biano usata, se non nelle Compositioni de più uoci.
Cap. V.
ro delle Consonanze; poi che fin'hora da i Prattici sia stata collocata tra le
Dissonanze. Onde, accioche di tal cosa si habbia qualche notitia, si dè auer
tire; che la Quarta ueramente non è Dissonanza, ma Consonanza; come
si può prouare in tre modi; prima per l'Autorità de i Musici antichi, la quale non è da
sprezzare; dopoi per Ragione; & ultimamente per essempio. Per l'autorità de gli An-
tichi prima; percioche da ogni dotto Scrittore Greco & Latino è collocata tra le Con-
sonanze. Tolomeo (lasciandone molti altri più antichi di lui) in molti luoghi de gli Har
monici, & specialmente nel Cap. 5. del Primo libro, la nomina Consonzanza. Il mede-
simo fà Boetio nella Musica molte fiate, & massimamente nel Cap. 7. del Primo libro,
& nell'Vndecimo del Quinto. Et Dione historico nel Lib. 37. con l'autorità de i più an-
tichi di lui, la chiama Harmonia. Euclide nel Cap. Primo; & Gaudentio filosofo nel
Cap. 7. de i loro Introdottorii. Macrobio nel Primo capitolo del Secondo libro del So
gno di Scipione la connumera tra le Consonanze. Vitruuio anco nel Cap. 4. del Quin-
to libro della Architettura è di parere, ch'ella sia Consonanza; & Censorino in quello,
che scriue à Q. Cerellio, hà l'istessa opinione. Si proua dopoi per ragione in cotal modo:
Quell'Interuallo, che in una compositione harmonica si ode consonare perfettamente;
posto da per sè, non può essere à patto alcuno dissonante: Essendo adunque la Diates-
saron, ò Quarta di tal natura, che accompagnata con la Quinta in una harmonica com
positione, rende soaue & harmonioso concento; seguita ch'ella sia anco fuori della com
positione consonante; cioè, quando è posta sola. L'Assonto di tal ragione è manifesto
per il suo contrario; cioè, per le dissonanze, che sono la Seconda, & la Settima, con le
loro Replicate; le quali non essendo nella compositione per alcun modo consonanti, so-
no etiandio fuori della compositione dell'istessa natura; com'è manifesto. Oltra di ciò
si proua per un'altra ragione. Quello, che hà Ragione de numeri nell'acuto & nel gra-
ue è consonante; com'è manifesto per la definitione del Filosofo posta nel Cap. 13. del-
la Seconda parte; la onde hauendo la Quarta cotal ragione, è manifesto, ch'ella sia con
sonante. Et questa propositione minore si proua per Giouanni Grammatico detto Fi-
page 187lopono sopra la Definitione data dal Filosofo nel Lib. 2. de i Posteriori, ilquale chiama
la Sesquiterza, ch'è la sua uera forma, Ragion de numeri. Ma perche gli essempii ua-
gliono più appresso alcuni, che l'autorità & le ragioni; però è necessario uenire alla ter-
za proua. Onde dico (lasciando di replicare in questo luogo quello, ch'io dissi sopra
la Decima definitione del Secondo delle Dimostrationi in questo proposito) che, quan-
do tal Consonanza si ridurrà in atto, nella sua uera proportione ouer'Interuallo, ogn'
uno di sano giudicio dirà sempre, che ueramente è Consonanza; & di questo ogn'uno
da sè potrà farne la proua, accordando un Liuto, ouero un' Violone perfettamente;
imperoche tra la chorda, che chiamano il Basso, & quella, che nominano Bordone; oue
ramente tra questa & quella, che chiamano il Tenore; & tra quell'altre tre chorde, che
sono più acute, udirà che la Diatessaron, ò Quarta farà marauiglioso concento. Et se
pure alcuno uorrà dire, ch'ella sia dissonante, questo auerrà, perche seguirà l'uso de i
Prattici, i quali non sapendo addur ragione alcuna, à gran torto cosi la chiamano, & la
separano dal numero delle Consonanze; ponendola tra le Dissonanze; ma in fatto non
è cosi; percioche quando si riducono ad udirla sopra alcun'Istrumento, che sia accordato
perfettamente, s'acchetano. Et se fusse ueramente dissonante, come dicono, non la usareb
bono nelle compositioni; & similmente i moderni Greci non la porrebbono ne i lor Can
ti à più uoci; i quali si odono qui in Vinegia ogni giorno solenne nella lor Chiesa, ne i lor
Canti ecclesiastici; ne i quali cantano essa Diatessaron nella parte graue, senza porre per
sua base (dirò cosi) alcun'altra Consonanza. Qui dirà forse alcuno; da che nacque adun-
que, che i nostri Prattici la posero nel numero delle Dissonanze? Penso che questo na-
scesse, per la discordia, ch'era tra i Pitagorici & Tolomeo; perche quelli uolendo, che
ciascuno Interuallo, il quale fusse contenuto da altro Genere di proportone, che dal
Molteplice & Superparticolare; come molte fiate hò detto; non fusse atto, à far Con-
sonanza alcuna; non acconsentiuano, che la Diapasondiatessaron, contenuta dalla pro
portione Dupla superbipartienteterza, fusse consonante; ancora che Tolomeo si sfor-
zasse di mostrare, che era il contrario, adducendo (come sopra la Quarantesima del Se-
condo delle Dimostrationi habbiamo ragionato) tal ragione: Che si come la Diatessa-
ron semplice è consonante, cosi aggiunta all'Ottaua, l'estreme chorde di tale aggiuntio-
ne non possono esser dissonanti; imperoche quei Suoni, che s'aggiungono alla Diapa-
son, si uedono esser aggiunti quasi ad un Suono solo; come (per quello che mostra Boe
tioMusic lib.
5. cap. 19.) è la natura di tal Consonanza. Onde vedendo i Musici Latini la lite, ch'era tra co-
storo, & parendoli che le ragioni che adduceuano erano buone; non uolsero far giudi-
cio determinato di questa cosa; ma per non dare una certa libertà di por nelle cantile-
ne questa Consonanza & la sua semplice senza qualche consideratione, le separarono
dal numero & ordine dell'altre; non perche ueramente siano dissonanti; percioche non
hauerebbono comportato, che fussero poste nelle compositioni; ma accioche si haues-
sero à porre con qualche buon'ordine, & con giudicio. Et che questo sia uero, si può
uedere; che quelli c'hanno hauuto qualche giudicio nella Musica, l'hanno usata, non
solamente accompagnata con altre Consonanze, ma etiandio senz'alcuno accompa-
gnamento ne i canti de due uoci; tra i quali fu uno Giosquino, che nel principio di
quella parte; Et resurrexit tertia die, della Messa detta l'Homme armè à quattro uoci, po-
se tal consonanza semplicemente, senz'accompagnarle alcun'altro Interuallo dalla parte
graue; il che si può etiandio uedere in molte altre cantilene antiche & moderne, le quali
non pongo per non fastidire il Lettore. Et benche tali Consonanze si ritrouino esser po
ste in opera rare uolte; nondimeno si uede, che le usarono; & se hauessero hauuto opi-
nione, che fussero state dissonanti, credo, che non le hauerebbono usate. Hora da
quello, che si è detto, si può comprendere, che la Quarta, & le Replicate sono conso-
nanti, & per qual cagione i Musici le collocarono tra quelli Interualli, che sono disso-
nanti. In qual maniera poi ella si dica Perfetta, & in qual modo si habbia à porre nelle
Compositioni, lo uederemo al suo luogo. Ma la Diapason diatessaron qual Conso-
page 188nanza ella sia, & come s'accordi l'opinione de Pitagorici, con quella di Tolomeo;
ciascheduno che uedrà la sopranominata Quarantesima proposta del Secondo lo po-
trà sapere.
Diuisione della Consonanze nelle Perfette, & nelle Imperfette.Cap. VI.
no Perfette, & alcune Imperfette; Le Perfette sono l'Vnisono, la Quarta,
la Quinta, la Ottaua, & le Replicate; ancora che AristoteleProbl. 18.
parti. 19. attribuisca tal
perfettione all'Ottaua solamente; & per certo è uero; conciosia che la Quar-
ta & la Quinta sono mezane tra la perfettione & la imperfettione; come uederemo;
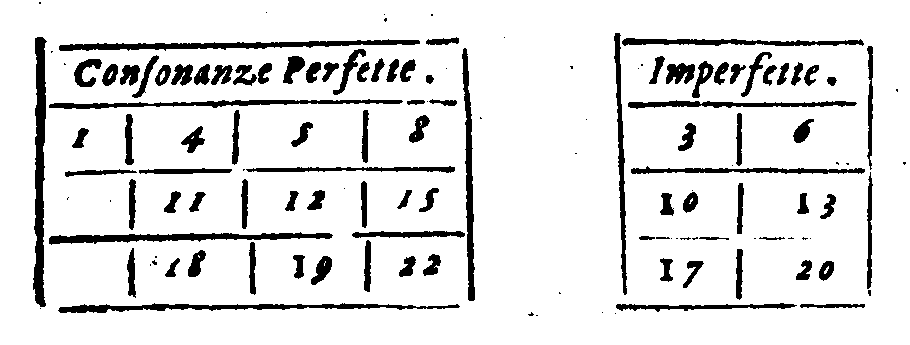
& quelle, che nascono da queste ag-
giunte alla Ottaua; come nell'essem-
pio si uedono. Et dicono le prime
esser perfette, forse perche hanno la
lor forma dalle proportioni contenu
te tra le parti del numero Quaterna-
rio nel genere Moltiplice, & nel Su-
perparticolare; tra 4. 3. 2. 1. il qual numero (come altroue hò dettoPars. 2. c. 2.) appresso i Pita-
gorici era tenuto Perfetto; dalle sue parti aliquote & non aliquote, che
sono i quattro mostrati numeri, risultaua un'altro numero, ilquale medesimamente chia
mauano Perfetto, ch'è il Denario. Ma in uero le nominarono Perfette; per che po-
ste da per sè, oueramente accompagnate ad altre Consonanze hanno possanza al primo
apprenderle, che fa il Sentimento, di acchetarlo & satisfarli à pieno, quando da loro è
mutato; imperoche mentre se ne ode una posta nel graue, ouer nell'acuto, contenu-
ta nella sua uera forma, si fortifica l'Vdito, & fà che niente desidera più oltra, che faccia
alla sua perfettione, & la faccia più soaue & più grata. Ne altra differenza si ritroua tra
le dette Consonanze poste nel graue, di quello che si troua, quando sono poste nell'acu
to; se non che quelle, che sono poste nell'acuto, feriscono più uelocemente l'Vdito,
che non fanno quelle, che sono poste nel graue; per le ragioni dette nel Cap. 11. della
Seconda parte; percioche sono contenute da una istessa proportione: ma l'altre chiama-
rono Imperfette; conciosia che hanno la forma loro dalle proportioni, i cui termini sono
contenuti da numeri, che si ritrouano oltra il Quaternario, che sono 6. 5. 4. Onde il Di-
tono nasce dalla proportione Sesquiquarta, & il Semiditono dalla proportione Sesqui-
quinta, nel genere Superparticolare. Questi due Interualli aggiunti alla Diatessaron ge
nerano due Hexachordi; l'uno il Maggiore, & l'altro il Minore, le cui proportioni han-
no luogo nel genere Superpartiente, dalla Superbipartienteterza, & dalla Supertripar-
tientequinta; come nella Prima parte hò dichiarato;Cap. 16 lequali (secondo il parer de i Pi-
tagorici) non fanno Consonanza. Et sono queste di tal natura, che poste in essere da
per sè nelle loro forme, non hanno possanza di acchetare l'Vdito, di modo, che non desi
deri altro Suono più grato, più dolce & più soaue; come è manifesto à tutti coloro, che so
no periti nella Musica; ma si bene quando sono accompagnate con altri Interualli in tal
maniera, che gli estremi della compositione faccino una Cōsonanza perfetta, ouero una
delle Imperfette replicate; come uederemo altroue. Et benche costoro faccino tal dif-
ferenza; nondimeno tutte si possono chiamar Perfette, quando sono contenute nella
uera & naturale forma loro; cioè, nella loro propria proportione. Ma quali siano i
lor ueri & naturali luoghi nell'Ordine delle Consonanze, leggendo accuratamente quel
lo, ch'io hò discorso nel principio delle Dimostrationi, & nel Cap. 5. del 3. lib. de i Sop
plimenti; sarà manifesto.
page 189
Che la Quinta & la Quarta sono mezane tra le Consonanze perfette & l'Im-
perfette.Cap. VII.
nanze perfette; nondimeno l'Ottaua è solamente perfetta, & la Quinta men
perfetta dell'Ottaua, & la Quarta men perfetta della Quinta. Onde si può di-
re, che cosi come quella cosa, la quale è più uicina alla sua origine, ouero alla
sua cagione, ritiene maggiormente la natura di quella, & è più perfetta in quel genere,
che non sono quelle, che le sono lontane; come si uede nella Luce; che quella parte, la
quale è più uicina alla sua origine & alla sua cagione, ch'è il Sole, hà più chiarezza, &
risplende più eccellentemente, & è più perfetta di quella, che l'è piu rimota, ò lontana;
cosi quella Consonanza, la quale è più uicina alla sua cagione, & alla sua origine, ch'è
l'Vnisono, il quale è contenuto nella proportione della Equalità, & nelle Voci Vniso-
ne, è maggiormente perfetta d'ogn'altra Consonanza; & questa è la Ottaua, la quale
hà la sua forma dalla Dupla, ch'è la più uicina alle proportioni della Equalità, & è con-
tenuta tra le voci Equisone, che sono più uicine alle Vnisone; come di sopra habbiamo
ueduto. Onde la potiamo chiamar Più semplice & più perfetta d'ogn'altra Consonan-
za. Dico più semplice & più perfetta; percioche Qualunque uolta si ritroua una dispo-
sitione, che riceui il più & il meno, & denomini formalmente la cagione & l'effetto, &
conuenga cotal cosa all'Effetto, per la Cagione; sempre si denominerà primieramente
la Cagione semplicemente; & dopoi l'Effetto si denominerà, ouero si dirà tale, ad un
certo modo; & questo in tutti i generi delle cagioni. La onde dico; Quella cosa, che per
un'altra è tale, quella che n'è cagione, è detta maggiormente tale. Però, si come di-
ciamo, essendo la mano calda per il fuoco, il fuoco esser maggiormente caldo; cosi di-
ciamo, essendo l'Ottaua semplice per l'Vnisono, che l'Vnisono è maggiormente sem-
plice. Ma perche l'Vnisono non è considerato dal Musico come consonante, ma come
principio della Consonanza, però parlando delle Consonanze diciamo, che l'Ottaua
semplicemente è semplice, la prima & la più perfetta d'ogn'altra Consonanza; & in fat-
to è cosi; percioche da lei ogn'altro Interuallo hà il suo essere, & diciamo perfette le al-
tre consonanze, non semplicemente, ma ad un certo modo. La onde essendo la Quin-
ta piu uicina all'Ottaua, che non è la Quarta; diciamo, che la Quarta è men perfetta
della Quinta; percioche la sua proportione è piu lontana dalla proportion Dupla, ch'è
il principio dell'Inequalità, & cagione d'ogn'altra proportione. Similmente diciamo,
che la Quarta è più perfetta, che non è il Ditono, & questo più perfetto del Semiditono;
conciosia che la Sesquialtera, ch'è la forma della Diapente, è contenuta tra 3 & 2. & è
più uicina alla Dupla, la quale è la forma della Diapason, contenuta tra questi termini
2 & 1. ilche si può dire anco dell'altre. Ma se il principio d'alcuna cosa è piu perfetto di
quelle cose che seguono dopo; non è cosa ragioneuole, che noi diciamo, che la Quinta,
ò la Quarta siano equali nella perfettione all'Ottaua; percioche da essa Ottaua dipendo-
no. Et ben ch'io habbia detto, che la Quinta & la Quarta, con le lor Replicate siano Con
sonanze perfette; secondo il mostrato modo; nondimeno la Ottaua solamente, & le Repli
cate sono semplicemente perfette; essendo che non se le può aggiungere; ne leuare alcuna
cosa; cioè non si possono accrescere, ò diminuire d'Interuallo, fuori delle lor uere & le-
gittime proportioni per modo alcuno, se non con grande offesa dell'Vdito. Essendo poi
la Quinta, la Quarta, & le Replicate sottoposte à cotal passione; come nel Cap. 42. del-
la Seconda parte hò mostrato; però dico, ch'elle sono mezane tra le Consonanze per-
fette & le imperfette; oueramente mezane tra la perfettione & la imperfettione. Et
perche etiandio quelle, che si chiamano Imperfette, à ciò sono sottoposte; però si pos-
sono chiamare non solo Imperfette, ma anco Imperfettissime; poiche oltra l'imperfet-
page 190tione, che si ritroua in loro al modo detto, si possono anco accrescere & minuire, nel
modo che si fà la Quinta & la Quarta.
Quali Consonanze sino più piene, & quali più uaghe.Cap. VIII.
sonanza uaga; onde mi pare, inanti che si uada più oltra, di uoler dire, quel,
ch'importino, & quali siano tali Consonanze. Però è da auertire, che i Mu-
sici rare uolte hanno usato questi due termini, senza aggiungerli l'una de que-
ste due particelle; Piu, ò Meno; onde hanno detto, Consonanza piu piena, ò piu
uaga, & Consonanza men pienza, ò men uaga; hauendo hauuto sempre rispetto ad un'
altra Consonanza. La onde chiamano piene quelle Consonanze, le quali hanno mag-
gior possanza d'occupar l'Vdito, con Suoni diuersi; perilche si può dire, che la Quinta
sia piu piena della Ottaua; percioche i suoi estremi occupano maggiormente & con piu
diletto l'Vdito con diuersi Suoni, che non fanno gli estremi della Ottaua, i quali sono
equisonanti, & s'assimigliano l'un l'altro. Di modo che lasciando da un canto essa Otta-
ua, tutte l'altre si dicono esser piu piene l'una dell'altra, in quanto l'una hà maggior for-
za di contentare l'Vdito; come sono quelle, che sono piu uicine al loro principio, &
hanno maggior perfettione de tutte l'altre. Si che de qui si può cauare una Regola; che
Tutte quelle, che sono di maggior proportione sono piu piene, lasciando (come hò det-
to) da un canto la Ottaua, & le Replicate anco. Quelle poi chiamano piu uaghe, le qua
li sono contenute da minori proportioni. Et è cosi in fatto, massimamente quando sono
collocate à i loro proprij luoghi; conciosia che quelle Consonanze, c'hanno le lor pro-
piu uicine alla Dupla, per loro natura amano la parte graue, come proprio
luogo, & uengono ad esser piu piene di quelle, che hanno cotali proportioni piu lontane
da essa Dupla; imperoche queste sono di minor proportione, che non sono le prime, &
per loro natura amano l'acuto. Onde poste à i luoghi proprii, uengono ad esser men pie-
ne & piu uaghe dell'altre; percioche stando nell'acuto, per la uelocità de i mouimenti
penetrano piu uelocemente l'Vdito, & con maggior diletto, si fanno udire. Et tanto piu
sono uaghe, quanto piu si partono dalla semplicità, della quale i nostri sentimenti non
molto si rallegrano, poi che amano maggiormente le cose composte, che le semplice, &
s'accompagnano ad altre Consonanze. Per la qual cosa intrauiene all'Vdito intorno i
Suoni, udendo le Consonanze prime, quello, che intrauenire al Vedere intorno
à i principali Colori, de i quali ogn'altro color mezano si cōpone; che si come il Bianco, &
il Nero li porgono minor diletto, di quello che fanno alcuni altri colori mezani & misti;
cosi porgono minor diletto le Consonanze principali, di quello che fanno l'altre, che so-
no men perfette. Et si come il Verde, il Rosso, l'Azuro, & gli altri simili piu gli diletta-
no, & tanto piu si dimostrano à lui uaghi; percioche sono lontani da i principali; che non
fà il colore, che chiamano Roano, ouero il Beretino, de i quali l'uno è piu uicino al
Nero, & l'altro al Bianco; cosi l'Vdito piu si diletta nelle Consonanze, che sono piu lon
tane dalla semplicità de i Suoni; conciosia che sono molto piu uaghe, di quelle che le so-
no piu uicine. Et quasi all'istesso modo si diletta l'Vdito della compositione de i Suoni,
che fà il Vedere della compositione de i Colori; poiche la compositione de i Colori, oue
ro che non può esser senza qualche harmonia, ouero che hà con l'harmonia qualche con
uenienza; essendoche l'una & l'altra si compone di cose diuerse. Onde potiamo dire,
che si come le dette Consonanze maggiori sono piu piene, che non sono le minori; cosi
le minori sono piu uaghe, di quello che sono le maggiori; & tanto piu si rendono sono-
re & grate all'Vdito, quanto sono poste ne i luoghi loro proprii; come al di-
remo. Si potrebbe anco dire, che nell'istesse perfette la Quinta è piu uaga della Ottaua,
& la Quarta piu uaga della Quinta; com'è manifesto; percioche sono piu lontane dalla
page 191Equalità; poiche etiandio le Consonanze perfette non sono priue di tal uaghezza; ma
questo basti; percioche quali siano i ueri & naturali luoghi delle Consonanze, coppiosa-
mente nel principio del Primo delle Dimostrationi ne hò à sufficientia ragionato.
Della Differenza, che si troua tra le Consonanze Imperfette.
Cap. IX.
differenza; che quelle, che sono d'una istessa denominatione, alcune sono
maggiori, & alcune minori. Le maggiori sono quelle, i cui estremi sono
contenuti da proportioni maggiori, & da maggiori interualli; & sono il Di-
tono; & l'Hexachordo maggiore; de i quali il primo si chiama Terza, & il secondo Sesta,
& l'una & l'altra maggiori. Et le minori sono quelle, che sono di proportione minore, &
hanno minor interuallo; & queste sono il Semiditono, ilquale chiamano Terza minore;
& l'Hexachordo minore, chiamato Sesta minore. Et se ben disopra hò nominato le dette
Consonanze col nome semplice di Terza, & di Sesta, senza fare alcuna mentione di
maggiore, ò di minore; & hora gli aggiungo tali differenze; l'hò fatto per seguire il mo
do, che tengono i Prattici, & per poterle ridurre prima sotto un Genere, & mostrar do-
poi le loro Specie, & le loro Differenze; accioche da i Prattici (à i quali uoglio in que-
ste due parti satisfare quanto io posso) siano conosciute; percioche da loro non sono al-
tramente nominate. E' ben uero, che tra loro pongono la differenza di Maggiore &
di minore; come di sopra si è detto, & come qui sotto sono notate.
| Consonanze imperfette Maggiori. | Consonanze imperfette Minori. |
| Ditono, ò Terza maggiore. | Semiditono, ò Terza minore. |
| Hexachordo, ò Sesta maggiore. | Hexachordo, ò Sesta minore. |
| Et le Replicate. | Et le replicate. |
nanze imperfette; nondimeno le Specie, ouer Interualli dissonanti anco possono haue-
re tal differenza; ancora che non siano considerati dal Musico, se non in quanto hanno
ragione d'Interuallo; come altroue uederemo; percioche la Seconda è di due sorti ap-
presso i Prattici; cioè, il Tuono maggiore, ò minore, & il Semituono; onde si può dire
Seconda maggiore, & Seconda minore. Et la Quarta è di tre sorti; cioè, la Diatessa-
ron consonanza, il Tritono, ch'è una compositione di tre Tuoni; & la Semidiatessaron,
ch'è una compositione di un Tuono & di due Semituoni; i quali due Interualli ne i loro
estremi sono dissonanti. Questo istesso si potrebbe etiandio dire della Quinta, della Ot-
taua, & delle Replicate, le quali si lasciano per non andare in lungo.
Della Propietà, ò Natura delle consonanze Imperfette.Cap. X.
uiue & allegre, accompagnate da molta sonorità; & alcune, quantunque
siano dolci & soaui, declinano alquanto al mesto, ouer languido. Le prime
sono le Terze & le Seste maggiori, & le Replicate; & l'altre sono le minori.
Tutte queste hanno forza di mutare ogni cantilena, & di farla mesta, ouero allegra, se-
page 192condo la sua natura. Ilche potiamo uedere da questo; che sono alcune Cantilene, le
quali sono uiue, & piene d'allegrezza, & alcune altre per il contrario, sono alquan-
to meste, ouer languide. La cagione è, che nelle prime, spesso si odono le Maggiori
consonanze imperfette sopra le chorde estreme finali, ò mezane de i Modi, ò Tuoni,
che sono il Primo, il Secondo, il Settimo, l'Ottauo, il Nono, & il Decimo; come ue-
deremo altroue; i quali Modi sono molto allegri & uiui; conciosia che in essi udimo spes-
se fiate le Consonanze collocate secondo la natura del Numero sonoro; cioè, la Quin-
ta tramezata, ò diuisa harmonicamente in una Terza maggiore, & in una minore; il
che molto diletta all'Vdito. Dico le Consonanze esser poste in essi secondo la natura del
Numero sonoro, percioche allora le Consonanze sono poste ne i lor luoghi naturali; on-
de il modo è più allegro, & porge molto piacere al sentimento, che molto gode & si di-
letta de gli Oggetti proportionati, & per il contrario, hà in odio, & abhorrisce i spropor
tionati. Ne gli altri Modi poi, che sono il Terzo, il Quarto, il Quinto, il Sesto, l'Vndeci
mo, & il Duodecimo, la quinta si pone al contrario; cioè, mediata arithmeticamente da
una chorda mezana; di modo che molte uolte udimo le Consonanze poste contra la na
tura del nominato Numero. Per ilche, si come ne i primi la Terza maggiore si sotto-
pone spesse uolte alla minore; cosi ne i secondi si ode spesse fiate il contrario; & si ode un
non sò che di mesto ò languido, che rende tutta la cantilena molle; il che tanto più spes-
ode, quāto più spesso in esse sono poste à tal modo; per seguir la natura & la proprietà
del Modo, nel quale uiene ad esser composta. Hanno oltra di questo le Consonanze im
perfette tal natura, che i loro estremi con più cōmodo & miglior modo si estendono uerso
quella parte; ch'è piu uicina alla sua perfettione; che uerso quella, che le è più lontana; per
cioche Ogni cosa naturalmente desidera di farsi perfetta, con quel modo piu breue & mi
gliore, che puote. Onde le Imperfette maggiori desiderano di farse maggiori, & le minori
hanno natura contraria; conciosia che 'l Ditono & l'Hexachordo maggiore desiderano
di farsi maggiori, uenendo l'uno alla Quinta & l'altro alla Ottaua, & il Semiditono & l'He
xachordo minore amano di farsi minori, uenendo l'uno uerso l'Vnisono & l'altro uerso
la Quinta; come è manifesto à tutti quelli, che nelle cose della Musica sono periti, & han
no il lor giudicio sano; percioche tutti i mouimenti, che fanno le parti uengono à farsi
col mouimento d'alcuno Interuallo, nel quale si contiene il Semituono; ch'è ueramen-
te il Sale (dirò cosi) il condimento & la cagione d'ogni buona Modulatione & d'ogni
buona Harmonia; le quali modulationi senza il suo aiuto, sarebbono quasi insopporta-
bili di udire. Ma in qual maniera ogni consonanza si dica Arithmeticamente, ouero
Harmonicamente mediata; quello che si dirà nel Cap. 31. & quello, che ragioneremo
intorno le Consonanze Diapason nel Cap. 9. della Quarta parte, lo farà manifesto.
Ragionamento particolare intorno all'Vnisono.Cap. XI.
ueduto; che gli Elementi semplici, ouero Specie semplici del Contrapunto;
si consonanti, come etiandio dissonanti, siano Dodeci; cioè, l'Vnisono, il
Semituono, il Tuono, il Semiditono, il Ditono, la Diatessaron, la Diapen-
te, l'Hexachordo minore, il maggiore, l'Heptachordo minore, il maggiore & la Dia-
pason; delle quali Specie si ragionerà al presente di ciascuna particolarmente; percio-
che se bene il Contrapunto si compone principalmente de Consonanze; nondimeno
per accidente anco si compone de Dissonanze; accioche sia più allegro, & più bello. Vo
lendo adunque ragionar de tali Specie; tenirò quest'ordine; che dopo c'hauerò ragio-
nato dell'Vnisono; come porta il douere; percioche è il principio, dal quale nascono le
Consonanze, & senza lui ogn'altro Interuallo non hauerebbe il suo essere; uerrò à
page 193parlare dell'altre Specie; non già secondo l'ordine proposto, il quale è tenuto da i Pratti
ci ma secondo che l'una si ritroua esser più perfetta dell'altra; & secondo che sono collo-
cate per ordine nel progresso naturale de i Numeri sonori, ouer delle Proportioni; inco-
minciando prima da quelle che sono contenute nel genere Molteplice; dopoi da quel-
le, c'hanno le lor forme nel genere Superparticolare; le quali espedite, ragionerò di
quelle, c'hanno ne gli altri Generi il loro essere. Pigliaremo adunque il principio del no-
stro ragionamento dalla Definitione dell'Vnisono dicendo; Vnisono è una adunanza di
due ouer più Suoni, ò Voci equali, che non fanno alcuno interuallo, ma sono conte-
nute in un medesimo punto, & in un medesimo luogo; & si ritroua nella proportione
della Equalità tra 1 & 1. ouero tra 2 & 2. & altre simili; la qual proportione è princi-
pio della Inequalità. Questo non si pone tra le Consonanze, ne tra gli Interualli; per-
cioche tanto è l'Vnisono appresso il Musico, quanto è il Punto appresso il Geometra.
Onde si come il Punto è principio della Linea, ma non è però linea; ne la Linea è com-
posta da Punti; imperoche 'l Punto non hà lunghezza, ne larghezza, ne altezza, che si
possa continuare, ò congiungere con un'altro Punto; cosi l'Vnisono è solamente princi-
pio della Consonanza, ò dell'Interuallo; ma non è consonanza, ne Interuallo, essendo
che non si può continuare; come non si può continuare il Punto. Et perche ogni
Consonanza si ritroua tra due suoni distanti per il graue & per l'acuto, i quali fanno un'
Interuallo, & è (come uedemmo nella Seconda parteCap. 12) mistura, ò compositione di
suono graue & di acuto; però non hauendo l'Vnisono alcuna di queste qualità, non lo
potiamo chiamare per alcun modo ne Consonanza, ne Interuallo. La qual cosa si pro-
ua dalle parole del Filosofo, il quale riprendendo nella Politica il porre in una Città la2. Pol. c. 3.
robba in commune, & facendo tal cosa impossibile, conferma la sua opinione con uno
essempio musicale, dicendo; che sarebbe non altramente, come se uno uolesse fare di
una Consonanza, una Voce unisona, oueramente del Verso, un solo piede. Onde si
uede, che la Consonanza è presa da lui diuersa dall'Vnisono. Meritamente adunque è
chiamato Vnisono, quasi d'un suono solo; la onde quando ritrouaremo in una parte d'una
Canzone due, ò più figure in una istessa lettera, ò chorda; siano poste in riga, ouero in
spacio; diremo che quelle saranno Vnisone, & di un solo suono; & che quel passaggio,
che si troua dall'una all'altra è Vnisono; come nell'essempio si uede.
 Il medesimo potremo anco dire, quando due ò più parti di tal Canzone si ritroueranno
Il medesimo potremo anco dire, quando due ò più parti di tal Canzone si ritroueranno essere in una medesima chorda; come sono le due sottoposte.
 page 194
page 194Della Prima consonanza detta Diapason, ouer'Ottaua.
Cap. XII. >
le cose più semplici, le quali per loro natura sono maggiormente comprese
da i nostri sensi, & sono più manifeste, & più intelligibili; accioche da que-
ste più ageuolmente passiamo alle meno semplici; però daremo principio al
ragionamento delle Consonanze dalla Diapason, ouer'Ottaua; conciosia che di lei
non si ritroua alcun'altra Consonanza, che sia più semplice, & maggiormente cono-
sciuta dal Senso di lei. Ma perche sommamente desidero, che i Prattici non solo cono-
scano gli Interualli musicali in quanto sono consonanti, ò dissonanti, & le loro specie;
ouero in quanto sono perfetti, ò men perfetti; ma etiandio da che Proportione siano con
tenuti; però incominciando da essa Diapason, la quale è la Prima consonanza; per ser-
uar l'ordine proposta, dico ch'ella è contenuta dalla proportion Dupla prima nel ge-
nere Molteplice tra questi termini radicali 2 & 1. & è prima tra quelli Suoni, che hanno
la forma loro delle proportioni della Inequalità. Onde mi penso ch'ella fusse chiamata
da i Musici con tal nome; percioche (come altroue hò detto2. Pars.
cap. 48.) hà iurisditione in ogni
Consonanza, & in ogni Interuallo, che sia maggiore, ò minor di lei, Il che è manife-
sto dal nome; che tiene; percioche è composto da Διὰ, ch'è parola Greca; che signifi-
ca Per; & da Πᾶσα, che uuol dire Vniuersità, ouero Ciascuno; onde è chiamata Διὰ
πασῶν; quasi uoglia dire Vniuersità di concento. Meritamente adunque, & non sen-
za proposito i Musici l'hanno chiamata Genetrice, Madre, Fonte, Origine, Princi-
pio, Luogo, Ricetto, & Soggetto uniuersale d'ogni Consonanza, & d'ogni Interual-
lo, quantunque minimo. Questa quando è considerata dal Musico semplicemente
& in generale; cioè, quando i suoi estremi sono senz'alcuna uoce mezana; ouer altro
suono; & fanno un solo interuallo, si ritroua hauere una sola specie; imperoche tanto è
contenuta dalla proportione Dupla ne i suoi estremi una Diapason, che sia posta nell'
acuto, quanto un'altra, posta nel graue; ma quando è considerata particolarmente, &
secondo ch'ella è diuisa diatonicamente in Tuoni & in Semitnoni; ouer mediata d'altri
Interualli, allora dico, che le sue specie sono Sette, secondo che gli Interualli de i suoni
mezani si possono diuersamente, secondo la natura del genere Diatonico naturale ordi-
nare in sette maniere; percioche ciascuna Consonanza (come dice Boetio,Musicae li.
4. cap. 13. parlando del
le Perfette) produce vna specie meno di quello, ch'è il numero delle sue chorde; ilche
etiandio intenderemo de quelle semplici Consonanze, le cui forme sono contenute tra
le proportioni superparticolari; come sono la Diapente, la Diatessaron, il Ditono &
lo Semiditono; percioche de gli Interualli dissonanti si dè hauere altra consideratione.
Et nasce cotal uarieta delle Specie, dalla uarietà de i luoghi, che contengono in esse il
Semituono; conciosia che nella prima, che si troua da C in c. il Semituono, ilquale è
la cagione della distintione delle Specie, è contenuo nel terzo & nel settimo Interual-
lo di essa Diapason; procedendo dal graue all'acuto; ma nella Seconda specie, che è
posta tra D & d, tal Semituono si ritroua nel secondo & nel sesto; & cosi di mano in ma-
no, secondo l'ordine delle mostrate Sette lettere; tanto ascendendo, quanto discen-
dendo; come nella Ottaua definitione del Quinto delle Dimostrationi hò dichiarato.
Onde essendo in tal maniera mediata, dicono i Musici, che la Diapason. è una compo-
sitione de otto Suoni diatonicamente, & secondo la natura del Numero sonoro accom-
modati, & ordinati in essa; da i quali la nominarono etiandio Ottaua; & contengono
in se cinque Tuoni, tre maggiori, due minori; & due Semituoni maggiori; come ne i
sottoposti essempi si ueggono.
page 195
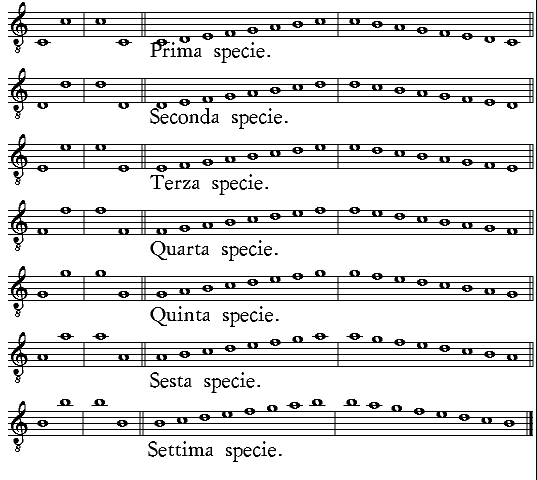 Quando adunque nelle compositioni ritrouaremo due parti, l'una distante dall'altra
Quando adunque nelle compositioni ritrouaremo due parti, l'una distante dall'altra per un simile Interuallo, di modo che la graue occupi il luogo graue, & l'acuta, il luogo
acuto di qual si uoglia dell'una delle Specie de i mostrati essempi; allora diremo, che cota-
li parti saranno distanti tra loro per una Ottaua; come in questo essempio si uedono.
 Ilperche quando alcuno uorrà porre in una sua cantilena l'Ottaua, potrà porre la par-
Ilperche quando alcuno uorrà porre in una sua cantilena l'Ottaua, potrà porre la par-te graue lontana dall'acuta per uno de mostrati Interualli, sopra le notate chorde, &
ottenerà il suo proposito.
Della Diapente, ouer Quinta.Cap. XIII.
te; che Ogni Cōsonanza, ouer altro Interuallo quantunque minimo, che sia mi-
nor della Diapason, nasce non per aggiuntione de più proportioni insieme; ma
per la diuisione della Dupla, che contiene la Diapason. Ilche habbiamo potuto uede-
re, non solo da i Numeri, & dalle Proportioni poste nel Cap. 15. della Prima parte, ma nel
page 196Cap. 39. della Seconda per uia della diuisione Harmonica; percioche dalla diuisione del-
la Diapason contenuta dalla Dupla, nacque la Diapente & la Diatessaron. La Diapente
(dico) contenuta tra questi termini radicali 3 & 2. & la Diatessaron tra 4 & 3. Et perche
la proportione, che si troua tra 3 & 2. segue immediatamente dopo la Dupla; però ha-
uendo prima ragionato della Diapason, mi par cosa honesta di ragionar della Diapen-
te, & dopoi della Diatessaron; imperoche si come la proportione della Diapason è la pri
ma nel genere Molteplice; cosi quella della Diapente è la prima nel genere Superparti-
colare. Onde non è fuori di ragione, che noi incominciamo da questi principii; essen-
do bisogno, che siano conosciuti prima d'ogn'altra cosa. Ritornando adunque alla Dia-
pente dico; quando ella è considerata semplicemente, nel modo ch'è contenuta ne i suoi
estremi termini senz'alcun mezo, si può dire, che tal Consonanza sia d'una sola specie;
percioche non si ritroua alcuna Diapente, che sia maggiore, ò minore d'un'altra di pro-
portione; ne meno che gli estremi dell'una siano più distanti, ò più ristretti di proportio
ne de quelli d'un'altra. Ma quando la consideriamo tramezata ne i suoi estremi d'altre
chorde, & d'altre proportioni nell'ordine Diatonico; allora diciamo, che le sue Specie
sono quattro; imperoche essendo tali estremi tramezati da altre chorde diatonicamente,
il maggior Semituono è posto tra loro in quattro modi diuersamente;Vide c. 8.
Lib. 5. Sup-
ple. lasciando però d'
hauer consideratione alcuna de i Tuoni maggiori, ò minori si in questa, come in ogu'al-
tra Consonanza; percioche generarebbono etandio altre Specie differenti, quando si
considerassero minutamente tali Interualli collocati tra esse. Di quelle adunque che so-
no tra loro solamente differenti per le trasportatione del Semituono, quella è la Prima
specie, che hà il Semituono nel terzo interuallo nel graue; la Seconda è quella, che l'hà
nel secondo; la Terza nel primo; & la Quarta nel quarto; tanto ascendendo, quanto
discendendo; come nella Nona definitione del Quinto delle Dimostrationi si contiene;
& qui sotto si uedono.
 Et ciascuna de loro contiene in se cinque Voci, ò Suoni & quattro Interualli, c'han-
Et ciascuna de loro contiene in se cinque Voci, ò Suoni & quattro Interualli, c'han-no tra loro due Tuoni maggiori, un minore, & un Semituono maggiore; & per questa
cagione, dal numero delle chorde, che contiene, è detta Quinta da i Prattici; ma i
Greci la chiamano Diapente, con queste due parole; Διὰ, che significa Per; & Πέντε,
che uuol dir Cinque; quasi uolendo dire, Consonanza, che procede Per cinque voci,
ò Suoni. Quando adunque sarāno due parti lontane l'una dall'altra di maniera, che l'una
tenga la parte graue di ciascuna delle dette specie, & l'altra l'acuta; allora diremo, che sa-
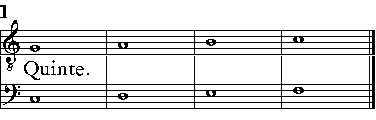 ranno lontane l'una dall'altra per una Diapente, ò pervna Quinta;
ranno lontane l'una dall'altra per una Diapente, ò pervna Quinta; come qui si uede. Boetio nel Cap. 13. del Quarto Libro della Mu-
sica, pose la specie di questa consonanza tra le chorde Hypate hy-
paton & Parhypate meson, che è una Quinta diminuta; essen-
do che contiene due Tuoni & due Semituoni; ma credo, che
forse s'ingannasse nel porre l'essempio; oueramente che non
curasse di porre essattamente il uero della cosa, pur che mostrasse
page 197col numero delle chorde quello, che uolea intendere. Sia però stato quel che si uo-
glia, basta sapere almeno, che cotale essempio sia falso; acciò alcuno non piglias-
se errore.
Della , ouer Quarta.Cap. XIIII.
ma è contenuta nel secondo luogo del genere Superparticolare tra questi ter
mini 4 & 3. essendo considerata senz'alcun mezo, non si ritroua di lei se
non una sola Specie, per le ragioni dette di sopra della Diapason & della
Diapente; ma quando è considerata tramezata diatonicamente da altri suoni, ò uo-
ci, allora si ritrouano tre specie, che nascono dalla uarietà del Semituono; lasciando
la consideratione de i Tuoni; il qual Semituono è diuersamente collocato tra esse
nelle lor chorde mezane; come hò detto della Diapason, & della Diapente; per-
cioche hauendo la prima specie il Tuono nel primo & nel secondo luogo più graue;
hà dopoi nel terzo il Semituono maggiore. Ma la seconda hà il Semituono nel se-
condo luogo; & la terza nel primo; essendo i Tuoni accommodati per ordine; come
qui si uede, & nella Decima definitione del Quinto delle Dimostrationi hò dichiarato.
 Questa da i Greci è chiamata prima Sinfonia, ouer (come la nomina Filon GiudeoDe
Questa da i Greci è chiamata prima Sinfonia, ouer (come la nomina Filon GiudeoDe cio )
prima Harmonia, & BoetioM
1. c la dimanda Minima consonanza; la onde si uede, che non
hebbero il Ditono, ne il Semiditono per consonanze, come nel principio del Primo li-
bro delle nominate Dimostrationi hò anco dichiarato. La chiamarono etiandio Dia-
tessaron dal numero delle chorde, ò uoci, che in se contiene; percioche ogni Diates-
saron procede al modo mostrato per quattro uoci; imperoche è detta da Διὰ, ò Per, &
da Τέσσαρα, ò Quattro; cioè, Consonanzadi quattro uoci, ò suoni; dal qual nume-
 ro i nostri Moderni la chiamarono Quarta. Quando adunque
ro i nostri Moderni la chiamarono Quarta. Quando adunque uorremo far due parti nelle nostre compositioni, lequali siano tra
loro distanti per una Diatessaron; porremo in una delle chor-
de estreme di uno de i sopraposti essempi la uoce graue, & nell'al-
tro l'acuta; come si uede nell'essempio. Il perche ritrouandosi an-
co nelle Cantilene due parti accōmodate l'una con l'altra in cotal
modo; potremo dire, che l'una sia distante dall'altra per una Dia-
tessaron, oueramente per unaQuarta.
page 198
Del Ditono, ouer Terza maggiore.Cap. XV.
tono, che è tra questi termini 5 & 4. nel terzo luogo del genere Superparti-
colare, contenuta dalla proportione Sesquiquarta. Questo è ueramente ma-
rauiglioso, che la Natura habbia ordinato in tal maniera l'una Consonanza
dopo l'altra; che ritrouandosi tra le parti del Senario la forma della Diapente diuisa
Arithmeticamente in due parti, tra questi termini 6. 5. 4. il Musico con un'ordine contra-
rio, tra l'istessa Diapente diuisa harmonicamente in due parti, ritroua le istesse tra que-
sti termini. 15 12. 10. Considerato adunque il Ditono senz'alcun mezo, secondo ch'è
contenuto semplicemente ne i suoi termini radicali, potiamo dir quello, che si è detto
dell'altre consonanze; che non se ne troua se non una specie; percioche tanto distanti
in proportione sono gli estremi di un Ditono posto nell'acuto, quanto quelli d'un'altro
posto nel graue; ma considerandolo tramezato diatonicamente, & diuiso in due Tuo-
ni, dico che le sue specie sono due; come qui sotto appare.
 Et tal differenza nasce dalla uarietà de i suoi Interualli; conciosia che nel primo Inter-
Et tal differenza nasce dalla uarietà de i suoi Interualli; conciosia che nel primo Inter-uallo della prima specie si ritroua il Tuono maggiore, & nel secondo il minore, ascen-
dendo dal graue all'acuto, & cosi discendendo; & nella Seconda specie si ritroua il con-
trario; cioè, il Minore nel primo, & nel secondo il Maggiore: Differentia c'haurebbe
accresciuto maggior copia nella Diapente, ò Quinta; come accennai, parlando di essa.
 Diremo adunque, che allora le parti de i Contrapunti sono distan
Diremo adunque, che allora le parti de i Contrapunti sono distanti l'una dall'altra per un Ditono, quando l'una di esse si ritroua in
alcuna delle chorde estreme graui de i mostrati essempi & l'altra
nell'estreme acute; come nell'essempio si uede. Questa Consonan-
za è detta Ditono, perche contiene in sè due Tuoni; quantun-
que i Prattici la dimandano Terza maggiore; perch'è diuisa in due
Interualli contenuti da tre chorde; delle quali l'estreme sono più
distanti di quello, che sono l'estreme del Semiditono per un Se-
mituono minore; come à mano à mano uederemo.
Del Semiditono, ouer Terza minore.cap. XVI.
quale è contenuta nel Genere Superparticolare dalla proportione Sesqui-
quinta nel Quarto luogo. Questa da i Prattici etiandio è detta Terza mi-
nore, & le sue Specie sono due, considerandola diuisa diatonicamente
in un Tuono maggiore, & in un maggior Semituono; imperoche la prima contiene
page 199tal Semituono nel suo secondo interuallo, & la seconda lo contiene nel primo, salen-
do dal graue all'acuto, & anco discendendo dall'acuto al graue, come qui si uede.
 Ma considerandola senz'alcun mezano suono; cioè, ne i suoi estremi solamente, è di
Ma considerandola senz'alcun mezano suono; cioè, ne i suoi estremi solamente, è di una sola specie; conciosiache le chorde estreme d'uno posto nel graue, & quelle d'un'al-
tro posto nell'acuto, sono contenute da un'istessa proportione. Dicono i Prattici, che
quando le Parti delle lor Compositioni sono distanti l'una dall'altra di maniera,
che l'una parte occupi qual chorda si uoglia graue, & l'altra occupi qual si uoglia
acuta d'uno de gli essempi mostrati di sopra; sono lontane per un Semiditono, ouer
Terza minore; come sono le due sottoposte. Questo Interuallo è chiamato Semidito-
no; non già da Semis parola latina, che uuol dir Mezo; come fusse mezo Ditono à pun-
 to; ma si bene da Semus, che significa Sciemo; percioche (co-
to; ma si bene da Semus, che significa Sciemo; percioche (co-me uuole Boetio1. Music.
Cap. 16.) in tal maniera si chiama quella cosa, che non è
l'intero mezo del suo Tutto; onde si dice Semituono quell'Inter-<
uallo, che non arriua all'intiero del Tuono; ma è Tuono imper-
fetto. Si dice adunque il Semiditono, Ditono imperfetto; con-
ciosiache è diminuto di un Semituono minore, contenuto dalla
proportione Sesquiuentesima quarta. Lo nominano anco Terza,
dal numero delle chorde; & le aggiungono, Minore; percioche
i suoi estremi sono più ristretti, & di minor proportione, che
non sono quelli del Ditono. Ma questo sia detto à bastanza intorno à quelli Interual-
li, che sono ueramente consonanti.
Dell'vtile che apportano nella Musica gli Interualli dissonanti.Cap. XVII.
& non le Dissonanze; percioche compone di esse principalmente le sue Can-
zoni; nondimeno par (come dice Plutarco nella uita di M. Tullio) che con-
sideri anco quelle Voci, che sono dissonanti; cioè, quelli Interualli, che
non fanno la Consonanza; accioche sappia elegger quelle cose, che li apportano utile
& commodo, & fuggir quelle, che poco fanno al suo proposito; essendo che quelli In-
terualli, i quali sono dissonanti, generano ingrato suono all'Vdito, & fanno la cantilena
aspra, & senz'alcuna soauità. Ma perche è impossibile, che nel cantare si possa an-
dar da una Consonanza all'altra, procedendo dal graue all'acuto, ò per il contrario, se
non col mezo, & con l'aiuto di tali Interualli; pero è dibisogno, che 'l Musico non
solamente li conosca, accioche non li ponga in luogo de quelli, che sono conso-
nanti; ma etiandio fà dibisogno, c'habbia notitia di loro, per poterli usare tra le par-
ti della cantilena, nel modo, ch'io mostrerò altroue. Onde essendo utili, & anco ne-
cessarii, è cosa conueniente, che si dica alcuna cosa in particolare di loro; percioche se
bene non hanno ragione di Consonanza, hanno almeno ragione d'Interuallo. Ne
sono però tutti gli Interualli necessarii al Musico; ma solamente quelli, che seruo-
no alle modulationi diatoniche, i quali sono minori del Semiditono, & maggiori del
page 200Semituono minore; & senza alcun dubbio sono contenuti tra le Otto chorde di ciascu-
na Diapason; conciosia che sono separate l'una dall'altra harmonicamente per diuisio-
ne diatonica. Essendo adunque utili & anco necessarii all'uso dell'Harmonie, fa dibiso-
gno che si conoscano, & si sappia la loro ragione, il numero loro; & la loro utilità.
deremo hora il numero. Onde dico che ueramente non sono più ne meno di Tre;
cioè, il Tuono maggiore, il Minore, & il maggior Semituono, che sono ueri & legitti-
mi Interualli del genere Diatonico, nel quale s'adoperano. Et si chiamano ueri & legit-
mi di tal genere; percioche nascono da Numeri sonori, & sono contenuti nel suo Te-
trachordo come nel Cap. 39. della Secōda parte habbiamo ueduto. Si trouano etiandio
altri Interualli, che sono dissonanti; si come si può ueder nella diuisione, ò compositione
del Monochordo, mostrata nella Seconda parte; & in qualunque altra, che si potesse fa-
re con l'aiuto de i Numeri harmonici; ma perche sono minori de i Tre sopra nominati,
il Musico non hà dibisogno di essi; & questi sono il Semituono minore, che si troua tra
le Chorde S B & K B; & il Comma, ch'è posto tra le chorde R B & M B. della sopra-
detta diuisione. Et se ben si uede in lei, ch'alle volte sia impossibile di proceder dal gra-
ue all'acuto, ò per il contrario; & da vna Consonanza all'altra, senza l'aiuto di uno de
questi Interualli; questo importa poco; percioche in tali Istrumenti simili aggiunti so-
no necessarij; ma non è però necessariò, che in un proceder Diatonico si odono; ne
anco è utile l'Interuallo del Comma; percioche generarebbe molto fastidio à chi l'udis-
se; tanto più, che nelle Voci questo non si ode; essendo che si possono fare acute & gra-
ui, come torna meglio; & col mezo loro si può ridurre à perfettione ogni cantilena, sen-
z'alcuno incommodo; ilche non intrauiene ne gli Istrumenti arteficiali; conciosia che
l'Arte (come habbiamo detto nel Cap. 4. del Primo libro de i Sopplimenti) mai non
può in cosa alcuna agguagliarsi alla Natura. Ma perche uediamo, che le Voci maggior-
mente s'accostano alla natura de gli Istrumenti ridotti al numero delle chorde Pitago-
riche, ne i quali non si ritrouano queste minutie; che alla natura de gli accordati per-
fettamente secondo le forme de i Numeri harmonici; però si potrebbe dire, che la Par-
tecipatione fusse più utile al Musico, che l'Accordo perfetto. Laonde si debbe auertire,
che in quanto alla Scienza questo è più utile; perche da lui si può cauar la Ragion uera
d'ogni Interuallo, che sia accommodato perfettamente alla sua proportione; massima-
mente perche le Voci seguono la perfettione de gli Interualli; ma quanto all'uso, & alla
Prattica, è più commodo quello. E' ben uero, che l'uno & l'altro si può dir perfetto
nella loro specie, nel modo ch'altre uolte hò detto, & mostrato. Tale utile adunque
apportano alla Musica i nominati Interualli; che uolendo passare da una Diatessaron
ad una Diapente, ò per il contrario, non si può uenire con altro mezo, che col Tuono
maggiore; cosi procedendo dal Semiditono alla Diatessaron, oueramente da questa à
quello, & dalla Diapente all'Hexachordo maggiore, ò per il contrario; non si uiene, se
non col mezo del Tuono minore. L'utile poi che si caua dal Semituono maggiore è
questo; che dal Ditono si può uenire col suo mezo alla Diatessaron, & per il contrario;
& dalla Diapente all'Hexachordo minore, ò da questo à quella. La onde hauendosi da
loro un tal commodo, non sarà fuor di proposito, che ragioniamo alcuna cosa di loro
particolarmente; lasciando quelli, che sono contenuti ne gli Istrumenti arteficiali;
conciosia che non solo non si adoperano; ma è anco impossibile di potere hauere la pro
portione rationale de quelli, che s'accrescono, ò diminuiscono d'alcuna partedel Com
ma; come altroue hò mostrato.
page 201
Del Tuono maggiore, & del minore.Cap. XVIII.
ricordarsi quello, che si è detto, & mostrato nel Cap. 39. della Seconda par
te; che 'l Ditono si diuide harmonicamente in due Tuoni, non già Sesquiot-
taui, come da molti Antichi, & moderni Musici è stato affermato; percio-
che generarebbono ne i loro estremi dissonanza; ma si bene in uno contenuto dalla
proportione Sesquiottaua, & l'altro dalla proportione Sesquinona; & l'uno si chia-
ma maggiore, & l'altro minore. Onde per maggiore intelligenza de i Studiosi del-
la Musica, mostrarò tra quali chorde diatoniche l'uno & l'altro siano contenuti. In-
cominciando adunque dal Maggiore dico, ch'è quello, che segue immediatamente
uerso l'acuto nelle chorde diatoniche nominate il Semituono maggiore in ogni Tetra-
chordo; & è quello anco, che si troua collocato tra le chorde A
 , & a
, & a  . senz'alcun me
. senz'alcun mezo; Mà il Minore segue sempre il maggiore uerso l'acuto; & tiene sempre l'Interuallo,
che è il terzo di ciascun Tetrachordo nella parte acuta; come nell'essempio si uede.
 Habbiamo adunque nel genere Diatonico due specie di Tuono; cioè, il Maggiore, &
Habbiamo adunque nel genere Diatonico due specie di Tuono; cioè, il Maggiore, & il Minore; però quando ritrouaremo due parti ne i Contrapunti, che saranno di-
stanti l'una dall'altra per uno de questi Interualli; diremo, che quelle sono lonta-
ne per un Tuono maggiore, ouer minore; oueramente diremo, che siano distanti
per una Seconda maggiore; conciosia ch'è cosi nominato da Prattici tale Interuallo,
per differenza della minore, ch'è il Semituono maggiore; & è cosi chiamata dal nume
ro delle sue chorde, lequali contengono questi Interualli, che sono diatonici; come
nell'essempio si ueggono.
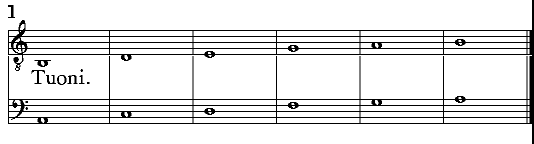
Del Semituono maggiore, & del minore.Cap. XIX.
quiquintadecima. Questo congiunto al Tuono maggiore ne dà il Semiditono.
Et se bene non nasce per la diuisione d'alcun'Interuallo, fatta per uia della
Proportionalità harmonica; nasce almeno per la reintegratione della Diates-
saron, quando dal Ditono peruenimo à i suoi estremi; perioche è impossibile di uenirui
senza 'l suo mezo; come nel Cap. 39. della Seconda parte, & di sopra anche hò dimostra
to. Onde tanta è la sua proportione, quanta è la differenza, che si ritroua tra la Sesqui-
page 202quarta, che contiene il Ditono, & la Sesquiterza, che è la forma di essa Diatessaron.
mezo nella parte graue nel principio di ciascun Tetrachordo; come si è potuto uedere;
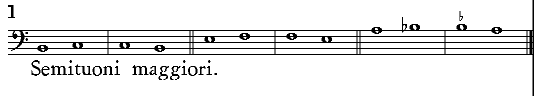 & è collocato naturalmente
& è collocato naturalmente tra le chorde poste in questo
essempio. Guidone pose il Se
mituono nel mezo di ciascun
Hexachordo, come in luogo
più degno, & più honorato,
nel quale (come si dice) consiste la Virtù; conciosia che l'eccellenza & nobilità sua è ta-
le, che senza lui ogni Cantilena sarebbe aspra & insopportabile da udire; ne si potrebbe
hauere alcuna Harmonia, che fusse perfetta, senza il suo mezo. Questo è detto Maggio
re, à differenza del Minore, che si ritroua in acuto ascendendo tra le chorde b. &
 . ò
. ò per il contrario; ilquale non si adopera nel genere Diatonico, & è il sottoposto.
 na dall'altra per uno de i gradi acuti de i mostrati essempi, & l'altra
na dall'altra per uno de i gradi acuti de i mostrati essempi, & l'altra per uno de i graui, allora diremo, che quelle sono distanti per un Se
mituono maggiore, ouer per una Seconda minore; come nell'essem
pio seguente si uede. Fu chiamato Semituono, per le ragioui, che
io dissi parlando nel Cap. 16. del Semiditono, da questa uoce Semus,
che uuol dir Sciemo, & Imperfetto; percioche il Tuono non è mai
diminuto, ouer fatto imperfetto della sua meza parte intera; come
l'esperienza lo dimostra; essendo che niuna proportione Superparti
colare (come hò detto più uolte) si può diuidere in due parti equali.
Et Guido monaco Aretino nel Primo libro detto Micrologo chia-
ma il Semituono, Non pieno Tuono. Ma questo sia detto à bastan-
za intorno queste due specie de Semituoni; che si ritrouano di Cin-
que specie; come si è mostrato nel Cap. 11. del Libro de i Soppli-
menti: & circa gli Interualli diatonici contenuti dalle proportioni Molteplice, &
dalle Superparticolari.
Dell'Hexachordo maggiore, ouero Sesta maggiore.Cap. XX.
re Superpartiente, dico; che l'Hexachordo maggiore hà la sua forma dalla
Superbipartiente terza; la quale è la prima proportione di que
sto genere, tra questi termini radicali 5 & 3. Et benche questo Interuallo
non si possa chiamare assolutamente Semplice, se non ad un certo modo; percioche gli
estremi della sua proportione possono esser tramezati dal numero Quaternario, in cotal
maniera 3. 4. 5. & lo potiamo dire Composto della forma della Diatessaron, & della for
ma del Ditono; tuttauia lo chiamaremo Semplice in un certo modo; non già perche sia
composto di due Interualli, ma perche non è composto dell'interuallo della Diapason,
ch'è il Tutto, & d'alcuna sua parte. Quādo adunque consideraremo questo Interuallo ne
i suoi estremi solamente, & senz'alcun mezo; ritrouaremo, che è d'una sola specie, anco-
ra che fusse posta nel graue, ò nel acuto; ma quando lo consideraremo diuiso diato-
nicamente; tante saranno le sue Specie, quanto saranno le uariationi de i luoghi del
Semituono compreso in esso, secondo i modi delle diuisioni, che fanno le sue chorde
page 203mezane, lasciando però la consideratione de i luoghi de i Tuoni maggiori, ò minori;
perche darebbono altre Specie; come altroue dicemmo; le quali saranno tre; co-
me qui si uede.
 I Musici chiamano questo Interuallo Hexachordo, per il numero delle chorde, che
I Musici chiamano questo Interuallo Hexachordo, per il numero delle chorde, che contiene, che sono Sei; Percioche appresso de i Greci tanto uuol dire Ε῞ξ, quanto Sei
appresso de noi; & similmente tanto uuol dire Χορδή, quanto Chorda. Onde è detto In-
teruallo, che contiene Sei chorde, ouer Consonanza de sei Voci; percioche è com-
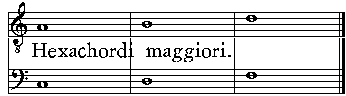 preso da tal numero de chorde. La onde i Prattici lo chiamano
preso da tal numero de chorde. La onde i Prattici lo chiamano Sesta maggiore, à differenza della minore, la quale è compresa
da minor proportione; & dicono, che la Sesta maggiore, oue-
ro il maggiore Hexachordo è una compositione de sei uoci, ò
suoni, che contiene quattro Tuoni, & un Semituono maggiore.
Quando adunque saranno due parti ne i nostri Contrapunti di-
stanti l'una dall'altra per il graue & per l'acuto, secondo la ra-
gione de gli estremi d'alcuno de i sopraposti essempi; allora di-
remo, che tali parti seranno distanti l'una dall'altra per un'He-
xachordo, ouer Sesta maggiore; come nel essempio si uede.
Dell'Hexachordo minore, ouer Sesta minore.
Cap. XXI.
ta, è (secondo che lo definiscono i Prattici) una compositione de sei uoci, ò
suoni, dalle quali prende il nome di Sesta; che contiene tre Tuoni, & due
Semituoni maggiori, hauendo riguardo al modo, che è tramezato diatonicamente da
Quattro chorde. Et perche è tramezato solamente in tre modi; come dalla uaria po-
sitione de i Semituoni si può comprendere; però tre solamente sono le sue Specie, le
quali si ueggono qui sotto in essempio.
 Ma quando fusse considerato ne i suoi estremi solamente, senza esser tramezato d'alcu-
Ma quando fusse considerato ne i suoi estremi solamente, senza esser tramezato d'alcu-na chorda mezana; si trouerebbe di lui una sola specie per le ragioni dette de gli altri
Interualli. Et ancora che non si possa chiamare assolutamente Semplice; percioche i suoi
termini radicali sono tramezati dal numero Senario in cotal modo 5. 6. 8. come si può
uedere tra i Numeri harmonici posti nel Cap. 15. della Prima parte; onde lo potiamo
chiamar composto della Diatessaron, & del Semiditono; tuttauia per le ragioni dette
dell'Hexachordo maggiore, lo chiamaremo anco lui Semplice ad un certo modo. Quan
do adunque due parti de i nostri Contrapunti saranno distanti l'una dall'altra per il gra-
 ue & per l'acuto, secondo la ragione delle chorde estreme d'al-
ue & per l'acuto, secondo la ragione delle chorde estreme d'al-cuno de i mostrati essempij; allora potremo dire, che saran-
no distanti per uno Hexacordo, ò Sesta minore; come nell'
essempio si ritroua. Questo etiandio si chiama Hexachordo per
le ragioni dette dell'Hexachordo maggiore; la onde à sua
differenza gli aggiunsero Minore; & tanto l'uno, quanto
l'altro non erano connumerati da gli antichi tra le consonan-
ze; conciosiache le loro estreme chorde sono tirate sotto le
ragioni delle proportioni predette, lequali si ritrouano esser
connumerate tra quelle del genere Superpartiente. Ma perche i Musici moderni le
pongono in cotale ordine; & perche sono composte (se cosi le uoglian considerare)
della Diatessaron & del Ditono, ouer del Semiditono; che poste insieme, non pos-
sono esser se non consonanti, quando sono collocati à i loro luoghi proprij; però hò
uoluto far di loro particolar mentione, & mostrar le loro Specie. Onde facendo fine
di ragionar più de quelli Interualli, le cui proportioni, sono comprese nel genere Mol-
teplice & nel Superparticolare, & de quelli, c'hanno le lor forme nel genere Superpar-
tiente, & sono accettati da ciascun Musico per consonanti; verrò à ragionar de quelli,
c'hanno le lor forme in questo genere istesso, & sono al tutto Dissonanti.
Della Diapente co 'l Ditono, ouer Settima maggiore.
Cap. XXII.
mi suoni della Diapente co 'l Ditono la loro forma. Hò detto gli Estremi
suoni; percioche se ben questo Interuallo si può chiamar Composto; per-
che i suoi termini radicali, che sono 15. & 8. possono esser tramezati in co-
tal modo 15. 12. 10. 9. 8. come nel Cap. 15. della Prima parte si può uedere; tuttauia,
per le ragioni dette di sopra, lo chiamaremo Incomposto. E' posto questo Interuallo
nell'ordine de gli Interualli dissonanti; percioche la sua proportione non hà luogo
tra i Numeri harmonici. Questo, essendo prima considerato semplicemente, & sen-
z'alcun mezo, non hà sotto di sè alcuna specie; ma dopoi considerato diuiso dia-
tonicamente in Tuoni, & in Semituoni, le sue specie sono due. Dicono i Pratti-
ci, che questo Interuallo tramezato è una compositione di Sette suoni ouer Sette
uoci, che contiene Sei interualli, tra i quali sono cinque Tuoni, & un Semituono
maggiore; come qui si uede.
page 205
 I Prattici lo nominano Settima dal numero delle uoci, ò de i suoni, che sono contenuti
I Prattici lo nominano Settima dal numero delle uoci, ò de i suoni, che sono contenuti 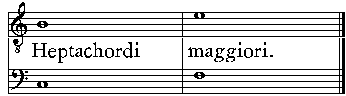 in esso; & lo chiamano anco Heptachordo, de Ε'πτὰ, Sette, & da
in esso; & lo chiamano anco Heptachordo, de Ε'πτὰ, Sette, & da Χορδή, Chorda; & à differenza del minore gli aggiungono questa
parola, Maggiore. Diremo etiandio di esso quello, che si è det-
to de gli altri Interualli; che tutte le uolte, che si ritrouerà in
alcuna cantilena due parti, che siano poste l'una nelle chorde
graui de i mostrati essempi, & l'altra nell'acuta; che tali Parti
saranno distanti l'una dall'altra per una Settima maggiore, ouera-
mente per un'Heptachordo maggiore; come sono le due poste
nell'essempio.
Della Diapente co 'l Semiditono, ouer Settima minore.Cap. XXIII.
miditono nelle sue estreme chorde. Et ancora che si possa chiamar Composta;
conciosiache i suoi Termini radicali 9 & 5. siano tramezati nell'ordine natu-
rale de i Numeri harmonici da 8 & 6. come nel Cap. 15. della Prima parte si
può uedere; nondimeno per essere Interuallo minore della Diapason, lo chiamare-
mo Incomposto. Questo considerato senz'alcun mezo (per le ragioni addotte altre uol
te) non hà sotto di se alcuna Specie; ma considerato tramezato secondo la natura del
genere Diatonico, i Prattici dicono, ch'è un composto de sette uoci, ò suoni, che con-
tengono sei Interualli; tra i quali si trouano quattro Tuoni, & due Semituoni maggio-
ri; & le sue Specie sono Cinque, che nascono dalla diuersità de i luoghi, che occupano
i Semituoni; come qui si uede.
 Dal numero delle chorde i Prattici lo chiamarono Settima; è ben uero che u'aggiunse-
Dal numero delle chorde i Prattici lo chiamarono Settima; è ben uero che u'aggiunse-ro questa parola, Minore, per farlo differente dal Maggiore. Lo nominarono etiandio
Heptachordo da quelle due parole greche poste nel Capitolo precedente. Quando adun
que saranno due parti distanti l'una dall'altra, come sono le chorde estreme de i sopra-
posti essempi, allora diremo, che sono lontani per una Settima minore; come sono le sot-
 toposte. Qui porrò fine al ragionar delle Consonanze, &
toposte. Qui porrò fine al ragionar delle Consonanze, & de gli Interualli semplici; lasciando etiandio, per più breui
tà, di ragionar de i Composti; conciosiache ogn'altro, qual
si uoglia, che sia maggior della Diapason, si considera com
posto di lei, & di una sua parte, & non sarà molto difficile il
uoler sapere la loro ragione; laquale sempre si potrà hauere,
quando aggiungeremo sopra la proportione della Diapason
quella dell'Interuallo, che le uorremo porre appresso, som-
mando insieme i termini radicali, che contengono tali pro-
portioni. Dirò ben questo, che gli estremi suoni della Diapasondiapente, ouer Duode-
cima sono contenuti dalla proportione Tripla; quelli della Disdiapason, ouer Quinta-
decima dalla Quadrupla; quelli della Disdiapason co 'l Ditono, ouer Decimasettima
dalla Quintupla; & quelli della Disdiapasondiapente, ouer Decimanona dalla Sestu-
pla: come si è detto altroue ma gli altri si potranno inuestigar facilmente con la ra-
gione al modo detto.
In qual maniera naturalmente, ò per accidente tali Interualli da i Prat-
tici alle volte si ponghino superflui, ò diminuti.
Cap. XXIIII.
possa denominar (come habbiamo ueduto) dal Numero delle chorde; tutta-
uia si debbe auertire, di non cascare in un'errore commune, nelquale sono ca
scati spesse uolte alcuni Prattici, i quali considerando gli Ordini de Suoni nel
numero delle chorde solamente, & facendo poca stima de gli Interualli contenuti in essi;
hanno posto tallora nelle compositioni loro sotto 'l titolo, ò nome d'alcuna delle predet
te Consonanze il suo Interuallo superfluo, ouer diminuto, in luogo della uera, & legiti
ma specie. Et ciò hanno fatto, come poco intendenti delle cose della Musica, non con-
siderando, che gli estremi di qual si uoglia ordine de Suoni che pigliano, diatonicamen
te ordinato nel numero delle sue chorde, si possono considerare, ò ritrouar di tre manie
re: imperoche ouero che sono Consonanti, ò Dissonanti, ò che ueramente sono Falsi.
I due primi sono quelli, c'hanno i loro estremi contenuti da una proportione compresa
tra quelle, che sono collocate ne i Numeri harmonici; come sono gli Interualli già mo-
strati, i quali ageuolmente cantar si possono, quantunque ue ne siano tra loro de Disso-
nanti. Ma i Terzi sono quelli, che sono compresi da una proportione, che non hà luogo
tra i nominati Numeri, ne sono compresi tra gli harmonici Interualli, i quali di sopra
habbiamo dichiarato; & difficilmente, & senza suauità alcuna si possono cantare; anco
ra che l'ordine tutto sia composto d'Interualli diatonici; de i quali al presente parlaremo.
page 207Questi si ritrouano etiandio esser di due sorti facendosi il cōto dal numero delle lor chor-
de solamente; percioche, ouero che l'Interuallo è diminuto, per contenere in se alcun'
Interuallo minore in luogo d'un maggiore; come il Semituono maggiore in luogo del
Tuono; ouero ch'è superfluo, perche contiene un'Interuallo maggiore in luogo d'un mi
nore; come il Tuono in luogo del Semituono. Onde quella Quinta, che naturalmente
si troua da
 ad F. collocata tra cinque chorde, è senza dubbio alcuno diminuta d'un Se
ad F. collocata tra cinque chorde, è senza dubbio alcuno diminuta d'un Semituono minore; percioche in luogo di tre Tuoni, & di un Semituono maggiore, con-
tiene due Tuoni, & due Semituoni; & è ne i suoi estremi dissonante; perche è contenu-
ta dalla proportione Super 19. partiente 45. che non hà luogo tra i Numeri harmonici;
& però la chiamano Semidiapente, & Quinta imperfetta, ouer diminuta. Il medesimo
potiamo dire della Quarta contenuta nel Numero de quattro chorde tra F. &
 , che per
, che per ritrouarsi in lei tre Tuoni, è chiamata Tritono; & è superflua d'un Semituono minore.
La onde non essendo le sue chorde estreme contenute sotto le proportioni de gli harmo-
nici Numeri; percioche la sua forma è contenuta dalla Super 13. partiente 32. è sopra-
modo dissonante; come qui in essempio si uede.
 Questo errore non solamente può accascare nella Quinta, & nella Quarta tra le chorde
Questo errore non solamente può accascare nella Quinta, & nella Quarta tra le chorde pure diatoniche; ma etiandio nell'Ottaua tra le chorde naturali de i modi, & le acciden
tali chromatiche; percioche se 'l si hauerà riguardo al Numero delle chorde solamente,
che si ritrouano tra la chorda
 . & la b. diremo che tale Ottaua sia senz'alcun dubbio di-
. & la b. diremo che tale Ottaua sia senz'alcun dubbio di-minuta d'un Semituono minore; essendo ch'è contenuta nelle sue estreme chorde dal-
la proportione Super 21. partiente 135. onde è dissonante, quanto dir si possa; & si uede
posta tra le chorde diatoniche del sottoposto essēpio, & si può anco nominare Semidia-
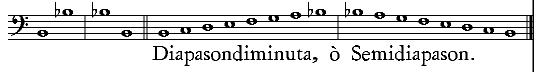 pason. Simili errori si possono ancora commettere tra la chorda b. che si pone alcune uol
pason. Simili errori si possono ancora commettere tra la chorda b. che si pone alcune uolte nel graue, tra A. & la
 . la quale corrisponde alla
. la quale corrisponde alla  . & alla E. poste nel acuto & tra essa
. & alla E. poste nel acuto & tra essa b. & la
 . Si trouerà la Diapason superflua, di proportione Dupla super 7. partiente 64.
. Si trouerà la Diapason superflua, di proportione Dupla super 7. partiente 64. & tra l'istessa b & la E. il Tritono, di proportione Super 13. partiente 32. ilche hauerà
simigliantemente tra le chorde diatoniche, & le chromatiche; percioche se noi porre-
mo la chorda
 . posta in acuto tra la c. & la d. per l'uno de gli estremi della Ottaua;
. posta in acuto tra la c. & la d. per l'uno de gli estremi della Ottaua; & la chorda C. posta nel graue per l'altro estremo; haueremo una Ottaua Dissonantissi-
ma, cōtenuta dalla proportione Dupla sesquiduodecima; & sarà una Diapason superflua
d'un Semituono minore. Onde se di nouo pigliaremo la detta chorda
 con la F. ha-
con la F. ha-ueremo una Quinta dissonante, contenuta dalla proportione Super 9. partiente 16. detta
Diapente superflua. La medesima chorda ancora accompagnata alla G. ne darà il
Tritono, che contiene tre Tuoni; & la proportione Super 7. partiente 18. come
sottoposti essempi si uede.
page 208
 Tutti questi Interuali si potranno etiandio diminuire dell'istessa quantità, quando pi-
Tutti questi Interuali si potranno etiandio diminuire dell'istessa quantità, quando pi-gliaremo la chorda chromatica
 posta nel graue tra la C. & la D. in luogo della C. & fa-
posta nel graue tra la C. & la D. in luogo della C. & fa-remo la Ottaua
 & c; percioche allora tale Ottaua sarà diminuta d'un Semituono mino
& c; percioche allora tale Ottaua sarà diminuta d'un Semituono minore, & contenuta dalla proportione Super 23. partiente 25. ch'è minor della Dupla; la on
de si chiama Semidiapason. Similmente tal chorda accompagnata con la G. ne darà vna
Semidiapente, contenuta dalla Super 11. partiente 25. & accōpagnata con la F. ne darà
la Semidiatessaron, cōpresa sotto la forma della proportione Super 21. partiēte 75. laqua
le insieme con l'altre sono contenute nel sottoposto essempio, & sono al tutto dissonanti.
 Questi, & tutti gli altri Interualli mostrati di sopra sono disonantissimi, & non si debbo-
Questi, & tutti gli altri Interualli mostrati di sopra sono disonantissimi, & non si debbo-no porre ne i Contrapunti; perche generano fastidio all'Vdito. Onde non senza giudicio,
i Musici prattici più periti diedero una Regola, per schiuar questi errori; Che non si do
uesse mai porre la uoce del Mi, contra quella del Fa, nelle Consonanze perfette. Si deb
be però auertire, ch'alle uolte si pone la Semidiapente ne i Contrapunti in luogo della
Diapente; similmente il Tritono in luogo della Diatessaron, che fanno buoni effetti; ma
in qual maniera s'habbiano à porre lo dimostrerò più oltra. Quando adunque ritrouare
mo due parti, l'una delle quali nell'acuto tenga il luogo d'alcuna delle chorde estreme d'
alcuno de i mostrati essempi, & l'altra tenga il luogo d'alcuna posta nel graue; allora di-
remo, che saranno distanti l'una dall'altra per uno de i detti Interualli; come si uede.
 Qui si haurebbe potuto porre
Qui si haurebbe potuto porre molti altri essempi, & mostrar
più in lungo in quante maniere
cotali Interualli si accrescono,
& minuiscono col mezo delle
chorde chromatiche; ma per nō
andare in lungo hò uoluto la-
sciarli. Similmente si hauerebbe
page 209potuto mostrare, in qual modo, per uia dell'istesse chorde chromatiche, il Ditono diuen-
ti Semiditono; & il Semiditono Ditono. Ma perche cambiandosi in tal maniera, non
fanno alcun'Interuallo dissonante; però hò uoluto etiandio lasciar da parte tal ragiona-
mento; accioche io possa dichiarare, & mostrar gli effetti, che fanno questi tre segni
 .
. quadrato, b molle, &
 Diesis.
Diesis. De gli Effetti che fanno questi segni.  . b. &
. b. &  .Cap. 25.
.Cap. 25.
che dimostrano l'aggiungere al Semituono maggiore il minore; oueramente
il leuarlo dal Tuono, & di far diuentare minore alcuna Consonanza maggio-
re; ò per il contrario la maggiore minore. Il Semituono minore; ancora che
non s'adoperi nelle modulationi del genere Diatonico; si ritroua tuttauia essere stato usa
to alcune fiate da i Compositori nelle lor cantilene; & massimamente tra le modulatio-
ni, che fanno due parti ascendendo, ouer discendendo insieme col mouimento della Ter
za; si come si può uedere, essaminando molte compositioni tanto de gli Antichi, quan-
tode i Moderni compositori. Ma Cipriano di Rorè lo adoperò in una parte sola
in quella Canzone à quattro uoci, che incomincia; Helas coment; si nella parte piu gra-
ue, come anco nella parte piu acuta. Et tal Semituono si ritroua naturalmente tra la
chorda Tritesynemennon, & la Paramese; come nel Cap. 19. di sopra hò mostrato. Di
cono i Prattici, che tal Semituono è descritto tra queste due cifere, b &
 . & tra queste
. & tra queste due uoci, ò sillabe Fa & Mi, stando il Mi sopra il Fa; le quali cifere sono differenti di for
ma; come si ueggono descritte nel sottoposto essempio; percioche la uoce, ò chorda se-
gnata col
 è più acuta di quella, ch'è segnata col b. La onde Guido Aretino, per non
è più acuta di quella, ch'è segnata col b. La onde Guido Aretino, per non 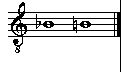 confondere i Cantori, pose nel suo Introduttorio queste due Let
confondere i Cantori, pose nel suo Introduttorio queste due Lettere, ò Cifere differenti, in un'istesso luogo; & uolse, che per l'una
di esse s'intendessela chorda Tritesynemennon, & per l'altra la
Paramese. Vedendo dopoi i Musici questa differenza, ordinaro-
no due sorti di cantilena, l'una delle quali chiamarono di Natura
& di
 . quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, &
. quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, & per quelle del Diezeugmenon; & non poneuano nel principio delle parti della can-
tilena alcuna delle mostrate cifere. L'altra nominarono di Natura, & di b molle;
& questo quando le parti procedeuano per le chorde del Tetrachordo Synemen-
non & quelle del Meson; lasciando da un canto quelle, che sono del Tetrachordo
Diezeugmenon; & in questa sorte di canzone poneuano nel principio delle Parti
della cantilena la cifera, ouer segno del b molle, auanti i segni del Tempo. Et
se ben nelle Cantilene, che procedeno per il Tetrachordo Meson, & per il Die-
zeugmenon, non si costuma di porre la cifera del
 . nondimeno i Moderni ue la in-
. nondimeno i Moderni ue la in-tendono; & tal Cifera si ritroua ne i Libri ecclesiastici; cioè ne i Canti fermi molto spes
so, se ben ne i Canti figurati sia stata & è anco poco usata; percioche quādo uogliono por
re alle uolte la chorda Paramese in luogo della Tritesynemennon, pongono la cifera
 . in
. in luogo del
 . ancora che tal cosa si faccia impropriamente; conciosia che si douerebbe u-
. ancora che tal cosa si faccia impropriamente; conciosia che si douerebbe u-sar la propria cifera della cosa, che uogliono intendere, & non un'altro segno forestiero;
quantunque questo importi poco; percioche hormai ogn'uno conosce, qual chorda si hà
da usare in luogo della Tritesynemennon, quando pongono la cifera del
 . Ma in uero
. Ma in uero io lodarei molto, che si usasse il segno propio. Per tornare adunque a gli Effetti, che fan
no cotali Cifere, dico; che dinotano che si leua, ouer aggiunge il sudetto Semituono
minore nel cantare; Imperoche se noi uorremo essaminare con diligenza il Primo de
i due sequenti essempi; ritrouaremo, che dalla prima figura alla Seconda, ui è l'Inter-
page 210uallo del Tuono, onde se tra loro porremo il segno del b, come si uede nel secondo; non
è dubbio, che uorremo à leuare della parte acuta del detto Tuono il Semituon minore,
& tra le sue figure si ritrouerà il maggiore; perche dalla diuisione del Tuono, fatta per la
chorda Tritesynemennon, nasce il Semituono maggiore & il minore; com'altroue si è
detto. Similmente il
 . fà un tale effetto nel Quarto essempio; perche, si come tra le fi-
. fà un tale effetto nel Quarto essempio; perche, si come tra le fi-gure del Terzo si ritroua il Tuono; cosi posta la Chorda
 . in luogo della b. è rimosso dal
. in luogo della b. è rimosso dalla parte graue il minore, & resta il maggior Semituono. Tal'effetto fà anco il
 . percio-
. percio-che, si come tra le figure del Quinto essempio si scorge il Tuono, cosi tra quello del Sesto
è posto il Semituono maggiore. Et tutto questo si è detto per la diminutione dell'Inter-
uallo del Tuono, col mezo delle mostrate cifere, ò chorde, leuandoli il Semituono mino
re. Ma se noi uorremo accrescere l'Interuallo del Semituon maggiore, per passare al Tuo
 no, con l'aggiungerli il Minore, si potrà far l'istesso con le predette cifere, ò chorde; co-
no, con l'aggiungerli il Minore, si potrà far l'istesso con le predette cifere, ò chorde; co-me ne i sottoposti essempi si uede.
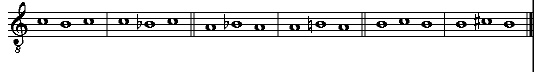 Dobbiamo però auertire, accioche le parti della Cantilena riuscischino più facili, & più
Dobbiamo però auertire, accioche le parti della Cantilena riuscischino più facili, & più ageuoli da cantare; & gli Interualli siano piu facili da proferire; che quando si uorrà por
re la chorda del b. che la Figura cantabile, laquale è posta auanti quella, che si uuol se-
gnare con tal segno, proceda dal graue all'acuto; & quando si uorrà porre il
 . ouero il
. ouero il  . fare, che procedino al contrario; cioè, dall'acuto al graue; ancora che non sarebbe
. fare, che procedino al contrario; cioè, dall'acuto al graue; ancora che non sarebbe grande errore, & di molta importanza, quando si facesse altramente.
Quel che si ricerca in ogni Compositione, & prima del Sogetto.
Cap. XXVI.
tal ragionamento, fa dibisogno sapere, che In ogni buon Contrapunto,
ouero in ogn'altra buona Compositione si ricercano molte cose, delle quali
se una ne mancasse, si potrebbe dire, che fosse imperfetta. La Prima è il
Soggetto, senza il quale si farebbe nulla; imperoche si come l'Agente in ogni sua ope-
ratione hà sempre riguardo al fine, & fonda l'opera sua sopra qualche Materia, laquale
chiama il Soggetto; cosi il Musico nelle sue operationi, hauendo riguardo al fine, che
lo muoue all'operare, ritroua la Materia, ouero il Soggetto, sopra 'l quale uiene à fon-
dar la sua Compositione; & cosi uiene à condurre à perfettione l'opera sua, secondo 'l
fine proposto. La onde, si come il Poeta, ilquale è mosso da questo fine, di giouare & di
dilettare; come Horatio chiaramente dimostra nella sua Poetica, dicendo:
Aut prodesse volunt, aut delectare Poeta:
Aut simul & iucunda, & idonea dicere vitae.
page 211Hà nel suo Poema per soggetto l'Historia, ouer la Fauola; la quale, ò sia stata ritrouata
da lui, ouer se l'habbia pigliata d'altrui; adorna & polisse in tal maniera con uarij costu-
mi, come piu gli aggrada; non lasciando da parte alcuna cosa, che sia degna & lodeuo-
le, per dilettar l'animo de gli uditori; onde hà poi del magnifico & marauiglioso; cosi il
Musico, oltra che è mosso dall'istesso fine di giouare & dilettare gli animi de gli ascoltan-
ti con gli accenti harmonici; hà il Soggetto, sopra il quale è fondata la sua Cantilena;
la quale adorna con uarie modulationi & uarie harmonie, di modo che porge grato pia
cere à gli Ascoltanti. La Seconda è, che sia composta principalmente de Consonan-
ze; dopoi habbia in sè per accidente molte Dissonanze collocate in essa con debiti mo-
di; secondo le Regole, le quali piu abbasso uoglio mostrare. La terza è, che le parti del-
la Cantilena procedino bene; cioè, che le Modulationi procedino per ueri & legitimi
Interualli, che nascono da i Numeri sonori; accioche per il mezo loro s'acquisti l'uso
delle buone Harmonie. La Quarta conditione, che si ricerca, è; che le Modulationi,
& il Concento sia uariato; percioche da altro non nasce l'Harmonia, che dalla diuersi-
tà delle modulationi, & dalla diuersità delle Consonanze messe insieme con uarietà. La
Quinta è, che la Cantilena sia ordinata sotto una prescritta & determinata Harmonia, ò
Modo, ò Tuono, che uogliamo dire; & che non sia disordinata. Et la Sesta & ultima
(oltra l'altre, che si potrebbono aggiungere) è; che l'Harmonia, che in essa si contie-
ne, sia talmente accommodata all'Oratione; cioè, alle Parole; che nelle materie alle-
gre l'Harmonia non sia flebile; & per il contrario, nelle flebili, l'Harmonia non sia alle-
gra. Onde accioche del tutto si habbia perfetta cognitione, uerrò à ragionar de tutte
queste cose separatamente, secondo che mi uerranno al proposito, & secondo 'l bisogno.
Incominciando adunque dalla Prima, dico. Il Soggetto d'ogni compositione musica-
le chiamarsi quella Parte, sopra la quale il Compositore caua l'Inuentione di far l'altre
Parti della cantilena, siano quante si uogliano; & tal Soggetto può essere in molti modi:
prima può essere inuentione propria; cioè, che 'l Compositore hauerà ritrouato da sè;
dopoi può essere, che l'haurà pigliata dall'altrui compositioni, accommodandolo al-
la sua cantilena, & adornandolo con uarie parti, & uarie modulationi; come piu gli
aggrada, secondo la grandezza del suo ingegno. Et tal Soggetto si può ritrouare de
piu sorte; percioche può essere un Tenore, ouero altra Parte di qual si uoglia cantilena
di Canto fermo, ouer di Canto figurato; ouer potrà esser due, o piu Parti, che l'una
seguiti l'altra in Consequenza, ouero à qualunque altro modo; essendo che i uarij mo-
di de tali Soggetti sono infiniti. Ritrouato adunque che hauerà il Compositore il Sog-
getto; farà l'altre Parti, nel modo che piu oltra uederemo; ilche fatto, cotal maniera di
comporre si chiamerà, secondo i nostri Prattici, Far contrapunto. Ma quando non
hauerà ritrouato prima il Soggetto; quella parte, che sarà primieramente messa in atto;
ouer quella, con la quale il Compositore darà principio alla sua cantilena; sia qual si uo-
glia, & incomincia à qual modo piu li piace; ò sia graue, oueramente acuta, ò mezana;
sempre sarà il Soggetto, sopra 'l quale poi accommodarà l'altre in Consequenza, oue-
ro ad altro modo; come piu li piacerà di fare; accommodando l'Harmonie alle Parole,
secondo che ricerca la materia contenuta in esse. Ma se 'l Compositore andrà cauando
il Soggetto dalle Parti della cantilena; cioè, quando cauerà una parte dall'altra; & an-
drà facendo insieme la Compositione; come uederemo altroue; quella Particella, che
lui cauerà fuori dell'altre, sopra la quale dopoi componerà le parti della sua composi-
tione, si chiamerà sempre Soggetto. Et tal modo di comporre i Prattici dimandano
Comporre di fantasia; ancora che si possa etiandio nominare Contrapuntizare, ò Far
contrapunto; come dicono.
page 212
Che le Compositioni si debbono comporre primieramente di Consonan-
ze, & dopoi per accidente di Dissonanze.
Cap. XXVII.
la, ogni Harmonia si componi de Consonanze principalmente & primieramē
te; nōdimeno per maggior bellezza & leggiadria, s'usano anco secondariamen
te in essa, & per accidente, le Dissonanze; le quali quantunque poste sole all'
Vdito non siano molto grate; nondimeno quando sono collocate nel modo, che regolar
mente debbono essere, & secondo i Precetti, che dimostraremo; l'Vdito talmente le
sopporta, che non solo non l'offendono; ma li danno grande piacere & diletto.
lore; la Prima è stata detta di sopra; cioè, che con l'aiuto loro si può passar da una Con
sonanza all'altra; la Seconda è, che la Dissonanza fa parer la Consonanza, laquale
immediatamente la segue, più diletteuole, & con maggior piacere dall'Vdito è com-
presa & conosciuta; come dopo le tenebre è più grata & diletteuole alla uista la Luce;
& il dolce dopo l'amaro è più gusteuole & più soaue. Prouiamo per esperienza ogni
giorno ne i Suoni; che se per alquanto di tempo l'Vdito è offeso d'alcuna Dissonanza;
la Consonanza, che segue dopo, se li fà più soaue & più diletteuole. La onde gli anti-
chi Musici giudicarono, che nelle Compositioni hauessero luogo non solo le Conso-
nanze, che chiamano Perfette, & quelle, che nominano Imperfette; ma le Dissonan
ze ancora; percioche conobbero, che con più bellezza & maggior leggiadria pote-
uano riuscire, di quello c'hauerebbono fatto, non le hauendo; conciosiache se fusse-
ro composte di Consonanze solamente, con tutto che facessero bello udire, & da loro
ne uscissero buoni effetti, hauerebbono tuttauia tali compositioni (non essendo mesco-
late le Consonanze con le Dissonanze) quasi dell'imperfetto; si dalla parte del cantare,
come anco per l'aiuto della compositione; perche mancarebbono d'una gran leggia-
dria, che nasce da queste cose. Et bench'io habbia detto, che nelle Compositioni si
usino principalmente le Consonanze, & dopoi per accidente le Dissonanze, non si debbe
per questo intendere, che si habbiano à porre ne i Contrapunti, ò Compositioni, come
uengono fatte, senz'alcuna Regola, & senz'alcuno ordine; percioche ne seguirebbe
confusione; ma si dè auertire, di porle con ordine & con regola, acciò il tutto tor-
ni bene. Si debbe sopra 'l tutto hauer riguardo (oltra l'altre) à due cose; nellequa-
li (per mio giudicio) consiste tutta la bellezza, tutta la leggiadria, & tutta la bon-
tà d'ogni compositione; cioè, à i Mouimenti, che fanno le parti della cantilena ascen
dendo & discendendo per mouimenti simili, ouero contrarii; & alla Collocatione del-
le Consonanze à i luoghi proprij nelle harmonie; delle quali cose, con l'aiuto di Dio,
intendo ragionarne, secondo che tornerà il proposito; imperoche questo è stato sem-
pre il mio principale intendimento. Et per introduttione di questto ragionamento in-
tendo di esporre alcune Regole date da gli Antichi, i quali conobbero la necessità de co
tali cose; con le quali insegnando il modo, che si hauesse da tenere nel porre regolarmen-
te le Consonanze & anco le Dissonanze l'una doppo l'altra nelle compositioni, ueni-
uano à dare etiandio alcune Regole de tali Mouimenti; ancora che questo facessero im
perfettamente. Queste Regole adunque porrò io conseguentemente per ordine, &
porrò la sua dichiaratione; con la quale uerrò à mostrar quello, che si hauerà da fare;
& con ragioni euidenti mostrarò, in qual maniera s'haueranno da intendere; aggiun-
gendouene etiandio alcun'altre, che saranno non solo utili, ma anco necessarie
molto à tutti coloro, che desiderano di ridursi in un modo regolato & ordine buono di
comporre dottamente & elegantemente, con buone ragioni & buoni fondamenti, ogni
page 213cantilena; & per tal modo ciascuno potrà conoscere, in qual parte haurà da colloca-
re le Consonanze & le Dissonanze; & in qual luogo potrà porre le Maggiori & le Mi-
nori nelle sue Cantilene.
Che si debbe dar principio alle Compositioni per una delle Consonanze
perfette.Cap. XXVIII.
Moderni; che nel dar principio à i Contrapunti, ouero ad altre Compositio
ni musicali, si douesse porre una delle nominate Consonanze perfette; cioè,
l'Vnisono, ò la Quinta, ò la Ottaua, ouer'una delle Replicate. Laqual Re-
gola non uolsero però che fusse tanto necessaria, che non si potesse fare altramente; cioè
che non si potesse anco incominciare per una delle Imperfette; poi che La perfettione
sempre si attribuisce al fine, & non al principio delle cose. La onde dobbiamo notare
per maggiore intelligenza di cotal Regola: che quando la parte del Contrapunto inco-
mincierà à cantare insieme con la parte del Soggetto; allora si potrà incominciar per
una delle Perfette già dette: ma quando per maggior bellezza & leggiadria del Con-
trapunto; & anco per maggior commodità, i Musici facessero, che le Parti non in-
cominciassero à cantare insieme; ma l'una dopo l'altra con l'istesso progresso de fi-
gure, ò note, ch'è detto Consequenza; ilquale rende il Contrapunto non pur dilette-
uole, ma etiandio arteficioso; allora potranno incominciare da qual Consonanza
uorranno; sia perfetta, ouero imperfetta; percioche intrauengono le Pause in una del
le parti. Si debbe però osseruare, ch'almeno i Principij dell'una, & dell'altra Parte
habbiano tra loro relatione ad una delle nominate Consonanze perfette, ouer d'una
Quarta; & ciò non sarà fatto fuor di proposito; conciosia che si uiene à incominciare
sopra le chorde estreme, ouer sopra le mezane de i Modi, sopra i quali sarà fondata
la cantilena; che sono le lor Chorde naturali ouero essentiali; come altroue uederemo.
Et questo credo, che intendessero gli Antichi, quando dissero, che nel principiare i
Contrapunti si douesse dar principio ad una delle Consonanze perfette; la qual Rego
la non è fatale, ò necessaria; ma si bene secondo 'l uoler di colui, che compone.
Quando adunque uorremo incominciare alcun Contrapunto in Consequenza, lo po-
tremo incominciare per qual si uoglia delle Perfette, ouero Imperfette, & per Quar-
ta anche; non che le Parti incomincino à cantare per questo Interuallo; ma dico
per Quarta rispetto al principio del Soggetto, con la parte del Contrapunto, ò per
il contrario; come si uede tra le parti del Soggetto posto qui di sotto, laquale è u-
na Cantilena dell'Ottauo modo, & tra la parte del Contrapunto del Quarto essempio
nel graue; imperoche l'una incomincia nella chorda F. & l'altra nelle chorda C. &
sono distanti per Quarta, rispetto al principio dell'una & dell'altra; & cosi osserua-
remo la Regola data, di cominciar per una delle Consonanze perfette; facendo in-
cominciar le Parti à cantare insieme in una Terza maggiore; percioche l'una in-
comincia insieme nella chorda E. & l'altra nella chorda C. come nel detto Quarto
essempio si uede. La onde tal Principio dimostra ueramente, che tal precetto non è
fatale, ò necessario; ma si bene arbitrario. Ne possono queste due parti generar cosa
alcuna di tristo all'Vdito; essendo che se bene i loro principij corrispondono per u-
na Quarta; tuttauia nel principiare il canto insieme si ode il Ditono, ouer la Ter-
za maggiore.
page 214
 Il medesimo dobbiamo osseruar ne i Principij de i Contrapunti, ò Compositioni, quan
Il medesimo dobbiamo osseruar ne i Principij de i Contrapunti, ò Compositioni, quando nella parte del Soggetto si ponesse alcuna Pausa; com'intrauiene, quando si piglia un
Tenore di qualche Canzone, ò di qual si uoglia Cantilena, per comporli sopra l'altre Par
ti; percioche allora le Parti, che s'aggiungono, si debbono incominciare al modo mo-
strato; osseruando quello, ch'intorno ciò è stato detto; come si uede ne i sottoposti es-
sempi, de i quali il Soggetto è composto nel Sesto modo.
 Si debbe etiandio auertire (ilche è cosa di non poca importanza) & corrisponde quasi à
Si debbe etiandio auertire (ilche è cosa di non poca importanza) & corrisponde quasi à quello c'habbiamo detto disopra) di ordinar nelle Cōpositioni & ne i Contrapunti a più
uoci in tal maniera le Parti, che i loro principij corrispondino tra & habbiano rela-
tione per una delle Consonanze perfette, ouero imperfette; di modo che uolendole can-
page 215tare nel pigliar le uoci delle parti, non si oda alcuna dissonanza; essendo che que-
sto non solo porge fastidio à i Cantori; ma alle uolte è cagione di farli errare più
facilmente, pigliando una uoce per un'altra; massimamente quando non sono mol
to sicuri nel cantare. E' ben uero, ch'è lecito porre nel graue il principio de
due parti, che siano distanti l'una dall'altra per una Quarta, senza esserui alcun'al-
tra parte piu graue, alle quali l'altre corrispondino per Ottaua; massimamente ne i
Modi Placali, ouero Impari, che li uogliamo dire; quando le Parti della cantile-
na incominciano à cantar sopra le chorde principali de i loro Modi, ne i quali è
composta; conciosiache uolendo torre la libertà al Compositore di poter porre due
parti in tal maniera, non è cosa honesta; massimamente potendolo fare à due uo-
ci; & sarebbe farlo Soggetto & obligato ad una cosa fuori d'ogni proposito; essen-
doche l'Incominciare in tal modo è stato posto in uso da molti Prattici periti; co-
me da Giosquin de Pris, da Motone, & da altri antichi & moderni Composito-
ri; & di ciò potiamo hauer l'essempio nel Canto, che fece Adriano à cinque uo-
ci. Laus tibi sacra rubens; lasciandone infiniti altri. Tal licenza presi anch'io in quel-
li tre Canti; Osculetur me osculis oris sui; Ego rosa Saron; & Capite nobis vulpes paruu-
las; i quali già composi à Cinque uoci; come ogn'un potrà uedere; & saranno es-
sempio alle cose che di sopra sono state dette. Questo adunque si concede à tutti
li Compositori; ma non è però anco da lodare, che due parti siano distanti ne i
loro principij dalla parte del Soggetto, ò nel graue, ò nell'acuto, l'una per una
Quarta, & l'altra per una Quinta; percioche allora queste parti uerrebbono ad es-
ser distanti l'una dall'altra per una Seconda; & nel pigliar le uoci farebbono dissonan-
za; & potrebbe essere, che l'una di esse parti facesse il suo principio sopra una chor-
da, che non fusse del Modo, sopra 'l quale è fondata la compositione, ò cantile-
na. Et quantunque tale auertimento sia buono; tuttauia non è anco necessario,
quando 'l Soggetto principale della compositione fusse composto con tale arteficio,
che l'una parte cantasse sopra l'altra in Consequenza, di modo che due di loro can-
tassero sopra la principale di cotal Soggetto nell'acuto, ouer nel graue, l'una di-
stante dall'altra per una Quinta, ouer per una Quarta; oueramente che l'una fus-
se distante dal Soggetto per una Quarta, & l'altra per una Quinta, ò per altro In-
teruallo; come si può uedere nel Canto fatto à sei uoci; Pater de coelis Deus: che
fece P. della Rue, & nel Canto Virgo prudentissima; ch'io composi simigliantemen-
te à Sei uoci; nel quale tre parti cantano in Consequenza, due uerso l'acuto, &
una uerso il graue per gli istessi Interualli; & nel pigliar le uoci si ode un tal incommo-
do. Ma si debbe auertire, ch'io chiamo la Parte del Soggetto, quella sopra la quale so
no accommodate l'altre Parti in consequenza; & è la Principale & la Guida de tutte l'al
tre. Io non dico quella, che prima d'ogn'altra incomincia à cantare; ma quella, che
osserua & mantiene il Modo, sopra laquale sono accommodate l'altre distanti l'una
dall'altra per qual si uoglia interuallo; Come si potrà uedere nella Oratione domini-
cale, Pater noster; & nella Salutatione angelica, Aue Maria; ch'io composi à Sette uo-
ci; doue il principale Soggetto di quelle tre parti, che cantano in Consequenza, non
è quella parte, che prima incomincia à cantare, ma la seconda. In simili casi adunque
sarà lecito porre in una compositione molte Parti tra loro discordanti ne i loro princi-
pij; massimamente non uolendo, ne potendo ueramente discommodar l'arteficioso Sog
getto; che facendolo sarebbe pazzia; ma ne gli altri non si debbe (per mio consiglio)
dar tal incommodità à i Cantanti.
page 216
Che non si debbe porre due Consonanze contenute sotto un'istessa proportio-
ne l'una dopo l'altra ascendendo, ouer discendendo senz'alcun
mezo.Cap. XXIX.
fette d'un'istesso genere, ò spccie, contenute ne i loro estremi da una pro-
portione istessa, luna dopo l'altro; mouendosi le modulationi per uno,
ò per più gradi; come il porre due, ò più Vnisoni; ouer due, ò più
Ottaue; oueramente due, ò più Quinte, & altre simili; come ne i seguenti es-
sempi si uede.
 Conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra
Conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra loro diuerse, discordanti, & contrarie; & non da quelle, ch'in ogni cosa conuengono.
La onde se da tal uarietà nasce l'Harmonia; sarà dibisogno, che nella Musica, non solo
le Parti della cantilena siano distanti l'una dall'altra per il graue & per l'acuto; ma
etiandio che le lor modulationi siano differenti ne i mouimenti; & che contenghino
uarie Consonanze, contenute da diuerse proportioni. Et tanto più potremo allora giu-
dicar, che quella cantilena sia harmoniosa, quanto più si ritrouerà nella compositione
delle sue parti, diuerse distanze tra l'una & l'altra per il graue & per l'acuto; diuersi moui-
menti, & diuerse proportioni. Videro forse gli Antichi, che le Consonanze poste in-
sieme in altra maniera, di quella, ch'io hò detto; ancorache fussero alle uolte uarie ne i
loro estremi per il graue & per l'acuto; erano simili nel procedere, & simili di forma
nelle loro proportioni; però conoscendo, che tale simiglianza non generaua alcuna
uarietà di concento, & giudicando (com'era uero) che la perfetta Harmonia consi-
stesse nella uarietà, non tanto de i Siti, ò Distanze delle parti della cantilena, quan-
to nella varietà de i Mouimenti, delle Modulationi, & delle Proportioni; giudica-
rono, che 'l por due Consonanze l'una dopo l'altra simili di proportioni, uariauano se
non il luogo di graue in acuto, ò per il contrario; senza fare alcuna buona Harmonia;
ancorache i loro estremi fussero uariati luno dall'altro. Però non uolsero, che due, ò
più Consonanze perfette contenute daun'istessa proportione, ascendenti insieme, ò di-
scendenti le parti, si potessero porre nelle compositioni l'una dopo l'altra, senz'alcun'al
tro mezano interuallo. Et massimamente uietarono gli Vnisoni, i quali non hanno
alcuno estremo ne i suoni, ne sono differenti di sito, ne sono distanti tra loro, ne fan-
no uariatione alcuna nel procedere, & sono simili in tutto & per tutto; ne si ritroua in lo
ro cantando differenza alcuna di graue, ò di acuto; non cadendo tra l'uno, & l'altro
suono alcun'Interuallo; percioche le uoci di una parte si ritrouano in quell'istesso luogo,
che si ritrouano le uoci dell'altra; come nell'essempio posto di sopra, & nella definitio-
ne posta al Cap. 11. dell'Vnisono, si può uedere; ne anco si ritroua diuersità alcuna di
modulatione; percioche quell'istessi Interualli canta una parte, per i quali procede
l'altra. Il medesimo si potrebbe etiandio dire di due, ò più Ottaue; se non fusse, che
page 217i loro estremi sono differenti l'un dallaltro per lo graue, & per lo acuto; cosa che porge
all'Vdito alquanto più diletto, di quello, che non fanno gli Vnisoni; per esser l'Ottaua
ne i suoi estremi alquanto uaria. L'istesso si può dire di due, ò più Quinte; che per il pro
ceder che fanno per gradi & per proportioni simili, alcuni de gli Antichi hebbero
opinione, che più presto ne uscisse ad un certo modo Dissonanza, che Harmonia, ò
Consonanza. Onde hebbero per uero, che qualunque uolta si perueniua ad una Con-
sonanza perfetta, se fusse uenuto al fine & alla perfettione, alla quale tende la Musi-
ca; la qual perfettione non uolsero che si replicasse molte uolte, per non generare sa-
cietà all'Vdito. Questo bello & utile auertimento conferma esser uero & buono l'ope-
rationi della Natura, la quale nel produrre in essere gli Indiuidui di ciascuna specie,
mai li produce di maniera, che s'assimiglino in tutto l'uno all'altro; ma uariati per qual-
che dfferenza, la qual differēza, ò uarietà molto piacere porge à i nostri Sentimenti. Deb
be adunque ogni Compositore im tare un tale & tanto bell'ordine; percioche sarà riputa
to tanto migliore, quanto le sue operationi s'assimiglieranno à quelle di una si gran Ma-
dre. A tale osseruanza ne inuitano i Numeri & le Proportioni, percioche nell'ordine
loro naturale non si troua due Proportioni l'una immediatamente dopo l'altra, che sia-
no simili; come è un simil progresso, 1. 1. 1. oueramente 2. 2. 2. & altri simiglianti,
che sarebbono le forme di due Vnisoni; ne meno un tal progresso 1. 2. 4. 8. il qual non
è Harmonico; ma Geometrico, nel quale si contengono le forme di tre Ottaue conti-
nue, ne meno si ritroua un tal'ordine 4. 6. 9. che contiene le forme di due Quinte con-
tinuate. Non dobbiamo adunque per alcun modo porre due Vnisoni l'uno dopo l'altro
immediatamente, ne due Ottaue, ne due Quinte; poiche naturalmente la cagione del-
le Consonanze, che è il Numero harmonico, non contiene nel suo progresso, ouer'ordi
ne naturale due proportioni simili l'una dopo l'altra, senz'alcun mezo; come nel Cap. 15.
della Prima parte si può uedere; percioche se ben queste Consonanze; quando fussero
poste in tal maniera; non facessero euidentemente alcuna Dissonanza tra le parti; tutta-
uia farebbono udire un non so chè di tristo, che dispiacerebbe. Per tante ragioni adun-
que non dobbiamo à patto alcuno far contra questa Regola; cioè, non dobbiamo por-
re le Consonanze l'una dopo l'altra al modo mostrato di sopra; ma dobbiamo cercare
di uariar sempre i Suoni, le Consonanze, i Mouimenti, & gli Interualli; & per tal mo-
do, dalla uarietà di queste cose uerremo à fare una buona & perfetta harmonia.
sto per presuntione, & propria autorità, che per ragione alcuna, che loro habbia-
no hauuto; come uediamo nelle loro compositioni; Conciosia che non si deue imitar
coloro, che fanno sfacciatamente contra i buoni costumi & buoni precetti d'un'Ar-
te, & di una Scienza, senza renderne ragione alcuna; ma dobbiamo imitar quelli,
che sono stati buoni osseruatori; & accostarsi à loro, & abbracciarli come buoni
maestri; lasciando sempre il tristo, & pigliando il buono; & questo dico, perche si
come il uedere una Pittura, che sia dipinta con uarii colori, maggiormente diletta l'Oc-
chio, di quello che non farebbe se fusse dipinta con un solo colore; cosi l'Vdito maggior-
mente si diletta & piglia piacere delle Consonanze & delle Modulationi variate poste
dal diligentissimo Compositore nelle sue compositioni, che delle semplici & non ua-
riate. Questo adunque uolsero che si osseruasse i Musici antichi più diligenti; à i quali
siamo molto debitori; & aggiungeremo à questo; che, per le ragioni già dette, non si
debbe anco porre due, ò più Imperfette consonanze insieme ascendenti, ò discenden-
ti l'una dopo l'altra, senz'alcun mezo; come sono due Terze maggiori, due minori,
due Seste maggiori anco & due minori; come nell'essempio si ueggono. Conciosia
che non solo si fà contra quello, c'hò detto delle Perfette; ma il loro procedere si fà
udire alquanto aspro; per non hauer nella lor modulatione da parte alcuna l'interuallo
del Semituono maggiore, nel quale consiste tutto 'l buono nella Musica, & senza lui ogni
Modulatione & ogni Harmonia è dura, aspra & quasi inconsonante. Etciò nasce an-
page 218
 co, cōciosiache tra le parti, ouer tra le uoci delle due Terze maggiori & delle due Seste mi
co, cōciosiache tra le parti, ouer tra le uoci delle due Terze maggiori & delle due Seste minori nō si troua la Relatione harmonica; ilche fa, che siano alquanto più triste dell'altre; co
me più oltra uederemo. Laonde dobbiamo sommamente auertire, ch'in ogni progresso,
ouer modulatione, che fanno le parti cantando insieme, almeno una di quelle si muoua,
ò faccia l'interuallo del Semituono maggiore, potendolo fare; accioche la modulatio-
ne & l'harmonia, che nasce da i mouimenti, che fanno insieme le parti della cantilena,
siano più diletteuoli, & più soaui. La qual cosa si hauerà facilmente, quando le Conso-
nanze si porranno l'una dopo l'altra, che siano diuerse di specie; come dopo la Terza, ò
la Sesta maggiore si porrà la Minore, ò per il contrario; & dopo la Terza maggiore si
porrà la Sesta minore, ouer dopo questa si porrà quella; & dopo la Terza minore la Se-
sta maggiore, similmente dopo la Sesta maggiore la Terza minore. Ne ui è maggior ra-
gione, che più ne uieti il porre due Perfette, che due Imperfette consonanze immedia-
tamente l'una dopo l'altra; percioche se ben le prime sono consonanze Perfette; tutta-
uia ciascuna dell'Imperfette si ritroua esser perfetta nella sua proportione. Et si come non
si può dire con uerità, ch'un'Huomo sia più Huomo d'un'altro; non si può dire, ch'una
Terza maggiore, ouero una minore; & cosi l'una, ò l'altra delle due Seste posta nel gra-
ue, sia maggiore, ò minore di un'altra posta nell'acuto, ò per il contrario; di modo che
si come è uietato il porre due Consonanze perfette d'una istessa specie l'una dopo l'altra;
cosi maggiormente non dobbiamo porre due Imperfette d'una istessa proportione; con-
ciosiache non sono tanto consonanti, quanto sono le Perfette. E' ben uero, che due Ter
ze minori poste l'una dopo l'altra ascendenti insieme, ouer discendenti per grado; Simil-
mente due Seste maggiori si potranno sopportare; percioche se ben nelle lor modulatio-
ni non si ode cantare il Semituono maggiore, & le Terze siano per loro natura alquanto
meste, & le Seste alquanto dure; quella poca differenza, che si troua ne i mouimenti,
che fanno le parti, uiene, à fare alquanto di uarietà; conciosiache la parte graue sem-
pre ascende, ò discende per un Tuono minore, & l'acuta per un maggiore, ò per il con-
trario, & fà un non sò che di buono all' ; tanto più quanto che le Voci delle parti so
no lontane tra loro in harmonica relatione. Ma quando le parti si mouessero per salto;
allora per niun modo porremo due, ò piu simili ascendenti, ò discendenti l'una dopo
l'altra; percioche, oltra il non osseruar le conditioni toccate di sopra, le Voci delle
parti non sarebbono distanti l'una dall'altra in harmonica relatione; come qui sot-
to si ueggono.
 page 219Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre
page 219Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre due Terze, ò due Seste l'una dopo l'altra; osseruaremo di porre primieramente la mag-
giore, & dopoi la minore; ò per il contrario; pongansi poi in qual maniera si uoglino, ò
cō mouimenti di grado, ouer di salto; percioche ogni cosa tornerà bene. Ma si debbe auer
tire, che quando si porrà la Terza dopo la Sesta; oueramente la Sesta dopo la Terza, di
fare, che l'una sia maggiore & l'altra minore; & ciò faremo quando ciascuna delle parti
farà il mouimento nel graue, ouer nell'acuto. Ma quando l'una di esse non facesse al-
cun mouimento; allora tal Regola non si potrà osseruare, senza partirsi dalle Regole,
che più oltra daremo; che saranno per il ben'essere della cantilena; conciosiache allora
dopo la Terza maggiore sarà dibisogno darli la Sesta maggiore, & dopo la minore, la Se
sta minore; ouer per il contrario; come nel sottoposto essempio si uede.
 Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette,
Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette, nel modo ch'io hò mostrato; che non si douerebbe anco porre due Quarte, in qual si uo-
glia compositione, come fanno alcuni in alcune particelle delle loro Canzoni, che chia-
mano Falso bordone; conciosia che, senza dubbio alcuno, la Quarta è consonanza perfet
ta: ma di questo ne ragionerò, quando mostrerò il modo di comporre à più uoci.
Quando le Parti della Cantilena hanno tra loro Harmonica relatione; & in qual
modo potiamo usare la Semidiapente & il Tritono nelle com-
positioni.Cap. XXX.
no le Parti della cantilena; cioè, quando le Voci tallora hanno, & tallora non
hanno relatione Harmonica tra loro. Onde si dè sapere; che tanto è dire, che
le Parti della cantilena non habbiano tra loro relatione Harmonica nelle loro
uoci; quanto à dire, che tra due Consonanze uicine l'una all'altra, che fanno can-
tando insieme due parti ascendendo, ò discendendo; ouero insieme ascendendo &
discendendo; si uenga à udire la Diapason superflua, ò la Semidiapente, ouero il Tri-
tono. Il che si troua fatto nello incrociamento della prima Figura, ò Nota di una par-
te acuta, con la seconda Figura, ò Nota di una parte graue; ouero tra la prima della
parte graue & la seconda della parte acuta. La onde tal Relatione si troua sempre tra
page 220quattro figure, ò note, & non meno; cioè, tra due poste nel graue, & due nell'acuto di
due Consonanze; come qui si uedono.
 E' ben uero che due parti, ch'insieme ascendono, & habbiano un mouimento, che conten
E' ben uero che due parti, ch'insieme ascendono, & habbiano un mouimento, che contenga il Semituono, tanto in una quanto nell'altra; par che sian tollerate dall'Vdito; per ca-
gione de i mouimenti fatti per cotali Semituoni; come sono quelli del primo luogo, della
Diapason superflua, & della Semidiapente, posti nel primo & nel terzo luogo dell'essem
pio. Onde accioche le nostre compositioni siano purgate d'ogni errore, & siano corrette,
cercaremo di fuggir tali relationi, quanto più potremo; massimamente quando compone
remo à Due uoci; percioche genera alle purgate orecchie alquanto di fastidio; essendo
che simili Interualli non si ritrouano esser collocati tra i Numeri sonori, & non si canta-
no in alcun genere di Cantilena; ancora ch'alcuni habbiano hauuto contraria opinione;
ma sia come si uoglia, sono molto difficili da cantare, & fanno tristo effetto. Et molto
mi merauiglio di coloro, che non si hanno punto schiuato di far cantare ò modulare in
alcuna delle parti delle lor cantilene alcuno de questi Interualli; ne mi sò imaginare, per
qual ragione l'habbiano fatto. Et ancorache sia minor male il ritrouarlo per relatione
tra due modulationi, che udirlo nella modulatione di una parte; tuttauia quel male istes-
so, che si ode in una parte sola, si ritroua diuiso tra due; & è quella istessa offesa dell'Vdi-
to; percioche nulla, ò poco rileua l'essere offeso d'uno istesso colpo, più da uno, che da
molti; quando il male non è minore. Questi Interualli adunque, che nel modulare non
si ammettono, si debbono schiuare nelle cantilene di maniera, che non si odino per
relationi tra le parti; laqual cosa uerrà fatta, quando le parti si potranno mutar fra loro
con interualli Harmonici proportionati, contenuti nel genere Diatonico; cioè, quan-
do da una voce della parte graue, potrà ascender alla seguente della parte acuta per un
spatio legittimo & cantabile, & cosi per il contrario; ma non già quando tra le parti di
qual si uoglia Compositione, tra quattro uoci, al detto modo, non si vdirà la relatione
de i detti Interualli; perche non si potranno, se non con gran discommodo, mutare; co-
me ne i sottoposti essempi tutti gli Interualli dell'altro essempio mutati si ueggono.
 Tutte le volte adunque che le Parti della compositione, ò cantilena non si potranno mu-
Tutte le volte adunque che le Parti della compositione, ò cantilena non si potranno mu-tar l'una nell'altra, dalla qual mutatione ne nasca il procedere per ueri & legittimi in-
terualli cantabili, tal compositione si debbe fuggire; massimamente se noi desideriamo
d'hauere una corretta compositione, & purgata da ogni errore. E' ben uero, che nelle
page 221compositioni de più uoci molte volte è impossibile di poterli schiuare, & di non incorre-
re in simili intrichi; percioche accade alle volte, che 'l Compositore componerà sopra al-
cun Soggetto, che lo inuiterà spesse uolte à far contra questo precetto; onde astretto dal-
la necessità lo lascierà scorrere; come quando lui uedesse, che le parti della compositio-
ne non potessero cantare commodamente; ouero quando uolesse accommodare una
Consequenza; che si potesse cantare commodamente; come altroue uederemo; ma
quando la necessità l'astringesse, debbe almeno hauer riguardo, che tal diffetto si com-
metta nelle chorde diatoniche, & in quelle, che sono proprie & naturali del Modo, &
non tra quelle, che sono accidentali, che nel mezo delle Cantilene si segnano con que-
sti segni
 .
.  . & b; percioche allora non generano tanto tristo effetto. Si debbe però
. & b; percioche allora non generano tanto tristo effetto. Si debbe però notare, ch'io chiamo Errori naturali quelli, che nascono nel modo mostrato di sopra nel
primo essempio; & quelli dico nascere per accidente, quando tra le uere chorde d'alcun
Modo se ne pone un'altra, che non è di quell'ordine, & da tal chorda nasce un tale in-
commodo; come può accascare nel Quinto Modo, del quale molte fiate la mezana chor
da, che è la
 , è lasciata da un canto, & in suo luogo si pone la b. per accidente. Onde
, è lasciata da un canto, & in suo luogo si pone la b. per accidente. Onde tra questa & la precedente, ò la seguēte nasce uno de i mostrati disordini; come nel primo
essēpio seguēte si uede. Et tanto più è senza soauità, quanto che la chorda
 . che è la prin
. che è la principale del Quinto modo, è rimossa dal suo proprio luogo, & posto la chorda b, laquale è
accidentale. Et benche per le ragioni dette non si possa usar tali Interualli accommoda-
ti in cotal maniera nelle cantilene; nondimeno potremo usare alle uolte la Semidiapen-
te in una istessa percussione; & ciò faremo, quando immediatamente da essa uerremo al
Ditono; come nel secondo essempio uediamo; percioche le parti si possono mutar tra
loro senz'alcun discommodo; come nel terzo essempio si può uedere. Et questo si osser-
ua da i migliori Musici moderni; com'è stato etiandio osseruato per il passato d'alcuni de
i più Antichi. Ne solamente sarà lecito usar la Semidiapente, ma il Tritono anco alle
uolte; come uederemo al suo luogo. E' ben uero, che tornerà meglio vsar la Semidia-
pente, che 'l Tritono; percioche allora le Consonanze saranno poste à i lor propri luo-
ghi; il che non sarà quando si porrà il Tritono. Si debbe però auertire, che quelle parti,
c'haueranno la Semidiapente, ouero il Tritono, debbono hauere primieramente auan-
ti essa Semidiapente ò Tritono senz'alcun mezo una Consonanza, sia poi perfetta ouer'
imperfetta, che questo non fà cosa alcuna; percioche dalla Consonanza precedente, &
dalla seguente, la detta Semidiapente uiene à temperarsi di maniera, che non fà tristo ef-
fetto, anzi buono; come si proua con la esperienza, & si ode ne i seguenti essempij.
 page 222
page 222Che rispetto si de hauere à gli Interualli relati nelle Compositioni di più
voci.Cap. XXXI.
midiapenti, de Semidiapason, & altri simili, quando si trouano posti ne i
Contrapunti, che non sono accompagnati con altri Interualli, sono con-
numerate tra quelle cose, che nella Musica possono dar poco diletto. On-
de dobbiamo sforzarsi di non porle nelle compositioni semplici, che sono quelle di due
uoci, come hò detto; ouer quando due parti d'ogn'altra cantilena cantano sole; concio
siache allora simil cose si odono manifestamente, per non ui esser quella Harmonia, che
noi chiamiamo Propria; nella quale si ode un Corpo pieno di consonanze & d'harmo-
nia; per hauer gli estremi suoni tramezati d'altri mezani; ma solamente si ode quella,
ch'è detta Impropria, nellaquale si odono solamente due parti, che cantano insieme
senza esser tramezate d'alcun'altro suono; le quali sono maggiormente comprese dal sen
so, che non sono tre, ouer quattro. La onde tra le due dobbiamo uariar quanto po-
temo l'Harmonia, & osseruar di non porre cotali relationi; cosa che si può fare senza
difficultà alcuna; ma nelle compositioni de più uoci tal rispetto non è molto necessario;
si perche non si potrebbe sempre osseruare cotal cosa, se non con grande incommo-
do; come etiandio perche la uarietà consiste non solo nella mutatione delle Consonan-
ze; ma etiandio dell'Harmonie, & de i luoghi; il che non accade nelle Compositioni,
che si compongono à due uoci. Et questo dico; percioche, si come alle uolte si troua-
no molte cose, che da per sè sono triste & nociue, & accompagnate con alcun'altre sono
buone & salutifere; come si uede di quelle, ch'entrano nelle Medicine, & altri Elettua-
ri, che da sè sono insuaui, & anco mortifere; ma accompagnate con alcun'altre, che iui
entrano, senza dubbio fanno men tristo effetto, & danno salute; cosi ancora fanno co-
tali Relationi nella Musica: & ui sono alcuni altri Interualli, che da per sè danno poca
dilettatione; ma accompagnati con altri fanno mirabili effetti. Però adunque altra con-
sideratione dobbiamo hauer di loro, quando si uogliono usare semplici, di quello, che
facciamo uolendoli usare accompagnati; conciosia che la uarietà dell'Harmonia
in simili accompagnamenti non consiste solamente nella uarietà delle Consonan-
ze, che si troua tra due parti; ma nella varietà anco dell'Harmonie, la quale consi-
ste nella positione della chorda, che fà la Terza, ouer la Decima sopra la parte graue del
la cantilena. Onde, ouer che sono minori, & l'Harmonia che nasce, è ordinata, ò
s'assimiglia alla proportionalità, ò mediatione Arithmetica; ouer sono maggiori, & ta-
le Harmonia è ordinata, ouer s'assimiglia alla mediocrità Harmonica; & da questa ua-
 rietà dipende tutta la diuersita, & la perfettione dell'Harmonie; conciosiache è neces-
rietà dipende tutta la diuersita, & la perfettione dell'Harmonie; conciosiache è neces-sario (come dirò altroue) che nella Compositione perfetta si ritrouino sempre in atto la
page 223Quinta & la Terza, ouer le sue Replicate; essendo che oltra queste due consonanze l'Vdi-
to non può desiderar suono, che caschi nel mezo, ouer fuori de i loro estremi, che sia in
tutto differente & uariato da quelli, che sono ne gli estremi di queste consonanze poste
insieme; ritrouandosi iui tutti quelli Suoni differenti, che possono far l'Harmonie diuer
se. Ma perche gli estremi della Quinta sono inuariabili, & sempre si pongono contenuti
sott'vna istessa proportione; lasciando certi casi, ne i quali si pone imperfetta; però gli
estremi delle Terze si pongono differenti tra essa Quinta. Non dico però differenti di
proportione, ma dico differenti di luogo; percioche (come hò detto altroueSupra.
cap. 10.) quando
si pone la Terza maggiore nella parte graue, l'Harmonia si fà allegra; & quando si pone
nell'acuto si fà mesta. Di modo che dalla positione diuersa delle Terze, che si pongono
nel Contrapunto tra gli estremi della Quinta, ouer si pongono sopra l'Ottaua, nasce la
uarietà dell'harmonia. Se adunque noi uorremo uariar l'harmonia, & osseruare più che
si può la Regola posta di sopra nel Cap. 29. (ancora che nelle compositioni di piu uoci
non sia tanto necessaria, quanto è in quelle di due uoci) è dibisogno, che noi poniamo
le Terze differenti in questa maniera; c'hauendo prima posto la Terza maggiore, che
faccia la mediatione Harmonica; poniamo dopoi la minore, che farà la diuisione Ari-
thmetica; la qual cosa non si potrebbe osseruar cosi di leggieri, quando s'hauesse rispet-
to à queste relationi; conciosiache mentre si cercasse di fuggirle, si uerrebbe à continua-
re il concento per alquanto spatio di tempo in una delle sopradette diuisioni, senz'alcun
mezo; & far che la cantilena alle uolte si udirebbe mesta nelle parole, che portano seco
allegrezza, ouer si udirebbe allegra in quelle, che trattano materie meste, senz'alcun
proposito. Io non dico già, che 'l Compositore non possa porre due diuisioni Arithme-
tiche l'una dopo l'altra; ma dico, che non dee continuare in tal diuisione lungo tempo;
perche farebbe il concento molto maninconico. Ma il porre molte diuisioni Harmoni-
che l'una dopo l'altra, non potrà mai dar noia; purche siano fatte nelle chorde na-
turali, & con qualche iudicio, & proposito nell'accidentali; percioche allora l'Harmo-
nia hà le sue parti collocate secondo i lor gradi, & tocca il suo ultimo fine, & fà ottimo ef-
fetto. E' ben uero, che quando due parti ascendessero, ò discendessero per un grado,
ouer per due, la mediatione si debbe porre diuersa; massimamente quando tra le due
parti, che fanno tali ascese & discese, può cascare il Tritono, ò la Semidiapente per re-
latione; che è quando si pone nel primo modo due Terze maggiori l'una dopo l'altra, &
nel secondo due minori; ma quando la relatione fusse d'una Semidiatessaron; & fusse
tra i segni accidentali; come sarebbe il b. & il
 ; oueramente quando concorresse un so-
; oueramente quando concorresse un so-lo de questi segni solamente, non ci dobbiamo per niente schiuare; perche essendo due
mediationi harmoniche, fanno buono effetto; com'è manifesto; ancora che non sia-
no uariate. Et di ciò alcun non si debbe marauigliare; percioche quando uorrà con di-
ligenza essaminar le Consonanze poste in cotali ordini; ritrouerà, che quell'ordine,
ch'è Aritametico, ouer s'assimiglia alla proportionalità Arithmetica, si lontana un po-
co dalla perfettione dell'harmonia; conciosia che le sue parti vengono ad esser colloca-
te fuori de i lor luoghi naturali. Per il contrario ritrouerà, che l'Harmonia, che nasce
dalla diuisione Harmonica, ouero à quella si s'assimiglia, consonerà perfettamente; per-
che le parti di tal diuisione saranno collocate & ordinate secondo i proprii gradi di tal
proportionalità; & secondo l'ordine, che tengono i Numeri sonori nel loro ordine
naturale; come si può uedere nel Cap. 15. della Prima parte. Et questo sia detto à ba-
stanza per hora; percioche forse un'altra fiata, per maggiore intelligenza di questo, ch'io
hò detto, ne toccherò una parola.
page 224
In qual Maniera due, ò più Consonanze perfette, ouero imperfette contenute sotto
vna istessa forma, si possino porre immediatamente l'una dopo
l'altra.Cap. XXXII.
trapunti due Consonanze simili in proportione, che insieme ascendino, ouer
discendino; si concede nondimeno il porre due Consonanze contenute da un'
istessa forma; siano perfette, ouero imperfette; come sono due Ottaue, due
Quinte, due Ditoni, due Semiditoni & altri simili, l'una dopo l'altra; senza por di me-
zo alcuna consonanza; quando che scambieuolmente per contrarij mouimenti la uoce
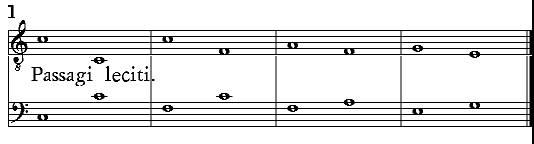 graue d'una parte della cantilena si pone nel luo-
graue d'una parte della cantilena si pone nel luo-go della uoce acuta dell'altra, & per il contrario;
come qui si uede. Percioche nel mutare, ò cam-
biare tali chorde tra loro la Consonanza non si
trasporta dall'acuto al graue, ouer dal graue
all'acuto; ma resta nelle sue prime chorde, non
mutando ne luogo, ne suoni; la onde non si ode
alcuna uarietà di graue, ò di acuto. Non si uden
do adunque tal uariatione; non si può dire, che
siano due Consonanze contenute da un' istessa
forma, poste l'una dopo l'altra, nel modo che s'intende di sopra; ma si bene una sola
consonanza replicata nell'istesse chorde; com'è manifesto al senso. Et quantunque le
parti si mutino tra loro ascendendo & discendendo, & che l'una piglia il luogo dellal-
tra, & le lor modulationi siano uariate per i mouimenti contrarii, che fanno; non sono
però uariati i lor suoni; ancora che si potesse udire qualche uarietà, quando la parte, che
era nel graue, s'udisse più nell'acuto, & quella ch'era nell'acuto, più si udisse quando
fusse nel graue. Ma tal cosa non farebbe assolutamente uarietà alcuna secondo 'l propo-
sito; ma si bene ad un certo modo; come si può comprendere dal sottoposto essempio;
che quando le parti non mutassero luogo, necessariamente le modulationi di ciascuna
uerrebbono ad essere unisone.

Come due, ò più Consonanze perfette, ouero imperfette, contenute sotto diuer-
se forme, poste l'una immediatamente dopo l'altra si concedono.
Cap. XXXIII.
cioche dalla uarietà delle Consonanze poste nelle compositioni con tanto
bell'ordine nascesse l'Harmonia soaue & diletteuole. La onde osseruate
tutte queste cose, i Musici presero dopoi tal libertà, che ne i loro Contra-
punti poneuano le Consonanze, come meglio li tornauano in proposito; & non si schi-
page 225uauano di porre due Consonanze perfette, ouero imperfette, che fussero; l'una dopo
l'altra uariando il luogo; senza esser tramezate d'alcun'altra consonanza mezana; pur
che fussero contenute sotto diuerse forme. Noi adunque per seguir tal'uso; per esser mol-
to commodo & ragioneuole, porremo ne i nostri Contrapunti le Consonanze nel mo-
do predetto; ponendo (quando tornerà commodo) l'Ottaua immediatamente dopo
la Quinta, ò per il contrario; & dopo ciascuna di queste la Terza maggiore, ouer la
minore. Similmente potremo porre dopo la Terza l'Hexachordo, & dopo questo
quella; come tornerà meglio, uariando sempre le consonanze; come nell'essempio
sequente si uede.
 Osseruando però, che le Parti procedino nelle lor modulationi per Interualli cantabili,
Osseruando però, che le Parti procedino nelle lor modulationi per Interualli cantabili, & con bel procedere, accioche ne risulti buona & diletteuole harmonia.
Che dopo la Consonanza perfetta stà bene il porre l'Imperfetta: ouero per il
contrario.Cap. XXXIIII.
nanze perfette prima si ritrouino l'una dopo l'altra, senza esserui interposta al
cuna forma dell'Imperfetta; come si può uedere nel Cap. 15. della Prima par-
te; & dopoi quelle dell'Imperfette, seguitando per ordine, senza essere trame-
zate d'alcuna forma delle Perfette; tuttauia non dobbiamo credere; se ben ci dobbiamo
reggere sempre da cotali numeri; che gli Antichi habbiano tenuto tal'ordine nel porre le
Consonanze ne i lor Contrapunti; percioche molto ben conobbero, che 'l continuare
nelle Consonanze perfette, ouer nelle imperfette; oltra che haurebbono apportato se-
co quasi fastidio; haurebbono etiandio aggiunto difficultà. Et ueramente sarebbe stato
quasi impossibile, che le modulationi delle parti hauessero hauuto in se una certa perfet-
tione, la qual si ricerca; conciosia che sarebbe stato difficile d'accommodarle con quella
uaghezza, che fà dibisogno, che si ritroui nella cantilena. Perilche adunque acciò si le-
ui questa difficultà, osseruaremo quello, che etiandio da loro è stato osseruato di porre
& collocar ne i Contrapunti una delle Cōsonanze imperfette dopo una perfetta; ouero
per il contrario; come dopo l'Ottaua, ouer la Quinta porre la Terza, ò la Sesta, ouer le
Replicate; & cosi dopo queste porre una de quelle; come uediamo fatto qui sotto.
 Imperoche da tal uarietà non potrà nascere se non buona, uaga, diletteuole, & perfetta
Imperoche da tal uarietà non potrà nascere se non buona, uaga, diletteuole, & perfetta Harmonia. Osseruando sempre (com'hò detto ancora) che le Parti della cantilena sia
page 226no cantabili; cioè, che cantino bene, accioche dalla compositione de tante cose ben po
ste insieme, habbiamo l'uso delle perfette harmonie.
Che le parti della Cantilena debbono procedere per mouimenti contrarij.
Cap. XXXV.
onde intendendosi etiandio de i Mouimenti, che fanno le parti cantando in-
sieme, si debbe osseruare quanto più si puote; ilche non sarà fuori delle osser-
uanze de gli Antichi; che quando la parte, sopra la quale si fà il Contrapun-
to; cioè, quando il Soggetto ascende, che 'l Contrapunto discenda; & cosi per il con-
trario, ascendendo questo, quella discenda; ancora che non sarà errore, se alle uolte
insieme ascenderanno, ouer discenderanno, per accommodar le parti della cantilena,
che procedino con acconci mouimenti. Onde se noi oseruaremo, che quando l'una
delle parti ascenda, l'altra discenda; non è dubbio, che le modulationi, faranno buono
effetto; come dal sottoposto essempio si potrà conoscere.

In qual maniera le Parti della Cantilena possino insieme ascendere, ò di-
scendere.Cap. XXXVI.
gola) ch'ella sia in tal modo fatale & necessaria, che non si possa alle uolte
fare il contrario; percioche sarebbe un uoler legare il Musico senza proposi-
to ad una cosa non molto necessaria, & leuargli il modo di procedere con
leggiadria, & eleganza, & l'uso insieme del cantare con harmonia; conciosiache se fus-
se bisogno d'osseruar sempre cotal cosa, non potrebbe (quando gli occorresse) usare il
procedere per Consequenza; il che è molto lodeuole à i tempi nostri in un Composito-
re, & si usa quando una parte della cantilena segue l'altra, nel modo che uederemo. Os-
seruando adunque la sopradetta Regola, più che si potrà; quando ne occorrerà di fare
che le parti della compositione ascendino, ò discendino insieme; allora cercaremo di re
plicare i lor mouimenti, che non habbiano à generare allVdito tristo effetto. Onde
quando si uorrà porre due Consonanze perfette l'una dopo l'altra, auertiremo che 'l si
proceda dall'una all'altra in cotal modo; che mouendosi l'una per salto, l'altra si muo-
ua per grado; percioche allora si potrà passar dalla maggiore alla minore; come dall'Ot-
taua alla Quinta; & per il contrario dalla minore alla maggiore, senz'alcuna offesa del
sentimento; come dal sottoposto essempio si può comprendere.
page 227
 E' ben uero, ch'è molto più lodeuole, quando le parti discendono insieme nel graue;
E' ben uero, ch'è molto più lodeuole, quando le parti discendono insieme nel graue; percioche allora necessariamente i Mouimenti loro si fanno tardi; & tanto più è lode-
uole, quanto più sono graui; perche per la tardità si comprende facilmente la diuersità
delle specie; Il che non cosi facilmente si comprende ne i suoni acuti nati dalla uelocità
de i mouimenti; conciosiache tendono quasi ad una simiglianza; massimamente quan-
do le parti ascendono insieme dalla Perfetta minore alla Perfetta maggiore. Ma per-
che queste cose non sono hoggidi considerate da i Prattici; essendoche pongono tali
passaggi ne i lor Contrapunti senz'alcuno auertimento; però dico solamente, che non si
debbono vsare spesse fiate ne i Contrapunti à due uoci; conciosia che dal Senso sono
maggiormente compresi, di quello che sarebbono, se tali mouimenti si ritrouassero in
una cantilena à più voci; percioche allora la diuersità de mouimenti, che farebbono
le parti tra loro, & la loro moltitudine non lasciarebbono udire ne questi, ne altri simili.
Ne anco è cosa lodeuole che si oda ne i Contrapunti due parti, che ascendino insieme da
una consonanza maggiore, che sia di specie Imperfetta, ad una minore, che sia Perfet-
ta, & facino i loro mouimenti per salto; cioè, per più d'un grado; oueramente due par-
ti, che ascendino, ò discendino insieme per detti mouimenti da una consonanza conte-
nuta da una proportione maggiore, sia perfetta, ouero imperfetra, ad una che segue, che
sia perfetta; come dalla Terza all'Vnisono, & dalla Decima all'Ottaua; percioche sem-
pre darà qualche noia alle purgate orecchie. Ne anco torna bene il por la Sesta auanti
la Quinta, quando le parti ascendono, ò discendono insieme; ancora che l'una si muoui
per grado, & l'altra per salto; come nel sotto posto essempio si può comprendere.
 Quanto poi siano grati questi mouimenti all'Vdito, l'Esperienza maestra delle cose,
Quanto poi siano grati questi mouimenti all'Vdito, l'Esperienza maestra delle cose, per uia del senso, ce lo manifesta; essendo che la Natura hà in odio le cose senza pro-
portione & senza misura, & si diletta di quelle, c'hanno tra loro conuenienza. Per il-
contrario adunque sarà lecito il porre una Consonanza maggiore, che sia imperfetta,
auanti una minore, che sia perfetta; quando le parti ascenderanno, delle quali l'una,
cioè, l'acuta ascendi per grado, & la graue per salto. Starà anche bene, che da una Con-
sonanza imperfetta minore si uada ad una perfetta maggiore, ascendendo la parte gra-
ue per grado, & l'acuta per salto; ouero ascendendo l'acuta per grado, & la graue per
salto. Si concede etiandio che dalla Consonanza imperfetta, che sia minore di propor
page 228tione della seguente, si uadi all'Ottaua; quando insieme ascendono, ouer discendono
le parti; pur che una di esse faccia il Mouimento di grado, & tal Mouimento sia d'un
Semituono maggiore; come nell'essempio seguente si uede.
 E' concesso etiandio il venire dalla Consonanza perfetta all'imperfetta; quando le parti
E' concesso etiandio il venire dalla Consonanza perfetta all'imperfetta; quando le parti ascendono, ouer discendono insieme; pur che l'una di esse si muoua per grado, & la Con
sonanza imperfetta sia di maggior proportione della perfetta. E' lecito etiandio por due
Consonanze l'una dopo l'altra, che faccino tra due parti il mouimento di salto; pur che
l'una di esse si muoua per un Semiditono; come qui si uede.
 Si può ancora con mouimenti di salto por due parti ne i Contrapunti, che insieme
Si può ancora con mouimenti di salto por due parti ne i Contrapunti, che insieme ascendino ò discendino, quando la parte acuta discende per una Terza, & la graue per
una Quinta, & si uiene dalla Terza alla Quinta; ouer per il contrario, si ascende dalla
Quinta alla Terza, & l'una delle parti; cioè, la graue ascende per una Quinta, & l'acuta
per una Terza. E' ben uero, che quando una de loro facesse il moto per un Ditono; mas-
simamente discendendo, che tali mouimenti si potranno schiuare; percioche 'l procedere
in cotal modo è alquanto aspro; come l'esperienza ce lo manifesta. Ma l'ascendere dalla
 Quinta al Ditono si concede; percioche le parti procedono per alcuni mouimenti, i qua
Quinta al Ditono si concede; percioche le parti procedono per alcuni mouimenti, i quali non solamente sono sopportabili; ma anco molto dilettano; essendo che sono molto so
nori; & questo percioche procedono uerso l'acuto, onde si generano i Mouimenti ueloci,
da i quali sono ascose le durezze, che per la tardità de mouimēti si manifestano, quādo uā
no uerso 'l graue. Lūgo sarebbe il voler porre d'uno in uno tutti i Mouimēti & passaggi, che
page 229possono far le parti de i Contrapunti; & di uno uolerne assignare la ragione paticola-
re; ma di ciò sia detto à sufficienza, poi che da quello, che si è detto, si può hauere un
modo, ò Regola generale di conoscere i buoni passaggi da i tristi; laqual cognitione
non sarà molto difficile d'acquistare à tutti coloro, che si uorranno essercitare nell'osser-
uanza delle nostre Regole.
Che si debbe schiuare più che si può, i Mouimenti fatti per salto; & similmen-
te le Distanze, che possono accascare tra le Parti della cantilena.
Cap. XXXVII.
solo quando ascendono insieme, ò discendono; ma etiandio quando si muo-
uono in diuerse parti, procedino più che sia possibile per Gradi, & si deb-
be fare, che l'una parte non molto s'allontani dall'altra con Salti; come quan-
do l'una procedesse per salto d'Ottaua, & l'altra per salto di Quinta, ò di Quarta, ò per
altri simili ; come sono quelli del seguente essempio.
 Conciosia che tali distanze, oltra che sono difficili da cantarsi; percioche non cosi fa-
Conciosia che tali distanze, oltra che sono difficili da cantarsi; percioche non cosi fa-cilmente si possono formar le Voci & proportionare gli Interualli, & le Consonanze in
quelle modulationi, che procedono in cotal modo; come quelle, che si cantano l'una
per grado & l'altra per salto; generano etiandio alcuni effetti, ch'alle uolte all'Vdito
non sono molto grati. Onde è da notare, che i Mouimenti quanto più sono uniti; cioè,
non molto lontani, come sono quelli, che si muouono per grado, sono senza dubbio più
cantabili, & con maggior diletto fanno udire l'Harmonia, che nasce da loro tra le parti;
che quelli, che sono lontani; & ciò nasce; perche quanto più sono congiunti, tanto più
sono naturali; essendo che allora si procede naturalmente, quando si uà dall'uno estre-
mo all'altro d'alcuna cosa per i debiti mezi. Di maniera che molto è da lodare & da
commendare tale uicinità; come quella, che s'accosta più alla natura. Il che molto lo-
dò anco Agostino il Santo nel Cap. 10. del 2. lib. della Musica, dicendo; La uicinità
delle parti, tanto è più degna d'essere approuata, quanto è più uicina all'equalità; an-
cora che iui ragionasse in altro proposito. Et quantunque queste distanze da sè non sia-
no dissonanti, generano nondimeno un non sò chè di tristo all'Vdito, che non si può
udir con diletto. Schiuaremo adunque queste distanze, accioche i nostri Contrapunti
siano grati, dolci, sonori, & pieni di buona harmonia.
page 230
In qual maniera si debba procedere da vna Consonanza ad vn'altra.
Cap. XXXVIII.
teuano occorrere contra la data Regola, alcuni Musici ordinassero, che
Quando si procedeua da una Consonanza all'altra, che se li douesse anda-
re con la piu uicina; come dall'Vnisono alla Terza, da questa alla Quin-
ta, dalla Quinta alla Sesta; cosi da questa all'Ottaua, & per il contrario; per non ue-
nire à i mouimenti distanti. La qual Regola, ancora ch'al primo incontro pari che
sia facile da intendere; nondimeno hà di bisogno di qualche consideratione; per-
cioche contiene alcune cose non solo utili, ma anco necessarie à tutti quelli, che
uorranno seguir l'uso delle buone harmonie, & condurre à perfettione l'opere loro;
lequali non solamente l'Arte, ò la Scienza ricerca, ma sono etiandio osseruate na-
turalmente da molti. Quando adunque dicono, che si dee procedere da una Con-
sonanza ad un'altra con la più uicina; si debbe intendere in cotal modo; che parten-
dosi il Compositore da una consonanza Imperfetta, & uolendo andare alla Perfetta;
debbe fare, che quella Imperfetta, che precede, le sia ueramente la più uicina; per-
cioche facendo altramente non osseruarebbe tal Regola, la quale è sommamente ne-
cessaria. La onde si dee prima auertire, che quando uorremo uenire dalla Sesta al-
l'Ottaua, tal Sesta dè esser la maggiore, come a lei più uicina; & non dobbiamo por-
re la minore; percioche (come più oltra uederemo) l'è più lontana. Et ciò dobbia-
mo osseruare, non solo quando le parti della cantilena fanno contrarii mouimenti,
ma etiandio quando una di esse non si mouesse dal proprio luogo, & l'altra ascendesse,
ò discendesse per salto di due gradi. Similmente quando dalla Sesta uorremo uenire
alla Quinta, tal Sesta debbe esser minore; come quella che à lei è piu propinqua;
& non la maggiore; perche le è piu lontana; massimamente quando una delle parti
della cantilena non fà mouimento alcuno, & l'altra ascende, ò discende per grado;
& quando dalla Terza uorremo uenire all'Ottaua, la Terza debbe esser la maggio-
re; come quella, ch'è più uicina ad essa Ottaua, & non la minore. Et fa dibiso-
gno che le parti si muouino per mouimenti contrarii; l'una per Grado, & l'altra per
Salto. Ma quando dalla Terza uorremo uenire alla Quinta, & una della parti non
farà mouimento alcuno; sarà dibisogno, che la Terza sia la maggiore. Ma la Ter-
za allora sarà minore, massimamente nelle cantilene di due uoci, quando le parti
procederanno per Gradi, & anco per Mouimenti contrarii; oueramente quando
l'una di esse discenderà per grado, & l'altra similmente discenderà per Salto; ancora
che in quelle parti, che procedono per Mouimenti contrarij si pone la Terza mino-
re, per schiuar la Relation del Tritono tra le parti, la quale non le è più uicina,
ma più lontana. Quando poi dalla Terza uorremo uenire all'Vnisono; ancora che
non sia posto nel numero delle Consonanze, se non in quanto è il loro principio;
la Terza sarà sempre minore, come più uicina; ma bisogna che le parti si muoui-
no per Contrarii mouimenti, & che tali mouimenti siano per grado; percioche
quando le parti ascendessero insieme, l'una per grado & l'altra per Salto, allora
la Terza si porrà maggiore. Et se una delle parti non si muouesse, & l'altra ascen-
desse, ò discendesse per Salto, allora la Terza si porrà sempre minore. Et ciò dico,
hauendo sempre riguardo à i luoghi, ouer termini della Consonanza perfetta, che
saranno le chorde, sopra le quali essa Consonanza hauerà à terminare; come si uede
ne i sottoposti essempi.
page 231
 Quando poi si porrà la consonanza Imperfetta dopo la Perfetta, allora non è neces-
Quando poi si porrà la consonanza Imperfetta dopo la Perfetta, allora non è neces-sario hauere questa consideratione; pur che si osserui che i mouimenti, che fanno
le parti, siano regolati, secondo 'l modo mostrato di sopra. Io dico dalla Perfetta
all'Imperfetta, per questa ragione; percioche Ciascuna cosa desidera naturalmente
la sua perfettione, alla quale desidera di peruenire più presto, & col migliore & più
breue modo, che puote; la qual perfettione in questo genere s'attribuisce alle Con-
sonanze perfette. La onde ciascuna cosa facilmente (come ad ogn'uno è manifesto)
dalla perfettione può passare all'imperfettione, ma non per il contrario; percioche
è cosa più difficile fare una cosa, che non è il distrugger la & roinarla. Di modo che
quando si operasse altramente di quel che hò detto, sarebbe un'operare contra l'or-
dine & contra la natura delle cose; conciosia che le Imperfette tanto più parteci-
pano della perfettione, quanto più s'accostano alla lor uicina Perfetta, & si ren-
dono etiandio all'Vdito tanto più dolci & più soaui. Mi potrebbe alcun dire; Se
la Sesta maggiore è più uicina alla Quinta, che non è all'Ottaua, com'è manifesto;
per qual cagione la dobbiamo maggiormente porre auanti la Ottaua, che la Quin-
ta; poi c'habbiamo d'andare dalla consonanza Imperfetta alla Perfetta con la più
uicina? Dico, che quantunque la Sesta maggiore sia più uicina alla Quinta, che
all'Ottaua; per questo non è uero, che la Minore non sia più uicina alla Quinta
della Maggiore. Onde dobbiamo sapere, che essendo tra le Consonanze perfette
l'Ottaua maggior della Quinta; & tra le Seste, la maggiore di maggior quantità,
che non è la minore; dobbiamo accompagnar la maggiore delle Perfette con la mag-
giore dell'Imperfette; per la simiglianza (dirò cosi) ò consenso, che è tra loro;
percioche facil cosa è di passar da una cosa ad un'altra & senza molta fatica, quan-
do tra loro si ritroua qualche simiglianza. Onde dobbiamo andare alla Quinta
con la Sesta minore; percioche hà tal consentimento con lei, & à lei è più uicina.
so, & è à lei più propinqua. Ne sò ueder ragione alcuna, che dimostri, che ad una
cosa, alla quale s'habbia solamente un rispetto, se le conuenga due cose diuerse, &
quasi contrarie; & parmi, che usandole ad altro modo, sarebbe fare, come fà quel
Medico, che GalenoDe Sectis. chiama Empirico, ilquale con una istessa medicina uuol curare
diuerse egritudini; non facendo caso alcuno, che 'l male procedi più da humor cali-
do, che da frigido; conciosiache non conosce l'humore peccante. Alla Ottaua uera-
mente si conuiene la Sesta maggiore, & non la minore; & questa s'accompagna ot-
timamente con la Quinta; come si può prouar con ragione, con autorità, & con l'es-
sempio. Et primieramente si proua con ragione; come hò mostrato di sopra; & anco,
perche se noi haueremo riguardo al Numero harmonico, dal quale hà la sua forma ogni
Consonanza musicale; ritrouaremo, che la Sesta maggiore hà la sua forma dalla pro-
portione Superbipartienteterza, contenuta tra questi termini 5 & 3. che sono la Radice
tal proportione. Onde se noi procederemo più oltra nell'ordine naturale de i Numeri
sopradetti; ritrouaremo, che dopo 'l 5. senz'alcun mezo succede il 6. che col 5. contiene
page 232la forma della Terza minore; la quale se noi accompagnaremo con la detta Sesta, haue-
remo à punto la Ottaua. Per la qual cosa se noi porremo il 3. che habbia due relationi;
com'è al 5. & al 6. procedendo per ordine naturale in questo modo. 6. 5. 3. qua-
si nella maniera, che procedono due parti, delle quali l'una uadi dall'acuto al graue &
l'altra non si muoui; oueramente se noi porremo l'istesso ordine tra 10. 6. 5. quasi nel
modo, che procedono due parti, delle quali l'una si parta dal graue & uada uerso l'acu
to, procedendo per un Semiditono, & peruenga all'Ottaua; & l'altra stia ferma; mede-
simamente uederemo quanto sia necessaria l'osseruatione della predetta Regola. Que-
sta osseruanza ritrouaremo etiandio in tale ordine tra il 15. & 9. che contengono la for-
ma della Sesta maggiore fuori de i suoi termini radicali; perche, si come due parti, l'una
delle quali ascendi per un Tuono maggiore, & l'altra discendi per un maggiore Semi-
tuono, uengono all'Ottaua con mirabil modo; cosi ponendo l'8. sopra il 9. & aggiun-
gendo 'l 16. sotto 'l 15. ritrouaremo la forma della Diapason fuori de i suoi termini radi-
cali, tra il 16. & l'8. in questo ordine naturale 16. 15. 9. 8. Et si come non si ritroua in un
tal'ordine, che dalla forma della Sesta maggiore si possa uenire alla forma della Quinta,
se non con l'aiuto del Tuono; cosi mai si potrà procedere dalla Sesta minore alla Quin-
ta, se non con l'aiuto del Semituono; come si può comprendere da questi quattro ter-
mini 50. 45. 30. 27. tra i quali commodamente si ritroua la forma della Quinta tra 45.
& 30. & quella del Tuono minore da ogni parte; & tra questi 24. 16. 15. 10. la forma del
Semituono maggiore nel luogo di mezo, & quella della Quinta da ogni parte tra 24 &
16. & tra 15. & 10. à guisa d'una parte, che proceda dal graue all'acuto, ò per il contra-
rio; & l'altra posta nel graue, ò nell'acuto non faccia mouimento alcuno; & questi termi
ni nō si potranno ritrouare in altra maniera nell'ordine naturale de i detti Numeri harmo
nici, se non con grande difficultà, & non saranno posti nel detto ordine se non per ac-
cidente. Et quelle ragioni, ch'io hò detto della Sesta maggiore con la Ottaua, si possono
applicare alla minore con la Quinta, & all'altre Consonanze ancora, le quali lascio per
breuità. Ecci un'altra ragione ancora, per dimostrare cotal cosa; che di due Conso-
nanze imperfette proposte, siano qual si uogliano, pur che siano denominate da un'
istesso numero di chorde; sempre la maggiore è più atta à pigliare accrescimento nel gra-
ue, ò nell'acuto, che la minore, laquale hà natura di restringersi, & farsi anco minore,
conciosia che la maggiore hà più del continuo, che non hà la minore. Laonde auiene, che
desiderando & appetendo ogni cosa simile naturalmente il suo simile, la Sesta maggiore,
per hauer più perfettione della minore, maggiormente desidera di auicinarsi all'Otta-
ua, la quale per sua natura è più perfetta della Quinta; anzi d'ogn'altra è perfettissi-
ma, com'altre uolte hò detto; & la Sesta minore, come meno perfetta, da qual parte
si uoglia, sia graue, ò acuta, appetisce quella, ch'è piu conforme alla sua natura, che è
la Quinta. Questa istessa osseruanza si conferma con la autorità de molti Musici mo-
derni,Franchi-
nus Gaffu-
rus.
Pract. lib.
3. cap. 3.
Regu. 7. i quali seguendo le ragioni & l'autorità de quelli, che erano più antichi di loro, uo-
gliono, che 'l proprio della Sesta maggiore sia di uenire all'Ottaua, & il proprio della Mi
nore d'auicinarsi alla Quinta. Essendo adunque tale la Natura de queste Conso-
nanze, bisogna dire, che sempre habbiano tal natura & inclinatione; & che quando
si pongono altramente nelle compositioni, si ponghino contra la natura loro. Onde se
quelle cose, che si pongono contra la lor natura in opera, non possono far buono effetto;
percioche sono ritirate dal proprio loro fine; potremo dire, qualunque uolta che tali Con
sonanze si porranno ne i Contrapunti contra la loro natura, che non potranno apporta
re all'Vdito cosa che molto diletti. Potiamo hora uedere cotal cosa esser uera con l'espe-
rienza in mano, & uenire all'essempio promesso; conciosia che migliore effetto fanno
poste ne i Contrapunti al modo mostrato di sopra, che in altra maniera. La onde la
Natura, la quale hà iurisdittione in ogni cosa, hà fatto, che non pur quelli, che so-
no periti nella Musica; ma gli Idioti & Contadini, i quali cantano al modo loro sen-
z'alcuna ragione, usano di andare (come spinti, & quasi uiolentati dalla Natura)
page 233dalla Sesta maggiore all'Ottaua; ilche si ode maggiormente nelle Cadenze, che in ogn'
altra parte delle lor Canzoni; come è manifesto à ciascun perito nella Musica. Et forse,
che Franchino Gaffuro, da questo prese ardir di dire, che l'andare dalla Sesta maggiore
all'Ottaua, si douea osseruare solamente nelle Cadenze; percioche in esse si fanno le ter-
minationi delle cantilene; ma parmi (come si può comprendere) da quello che si è det-
to di sopra, che ciò non sia detto con ragione; se uorremo attendere alla natura dell'u-
na & dell'altra. Non sarà adunque lecito (uolendo osseruar cotal Regola) di passar dal-
la Sesta maggiore alla Quinta, ne anco dalla minore all'Ottaua, senza deprauatione del
la natura delle predette Consonanze. Onde bisogna auertire; accioche con facilità si
osserui questa Regola; che qualunque uolta si uorrà procedere dalla Consonanza Im-
perfetta alla Perfetta; di fare, che almeno una delle parti si muoua con un mouimento,
nel quale sia il Semituono maggiore, tacito, ouero espresso. Et per conseguire tal cosa
giouerà molto l'uso delle chorde Chromatiche, & dell'Enharmoniche, adoperandole
nel modo, ch'altroue son per dimostrare. Ma perche, si come non torna sempre commo
do al Compositore di passar dalla Sesta maggiore all'Ottaua, ne dalla Minore alla Quin-
ta; cosi non torna alle uolte commodo di procedere dalla Terza minore all'Vnisono,
nel modo chio hò mostrato di sopra; per tanto accioche ogn'uno sappia in qual modo
habbia da fare in simil casi; porrò i sottoposti essempi, ne i quali si potrà uedere, in quan
ti modi si può passar dall'una all'altra Sesta; & cosi dalla Terza maggiore & dalla mino-
re & altre simili ad un'altra Consonanza.
 Questo è ultimamente da notare; che quello, che si è detto delle Consonanze semplici,
Questo è ultimamente da notare; che quello, che si è detto delle Consonanze semplici, si dee anco intender delle Replicate. Similmente si debbe auertire; che quando due
 parti della cantilena discenderanno insieme, &
parti della cantilena discenderanno insieme, & dalla Sesta maggiore uerranno alla Terza, che sia
Maggiore; allora la parte acuta cascherà meglio,
& farà megliore effetto, che se cascasse sopra la
Minore; ancora che l'uno & l'altro modo sia buo-
no; percioche cascherà senza dubbio alcuno so-
pra una Consonanza, che più si auicina alla per-
fettione, che non fà la Terza minore; come si
potrà udire & essaminare in questi due essempi, po-
sti qui da canto.
In qual maniera si debba terminare ciascuna Cantilena.Cap. XXXIX.
delle Consonanze perfette; percioche uidero ueramente, che per ogni do-
uere la Perfettione della cosa si attribuisce al fine, dal quale si fà poi giudicio.
Et perche uidero, che non si poteua ritrouar maggior perfettione nelle Con-
sonanze di quello, che si troua nell'Ottaua, per esser la piu perfetta d'ogn'altra; uolsero
page 234che tal Regola fusse fatale, & che si douesse finire le cantilene nell'Ottaua, oueramente
nell'Vnisono, & per alcun modo non si facesse al contrario; ancora che questa Regola d'
alcuni di non molto giudicio sia stato poco osseruata. Se adunque noi desideriamo di se
guir tutti quelli, che sono stati Istitutori & Osseruatori delle buone Regole, quando ha-
ueremo da concludere alcun de i nostri Contrapunti, lo terminaremo per una delle no-
minate Consonanze; percioche sono le piu perfette de tutte l'altre. Questa Regola ue-
ramente fù molto bene istituita; conciosia che se le cantilene finissero altramente, l'orec
chie de gli Ascoltanti starebbono sospese, & desiderarebbono la lor perfettione. Onde
intrauerrebbe quello, che suole intrauenire à coloro, che odono recitare alcuna Oratio
ne; che stando con l'animo attenti ad ascoltare; desiderano & aspettano in un tempo il
suo Epilogo & la Conclusione, nella quale l'Oratione si riduce alla sua perfettione. Na
scerebbe etiandio un'altro incommodo, quando la Cantilena si terminasse altramente;
che essendosi attribuito il giudicio, che si fà, di qual Modo ella sia composta, all'Vlti-
ma chorda di ciascuna cantilena, per conoscere se l'Harmonia, che nasce da lei, sia del
Primo, ouer del Terzo, ò d'altro Modo; come uederemo nella Quarta parte; si potreb
be allora pigliar la chorda finale di qual parte si uolesse, ancora che non fusse la pro-
pria del Modo; fusse poi la graue, ouer l'acuta; & giudicar per quella, che non è la
propria, un Modo per un'altro; & cosi si farebbe giuditio falso; il che ueramente aue
rebbe, quando detti Contrapunti finissero per Quinta, ouer per Terza, ò per una del
le Replicate; massimamente stando la parte piu graue nella chorda confinale del Mo-
do, sopra 'l quale è fatta la cantilena; conciosiache allora non si saprebbe cosi facilmen-
te, qual chorda si douesse pigliare, ò l'acuta, ouer la graue, per far tal giudicio; ancora
che si potesse giudicare, cotal cosa nel mezo udendola & uedēdola dalla sua forma; cioè,
dal procedere, ch'ella farebbe. Con gran giudicio adunque ordinarono gli antichi Musi
ci questa & l'altre sopra date Regole, molto utili & grandemente necessarie à ciascuno,
che desidera di comporre correttamente ogni cantilena. La onde ciascuno si sforzerà di
porle in uso; accioche delle sue fatiche ne possa acquistare honore. Ma questo sia detto
à sufficienza intorno le Regole essentiali di comporre i Contrapunti semplici de due uo-
ci, che si chiamano di Nota contra nota; le quali non solamente seruono à queste com-
positioni; ma etiandio à qualunque altro modo di comporre, sia qual si uoglia, sempli-
ce, ò diminuito, che sia il Contrapunto; come si potrà uedere.
Il modo che si dee tenere nel far i Contrapunti semplici à due voci,
chiamati di Nota contra nota.Cap. XL.
nere nel far i Contrapunti; incominciando da quelli, che si compongono sem
plicemente à due uoci di Nota contra nota; accioche da loro si possa passare à
i Diminuiti, & all'uso dell'altre compositioni. Volendo adunque osseruar quel
lo, che da tutti i buoni Scrittori & Compositori di qualunque altra materia è stato os-
seruato, ragioneuolmente incominciaremo dalle cose più leggieri; accioche 'l Lettore
più facilmente si renda docile, & non ne segua confusione. Primieramente adunque ha-
uendo riguardo à quello, che si è detto di sopra nel Cap. 26. fà dibisogno di ritrouare
un Tenore di qual si uoglia Canto fermo, il quale sia il Soggetto della Compositione;
cioè, del Contrapunto; dopoi bisogna essaminarlo con diligenza, & ueder sotto qual
Modo ello sia composto; per poter far le Cadenze à i loro luoghi proprij con proposito,
& conoscer da quelle la natura della compositione; accioche facendole per inauertenza
fuor di proposito, & fuor de i loro proprij luoghi, mescolando quelle d'un Modo con
quelle d'un'altro, non uenga poi il fine ad esser dissonante dal principio & dal mezo del-
page 235la cantilena. Ma poniamo che 'l ritrouato Soggetto sia il sottoposto Tenore di canto fer
mo, contenuto nel Terzo Modo; si dè auertire auanti tutte l'altre cose quello, che nel
Cap. 28. di sopra si è detto, intorno al modo di dar principio alla compositione; On-
de porremo la prima figura, ò nota del Contrapunto lontana dalla prima del Soggetto
in tal maniera, che siano distanti per una delle Consonanze perfette. Fatto questo ac-
compagnaremo la seconda nota del Contrapunto con la seconda del Soggetto distanti
l'una dall'altra per una Consonanza, sia Perfetta, ouer'Imperfetta; pur ch'ella sia diuer
sa dalla prima; acciò non si facesse contra quello, che si è detto nel Cap. 29. hauendo sem
pre l'occhio à quello, ch'è stato determinato nel Cap. 38. facendo che le parti della canti
lena stiano piu unite, che sia possibile; & che l'una & l'altra non faccino mouimenti di
grande interuallo; accioche le parti non siano tra loro molto lontane, secondo la dottri-
na del Cap. 37. Fatto questo si potrà uenire alla terza figura, ò nota del Contrapunto,
& accompagnarla con la terza del Soggetto; uariando non solamente le chorde, ò luo-
ghi; ma etiandio la consonanza; accompagnando la Perfetta dopo l'Imperfetta, & co-
si per il contrario; oueramente ponendo due Perfette, ouero Imperfette differenti di spe
cie l'una dopo l'altra, secondo le Regole date nel Cap. 33. & 34. Il medesimo faremo
della quarta figura del Contrapunto, con la quarta del Soggetto; & cosi della quinta,
della sesta, & dell'altre per ordine, fin tanto, che si uenghi all'ultima; & secondo la
Regola data nel Capitolo precedente, finiremo il Contrapunto per una delle Con-
sonanze perfette. Ma sopra ogn'altra cosa si dee cercare, che la parte del Contra-
punto sia uariata, non solamente per diuersi mouimenti; toccando diuerse chorde
hora nel graue, hora nell'acuto & hora nel mezo; ma che sia anco uariata di con-
sonanze con la parte del Soggetto. Et si dè fare, che la parte del Contrapunto canti
bene, & proceda piu che sia possibile per Gradi; percioche in questo consiste una
parte della bellezza del Contrapunto; la quale aggiunta à molte altre, che si ricer-
cano in esso (come uederemo) lo rende alla sua perfettione. Onde ciascuno, che si esser
citerà primieramente in questa maniera semplice di comporre; potrà dopoi facilmente
& presto peruenire à cose maggiori; imperoche cercando di far sopra un Soggetto ho-
ra nel graue, hora nell'acuto, uarie Compositioni & Contrapunti, uerrà à farsi buon
prattico delle chorde & delle distanze di ciascuna Consonanza; & potrà secondo i pre
cetti, che io son per mostrare, uenire alla diminutione delle figure; cioè al Contrapun-
to diminuito; ponendo alle uolte le parti de i Contrapunti in Consequenza con quelle
del Soggetto, & alcuna uolta imitandole, & ad altri modi facendo; come uederemo;
& dopo questo potrà uenire alle Compositioni de piu uoci; conciosiache aiutato da i no
stri auertimenti, & dal suo ingegno diuenterà in tempo breue un buono Compositore.
nel far la parte del Contrapunto sopra un Soggetto, ma solamente la pongo uniuersale;
onde da quelle Regole, che sono poste di sopra, è dibisogno, che 'l Compositore col suo
intelletto caui cotal Parte, operando con giuditio; all'acquisto del quale uagliono poco
le Regole & li Precetti, quando dalla Natura non è aiutato. Ne di ciò prenda al-
cun marauiglia, essendo questo commune ad ogn'Arte & ad ogni Dottrina; per-
cioche tutti quelli, c'hanno uoluto dar notitia & insegnare alcuna Arte, ò Scienza,
hanno sempre proposto l'Vniuersale; essendo che la Scienza non è de i Particolari,
i quali sono infiniti; ma si bene de gli Vniuersali. Vediamo, che i Precetti della
Poesia, & dell'arte Oratoria; scritti da Platone, da Aristotele, da Hermogene, da
Demetrio Falereo, da Cicerone, da Quintiliano, da Horatio, & d'altri ancora; so-
no intorno l'Vniuersale, & non intorno al Particolare. Et per dar'un'essempio, mi
souien quello, che scriue Horatio parlando in uniuersale dell'ordine, c'hanno da te-
nere i Poeti nel disporre il Soggetto, che è la Historia, ouer la Fauola nelle lor nar-
tationi; dicendo:De arte
Poetica.
page 236
Ordinis haec virtus erit, & Venus, aut ego fallor.
Vt iam nunc dicat: iam nunc debentia dici
Pleraque differat, & praesens in tempus omittat.
La qual Regola molto ben sapea il dottissimo Virgilio, come si può comprendere; c'
hauendo preso un Soggetto determinato, ch'era di scriuere la Roina, & l' di
Troia, & la Nauigatione di Enea; incominciò primieramente dalla Nauigatione, inter
rompendo l'ordine; nondimeno la Nauigatione fù dopo; ma comprese, che con mag-
giore arteficio, & con maggior maestà sarebbe riuscito il suo Poema,2. Aenei. se hauesse fatto re-
citar l'Historia per ordine da Enea alla presentia di Didone, come fece; prendēdo l'occa
sione dalla fortuna ch'ei hebbe riducēdolo in Cartagine. Cosi sogliono fare i Poeti, & nō
solo i Poeti; ma anco i Pittori; i quali accommodano le historie, ò fauole, come meglio li
tornano in proposito; percioche la Pittura nō è altro, che una Poesia muta. Onde il Pitto
re hauendosi proposto alcuna uolta di dipingere un'historia, ò fauola, accōmoda le figure
& le accompagna insieme, secondo ch'à lui pare, che stiano meglio, & che faccino me-
gliori effetti; ne fà caso alcuno di porne una più in un modo, che in un'altro; cioè, che
più stia in piedi, ouer'à sedere in una maniera, che in un'altra; pur che osserui l'ordine
della Historia, ò fauola, che vuol dipingere; ilche si uede, ch'infiniti Pittori haueranno
dipinto una cosa istessa in infinite maniere; come più uolte hò ueduto l'historia di Lucre
tia Romana moglie di Collatino; quella d'Horatio Cocle, & molte altre; nondimeno
tutti haueranno hauuto un'istesso fine, di rappresentar le dette historie. Et non solamen
te questo si uede fatto da diuersi Pittori d'un'istesso soggetto; ma etiandio da un solo, il-
quale haurà dipinto una cosa istessa in diuersi modi. Debbe adunque il Musico etiandio
cercare di uariar sempre il suo Contrapunto sopra un Soggetto; & potendo far molti pas
saggi, eleggerà quello, che sarà il migliore, che li tornerà più in proposito, & che farà il
suo Contrapunto più sonoro & meglio ordinato, & lascierà da un canto gli altri. Però
adunque quando gli occorrerà di poter fare un passaggio; come sarebbe dire una Caden
za, & non tornerà bene secondo 'l proposito, la debbe riseruare ad un'altro luogo piò cō
modo; & ciò farà, quando la Clausula, ouer il Periodo nelle Parole, ouer'Oratione non
sarà terminato; conciosia che debbe sempre aspettare, che ciascun de questi sia finito; &
similmente auertir debba, che sia il luogo proprio, & che 'l Modo, sopra il quale è fonda
ta la cantilena, lo ricerchi. Tutte queste cose debbe osseruar colui, ilquale desidera di
introdursi bene nell'arte del Contrapunto; ma sopr'ogn'altra cosa dee con ogni studio es
sercitarsi primieramente molti giorni in tal sorte di compositione; accioche con più fa-
cilità possa uenire dopoi all'uso del Contrapunto diminuito, nel quale potrà usar molt'al
tre cose; come uederemo à i loro luoghi. Ma accioche si habbia qualche intelligenza di
tutto quello, c'hò detto, porrò qui sotto alcuni Contrapunti di Nota contra nota uaria-
ti, composti sopra 'l Soggetto nominato, hora nell'acuto & hora nel graue; i quali prima
essaminati, si potranno dopoi facilmente intender quelle cose, che mostrerò altroue; & si
potrà operare con minor fatica. Ciascun però debbe esser'auertito, che 'l fare del Contra
punto di Nota contra nota, par che sia & è ueramente alquanto più difficile di quello,
che non è, il farlo diminuito; & questo procede, perche in questo non gli è quella libertà
che si ritroua in quello; essendo che nel primo è dibisogno, ch'ogni Nota, ò Figura can
tabile habbia una Consonāza solamente; & nel secondo se ne pongano molte mescola-
te con Dissonanze, secondo l'arbitrio & il buon giudicio del Compositore Onde nel pri
mo modo non si può cosi bene, & à suo uolere ordinar le parti, che siano senza salti; mas-
simamente quando sopra un'istesso Soggetto si uolesse comporre molti Contrapunti, che
fussero in ogni parte uariati. Ne per questo alcuno si debbe attristare; conciosiache quā
tunque da questa radice si gusti alquanto di amaritudine; dopo non molto tempo si godo
no i frutti, che da essa nascono, che sono dolci soaui & saporiti; essendo che la Virtù (co
me affermano i Sauij) consiste intorno al difficile, & non intorno alla cosa facile.
page 237

Che ne i Contrapunti si debbono schiuar gli Vnisoni, più che si puo-
te; & che non si dè molto di lungo frequentare le
Ottaue.Cap. XLI.
letto all'Vdito; auanti ch'io uada piu oltra, darò alquanti auertimenti molto
utili per la bellezza, & per la leggiadria del Contrapunto; il primo de i quali
sarà; Che 'l compositore debba, più che sia possibile, schiuarsi di porre ne i suoi contra-
punti gli Vnisoni; & non debbe usar molto spesso le Ottaue; percioche quelli non sono
(come altroue hò detto) posti nel numero delle Consonanze, & queste per una certa si-
miglianza, che hanno con l'Vnisono, non sono cosi uaghe all'Vdito, come sono l'altre.
Et ciò non sarà fuor di proposito; perche se gli Antichi hanno col mezo della Musica mo
derato & regolato non solo le Arti, ma anco molte Scienze, si intorno à i Suoni, come
etiandio intorno à i Numeri & le Proportioni; come si può considerar della Grammati-
ca & della Rhetorica; similmente della Poesia & de molte altre simili; che ciò c'hanno di
buono & di bello, l'hanno (dirò cosi) per la Musica; essendo ella veramente quella (co-
me dimostra il Sant'huomo AgostinoDe Doctr.
Christiana
lib. 4. c. 20.) dalla quale tutte queste cose s'imparano; non sa-
rà cosa disconueneuole, ch'ella sia ordinata, come sono l'altre Arti & l'altre Scienze.
z'alcuna regola in quelle cose, per le quali l'altre Scienze & l'altre Arti sono state ordina
te & ben regolate. La onde se 'l Grāmatico, il Rhetore, & il Poeta hanno dalla Musica
questa cognitione, che la continuatione d'un suono, che si fà nel replicar molte uolte
page 238una Sillaba, ò una lettera istessa in una clausula d'una Oratione, genera un nō so chè di tri
sto da udire, che i Greci chiamano Κακόφατον; ò Cattiuo parlare, ò Cattiua Consonan
za; come si ode in quel uerso;
O fortunatā natam me consule Romam;per il raddoppiamen-
to delle due insieme aggiunte sillabe, Natam, & per la terminatione del uerso nella sil-
laba Mam; & nel principio di quella Epistola, che scriue Cicerone à Lentulo Procon-
suleEpist. fam.
lib. 1. epist.
1.,
Ego omni officio; che in tre parole si legge quattro uolte la lettera O, & in altri luoghi
quasi infiniti; onde si ode un non so chè di tristo, che le orecchie purgate non possono
udire; sarebbe ueramente il Musico degno di reprensione, quando comportasse un simi-
le disordine ne i suoi componimenti; conciosiache se tutti costoro di commun parere han
no con leggi uniuersali concluso, che non è lecito, ne in Prosa, ne in Verso (saluo se nō
fusse posto cotal cosa arteficiosamente, per mostrar qualche effetto) porre questi modi
strani di parlare; maggiormente il Musico debbe bandire dalle sue compositioni ogni tri
sto suono, & qualunque altra cosa, che potesse offendere il senso. Debbe adunque il Cō
positore auertire, di non commetter simil cose nelle sue cantilene; & di regolare in
tal maniera i suoi concenti, che in loro si odi ogni cosa buona. Non debbe adunque fa-
re udire ne i suoi Contrapunti (come hò detto) molti Vnisoni, ò molte Ottaue l'una do
po l'altra, che siano tramezate solamente da un'altra Consonanza; massimamente quan
do sono poste sopra una chorda istessa, ancora che procedessero le parti per salti; im-
peroche quando fussero collocate in cotal maniera, dal sequente essempio si potrà cono
scere quanto sarebbono grate à ciascun di sano giudicio.
 Io non dico però che non si debbino adoperare; ma dico, che non si debbono usare trop
Io non dico però che non si debbino adoperare; ma dico, che non si debbono usare troppo spesso; percioche quando occorresse, che 'l Compositore non potesse accommodare
una buona & commoda modulatione, & un bello & elegante procedere, con un bello
& leggiadro cantare; le debbe per ogni modo usare, tramezate però d'alcun'altre Con-
sonanze; & debbe più presto porre sempre l'Ottaua, che l'Vnisono quando li tornerà
commodo.
De i Contrapunti diminuiti à due voci; & in qual modo si possino vsar le
Dissonanze; & de molte Regole che si deono osseruare
in essi.Cap. XLII.
trapunto di Nota contra nota, il quale sommamente è necessario à tutti i Prin
cipianti, per far la Prattica di conoscere il sito & le distanze delle Consonan
ze; poi che haurà conosciuto di farlo bene & correttamente; allora potrà
passare al Contrapunto diminuito, ritrouando primieramente il Soggetto, secondo
che facemmo ne i Contrapunti semplici. Et perche in quelli si poneuano solamente fi-
page 239gure equali, & d'un'istessa specie, però in questo si potrà porre figure differenti, di mo-
do che si come il Semplice si componeua de Consonanze solamente, senza esserui mesco
lata alcuna Dissonanza; cosi il Diminuito sarà capace non solamente delle Consonanze,
ma anche delle Dissonanze, & ciò per accidente; come uederemo; le quali non sono da
porre in essi senza consideratione; acciò non seguiti confusione; laquale se ben si dee
schiuare in ogni cosa, si debbe sommamente uietare nella Musica. Adunque dee prima
auertire, che si come ne i Cōtrapunti semplici, si poneua ogni figura del Soggetto corrispō
dente ad un'altra cōtenuta nella parte del Contrapunto; cosi hora sopra qualūque figura
di tal Soggetto sarà lecito porne quāte, & quali tornerāno al proposito; purche quelle, che
si porrāno nella parte del Contrapūto, siano equiualenti à quelle, che sono nella parte del
Soggetto. Onde sopra ogni Semibreue contenuta nel Soggetto potremo porre due Mini
me, ouer quattro Semiminime; & cosi una Minima & due Semiminime & altre simili, co
me tornerà meglio; con quest'ordine però, che ponendo due Minime nella parte del Con
trapunto sopra una Semibreue della parte del Soggetto, ciascuna di loro siano consonan
ti; percioche queste due parti della Semibreue sono considerate grandemente dal senso,
per rispetto della Battuta, la quale si considera in due modi; cioè, nel Battere, & nel Le-
uare; come altroue uederemo; delle qual parti, alla prima si dà una Minima, & l'altra alla
seconda; le quali sono equali alla Semibreue posta nel Soggetto. Quando poi si uorrà por
re nel Contrapunto quattro Semiminime equiualenti à tal Semibreue, allora si osseruerà
che quelle Semiminime, che cascherano sopra 'l battere, & sopra il leuare della Battuta sia
no consonanti. Per il che sarà dibisogno, che tali siano la Prima & la Terza semimini-
ma; l'altre poi (com'è la Seconda & la Quarta) non è necessario, che siano in tal numero;
ancora che quando occorresse, che si ponessero consonanti tornerebbe meglio. Et tutto
questo c'hò detto si debbe intendere, quando la parte del Contrapunto procede per
Gradi; percioche procedendo per Salti, è necessario, che quelle figure, che contengo-
no tali mouimenti siano consonanti con la parte del Soggetto. Ma perche alle uolte; per
leggiadria, si suol porre la Minima legata; cioè, la Minima accompagnata con un pun
 page 240to; però è da auertire di porre il Punto, che sia consonante; percioche se 'l si ponesse altra-
page 240to; però è da auertire di porre il Punto, che sia consonante; percioche se 'l si ponesse altra-mente, ciascun potrebbe da se stesso conoscere, quanto fusse grato da udire. Et benche la
Minima legata in cotal modo si possa porre in due modi ne i Contrapunti; prima nel bat
tere, ò nel principio della Battuta; dopoi nel leuare; però il primo modo si debbe porre
solamente nel principio de i Contrapunti & non nel mezo; & questo dico ne i Contra-
punti di due uoci; ma il secondo modo si può porre non solo nel principio, ma etiandio
nel mezo, come nel sopraposto essempio si è ueduto. Potrà anco alle uolte il Contrapun
tista porre scambieuolmente due minime, delle quali l'una sia consonante, & l'altra dis-
sonante; pur che la consonante caschi nel battere, & la dissonante nel leuar la battuta;
ma debbono procedere uerso il graue, ò uerso l'acuto per molti gradi continuati senz'al
cun salto. Et quando un simil procedere incominciasse nel principio del Contrapunto;
allora potrà auanti ogn'altra cosa usar la Semibreue col punto; purche torni bene, ma
non già nel mezo; conciosia che anco non si usa in simil luogo la Semibreue semplice, ne
la Minima puntata, se non sincopata; anzi (fuori di tal caso) ogni figura del Soggetto,
che sia Canto fermo, debbe hauere almeno sopra di se due consonanze, l'una nel batte-
re, & l'altra nel leuare della battuta nel Contrapunto diminuito; percioche poste in tal
maniera hanno molta gratia; come l'esperienza ce lo manifesta. Ma quando 'l Soggetto
fusse diminuito; cioè, una parte di Canto figurato, allora le figure del Contrapunto si pos
sono fare equali alle sue figure; pur che procedino in tal modo insieme; che se ben è di-
minuito, il Contrapunto habbia in se qualche leggiadria; & tal uolta procedi con figure
d'alquanto più ualore, che quelle, che sono contenute nel Soggetto; percioche fà dibiso
gno, che si oda almeno una parte, che faccia mouimento, si nel battere, come anco nel
leuar della Battuta. Quando adunque tra molte Minime se ne ritrouasse alcuna, che nō
procedesse per grado; non sarà mai lecito, ch' ella sia disonante, anzi l'una & l'altra de
due figure, che faranno tal Grado, si debbono porre consonanti; Conciosia che se ben
la Dissonanza è posta nella seconda minima nel mouimento di grado; tal mouimento &
quel poco di uelocità, che si ritroua nel proferir simili figure, non lasciano udir cosa ue-
runa, che dispiaccia. Ma non è già cosi ne i Mouimenti di salto; percioche per tal sepa-
ratione la Dissonanza si fà tanto manifesta, ch'apena si può tolerare; com'è manifesto à
tutti quelli, c'hanno giudicio di cotal cosa. Si potrà nondimeno porre la Prima parte del
la battuta, che sia dissonante, quando sarà la seconda minima d'una Semibreue sincopa-
ta del Contrapunto; percioche la prima parte di tal figura sarà posta, senza dubbio, nel
leuar la battuta, & la seconda nel battere, & tal Dissonanza si potrà sopportare; percio-
che nel cantar la Semibreue sincopata si tiene salda la uoce, & si ode quasi una sospensio-
ne, ò taciturnità, che si troua nel mezo della percussione, dalla quale nascono i suoni;
& per essa si discernono l'un dall'altro, & consiste nel tempo; onde l'Vdito quasi non la
sente; perche da lei non è mosso di maniera, che la possa comprendere , per
non esser da lei percosso, & anco per la debolezza del mouimento, che si scorge in essa;
perche manca della percussione, che lo muoue; la onde la Voce allora nel perseuerar
della Sincopa perde quella uiuacità, c'hauea nella prima percussione, di modo che fatta de
bole, & essendo percossa da un mouimento più gagliardo d'un'altra uoce forte, che si muo
ue da un luogo all'altro con più gagliardo mouimento, nella quale è nascosta la Disso-
nanza sopra la sua seconda parte, tal Dissonanza à pena si ode; essendo anco che
prestamente se ne passa. Et se pure il Senso è da qualche parte offeso; è dopoi ragguaglia
to per tal maniera dalla Consonanza che succede senz'alcun mezo, che nonsolamente tal
Dissonanza non li dispiace; ma grandemente in lei si compiace; perche con maggior
dolcezza & maggior soauità fà udire tal Consonanza. Et questo forse auiene; perche
Ogni contrario maggiormente si scopre & si fà al sentimento più noto per la comparatio
ne del suo Opposto. Ma non si debbe giamai por la Prima parte della Semibreue, che
sia dissonante; sia poi sincopata, ò non sincopata; & si dee auuertire pero gni modo due
cose; la prima, che Dopo la Dissonanza segua una Consonanza à lei più uicina; la secon
page 224
 da, che 'l Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, &
da, che 'l Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, & esser di grado, & non ascendere. Onde potrà esser utile questa Regola: Quando la Disso-
nanza sarà posta nella seconda parte della Semibreue sincopata, la quale sarà una Se-
conda; allora dopo lei accommodaremo ottimamente la Terza, che le è più uicina.
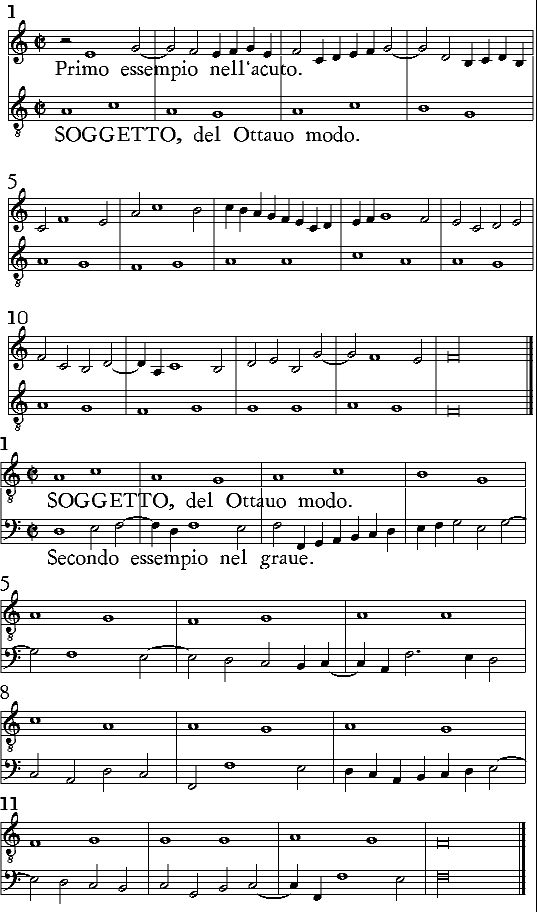 page 242Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Setti-
page 242Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Setti-ma poi se le accompagnerà la Sesta; percioche le è più uicina. si potrebbe dir
delle Replicate; come della Nona, dopo la quale si accompagna la Decima; & della
Vndecima, che riceue la Decima; come si può uedere nell'essempio: Ma basterà quel
che detto habbiamo, & mostraremo più oltra, dicendo; che Si potrà anco alle uolte (co
me costumano fare i buoni Musici, non senza suo gran commodo) dalla Seconda sinco-
pata uenire all'Vnisono, & ciò quando le parti sarano ordinate in tal maniera, che l'una
faccia il mouimento di Tuono & l'altra di Semituono. Vsaremo etiandio la Quarta sin-
 copata, dopo la quale segua senz'alcun me
copata, dopo la quale segua senz'alcun mezo la Semidiapente, & dopo questa imme
diatamēte succeda la Terza maggiore; per
cioche la Semidiapēte è posta in tal manie
ra, che fà buono effetto; essendoche tra
le parti non si ode alcuna trista relatione.
do casca il Tritono per relatione, secondo
il modo mostrato di sopra; come si può udire ne i due sottoposti essempi. Sogliono anco
ra i Prattici usar di porre la Nona, quando dopo essa si uiene all'Ottaua per contrarij Mo
 uimenti, & l'una delle parti ascenda per Quarta,
uimenti, & l'una delle parti ascenda per Quarta, ò discenda per Quinta, & l'altra discenda per
grado; come più oltra nell'essempio si uede.
quel modo migliore, che far si pote; che quella figu
ra la qual segue la Dissonāza & discende, nō sia le-
gata ad un'altra Consonanza; cioè che non faccia
un'altra sincopa, che sia tutta consonante, ma che
di due cose sia l'una; ouer che tal Figura, la qual sarà sempre di ualor della metà di quel-
la che contiene la sincopa, ne habbia un'altra dopo sè, sia qual si uoglia, la quale discen
da, ò pure ascenda per grado, ò per salto; ouero ch'ella sia legata ad un'altra figura, che
sia simigliantemente dissonante, & che tra loro facciano un'altra Sincopa; come nell'es-
sempio si uede.
 Hò detto legata ad un'altra figura; percioche quādo si risolue la sincopa di Semibreue, nel
Hò detto legata ad un'altra figura; percioche quādo si risolue la sincopa di Semibreue, nellaquale sia la dissonāza, allora seguita la Minima senz'alcuna figura mezana; laquale dico
allora esser legata, quando dopo la Dissonanza segue non la Minima, ma un'altra Semibre
ue sincopata, ouero una Minima col punto; della qual Semibreue la secōda parte battuta
sia cōsonante, ò dissonante; & cosi ancora dico del Punto, che stà appresso la nominata Mi
nima. La onde dico, che al primo modo la Minima è legata ad un'altra Minima; & al secō
do modo la Minima è legata alla Semiminima, ch'è il Punto. Quelle adunque, che nel
le cātilene si cōcedono sono le sottoposte; perche hāno molta gratia; ma quelle ueramēte
che i boni Cōpositori nō vsano, sono quelle, che seguitano; īperoche quādo nō si osserua in
page 243
 la sopradetta Regola, la figura, che segue la Dissonanza, non fà bene il suo officio, &
la sopradetta Regola, la figura, che segue la Dissonanza, non fà bene il suo officio, & quel che debitamente à lei appartiene. Onde non hà in se quella gratia, c'hà la prima;
percioche la Dissonanza si risolue con un modo freddo (dirò cosi) essendo che non rag-
guaglia pienamente l'Vdito di quello; che forse per auanti in qualche modo fu off so dal
la Dissonanza; come nel seguente essempio si potrà udire. Et perche g[gap — ] Antichi Prat-
 tici hanno , & i Moderni ancora usano, di porre alle uolte confusamente ne i loro
tici hanno , & i Moderni ancora usano, di porre alle uolte confusamente ne i loro Contrapunti hora la prima, & hora la seconda Semiminima, che seguono la Minima
battuta, ouer la Semibreue col punto, ò pur la detta Semibreue senza 'l punto sincopata
consonante; massimamente quando il loro procedere è per Mouimenti di grado uerso la
parte graue; però accioche non si generi confusione nell'animo del Compositore, deter
minaremo hora, quale delle due Semiminime si habbia da porre, che sia consonante.
le seguente figura, sia qual si uoglia, dopo la seconda delle nominate Semiminime imme
diatamente discende, ouer quando ascende per grado; dopoi, quando ascende per sal-
to ciascheduno de i quali modi, ouer che si fà nella parte del Contrapunto posta in acu
to sopra la parte dun Soggetto, che sia Canto fermo; ouer nel graue sotto la parte di es-
so Soggetto. Il perche, quando 'l Canto fermo farà la Parte graue, & discenderà per
grado, & la Parte, che farà il Contrapunto, hauerà la Minima, che precede le due Se-
miminime, Quinta sopra la prima nota del Canto fermo; allora la seconda delle due Se
miminime del primo modo si porrà Terza, percioche la figura seguente con quella del
Canto fermo farà simigliante Terza. Il simile si farà quando la predetta Minima fusse
Decima, & il Canto fermo ascendesse per grado, ouer per salto di Terza; percioche al
lora le figure seguenti sarebbono insieme Sesta, ouer Quinta. Ma quando 'l Canto fer-
mo non si muouesse da un luogo all'altro, allora si porrà la prima delle due Semiminime
consonante; quando però la Minima, che le uà inanti, sarà Sesta minore; essendo che
la seguente figura del Soggetto uerrebbe à far con quella del Contrapunto Terza; ilche
si farà etiandio quādo la prefata Minima sarà collocata nella sincopa di Semibreue, & fa-
rà co 'l Canto fermo la Quarta, & il detto Canto fermo discenderà per salto di Terza;
percioche le note seguenti faranno la Terza; & l'istesso auuerrà anco, quando 'l Canto fer-
mo salirà per salto di Quarta, & la detta Minima sincopata sarà Vndecima percioche le se
guenti figure faranno insieme la Quinta. Ma quando 'l Canto fermo sarà con la sudetta
Minima posta in Quinta, & la Nota seguente la seconda Semiminima ascenderà un gra-
page 244do, nel secondo modo, & il Canto fermo simigliantemente descenderà per grado; allo-
ra si porrà consonante la seconda Semiminima; & tutto questo si farà quando 'l Canto
fermo sarà il Soggetto, & la parte graue del Contrapunto. Ma quando esso Canto fermo
terrà la parte acuta, & il Contrapunto si farà nel graue; la prima delle due nominate Se-
miminime descendenti nel primo modo per grado si porrà consonante; quando la Mini-
ma, che la precederà, sarà la secōda parte della Semibreue sincopata, & sarà col Canto fer
mo una Seconda, & esso Canto fermo discenderà per salto di Terza; percioche le seguē
ti figure conteneranno simigliantemente la Terza. Il simile si osseruarà, quando 'l Canto
fermo salirà per salto di Terza, & la detta Minima sarà Terza; ouer quando non farà mo
uimento alcuno, & la Minima predetta sara Sesta; essendo che le seguenti figure faranno
la Ottaua. Si porranno etiandio à cotesto modo cotali Semiminime, quando la detta
Minima sarà Vnisona col Canto fermo, & il detto Canto discenderà per Grado.
Quando poi la detta Minima sarà la Terza col Canto fermo, & la seconda Semiminima
al primo modo si mouerà per grado uerso l'acuto, & il Canto fermo salirà per salto di Ter
za; allora si porrà la seconda delle due Semiminime consonante. Ilche si farà etiandio,
quando la Minima farà la Sesta; come nel sottoposto essempio si può uedere.
 Ma quando per Soggetto si piglierà una parte di Canto figurato; allora si osseruarà di por
Ma quando per Soggetto si piglierà una parte di Canto figurato; allora si osseruarà di porre cotali Semiminime consonanti; secondo la dispositione, si della parte del Contrapun-
to; come ancora del Soggetto; come à i luoghi proprij son per dimostrare.
Il modo che hà da tenere il Compositore nel fare i Contrapunti sopra vna Parte,
ò Soggetto diminuito.Cap. XLIII.
per molti giorni nel fare il Contrapunto sopra vn Soggetto di Canto fermo;
conoscendo di farlo senz'alcuno errore, vorrà passar più oltra, & venire ad
vn'altra compositione, pur de Due voci; la onde per assuefarsi alla buoua &
bella inuentione, non sarà fuori di proposito, se' gli pigliarà primieramente per Soggetto
vna Parte d'alcuna cantilena di Canto figurato, & dopoi ne comporrà vn'altra; secondo
 page 246che li tornerà più al proposito, & se ciò non vorrà fare, potrà comporre tal Parte da se
page 246che li tornerà più al proposito, & se ciò non vorrà fare, potrà comporre tal Parte da se stesso; & secondo il suo ingegno comporne vn'altra nel graue; ouer, secondo che li verrà
meglio fatto, nell'acuto. E' ben uero, che uolendo comporre il Soggetto da se stesso, potrà
aiutato da vna Parte della sua compositione comporre l'altra, di modo che tutto in vn
tempo uerrà à comporre il Soggetto, & à dar fine alla Cantilena. La onde tanto più age-
uolmente lo potrà fare; quanto più vorrà osseruar quelle Regole, lequali hauera osser-
uato nel fare i Contrapunti sopra il Canto fermo. Ben'è uero, che questo modo di com-
porre gli sarà più libero & più espedito; percioche potrà, diminuire qual si uoglia par-
te, sia graue, ouero acuta; lasciando vna di esse parti con le Figure di alquanto maggior va
lore; ouero ponendo le Figure tra tutte due, che siano simili, ò diuerse l'vna contra l'altra,
ilche non poteua fare nel primo modo. Potrà adunque il Compositore far quello che li
tornerà più commodo; auertendo però di accommodar sempre in tal maniera le Parti
della cantilena, che cantino bene, & habbiano bello & elegante procedere, con un non
 page 247sò che misto di grauità. Et accioche si vegga il modo, che hà da tenere nel comporre si-
page 247sò che misto di grauità. Et accioche si vegga il modo, che hà da tenere nel comporre si-mili Contrapunti, ò Compositioni (poiche non si può dar Regola particolare d'ogni co-
sa, per essere infiniti gli indiuidui) hò posto due essempi, l'uno de i quali è fondato sopra
il Soggetto, ch'incomincia; Scimus hoc nostrum meruisse crimen: ilquale è una Parte d'u-
na leggiadra compositione à due voci d'Adriano, composta del Primo modo. L'al-
tro poi è tutto composto di fantasia. Di maniera che vedendo & essaminando queste
due, & altre simili compositioni, potrà venire all'uso di comporre à cotesto modo facil-
mente & bene.
Quando è lecito vsare in vna parte della Cantilena due, ò più volte vn passaggio,
& quando non.Cap. XLIIII.
istessa troppo vsata, alle uolte genera noia & fastidio. La onde dobbiamo
cercare sopra ogn'altra cosa, per non cascare in alcuni errori communi, che i
nostri Contrapunti siano uariati di maniera, che non si odi due, ò più uolte
vn passaggio & vn'istesso concento replicato nelle istesse Consonanze, ne gli istessi mo-
uimenti, & nelle istesse chorde. Et benche sia impossibile, che in questi Contrapunti
fatti à questo modo, quando saranno bene ordinati, si oda alcuna cosa, che sia dissonan-
te, & che non sia grata all'Vdito; tuttauia il replicar tante volte un'istessa harmonia non
dà quel piacere, che darebbe, quando fusse uariato; oltra che 'l Compositore sarebbe
giudicato molto pouero d'inuentione da quelli, che sono intelligenti dell'Arte; conciosia
che pensarebbeno (hauendo egli usato l'istesso passaggio più d'una uolta) che non haues-
se alle mani altro Contrapunto. Debbe adunque ciascuno essere auertito, di non com-
mettere cosa simile à quella, che si ritroua nell'essempio seguente; poiche cotal cosa se gli
può attribuire à vitio.
 Hò detto, che non si debbe usar molte uolte un passaggio, intendendo del Contrapunto
Hò detto, che non si debbe usar molte uolte un passaggio, intendendo del Contrapunto replicato nelle istesse consonanze, ne gli istessi mouimenti, & nelle istesse chorde; percio-
che non solo è lecito, ma è molto lodeuole il Replicar quante uolte si vuole, ò puote una
modulatione istessa, & un'istesso passaggio; pur che 'l Contrapunto sia sempre differente
& uariato; essendo che tali Repliche hanno un non so chè d'ingegnoso; la onde ogn'uno
si dee sforzare di far tali Repliche, qualunque uolta gli occorrerà di poterle fare, che stia-
no bene, senza esserli alcuno errore; percioche sarà riputato da gli Intelligenti huomo di
page 248pellegrino ingegno, & abondante d'inuentione. Hò detto, che si dee sforzare; percioche
à far questo il Contrapuntista non è obligato di maniera, che nō possa mutare & cambiar
simili passaggi secondo 'l suo uolere; essendo che replicati in cotal modo, non si potreb-
beno vsar troppo di lungo, se non con gran discommodo delle Parti; cioè, con sini-
stre modulationi. Ma quando non accaderanno cotali inconuenienti; si potranno repli-
care; percioche fanno buono effetto; come ne i sottoposti essempi si puo vdire.

 page 249Et perche alle uolte i Musici si sogliono obligar di fare il Contrapunto, vsando sempre
page 249Et perche alle uolte i Musici si sogliono obligar di fare il Contrapunto, vsando sempre vn passaggio, & replicarlo; uariando però il concento; il qual modo dicono Far con-
trapunto con obligo; onde tali Repliche, ò passaggi chiamano Pertinacie; però quando
alcun uorrà obligarsi ad una cosa simile, piglierà un Thema, ò Passaggio, & incomincie-
rà à fare il Contrapunto sopra il proposto Soggetto. Ma perche questa maniera di far
Contrapunto è molto difficile; però il Contrapuntista potrà prendere alcune licenze; co-
me sarebbe dire, usare alle uolte alcune modulationi, che non fussero cosi ageuoli al can-
tare; come portarebbe il douere, quando il Contrapunto si ponesse in iscritto, & fusse
senza obligo alcuno. Et potrà usar quelle Figure, che piu gli torneranno commode,
uariando il concento, usando hora le Breui, hora le Semibreui, hora le Minime, & altre
Figure; le quali potrà porre hora sincopate, & hora senza la sincopa; acciò possa satisfa-
re all'obligo. Debbe nondimeno sempre hauer l'occhio all'osseruanza di quello, ch'è
stato detto di sopra & mostrato; & di schiuar quanto potrà gli errori; accioche il Con-

 page 250trapunto non sia più tosto biasimato, che lodato; percioche Quella cosa, che si fà ben nel
page 250trapunto non sia più tosto biasimato, che lodato; percioche Quella cosa, che si fà ben nel difficile, è molto più da lodare, che non è quella, ch'è fatta bene senz'alcuna difficultà.
Adunque accioche si habbia di cotal cosa piena cognitione, hò posto due essempi, da i
quali si potrà conoscer quello, che si potrà far ne gli altri simili.
Che non è necessario, che la del Soggetto & quella del Contrapunto incomincino insieme;
& di quattro differenze che si trouano delle Figure cantabili.Cap. XLV.
si) superstitione, che ciascuno fusse tenuto per legge fatale, di dar prin-
cipio à i suoi Contrapunti in un sol modo; facendo sempre che la Parte del
Soggetto incominci à cantare insieme con quella del Contrapunto; & che
non fusse lecito d'vsar le Pause nel principio di qual Parte si uoglia; Conciosia che l'vso
delle Pause non solamente fù ritrouato per ornamento della cantilena; ma etiandio per
necessità; come dirò altroue. Onde quando tornerà commodo di porle nel principio di
qual Parte si uoglia lo potrà fare, senza esserui alcuno errore; & potrà porre non solo le
Pause di Breue, ò di Semibreue; ma quelle di Minima ancora. Et ciò non sarà fuori del-
l'vso de gli Antichi & de' Moderni Compositori; i quali presero tal licenza, vedendo
che tal cosa li tornaua molto commoda. Volendo adunque dar principio à i Contrapun-
ti in cotal maniera, si dee far cantare primieramente qual Parte si uoglia delle due; inco-
minciando nel principio della Battuta; l'altra poi si potrà far cantare, ponendo nel prin-
cipio auanti la prima Figura cantabile la Pausa di Minima, che si chiama uolgarmente
Sospiro; dopò laquale si potrà porre qual Figura tornerà meglio, pur che 'l suo valore non
ecceda il ualor della Semibreue; la qual posta dopo la Pausa di Minima, verrà necessaria-
mente ad esser sincopata. Ma si debbe schiuare di dar principio alla parte del Contra-
punto & à quella del Soggetto nel principio della Battuta per altre figure, che siano di mi-
nor valore della Semiminima; percioche si verrebbe à dar principio alla cantilena per
vn mouimento molto veloce, anzi velocissimo. Incominciando poi dalla Semimini-
ma, sempre se le porrà auanti la Pausa di minima. Et veramente in ciò & in ogn'altra
cosa dobbiamo imitar la Natura, il cui procedere si vede esser molto regolato; conciosia
che se noi haueremo riguardo à i Mouimenti naturali; ritrouaremo, che sono ne i loro
principij alquanto più tardi, di quello, che non sono nel mezo & nel fine; come si può ve-
dere in vna Pietra, che sia lasciata cadere dall'alto al basso; della quale il Mouimento è
più veloce, senza dubio, nel fine, che nel principio; contrario di quello che fà; quando
con è gettata in alto. Imitaremo adunque la Natura & procederemo in ma-
niera, che i Mouimenti, che faranno le parti de i Contrapunti non siano molto veloci nel
principio; ilche osseruaremo etiandio nel mezo & nel fine di ciascuna Parte, quādo dopo
le Pause incomincieranno à cantare, & il loro principio sarà per vna Figura di qualche va
lore; come per vna Semibreue, ouer'altra maggiore. Et volendo procedere per Moui-
menti alquanto più veloci, faremo, che dopo quella ne seguiti vn'altra, che le sia più
vicina & di minor valuta; come sarebbe la Minima, & dopo lei la Semiminima. Io
non dico già, che dopo la Minima non si possa porre due, ò più Figure simili l'vna dopo
l'altra; percioche dopo vna Seminima se ne può porre un'altra, & più anche, & cosi do-
po la Minima; ma dico, che volēdo procedere da vna Figura maggiore ad vna minore, il
douere vuole, che la figura seguente sia la più vicina alla precedente. Ne voglio anco,
che alcuno creda, ch'io ponghi tal Regola per si fatto modo necessaria, che non si possa fa-
re altramente; conciosia che quello, c'hò detto, è stato per dare un poco di lume & di
giudicio al Compositore. Et perche hò detto di sopra, che si debbe procedere da vna Fi-
gura cantabile all'altra con la sua più vicina; però è da auertire, ch'alcuni Musici esser-
citati intorno vn certo loro Genere detto Quantitatiuo; hanno posto le Figure can-
page 251tabili in quattro differenze; percioche alcune hanno nominato Parte propinque d'un'al-
tra, alcune altre Parti remote, alcune Parti più remote, & alcune altre Parti remotissi-
me. La onde dicono, che quella Figura è Parte propinqua d'un'altra; che nell'ordine
posto di sopra nel Cap. 2. la segue senz'alcun mezo. Però si può dire, che la Breue sia
Parte propinqua della Lunga, & la Semibreue della Breue, & la Minima della Semi-
breue, & cosi l'altre che seguono; ancora che in tal consideratione non passassero ol-
tra la Minima, per essere vltima figura tra quelle, che patiscono alteratione; come for-
se mostrerò altroue. Ma quando lasciauano una figura di mezo & pigliauano la se-
guente, chiamauano tal figura Parte remota della prima. La onde si può dir con veri-
tà, che la Semibreue è Parte remota della Lunga, & la Minima Parte remota della
Breue, & cosi l'altre per ordine. Quando poi lasciauano le due mezane; quella, che
era seguente alle due lasciate, chiamauano Parte più remota della prima; come potia-
mo dire della Minima rispetto alla Lunga, & dell'altre ancora. Ma quando ne lascia-
uano tre, la seguente dimandauano Parte remotissima; come la Minima rispetto alla
Massima. Tornando hora al nostro primo proposito, dico; ch'è concesso à ciascuno di
porre due Semiminime & più ancora dopo il Sospiro; come si possono porre dopo la
Minima; percioche questa è di valore equale al Sospiro, & ciascuna di esse è la sua Par-
te propinqua; quantunque tal Sospiro, ò Pausa non si canti. Ma non si accom-
moderanno cosi bene tali Semiminime dopo la Pausa di Semibreue, ò dopo vn'altra
maggiore; essendo ch'elle sono Parti remote; ne tornerà etiandio beue il porre dopo il
Sospiro molte Chrome. Sarà però lecito il porre due Semiminime dopo la Semibreue
col Punto, ouer dopo la Semibreue sincopata; percioche nella parte, sopra la quale casca
la Battuta, che è sopra il Punto, ouero sopra la seconda parte della Sincopa; si consi-
dera come separata dall'altra per la Battuta; cioè, si piglia per vna Minima separata, so-
pra laquale casca la detta Battuta. Non è però lodeuole (quantunque pochi se ne guar-
dino) il por le Figure con tal ordine, che dopo la Semibreue, che sia battuta senza il
punto, ne segua due, ò più Semiminime; percioche sono parti remote, & non propinque
della Semibreue; lequali poste in tal maniera, quanto siano grate & commode à i Can-
tori, ciascuno da sè lo potrà comprendere, quando vdirà procedere da vna figura can-
tabile ad un'altra con vna subita mutatione di tempo tardo al veloce, senz'alcun'altra
mezana dispositione.
Che le Modulationi debbono essere ben regolate; & quel che dee osseruare il Can-
tore nel cantare.Cap. XLVI.
tori, s'io uolesse ragionar d'ogni minima cosa, che può occorrere nel com-
porre. La onde lasciando da un canto quelle cose, che non sono cosi necessa-
rie, verrò à quelle, che sono di qualche importanza; delle quali alcune appartengono
al Compositore, & alcune al Cantore. Quelle ch'appartengono al Compositore so-
no queste; Primieramente debbe comporre le sue cantilene, secondo le Regole date
di sopra, non si partendo da i Precetti, i quali più oltra son per dimostrare; dopoi deb-
be porre ogni studio, che 'l Contrapunto; cioè, le Parti della sua cantilena siano or-
dinate & regolate in tal maniera, che si possino cantare ageuolmente, & che siano sen-
z'alcuna difficultà; percioche se l'Harmonia nasce (come vedemmo nella Seconda par-
teCap. 12.) dal cantare, che fanno insieme le parti della cantilena; senza offesa alcuna dell'Vdi-
to; non potrà ella già mai nascer da cose, che siano tra loro senz'alcuna proportione.
Sarà adunque auertito di fare, che le Parti si possino cantar bene, & che procedino
per veri & legittimi interualli, contenuti tra i Numeri harmonici; consonanti ò
dissonanti, che siano. Consonanti dico; come di Ottaua, di Quinta, di Quarta, di
page 252Terza & d'altri simili; come sono quelli di Decima ancora, che sarà fatto senza errore al-
cuno; poiche Giosquino, non pure hà vsato vn tale Interuallo; ma etiandio vsò quello di
Duodecima; come si può uedere nel Canto, che si canta à cinque voci: Inuiolata, integra,
& casta es Maria. dissonanti etiandio; come sono quelli del Semituono maggiore & quelli
del Tuono, che sono le differenze, per le quali l'una Consonanza supera laltra; come hò
mostrato nel Cap. 39. della Seconda parte. E' ben uero, ch'alle uolte si pone quello di
Settima & di Nona; ancora che di raro; come hanno vsato & usano anco alcuni buoni
Compositori. Ma quelli del Tritono, della Semidiapente & altri simili non si debbono
vsare, come fanno alcuni Moderni; uolendo ciò attribuire al proceder delle Modulationi
chromatiche; conciosia che ueramente questi Interualli non hanno le forme loro conte-
nute tra i Numeri harmonici; la onde non è possbile che possino far nelle Modulationi
alcun buono effetto; anzi offendono grandemente il sentimento; come la esperienza ce
lo dimostra. Et se la Musica (come la definisce il P. S. AgostinoMusices lib. 1. c. 2.) è Scienza di ben canta-
re, ò ben modulare, & ad altro non attende, che à questo; in qual maniera si potrà porre
quella cantilena nel numero di quelle, che osseruano & tendono à questo fine; laquale ha-
urà le sue modulationi piene de simili errori, & sarà in tal modo disordinata, ch'apena si
potrà sopportar di uederla, non che di cantarla? A' questo anco si ricerca quello, che nel
Cap. 37. si è detto; che le Parti procedino, più che sia possibile, per mouimenti di grado;
percioche sono più naturali, de quelli che sono di salto. Cercarà adunque il Composito-
re di fare, che le Parti della sua cantilena si possino cantar bene & ageuolmente; & che
procedino con belli, leggiadri & eleganti Mouimenti; accioche gli Vditori prendino di-
letto de tali modulationi, & non siano da veruna parte offesi. Quelle cose poi ch'apparten-
gono al Cantore sono queste: Primieramēte dee cō ogni diligenza proueder nel suo Can
tare, di proferir la modulatione in quel modo, che è stata composta dal Compositore; &
non far come fanno alcuni poco aueduti, i quali per farsi tenere più valorosi & più sapiē-
ti de gli altri, fanno alle uolte di suo capo alcune diminutioni tanto saluatiche (dirò cosi)
& tanto fuori d'ogni proposito; che non solo fanno fastidio à chi loro ascolta; ma insieme
commettono nel cantare mille errori; percioche alle uolte uengono à fare in un colpo
con molte Discordanze; due, ò più Vnisoni; ò due Ottaue, oueramente due Quinte &
altre cose simili, che nelle Compositioni senz'alcun dubio non si sopportano. Sono poi
alcuni, che nel loro cantare fanno alle uolte la Voce più acuta, ò più graue di quello, che
è il douere; cosa che non hebbe mai in mente il Compositore; come quando in luogo del
Semituono cantano il Tuono, ò per il contrario, & altre simili cose; la onde, oltra l'offesa
del Senso, ne seguono infiniti errori. Debbono adunque i Cantori auertire, di Cantar
correttamente quelle cose, che sono scritte secondo la mente del Compositore; intonan-
do bene le voci, & ponendole à i loro luoghi; cercando d'accommodarle alla Consonan-
za, & cantar secondo la natura delle Parole contenute nella compositione in tal manie-
ra; che quando le Parole contengono materie allegre, debbono cantare allegramente &
con gagliardi mouimenti; & quando contengono materie meste, mutar proposito. Ma
sopra 'l tutto (accioche le Parole della cantilena siano intese) debbono guardarsi da uno
errore, ch'è in uso appresso molti; com'è il mutar le Lettere uocali nel proferir le parole;
dicendo A in luogo di E, I in luogo di O, ouero V in luogo d'una delle nominate; ma
debbono proferirle secondo la lor uera pronuncia. Et è ueramente cosa vergognosa &
degna di mille reprensioni, l'udir cantare alle uolte alcuni sciocchi & goffi; tanto ne i Cho
ri & nelle Cappelle publiche; quanto nelle Camere priuate, tanto sgarbatamente; pro-
ferendo le Parole corrottamente, quando le douerebbono proferir chiare, espedite &
senz'alcuno errore. La onde se (per cagione di essempio) udimo in una Canzone al-
le fiate alcuni di poco giudicio sgridacchiare (non dirò cantare) come Cornacchie;
con uoci molto sgarbate; & con atti & modi anco tanto contrafatti, che ueramente
paiono Simie, ò Buffoni; & proferir le parole in questa maniera: Aspra cara, e sal-
uaggia e crada uaglia; in luoco di dire; Aspro core, e seluaggio, e cruda uoglia;
page 253chi non riderebbe? anzi (per dir meglio) chi non andrebbe in colera; udendo una co-
sa tanto contrafatta, tanto brutta, & tanto horrida? Non debbe adunque il Cantore
mutare il suono delle Lettere; ne meno nel cantar mandar fuori la uoce con impeto, &
con furore à guisa di Bestia; ma debbe cantar con uoce moderata, & proportionarla
cō quelle de gli altri Cantori, di maniera che non superi, & che non lascia udir le uoci de
gli altri; facendo piu presto strepito, ch'Harmonia; conciosia ch'ella non nasce da altro,
che dalla temperatura de molte cose poste insieme in tal maniera, che l'una non superi
l'altra. Hauerà etiandio il Cantore questo auertimento, che ad altro modo si canta nel-
le Chiese & nelle Cappelle publiche; & ad altro modo nelle priuate Camere; imperoche
iui si canta à piena uoce; con discretione però; & non nel modo detto di sopra; & nel-
le Camere si canta con uoce più sommessa & soaue, senza far'alcuno strepito. Però quan-
do cantarà in cotali luoghi, procederà con giudicio, acciò non sia (facendo altramente)
degnamente biasimato. Debba oltra di questo osseruare, di non cantar con mouimenti
del corpo, ne con atti, ò gesti, che induchino al riso, chi lo uedono & ascoltano; come
fanno alcuni; i quali per si fatta maniera si muouono, il che etiandio fanno alcuni So-
natori, che par ueramente, che ballino, & saltino al loro Suono. Ma se 'l Compositore,
& il Cantore insieme osseruaranno quelle cose, che appartengono al loro officio; non
è dubbio, ch'ogni Cantilena sarà diletteuole, dolce & soaue, & piena di buona harmonia,
& apporterà à gli Vditori grato & dolce piacere.
Che non si dè continuar molto di lungo nel graue ò nell'acuto nelle modulatio-
ni.Cap. XLVII.
alquanto più del douere nel graue ouer nell'acuto, è cagione che 'l Cantore
si stanchi; massimamente quando hà la uoce graue, & dimora nell'acuto:
ouer quando hà la uoce acuta; & è sforzato di stare nel graue; onde uiene
à far debole la uoce, & abbassarla, s'è nell'acuto; ouero ad alzarla, se 'l si ritroua nel gra-
ue; & à far molta dissonanza, però uorrei; per leuar cotal discommodo & disor-
dine; che 'l Contrapuntista hauesse auertenza à cotal cosa, & accommodasse la can-
tilena in tal maniera, che le Parti non cantassero per lungo tempo nel graue, ne anco mol
to di lungo stessero nell'acuto; in cotali estremità; ma tutte le uolte ch'ascendessero,
ò discendessero, non fussero poste in cotal maniera senza proposito. Hò detto; sen-
za proposito; percioche i compositori moderni hanno per costume (il che non è da bia-
simar, se non da quelli, che sono troppo sauii) che quando le parole dinotano cose gra-
ui, basse, profunde, discesa, timore, pianti, lagrime & altre cose simili, fanno conti-
nuare alquanto le lor modulationi nel graue; & quando significano altezza, acutezza,
ascesa, allegrezza, riso, & simili cose, le fanno modular nell'acuto: del che habbia-
mo ragionato nel Cap. 11. dell'Ottauo Lib. De i Sopplimenti. Ben è uero, che non deb-
bono far continuare di lungo l'Harmonia in tali estremi; ma debbono fare, che le mo-
dulationi tocchino le chorde graui, & anco le acute, con le mezane delle parti della
cantilena; uariando sempre le modulationi. Ne debbono comportare, che l'estremità
delle parti trappassino nel graue, ò nell'acuto fuora de i loro termini, contra la lor na-
tura, & contra la natura del Modo, sopra il quale sarà fondata la cantilena; cioè, non
debbe fare, che 'l Soprano pigli il luogo del Tenore, ne questo il luogo del Soprano;
ma far, che ciascuna parte stia ne i suoi termini; come uederemo nella Quar-
ta parte, quando parlaremo intorno al modo, che si hà da tenere nell'accom-
modar le Parti nella Cantilena; ancorache in alcuni casi questo sia concesso per
page 254poco spacio di tempo; percioche ordinandole, che non trappassino i lor termini, non
potrà seguir se non commodo grande al Cantore, & nascere buoni & perfettti concenti.
Che 'l porre vna Dissonanza, ouer vna Pausa di minima tra due Consonanze
perfette d'una istessa specie, che insieme ascendino, ò discendino; non fà,
che tali Consonanze non siano senz'alcun mezo.Cap. XLVIII.
sonanze d'vna istessa specie, l'una dopo l'altra nelle lor compositioni, che insie
me ascendino, ò discendino, senza porui di mezo alcun'altra Consonanza;
percioche s'auisano, che 'l por tra loro una Dissonanza, oueramente una Pau-
sa di minima, faccia uariar le specie; & che per questo non si faccia contra la Regola
data nel Cap. 29. Ma in uero quanto costoro s'ingannino, ciascun lo potrà conoscere dal
la esperienza istessa; dopo che hauranno udito quello, che ne i seguenti essempi si contie
ne; percioche conosceranno, che la Dissonanza posta tra due Consonanze perfette,
non fà uarietà alcuna di concento; ne anco leua, che tali Consonanze non siano poste
l'una dopo l'altra senz'alcun mezo; essendo le Consonanze considerate dal Musico per
sè, & le Dissonante per accidente solamente; com'hò detto altroue. Et se la Dissonan-
za, ch'è suono, posta tra le dette Consonanze, non hà forz'alcuna di fare alcuna uarie-
tà; minormente haurà tal forza la Pausa di minima, che non rappresenta suono, ma
taciturnità & priuatione. Non sarà adunque lecito por due Ottaue l'una dopo l'altra,
tramezate solamente dalla Settima, ouer dalla Nona; ne due Vnisoni tramezati dalla
Seconda. Et quantunque la Quarta & la Sesta siano Consonanze; come fù determinato,
& si possa dire, che l'una, ò l'altra posta tra due Quinte faccia alcuna uarietà di concen-
to; nondimeno non si debbono usare, se non nelle compositioni de più uoci; percioche
nelle semplici generano non so chè di tristo; come si udire ne i seguenti essempi.
 page 255Sogliono anco alle uolte i Compositori in una particella della compositione, dopo l'Ot-
page 255Sogliono anco alle uolte i Compositori in una particella della compositione, dopo l'Ot-taua posta sopra una figura di Semibreue, che discenda, & habbia sopra, ò sotto di se una
Minima, porre immediatamente due Semiminime, lequali descendino per gradi & senz'
altro mezo; & dopoi la figura seguente ascendi & uenghi all'Ottaua. Simigliantemente
sogliono, dopo una figura di Semiminima posta in Ottaua sopra una Minima, che discēdi,
porre un'altra Semiminima, laquale si muoua per salto, & uenghi medesimamente all'
Ottaua; & non solo ciò fanno, ma etiandio pongono in luogo delle Semiminime la Mi
nima col punto, con due chrome seguenti, & altre cose simili; come qui si uedono.
 Le quali, auenga che non si possa dire con uerità, che facciano due Ottaue poste l'una do
Le quali, auenga che non si possa dire con uerità, che facciano due Ottaue poste l'una dopo l'altra, senz'alcun mezo; percioche si ritroua un'altra Consonanza posta tra loro, ch'è
la Sesta, ouer la Decima; nondimeno non si debbono usar di lungo per due ragioni. La
prima delle quali fù detta nel Cap. 4. & la seconda è, che per la mutatione ueloce, che fà
la Sesta, ò la Decima poste tra loro; ouero per il ueloce mouimento, che fanno, quasi nō si
ode; tanto più, che nelle due Semiminime, che seguono la minima, ouer la semibreue sin-
copata, la prima è posta nel numero delle dissonanze. Onde maggiormente tali Ottaue
si odono, & si uiene à far contra quello, che si è detto nel sudetto Capitolo, che non si
douessero usar molto spesso accommodate nel Contrapunto in cotal maniera. Et per di-
re il uero, i passaggi, che fanno le due Semiminime con la Minima inanti, ouer la Mi-
nima col punto, & le due Chrome sequenti; non sono altro, che la diminutione del
mouimento di grado, che fanno insieme due Semibreui. A cotesti anco s'aggiunge, che
non si dè usar quel passaggio, che fanno due parti ascendendo, ò discendendo insieme,
l'una per i gradi della Quinta, procedendo per quattro semiminime, & l'altra per il sal
to di Quinta, ascendendo per semibreui senz'alcuna diminutione; & le Consonanze,
che cascano nel battere sono due Quinte; come nell'essempio si uede; percioche se ben
 sono tramezate dalla Terza, hanno però poca gratia.
sono tramezate dalla Terza, hanno però poca gratia. E' ben uero, che 'l secondo passaggio è più sopporta-
bile del primo; ma non è però lodeuole; percioche
nel cantar la parte diminuita, si ode la Terza posta
tra due Quinte nella terza semiminima, laquale è con
sonante, & è percossa nella seconda parte della Battu
ta. Et tanto più si possono sopportare, quanto che le
Quinte tramezate in cotal maniera, non sono cosi
facilmente comprese dall'Vdito; perche non sono semplici, com'è l'Ottaua; & i moui-
menti, che fanno le parti, che contengono le Semibreui, non sono di grado, come sono
quegli altri, c'hò mostrato. Ma perche alcuni cantano tali passaggi per diminuire il sal-
to di Quinta, che fanno alle uolte le parti; però dico, che si debbono fuggire per ogni
modo. Et se pure ad alcun paresse d'usare non solamente questi, ma gli altri ancora mo-
strati di sopra, non debbe però usarli molto spesso, percioche quando non ui fussero al-
tre ragioni, ui sono almeno queste, che si uiene à far contra quella Regola, che dice;
Che dobbiamo procedere da una Consonanza all'altra per mouimenti contrarii; & con
tra quella, che ne auertisce, Che facciamo muouere le parti insieme, quando ascendo-
no, ò discendono, l'una di esse almeno per grado, che dourebbono ritrouarsi in quelle
page 256parti, che si muouono per salto, & contengono le Semibreui; & nondimeno non lo fan-
no; come si può chiaramente uedere. Ma questo basti intorno à i mouimenti, che fan-
no due parti cantando insieme.
Della Battuta.Cap. XLIX.
ragioneuole, auanti che si uada più oltra, che uediamo quello che sia ciascu-
na da per se; accioche non procediamo per termini non conosciuti, i quali non
possono apportare alcuna scienza; Laonde dobbiamo sapere, che i Musici
uedendo, che per la diuersità de i mouimenti, che fanno cantando insieme le Parti del-
la cantilena, per esser l'un più ueloce, ò più tardo dell altro, si poteua generar qualche
confusione; ordinarono un certo Segno, dal quale ciascun Cantante s'hauesse da regge-
re nel proferir la uoce con misura di tempo ueloce, ò tardo, secondo che si dimostra con
le Figure diuerse cantabili, le quali sono poste nel Cap. 2. Et s'imaginarono che fusse be-
ne, se cotal segno fusse fatto con la mano; accioche ogn'uno de i Cantori lo potesse ue-
dere, & fusse regolato nel suo mouimento alla guisa del Polso humano. Onde dopoi da-
to tal'ordine, alcuni de i Musici chiamarono cotal segno Battuta, alcuni altri Tempo so-
noro, & alcuni altri; tra i quali è Agostino dottore Santissimo nel Cap. 10. del Secondo
libro della Musica, lo nominano Plausum; che uiene da Plaudo uoce latina, & uuol dire
il Battimento delle mani. Et ueramente parmi che pensassero bene; percioche non
sò uedere, qual mouimento poteuano ritrouare, che fusse fatto naturalmente; &
potesse dare à loro la regola & proportione, fuori che questo. Percioche se noi considera-
remo le qualità, che si ritrouano in uno & l'altro; cioè, nella Battuta & nel Polso, che da
i Greci è detto Σφυγμός, ritrouaremo tra loro molte conuenienze; conciosiache essendo
il Polso (come lo definisce GalenoDe Diffe.
pub. lib. 4.> & Paulo EginetaLib. 2. ca.
12.
Dct. 3.
Sum. 1.) un certo Allargamento & Ristren-
gimento; ò pur uogliamo dire Alzamento & Abbassamento del cuore, & delle arte-
rie; uiene ad esser composto (come uuole Auicenna nel Secondo Fen del Lib. 1.)
di due mouimenti, & di due quiete; dellequali cose similmente la Battuta uiene ad
esser composta; & prima di due mouimenti, che sono la Positione, & la Leuatio-
ne, che si fà con la mano; ne i quali si troua lAllargamento & il Ristringimento; o-
uero l'Alzamento & Abbassamento nominato, che sono due mouimenti contrarij; &
dopoi due quiete; percioche (secondo la mente d'Aristotele8. Thy.
cap.) tra questi mouimenti,
come (etiandio nel Cap. 42. di sopra commemorai) sempre si ritrouano; massima-
mente perche è impossibile, che simili mouimenti si possino continuare l'un con l'al-
tro. Et si come la Medicina chiama il primo mouimento Συστολὴ, & il secondo Διαστολὴ;
cosi la Musica nomina la Positione, ouero il Battere Θέσις, & la Leuatione Α῎ρσις. Simi-
gliantemente; si come il Polso si ritroua di due maniere, secondo l'autorità de i comme-
morati Prencipi della Medicina; cioè, Equale & Inequale; pigliando però solamente
quella equalità & inequalità, che nasce della uelocità & tardità, onde si fà il Rhythmo,
dal quale nasce molti mouimenti proportionati, contenuti ne i generi Molteplice, & Su
perparticolare, oltra gli altri, che si lasciano, che non sono contenuti sotto cotali generi;
cosi la Battuta si ritroua di due maniere, Equale & Inequale; oue si riduce ogni moui-
mento proportionato, che si fà con la uoce. Et questo dico, perche gli Antichi Musici,
& i Poeti anco, i quali già erano riputati una cosa istessa; per un certo loro istinto naturale
diuisero le Voci in due parti, & attribuirono ad alcune il Tempo breue, & ad alcune
il Tempo lungo; & al Tempo lungo applicarono due Tempi breui, & posero nel pri-
mo luogo quelle Sillabe, ò Voci del Tempo breue, che sono di minor quantità, & nel
secondo quelle del lungo, che sono di maggiore; com'è il douere; essendo che si co-
me la Vnità tra i numeri è inanti il Binario, che contiene due Vnità; cosi il Tem-
page 257po breue debbe tenere il primo luogo, & il lungo il secondo. Ma si dè auertire, che
considerarono la Battuta in due parti; & tanto alla prima, quanto alla seconda attribui-
rono la misura del Tempo breue, ò lungo; come li tornaua più commodo. E' ben uero
che i Moderni applicarono primieramente alla Battura hora la Breue, & hora la Semi-
breue imperfette; facendole equali al tempo del Polso distinto in due mouimenti equa-
li; onde cotale Battuta si può ueramente chiamare Equale; conciosia che tra la Posi-
tione & la Leuatione si ritroua la proportione d'Equalità; essendo che tanto alla Posi-
tione, quanto alla Leuatione si attribuisce il Tempo lungo, oueramente il breue. Do-
poi le applicarono hora la Breue con la Semibreue, & hora la Semibreue con la Mini-
ma, & la in due mouimenti inequali, applicando alla Positione il Tempo lun-
go, & alla Leuatione il breue, ponendole in Dupla proportione. Et perche tra la Posi-
tione & la Leuatione casca la proportione d'Inequalità, però cotal Battuta si può con
uerità chiamare Inequale. Hauendo dopoi essi Musici cotal rispetto, quando intende-
uano la Battuta equale, segnauano le lor Cantilene nel principio col Circolo, ò Semi-
circolo intieri; ouer da una linea in due parti tagliati; & quando intendeuano l'Inequale
aggiungeuano à cotali segni, ò cifere il Punto; come in questi essempi si uede.

quale, con i segni del Tempo non puntati; po-
neuano dopo il Segno del Tempo la cifera del Ter-
nario sopra quella del Binario in cotal modo 3/2.
& cotali Cifere nominauano della Sesquialtera, &
forse non senza ragione; percioche (secondo la
dottrina del loro Genere Quantitatiuo) si possono
considerare in quattro maniere; Prima, quando
sono poste nel principio de tutte le parti della Can-
tilena; & allora si usa la Battuta inequale; Seconda,
quando sono collocate medesimamente nel principio, ma nō in tutte le parti; onde ciascu
na parte si uiene à regolar sotto la Battuta equale; Terza, quando sono poste nel mezo del
la cātilena in ciascuna parte, & si usa medesimamēte la Battuta inequale; & Quarta, quādo
sono poste nel mezo d'alcuna parte solamente, & le parti si uengono à regolare similmente
dalla Battuta equale. Onde cotali Cifere possono significar due cose; prima (com'è opinio
ne de i Moderni) c'hauendo rispetto al Segno del tempo; si uiene à porre la Misura ine-
quale contra la equale; cioè, tre tēpi lunghi, ò breui contra due; dopoi significano, che nel
la Battuta intera sono contenuti Tre tempi lunghi, ò breui che siano, de i quali due si pon-
gono nella Positione, & uno nella Leuatione; massimamente quando non ui concorro-
no altre cifere numerali, che denotino alcuna proportione nelle figure, ò note della can-
tilena; come gia faceuano alcuni Musici; ilperche per tal modo ueniuano à uariar la Pro
latione, ouer Pronuncia delle figure; la qual segue senz'alcun dubio i segni; onde inte-
sa la Battuta in questa maniera, leua molte difficultà, che possono occorrere à i Compo
sitori, & à i Cantori. Potiamo hora ueder da quel che si è detto, che la Battuta non è
altro, che un Segno fatto dal Musico equalmente, ouero inequalmente, secondo alcu-
na proportione, con la Positione & con la Leuatione della mano, à simiglianza del Pol-
so humano. Essendo adunque la Battuta di due sorti; com'habbiamo ueduto; tanto il
Musico quanto il Poeta potranno in esse accommodar la Misura del tempo di ciascun
piede del Verso. Imperoche nella Equale potranno accommodare il Pyrrhichio, ch'è
un Piede composto de due sillabe breui, le quali i Poeti sogliono segnare con tali cifere
˘˘; onde i Musici sogliono porre i loro Tempi, che sono due tempi breui con due figu-
re equali; come sono due minime, ouer due altre simili; conciosia che 'l Poeta considera
solamente la Sillaba s'è Lunga; laqual segna con questa cifra ¯. ouero se è Breue, notan-
dola con quest'altra ˘. & il Musico considera 'l Tempo lungo, ò breue, & lo segna con
una delle Otto figure cantabili; come li torna più commodo. Potranno anco accom-
page 258modar lo Spondeo, che segnano con queste due ¯¯. che dinotano due sillabe lunghe,
con due Semibreui, che significano due tempi lunghi, de i quali è composto; & il Dat-
tilo, il quale contiene una sillaba lunga & due breui, ouer un tempo lungo & due breui,
in cotal modo ¯˘˘, ouer con una Semibreue & due Minime. Similmente potranno ac-
commodar l'Anapesto in questo modo ˘˘¯. oueramente con due Minime, & una Semi
breue; perche contiene due sillabe breui & una lunga; ouer due tempi breui & uno lun-
go; & in tal guisa lo Proceleumatico ˘˘˘˘. con quattro Minime; conciosia che tutti
questi piedi sono contenuti sotto una proportione equale; com'è noto à tutti gli Intelli-
genti. Sotto l'Inequale poi si può accommodar lo Iambo ˘¯. con una Minima & una
Semibreue; percioche è composto d'una sillaba breue, & d'una lunga; ouer d'un tempo
breue & di un lungo. Cosi anco si potrà accommodare il Trocheo ¯˘. con una Semi-
breue & una Minima; perche contiene una sillaba lunga, & una breue, che contengo-
no un tempo lungo, & un tempo breue. In cotal modo si potrà accommodar lo Tri-
bracho ˘˘˘. con tre Minime; cosi lo Ionico maggiore ¯¯˘˘. lo minore ˘˘¯¯. il Cho-
riambo ¯˘˘¯. l'Antispasto ˘¯¯˘. & molti altri piedi, hora sotto l'una, & hora sotto l'al-
tra Battuta; ancorache ciascuno de i Nominati sotto la Battuta inequale, etiandio sotto
la equale accommodar si possino. Et non pur questi, ma tutti gli altri Piedi ancora;
siano di che quantità si uogliano, per molti che ue ne siano, di due fino à Sei sillabe, i
quali arriuano al numero di Cento & uenti quattro. Ma quelli, ch'io di sopra hò nomi-
nato si potranno conoscere esser compresi in questi tre Versi.
 Imperoche il Pyrrhichio si troua tra questi due tempi, ò sillabe breui ˘˘, uane; lo Spon-
Imperoche il Pyrrhichio si troua tra questi due tempi, ò sillabe breui ˘˘, uane; lo Spon-deo tra queste due tempi lunghi, ò sillabe ¯¯, sù co; il Dattilo ¯˘˘, Giouane; l'Ana-
pesto ˘˘¯, cominciò; lo Procelesmatico ˘˘˘˘, uane comin; lo Ionico maggiore ¯¯˘˘,
sù come fan; lo minore ˘˘¯¯, so la sù co; il Coriambo ¯˘˘¯, noi salirem'; l'Antispasto
˘¯¯˘, la sù come; lo Iambo ˘¯, gridan; & lo Tribracho ˘˘˘, bile ca; i quali piedi
(com'hò detto) tutti si possono ridurre anco sotto la Battuta equale. Ma di questo leggasi
il Cap. 13. del Lib. 8. De i Sopplimenti, acciò non si prenda errore. Et perch'è costume de
i Musici, di porre il più delle uolte nella Battuta equale una Breue imperfetta, la quale
contenga due Tempi lunghi, & nella inequale una Breue perfetta, che ne contenga tre;
però ci contentaremo al presente di queste due; percioche ciascun'altra Battuta, che
l'Huomo si potesse imaginare, si potrà sempre ridurre à queste; la prima delle quali si
potrà veramente chiamar battuta Spondaica, & la seconda Trochaica. Et s'alcuno
prendesse di ciò marauiglia, com'io introducessi cosa nuoua, legga Boetio nel proemio del
la Musica, oue ritrouerà, che Pitagora volendo ritrahere un giouine Taurominita-
no dalla furia alla quiete, commandò che 'l Musico douesse cantar lo Spondeo; il quale
ueramente s'vdiua, come etiandio si ode à i nostri giorni ne i Balli, che dimandano
page 259Passo è mezo, & Padoane; & in quelli, che nominano Balletti, udimo la Battuta del
Trocheo. Dobbiamo oltra di ciò auertire, accioche alcuno non si marauigli, che essen-
do necessario, ch'ogni Compositione incomincia & finisca ancora nella Positione della
mano; cioè, nel principio della Battuta; di sopra hò detto, che lo Iambo si può accom-
modare sotto la Battuta inequale, pur che la Cantilena uenghi à terminar sccondo 'l co-
stume de i Musici moderni. Ma questo sia detto à bastanza intorno alla Battuta.
Della Sincopa.Cap. L.
della Battuta: ond'era necessario, che primieramente si ragionasse di lei, come
di quella, ch'è molto necessaria alla sua cognitione; & dopoi dichiarar quello,
ch'importa questo nome Sincopa. Ma si dè sapere, che la Sincopa non è con-
siderata dal Musico, come la considera il Grammatico; il qual uuole, ch'ella sia una fi-
gura di Dittione, ò Parola, che uogliamo dire, che si fà quando se le taglia, ò rimuoue
una lettera, ò sillaba nel mezo; come si fà, quando per commodità del Verso, in luogo
di porre Audaciter, si dice Audacter; oueramente bisognando dire Vendidit, si dice Ven-
dit; ma la considera come Trasportatione, ò Riduttione d'alcuna figura, ò nota canta-
bile minore, oltra una, ò più maggiori alla sua simile, oue conuenientemente si possa
applicare & numerare, per finire il numero della misura del suo tempo. Et questo acca-
sca non solamente nel Tempo perfetto, inteso per il circolo intero, ouer tagliato, che si
termina per il numero Ternario; ma etiandio nell'imperfetto, che s'intende per il Mezo
circolo intiero, ò tagliato terminato nel numero Binario; percioche il Tempo (come
uederemo al suo luogoInfra
cap. 67.) appresso il Musico è di due sorti. Onde quella Figura, ò Nota si
chiama Sincopata; ouer si dice, che fà la Sincopa; quando incomincia nella leuatione
della Battuta, & è sotto posta anco alla positione; ne mai puo cascare (come porta la
sua natura) sotto la positione, fino à tanto, che non ritroui una figura minore, ouer'
altre figure, che siano equali à questa di ualore, con lequali s'accompagni & ritorni,
oue la Battuta hebbe principio. Per il che è da notare; per dare uno essempio; che 'l pro-
prio della Semibreue è di cascare, & di essere insieme cantata nel Tempo perfetto, &
nell'Imperfetto anco; cioè, sotto questi due segni O & C nel principio della Battuta;
& la Breue sotto 'l Semicircolo tagliato. Ma se auiene, che l'una, ò l'altra si canti, ò
proferisca nel leuare della Battuta, tal figura, ò Nota è detta Sincopa, ouer Sincopata;
come ne i due essempi posti qui di sotto si uede.
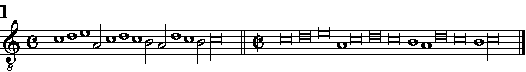 Si può etiandio chiamar Sincopata quella Minima, c'hà appresso di sè il Punto, ne
Si può etiandio chiamar Sincopata quella Minima, c'hà appresso di sè il Punto, ne i primi segni, quando è posta nel leuar della battuta; & cosi la Semibreue col punto, sot
to l'altro segno; come qui sotto si uedono; ancora che si possa veramente dire, che nō siano
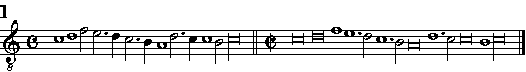 Sincope, se non impropriamente. E' ben uero, che la Semibreue si chiama sincopata, sot
Sincope, se non impropriamente. E' ben uero, che la Semibreue si chiama sincopata, sotto qual segno si uoglia, che dimostri il Tempo perfetto, ò imperfetto; quando uien posta
page 260da i Compositori ne i loro contrapunti al detto modo. La Sincopa adunque si fà da una
figura, ò nota, che le uadi auanti, la qual sia di ualore della metà della figura sincopa-
ta; oueramente si fà, quando se le pone auanti due, ò più figure, che siano equiualenti à tal
metà. Sono anco tali figure sincopate alle uolte dalle Pause, che si pongono à loro inan-
ti; & tali Pause sono di ualore della meza parte delle figure sincopate; come qui si
ueggono.
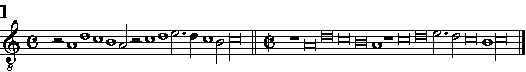 Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne stà bene il sin-
Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne stà bene il sin-copar le Pause; siano poste sotto qual segno si uoglia, ò perfetto, ouer'imperfetto che
sia il Tempo; come sono le sequenti:
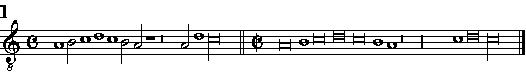 Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il prin-
Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il prin-cipio di ciascuna, sotto i lor Segni proprii; come mostrerò altroue; & genera anco in-
commodo à i Cantori, i quali confidandosi spesse uolte nella loro integrità, non pensan-
do che 'l Tempo sia in loro uariato, senza tenerne memoria & conto alcuno, pongono la
Battuta nel loro principio; & per tal maniera ingannati, uengono necessariamente ad
errar cantando. Questi incommodi adunque si debbono per ogni modo schiuare; percio
che non furono mai sopportati da i buoni & discreti Musici; come si può ueder nelle
compositioni d'Ocheghen, di Giosquino, di Motone, & d'altri più Antichi di loro; pur
che non siano state guaste d'alcuno ignorante Scrittore. Per la qual cosa, quando oc-
correrà di por le Pause di breue ò di semibreue, & non nel principio della
Battuta, & del loro Tempo, allora si debbono ridurre sotto l'uno & l'altro; come nel
seguente essempio si uede.
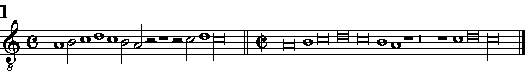
Della Cadenza, quello ch'ella sia, delle sue Specie, & del suo
uso.Cap. LI.
ro) è la più bella parte, che si ritroui nelle cantilene; perche si uede, che ritro-
uandosene alcuna, che sia priua di essa, si ode in lei un non so chè d'imperfet-
to; percioche quelle Cantilene maggiormente dilettano, & più illustremen-
te risonano, che ritengono in se cotali Cadenze, di quello che non fanno quelle, che
di esse sono priue; il perche hauendo di sopra fatto commemoratione della Cadenza,
& ragionato della Sincopa; essendo la maggior parte delle Cadenze formate dalle Sin-
cope; parmi che 'l tempo & il luogo ricerchi, ch'auanti che più oltra si passi, di essa Ca-
denza si ragioni, Adunque dirò hora quel ch'ella sia, & mostrerò le sorti della Ca-
denza, & insegnarò in qual maniera s'usino. La Cadenza adunque è un certo atto,
page 261che fanno le parti della cantilena cantando insieme, la qual dinota, ò quiete generale
dell'Harmonia, ò la perfettione del Senso delle parole, sopra lequali la cantilena è com-
posta. Oueramente potiam dire, ch'ella sia una certa terminatione d'una parte di tut-
to 'l concento, & quasi mezana, ò uogliamo dir finale terminatione, ò distintione del
contesto dell'Oratione. Et benche la Cadenza sia molto necessaria nell'Harmonie; per-
cioche quando nō l'hanno mancano (com'hò detto) d'un grande ornamento necessario,
si per la distintione delle sue parti, come anco di quelle della Oratione; non è però da
usarla; come fanno alcuni, che non sanno far'altro che Cadenze nelle loro compositio-
ni; se non quando s'arriua alla Clausula, ouer al Periodo contenuto nella Prosa, ò nel
Verso; cioè, in quella parte, che termina il Membro di essa, ouer'una delle sue parti.
Onde la Cadenza è di tanto ualor nella Musica, quanto è il Punto nella Oratione; & si
può ueramente chiamar Punto della Cautilena. E' ben uero, che si pone anco doue si ri
posa; cioè, doue si troua la terminatione d'una parte dcll'Harmonia, nel modo che si
fermiamo etiandio nel contesto dell'Oratione, quando si troua non solamente la distin-
tione mezana, ma anco la finale. Ne la douemo porre sempre in un luogo, ma si bene in
luoghi diuersi, accioche dalla uarietà ne seguiti più grata & più diletteuole Harmonia.
Et debbono terminare insieme il Punto dell'Oratione, & la Cadenza; non già sopra
qual si uoglia chorda, ma nelle proprie chorde regolari de i Modi, ne i quali sarà cōposta
la cantilena; le quali chorde mostrerò nella Quarta parte, quando ragionerò separatamē-
te di ciascun di loro. Ma si debbe auertire, che le Cadenze ne i Canti fermi si fanno in
una parte sola; ma ne i Figurati s'aggiungono altre parti. Et in quelli si pongono fini-
ta la sentenza delle parole; in questi poi non solamente si fanno, quando si ode la Clau-
sula perfetta nell'Oratione; ma alle uolte s'usano per necessità, & per seguire un cert'or-
dine nel Contrapunto principiato dal Compositore. E' ben uero, che quelle del Can-
to figurato si trouano di due sorti; cioè, quelle, che terminano tra due parti per l'Vniso-
no, & quelle che finiscono per la Ottaua. Et benche ue ne siano alcun'altre, che finisco-
no per Quinta, alcun'altre per Terza, & alcune per diuers'altre consonanze; non sono
però da esser dette assolutamente Cadenze, se non ad un certo modo, & con una aggiun
tione; cioè, Cadenze imperfette, Si trouano tutte le sorti de Cadenze in due modi; ouer
che sono Semplici; oueramente che sono Diminuite. Le Semplici sono quelle, le cui
parti procedono per figure, ò note simili, & contengono alcuna Dissonanza; & le Di-
minuite sono quelle, che contengono tra le parti della cantilena uarie figure, & alcune
Dissonanze. Et ciascuna di loro è contenuta almeno da tre figure, sia nella parte graue,
ouer nell'acuta della Cantilena; & si fanno almeno tra due parti, che procedino per moui
menti contrarii. La prima sorte di Cadenza adunque terminata per l'Vnisono è quel-
la, che contiene in se un progresso, che fanno due parti l'una con l'altra; delle qua-
li l'una ascendendo & poi discendendo; ouer discendendo solamente con le sue figu-
re per gradi, & l'altra discendendo, & poi ascendendo per gradi simili, essendo la secon-
da figura della parte graue, con la seconda dell'acuta distante per una Terza minore, le
Terze figure di ciascuna parte uengono à finire & congiungersi in una chorda istessa, cioè,
in un'istesso suono. Questa Cadenza si può fare etiandio in diuersi altri modi; ma facciasi
in qual maniera si uoglia, che importa poco; purche le sue ultime figure siano con le an-
tecedenti collocate al modo detto, & come nel sottoposto essempio si può uedere.
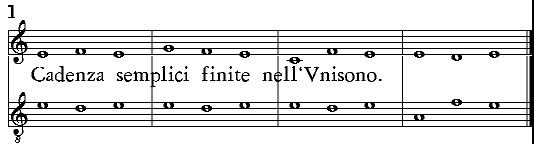 page 262Le Diminuite terminate per l'Vnisono sono quelle, che contengono un simil procedere;
page 262Le Diminuite terminate per l'Vnisono sono quelle, che contengono un simil procedere; ma si fanno con diuerse figure, tra le quali si ritroua la Sincopa, della quale la sua secon-
da patte, ch'è quella, ch'è percossa dalla Battuta, si troua dissonante; cioè, una Se-
conda. Onde dopo essa immediatamente seguendo la Terza minore, si uiene à fini-
re all'Vnisono.
 Et perche i Prattici sogliono il più delle uolte diminuire quella parte della Cadenza,
Et perche i Prattici sogliono il più delle uolte diminuire quella parte della Cadenza, che contiene la Sincopa, per potere, secondo che li torna commodo, accommodar le
Harmonie alle Parole; però auanti ch'io uada più oltra, uoglio porre tali Diminutioni,
che si ueggano; & saranno le seguenti, le quali potranno apportar molto utile nell'accom
modar le Figure cantabili alle Parole soggette; come uederemo nella Quarta parte.
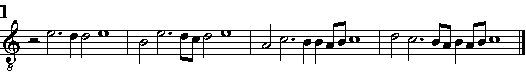 Qui debbe ciascun Compositore auertire, che quantunque le Cadenze siano poste so-
Qui debbe ciascun Compositore auertire, che quantunque le Cadenze siano poste so-lamente ne i mostrati luoghi; nondimeno si possono fare anco in qualunque altro luogo,
oue torna più commodo, pur che si osserui la Regola data di sopra nel Cap. 38. di anda
re dalla Consonanza imperfetta alla Perfetta con la più uicina. La onde fà dibisogno,
che nelle penultime figure di queste Cadenze sia la Terza minore, la qual sempre si udi-
rà, quando faranno il mouimento all'Vnisono di maniera, che l'una discenda per grado
di Tuono, & l'altra con un simile mouimento di Semituono maggiore ascenda, ò per il
contrario. Et ciò si potrà sempre fare in ciascun luogo, senza porre il segno
 della chor-
della chor-da chromatica, per far dell'interuallo del Tuono un Semituono; imperoche in quel-
la parte, che la penultima Figura & l'ultima si troua il mouimento, che ascende, sempre
s'intende esser collocato il Semituono; pur che l'altra parte non discenda per simile In-
teruallo; conciosiache allora il Semituono non si potrebbe porre da due parti; cioè, nel-
la parte graue, & nell'acuta; perche s'vdirebbe un'Interuallo minore d'un Semiditono,
che sarebbe dissonante. Ma la Natura hà prouisto in simil cosa; percioche non solamen-
te i periti della Musica, ma anco i Contadini, che cantano senz'alcuna arte, procedo-
no cantando à questo modo per l'interuallo del Semituono. Queste sono dette
Cadenze propriamente; ancora che quando le lor prime Figure si ritrouassero distanti
page 263l'vna dall'altra per Quinta, & le seconde per un Semiditono, & le ultime finissero per
l'Vnisono; come sono le sequenti non farebbono, che non si potessero anco chiamare Ca-
denze; quantunque si potesse dire, che si chiamassero impropriamente. La Cadenza ter-
 minata per Ottaua è di tal sorte, che le sue Figure vo-
minata per Ottaua è di tal sorte, che le sue Figure vo-gliono esser ordinate di modo; che la prima, la seconda,
& la terza della parte acuta; & la prima, la seconda, &
la terza della parte graue, si muouino con mouimen-
ti contrarij di grado l'una parte contra l'altra; & le se-
conde Figure delle parti siano distanti l'una dall'altra
per una Sesta maggiore, & le ultime per una Ottaua. Et
quantunque potesse essere alcuna differenza de moui-
menti tra le prime & le seconde Figure; percioche fa-
cendo le Figure della parte acuta i loro mouimenti sem-
pre di grado, quelle della parte graue alcune uolte potranno procedere per mouimenti
di salto, discendendo alcuna uolta insieme; tuttauia siano accommodate in qual manie-
ra si uogliano, le seconde Figure della Cadenza si porranno sempre distanti l'una dall'al-
tra per l'interuallo di Sesta maggiore, & le ultime finiranno in Ottaua. Et ciò sempre tor-
nerà bene, quando una parte farà il mouimento de grado de Semituono, ò nel graue,
oueramente nell'acuto; & l'altra quello del Tuono, cosi in queste come in ogn'altra sorte
di Cadenza, sia semplice, ò diminuita. E' ben uero che le Cadenze diminuite hanno la
Sincopa, nella quale si ode la Settima sopra la sua seconda parte; cioè, nel battere; ma la
Cadenza semplice è tutta consonante; percioche le sue figure sono tra loro equali; come
ne i sequenti essempi si può uedere.
 Si può etiandio uedere, in qual maniera spesse uolte si potrà
Si può etiandio uedere, in qual maniera spesse uolte si potrà cambiar le parti della Cadenza tra loro, & porre quel passag-
gio, che fà la parte posta nel graue, nella parte acuta; & per
il contrario, quel che fà la parte acuta, nella parte graue, che
corrispondino per una Ottaua, percioche tali mutationi sono
molto commode à i Compositori. Oltra queste due sorti di
Cadenza, ue n'è un'altra terminata per Ottaua, ouer per Vni-
sono; laqual si fà, quando si pone le seconde Figure della par-
te graue & quelle della parte acuta distanti tra loro per un Ditono; facendo discende-
re la parte graue per un salto di Quinta, ouero ascendere per quello di Quarta; & ascen-
dere la parte acuta per grado; come si uede.
 Et sono queste Cadenze di due sorti medesimamente; Semplice & Diminuite; come si
Et sono queste Cadenze di due sorti medesimamente; Semplice & Diminuite; come si può vedere. Quelle che sono Semplici, hanno le Figure simili; & le Diminuite hanno
le Figure diuerse; & tra loro si ritroua la Sincopa, che hà nella sua seconda parte la Quar-
ta, dopo la quale segue immediatamente la Terza maggiore; come hò mostrato. Ma per-
che queste Cadenze non si vsano molto nelle Compositioni de due voci; conciosia che
l'ascēdere per i mostrati salti, & lo discendere anco è proprio della parte grauissima di al-
cuna compositione composta à più voci; però si guardaremo di porle spesso; & quando
le vorremo porre, sempre le porremo nel mezo, & non nel fine della Cantilena; & quan-
do la necessità ciò fare ne astringesse; cioè, quando volessimo porre le Parti della compo-
sitione in Consequēza, ouero nella Imitatione; Secondo i modi che si mostrerà più oltra;
& quando non si potesse hauere per altra via vn passaggio commodo al cantare, & vna
grata . E' ben uero, che questo voglio che più tosto sia conseglio, che pre-
cetto; percioche quando si ponessero anco nel principio & nel fine, non sarebbe errore.
Oltra di questo si troua la Cadenza terminata per Quinta, ouero, per Terza, ò per altra
Consonanza; la quale è detta Cadenza impropriamente; & è contenuta similmente da
vn numero simile de Figure; & è ordinata in tal modo, che essendo le Seconde figure del
l'una & dell'altra parte distanti per vna Terza, le vltime vengono à cascare in vna delle
nominate Consonanze; & questo quando la parte acuta fà il mouimento di grado ascen-
dendo; & è di due sorti, Semplice & Diminuita; ciascuna delle quali hormai per tanti es-
sempi dati di sopra, credo che sia da ogn'vno conosciuta; la onde bastarà dire solamente,
che nella Diminuita si ode la Quarta nella seconda parte della Sincopa & non altra disso-
nanza; come si può udire in ciascuna, che si troua ne i sottoposti essempi.
page 265
 Ne in queste (quando si fanno à due uoci) è necessario, che sempre si odi in vna parte il
Ne in queste (quando si fanno à due uoci) è necessario, che sempre si odi in vna parte il grado del Semituono maggiore, ò graue, ouero acuta ch'ella sia; percioche si vdirebbe al-
le volte tra le Parti la relatione, che non sarebbe harmonica; come nel Cap. 30 hò dichia-
rato. Sarebbe cosa molto tediosa, s'io volesse dare essempio particolare d'ogni Ca-
denza propria & non propria; conciosia che sono quasi infinite; onde è dibisogno, che 'l
Contrapuntista s'ingegni di ritrouarne sempre di nuoue, inuestigando di continuo nuo-
uemaniere; & guardandosi di non commettere errore. Et accioche ei possa vedere in
qual modo le Cadēze si possono per diuersi modi ordinare, & in qual maniera si possono
usare; per non andare in lungo; porrò molti essempi, da i quali potrà scorger quello, che
hauerà da fare nella inuentione delle altre.
 Non voglio etiandio restar di dire, che i Prattici sogliono vsare alle uolte nelle Cadenze,
Non voglio etiandio restar di dire, che i Prattici sogliono vsare alle uolte nelle Cadenze, & in altri luoghi ancora, in vece della Semibreue sincopata la Semibreue col punto, che
sia dissonante; vsando poi quelle circonstanze, che conuengono alla Cadenza & alla Sin-
copa posta in cotal modo. Et benche cotal cosa sia tollerata, nondimeno non sodisfà à
pieno il sentimēto. La onde essortarei il Compositore à non far simil passaggi molto spes-
so nelle sue compositioni, se non sforzato da necessità; percioche (secondo 'l mio giudi-
cio) parmi, che non siano da esser poste nel numero delle Cadenze; massimamente non
page 266osseruando tutto quello, che ricerca la Cadenza; come ogn'vno potrà giudicare, dopo
c'haurà vditi & essaminati i sequenti essempi.
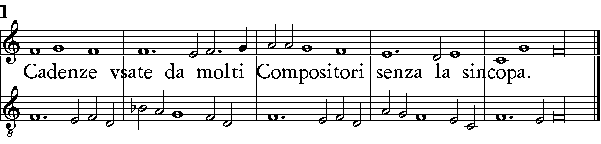 Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfet-
Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfet-tione delle parti di tutto il concento; come anco, accioche per il loro mezo si hauesse à fi-
nire la Sentenza perfetta delle parole; è honesto, che volendola terminare per esse, che si
finisca per una delle consonanze perfettissime; cioè per la Ottaua, ò almeno per l'Vniso-
no; accioche il Perfetto proportionatamente si uenga à finire col Perfetto. Ma quando
si vorrà fare alcuna distintione mezana dell'Harmonia & delle Parole insieme, le quali
non habbiano finita perfettamente la loro sentenza, ò pericolo; potremo vsar quelle Ca
denze, che finiscono per Terza, per Quinta, per Sesta, ò per altre simili consonanze; per-
che il finire à cotesto modo, non è fine di Cadenza perfetta; ma si chiama fuggir la Ca-
denza, come hora la chiamano i Musici. Et fù buono il ritrouar; che le Cadenze finisse-
ro anco in tal maniera; conciosia che alle uolte accasca al Compositore, che venendoli
alle mani un bel passaggio, nel quale si accommodarebbe ottimamente la Cadenza, &
non hauendo fatto fine al Periodo nelle parole; non essendo honesto, c'habbiano à finire
in essa; cerca di fuggirla, non solamente al modo mostrato; ma nella maniera ch'io mo-
strerò nel seguente Capitolo. Et se ben da quello c'hò detto, si possa concludere, che
qualunque uolta alcuna Cadenza non finirà nella Ottaua, ouer nell'Vnisono, si potrà
chiamare Imperfetta; perche si fugge il fine perfetto; tuttauia perche il fuggir la Ca-
denza si fà in molti altri modi, voglio che uediamo hora in qual guisa la si possa fuggire,
& il modo che si potrà tenere, quando vna parte del Contrapunto farà il mouimen-
to di salto; cioè, si mouerà di due, ò più gradi; come accade molte volte nel-
le Compositioni.
Il modo di fuggir le Cadenze; & quello che si haurà da osseruare, quando il Soggetto fa-
rà il mouimento di salto.Cap. LII.
lo che fin'hora si è detto & mostrato, che ciascun possa hormai molto ben'es-
sere istrutto in cotal materia, & nelle cose etiandio, che sono vtili & necessarie
all'arte del Contrapunto. La onde (come mi aueggo) bastarà solamente dire,
che 'l Fugir la Cadenza sia (come habbiamo veduto) un certo atto, il qual fanno le Parti,
accennando di voler fare una terminatione perfetta, secondo l'uno de i modi mostrati di
sopra, & si riuolgono altroue; & basterà porre uno essempio, dal quale si potrà compren-
dere in quante maniere la si potrà fuggire, quando tornerà in proposito; & anco si potrà
veder quello, che si haurà da osseruare, quando il Soggetto farà alcuni mouimenti di Ter
za, ò di Quarta, ò d'altri simili Interualli di salto. Di modo che quando alcuno sarà in
ciò molto bene instrutto, potrà saper quello, c'hauerà da fare, quando gli accaderà vsar
simili passaggi.
page 267

Delle Pause.Cap. LIII.
presentano le Voci, ò i Suoni, da i quali nascono l'Harmonie; & la varietà lo
ro rappresenta il mouimento ueloce, ò tardo del Tempo, che si tiene la uo-
ce; cosi le Pause si chiamano figure Priuatiue; percioche sono indicio della
taciturnità, ò silentio; & rappresentano il Tempo, che si hà da tacere, ilqual si scor-
ge dalle loro diuersità. Queste sono alcuni segni fatti dal Musico con alcune linee
tirrate diuersamente secondo 'l suo arbitrio; le quali perpendicolarmente cadono so-
pra una, ò più delle cinque mostrate Linee parallele. Et le specie sono tante, quan-
te sono le figure cantabili, due meno; incominciando dalla Lunga, lasciando quella
della Massima; essendo che in suo luogo si pone quella della Lunga raddoppiata. Et quel-
la della Semichroma anco si lascia; percioche per esser di minimo ualore, nō si usa. Et sono
dell'istesso ualore, & denominate con l'istesso nome della figura, ò nota, che rappresētano.
page 268Le quali Pause quantunque alle uolte dinotano Modo maggiore & minore perfetto, oue
ro imperfetto ch'esso sia; non però mai abbracciano più de quattro delle sopradette li-
nee; come qui sotto si uede.
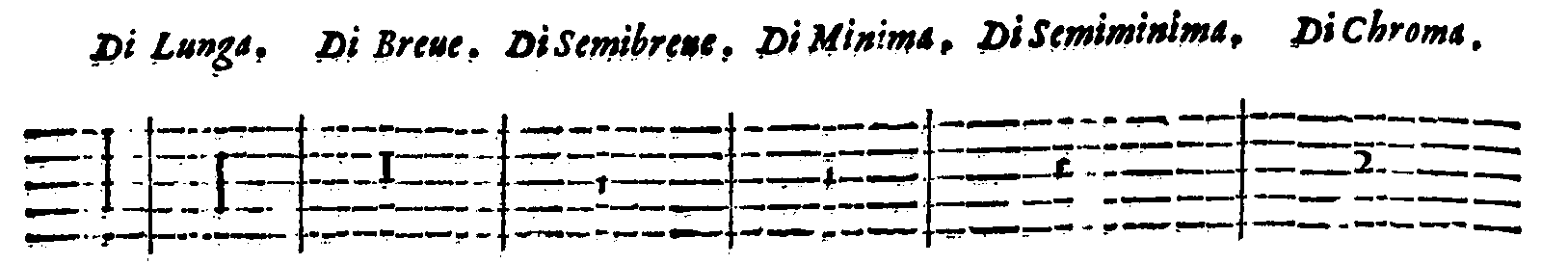
Cantore, per due ragioni; l'una per Necessità, & l'altra per Ornamento delle cantilene.
Per necessità prima; perche era impossibile, che i Cantori potessero peruenire dal princi
pio al fine della cantilena, senza mai posarsi, se non con loro grande incommodo; ne
ueramente haurebbono potuto durare. Onde i Musici forse ricordeuoli di quello, ch'è
detto da Ouidio nelle sue amorose Epistole.Phdrae.
Hippolito
epist. 4.
Quod caret alterna requie, durabile non est.
Ritrouarono questo opportuno rimedio. La onde si può dir con uerità della Pausa
quello che segue.
Haec reparat vires, fessaꝗ membra leuat.
Furono poi ritrouate le Pause per ornamento della cantilena; percioche per mezo lo-
ro, le Parti si possono porre l'una dopo l'altra in Consequenza; come uederemo; il qual
modo fà la cantilena non solo arteficiosa, ma etiandio diletteuole; conciosia che 'l canta
re di continuo, che fanno cotali parti insieme genera noia non solamente à i Cantori, ma
anche à gli Ascoltanti induce sacietà; & il farle tacere alcune uolte con qualche proposi-
to, facēdone cantare hora due, hora tre, hora quatro, & tallora (essendo la compositione à
più voci) tutte insieme, massimamente nel fine, conciosia ch'è necessario, che tutte le par-
ti insieme cantino & insieme finiscano; fà, che le compositioni per tal uarietà riusci-
scono più uaghe, & più diletteuoli. Onde ritrouarono un segno, che rappresentas-
se questa taciturnità, ò silentio; & l'usarono per la cosa significata, & lo nominarono
Pausa; la quale, dal suo officio dissero esser'un' certo Intralasciamento arteficioso di uo-
ce. Et ben dissero Arteficioso intralasciamento; uolendoci auertire, che non douessi-
mo por le Pause nelle cantilene fuor di proposito, & senz'arteficio, ma collocarle di ma-
niera che si ueda, che la necessità, & l'arteficio lo richieda. Imperoche si come è ui-
tiosa cosa ad alcuno, che parli sempre, & non sappia por fine, ò meta al suo parla-
re; cosi è cosa uitiosa al Musico, che non sappia à tempo & luogo dar riposo alle parti del
la sua compositione. Di modo che; si come non è senza uirtù il saper ragionare, & tace-
re con proposito; cosi ancora non è senza uirtù, che 'l Musico sappia far tacere, & can-
tare le parti della sua cantilena à tempo & luogo. Ma si debbe auertire, che doue ac-
cascasse di porre più Pause, le quali eccedessero il ualore di quella della Lunga, al-
lora questa si debbe raddoppiare; come auerebbe, quando si uolesse segnar la Pausa della
Massima; ma quando si uolesse raddoppiar le Pause, che rappresentano essa Massima,
ouer porle appresso altre pause minori, allora si potrà por quelle, che si aggiungono sopra
l'altre linee; percioche non si costuma tra i Musici di porre insieme tante Pause sopra
quelle righe istesse, che sopr'auanzino il ualore di essa Massima; come in questo es-
sempio si ueggono.
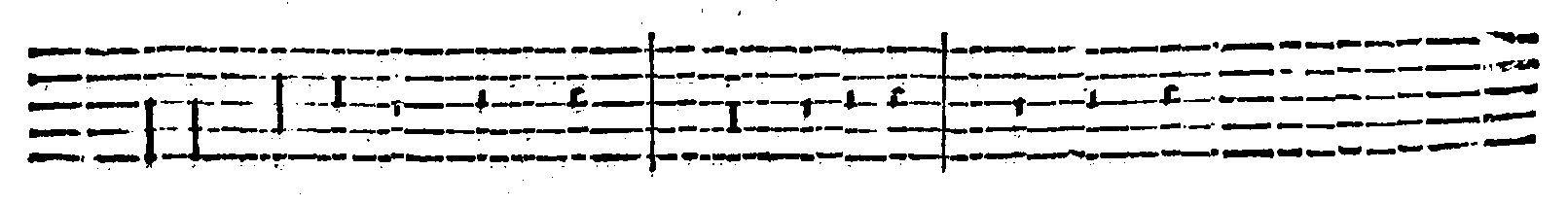 page 269Sono state uarie opinioni di questo nome Pausa; percioche alcuni hanno hauuto pare-
page 269Sono state uarie opinioni di questo nome Pausa; percioche alcuni hanno hauuto pare-re, che sia stata detta da Παύομαι parola Greca, che significa Cessare, Posare, ò Lasciare.
Altri hanno uoluto, che sia cosi chiamata dal Batter delle mani, che da i Latini è detto
Plausus; conciosia chè misurata dalla Positione & dalla Leuatione della Battuta, la quale
si conosce dal segno formato dalla mano, come di sopra habbiamo ueduto.Supra
cap. 49. Et forse, che
non fù detta da principio ne all'uno, ne all'altro modo de i due nominati; ma piò presto
(come pare ad alcuni) da Posa parola Francese, che significa Posata. Onde si suol dire
Vna pausa, due pause, & l'altre; cioè, una posata, due posate, & cosi il resto. Ma sia
detta da che si uoglia, questo importa poco; purche si sappia, che quando 'l Composito
re pone le Pause nella cantilena, uuole, che iui il Cantore taccia per tanto spacio di tem
po, quanto significa il ualor delle Pause. Gli Ecclesiastici etiandio pongono le Pause ne
i lor canti, non già per ornamento, ma per necessità; perche è impossibile di poter perue
nire al fine di cotali cantilene, senza pigliare alcun riposo. La onde di ciò aueduti, ritro
uarono un segno, dal quale ciascuno Cantore è auertito, che arriuando à quello, s'hab-
bia da fermare, & pigliare Spirito, ò fiato. Perilche da un tale effetto lo chiamarono
Πνεῦμα, che uuol dire Spirito. Posero etiandio cotal segno, accioche ogn'uno de i Can
tori concordeuolmente si hauesse da fermare; onde lo dimandarono Νεῦμα; che uuol dir
Cenno & Consenso. E' ben uero, che non pongono tali Pause nel modo, che si pon-
gono l'altre mostrate di sopra; percioche le pongono di maniera, che cingono & abbrac
ciano tutte le linee della cantilena; tallora ponendole semplici, & tallora raddoppiate;
come qui si ueggono. Et si debbe per ogni modo osseruar quello, che già molti de gli
 Antichi hanno osseruato; di non porre tali Pause, se non nel fine
Antichi hanno osseruato; di non porre tali Pause, se non nel fine delle Clausule, ò punti della Oratione, sopra la quale è composta la
cantilena; & simigliantemente nel fine d'ogni Periodo. Ilche fà dibi
sogno, che i etiandio auertiscano; accioche i Membri
dell'Oratione siano diuisi, & la Sentenza delle parole si oda & intenda interamente; per
cioche facendo in cotal modo, allora si potrà dire, che le Pause siano state poste nelle Par
ti della cantilena con qualche proposito, & non à caso. Ne si debbono per l'auenire por
re per alcun modo, auanti che sia finita la Sentenza nel mezo della Clausula, conciosia
che colui, che le ponesse à cotal modo, dimostrarebbe ueramente essere un pecora cam
pi, un goffo & un'ignorante. Però adunque il Musico si sforzerà di non cascare in simili
errori; accioche non dia à i dotti di sè mala opinione.
Delle Consequenze.Cap. 54.
Compositioni alcuna cosa, che fusse degna di riprensione, essendo purgate
& limate da ogni errore; ne si udisse in esse, se non buona & soaue Harmonia;
li mancherebbe nondimeno un non so chè di bello, di leggiadro & elegante,
che à nostri tēpi si usa; & fù usato anco da gli Antichi; come si uede nelle loro compositio
ni; quando in esse non si udisse alle fiate (poi ch'è impossibile di poter lo far sempre) alcu-
ne Repliche, ò Reditte d'una particella, & tallora di tutta la Modulatione d'una parte
contenuta nella Cantilena, fatte da un'altra, ouer da più dell'altre parti; quando tra lo
ro uanno cantando insieme, dopo un certo spacio di tempo l'una all'altra, quasi à guisa
d'uno riflesso di uoce, il quale è detto Echo, rispondendosi; intorno alle quali arteficiosa
mente si affatica ogni buon Compositore. Et tal modo di far cantare le parti in cotal ma
niera da i Prattici diuersamente è stato nominato; percioch'alcuni considerando, che le
Parti cantando insieme al modo detto, l'una segue l'altra à guisa d'uno, ilquale fuggen-
do sia seguitato da un'altro, l'hanno chiamato Fuga, alcuni Risposta; percioche tra lo-
page 270ro cantando par che l'una parte all'altra quell'istessa modulatione risponda cō proposito;
alcuni l'hanno addimandato Reditta, essendo che l'una parte uiene à redire, & à referir
quello, che l'altra hà detto, ò cantato prima; alcuni altri lhanno chiamato Conse-
quenza, & meglio forse; percioche questo è più proprio, & più al proposito; essendo
che si come dal dire, che Essendo ogn'Animale Sostantia, & essendo l'Huomo animale,
nasce questa Consequentia, che l'Huomo sia Sostantia; cosi da quell'ordine, ò modula-
tione, che è posta in alto dal Compositore, ne segue che in Consequenza si possa da un'
altra parte cantare l'istesso ordine, ò modulatione, senza lasciarui cosa alcuna, ò nell'i-
stesso suono, ò più graue, ò più acuto. Ma sotto questo nome porrò una specie di Con-
sequenza; la quale nominaremo Imitatione; perche è diuersa dalla Consequenza, co-
me uederemo; essendoche l'una & l'altra tendono ad un'istesso fine. Onde la Consequen
za diciamo essere una certa Replica, ò Reditta di modulatione d'una parte, ouer di tutta
la modulatione, che nasce da un'ordine & collocatione de molte Figure cantabili, fatta
dal Compositore, in una parte della Cantilena; dalla quale ne seguiti unaltra, ò più, ò
nel graue, ò nell'acuto, ò nell'istesso Suono, per una Diapason, ò per una Diapente, ò
per una Diatessaron, ouero all'Vnisono; dopo un certo & limitato spatio di tempo; pro-
cedendo l'una dopo l'altra, per gli istessi Interualli; ma l'Imitatione diremo esser una Re-
plica, ò Reditta, la quale non procede per gli istessi Interualli; ma per quelli che sono in
tutto differenti da i primi; essendo solamente i mouimenti che fanno le parti cantando,
& le figure ancora simili. Il perche è da sapere, che tanto la Consequenza, ò Fuga, quan
to la Imitatione, si ritroua esser di due maniere; l'una delle quali nominaremo Sciolta,
& l'altra Legata. La prima, perche è in tal maniera ordinata dal Compositore tra le parti
di qual si uoglia Cantilena, che una di esse hà un certo numero di figure solamente, ouer
una terminata particella di Modulatione, laquale da una, ò più dell'altre Parti può esser
replicata; non essendo però il resto della Cantilena sottoposta à cotal legge; ma si bene
al tutto libera: Ma la Legata chiamaremo quella, che in tal modo è ordinata & con obli
go tale, che tutta la modulatione d'una parte del concento; sia poi graue, ouero acuta;
da un'altra, ò più parti si può cantare, seguendo l'una dopo l'altra per un spacio di tempo
determinato; & in tal maniera ordinata, che in tutte le parti si possono scriuere & cantar
sopra una parte sola; come costumano di fare i Compositori, acciò si ueda l'arteficio da
loro osseruato nel comporre la Cantilena in simili modi di comporre; facendo che l'una
seguiti l'altra, secondo un certo spacio di tempo (come hò detto) determinato & asse-
gnato. Questo si può ueramente chiamar Consequenza; percioche si come nel Sillogis
mo formale (come hò detto) ui entra l'Oratione, nella quale essendo poste alcune cose,
di necessità ne segue un'altra; cioè, la Conclusione, ò Consequenza; cosi nella Canti-
lena, essendo accommodata dal Compositore una sorte di modulatione con debita for-
ma, fatta in una parte del concento, la quale chiamaremo GVIDA; ne seguita necessaria
mente oltra di esse un'altra, come conclusione, & consequenza; ch'è quella parte; che
chiamaremo CONSEQVENTE. La onde in queste Consequenze fà dibisogno dosseruare,
che quelle Parti, che seguitano la prima in cotale maniera, habbiano da cantar non so
lamente quello, che rappresentano le Figure cantabili; ma debbono osseruare il nume
ro delle Pause, & ogn'altro accidente; come si costuma di fare alle uolte; quantunque
una delle parti raddoppiasse, ò minuisse nel cantare il ualor delle Figure, & delle Pause; &
l'altra cantasse due fiate replicando quello, che contiene la prima. Ma per uenire à mo-
strar queste cose; accioche si conoschino; incominciaremo dalla Consequenza, ò Fuga
sciolta, nella quale il Compositore non è obligato di osseruar l'equalità delle figure, & di
por le Pause simili, ne osseruare altri simili accidenti; ma può far quello, che più li tor-
na commodo; come ch'una parte proceda per Minime, & l'altra per altre figure; cioè,
per Semibreui, & similmente per Minime & Semiminime insieme mescolate; come s'os
serua di far ne i Contrapunti fatti sopra 'l Canto fermo. Si debbe però auertire, che quel
la parte, che incomincia la Fuga, ò legata, ò sciolta ch'ella sia, è detta Guida; come ha
page 271uemo detto di sopra, & quella che segue è chiamata Consequente. Et perche quelle Con
sequenze, che si fanno distanti l'una dall'altra per lo spacio, ò tempo d'una Pausa di Mi-
nima, ò di una Semibreue, & d'alcun'altre ancora; per la lor uicinità sono più intelli-
gibili; percioche dal sentimento sono facilmente comprese; però si sforzarono i Musici
di fare, che le parti delle lor cantilene fussero più uicine nella Consequenza, che fusse
possibile; Ma il troppo continuare cotal uicinità fece, che si cascò in un certo modo com
mune di comporre, ch'al presente non si ritroua quasi Consequenza, che non sia stata
mille migliaia di uolte usata da diuersi Compositori. La onde accioche per l'aueuire nel-
le cantilene si oda qualche uarietà, si sforzaranno di usar più di rado le Consequenze co
 si uicine & unite; & si allontanarono alquanto da quelle, che sono tanto communi; & cer
si uicine & unite; & si allontanarono alquanto da quelle, che sono tanto communi; & cercaranno con ogni lor potere di farle, che fussero più noue; conciosiache quando si faran
no la Guida & il Consequente alquanto distanti l'uno dall'altro per tre Pause di Mini-
ma, ouer per cinque, ò per altre simili; uerranno senza dubbio, à far qualche noua ua
riatione. Io non dico già che le Consequenze distanti per l'una Pausa di Minima, ò di
Semibreue non si debbino usare; ma dico, che non si debbono usar molto spesso; per nō
cascare in quello, ch'è tanto commune; che non si ritroua libro, nel quale non sia molte
& molte uolte replicato; il qual lascio di mostrare, per non esser tedioso, & per non of-
fender alcuno. Ma accioche si caui qualche frutto da quello, ch'io hò detto; porrò pri-
ma l'essempio delle Consequenze sciolte, le quali si fanno sopra i Canti fermi à loro
imitatione; percioche di quelle che si trouano tra due parti diminuite, se ne potrà
hauere due accommodati essempi, posti di sopra nel Cap. 43. Ma delle legate, che
si fanno in molte maniere, ne porrò qui alcune solamente: essendo ch'è impossi-
bile di poterle por tutte, & dimostrarle con breuità in poche carte; nelle quali s'hauerà
da osseruar questo nella prima maniera, che siano poste l'una con l'altra in Con-
sequenza all'Vnisono, ouero alla Quarta, oueramente alla Quinta, ò pure all'Ot-
taua incominciando da qual parte si uoglia, sia la graue, ouer l'acuta, che que-
sto importa poco. La onde finito che sarà il tutto; come qui si uede; si piglierà la par-
page 272
 te, che incomincia à cantare; cioè, la Guida, & si scriuerà di lungo & doue 'l Con-
te, che incomincia à cantare; cioè, la Guida, & si scriuerà di lungo & doue 'l Con-sequente hà da incominciare à cantare; cioè, sopra la figura posta nella Guida, si porrà
un segno tale, [[mus.sigcon]] il qual da i Musici uien detto Presa; Et nel fine, ou'hà da fermarsi, si
segnarà la parte della Guida col detto segno, ouer con questo [[mus.ferm]] ponendolo sopra la fi-
gura finale, oue si hà da fermare il Consequente; & cotal segno chiamano Coronata.
Regola sopra la parte della Guida, la quale essendo chiamata da i Greci Κανὸν, alcuni
Musici poco intelligenti dicono Canon quello, che douerebbono dire Consequenza.
te è più acuto della Guida, s'aggiunge, In acuto; aggiungendoui oltra di ciò il Tempo
che hà da aspettare la parte del Consequente, auanti ch'incomincia à cantare; ancora
che sia segnata il luogo col segno [[mus.sigcon]] La onde si scriue.
 Oltra di ciò se 'l Consequente cantasse nel graue in luogo didire, Acuta; si porrebbe,
Oltra di ciò se 'l Consequente cantasse nel graue in luogo didire, Acuta; si porrebbe, Graue. Et se la Consequenza fusse fatta per una Quarta, allora si direbbe; In Diatessa-
ron; & se cantasse per una Quimta, si direbbe; In Diapente; & se per l'Vniso-
no, si direbbe; All'Vnisono, oueramente, Nell'istesso suono, ò uoce istessa. Lungo sa
rebbe il uoler raccontare tutte le specie delle Consequenze d'una in una; & il uoler dar'
un'essempio particolare; ma perche de queste ne sono i Libri pieni; però lasciarò di ra-
gionarne più oltra, rimettendo 'l resto al buon giudicio del Compositore; che uedendo
page 273& essaminando gli essempi sopra detti, li saranno guida & lume di ritrouar cose assai mag
giori. Non voglio però restar di dire, che si troua etiandio vn'altra sorte di Consequen-
za, la quale si fà per gli istessi Interualli, per mouimenti contrarij, detta Consequenza
per Α῎ρσιν, & Θέσιν; cioè, per Leuatione & Abbassamento di voce; il qual modo è vsa-
to da i buoni Prattici; & nel comporla si procede à quell'istesso modo, col quale si pro-
cede nell'altre. Sono nondimeno due le sue Specie; Legate, & Sciolte. Le Legate po-
tremo conoscere, quando haueremo piena cognitione delle precedenti; il simile anco
auerrà delle Sciolte. Ma perche, considerato quello, che di sopra hò detto, con facili-
tà si può fare, ò compor le Sciolte; lasciandole da vn canto, verrò à mostrar le Legate,
che sono alquanto più difficili, & porrò solamente alcuni essempi, da i quali si potrà co-
noscere & comprender quello, che si dè osseruare, quando si vorrà comporre in tal
maniera. Se noi adunque ordinaremo la Guida col Consequente, che procedino l'vno
contra l'altro per contrarij mouimenti, osseruando di porre quelli istessi Interualli de Tuo
ni, de Semituoni & gli altri in vna parte, che si pone nell'altra; non è dubbio, che que-
ste Parti si potranno ordinare in diuerse maniere; percioche si potrà porre il Conse-
quente sopra la Guida distante per lo spatio del Semiditono, aspettando due Tempi in-
teri di Breue imperfetta; cioè, dimorando all'incominciare per lo spatio di vna Pausa
di Lunga, & cosi haueremo il seguente essempio: Ouero si potrà porre l'vna delle par-
 ti; cioè, il Consequente lontano dalla Guida per vna Settima, & haueremo la seguente
ti; cioè, il Consequente lontano dalla Guida per vna Settima, & haueremo la seguente cantilena; nella quale il Consequente seguirà la Guida per due tempi di Breue imperfet-
ta; cioè, dopo vna Pausa di Lunga.
page 274
 Volendo poi scriuere in lungo cotali essempi, ò cantilene, si potranno ordinare di manie
Volendo poi scriuere in lungo cotali essempi, ò cantilene, si potranno ordinare di maniera, che i Consequenti potranno hauer le loro chiaui, che dimostreranno, per quali chor-
de haueranno à procedere nel cantare, come hà la Guida. Lequali Chiaui si porranno
sempre auanti quella, che serue ad essa Guida; & tra queste & quelle si porranno le Pau-
se, che 'l Consequente haurà da fare, auanti che incominci à cantare; ancora che la Re-
gola posta sopra di loro gli insegni, in qual maniera si habbia da procedere; come ne i
due sottoposti essempi si uede.

 page 275Vedremo poi al suo luogo, quel ch'importi vn tempo, due tempi, & più ancora; concio-
page 275Vedremo poi al suo luogo, quel ch'importi vn tempo, due tempi, & più ancora; concio-siache allora mostrarò etiandio, quante Figure in esso si pongano, & à qual figura il Tem
po s'attribuisca. Si debbe oltra di ciò auertire, che queste maniere di Consequenza non
sono per alcun modo da sprezzare; anzi si debbono abbracciare; percioche oltra che so-
no belle, eleganti & ingegniose; hanno anco un certo non sò che di grandezza, essendo
che un tal modo di comporre non è cosi commune, come sono gli altri modi. Però adun-
que, chi si uorrà essercitare nel comporre simili maniere, non è dubbio, che in breue tem-
po diuenterà buon Musico. Et quello c'hò detto nelle Consequenze legate, uoglio che
s'intenda anco delle Slegate, ò Sciolte, che si compongono senza obligo alcuno. Ne si
debbe alcuno imaginare; hauendo io solamente posto i mostrati essempi; che queste sola-
mente siano tutte le maniere delle Consequenze, & che non se ne possa fare alcun'altra,
per altra maniera; come il porre più, ò meno tempi; & che la Guida non si possa porre
nell'acuto, & il Consequente nel graue; conciosia che sono quasi infiniti li modi, & lungo
sarebbe il raccontarli di uno in uno; ma hò posto solamente questi pochi, accioche siano
vn lume & una guida à ciascuno, che uorrà sotto à questa bella, ingegnosa, & ho-
noreuol fatica.
Delle Imitationi, & quello che elle siano.Cap. LV.
mento, che apporta alla cantilena, è cosa d'ingegno & molto lodeuole; & è di
due sorti, come è la Consequenza; cioè, Legata & Sciolta. E' da i Prattici
etiandio chiamata Consequenza; ma in uero tra questa & la Imitatione è co-
tal differenza; che la Consequenza legata, ò Sciolta, ch'ella si sia, si ritroua tra molte
parti della cantilena; le quali, ò per mouimenti simili, ò per contrarij, contengono quel-
l'istessi Interualli, che contiene la lor Guida, come hò mostrato: ma la Imitatione sciolta,
ò legata, come si vuole; quantunque si ritroui tra molte parti (come mostraremo) & pro-
cedi all'istesso modo; nondimeno non camina per quell'istessi Interualli nelle parti con-
sequenti, che si ritrouano nella Guida. La onde; si come la Consequenza si può fare
all'Vnisono, alla Quarta, alla Quinta, all'Ottaua, ouero ad altri Interualli; cosi la
Imitatione si può accommodare ad ogni Interuallo; dall'Vnisono & da i nominati in
 page 276fuori. Il perche, si potrà porre alla Seconda, alla Terza, alla Sesta, alla Settima & ad altri
page 276fuori. Il perche, si potrà porre alla Seconda, alla Terza, alla Sesta, alla Settima & ad altri Interualli simili. Diremo adunque che la Imitatione è quella, che si troua tra due, ò più
parti; delle quali il Consequente imitando i mouimenti della Guida, procede solamente
per quell'istessi Gradi, senz'hauer'altra consideratione de gli Interualli. Et la cognitio-
ne tanto della Legata, quanto della Sciolta si potrà hauer facilmente, quando s'hauerà
conosciuto quello, che uoglia dire Consequenza legata & Consequenza sciolta. Ma per
maggior chiarezza uerrò ad uno essempio particolare, dal quale si potrà conoscer quel-
lo, c'hò voluto dire in vniuersale. Le Imitationi adunque, che si fanno per contrarij mo-
uimenti, hanno al medesimo modo, che hanno le Consequenze, la Guida & il Con-
sequente; onde si usa anco nel scriuere la Guida in lungo gli istessi modi, che furono usati
nelle Consequenze; cioè, porre le lor Prese & le Coronate, come hò mostrato. Ma il Ca-
none, ò Regola de queste si scriue in cotal Guisa. Si canta alla Seconda, ouero alla terza, ò
pur ad altre simili; acuta, ouer graue, pausando due tempi, ò più, ò meno. Et se le Parti procedono
per mouimenti contrarij, s'aggiunge queste parole; Per mouimenti contrarij. Si debbe do-
poi auertire, che nelle Sciolte si può cauare il Consequente dalla Guida, parte per imita-
tione & parte in consequenza. Cosi parte in mouimenti simili & parte in mouimenti
contrarij; onde sarebbe cosa troppo lunga, se 'l si uolesse dar notitia particolare d'ogni co-
sa minima. Ciascuno però sarà auertito per sempre, di ordinare in tal maniera le Parti
della sua compositione, massimamente nelle Fughe & Imitationi legate, che procedono
per mouimenti contrarij; che si possino cantar senza discommodo. Et per dare di ciò
qualche lume, hò posto di sopra lo essempio particolare delle Imitationi sciolte; accioche
da esso si possa trar frutto di quello, c'hò detto di sopra; & hora uerrò à mostrare gli es-
sempi delle Imitationi legate. La Imitatione legata si potrà conoscer da questo, che ha-
uerà la Guida & il Consequente, che l'uno seguiterà l'altro; non per gli istessi Interualli;
 page 277ma per quelli istessi Mouimenti, ouer Gradi; come nell'essempio seguente si uede. Et
page 277ma per quelli istessi Mouimenti, ouer Gradi; come nell'essempio seguente si uede. Et questa si conosce esser manifestamente Imitatione, & non Fuga; percioche il Consequen
te canta per un Ditono più acuto della Guida. Et ancora che l'uno, & l'altro procedino
per gli istessi Gradi; non procedono però per gli istessi Interualli; come hò detto. Vo-
lendo adunque ridurre tale Imitatione in vna parte sola, la disponeremo à questo modo;
ponendole di sopra la Regola, ch'insegnerà quello, che si hauerà da tenere nel cantarla,
in questa maniera.
 Ma in quelle Imitationi, che procedono per Mouimenti contrarij, si tiene altro modo;
Ma in quelle Imitationi, che procedono per Mouimenti contrarij, si tiene altro modo; come nell'essempio seguente si può vedere.
 page 278Et acciò si uegga in qual maniera per l'auenire s'habbia da procedere, quando si vor[gap — ]
page 278Et acciò si uegga in qual maniera per l'auenire s'habbia da procedere, quando si vor[gap — ] porre insieme la Guida & il Consequente; scriuerò tale Imitatione in lungo, col suo Ca-
none, ò Regola in cotal modo.
 Si troua etiandio una sorte di Compositione simile, laqual contiene la Guida & il Conse-
Si troua etiandio una sorte di Compositione simile, laqual contiene la Guida & il Conse-quente, parte in Consequenza & parte in Imitatione; come quì si uede.
 page 279La quale si suol ridurre sopra vna parte sola, col suo Canone, ò Regola in questo modo.
page 279La quale si suol ridurre sopra vna parte sola, col suo Canone, ò Regola in questo modo. 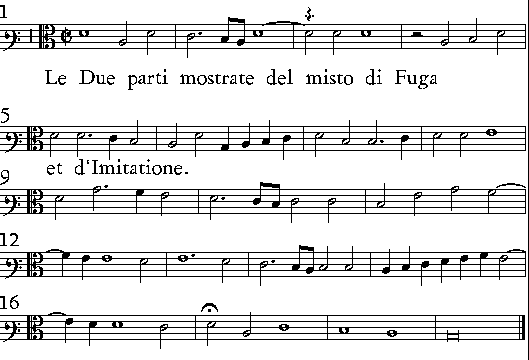 Questa communemente da i Prattici è detta Fuga; & si usa molto spesso nelle Composi-
Questa communemente da i Prattici è detta Fuga; & si usa molto spesso nelle Composi-tioni à più voci; come si può uedere in molte cantilene. Et in uero non è da sprezzare,
anzi da porla spesse volte in uso; percioche fà la compositione ingegnosa, & fà anco buo-
nissimo effetto. Ma si dee sapere, che nelle Consequenze & nelle Imitationi, che si troua-
no nelle compositioni à più voci, Legate, ò Sciolte che siano, si possono por le Quarte, &
far molti passaggi, che ritornano bene; percioche l'altre parti sono di grande aiuto al
compositore; ancora che nelle compositioni de due voci le Quarte non si ponghino; per
che non fanno quel buono effetto, che fanno l'altre Consonanze. Però sarà bisogno, che 'l
Compositore stia auertito, acciò non cada in qualche errore. Ma questo sia detto à suffi-
cienza intorno alle Consequenze & alle Imitationi; percioche d'alcune di quelle, che si
pongono nelle compositioni à più uoci, ragionaremo altroue.
De i Contrapunti doppij, & quello che siano.Cap. LVI.
punto à due voci; uoglio che uediamo hora, in qual modo si possa fare alcu-
ne sorte arteficiose di Contrapunto à due uoci medesimamente, sopra qual
Soggetto si uoglia; che si chiama Contrapunto doppio; il quale non è altro,
che vna compositione fatta ingegnosamente, che si può cantare à più modi, mutando
le parti di maniera, che replicata si oda diuerso concento da quello, che nell'istesse pri-
mieramente si udiua. Onde dobbiamo sapere, che tal Contrapunto si troua essere di
due sorti; la prima è, quando il Principale; cioè, il primo, che si compone & la Re-
plica; cioè, quello, che s'intende dopo il primo; si cantano mutando le parti in questo
modo, che l'acuta diuenti graue, & graue l'acuta, senza variatione alcuna de moui-
menti. Et questa si ritroua etiandio de due sorti; Imperoche mutate le parti; ouero
procede per gli istessi Interualli, oueramente per variati; Se per gli istessi, il Contrapun-
to replicato si canta facendo la parte acuta del principale più graue per vna Quinta; &
la graue più acuta per una Ottaua; & se 'l si procede per uariati, si canta la parte acuta
del principale vna Decima più graue, & la graue una Ottaua più alta. La secon-
da poi è, quando dopo il Principale si canta la Replica, che procede per mo-
uimenti contrarij; cambiate primieramente le parti, come si è detto; cioè, la gra-
ue nell'acuta, & questa nella graue. Quando adunque si uorrà comporre al pri-
mo modo, che procede per gli istessi Mouimenti, & per gli istessi Interualli; osserua-
remo di non porre mai la Sesta nel Principale; imperoche nella Replica non può
page 280far consonanza. Ne porremo mai le Parti della cantilena tanto distanti l'una dall'altra,
che trappassino la Duodecima chorda; ne mai porremo la Parte acuta nel luogo della
graue; ne per il contrario, la graue nel luogo della acuta; conciosia che non solo le figu-
re, che passano la Duodecima; ma etiandio quelle, per le quali si uiene ad occupare con
vna parte il luogo dell'altra, uengono à far dissonanza nella R eplica. Non porremo
anco la Sincopa, nella quale si contenghi la Settima; percioche nella Replica non tor-
na bene. Potremo però vsar la Sincopa, nella quale sia la Seconda & la Quarta; essen-
do che queste vengono à far nella Replica buonissimi effetti; massimamente quando è
risolta secondo i modi mostrati altroue. Et accioche tra le parti della Replica non si oda
alcuna relatione, che non sia harmonica; si dè auertire, di non porre per alcun modo
nel Principale la Decima minore, dopo la quale uenghi la Ottaua, ò la Duodecima, ne
la Terza minore auanti l'Vnisono, ò la Quinta; quando le parti procedono per contra-
rij mouimenti; percioche poste in cotal modo, ne segue il Tritono, ouer'altro incom-
modo tra le parti. Debbesi oltra di ciò auertire, ch'ogni Duodecima nel Principale,
viene ad esser nella Replica Vnisono, & ogni Quinta torna Ottaua. Etiandio si dè os-
seruare, che ogni Regola mostrata di sopra sia nel Principale intieramente osserua-
ta; percioche la Replica verrà ad essere senz'alcuno errore. E' ben uero, che uolen-
do finire il Contrapunto con la Cadenza, sarà necessario, che 'l Principale, ò la Re-
plica habbia la Cadenza terminata per Quinta, ò per Duodecima; ilche auiene etian-
dio nelle Cadenze mezane; se bene tra le parti si udirà la relatione del Tritono; Ma que-
sto sarà di poca importanza, quando il resto sarà ordinato regolatamente; come si
può vedere nel Principale. Cantaremo poi la Replica in questo modo, facendo acu-
ta la parte graue per una Ottaua, & graue la acuta per una Quinta; procedendo per
gli istessi Mouimenti, & per gli medesimi Interualli, come più oltra si uede nello essem-
pio; dal quale si potrà comprendere, che 'l suo Contrapunto & il suo concento è mol-
to uariato da quello del Principale; & questo si chiama Contrapunto doppio alla Duo-
 decima. Ma uolendo comporre quello, che tiene il Secondo luogo nella Prima manie-
decima. Ma uolendo comporre quello, che tiene il Secondo luogo nella Prima manie-ra; cioè, quello, che nella Replica procede per gli istessi mouimenti; ma per Interualli
differenti da quelli, che sono nel Principale; osseruaremo di non porre per alcun modo
nel Principale due Consonanze simili; come sono due Terze, ò due Seste, l'vna dopo l'al-
tra, senz'alcun mezo; ancora che l'una fusse maggiore, & l'altra minore; & di porre le Sin-
cope, che siano in tutte le lor parti consonanti. Io dissi, che non si pone due Seste; per-
cioche in questi & in altri simili Contrapunti la Sesta si può vsare, che fà buono effetto; &
si può far che la Parte graue piglia il luogo dell'acuta, & questa quella del graue; come tor-
na più commodo; con questa conditione però, che quando saranno poste in tal maniera;
l'una non sia lontana dall'altra per più d'vna Terza; essendo che restando ciascuna ne i
suoi termini, allora si potranno porre distanti l'una dall'altra per vna Duodecima. E' ben
uero, che se ben passasse più oltra, non bisognarebbe porre per alcun modo la Terzade-
cima; perche non tornarebbe molto commoda. Non passaremo adunque la Duodeci-
ma, & osseruaremo le Regole date, & faremo, che le Parti della cantilena cantino commo
damente, con mouimenti di grado, più che sia possibile; percioche quelli di Quarta & di
Quinta possono in alcuni luoghi della Replica generar qualche discōmodo; Il che osser-
uato, potremo hauere un Contrapunto purgato da ogni errore simile à quel che seguita.
Dal quale potremo hauere non solo vna; ma due Repliche; l'una quando prima fare-
mo la sua parte graue più acuta per vna Ottaua, & l'acuta più graue per una Decima;
Et l'altra, quando si farà graue la Parte acuta per una Ottaua, & la graue si cantarà acuta
per vna Decima; & più piacerà, perche si udirà il Modo mantenuto maggiormente ne i
suoi termini, con altr'harmonia. Et queste sorte de Contrapunti si potranno cantare
etiandio à Tre voci; facendo prima cantare sotto la parte acuta del Principale un'altra
parte distante nel graue per una Decima; & dopoi nella prima Replica l'acuta, si cantarà
più graue, per una Diapason; & restando la graue nel suo essere; si farà cantare una Ter-
za parte nel graue, distante per una Decima da quella che si canta più graue nella Repli-
ca per una Diapason. Fatto questo, nella Seconda replica si fara cantare una parte più
acuta per una Terza, sopra la parte graue della Replica, & si haurà il proposito; cioè,
Tre maniere di contrapunto à Tre uoci, che saranno l'una dall'altra differenti. E' ben
uero che 'l Contrapunto non verria ad esser cosi bene espurgato da errori; come sarebbe
il douere. Ma perche il fare questa sorte di Contrapunto è molto difficile, uolendolo
far, che uenghi nella Replica senza errore; però voglio porre alcune regole generali,
page 282
 page 283delle quali la prima sarà (lasciando molt'altre cose alla discretione & al buon giudi-
page 283delle quali la prima sarà (lasciando molt'altre cose alla discretione & al buon giudi-cio del Compositore) che non si dè por mai la Terza dopo l'Vnisono, ne la Terza me-
desimamente, ouer la Decima dopo la Ottaua, quando le parti della cantilena discen-
deranno insieme. Osseruaremo, anco che quando le parti ascenderanno, di non por
dopo la Quinta la Sesta, ne meno la Decima dopo la Duodecima; massimamente
quando la parte acuta non procederà per grado, il quale è alquanto più tolerabile del
mouimento per salto. Similmente si auertirà, di non procedere dalla Ottaua alla De-
cima minore, se non quando la parte acuta farà il mouimento di Tuono, & la graue
quello del Semituono; ne meno dalla Terza, ò dalla Quinta alla Decima minore, per
contrarij mouimenti. Schiuaremo il porre la parte acuta, che si muoua dalla Quinta
alla Terza maggiore, quando la graue non farà mouimento alcuno. Cosi quando la
parte acuta non farà mouimento, & la graue si muouerà, procedendo dalla Quinta al-
la Terza minore, ouer dalla Duodecima alla Decima minore; Imperoche la Replica
non uerrebbe secondo le Regole date. In questa maniera di Contrapunto ogni Deci-
ma, che si pone nel Principale, diuenta Ottaua nella Replica; & ogni Terza ritorna
Quintadecima. Ma debbe il Cōtrapuntista comporre insieme il Principale & la Replica;
& cosi il tutto verrà ad esser senza errore. Quanto al Secondo modo, oue la Replica và
modulando per mouimenti contrarij à quelli, che sono contenuti nel Principale, osser-
uando pero nelle sue parti gli istessi Interualli; fà dibisogno, ch'esso Principale habbia
Sincope (se ne hauerà alcuna) che siano tutte consonanti; siano poste poi à qual mo-
do si uoglia; percioche se hauesse alcuna dissonanza, non verrebbono à far buoni ef-
fetti nella replica. Qui si potrà vsare (facendo bisogno) la Sesta nel principale; ma
bisogna auertire, di non porre la Decima, dopo la quale seguiti la Ottaua; ne la Ter-
za auanti l'Vnisono, quando le parti ascendono insieme; come nel sottoposto essem-
pio si è osseruato.
 Haueremo la Replica, ponendo graue la parte acuta, & l'acuta graue; questa distante
Haueremo la Replica, ponendo graue la parte acuta, & l'acuta graue; questa distante dalle parti principali per una Settima, & quella per vna Nona; come quì si vede.
page 284
 Componendo in cotal maniera, le Parti della compositione si possono porre nel Principa-
Componendo in cotal maniera, le Parti della compositione si possono porre nel Principa-le distanti l'vna dall'altra per qual si uoglia Interuallo; se bene ariuassero alla Quintade-
cima; perche nella Replica tornano bene; ma non si debbe porre le Parti molto lontane


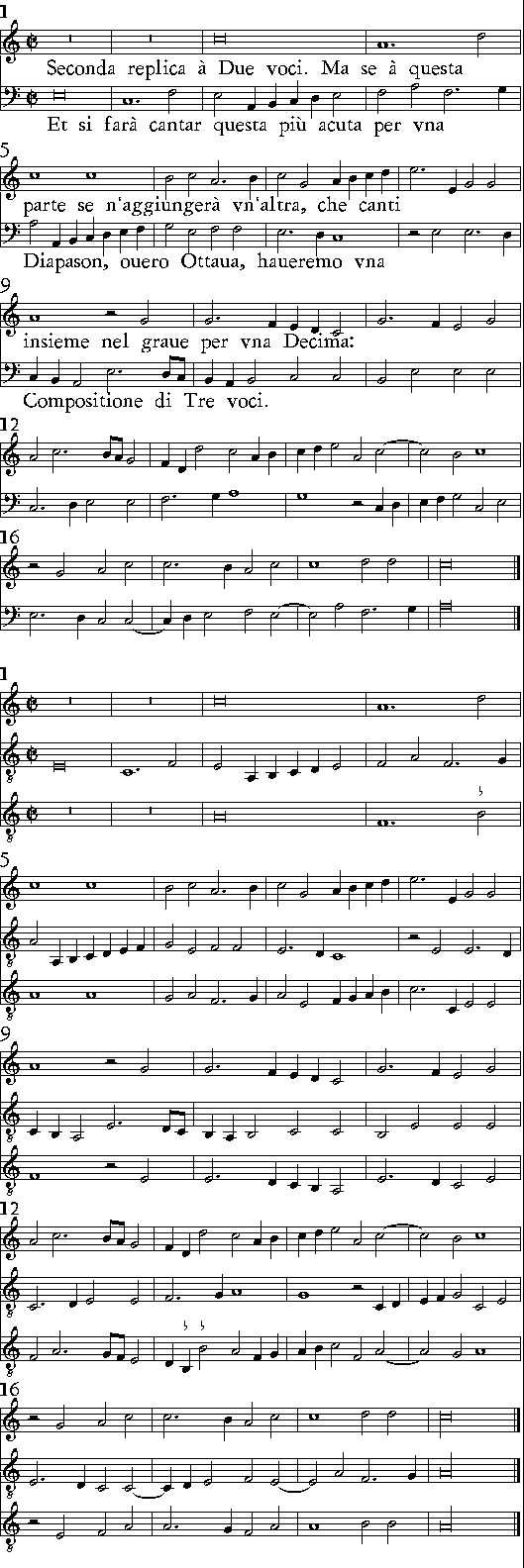
 page 286l'vna dall'altra. Hò uoluto dar questi pochi essempi; accioche essaminati, il diligente
page 286l'vna dall'altra. Hò uoluto dar questi pochi essempi; accioche essaminati, il diligente Compositore possa ritrouare col suo intelletto altre noue, & belle inuentioni. La onde
voglio etiandio auertire vna cosa; che se 'l si osseruarà tutto quello che le Regole ne to-
glie, di potere vsare alcuna cosa ne i Contrapunti mostrati di sopra; potremo comporre
vn Contrapunto di tal sorte, che si potrà cantare à ciascuno de i modi mostrati, con gran-
de uarietà d'harmonia; come ne i poco fà mostrati si potrà conoscere. Non voglio ta-
cere anco questo, acciò si ueda l'arteficio di questa sorte di Contrapunto; che se noi ag-
giungeremo à qual si uoglia parte delle Cantilene, che si cantano à Due voci, un'altra
nel graue, ò nell'acuto; secondo c'hò notato in esse particolarmente; ciascuna da per sè
si potrà cantare à tre uoci. E' ben vero, che le parti aggiunte non ueranno fatte con l'os-
seruanza delle Regole date di sopra: Ma questo basti. Si debbe etiandio sapere; che ol-
tra le mostrate maniere di Contrapunto doppio, se ne ritrouano molt'altre; le quali uo-
lendole raccogliere insieme sarebbe cosa lunga & difficile; ma per hora basterà di mo-
strarne alcune, che si fanno in Consequenza; le quali sono marauigliose. La onde (per
venire al fatto) dico; che se nella Consequenza fatta per mouimenti contrarij osserua-
remo di non por mai alcuna Dissonanza; verrà una Compositione di tal maniera, c'ha-
urà una Replica, nella quale, quella parte, ch'era nel Principale Consequente, potrà esser
Guida; come nel sequente essempio, il quale corrisponde alla Seconda maniera di Con-
sequenza legata, posta nel Cap. 54. si può comprendere.
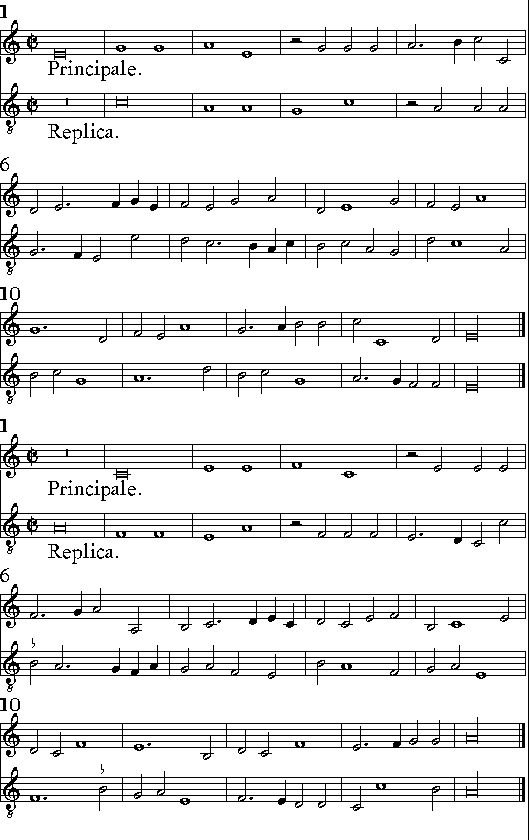 Percioche essendo la parte acuta Guida nel principale, & la graue il Consequente; nella
Percioche essendo la parte acuta Guida nel principale, & la graue il Consequente; nella Replica viene il contrario; cioè, la graue Guida, & l'acuta Consequente. Questo istesso
ne verrà fatto nelle Imitationi per contrarij mouimenti; quando osseruaremo medesi-
mamente di non far mai alcuna Dissonanza. Onde nascerà una compositione simile alla
sequente; corrispondente al Secondo modo d'Imitatione legata posta nel Cap. 55. La
quale hauerà la sua Replica.
 Ma al misto di Consequenza, & d'Imitatione posto nel nominato Cap. 55. corrispon-
Ma al misto di Consequenza, & d'Imitatione posto nel nominato Cap. 55. corrispon-de il sequente essempio; nel quale se 'l si osseruerà, sopra ogn'altra cosa, di non fare
Sesta; onde ne uiene, che non si può fare la Sincopa, nella quale sia nascosta la Settima;
& haueremo una Replica; nella quale il Consequente del principale diuenterà Guida,
& la Guida ritornerà Consequente; come nel sequente essempio si può vedere.
Imitatione legata, posta nel detto Cap. 55. osseruaremo primieramente queste cose, che
sono di maggiore importanza; cioè, di non far mai due Interualli, ò Consonanze, che
siano simili; siano poi qual si voglino; ne di usar mai la Quinta; ne di far mai la Sinco-
pa, che habbia la Settima; ancora che si possa vsar la Sesta; ma non mai sotto 'l Conse-
quente; ne mai sotto di questo si fà Quinta, dopo la quale ne venga la Terza insieme
page 288
 discendendo; & haueremo una Cantilena, com'è la sequente, con due Repliche; nella
discendendo; & haueremo una Cantilena, com'è la sequente, con due Repliche; nella Prima delle quali, quello ch'era Consequente nel Principale, & cantaua dopo la Gui-
da per l'Interuallo de due Tempi, per vna Terza più graue; potrà cantar per lo spacio di
essi due Tempi per vna Diapente simigliantemente più graue; Ma nella Replica, l'uno
& l'altro de i due Consequenti; cioè, quello del Principale, il quale cantò dopo la Gui-
da per vna Terza più graue; & anco questo che cantò per vna Diapente, potranno can-
tare insieme con la Guida, facendo prima ciascheduno due Tempi, come haueano fat-
to prima; & cosi si potrà hauere vna cantilena à tre Voci; come nel sequente essempio
si potrà vdire. Ma bisogna auertire, di non procedere molto per salti di Quarta & di
 Quinta; essendo che ne i Consequenti alle fiate vengono discommodi, per li salti di Tri
Quinta; essendo che ne i Consequenti alle fiate vengono discommodi, per li salti di Tritono & Semidiapente. Poniamo hormai fine à coteste cose; essendo che (per quello ch'io
m'aueggio) fin'hora ne hò insegnate tante, che ogn'uno di eleuato ingegno da se stesso
potrà non solamente accommodarle nelle sue Compositioni; ma etiandio ritrouarne
dell'altre; con nuoue & belle inuentioni; percioche seguitando i modi, c'hò insegnato
di sopra, non li sarà difficile. Ma di questo sia detto à sufficienza.
page 289
Quel che dè osseruare il oltra le Regole date, & d'alcune licenze,
che potrà pigliare, quando li tornaranno commodo.Cap. LVII.
per il quale il Compositore potrà comprendere l'Vniuersale; accioche dalla
lor'osseruanza la sua cantilena, uenghi ad esser piena di soaue harmonia; & il
concento apporti diletto à tutti coloro, che l'udiranno. La onde dico, che
oltra l'osseruanza delle Regole date di sopra, fà dibisogno, che primieramente il Com-
positore accompagni in tal maniera le Parti della cantilena, che se una sarà contenuta
per essempio tra le chorde del primo Modo, l'altra sia compresa da quelle del Secondo,
com'io intendo di mostrare nella Quarta parte. Et perche nel fare i Contrapunti, alle
uolte il Compositore ritrouarà molte figure sopra una chorda della parte del Soggetto,
essendo necessario, che 'l Contrapunto faccia mouimento; onde spesse fiate non porrà
continuar nella uarietà delle Consonanze molto di lungo, se non con grande difficultà;
però in tal caso potrà usar molte figure sincopate; come sono la Semibreue, & la Mini-
ma col Punto uariando sempre le chorde & li suoni; & cosi le figure poste in questo mo-
do, faranno passare il Contrapunto con molta gratia, & apporteranno gran commodo
al Compositore; perche uerrà ad esser legato di maniera, che farà buonissimo effetto.
Ma si dè sapere, che allora il Contrapunto si potrà chiamar legato, quando sarà sincopa-
to in tal maniera, che la Semibreue del Soggetto non cascarà interamente battuta sopra
la Semibreue del Contrapunto, ma si bene sopra la sua metà; il che auerrà, quando sa-
rà posta Sincopata, ouer quando cascarà sopra 'l punto della Minima. Sarà etiandio det-
to legato, quando la parte del Soggetto starà ferma; cioè, non si muouerà da una chor-
da all'altra, & il Contrapunto si muouerà, & andrà modulando per diuerse chorde. Si-
milmente sarà chiamato legato, quando 'l Contrapunto starà fermo, & il Soggetto pas-
sarà per uarie chorde; & ciò accaderà quando sarà diminuito. Quando occorrerà poi di
uolere usar gli Vnisoni, ò per necessità, ò per altra cagione, si potranno porre sopra la se-
conda parte della Semibreue, pur che la parte del Soggetto, & il Contrapunto nel bat-
tere, ò nel leuare, in un tempo non s'incontrino à proferir l'Vnisono; conciosia che po
sto sopra la seconda parte di qual figura si uoglia, quasi non si ode; come si udirebbe quan
do s'incontrassero insieme nella prima parte. Onde per questa ragione si potrà anco por
re quando cascherà sopra 'l punto della Semibreue, ò della minima, posto in qual parte
si uoglia; pur che tal parte sia diminuita; & ciò torna bene nelle compositioni de più uoci;
essendo che quell'Vnisono uiene à pigliare il luogo di quella Minima, dellaquale il punto
tiene il suo luogo; che non solamēte quasi non si ode, ma tal punto alle uolte da Cantori si
tace; onde è cagione spesse fiate di fare, che l'harmonia resta priua d'alcune delle sue par
ti; cioè, della Quina, ò della Terza; com'altroue uederemo; & per tal maniera resta im-
perfetta. Ma perche l'osseruanza delle mostrate Regole lega alle uolte il Compositore
in tal guisa, che non solo ne i Contrapunti può far'acquisto d'una bella & leggiadra
modulatione, che diletti; ma non può anco por le parti della cantilena in Conse-
quenza, secondo che sarebbe il suo desiderio; però, secondo ch'à i Poeti è concesso al-
cuna uolta di far contra le Regole metriche, & di usare una locutione per un'altra, &
una sillaba lunga in luogo d'una breue, ò per il contrario; cosi sarà lecito al Musico
alle uolte, di poter porre in carte alcune cose, contra le date Regole. Ma non però li
sarà concesso il troppo continuarle; come etiandio non è permesso al Poeta di usar spesse
uolte cotal licenze. Potrà adunque il Musico, quando gli uerrà commodo, & non
potrà far'altramente, per qualche accidente, por la Quinta dopo la Sesta maggiore,
contra la Regola data di sopra nel Cap. 38 quando la Sesta sarà posta nella seconda par-
page 290te della Semibreue sincopata; come nell'essempio si uede; percioche se la Seconda & la
Settima, che sono dissonanze, poste nelle Sincope sono sopportate; quanto maggior-
 mente si dè tollerar la Sesta, che
mente si dè tollerar la Sesta, che non solamente non è dissonante,
ma appresio d'ogn'uno è riceuuta
per consonante? Potrebbe forse
alcun dire, che con questa licen-
za, & con l'istesso modo si potreb-
be anco peruenire dalla Sesta mi-
nore all'Ottaua: Rispondo, che
questo si farebbe contra ogni do-
uere; imperoche quantunque la
Maggiore habbia natura di per-
uenire all'Ottaua, come alla sua
propinqua, è nondimeno più uicina alla Quinta, che non è la Minore all'Ottaua. La
 onde si uede, che douendosi (co-
onde si uede, che douendosi (co-m'è il douere) andar dalla Con-
sonanza imperfetta alla perfetta
con la più uicina; stando in que-
sta licenza, la Sesta maggiore con-
uiene più alla Quinta, che la mi-
nore all'Ottaua. Non gli è adun-
que ragione alcuna, che scusi, ò
diffendi, quando si uolesse com-
mettere un tal disordine. E' ben
uero che dalla Sesta minore potrà alle fiate andare all'Ottaua con una figura di Semimi-
nima; perche la Quarta semiminima, che si parte dalla Terza co 'l mouimento di grado,
si può sempre pigliar per non buona; come nel Cap. 42. fu detto. Onde se una Secon-
da, ouer'una Settima, ò qualunque altra dissonanza posta in cotal modo si sopporta,
quanto maggiormente si può tollerare una Sesta? Et tanto più è da tollerare, quanto
spesse fiate da i Cantori periti, non potendo il lor'udito sentire alcun discommodo in al-
cuna cosa, quantunque minima, è fatta maggiore. Ma ueramente questi passaggi non
 sono altro, che la diminutione de quelli,
sono altro, che la diminutione de quelli, che sono posti qui da canto; per iquali non
si toglie ad alcuno, che non possa aggiunge
re à suo bel piacere à tal Semiminima po-
sta ne i primi essempi, il segno
 , & far la Se
, & far la Sesta di minore maggiore per virtù della chor
da Chromatica; & cosi quella del b, secon
do che occorrer puote nel fare i Con-
trapunti; & se ben tali chorde non si segnassero, non si debbe attribuire al Compositore,
che l'habbia fatte per errore; massimamente in cotali cose che sono minime. Potrà simil-
 mente usar'alle volte; ma non spesso; una
mente usar'alle volte; ma non spesso; una modulatione d'una Semidiapente, quan
do tornarà cōmodo nell'accommodar la
modulatione alle parole, e procederàper
le chorde diatoniche naturali del Modo,
sopra 'l quale è fondata la cantilena; co-
me qui si uede. Ma quando ui entrasse
alcuna delle chorde chromatiche (quan
tunque si ponesse per l'acquisto d'alcuna
page 291consonanza) non si debbe usare; conciosia che tali chorde non furono ritrouate à de-
struttione delle buone harmonie, & de i buoni costumi Musicali, ma si bene alla loro edi-
ficatione, & al lor bene essere. Non sarà adunque lecito di usare alcun passaggio, che sia
 simile ad uno de questi qui in essem
simile ad uno de questi qui in essempio; percioche le chorde chroma-
tiche haueranno sempre nella mo-
dulatione una chorda diatonica cor
rispondente pervna Semidiapente,
ouer per un Tritono, ò Semitrito-
no, secondo l'ordine della compo-
sitione; i quali sono Interualli, ò Mo
dulationi senz'harmonia. Gli sarà
anco permesso di potere usare alle
uolte le chorde chromatiche, quan-
do uorrà procedere da una Sesta
fatta maggiore per uirtù de tali chorde alla Decima; ò Terza maggiore, col mouimen-
to di Quarta, ò di Quinta; per poter da quelle peruenire all'Ottaua, oueramente all'
Vnisono; come qui si uede; & ciò per due ragioni, l'una delle quali è; perche il proce-
dere è Diatonico nelle chorde chromatiche; l'altra perche i mouimenti, che fanno le
parti, procedono per Interualli harmonici, & sono anco regolati secondo i precetti mo-
strati di sopra. Queste chorde si debbono segnar col segno
 per molti rispetti; & mas-
per molti rispetti; & mas- simamente per i poco accorti Can-
simamente per i poco accorti Can-tori; acciò non commettessero alle
uolte qualche errore, ponendo una
chorda in luogo d'un'altra; cioè, la
Diatonica in luogo della Chroma-
tica, & ne segua la dissonanza. E' ben
uero, che nelle modulationi si troua
no alcun'Interualli, come sono quel
li di Quarta, di Quinta, & di Otta-
ua; ne i quali il Cantore dè porre la
chorda chromatica, ancora che non
sia stata segnata dal Compositore;
accioche la modulatione delle parti sia drittamente ordinata. Ne il Compositore la deb
be porre, perche è superfluo; essendo che ueramente non si dè cantare se non quelli In-
terualli, che sono harmonici; come qui si uede. Ne debbe far, come fanno alcuni, iqua
 li fuori d'ogni proposito, & senz'alcuna utilità, ò necessità danno principio alle lor can-
li fuori d'ogni proposito, & senz'alcuna utilità, ò necessità danno principio alle lor can-tilene sopr'alcune chorde, che non sono naturali de i Modi, & mescolano le chorde
chromatiche con le diatoniche di maniera, che non solamente nel principio; ma nel
mezo, & nel fine anco non si uede altro che
 Diesis & b molli; la qual cosa; quando la
Diesis & b molli; la qual cosa; quando la compositione la ricercasse, sarebbe da sopportare. Però sarà auertito ciascuno d'aste-
nerse più che potrà da simil cosa, se non fusse costretto dalle parole, ouer d'altra cosa,
che accade nella cantilena; conciosia che per il lungo continuare in essi, la cantilena
page 292viene à mutare il Modo, entrando d'uno nell'altro; com'è uitio particolare di qualche
Compositor moderno. Et sopra 'l tutto si dè guardare, da porre tali chorde nel princi-
pio senza proposito; come fanno alcuni, che non solamente segnano la Seconda figura
della modulatione col segno
 Chromatico, ma etiandio la prima; & fanno, che spesse vol
Chromatico, ma etiandio la prima; & fanno, che spesse volte, credendosi dar principio ad una modulatione del terzo Modo (per dar un'essempio)
non si accorgendo, incominciano una cantilena del Nono; come si può uedere nel prin
 cipio dell'essempio posto qui da canto. A-
cipio dell'essempio posto qui da canto. A-uertisca etiandio ogni Compositore, che si
pone alle uolte tra la chorda g. & la aa. un'al-
tra chorda, segnata col segno commune
chromatico
 ; onde nascono alcune modu-
; onde nascono alcune modu-lationi, che non si possono chiamar Diato-
niche semplicemente, ne Chromatiche;
percioche tanto nell'acuto quanto nel gra-
ue, non si possono accommodar tra le chor-
de naturali Diatoniche ad una modulatio-
ne, che sia diatonica; come sono le sequen-
ti conciosia; che essendo 'l primo Interuallo, che fanno le tre prime figure il Semituo-
no maggiore, & quello che fanno la terza & la quarta il Ditono, & medesimamente è
il Semituono maggiore quello, che è contenuto tra le due ultime; se noi discorreremo
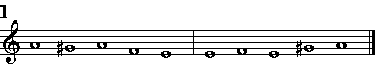 tutte le chorde diatoniche, & anche le Chro
tutte le chorde diatoniche, & anche le Chromatiche insieme, non ritrouaremo, ne uer-
so 'l graue, ne uerso l'acuto, di poter accom-
modar questi Interualli, senza l'aiuto d'un'
altra chorda forastiera, la qual segnaremo con questo segno X, col quale si segna
ogni seconda chorda d'ogni Tetrachordo Enharmonico; Et questa chorda non si po-
trà chiamar Diatonica; perche non hà luogo tra le chorde diatoniche; ne anco
Chromatica; conciosia che per il suo mezo da parte alcuna non si può hauere il Trihe
mituono; ne meno la potremo nominare Enharmonica, essendo che non diuide il Se-
mituono maggiore in due Diesis; il che è ufficio della uera chorda Enharmonica; come
si può uedere in ciascuna diuisione fatta nella Seconda parte. Et bench'ella si possa chia
mar Diatonica, perche si troua in una compositione diatonica, & fà il Semituono, ch'è
diatonico; tuttauia è nominata impropriamente; essendo che allora sarà detta Diato-
nica, ò Chromatica, oueramente Enharmonica, quando sarà posta in luogo, oue po-
trà in uno de i detti Generi fare 'l suo ufficio; ma non giamai altramente; com'auiene
di quella, ch'è posta nel quarto luogo del Quarto essempio qui di sotto.
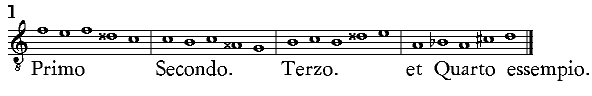 Et se ben tal chorda posta in cotal maniera non è Diatonica, non si debbe restar di usar
Et se ben tal chorda posta in cotal maniera non è Diatonica, non si debbe restar di usarla, poi che in questi, & altri simili passaggi, non fà alcun tristo effetto, & torna mol-
to al proposito alle uolte al Compositore. Et perche si ritrouano infinite cantilene Dia
toniche, le quali sono piene di questi, & d'altri simili passaggi, & non sono considera-
ti da i Prattici; però ne hò uoluto far qui mentione, & rimettere cotal cosa al sa-
no giudicio de i buoni & eccellenti Compositori, acciò uedino, in qual maniera si
debbino usare. Rimetto etiandio molt'altre cose, dellequali non uoglio tacere que-
sta; che non è il douere, che si ponga la Semibreue sincopata, in modo, che dopo le
seguiti immediatamente la Minima dissonante col mouimento di grado; conciosia che si
page 293farebbe contra quello, che si conuiene alla natura della Sincopa tutta consonante, la qua
le non riceue dopo se alcuna dissonanza, ma si bene la Consonanza. Però quando uorre
mo porre tal Minima dissonante, porremo sempre la battuta sopra la Semibreue; po-
nendo appresso il punto, il qual dè esser sempre consonante; uenga poi la Minima à
qual modo si uoglia, ò consonante, ò dissonante, pur che procedi per grado; come qui
si uede. Debbe oltra di questo auertire, che tutte le uolte, che uorrà fare il Contrapun-
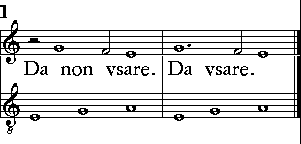 to alquanto languido ò mesto; simigliantemente dolce, ò
to alquanto languido ò mesto; simigliantemente dolce, ò soaue, debbe procedere anco per mouimenti dolci & soa-
ui; come sono quelli, che procedono per il Semituono,
per il Semiditono, & altri simili; usando le Consonanze
imperfette minori, che sono il Semiditono, l'Exachordo
minore, & l'altre Replicate; le quali Consonanze per sua
natura sono (come hò detto nel Cap. 10.) atte à tali cose.
Per il contrario uolendolo fare allegro, usarà il mouimento
del Tuono, quello del Ditono; & d'altri simili, con i suoi
Interualli. Et uolendolo far, che qualche uolta habbia dell'aspro, potrà usar le Maggiori,
che sono il Ditono, l'Hexachordo maggiore, & le Replicate nelle parti graui della can-
tilena. Et tanto più sarà aspro, quanto maggiormente hauerà in sè il detto Hexachor-
do, nelle figure di alquanto ualore, nella parte graue del concento. E' cosa difficile uera-
mente il uolere insegnare particolarmente, in qual maniera, & à che tempo s'habbiano
da usar cotal cose; ma perche questo c'hò detto potrà molto giouare, quando si uor-
rà alle uolte usar cotali maniere; però bastarà questo per hora; percioche forse un'al-
tra uolta ne dirò più diffusamente.
Il modo che si hà da tenere nel comporre le Cantilene à più di due voci; & del
nome delle parti.Cap. LVIII.
& insegnare il modo, che si hà da tenere nel compor le Cantilene à Due uo-
ci; parmi esser tempo di rimetter tutte l'altre cose, che intorno ciò potesse-
ro accascare al buono & giudicioso Lettore; percioche uedendo & essaminan
do le dotte compositioni de i buoni & eccellenti Compositori, potrà esserchiaro di tutto
quello, che gli potrà occorrere; onde uerrò à mostrare il modo, che haurà da tenere, uolen
do comporre quelle, che si fanno à più uoci. Ma auanti che passiamo più oltra, si dè auer-
tire; che i Musici nelle lor cantilene sogliono il più delle uolte porre Quattro parti, nel-
le quali, dicono contenersi tutta la perfettione dell'harmonia. Et perche si compongo-
no principalmente de cotali parti; però le chiamarono Elementali della compositione,
alla guisa de i quattro Elementi; percioche, si come ogni Corpo misto di essi si compone;
cosi si compone di quelle ogni perfetta cantilena. La onde la Parte più graue nominaro-
no Basso, ilquale attribuirono all'Elemento della Terra; cōciosia che si come la Terra tra
gli altri Elementi tiene il luogo infimo, cosi 'l Basso occupa il luogo più graue della Canti
lena. A questa, procedendo alquanto più in sù uerso l'acuto, accommodarono un'al-
tra parte, & la chiamarono Tenore, il quale assimigliaremo all'Acqua; la quale, si
come immediatamente segue, nell'ordine de gli Elementi, dopo la Terra, & è con es-
sa abbracciata; cosi nell'ordine delle dette parti il Tenore senz'alcun mezo segue il
Basso, & le sue chorde graui non sono in cosa ueruna differenti da quelle del Basso, po-
ste in acuto. Simigliantemente accommodarono laTerza parte sopra 'l Tenore, la qua-
page 294le alcuni chiamano Contratenore, alcuni Contralto, & altri la nominano semplice-
mente Alto; & la posero nel terzo luogo, ch'è mezano nella cantilena; & si puo assimi-
gliar veramente all'Aria; ilquale, si come si conuiene con l'Acqua, & col Fuoco in al-
cune qualità; cosi anco le chorde graui dell'Alto conuengono con l'Acute del Teno-
re, & l'acute conuengono con le graui della Quarta parte posta più in acuto, chia-
mata Canto; il quale accommodarono nel luogo supremo della Cantilena; la onde
dal luogo che tiene, alcuni etiandio la chiamano Soprano; il quale potremo assimiglia-
re al Fuoco, che segue immediatamente dopo l'Aria, nel grado supremo di tale or-
dine; & ciò non sarà fatto senza qualche ragione; percioche tenendo la parte graue
il luogo inferiore della cantilena, & procedendo per mouimenti tardi & rari, da i qua-
li nascono i Suoni graui, che per loro natura sono (com'hò detto nel cap. 11. della Se-
conda parte) uicini alla taciturnità; hà grande conuenienza con la Terra, la quale per
sua natura è immobile, & non può far nascere alcun suono. Et se la parte più acu-
ta d'ogn'altra assimigliai al Fuoco; ciò feci, percioche hauendo i Suoni acuti, che na-
scono da i mouimenti ueloci & spessi, tal natura, che per la loro subita & ueloce per-
cussione si fanno udire, rappresentandosi all'Vdito con prestezza, uengono à ritenere
in loro quasi la natura del Fuoco; il quale, non solo è acuto & raro; ma etiandio
ueloce & attiuo per se stesso. L'altre parti mezane, per la temperatura de i loro moui-
menti, & per la simiglianza del sito, io l'assimigliai à gli altri due Elementi mezani;
perche tengono secondo 'l sito diuerso la natura loro. In qual maniera s'habbiano
poi da ordinare queste Parti & disporre, & quanto l'una dall'altra debbiano esser lon-
tane, ciò uederemo nella Parte, che segue. Se hora da quello, che si è detto, vor-
remo essaminar la proprietà di queste Parti, ritrouaremo che 'l soprano; come quel-
lo, ch'è più acuto d'ogn'altra parte, & più penetratiuo all'Vdito, farsi udire anco pri-
ma d'ogn'altra; la onde si come 'l Fuoco nutrisce, & è cagione di far produrre ogni co-
sa naturale, che si troua ad ornamento, & à conseruatione del Mondo; cosi il Com-
positore si sforzarà di far, che la parte più acuta della sua cantilena habbia bello, or-
nato & elegante procedere, di maniera che nutrisca, & pasci l'animo de quelli, che
ascoltano. Et si come la Terra è posta per fondamento de gli altri Elementi; co-
si 'l Basso hà tal proprietà, che sostiene, stabilisce, fortifica, & da accrescimento
all'altre parti; conciosiache è posto per Basa & fondamento dell'Harmonia; onde
è detto Basso, quasi Basa, & sostenimento dell'altre parti. Ma si come auerrebbe,
quando l'Elemento della Terra mancasse (se ciò fusse possibile) che tanto bell'ordine
di cose ruinarebbe, & si guastarebbe la mondana, & la humana Harmonia; cosi quan-
do 'l Basso mancasse, tutta la cantilena si empirebbe di confusione, & di dissonanza, &
ogni cosa andarebbe in ruina. Quando dunque il Compositore componerà 'l Basso del-
la sua compositione, procederà per mouimenti alquanto tardi, & separati alquanto, ouer
lontani più de quelli, che si pongono nell'altre parti; accioche le parti mezane possino
procedere con mouimenti eleganti, & congiunti, & massimamente il Soprano; percio-
che questo è 'l suo proprio. Debbe adunque esser'il Basso non molto diminuito; ma pro
cedere per la maggior parte cō figure d'alquanto più valore, di quelle, che si pongono nel
l'altre parti; & debbe esser'ordinato di maniera, che faccia buoni effetti, & che non
sia difficile da cantare; & cosi l'altre Parti si potranno collocare ottimamente ne i pro-
prij luoghi nella cantilena. Il Tenore segue immediatamente 'l Basso uerso l'acuto, ilqua
l'è quella parte, che regge, & gouerna la cantilena, & è quella, che mantiene 'l Modo,
sopra il quale è fondata; & si debbe comporre con eleganti mouimenti, & con tale ordi-
ne, che osserui la natura del Modo, ò Tuono, nelquale è composto; sia primo, secondo, ter
zo, ouer'altro qual si uoglia; osseruando di far le Cadenze à i luoghi proprii, & con propo
sito. Ma si come, essendo l'Aria illuminata da i raggi del Sole, ogni cosa rasserena, & ogni
cosa si uede ridere di qua giù, & esser piena d'allegrezza; cosi quando l'Alto è ben
page 295ordinato, & ben composto, ornato de belli, & eleganti passaggi, adorna sempre, & fà
uaga la cantilena; la onde debbe il Compositore auertire, di compor la parte dell'Alto
per tal maniera, che canti allegramente, & faccia buoni effetti. L'ufficio, & la natura
di queste Parti giocosamente, & con grande arteficio espresse quel faceto Poeta Man-
toano con grossi uersi, dicendo;Merlinus
Stryaecis
lib. 1.
Plus ascoltantum Sopranus captat orecchias.I quali hò uoluto porre, accioche 'l Compositore ricordandoseli, possa saper quello,
Sed Tenor est, vocum rector, uel Guida canentum.
Altus Apollineum carmen depingit, & ornat.
Bassus alit voces, ingrassat, fundat, & auget.
c'haurà da fare, componendo coteste parti. Queste sono adunque le Parti principali, &
Elementali d'ogni compositione perfetta; delle quali, ancora che l'Alto sia l'ultimo à cō
porsi; percioche composte l'altre parti, uiene a supplire, & à far perfetta l'Harmonia,
che tra loro non si potea (doue mancauano) hauere; nondimeno non è legge fatale, che 'l
si habbia da porre sempre ultimo nel comporre; come etiandio non è cosa alcuna, che ne
astringa, à compor prima l'una, che l'altra Parte della compositione. Si debbe però auer-
tire, che quando i Musici uogliono comporre alcuna cantilena à Tre uoci, il più delle
uolte lasciano fuori il Contralto, ouer il Soprano, & pigliano l'altre parti; Et se uoglio-
no procedere oltra le Quattro nominate, non ui aggiungono alcuna parte nuoua; ma
le uengono à raddoppiare, facendo due Soprani, ò due Alti, ò due Tenori, & cosi
due Bassi; & hanno il loro proposito. Qualunque uolta adunque che si uorrà compor-
re alcun concento sopra un Soggetto ritrouato, sia Canto fermo, ò figurato; ouer se l
si uorrà comporre alcuna Canzone, Madrigale, ouer altra cosa, & faccia dibisogno, che 'l
Compositore sia l'Inuentore di tal Soggetto; debbe prima auertire di qual Modo ella
sia; oueramente sopra qual modo uorrà comporre la cantilena, accio conosca le chor
de, sopra le quali si haueranno da far le Cadenze, per poter comporre il concento in tal
maniera, che 'l fine non sia dissonante dal mezo, & dal principio. La onde considera-
te queste cose, potrà incominciare, da qual parte li tornarà più commodo; incomin-
ciando però sempre in una chorda, la quale sia regolare del Modo, sopra 'l quale ha-
urà da fondar la cantilena; osseruando quello, ch'in molte Regole poste di sopra si con-
tiene. Ma perche i Musici costumano di dar principio alle lor Compositioni il più del-
le uolte per il Tenore; & dopoi pongono il Soprano, alquale Aggiungono il Basso,
& ultimamente l'Alto; hauendo di sopra mostrato molti essempi, contenuti tra
queste due parti, Soprano, & Tenore; però non accade, se non porre la se-
guente Tauola, nella quale si potrà comprender senza molta fatica tutti gli accor-
di, che potranno far le Parti aggiunte insieme alle due nominate, siano quante si
uogliono. Et hò tenuto tal'ordine, di porre primieramente gli accordi, che dan-
no insieme il Soprano col Tenore; dopoi quanto potrà essere il Basso lontano dal Te-
nore nella parte graue; accioche il tutto s'accordi; & cosi stante le nominate parti,
quel che fà dibisogno, che sia l'Alto sopra 'l Basso; accioche l'Harmonia uenghi ad
esser perfetta. Ma si dè auertire, che si trouarà alle uolte nell'Alto più d'uno accordo;
onde tali accordi potranno seruire non solamente ad esso Alto; ma etiandio all'altre
Parti, che si aggiungessero alla cantilena, oltra le Quattro nominate. Ne si troua-
rà il Contralto posto con l'altre parti in Vnisono, ne in Ottaua, se non in quattro
luoghi; percioche quando l'altre Parti haueranno tra loro la Quinta, & la Terza,
ouer una delle Replicate; allora le aggiunte à queste, siano quante si uogliano, ne-
cessariamente uerranno ad esser con una delle tre nominate in Ottaua, ouero in Vniso-
no. Ma accioche si habbia piena intelligenza di quello, che si è detto, porrò un'essem-
pio primieramente delle Compositioni, che si uorranno fare à Tre uoci; le quali si com-
pongono senza la parte dell'Alto; dopoi ne porrò un'altro di quelle, che si fanno à Quat-
tro. Sia adunque che noi uogliamo comporre una Cantilena à tre uoci; & che 'l
page 296s'habbia posto il Soprano Vnisono col Tenore; dico, ch'allora bisognerà porre la parte
del Basso, Terza, ò Quinta, ò Sesta; ouer Ottaua, ò Decima, ò Duodecima, ò Terza-
decima, oueramente Quintadecima, sotto 'l Tenore. Simigliantemente quando si ha-
uesse posto il Soprano in Terza col Tenore; bisogno sara di porre il Basso Terza, ò Se-
sta, ouer'Ottaua, ò Decima sotto 'l detto Tenore. Si potrebbe anco dire, che quan-
do le dette due parti si ponessero lontane l'una dall'altra per una Quarta, che 'l Basso si
potrebbe porre Quinta, ò Duodecima sotto 'l Tenore, & cosi dell'altre; ma perche tut-
ti questi & altri accordi si possono ueder nella Tauola seguente; però passarò più oltra,
& dirò, che nelle Compositioni de Quattro uoci bisogna tener quest'ordine; che quan-
do nella compositione il Soprano sarà posto Vnisono col tenore; cioè, quando l'uno &
l'altro staranno sopra una chorda istessa; uolendo aggiunger la Terza parte à queste due,
sarà dibisogno di porre il Basso distante per una di queste consonanze; Terza, ò Quin-
ta, ò Sesta, ouer'Ottaua, ò per qualunque altra (come si uede nella Tauola) sotto 'l Te-
nore; onde essendo il Basso lontano per una Terza; l'Alto potrà esser distante dal Basso
nell'acuto per vna Quinta, ò per una Sesta, & l'altre parti (se fussero più di Quattro)
potranno esser Vnisone, ouer distanti per una Ottaua dall'una di queste quattro. Ma se 'l
Basso fusse distante dal Tenore nel graue per una Quinta, & l'Alto si potrà porre sopra 'l
Basso distante per una Terza, ouer per una Decima; & l'altre parti, che s'aggiungessero
sarebbono Vnisone, ouer lontane dall'una di queste quattro per una Ottaua. Et se 'l
Basso fusse anco distante per una Sesta, riguardando nel Terzo essempio della Tauola, si
trouerà quello, che potrà essere il Contralto; il che si potrà etiandio uedere dell'altre
qui di sotto, chiaramente & distintamente per ordine.
SEGVITA LA TAVOLA DE GLI ACCORDI, CHE
POSSONO FARE CANTANDO INSIEME LE PARTI
DELLE CANTILENE.
| DELL'VNISONO. |
|
| DELLA TERZA. |
|
| DELLA QVARTA. |
|
| DELLA QVINTA. |
|
| DELLA SESTA. |
|
| DELLA OTTAVA. |
|
lontano dal Tenore per un'altra Consonanza, & il Basso fusse per alcun'altro Interuallo
sotto 'l Tenore, quello che necessariamente sarebbe dibisogno, che 'l Contralto fusse di-
stante nell'acuto dal Basso; ilche si lascia al giudicio del discreto Compositore, per non
andare in lungo. Debbe però auertire, ch'alle uolte (secondo 'l uolere de chi compone)
la parte del Basso si pone nel luogo del Tenore; ancora che ciò intrauenga di raro, & per
il contrario, quella del Tenore nel luogo del Basso; cosi ancora il Soprano alle fiate si
pone nel luogo dell'Alto, & questo in quello del Soprano; ouer si pone il Tenore nel luo
go del Contralto, & cosi per il contrario; Però ciascuno sarà auertito, che in questa Ta
uola sempre si piglia il Soprano per la parte più acuta, & il Basso per quella, che è più gra
ue; quantunque alle uolte le Parti nominate con questi nomi cambiano per accidente i
loro assignati & proprij luoghi. Debbe etiandio intendere per il Tenore quella parte,
che segue immediatamente il Basso uerso l'acuto; & per il Contralto quella, che si com-
pone dopo le tre nominate; Imperoche intesa la cosa per tal maniera, ciascun po-
trà commutar le parti l'una nell'altra; secondo che li tornerà commodo, senz'alcu-
no errore.
Delle Cantilene che si compongono à Tre voci; & di quello, che si dè osseruar
nel comporle.Cap. LIX.
Tre uoci; accioche da queste si possa con facilità uenire alla compositione di
quelle, che si compongono à Quattro & à più ancora, dico; ch'è dibisogno
sapere, che oltra l'osseruanza delle Regole date, è necessario di osseruare etiā
dio alcun'altre cose, le quali di mano in mano uerrò mostrando, secondo che mi occor-
reranno. Et per incominciare; poniamo, che si hauesse à far un Contrapunto à Tre uo
ci sopra un Soggetto, che fusse il Tenore posto più à basso nell'essempio. Dico, che do-
po che si haurà accommodato & ordinato le parti, ch'entrano nella Compositione l'una
sotto l'altra; ponendo prima il Soggetto di sopra, & dopoi l'altre per ordine, facendo
che la parte graue sempre tenghi il luogo più basso, & l'acuta il piu alto; si potrà (secon-
do le Regole date) auanti che s'incomincia à far cantare la parte del Soggetto, compor-
re l'altre due à sua imitatione. Dopoi facendolo entrare nella cantilena con gratia, tenen
do quell'ordine nella diminutione della parte, che s'aggiunge, che fù tenuto nelle com-
positioni à due uoci, aiutati dalla Tauola posta di sopra, si potrà continuar di maniera,
che si haurà la cantilena sequente per essempio. Ma si dè auertire, che quando una delle
parti del Cōtrapunto darà principio alla cantilena, dee incominciar sopra quella chorda,
ch'incomincia la prima figura del Canto fermo; come porta 'l douere; imitandolo piu
che sia possibile; ponendo le parti del Contrapunto tra loro in Consequenza; & se be-
ne si porranno etiandio col Canto fermo non sarà male; è ben uero, che 'l porle à que-
sto secondo modo, non è noua maniera, ne inuention noua; perche non si può far cosa
alcuna, che non sia stato fatta le migliaia di uolte. Ma dirò bene, che 'l primo modo, se
non sarà cosa noua, almen sarà poco usato; anzi potrà etiandio, con grandissimo com
modo (ilche è anco lodeuole) porre in Consequenza le parti tra loro; non con quell'ordi
ne istesso & dispositione, come si usa nella legata; ma con un'ordine interrotto; ponendo
parte delle figure ascendenti & parte discendenti; & porre solamente il numero delle fi-
gure, che siano d'un'istesso ualore; ponendo tallora una Imitatione de figure al contra-
rio; cioè, la Guida, ò Principale, che procedi per un numero de figure ascendenti, &
il Consequente, che con l'istesso numero discendi; come da i sottoposti essempi si può
page 299
 comprendere; ne i quali hò uoluto porre una parte sola per due cagioni; prima, perche
comprendere; ne i quali hò uoluto porre una parte sola per due cagioni; prima, perche non mancano le dotte compositioni de molti eccellenti Musici, che sono piene di
queste cose; dalle quali si potrà comprendere il modo, che si haurà da tenere nella com
positione dell'altre cantilene; dopoi per non accrescere il uolume con tanti essempi;
essendo che da questa sola parte si potrà comprender quello c'hò uoluto dire, & in qual
maniera si potrà procedere, cauando l'Inuentione d'una parte dal proceder dell'altra,
per potere impire il Contrapunto di belle fantasie & leggiadre inuentioni. Ma si
debbe anco auertire, che quantunque il basso possa alle uolte tenere il luogo del
Tenore, & cosi l'una dell'altre parti, quel dell'altra; nondimeno si dè fare, che 'l Bas-
so finisca sempre sopra la Chorda regolare & finale del Modo, sopra 'l quale è compo-
sta la cantilena, & cosi l'altre parti à i lor luoghi proprij; percioche da tal chorda ha-
ueremo à giudicare il Modo. Et se bene il Tenore uenisse à finire in altra chorda, che
nella finale, questo non sarebbe di molta importanza; pur che si habbia proceduto nel-
la sua modulatione secondo la natura del Modo della cantilena; Ilche si debbe anche in-
tendere di ciascuna dell'altre parti. Oltra di questo è da auertire, che quella Composi-
tione si può chiamar Perfetta, nella quale in ogni mutatione di chorda, tanto uerso 'l
graue, quanto uerso l'acuto, sempre si odono tutte quelle Consonanze, che fanno
uarietà di suono ne i loro estremi. Et quella è ueramente Harmonia perfetta; ch'in es-
sa si ode tal consonanze; ma i Suoni ò Consonanze, che possono far diuersità al senti-
page 300
 mento sono due, la Quinta & la Terza, ouer le Replicate dell'una & dell'altra; percio-
mento sono due, la Quinta & la Terza, ouer le Replicate dell'una & dell'altra; percio-che i loro estremi non hanno tra loro alcuna simiglianza, come hanno quelli dell'Ottaua;
essendo che gli estremi della Quinta non mouono l'Vdito nella maniera, che fanno quel-
li della Terza, ne per il contrario; onde aggiunto il Ditono al Semiditono, generano la
Quinta, la quale è ne i suoi estremi contenuta da suoni molto uariati da quelli, che si odo
no ne gli estremi del Ditono, ò del Semiditono; perche gli estremi del Ditono sono an-
co molto differenti da quelli del Semiditono. Et ciò non si ritroua nell'Ottaua; impero-
che i suoi estremi hanno tal simiglianza, che paiono un solo suono, & s'assimigliano di ma
niera allVnisono, che aggiungendole qual Consonanza si uoglia; par che sia congiunto
(come etiandio hò detto altroue) quasi ad un solo suono. Ritrouandosi adunque la uarie
tà solamēte tra gli estremi della Quinta & quelli della Terza; & cōponendosi l'Harmonia
di cose, che tra loro sono diuerse; dobbiamo per ogni modo (accioche habbiamo perfetta
cotale harmonia) cercare cō ogni nostro potere, di fare udir nelle nostre Cōpositioni que
ste due consonanze, più che sia possibile, ouer le loro Replicate. E' bē uero, che molte uol
te i Prattici pongono la Sesta in luogo della Quinta, & è ben fatto. Ma si de auertire, che
quando si porrà in una delle parti la detta Sesta sopra 'l Basso, di non porre alcun'altra
parte; che sia distante per una Quinta sopra di esso; percioche queste due parti uerrebbo
no ad esser distanti tra loro per un Tuono, ouer per un Semituono; di maniera che si
udirebbe la dissonanza. Hò detto però, che dobbiamo far ogni nostro potere, di por sem-
pre queste due Consonanze nelle compositioni; conciosia che sempre non si possono por
re; massimamente nelle compositioni di Tre uoci; perche in luogo d'una di loro si pone
spesso l'Ottaua, per non guastar il bello, elegante & facile cantare, che fanno le parti; la
onde uolendo osseruare di por sempre cotali Consonanze in simili compositioni, sareb-
be quasi impossibile; massimamente uolendo far cantare cotali parti, & uoler'acquistar le
sudette Consonanze; percioche si potrebbe procedere per alcuni mouimēti tanto discō
modi, che sarebbono cagione di roinare in parte la compositione; ma nelle Compositio-
ni de Quattro ò più uoci, sarebbe più errore lasciarne una delle due nominate, che in quel
le, che si compongono di Tre; conciosia che oue non si può osseruar cotal Regola con tre
parti, la quarta parte ce lo permette; & tanto maggiormente siamo obligati all'osseruan-
za di cotal Legge, quanto più cresce 'l numero delle parti: la onde non osseruando quel-
lo che si è detto, si uerrebbe à mostrar quanto si fusse stato buoni Imitatori della Natura;
la quale, quando non è deprauata, riduce tutte le cose alla loro perfettione. Ma ueramen
te è gran uergogna d'alcuni, che non solo fanno pouere le lor compositioni de Quattro
uoci d'una delle dette consonanze; ma fanno anco peggio, che pongono le parti in tal
page 301maniera, che sono tra loro Vnisone, ouer lontane l'una dall'altra, per un'Ottaua sola-
mente; onde simili Ottaue, si chiamano Raddoppiate, & fanno l'harmonia molto smem
brata & pouera. Et questo sarebbe anco di poco momento, quando non si ritrouasse l'
istesso errore nelle compositioni de Cinque, de Sei, de Sette, & de più uoci; nelle qua-
li sono alcuni luoghi smembrati & poueri in tal maniera; che s'odono con poca satisfat-
tione dell'vdito. Però il Contrapuntista si debbe guardare da commettere tali mancamē
ti, degni ueramente di correttione; & debbe sapere, che tali errori si commettono non
solamente nelle figure, che si proferiscono nel battere, ò leuare della battuta; ma anche
in ogni figura cantabile, che si pone nel numero delle Consonanze. Osseruarà adunque
il Compositore questo, c'hò detto nelle sue compositioni; cioè, di far più ch'ello po-
trà, che si ritroui la Terza, & la Quinta, & qualche fiate la Sesta in luogo di questa, ò
le Replicate; accioche la sua cantilena uenghi ad esser sonora & piena; & accioche
contenga in sè ogni perfettione d'harmonia. Ma non per questo dè intendere, ch'
ei debba osseruar cotal legge dal principio della compositione infin'al fine; impe-
roche dè anco auertire in ogni cantilena, di dar qualche riposo alle parti; & di non
farle cantare sempre insieme; ma far che se ne odi hora due, hora tre, hora quattro,
 page 302secondo 'l numero che saranno, & tallora tutt'insieme, & massimamente nel fine; percio-
page 302secondo 'l numero che saranno, & tallora tutt'insieme, & massimamente nel fine; percio-che tal uariatione uerrà à portar seco commodo al Compositore & al Cantore; bellezza
alla cantilena, & diletto & piacere all'udito. Oltra di questo si debbe sapere, ch'accom-
modato che si haurà tre parti di qualunque compositione, le quali tra loro contenghino
le già dette Consonanze, ouer la Sesta in luogo della Quinta; l'altre parti, che s'aggiun
gessero à queste, uerrebbono ad esser necessariamente Vnisone, ouer in Ottaua con una
delle tre nominate; siano poi quante si uoglino le Aggiunte; come di sopra nell'essem-
pio in molti luoghi si può comprendere. Però il Compositore potrà accommodarle alla
Cantilena, come meglio li tornerà commodo; E' ben uero, che più tosto debbe porre
nella sua Compositione l'Ottaua, che l'Vnisono; percioche (come dicemmo altre uolte)
non è consonanza.
In qual maniera la Quarta si possa porre nelle Compositioni.
Cap. LX.
pata, & in queste si possa porre etiandio non sincopata, come torna meglio;
percioche 'l suo uso non solamente è utile, ma anco necessario; tuttauia è da
sapere, ch'essendo la Quarta Consonanza; com'altroue hò prouato;Supra
Cap. 5. ella si
può accommodar nelle compositioni in due maniere, come costumano di fare i Musici
moderni; prima ponendo il Basso & il Tenore distanti l'un da l'altro per una Quinta, ag-
giungendouene à queste due parti un'altra lontana dal Basso per una Ottaua; di maniera,
che la chorda del Tenore uenga à diuidere, ò tramezare tal'Ottaua in harmonica propor
tionalità; ilperche essendo collocate le Parti in tal maniera, nasce diletteuole & soaue
harmonia; ne mai fin'hora i Musici, l'accompagnarono con la Quinta altramente. L'ac
compagnarono poi con la Terza, & ciò in due maniere; percioche, ouer l'accompagna
rono con la Terza posta nel graue, ouer con la Terza posta nell'acuto; & ciascuno
di questi due accompagnamenti si può far etiandio in due modi; essendo che quan-
do se le accompagna la Terza nel graue; oueramente che ella è la maggiore; oue-
ro che è la minore. Il perche dobbiamo sapere, che la Quarta accompagnata in
tal maniera farà sempre migliore effetto accompagnata con la Terza minore, di quel-
lo, che farebbe, s'hauesse sotto di sè la maggiore; essendo che posta in cotal mo-
do, è collocata naturalmente secondo i gradi delle Consonanze; come si può ue-
dere nel Cap. 15. della Prima parte; nel quale si uede, che dopo 'l Semiditono con-
tenuto tra questi termini 6 & 5. segue immediatamente la Diatessaron, posta tra que-
sti termini 8 & 6. Ma quando è accommodata col Ditono, non può far quello effetto;
 perche non sono poste insieme secondo l'ordine naturale de cotali con
perche non sono poste insieme secondo l'ordine naturale de cotali consonanze; anzi sono aggiunte insieme in un'ordine ; per
che non si troua nell'ordine nominato, che 'l Ditono sia posto senz'al-
cun mezo auanti la Diatessaron; la Onde essendo queste due consonan
ze accommodate l'una dopo l'altra contra la loro natura; essendo posta
nell'acuto quella, che douerebbe esser collocata nel graue, & nel gra
ue quella, che douerebbe tener l'acuto; de qui uiene, che i Suoni, che
nascono dalle chorde ordinate in tal maniera, sono men grati all'udi-
to, de quelli, che nascono dalle chorde tese secondo i lor gradi natu-
rali; Il perche ciascuno da se stesso con l'esperienza potrà conoscer da
i seguenti essempi sensatamente, & euidentemente comprender delli
due accompagnamenti qual sia ueramente il Buono. Quando poi s'ac-
page 303compagna la Quarta con la Terza posta in acuto; ciò si può fare simigliantemente in due
modi; percioche, ouer se le aggiunge la Terza maggiore, ouer se le accompagna la mino
re. Quando è accompagnata con la maggiore fà buon effetto; ma quando è accompagna
ta con la minore, fà quasi dissonanza. Et ciò non è senza cagione; percioche oltra che si
potrà comprendere da i due essempi seguenti, quando le uoci, ò i suoni saranno ridotti
in atto; l'ordine naturale de i Numeri harmonici ce lo dimostra; nel quale ritrouandosi la
proportione della Diatessaron tra questi termini 4 & 3. come si può uedere nel detto luo
go; segue senz'alcun mezo la proportione del Ditono posta tra 5 & 4. Ma in cotal'ordine
non si troua, che dopò la proportione, ò forma della Quarta segua immediatamente quel
la della Terza minore, come ogn'un può uedere. Per questo adunque auiene, che quel
 le Consonanze, che sono fuori de i loro luoghi naturali, & non so
le Consonanze, che sono fuori de i loro luoghi naturali, & non sono ordinate, secondo channo le forme tra i Numeri harmonici,
senz'alcun dubbio fanno qualche rumore. Onde dico, che la Quar
ta accompagnata con la Terza minore posta nel graue, si potrà sem
pre usare, & quella etiandio, che haurà la Terza maggiore nell'a-
cuto; percioche non potranno far se non buoni effetti; ma quando
hauerà la Terza maggiore nel graue, ouer la minore nell'acuto, sē-
pre s'udirà qualche effetto tristo. Ne ciò debbe parer strano ad alcu
no; cōciosiache quello ch'intrauiene al Vedere intorno la cosa Visi
bile, ītrauiene anco all'Vdito ītorno l'Vdibile. Onde si come sareb
be strana cosa da uedere in un'edificio una parte posta nel luogo d'
un'altra; come sarebbe; se i Fondamenti fussero posti nel luogo del
Tetto, & nel luogo delle Porte le Finestre, & tutte le cose fussero
poste al contrario fuori de i loro luoghi, & senz'alcuna propor-
tione; cosi sarebbe cosa strana da udire una massa de Suoni, ò Consonanze poste in-
sieme senza proportione, & fuori de i lor luoghi naturali; i quali parmi che d'alcuni mo-
derni Scrittori, fin hora siano stati male intesi; tra i quali è uno Andrea Papio nel Cap.
20. del Lib. 2. del suo Trattato De Diatessaron. Si ritrouerà etiandio, uolendo inuesti-
gar più oltra, che la Quarta, laquale hà nell'acuto il Ditono, è più grata all'Vdito di quel
la, che l hà nel graue; come etiandio è più grata quella, c'hà il Semiditono nella parte
graue, di quella che l hà nell'acuta; & che di queste due compositioni, quella Quarta,
che sarà accompagnata con la Terza minore nel graue, farà miglior'effetto di ciascun'al
tro accompagnamento; come si potrà comprendere da i seguenti essempi.
 Percioche quantunque le Seste, che contengono gli estremi de
Percioche quantunque le Seste, che contengono gli estremi de queste parti poste insieme, non siano l'un dall'altro differenti nella
proportione, & non faccino variatione de suoni & di consonan-
ze; nondimeno la uarietà delle chorde, che riceuono nel loro me
zo, è cagione, che l'accompagnamento s'udirà esser migliore del-
l'altro, & di far la differenza tra due accompagnamenti, che siano
buoni, dal buono al migliore. Tanta è la possanza delle Consonan
ze quando sono poste ne i lor proprij luoghi & naturali, che non so
lamente quelle, che sono tramezate in cotal maniera secondo la
natura de gli Harmonici numeri, sono più grate all'udito di quelle,
che sono poste al contrario; ma anche fanno più allegra & più so-
nora ogni compositione, nellaquale sono poste. Questo adunque
raccoglieremo da quel che si è detto; che le Quarte si potranno por
re ottimamente nelle compositioni, quando saranno collocate in
tal maniera, che sotto di loro nel graue habbiano la Quinta, ouer la Terza; come hò
mostrato di sopra; & etiandio si potrà porre alle uolte con la Terza nellacuto; massima-
mente quando sarà la maggiore; ancora che questo dall'uniuersità de i Musici Prattici
fin'hora sia stata poco considerata; percioche se l'accompagnamento della Quarta con la
page 304Terza maggiore posta nel graue, che non è ueramente molto consonante è sopportata;
non sò ueder ragione perche non si dè sopportare l'accompagnamento della Terza mag
giore posta nell'acuto; essendo che questo ueramente è migliore, come la esperien-
za ce lo farà sempre uedere. Non bisogna pero fermarsi molto sopra tale Composi-
tione; come anco non si dimora per molto tempo sopra la Sesta, ò maggiore, ò mino-
re che ella sia.
D'alcune Regole poste in commune.Cap. LXI.
pitolo precedente, in qual modo s'habbia da comporre con la Quinta & con
la Terza; che qualunque uolta sarà accompagnata, nelle maniere c'hò mo-
strato, farà sempre buono effetto nella compositione. Qualunque uolta adū
que che uorremo usarla, potremo senza porre la Quinta, ò la Terza nel graue, por la Ter
za maggiore nella parte acuta, massimamente quando le Parti procederanno per ordi-
ne naturale, nel modo che si uede ne gli essempi; percioche apporterà gran commodo al
Compositore, aiutandolo la uaghezza delle modulationi, & lo schiuare il Tritono, che
potrebbe nascere alle uolte tra le parti della cantilena; come nel secondo essempio si può
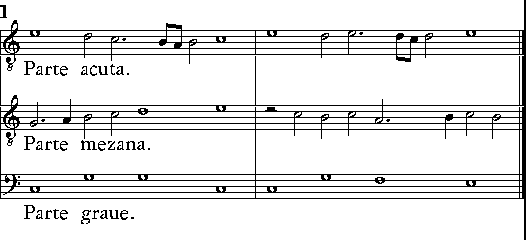 comprendere. Potrà ancora usar la Vnde
comprendere. Potrà ancora usar la Vndecima; come più à basso si uederà; la qual
si compone dellOttaua & della Quarta;
poi che Tolomeo nel Cap. 5. del Primo li
bro de gli Harmonici, & Boetio nel Cap.
10. del Libro primo della Musica, la pon-
gono tra le Consonanze;Vide Def.
Demonst. di modo che da
questi essempi si potrà conoscere la loro
natura, & quāto possano esser grate all'V-
dito; ancora che ne potrebbe bastar l'uso
de i Moderni, & de gli Antichi Composi-
tori, i quali molte uolte l'hanno accompa
gnata in tal maniera. Vsano alcuni di por-
re la parte acuta con la mezana distante
per una Quarta, & questa con la graue per
una Terza di maniera che 'l Basso uiene ad
esser lontano dal Soprano per una Sesta, tramezata dalla Terza, ò maggiore, ò minore:
 Onde essendo le parti composte in tal maniera, sogliono farle ascendere, ò discendere in
Onde essendo le parti composte in tal maniera, sogliono farle ascendere, ò discendere insieme più gradi, & tal modo di procedere chiamano Falso bordone. Ma in uerità, anco-
ra che tal maniera sia molto in uso, & che con difficultà grande si potesse leuare, non è pe-
rò molto lodeuole: imperoche, oltra che la Quarta è consonanza perfetta; com'altroue hò
mostrato;Supra
Cap. 5. & che non dobbiamo far contra la Regola data nel Cap. 29. genera alle uolte
tra le parti alcune relationi, che non sono harmoniche; la onde poco diletto apportano
all'Vdito; come ciascuno col mezo dell'essempio posto qui di sotto potrà conoscere.
 L'errore di cotesto abuso si manifesta da questo; percioche se noi uorremo porre le Terze
L'errore di cotesto abuso si manifesta da questo; percioche se noi uorremo porre le Terze à i lor luoghi naturali, oue si debbono ragioneuolmente porre; ouer sopra l'Ottaua alme-
no; si potrà conoscere con quanta ragione si possa fare una cosa simile; conciosia che si co
me nel mostrato essempio si udiuano molte Quarte, cosi nel sottoposto potremo udire al-
tretante Quinte.
 Io sò ben ch'appresso de molti più uarranno le autorità d'alcuni, che si habbiano usurpa
Io sò ben ch'appresso de molti più uarranno le autorità d'alcuni, che si habbiano usurpata cotal licenza, che le ragioni addotte di sopra; ma faccino pur'il peggio, che sanno, con
dire questa cosa è stata usata da molti, che poco mi curo; poi che non sono, ne uogliono
esser capaci di ragione. Et benche la Terza sia consonanza, & si possa porre in qual luogo
torna commodo; tuttauia il suo uero luogo non è nel graue, ma nell'acuto, sopra la Disdia
pason, ouer Quintadecima: Imperoche naturalmente l'Ottaua posta nel graue, non può
esser tramezata d'altro suono; ma uuol'esser posta semplice, senz'alcuna mediatione;
come hò raccontato nel principio del Primo libro delle Dimostrationi; & come etian-
dio ci mostrano i Numeri harmonici, posti nel Cap. 15. della Prima parte; tra i quali,
si uede la prima Dupla contenuta nel Senario tra 2 & 1. ch'è la sua forma, la quale
non è mediata d'alcun termine mezano, ma si bene la seconda posta tra 4. & 2. la-
quale è diuisa dal 3. in una Sesquialtera, che si troua tra 3 & 2. & in una Sesqui-
terza, che si troua tra 4 & 3. che sono le forme della Diapente, & della Diates-
saron consonanze. Onde la Sesquialtera nella detta seconda Diapason resta non diui-
sa & intera; ma oltra la Quadrupla, ch'è la forma della Disdiapason, si troua diuisa in due
parti; cioè, in una Sesquiquarta, chè la forma uera del Ditono, & in una Sesquiquin-
ta, ch'è quella del Semiditono; delle quali, l'una è collocata tra 5 & 4. & l'al-
tra 6 & 5. Si uede adunque, che la prima Ottaua è collocata naturalmente tra i
Numeri sonori senz'alcun altro numero mezano; & che la Quinta le succede senz'
alcun mezo; dopoi segue la Quarta, & da queste due parti maggiori si compone la
seconda Diapason, onde nasce la Disdiapason; ò Quintadecima. Dopo queste uie-
ne il Ditono, & immediatamente dopo lui segue il Semiditono; di maniera che, se
tali consonanze fussero poste ne i Contrapunti (se ciò si potesse far sempre commoda-
mente) à i lor luoghi proprij & naturali; non è dubbio, che nascerebbe un concento
tanto harmonioso, quanto l'Huomo si potesse imaginare. Et di ciò potiamo ueder l'espe
rienza sempre ne gli Istrumenti arteficiali; massimamente nell'Organo, oue poste le con
sonanze nominate per ordine l'una dopo l'altra, secondo c'hò mostrato; non si può dire
il buono effetto che fanno. Ma se per caso la prima Ottaua si pone tramezata nel graue,
dalla Quinta; allora il concento si fà alquanto tristo; & se tal Quinta si diuidesse in
due Terze, non si potrebbe à pena udire tal composto, massimamente se la Terza mino-
re tenesse il luogo della maggiore; cioè, s'ella fusse posta nel graue. E' nondimeno sop-
portabile la prima Ottaua tramezata in proportionalità harmonica per la Quinta; & quā
do sopra di essa si pone la Terza, non fà tristo effetto; ancora che cotali Consonanze
non siano poste à i lor luoghi proprij; & ciò intrauiene; percioche tengono il luogo
mezano nell'istrumento, oue si contiene tale ordine. Si debbe adunque porre la
page 306Terza immediatamente dopo la Quintadecima, ò almeno dopo l'Ottaua in ordine; &
debbe esser la maggiore, acciò che 'l concento sia più allegro & più pieno; ma se 'l si ab-
batterà, ch'ella sia la minore; come infinite uolte suole accascare, allora il concento sa-
rà più mesto. Queste cose ueramente sono poco considerate da i Prattici; percioche sen-
z'alcun riguardo pongono la Quinta tra le chorde graui, & anco la Terza, come torna à lo
ro più commodo; la qual cosa quanto diletto apporti all'Vdito lasciarò considerare à
coloro c'hanno giudicio. Onde uoglio dir questo solamente, che douendosi porre la Ter-
za nella compositione, è meglio porla sempre sopra l'Ottaua, che tra essa; Voglio inferi-
re, che migliore effetto farà sempre la Decima, che la Terza. Et quantunque si potreb-
be dire, che meglio sarebbe anco, porre la Quinta sopra l'Ottaua posta nel graue della
cantilena; come cosa più propinqua, secondo la natura de i Numeri harmonici; che la
Terza, come più lontana; tuttauia pongansi à qual modo si uoglia, tornarà sempre bene.
Ma quanto miglior'effetto faccia la Decima, che la Terza, da questi due essempi, ciascu
no, che hà giudicio, lo potrà conoscere. Si debbe però auertire, ch'in uno essempio; cioè,
 nel primo si contiene il Tritono, & nel secondo la Semidiapente; i quali tanto più sono
nel primo si contiene il Tritono, & nel secondo la Semidiapente; i quali tanto più sono sopportabili, quanto che dopo sè l'uno hà la Terza, & l'altro la Decima maggiori, che
fanno relatione harmonica con le uoci, che contengono il Tritono, ouer la Semidiapen
te. Et se bene gli Interualli, che sono nelle seconde figure de i mostrati essempi, sono uera
mente dissonanti; tuttauia sono in tal maniera collocati, che per il procedere, secondo
lordine mostrato nelle Regole, se ne passano, che l'Vdito se ne contenta. Si debbe oltra
di ciò auertire, che quando dissi, che La prima Ottaua si pone senz'alcun mezo, potiamo
intendere tale Ottaua esser quella, la quale incomincia nella chorda più graue del Basso
della cantilena, salendo di mano in mano allacuto fin'all'Ottaua chorda; & per la secon
da si può intender quella, ch'incomincia dalla chorda estrema acuta di tale Ottaua, & uà
fino alla Quintadecima. Pongono i Prattici alle uolte il Tritono tra due parti, il quale ca
sca sopra la seconda parte d'alcuna Semibreue sincopata posta nel graue in cotal manie-
ra; il quale si ode nella loro relatione; ma non è percossa l'una delle parti acute con la par
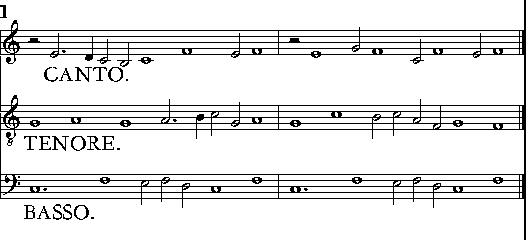 te graue di tale Interuallo. Et perche le parti procedono in cotal modo, & sono concate-
te graue di tale Interuallo. Et perche le parti procedono in cotal modo, & sono concate-nate tra loro di maniera, che senza partirsi dall'osseruanza delle Regole date, fanno buo-
page 307no effetto; però queste parti porgono all'Vdito & grato & soaue piacere; perche quel po
co di dissonanza, che si ode nel Tritono & nella Semidiapente, se ne passa presto, & aggiū
ge soauità alla consonanza seguente, più di quello, che si udirebbe, se non ui fusse; essendo
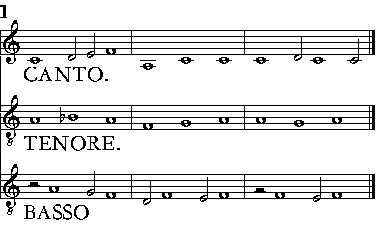 che Di due opposti l'uno si conosce maggior
che Di due opposti l'uno si conosce maggiormente per la comparatione, che si fà con l'al
tro. Frequentano i Moderni molto spesso ta
li passaggi; onde parendoli la cosa riuscibile
pongono alle uolte la parte graue sincopata
in tal maniera, che la secōda parte della Sin-
copa contiene col Tenore la Seconda, & il
Tenore col Soprano hora la Terza, hora la
Quarta, & tallora la Quinta; come si uede
nell'essempio. Ma quello, che contiene la
Quarta, senza dubio è men buono de gli al-
tri; percioche si ode tale Interuallo senz'al-
cun'accompagnamento. Oltra di questo si
dè auertire, che alle uolte si potrà passare
dalla Sesta minore all'Ottaua, quando le par
ti saranno collocate in tal maniera, che 'l Bas
so col Tenore procedino ordinatamente secondo l'ordine & modo dato nelle Regole u-
niuersali; & il Soprano procedi per Decima sopra 'l Basso; come qui si uede.
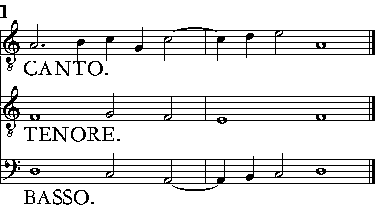 Si potrà anche dalla Terza maggiore passare all'Vnisono, quando 'l Soprano pro-
Si potrà anche dalla Terza maggiore passare all'Vnisono, quando 'l Soprano pro-cederà dall'acuto al graue col mouimento del Ditono; & il Basso col Soprano sarà ordina
to secondo i precetti dati di sopra, stando il Tenore, senza mutar luogo; come si uede; per
cioche essendo le parti estreme, che sono più dell'altre comprese dal senso, ben regola
te; s'alle uolte uerrà qualche cosa nell'altre, che non sia cosi ben regolata, si potrà soppor-
 tare. La onde si concede al compositore, che possa pigliare alle fiate qualche licenza fuo-
tare. La onde si concede al compositore, che possa pigliare alle fiate qualche licenza fuo-ri della Regola data di sopra nel Cap. 38. Gli sarà etiandio lecito di passar dalla Terza mi
nore, per contrarij mouimenti, all'Ottaua; quando le parti saranno ordinate in tal manie
ra, che quella, che si trouerà lontana per simile consonanza, & dopoi passarà all'Ot-
taua, habbia nel graue la Terza maggiore, di maniera che la parte acuta sia lontana dalla
graue per una Quinta; come nell'essempio seguente si uede. Anzi dirò di più; che
 sarà necessario, che le Parti stiano in cotal mo-
sarà necessario, che le Parti stiano in cotal mo-do; perche se si ponessero altramente, facen-
do maggiore quella Terza, ch'è minore, col se-
gno
 . accioche (secondo le date Regole) dal-
. accioche (secondo le date Regole) dal-la Imperfetta più propinqua si peruenghi alla
page 308Perfetta; non si potrebbe far tal cosa per alcun modo, senza grande offesa dell'Vdito; con
ciosia che si uerrebbe à fare una Quinta, che hauerebbe due Terze maggiori. Ma ciò sia
detto per sempre, che l'obligo stà nelle cose possibili, & non nelle impossibili; al quale
niuno è obligato. Dobbiamo oltra di questo osseruare, che nelle Cadenze principali del
la cantilena, le parti siano ordinate & accommodate in tal maniera, che la seconda parte
della figura sincopata, la qual si pone dissonante, sia sempre con la parte graue distante
per una Quarta, oueramente per una Vndecima; & con l'altra sempre lontana per una
Seconda, ò per una Settima; ilche si debbe osseruare etiandio in ogni figura sincopata,
nella quale sia la dissonanza; come si uede ne i seguenti essempi; da i quali si potrà com-
prender il modo, che si haurà da tenere in altre simili; quando accascheranno. Ma se uor
remo aggiunger la Quarta parte à queste, sempre ella si porrà in Ottaua dell'una delle due,
che sono distanti tra loro per Quinta, ò per Duodecima; accommodando la hora in un
luogo & hora in un'altro secondo che tornerà meglio.
 Et perche la Cadenza si può fare in molte maniere con uarietà delle parti; però uoglio
Et perche la Cadenza si può fare in molte maniere con uarietà delle parti; però uoglio por qui molti essenpi accommodati sopra Quattro parti; i quali potranno etiandio ser
 uire alle compositioni di Tre uoci; ouer se li potrà aggiunger nell'altre, quando fusse bi-
uire alle compositioni di Tre uoci; ouer se li potrà aggiunger nell'altre, quando fusse bi-sogno; accioche io non habbia da replicar più cosa alcuna in questa materia. Ma non uo
glio restar di dire, che si conosce per esperiēza, che quella Cadenza non hà gratia alcuna
ò leggiadria in sè, la qual sia senza la Dissonanza, che si troua nelle mostrate; mas-
simamente quando le parti procedono insieme per l'istesse figure; ancora che siano
sincopate, ouer non sincopate, che si proferiscono nel leuare, ò nel battere della bat-
tuta; come sono queste.
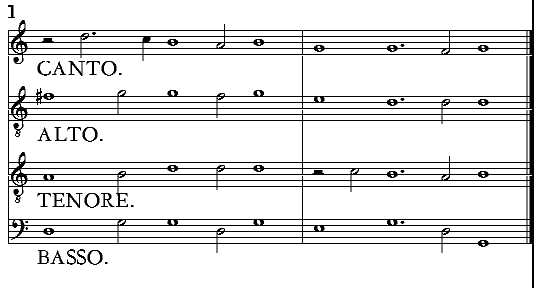 Però il Contrapuntista si guardarà di usarle, & debbe schiuare al tutto, di fare ch'alcu-
Però il Contrapuntista si guardarà di usarle, & debbe schiuare al tutto, di fare ch'alcu-na parte della cantilena non faccia la Cadenza, quando l'altre parti fussero ordina-
te in un modo, che qualunque altra delle più graui facesse la Quinta con la figura meza-
na della cadenza posta nell'acuto, mouendosi per l'interuallo del Semituono, quando tal
figura si potrà segnare con la cifra
 . Chromatica; percioche (com'hò detto altroue) pro
. Chromatica; percioche (com'hò detto altroue) proferendosi tal parte della Cadenza naturalmente col Semituono, sarebbe cosa difficile,
che l Cantore potesse hauer'in tal caso riguardo, di non proferirla, con quel modo che si
proferisce naturalmente. Onde uerrebbe poi à commettere errore, & à porre una dis-
sonanza in luogo della consonanza; cioè, uerrebbe à porre la Diapente superflua in
luogo della uera; come qui si uede.
page 310
 Accascherà anco un simile errore, quando le parti à Tre uoci saranno ordinate in tal ma
Accascherà anco un simile errore, quando le parti à Tre uoci saranno ordinate in tal maniera, che essendo 'l Tenore sopra 'l Basso lontano per una Terza, discendendo per salto
di Quarta sotto 'l Basso una Terza, ascendendo il Basso per grado di Tuono; & ritornan
do dopoi ciascun'à i suoi primi luoghi; il Soprano farà la Cadenza distante dalla parte
graue per una Quinta uerso l'acuto; come in questo essempio si uede.
 Seguirebbe anco un'altro errore, che qualunque uolta si uolesse sonar queste tre parti so-
Seguirebbe anco un'altro errore, che qualunque uolta si uolesse sonar queste tre parti so-pra un'Istrumento, si udirebbe senz'alcun' dubio tre Quinte. La onde i Compositori deb
bono auertire cotal cosa, & non far che le parti mutino luogo tra loro in questa maniera;
percioche tale inconueniente apportarebbe all'Vdito cosa, che non molto li piacerebbe;
ancora che nel cantar le parti non si potessino udire tali Quinte. Et perche da molti Prat-
tici questo non è molto auertitò; però hò uoluto toccarne una parola. Hora hauendo à
bastanza ragionato intorno alle cose necessarie à simili compositioni; lasciarò l'altre co-
se, che possono accascare & non sono di molto momento, al giudicio del Compositore;
imperoche col mezo delle Regole date, potrà quando gli occorrerà alcun dubio, quan-
tunque fusse di molta importanza, darne perfetta risolutione. Lasciando adunque di par
lare più intorno à cotal materia, uerrò à ragionar de i Contrapunti, che arteficiosamen
te si compongono à tre uoci, i quali si chiamano Doppij, & de quelli che si fanno con
qualche obligo. Ma perche i primi con maggior libertà da i Compositori, & più corret
tamente secondo i nostri precetti possono esser composti, ma non già i secondi; percio-
che 'l Compositore non può cosi ben purgare il suo Contrapunto, per esser li leuato il po-
tere dalla natura della cosa in sè; la quale ricerca (come uederemo) alcune osseruanze,
che non si possono lasciare, uolendo condur l'opera sua al desiderato fine; però ragione-
rò prima de i primi; dopoi dimostrerò gli altri; scoprendo quelle Regole & precetti, che
concorrono alla lor compositione; accioche ogn'uno possa restar (per quanto si potrà da
me fare) satisfatto.
Delle varie sorti de i Contrapunti arteficiosi; & prima de quelli, che
si chiamano Doppij.Cap. LXII.
tre uoci è quasi quell'istesso, che si compone à due, il quale nel Cap. 56. di so
pra, hò dichiarato & mostrato; conciosia che tra l'uno & l'altro si troua tal dif
ferenza, che l'uno non si può cantare à più che due, ouer tre, aggiungendoli
una parte, che canti nell'acuto, ò nel graue, di sopra, ò di sotto d'una delle Parti
principali per una Decima; ma l'altro non si può cantare se non con quelle parti,
che si compongono principalmente; cioè, à tre uoci, con grande uarietà d'harmonia nella
page 311
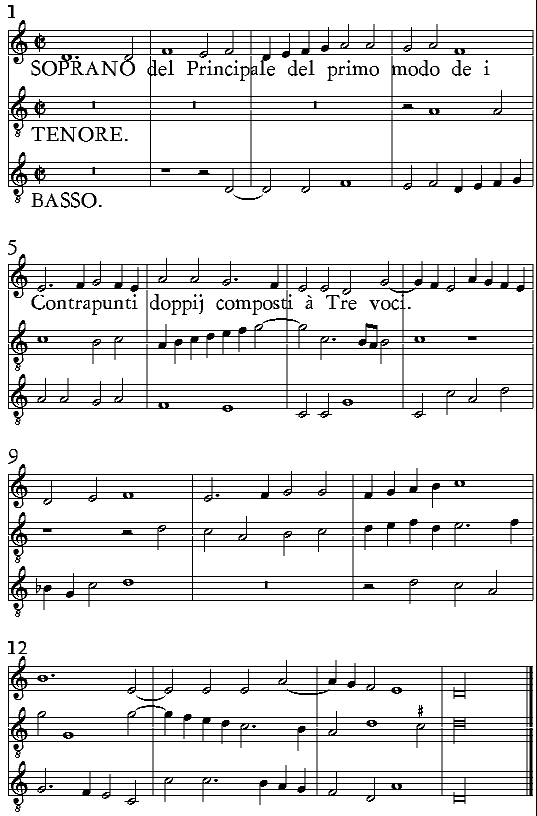
 page 312Replica, & molto differente da quella, che si ode nel principale. Però adunque ricordan-
page 312Replica, & molto differente da quella, che si ode nel principale. Però adunque ricordan-dosi quello, ch'è Contrapunto doppio à due uoci; è superfluo il uoler replicare, & dir quel
lo, che sia Contrapunto doppio à tre uoci; percioche sapendo quel ch'importa il primo, fa
cilmente si può hauer notitia di quel ch'importa il secondo. Volendo adunque ragionar
de quei Contrapunti doppij, che si compongono à tre Voci, dico; che le Specie loro son
molte; imperoche si possono comporre in uarie maniere, con l'osseruanza d'alcune Re-
gole; che cantandosi prima ad un modo nel Principale, & udendosi una sorte d'harmo-
nia, nella Replica poi diuersamente si cantano le Parti con quelle figure & interuall'istes
si, & si ode gran diuersità di concento. Ma ancora che molti siano i modi di comporre ta
li Contrapunti; come hò detto; porrò solamente quelli, che mi sono paruti più difficili &
più eleganti; acciò non sia tedioso à i Lettori; da i quali ciascuno ingegnoso potrà com-
prēdere, come si haurà da reggere in qualunque altra maniera de simili compositioni. Il
primo modo adunque sarà, che composto che si haueranno prima Tre parti principali, cō
l'aiuto d'alcune auertenze molto necessarie ad un tal negotio; haueremo la prima Specie;
percioche Quādo uorremo la Replica, porremo poi il Basso del Principale nel luogo del
Soprano più acuto per una Quinta; & il Soprano in quello del Tenore; & il Tenore nel luo
go del Basso, l'uno & l'altro più graue per una Ottaua; come nell'essēpio si uede. Ma sareb
be ueramente impossibile, che potesse riuscir bene, quando non si osseruasse, di non por
mai il Basso nel Principale cō l'altre parti distante per una Sesta; ancora che l'altre due tra
loro si possino porre; ne di porre la Quarta tra le due parti piu acute. Similmēte bisogna os
seruare, di non por mai il Basso co 'l Tenore in Terza, dopo la quale seguiti la Quinta; ne il
Basso col Soprano in Decima, dopo la quale uenghi la Duodecima, quando le parti insie
me discendono; percioche la Duodecima, che si pone nel Principale tra 'l Basso, & il So-
prano; nella Replica uiene Vnisono tra 'l Tenore & il Soprano; & la Quinta simigliante-
mente uiene Ottaua, & l'Vnisono del Basso co 'l Tenore diuenta Duodecima. Potiamo
hora uedere, che in simil sorte di Contrapunto, ò Compositione, nel Principale non si
può far la Sincopa di Settima; conciosiache non si può risoluere con la Sesta. In questa
sorte di Contrapunto, il Tenore potrà discendere sotto 'l Basso per Terza & Sesta; ma
non per Quinta: ma bisogna auertire, che non passi la Sesta; percioche le parti uengono
ad esser distanti l'una dall'altra per lungo spacio. Molt'altre cose sarebbe da mostrare, per
hauer'il modo facile da comporre; ma per non andare in lungo, & per non esser molto ne
cessarie, si lasciano. Et ueramente questa cagione mi muoue à lasciarle; perche desideran
do alcuno di uoler far cosa ottima, è dibisogno che faccia insieme il Principale & la Repli
ca; & cosi potrà uedere tutti gli incommodi, che potranno occorrere. Vltimamente è di
bisogno sapere, che se 'l si componerà il Principale secondo l'osseruanza delle Regole no-
stre mostrate di sopra, la Replica similmente uerrà ad esser'osseruata; & se 'l si farà altramē
te, ne seguirà il contrario. Et ciò sia detto à bastanza intorno la Prima sorte di Contra-
punto doppio à Tre uoci, la cui Replica procede per gli istessi mouimenti, che sono con-
tenuti nel Principale; perciò la seconda è quella, della quale la Replica procede per moui
menti contrarij a quelli, che si trouano nelle parti del suo Principale; come ne i seguenti
essempi si può uedere. Ma la Replica non potrebbe mai tornar bene, se non si osseruas
se alcune cose; come sarebbe dire; far che tutte le parti delle Sincope, che si pongono
nel Principale siano consonanti; & non por mai il Tenore distante dal Soprano per una
Quarta. Queste cose si debbono principalmente per ogni modo osseruare; l'altre poi,
che potrebbono accascare non saranno difficili; quando si componerà la Replica insie-
me col Principale. In simil sorte di Contrapunto si potranno usar le Seste, & por-
re le parti lontane l'una dall'altra per qual'Interuallo si uorrà. Il Tenore potrà
pigliare il luogo del Basso; & il Soprano quello del Tenore, & quello del Basso
anco. Et per hauer la Replica, si porra il Basso del nel luogo del Soprano
più acuto per una Sesta; il Soprano nel luogo del Basso più graue per una Decima; & il
Tenore più graue per un Tuono; facendo, che le Parti procedino per contrarij mouimēti
page 313
 di quelli, che si trouano nel Principale; & cosi haueremo l'harmonia differente; come ua
di quelli, che si trouano nel Principale; & cosi haueremo l'harmonia differente; come uarii & differenti sono i siti & li mouimenti dell'uno & dell'altro. Et se noi osseruaremo
 page 314nella compositione del Principale le Regole, che di sopra nel far le sudette due sorti de
page 314nella compositione del Principale le Regole, che di sopra nel far le sudette due sorti de Contrapunti sono state dichiarate; non è dubbio che la Replica (se non in tutto, almeno
in molte parti) uerrà ad esser osseruata. Si potrà anco comporre una Terza specie di Con
trapunto doppio, che participarà dell'una & dell'altra sorte de questi Contrapunti: quan
do si osseruarà tutte quelle Regole, che s'osseruano nelle compositioni; delle due mo-
strate specie; le quali Regole sono negatiue; cioè, uietano il far'alcuna cosa; Il che
fatto haueremo poi un Contrapunto, che potrà hauer la Replica simile à quella del
Primo & del Secondo modo mostrati; come qui si può uedere.


 Ma quando prima si componerà il Principale di maniera, che dopoi il Basso resterà nel-
Ma quando prima si componerà il Principale di maniera, che dopoi il Basso resterà nel-le sue chorde principali senz'alcuna mutatione; & il Soprano diuenterà nella Replica il
Basso, trasportato per una Duodecima più graue; & il Tenore si trasportarà per una Quin
ta; si haurà una Quarta specie di Contrapunto doppio; nel modo che qui di sotto si uede.
E' ben uero, che questo modo è più difficile di ciascuno de i mostrati; onde uolendolo fa-
re, acciò la Replica torni bene; bisogna osseruar molte cose, & prima. Quando 'l Tenore
si farà cantare col Basso à due voci; non bisogna, che le parti siano distanti l'una dall'al-
tra per Ottaua, ne per Sesta; massimamente quando 'l Tenore si porrà sopra 'l Basso; ma
quando si porrà di sotto, non si dè porre distante da esso Basso, ne per Terza, ne per
Quinta; ma si ben per Sesta, ò per Ottaua, & per Quinta ancora; con questa condi-
tione, che tal Quinta si troui nella seconda parte della sincopa, dopo la quale senz'al-
cun mezo ne uenga la Sesta; percioche quando queste due parti si pongono à i loro
luoghi proprij, non possono esser distanti l'una dall'altra per maggiore spacio, che di
page 315
 quello della Quinta; & tal Quinta nella Replica uiene à far l'Vnisono. Simigliante-
quello della Quinta; & tal Quinta nella Replica uiene à far l'Vnisono. Simigliante-mente, quando il Soprano & il Basso canteranno soli, bisogna auertir di non fare, che 'l
Soprano passi sotto 'l Basso; ne si debbe porre la sincopa di Settima; benche quella di Se-
conda & di Quarta si possa vsar'ottimamente nel Soprano; ne si debbe por queste par-
ti lontane l'una dall'altra per una Sesta, ne uogliono esser più distanti d'una Duodeci-
ma. Non si fà laTerza & dopoi la Quinta; ouer non si fà la Decima & dopoi la Duo-
decima, quando le parti discendono. Quando poi il Tenore & il Soprano cante-
ranno insieme, non si dè far la Quinta, se non quando il Tenore sarà la sincopa, nella se-
conda parte della quale tal Quinta sia contenuta; & dopo lei bisogna che seguiti, senz'
alcun mezo, la Sesta; & dopo questa la Terza, ouer un'altra Sesta. Non si fà Sesta &
dopoi Ottaua, quando le parti discendono; ma si pone la Sesta ad un'altro modo, che
uenga bene. Il Soprano può discendere sotto 'l Tenore fin'alla Ottaua uoce, quando
torna commodo, & quando si porrà la sincopa di Quarta nell'una & nell'altra di que-
ste due parti, tornerà molto bene. Bisogna auertire di non dimorar lungo tempo so-
pra la Terza, percioche nella Replica uiene Sesta col Basso; ne dobbiamo anco fer-
mar le parti sopra l'Ottaua, conciosia che torna Vnisono. Tutte queste cose si debbo-
no osseruare, accioche si possa peruenire con qualche facilità al fine desiderato. Et per-
che osseruando queste Regole, sarà facile il comporre questi contrapunti à Tre uoci;
page 316tanto più, componendo in un tempo il Principale & la Replica, accioche il Com-
positore possa ueder gli incommodi, che possono occorrere in tali compositioni.
Pero si dè auertire per ultima conclusione, che quantunque il Principale si purgasse da
ogni errore, che si potesse commettere contra le date Regole uniuersali, è impossibile
che la Replica in tutti possa venire osseruata. Questi pochi essempi hò uoluto porre,
da i quali ciascun potrà uedere il modo, che haurà da tenere uolendone comporre
de gli altri.
Delle varie sorti de Contrapunti à Tre uoci, che si fanno à mente in Consequenza so-
pra un Soggetto; & d'alcune Consequenze, che si fanno di fantasia; & quel
che in ciascheduna si hà da osseruare.Cap. LXIII.
i Numeri harmonici; quando dal Musico, il quale sappia conoscer la natu-
ra loro, sono posti in atto; che se non si udissero & anco vedessero, impossibi-
le sarebbe quasi di poterle credere. La onde è da sapere, che si come l'inge-
gnoso Prospettiuo col mezo della Linea dritta & della obliqua, prima materia della sua
Arte, essendo condutte in diuerse parti, rappresenta al Senso del Vedere tante cose &
diuerse, che paiono miracolose; col far parere vna cosa picciola grande; & quello che
non si muoue girarsi & quasi andar dietro in ogni parte à chi la mira; simigliantemente il
far'una Figura, che parerà che guardi ogn'uno, sia da qual parte, & in qual luogo si uo-
glia, che riguarda in quella; cosi il Musico; ilquale conosca la natura de i nominati nu-
meri & li ponga in atto; come si debbe, rappresenterà al senso dell'Vdito tante & tante
harmonie, con nuoue foggie & uariate, che sarà un stupore di vdirle; cantando lui vna
sola parte, tirandosene (dirò cosi) dietro una, ò più in Consequenza. Et perche di que-
sto fin'hora non credo, ch'alcuno s'habbia mosso à scriuere, dando Regole ferme di
poter con breue studio far coteste cose; dopo l'hauer scoperto di sopra molti belli Se-
creti di quest'Arte, i quali da molti (com'io credo) non furono stati mai imagina-
ti; uoglio ancora scoprirne alcun'altri, i quali (com'io penso) saranno di gran gioua-
mento, & di non poca satisfattione à i Studiosi di questa nobile Arte; & saranno i se-
quenti. Però è d'auertire, che oltra le uarie maniere de Contrapunti, tanto sempli-
ci, quanto doppij & uarie Consequenze & Imitationi, che sono quasi infinite; lequa-
li si compongono à mente sopra 'l Canto fermo à tre uoci; se ne trouano alcune, che so-
pra di esso, ouer sopra qualch'altro Soggetto in Consequenza, & in Imitatione; il
Conseguente seguiterà la Guida per un certo spacio di tempo, hora cantando per l'
Vnisono, hora per la Diapente, & hora per la Diapason; cosi graue, come etian-
dio acuta; il qual modo, quantunque sia di fatica, quanto alla inuentione nel por
le Consonanze nella Guida di maniera, che nel Consequente tornino commode;
riuoltando i Numeri & le Proportioni, che l'un dopo l'altro consonino; è nondime-
no ingegnoso, & da udir diletteuole; ancora ch'alle fiate non si possa far quel Con-
trapunto in esse cosi candido & netto, quanto ricerca l'ordine & precetti contenuti
nelle Regole date di sopra. Il perche uolendo io al presente di queste copiosamen-
te ragionare; accioche i Spiriti gentili, uirtuosi, & nobili non siano priui di que-
sti Secreti, non solamente uolendoli fare à mente; ma acciò che etiandio (sa-
pendoli) accommodar li possino nelle lor Compositioni; & ritrouare in esse col
loro mezo infinite altre belle Inuentioni, si debbe sapere; che i Contrapunti, che si
fanno nel modo, ch'io dimostrerò al presente, sono de più maniere; imperoche il
Consequente si ritroua esser con la Guida di due sorti; se ben possono esser molte le sue
page 317Specie; lequali è impossibile di poterle trattare in breue tempo, & in poche carte; im-
peroche ouer che 'l Consequente canta dopo la Guida per una Pausa di Minima, ouer
per una di Semibreue; Et di questa Seconda maniera ne porrò solamente una specie; &
sarà di quella, che si canta per una Diapente più acuta dopò la Guida; ma della prima
maniera se ne trouano molte; essendoche in questo il Consequente può seguitar la Gui-
da in molti modi; onde prima ne porrò due di quelle, che si possono cantare all'Vniso-
no, tanto di sopra, quanto di sotto la parte del Soggetto; dopoi una di quelle, che si po-
trà cantare alla Diapason sopra la Guida; stando essa Guida sotto la parte di esso Sog-
getto; simigliantemente ne dimostrerò Quattro, nelle quali la Guida sarà seguitata dal
Consequente per una Diapente. La onde due di queste saranno, nelle quali il Conse-
quente seguiterà la Guida in acuto, tanto di sopra quanto di sotto la parte di esso Sog-
getto; & due, ch'esso Consequente la seguiterà nel graue, tanto di sotto, quanto di so-
pra la parte nominata. Ma per incominciar dalle cose, che sono men difficili, daremo
principio à quelle, nelle quali dopò una Pausa di minima il Consequente seguita la Gui
da per Vnisono, sopra la parte del Soggetto. Si dee però sapere, che in questo, & ne
gli altri ancora di questa sorte, si hanno da osseruare tre cose; La prima, che 'l Contra-
punto, che si fà, consiste in due Figure, ò Note del Soggetto; il quale sarà di Canto
fermo; cioè, in quella, sopra la quale allora si canta, ò fà il Contrapunto; & in quella,
che segue immediatamente; sopra la quale si hà da cantare. Quella nominaremo Pri-
ma, & questa Seconda; & chiamaremo quella sempre Prima; sopra la quale allora si fà
il Contrapunto; & dopo essa ne segua un'altra; la quale adimandaremo prima anco, se
bene ella sia stata seconda, à quella, che le andaua inanti. La Seconda cosa è, ch'es-
sendo la Semibreue di ualor di due Minime; cosi faremo etiandio ualere le figure del
Soggetto, quando sarà di Canto fermo; la onde la cosa uiene à consistere, che la Gui-
da habbia da collocare ogni seconda Minima sopra la prima Semibreue in tal maniera,
che quando il Consequente incomincierà à cantare, quella istessa che sarà (necessaria-
mente) sopra essa prima Semibreue, non ne habbia da seguitare alcuna discordanza; il
che si farà anco quando canterà la prima Minima sopra la seguente Semibreue; che sa-
rà la seconda, della seguente seconda Semibreue; accioche nella seconda della prima Se-
mibreue il Consequente accordi con la detta prima minima della Seconda. Et perche
ogni mouimento, che fà il Canto fermo da una figura, ò nota all'altra; per uenire alla
Terza cosa; ouer ch'è di Vnisono, ò di Seconda, ò di Terza, ò di Quarta, ò di Quinta;
ò pur (com'auiene alle fiate) di Sesta, ò di Ottaua; però lasciando quelli dell'Vnisono, di-
co, che gli altri, ouero uanno uerso l'acuto; ouero uerso il graue; onde in ciascheduno
de questi mouimenti bisogna sapere in qual modo s'habbia à porre la detta Seconda mi-
nima della prima Semibreue; acciò che 'l Consequente accordi cantando sopra la sua
prima. Et perche uarii sono i modi, uarii anco saranno le Regole; perciò bisogna auer-
tire oltra l'altre cose; il che è di molta importantia; di non far mai alcun mouimento
di grado passando d'una Minima ad un'altra; & che quando si trouerà la modulatione fat
ta per Vnisono, che nelle due prime Semibreui la seconda minima della prima Semibre-
ue (lasciando di dir della prima minima; percioche si può accōmodar come si uuole: pur
che accordi) si porrà Vnisona, ò Terza ouer Quinta, & anco Ottaua; ma quando 'l Sog-
getto ascenderà per grado, allora tal minima sarà Sesta; oueramente (per un certo com-
modo, che ne risulta; ancora che non sia troppo reale; essendo un passo strauagante;
& per acquistare un poco più di uarietà) la prima minima della prima Semibreue sarà Ter
za, & l'altra, ch'è la seconda, farà due Semiminime uerso 'l graue; delle quali la prima fa-
rà Seconda & l'altra l'Vnisono col Soggetto. Quando poi tal grado sarà discendente, al-
lora la Seconda minima nominata sarà Quinta. Ma quando 'l Canto fermo si muouerà
per salto di Terza all'insù; tal minima dourà essere Terza, ò Quinta, ouer'Ottaua, & an-
co Decima. Et quando farà il mouimento di Terza all'ingiù, la detta minima si sa-
rà Vnisono, ò Terza, ò Sesta, ò pur'Ottaua, oueramente Decima. Nel salto di Quar-
page 318ta all'insù tal Minima si porrà Sesta, ouer Ottaua; & all'ingiù sarà Terza, ò Quinta,
ouer'Ottaua. Se 'l salto sarà di Quinta uerso l'acuto, la Minima si porrà Terza, ouer
Quinta; & se uerso 'l graue, Vnisono, ò Sesta, ò pure Ottaua. Et se per caso tal salto
fusse di Sesta (come suole alle fiate auenire) all'insù, si porrà tal Minima Decima; ma se
all'ingiù, Terza, ouer'Quinta. Vltimamente nel salto d'Ottaua uerso l'acuto tal mini-
ma si porrà Ottaua, ò Decima, ò Duodecima. Et uerso 'l graue s'accommoderà Vniso-
no, ò Terza, ò Quinta; delle quali Regole se ne potrà ueder molte osseruate nel sequen-
te essempio; percioche hò pigliato questa impresa, di uoler dimostrar tutte queste sorti de
Contrapunti fatti in Consequenza sopra un Soggetto di canto fermo: però cotal Sogget
to sarà l'Hinno dello Spirito santo; Veni creator Spiritus; al cui nome cantaremo il seguen
te primo, che sarà più d'ogn'altro semplice, per maggiore intelligenza di quello, che
si è detto.
 page 319L'altra sorte de Contrapunto all'Vnisono si fà sotto la parte del Soggetto, con l'istess'os-
page 319L'altra sorte de Contrapunto all'Vnisono si fà sotto la parte del Soggetto, con l'istess'os-seruanze de gradi & salti; nel quale si dè anco sommamente auertire; come ho detto del
la mostrata di sopra; di non far alcun mouimento di grado da una Minima all'altra, ne
uerso 'l graue, ne uerso l'acuto; & in questa particolarmente non si farà alcun salto di
Quarta. Et quando le due nominate Semibreui saranno unisone, la detta Secōda minima
della prima potrà esser'Vnisono, ò Terza, ouer Quinta. Ma quando conteneranno il
mouimento di grado ascendente, tal minima si porrà Terza, ò Quarta, oueramente
Quinta; & uorrà esser Quinta, ò Sesta quando tal grado sarà discendente. Il salto di Ter
za ascendente uorrà Vnisono, ò Terza; & quel di Terza discendente, uorrà Vnisono,
ò Terza, oueramente Quinta. Quel di Quarta ascendente, uorrà Vnisono, ò Terza,
ò Quinta, & Sesta; oueramente Ottaua dourà essere quello di Quarta, discendente.
Quando tal salto sarà di Quinta, ascendente, tal Minima dourà essere Vnisona, ò quar-
ta, ouer Sesta, & anco Terza sopra 'l Soggetto. Ma quando sarà discendente, potrà es-
ser Decima, ouer Duodecima. In quello di Sesta ascendente potrà esser Terza, ouera-
mente Quinta; & in quello che sarà di Sesta discendente, sarà dibisogno che sia Quar-
ta, ò Sesta, ouer'Ottaua, & anco Decima. Ma in quelli d'Ottaua, s'accommoderà l'Vni-
sono, ò la Terza, oueramente alla Quinta; come nel sequente essempio si uede osseruato.
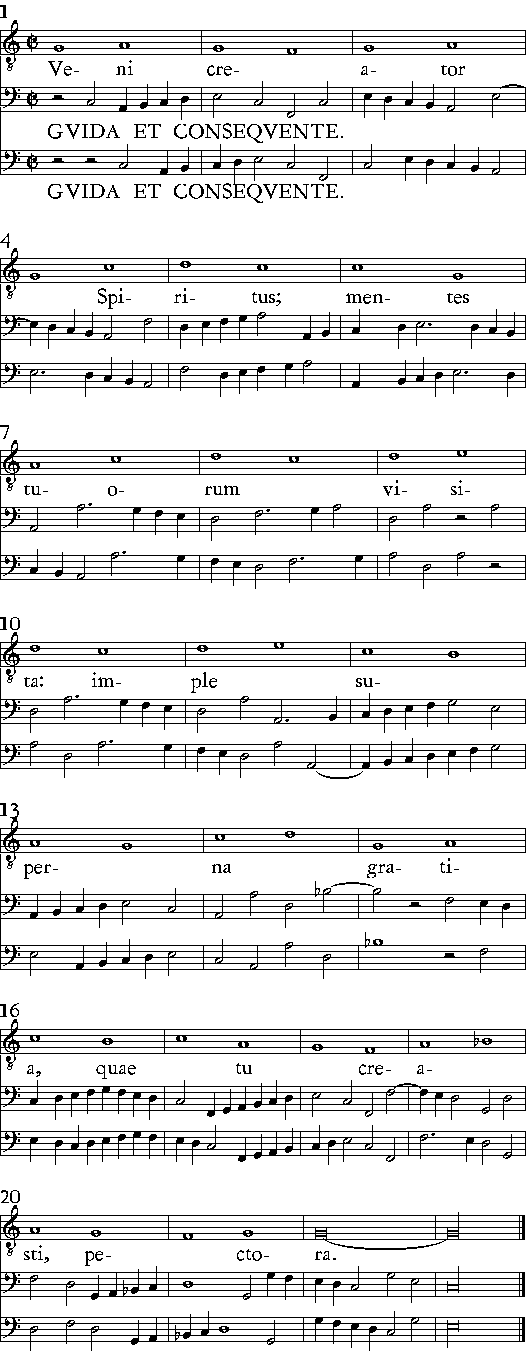 page 320Et questo è quanto à i due primi modi, ne i quali il consequente canta all'Vnisono con
page 320Et questo è quanto à i due primi modi, ne i quali il consequente canta all'Vnisono con la Guida dopo 'l tempo d'una Minima; tanto di sopra, quanto di sotto la parte del Sog-
getto. Ma se 'l Consequente si urrà far cantare in Diapason nell'acuto con la Guida, do-
po il tempo, che importa una Minima, facendo ch'essa Guida canti sotto la parte del
Soggetto; si potrà ottimamente fare, quando si osseruarà, sopra ogn'altra cosa, alcune
Regole molto necessarie; come è di non far mai mouimento nel Contrapunto per gra-
do; ne mai salto di Quarta all'ingiù. Ancora di non fare la Sesta, dopo la quale ne uen-
ga l'Ottaua, quando 'l Soggetto discende per grado; ne anche Ottaua, quand'è salto di
Quarta. Il Grado etiandio non uuole Ottaua; ne il Salto di Terza ascendente vuol
Quinta. Il mouimento del Soggetto fatto di Vnisono vuole hauer la Seconda minima
Vnisona, ò Terza, ouer Quinta sopra, ouer sotto la parte del Soggetto; ma 'l grado
ascendente uuol Terza, ouer Quinta; & il descendente Quinta, ò Sesta. Quel salto, che
si fà per Terza ascendente uuole Vnisono, oueramente Terza, ò Quinta, ouer'Ottaua
sopra 'l Soggetto; & lo discendente vuole Vnisono, ò Terza, ò Quinta, & anche Otta-
ua sotto esso Soggetto, oueramente Terza di sopra. Il salto di Quarta ascendente uuol
Terza ò Quinta, oueramente Sesta sopra la parte del Soggetto; & quel di Quar-
ta discendente uuol Sesta, ouer'Ottaua nel graue. Salto di Quinta all'insù uuol Sesta,
ouer Ottaua, ò pur Quinta sopra 'l Soggetto; & quello all'ingiù uuol Terza, pur di sopra,
 page 321oueramente Ottaua, ò Decima, ò Duodecima di sotto. Quel di Sesta, ch'ascende; uuo-
page 321oueramente Ottaua, ò Decima, ò Duodecima di sotto. Quel di Sesta, ch'ascende; uuo-le Vnisono, ò Terza, ò Quinta, ouer la medesima Terza sopra cotal Soggetto; come
quello che discende uuole Ottaua, ò Sesta, ouer Decima. Et si come il salto d'Ottaua
ascendente uuole Vnisono, ò Terza, ò Quinta; cosi quel della discendente uuole
Ottaua, ouer Decima; come si può considerare nel sequente essempio.
 Et questo sia detto intorno à i Consequenti d'Vnisono & di Ottaua. Ma per uenire à quel
Et questo sia detto intorno à i Consequenti d'Vnisono & di Ottaua. Ma per uenire à quelli, che seguono la Guida per una Diapente acuta, ouer graue; incominciaremo da quel-
li, che si fanno sopra la parte del Soggetto, & hanno il Consequente in acuto. Onde tra l'
altre cose, che sono d'importanza in questa sorte de Consequenti, si dè osseruar di fare,
che la Guida nō faccia mai salto ne di Quarta, ne di Sesta all'insù; ne anche salto di Terza,
ne di Quinta all'ingiù. Et quando le due nominate Semibreui saranno l'una dall'altra lon
tane per Vnisono; sarà dibisogno, che la Seconda minima, che casca sopra la prima di
esse, sia Ottaua sopra, ouer Terza sotto 'l Soggetto. Ma quando conteneranno il mouimen
to di grado all'insù, tal minima sarà Terza, ouer Quinta sopra di esso; oueramente si por-
rà tutta la prima Semibreue, che sarà Ottaua; onde nel Consequente nascerà la Sinco-
pa di Vndecima, che si haurà da risoluere; come di sopra si è mostrato, con la Decima; per
page 322cioche allora necessariamente bisognerà che la Guida faccia la prima Minima della se-
conda Semibreue Sesta, & la seconda Quinta; similmente si potrà porre la prima semibre
ue, che nella prima minima siano due semiminime, l'una Terza & l'altra Seconda; & che
la seconda minima sia tutta Terza. Ma quando le due Semibreui conteneranno il gra-
do ascendente; allora la detta seconda minima sarà Terza, ouer Quinta. Quando poi il
salto sarà di Terza ascendente, la detta Minima sarà Vnisona ò Terza; & se 'l sarà di-
scendente, si farà Terza sotto la parte del Soggetto. Salto di Quarta ascendente uuol
Terza; & discendente uuol simigliantemente Terza, ouer Quinta. Il salto di Quinta
ascendente uuol Quinta, & quel che discende uuol medesimamente Quinta; ma sotto
esso soggetto. Quel di Sesta ascendente uuol Sesta, & quello che discende uuol Terza.
Salto d'Ottaua ascendente uuol Sesta; & quando è discendente uuol Quinta, ò pure Ot
taua, l'una & l'altra sotto la parte del Soggetto. La onde osseruando queste cose primie
ramente, che sono necessarie, & continuamente essercitandosi; potrà nascere un tal
Contrapunto con la sua Guida & Consequente; come è quello, che segue.
 Dopo questo seguita il Quinto modo, doue 'l Consequente segue la Guida, la quale can-
Dopo questo seguita il Quinto modo, doue 'l Consequente segue la Guida, la quale can-ta sotto la parte del Soggetto nel graue per una Diapente acuta; nel qual modo si dè os-
seruar sopra ogn'altra cosa, che la Guida non faccia salto di Terza, ne di quinta all'in-
giù; ne di Quarta ne di Sesta all'insù. Et quando 'l Soggetto canterà le due nominate
Semibreui, che saranno Vnisone, la Guida sarà la detta seconda minima della prima
Semibreue, Vnisono, ò Terza; ò Quinta, ouer'Ottaua, come li tornerà piu commo-
page 323do; & quando farà il mouimento di grado all'insù, porrà tutta la detta minima Sesta; ouer'
Ottaua, oueramēte porrà tutta la prima Semibreue Vnisona, ouer Terza; onde nascerà la
Sincopa nel Consequente. Et quando tal mouimento sarà fatto all'ingiù, la detta Minima
sarà Terza, ò Sesta, oueramente Ottaua. Al salto di Terza ascendente si darà l'Vnisono,
ò Terza, ò Quinta, ò Sesta, ouer'Ottaua, secondo che si ritrouerà ordinata la parte del
Soggetto; ma à quello di Terza discendente si darà la Quinta, ouer Decima. Quello di
Quarta ascendente vuole la detta seconda minima, che sia Sesta; & la discendente, quel-
la che sia Ottaua, ò Decima. Salto di Quinta ascendente ricerca la Terza, ò Sesta, ouer
l'Ottaua; & quella della descendente ricerca la Sesta, ò la Duodecima. A quello di Se-
sta ascendente s'accommoda la Terza, ò la Quinta; & à quello di Sesta discendente se
li dà l'Ottaua, ò la Decima. Quel di Ottaua ascendente uuole Vnisono, ò Terza, ò
Quinta, ouer'Ottaua; & quello di discendente ricerca Ottaua, ò Decima, ò Duodeci-
ma: come nel sequente essempio in gran parte si può uedere.
 Et questo sia detto intorno à quelle Consequenze, che si cantano alla Diapente acuta.
Et questo sia detto intorno à quelle Consequenze, che si cantano alla Diapente acuta. Ma quando uorremo far quelle, che si cantano alla Diapente graue, sopra la parte
del Soggetto; bisognerà osseruar sopra ogn'altra cosa, di non far che la Guida canti
per salti di Quarta all'ingiù; se non quando si porrà la prima Minima della prima
page 324delle due nominate Semibreui, & due Semiminime sequenti, che uadino per gradi uer
so 'l graue; percioche torna alle fiate commodo. Ne debbe far due salti di Quarta l'una
dopo l'altra. Ma quando la parte del Soggetto si muouerà da una figura all'altra per
Vnisono; la seconda minima, già tante fiate nominata, si porrà Vnisona, ò Terza,
ouer Quinta sopra la prima delle due nominate Semibreui. Facendo poi il passag-
gio di grado uerso l'acuto, potrà porsi Ottaua, ouer Decima. Et non solamente si po-
trà far questo, ma etiandio si potrà far la detta prima Semibreue, che sia tutta Duode-
cima; percioche nel Consequente uerrà la Sincopa. Ma quando tal passaggio sarà
uerso 'l graue, cotal Minima potrà esser Quarta, ò Sesta, oueramente Ottaua. E'
ben uero, che la detta prima Semibreue potrà anco esser tutta Decima; percioche me-
desimamente 'l Consequente contenerà la Sincopa. Quando 'l salto sarà di Terza,
all'insù, allora si porrà la seconda minima Duodecima; & anco si potrà far la pri-
ma, che sia Decima, con due Semiminime sequenti, che discendino per grado;
delle quali l'una sia Nona & l'altra Ottaua; che saranno (come di sopra hò detto) di
gran commodo. Il salto etiandio di Terza all'ingiù ricerca, che tale Minima si pon-
ga Terza, ò Quinta, ouer Decima; ma 'l mouimento di Quarta all'insù uuole Otta-
 page 325ua, ò Decima; come quell'all'ingiù uuol Sesta. Quel di Quinta uerso l'acuto uuol la
page 325ua, ò Decima; come quell'all'ingiù uuol Sesta. Quel di Quinta uerso l'acuto uuol la Prima minima della prima semibreue Duodecima, & la Seconda diuisa in due Semi-
minime, delle quali la prima sia Vndecima & Decima l'altra. Ma all'ingiù uuol Ter-
za, ouer Quinta. Il mouimento di Sesta uerso l'acuto uuole Ottaua, ò Decima, ouera-
mente Duodecima; & quello uerso il graue uuol la prima Minima, che sia Terza, & Quar
ta la seconda. Ma i mouimenti d'Ottaua all'insù uogliono la Duodecima; & quelli
all'ingiù uogliono Quinta; come nell'essempio una buona parte delle nominate co-
se si possono ottimamente uedere osseruate. Se uorremo dopo questa far quella ma-
niera di Consequenza alla Quinta graue, sotto la parte del Soggetto; sopra tutte l'altre
cose osseruaremo di non far salto di Quarta all'ingiù. Però quando il Canto fermo pro-
cederà da una figura all'altra per Vnisono, osseruaremo di far, che la Guida faccia
la sudetta seconda Minima della prima Semibreue, che sia Vnisono, ouer'Otta-
ua. Ma quando si muouerà di grado uerso l'acuto, la detta minima farà Terza,
ouer Quinta; imperoche 'l grado discendente uuol Quinta, ouer Decima; ò pur
la prima Minima della prima Semibreue, si farà Sesta, & la seconda sarà di-
uisa in due Semiminime, delle quali l'una sarà Settima & l'altra Ottaua con
 page 326la parte del Soggetto. Il salto di Terza all'insù uuol Sesta, ouer che la prima minima
page 326la parte del Soggetto. Il salto di Terza all'insù uuol Sesta, ouer che la prima minima sia Vnisono, & delle due sequenti Semiminime l'una sia Seconda & l'altra Terza, & quel
di Terza all'ingiù uuol Sesta, ouer'Ottaua. Salto di Quarta all'insù vuol Terza, ò
Quinta; & quello all'in giù vuol Quinta, ouer che la prima minima sia Ottaua, & la se-
conda sia diuisa in due Semiminime, delle quali la prima faccia Nona, & l'altra Decima.
Quel di Quinta uerso l'acuto uuol Quarta, oueramente Quinta; & uerso 'l graue uuol Se-
sta, ouer Ottaua, ò Decima. Quando la parte del Soggetto fà il salto di Sesta in sù, tal mi
nima uorrà esser Sesta, ouer'Ottaua, ò Decima; & quando in giù, si sarà la prima minima
Ottaua, & la seconda due Semiminime Nona & Decima; oueramente si farà la prima mi
nima Sesta, & le Seminime Settima & Ottaua. Ma 'l mouimento di Ottaua tanto all'insù
quanto all'ingiù uuol Sesta. La onde osseruando cotali Regole, nasce la compositione,
che si uede nello essempio, & altre simili. Et tutte queste sono Consequenze fatte al-
la Diapente hor'acuta, & hora graue, si di sopra, come anco di sotto la parte del Sog-
getto. Ma per uenire all'Ottaua maniera di Consequenza, nella quale il Consequen
te seguita per una Diapente acuta la Guida dopo una pausa di Semibreue; bisogna
auertire, che questo modo è alquanto più difficile de gli altri; percioche, si come in
quelle, che fin qui habbiamo mostrato, il Consequente seguitaua la Guida dopo una
pausa di Minima, & si hauea à considerar due Semibreui l'una sequente l'altra, per ca-
gione de i Mouimenti, che conteneuano; cosi in questa fà dibisogno considerarne, &
hauer l'occhio à tre; però bisogna osseruar nelle due prime (secondo i gradi & salti, che
faranno insieme) la seconda Minima della prima, & la prima della seconda Semi-
breue; & saper la consonanza, che si ritroua nella seconda, quel ch'ella potrà fare,
ò ritorni nella Terza; acciò il Consequente con la Guida non faccino dissonanza, nel
muouersi la parte del Canto fermo, ouer Soggetto da un luogo all'altro, cosi uerso l'acu-
to, come etiandio uerso 'l graue. Bisogna adunque auertire, che nelle due prime Se-
mibreui, quando si trouerà la modulatione fatta per Vnisono, allora la Seconda mini-
ma della prima Semibreue sarà Quinta graue sotto la parte del Soggetto, & la pri-
ma della Seconda sarà simigliantemente Terza graue; oueramente l'una Terza gra-
ue & l'altra Vnisona, ouer Terza graue: simigliantemente l'una & l'altra si porrà
Vnisona, oueramente l'una Vnisona & l'altra Terza; ouer che nella prima si farà la
Pausa & l'altra farà la Quinta; ancora la Seconda si porrà Sesta & la prima nominata
si farà Quinta. Ma nel grado ascendente la Seconda & la Prima saranno Terze;
ouer la seconda sarà Quinta & la prima Terza; oueramente l'una sarà Quinta & l'al-
tra Quarta acuta; ò pur l'una Terza & l'altra simigliantemente Terza; graue però, &
sotto la parte del Soggetto; & si potrà far anco, che la Semibreue haurà la prima
Minima unisona, la seconda due Semiminime, che faranno Seconda & Terza;
& la prima minima della seconda Semibreue farà Terza graue; ancora la prima
Semibreue potrà hauer la prima minima Terza, & la seconda due semiminime Se-
conda & Vnisono; & cosi la prima minima della sequente Semibreue potrà esser Ter-
za graue. Ma nel grado discendente la detta seconda minima sarà Terza, & la prima
della seguente simigliantemente Terza; oueramente l'vna sarà Terza & l'altra Quin-
ta; ouer'Vnisona la seconda & Terza la prima; ancora la seconda potrà esser Ter-
za, & la prima Quarta; ouer la seconda Quinta, & la prima Sesta; etiandio l'una
farà Terza nel graue, & l'altra farà la Seconda sincopata. Il salto di Terza all'
insù uuol la seconda Vnisona, & la prima Terza graue, ouer l'una & l'altra di
queste Terza; oueramente che la seconda sia Terza & la prima Vnisona; co-
m'anco à tutta la prima Semibreue si dà la prima minima, che sia Quarta sin-
copata dopo la quale ne seguino due Semiminime, che l'una sia Terza & Secon-
da l'altra; ò pur la seconda minima Terza, & Terza nel graue la prima mini-
ma della seguente Semibreue. Il salto ueramente di Terza all'in giù uuole la det-
ta seconda minima, che sia Terza graue, & la prima Vnisona, ouer Terza; &
page 327anco la detta seconda, che faccia Quinta, & Terza la prima. Ma 'l salto di Quar-
ta verso l'acuto uuol Terza nella seconda, & Terza, ò Quinta nella prima; oueramente
che vuol nella seconda la Quinta, & nella prima l'Vnisono, ò Terza; come il salto di
Quarta verso 'l graue vuol la seconda, che sia Terza, & la prima che sia Quinta, ò Sesta,
ouer'Ottaua. Simigliantemente il salto di Quinta all'insù vuol la seconda, che sia Quin-
ta, & la prima Vnisono; come quando uà all'in giù, vuole la seconda, che faccia una
Pausa, ouer che sia Quinta graue, & che la prima sia Quinta, ouer Vnisono; ò pur che
la seconda habbia la Pausa, & la prima sia Ottaua. Quanto al salto di Sesta uerso l'acu-
to, la seconda minima della prima semibreue vuol esser Quinta, & la prima della secon-
da Terza graue; & quel che uà uerso 'l graue, vuol la seconda, che sia Terza graue, &
la prima, che sia Terza acuta. Il salto d'Ottaua all'insù uuol la detta seconda Vnisona,
& la prima che sia Quinta; & quella che uiene all'in giù, vuol la seconda che sia Quin-
ta, & la prima che sia Terza, ouer Quinta. Et queste sono una parte de quelli auer-
timenti, che si debbono hauer nel passare dalla prima alla seconda Semibreue delle tre
nominate di sopra. Ma bisogna di nuouo auertire; accioche la Terza semibreue ac-
cordi nel Consequente; di porre sopra la Seconda tal Consonanza nella Guida, che ac-
cordi nella Terza col Consequente; però è da auertire, che nella modulatione, che fà il
Soggetto per Vnisono; l'Vnisono che fà la Guida nella seconda semibreue delle tre già
nominate, torna al Consequente Quinta sopra la detta terza Semibreue. Nel gra-
do ascendente primieramente la Quinta torna Ottaua, & la Terza torna Sesta; ma di-
poi nel grado discendente l'Vnisono torna Sesta, la Terza uiene Ottaua; & la Quinta
torna Decima. Nel salto di Terza verso l'acuto, l'Vnisono uien Terza, la Terza gra-
ue Vnisona, & la Sesta Ottaua, & la Ottaua torna Duodecima; ma à quello di Terza
verso 'l graue la Sesta torna Duodecima, & la Terza graue uiene Quinta. Nel salto di
Quarta all'insù la Sesta torna Settima, & la Terza uien Quarta; & in quello, ch'è al-
l'in giù, l'Vnisono torna Ottaua, la Terza Decima, & la Quinta Duodecima. Et si
come nel salto di Quinta all'insù l'Ottaua torna Ottaua, la Quinta uiene Quinta, &
la Terza uiene Terza graue; cosi all'in giù la Quinta graue ritorna Quinta acuta. Il
salto di Sesta ascendente fà, che la Sesta venga Quinta, & quel di Sesta discenden-
te fà che l'Vnisono torna Decima. Hauendo adunque il Contrapuntista riguardo à tut-
te queste cose, potrà compor la Guida sopra 'l suo Soggetto di maniera, che 'l Consequen
te la seguiterà senz'alcuno discommodo, come nel sequente essempio si può uedere.
Ma queste Consequenze siano per una parte di quelle, che si possono dimostrar, per
fare à mente sopra un Soggetto qual si uoglia, poi che le maniere sono quasi infinite;
le quali giudico essere à bastanza à i Studiosi di pronto & viuace ingegno; essendo
che da queste maniere ne potranno cauar dell'altre con lo studio, che ui porranno.
Debbe però auertire ciascheduno, che in queste sorti de Contrapunti, ò Compo-
sitioni, con simili osseruanze & oblighi, il Compositore non può à suo piacere li-
mare (dirò cosi) & correggere 'l suo Contrapunto, secondo quelle Regole, che di so-
pra habbiamo mostrato; percioche non è libero; ma è sforzato di por le Consonan-
ze l'una dopo l'altra, secondo che richiede la natura del Soggetto; La onde tali Con-
trapunti, ò Compositioni si possono chiamar veramente Sforzati; & chi non lo
uorrà credere, facendone la proua da se stesso potrà esser chiaro; che in queste co-
se è gran pazzia il volere ostinarsi, & cercar quello, che per uia alcuna mai si potrà
ritrouare. E' ben uero, che colui il quale si esserciterà in simili Contrapunti, po-
trà correggerli con qualche facilità. Hora lasciando da un canto queste maniere de
compositioni, voglio che veniamo à dimostrare alcune sorti de Consequenze dop-
pie, che si fanno à mente senza Soggetto; le quali dico esser de molte maniere; Et
porrò questa per la prima, laquale primamente dà un Contrapunto doppio à Due vo
ci; doue 'l Consequente nel Principale canta dopo la Guida per una Diapente graue,
hauendo fatto una Pausa di lunga, & nella Replica, quel ch'era Consequente diuen-
page 328
 ta Guida, & la Guida consequente, ilquale canta dopo essa Guida per una Diapason
ta Guida, & la Guida consequente, ilquale canta dopo essa Guida per una Diapason acuta, dopo lo spacio di tanto tempo, quanto cantarono prima; cioè, della pausa di
Lunga. La onde si ode un Contrapunto molto diuerso dal primo. Dopoi se 'l si ritor-
nerà à far cantare il Principale, & la Replica con i loro Consequenti dopo le lor Gui-
de per ordine, come prima si fece; haueremo una Doppia consequenza, che si po-
trà cantare à tre uoci insieme; come nel sequente essempio si può udire & uedere.
Ma in questa sorte di doppia Consequenza sopr'ogn'altra cosa si dè osseruare, che
nel Principale non ui sia Sesta per niun modo; ne si dè far, che la Guida passi sot-
to 'l Consequente; ne si dè por mai Terza, & poi Quinta descendendo l'una & l'al-
tro; ne si passa dall'Ottaua alla Quinta per contrarii mouimenti; percioche nella
Replica il Contrapunto non ritornarebbe bene. Et perche in tal sorte de Contra-
punti la Quinta, che si pone nel Principale, ritorna Ottaua nella Replica; però
cotal Quinta non si haurà da continuare molto di lungo. Si debbe etiandio sa-
pere, che quando questa sorte di Consequenza si ristringe à far che 'l Consequente
page 329
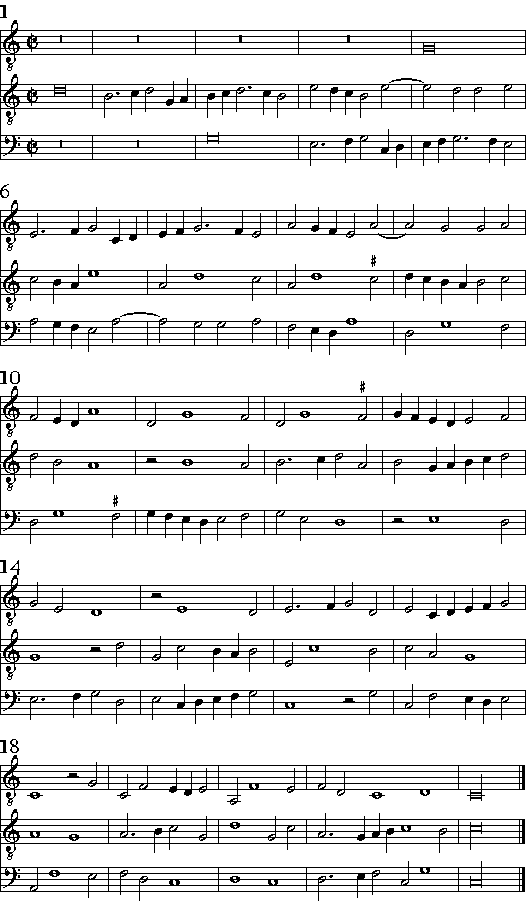 seguiti la Guida per poco spacio di tempo; come sarebbe dire, d'una pausa di Semibre-
seguiti la Guida per poco spacio di tempo; come sarebbe dire, d'una pausa di Semibre-ue come nel seguente essempio si uede oltra quello, che si hà osseruato di sopra, bisogna
 anco auertire, non solamente di non continuare quattro Terze l'una dopo l'altra ascen-
anco auertire, non solamente di non continuare quattro Terze l'una dopo l'altra ascen-dendo, ouer discendenti le parti; percioche non tornarebbono bene, quando cantasse
ro le Guide & li Consequēti insieme; ma che i mouimenti nel discendere siano di Terza,
ò di Quinta; & nellascendere non siano minori de quelli di Quarta. Non si farà Terza
& poi Decima per contrarij mouimenti; & sopra ogn'altra cosa bisogna auertire di non
replicare immediatamente alcun passaggio in Quarta più acuta, il qual passaggio conten
ga tante figure, che siano equiualenti ad un Tempo; cioè, à due Semibreui; & questo
perche nel secondo Consequente ritornano tante Ottaue. Vltimamente, quando si por
rà il Soprano, che sia Guida del Tenore & questo dell'Alto, & siano l'uno all'altro Con-
sequenti; & che l'uno canti dopo l altro per una Pausa di Semibreue; cioè, il Tenore do
po il Soprano, per una Diapason graue, & l'Alto sopra esso Tenore per una pausa simigliā
temente di Semibreue per una Diapente acuta; oueramente sotto esso Soprano dopo
un Tempo, ò pausa di breue, per una Diatessaron graue; ne uerrà una Cantilena co-
me è la sequente.
page 330
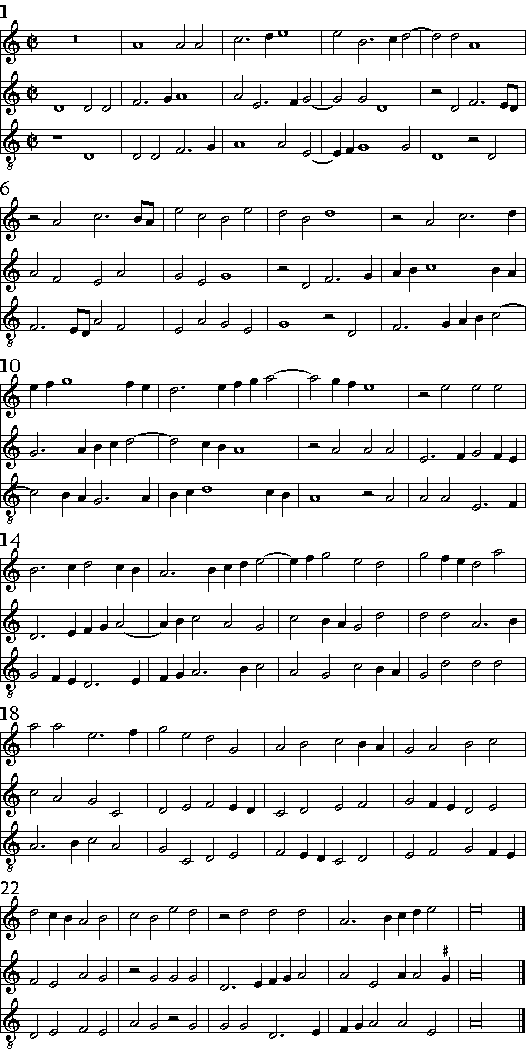 Quando però si osseruarà di non far mai Sesta; ne due Terze, che ascendino, ò discen-
Quando però si osseruarà di non far mai Sesta; ne due Terze, che ascendino, ò discen-dino l'una dopo l'altra; ne di far Sincopa alcuna, nella quale sia alcuna dissonanza. Quel
li gradi, che si osseruano nel modulare, ò Cantare, sono, che si ascende per Terza, ouer
per altro salto maggiore; ma non si discende per minore di quello di Quarta. Et questo
basti intorno à quelli Contrapunti & Consequenze, che si fanno à mente. Non creda
però alcuno, ch'io habbia posto in ciascheduna sorte di esse tutte quelle Regole, che osser
uar si debbono, percioche sarebbe in errore; essendo che solamēte hò posto quelle, che mi
è paruto esser di maggior'importanza, & essentialmente fanno alla natura del Contrapū
to; però colui, il quale si uorrà essercitare in simili maniere di Consequenze & Contra-
punti; dando opera allo studio, potrà ritrouar quello, da che si haura da guardare, &
quel che douerà osseruare, accioche il suo Contrapunto uenga netto, & purgato da mol-
ti errori, i quali possono occorrere, facendo dette sorti di Contrapunto. Si dè però sa-
pere, ch'è impossibile in tutte queste sorti de Contrapunti Doppij, quando sono fatti cō
simili oblighi, di potere osseruar pienamente le Regole date di sopra, come hò detto an
cora; massimamente quando cotali oblighi crescono; essendo che non si può osseruar in
essi la bellezza & il decoro, si quanto alla Modulatione, quanto ancora intorno all'in-
uentione, & il modo di por le Consonanze; percioche è leuata la libertà al Composito-
re, c'hauea nel comporre gli altri senz'alcun obligo; & questo dico, accioche 'l diligen-
te Osseruatore de i nostri Precetti, uedendo alcune cose, che non uengono cosi ben cor
rette, non si marauigli; perche non hò posto qui cotali Compositioni, accioche lunga-
mente, & per sempre s'habbiano da usare; ma si bene alle uolte, quando li tornerà in
proposito, per mostrar la uiuacità del suo ingegno, & la prontezza del suo intelletto
con alcuni, che ad altro non attendono, che à simil cose, & poi nel resto si ritrouano es-
sere nudi, come una pietra. Sono queste maniere ueramente molto ingegnose; percio-
che scoprono, quanto possa fare il Musico, il qual sappia adoperare gli Harmonici nu-
meri; ancora che si oda alle uolte qualche cosa, che sia strana da udire; ma è buono
saper tutte le cose (se fusse possibile) massimamente le necessarie & le utili in ciascun'Ar-
page 331te & in ciascuna Scienza; & non solo queste, che sono buone; ma l'altre ancora quan-
tunque siano triste; l'une per mettere in opera, l'altre poi per sapersi guardare, & seruir-
sene di esse à tempo & luogo conueniente. Et s'alle uolte hò mostrato delle cose, che nō
sono molto buone; hò uoluto in ciò imitare il Filosofo, il quale, hauēdo mostrato il buo
no della Logica & della Filosofia; & mostrato il uero modo d'argumentare; dopo l'hauer
scritto molte cose nell'una & nell'altra facultà; scrisse etiandio i Libri de i Sillogismi falla
ci, ò Soffistici, i quali chiamò Elenchi; non perche s'hauessero da usare; ma accioche
(accadendo) ogn'uno si sapesse guardare da gli intrichi de i Sofisti, che uogliono esser te
nuti dotti, ancora che non siano. Buona cosa è ueramente & ottima il sapere cotali Con
trapunti, & usarli quando torna cōmodo; ma il frequentarli nelle compositioni non lo-
do molto; conciosia che non si può far, ch'essendo 'l Contrapuntista obligato all'osser-
uanza de tante cose, il Contrapunto uenga ad essere in tal maniera elegante & sonoro,
che porga in tutto & per tutto grato piacere all'Vdito.
Quel che si dè osseruare, quando si volesse fare vna Terza parte alla sproueduta
sopra Due altre proposte.Cap. LXIIII.
ria, quando si canta alcuna cantilena à Due uoci, aggiungere alla sproueduta
elegantemente una Terza parte di maniera, che fanno udire il concento à Tre
voci. Onde io per non lasciare alcuna cosa indietro, che sia utile & di qualche
honore in quest'Arte; hò deliberato; oltra l'hauer mostrato il modo, che si hà da tene-
re nel comporre à Tre uoci diuerse sorti de Contrapunti; dimostrare il modo, che si ha-
urà da tenere, uolendosi essercitare nel cantare cotal parte in cotal maniera. Et questa
impresa hò pigliato uolentieri; conciosia ch'alle uolte hò udito alcuni, non dirò sciocchi,
ma presontuosi à fatto & arroganti, che per dar'ad intendere al uolgo, che siano di molto
ualore; si pongono à uolere etiandio passar più oltra; imperoche non solamente si conten
tano di uoler fare cotal Parte; ma di più sopra qual si uoglia altra cantilena se ben fusse à
Dodici uoci ne uogliono aggiungere una Terzadecima; la qual fanno in questo modo,
facendo solamente Contrapunto sopra 'l Basso senza uedere alcuna dell'altre parti; &
spesso si uagliono d'una loro Regola sciocca, la quale hanno per un bel secreto, di por
spesso la parte, ch'aggiungono lontana dal Basso per una Terza, oueramente per una
Decima; & per tal modo danno ad intendere à i sciocchi, come loro; & che non intendo
no più oltra, che fanno miracoli. Ma quanto ciò sia ben fatto, lasciarò giudicare à cia-
scuno, c'hà qualche giudicio; essendo che quando queste lor Parti aggiunte si uedessero
scritte nel modo, che le cantano; oltra che da i periti della Musica si odono le cose, che
fanno contra l'arte; se ben non sono in scrittura; si scoprirebbono mille errori, che fan
no contra le Regole communi, & si uederebbono esser piene d'infinite dissonanze. Ho-
ra per uenire al mio primo intendimento dico: Dopo che ciascuno si hauerà ottimamen
te essercitato nella compositione de i mostrati Contrapūti, & uorrà aggiungere alla spro
ueduta cotal parte; sarà dibisogno, che lui dia opera separatamente per qualche giorno
à tal cosa in questa maniera. Proposto che lui si haurà alcuna Cantilena composta à
due uoci, alla quale uorrà aggiungere la Terza parte, debbe con diligenza por mente à
i passaggi & alle modulationi, che fanno insieme le due Parti proposte; acciò possa com-
prendere, in che maniera il loro Contrapunto sia ordinato, & possa dopoi aggiunger, sen-
z'alcun'errore, quella parte, che lui uorrà aggiungere. Et debbe per ogni modo tenere
quest'ordine; perche non è sufficiente (come s'auisano molti, che non sanno) una parte so
la, à mostrar'il Contrapunto, che s'hà da aggiungere con la Terza parte; massimamente
potendosene aggiungere molti & uariati sopra un'istesso Soggetto. Hauendo adunque il
page 332
 page 333
page 333 Contrapuntista tal riguardo, potrà ottimamente accommodare 'l suo Contrapunto, in
Contrapuntista tal riguardo, potrà ottimamente accommodare 'l suo Contrapunto, in quella maniera, che li parerà meglio, & li tornerà più commodo; tanto uolendo aggiun
gere una parte acuta sopra la parte graue delle due proposte; quanto uolendo far sotto di
esse una parte graue. E' ben uero, che 'l porre alle uolte la parte, che si aggiunge distante
per una Decima, ouer per una Terza dall'una delle due, torna molto commodo; ma bi-
sogna auertire, che quando le parte proposte fussero per una Terza lontane l'una dallal-
tra, & quella che s'aggiunge cantasse per una Decima, tra l'aggiunta & l'una delle due, che
sarebbe la graue; quando la parte s'aggiungesse nell'acuto; ouer sarebbe l'acuta, quando
l'aggiunta fusse più graue; sempre si udirebbe l'Ottaua; & cosi dico, quando fussero di-
stanti per una Decima, & l'aggiunta cantasse per una Terza; onde se le Due proposte
hauessero molte Terze, ò Decime l'una dopo l'altra; come si sogliono porre alle uolte, s'
udirebbono con l'aggiunto tante Ottaue senza mezo alcuno, quante erano le Terze, ò
le Decime contenute tra le parti; & per tal maniera si uerrebbe a far errore. Però è cosa
buona, anzi necessaria il uedere il Contrapunto delle Due proposte, per potere schiuare
gli errori, che potessero occorrere; percioche; quando si facesse altramente, sarebbe im-
possibile di far cosa buona, s'almen non s'hauesse alla memoria ciascuna delle due par-
ti della Cantilena proposta. Et perche può occorrere d'accommodare, ouero aggiunge-
re tal parte in due maniere; Prima ad alcune cantilene, che non saranno composte secon
do gli auertimenti, ò Regole date; dopoi ad alcune, che saranno ordinate secondo i mo-
di mostrati; però il Contrapuntista non sarà obligato cosi strettamente d'osseruare i Pre-
cetti dati di sopra, nel fare la Terza parte sopra quelle, che saranno composte senza i da
ti auertimenti; ancora che sarà sempre lodeuole, quando potrà fare, che tal parte aggiun
ta sia posta con quelle conditioni, che si ricerca in ciascuna buona cōpositione. Ma quan-
do la Cantilena sarà composta regolatamente, debbe per ogni modo star nell'osseruan-
za de i mostrati precetti, più che puote; percioche è il douere. Ma accioche si possa com
prendere il modo, che si dè tenere in un tal negotio, hò uoluto prima aggiungere due
page 334
 page 335
page 335 Terze parti uariate l'una dall'altra; ad una compositione de due uoci di Giosquino, che
Terze parti uariate l'una dall'altra; ad una compositione de due uoci di Giosquino, che si troua nel Canto Benedicta es coelorum Regina; à sei uoci; & dopoi n'hò aggiunto due al-
tre ad una leggiadra compositione d'Adriano, fatta pure à due uoci; le quali, dopoi che
saranno state uedute & essaminate, si potrà uedere il modo, che si haurà à tenere uolen-
do aggiungere tal parte in alcun'altra compositione, composta pure à Due uoci. Si deb-
page 336be però auertire, che se le parti aggiunte alcune uolte procedessero per alcuni mouimen
ti alquanto lontani; questo sarà soppportabile, per la difficultà, che si troua nell'accōmodar
tal parte alla modulatione continua della cantilena; essendo che, altro è il Cōporre insie-
me tutte le parti; & altro è aggiūgere à Due parti la Terza, ch'è cosa molto difficile, & da
Huomo consumato nella Musica; & è cosa molto lodeuole, quando s'aggiunge, che stia
bene. Et quello, c'hò detto dell'aggiungere una parte à Due, si può anco intendere, quan
do se ne uolesse aggiungere una a Tre, & anco à Quattro; percioche non è cosa impos-
sibile, se ben è difficile. E' ben uero, che quanto più sarà il numero delle Parti, tanto
più difficultà apporterà à colui, che uorrà aggiungere cotale Parte. Ma bisogna sopra il
tutto tre cose; Buona memoria, & Lunga essercitatione; & Buon occhio per potere rac
cogliere con prestezza le parti della Cantilena, sopra le quali s'haurà da aggiungere co-
tal Parte: Senza le quali cose nulla, ò poco almeno si farebbe.
Quel che bisogna osseruare intorno le Compositioni de Quattro, ò de più uoci.
Cap. LXV.
à Tre uoci; è conueneuole, che hormai mostriamo quelle cose, che concorro-
no nelle cantilene, che si compongono à Quattro, & anco à più uoci. Però è
d'auertire, che si dè osseruare in queste Compositioni tutte quelle cose, che fu
rono osseruate nell'altre. Onde la maggior difficultà, che possa occorrere è, d'accommo
dar le parti della cantilena in tal maniera, che l'una dia luogo all'altra, che siano facili da
cantare, & habbiano bello, regolato, & elegante procedere. Queste cose non si possono
cosi facilmente in carte insegnare; la onde si lasciano alla discretione, & al giudicio del
Compositore. Voglio ben dire, che suole intrauenir'al Musico quello, che intrauiene an
co al Medico; che si come questo non può hauer cognitione perfetta della Medicina per
hauer solamēte studiato Hipocrate, Galeno, Auicēna, & molti altri eccellētissimi Scritto
ri; se nō dopoi, che hauerà pratticato con altri Medici, & spesse uolte ragionato & discorso
seco molte cose appartenenti à tal'Arte; & toccato molti Polsi, ueduto gli escrementi, &
fatto mille esperienze; cosi quello non potrà esser perfetto, per hauer letto, & riletto mol
ti libri; ma li sarà dibisogno alla fine d'intender bē quello, c'hò mostrato di sopra, & mol
t'altre cose, che son per mostrare; che si riduchi alle uolte à ragionar con alcuno, c'hab-
bia cognitione della Prattica, ò Contrapunto; accioche se hauesse pigliato alcun uitio,
& intendesse qualche cosa al contrario di quello, che si dee intendere; si possa corregge-
re; conciosia che 'l Vitio preso dal principio si conuerte in habito, quando molto si conti
nua; ilquale habito si può difficilmente lasciare; come dimostra Horatio, dicendo;Epist lib.
1. ad Loliū.
Quo Semel est imbuta recens, seruabit odoremEt se la Speculatiua senza la Prattica (com'altre uolte hò detto) ual poco; atteso che la
Testa diu.
Musica non consiste solamente nella Speculatiua; cosi questa senza la prima è ueramente
imperfetta. Et questo è manifesto; conciosia c'hauendo uoluto alcuni Theorici trattar le
cose della Musica; per non hauer'hauuto buona cognitione della Prattica, hāno detto mil
le chiachiere, & commesso mille errori. Simigliantemente alcuni, che si hanno uoluto
gouernare con la sola Prattica, senza conoscere alcuna ragione; hanno fatto nelle loro
compositioni mille & mille pazzie, senza punto auedersene di cosa alcuna. Ma per ritor
nare al nostro proposito, dico; che uolendo dar principio alle Compositioni nominate
di sopra; primieramente si ritrouerà il Soggetto; dopoi ritrouato, si potra incomincia-
re 'l Contrapunto da quella parte, che tornarà più commodo. La onde poniamo, che si
uolesse dar principio alla Cantilena con la parte del Basso, subito il Compositore potrà
page 337conoscere il luogo del Contralto, del Soprano, & quello del Tenore. Cosi ancora uo-
lendo dar principio per il mezo di qualunque altra parte; come per il Tenore, ò per il
Contr'alto; saprà i luoghi dell'altre parti per ordine, reggendosi secondo 'l modo mostra
to nella Tauola; osseruando anche quelle Regole, che di sopra in molti luoghi hò dichia
rato, quando fù ragionato intorno il modo di comporre à Due & à Tre uoci. Per la qual
cosa osseruando il tutto, potrà hauere il desiderato fine, & acquistarsi honore; al quale
spesse fiate ne conseguita grande utile ancora. Ma accioche si uegga 'l modo, che si ha-
urà da tenere, & il procedere in simili compositioni; ancora che siano infiniti gli es-
sempi à Quattro uoci, composti da molti compositori eccellenti; porrò solamente
due Compositioni sopra 'l Canto fermo, dalle quali (poi che si haueranno essaminate) si
potrà hauer qualche lume, per poter seguire più oltra di bene in meglio, & porsi à
maggiori imprese, & comporre altre cantilene di fantasia; preparandosi il Sogget-
to, ò pigliando alcun'altro Canto fermo, ouer qualunque altra parte, come pare-
rà meglio al Compositore. Et benche in ogni compositione perfetta Quattro parti sola-
mente siano basteuoli; come il Soprano, l'Alto, il Tenore, & il Basso; tuttauia quando
si uorrà passar più oltra & hauer maggior numero de Parti, bastarà solamente raddoppia
re (com'hò detto altroueSupr. c. 58.) una delle Quattro nominate; & cotal parte aggiunta si chia-
mera medesimamente Soprano, ò Tenore, ouer Alto, ò Basso; secondo la parte, che si
hauerà doppiata; aggiungendoli questa parola Secondo, ò Terzo, secondo 'l numero de
quelle parti, che si troueranno aggiunte. Et le chorde estreme della Parte aggiun-
ta, si fanno equali à quelle della Parte, che uiene raddoppiata; ancora che non sarebbe
errore, quando non fussero equali, & le chorde della parte aggiunta si estendessero più
uerso 'l graue, ò uerso l'acuto, che quelle della raddoppiata; cioè, della parte principa-
le. Si debbe però auertire, ch'alle uolte si costuma di compor la cantilena senza 'l Sopra
no, nel luogo del quale si pone un Contr'alto, alquanto più acuto del principale per una
Terza più, ò meno, che importa poco. Il medesimo si fà, lasciando il Soprano & l'Alto,
componendo con tre Tenori, & un Basso; oueramente con tre Bassi & un Tenore; & al
le uolte con quattro Bassi, & ad altro modo anco, come torna più commodo; ilqual mo-
do di comporre si chiama à Voci mutate, ouer'à Voci pari. Si compone anche con due
Soprani & un Contr'alto, ouer'un Tenore & il Basso; alle uolte con tre Soprani & un
Basso; & tal fiata con quattro Soprani, tanto à quattro uoci, quanto à cinque, & piu oltra;
sēpre aggiungendo quelle parti, che fanno dibisogno; come si uede ogni giorno nelle mo
derne compositioni. Ma questa maniera di comporre; ancora che le parti si uenghino à
molteplicare & accommodare altramente di quello, che si fà nell'altre; non fà però uarie
tà alcuna di concento; cioè, non partorisce uariatione d'accordi, oltra quelli che nel
Cap. 58. di sopra hò mostrato. E' ben uero, che si troua tal differenza tra le prime &
queste seconde compositioni; che essendo in quelle il campo piu largo; cioè, piu lontana
la parte graue dalla parte acuta di tutto il concento, in questo luogo è piu ristretto; per-
cioche gli estremi delle parti graui & dell'acute insieme si conchiudono commodamente
tra Quindeci Chorde al più, & meno anco, secondo che fà dibisogno; & in quelle si
conchiudono in Venti; come nella Quarta parte uederemo.Cap. 31.
page 338
 page 339
page 339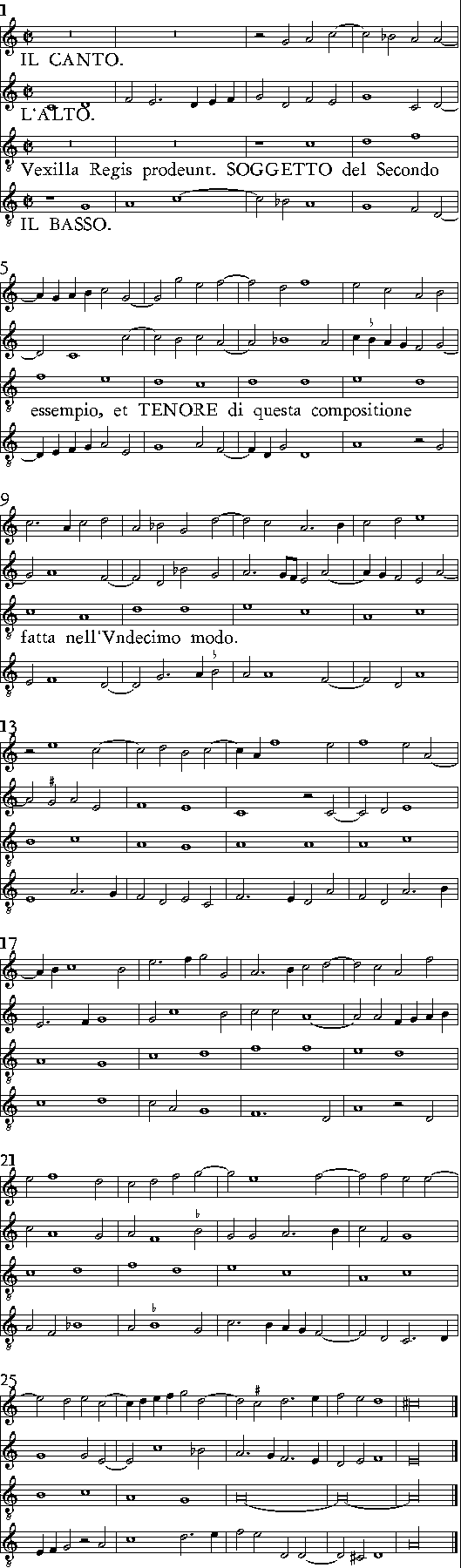 page 340
page 340Alcuni auertimenti intorno le Compositioni, che si fanno à più di
Tre voci.Cap. LXVI.
troue, che si debba sforzare di por le parti della cantilena, che procedino per
mouimenti contrarij; che nelle Compositioni de più uoci, questa Regola s'in-
tenderà esser'osseruata, quando farà, ch'almeno vna delle nominate parti ascē
di, ò discendi per contrarij mouimenti; imperoche se 'l si uolesse osseruar cotal Regola in
tutte le parti; questo, se non fusse impossibile, sarebbe almen difficile. Debbe anco auer
tire, ch'in simili Compositioni, quando si porrà alcuna figura sincopata, nella quale si tro
ui la Dissonanza nella sua seconda parte; di por tutte l'altre Parti della Compositione, sia
no quante si uoglino, ch'accordino tra loro; percioche (come si è detto altroueSup. c. 42.) la Dis-
sonanza posta nella sincopa; per molte ragioni non è quasi compresa dal senso; Et se pu-
re in alcuna parte dalla Dissonanza posta in tal maniera è offeso, non debbono l'altre par-
ti esser tra loro dissonanti; acciò non offendino doppiamente. Onde quando si porrà la
seconda parte della figura sincopata dissonante; quelle parti, che percuoteranno insieme
sopra quella parte dissonante, debbono esser tra loro consonanti. Quando adunque si
trouerà la Dissonanza posta in tal maniera, allora potremo porre Quattro parti l'una dal
l'altra distanti per una Terza, tra le quali non si udirà l'Ottaua; come qui si uede.
 Et perche accaderà alle uolte di compor sopra alcune Parole, le quali ricercano l'Harmo
Et perche accaderà alle uolte di compor sopra alcune Parole, le quali ricercano l'Harmonia alquanto dura & aspera; acciò si uenga con gli effetti (quanto può fare il Musico)
ad imitar'il Soggetto contenuto nell'Orattione; però, quando bisognarà usar simi-
li durezze, allora si potranno porre le Seste, nelle quali siano le figure d'alquan-
to ualore; come de Breui & de Semibreui mescolate; oueramente si porranno le
Dissonanze tra loro, che siano ordinate secondo le Regole & modi mostrati di so-
pra; & si hauerà il proposito; come auerrebbe ponendo la Quarta, ouer l'Vnde-
cima nella Sincopa; come ne i sottoposti essempi si può uedere. Accascherà alle
uolte, che nella prima, ò nella seconda parte della Battuta si troueranno due Parti so-
pra una medesima chorda Vnisone; ouero si troueranno in un'istesso tempo esser lontane
l'una dall'altra, per una Diapason; dico, se bene tali Parti ascendessero, ò discendes-
sero dopoi per un sol grado, & per più gradi ancora, & toccassero un'istessa chorda:
page 341
 pur che ascendessero, ò discendessero una dopo l'altra; & che quella, che sarà la prima
pur che ascendessero, ò discendessero una dopo l'altra; & che quella, che sarà la prima à toccar la seconda chorda, non aspetti l'altra parte; ma subito muti luogo; hauendo la
seconda primieramente una Pausa, che sia di ualore della figura posta sopra la seconda
chorda; se ben l'una & l'altra di queste due parti toccassero cotal chorda; che mai si potrà
con uerità dire, che tra loro siano fatti due Vnisoni, ouer due Ottaue. Et se ben hò già
detto nel Cap. 48. che la Pausa, ò la Dissonanza posta tra due Consonanze perfette di
un'istessa Specie, che ascendino, ò discendino, non è atta à far uarietà alcuna di concen
to; & non fà, che elle siano senz'alcun mezo; dico hora, che iui mostrai le Figure, che
fanno il Contrapunto, esser poste in altra maniera, di quello, che sono poste in simili
Contrapunti; percioche ueramente allora si fanno due Vnisoni, ò due Ottaue, quando
le parti ascendono, ò discendino, insieme senza esser tramezate d'alcuna Pausa; ouer quā-
do dopo la Pausa, l'una delle Parti casca sopra l'altra, senz'alcun mezo. Quando adun-
que s'interpongono le Pause, & l'una Parte fugge, auanti che l'altra arriui alla già toccata
chorda, non s'intendono, ne sono, ne si potrà mai dire per alcun modo, che siano poste
contr'alcune delle date Regole; come qui sotto in essempio si uede.
 Il perche quando si porranno in tal maniera, si potranno sempre usare in ciascuna com-
Il perche quando si porranno in tal maniera, si potranno sempre usare in ciascuna com-positione di Quattro, di Cinque, ò di qual'altro numero si uoglia de uoci. Ne si potrà
anco dire; se ben quello, c'hò detto nel Cap. 48. pare che sia contrario à questo; che due
parti distanti l'una dall'altra per una Diapente ascendendo, ouer discendendo insieme per
grado, faccino due Quinte; quando l'una di esse haurà la Pausa inanti la seconda figu-
ra; & un'altra parte del Contrapunto farà Sesta nel luogo della Pausa, sopra la se-
conda figura di quella parte, che si muouerà senza pausa; come qui si uede tra la
 page 342Quarta & la Quinta figura posta nel Basso, con la parte del Tenore, & quella dell'Alto.
page 342Quarta & la Quinta figura posta nel Basso, con la parte del Tenore, & quella dell'Alto. Et questo ch'io dico in questo essempio, uoglio che s'intenda in altri simili; che potran-
no occorrere; percioche allora ciascun potrà hauer da quello, che si è detto, piena reso
lutione; La onde non mi estenderò più oltra, per non perder tempo. Qualunque uolta
etiandio occorrerà di uoler comporre alcuna cantilena à Cinque, ouer'à Sei, oueramē
te à più uoci; si potrà osseruar quello, che da molti Musici celebratissimi è osseruato; con
ciosia che prima pigliano alle uolte per Soggetto un Tenore di Canto fermo, & dopoi l'
accommodano con uarie figure, come li tornaua più commodo; & fondano la Composi
tione sopra tal Tenore, & fanno cantar le Parti à quel modo, che li tornano meglio, di
maniera, che facciano buona Harmonia; usando di porle in Consequenza l'una con l'al
tra; ouer di fare, che l'una imita l'altra, nel modo, c'hò mostrato di sopraSupra cap.
54. & 55.. Il che si può
uedere, uolendo di ciò qualche essempio, in più Canti già composti d'Adriano; come
in quello, che incomincia; Nil postquam sacrum, à Sei uoci; & in quelli; Victor, io salue; &
Inclyte sforciadum; composti à Cinque uoci; & in molt'altri fatti d'altri Compositori.
ti in Consequenza; & dopoi sopra di quelle fanno l'altre; & di ciò si può hauer l'essem-
pio ne i Canti Verbum supernum; sopra 'l canto di, O salutaris hostia; & in quello ch'inco-
mincia, Praeter rerum seriem; composti dal medesimo Adriano à Sette uoci. Nella mede
sima maniera si ritrouano i Canti; Miserere mei Deus, miserere mei, con tre parti, fatto so-
pra l'Antiphona Ne reminiscaris Domine: & il Canto Misereris omnium Domine, fatto so-
pra due Soggetti; cioè, sopra la sudetta Antiphona Ne reminiscaris; & sopra un Tenore,
Miserere mei Deus; i quali composi à Sei uoci. Vi è anco la Oratione Dominicale, Pater
noster, con la Salutatione Angelica Aue Maria, ch'io composi à Sette uoci. Debbe però
auertire il compositore, che in quelle Consequenze, le quali si fanno sopra cotali Teno-
ri, le parti possono esser tra loro distanti per Terza, Quarta, Quinta, Sesta, & per altre
simili Consonanze; ma di raro si pone la Quarta, dopo la quale segua immediatamente
la Sesta; ò per il contrario. Similmente rare uolte si pongono due Seste; percioche sono
difficili d'accompagnare con l'altre parti. Tali Consequenze si sogliono & si debbono ue
ramente comporre, prima che si componghino l'altre parti; ma bisogna hauer sempre ri-
guardo nel comporle, in qual maniera le parti, che si hauranno d'aggiungere, si possino
accommodar nella cantilena; accioche non si habbia doppia fatica nel comporre tutto
il corpo della Compositione, quando uenisse alcuna cosa di sinistro in tali Consequenze.
Et se nell'aggiunger l'altre parti, si trouasse qualche discommodo, ouer che per mutar le
parti del Canto fermo posto in tali Consequenze, facesse miglior'effetto; allora non
dè il Compositore perdonare à fatica; ma debbe mutar proposito, aggiungendo, ò le-
uando alle dette Parti quel, che farà dibisogno; Il che sarà facile, quando le parti saran
no state ben ordinate da principio. Ma si dè auertire, che le Parti che cantano in Con-
sequenza, non si possono sempre ordinare in tal maniera, che 'l Consequente canti
tutto quello, che canta la Guida; onde è necessario, che seguendo la Guida il can-
tare in fino al fine, il Consequente si uenga à fermar poco lontano; come si può
vedere in molte cantilene composte à tal guisa; & massimamente in quelli Canti,
Veni sancte Spiritus d'Adriano composto à Sei uoci, & O beatum Pontificem, ch'io
composi ad imitatione del Canto fermo à Cinque uoci. Si debbe usare etiandio
tal discretione nell'accommodar le parti; che quella che canta nel suo luogo pro-
prio il Canto fermo, dopo l'hauer cantato tutto quello, che fà dibisogno, ò sia Can-
to fermo, ouer sua Imitatione; quel che haurà da cantare più oltra, di quello, che
dè cantare 'l Consequente, sia almen quasi replicato. Il Consequente, poi debb'esse-
re ordinato in tal modo, che canti & finisca tutto 'l Canto fermo, & non fuori del
suo ordine. De questi si potrà hauer molti essempi accommodati; come sarebbe il Can
to: Salue regina misericordiae; & quello, che incomincia; Litigabant Iudaei, sopra 'l
canto fermo, Comedite pinguia; i quali composi à Sei uoci. Si potrà anco pi-
page 343gliare una, ò due parti de Canto fermo, & ordinar sopra quelle molte parti in Conse-
quenza continua, ò legata; come uogliamo dire; come fece Adriano nella Cantilena;
Salue Sancta parens, à Sei uoci. Potremo simigliantemente pigliare un Tenore, & ordi-
narlo con un'altra parte in Consequenza in tal maniera, che uolendo replicar le parti,
facino una seconda parte, di modo, che quella che prima fù la Guida, diuenti il Conse-
quente; & similmente quella, che era 'l Consequente diuenti la Guida. Di questa ma-
niera si trouano molte compositioni, tra le quali è il Canto d'Adriano; Venator lepores,
sopra 'l Canto fermo, Argentum & aurum non est mihi; & il Canto in principio Deus ante-
quàm terram faceret, sopra quel Canto fermo, Omnis sapientia; il quale composi da canta
re à Sei uoci; come si canta etiandio il sopradetto. Vsano etiandio alle uolte i Prattici,
imitando due, ò più Tenori diuersi de uarij canti Ecclesiastici, comporre alcune cantile
ne à più uoci, di maniera, che l'una delle parti uēga ad imitar l'uno & l'altra l'altro; come
fece Giosquino, il quale in cotal maniera in una compositione di Sei uoci ne imitò Quat-
tro; cioè, Alma redemptoris mater: Aue regina coelorum; Inuiolata, integra, & casta; & Re-
gina Coeli; & Gomberto in una Cantilena à Quattro uoci, ne imitò pur Quattro; cioè,
Salue regina; Alma redemptoris; Inuiolata, & Aue regina coelorum; come si può uedere; ilche
potrà etiandio far ciascuno, imitandone diuerse altre; percioche ueramente cotal cosa
è molto lodeuole, per esser ingegnosa. Si potrà anco pigliar due Tenori di canto fermo,
& accommodarli, come torna meglio alla cantilena, & sopra di essi comporre l'altre par
ti; come fece Costanzo Festa nel Canto Exaltabo te Domine; à Sei Voci, ch'accōmodò l'
Antifona; Cum iucunditatem, & il primo uerso del Cantico di Zaccaria: Benedictus Domi-
nus Deus Istrael. Potremo etiandio (com'han fatto de gli altri) por due parti della cantile
na, lasciando da parte 'l canto fermo, in Consequenza; oueramente porle legate insie-
me con la Imitatione; delche si può hauer l'essempio nel Canto; Ecce tu pulchra es, ilqua
le composi à Cinque uoci. Si potrebbe anche comporre le Cantilene facendo le parti rad
doppiate; cioè, ponendo le parti à due à due in Consequenza, ouer nella Imitatione,
come fece Motone nel Canto: Nesciens mater; & Gomberto nel Canto Inuiolata, integra
& casta, l'uno, & l'altro composto à Otto uoci; & Adriano il già nominato Canto: Sal-
ue sancta parens, & la Canzone Sur l'herbe brunette, che l'una & l'altra si cantano à Sei uo-
ci. Oltra di questo si potrà comporre à Quattro à Cinque & à più uoci in mille modi; di
rò cosi; ponendo le parti hora in Consequenza, hora nella Imitatione; oue si ritrouerà
esser tanti i Consequenti, quante saranno le Guide; come si può uedere in quel Canto
d'Adriano: Sancta immaculata virginitas; & in una sua Canzone: Petite camusete, à Quat-
tro uoci. Sarà anco lodeuole il comporre Quattro parti sopra una, ponendone alcune
in Consequenza, & alcune nella Imitatione; come fece P. della Rue nella messa: O sa-
lutaris hostia; & Adriano anche, con molta leggiadria, nella Messa, Mente tota; delle qua
li l'una & l'altra si troua à Quattro uoci. Infiniti sono i modi del cōporre in simili manie
re, & difficile, anzi impossibile sarebbe il uoler raccontare d'una in una le dispositioni del
le parti, & dell'ordine tenuto; ma per non esser lungo farò fine; massimamente perche
ogni giorno si ueggono molt'altre Compositioni, composte dall'Eccellentissimo Adria-
no Vuillaert; le quali, oltra che sono piene de mille belle & leggiadre Inuentioni; sono
anche uaghe, dottamente & elegantemente composte. Infinite altre etiandio ue ne so-
no, composte da altri Eccellentissimi Musici; delle quali molte se ne ritrouano in un Li-
bretto, che già fù stampato in Vinegia da Andrea antico in ottauo foglio; le quali uedu
te, potranno esser di grande aiuto per ritrouar'altre simili inuentioni; percioche da quel
le, si hauerà un tal lume, che ciascun dopoi si potrà porre à maggiori & più difficile im-
prese & honorate. Non mancarebbono ueramente oltra di queste mille leggiadre inuen
tioni, che si potrebbono fare; come sarebbe il uoler cōporre Tre parti sopra unTenore di
canto fermo in questa maniera; che due in Cōsequēza si seguitino per mouimēti contra-
rij, & laltra sia cōposta secondo 'l uolere del Cōpositore; come qui in essempio si ueggono.
page 344
 Et comporre etiandio Quattro parti in tal maniera, che 'l Soprano co 'l Basso, & il Con-
Et comporre etiandio Quattro parti in tal maniera, che 'l Soprano co 'l Basso, & il Con-tralto co 'l Tenore cantino in Consequenza per contrarij mouimenti; come nell'essem-
pio posto qui di sotto si uede.
 Ma si debbe auertire, di non por mai l'Alto col Soprano, che facino Quarta; percio-
Ma si debbe auertire, di non por mai l'Alto col Soprano, che facino Quarta; percio-che l'altre parti non tornarebbono bene. Quattro simili compose etiandio l'Eccel-
lentissimo Adriano di maniera, che quando si è arriuato al fine, di nuouo si può incomin
ciare dal principio, & ritornar quante fiate si uuole; come dimostrano i Ritornelli posti
nel fine di ciascuna di esse; & nell'essempio dal quale si potrà comprendere, come elle
si componghino.
 Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osser-
Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osser-ua, di non comporre il Canto di alcuna Messa, se non sopra qualche Soggetto; il mede
simo si farà etiandio per l'auenire. Ma bisogna sapere, che tal Soggetto può essere fat-
to dal Compositore; come fece Giosquino i Tenori La, sol, fa, re mi; & Her-
page 346cules Dux Ferrariae, cauati dalle uocali de cotali parole; sopra i quali Tenori ei compose
il canto de due Messe à Quattro uoci, che sono degne d'essere udite; Oueramente tal Sog
getto lo piglia da altri; percioche si piglia alcun Tenore di Canto fermo; come fece il me
desimo Giosquino, quando compose il canto delle Messe Pange lingua, Gaudeamus, & Aue
maris stella, & Brumello in quello de i Defunti, tutte à Quattro uoci; percioche molto si
dilettauano di comporre sopra i Canti fermi, sopra i quali se ne uedono infinite altre, che
sarebbe impossibile à numerarle. Quando adunque uorremo comporre il canto di alcu-
na Messa, ritrouaremo prima il Soggetto, sia di Canto fermo, ò qualche altro canto di
Musica figurata, come si usa, oueramente altro simile; & dopoi cercaremo d'accommo-
darlo à diuersi modi; ritrouando noue inuentioni & belle fantasie, imitando gli Antichi;
pigliando l'essempio da quella Messa, che fece P. Molù; Alma redemptoris, la quale com-
pose in tal maniera, che si può cantar con le Pause & senza, & torna molto bene; & da
quella, che fece Giouanni Occheghen, maestro del sudetto Giosquino, la qual compose di maniera, che si poteua cantare sotto diuersi tempi & diuerse Prolationi, che faceua buō
effetto. Accaderà di cōporre alle uolte alcuni Salmi in una maniera, che si chiama Choro
spezzato, i quali spesse uolte si sogliono cantare in Venetia ne i Vesperi & altre hore delle
feste solenni; & sono ordinati & diuisi in due, ò più Chori, ne i quali cantano Quattro
ò più uoci; & li chori si cantano hora uno hora l'altro à uicenda; & alcune uolte (secon-
do 'l proposito) tutti insieme; massimamente nel fine; il che stà molto bene. Et perche
cotali Chori si pongono alquanto lontani l'un dall'altro; però auertirà il Compositore
(acciò non si odi dissonanza in alcun di loro tra le parti) di fare in tal maniera la compo-
sitione, che ogni Choro sia consonante; cioè, che le parti d'un Choro siano ordinate in
tal modo, quanto fussero composte à Quattro uoci semplici, senza considerar gli altri
Chori; hauendo però riguardo nel por le parti, che tra loro insiememente accordino, &
non ui sia alcuna dissonanza; percioche composti i Chori in cotal maniera, ciascun da per
sè si potrà cantare, che non si udirà cosa alcuna, che offendi l'Vdito. Questo auertimen-
to non è da sprezzare; percioche è di gran commodo; & fù ritrouato dall'Eccellentissi-
mo Adriano. Et benche si rendi alquanto difficile, non si debbe però schiuar la fatica;
percioche è cosa molto lodeuole & virtuosa; & tal difficultà si sarà alquanto più facile,
quando si hauerà essaminato le dotte compositioni di esso Adriano; come sono questi Sal
mi: Confitebor tibi domine in toto corde meo in consilio iustorum. Laudate pueri dominum: Lau
da Ierusalem dominum: Deprofundis: Memento domine Dauid, & molti altri; tra i quali sono i
Salmi; Dixit Dominus Domino meo: Laudate pueri dominum: Laudate Dominum omnes gen-
tes: Lauda anima mea Dominum; Laudate Dominum quoniam bonus est Psalmus. Lauda Ierusa-
lem Dominum; & il Cantico della Beata Vergine; Magnificat anima mea Dominum, ilquale
composi già molt'anni fà à tre Chori, per uso della Cappella del Famosissimo Tempio di
S. Marco; della quale da questi Sig. Illustriss. già uentiquattro anni sono, mi fù dato il go-
uerno. Queste compositioni vedute & essaminate saranno di gran giouamento à tutti colo
ro, che si dilettaranno di comporre in tal maniera; conciosiache ritrouerāno, che i Bassi de i
Chori si pongono tra loro sempre distanti; per Vnisoni, ouer per Ottaua; ancora ch'alcu-
ne uolte si pongano in Terza; ma non si pongono però in Quinta; se non sopra la parte del
Tenore; percioche altramente torna molto incommodo; & oltra la difficultà che nasce;
è impossibile di far cosa, che torni bene secondo il proposito; essendo che si ode sempre
nel cantare qualche asprezza. Et questa osseruanza uien'ad essere molto commoda à i
Compositori; percioche lieua à loro la difficultà di far cantar le parti de i Chori, che
tra loro non si ritroua dissonanza. Lodarei però, ne haurei per inconueniente quello, che
molte fiate hò fatto anch'io; che quando si passasse 'l numero de due chori, & anco
nell'istessi due chori, che i Bassi d'un Choro cantasse anco la parte dell'altro; percioche
ne seguitarebbe, che 'l Canto tutto & l'Harmonia tutta, hauerebbe una base, & un fon
damento, dirò cosi, che la sustentarebbe di maniera, che la farebbe comparere altra
tanto; essendoche quella parte che è raddoppiata si uiene più à udire, che se la si cantas-
page 347se semplicemente da una uoce; come ben lo dimostra Aristotele nel Problema 2. della
19. Settione. Oltra di questo il Compositore potrebbe uariare l'Harmonia, piu che non si
fà; percioche ponendo i Bassi differenti di modulatione, non si può far molta uarietà d'
Harmonia nelle Compositioni. Et chiunque prouerà cotesta cosa, potrà conoscer l'uti-
le, ch'ella potrà apportare. Nè però alcuno si dee conturbar di questo; percioche se 'l bi
sognasse hauere cotal rispetto; per dire che canteranno quest'istesso l'una parte che can-
teranno l'altre parti; non bisognerebbe anco che nelle capelle, ne i chori, non ui fusse al-
tro che una uoce per parte, nel cantar le compositioni che iui si cantano. Hora per conclu
der questo ragionamento, dico; che hauendo il Compositore intese tutte queste cose, dè
auertire anco à quello ch'è obligato; poi ch'è legge osseruata da gli Antichi; di terminare
il numero delle Figure di ciascuna sua compositione, secondo che ricercano il Tempo, il
Modo, & la Prolatione, sotto i quali Accidenti componerà la cantilena. Er perche simi
li accidenti erano già in grande consideratione, & anco appresso d'alcuni sono in uso;
però accioche ciascun habbia cognitione di simil cose, uerrò à ragionar di quelle;
che sono più bisognose; lasciando quelle, che sono superstitiose, & fanno poco al pro-
posito; & incomincierò dal Tempo, come da quello, ch'è (secondo 'l mio parere)
più uniuersale, & primo d'ogn'altro accidente.
Del Tempo, del Modo, & della Prolatione; & in che Quantità si debbino fini-
re, ò numerare le Cantilene.Cap. LXVII.
sica, di non uoler ragionar cosa alcuna, oltra quello, ch'è necessario alla co-
gnitione delle Proportioni, de i Suoni, delle Voci, & de tutte quelle cose,
che concorrono alla costitutione della buona Harmonia, & alla cognitione
di quelle, ch'appartengono à questa Scienza; Ma perche alle uolte uengono alle mani
del Musico moderno alcune cantilene antiche, le quali sono composte sott'alcune os-
seruanze del Tempo, del Modo, & della Prolatione; delle quali non ne sapendo ren-
der ragione, resta (per cosa di si poca importanza) con uergogna; però hò mutato pro-
posito; & essendomi necessario ch'io ragioni alcune cose del Tempo, ragionerò etiandio
dell'altre due seguenti, cioè, di quelle, le quali saranno le più reali, & più importanti. Di-
co adunque, ch'essendo la Breue (com'hò detto altroue2. Partis.
cap. 2.) madre & genetrice di qualun- que altra figura cantabile; è dibisogno primieramente ragionar de tutti quelli Acciden-
ti, che possono accascare intorno à lei; percioche gli Antichi le attribuirono il Tempo;
& dopoi de gli altri, che accascano intorno l'altre Figure, che sono sottoposte alla mu-
tatione. La onde dico, che in questo luogo io non chiamo Tempo quello, che significa
lo Stato buono, ò la buona Fortuna d'alcuno; come quando si dice; Francesco è huo-
mo di buon tempo; cioè, mena tranquilla & lieta uita; ne meno quella buona tempera-
tura d'Aria, come si suol dire; Hoggi è buon tempo; cioè, hoggi è giorno sereno, chia-
ro, & lieto; ne anco nomino Tempo quello, che 'l Filosofo4. Phy.
cap. 5. definisce esser Numero, ò
Misura di mouimento, ò d'alcun'altra cosa successiua; ma dico Tempo; secondo la defi-
nitione de gli Antichi Musici; essere una certa & determinata quantità de figure mi-
nori, contenute, ò considerate in una Breue. Et questo Tempo è di due maniere; Per-
fetto, & Imperfetto, Il Perfetto si troua nella cantilena, segnata nel suo principio col
circolo O; per il quale si denota, che la Breue in essa cantilena è perfetta; cioè, si pone
in luogo di tre Semibreui; ò per il contrario tre Semibreui in luogo di una Breue; ma
l'Imperfetto, si troua quando nel detto principio è posto il Semicircolo C. in luogo del
circolo; per il quale si comprende, che la Breue si pone imperfetta; cioè, in luogo di
due Semibreui; ò per il contrario, due Semibreui in luogo di una Breue. Quando adun-
page 348que gli Antichi componeuano alcuno Canto sotto 'l segno del Tempo perfetto, inteso
per il Circolo, che dinota il numero Ternario; secondo alcuni rispetti; detto numero
Perfetto, lo numerauano à Breui perfette; cioè, à tre Semibreui per ogni tempo; ma
quando lo componeuano sotto 'l segno dell'Imperfetto; dinotato per il Semicircolo; lo
numerauano à Breui imperfette; cioè, à due Semibreui per ogni Tempo; essendo che
in questo si considera 'l numero Binario, chiamato d'alcuni numero Imperfetto. Bisogna
però auertire, che l'ultima Figura, ò Nota d'ogni cantilena non è da porre in tal nume-
ro; conciosiache essendo finale in essa si termina il concento & il Tempo; & ciascun de
questi terminano sopra quella figura, nella quale hebbero principio; ch'è la prima Se-
mibreue. ll Modo (lasciando da parte quello, del quale si ragiona nella Quarta parte)
gli Antichi diceuano esser una Quantità de Lunghe considerata nella Massima; ò di Bre
ui considerata nella Lunga, secondo la diuisione binaria, ò ternaria; percioche lo diui-
sero in due parti; cioè, in maggiore, & in Minore; & ciascun de questi considerauano
Perfetto, ouer Imperfetto. Intendeuano il Maggiore, quando poneuano due Pause di
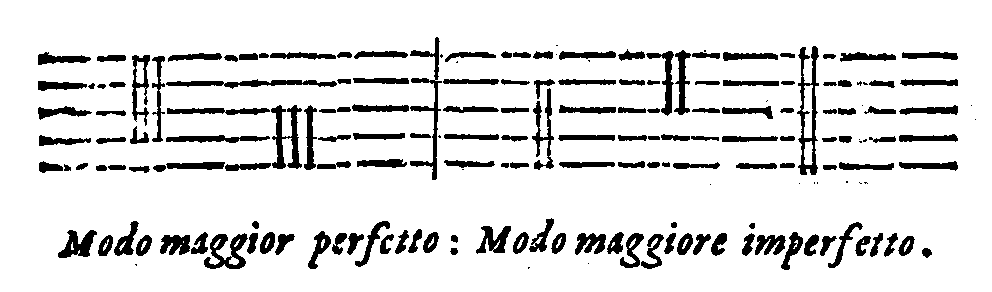
pigliassero due, ouer tre spacii, &
tre, ò Quattro linee delle cinque
già mostrate; come si uede nell'es-
sempio; ma 'l Minore si considera
uano quando poneuano una sola
Pausa, ch'abbracciasse tre, ouer
quattro delle predette linee. Il Modo perfetto maggiore intendeuano, quando poneuano
tre delle mostrate Pause insieme; & l'Imperfetto maggiore, quando erano solamente

lo, c'hauea una Pausa, ch'abbracciaua quattro
linee, & tre de i sopranominati spacii; & il Mi-
nore imperfetto, quando la detta Pausa posta
in tal maniera abbracciaua solamente tre linee
& due spacij; di maniera, che nel Modo mag-
gior perfetto faceuano ualer la Massima tre Lunghe, & nell'Imperfetto due. Similmen-
te nel Modo minor perfetto faceuano ualer la Lunga tre Breui, & due nell'Imperfetto.
La onde quando componeuano, ordinauano in tal maniera le lor cantilene; che nel Mo
do maggior perfetto numerauano di tre in tre Lunghe, ò perfette, ouer imperfette che
fussero; & sotto 'l Modo maggiore imperfetto, di due in due. Simigliantemente nel Mo
do minor perfetto numerauano di tre in tre Breui, & nell'Imperfetto di due in due. La
onde quando 'l moderno Compositore componerà sotto'alcuno de questi Modi, & non
numererà la cantilena secondo 'l detto numero, al modo detto; si potrà ueramente dire,
che sia stato poco considerato, & che nō habbia hauuto cognitione alcuna di tal cosa. E pe
rò d'auertire, che gli Antichi poneuano le nominate Pause in due maniere; imperoche ne
poneuano alcune auanti i segni del Tempo, & alcune dopo. Le prime chiamauano In-
diciali solamente; percioche non si numerauano nella compositione; ma erano poste
in cotal luogo per dimostrar solamente il Modo, ò maggiore, ò minor, che si fusse; ò
perfetto, ouer'imperfetto, sotto 'l quale era composta la cantilena. Le seconde nomi-
nauano Indiciali, & essentiali; conciosiache non solo seruiuano à dimostrar qual si fusse
il Modo; ma seruiuano etiandio alla cantilena; come nel sottoposto essempio si può
comprendere.
page 349

te altre cose) diceuano, ch'era una Quantità de Minime considerata, ouer'applicata ad
una Semibreue; & la dimostrauano col segno circolare, ouer semicircolare: onde la fa-
ceuano de due sorti; percioche l'una nominauano Perfetta, & l'altra Imperfetta. In-
tendeuano la Perfetta, quando poneuano nella cantilena i mostrati segni puntati in que
sta maniera

 ; & l'Imperfetta quando erano posti senza i punti
; & l'Imperfetta quando erano posti senza i punti 
 & face-
& face-uano ualere la Semibreue tre Minime sotto i due primi; & sotto quelli che non erano
puntati due; il perche nelle cantilene numerauano in questa maniera; che quelle ch'era-
no poste sotto la Prolation perfetta procedeuano & erano numerate di tre in tre mi-
nime; & quelle ch'erano composte sotto la Imperfetta, di due in due. Et perche ne i Mo-
di spesse uolte s'aggiungeuano insieme questi gradi, cioè, Maggiore & Minore; & an-
co il Perfetto & l'Imperfetto, de i quali, il maggiore include, ouero in sè contie-
ne il minore; il che fà etiandio il Perfetto, che in sè contiene l'Imperfetto, ma
non per il contrario; però auertiuano in tale congiuntione; che se 'l Modo mag-
giore era congiunto col minore; & l'uno & l'altro fussero stati Perfetti; allora nu-
merauano la cantilena di tre Lunghe, in tre perfette; ma se 'l Modo fusse stato mag-
giore perfetto, & minore imperfetto; la numerauano di tre Lunghe, in tre Lun-
ghe, lequali fussero imperfette. Oltra di questo, quando 'l Modo maggior imperfet-
to era posto insieme col minor perfetto, numerauano le lor compositioni di due in due
Lunghe perfette; & se l'uno & l'altro modo erano imperfetti, numerauano quelle di due
Lunghe in due, l'una & l'altra imperfette. Ancora quando 'l Modo era solamente Mi-
nor perfetto, le numerauano con due lunghe perfette; & quando era imperfetto, nume-
rauano quella à Lunghe imperfette; cioè, d'una in una. Et con simile consideratione
procedeuano ne gli altri gradi; come nel Tempo, & nella Prolatione, perfetti & imper
fetti; percioche ne i Perfetti numerauano di tre, in tre; & ne gli Imperfetti numeraua-
no di due, in due. Potiamo hora uedere, che per i Segni; cioè, per il Circolo, & per lo
Semicircolo dauano la cognitione del Tempo perfetto, ouer'imperfetto; per le Pause,
quella del Modo maggiore, ò minore perfetto, ouer imperfetto che 'l si fusse; & per i se-
gni del Tempo puntati, ò non puntati, intendeuano la Prolatione perfetta, ouer imper
fetta. Di maniera che potiamo etiandio comprēdere, che attribuirono il Modo maggior
perfetto alla Massima di ualore di tre Lunghe, & à quella di ualor di due il Modo mag-
giore ; similmente alla Lunga di ualor di tre Breui attribuirono il Modo mi-
nor perfetto, & à quella di ualor di due il Modo minore imperfetto. Il Tempo perfetto
attribuirono alla Breue di ualor di tre Semibreui, & l'Imperfetto à quella, che ual due;
& la Prolatione perfetta alla Semibreue di ualor di tre Minime; ma la imperfetta diede-
ro à quella di due. Soleuano anco gli Antichi tagliare i segni del Tempo in tal maniera;
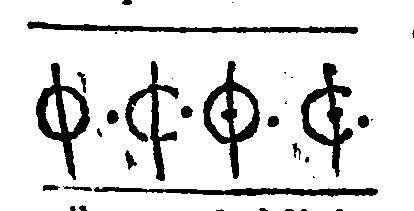 & questo faceuano, quando uoleuano, che le Figure sottoposte
& questo faceuano, quando uoleuano, che le Figure sottoposte alla perfettione & all'imperfettione, & anche all'Alteratione nel
Tempo perfetto & nell'imperfetto, fussero più ueloci; lequali figu-
re (come uederemo) sono cinque; Massima, Lunga, Breue, Se-
mibreue, & Minima. E ben uero, che ne per il tagliare i Segni, ne per il far nere le det-
te Figure; come molte fiate accade, & più oltra uederemo; leuauano à loro il nome,
ma lo riteneuano tanto, quanto che tali Segni fussero stati intieri, & le Figure senza co-
lore. Ne per il tagliare de i detti segni si leuaua la perfettione, ò l'Imperfettione, ne
page 350meno l'Alteratione; ma tanto erano sottoposte à tali accidenti & passioni; quanto s'essi
Segni fussero stati intieri. Bisogna però sapere, che nella Prolatione perfetta gli Anti-
chi vsarono la figura della Chroma bianca in luogo di quella, che è di ualore della metà
della Minima; la quale noi chiamiamo Semiminima; come son per dimostrare;Infra cap.
70. & questo
fecero, accioche se per caso bisognasse fare tal Minima nera, per rispetto di leuar l' à cotale figura; il che può intrauenire molte fiate; rispetto à diuersi accidenti,
che occorrer possono; ch'ella non fusse riputata esser cotale Semiminima; la qual (com'
altroue hò mostratoSupra c. 2.) si diuide in due Chrome, & la Chroma in due Semichrome. Ha-
ueano etiandio gli Antichi sotto 'l segno del Tempo perfetto tagliato doppia considera-
tione nel numerar componendo le Cantilene; percioche numerauano à tre à tre, & an-
co à due à due; cioè, di due Breue perfette in due, oueramente di tre Semibreui in tre;
di maniera che 'l numerar delle Semibreui finiua nel numero Senario; conciosia che se mi
surauano altramente non ritrouauano nelle lor cantilene la misura della Breue. Il che pa
rimente cercaremo anche noi di osseruare, non solo nel Tempo perfetto; ma anco nell'
Imperfetto tagliato, procedendo in questo de due Breui imperfette in due; acciò la can
tilena finisca nel numero Quaternario. Ma che diremo hora d'alcuni compositori moder
ni, i quali non solamente non osseruano la misura del numero Senario, ò Quaternario
nelle lor Cantilene; ma di più non osseruano il numero Ternario nel Tempo perfetto,
ne meno nell'Imperfetto il Binario, siano pur tagliati, ò non tagliati; ilche ueramente
è gran uergogna; conciosiache uengono a rompere il Tempo & la misura, delle quali co
se gli Antichi furono osseruatori molto diligenti; & per tal maniera guastano & confon-
dono ogni cosa di buono; dimostrandosi essere poco intelligenti delle cose della Musica.
Della Perfettione delle Figure cantabili.Cap. LXVIII.
ua Tempo, Modo, & Prolatione; sotto i quali accidenti ciascuna delle cinque
Figure nominate uiene à uariare il suo ualore, secondo ch'è accompagnata
con altri accidenti. La onde è da sapere, che gli Antichi osseruarono di nomi
nar le dette Figure da gli effetti, alcune Agenti, & alcune Patienti. Nominarono prima
la Minima agente; percioche la posero immutabile; cioè, che non potesse riceuere al-
cuna Perfettione; ma potesse far l'Imperfettione. Io dissi Immutabile; conciosiache non
si può diuidere in alcune dell'altre nominate; per esser quella, che in questo Genere è la
minima d'ogn'altra di ualore; ancora ch'ella sia diuisibile in due Semiminime & in quat
tro Chrome; come altroue s'è detto.Supra c. 2. La Massima poi chiamarono Patiente; imperoche
essendo la maggior de tutte l'altre, può patire imperfettione; ma la Lunga, la Breue, &
la Semibreue dissero Agenti & Patienti; percioche possono far perfetto & imperfetto;
& esse non solamente si possono far perfette, ma etiandio patiscono imperfettione. On-
de è da notare; che nominarono Perfetta quella Figura, che ual tanto, quanto uaglio-
no tre delle figure, che le sono parti propinque; come la Massima, la quale è detta Per-
fetta, quando ual tre Lunghe; & la Lunga, quando è di ualore di tre Breui; & la Breue,
quando ual tre Semibreui; & la Semibreue, quando è di ualore di tre Minime. Simil-
mente chiamarono cotali Figure imperfette, quando ualeuano due; come la Massima
due Lunghe, la Lunga due Breui, la Breue due semibreui, & la Semibreue due mini-
me. Considerarono oltra di ciò queste Figure in molt'altre maniere; come Parte propin
que, ò remote, ò più remote, oueramente remotissime, l'una dell'altra; come nel Cap.
45. hò mostrato. La onde la Lunga non hà parte remotissima, ne la Breue hà parte più
remota, ne remotissima; & la Semibreue non hà la parte remota, ne la più remota, ne
meno la remotissima. Et perche alcun potrebbe dubitare, se le Figure sottoposte al Tem
page 351po, al Modo, & alla Prolatione possono esser sempre perfette; però è da sapere (per non
partirsi dall'autorità de gli Antichi) che ueramente possono esser Perfette, & anco Im-
perfette, secondo 'l uolere del Compositore. Il perche si dee notare, che gli Antichi uol
sero, che qualunque Figura posta auanti un'altra simile bianca, ò nera, sempre fusse per-
fetta; come nel modo maggior perfetto una Massima auanti un'altra, bianca, ò nera
ch'ella fusse. La Lunga nel Modo maggiore imperfetto & minore perfetto: La Breue nel
Tempo perfetto; & la Semibreue nella Prolation perfetta. Et ciò fecero con qualche ra-
gione; percioche il Simile non patisce imperfettione alcuna dal suo simile; come si com
prende in due cose, che siano equali in uirtù & possanza, che l'una nō può superar, ne me
no può esser superata dall'altra. Mala simiglianza nelle Figure s'intende rispetto alla for-
ma, & non al colore; imperoche la Forma è quella, che ueramente dà l'essere alla cosa;
onde l'esser nera non le toglie la forma; come il color nero non lieua all'Ethiope essere
Huomo & rationale; conciosia che 'l Colore non è altro, che accidente; quantunque alle
uolte sia inseparabile dal Soggetto. Onde niuna Figura può esser fatta imperferta da una
sua maggiore, ma si bene da una sua minore essendo; che la maggiore rispetto alla minore
è sempre patiente; & per il contrario la minore rispetto alla maggiore è sempre agente. Et
anco si osserua questo in ogni Figura; quando è posta auanti le Pause della sua propria
denominatione; si come la Massima auanti tre pause, che dinotano il modo maggior
perfetto; ò siano pause di tre tempi, ouer de due; per esser le dette Pause la quantità & il
ualore d'una Massima è perfetta. Cosi la Lunga del Modo minor perfetto appresso la Pau
sa di tre tempi, ò di due; & la Breue & la Semibreue del Tempo perfetto & della Prola-
lation perfetta, auanti le lor Pause; come qui si uede.

ti quella di due Breui; & la Breue auanti quella di due Semibreui, ouer'auanti due pause
di Semibreue poste sopra una linea istessa, sempre saranno perfette; essendo che tali Lega
ture, ò pause poste in cotal maniera hanno uirtù di unione; percioche la Legatura con-
tiene sempre in se un tempo perfetto; se ben alle fiate l'ultima sua figura è fatta imperfetta
dalla figura propinqua, che la segue: & le Pause hāno in quel caso questo priuileggio, che
sono come se fussero la Figura che rapresentano; imperfetta però, & non altramente; il
che auiene anco nella Semibreue, quando è posta auanti due pause di minima poste all'
istesso modo. Ma se tali Pause fussero separate, tal Regola non haurebbe luogo. Et s'al-
cun uolesse dire, che la Figura posta auanti la Legatura non può esser perfetta; adduca
che ragione si uoglia, si potrà rispondere, che se la Breue è perfetta, quando è posta auan
ti due pause di Semibreue, poste sopra una istessa linea sotto 'l segno del Tempo perfetto;
maggiormente dee esser perfetta auanti la Legatura, poiche le Pause sono priuatiue &
non dinotano altro, che priuatione di suono, ò di uoce, & la Legatura è positiua, & di-
nota positione, & pone il Suono, in essere, come qui si uede.

che cagione; se gli porrà appresso il punto di perfettione; come la Massima nel Modo
maggior perfetto; la lunga nel Modo minor perfetto; la Breue nel Tempo perfetto; &
la Semibreue nella Prolation perfetta; come qui in essempio si uede. Quando saranno

ò tre minori propinque, la prima maggiore
sempre sarà perfetta. Come per essempio
nel modo maggior perfetto due, ò tre Lunghe
poste tra due Massime fanno che la prima Mas
sima sia perfetta; nel Modo minor perfetto
due, ò tre Breui poste tra due Lunghe fanno, che la prima Lunga sia perfetta. Quest'
istesso fanno della Breue due, ò tre Semibreui poste tra due Breui nel Tempo perfetto;
& della Semibreue nella Prolation perfetta, due, ò tre Minime poste tra due Semi
breui; percioche la prima Breue & la prima Semibreue diuentano perfette. L'istesso fa-
ranno le Figure & le Pause insieme d'un istesso ualore nell'istessa maniera collocate. Ma
si dè auertire; uolendo che la prima maggiore sia perfetta; che quando si porrà tra due
maggiori una sola minore & la sua Pausa, si porrà primieramente la Pausa, & dopoi la
Figura; ma quando si porrà due Figure minori & una Pausa, allora la Pausa si potrà por
re in qual luogo tornerà più commodo; come nel sottoposto essempio si può uedere.

ma Breue sarà perfetta, & l'ultima delle cinque Semibreui alterata; cioè, raddoppiata;
ma la prima Breue posta auanti le sei Semibreui sarà sempre perfetta, senz'alteratione
d'alcuna delle Semibreui; percioche le sei Semibreui sono poste per due Tempi intieri;
come qui si uedono. Ma per qual cagione le mostrate Pause si ponghino più in un luogo,
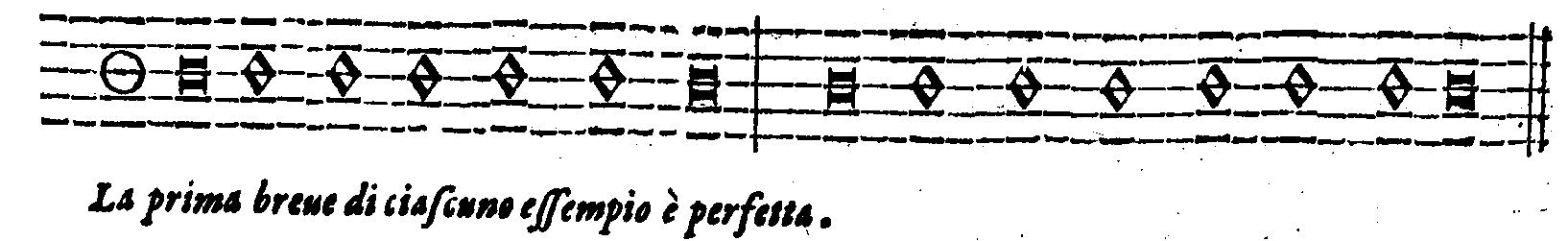
habbia in quest'ultimo essempio posto solamente la Breue nel Tempo perfetto; si può in-
tendere tutto quello, c'hò detto etiandio della Massima & della Lunga nel Modo mag-
giore & minore perfetti; & della Semibreue nella Prolatione; imperoche non si troua
ragione, che maggiormente ne costringa à far Perfetta più l'una che l'altra; massimamen
te essend'accommodate à lor luoghi, & sotto i segni loro proportionatamente.
Dell'Imperfettione delle Figure cantabili.Cap. LXIX.
mentione della Perfettione delle Figure cantabili, resta che noi uediamo i mo-
di, per i quali ogn'una di esse si possa fare, ò chiamare imperfetta. Onde s'è ue
ro quel, che dice il Filosofo,1. Topic.
cap. 2 ch'egli è un'istessa disciplina quella de i contra-
rij; c'hauendo ueduto quello, che si ricerca alla Perfettione, sarà facil cosa di cono-
scer quello, che si ricerca intorno alla lor Imperfettione; imperoche si ritroueranno es-
sere Imperfette, quando non saranno accompagnate con gli accidenti mostrati di sopra.
Ma auanti che si uada più oltra; uederemo prima alcune cose generali intorno tal ma-
teria; & dopoi discenderemo al particolare. Dico adunque che le Figure, che si posso-
no fare imperfette sono Quattro; & sono tutte le Patienti mostrate di sopra; cioè, la
Massima, la Lunga, la Breue, & la Semibreue. Et quella, che patisce l'Imperfettione,
è sempre maggior di quella, che la fà; per il contrario, quella ch'è cagione della im-
perfettione; è sempre minore. Et quella Figura; ch'è cagione di tal'imperfettione, si
hà da considerar quanto alla Quantita perfetta; cioè, quanto à quelle figure, che sono
sottoposte al numero Ternario, & non à quelle che sono sottoposte al Binario; come la
Massima nel Modo maggiore, la Lunga nel Modo minor perfetti, la Breue nel Tem-
po perfetto, & la Semibreue nella Prolation perfetta. Et perche la Massima (com'hò
detto) è solamente patiente; però non dà, ma imperfettione. Cosi la Minima;
per esser solamente agente, non patisce; ma è cagione dell'imperfettione. La onde la
Lunga, la Breue, & la Semibreue sono quelle, che per esser non solo agenti, ma etian-
dio patienti; fanno & patiscono l'imperfettione. Ma bisogna auertire, che l'esser perfet-
to si considera in due modi; prima in quanto al Tutto; dopoi in quanto alle Parti. In
quanto al Tutto s'intende imperfetta quella Figura, ch'è imperfetta d'una sua Parte pro
pinqua; & questa è la maggiore imperfettione, che se le possa dare; ma in quanto alla
Parte s'intende, quandè fatta imperfetta d'una parte remota, ò più remota, ò remo-
tissima. Et la Figura, che si può far imperfetta, non solo si può far imperfetta quanto
al Tutto con la parte propinqua; ma con le parti remote, & con l'altre ancora; pur che
la quantità sia equale alla Terza parte del suo Tutto; imperoche l'Imperfettione nelle
Figure non è altro, che una certa diminutione d'una Terza parte, riducibile alla figu-
ra nella perfettione del numero Ternario. Le Figure, che fanno l'Imperfettione, si
pongono in tre maniere; imperoche, ouer si pongono dopo quella, che si fà imperfet-
ta, ouero inanti, oueramente inanti & dopoi; essendo ch'Ogni figura si può far'imper-
fetta solamente in uno de i tre modi. Et tanto si leua à ciascuna figura, che si fà im-
perfetta, quanto è il ualore delle figure, che fanno tale imperfettione. Et se ben la Mi-
nima è figura agente; non può però far imperfetta alcuna figura, che non sia sottopo-
sta alla Prolatione perfetta. Nè si dè credere, che tali Imperfettioni si facciano sola-
mente con tali figure, nel modo c'hò detto; imperoche le Pause, il Colore, & etiandio
i Punti hanno l'istessa forza. E' ben uero, che le Pause, non sono sottoposte all'Imperfet-
page 354tione; percioche sono solamente agenti, ma non patienti; cioè, fanno perfetto & imper
fetto; & esse, per qual si uoglia accidente, non si fanno imperfette. Il Colore leua sem-
pre la Terza parte del Tutto alle figure sottoposte alla perfettione; ma nell'Imperfettio-
ne (come usano & non bene i Moderni) leua sempre la Quarta parte. L'imperfettione
adunque delle figure è, il leuarle una Terza parte del loro ualore, ch'è la Parte loro pro
pinqua; & questa è l'imperfettione quanto al Tutto. Ciascuna delle dette figure adun-
que è imperfetta quanto al suo Tutto, quando senz'alcun mezo le segue la sua parte pro-
pinqua; come dopo la Massima la Lunga; dopo questa la Breue; dopo la Breue la Semi
breue; & dopo questa la Minima, sotto i lor segni di perfettione; come si può vedere
nel sottoposto essempio.

mente segue alcuna Pausa di ualor della lor Parte propinqua; Similmente il Colore, ò
Nero, oueramente Rosso, ch'ello si sia; come usauano gli Antichi; è cagione di tal'imper-

non è in cosa alcuna differente dalla Figura semiminima; però bisogna sapere, che gli
Antichi (come hò detto altroueSupra cap.
67.) acciò si conoscesse tal diuersità, giudiciosamente vsa-
rono di porre in cotali modulationi la Chroma bianca in uece della sudetta Semimini-
ma; come si uede fatto nella Prima parte del Canto; Optime diuino date munere pastor; d'
Henrico Izac à Sei uoci. Laonde molti de i Moderni, i quali non hanno osseruato cotal
cosa, hanno ciò fatto con poca consideratione; non attendendo, che se bene la minima
colorata per rispetto dell'Alteratione, non è quanto à questo Accidente del colore diuer
sa dalla Semiminima; è nondimeno differente quant'al ualore; percioche ò colorata, ò
non colorata, sempre uale una Minima. La onde il non osseruar cotal cosa è cagione spesse
fiate, che i Cantori pigliando l'una per l'altra, errando discordino nel cantare; com'è ad

no esser fatte Dalla parte dopo: imperoche Dalla parte ināti si fanno cotali imperfettioni,
quando le Figure sono poste al contrario; come quando le Pause, ò le Figure minori so
no poste inanti le maggiori. Tali Figure saranno etiandio imperfette, tanto Dalla parte do
po, quanto Dalla parte inanti; cioè, dalla seguente & dalla antecedente, per il Punto;
quando tra due figure maggiori saranno poste due figure minori propinque; tra le quali
sia il Punto; come; qui si uede.
page 355

tù del Punto posto tra le minori, che si chiama di Diuisione; come più oltra uederemo.
Saranno etiandio imperfette cotali Figure, quando tra due maggiori, dalla parte sini-
stra sarà collocata una figura, che le sia Parte propinqua, alla quale senz'alcun mezo
succeda una Pausa dell'istesso valore; come qui si uede. In molt'altre maniere le Figure
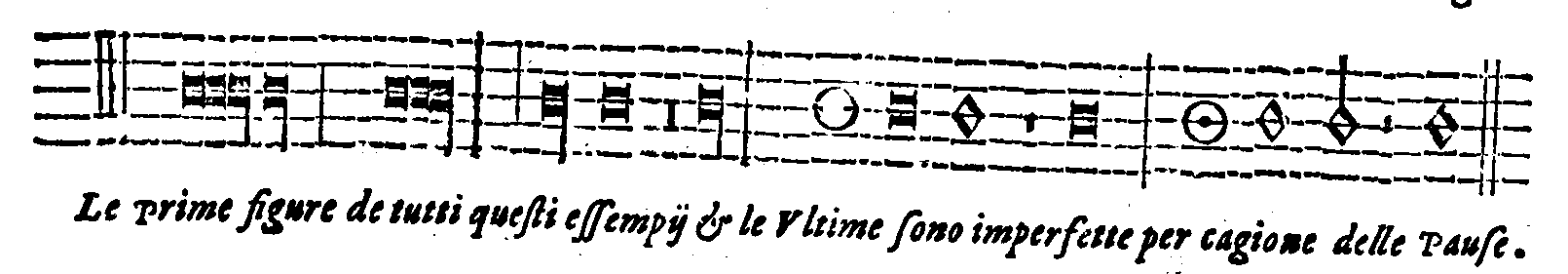
tiosi, bastarà solamente quel, c'hò detto intorno all'Imperfettione loro, quanto al Tut-
to; cioè, quanto alla Parte propinqua; imperoche quanto all'Imperfettione dell'altre
loro parti; dopo che si hauera considerato tutto quello, c'hò detto di sopra, ritrouare-
mo, che tal Imperfettione si fà, quando sono fatte imperfette d'una quantità minore
delle mostrate; siano poi imperfette Dalla parte inanti, ouer Dalla parte dopo; ò pur
dall'una & l'altra delle nominate. Ma uediamo quel che sia Punto nella Musica, & di
quante sorti si troui.
Del Punto, delle sue specie; & de i suoi effetti.Cap. LXX.
metra; il qual uuole (come dimostra EuclideElement.
li. 1. Def. 1.) che non habbia alcuna parte,
& che sia indiuisibile. Ne lo considera come Vnità, la quale habbia positio-
ne; come lo definisce il Filosofo;De Ani-
ma lib. 1.
c. 4. 5. Me-
tap. cap. 6. ma dice, che 'l Punto è una minima parti-
cella, ouer una certa quantità indiuisibile; oueramente un minimo segno, che s'aggiun
ge alle figure cantabili per accidente, hora dopo, hora di sopra, & alle uolte si pone tra
loro; & lo considera in Quattro modi; cioè, in quanto fà perfetto, in quanto accresce,
in quanto diuide, & in quanto altera, ò raddoppia le dette Figure. Onde i Musici, con
siderando i suoi ufficii, dicono; che si troua de Quattro maniere; lasciando gli altri, che
fanno poco al proposito; cioè, di Perfettione, d'Accrescimento, di Diuisione, & d'Al-
teratione, ouer Raddoppiamento. Punto di Perfettione chiamano quello, che si pone
alle fiate immediatamente dopo la figura, che si può fare, ouer può esser perfetta ne i
Segni di perfettione solamente, per conseruar la perfettione di tal figura; come qui
di sotto si uede.
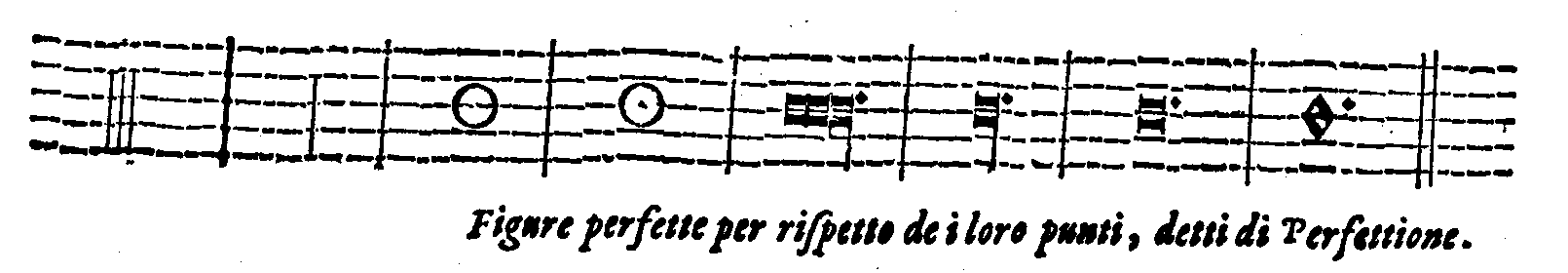
non può essere, ne si può far perfetta per alcun modo; come è ciascuna che è posta ne i
Segni d'imperfettione, & ne i Segni della perfettione à quelle, che sono di minor ualo-
re Semibreue; come qui si ueggono.

lato destro della figura, tanto perfetta, quanto imperfetta; onde fanno maggior la
figura Imperfetta di tanta quantità, quanta è la metà di essa figura; cioè, quanta è la
metà del suo Tutto; come per essempio nella lunga, che ual Quattro Semibreui, ag-
giuntole il Punto uarrà Sei; ma quando s'aggiunge à quelle, che si possono far perfet-
te, sempre il Punto ual la Terza parte della figura perfetta, alla quale si pone appresso;
Per il che si uede la differenza, che è tra 'l Punto di Perfettione, & quello d'Accre-
scimento; che l'uno si pone solamente appresso quelle figure, che si possono far per-
fette sotto i Segni della loro perfettione; & l'altro si pone à canto quelle, che non si
possono far perfette. Et tali Punti tanto operano nelle Figure legate, quanto nelle
sciolte. Il Punto di diuisione è quello, che si pone tra due figure simili minori & pro-
pinque, poste tra due maggiori, ne i Segni della perfettione; il cui vfficio è di diuidere, &
di far imperfetta l'vna & l'altra delle figure maggiori, come la prima dalla parte dopo, &
l'altra dalla parte inanti. Et si scriue sopra tale figure nel mezo de loro; & tal punto non si
canta. Di maniera ch'inquanto separa l'una figura dall'altra delle due minori, & le accom
pagna con le maggiori, è chiamato di Diuisione; ma in quanto fà la imperfettione delle
maggiori, si può nominare anco Punto d'Imperfettione; percioche (cō ogni douere) sem
pre si dè porre nel fine del Tempo passato; & nel principio di quello, ch'al presente; il
ch'è poco osseruato da i Compositori moderni. Et si pone etiandio tra la Pausa, che
tiene il primo luogo, & una Figura, che tenga 'l secondole quali siano d'un'istesso ua-
lore; come nel sottoposto essempio si uede.

due Figure minori poste auāti una maggior propin-
qua; il cui officio è di raddoppiar la Seconda figura
minore, che segue dopo lui; & è posta inanti la mag
giore, accioche tra queste due minori si ueda il Tempo perfetto. Et si dè osseruar di por-
re tal Punto in tal maniera, che sia nel fine del Tempo precedente, & nel principio del
seguente; com'hanno osseruato i buoni Musici Antichi; & tal Punto (come anco quel-
lo di Diuisione) non si canta. Ne altro uuol dire Alteratione, che Raddoppiamento,
che si fà nelle Parti propinque delle Note, ò Figure, che si cantano; le quali si posso-
no far perfette sotto i lor segni; & questo sempre (com'hò detto) nella Seconda fi-
gura, che si pone dopo lui; perche hauendo la Prima ragione d'Vnità, & la Seconda
ragione di Binario, è il douere che 'l Binario sia posto dopo tale Vnità; onde tal Punto
si pone in questo modo.
page 357

lo nelle Figure poste in tal maniera; ma etiandio in molt'altri modi; come era quando po
neuano due Figure minori, parti propinque, tra due maggiori, sotto i lor segni. Onde
faceuano perfetta la prima maggiore, & la seconda minore raddoppiata, ouer'altera-
ta; come qui si uede. Il medesimo faceuano, quando poneuano queste minori tra due

conda minore; come nel sottoposto essempio si può uedere. Faceuano alterare, ò rad-
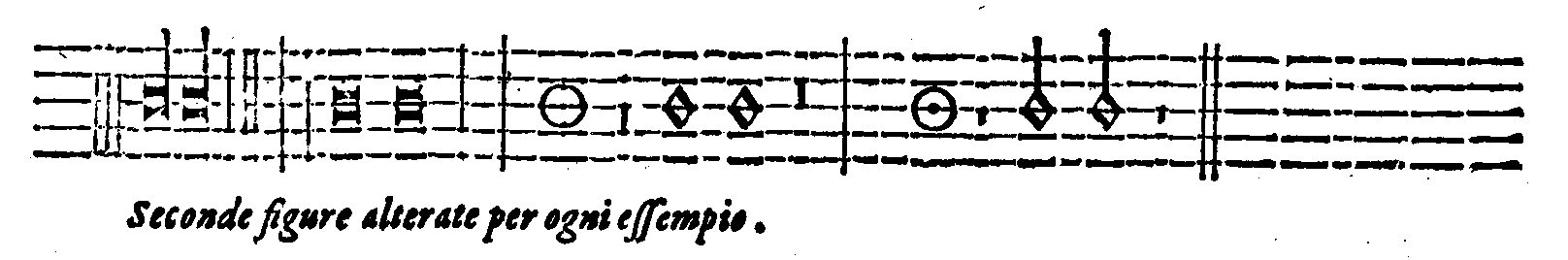
giore, & dopoi due Figure minori proprinque, & una Pausa di ualor della maggiore; co-
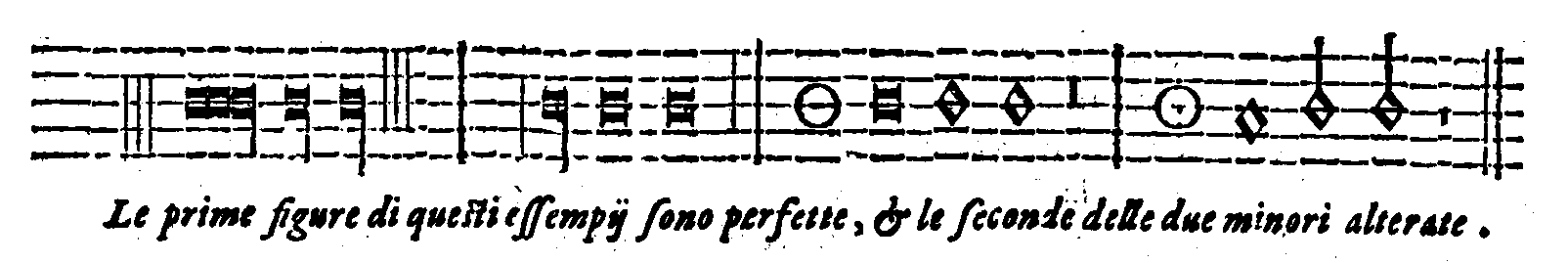
due maggiori una Pausa di ualor della minore proprinqua à banda sinistra, & alla parte
destra poneuano cotale minore; come qui si uede. Si debbe però auertire, che le Figure

breue, & la Minima; ma la Massima, per non esser Parte proprinqua d'alcun'altra figura,
non si può alterare. Similmente la Minima è fine di tale alteratione; essendo che non si
può diuidere in due parti equali; & se fusse altramente, sarebbe non solamente agente,
ma anco patiente. Onde casca l'Alteratione sopra quelle Figure, che sono Parti propin
que delle maggiori; ne mai alcuna Pausa è sottoposta all'alteratione; & tale Alteratio-
ne si ritroua solamente ne i Segni di perfettione; & si fà per il diffetto d'una figura, che
page 358manca al compimento del numero Ternario. Le due Figure minori etiandio poste tra le
due maggiori, possono esser collocate in tal maniera; ch'in luogo della prima si può porre
la sua Pausa; ilche non auiene nella seconda; com'habbiamo veduto; percioche sempre
si raddoppia la Seconda figura tanto nelle figure legate, quanto nelle sciolte, & non mai
la prima. Ma la Negrezza, ouero il Colore, & spesse volte il Punto di diuisione, scaccia
tale Alteratione; come hò mostrato. Si debbe oltra di ciò auertire, che la Perfettione
delle figure si può considerare in tre maniere; Prima per virtù delle Pause; dapoi per vir-
tù del Segno, come del Circolo; Vltimamente per virtù del Punto posto in esso circolo,
ouer semicircolo. Però la Massima & la Lunga sempre saranno perfette per virtù delle
Pause, siano sottoposte à qual segno si vogliano; la Breue si fà perfetta per virtù del Cir-
colo; & la Semibreue per virtù del Segno puntato. Onde si debbe notare, che niuna Figu
ra è perfetta per virtù del segno, se non la Breue; & per il punto che è nel segno la Semibre
ue; l'altre poi, che sono la Massima, & la Lunga, sono perfette (come si è detto) per virtù
delle Pause. Oltra di ciò si debbe auertire, che tali accidenti si considerano; non sola-
mente in quelle cantilene, che sono contenute sotto i Modi, Tempi, & Prolationi mo-
strate; ma etiandio in quelle, nelle quali si pone la Battuta inequale, che nel Cap. 49. chia
mai Trochaica; laquale si dimostra per le Cifere ternaria & binaria, & la nominano Ses-
quialtera; come iui hò commemorato; & come nell'essempio che segue si può vedere; an-
cora che i Prattici intendino etiandio tal Battuta, quando pongono le figure tutte nere;
senz'alcuna cifera; ma allora la addimandano Hemiolia, da Η῾μιόλιος parola Greca, che
tanto importa, quanto appresso di noi Sesquialtera, ò Meza parte; & allora uon vi accasca
alcuno de i predetti accidēti; imperoche 'l Colore leua tutte queste cose; come qui di sotto
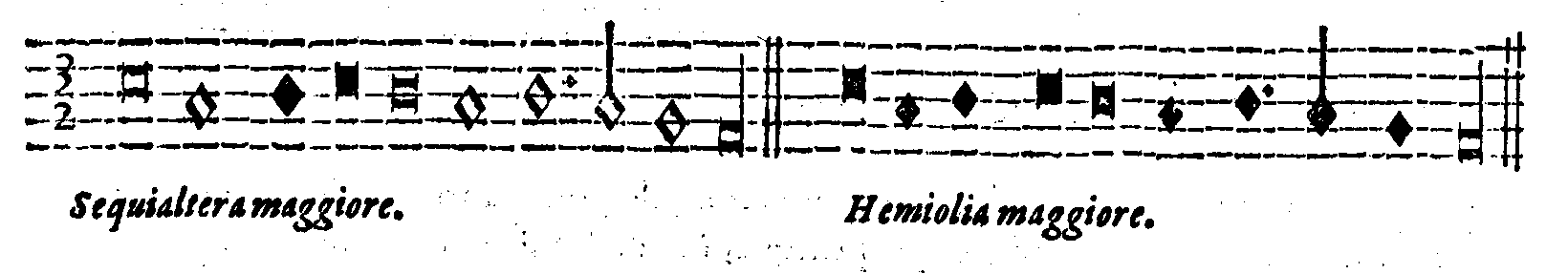
to puntati, & tagliati; ma anche ne i semplici, i quali si pongono senza i punti, & senza il
taglio. E' ben vero, che tra questi & quelli si ritroua qualche differenza; che ne i tagliati
senza punti vsano di porre la Breue & la Semibreue, l'vna nel battere & l'altra nel leuare
della Battuta; & ne i semplici, la Semibreue & la Minima. La onde quando pongono la
Breue & la Semibreue nella Battuta; tal Battuta, ò Prolatione chiamano Sesquialtera,
ouer'Hemiolia maggiore; & quando pongono la Semibreue & la Minima, la nominano
minore. Ma tutto questo si può far commodamente nella Prolatione perfetta; come qui
sotto si può vedere nel terzo essempio, tāto nel perfetto, quanto nello imperfetto. Bisogna

altere; ouer'Hemiolie maggiori, quanto nelle minori, secōdo 'l modo, che ricercano il Mo
do, il Tēpo, & la Prolatione; come nel Cap. 67. hò mostrato; & di por la Breue, & la Semi-
breue cōtenuta nella Sesquialtera, ò nell'Hemiolia maggiore, per vn sol Tēpo, cosi anco la
Semibreue cō la Minima posta nella Sesquialtera, ouer'Hemiolia minore per vn mezo Tē
page 359po; il che da pochi è osseruato; sia poi sottoposta la cantilena à qual segno si voglia, Perfet-
to, ouer'Imperfetto, che 'l si sia. Et perche i Musici sogliono alle volte lasciar da parte non
solo le Pause, che sono Indiciali ne i Modi maggiore & minore; ma alle volte etiandio non
gli accasca di porre le Essentiali; però sarà auertito il Cantore, che le Perfettioni & l'Im-
perfettioni si conoscono alcune volte d'alcuni segni, i quali chiamano Intrinsechi; come
sono i Colori, & li Punti; conciosia che tali segni sono di due maniere; come sono i no-
minati; & gli Estrinsechi, che sono le Pause, i Segni del Tempo, & quelli della Prolatione.
Però quando sitroueranno tali Segni intrinsechi, si potrà giudicar facilmente, sotto qual
Modo, ò Prolatione sia composta la cantilena; come si potrà giudicare il seguente Teno-
re, esser composto sotto 'l Modo maggiore & minor perfetto: percioche nelle figure sotto-
poste alla perfettione ne i sopra nominati Modi si troua il Punto di Diuisione, & quello
d'Alteratione, & il Colore; come in esso si vede.
 Haueano oltra di questo gli Antichi nelle loro compositioni molti altri Accidenti, & Ci-
Haueano oltra di questo gli Antichi nelle loro compositioni molti altri Accidenti, & Ci-fere di più maniere: ma perche poco più s'vsano, & non sono d'vtile alcuno alle buone, &
sonore harmonie; però lasciaremo il ragionar più in lungo di simil cose à coloro che sono
otiosi, & che si dilettano di simili Cifere più di quello, che facciamo noi.
Dell'vtile, che apportano i mostrati Accidenti nelle buone
Harmonie.Cap. LXXI.
cidenti alle buone & sonore Harmonie; ma per maggiore intelligenza (piglian
do 'l nostro parlare alquanto in alto) è dibisogno sapere, che essendo 'l vero
Oggetto del Senso, il Corpo, che lo muoue mediante l'organo; in quanto tal
Corpo è considerato secondo diuerse ragioni di mouimenti, viene à porre necessariamen
te nel Senso diuerse possanze; essendo che considerato in quanto si può vedere, è detto Vi
sibile, & non si può sentire da altro sentimento, che dal Vedere; & questo Oggetto è ve-
ramente di due maniere; conciosiache, ouer'è Principale, com'è il Colore, che si vede pri
ma dogn'altra cosa; ouero ch'è Adequato, ò vogliamo dir Proportionato; & questo non
è il Colore; & si ritroua in molte cose, che non sono colorate; come è il Fuoco, la Lu-
na, il Sole, le Stelle, & altre cose simili. Quest'Oggetto per tal cagione non hà veramen-
te proprio nome; ma si dice solamente Visibile, & sotto di lui si contengono tutte quel-
le cose, che si veggono per il Lume; come sono tutti i Corpi lucidi, che sono quelli c'hò
nominato di sopra. In quanto tal'Oggetto si può vdire; come sono le Voci, & li Suo-
ni, si chiama Vdibile, & non si può sentire d'altro sentimento, che dall'Vdito; ilche si
potrebbe anche dire de gli altri. Questi Oggetti sono detti Proprij sensibili; percioche
qual si voglia di loro può esser compreso da vno de i nominati sentimenti solamente. E
ben verò, che si trouano alcuni Oggetti, che si chiamano Communi, i quali possono esser
compresi da molti sentimenti; come è il Mouimento, la Quiete, il Numero, la Figura, &
ogni Grandezza, che si possono vedere, vdire, & toccare; com'è manifesto. Sono etiandio
alcuni altri Oggetti sensibili per accidente, i quali sono quelli, che nō si possono sentire, se
non col mezo d'vn'altra cosa; come sono i Corpi sonori; che non si possono udire, senō per
il Suono, che si fà nell'Aria; come nella Seconda parte hò mostrato;Cap. 10. i quali Oggetti tanto
più sono grati al proprio sentimēto, & tanto più soaui, quāto più sono à lui proportionati;
page 360& cosi per il contrario; come si uede dell'Occhio nostro, ilquale riguardando nel Sole è
offeso; perche tale Oggetto non è à lui proportionato, & quel che dicono i Filosofi;De Ani-
ma. lib. 2.
cap. 12. &
lib. 3. c. 13. che
l'Eccellente sensibile, se non corrumpe il Sentimento, almen corrumpe il suo Istru-
mento, è uero. Se adunque i Proprii oggetti sensibili non si possono sentire, ne giudica-
re d'alcun'altro sentimento, che dal loro proprio; come 'l Suono dall'Vdito, il Colore
dal Vedere, & cosi gli altri per ordine. Dicami hora (di gratia) quelli, che tanto s'af-
faticano & pongono cura di por nelle lor Cantilene tanti intrichi; quale & quanto dilet-
to & utile possino porgere al sentimento; & se sono più uaghe, & più sonore di quelle,
che non hanno tali cose, le quali sono se non uisibili, & non cadono sotto alcun senti-
mento, che sotto quello del Vedere; ne si possono per alcun modo udire; percioche non
sono Oggetti communi; come sono i sudetti, che possono esser compresi da molti senti-
menti. Io sò che risponderanno, s'haueran giudicio, che non danno in questo utile alcu-
no; percioche quando saranno ridutte ad un modo semplice, & commune, fuori de ta-
li cifere; tale & tanta sarà l'Harmonia, che si ode in quelle; quale & quanta è quella, che
si ode in queste. Se adunque non sono d'alcun'utile per l'acquisto delle buone Harmo-
nie, ne apportano utile alcuno al senso, à che proposito aggiungere obligo & accrescer
fastidio al Cantore con simili cose, senza proposito? Perche quando douerebbe esser in-
tento à cantare allegramente quelle cantilene, che si sono proposte; gli è dibisogno, che
stia attento à considerare simili chimere, che cadono (secondo i uarij accidenti) sotto 'l
Modo, sotto il Tempo, & sotto la Prolatione; & che non lascia passar cosa che sia dipin-
ta, che non ne habbia grande consideratione; essendo che se facesse altramente, sarebbe
riputato (dirò cosi) un goffo & un'ignorante. Et se non danno utile alcuno; come ue-
ramente non danno; parmi ueramente gran pazzia, ch'alcuno d'eleuato ingegno hab-
bia da fermare il suo studio, & spendere il tempo & affaticarsi intorno à simili cose im-
pertinenti; la onde consiglierei ciascuno, che mandasse da un canto queste cifre, & atten
desse à quelle cose, col mezo delle quali si può acquistar le buone & soaui harmonie. Di-
rà forse alcuno, non è bella cosa uedere un Tenore ben ordinato sotto i segni del Modo,
del Tempo, & della Prolatione come faceuano quelli antichi Musici, i quali ad altro
quasi non attendeuano? Si ueramente, ch'è cosa bellissima; massimamente quand'è scrit
to, ò dipinto, & miniato anche per le mani d'un'eccellente Scrittore & Miniatore con ot-
timi inchiostri, colori fini, & con misure proportionate; & li sarà aggiunto uno Scudo
(come hò già ueduto) una Mitra, ò Capello, con qualche altra bella cosa appresso; ma
che rileua questo? se tanto sarà sonora, ò senz'alcuna gratia quella cantilena, c'hauerà
un Tenore scritto semplicemente & senz'alcun intrico, ridotto ad un modo facile; quan
to se fusse pieno di queste cose. Adunque si può ueramente dire, ch'un tal modo di com
porre non sia altro, che un molteplicar difficultà senza necessità alcuna, & non un molte-
plicar l'Harmonia; & che tal cosa si fà senza utile alcuno, poi che uanamente si moltepli
cano le cose senz'alcuna necessità; come uogliono i Filosofi; Perche essendo la Musica
scienza, la qual tratta de i Suoni & delle Voci, che sono Oggetti proprii dell'Vdito; uà
speculando solamente il Concento (come dice Ammonio In Praedi-
cabilibus.) che nasce dalle chorde &
dalle uoci; & non considera tant'altre cose. La onde parmi che tutto quello, che nella
Musica si uà speculando, & non si indriccia à tal fine, sia uano & inutile; conciosia che
essendo stato ueramente ritrouata la Musica non ad altro fine; come altre uolte dicem-
mo; che per dilettare & per giouare; niun'altra cosa hà possanza, dalle Voci & da i
Suoni in fuori, che nascono dalle chorde; le quali come s'imaginò Aurelio Cassiodo
roPar. 1. c. 3.
& Lib. 2.
ad Boetiū
Patriciū.) sono in tal maniera nominate; percioche muouono i Cuori; come lo dimostra cō mol-
ta gratia con queste due parole latine Chorde & Chorda; & per tal uia sentiamo il pia-
cere & il giouamento, che noi pigliamo nell'udire l'Harmonie & le Melodie. Conclude
remo adunque da quel, che si è detto; che 'l modo di comporre in tal maniera, non sola-
mente non sia utile, ma anco dannoso; per la perdita del tempo, ch'è più pretioso d'ogni
altra cosa; & che i punti, le Linee, i Circoli, i Semicircoli, & altre cose simili, che si
page 361ipingono in carte, sono sottoposte al sentimento del Vedere, & non à quello dell'Vdi-
o; & sono cose considerate dal Geometra; ma i Suoni & le Voci (come quelli, che uera
mente sono il proprio Oggetto dell'Vdito, da i quali nasce ogni buona Consonanza & o-
gni Harmonia) sono principalmente dal Musico considerate; ancora che consideri per ac
cidente etiandio molt'altre cose. Vorrà forse alcuno qui riprendermi & biasimarmi, at-
tesoche molti dotti & celebratissimi Musici antichi, de i quali il nome loro ancora uiue
appresso di noi, hanno dato opera ad un tal modo di comporre; & che li uoglia hora bia
simare. Dico à questo, che se tali biasimatori consideraranno la cosa, non ritrouaranno
maggiore utile nelle lor compositioni inuiluppate in tal legami, di quello, che ritrouareb
bono se fussero nude, & pure senz'alcuna difficultà; & uedranno, che si dolgono à
gran torto; & comprenderanno, loro esser degni di riprensione; come quelli, che s'op-
pongono al uero; percioche se bene gli Antichi seguitarono un tal modo; conosceuano
molto bene, che tali accidenti non poteuano apportare alcun accrescimento, ò deminu
tioni d'harmonia; ma dauano opera à simil cose, per mostrar di non essere ignoranti di
quella Theorica, che da alcuni otiosi Speculatiui de quei tempi era stata posta in uso; es-
sendo ch'allora la cosa era ridotta à tal fine, che la parte Contemplatiua della Scienza
consisteua più tosto nella contemplatione de simili accidenti, che nella consideratione
de i Suoni, delle Voci & dell'altre cose mostrate nella Prima & nella Seconda parte di
queste mie fatiche. Et di ciò fanno fede molti Libri composti da diuersi Autori, che non
trattano se non di Circoli & Semicircoli, puntati & non puntati, interi & tagliati, non
solo una uolta, ma anco due & tre fiate; ne i quali si ueggono tanti Punti, tante Pause,
tanti Colori, tanti Cifre, tanti Segni, tanti Numeri contra numeri, & tant'altre cose stra
ne; che paiono alle uolte Libri d'un'intricato mercatante. Ne altro si legge in cotesti lo-
ro libri, che possa condur l'Huomo alla intelligenza d'alcuna cosa, che caschi sotto 'l giu
dicio del senso dell'Vdito; come sono le Voci, ò i Suoni, da i quali nascono le Harmonie,
& le melodie, che le cose nominate. Et se ben uiue ancora honoreuolmente il nome d'
alcuni Musici appresso di noi; non s'hāno però acquistato riputatione alcuna con tali chi
mere; ma con le buone harmonie & harmoniosi concenti & con le belle Inuentioni, i
quali si uedono & odono nelle lor compositioni. Et quantunque mescolassero in quelli
cotali intrichi, si sforzarono anco, se non con la speculatione, almeno aiutati dalla pratti
ca & dal lor giudicio, di ridur le loro Harmonie à quella ultima perfettione, che dare le
poteuano; ancorache da molti altri fusse mal'intesa & malamente usata; del che ne fanno
fede molti errori commessi da i Prattici Compositori nelle lor compositioni. Quanto poi
alle Ragioni; cioè, in quanto alla speculatiua; pochi si uedono essere stati quelli, c'hab-
biano tenuto la buona strada; conciosiache, oltra quello che scrisse Boetio in lingua lati
na di tal scienza, che si troua anco esser'imperfetto; non si troua alcuno (lasciando Fran-
chino & il Fabro da un canto,Nota per i
maligni. i quali sono stati, si può dire, commentatori di
Boetio) che habbia procedesto piu oltra speculando intorno le cose appartinenti alla Mu
sica, ritrouando le uere Proportioni de gli interualli Musicali; da Ludouico Fogliano da
Modena in fuori; il quale hauendo forse considerato quello, che Tolomeo lasciò scritto
del Diatonico syntono, s'affaticò nel scriuere un uolume latino in tal facultà; per mo-
strare com'ei puote, le uere Proportioni de i nominati Interualli. Il resto poi de i Musici
Theorici, stando à quel che scrisse Boetio intorno à simili materie, non uolsero, ò non po
tero passar piu oltra; ma si diedero à scriuere le cose mostrate, le quali chiamarono del
genere Quantitatiuo; che sono contenute nel Modo, nel Tempo, & nella Prolatione;
come nel Recaneto di Musica, nel Toscanello, nelle Scintille, & in mille altri libri simi-
li si può uedere. Et di più si trouano anco sopra tali materie uarie opinioni & disputatio-
ni lunghissime, da non uenire mai al fine. Si trouano etiandio molti Trattati, Inuettiue
& molte Apologie d'alcuni Musici, scritti contr'alcun'altri, ne i quali (se bene si leggessero
mille fiate) dopo letti, riletti, & essaminati, non si ritroua altro, che infinite uillanie & male-
dicentie, che dicono l'uno dell'altro (ò che uergogna) senz'alcuna modestia; & finalmen-
page 362te poco di buono; di maniera ch'è vn stupore. Ma veramente cotali Scrittori sono anco
escusabili; percioche si come al tempo di Socrate & di Platone erano i Sofisti; cosi anco si
trouauano costoro à quei tempi, i quali erano stimati tanto, quanto erano quelli nella età
loro; & tanto si essercitaua allora questo loro genere Quantitatiuo, che si può vera-
mente chiamare Arte sofistica nella Musica, & tali Musici Sofisti; quanto i Sofismi à i
tempi de i detti Filosofi. La onde dobbiamo di continuo lodare & ringratiare Iddio, ch'à
poco à poco (non sò in che maniera) cotal cosa sia quasi spenta; & estinta; & che n'habbia
fatto venire ad vna età, nella quale non si attende ad altro, che alla moltiplicatione de i
buoni concenti & delle buone Melodie; com'al vero fine al quale debbe il Musico indric-
ciare ogni sua opera.
Delle Chorde Communi, & delle Particolari delle cantilene Diatoniche, Chromatiche,
& Enharmoniche.Cap. LXXII.
positione delle Cantilene del genere Diatonico; è ragioneuole (per non la-
sciar'in dietro alcuna cosa degna di consideratione) ch'io ragioni vn poco in-
torno gli altri Generi, che sono il Chromatico, & l'Enharmonico; massimamē-
te perche hoggidi alcuni Prattici poco intendenti di cotal cosa, molto s'affaticano, &
pongono ogni lor cura per volerli porr'in vso. Ma inanti ch'io venga à ragionar cosa al-
cuna; parmi che sarà ben fatto, ridur le Chorde di ciascun de questi tre Generi à i luo-
ghi loro per ordine tra l'usate linee & spatij; secondo 'l modo, che tengono costoro; & mo-
strar tutte quelle, che sono Communi & seruono à ciascun Genere, & anco le Particola-
ri; accioche più facilmente s'habbia da intender quello, c'haurò da dire. Onde si dè sa-
pere, che ritrouandosi nel Systema massimo di ciascun genere, da Proslambanomenos à
Netehyperboleon, Diciotto chorde, diuise & ordinate in cinque Tetrachordi; com'etiā-
dio mostra Boetio;Musicae l. 1
cap. 22. alcune si chiamano Naturali & Essentiali del genere, & alcune Acci-
dentali. Le Naturali sono quelle, che sono contenute tra i quattro Tetrachordi, Hypa-
ton, Meson, Diezeugmenon, & Hyperboleon, & le Accidentali quelle, che sono conte-
nute nel Tetrachordo synemennon. Et queste si nominano Accidentali; percioche so-
no collocate tra le prime per accidente; come si può comprendere; essendo che poche
di loro si trouano, ch'habbiano corrispondenza con alcun'altra chorda posta tra Pros-
lambanomenos & Mese per vna Diapason; com'hanno quelle de gli altri Tetrachordi
Diezeugmenon & Hyperboleon; anzi molte di loro non sono differenti d'alcune chor-
de di questi due Tetrachordi, se non per il nome; di maniera che le chorde Naturali &
essentiali di ciascun genere uengono ad essere Quindeci, & Tre si trouano esser le acci-
dentali; conciosia che la chorda Mese è il fine del Tetrachordo Meson, & il principio del
Synemennon; come in più luoghi si può vedere. Et benche tali chorde siano state de-
nominate secondo l'ordine mostrato nel Cap. 28. della Seconda parte; di maniera che, in
quanto alla loro denominatione, non si ritroua alcuna differenza dalla Parhypate, & la
Lychanos del Diatonico, da quelle del Chromatico & dell'; tuttauia quā-
do ciascuna di loro è collocata in vn'Istrumento, sono differenti in quanto alla positione,
ouer'in quanto al sito; conciosia che l'una sia più verso 'l graue, ò verso l'acuto dell'al-
tra; come si può uedere nella Parhypate enharmonica, laquale è più graue della Parhy-
pate de gli altri due generi; & similmente nella Lychanos diatonica, ch'è più acuta della
Lychanos chromatica & della enharmonica; come nel Cap. 38. della Seconda parte si
può comprendere. Onde accioche manifestamente appari, quali siano le chorde Propie
& Naturali, & quali le Accidentali & le Communi di qualunque de i tre nominati Gene-
ri, porrò tre ordini de chorde; il primo de i quali contenerà solamente quelle, che seruo-
no al Diatonico, senza porli alcun'altra chorda, che sia (dirò cosi) forestiera; & le ridurrò
page 363nell'ordine commune vsato da i Prattici; Il secondo contenerà quelle, che seruono al
Chromatico; ancora che ne ritrouaremo molte tra loro, che saranno communi à ciascun
genere; ma non saranno però particolari Diatoniche, ouer particolari Enharmoniche; &
in questo ordine potremo conoscer le particolari chromatiche dalle particolari de gli al-
tri due generi; percioche saranno tutte segnate col
 , & le communi saranno senza. Et
, & le communi saranno senza. Et se bene le chorde b &
 . fanno in questo genere il Tetrachordo Synemennon, non saran-
. fanno in questo genere il Tetrachordo Synemennon, non saran-no però particolari; ma communi à ciascun genere; perche tal Tetrachordo si congiunge
à i quattro primi per accidente; com'hò detto. Il Terzo ordine poi contenerà quelle
chorde, che seruono all'Enharmonico, nel quale ritrouaremo le chorde particolari di
questo Genere, che saranno segnate con questo segno [[mus.hsharp]]. à differenza di quelle, che so-
no particolari & anco communi de gli altri due generi; come si può vedere ne i seguenti
ordini.
 Onde le chorde particolari de questi Generi saranno queste. Primieramente la Terza
Onde le chorde particolari de questi Generi saranno queste. Primieramente la Terza chorda d'ogni Tetrachordo del primo ordine, procedendo dal graue all'acuto, sarà par-
ticolare Diatonica; dopoi la Terza d'ogni Tetrachordo posto nel secondo ordine segna-
ta con questo segno
 . sarà particolare Chromaticha; ma ogni Seconda chorda d'ogni
. sarà particolare Chromaticha; ma ogni Seconda chorda d'ogni Tetrachordo del Terzo ordine segnata con tale cifera [[mus.hsharp]]. sarà particolare Enharmonica;
l'altre poi, che non saranno segnate con alcuni de questi caratteri, saranno communi à
ciascun de i nominati Generi. Et se ben tali ordini sono ristretti in poche chorde; tutta-
uia si potranno far maggiori, secondo che tornarà commodo; come fin'hora nelle cose
della Prattica è stato fatto da i Compositori; il che si può veder nelle loro cantilene. Ne
alcun dè prender marauiglia, ch'io habbia posto in uso cotal segno [[mus.hsharp]]. forse non più vsato
per auanti; percioche non hò ritrouato segno più commodo, che sia stato posto in vso
d'alcuno, col mezo del quale potessi mostrar la chorda Enharmonica, & l'Interuallo, fuori
che questo. Ma s'è lecito à i Filosofi (come vuole Aristotele ne i PredicamentiCap. De
Relatione.) fingere,
ò comporre nuoui Nomi, ò Vocabuli, per manifestare i lor concetti; perche non è anco
page 364lecito al Musico di ritrouar nuoui Segni, per manifestar quelle cose, che fanno al propo-
sito dell'Harmonie? tanto più, che (com'è noto ad ogni studio) la Musica è parte della
Filosofia.
Se l'uno de i due vltimi Generi si possa vsar semplice nelle sue chorde naturali, senz'adope-
rar le Chorde particolari de gli altri.Cap. LXXIII.
scun può comprendere, se tal Genere si possa vsar perfettamente nelle sue chor-
de naturali, oueramente non; però essendo tal cosa manifesta, mi par fuora di
proposito sopra di ciò farne più parola. Passando adunque più oltra, vedere-
mo se 'l si potrà far l'istesso anco ne l'uno de gli altri due senz'adoperar le chorde partico-
lari d'un'altro, & senza la perdita de molte Consonanze, che fanno alla generatione delle
perfette Harmonie. Ilche potremmo conoscer facilmente da questo; che se noi pigliare-
mo per Soggetto della compositione il Tenore posto qui sotto, ch'è del Terzo modo, con-
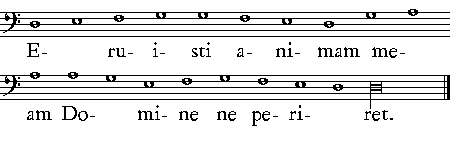 tenuto tra le chorde naturali del genere Diatonico; non è dubbio alcuno, che se lo vor-
tenuto tra le chorde naturali del genere Diatonico; non è dubbio alcuno, che se lo vor-remo accommodare ad vna cantilene de Quattro & de più voci, noi potremmo proce-
dere dal principio al fine per le Chorde naturali di questo Genere per ogni uerso, senza
toccare alcuna chorda particolare de gli altri Generi; come ciascuno potrà uedere. Ma
se lo uorremo ridurre nelle chorde Chromatiche, che saranno le contenute nel sequente
Tenore; ogn'uno, c'hauerà giudicio, potrà conoscere, ciò essere impossibile; conciosia-
che quando non si vorremo partire dalle sue chorde essentiali, contenute nel Secondo
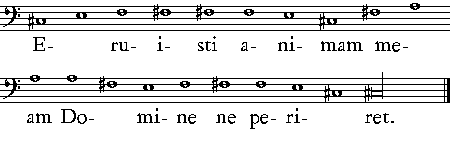 ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri Generi; ri-
ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri Generi; ri-trouaremo, che molte chorde di questo Tenore, non potranno hauer quelli accompa-
gnamenti perfetti, che ricerca ogni perfetta compositione. La onde senz'alcun dubbio
potremo comprendere, che in tal Genere non si potrà comporre perfettamente alcuna
cantilena; com'alcuni s'hanno sognato; oltra che ritrouaremo etiandio alcune modula-
tioni molto strane, i cui Interualli saranno molto lontani dalle forme, che sono contenu-
te nel Numero sonoro. Ma lasciamo questo; percioche credo che sia manifesto à tutti
quelli, c'hanno intelligenza dell'Arte; & passiamo all'Enharmonico, che noi vedremo
quanto poco sapienti siano stati quelli, che hanno detto, che si può comporre in questo
Genere qual si voglia cantilena, non si partendo dalle sue chorde propie & naturali, sen-
z'hauer'aiuto alcuno dalle chorde particolari de gli altri Generi; percioche riducendo il
mostrato Tenore nelle chorde Enharmoniche nella maniera che si uedono; se nō si vorrà
passar fuori delle chorde mostrate in questo Terzo ordine; ritrouaremo molte figure, che
nō si potranno accōpagnare in modo, che dapoi accōpagnate s'odi l'Harmonia perfetta;
page 365
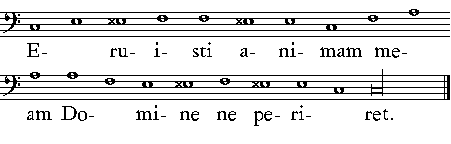 me ricercano le buone, sonore & perfette compositioni; anzi ritrouaremo molte chorde,
me ricercano le buone, sonore & perfette compositioni; anzi ritrouaremo molte chorde, che non potranno hauer quelle Consonanze, che si desiderano; & se pur l'haueranno in
alcuni luogni, sarà necessario, che le parti cantino in tal maniera, che rendino ingrato &
insoaue suono all'orecchie de gli ascoltanti; come l'esperienza sempre ce lo farà vedere.
Potiamo adunque concludere, ch'è impossibile di potere, vsar semplicemente, & da per
sè questi due Generi ultimi, di maniera che vi sia l'Harmonia perfetta, senza l'uso delle
chorde particolari d'alcun'altro Genere.
Che la Musica si può vsare in due maniere; & che le Cantilene, che compongono alcuni de
i Moderni, non sono d'alcuno de i due nominati Generi.Cap. LXXIIII.
chi; com'hò mostrato nella Seconda parte,Cap. 4. & di nuouo son per mostare; & nel
modo che la vsano i Moderni; è da notare, che quando alcun la uolesse usare
nel primo modo, non sarebbe impossibile, che potesse osseruar tutto quello,
ch'osseruarono gli Antichi nelle lor Melodie; ma quando la volesse vsar secondo 'l modo
de i Moderni, con la moltiplicatione de molte parti, & far che in essa si vdisse l'Harmonia
perfetta; qualunque volta pigliasse questa impresa, & volesse porre in uso i due mostrati
Generi, s'affaticarebbe in uano; come si può comprendere da quello, che s'è detto nel
Capitolo precedente; massimamente non si uolendo partire da i precetti dati da gli anti-
chi Prattici, & da me mostrati di sopra nel compor le cantilene.Vedi il cap.
9. de. 6. De
i Sopplimē-
ti. Et se bene alcuni han-
no opinione di cōporre à i nostri giorni le antiche harmonie Chromatiche & le Enhar-
moniche; non è però cosi; percioche ueramente non le conoscendo; passano i termini, &
non usano quelle cose, che concorrono alla compositione loro, che sono l'Harmonia, il
Numero, & le Parole poste insieme. Ne solamente si seruono delle chorde proprie di quel
Genere, del quale dicono, ch'è la compositione; ma etiandio di quelle, che sono proprie,
& seruono particolarmente à gli altri Generi, & d'alcun'altre, che sono al tutto forestiere;
& usano anco molti Interualli diatonici & modulationi tanto strane, quanto si possa dire;
come sono Interualli de Tritoni, Semidiapente, & altri simili, i quali da gli Antichi era-
no molto schiuati; percioche non solamente offendono il sentimento; ma anche contra-
dicono alla ragione; come nelle lor compositioni si può insiememente udire & uedere; le
quali, per non contener'alcuna delle già dette cose, non si possono chiamar composte in
alcun de questi due Generi, che usauano già i Musici antichi; ma in un Genere ritrouato
& fatto ad un modo loro, molto conforme à i loro capricci.
Che 'l Diatonico può procedere nelle sue modulationi per gli Interualli di Terza maggiore, &
di minore; & che ciò non faccia variatione alcuna di Genere.Cap. LXXV.
sino mostrare, che le lor compositioni siano pure Chromatiche, ouer'Enharmo-
niche; tuttauia si sforzano di prouar, che sia cosi in fatto, col dire, che 'l Diatoni-
co procede per due Tuoni & un Semituono per ogni suo Tetrachordo; il Chromatico
per due Semituoni & vn Trihemituono, ch'è la Terza minore; & l'Enharmonico per due
page 366Diesis & un Ditono, ch'è la Terza maggiore; & non potendo il Diatonico procedere per
il Ditono, ne meno per il Semiditono; segue, che quando si usano quest'Interualli, la can-
tilena uenga à uariar Genere. Questo loro argumento ueramente concluderebbe, quan-
do quel, che dicono, fusse uero; ma secondo 'l mio giudicio parmi, che s'ingannino; con-
ciosiache ritrouandosi nel Diatonico tutti quest'Interualli; come nella Seconda parte in
più luoghi habbiamo ueduto; non è inconueniente, che si possano usar'alle uolte in tal
Genere, senza essere tramezati; ne per questo la cantilena uiene ad esser Chromatica, ne
Enharmonica; come si pensano; essendo che quando s'usano in cotal maniera, non s'usa-
no come Elementi, ò semplici parti di tal Genere; ma come Misti, ò parti composte de i
Primi interualli, che sono cotali Elementi. Et che questo sia uero, si può comprender da
quello, che dice Boetio nel Cap. 23. del Primo libro della Musica; ilquale parlando in
questo proposito, dice; ch'anco il Tuono & lo Semituono si può chiamare Trihemituono
nel genere Diatonico; ma non è Incomposto; percioche si fà de due Interualli. Di mo-
do che si può vedere (come etiandio hò mostrato nella Seconda parteCap. 17) che Boetio piglia
il Trihemituono incomposto per Elemento del Genere chromatico & nel Diatonico lo
piglia per un Misto, ò composto de due elementi, che sono il Tuono, & lo Semituono; il
che si può anco dire del Ditono nel Diatonico, ch'è Composto & non Semplice; & nel-
l'Enharmonico è Incomposto; cioè, Elemento di tal Gcnere. Ma anco meglio si com-
prende da questo, che quando parla de cotali Interualli, sempre dice; Si chiamano; ne
mai dice, sono Incomposti; percioche molto ben sapea, che i due ultimi Generi pi-
gliauano i loro Interualli (come si dice) à prestanza dal Diatonico; come in molti luoghi
nella Seconda parte si è potuto uedere. Ne può esser'inconueniente, che da i Semplici
si possa passare à i Composti; percioche cosi porta l'ordine delle cose; ma ben sarebbe im-
possibile, quando da i Semplici, ouer'Elementali si volesse passare ad altre cose più sempli-
ci nell'istesso Genere; come per essempio uediamo nelle Lettere, delle quali si compon-
gono tutte le Parole; che uolendo passare à cose più semplici di quello, che sono, non è
possibile; percioche nel loro Genere non si troua alcuna cosa più semplice. Ne ueramen-
te è impossibile, ch'una cosa Composta in un Genere sia Semplice, ouer'Elementale in
un'altro; conciosia che in un Genere si può cōsiderare ad un modo, & in un'altro ad un'al-
tra maniera. La onde non è errore, che 'l Trihemituono & lo Ditono, che si trouano nel
Diatonico composti, si pongano ne gli altri due Generi per Elementi. Et se ben questi
due Interualli nō si trouano nel genere Diatonico incōposti in atto; sono tuttauia in potē-
za; essendo che si possono ridurre à cotal modo facilmēte, altramente tal potēza sarebbe
uana. Et ciò nō debbe parer strano; perche si come l'Huomo, ch'è Animal risibile, nō si ue-
de che in atto sempre rida; cosi nel genere Diatonico non si troua che sempre si proceda
per Tuono, Tuono, & Semituono per ogni suo Tetrachordo. Onde dico, che 'l passar da
un Genere all'altro nō si può intendere, quādo si usa i Composti, i quali seruono per Ele-
menti dun'altro Genere; ma quādo si usano i Semplici interualli, che sono proprij, & s'a-
doperano particolarmente in quel Genere, che nō si possono ritrouar ne semplici, ne cō-
posti in vn'altro. Però non varrà la Consequenza, che fanno costoro, dicendo; In questa
cantilena si troua l'Interuallo del Ditono & quello del Semiditono posti senz'alcun me-
zo; adunque è Chromatica, ouero Enharmonica; ma si bene varrà à dire; Questa canti-
lena procede per il Semituono minore, adunque è Chromatica; & questa procede per il
Diesis, adunque è Enharmonica; come uale a dire; Questo è animale rationale; ouer,
Questo è risibile; adunque è Huomo; essendo che la differenza specifica è quella, che co-
stituisce la Specie; come fanno quest'ultime differenze del Semituono & del Diesis, che
sono proprie de questi due generi. La onde è da sapere, che gli Interualli, che si trouano ne
i Tetrachordi diatonici, si possono considerare in due modi: cioè, Semplici, come sono i
poco fà nominati; & Composti, come sono quelli di Terza maggiore & di minore; il per-
che considerati con alcun suono mezano, li potremo chiamar'insieme con i Greci Sy-
stemati, quasi Complessioni, ouer'Ordinate compositioni; & considerati senza mezo al-
page 367cuno, si potranno dire Diastemati; cioè, Spacij, ouer'Interualli senza mezo alcuno. Sareb-
be veramente gran pazzia à credere, che noi hora & inanti à noi gli Antichi, prima che
fussero in vso gli altri due Generi, non hauessero potuto vsar se non vna sorte dInterual-
li minori; che sono quelli, che sono contenuti ne i Systemati; & non possono esser Syste-
mati; & non quelli, che sono maggiori, & possono anco esser Systemati; percioche se non
vi fusse stato, & non ui fusse tal libertà; non sò vedere, in qual maniera potessero riuscir
bene l'Harmonie; atteso che sarebbe stato, & sarebbe anco dibisogno che qualunque vol-
ta s'incominciasse à cantare, incominciando nel graue salissemo nell'acuto, per gli In-
terualli minori solamente; & tanto salire, che si venisse à finire poi nell'acuto, & non ri-
tornar mai nel graue, & ripigliare alcuna delle prime voci; & cosi per il contrario. Ma
di gratia qual dolcezza, ò qual soauità d'harmonia potrebbe esser questa? Parmi, ch'in-
tendendola à questo modo, che tanto sia dire, quanto ch'incominciando noi à Parlare da
qual lettera si uoglia dell'Alfabeto, fusse dibisogno di seguitar per ordine tutte l'altre, co-
me sono poste fino al fine, & non ne lasciare alcuna; ma in qual maniera si potrebbe espri-
mere i concetti? Dirà forse alcuno, che i ripigliamenti de voci sono leciti, quando si ripi-
glia la voce per una Ottaua, ò per una Quinta, ò per vna Quarta. Se ciò è lecito; adun-
que erano leciti i Diastemati, ouer'Interualli maggiori; & se era lecito usar non solamen-
te questi ne i ripigliamenti; ma anco i Tritoni; iquali sono interualli dissonanti; come vsa-
no costoro, non sò vedere per qual cagione non erano leciti anco in ogni parte della can-
tilena tanto questi, quāto etiandio i minori de questi, che sono quelli del Ditono & quel-
li del Semiditono; poi c'hanno le lor forme contenute tra i Numeri sonori; & sono con-
sonanti; La onde non vi essend'altre ragioni, potiamo dire, ch'essendo leciti nel genere
Diatonico i Diastemati maggiori, erano anco leciti gli altri mostrati; & per questo non
impediuano, che tal Genere non fusse Diatonico; & non solamente Diatonico; ma Sem-
plice anco, senz'alcuna mistione d'alcun'altro Genere; ilche non aueniua ne gli altri due;
percioche qualunque uolta procedeuano per Tuono maggiore, ò minore, ueniuano à ri-
ceuere, un'interuallo, che è proprio del Diatonico; & per tal maniera tali Generi si pote-
uano chiamar Misti. Et quello, che hò detto di un Genere intendo anco de gli altri in-
torno al procedere per i Diastemati, ouer'Interualli maggiori; essendo che quando nelle
cantilene Diatoniche si vdisse una modulatione del Semituono minore, ouer del Diesis,
quella modulatione si potrebbe chiamar mista; ilche si potrebbe anche dire delle Chro-
matiche Ma dobbiamo auertire, che quantunque la modulatione diatonica sia propria-
mente di modulare dal graue all'acuto per vn Semituono, & per due Tuoni per ogni Te-
trachordo, & la Chromatica per un Semituono maggiore, per un minore, & per un Tri-
hemituono; & l'Enharmonica per due Diesis, & per un Ditono; & cosi per il contrario,
procedendo dall'acuto al graue; nondimeno cantandosi i Diastemati maggiori, molti di
questi uengono ad esser communi; onde resta solamente di propio al Genere Diatonico
la modulatione del Tuono; al Chromatico quella del Semituono minore; & all'En-
harmonico quella del Diesis; come facendone l'esperienza ciascun potrà conosce-
re. Concludendo adunque diremo, che se la Consequenza hor uale à dire; In questa
cantilena si canta la Terza maggiore senz'alcun mezo, adunque è Enharmonica; ouer si
canta la minore, è Chromatica; tal Consequenza ualeua etiandio, auanti che
fossero ritrouati tali Generi, quando semplicemente s'usaua il Diatonico, & non erano
altramente in uso il Semituono Chromatico, ne anco 'l Diesis; poi che (come si può ue-
ramente tener per certo, per le ragioni addotte di sopra) gli Antichi modulauano tali
Interualli senz'alcun mezano suono. La qual cosa, quanto sia fuor di ragione, lasciarò
considerare à ciascuno, c'habbia ogni poco di giudicio nelle cose della Musica. Ma di que
sta materia ueda il Lettore quello ch'io hò discorso nel Cap. 9. del Libro Sesto de i Sop-
plimenti; acciò intendi meglio quello c'hò detto.
page 368
Che doue non si ode nelle Compositioni alcuna varietà d'Harmonia, iui non può esser
varietà alcuna di Genere.Cap. LXXVI.
por la Terza maggiore, ò la minore tramezate, ò non tramezate d'alcun'altro
suono; ma nella modulatione de gli Interualli proprij de i Generi; resta hor'à
dire, che la mutatione d'un Genere nell'altro similmente consiste nella muta-
tione dell'Harmonie; come la mutatione d'un Modo nell'altro consiste nella mutatione
delle modulationi d'vna specie di Systema nell'altra, & nella mutatione delle Cadenze;
percioche s'io udirò quell'istessa Harmonia in una cantilena, le cui parti procedino per
un Systema di Ditono, ouer di Semiditono; ch'io odo in una, le cui parti procedino per
il loro Diastema; & che in quella maniera mi muouerà l'udito l'una, che mi muouerà l'al-
tra; io non sò ueder, che differenza grande possa esser tra queste due cantilene. Però di-
co, che non può esser'alcuna differenza di Genere in quelle compositioni, che non si ode
differenza alcuna d'Harmonia; come non può esser differenz'alcuna di Modo, oue non è
differenza di modulatione & di cadenze; & soggiungo etiandio, che allora si potrà dir'
essere differenza & uarietà di Genere in quelle, quando s'udirà uarietà di Harmonia, che
sia numerosa, con Parole conuenienti accommodate in essa. Non dico però, che la ua-
rietà sia nelle Harmonie d'un Modo ad un'altro; come del Modo primo al terzo; percio-
che questa uarietà senza dubbio si troua nelle cantilene Diatoniche; ma dico uarietà
d'Harmonia, ch'in tutto & per tutto sia differente dall'Harmonia, che nasce dalle com-
positioni Diatoniche; & che usata nel modo, che faceuano gli Antichi accompagnata
col Numero, per un'altra maniera insolita muouino l'Vdito, di quel che fanno le commu
ni Harmonie, che s'odono di cōtinuo composte d'alcuni sciocchi Compositori, & Orga-
nisti; & faccia udir diuersità de Modi; la qual diuersità, se si ode, ò non nelle Composi-
tioni moderne, lequali chiamano Chromatiche & semplici, lasciarò di dire; & lasciarò
giudicare à quelli, che sono periti nell'Arte & nella Scienza della Musica.
Dell'vtile ch'apportano i predetti due Generi; & in qual maniera si possino vsare,
che faccino buoni effetti.Cap. LXXVII.
mistione del Genere Diatonico; parmi ciò non hauer detto fuori di ragione; im-
peroche non hò ritrouato alcun Scrittore ne Greco, ne Latino, che dica vera-
mente, che s'usassino, ò si possino vsar separatamente & semplici, dal Diatonico in fuori;
come hò mostrato. Et per confirmatione di questo; Boetio nel Cap. 4. del lib. 4. della
Musica, pone la diuisione del Modo Lidio nel Genere Diatonico semplice, ancora che
non mostri la diuisione de gli altri Modi; & nel principio del Cap. 5. lo chiama non sola-
mente Più semplice; ma anco Principe de tutti gli altri; nella qual diuisione (per confir-
mare etiandio con un'essempio quello, che hò detto di sopra) pone prima quattro uolte
l'Interuallo della Terza minore, senza por di mezo alcuna chorda. Nel Cap. 3. poi pone
le Cifere del detto Modo de tutti tre i Generi ridotti in uno, riseruandosi di por quelle de
gli altri Modi in un'altro tempo & luogo più commodo; tuttauia non hò trouato essempio
alcuno de gli altri Generi semplici; percioche se ben Tolomeo nel Cap. 15. del Secondo
libro de gli Harmonici, pone gli essempi de i Modi ne gli altri Generi; nondimeno non li
pone senza mistione; com'ogn'uno potrà vedere. Quest'hò uoluto dire; percioche altro
è il porre gli Interualli d'un Genere in un'ordine de Suoni, & altro è dire, che si possino
usar semplicemente nel loro Genere, che facino buono effetto; conciosia che si ritrouano
page 369molte cose, che sono semplici nel loro essere, lequali da sè sono poco buone; ma accom-
pagnate con altre cose, & vsate con i debiti mezi sono buone, & fanno mirabile effetto;
come vediamo della Farina, tra l'altre cose; che da sè, non sò veramente ,
quanto possa esser'al gusto nel mangiarla diletteuole & buona, ma accompagnata con al-
tre cose, & posta in vso con i debiti mezi, habbiamo il Pane & altre compositioni, che ap-
portano gran commodo & gran diletto al Genere humano. La onde si può dir il medesi-
mo de questi due Generi vltimi, i quali da sè non possono esser sufficienti à dar diletto al-
l'Vdito; ma accompagnati al Diatonico sono di grande vtilità, & di molto commodo,
vsandoli & accompagnandoli l'vno con l'altro con quei modi, che si ricerca nella Com-
positione; & questo da quello, ch'io son per dire, si potrà comprendere. Primieramente
da loro potiamo hauer questo utile, che col mezo delle lor Chorde accommodate tra le
Chorde diatoniche, potiamo passare all'vso dell'Harmonie perfette; accommodandosi di
loro per l'acquisto de molte Consonanze imperfette maggiori, ò minori; le quali in mol-
ti luoghi non si possono hauere nell'ordine delle Chorde diatoniche; com'è manifesto à
ciascun, che sia essercitato nell'Arte del comporre; le quali uengono alle uolte al propo-
sito, per fare lHarmonia, che corrispondi allegra, ò mesta secōdo la natura delle Parole.
Potiamo dopoi col mezo delle Chorde di questi Generi far le Trasportationi de i Modi
uerso l'acuto, ouero verso 'l graue; le quali Trasportationi sono molto necessarie à gli
Organisti, che seruono alle Cappelle; cōciosia che fà dibisogno, ch'alle volte trasportino il
Modo, hora dall'acuto nel graue, & tallora dal graue nell'acuto; secōdo che la natura del-
le Voci, che si trouano in quelle, lo ricerca; che senza 'l loro aiuto sarebbe impossibile po-
terlo fare. Et quantunque tali Chorde s'vsino spesse fiate in simili occasioni, tuttauia nō si
procede per esse se non diatonicamente, secondo i modi mostrati di sopra; di maniera che
nasce sommo piacere & diletto à tutti quelli, ch'ascoltano: per il contrario molto fastidi-
scono gli audienti, & molto gli offendono il senso, quando sono vsate fuor di proposito,
senza regola & senz'alcun'ordine; & quando si passa per queste Chorde tanto strane la-
sciando da vn canto le Diatoniche, fuori di proposito, nasce quel, che dice Horatio in
questo proposito;De Arte
Poetica. che allora
Citharoedus
Ridetur, chorda qui semper oberrat eadem.
Et non si marauiglia alcuno, ch'io habbia detto, che s'vsino le Chorde de i Generi, &
si proceda secondo i modi mostrati di sopra; imperoche vsiamo veramente le Chorde;
ma non essi Generi, cioè, vsiamo le Parti, ma non il Tutto; essendo che (come più oltra
vederemo) l'uso intiero del Genere non può far buon'efferto, ma si bene lvso delle Par-
ti; cioè, delle Chorde segnate con questi segni accidentali
 . b. &
. b. &  . & anche con que-
. & anche con que-sto [[mus.hsharp]]. vsandole nel modo, che di sopra ho mostrato. Et s'alle uolte ritrouaremo al-
cuna cantilena libera al tutto da queste cifere, potremo dir (com'è uero) che proce-
da per le Chorde diatoniche solamente; ma quando ne ritrouaremo alcuna, ch'hab-
bia in se simili caratteri b &
 . allora diremo, che procede per le chorde Chromati-
. allora diremo, che procede per le chorde Chromati-che, mescolate con le Diatoniche. Et se ne ritrouaremo alcuna, la quale hauesse al-
cuna chorda, che non si ritrouasse connumerata tra le Diatoniche, ne tra le Chromati-
che, la potremo nominar'Enharmonica; pur che tal chorda si possa segnare con questo
segno [[mus.hsharp]]; & possa diuidere il Semituono maggiore in due Parti; imperoche tal chorda
verrà ad essere vna di quelle, che si ritrouano nel Terzo ordine mostrato di sopra; & po-
tremo dire, che tal Cantilena proceda per le chorde di ciascun de i tre nominati
Generi. Ma si debbe auertire, che tal mistione si può fare in più maniere, secondo 'l
voler de i Compositori, & de i Sonatori, trasportando i Modi più nel graue, ouer nell'a-
cuto fuori delle lor chorde naturali, cōtenuti nelle chorde del Genere Diatonico; & la cō
positione (come dicono impropriamente) si canta per Musica finta. La Prima delle qua-
li è (lasciando da parte quelli, che non sono cosi in vso) quando le cantilene procedono
per le chorde segnate col b. rotondo dal loro principio; trasportate verso 'l graue per vn
page 370Tuono; come è il canto, Verbum iniquum & dolosum; di Morale Spagnolo à cinque; & il bel-
lissimo & arteficioso Aspice Domine; d'Adriano à sei uoci. La Seconda maniera è quella,
nella quale si procede per le chorde segnate dal principio della cantilena colsegno
 . &
. & si trasporta il Modo per un Tuono uerso l'acuto. Et nell'vna & l'altra sorte di queste can-
tilene alle uolte si tocca le chorde Enharmoniche, per poter'hauer le consonanze Imper-
fette maggiori & le minori secondo 'l proposito; à benche si tocchino di raro; di modo
che per tal maniera venimo ad usare i due Generi detti; che fanno mirabilissimi effet-
ti. Non dico già (come anc'hò detto) che usiamo tutto 'l Genere; ma si bene alcuna parte
del Genere; cioè, alcune chorde; accommodandole al Genere Diatonico, & proceden-
do secondo la sua natura per Tuoni & Semituoni maggiori; com'a ciascuno è manifesto.
Per qual cagione le Compositioni, che compongono alcuni Moderni per Chromatiche,
facciano tristi effetti.Cap. LXXVIII.
che vogliono, che noi allora vsiamo il Chromatico, & l'Enharmonico nelle
compositioni, quando vsiamo le chorde de i già detti Generi; ma ueramen-
te altro è vsare il Genere, & altro accommodarsi d'alcune Chorde di tal gene-
re; ouer'accommodarsi anco d'alcuni suoi Interualli; come etiandio altro è l'uso del
Tutto, & altro quel delle Parti. Onde l'uso delle chorde & anco d'un'Interuallo, che
sia sonoro si può concedere; percioche fà buono effetto; & tal'è l'uso delle Parti;
ma quello del Tutto; cioè, de tutte le chorde di vn Genere & de tutti i suoi Interual-
li non è lecito; conciosia che fà tristo effetto. Per la qual cosa l'uso del Genere, è usar
tutte le sue chorde & quelli Interuali tutti, che sono considerati dal Musico in tal Ge-
nere, & non alcun'altro; & questo dico nelle modulationi, che fanno le parti della can-
tilena; ma l'uso delle Chorde, non è altro, che l'accommodarsi di esse nelle modulatio-
ni delle cantilene ; procedendo per quelli Interualli, che si ritrouano &
anco si potessino ritrouare nel Genere Diatonico; come da molti sono state & anco
sono felicemente usate; lasciando da un canto quelli, che sono propij de quelle chor-
de Chromatiche & Enharmoniche, che noi usiamo; cioè, il Semituono minore, &
li Diesis. Et perche sono alcuni che dicono, che se l'uso delle Chorde chromatiche
(se bene non s'usa il Genere) fà nelle cantilene effetti mirabili, che quando si vdisse l
Genere puro, si moltiplicarebbe la Melodia; però dico, che quantunque à questi ba-
starebbe la risposta data di sopra; cioè che 'l Genere semplice Chromatico & l' non si possano usare; si può anche dire (poniamo che si potesse usare 'l Genere) che
non uale sempre la consequenza à dire; l'uso delle Parti torna commodo; adunque
maggiormente l'uso del Tutto; conciosia che si troua in fatto, che non è uera; come cia-
scheduno sano di giudicio può esser certo. Et questo non solamente si uerifica nella
Musica; ma anche nell'altre Arti; come uediamo nell'Arte del Scultore; che tutto quel
Marmo, ch'ei piglia per far'una Statua, non torna al suo proposito, ma alcune parti;
essendo che prima lo elegge, dopoi s'accommoda à quelle parti, che gli tornano più
al proposito, leuandogli il superfluo; & conduce l'opera al fine desiderato. Non pi-
glia adunque il Scultore tutta quella pietra, che s'hauea posto inanti; ma quella parte
solamente, ch'ei uede esser necessaria al suo bisogno. Onde i Musici etiandio conoscen-
do, che l'uso delle Chorde chromatiche li tornaua molto al proposito; & che l'uso de i Ge
neri era molto incommodo; presero quella parte, che faceua per loro, à far più bello
& più leggiadro il Diatonico, & con tal mezo lo ridussero alla sua perfettione; concio-
sia che in esso (secondo i propositi) si possono far'udire ogni maniera di concento, sia dol-
ce, ouero aspro, ò come si uoglia; massimamente quando le Consonanze sono adoperate
con proposito dal Compositore, c'habbia giudicio. L'uso adunque delle Parti è uti-
page 371le, anzi dirò necessario, & non quello del Tutto; percioche con l'aiuto d'vna chorda chro-
matica potiamo peruenire all'uso d'una buona & sonora Harmonia, & schiuar nel genere
Diatonico alcune discommode relationi de Tritoni, Semidiapenti, & d'altri simili Inter-
ualli, che fanno le parti cātādo insieme; com'altroue hò mostrato, senza l'aiuto delle quali
molte uolte si potrebbe vdir non solamente assai durezze; ma anco alcune disconze mo-
dulationi. Et quantunque tutti questi inconueniēti si potessero schiuare, vsando solamen
te le chorde diatoniche; tuttauia ciò si farebbe alquanto più difficilmente; massimamen-
te volendo (come porta 'l douere) cercar di uariar l'Harmonia; la onde auiene, che per l'u-
so di tal chorda i Modi si fanno più dolci & più soaui. Io uoglio credere, che gli Anti-
chi non chiamassero il Diatonico più duro & più naturale de gli altri due Generi per al-
tro, se non perche videro, che dalle chorde chromatiche gli era moltiplicata l'Harmonia,
& si faceua più lasciuo; & stando nelle sue proprie chorde, era alquanto più virile, & più
hauea del forte. Et credo etiandio, che 'l Chromatico pigliasse il nome di lasciuo, di
molle, & di effeminato, dall'effetto, che faceuano le sue chorde poste tra quelle del
Diatonico; & ciò mi fà credere Boetio,Musicae li.
1. cap. 1. quando dice, ch'vna chorda sola posta da Ti-
motheo nell'Istrumento antico, ilquale era ordinato in vn'ordine de Suoni diuisi diato-
nicamente, faceua un tal'effetto; come anco faceua quella aggiunta da Terpandro (co-
me si legge) nell'istesso Istrumento; il perche si può etiandio comprendere, che non
vsassero il Chromatico semplice, & anco che non adoperassero tal chorda se non per
ornamento del Diatonico. Et perch'io uedo che 'l passar per le chorde Enharmoni-
che poste ne i nostri Istrumenti moderni, è cosa alquanto più difficile, & vuole il Sonato-
re alquanto più esperto, di quel, che non vuole, quando passa insieme per le chorde dia-
toniche & per le chromatiche; però questo mi fà pensare, che gli Antichi, hauendo ri-
spetto à cotal cosa, chiamassero l'Enharmonico difficile; ancora che la difficultà era
posta in molt'altre cose; come più oltra son per dimostrare. Diremo adunque ritor-
nando al nostro proposito, che l'vso delle Parti è buono, & torna molto commodo al
Compositore, & che l'uso del Tutto (oltra l'incommodità) fà la Cantilena senz'alcuna
vaghezza; perche nella sua compositione entrano alcune cose, le quali senza dubbio
sono molto sproportionate & fuori d'ogni Harmonia, & non possono far'alcuno buon
concento. Et s'alcuno dirà, che tali cose spiacciono, non perche siano triste da sè, ma
perche l'Vdito non è assuefatto ad udirle. Parmi, che costui voglia dire, ch'vn cibo tri-
sto & insipido habbia da piacere, dopò che lungamente si hauerà assuefatto il Gusto;
ma sia pur come si uoglia io non credo, che cosi come colui, il quale haurà usato il suo
Gusto ad un cibo tristo (se non fusse al tutto fuori di se) dopo che n'haurà gustato
un'altro, che sia buono & perfetto; non conosca, & insieme non confessi , tal cibo esser buono, diletteuole, & soaue; & che quello, che mangiaua prima era
tristo & senza soauità alcuna; cosi non credo, che ciascuno, il quale haurà assuefat-
to il suo Vdito à cotali cantilene; dopo l'hauerne udito una diatonica ben ordinata,
non confessi ueramente quella esser buona, & l'altre triste. Et accioche non pari, che
quel ch'io hò detto, sia detto senz'alcuna ragione, voglio ch'inuestighiamo hora la ca-
gione; perche queste Cantilene non possino esser buone. La onde è da sapere, che si co-
me è impossibile, che quella cosa, la quale hà le sue parti, che tra loro hanno vna certa cor
rispōdente proportione; la quale da i Greci è chiamata Συμμετρία, non diletti 'l Senso; che
si diletta grandemente de gli Oggetti proportionati; cosi è impossibile; che quella, che hà
le sue parti fuori di tal proportione, possa dilettare. Il perche dico, che hauendo il Ge-
nere Diatonico in sè cotale proportione; corrispondente (come son per dichiarare) non
può far che ueramente non diletti, & che 'l Senso di tal cosa non ne piglia sommo piace-
re. Per contrario, essendo le Parti del Chromatico, & quelle dell'Ennarmonico dispropor
tionate col Tutto, è impossibile, che possino dilettare. Però è da notare, ch'io chiamo il
Tutto in questo luogo, tutto 'l Corpo della cantilena; cioè, tutte le Parti insieme; & la
Parte nomino la modulatione d'una di esse. Similmente chiamo 'l Tutto una consonan-
page 372za, & la Parte ciascun'interuallo contenuto nel Systema di tal consonanza. Hora in-
teso questo, dico; ch'è impossibile, che 'l Diatonico non diletti, hauendo le Parti propor-
tionate col tutto; conciosia che non si troua nelle sue parti alcun'Interuallo cantabile,
che non sia simile ad una Consonanza, che si pone nel Contrapunto; come potiamo ve-
der per essempio; che 'l Diastema dell'Ottaua cantato nelle parti è simile in proportione
all'Interuallo dell'Ottaua, che si troua collocata nel Contrapunto tra vna parte & l'al-
tra. Simigliantemente l'interuallo della Quinta cantato, è simile à quel della Quinta po-
sta nel Contrapunto; Ilche si può anche dire dell'interuallo della Quarta, delle due Ter-
ze, delle due Seste, & de quelli de i Tuoni, & del Semituono maggiore; che di quell'istes-
sa proportione si pongono ne i Contrapunti, nella quale si trouano esser cantati nelle
parti della cantilena. Onde non è marauiglia, sio ho detto, che 'l genere Diatonico
non può far se non buono effetto; per il contrario, che 'l genere Chromatico lo fà tristo
& simigliantemente l'Enharmonico; percioche gli Interualli dell'vno & dell'altro posti
ne i Contrapunti non sono proportionati con quelli, che si cantano nelle parti, ne per
il contrario; imperoche l'interuallo del Semituono minore, che si canta nel Chromati-
co, non è proportionato con alcun de quelli, che si pongono nel Contrapunto. Ne ve-
ramente si pone nel Contrapunto cotale interuallo; percioche farebbe tristo effetto, co-
m'è manifesto; ancora che si ponesse sincopato, non essendo contenuto da tal propor-
tione, ch'aggiunto ad vn'altro qual si uoglia Interuallo possa far'vna consonanza; impe-
roche è connumerato tra quelli, che si chiamano Ecmeli, i quali hò mostrato di sopra nel
Cap. 4. Tra questi etiandio si pone il Diesis Enharmonico, il quale è in tutto fuori d'ogni
proportione con gli interualli posti nel Contrapunto; percioche à niun di essi s'assimiglia,
& è molto più lontano da tal proportione, che non è il Semituono minore. Onde auiene,
che meno harmonioso è l'Enharmonico nel Contrapunto, che 'l Chromatico; essendo
che quanto più alcun Genere si lontana da tale proportione corrispondente, tanto più
offende 'l sentimento. Et se ben l'Enharmonico è detto da molti Harmonico dalla com-
mune Harmonia, & uogliono, che sia Genere bonissimo; percioche (nel modo ch'io hò
dichiarato) quādo entra nella modulatione de gli altri Generi, può far buono effetto; tut
tauia, come dice Psello;In Musica. Δυσμελωδικώτατον μέντοι τὸ ἁπμονικὸν γένος τῆς μελωδίας ἐστὶ; cioè,
il Genere Harmonico hà tristissima Melodia nella Melodia; ancora che alcuni uogliano
che s'intenda, che in cotal Genere con gran difficultà si possa essercitare l'Harmonia; & è
troppo uero, che hà tristissima Melodia; cōciosia che quādo si uiene al suo Contrapunto,
fà tristissimo effetto; nō hauēdo (come hò detto) gli Interualli cantati simili in proportio-
ne à quelli, che si pongono ne i Contrapunti. Per questo adunque dico, che 'l Cōtrapun-
to, ouer l'Harmonia de questi due Generi ultimi non può per alcun modo esser buono;
E' ben uero, che l'Harmonia è tanto men trista, quanto più s'accosta alla proportione
corrispondente, già nominata.
Delle cose che concorreuano nella compositione de i Generi.Cap. LXXIX.
& 7. mostrai il modo, che teneuano gli Antichi nel re-
citare la Musica, & quelle cose, che concorreuano nella Compositione delle lor
Melodie; & ciò potrebbe bastare al Lettore per conoscer la differenza in quan-
to all'uso & alla compositione della Musica moderna dalla anticha; tuttauia
uoglio (per non lasciar alcuna cosa, che sia degna di consideratione) che vediamo hora
alcune cose, che gli Antichi osseruauano nella compositione delle Melodie de questi Ge-
neri, accioche manifestamente si possa conoscere, se i moderni Chromatisti si accostano
al uero, ò se pur sono al tutto fuori della buona strada. Ci dobbiamo adunque ricorda-
re, ch'io dissi, che gli Antichi nelle loro cantilene considerauano una compositione di
Numero, d'Harmonia, & di Parole; la qual compositione nominarono Melodia;
page 373ma si dè auertire, che nella compositione de i Generi haueuano non solamente l'Harmo-
nie differenti; ma anco il Numero, ò Metro, che lo uogliamo chiamare, determinato, &
diuerso; percioche quei Piedi contenuti in un Verso, che poneuano in un Genere,
non poneuano nell'altro. Et ciò si può comprendere, leggendo la Musica di Plutarco,
ou'ei parlando manifestamente de i Piedi, che si poneuano ne gli Enharmonij, oltra mol-
te altre parole, che cio manifestano, dice; che nel primo luogo si poneua lo Spondeo; &
più à basso parlando de gli Enharmonij d'Olimpo, si vede, che fà manifestissimamente cō
memoratione del Peone, & del Trocheo, ch'intrauano nella compositione di cotal Ge-
nere; come si può anco vedere nel Cap. 9. del 6. Libro De i Sopplimenti Musicali. Et non
solamente vsauano tal cosa ne gli Enharmonij; ma etiandio ne gli altri; come si può com-
prendere dalle parole di Boetio, poste nel Cap. 3. del Quarto libro della Musica; le qua-
li dicono breuemente; che gli Antichi per non por sempre i nomi intieri delle chorde nel-
le lor cantilene, ritrouarono alcune cifere, con le quali notauano cotali nomi, & le diui-
sero per i Generi & per i Modi; & cercarono di far con breuità, quando voleuano scri-
uere alcuna lor cantilena sopr'alcuna compositione fatta in uersi, di porre cotali cifere;
onde non solamente veniuano ad esplicar le Parole contenute in tali Versi, ma etiandio
la cantilena. Plutarco ancora dice più auanti, che le prime Leggi delle cantilene, che
si cantauano con gli Istrumenti da chorde, erano mescolate con Versi, ne i quali si can-
taua la Dittione, ò Parola dithyrambica; & questa parola era prima composta de più pa-
role; come è questa Σελαννεοάεια, posta da Platone nel Cratilo, che è composta di tre; cioè,
di Σέλας, che vol dir Lume; di Νέον, che significa Nuouo, & di Ε῎ννον, che importa Vec-
chio; col qual nome dice, che si dourebbe chiamar la Luna, che di continuo uiene à cam-
biare il lume, & à rinouarsi; delle quali parole n'è copiosissimo Aristofane nelle Comme-
die; & sono forse quelle ch'Horatio chiama Sesquipedalia verba;Ad Piso-
nes. Et dopoi la parola Dithy-
rambica era contenuta sotto alcuni Piedi veloci più d'ogn'altro Piede; & da cotali Piedi,
ch'erano posti ne i Versi, haueano la Misura de i mouimenti dell'Harmonia; laquale Har-
monia era terminata & costituita sott'vn certo Modo, ouer'Aria, che lo vogliamo dire, di
cantare; come sono quei Modi, sopra i quali cantiamo i Sonetti, ò Canzoni del Petrar-
ca; oueramente le Rime dell'Ariosto. Ne cotali Modi si poteano mutare, ouer'alterare
in parte alcuna fuora del loro terminato Numero, ò Metro, senz'offesa dell'Vdito; come
vediamo nell'Harmonia de i Balli, laquale offende grandemente, quando è alterata in
vn minimo piede. Onde si vede manifestamente, che nella compositione de i Gene-
ri intraua 'l Numero, ò Metro, contenuto ne i Piedi de i Versi. Et non solamente il Nu-
mero, parlando assolutamente; ma questo, ouer quel numero; cioè, questo, ò quel Pie-
de; ò Datilo, ò Spondeo, ò Trocheo, ouer'altro simile, che fusse. Il perche è pur troppo
manifesto, che gli Antichi vsauano incotali Generi vna sorte de Versi terminata; anco-
ra che non si possa fermamente sapere, qual maniera fusse; come anco non potiamo hauer
cognitione alcuna del Modo, ouer'Aria del loro cantare; poiche da niuno (per quanto
si vede) è stato lasciato scritto cosa alcuna. Ne si ritroua anco, che gli Antichi faces-
sero cantar molte parti (come faciamo noi) in un concento; ma cantauano soli, accom-
pagnando la lor voce col suono d'un'Istrumento; il che faceuano anco gli Hebrei; come
di ciò ne fà fede Gioseffo,De Antiq.
lib. 6. c. 9. & il Diuino Hieronimo;Ad Mar-
cellum. i quali dicono, ch'anticamente i sa-
cri Salmi si cantauano con la voce congiunta all'Organo. Et io tengo per fermo, ch'al-
cune delle chorde de i loro Istrumenti erano accordate (come n'hò veduto & vdito mol-
ti antichissimi) per Ottaua, per Quinta, & per Quarta; & l'Harmonia, che vsciua da
queste chorde, sempre si vdiua continuata & senz'alcuna quiete, mentre sonauano;
& dopoi sopra di esse faceuano vna parte al modo loro con l'altre chorde più acu-
te. Et quel, che mi fà creder questo è; ch'io vedo, che fin'hoggidi si ritrouano alcuni
Istrumenti antichissimi, i quali sono in tal modo fatti, che si sonano, come hò det-
ro, & in essi si cantano; tra i quali si troua quello, che da i Toschani si chiama Sin-
fonia; ilquale alcuni uogliono, che fusse la Lira antica. Et forse Ottomaro Lusci-
page 374nio nel Lib. 1. della Musurgia hauendo tal'opinione lo nominò Lira. Et potrebbe facil-
mente esser quello, che commemora Horatio, dicendo;De Arte
Poetica.
Vt gratas inter mensas Symphonia discors,
Si ritroua etiandio vn'altra sorte d'Istrumento lungo intorno vn braccio, il cui nome
si chiama in Vinegia Altobasso, & è quadrato & uacuo; sopra 'l quale sono tese alquante
chorde accordate tra loro per una delle nominate consonanze, & s'vsa in questa manie-
ra; che mentre 'l Sonatore di questo Istrumento sott'un certo numero, ò tempo percuote
con una mano le sue chorde con vna bachetta, con l'altra sona un Flauto, & fà vdir'vn'a-
ria di cantilena, fatto à suo modo. Et non solamente si trouano cotali Istrumenti da
chorde; ma etiandio se ne troua tra quelli da fiato vno ch'in Thoscana si chiama Corna-
musa; nel quale già si soleua vdire, due ò tre suoni continui accordati insieme consonan-
ti, che nasceuano da due, ò tre Pifferi graui, accordati al sudetto modo; ancora ch'al pre-
sente se ne odi solamente uno, & dapoi si ode vn'aria di cantilena, che si fà da un Piffero
acuto; che se ben non accorda col concento de tali Pifferi in ogni parte, almeno s'ac-
corda nel fine & in alcune cadenze; come si fà etiandio in ciascuno de i nominati Istru-
menti; al suono de iquali cantano i Rustici le lor Canzoni; simile à quella ch'io hò po-
sto nel Cap. 2. del Lib. 8. De i Sopplimenti. L'uso di quest'Istrumento & l'istrumento an-
cora è descritto da Battista Mantoano; ilquale parlando d'un suo Tonio sonatore di co-
tale Istrumento, nella sua Bucolica dice;
Et cum multifori Tonius cui tibia buxo.
Tandem post epulas & pocula multicolorem
Ventriculum sumpsit, buccasꝗ inflare rubentes
Incipiens, oculos aperit, cilijsꝗ leuatis
Multotiesꝗ altis flatu à pulmonibus hausto
Vtrem implet, cubito vocem dat Tibia presso.
Nunc huc, nunc illuc digito saliente vocauit
Pinguibus à mensis iuuenes ad compita cantu,
Saltidico, dulciꝗ diem certamine clausit.
Quest'istesso si ritroua etiandio nelle Trombe, che s'usano ne gli Esserciti & nelle Ar-
mate di mare; percioche mentre molte di loro sonano con un suono continuo, fuora di
quelle se ne ode una, che chiamano Chiareto; che fà udire nell'acuto un aria di Can-
zone; nel modo di quella ch'io hò nominato poco fà, che rende mirabile effetto ne gli au-
ditori; oltra che dà segno all'Essercito di combattere, ò di dar'all'arme, come dicono; &
finalmente il raccoglierlo in uno. La onde mi penso, che quei Pifferi, che gli Antichi chia
mauano Destri & Sinistri, iquali usauano (com'altre uolte hò detto2. Par. c. 4.) nelle Comedie, fus-
sero accordati in tal maniera. Gli Organi Antichi etiandio à tal maniera s'accostauano;
percioche non erano fatti, come moderni; & di ciò me n'hà fatto fede il rarissimo Fabri-
catore de simili Istrumenti Maestro Vincenzo Colombi da Casal Sanuas; ilquale ritro-
uandosi già molt'anni nel Piemonte appresso Turino, ne ritrouò un molto antico, ch'era
senza canne, & tutto marcio; & hauea un Tastame di tal maniera, che dalla parte sinistra;
cioè, nel graue, hauea i Tasti tanto larghi, che per man grande che fusse stata, apena pote-
ua arriuare il Quinto tasto; & cotale Tastame, tanto più che si andaua uerso la banda de-
stra; cioè, nell'acuto, tanto più si faceua minore. Vn Tastame quasi simile anco taccato al
Somiero, mi trouo hauer nelle mani; che mi diede M. Vincēzo Colōna nella sudetta Ar
te à niuno inferiore de nostri tēpi; ritrouato in un'Organo antichissimo; i fori del qual So
miero, & dalla lōtanāza d'uno d'all'altro si cōprēde, che le canne dell'Organo, di cui era, &
dal Tastame, erano d'una istessa grossezza; onde nella lunghezza di necessità, doueano
proportionatamēte esser differēti; la cui forma si può vedere nel Cap. 3. del suddetto lib.
De i Sopplementi & fù d'una Chiesa di Grado. Et (per quel che l'uno & l'altro uidero)
tēgono per fermo, che si doueano anco accordare in altra maniera di quel, che s'accorda-
page 375no i nostri moderni. Si ritrouano etiandio à i nostri tempi molti altri Istrumēti, si da chor-
de, come da fiato, che si sonano in tal modo; i quali (per non esser lungo) lasciò de nomina-
re. Erano adunque composti i Generi d'Harmonia, di Numero, & d'Oratione: ne intra
uano nelle Compositioni loro tutte le sorti de Versi, ò piedi; ma questo, ò quello; cioè, un
terminato Numero; & per tal maniera i Musici Antichi essercitauano la Musica ne i lo-
ro Generi; ne ciò era à loro difficile, ne anco impossibile; perche poteuano, vsandola in
cotal modo, far vdire quale Interuallo voleuano nelle lor canzoni; che non poteua ge-
nerar fastidio di maniera, che non si potesse tollerare; conciosia che non vsauano i Con-
trapunti, che usiamo nelle nostre Compositioni; anzi vsauano vn semplice modo d'Har-
monia, come si è potuto vedere.
Opinioni de i Chromatisti ributtate.Cap. LXXX.
possino vsar qual si voglia Interuallo cantando, quantunque non habbia la
sua forma, ò proportione collocata tra i Numeri harmonici; & si muouono
con questa ragione; che potendo la Voce formare ogn'Interuallo, & essendo
necessario d'imitare il Parlar famigliare nel proferir le Parole; come vsano gli Oratori,
& come vuole anco il douere; non è inconueniente, che si possa usar tutti quelli Interual-
li, che fanno al proposito, per potere esprimere i concetti, che sono contenuti nelle Paro-
le, con quelli accenti, & altre cose, nel modo che ragionando li proferimo, acciò muoui-
no gli affetti. A i quali si risponde, che veramente è grande inconueniente; imperoche al-
tro è parlare famigliarmente, & altro è parlar modulando, ò cantando. Ne mai hò vdito
Oratore (poi che dicono, che bisogna imitar gli Oratori, accioche la Musica muoua gli af-
fettiVide cap.
11. lib. 8.
Supple.) che usi nel suo parlare quei cosi strani & sgarbati Interualli, ch'vsano costoro; per-
cioche quando li usasse, non sò uedere, in qual maniera potesse piegar l'animo del Giu-
dice, & persuaderlo à far'il suo uolere; com'è il suo fine; se non per il contrario; conciosia
che quantunque si potesse far'il tutto commodamente in una parte della cantilena, &
si udissero tali accenti fatti con proposito, & che facessero buoni effetti; tuttauia ne i ac-
compagnamenti si udirebbono cose tanto ladre, & assassine; dirò cosi; che sarebbe di-
bisogno chiudersi l'orecchie. Ne uale cotesta loro consequenza; La uoce può far'ogni
Interuallo; adunque si può & si debbe usar'ogn'Interuallo; perche tanto sarebbe dire,
quanto, che potendo far l'Huomo bene & male; li fusse lecito di fare ogni sceleraggine,
& usar'ogni modo illicito contra i buoni costumi, contra ogni douere, & contra ogni giu-
stitia. Ma ueramente gli Antichi non hebbero mai opinione tanto maligna, ne presero
licenza alcuna tanto presontuosa, che uolessero guastare cosa alcuna di buono della Mu-
sica; anzi cercarono d'acconciare il tristo, d'accrescere il buono, & di farlo anche miglio-
re. Per la qual cosa quanto fusse lodeuole appresso di loro cotali licenze, si può cōprender
da , che scrisse in molti luoghi il Prencipe de i Musici de suoi tempi Tolomeo con-
tr'Aristosseno, Didimo, Archita, & Eratosthene, che non uolse lodare, anzi biasimò alcu-
ne loro Diuisioni de Tetrachordi; percioch'erano fatte di maniera, che i loro Interualli
non erano contenuti dalle Proportioni, che sono del Genere Superparticolare. Et se per
la modulatione d'un Tetrachordo, che nō faceua (come diciamo al presente) Contrapun
to, quelli furono tanto biasimati & tanto ripresi; quanto sarebbono stati ripresi questi no-
stri Compositori moderni, s'ei hauesse ueduto le loro cantilene? che nō solamente in una
delle parti; ma alle uolte in tutte procedono insieme per discommodi & disproportionati
Interualli. Veramēte, come huomo di grāde autorità, & come buon maestro nō haureb-
be fatto molte parole; ma gli haurebbe dato tal castigo, che sarebbe stato degno della loro
presuntione & arroganza. Dicono etiandio, che si debbono adoperar tutte quelle chorde,
che sono in un'Istrumento, accioche nō siano poste in esso uanamente; Veramēte dicono
page 376il uero; percioche quando non s'adoperassero, sarebbono poste fuori di proposito; ma biso
gna adoperarle con ragione & cō proposito; essendo che fuori di ragione, & fuori di pro-
posito non si vsano bene; ma si adoperano male. Et se bisognasse adoperare tutti gli In-
terualli, che sono in vno Istrumento, che alle volte fanno vn gran numero, con dire
che sono in vn tale ordine; si potrebbe anche dire l'istesso, quando questi Interualli fus-
sero diuisi in due parti, & gli altri in due ancora, & cosi procedendo in infinito, molte-
plicando gli Ordini de i suoni, per hauer (come dicono) ogni sorte di voce, per potere
esprimere ogni sorte di accento; la qual cosa quanto sia ridicolosa, lasciaro giudicare
à tutti coloro, che sono capaci di ragione. Et se ben sono molte Chorde in vno Istrumen-
to, tra le quali si trouano molti & uariati interualli; non si debbono però adoperar se
non con proposito, & quando la cantilena & il Modo lo ricerca; conciosia che l'adopera-
re qualunque cosa senza necessità & senza proposito, è cosa veramente vana, & dino-
ta poca prudenza; oltra che genera al proprio sentimento di tale Oggetto gran fastidio-
E ben uero che molti non sentono tal noia, pur che odino cose nuoue & fantastiche; sia-
no buone, ò triste quanto si uogliono; perche ne tengono poco conto. Ma quelli, che si di-
lettano delle cose rare & buone, non possono patire alcuna cosa di tristo. Sono però alcu-
ni che sono ingannati dalla opinione de molti, & non hauendo giudicio più che tanto, si
attengono alle Parole d'alcuni, che hanno più autorità di loro, & dicono questo è buono
& questo è tristo; ma se à questi fusse mostrato il uero, mutarebbono consiglio subito, &
sarebbono d'altro parere. Questi si possono assimigliare à quelli, che non hanno giudicio
alcuno di Gioie, che quando à loro ne è mostrata una di quelle, che sono contrafatte &
false, la qual sia bella; & sia à loro detto, ch'è di gran ualore, l'appreciano molto; per-
che non la conoscono; per la opinione, c'hanno, che le Gioie uaglino assai denari; &
quella, che sarà la buona, ma non cosi bella, appreciano poco; ma quando gli è detto,
quella esser la falsa, & questa esser la buona, subito mutano consiglio, & hanno altra
opinione. Hò uoluto dir tutto questo, per quelli, che credono, che vn Pulice sia uno Ele-
fante; accioche possino uedere & udire, che mai sono per hauer cosa buona, fuori del no-
stro Genere che usiamo; usando nel modo che facēmo in esso le chorde Chromatiche &
le Enharmoniche cō proposito; se non si ritornasse à coniungere insieme (come faceuano
gli Antichi) il Numero, l'Harmonia, & le Parole, nelle quali si cōtenessero le cose mostra-
te nel Cap. 7. della Seconda parte; percioche se 'l si hauesse potuto ritrouare alcuna cosa di
buono, oltra il nostro vso; nō è dubbio, che già tanti & tanti anni sono, che la Musica è in
essere; dopò l'hauersi dismessi i due ultimi Generi; è impossibile che non fusse stato alcuno
d'ingegno tanto eccellente, che non hauesse posto in uso almeno uno di essi; essendo uera
mēte stati alcuni, che già più anni sono (come hò udito dire da molti) intorno questa cosa
ci sono affaticati, ne mai poterono ritrouar cosa alcuna, che li dilettasse. Veramēte sareb-
be stato la Musica tra l'altre Arti & Scientie molto infelice; che il buono & il bello d'essa si
hauesse lasciato da un canto, & il men buono ritenuto. Ma ciò non è credibile; percio-
che si come nell'altre Arti & nell'altre Scienze, che sono di grande speculatione & di
poco utile, sempre si è riseruato il buono; & lo tristo, come cosa inutile, si è lasciato sma-
rire; cosi credo, che sia stato nella Musica; à benche spero di uedere vn giorno darsi ope-
ra à questa Scienza di tal maniera, che io la vederò in tal modo perfetta, che non si potrà
desiderare in essa cosa alcuna, oltra quello, che si porrà in uso. Et questo dico; percioche
non la uedo ancora in quella perfettione, che può uenire; la quale si riserua in tal modo
in me; che ueramente nō la posso esprimere ne dire. Il che auerra; quādo sarà abbracciata
da qualche Spirito gentile, che non haurà per ultimo fine il guadagno, ch'è cosa da uile
& mecanico, ma si bene l'honore & la gloria immortale, che potrà acquistare, dopò lha-
uersi affaticato intorno tal Scienza, & accresciuta à quel grado ultimo, ch'io hò detto.
LA QVARTA ET VLTIMA PARTE
DELLE ISTITVTIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
Compositioni Musicali; & è la Seconda della Seconda parte
della Musica detta Prattica.
Quel che sia Modo ò Tuono; & delle sue specie.Cap. I.
do, che s'hà da tener nel compor le cantilene; & in qual maniera,
& con quanto bello & regolato ordine le Consonanze l'una con
l'altra, & etiādio le Dissonanze, si cōcatenino; uerrò hora à ragio-
nar de i Modi, ò Tuoni. Et benche tale impresa sia non poco diffi
cile; massimamente uolendo ragionare alcune cose di loro secon
do l'uso de gli Antichi; si perche (com'altre uolte hò detto2. Parte
cap. 4.) la Mu-
sica moderna dall'Antica è uariatamente essercitata; com'anco
per non ritrouarsi alcun'essempio, ò uestigio alcuno di loro, che ne possa condurre in
una uera & perfetta cognitione; tuttauia non uoglio restar di discorrere prima alcune
cose; & con quel meglior modo ch'io potrò, ragionando in uniuersale & in particolare
anco, di toccare alcune delle più notabili, secondo che mi soueniranno alla memoria,
& anco mi torneranno in proposito; dalle quali i Studiosi potranno uenire alla risolu-
tione di qualunque dubbio, che sopra tal materia li potesse occorrere; Il che fatto, uer-
rò à mostrar dopoi, in quai maniera i Musici moderni li usino; & dirò de quante sorti si
trouino, l'ordine loro, & in che maniera l'Harmonie, che nascono da loro s'accommodi-
no al Parlare; cioè, alle Parole. Douendo adunque dar principio à tal ragionamento, ue-
deremo prima quello, che sia Modo, ò Tuono; acciò possiamo sapere, che cosa sia quello,
di cui intendiamo ragionare; ne ciò sarà fatto fuori di proposito; poi che 'l Modo è il prin
cipal Soggetto di questo nostro ultimo ragionamento. Si debbe adunque auertire, che
questa Parola Modo (oltra d'ogn'altra sua significatione, che sono molte) significa pro-
priamente la Ragione; cioè, quella Misura, ò Forma, ch'adoperiamo nel fare alcuna
cosa, la qual ne astrenge poi a non passar più oltra; facendone operar tutte le cose con
una certa mediocrità, ò moderatione; & è ben detto ueramente; imperoche (come di-
ce Pindaro)Olimp.
ode. 13.
Ε῎πεται δ'ἐν ἑκάστω μέτρον. cioè;
In ciascuna cosa è Modo, ò Misura.
page 378il che dice anco Horatio dopo lui.Ser. lib. 1.
Saty. 1.
Est modus in rebus, sunt certi denique fines:
Quos vltra citraꝗ nequit consistere rectum.
Imperoche tal mediocrità, ò moderatione non è altro, che una certa maniera, ouer
ordine terminato & fermo nel procedere, per il quale la cosa si conserua nel suo essere,
per uirtù della proportione, ch'in essa si ritroua; che non solo diletta; ma etiandio mol-
to giouamento apporta. De qui uiene, che se per caso, ouer'à bello studio tal'ordine
da essa si allontana, non si può dire, quant'offendi; & quanto il sentimento abhorrisca.
Hauendo adunque i Musici & i Poeti Antichi considerato tal cosa; perche gli uni & gl'al
tri erano una cosa istessa (come hò detto altroueIn Proe-
mio et c. 6.
Secun. par.) chiamarono le loro compositioni Mo
di; nelle quali sotto uarie materie per uia del Parlare accompagnate l'una all'altra con
proportione esprimeuano diuersi Numeri, ò Metri, & diuerse Harmonie. Onde nac-
que, che posero tre Generi de Modi, non hauendo consideratione al Suono, ouer all'
Harmonia che nasceua, ma solamente all'altre parti aggiunte insieme; l'uno de i quali
chiamarono Dithyrambico, l'altro Tragico, & il Terzo Nomico; de i quali le lor specie
furono molte; come Epithalamij, Encomij, Hinni, Peani, & altri simili; come si è dichia
rato ne i Sopplimenti.Cap. 2 del
7. lib. &
nel Cap. 1.
del lib. 8. Considerando dopoi l'Harmonie da per sè, che usciuano da tali
congiungimenti, perche riteneuano in loro una certa, propria, & terminata forma, le
nominarono simigliantemente Modi; aggiungendoli Dorio; ò Frigio; ouer'altro no-
me secondo 'l nome de i Popoli, che furono Inuentori di quell'Harmonia; ouer da quel-
li, che più si dilettauano di una specie, che d'un'altra; imperoche l'Harmonia Do-
ria fù denominata da i Doriensi, che furono i suoi inuentori; la Frigia da i popoli,
che habitauano la Frigia; & la Lidia da quelli di Lidia, & cosi l'altre per ordine. E' ben
uero, c'hauendo ciascuna di esse in sè alcuna cosa propria nel suo canto, & essendo ac-
compagnata con diuersi Numeri, chiamarono alcune di esse graui & seuere, alcune
baccanti & furiose, alcune honeste & religiose, & alcun'altre nominarono lasciue &
bellicose. Onde per questo rispetto hebbero grand'auertimento nell'accompagnar co-
tali Harmonie à i Numeri, & questi insieme con proposito à materie conuenienti, lequa
li esprimeuano nell'Oratione, ò Parlare, secondo la lor natura. Il perche hauendo con-
sideratione à tutte queste cose, nominarono le lor Compositioni secondo la natura del
composto; come sarebbe dire, Modi flebili, i quali sono le Elegie; imperoche conten-
gono materie meste & flebili; come si può ueder espressamente in quelli due uolumi;De Tristi-
bus: & De
Ponto. ol-
tra gli altri quasi infiniti, che sono d'altri autori; iquali scrisse Ouidio, dopo che fù man- dato in essilio in Ponto da Augusto; & da quell'anco, che scriue nella Epistola di Saffo
à Faone; uolendo mostrar, che le cose amatorie sono materie flebili, & che conuengo-
no alla Elegia, dicendo.
Forsitan & quare mea sint alterna requiris
Carmina, cùm lyricis sim magis apta modis:
Flendus amor meus est. Elegëia flebile carmen
Non facit ad lacrymas barbitos vlla meos.
Fece anche Horatio mentione de questi Modi, dicendo;1. Carmi.
ode. 9.
Tu semper vrges flebilibus modis
Mysten ademptum.
Et anco Boetio nel lib. 3. della Consolatione Filosofica;Metro 12.
Quondam funera coniugis
Vates threicius gemens,
Postquàm flebilibus modis,
Syluas currere, mobiles
Amnes stare coegerat;
Come li commemorò etiandio Cicerone nelle Tuscolane,Tus. lib. 1. quando (facendo insieme
mentione de gli humili & depressi) disse;
Hac cum pressis & flebilibus modis, qui totis thea-Et in un'altro luogo, facendo mentioni de i tardi;De Orat.
page 379tris moestitiam inferant, concinuntur.
lib. 1.
Solet idem Roscius dicere, se quo plus aetatis sibi accederet, eo tardiores tibicinis modos, & can-Altre nominarono Modi lamenteuoli; come si può uedere
tus remissiores esse facturum.
appresso Apuleio, quando dice;
Et sonus tibiae Zigiae mutatur in quaerulum Lydij modum.
Alcune poi chiamarono Modi dolci; come ne mostra l'istesso Horatio in un'altro luo-
go, quando dice;Car. lib. 3.
ode. 9.
Me nunc Tressa Chlöe regit,Et Seneca anco:In agamē.
Dulces docta modos, &
Citharae sciens.
Sacrifica dulces tibia effundat modos.Nominarono etiādio alcun'altri Modi mesti; come si può uedere dall'autorità di Boetio;
Carmina qui quondam studio florente peregi.1. De Cōsi.Et alcune Modi impudici, i quali commemora Quintiliano, dicendo:Institu. o-
met. 1.
Flebilis heu moestos cogor inire modos:
rat. lib. 1.
cap. 10.
Apertius ta-Altre chiamarono Modi rudi, ò grossi; ilche dimostra Ouidio;1. De Ar-
men profitendum puto, non hanc à me praecipi, quae nunc in scenis effoeminata, & impudicis mo-
dis fracta.
te amādi.
Dumꝗ, rudem praebente modum tibicine Tusco,Et altre Modi discordanti; & de questi ne fa mentione Statio.Sylua. lib.
Lydius aequatam ter pede pulsat humum:
5. Epicedii
in filium.
Discordesꝗ modos, & singultantia verbaVltimamente (lasciandone molt'altri per breuità) chiamarono in uniuersale alcune
Molior.
compositioni Modi lirici; come dall'autorità d'Ouidio commemorata di sopra si può
comprendere. Et le loro materie nō si esprimeuano cō la Voce solamente; ma se le ac-
compagnaua l'Harmonia, che nasceua d'alcuno Istrumento, fusse stato poi Cetera, ò Li
ra oueramente Piffero, ò di qualunque altra sorte. Si trouaua nondimeno gran differen
za tra questi Modi; essendo che i popoli di questa prouincia usauano una maniera de Ver
si & un Istrumento, & quelli di quella ne usauano un'altro & un'altra maniera de Versi.
Et non erano differenti solamente in questi, ma nelle Harmonie ancora; imperoche
una sorte d'Harmonia usaua un popolo, & un'altro un'altra; di maniera ch'erano anco
differenti ne i Numeri; i quali si ritrouauano ne i Versi. De qui nacque dopoi, che i Mo-
di erano denominati da quei popoli (come di sopra hò detto) che più si dilettauano di
quella maniera, ouer erano stati gl'Inuentori. La onde da questo si può comprendere,
che se un popolo; come quello di Frigia, udiua alcuna maniera forestiera, diceua, quel-
lo essere Modo di quella , oue più si usaua, oueramente ou'era stato ritrouato;
di maniera, che chiamauano il Modo Eolio da i popoli della Eolia suoi inuentori, ch'era
contenuto in un certo Hinno, composto nel Modo lirico sott'alcuni Numeri; concio-
siache questi popoli si dilettarono molto della Lira, ò Cetera; che secondo l'opinione d'al
cuni (la qual reputo falsa) à quei tempi erano una cosa istessa; al suono della quale canta
uano il sudetto Hinno; ma di questo si legga il Cap. 16. del lib. 1. De i Sopplimenti, che
si potrà conoscere il uero di cotal cosa. Tal'Istrumento usauano similmente i Doriesi,
ancora che forse cātassero altra maniera de Versi, & usassero l'Harmonia molto differen-
te; del che ne fà fede Pindaro,Olymp. o-
de. 1. quando nomina simili Istrumento Δορίαμ φόρμιγγα; cioè,
Dorica cetera; & Horatio,In Epodo.
ode. 7.
Sonantem mistum tibijs carmen lyra,Onde si può uedere dalla parola Barbarum, la quale s'intende per il modo Fri-
Hac Dorium, illis Barbarum.
gio, ch'anco i popoli della Frigia usassero i Pifferi. Et cotal Modo ueramente sole-
uano sonare con simili Istrumenti; come potrei mostrar con molti essempi, i quali
lascio per breuità; bastando solamente uno di Virgilio, il quale dice in tal ma-
niera.
page 380Aeneid. 9.
O vere phrigiae (neque enim phryges) ite per alta.Et uno d'Ouidio.Fast. lib. 4.
Dyndima, ubi assuetis biforem dat tibia cantum:
Tibia dat phrygios, ut dedit ante modos;
Da i quali si può comprendere, esser uero quel, c'hò detto. Con questo Istrumento
similmente quei popoli, c'habitauano la Lidia, faceuano le lor Harmonie; & di ciò n'è
testimonio Horatio dicendo;Car. lib. 4.
ode. 15.
Virtute functos more patrum ducesEt Pindaro,Olimpi.
Lydis remisto carmine tibijs,
Troiamꝗ, & Anchisen, & alma
Progeniem Veneris canemus;
ode. 5. ilquale, auanti di lui, supplicando Gioue per Psaumido Camarineo vin-
citore ne i giuochi Olimpici, dice;
Io uengo à te supplicheuole ò Gioue sonando Λυδίοις ἀυλο͂ις:Non manca per dimostrar questo etiandio il testimonio d'Apuleio,
con Pifferi Lidij.
con l'Autorità addutta di sopra, & de molti altri; ma questi bastino. Da questo adun-
que potiamo comprendere, che i Modi anticamente consisteuano nell'Harmonie & ne
i Numeri espressi da una sorte d'Istrumento; & che la diuersità loro era posta nella uaria-
tione dell'Harmonie, nella diuersità de i Numeri, & nella maniera dell'esprimere;
cioè, dell'Istrumento. Et se bene alcuni popoli conueniuano con alcun'altri nelle Har-
monie, ouer ne gli Istrumenti; erano poi differenti ne i Numeri; & se in questi erano
concordi, discordauano poi nelle Harmonie & ne gli Istrumenti; di maniera che se in
una cosa, ouer in due erano conformi, variauano poi nel resto. Questo istesso uedia-
mo etiandio hoggidi in diuerse nationi; imperoche l'Italiano usa 'l Numero, ò Verso de
piedi, ò sillabe commune col Francese & col Spagnolo; com'è quello d'Vndici sillabe;
nondimeno quando s'odono cantar l'uno & l'altro, si scorge un'Harmonia differente,
& altra maniera nel procedere; conciosia che altramente canta l'Italiano, di quello che
fà il Francese; & in altra maniera canta lo Spagnuolo, di quel che fa 'l Tedesco; lascian-
do di dire delle nationi barbare & infideli; com'è manifesto. Vsa l'Italiano & anco il
Francese grandemente 'l Leuto, & lo Spagnolo usa il Ceterone; ancora che questo uaria
poco da quello, & altri popoli usano il Piffero. Ne i Numeri, ò Versi, quanta differenza sia
tra i popoli, & quanto un popolo habbia differente maniera dell'altro, si può conosce-
re; incominciando da questo capo; che se ben fuori dell'Italia in alcuna parte non si
usa 'l Verso legato, ò sciolto d'Vndeci sillabe, fatto alla simiglianza dell'Endecasillabo
latino; tuttauia nella Italia, nella Franza, & nella Spagna molto si usa. Et quel, che in
Italia si chiama Rima, credo che sia detto da questa parola greca Ρυθμὸς, che significa
(com'altroue hò detto) Numero, ò Consonanza;2. Partis
cap. 8. percioche da quelle corrisponden-
ze & legature, che si trouano nel fine de i Versi, le quali chiamano Cadenze, nasce la
Consonanza, ouer Harmonia, che si troua in essi.Vedasi il
cap. 13. del
lib. 8. De i
Sopplim. Vsano gli Italiani cotali Cadenze,
non tanto in quella maniera de Versi, che si trouano nell'Ottaue rime, ò Stanze, ne i
Sonetti, ne i Capitoli, & altri simili, che dimandano Intieri; quanto nelle Canzoni an
cora & Madrigali; oue si pone molte sorti de Versi; come sono quelli di Sette sillabe &
altri simili, che chiamano Versi rotti; com'è manifesto; imperoche nell'Italia madre de
i buoni & rari intelletti s'usa uarie maniere di comporre; come si può comprendere dal-
le nominate Ottaue rime, ò Stanze; che dir le vogliamo, da i Terzetti, dalle Sestine,
da i Sonetti, & da i Capitoli, ne i quali s'adoperano una sola maniera de Versi, che so-
no gli Intieri & nelle Canzoni & ne i Madrigali con altri simili, ne i quali si pongono
uarie sorti de Numeri ad imitatione dell'Ode d'Oratio; à benche i Numeri Horatiani sia
no senza le commemorate Cadenze, & gli Italiani siano per esse Cadenze al det-
to modo legati; come nelle dotte & leggiadre Canzoni del Petrarca & de molt'altri
eccellentissimi huomini si può uedere; delle quali tengo per certo, che i dotti spiriti Ita-
liani siano stati Inuentori; conciosiache non mi ricordo hauer mai trouato appresso
d'alcun'altro Poeta, ne Greco, ne Latino un simil modo di comporre, con tali Ca-
page 381denze; con tutto che 'l Dottissimo Horatio habbia cantato assaissime Ode in molte ma-
niere. E' ben uero, ch'altri Poeti latini (ancora che non molto spesso) hanno usato
simili Cadenze, ò Corrispondenze nelle mezane sillabe, & nell'ultime d'alcuni lo-
ro Versi, i quali chiamano Leonini, ò Canini; come in ciascun de questi hà fat-
to il Poeta;
Ad terram misêre, aut ignibus aegra dedére. Aeneid. 2.Ibidē 12.
Cornua vellatarum obuertimus antennarum.Ibidem 3.
Illum indignanti similem, similemꝗ minanti.Ibidem 8.
Tum caput orantis nequicquàm, & multa precantis.Ibidē 10.
Ora citatorum dextra contorsit equorum:
Et Ouidio anche in questo hà osseruato cotal legge.In Epistola
Helenae ad
Paridē. 8.
Vim licet appelles, & culpam nomine veles;
& in molt'altri, che non si mettono, per non crescere 'l volume. Onde 'l Petrarca (com'
io credo) imitando tal maniera di comporre, le pose in un'altro modo, accordando 'l
fine del Verso precedente, col mezo del seguente in cotal guisa:Canz. 22.
Mai non uò più cantar com'io soleua:
Ch'altri non m'intendeua: onde hebbi scorno.
E puossi in bel soggiorno esser molesto;
Et cosi il restante di tal Canzone. Ilche osseruò etiandio nella Canzone, Vergine bella.Canz. 49.
Quest'istesso fece il Sanazaro nel principio dell'Arcadia in quella parte, quando parlan-
do Ergasto con Seluaggio pastore, dice:
Menando un giorno li agni appresso un fiume.
Vidi un bel lume in mezo di quell'onde.
Che con due bionde treccie allor mi strinse,
Et mi dipinse un uolto in mezo 'l cuore.
& il resto, che segue. Ma quando ben si ritrouasse tra i Greci, ò tra i Latini poeti una
tal maniera di comporre, con simili Cadenze, questo poco importarebbe; essendo
che tanto si potrebbe gloriare il primo Inuentore d'una tal maniera di comporre Ita-
liano, se bene hauesse pigliato l'Inuentione d'alcun poeta Greco, ò Latino; quanto si
gloriaua Horatio d'esser stato il primo, che ritrouato hauesse il modo di comporre in
Latino i Versi lirici alla guisa de i Greci; ilche si può comprender dalle sue parole;
quando dice;Carmi. lib.
3. Ode. 31.
Dicar, quà violens obstrepit Aufidus,Delche si può etiandio gloriare Claudio Tolomei Sanese d'essere stato il primo, che
Et qua pauper aquae Daunus agrestium
Regnator populorum, ex humili potens
Princeps Aeolium carmen ad Italos
Deduxisse modos.
habbia espresso 'l Verso Heroico & l'Essametro & lo Pentametro nelle Italiane muse;
ancora che da pochi, fin'hora, cotal cosa sia stata abbracciata. Vogliono alcuni, che 'l
Dottissimo Dante Aliglieri poeta Fiorentino fusse 'l primo inuentore de i Terzetti, & il
Boccaccio dell'Ottaua rima; per ilche quando à cotali maniere di comporre si uolesse
dare un nome particolare; uolendole denominar dalla ragione, nella quale furono ritro
uate; l'una & l'altra maniera si chiamarebbe (come ne inuita Horatio con l'autorità
posta di sopra) Modi Italiani; ò uolendole denominar dalla Patria, si chiamarebbono
Modi thoscani. Ma se si uolessero denominar da i Proprii inuentori, la prima maniera
si nominarebbe (dirò cosi) modo Dantesco, & la seconda maniera modo Boccacciano;
come le legge Citaristice & le Tibiali (il che habbiamo ueduto nella Seconda parteCap. 5.)
furono denominate parte de i Popoli, & parte da gli Inuentori. Et se ben nell'Italia si tro
ua non solo una maniera de Versi, ma anco più maniere particolari; come hò mo-
strato; tuttauia i Greci à i nostri giorni, oltra l'altre loro maniere hanno il Ver-
page 382so de Quindeci sillabe; come sono questi, che sono di Constantino Mannasì loro
Filosofo.
Ο῾ τοῦ θεοῦ παντέλειος, καὶ παντοκτίστωρ λόγος,& uogliono dire; La parola di Dio in tutto è perfetta; & colui, che fabricò tutte le cose del
Τὸν ὀυρανὸν τὸν ἄναστρον παρήγαγεν ἀρχῆθεν
Mondo, da principio fabricò il Cielo senza stelle; de i quali Versi tutto 'l suo Hexameron è
pieno; & li cantano sotto un Modo particolare, secondo 'l costume loro; il che non si
usa nella Italia. Perilche (lasciando di dir de gli altri Popoli) da questi due potiamo ue
der la differenza, che poteua esser de i Numeri, & delle Harmonie ne i Modi de quei
popoli, nel tempo che nella Grecia la Musica era in fiore. Percioche come uediamo
questi due popoli à nostri tempi hauere una maniera particolare di Verso, & una ma-
niera particolare di cantare; il simil douemo creder, che fusse anticamente tra quei popoli.
Et ancora che à i nostri giorni alcuni popoli di natione diuersa conuenghino insieme nel
Numero, ò ne i Piedi del Verso, & nella maniera della compositione delle lor Canzoni;
tuttauia sono differenti intorno la maniera del Cantare. Et non solamente si troua tra
diuerse nationi tal differenze; ma anco in un'istessa patria; come si può ueder nell'Ita-
lia; percioche in una maniera si cantano le Canzoni, che si chiamano Villotte nella pro-
uincia di Venetia, & in un'altra maniera nella Toscana, & nel Reame di Napoli; com'
era anco appresso gli Antichi; percioche se bene i Popoli della Doria, & quelli dell'Eo-
lia vsauano un'istessa qualità ò sorte di Verso, & un'istesso Istrumento; le Harmonie loro
poi erano in qualche parte differenti. De qui si può comprendere adunque la diuersità
de i nomi ne i Modi; che si come in alcun Modo si trouaua il Numero, l'Istrumento, &
l'Harmonia differente da un'altro Modo; cosi anco nacque la diuersità de i nomi. La
onde credo, che 'l Modo Dorio fusse differente dall'Eolio, come il Frigio era diuerso
dal Lidio; & ciò non solamente nell'Harmonie; ma etiandio ne i Numeri; come si può
comprendere da i uarii effetti, che nasceuano dall'uno & dall'altro, i quali uederemo al
suo luogo. Però adunque quando leggiamo di Filosseno 8. Politic.
cap. 7., hauendo ei tentato di fare il
Poema Dithyrambico nel modo Dorico, che non lo puote mai condurre al desiderato
fine; percioche dalla natura del Modo fu tirato di nuouo nell'Harmonia Fr igia, conue-
neuole à tal Poema; non dobbiamo prendere ammiratione; essendo che i suoi Piedi, &
il suo Numero è più ueloce d'ogn'altro Poema; & per il contrario, i Numeri del modo
Dorico più tardi & più rimessi. Perilche essend'altri Numeri nella Dorica, & altri nella
Frigia Harmonia (come si è detto) era impossibile, che Filosseno potesse far cosa alcu-
na, che fusse buona; come anco sarebbe impossibile, quando sotto i Numeri d'un Verso
Saffico, che si compone del Trocheo, dello Spondeo, del Dattilo, & nel fine di due
Trochei, ouer d'un Trocheo & uno Spondeo; come sono questi due Horatiani.1. Carm.
Ode. 10. &
38.
Mercuri facunde nepos Atlantis:&
Persicos odi puer apparatus;
si uolesse cantare, ò tirare in uerso Heroico, che si compone di Sei Piedi diuersamen-
te con Dattili & Spondei; come si può comprendere in ciascun de i due Virgilia-
ni sequenti:
Georgic. 3.
Sed fugit interea, fugit irreparabile tempus.&
Aeneid. 6.
Parcere subiectis, & debellare superbos.
Tutto questo discorso hò uoluto fare, non ad altro fine; se non accioche più facilmen-
te si potesse comprendere, quel ch'era il Modo nella Musica. Onde potiamo ueramen-
te dire, che 'l Modo anticamente era una certa & determinata forma di Melodia, fatta
con ragione & con arteficio, contenuta sotto un determinato & proportionato ordine
de Numeri & d'Harmonia, accommodati alla materia contenuta nell'Oratione. Et
benche i Musici moderni non considerino nelle lor cantilene se non un certo ordine di
cantare & una certa specie d'Harmonia; lasciando da parte il considerare il Numero, ò
Metro determinato; percioche dicono, che questo appartiene à i Poeti; massimamente
page 383essendo la Musica à i nostri tempi separata dalla Poesia; tuttauia considerano cotal ordi-
ne in quanto è contenuto tra una delle Sette già mostrate specie della Diapason harmo-
nicamente, ouero arithmeticamente mediata; come più oltra vederemo; tra le quali si
troua una certa maniera di cantare in una, che in un'altra è uariata. Et tal'ordine di
cantare con diuersa maniera, ouero Aria dimandano Modo, & alcuni lo chiamano
Tropo, & altri Tuono. Nè di ciò dobbiamo render marauiglia, poi che Τρόπος è Pa
rola greca, che significa Modo, ò Ragione, dalla quale uogliono, che siano cosi detti.
Et se fusser'anco nominati da Τροπὴ, che uuol dire, Conuersione, ò Mutatione, staria
medesimamente bene; essendo che l'uno si conuerte & muta nell'altro; come uederemo;
& i Grammatici alle uolte chiamano Tropi quelle conuersioni, che si fanno d'una parola
ò uoce, dal proprio significato, in un'altro. Lo nominano etiandio Tuono, & ciò non è
maldetto; percioche per il Tuono (come mostra Euclide nel suo Introdottorio) si può
intendere Quattro cose; Primieramente, quel, che i Greci chiamano φθόγγος, che signi-
fica ogni Suono, ò Voce inarticolata, la quale non si estende ne uerso il graue, ne uer-
so l'acuto; secondariamente, quelli due Interualli mostrati nel Cap. 18. della Terza par-
te; dopoi una forte & sonora Voce; come quando diciamo, Francesco hà un buon tuo-
no, sonoro, & gagliardo; cioè, una buona; sonora, & gagliarda Voce. Vltimamente
s'intende per quello c'habbiamo nominato di sopra; come quando si dice; il Tuono Do-
rio, il Frigio, & gli altri; cioè, il Modo Dorio, il Frigio, & li seguenti per ordine. Et
perche questo nome Tuono si estende in più cose, come uedemmo; però per schiuar la
Equiuocatione, più c'hò potuto, hò uoluto nominarli Modi, & non Tuoni. Volendo
adunque dichiarar quello, che sia Modo, diremo con Boetio,Musicae
lib. 4. c. 4. il quale parla de i Modi
ò Tuoni antichi; che Modo è una certa Costitutione in tutti gli ordini de uoci, differente
per il graue & per l'acuto; & tale Costitutione è come un corpo pieno di modulatione,
la quale hà l'essere della congiuntione delle Consonanze; come è la Diapason, la Dia-
pasondiapente, ouer la Disdiapason. Di maniera che da Proslambanomenos à Mese uie
ne ad essere una Costitutione, connumerando le Chorde, ò uoci mezane; cosi ancora da
Mese à Netehyperboleon, intendendoui sempre i suoni mezani. Ma perche queste Co-
stitutioni sono ueramente le uarie specie della Diapason, che si trouano dall'una lettera
all'altra; come nel Cap. 12. della Terza parte habbiamo ueduto; numerando le lor Chor
de mezane; però diremo; come dicemmo etiandio nell'Vndecima definitione del Quin
to delle Dimostrationi, & anco habbiamo detto di sopra; che 'l Modo secondo i Moder
ni è una certa forma, ò qualità d'Harmonia, che si troua in ciascuna delle nominate
Sette specie della Diapason, le quali tramezate harmonicamente, secondo che si con-
siderano hora, ne danno Sei Modi principali & autentichi; da i quali poi nascono i suoi
collaterali per la diuisione arithmetica, che si chiamano (come uederemo) Plagali,
ouer Placali.
Che i Modi sono stati nominati da molti diuersamente, & per qual
cagione.Cap. II.
alcuni, i quali etiandio li hanno chiamati Harmonie, alcuni Tropi; come hab
biamo detto di sopra: alcuni Tuoni, & alcuni Systemati, ouer Intiere consti-
tutioni. Quelli che li chiamarono Harmonie furono molti, tra i quali fù Pla-
tone,De Rep.
lib 3. Plinio,2. Nat. his.
cap. 22. & Giulio Polluce.Onomast.
Lib. 3. cap.
9. 4. E ben uero, che 'l Polluce (secondo 'l mio parere) po-
ne differenza tra l'Harmonia & il Modo; essendo che prima piglia l'Harmonia per il con
cento solamente, che nasce da i Suoni, ò dalle Voci aggiunte al Numero; & dopoi pi-
glia il Modo per il composto d'Harmonia, di Numero, & d'Oratione, che Platone no-
page 384mina Melodia; & fà veder, quanto il Modo sia differente dall'Harmonia. La onde essen-
do à i nostri tempi l'uso della Musica molto differente dall uso di quella de gli Antichi; co
me altroue hò mostrato; ne osseruandosi in essa alcuna cosa intorno al Numero (lasciādo
quell'Harmonie, che si odono ne i Balli; percioche uengono necessariamēte ad esser con-
giunti à cotal numero) secondo l'opinione di costui li doueressimo più presto chiamare
Harmonie, che Modi; ma ciò si è fatto; perche questo nome è più commune tra i Musici
in simil cosa, che non è Harmonia. Quando adunque il Polluce li chiama Harmonie, nō
discorda punto da Platone, intendendo quel concento, che nasce da i Suoni, ò dalle Voci
congiunt'al Numero; ma quādo li nomina Modi, allora intende la Melodia; cioè, il com-
posto delle nominate tre cose. Ne dobbiamo prender marauiglia, ch'una istessa cosa sia
denominata in tante maniere; percioche non è inconueniente, che quando ella è conside-
rata diuersamente, sia anco diuersamente nominata. Però quando Platone & gli altri le
nomina Harmonie, può essere, che lo dica indotto dalla concordanza de molti suoni, ò
uoci dissimili, che ritrouò tra loro; & dalla cōgiuntione anco de molte Consonanze vnite
insieme, che si troua tra molte parti, & anco in una sola; imperoche, Α῾ρμονία secondo 'l
parere di Quintiliano, si chiama quella concordanza, che nasce dalla congiuntione de
più cose poste insieme, tra loro dissimili. Et s'alcuni altri li chiamarono Tropi, fù anco
ben detto; come ho dimostrato nel Capitolo precedente, per le qualità per le quali sono
tra loro differenti; percioche essendo tutte le chorde d'un Modo più graui ò più acute per
un'interuallo di Tuono, ò di Semituono delle chorde di quello, che gli è più uicino; con-
siderando eglino il passaggio, che fanno l'un nell'altro per l'ascendere, ò discendere con
le Chorde d'un'ordine nelle Chorde dun'altro; furono da essi nominati in tal maniera;
quasi che uolessero dire; Voltati dal graue all'acuto, ò per il contrario. Ma se noi li con-
siderassimo secondo l'uso moderno; cioè, inquanto alla conuersione ò trasportatione del-
le loro Diatessaron, le quali si pongono (come uederemo) tallora sotto, & tallora sopra la
Diapente commune; si potrebbono etiandio chiamare Tropi. La onde parmi, che non
fuor di proposito alcuni dimādarono le due nominate specie; cioè, la Diapente & la Dia-
tessaron Lati, ouer Membra della Diapason, & essa Diapason Corpo; poi che ne segue
una tale & tanta uarietà, che fa un'effetto mirabile. De quì uiene, ch'alcuni chiamarono
parte di essi; Modi laterali; come sono i Plagali, dall'uno de i loro lati, che si muta, ch'è la
Diatessaron. Et quelli, che i nominarono Tuoni, non lo fecero senza ragione, de i quali
l'uno fù Tolomeo; ilqual dice, che forse si chiamarono in cotal modo, dallo spacio del
Tuono, per il quale i tre Modi principali Dorio, Frigio, & Lidio (come dimostra nel
Cap. 7 & nel 10. del 2 lib. de gli Harmonici) sono lontani l'uno dall'altro; ancora ch'alcu-
ni vogliano, che siano nominati in tal maniera, da una certa soprabondanza d'Interualli;
come da i Cinque Tuoni, che sono in ogni Diapason, oltra i due Semituoni maggiori;
oueramente dall'ultimo suono, ò uoce finale di ciascuno (come uogliono alcuni altri) me-
diante ilquale, cauano una Regola di conoscere & giudicare dall'ascesa & dalla discesa
delle lor Modulationi, qual si uoglia cantilena, sotto qual Modo sia composta. Ma que-
st'ultima opinione à me non piace; conciosia che non hà in se alcuna ragione, che accheti
l'intelletto. Sono anco detti Modi da questa parola latina Modus, che deriua da questo
verbo Modulari, ilquale significa Cantare; ouer sono detti Modi dall'ordine moderato,
che si scorge in loro; imperoche non è lecito, senz'offesa dell'Vdito passar'oltra i loro ter-
mini, & di non osseruar la proprietà & natura di ciascuno. Quelli, che li nominarono
Systemati, ouero Intiere costitutioni; tra quali uno è Tolomeo; si mossero da questa ra-
gione; perche Systema vuol significare una Congregatione de uoci, ò suoni, che contiene
in se vna certa ordinata & intera modulatione, ouer congiuntione delle Consonanze; co
me sono della Diapente & della Diatessaron, & dell'altre ancora. Di maniera, ch'ogni
Modo si colloca interamente in una delle Sette specie della Diapason, ch'è la più perfetta
d'ogn'altra qual si uoglia costitutione; se bene la Disdiapason dal sudetto Tolomeo,2. Harmo.
cap. 4. & nō
alcun'altra, è detta perfetta & intiera Costitutione, ò Complessione.
page 385
Del Nome & del Numero de i Modi.Cap. III.
uede gran uarietà intorno al loro nome in generale, come habbiamo uedu-
to; cosi anco l'istesso è intrauenuto intorno ad alcuni nomi particolari, & in-
torno al numero loro; imperoche se noi uorremo hauer riguardo à quel, che
scriue PlatoneDe Rep. 3. in tal materia; ritrouaremo, che pone sei Modi solamente di Harmo-
nie, chiamando alcune di esse Harmonie Lydie miste, alcune Lydie acute, altre Ioni-
che, & altre Lydie, senz'aggiungerui cosa alcuna. Aggiunge poi à queste la Dorica,
& la Frigia; lodando solamente & approuando sopra tutte l'altre queste due vltime, co-
me molto utili ad vna bene istituita Republica. In un'altro luogo In Lache-
te. poi commemora so-
lamente la Dorica, la Ionica, la Frigia, & la Lydia; & cosi tra queste, par che lodi sola-
mente la Dorica, come più seuera & miglior d'ogn'altra. Aristosseno anco lui (come
vuol Martiano CapellaLib. 9.) pone Quindeci modi; cioè, Cinque principali Lydio, Iastio,
Eolio, Frigio, & Dorico, con Dieci collaterali; aggiungendo à ciascun di loro queste
due particelle Greche Υ'πὲρ; che vuol dire Sopra, & Υ'πὸ; che significa Sotto; onde fà
nascer due altri Modi, l'un de i quali chiama Hyperlydio & l'altro Hypolidio; & cosi fà
de gli altri per ordine. L'istesso numero con nomi simili pone Cassiodoro nel suo Com-
pendio di Musica; & scriuendo à BoethioEpist. li. 2.
Ad Boe-
thum. ne pone Cinque; cioè, il Dorio, il Frigio, l'Eo-
lio, l'Iastio, & il Lydio; & dice, ch'ogni Modo hà l'Alto & il Basso; & questi due so-
no cosi detti per rispetto del mezo; uolendo inferire, che ciascun de i nominati hà due
Modi collaterali; come dimostra dopoi, quando dice; che la Musica arteficiata è con-
tenuta da Quindeci modi, & in ciò è concorde con Martiano. Ma Euclide,InIsagoge. il quale se-
guitò anche lui l'opinione d'Aristosseno, ne pone Tredeci solamente; il che fà medesi-
mamente Censorino.De Die na
tali ad Q.
Caerelium. La onde si uede due seguaci d'un'istesso autore, esser molto di-
scordi & uarij nel numero. Tolomeo,Har. lib. 2.
cap. 10. quando ragiona di tal cosa, ne pone Sette;
l'Hypodorio, l'Hypofrigio, l'Hypolidio, il Dorio, il Frigio, il Lydio, & il Mistolydio;
à i quali Boetio nel suo ordine aggiunge l'Ottauo, chiamato da Tolomeo istesso Hyper-
mistolydio, & da Euclide Hyperfrigio; & questo fece acciò che 'l Systema massimo; cioè,
le Quindeci chorde, da Proslambanomenos à Netehyperboleon, fussero comprese
dalle chorde de questi Modi. Et quantunque TolomeoHarmo. li.
1. cap. 16.
& Lib. 2.
cap. 15. conoscesse molto bene, ch'oltra
de questi Sette Modi & lo suo aggiunto, se ne ritrouano molt'altri; come si può uede-
re, quando commemora l'Ionico & l'Iastioeolico, nominandoli Harmonie; tuttauia
non uolse passar tal numero; forse perche hauea fatto disegno, d'accommodare à ciascu-
na Sphera celeste uno de i suoi nominati sette Modi; come si può uedere nel Cap. 9. del
Terzo libro de gli Harmonici; nella maniera, che gli Antichi etiandio haueuano disse-
gnato; come mostra Plinio nell'Historia naturale.Lib. 2. cap.
22. Giulio PolluceOnomast.
lib. 4. cap.
9. & 10. s'accorda con Pla-
tone nel numero; ma discorda nel nome; percioche pone 'l Dorico, l'Ionico, & l'Eolio,
& li nomina Prime Harmonie; alle quali aggiunge la Frigia, la Lydia, la Ionica, & Lo-
crense; con quella che nomina Continua; come vna di quelle Harmonie, che seruiuano
al suono de i Pifferi. Aristide Quintiliano nel Primo lib. della Musica pone sei Modi, i
quali dimanda Tuoni; che sono il Lydio, il Dorio, il Frigio, l'Iastio, il Mistolidio, & il
Syntonolydio, il quale potiamo nominare Lydio acuto. Ma Gaudentio filosofo ha-
uendo nel suo Introdottorio fatto mentione del Mistolydio, del Lydio, del Frigio, del
Dorio, dell'Hypolydio, dell'Hypofrigio, & di quel che chiama Commune, nominan
dolo Locrico & Hypodorio; aggiunge dopoi ne gli essempi, che pone quello dell'Eo-
lio, & quello dell'Hypoeolio. ApuleioFloridorū
lib. 1. oltra costoro ne commemora cinque l'Eolio, l'Ia
stio, il Lydio, il Frigio, & il Dorio; & LucianoIn Harmo
nide. ne racconta quattro; il Frigio, il Lydio, il
Dorio, & l'Ionico. Lasciarò di dir, oltra di questi quello, che faccia Boetio; poi
che nel Capitolo 14. & nel 15. del 4. Libro,In Musica. non discorda in cosa alcuna da i Mo-
page 386di posti da Tolomeo, se non nell'Ottauo; nel modo ch'io hò detto di sopra. Et quan-
tunque PlutarcoIn Musi-
ca. uoglia, che i Modi siano Tre solamente, Dorio, Frigio, & Lydio; tut-
tauia dice questo, commemorandoli come Principali; perche soggiunge dopoi, che qua-
lunque altro Modo dipende & deriua da questi. Et ciò disse; imperoche uide non esserli
più de Tre sorti di Diatessaron; come nel Cap. 14. della Terza parte hò mostrato; dalle
quali nasce la uarietà de i Modi. Non mancano quelli (lasciando da parte il raccontare 'l
loro nome, che quasi sono infiniti) che hanno fatto mentione solamente del Dorio, del-
l'Eolio, & dell'Ionico; come di quelli, ch'erano ueramente Modi greci, percioche (come
mostra CiceronePro L. Fla
co.) la Grecia era diuisa in tre parti; nella Doria, nella Eolia, & nella Io-
nia; come racconta anche Plinio nel libro Sesto al Cap. 2. della sua Historia naturale. Al-
tri hanno fatto mentione incidentalmente d'vna parte di loro; come ,Olim. ode
1. che no-
minò il Dorio sotto 'l nome della Cetera dorica, & cosi l'Eolio; & Horatio in diuersi luo-
ghi nomina l'Ionico, l'Eolio, il Dorio, & il Lydio. Di maniera che dalla diuersità dell'or-
dine, dalla uarietà del numero, & dalla differenza de i lor nomi, che si troua in tutti
questi autori; non si può cauare altro, che confusione di mente. Ma siano à qual modo
si uogliano collocati, ouer'ordinati; siano anco quanti si uogliono in numero, & habbia-
no qual nome si uogliano, appresso gli Antichi; questo importa poco à noi; ci basta sa-
per questo per hora, ch'essi Antichi usauano i lor Modi nella maniera, che di sopra hò
mostrato; & che considerandoli secondo l'uso de i Musici moderni collocati in una delle
Sette specie della Diapason harmonicamente, ouer'arithmeticamente mediata & diui-
sa, siano Dodici; imperoche in Dodici maniere solamente & non più, commodamente
si possono diuidere; de i qual Sei sono i Principali, & Sei loro Collaterali; come uede-
remo; habbiano poi hauuto gli Antichi quanti Modi si uogliano; Da che ueramente
nascesse una tanta discordia tra i Scrittori; si intorno al numero, com'anco intorno al
nome & all'ordine loro; è cosa difficile da giudicare; se non uolessimo dire, che ciò acca-
scasse, perche ouer ch'al tempo d'alcun di loro tutti i Modi non erano ancora conosciu-
ti; ò che non facessero mentione se non de quelli, che li ueniuano in proposito à tempo &
luogo commodo. Potiamo adunque da quel, che si è detto ricogliere, come è anco il
parere d'alcuni altri; che i Modi principali appresso gli Antichi erano Sei; Dorio, Frigio,
Lydio, Mistolydio, Eolio, & Ionico. Et se ben Tolomeo con Apuleio & molt'altri anco
chiamano il modo Ionico, modo Iastio; questo nulla, ò poco rileua; imperoche conside-
randoli l'vno & l'altro nella lingua Greca, tanto importa l'vno, quanto l'altro; poi che
anco il modo Mistolydio da Giulio Polluce è chiamato Locrico, ouer Locrense; & Athe
neo; tenne per cosa certa, che l'Hypodorio fusse l'Eolio. Cosa molto difficile è ueramen-
te il uoler'hauer di ciò chiara & perfetta cognitione, uolendo seguir l'vso de gli Anti-
chi; percioche questo non si può dimostrar per alcuna uia, per esser il loro vso total-
mente spento, che non potiamo ritrouar di loro uestigio alcuno. Ne di ciò si dobbia-
mo marauigliare; essendo che il tempo consuma ogni cosa creata; ma più presto si dob-
biamo marauigliar d'alcuni sciocchi, che credendosi porr'in uso il genere Chromatico &
l'Enharmonico, già per tanto, & tanto spacio di tempo lasciati; non conoscendo di lo-
ro maniera, ne hauendone ueduto uestigio alcuno; non si accorgono, che non hanno an-
cora intiera cognitione del Diatonico; percioche ueramente non sanno in qual manie-
ra cotali Modi si ponessero in uso, secondo 'l costume de gli Antichi. La onde credo,
che se ben uorranno essaminar la cosa, ritrouaranno senza dubio alcuno, doppo l'ha-
uersi lungamente lambicato il ceruello con molte fatiche & stenti, che haueranno get-
tato uia il tempo, più pretioso, ch'ogn'altra cosa; & esser stati ingannati alla guisa de
gli Alchimisti, intorno il uoler ritrouare quello, che mai ritrouar potranno; quello di-
co, che chiamano Quinta essentia.
page 387
De gli Inuentori De i Modi.Cap. IIII.
mo inuentore de i Modi moderni; percioche fin'hora non hò ritrouato alcu-
no, che lo dica; ancora che sia manifesto à tutti quelli, che leggono il Plati-
na,De Vitis
pontificū. che Papa Gregorio primo, huomo di santissima vita, & piena di mirabil
dottrina, fù quello, ch'ordinò, che si cantasse gli Introiti, il Κύριε ἐλέησον noue uolte,
l'Haleluiah, & l'altre cose, che si cantano nel nostro Santissimo sacrificio. Similmente,
che Vitaliano primo di questo nome ordinò il Canto, & aggiunse insieme gli Organi
(come uogliono alcuni) per consonanza. Ma Leone secondo, huomo perito nella Mu-
sica compose 'l canto de i Salmi; cioè, ritrouò le loro Salmodie, ò Intonationi; cioè, il
modo, che si cantano; & ridusse gli Hinni à miglior consonanza; hauendo Damaso pri-
mo per inanti ordinato, che tali Salmi si cantassero in Chiesa cambieuolmente un uerso
per Choro, & nel loro fine s'aggiungesse il uerso Gloria patri, co 'l resto. Et per quello, che
racconta Socrate nel Cap. 9. del Lib. 10. della Historia tripartita di Cassiodoro; & anco
di questo ne scriue Giouanni Gerson;De Canti-
cis Trac.
3.Ignatio huomo santissimo & martire di Christo fù
quello, che ritrouò l'Antifone; il che manifesta, dicendo;>
Antiphonas dedit ad Psalmos Ignatius aptas.
Monte prout quodam desuper audierat.
Tutto questo è stato detto intorno al Canto ecclesiastico; ancora che di esso non si
possa ritrouare il Primo inuentore; se bene alcuni l'attribuiscano al Dottore di S. Chiesa
Gregorio primo sudetto; ma inquanto all'Inuentione de quei Modi, che sono nel Can-
to figurato, & l'Inuentione di comporre nella maniera, che faciamo al presente; non è
dubio, che di ciò non ne potiamo hauer'alcuna certezza; ancora che (per quello, che si
può uedere) non è molto tempo, rispetto al Canto ecclesiastico; che un tal modo di
comporre, fù ritrouato. Et benche intorno gli Inuentori de i Modi antichi nasca qua-
si l'istessa difficultà; tuttauia potiamo hauer'alcuna cognitione de gli Inuentori de molti
de loro; imperoche PlinioNatur.
his. lib. 7.
cap. 56. vuole, che Anfione figliuolo di Gioue, ò come alcuni vo-
gliono di Mercurio & di Antipa, fusse inuentor dell'Harmonia Lydia, con la quale (se-
condo che riferisce Plutarcho di Aristosseno nel Libro della Musica) Olimpo fù
quello, che sonò col Piffero i funerali nella sepoltura del Serpente Pithone; la qual Har-
monia s'adoperò anco nella pompa funebre della vergine Psiche; come di sopra fù com-
memorato. E' ben uero, che Clemente AlessandrinoStromat.
lib. 1. attribuisce l'Inuentione dellHar-
monie Lydie ad Olimpo di Misia, ilquale fu forse il disopra nominato; & altri uoglio-
no, che la melodia Lydia fusse ritrouata non ad altro effetto, che per usarla ad un tale
ufficio; come è detto di sopra. Dicono ancora, che tal Melodia usauano i Rustici ne i triuij
& ne i quadriuij in honore di Diana, ad imitatione di Cerere, che con grande gridi cer-
caua la rapita Proserpina; come accenna il Poeta, quando dice; In Palae-
mone.
Non tu in triuijs indocte solebas
Stridenti miserum stipula disperdere carmen?
Oue si uede, che non faceuano vn tale vfficio con molti Istrumenti; ma con un Piffe-
ro solo, del quale (come vuole ApuleioFloridorū
lib. 1.) Iagne Frigio, che fù padre di quel Marsia, che
fù punito grauemente da Apollo della sua arroganza, fù l'inuentore. Questo istesso fa-
ceuano etiandio col Zuffolo, del quale (come vogliono alcuni, & massimamente Virgi-
lio) Pan dio de pastori fù l'inuentore; perche, com'egli dice. In Alexi
de.
Pan primus calamos caera coniungere pluresMa le melodie Dorie, secondo l'istesso Clemente; del qual parere fù anche
Instituit.
Plinio, furono ritrouate da Thamira di Thracia. Le Frigie, la Mistalydia, & la Mista
frigia (come vuole il detto Clemente) furono ritrouate da Marsia, che fù di Frigia; quan-
page 388tunque alcuni uogliano, che Saffo Lesbia poetessa antica fusse l'Inuētrice delle Mistely-
die & altri attribuiscano tale inuentione à Thersandro; & altri ad un Trombetta chiama-
to Pithoclide; ma Plutarco, pigliando 'l testimonio d'un Lisia, vuole, che Lamprocla d'A-
thene fusse l'inuentore de tali Melodie. Alcuni anco vogliono, che Damone Pitagorico
fusse inuentor dell'Hypofrigio, & Polimnestre dell'Hypolydio. De gli altri Modi non hò
ritrouato gli Inuentori; ma quando l'autorità d'Aristotele posta nel lib. 2. della MetafisicaCapit. 1.
ualesse in questo proposito, si potrebbe dire, che Timotheo fusse stato l'Inuentore del re-
sto; ancora che Frinide musico perfetto de quei tempi fusse auanti lui; percioche (com ei
dice) se non fusse stato Timotheo non haueressimo molte Melopeie, & non molti Modi.
Ma inuerità parmi che siano più antiche di Timotheo; come legendo molti autori & es-
saminandoli intorno al tempo, si può uedere. Qual di loro fusse il primo ritrouato; questo
è non dirò difficilissimo, anzi impossibile da sapere; ancora ch'alcuni uoglino, che 'l Ly-
dio fusse 'l primo; alla quale opinione si potressimo accostare, quando l'ordine de i Modi
posti da Platone, da Plinio, da Martiano, & da molt'altri, fusse posto, secondo che l'un fù
ritrouato prima dell'altro; ma ueramente è debile argomento; percioche
l'istesso di qualunque altro Modo, che fusse posto primo in qualunque altro ordine; come
del Frigio, ch'è posto da Luciano primo, & dell'Eolio, che è posto in cotal luogo da Apule
io. Lasciaremo hora di ragionar più di cotali cose, & uerremo à dir della loro Natura;
percioche della Proprietà de i Modi moderni vn'altra fiata ne parlaremo.
Della Natura, ò Proprietà de i Modi.Cap. V.
sitione de più cose poste insieme; dalla uarietà loro nasceua una certa differen-
za, dalla quale si poteua comprendere, che ciascun di essi riteneua in se un
certo non sò chè di uario; massimamente quando le cose, ch'entrauano nel
composto, erano poste insieme proportionatamente. Ond'era potente con l'altre par-
ti che concorreuano, d'indur ne gli animi de gli ascoltanti uarie passioni; inducendo
in loro nuoui, & diuersi habiti & costumi. De qui uenne, che tutti quelli, c'hanno scrit-
to alcuna cosa di loro, attribuirono à ciascuno la sua proprietà, da gli effetti, che ue-
deuano nascer da loro. Onde chiamarono il Dorio Stabile, & uolsero che fusse per sua
natura molt'atto à i costumi dell'animo de gli huomini ciuili; come dimostra Aristo-
tele nella Politica;Lib. 8. ca-
pit. 7. ancora che LucianoIn Harmo
nide. lo chiami Seuero; perche serua in se una certa
seuerità; & ApuleioFlorid. 1. lo nomini Bellicoso; ma Atheneo
14. ca. 10.
& uehementia; & Cassiodoro
lib. 2. ad
Boethum dice, ch'è donatore della pudicitia, & conseruator della
Castità. Dicono etiandio, ch'è Modo, che contiene in se grauità; per il che Lachete
appresso di Platone soleua comparar quelli, che ragionauano, ò disputauano de cose
graui & seuere; come della Virtù, della Sapienza, & d'altre cose simili; al Musico, che can-
tasse al suono della Cetera, ò Lira, non la melodia Ionica, ne la Frigia, ò la Lydia; ma
si bene la Dorica, la quale istimaua, che fusse ueramente la uera harmonia Greca; & ciò
massimamente quando erano huomini degni de tal parole, & tra loro & le parole dette si
comprendeua una certa Consonanza. Et perche i Doriensi usauano vn'Harmonia al-
quanto graue & seuera, con numeri non molto ueloci, i quali accompagnauano con la
Oratione, & conteneua in sè cose seuere & graui; però uoleuano gli Antichi, che per il
mezo del modo Dorio s'acquistasse la prudenza, & per esso s'inducesse in noi un'animo
casto & uirtuoso. Et ciò non era detto senza qualche ragione; come si può compren-
dere da gli auenimenti; imperoche (come racconta StraboneDe Situ or
bis lib. 3.) il Re Agamennone,
auanti che si partisse dalla patria, per andar'alla guerra Troiana, diede la moglie
Clitennestra in guardia ad un Musico Dorico; perche conosceua, che mentre 'l Musico le
page 389so, non poteua essere uiciata d'alcuno; della qual cosa accorgendosi il uitioso
uandoselo da gli occhi, diede fine à i suoi sfrenati desiderij. Ma perche que-
ebbe parer'ad alcuno cosa strana; però considerato quel, c'hò detto nella Secon-
rte,Cap. 7. &
8. ritrouerà, che non è impossibile; imperoche è da credere, che 'l buon Musico fus-
ale, che la stimolasse continuamente con dotte narrationi, accompagnate con Har-
monie appropriate, all'operationi uirtuose, & al dispreggio de i vitij; essortandola al uiuer
; co 'l preporle molti essempi de castissime & ben'accostumate Matrone, da
douer'imitare; insegnandole il modo, che hauesse da tenere per conseruar la sua castità, &
la intratenesse etiandio con narrationi filosofiche, & soauissime cantilene; come si conue-
niua à donna casta & pudica. In tal maniera anco Didone appresso di VirgilioAEneid.
lib. 1. con seue-
re & graui canzoni dal buon Musico Ioppa era tratenuta; il che si costuma di far tra l ho-
neste & caste donne; ma non già tra le lasciue, & men che honeste; come leggiamo ap-
presso l'istesso VirgilioGeorgi.
lib. 4. delle Ninfe;
Inter quas curam Clymene narrabat inanemPer tali effetti adunque gli Antichi
Vulcani, Martisꝗ dolos, & dulcia furta.
attribuirono le narrate proprietà al modo Dorico; & ad esso applicauano materie seuere,
graui, & piene di sapienza. Et quando da queste si partiuano & passauano à cose piace-
uoli, liete, & leggieri, vsauano 'l Modo Frigio; essendo che i suoi Numeri erano più ue-
loci de i numeri di qualunque altro Modo, & la sua Harmonia più acuta di quella del
Dorio; onde da questo, credo io, che sia uenuto quel Prouerbio, che si dice; Dal Do-
rio al Frigio; che si può accommodar, quando da vn ragionamento di cose altissime &
graui, si passa ad uno, che contenga cose leggieri, basse, non molto ingegnose, & simi-
gliantemente cose liete & festeuoli, & anche non molto honeste. Clemente Alessandri-
no,Stromat.
lib. 6. seguitando l'opinione d'Aristosseno, vuole; che 'l genere Enharmonico conuenghi
grandemente all'Harmonie doriche, come genere ornato & elegante; & alle Frigie il
Diatonico, come più uehemente & acuto. Fù già tanto in ueneratione il Dorio, che
niun'altro, da lui & il Frigio in fuori, fù approuato, & admesso da i due sapientissimi
Filosofi Platone & Aristotele; percioche conosceuano l'utile grande, che apportauano
ad una ben'istituita Republica; istimando gli altri di poco utile & di poco ualore. Onde
uolsero, che i dalla lor tenera età fussero istrutti nella Musica. Voleuano etian-
dio gli Antichi, che l'Hypodorio hauesse natura in tutto diuersa da quella del Dorio; im-
peroche si come il Dorio disponeua ad una certa costanza uirile, & alla modestia; cosi
l'Hypodorio per la grauità de i suoi mouimenti inducesse una certa pigritia & quiete.
lib. 3. c. 7 & QuintilianoInstitut.
lib. 9. c. 4.) i Pitagorici haueano cotale usan-
za, che soleuano col mezo dell'Hypodorio tra 'l giorno, & quando andauano à dormire,
mitigar le fatiche & le cure dell'animo del giorno passato; & nella notte suegliati dal son-
no, col Dorio ridursi à i tralasciati studij. Ma AtheneoDipnos.
lib. 14. (com'altroue hò anco detto) si pen-
sò, che questo fusse l'Eolio, & gli attribui, che inducesse ne gli animi un certo gonfia-
mento & fasto; per esser di natura alquanto molle. Attribuirono anco gli Antichi al Fri-
gio (come ci manifesta PlutarcoIn politi-
cis.) natura d'accender l'animo; & d'infiammarlo all'ira &
alla colera; & di prouocare alla libidine & alla lussuria; percioche lo istimarono Modo al-
quanto uehemente & furioso; & anco di natura seuerissimo & crudele; & che rendesse
l'Huomo attonito. La onde (secondo 'l mio parere) Luciano toccò molto ben la sua na-
tura con queste parole;In Episto.
ad Nigri-
num. Si come quelli (dice egli) i quali odono il Piffero Frigio, non tut-
ti impaciscono; ma solo quelli, i quali sono tocchi da Rhea, & questi hauendo udito il
Verso, si ricordano del primo affetto, ò passione prima, & etiam della prima perturba-
tione; cosi quelli, ch'odono i Filosofi, non tutti si partono attoniti & impiagati; ma sola-
mente quelli, ne i quali si ritroua un certo incitamento intrinseco alla Filosofia. Simil-
mente Ouidio l'accennò in questi due uersi, dicendo;In Ibin.
Attonitusꝗ seces, vt quos Cybeleia mater
Incitat, ad Phrygios uilia membra modos.
page 390Aristotele8. Polit.
Cap. 5. l'accenna Bacchico; cioè, furioso, & Baccante; & LucianoIn Harmo
nide. lo chiama furio-
so, ò impetuoso; ancora ch'Apuleio1. Flori-
dorum. lo nomini Religioso. Questo Modo (come hab-
biamo veduto) si sonaua anticamente col Piffero, il quale è Istrumento molto incitati-
uo; per ilche (come dicono alcuni) col mezo del suono de i Pifferi i Spartani inuitaua-
no i soldatià pigliar l'arme; & (come narra ValerioDictor. &
Fact. lib.
2. cap. 1.) costretti dalle seuerissime leggi di Li-
curgo, osseruauano di non andar mai cō l'essercito à combattere, se prima non erano be-
ne inanemiti & riscaldati dal suono de i detti Istrumenti, con la misura del piede Ana-
pesto; il qual si compone di tre tempi; due breui, & uno lungo. La onde da i due primi,
i quali fanno la battuta più spessa & più ueloce, comprendeuano, d'hauer'assalire l'ini-
mico con grand'empito; & dal lungo, d'hauere à fermarsi & resistere animosamente,
quando non l'haueano rotto nel primo assalto. Il che faceuano anco i Romani; come
narra Tullio;Tuscul.
lib. 1. i quali non pur col suono della Tromba; ma col canto accompagnato à co-
tal suono, soleuano incitare gli animi de i Soldati à combattere virilmente; & ciò ne
mostra anco Virgilio,Aeneid.
6. parlando di Miseno.
Quo non praestantior alter,
Aere ciere viros, Martemꝗ cantu.
Et Horatio parlando di Tirteo, dice;De Arte
poetica.
Tyrtheusꝗ mares animos in martia bella
Versibus exacuit.
Imperoche gli Italiani usarono la Tromba, che fù inuentione de i popoli Tirrheni,
come vuol Diodoro;Hist. li. 6. & PlinioHisto. na-
tu. lib. 7.
c. 56. vuole, che l'Inuentore fusse un nominato Piseo, pur Tir-
rheno. Di questa inuentione Virgilio ne tocca una Parola, quando dice;Aeneid.
8.
Tyrrhenusꝗ tubae mugire per aethera clangor.
Ma Gioseffo nel Primo libro delle Antichità giudaiche vuole, che l'Inuentore sia sta-
to Mosè, & Homero dice, che fù Dirceo, alcun'altri Tirteo, & alcuni Maleto; col
suono della quale, ch'era aspro, ueloce, gagliardo, & forte (come si può comprende-
re dalle Parole di Ennio poeta antico, in quale esprimendo la natura di questo istru-
mento disse;
At Tuba terribili sonitu taratantara dixit.)
Proferiuano il modo Frigio. Inuitati i Lacedemoni, ò Spartani adunque al cōbattere
con grande vehementia dal suono del detto Istrumento, erano dalla tardità del suono;
cioè, dalla tardità del mouimento, & dalla grauità del Modo inuitati à lasciar di combat-
tere. Il grande Alessandro anco col mezo d'un Piffero come narra Suida) fù inuitato da
Timotheo à pigliar l'arme, recitando la legge Orthia nel modo Frigio. Similmente vn
giouine Taurominitano (come recita Ammonio In predi-
cabilibus. & Boethio,Musicae
lib. 1. cap.
1. & come molte volte hò
commemorato) fù da questo Modo riscaldato. Per il che uoleuano gli Antichi; che le
materie, che trattauano di guerra, & fussero minaccieuoli & spauētose, si accommodasse-
ro à cotale Modo; & che l'Hypofrigio moderasse & sottrahesse la natura terribile & con-
citata del Frigio. Onde dicono alcuni, si come i Spartani, & li Candioti inanemiuano
i soldati al Combattere col modo Frigio; cosi li riuocauano dalla pugna con l'Hypofri-
gio al suono de i Pifferi. Vogliono anco, che Alessandro fusse riuocato dalla battaglia
da Timotheo col mezo di questo Modo, recitato al suono della Cetera; & che 'l gio-
uine Taurominitano commemorato col mezo di questo Modo, & col canto dello Spon-
deo fusse placato. Vuol CassiodoroVariarū.
lib. 1. Boe
thum., che 'l Frigio habbia natura di eccitare al combatte-
re, & d'infiammare gli huomini al furore, & che 'l Lydio sia rimedio contra le fatiche del-
l'animo, & similmente contra quelle del corpo. Ma alcuni uogliono, che 'l Lydio sia
atto alle cose lamenteuoli & piene di pianto, per partirsi dalla modestia del Dorio, in
quanto è più acuto, & dalla seuerità del Frigio. Sotto questo Modo, Olimpo (come nar-
ra PlutarcoIn Musi-
ca.) al suono del Piffero nella Sepoltura di Pithone cantò gli Epicedij; che sono
alcuni versi, che si cantauano auanti 'l Sepolchro d'alcun morto; imperoche antica-
mente era usanza di far cantare al suono del Piffero, ò d'altro Istrumento nella morte de
page 391i parenti, ò de gli amici più cari; dal qual canto erano indotti à piangere i circostanti la
lor morte; & ciò faceuano fare ad una femina vestita in habito lugubre; come anco si
osserua al presente in alcune città, massimamente nella Dalmatia, nella morte d'al-
cun'Huomo honorato. Tale vsanza commemorò Statio Papinio, dicendo;Theb. lib.
6.
Cum signum luctus cornu graue mugit adunco
Tibia, cui teneros suetum producere manes,
Lege Phrygum mesta.
Onde si uede, che tali Harmonie erano fatte nel modo Frigio, ouer nel Lydio; co-
me dall'autorità d'Apuleio addotta di sopra si può uedere. Alcuni hanno chiamato
il Lydio da gli effetti, horribile, tristo & lamenteuole; & LucianoIn Harmo
nide. lo nomina furioso,
ouero impetuoso; è ben uero, che Platone pone tre sorti d'Harmonie Lydie; cioè, Mi-
ste, Acute, & Semplici, senza porui alcun'aggiunto. Hanno hauuto opinione alcuni,
che l'Hypolydio habbia natura differente & contraria à quella del Lydio; & che conten-
ga in se una certa soauità naturale & abondante dolcezza, che riempia gli animi de gli
ascoltanti d'allegrezza & di giocondità, mista con soauità, & che sia lontano al tutto
dalla lasciuia & da ogni uitio; perciò l'accommodarono à materie mansuete, accostu-
mate, graui, & continenti in se cose profunde, speculatiue, & diuine; come sono quel-
le, che trattano della gloria di Dio, della felicità eterna; & quelle, che sono atte ad im-
petrare la Diuina gratia. Et uolsero similmente, che 'l Mistolydio hauesse natura d'in-
citar l'animo, & di rimetterlo. Apuleio dimanda l'Eolio semplice; & Cassiodoro vuole,
che habbia possanza di far tranquillo & sereno l'animo oppresso da diuerse passioni; &
che dopo scacciate tali passioni, habbia possanza d'indurre il sonno; natura & proprie-
tà veramente molto conforme à quella dell'Hypodorio. Onde non è da marauigliarsi,
s'Atheneo, adducendo l'autorità d'Eraclide di Ponto, fù di parer, che l'Eolio fusse
l'Hypodorio; ò per il contrario. Vogliono alcuni, che all'Eolio si possino accommodar
materie allegre, dolci, soaui, & seuere; essendo che (come dicono) hà in se vna grata
seuerità mescolata con vna certa allegrezza & soauità oltra modo; & sono di parer, che
sia molto atto alle modulationi de i Versi lirici, come Modo aperto & terso. Ma s'è ue-
ro quel, che si pensò Eraclide, sarebbe à tutte queste cose contrario molto; percioche
hauerebbe diuersa natura; come di sopra hò mostrato. Apuleio chiama lo Iastio, oue-
ro Ionico (che tanto vale) vario; & Luciano lo nomina allegro; per essere (secondo 'l
parere d'alcuni) molto atto alle danze & à i balli. La onde nacque, che lo dimandaro-
no lasciuo; & i popoli Inuentori di tal Modo, che furono gli Atheniesi, popoli della Io-
nia, amatori de cose allegre & gioconde; & molto studiosi della eloquenza, chiamaro-
no Vani & leggieri. Cassiodoro vuole, che habbia natura d'acuire l'intelletto à quelli,
che non sono molto eleuati; & d'indurre vn certo desiderio delle cose celesti in coloro,
i quali sono grauati da un certo desiderio terrestre & humano. Queste cose dicono in-
torno la natura de i Modi; la onde si scorge vna gran varietà ne i Scrittori, volendo
alcuni una cosa, & alcuni vn'altra. Il perche mi penso, che tal varietà poteua nascere
dalla uarietà de i costumi d'una Prouincia, ch'essendo dopo molto tempo uariati, va-
riassero ancora i Modi; & che una parte de i Scrittori parlasse di quei, che perseueraua-
no d'esser nella lor prima & pura semplicità; & l'altra parte parlasse di quelli, che già
haueano perso la loro prima natura; come per cagione d'essempio diremo del Dorio,
ch'essendo prima honesto, graue, & seuero; per la uariatione de i costumi fusse ua-
riato anche lui; & dopoi applicato alle cose della guerra. Et per questo non ci dob-
biamo marauigliare; percioche se dalla varietà dell'Harmonie nasce la uariatione de i
costumi; com'altroue si è detto; non è inconueniente anco, che dalla variatione de i
costumi si uenga alla uarietà dell'Harmonie & de i Modi. Poteua anco nascere dal-
la poca intelligenza, ch'haueano i Scrittori di quei tempi intorno à cotal cosa; co-
me suole accascare etiandio à i tempi nostri, ch'alcuni si porranno scriuere alcune
cose, che non intendono; ma si rimettono al giudicio & alla opinione d'vn altro,
page 392il quale alle uolte ne sà men di lui; & cosi molte uolte pigliano una cosa per un'altra, &
attribuiscono à tal cosa alcune proprietà, che considerandola per il dritto, è da tal pro-
prietà tanto lontana & diuersa, quanto è lontano & diuerso il Cielo dalla Terra. Et mol-
te volte vediamo, che pigliano una cosa per un'altra; come si può uedere in quello, che
scriue Dion Chrisostomo d'Alessandro Magno ne i Commentarij del Regno,Orat. 1. essempio
addutto da molti; oue dice, che fù costretto da Timotheo a pigliar l'arme col mezo del
Modo Dorio; tuttauia è solo di questo parere, per quello c'hò potuto comprendere;
imperoche il Magno Basilio (com'altre fiate hò detto) & molt'altri auanti lui, uuole, che
fusse costretto a fare un simile atto dal Frigio. Ma di questo sia detto à bastanza; impero-
che è dibisogno, che si uenghi à ragionare intorno all'Ordine.
Dell'Ordine de i Modi.Cap. VI.
ri intorno à i nomi de i Modi, & intorno alle lor proprietà; cosi furono diffe-
renti anco dell'ordine & del sito loro; imperoche alcuni li ordinarono in vna
maniera & altri in un'altra. PlatoneDe Rep. 3. prima d'ogni altro pose nel suo ordine
l'Harmonie Lidie miste nel primo luogo, alle quali soggiunse le Lydie acute; nel secon-
do luogo accommodò le Ioniche, & quelle che chiama semplicemente senz'altro ag-
giunto Lidie; & nel terzo la Doria & la Frigia harmonia. E ben uero, che si può dir, che
non habbia posto tal'ordine, come naturale; ma à caso & accidentalmente, secondo che
nel suo ragionamento li tornaua in proposito; come fece anco in un'altro ragionamento,In Lache-
te.
nel quale pose prima la Dorica, dopoi la Ionica soggiungendole la Frigia, & dopoi que-
st'aggiunse la melodia Lidia nell'ultimo luogo. Altri tennero altro ordine; imperoche
posero l'Hypodorio nella parte graue del loro ordine primo d'ogn'altro, & il Mistolidio
nell'acuta; ponendoli di sopra l'Hypermistolidio, & sopra l'Hypodorio l'Hypofrigio;
dopo questo l'Hypolidio, aggiungendoli il Dorio, dopo il quale seguiua immediatamen
te il Frigio; di maniera che fecero, che 'l Lidio era posto di sopra à questi quattro meza-
ni; & tra costoro si ritrouano Tolomeo & Boetio. Et quantunque alcun'altri tenessero
un'altro ordine; come fece Apuleio,Florido-
rum. 1. il quale pose l'Eolio auanti d'ogn'altro, dopoi l'Ia-
stio & gli altri, secondo che si uedono nel suo ordine; tuttauia Martiano pone primo il
Lidio, dopoi soggiunge l'Iastio, & cosi gli altri; ma altri posero primo il Mistolidio, tra
i quali sono numerati Euclide & Gaudentio. Giulio polluce in due luoghi pone il Dorio
prima d'ogn'altro; come fecero Plutarcho & Cassiodoro; ma Aristide Quintiliano ac-
commodò il Lidio, come fece Martiano; ancora che Luciano habbia posto il Frigio nel
primo luogo. Onde da tal diuersità non ne segue altro, che confusione grande di men-
te; & questo può nascere, perche alcuni scriuendo in tal maniera tennero un'ordine na-
turale nel porre i Modi l'vn dopo l'altro; & altri (non attendendo à tal cosa) posero un'
ordine accidentale. I primi furono quelli, che ragionarono de tali cose secondo l'ordi-
ne della Scienza, & anco in maniera dimostratiua; come fù Euclide, Tolomeo, Gau-
dentio, Briennio, Aristide, Boetio, Cassiodoro, & Martiano. Ma gli altri ragionaro-
no di essi à caso, secondo che li tornauano in proposito; oue non faceua dibisogno, che li
ponessero, secondo che si debbono porre l'un dopo l'altro, seguendo l'ordine naturale;
ma in quel modo, che tornauano à loro più commodi. Tra questi fù Platone, Plutar-
co, Luciano, il Polluce, & Apuleio. Non è però da marauigliarsi, che questi, tra loro
tenessero un'ordine diuerso; ma ci dobbiamo marauigliare de i primi, che trattando vna
cosa istessa scientificamente, fussero cosi differenti di parere. Ma cessi tal marauiglia, poi
che (come disssi altroue1. Supple.
cap. 15.) si come suole auenire nell'altre Scienze, nelle quali si trouano
molte Sette; cosi nella Musica si ritrouauano à quei tempi esser due Sette principali; l'una
page 393delle quali si chiamaua Pitagorica, la qual seguitaua la dottrina di Pitagora; & l'altra
Aristossenica, ch'era de quelli, che seguitauano i pareri d'Aristosseno. Essendo adun-
que tra costoro molte differenze & pareri diuersi intorno ad una cosa istessa; percioche
alcuni la uoleuano ad un modo, & alcuni ad un'altro, dalla uarietà de i loro Principii non
nasceua altro, che uarietà di conclusioni. La onde nacque, che si come furono diffe-
renti in molte cose (come in alcuni luoghi, secondo che mi tornaua in proposito, hò mostra
to) cosi ancora furono discordanti nel numero, nel sito, & nell'ordine de i Modi, Impero
che se noi haueremo riguardo à quel che scriuono Tolomeo & Boetio in questa materia,
ritrouaremo, che pongono il Modo Mistolidio nella parte acuta de i lor ordini; & uoglio
no, che la chorda grauissima di ciascun si chiami Proslambanomenos, la mezana Mese &
l'acuta Nete; & Boetio vuole, che le distanze & gli Interualli che si trouano in ciascun
Modo, siano solamente di Tuono, ò di Semituono; nondimeno Euclide numerando le spe
cie della Diapason pone la prima specie ne i suoni graui spessi, i quali chiama Βαρύπυκνοι
da Hypate hypaton à Paramese; & dice, che quest'era chiamata da gli Antichi Misto-
lidio; la seconda pone tra i mezani spessi, i quali dimanda Μεσόπυκνοι, da Parhypate hy-
paton à Tritediezeugmenon, & la nomina Lydio. Et la Terza tra gli Ο'ξύπυκνοι; cioè,
acuti spessi, & la chiama Frigio; nominando la quarta Dorio, la quinta Hypolidio, la
sesta Hypofrigio, & la settima non solamente nomina Hypodorio, ma anche Lochrica,
& Commune; la qual cosa fà etiandio Gaudentio; come si può vedere appresso di loro.
Ilperche si uede manifestamente, che fà l'una de due cose, ouer che pone il modo Mi-
stolidio nella parte graue del suo Monochordo; com'è ueramente, & lHypodorio, ò
Lochrico più acuto; ouer che pone le chorde nel detto Istrumento ad altro modo, di quel
che fanno gli altri Musici. La onde uediamo hora uerificarsi quella opinione, ch'io toc-
cai nel Cap. 29. della Seconda parte, ragionando dell'opinione, che hebbero gli Anti-
chi dell'Harmonia celeste. Ma chi uolesse narrar il modo, che teneuano nel cantare i det
ti Modi, sarebbe cosa difficile; prima, perche non si ritroua alcuno essempio di cotal co
sa; dopoi, perche (quantunque BoetioMusicae li.
4. c. 14. &
15. ponga gli Interualli, che si trouauano da una
Chorda all'altra di ciascun Modo) Tolomeo & Aristide pongono altri Interualli diuersi;
ne però l'uno nell'altro pone la maniera del procedere, quando cantauano dal graue al-
l'acuto, ò dall'acuto al graue. Et se ben si trouano molti essemplari scritti à mano di To
lomeo, che dimostrano tali Interualli; tuttauia sono talmente ne gli essempi & in altri luo
ghi, ò peril tempo, ò per l'ignorantia de i Scrittori, in tal maniera imperfetti; che si può
da loro cauar poco di buono. E' ben uero, che nel Cap. 1. del 3. Libro applica manife-
stamente la Diatessaron, ch'è il Tetrachordo Diatonico diatono al Modo Eolio; de gli
altri poi non ne hò potuto hauer ragione alcuna. Ma cotali distanze sono alquanto me-
glio poste da Aristide,De Musica
Lib. 1. di maniera che si possono intendere; ancora che due essemplari,
che mi sono peruenuti alle mani siano in tal modo scorretti; che à pena hò potuto cauar
queste poche parole, che seguono; le quali uoglio porre come stanno, accioche si ueda in
qualche parte la diuersità de i Modi antichi, & quanto siano differenti da i nostri Mo-
derni; & dicono:
Τὸ μὲν οὖν Λύδιον διάστημα συνετίθεσαν, ἐκ διέσεως καὶ τόνου καὶ τόνου, καὶ διέσεως καὶ διέσεως,
καὶ τόνου καὶ διέσεως. Καὶ τοῦτο μὲν ἦν τέλειεον σύστημα. Τὸ δὲ Δώριον, ἐκ τόνου καὶ διέσεως, καὶ
διέσεως καὶ τόνου καὶ τόνου καὶ διέσεως καὶ διέσεως καὶ διτόνου. ἦν δὲ τοῦτο, τόνῳ τοῦ Διὰ πασῶν
ὑπερἐχον. Τὸ δὲ Φρυγϊον, ἐκ τόνου καὶ διέσεως καὶ διέσεως, καὶ
διτόνου καὶ τόνου, καὶ διέσεως καὶ
τόνου. ἦν δὲ καὶ τοῦτο τέλειον Διὰ πασῶν. τὸ δὲ Ιάστειον, συνετίθεσαν ἐκ διέσεως καὶ διέσεως καὶ
διτόνου, καὶ τριημιτόνου καὶ τόνου. ἦν δὲ τοῦτο τοῦ Διὰ πασῶν ἑλλεῖπον τόνῳ. Τὸ δὲ Μιξολύδιον, ἐκ δύω
διέσεων κατὰ τὸ ἑξής κειμένον, καὶ τόνου, καὶ τόνου, καὶ διέσεως καὶ τριῶν τόνων. ἧν δὲ καὶ τοῦτο τέ-
λειεν σύστημα. τὸ δὲ λεγόμενον Σύντονον λυδϊον, ἧν διέσεως καὶ διέσεως καὶ διτόνου καὶ τριημιτό-
νίου. Δίεσιν δὲ νῦν ἐπὶ πάντων ἀκουστέον, τὴν ἐναρμόνιον: cioè, Hanno adunque composto il
Lydio diastema di diesis & di tuono & tuono, & di diesis & diesis, di tuono & diesis; &
questo è Systema perfetto. Ma il Dorio di tuono, & diesis, & di diesis, & tuono; & di tuo
page 394no & diesis, & di diesis & Ditono; & questo superaua la Diapason per un tuono. Il Fri-
gio poi di tuono & diesis, & di diesis & ditono & tuono, & di diesis & tuono; & questo
era una Diapason perfetta. Ma composero l'Iastio di diesis & diesis, di ditono & trihe-
mituono & di tuono; & mancaua della Diapason d'un tuono. Il Mistolidio poi di due
diesis posti l'un dopo l'altro, & di tuono & tuono, & d'un diesis & tre tuoni; & quest'e-
ra vn Systema perfetto. Ma quel ch'era detto Syntono lidio, era composto di diesis &
diesis, & d'un Ditono & un Trihemituono. Ma il Diesis hora in tutti si hà da intender
quello dell'Enharmonico. Il perche dalle parole di Aristide potiamo comprendere, che
i Modi (secondo la sua opinione) erano varij non solamente ne gli Interualli; ma anco
nel numero delle Chorde; quantunque Boetio nel Cap. 4. del lib. 4. della Musica ponga
solamente undici Chorde nel Lydio, & nel Cap. 14. & nel 15. ne ponga per ogni modo
Quindeci; alle quali aggiunge anco il tetrachordo Synemennon. Ma per quel che po-
tiamo comprendere dalle parole d'Euclide & di Gaudentio poste di sopra, ciascun de i
Modi, quando era perfetto, era compreso sott'una specie della Diapason; cioè, tra Ot-
to Chorde; & cotal'uso è anco appresso i Moderni; imperoche tra la Prima specie della
Diapason C & c (per tener il modo, ch'io hò tenuto ragioneuolmente nella Terza par-
te, & nel Quinto delle Dimostrationi intorno alle Dimostrationi de i Modi) porremo il
Primo & l'Ottauo modo; il Terzo & il Decimo, tra la Seconda specie D & d. simiglian-
temente tra la Terza E & e. il Quinto & il Duodecimo; & tra la Quarta F & f. il Settimo.
Ma tra la Quinta Γ & G. ouer G & g. porremo il Nono & il Secondo; & tra la Sesta A
& a. oueramente a & aa. l'Vndecimo, & il Quarto. Vltimamente tra la
 &
&  . che è la
. che è la Settima specie porremo il Sesto modo; come più à basso vederemo. Et sono al numero
de Dodici, non solamente appresso i Compositori prattici, ma etiandio appresso gli Ec-
clesiastici; ancora che da molti non siano considerati in tanto numero; de i quali intendo
ragionar particolarmente, & mostrare in qual maniera al presente si vsi ciascuno di loro.
Che l'Hypermistolidio di Tolomeo non è quello, che noi chiamiamo
Decimo modo.Cap. VII.
do, che noi vsiamo sia l'Hypermistolidio di Tolomeo; del quale ne fà mentione
nel Cap. 10. del Lib. 2. de gli Harmonici, posto nell'Ottauo luogo dell'ordine
commemorato nel Capitolo precedente; ma ueramente costoro di gran lunga
s'ingannano; Imperoche 'l Decimo (come vederemo) è contenuto tra la Seconda specie
della Diapason D & d. ouer tra Lychanos hypaton & Paranete diezeugmenon arithme-
ticamente tramezata; & l'Hypermistolidio è contenuto tra la Sesta a & aa. cioè, da Mese
à Netehyperboleon; come ne mostra chiaramente Boetio nel Cap. 17. del Lib. 4. della
Musica. Onde insieme si può ueder la differenza, che si troua tra l'uno & l'altro; & l'er-
rore, che costoro pigliano. Et ben ch'alcun'altri habbiano hauuto parere, che dall'Hy-
podorio loro, ilquale è più graue d'ogn'altro modo, all'Hypermistolidio posto nella parte
più acuta, non si troua alcuna differenza, se non di graue & d'acuto; percioche l'un & l'al-
tro sono contenuti sotto un'istessa specie della Diapason; tuttauia parmi (secondo 'l mio
giudicio) che costoro siano in grand'errore; imperoche tanto sarebbe dire, che Tolomeo
hauesse replicato nell'acuto quel ch'era posto nel graue, senza far'alcun'altra differenza
d'Harmonia. Ma ciò non è credibile; essendo che un si gran Filosofo, & Mathematico,
com'era Tolomeo, non sarebbe stato si priuo di giudicio, c'hauesse molteplicato una
cosa fuor di proposito, com'era questa; tanto più, che quest'era tra Filosofi un grande in-
conueniente. Bisogna adunque dire, che tali Modi fussero differenti l'un dall'altro, non
solamente per il sito; ma anco per natura, mediante la Melodia, ch'era diuersa; & che
page 395Tolomeo hauesse tal intentione quando nominò lo Hypermistolidio; come si può com-
prendere dalle sue parole, poste nel sudetto Capitolo. Alcuni altri hanno uoluto chia-
mar cotal modo Eolio; & ueramente ciò parmi esser fatto senz'alcuna ragione; essendo
ch'esso Tolomeo nel Cap. 1. & nel 15. del lib. 2. de gli Harmonici fà mentione dell'Eolio,
nominandolo Eolia harmonia. Potrebbe forse alcun'addimandare; per qual cagione
Tolomeo non habbia aggiunto 'l suo collaterale, ò placale all'Hypermistolydio; ne meno
habbia posto l'Eolio in cotal'ordine, ne anco l'Ionico, ilquale chiama Iastia harmonia;
ma perche ciascun leggēdo il sudetto Cap. 10. & il Cap. 3. di questo; & il Cap. 8. del 6. Lib.
De i Sopplimenti; di tal dubbio, ò questione proposta potrà hauer risposta sufficiente;
però non mi par di replicar cosa alcuna.
In qual maniera gli Antichi segnauano le Chorde de i loro
Modi.Cap. VIII.
Greco, ne Latino pur vn'essempio, per il quale si possa comprendere, in qual
maniera gli Antichi facessero cantare molte parti insieme; se non il modo, che
teneuano nel scriuer le Chorde de i lor Modi, ò Cantilene separatamente, &
in che proportione poneuano le voci lontane l'una dall'altra; più mi con fermo nel cre-
dere, che mai non vsassero la Musica altramente di quello c'hò mostrato nel Cap. 14. del-
la Seconda, & nel Cap. 79. della Terza parte; oltra ch'è manifesto, che non usauano quel-
le figure, ò caratteri nelle lor Cātilene, ne meno quelle linee & spacij mostrati nel Cap. 2.
della Terza parte, i quali vsiamo al presente; imperoche (come dice BoetioMusicae
lib. 4. c. 3.) haueano al-
cune loro Cifere, le quali poneuano sopra le sillabe de i loro Versi, & da quelle compren-
deuano in qual maniera douessero cantare, mouendo la uoce verso 'l graue, ouer uerso
l'acuto. E' ben uero, che tali Cifere poneuano raddoppiate, l'una sopra l'altra; & dice
l'istesso Boetio, che quelle, ch'erano le prime poste di sopra, erano le Note, ò Caratteri
delle Dittioni, ò Parole; & le seconde ch'erano di sotto, quelle delle Percussioni; uolendo
inserire (com'io credo) che le prime dimostrauano le Chorde, & le seconde il Tempo
lungo, ò breue; ancorache tal breuità ò lunghezza poteuano apprendere dalla sillaba
posta nel Verso, la quale era non altramente, che ò lunga, ò breue. Tali cifere poi erano
l'una dall'altra differenti; percioche à ciascuna Chorda haueano segnato una cifera par-
ticolare, di maniera che la Cifera di Proslambanomenos era differente da quella d'Hy-
pate hypaton & dall'altre; & simigliantemente la cifera di Proslambanomenos del modo
Dorio era differente dalla cifera di Proslambanomenos del modo Frigio & cosi l'altre.
dottore Santo, ritrouò (come uogliono i moderni) altri caratteri nuoui, iquali accommo-
dò alle cantilene Greche ecclesiastiche di maniera, che non significano le Chorde, come
faceuano i nominati caratteri, ò cifere; ma dimostrano l'Interuallo, che si hà da cantare
ascendendo, ò discendendo; percioche hanno i suoi Caratteri ò Cifere diuise in due
parti; onde una parte serue cantando nell'ascendere, & l'altra nel discendere; & per tal
modo ogni Interuallo cantabile hà la sua cifera; di maniera, che quella del Tuono è diffe-
rente da quella del Semituono; & quella della Terza minore, da quella della maggiore, &
cosi l'altre, che ascendono; & sono differenti tra loro etiandio quelle cifere di Tuono, di
Semituono & altri Interualli che discendono, da quelli, che ascendono; alle quali tutte
s'aggiungono i lor Tempi; di modo che si può ridurre ogni cantilena sotto cotali caratte-
ri, ò cifere con maggior breuità, di quel che facciamo noi adoperando i nostri; come po-
trei mostrare in molte mie compositioni; nelle quali sono commodati tutti quelli acciden
ti, che in esse concorrono, sia qual si uoglia; secondo che tornano al proposito. Ma dob-
page 396biamo auertire, acciò non si prendesse errore, che se noi cōsideraremo le parole di Boetio
poste nel Cap. 14. & nel 16. del lib. 4. della Musica, le quali trattano della materia de i Mo
di, potremo comprender due cose, dalle quali si scoprono due grand'inconuenienti; se-
condo 'l mio giudicio; il primo de i quali è, che non potremo ritrouar'alcuna differenza
de Interualli più in un Modo, che in un'altro; essendo che vuole, che tutte le Chorde del-
l'Hypodorio, nella maniera che sono collocate, siano fatte più acute per vn Tuono; acciò
si habbia il modo Hypofrigio; & che tutte le Chorde di questo Modo siano medesimamē-
te fatte acute per vn'altro Tuono, per hauer quelle della modulatione (com'egli dice)
dell'Hypolydio; La onde se tutte queste Chorde si faranno più acute per un Semituono,
vuole che ne uenga 'l Dorio; & cosi segue dicendo de gli altri Modi. Per il che se in tal
maniera si hà da procedere, per far'acquisto de i Modi; non sò comprendere tra loro al-
cuna uarietà; se non che accommodati tutti per ordine in un'istesso Istrumento, l'un sarà
più acuto dell'altro per un Tuono, ouer per un Semituono, procedendo per gli istessi in-
terualli. Ma che differenza, di gratia, si trouerebbe tra l'uno & l'altro Modo, quando nel-
le Chorde graui, nelle mezane & nelle acute di uno, si trouasse quell'istessi Interualli tra
le graui, le mezane & le acute d'un'altro? se bē fussero più acuti l'un dell'altro, ò più graui
per qual si uoglia distanza; essendo che gli Interualli, che fanno la forma de i Modi, sono
quelli, che fanno la differenza loro, & non l'essere vn poco più acuto, ouer'vn poco più
graue. Il Secondo è, che dalle sue Parole & da gli essempi, come male intesi, potremo
comprendere, che i Musici moderni parlando in simil materia molto s'ingannano; per-
cioche credono, che 'l Settimo modo moderno, secondo l'ordine che tenimo, sia il Lidio
antico, & lo fanno più graue del Nono, ilquale chiamano Mistolydio, per un Tuono; essen
do che pongono, che questo lor Lydio sia contenuto tra la Quarta specie della Diapason
F & f. & il Mistolydio tra la Quinta G & g. iquali sono distanti l'un dall'altro per un Tuo-
no; nondimeno Boetio mostra chiaramente, che 'l Lydio antico è distante dal Mistolydio
per un Semituono. Similmente vuole, che 'l Dorio sia lontano dal Frigio per un Tuono;
ilche dimostra anche Tolomeo nel Cap. 10. del Lib. 2. de gli Harmonici; & questo dal Ly-
dio per un'altro Tuono; & pur uogliono i Moderni, che 'l Terzo Modo del nostro ordine
sia anco il Dorio antico, il Quinto il Frigio, & il Settimo il Lydio; il che uerrebbe ad essere
tutto 'l contrario di quello, che costoro tengono; perche 'l Terzo è distante dal Quinto per
un Tuono; & questo dal Settimo per un Semituono; di maniera che potiamo dire, che so-
no in grande errore, quando nominano il Terzo Dorio, il quinto Frigio, & cosi gli al-
tri, secondo che sono collocati da Tolomeo & da Boetio; imperoche se pur si uoles-
sero nominare per tali nomi; quando i Modi moderni fussero simili in qualche parte à gli
Antichi; più presto douerebbono chiamar'il Primo Dorio, il Terzo Frigio, & Lydio il
Quinto, come facciamo, che altramente; essendo che in tal modo sono distanti l'un dal-
l'altro per gli Interualli, che li pongono Tolomeo & Boetio. Questa è stata ueramente
una delle cagioni, oltra l'altre (acciò ch'alcun non si marauigli) che hà fatto, ch'io non
nomini i Modi ne Dorio, ne Frigio, ne Lydio, ò con simili altri nomi; ma Primo, Secondo,
Terzo, & gli altri per ordine; & ch'io hò tenuto nell'ordinarli l'un dopo l'altro, altra ma-
niera di quel che hāno tenuto tutti i nostri Moderni, & anco i nostri Antichi; percioch'io
uedeua, che 'l nominarli in tal maniera, & ordinarli per altro modo, non era ben fatto.
Et benche Franchino Gaffuro nella sua TheoricaLib. 5. c. 8. tenga un'altr'ordine, nel situare & por-
re i Modi l'un più acuto, ò più graue dell'altro; tuttauia non pone gli d'un Modo
differenti da quelli d'un'altro; ma solamente pone gli istessi più acuti, hora d'un Tuono,
hora d'un Semituono; & non uaria altramente la modulatione. Quest'hò voluto dire, non
già per parlar contra alcuno de gli Antichi, ne de i moderni Scrittori, à i quali hò sempre
portato & portarò somma riuerenza; ma accioche i Lettori siano auertiti, & considerino
bene cotal cosa con diligenza, & possino far giudicio, & conoscer sempre il buono dal tri
sto, & il uero dal falso nelle cose della Musica. Ne credo che sarebbe grande inconuenien-
te, quando alcuno uolesse dire, che se ben Boetio sia stato dottissimo delle cose speculati-
page 397ue della Musica; che poteua essere, che delle cose della prattica non fusse cosi bene intel-
ligente; il che ueramente si può confermare con quello, che si è detto di sopra, & con
quello che hò mostrato nel Cap. 13. della Terza parte; quando ragionai delle Quatrro spe
cie della Diapente. Ne di ciò habbiamo da marauigliarsi; percioche ciascuno in quan-
to è Huomo dalla propria opinione può esser'ingannato; ma ricordiamoci quel, che scri-
ue Horatio nella Epistola dell'Arte Poetica, quando dice;
Verùm opere in longo fas est obrepere somnum.
Percioche potrà essere ottima iscusatione à questo grauissimo autore, & etiandio à cia-
scun'altro, che scriue molto di lungo.
In qual maniera s'intenda la Diapason esser'Harmonicamente, ouer'Arithme-
ticamente mediata.Cap. IX.
te specie della Diapason fatta hor'Harmonicamente, & hor'Arithmeticamente;
però uoglio che uediamo in qual maniera s'intenda la Diapason esser mediata, ò
diuisa all'uno & l'altro modo. Si debbe adunque auertire, che la Diapason, laquale è la
Prima consonanza (com'altroue hò mostrato1. Partis
cap. 13.
2. Partis
cap. 39.
Et 3. part.
cap. 3
) si diuide primieramente per una chorda
mezana nelle sue parti principali, che sono la Diapente, & la Diatessaron; le quali parti
(perche spesse uolte si uniscono insieme, ponendosi hor la maggiore, & hor la minore nel
graue) ne danno due congiuntioni, ouer'unioni; delle quali l'una non essendo in tutto
sonora, l'altra uiene ad esser molto buona & soaue. Et tal soauità nasce, quando la Dia-
pente si pone sotto la Diatessaron; percioche essendo congiunte & unite in cotal manie-
ra, gli estremi della Diapason viene ad esser tramezati da una chorda mezana, la quale è
l'estrema acuta della Diapente, & l'estrema graue della Diatessaron; onde tal diuisione,
anzi congiuntione, si chiama Harmonica; percioche i termini delle proportioni, che dan-
no la forma alla Diapente & alla Diatessaron, che sono 6. 4. 3. sono posti in Proportiona-
lità harmonica; essendo che 'l mezano diuide i due estremi nel modo, ch'ella ricerca; se-
condo ch'io hò mostrato nel Cap. 39. della Prima parte. L'altra, la quale è men buona;
perche ueramente non è cosi sonora, per non esser'in essa collocate le Consonanze à i
proprij luoghi; si dice Arithmetica; & si fà quando le sudette parti s'uniscono per una
Chorda mezana al contrario; cioè, quando la Diatessaron tiene la parte graue, & la Dia-
pente la parte acuta. Et perche i termini continenti le proportioni, che danno la forma
alla Diatessaron & alla Diapente, i quali sono 4. 3. 2. si ritrouano esser posti in Diuisione
arithmetica; essendo che 'l mezano, ch'è 3. diuide gli estremi 4 & 2. nel modo che ricer-
ca tal diuisione; come nel Cap. 36. della Prima parte si è mostrato; però meritamente è
detta Arithmetica. Et la prima unione è tanto miglior della seconda, quanto che l'or-
dine delle Consonanze, che sono collocate in essa, si ritroua hauer tutte le sue Chorde
nel loro proprio luogo naturale, secondo la natura delle forme delle Consonanze conte-
nute in esso; Percioche nel secondo ordine le Consonanze sono poste in tal maniera, che
più presto si può nominare ordine accidentale, che naturale. Però adunque tutte le uol-
te, che ritrouaremo alcuna Diapason diuisa nel primo modo; si potrà dire, che ella sia
tramezata Harmonicamente; & quando si ritrouerà tramezata al secondo, si potrà dire
(per le ragioni dette) ch'ella sia diuisa arithmeticamente; il che si potrà anco dir del-
la Diapente, quando sarà diuisa in un Ditono & in uno Semiditono; come nel Cap. 31.
della Terza parte si è dimostrato; ma poniamo gli essempi.
page 398

Che i Modi moderni sono necessariamente Dodici; & in qual maniera
si dimostri.Cap. X.
Modi moderni; come uogliono i Prattici; potremo hora dimostrar, che cotali
Modi necessariamente ascendono al Numero de Dodici; ne possono esser me-
no, siano poi posti quanti si voglino i Modi antichi; percioche nulla, ò po-
co fanno più al nostro proposito; massimamente, perche hora li usiamo (come s'è det-
to) in un'altra maniera molto differente dall'antica. Et per mostrare cotal cosa piglia-
remo per fondamento quel, che supponemmo di sopra; cioè, l'Vnione delle Quattro spe-
cie della Diapente con le Tre specie della Diatessaron mostrate nel Cap. 13. & nel 14. del-
la Terza parte. La onde quante saranno le maniere, che potremo unire commodamen-
te queste parti insieme; ponendo hora di sopra, hora di sotto la Diatessaron alla Diapen-
te; tanto sarà anco 'l numero de i Modi. Incominciando adunque per ordine; Se noi pi-
gliaremo la Prima specie della Diapente collocata tra C & G. & la uniremo nell'acuto
con la Prima specie della Diatessaron, contenuta tra G & c. non è dubbio, che da tale
unione, ò congiuntione haueremo quel, che hora chiamiamo Primo modo, contenuto
tra la Prima specie della Diapason posta tra C & c. Similmente se noi pigliaremo l'istessa
Prima specie della Diapente, & le aggiungeremo dalla parte graue la Prima specie della
Diatessaron, posta tra C & Γ. senz'alcun dubbio ne risulterà la Quinta specie della Dia-
pason, collocata tra G & Γ. laquale contenerà quello, che noi chiamiamo Secondo mo-
do. Hora se noi pigliaremo la Seconda specie della Diapente, contenuta tra D & a. &
le aggiūgeremo nell'acuto la Secōda della Diatessaron, posta tra a & d. haueremo quello
che nominiamo Terzo modo, contenuto tra la Seconda specie della Diapason D & d. Et
se alla detta Diapente aggiungeremo nel graue la nominata Diatessaron, collocata tra le
chorde D & A. haueremo la Sesta specie della Diapason a & A. laqual ne darà un Modo
diuerso da i tre primi, che sarà quello, che noi dimandiamo Quarto. Pigliaremo hora la
Terza specie della Diapente, collocata tra E &
 . & le aggiungeremo nell'acuto la Terza
. & le aggiungeremo nell'acuto la Terza della Diatessaron, posta tra
 & e. & haueremo tra la Terza specie della Diapason E & e.
& e. & haueremo tra la Terza specie della Diapason E & e. quel che noi dimandiamo Quinto modo. Se pigliaremo hora l'istessa Diapente, & le ag-
giungeremo nel graue la Diatessaron E &
 . haueremo la Settima specie della Diapason
. haueremo la Settima specie della Diapason  &
&  . & insieme quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei
. & insieme quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei unioni, ò congiuntioni; cioè, quelle della Prima specie della Diapente con la Prima della
Diatessaron, tanto nel graue, quanto nell'acuto; & quelle della Seconda di ciascuna si-
milmente nel graue, & nell'acuto; cosi quelle della Terza specie fatte hora nel graue, hora
nell'acuto; & per tal uia haueremo Sei modi. Resta hora d'accompagnar la Quarta spe
cie della Diapente con la Prima della Diatessaron, che si può accompagnar commoda-
mente. Onde è d'auertire, che tutte le specie della Diatessaron si possono di nuouo ac-
commodare & accompagnar con la Diapente in tre maniere; percioche la Prima specie si
può accompagnar con la Quarta specie della Diapente, la Seconda con la Prima, & la
page 399Terza con la Seconda specie di essa Diapente; ne tali specie si possono congiungere insie-
me commodamente in altra maniera; come è manifesto. Pigliando adunque la Quarta
specie della Diapente posta tra F & c. le accompagnaremo la prima della Diatessaron c &
f. & tra le chorde F & f. estreme dalla Quarta specie della Diapason con le sue mezane,
haueremo il Modo, che chiamiamo Settimo. Il perche se di nuouo pigliaremo la Dia-
tessaron, posta tra F & C. & l'accompagnaremo nel graue con la nominata Diapente, ha-
ueremo tra la Diapason c & C. Prima specie, il modo chiamato Ottauo. Aggiungeremo
hora la Seconda specie della Diatessaron posta tra d & g. alla Prima della Diapente, col-
locata tra G & d. dalla parte acuta; ilche fatto tra la Quinta specie della Diapason G &
g. haueremo un'altro Modo; il quale per esser da gli otto Modi mostrati differente, lo no-
minaremo Nono modo. Dalla parte graue poi di tal Diapente congiungeremo l'istessa
Diatessaron g & D. & haueremo tra la Seconda specie della Diapason d & D. quel, che
drittamente chiamiamo Decimo modo. Vltimamente se noi accompagneremo la Ter-
za specie della Diatessaron postatra e & aa. dalla parte acuta, con la Seconda della Dia-
pente posta tra a & e. nella Sesta specie della Diapason a & aa. haueremo il Modo, che si
chiama Vndecimo; imperoche s'accompagnaremo le dette specie per il contrario, ponen
do la Diatessaron nella parte graue tra le chorde a & E. haueremo l'Vltimo Modo, detto
Duodecimo; contenuto nella Terza specie della Diapason e & E; come quì in essempio
si vede.
 Et per tal maniera non haueremo più, ne anco meno de Dodici Modi, imperoche cotali
Et per tal maniera non haueremo più, ne anco meno de Dodici Modi, imperoche cotali Specie non si possono accompagnar'in altro modo l'una con l'altra, se non con grande in-
commodo; come è manifesto à ciascheduno perito nella Musica.
Altro modo da dimostrar'il Numero de i Dodici Modi.Cap. XI.
tro mezo, il quale è la Diuisione della Diapason, hora secondo l'Harmonica, &
hora secondo l'Arithmetica diuisione. Et per osseruar'un buon ordine inco-
minciaremo dalla Prima specie, & dopoi seguitaremo all'altre, diuidendole
prima nell'Harmonica, & dopoi nell'Arithmetica. Se adunque noi pi gliaremo la Prima
specie della Diapason contenuta tra C & c. & la diuideremo harmonicamēte in due parti
con la chorda g. non è dubbio, che nel graue haueremo tra C & g la Prima specie della
page 400Diapente; & tra g & c. la Prima della Diatessaron; le quali, come di sopra s'è ueduto,
costituiscono (aggiunte insieme) il Primo modo. Per il che pigliando dopoi la Seconda
specie tra D & d. & diuidendola in tal maniera con la chorda a. haueremo la Diapente
D a. Seconda specie, & la Seconda della Diatessaron a & d. le quali aggiunte insieme al
mostrato modo, ne danno il Terzo. Ma pigliando la Terza specie E & e. & diuidendola
in tal maniera con la chorda
 . haueremo il Quinto, ilquale medesimamente nasce dal-
. haueremo il Quinto, ilquale medesimamente nasce dal-la congiuntione della Terza specie della Diapente, & della Terza della Diatessaron, che
sono E &
 . &
. &  & e. come s'è detto. Presa dopoi la Quarta specie della Diapason, con-
& e. come s'è detto. Presa dopoi la Quarta specie della Diapason, con-tenuta tra F & f. & diuisa harmonicamente con la chorda c. haueremo la Quarta specie
della Diapente F & c. aggiunta alla Prima specie della Diatessaron c & f. & il Settimo mo-
do. Dopoi pigliata la Quinta specie della Diapason collocata tra G & g. diuisa harmoni-
camente dalla Chorda d. haueremo la Prima specie della Diapente G & d. & la Seconda
della Diatessaron d & g. ch'insieme aggiunte ne danno il Nono. Pigliaremo hora la Se-
sta a & aa. & la diuideremo al sopradetto modo con la chorda e. & da tal diuisione na-
scerà la Seconda specie della Diapente a & e. & la Terza della Diatessaron e & aa. &
l'Vndecimo modo; come qui si vede. Et perche; per la Decima proposta del Quinto

zana, ch'harmonicamente in due parti diuider la possa, però dalle diuisioni delle Sei
prime specie fatte di sopra al modo mostrato, haueremo solamente Sei modi; ma dalla
diuisione arithmetica de Sei specie sole ne haueremo altri sei; Imperoche s'incomincia-
remo dalla Quinta specie della Diapason posta tra Γ & G. ouer da quella, che è posta tra
G & g. che non fà uarietà alcuna se non di graue, & di acuto; percioche; per l'Vltima del
Quinto delle dette Dimostrationi; ogni Modo si può trasportare più acuto, ò più graue
per una Diapason; & la diuideremo arithmeticamente con la chorda C. pigliando però
la Γ & G. haueremo la Prima specie della Diatessaron C & Γ. posta nel graue, & la Prima
specie della Diapente G & C. posta nell'acuto, lequali unite insieme nella maniera, come
habbiamo ueduto, ne danno quel Modo, che noi dimandiamo Secondo. Pigliaremo
poi la Sesta specie della Diapason posta tra A & a. & la diuideremo al mostrato modo con
la chorda D. & haueremo tra D & A. la Seconda specie della Diatessaron, & tra A & D. la
Seconda della Diapente, lequali vnite insieme ne daranno medesimamente il Quarto mo
do. Ma la Settima specie della Diapason
 &
&  . diuisa per la chorda E. ne darà il Sesto;
. diuisa per la chorda E. ne darà il Sesto; percioche la Terza specie della Diatessaron E &
 . posta nel graue, s'vnisce con la Ter-
. posta nel graue, s'vnisce con la Ter-za della Diapente
 & E. posta in acuto. Ma se pigliaremo la Diapason C & c. Prima spe-
& E. posta in acuto. Ma se pigliaremo la Diapason C & c. Prima spe-cie, diuisa dalla chorda F. arithmeticamente, haueremo l'Ottauo modo; percioche F &
C Prima specie della Diatessaron, si congiunge con la Quarta della Diapente c & F nel
graue. Hora prenderemo la Seconda specie della Diapason D & d. & la diuideremo al
page 401modo mostrato con la Chorda G, & haueremo la Seconda della Diatessaron G, & D,
& la prima della Diapente d & G, che costituiscono il Decimo modo. Pigliando ultima-
mente la Diapason E & e, Terza specie (lasciando la F & f Quarta specie; percioche,
per la Duodecima proposta del Quinto delle Dimostrationi non si può diuidere in tal ma
niera) se noi la diuideremo con la Chorda a, haueremo il Duodecimo modo, percioche
per tal diuisione nascerà la Terza specie della Diatessaron a & E. nella parte graue, uni-
ta alla Seconda della Diapente e & a; come qui sotto si può uedere.

Sei dall'arithmetica, come hò mostrato. Et benche la Settima specie della Diapason
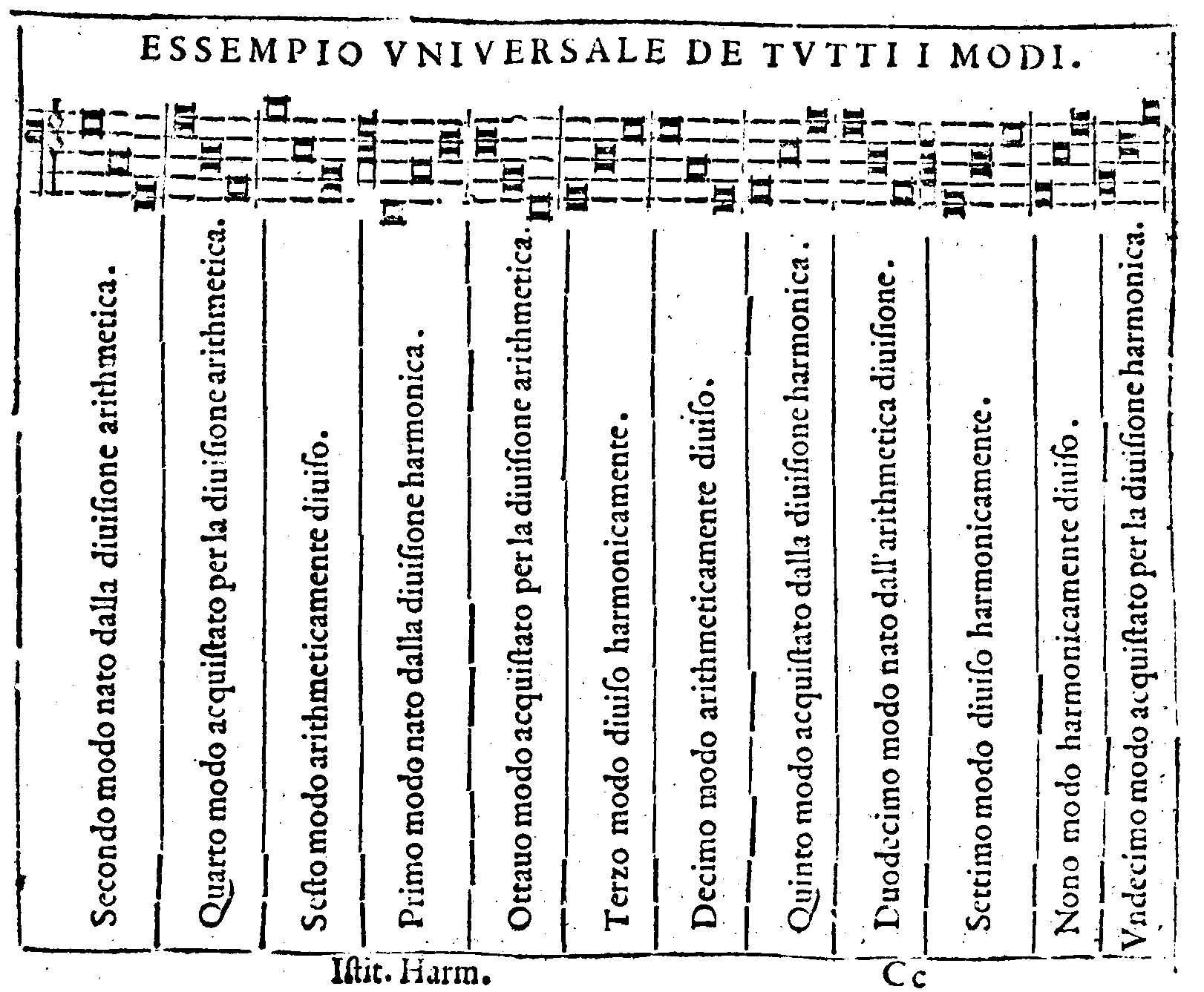
 &
&  non si possa diuidere harmonicamente; com'hò detto; percioche dalla parte gra-
non si possa diuidere harmonicamente; com'hò detto; percioche dalla parte gra-ue uerrebbe la Semidiapente
 & F, & il Tritono F &
& F, & il Tritono F &  nella parte acuta, quando fusse
nella parte acuta, quando fusse tramezata dalla chorda F; ne meno la Quarta specie F & f arithmeticamente, essendo
che si udirebbe nel graue tra la Chorda
 & F il Tritono, quando fusse diuisa dalla
& F il Tritono, quando fusse diuisa dalla  , &
, & dalla parte acuta la Semidiapente f &
 ; tuttauia sono stati alcuni, che oltra i Dodici mo
; tuttauia sono stati alcuni, che oltra i Dodici mostrati, le hanno attribuito altri Modi; come alla prima diuisione il Terzodecimo, & alla
seconda il Quartodecimo; ma ueramente non possono esser più de Dodeci, i quali sono no
tati per ordine nell'essempio di sopra, come habbiamo anco dimostrato nella Quartade
cima proposta del Quinto & ultimo ragionamento delle Dimostrationi. Et nel Cap. 3.
del Lib. 6. de i nostri Sopplimenti.
Diuisione de i Modi in Autentichi & Plagali.Cap. XII.
derni alcuni sono chiamati Principali, ouer'Autentichi, & di numero Impa-
ri; & alcuni sono dimandati Laterali, & Plagali, ouer Placali, & di numero
Pari. I primi sono il Primo, il Terzo, il Quinto, il Settimo, il Nono, & l'Vn-
decimo; ma i Secondi sono il Secondo, il Quarto, il Sesto, l'Ottauo, il Decimo, & il
Duodecimo. I Primi furono chiamati Principali; perche l'honore & la preeminenza si
dà sempre a quelle cose, che sono più nobili; onde considerando il Musico principal-
mente le Consonanze tramezate harmonicamente, che sono più nobilmente diuise, di
quello, che non sono l'altre; & dopoi quelle, che si ritrouano diuise in altro modo; merita-
mente gli attribuirono questo nome; essendo che in essi si troua l'Harmonica medietà tra
le due parti maggiori della Diapason, che sono la Diapente, & la Diatessaron; l'una posta
nel graue, & l'altra nell'acuto; il che ne gli altri non si rirtoua. Ma alcuni uogliono, che sia
no detti Autentichi; perche hanno più autorità de gli altri, ouer perche sono augumenta-
tiui; atteso che secondo una certa loro regola, possono ascendere più sopra il loro fine, di
quel che non fanno i Secondi. Sono anche detti di numero Impari; percioche posti con
i Secondi in ordine naturale in cotal maniera. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. tengono il
luogo de i numeri Impari. I Secondi sono chiamati Laterali, da i lati della Diapason,
che sono (com'altroue hò detto) la Diapente & la Diatessaron; percioche pigliate le par
ti, che nascono dalla diuisione de gli Autentichi, ò Principali, che sono le due nomina
te; da quell'istesse poste al contrario (rimanendo la Diapente commune & stabile) na-
scono cotali Modi. Il che si può uedere nel Primo & nel Secondo de i mostrati; che rima
nendo la Diapente C & G stabile, dall'aggiuntione della Diatessaron G & c, posta in acu
to nasce 'l Primo modo autentico, & aggiungendola nel graue tra C & Γ, nasce il Secon
do, ch'è il suo collaterale. Il medesimo anche accasca ne gli altri; come si può ueder ma
nifestamente ne gli essempi. Però alcuni meritamente li chiamarono Plagii, ò Plagali;
essendo che tali nomi deriuano dal Greco, Πλάγιον, che uuol dire Lato; ouer da Πλάγιος;
che significa Obliquo, ò Ritorto; quasi obliqui, ritorti, ò riuoltati; essendo che proce-
dono al contrario de i loro Autentichi; procedendo questi dal graue all'acuto, e i Plaga-
li dall'acuto al graue; Ben è uero, che alcuni li dimandarono Placali, quasi che uolessero
dire Placabili; imperoche hanno il lor cantare & la loro harmonia più rimessa, di quello,
che non hanno i lor Principali; ouer perche hanno (come dicono) natura contraria à
quella de i loro Antentichi; percioche se l'Harmonia che nasce dall'Autentico dispone
l'animo ad una passione, quella del Placale la ritira in diuersa parte. Sono poi detti Pa-
ri di numero, perche nel sudetto ordine naturale de numeri tengono il luogo de i
Pari. Ma perche ogni cosa sia naturale, ouero arteficiale, la quale habbia hauuto
principio, è necessario anco, chabbia fine; riducendosi in esso il giudicio, come à
cosa perfetta; però uoglio mostrare in qual maniera ciascun di loro si habbia da termi-
page 403nare regolatamente; mostrando insieme i termini de i Principali, & de i Collaterali;
& quanto possino ascendere & discendere di sopra & di sotto la Chorda ultima del loro
fine; accioche possiamo comporre le Cantilene con giudicio & con buon'ordine; oue-
ramente che vedendole composte, possiamo giudicare, & sapere in che Modo, & sotto
qual modulatione si ritrouino.
Delle chorde finali di ciascun Modo; & quanto si possa ascendere, ò discendere
di sopra & di sotto le nominate chorde.Cap. XIII.
rata la sua compositione; cioè, l'Vnione della Diatessaron con la Diapente;
ouer considerata la sua origine dalla Diuisione delle maniere mostrate di so-
pra; imperoche i Musici moderni pigliano per tal Chorda la più graue di cia-
scuna Diapente; come nella definitione Decimasettima del quinto delle Dimostrationi
hò dichiarato; sia poi la Diatessaron posta nell'acuto, ouer nel graue, che non fà co-
sa alcuna di uario. Et perche la Chorda grauissima di ciascuna Diapente è commune à
due Modi, per esser anco esse Diapenti à due Modi communi; però usano d'accom-
pagnarli à due à due; percioche essendo la Chorda grauissima della Prima specie della
Diapente posta nel primo & nel secondo Modo in C. & commune à questi due Modi;
uiene ad esser la finale non solamente del Primo; ma etiandio del Secondo. La onde
per tal legamento & parentella (dirò cosi) che si troua tra loro, sono in tal maniera
vniti, che quando bene alcuno li uolesse separar l'un dall'altro non potrebbe; come
vederemo, quando si ragionerà di quello, che si hà da fare nellaccommodar le Parti
nelle cantilene. Meritamente adunque accompagnano il Primo col Secondo modo, il
Terzo col Quarto, & cosi gli altri per ordine; poi che la chorda più graue della prima
specie della Diapente C & G. è commune finale de quelli & è la C. & di questi la D.
laquale è la grauissima della Seconda specie della Diapente, commune all'uno, & l'al-
tro di questi due. Pongono poi commune la E. grauissima della Terza specie della
Diapente al Quinto & al Sesto modo, & li vniscono insieme; percioche tal Diapen-
te è commune all'vno & all'altro: come si può uedere. Accompagnati questi, ac-
compagnano il Settimo con l'Ottauo; perche hanno la Quarta specie della Diapen-
te tra loro commune; onde la grauissima chorda F. uiene ad esser la finale di questi
due Modi. Ma pongono la chorda G. commune finale del Nono & del Decimo;
percioche è la grauissima della Prima specie della Diapente, & uniscono questi due
Modi insieme; essendo che tal Diapente si troua esser commune all'uno & l'altro.
uiene ad esser la più graue della Seconda specie della Diapente, & accompagnano
questi due insieme, per rispetto di tal Diapente, ch'è all'vno & l'altro commune.
pagnare il Modo Autentico col suo Plagale; massimamente conoscendo, che la chor-
da finale del Primo & del Secondo modo è la C. quella del Terzo & del Quarto la D.
quella del Quinto & del Sesto la E. quella del Sesto & del Settimo la F. quella del Nono
& del Decimo la G. & quella dell'Vndecimo & del Duodecimo la a. come piu oltra si ue
de. Et non solamente hanno le chorde finali communi, ma hanno etiandio i luoghi del-
le Cadenze come uederemo. Si dee però notare, che i Modi, quando sono Perfet-
ti, toccano le Otto chorde della loro Diapason; è ben uero, che si troua questa diffe-
renza tra gli Autentichi & li Plagali: che questi ascendono solamente alla Quinta chor-
da sopra il loro fine, & discendono alla Quarta; ma quelli toccano l'Ottaua acuta sola-
mente & alle uolte discendono sotto la lor Diapason per un Tuono, ò per un Semi-
page 404tuono; & li Plagali simigliantemente ascendono sopra la loro Diapente per un Tuono,
ouer per un Semituono; come si uede in molti canti Ecclesiastici. Di maniera che l'Auten-
tico si troua tra Otto chorde tramezate Harmonicamēte, & lo Plagale tra Otto arithme-
ticamente diuise; nel modo che si può uedere di sopra, & ne i seguēti essempi. Estendēdosi
 adunque i Modi di sopra & di sotto il loro fine à cotal modo, si possono chiamare Per-
adunque i Modi di sopra & di sotto il loro fine à cotal modo, si possono chiamare Per-fetti. Perilche l'Introito, che si canta nella Messa della quarta Dominica dell'Aduen-
to; Rorate coeli desuper; si chiamerà Terzo modo secondo 'l nostro ordine naturale, &
quello, che si canta nella Messa dell'Ottaua della Natiuità del Signore; Vultum tuum
deprecabuntur; si potrà dimandar Quarto modo l'uno & l'altro perfetto. Ma quando i
Plagali nel graue passassero più oltra, ouer gli Autentichi nell'acuto; cotali Modi si
potranno nominare (come li nomina Franchino GaffuroPract. lib.
1. Cap. 8.) Superflui; com'anco si chia-
marebbono Imperfetti, ò Diminuti, quando non arriuassero alla loro Ottaua chorda
acuta, ouer'alla Prima graue delle loro Diapason. De i primi habbiamo un'essempio
nell'Introito; Iustus es Domine del Terzo modo, che si canta nella Messa della Domi-
nica Decimasettima dopo la solennità delle Pentecoste; Ma de i secondi sono quasi in-
finiti gli essempi, tra i quali si ritroua l'Introito; Puer natus est nobis del Nono modo;
che si canta alla Terza Messa il Sacrosanto giorno della Natiuità del Figliuolo di Dio.
Si debbe hora auertire per sempre, che quel c'hò ragionato intorno à i Modi del
Canto fermo, intendo anco, che sia detto intorno le parti de i Modi del Canto figu-
rato; se ben io non pongo di loro gli essempi; percioche uoglio, che cotal ragionamen-
to sia commune all'vno & l'altro. Ma perche hò detto di sopra, ch'Ogni cosa si debbe
denominare dal fine, come da cosa più nobile; però da ogni Chorda finale haueremo da
giudicar ciascun Modo, di maniera che quello, che terminerà nella Chorda C. & sa-
lirà alla Chorda c. dimandaremo Primo modo perfetto; & quando non arriuarà (come
hò detto) lo nominaremo Imperfetto; & quel che finirà nell'istessa C. & ascenderà
alla Chorda G. discendendo anco alla Γ. chiamaremo medesimamente Secondo mo-
do perfetto; & simigliantemente Imperfetto, quando non ui arriuasse. Cosi anco l'uno
& l'altro si addimandarebbe Superfluo, ò Abondante, quando 'l Primo passasse la Otta-
ua Chorda sopra il suo fine, & il Secondo la Quarta sotto di esso. Et ciò dico, quando fi-
nissero nelle lor Chorde proprie finali, & tenessero la lor forma propria; percioche se fi-
nissero nelle lor Chorde, che si chiamano Confinali, ouer'in altre Chorde, & tal forma
non si comprendesse esser in loro; allora haueremo da far'altro giudicio; come altroue
son per dimostrare.
De i Modi Communi, & de i Misti.Cap. XIIII.
pari & li Pari anco trappassassero le loro Diapason, questi nell'acuto & quel-
li nel graue; & arriuassero alla quarta chorda; tali Modi si chiamarebbono
Communi; essendo che sarebbono composti del Principale & del suo Collatera-
page 405le, & tutta la compositione di cotal Modo si ritrouarebbe tra Vndici chorde communi
all'Autentico & al Plagale, i quali hanno vn'istessa Diapente & un'istessa Diatessaron
commune; come ne gli essempi si può uedere. Et di questi Modi communi si trouano
molte cantilene appresso gli Ecclesiastici; come quella Prosa, ò Sequenza (ch'in tal
maniera dimandano) che si canta dopo la Epistola il Sacratissimo giorno della Resur-
rettione di GIESV CHRISTO Figliuoio di DIO; Victimae paschali laudes immolent
Christiani; l'Antifona Salue regina misericordiae; & li due Responsorij; che si cantano al
matutino, Duo Seraphin; & Sint lumbi uestri praecincti; lequali tutte sono denominate dal
Modo principale; cioè, dal Terzo; percioche (com'è il douere) Ogni cosa debbe es-
ser denominata dalla cosa più perfetta, più degna, & più nobile. E' ben uero, che que-
sti Modi communi si possono chiamare alle uolte Imperfetti; massimamente quando non
abbracciano le dette Vndici chorde; ma quando in alcuno de i mostrati Modi, fusse
Autentico, ò Plagale; Perfetto, ò Imperfetto; Superfluo, ò Diminuto; & ne i Com-
muni anco accadesse, che fusse composto sott'un Modo terminato; come sarebbe dire
del Terzo, ò del Quarto, ò d'altro simile; & in esso si udisse replicar molte volte una
Diapente, ò una Diatessaron, che seruisse ad un'altro Modo; come al Quinto, al Sesto,
ouer'ad un'altro, tal Modo si potrà chiamar Misto; percioche le Diapenti, ò Diatessa-
ron d'un Modo, si uengono à mescolare con la cantilena d'un'altro; come si può ueder
nell'Introito; Spiritus Domini repleuit orbem terrarum; che si canta nella Messa della so-
lennità delle Pentecoste, ilquale è stato composto del Decimo modo, & hà nel suo prin-
cipio la Seconda specie della Diapente, che serue al Terzo; & replica molte uolte nel me-
zo la Quarta specie, che serue solamente al Settimo & anco all'Ottauo; come in esso si
può vedere.
Altra diuisione de i Modi; & di quello, che si hà da osseruare in ciascuno, nel com-
porre le cantilene; & in qual maniera le Otto sorti di Salmodie
con essi s'accompagnino.Cap. XV.
ne sono alcuni, sotto i quali si cantano i Salmi di Dauid & li Cantici euange-
lici; che si chiamano Salmodie; come le nomina anco Dante Alighieri nel prin-
cipio del 33. Canto del Purgatorio; quando dice;
Deus venerunt gentes, alternando
Hor tre hor quattro dolce Salmodia
Le Donne incominciaro lagrimando.
Et alcuni sotto i quali si cantano le Antifone, Responsorij, Introiti, Graduali, & simi-
li altre cose. Questi si possono chiamare Modi varij; essendo che non gli è di loro un so-
lo canto, ouer'una sola & determinata forma di cantare per tutti i Modi, nella qua-
le si habbiano da cantar tutte le Antifone, Responsorij, & altre cose simili nel Pri-
mo modo (dirò per essempio) sotto un Tenore, ò aria, nella maniera che cantano i
Salmi & li Cantici; & sotto un'altro tutte quelle del Secondo; & cosi tutte quelle de gli
altri Modi, ma si bene è uariato; come si può vedere in molte cantilene; percioche can-
tano sotto un Tenore, ouer modulatione l'Introito Gaudete in Domino; che si canta la
Dominica terza dell'Aduento del Signore; & sotto un'altro Suscepimus Deus misericor-
diam tuam, che si canta la Domenica ottaua dopo la solennità delle Pentecoste, l'uno
& l'altro de i quali è composto nel Terzo modo. Ma non auiene cosi de i primi, iquali
page 406potiamo chiamar Stabili; percioche sempre si cantano tutti i Salmi con i suoi Versi
di qual si voglia Salmodia sotto un Tenore, ò modulatione determinata, senz'alcuna mu-
tatione, & non è lecito uariar cotal Tenore; essendo che ne seguirebbe confusione. Et
benche si trouino molte Forme uariate de tali Salmodie, ò Modi di cantare, che le uoglia-
mo dire; come sono alcune, che chiamano Patriarchine, & alcune Monastiche; tutta-
uia in ciascuna Chiesa non se ne vsa communemente più che Otto, lequali dimandano
Regolari; & li Cantori le riducono sotto l'Antifone contenute ne gli Otto Modi mezani
de i Dodici mostrati, lasciandone i Quattro estremi; cioè, il Primo, il Secondo, & l'Vnde-
cimo, col Duodecimo in questa maniera; percioche la Prima sempre cantano dopo tut-
te quelle Antifone, che sono contenute nel Terzo modo; la Seconda dopo quelle, che so-
no comprese nel Quarto; & la Terza intonano dopo ciascheduna, che sia del Quinto mo-
do; & il medesimo fanno dell'altre, per ordine; di maniera che l'Ottaua delle Salmodie
uiene à finire quelle Antifone, che sono composte nel Decimo modo. Il perche hanno
questa Regola, per sapere applicar bene cotali Salmodie alle dette Antifone; che ri-
guardando il loro Fine, & il Principio del SEVOVAE, il qual segue subito dopò loro;
che contiene le Lettere vocali de queste parole Seculorum Amen; hanno cognitione del
tutto. Percioche à quella cantilena, che finisce in D. & il Principio del suo SEVOVAE
sia in a. applicano la prima Salmodia; & quando tal fine medesimamente è posto in
D. & il nominato Principio sia in F. gli applicano la Seconda. La onde applicando
la Terza à quella che è terminata in E. & il detto Principio sia posto in c. & la Quarta,
à quella il cui fine si troua etiandio essere in E. & il Principio sia in a. le uanno applican-
do all'altre Antifone per ordine. Ma perche ne i sequenti Versi; acciò più ageuol-
mente ogn'uno ricordar si possa quello, che detto habbiamo; sono contenute cotali Re-
gole; essendo che mostrano qual Fine, & qual Principio de i nominati ricerca l'un de i
Tenori, ò Forme delle otto Salmodie commemorate; però contentandomi di por
solamente cotali Versi; i quali saranno i seguenti; non ne farò d'essi più altro ragio-
namento.
Psalmodiam Primum Re La, Re Faꝗ Secundam,
Per Sextam Mi Fa ternam praebent, & Mi La Quartam.
Fa Fa dant Quintam, Fa La ostendunt tibi Sextam,
Vt Sol Septenam, Vt Fa demonstrantꝗ Octauam.
Ma i Principij delle Forme, ouero Intonationi delle dette Salmodie, acciò più facil-
mente ricordar si possino, saranno etiandio ridotti in questi altri quattro Versi se-
quenti.
Psalmodiam retinent Primam, Sextamꝗ Fa Sol La,
Vt Re Fa Octauam, sic Ternam, sicꝗ Secundam:
La Sol La Quartam, Fa Re Fa dant tibi Quintam,
Septenam vero Fa Mi Fa Sol tibi monstrant.
La onde da cotali mezi aiutati, facilmente possono conoscere, qual Salmodia hanno da
intonare, & sotto qual Tenore, ò Forma l'habbiano da cantare. Otto adunque sono le
Salmodie, ouero Intonationi, che usano communemente gli Ecclesiastici (com'è ma-
nifesto) ne i loro Diuini officij; & se alle fiate accascherà di cantarne alcuna sotto un'al-
tro Tenore, che sia oltra le Otto forme nominate, le quali chiamano Principali; come è
quella posta nel Cap 28. più a basso, che serue all'Vndecimo modo, & al Salmo In exitu
Israel de Aegypto; come uederemo al suo luogo; cotali Salmodie dicono Irregolari;
ancora che impropriamente; ma in questo proposito fà dibisogno uedere & leggere i
Cap. 2. 3. 11. 12. & 13. del 24. Lib. De Re Musica; acciò si habbia maggior lume di questa
cosa; & si leui ogni confusione, che potrebbe accadere. Tali Intonationi sono anco uaria-
te per ogni Modo, quantunque non sia uariato il Tenore della Prima maniera, col quale
cantano hora un Salmo, da quello che cantano dopoi l'istesso Primo modo un'altro. Et
benche queste uarietà nel cantar diuersi Salmi sotto un'istesso Tenore non si odono; tut-
page 407tauia si troua un'altra differenza; percioche gli Ecclesiastici hanno due sorti di Salmo-
die; Festiue, & Feriali; & ciò auiene, perche altra maniera & più breue tengono nel
cantare i Salmi feriali, di quel che fanno i festiui; ancora che si troua poca differenza tra
l'una & l'altra. Ne si troua differenza alcuna tra le Salmodie tanto festiue, quanto fe-
riali, con i quali cantano i Cantici euangelici, da quelle, che cantano i Salmi; se non,
che nelle festiue del Cantico euangelico Magnificat anima mea Dominum; sogliono uaria-
re alquanto i principij solamente di quelle, che seruono al Quarto, al Nono, & al De-
cimo Modo; come si può veder nel Primo libro della Prattica di Fanchino Gaffuro dal
Cap. 8. insino al fine di tal Libro; & nel Recanetto di Musica nel Cap. 59. & nel 60. del
Primo libro; oue si può etiandio vedere, in quante maniere vsino gli Ecclesiastici di fi-
nir cotali loro Salmodie. Et benche ne i Tenori, con i quali cantano i Versi de i Salmi
ne gli Introiti delle Messe & il loro Gloria patri; si trouino alcune forme alquanto varia-
te da quelle che si cantano ne i Salmi del Vespero & dell'altre Hore canoniche; come si
può vedere nel Cap. 62. del nominato Recanetto; tuttauia anche loro si cantano sempre
sotto un Tenore terminato senz'alcuna varietà; il che etiandio si osserua ne i Versetti de
i Responsorij; che si cantano nel Matutino; imperoche vanno cantati sott'una Modula-
tione non uariata, se non in alcuni luoghi, che si allungano, ò si accorciano per cagione
della breuità, ò lunghezza delle Parole, che in essi si canto. Ma il loro Gloria patri, cauati
de i predetti Versetti; sempre si canta secondo un Tenore prescritto; come nel Cap. 64.
del nominato Recanetto si può vedere. Tutto questo hò uoluto dire, accioche se accade-
rà al Compositore di comporre alcuna cantilena, uolendo seguitar l'ordine de cotali Mo
di habbia da saper quello, che haurà da fare; Percioche quando vorrà comporre sopra le
Parole del Cantico euangelico nominato, che si canta nel Vespero, fà dibisogno, che se-
guiti la Salmodia & l'Intonatione, che si canta ne i Canti fermi cantandosi il detto Can-
tico; il che leggiadramente (per dare un'essempio) è stato osseruato oltra molti altri da
Morale Spagnolo. Quel medesimo debbe anco osseruare, quando componerà sopra le
Parole d'alcun Salmo, che si canta nel Vespero, ouero in altre hore canoniche; sia poi tal
Salmo composto in maniera, che i suoi Versi si possino cantare con un'altro choro scam-
bieuolmente; come hà composto Giachetto & molti altri; ò pur siano tutti intieri, come
compose Lupo i Salmi In conuertendo Dominus captiuitatem Sion, & Beati omnes qui timent
Dominum, à Quattro voci sotto 'l Modo ottauo delle Salmodie; oueramente siano com-
posti à due chori; come i Salmi d'Adriano Laudate pueri Dominum, Lauda Ierusalem Domi-
num, & molti altri: che si chiamano à choro spezzato. Ma quando haurà da compor'al-
tre cantilene, non debbe seguitare 'l canto, ò Tenore de tali Salmodie; percioche non è
obligato à questo; anzi quando ciò facesse, se li potrebbe attribuire à vitio, & che non
hauesse inuentione. Ne dè per cosa alcuna far quello, che fanno alcuni Compositori,
i quali componendo (per modo di essempio) alcuna cantilena sotto 'l Decimo modo,
non sanno partirsi dal fine dell'Ottaua Salmodia; ilche fanno ancho ne gli altri Modi; di
maniera che par, che vogliono, che sempre si canti 'l SEVOVAE posto ne gli Antifonarij
nel fine di ciascuna Antifona. Quando adunque uorrà comporre alcuna cantilena fuo-
ri delle Salmodie, allora sarà libero, & potrà ritrouare quella inuentione, che li tor-
nerà più commoda. Ma ne i Modi sudetti debbe spesso far cantare i proprij membri
della Diapason, che contiene il Modo sopra il quale si comporrà la cantilena; che so-
no la Diapente & la Diatessaron. Dico i proprij, & non quelli d'un'altro Modo, co-
me fanno alcuni; percioche dal principio al fine fanno vdire un procedere d'un Modo,
toccando spesso le sue Diapente, & le Diatessaron in ogni parte; ma quando arriuano à
tal fine, entrano fuori di proposito in un altro; ilche fà tristissimo effetto. Et perche io
veggio, ch'alcuni fanno poca differenza nel procedere che si fà in un Modo Principale,
dal procedere che si usa nel suo Collaterale; essendo che quelli istessi mouimenti & pas-
saggi, che usano in uno, usano anco nell'altro; oue poi non si ode alcuna uariatio-
ne di concento, & poco di uario si troua tra loro; però auertirà etiandio il Composi-
page 408tore, che desidera di fare il tutto con ragione, di usare i mouimenti & passaggi Princi-
pali, che uadino (più che si potrà fare) uerso l'acuto; massimamente quelli della Diapen-
te & quelli della Diatessaron; ripigliando sempre (quando tornarà commodo) nel graue;
& li mouimenti de i Collaterali, per il contrario; cioè, nel graue; massimamente quel-
li, che procedono per le due nominate specie; percioche è il douere, essendo ueramen-
te situate ne i Modi al contrario l'una dell'altra; cioè, la Diapente nel graue, & proce-
dendo più oltra, & la Diatessaron nell'acuto nel Principale; & nel suo Collaterale la Dia-
pente collocata nell'acuto, & la Diatessaron nel graue. Veramente è cosa giusta, hauen-
do il Collaterale (come hò detto) natura contraria à quella del suo Principale; di ma-
niera ch'essendo per natura differenti, debbono esser anche differenti ne i mouimenti;
conciosia che da tali membri uien tal differenza, & anche da i mouimenti ueloci, ò tardi.
Onde s'al Principale uorremo attribuire i mouimenti uerso l'acuto, & al suo Collaterale
uerso 'l graue, il tutto sarà fatto con ragione; prima, perche 'l Modo principale si ritroua
più acuto del suo Collaterale per una Diatessaron; la onde à questo conuiene i mouimen-
ti tardi; i quali (com'altre uolte si è detto2. Partis
cap. 11.) fanno la grauità, & à quello i ueloci, da i quali
è generata l'acutezza; dopoi, perche usando i mouimenti tardi nel Collaterale, & li veloci
nel Principale, uerremo à commodare il tutto al suo propio luogo. Però parmi, che fuo-
ri d'ogni proposito alcuni habbiano usato alle uolte le parti graui delle loro con mouimenti troppo ueloci, & molto diminuite; & le acute con troppo tardi; cioè,
con mouimenti molto rari; ancora che non biasimo, che alle fiate non si possa porre nel-
l'acuto il mouimento tardo, & nel graue il ueloce, quando la materia lo ricerca; ma
in ogni cosa bisogna adoperare 'l giudicio, senza 'l quale poco si può far di buono. Et
questo sia detto à bastanza intorno tali materie; imperoche auanti ch'io passi più oltra,
uoglio che ueggiamo vn'errore, che si troua tra alcuni poco periti delle cose della Mu-
sica; il quale mostrato, seguiremo al particolare ragionamento di ciascuno de i nomi-
nati Dodici modi.
Se col leuare da alcuna cantilena il Tetrachordo Diezeugmenon, ponendo il Synemen-
non in suo luogo, restando gli altri immobili, vn Modo si possa nell'altro.Cap. XVI.
rere, che pigliata qual si uoglia specie della Diapente, ò della Diapason, che
contenesse tra le sue chorde essentiali il Tetrachordo diezeugmenon; se 'l si le-
uasse il detto Tetrachordo, ponendoui in suo luogo il Synemennon, che tal
mutatione non haueria forza di mutare il Modo; perche dicono; che 'l Tetrachordo Sy-
nemennon non è naturale, ma accidentale, & che non hà forza di poter trasmutare in
tal maniera i Modi l'vn nell'altro. Io non starò hora à disputar, se questo Tetrachor-
do sia naturale, ouero accidentale; ma dirò ben, che se quel, che dicono fusse uero, ne
seguirebbe, che 'l Semituono fusse superfluo nella Musica, & che non hauesse alcuna pos-
sanza di uariar le Specie delle Consonanze. Il che quanto sia uero, si può ueder nella
Terza parte in molti luoghi; oue si mostra, che per il Semituono si ritroua la uarietà del
le dette Specie, che si fà per la sua trasportatione da un luogo all'altro. E' ben uero, che 'l
leuare un Tetrachordo da una cantilena, & poruene un'altro, si può fare in due manie-
re; la Prima è quando in una Parte sola della cantilena; cioè, in una particella del Teno-
re, ò d'altra Parte (ma non per tutto) si pone la chorda b. che è la Trite synemennon
incidentalmente vna, ò due fiate, tra la Mese & Paramese; & cosi potiamo dire, che 'l
leuare il Tetrachordo Diezeugmenon, il cui principio habbiamo nella Chorda
 ; cioè,
; cioè, in Paramese, & il porre il Synemennon, che hà il suo principio nella Chorda a. ch'è il
page 409porre la b. sopradetta, non hà forza di trasmutare un Modo nell'altro; & che tal Tetra-
chordo posto nella cantilena non sia naturale, ma accidentale; & in questo caso dicono
bene. Ma la Seconda maniera si fà, quando per tutta la cantilena; cioè, in ciascuna parte,
in luogo del Tetrachordo Diezeugmenon, vsiamo il Synemennon; & in luogo di cantar
la detta cantilena per la proprietà del
 . quadrato, la cantiamo per quella del b, molle; la
. quadrato, la cantiamo per quella del b, molle; la onde essendo posto in cotal maniera, non dicono bene; percioche questo Tetrachordo
non è posto accidentalmente nella cantilena; ma è in essa naturale, & il Modo si chiama
; come più à basso uederemo, & cotale Tetrachordo hà possanza di trasmu-
tare un Modo nell'altro. Et che ciò sia uero, facilmente potremo conoscere con un'ac-
commodato essempio, Poniamo il sottoposto Tenore del Nono modo, contenuto nel-
le sue chorde naturali; cioè, ne i suoi proprij & naturali luoghi, tra la Quinta specie della
 Diapason. Dico, che se in tal Tenore, ouer'in un'altro simile si mutasse lachorda
Diapason. Dico, che se in tal Tenore, ouer'in un'altro simile si mutasse lachorda  . so-
. so-lamente vna ò due uolte nella b. questa non farebbe, che tal Modo si trasmutasse, se non
in quella parte oue fusse posto; & non hauerebbe possanza di far, che tal Modo non fusse
anche Nono; imperoche se bene tal chorda posta in cotal maniera è necessaria per po-
ter regolare la modulatione; tuttauia essendo accidentale, non muta la forma del Mo-
do di sorte, che non si habbia da conoscere per Nono; come da questo essempio si può
uedere.
 Ma se noi porremo nel principio de tali Tenori il segno b. ilquale dimostra, che per tut-
Ma se noi porremo nel principio de tali Tenori il segno b. ilquale dimostra, che per tut-ta la Cantilena dobbiamo procedere per le chorde del Tetrachordo synemennon; di-
co, che allora tal chorda sarà naturale, & non accidentale; & hauerà possanza di
mutare il Nono modo nel Terzo; percioche uaria la specie della Diapente, ch'era
Prima per inanti tra G & d. & pone in essere la Seconda tra le istesse chorde; come qui
si uede.
 E' ben uero, che 'l Modo non si troua nelle sue chorde naturali; percioche è trasportato,
E' ben uero, che 'l Modo non si troua nelle sue chorde naturali; percioche è trasportato, per una Diatessaron più acuta; il perche quando si uolesse porre al suo luogo, si ritroua-
rebbe collocato in cotal maniera tra le chorde della Diapason D & d.
 page 410Non è adunque uero assolutamente, che 'l porre il Tetrachordo Synemennon in una
page 410Non è adunque uero assolutamente, che 'l porre il Tetrachordo Synemennon in una cantilena in luogo del Diezeugmenon, non habbia forza di mutar quel Modo, in cui
si pone, in un'altro; ma è ben uero, quando è posto secondo 'l modo mostrato. Diremo
adunque, se per la varieta del Tetrachordo, segue la uariatione della Diapason; & dal-
la uarietà della Diapason la uarietà del Modo; procedendo dal primo all'vltimo; che tal
Tetrachordo posto al secondo modo, habbia possanza di mutare vn Modo nell'altro.
tifona Argentum & aurum non est mihi; la quale Antifona è del Nono; percioche traspor-
tando in essa il Tetrachordo Diezeugmenon, ouer mutandolo nel Tetrachordo meson, la
fece del Primo. Concluderemo adunque, che qualunque uolta porremo in una cantile-
nala Chorda b. in luogo della
 , che tal Chorda farà sempre uariare il Modo; & cosi per
, che tal Chorda farà sempre uariare il Modo; & cosi per il contrario, ponendo la
 . in luogo della b. come ne mostra l'esperienza.
. in luogo della b. come ne mostra l'esperienza. Della Trasportatione de i Modi.Cap. XVII.
ne d'una Chorda nell'altra; cioè, per il porre la Chorda b. in luogo del-
la
 ; ouero per dir meglio, per la trasportatione del Semituono, si possa
; ouero per dir meglio, per la trasportatione del Semituono, si possa variare vn Modo nell'altro; & di Terzo farlo diuentar Nono, & di No-
no Terzo; non è dubio, che qualunque Modo sia Primo, Secondo, Terzo, Quar-
to, ouero alcuno de gli altri, col fauore d'alcuna Chorda, che muti vna Diapason nel-
l'altra, si potrà trasportare uerso l'acuto, ò uerso 'l graue, à nostro bel piacere. Il che
quanto alle uolte possa tornar commodo, lasciarò giudicare à ciascuno, che habbia giu-
dicio; percioche tali Trasportationi non sono utili solamente, ma sommamente necessa-
rie anco ad ogni perito Organista, che serue alle Musiche choriste; non solo nelle Messe,
& ne i Vesperi; ma anco nell'altre Hore canoniche & ad altri Sonatori similmente, che
sonano altre sorti d'Istrumenti, & che non sono cosi bene istrutti, come douerebbo-
no essere; per accommodare il suono de quelli alle Voci, lequali alle uolte non possono
ascendere, ò discendere tanto, quanto ricercano i luoghi proprij de i Modi accommo-
dati sopra i detti Istrumenti. Et tali Trasportationi sono hora in uso appresso i Mu-
sici moderni; come furono anche appresso gli Antichi, Ocheghen, & il suo discepolo
Giosquino, & infiniti altri; come nelle loro compositioni si può uedere; & furono anco
in uso appresso gli antichi Greci; come si può uedere nel Cap. 3. del Lib. 7. De i nostri
Sopplimenti; percioche chiamarono cotale Trasportatione Μεταβολὴ; la quale è di
più maniere, come si potrà uedere. Quando adunque accascarà, che per necessità, ò
per qualunque altr'accidente farà dibisogno di trasportare il Modo contenuto in alcuna
cantilena; sopra ogn'altra cosa bisognarà auertire d'accommodarlo in tal maniera &
in tal luogo, che si possa ascendendo & discendendo hauer tutte quelle chorde, che so-
no necessarie alla costitutione di tal Modo; cioè, che diano gli interualli e i Tuoni, &
i Semituoni necessarij al suo esser'essentiale. Et ciò debbono sommamente osseruare i
Compositori, quando uorranno compor tali cantilene, per sonare sopra qualche Istru-
mento; Imperoche quando le uorranno comporre per cantare solamente, non sarebbe
grande errore, quando segnassero alcune Chorde con alcun segno accidentale, che non
si ritrouassero sopra l'Istrumento; massimamente sopra il Grauocembalo; come sono le
Enharmoniche, le quali si trouano in pochi Istrumenti arteficiali. Et questo hò detto;
percioche la Voce si può fare acuta & graue; ouer si può vsare in qualunque altra ma-
niera, secondo 'l uoler del Cantore, che non si può far cosi liberamente con tali Istrumen-
ti. Hora per mostrare in qual maniera commodamente si possa trasportare qual si uoglia
cantilena fuori delle sue Chorde naturali, non pigliaremo altro essempio, che 'l Terzo,
& il Quarto, posto nel Capitolo precedente; percioche ne potranno ottimamente mo-
page 411strare in qual maniera ogni cantilena, che procede per la Chorda
 . si possa trasportare
. si possa trasportare per una Diatessaron in acuto, con l'aiuto della Chorda b. ouer per il contrario, quan-
do il canto procedesse per la Chorda b. in qual maniera si potesse trasporre nel graue
commodamente per un simile Interuallo, con l'aiuto della
 . Ma perche alle uolte i Mu-
. Ma perche alle uolte i Mu-sici, non già per necessità, ma più presto per burla & per capriccio; ò forse per uolere
intricare il ceruello (dirò cosi) à i Cantanti, sogliono trasportare i Modi uerso l'acuto,
ouero uerso il graue per un Tuono, ò per altro lnteruallo, adoperando non solamente
le Chorde chromatiche, ma anco l'Enharmoniche, per poter commodamente, quando
li fà dibisogno, trasportare à i loro luoghi i Tuoni & li Semituoni, secondo la propria for-
ma del Modo; però mostraremo il modo, & come si potranno trasportare. Et benche so-
gliono usar di trasportarli in più maniere; tuttauia ne porrò qui due solamente più vsate,
fatte nel Terzo modo; dalle quali potrà ogn'vno comprendere il modo, che hauerà da
tenere nell'altre; & saranno le sottoposte; l'una delle quali si fà con l'aiuto delle Chorde
segnate col b. & l'altra con l'aiuto di quelle, che sono segnate col
 . Bisogna auertire, che
. Bisogna auertire, che i Moderni chiamano queste Trasportationi Modi trasposti per Musica finta, laquale (se-

 condo che la dichiarano) dicono essere una Trasportatione de Figure (intendendo però
condo che la dichiarano) dicono essere una Trasportatione de Figure (intendendo però di tutto l'ordine, che si troua in ciascun Modo) dalla lor propria sede in un'altra. Ma
questo si dè saper sopr'ogn'altra cosa; che quantunque habbia posto gli essempi solamen-
te del Terzo modo, che tali Trasportationi si possono far nell'altre cantilene de al-
tri Modi; il che nella Ventesimaquinta del Quinto delle Dimostrationi hò chiaramen-
te dimostrato, & nel Cap. 3. De i Sopplimenti hò simigliantemente dichiarato.
Ragionamento particolare intorno al Primo modo, & nella sua Natura, de i suoi Prin-
cipij, & delle sue Cadenze.Cap. XVIII.
incominciando dal Primo; acciò procediamo con ordine; & mostrerò primie-
ramente, che non solamente appresso tutta la scuola de i Musici è in uso; ma
etiandio appresso gli Ecclesiastici; dopoi dimostrerò, doue regolarmente si possa dar
principio ad esso Modo; & doue (tanto in questo, quanto in ciaschedun de gli altri) si
possano far le Cadenze; non lasciando di ragionare alquanto intorno la sua natura &
proprietà; & secondo che mi uerrà in proposito. Dico adunque che 'l Primo modo è
quello, come hò mostrato; il quale nasce dalla Prima specie della Diapason C & c. dal-
la Chorda G. harmonicamente mediata. La onde dicono i Prattici, che questo si com-
pone della Prima specie della Diapente & C & G posta nel graue, & della Prima della
Diatessaron G & c. posta in acuto; Et dicono ch'è di natura molto atto alle Danze &
à i Balli; il perche vediamo, che la maggior parte di quelli, che vdimo hora in Italia,
sono composti sotto questo Modo; onde nacque, che à i nostri tempi alcuni lo chiamano
page 412Modo lasciuo. Di questo Modo ne i Libri Ecclesiastici; massimamente ne gli antichi; de
i quali ne hò uno appresso di me, si trouano molte cantilene; come la Messa, la qual
chiamano De gli Angioli, le Antifone Alma redemptoris mater, Reginae coeli laetare Hale-
luiah, & molt'altre; oltra quelle ch'erano del Settimo, contenuto nella Quarta specie
della Diapason E. & f. le quali sono state ridotte sotto questo modo con l'aggiungerle la
Chorda b. in luogo della
 . I moderni Compositori hanno etiandio composto in questo
. I moderni Compositori hanno etiandio composto in questo Modo un numero quasi infinito d'ogni maniera di Cantilena; come sono Messe; Hinni, &
altre sorte de Cāzoni; tra le quali si ritrouano Stabat mater dolorosa di Giosquino à cinque
uoci. O salutaris hostia; Alma redemptoris mater; Pien d'un vago pensier; d'Adriano; Descen-
di in ortum meum di Giacchetto; tutti composti à Sei uoci. Cosi anco il canto Audi filia
& vide di Gomberto; con Ego ueni in ortum meum, il quale composi à cinque voci; & in-
finiti altri; che 'l uoler riferirli d'uno in uno sarebbe impossibile. Et benche i ueri & natu-
rali Principij non solamente di questo, ma etiandio di qual si uoglia altro Modo, siano nel
le Chorde estreme della loro Diapente & Diatessaron, & nella Chorda mezana, la qual
diuide la Diapente in un Ditono & in un Semiditono; tuttauia si trouano molte cantilene,
c'hanno i lor principii sopra l'altre Chorde, lequali non starò hora à commemorare. Ma di
rò solamente, ch'osseruarono gli Ecclesiastici ne i lor Canti alcuni fini mezani, nel fine d'o-
gni Clausula, ò Periodo & d'ogni Oratione perfetta, i quali chiamarono Cadenze, che so
no molto necessarie per la distintione delle Parole, che generano il senso perfetto; le quali
s'alcun uorrà saper quello, ch'elle siano, potrà leggere il Cap. 51. della Terza parte, percio
che iui di tal materia hò à sufficienza ragionato; & potrà hauer di loro piena cognitione.
La onde basterà in questo luogo dir hora per sempre; che le Cadenze si trouano esser di
due sorti; Regolari, & Irregolari. Le Regolari sono quelle, che sempre si fanno ne gli
estremi suoni, ò Chorde de i Modi, & doue la Diapason in ciaschedun Modo harmo-
nicamente, ouer'arithmeticamente è mediata, ò diuisa dalla Chorda mezana; le
quali Chorde sono l'estreme della Diapente & della Diatessaron, nelle quali è diuisa
simigliantemente doue la Diapente è diuisa da una Chorda mezana in un Ditono & in
un ; & per dirla meglio, oue sono i ueri Principii & naturali di ciaschedun
Modo; l'altre poi facciansi doue si uogliano, si chiamano Irregolari. Sono adunque le
Cadenze regolari di questo Modo quelle, che si fanno in queste Chorde C, E. G & c.
& le Irregolari sono quelle, che si pongono nell'altre. Ma accioche più facilmente si co-
nosca quello, che si è detto, porrò un'essempio composto à Due uoci; dal quale si potrà
conoscere i proprij luoghi delle Regolari, & uedere il modo, che si haurà da tenere nel
compor le sue modulationi; il che non solamente osseruarò in questo Primo modo, ma
ne gli altri Modi ancora; & sarà quel, che segue.
 Si debbe però auertire, che le Cadenze delle Salmodie si debbono sempre far doue
Si debbe però auertire, che le Cadenze delle Salmodie si debbono sempre far doue casca 'l termine della mediatione delle loro Intonationi. La onde le Cadenze della me-
diatione, ò mezano punto della Prima, della Quarta, & della Sesta si faranno in a; quel
la della Seconda in F; quella della Terza, della Quinta & dell'Ottaua in c; & quella
della Settima in e; essendo che tali mezi, ò punti mezani finiscono iui; come si può ue-
dere nel sopranominato libro Recanetto, & in molti altri, i quali contengono simili Sal
modie, ouero Intonationi, che dir le uogliamo. Le Finali poi si fanno sempre nel luogo,
che ciaschedun verso di tali Salmodie, ouer di ciaschedun Salmo si fanno finire. Dobbia-
mo etiandio sempre osseruar, di far le Cadenze principalmente nel Tenore; essendo que
sta parte la Guida principale di caschedum Modo, sopra il quale si compone la Cantile-
na; & da esso debbe il Compositore pigliar l'Inuentione dell'altre parti; è ben uero che
tali Cadenze si fanno anco nell'altre parti; & questo secondo che tornano più commo-
de. Questo Modo si trasporta fuori delle sue Chorde naturali per vna Diatessaron uer-
so l'acuto, tra la Diapason F. & f, passando per le Chorde del Hexachordo Synemen-
non, nelle quali si troua la Chorda b; come si può uedere in tutte quelle Compositioni
che di sopra hò nominato.
page 414
Del Secondo modo.Cap. XIX.
le è contenuto tra la Quinta specie della Diapason G. & Γ, diuisa arithmeti-
camente dalla sua Chorda finale C. Questo (come dicono i Prattici) nasce
dal congiungimento della Prima specie della Diatessaron C, & Γ, posta nella
parte graue, con la prima della Diapente G. & C, posta in acuto. Tal Modo appresso gli
Ecclesiastici anticamente fù molto in uso nelle sue Chorde naturali; come ne i Libri lo-
ro antichi si può uedere; ma i Moderni, con l'aiuto del Hexachordo synemennon, nel
quale si troua la Chorda b. hanno fatto la maggior parte delle lor Cantilene, ch'erano
dell'Ottauo modo, del Secondo; & li più moderni anco hanno composto nuoue Can-
tilene di questo Modo, tra lequali si troua l'Antiphoua Aue Regina coelorum, & molt'altre.
Questo, quanto alla sua Salmodia, la quale è la Sesta, è atto ad esprimer cose amatorie,
che cōtengono cose lamenteuoli; onde è deto Modo lamenteuole; percioche contiene in
se una modulatione (secondo 'l parere de i Musici) alquanto mesta & languida; tuttauia
considerato come Secondo modo nella sua propria forma, è Modo allegro; & da que-
sto si può conoscere, che ciaschedun Compositore, il qual desidera di comporre alcuna
cantilena, che sia allegra, non si parte da questo Modo. I suoi Principii regolari si pon-
gono insieme con le sue regolari Cadenze (come nell'essempio si uede) nelle Chorde Γ,
C. E, & G; & le Irregolari sopra l'altre Chorde.
 Si trouano composte sotto questo Modo innumerabili Compositioni da molti Musici
Si trouano composte sotto questo Modo innumerabili Compositioni da molti Musici prattici; tra le quali è il Canto Mittit ad Virginem, à Sei uoci; & Quando nascesti Amor?
à Sette uoci; I vidi in terra angelici costumi, à Sei: & Quando fra laltre donne, à Cinque uo
ci, tutti composti d'Adriano; oltra il canto Inuiolata, integra, & casta es Maria, di Giosqui-
no à cinque uoci, & d'Adriano à Sette, à i quali s'aggiunge il canto à cinque uoci di Gia
chetto Decantabat populus; & Litigabant Iudaei; & O quàm gloriosum est regnum, i quali hò
composto da cantar con Sei uoci. Et se ben le chorde naturali di questo Modo sono le
mostrate di sopra, tuttauia i Musici con l'aiuto della chorda b. dell'Hexachordo synemen-
non lo trasportano nell'acuto per una Diatessaron, tra le chorde della Diapason c. & C;
come nella maggior parte delle Compositioni nominate si può chiaramente uedere.
Del Terzo modo.Cap. XX.
presente del Terzo modo, il quale fin'hora con poca ragione, dall'Vniuersità
de i Musici è stato posto, nel Primo luogo; & hora (per le ragioni, addotte
nel Quinto libro delle Dimostrationi, & nel Sesto de i nostri Sopplimenti) me-
ritamente possede il Terzo. Questo è contenuto tra la Seconda Specie della Diapa-
page 416son che si ritroua tra queste due chorde estreme D. & d. diuisa harmonicamente; dalla
qual diuisione dicono i Prattici; che tal Modo è contenuto dalla seconda specie della Dia
pente D & a, & dalla Seconda della Diatessaron a, & d. posta di sopra di essa Diapente.
Di questo modo quasi infinite sono le Cantilene, le quali si trouano ne i Libri Ecclesia-
stici; come sono Introiti, Graduali, Haleluiah, Antiphone, Responsorii, Prose, & altre
cose simili. Ma appresso gli altri Musici non si possono numerare le Messe, gli Hinni, &
altre sorti di Canti Latini & Volgari, che sono state composte nelle due modulationi;
tra le quali si trouano i canti Veni sancte Spiritus composto à Sei uoci, & il Giunto m'ha
Amor, à Cinque d'Adriano. Composi ancora io molte cose, tra le quali sono i canti Ho-
die Christus natus est, con Victimae pascali, & Salue regina misericordiae, à Sei uoci, & uno à
cinque Nigra sum, sed formosa. Si trouano anco molt'altre compositioni composte d'al-
tri Compositori; le quali lascio di nominar, per non esser lungo. I ueri & naturali Prin-
cipii di questo Modo sono nelle Chorde D, F, a. & d. simigliantemente le sue Cadenze
regolari; come nel seguente essempio si uedono.
 Et non solamente i Principij irregolari; ma anco le irregolari Cadenze si ritrouano esser
Et non solamente i Principij irregolari; ma anco le irregolari Cadenze si ritrouano esser fatte nellaltre Chorde; come si uede in molte Cantilene, non solamente Ecclesiastiche,
ma etiandio nell'altre. Questo Modo hà strettissima parentella (dirò cosi) con l'Vndeci
mo, il quale è contenuto tra le Chorde a. & aa, percioche i Musici compongono nelle
sue Chorde le lor Canzoni del Modo Vndecimo, trasportandolo nell'acuto per una Dia
tessaron; lasciando da un canto la chorda
 , & ponendoui la b, la qual serue all'Hexa-
, & ponendoui la b, la qual serue all'Hexa-chordo synemennon, come fece Morale Spagnuolo nel Canto Sancta & immaculata virgi-
nitas; & Giachetto nel Spem in alium; l'uno & l'altro composto per cantare à quattro uo
ci. Et perche il Terzo modo hà un certo mezano effetto tra 'l mesto & l'allegro, per cagio
ne del Semiditono, che s'ode nel concento sopra le Chorde estreme della Diapente &
della Diatessaron; non hauendo altramente il Ditono dalla parte graue; però per sua na
tura è riputato dolce & alquanto mesto. Onde potremo ad esso accommodare ottimamen
te quelle parole, le quali saranno piene di grauità, & che tratteranno di cose alte & sen-
tentiose; accioche l'Harmonia si conuenghi con la materia, che in esse si contiene.
page 418
Del Quarto Modo.Cap. XXII.
non adulatoria; & che la sua natura fusse lagrimeuole, & humile; di maniera che
mossi da questo parere, lo chiamarono Modo lagrimeuole, humile & deprecatiuo.
La onde si uede; che hauendo gli Ecclesiastici questo per fermo, l'hanno usato nelle cose
meste & lagrimose; come sono quelle de i tēpi Quadragesimali, & d'altri giorni di digiuno;
 & dicono, ch'è Modo atto alle Parole che rappresentano pianto, mestitia, sollicitu-
& dicono, ch'è Modo atto alle Parole che rappresentano pianto, mestitia, sollicitu-dine, cattiuità, calamità, & ogni generatione di miseria; & si troua molto in uso ne i
loro canti; & le sue Cadenze principali & regolari (per esser questo dal Terzo Modo
poco differente; percioche l'uno & l'altro si compongono dell'istesse specie) si pongono
nelle Chorde a, F, D, & A; che si uedono nell'essempio; l'altre poi, che si pongono ne gli
altri luoghi sono tutte Irregolari. Imperoche i Prattici dicono, questo Modo compor-
si della Seconda specie della Diapente a. & D. posta nell'acuto, & della Seconda della
Diatessaron D. & A. posta nel graue; & lo chiamano Collaterale, ouer Plagale del Ter-
zo. Si trouano molte compositioni del Quarto modo, composte da molti Antichi & da
moderni Musici; tra le quali è il canto Praeter rerum seriem, composto à sei uoci da
Giosquino, & da Adriano à Sette uoci; & Che fai alma, simigliantemente à sette; con
Auertatur obsecro Domine, & Oue ch'i posi gli occhi; l'uno & l'altro à sei uoci dal detto
Adriano, con molt'altri composti. Composi anch'io in tal Modo l'Oratione Domi-
nicale Pater noster; con la Salutatione angelica; Aue Maria, à sette uoci; & li canti.
Ego rosa Saron, & Capite nobis vulpes paruulas; à cinque uoci. Si trouano etiandio
molte altre compositioni fatte da diuersi compositori, le quali per esser quasi infinite
si lasciano. Questo Modo rare uolte si troua ne i Canti figurati nelle sue Chorde
proprie; ma il più delle uolte si ritroua trasportato per una Quarta; come si può
ueder ne i Canti nominati; & questo, percioche si può trasporre; come anco si
può trasporre il Terzo con l'aiuto della Chorda Tritesynemennon, uerso l'acuto.
Et si come il Terzo col Vndecimo hà molta conuenienza, cosi questo l'hà ueramen-
te col Duodecimo.
page 420
Del Quinto Modo.Cap. XXII.
te della chorda
 ; ouer dall'unione della Terza specie della Diapente E, &
; ouer dall'unione della Terza specie della Diapente E, &  , po
, posta nel graue, con la Terza della Diatessaron
 . & e, posta nell'acuto. Questo Mo
. & e, posta nell'acuto. Questo Modo hà la sua Chorda finale E. cōmune col Sesto; & gli Ecclesiastici hanno infinite cantile
ne; come ne i loro libri si può uedere. Le sue Cadenze principali si fanno nelle Chorde de i
suoi principii regolari, iquali, sono le chorde mostrate E, G,
 , & e; che sono l'estreme della
, & e; che sono l'estreme della sua Diapēte & della sua Diatessarō, & la mezana della Diapēte; l'altre poi, che sono Irrego
 lari, si possono far sopra l'altre chorde. Ma perche conosciuto le Regolari, facilmente si
lari, si possono far sopra l'altre chorde. Ma perche conosciuto le Regolari, facilmente si può conoscer le Irregolari; però hò dato l'essempio delle prime; acciò ueniamo in co-
gnitione delle seconde. Si debbe però auertire, che tanto in questo, quanto nel Sesto,
nel Nono, & nel Decimo modo, regolarmente si fanno le Cadenze nella Chorda
 ma
ma perche tal Chorda non hà corrispondenza alcuna per Quinta nell'acuto, ne per Quarta
nel graue; però è chorda alquanto dura, ma tal durezza si sopporta nelle cantilene com
poste à piu di due uoci; percioche si tiene tal'ordine, che fanno buono effetto; come si
può ueder tra le Cadenze poste nel Cap. 51. della Terza parte. Molte compositioni si
trouano composte sotto questo modo, tra le quali è questa O Maria mater Christi, à quat-
tro uoci di Izac; & d'Adriano i canti Te Deum patrem, Huc me sydereo; & Hac est domus
domini, composti à sette uoci, & I mi riuolgo indietro, composto da lui medesimamente
à cinque uoci; à i quali aggiungeremo Ferculum fecit sibi rex Salomon, il quale composi
simigliantemente à cinque uoci. Se questo Modo non si mescolasse col Nono, & si
udisse semplice, hauerebbe la sua Harmonia alquanto dura; ma perche è temperata dal-
la Diapente dell'Vndecimo, & dalla Cadenza, che si fa in a, che in esso grandemente si
usa; però alcuni hanno hauuto parere, c'habbia natura di commouere al pianto; la on-
de gli accommodarono uolontieri quelle parole, che sono lagrimeuoli & piene di lamen
ti. Ha grande conuenienza col detto Vndecimo; percioche hanno la Terza specie della
Diaressaron commune tra loro, & spesse uolte i Musici moderni lo trasportano fuori del-
le sue Chorde naturali per una Diatessaron più acuta, con l'aiuto della Chorda b; anco
ra che 'l più delle uolte si ritroui collocato nel suo proprio & natural luogo.
Del Sesto Modo.Cap. XXIII.
pason
 . &
. &  , mediata dalla sua Chorda finale E. arithmeticamente. Que-
, mediata dalla sua Chorda finale E. arithmeticamente. Que-sto (come dicono i Prattici; si compone della Terza specie della Diapente
 & E, posta in acuto, & della Terza della Diatessaron E &
& E, posta in acuto, & della Terza della Diatessaron E &  , congiunta al-
, congiunta al-la Diapente dalla parte graue. Questo medesimamente, secondo la loro opinione,
s'accommoda marauigliosamente à parole, ò materie lamenteuoli, che contengono tri-
stezza, ouer lamentatione supplicheuole; come sono materie amorose, & quelle che
significano otio, quiete, tranquillità, adulatione, fraude, & detrattione; il perche
dall'effetto alcuni lo chiamarono Modo adulatorio. Questo è alquanto piu mesto del
suo Principale, massimamente quando procede dall'acuto al graue per mouimenti
tardi & contrarij. Credo io che se 'l si usasse semplicemente, senza mescolarui
la Diapente, & la Cadenza posta in a, che serue al Duodecimo; che hauereb-
be alquanto più del uirile, di quello, che non hà cosi mescolato; ma accompagna-
page 422to in tal maniera, s'usa grandemente, di modo, che si trouano molte cantilene compo-
ste sotto questo Modo, tra le quali si troua Deprofundis clamaui ad te Domine, à quattro uo
ci di Giosquino; & Peccata mea Domine, con Rompi dell'empio cor'il duro scoglio, & In quel
parte del ciel; composti da Adriano, l'uno & l'altro à sei uoci. Composi anch'io molte
cantilene, tra le quali si troua à sei uoci il canto Miserere mei Deus, miserere mei; & anco
Misereris omnium Domine; & una Messa, senza usar in essa le osseruanze mostrate nella Ter
za parte; & ciò feci, non per altro se nō per mostrare, che ciascuno il quale uorrà cōpor sen
za partirsi dalle date Regole, potrà etiandio comporre facilmente senza queste osseruāze,
& assai meglio di quello, che fanno alcuni, che non le fanno. Si trouano di questo Modo
quasi infinite Cantilene ecclesiastiche, nelle quali rarissime uolte (anzi s'io dicesse mai,
non errarei) si uede toccar la Chorda
 . Ben è uero, che passa nell'acuto alla chorda c,
. Ben è uero, che passa nell'acuto alla chorda c, di maniera che quando 'l Semituono douerebbe udirsi nel graue, si ode nell'acuto; & cosi
gli estremi di cotal Modo uengono ad esser le chorde c. & C. I suoi Principii Irregolari ap
presso gli Ecclesiastici si trouano in molti luoghi; ma li Regolari sono nelle Chorde
 , E
, E G. &
 solamente che si trouano anco le sue Cadenze regolari, che sono le sottoposte;
solamente che si trouano anco le sue Cadenze regolari, che sono le sottoposte; ancora che molte siano le Irregolari. Il più delle uolte i Prattici lo trasportano per una
Diatessaron nell'acuto, ponendo la Chorda b, in luogo della
 ; come si può ueder'in in-
; come si può ueder'in in-finite cantilene; il che fanno etiandio (come hò detto) ne gli altri Modi.
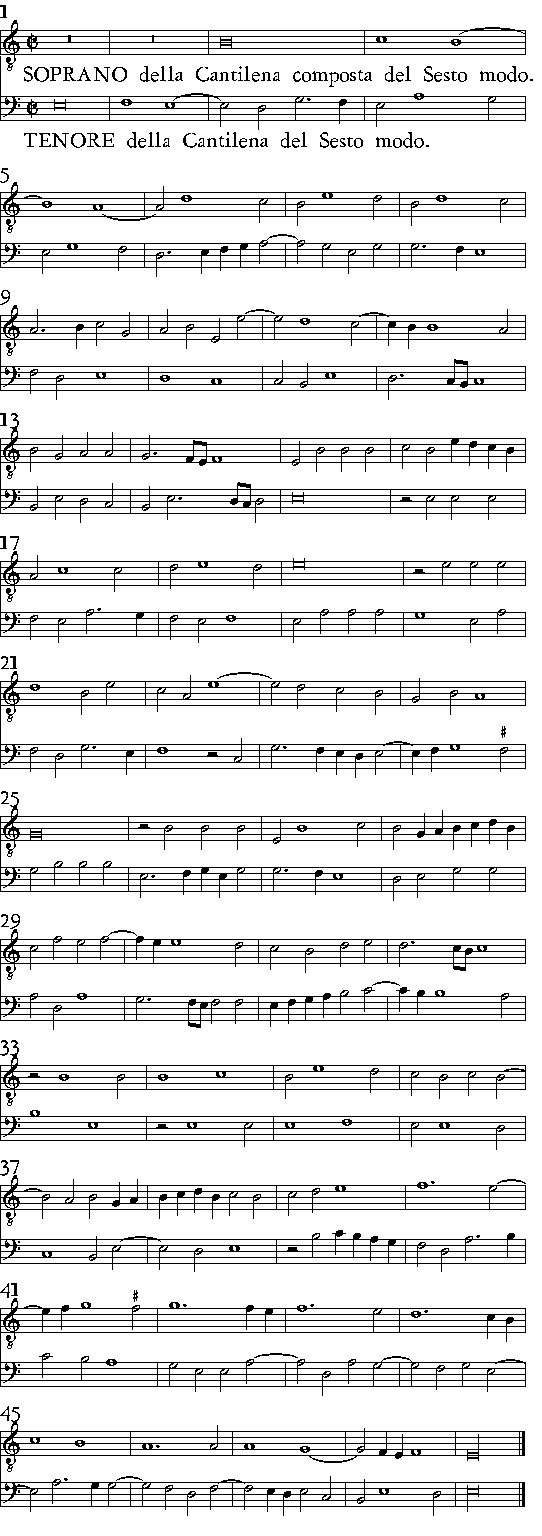
Del Settimo Modo.Cap. XXIIII
mezata Harmonicamente dalla Chorda c. Dicono i Prattici, che si compone
della Quarta specie della Diapente F. & c, & della Prima della Diatessaron
c. & f. posta nella parte acuta della Diapente; del quale la Chorda F. è Chor
da commune finale con l'Ottauo modo suo collaterale. Da tal specie di Diapason hab-
biamo solamente questo Modo; percioche non riceue altra diuisione, che l'Harmonica.
Alcuni uogliono, che nel cantar, arrechi modestia, letitia, & solleuatione à gli animi
dalle cure noiose. Però gli Antichi usarono di accommodarlo alle Parole, ò materie,
che contenessero alcuna uittoria; onde da tal cose alcuni lo dimandarono Modo giocon
do, modesto, & diletteuole. Et quantunque i suoi Principii naturali si pongano nelle
Chord F, a, c & f; percioche sono Chorde regolari; tuttauia appresso gli Ecclesiastici si
ritrouano altri Principii in diuerse altre Chorde; come si può uedere ne i libri loro. Le
Cadenze regolari di questo Modo si fanno nelle nominate quattro chorde, come nell'es-
sempio si ueggono; & le Irregolari, quando si uogliono usare, si fanno nell'altre. Molte
cantilene si trouano ne i Libri Ecclesiastici che contengono la forma di questo Modo,
ancora che non sia molto in uso appresso i compositori moderni; percioche par à loro che
sia Modo più duro, & più insoaue di qualunque altro; tuttauia si trouano composte in
esso molte cantilene; come l'Hinno di S. Francesco, Spoliatis aegyptijs. d'Adriano, & due
altri canti di Ciprian di Rore, Di tempo in tempo mi fà men dura; & Donna che ornata se-
te; con quel di Francesco Viola, Fra quanti amor; tutti composti à quattro uoci; & molt'
altri ancora, che non mi soccorrono alla memoria Questo si può trasportare per una Dia
pente nel graue, con l'aiuto della chorda b, lasciando la
 ; come de gli altri si è fatto, nel
; come de gli altri si è fatto, nell'acuto & la sua chorda finale uerrà ad essere la b; ilche ciascun potrà uedere.
page 424
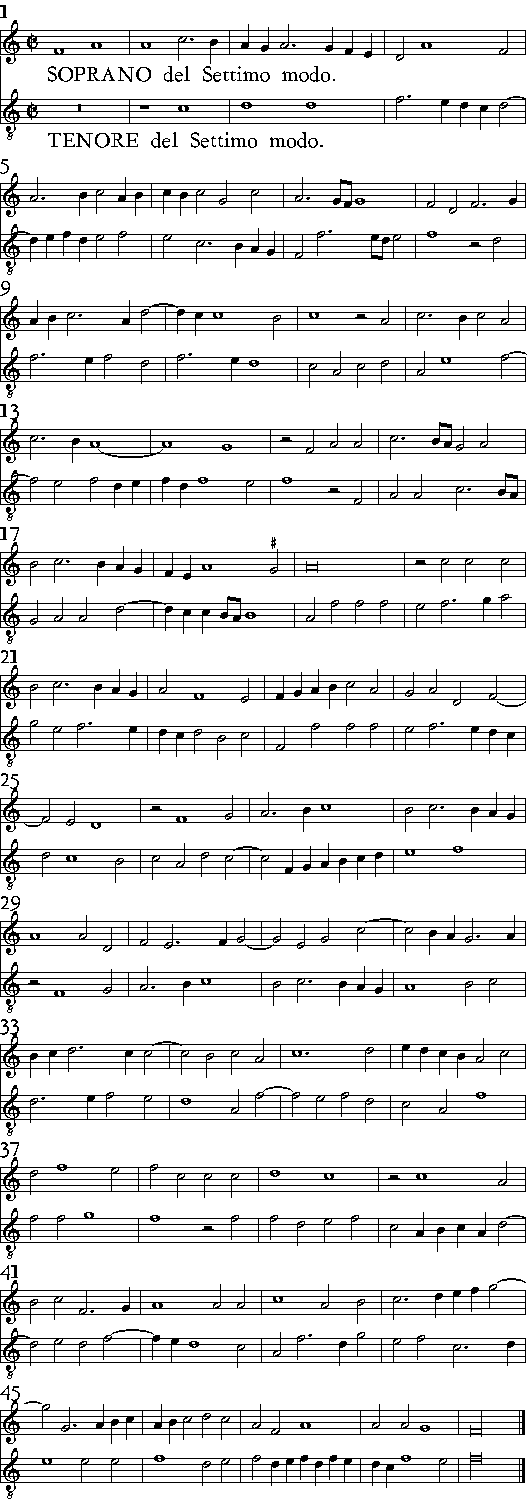
Dell'Ottauo Modo.Cap. XXV.
Diapason c. & C, diuisa arithmeticamente. Dicono i Prattici, che questo
Modo si forma & nasce dalla congiuntione della Quarta specie della Diapen
te c. & F, posta nell'acuto, con la Prima della Diatessaron F. & C. accom-
pagnata nel graue; & che la Chorda F. è la sua Chorda finale. Questo da gli Ecclesiasti
ci è stato molto frequentato, come era frequentato anche molto il suo Principale; im-
peroche si troua ne i loro libri molte cantilene, composte di questo Modo, il quale di-
cono, non esser molto allegro, ne molto elegante; & però l'usarono nelle cantilene gra
ui & deuote, che contengono commiseratione; & l'accompagnarono à quelle mate-
rie che contengono lagrime. Di maniera che lo chiamarono Diuoto & Lagrimeuole,
à differenza del Quarto, il quale è più tosto funebre & calamitoso, che altro. I Princi-
pii regolari di tal Modo & le sue Cadenze regolari si fanno nelle Chorde c, a, F & C;
nell'altre poi si fanno le Irregolari. Ma perche conosciute le prime è facil cosa di cono-
scer le seconde; però non sarà fuor di proposito, porre di loro un'essempio, accioche
più facilmente si conosca l tutto, & sarà il posto qui di sotto. Molte cantilene mi ricor-
do hauer ueduto composte in questo Modo; ma al presente mi soccorrono alla memoria
solamente queste; Vn canto di Giouan Motone à quattro uoci, Ecce Maria genuit no-
bis Saluatorem, & un Salmo à due chori spezzati di Adriano à otto uoci In conuertendo
Dominus captiuitatem Sion; composto sopra la Sesta Salmodia. Questo etiandio si può
trasportare nell'acuto per una Quarta, con l'aiuto dell'Hexachordo synemennon; cioè
con la Chorda b. che contiene; come si trasportano gli altri; il che quanto sia facile,
ciascun lo potrà conoscere dalle due nominate cantilene.
page 426
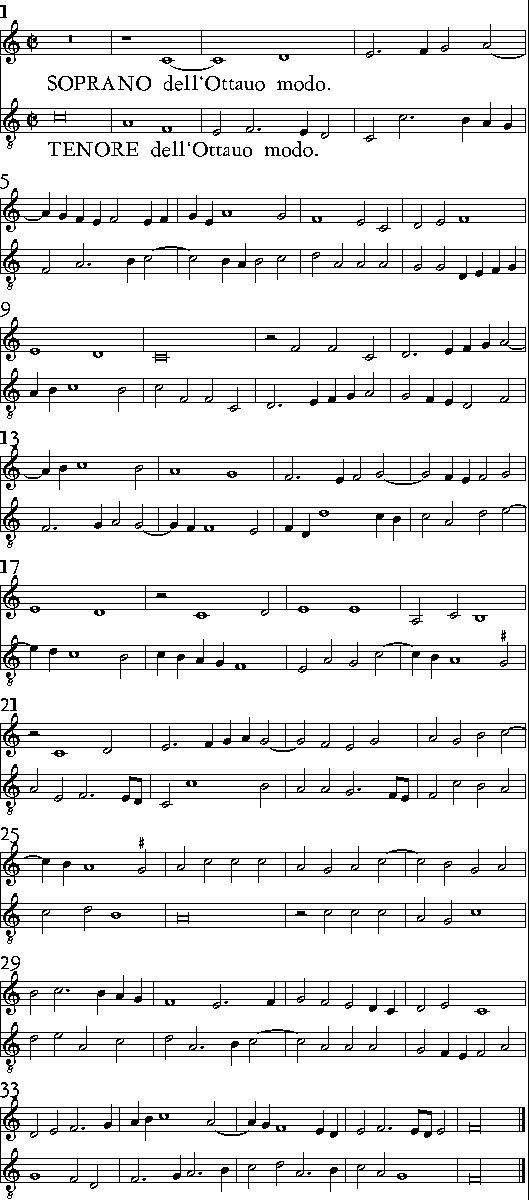 page 427
page 427Del Nono Modo.Cap. XXVI.
tenuto il Nono modo; il quale (come dicono i Moderni) nasce dalla congiun
tione della Seconda specie della Diatessaron d. & g, con la Prima specie della
Diapente G. & d; questa posta nel graue, & quella posta nell'acuto. A questo
 (secondo che dicono) si conuiene Parole, ò materie, che siano lasciue, ò che trattino
(secondo che dicono) si conuiene Parole, ò materie, che siano lasciue, ò che trattino di lasciuia, lequali siano allegre, dette però con modestia, & quelle, che significano mi-
naccie, perturbationi, & ira. I suoi Principii regolari & le sue Cadenze principali & re-
golari si pongono nelle Chorde G,
 , d, & g; come qui sotto si ueggono; ma le Irregola-
, d, & g; come qui sotto si ueggono; ma le Irregola-ri si pongono sopra l'altre. Molte cantilene si trouano composte da i Musici sotto questo
Modo, tra le quali sono, Pater peccaui, & I piansi, hor canto, d'Adriano à sei uoci. Que
sto Modo è molto in uso appresso gli Ecclesiastici, & nelle cantilene de gli altri Musici si
troua il più delle uolte nelle sue Chorde naturali; ma molte uolte con l'aiuto della Chor
da b, cioè, col mezo dell'Hexachordo synemennon, è trasportato nel graue per una Dia
pente, senz'alcun'incommodo.
Del Decimo Modo.Cap. XXVII.
la Diapason d & D, diuisa arithmeticamente dalla chorda G; & (come dico-
no) nasce dalla congiuntione della Quarta specie della Diapente d. & G. po-
sta nell'acuto, con la Prima della Diatessaron G. & D posta nel graue. Que-
sto col Nono hà la chorda commune finale la G; & dicono i Prattici, che hà natura di con
tenere in se una certa naturale soauità, & abondante dolcezza, che riempie d'allegrez-
za gli animi de gli ascoltanti, con somma giocondità & soauità mista; & uogliono, che
sia al tutto lontano dalla lasciuia & da ogni uitio. La onde l'accompagnarono con paro-
le, ò materie mansuete, accostumate, graui, continenti cose profonde, speculatiue, &
diuine; come sono quelle che sono accommodate ad impetrar gratia da lddio. Molte
cantilene si ritrouano ne i libri Ecclesiastici di questo Modo, il quale hà i suoi Principii
regolari nelle chorde d,
 , G. & D; ma gli Irregolari si trouano nell'altre; & le sue Ca-
, G. & D; ma gli Irregolari si trouano nell'altre; & le sue Ca-denze regolari si pongono simigliantemente nelle mostrate quattro chorde; come nel se
guente essempio si può uedere; ma le Irregolari si pongono sopra laltre ancora. Ap-
presso gli altri Musici si trouano molte compositioni, tra le quali si trouano Benedicta es coe-
lorum regina, di Giosquino, à sei Voci; & Audite insulae, pur à sei uoci; con il canto Ver-
bum supernum prodiens, & Liete & pensose, accompagnate & sole Donne, tutti d'Adriano à
sette uoci, & molt'altri. Questo modo si può trasportar come gli altri, fuori delle sue
chorde naturali, ponendolo in acuto per una Diatessaron, con l'aiuto della chorda b, ò
dell'Hexachordo synemennon; imperoch'altramente sarebbe impossibile. Gli Eccle-
siastici sogliono à tutte quelle Antifone che incominciano nella chorda C. ouer D,
& finiscono nella sua finale G; le quali sono (considerata la loro forma) del Terzo modo;
quantunque finiscano nella sopra detta chorda G, applicare la Salmodia, che è posta nel
cap. sequente del Salmo In exitu Israel de Aegypto: come sono le Nos qui uiuimus, & Mar-
tyres Domini, con molt'altre simili, che si trouano ne gli Antifonarii uecchi; il che dimo-
stra il loro SEVOVAE. La onde per non lasciare indietro cosa, che al Musico ap-
partenga, ne hò uoluto far mentione, accioche occorrendoli ueder cotal cosa, non si ma
rauigli; percioche si può ueramente dire, che tale Salmodia sia più al proposito di quel-
lo che non è l'Ottaua, laquale applicano all'altre Antifone di questo Modo; essendo
che la sua Modulatione è molto conforme alle modulationi delle già commemorate An
tifone. Ma ueniamo à ragionare dell'Vndecimo.
page 429

Dell'Vndecimo Modo.Cap. XXVIII.
la Seconda specie della Diapente A. & E, ouero a. & e (come più piace) con
la Terza della Diatessaron E. & a; ouero e. & aa; & per dir meglio, è contenuta
nella Sesta specie della Diapason A. & a, ouero a. & aa, mediata Harmonicamente dal-
la Chorda E, ouer dalla e. Non si potrà mai dire con uerità, che questo sia Modo nouo,
ma si bene antichissimo; ancora che fin qui sia stato priuo del suo nome, & del suo luogo
proprio; percioche alcuni l'hanno posto tra alcuni lor Modi, che dimandano Irregola-
ri, quasi che non fusse sottoposto à quell'istessa Regola, alla quale gli altri si sottopongo-
no; & che la sua Diapason non fusse tramezzata Harmonicamente, come quella de gli al-
tri Modi, ma à qualch'altra maniera strana. E ben uero (com'hò dett'altroueSupra
Cap. 15.) ch'alle
Intonationi de i Salmi, ò Salmodie, che dir le uogliamo gli Ecclesiastici ne hanno segna-
to solamente Otto modi; al Terzo, al Quarto, al Quinto, al Sesto, al Settimo, all'Otta-
uo, al Nono & al Decimo; come si può uedere ne i loro libri; ma per questo non si può
dire, che sia Irregolare; conciosia ch'altra cosa è la Salmodia, ouer'Intonatione de i Sal-
mi, & altra le Modulationi che si trouano in diuersi Modi, si ne i Canti fermi, com'anco
ne i figurati. Ne si dee creder per cosa alcuna, che qualunque uolta si trouasse una Anti-
fona, che fusse composta sott'alcun de questi Modi, Primo, ouer Secondo, Vndecimo, ò
Duodecimo; non se le potesse applicare una delle otto Intonationi nominate, ò Salmo-
die, massimamente hauendo ciascuna da esse varij fini; com'è manifesto à tutti quelli, che
sono prattici in cotal cosa; percioche al Primo modo si può applicar la Quinta Salmodia
commodamente; al Secondo la Sesta; all'Vndecimo la Prima; & anco la Quarta, come
più à basso dimostraremo & al Duodecimo la Seconda, procedendo per quella specie di
Diapente & Diatessaron, che ricercano i nominati quattro modi; come si è mostrato nel
Lib. 24. De Re Musica. Questo modo, alcuni l'hanno chiamato aperto & terso, attissimo
à i Versi lirici; la onde se li potranno accommodar quelle parole, che contengono ma-
terie allegre, dolci, soaui, & sonore; essendo che (come dicono) hà in sè una grata seueri-
tà, mescolata con una certa allegrezza & dolce soauità oltra modo. E cosa notissima à
tutti i periti della Musica, che questo Modo col Terzo sono tra loro molto conformi;
percioche la Seconda specie della Diapente è commune à l'uno & l'altro, & si può passar
dall'uno in l'altro facilmente; il che si può anco dire del Quinto & del Primo modo. So-
no di questo Modo molte cantilene ecclesiastiche, che longo sarebbe il referirle, tra le
quali si troua il canto dell'Oratione Dominicale, Pater noster, la quale hà la sua forma
contenuta tra la Sesta specie della Diapason A. & a. & finisce nella chorda A. in tal ma-
niera; come si può uedere in alcuni essemplari antichi corretti. Si troua anche di questo
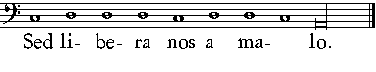 Modo il canto del Symbolo Niceno, Credo in unum
Modo il canto del Symbolo Niceno, Credo in unum Deum; il quale hà principio per la sua Intonatione
nella chorda D, & uiene à terminare (come si uede
ne i detti corretti essemplari) nella chorda A. mede-
simamente, & non nella
 , ouer nella E. trasporta-
, ouer nella E. trasporta-to per una Diatessaron nell'acuto con l'aiuto della
chorda b; come ne i moderni Libri si uede; il qual
canto trasportato douerebbe per il douere finir nella chorda D. ma è stato guasto & scor-
retto per l'ignoranza de i Scrittori; & per la presuntione & temerità d'alcun'altri; co-
 page 431m'intrauiene anco nell'altre cose di maggiore importanza. Et non solamente i fini de i
page 431m'intrauiene anco nell'altre cose di maggiore importanza. Et non solamente i fini de i mostrati canti si ritrouano fuori della lor propria & natural chorda; ma de gli altri anco-
ra, che si trouano in tal maniera guasti & corrotti, che sarebbe cosa troppo lunga da mo-
strare, quando si uolesse dar di ciascuno uno essempio particolare. Ma quanto sia facile
il trasmutare ne i Canti ecclesiastici un Modo nell'altro, variando solamente la chorda
finale, ouer trasportandolo dall'acuto al graue, ouer dal graue all'acuto, senz'alcun'aiu-
to dalla chorda b, questo sarebbe facil da uedere, quando si uorrà essaminar minuta-
mente le modulationi loro & il lor procedere. In questo modo si ritroua composta l'An-
tifona Aue Maria gratia plena. la quale ne i libri antichi si troua terminata tra le sue chor-
de naturali; come qui si uede; che ne i moderni si troua scritta più graue per vna Dia-
pente, & la sua Salmodia è la Prima; la quale incomincia nella chorda c. Et che ciò sia
 uero, da questo lo potiamo comprendere, che P. della Rue compose una Messa à quat-
tro uoci sopra questa Antifona nelle chorde uere & essentiali di cotal Modo; nel quale si
uero, da questo lo potiamo comprendere, che P. della Rue compose una Messa à quat-
tro uoci sopra questa Antifona nelle chorde uere & essentiali di cotal Modo; nel quale si troua etiandio composto l'Introito, Gaudeamus omnes in Domino. Ne alcuno prenda di
questo marauiglia; massimamente uedendo, che la Salmodia, che segue sia la Prima,
percioche (com'hò detto ancora) non è inconueniente, che ciascun de i Quattro ultimi
Modi poco fà nominati, si ridurre all'Intonatione d'alcuna delle Otto nominate. Et
se la chorda b. posta in luogo della
 . hà possanza di mutare un Modo nell'altro; non è
. hà possanza di mutare un Modo nell'altro; non è dubbio, che ritrouandosi 'l detto Introito collocato nella Seconda specie della Diapason,
& cantandosi per la proprietà di b. molle, non sia anco dell'Vndecimo modo; come essa-
minando il tutto, & quello ch'hò detto di sopra nel Cap. 16. manifestamente si può uede-
re. Ma quando si uolesse ridur nelle sue uere chorde naturali, trasportandolo nell'acuto
per vna Diapente, si trouerebbe collocato tra la Sesta specie della Diapason a. & aa; come
fece Giosquino, che compose à quattro uoci la Messa sopra il sudetto Introito, & la ritirò
nelle sue chorde naturali; come si può uedere. Mi souiene hora, ch'alcuni non hanno
detto male, quando giudicarono, che l'Intonatione ò Salmodia del Salmo. In exitu Is-
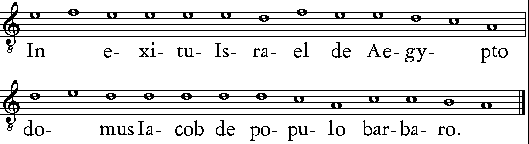 rael de Aegypto, fusse la Nona; percioche uogliono, che la Antifona Nos qui viuimus sia sta-
rael de Aegypto, fusse la Nona; percioche uogliono, che la Antifona Nos qui viuimus sia sta-ta guasta & trasportata fuori del suo luogo da alcun Scrittore, che habbia uoluto mostrar-
si più sauio de gli altri; com'han fatto molti anco dell'altre; ma di questo si è detto à ba-
stanza nel Capitolo precedente. Questo Modo hà, com'hanno gli altri, i suoi Principij &
le sue Cadenze regolari & irregolari. I Regolari sono quelli, che si pongono nelle chor-
de A, C, E, & a, come etiandio le Cadenze, che si uedono in questo essempio. ma i
page 432
 Principii & similmente le Cadenze irregolari si pongono nell'altre Chorde. Trouansi in
Principii & similmente le Cadenze irregolari si pongono nell'altre Chorde. Trouansi in questo Modo composte uarie cantilene, tra le quali è il canto Spem in alium numquàm ha-
bui di Giachetto, & Sancta & immaculata virginitas, di Morale Spagnuolo, l'uno & l'altro
composto à quattro uoci, & le due nominate Messe. Composi anch'io sotto questo Mo
do il canto. Si bona suscepimus de manu Domini, I uò piangendo il mio passato tempo, à cinque
uoci, la Messa sopra il canto Benedicam Dominum in omni tempore di Gian Motone à Sei uo
ci; & altre cose, lequali non nomino. Ma questo Modo si può trasportar per una Dia-
pente nel graue, con l'aiuto della Chorda b; come si trasporta etiandio gli altri.
Del Duodecimo & vltimo modo.Cap. XXIX.
trouano ne i libri Ecclesiastici, composte sotto 'l Primo & Secondo modo, & an-
che sotto l'Vndecimo & Duodecimo, che sono per la maggior parte Graduali,
Offertorij, Post communioni, & altre simili, & non sono tanto facili da cono-
scere da quelli, che non sono nella Musica ben'istrutti; ma lascierò da un canto cotesta
cosa, & uerrò à seguitar 'l mio principale intendimento; & dirò solamente, che uolen-
do hauer perfetta cognitione del Duodecimo modo, il quale è l'Vltimo de i Dodici,
s'auertirà, che egli è contenuto nelle Chorde della Terza specie della Diapason E. & e,
diuise arithmeticamente dalla Chorda a. & per questo dicono alcuni, che 'l detto Modo
si compone della Seconda specie della Diapente e. & a, posta nell'acuto; & della Terza
della Diatessaron a. & E, posta nel graue, congiunta alla Chorda a; la quale è la sua fina-
le. Potiamo dir, che la natura di questo Modo non sia molto lontana da quella del Quar
to, & del Sesto, se tal giudicio si può far dall'Harmonia, che da esso nasce; imperoche
si serue della Diapente, ch'è commune col Quarto; & della Diatessaron, che serue an-
ch'al Sesto Modo. I suoi Principii regolari sono nelle chorde e, c, a & E; similmente le
sue Cadenze. Ma perche hauendo cognitione delle Cadenze regolari, facilmente si
può saper'in quali chorde si fanno le Irregolari; però solamente delle prime darò un'es-
sempio, ilquale sarà il seguente. Di questo Modo si trouano molte compositioni; co-
me, Gabriel Archangelus locutus est Zachariae di Verdeloto; similmente, Flete oculi, rorate
genas, d'Adriano, l'uno & l'altro à quattro uoci, & molt'altre: & trasportasi per una Dia-
pente nel graue con l'aiuto della chorda b. senza la quale poco si farebbe, che fusse
buono & stesse bene. Ma quello, che io hò detto fin'hora intorno la Natura & Proprie-
tà de i Modi, & circa l'uso, i Principii & le Cadenze di ciascheduno, uoglio che sia det
to à sufficienza; imperò che fà dibisogno hormai che si ragioni & tratti alcun'altre co-
se, che saranno molto utili & anco necessarie al Compositore, le quali uedute, par-
laremo prima del ualore d'alcune delle Figure cantabili, che insieme si legano; il che
fatto dopoi (à Dio piacendo) faremo fine.
page 434

In qual maniera si debba far giudicio de i Modi; & quelche si dè osser-
uare nelle Compositioni.Cap. XXX.
infinite le Cantilene di ciascun de i mostrati Modi; nondimeno molte di
loro si trouano, le quali sono composte ne i lor Modi semplici; ma ne i
Misti; Imperoche ritrouaremo il Quinto modo mescolato col Duodeci-
mo, il Decimo co 'l Primo, & cosi gli altri; come si può comprendere essaminando
le dette cantilene; massimamente quelle del Quinto modo, le quali in luogo della Ter-
za specie della Diapente E. &
 . posta nel graue, hanno la Terza della Diatessaron E.
. posta nel graue, hanno la Terza della Diatessaron E. & a; & in luogo della Terza della Diatessaron
 , & e, si troua la Seconda specie del-
, & e, si troua la Seconda specie del-la Diapente a, & e, posta nell'acuto; di maniera che se ben le dette specie sono contenu-
te sott'un'istessa Diapason, che è la E & e; nondimeno si troua in uno de i Modi trame-
zata harmonicamente, & tiene la forma del Quinto modo; & nell'altro arithmetica-
mente, & tiene la forma del Duodecimo; la onde udendosi tali specie tante & tan-
page 435te uolte replicate, non solamente la maggior parte della compositione uiene à non ha-
uer parte alcuna del Quinto, ma tutta la cantilena uiene ad esser composta sotto 'l Duode
cimo modo. Et che ciò sia uero, da questo si può comprendere, che se noi aggiungere-
mo queste due specie insieme, la Diatessaron E. & a, con la Diapente a. & e, collocan-
do questa nell'acuto, & quella nel graue; non è dubbio, c'haueremo la forma di cotal
Modo, contenuto tra la Terza specie della Diapason arithmeticamente mediata. Di ma
niera che quella compositione, che noi giudichiamo esser del Quinto modo, non uiene
ad hauer cosa alcuna, per la quale possiamo far giudicio, che sia tale, se non il fine; percio
che finisce nella Chorda E, il che è cosa molto fallace. Però adunque; se ben la Chorda
finale del Modo è quella; dalla quale (come dal fine & non auanti) dobbiamo far giu-
dicio della cantilena, com'alcuni uogliono; essendo ch'Ogni cosa da esso ò in esso dritta-
mente si giudica; non dobbiamo però intender, che per tal Chorda semplicemente noi
possiamo uenire in cognitione del Modo, sopra il quale è fondata la cantilena; percio-
che non si dè credere, che semplicemente da lei si debba far giudicio; ma che debbia-
mo aspettar tanto, che la cantilena sia condotta al fine, & iui giudicare, secondo il drit-
to; cioè secondo la sua forma; conciosia che allora la cantilena è perfetta, & hà la sua for
ma, dalla quale si prende la occasione di far tal giudicio. Ma si dè notare, che da due co
se si può pigliar simile occasione; prima dalla forma di tutta la cantilena; dopoi dal suo
fine; che è la sua Chorda finale. La onde essendo la Forma quella, che dà l'essere alla co
sa, giudicarei, che fusse ragioneuole, che non dalla Chorda finale semplicemente, come
hanno uoluto molti; ma dalla Forma contenuta nella cantilena, s'hauesse da far tal giu-
dicio. Onde hauendosi da giudicar la cantilena da tal forma; cioè, dal procedere, com'è
il douere; non è inconueniente, che 'l Modo principale possa finir nella Chorda mezana
della sua Diapason harmonicamente tramezata; & cosi 'l Modo collarerale nell'estreme
della sua Diapason arithmeticamente diuisa; lasciando da un canto la Chorda finale. Il
che quanto gentilmente si possa fare, si può comprendere dal canto. Si bona suscepimus de
manu Domini, composto da Verdeloto à cinque uoci, & dal canto. O Inuidia nemica di vir-
tute, composto medesimamente da cantare con cinque uoci da Adriano; i quali da un
capo all'altro l'uno hà il procedere dell'Vndecimo, & l'altro del Quarto modo; tuttauia
non finiscono nella loro uera Chorda finale, ma nella mezana. Et questo ch'io dico del
Quinto & del Duodecimo, si può anche mostrar ne gli altri modi, i quali per breuità
lascio da un canto. Per la qual cosa non è da marauigliarsi, se molte uolte non si ode al-
cuna differenza tra un Modo, che finisca nella Chorda E, & tra un'altro, che termini
nella a, poi che nella maniera, che s'è detto, si compongono misti; ma se si compones-
sero semplici; non è dubio, che si udirebbe tra l'uno & l'altro gran uarietà d'Harmonia.
Quando adunque haueremo da far giudicio, di qual si uoglia cantilena, haueremo da
considerarla molto bene dal principio al fine, & ueder sotto qual forma ella si troua esser
composta; se sotto la forma del Primo, ò del Secondo, ò di qualunque altro Modo; ha-
uendo riguardo alle Cadenze, le quali danno gran lume in tale cosa; & dopoi far giudicio;
ancora che non hauesse il suo fine nella sua propria Chorda finale, ma nella mezana, ouer'
in qualunque altra, che tornasse al proposito. Et se noi usaremo nelle Compositioni
una tal maniera di finire, non sarà fatto fuori di proposito; essendo che gli Eccle-
siastici anco hanno usato un tal modo nelle lor cantilene; come si può uedere nell'ul-
timo de i Κύριε ἐλέησον, i quali chiamano il Doppio minore, ouer de gli Apostoli; la
cui forma (com'è manifesto) è del Terzo modo; nondimeno finisce nella chorda a. laqua
le chiamano Confinale, & è la mezana delle Diapason D. & d, continente la forma
di cotal Modo; oltra che si troua l'Offertorio, che si canta nella Messa della Quarta feria
della Dominica terza di Quadragesima, Domine fac mecum, contenuto tra le sue Chorde
estreme F. & e. Et due cantilene, la prima delle quali è, Tollite hostias, contenuta tra le no-
minate Chorde estreme, che si canta fatta la Cōmunione della Messa della Dominica De
cima ottaua dopo la Pentecoste; la secōda è, Per signum Crucis, che si canta ne i giorni solen
page 436ni dell'Inuentione & Essaltatione di Santa Croce; & è contenuta tra le Chorde estre-
me F. & g. le quali cantilene tengono in se la Forma del Nono modo; percioche in esse si
troua la modulatione della sua Diapente G. & d. & della sua Diatessaron d. & g, & finisco
no nella Chorda
 , la quale è la mezana della detta Diapente. E' ben uero, ch'alcuni
, la quale è la mezana della detta Diapente. E' ben uero, ch'alcuni Moderni secōdo il lor parere) attribuiscono tali canti al Quartodecimo modo; ma di que-
sto lascierò far giudicio ad ogn'uno, c'habbia intelletto. Tali canti, in alcuni de i libri
moderni, si trouano trasportati nel graue per una Diapente senza l'aiuto della chorda b.
fuora delle loro chorde naturali; sia stata lor'ignoranza, ouer dapocagigne de i scrittori, ò
pur la presuntione d'alcuni poco intendenti; ma ne i buoni & corretti essemplari, de i
quali ne hò un appresso di me antico & scritto à mano, che si può ancora uedere & essa-
minare; si trouano tra le chorde nominate di sopra. Si dè però auertire, ch'io nomino la
forma del Modo, la Ottaua diuisa nella sua Quinta & nella sua Quarta, & anco queste due
parti, che nascono dalla diuisione harmonica & arithmetica, che si odono replicate mol
te fiate ne i proprii Modi. Quando adunque haueremo da comporre, potremo saper da
quel, che si è detto, il modo, c'haueremo da tenere nel far cantar le parti della cantile-
na; & nel por le Cadenze à i luoghi conuenienti per la distintione delle parole. Et simi-
gliantemente potremo saper quello, c'haueremo da fare nel giudicar'ogn'altra Compo-
sitione, sia poi in qual maniera si uoglia composta, tanto nel Canto fermo, quanto nel
Canto figurato.
Del modo che si hà da tenere, nell'accomodar le Parti della cantilena; & del-
l'estremità loro.Cap. XXXI.
porre, & nell'accommodar le parti nella Cantilena, che le fanno passar'alcu-
na uolta oltra modo nel graue, ouer nell'acuto, che non si possono cantar se
non con gran fatica; però accioche si leui in questa Arte tutti gli incommodi,
che possono occorrere, & si componi di maniera, ch'ogni Cantilena si possa cantar com-
modamente; mostrarò in qual modo le Parti si uenghino à commodar tra loro, & quanto
possino simigliantemente ascendere, ò discendere, & quanto l'estreme Chorde di cia-
cuna cantilena uogliono esser distanti l'una dall'altra. Dico adunque, che qualunque
uolta il Musico haurà proposto di comporre alcun canto; considerato prima ch'egli ha-
urà ben le Parole del Soggetto, dee dopoi eleggere il Modo conueniente alla loro natu-
ra. Ilche fatto osseruarà, che 'l suo Tenore procedi regolatamente modulando per le chor
de di quel modo, che si haurà eletto, facendo le Cadenze, secondo che ricerca la perfet
tione della Oratione, & il ne de i suoi Periodi. Et sopra 'l tutto cercarà con ogni dili-
genza di far, che tal Tenore sia tanto più regolato & bello, leggiadro & pieno di soauità;
quanto più che la cantilena si suol fondare sopra di lui; accioche uenga ad esser'il neruo
& il legame de tutte l'altre Parti; lequali debbono essere unite insieme in tal maniera & in
tal modo congiunte, che occupando il Tenore le chorde d'un Modo autentico, ò pla-
gale, il Basso sia quello, ch'abbraccia le chorde del suo compagno. Et se bene il Tenore
trappassasse oltra le chorde della Diapason continenti il Modo nel graue, ò nell'acuto per
una chorda, ouer per due; questo importarebbe poco; imperoche i Musici non curano,
che i Tenori, & l'altre parti de i lor Modi siano perfetti, ouero imperfetti, ò soprabon-
danti; pur che le parti siano commodate bene alla modulatione, di maniera che faccino
buona harmonia. Sarebbe il douere che ciascuna di esse non passasse più d'otto Chorde,
& stesse raccolta nelle Chorde della sua Diapason; ma perche torna alle uolte cōmodo grā
demente à i Cōpositori il passar più oltra; però questo attribuiremo più tosto ad una cer
ta licēza, che si pigliano, ch'alla perfettione della cosa. Le parti però debbono esser'ordina
page 437te in tal maniera, che fondando il Modo, sopra il quale si compone la cantilena, nel Teno
re; se 'l Modo occuparà in tal parte le chorde dell'Autentico; com'hò detto; il Basso con-
tenga nelle sue il Modo collaterale, ò plagale. Cosi per il contrario, se 'l Tenore occupa-
rà nelle sue Chorde il Modo plagale, il Basso uenghi à contenere l'Autentico; di manie-
ra, che quando saranno collocate in tal maniera, l'altre poi s'accommodaranno ottima-
mente, senz'alcun incommodo della cantilena. La onde si dè auertir di far, che le chor-
de estreme del Basso non siano più distanti dall'estreme del Tenore, di una Diatessaron,
ouer per una Diapente; ancora che non sarebbe errore, se passassero più oltra per un'altra
Chorda. Stando poi in tal guisa legati il Basso col Tenore, sarà facil cosa di porre al suo
luogo, & collocar nella cantilena l'altre parti; imperoche le Chorde estreme del Soprano
si porranno con l'estreme del Tenore distanti per una Diapason; & cosi tanto il Tenore,
quanto il Soprano uerranno à cantar nelle chorde del Modo autentico. Simigliantemen
te si porranno quelle dell'Alto con quelle del Basso distanti per una Diapason; & queste
parti uerranno collocate in tal maniera, ch'occuparāno le chorde del Modo plagale. Col-
locate adūque in tal guisa, il Soprano tenerà il luogo più acuto della cantilena; & il Basso
il più graue; & il Tenore & l'Alto saranno le parti mezane con questa differenza però;
che le chorde dell'Alto saranno più acute di quelle del Tenore per una Diatessaron, poco
più, ò poco meno. Et tanto saranno le chorde estreme del Soprano lontane da quelle del
l'Alto, quanto quelle del Tenore da quelle del Basso. Et benche (com'hò detto) tali Par
ti si possino estender alle uolte per una chorda nel graue & anche nell'acuto; & per due an
co & più (se fusse dibisogno) oltra le loro Diapason; tuttauia si debbe cercare, che le par-
ti cantino commodamente, & che non trapassino la Decima, ouer la Vndecima chorda
ne i loro estremi; essendoche uerrebbono ad esser sforzate, faticose, & difficili da cantarsi
per la loro ascesa & discesa. Si debbe oltra di ciò auertire, che 'l Basso non si estenda mol-
to fuori delle Chorde della sua Diapason continenti il Modo nel graue; ne 'l Soprano me
desimamente nell'acuto; percioche questo sarebbe cagion di far che la cantilena si fareb
be estrema; la onde ne seguitarebbe discommodo grande à i cantanti. Debbe adunque
fare il Compositore, che computando l'estrema chorda graue del Basso della cantilena,
con l'estrema acuta del Soprano, non trappassi la Decimanona; ancora che non sarebbe
molto incommodo, quādo s'arriuasse alla Ventesima, ma nō più oltra; percioche osseruan
dosi questo, le Parti resteranno ne i lor termini, & saranno cantabili senza fatica alcuna.
Et perche alle uolte si suol comporre senza 'l Soprano, & tal maniera di comporre si chia-
ma da i Prattici comporre à uoci mutate; ouer componendo solamente più Tenori & il
Basso, lo chiamano comporre à uoci pari; però uoglio, che si sappia, che nelle prime com-
positioni si piglia il Contralto in luogo del Soprano, & l'altra parte uiene ad esser conte-
nuta tra l'istesse chorde del Contralto, ouer nelle chorde del Tenore; di maniera che tal cā
tilena uiene ad esser cōposta con due Contralti, ouer cō tre Tenori. E' ben uero, che si hà
rispetto alla parte, che si piglia per il Soprano; percioch'è alquāto più acuta sempre di quel
la, che si piglia per l'Alto; essendo che questa procede in una maniera alquanto piu rimes
sa. Ma sia come si uoglia, bisogna compor le parti della cantilena in tal guisa, che i lor
estremi non passino oltra la Quintadecima chorda; connumerando l'estrema graue, &
l'estrema acuta. E se altre parti s'aggiungessero oltra le quattro nominate, come si è det-
to nel Cap. 65. della Terza parte; non si potrebbono aggiungere in altra maniera, se non
raddoppiando l'una di esse; & si chiamarebbe Tenor secondo, ò Secondo Basso; & cosi di
co dell'altre; & sempre quella parte, che continuasse di star piu nell'acuto, che nel graue;
& arriuasse più in alto dell'altre; quella ueramente si potrà chiamar Soprano. Ma si dè
auertire, che le Chiaui de i Soprani, & de i Tenori in tutti i Modi, si scriuono, & accommo
dano, come si è mostrato di sopra ne gli essempij di ciascun Modo; & quelle de i Bassi s'ac-
commodano di maniera, che le lor Chorde possino esser (come hò detto) distanti da quel
le de i Tenori per una Diatessaron, ouer per una Diapente; il che dico etiandio de i So-
prani da quelle de i Contralti. Et si dè auertire ancora, che nel principio delle Seconde
page 438parti delle cantilene, le parti ch'incominciano à cantar sole, ripiglino le lor modulatio-
ni sopra una Chorda d'alcun principio regolare del Modo, sopra il quale è fondata la can
tilena; ouer sopra qualunque altra Chorda, pur che ella sia Chorda naturale di tal Mo-
do; perche non è lodeuole, che nel fine d'alcuna prima parte termini il Contralto, ò Te-
nore, ò Soprano sopr'una Chorda; come sarebbe dire sopra la
 ; & nella Seconda parte
; & nella Seconda parte dia principio sopra la Chorda b; ò per il contrario. Sarà adunque auertito il Composito
re di tal cosa, accioche la sua compositione sia purgata da ogni errore & da ogni discom
modo; & lui sia riputato buono & perfetto Musico.
In qual maniera l'Harmonie s'accommodino alle soggette Parole.
Cap. XXXII.
niera si debba accompagnar l'Harmonie alle soggette Parole. Dico accompa
gnar l'Harmonie alle Parole, per questo; perche se bene nella Seconda parte
(secondo la mente di PlatoneDe rep. 3.) si è detto, che la Melodia è un composto
d'Oratione, d'Harmonia, & di Numero; & par che in tal compositione l'una di que-
ste cose non sia prima dell'altra; tuttauia pone l'Oratione, come cosa principale, &
l'altre due parti, come quelle che seruono à lei; percioche dopo che hà manifesta-
to il tutto col mezo delle parti dice; che l'Harmonia & il Numero debbono seguitar
l'Oratione; & ciò è il douere; imperoche se nell'Oratione, ò per uia della narratione
ò della imitatione (cose, che si trouano in lei) si può trattare materie, che siano allegre
ò meste; oueramente graui, & anco senz'alcuna grauità; simigliantemente materie ho-
neste, ouer lasciue: fà dibisogno, ch'ancora noi facciamo una scielta d'Harmonia & di un
Numero simile alla natura delle materie, che sono contenute nell'Oratione; accioche dal
la compositione di queste cose messe insieme con proportione, risulti la Melodia secon-
do 'l proposito. Et ueramente dobbiamo auertire à quello che dice Horatio nella Epi-
stola dell'arte poetica, quando dice;
Versibus exponi Tragicis res Comica non uult:
Et anco Ouidio in questo proposito dice.Lib. 1. de
rem. Am.
Callimachi numeris non est dicendus Achilles,
Cydippe non est oris Homere tui.
Percioche se non è lecito tra i Poeti comporre una Comedia con uersi Tragici; non sa
rà anco lecito al Musico daccompagnar queste due cose; cioè, l'Harmonia & le Parole
insieme, fuor di proposito. Non sarà adunque conueniente, ch'in una materia allegra
usiamo lHarmonia mesta & i Numeri graui; ne doue si tratta materie funebri & piene di
lagrime, è lecito usar'un'Harmonia allegra & Numeri leggieri, ò ueloci, che li uoglia-
mo dire. Per il contrario bisogna usar l'Harmonie allegre, & i Numeri ueloci nelle ma-
terie allegre, & nelle materie meste l'Harmonie meste, & i Numeri graui; accioch'ogni
cosa sia fatta con proportione. Il che penso, che ciascun saprà fare ottimamente,
quando haurà riguardo à quel, c'hò scritto nella Terza parte, & considerato la natura
del Modo, sopra 'l quale uorrà comporre la cantilena. Et debbe auertire d'accom-
pagnare, quanto potrà, in tal maniera ogni parola, che doue ella dinoti asprezza,
durezza, crudeltà, amaritudine, & altre cose simili, l'Harmonia sia simile à lei; cioè,
alquanto dura, & aspra; di maniera però che non offendi. Simigliantemente quando
alcuna delle parole dimostrerà pianto, dolore, cordoglio, sospiri, lagrime, & altre cose si-
mili; che l'Harmonia sia piena di mestitia; ancora che questo d'alcuni moderni Aristarchi
sia biasimato: ma di questo si ueda il cap. 11. del lib. 8. de i Sopplimenti. Il che farà ottima
mente, uolēdo esprimere i primi effetti, quando usarà di por le parti della cantilena, che
page 439procedino per alcuni mouimenti senza 'l Semituono; come sono quelli del Tuono, &
quelli del Ditono; facendo udire la Sesta, ouer la Terzadecima maggiori, che per loro na
tura sono alquanto aspre, sopra la chorda più graue del concento; accompagnandole an
co con la Sincopa di Quarta, ò di Vndecima sopra tal parte, con mouimenti alquanto
tardi, tra i quali si potrà usar'etiandio la sincopa della Settima. Ma quando uorrà espri-
mere i secondi effetti, allora usarà (secondo l'osseruanza delle Regole date) i mouimenti,
che procedono per Semituono, & per quelli del Semiditono, & altri simili; usando spes-
so le Seste, ouer le Terzedecime minori, sopra la chorda più graue della cantilena, che
sono per natura loro dolci & soaui; massimamente quando sono accompagnate con i de
biti modi, & con discretione & giudicio. Ma si debbe auertire, che la cagione d'espri-
mere simili effetti non s'attribuisce solamente alle predette consonanze poste in tal ma-
niera; ma etiandio à i mouimenti, che fanno cantando le parti; i quali mouimenti sono
di due sorti, Naturali & Accidentali. I Naturali sono quelli, che si fanno tra le chorde
naturali della cantilena, oue non intrauiene alcun segno, ò chorda accidentale, & que-
sti mouimenti hanno più del uirile, che quelli, che si fanno col mezo delle chorde acci-
dentali segnate con tali segni
 . & b; i quali sono ueramente accidentali, & hanno alquan
. & b; i quali sono ueramente accidentali, & hanno alquanto del languido, da i quali nasce similmente una sorte d'Interualli, chiamati Acciden-
tali; ma da i primi nascono quelli Interualli, che si chiamano Naturali. La onde dob-
biamo notare, che i primi mouimenti fà la cantilena alquanto più sonora, & uirile; & li
secondi più dolce, & alquanto più languida. Per il che i primi potranno seruire ad
esprimere i primi effetti; & li secondi mouimenti potranno seruire à gli altri; di maniera
che accompagnando gli Interualli delle maggiori & delle minori consonanze, con li
mouimenti naturali & accidentali, che fanno le parti con qualche giudicio; si uerrà ad
imitare le parole con la ben'intesa harmonia. Quanto poi all'osseruanza de i Numeri,
considerata primieramente la materia contenuta nell'Oratione; se sarà allegra, si dè
procedere con mouimenti gagliardi & ueloci; cioè, con Figure, che portano seco uelo-
cità di tempo; come sono le Minime & le Semiminime; ma quando la materia sarà
flebile, si dè procedere con mouimenti tardi & lenti; come n'hà insegnato Adriano ad
esprimere l'uno & l'altro modo in più cantilene, tra le quali si troua queste: I vidi in ter-
ra angelici costumi: Aspro core e seluaggio: Oue ch'i posi gli occhi; tutte composte à sei uoci;
& Quando fra l'altre donne: & Giunto m'ha Amor, à cinque uoci; & infiniti altri. Et
questo non solamente si dè osseruare intorno i Numeri, ancora che gli Antichi inten-
dessero tal cosa in un'altra maniera, di quello, che fanno i Moderni; come si uede chia-
ramente in molti luoghi appresso di Platone; ma etiandio dobbiamo osseruar, di accom
modare in tal maniera le parole dell'Oratione alle figure cantabili, con tali Numeri,
che non si oda alcun Barbarismo; come quando si fà proferire nel canto una sillaba lon
ga, che si douerebbe far proferir breue; ò per il contrario una breue, che si douerebbe far
proferir longa; come in infinite cantilene si ode ogni giorno; ilche ueramente è cosa uer-
gognosa. Ma di questa cosa si dee ad ogni modo molto ben considerate quello che si è
detto nel cap. 13. dell'Ottauo libro de i Sopplimenti: acciò le cose passimo bene; & non
si commetta errore ueruno. Ne si ritroua questo uitio solamente ne i Canti figurati, ma
anco ne i Canti fermi; com'è manifesto à tutti coloro, che hanno giudicio, conciosia
che pochi sono quelli, che non siano pieni di simili barbarismi, & che in essi infinite
uolte non si odi proferire le penultime sillabe di queste parole Domìnus, Angèlus,
Filìus, Miracùlum, Glorìa, & molt'altre, che sono breui, & passano presto, con lon-
ghezza di tempo; ilche sarebbe cosa molto lodeuole, & tanto facile da correggere,
che mutandoli poco poco, si accommodarebbe ottimamente la cantilena, ne per
questo mutarebbe la sua prima forma; essendo che consiste solamente nella Legatu-
ra di molte figure, ò note, che si pongono sotto le dette sillabe breui, senz'alcun pro-
posito fatto lunghe; quando sarebbe sofficiente una sola figura. Si debbe similmen-
te auertire, di non separare le parti della Oratione l'una dall'altra con Pause; co-
page 440me fanno alcuni poco intelligenti; fino à tanto, che non sia finita la sua Clausula, ouer
alcuna sua parte, di maniera che 'l sentimento delle parole sia perfetto; & di non far la
Cadenza, massimamente l'una delle principali; ò di non porre le Pause maggiori di
quelle della Minima, se non è finito 'l Periodo, ò la sentenza perfetta dell'Oratione;
& di non por quella di Minima ne i punti mezani; percioche ueramente è cosa uitiosa;
la quale quanto sia osseruata d'alcuni Prattici poco aueduti de nostri tempi, ciascuno che
uorrà por mente à tal cosa, lo potrà con facilità uedere & conoscere. Debbe adunque
il compositore in cose simili aprir gli occhi, & non li tenir chiusi; percioche è di molta
importanza; accioche non sia riputato ignorante d'una cosa tanto necessaria; & deb-
be auertire di porre la Pausa di Minima, ò di Semiminima (come li torna commodo)
in capo de i mezani punti dell'Oratione; percioche seruiranno in essa per i Comma; ma
in capo de i Periodi potrà porre quanta quantità de pause, ch'ei uorrà; percioche
mi pare, che poste in cotal maniera, si potrà ottimamente discernere i membri del
Periodo l'un dall'altro; & udir senz'incommodo alcuno il sentimento perfetto del-
le Parole.
Il modo, che si hà da tenere, nel por le Figure cantabili sotto le Parole.
Cap. XXXIII.
han tenuto molti Prattici, & quanta confusione hanno fatto nellaccommo-
dar le Figure cantabili alle parole dell'Oratione proposta? se non con gran
difficultà. Però quand'io mi penso ch'una Scienza, la quale hà dato leggi &
buoni ordini all'altre, sia in alcune cose tanto confusa, che à pena si può tollerare, io non
posso fare, che non mi dolga; percioche è ueramente un stupore, l'udire & il uedere al-
cune cantilene, le quali oltra che in esse si odono, nel proferir delle parole, i Periodi con
fusi, le Clausule imperfette, le Cadenze fuor di proposito, il Cantar senza ordine, gli
errori infiniti nell'applicare l'Harmonie alle parole, le poche osseruationi de i Modi, le
mal'accommodate parti, i passaggi senza uaghezza, i Numeri senza proportione, i Mo-
uimenti senza proposito, le Figure ne i Tempi & Prolationi mal numerate, & infinitaltri
disordini; si troua anco in esse le Figure cantabili accommodate in tal maniera alle paro-
le, che 'l Cantore non si sa risoluere, ne ritrouar modo commodo, da poterle proferire.
Hora uede sotto due Sillabe contenersi molte figure, & hora sotto due figure molte silla-
be. Ode hora una parte, che cantando in alcun luogo farà l'Apostofe, ò collisione nel-
le lettere uocali, secondo che ricercano le Parole; & uolendo lui far l'istesso cantando la
sua parte, gli uiene à mancar il bello & l'elegante modo di cantare, col porre una figu-
ra, che porta seco il tempo lungo sotto una sillaba breue; & cosi per il contrario. La onde
tallora ode proferire nell'altre parti quella sillaba lunga, che nella sua necessariamente gli
è dibisogno di proferirla breue, di maniera che sentendo tanta diuersità, non sà che si fa-
re; ma resta in tutto attonito & confuso. Et perche 'l tutto consiste nell'accommodar le
Figure cantabili alle soggette parole; & nelle cantilene si ricerca, che le chorde, siano
con esse descritte & notate, accioche i Suoni & le Voci si proferiscano bene in ogni mo-
dulatione; essendo che col mezo di tal Figure si uiene à proferire il Numero; cioè, la lun
ghezza & la breuità delle sillabe contenute nell'Oratione, sotto le quali sillabe spesse uol-
te si pone non solamente una, due, tre; ma più delle nominate figure, secondo che ricer
cano gli Accenti posti nell'Oratione proposta; però accioche non intrauenga confusio-
ne alcuna nell'accommodarle alle Sillabe & alle parole; uolendo leuare (s'io potrò)
tanto disordine; oltra le date Regole in diuersi luoghi, che sono molte, accommodate
alle materie secondo 'l proposito, porrò hora queste, le quali seruiranno non solo al Com
page 441positore; ma anche al Cantore; & saranno secondo 'l nostro proposito. La Prima Rego-
la adunque sarà, di por sempre sotto la sillaba longa, ò breue una figura conueniente, di
maniera, che non si odi alcun Barbarismo; percioche nel Canto figurato ogni figura can-
tabile, che sia distinta, & non legata (dalla Seminima & tutte quelle che sono di lei mino-
ri in fuori) porta seco la sua sillaba; ilche si osserua etiandio nel Canto fermo; essendo
ch'in ogni figura quadrata si accommoda la sua sillaba; eccettuandone alcune volte le
mezane, che si mandano come le Minime, & anche come le Semiminime; ilche si com-
prende in molte cantilene, & massimamente nella cantilena del Symbolo Niceno, Credo
in vnum Deum, ilquale chiamano Cardinalesco. La Seconda regola è, che ad ogni Le-
gatura di più figure, ò note, sia posta nel canto figurato, ò nel piano, non se le accommoda
più d'una sillaba nel principio. La Terza, ch'al Punto, ilqual si pone vicino alle figure
nel canto figurato, ancora che sia cantabile, non se gli accommoda sillaba alcuna. La
Quarta, che rare volte si costuma di por la sillaba sopra alcuna Semiminima; ne sopra
quelle figure, che sono minori di lei; ne alla figura, che la segue immediatamente. La
Quinta, che alle figure, che seguono immediatamente i Punti della Semibreue & della
Minima, le quali non sono di tanto valore, quanto sono cotali Punti; come la Semimi-
nima dopo 'l punto della Semibreue, & la Chroma dopo 'l punto della Minima; non si
costuma d'accompagnarle alcuna sillaba; & cosi à quelle, che seguono immediatamente
tali figure. La Sesta, quando si porrà la sillaba sopra la Seminima, essendo bisogno, si
potrà anco porre un'altra sillaba sopra la figura seguente. La Settima che qualunque fi-
gura, sia qual si uoglia, che sia posta nel principio della cantilena, ò sia nel mezo dopo
alcuna pausa, di necessità porta seco la pronuntia d'una sillaba. La Ottaua, che nel Can-
to piano non si replica mai parola, ò sillaba; ancora che si odino alle uolte alcuni, che lo
fanno, cosa ueramente biasimeuole; ma nel figurato tali repliche alle fiate si comporta-
no; non dico già d'una sillaba, ne d'una parola; ma d'alcuna parte dell'Oratione, quan-
do 'l sentimento è perfetto; & ciò si può far, quando ui sono figure in tanta quantità, che
si possino replicar commodamente; ancora che 'l replicar tante fiate una cosa (secondo 'l
mio giudicio) non stia troppo bene; se non fusse fatto, per isprimere maggiormente le
parole, che hanno in se qualche graue sentenza, & fusse degna di consideratione. La
Nona, che dopo l'hauer'accommodato tutte le sillabe, che si trouano in un Periodo, oue-
ro in una parte dell'Oratione, alle figure cantabili; quando resterà solamente la penul-
tima sillaba & l'ultima; tale penultima haurà questo priuilegio, che potrà hauer'alquan-
te delle figure minori sotto di se; come sono due, ò tre, & altra quantità; purche la det-
ta penultima sillaba sia longa & non breue; percioche se fusse breue, si uerrebbe à com-
mettere il Barbarismo; il perche cantando in tal modo si uiene à far quello, che molti
chiamano Neuma; che si fà, quando sott'una sillaba si proferisce molte figure; ancora che
essendo poste cotali figure in tal maniera, si faccia contra la Prima regola data. La De-
cima & Vltima regola è, che la sillaba ultima dellOratione dè terminare, secondo l'os-
seruanza delle date Regole, nella figura ultima della cantilena. Ma perche in questa ma-
teria si potrà hauer'infiniti essempi, essaminando le compositioni d'Adriano, & de quel-
li, che sono stati & sono suoi discepoli, & sono osseruatori delle buone Regole; però sen-
za mostrare altro essempio passarò à ragionar delle Legature, che si fanno con alcune
delle figure cantabili, & seruono ad un tale negotio.
Delle Legature.Cap. XXXIIII.
percioche tornano commode non solamente à i Compositori nell'accommodar
le figure, ò note cantabili alle sillabe dell'Oratione proposta; ma anco perche al-
le uolte pigliano per Soggetto un'Antifona di canto fermo, nella quale entrano molte
page 442figure legate, sopra la quale uolendo fondar la cantilena, & uolendola imitare, li fà dibi-
sogno, che nel medesimo modo vsino le dette Legature; non però tutte, percioche alle
uolte torna discommodo; ma si bene alcune; ne anche con quelle istesse figure, ma con
diuerse, secondo che pare al compositore. Però accioche shabbia piena cognitione di
tal cosa, & si sappia in qual maniera si habbiano da fare; & quali figure si habbiano da
legare, & quanto sia il lor ualore, trattaremo di esse al presente; ma prima è da ueder
quello, che sia Legatura. Dicono i Prattici, che la Legatura è una certa colligatione, ò
congiuntione di due, ouero più semplici figure cantabili; fatta con tratti, ò lineamenti
conuenienti; nella quale si forma ciascuna Figura, che si può legare, di corpo quadra-
to, ouer'obliquo. Et la Legatura si fà con tre sorti di figure; con la Massima, con la Lun-
ga, & con la Breue; delle quali le due estreme, la Massima & la Breue uariano il lor ualo-
re, secondo che sono diuersamente legate, & secondo i uarij accidenti, che riceuono;
la onde la Massima è figura passiua; sottoposta alla diminutione del suo ualore, & non
può mai esser'accresciuta; & la Breue è similmente passiua; conciosiache può esser'accre-
sciuta & diminuita, secondo 'l modo, ch'è posta, & secondo il luogo che tiene nella Le-
gatura; ma la Longa non è sottoposta à cotal cosa, essendo che non riceue augumento,
ne discressimento alcuno; & questo, perche sempre si pone nella Legatura senz'alcuna
uariatione della sua forma; sia posta da qual parte si uoglia. Ogni Legatura si considera
in due maniere; prima quando la figura seguente è posta più in alto dell'antecedente,
onde è detta Ascendente; dopoi per il contrario, quando l'antecedente è posta più in
alto della seguente, & si chiama Discendente. E' ben uero, che si suol fare una Lega-
tura, le cui figure sono legate ascendenti & discendenti, come uederemo; la onde si dè
auertire, che la Massima si pone nella Legatura in due maniere; prima secondo la sua ue-
ra forma, cioè, col corpo lungo dritto; dopoi col corpo lungo obliquo, ò ritorto, che
dir lo uogliamo. Quando si pone senza l'obliquo, si pone in due maniere; prima con
la coda, ò gamba, che la uogliamo chiamare, della parte destra; ouer si pone senza;
& posta in cotali maniere, sia nel principio, ò nel mezo, ò nel fine della Legatura, sem-
pre resta nel suo ualore; cioè, uale due Lunghe, ouer quattro Breui; dopoi si pone ob-
liqua simigliantemente in due modi; percioche, ouer che ascende dal graue; cioè, dal-
la sua prima parte, ch'è quella, ch'è posta à banda sinistra, all'acuto, con la sua secon-
da parte; la quale si chiama quella, che è posta alla banda destra; oueramente che dal-
l'acuto, cioè, della sinistra discende alla destra nel graue; & questo in due maniere; ha-
uendo la gamba dalla sinistra parte, ouer essendo senza. S'è posta con la gamba; ouer
l'hà all'ingiù; oueramente l'hà all'insù. Quando hà la gamba all'ingiù, & è obliqua uer-
so 'l graue; tanto la sua prima parte, quanto la seconda uale una Breue; cosi ancora
quando è obliqua all'insù; ancora che questa poco sia in uso. Ma quando hà la gamba
uoltata insuso, & è similmente obliqua, tanto uerso 'l graue, quanto uerso l'acuto (se
ben questa anco non si usa) sempre la prima & la seconda parte di ciascuna da per sè ua-
gliono vna Semibreue. Quando poi tali oblique non hanno la gamba; se la sua secon-
da parte uà uerso 'l graue, la prima parte uale una Lunga, & la seconda una Breue; ma
quando uà uerso l'acuto; il che più non usano i Musici di fare; tanto la prima, quanto
la seconda parte; ciascuna da per se uale una Breue; & ciò s'intende, quando non sono
accompagnate, ò legate con altre figure; percioche quando sono accompagnate, ò le-
gate, si hà altra consideratione. In quanto alla Breue dico, che si troua collocata in det-
te Legature in due modi; cioè, con la gamba, & senza. Quando hà la gamba, si troua
di due maniere; con la gamba della parte sinistra uolta in giù, & con la gamba uoltata
in sù; di modo che posta nella Legatura in cotal maniera si fà altra consideratione; im-
peroche Ciascuna figura, che si può legare, si pone nella Legatura in tre modi; nel prin-
cipio, nel mezo & nel fine; & cosi dal principio, dal mezo, & dal fine si conosce il ualo-
re delle parti di ciascuna Legatura. Volendo adunque hauer cognitione perfetta del
ualore di qual si uoglia figura, posta nella Legatura; si danno molte Regole, la Prima
page 443delle quali è; Ogni massima che sarà obliqua all'in giù, & sarà senza gamba; haurà la sua
prima parte; che sarà di ualor d'una lunga. Ma hò detto Prima parte; percioche quella
è ueramente Prima d'una figura, che per la sua obliqua nel principio sia posta sopra una
chorda della cantilena, & nel fine ne occupa un'altra diuersa, com'è ueramente il proprio
della Massima obliqua; habbia poi la gamba uoltata all'insù, ò all'ingiù, ò sia anco senza.
La Seconda regola è; Ogni figura quadrata senza gamba, posta nel principio della Lega-
tura; dalla quale ne discenda un'altra; tal Figura sempre è di ualor d'una Lunga. La Ter-
za Regola è; ch'ogni Prima figura quadrata, ò prima parte d'alcuna figura obliqua;
laquale habbia la gamba dalla parte sinistra uoltata all'ingiù; sempre è di ualor d'una Bre
ue. La Quarta; Quando alcuna figura senza gamba è posta nel principio, & la seconda
che segue ascende, è tal figura di ualor d'una Breue. La Quinta; Ogni figura posta nel
principio di qualunque Legatura si sia, la qual'habbi la gamba uoltata all'insù à banda
sinistra, ascendendo, o discendendo la seconda, sia poi quadrata, ouer obliqua; tanto lei,
quanto la seguente sempr'è di ualor d'una Semibreue; come si può uedere. Et queste Re
gole siano dette intorno le Prime figure: ma intorno le mezane s'ha d'hauere altra conside
ratione; imperoche tutte le Figure mezane, siano quadrate, ouer oblique; dalla mostra
ta seconda Semibreue in fuori; sempre saranno di ualore d'una Breue. L'ultime poi,
quando saranno la seconda parte d'alcuna Obliqua senza gamba ascendente ò discen-
dente: ò se pur haurà la gamba dalla sinistra parte ingiù; sempre sarà di ualor d'una Bre-
ue. Et le figure quadrate, che discenderanno da qual si uoglia prima, ò mezana Figura;
tutte saranno di ualore d'una Lunga. L'ultime poi, quando saranno quadrate, & discen-
deranno da qual si uoglia figura; saranno tutte di ualor d'una Lunga. Et se saranno la secon
da parte d'alcuna Obliqua tanto ascendente, quanto discendēte c'habbia la gamba ingiù
ò senza dalla sinistra parte sempre sarà del ualor d'una Breue. Ma quando da qual si uoglia
legatura sarà ascendente, il suo ualor sarà sempre d'una Breue, come anco sarà la seconda
parte dell'Obliqua legata discendēte. Ma se discenderanno da una quadrata ouer da qual
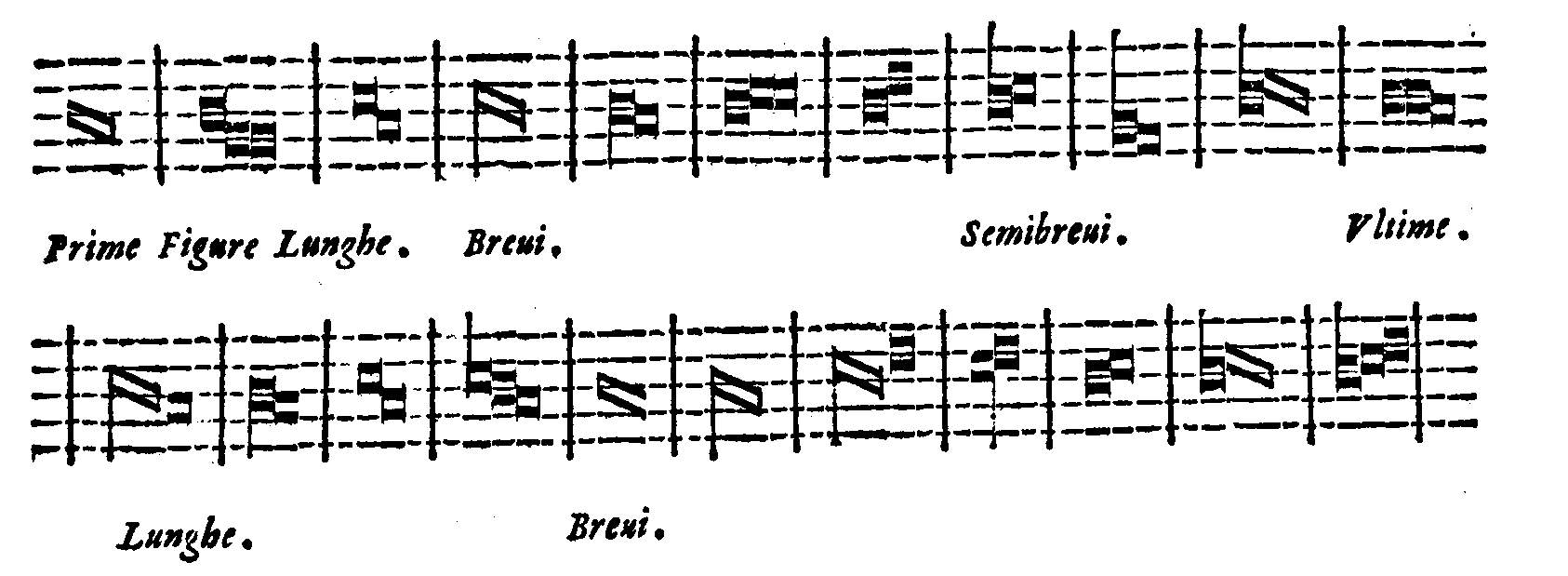
Bisogna però auertir tre cose; la prima, che 'l ragionamento de tali Figure è stato intorno
la Forma del corpo loro, & non intorno ad altro accidente; la Seconda, che qual si uoglia
figura posta nelle nominate Legature è sottoposta à quelli istessi accidenti, che sono sot-
toposte le Figure semplici non legate; quantunque alcuni habbiano tenuto il contrario;
ma la Terza è, che ciascheduna Legatura (come hò detto altroue) contenerà interamen
te i suoi tempi, che rappresentano; tanto quando sono sottoposte al tempo perfetto,
quanto all'imperfetto; pur che non siano alterate della sua natura per qualche acciden-
te, di maniera che nel Tempo perfetto, se quella Nota, che è posta prima nella Lega-
tura di tre Note, come quella che è posta ultima nell'essempio; ualerà una Semibreue,
l'altra uerrà à ualerne due, cioè una Breue imperfetta; percioche sempre s'intenderà esser
page 444alterata; Et la sequente terza sempre sarà perfetta; pur chenon sia fatta imperfetta per
qualche accidente; percioche bisogna che si troua in essa i tempi perfetti, & il numero
Ternario: onde le mezane uarranno sempre una Breue perfetta, & l'ultima sempre sarà
etiandio perfetta; pur che da qualche altro accidente non siano fatte imperfette; ma
nel Tempo imperfetto si considerano i Tempi perfetti, & il numero Binario. Et perche
tal Legature (come io credo) sono state ordinate in tal maniera dal Primo inuentore, &
appreciate d'una certa quantità, secondo i diuersi modi delle figure poste in esse, & se-
condo i luoghi differenti, come gli è paruto; però ciascun si potrà contentare, di quanto
hò parlato intorno ad esse; non cercando per qual cagione ei habbia uoluto appreciar
più l'una, che l'altra; & porre in ordine tal Legature più in una maniera, che in un'al-
tra; percioche sarebbe cosa uana & superflua; poi che poco importa il saperlo & non
saperlo.
Quel che dè hauer ciascuno, che desidera di venire à qualche perfettione nel-
la Musica.Cap. XXXV.
di queste mie fatiche; auanti ch'io concluda questo ragionamento, uoglio
che uediamo due cose; l'una delle quali sarà; Che noi mostriamo quelle cose,
che richiedono ad uno, che desidera di peruenire all'ultimo grado di questa
Scienza; l'altra, Che noi diciamo, che nel far giudicio delle cose della Musica, non dob-
biamo attribuire tal giudicio in tutto al Senso, percioche è fallace; ma si bene accom-
pagnarli la Ragione; come habbiamo dimostrato nel Cap. 13. del Primo libro De i Sop-
plimenti; secondo il consiglio di due eccellentissimi Musici & Filosofi, Aristosseno & To-
lomeo; conciosiache essendo queste due parti insieme aggiunte concordi, non è dubbio,
che non si potrà commettere alcun'errore, & si farà il giudicio perfetto. Incomincian-
do adunque dalla prima dico; che colui, il quale desidera di uenire à quella perfettione
delle cose della Musica, alla qual si può arriuare; & di ueder tutto quello, che n'è per-
messo in cotale Scienza; fà dibisogno, c'habbia in sè molte cose; accioche facilmente
possa uenire in cognitione di quelle, che sono à molti occulte in questa facultà, senza
l'altrui mezo; delle quali quando una ne mancasse, non potrebbe sperar, di poter'arri-
uare à quel segno, dou'ei hauea dissegnato. La onde è da sapere, che essendo la Musica
scienza subalternata alla Arithmetica; come hò dichiarato nel Cap. 20. della Prima par-
te; perche le forme delle Consonanze sono contenute sott'alcune proportioni determi-
nate, le quali sono comprese ne i Numeri, per poter'haueria ragione de tutti quelli acci-
denti, che accascano intorno di esse; è dibisogno, che sia bene istrutto nelle cose del-
l'Arithmetica, nel maneggio de i Numeri & delle Proportioni; oueramente, che uolen-
do da queste mie fatiche imparar quelle cose, che sono solamente dibisogno à tal nego-
tio; almeno sappia il maneggio de i Numeri mercanteschi; accioche uenendo all'uso del-
le Proportioni, trattate nella Prima parte; possa hauer facilmente quello, che desidera.
Et perche le ragioni de i Suoni non si possono sapere, se non col mezo de i Corpi sonori,
che sono Quantità, che si può diuidere; & sono ueramente quelli, che danno la Materia
delle Consonanze; però fà dibisogno, che sia istrutto nelle cose della Geometria; oue-
ramente, che sappia almeno adoperar bene il Compasso, ò Sesto nel diuidere una linea;
& sappia quello, ch'importi un Punto, una Linea; sia ritorta, ouer dritta; una Superfi-
cie, un Corpo, & altre cose simili, ch'appartengono alla Quantità continua; accioche
nelle sue speculationi, possa con più facilità hauer'aiuto da questa Scienza, nel diuider
qual si uoglia Quantità sonora; come si è dimostrato nella Seconda parte. Debbe anco,
se non perfettamente, almeno mediocremente saper sonar di Monochordo, ò Arpi-
chordo; & questo perche è il più perfetto, & il più stabile ne gli accordi d'ogn'altro
page 445Istrumento; accioche possa da quello, hauer cognitione de gli Interualli sonori conso-
nanti & dissonanti, & possa ridurre alle uolte in atto quelle cose, ch'ogni giorno uà ritro-
uando di nuouo; & farne la proua per sapere inuestigar con la proua in mano le Passio-
ni proprie de i Numeri sonori. Ma questo presuppone, ch'ei sappia accordar perfetta-
mente cotale Istrumento; & c'habbia l'Vdito perfetto; accioche possa conoscere & di-
scernere ogni picciola differentia tra suono; & suono uolendo inuestigar (come accade al-
le uolte) molte differenze de gli Interualli; & possa far giudicio perfetto, senza commet-
ter'errore; & uolendo accordar'ogn'altro Istrumento, sappia quel, che bisogna opera-
re. Fà dibisogno etiandio, che sia istrutto nell'Arte del Cantare principalmente, & nel-
l'Arte del Contrapunto, ouer Comporre, & che n'habbia buona intelligenza; accioche
sappia porr'in atto tutto quello, che occorre nella Musica; & sappia farne giudicio, se è
riuscibile, ouer non; percioche il porre in esser le cose della Musica, non è altro vera-
mente, che il ridurle nel loro vltimo fine, & nella loro perfettione; come intrauiene
etiandio nell'altre Arti & nell'altre Scienze, che hanno in sè queste due parti, la Specu-
latiua & la Prattica; come è la Medicina. Non lasciarò hora di dir breuemente, di quan-
to commodo li potrà esser la cognitione dell'altre Scienze; prima della Grammatica,
per laquale s'hà perfetta cognitione delle Sillabe lunghe & breui, mediante le Regole
che danno i Grammatici; & la cognitione delle Lingue, per il cui mezo s'intendono di-
stintamente gli Autori, che trattano la Musica; & anco l'Historie, come parte della Mu-
sica; del che si è ragionato nel Cap. 2. del Primo Lib De i Sopplimenti; nelle quali si ritro-
uano alle fiate molte cose, che sono di grand'aiuto, & danno gran lume, uolendo essa-
tamente hauer cognitione delle cose di cotale Scienza; oltra che uolendone di essa scri-
uere qualche cosa è molto necessaria la Dialettica; accioche col suo mezo si possa discor-
rere con ragione & buoni fondamenti, & uenire alle Dimostrationi; senza le quali nul-
la, ò poco di buono si farebbe; essendo la Musica scienza mathematica, che si serue gran-
demente di esse come per tutti i Cinque Ragionamenti dell'Harmoniche dimostrationi
si può uedere. La Rethorica di quanto utile possa essere à i Studiosi di questa Scienza,
per potere esprimer con ordine i loro pensieri; & l'essere istrutto anco nelle cose della
Scienza naturale, lasciarò giudicare ad ogn'uno, c'habbia punto di giudicio; poi che
la Musica non solamente è sottoposta alla Scienza mathematica, ma anco alla Filosofia
naturale; com'altroue hò dichiarato;Cap. 20.
Primae par
tis. & non pur queste; ma la cognitione di molte altre
Scienze ancora non li può senon giouare. Et se bene il fine della Musica cōsiste nella ope
ratione, che è l'esser ridotta in atto; & che l'Vdito, quando è purgato, non possa esser facil-
mente defraudato dal Suono; tuttauia possono occorrer alle uolte alcune cose, che l'Huo
mo (essendo priuo d'alcuna delle nominate cose, che fanno grande vtile à conoscere le Ca
gioni di esse) resta di gran lunga ingannato. A' Ciascuno adunque che uorrà acquistar la
perfetta cognitione della Musica, sarà dibisogno, che sia dotato di tutte queste cose; per-
cioche qualunque uolta mancherà d'alcuna di esse, tanto meno potrà peruenire à quel gra
do ch'ei desidera di peruenire; & cō tanta maggior difficultà li potrà arriuare, quanta mag
gior sarà l'ignoranza delle cose nominate, che saranno di maggior importanza & più
necessarie. Ma perche diffusamente hò trattato questo nel Libro titolato Il MELO-
PEO ouer MVSICO PERFETTO; però basterà d'hauer toccato al presente queste po-
che cose, & quasi accennate; percioche colui che più minutamente vorrà ueder la neces-
sità di cotal cosa; leggendolo potrà pienamente esser satisfatto.
Della fallacia de i Sentimenti; & che 'l Giudicio non si dè far solamente con loro mezo;
ma se li debbe accompagnar la Ragione.Cap. XXXVI.
ma. tex. 63 questa propositione sia molto famosa; che 'l Senso in-
torno al proprio sensibile, ouer'Oggetto proprio mai non erra; tuttauia se tale
propositione s'intendesse semplicemente, come le parole suonano, alle volte sa-
page 446rebbe falsa; imperoche il Proprio oggetto si piglia in due maniere; Prima per quello, che
d'altro sentimento non è compreso, & per se stesso muta il senso, & contiene sotto di se
tutte quelle cose, che per se stesse sono comprese solamente da cotal senso; come il Co-
lore, ò la Cosa uisibile, che è proprio oggetto del Vedere; & il Suono, che è oggetto pro
prio dell'Vdito; & cosi de gli altri; come hò dichiarato nel Cap. 71. della Terza parte;
Dopoi per quello, che per sè muta il Senso, & non può esser sentito, ò compreso da al-
tro senso. Di maniera che la Specie contenuta sotto 'l proprio oggetto preso al primo mo
do, è detto Proprio sensibile, come la bianchezza & la negrezza è il Proprio oggetto del
Vedere; essendo che lo mutano, imprimendo in esso la sua specie, la qual specie non è
compresa per sè, se non da esso Vedere; & cosi s'intende delle specie de i Suoni & dell'
altre cose. Laonde quantunque il Senso non erri intorno all'Oggetto proprio nel pri-
mo modo; può molto bene errar nel secondo; massimamente non si trouando quelle con
ditioni, che si ricercano; cioè, che 'l Senso sia debitamente propinquo allOggetto; che
l'Organo sia debitamente disposto; & che 'l Mezo sia puro, & non deprauato. Et se bene
non errasse (com'intende il Filosofo) intorno al proprio oggetto al secondo modo, stan-
te le conditioni già dette; può nondimeno errare intorno al Soggetto de i proprij ogget
ti sensibili; cioè, intorno al luogo, & doue sia posto; percioche questo non appartiene al
sentimento esteriore, ma all'interiore; ch'è la uirtù, ò potenza cogitatiua, laquale è la più
nobile tra le potenze sensitiue; per esser più d'ogn'altra uicina all'Intelletto. Et ciò hò uo
luto dire; percioche molti credono, c'hauendo hauute le Scienze origine da i Sensi, noi
doueremmo maggiormente prestare à loro fede, che ad ogn'altra cosa; essendo che non
si possono ingannare intorno à i loro proprii oggetti. Ma ueramente costoro credendo
questo, sono grandemente lontani dalla uerità; Percioche se bene è uero ch'ogni Scien-
za habbia hauuto principio da loro; tuttauia non hà da essi acquistato il nome di Scienza,
& da loro non si hà hauuto la certezza di quello; che in essa si ricerca; ma si ben dalle Ra-
gioni, & dalle Dimostrationi fatte per uia de i Sensi interiori; cioè, per opera dell'Intel-
letto, ch'è il Discorso. Et se l Intelletto può errare alle uolte discorrendo, come uera-
mente erra; quanto maggiormente potrà errare il Senso? La onde dico, che ne il Senso
senza la ragione, ne la Ragione senza il Senso potranno dar buon giudicio di qualunque
oggetto si uoglia scientifico; ma si bene quando queste due parti saranno aggiunte insie-
me. Et che ciò sia uero, lo potiamo conoscere facilmente da questo: che se noi uorremo
(per dar un'essempio accommodato) diuidere solamente col mezo del Senso alcuna co-
sa in due parti, lequali siano equali; mai la potremo diuidere perfettamente. Et se pure
auenisse, che dopo fatta la diuisione fussero equali; ciò sarebbe fatto à caso, & non po-
tressimo mai esser certi di tal cosa, se non si facesse altra proua. Et tanto più difficile sarà
ogni diuisione fatta in cotal modo, quante più parti uorremo fare della cosa, che si ha-
urà da diuidere; ne mai l'Intelletto si potrà acchetare, fino à tanto, che la Ragione non
li mostri ciò esser fatto bene; & questo auiene, perche il Senso non può conoscer le mi-
nime differenze, che si trouano tra le cose; essendo che dal troppo, & dal poco resta con-
fuso, & si corrompe anco; come si comprende del sentimento dell'Vdito intorno i Suo-
ni, che dalla grandezza d'alcun strepito è offeso, & della picolezza, ò quantità minima
non è capace. Però adunque non seruendo à ciò il Sentimento solamente, sarà dibisogno
accompagnarlo con una pensata ragione, per uoler ritrouar simili differēze. Si uede anco;
che se da un gran monte di grano se ne leuasse uenticinque, ouer cinquanta grani, ouero
altra quantità minore, ò maggiore; pur che non fusse una disconcia, il Vedere non sareb
be capace di tale alteratione; per esser la quantità quasi insensibile, rispetto al monte;
come non potrebbe anche far giudicio alcuno, se 'l si aggiungesse il predetto numero de
grani à tal monte; onde uolendo conoscere tal cosa, bisognarebbe procedere altramen-
te, che per uia del senso. ll simile ueramente intrauiene intorno i Suoni, che quantun-
que lVdito non possa errare al primo modo, nel giudicar gli Interualli consonanti da i
dissonanti; tuttauia il suo ufficio non è di giudicar quanto l'uno sia lontano dall'altro se-
page 447condo 'l graue & l'acuto, & di quanta quantità l'vno superi ò sia superato dall'altro; es-
sendo che se l senso non potesse errare intorno cotali cose; ueramente in uano si adope-
rarebbono tante ritrouate misure, & tanti pesi, & altre cose simili. Ma ueramente co-
tale cose non furono ritrouate in uano; percioche gli antichi Filosofi conobbero molto
bene, che 'l Senso intorno ciò si poteua ingannare. Ma diciamo quello che è uero, che
quantunque la scienza della Musica habbia hauuto origine dal Senso dell'Vdito; come
nel Cap. 1. della Prima parte si è detto; & l'ultima sua perfettione & fine ultimo sia di es-
ser ridotta in atto, & essercitata; ancora che 'l Suono sia il proprio sensibile, ouer'oggetto
dell'Vdito; non è perciò da dar questo ufficio di giudicare al Senso solamente nelle cose
de i Suoni, & delle Voci; ma li dobbiamo accompagnar sempre la Ragione. Ne meno
si debbe dare tutto 'l giudicio alla Ragione lasciando da parte il Senso; percioche l'uno
senza l'altro potrà sempre essere cagione d'errore. Douendo adunque hauer cognitione
perfetta delle cose della Musica, non bastarà riportarsi al Senso; ancora ch'alcun fusse di
ottimo giudicio; ma si debbe cercar d'inuestigare & di conoscere il tutto di maniera, che
la Ragione da esso non sia discordante, ne il senso dalla Ragione, & allora il tutto starà
bene. Ma si come à far questo giudicio nelle cose della Scienza, fa dibisogno, che concor-
rino queste due cose insieme; cosi fà dibisogno, che colui, ilquale uorrà giudicare alcuna
cosa che appartenghi all'Arte, habbia due parti; Prima, che sia perito nelle cose della
scienza cioè della speculatiua; dopoi in quelle dell'Arte, che consiste nella prattica; &
bisogna che habbia buono Vdito, & sappia comporre; Imperoche niun potrà mai drit-
tamente giudicar quella cosa, che lui non conosce; anzi è necessario, che non la cono-
scendo la giudichi male. La onde si come uno ilquale sia solamente dotto nella parte
della Medicina detta Theorica, non potrà mai far giudicio perfetto d'una egritudine, se
non hauerà posto mano alla Prattica; ouer potrà sempre errare, confidandosi solamente
nella Scienza; cosi il Musico prattico senza la speculatiua; ouer lo Speculatiuo senza la
prattica, potrà sempre far'errore, & far cattiuo giudicio delle cose della Musica. Onde
si come sarebbe pazzia il fidarsi d'un Medico, che non hauesse l'una & l'altra delle cose
nominate aggiunte insieme; cosi sarebbe ueramente balordo & pazzo colui, che si uoles-
se fidar del giudicio d'uno, che fusse solamente prattico, ouer hauesse dato opera sola-
mente alla Theorica. Questo hò uoluto dire, perche si trouano alcuni di si poco giudi-
cio & tanto temerarij, & presuntuosi, che quantunque non habbiano alcuna di queste
parti uogliono far giudicio di quello, che non conoscono. Et sono alcuni altri, che per
loro trista natura, per mostrar di non essere ignoranti, biasimano tanto le buone, quan-
to le triste fatiche d'ogn'uno. Alcuni altri sono che non hauendo ne giudicio ne cognitio-
ne, seguono quello, che piace al uolgo ignorante, & tallora della sufficienza d'alcuno
vogliono far giudicio dal nome, dalla natione, dalla patria, dalla seruitù che tiene con
alcuni, & dalla persona; che se l'essere eccellente & raro in una professione consistesse nel
nome, nella natione, nella patria, nella seruitù, nella persona, & in altre cose simili; io
credo per certo, che non passarebbe molti anni, che non si trouarebbe huomo, che se gli
potesse dire che fusse ignorante percioche ciascun Padre aprirebbe gli occhi bene in co-
tal cosa, & farebbe tutto quel, che fusse possibile, per hauere Figliuoli segnalati in qua-
lunque si uoglia professione; essendo che non si ritroua (come mi penso) Padre, che non
habbia questo desiderio naturale, che i lor Figliuoli siano superiori à ciascuno in qual si
uoglia scienza & professione. Ma in uero si uede il contrario; che doue sono nati gli huo-
mini grandi & famosi d'alcuna professione, i quali sono stati pochi, rispetto al numero;
ui sono nati le migliaia & migliaia d'huomini oscuri, ignoranti, goffi, & pazzi; come
discorrendo si potrebbe uedere. Questo hò uoluto dire; percioche tanto uale, alle uolte
un publico grido, & una fama publica, non solamente appresso gli huomini idioti & pri-
ui di ingegno; ma anco appresso quelli di qualche giudicio; che cotal cosa fà, che niuno
ardisce di dir contra la commune opinione (quantunque la comprendino alle uolte es-
sere euidentissimamente falsa) cosa alcuna; anzilo fà tacere, & starsi sospeso & mutolo.
page 448Et per dar qualche essempio accommodato di questo, mi ricordo, che leggendo per mio
diporto vna fiata il CortigianoLibro 2. del Conte Baldessara Castiglione ritrouai, ch'essendo
appresentati nella corte della S. Duchessa d'Vrbino alcuni Versi sotto 'l nome del Sanna-
zaro, da tutti prima giudicati essere molto eccellenti, & li lodarono sommamente; ma
dopoi saputo per cosa certa, che non erano suoi; ma che erano stati composti da un'altro,
subito persero la riputatione, & furono giudicati men che mediocri. Simigliantemente
ritrouai, che cantandosi in presentia della nominata Signora un canto; non piacque, ne
fu riputato nel numero de i buoni; fino à tanto, che non si seppe, che la compositione
era di Giosquino; la onde allora allora riputato; per il nome ch'hauea esso Giosquino à
quei tempi; cosa rara. Quanto possa etiandio alcuna uolta la malignità & la ignoranza
insieme de gli huomini, uoglio dir quello che intrauenne all'Eccellentissimo Adriano
Vuillaerte in Roma nella capella del Pontefice, quando uenne di Fiandra in Italia al
tempo di Leone Decimo; che cantandosi sotto 'l nome del sudetto Giosquino il canto
Verbum bonum & suaue; il quale si soleua cantare ogni festa di nostra Donna, & era tenu-
to per una delle belle Compositioni, che à quei tempi si cantasse hauendo detto à i Can-
tori, che cotal Canto era il suo; com'era ueramente; tanto ualse la ignoranza, ouer (di-
rò più modestamente) la malignità & la inuidia de quei Cantori, che mai più non lo uol-
sero cantare. Di costoro, che sono senz'alcun giudicio, soggiunge in quello istesso luo-
go il Conte Baldessara un'altro essempio d'uno, che beuendo d'uno istesso uino, diceua
tallora, che era perfettissimo, & tallora insipidissimo; percioche gli era persuaso, ch'e-
rano di due sorti uino. Veda hora ogn'uno, che 'l giudicio non è dato à tutti; & da que-
sto impari, di non esser cosi precipitoso nel lodare, ò biasimare alcuna cosa, cosi nella
Musica, come etiandio in ciaschedun'altra Scienza, ouer'Arte; secondo che s'è discor-
so nel Cap. 14. dell'Ottauo lib. De i Sopplimenti; poi che per tante cagioni; come sono
molti impedimenti che possono occorrere, & molte cose delle quali non si può saper le lo-
ro cagioni; onde il giudicare è cosa molto difficile & pericolosa; tanto più, che si troua-
no diuersi appetiti; di maniera, che quello, che piace ad uno non piace all'altro; & di-
lettandosi costi di un'Harmonia dolce & soaue; quello poi la uorrà alquanto più dura &
più aspera. Ne anco per udir simili giudicij, i Musici debbono disperare; se bene anco
udissero costoro biasimare & dire ogni male delle loro compositioni; ma debbono pi-
gliar animo & confortarsi; poi che 'l numero de quelli che non hanno giudicio,
è quasi infinito; & pochi si ritrouano esser quelli, iquali non si giudichino esser
degni da esser connumerati tra gli huomini prudenti & giudiciosi. Assai
cose si potrebbe dire oltra di queste; ma perche mi accorgo d'ha-
uere sopra tal cosa hormai detto più, che forse non conue-
niua; però rendendo gratie à IDDIO larghissimo
donatore de tutti i beni, à queste fatiche con
questo ragionamento darò
FINE.