Title: Dimostrationi harmoniche
Author: Gioseffo Zarlino
Publication: Francesco de' Franceschi (Venezia, 1589)
Principal editor: Frans Wiering
Funder: Utrecht University Netherlands Organization for Scientific Research (NWO)
Edition: 2000
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht NetherlandsDA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria di Venetia,
Secondo Volume.
Contenente
LE DIMOSTRATIONI HARMONICHE
DIVISE IN CINQVE RAGIONAMENTI.
NE I QVALI SI DISCORRONO ET DIMOSTRANO
le cose della Musica; & si risoluono molti dubij d'importanza à tutti quelli,
che desiderano di far buon profitto nella Intelligentia di cotale Scienza.
Con la Tauola delle materiali notabili contenute nell'opera.
Καὶ καμάτῳ ἀκαματῳ ἅμα εὔξησα,
Εὐνόῳ νῆν νόῳ, καὶ ὁδῳ εὐόδῳ ἐδιδαξα.

Καὶ μὴ διδόντος, ὀυδὲν ἰσχύι πόνος.IN VENETIA, MDLXXXIX.
Appresso Francesco de' Franceschi Senese.page iipage iii

AL SERENISSIMO
PRENCIPE DI VENETIA
ALVIGI MOCENIGO
 GIOSEFFO ZARLINO DA CHIOGGIA.
GIOSEFFO ZARLINO DA CHIOGGIA.
un certo modo & molto imperfetto cognitione di Dio; tra l'altre
cose, che gli attribuirono, questa fù una; il Conseruar la sua crea-
tura & farle benificio. Et questo tennero di modo esser uero, che
hebbero opinone, che colui, il quale apportaua qualche bene à
mortali,usaua quell'officio, che apparteneua ad esso Dio; come
benefattore (parlando al modo loro) era fatto Iddio, à cui soccor-
reua. Da questo auenne, che gli Inuentori de quelle cose, ch'erano utili à gli Huomini,
Dei furono riputati; ancora (come si uede appresso Diodoro SicoloRerum an-
tiquarum.
lib. 1. ca. 2.) posti nel nu-
mero de i lor Dei. Onde nacque tra loro il Prouerbio: Α῎νθρωπος ἀνθρώπου δαιμόνιον:
L'Huomo è Dio dell'Huomo; il qual Prouerbio accommadarono non solo alle priuate
persone; ma à i Prencipi ancora; & maggiormente à gli Imperatori; che con la lor
possanza & somma autorità poteuano conseuar le Città, i Popoli & i Regni: imperoche
essendo ancora tra mortali, li chiamauano Dei; & dopo la morte loro, tra i Dei, con al-
cune ridicolose ceremonie (come narra Erodiano Greco ScrittoreHist. lib. 4.
Pet. Messia
in Vita Bas
siani Imp.) tra gli altri Dei li po
neuano & consacrauano. Questo fù cagione; che si come gli Huomini per natura erano
inuitati ad offrir'à Dio doni, & sacrificij, & anco far uoti, acciò lo hauessero propitio;
cosi anco si mouessero ad offrirgli in uita loro quei doni, che li pareuano più conue-
neuoli. La onde un numero quasi infinito de Scrittori (lasciando molte altre cose, che
potrebbero far à questo proposito) dedicarono & consacrarono à i loro Prencipi,
come à loro Dei, l'Opere loro. Percioche Vitruuio dedicò il suo Volume d'Architte-
tura all'Imperatore Ottauiano Augusto; Valerio Massimo i Libri de i Detti & Fatti no-
tabili de gli Antichi à Tiberio Cesare; Plinio l'Historia naturale à Tito Vespasiano.
Ilperche mosso dall'essempio di costoro; hauendo Io gli anni passati, dopo le Istitutio-
ni, composto le presenti Dimostrationi di Musica; & essendo hormai tempo, à benefi-
cio de quelli, che sono studiosi de questa nobil Scienza, ch'elle debbano uscir in publi-
co; hò uoluto offerirle & dedicarle à V. Sublimità, come ad Ottimo Prencipe & mio
Signore. Et spero, che non minormente le saranno grate, di quel, che furono grate à
quei grandi Imperatori le fatiche de quei eccellenti Scrittori; non essendo la Musica
page iv punto all'Archittetura in cosa ueruna inferiore; anzi di gran lunga superiore. Perche se
bene Vitruuio dice,Architec.
lib. 1. ca. 1. che l'Archittetura è scienza ornata di molte discipline & uarie eru-
ditioni; non è però Scienza; ma Arte fattiua, la qual tiene il terzo luogo tra le Arti; &
la Musica,1. Demon.
Def. 1. oltra ch'ella non si può trattare (secondo 'l parer di PlatoneDe Legi-
bus. 1.) senza la Vniuer-
sal disciplina; è Scienza; non solo per il Soggetto, ma etiandio per la certezza della
Dimostratione, senza dubio alcuno, dell'Archittetura assai più mobile & più eccellente.
Et se le fatiche di Valerio & di Plinio nell'adunare insieme da diuidersi autori Greci & La-
tini uarie cose, furono con quelle di Vitruuio al mondo grate; credo per certo, che que-
ste mie habbiano simigliantemente à piacere, & esser di grande utile, non solo per il di-
letto, che da sè porta all'Huomo lo studio di questa Scienza; ma etiando per il com-
modo & utilità, che ne sentiranno i Studiosi dell'altre Arti, & Scienze nella cognitio-
ne del buono & del bello, che ritrouaranno in esse; conciosiache si può dir con uerità,
che l'habbiano acquistato col mezo della Musica. Et quantunque à me sia stato cosa
trauagliosa il raccorre, l'ordinare & dimostrare insieme le cose di questa Scienza; le qua-
li ueramente erano poste senz'alcun'ordine, & anco non erano intese, secondo ch'inten-
der si deono; tuttauia con la patienza hò superato la difficultà, & uinto la fatica col pia-
cere; di modo che, per la gratia di Dio, le hò ridutte in tal'essere, che se prima la Musi-
ca pareua esser priua del suo antico honore, hora con maestà & decoro, come nobilissi-
ma & come una delle principali tra l'altre scienze; può comparere. Hauendo io adun-
que à porre in luce queste mie fatiche, le quali trattano le cose di cosi nobile Scienza, &
una delle prencipali; à chi doueua io dedicarle & offerirle, se non ad un Prencipe Illu-
strissimo & Nobilissimo, come è la Serenità uostra? non altramente da me istimata,
per la Religione incontaminata, per la Vita innocentissima, per il Consiglio gra-
ue, & per molt'altre sue eccellenti qualità, di quello che istimassero Vitruuio, Va-
lerio, Plinio quei sommi Imperatori. Essendoche non con altro mezo, che con
quello del suo ualore; dopo molti gradi de i maggiori ottenuti in questa Eccelsa Re-
publica; meritò sedere in quel seggio sublime, nel quale già sedettero molti Pren-
cipi Serenissimi, la cui Pietà & Religione uerso Dio, accompagnate dall'Amore &
Charità uerso la Patria, tanto puotero, che alla Città, la quale intorno Mille Cento
& Quindici anni Vergine & immaculata ancora si conserua; allargarono i confini,& ac-
crebbero il Dominio; tra i quali furono Tomaso, Pietro, & Giouanni Mocenighi, auo-
li & progenitori suoi di nome immmortale per i fatti illustri loro; à cui s'aggiunge Vostra
Sublimità, che non è, ne sarà à loro punto inferiore. Riguardi adunque la Serenità Vo-
stra col guardo della sua clemenza la mia uerso lei diuotione, & riceua con allegro ani-
mo il dono, ch'io offerisco & dedico al suo gran nome, & me faccia degno di conseruar-
mi nella sua buona gratia; percioche mi parerà hauer'ottenuto grande & singolar bene-
ficio; che di continuo terrò uiuo nella memoria, & con gli Antichi (religiosamente par
lando) potrò dire: Α῎νθρωπος ἀνθρώπου δαιμόνιον: & insieme pregar nostro Signor Iddio,
che le dia lunga uita & felice, & gratia di essere sempre uittoriosa contra gli ini-
mici de questa Serenissima christiana Republica.
page v
TAVOLA DI TVTTE
LE COSE NOTABILI CONTENVTE
NELL'OPERA.
A
tia, 1. f. studiò à Parigi in Legge.
8. f. 12. p. 201. p. Fu cagione del stu-
dio dell'Autore nelle cose della
Musica. 12. p
diapente 123. f. Il Tuono maggiore, ouero il mi
nor Semituono alla Diapente non fà consonanza
alcuna. 126. f
è riceuuto con solennissima pompa da i Signori
Venetiani 1. m
Semitono. 3. f. Non passarono la Quintadeci-
ma uoce, ne la Quadrupla proportione. 3. f. Nō
intesero i Luoghi & Siti delle consonanze. 4. p.
6. m. 60. f. Non consideranno altra diuisione har
monica, che quella della Dupla. 60. f. In qual mo
do denominarono le Proportioni. 88. f. Attribui
rono la ragione de numeri al Quaternario. 81. p
Posero la Diatessaron nel numero delle conso-
nanze nelle loro Compositioni, 84. p Qual chia-
massero Massima & perfetta harmonia. 103. f. Per
che facessero due generi del Pentachordo, & tre
dello Hexachordo. 194. m. Nelle dimostrationi
de generi, perche tolsero il Tetrachordo & non
altro numero di chorde.196. m Perche colloca-
rono la prima specie della Diapason nella chor-
da. A. 287. m
che sia. 91. m 164. m. E minore del Semituono
maggiore. 164. m
Diapason solamente Cōsonanza perfetta. 245. p
consistere nella figura circolare, compresa da
una sola linea. 16. m.
gli Antichi; ma più presto renderle facili. 248. p
Per qual cagione non habba uoluto passare il nu
mero delle Dicisette chorde nelle dimostrationi
fatte nel Quinto ragionamento. 254. m
C
quelli Interualli che sono minori della Diates
saron siano dissonanti. 3. m Propria del non respi
rare qual sia 13. m. perche l'Autore non habbia
uoluto trappassare il numero di Quindeci Chor-
de nelle sue dimostrationi. 203. m. Della parteci
patione fatta nella Quinta parte ināti l'altre dimo
strationi. 242. m Che muoue l'autore à porre al-
tro ordine nelle Specie delle consonanze 246. m
tore di porre altr'ordine nelle specie delle Con-
sonanze semplici: & ne i modi. 246. m.
Diatessaron: & questa cauata da quella, resta il
Tuono. 133.
no: & lo Semiditono cauato, resta il Ditono. 123. p
le distanze de i Suoni l'uno dall'altro. 23. f Meza
na proportionale come tra due date trouarsi pos
sa: la quale partisca il Tuono in due equali.
148. m quādo inutilmēte si aggiūga in uno istru
mēto. 216. f. Vera finale de i Modi qual sia. 253.s.
Stabili quali siano. 197. f. Stabili quāte in ciasche
duno de i tre Generi 230. m Mobili quali siano.
197. f Mobili quante siano in ciaschedun Gene-
re. 230. m. Neutrali quali siano. 197. f Neutrali
quante siano in ciaschedun de i tre Generi. 230. f
Delle diuisioni Diatonica & Chromatica in qual
page vi modo l'una all'altra corrispōdino. 194. m. 223. p
Finali delli Sei modi principali. 253. f. Cō
muni al Diatonico & Chromatico genere. 194.
m. 223. p. Quanto siano più acute quelle di uno
Modo, che quelle di un'altro.279. f De i Modi
principali più acute di quelle delli Non principa
li per una Diatessaron. 280. m. De tutti li Modi
abbracciano tutte le Sedeci chorde. 284. f
re se non col mezo de i Corpi sonori. 11. m. della
Natura, & Nostra molto diuerse. 14. m
appresso gli Antichi. 93. p. 113. m 154. p 142. f. Di
donde sia cosi detto. 93. p. In qual modo di accō-
modi alla sua proportione sopra una chorda.
172. p. Minimo interuallo musicale. 171. f.
co. 198. p Del Monochordo regolare Chromati
co 201. f. Del Monochordo regolare Enharmo-
nico. 202. f
te considerata dal Musico. 77. f. Et Dissonanza so-
no due estremi nella seconda specie de gli Oppo
siti. Di due specie. Propriamente detta 78. f.. Cō
munamente detta. 79. m Semplice raddoppiata
non dà nelli suoi estremi interuallo alcuno con-
sonante. 94. f
gono quei luoghi, che tengono le lor forme tra i
numeri 4. f Musicali come nascono. 7. p. Della
prima materia sono tutte Moltiplici, ò Superpar
ticolari 79. p. della Seconda maniera sono tutte
de gli ultimi tre Generi di proportione. 79. f. 80.
p. Di due forti. Semplici quali siano. Composte.
82. f. Tutte come l'una all'altra ne i loro luoghi si
soggiunghino 176. f. Diapason, Diapente, & Dia
tessaron quante fiate si ritrouino nelle Quindeci
chorde Diatoniche 231. f. Et quante tra le Chro-
matiche.234. f. Et quante tra le Enharmoniche.
237. m. Quanto alla forma loro sono immutabi-
le: ma non quanto à gli accidenti. 248. m
l'uno dopo l'altro, come si possa fare. 36. m. ouer
differenti di proportione. 36. f
sica.10. p 11. m 182. f. quello che sia. 23. f E diui-
sibile in infinito. 55. m
metà intiera. 34. m Che raddoppiata trappassa
un'altra cosa, ella è piu della sua metà. 34. f. Che
raddoppiata non arriua allo intero di un'altra. el
lanon può essere la sua metà 35. m. Ridocolosa
osseruata da i moderni. 193. p
sono mai nella materia. 9. f. Che uniuersalmente
non sono mai nella materia. 9. f. Che cadono sot-
to la Scienza Metafisica. 9. f. Che necessariamen-
te sitrouano nella proposta. 17 f. Che non si tro
uano molte fiate in molti Theorema. Ch'appar-
tengono al Dato. 18. p. Poste in atto nella Musica
non sempre restano 22. f. Che sono ad un'altra
equali, tra loro sono equali. 33. p Che tra loro so
no equali ad una istressa, sono equalmente Molte
plici, ò Superparticolari, ò di altro Genere. 33. m
Che hanno i loro tutti equali, hanno anco tra lo-
ro le parti equali. 33. f
D
m. 20. p. 89. p E quella che ci fa uenire in cogni-
tione della cosa. 9. m. Quello che sia. 10. m. Si pi-
glia in luogo della Descrittione. 10. f. Che si po-
ne nella Dimostratione qual sia 10. f. Di tre sorti:
cio è Formale & Finale 11. p. Delle Di
mostratione di due sorti 14. p. Delle cose non si
può dimostrare. 15. m. Del Suono data da Boetio
non è al proposito del Musico. 20. m. Di Euclide
del Genere.192. f. Del modo. 250. p. De tutti i
Dodeci modi. 251. m
cose. 9. m. Per qual cagione si pōgono inanti ogn'
altra cosa nelle Scienze . 19. f. Quel
che fanno. 20. p
tutti gli altri Interualli 5. p. Esser composta de
Tuoni & Semituoni non è mal detto. 7. p. Quel
lo che sia. Tra l'altre consonanze tiene il primo
luogo. Presa dal musico per il tutto diuisibile.
83. p. Piu d'ogni altra conosciuta dal senso. 86. f.
Come nasca 96. p. Minor de sei & maggiore di
cinq Tuoni maggiori. 128. p Quāti Tuoni & Se
mituoni contenga. 128. f. Conserua inuiolata
quella consonanza, che à lei s'accompagna.
129. p Regina de gli altri interualli. 83. f. 205. p.
Detta da Aristotele Consonanza perfetta. 245. p
Ha Sette specie. 245. f. In ogni caso temperamento re
sta nella sua uera forma. 245. m. Non si può alte-
rare senza offesa dell'Vdito. 243. p. Quando sia
detta harmonicamente, ouero arithmeticamen-
te diuisa. 250. m. Quante fiate sia contenuta tra
le Dicisette chorde temperate. 167. f.
fatta della Diapason harmonicamente. 83. f. Re-
integrata dal Ditono & dal Semitono. 98. p
Quanti Tuoni & Semituoni contenga. 123. m
Come nasca 123. f Quanto resta sciema nel tem-
peramento de gli Istrumenti. 243. p. di Quattro
specie.249. m. 245. f. Quante fiate sia contenuta
tra le Dicisette chorde temperate.267. f. Non ha
luogo tra la Terza & la Settima chorda. 269. m
fatta harmonicamente della Diapason. 83. f. Po-
sta nel numero delle Consonanze. 84. p. E conso
nanza perfetta. 85 p. Hauuta appresso gli Anti-
chi per consonanza. 2. m. 85. f. Quanti Tuo
ni & Semituoni contenga. 120. f. Come si ac-
commodi alla sua proportione con la Diapente
& la Diapason insieme. 175. f. Quanto si accre-
sca nella Participatione. 243. m. Di tre specie.
249. f. Quante fiate sia contenuta tra le Dicisette
chorde temperate. 270. m. Non si troua tra la
Settima & la Decima chorda. 271. p
pitagorico. 86. p. Principio & Elemento de gli
Interualli musicali. 91. p. Detto Apotome secon-
do. 164. p. Minore Enharmonico quello che sia.
92. p. Apotome secondo. E minore del Semituo-
no maggiore. 164. m. Di Martiano capella. Tris
temoria. Tetartemoria. 153.
ci. 16. p. Tra il Diatonico & Chromatico gene-
re consiste in una sola chorda. 194. m. Ch'è tra la
Participatione fatta nelle Istitutioni & quella del
le presenti Dimostrationi. 200. f
12. m. E come uno istrumento, che ne conduce
al Sapere.12. m Potissima qual sia. Potissima ca-
giona in noi il Sapere. Chiamata A priori & Pro
pter quid. A posteriori & Quia, quello che sia.
13. f. Della Prima proposta del lib.1. di Euclide
18. f. Della Partecipatione, ò Temperamento de
gli Interualli de gl'Istrumenti ritrouata dall'Au-
tore. 200. m
me sono dette Elemēti delle Sequēti. 40. m. 124. f
che cōposta di due Diapason.86. f. Come nasca,
& quanti Tuoni & Semituoni cōtenga. 131. m
gli Opposti.78. p. Et consonanza sono come due
estremi nella Seconda specie de gli oppositi.78. f
Quello che sia.80. f. Al tutto priua della Ragione
de numeri.81. m. Hauer Ragion de Numeri, co-
me s'intenda. 81. p
effetto. 4. m. Collegato nel graue della Cātilena fa
cattiuo effetto.4. f. Posto nell'acuto diletta.4. m
Et Semituono posti nel graue perche siano tāto
poco grati.5. f Quello che sia. Serue al genere En
harmonico. Vna delle prime parti della Diapen-
te, & delle seconde della Diapason.85. f. Et Semi
ditono come nascano. 97. f. Quanti Tuoni & qua
li cōtenga.120. m. Come si accōmoda alla sua pro
portione.174. m. E minore di due Tuoni Sesqui-
ottaui per un Cōma.174. f Et Semitono sono
anco del Diatonico genere.193. m. E contenuto
nella sua uera forma nella Partecipatione. 242. f
equali come si possa fare. 148. p. 150. m La diffe
renza del Tuono in due parti equali, non è la Re
gola di trouare i Semituoni. 161.
page viii
Stiffelio, & da Nicolò Tartaglia.146. p. Di qual si
voglia Interuallo in più parti equali, come si pos
sa fare. 150. m. Del Tuono fatta da Aristosseno va
namente. 153. m. Di Martiano Capella fatta del
Tuono. 153. f. Fatta del Tuono da Filolao pitago-
rico in due parti. 154. m. Del monochordo rego
late Diatonico. 198. p. Del monochordo Chro-
matico regolare. 201. f. Dell'Enharmonico mono
chordo regolare. 202. f
tionali. 118. m. dello Schisma, & del Diaschisma
non si possono far realmente, se non col mezo
della Geometria. 94 p. Delle proportioni quādo
siano incognite, & irrationali. 119. m
portione della Diapason col ditono. 88. m. So-
pra il Semituono minore. 90. f Et solutione intor-
no l'ordine de gli Interualli del Monochordo
Diatonico. 199. m. Intorno la specie delle Conso
nanze. 246. p
li, ò più communi da vna istessa proportione ne i
estremi non fanno consonanza alcuna.38. f. Ses-
quiottaui sono minori di uno Sesquiterzo: &
maggiori di un Sesquiquarto. 70. f. Consonanze
prime, & maggiori diuise in due semplici mino
ri. 102. f. Diatessaron aggiunte insieme, di quan
to trappassino la Diapente. 124. p. Consonanze
semplici contenute da vna proportione insieme
aggiunte ad vna chorda mezana commune, dalla
Diapason in fuori, non fanno alcuna maniera
di Harmonia. 180. f
terza. 54. p. E prima d'ogn'altra proportione.
83. p
terzo non è cagione della proportionalità har
monica. 55. p
E
F
Seguirò le ragioni de i Numeri nella diuisione
del Tuono. 153. f
tra i termini, & le differenze dell'Harmonica, &
Contraharmonica proportionalità. 101. p Conte
nute nella Progressione Arithmetica. 102. f Nel-
la Massima, & perfetta harmonia. 106. f Conte-
nute tra le parti delle Linee fatte nella diuisione
del Quadrato. 108. f
G
H
Semplicemente detta qual sia. 81. f Ad vn
certo modo detta quello che sia. 81. f Ad un
certo modo detta si fà per l'ordine, & non per le
Consonanze, che ella contiene. 87. p. Geometri
ca qual sia 105. m. Tra le qualità del Corpo cubo.
105. f. Semplicemente detta oue si ritroui. 181. p
Detta ad un certo modo oue sia posta. 181. f
Consiste nell'ordine. 55. p. Perche sia cosi det-
ta. 105. f
sempre, che dimostri, che la donna habbia par-
torito. 13. p
ma non della istessa natura, che è il Ditono, & lo
m. minore ꝗllo che sia. 87. f. Maggiore, & mino-
re come si facciano. 87. m. Maggiore di quanto
sopr'auanz' la Diapēte, & la Diatessaron. 125. f.
Minore di quanto sopr'auanzi la Diapente, & la
Diatessaron 126. m. Maggiore quanti Tuoni, &
Semituoni contenga. 127. f. Minore quanti Tuo
ni, & Semituoni contenga. 127. m Minore co-
me sia contenuto nella sua forma nella Partecipa
tione. 242. m. Hypaton. 216. p. Meson. 256. m.
Diezeugmenon. 256. f. Hyperboleon. 256. f. Sy-
nemennon. 257. p. Synemennon come si aggiun
ga à i quattro primi. 209. p. Della propietà di b
molle 257. p. 267. f Della propietà di Natura.
267. f. Della propietà di
 quadro. 267. f. Con
quadro. 267. f. Contiene tutte le Specie della Diatessaron. 256. p
255. m. Tra le Dicesette chorde tēperate. 267. f.
In qual modo siano nominati da i Moder
ni. 255. f. 265. f
I
no. 247. p. Dell'Autore nello scriuere le cose del
la Musica; tanto nella Speculatiua, quanto nella
Prattica. 190. m
Primo considerato dal Musico ad un certo mo-
do. 23. p. Molteplice. 24. p. Superparticolare.
24. m. Superpartiente. 24. f. Molteplice superpar
ticolare. 25. p. Molteplice superpartiente. 25. m.
Qual sia maggiore l'vno di due. 32. p. Moltepli-
ce doppiato genera un Molteplice. 39. p. Raddo
piato se produrrà un molteplice, anche lui sarà
molteplice. 41. f. Superparticolare è indiuisibile
in parti proportionali cō numeri rationali. 44. p
Non molteplice raddoppiato nō fa alcuno Mol
teplice,nè Superparticolare. 45. p. Raddoppia-
to, che non da il Moltiplice, non può essere
molteplice. 45. f. Ne i suoi termini radicali co
me moltiplicar si possa con Numeri composti.
51. m. Duplo da che nasca. 53. f. Triplo come si
faccia. 59. m. Quadruplo da che nasca. 60. p. Ses-
quiottauo de quali interualli sia la differenza.
62. f Sesquinono qual differenza sia. 63. f. Sequi
quintodecimo de quali interualli sia la differen
za. 64. f. Sesquiuentesimo quarto di che sia la
differenza. 65. f. Sesquiottantesimo qual differē
za sia. 68. p. Supertripartiente. 125. qual differen
za sia 68. m Del Tuono maggiore, & quello del
minore sono Superparticolari. 100. m. Del Se-
mituono maggiore è Superparticolare. 111. m.
Del Semituono minore è Superparticolare. 111.
m. del Semituono maggiore è il primo de i Te
trachordi Diatonico, & Chromatico. 223. p. Del
Semituono maggiore è Elemēto del Diatonico,
& del Chromatico. 223. p. Del Tuono diuiso in
due parti equali, in quali proportioni sia diuiso.
144. f. Del Semituono maggiore è minore dello
Apotome. 163. m. Qual si uoglia come si possa
diuidere in due, ò più parti proportionali. 148. p
150. m. Fatto maggiore, ò minore quando s'in-
tenda. 257. p. Farsi più graue, ò più acuto,come
s'intenda. 258. p
to. 3. f. Quando si dicano simili. 32. p. Come si
possano l'uno dopo l'altro. 37. p. mol
teplici raddoppiati quello che facciano. 59. p.
Minore della Diatessaron hauuti da gli Antichi
per Dissonanti. 77. f. Mezani tra la Consonanza,
& la Dissonanza sono molti. 78. f. Dissonanti mi
nori del Semitono sono le differēze de i mag-
giori consonanti. 89. m. del Ditono, & del Se
miditono sono Superperticolari. 98. m. Fatti da
Filolao, & da Aristosseno nelle loro diuisioni
del Tuono aggiunti à due Tuoni Sesquiottaui,
ouero al Ditono non fanno Consonanza alcu
na. 165. m. Vsati da Chromatisti nelle loro com
positioni. 215. p
rare con ragione gl'istrumenti da chorde, è di
tre sorti. 200. m.
mento de gli Istrumenti non si fa chi si fus-
se. 214. p
Spesso allegate dall'Autore, & per qual cagio
ne. 40. p
L
voglia dire. Da che proportione sia contenu-
to. 91. p
vno Interuallo minore da vn maggiore; quello
che viene è Superparticolare. 66. p
M
Perche in tal modo la chiamassero. 103. f. Tra
cinque termini, & quattro interualli. 105. p. Che
tra i termini, & le differenze loro contiene i
Tuoni maggiore, & minore, con l'altre Con-
sonanze. 106. f
del Tuono doue cada. 156. f. Del Tuono minore
doue caschi. 158. m
le cagioni formali, finali, & efficienti. 11. f
& la Dissonanza. 78. f. Nascono da altre propor
tioni, che da Molteplici, ò Superparticolari, col
locate però tra le parti del Senario, & dall'Otto
nario numero. 78. f
siano consonanti. 6. m. Non hanno hauuto suffi
cienti Principij, nè anco esperienza delle cose
della Mathematica. 6. f. Perche trappassarono il nume
ro delle chorde de gli Antichi. 205. p
Perche siano l'vno dall'altro differenti. 249. f Se
condo l'vso de gli Antichi parte molo difficile
da intendere. 251. f. Distanti l'vno dall'altro per
vn Tuono, ouer per vn Semituono. 278. p Prin
cipali posti per ordine. 275. p. Nō principali po
sti per ordine. 278. p. Tutti l'vno dopo l'altro
per ordine. 281. p. Principali tutti contenuti so
no tra le Tredici più acute chorde delle Sedici.
283. f. Non principali contenuti tra le Tredici
più graui del numero de Sedici. 184. m. Si pos-
sono trasportare dal graue all'acuto; & per il cō
trario. 285. p. Non possono essere nè più nè meno
de Dodici. 251. m. 275. m
il suo nome. 192. p. Regolare perche cosi si di
ca. 198. p
10. p E scienza di Relatione. 10. p. Hà per Sog-
getto il Numero sonoro. 10. p. Hà per Soggetto
il Corpo Sonoro proportionato. 10. p. Risolta
nel suo fine è cosa attiua. 22. f. A qual Genere sia
sottoposta. 22. f. Da qual parte è detta Theorica;
& come sia detta Prattica. 22. f. Subalternata alla
Arithmetica. 38. p. Et Poesia arriuate ad vna istes
sa conditione. 190. p. Ripiena di Compositori.
190. p. Senza Artefici, che habbiano cognitione
di essa; & per qual cagione. 190. m. Guasta da
Chromatisti. 215. f
Consonanza, & d'ogn'altro interuallo 20. m
Non considera il Suono nella lunghezza. 20. f.
Come dè vsare i Principij, che piglia da vn'al
tra Scienza. 38. p. Caua le sue ragioni dal
Tutto, & dalle parti del Corpo sonoro. 55. m.
Poco conto fà de i Numeri irrationali. 146. m
N
do & riuerendo. 203. f. De gli Hexachordi ap-
presso i Prattici. 255. f
gli Antichi. 195. m. Et ordine de i Modi. 252. m.
Secondo i Moderni. 254. p
glia che moltiplica, ò parti i termini di una pro-
portione, produce la istessa. 31. m. Qual si uoglia
si può porre per la differenza di qual si voglia
proportione. 43. f. Composto quello che sia. 51.
m. Maggiore di qualunque ordine dinota il
Tutto del Corpo sonoro. 55. m. Numerante è
vno Essemplare, & vna Idea nell'Anima nostra.
49. f. Posto in Atto dal Musico quello che si deb
ba intendere. 55. m. Esser aggiunto à se stesso
quello che s'intenda. 102. f. Ternario perche nō
si possa diuidere in due parti equali. 99. m. Ter
nario è perfetto. 153. f. De Cōpositori oltra mo
do cresciuto nella Musica. 190. m. Maggiore di
qual si uoglia ordine rappresēta la parte più gra
ue. 251. p. Di Quindeci chorde, perche non sia
trappassato nelle dimostrationi, & ordini de
Suoni. 203. m
portioni. 25. m. Tra loro composti, ò Communi-
canti quali siano. 25. f. Di due sorti. 28. f. 49. f. Et
proportioni sono imagini de i Suoni, & delle
Cōsonanze. 41. p. O proportioni del Monochor
do Diatonico. 211. p. Della Deuisione Chromati
ca. 220. f. Del Monochordo Enharmonico co
me si possono adunare insieme. 226. f
O
2. m. De gli Antichi intorno à gli Interualli del
la Musica. 76. m. De gli Antichi intorno alla lo
ro Massima, & perfetta harmonia. 103. f. Di To
lomeo, & de Pitagorici intorno alla Diapason
Diatessaron. 129. p. De' Moderni Chromatisti
nel cantare. 193. p. Di Boetio intorno i Mo-
di. 252. p
dine nelle Voci diuerso da quello, che si troua
ne gli Istrumenti arteficiali. 234. m. Interrotto
de i Modi. 247. m. Non varia la essenza delle Cō
sonanze. 248. m
bito, è cagione di ordinare i Modi con buon or
dine secondo la mente de gli Antichi. 247. f
P
Aliquota, & non Aliquota di vn numero dato
come si troua. 49. f. Qual si voglia come si caua
da un'altra. 69. f. Minore della proportionalità
harmonica non è atta ad esser diuisa, di modo
che produca i suoi interualli consonanti. 99. p
la Diapente. 90. m. Diuerse de' Nominatori, co
me si riduchino sotto vn solo Denominatore.
72. f. Come insieme si sommano. 72. f.
mostri. 259. p. Si può fare in tre maniere.200. f.
De gran commodo nella musica. 210. p
le loro forme da altro Genere di proportione,
che dal Molteplice, ò Superparticolare. 3. m
nori della Diatessaron esser consonanti. 2. m.
Per qual cagione si mouessero à dire, che quelli
interualli, che sono minori della Diatessaron
non sono consonanti. 3. m Non hebbero cogni
tione de i Gradi, & propij Luoghi delle Conso
nanze. 4. p. 6. p
page xii sua cagione. 14. m. Debbono esser vere. 14. m.
Debbono esser più note della conclusione. 14. f.
Debbono esser prime, & senza mezo alcu-
no. 14. m
15. f. Della Geometria. 15. f. Dell'arithmetica.
15. f. Della Musica. 16. p. Communi chiamati Di
gnità. 16. m. Di vna Scienza in quella sono inde
mostrabili. 16. m. Della Musica da chi si piglia-
no. 38. p
strare si possa diuidere il Tuono in due
parti equali. 148. m
p. Contr'harmonica. 27. m. Arithmetica più to-
sto detta Progressione. 26. p. 55. m. Harmonica
detta Mediocrità. 39. m. 55. m. Harmonica consi
ste nell'ordine. 55. p.Harmonica come si troua.
55. m. Contr'harmonica come si troui. 55. f. 57.
p. Continua, & discōtinua, ò discreta. 105. m. Geo
metrica discontinua. 105. f
Antichi. 3. m. Di graue, & di acuto tra i Corpi so
nori. 11. m. Quando è capace di un termine me-
zano, quello che debba hauere. 43. m. 119. p.
Qual sia maggiore di due contenute fra tre ter-
mini. 72. f. Di suono à suono è tanta, quanta quel-
la di Spacio à spazio. 135. f
tonico diatono. 3. m. Quando siano fuori delle
loro Radici. 25. f. Et Numeri sono le imagini de
i Suoni, & delle Consonanze. 41. p. Dello Schis-
ma, & del Diaschisma sono irrationali. 118. m.
Incognite, & irrationali quali siano. 118. m. Che
superanno l'intera metà del Tuono quali siano.
155. f. 157. m. Delle parti fatte vn Spacio di-
uiso, quali siano maggiori, ò minori. 142. m.
Delle consonanze come si possano descriuere
con numeri. 178. f. Della diapente della diatessa-
ron, del Tuono, & quella del Semituono mag-
giore sono sordi, & irrationali nella Partecipa-
tione. 200. f. 263. f.
duce alla Speculatione, oueramente che ne fà
operare. 17. m. Prima del lib. 1. di Euclide minu
tamente dimostrata. 18. m. Del Lib. 6. di Euclide
vsata per ritrouar la mezana chorda proportio
nale tra due date. 148. m
Q
26. p. In geometrica proportionalità. 26. f. In
Harmonica mediocrità. 27. p. In Proportionali
tà Contr'harmonica. 27. f
che dalla misurata è misurato. 30. p. Che misura
il cauato, & il restante di vna quantità; misura
anco il Tutto. 31. f
R
11. m. Noua, la qual proua da Diatessaron essere
consonanza, & perfetta. 84. m. Addutta da Tolo
meo à prouare, che la Diapason diatessaron sia
Consonanza. 129. p. De i Pitagorici, la qual pro
ua, che la Diapason diatessaron non è consonan
za. 129. m. Del Temperamento de gl'istrumenti
inuentione dell'Autore. 200. f
è tenuto vna Listella fatta di legno. 134. f. 198. m
diuidendo la differenza del Tuono in due parti
equali. 161. f
mero, & il primo numero Cubo, sono Venti-
una. 79. f
S
12. m. Per se. 12. m. Per accidente. 12. m. Per se
è vero sapere. 13. m. Per accidente non è vero
sapere. 12. f. Per se di due sorti. 12. f. Semplice-
mente. 12. f. Ad vn certo modo. 12. f. Per se
semplicemente quello che sia. 12. f. Che si acqui
sta col mezo de i segni probabili. 13. f. Con la
Scienza sono correlatiui. 13. f. Per negatione
quello che sia. 214. f
della Dimostratione. 9. m. Diuerse nascano da i
Generi diuersi delle cose, che si possono sape-
re. 9. m. 15. f
ma perfetto. 17. m. Interualli Sesquiottaui sopr'a-
uanzano il Duplo. 74. f Specie sole delle Diapa-
son si possono diuidere harmonicamente. 272. f
nel graue della Cantilena, perche siano poco
grati. 5. f. Detto Sesquituono, & Trihemituono,
ò Trisemituono. 86. p. Serue al genere Chro-
matico. 86. p. E la minor consonanza de tutte
l'altre. 86. p. Quanti Tuoni, & Semituoni con-
tenga. 120. p. Et Ditono come nascano. 97. f. Co-
me si colloca alla sua proportione. 173. p. Quāto
sia minore di due Tuoni Sesquiottaui. 173. f. Et
Ditono sono contenuti nel genere Diatonico.
193. p. Posto da Tolomeo nel Chromatico mol
le. 216. m
Apotome. 90. m. Adoperato nel Diatonico gene
re in ogni Tetrachordo. 90. m. E maggior di cin
que, & minor di sei Comma. 115. f. Qual propor
tione habbia. 111. m. Come si soggiunga al Tuo-
no maggiore. 158. f. Come si proponga al Tuono
maggiore, & al minore. 159. m. Come si accom
modi tra il Tuono maggiore, & minore. 159. f.
Consiste in maggior proportione della Sesqui-
decimasesta. 160. m. Consiste in maggior propor
tione della Sesquidecimasettima. 161. m E col
locato tra la Sesquiquartadecima, & la Sesquide
cimasesta proportione. 163. m. E minore dell'A-
potome. 163. f. Elemēto del Diatonico, & Chro
matico genere. 223. p. Quanto si accresca nel Tē
peramento de gl'Istrumenti. 244. f
Diesis maggiore Enharmonico. 90. f. Detto da i
Greci Limma. 90. f. E detto Diesis da Filolao.
91. f. 170. m. Perche non sia detto Minimo. 90. f.
Da che proportione sia cōtenuto. 112. p. E mag
giore di tre, & minore di quattro Cōma. 117. m.
Come si accommodi alla sua proportione. 168. f
Come si soggiunga al maggiore. 169. f. E minore
interuallo del Lemma. 170. m
Di Hermete, ò Mercurio Trismegisto. 133. m.
Di Hesiodo. 188. f
ghi si fanno per la moltiplicatione de gli inter-
ualli di vna istessa proportione. 143. m
sette. 245. f. Della Diapente sono quattro. 245. f.
249. m. Della Diatessaron sono tre. 256. p. 245. f
249. f
sonanza 20. m Quando si dice esser Voce. 20. f.
Da Greci detto Φθόγγος. 20. m. Considerato secō
do diuerse estentioni cade sotto la qualità di
Graue, & di Acuto. 21. p. Si vede quasi cadere dal
Corpo sonoro ad un certo modo. 21. f. Conti-
nuo. 21. f. Considerato secondo la duratione. 21.
m. Sottoposto al Genere di cose, che l'vna all'al-
tra succedono. 22. f. Quando si estende uerso il
graue,ò verso l'acuto, fa l'Interuallo. 23. p. Più
graue, ò più acuto da che uenga. 136. f. Di una
chorda mezana di un Spacio diuiso in due parti
equali, come sopr'auanza gli estremi. 145. p
page xiv
Adunati in un luogo istesso si chiamano Vniso-
ni. 21. p. Diuersi da che nascono. 21. p. Conside-
rati dal Musico quanto alla loro duratione. 21. f
Che fanno l'interuallo debbono esser differen-
ti. 21. p. Della Diapason niente differenti in uir-
tù & possanza da un solo Suono. 129. m. De gli
Istrumenti arteficiali sono stabili. 200. m
T
tre modi. 200. f. Quando si fà, che utilità ap-
porti. 241. p
torno al Suono. 22. p. Non ha parte alcuna indi-
uisibile, se non lo Istante. 22. m
proportioni Superparticolari si uoglia, come si
possa trouare. 60. f. Maggiore etiandio in qual
maniera trouar si possa. 61. f
all'altro proportionali. 40. f Maggiori di uno in-
teruallo à quanti corrispondino de i minori in-
sieme adunati. 47. f Maggiori di uno interuallo,
come siano equali à i minori. 48. f. Incogniti qua
li siano. 50. f. Che usa il Musico sono le parti del
corpo sonoro. 55. m. Che adopera l'Arithme-
tico. 55. m
riceuuto da i Pitagorici. 3. m. Di donde sia detto.
192. p. Quello che sia. 196. p. Hypaton nel mo-
no chordo diatonico. 204. p. nel Chromatico.
214. m. & nello Enharmonico. 224. p. Meson nel
diatonico. 205. m. nel Chromatico. 217. f. &
nello Enharmonico. 224. f. Diezeugmenon nel
diatonico. 206. m. nel Chrommatico. 218. m. &
nello Enharmonico. 225. m. Hyperboleon nel
diatonico. 207. f. nel Chromatico. 218. m. & nel
lo Enharmonico 225. f Synemennon nel dia-
tonico. 209. p. nel Chromatico. 219. f & nello
Enharmonico. 225. f. Congiunto. 197. p. Sepa-
rato. 197. m. Symennon è accidentale. 208. f
discepolo. 239. m. Inuentore del Genere Chro-
matico fù bandito da i Lacedemoni: & per
che. 215. f
Tiene, che la Diapason diatessaron sia conso-
nanza. 129. p. Nel Chromatico molle dimostrò
la forma del nostro Semiditono. 216. m.
li Sesquiottaui sopr'auāzano un Sesquiterzo: &
sono minori di un Sesquialtero. 71. m. Tuoni
maggiori: ò due maggiori & uno minore sopr'
auanza la Diatessaron. 121. m. Tuoni maggiori
sono minori di una Diapente; & quattro sono
maggiori. 124. m
tramente definito da gli Antichi. 106. m. Et lo
minore come nascano. 99. p. E Sesquiottauo.
100. p. E maggiore di noue, & minore de dieci
Comma. 14. p. Come si accomodi alla sua pro
portione. 139. m. è detto maggiore per eccellen
za. 138. m. Di quanto resta sciemo nella parte-
cipatione. 144. m
100. p. Di che si faccia. 112. f. E maggiore di
otto & minore di noue Comma. 115. f. Come
accomodar si possa alla sua proportione.
138. m. Di quanto si accresca nella participa-
tione. 244. m
consonanza, secondo gli Antichi. 89. f. Misura
d'ogni Consonanza musicale, secondo gli An-
tichi. 104. f. Come si accommoda alla sua pro-
portione. 137. m. 138. f. Come si possa soggiun-
gere ad un'altro, sopra una chorda. 139. p. Co-
me si possa preporre. 140. p. Diuiso in due parti
nelle estremità, non è diuiso equalmente. 143. f
Non si può diuidere in due parti equali con nu
meri rationali. 145. f. Come si possa diuidere in
due parti equali. 148. p. Come si possa diuidere
in più equali. 150. m
V
fonso Duca di Ferrara. 1. m. Religiosi, & à Dio
deuoti. 1. m
dell'Harmonica, & Cōtr'harmonica proportio
nalità. 57. f. Di Horatio contra gli Inuidi, & ma-
ligni. 77. m
28. f. 49. f. Del numero numerato si può diuide
re. 28. f. 50. p. E parte di qual si uoglia Numero.
30. f. Moltiplicata in qual si uoglia numero, pro
duce l'istesso. 31. p
siderati dal Musico quanto alla loro duratio-
ne. 21. m. Da ogni parte piegar si possono 200.
p.234. m
 page xvi
page xviLETTORI STVDIOSI.
legio de Stampatori, che hanno di non stampar mai Libro alcuno
senza errori: col riportare queste poche correttioni, che sono di qual-
che importanza, à i loro luoghi.
| Facciata. | Linea. | leggi. |
| . | 48. | senza aspettar altra. |
| 50. | che conoscessero. | |
| 12. | 16. | che cosi fusse, |
| 23. | 32. | hauete dichiarato |
| 27. | nel principio della seconda li nea dell'essempio manca la lettera f. |
|
| 12. | Sesquiquarta; & quella che si troua tra ac. è Dupla, come quella che si troua tra fg. |
|
| 30. | 32. | bene, dissi; onde. |
| 38. | 6. | che non ui sono. |
| 39. | 1. | PROPOSTA III. |
| 48. | nell'ordine de i Molteplici. superparticolari. d.10. |
|
| 93. | 2. | Messer Claudio; lasciamo |
| Facciata. | Linea. | |
| 105. | 33. | compreso da i Quattro primi che si uedono, che anco gli al tri sono Quattro, |
| 213. | 11. | Semituono. |
| 135. | di sopra. | TERZO. |
| 137. | di sopra. | TERZO. |
| 137. | 28. | per la terza. |
| 139. | di sopra. | TERZO. |
| 144. | 4. | & cb. è quello |
| 146. | 14. | cifera √ la |
| 149. | 12. | & eg faranno. |
| 214. | 29. | studiano |
| 246. | 20. | ch'io non faccia. |
| 254. | 1. | (per tornar al proposito) |
| 44. | gli Istrumenti Naturali. | |
| 183. | 46. | PROPOSTA L. |
 page 1
page 1DIMOSTRATIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
Diuise in Ragionamenti.
RAGIONAMENTO PRIMO.
&era il Mese d'Aprile quando l'Illustrissimo Sig. Donno Alfonso d'
Este Duca di Ferrara, per cagione di uedere una bella, nobile & ricca
Città; non solamente gloria, splendore & riputatione della bella Ita
lia; ma anco di tutto 'l Christianesimo; & forse per altri suoi negotij
d'importanza, uenne à Vinegia; onde da i nostri Sig. Illustrissimi Ve
netiani con solennissima pompa & regali apparati; com'è lor costume
di riceuere tutte quelle Persone, che sono d'alto affare; fu riceuuto. Hauea questo Sig.
seco menato i miglior Musici, ch'appresso di lui si ritrouauano; tra i quali (lasciando
gli altri, per non esser lungo) era Francesco Viola suo Maestro di Cappella & mio sin-
golare amico. Questi uenuto un giorno à ritrouarmi alla mia stanza, & presomi in sua
compagnia, s'auiassimo uerso la bellissima piazza di S. Marco. La onde uedendo aperto
il suo famoso & ricco Tempio, che de belli & finissimi marmi, con una gran copia di co-
lonne, è fabricato; percioche già era l'hora del Vespero, entrammo in esso; & pascendo
la vista per un buon pezzo di tempo, con belle pitture, che iui si ritrouano da buoni & ec
cellenti maestri di Mosaico antico & moderno lauorate; insieme andauamo ragionando
della lor bellezza & della ricchezza del Tempio, & della spesa grande, ch'in esso faceua
no i nominati Signori Illustrissimi, come quelli, che sono stati sempre religiosi, & à Dio
deuoti; per adornarlo di quelle cose, che uedono esser necessarie & conueneuoli, & por
tino bellezza, decoro & maestà al culto Diuino. Hora mentre che noi con sommo piace
re & nostro gran gusto andauamo discorrendo molte cose; essendo già finito il Vespero; ec
coti comparere il gentilissimo M. Claudio Merulo da Correggio, soauissimo Organista;
il quale uedutoci, s'accostò à noi; & conosciuto il Viola; dopo gli abbracciamenti fat-
tisi l'un con l'altro, ci ponemmo à sedere. Il perche essendosi tra noi de molte cose degne
& honorate, come 'l luogo richiedeua, per un buon pezzo ragionato, fatto dissegno di par
tire; prendemmo tutti d'accordo il camino uerso la stanza di M. Adriano Vuillaert, allo-
ra Maestro di Cappella di questa Serenissima Signoria; il quale poco lontano dimora-
ua, per conto di uisitarlo; & essendo molestato dalle podagre, non si partiua di ca-
sa; à fine che la presenza de i suoi amici amoreuoli & carissimi, gli apportasse qual-
che solleuamento. Arriuati adunque che noi fussemo, & ritrouato, che 'l sudetto Sig.
poco inanzi era stato à uederlo con una bella, degna & honorata copia de Signori &
Gentil'huomini; dopo molti ragionamenti hauuti da una parte & l'altra; i quali com-
page 2 memorauano le cortesie, che questo Sig. eccellētissimo molte uolte usato gl'hauea; & quā
to care gli erano le sue cōpositioni; & come per lui erano uenute à luce una grandissima
parte di quelle cose, ch'egli hauea gia cōposto; le quali stauano quasi sepolte. Et hauendo
insieme con buon proposito discorso molte cose della Musica, & della nostra amicitia; à
caso arriuò un degno & honorato Gentil'huomo forastiero amico di M. Adriano, uenuto
simigliantemente per cagione di uisitarlo. Questi grandemente si dilettaua della Musica;
ma sopra ogn'altra cosa desideraua udir ragionar delle cose dell'Arte, & della Sciēza; per
cioche per molt'anni ināzi studiato hauea nella Filosofia, & hauea letto molti Autori Gre
ci & Latini, i quali di Musica trattauano. Di questo il nome era Desiderio; & era di natio
ne Lōbardo, da Pauia; ilquale dopo un lungo ragionamento de uarie cose insieme fatto;
hauendo da quel, che detto si hauea compreso, chi erauamo, il nome di ciaschedū de noi,
il cognome, la patria, & la particolare professione; cosi ancora noi hauendolo dal suo par
lare à pieno conosciuto, & informatoci delle sue qualità & conditioni; uoltatosi questo
Gentil'huomo uerso di me; in cotal guisa incominciò à dire. Veramente credo M. Gio-
seffo, al desiderio chio tengo di potermi risoluere d'alcuni dubij, che mi uanno per la mē
te già molt'anni sono, dopo chio uidi & studiai insieme cō molt'altri libri di Musica le uo
stre Istitutioni harmoniche; che non mi potea abbatter meglio di quello, c'hoggi mi son
abbattuto. Percioche ricordandomi molte cose, mi par uedere, che tutto quello,ch'io leg
go in molti Autori, & che di continuo odo da Musici ricordare, mi generi nell'animo tan
ta confusione,ch'io per me non mi sò risoluer'in molte cose, di quel ch'io habbia da tene-
re & credere. Et per diruene una, che mi fà molto dubitare; ritrouo, che Pitagora negādo
di potersi passare oltra la Quadrupla; come nel Cap. 2. delle nominate Istitutioni nella Se
conda parte hauete detto; non acconsentiua, che quelli Interualli, i quali hanno la forma
loro da i Numeri, che sono maggiori del Quaternario, fussero consonanti. La quale opi-
nione fù tenuta da molti; imperoche Euclide Prencipe de Mathematici nel suo Introdot
torio di Musica chiaramente manifesta cotali Interualli dicendo: Διάφωνα δὲ τὰ ἐλάττονα
τοῦ Διατεσσάπων, Δίεσις, ἡμιτόνιον, τόνος, Τριημιτονιον, Δίτονον, Lequali parole uogliono di-
re; Ma le Dissone sono quelle, che sono minori della Diatessaron; il Diesis, lo Semituono,
il Tuono, il Trihemituono, il Ditono; hauendo egli prima detto; Σύμφωνα μὴν οὖν ἐστὶν Δια-
τεσσάρων, Διαπέντε, Διαπασῶν, καὶ τὰ ὅμοιοα; cioè, Adūque le Cōsonanze sono la Diatessarō
la Diapēte, la Diapasō, & altre simili. Et Aristosseno antico Musio nel Lib. 2. de gli Ele-
mēti Musicali dice; ἔστω δὴ τῶν συμφώνων ὀκτὼ μέγεθα. ἐλαχιστον μην τὸ διὰ τεσσάρν. συμβέβη
κε δὲ τοῦτο τῇ αὑτοῦ φύσει ἐλάχιστον εἶναι. σημεῖον δὲ τὸ μελοδεῖν μὴν ἡμᾶς πολλὰ τοῦ διατεσσάρων
ἐλάτω, πάντα μέντοι διάφωνα; cioè, Siano hormai Otto le magnitudine de i consonāti, de i
quali sia minima la Diatessarō: ma ciò auien'ancora naturalmēte esser minimo; del che n'è
segno, che noi cātiamo molti Interualli, che sono minori della Diatessaron; che sono tut-
ti dissoni. Tolomeo etiādio, chiama la Diatessarō col nome d'ἐλαχίστης, καὶ πρώτης συμφω-
νίας; cioè, Minima & prima Cōsonanza. La si uede, che cotal cosa appres
so de costoro era tenuta per uera. Et perche uedo in fatto, & intendo da uoi Musici esser'il
contrario; però non sò in qual maniera possa credere; che se ben Pitagora & gli altri, che
lo seguirono, negaua cotal cosa, la negasse semplicemente; come le parole à noi suonano.
Ne mi par, che questo habbia del uerisimile; essendoche Pitagora & li Pitagorici sono sta
ti huomini saputi, di gran giudicio, & d'eleuato ingegno; & hāno hauuto quel buon senti-
mento; come si può credere, che habbiamo noi; col quale si poteuano certificar, se la cosa
era in fatto, come la credeuano & teneuano; delche forte mi marauiglio. Però desidero
grandemente intender da uoi, donde cotal cosa nascer potesse; la quale appresso di me è
tanto difficile; ch'io nō posso far, che ricordandomi non la chiami errore. Soggiūse M. A-
driano à questo, sēz'aspettar'altra risposta: Io ancora già molto tēpo è, ch'io desidero d'in
tender questa cosa; poscia ch'io tēgo fermamēte; come diceua il S. Desiderio, che gli Anti
chi nō fussero priui ne del sentimento dell'Vdito, neanco di giudicio; ma che conosces-
sero cosi bene il buono & il tristo, come conosciamo noi: ma che dite uoi di questo M. Frā
page 3 cesco? credete anco uoi, che questo sia uero? Io l'hò per fermo Messere, rifpose M. France
sco, che gli Antichi hauessero tanta cognitione del buono & del tristo, quanta ne habbia-
mo noi. Et forse, che come quelli, che dauano grandemente opera alle speculationi, più
di quel, che facciamo noi, hauessero 'l Senso più purgato; ma per qual cagione ciò facesse-
ro, haurò anch'io molto grato il saperlo da M. Gioseffo. Allora tacēdo ogn'uno, dissi: Sig.
Desiderio, ancora che questa cosa sia molto difficile, & alle spalle mie carico troppo gra-
ue, & cosa ueramente da ricusare; tuttauia desiderando di satisfare in qualche parte al uo
stro desiderio; poi che questa è la prima uolta, che s'habbiamo ueduto, & lo primo appia-
cere anco, che m'hauete richiesto; non resterò di dirui tutto quello, ch'io sento sopra que-
sta dimāda; tanto più ch'io ui uedo tutti d'un'istesso uolere, & accesi d'un buon desiderio;
ond'io per satisfarui, non porrò tēpo alcuno di mezo. Pregate adunque Dio, che mi illumi
ni la mente à dir cose, che ui siano di satisfattione. Cosi faremo, rispose M. Adriano; & ui
preghiamo tutti ad incominciare. Auertite adunque, soggiunsi; c'hauendo Pitagora hauu
to opinione, che tutti quelli Interualli, che sono consonanti, hauessero le forme loro con-
tenute dalle Proportioni del genere Molteplice, ò Superparticolare solamente; hebbe
per fermo, che tutti quelli, che le hauessero contenute sott'altri generi, fussero al tutto
dissonanti. La onde, uedendo che i Tetrachordi del genere Diatonico diatono, ilquale
più d'ogn'altro da lui, & da i suoi seguaci era riceuuto, procedeuano dal graue all'acuto
per due Tuoni di proportione Sesquiottaua, & per un Semituono contenuto dalla pro-
portione Super 13. partiente 243. & che i due Tuoni, i quali formauano il Ditono, era-
no contenuti ne i loro estremi dalla proportione Super 17. partiente. 64. & che un Tuono
col nominato Semituono, dal quale si poteua formare un Semiditono, erano contenuti
dalla proportione Super. 5. partiente. 27. ritrouandosi queste due proportioni tra quelle
del genere Superpartiente, veniua à concludere; per la prima ragione, che ui posso dire;
che quelli Interualli, ch'erano contenuti tra queste forme, ne i loro estremi fussero; come
ueramente sono; dissonanti. Dalla qual Regola non escludeua i due Hexachordi maggio
re & minore; essendo c'hanno in tal genere le forme loro. Et questo è troppo uero; percio-
che cotali Interualli ridotti in atto, si conoscono esser poco grati all'Vdito. Onde tale opi
nione non è da esser giudicata falsa, quanto à questa ragione; & non dee parer cosa stra-
na. Quel che uoi dite; rispose M. Adriano; è uerissimo; ma mi par gran cosa da dire; essen-
do (come chiaramente da ogn'uno di giudicio si comprende) che tutta la uaghezza & la
leggiadria della Musica, & dirò anco ogni sua diuersità, è posta nelle due Consonanze
minori della Diatessaron; cioè, nel Ditono & nel Semiditono, & anco nei due Hexachor
di maggiore & minore; che gli Antichi non hauessero mai udito tra Sette spacij contenuti
nella Diapason; & nō hauessero conosciuti i nominati Interualli essere cōsonanti. E' ben
uero, che 'l non hauerli per cōsonanti, crederò, che fusse fatto non senza qualche ragione.
Messere, risposi; à questo, che uoi hauete detto, risponderò con un'altra ragione. Bisogna
che uoi cōsideriate, che se gli Antichi hanno uoluto udire gli Interualli nominati, facea di
mestieri, che eglino li hauessero uditi in uno de due modi; prima sotto le Forme contenu
te tra i Sette nominati spacij, ouer'Interualli della Diapason; dopoi sotto altre forme ua-
riate da quelle. Quanto d'hauerli udito nel primo modo; credetemi, che li udirono disso-
nanti; percioche le dette forme sono sottoposte al genere Superpartiente; ma in quanto
l'hauerli udito sott'altre forme; sia poi nelle uoci, ò ne i suoni; questo è ben possibile d'
hauerli udito consonanti. Auertite però, che in due modi li poteuano udire nella secon-
da maniera; prima ne i proprij, ueri, & naturali luoghi; dopoi fuori di essi. Se li uole-
uano udire ne i proprij & ueri luoghi sopra i loro Istrumenti, quest'era impossibile; percio
che cotali Istrumenti nō erano sufficiēti; essendo che (come hò detto nel cap.2. della Secō
da parte dell'Istitutioni) gli Antichi non passarono mai la Quintadecima uoce, ò chor-
da; ne mai passarono (secondo 'l precetto di Pitagora) la proportione Quadrupla;
se ben si legge appresso di Giulio Polluce di due Istrumenti, l'uno de i quali chiama Epi
gonio, dal nome dell'Inuentore chiamato Epigono ambraciota, che hauea 40. chorde; &
page 4 l'altro Simico, ilqual n'hauea 35. i quali Istrumenti credo, che fussero molto dopoi quella
età nella quale fiorirono i primi & più illustri Musici & che di loro ne fusse fatto poco cōto:
percioche tra quelli, che trattano le cose della Musica, non se ne troua alcuna memoria; se
nō (come ho detto) appresso il Polluce, che uisse ne i tēpi dell'Imperatore Comodo di no
me; ma incōmodo al mondo; alquale egli dedicò la sua opera, intorno gli Anni di Christo
190. Onde essendo cosi; necessariamente gli udiuano fuori de i loro luoghi, & ne i luoghi
nō proprij. Et se ne i luoghi nō proprij le udirono, nō poteuano pienamente satisfare al sē
so; ilperche sforzatamente le giudicarono dissonāti più tosto, che cōsonanti; per laqual co
sa son di parere, ch'essi non per altro giudicassero gli Interualli, che sono minori della Dia
tessaron dissonanti, se non perche non hebbero cognitione, ò per dir meglio, non intesero
i ueri, legittimi, proprij & naturali Luoghi delle Consonanze; cioè, doue ciascheduna si
douea naturalmente collocare; essendoche (come tutti uoi sapete) se bene il Ditono è cō
sonanza, tuttauia posto fuori del suo luogo naturale, & collocato nel luogo d'un'altra con
sonanza, più tosto rende dissonanza, che buon concento; ilche dir si può anco della Dia-
tessaron; percioche posta per base della Diapente tra la Diapason; non dà quella satisfat
tione all'Vdito, che fà quando si pone essa Diapente per base della Diatessaron nella Dia
pason. Questo è purtroppo uero, rispose il Merulo, & l'esperienza, ch'io fò ogni giorno
nel sonar l'Organo lo dimostra; perche quando il Ditono si ode nelle uoci, ò ne i suoni col
locato nel graue, allora parmi di udire un non so chè di tristo, che nasce nella compositio
ne da tale Interuallo, che sōmamente mi offende il sentimento. Et questo ueramēte nō si
potrà da alcū di sano giudicio negare. Ma se cotale Interuallo si uà riportādo uerso l'acu-
to, quanto più si trasporta, tāto più rende maggior dilettatione al senso; di maniera che se
quel Ditono, ilquale è posto nella parte graue d'alcuna cantilena, offende alquanto l'Vdi
to; quel ch'è posto tra 'l graue & l'acuto, non solo non offende, ma anco diletta. Quando
poi è posto nella parte più acuta, dà maggior diletto ancora, di quello, che non danno i
due nominati, posti nella maniera già detta. Disse allora il S. Desiderio; Parmi che questa
cosa sia di non picciola importanza da sapere; Ma poniamo che 'l Ditono, il quale hauete
nominato, posto in luogo graue in cotal maniera faccia tristo effetto: farà forse quell'istes
so il Semiditono? Non solamente; rispose il Merulo, lo farà tristo; ma tristissimo, di tal sor-
te, che quasi non si potrà udire; & questo è uero, credetelo a me, che spesso l'hò prouato
nell'Organo; come ho detto; perche se quando si uien'à toccar nella parte graue il Dito
no, s'ode tristissimo effetto; se per caso si tocca il Semiditono, fà una ruina tanto grande,
che à pena si può udire. Ma quando questi Interualli sono toccati nel mezo Istru
menti ne i loro gradi, fanno udire suono grato & soaue. Et se si toccano ancora più uerso
l'acuto, fanno migliori effetti; di maniera che quel, c'hò detto è uerissimo. A fè, rispose il
S. Desiderio, che mi piace questa cosa, & credo che pochi siano quelli, che cotali cose con
siderino. Pochi sono ueramente Sig. mio; rispose allora M. Francesco; & tanto pochi, che
io non ue ne saprei ritrouar molti. Voglio dire anche più oltra (soggiunsi io) che non so-
lo quest'Interualli, quando sono posti nel graue, possono offender l'Vdito; ma etiandio
quando sono posti nell'acuto; percioche quando 'l Ditono tiene il luogo del Semidito-
no, ò per il contrario; se pure non discordano, almeno danno manco dilettatione.
Et sappiate, che la maggior parte de tutte quelle compositioni Musicali, che poco
dilettano; tra gli altri difetti, che hanno, questo è un de quelli. Veramente è cosi;
disse Messer'Adriano; percioche hò posto mente, che in tutte quelle Canzoni, che mi
dilettano, si troua 'l Ditono esser replicato tra le parti, sopra la parte del Basso; al contra
rio in quelle, che poco mi piacciono, hò compreso, che 'l Basso sopra di sè molte fiate hà il
Semiditono. Douete sapere Sig. (risposi io) com'io hò detto & replicato molte fiate nelle
Istitutioni,1. Par. c.
13. & 3.
par. c. 60. che le Cōsonanze nella Musica hanno i lor gradi, & naturalmente occupano
quei luoghi, che tengono tra i Numeri harmonici le lor forme. Et quando tali Consonan
ze sono poste al contrario; se non fanno tristo effetto; almeno lo fanno mē buono,di quel
che farebbono, se ne i lor proprij luoghi fussero collocate. Però, si come la Dupla, che è
page 5 la uera forma della Diapason, collocata ne i numeri tra 2 & 1. per darui un'essempio; tie
ne il primo luogo tra essi, & tra le proportioni è la prima; essendo che inanzi de questi due
termini 2 & 1. non si troua numero, che sia minore; cosi tra le Consonanze non se ne ritro
ua alcun'altra, che per origine sia prima della Diapason; onde la Diapason tiene 'l primo
luogo nel graue, & inanzi non si ritroua Consonanza alcuna, che sia maggior, ò minor di
lei. Il perche hò detto molte fiate, che la Diapason è la Prima consonanza, dalla qual na
scono tutte l'altre, siano poi di essa maggiori, ò minori. Soggiungo anco di nuouo, che el
la è non solo Principio; ma Elemento de tutte l'altre. La onde si come la sua forma sem-
plice, contenuta ne' suoi termini radicali 2 & 1. non riceue altro numero, ò termine meza
no, che la diuida in due parti; cosi essa non admette nel primo luogo & grauissimo dell'ordi
ne delle Consonanze alcuna chorda mezana, ne anco nella parte grauissima di qual si uo
glia Istrumento, che la partisca in due Interualli; onde si possa udir'alcun'effetto, che nō
sia men grato di quello, che si ode, quando si fà udir semplicemente. Nel secondo luogo si
ritroua la Diapente, la cui forma è 3 & 2. che tra l'ordine naturale de' numeri tiene pure il
secondo; il perche uà posta senza mezo alcuno dopo la Diapason. Et si come tra 3 & 2. nō
ui può capire alcun mezano numero; cosi tra l'estreme chorde della Diapente non può ca
scar'alcuna chorda mezana, che in qualche parte non offenda il sentimento. Dopo que-
sta segue nel terzo luogo la Diatessaron tra 4 & 3. nell'ordine naturale de numeri, la qua-
le non riceue alcun mezo, che operi buono effetto; onde essendo poste tutte queste Con
sonanze l'una dopo l'altra (come altroue ho dettoInst. lib. 1.
cap. 15.) sopra d'un'Istrumento per ordine, sen
za porui in mezo alcun'altra chorda, gratissimo suono & soaue concento udir fanno. Ma
se per auentura nel graue la Diapason uenisse ad esser tramezata, di modo che nella parte
graue s'udisse la Diapente, & nell'acuta la Diatessaron, subito si udirebbe mutar forma il
concēto, & un non so chè di non cosi grato, com'era 'l primo, all'Vdito. Et se ancora tra
questa Diapente si interponesse una chorda, la quale uenisse à diuiderla in due parti; cioè,
in un Ditono & in un Semiditono, & questo fusse collocato nella parte acuta, & quello
nella parte graue; allora s'udirebbe cosa, che all'Vdito apportarebbe gran dispiacere.
Questo, però non è l'ultimo grado della poco grata adunanza delle Consonanze; percio
che ancora si troua di peggio; & ciò intrauiene quando 'l Semiditono uiene à tenere il luo
go del Ditono, & questo il luogo del Semiditono, & sono posti tra la Diapente al contra
rio di quello, ch'erano prima; cioè, che 'l Ditono tenesse il luogo acuto, & lo Semiditono
il graue; perche allora si udirebbe quella ruina estrema, che possono far le Consonanze a-
dunate insieme; essēdoche questo ordine allora sarebbe posto alla riuersa; cioè, che 'l Semi
ditono occuparebbe il primo luogo nel graue, il Ditono il secondo, la Diatessaron il ter-
zo, il quarto la Diapente, & la Diapason tenerebbe nell'acuto il sesto & ultimo luogo. Et
credo, che tutti quelli, c'hanno giudicio, & hanno prattica de gli Organi, possono questo
molto ben sapere; percioche, quando cotali Istrumenti sono sonati à pieno, maggiormen
te di quel che non fanno gli altri Istrumenti, che hanno poco spirito; scuoprono tale con-
quassamento. Si che S. Desiderio; mi par che hora si possa comprendere, in che consista,
& quel che sia la già addimandata à me da uoi differenza; laquale à gli huomini d'inge-
gno eleuato, non è difficile d'apprendere; ma si bene à quelli, che sono di poca tenuta; tra
i quali se ne trouano al presente de quelli, che questa cosa non capiscono, come se fusse co
sa della quale non si potesse hauer esperientia alcuna; Onde non la intendendo, la biasi-
mano. Hauend'io detto questo; riuoltatosi à me disse, il S. Desiderio; Ditemi ancora que
sto; per uostra fè; perche maggiormēte tanta ruina fanno questi due Interualli, ch'ultima-
mente hauete nominato, posti nel graue, che non fanno quādo sono situati nell'acuto? Per
due cagioni, risposi; l'una, perche 'l luogo del Ditono & del Semiditono nō è l'esser posto
nel graue, ma nell'acuto; l'altra, perche posti al modo detto, non sono collocati per ordi-
ne, secondo i gradi & i luoghi loro, ma al contrario: essendo che quell'Interualli, che so-
no di maggior proportione naturalmente uogliono il luogo più graue, & queli di mino-
re, il luogo più acuto. Ne mai ritrouarete nell'Ordine naturale delle Consonanze, che
page 6 il Ditono segua uerso l'acuto immediatamente 'l Semiditono; ma ritrouerete il contra-
rio; che tenendo 'l Ditono il luogo più graue, il Semiditono immediatamente lo segue uer
so l'acuto; di maniera che un tal disordine nasce da queste cagioni, quantunque l'uno
& l'altro siano consonanti. Adunque; soggiunse il Sign. Desiderio; per quel ch'io ueg-
gio il poco accordo, che tallora fanno le parti d'una compositione, procede non solamen
te dal mescolamento delle Dissonanze, ch'alle fiate ui si fà per dentro; ma dal porre in esse
con male ordine le Consonanze. Cosi è in fatto, rispose M. Claudio. Non è stato adun-
que fuor di proposito, disse M. Adriano, che nelle mie compositioni habbia schiuato, più c'
hò potuto, di por cotali Consonanze nella parte graue; al modo c'hauete dichiarato; per
che pur troppo mi parea, che non stauano bene; quantunque io non ne sapesse render ra-
gion'alcuna; ma udiua, che non mi contentauano à pieno il senso. Vi sono anche dell'al
tre osseruanze Messere (gli risposi) nelle uostre Compositioni; lequali hauete imparato
co 'l mezo del senso; come quello, che è il principio del nostro sapere, che non sono di po
ca importanza; delle quali, se ben non ne sapete dire la ragione, non mancano quelli, che
la dicono per uoi. Ma per ritornar al nostro proposito, dico; che la cagione, che mosse i
Pitagorici, & Pitagora prima à dir, che tutti gl'Interualli, i quali erano minori dell'Dia
tessaron fussero dissonanti, è questa; secondo 'l mio giudicio, & come ui hò dichiarato; per
che non hebbero cognitione de i Gradi & proprij luoghi delle Consonanze, & in qual
maniera si hauessero à disporre & collocare in ordine. Onde hauendo essi conosciuto, se
pur lo conobbero, che quelle consonanze, che sono minori della Diatessaron; come so-
no il Ditono & lo Semiditono, à noi tanto grate; poste nella parte graue, generauano più
tosto dissonanza, che consonanza; per non essere stato conosciuto da loro tale differēza;
cioè, che poste ne i loro proprij & naturali luoghi, generano grato suono all'udito; & per
il contrario ingrato, quando fuori de i loro naturali luoghi sono collocate; però giudicaro
no, che per ogni modo fussero dissonanti. Adunque dal non conoscere i gradi, & l'ordine,
& i proprij luoghi delle consonanze nacque, che gli Antichi negarono quelli Interualli,
che sono minori della Diatessaron, esser consonanti. Non li bastaua almeno sapere; disse
il S. Desiderio; che posti nell'acuto, & à i loro luoghi proprij erano & sono cōsonanti? Già
ho detto (soggiunsi) che nō cōsiderarono questo, anzi mai lo sepero; essendo che se l'haues
sero saputo, nō è dubio, che l'haurebbono posto in uso, ouero ne haurebbono almē lascia
to qualche memoria di loro; com'hāno fatto alcuni de i nostri Moderni, i quali se ben nō
hāno dimostrato, che 'l Ditono cōtenuto dalla proportione Sesquiquarta, & lo Semidito
no contenuto dalla Sesquiquinta, fussero consonāti, hanno almeno con grāde dubitatio-
ne affermato, che 'l Ditono cōposto di due Tuoni sesquiottaui, & il Semiditono, che con-
tiene un Tuono sesquiottauo, & un Semitono minore, cōsiderati dalla parte delle loro pro
portioni, erano dissonanti; appoggiati à questa opinione; che d'altre Proportioni, che dal
le Molteplici & dalle Superparticolari in fuori, le Cōsonanze non potessero hauer le loro
forme, & che considerate in atto ne i Suoni, ò nelle Voci, fussero consonāti;Vide cap.
12. lib. 4.
supple. perciò che
quando uoleuano, tali le udiuano. Ma s'ingānauano; perche quando le udiuano cōsonan
ti; erano cōtenute da proportioni Superparticolari, & nō da Superpartiēti, come credeua
no; & poteua nascer l'errore di costoro, dal non hauer'hauuto sufficiēti principij; nelle lor
dimostrationi, & poca isperienza delle cose della Musica; percioche non era basteuole il
dir solamente, che le Consonanze erano quelle, le quali haueano la forma loro dal gene
re Molteplice, ò Superparticolare, contenute tra le parti del numero Quaternario; ma bi-
sognaua più tosto dire, che erano quelle, le quali haueano le forme loro da quelle propor
tioni, che si trouano in atto tra le parti del Senario. Adunque; disse M. Francesco; nō pote
uano costoro dimostrar le cose della Musica perfettamēte, nō hauēdo essi cotali principij;
essēdo che da loro si hà la cognitione (come molte fiate dire) de tutte le cose, che
si trattano in qual si uoglia sciēza. Dite troppo il uero; risposi; onde bisogna sapere, ch'à uo
ler dimostrar perfettamente le cose della Musica, bisogna à quei Principij, co 'l mezo de i
quali altri hanno dimostrato, aggiungerui quelle, cose, che ne cōducono al fine di quello,
page 7 che cerchiamo. Et ricordarsi quel c'hò detto nelle Istitutioni;1. Part. c. 13. et. 3.
par. cap. 3. che le Consonanze, ò In-
terualli musicali non nascono primieramente; com'hanno tenuto alcuni; per l'aggiuntio
ne de molti Interualli minori posti insieme; ma per la Diuisione della Diapason, la quale
chiamai Madre & Fonte dogni altra consonanza & interuallo. Questo credo, ch'ogn'un
de noi l'habbia in memoria; disse M. Adriano; ma parmi, che al tutto non sia mal detto,
che la Diapason si componga de tre Tuoni maggiori, de due minori, & de due maggiori
Semituoni; percioche si uede pur che contiene in se ueramente, & camina per tali Inter
ualli. Vdite Messere; risposi; nella Musica hauete da considerar due cose; prima l'Interual
lo, il quale da Greci è detto Διάστημα; & gli ordini, ò scale, cosi detti d'alcuni moderni, ò
pur Costitutioni, che nominar le uogliamo; chiamate separatamente, & ciascheduna da
per se Σύστημα; però dico, che se parlate di questa ultima; nō è inconueniente dire, ch'una
Diapente sia composta de due Tuoni maggiori, d'un minore, & d'un maggior Semituo-
no, come da due parti: Ma parlando della prima, questo non si uerifica; percioche nasco
no dalla diuisione della Diapason; & non è senza proposito il dire, che fatto molte parti
d'una Diapason, de quelle istesse si possa reintegrare, & comporre un'ordine, ilquale con-
tenga quanti Tuoni & Semituoni possa accascare in quella compositione, secondo la qua
lità dell'ordine, che uolete comporre; come sarebbe dire; comporre una Diapason, nel-
la quale entrino gli Interualli nominati di sopra, & altri simili. Et à questo modo non è
errore à dire, ch'una Consonanza; cioè, uno de questi ordini sia composto. Ma si ben
sarebbe, quando si dicesse, ch un'Interuallo de i primi fusse composto. Voi dite bene sog
giunse M. Adriano; ma di gratia fatemi un piacere, & à tutti gli altri, che sono qui adu-
nati & si dilettano della Musica; ragionateci un poco di queste cose; acciò sappiamo an-
che noi ragionarne, quando farà dibisogno, qualche cosa; perche io desidero grande-
mēte uedere un giorno le cose della Musica dimostrate, come star debbono. Et se uoi uo
leste pigliar questa impresa, ci fareste cosa grata; percioche credo, che nō sia alcun de noi,
che nō l'hauesse in piacere, & nō ne hauesse da hauer obligo. Cosi è ueramente; rispose il
S. Desiderio; & io in particolare lo desidero molto; percioche da queste imparerò la uia,
che tiene il Musico, nel dimostrar le sue cōclusioni, & uedrò la differenza, ch'è tra le dimo
strationi, che fà il Musico, le quali nō hò mai cōpitamente ueduto; & quelle che fà l'Arith
metico & il Geometra; hauēdo io queste due ultime molte fiate ueduto porre in atto. Si-
gnor; risposi io; nō bisogna in queste cose hauer fretta; ma bisogno è di andare adagio. Et
ui prometto, che ui andrebbe più tempo di quel, che u'imaginate, quandio uolessi tuor l'
impresa di ragionar, come si debbe, le cose della Musica; percioche bisognerebbe prima
dichiarare alcune cose à quelli, che non hanno ueduto, ò letto, che concorrono nel-
la Dimostratione; uolendoui di questa materia ragionar con la Dimostratione in mano;
& bisognerebbe oltra di questo dichiarar quello, che sia Dimostratione, & di che si cōpo
ne, & molt'altre cose, lequali portarebbono seco molto tempo. Et bisognarebbe, che u'i-
maginaste dhauere più d'uno ragionamento; essendo che nella Musica l'una cosa è
concatenata con l'altra, come sono gli annelli, che si trouano congiunti insieme in
una catena. Rispose allora M. Adriano, uoi mi accrescete la uoglia, dicendo coteste cose;
on d'io ui prego à pigliar uolōtieri questa impresa; perche mi sarà un grande solleuamēto
del mio male. Et ui giuro, che s'io fusse più giouane di quel, ch'io non sono; uorrei di nuo
uo diuentar Discepolo, & dar'opera per si fatta maniera all'intender la ragione delle cose
della Musica; che non uorrei, ch'alcun mi dimandasse cosa alcuna, che io non lo potesse sa
tisfare. Questo à me sarebbe etiandio ueramente oltra modo grato; disse M. Francesco;
acciò mentre stò in Vinegia, acquistassi qualche cosa da portar meco à Ferrara; onde ui
essorto & prego M. Gioseffo à pigliar questo carico. Ma ui dico hora Messere, che ui doure
ste contentar d'esser il primo de nostri tempi nelle cose della prattica, laquale hauete an-
co non senza qualche cognitione della Theorica; essendoui sempre dilettato di pratticar
cō huomini dotti in questa professione. Et se ben nō sete in tutto della Theorica colorito,
almen sete molto . Et ui douete allegrar di questo, percioche sono doni, che nō si
page 8 danno cosi à tutti, & ringratiatene la Diuina bontà. Veramente di continuo la rin-
gratio; rispose egli; ma per questo non si estingue la sete, ch'io hò di sapere; perche è co-
sa naturale ad ogn'uno;Metaph. 1.
cap. 1. anzi di giorno in giorno più mi uà crescendo. Ne mi doglio d'es-
ser uicino à gli anni della decrepità; ma ben mi doglio, che mi conuerrà morire allora,
ch'io incomincierò ad imparare. Sia però sempre fatta la uolontà del Signore. Hora 'l de-
siderio ch'io tengo di sapere, mi fà di nuouo pregarui M. Gioseffo, à far quello, che ui ho
proposto. Non minor sete ho io di cotal cosa soggiunse il S. Desiderio, che l nostro M. A-
driano habbia; percioche se bene ho ueduto & letto appresso dalcuni Autori molte cose
dimostrate; tuttauia non son restato à pieno satisfatto. Gli uorrebbe (risposi) un fiume
de i maggiori, non dirò che sia in Italia, ma de i maggiori che sia nel mondo; & non un pic
ciolo riuo, com'è 'l mio, à uolere estinguere queste seti tanto ardenti; però ui uoglio dire;
che se tanti, i quali hanno scritto, & hanno trattato queste cose auanti di me, non ui han
no potuto cauar questa sete, che debbo sperare io? Ma perche sō molto tenuto à M. Adria
no; & gli hò quell'obligo, come se mi fusse padre; & una certa honestà nō sopporta, chio ri
cusi questo carico; per satisfare à questa honorara & uirtuosa compagnia; però non uo-
glio restar, di far quello ch'io potrò con tutte le mie forze; perche se bene da me non ha-
ueste quel tutto, che desiderate; uedrete almen, che la mia uolontà è pronta nel seruir-
ui. Et prego Iddio, che questa fiata io sia & Musico & Medico insieme, il che mi sarà di
gran contento l'hauer fatto in un solo colpo due operationi; cioè, dato l cibo conue-
niente all'Intelletto de chi m'ascolta; & leuato 'l male à quelli, c'hanno bisogno di sanità.
Nel nome del Signore adunque uoglio pigliar questo carico uolontieri; E' ben uero, ch'
io non mi uoglio obligar à dimostrarui & risoluerui tutte quelle difficoltà, che possono ac
cascar nella Musica; essendo che se 'l si uolesse dimostrare ogni cosa; oltra la difficoltà & la
lunghezza del tempo sarebbe se non impossibile, almeno difficile il raccoglierle tutte d'
una in una insieme, & dimostrarle per ordine. A questa legge (rispose M. Adriano) non
ui uogliamo sottoporre; essendoche troppo ben sappiamo, che questè un'impossibile. Sog
giunse allora il Sig. Desiderio; Date pur principio da qual capo ui piace; perche quando ci
nascerà alcū dubio, ue lo andaremo proponēdo; & uoi ce lo risoluerete, uolēdo. Cosi farò
adūque soggiunsi; Ma auertite,Nota per
i maligni. che quand'alle fiate ui proponerò alcuna cosa, che per inā
zi l'habbiate udita, letta, ò conosciuta in alcun Autore, di nō m'accusar di furto; come fan
no alcuni poco giudiciosi, & poco prudenti; accusando questo & quello Scrittore; ne an-
che dir, che non faceua dibisogno di commemorarla; percioche uolendoui dimostrar per
ordine le cose della Musica; non posso far, che nō vi discorra alcune cose necessarie à tali
ragionamenti; massimamente conoscendo la maggior parte de uoi non hauer dato opera
allo studio dell'Arti, & non saper quello, ch'importi questo nome Dimostratione, & quel
le parti ch'entrano in essa. Questo disse M. Francesco; mi piace sommamente; perche se
ben può esser, ch'io habbia udito alle fiate quel che sia Dimostratione, da i colloquij del
Maggio & del Pigna nostri, grand'huomini nelle lettere; hauuti spesse fiate co 'l nostro
Sig. Duca, & con altre persone segnalate; tuttauia, per non esser mia professione, non me
ne posso cosi à pieno ricordare. La onde facendo quel, che detto hauete, non potrà esser'à
noi se non di grande utilità. Lo douete far per ogni modo; disse M. Adriano; perche anco
ra io non mi ricordo troppo ben queste cose, se bene essendo giouane le udì in Pariggi,
quando mi diedi allo studio delle Leggi imperiali. Ancora io lhaurò in grande piace-
re disse M. Claudio: perche di queste cose, credo saperne poche: quantunque io ne hab-
bia udito molte ne i ragionamenti de quelli Huomini eccellēti, co i quali praticaua di cō
tinuo; onde mi verrò à ricordar qualche cosa, & la terrò ben'in memoria. Poi che cosi
ui contentate, cosi farò; risposi; onde parlerò hora con uoi Sig. Desiderio; il quale, co-
nosco dal ragionamento poco fà hauuto con noi, esser molto istrutto. Auertisca però ogn'
uno, che in questo Ragionamento io non posso far, che io non faccia quello, che etiandio
hāno fatto la maggior parte de quelli, c'hāno inanzi à me scritto di queste cose & ragiona
to; cioè, ch'io non piglia una parte de quei mezi, che mi seruono à uenire all'atto dimostra
page 9 tiuo; essendoche senza loro non potrei far cosa buona. E' ben uero, ch'io uene aggiūgerò
alquanti altri, per condur questa mia impresa al desiderato fine; conciosiache quelli, i
quali sono stati proposti da altri, non sono à bastanza; & con questi & quelli insieme uer
rò à ragione di quello, che io ui son per dire, & mi sarà da uoi proposto. I biasi-
matori de quelli, che hanno scritto alcune cose nelle scienze, & hanno pigliato i princi-
pij da quelli, che hanno scritto per inanzi; rispose il Signor Desiderio; hanno poco giu-
dicio. Chi non sà, che uolendo scriuere, ò parlar di alcun'Arte, ò Scienza, bisogna di
due cose farne una; ò ritrouar nuoui principii; oueramente usar quelli, ch'altri professo-
ri di quell'Arte, ò Scienza hanno usato? Però Platone, Aristotele, & altri eccellen-
tissimi Filosofi, molte cose s'hanno fatto proprie; quantunque fussero inuentioni d'altri;
come chiaramente ne i Scritti loro si comprende. Ma più si scorge ne i scritti d'Euclide,
che in altro autore; poi che siamo à ragionar della Dimostratione; il quale pose insieme
tante & tante Dimostrationi fatte da altri, facendosele sue, & anco i Principii, col bel-
l'ordine, che le diede; come racconta Proclo, ne i CommentariLib. 2. c. 4.i fatti sopra il Lib.1 de
gli Elementi d'esso Euclide, ch'à molti è di gran merauiglia, ch'un tant'huomo lo faces-
se; quasi che l'età d'un'huomo fusse à bastanza di ritrouar, porre insieme, & dar perfet-
tione à tante cose. Ma lasciamo questo da un canto & diciamo, che se ciò si permette &
concede à tanti & tali huomini; ne à loro si attribuisce uitio alcuno; per qual cagione
non ui sarà concesso quest'istesso anco à uoi? poi ch'io non uedo, ch'essi habbiano hauu-
to dal mondo maggior priuilegio di quello, che hauete uoi. Questo è il douere; disse
M. Francesco: Ma lasciamo, per uostra fè, questo da un canto, & attendiamo à quel,
che importa à noi, senza perder tanto tempo. Volendo adunque (soggiunsi io) hauer pie
na notitia di quello, che ui hò da dire; fa dibisogno che uoi sapiate; Ch'essendo ogni
Scienza posta nell'intelletto; tutte le cose si rendono intelligibili in atto, secondo che ad
alcun modo si considerano lontane dalla materia. Onde secondo che diuersamente han-
no (dirò cosi) proportione con essa lei, la lor consideratione appartiene à diuerse Scien
ze; lequali acquistar non si possono, se non con l'aiuto della Dimostratione; il me-lb> zo della quale, è la Definitione. Onde essendo la Definitione quella, che ci fà uenire in
cognitione della cosa; esprime le cose essentiali di essa; è necessario, che si co
me elle differenti sono tra loro, che anco siano differenti le Definitioni, ò mezi, che le
vogliamo dire. La onde nasce la diuersità delle Scienze dalla uarietà delle cose in mol-
te maniere considerate; lequali in tre modi considerar si possono;Vide ca. 7.
& 12. lib.
1. Supple. Imperoche primiera-
mente ne sono alcune, le quali hanno il loro essere, che dipende dalla Materia, ne sen-
za essa definire si possono; Secondariamente ne sono alcune, le quali non possono star
da essa materia lontane, & nelle definitioni loro non si pone cotal materia; Oltra di que-
sto alcun'altre ue ne sono, che non solamente da tal materia non dependono secondo 'l
loro essere, ma ne anco secondo la ragione ò definitione; & queste sono quelle, che ca-
dono sotto quella Sciēza diuina, che noi chiamiamo Metafisica; percioche quelle cose, le
quali considera; ouer che mai si trouano esser nella materia; com'è Iddio benedetto, &
l'altre sostanze separate; ouer perche non sono uniuersalmente in essa; come è la
Sostanza, la Potenza, & l'Atto, & quell'anco che i filosofi chiamano Ente; il per-
che nella loro definitione; per non esser cose corporali; non si pone la materia. Ma le
prime; che sono cose naturali, & sono considerate nella Scienza naturale, la quale chia-
mano Fisica, & hanno l'esser loro nella materia sensibile, & sono sottoposte al moui-
mento, si definiscono per la materia nominata; onde quando definiamo quel che sia Huo-
mo, diciamo; che è Animal rationale & mortale; & l'Animale, senz'alcun dubio, è co-
sa naturale, & hà l'esser suo tra le cose della natura. L'altre poi sono tutte cose appar-
tenenti alle scienze Mathematiche, come sono punti, linee, superficie, corpi, & tutte
quelle cose insieme, che appartengono alla Moltitudine & alla Grandezza; onde nella lo
ro definitione non si pone la materia sensibile; se bene non possono star senza lei, essen-
do che non si dice, che 'l Triangolo sia figura di legno, ò di pietra, ò di ferro, ò di qua-
page 10 lunque altro metallo, ò materia, che si uoglia; ma si dice, ch'ello è figura, la quale hà
in se tre angoli equali à due retti, quantunque il Triangolo habbia l'esser suo nella mate-
ria; come discorrendo potrete conoscere. Questo discorso tanto più mi è piaciuto; dis-
se M. Adriano; quanto più uedo quasi una cosa noua; che ne i ragionamenti di Musica,
si parla anco delle cose appartenenti alla Filosofia. Non sapete messere, soggiunsi io, che
la Musica, per esser Scienza parte mathematica, & parte naturale; com'hauete potu-
to uedere nelle Istitutioni;1. Par. cap.
20. è sottoposta alla Filosofia? Io per me lo sò per certo; ma mol-
to mi dilettano (rispose egli) queste cose; tanto più, quando le uedo tirate à qualche bel
proposito. Sappiate dissi io, che tutto questo discorso si è fatto, accioche essendo la Musi
ca, come già dimostrai nelle sudette Istitutioni,1. Par. cap.
18. et 29. scienza di Relatione; & hauendo per sog
getto il Numero sonoro; ò Corpo sonoro proportionato; come forse dimostrerò un'al-
tra fiata;Vide c. 14.
lib. 8. Sup-
ple. non senza proposito uiene ad esser parte Mathematica, & parte Naturale; es-
sendoche considerata nel primo stato; già che da i numeri dipende il suo essere; è con-
numerata tra le cose già dette, poste nel terzo luogo; ma considerata al secondo modo,
hauendo i Suoni l'esser loro tra cose naturali, è posta tra quelle cose, che posseggono il
Secondo. Però credo, che ui ricordate quel, ch'io chiamo Materia; & quello ch'io no
mino Forma delle consonanze; onde non starò à replicarlo.Vide cap.
primae par-
tis Instit. Onde hauete à sapere; che
se ben co 'l mezo delle Quantità habbiamo la cognition uera delle cose della Musica;
non essendo ella semplice mathematica; nella definitione della Consonanza, & di qua
lunque altro Interuallo, i Musici sogliono alle fiate porre la materia; come habbiamo
potuto uedere in molte definitioni, nelle quali si pongono i Suoni, ò le Voci, che sono
la Materia delle consonanze, & d'ogn'altro Interuallo; essendoche i Musici contempla-
no tali Interualli in atto, i quali non sono senza materia; il che non fanno gli Arithme-
tici, ne anco i Geometri; percioche i primi con templano il Numero; & i secondi le
Quantità misurabili, in quanto sono lontane da essa. Per questo adunque; soggiunse il
S. Desiderio; alcuni han detto, che la Consonanza è distanza di suono graue & di acuto.
E' cosi; dissi io; ma sono stati etiandio alcuni altri, c'hanno detto la Consonanza esser
Aria formato; però auertite, che nell'esplicar quello, che siano le cose (io parlo con
quelli, che non lo sanno) usiamo due sorti di Dichiaratione; La prima è detta Defini-
tione, & è quella, che esplica la cosa per le cose essentiali; & la Seconda è chiamata De-
scrittione, & è quella, che non dice la cosa per gli essentiali; ma per i suoi accidenti. La
prima è, quando noi definiamo l'Huomo, & diciamo, che è Animal rationale & mor-
tale; che sono cose essentiali dell'Huomo. La seconda è quella, con la quale; uolendo
dar'ad intendere ad alcuno quello, che sia Huomo; non sapendo, ò non uolendo espri
mer le cose sue essentiali, diciamo; ch'ello è Animale politico, di statura dritto, & altre
cose simili, le quali non esplicano la natura dell'Huomo. E' ben uero, che molte fia-
te si prende l'una per l'altra; percioche tallora, si piglia la Definitione in luogo della De-
scrittione; & alle uolte questa in luogo di quella; quanto alla uoce; & si chiama senz'al-
cuna differenza Definitione; ancora che quanto all'esser della cosa sia altramente. Qual
di queste due si pone nella Dimostratione? disse allora M. Adriano. La prima (risposi) co
me uederete. Dichiaratemi un dubio, soggiunse M. Francesco, & poi seguitate. Se d'una
cosa sola (come molte fiate hò udito dire) gli è solamente una definitione; da che uiene,
che alle fiate non solo se ne ritroua una; ma anco più? A questo, risposi subito, Bel du-
bio ueramente proponete M. Francesco; però auertite, che nasce da questo; che non so-
no propriamente Definitioni, ma Descrittioni; il perche se ben'alcuna cosa non si può
definir più d'una uolta; si può nondimeno molte fiate descriuere; percioche porta seco
molti accidenti. La onde tale proposta non è uera in questo caso, ma si bene nelle Defini
tioni perfette; essendoche se fusse altramente, sarebbe falsa. Soggiunse allora M. Clau-
dio, dopo l'hauer per un poco di tempo tacciuto; Da che uiene adunque, che nel Cap.
12. della Seconda parte dell'Istitutioni, hauete posto due definitioni della Consonan-
za? Alquale risposi. Mi piace grandemente, che 'l uostro dubitare torni al proposito di
page 11 quello, che io uolea dire. Però notate, che la Definitione si troua esser di tre sorti; La
prima si chiama Materiale, & è quella, che contiene la materia, la quale entra nella co-
sa definita; come s'io uolessi definire l'Huomo, & dir quel che ello fusse, direi, ch'è co-
sa composta di carne, d'ossa, de nerui & d'altre cose simili, ch'entrano nella sua mate-
riale compositione; La Seconda si chiama Formale; & è quella, che contien la forma
della cosa, che si definisce; come s'io dicesse: l'Huomo è animale ratione; conciosia che
la Rationalità è la propria & uera forma dell'Huomo; Ma la terza si chiama Finale; & è
quella che contiene, & esplica il fine della cosa; come quando io dicesse; l'Huomo è Ani
male rationale & mortale, capace della Beatitudine; di maniera, che la Beatitudine è il
fine dell'Huomo. Disse allora M. Adriano; Si troua alcuna definitione, che contenga
tutte queste tre cose? Ben sapete; risposi. Ditene una adunque; disse egli; & poi segui-
tate quel che ui piace. La Definitione soggiunsi, che contiene ciascheduna di queste co-
se sarà, quando uorrò definire alcuna cosa; come sarebbe dire la Consonanza, & porrò
nella sua definitione i suoni, la Ragione de Numeri, & quel ch'ella può fare; come sa-
rebbe dir; Consonanza è ragion de Numeri contenuta da due suoni, ò uoci l'uno graue
& l'altro acuto; la quale soauemente uiene al nostro udito. Stà molto bene, disse
M. Adriano; poi che (com'hauete altre fiate detto) i Suoni, ò le Voci sono la materia,
la Ragione de Numeri la forma, & lo Soauemente uenire all'Vdito è il fine della Con-
sonanza. Allora il S. Desiderio, desideroso di saper più oltra, soggiunse; Diteci per uo-
stra fe; questa Consonanza ha ella altro fine? Et io, per satisfarlo, dissi; Hà per certo; &
ue lo potrete ricordar da quello, c'hauete letto; com'è il mutare il senso, nella maniera,Inst. 2. par.
c. 8. & 12.
che hà l'Harmonia di dilettare, & anco d'indurre in noi passioni diuerse. Cosi è in fat-
to rispose egli. Onde M. Francesco; Io credo che saria bene, disse che hormai passaste
piu oltra; perch'io penso, che tutte queste cose s'intendino bene. Sarà bene; soggiun-
se M. Claudio; perche se l'occorrerà alcuna cosa difficile, ue la andaremo dimandando.
Allora il S. Desiderio uoltato à me, disse; Ne date forse questa licenza M. Gioseffo? Per
qual cagione uolete, che io non ue la dia? risposi. Io son qui per satisfarui; onde facen-
dolo mi farete sommo piacere. Hor sù adunque, per non por tempo di mezo dico; ch'
essendo 'l Soggetto della Musica il Numero sonoro, ouero il Corpo sonoro proportiona-
to, & non potendosi hauer alcuna cognitione uera della quantità de i suoni, se non co 'l
mezo de i Corpi sonori, che sono le chorde, le quali sono quantità, che si misurano, ne
potendosi hauer Scienz'alcuna de gli Interualli, se non per uia della misura di essi corpi;
cioè, dalla misura di due di essi, ò ueramente d'un'almeno diuiso in molte parti; è neces-
sario, che tra loro intrauenga una certa proportione di suono graue & d'acuto. La onde
per la comparatione della quantità della chorda, che dà il suono graue, con quella che
rende il suono acuto, diciamo, che la Musica è sottoposta alla Quantità relata; mediante
la quale potiamo con diuersi mezi tutte quelle cose, che sono dimostrabili
nella Musica. Ma per hauer' cognitione perfetta de cotali cose; fà dibisogno ricorrere à
quell'Istrumento, il quale da ogni Scienza è adoperato, che si chiama Dimostratione;1. Post. ca-
pit. 2.
la quale è quella, che ne fà ueramente sapere. E' ben uero, che non tutte le Scienze usa-
no gli istessi mezi; percioche essendo Quattro le cagioni; come nelle Istitutioni dichia-
rai;1. Par. cap.
41. non tutti dimostrano per tutte quattro; conciosiache la Metafisica dimostra solamen
te per le cagioni formale & finale, & anco per la efficiente. Il Naturale dimostra per
ogni cagione; ma il Mathematico (lasciando qualch'altra opinione da un canto) dimo-
stra solamente per la cagione formale. A questo disse . Adriano: Per le cagioni forma-
li adunque hauerete à dimostrarci le cose della musica. Et io à lui; Cosi sarà, in quanto
Mathematica; però quando s'hauesse à dimostrar come naturale; essendo la Musica col
locata tra questi due generi, si procedebbe altramente. Ma inanzi che passiamo à dimo-
strar cosa alcuna sarà ben fatto; per alcuni de uoi, che non sete cosi bene essercitati ne i
studii delle lettere; d'andar ricordando (com'hò detto ancora) quel che sia Dimostra-
tione, & mostrar le sue conditioni, & come debbono esser le sue premesse, ò propor
page 12 tioni, di che ella si compone. Sarà ben fatto; disse il Signor Desiderio; per non star poi
à dichiararle fuori di tempo. Questo apunto ui uolea dire; soggiunse M. Claudio; quan-
tunque ne habbia un poco di prattica; perche molte fiate io ne hò (come hò detto anco)
udito ragionare. Veramente è necessaria la cognitione di queste cose, disse M. Adriano;
percioche non le intendendo, non s'haurebbe quel spasso & quella dilettatione; ne si
cauerebbe quella utilità, che bisognerebbe. Ma credo, che mi ricorderò il tutto quan-
do l'andarete commemorando. Vdito questo il S. Desiderio, le disse. Voi sete stato in Pa-
riggi M. Adriano; per quel c'hauete detto. Alquale rispose M. Adriano; Fui, & inco-
minciai à studiare; ma Iddio ha uoluto, ch'io insegni Musica alla fine. Allora uoltatomi
uerso lui, dissi: Messer Domenedio molto ben sapea, che 'l mondo hauea dibisogno d'un
uostro pari, però ci diede uoi, à fine che haueste ad illuminar quelli, che si dilettano di
quest'Arte cosi nobile, & dirò anco di questa Scienza; percioche se non foste stato uoi,
che mi hauete aiutato nella Prattica, non mi sarei posto à ueder cosi intrinsecamente,
com'io hò fatto, & cosi minutamente le cose della Musica; ma mi sarei riportato, come
han fatto molti, al giudicio d'altri; & mi sarei attenuto à quel c'hauessi ritrouato scritto
d'altri Scrittori, credendoli & persuadendomi, cosi fusse, come hanno scritto. Pe-
rò fù ben fatto, che lasciaste lo studio delle Leggi, & attendesti alla Musica; essendoche
in questa tenete il primo luogo, & Iddio lo sà; se ben non sete senza giudicio: s'in quel-
la professione hauesti tenuto il terzo. Cosi hà piaciuto à Dio; rispose egli; & me ne con-
tento. Disse allora M. Francesco; Ve ne potete contentar Messere; ma lasciamo da un
canto queste cose; perche 'l tempo scorre, & ancora non si è incominciato à ragionar di
quello, ch'è stato proposto. Sappiate adunque (io seguitai) acciò continui quello ch'in-
cominciato hauea, che la Dimostratione è proprio come un'Istrumento, che ci conduce
al Sapere, & all'acquisto della Scienza, & questo è il suo uero fine, al quale tendiamo. Ma
auertite, che qui per il Sapere nō intendo altro, che il conoscer le cose col mezo delle lor
uere & proprie cagioni; di maniera che manifestamente si cōprenda, che non possino esse
re, ne stare possino altramente di quello, che si conoscono. Et questo dico, ch'è il uero Sa-
pere, & la uera Scienza. Sappiate però, che il Sapere si ritroua esser di due maniere; Il
primo è detto Sapere per sè, & l'altro Sapere per accidente. Il primo è quello, quando
noi conosciamo la conclusione col mezo delle propositioni, ò premesse, che sono per se.
Riducetemi di gratia (disse M. Francesco) alla memoria quel che intendiate per queste pro
positioni, ò premesse, che sono per sè. Lo farò à mano à mano, risposi; ma soggiunse subi-
to M. Adriano, Dateci anco un'essempio di quello, che detto hauete. Son contento; ri-
sposi; ma non habbiate pressa. Dico, che 'l primo modo è, quando si conosce l'Huomo
esser risibile, col mezo di questa propositione, ò proposta maggiore; quando dico; l'Ani-
male rationale è risibile; & col mezo di questa minore, che è; l'Huomo è animal ratio-
nale; da questa cauo la conclusione, & dico; Adunque l'Huomo è risibile. Questo adun
que è il Sapere per se; soggiunse M. Adriano; per quello ch'io m'accorgo. Cosi stà la
cosa, soggiunsi. Seguitate adunque il Sapere per accidente, disse egli. Notate a-
dunque Messere, risposi, che il Saper per accidente (per dichiararui il secondo modo)
è conoscer la cosa col mezo delle premesse, che sono per accidente. Allora M. Clau-
dio, Dateci l'essempio di gratia, soggiunse. Et io à lui; eccolo, come s'io uolessi prouar,
che l'Huomo compone, io direi; Il Musico compone; l'Huomo è Musico; adunque
l'Huomo compone; & questo sarebbe Sapere per accidente; essendo che le premesse & la
conclusione sono per accidente; conciosia che l'esser Musico non è per se nell'Huomo, ma
per accidente; & questo sapere non è uero sapere. Soggiunse M. Adriano; Da quel che
detto hauete adunque; potiamo dire, che 'l primo modo è il uero sapere, ma non il secon
do. E' uero, risposi; ma questo primo modo etiandio è di due sorti; imperoche l'uno si
chiama Saper semplicemente, &l'altro Sapere ad un certo modo. Il primo de questi è sa-
per la conclusione col mezo della propria cagione & immediata; & il Secondo è Saper
col mezo d'alcun segno, ò per alcun'effetto, o ueramente per alcuna cagione uniuersa-
page 13 le & rimota. Desidero, disse M. Francesco, l'essempio di una & dell'altra maniera. On-
de li dichiarai, che Della prima maniera sarà; quando saperemo l'Huomo esser risibile,
perche è rationale; percioche la Rationalità è propria & immediata cagione della Risi-
bilità, ò del Ridere, che uogliamo dire: Della seconda; quando saperemo, che la Don-
na hà partorito, perche hà il latte; essendoche l'hauere il latte non è segno fermo, che
sempre ne dimostri, che la Donna habbia partorito; massimamente perche si ritro-
uano molte Donne hauer il latte, & non per questo hauer partorito. Et non sola-
mente si trouano le Donne, ma anco (per dirui cosa forse, che ui parerà incredibile) hò
ueduto de gli huomini, che hanno il latte, & per questo non si può dire, che habbiano
partorito. Soggiunse, ridendo M. Claudio. Questa è ben cosa rara & ridicolosa; ma per-
che si è inteso benissimo il tutto, ui preghiamo à seguitare. Dico adunque (soggiunsi) che
la Dimostratione fatta nel primo modo, fà sapere per sè semplicemente, & in uno modo
perfettissimo, ma quella fatta nel secondo, fa sapere per sè ad un certo modo, & molto
imperfettamente; come da gli essempii posti di sopra hauete potuto comprendere. Di-
teci adunque, disse M. Adriano, quello che sia questo Sapere. Auertite, diss'io, che io non
ui uoglio definire il Sapere pigliato uniuersalmente, secondo tutti quei modi, ch'io hò
dichiarato di sopra; ma secondo quello, ch'io nomino Sapere per sè semplicemente, &
con modo perfettissmo; delquale questa sarà la sua definitione. Il Sapere è conoscer la
cosa per la sua cagione, per la quale è, & non può essere in alcun'altra maniera. Et nota-
te, ch'io hò detto, che 'l Sapere è conoscer la cosa per la sua cagione; accioche da questo
comprendiate, che non intendo il Sapere dall'effetto; anzi uoglio che sappiate, ch'io
uengo à distinguer quello da questo. Soggiunsi poi: Per la quale è; facendoui auertiti,
che tal cagione è propria non commune à tal cosa & ad un'altra; accioche da questo pos-
siate conoscere, quanto sia differente il Sapere, ch'io intendo di sopra, da quello, che
si uiene ad acquistare dalla cagione uniuersale & rimota. Imperoche quando noi sap-
piamo, che una pietra, ouer un legno secco non respira, perche non hà anima, tal Sa-
pere non nasce dalla cagione propria & propinqua; essendoche si trouano molti animali;
come sono arbori, ostreghe, uermi, mosche, & infiniti altri imperfetti, i quali non respira-
no. Ma la propria cagione & propinqua del non respirare è, che non hanno il polmo-
ne. Adunque quand'io dico; Et non può esser'in altra maniera; tale aggiungimento
è, accioche conosciate tal cagione essere infallibile & necessaria; & anco accioche co-
nosciate 'l Sapere, che s'acquista col mezo de i segni probabili; come quando sappiamo,
che l'Infermo si dè sanare; perche fà la urina chiara, mangia con appetito, dorme soa-
uemente, & fà altre cose simili; di maniera che queste attioni s'assimigliano à quelle d'un
sano. Et questo segno alle fiate è molto fallace; percioche spesso intrauiene il contra-
rio. Bisogna adunque, disse M. Francesco, che la cagione, col mezo della quale sappia-
mo semplicemente alcuna cosa, sia necessaria. Cosi bisogna che sia; risposi; percioche
è il mezo della conclusione. Et perche quello, che si hà da sapere, & la Scienza sono
correlatiui, & l'uno all'altro corrispondenti; è necessario, che si come la cagione del Sa
pere è necessario, che anco necessario sia quello, che si hà da sapere, che è la conclusione:
Percioche non potiamo saper semplicemente una conclusione, la quale può accascare,
che è detta Contingente; ma si ben potiamo hauer di essa opinione. Queste cose tutte, ri-
spose M. Adriano, fin qui intendiamo benissimo. Passaremo adunque (soggiunsi) al-
l'Istrumento dell'Intelletto, al Sapere & all'acquistar la Scienza, & lasciaremo di defi-
nire la Dimostratione uniuersalmente presa; come habbiamo lasciato anche da un can
to il definire il Sapere uniuersalmente, & uerremo alla definitione della Dimostratione,
la quale è chiamata da i Filosofi Potissima, & è quella, che cagiona in noi il Sapere so-
pra la cosa definita. Aggiungereremo anco, di che, & di quali Premesse si compone:
Et tal Dimostratione i nostri addimandano A' priori; & dimostratione Propter quid,
la quale è differente dalla Dimostratione, che si chiama A' posteriori & Quia, ch'è quel
la, la quale si piglia da i segni & dalle cagioni uniuersali, come del secondo modo di Sa-
page 14 pere di sopra hò dichiarato. Sono cose (disse M. Francesco) queste, che si lasciano inten-
dere; però non ui dia noia il seguitare. Seguitando il mio ragionamento, dissi; Vi porrò
adunque inanzi due definitioni della Dimostratione, l'una sarà della cagione finale, &
l'altra della materiale. Douete adunque auertire; che si come diciamo; uolendo definire la
Casa dal fine, ilquale ci muoue ad edificare; ch'ella è cosa, che ci copre & difende dal fred
do, dalla pioggia, dalla neue, & dal caldo; essendoche à questo fine la edifichiamo; oue-
ramente, pigliando la definitione dalla materia, della quale ella si compone, uenimo à
dire; che è cosa composta de pietre, di calzina, de legni & altre cose simili; cosi pren-
dendo la Definitione della Dimostratione dal fine, dicemo; che la Dimostratione (come
la dichiara Aristotele nel.1. de i posteriori) è un Sillogismo scientifico, ouer'è Sillo-
gismo della scienza; come à noi torna più commodo à dire, il quale ueramente cagiona,
ò partorisce in noi la Scienza, ouer il Sapere, che di sopra habbiamo definito. Questo in
tendo benissimo; disse M. Claudio; ne hò dibisogno d'altra dichiaratione; però segui-
tate, che se tutto quello che direte apprenderò cosi facilmente, come ho appreso quello,
che fin'hora detto hauete, le cose passaran bene. La Definitione della Dimostratione,
risposi, che si piglia dalla materia, M. Claudio, si darà in questo modo. La Dimostra-
tione è un Sillogismo, che si compone di Premesse uere, prime, immediate, ò sen-
za mezo alcuno, & cagioni piu note; & maggiormente prime, & conosciute della con-
clusione. Et quantunque tutte queste cose si ricercano; fà dibisogno ancora, che tali
Premesse siano inanzi, ò precedino la conclusione; & siano la sua cagione; di maniera
che dall'una & l'altra di queste due Definitioni potete comprender quello, ch'entra nel-
la Dimostratione, & il fine, à che ella sia stata ritrouata. Dopo questo M. Francesco
aggiunse; Veramente che appresso di me la prima definitione è chiara; ma la seconda mi
fà stare alquanto dubioso, per non ricordarmi cosi ben quello, che s'intenda Premesse
uere, prime, immediate, & cagioni più note, & maggiormente prime della conclusio-
ne. Però ui prego, che ci dichiarate questi termini, che credo, che qui sia il luogo.
Adunque (dissi io) accioche di queste cose ne habbiate buona cognitione, statemi ad
ascoltare. Io dissi di sopra, che le Premesse debbono esser uere, percioche douendo far
sapere la conclusione di maniera, che sia impossibile, che nasca d'altro luogo, che dal-
la cagione contenuta in esse; è sommamente necessario, che tali Premesse siano uere, &
per consequente cagione della Conclusione. In qual maniera cagione della conclusio-
ne? disse M. Adriano. Cagione, dissi, non solamente della Consequenza, come ne gli
altri Sillogismi intrauiene per la forma loro, che si richiede ch'auenga, ma cagione del
uero esser della Conclusione; ilche è proprio del Sillogismo dimostratiuo, del quale ho
ra parliamo. Questo s'intende benissimo, disse M. Claudio. Le premesse (soggiunsi) à que
sto debbono etiandio esser più note della conclusione, & anco le debbono precedere.
Allora M. Francesco mi fece questa dimanda; Che intendete uoi per questo precedere,
& per più noto? Allaquale risposi. Che non siano tali inquanto à noi, ma in quanto al-
la Natura istessa; la notitia della quale non sempre concorre con la nostra. Disse à que-
sto M. Francesco. Fate di gratia che meglio u'intendiamo. Notate adunque, dissi; che
rispetto alla Natura habbiamo à dire, che più note siano à lei le cagioni con le quali el-
la opera gli effetti, che essi effetti non sono; & consequentemente, che ad essi effetti nel-
la sua cognitione uadino auanti le cagioni; si come etiandio nell'atto parimente prece-
dono; poi che senza dubitatione alcuna ella produce col mezo loro tutti gli effetti. On-
de hauendo rispetto à noi, che non operiamo detti effetti, col mezo del senso, che ce li
mostra; quelli il più delle uolte prima si offeriscono alla nostra cognitione, che non fan-
no le cagioni, le quali, discorrendo noi col mezo de tali effetti, conosciamo nell'ulti-
mo luogo. Di modo che l'ordine della nostra cognitione, il più delle uolte si troua esser
contrario à quello della Natura; la qual Natura operando da quel che produce, à quel
che segue; simigliantemente per la , ch'ella hà seco, conosce col mezo
dell'ordine detto. Ma noi da quel che seguita, spesse fiate procediamo à quello che uà
page 15 inanzi, per la ragione detta. Rispose à questo M. Claudio. Diremo adunque, ch'ogni
fiata ch'io dico, che le premesse della Dimostratione hanno da esser piu note, che la con-
clusione, & preceder quella; che sempre intender debbiamo secondo 'l proceder della
natura. Cosi è in fatto, dissi. Adunque, soggiunse M. Adriano, in cotale Sillogismo se-
guitiamo l'ordine della natura, & il suo procedere. Senza dubio alcuno; risposi io; ma
ciò non accasca molte uolte. Per qual cagione? disse M. Francesco. Per la nostra imper-
fettione; risposi io; onde nasce, che simigliantemente rare uolte i Filosofi pongono in es-
sere questi Sillogismi Questo intendiamo bene; disse M. Claudio; ma resta che ancora ci
andiate dichiarando quel che s'intende, che le Premesse siano prime, & senz'alcun me-
zo. L'esser senza mezo (replicai) s'intendono, quando 'l mezano termine, che si pren-
de nella dimostratione è cosi congiunto al maggiore, che si piglia; & al maggiore, che si
hà da concludere; che niun'altra cosa si può ritrouar di mezo; ouer è il mezo tra loro per
grado predicamentale; & ciò potrete comprendere (per dare un'essempio) auenire tra
la Definitione & il Definito; non essendo tra l'Huomo, ch'è definito, & l'Animale di-
scorsiuo, ch'è la definitione; alcun mezo, per il quale si possa mostrar, che l'Huomo sia
tale. Non si potendo dimostrar la definitione delle cose. L'essempio c'hauete addutto,
rispose M. Claudio; hà di maniera illustrato questo ragionamento, che sin'hora s'inten-
de benissimo quel c'hauete detto; però seguitate il resto. A questo aggiunsi, che le Pre
messe debbono oltra ciò esser prime; cioè, debbono esser tali, che non si ritroui in alcu-
na Scienza (dirò cosi) più alta proposta & più nota di quelle; & è forza, che si prendino
come note, senz'alcuna proua. Adunque; disse M. Adriano; per tal cagione saranno, ò si
chiameranno Indemostrabili. Sta molto ben Messere; gli risposi; percioche douendo
nascer quello, che si dimostra dalle Premesse precedenti & più note; se le Premesse tutte
s'hauessero sēpre da dimostrare, & anco le Premesse delle Premesse; bisognerebbe, ch'al
tre più note, & più precedenti, sempre salendo in infinito; fusse 'l nostro procedere. La on
de non si potendo poi arriuar mai à quelle, che per se stesse fussero tali, ne si potendo trap
passir l'infinito; saria forza, fermarsi in alcune di esse, le quali, per dipendere da più alte
premesse, non sarebbono da noi per se stesse conosciute; & per consequente le conclusio
ni, che da esse nascessero, non potrebbono rendersi manifeste; da che ne seguirebbe
quello, che molti s'hanno imaginato; che niuna propositione dimostrar si potesse. Do-
po questo disse M. Francesco; Questo discorso mi è stato molto utile; percioche m'ha rid
dotto alla memoria molte cose, le quali già (per non attender'à questi studii) mi erano
di mente uscite. Et mi souiene, ch io udì spesse fiate dire; che in qualunque Scienza,
auanti che si uenga al discorrere in essa cosa alcuna; si suppongono alcune Propositioni
manifeste, lequali nō debbeno esser negate d'alcuno, che si vuol essercitare in quella Sciē
za. Vi ricordate molto bene per mia fè; gli risposi; & mi rallegro, che non haurò fati-
ca di replicar più cotal cosa; ne meno molt'altre, che concorrono alla Dimostratione,
per causa uostra; delle quali ui conosco insieme con gli altri istrutto; però seguitando do-
ue hò lasciato, dirò, che tali Principij alcuni si chiamano Positioni; & sono queste Posi-
tioni, ouer Principii di più maniere: Imperoche alcuni sono detti Communi, & alcuni
sono chiamati Proprii. I Proprij sono quelli, che seruono ad una Scienza particolare;
ne bisogna che ui pensiate, che questi siano i Principij istessi d'un'altra; perche sareste in
errore: Ma douete sapere (com'hò anco detto di sopra) che da i Generi diuersi delle cose
scibili, nascono diuerse Scienze. Onde si come la Quantità continua è differente in ge-
nere dalla Discreta; cosi è differente l'Arithmetica dalla Geometria. Et si come la Gran
dezza è differente dal Numero; cosi sono differenti i principij della Geometria, co i qua-
li si dimostrano le sue conclusioni, da quelli dell'Arithmetica. Onde i principij proprii
della Geometria sono (per darui un'essempio) questi; Si può condurre una Linea da un
punto all'altro; Il continuo è diuisibile in infinito, & altri simili. Ma quelli dell'Arithmeti-
ca sono; Il Numero è moltitudine ordinata di Vnità, Le parti del numero non si congiun
gono ad un termine commune. I Numeri procedono oltra l'Vnità in infinito; & gli altri.
page 16 Et quelli della Musica sono; L'Interuallo è habitudine de spacij del suono graue & del-
l'acuto; & altri simili, come presto uederete; & questi si chiamano Principij proprij.
Ma i Communi sono cosi nominati, che non solo in questa, ò in quella Scienza si posso-
no supporre; ma in tutte l'altre vniuersalmente; percioche sono tali, che l'Huomo per
natura; inteso che hà la significatione delle parole, che contengono; subito aiutato
dall'Intelletto conosce chiaramente la uerità loro: Come per essempio quando si dice;
che 'l Tutto è maggior della Parte; saputo che si hà il significato di queste due parole Tut
to & Parte; si conosce, senz'altro aiuto, di maniera esser uera tal positione;
che chi altramente uolesse far credere, non si darebbe fede alle sue parole; & sarebbe
riputato pazzo. In uano ueramente si affaticherebbe, disse allora M. Claudio; chi uo-
lesse persuadermi il contrario. A questo soggiunsi: Questo principio è detto Commu-
ne; percioche serue in diuerse Scienze, onde nella Geometria il Geometra l'applica al-
le quantità misurabili; nella Arithmetica l'Arithmetico l'accommoda alle quantità nu-
merabili, & nella Musica il Musico se ne serue & lo addatta à gli Interualli, ouero alle
Quantità ò Corpi sonori. Sono questi Principii communi, ò propositioni, chiamati Di
gnità; & per la loro eccellente notitia che tengono, sono supposti per principij notissi-
mi, & principali d'ogni Scienza; ma gli altri Principii & altre Proposte sono d'altra na-
tura; percioche se ne ritrouano alcune di esse, che se ben non sono naturalmente cono-
sciute da Colui, che vuole apprendere alcuna Scienza; nondimeno è forza, ch'egli le
conceda per uere, & non cerchi in tal Scienza di loro altra dimostratione, per non ha-
uer quiui elle cosa alcuna più nota, che vi stia sopra. Et queste tali Propositioni sono di
due sorti; l'una è che affirmando, ò negando alcuna cosa, si chiama Definitione, la qua
le dichiara molti termini necessarii à quella Scienza; & tali Definitioni si accettano per
uere, senza uerun'altra proua; come trattandosi nell'Astrologia delle Sfere, de i circoli,
& d'altri cosi fatti termini; auanti tutte le cose si suppone, che la natura del Circolo cele-
ste consista nella figura circolare, compresa da una sola linea, che hà nel mezo il punto,
dal quale tirrate le linee alla sua circonferenza, tutte sono equali. Il simile si può anche
dire della Sfera; disse il Signor Desiderio; & d'ogni altro termine in cotale Scienza neces-
sario. Cosi è, risposi; onde gli Astrologi col mezo de tali definitioni prouano le proprie-
tà de i Corpi celesti, che sono ueramente il loro Soggetto. A questo M. Francesco dis-
se; Questo istesso si potrebbe anco dir nella Musica de i Corpi sonori, i quali contengo-
no l'Interuallo; come sono le Chorde; percioche col diuidere, ò misurare vna linea retta,
posta in luogo di chorda tirrata sopra vn spacio; è mezo molto accommodato al Musi-
co, per prouar le conclusioni del suo Soggetto. Voi la intendete benissimo; dissi io, però
passaremo à dir dell'altre sorti de propositioni, che sono Dignità; & saranno, quando in
una Scienza si suppone alcune cose, le quali contengono in se affirmatione, ò negatione;
& si debbono chiamare & stimare propositioni. Et se ben per loro natura manifeste non
sono; si hanno però da supporre nelle Scienze per note, & queste sono di due maniere.
Non mancate, disse M. Claudio, vi prego, di porre gli essempij. Cosi farò; risposi; state-
mi pure ad vdire. La prima maniera è quando colui, che hà da imparar quella Scienza;
udendo cotali proposte, à loro assentisce facilmente; non essendo prima per se stesso dispo
sto più ad accettarle per uere, che à negarle come false. Et per darui un essempio: S'io di-
cesse, che colui, il quale vuole imparare & apprender la Musica, hà da supporre, che tutti
gli Interualli della Diapason sono eguali di proportione; & uoi vdēdo questo lo credeste;
per non hauer prima uoi stessi opinione, che siano più equali, che inequali, queste Po-
sitioni si chiamano Suppositioni. Io intendo benissimo, disse M. Adriano, onde potete
seguitare. Il perche seguitai, cosi dicendo; La seconda maniera de queste Positioni sono
quelle, che quando, per il contrario, colui c'ha da imparar la Scienza, vdendo le Po-
sitioni, che li sono proposte da credere, assentisce à quelle, perche gli vien detto, che
cosi bisogna fare, ma non perche egli conosca, ò li paia, che sia cosi; hauendo egli uera-
mente prima per se stesso piu tosto tenuto 'l contrario. Et per uenire all'essempio; dirò;
page 17 Se à uoi, che desiderate di apprender le cose della Musica, si proponesse; che si hà da
supporre, che l'Vnisono sia quello, che non hà alcun Interuallo, nella qual Positione
forse ui marauigliareste, parendoui strano; se non haueste cognitione di questa Scienza;
c'he si possa ritrouar cosa, che non sia dissonante, & che non habbia interuallo. Soggiun-
se à questo M. Adriano; Adunque hauendo inteso il tutto bene, potiamo dire, che tut-
te le Positioni, Dignità, Definitioni, Suppositioni, & le Petitioni, ò Dimande ancora,
si hanno da stimare per Principii di quella Scienza, nella quale si pongono. Cosi è ue-
ramente; risposi; ma auertite ancora; che se bene alcuna delle nominate Petitioni & Sup
positioni in un'altra Scienza dimostrar si potesse; tuttauia in quella facultà, nella quale è
posta per Principio, non si potrebbe ritrouar modo alcuno di dimostrarla; essendoche uo-
lendola dimostrare, bisognerebbe altri principii; di maniera che cotali Suppositioni, &
Petitioni uerrebbono à non esser Principii. Ma pigliandosi per sapute & per note; da
quelle, come da sufficienti premesse, si dimostrano poi le conclusioni, le quali alla det-
ta facoltà appartengono. La onde se in alcuna Scienza particolare; come è la Musica,
& l'Astrologia, ò in qualunque altra, alcun uorrà negar qual si uoglia principio; in co-
tal Scienza non li sarà concesso disputare; ne sarà atto à modo alcuno d'impararla.1. Phy. c. 2.
Et Quanto à questa parte non ui uoglio dir'altro; ma credetemi Messere, che hora in
comincia il buono. Lodato sia Iddio adunque, disse egli, & seguitate pure, & dite
quel che uolete, perche siamo apparecchiati ad ascoltarui. Seguitai, inteso questo, in
cotal maniera; Voglio, che sappiate; ch'ogni Proposta, che si propone à dimostrare;
può essere di due sorti; imperoche oueramente ch'ella ci conduce alla Speculatione; ò
ueramente che ci fà operare. Quella, che ci conduce alla speculatione, è detta Θεώρη-
μα; ma l'altra è chiamata Πρόβλημα; & questa è dimandata per tal nome; percioche da
lei impariamo il modo di diuidere, comporre, descriuere, disegnare, & formare ogni
qualità di figura superficiale, con tutti quei accidenti, che concorrer possono in molte
Arti; come nella pittura, prospettiua, corographia, cosmographia, geographia, scol-
tura, architettura, & altre simili. Oltra di ciò ui uoglio dire, ch'ogni Theorema, ò
Problema, il quale sia compiuto dalle sue parti, debbe hauere in se Sei cose; la prima
è la Proposta, che da Greci è detta Πρότασις; nella quale si contiene il Dato, & il Que-
sito; delle quali due cose si compone ogni perfetta Proposta; Et l'officio di questa parte
è d'isegnar quello che si cerca dal Dato. La Seconda è chiamata Espositione, ouer
Esplicatione del Dato; detta Ε῎κθεσις; il cui officio è di riceuere in se il Dato, & appa-
recchiarlo alla Questione. Qui disse M. Claudio Merulo, Diteci di gratia quel che
sia ciascheduna di queste due cose. Vi farò capace (risposi) con un'essempio. S'io di-
cesse; Si può sopra una chorda data collocare il Tuono alla sua proportione; la chor-
da data si chiama ueramente il Dato; & il collocare il Tuono è il Quesito. Io in-
tendo benissimo; disse il Merulo; seguitate il uostro parlare, & perdonatemi, s'alle
fiate ui dò disturbo. Anzi mi date piacere; gli risposi; Ma per ritornar al nostro pro-
posito, dico; che la Terza parte si nomina Διορισμὸς; cioè, Determinatione del
Quesito; il cui officio è di esporre da parte quello, ch'ello sia. La Quarta è detta Co-
struttione, chiamata da i Greci Κατασκευὴ; la quale è quella, che per ritrouare il
Quesito, aggiunge quelle cose, che mancano al Dato. S'aggiunge à queste la Quin-
ta, detta Α'πόδεξις; cioè; Dimostratione; la quale scientificamente ci dà il proposito,
col mezo delle cose concesse, & presupposte. Vltimamente ui è la Sesta, detta
Συμπέρασμα; la quale Epilogo, ò Conclusione potiamo dire; che di nuouo si uolta
alla Proposta, confirmando quello, ch'è dimostrato. Dimandò allora M. Adriano; se
si trouano tutte queste cose in ogni Theorema, ò Problema? A cui risposi; Messer
nò; ma in ciascheduno si ritrouano necessariamente la Proposta, la Dimostratione,
& la Conclusione; percioche fà bisogno conoscer primieramente il Quesito; cioè, quello,
che si propone nella questione; & dopoi dimostrarlo cō i debiti mezi; & dopo dimostrato
concluderlo. Di modo che nō può mai mācare alcuna di queste tre cose. In alcuni luoghi
page 18 l'altre molte uolte s'adoperano, & in molti da un canto si lasciano; come si può uedere
nella 10. del 4. di Euclide; la qual dice; Potiamo constituire il Triangolo de due lati egua
li; che habbia all'uno, & laltro de gli angoli alla base il doppio de gli altri angoli; doue
mancano la Determinatione, & la Espositione; massimamente quando l'Esplicatione
del Dato è sufficiente, di maniera che non faccia dibisogno altra aggiuntione, per dimo
strar quello, che si propone. Ma la Costruttione spesse fiate non si troua in molti Theo-
rema. Et quando nella Proposta non sarà alcun Dato; allora mancherà la Espositione.
Ma la proposta il più delle uolte haurà il Dato & il Quesito, non però sempre: percio-
che alle uolte haurà solo il Quesito, il quale fa dibisogno di conoscere, ouero di farlo,
ò ridurlo ad effetto; come già nel detto Problema, ò Proposta si uede, percioche non
si dice; Di qual Dato bisogna costituire il Triangolo de due lati equali, c'habbia l'un
de i lati equali doppio all'altro; ma solamente si propone, che tal Triangolo da farsi,
sia Equicruro. Quando ueramente la Propositione haurà l'uno & l'altro; allora si ritro-
ueranno la Determinatione & l'Espositione. Ma quando 'l Dato non ui sarà; manche-
ranno etiandio tutte queste cose; percioche l'Espositione & la Determinatione, sono co-
se, ch'appartengono al Dato. Disse à questo il Sig. Desiderio; Veramente che la co-
gnitione di queste cose è molto necessaria, à uolere hauer piena notitia della Dimostra-
tione; ma forse ch'alcuno de questi Sig. non si contenta ancora; perche uorrà un parti-
colare essempio delle Sei cose nominate di sopra. Voi hauete toccato il segno, disse M.
Francesco; questo è quello, che uolea à punto dimandare; però M. Gioseffo non ui sia
noioso il darci ad intendere coteste cose essemplarmente. Io credea, dissi; che il mio
parlar cosi lungo ui douesse rincrescere, ma per quel ch'io uedo, è tuttto al contrario;
hora perche cosi ui piace, statemi ad udire. Sia adunque per fondamento di quello, che
ui son per dire, la Prima proposta del 1. de gli Elementi d'Euclide; come più facile, più
breue, & come quella, che contiene tutte queste Sei cose; la qual dice; Possiamo sopra
una data linea retta terminata costituire un Triangolo equilatero. Tutta questa diceria
si chiama Proposta, & si diuide in due parti; cioè, nel Dato, ch'è la Linea retta termi-
nata; & nel Quesito ch'è il Triangolo equilatero. Hora s'io ui uoglio dimostrar questa
cosa, incomincierò prima dall'Espositione del Dato, & dirò; Sia la data linea finita ab;
dopoi uerrò alla espositione del Qesito, dicendo, Fa dibisogno sopra di essa ab. linea
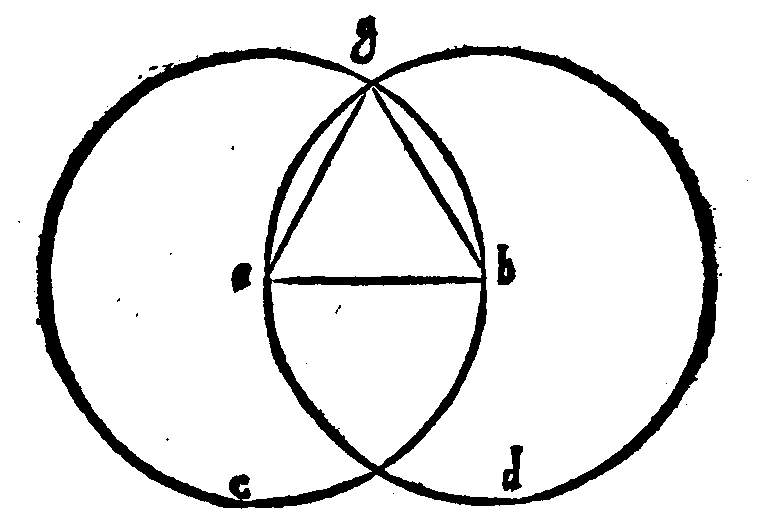
rò; Sopra 'l centro a, secondo la quantità della linea ab, discriuerò il circolo bgc. Si-
migliantemente sopra il centro b, secondo la quantità della istessa linea ab, descriue-
rò il circolo agd. Il che fatto, tirerò le linee ag. & gb. Hora pronuncio la Costruttio-
ne, dicendo; Dico; che 'l Triangolo agb. è equilatero. Vengo (fatto questo) alla Di-
mostratione, & dico; In ogni circolo, le linee tirate dritte dal centro alla circonferenza
sono equali; la figura bgc. è circolo, & il suo centro è a; adunque la ag. è equale alla ab.
Et per prouar l'una & laltra delle propositioni assonte; & mostrar che 'l Sillogismo non
è difettiuo nella materia, perche quanto alla forma e della Prima figura, & in essa non
ui è difetto alcuno; dico, che la maggior proposta è la Definitione del circolo, & la mi-
page 19 nore è nota dalla costruttione. Dico ancora; In ogni circolo le linee dritte, che uanno
dal centro alla circonferenza, sono equali; la figura agd. è circolo, & il suo centro è b;
adunque la linea gb. è equale alla ba. Et per prouar questo secondo Sillogismo, faccio
quello, ch'io feci nel primo, & dico, che la maggiore è la definitione del circolo, con-
tenuta ne i principii; & la minore è manifesta dalla Costruttione. Vengo hora ad uno
terzo Sillogismo & dico; Quelle cose, che sono equali ad un'altra, tra loro sono anco
equali; ciascuna delle linee rette ag, & gb, si troua equale alla linea retta ab; adun-
que la retta ag. è equale alla retta gb. Et prouo questo sillogismo, dicendo; La mag-
gior propositione è Commun parere; & la parte prima della Minore è la conclusio-
ne del primo sillogismo; & quella che segue, è la conclusione del secondo. Ho-
ra uengo al quarto sillogismo, & dico; Ciascun Triangolo contenuto da tre linee
rette equali, è Triangolo equilatero; Il Triangolo agb. è contenuto da tre linee
rette equali; adunque il Triangolo agb. è equilatero. La proua di questo Sillo-
gismo è tale; la maggior proposta è la definitione del Triangolo; & la minor è la conclu-
sione del terzo sillogismo; & cosi è finita tutta la dimostratione. Onde fatto questo aggiun
go la Conclusione, & dico, il Triangolo agb. è equilatero, & posto sopra la data linea
ab; Adunque sopra la data linea retta terminata è costituito il Triangolo equilatero;
come bisognaua fare. Et cosi è compito il tutto; come potete uedere. Vi hò uoluto far
questo cosi lungo discorso inanzi ch'io ui ueng'à dimostrar le cose della Musica, à questo
fine, per non hauer da replicarui in ogni dimostratione più cosa alcuna; però tenete à
memoria, quello che fin qui u'hò detto. Ho inteso, disse il Viola; & molto bene consi-
derato 'l tutto di maniera, che non haurò più cagione di farui replicar sopra queste cose.
Voltatosi allora M. Adriano al Sig. Desiderio, disse; Vedete di gratia quanto bell'ordi-
ne si tiene nel dimostrare; & quanto sensatamente si capisce ogni cosa; il qual gli rispo-
se; Questa è la natura delle Scienze, che dimostrano; che fatta la dimostratione d'una
cosa; tanto ne intende 'l Maestro, quanto 'l Discepolo; & tanto 'l Discepolo, quanto 'l
Maestro. Cosi è dissi io, & si potrebbe ueramente dire ancora molte cose; ma perche
comprendo, che sete molto bene istrutti di quelle, che fin'hora hò ragionato; però pre-
suppono (essendo queste le più difficili, & più necessarie da sapere) che l'altre ui saran-
no facili, quando ue le porrò inanzi; per essere ancora cosa di poca importanza. Onde
passaremo più oltra, & uerremo al nostro principale intendimento; percioche queste
cose, che fin'hora ui hò discorso, non sono quelle, che ui era per dire; ma un pre-
paramento à quei ragionamenti, che seguiteranno. Disse allora il Sig. Desiderio; E' sta
to molto utile ueramente M. Gioseffo & molto necessario questo discorso, c'hauete fat-
to, percioche non attendendo questi nostri amici cari à queste cose; ancora che molte
fiate habbiano udito di esse ragionare, bisognaua dimostrarli, come tornano bene & com
modo à quello, che uolete dire; però passate pure inanzi, quando ui piace, che mi par
che fin'hora habbiamo hauuto una buona lettione. Ripigliai dopo queste parole il mio
ragionamento à questo modo: Volendo adunque dar principio alle dimostrationi, è ne-
cessario primieramente porre i Principii di questa Scienza; accioche col mezo loro si
possa uenir'alle Conclusioni; dimostrando quelle cose, che ci pareranno necessarie. I
quali Principij da uoi, com'io credo, non mi saranno negati; se uorrete ch'io uenga al-
l'atto dimostratiuo. Ma per seguitar l'ordine tenuto da i nostri Maggiori, & da i moder-
ni Mathematici ancora; porrò primieramente le Definitioni per ordine, dopoi le Di-
gnità, ò Massime, ò ueramente Communi pareri, che dir li uogliamo; & ultimamente
le Dimande, senza le quali poco, anzi nulla potrei dimostrare. Niun di noi; disse M.
Adriano; non haurà mai ardimento di negarui cosa alcuna; essendo che sappiamo trop-
po bene, che non ci proponereste cosa falsa. Ma diteci ui prego; per qual cagione po-
nete inanzi ogn'altra cosa le definitioni? Alquale risposi; Bella dimanda ueramente, &
necessaria Messere mi fate; & anco non fuori di proposito, & di grande utile à saperla; pe-
rò sappiate, che se bē ui hò detto di sopra, ch'io lo faccio per seguitar gli Antichi; nōdime
page 20 no questa non può esser buona ragione, anzi la uera è, che le Definitioni sono quelle, che
ci danno ad intender quello, che sono le cose, che si hanno da trattare. Percioche ogni ra-
gion vuole, che prima si sappia quel che sia la cosa, di che si uuol ragionare, almeno
quanto al nome; inanzi che ella si tratti; acciò non si proceda per termini non conosciu-
ti. Oltra di ciò; perche la Definitione è (come tengono i Filosofi, & come hò detto più
inanzi) il mezo della Dimostratione; la onde potete uedere, per qual cagione io mi sia
mosso à uolerla porre inanzi ogn'altra cosa. Io son satisfatto; rispose M. Adriano; però
incominciate doue, & quando vi piace. Darò adunque principio (dissi io) col nome
del Signore alla prima Definitione, la quale sarà questa.
DEFINITIONE
PRIMA.
no prima d'ogn'altra cosa? Gli risposi; percioche il Suono, ilquale hò defi-
nito è detto da Greci φθόγγος, & non ψόφος. il quale significa ogni Strepito; &
è principio della Consonanza, & ogni altro Interuallo qual si uoglia della Mu
sica; com'è il Ponto nella Geometria principio della quantità, che da lui nasce & di-
pende; à questo rispose; dicendo. Questa uostra risposta mi satisfa assai; ma ditemi per
uostra fè; non è buona la Definitione del Suono data da Boetio,Music lib.
1. cap. 3. la qual dice, ch'è riper-
cussione d'aria, che uien fino all'udito? Non è in uerità Sig. Desiderio risposi; questa
sua Definitione al nostro proposito; imperoche il Musico considera 'l Suono in un'altra
maniera, di quel che lo definisce Boetio. Egli definisce il Suono, come cosa naturale in
uniuersale; & il Musico lo definisce in particolare, & lo considera come principio della
Consonanza, & d'ogn'altro interuallo Musicale, quando dice; Il Suono esser cadimento
di uoce atta alla modulatione, fatto sotto una estensione; ò come lo definisce Aristosseno
nel primo de gli Elementi harmonici; dicendo: Il Suono è cadimento di Voce in una
estensione: intendendo per tale estensione la mansione, & lo stato della uoce; Percio-
che pare ch'allora il Suono stia, cadendo la Voce in un stato conueneuole al Canto;
mentre iui cessa in una estensione: La onde quando ella si uede essere in cotale estensio-
ne, allora diciamo il Suono esser voce ordinata alla modulatione; & cadere da tal prin-
cipio, quasi come fà la Linea dal punto: come potrete uedere dichiarato nel Cap. 6.
del Secondo libro de i Sopplimenti; à i quali presto darò fine, à Dio piacendo, & por-
rò in luce. Laonde udendo, questo il Signor Desiderio, disse; mi piace grandemente
questa noua, che ci hauete dato; poi che haueremo di nuouo quello che non aspet-
tauamo; Onde ciascuno Studioso ue ne haurà d'hauere obligo, per le uostre fatiche:
ma non uò restardi dirui; che se 'l Suono è cadimento di uoce, tal cadimento non si può
far senza mouimento; onde non si ritrouando mouimento senza tempo, ne tempo sen-
za quantità; essendo che se gli attribuisce lunghezza, & breuità, secondo diuersi rispet-
ti; Seguita, che non si può dire, come à me pare, che 'l Suono sia principio della Consonan
za, come il Punto è principio della Linea; ma più tosto sia quantità, com'è essa linea; la-
quale si può diuidere in infinito; percioche hà le sue parti aggiūte ad vn termine cōmune,
ch'è l'Instante. Voi argomentate molto bene, Sig. Desiderio risposi; & ueramente il uostro
argomento concluderebbe, quando 'l Musico considerasse 'l Suono, che ho definito, nella
page 21 lunghezza; ma non è cosi; percioche lo considera con altro rispetto. Onde douete sape-
re, che tre cose accadono intorno al Suono; la prima è il Luogo; la seconda il Tempo; &
la terza il Colore, diremo cosi. Quanto alla prima; il Luogo del Suono si considera, in
quanto ad una certa Relatione di graue, & d'acuto; imperoche quei Suoni, che sono in
un'istesso luogo; cioè in un'istesso punto, dirò cosi; il Musico li chiama Vnisoni, & sono
senz'alcun'interuallo tra loro, & sott'una istessa estensione, ò qualità. Ma quando si
fanno più acuti, ò più graui l'un dell'altro; cioè, quando alcuni de quelli si partono dal
detto punto, & uanno in altra parte: allora diciamo, che si trouano in diuersi luoghi, &
hanno tra loro Interuallo, & diuerse estensioni, & riceuono tra loro molti Suoni, nel mo
do ch'in molti luoghi delle Istitutioni hò dichiarato, & altroue son per dichiarare; essendo
che allora tale estensione si muta, & li Suoni diuersi nascono dalla estensione uaria della
chorda; percioche i Suoni graui nascono, quando si rallenta alcuna chorda tirata sotto
qual si uoglia estensione; & gli acuti, quando tal chorda è più tirrata. Et quanto più si
ralenta la detta chorda, tànto più graue rende 'l Suono; & per il contrario, quanto piu
si tira, tanto maggiormente rende il Suono più acuto; come anco dissi nel cap. 1. del Se-
condo Libro sudetto. Il perche considerata la Voce, ouero il Suono dal Musico sola-
mente secondo l'Estensione, & non secondo la Duratione, non cade sotto 'l tempo; ma
sotto la qualità di graue & d'acuto; comparando l'uno all'altro Suono;Vide c. 16.
Lib. 2. Sup-
ple. ma considerato
nella sua Duratione, non è dubio, che non sia sottoposto ad esso tempo. La Estensione
adunque semplicemente considerata, com'è il Punto, non è diuisibile; ma si bene quando
è considerato & riceuuto nella sua Duratione, come Linea. Potiamo adunque dire, che
quantunque il Suono sia diuisibile per la duratione, quanto alla lunghezza, e però indi-
uisibile quanto alla larghezza & alla distanza di graue, & di acuto nella Estensione; essen
do che non hà alcuno Interuallo. Onde essendo considerato come Punto, & essen-
do il Punto indiuisibile; segue anco, che gli Indiuisibili sia; poi che non hà distanz'al-
cuna in atto di luogo, ò sito, alla simiglianza del punto; se ben l'hà nella Duratione,
come hà il punto nella Positione. Ma si come quando tal punto si muoue, uiene à far la
Linea; cosi anco mosso il Suono uerso 'l graue, ouero uerso l'acuto, fà l'Interuallo; il
quale in larghezza è diuisibile. Il Suono adunque pigliato al primo modo; non si può
diuidere; come hò detto; & essendo indiuisibile (ripugnando la diuisibilità all'esser
principio) resta, che senz'alcuna con tradittione esso Suono sia anche principio. Se
il Suono col tempo dura; disse allora il Signor Desiderio; ello hà lunghezza, es-
sendo misurato dal tempo lungo, ò breue; & se cosi è, si può diuidere: per la qual
cosa di nuouo ui dico; che essendo diuisibile, ripugna ch'ello sia principio. A que-
sto risposi; Già ui hò detto, che quantunque il Suono, quanto alla sua duratione hab-
bia lunghezza & da questa parte non sia considerato dal Musico; essendo che lui non
considera quella particola, che pone Boetio nella sua Definitione del Suono: Che
peruiene all'udito; essendo che troppo ben sà, che bisogna che sia cosi, se 'l si hà da udi-
re; tuttauia lo considera per cadimento di uoce solamente; & ui aggiunge; Ad una
estensione; percioche quando nasce il Suono, si uede quasi cadere ad un certo mo-
do dal Corpo sonoro, di doue ello deriua; ma non si ode mutatione alcuna di suono
dal graue all'acuto, ò per il contrario; percioche haurebbe più d'una estensione; co-
me da quello, ch'io hò detto, si può comprendere; ma hà una sola qualità, & è
di un sol tenore; & tal suono si chiama continuo, mentre che resta in questa e-
stensione. Et uoi sapete, che la uoce continua; essendo che non fà consonanza,
ne harmonia alcuna; non è considerata dal Musico, ma si bene la discreta. Et
quantunque il nostro parlare familiare (come forse potreste dire) habbia un non
sò che di graue & d'acuto; tuttauia al suono, che habbiamo dichiarato, non si ue-
de aggiunta alcuna di queste qualità, che da essa si possa tenere il contrario di quel-
lo, che si è detto. Non uoglio però che pensiate, che 'l Musico tenga poco conto
de cotali Suoni, ò Voci, quanto alla loro duratione; essendoche cascano sotto 'l senso
page 22 dell'Vdito; & è cosa, che appartiene à lui; per ilche notate la seconda cosa, che accasca
intorno al Suono, ch'è il Tempo; il quale è considerato, come quel che comprende Nu-
mero, ò Rhythmo; onde da questa parte è cōsiderato secondariamente secondo la sua du
ratione, nella prolatione delle sillabe lunghe ò breui, contenute nella Prosa, ouer nel
Verso: come dichiarai nel cap. 16. del Secondo libro,Vide c. 16.
Lib. 2. Sup-
pli. c'hò nominato poco fà. Inteso
questo, disse il Sig. Desiderio; Io son benissimo satisfato del uostro parlare, di quello
ch'io dubitaua; ma non però di dir la terza cosa, che segue 'l Suono, ch'è il Co
lore. Non mi son per questo scordato; risposi; però ui dico, che 'l Colore è quello, per
il quale sono le Voci & i Suoni l'un dall'altro; com'è nelle cantilene, le
quali consistono nelle uoci, ò ne i suoni, i quali sono tutti sotto diuersi estensioni; & so-
no (dirò cosi) tortuosi & piegati hor da una parte & hora dall'altra; cioè, hora uerso l'a-
cuto & hora uerso 'l graue; contrario di quel che fanno gli Vnisoni, i quali dal principio
loro per tutta la lor duratione, fino al fine sono sotto vna sola estensione; & sotto vna sola
qualità, & sotto un solo tenore, alla similitudine della linea retta, la quale giace di pari
tra i suoi punti, & si troua esser senz'alcuna larghezza. Tornò di nuouo à dire il Sig. De
siderio: Voi uenite pure à confessar, che 'l vostro suono definito habbia duratione, la
quale consiste nella lunghezza. Et io à questo risposi; Non hò mai negato questo; come
si può conoscere da quello che fin'hora hò detto: Ma che importa questo, purche al mo
do che lo considera il Musico, come principio sia indiuisibile. Vi voglio ancor dir una co-
sa, & poi far fine di ragionar sopra questo principio. Non sapete che quando la Musica è
considerata & ridutta nel suo fine, ella è ueramente cosa attiua? & è posta in atto col
mezo di quelle cose che sono sottoposte à quel Genere di cose, che succedono l'una al-
l'altra? com'è il Suono, & non in quello, ch'è di cose durabili & permanenti? come vo-
lete voi adunque ch'ella si ponga in atto, se i Suoni non restano, & non si fanno vdire per
qualche spacio di tempo? il quale non hà alcuna parte, che indiuisibile sia, se non l'In-
stante? Ma in vero altro è la cosa quanto al suo essere; & altro quanto all'esser conside-
rata; come uediamo delle quantità mathematiche, le quali ancorache non possino esser
lontane dalla materia; sono però considerate come da essa lontane. In fatto è cosi; disse
egli; come detto hauete, & hauete ragione; però seguitate quello, che più ui piace.
Cosi voglio fare, dissi. Allora M. Claudio hauendo inteso questo, disse; M. Gioseffo,
hauete posto la Musica nel Genere attiuo; & hauete detto, che i Suoni sono sotto 'l Ge-
nere delle cose che succedono l'vna l'altra; di gratia fatteui vn poco meglio intendere; &
poi farete quel che più u'aggradirà. Son contento soggiunsi; Auertite adunque che l'Ar
ti si ritrouano esser di quattro maniere; imperoche l'vna è detta da i nostri maggiori
Θεωριτικὴ; ò Contemplatiua, la quale hà il suo fine nella speculatione; come è l'Arith-
etica, l'Astronomia & altre simili. L'altra è πρακτικὴ; oueramente Attiua,
o Prattica, che la vogliamo dire, com è l'arte del Saltare, ò Ballare, del Sonare di cetera,
& del Cantare. La è nominata ποιητικὴ, ò Fattiua; com'è l'arte del Fabro, la Pittu-
ra, la Scoltura & altre simili. Ma la quarta è detta Κτητικὴ; ò Indagatrice, ò Cercatrice;
com'è l'Arte del pescare & quella della Caccia. Onde alcune Arti fāno le cose, com'è l'Ar
te del Testore, del Calzolaio & altre simili; alcune cōseruano le cose fatte; come l'Arte del
gouernar la naue; & altre fanno l'vno & l'altro, com'è l'Arte dello edificare. Et se bē la Mu
sica dalla parte speculatiua è detta Theorica; tuttauia dal porre in atto & nel suo fine le co
se, è detta Attiua, ouer Prattica. Ma le cose poste in atto nella Musica non sempre restano,
se non tanto quanto elle sono essercitate; imperoche tanto dura il Ballo, quanto colui, che
l'essercita si muoue; & tanto si ode la Cetera, quanto sono mosse le chorde da colui, che le
percuote: simigliantemēte, tāto si ode la , quanto colui, che canta, manda fuori la
voce. Et perche tutti i mouimēti, che sono fatti in questi atti, sono violenti; però non sono
durabili; onde passato l'vno, di necessità bisogna che l'altro succeda, se 'lsi uuole, che la cosa
stia in atto; oueramēte essendo tali mouimēti giūti al fine, è necessario che da capo si rinuo
uino; però hò detto che la Musica è cosa attiua, & che le cose, di ch'ella si serue, nō sono tra
page 23 quelle, che rimangono; come quelle dell'arte fabrile, ma tra quelle, che l'una all'altra suc
cedono, hanno luogo. Vdito questo M. Claudio restò satisfatto, onde disse; Non mi pen-
tisco di hauerui fatto ragionar queste quattro parole; perche in uero è stata una buona
lettione; Onde ui prego à darci spesso de questi buoni cibi; il che farete seguitando quel-
lo, c'hauete principiato, secondo che ui uerrà commodo. Cosi son per fare, dissi; Ma
perche quando 'l Suono si estende uerso il graue, ò uerso l'acuto, immediatamente si ge-
nera l'Interuallo, il quale è il primo considerato dal Musico ad un certo modo, & non
semplicemente; percioche il Musico semplicemente, & prima d'ogni altra cosa con-
sidera la Consonanza, della quale intende comporre la sua cantilena; però senza por-
re alcun tempo di mezo, definirò l'Interuallo à questo modo.
DEFINITIONE II.
to; i quali nascono da i corpi ò quantità sonore.
anco ui dirò le sue specie; percioche credo, che ue lo ricordiate; Ma ui dirò sola-
mente, che questa definitione è dell'Interuallo propriamente, & non del com-
munemente, detto. Et se hauete in memoria quel c'hò detto di sopra, sappiate, che fà di
bisogno, che questi Suoni siano differenti di estensione; percioche se tutti hauessero una
estensione istessa, non si farebbe altramente l'Interuallo; essendo che questi Suoni parreb-
bono essere & sariano anche in un'istesso luogo; di modo che la differenza, ò distanza,
che si troua tra 'l suono graue, & l'acuto; ò trà l'acuto & il graue, si chiama Interuallo.
Questo è chiaro, disse M. Adriano, & s'intende benissimo, & non hà bisogno d'altro
commento. Allora seguitai, dicendo: Quantunque creda, che uoi sappiate quello che
sia Corpo sonoro; tuttauia lo uoglio da bel nuouo definire, accioche habbiate di lui
più certa & più ferma cognitione. Onde dirò, che appresso il Musico.
DEFINITIONE III.
cun suono.
ciaschedun'Istrumento musicale; Et non solo questa, ma etiandio le Campane,
& qualunque altra cosa fatta di metallo, ò d'altra materia, dalla quale nasca suo-
no; come hò dichiarato di sopra, serà Corpo sonoro. Cosi è, risposi; & di più anco, che
ciascheduna Canna fatta di qual materia si voglia, che poco importa, pur che man-
di fuori suono, è Corpo sonoro. Ma perche ogn'Interuallo musicale (com'hò det-
to poco fà) hà distanza, che si troua tra 'l suono graue, & l'acuto; la quale senza du-
bio cade sotto alcuna proportione; però uolendo i Musici hauer la ragione di ta-
le distanza, non hanno ritrouato miglior mezo, quanto la misura de i nominati
Corpi, da i quali nascono i Suoni; onde come cosa più sicura, & men uariabile, eles-
sero la Chorda sonora; & dalle parti fatte di essa, comparate l'una all'altra, ritrouarono
quel che cercauano. Ne solamente tal cosa ritrouarono, adoperando una sola chorda; ma
page 24 ancora ponendone in opera due tre, & quante più di queste ne facea bisogno; come nel-
le Istitutioni mostrai.2. par.
Cap. 20. Et perche le diuisioni sono quasi infinite, & le parti sono di uaria-
te lunghezze, & cadono (comparate esse Parti al tutto, ouero tra loro; oueramente com-
parati i corpi, da i quali nascono i Suoni, l'uno con l'altro) sotto l'uno de i Cinque generi
di proportione di Maggiore inequalità; però auertirete, che nel primo.
DEFINITIONE IIII.
uolte interamente; come sarebbe due, tre, quattro & più fiate ancora, si chiama
Molteplice; il primo de i quali si nomina Duplo, il secondo Triplo, il terzo Qua
druplo, & cosi di lungo.
chiarai quello che sia Genere; & mostrai anco le sue Specie. Ma nel secon-
do luogo diremo, che
DEFINITIONE V.
te Aliquota, si chiama Superparticolare; come, se la maggior contiene la minore una
sol volta, & una sua meza parte, è detto Sesquialtero; & se la contiene una fiata;
& la sua terza parte, è chiamato Sesquiterzo; & cosi gli altri per ordine.
uengono denominate dalla parola Sesqui, aggiuntaui la parte nominata; la
qual parte, quello ch'ella sia, nelle Istitutioni dichiarai.1. parte
ca. 23. 25. Et perche sò che
tutti uoi l'hauete studiate; credo che ue lo ricordate; onde di essa non ne dirò
più cosa alcuna. Veramente ce lo ricordiamo, disse M. Adriano, & non habbiamo di-
bisogno di replica. Seguitiamo adunque (dissi) più oltra, & diciamo che nel Ter-
zo genere
DEFINITIONE VI.
ta & più parti di essa, che si chiamano parte Nonaliquota, è detto Superpartiente.
Onde se la maggior contiene la minore una fiata con due terze parti, è detto Super-
bipartiente terzo, & cosi gli altri di lungo.
finitioni de due, composti del Primo & dell'uno de gli altri due Generi nomina-
ti; & questa sarà la Prima, & terrà il Quarto luogo. Laonde dico; che
page 25
DEFINITIONE VII.
contien la minore due, ò più volte, & vna sua parte Aliquota; come se la maggior
contiene la minor due fiate con la sua metà, è detto Duplosequialtero.
che nel Quinto luogo si troua il Secondo de i due Generi composti: Il per-
che diremo:
DEFINITIONE VIII.
re due, ò più fiate con vna sua parte Nonaliquota; di modo che quella quantità mag-
giore, la qual contiene la minore due fiate, & due terze parti fà la proportione Du-
plasuperbipartiente terza.
tal diuersità uiene da quella de i loro Denominatori; come, ragionando nel-
le Istitutioni1. Par.
Cap. 25. intorno à i Denominatori delle proportioni de i numeri, ui di-
chiarai. Ma sappiate (per uenire ad un'altra Definitione) che,
DEFINITIONE IX.
chiarai nelle Istitutioni.1. Par.
Cap. 13. Et tanto questi, quanto quelli, che sono detti numeri
Tralorocomposti, sono numeri Relati. Auertite però; che,
DEFINITIONE X.
meri Tralorocomposti, ò Communicanti.
delle Istitutioni) niū'all'altro è primo; & possono esser numerati & diuisi d'altro nu
mero, che dalla Vnità. Et perche la Definitione da sè è chiara; però non ui repli
cherò altro sopra di essa; ma hauendo qualcheduno de uoi da dirmi cosa alcuna, si lascia
intendere, auanti che si uada più oltra. Allora M. Adriano disse; Gli altri numeri, come
sono Pari, Impari, Parimente pari, Primi & incomposti, Composti, Quadrati, Cubi, &
Perfetti, non sono eglino tutti Numeri semplici, & senz'alcuna relatione? Cosi è Messe-
re, risposi; & dimostrate molto ben di hauere studiato le mie Istitutioni; però con uostra
licentia passarò ad un'altra la qual sarà questa.
page 26
DEFINITIONE XI.
differenza, che si troua tra la maggiore & la mezana, sia equale à quella, ch'è tra
questa & la minore; & che tra le minori si troua la maggior proportione, & la
minore tra le maggiori; allora si diranno esser collocate & ordinate in Arithmetica
progressione.
Differenza quella Quantità, per la quale una maggiore sopr'auanza una mino-
re; come è manifesto dalla Quarta definitione del Lib. 7. d'Euclide, secondo la
tradottione del Campano. Hora ui dò lessempio di quello, c'hò detto della definitione.
Poniamo che a b. & c. siano le quantità nominate, & che d. sia la differenza, che si tro-
ua tra a. & b. & e. sia la differenza, che è tra b. & c. Dico, essendo queste due differenze

4. & 3. termini maggiori; che tali quantità si dicono esser'ordinate secondo la Progres-
sione arithmetica. A questo disse M. Adriano; Questo habbiamo facilmente inteso, per
il lume c'habbiamo hauuto dalle uostre Istitutioni; però seguitate il resto. Allora Sog-
giunsi; Verrò adunque all'altra definitione, & dirò.
DEFINITIONE XII.
la Geometrica proportionalità, quando le proportioni, che si trouano tra la maggiore &
la mezana; & tra questa & la minore; & anco tra i termini delle lor differenze, saran-
no simili & equali.
a. b. & c. le quantità nominate; & d. sia la differenza di a. & b. & f. quella di b. &
c. Dico, essendo le proportioni a. & b. b. & c. con d. & f. Duple; che tali quan-
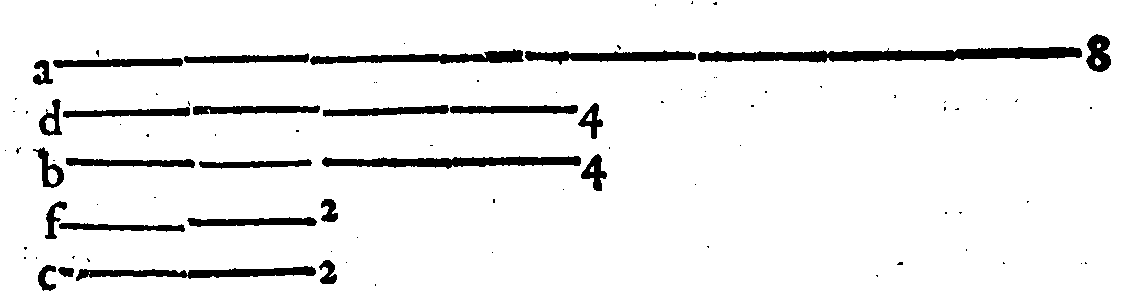
nalità. Questa etiandio; disse M. Francesco; non hà dibisogno di replica; Onde soggiun
si subito; Passarò adunque ad un'altra definitione, & dirò.
page 27
DEFINITIONE XIII.
zana sarà maggior proportione di quella, ch'è tra la mezana & la minore; & anco quel-
la, che si troua tra le differenze della quantità maggiore alla mezana, & di questa alla
minore, sia equale à quella, ch'è posta tra gli estremi; allora tal ordine si dirà esser fat-
to secondo la Proportionalità, ò mediocrità Harmonica.
(diss'io) Siano a. b. & c. tre quantità, & sia f. la differenza di a. & b. & g. sia quel
lo di b. & c. Dico, che le dette quantità si diranno collocate in Proportionalità,
ouer Mediocrità harmonica; poi che la proportione, che si troua tra a. & b. la quale dal
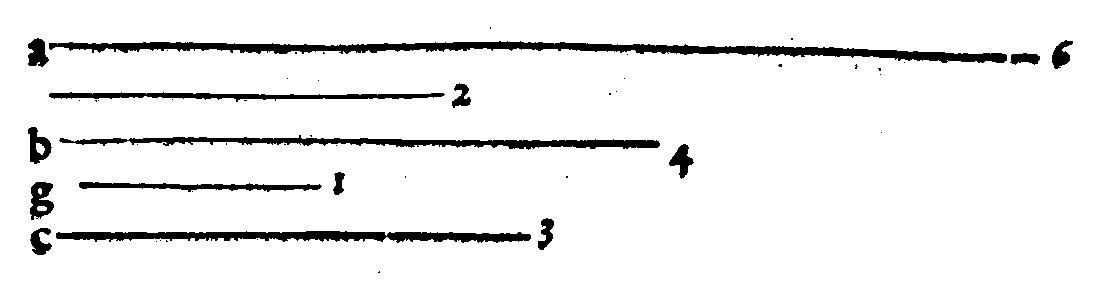
gior di quella, che è tra b. & c. Sesquiquarta; com'è il proprio di questa Mediocrità. Che
segue dopoi, sogiunse M. Desiderio; Segue (& io dissi) che,
DEFINITIONE XIIII.
due minori si troui maggior proportione di quella, ch'è contenuta tra le due maggiori;
& quella che si troua tra le due estreme, s'assimigli à quella ch'è posta tra le differen-
ze, le quali sono tra la maggiore & la mezana, & tra questa & la minore; tal'ordi-
ne si dirà fatto secondo la proportionalità Contr'harmonica.
pio; percioche di questa mai più non ne hò udito cosa alcuna. Se haueste uedu-
to Boetio,:2. Arith.
cap. 51. risposi, & Giordano,10. lib. Arith. questo non ui parrerebbe cosa nuoua, Messere
Ma ueniamo pur'all'esempio. Siano a. b. & c. le nominate quantità, sia & d.la differenza
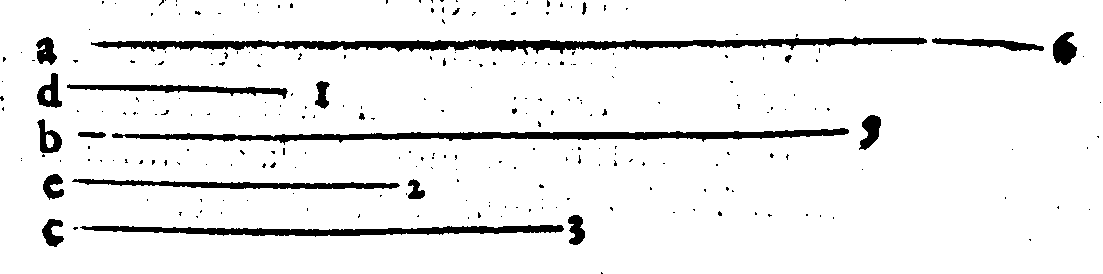
tra a. & c. ch'è Dupla, s'assimigli à quella, ch'è posta tra d. & e. Subdupla; dico queste
quantità esser'ordinate secondo la Contr'harmonica proportionalità, percioche etiandio
tra le due minori si troua maggior proportione di quella, ch'è collocata tra le due mag
page 28 giori. Ma notate, c'hò detto, s'assimiglia; percioche la comparatione, che si fà della mag
giore alla minore quantità, è alquanto differente da quella, che si fà delle differenze, che
si trouano tra le quantità nominate; essendoche per il contrario (uolendo seguir l'ordine
incominciato) si compara la differenza minore alla maggiore; onde nasce la proportio-
ne Subdupla, che ne i termini alla Dupla s'assimiglia; come nelle Istitutioni1. par. cap.
21. & 30.
& 2. part.
cap. 50. hò dichiara
to. Ho inteso il tutto benissimo; disse M. Adriano; però proponete quel che ui piace. Sog
gionsi allora; S'alcuno de uoi hà da dire alcuna cosa, sopra di quel, che fin'hora si è det
to, non ponga tempo alcuno di mezo, acciò possiamo ragionar senza interrompimento,
quelle cose, che seguono. Rispose il Sig. Desiderio; Non habbiamo altro che dirui; se
non ch'à queste Definitioni ci par, che debbano succedere i Pareri communi; che ne di-
te di questo? non è cosi? Cosi è (risposi io à questo) essendo che sono stati alcuni,
i quali hanno tenuto tale ordine; non sò però con che ragione; percioche quei Principij,
che seruono à più Scienze, si debbono porre separati da i Principij proprij d'alcuna
Scienza, & non mescolarli tutti insieme. Però in questo, parmi, di uoler tener'altr'ordi-
ne, & di seguitare insieme con la ragione quelli, che sono stati i migliori; i quali hanno
scritto delle cose dimostratiue; che dopo le Definitioni hanno posto le Dimande, & do
po queste le Dignità, ò i Communi pareri. Incomincierò adunque da quelle, le quali
sono Proprij principij, & il Musico, per dimostrar le cose della Scienza, dimanda che li
siano concessi; percioche ogni uolta, che negati li fussero, si negarebbe tutta la scienza
della Musica, la quale dipende da essi; ne accascarebbe disputar più di essa cosa alcuna;
ilche fatto porrò dopoi quelle. Parue à M. Adriano, che ciò fusse ben fatto, onde disse;
E' cosa ragioneuole; bisogna adunque prima che uoi concediate, dissi allora; che,
DIMANDA
PRIMA.
ro, ò mezano termine.
non si può porre altro numero. E' uero Messere, risposi; perche l'Vnità non si
può partire in due parti; ma resta nella Musica indiuisibile. Notate però, ch'
io parlo dell'Vnità discreta, & non della Continua; essendo che qual si uoglia
Continuo si può diuidere in infinito in parti infinite, in potenza almeno, se non in atto.
Perche rispetto; disse il Viola. Per questa ragione, soggiunsi; che ui basterà solamente;
perche non si dà nella natura una cosa infinita in atto, secondo 'l Filosofo.3. phy. c. 1.
Ibidē. c. 4.
& 11. Me
taph. c. 9.
4. Physi.
cap. 9. La onde doue-
te sapere, che i Numeri sono di due sorti; l'un de i quali si chiama Numero numerante, &
l'altro Numero numerato. La Vnità del primo non si può diuidere in atto; ma quella del
secondo è troppo ben diuisibile; essendo che questo non è altro, che una moltitudine di co
se numerate. Allora M. Claudio disse; Mi piace questa bella distintione del Numero, &
la espositione, di questo principio.All'altro adūque, dissi; bisogna che mi concediate; che,
DIMANDA II.
ni l'istesso numero dato.
6. ne uiene 144. & diuiso tal prodotto medesimamente per 6. senza dubio ritor-
na 24. il che manifesta quel che s'habbia da intendere in questa seconda diman-
da. Disse allora il Merulo; A fè M. Francesco, che uoi siete un buon mathematico, & mi
allegro; però M. Gioseffo ponete fuori la terza se fa dibisogno; poi che questa s'intende.
Concedetemi etiandio, se cosi uolete, ch'io uada più oltra, dissi; che,
DIMANDA III.
uisore; che ritorni il primo Numero dato.
Questo, rispose egli; è il cōtrario di quello, ch'inanzi s'è detto, per quel ch'io m'ac
corgo. Percioche se diuideremo 144. per il 6. ne uerrà 24. onde tal prodotto mol
tiplicato per il 6. darà senza dubio alcuno 144. secondo che dice questa dimanda. A que-
sto disse M. Francesco; Che ui pare M. Gioseffo del nostro Messere? Parui forse, che egli
non sappia far conto? Cosi fà, risposi; chi hà Denari assai. Burlate M. Gioseffo; disse M.
Adriano; per quel ch'io uedo. Al quale disse M. Claudio; A fè, che non burla ello, anzi di
ce il uero; perche n'hauete guadagnato assai col mezo del uostro ualore. Ne hò guadagna
to assai ueramēte, rispose egli; ma holli anco dispensato à i miei più stretti parenti; il perche
pochi ne posso hauere. Ond'io soggiunsi; Voi hauete fatto da huomo da bene, come uoi
sete; però non ui hò dato la burla à dire, che chi ha assai Denari, sà far ben conto. Ma nō
più di questo: Vltimamente concedetemi; che,
DIMANDA IIII.
simo & il Minimo, risposi io. Dechiarateci questa, disse M. Adriano; & poi segui-
tate à dir quello, che più ui piace. E' molto ben honesto Messere, risposi; hauen-
domi tolto questo carico: però attendete. Se fussero quattro termini a. b. c. & d. & a. d. fus sero gli estremi; cioè a. il Massimo, & d. il Minimo, i quali contenessero la proportione
Dupla; allora diressimo, che questa proportione contenuta da tali estremi fusse composta;

d. fanno aggiunte insieme la Dupla proportione a. b. Oueramente si direbbe, ch'aggiun-
gendo la proportione Sesquiquarta b. c. alla Sesquiquinta a. b. si farebbe la Sesquialtera
a c. che congiunta alla Sesquiterza c. d. farebbe la Dupla contenuta tra a. & b. Et questo
è tanto manifesto, che non hà dibisogno d'altra proua. Niuno di noi haurà ardimento,
disse il Sig. Desiderio; di negarui questo principio; perche, com'hauete mostrato, da se
stesso è chiaro; inteso che si hà i termini della cosa. Voglio adunque, dissi che queste Di
page 30 mande siano basteuoli à quelle cose, ch'à mano à mano son per dirui; dopo ch'io ui haurò
proposto i Communi pareri, ouer Massime; dette da i Greci Α'ξιώματα; le quali, per la
loro euidente uerità, si chiamano anche Dignità; la prima delle quali sarà questa.
DIGNITA'
PRIMA.
ta è misurato.
tre quantità a. b. & c. delle quali a. misuri, ò numeri due fiate la b. & questa
sia la misurata, che numeri, ò misuri la c. due fiate. Dico che a. numera la c.
quattro fiate, che fù dalla b. misurata due. Et questo è quello, che questa
Dignità uuol inferire. Disse allora Messer'Adriano; La cosa è chiara, & non ha di-
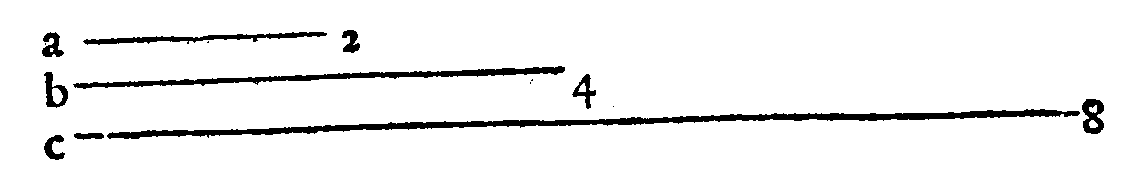
giunsi; dirò; che,
DIGNITA' II.
Metafisica, & anco nel Libro 3. del Cielo. E' uero, risposi; la onde M. Francesco
aggiunse; Questo par che sia difficile, & è ueramente facile da intendere; pur de-
sideriamo, che sopra di questo (per maggior nostra intelligenza) ragionate qualche cosa.
Notate adunque, soggiunsi; che tutta la scuola de i Filosofi chiama Elemento quella cosa,
della quale primieramente un naturale Indiuiduo si compone; di maniera che nel-
la resolutione tale Indiuiduo non si può risoluere in altri corpi, che siano primi.
Del che (per darui un'essempio) piglierò l'Huomo, il quale è composto de i Quattro
elementi Terra, Acqua, Aria, & Fuoco; onde, perche niun de questi quattro si ri-
solue in altro corpo, che sia primo di loro; essendo che non si ritroua alcun Corpo corrut
tibile, che sia primo de i Quattro nominati Elementi; però è neccssario, che morendo l'
Huomo, si risolua il corpo ne i detti Elementi, & non in altri corpi; percioche tali Elemē
ti sono corpi semplici, de i quali è composto; & ciascheduno altro corpo è de questi com
posto, ouer Misto. Questo s'intende, disse Messer'Adriano; & uolete dire; se un Interual-
lo fusse composto de Tuoni & Semituoni; che risoluendosi, in Tuoni & Semituoni,
etiandio si risoluerebbe. Stà molto bene; onde passarò alla terza Dignità; è dirò.
DIGNITA' III.
la quale per esser'una delle parti del Binario, tal parte si dice la Metà. Simiglian-
temente, perche nel Ternario si trouano tre unità; la vnità è detta Terza parte
di esso. Il che si può anco dir de gli altri Numeri; ma è cosa tanto chiara, che non fà di-
bisogno dirne più parola. Ma per il Quarto parer commune, ò Dignità, dirò;
DIGNITA' IIII.
per la Vnità, uerrà l'istesso Senario; com'è noto à ciascheduno, che sia essercita
to nell'Arithmetica. Et anco questa Dignità è di Euclide nel luogo nominato.
Qui non è dibisogno di commento, disse il Viola. Adunque uerrò all'altra, dissi; &
sarà questa.
DIGNITA' V.
duce la proportione medesima.
uero, che le aggiungete il Partire; ma qui non è dubitatione alcuna, che cosi sia.
Cosi è Messere, gli dissi; pur uoglio dirui una parola; che se noi moltiplicheremo
3. & 2. termini radicali della proportione Sesquialtera, per il 4. ne uerrà 12. & 8. i quali
conteneranno la medesima Sesquialtera, tra i numeri Tralorocomposti; essendo però
1 1/2 il Denominator dell'una & dell'altra. Ma se diuideremo 12. & 8. per il medesimo 4. na
scerà 3. & 2. i quali senza dubio alcuno contengono quella proportione istessa, che con-
tengono i primi; che sono 12. & 8. Ma passiamo un poco più oltra.
DIGNITA' VI.
to di quella.
24 leuaremo 18. ne resterà 6. Onde dico, che se 'l 3. numera, ò misura il 18. ch'è
il cauato di 24. & il 6. ch'è il restante; al medesimo modo misurerà, ò numererà
etiandio il Tutto, ch'è il 24. Et è uero; perche il 3. numera il 6. due fiate; il 18. sei; & il 24.
otto uolte. Allora soggiunse il Merulo; Meritamente si chiamano Communi pareri, ò
Massime, ò ueramente Dignità, che dir le uogliamo, essendo che non sò pensarmi, chi sa
rebbe quel tanto pazzo, che uolesse tenere il contrario. Che ne dite uoi Messere di que-
sto? Sarebbe ueramente da connumerar tra i balordi, ; & priui d'ogni sentimen-
to. Però seguitando ripigliai il mio ragionamento in cotal modo.
page 32
DIGNITA' VII.
le Denominationi loro da vn'istesso Denominatore. Ancora quando diuiso 'l mag-
gior termine d'vno, secondo il maggior dell'altro; & il minore, secondo 'l minore. Simi-
gliantemente, quando moltiplicato il maggior di vno scambieuolmente secondo il minore
dell'altro; i prodotti vengono equali.
& la equalità si piglia dalla parte della forma, & non della materia; & del resto hab
biamo la proua in mano; percioche noi sappiamo, che tanto la proportione, che
si troua tra 3. & 2. quanto quella, ch'è contenuta tra 9. & 6. è detta Sesquialtera, dal
Denominatore dell'una & dell'altra, il quale è 1 /2. se ui ricordate quello, ch'io dis-
si in questo proposito nelle Istitutioni.1. Part.
Cap. 25. Et se noi partiremo il 9. termine maggiore della se
conda data proportione, per il 3. pur termine maggiore della prima; & il 6. minore ter-
mine dell'una per il 2. termine minore dell'altra; tanto da una parte, quanto dall'altra uer
rà 3. Onde uerrà anco 18. moltiplicando 'l 9. per il 2. & il 6. per il 3. ch'è segno manife-
sto esser uero quello, c'habbiamo detto. Il perche aggiungeremo à questo:
DIGNITA' VIII.
è minore, ch'è denominato da minore.
com'è maggiore 1 1/2. Denominator del primo, di 1 1/3. Denominator del secon
do. Aggiunse il S. Desiderio; Questo è troppo manifesto; & però stà be-
ne, che questo principio sia numerato tra le Dignità. Seguitai dopo questo: Vi uoglio
etiandio aggiungere; che simigliantemente.
DIGNITA' IX.
tore, & minor quella, che l'hà minore.
questa douerebbe porsi auāti di quella; tuttauia hò uoluto, che qui sia il suo luo-
go; essendo che sempre il Tutto uà inanzi le Parti. Et perche quella Parte, ch'è
la metà d'alcuna cosa, sempre è maggior di quella, la quale è la terza parte; però nō è du
bio che quella parte, ch'è denominata dalla metà, sia maggior di quella, ch'è denomi-
nata dalla terza. La onde perche questo è pur troppo noto à tutti quelli, c'hanno
qualche intelligenza delle cose; pero uerremo ad un'altra Dignità, ò parer commu-
ne, il quale sara questo.
page 33
DIGNITA' X.
che se a. & b. saranno separatamente l'una dall'altra equali alla c. la a. sarà al me
desimo modo equale alla b. Et quello che si uerifica in una sorte di quantità, si
uerifica etiandio in un'altra. Questo non hà bisogno d'altra proua, disse M. Adriano; pe

Auertite che,
DIGNITA' XI.
perparticolari; ò d'alcun de gli altri Generi.
adunque, soggiunsi; & siano tre quantità a. b. c. per essempio, delle quali a. & b.
siano equali; & l'una & l'altra sia il doppio della c. E' manifesto da quel che det-
to habbiamo di sopra, che quella proportione, che si troua tra a. & c. si troui anco tra b.
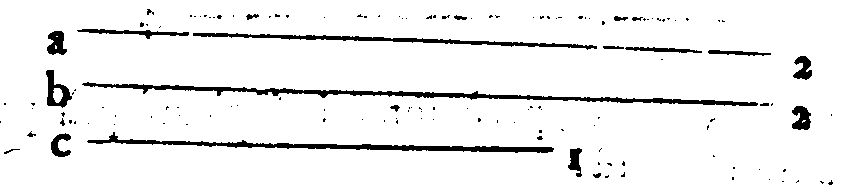
que, soggiunsi da nouo; che,
DIGNITA' XII
tità; & sia c. d'una & l'altra la Terza parte. Dico, che se 'l si farà a. & b. equali in d.
& e. secondo la quantità di c. quel che nascerà dalle dette quantità, sarà cambie
uolmente equale. Oltra di questo, se 'l si farà equale la c. f. alla Terza parte di tutta la c.
quella proportione, ch'era prima tra tutta la a. ouer la b. con tutta la c. si trouerà anco tra
le parti loro; cioè, tra la a. d. ouer b. e. con la c. f. & etiandio tra tutta la d. ouer tutta la e.
con tutta la f. la quale senza dubio alcuno è Tripla medesimamente. Veramente è cosi,
affermò il Sig. Desiderio; percioche, secondo 'l principio d'Euclide, Se da cose equali
si leueranno cose equali; i rimanenti saranno equali; onde si come tra a. & c. & tra b. & c.
page 34
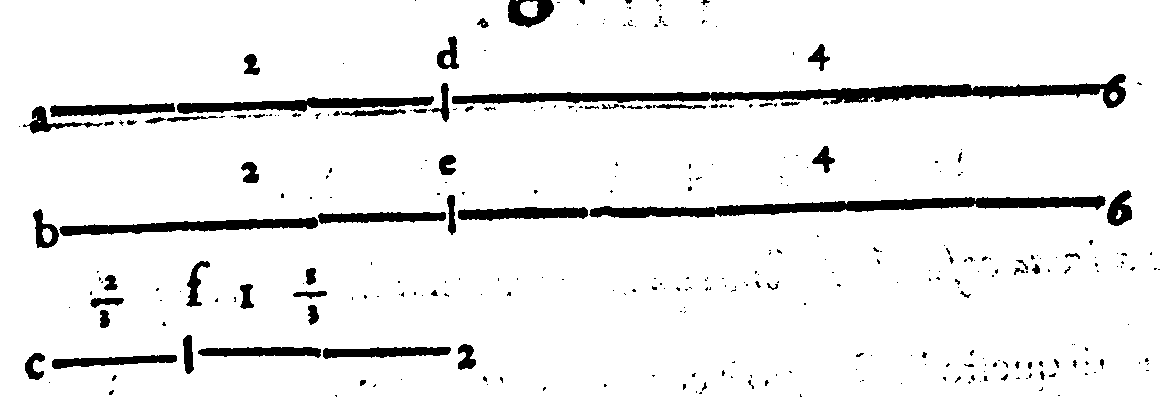
ta la b. leuata la be. ne uiene la d. & la e. ciascheduna delle quali con c. uengono ad esse-
re in Dupla proportione. E' cosi in fatto, dissi; & il Principio, che hauete allegato è il
Terzo Commun parere, che Euclide pone nel principio del lib. 1. de suoi Elementi. Di
rò; disse hora M. Francesco; che questo è tanto manifesto, che chi lo uolesse negare, sa-
rebbe riputato un pazzo. Seguiterò l'altro, risposi; ilquale è,
DIGNITA' XIII.
la ua metà.
di maniera, che ne uenga b. la quale è di tanta quantità, quanta è la c. ch'è il
doppio di a. bisogna necessariamente confessare, che a. sia la intera metà della quā
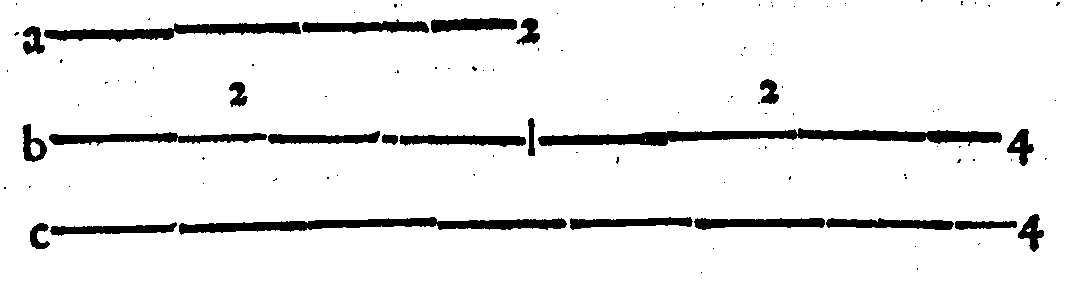
tendere; ma passarò ad un'altra Dignità.
DIGNITA' XIIII.
sia più della sua metà intiera.
a. sia minore della b. dico, che essendo c. la quantità a. raddoppiata; se la c. trapas
sarà la b. ch'essa a. sarà più della metà intera della b. Ecci un'altro parer commu

DIGNITA' XV.
metà.
trarij: che se la quantità a. sarà il doppio della quantità b. & non arriuerà alla
quantità c. che b. non sarà la metà della c. come ciaschedun de uoi può com-

paci di ragione.
DIGNITA' XVI.
sia maggiore di essa, & l'altra minore.
za, porrò la quantità a. la quale è la metà della b. onde è cosa assai ben chiara,
ch'essendo la c. minore di essa a. & la d. maggiore; ch'essa a. casca nel mezo della

sto, ultimamente?
DIGNITA' XVII.
cora campi; essendo che tanto sarebbe dire, che la quantità a. che ui dimostro so
pra quest'asse, & è minore & parte della b. fusse ad essa b. equale, oueramente
maggiore; cosa molto lontana; anzi dirò lontanissima dalla uerità. Tanto sarebbe anco,
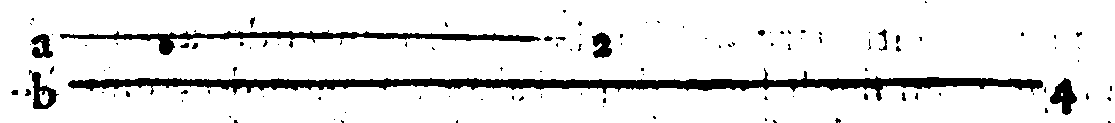
che detto hauete, fusse uero; percioche se questa è uera; La parte è maggior
del suo Tutto; uale anco à dire per il contrario; Il tutto è minor della sua parte;
page 36 essendo che sono relatiui l'uno all'altro. Messere, dissi; uoi sete diuentato un gran Logi-
co, & sapete molto bene riuoltare una propositione; & parmi che l'esser stato à Pariggi ui
ha giouato molto; perche la uostra conclusione è uera; ma veniamo ad altro. Io non son
per proponerui per hora altri Principij: ma quando 'l tempo & il luogo lo ricercheranno,
allora ue ne proponerò de gli altri, che faranno al proposito. Onde questi, che mostrato
& proposto ui hò, saranno à sufficienza per dimostrarui quello, di che habbiamo à ragio-
nare. Parmi hora di uedere, disse il S. Desiderio; verificarsi quello, che detto hauete nelle
Istitutioni;1. Par.
c. 20 ch'essendo la Musica subalternata alla Arithmetica, ella piglia una gran par-
te de questi Principij ad imprestido da questa Scienza; massimamente de questi ultimi,
che hauete chiamato Dignità. Onde si uede, ch'una Scienza porge aiuto all'altra; secon
do che più fiate hò ueduto in quel, ch'io hò studiato, & hora lo uedo in fatto. Questo
non è dubioso appresso d'alcun Dotto (dissi io) che la Scienza subalternata non usi alcu-
no de i principij della Scienza subalternāte. Ma bisogna che l Musico habbia questa auer
tenza, di pigliarne meno, che ei puote; & quando è sforzato d'usarli, bisogna che li usa
in un'altra maniera di quello; che si usano nell'Arithmetica. La onde si debbono usar secō
do 'l modo, che si tiene nelle dimostrationi della Musica; applicandoli à i Suoni, à i mu-
sici Interualli, & à i Corpi sonori; accioche l'una con l'altra corrispondino in una certa
proportione. Mi par mille anni, soggiunse M. Adriano; che incominciate à dimostrar
qualche cosa. Non andrà molto in lungo Messere, risposi; che in fatto lo uedrete; ma
per hoggi non intraremo à dimostrar quelle cose, che uoi desiderate di uedere in-
torno à gli Interualli della Musica: dimane poi, piacendo à Dio, sarete piena-
mente satisfatto; percioche bisogna prima trattar quelle, che più presto appartengo-
no ad un certo uniuersale nelle cose delle Proportioni, che à gli Interualli, ò Con-
sonanze istesse. Ma per non proceder più in lungo, uerrò alle Proposte; delle qua-
li la Prima sarà.
PROPOSTA
PRIMA.
tione.
uer ueduto & letto nell'Istitutioni; parmi che non sia necessario nella Musica,
il continuar due, ò più Interualli d'un istessa proportione l'un dopo l'altro; per
cioche ne i loro estremi non fanno consonanz'alcuna, & i ueri Numeri harmo
nici non comportano cotale continuatione. Ancorache questo non sia uniuersalmente
uero, risposi; percioche falla in molte delle proportioni Molteplici; tuttauia non hà da es
ser fatto fuori di proposito, per quel ch'io son per dimostrarui; percioche se ben alle co
se della prattica non fà dibisogno soggiungere, ò preporre tanti Tuoni, ò altri In-
terualli simili di proportione, continuati l'un dopo l'altro; nondimeno nelle cose
speculatiue alle fiate occorre di adoperar tali modi. Onde non uoglio lasciar di di-
mostrarui questa cosa; acciò dimostrar ui possa quel che farà dibisogno. Ma auerti-
te, che per questo continuare, ch'io dico; non intendo altro, che 'l Moltiplicar
due, ò più proportioni simili l'una dopo l'altra. V'intendo, disse M. Adriano; &
comprendo hora l'utile, che si potrà hauere di questa cosa; però seguitare il uostro
parlare. Soggiunsi allora; Siano a & b. i minimi termini della proportione di
qual si uoglia Interuallo, che noi uogliamo molteplicare. Dobbiamo prima mol-
tiplicare a. in se stesso, & ne uerrà c. dopoi lo moltiplicheremo co 'l b, & ne nasce-
page 37

& e. esser due Interualli simili continuati & insieme congiunti; cioè, c. d. il primo; & d. e.
il secondo. Percioche c. & d. nascono dalla moltiplicatione di a. in se stesso, & anco in b.
però (per la Quinta dignità) tanta è la proportione di c. & d. quanta quella di a. & b. Più
oltra; perche d. & e. nascono dalla moltiplicatione di b. in se stesso & in a. però (per l'istes
sa Dignità) tanta è la proportione di d. & e. quanta quella di a. & b. Onde se tanta è la pro
portione di c. & d. & anco di d. & e. separatamente, quanto è quella di a. & b. seguita, che
habbiamo tra c. d. & e. due Interualli continuati da un'istessa proportione contenuti; co-
m'è il proposito. Ma per hauere un terzo Interuallo; moltiplicheremo di nuouo c. d. & e.
per a. & ancora e. per b. & ne uerrà f. g. h. & k. i quali simigliantemente, per la già allega-
ta quinta Dignità; saranno tre proportioni, ò Interualli simili à quel ch'è contenuto tra
a. & b. cioè, f. g. per il primo; g. h. per il secondo; & h. k. per il terzo. Et per hauer'il quar-
to à questi tre congiunto, di nuouo moltiplicheremo a. con f. g. h. & k. & anco b. con K. &
haueremo, per la Quinta nominata, quattro proportioni simili alla a. b. continuate &
moltiplicate l'una dopo l'altra; cioè, l. m. la prima, m. n. la seconda; n. o. la terza; & o. p,
la quarta, secondo 'l proposito. Et questo è tutto quel che dimostrar ui douea. La onde
operando in questo modo, si potrà continuar quanti Interualli faranno dibisogno l'un
dopo l'altro, i quali saranno etiandio contenuti da una proportione istessa, in un'ordine
Radicale; ilche farà qual si uoglia Interuallo, quando sarà moltiplicato ne i suoi minimi
termini. Hora si uede, disse M. Adriano, la grandezza della Dimostratione; la quale con
firmata da i Principij, fà che ueramente sapiamo le cose; essendo ch'è impossibile, che
stiano altramente di quello, che sono dimostrate. In fatto è cosi Messere, soggiunse M
Claudio; ma ui uoglio dir, che se ben questa cosa, che hà dimostrato hora Messere Gio
seffo, non s'adoperasse mai, non mi dispiace d'hauerla imparata; percioche è molto bel-
la, & à me ueramente noua. Ma come potrei far, s'io uolesse in cotal maniera continua
re l'un dopo l'altro due Interualli, che non fussero di proportione simili? Bene, risposi;
se terrete quest'ordine istesso; è ben uero, che bisognerà por sempre gli Interualli
(come ui mostrerò) l'un sopra l'altro; di modo che sempre dalla parte di sopra stia-
no i termini di quel che uorrete soggiungere, & di sotto i termini di quel che uor-
rete preporre. Ma acciò che meglio m'intendiate, ui uoglio far la dimostratione.
Ascoltate adunque la proposta.
PROPOSTA II.
ritrouar l'Ordine radicale de i prodotti termini.
dotti; percioche alle fiate auerrà; ma non sempre, che aggiungendo due propor
tioni diuerse insieme, i prodotti saranno collocati ne i numeri Tralorocompo-
sti. Però accioche con più facilità possiate intender'il Tutto, & adoperar questi Inter-

che ui sono incogniti questi termini; cioè, Ordine radicale, & Radice delle proportioni;
però non ui starò à replicar cosa alcuna; ma uenirò alla Dimostratione. Siano a. b. & c. d.
minimi termini de due Interualli, quali si uogliano, differenti di proportione; cioè, a. &
b. di uno, & c. & d. dell'altro, che uogliamo insieme moltiplicare. Moltiplico primieramē
te a. in c. & in d. dopoi b. in d. onde ne uiene e. f. & g. Dico hora e. f. & g. contenere l'Inter
uallo a. b. & lo c. d. cioè, e. f. il primo, & f. g. il secondo. Et perche, per la Quinta dignità;
Qualunque numero moltiplicato ne i termini di qual si uoglia proportione, produce la
proportione medesima; nascendo e. & f. dalla moltiplicatione di a. ne i termini c. & d. di-
co e. & f. esser di tanta , quanta è c. & d. Simigliantemente dico, risultando
f. & g. dalla moltiplicatione di d. in a. & b. per l'istessa dignità; f. g. contener la proportio
ne istessa, che contengono a. & b. secondo 'l proposito. Il perche, se tanta è la proportio-
ne di e. & f. quanta è quella di c. & d. & tanta quella di f. & e. quanta è quella di a. & b. se
guita, che tra questi termini e. f. & g. habbiamo continuato due Interualli differenti di
proportione l'un dopo l'altro; come dice la proposta, & secondo che ui douea dimostra-
re. Ma perche per la Decima definitione, e. f. & g. sono tre Numeri Tralorocomposti, i
quali possono esser numerati d'altro numero, che dall'Vnità però, come c'insegna il Cap.
43. della Prima parte delle lstitutioni, ritroueremo un numero, ò termine, il maggior,
che si possa ritrouare, che numeri ciafchedun da persè & insieme de i nominati tre nume
ri; il quale sarà h. onde diuiso e. f. & g. per h. nascerà k. l. m. i quali dico, per la Nona de-
finitione, esser Numeri Contraseprimi, & per consequente minimi termini & radicali di
questi due Interualli, i quali, per la già detta Quinta dignità, contengono quell'istesse pro
portioni, che tra e. f. & g. sono contenute; percioche Ciaschedun numero, il quale parti
sca i termini di qua si uoglia proportione, produce la proportione medesima. Et questo
è tutto quello, che secondo la proposta ui douea dimostrare. Notate ancora, che s'à que
sti due Interualli ne uoleste aggiungere un terzo; moltiplicando il suo maggior termine
radicale con k. l. & m. & il minor di nuouo con m. si haurà il proposito; riducendo poi li
termini, quando fusse bisogno, se fussero numeri Tralorcomposti alla Radice; seguendo
l'ordine mostrato nel detto Cap.43. onde si potrà proceder in infinito. Ma se per caso uo
leste per il cōtrario, che la proportione, ò interuallo c. d. fusse preposto, & a. b. fusse sog-
giunto; allora non si haurebbe da far altro, se non di cambiare i luoghi, & porre lo a. b.
nel luogo dello c. d. & questo nel luogo di quello, & haureste il proposito. Queste cose so
no molto diletteuoli, disse il Sig. Desiderio; percioche in esse si uede un'aperta uerità; es
sendo che subito dimostrate; achettano l'intelletto. Et però ben disse quel gran Filosofo;Auer. 2.
Metap.
com. 1.
che le dimostrationi Mathematiche sono nel primo grado di certezza collocate; & che le
Naturali seguitano quelle. Questo è uero risposi; ma udite un'altra proposta.
page 39
PROPOSTA .
to sarà etiandio Molteplice.
sieme due Interualli, che siano contenuti da un'istessa proportione. Però dico:
Sia nel sottoposto essempio a. b. l'Interuallo Molteplice semplice, che uogliamo
raddoppiare; & sia c. d. e. l'Interuallo proposto; cioè, a. b. raddoppiato; come c'insegna
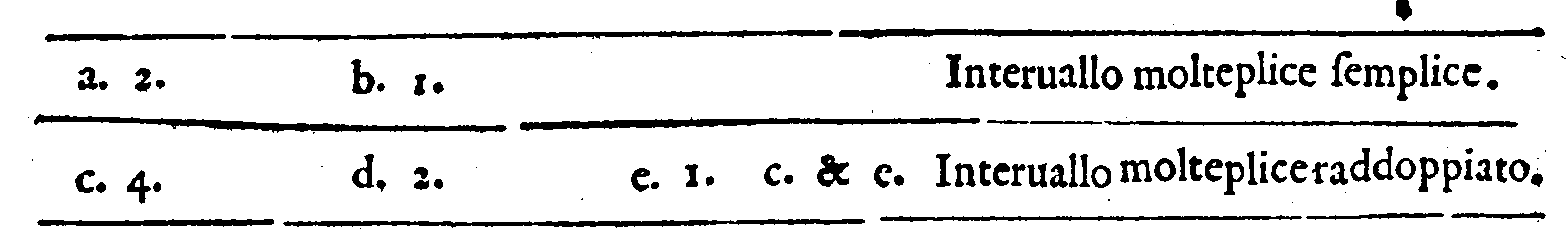
il d. all'e. Dico etiandio il prodotto Interuallo c. & e. esser Molteplice. Et perche d. è mol
teplice di e. però, per la Definitione de i Molteplici, e. misura il d. interamente più d'u-
na uolta. Ma dalla suppositione fatta di sopra; si come d. è molteplice con e. cosi c. è mol-
teplice con d. il perche e. misura esso c. più fiate interamente. Adunque, per la sopradet-
ta Definitione, il c. è molteplice di esso e. come bisognaua dimostrare. Ditemi di gratia,
disse M. Adriano; & perdonate alla mia curiosità; percioche la facilità di questa dimostra
tione mi fà, ch'io ui dimandi, se questa Proposta si può dimostrar'in altro modo. Si può
ueramente, dissi; Messere. Adunque, soggiunse M. Claudio; si può fare in una proposta
istessa diuerse dimostrationi. Ben sapete, gli risposi; percioche essendoui molti mezi; ui so
no ancora molte dimostrationi. adunque per uostra fè, disse il Viola. Cosi
uoglio fare, per satisfarui, dissi. Sia adunque di nuouo l'Interuallo a. & b. molteplice; co
me propone la proposta; il quale per la Prima di questo, sia raddoppiato; & sia c. & e. il
doppio; & la proportione, che si troua tra c. & d. & sia anco tra d. & e. Dico l'Interuallo c.
& e. esser simigliantemente Molteplice. Et che cosi sia lo dimostro. La proportione, che
si troua tra a. & b. per la Settima dignità; è quella, che si troua anco tra c. & d. & simiglian
temente tra d. & e; onde ciascheduna da per se è la metà della raddoppiata c. & e. ma la
proportione a. & b. è posta Molteplice; adunque la proportione c. & d. medesimamente
è Molteplice. Il d. adunque, per la Quarta Definitione, misura 'l c. due, ò più fiate; & all'i-
stesso modo tante fiate e. misura il d. per il che etiandio medesimamente, per il Primo cō
mun parere, ò Dignità, che dice; che Quella cosa, che misura un'altra, misura anco quel
la, ch'è misurata da lei; e. misura esso c. Adunque per la Definitione de i Molteplici, l'In-
teruallo c. & e. uiene ad esser Molteplice; come faceua dibisogno di mostrare. Ogni cosa
torna molto bene, disse M. Adriano; ma inanzi che si proceda piu oltra ditemi. Voi ha-
uete allegato molte fiate il modo d'operare alcuna cosa; secondo le uostre Istitutioni; non
dimeno in esse dimostrate poche cose, per quel che mi ricordo; anzi piu tosto procede-
te con un'atto prattico; però desidero, che sopra di questo mi diciate qualche co-
sa. Soggiunsi allora; Questo Messere è di poca importanza; ne in questa parte, che serue
all'accommodar l'essempio, ò figura alla Dimostratione; la quale nominai Κατασκευὴ, ò
Costruttione (stando nelle già nominate cose, ch'entrano in ciaschedun Theorema, ò
Problema) fà molto dibisogno, che tale operatione nasca dalla Dimostratione; pur che
quel che si opera sia fatto senza errore, & secōdo 'l proposito. Imperoche quādo si uiene poi
alla Quinta, ch'è la Α'πόδειξις, ò Dimostratione; allora si fà noto il uero, oueramēte il falso
dalle premesse. Ma uoglio che sapiate; se ben nelle Istitutioni hò proceduto nel mostrar le
cose con atto prattico, com'hauete detto; che tali operationi non son fatte à caso; anzi so-
page 40 no cauate dal fonte delle Dimostrationi, c'hanno fatto de loro i Mathematici. Di modo
che il tutto uiene ad esser fatto senz'alcun'errore; essendo c'habbiamo anco la proua, la
quale non è altro, ch'un certo mezo, & una dimostratione, che scuopre, se quel che noi
operiamo nel cercar la uerità d'alcuna cosa, habbiamo operato senz'errore. Et se ben per
l'auenire potessi allegare un modo di operar, secondo le Dimostrationi fatte d'alcuno Au
tore; tuttauia uoglio anco seruirmi di quel c'hauete ueduto ne i miei Scritti, che ui stà (co
me posso comprender) nella memoria; accioche più facilmente m'intendiate, & ne ripor
tiate quel frutto, ch'io desidero, & che desiderate anche uoi d'hauer da questi miei Ragio
namenti. Però quando udirete nominare alcuna cosa mostrata nelle Istitutioni, non ui
scandalizate; perche hò dimostrato iui il tutto con ogni uerità, & con ogni proua; onde
non fà dibisogno di farne altra dimostratione. Rispose à questo M. Adriano; Se ben ui
hò fatto questa dimanda M. Gioseffo, non pensate che sia stato per altro, se non per saper
la uostra intentione; accioche rispondendomi al proposito, com'hauete risposto; io ne ri-
portasse, com'hò fatto, qualche guadagno. Et mi contento, percioche è stata una buona
istruttione fin qui, quel che hauete detto; & me la terrò molto bene à memoria. Et perche
d'ogni cosa restiamo benissimo satisfatti; però nō sarà se nō bene, ch'uoi andiate più oltra.
Adunque auertite, ui prego, risposi; di tenere apunto bene à memoria tutto quello, ch'io
ui dimostro; percioche quando non ui ricordaste una di queste dimostrationi; malamen-
te potresti intender le seguenti; essendo che l'una dipende dall'altra; & le prime son chia
mate Elementi delle sequenti; perche co 'l mezo loro, queste si uengono à prouare. Io per
me sforzerōmi di ritenerle; disse il Merulo; & sò troppo bene, per quel poco d'esperien-
za, che io tengo; che 'l domenticarsi le cose precedenti, causa l'ignoranza delle sequenti.
La onde hauendo udito M. Adriano queste parole, soggiunse; Se ben la maggior parte
de i uecchi mancano di memoria; tuttauia ringratio Dio, che m'hà concesso questa gra-
tia, che nella mia uecchiezza nō ne son di essa priuo. Et ui prometto, che questa cosa tan
to mi diletta, che in questa età mi potrei ben stancare di udir quel che nella mia giouanez
za non ho mai potuto ne udire, ne imparare; ma satiare non mi potrò già mai. Verremo
adunque, soggiunsi; alla Quarta proposta.
PROPOSTA IIII.
tionali; & costituiscono la Geometrica proportionalità.
etiandio altroue1. Istitut.
cap. 36. 37.
& 39.) intēdo, & si dè intēder della Geometrica; percioche l'Arithme-
tica più tosto si chiama Progressione, & l'Harmonica maggiormente si dee nomi-
nar Mediocrità, che Proportionalità, ò Progressione; onde i termini della Geometrica
si nominano drittamente Proportionali; per il che, se ben quest'importa poco; tuttauia
hò uoluto farui sapere, che s'alle fiate m'udirete usar questi termini, senz'alcun'ag-
giunto; uoi li dobbiate riceuer per quello, ch'io li ho dichiarati. Et queste cose ui
saranno à memoria; onde passaremo alla Dimostratione. Siano a. b. & c. tre termini dell'
interuallo Molteplice raddoppiato per la precedente; & sia d. la differenza, che si troua
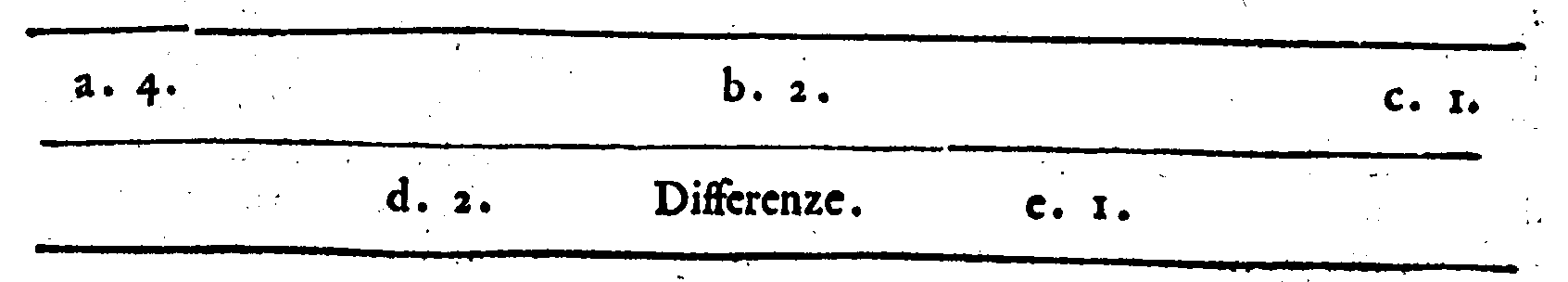
all'altro proportionali, i quali costituiscono la Geometrica proportionalità. Et perche i
termini b & c. sono simili à i d & e, com'è manifesto; però, per la settima Dignita, tanta è
la proportione, che si troua tra b & c; quanto quella, che è posta tra d & e: ma per la Pre-
cedente, ab & bc. sono simili di proportione: adunque, per la Duodecima definitione,
a. b & c. sono l'un'all'altro proportionali, & costituiscono la proportionalità Geometri-
ca; poi che Tre quantità si chiamano Proportionali, & la costituiscono allora; quando
le proportioni, che si trouano tra loro sono equali & simili à quella, che si troua tra
i termini delle lor differenze. Et tutto questo è quello, ch'io ui douea, secondo
la proposta, dimostrare. E' possibile, disse il Signor Desiderio; che queste dimo-
strationi di numero à numero, le quali seruono piu tosto all'Arithmetica, ch'alla
Musica, habbiano à tornare al uostro proposito? Non ui ricordate, soggiunsi, ch'
io dissi nelle Istitutioni, che i Numeri & le Proportioni sono le imagini de i Suoni
& delle Consonanze? Me ne ricordo; rispose. Et io dissi; Habbiate adunque pa-
tienza, & statemi ad ascoltare, che non andrà molto di lungo, che conoscerete, che
non sono fatte uanamente. Sappiate però che la Quinta proposta; dipenderà dalle due
poco fà mostrate, & sarà.
PROPOSTA V.
il maggiore; misurerà etiandio quelli di mezo.
Dico, che c. simigliantemente misurerà il b. termine mezano. Riduco prima
a. b. & c. ne i lor minimi termini & radice di quest'ordine, nel modo mostrato
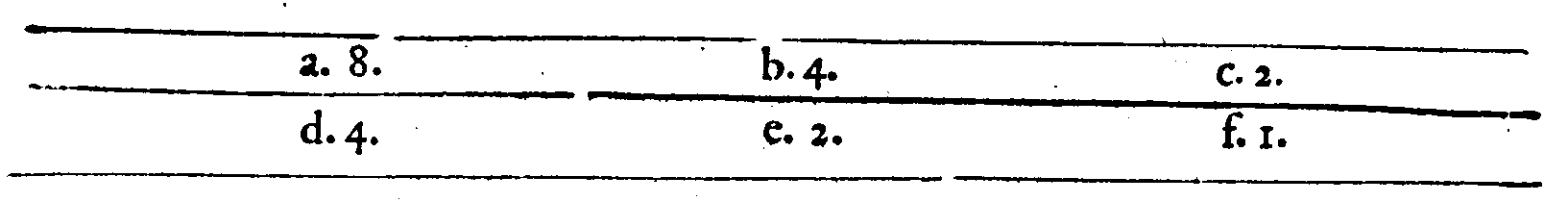
che, per la settima Dignità, tant'è la proportione di de, & di ef; quanto quella di ab,
& di bc; però, per l'Equale proportionalità, dico; tanto esser la proportione, che si
troua tra d & f, quanto quella, ch'è tra a & b. Ma, per la Suppositione, c. minore
misura a. termine maggiore; adunque f. misurerà d. maggior termine de i minimi ri-
trouati. Et perche d. e. f. si trouano Contraseprimi, & sono, per la Nona definitione,
minimi termini di tal'ordine; per tanto d. f. sono anco contraseprimi. Simigliantemente
perche f. misura se stesso & d. ancora; però per la Definitione detta, f. uiene ad esser l'Vni
tà. Ma l'Vnità, per la Terza massima, ò Dignità, è parte di qual si uoglia numero;
adunque f. misurerà anco e. La onde essendo tanta la proportione, che si troua dal b. al
c, quanta quella, che si troua tra e & f; seguita, che c. minore de i dati termini misura
il b, il quale è il secondo & mezano; il che era il proposito di dimostrare. Aggiungerò
à questa; che,
PROPOSTA VI.
anche Molteplice.
ramente; risposi io. Come farete adunque à dimostrar questa; soggiunse M.
Adriano. Ben Messere; risposi; ascoltate pure. Essendo l'Interuallo a. b. c. rad-
raddoppiato; per la Terza proposta, Moltiplice; & anche a. cō c. Molteplice: Et la proportio
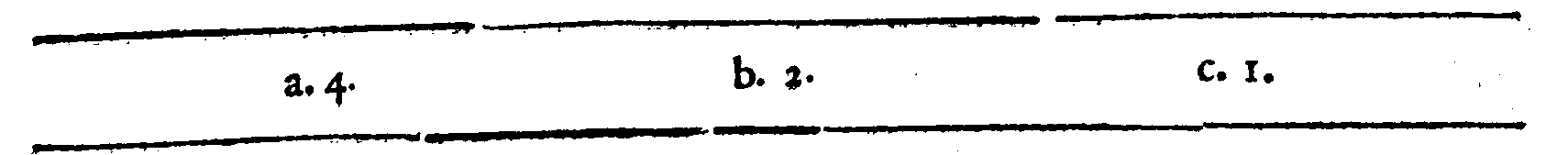
Molteplice, il c, per la Quarta definitione, misurerà esso a. più fiate; il perche, per la Prece
dente, c. misurerà anche 'l b. Adunque l'Interuallo bc. sarà semplice; & per la detta De-
finitione, anco Molteplice; come fù il proposito di dimostrarui. Disse allora di nuouo
M. Claudio: Stà bene; ma diteci; si potra dimostrar questa proposta per altra uia? Si
può ueramente; risposi; statemi à udire. Essendo ac. Interuallo composto; & risoluen-
dosi, per il secondo parer commune, ò Dignità, in quell'Interualli, che dalla molti-
plicatione, ò raddoppiamento è generato, ò composto; poi ch'ogni si ri-
solue in quelle cose simplici, delle quali si troua esser composto; non è da dubitare; che,
si come s'è dimostrato nella Terza proposta, d'un'Interuallo molteplice, raddoppiato;
che si generò un molteplice composto; cosi per il contrario, risoluendosi tal composto
ne i suoi semplici; se tali semplici furono Molteplici; che siano anco dopo la
Molteplici, il ch'è secondo 'l proposito; come bisognaua dimostrare. Qui disse il Signor
Desiderio; Questa dimostratione ultima, più tosto hà del Naturale, che del Mathema-
tico; onde mi è forte piaciuta. Questo è ben detto; risposi; onde passarò alla Settima.
PROPOSTA VII.
ne; è necessario, che tanti siano i mezi proportionali dell'uno, quanti quelli dell'altro.
par, che sia alquanto difficile da intendere. Hor'hora la farò facile; soggiunsi.
Siano ab & de. due, qual si uogliono, Interualli proposti; contenuti da un'istes-

contenuto ne i suoi termini radicali. Dico, che simigliantemente tra a & b. può cascar'
un termine mezano; Onde dico argumentando per la Vndecima dignità dalla Equale
proportione: Tanta è la proportione di df, quanto quella di ac; & tanta quella di fe,
quanta di cb; Adunque tanta è quella di de, quanta è quella di ab. Ma se i termini ab.
sono contenuti da un'istessa proportione co i termini de; manifesta cosa è, che tra ab.
casca ancora un termine mezano proportionale, ch'è il c. Et se ciò non è; d & e. misu-
page 43 reranno a & b. equalmente; & questo secondo 'l g. Molteplico adunque g in d. f. & e;
& ne uiene a. c. b; di modo che tra ac. si troua esser quella proportione istessa, che si tro-
ua tra df; & tant'è quella, che si troua tra c. b; quanto quella, ch'è posta tra fe; il che
proportionatamente c. uiene à cascar nel mezo di a & b; come bisognaua dimostrare.
Intendo hora quello, disse M. Claudio, che hauete uoluto dire nella uostra proposta:
Però seguitate 'l resto à uostro bel piacere. Notate adunque, soggiunsi; che nella pro-
posta, che ui son per proporre, uoglio ch'intendiate, che niun Superparticolare In-
teruallo si può diuidere in due parti equali, ò proportionali, con certi & determinati
Numeri rationali; se ben si può diuidere con irrationali; come in qualche buon propo-
sito son per dichiararui. Onde da questo, che ui dimostrerò spero, che ui sarà manife-
sto. Vorrei saper più inanzi; disse M. Adriano; S'ogni Interuallo Molteplice può esser
capace di uno, è piu termini, che lo diuida in due, ò più parti simili. Ricordateui; ri-
sposi; quel ch'io dissi nelle Istitutioni,1. Par. cap.
37. & Co-
rol. 25. Se-
cūdi huius. & uederete quali siano capaci, & quali non. Mi
ricordo hora, rispose egli; essendo che bisogna, che la proportione, la quale può esser
capace di cotal mezo, ne i suoi termini radicali habbia tal conditione, che 'l maggior
sia numero Quadrato, ouer Cubo; & il minore sia l'Vnità. A questo soggiunsi subito; Io
non dissi già, che cotal numero fusse Cubo, ma Quadrato; percioche iui parlai dell'In-
uentione d'un sol termine mezano, il quale diuidesse la proportione in due parti equali.
Ma quando si uolesse pur diuidere cotal proportione in tre parti equali, tal numero sa-
rebbe necessario; percioche come uoi potrete comprendere da quello ch'io mostrarò
nel cap. 6. dell'Ottauo Lib. De i Sopplimenti; quando l'Vnità sarà il minor termine della
proportione, & il primo numero Cubo sarà il maggiore; allora tal proportione potrà
esser diuisa dal Binario & dal Quaternario insieme, in tre proportioni equali; come tra
questi termini. 8. 4. 2. 1. Intendo molto ben la cosa; disse M. Adriano; però seguitate
quello, che più ui piace, senza tardare. Cosi farò dissi; Ma prima che 'l si uenga à dimo
strarui quel che ui hò dichiarato, uoglio che uediamo questa. Che
PROPOSTA VIII.
proportione Superparticolare.
sia c. che è l'Vnità, la lor differenza: essendo che a. si troua per tanta quantità
differente dal b. Volendo porre il d. per differenza de tali estremi, si moltepli-

mente gli estremi della proportione proposta a & b. Ma quel che nasce dal d. moltiplica-
to in a. è tanto quanto quel che nasce dal d. moltiplicato in b. & c. i quali sono equali ad
esso a. Imperoche moltiplicato d. in b. nasce f; & ancora moltiplicato in c, che è l'Vnità
nasce il g; i quali aggiunti insieme & composti fanno h; essendoche moltiplicato d. in c,
ch'è Vnità, produce, per la Quarta dignità, se stesso d; adunque il g è posto per la dif-
ferenza di e. & f. Superparticolare proportione; come dimostrar ui douea. Et questo
etiandio si potrà far quando si uorra porre altro numero per tale differenza; sia Ter-
nario, ò Quaternario; moltiplicando sempre i termini radicali, ò non radicali di quell'
page 44 Interuallo, alquale si uorrà porre cotal numero per differenza de i suoi estremi: A questo
replicò M. Adriano: Spero d'auanzar molto da questi uostri Ragionamenti; & uscir fuori
della prattica; però seguitate, ui prego, à dimostrarci quello, che uoleuate dimostrare;
Et io soggiunsi à queste parole:
PROPOSTA IX.
partisca in due, ò più parti equali & proportionali.
renti per il Binario; onde uengono ad esser capaci d'un termine mezano; il qua
le Interuallo uogliamo diuider (se sarà possibile) in due parti equali rationa-
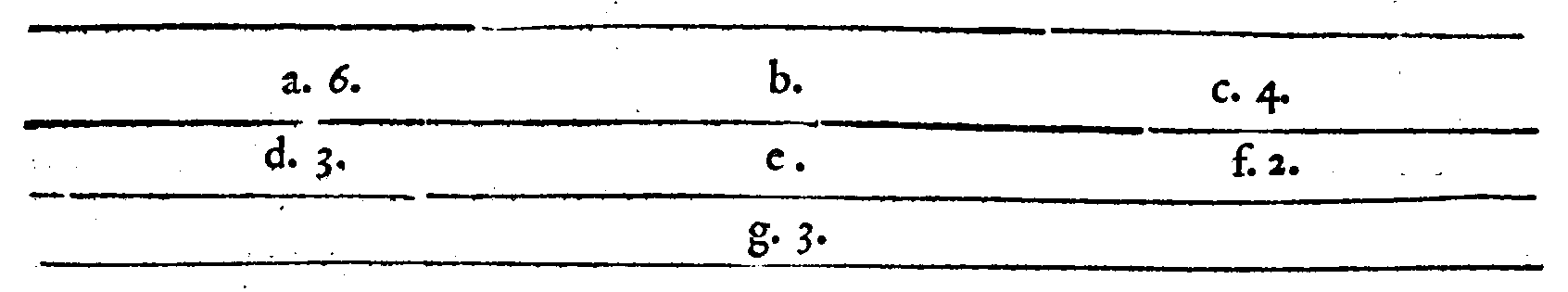
a & b. Riduco a. b. & c, secondo 'l modo mostrato nel Cap. 42. & 43. della Prima parte del
le Istitutioni, alla sua Radice, & ne uiene d. e. f. tre termini proportionali nella propor-
tione a & b. Et perche de. si troua, come è ab; & ef. come bc; adunque, per l'equale pro
portionalità df. è come ac. Ma ac. è posto Interuallo superparticolare; però df. simi-
gliantemente è Superparticolare. Ma perche d. e. f. sono i minimi termini di tal'ordine;
però d. & f. primo & ultimo, per la nona definitione, sono numeri Contraseprimi. Hauen
do adunque mostrato d. con f. esser Superparticolare; per la Quinta Definitione, il d.
contiene f. & una sua parte Aliquota; la qual parte però, per quello, ch'io dichiarai nel
Cap. 23. della sudetta Prima parte, misura esso f. Et se tal parte uiene ad esser Numero;
misurando, per il Sesto parer commune, il d; misurerà anco se stesso, ch'è la parte caua-
ta, & lo restante, che uiene ad esser equale ad f. Et per tal modo d. & f. non uerranno ad
essere Insieme, ò Contraseprimi; della qual cosa già si è mostrato l'opposito, & l'impos-
sibile. Sarà adunque necessariamente tal parte la Vnità. Disse allora M. Desiderio; Que
sto è ueramente necessario; ma che ne segue per questo? Soggiunsi, ne segue, ch'io ag-
giungo essa Vnità ad esso f, & ne uiene g; di maniera, che g. & f. uengono ad esser lon-
tani l'un dall'altro per la Vnità solamente. Dico hora, per la Settima dignità, che quella
proportione, ch'è tra d. & f, è quella etiandio, che si troua tra g. & f; ma tra d. & f. fù
supposto, che casca un solo mezo; adunque, per la Penultima proposta simigliantemen
te tra g. & f; che sono numeri differenti per la Vnità; cascherà alcun numero mezano;
il che, per la Prima dimanda, è impossibile. Concludiamo adunque, che se l'Interual-
lo Superparticolare non riceue un termine mezano rationale, che lo diuida in due par-
ti equali & proportionali; che minormente ne riceuerà, per l'istesso argomento, molti;
come dice la proposta. Et questo è tutto quel, che si douea dimostrare. Allora M. Fran
cesco; Questo è troppo il uero; disse; ma non bastaua la Regola dell'Vnità, & del nume-
ro Quadrato, & del Cubo, che uoi diceste poco fà, per saper cotal cosa? Bastaua, dissi,
quanto al saper'ad un certo modo; ma per questo cotal cosa non si sapea semplicente; per
ciò che questo saper s'acquista col mezo della Dimostratione, la qual com'hauete ue-
page 45 duto) lieua ogni dubitatione. Intendo hora 'l tutto, rispose M. Francesco. Passiamo
adunque alla Decima proposta, dissi io.
PROPOSTA X.
mento non sarà ne Molteplice, ne Superparticolare.
b; & lo raddoppiato sia a & c; di maniera, che l'istessa proportione sia tra a & b,
che si troua tra b & c. Dico, che l'Interuallo a & c. non è Molteplice, ne Su-
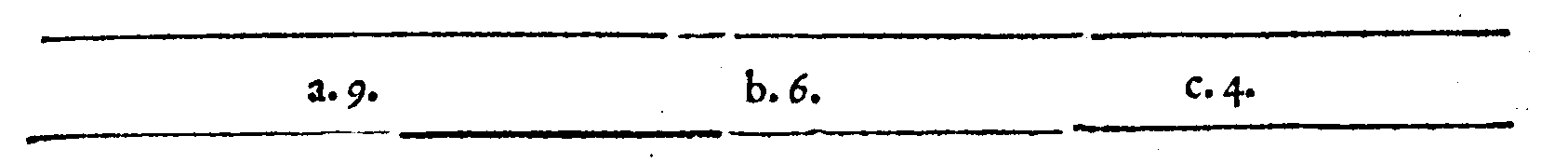
posta, l'Interuallo a & b. sarà anco lui molteplice. Ma già habbiamo detto ciò esser im-
possibile; adunque senza contradittione alcuna, ne uiene il proposito. E' uero disse il Me
rulo; che non è Molteplice; ma non potrebbe egli esser forse Superparticolare? Questo è
anco impossibile; risposi. Et che questo sia uero, uerremo alla dimostratione, che farà
ogni cosa chiaro. Essendo a & b. di tanta proportione, di quanta è b & c; non è dubio,
che a & c. haurà un termine mezano proportionale, che lo diuiderà in due parti equali;
il che essendo palese, per la Precedente, esser'impossibile; è cosa anco per se stessa mani-
festa; che Se un'Interuallo non molteplice si uorra raddoppiare, che l'Interuallo com
posto non potrà esser, ne Molteplice, ne meno Superparticolare; secondo 'l nostro pro
posito. Non pote allora M. Adriano contenersi, che non dicesse; O come mirabilmente
tali dimostrationi sono insieme concatenate, che l'una con l'altra si uiene à porgere aiu-
to, non altrimente di quello che fanno le dimostrationi Geometriche; però meritamen-
te sono chiamate Elementi. Rispose il Viola; Veramente c'han detto bene quelli, che
l'hanno nominate con tal nome; percioche (come si uede manifestamente) l'una uiene
ad esser'elemento dell'altra. Et bene; disse il Signor Desiderio; poi che Elemento si chia-
ma quello, del quale si compone primieramente (come altre fiate si è dettoSupra dig.
2.) alcuna co-
sa. Che ne dite uoi M. Claudio di questo? A questo ei rispose; Hò sempre udito dire,
che le Mathematiche sono Scienze, che hanno del diuino, & lo uedo hora in effetto,
con mia grande satisfattione. Soggiunsi allora. Poi che fin qui ui sete compiaciuti
di tutto quel ch'io hò detto; non mi rincrescerà di seguitar il resto; però notate quel
che in questa proposta ui uoglio dimostrare.
PROPOSTA XI.
sarà Molteplice; esso Interuallo etiando non sarà Molteplice.
hauete dimostrato; percioche in quella l'antecedente dalle Parti aggiunte in-
sieme, nega il tutto; & in questa dal tutto si negano le Parti. Voi dite bene;
diss'io; però seguitando l'impresa dirò; Sia a. & c. l'Interuallo raddoppiato, come è po-
page 46 sto nella Precedente; & non sia a. & c. Interuallo molteplice. Dico simigliantemente,
l'Interuallo a & b. non esser molteplice. Percioche se a & b. è Interuallo molteplice;
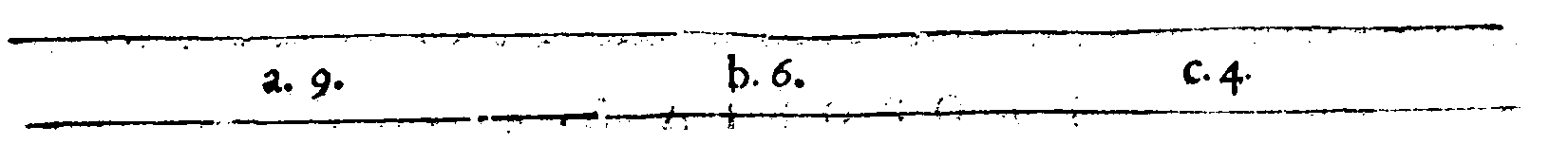
la Terza proposta di questo ragionamento, l'Interuallo a & c. sarà etiandio Molteplice.
Ma quel ch'è posto non è molteplice; adunque, Se l'Interuallo non Molteplice nasce-
rà dal raddoppiamento d'alcun Interuallo, ne anco esso raddoppiato sarà Molteplice.
Et questo è quello, ch'io intendea di dimostrarui. Disse qui il Viola; Fin'hora hauete
proceduto chiaramente tanto, ch'io credo, che cosa alcuna non resti, che non sia chia-
ra & palese; però ui preghiamo à seguitar cosi facilmente il resto; che ui udiremo con gran
piacere. Mi sforzerò, dissi; di satisfarui. Ma notate, auanti ch'io uenga all'altra Propo-
sta: percioche è cosa alquanto difficile; che le Parti, che si nominaranno in essa, si ha-
urano da intendere, per quei Numeri, per i quali i Termini maggiori continenti l'In-
teruallo sopr'auanzaranno i minori, di una delle lor parti Aliquote; come della loro Me-
tà, ò della Terza, ò della Quarta, ò d'altra parte simile. Onde auiene che tali Termini
si hauranno da considerar, come un Tutto aggregato de tante delle sudette Parti; quante
sono l'Vnità che contengono. Et accioche mi possiate meglio intendere; proponerò i
termini del primo Interuallo superparticolare, detto Sesquialtero; che sono 3. & 2. de i
quali il 3. sopra'auanza il 2. per la Vnità; la qual senza dubio uiene ad essere la sua Me-
tà intiera; ò Meza parte, come dir la uogliamo. Laonde il 3. è considerato come
Tre meze parti; & il 2. come due metà; come si può dir anco nel Sesquiterzo, contenu-
to tra i termini 4 & 3. dell'Vnità; percioche il 4. superando il 3. per essa Vnità ella uien
ad esssere la Terza parte del minore. Onde cotali termini uengono à rappresentare tante
delle sudette parti, quante Vnità contengono. Però si dè auertire prima questo, che
poste insieme al numero de tante, quante Vnità si trouano nel termine minore; si dicono
restituire il loro Tutto, intesa la cosa à cotal modo, Dopoi à questo numero se n'aggiun
ge un'altra maggiore per una unità; & per tal modo questi due Numeri saranno quei
mezi, da i quali nascerà la Dimostratione. Et perche credo che habbiate inteso quello,
ch'io uoglio dire; però senza dir'altro, uerrò alla Dimostratione. Allora ch'io hebbi fini-
to di dire; disse il S. Desiderio; questa è stata una buona & necessaria preparatione; sen-
za la quale potea essere qualche difficultà; ma questa leuarà ogni cosa: però M. Giosef-
fo ui preghiamo à seguitare il uostro ragionamento; & dimostrar questa cosa con quella
breuità & facilità, più che sia possibile. Ilche hauendo inteso, dissi; Attendete alla pro-
posta la qual sarà questa.
PROPOSTA XII.
me facciano un Tutto; et un'altro Numero maggior di esso per l'Vnità; ci di-
mostra, quanti maggior termini dell'Interuallo, à i minori insieme aggiunti corri-
spondono.
ui. Incomincierò adunque con l'aiuto del Signor Iddio. Sia a & b. Interual-
lo Superparticolare; è manifesto dalla Quinta definitione de i Superparticolari,
a. contenere il b. & una delle sue Parti; la quale sarà c. & costituirà b. suo Tutto, secon- page 47 do 'l numero d. Ma sia oltra di questo e. numero maggior di d. per l'Unità. Dico
hora a. preso secondo 'l numero d. esser equale à b. preso secondo 'l numero e. Impero-

secondo d. Ma si è detto, queste hauer già costituito un b. adunque a: preso secondo d.
contiene b. preso secondo 'l numero maggiore di d. per una unità; Ma e. è posto numero
maggiore di d. per una Vnità; adunque a. preso secondo d. contiene il b. preso secondo
e. come douea dimostrare. Ma di bisogno è, che cotal cosa si consideri in uniuersale; an
cora che nell'essempio habbia posta la proportione & Interuallo particolare. Conside-
rasi però à qual modo si uoglia; sempre tornerà bene, & si dimostrerà quest'esser uero. De
sidero, disse M. Adriano; che ui lasciate intender un poco meglio, s'è possibile; pur con l'
essempio posto di sopra, col chiamar l'Interuallo col suo proprio nome; acciò s'inten-
da meglio. Messere ui uoglio al tutto satisfare; risposi. Poniamo adunque a & b, come di so-
pra facemmo, Interuallo Sesquialtero; Et perche a & b. è Sesquialtero; però per la Quin
ta definitione, a. contiene il b. & la sua metà; Ma due metà, per la Terzadecima dignità,
restituiscono il loro Tutto; adunque due a. che sono d, sono tanto, quanto sono tre b.
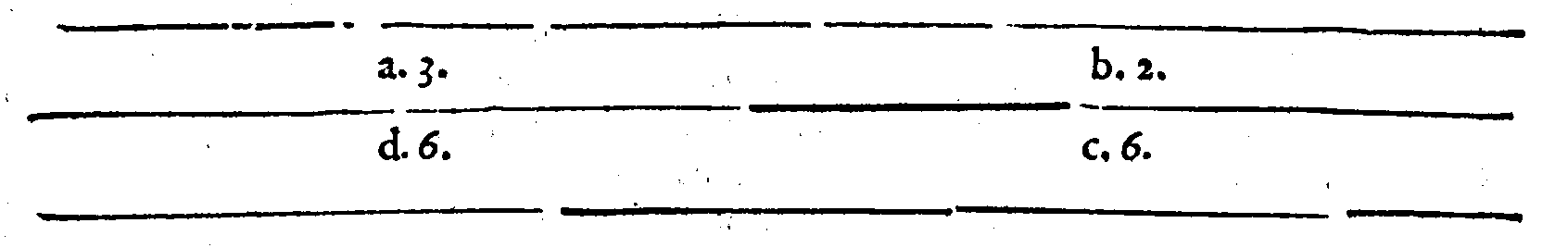
un b. intiero; però due a. contengono tre b. & diuengono à tre equali. Di maniera, che
data qual si uoglia Superparticolare, i maggior termini, secondo 'l minor numero della
proportione, sono equali à i minori, pigliati secondo 'l minore; come bisognaua dimo-
strarui. Io son satisfatto; disse M. Adriano; & credo, che chi uolesse dimostrar l'altre
Specie di questo genere, ch'altra differenza non ui sarebbe, che le Parti; percioche
nell'Interuallo Sesquiterzo u'intrarebbe la terza; nel Sesquiquarto la quarta; & cosi per
ordine l'altre: di maniera ch'essendo cosi, non accade sopra ciò far altra diceria. Però buō
sarebbe, che 'l si andasse di lungo, senza perder tempo sopra questa cosa. Poi che cosi ui
piace; risposi; seguirò à proporui la Terzadecima proposta, la quale sarà questa:
PROPOSTA XIII.
sono equali à minori presi secondo 'l numero de i maggiori.
particolari; ma etiandio ne gli altri Generi di proportione. Sia adunque a
& b. qual si uoglia proportione; & sia a. il suo termine maggiore, & b. il mino-
re. Dico che a. preso (per la precedente) secondo 'l numero b, ch'è minore, è equale à b,
pigliato secondo a. numero maggiore. Imperoche è manifesto, che quel che nasce del-

di b in a, che è d. Ma quel che nasce dalla moltiplicatione di a. in b, è a. preso secondo 'l
b; & quel che nasce dalla molteplicatione di b in a, è b. preso secondo a; come dimo-
stra la Precedente; adunque a. preso secondo il b, è equale à b. preso secondo a; come do
uea dimostrare. Et se uolete, ch'io discenda al particolare, com'hò fatto nella Preceden
te, lo farò uolentieri; acciò restiate da me satisfatti. Non accade; disse M. Francesco;
percioche la cosa è tanto da sè chiara, che non fà dibisogno d'altra espositione. Verre-
te adunque all'altra proposta, se ui è in piacere. L'altra proposta, che segue, soggiun-
si, è questa.
PROPOSTA XIIII.
minori; si ritroua quella proportione tra uno de i maggiori & uno de i minori, che si
troua etiandio in uno de i minori adunati insieme, ad uno de i maggiori insieme
aggiunti.
Non u'ingannate punto Messere; dissi; Auertite adunque che, per la Preceden
te, i Numeri minori raccolti insieme secondo 'l Numero maggiore, sono equali
à i maggiori adunati secondo 'l numero de i minori; ma 'l Numero de i maggiori è un ter
mine maggiore; Adunque quellistessa proportione si troua tra un de i maggiori ad uno de
i minori, che si troua anco tra uno de i numeri minori raccolti, al numero de i maggio-
ri posti insieme. Parmi, disse il Merulo, che cosa sia molto , & che questo
page 49 forse auenga, perche non è troppo in uso; però dateci per uostra fè meglio ad intender
questa proposta con un'essempio; accioche quello, che à noi è tanto oscuro, si faccia lu-
cido & chiaro. Sono queste cose ueramente difficili, M. Claudio; risposi; ma l'uso di es-
se ui leuerà nelle sequenti dimostrationi la difficultà. Ascoltate però quel ch'io ui uo-
glio dire. Habbiamo, per la Precedente, che In ogni genere di proportione, se 'l nu-
mero maggiore è comparato al minore, che 'l maggiore preso secondo 'l numero del mi-
nore, è equale al minore, preso secondo 'l numero del maggiore; onde si uede nella Ses-
quialtera; che due 3. numeri maggiori sono equali à tre 2. numeri minori. La onde in
ogni Genere di proportione, tanta è la proportione contenuta ne i termini radicali di
qual si uoglia Interuallo; quanta è quella, ch'è contenuta ne i termini non radicali mol-
tiplicati ò raddoppiati essi radicali termini. Et per darui un'essempio ne i Superparti-
colari; dico; Quando due maggiori sono equali à tre minori, Quattro à sei, Sei à noue,
& Otto à dodici, l'un de i maggiori ad uno de i minori, & tale Interuallo è Sesquialte-
ro; allora quella proportione, che si troua tra 3 & 2. numeri radicali, ch'è Sesquialtera;
si troua anco tra 6 & 4; & tra 9 & 6; come anco si troua tra 12. & otto; i quali sono Nu-
meri non radicali di tal proportione. Et ne i Molteplici, quando Vno sarà equale à Due,
due à Quattro; & quattro ad Otto; & il maggior è duplo al minore; allora tanta sarà la
proportione dupla tra 2 & 1. quanto tra 4 & 2. & anco tra 8 & 4. percioche 'l maggior è
doppio al minore, il che si può dire anco de gli altri Generi; che per esser cosa chiara,
non mi uoglio sopra ciò molto distendere. Ma ne i Numeri composti, ò Composte pro-
portioni è da auertire; che quando 2. saranno equali à 4 1/2. allora saranno due congiun
te Sesquialtere; & quando 2. saranno equali à 6. 3/4. saranno tre; com'allora saranno
due congiunte Sesquiterze, quando 3. saranno equali à 5 1/3. & 3. saranno equali à 7 1/9.
ò in altre simili, che nascono dal loro raddoppiamento & più oltra. Ma allora cotal co-
sa ui sarà facile da intendere; quando hauerete compreso tutto quel ch'io ui son per di-
re. Ascoltate dunque attentamente, & tenetelo à memoria. Ma auanti ch'io ui dimo-
stri in qual maniera si componghino, ò molteplicano questi Interualli ne i Numeri com-
posti; uoglio che uediamo, in qual maniera.
PROPOSTA XV.
rollario, che gentilmente da essa nasce; accioche habbiate la cosa perfetta; il
qual sarà questo.
COROLLARIO.
ta dal Denominatore di cotal parte.
à replicar cosa alcuna. Chiaritemi hora d'un dubio; disse il Sig. Desiderio; & poi se
guitate il uostro parlare; Si può diuider l'Vnità, essēdo appresso i Mathematici in
diuisibile? A questo risposi; Io dissi ancora, dichiarādoui la prima Dimāda, che i Numeri ap
presso i Filosofi4. Phy.
cap. 3. si trouano esser di due maniere, delle quali la prima, è detta Numero nume
rāte; & la secōda Numero numerato. I primi sono un'essēplare & una Idea nell'Anima no
page 50 stra; & la lor Vnità non si può à patto alcuno diuidere; ma ne i secondi; come sono nelle
Cose naturali i numeri de i Mouimenti; nelle Geometriche le Linee, Superficie, Corpi
& altri simili; nell'Astronomiche i Numeri de i tempi; & nelle Musicali il Numero de gli
Interualli. l'Vnità loro; anzi per dir meglio; la cosa intesa per l'Vnità, è diuisibile in più
parti, senza contradittione alcuna. V'hò inteso, disse allora il Sig. Desiderio; che uoi
intendete del Numero numerato, & della sua Vnità in questa proposta; se ben'hauete
fatto quel discorso sopra la prima dimanda, il quale troppo ben mi ricordo; tuttauia hò
uoluto chiarirmi; acciò non prendessi errore. Cosi bisogna intender (soggiunsi) questa
cosa, come u'hò detto; onde tornando al mio primo proposito, dico; Sia a. qual numero
si uoglia, del quale sia ricercata una delle Parti denominata da b. Riduco prima a. in tut
te le sue parti denominate dal b. Denominator della parte; Moltiplicando esso b. Deno
minator del numero a. di modo che ne nasce c. E' manifesto, che le parti c. denominate
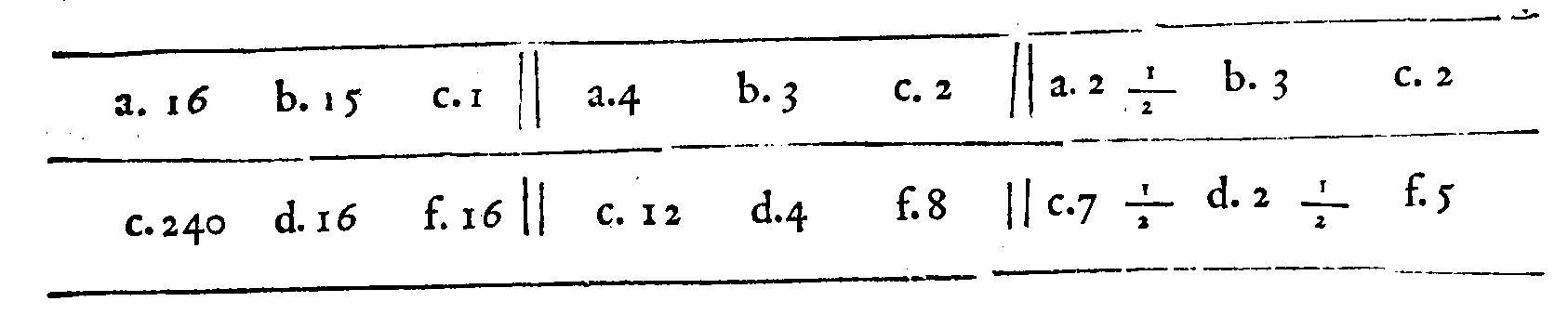
il b. Denominatore, & risulta d. onde dico d. esser la parte Aliquota di a. ricercata; & da
esso a. numerata; cioè, dal numero b. denominante esso a. Ma che d. sia la parte di a. de-
nominata dal Denominator b. come contiene il Corollario; da questo sarà manifesto;
perche molteplicato b. in d. per la Terza dimanda, di nuouo produce il c. però d. è par-
te di c. denominata dal Denominator b. Ma d. si agguaglia alla a. adunque d. è parte di
a. denominata dal b. Et che 'l d. sia numerato da a. è manifesto; perche molteplicato a nel
b. produce il c. Adunque, per la Seconda Dimanda, il c. diuiso per il b. ritorna a. Ma
essendo diuiso l'istesso c. per il b. prima ueniua d. adunque a. numera il d. una fiata: & per
tal modo la proposta uiene ad esser manifesta insieme col suo Corollario. Disse allora il
Viola; Voi proponeste di dimostrarci anco la parte Nonaliquota; nondimeno non l'ha-
uete ancora dimostrata; però se 'l ui piace di pagar'il uostro debito, fate uoi. E' il doue
re, risposi, & uoglio; ma non m'hauete lasciato finir di dir quello, ch'io uolea; percio-
che bisognaua prima ragionar sopra il Corollario, & dimostrar ch'era uero; però per sa-
tisfare alla proposta, dico; che se la parte, che si uorrà cauar del Numero dato sarà Non-
aliquota; è necessario, ch'ella habbia il Numeratore, che sia altro numero, che la Vnità.
Onde poniamo, che 'l Numerator della parte ricercata secondo 'l Denominator b. sia e.
molteplicheremo e. in d. & haueremo f. la quale dico esser la parte Nonaliquota di a. per
cioche f. uiene ad essere il d. molteplicato secondo 'l Numeratore e. Et questo è tutto quel
lo, che per pagare il mio debito ui doueua dire. Allora disse il Viola; Son in tutto satis-
fatto: però seguitate quello, c'hauete da dire. La onde seguitai in questo modo; per fi-
nir quello c'hauea da dire. Vi uoglio oltra di ciò auertire; che d. è il Numerator della par-
te Aliquota ritrouata di a. numero dato, & f. è il Numerator della Nonaliquota; Ma il
b. uiene ad esser il commune Denominator dell'una & l'altra. Allora disse M. Adriano;
Haurei molto caro, se far si potesse, che questa proposta ci dimostrasti con Numeri sem-
plici; percioche questi termini a. b. c. & gli altri, che da i Filosofi sono detti Termini igno
ti, ouero Incogniti, alle fiate non hanno quella forza, che hanno i Numeri semplici; massi
mamente quando sono posti in prattica; ancora che non si può negare, che la dimostratio
ne, che hauete fatto con tali termini, & con i numeri dati ancora, sia chiara. Io ui uoglio
al tutto satisfare dissi; s'io potrò Messere; & accioche con un'essempio uediate il tutto;
page 51 Sia ricercato, come di sopra ho dimostrato, la Parte della somma di 16; & sia tal parte
1/15; Molteplico primieramente 16 & 15. denominatori & numeratori de cotali parti l'un
cō l'altro, & ne uiene 240/15; imperoche tante Quintedecime contiene il 16. risolto in parti.
Diuido poi 240. per il 15, & ne risulta 16/15; i quali sono la Quintadecima parte di tutta
la somma de 240. parti. Onde il 16. anco uiene ad esser la Quintadecima parte. Ma
16/15 contengono la Vnità & 1/15; adunque la Vnità con 1/15 appresso sarà la Quintadeci-
ma parte di 16. numero dato; la quale è parte Aliquota. Ma per hauer la parte Non-
aliquota; moltiplicando la parte Aliquota per il Numerator della parte Nonaliquota,
haueremo sempre quel che cerchiamo; come si uede nell'essempio posto di mezo; che
moltiplicato il 4. per il 2. Numerator della parte 2/3, hauemmo 8/3; cioè, 2 2/3, ch'è la
parte non Aliquota di 4. ricercata. Di modo che uolendo la Parte di qual si uoglia nu-
mero proposto; operando à questo modo; sempre si quel che si cerca. Ma uenia-
mo all'altra proposta.
PROPOSTA XVI.
fiate si vuole tra Numeri composti.
ro composto. Al quale risposi; Io chiamo in questo luogo Numero composto
quello; che contiene in sè un numero intero, & qual si uoglia sua parte; come è
3 1/8; ouer 4 2/3 de i quali, il 3. & il 4. non sono numeri composti; ma semplici, &
1/8 & 2/3 sono le parti; di modo che 3 1/8. è composto di 3. numero semplice, & di
1/8. sua parte; & 4 2/3. è composto di 4. numero semplice medesimamente, & di 2/3, che
sono parti di esso 4; cioè, parte Nonaliquota. Siano adunque a. & b. i minimi termini
di qual si uoglia Interuallo, il quale uogliamo moltiplicare. Ritrouo prima, secondo 'l
modo mostrato nel Cap. 25. della Prima parte delle Istitutioni il Denominatore della
sua Proportione; il quale è c, che contien l'Vnità; la quale dimandarò Numero; & una
parte, sia poi Aliquota, ò Nonaliquota; oueramente un Numero, con la nominata
Parte. Moltiplico poi il numero c in a, & ne uiene d; il che fatto, per la Precedente, ri-
trouo la parte di a, secondo la parte di c; la qual uiene e; & questa aggiungo con d. &
ne nasce f. Dico hora, per la Settima dignità, che la proportione; che si troua tra f. & a.
è simile à quella, ch'è posta tra a. & b. percioche tanto uiene c. diuiso f. maggior termi-
ne della proportione fa. per a. termine della proportione a. b. quanto diuiso a. minor
termine della fa. per il b. minor termine di essa ab. Habbiamo adunque secondo la pro
posta, molteplicato l'Interuallo fa. con Numeri composti al dato ab. contenuto ne i
suoi radicali Termini; come ui douea dimostrare. Chi uorrà; disse il Merulo; à questi due
moltiplicar'un'altro Interuallo simile, tra gli istessi Numeri composti, che ordine haurà
egli da tenere? L'ordine istesso, risposi. Soggiunse ancora M. Claudio; Per uostra fè di-
mostrateci il modo. Bisognerà dissi, primieramente moltiplicar'il numero di c. in f. & ne
uerrà g. dopoi bisognerà cauar, per la Precedente, la parte di g. secondo la parte di c. on
de ne uerrà h. la quale aggiungeremo con g. & nascerà K. che con f. senza dubio alcuno,
per la Settima dignità nominata; contenerà quella proportione istessa, che si troua tra a
& b. percioche molteplicando b. maggior termine di Kf. per il b. minor termine di ab. ne
nascerà l. come etiandio nascerà, moltiplicando f minor termine di Kf. con a. maggior ter
page 52
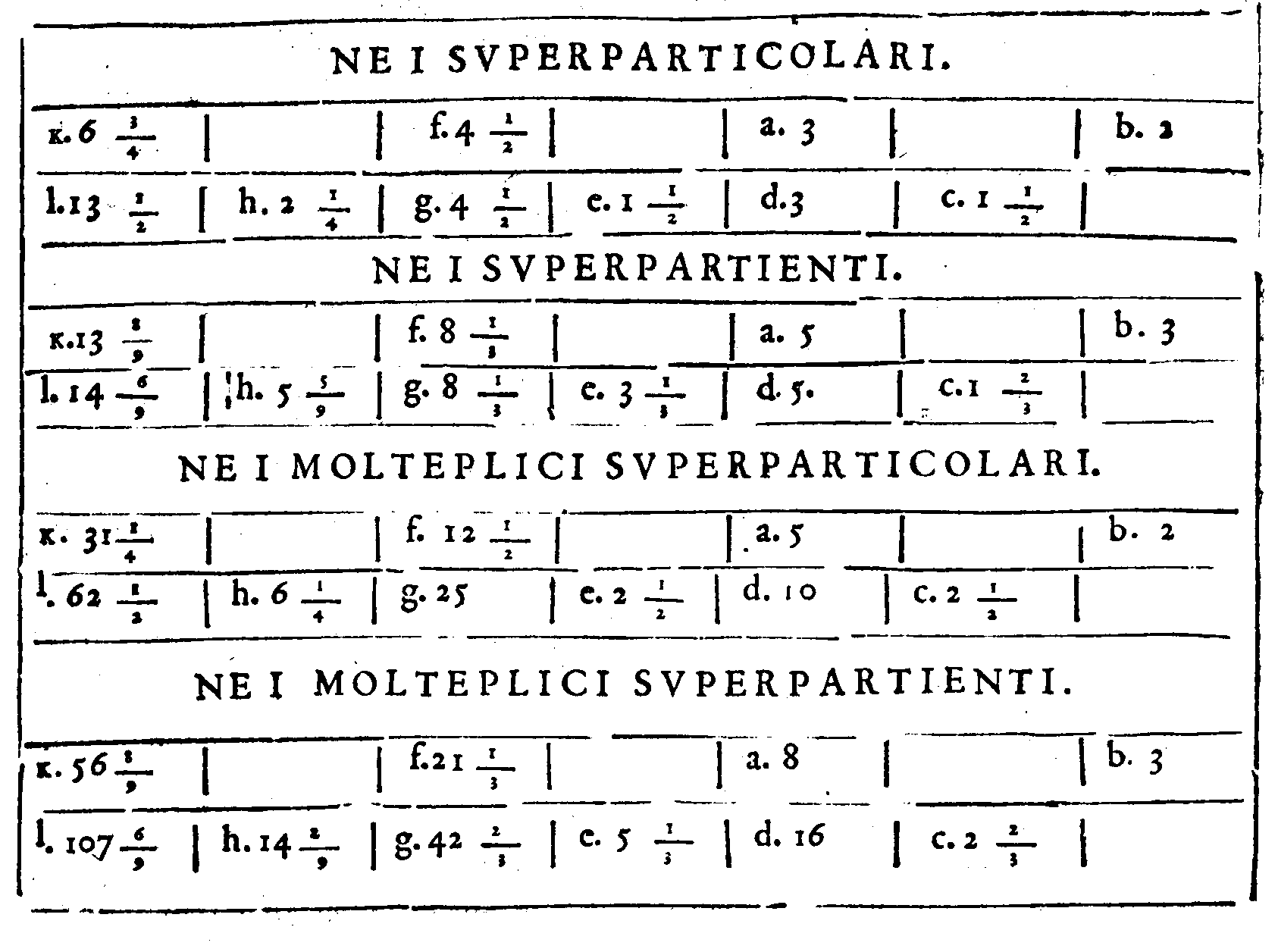
dimostrare. Onde uolendone ancora aggiunger un'altro, & poi un'altro; tenendo
quest'ordine, si potrà andare in infinito, & hauere il proposito. Che ui par Messe-
re? disse il Viola; parmi che bisogna saper'adoperar ben la penna, & far ben con-
to, à chi uuol intendere, & porre in atto queste cose. Vi sò che dire, che non biso-
gna esser grosso di ceruello; rispose M. Adriano; per che non si farebbe cosa alcuna
di buono. Ma che uorrete soggiungere à questa M. Gioseffo? Questa; risposi io; che
PROSTA XVII.
lari.
Sesquialtero, & bc. Sesquiterzo. Dico ac. nascer dalla congiuntione di ab.
con bc. Et perche ab. è Sesquialtero; però, per la Quinta definitione, a. con-

due a. sono equali à tre b. Et di nuouo; perche b & c. è Sesquiterzo; però, per l'istessa De-
finitione, il b. contiene il c. una fiata & una sua Terza parte. Adunque tre b. sono equali
à quattro c. & due a.sono posti equali à tre b. adūque due a. sono equali à quattro c. Essen
do per il Decimo parer commune, che Quelle cose, lequali ad una cosa istessa sono equa
li, tra loro etiandio sono equali. Et 4. numero de i minori adunati insieme è il doppio,
per la Quartadecima proposta, de due maggiori posti insieme: adunque, per l'istessa Quar
tadecima, uno a. sarà doppio ad un c. Ma perche 'l Sesquialtero & lo Sesquiterzo: per
l'Ottaua, & per la Nona dignità; sono tra i Superparticolari i due maggiori; però dico,
che l'Interuallo Duplo nasce dalla congiuntione de i due maggiori Superparticolari, co-
sa, che ui douea dimostrare. Dopo questo aggiunse M. Adriano: Si può anco dimostrar
questa propositione, secondo che mi pare, per un'altra strada; & questo col mezo della
Duodecima dignità; & mi dà l'animo di saperlo fare. E' uero quel che uoi ditte Messe-
re; risposi; & quando la dimostraste, dareste da intendere in fatto, che uoi intendiate
benissimo quel che fin'hora hò detto; però fate quel che ui piace. Voglio prouar per
ogni modo; soggiunse egli. Dico adunque, ch'essendo due a. del uostro proposto essem-
pio equali à quattro c; come hauete concluso; uno a, per la Dignità nominata, uiene à
farsi equale a due c. Imperoche, Di quelle cose, delle quali Tutti sono equali, equali so-
no etiandio le lor parti: Ma perche due c. sono il doppio di uno; adunque uno a. equale
à due c, sarà il doppio di un c. Ma a & c, nasce dalla congiuntione di ab. & ac, che so-
no (come hauete prouato) due maggiori superparticolari; adunque l'interuallo Duplo
nasce dalla congiuntione de i due maggiori superparticolari. Fatto che egli hebbe cota-
le proua egli dissi: Voi sete in fatto un gran picciolo, Messere; sete come 'l Pepe, il-
quale è piccolo in quantità, ma è grande in uirtù & possanza; percioche ui sete dimo-
strato un gran Discepolo in poco tempo. Che ui par Signor Desiderio, non s'hà egli
diportato bene? Ben ueramente; rispose egli; & non m'ha ingannato punto, di quel ch'
io credeuo di lui; percioche sempre hò hauuto M. Adriano, per huomo di bello ingegno.
Ringratio V. Signoria (rispose M. Adriano) di questo fauore; ma lasciamo per uostra
fè queste parole da un canto, & stiamo à ueder quello che uorrà aggiungere M. Giosef-
fo; & non ci partiamo dall'ordine incominciato. Quello, ch'io uoglio aggiungere, dissi;
sarà; che quest'istessa proposta ui uoglio dimostrare con un'altro mezo, se non ui rincre-
sce l'ascoltarmi. Come rincresciere? soggiunse M. Desiderio; non ci potete fare il mag-
gior fauore, ne apportarci maggior diletto, che seguitar quello, c'hauete ;
percioche io per me non credeua di ueder cotante cose uarie della Musica. Co 'l no-
me di Dio adunque; dissi; & ripigliai il ragionamento in questo modo. Sia ab. Inter-
uallo Sesquialtero; & bc. Sesquiterzo. Dico a. con c. esser'Interuallo Duplo. Faccio prima
a. equale al b, & ne uiene d; & sopra auanza e; dopoi faccio b. equale al c; & nasce f, & auan
za g. il che fatto, dico; perche a. è Sesquialtero con b; e. uiene ad esser la Terza parte di a

parte di b. & la Terza di c. Onde essendo g Quarta parte di b; & e. la sua metà; g sarà la me
COROLLARIO.
quialtera & Sesquiterza proportione, come da sue parti principali.
de gli estremi di qual proportione si uoglia, ouer Interuallo, si dice esser com-
posta de i suoi mezi proportionali; come da sue parti. Bella dimostratione ue-
ramente è stato questa; disse il Signor Desiderio; & mi è sommamente piaciuta; però
seguitate quello, che ui torna più al proposito. Mi torna hora commodo il dimostrarui,
soggiunsi; che
PROPOSTA XVIII.
lità.
de i due maggiori superparticolari; ab. Sesquialtero, & bc. Sesquiterzo. Dico
dall'Interuallo a & c. composto in tal maniera nascer l'Harmonica proportiona
lità. Faccio adunque primieramente a. equale al b, di modo che sopr'auanzi d; il qua-
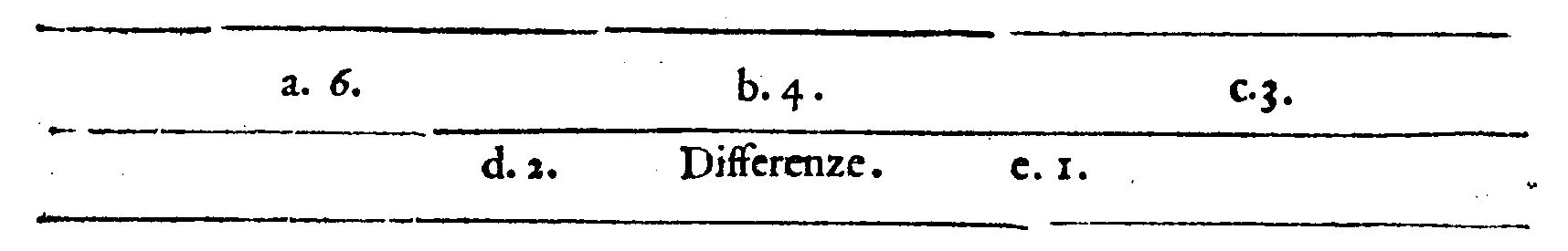
tal sorte, che soprauanzi e. & e. sia la differenza che si troua tra b & c. Dico hora; per-
che d. contiene e. due fiate di punto, per la Quarta definitione, d. uiene ad esser duplo
allo e; ma a. simigliantemente; per la Precedente; è posto duplo al c. adunque, per la
Settima dignità; ac. & de. sono Interualli contenuti da un'istessa proportione. Et per-
che tra i maggiori termini ab. per la Ottaua dignità; si troua la proportione maggio-
re, & tra i minori, che sono bc. si troua la minore; però, per la Terzadecima de-
finitione, dico; che tra i termini a. b. c. si troua la proportionalità, ò mediocrità
Harmonica; essendo aggiunti i due maggiori Superparticolari interualli insieme; come
proposi à dimostrarui. Ogni cosa torna bene; disse allora M. Adriano; Ma ditemi per
nostra fè; s'io trouerò l'Interuallo Duplo composto (per dir com'hauete detto) d'una
page 55 Sesquiterza & d'una Sesquialtera, tra questi termini. 4. 3. 2. ouer'altri simili; come mol
te fiate n'hò ritrouato, non si potrà forse dire, che tali Interualli si trouano in Harmoni-
ca proportionalità ordinati? Si potrà ben dire, diss'io, Messere; ch'ello sia Interuallo
cōposto de i due nominati; ma non già, che tal ordine posto sia in proportionalità har-
monica. Per qual cagione? disse egli; non è ello composto de quelli Interualli, che en
trano nella uostra proposta? Che l'interuallo Duplo sia composto d'un Sesquialtero &
d'un Sesquiterzo semplicemente; risposi; non è cagione, che tale Interuallo contenga
la Proportionalità harmonica; ma si ben consiste nell'ordine; percioche bisogna, che le
Proportioni siano ordinate in tal maniera; oltra le proportioni, che si trouano tra le diffe-
renze, & tra gli estremi, lequali uogliono esser simili; che ne i termini maggiori si troui
la maggior proportione, & tra i minori la minore. Percioche (come nel Cap. 40 della
Prima parte delle Istitutioni, degno di esser considerato dichiarai) il Musico se ui ricor-
date Messere) uà facendo & cauando sue ragioni dal Tutto & dalle Parti fatte del Cor-
po sonoro; sia poi chorda, ò qual si uoglia altra cosa, che torni al proposito; ilqual Cor-
po è diuisibile in infinito. Onde intende & piglia in qual ordine si uoglia di proportio-
ne il numero maggiore per il Tutto del Corpo sonoro diuiso in tante parti & non il mi-
nore. Il perche accommoda sempre i termini maggiori de gli interualli al Tutto fatto in
parti, & gli altri nel restante; secondo le parti, che considera; & come che per loro natura
accommodar si debbono, secondo i loro gradi per ordine. Però uedete, che i termini,
i quali hauete proposto, sono posti al contrario; perche tra i numeri maggiori si ritroua la
proportione minore, & tra i minori la maggiore. La onde si uede dalle differenze loro,
che sono Vnità tra loro equali, che tali termini sono ordinati in progressione, ò come
più ui piace di dire, proportionalità Arithmetica, & non in mediocrità, ò proportio-
nalità Harmonica; come dall'Vndecima definitione si può comprendere. Intendo ho-
ra il tutto; disse M. Adriano; poi che mi hauete ridutto alla memoria questo Capitolo;
ma in uero non mi ricordaua tanto inanzi. Et quando non haueste hauuto altra ragio-
ne, che dirmi; era a bastanza la Definitione, c'hauete allegato. Ma non mi scorderò più
quello chauete detto in esso; cioè, che i Termini, che usa il Musico sono parti del Cor-
po sonoro; & quelli che usa l'Arithmetico, sono cose, ouer'Vnità moltiplicate; come
sono quelle che sono contenute ne i termini, ch'io ui proposi, & non le parti del nomina-
to Corpo. Cosi è ueramente; soggiunsi; però per l'auenire quando uedrete ch'io pro-
ponerò un numero in atto; sempre lo prenderete per tante parti fatte del Corpo sonoro,
le quali dinota esso Numero. Et quando ne uedrete più di uno in un'altro ordine; sempre
piglierete il maggiore per il Tutto del detto Corpo fatto in tante parti, & gli altri intende
rete per quelle che succedono. Questa disse M. Francesco; è stata un'altra buona lettione
& molto utile; percioche ancora non hauea inteso, in qual modo applicauate questi Nu-
meri, ò termini al detto Corpo Attendete adunque, dissi io, & non ui lasciate uscir di
memoria quello, ch'io uò dimostrando; percioche potrebbe esser causa di confusione.
Ma uenendo alla proposta, dico:
PROPOSTA XIX.
costituisca la Proportionalità harmonica; ouer quello che faccia la Contr'harmonica,
ne i suoi termini radicali.
da ritrouar il mezan Termine, ouer'harmonico Diuisore. Et perche a. & b. so-
no termini differenti l'un dall'altro per l'Vnità; & non riceuono, per la prima
Dimanda, tra loro alcun mezano termine; però adunaremo prima insieme a & b. & ne
page 56 nascerà c. Questo molteplicato con i detti a & b. ci darà d & e. i quali conteneranno, per
la Quinta Dignità, l'istessa proportione, che contiene ab; & saranno capaci di cotale ter
mine nominato. Onde moltiplicando poi a. co 'l b. haueremo f. che, raddoppiato, ci darà
g. il quale senza dubio alcuno sarà il ricercato Mezano termine, che costituirà l'Harmo
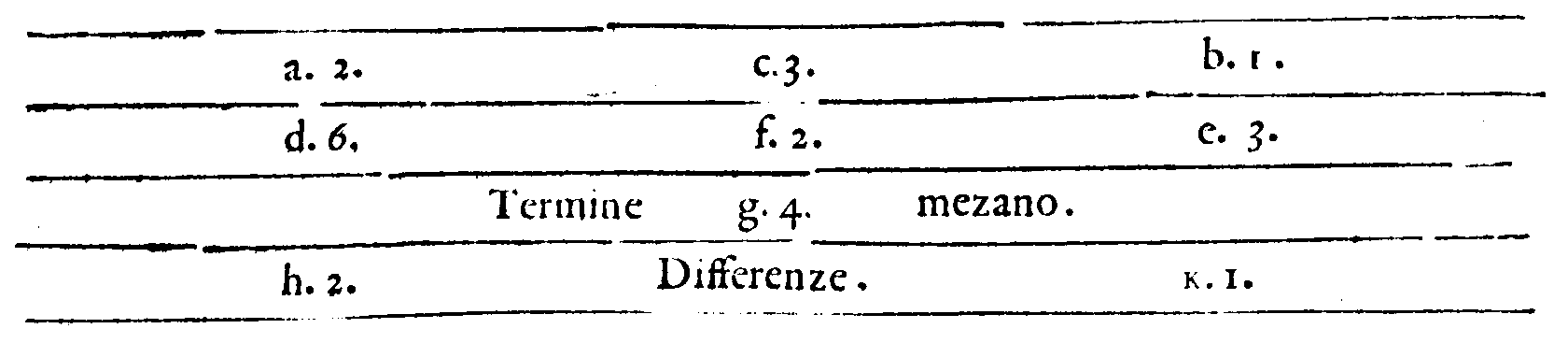
piglio la differenza, che si troua tra d & g, la quale è h. & quella, ch'è posta tra g & e. la-
quale è k. & dico: perche la proportione h & k. hà gli istessi termini, da i quali è conte-
nuta etiandio la proportione a & b. però, per la Settima Dignità, tanta è la proportione
h & k. quanta quella de i dati termini a & b. M'habbiamo già detto, che tanta è la pro-
portione di d. & e. quanta quella di a. & b. adunque tanta è quella delle due differenze
h. & k. quanta quella de gli estremi d. & e. Onde, per la Terzadecima definitione, la
qual dice; che Se saranno tre quantità sonore poste in ordine di maniera, che la proportio
ne, la qual si troua tra le differēze del maggiore al mezano, & di questo al minore, sia equa
le à quella, che si troua tra le differenze de i nominati termini; dico, che tra due dati termi
ni habbiamo ritrouato 'l mezano, il quale costituisce l'Harmonica proportionalità. Et per
che d. g. e. sono numeri Contraseprimi; percioche non hanno altra misura tra loro com
mune, che l'Vnità; però dico, per la Nona definitione, tal proportionalità esser con-
tenuta ne i suoi termini radicali; come dice la proposta. Et questo è tutto quello, ch'io
ui douea dimostrare. A questo disse M. Adriano; Questa cosa è molto bella & ingegnosa;
onde io soggiunsi; E' anco una delle mie Inuentioni; & non sono molti giorni, che af-
faticandomi di ritrouar il mezan termine della Contr'harmonica, ritrouai questo bel
modo, facile & presto. Soggiunse anco M. Adriano; Voi tenete, se ben mi ricordo, un'
altro ordine, nel ritrouar questo termine mezano nelle Istitutioni.2. par. Cap.
39. E' uerò, risposi; & co
tal modo serue molto à dimostrar (se ui ricordate1. par. cap.
40.) la conformita della proportionalità
Arithmetica con l'Harmonica; la qual cosa mi diede occasione di discorrere sopra dell'
una & dell'altra molte cose. Mi ricordo; ei rispose; ma ditemi per uostra fè; questa maniera
di ritrouar questo mezano termine, è ello commune à gli altri Generi di proportione?
E commune per certo, dissi; & serue à qual Genere si uoglia; purche si tenga 'l modo &
l'ordine, c'hò dimostrato. Aggiunse anco egli; Nella Contr'harmonica poi, come si ri-
troua questo mezano termine? Et io; In un modo bello & anco breuissimo. Ma sappia-
te, che se ben questa proportionalità è Antichissima, & che di lei molti n'habbiano fat-
to mentione; tuttauia quanto all'uso di essa, non sò se ritrouarete alcuno, che n'habbia
parlato, & c'habbia detto, in qual cosa l'Huomo di essa se ne possa seruire. A questo dis-
se il Signor Desiderio; Io mi ricordo d'hauerla ueduto ueramente in Boetio;Arith. lib.
2. cap. 51.
& 53. ma non mi
poteua imaginare, à che potesse seruir nella Musica; onde la teneua quasi per cosa su-
perflua. Ma non mi dispiacerà conoscere, in qual modo ella sia utile in questa Scienza,
la quale col mezo delle sue Dimostrationi si mostra tanto copiosa, tanto ricca, & tanto
abondante de cose; che non credo, ch'alcuni sciocchi potranno più dire, che la Musica
non sia speculatiua. O ueramente sciocchi, gli risposi; anzi goffi che sono costoro, se si
penssassero, che si potesse dire, ò scriuere ogni cosa, che si ritroua in questa Scienza; per-
cioche ogni giorno nasce qualche bel dubio; & qualche bella consideratione di maniera,
che la cosa uà in infinito. Ma ritorniamo al nostro proposito. Siano (come di sopra) a.& b.
page 57 termini radicali d'alcuna proportione, tra i quali uogliamo ritrouare un Mezan termi-
ne contr'harmonico; & siano d. & e (com'anno di sopra) termini capaci di cotal me-
zo, continenti la proportione, che si troua tra a & b. Dico, che se noi cauaremo b. mi-

b. & quello che uerrà da tal molteplicatione cauaremo dal d. maggior de i secondi; uer-
rà f. che sarà il Mezano termine, ò ricercato Diuisore, che costituirà la Contr'harmoni-
ca proportionalità. Et per dimostrar questo; cauo prima la Differenza, che si troua tra
d. & f. maggiori termini de i secondi, & ne nasce g. dopoi cauo quella, che si troua tra f.
& e. & ne uiene h. onde dico; perche tra a. b & g. h. ui è simiglianza de termini; però,
per la Settima Dignità, ui è anco simiglianza di proportione. Ma, per la Definitione
Decimaquarta; Quando tra le differenze di tre dati termini, & i loro estremi si trouerà si
miglianza di proportione, allora si dirà che tal ordine sia fatto secondo la proportionalità
Contr'harmonica; il perche ritrouandosi tale simiglianza tra de. & gh. seguita, che tra d. f.
& e. sia costituita la proportionalità nominata. Tra due termini dati, adunque, di qual
si uoglia proportione, habbiamo ritrouato 'l Mezano, il quale costituisce la Contr'har-
monica proportionalità, secondo ch'io ui douea dimostrare. Questo modo; disse M.
Claudio; è ello, commune ad ogni sorte di proportione? Ben sapete, risposi. In ueri-
tà; soggiunse il Signor Desiderio; ch'è anche lui molto bello & facile. Ma uenite à di-
mostrarci qualche altra cosa. Cosi uoglio fare, risposi; ascoltatemi prima, & manda-
te alla memoria questi Versi ch'io ui reciterò; acciò più facilmente ui ricordate le Re-
gole, ch'io ui hò dato per ritrouare i Mezani termini de queste due proportionalità; &
sono cotesti.
Se vorrai ritrouare tra due numeri
Dati, che un terzo sia Mezano harmonico;
Fà che tu aggiunga insieme cotai numeri;
Et quel che nascerà con quei molteplica;
Et ne uerrà due altri maggior numeri.
Fatto questo, bisogna che molteplichi
I due Dati tra loro, & che raddoppij
Il prodotto, & uerrà 'l sudetto harmonico.
S'anco delli due Dati il minor numero
Leuarai dal maggior; fà che 'l residuo
Con il minor insieme tu molteplichi;
Et quel che nasce dal maggior de i termini
Leua, e tra lor quello ch'auanza colloca,
C'hauerai lo mezano Contr'harmonico.
Questi Versi non mi dispiaceno, allora disse il Signor Desiderio; poiche le cose mathe-
matiche per la lor natura presto si partono delle menti nostre; onde saranno cagione di
far, che nō cosi facilmente cotesta cosa si scompagnarà da noi; essendo che 'l Verso per sua
natura non si domentica tanto facilmente, quanto auiene della Prosa; però hauendo fat-
to questo poco di guadagno, ui prego M. Gioseffo, à seguitare il resto. Sappiate adun-
que questo, dissi, essere infallibilmente uero, come ui dimostrerò, che:
page 58
PROPOSTA XX.
quarto & un Sesquiquinto.
termine harmonico, in ab. & bc. dico da tal diuisione nascere il Sesquiquarto,
& lo Sesquiquinto; il primo tra ab, & lo secondo tra bc. Et perche a. contiene

quiquarto. Simigliantemente, perche b. contiene c. una fiata & una sua Quinta parte;
però, per la Definitione nominata, b. con c. è Sesquiquinto. Ma perche ac. è interuallo
Sesquialtero, & da b. termine Mezano harmonico è diuiso in ab. Sesquiquarto, & in b
c. Sesquiquinto; però dico, che Diuiso l'Interuallo Sesquialtero da un termine harmo-
nico mezano, nasce un Sesquiquarto & un Sesquiquinto; come dimostrar ui douea.
Et à questo aggiungerò, il seguente Corollario, ilquale sarà; che
COROLLARIO.
Sesquiquinto, come da sue parti principali; & che cauato l'uno de questi da esso ne-
cessariamente, resta l'altro.
trebbe porre nel Numero de i pazzi. A questo, dissi; uoglio hor'aggiunge-
re; che.
PROPOSTA XXI.
uo, & in un Sesquinono.
ste parole; Mi souiene hora, che io non hò mai ritrouato, che gli Antichi hab-
biano considerato altra diuisione Harmonica, che quella della Dupla; on-
de mi pare, che ciò potesse procedere, ò da ignoranza, ò da troppo superstitione.
O, non dite cosi; gli risposi à questo; credo che più tosto gli Antichi fussero super-
stitiosi, che ignoranti; se ben si può credere, che dalla ignoranza de molte cose, da
quel che già dissi, & da quello che uederete scritto ne i miei Sopplimenti;Lib. 3. c. 5.
& 6. non fussero al
tutto liberi; poi che loro non intesero i Gradi delle Consonanze. Onde procedeua 'l tut-
to, dal non uolere admettere alcuno Interuallo, che fusse minor della Diatessaron, nel
numero loro; del che quanto s'habbiano ingannato, la proua, che facciamo ogni gior-
page 59 no del Ditono & del Semiditono, che sono due parti, che nascono dalla proposta & dimo
strata diuisione, ce lo manifesta: Ma ueniamo alla sua dimostratione. Siano a. b. c. l'inter
uallo Sesquiquarto, diuiso, per la proposta, dal b. Mezano termine Har
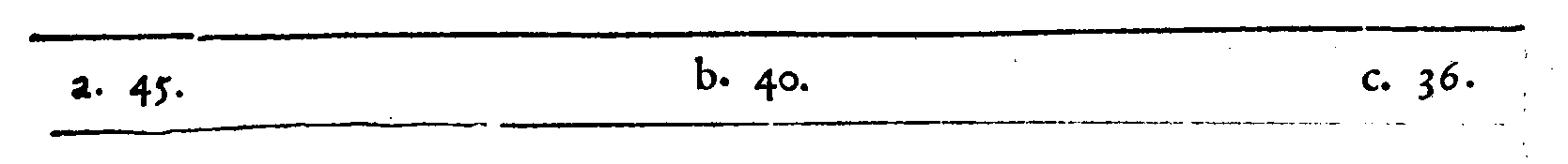
tauo, & lo Sesquinono; percioche se a. contiene il b. con una sua Ottaua parte, non è du-
bio; per la Definitione de i Molteplici, che a. & b. sia Interuallo Sesquiottauo. Al medesi
mo modo; perche b. contiene il c. una fiata & una sua Nona parte; però, per l'istessa De
finitione, il b. & c. sarà interuallo Sesquinono. Il perche dico, Diuiso l'interuallo Sesqui-
quarto da un mezano termine Harmonico, come dice la proposta, si diuide in un Sesqui
ottauo & in un Sesquinono; come ui douea dimostrare. A questa etiādio aggiūgerò; che,
COROLLARIO.
grato, come da sue parti principali.
giori della Dupla. Et io à lui; Anzi ue ne uoglio hora dire; perche questo è il
suo luogo; che,
PROPOSTA XXII.
contiene l'Harmonica proportionalità.
alcuna delle già dimostrate. Questo è uero, soggiunsi; però uolendola dimo-
strare, dirò in questo modo. Sia prima a. b. c. Interuallo composto di a. b. Du-
plo, & di b. c. Sesquialtero. Dopoi sia la d. la differenza, che si troua tra a. & b. & sia anco
c. quella, che si troua tra b. & c. Dico hora a. esser Triplo al c. & a. b. c. esser ordinati in Har
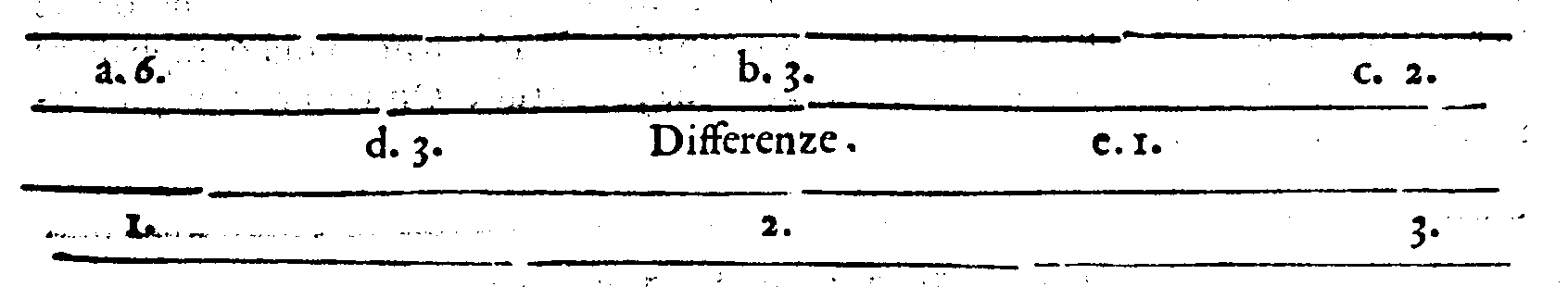
finitione, contiene il b. due fiate; adunque per la Duodecima proposta, uno a. si troua es
ser equale à due b. Simigliantemente; perche b. c. è Sesquialtero; però il b. contiene, per
la Quinta definitione, il c. una fiata & la sua metà; Adunque per l'istessa Duodecima, due
b. sono equali à tre c. & due b. erano equali ad uno a. adunque tre c. simigliantemente so
page 60 no equali ad uno a. Ma tre sono Tripli ad uno; adunque, per la quarta decima, uno a. è
Triplo ad uno c. come primieramente dimostrarui douea. Ma perche la proportione del
le differenze contenute ne i termini d. & e. uiene ad esser Tripla; essendo che 'l d. contiene
tre fiate e. & già per la Dimostratione habbiamo a. & c. esser Triplo; però, per la Settima
dignità, & per la Decimaterza, ne segue; ch'essendo d. & e. differenze de i sopra dati ter
mini a. b. c. simili in proportione con a. c. estremi termini; che a. b. c. siano collocati in Har
monica proportionalità; come secondariamente ui douea dimostrare. Hora dopo que-
sta seguitarò dirui; che,
PROPOSTA XXIII.
trica proportionalità.
& b. c. simigliantemente Duplo. Dico a. esser Quadruplo al c. Et perche a. è dop
pio al b. però due b. sono equali ad uno a. Et di nuouo; perche b. è doppio al c.
però due c. sono equali ad uno b. Ma se due c. sono tanto quanto è un b. quattro c. saran-
no equali à due b. ma due b. sono posti equali ad uno a. adunque quattro c. saranno equa
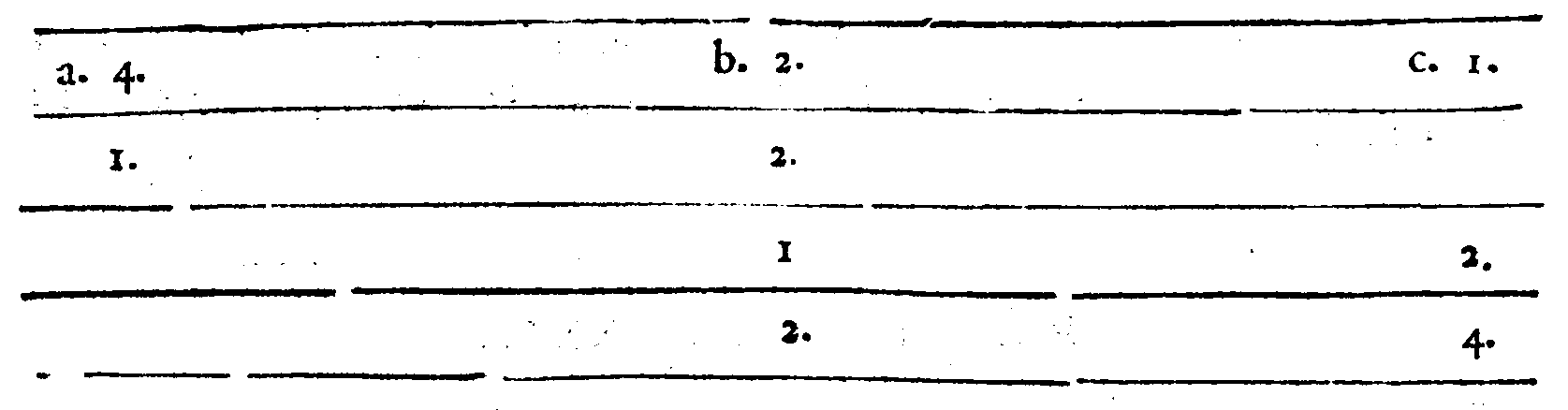
tadecima proposta, uno a. è Quadruplo ad un c. Et questo è quello, che primieramente
douea dimostrare. Ma perche a. b. c. è interuallo d'un Duplo raddoppiato; & il Duplo,
per la Quarta definitione, è Molteplice; però seguita, che l'Interuallo a. b. c. sia interual-
lo Molteplice raddoppiato. Ma i termini di qual si uoglia interuallo Molteplice raddop-
piato, per la Quarta proposta, constituiscono la proportionalità Geometrica; adunque
a. b. c. interuallo Duplo raddoppiato constituisce la proportionalità Geometrica. Et que
sto è quello, che secondo la proposta, ui douea secondariamente dimostrare. Sete arriuato
alla Quadrupla, disse M. Adriano; non credo già, che uorrete passar più oltra; però c'ha
uerete più da dirci? Attendete pur Messere, risposi; che se ben non uoglio trappassare
i termini della Quadrupla, non mancano le cose da proporui. Onde hora ui uoglio di-
mostrare; come noi.
PROPOSTA XXIIII.
perparticolari vorremo.
per satisfarui, gli risposi. Sia adunque il nostro principale intendimento, di ritro
uar un Termine, ò Numero minore, al quale possiamo assegnar due, ò più In-
terualli diuersi di proportione; & siano a. b. & c. d. le proportioni, che uogliamo assegna

ni minori de gli Interualli: a. b. & c. d. onde ne uiene e. il quale dico esser il Numero mino
re ricercato; percioche cauando primieramente, per la Quintadecima proposta, la par
te di e. secondo 'l d. uiene f. il quale aggiunto con e. nasce g. Et perche g. contiene e. & u-
na sua parte; come etiandio contiene al medesimo modo c. il d. però dico, per la Settima
dignità, tanto esser la proportione di g. con e. quanta quella di c. con d. Cauo secondaria
mente, per l'istessa Quintadecima, al medesimo modo, la parte di e. secondo b. la qual
uiene h. & questa aggiungo con e. onde risulta k. Ma perche k. contiene e. una fiata &
una sua parte; come anco a. contiene al modo medesimo il b. però dico, per l'istessa Set-
tima dignità, tanta esser la proportione di k. e. quanta quella di a. b. Et perche habbia-
mo assegnate le Proportioni proposte a. b. & c. d. al numero e. però dico, che habbia-
mo ritrouato un numero minore, al quale potiamo assegnar quante proportioni Super-
particolari uogliamo; secondo la proposta. Et questo è quello, ch'io ui uolsi dimostrare.
Vi uoglio anco auertire una cosa; che si può ritrouar cotale termine, il quale sarà il mag-
giore; operando però tutto al contrario di quello, che habbiamo fatto à ritrouar'il mino
re; onde questa sarà la proposta.
PROPOSTA XXV.
particolari farà dibisogno.
che uoi insegnate nelle Istitutioni;3. par. cap.
56. & 62. ilche molto mi diletta; però dimostrateci que
sta anco; poi che si procede al contrario della Precedente. Onde soggiunsi; Vo-
lendo ritrouar'il proposto termine, dico: Sia il proposito nostro di ritrouar un Numero, ò
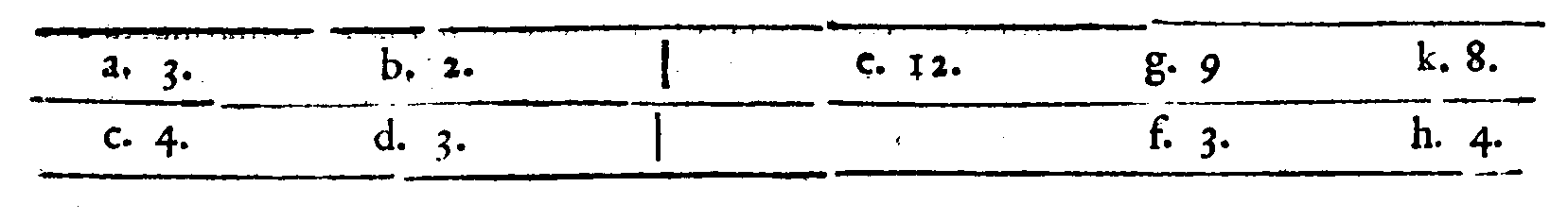
ti di proportione; & siano a. b. & c. d. constituiti ne i lor termini radicali. Molteplico pri-
ma a. & c. maggiori termini delle proposte proportioni a. b. & c. d. & ne risulta e. Dico e.
esser'il Termine maggiore, al quale potremmo assegnar le date proportioni a. b. & c. d. on
de fatto questo, dopoi per la Quintadecima di questo nostro ragionamento, piglio la par
te di e. secondo c. maggior termine della proportione c. d. la quale uiene f. questa cauo
di e. & ne nasce g. Dico hora, per la Settima dignità, tra e. & g. esser quella medesima pro
page 62 portione, ch'è collocata tra c. & d. percioche tante fiate contiene e. il g. & una sua parte;
quante fà il c. il d. Piglio di nuouo, per la nominata Quintadecima, la parte di e. secon
do a. maggior termine della proportione a. b. & ne uiene h. ilquale cauo di e. & ne nasce
k. la onde dico, per l'istessa Dignità, tanta esser la proportione di g. & k. quanta quella di
a. b. percioche g. contiene tanto una fiata il k. & una sua parte; quanto fà a il b. Ma per
che habbiamo assegnato al numero e. le proportioni proposte a. b. & c. d. secondo 'l pro-
posito; però dico e. esser'il ritrouato numero, ò termine maggiore, secondo la proposta.
Et questo è tutto quello, ch'io ui douea dimostrare. Ma auertite, che nella Precedente
bisogna incominciare à giunger le Parti dalle proportioni, che minor denomina-
tore; & in questa, da quelle, che l'hanno maggiore. Disse allora M. Claudio; Si può ben
ueramente dire, che si proceda al contrario; & pur troppo mi son accorto nel dimostrar
la proposta, che l'hauete osseruato; però dimostrateci qualch'altra cosa. Io uoglio ch'in-
cominciamo hora, risposi; adoperar queste proposte; però ascoltate.
PROPOSTA XXVI.
ottauo.
sesquiterzo, & c. Sesquialtero. Da a. c. cauo a. b. Sesquiterzo, lasciando da un
canto b. c. il quale dico esser Sesquiottauo. Imperoche essendo a. Sesquialtero
al c. a. contiene esso c. una fiata & la sua metà. Il perche, per la Duodecima di questo,
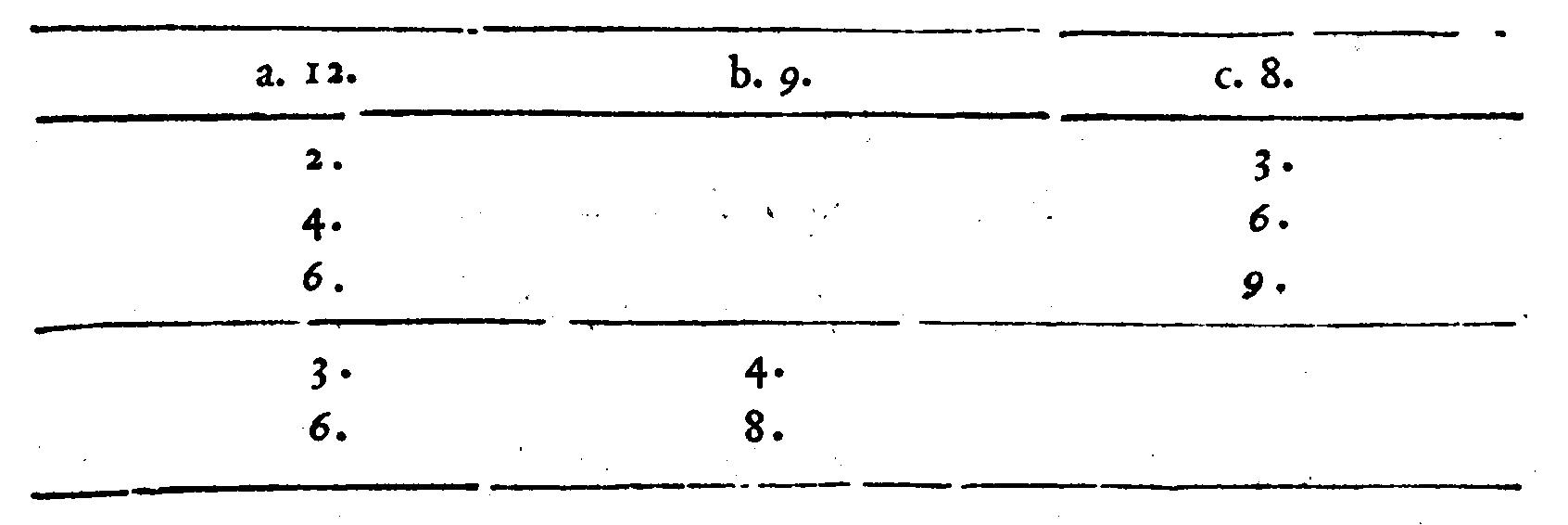
Sesquiterzo di a. adunque a. contiene in se il b. & una sua Terza parte; onde nasce, che,
per la nominata Duodecima, Tre a. sono equali à quattro b. & Sei ad otto. Ma Sei a. so-
no già equali à Noue c. adunque Otto b. sono equali à noue c. per la Decimaquarta adū-
que; il b. contiene il c. & la sua ottaua parte; & b. e. per la 5. Definitione; Sesquiottauo
al c. come ui douea dimostrare.
COROLLARIO.
pr'auanza il Sesquiterzo interuallo.
re. Onde ripigliai dopo questo il mio ragionamento in questo modo. Dirò adun
que aggiungendo la uentesimasettima proposta.
PROPOSTA XXVII.
quinono.
quale sia assegnato il b. Sesquiquinto, & il c. Sesquiterzo. Leuo da a. c. Sesqui-
terzo, a. b. Sesquiquinto; lasciando da un canto b. c. & dico b. c. esser'Interual
lo Sesquinono. Imperoche essendo a. Sesquiterzo al c. a. contiene il c. una fiata & una
sua terza parte; onde Tre a. uengono equali, per la Duodecima proposta, à quattro c.
Sei, ad otto; Noue, à dodici; Dodeci, à sedici; & Quindeci, à uenti. Simigliantemen
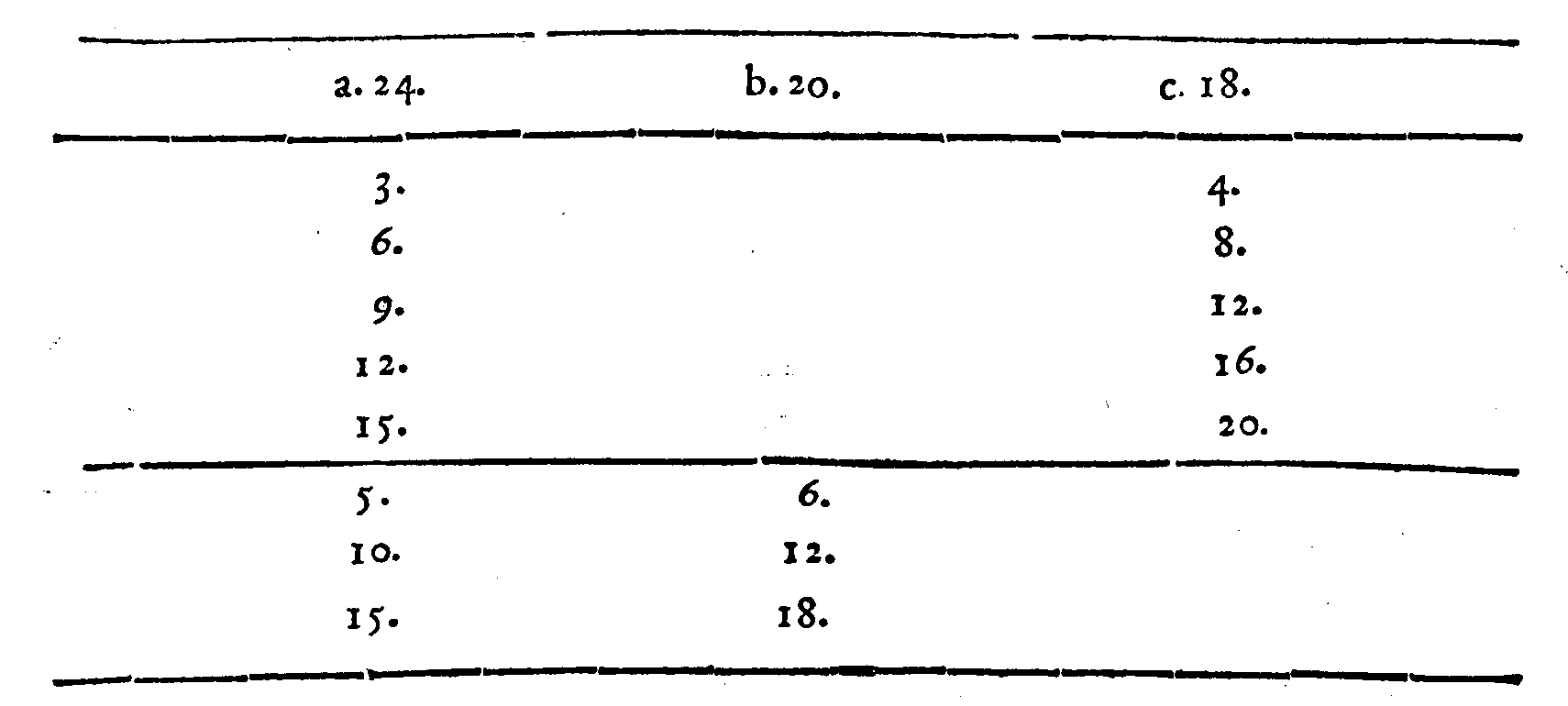
te; onde, per l'istessa Duodecima, Cinque a. sono equali à sei b. Dieci, à dodici; & Quin
deci, à diciotto. Ma Quindeci a. sono posti equali à Venti c. adunque Venti c. sono equa
li à Diciotto b. La onde, per la Decimaquarta proposta di questo nostro ragionamen-
to, il b. contiene il c. & la sua Nona parte; adunque b. c. per la Quinta definitione, è Ses-
quinono; come ui douea dimostrar, secondo la proposta.
CORROLLARIO.
& la Sesquiquinta proportione; per laquale quella viene ad esser'à questa superiore.
espositione; però al uostro bel piacere seguitarete quello, che più ui torna com-
modo. Cosi son per fare, risposi; la onde dico; che,
page 64
PROPOSTA XXVIII.
todecimo.
Ventesimaquarta, ritrouato. Faccio b. Sesquiquarto con a. & c. Sesquiterzo an
cora con a. il che fatto, leuo b. a. Sesquiquarto, da c. a. Sesquiterzo; & lascio da
un canto c. b. il perche quest'Interuallo; senza dubio alcuno, è Sesquiquintodecimo.
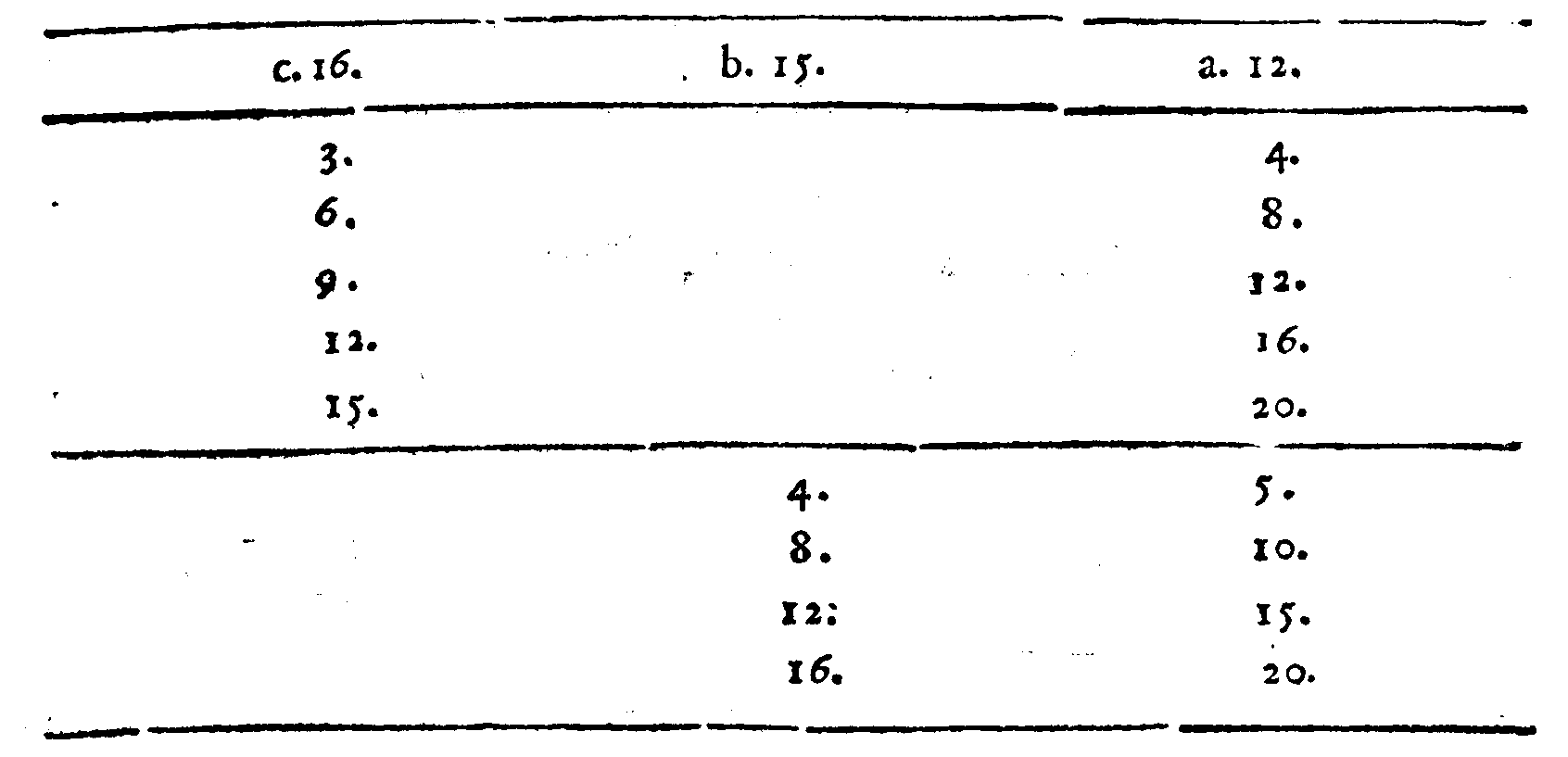
te; la onde, per la Duodecima proposta, tre c. sono equali à quattro a. sei, ad otto; no-
ue, à dodeci; dodeci à sedeci; & quindeci, à uenti. Oltra di questo; perche b. con a. è
Sesquiquarto; però b. contiene a. & una sua Quarta parte; onde auiene, per la detta
Duodecima, che quattro b. sono equali à cinque a. otto, à dieci; dodici, à quindeci;
& sedeci, à uenti. Ma Quindeci c. erano equali à uenti a. adunque sedici b. sono equali à
quindeci c. Per la Quartadecima adunque già nominata, il c. contiene il b. & una sua
Quintadecima parte; & c. per la Quinta definitione, è al b. Sesquiquintodecimo; come
ui douea dimostrare.
COROLLARIO.
quiterza & la Sesquiquarta proportione.
che quando à questo ultimo Interuallo si aggiungerà il primo; che 'l secondo
uerra ad esser integrato di tutta la sua proportione. Non ella cosi M. Gioseffo?
Cosi è senza fallo, gli risposi; onde uerrò ad un'altra proposta.
page 65
PROPOSTA XXIX.
uentesimoquarto.
mieramente faccio b. Sesquiquinto con esso a. dopoi faccio c. etiandio con esso
lui Sesquiquarto; & da a. c. cauo a. b. Sesquiquinto; onde resta da una parte l'in-
teruallo b. c. il quale dico essere Sesquiuentesimoquarto; dimostrandolo à co-
testo modo. Essendo a. Sesquiquarto al c. non è da dubitare, che a. contenga il c. & una
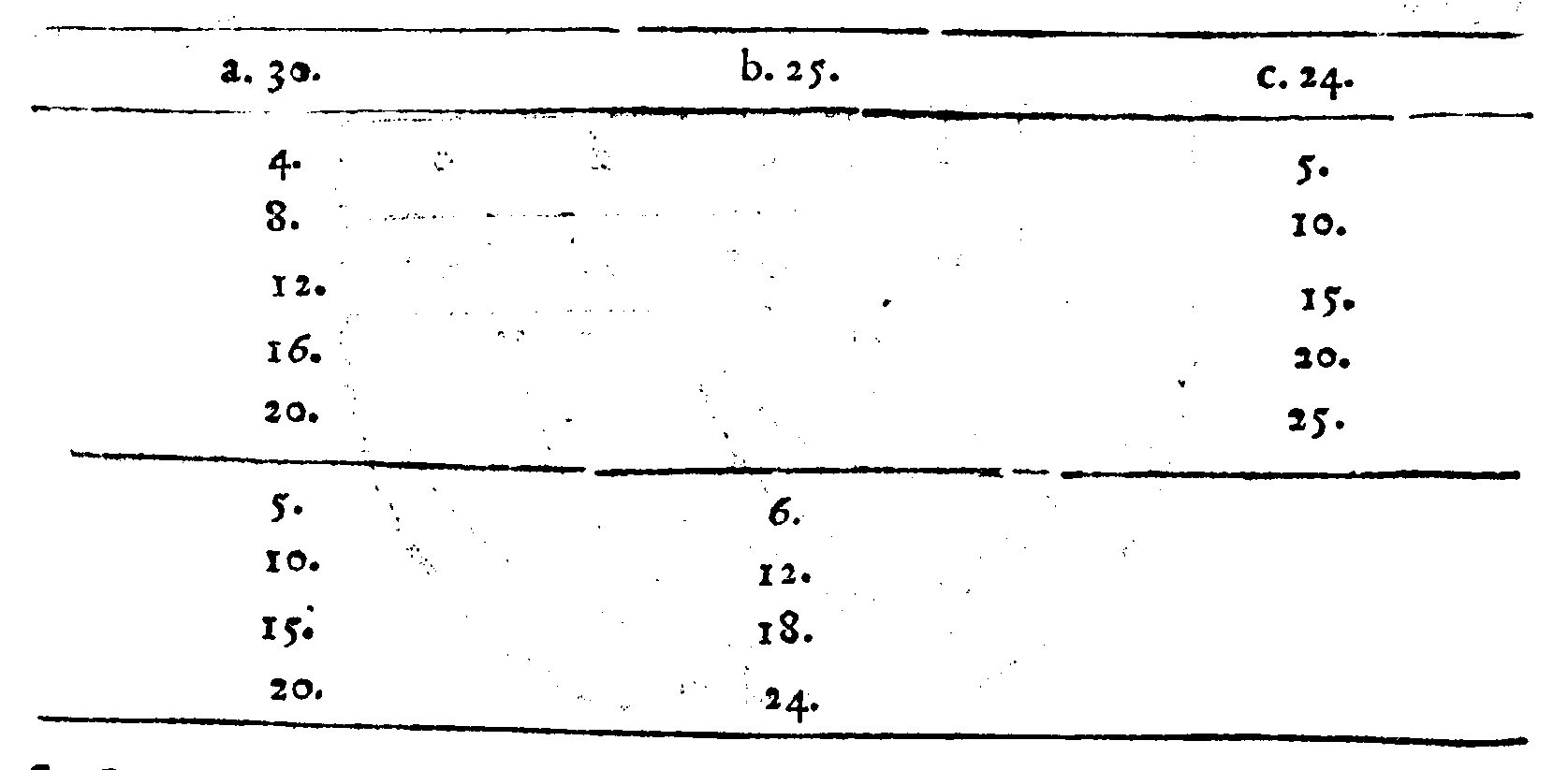
à quindeci; sedeci, à uenti; & uenti, à uenticinque. Et perche b. etiandio è Sesquiquin-
to di a. però a. contiene il b. & una sua Quinta parte. Onde nasce, che cinque a. sono e-
quali à sei b. dieci, à dodici; quindeci, à diciotto; & uenti, à uentiquattro. Ma perche
hò detto, uenti a. essere tanto quanto uenticinque c. però dico ancora, che uentiquattro
b. sono equali à uenticinque c. Et per la Quartadecima proposta simigliantemente dico,
che il b. contiene il c. una fiata & una sua Ventesimaquarta parte. Onde b. c. uengono à
contenere l'interuallo Sesquiuentesimoquarto; come ui douea, secondo quello, ch'io hò
proposto, dimostrare.
COROLLARIO.
to supera lo Sesquiquinto.
non cosi esposto da ogn'uno del dimostrare, disse; O' quanto sono chiare que-
este dimostrationi; onde chi uolesse opponersi, per mia opinione, haurebbe gran
demente del pazzo. Veramente, che cosi sarebbe, gli risposi; ma ueniamo pur'ad un'
altra proposta.
page 66
PROPOSTA XXX.
si voglia de i tre minori; quel che nascerà, sarà etiandio Superparticolare.
a. e. Sesquialtero, a. d. Sesquiterzo, a. c. Sesquiquarto, & a. b. Sesquiquinto;
assegnati, per la Ventesima quinta, al termine a. Et siano a. e. a. d. & a. c. i tre
maggiori; & a. d. a. c. & a. b. i tre minori. Dico, sel si leuarà un de questi, sia qual si
voglia, da uno de i tre primi; che quello che uscirà, sarà simigliantemēte Superparticola
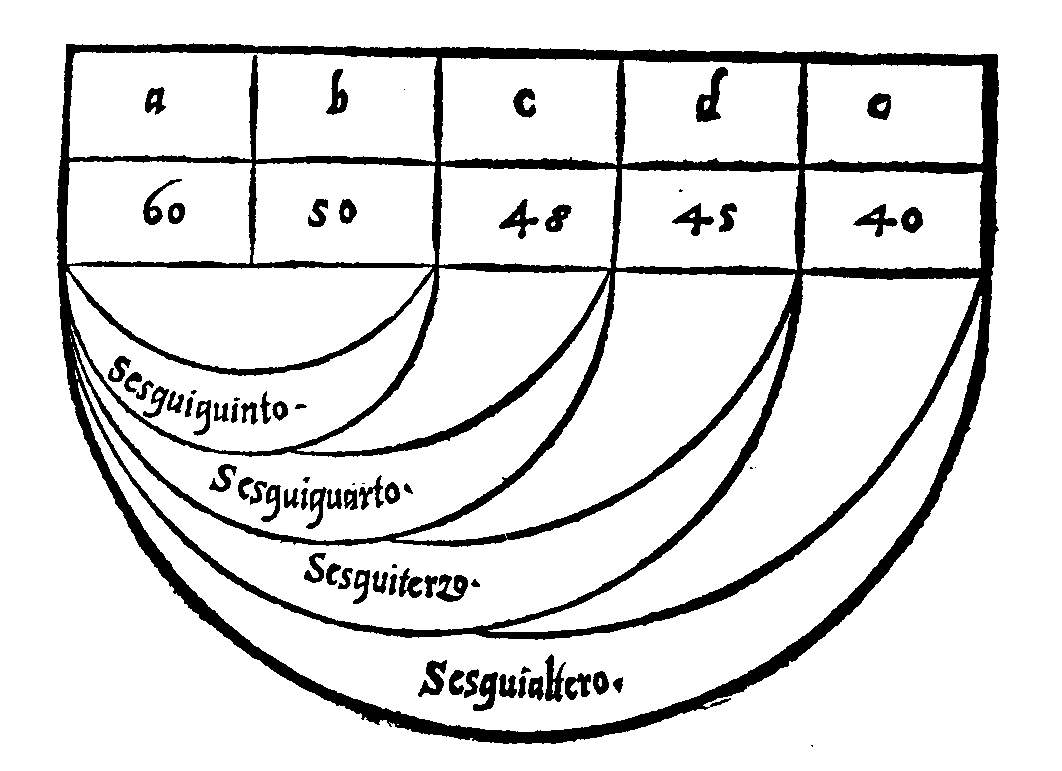
esser Massimi superparticolari; & per l'Ottaua dignità; l'interuallo Sesquialtero è mag-
gior del Sesquiterzo; percioche anco il suo Denominatore è maggiore. Se noi adunque
dall'interuallo Sesquialtero a. & e. il quale è il primo & maggior de i tre maggiori de i su
detti quattro Superparticolari, leuaremo il Sesquiterzo a. & d. che è il primo & maggio-
re di ciascheduno de i tre minori; resterà d. & e. il quale dico, per la Ventesimasesta pro-
posta, esser Sesquiottauo. Et perche d. contiene e. una fiata & una sua parte Aliquota; pe
rò, per la Quinta definitione, d. & e. uiene ad esser'interuallo Superparticolare. Hora se
da a. & e. Sesquialtero leuaremo a. & c. Sesquiquarto, ilquale è il secondo de i minori; per
il Corollario della Ventesima proposta; resterà c. & e. Sesquiquinto. Et perche c. cōtiene
e. una fiata, & una sua Quinta parte; però, per la istessa Quinta definitione, c. & e. uiene ad
esser collocato tra i Superparticolari. Ma se da a. & e. di nuouo cauaremo a. & b. Sesqui
quinto, ultimo Interuallo de i minori; per l'istesso Corollario, ne uerrà b. & e. Sesqui-
quarto, il quale medesimamente, per la Suppositione, è Superparticolare. Et que-
sto sia detto intorno quello, che si può dire del Primo interuallo de i tre maggiori. Ma
uenendo al Secondo dico; essendo a. & d. Sesquiterzo; se da lui cauaremo a. & c. Ses-
quiquarto; quel che uerrà, per la Ventesimaottaua, sarà c. & d. Sesquiquintodecimo.
Et perche c. contiene il d. & una sua Quintadecima parte; però, per la sudetta Definitio-
ne, c. d. è interuallo Superparticolare. Ma se di nuouo da a. & d. Sesquiterzo cauaremo
a. & b. Sesquiquinto; ne uerrà, per la Ventesimasettima, un Sesquinono; il quale dico es-
ser'interuallo Superparticolare; percioche d. contiene una fiata il b. & una sua Nona par
te. Vltimamente; se da a. c. Sesquiquarto leuaremo a. b. Sesquiquinto; per la Precedēte,
page 67 ne uerrà b. c. Sesquiuentesimoquarto. Et perche b. contiene il c. intieramente una fiata &
una sua Ventesimaquarta parte, chiamata Aliquota; però b. c. per la detta Quinta defi-
nitione, uiene connumerato tra gli interualli Superparticolari. Adunque; Se da uno de
i tre maggiori de i quattro primi interualli Superparticolari, si leuerà qual si uoglia de i
tre minori; quel che uerrà, sarà etiandio Superparticolare. Et questo è tutto quello, che
secondo la proposta ui douea dimostrare. A questo M. Adriano tutto allegro disse; Que-
sta dimostratione mi è molto piaciuto, perche hà dell'ingegnoso; però seguitate pur'un'al
tra; che queste cose non mi lasciano sentir dolore alcuno. Mi piace Messere, dissi; che que
sti Ragionamenti seruino per medicina al uostro male; però molto uolentieri uoglio se-
guitare, & dimostrarui; che,
PROPOSTA XXXI.
tesimo.
no, & a. c. Sesquiottauo. Leuo da a. c. l'interuallo a. b. onde ne resta b; c. il quale
dico infallibilmente esser Sesquiottantesimo; percioche, essendo a. c. Sesquiotta
uo; a. contiene il c. una fiata & la sua Ottaua parte; Onde per la Duodecima di questo, Ot

andar'in lungo) Ottantauno c. sono equali à Settantadue a. Di nuouo dico; perche a. è
Sesquinono di b. contiene a. il b. una fiata, & la sua Nona parte. Onde auiene, per la sudet
ta Duodecima, che Noue a. sono equali à dieci b. Diciotto, à uenti; & cosi (ascendendo
con l'istessa progressione, & con l'istess'ordine) Settantadue a. saranno equali ad Ottanta
b. Ma habbiamo già detto, che Settantadue a. sono equali ad Ottantauno c. adunque
Ottantauno c. sono tanto, quanto Ottanta b. Il b. adunque contiene il c. una fiata & la sua
Ottantesima parte. Et b. c. come ui douea dimostrare, è interuallo Sesquiottantesimo;
secondo che si è proposto.
page 68
COROLLARIO.
troua tra 'l Sesquiottauo & il Sesquinono interuallo.
tione, laquale sarà la sequente.
PROPOSTA XXXII.
zerà sarà Supertripartientecentesimouentesimoquinto.
b. Sesquiuentesimoquarto, & c. Sesquiquintodecimo. Dico, che cauando b.
a. interuallo Sesquiuentesimoquarto da c. a. Sesquiquintodecimo, ne rimane-
rà c. b. il quale è Supertripartiente 125. Imperoche c. contiene a. & una sua
Quintadecima parte; onde, per la Duodecima proposta, Quindeci c. sono equali à sede ci a. Trenta, à trentadue; Quarantacinque, à quarantaotto; & cosi ultimamente, accre
scendo secondo l'Arithmetica progressione, Trecento settantacinque c. saranno equali
à Quattrocento a. Et perche b. a. è Sesquiuentesimoquarto; però b. contiene a. & una sua
Ventesimaquarta parte; onde nasce, per la sudetta Proposta, che Ventiquattro b. sono e-
quali à uinticinque a. Quarantaotto, à cinquanta; & cosi per Arithmetica progressione,
per non andar più di lungo; Trecento ottantaquattro b. sono equali à Quattrocento a.
Ma habbiamo già detto, che Trecentosettantacinque c. sono equali à Quattrocento a.
adunque Trecentoottantaquattro b. sono equali à Trecentosettantacinque c. Et per la
Quartadecima proposta, dico; che 'l c. contiene il b. una fiata & tre centesimeuentesime

al b. Ilche si può facilmente scorgere da i termini radicali di c. & b. i quali sono d. & e. ac
quistati dalla diuisione del Ternario, secondo 'l modo mostrato nel Cap. 43. della Prima
parte delle Istitutioni, ne i termini c. b. a. onde nasce d. e. f. che sono Numeri Contrase-
primi; & per la Nona Definitione, Radice delle proportioni c. b. a. Il perche; Se dall'
interuallo Sesquiquintodecimo si leuerà il Sesquiuentesimoquarto, quel che uerrà, sarà
Supertripartiente centesimouentesimoquinto; Come ui douea dimostrare.
COROLLARIO.
za, che si troua tra lo Sesquiquintodecimo, & lo Sesquiuentesimoquarto; Et che l'inter
uallo Sesquiquintodecimo è reintegrato dal Sesquiuentesimoquarto & dal Supertripar-
tiente centesimouentesimoquinto; come da sue parti.
hormai son stanco per il molto ragionare; ma di gratia non ui rincresca l'ascol-
tarmi ancora un poco; Percioche desidero di finir di dimostrarui alcune cose, per non
hauer poi al nostro ritorno da far'altro, che dar principio à quello, ch'è il nostro princi-
pale intendimento, applicando tutte queste dimostrationi fatte fin'hora, & quelle poche,
ch'io son per dimostrarui, alle Consonanze & à tutti quelli Interualli, che sono nella Mu-
sica; essendo che queste sono come fondamento de quelle cose, che ui son per dire. Io
non desidero altro, disse il Sig. Desiderio; se non di udirui ragionare; perche mi pare,
che queste hore siano ben spese; & uoi credete, che m'habbia da rincresciere? seguitate
pur quel che ui piace, che tutti noi ui ascoltiamo uolentieri; perche in uero tutta la fati-
ca è uostra. Questa non mi è fatica, risposi; anzi piacere: la onde poi che non ui rincre-
sce, Seguiterò à dar fin'à quello, che dir ui uolea; il perche dico; che,
PROPOSTA XXXIII.
tinua di qual si voglia Interuallo, aggiunto alla seconda, produce la prima.
glio dire; per farui capaci di questa cosa cō un particolar'essempio; che se da una
Terza parte di qual si uoglia Interuallo, leuarete la Quarta, che l'è minore & continua,
ò uogliate dir' uicina; quel che uerrà, che sarà il restante; aggiunto alla Quarta parte fa-
rà medesimamente la Terza. Et che questo sia uero, lo uederete prima in prattica; dopoi
ve lo dimostrerò, acciò lo sapiate, come saper si debbe. Quando adunque uorrete ca-
uare 1/4 di 1/3; che sono parti propinque l'una all'altra; prima molteplicarete cambieuol-
mente il Numerator dell'una co 'l Denominator dell'altra; ilche fatto, uerrà 3. & 4. che
saranno i Numeratori delle due parti, che nasceranno, simili alle parti proposte. Dopoi
molteplicarete i Denominatori delle proposte parti insieme, & ne uerrà 12. ilquale sarà
il Denominator de i detti due Numeratori; Percioche altro non è quel ch'io hò operato
fin'hora, che un ridur molte parti de diuersi Denominatori, sotto un solo. Onde da co-
page 70
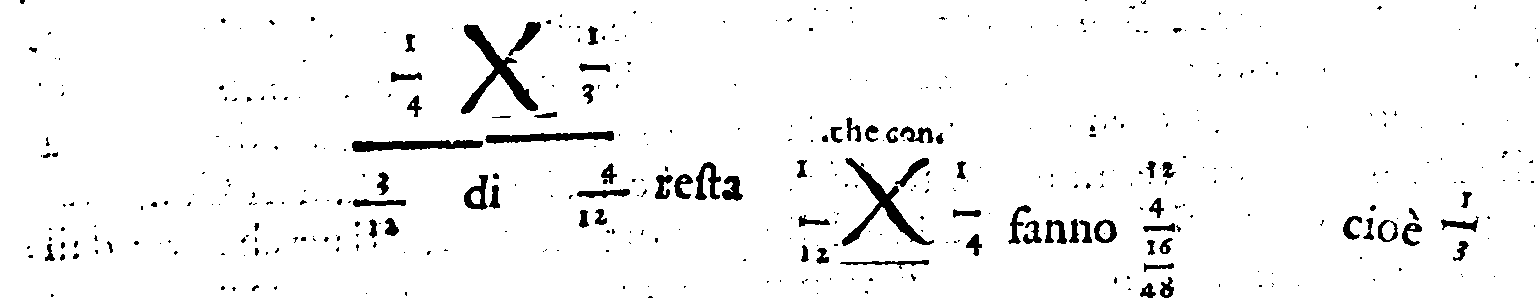
do à 1/3. Fatto questo, cauareteli 3/12 de i 4/12, & ne uerrà senza fallo1/12; il quale s'aggiun
gerete à 1/4, hauerete 1/3. Il che ui uerrà fatto, quando molteplicherete i Numeratori di
1/12 & di 1/4 scambieuolmente, per i Denominatori; sommando insieme i prodotti, &
molteplicando etiandio l'un per l'altro i Denominatori; ponendo il prodotto di questi
sotto una linea, & quello di quelli sopra; come uedete nell'essempio, che ui hò formato,
accioche piu facilmente m'haueste da intendere. Hora potrete dire, che cauato 1/4 di 1/3,
ne uiene 1/12; il quale aggiunto ad 1/4 rende di punto 1/3. Et questo si fà manifesto con la
Dimostratione, per tal modo. Se Tre terze parti d'un Interuallo fanno tutto l'Interual-
lo intiero, il che fanno etiandio Quattro quarte parti, ò Dodici duodecime parti; Tre
terze parti, & parti, simigliantemente Dodici duodecime parti sono
traloro equali. Onde auiene, che 2/4 sono equali à 6/12, & 1/4 à 1/12 & 2/3 sono anco equali à
1/12, & 1/3 à 4/12. Imperoche, per la Duodecima dignità; De quelle cose, delle quali i Tut
ti sono equali, equali etiandio sono le Metà loro. Ma 4/12 sono 1/3; adunque sono una Ter
za parte di tutto l'Interuallo, al quale Dodici duodecime sono equali, & con esso sono
una cosa istessa. Però adunque 1/4 minor parte di tutto l'Interuallo, ch'è equale (come
è mostrato) à 3/12, & 1/12 aggiunto ad 1/4, restituiscono 1/3; il quale è la parte maggiore
di esso Interuallo. Sono adunque l/4 & 1/12 equali ad un Terzo; come ui hò mostrato. On
de il restante d'una parte maggiore di qual si uoglia Interuallo, dalla quale sia cauata una
minore à lei piu uicina, ò continua, aggiunto alla seconda, produce la prima. Et que-
sto è quello, che secondo la proposta, dimostrarui douea. Et ancora che questa dimostra
tione sia ristretta in un particolare; tuttauia si uerifica uniuersalmente in due qualunque
si uogliano parte propinque & nell'Vniuersale, come sono una Quarta & Quinta parte;
perche aggiunto una Ventesima alla Quinta parte, uiene una Quarta intera. Simiglian
temente aggiunta una Sesta parte & una Trentesima, ne nasce una Quinta; il che si po-
trebbe anco dir dell'altre, le quali lascio per breuità. Il Merulo; hauendo io dato fine à
questa dimostratione; allora disse; Questo intendo hora benissimo, & ui ringratio della
fattica, c'hauete fatto à mia istantia. Al quale soggiunsi; Accioche uediate à che pro-
posito habbia introdotta questa proposta, hora lo mostrerò, & dirò in questa maniera.
PROPOSTA XXXIIII.
quarto.
ma proposta di questo, molteplicati; di modo che a. b. sia il primo, & b c. il secondo,
a i quali (per più facilità) corrispōdino l. k. h. ancora per la Decimasesta, due inter
ualli Sesquiottaui moltiplicati tra i Numeri cōposti; cioè h. ad. a. k. al b. & l. al c. Et sia anco
a. & d. interuallo Sesqui 3. & a. cōe. Sesqui 4. Dico a. c. esser minor'Interuallo di a. d. & mag
page 71

no equali à noue b. Simigliantemente, perche b. è Sesquiottauo al c. per l'istessa Duode-
cima, Otto b. fanno tanto, quanto noue c. Ma essendo (per la 14. proposta) un de i b. equa
le ad un de i c. & ad una sua Ottaua parte; 9. b. uengono equali à 10. c. & ad una Ottaua
parte, d'esso c Habbiamo però detto, 9. b. esser'equali ad 8. a. adunque 8. a. sono equali
à 10. e. & ad 1/8 parte. Ma 10. & 1/8 contengono 8. una fiata & 17/64. che sono una sua Quar
ta parte con 1/64. adunque per l'istessa Quartadecima proposta, uno a. contiene un c. & una
sua Quarta parte con 1/64. Et una Quarta parte con 1/64 sono il Denominatore dell'Inter-
uallo de due Tuoni molteplicati; & per l'Ottaua Dignità; minor di 1/3 parte, ch'è il De-
nominatore del Sesquiterzo, & maggior di 1/4. ch'è Denominatore del Sesquiquarto. Im
peroche, come anco particolarmente dimostrai nella Precedente 1/4 & 1/12. fanno una
Terza parte, ch'è maggiore, per l'istessa Nona Dignità, che non è 1/4 & 1/64 come questa
è maggior della Quarta parte; percioche la supera per 1/64. La onde, perche 10. & 1/8
parte, con 8. per la Sestadecima proposta, sono due Sesquiottaui insieme moltiplicati
tra i Numeri composti; però potiamo concludere, che due Sesquiottaui sono minori d'
un Sesquiterzo, & maggior d'un Sesquiquarto interuallo; come bisognaua dimostrare.
Questo non si può negare, disse M. Adriano. Ne questo anco, soggiunsi io, si potrà nega
re; cioè, che,
PROPOSTA XXXV.
ti, per la Prima di questo; di modo che a. b. sia il primo, b. c. il secondo, & c.d. il
terzo. Et siano anco h. k. l. m. tre Sesquiottaui per la Decima sesta, moltiplicati
tra i Numeri composti, di modo che 'l maggior de questi corrispondi al minor de i primi;
& per ordine, il minore al maggiore. Dico primieramente a d. esser maggior d'un inter-
uallo Sesquiterzo; percioche essendo a. b. & b. c. due Sesquiottaui, per la Precedente;
per la Duodecima 8. a. sono tanto quanto 10. c. & 1/8 parte. Ma c. anco è Sesquiottauo al
d. per la detta Duodecima adunque; 8. c. sono equali à 9. d. & 9. c. sono equali à 10. d.
& 1/8 sua parte; & anco 10. c. & 1/8 numero composto è equali ad 11. d. & 25/64 pur compo
sto. Ma poi che 8/8 di c. contengono 9/8 di d. adunque, per la Quartadecima proposta, 1/8 di
c. contiene 1/8 di d. & la sua Ottaua parte, ch'è 1/64. Adunque 10. c. & 1/8 sono equali à 11.
d. & 25/64, che sono 3/8 & 1/64. & per la Decimaquarta nominata; si come 11. 3/8 & 1/64 sono
in proportione ad 8. cosi si troua esser'a. con il d. Ma 11. contiene una fiata 8. con 3/8 & 1/64.
Et queste parti col resto, che sono Denominatori dell'Interuallo, che fāno i quattro Tuo
ni proposti; per la Nona dignità, sono più della Terza parte del Denominator loro Adūꝗ
necessariamēte seguita; che 3/8 con 1/64 siano più della sudetta Terza parte. Imperoche 11.
page 72 & 3/8 di uno & 1/64 contengono gli Ottaui una fiata & più della Terza parte loro. Onde
seguita, che a. contien d. & più d'una sua terza parte. Et perche a. con d. ouer h. cō m. per
la Decimasesta proposta, sono tre Sesquiottaui insieme aggiunti; però tre Sesquiottaui
sono più d'un Sesquiterzo interuallo. Secondariamente dico a.d. esser minore del Sesqui
altero; essendoche 11. contiene 8. & i suoi 3/8; adunque manca 1/8 al compimento di
4/8, i quali sono la metà de i Otto; che è il Denominatore dell'interuallo Sesquialtero. Ma
quelle parti, che superano, sono i 3/8 di 1/8 & 1/64, & fanno meno della metà di 1/8; ilche
anco minormente faranno. 1/8. Adunque 11. & 3/8 & 1/64 di uno contengono 8. una fia
ta & meno che la metà di 8/8 parti. Adunque, per la Quartadecima nominata, a. con-

Sesquialtero. Et questo è tutto quello, che in tal proposta bisognaua dimostrare. Que-
sta è stata una lunga diceria, disse il Viola; & bisogna che tanto colui, che ascolta, quan-
to quel che dimostra, stia in ceruello; altramente le cose non passariano troppo bene. In
fatto, rispose M. Adriano; il commemorar tante parti contante minutie, fanno un gran
garbuglio à quelli, che non hanno molta prattica de i Numeri. Soggiunse à questo il
Sig. Desiderio; Veramente, che colui, ilquale non hà prattica delle cose dell'Arithme-
tica, non può ben intender le cose della Musica. Et però non è da marauigliarsi, s'alcu-
ni de i uostri Musici; dico de i bassi d'ingegno & di grosso & ottuso intelletto, non la uo
gliono assaggiare; anzi la sprezzano; Et questo auiene per la lor dapocaggine. Ma biso
gna hauer patientia; però non perdiamo tempo intorno à costoro. Voglio adunque dis-
si; che uediamo; che,
PROPOSTA XXXVI.
gior, che quella di ciaschedun di loro da persè co 'l Termine mezano.
posti per ordine; dico che maggior'è la proportione, che si troua tra a. & c. ter-
mini estremi, che non è quella di b. mezano termine con a. oueramente con
c. Imperoche essendo, per la Quarta dimanda, la proportione de gli estremi a. & c. com-
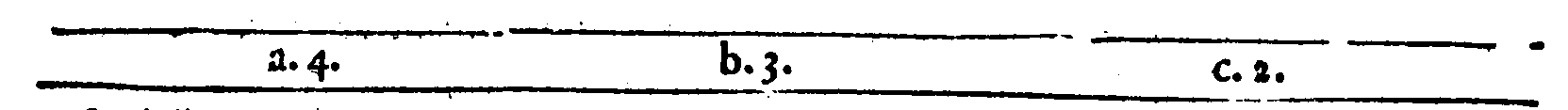
parti della a. c. & la a. c. è il Tutto. Ma perche, per l'Vltima dignità, Ogni tutto è mag-
page 73 gior della sua parte; però è maggior la proportione di a & c. che non è quella di a & b.
ouer di b & c. come dice la proposta. Et questo è quello, che dimostrarui uolea. Et
questa maniera d'argomento seruirà ad ogni proposta simile. Veramente, disse M Adria
no, ch'è bella, & anco; com'hauete detto, è facile molto; onde assai mi piace. Però se-
guitate 'l resto. Voglio che hora dimostriamo; soggiunsi; che
PROPOSTA XXXVII.
quattro Interualli insieme congiunti; & sia ab. il primo; bc. il secondo; cd. il
terzo: & de. il quarto. Et siano etiandio h. K. l. m. n. quattro Sesquiottaui,
per la Decimasesta proposta, insieme adunati; di modo che h. corrispondi ad a. K al b.
l al c. m al d. & n ad e. Dico hora, che l'Interuallo ae. si ritroua esser maggior dell'inter
uallo Sesquialtero. Imperoche, come hò dimostrato nella penultima. 10. a. sono tanto
quanto undeci d. & 25/64. Et Vndici d. & 25/64 sono equali à dodici e. & 417/512 Adunque Ot-
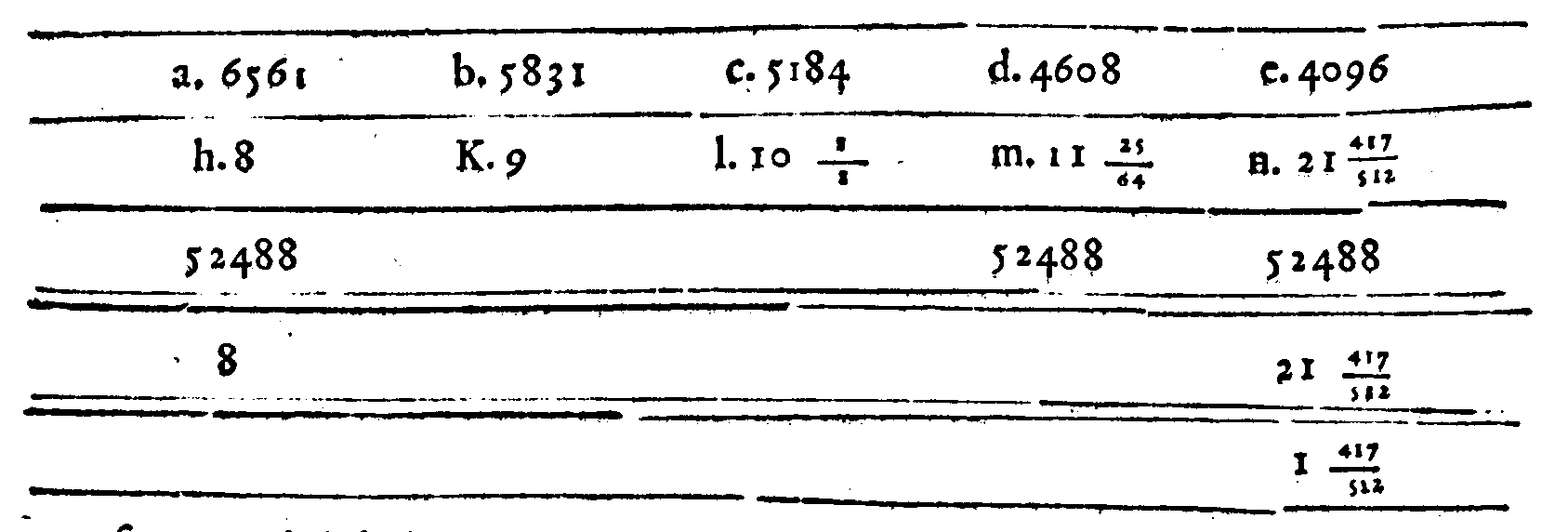
metà d'Otto ottaue parti; percioche 12. contengono 8. una fiata & la sua metà; Onde,
per la Definitione, sono in proportione Sesquialtera; ma il 12. oltra di questo contiene
la 417/52 parte di Vno; onde, per la Precedente, haurà maggior proportione 8. con 12
& 417/512 numero composto; che non haurà con 12. numero semplice. Onde, per la Quar
tadecima proposta, a. contiene e. una fiata & più della sua metà. Et essendo a & e. Inter
uallo congiunto de quattro sesquiottaui; quattro Sesquiottaui insieme adunati superano
l'Interuallo Sesquialtero; com'era il proposito di dimostrarui. Credo; disse allora M.
Claudio; che si potrà dimostrar, che cinque Sesqiuiottaui sono minori (come sono cer-
tamente) d'un interuallo Duplo. Questo si può anco dimostrar per questa strada; risposi;
ma io per schiuar la lunghezza, uedrò di tener altro mezo, di quel ch'io ho tenuto di
sopra. Et qual mezo sarà questo? disse M. Adriano; onde io risposi; Ascoltate prima la
Proposta, Messere; & dopoi udirete la dimostratione.
PROPOSTA XXXVIII.
mo già dimostrato nella Decimasettima proposta, che l'interuallo Duplo si fà di
due maggiori interualli Superparticolari, i quali sono Sesquialtero & Sesquiter-
zo. Ma per la Trentesima quinta proposta Tre interualli Sesquiottaui, sono minori d'un
Interuallo Sesquialtero; & due, per la Trentesima quarta, sono minori d'un'Interuallo
Sesquiterzo; adunque tutti insieme aggiunti sono minori d'un Interuallo Duplo; come
dice la Proposta. Io staua pur à ueder, disse M. Francesco; doue poteua uscir un'altro
modo differente dimostrati; ma mi hauete satisfatto benissimo; percioche è bello, fa-
cile, & breue. Et credo, che (come già dicesti) quanti sono i mezi, tante siano le Dimo
strationi; però, uorrei sapere, se questa ancora si potesse dimostrare in un'altro modo.
Si può ueramente, risposi, & in questa maniera. Siano a & f. gli estremi termini di cin-
que interualli Sesquiottaui, per la Prima di questo, adunati insieme; oueramente siano
h & o. medesimamente cinque Interualli Sesquiottaui molteplicati, per la Decimasesta,
tra numeri composti; di modo che h. corrispondi con a. & o. con f. Sia oltra di questo p.
il quale con a. contenga l'Interuallo Duplo. Dico, che a. & f. non fanno cotale Inter-
uallo; percioche, per la Trentesima sesta proposta, è maggior la proportione, che si tro-
ua tra a. & p. due estremi, che non è quella laquale si troua tra un'estremo & un mezano
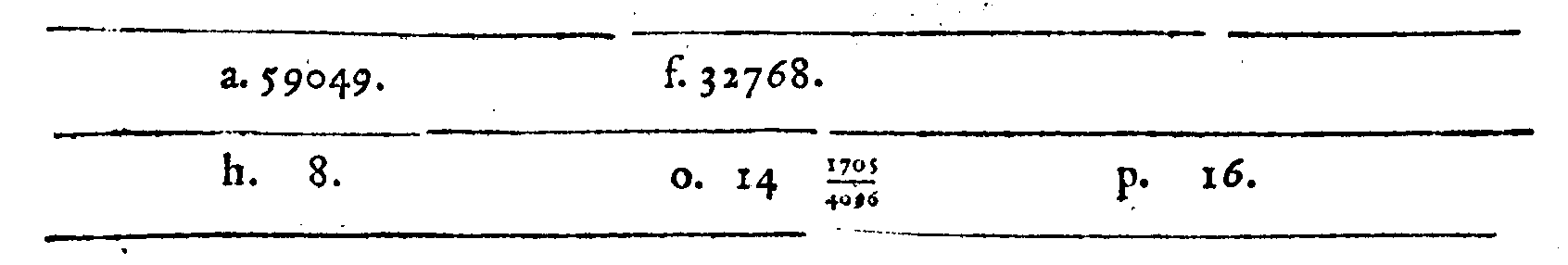
con p. l'Interuallo Duplo; seguita che cinque interualli Sesquiottaui posti insieme non
faciano quest'Interuallo, come douea dimostrare. Ancora ui uoglio dire; perche a &
f. sono cinque Interualli Sesquiottaui; & a. p. Duplo; essendo che a. contie-
ne f. solamente una fiata con 3/4 parti, & di più 1705/4096, le quali parti aggiunte insieme
non arriuano all'intero di esso p. ch'è il termine della Dupla; de qui nasce, che cinque
interualli Sesquiottaui aggiunti insieme non fanno un'interuallo Duplo; come dice la
Proposta. Ma per dar fine à questo ragionamento, ui dico; che
PROPOSTA XXXIX.
credo, che uogliate prouar questa proposta contra l'opinione d'Aristosseno, &
riprobar, che Sei tuoni (com'ei teneua) facessero una Diapason. Cosi è uera-
mente; dissi; ma ueniamo al proposito della proposta. Sia a & g. interuallo, che conten
ga Sei sesquiottaui congiunti; di modo che ab. sia il primo; bc. il secondo; cd. il Terzo;
de. il Quarto; ef. il Quinto; & fg. il Sesto. Et siano anco h. K. l. m. n. o. p. simiglian-
temente Sei sesquiottaui interualli, molteplicati, per la Sesta decima, tra Numeri com
posti; & accommodati di maniera, che h. corrispondi ad a. per ordine, & p. al g. Dico
che ag. è maggior d'uno interuallo Duplo. Et perche ab. è Sesquiottauo; però, per
la Duodecima proposta, 8. a. sono equali à 9. b. &, per l'istessa, sono equali à 10. c. &
1/8 Et per la Trentesima quarta, 10. c. & 1/8 sono equali ad 11. d. & 25/64. Et, per la
Trentesimaquinta, 11. d. con 25/64. sono equali à 12. e. & 417/512. Simigliantemente 12.
page 75 e. col resto sono equali à 14. f. & 1705/4096; & tutta questa somma è equale à 16. g. & 7153/32768. On-
de 16. con 7153/32768 contengono 8. due fiate & anco più; di modo che per la Quartadeci-
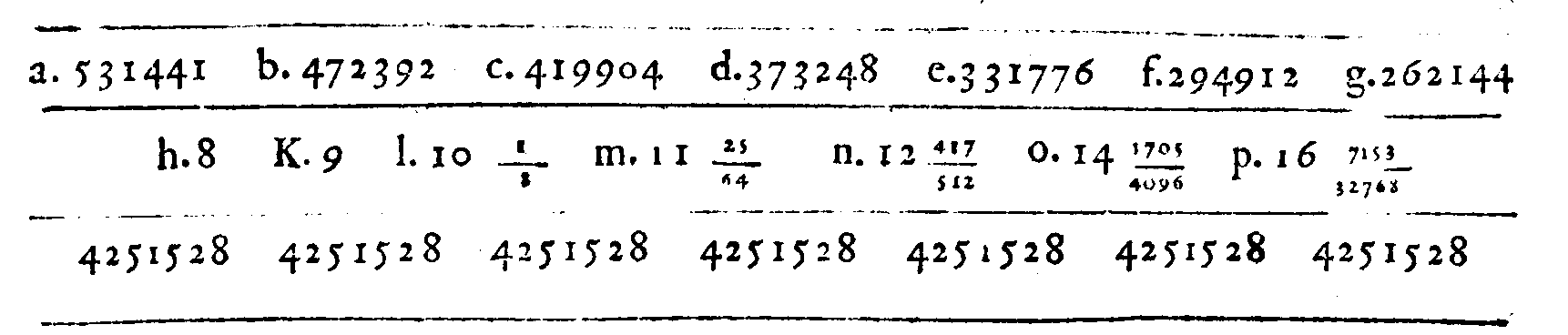
Sei Sesquiottaui adunque congiunti insieme sono maggiori d'un'interuallo Duplo; com'
era 'l mio proposito di dimostrarui. Et qui cō la uostra buona gratia uoglio far fine per hog
gi di ragionar più alcuna cosa della Musica; percioche hormai son stanco. Hauete mol-
to ben ragione; disse M. Adriano; & credo che sia cosi; Ma queste ultime dimostratio-
ni mi paiono molto difficili da mandare alla memoria, & che habbiano dibisogno di mol
to essercitio delle Mathematiche. Sono ueramente difficili Messere; dissi io; ma quan-
do si possederà bene la Duodecima proposta, & le due sequenti, allora il tutto parerà fa-
cile. Ma qui stà il peso della cosa; che uolendosi far patroni de queste Dimostrationi, bi
sogna affaticarsi & essercitarsi; non solamente nel porre insieme molte Proportioni d'un
solo genere; ma etiandio de gli altri; raccogliendo molte parti insieme, & diuidendo l'una
per l'altra, & facendo molt'altre cose simili; percioche cosi facendo, si uiene à far la pratti-
ca; onde nel dimostrar, non lasciano parer le cose tanto strane. Ma non più di questo;
di gratia; perch'io credo, che ancor uoi hormai tanto sete stanchi di ascoltarmi, quant'
io di ragionare. Può ben essere, disse M. Francesco; che siamo stanchi, ma non già sa-
tij; essendoche troppo diletteuole & troppo utile è l'imparare. Diciamo pur quello ch'è
ueramente; soggiunse M. Claudio; l'hora è tarda, & il tempo non ci concede, ch'andia
mo più oltra. Quanto poi alla stanchezza, non credo ch'alcun di noi si possa chiamar
stanco; essendo stata la fatica tutta di M. Gioseffo. Questo è pur troppo uero; aggiunse
M. Adriano; ma ui prego à farmi questo fauore, di ritornar dimane all'hora, che sete
uenuti hoggidì à uedermi; poi ch'io non mi posso partire, come uedete; perche se mi
fusse concesso, uerrei à ritrouar uoi. Et questo dico; accioche potiamo udire il fine di
questa cosa, & non lasciamo l'incominciata opera imperfetta. Cosi faremo Messere dis-
si; rimaneteui adunque in pace. La onde M. Adriano soggiungendo; Andate tutti ch'Id
dio u'accompagni; tutti noi partissemo insieme, & ciascuno andò per diuerse strade al
suo alloggiamento.
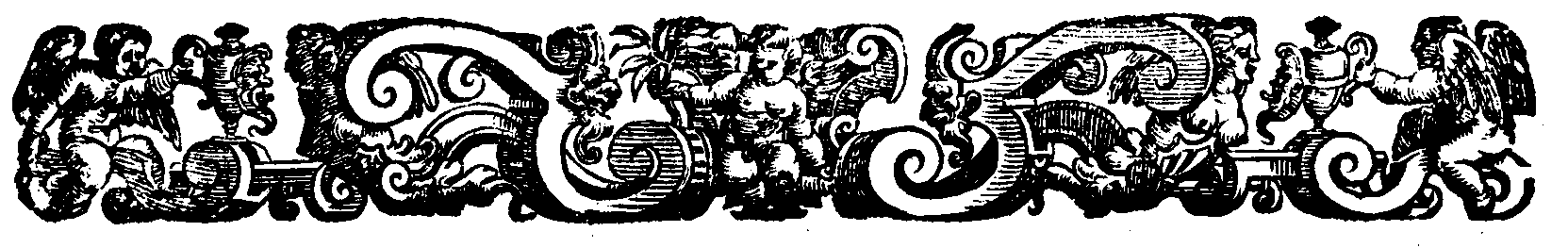
DIMOSTRATIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
RAGIONAMENTO SECONDO.
ritornassimo à casa di M. Adriano; per cagione di seguitare i nostri
diletteuoli & utili già incominciati ragionamenti. Onde hauendosi
prima discorso sopra diuierse cose, ragionate 'l giorno inanti; quan-
do mi parue tempo, con licentia de tutti, incominciai à parlare in
cotal guisa. Io conosco Signori miei da molti segni, & massima-
mente da questo; che inanzi l'hora costituita il giorno precedente
insieme ui sete adunati; che i nostri Ragionamenti passati ui siano piaciuti. Il che heri lo conobbi dalla patientia, c'haueste in ascoltarmi; però penso di dirui
hoggi cose, che maggiormente ui dilettaranno; percioche entraremo à ragionare un
poco più particolarmente della Musica; Essendo che 'l ragionamento hauuto heri fù in-
torno al dimostrarui molte cose de Numeri & Proportioni; Ma hoggi descenderemo à
dare una cognitione particolare de gli Interualli Musicali, & à dimostrarui in qual ma-
niera nascono i consonanti, & anco i dissonanti, i quali seruono alle compositioni delle
nostre Cantilene; & sarui conoscere, quanta differenza si troui tra quelli, che usauano
gli Antichi, i quali erano minori della Diatessaron, tenuti da loro per dissonanti, &
quelli che usiamo al presente. Onde potrete dopoi conoscere in quanto errore siano quel
li, ch'à i giorni nostri credono, & ostinatamente affermano, che tali Interualli da gli An-
tichi prohibiti entrino nel numero delle nostre Consonanze. Le quali cose spero dimo-
strar tanto facilmente, & tanto chiaramente, ch'ogn'un de uoi potrà restar satisfatto.
Et s'alcun de uoi hebbe mai contraria, da quel che son per dirui & dimostrar-
ui; son certo che si ridurrà à creder quello, ch'è uero, & che in fatto non può esser altra-
mente; & si leuarà dal credere il falso. Qui incominciò il Viola à dire; Fin hora si può
troppo ben conoscer l'errore de questi tali, quando si hà inteso quel c'hauete scritto nelle
Istitutioni; percioche tanto manifesto appare, che non hà dibisogno d'altre dimostratio
ni. Alle quali parole, uoltatosi M. Claudio uerso M. Adriano, soggiunse; Che direte
uoi di questo Messere; ch'alcuni, forse per parer d'intender meglio di ciaschedun'altro
le cose della Musica; quando odono dire, che noi adoperiamo il Semituono maggiore
nelle nostre compositioni, & non il minore; simigliantemente, quando odono far la dif-
ferenza di Tuono maggiore & di minore; mostrano di merauigliarsi di queste cose; il che
fanno ancora, quando odono dire, che i Modi, ò Tuoni arriuano al numero de Dodi-
ci; quasi, che non fussero uere, & che non fussero state dimostrate da M. Gioseffo otti-
page 77 mamente; & che la cosa non fusse tanto chiara, ch'ogn'un di mediocre intelletto potesse
esser capace; ma consistesse più presto in opinione, che in altro. Non ui fate marauiglia
disse M. Adriano; di questo perche si trouano etiandio alcuni, i quali se ben non si posso-
no numerar tra gli ignoranti; almeno si possono porre tra i Maligni; che quando cono-
scono, ch'una cosa sia per apportar qualche utile & qualche honore ad alcuno per scie-
mar le laudi che gli conuengono; da una certa loro passione uinti; più tosto uogliono con
lor biasimo & contra la conscienza loro occultar'il uero & contrastare; che affirmar quel-
lo, che sentono nell'animo non esser falso. Questa è una mala razza d'huomini Messere,
disse il Viola; Ma che direte de quegli altri, che non potendo apertamente biasimare il
buono; perche uedono, che in fatto non gli riuscirebbe il lor pensiero; cercano d'offus-
care in qualche parte la gloria di coloro, che per qualche buona opera fatta, la merita-
no; col lodarli frigidamente insieme con l'operationi loro; ch'è peggio assai; come so-
leua dir Fauorino appresso Aulo Gellio;Lib. 19.
Cap. 3. che s'apertamente le biasimassino; oueramen-
te almeno col lodare estremamente l'opere di qualchedun'altro; quantunque conosca-
no, che non meritano laude; & tutto fanno à fine d'abbassarli, se ben si ritrouano esser
presenti. Ancora, s'altro non sanno fare, lodano almeno tanto gli Antichi, quantunque
non habbiano cognitione delle cose loro; che con ogni lor potere cercano di leuar quel
poco di riputatione, che i Moderni s'hanno delle buone opere loro fatto acquisto. A co
storo si conuiene soggiunse M. Adriano; quel bel detto d'Horatio, il qual torna benissimo
à questo proposito de cotali Huomini rabiosi, inuidi, ignoranti & maligni; quando dice:Epistol. lib.
2. pist. 1.
Iam saliare Numae carmen, qui laudat, & illud,
Quod mecum ignorat, solus uult scire uideri.
Ingenijs non ille famet, plauditꝗ sepultis:
Nostra sed impugnat; nos, nostraꝗ liuidus odit.
Veramente Messere, che uoi sete un buon scolare; dissi; perche ui hauete tenuto
molto bene à memoria la lettione, ch'io già ui lessi sopra questi Versi; à proposito de
quei maligni, che cantando una fiata le uostre compositioni, le biasimauano molto; lo-
dando fuor d'ogni proposito grandemente quelle di Giosquino con parole; ma con i fat
ti, al lor dispetto lodauano uoi, & ueniuano à biasimare il lodato; percioche ne i con-
serti loro non adoperauano cosa alcuna di Giosquino, ne d'alcuna sua cosa se ne serui-
uano, ma si ben delle uostre; il che ui è di somma laude. Onde ui dico, che questo Ho-
ratio è stato & è un gran Poeta. Vedete, com'egli ci pone auanti gli occhi questa mala
generatione d'huomini dipingendoci la lor natura; perch'ancora lui à i suoi tempi da
simil Gente inuida, maligna, & peruersa era bersagliato. Ma di gratia non parliamo
più cosa alcuna di costoro; percioche non uoglio c'habbiamo da far con loro; & desi-
dero, che ritorniamo à ragionar di quelle cose, delle quali heri incominciassemo il nostro
ragionamento. Sarà ben fatto M. Gioseffo; disse il Signor Desiderio; & incominciarete
da quello che ui torna più commodo. Ripigliai adunque il mio ragionamento in questo
modo. Hauendoui à ragionar de quelle cose, che fanno alla cognitione delle Con-
sonanze, & anco delle Dissonanze, & à dimostraruene molte, che accascano intorno
ad esse, secondo la uerità, & come la Scienza richiede; è necessario il porui prima inan
zi quei Principij, da i quali dipendono tutti i nostri Ragionamenti, & dichiararui quel
ch'importino alcuni termini, & il Nome d'alcuni Interualli usati nella Scienza; ancora
che della maggior parte de loro ne habbiate acquistato la cognitione, col mezo delle Isti
tutioni; accioche per auentura non procediamo per cose non conosciute. Et ciò non
sarà senza utilità; percioche non resterò di dichiararui alcune cose, & aprirui alcuni
secreti, che ui saranno di gran contentezza & giouamento. Et per non andar molto in
lungo, darò principio alla definitione della Consonanza; laquale (com'altroue hò det-
to) è primieramente dal Musico considerata; & dopoi dirò quel che sia la Dissonanza,
ch'è il suo Opposito, ò contrario; la qual'è considerata nel secondo luogo, & per acci-
dente. Ma auanti, che passiamo più oltra, ui uoglio fare un poco di discorso, che ui sarà
page 78 di grande utile, & forse non più udito in questo proposito; & tornerà bene, per poter ri-
soluere alcune cose, che ui son per dimostrare. Attendete adunque prima, & dopoi uer-
remo senza por tempo di mezo, à por le Definitioni l'una dopo l'altra. Dico adunque
incominciando, che la Oppositione, secondo 'l Filosofo,Prd. Trat.
3. cap. 1. si troua esser de Quattro ma-
niere; acciò sappiate per qual cagione hò detto, che la Dissonanza è opposita ò contra-
ria alla Consonanza; come è, Relatiua, Contraria, Priuatiua, & Contradittoria. Ma
perche la prima & le due ultime non fanno al nostro proposito; però le uoglio lasciar da
un canto, & dir solamente della Seconda; la quale non è altro, che la Ripugnanza de
due contrarij, che non conuengono insieme in un'istesso Soggetto; ma per lor natu-
ra l'un scaccia ò destrugge l'altro. Et questi Contrarij ono de due maniere; percioche
ouer che sono mediati, oueramente immediati. I primi sono quelli che riceuono alcu-
ni mezi ne i loro estremi; come tra 'l Nero & il Bianco molti mezani colori. Onde non è
necessario sempre, che l'un de i due estremi sia nel soggetto; percioche 'l Corpo può es-
ser Rosso, ò Verde, ò di qualch'altro colore; se ben non è Nero, ò Bianco. Ma i Secon
di sono quelli, che non riceuono cosa alcuna mezana dell'istesso Genere; com'è la Sani-
tà & la Infermità; tra lequali non ui si dà mezo alcuno, secondo i Filosofi; ancora che i
Medici habbiano altra opinione. Il Mezo però in questo luogo è di due sorti; prima per
Participatione dell'uno & dell'altro estremo, come sono i mezani Colori & Sapori; dopoi
per Negatione dell'uno & dell'altro de gli nominati estremi; & quando si troua un Sogget
to, il quale non habbia estremo alcuno. Onde da quel c'hò detto potete comprendere,
che essendo la Consonanza & la Dissonanza senz'alcun dubio Suono, uengono ad esser
Qualità passibili; percioche da l'una & da l'altra il Senso è mutato; la onde essendo à
questo modo; chiara cosa è, che si hanno à porre nel Predicamento della Qualità, & si
debbono collocar come due estremi nella Seconda specie de gli Oppositi; essendo che rice
uono molti mezi tra loro. Et questo è uero; percio che, si come il Corpo uisibile non è per
necessità sempre bianco, ò nero; ma tallora è rosso, tallora uerde, & tallora di qualch'altro
colore; ne anco il Tangibile, è sempre freddo, ò caldo; ò duro ò tenero; ma alle fiate te-
pido; & hora più & hora men caldo ò freddo; oueramente di qualch'altra mezana qua-
lità; come anco il Gustabile, che non è sempre per necessità dolce, ouer'amaro; ma gar-
bo, ò acerbo, oueramente in altro modo; cosi l'Vdibile non è sempre semplicemente
Consonante, ò Dissonante; ma alle fiate partecipa d'una qualità mezana, che tiene
dell'uno & dell'altro, più & meno, secondo che più s'auicina all'un de i nominati estre-
mi. Per il che non sò ueder, ne ritrouar ragione, che mi costringa à dire & credere;
che tra gli estremi Oggetti de gli altri Sensi possano cascar molti mezi, & non in quel-
li dell'Vdito. Però adunque diciamo, che tra la Consonanza, & la Dissonanza, che
sono due estremi nella Seconda specie de gli Oppositi; ui cascano; contra l'opinione de
molti; per non hauere di questa Aristotele fatto mentione alcuna; molti mezani inter
ualli, i quali partecipano (secondo che maggiormente saccostano più all'una, che al-
l'altra) de questi due estremi udibili. Et questi saranno quelli (lasciando di por qual-
ch'altra differenza tra loro, che si potrebbe fare) che nascono d'altra proportione, che
da alcuna de quelle, che sono contenute nel Genere Molteplice & Superparticolare,
collocate tra le parti del numero Senario. La onde diuideremo la Consonanza in due
specie; delle quali la prima chiamaremo Consonanza propriamente detta, & la secon-
da Consonanza detta Communemente. Le quali uolendo conoscere, incomincian-
do dalla prima; diremo.
DEFINITIONE
PRIMA.
page 79 la quale soauemente & uniformemente uiene all'Vdito; la cui forma è contenuta da
proportione Molteplice, ò Superparticolare, che si troua in atto tra le parti del primo
Numero perfetto; cioè, del Senario.
to nouo; essendoche non hò mai più inteso cosa alcuna di queste Qualità ò dette d'alcuno in uesto proposito; ne meno hò ritrouato cotal cosa ap
presso d'alcun'autore, ch'io habbia studiato; Onde mi piace molto questa noua distintio
ne, & di questo hauete una gran ragione. Et quando non diceste altro in tutto il Ragiona-
mento, c'habbiamo da fare insieme; questo pagherà ogni cosa. Che ne dite uoi di que-
sto Messere Adriano? Questa cosa (rispose egli) mi hà leuato molti dubij, ch'io hauea nel
capo; percioche nella prattica udiua tutte queste cose; ne sapea dir, come la cosa pote-
ua stare; ma hora son chiaro, ch'è quello, che detto ha M. Gioseffo; percioche spesse
fiate udimo nella Musica alcun'Interualli, che non si possono chiamar dissonanti, ne anco
li potiamo nominar semplicemente consonanti; Onde questa cosa assai assai mi è piaciu
ta; però M. Gioseffo seguitate à dirci quel che sia l'altra sorte di Consonanza; acciò sap
piamo conoscer l'una dall'altra, col mezo delle definitioni. Vedete Messere dissi, ch'
io ui dirò sempre qualche cosa di nouo; però ascoltate questa.
DEFINITIONE II.
quale, se ben non è interamente soaue all'Vdito, è però sopportabile; & la sua for-
ma à contenuta da altra proportione, che Molteplice, ò Superparticolare; la qual si
troua in atto tra le parti del Senario, & il primo Numero cubo.
chiaratione; percioche hauendoci proposto due maniere de Consonanze; fà bi-
sogno, che ce le dimostrate particolarmente. Cosi farò Messere, risposi, non du-
bitate: onde douete sapere, che la prima maniera è riceuuta da tutti per tale; ch'essen-
do i suoi Indiuidui &Interualli collocati ne i loro proprij & naturali luoghi; come heri fù
dichiarato; sono in tal modo grati all'Vdito; che nō si può desiderar cosa più perfetta. Ma
la seconda, contien quelli, che fanno un non sò che di poca poca offesa al senso; la qua-
le però è sopportabile. Onde i primi hanno le forme loro contenute in atto tra le parti
del Senario, che tra loro fanno le proportioni del genere Molteplice, ò Superparticola-
re; & i secondi le hanno contenute tra le proportioni de gli altri Generi; tra le nomina-
te parti & il primo numero Cubo, ch'è l'Ottonario. Et accioche meglio m'intendiate;
douete sapere, che tra le nominate Parti, & il detto numero Cubo; che sono 1. 2. 3. 4. 5.
6. 8. ui cadono Ventiuna relatione; Sei tra ciascheduno de gli altri numeri & l'Vnità;
Cinque tra i cinque numeri maggiori & il Binario; Quattro tra i quattro numeri mag-
giori & il Ternario; Tre tra i primi tre
maggiori & il Quaternario; Due tra i due
maggiori & il Quinario; & Vna tra il Se-
nario & l Ottonario. Delle quali, Vndici so
no Molteplici, Sei Superparticolari, Due Su
perpartienti, Vna Molteplice superpartico-
lare, & Vna Molteplice Superpartiente. On-
| 2. 1. | Diapason. |
| 3. 1. | Diapason diapente. |
| 4. 1. | Disdiapason. |
| 5. 1. | Disdiapason ditona. |
| 6. 1. | Disdiapason diapente. page 80 |
| 8. 1. | Trisdiapason. |
| 3. 2. | Diapente. |
| 4. 2. | Diapason. |
| 5. 2. | Diapason ditona. |
| 6. 2. | Diapason diapente. |
| 8. 2. | Disdiapason. |
| 4. 3. | Diatessaron. |
| 5. 3. | Hexachordo maggiore. |
| 6. 3. | Diapason. |
| 8. 3. | Diapason diatessaron. |
| 5. 4. | Ditona. |
| 6. 4. | Diapente. |
| 8. 4. | Diapason. |
| 6. 5. | Semiditono. |
| 8. 5. | Hexachordo minore. |
| 8. 6. | Diatessaron. |
le Sei superparticolari sono contenute tut-
te le forme delle Consonanze della Prima
maniera; & nelle due, con l'altra seguente,
si ritrouano le forme delle Consonanze del-
la Seconda; percioche tra 2. & 1, 4. & 2, 6.
& 3, 8. & 4, che sono tutte Duple, si troua
la forma della Diapason. Tra 3. & 1, 6. &
2, che sono Triple; si troua la forma della
Diapasondiapente. Tra 4. & 1, 8. & 2. che
sono Quadruple, si troua quella della Dis-
diapason. Tra 5. & 1, che fanno la Quin-
tupla, si troua la forma della Disdiapason-
ditono; tra 6. & 1, ch'è la Sestupla, si tro-
ua la forma della Disdiapason diapente; &
tra 8. & 1, che contiene l'Ottupla propor-
portione, si troua la forma della Trisdiapa-
son. Et queste sono tutte Molteplici. Simi
liantemente tra 3. & 2, & anco tra 6. & 4,
che sono Sesquialtere, si troua la Forma della Diapente; tra 4. & 3, ancora tra 8. & 6,
che sono Sesquiterze, quella della Diatessaron; & tra 5. & 4, che è Sesquiquarta, quel-
la del Ditono. Vltimamente tra 6. & 5, che è Sesquiquinta, è quella del Semiditono.
Et tutte queste proportioni sono Superparticolari. Onde queste con le Molteplici sono
contenute nella Prima schiera delle Consonanze, & hanno il loro essere in atto tra i nu-
meri; ò parti nominate. Ma quelle della Seconda, si trouano tra l'altre, percioche nel Su-
perpartiente tra 5. & 3, ch'è Superbipartiente terzo, si troua la forma dell'Hexachordo
maggiore; & tra 8. & 5, che è Supertripartientequinto; si troua quella del minore. Ma
nel Molteplice superparticolare tra 5. & 2, ui è la Dupla Sesquialtera; la quale è la for-
ma della Diapasonditona; & tra 8. & 3. nel Molteplice Superpartiente, ch'è la Dupla
superbipartiente terza, si troua la forma della Diapason diatessaron. M'hauete intera-
mente satisfatto; disse M. Adriano & mi piace grandemente questa noua distintione;
percioche mi par uedere, ch'ella habbia à portar grande utile, & d'accordar molte di-
scordie & liti, che già gran tempo sono tra i Musici; & non sono ancora finite. Cosi cre-
do, che sarà; risposi; ma acciò non perdiamo tempo, definirò la Dissonanza; la quale è
oppositamente contraria alla Consonanza propriamente detta; onde dirò.
DEFINITIONE III.
con l'altro mescolare, ouer vnire non si possono; & percuote l'Vdito aspramente, &
senz'alcun piacere; & nasce da proportioni differenti di denominatione da quelle,
che si trouano collocate in atto tra le parti del Senario, & l'Ottonario numero.
Cōsonanza; può anco intender quella della Dissonanza; se per caso non uoleste
far'alcuna distintione di essa; com'hauete fatto della Consonanza. Non uoglio;
disse M. Claudio; porre altra distintione al presente; ma uoglio dir solamente che secon
do la definitione del Filosofo,2. post. c. 2. il quale definisce, che la Consonanza è ragion de Nume
page 81 ri, che etiandio nella Dissonanza si troua una certa ragione de Numeri; onde aggiunsi;
Contenuta da proportioni differente de denominationi da quelle, che si trouano in atto
tra le parti del Senario & dell'Ottonario numero, collocate; accioche conosciate, che
la Dissonanza sia al tutto priua della Ragione de quei Numeri, che intende il Filosofo;
& anco quel ch'io hò dichiarato altroue in questo proposito.Istitut. 2.
par. c. 11.
& 3. par.
cap. 5. Vi uoleua apunto dire;
disse M. Adriano; S'ogni Consonanza & ogni Interuallo Musicale rationale è contenu-
to sotto una determinata proportione di numero à numero; come più fiate ui hò udito
dire; come potea stare, che solamente la Consonanza fusse Ragione de Numeri, &
non la Dissonanza? Non si può negare (dissi) Messere, che la Dissonanza, essendo conte-
nuta da proportione rationale di numero à numero; habbia Ragione de Numeri; essendo
che quella Ragione si considera, & si scorge in quanto 'l maggior termine contiene lo mi-
nore, una due, ò più fiate, con alcuna sua parte Aliquota, ò Non aliquota; Ma l'hauer ra-
gion de Numeri, ò esser ragion de Numeri, per una certa eccellenza conuiene al pri-
mo Numero perfetto, ch'è il Senario ancora che gli Antichi attribuissero tal Ragione al
Quaternario, chiamandolo per alcune ragioni anco lui Perfetto. La onde le Consonan
ze, che ueramente hanno le lor uere forme dalle proportioni contenute tra le parti del Se
nario; si chiamano hauer ragione de Numeri; oueramēte esser ragione de Numeri. Ma le
Dissonanze non possono esser dette, ne hauer cotali ragioni; percioche hanno le propor
tioni loro contenute tra altri numeri, che tra quelli che sono posti tra le parti nominate.
Son satisfatto benissmo; soggiunse M. Adriano; seguitate il resto. Allora dissi; Ha-
uendoui definito la Consonanza secondo le due maniere dichiarate, & la Dissonanza an
cora; fà dibisogno ch'io ui definisca l'Harmonia, la quale si compone di due consonan-
ze almeno. Onde hauete prima à sapere; che quella distintione, che hò posto della Con
sonanza, è necessario che anco sia fatta dell'Harmonia; intendendo però dell'Harmonia
non propria; secondo 'l modo dichiarato nel Cap. 12. della Seconda parte delle Istitu-
tioni; percioche è di due sorti anch'ella; cioè, Semplicemente, & Detta ad un certo mo-
do. Onde dichiarando la prima, dirò che:
DEFINITIONE IIII.
me unite, secondo i gradi dell'Harmonica proportionalità, laquale soauemente per-
uiene all'Vdito.
ceuono un mezano suono, che diuida l'Interuallo, che si troua tra loro, in
due Consonanze, secondo i gradi della proportionalità Harmonica; allora si
fà questa compositione, che intendiamo nella definitione, che si chiama Harmonia
Semplicemente detta. Ma per dichiararui il secondo membro dell'Harmonia non pro-
pria; dico, che
DEFINITIONE V.
ste insieme; ma non secondo i gradi della mediocrità Harmonica, la quale non cosi soa-
uemente, come la Semplicemente detta, uiene al senso dell'Vdito.
meglio, disse; Questa anco mi pare, che hà dibisogno d'un poco del uostro lu-
me; perche à me, ch'io nō son molto prattico delle cose della Musica, è alquan-
to oscura; Però sarete contento di darmi meglio ad intendere questa cosa con
vno essempio. E' il douere risposi, Dico adunque, che poco fà mostrandoui le Propor-
tioni, che nascono dalle parti del Senario & dall'Ottonario; breuemente ui dichiarai, &
dimostrai anco le forme de tutte le Consonanze; il che ricordandoui dico, che quando ri
trouarete due consonanze unite insieme, le cui proportioni saranno in cotal modo ordi-
nate. 6. 4. 3. direte, che elle fanno lHarmonia Semplicemente detta; percioche tra loro si
troua l'Harmonica mediocrità; come la Quintadecima definitione di heri sempre lo farà
manifesto. Il che direte anco dell'altre simili; & questo è quanto alla Semplicemente det-
ta. Ma la Detta ad un certo modo, si fà, quando tra due consonanze ordinate al modo
detto, non si troua tale Mediocrità; come sarebbe dire; quando le sue proportioni fussero
collocate tra questi terimini 4. 3. 2. percioche se ui ricordate la Terzadecima Definitione
di heri, sono collocate in Arithmetica progressione, ò proportionalità; come più ui piace
dire. Essendo che nella prima la forma della Diapente, anzi la Diapente istessa è colloca-
ta nel graue, & la Diatessaron nell'acuto; & in questa il tutto è posto al contrario; percio-
che la Diatessaron tiene il luogo graue, & la Diapente occupa l'acuto; cosa che non si tro-
ua tra le proportioni, che sono collocate nell'ordine naturale de i Numeri Harmonici. On
de, quello aggiunto: Meno che soauemente peruenire all'Vdito: che si è detto nella sua
Definitione, non è causato da gli interualli nominati; percioche sono consonanti; ma si
ben dall'ordine, ch'è posto al contrario del primo; il perche Meno che soauemente muo-
uono l'Vdito. Questa è bella consideratione; disse il Sig. Desiderio: Et la intendo hora; pe
rò passate ad un'altra proposta; s'altro sopra di questo non uolete dire. Non uoglio dire
altro risposi: Ma uoglio che sappiate, che le Consonanze; parlando uniuersalmente; so-
no de due maniere; percioche alcune si chiamano Semplici, & alcune Composte; & ac-
cioche conosciate l'une & l'altre, uerremo alla lor definitione; onde incominciando dal-
le prime, diremo.
DEFINITIONE VI.
Diatessaron, il Ditono, il Semiditono, & essa Diapason; le cui forme sono contenute
tra le parti del numero Senario ne i Generi Molteplice & Superparticolare.
13. & 16. hauete connumerato etiando
i due Hexachordi; Maggiore & Minore; onde non credo che hora li uogliate
escludere. E' uero, dissi, ch'io chiamai l'Hexachordo semplice consonananza; non
però semplicemente; ma ad un certo modo, & per un certo rispetto; percioche è minore
della Diapason; onde essa Diapason non entra nella sua compositione; Ma qui chiamo so
lamente semplici quelle Consonanze, c'hò nominato, & non l'altre; onde seguitarò à di-
re; che
DEFINITIONE VII.
diapente, la Disdiapason, & tutte l'altre Maggiori di queste.
uno Interuallo, che si potrà dir Composto; per quello, ch'io ueggio; disse il Vio
la. A' cui risposi; Cosi è in fatto; ma senza por tempo di mezo, uerremo alla par-
ticolar Definitione di ciascheduna Consonanza; onde incominciando da quella, ch'è
Regina de tutte l'altre, la Diapason, diremo.
DEFINITIONE VIII.
tra i numeri semplici non si troua maggior proportione nell'ordine naturale di
numero à numero, l'uno all'altro più uicino, della Dupla; essendo ch'ogni altra,
che si troua, se è minore, è sua parte, & se è maggiore, è collocata tra numeri, i quali non so
no uicini, & è composta di lei & d'una sua parte; Cosi la Diapason tra l'altre Consonanze
& Interualli tiene il primo luogo; & nō si troua alcun'altro Interuallo, sia qual si uoglia, che
di lei sia maggiore; essendo che se è minore, è sua parte; & se è maggiore, è composto d'una
sua parte & del suo Tutto, com'altroue ho dichiarato;1. par. cap.
13. & dal Musico è presa per il suo Tut-
to diuisibile. Ma si come non si troua proportione, che sia auanti la Dupla; cosi non si
troua Consonanza, che sia prima della Diapason;2. par. cap.
48. poi che la Dupla è la sua uera forma;
essendo il Tutto diuisibile, senza dubio alcuno, prima delle sue parti; come è noto à tut
ti gli intelligenti; hora hauendoui definito il Tutto, ui uerrò à definire di una in una tut-
te le sue parti; le quali nascono dalla diuisione harmonica di esso Tutto; come nelle Istitu-
tioni si è dimostrato; & incominciando dalla maggiore, dirò in cotal modo.
DEFINITIONE IX.
tione Sesquialtera.
diuisione fatta harmonicamente; come uederemo al suo luogo. Et perche in-
torno ad essa non ui cade difficultà alcuna; però passarò all'altra definitione.
DEFINITIONE X.
giore della Diapason; non è dubio, che la Diatessaron farà la sua parte minore;
poi ch'aggiunte queste due parti insieme, fanno di punto la Diapason. Et mi
ricordo, che heri dimostrate,Propo. 17 che l'Interuallo Duplo nasce dalla congiuntione de i
due primi maggiori Superparticolari; Onde se la Diapente è contenuta dalla Sesqui-
altera, & la Diatessaron dalla Sesquiterza; non è dubio, che diuisa la Diapason in que-
ste due parti; per il conuerso della detta proposta; elle non siano le sue parti mag-
giori; come sono ancora maggiori d'ogn'altra Superparticolare le loro proportio-
ni. Voi l'intendete benissimo, Messere risposi; perche è cosi in fatto. Aggiunge-
te anco disse M. Claudio; che se poste insieme, come dimostra la Decimaottaua,1. Huius.
page 84 fanno la Proportionalità harmonica, che queste due parti nascono dalla diuisione di es-
sa Diapason, fatta per la istessa Proportionalità. Qui non può nascer difficultà alcuna;
gli dissi. Il perche il Signor Desiderio soggiunse; in fatto hauete ragione à dire, che la
Diatessaron sia consonanza; & hanno il torto tutti quei Prattici, che la pongono nel nu
mero delle Dissonanze; ma sono da iscusare in questo, che non sanno quel, che si faccia
no. Questi c'hanno questa opinione; disse M. Adriano; sono in errore. Et mi ricordo, ch'
inanzi de noi quei buoni Antichi Giosquino, il suo Maestro Gio. Ochegen; Gascogne,
& il mio precettore Gio. Motone in molti luoghi delle loro compositioni l'hanno posta
nella parte graue, senz'aggiungerle altro Interuallo. Messere; gli risposi; Se la Diatessa-
ron fusse dissonanza, non la porreste ne i uostri Contrapunti, nel modo che la ponete,
sopra la Diapente, ò sopra il Ditono, ò lo Semiditono; ne anco questo farebbono gli
altri compositori. Ne anco; soggiunse il Merulo; si potrebbe accordar col mezo di que
sto Interuallo alcuna sorte d'Istrumenti, se non fusse consonante; tuttauia se n'accorda-
no de molte sorti; come sono Organi, Viuole, Leuti, Lire & altri simili, tanto bene;
come si fà col mezo della Diapente & della Diapason. Ascoltate di gratia, dissi, ch'io ui
uoglio dire una ragione; la quale hor'hora mi souiene; alla quale non si può con ragione
contradire. Ditela di gratia, soggiunse M. Adriano. Ascoltate, adunque Messere, rispo-
si; & uoglio che oltra quello, ch'à questo proposito hò detto nelle Istitutioni; habbiate
questa per una Massima; che Quando si muta alcuno de gli estremi di qual si uogla In-
teruallo, sia consonante, ò dissonante; facendolo d'acuto graue; ò per il contrario di gra-
ue acuto per una Diapason, si hà uno corrispondente Interuallo nell'acuto, ò nel graue,
il quale è della istessa natura del primo. Et accioche m'intendiate, ui uoglio parlare prat
ticamente. Poniamo, che sia quell'Interuallo, che noi chiamiamo Seconda; Questo (co-
me è noto à ciascheduno) è Interuallo dissonantissimo; però se trasportaremo il suo estre
mo graue nell'acuto, ouer'il suo acuto uerso 'l graue, per una Ottaua; rimanendo gli
altri termini à i loro luoghi; non è dubio, che haueremo un'Interuallo à lui corrisponden
te, nella parte acuta, ouer nella parte graue, che sarà dell'istessa natura di essa Secon-
da, & sarà una Settima; la quale ciascheduno di uoi conosce essere dissonante. Il che an
cora auerrà facendo 'l contrario; cioè, quando si trasporterà l'estremo acuto dalla Set-
tima uerso il graue; ouer l'estremo suo graue uerso l'acuto; percioche ne nascerà la Secon
da nominata. Onde non si può negare, che l'uno & l'altro de questi due Interualli sia d'
una istessa natura, & siano comprese sotto un'istesso Genere di Dissonanza. Questo istes-
so auerrà nella Semidiapente, che trasportato il suo estremo acuto uerso 'l graue, ouer
l'estremo graue uerso l'acuto, uerrà il Tritono; & trasportati in cotal maniera gli estremi
di esso Tritono; nascerà la Semidiapente; de i quali Interualli l'uno & l'altro sono con-
tenuti sotto questo genere di Falso interuallo. In fatto è cosi; disse il Viola; ma non ue-
do, doue uogliate arriuare. Andrà poco lontano la cosa, risposi; che lo uederete. Dico
ancora; che se di nuouo pigliaremo una Terza, la quale sapete, ch'è posta nel numero
delle Consonanze imperfette; & faremo il simile, trasportando in acuto il suo estremo
graue per una Ottaua; oueramente ponendo il suo estremo acuto nel graue, per un simi-
le Interuallo; subito ne uerrà la Sesta, la quale etiandio è connumerata tra le Conso-
nanze imperfette. Il che auerrebbe anco, trasportando all'istesso modo gli estremi di que
sta; percioche ne risultarebbe la Terza; cosa che ueramente non si può da niun sano di
giudicio negare. La onde, se usando simili modi, di trasportare i detti termini, si uede;
ch'una Dissonante ne produce un'altra; come fa anco il Falso interuallo; & una Conso-
nanza imperfetta ce ne da un'altra simile di genere, ò specie; che maggior priuileggio in
questo debbono hauer le Dissonanze, i Falsi interualli & le Consonanze imperfette; del-
le perfette Consonanze? Niuna certamente; percioche non ui è maggior ragione delle
prime, che di queste ultime. Diremo adunque con l'istessa ragione, che se 'l si riporterà l'e-
stremo graue d'una Quinta uerso l'acuto per una Ottaua; oueramente l'estremo acuto
uerso il graue per un simile interuallo; quello, che uerrà sarà una Quarta, la quale, per
page 85 le ragioni addotte nelle Dissonanze, ne i Falsi Interualli & nelle Consonanze imperfette,
dico esser della natura della Quinta, & esser sottoposta ad un'istesso genere, ò specie di
Consonanza. Et si come la Quinta per diuersi rispetti è detta Consonanza perfetta; co-
si ancora, per quelli istessi, la Quarta è detta Cōsonanza perfetta. Percioche ancora ripor
tando gli estremi della Quarta nell'acuto & nel graue, come facemmo quelli della Quin
ta; nasce al medesimo modo essa Quinta; Onde siamo sforzati uolendo, o non uolendo, di
re; che se la Quarta è dissonante, che dissonante sia all'istesso modo la Quinta; ouero che se
questa è cōsonante, che anco quella sia di tale natura. Ilche non credo che sia negato da
Huomini di sano intelletto. Disse allora M. Adriano, Questa ragione è ben ueramente no
ua, & è una delle belle, che si possa addurre in confirmatione delle uostre ragioni. E quan
do non imparassi mai altro hoggi di questo, me ne contento assai. Spero di dirui dell'al-
tre cose Messere, diss'io; che ui piaceranno, però state allegro. Replicò anco il Viola
in questo modo, Io dirò M. Gioseffo, che la ragione della Seconda & della Settima uà
bene; percioche sono tutte due dissonanti; simigliantemente quella della Terza con la
Sesta & delli due Falsi interualli, che hauete nominato: ma quella della Quinta con la
Quarta mi par differente. Et ciò dico; accio che sopra di questo diciate qualche cosa;
essendo che tra le parti de i Contrapunti senz'alcuna differenza si pone la Terza & la
Sesta per buone consonanze, che fanno buono effetto; ma non auiene cosi della Quar
ta. A questo risposi & dissi, La differenza, che si troua tra la Quinta & la Quarta consonan
za della prima maniera, è quasi l'istessa, che si troua tra la Terza consonanza della pri-
ma, & la Sesta consonanza della seconda; Imperoche si come la Sesta per sua natura
non è molto consonante, & è men buona della Terza; massimamente della maggiore;
come si uede, che non la lasciate ne i Contrapunti dimorare in un luogo per molto tem
po, perche offende il senso; ne mai date fine ad una uostra cantilena per il detto Inter-
uallo; ma si ben per Ottaua & per Quinta; cosi la Quarta, comparata alla Quinta, non
è molto consonante, & è men buona di essa Quinta; come anco essa Quinta è men buo
na della Ottaua, la quale più d'ogn'altra perfettamente consona. La onde dico la Dia-
tessaron esser Consonanza & perfetta; ma non però dico, che ella sia tanto consonante
& tanto perfetta, com'è la Diapente; ne meno com'è la Diapason; come etiandio dico
l'Hexachordo (per ritornar ne i nostri termini primi) esser consonante; ma non di quell'
istessa & propria natura, ch'è il Ditono, ò lo Semiditono; percioche secondo che nell'
altre cose si ritrouano gradi tra loro; cosi ancora ui sono i suoi gradi tra le consonanze,
& gli interualli dissonanti; ma questo ui basti. Io resto benissimo satisfatto; rispose il
Viola. Onde il Sig. Desiderio soggiunse subito; Questo è stato un ragionamento molto
utile; & credo che non si ritrouerà più alcuno, dopo c'haueranno inteso queste ragioni,
che uoglia dire, che la Diatessaron sia dissonante. Noua & bella ragione è stata uera-
mente; aggiunse M. Claudio; onde dobbiamo desiderar che 'l si uada più oltra; acciò in-
tendiamo di nouo qualch'altra cosa. Notate, adunque soggiunsi; che della Diapente
harmonicamente diuisa, si fanno due parti, come son per dimostrarui; l'una delle quali si
chiama Ditono, che è la maggiore; l'altra, ch'è la minore, è nominata Semiditono; &
la definitione della prima sarà di questa maniera.
DEFINITIONE XI.
zana chorda, serue etiandio al Genere Enharmonico. Et si può chiamare una
delle prime parti della Diapente, & delle Seconde della Diapason; come anco si
può nominare al modo medesimo il Semituono, del quale porremo questa definitione.
page 86
DEFINITIONE XII.
no chiamato Sesquituono; quasi uolendole dire d'un Tuono & mezo; ma quel,
ch'io scrissi nel Cap. 25. della Prima parte delle Istitutioni, sopra questa paro-
la Sesqui, ui potrà chiarire; se 'l si può dire di un Tuono & mezo. Altri l'hanno detto
Trihemituono, ò Trisemituono; hauendo consideratione, che serue al Genere chro-
matico, quando è pigliato senza ueruna chorda mezana. Ma non stiamo hora sopra la
consideratione de i nomi; noi lo chiamaremo Semiditono, il quale è la minor conso-
nanza, che si troui. Imperoche non ui è alcun'Interuallo, sia qual si uoglia, il quale sia
minor di lui; che sia consonante. Et da questo si può conoscere, che la sua proportione
tiene l'ultimo luogo tra i numeri delle parti del Senario. La onde, credo, c'habbiate da
uoi stessi compreso, che tutte le Consonanze, lequali fin'hora habbiamo definito, siano
semplici, & tutte minori della Diapason; però uerremo hora à quelle, che sono di lei mag
giori, & si chiamano Composte.
DEFINITIONE XIII.
sendo che dell'una & dell'altra di queste due si cōpone; come si conosce dalle lor
forme 3. 2. 1. contenute nel Senario tra i numeri Arithmetici; ouer da 6. 3. 2. Nu
meri harmonici. Ma,
DEFINITIONE XIIII.
Consonanza si può considerar composta in due maniere; prima, della Diapason,
della Diapente, & della Diatassaron; come si scorge tra questi numeri. 4. 3. 2. 1.
ouer tra questi. 12. 6. 4. 3. dopoi, de due Diapason; come si uede tra questi termini. 4. 2. 1.
per qual cagione adunque si dice da molti, che la Disdiapason si compone di due Diapa-
son maggiormente; che di una & delle due altre nominate consonanze? Questo auie-
ne Messere; risposi; perche gli Antichi; prima la considerarono come composta
de due consonanze piu note: come sono due Diapason; che dal senso sono maggior-
mente conosciute, che non è qual si uoglia altra consonanza; dopoi perche la conside
rarono composta della più nobile consonanza replicata, ch'è la Diapason; che sia tra
l'altre consonanze. Et se bene la prima Diapason si pigliasse semplice & l'altra composta
delle due maggiori sue parti, questo importarebbe poco; percioche per ogni modo
contiene & contenerebbe due Diapason. Ma per dirui;
DEFINITIONE XV.
maggiormente composta della Disdiapason & del Ditono, che d'altre conso-
nanze; poi che i termini della Quintupla stanno tramezati in questo modo. 5. 4.
3. 2. 1. oueramente tra i Numeri Harmonici. 60. 30. 20. 15. 12. sò che mi risponderete, co-
me hauete fatto à M. Adriano; però senza por tempo di mezo, seguitate 'l uostro ra-
gionamento; ch'altro non uoglio dire. Voglio che anco ui ricordiate; soggiunsi; che
DEFINITIONE XVI.
Sestupla.
i termini della sua forma in tal maniera tramezati sono. 6. 5. 4. 3. 2. 1. ouerame
te. 60. 30. 20. 15. 12. 10. la ragione detta di sopra ui può bastare. Onde uerremo
alla Decimasettima definitione.
DEFINITIONE XVII.
perbipartiente terza.
sendo che prima hauete definito le Consonanze, incominciando dalle Sempli-
ci, uenendo alle Composte, & sete uenuto dalle minori alle maggiori; hora di
nuouo ritornate da capo; & per qual cagione lo fate, per uostra fè? Quelle Consonan
ze, dissi; che fin'hora hò definito, sono contenute ne i generi Molteplice & Superpar-
ticolare, che sono Generi semplici di proportione; il perche hauendo posto fine à quel-
le, che sono contenute sotto questi due Generi; uengo hora à definir quelle, che sono
contenute ne gli altri; per poter seguitar un buon'ordine. Ne mi curo, che queste
ch'al presente definisco siano maggiori, ò minori; essendoche questo è di pochissima
importanza. Ma ui basta à sapere; che questa proportione Superbipartienteterza, no-
minata di sopra, è compresa nel Terzo genere di proportione, detto Superpartiente,
& è la prima di cotal genere. Mi piace l'ordine, & resto satisfatto, rispose il Viola;
però seguitate quello, che ui piace. Soggiunsi adunque; Ancora che tra le parti del
Senario non ui sia la forma dell'Hexachordo minore in atto; tuttauia per esserui (com'
hò dichiarato altroueInstitut. 1.
part. c. 16.) in potenza; & tra 'l primo Cubo & il Quinario in atto: non uoglio
restar, già ch'è contenuta la sua forma nel Genere sopradetto, di darui la sua definitio-
ne; onde diremo.
DEFINITIONE XVIII.
tione Supertripartiente quinta.
nel secondo luogo del nominato Genere, tra questi numeri, ò termini. 8 & 5.
Ma per uenire à gli altri due Generi, che sono composti; per dimostrarui, ch'
in ogni Genere di proportione si troua alcuna consonanza; se non semplice, almeno
Composta; porrò senza por tempo alcun di mezo, la definitione della Diapason col Di-
tono; in questa maniera.
DEFINITIONE. XIX.
Dupla sesquialtera.
nario, tra questi termini. 5. & 2. Fermateui di gratia un poco M. Gioseffo; disse
qui M. Adriano; & lasciatemi addimandarui un dubio. Voi dite, che la Diapa-
sonditona ha forma dalla Dupla sesquialtera; nondimeno questo Interuallo è com
posto d'una Diapason, la quale hà la forma dalla proportione Dupla, & di un Ditono,
che hà la forma della Sesquiquarta; com'hauete posto nelle loro definitioni. Ma se la
Sesquialtera, è la forma della Diapente; com'è possibile, che la Diapason col Ditono
habbiano la forma della Dupla sesquialtera, & non dalla Dupla sesquiquarta? Com-
prendo dalle uostre parole; dissi; che uorreste, che più tosto si dicesse, che la proportio-
ne Dupla sesquiquarta fusse la forma della Diapasonditona; la quale è composta della
Diapason & del Ditono, che la Dupla sesquialtera; perche ui pare, che da questa de-
nominatione più tosto si douesse denominar la Diapason diapente, che la Diapasondi-
tona; poi che la Dupla è la forma della Diapason; & la Sesquialtera quella della Dia-
pente. Non è com'io dico? Stà bene; rispose egli. Allora soggiunsi; Se è dibisogno che
sia cosi; sommaremo nel modo, ch'io dimostrai nel Cap. 33. della Prima Isti-
tutioni, la Dupla insieme con la Sesquiquarta, & se uerrà la proportione, c'hauete no
minato, la cosa andrà bene. Ma noi uediamo, che ella uà ad'un'altro modo; essendo
che uiene una Dupla sesquialtera, come contiene la Definitione; adunque la cosa non
uà bene. Onde sommando insieme anco al modo detto la Dupla con la Sesquialtera,
non nasce la Dupla sesquialtera, ma si bene la Tripla, ch'è la forma della Diapason dia-
pente. Il perche si uede, che à dir Tripla, & dir Dupla sesquialtera, non è dire una pro-
portione istessa; ma due diuerse. Questo di nuouo uediamo, che sommando insieme la
proportione della Diapason, & quella della Diatessaron; non uiene la Dupla sesquiter-
za; se ben la Dupla è la forma della Diapason, & la Sesquiterza quella della Diatessaron;
ma la Supertripartiente quinta; ch'ella della Diapason diatessaron; come nella seconda
Definitione dichiarai. Onde è manifesto, che gli Antichi all'uniuersale più attesero, che
al particolare, & al leuar la confussione dalle menti de gli huomini. Et uolsero (com era 'l
douere) denominar le Proportioni in ogni Genere da i modi che 'l maggior termine con-
tiene il minore più fiate interamente; ouero più fiate con una, ò più parti del minore; ac
cioche queste denominationi seruissero non solo alle Proportioni & à gli Interualli della
Musica particolarmente; ma etiandio è quelle, che seruono all'altre Scienze. Et ancora
che mi potreste dire, che questa parola Sesqui; come dichiarai nelle Istitutioni;1. Par. cap.
25. uoglia di
re Tutto, & Altera significhi l'una de due parti fatte d'alcuna cosa; & che meglio sareb-
be dire, Dupla & Altera, che Duplasesquialtera; responderò, che questo non sareb-
be mal fatto; quando in ogni Genere, la parola Sesqui si pigliasse solamente per una addi
tione sillabica; come uoleuano alcuni; ne altro uolesse significare. Ma diciamo pure con la
page 89 sua significatione; che Dupla sesquialtera uoglia dire; Due fiate il Tutto & una parte del
la minor quantità comparata alla maggiore; percioche questo non è di molta importan-
za, che se le aggiunga, ò leua tal particella; essendoche già è riceuuta per tale; & s'aggiū
ge oltra questi termini Dupla, Tripla, & gli altri. Et simili denominationi; come Sesqui
altera, Sesquiterza, & l'altre per ordine, sono le denominationi delle parti, per le qua-
li il maggior termine, che si ritroua ne i Denominatori delle Proportioni; sopr'auanza il
minore. Et questo per hora ui potrà bastare. Son satisfatto benissimo, soggiunse M. Adria
no . Passarò adunque auanti, risposi; & dirò, che tutte queste Definitioni, che io hò da
to sono à bastanza intorno à quelli Interualli, che sono Consonanti; percioche bisogna
hormai definire i Dissonanti, i quali seruono alla cognitione delle cose della Scienza &
anco dell'Arte; accioche nelle Dimostrationi, che siamo per fare, non ci manchino quei
Principij, che sono necessarij per concluder quello, c'habbiamo da preporre: Tanto
più, che le Definitioni (com'altroue hò dettoSupra ante
prima Defi
nitionem.) sono i Mezi delle Dimostrationi. Ascolta
te adunque, che hora ui definirò tutti quelli Interualli dissonanti, che io ui son per defi-
nire, l'un dopo l'altro, & senza hauer rispetto à Genere alcuno. Onde incominciando
dal Maggiore, dirò in questo modo.
DEFINITIONE XX.
la Diatessaron.
il Tuono esser principio della Consonanza; il quale nasce, producendo da suo
no à suono, dalla proportione Sesquiottaua. Disse allora M. Adriano; Per
qual cagione adunque non hauete detto nella definitione, come hauete fatto nell'altre,
che questo Tuono nasce da simil proportione; poiche nell'Istitutioni molte fiate l'hauete
. Perche uoglio, risposi; che ella sia uno de i Principij, ch'io adopererò in questo &
ne gli altri Ragionamenti. Et s'io hauesse posto nella Definitione, che ella nasce dalla
proportione Sesquiottaua, non lo potrei dimostrare; perche i Principij non si dimostra-
no; ma perche son per dimostrarui cotal cosa; però ui hò detto solamente, ch'è la diffe-
renza, che si troua tra la Diatessaron & la Diapente; essendo che ui uoglio far col mezo
di queste Definitioni auertiti; che tutti quelli Interualli, che sono minori del Semidito-
no, & sono dissonanti, altro non sono che le differenze, che si trouano tra un'Interual-
lo Maggiore & un Minore. Questo mi piacerà assai, soggiunse M. Claudio; ma diteci, ui
prego, che uuol dir questa parola Tuono. E' Greca, risposi; & si dice Τόνος, che impor-
ta Fermezza, ò Stabilità. Et perche non si troua alcuno Interuallo consonante, il quale
non ritenga questo Interuallo; cioè, la sua proportione almeno; però gli Antichi lo chia
marono Principio della Consonanza. Essendo c'haueano opinione, ch'ogni interuallo
Maggiore di lui fusse, ò si douesse di lui & del suo minor Semituono comporre. Onde da
questa credula fermezza & stabilità, ch'in esso uedeano, lo chiamarono Tuono. Disse à
questo M. Adriano; Non sono de due sorti Tuoni? Sono per certo, diss'io; & da questo
si conosce, ch'à questo aggiungo la parola, Maggiore, che lo fà differente dall'altro, che
ui definirò hor'hora, che sarà il Minore.
DEFINITIONE XXI.
ni, mi disse; Questo Tuono fu egli mai conosciuto da gli Antichi? Allora gli ri-
sposi; Quando sarà il suo Tempo, ui dimostrerò in che proportione ello si troui,
Harm. lib.
1. cap. 15.& allora conoscerete, se hauerete à memoria le cose di Tolomeo, hauendole uedute, che
questo Interuallo entraua nella compositione della specie Diatonica, chiamata Diato-
nico syntono; se bene da lui non è chiamato col nome di Tuono, & era conosciuto.
Ma noi lo nomineremo Tuono aggiungendoui questa parola Minore, à differenza
del primo, che già habbiamo definito. Essendo che tra l'uno & l'altro ui cade po-
ca differenza; come potrete uedere, Ma passiamo un poco più oltra, acciò non
perdiamo tempo.
DEFINITIONE XXII.
Ditono.
Semituono Apotome. E' uero, dissi; che chiamarono Α'ποτομὴ il Semituono
maggiore; ma questo ch'io hò definito non è quello de i Greci; essendoche è cō
tenuto d'altra proportione, che dalla Super. 139. partiente. 2048. dalla quale è contenu-
to quello, com'io son per dimostrarui. Per qual cagione lo chiamauano con tale nome?
dimandò il Viola. Perche diceuano, risposi io; che è Quasi tagliato fuori del Tuono, co
me superfluo; essendo che gli Antichi non adoperauano tal Semituono ne i loro Tetra-
chordi. Onde Α'ποτομὴ appresso di loro significa Tagliamento. Auertite però; che,
DEFINITIONE XXIII.
tono viene à superare il Semitono, ouer il Tuono minore il maggiore Semituono.
che è Interuallo, il quale serue al Genere Enharmonico; come udirete & uede
rete al suo luogo ne i nostri ragionamenti. Questo intendiamo bene, disse Me-
ser'Adriano; ma sopra la definitione, che ci hauete proposto, ui uoglio dir due cose; del-
le quali la prima è, che i Greci chiamauano Lemma il lor Semituono minore. La secon-
da, che se noi consideriamo il Tuono maggiore diuiso in due parti; cioè, in due Semituo
ni, secondo la ragione, ch'io feci già, leggendo un giorno le uostre Istitutioni, ritrouo,
che se noi cauaremo il maggior Semituono dal Tuono maggiore, quella parte, che uer-
rà, sarà maggiore di questo Semituono, che ponete per la differenza, che si troua tra il
Ditono & lo Semiditono, ouer tra 'l Tuono minore & lo maggiore Semituono, che ha-
uete definito, & sarà etiandio di questo maggiore; tuttauia chiamate questo Minore, che
si douerebbe dire Minimo. Et non fate mentione alcuna di quello, ilquale sarebbe uera
mente il Minore; diteci adunque doue nasce questa cosa. Messere; dissi allora; Voi sete
in poco tempo fatto un'huomo molto sottile. Et mi diletta molto il uostro dubitare, il
quale è di gran giouamento; essendo che egli è uicino al Sapere. Percioche il dubitare
di ciascheduna cosa, nelle Scienze (secondo il FilosofoPraedica-
mēt. c. 3.) non è senza utilità. Et mi pia-
ce, che uoi penetriate alle cose difficili col uostro intelletto, il quale è stato sempre bello,
& arteficioso. Però risponderò uolontieri à quel, che dimandato m'hauete; & prima al
page 91 la Prima cosa; dopoi uerrò alla seconda. Quanto alla prima ui dico, che è uero: che i Gre
ci chiamarno il lor Semituono minore Λεῖμμα; ma (come u'hò detto anco del Maggiore)
questo Semituono, che hò definito, non è quello, che da i Greci è chiamato per cotal
nome; ma si ben quello il quale da noi è usato al presente; essendo che il loro era conte-
nuto dalla proportione Super. 13. partiente. 243. & il nostro è contenuto d'altra propor-
tione; come son per dimostrarui. Onde appresso de loro tanto uuol dir Λεῖμμα, quanto
Residuo, ò Restante appresso di noi; percioche i Pitagorici chiamarono con tal nome la
parte minore d'una cosa diuisa in due parti inequali. Questo fù anco detto Δίεσις da Filo-
lao pitagorico. Ma di quel Δίεσις, del quale alcuni hebbero parere, che fosse Principio,10. Meta-
phy. c. 2.
Et 1. poste.
cap. 17.
& Elemento de gli altri Interualli della Musica; & uoleuano, che fusse come l'Vnità ne i
Numeri, la quale è la lor cōmune misura; hora non ui uoglio dir cosa alcuna; ma leggere
te il Cap. 48. della Seconda parte delle Istitutioni, se uorrete intender di lui qualche cosa;
& uoglio che questo ui sia basteuole intorno alla prima cosa, che m'hauete richiesto. Quā
to poi alla Seconda douete sapere; ch'io hò definito il Semitono minore esser quell'Inter
uallo, per il quale il Ditono sopr'auanza il Semiditono, oueramente il Tuono minore su-
pera 'l maggior Semituono; & non quello, per il quale il Semituono maggiore definito di
sopra dal Tuono maggiore è superato; percioche questo, ch'io hò definito, è quello, ch'a-
doperano al presente i Musici, & fà più al proposito nostro, di quell'altro; ancora che nel
Genere diatonico s'adoperi solamente 'l Maggiore in ogni suo Tetrachordo, & non il
minore. Onde non hauete dubitato fuor di proposito Messere. Et ui uoglio dire, che chi
uolesse minutamente considerar gli Interualli, che nascono in una ordinatione de Suoni
nelle lor proportioni, si trouerebbe esserui non solamente il Maggiore & lo Minor semi-
tuono, ma anco il Massimo, il Minimo, & il Mezano: onde si uerrebbe quasi à confonde
re l'intelletto de chi ascoltasse. Et perche queste minutie non fanno al nostro proposito;
perche dal Senso non sono comprese, per la poca differenza, che cade tra l'uno & l'altro;
Simigliantemente, perche ne gli Istrumenti arteficiali la Partecipatione & il Tempera-
mento loro non lascia conoscer cotali cose; però si lasciano da un canto. E' ben uero, che
quando queste minutie si uorranno trattare, & dimostrare il luogo doue accascano & si
ritrouano in un'ordine de suoni, noi sarà cosa impossibile, quantunque difficile; & già so-
pra un'Istrumento fabricato à tal proposito molt'anni sono le ridussi in atto, & le uolsi udi
re; come potrete uedere à Dio piacēdo ne i miei SopplimētiLi. 4. c. 11. già promessi. Mi ricordo del
l'Istrumēto, disse il Viola; & mi accorgo hora; per qual cagione non hauete fatto mentio
ne alcuna cosi minutamente de questi Semituoni nelle Istitutioni; massimamente di que
sto Minore, quando ne parlaste. A questo dissi; Voi hauete udito la cagione; ma nel Cap.
46. della Seconda, & nel 19. della Terza parte, non solamente l'hò nominato, ma pongo
anco la sua proportione, se ue lo ricordate. A questo disse; Me ne ricordo; & ricordomi an
co, che nel Cap. 15. della Prima, è compresa la sua proportione nell'ordine de i Numeri
harmonici. Per qual cagione adunque; interrogo M. Adriano; per ritornar'à dir qualche
cosa ancora di questo Semituono, lo chiamate Minore, essendo Minimo? Risposi Per due
cagioni; l'una è, perche per la moltiplicatione delle parti del Senario tra loro secondo 'l
proposito, non si passa il numero 36. Onde tra quei numeri, che sono minori di questo,
non si troua la proportione del Minore, che uoi intēdete; ma si bene del Minimo, ch'è que
sto ilquale chiamo Minore; ilperche douendo dir Minimo, era necessario, che ui fusse auā
ti il Minore, ò dopoi almeno; essēdo che Minimo è relatiuo di Minore, ne i gradi della Cō
paratione; onde non mi parue cosa conueniente di nominare il Minimo, non ui essendo
il Minore; però lo nominai Minore, per rispetto del maggiore. L'altra cagione fù; perche
il Minore, che uoi dite non fà al proposito nostro. Son satisfatto, rispose M. Adriano; se-
guitate pur quel, che più ui piace. Soggiunsi allora; Dandoui di sopra la Definitione del
Semituono minore, io uenni à definire insieme il Diesis maggiore, che serue al Genere
enharmonico, percioche è quell'Istesso Interuallo; per il che hora seguiterò à dirui la de
finitione dell'altro, ch'è il Minor, & dirò à questo modo.
page 92
DEFINITIONE XXIIII.
no supera il Diesis maggiore, ò Semituono minore.
tuon maggiore, il quale è commune al Diatonico; & l'Enharmonico usa il mino
re, ch'è commune al Chromatico; di maniera che potete comprendere, quanto
la Natura maestra delle cose sia mirabile. Vedete ancora, soggiunse M. Claudio; che bell'
ordine & regolato è questo; che 'l Semiditono, il quale si troua nel Diatonico tra la prima
& la terza chorda del suo Tetrachordo; nel Chromatico si ritroua tra la terza & la quar-
ta; & il Ditono, che nel Diatonico tra la seconda & la quarta è collocato, nell'Enharmo
nico è posto tra la terza & la quarta medesimamente. Che uorranno adunque dir questi
Chromatisti; soggiunse il Sig. Desiderio? staranno forse ancora ostinati? uorranno forse
dire ancora, che 'l Ditono & lo Semiditono non siano del Diatonico, ma si bene, che l'u-
no sia dell'Enharmonico, & l'altro serui al Chromatico. Lo diranno certo, disse M. Adria
no; & senza ragione; Et se dicessero almeno, che 'l Semiditono, che si troua tra la chor-
da E. parlando come prattico, & la chorda C. segnata con questo segno
 . il quale chia-
. il quale chia-miamo Diesis, & ciò discendendo; quasi quasi, che si potrebbe, se non in tutto, almeno
in parte, tener da loro; ma non già altramente. In che modo Messere, soggiunse il Vio-
la ; uorreste tenere con loro in questa cosa. In questo, rispose; quando la nominata Con
sonanza si ritrouasse esser collocata tra una chorda Diatonica, segnata E. & una Chroma
tica, segnata
 . com'hò detto di sopra; perche allora non si ritrouerebbe esser semplice
. com'hò detto di sopra; perche allora non si ritrouerebbe esser semplicemēte tra le chorde Diatoniche; ma tra una segnata E. Diatonica, & una signata
 . Chroma
. Chromatica; & à questo modo potrei tener dalla sua. Ma che quest'Interuallo nō si troui nel Dia
tonico tra le chorde
 . & d. & tra e. & g. & non si possa cantare, senza interponerui una
. & d. & tra e. & g. & non si possa cantare, senza interponerui una chorda mezana; & ch'ello non sia interuallo Diatonico, questo non li consentirò mai; per
cioche se 'l si canta la Diatessaron senz'esser tramezata d'alcun'altro suono, & in un solo
Interuallo, & questa non faccia alcuna uarietà di Genere; il simile etiandio bisogna che
auenga, quando si canta il Ditono, ò lo Semiditono con un solo Interuallo; percioche nō
ui sò uedere, ne ritrouar maggior ragione, c'habbia l'un più che l'altro de questi Interual
li; essendo tutti consonanti. Anzi se 'l si douesse hauer qualche rispetto ad alcun di loro;
che, come più consonanti, si potessero cantar tramezati & non tramezati, & non fa-
cessero uarietà alcuna di Genere, come forse questi potrebbono dire della Diatessa-
ron; percioche da gli Antichi era tenuta la Prima consonanza; maggiormente do-
urebbe hauer questo priuilegio il Ditono & lo Semiditono; percioche tra i Mo-
derni fin'hora la Diatessaron da molti non è posta nel numero delle Consonan-
ze; come sono la Diapason & la Diapente; ma si bene il Ditono & lo Semiditono.
Et che questo sia uero, uedete questi due Interualli consonanti, che scambieuol-
mente tanto si pongono nella parte graue delle nostre compositioni l'uno sotto, ouer
sopra l'altro, quanto nell'acuto; il che non si fà della Diatessaron con la Diapente; per-
cioche questa sempre si pone sotto la Diatessaron, & questa le stà di sopra; oueramente
costumiamo di porle sotto il Ditono, ò lo Semiditono. Io uoglio dire, disse il Merulo,
una parola Messere, & poi seguitarete. Ditemi per uostra cortesia; di che Genere fanno
costoro, che sia il Tritono, il Semidiatessaron, la Diapente superflua, la Semidiapente, &
altri simili Interualli saluatichi, i quali non sono consonanti, ch'essi pongono nelle lor
compositioni? Voleua anch'io à punto dimandarui, soggiunse il Viola; Di che Genere
li fanno. Dicono, rispose egli all'uno & l'altro; che sono di un Genere misto, questi ga-
page 93 lant'huomini; ma non conoscono però la sua mistura. Vdita questa Conclusione, dissi;
Horsu Messere; lasciamo hormai queste cose da un canto, & torniamo al nostro proposi
to, che sarà cosa più utile: & sarà la Definitione del minimo Interuallo rationale, che si
troua nella Musica, il quale è chiamato Comma; onde diremo.
DEFINITIONE XXV.
chiamano etiandio i Grammatici una parte dell'Oratione. Disse allora il Meru-
lo; Questo nostro Comma non s'assimiglia à quello de gli Antichi, per quel ch'
io hò potuto uedere. Non solamente, dissi; non s'assimiglia nella proportione; ma ne an
co nella origine; percioche il Comma antico è quello, per il quale il Tuono sesquiottauo
è maggiore di due loro Semituoni minori, ouero è quella differenza, che si troua l'Α'πο-
τομὴ & il Λεῖμμα; & è contenuto dalla proportione Super. 7153. partiente. 524288. come
porta la natura di cotal cosa; ma quel, che hò definito, è contenuto d'altra proportione;
come al suo luogo son per dimostrarui. Et è differente per la origine, il che ci manifesta
la definitione. Disse allora M. Adriano; Ci direte cosa alcuna de i loro Schisma & Diaschis
ma? poi ch'io uedo che procedete per un'altra strada fuori di quella che faceuano gli An-
tichi. Dirouui gli risposi; & questo sarà il luogo; per non andare più in lungo: essendoche
lo Schisma nasce dal Comma, & lo Diaschisma del Semituono minore, come udirete.
Diremo adunque,
DEFINITIONE XXVI.
de gli Antichi? A' questo soggiunsi; Quantunque si habbia da intender di quel-
lo de gli Antichi; percioche da loro sono uenuti questi termini, & queste diui-
sioni; tuttauia non uoglio che facciamo tra 'l nostro & il loro alcuna differenza; ancora
che quello sia molto differente da questo di proportione; pur che ui dimostri quello, ch'
io intendo di dimostrarui al suo luogo. Sopra di questo Soggiunse M. Claudio; Che uuol
dire ueramente Schisma? Σχίσμα, risposi; è uoce Greca, & uuol dire Diuisione; percio-
che, come hauete udito nella sua definitione, gli Antichi faceuano due parti equali,
ouer l'intendeuano del Comma, & ciascheduna di esse chiamauano Schisma. Stà bene,
disse M. Adriano; ma che sarà poi lo Diaschisma? Quello, che ui hò detto di sopra, rispo
si; il quale diffiniremo à questo modo.
DEFINITIONE XXVII.
pur del nostro? Sete molto diligente Messere, gli dissi; Ma qui non uoglio far dif
ferenza alcuna; percioche importa poco hauendoui à dimostrar solamente, che
le sue diuisioni sono Irrationali; essendoche non si possono denominar con Numeri deter
page 94 minati & rationali; ma con irrationali & sordi. Et realmente le loro diuisioni non posso-
no farsi se non col mezo della Geometria; cioè, con l'aiuto d'un'istrumento Geometri-
co, come ui dimostrerò quando sarà il tempo. Ma quel che fin'hora hò detto ui potrà es
sere à bastanza intorno alle Definitioni; percioche uoglio, che ueniamo alle Proposte.
Non sarà fuori di proposito, aggiunse il Sig. Desiderio; non hauendoci altro da dire so-
pra questi Principij; però incominciate da quello, che ui torna commodo, che noi ui a-
scoltaremo attentamente. Voi dite bene, risposi; però ascoltate la prima Proposta, la
quale sarà,
PROPOSTA
PRIMA.
sonanza.
secondo la Decimanona del primo nostro Ragionamento, dal c. Harmonica-
mente in due parti in a. c. & in c. b. diuisa. Dico di tal diuisione nascer la conso-
nanza Diapente & la Diatessaron; & lo prouo. Perche a. contiene il c. & la sua
metà; però, per la Quinta definitione di heri, a. co 'l c. uiene ad essere interuallo Sesqui-

per l'istessa definitione, dico c. b. esser'interuallo Sesquiterzo. Ma perche, per la Nona
& decima definitione d'hoggi, la Sesquialtera è la forma della Diapente, & la Sesquiter
za è quella della Diatessaron; però dico a. c. esser la Diapente, & c. b. la Diatessaron, le
quali nascono dalla diuisione della Diapason a. b. Harmonicamente fatta, secondo che
era 'l proposito di dimostrarui. Ancora che queste cose siano palesi al senso, disse Messer'
Adriano; non sono però considerate per il uerso che uanno; Percioche se bene io sò, che
una Diapente & una Diatessaron aggiunte insieme fanno una Diapason; tuttauia non
sapea, che fussero parti della Diapason; & che nascessero dalla sua diuisione Harmoni-
camente fatta, come hora hauete dimostrato. Se ben tutte ui erano note; Messere, gli
dissi; non però le sapeuate dimostratiuamente, & per le lor cagioni; però ascoltatemi,
che à poco à poco uerrete à sapere il tutto. Onde auertite; che,
PROPOSTA II.
fuori; non dà alcun'Interuallo, che sia consonante.
per la Decimasesta del giorno passato, sia raddoppiata tra c. a. & b. & siano a. &
b. numeri semplici, & d. sia numero composto di Numero & Parte; & tra c. & a.
si troui quell'istessa proportione, che si troua tra a. & b. Dico, che gli estremi termini c.
page 95 & b. di tal raddoppiamento non danno consonanza alcuna. Imperoche, non vi essendo
consonanza, che non sia della prima, ò della seconda maniera; & hauendo cotali Con-
sonanze; per la Prima & per la Seconda Definitione di questo ragionamento; le forme lo-
ro tra i numeri, ò termini, che sono le parti del Senario, col primo numero Cubo; i quali
sono Numeri semplici; poi che c. numero & parte uiene ad esser numero Composto; ne
segue che tra c & b. non ui possa cascare forma d'alcuna consonanza. Ma perche c. nu-

però dico, che Raddoppiata qual si uoglia semplice consonanza; ne i suoi estremi non dà
alcun'interuallo, che sia Consonante. Et perche, per la Ventesimaterza del ragionamen
to del giorno passato; raddoppiato l'interuallo Duplo, costituisce il Quadruplo; & per
l'Ottaua definitione d'hoggi, il Duplo è la forma della consonanza Diapason; &, per la
Quarta decima, il Quadruplo è quella della Disdiapason; però raddoppiato l'interuallo
della Diapason ne gli estremi produce la Disdiapason; la quale, per la Settima & per la
Quartadecima nominata definitione; è interuallo . Raddoppiata adunque
qual si uoglia semplice consonanza dalla Diapason in fuori, ne i suoi estremi non dà al-
cun'Interuallo, che sia consonante. Et questo è tutto quello, che secondo la proposta,
ui douea dimostrare. Onde passarò à dirui, che
PROPOSTA III.
b & cd. esser collocate tra le maggiori Superparticolari. Molteplico adunque,
ò raddoppio; per la Decimasesta del giorno passato, l'interuallo ab. & lo cd.
di maniera, che ne uenga eb. due Diapente, & fd. due Diatessaron. Et per-
che eb & fd; per la Precedente; non fanno alcuna consonanza; però dico; per la Prima
definitione d'hoggi; che ne eb & fd; simigliantemente, ne anco ab & cd; per la Vnde-
cima proposta di hieri; possono tra le Molteplici esser collocate. Ma ab. Diapente, & c
d. Diatessaron; per la Sesta definitione d'hoggi; sono Consonanze semplici, & le forme lo
ro sono collocate tra le Molteplici, ò Superparticolari, & non tra altri Interualli; Adun-
que ab & cd. non hauēdo luogo tra le prime, di necessità l'haueranno tra le seconde; che
sono le Superparticolari. Ma la Diapente & la Diatessaron; per le loro Definitioni; han-
no le forme dalla Sesquialtera, & dalla Sesquiterza proportione; delle quali, per l'Otta-
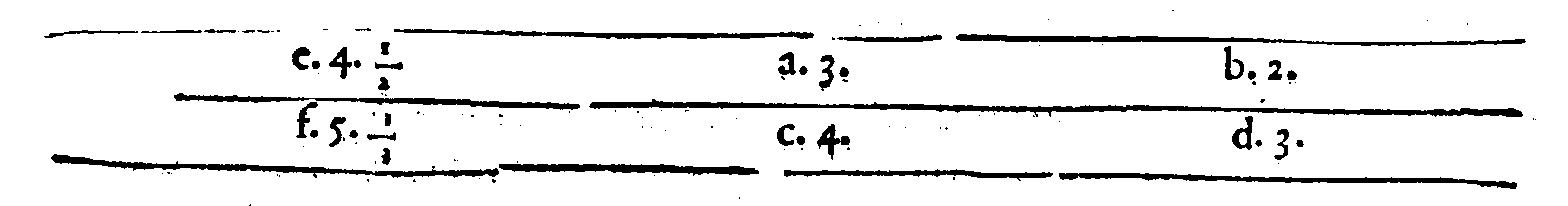
la Diatessaron sono collocate tra le maggiori Superparticolari; come ui douea dimostra-
page 96 re. Piu oltra. Per la Decimasettima proposta del giorno inanti, ui dimostrai, che l'Interual-
lo Duplo nasce dalla congiuntione dei due maggiori Superparticolari; cioè, Sesquialtero
& Sesquiterzo. La onde, essendo, per la Nona definitione d'hoggi, la Sesquialtera forma
della Diapente; & per la Decima, la Sesquiterza forma della Diatessaron; seguita che la
Diapente & la Diatessaron siano collocate tra le maggiori Superparticolari; come dice la
proposta. Et questo è tutto quello, che dimostrar ui douea. Et perche ui uedo attentamen
te ascoltarmi; seguitarò dicendo; che
PROPOSTA IIII.
di quello, che poponeste nella Prima proposta. Come adunque può stare, che
di queste due consonanze si componi la Diapason, se hauete detto prima che
dalla diuisione di essa nascono le due altre? Questo non è inconueniente (gli dis-
si) à dire, & anco ad essere; come dissi heri; che di una cosa diuisa in più parti, se ne compo
ni in'altra & quell'istessa, di quelle parti istesse. E' ben uero; ei rispose; ma genera fastidio
udire, che questi due termini cōtrarij possino stare insieme Diuiso & Cōposto, in un'istes-
so soggetto. Sono possibili, dissi io, quando sono considerati secondo diuersi rispetti. Ma
ueniamo al nostro proposito. Vi dimostrai nella Precedente, che la Diapente & la Dia-
tessarō sono collocate nelle maggiori Superparticolari. Dimostrai ancora heri; per la De-
cimasettima; che l'Interuallo Duplo si sà de due Massimi superparticolari; la onde essendo
l'Interuallo Duplo la forma della Diapason; & la Sesquialtera quella della Diapente; &
quella della Diatessaron la Sesquiterza; seguita che la Diapason nasca, quando la Diapē
te con la Diatessaron insieme si congiungono; come dice la proposta. Et questo è quello,
che bisognaua dimostrare; al che aggiungeremo:
COLLORARIO.
saron; & cauatane la Diatessaron resti la Diapente.
tra dimostratione: percioche se da ab. interuallo della Diapason; come hauete
dimostrato nella Prima; leuaremo ac. Diapente; ne resterà senza dubio cb. Dia-
tessaron: come anco, se da ac. si leuarà cb. Diatessaron, necessariamente resterà ac.
Diapente. Questo è uero, risposi, & si tocca con le mani; onde uerrò all'altra proposta;
la quale sarà questa.
PROPOSTA V.
d'hoggi, & per la Terza del primo la Dupla la sua proportione; & sia oltra di que-
sto c & b. tale Interuallo raddoppiato. Dico a & b. essere interuallo Molteplice.
Per la Ventesima terza di heri; l'interuallo Duplo raddoppiato costituisce il Quadruplo;
ma il Quadruplo, per la Quarta definitione di heri; è Molteplice; adunque raddoppia-
page 97
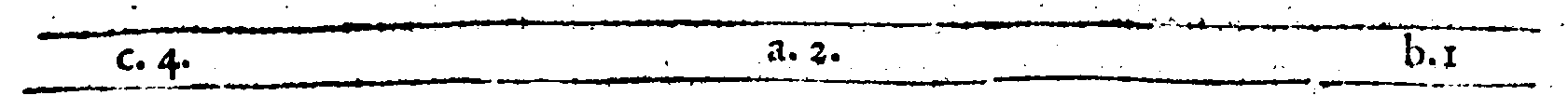
lo molteplice; però a & b. Interuallo raddoppiato in c & b. per la Sesta proposta di heri; fa-
rà etiandio molteplice. Ma tra a & b. ui è l'Interuallo della Diapason; adunque (come
dimostrar ui douea) tale Interuallo è molteplice. Ancora; per la Decimasettima di he-
ri, habbiamo; che l'Interuallo Duplo nasce dalla congiuntione de i due maggiori super-
particolari; Sesquialtero & Sesquiterzo. Et per la Precedente, habbiamo dimostrato; che
la Diapason nasce dalla congiuntione della Diapente con la Diatessaron; lequali hanno
le forme loro dalle due nominate proportioni, ouero interuallo; Onde non è dubbio, es-
sendo l'interuallo Duplo (per la Quarta definitione di heri) Molteplice; che anco l'inter-
uallo della Diapason sia molteplice; poiche, per la Definitione, la Dupla è la sua vera for-
ma. Ancora; Per la Ottaua definitione d'hoggi, l'interuallo della Diapason, ò uogliamo
dire la Diapason cononanza è contenuta dalla Dupla proportione; ma, per la nominata
Quarta definitione di heri; tale interuallo è Molteplice; adunque l'interuallo della Dia-
pason è Molteplice; come, secondo quello, che ui hò proposto, vi douea dimostrare. Stà
bene, disse M. Francesco; ma ditemi perche non dimostrate, che l'interuallo della Diapa-
son sia Duplo? Perche già lo sapete per uia della sua Definitione, risposi; che dice; che è
contenuta nella sua uera forma dalla proportione Dupla. Et già vi hò detto, che le De-
finitioni sono Principij, i quali non si possono in quella Scienza, della quale sono Princi-
pij, dimostrare; altramente non si potrebbono dire Principij, però non aspettate, ch'io
ue lo dimostri. Soggiunse allora M. Claudio; Poniamo, che non haueste detto, che la
forma della Diapason fusse la proportione Dupla; la potreste uoi allora dimostrare? Si be-
ne, dissi. Fatemi adunque di gratia questo fauore; soggiunse egli; dimostratecela. A que-
sto gli dissi; vi uoglio satisfare al tutto. Vi hò già dimostrato; che questo interuallo è Mol-
teplice; non è cosi? Cosi è in fatto replicò M. Claudio; Adunque, dissi io; ouero ch'ello
è Duplo, oueramente maggiore del Duplo. Ma perche il giorno auanti hò dimostrato,
per la già nominata Decimasettima proposta, l'interuallo Duplo nascere dalla congiun-
tione de i due Massimi superparticolari; però se l'Interuallo è maggior del Duplo; il Du-
plo non si componerebbe solamēte de due interualli Superparticolari, ma de più de due.
Nondimeno, hò dimostrato nella Penultima, che la Diapason si compone de due Con-
sonanze & superparticolari Interualli, che sono la Diapente, & la Diatessaron; adunque
la Diapason non è maggior dell'interuallo Duplo. Et se non è maggiore, adunque è Du-
plo; come vi douea dimostrare, secondo la uostra richiesta. Siamo benissimo satisfatti;
disse M. Claudio; & ui ringratiamo. Verremo adunque ad un'altra proposta, soggiunsi;
la quale sarà.
PROPOSTA VI.
fatta.
mine Harmonicamente in due parti; in ac. & in cb. Dico da tal diuisione nasce-
re il Ditono & lo Semiditono. Onde perche a. contiene c. & la sua Quarta par-
te; però, per la Quinta definitione di heri, ac. uiene ad essere Sesquiquarto; Ma il
Sesquiquarto, per la Vndecima definitione d'hoggi, è la forma del Ditono; adunque a &
c. uerranno ad essere il Ditono. Ancora; perche c. contiene il b. & una sua Quinta parte;
page 98 però dico cb. essere, per la Quinta definitione nominata, interuallo Sesquiquinto. Ma lo
Sesquiquinto, per la Duodecima Definitione d'hoggi, è la Forma del Semiditono, adunque

del primo, diuiso Harmonicamente in un ditono & in un Semiditono; però dico, ch'el
Ditono & lo Semiditono nascono dalla diuisione Harmonicamente fatta della Diapen-
te. Et questo è quello, che secondo la Proposta douea dimostrarui.
COROLLARIO.
parti.
Dimostratione chiarisce il tutto. Onde si uede M. Gioseffo, che quello che uoi
dite, è vero in effetto; che dalla diuisione della Diapason nelle sue parti, nascono
gli altri Interualli, che seruono alla Musica; cosa, che mai più hò inteso da altri, che da
uoi. Ma che ci proporrete hora da dimostrare? Subito soggiunsi; Che
PROPOSTA VII.
piato, & sia a & c. due Ditoni. Dico ab. ouer bc. esser'Interuallo Super-
particolare. Et perche ac. per la Seconda di questo; è impossibile, che fac-
cia consonanza alcuna; però ac. non può esser Molteplice, ne meno per la
Vndecima del passato ragionamento ab. ouer bc. sarà Molteplice. Ma per la Sesta de
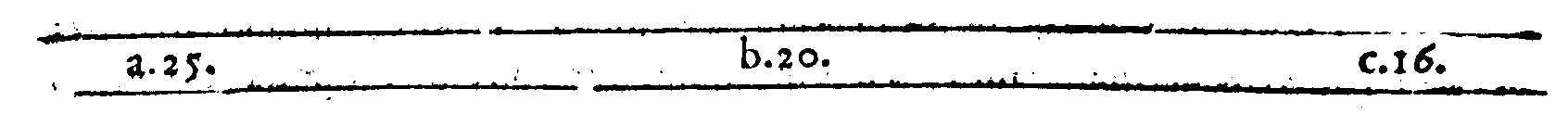
i Molteplici, ouer tra i Superparticolari; però se ab. ouer bc. non è Molteplice; bisogna
necessariamente, ch'ella sia Superparticolare. Ilche è quello, che vi douea dimostrare.
Allora il Viola; Stà bene, disse, Hauete detto del Ditono; ma come si farà à prouar, che 'l
Semiditono sia anche lui Superparticolare? Si tenerà l'istesso ordine, soggiunsi; & si use-
ranno le ragioni istessse, che habbiamo usate nel Ditono; raddoppiando 'l Semiditono; co-
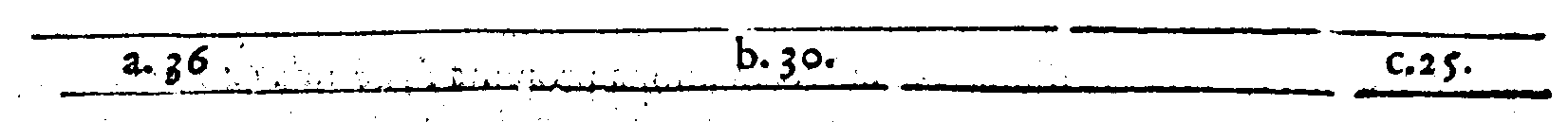
verrò all'altra, che segue; la quale sarà questa.
page 99
PROPOSTA VIII.
mente.
uiene, ch'in tutte le Diuisioni, fatte fin'hora harmonicamente, hauete sempre
pigliato la Parte maggiore della diuisione precedente, & non minore? Perche
la minore, dissi non dà quelli Interualli, che fanno al proposito, ne consonanti, ne anco
dissonanti; come da questo potrete comprendere; che diuidendosi la Diatessaron harmo-
nicamente in due parti, dirò cosi; ne uengono due Interualli, de i quali il maggiore è con-
tenuto dalla Sesquisesta, & lo minore dalla Sesquisettima proportione; che se ben sono
Superparticolari, non fanno però Consonanza alcuna; percioche i loro termini non so-
no contenuti tra le Proportioni delle parti del Senario, secondo la Definitione; Onde nō
seruono alle nostre Harmonie, essendo che non sono Interualli, per i quali l'uno maggio-
re de i consonanti superi un'altro minore; come sono gli interualli de i Tuoni & Semituo-
ni, & altri ancora, i quali habbiamo definito. Detto ch'io hebbi questo, replicò & disse,
Da che nasce questo? Nasce; risposi; che tali Interualli per loro natura & proprietà non
sono atti à riceuer tal diuisione, che possa produrre i suoi Interualli consonanti; come
fà quello della Diapente; ouer se non sono consonanti, ch'almeno seruino alle modula-
tioni delle cantilene; come quelli, che nascono (come ui dimostrerò) dalla diuisione del
Ditono; il che dico etiandio de gli altri. Questa ragione è molto commodo; soggiūse egli.
Et io per hora (risposi) nō ui sò dir'altro; ma quando ne direte un'altra più particolare, &
più propria; la mia le darà luogo. Ma ditemi per uostra fè; per qual cagione il numero Ter
nario non si può di uidere in due altri numeri, che siano equali? Ei rispose; Per la ragione
istessa c'hauete detto della Parte nominata; però con questa uostra dimanda m'hauete
fatto accorgere, ch'è buona ragione quella, c'hauete addotto; se ben non è propria, essendo
che in uerità altro nō si può dir sopra questo fatto; se non che tali proprietà uenghino dal-
la lor Natura. Seguitate adunque quello c'hauete principiato; percioche di questo resto sa
tisfatto. Sia adunque soggiunsi ab. il Ditono diuiso dal c. harmonicamēte in due parti ac.
& cb. come c'insegna la Decimanona del Primo. Dico da tale diuisione esser prodotto il
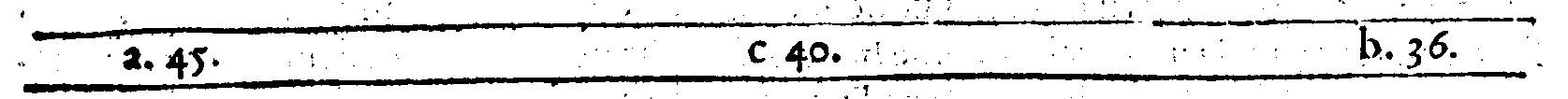
dico, per la Quinta definitione del primo, ac. esser'interuallo Sesquiottauo. Ancora; per
che cōtiene b. & la nona parte di esso b però, per la istessa Definitione, cb. uiene ad esser
Sesquinono. Ma perche ac. è Sesquiottauo, & il Sesquiottauo, per la Ventesima sesta pro
posta di heri, & per il suo Corollario, è la differenza, che si troua tra lo Sesquialtero forma
della Diapente, & lo Sesquiterzo forma della Diatessaron; la quale, per la Ventesima defi-
nitione d'hoggi, è Tuono maggiore; però dico ac. esser Tuono maggiore. Simigliātemēte;
perche cb. è Sesquinono, & questo, per la Ventesima settima proposta del giorno passato,
& anco per il suo Corollario, è la differenza, per la quale la Sesquiterza; cioè, la Diatessa-
ron sopr'auanza la Sesquiquinta, che è il Semiditono; & tale differenza è Tuono minore;
però dico cb. esser Tuono minore. Diremo adunque, che dalla diuisione del Ditono fatto
harmonicamente nascono il Tuono il maggiore & lo minore; come ui douea dimostrare.
Si può egli dimostrare, disse M. Adriano; che 'l Tuono maggiore sia Sesquiottauo, & lo mi
nore Sesquinono. Si può; Messere; & si debbe anco dimostrare; dissi; se bē da quello, che di
page 100 sopra detto habbiamo, tal cosa si possa comprendere; essendo che nella loro Definitione
non ui è posto la lor forma. Allora ei soggiunse; Adunque se 'l non ui rincresce dimostra-
teci cotal cosa. Et io dissi. Voglio satisfarui Messere per ogni modo; onde diremo.
PROPOSTA IX.
l'Interuallo, per il quale la Diapente sopr'auanza la Diatessaron. La onde
essendo, per la Ventesimasesta proposta del primo, tale interuallo Sesquiotta-
uo; com'anco si è detto nella Precedente; ne uiene, che l'interuallo del Tuono maggio-
re sia Sesquiottauo. Simigliantemente, per la Definitione Ventesimaprima di questo
Ragionamento; chiaramente si uede & conosce, che 'l Tuono minore è la differenza,
che si troua tra la Diatessaron & lo Semiditono, di quanto l'un supera l'altro; & già si è
dimostrato nel Ragionamento passato, nella Ventesimasettima proposta & nel suo Corol-
lario, che tal differenza è un Sesquinono; però necessariamente seguita, che l'interuallo
del Tuono minore sia Sesquinono. Et questo è quello, che m'hauete richiesto, ch'io ui
douesse dimostrare. Son satisfatto; disse M. Adriano. Io adunque seguiterò; soggiunsi;
dimostrandoui; che
PROPOSTA X.
Definitione, Quell'interuallo è Superparticolare, ilquale hà i suoi termini in
tal maniera, che 'l loro maggiore cōtenga il minore & di più una sua parte Ali-
quota; l'interuallo del Tuono maggiore & quello del minore, senza dubio
sono Superparticolari; perche, come hauete dimostrato nella Precedente; l'uno è Ses-
quiottauo, & l'altro Sesquinono, & ne l'uno & ne l'altro di essi il termine maggiore con-
tiene il minore & la sua nominata parte Aliquota. Onde posso dire, che questo è quello,
che uoi poteuate dimostrare. La cosa và bene; risposi; però andaremo un passo più auan-
ti. Il perche hauendo espedito di dimostrare, in qual maniera tutti quelli Interualli, che
sono semplici, nascano dalla diuisione harmonica della Diapason, fatta nelle sue parti;
uoglio ch'al presente dimostriamo alcune cose, che vi saranno di molta contentezza l'ha-
uerle uedute; percioche da esse comprenderete, come la madre Natura, Istrumento
del Sommo fattore, sia mirabilissima nel produrre & nell'ordinar le sue cose. Et uede-
rete, che quelle della Musica non sono fatte dall'Arte; ne accascano casualmente; ma
necessariamente sono per lor natura tali; & per tali debbono dal Musico esser considera-
te. Però; accioche incominciate à uedere in quante cose, che sono quasi infinite, l'ordi-
ne delle Consonanze & Interualli Musicali si ritroui; ui proponerò & dimostrerò la pro-
posta, che segue.
page 101
PROPOSTA XI.
monica proportionalità, & anco tra le loro differenze; si trouano le forme de tutte le Con
sonanze musicali.
cagione non hauete cosi detto d'un'altra Consonanza; com'hauete detto della
Diapason? Onde gli risposi in cotal modo; Perche dalla sua diuisione, per es-
ser Prima consonanza, com'hò detto altroue;Cap. 13.
Inst. 1. par. hanno origine tutte l'altre. Et perche
ogn'altro Interuallo minor di lei, è come sua parte; ò maggior, come composto di essa &
d'una sua parte, non è atto à darci tutte queste cose. Vi hò inteso, disse egli; però segui-
tate, ch'io haurò molto caro di ueder questa cosa. Cosi farò Messere, per satisfarui, sog-
giunsi. Siano adunque a & b. minini termini della Dupla, la quale, per la Definitione,

diuisa da e. termine mezano harmonicamente. Et sia etiandio a. la differenza di d &
e. & b. quella, che si troua tra e & c. Dopoi, sia; per l'istessa Decimanona, da f. meza-
no termine posto tra c & d. diuisa secondo la proportionalità Contr'harmonica; di ma-
niera, che simigliantemente a & b. siano le differenze, che si trouano tra df. & fc. & a. sia
la differenza di f. & c. & b. quella di d & f. Onde tra d. e. c. sia l'Harmonica collocata;
& tra d. f. c. la Contr'harmonica; & a. con b. siano le nominate differenze. Dico, che
tra tutti questi termini. a. b. c. d. e. f. si ritrouano le Forme de tutte quelle Consonanze,
che seruono all'uso delle Compositioni moderne. Imperoche d & c. fatta la compara-
tione del Massimo termine al Minimo de i Quattro maggiori; contiene la proportione
Dupla. la quale si troua simigliantemente tra a & b. Onde per la Definitione, tale In-
teruallo contiene la Diapason consonanza. Al medesimo modo il d. contiene e. una fia-
ta & la sua metà; per tanto dico d & e. esser Sesquialtero, & per la Nona definitione di
questo, esser la forma della Diapente. Ancora; perche e. contiene il c. & una sua terza
parte; però dico ec. esser Sesquiterzo; onde la sua consonanza, per la Decima , sarà la Diatessaron. Comparato ancora f con e. si ritrouerà f contenere e. &
una sua Quarta parte; onde sarà la proportione Sesquiquarta; la quale, per la Vndeci-
ma definitione, è la forma del Ditono. Et quella del Semiditono sarà tra d & f. percio-
che il d. contiene f. una fiata & una sua quinta parte; onde nasce, per la Quinta definitio-
ne del Primo, la proportione Sesquiquinta; la quale, per la Duodecima definitione di
questo, è la sua uera forma. Tra c & b. ancora uiene ad esser la proportione Tripla; la
quale è la forma della Diapason diapente; come dalla propria Definitione si può com-
prendere; la quale è Consonanza composta; percioche il d. contiene il b. tre fiate à pun-
to. Et se 'l si farà comparatione tra e & b. si trouerà, che tra quei termini ui è la Quadru-
pla; dalla quale, per la Decima quarta definitione d'hoggi, nasce la Disdiapason; essen-
do che e. contiene il b. quattro fiate & non più. Tra f & b. si trouerà anco la Quintupla;
per la Quintadecima definitione, forma della Disdiapasonditona, poi che f. contiene b.
cinque uolte intere. Et tra d & f. sarà la forma della Disdiapason diapente; per la pro-
page 102 portione Sestupla, che si troua tra i nominati termini. Ma se faremo comparatione di
f. con c. ritrouaremo la Superbipartiente terza, dalla quale hà la sua forma; come per
la definitione Decimasettima è manifesto; l'Hexachordo maggiore. Percioche anco
tra f & a. si troua la Dupla sesquialtera, che è la forma della Diapasonditona; com'è pa-
lese dalla Decimanona definitione. Onde è manifesto, che tra i termini della Diapason,
diuisa secondo la proportionalità Harmonica, & Contr'harmonica, & le loro differen-
ze; si trouano tutte quelle Consonanze, che sono possibili da ritrouarsi, le quali à tempi
nostri i Musici pongono nelle lor Compositioni; come ui douea dimostrare. Disse qui
il Viola; Non hauete già fatto mētione alcuna dell'Hexachordo minore, ne della Diapa-
son col Semiditono, & de molt'altre Consonanze, che si pongono ne i Contrapunti. Al-
lora soggiunsi; Quando hò fatto mentione de tutte quelle Consonanze semplici, che si
possono porre in atto, & che nascono secondo l'ordine naturale de Numeri harmonici;
imaginateui, ch'io habbia fatto anco mentione di ciaschedun'altra Composta, & de tut-
te quelle, che nascono da un'ordine accidentale; come sono quelle, che nominato m'haue
te. Percioche (com'hò detto nelle Istitutioni1. par. c. 16.) tra questi termini, che ui hò mostrato in que
ste due Proportionalità congiunte, si ritrouano tutte le Parti del numero Senario; le quali
contengono in atto & in potenza tutte quelle Consonanze, che si può l'Huomo imagi-
nare, che possano seruire alla Musica. Me ne ricordo & resto satisfatto, soggiunse il Viola.
Che dite uoi Messere di questi cosi belli discorsi & dimostrationi? Veramente ch'io stu-
pisco; rispose M. Adriano; ne mai credeua di ueder tante cose, & tanto diuerse, & anco tan
to belle della Musica, com'io ueggio; del che ne sia lodato Iddio. Ma uoltatosi uerso di me
soggiunse; non ui uoglio più interrompere col mio parlare M. Gioseffo; percio che deside-
ro, che uoi seguitiate; essendo che u'ascolto molto uolentieri. Vi uoglio anco dire Messe-
re; risposi; che noi potremmo hauere quāte delle già dimostrate Proportionalità congiun
te piaceranno à noi; se molteplicheremo i termini d. f. e. c. per qual numero uorremo; per-
cioche, per la Quinta dignità, haueremo un'ordine, il quale contenerà quelle Proportio-
ni istesse, che sono contenute tra i primi termini. Et cosi si potrà hauer prontissimamente
quante proportionalità Harmoniche & Contr'harmoniche congiunte insieme, che sarà
dibisogno dhauere. Ma poi che siamo in questi dolci ragionamenti, ui uoglio dimostrar
l'istessa cosa, che u'hò dimostrato con un'altro mezo; accioche conosciate, quanto questa
Scienza si piena di belli concetti, & di dolcissime speculationi. Statemi adunque ad udire.
PROPOSTA XII.
aggiunto à se stesso, contiene le forme de tutte le Consonanze; tra le quali si trouano le
Due prime maggiori semplici, esser diuise in Due semplici minori.
rete al uostro piacere la dimostratione. Hauete ragione risposi. Notate adunque,
ch'io intēdo un Numero esser'aggiunto à se stesso Cinque fiate, quando primie-
ramete se gli aggiūge una fiata un'altro numero à lui equale dopoi due fiate, oltra di que
sto tre fiate, quattro anco, & ultimamente cinque fiate; onde nasce l'Arithmetica Progres-
sione; La onde dico, ch'ogni Progressione arithmetica, la quale incomincia da qual nu-
mero si uoglia aggiūto à se stesso in ꝗsto modo, cōtiene la forma d'ogni Musical cōsonāza.
Et di più ui dico; che le Due prime maggiori cōsonāze semplici; che sono la Diapason &
la Diapēte, ciascheduna per se, si troua in tal Progressione diuisa, alla similitudine dell'Har
monica proportionalità in due Cōsonanze minori. Hora u'intēdiamo benissimo; aggiūse
M. Claudio, seguitate il dimostrarci cotal cosa. Questa è cosa facile; dissi, & che ciò sia uero
page 103 lo vederete. Sia a. il numero, ilquale vogliamo aggiungere Cinque fiate à se stesso, di mo
do che produca l'Arithmetica progressione. Dico, che dobbiamo prima raddoppiare esso
a. & ne uerrà b. Et perche b. è duplo di a. però la Ottaua definitione, ba. contengono la for
ma della Diapason. Dopoi aggiungeremo a. al b. & ne uerrà c. Ma perche c. contiene a. tre
fiate & una il b. con la sua terza parte; però per le Definitioni, ca. è Tripla; & è la forma
della Diapason diapente, & cb. è Sesquialtera, & è la forma della Diapente. Di nuouo ag-
giungeremo a. col c. & ne risulterà d. Manifesta cosa è, che 'l d. contiene a. quattro fiate, &
c. una fiata con la sua terza parte; la onde, per le Definitioni; da. è Quadruplo; & uiene à
contener la Disdiapason; & cd. è Sesquiterzo, & contiene la Diatessaron. Al d. aggiunge-
remo di nuouo a & ne nascerà e. dico e. contenere a. cinque fiate, & esser Quintuplo; &
contenere il d. una fiata & la sua Quarta parte; il perche e & d. è Sesquiquarto. Onde dalle
Definitioni date al principio di questo ragionamento, è manifesto, che tra e & a. si troua la
forma della Disdiapason ditona; & tra e & d. quella del Ditono. Di nuouo aggiungendo
a. con e. nasce f. Onde, perche f. contiene a. sei fiate apunto; & e. una fiata con la sua Quinta
parte; dico, che f & a è Sestuplo, & per la Decimasesta definitione d'hoggi è la forma del-
la consonanza Disdiapason diapente, & fe. è Sesquiquinto, & è la forma del Semidito-
no. Ma perche e. contiene c. una fiata con due sue terze parti; però, per la Sesta definitione
del Primo ragionamento, ec. è terzo, & per la Decima settima di questo;
è la forma dell'Hexachordo maggiore. Oltra di questo; perche il d. contiene il b. due fiate;
però d & b. sono in Dupla proportione, & tale proportione è la forma della Diapason, &
è diuisa (come dice la Seconda parte della proposta) in due parti; in una Diapente cb &
in una Diatessaron dc. Simigliantemente, perche f. contiene il d. una fiata & di più la sua
metà; però dico, per la Definitione, f & d. esser Sesquialtero, & esser la forma della cōsonan
za Diapēte. Essendo poi tramezata da e. dico, ch'ella è diuisa in due parti, l'una delle quali
si troua tra e & d. ch'è il Ditono, & l'altra tra f & e. ch'è il Semiditono; come di sopra si è
mostrato. Ma perche qualchedun di uoi potrebbe dire, che i mostrati ordini non fussero
ordinati in Arithmetica progressione, ui uoglio aggiunger questo di sopr'abondante; che
dalla Vndecima definitione di heri, lo potrete comprendere; che le differenze, che si tro-
uano tra a. b. c. d. e. f. sono equali. La onde essendo tanta la differenza, laquale si troua tra
b & a. quanta quella, che si troua tra c & b. & d con c. e con d. & f. con e. la quale è uera-
mente a. dà segno manifesto, che questi Termini son'ordinati in Arithmetica progressio-
ne; come ui haueua proposto. Adunque Ogni arithmerica progressione, la quale inco-
mincia da qual si voglia numero, aggiunto cinque fiate à se stesso; contiene le forme de
tutte le Consonanze; Et ciascheduna delle due maggiori semplici si troua esser diuisa in
due minori; come v'hò dimostrato. Questa è una bella consideratione; disse il Viola; &
degna d'hauerla in memoria; percioche da tutti non è consideirata cosi minutamente, co-
me la considerate uoi; però ogn'animo uirtuoso ui hauerà da hauere grande obligo, poi
che u'affaticate per giouarli. Lasciamo andar da un canto questo; risposi; & lodiamo
DIO delle sue gratie & doni, che ci concede. Et perche siamo sopra le belle cose, ve ne
uoglio dimostrar'un'altra, che vi piacerà, la quale è degna di tenerla à memoria. Mi
farà molto grato; disse M. Adriano; però date principio. Allora soggiunsi; Perche ui
hò dimostrato, che tra Quattro termini continenti la Diapason diuisa secondo l'Harmo-
nica & la Contr'harmonica proportionalità, & anco, che nella Progressione arithmetica
d'un Numero cinque volte aggiunto à se stesso, si trouano le forme de tutte le Consonan-
ze; ui uoglio hora dimostrare, in qual modo Cinque termini più fiate si possino replica-
re, tra i quali si ritrouino, non solamentele nominate cōsonanze, ma anco il Tuono mag-
giore & lo iminore. Et per dimostrarui questo con qualche intelligenza, douete sapere;
che (come afferma Boetio2. Arith.
cap. 54) gli Antichi hebbero questo parere; che quella fusse una Massi-
ma & Perfetta harmonia, la quale in se contenesse quattro termini l'un dopò l'altro, che
fussero ordinati in tal maniera; che si come poco fà ui mostrai, tra questi Quattro
6. 5. 4. 3, numeri, si trouaua l'Harmonica & la Contr'harmonica proportionalità; cosi
page 104

nica insieme congiunte; di modo che tra 'l Massimo & lo Minore de i due mezani; & tra il
loro Maggiore & il Minimo, fusse la Geometrica; tra 'l Massimo, il Maggior de i mezani &
il Minimo, l'Arithmetica; & l'Harmonica tra 'l Massimo, lo Minor mezano & il Minimo.
Et uoleuano, che questa Massima & Perfetta harmonia hauesse gran forza nella Musica,
& nelle speculationi delle cose naturali; & che non si potesse ritrouar cosa alcuna più per-
fetta di questa medietà; & che contenendosi tra tre Interualli, hauesse presa la natura del-
la Sostanza d'un Corpo perfetto, il quale consta simigliantemente di tre interualli; che
sono lunghezza, larghezza & profondità, ouer'altezza; indotti dall'Harmonia, che si tro-
ua tra le qualità del corpo Cubo; ilquale essendo composto de Dodici lati, Otto angoli,
& Sei superficie; passando dalla lunghezza alla larghezza, & da questa alla profondità,
ouero altezza; equalmente crescendo & facendo il suo progresso da cose equali, & perue-
nendo à ; è tutto proportionato à se stesso: le quali cose tutte sono
veramente degne di gran consideratione. Onde per la conuenienza de tutte queste co-
se poste insieme, la quale è ueramente harmonica; la nominarono Geometrica har-
monia. Ne per altro chiamarono l'Harmonica mediocrità, ò progressione, Proportiona-
lità harmonica, se non per la grande conuenienza, che questa hà con quella. Ma per finir
di dirui, tra questa loro Massima harmonia, diceuano, che erano contenute tutte le sem-
plici Consonanze della Musica, & anco il Tuono; ilquale affirmauano esser misura com-
mune de tutti i Suoni musicali; essendo che uoleuano, ch'ello fusse il più picciolo d'ogn'al-
tro. Et se bene gli Antichi hanno dimostrato questa lor Massima harmonia contenersi tra
Quattro termini, & che tra loro si ritrouassero tutte le semplici Consonanze, che noi hora
page 105 chiamiamo perfette & anco il Tuono; tuttauia nō si ritrouādo in esso quelle Cōsonāze, le
quali chiamiamo Imperfette; che sommamēte sono all'Vdito grate; & da i Musici nelle lo
ro cātilene grandemēte poste in uso; ui uoglio dimostrar ꝗsta medesima Massima harmo-
nia accresciuta al numero de Cinque termini & Quattro interualli, i quali conteneranno
medesimamente nō solo la Geometrica, l'Arithmetica, & l'Harmonica al modo loro; ma
anco la Contr'harmonica, & qual si uoglia consonanza; insieme con le forme del Tuono
maggiore & del minore. Questo, disse M. Adriano; ci sarà molto caro; m'auanti che pas-
siate più oltra, dateci un'essempio di questa loro Massima perfetta & ueramente mirabi-
le harmonia, ui prego; percioche mi nasce di dimandarui un dubio sopra di essa. Io son
contento, risposi; & ui dò lo essempio de questi quattro termini; come uedete qui notato:
onde hauete à sapere, che Tutto quello, che ui hò descritto, intendono per Massima har
monia. Stà bene; soggiunse M. Adriano. Io uedo hora, che tra 12. 9. 6. ui è la propor-
tionalità Arithmetica, & tra 12. 8. 6. si troua l'Harmonica, ouer quella, c'hauete nomi-
nato di sopra Geometrica harmonia; ma per questo non ueggio la Geometrica. Et se è
quella, c'hauete detto di sopra, che si contiene tra 12 & 8; ancora tra 9 & 6; parmi che
questa non sia simile alla Geometrica, c'hauete mostrato nelle Istitutioni.1. par. c. 37. E' uero tutto
quello, che dicete; messere, risposi; ma gli Antichi intendeuano anco questa esser pro-
portionalità Geometrica; perche si assimiglia à quella, ch'io ui mostrai in questa cosa;
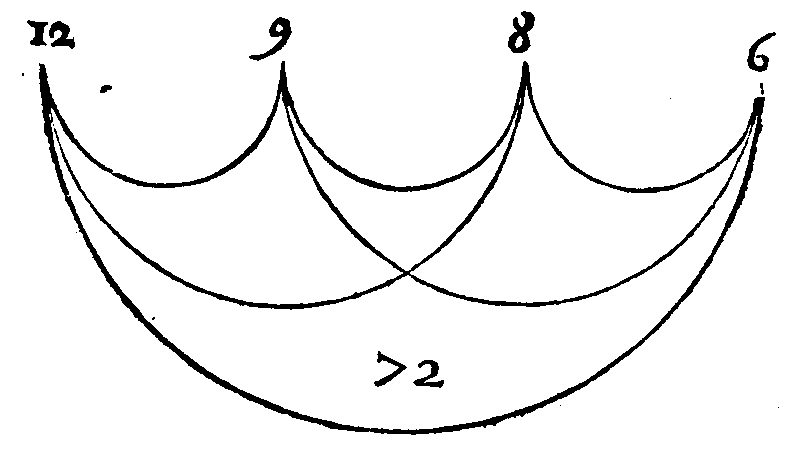
mezani tra loro; come potete uedere; percioche tanto uiene 72. molteplicato il 12. per
il 6. quanto il 9. molteplicato per 8. Ma questa maniera di Proportionalità i nostri Ma-
thematici nominano Discontinua, ò Discreta, come la uogliamo dire; & è (come haue-
te ueduto) costituita tra quattro termini. Quella poi, ch'è posta fra tre solamente,
chiamano Continua; come hauete ueduto nelle due altre. Adunque; soggiunse il Me-
rulo; chiamaremo questa proportionalità Geometrica discontinua, per quello ch'io in-
tendo. Cosi stà bene, risposi. Voglio anch'io (aggiunse il Viola) dimandarui una cosa;
Che cosa è corpo Cubo? del quale n'hauete fatto mentione. Corpo cubo (gli dissi) si no-
mina quello, il quale per ogni uerso si troua equale, & hà le sue superficie ò facciate, equa
li, & equali i suoi lati, & è fatto propriamente come un Dado, à questo modo. Hora
considero hora i Dodici lati, gli Otto angoli, & le Sei superfi-
cie; le quali di sopra hauete commemorato. Et hò finalmente
anche compreso Quattro angoli solidi. Ma ui uoglio ancor di-
re; ch'io non sò uedere in questi termini tanta Harmonia per-
fetta, com'essi dicono, che ui sia. Percioche, se li uogliamo con
siderare inquanto alla compositione; se fussero tirrate quattro
chorde sopra un'Istrumento sotto la ragione de tali proportioni,
& fussero insieme percosse; s'alcun uorrà dire, che facciano Con
sonanza, non che Massima & perfetta harmonia; costui si potrà ben connumerare con
page 106 quelli, che non hanno giudicio delle cose della Musica, perche l'Interuallo, ch'è compre
so tra i numeri, ò termini 9 & 8, è il Tuono; per quanto ci hauete insegnato, il quale
quanto sia perfettamente dissonante, lo dirà uno, che fusse al tutto sordo. Ma se 'l si di-
rà che non considerassero questa Massima harmonia à questo modo, ma in quanto con-
teneua tutte le Consonanze; questo sarebbe anco errore; essendo che (come detto
hauete) in quest'ordine mancano molti Interualli consonanti, iquali appresso de noi so
no in frequente uso. Però bisogna dir, che tale Harmonia non si possa chiamar da que-
sto, ne Massima, ne Perfetta; ma si bene secondo 'l loro modo: percioche contiene so-
lamente tutti quelli Interualli semplici, che appresso di loro erano riputati consonanti.
Voi dite bene M. Francesco, soggiunsi; ma mi penso che gli Antichi non la chiamasse-
ro Massima & Perfetta harmonia solamente per questo; ma ancora perche in se con-
tiene l'Harmonia del Cubo, di sopra da me dichiarata; & perche in lei (com'hò mo
strato) sono insieme aggiunte le tre nominate Proportionalità; percioche mi dò da in-
tendere, che molto ben sapeuano, che l'Tuono non è Interuallo consonante. Et se lo
chiamauano più picciolo d'ogn'altro suono; penso, che haueano rispetto à questo; per-
che essendo 'l Tuono la differenza della Diapente & della Diatessaron, con tal differen-
za ueniuano à misurar gli altri Interualli; essendo che li considerauano come composti
de Tuoni & de Semituoni. Onde lo chiamarono Misura commune; & Minimo de gli al-
tri suoni; rispetto alla Misura, la quale è sempre minor di quella cosa, che da lei uien
misurata. Intendendo però questo sanamente; come il Braccio che misura 'l panno;
ouer l'Vnità, che misura & numera gli altri numeri; percioche altramente non sarebbe
uero, poi che il Semituono è d'esso minore, & come sua parte. Questo credo anch'io;
disse di nuouo il Viola; ma perche non hò altro, che dimandarui sopra di questo, ui es-
sorto à seguitare il uostro ragionamento; & dir quello, che uoleuate. Cosi uoglio fare;
risposi: ma di questo ne ragionerò à Dio piacendo ne i Libri de i miei Sopplimenti.Lib. 8. c. 4.
5. & 6. La
onde douendo seguitar quello che segue, ascoltate la proposta.
PROPOSTA XIII.
scheduna da per sè il Tuono maggiore, & lo Minore, con tutte le Consonanze, tra
i suoi termini & le loro differenze.
proportionalità Harmonica & Contr'harmonica insieme aggiunte. Et sia cd.
Dupla; ce. Sesquialtera; cf. Sesquiquinta; fd. Superbipartiente terza; fe.
Sesquiquarta; & ed. Sesquiterza; alle quali dobbiamo aggiunger l'Arithme-
tica & la Geometrica. Per ritrouar l'Arithmetica, raddoppio, secondo 'l modo mostra-
to nelle Istitutioni;1. par. c. 36. c & d; & ne uiene g & h; i quali, per la Quinta dignità, conten-
gono quell'istessa proportione, che si troua tra c & d. La onde essendo cd. Dupla; gh.
simigliantemente uiene ad esser Dupla. Hora piglio la metà, di g. & h. aggiunti insieme,
& faccio i. Dico hora gi. esser Sesquiterzo, & ih. Sesquialtero; percioche essendo n. la
differenza, che si troua tra g & i; & contenendo g. quattro n. & i. contenendone tre; per
la Definitione, gi. è Sesquiterzo. Simigliantemente; perche i. contiene tre n. & h. ne
contiene due; però, per la Definitione, ih. uiene ad esser Sesquialtero. La onde, di-
co g. i. k. per la Vndecima definitione di heri; esser la ricercata proportionalità Arithme
tica; poiche le differenze, che si trouano tra i termini. g. i. k. sono tra loro equali & si-
mili alla differenza n. Fatto questo raddoppio simigliantemente f & e. & ne risulta k & l.
page 107 Onde dico, che tra g. k. l. h. sono contenute quelle proportioni istesse, che sono collo-
cate tra c. f. e. d. per la Quinta dignità nominata; cioè, gh. Dupla; gl. Sesquialtera; g
k. Sesquiquinta; k h. Superbipartienteterza; kl. Sesquiquarta; & lh. Sesquiterza. Ma
perche tanta è la proportione, che si troua tra g & i; quanta quella, ch'è tra l & h; &
tanto rende moltiplicati gli estremi g & h. essendo che l'uno & l'altro danno 72; però,
secondo che io dichiarai nella Precedente, dico; che tra g & i. & tra l & h. habbiamo la
proportionalità Geometrica. Hauendo ancora mostrato, che gh. è Duplo; per la De-
cimasettima di heri; gl. sarà Sesquialtero, & lh. Sesquiterzo. Certo è, per quello ch'io
hò mostrato, che i & h. è Sesquialtero; il perche, per l'istessa Decimasettima, g & i. uiene
ad esser Sesquiterzo. Se adunque da ih. che è Sesquialtero, leuaremo gi. Sesquiterzo;
per la Ventesima sesta del passato ragionamento, restarà i & l. che sarà Sesquiottauo. Si-
migliantemente; se da gi. Sesquiterzo leuaremo gk. Sesquiquinto, per la Ventesimasetti
ma di heri; uerrà k & i. Sesquinono. Onde si uede, che tra g. k. i. l. & h; sono contenu-
te le forme de tutti gli Interualli consonanti. Et anco quelle del Tuono maggiore & del

contiene ogni Consonanza, & il Tuono maggiore; con lo minore, i quali sono parti
d'esse Consonanze. Laonde hauendo prima dimostrato gh. esser Dupla; per la Defi-
nitione; gh. contiene la Diapason. Ma perche dimostrai gl. esser Sesquialtera; però
gl. contiene la Diapente. Habbiamo ancora detto g & i. esser Sesquiterzo; adunque
g & i. contiene la Diatessaron. Dimostrai ancora kl. esser Sesquiquarto; adunque kl. è
l'interuallo del Ditono. Dichiarai etiandio gk. esser Sesquiquinto; onde dico gk. esser
l'interuallo del Semiditono. Oltra di ciò mostrai i & l. esser Sesquiottauo: adunque i & l.
è l'Interuallo (per la Nona proposta di questo) del Tuono maggiore. Et perche k & i.
è Sesquinono; però (per l'istessa Nona) k & i. è quello del Tuono minore. Più oltra:
ui dimostrai kh. essere Superbipartienteterza; adunque, per la Decimasettima defini-
tione, c'hoggi u'hò mostrato, kh. è l'Interuallo dell'Hexachordo maggiore. Cosi an-
cora dimostrai hm. essere Tripla; adunque hm. è la forma della Diapason diapente.
Dimostrai simigliantemente lm. esser Quadrupla; per consequente lm. è l'Interuallo del
la Disdiapason. Ma quello della Disdiapasonditona è mk. percioche dimostrai tale inter
uallo esser Quintuplo: come etiandio dimostra il g. esser Sestuplo; onde nasce la Dis-
diapason diapente. Dico ancora i & o. essere Duplasesquiquarta, doue ha la sua for-
ma la Diapason col Tuono maggiore appresso. Et si come l & f. uiene ad essere Super-
tripartiente quinta, la quale, per la Deciaottaua definitione d'hoggi, è la forma dell'
Hexachordo minore; cosi kn. è Triplasesquiterza, & è l'interuallo della Diapason ac-
compagnata con l'Hexachordo maggiore. Per concludere adunque potete hora ueder
page 108 dimostrato tutto quello, che si contiene nella Proposta, come far douea. Et di più anco-
ra; hauendoui dichiarato molt'altre cose, le quali uoglio che crediate, che cosi siano; an
cora ch'io non l'habbia dimostrate; percioche quando poi uorrete, ui dimostrerò il tut-
to; acciò mi crediate, & mi habbiate per huomo senza inganno. Disse allora M. Adria
no; Queste cose sono quasi dimostrate; per qual cagione adunque uolete uoi, che
non ui prestiamo fede? Ma questo è stato un lungo tiro; & ui prometto, ch'io
mi son tanto satisfatto, quanto di cosa, che fin'hora habbiate dimostrato; percioche è
cosa molto bella, sottile, ingegnosa, & diletteuole. Il Signor Desiderio anche lui sog-
giunse; Veramente è cosa, che può dilettare; poiche dimostra congiunte insieme mol-
te cose, le quali, oltra l'esser (com'hauete detto M. Adriano) bella & ingegnosa; è anco
piena di dottrina. Ripigliò M. Adriano; Veramente ch'è cosi; ma queste cose non so-
no per ogn'uno; massimamente per quelli, che sono di grosso intelletto; perche oltra
le molte stenti, che farebbono nel uolerle apprendere; potrebbono anco forse impaz-
zire. Dite pure Messere la cosa come ella stà; disse M. Claudio; sono Noci moscate da
non porre auanti i porzi; ma si bene bisogna porli auanti le Ghiande, come cibo loro
proprio. La cosa è uera; dissi; & per dirui, resto molto consolato; poi ch'io uedo gli
amici miei tanto cari & di tanto sano giudicio, come sete uoi, restar satisfatti. Et ciò
mi dà animo di caminar più inanti, & di non temer fatica. Et per questo auanti che ui
dimostri alcun'altra cosa, ue ne uoglio dimostrare una molto bella, ingegnosa, & forse
(dirò cosi) anche noua; Però state ad udire.
PROPOSTA XIIII.
retta linea da un'angolo di esso Quadrato sopra il lato opposto; di modo che lo di-
uida in due parti equali; tra le linee de i lati de i Parallelogrammi, fatte da segamenti della retta, nasceranno tali parti, che paragonate l'una con l'altra, ci
daranno le forme de tutte le consonanze Musicali.
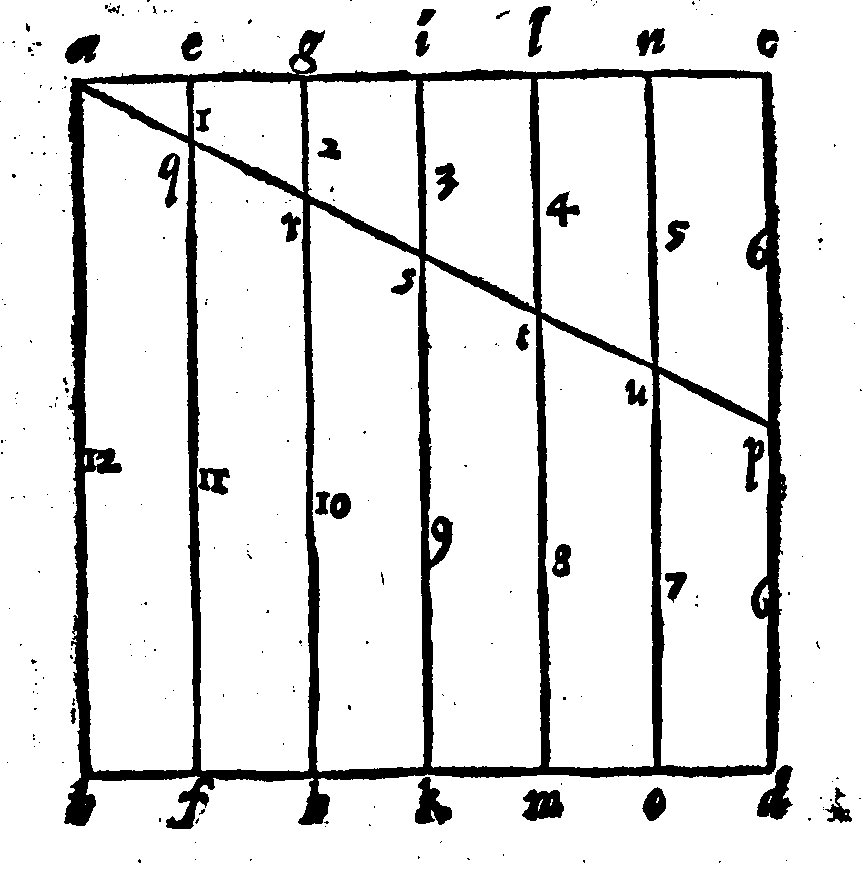
grammi equali a. b. e. f: e. f. g, h: g. h. i. k: i k l. m: l. m. n. o, & n. o. p. q. di maniera
che ciascun di loro sia la Sesta parte di tutto 'l Quadrato, a. b. c. d. Fatto que-
sto tiraremo dall'angolo a. la linea ap. di modo che tagli la cd. in due parti
equali in punto p. & sia cp. la metà intiera di cd. & il simile sia pd. Et la ef. uenga di-
uisa dalla ap. in due parti; cioè, in eq. & qf. la gh. in gr. & rh: la ik. in is. & sk: la
lm. in lt. & tm: & ultimamente la nq. in nu. & uo. di maniera che eq. uenga ad esser
la sesta parte dell'intiero lato di ciascun parallelogrammo; gr. due: is. tre: lt. quattro:
nu. cinque; & cp. ouer pd. sei. Et di nuouo: uo, uenga ad esser sette parti: tm otto:
sk. noue: r. h. dieci: qf. undeci; & ab. dodeci. Dico hora, che tra le parti de i lati ef.
gh. ik. lm. no. & cd. fatte da i segamenti della ap; & tra 'l lato ab. ritrouaremo le for-
me de tutte le Consonanze musicali. Percioche essendo ab. alla cp. ouer pd. Dupla; & la
Dupla, per la Definitione, la forma della Diapason; seguita, che ab. & cp. ouer. p. d. sia
la forma della Diapason. Et perche ab. contiene tutta la tm. & la sua metà; Però,
per la Definitione, queste sono in proportione Sesquialtera. Ma se la Sesquialtera,
per la Definitione, è forma della Diapente; adunque ab. & rm. contengono la Diapen
te. Ancora perche ab. contiene una fiata sk. & una sua terza parte; però ab. & sk.
contengono la Sesquiterza; essendo poi questa proportione la forma della Diatessaron;
seguita, che ab. & sk. sia la sua forma. Di più rh. & tm. sono in Sesquiquarta pro-
portione; percioche rn. contiene tm. & la sua quarta parte; essendo la Sesquiquarta
forma del Ditono; seguita che rh. & tm. sia la forma di esso Ditono. Oltra di que-
sto; perche ab. contiene rh. & di più una sua Quinta parte; però, per la Definitio-
ne, dico ab. & rh. esser Sesquiquinta; La onde essendo questa proportione la forma del
Semiditono; consequentemente ab. & rh. uiene ad esser la forma di questo Interuallo
consonante. Et perche sk. contiene tm. con una sua ottaua parte; Però dico, sk. &
tm. esser Sesquiottauo. Ma essendo, per la Nona di questo il Sesquiottauo la forma
del Tuono maggiore; però diremo, che sk. & tm. contengono la forma di questo Tuo-
no. Vltimamente (perch'io non uoglio perdere più tempo in dimostrarui tutto quello,
che si potrebbe) dico; perche rh. contiene sk. con una sua nona parte; ih. & sk. esser
Sesquinono. Ma 'l Sesquinono, per l'istessa Nona proposta, è la forma del Tuono mi-
nore; adunque rh. & sk. è la forma del Tuono minore. Et questo è tutto quello, che
sommariamente ui hò uoluto dire, & dimostrare; cioè, che tra queste Parti sono con-
tenute le forme delle Consonanze & Interualli semplici, & le Forme del Tuono maggio
re & del minore, lasciando da un canto il dimostrarui le forme delle Composte; percio-
che sono da se stesse, per quello che fin'hora habbiamo ragionato, conosciute. Onde
quando uorrete da uoi stessi potrete con facilità uedere, che cotali Forme di una in una
tra le già nominate parti si ritrouano; & per più uostra commodità potrete uedere, & far
da uoi stessi le dimostrationi de quelli Interualli, c'hò lasciati; aiutate dalla seguente Tauo
la, ch'io ui propongo; nellaquale trouarete. 45. Relationi di numero à numero, che so-
no le forme de quelli Interualli; à i quali saranno accommodati. Hauendo il Signor De
siderio ueduto cotal cosa, tutto ammiratiuo disse; Veramente che questa è stata una bel-
la inuentione; & si uede, che le proportioni della Musica sono tutte contenute (come
molte fiato hauete detto) nel numero Senario; perche alle proue, & alle Dimostrationi, c'
hauete fatto tante fiate, pazzo in tutto & balordo sarebbe colui, che negar le uolesse. Ma
passate pur innanzi, che ui sò dire, c'habbiamo hoggi hauuto alquante buone lettioni.
Già che hauete fatto mentione del Senario; risposi io ui uoglio anco auertire una cosa,
degna di consideratione; che se uoi porrete mente alle diuisioni fatte del proposto Qua-
drato, ritrouarete in lui non senza gran marauiglia una grande harmonia; Percioche se
lo considerarete diuiso ne i Parallelogrammi, ritrouarete per un uerso il numero Senario;
essendo di esso datto Sei parti; come si può dal Parallelogrammo e. f. g. h.
ouer dal l. m. n. o. imperoche ciascheduno di loro è la Sesta parte di tutto 'l Quadrato
page 110

rio; percioche il Triangolo a. c. p. uiene ad esser la Quarta parte di tutto il detto Quadra
to; come è noto à tutti quelli, c'hanno giudicio delle cose Geometriche; il che ui po-
trei anco facilmente dimostrare; che per non andare in lungo, lascierò à uoi altri questa
impresa. Solamente ui uoglio dire, che diuidendo questo Quadrato in Triangoli della
grandezza del Triangolo a. c. p. ne hauerete quattro, che saranno Orthogonii; cioè, che
haueranno un'angolo retto; com'è l'angolo a. c. p. del nominato Triangolo. Di manie-
ra che da questo potrete chiaramente comprendere, quanta forza habbiano questi due
numeri Quaternario & Senario nelle Musicali harmonie. Voglioui finalmente dire, che
se ui uerranno alle mani i miei Otto libri, ch'io chiamo Sopplimenti Musicali; i quali mol
te fiate ui hò nominati; & piacendo à Dio uederete un giorno & presto in luce, & leggere
te il Cap. 3. del Lib. 3. ritrouarete in questa materia cose che ui piaceranno assai; & forse
non più udite, ma non più di questo. Inteso questo M. Adriano, disse, Ancora io uoglio,
dire, che questa è una bella, sottile, & dotta inuentione; & che ui si potrebbe sopra di
essa far molti belli quesiti, che mi uanno per la mente; & dirui anco, che se haueremo
de queste lettioni, ui prometto ch'andranno per noi ben le cose; Però non ui uoglio più
tenere à bada; onde seguitate pur M. Gioseffo quello, che ci uolete dire. Fin hora Mes-
page 111 sere, gli dissi, habbiamo ragionato intorno quelli Interualli, che nascono dell'harmo-
nica Mediocrità; onde è cosa giusta hormai, che passiamo più oltra, & parliamo de quel-
li, che sono minori de loro, i quali non nascono per cotal modo; ma sono differenze,
che si trouano tra i nominati; come sono i due Semituoni, maggiore & minore, & il Com
ma. Però uederemo hora quali siano le forme loro, & in che Genere di proportioni
siano contenute. Incominciando adunque diremo.
PROPOSTA XV.
proposta disse; In qual modo la dimostrarete M. Gioseffo? Hora lo intenderete
gli dissi, ascoltate; Per il Corollario della Ventesima ottaua di heri, è manife
sto, l'interuallo Sesquiquintodecimo esser la differenza che si troua tra lo Sesquiterzo,
& lo Sesquiquarto; Ma essendo lo Sesquiterzo (come tante fiate hò replicato) la forma
della Diatessaron, & lo Sesquiquarto quella del Ditono, non è dubio, che 'l Semituono
maggiore (per la sua Definitione) uiene ad essere tal differenza. La onde essendo ella
contenuta dalla proportione Sesquiquintadecima; ne seguita ancora, che l'Interuallo
del Semituono maggiore sia contenuto dalla Sesquiquintadecima proportione. Et que-
sto è quello, ch'io ui douea dimostrare. Ogni cosa torna bene disse allora M. Claudio;
Et io seguiterò risposi à dimostrarui; che
PROPOSTA XVI.
Interuallo sia Superparticolare? Perche uoglio con ogni mio potere (risposi) le-
uarui totalmente dalla fantasia; che questo sia quello, che adoperauano gli An-
tichi ne i lor Tetrachordi, & usauano nelle lor cantilene. Non bastaua sapere aggiunse
ancora, che questo che usiamo sia il maggiore, & quello che elli adoperauano era il mi-
nore? Bastaua si, gli dissi; quanto al saperlo ad un certo modo; ma non bastaua al saper
lo semplicemente; acciò non haueste qualche fiata à credere, che 'l loro maggiore & mi-
nore siano simili à i nostri maggiore & minore. La onde ui uoglio dimostrare, che i no-
stri sono compresi da proportioni Superparticolari; essendo che i loro (come hauete
potuto comprendere dalla dichiaratione della Ventesima seconda, & della Ventesima
terza definitione d'hoggi) sono Superpartienti; se ui ricordate. Me ne ricordo & resto sa-
tisfatto; disse il Signor ; però seguitate il uostro parlare; & perdonatemi, s'al-
le fiate interrompo il uostro ragionamento. Questo importa poco; risposi; però ascol-
tate la dimostratione; la quale anderà in questo modo. Quell'Interuallo, del quale il ter
mine maggiore contiene il minore una fiata & una sua parte Aliquota; per la Quinta de-
finitione di heri, è Superparticolare; ma il Sesquiquintodecimo è sottoposto à tal leg-
ge; percioche 'l maggior termine, il quale è 16. contiene lo minore, ch'è 15. una fia-
ta, & di più una sua Quintadecima parte, la quale è detta Aliquota; adunque l'inter-
uallo Sesquiquintodecimo è Superparticolare. Ma perche, per la Precedente; il Semi-
tuono maggiore è compreso da tale Interuallo; però dico, che l'Interuallo del Semituo-
page 112 no maggiore (come dimostrar ui douea) è Superparticolare. Ma passiamo ad un'altra
Proposta; percioche il tutto è chiaro,
PROPOSTA XVII.
quello del Semiditono dalla Sesquiquinta; quell'Interuallo, anco per il quale
il Ditono uiene à superar lo Semiditono, per la Definitione, è il Semituono
minore; ma l'Interuallo, per il quale la Sesquiquarta sopr'auanza la Sesqui-
quinta; per la Ventesimanona proposta di heri; è la differenza, che si troua tra queste due
proportioni; adunque tale Interuallo è la differenza, che si troua tra 'l Ditono & lo Se-
miditono. Ma perche tal differenza è interuallo Sesquiuentesinoquarto; Però si con-
clude, il Semituono minore esser contenuto dalla proportione detta, come bisognaua
dimostrare. Et à questa uoglio, che aggiungiamo, per tener l'ordine, che si è tenuto
nell'altre; che
PROPOSTA XVIII.
giorno passato; che Quella proportione è Superparticolare, la quale hà il suo ter-
mine maggiore di tal maniera, che contenga il minore, & una sua parte Aliquo-
ta. Et perche la Sesquiuentesimaquarta è di tal natura; percioche il suo termine maggio-
re, che è 25. contiene il minore, che è 24. una fiata & una Ventesima sua quarta parte; pe-
rò dico, che la Sesquiuentesima quarta è contenuta nel Genere delle proportioni tra i Su-
perparticolari interualli; ma tale proportione; per la Precedente; è la forma, ouero in-
teruallo del Semituono minore; Adunque tale Interuallo è collocato tra i Superpartico-
lari. Et questo è quello, che breuemente, & succintamente; per non molteplicare in pa-
role; ui hò uoluto dimostrare. Questa cosa è espedita; disse à questo M. Adriano; onde
tocca la uolta ad un'altra. E' cosi Messere; però ascoltate, gli dissi;
PROPOSTA XIX.
no; & cd. quelli del Minore. Continuo, per la Seconda proposta di heri, questi
due Interualli l'un dopò l'altro; molteplicando a in c. & ne uiene e. & a in b. &
ne nasce f. Simigliantemente b. in d. & ne risulta g. Hora; perche e & f. nascono dalla
molteplicatione di c. in a. & in b. essendo ab. Semituon maggiore, per la Quinta dignità

che f. & g nascono dalla molteplicatione di b. in c. & in d. essendo c. et d. Semituon mino
re; dico, per l'istessa Dignità, f & g. esser'etiandio Semituono minore. Et perche e. contie-
ne il g. vna fiata & vna sua nona parte; Però, per la Definitione de i Superparticolari, e.
uiene ad esser con g. Sesquinono. Ma per la Nona proposta di questo, l'interuallo Sesqui-
nono è quello del Tuono minore; adunque e & g. è l'interuallo del Tuono minore. Ma e
& g. sono il Semituono maggiore & lo minore insieme aggiunti; adunque per la Quarta
dimanda; Se 'l si aggiungerà il Semituono maggiore al minore, nascerà il Tuono minore;
come ui douea dimostrare. Hora aggiungerò questo Corollario; che
COROLLARIO.
dal Tuono minore; necessariamente resta l'altro.
proposta, & sarà questa.
PROPOSTA XX.
pi, per quel che si può uedere. Prima volete dimostrare, che 'l Comma hà la sua
forma dalla Sesquiottantesima proportione; dopoi, che questa Forma sia collo-
cata tra i Superparticolari. Onde credo, che farete due dimostrationi. Cosi son per fare
Messere; risposi. Et per incominciar dalla prima, dico; Per la Trentesimaprima di heri fù
concluso; che Se da un Sesquiottauo si uorrà cauare vn Sesquinono, quel che uerrà, sarà
un Sesquiottantesimo. Et, per il Corollario dell'istessa proposta, habbiamo, che tale In-
teruallo è la differenza che si troua tra 'l Sesquiottauo & lo Sesquinono. Ma la forma del
Tuono maggiore, per la Nona proposta di questo, è il Sesquiottauo; & quella del mino-
re, per la medesima Proposta, è il Sesquinono. Et il Comma (per la Ventesimaquinta de-
finitione d'hoggi) è quell'Interuallo, per il quale il Tuono maggiore sopr'auanza 'l mino-
re; però essendo la proportione Sesquiottantesima la forma di tal differēza; Seguita, che 'l
Comma sia cōtenuto dalla proportione Sesquiottantesima. Et perche 'l termine suo mag-
giore, ch'è 81. contiene 80. ch'è il minore vna fiata, & una sua ottantesima parte, la quale
è parte Aliquota; però, per la Definitione de i Superparticolari, la quale è, che quell'in-
teruallo è Superparticolare, del quale il termine maggiore contiene lo minore una fiata,
& una sua parte Aliquota. Seguita (ritrouandosi l'interuallo Sesquiottantesimo sotto po-
sto à cotali conditioni) ch'ello sia collocato tra i Superparticolari. Et questo è tutto quel-
lo, che secondo la proposta dimostrar ui douea. Questo si è inteso benissimo; disse il Viola.
Ma già che siamo à ragionar del Cōma; diteci [[per]] vostra fè; Se 'l si può saper la quātità deter
minata de i Cōma, che sono contenuti ne i Tuoni & ne i Semituoni, che ci hauete dimo-
strato. Et se nō si può sapere, vi [[pre]]go à pigliar ꝗsta fatica, di dimostrarci il vero di cotesta co
sa, se 'l si può fare; acciò leuiate ogni dubio dalle menti nostre. Si può dimostrar benissimo;
risposi; & ui uoglio satisfare; per mostrarui, che quello, c'hò detto nelle Istitutioni2. par. c. 4. in que-
sto proposito, è uero. Ma perche 'l nostro Cōma è molto differēte da quello de gli Antichi;
come ui dichiarai sopra la Definitione Ventesimasesta d'hoggi; & etiādio sono quelli In-
terualli tutti, che sono minori della Diatessaron, dal Tuono maggiore in fuori; ch'appres-
so loro erano tenuti per dissonāti; Però di questo piglierò uolētieri l'assonto; accioche vi
page 114 dimostri questa uerità ne i nostri Interualli, per satisfarui; poiche ne i loro BoetioMusicae li-
bro 3. cap.
15. hà di-
ligentemente dimostrato quel, che si potea dimostrare; oue leggendole potrete il tutto
conoscere. Et accioche vediate, ch'io vi voglio seruire, incomincierò da questo capo, il
quale più vniuersalmente è considerato, & proponerò à dimostrarui questo; che
PROPOSTA XXI.
lib. 3. cap.
14. & 15. uoglia, che questo Tuono
sia minor di noue Comma, & maggior di otto. Onde si uede in questo, che discor
date da lui molto; doue nasce questo, di gratia? Nasce (dissi) che 'l Cōma di Boetio
è maggior del nostro; percioche la proportione Sesquiottantesima; la quale è la forma del
vero Comma; è minor della Super. 7153. partiente. 524288. che è la proportione del Cō
ma di Boetio; come conoscerete dalla dimostratione, onde dico. Sia a & b. la proportione
del Tuono, proposto ne i suoi minimi & radicali termini. Et siano c & d. il Comma, cōte-
nuto ne i suoi minimi termini, ò numeri. Molteplico prima a in c & in d. onde ne viene e
& f. dopoi molteplico c in b. & il prodotto sia g. Dico hora e & f. esser l'interuallo del
Comma; percioche, Ogni numero (per la Quinta dignità) molteplicato in due altri,
qual si vogliano; produce una proportione simile à quella, che tra i due numeri primi si
conteneua. La onde essendo molteplicato c & d per a. non è dubio, che tra e & f. sia quel-
l'istessa proportione, che si troua esser tra c & d. Il simile dico, ch'è tra e & g. percioche a
b. sono molteplicati per il c. onde, si come tra a & b. si troua la proportione del Tuono; co-
si quell'istessa si ritroua, per il detto Commun parere, ò Dignità, tra e & g. Fatto que-
sto molteplico c in e. & d in f. & ne nasce h & i. Simigliantemente molteplico c in g. &
ne uiene k. Dico hora h & i. esser la quantità de due Comma; cioè, del contenuto tra c &
d. & del compreso tra e & f. & hk. esser il Tuono. Di nuouo molteplico c in h. & d in i. &
ne risulta l & m. che sono tre Cōma sommati insieme; & molteplico simigliātemente c. in
k. & ne uiene n. La onde dico, per la Quinta dignità nominata, l & n. esser l'Interuallo
del Tuono. Molteplico ancora c in l. & d in m. & ne nasce o & p. che per le ragioni dette,
cōtiene quattro Cōma; & c in n. & ne viene q. il quale cō o. fà (per le ragioni addotte) l'in
teruallo del Tuono. Vn'altra fiata molteplico c in o. & d in p. & ne risulta r & s. i quali con
tengono cinque Comma; & c in q & nasce t. che con r. contiene simigliātemente il detto
Tuono; come vi potrei di nuouo dichiarare; che, per nō esser lungo, lascio da vn canto; es-
sendo che hormai è cosa à uoi manifesta. Più oltra; molteplico c in r. & d in s. & anco c. in
t. & ne uiene. u. x. y. di modo che tra u & x. sono sommati insieme sei Comma; & tra u &
x. viene à contenersi il Tuono. Fatto questo da capo molteplico c in u. & d in x. & uiene Z
& A. che contengono sette Comma; & molteplico c in y. & il produtto è B. il quale con Z.
cōtiene l'interuallo del Tuono, Quest'ordine istesso tengo, molteplicando un'altra fiata c
in z. & d in A. & c in B. & ne viene C. D. E. La onde dico, che C. D. contiene otto Cōma;
& C. E, il Tuono. Ancora con l'istesso modo molteplico c in C. & d in D. & ne risulta F. G.
che contengono noue Comma; & ancora c in E. & nasce H. il quale insieme con F. contie
ne medesimamente il Tuono. Fin qui vedete chiaramēte, che 'l Tuono è maggior de noue
Cōma. Percioche se 'l si farà comparatione del Numero F. al numero G. & di nuouo di es-
so F. al numero H. essendo 'l G. maggior numero di H. nō è dubio, che sarà anco (per la Trē
tesimasesta del Primo) minor la proportione di F. G. che quella di F. H. La onde essendo
FG. interuallo, il quale cōtiene noue Cōma; & FH. l'interuallo del Tuono Sesquiottauo
ò Tuono maggiore; senza dubio alcuno seguita, che 'l Tuono maggiore sopr'auanza il nu-
mero de noue Comma; come dice la Proposta. Ma per dimostrarui, ch'ello sia minor de
dieci, de nouo molteplico c in F. & d in G. onde ne uiene I & K. i quali contengono dieci
page 115 Cōma. Il perche molteplico anco c in H. & ne nasce L. che con I. simigliantemente, per le
ragioni addotte al tre fiate, contiene il nominato Tuono. Vedete hora, come la cosa và al

masesta nominata ancora, si conclude; che tra I & K. sia maggior la proportione, di quel-
lo ch'è tra I & L. Per il che essendo I & K. dieci Comma aggiunti insieme, & I L. l'inter-
uallo del Tuono; seguita, che maggior sia l'Interuallo de dieci Comma aggiunti insieme,
che nō è l'interuallo del Tuono maggiore. Et ꝗsto è tutto quello, che ui douea dimostra-
re, secondo la proposta. Questa è stata una lunga dimostratione; disse M. Adriano; ma non
già difficile; per il bell'ordine, c'hauete tenuto. Però non hauēdoci altro che dire sopra di
questo; perche il tutto è chiaro; passate più oltra, ch'io son risolto de i Diesis, de i quali i
nostri Moderni compositori segnano ne i loro canti, cō quattro, cinque, & noue Comma;
come nel Cap. 46. della Seconda parte delle Istitutioni hauete mostrato. Io non credo
Messere, gli risposi; che siate stato fin'hora à chiarirui. Ma ascoltate quest'altra ch'io vi vo
glio espedire in quattro parole.
PROPOSTA XXII.
mento, è Interuallo, per il quale il Tuono maggiore sopr'auanza 'l minore; adun-
que il Tuono minore è minor del maggiore per un Cōma. Se adūque il maggiore
è più de noue; com'habbiamo dimostrato nella Precedente, & men de dieci Cōma; il mi
nore (leuatogli un Cōma) verrà ad esser maggiore de otto, & minore de noue; come ha-
uea proposto di dimostrare. Disse allora quasi ridēdo M. Claudio; Queste dimostrationi co
si facili mi piacciono assai; ond'io uorrei, che si potesse procedere in tutte à ꝗsto modo; ma
perche sò, che nō attēdete ad altro, che à facilitar le cose; però non bisogna dirui altro; se
non che seguitate quello, c'hauete incominciato. Passarò adūque dissi à dimostrarui; che
PROPOSTA XXIII.
de Sei.
tenuto nella Precedente. Siano adunque a & b. minimi numeri del Semituono
maggiore, & cd. i minimi del Comma. Molteplico prima a in c & d. & ne uiene e
& f. dopoi molteplico c in b. ne nasce g. Dico hora ef. esser l'interuallo del Comma me-
desimamente; & e con g. esser quello del Semituono maggiore. Percioche, per la Quin-
ta dignità; I termini di qual si uoglia proportione molteplicati per qual si uoglia nume-
ro, rēdono l'istessa. La onde essendo cd. la proportione del Cōma, & essendo l'uno & l'al-
tro de questi due numeri molteplicati per lo a. seguita, che quel che uiene, che è e & f sia
l'istessa proportione, che si troua tra c & d. Il simile dico anco di e & g. percioche moltepli
cati a & b. che sono i minimi termini del maggior Semituono, [[per]] il c. ne uiene e & g. i quali;
per la nominata Dignità; con a & b. sono simili in proportione. Hora molteplico e per a.
& f per d. et ne uiene h & i. & molteplico anco g per c. & ne nasce k. Dico hora, che h & i.

ef. quella d'un'altro; sommati insieme ne risulta h & i. che fanno la proportione di due
Simigliantemente, dico h & k. esser la proportione del Semituono maggiore; essendo che
e. & g. è la proportione del detto Semituono; & essendo l'uno & l'altro de i due termini
molteplicati per il c. per la Dignità già allegata; h & k. uiene à cōtener l'istessa proportio-
ne, che contiene e & g. Di nuouo molteplico h per c. & i anco per d. simigliātemēte k. per
c. & ne risulta l. m. n. Onde dico, ch'essendo (come di sopra hò prouato) h & i. due Comma
sommati con cd il quale è uno lm. uengono ad essere tre Comma, & per la Dignità alle-
gata; essendo h & k. l'interuallo del detto Semituono; molteplicati questi due numeri per
il c. uengono medesimamente l & n. ad esser l'interuallo del Semituono maggiore. Que-
sto stà bene, disse M. Adriano, & non si può negare; ma qual segno mi farà certo, che cin-
que Comma siano minori, & sei siano maggiori del Semituono maggiore? Quell'istesso
Messere, risposi; che ui hò etiandio mostrato nella Precedēte; ilquale ui farò uedere, quan
do sarà il suo tempo. Soggiunse allora egli; Stà bene; seguitate pure. Et io seguitando
dissi. Molteplico hora l con il c. & m con il d. & ne uiene o & p. i quali dico esser l'Inter-
uallo di quattro Comma sommati insieme; per le ragioni addotte di sopra. Percioche
hauendoui dimostrato lm. essere tre Comma, & c. d. un Comma; è necessario, che som-
mati insieme questi Interualli, faciano il numero de Quattro. Ma molteplicato medesi-
mamēte n per c. nasce il q. il quale dico esser con o. il maggior Semituono; percioche (co-
me hò etiādio dimostrato) l & n. che sono i termini dell'istesso Semituono, sono cōmune-
mēte dal c. molteplicati. A' voi dico hora Messere; vedete questi tre termini, ò numeri o.
p. q. i quali sono in tal maniera ordinati l'un dopò l'altro, che 'l maggiore uà in anzi al mi-
nore; ò per il contrario il maggior segue il minore? Lo uedo disse; ma che uolere inferire
per questo? Voglio inferire; soggiūsi; che quando vederete nascere i numeri per altro uer-
so allora sarà segno manifesto, che quello ch'io uoglio dire, & ui hò detto, sia vero. Onde
state auertito, che resto lo uederete. Molteplico adunque di nuouo, seguendo l'istesso or-
dine, c in o. & d in p. & ne risultano r & s. i quali (per le ragioni addotte) contengono cin-
que Comma; come ui dissi; de i Quattro cōtenuti tra o & p. & di uno contenuto tra c & d.
Onde molteplicando ancora c in q. protiene il nominato Semi-
page 117 tuono; il perche si uede (per la Trentesima sesta di heri) che l'Interuallo rs. è minore del-
l'interuallo rt. & per cōsequente cinque Comma esser minori d'un Semituono maggio-
re. Ma se da capo, tenendo l'ordine, che fin'hora si è tenuto, molteplicaremo c in r. & d in
f. ne uerà u & x. che conteneranno; per le istesse ragioni sei Comma; cioè, cinque conte-
nuti tra r & s. & uno contenuto tra c & d Hora molteplicando di nuouo c in t. nascerà y.
il quale con u. contenerà (per le ragioni già tante volte dette) il maggior Semituono. Ma
vedete hora Messere, che questo ordine u. x. y. non è come gli ordini precedenti; percio-
che y. è maggior numero, che non è x. adunque u & y. contengono, per la Trentesima se-
sta nominata, minor proportione, che non contengono u & x. Et per consequente il Se-
mituono maggior è minore de sei Comma, & maggior de Cinque; come, secondo che ui
hò proposto, ui douea dimostrare. Questo non si può negare Messere; disse il Viola. Ma se 'l
Semituono maggiore è più de cinque, & meno de sei Comma; che pazzia è quella di co-
loro, i quali uogliono determinar quello; che la Scienza lascia indeterminato? Veramen-
te è pazzia, dissi. Ma quando ui uoleste anco chiarir per un'altra strada con la prattica, &
ueder di quanta quantità questi Comma, superano, ò sono superati dal Semituono no-
minato; sommando insieme cinque Comma, & cauādo quel, che nasce dalla proportione
del Semituono; vedreste, che ui auanzarebbe la proportione Super. 25406797. partien-
te. 10460353203. Et di tal quantità bisognerebbe dire, che 'l Semituono maggiore so-
pr'auanzasse cinque Comma. Ma se cauarete la proportione del detto Semituono dalla
proportione, che nasce de sei Comma adunati insieme, ritrouarete, che uerrà la propor-
tione Super. 8428209443. partiente. 838860800000. contenuta, com'è l'altra ancora
ne i suoi termini radicali. Et questa è quella quantità, per la quale Sei Comma sopr'a-
uanzano 'l maggior Semituono. Qui soggiunse il Merulo; Questo è per la dimostratione
tanto chiaro; che sarebbe al tutto balordo colui, che lo uolesse negare. Voglio ancora di-
mostrarui (allora soggiunsi) quest'altra in questo proposito.
PROPOSTA XXIIII.
ni del Semituono minore, & c con d. quelli del Comma. Primieramente molte-
plico a in c. & in d. & nasce e & f. dopoi molteplico c in b. & ne uiene g. Dico e &

massima, ò dignità; produce e & f. i quali contengono l'istessa proportione, chè contenu-
ta tra cd. Il simile dico di e & g. che contengono lo Semituono minore; percioche molte-
plicati a & b. che sono i suoi minimi termini, per il c. per l'istessa Dignità, produce e & g. i
quali cōtēgono la proportione cōtenuta tra a & b. Hora molteplico c in e. & di in f. & na-
sce h & i. che cōtengono due Cōma; percioche sono sommati insieme cd & ef. che fanno
tal somma. Molteplico etiandio c in g. & ne uiene k. il quale con h. cōtiene la proportione
di e & g. [[per]]cioche molteplicato il c cō e. & cō g. produce la proportione h & k. simile ad es-
sa e & g. Di nuouo molteplico h per il c. & i per il d. & producono l & m. che cōtēgono tre
page 118 Comma; percioche sono sommati insieme il Cōma cd. & li due h & i. Hora moltiplico k
per il c. & ne uiene n. il quale cō l. cōtiene il nominato Semituono; essendoche da un'istes-
so numero, che è c. sono moltiplicati h & k. La onde si uede, ch'essendo m. maggior nume-
ro di n. per la Trentesimasesta del passato giorno, si troua minor proportione tra lm. che
tra ln. & per cōsequente maggiore è la proportione del Semituono minore, che quella di
tre Comma. Se con quest'ordine istesso moltiplicherò etiandio c in l. & di in m. uerrà o &
p. i quali conteneranno quattro Comma sommati insieme; cioè, i tre l & m & uno colloca
to tra c & d. Resta hora à moltiplicar c. in n. percioche da tal molteplicatione nasce q. il
quale con o. cōtiene il Semituono minore essendoche c. fù molteplicato in l & in n. Et per
che q. è maggior numero, che non è p. però, per la Trentesimasesta nominata, è maggior
la proportione, che si troua tra o & p. che quella che è tra o & q. Ma perche tra o & p. si
trouano sommati quattro Comma, & tra o & q. si troua il nominato Semituono; però cō-
cludo & dico; che maggiore è l'Interuallo, ò quātità de quattro Comma, che non è quel-
lo del Semituono minore. Et per consequente questo Interuallo esser minore de quattro
Comma; come ui douea dimostrare. Io credo, disse M. Adriano, che si come hauete det-
to, che la uerità della Precedente si possa anco ritrouar con la prattica, sommando insie-
me i Comma; & sottrahendoli il Semituono; cosi anco si possa fare il medesimo in que-
sta; percioche da questa & da quella, mi par che si possa cauare una ragione istessa. Cosi
è ueramente Messere, risposi; ne ui uoglio sopra di questo fare altre parole; essendo ch'io
credo, che dalla Precedente uoi siate molto bene istrutto del caso. Allora M. Francesco
disse. Io hebbi sempre quest'opinione, che la Scienza non discordasse punto dalla buona
Prattica; Però di questo non ui è dubio alcuno; & sarà bene, che uoi seguitate qualch'al-
tra cosa. Parmi che qui sia il luogo; soggiunsi; de dirui qualche cosa dello Schisma & del-
lo Diaschisma, auanti che passiamo più oltra, i quali erano considerati da gli Antichi; ac-
cioche di loro ne sapiate ragionare qual che cosa; quando ui tornerà in proposito. Di-
co ui adunque; che
PROPOSTA XXV.
che non si possono descriuere con numeri Rationali; ma si bene con numeri Sor-
di & Irrationali; come diedi l'essempio, se ui ricordate, parlando nelle Istitutio-
ni1. par.
cap. 57. delle proportioni Rationali. Cosi dico esser le proportioni dello Schisma & dello
Diaschisma. Et per uenire alla Dimostratione; Siano a & b termini, ò numeri minimi del
Semituono minore; ouer c & d. quelli del Comma; gli uni & gli altri, per la Decimaotta-
ua proposta di questo giorno; & per la Ventesima etiandio, Superparticolari. Per la No-
na proposta del Primo nostro ragionamento, l'Interuallo superparticolare non riceue
ne uno, ne più termini mezani, che lo diuida rationalmente in due, ne in più parti equa-
li proportionali. La onde ab. & cd. restando in cotali parti in diuisibili; percioche sono
Superparticolari; è impossibile, quando si diuidessero, che le parti loro fussero cognite &
rationali. Onde ne segue; che non si potendo hauer la ragione de tal parti se nō incognite

Definitione di hoggi parti de ꝗsti Interualli, che tali parti siano incognite & irrationali;
page 119 secondo la proposta. Più oltra; nel luogo nominato delle Istitutioni dimostrai; che allora
una proportione costituita ne i termini suoi radicali, si può diuidere in due parti equali;
quādo il suo maggior termine è numero Quadrato, & il minore è la Vnità; percioche al-
lora il Quadrato & essa Vnita sono capaci d'vn termine mezano. Et perche tra a & b. si-
migliantemente tra c & d. non si ritrouano tali conditioni; ancora che a. sia Quadrato, &
anco c. però è impossibile, che ne ab. ne cd. si possa diuidere in due parti equali, delle
quali le proportioni siano cognite & rationali. Ma se pure è possibile; accioche tali par-
ti, le quali sono i due Schisma, & li due Diaschisma congiunti siano noti & rationali ne
i suoi minimi termini, i quali suppono, che siano e. f. g. procederemo in questo modo, di-
cēdo E' manifesto, che essendo lo Diaschisma la metà del Semituono minore, & lo Schis-
ma la metà del Comma; che è fg. & insieme congiunti faciano tutto 'l Semituono mino-
re; ouer tutto il Comma; & eg. sia l'interuallo del Semituono minore, oueramente quel-
lo del Comma. La onde essendo le proportioni ef. & gf. contenute ne i lor minini
termini; ef. simigliantemente è contenuta ne i suoi minimi termini; adunque sono i
minimi termini del Semituono nominato, ouer del Comma. Ma ab. & cd. si ri-
trouano di tal maniera; adunque ef. saranno quei numeri istessi, che sono ab. ouer c
d. cioè, è quell'istesso, ch'è b. ouer d. & g. quello, ch'è b. ouer d. Ma perche ab. & an-
co cd. sono numeri Contrase primi; però, per la Nona definitione di heri, non possono
esser diuisi da altro numero, che dall'Vnità. Onde ne auiene, che ab. & cd. sono rational-
mente indiuisibili. Et che se 'l si farà due parti de tali Interualli, & siano due Schisma, ò
due Diaschisma; tali parti saranno incognite & irrationali; secondo la proposta. Più
oltra; perche quella proportione, che si troua tra e & f. è quella, che si troua anco tra f &
g. adunque e. uiene ad esser numero Quadrato, come è a. ouer c. & g. uiene ad esser la
Vnità, come sono b. & anco d. ma il b. ouer il d. non è Vnità; adunque una cosa istes-
sa è quello, che è Vnità, & quello che non è Vnità. Ilche è ueramente impossi-
bile. Le proportioni adunque de i Schisma & de i Diaschisma non sono cognite & ra-
tionali; ma si bene incognite & irrationali; come ui douea dimostrare. Il perche da que-
sta dimostratione si caua questo Corollario.
COROLLARIO.
primi in
fine.
che sia numero Quadrato; & il minore, l'Vnità; le Proportioni delle sue diuisioni sono in-
cognite & irrationali.
lario, disse; Questo m'ha piaciuto grandemente; & credo anco, che quando i ter
mini della proportione non fussero radicali; come intrauerrebbe nella Qua-
drupla, contenuta tra 8 & 2. & il 2. hauesse forza d'Vnità; allora. 8. uerrebbe ad
essere il numero Quadrato, rispetto ad essa Vnità; & cosi tale proportione dal 4 si farebbe
diuisibile; che ne dite di questo M. Gioseffo? Cosi è; Sig. mio risposi. Ma hauendoui fatto
fin'hora questa cosi lunga digressione; uoglio che ritorniamo al nostro primo proposito.
Onde uoglio che uediamo gli Interualli, che sono maggiori del Tuono, quanti Tuoni &
Semituoni uengono à contenere; poi c'habbiamo incominciato à ueder, quante fiate il
Comma tra gli estremi de i due Tuoni, & due Semituoni; maggiore & minore sia con-
tenuto; acciò riportiate frutto da i nostri ragionamenti. Et per procedere ordinatamente
incomincierò prima da i minori contenuti da minori proportioni, & di mano in mano
uerrò à dirui de quelli, che saranno maggiori. Ascoltate adunque.
page 120
PROPOSTA XXVI.
il quale la Diapente sopr'auanza la Diatessaron; adunque la Diapente è mag-
gior della Diatessaron per vn tuono maggiore. Ancora, per la Ventesima se-
conda; il Semituono maggiore è quell'Interuallo, per il quale la Diatessaron è
maggior del Ditono; adunque la Diatessaron sopr'auanza il Ditono per vn Semituono
maggiore. Ma perche la Diapente sopr'auanza la Diatessaron per un Tuono maggiore, &
la Diatessaron sopr'auanza il Ditono per un Semituono maggiore; per tanto la Diapente
è maggior del Ditono per vn Tuono maggiore, & vn maggior Semituono. Ma per la Se-
sta proposta di questo si è dimostrato, che 'l Ditono & lo Semiditono nascono dall'harmo
nica diuisione fatta della Diapente; essendo 'l Ditono una parte di tal diuisione; seguita,
che 'l Tuono & lo Semituono l'uno & l'altro maggiore siano parti del Semiditono, il qua-
le è l'altra parte di tale diuisione; & che 'l Semiditono contenga un Tuono & vn Semi-
tuono, l'vno & l'altro maggiore; come dice la proposta, & come ui douea dimostrare. Ma
passiamo à dimostrar quella, che segue.
PROPOSTA XXVII.
Desiderio; percioche si uede le parti esser cōtenute nel loro Tutto. Mi piace; sog-
giunse M. Adriano; perche par, che si accordi con quelli, che componeuano
gli Interualli maggiori con i minori. Dite bene Messere, disse M. Claudio, che pare;
quantunque non sia cosi. Hor sù adunque, soggiunsi seguitādo, per dimostrar questa, dirò
in questo modo. Per la Ventesima definitione d'hoggi; il Tuon maggiore è interuallo, per
il quale la Diapente è maggior della Diatessaron; & per la Ventesima prima; il minore
è quella differenza, che cade tra la Diatessaron & lo Semiditono. Ma perche la Diapen-
te supera la Diatessaron per un tuono maggiore, & la Diatessaron sopr'auanza lo Se-
miditono per vn tuono minore; però il Semiditono è superato dalla Diapente per vn
Tuono maggiore & vn minore. Ma, per la Sesta proposta d'hoggi; la Diapente si diuide
harmonicamēte in vn Ditono, & in un Semiditono; adūque il Semiditono sarà vna par-
te di tal diuisione; & l'altra sarà il Ditono, & contenerà due Tuoni; l'vn maggiore & l'al-
tro minore; come dice la Proposta; & come ui douea dimostrare. Oltra di questo, per l'Ot-
taua proposta di questo; il Tuon maggiore & lo minore nascono dalla diuisione harmo-
nicamente fatta del Ditono; adunque il Tuono maggiore & minore, sono parti inte-
grali del Ditono. Ilche cosi essendo, dico che 'l Ditono, secōdo la proposta, contiene due
Tuoni, l'un maggiore & l'altro minore; come ui douea dimostrare. La onde à questa
soggiungerò, seguitando; che
PROPOSTA XXVIII.
è il maggiore, & l'altro è il minore; Et per la Ventesima seconda definitione, la
Diatessaron è maggior del Ditono per vn Semituono maggiore; ma il Ditono &
lo Semituono maggiore reintegrano la Diatessaron; adunque la Diatessaron contiene il
Tuono maggiore & lo minore, & anco il maggior Semituono. Più oltra; Per la Ventesi-
ma sesta proposta; il Semiditono contiene un uono & vn Semituono, l'uno & l'altro
maggiore; ma la Diatessaron (per la Ventesima prima definitione) è maggior del Semidi-
tono per vn Tuono minore; adunque la Diatessaron contiene due Tuoni l'un maggiore
& l'altro minore, con vn Maggior semituono; secondo la proposta, come ui douea dimo-
strare. Il Sig. Desiderio à questo soggiunse; Non contiene adunque la Diatessaron due
Tuoni sesquiottaui, & un minor Semituono; come uoleuano gli Antichi. Al quale rispo-
se M. Adriano; In fatto si uede, che non è, come loro teneuano; se uogliamo che 'l Ditono
& lo Semiditono siano consonanze. Et perche questo è cosa chiara; ascoltate quest'altra;
diss'io; che ueramente non si può negare; che
PROPOSTA XXIX.
saron.
& questo dal nome si può comprendere; siano poi tre maggiori, ouer due mag-
giori & un minore; poi che tra i primi & questi secondi non vi cade altra diffe-
renza, che quella del Comma; il che poco importa. Et ancora che questo sia manifesto
dalla Precedente, essendo ch'un Tuono maggiore & un minore, con un maggior Semi-
tuono sono equali alla Diatessaron; & tre Tuoni sono maggiori de i tre Interualli nomi-
nati; tuttauia uoglio che dimostriamo questo con un'altro modo. Dico adunque prima;
Per la Trentesimaquinta del primo ragionamento fù dimostrato; che Tre interualli Ses-
quiottaui sono più d'un'interuallo Sesquiterzo; Ma, per la Nona d'hoggi, tre Sesquiot-
taui sono tre Tuoni maggiori; & per la Decima definitione, l'interuallo Sesquiterzo è la
forma della Diatessaron; adunque Tre tuoni maggiori, ouero il Tritono; come dir uole-
te; superano la Diatessaron consonanza; secondo 'l proposito; come primieramente di-
mostrar ui douea. Dopoi; perche 'l Tuono maggiore supera 'l minore, per la Ventesima
quinta definitione riuoltata, per un Comma; però dico, Due tuoni maggiori & un mino-
re, esser minori di tre tuoni maggiori per l'interuallo d'un Comma, ilquale Interuallo pe-
rò non è maggior d'un Semituono minore; ne meno d'un maggiore; ne etiandio equale;
come dalla Decimaquinta, dalla Decimasettima & dalla Decimanona proposta d'hoggi;
& anco dalla Settima Dignità di heri, si può comprendere. Sopr'auanzano adunque due
Tuoni maggiori & un minore la Consonanza Diatessaron; come ui douea dimostrare.
Piu oltra ancora; nella Precedente hò dimostrato, che la Diatessaron contiene due Tuo-
ni; l'vn maggiore & l'altro minore; & un maggior Semituono. Et per la Ventesimaquin-
ta definitione di questo riuoltata, il Tuono maggiore supera 'l minore d'vn Comma; adun-
que due Tuoni l'vn maggiore & l'altro minore, sono minori de due maggiori per un Cō-
ma. Oltra di ciò; per la Ventesimaterza proposta d'hoggi; il Semituon maggiore è mi-
nore de Sei, & maggiore de cinque Comma; & per la Ventesima prima; Il Tuono mag-
giore è minore de dieci & maggiore de noue; adunque il Tuono sopr'auanza 'l Semituono
de quattro Comma. Et perche 'l secondo Tuono de i tre maggiori auanza il secondo &
minore della Diatessaron per un Comma; simigliantemente, perche il terzo de i tre mag-
giori sopr'auanza il maggior Semituono della Diatessaron per quattro Comma; però un
Tuon maggiore, un minore, & un maggior Semituono sono minori de tre Tuoni mag-
page 122 giori per la quantità de Cinque Comma. Adunque tre Tuoni maggiori sopr'auanzano
la Diatessaron, secondo 'l proposito; come secondariamente dimostrar ui douea. Ma que-
sto non è da lasciare indietro; essendo il Tritono corellatiuo alla Semidiapente, se noi con
sideraremo esso Tritono composto di Tre tuoni maggiori; uerrà ad esser contenuto nella
sua propria forma dalla proportione Super 217. partiēte 512. & la Semidiapēte uerrà ad
esser cōposta di Due tuoni maggiori, & li Due Semituoni minori, di proportione Super
13. partiente 256. & la sua forma sarebbe la Super 295, partiente 729. ambidue cōtenuti
nell'Antica specie detta Diatona Diatonica; nella quale il Tritono è senza dubio mag-
gior della Semidiapēte; come si puol prouare, che cauata la proportione Super 295. par-
tiēte 729. dalla Super 217. partiēte 512. ne nasce la Super 7153. partiēte 524288. ch'è la
quantità di quanto esso Tritono supera la Semidiapente; ò di quanto essa Semidiapente
da esso Tritono è superata. Ma se lo consideriamo composto secondo la Specie naturale
ò Syntona di due Tuoni maggiori, & d'uno minore; la sua proportione ò forma sarà la
Super 13. partiente 32. & la Semidiapente sarà composta d'una Terza minore & d'un
Tuono minore, con un Semituono maggiore appresso: & la sua forma sarà contenuta
dalla proportione Super 19. partiente 45. onde in questa Specie auerrebbe il contrario;
percioche la Semidiapente senza dubio sarebbe maggiore del Tritono: come si può di-
mostrare: percioche se dalla Super 19. partiente 45. cauaremo la Super 13. partiente 32.
ne uerrà la Super 23. partiente 2025. ch'è quella quantità di quanto essa Semidiapente
supera il Tritono; & questo da quella è superato. Queste dimostrationi, disse M. Claudio;
sono state molto belle; ma sommamente mi è piaciuto quella ultima de i Cōma & della
differentia, che si troua tra il Tritono & la Semidiapente del Diatonico diatono, & quelli
del Naturale, ò Syntono pur diatonico. Desidero però di saper quello, che uerrà da di-
mostrarsi dopò questa. Ne uerrà, gli risposi; che
PROPOSTA XXX.
tessaron contenere un Tuono maggiore, un minore & un maggior Semituono; &
per la Ventesima definitione riuoltata, la Diapente sopr'auanza la Diatessaron
per un Tuono maggiore; adunque la Diapente contiene due Tuoni maggiori; un mino-
re, & un maggior Semituono. Questa anco si può dimostrar con un'altro mezo, in co-
tal modo. La Sesta di questo dimostra, che 'l Ditono, & lo Semiditono nascono dalla Di-
uisione harmonica della Diapente; Onde il Ditono & lo Semiditono, per il suo Corol-
lario sono parti integrali di essa Diapente; Ma per la Ventesimasesta il Semiditono con-
tiene un Tuon maggiore & un maggior Semituono; & per la Ventesimasettima il Dito-
no contiene un Tuon maggiore & un minore; adunque la Diapente contiene due Tuo-
ni maggiori, & un minore, con un maggior Semituono; secondo 'l proposito. Si può an-
co ciò, dimostrar per un'altra maniera; & dire. Se da un'interuallo Sesquialtero, per la
Vētesimasesta di heri, si leuerà un Sesquiterzo; quello, che nascerà sarà Sesquiottauo; Ma
per le Definitioni date di sopra, la Sesquialtera è la Diapente; & la Diatessaron è la Ses-
quiterza; & lo Sesquiottauo è la forma del Tuono maggiore; per la Nona proposta dimo-
strataui di sopra adunque; leuata la Diatessaron dalla Diapente, il rimanente è il Tuono
maggiore. Più oltra; per la Ventesimaottaua di questo, la Diatessaron cōtiene due Tuo-
ni, l'un maggiore & l'altro minore con un maggior Semituono; ma questi Tre interualli
aggiunti ad un'altro Tuono maggiore, per il quale la Diapente sopr'auanza la Diatessa-
ron, fanno due Tuoni maggiori & un minore, con un maggior Semituono; adunque la
page 123 Diapente auiene à cōtenere due Tuoni maggiori, & un minore, & anco un maggior Semi-
tuono; come dice la proposta; & come ui douea dimostrare.
COROLLARIO I.
uno minore, & il maggior Semituono; cioè, la Diatessaron; & questa essendo cauata da
quella, resta il Tuono maggiore.
maggior Semituono; come habbiamo dimostrato; non è dubio, cauandone vn
Tuono maggiore, che il restante sia due Tuoni, l'un maggiore & l'altro mino-
re, con vn Semituono maggiore; i quali, com'habbiamo dimostrato nella
Ventesimaottaua di sopra, fanno la Diatessaron; come contiene la prima parte del Co-
rollario; & questa cauata dalla Diapente, resti, secōdo che dice la Seconda parte, il Tuon
maggiore. Et cosi potete uedere, che tutto quello; ch'è posto nel Corollario uiene ad
esser uero. Comprendo hora l'utile, che si caua da questi Corollarij; disse il Viola; cosa,
che per inanti non uedea. Ma ditemi di gratia, che vuol dire Corollario propriamente?
Questo è detto da Greci Πόρισμα soggiunsi; quasi Acquistato, ò Pensato; percioche (come
dice Proclo nel Terzo libro sopra la prima Proposta del Primo de gli Elemēti d'Euclide)
nasce come un'altro Theorema; non lo hauendo noi proposto da dimostrare. La onde
s'aggiunge alla Dimostratione già fatta, la quale genera scienza; come un certo guadagno
fatto oltra il proposito. Et ben che di due sorti siano tali Corollarij; tuttauia non uoglio
stare à perder tempo à dichiararui questa cosa; perche non è di molta importanza. Fa-
rete bene; ma da quello, c'hò compreso; soggiunse il Viola; credo, che questo sia etiandio
uero; che
COROLLARIO II.
precedente. Ma ui uoglio dimostrare, ancora che lo sapiate dalla Prattica; che
PROPOSTA XXXI.
uia non uoglio lasciar di dirui; che 'l Semiditono, per la Ventesimasesta propo-
sta (come poco fà ui diceua) cōtiene il Tuono maggiore & lo maggior Semituo-
no; & per la Ventesimasettima, il Ditono contiene il Tuono maggiore & lo minore. Ma
due Tuoni maggiori & un minore, con un maggior Semituono, per la Precedente, fanno
una Diapente; adunque aggiunto il Ditono al Semiditono, nasce la consonanza Diapen
te, secondo la proposta, & questo è quello, che ui douea dimostrare.
page 124
COROLLARIO.
da quella, ne viene il Ditono.
mostrarui breuemente quest'altra; che
PROPOSTA XXXII.
gior Semituono.
questo, contiene un Tuono maggiore, un minore, & un maggior Semituono; pe-
rò due Diatessaron uerranno à contenere due Tuoni maggiori, & due minori,
cō due maggiori Semituoni. Da questi adunque se noi leuaremo un Tuono minore & un
rnaggior Semituono; senza dubio restaranno due Tuoni maggiori, un minore & un mag-
gior Semituono; ma, per la Penultima, la Diapente contiene tutti questi Interualli; adun-
que la Disdiatessaron trappassa la Diapente per un Tuono minore, & un maggior Semi-
tuono. Et questo è quello, ch'intorno cotal cosa, secondo 'l proposito, ui douea dimo-
strare. Vi uoglio ancora dire, auanti ch'io passi piu oltra; che
PROPOSTA XXXIII.
minori d'un Sesquialtero. Et, per la sua Sequente, quattro sono di esso mag-
giori. E uoi già sapete, per la Nona definitione d'hoggi, che la Diapente hà
la sua forma dalla proportione Sesquialtera, & per la Nona proposta, lo Sesquiottauo è
la forma del Tuono maggiore; adunque Tre tuoni maggiori sono minori della Diapente,
& quattro le sono maggiori. Il che è secondo la proposta; come ui douea dimostrare.
Molto mi piacciono questa sorte de Dimostrationi; disse M. Adriano; le quali si conclu-
dono con le conclusioni fatte per altre dimostrationi precedenti. Per questo Messere
(dissi) sono chiamate Elementi; percioche l'una dipende dall'altra. Ma ascoltate questa,
che ui propongo.
PROPOSTA XXXIIII.
xachordo maggiore. Simigliantemente aggiungendo alla Diapente il maggior Semituo-
no; ouero alla Diatesseron il Semiditono, ne viene l'Hexachordo minore.
te; secondariamente c & d. quelli del Tuono minore. Moltiplico a. in c. & ne
viene e. il che fatto molteplico ancora b. in d. & ne nasce f. Dico hora e & f. con-
tenere la Sesquialtera con la Sesquinona proportione; Percioche (secōdo ch'io
mostrai nelle Istitutionipar. 1. c.
33.) sono sommate insieme queste sue proportioni; dalle quali ne uie-
ne vna terza, ch'è e & f. laquale contiene la Diapente col Tuono minore. Onde è manife-
sto da g & h. termini radicali di e & f acquistati dalla diuisione fatta di essi e & f. per il Se-
nario, & contenuti tra le parti di esso Numero; che e & f. sia Superbipartiente terza; per-
cioche g. contiene una fiata h. & due sue terze parti; la qual proportione (per la Decima-
settima definitione d'hoggi) è la forma dell'Hexachordo maggiore. Aggiunto adunque
il Tuono minore alla Diapente si fà l'Hexachordo maggiore; come dice la Prima parte
della proposta. Ma per l'altra parte; se di nuouo pigliaremo A & B. termini radicali della
Diatessaron, & CD. minimi termini del Ditono, & molteplicheremo A in C. & B in D.
nascerà E & F. i quali, per il Cap. 33. della Prima parte delle Istitutioni, conteneranno la

insieme aggiunti. La onde E & F. uiene ad esser simigliantenente l'Hexachordo mag-
giore. Percioche i termini radicali di E & F. che sono G & H. acquistati dalla diuisione
fatta di essi per il Quaternario; contengono la proportione Superbipartiente quinta; la
quale, per la nominata Decimasettima definitione, è la forma dell'Hexachordo maggio-
re; i quali termini potendosi tramezare da un termine mezano; come si uedono tra p. q. r.
de i quali p & q. contengono la forma del Ditono, & q. con r. quella della Diatessaron; ci
danno segno manifesto; ch'aggiungendo di nuouo alla Diatessaron il Ditono; si genera
l'Hexachordo maggiore; come douea dimostrarui.
COROLLARIO I.
la Diatessaron per un Ditono.
uo pigliaremo i minimi termini del Semituono maggiore, che sono i & k. &
molteplicheremo a in i & b in k. haueremo l & m. i quali (per il Cap. 33. allega-
to) conteranno la Sesquialtera & la Sesquiquintadecima proportione; & per conse-
quente la Diapente col Semituono maggiore. Hora è manifesto, che l & m. è proportio-
ne Supertripartiente quinta da i suoi termini radicali n & o, acquistati per la diuisione di
l & m. per il Senario. Percioche n. contiene o. una fiata & tre sue quinte parti; onde per
page 126 la Decimaottaua definitione, questa tal proportione è la forma dell'Hexachordo minore.
Adunque aggiunto 'l maggior Semituono alla Diapente, nasce l'Hexachordo minore; co
me dice la Prima parte della Seconda della proposta. Ma se di nuouo pigliaremo I & K.
radicali termini del Semiditono; & moltiplicheremo A in I. & B in K. ne risulterà senza
dubio alcuno L & M. i quali conteneranno la Sesquiterza & la Sesquiquinta proportio-
ne. Onde dico, che L & M. ci daranno l'Hexachordo minore simigliantemente, come si
può conoscere da N & O. che sono i termini radicali di L & M acquistati per la diuisione
fatta di L & M. col mezo del Ternario. Percioche contengono la Supertripartiente quin-
ta; la quale, per la nominata Decimaottaua definitione; è la forma del nominato Hexa-
chordo. I quali termini, poi che si possono tramezare da Q. come si uede tra P.Q.R. ci
danno manifesto segno, che tutto quel, che si è detto, sia uero; percioche tra P. & Q. è la
forma della Diatessaron, & tra Q. & R. quella del Semiditono. Dalla congiuntione del
Semiditono adunque con la Diatessaron, nasce l'Hexachordo minore; come dice la Secō
da parte della Seconda della proposta. Et questo è tutto quello, che ui douea dimostrare.
COROLLARIO II.
maggiore, & la Diatessaron per vn Semiditono.
uendo inteso questo M. Adriano; Ogni cosa torna bene. Et uoi sapete, che se 'l
si aggiunge il Tuono maggiore, ò lo minor Semituono alla Diapente, non può
far Consonanza alcuna; tuttauia desidero di uedere questa cosa di mostrata. Vedrete
poca varietà Messere; risposi; dal modo, che ui hò dimostrato nella Precedente, hor hora
dimostrata; però lasciatemi prima dirui la proposta, che dopoi ue la andrò dimostrando;
la quale è questa.
PROPOSTA XXXV.
scere consonanza alcuna.
& c. d. quelli del Tuono maggiore. Molteplico prima a in c. & ne uiene e. do-
poi molteplico b in d. & ne nasce f. Dico hora, per le ragioni addotte nella Pre-
cedente, che e & f. contengono la Sesquialtera & la Sesquiottaua
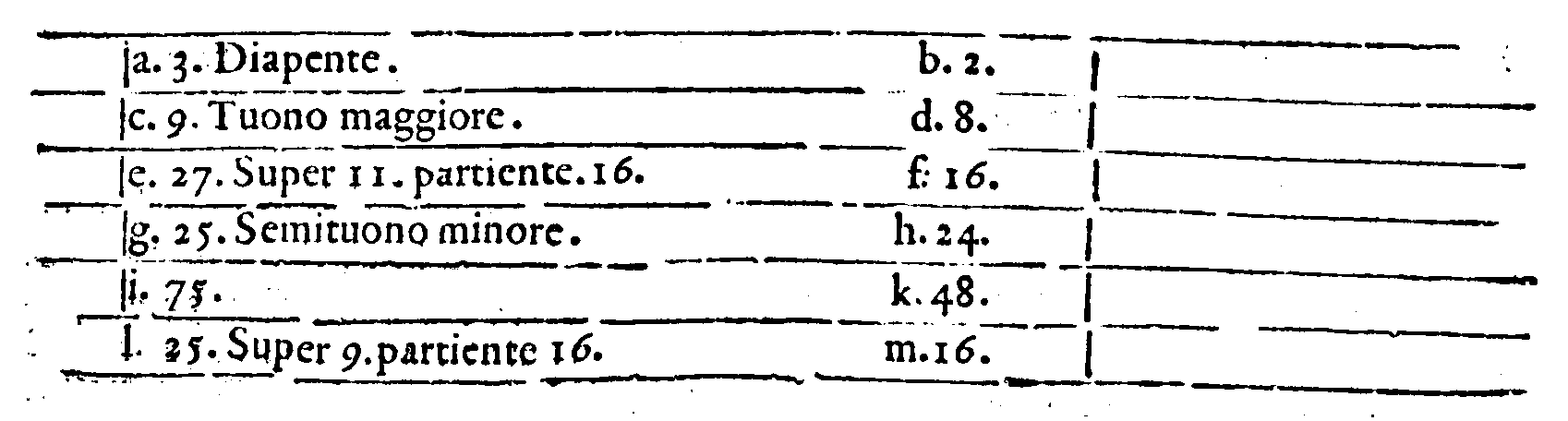
manifesto, per la Nona definitione di heri, che e & f. sono numeri Contraseprimi; per-
page 127 cioche non hanno altro numero, che li misuri, che la Vnità; onde sono Termini radicali
della proportione contenuta tra loro. I quali, per non ritrouarsi collocati tra le parti del
Senario, & il primo numero Cubo; per la prima & seconda Definitione d'hoggi; non
la forma d'alcuna Consonanza; ne semplice, ne composta. Onde si conclu-
de, per la Prima parte della Proposta; che aggiunto 'l Tuono maggiore alla Diapente,
non fà consonanza alcuna. Et quest'istesso argomento potiamo usare, à prouar, ch'ag-
giungendo 'l Semituono minore alla Diapente, non risulta alcuna Consonanza; Percio-
che presi i termini radicali del detto Semituono, che sono g & h. & molteplicati con quel-
li della Diapente a & b. cioè, a in g. & b in h. haueremo i & k. i quali contengono medesi-
mamente la Sesquialtera & la Sesquiuentesimaquarta proportione, & per consequente
la Diapente vnita al Semituon minore. Et perche i & k. nelle lor radici, che sono l & m.
vengono numeri Contraseprimi, i quali trappassano il primo numero Cubo; però, per la
prima & seconda Definitione nominate di sopra, non contengono forma d'alcuna Con-
sonanza. Adunque; Aggiungendo il Semituono minore alla Diapente, non genera Con-
sonanza alcuna. Et questo è tutto quello, che dice la Proposta, & che vi douea dimostra-
re. Son satisfatto; disse allora M. Adriano; & ui rendo gratie; però seguitate quello, che
vi torna più commodo, che v'ascolteremo uolentieri. Cosi uoglio fare, dissi; & proposi
à dimostrar; che
PROPOSTA XXXVI.
tuoni.
quarta d'hoggi; nasce dalla congiuntione del Semituon maggiore con la Dia-
pente. Ma, per la Trentesima, la Diapente contiene due Tuoni maggiori, un
minore, & un maggior Semituono; à i quali se aggiungeremo 'l maggior Semituono; fa-
ranno due Tuoni maggiori; un minore, con due Semituoni maggiori; Adunque l'Hexa-
chordo minore contiene due Tuoni maggiori, un minore, & due maggiori Semituoni.
Più oltra; la Trentesimaquarta nominata dimostra, che dalla Diatessaron & dal Semidi-
tono posti insieme, si fà l'Hexachordo nominato; Ma la Diatessaron, per la Ventesimaot-
taua, contiene un Tuono maggiore, un minore, & un maggior Semituono; simigliante-
mente il Semiditono, per la Ventesimasesta, contiene un Tuono & un Semituono, l'uno
& l'altro maggiore; i quali posti insieme fanno due Tuoni maggiori, un minore, & due
maggiori Semituoni; adunque l'Hexachordo minore contiene due Tuoni maggiori, un
minore & due Semituoni maggiori; come dice la Proposta, & come ui douea dimostrare.
Et per seguir l'ordine , dirò; che
PROPOSTA XXXVII.
tuono.
giuntione del Tuono maggiore con la Diapente; Ma perche, per la Trentesima
di questo, la Diapente contiene due Tuoni maggiori, un minore, & un maggior
Semituono; se à questi s'aggiunge 'l Tuono minore; uerranno ad esser due maggiori, due
minori, & un maggior Semituono; Adunque l'Hexachordo maggiore cōtiene due Tuoni
page 128 maggiori, due minori, & un maggior Semituono. Simigliantemente; per la nominata
Trentesimaquarta, l'Hexachordo maggiore nasce dall'aggiuntione fatta del Ditono al-
la Diatessaron; ma per la Ventesimaottaua, la Diatessaron contiene un Tuono maggio-
re, vn minore, & vn maggior Semituono; & il Ditono, per la Ventesimasettima, contie-
ne un Tuono maggiore & un minore; adunque l'Hexachordo maggiore contiene due
Tuoni maggiori, due minori, con vn maggior Semituono; come dice la Proposta. Et
questo è quello, che ui volea dimostrare. Sono hora espediti quelli Interualli, che sono
minori della Diapason; la onde verrò à trattare al presente di essa. Et perche alcuni de gli
Antichi hanno tenuto, che ella contenga Sei tuoni Sesquiottaui; però, uoglio dimostrar-
ui, che questo è impossibile; se bene da altri ancora cotal cosa non sia riceuuta per vera;
Onde proponerò a dimostrarui; che
PROPOSTA XXXVIII.
ragionamento di heri; Cinque interualli Sesquiottaui congiunti insieme sono
minori di un'interuallo Duplo; Et, per l'Vltima; Sei sono etiandio di esso Du-
plo maggiori; Et troppo bene sapete, che 'l Duplo è la forma della Diapason; & il Ses-
quiottauo è la forma del Tuono maggiore. Onde Cinque Tuoni maggiori sono meno
d'una Diapason, & Sei la trappassano. Et perche in fatto è cosi; la Diapason (secondo la
proposta) è minore de Sei tuoni maggiori; & è maggior de Cinque; come ui douea di-
mostrare. Dimostrateci anco; disse M. Adriano; secondo la uerità; quanti Tuoni & quan-
ti Semituoni contiene. Questo è molto necessario Messere; risposi; però vi dico; che
PROPOSTA XXXIX.
insieme; per la Quarta proposta d'hoggi; fanno la consonanza Diapason; Et ui
hò dimostrato, per la Ventesimaottaua, che la Diatessaron contiene un Tuono
maggiore, & vn minore, con un maggior Semituono; Et per la Trentesima fù concluso;
che la Diapente contiene due Tuoni maggiori, un minore, & un maggior Semituono; i
quali adunati insieme fanno tre Tuoni maggiori, due minori, con due maggiori Semi-
tuoni; Però la Diapason contiene Tre tuoni maggiori, due minori, con due maggiori
Semituoni; secondo ch'io douea dimostrare. Hora uoglio dichiarare una diffi-
cultà, & accordar (s'io potrò) due opinioni contrarie, de due fattioni molto segnalate nel-
la Musica; Però ascoltatemi; che ui uoglio prima dir la Proposta & dopoi dimostrarla; &
cosi nella dimostratione conoscerete la cagione che mosse i suoi Fautori ad hauer cotali
opinioni; & la uerità della cosa. Ascoltate adunque la Proposta; la quale è questa.
PROPOSTA XL.
no tenuto,Harmoni
lib. 1. c. 6.
Boeth. lib. 5. c. 8. Mu-
sicae. che quest'Interuallo sia dissonante, & voi uolete prouare 'l contrario;
per quello ch'io vedo; doue nasce questa cosa? Lo vederete tosto; risposi; ma
ascoltate prima l'opinioni di questo; e l'vna all'altra contrarie. Tiene Tolomeo, &
dopo lui molti altri, questa cōclusione per uera, contra i Pitagorici; che la Diapason dia-
tessaron sia Consonanza. Et se ben pare ad alcuni, che Tolomeo habbia ragione per
quello, che lui adduce in suo fauore; tuttauia non hanno anco il torto i Pitagorici. Dice-
ua Tolomeo questa ragione; tollendo da Aristosseno nel primo de gli Harmonici questa
conclusione; che Quando la Diapason consonanza hà i suoni, che la contiene ben'accor-
dati; niente sono differenti di virtù & possanza da un sol suono; onde applicata à qual si
voglia Interuallo semplice, che sia minore di lei, ò per il contrario; conserua quella specie
intera & inuiolata; come conserua 'l Denario in se stesso gli altri numeri, che sono di lui mi
nori. Il perche, si come quando alcun suono s'aggiunge alla Diapason dalla parte più gra-
ue, ouer dalla più acuta; si troua vna certa conuenienza & forza di muouer l'Vdito tra
esso & quello, che gli è più vicino; cosi appare esser tale conuenienza & forza tra lui & lo
più lontano. La onde la Diapente & la Diatessaron consonanze da se stesse hanno quella
sonorità in quella conuenienza da quella parte della Diapason, che gli è più uicina, onde
meritamente l'Vdito riceue all'istesso modo la Diapason diapente, ouer la Diapason dia-
tessaron, che riceue la Diapente, ouer la Diatessaron poste da per sè, & sole. La onde per
questa cagione seguita infallibilmente; ch'essendo la Diapente, & anco la Diatessaron,
Consonanze; che consonanti siano anco la Diapason diapente, & la Diapason diatessa-
ron; & ad vn modo esser riceuuta dall'Vdito ciascheduna di queste due, com'è riceuuta
la Diapente & la Diatessaron, ciascheduna da per sè & sola; come euidentemente appare
per l'esperienza. Finalmente conclude che tanto l'uno, quanto l'altro de questi due nomi
nati Cōposti interualli siano consonanti. Dall'altra parte i Pitagorici adduceuano in suo
fauore questa ragione, la quale teniuano per vera, anzi uerissima; che Ogni cōsonanza na-
sce, ouer dal Molteplice, oueramente dal Superparticolare, contenuti tra quei numeri,
che sono le parti del numero Quaternario, & non da altro Genere; & che non essendo la
Diapason diatessaron ne Molteplice, ne Superparticolare; essendo che la sua forma è
contenuta tra i Molteplici Superpartienti, dalla proportione Dupla superbipartiente ter
za; onde non poteua à patto alcuno esser Cōsonanza. Ma questo concluderebbe ottima-
mente; quādo semplicemēte fusse uero, che non si trouasse altre Cōsonanze, se non quel-
le, che nascono da i due nominati Generi, & le Sēplicemēte dette. Vediamo però in fatto
altramēte essere; come fin'hora dalla Esperienza & dalla Scienza siamo certificati. Et se
ben queste due opinioni sono cōtrarie; tuttauia si possono facilmente accordare; conside-
rato quello, c'hò detto nella Prima & Seconda definitione d'hoggi, sopra le Consonanze
Propriamēte dette, & le dette Cōmunemēte, & anco quello, che dissi heri intorno à i Luo
ghi, ouer Siti delle Consonanze; Percioche il tutto in queste due cose cōsiste; se ue le ricor
date. Cele ricordiamo benissimo, disse M. Adriano. Però adunque; soggiunsi; se bene al-
cun'Interuallo aggiunto à gli estremi della Diapason; come diceua Tolomeo; non fà va-
rietà alcuna di suono, di maniera che si oda diuersa dal Suono primo dell'aggiūto Inter-
uallo; come se aggiūta la Diatessarō alla Diapason, nō varia in tal maniera i suoni, , che parino d'un'altra Cōsonanza, ma simili alla Diatessaron, la quale è aggiunta;
tuttauia non si può dire, che tal Composto sia quell'istesso Semplice, che era inanzi ch'al-
la Diapason s'accompagnasse; come anco non si può dir con uerità, che 'l numero Duode
nario sia l'istesso numero, ch'è il Binario, per esser'esso Binario al Denario accompagnato;
essendo che se ben l'uno & l'altro di essi è Numero pare; non si può però dire, che 'l
Binario sia della natura del Duodenario, & habbia quelle proprietà istesse. Ne anco
si può dir senz'errore; ch'essendo la Diapasondiatessaron composta della Diapason &
della Diatessaron semplici consonanze; che tale interuallo Composto sia semplicemente
consonante, ouer semplicemente dissonante. Ma si ben si potrà dire; che necessariamen-
page 130 te caschi nel numero de quelle, che sono connumerate tra i due nominati estremi; cioè,
tra quelli Interualli, che consonanze Communemente dette, habbiamo nominato; Im-
peroche se haueremo riguardo alla proportione, che nasce dalla congiuntione de i due
nominati Interualli; ritrouaremo, che sarà la Duplasuperbipartienteterza, contenuta tra
8. & 3. la quale non è ne Molteplice, ne Superparticolare. Onde non può esser posta
tra quelle Consonanze, che sono contenute nel primo ordine, dette Propriamente; per
non esser la sua forma collocata tra le Parti del Senario; come nella Prima definitione fù
dimostrato; il perche non potrà essere à patto alcuno consonanza Propriamente detta; &
in questo si potrà tenere con i Pitagorici. Ma ch'ella non sia Consonanza della Seconda
maniera Communemente detta, questo non si può, ne potrà mai negare; se 'l si porrà men
te à quello, che nella Seconda definitione si è detto. Il perche quello, c'ha detto & con-
cluso Tolomeo, non sarà detto & concluso fuor di proposito. E' ben uero, che quando
si uolesse dire, che la mente di Tolomeo fusse, che questo Cōposto fusse consonanza Pro-
priamente detta; & di mente de i Pitagorici, ch'ello sia Interuallo dissonante; que-
sto sarebbe falso, & ripugnarebbe à i nostri Principij, iquali habbiamo posti nell'inco-
minciare di questo Ragionamento, & alla uerità istessa. Bisogna adunque tenere con To-
lomeo, ch'aggiunta la Diatessaron alla Diapason, faccia ne gli estremi una Consonanza,
non però Propriamente detta, ma si ben detta Communemente; & con i Pitagorici; che
la Diapasondiatessaron non sia ne possa esser Cōsonanza della prima maniera; se voglia-
mo accordar l'opinioni diuerse de questi Eccellentissimi Musici di modo, che non siano
l'uno dall'altro discordanti quanto al senso; nelle parole si vedino l'un'all'al-
tro contrarij. Et per tal uia l'uno & gli altri uerranno ad hauer detto bene. Hauete adun-
que inteso quel che si dee tenere, per intender queste due opinioni, che siano d'accor-
do. Et se sopra di ciò hauete cosa alcuna da dirmi; ditela auanti ch'io uada più oltra.
M'hauete hora dichiarato un dubio, disse M. Adriano; non ue lo dimandando, ilquale
mi daua molto trauaglio; che i Pitagorici concedeuano à Tolomeo la sua Premessa esser
vera, & negauano la Conclusione. Però questa uostra distintione, c'hauete fatto, nel por-
re questi Mezani interualli tra i Consonanti propriamente detti, & li Dissonanti, accon-
cia il tutto. Onde si possono accordar benissimo questi Pifferi, & dire; Che i Pitagorici
considerando tale aggiunto quanto alla vicinità della Dissonanza, diceuano ch'era Dis-
sonante; & che Tolomeo consideratolo, in quanto era (dirò cosi) la Diatessaron appo-
giata alla Diapason, & s'accostaua alla Consonanza; diceua ch'era Consonante; consi-
derando però il tutto quanto al Senso, & anco quanto alla ragione. Cosi stà la cosa in fat-
to; come vedete Messere, risposi. Soggiunse allora M. Adriano, vi prego adunque à se-
guitare; poi che da uoi uengo ad imparar molte cose degne di gran consideratione; le
quali da altri mai hò più udito. Soggiunsi adunque; Hauendo inteso, in qual maniera
queste due contrarie opinioni accordar si possono; seguitarò à dimostrar quello, che dice
la Proposta; & dirò in questo modo. Siano a & b. termini radicali della proportione
della Diapason, & c con d. numeri minimi continenti la proportione Diatessaron. Mol-
teplico (per la Seconda del ragionamento hauuto heri tra noi) queste due proportioni in-
sieme; & ne viene e. f. g. cioè, e & f. Dupla, & f con g. Sesquiterza; onde dico, che e & g.
uiene ad esser composto di ef. Dupla, & di fg. Sesquiterza; & contenere; la Diapason
& la Diatessaron consonanze. Ma perche e & g. non è Molteplice, ne anco Superparti-
colare; percioche e. contiene il g. due fiate & due sue Terze parti; ond'è detta Dupla su-
perbipartiente terza, contenuta nel Quinto genere di proportione, detto Molteplice su-
perpartiente; però, per la Prima definitione di questo, la Diapasondiatessaron non è
consonanza Propriamenta detta; ma per la Seconda, è ben detta Communemente; co-
me dice la Proposta; & come ui douea dimostrare. Voltosi allora M. Frācesco verso di me
disse; A' fe, c'hauete molto ben ragione; & il nostro Messere l'hà molto ben conosciuto;
percioche (come ancora hanno fatto i migliori Prattici) quando gli è tornato commo-
do; hà posto questo Interuallo con molta gratia nelle sue Cōposition. Et io per me l'userò
page 131 sempre, quando lo far con qualche buon proposito, senza schiuarmene; percio-
che mi pare, che in certi propositi faccia buonissimo effetto. Messer Francesco, dissi, se al-
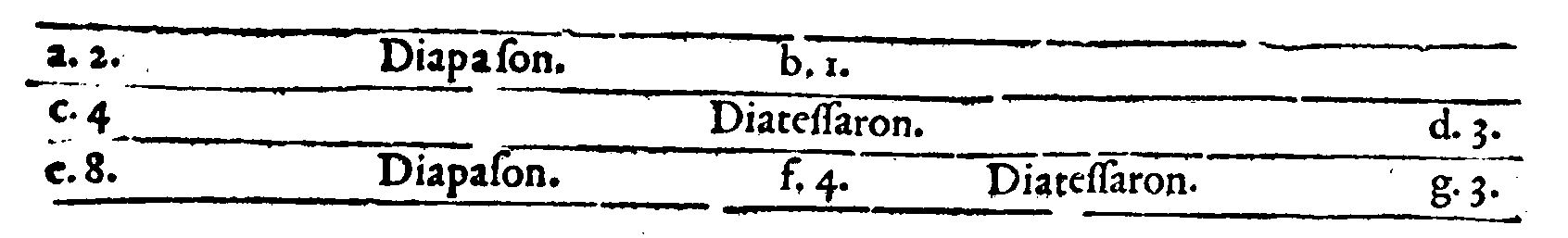
lizarebbe molto; essendoche hanno l'Vdito tanto delicato contra questa Consonanza,
che più tosto con miglior sua satisfattione potrebbe nelle sue Compositioni qualche stra-
na cosa, che una compositione di due consonanze fatta al mostrato modo. Ma lasciamo
costoro; percioche son certo, che di loro ue ne curate poco; & ritorniamo à seguitare il
nostro incominciato ordine, dicendo; che
PROPOSTA XLI.
ne cinque Tuoni maggiori, tre minori, & tre maggiori Semituoni.
del Primo giorno) l'interuallo Duplo & lo Sesquialtero aggiunti insieme fanno
l'interuallo Triplo; ma, per le Definitioni, il Duplo è la forma della Diapason, lo
Sesquialtero è quello della Diapente, & lo Triplo è quello della Diasondiapente;
Adunque aggiunto insieme la Diapason & la Diapente, nasce la Diapason diapente. Ol-
tra di questo; Se per la Trentesima d'hoggi la Diapente contiene due Tuoni maggiori, vn
minore, & un maggior Semituono; & , per la Trentesimanona, la Diapason contiene tre
Tuoni maggiori, due minori, & due maggiori Semituoni, & la Diapasondiapente (per la
Settima definitione) è Consonanza composta della Diapason & della Diapente; come
suona il suo nome: Seguita necessariamente; che quell'istessi Interualli, che sono conte-
nuti in questi due ultimi, siano etiandio contenuti nel primo. Et perche in questi due so-
no contenuti cinque Tuoni maggiori, tre minori, & tre maggiori Semituoni; però dico,
che la Diapasondiapente contiene cinque Tuoni maggiori, tre minori, & tre maggiori
Semituoni; come ui douea dimostrare. Aggiungerò etiandio; che
PROPOSTA XLII.
me; & contiene Sei tuoni maggiori, Quattro minori, & Quattro maggiori Se-
mituoni.
uallo Duplo costituisce il Quadruplo; ma per le Definitioni; il Duplo è la for-
ma della Diapason, & il Quadruplo della Disdiapason; adunque raddop-
piata la Diapason, ouero aggiunta una Diapason ad un'altra nasce la Disdiapason.
Et questo è quanto alla Prima parte della proposta. Ma uenendo alla Seconda dico;
Essendo la Disdiapason; per la Settima definitione; Consonanza composta; come 'l nome
page 132 suo dice; di due Diapason; ouer la Diapason raddoppiata; & contenendo la Diapason
semplice, per la Trentesimanona d'hoggi, tre Tuoni maggiori, due minori, con due mag-
giori Semituoni; è necessario, che la raddoppiata contenga sei Tuoni maggiori, quattro
minori, & quattro Semituoni maggiori; come vi douea dimostrare. Questo non si può
negare, disse il Sig. Desiderio; & mi piacciono assai quelle ragioni, che uoi dite nelle Isti
tutioni,2. parte
cap. 2. sopra quello; che gli Antichi, & massimamente i Pitagorici ui etauano il passare
oltra la Quadrupla, ouer'oltra la Disdiapason; onde statuirono, che quest'Interuallo fus-
se 'l termine delle Consonanze. Però, come tutti uoi sapete, si può passar più oltra; il che
fate ciascheduno de uoi; per quel poco di lume, ch'io hò di questa cosa; nelle uostre cō-
positioni. Et credo che ancor uoi M. Gioseffo uorrete seruar questo costume; & che non
vorrete in queste Dimostrationi passar più oltra; per non trapassare la Quadrupla pro-
portione; ò Disdiapason consonanza; doue pure alla fine con l'aiuto di Dio sete arriuato.
Son di questo parere ueramente, dissi; & non accade passar più oltra; ma star si può in que-
ste Proposte dimostrate fin'hora; percioche quantunque si potesse procedere più oltra
quasi in infinito; tuttauia non sono l'altre Dimostrationi, come sono queste, necessarie.
Il perche tutte le uolte, che uoi uorrete andar più di lungo; da quelle Dimostrationi, che
fin'hora ui hò posto inanzi, potrete commodamente per uoi stessi saper quello, che ri-
cercarete. Massimamente hauendoui ragionato, non solamente intorno alle Consonan-
ze semplici; ma etiandio intorno alle Composte. Onde con uostra buona gratia, per
questa fiata, farò fine. Dimane poi ritornarete di nuouo in questo luogo; per che ui son
per dir cose, che ui piaceranno. Hauete molto ben ragione di posarui; disse M. Claudio;
essendo ch'egli è in gran pezzo di tempo, che ragionate. Però è cosa honesta, che hor-
mai si ponga silentio. Mi pensaua; aggiunse M. Adriano; che haueste dimostrato tutto
quello, che si può dimostrare intorno questa materia; ma per quello ch'io uedo, ne resta
anco una buona parte; Però starò con gran desiderio ad aspettare, che venga dimane;
acciò possa udir quello, che hauerete da trattare. Ci manca da trattare (dissi) il più bello
Messere; però non vi date fastidio, che pur troppo presto verrà dimane; onde potrete ve-
dere, ch'io non u'inganno. Ma per finirla hormai rimaneteui tutti in pace. M. Francesco
andianci con Dio. Messere, dissse M. Francesco, state allegro, che di nuouo vi verremo
à uisitare. Di gratia fatelo. Egli rispose. Cosi faremo dissi, & presi la strada: & il Signor
Desiderio disse; Vengo anche io. Ne io ci uoglio restare, disse M. Claudio. A' Dio
adunque Messere; disse ogn'uno. A' Dio à Dio, rispose egli. Et cosi in un tratto tutti in-
sieme si partissemo.
DIMOSTRATIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
RAGIONAMENTO TERZO.
la & vera sentenza di Boetio;De Disci-
pli. Scho-
last. cap. 5. Ch'è cosa propria d'uno Ingegno
miserrimo & pouero, vsar sempre le cose, che sono state d'altrui
ritrouate, & non mai quelle, che ritrouar si possono; ch'io non hab-
bia hauuto cotal cosa nella memoria. Onde mosso prima dal natu-
rale desiderio, che hanno communemente gli Huomini di sapere;Metaphy.
1. cap. 1.
sapendo ch'è verissimo quello, che da quel gran Filosofo, il quale
per la sua eccellenza fù chiamato Tre fiate massimo; che La massima parte di quello
che sapiamo, è la minima di quello che ignoriamo. Dopoi mosso da quel che conti-
nuamente, hauendolo già ueduto, mi staua fisso nella mente; mi diedi à cercare & ue-
dere, se oltra le dette & mostrate cose da gli Antichi Musici ne fusse restato alcuna, che
si potesse da nuouo ritrouare; la quale apportasse qualche vtile à i Studiosi di questa
Scienza; il che dopò molte lunghe fatiche, varij & lunghi studij quanto bene mi sia
successo; lascierò, senza dir cosa alcuna, la cura di far giudicio à quelli; che si de-
gneranno (hauendo intelligenza delle cose della Musica) di ueder le mie fatiche.Nota per i
maligni.
Percioche, oltra quello, ch'io hò pigliato da gli Antichi, per l'ordimento di questa mia
tela; cioè, di quelle cose, c'hauea da dimostrare; ne hò dimostrate & dichiarate tante;
che se tutti coloro, c'hanno dato & danno opera alla Musica, affaticato si hauessero, &
anco si affaticassero nel modo, c'hò fatto io; credo, che non passarebbe molto tem-
po, che questa dignissima Scienza pigliarebbe tanto accrescimento, quanto habbia
fatto alcun'altra; sia qual si uoglia, ch'è compresa sotto questo titolo di Mathematica,
ò sotto qualunque altro. Io per me hò fatto la parte mia, & uoglia Iddio, che venga vo-
lontà à qualche Spirito nobile, di ridurre alla perfettione quello, che fin'hora hò (dirò
cosi) abbozzato; perche allora forse si potrà ueder quello, che sarà di gran contento à
quelli, che sono curiosi di sapere perfettamente, & secondo la verità le cose di questa
Scienza. Essendoche fin'hora ne hò posto tante in campo; che ciascheduno, che uorrà
seguitar più oltra, potrà hauer soggetto, & materia di ragionare ampiamente. Ma
non più di questo; percioche fà dibisogno ritornare al nostro proposito. Però dico;
che 'l Sole già per vna Duedecima parte del suo cerchio hauea passato la linea del Mezo
giorno; quando ciaschedun di noi, udito il segno del Vespero; senza dimorar punto, si
page 134 ridusse al solito luogo; onde dopò l'hauer discorso vn gran pezzo di tempo sopra quelle
cose che 'l giorno inanti furono ragionate; incominciò M. Adriano (volendo che si desse
principio ad un'altro ragionamento) in cotal modo à parlare. Il desiderio ch'io tengo
di udir cose noue, mi fà ch'io essorti M. Gioseffo à dar principio à quello, che segue à i
Ragionamenti hauuti insieme i due giorni passati. Però tanto più presto, che uoi inco-
minciarete; tanto più l'haueremo caro. Dopoi, finito quello, c'hauete da dire; se 'l tem-
po ce lo concederà; uolendo ragionar d'alcun'altra cosa; si potrà ragionar con più com-
modità. Veramente M. Adriano, disse il Signor Desiderio; che voi dite bene; però
quando ui piacerà di incominciar M. Gioseffo, noi v'ascoltaremo uolentieri. Io son quì
(risposi) per obedirui & satisfarui in questo fatto; & mi piace che non perdiamo 'l tempo
in altre cose; perche hoggidi hò da dirui cose assai. Ma douendo dar principio à questo
nostro Terzo ragionamento, ui uoglio fare auertiti; che fin'hora il parlar nostro è stato
tutto speculatiuo; ne mai habbiamo parlato (come ricordarui potete) d'alcuna cosa; on-
de ui sia stato bisogno di operar manualmente. Il perche si può dire, che le Proposte, le
quali fin'hora u'hò dimostrato; più tosto siano state Theoremi, che Problemi; essendoche
habbiamo trattato de Numeri & Proportioni, & ueduto come le Consonanze & gli In-
terualli minori habbiano l'origine loro dalla diuisione harmonicamente fatta delle Con
sonanze maggiori; & come queste siano reintegrate, ouer contengano quelle, come sue
parti. Hora farà dibisogno di uenir qualche fiata à i Problemi; & adoperare le mani, la ri-
ga & il Compasso; accommodando gli Interualli, de i quali habbiamo parlato, alle Pro-
portioni loro sopra 'l Corpo sonoro; accioche riduchiamo in atto le nostre speculationi, &
le potiamo udir col mezo loro, che ce le conduce sotto 'l giudicio del Senso. Ma uolen-
doci ridurre à quest'atto, vi concorrono alcuni Istrumenti; senza i quali non si può far
cosa buona; onde accioche si conoscano, porrò le lor Definitioni, delle quali la prima
sarà di quello, che nelle Istitutioni2. par. c.
27. nominai Monochordo; & Tolomeo,Har-
moni. lib.
1. cap. 8. con BoetioMusicae li.
5. cap. 2. &
molti altri lo chiamano Regola harmonica; co 'l mezo della quale ui ridurrò à memoria
quel ch'ello sia, & à che fine ei sia stato ritrouato. Ascoltatemi adunque.
DEFINITIONE
PRIMA.
do aggiunto 'l giudicio della Ragione con quello del Senso) in vna chorda, ò più tiratole
sopra, si và inuestigando le ragioni delle Consonanze, & delle parti loro.
do un giorno in casa uostra me lo mostraste. Anch'io l'ho ueduto; soggiunse
il Viola. Comprendo hora quello che volete dire, disse à questo il Signor
Desiderio; confrontando questa Definitione col Cap. 18. della Seconda parte
delle Istitutioni. A queste parole aggiunse il Merulo; Io posso saper quel ch'ello sia,
poi che n'hò uno in casa; il quale mi donò M. Vincenzo Colombi eccellente fabricato-
re d'Organi; onde non accade farui sopra altra espositione. E' vero; risposi; Ma auer-
tite ch'alcuni chiamano Regola harmonica vna Listella fatta di legno, nella quale pri-
ma da un capo all'altro ui sia tirato una Linea; sopra la quale si fà le Diuisioni, come ve-
drete, & dopoi si pone sotto quell'Istrumento, che chiamai Monochordo; sopra 'lquale
ui siano solamente tese le chorde; senza esserui Linea alcuna tirata nel mezo. Ma sia
page 135 come si uoglia: è quell'Istrumento, c'hauete ueduto in casa mia. Però uerrò à dirui quel
che sia Hemispherio. Dico adunque; che
DEFINITIONE II.
de tiratole sopra, come conuiene, per vdir gli Interualli in essa accommodati alle lor pro-
portioni.
il suo nome; dirò ch'ello è una meza Sphera. Quanto al nome (dissi) bisognereb-
be, che cosi fusse, ma in fatto è la Metà della metà, che uiene ad essere un quar-
to; come hora ui dipingo; sia poi di legno, ò di metallo, che questo importa poco. Et

hò vsato & mostrato nel Cap. 20. della Secōda parte delle
Istitutioni; hora mobile & hora immobile; il che si può
chiaramēte uedere nell'Vltimo Cap. del Lib. 4. della Musi-
ca di Boetio. Ma nō ui uoglio porre al presente altre Defi-
nitioni; perch'io uoglio che queste insieme con l'altre, ch'io
ui proposi ne i passati ragionamenti ui siano à bastāza per
il ragionamēto d'hoggi; ne gli altri poi ui proponerò quel-
le, che torneranno al nostro proposito. A questo, disse il
Signor Desiderio; Haueteci à proporre altre Dignità, ò
Massime, oltra quelle, che ci hauete proposto? Nò; gli risposi; percioche quelle ci ha-
ueranno à seruire sufficientemente in tutti i nostri ragionamenti. Intorno alle Dimande
poi; soggiunse M. Adriano; ui contentate forse di quelle cose solamente, che 'l primo gior-
no ci hauete richiesto? Messer nò; gli risposi; anzi uolendoui dimostrare operatiuamen-
te quello, che ui son per dimostrare; è necessario, che mi concediate molt'altre cose; al-
tramente non ui potrei dimostrar cosa alcuna. Et tra l'altre fà dibisogno, che mi conce
diate neccssariamente questa; che
DIMANDA
PRIMA.
troua da Spacio à spacio, quell'istessa anco sia da Suono à suono.
concedendo, non potreste dimostrar cosa alcuna non hauendo altra uia, che
sia più ferma & stabile di quella della Diuisione della chorda; al che soggiunse
M. Adriano; Anzi sopra di questa, mi pare, com'io lessi nelle Istitutioni;1. par. c.
19. & 2.
part. c. 18. che
fondate tutto 'l uostro parlare. Cosi è Messere: risposi. Et perche Vitelione dimanda;Perspec.
lib. 1. peti.
3.
che si gli conceda; che Quando due Superficie si toccano insieme, facciano una Super-
ficie sola; però ancora io ui dimando, che mi sia concesso da uoi; che
page 136
DIMANDA II.
me perfettamente vnisone, siano riputate, ouer faciano una chorda sola.
spose) è il douere che ui si conceda; essendo che (come dichiarate nelle Isti-
tutioni2. Instit.
cap. 11.) l'Vnisono non si fà maggior d'interuallo; come affirmatiuamente ten-
gono alcuni nouelli professori di questa Scienza; iquali dicono che due Vni-
soni aggiunti insieme fanno una Seconda; tre fanno una Terza; quattro fanno una Quar-
ta; & cosi aggiungendo gli altri per ordine vanno accrescendo l'Interuallo; il che è falsis-
fimo appresso d'ogni mediocremente essercitato nelle cose della Musica; essendo che fa-
cendosi à questo modo tale Interuallo (se cosi si può dire) non si fà altramente maggio-
re; come hò anco detto; percioche si potrebbe anche dire, che la Linea si facesse de Pun-
ti; aggiungendo l'uno all'altro; il che è impossibile: onde nel farsi cotali l'Interualli la
cosa uà altramente; essendo che non si aggiunge vno di essi ad vn'altro; ma si aggiun-
ge uoce à uoce, ouer suono à suono. Questo veramente hanno detto con poca consi-
deratione; disse il Signor Desiderio; & con poca intelligenza dalle cose; & una gran
pazzia; percioche (com'io credo) cosi come aggiungendo acqua ad acqua dell'istessa
qualità, non si uiene à comporre vn misto; ma si molteplica solamente cotale acqua; cioè,
la quantità douenta maggiore; cosi aggiungendo un Suono ad un'altro equale, non si
muta la prima qualità; ma si molteplica i suoni, ò le Voci. Dite bene per mia fè; risposi;
& la comparatione quadra benissimo, stando nella qualità; Però uerremo all'altra Di-
manda; la qual sarà questa.
DIMANDA III.
che essendomi stati fin'hora liberali, che per l'auenire vogliate essere auari; però
concedetemi anco; che
DIMANDA IIII.
il contrario; la Parte & il più tirato dia il suono più acuto.
diamo qual si uoglia Istrumento da chorde; vediamo esser uero quel che diman-
date. Questo vediamo etiandio ne gli altri Istrumenti da fiato, & maggiormen-
te ne gli Organi; imperoche s'io haurò una Canna, la quale sia più graue di quello, che la
uorrei; tanto più ch'io la faccio corta, tanto più il suono, che da lei uiene, si fà acuto.
A questo soggiunsi; Ancora che ad alcun di uoi parerà forse, ch'io replichi quasi la Pri-
ma dimanda; tuttauia quando considerarete quel, ch'io dimando hora, potrete cono-
scer la differenza; percioche quello, ch'io uoglio al presente è; che mi concediate.
page 137
DIMANDA V.
ma quella parla del Spacio referito al suono, & questa del Spacio referito al nu-
mero. Voi dite bene; risposi, Et queste saranno quelle cose, ch'io uoglio hauerui
dimandato; percioche con esse potrò dimostrar tutto quello, che hoggi ui uoglio propor-
re. La onde per non andar più in lungo; se cosi ui è in piacere; uerremo alle Proposte. Dis-
se à questo M. Adriano; Anzi tutti noi ui preghiamo à dar principio à quel che ui par,
che sia più espediente. Incomincierò adunque; soggiunsi; da una Dimostratione delle più
facili, che sarà come Elemento delle seguenti; la quale intesa, non è dubio, che l'altre non
ui saranno punto difficili; & sarà questa.
PROPOSTA
PRIMA.
strai nel cap. 18. & 19. della Seconda parte delle Istitutioni. Ce lo ricordiamo
benissimo, disse M. Adriano; Ma se ben mi ricordo quelle Sei cose, le quali
entrano in ogni perfetto Problema, ò Theorema; nella Proposta, ch'è Problema, non
Theorema; non si ritroua il Dato, & anco il Quesito; il primo de i quali è la data Chor
da, & il secondo è il Tuono? E' uero dissi; & ei subito soggiunse; A' questa non segui-
ta poi la Seconda cosa, che è la Espositione del Dato? Cosi è, risposi. Fatela adunque se 'l
vi piace, replicò egli. La onde cominciai in cotal modo; Sia adunque ab. la data chor-
da di stesa; sopra la quale habbiamo da collocare il Tuono alla sua proportione. Auer-
tite Messere, che in queste poche parole si ritrouano due cose; prima, quella che hauete
nominato; cioè, l'Espositione del Dato; quando dico; Sia ab. la data chorda distesa; ma
la seconda è la Espositione del Quesito; quando dico; Sopra la quale habbiamo da col-
locare il Tuono alla sua proportione; onde tutta questa prima parte è finita; & però uen-
go alla Costruttione, & dico; Diuido prima essa ab. Terza dimanda dhoggi in no-
ue parti equali; secondo 'l termine maggiore della proportione del Tuono; la quale, per
la Nona proposta di heri, è Sesquiottaua; di maniera, che cb. uenga à contenere otto
parti; secondo 'l termine minore della nominata proportione; & qui finisco la Costrut-
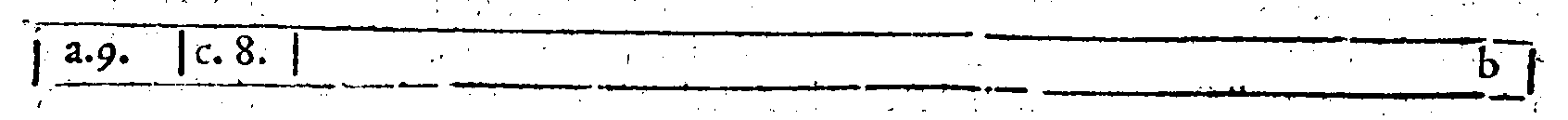
struttione. Cosi è risposi; però seguo in questo modo; & perche ab. & cb. contengono
il Tuono; però dico sopra la data chorda distesa esser collocato il Tuono alla sua propor-
tione. Fate hora, disse M. Adriano, la Dimostratione, che sarà la Quinta cosa. Voglio;
risposi; percioche senza essa haurei fatto nulla. Onde dico prima; Quell'Interuallo, del
quale la maggior de due quantità cōtiene la minore & una sua Ottaua parte; per la Quin
ta definitione del Primo ragionamento; è Sesquiottauo. Dopoi soggiungo, Tutto lo
Spacio della chorda ab. contiene lo Spacio cb. una fiata & una sua Ottaua parte; essendo
page 138 che ac. è equale ad una delle sue Ottaue parti; adunque, lo Spacio ab. allo Spacio eb. è
Sesquiottauo. La onde; per la prima Dimanda poco fà propostaui, quell'istessa pro-
portione sarà del Suono di tutta la chorda ab. alla chorda cb. che si troua dallo Spacio a
b. allo Spacio cb. Et anco per l'Vltima dimanda; Quella proportione, che si troua tra a
b. & cb. ne i Spacij, quell'istessa si trouarà tra Numero & numero; cioè, tra 9. & 8. La on-
de per aggiunger l'ultima parte; ch'è la Conclusione, dico; Ma la Sesquiottaua è la forma
del Tuono; Adunque tra le chorde ab. & bc. è contenuto il Tuono. Et cosi Sopra una
data chorda distesa habbiamo collocato il Tuono alla sua proportione; secondo la pro-
posta; & questo è quello, che ui douea dimostrare. Io hauea dibisogno, disse M. Adriano;
che di nuouo commemoraste quelle Sei cose, che di sopra habbiamo nominato; percio
che hauendole hora applicate alla proposta, la quale è musicale, mi sono tanto bene affis-
sate nella memoria; che mai più da me si partiranno. Ma parmi, che questa proposta sia
stata vniuersale; nondimeno l'hauete accommodata al Tuono maggiore; se ben si poteua
intendere anco del minore; questo importa pur qualche cosa. Auertite Messere, dissi;
per non replicar tante fiate 'l nome di maggiore, che quando per l'auenire nominerò il
Tuono, senza aggiunto alcuno di maggiore, ò di minore, d'intender sempre per una cer-
ta eccellenza il Maggiore, & non lo Minore. Percioche quando nominerò questo,
v'aggiungerò sempre questo termine Minore, per distinguerli l'un dall'altro. Deh di gra-
tia, disse M. Claudio; se non vi rincrescie, dimostrateci anco, in qual maniera.
PROPOSTA II.
distesa.
le Sei cose di sopra nominate. Però incominciando dico; Sia ab. la distesa
chorda, sopra la quale; nel modo c'habbiamo collocato il Tuono Sesquiottauo
& maggiore; uogliamo etiandio collocare lo Sesquinono & minore. Diuido
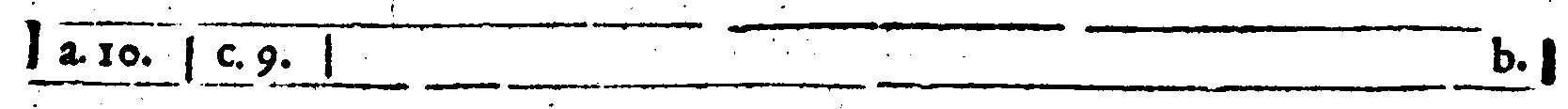
re della proportione Sesquinona, la quale è la forma del proposto Tuono; di tal sorte, che
cb. habbia noue parti, secondo 'l termine minore, & ac. sia una parte. Ilche fatto, Di-
co ab. & cb. cōtenere il Tuono minore, & sopra tal chorda esser collocato esso Tuono al-
la sua proportione. Et perche tutto lo Spacio ab. contiene cb. & la sua nona parte; essen-
do che ac. è equale ad una delle noue; però, per la Quinta definitione del primo giorno,
lo Spacio ab. è Sesquinono con cb. La onde la Prima dimanda d'hoggi ci concede; che
quella proportione istessa, che si troua tra la chorda, ò Spacio ab. con la cb. quell'
si troui ancora tra 'l Suono causato da tutta la chorda ab. con quel che nasce dalla cb. Et
per l'Vltima, quella proportione, che si troua tra ab. & cb. ne i Spacij, quell'istessa si tro-
ua tra Numero numero; cioè, tra 10 & 9. La onde essendo tra ab. & cb. la proportione
Sesquinona; & essendo questa proportione, per la Nona proposta del giorno preceden-
te, la forma del Tuono minore; seguita, che tra ab. & cb. sia collocato & accommodato
il Tuono minore sopra la data chorda alla sua proportione, secondo la vostra proposta;
come dimostrar ui douea. Resto di questo satisfatto, disse M. Claudio. Vi piaceranno
anco l'altre; come spero; risposi; però ascoltate questa Terza.
page 139
PROPOSTA III.
Tuono.
31. & 32.
Et. 2. part.
cap. 21. &
22. intorno la materia
del Soggiungere & del Preporre l'una all'altra le Consonanze, & anche le Pro-
portioni; onde non ui sarà difficile quel ch'in questa ui hò da dimostrare. Però
qui non replicherò altro; ma uerrò alla dimostratione. Sia adunque ab. la data chor-
da, sopra la quale, per la Prima proposta; sia accommodato ab. & cb. Tuono alla sua
proportione; al quale faccia dibisogno di soggiungerne vn'altro, ouer più, come torna
in proposito. Diuido, per la Terza dimanda di questo, cb. in noue parti equali, per il ter-
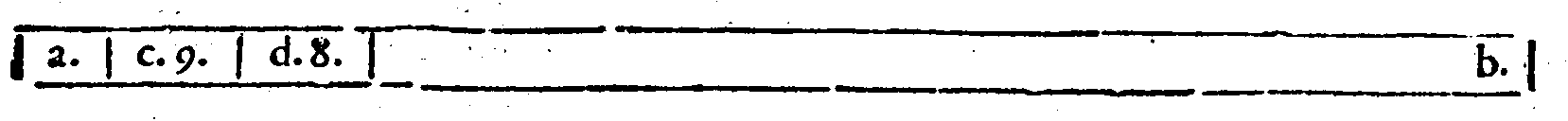
ne contenga otto, per il minor termine; & cb. ne contenga noue. Il perche è manifesto,
per la Prima proposta, che cb. & db. risonerà il Tuono. Ma perche ab. & cb. è Tuono,
& simigliantemente cb. & db. è Tuono adesso ab. & cb. congiunto; però dico, che so-
pra la data chorda habbiamo soggiunto un Tuono ad un'altro; secondo la proposta. Et
questo è quello, che vi douea di mostrare. Ne vi sarà cosa difficile da fare; quando à
questi due ne uoleste aggiungere un Terzo, oueramente qualunque altro Interuallo, che
più vi piacesse; percioche diuidendo 'l restante di tutta la chorda, che è db, secondo 'l ter-
mine maggiore radicale della proportione dell'Interuallo, che vorrete accommodare;
& pigliate quelle parti, che fanno per il numero delle Vnità, che sono contenute nel mi-
nore; come insegna la Prima proposta; potrete sempre hauer quello, che ricercarete. Io
intendo benissimo ogni cosa; à questo rispose M. Adriano; percioche mi ricordo quel-
lo, che hauete scritto in questa materia nelle Istitutioni;1. par cap.
31.
Et. 2. part.
cap. 21. onde intorno à questa cosa non
mi nasce dubio alcuno. Ma vi uoglio solamente dire; che mi pare, che questa cosa vadi
sempre ad vn modo; purche si osserui di diuider la chorda, sopra la quale si vuole accom-
modar l'Interuallo alla sua proportione, secondo i termini cōtenuti nella sua Radice. Que
sto è uero Messere; gli risposi; Percioche quanta varietà può intrauenire, lasciamo di dir
quanto al sito, è quella delle Proportioni; percioche l'vna può esser dell'altra maggiore;
ma quanto all'operare, è un'istesso modo di vna, con quello che serue all'altra. Que-
st'istessa anco uedete nella Geometria; percioche (per darui un'essempio) volendo di Tre
linee rette, che siano pari à Tre altre rette date, formare un Triangolo; sempre si fà ad un
modo; purche le Due in qualunque modo prese siano maggiori dell'altra; come per la
Ventesimaseconda del Primo de gli Elementi d'Euclide è manifesto; siano poi quan-
to si vogliano corte, ò lunghe le date Tre linee, che non fà caso alcuno. Et di questo cre-
do che il Sig. Desiderio, come quello, che ha veduto molti autori, se ne potra ricordare.
Me ne ricordo ueramente, rispose egli; Onde non ui è dubio alcuno, che la cosa non sia,
come l'hauete detta. Mi piace, dissi, che ue lo ricordate; Ma perche habbiamo nomina
to la Geometria, ui uoglio dire, ch'io spero, che vederete ne i miei Sopplimenti4. Supple.
cap. 21. un modo
nouo facile (com'io credo) di Molteplicare, soggiungendo l'uno all'altro quanti Inter-
ualli si uorranno, contenuti da un'istessa proportione; che verranno ad essere proportio-
nali; & questo col mezo della Geometria. Et credo che ui piacerà molto; percioche è
(com'hò detto) facile, breue & ingegnioso. Questo haueremo molto grato M. Gioseffo:
disse il Viola; però sforzateui di dar presto in luce cotali Sopplimenti; acciò potiamo
page 140 uedere qualche cosa di nuouo. Pregate il Sig. diss'io; che mi dia gratia di poterlo fare; poi
che ogni cosa è all'ordine. Ma non perdiamo il tempo, & passiamo un poco più oltra.
PROPOSTA IIII.
32. della Prima parte, & al 22. della Seconda delle Istitutioni; & però credo
anco, che non haurò difficultà d'intenderla; essendo che mi ricordo bene tut-
to quello, che contengono questi due Capitoli. Ma perche ui hauete obligato di dimo-
strar tutto quello, che uoi proponerete; però dimostratela. Credo; risposi; che ui ricor-
date, che ne i luoghi, che m'hauete allegato, voglia; percioche cosi fà dibisogno; che
primieramente si sommino insieme quelle proportioni, lequali si vogliano accommo-
dare & preporre l'una all'altra, & ridurle sotto una sola Denominatione. Però sia (co-
me dice la Proposta) che vogliamo preporre un Tuono ad un'altro sopra una data chor-
da; Sommaremo prima le proportioni de due Tuoni insieme, le quali sono due Sesqui-
ottaue, nel modo ch'io mostrai nel Cap. 33. della Prima parte delle Istitutioni, & haue-
remo questi termini 81. & 64. iquali, per la Nona definitione del Primo ragionamento
saranno radicali; percioche non possono esser numerati communemente da altro nu-
mero, che dall'Vnità, & conteneranno la Super. 17. partiente 64. che sono due Tuoni
Sesquiottaui sommati insieme. Dopoi, sopra la data chorda ab. accommodaremo questi
Tuoni; diuidendo, per la Terza dimanda, lo Spacio ab. in Ottantauna parte equale; di-
uidendola prima tutta in Noue; dopoi diuidendo quella parte, ch'è più vicina allo a. che
sarà ad. in altre Noue parti equali, perche faranno 81. per il Tutto di tutta la chorda a
b. Onde con l'istessa ragione & apertura di Compasso; aggiungendo à queste noue parti
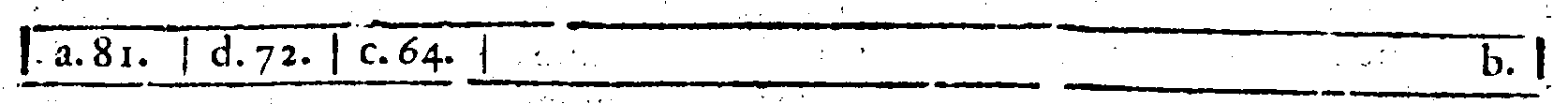
Il perche dico cb. contenere 64. parti di tutta la chorda ab. & esser per il termine mino-
re delle sommate proportioni. Dico hora ab. contenere la nominata proportione. Per-
cioche se tutto lo Spacio della chorda ab. cōtiene cb. una fiata & 17. Sessantesimequarte
parti; Adunque per la Sesta definitione del Primo; lo Spacio ab. sarà Super. 17. partien-
te 64 al cb. Et per la Prima dimanda, sarà l'istessa proportione di Suono à suono della
chorda ab. alla cb. che si troua tra lo Spacio ab. al spacio cb. & per la Quinta, quella
proportione, che si troua tra ab. & cb. ne i Spacij, quell'istessa si troua tra Numero & nu-
mero. Ma perche ab. & cb. è Interuallo composto di ab. & dh. & di db. & cb. che so-
no due Tuoni Sesquiottaui; però, per la Seconda dignità, risoluendosi il composto ab.
& cb. in ab & db. & in db. & cb. dico ab. & db. tanto esser Tuono, quanto è db. & cb.
Onde essendo db. & cb. Sesquiottauo; sarà anco Sesquiottauo ab. & db. Et, per la pri-
ma Dimanda di questo, tanta sarà la proportione di Suono à suono, quanta di Spa-
cio à spacio. Habbiamo adunque al Tuono cb. & db. preposto il Tuono ab. & db. secon-
do 'l nostro proposito; come vi doueà dimostrare. Auertite però, che questo modo di
preporre si fà, quando bisogna che 'l Tutto della chorda ab. sia l'estremo graue del Tuo-
no, che si hà da preporre. Et il sommare insieme le proportioni non si fà ad altro effetto;
se non accioche hauendo prima accommodato quell'Interuallo alla sua proportione,
al quale se ne uoglia un'altro preporre, dopoi quello, che si hà da preporre, habbia tan-
ta parte di chorda, che sia capace dell'Interuallo; percioche quando noi fussemo certi,
page 141 che tale Spacio fusse capace dell'Interuallo, che uogliamo preporre; ouer che prima fus-
se accommodato alla sua proportione quell'Interuallo, al quale ne vogliamo aggiungere
un'altro, nō accaderebbe fare altra somma. Però adunque poniamo, che per le due cose
nominate, fussemo certi, che nō bisognasse far'altra somma, & che euidentemente appa-
resse, che quella parte di chorda, sopra la simile tale Interuallo si uolesse accōmodare, fus-
se capace, procederemo à questo modo. Sia la chorda ab. sopra la quale sia accommo-
dato, per la Prima di questo, il Tuono cb. & db. alla sua proportione; al quale vogliamo
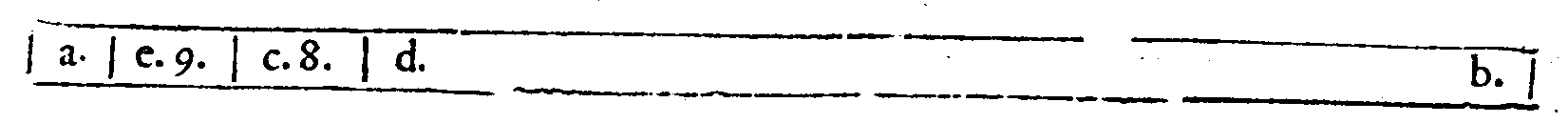
della proportione del Tuono; alle quali, secondo la ragione istessa, aggiungo la Nona, la
quale segno e. onde ne viene eb. Dico, che tra eb. & cb. habbiamo collocato il Tuono
alla sua proportione, & l'habbiamo preposto al Tuono cb. & db. Imperoche tutta la
chorda eb. cōtiene lo spacio cb. & una sua Ottaua parte; essendo che ec. viene equale ad
vna delle parti di cb. adunque per la Definitione, lo spacio eb. è Sesquiottauo allo spa-
cio cb. Et per la Prima Dimanda di hoggi, quell'istessa proportione è del Suono di tut-
ta la chorda eb. alla chorda cb. che si troua dallo Spacio eb. allo spacio cb. Et, per la
Quinta; quella proportione, che si troua tra eb. & cb. ne i Spacij, ò Interualli, quell'istes-
sa è tra Numero & numero; cioè, tra 9. & 8. Ma perche eb. è Sesquiottauo al cb. & è la for-
ma del Tuono; per la Nona di heri, è la Sesquiottaua proportione; però dico, che tra eb.
& cb. habbiamo collocato il Tuono alla sua proportione. Simigliantemente; perche eb.
& cb. proportione è proposta alla proportione cb. & db. essendo cb. & db. Tuono, &
anco eb. & cb. però dico, c'habbiamo preposto il Tuono eb. & cb. al Tuono cb, & db. il
che è secondo la proposta, & come ui douea dimostrare. Disse allora M. Francesco; Chi
uolesse preporre un'altro Interuallo, che fusse di proportione diuersa, credo, che si potreb-
be tener l'ordine istesso; s'io nō m'inganno. Al quale risposi; Non u'ingannate altramen-
te; purche si osserui la varietà de i termini delle proportioni. Onde se hauesti da prepor-
re il Tuono maggiore, contenuto dalla proportione Sesquiottaua, al minore, contenuto
dalla Sesquinona; bisognarebbe tener quell'ordine istesso; sommando prima i termini ra-
dicali delle lor proportioni, se fusse dibisogno, che sono. 9. 8. & 10. 9. Percioche ne verreb-
be 5. & 4. dopoi diuidendo tutta la chorda per il numero maggiore de i prodotti; si piglia-
rebbe le Quattro parti, secondo 'l numero delle Vnità contenute nel minor termine de i
prodotti, & si hauerebbe insieme accommodato alla sua proportione i sommati due Tuo-
ni; iquali pongo che siano tra ab. & cb. del primo essempio. Ma per preporre il maggio-
re al minore, diuideremo la chorda minore in Noue parti equali, per le Vnità contenu-
te nel minor termine del Tuono minore; Onde aggiungēdouene un'altra, secondo le Vni
tà del termine maggiore, haueremo proposto il Tuono maggiore al minore, secondo 'l
proposito; il quale per cagione d'essempio, diremo che sia ab. & db. & lo minore db. &
cb. Hora uolendo vdire in atto tutto quello, che si è operato; tirato che si haurà sopra la
Regola harmonica due chorde di grossezza vguale, di lunghezza della ab. & accordate
perfettamente insieme vnisone, saranno (per la Seconda dimanda di hoggi) riputate vna
chorda sola. Il perche posto l'Hemispherio sotto una di esse chorde nel segno d. & toccata
la ab. prima, & dopoi la db. oueramente percosse tutte due insieme; si udirà senza dubio
alcuno il suono di tutta la Chorda ab. col suono della Chorda db. mandar fuori l'inter-
uallo del Tuono. Et se 'l si porrà, ò spingerà l'Hemispherio della Chorda db. nel punto c.
dal percuotere prima la Chorda ab. & la cb. dopoi; oueramente del percuoter queste
due insieme, vdiremo l'Interuallo composto de due Tuoni Sesquiottaui, il quale senza
dubio non è consonante. Ma se sotto la Chorda ab. porremo un'Hemispherio in punto d.
tra la db. & la cb. si udirà un'altro Tuono più acuto del primo per una Sesquiottaua pro-
page 142 portione, il quale è della quantità del Tuono ab. & db. posto nella parte graue. Per co-
tal modo (adunque) qual si uoglia Interuallo si potrà porre sotto 'l giudicio del senso del-
l'Vdito; come mostrai etiandio nelle Istitutioni,2. par. c. 2. & udir anco, percotendo insieme cotali
chorde, ogni Consonanza & Dissonanza; & aggiungendoli una terza chorda, ogn'Har-
monia accommodate alla loro proportione. Qui disse M. Adriano; Parmi, che fin'hora
hauete dimostrato assai; & molto mi piace, ch'alle fiate ci andate riducendo alla memoria
alcune cose, c'hauete insegnato nelle Istitutioni; percioche tanto più si affisseranno nelle
nostre menti; quanto più ce le ricordarete; di maniera, che noi credo, che cosi tosto si par-
tiranno. Allora, disse M. Francesco; Queste cose Mathematiche sono à me tanto difficili,
quanto alcun'altra cosa; & cosi credo che sia anco à molti altri; da tenersi à memoria. On-
de non senza frutto si possono spesse fiate replicare. Il perche ne sento ueramente un gran
contento. A questo, disse M. Claudio; Sono di gran giouamento per ogni modo, tanto
più, quanto dalla uiua uoce procedono, & con gli essempij si pongono auanti gli occhi;
percioche queste due cose aggiunte insieme hanno grandissima forza. Questo è uero, dis-
si; la onde ui uoglio anco dire una cosa; che ritrouarete ne i poco fà nominati Soppli-
menti;4. Supple.
c. 22. &
23. aiutati dalla Geometria, il modo di molteplicare aggiungendo ò proponendo
quanti si uogliano Interualli, l'uno all'altro proportionalmente; modo poco differente
da quello, ch'io hò commemorato poco fà; sopra la Regola harmonica; & etiandio un
modo di riportar nell'acuto, ò nel graue qual si uoglia Ordine de proportioni accōmodato
nella detta Regola; senza far molte repliche di alcuna diuisione; operando il tutto con la
Riga solamente, & col Compasso. Questo credo ueramente, disse M. Adriano; che non
potrà essere se non grato; uenendo à minuire la fatica & la lunghezza del tempo nell'ope-
rare; cose à tutti molto noiose; però Iddio ui dia gratia, che li potiate porre in luce, &
presto. Cosi faccia il Sig. Iddio, risposi, à laude & gloria sua. Ma seguitando la nostra im-
presa, uerremo ad un'altra proposta.
PROPOSTA V.
Parte della vicina diuisione, che di essa Parte à tutto 'l restante delle parti, che seguono à
lei più vicine.
pere. Vi douete pure ricordar quello, ch'io chiamo Spacio, gli dissi. Benissimo,
rispose; onde il Sig. Desiderio soggiunse; Non chiamate uoi Spacio la Lunghez-
za de tutte quelle cose, le quali possono mandar fuori Suono? come sono Chorde, Ner-
ui, Aria mandato dal petto, & ogn'Istrumento qual si uoglia da fiato? come sono Canne
d'Organi, Pifferi, Trombe, Cornetti & altri simili? Queste cose tutte si chiamano uera-
mente Spacio, risposi; nelle quali si ritroua una certa proportione, col mezo della quale
ritengono quasi un'istessa natura. Però adunque sia tutto lo Spacio ab. diuiso, per la Ter-
za dimanda, in Noue parti equali; cioè, ac. cd. de. ef. fg. gh. hi. ik. & kb. Dico la pro-
portione ab. & cb. esser minore della proportione cb. & db. Imperoche essendo ab.
diuiso per i punti c. d. e. f. g. h. i. k. in Noue parti equali, cb. contiene Otto di esse parti,
delle quali ab. ne contiene Noue, & ab. contiene lo spacio cb. & una sua Ottaua parte,
la quale è ac. Ma perche cb. contiene Otto parti equali alla cd. però db. de tutte le par-
ti ne contiene solamente Sette. Adunque cb. contiene lo Spacio db. & una settima sua
parte, ch'è cd. Ma essendo la Ottaua parte, per la Nona dignità, minore della Settima;
per la Ottaua dignità di nuouo diremo, che ab. & cb. proportione Superparticolare sia
minore della cb. & db. come quella, ch'è denominata da parte minore. Essendo che dal-
page 143
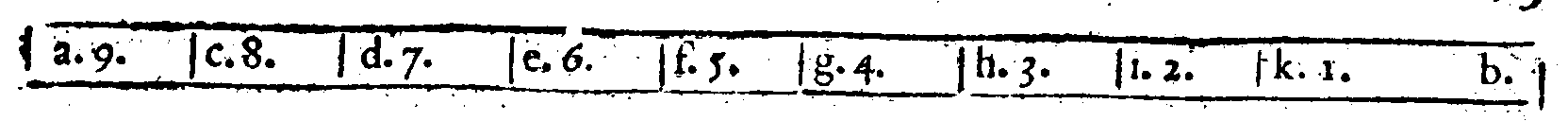
que; Qual si uoglia Spacio diuiso in molti Spacij equali, è minore la proportione del Tut
to à tutta la Parte della uicina diuisione, che di essa parte à tutto il restante delle Parti,
che seguono più uicine; come ui douea dimostrare. Allora M. Francesco disse, questo
hauete dimostrato benissimo nelle Istitutioni,1. par. cap.
40. parlando della Progressione, ò Propor-
tionalità arithmetica; percioche (per addur l'essempio che mostrate) tra 4. 3. 2. che sono
termini differenti per la Vnità; come sono etiandio le Parti fatte dello Spacio, che haue-
te diuiso tra 3. & 2. ui è la proportione Sesquialtera, & tra 4. & 3. la Sesquiterza, le quali
sono due proportioni differenti; come à ciaschedun di noi è manifesto. Voi hauete detto
bene; gli risposi; & questo istesso, che uoi dite (se ui ricordate) vi dimostrai heri nella
Duodecima proposta. Ma vdite che bel Corollario ne segue da quello, che detto hab-
biamo de i Spacij equali, in quelli che sono di proportione equali & proportionali.
COROLLARIO.
& l'uno all'altro si soggiungono; tanto più contengono i Spacij ristretti & minori. Et
quanto più nel graue l'uno all'altro si prepongono, tanto più i Spacij sono maggiori &
più larghi.
la Parte più grauemente, & la Parte rispetto al Tutto più acutamente suona.
Onde se al Tuono, il quale senza dubio è collocato tra ab. & cb. si aggiungerà
un'altro Tuono; quel che s'aggiungerà, sarà senza dubio più acuto di tanta proportione,
quanta è quella, ch'è contenuta nel primo. La onde se lo Spacio cb. si haurà da partire in
Noue parti equali, ciascheduna di essa uerrà minore dello Spacio cd. il quale è la sua
Ottaua parte. Imperoche è la Nona, & è denominata da maggior numero, che non è la
Ottaua. Sarà adunque ciascheduna delle Noue parti minore dello Spacio ac. essendo
che ac. & cd. sono equali. Et questo, ch'io hò detto d'un tuono, si potrà dire anco di cia-
schedun'altro, che si aggiungesse verso l'acuto. Non uoglio però, che vi ristringiate à cre-
dere, che questa Proposta sia uera nell'Interuallo, ò Spacio del Tuono solamente; ma sa-
piate, che è commune à qualunque altro Interuallo, sia qual si uoglia, ò grande, ò piccio-
lo; pur che s'osserui l'istessa proportione. M. Adriano à questo, disse; Questa cosa è chia-
ra, & non porta seco dubitatione alcuna. Seguitando adunque (dissi) è manifesto, che
quanto più in acuto un Tuono, ò altro Interuallo qual si uoglia d'un istessa proportione,
s'aggiunge all'altro; tanto contiene i Spacij più ristretti & minori ò per il contrario; nel
graue saranno tanto più larghi & maggiori; come dice la Proposta. Ma che direte di
questo? che
PROPOSTA VI.
parti proportionali.
Sia ab. & cb. l'interuallo del Tuono accommodato alla sua proportione, &
sia diuiso ab. come nella Precedente si è fatto; da c. d. e. f. g. h. i. k. in Noue
parti equali. Dico che 'l mezo delle estremità del Tuono, che sono ab. & cb. &
è quello Spacio, che si troua tra a & c. ilquale se bene è diuiso da l. in due parti equali, non
è però nella Regula harmonica diuiso in due parti proportionali. Adunque; soggiun-
se egli; uoi uolete inferire, che se 'l si diuiderà lo Spacio ac. della detta Regola in due par-
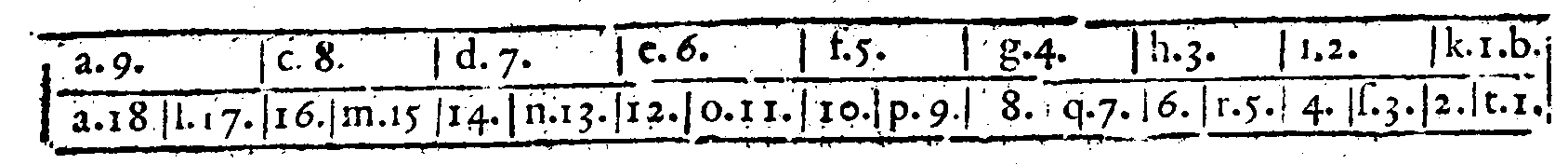
co, risposi; & il Sig. Desiderio soggiunse; Come è possibil questo? Lo vederete tosto, dis-
si, se hauete inteso la precedente. Ma notate, acciò non prendesti errore; ch'io dico di-
uidere in due parti equali tutta la proportione del Tuono geometricamente; & non la
sua differenza, ouero estremità; percioche facendo la diuisione della differenza per cotal
modo; tal diuisione è arithmetica, & non geometrica; & cosi le parti delle diuisioni sono
in proportione inequali & non equali. V'intendo hora benissimo; rispose egli; & mi ma-
rauigliaua grandemente di cotal cosa. Ma seguitate pure à dirci altro; che questa cosa à
me hora è chiara. Anzi ui uoglio dimostrar, soggiunsi, questa cosa minutamente; per ser-
uarui il patto, c'ho fatto con esso uoi. Questo non dico per interromperui; replicò il Sig.
Desiderio; percioche tanto ne dee esser cara la dimostratione delle cose facili; quanto
quelle delle difficili; poi che col suo mezo le uenimo à sapere. Perche se ben le sapiamo
senza 'l suo mezo; le sapiamo però ad un certo modo, che non è propriamente sapere; tan-
to più che non le sapiamo dalle lor cagioni. Essendo adunque diuisa la ab. risposi; in No-
ue parti equali, & essendo ab. & cb. le estremità del Tuono dico, che se 'l si diuiderà lo
Spacio ac. ch'è il mezano de queste due estremità, in due parti equali nel punto l. per
questo il Tuono non sarà diuiso in due parti proportionali & equali. Et che 'l Suono ab.
& lb. non sarà equale in proportione al Suono lb. & cb. lo prouo. Diuido ciascheduna
dell'altre parti, ouer'otto Spacij simigliantemente in Due parti equali, ne i punti m. n.
o. p. q. r. s. t. Hora è manifesto, che tutto lo Spacio ab. è diuiso in Diciotto parti equa-
li, che sono al. lc. cm. md. dn. ne. eo. of. fp. pg. gq. qh. hr. ri. is. sk. kt. & tb.
Adunque, per la Precedente, la proportione ab. & lb. è minore della lb. & cb. Et diuiso
il Tuono in questa maniera, non è però diuiso in due parti equali, ò proportionali; co-
me dice la Proposta. Et questo è quello, che ui douea dimostrare. Ma ascoltate quel
ch'io uoglio dire, che segue benissimo à quello, che ui hò dimostrato; & sarà questo.
PROPOSTA VII.
Sesquidecimosettimo, & in vn Sesquidecimosesto interuallo.
siano anco ab. & cd. l'Interuallo del Tuono diuiso similmente nel mezo de i suoi
estremi nel punto l. in due parti equali. Dico che l'Interuallo del Tuono ab.
& cb. è diuiso in un Sesquidecimosettimo ab. & lb. & in un Sesquidecimosesto lb. & c
b. Et perche ab. contiene Diciotto parti, & lb. ne contiene Dicesette; però dico, per la
Quinta definitione del Primo ragionamento, ab. & ln. essere interuallo Sesquidecimo-
page 145 settimo; percioche ab. contiene lb. una fiata & una sua Decimasettima parte, detta parte
Aliquota. Simigliantemente, perche lb. contiene Dicesette parti, & cb. ne contiene
Sedici; però dico lb. & cb. per la nominata Definitione, essere interuallo Sesquisesto-
decimo; essendo che lb. contiene cb. & una sua Sestadecima parte Aliquota. Diui-
so adunque l'Interuallo del Tuono nel mezo delle sue estremità in due parti equali, è di-
uiso in vn Sesquidecimosettimo, & in vn Sesquisestodecimo interuallo; come, secondo
la proposta, vi douea dimostrare. Ma Ascoltate quello, che ui uoglio dire in consequen-
za di quel, che ui hò dimostrato.
PROPOSTA VIII.
mezana chorda di tutto il partimento sopr'auanza il Suono del maggiore estremo per l'a-
cuto, & del minore per il graue.
to parti equali; di maniera che ab. & cb. sia il Tuono. Dico che 'l Suono, che uie-
ne dalla lb. sopr'auanza quello, che nasce da ab. per l'acuto; & l'istesso lb. uince
lo cb. per il graue. Et perche ab. è il Tutto, & lb. Vna delle sue parti; però, per la Quar-
ta dimanda d'hoggi; ab. fà il suono più graue, & lb. più acuto. Et per la istessa; perche il b.
è il Tutto di cb. & cb. sono parti; però il suono lb. è più graue del suono cb. Adunque
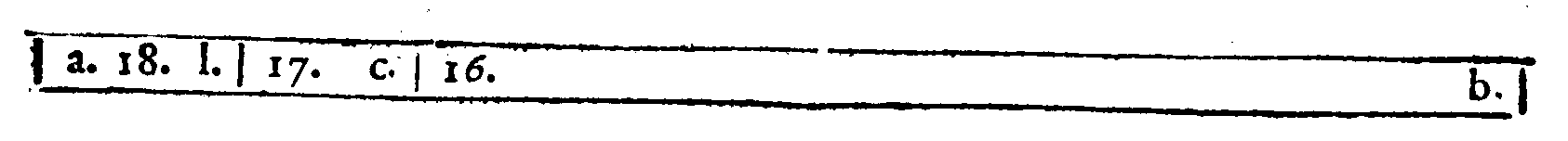
qual cosa ui era debitore di dimostrare. Siamo satisfatti, disse allora M. Claudio; & si
può seguitare. Dirò adunque, soggiunsi; in consequenza di quello che si è dimostrato;
che
PROPOSTA IX.
numeri rationali.
1. cap. 9. di dimostra-
re, contra quelli, che teneuano il contrario, che questo si può fare ottimamente?
& lo dimostrò ancora con numeri determinati; come può stare adunque, che
questo non si possa fare? Dissi à questo; Come lo dimostra il Stifellio? ue lo ricordate? Si
bene, soggiūse. Di gratia dimostratelo, gli dissi; perche ui uoglio far ueder l'errore di que-
sta cosa. Seguitò il Sig. Desiderio; Molteplica il Stifellio i termini radicali della propor-
tione Sesquiottaua; ch'è (com'hauete più uolte detto) la forma del Tuono; l'un nell'altro;
& lo produtto pone tra 'l maggior termine della proportione & il minore, ī questo modo
diuidendolo cō queste cifere ¯ & ˘ in due Semituoni minori, segnati cō la prima iquali
habbiano appresso loro lo Schisma rappresentato per la seconda cifera. Di maniera, che
page 146

lamente diuide quest'Interuallo, ma gli altri ancora, i quali sono più minuti assai; come
sono il Comma; oltra il Semituono maggiore & lo minore. Sta bene, risposi; Ma come
uorrete ridurre in atto cotal diuisione? Mi ricordo pur troppo la diuisione del Stifellio, &
mi ricordo anco, che Nicolò Tartaglia nella Seconda parte del suo general Trattatolib. 7. cap.
17. de
Numeri & Misure; corse la posta col Stifellio; percioche in questo luogo pose tutto quel-
lo, c'hauea scritto questo ueramente dotto nelle discipline Mathemati che; & ; ma (come ho detto) in qual maniera uorrete ridurre all'atto tal diuisione? Ve-
dete, ch'ella è irrationale; percioche tutte le uolte che si molteplica i minimi termini d'u-
na proportione tra loro; & che dal prodotto non si possa cauar la Radice quadrata; se li
pone appresso questa cifera √. la quale significa (come dimostrai nelle Istitutioni1. par. cap.
37.) quella
Radice, che si hà da cauar di quel tal numero. La onde il 72. il quale pone 'l Stifellio, ch'è
il produtto della molteplicatione di 9. con 8. non hà altramente Radice quadrata; & è
di altra specie, che non è il 9. & l'otto, che sono numeri semplici; come ei troppo bene lo
sapea; però gli hà posto appresso la cifera √. onde cotal diuisione si chiama Sorda & Ir-
rationale. Et però dico, che la proportione Sesquiottaua non si può diuidere in due par-
ti equali & proportionali, con numeri certi & determinati rationali. Et per conse-
quente ne anco il Tuono. Et che questo sia uero, uedete che 'l Stifellio nel fine del nomi-
nato Capitolo dice; che ne Giordano, ne il Fabro, ne alcun'Huomo dotto negò giamai,
che tal diuisione si potesse fare; parlando della sua; ma non già con numeri rationali &
determinati; come douete anco intendere la mia proposta. Di questo mi curo poco, dis-
se il Signor Desiderio; pur che si possa diuidere con certi numeri. Et io soggiunsi; di que-
sto poco conto tiene il Musico; ma si bene che siano certi & rationali. La onde ui uoglio
dire, che quelle tre quantità, che pone 'l Stifellio nella sua diuisione, sono non solamente
(comparando l'estreme con la mezana) irrationali; ma etiandio incerte. E come sono in-
certe? disse il Viola. Percioche le proportioni de i Schisma, gli risposi; per la Ventesima-
quinta proposta di heri, sono incognite & irrationali; le quali, se si aggiungeranno à qual
si uoglia proportione, che sia Rationale; quello che uerra, senza dubio alcuno, sarà Irratio
nale & incerto; come ui dimostrerò un'altra fiata; ma per hora di questo. Et
dico Incerto & Irrationale, in questo modo; perche 'l Musico non si può preualere di esse
in modo alcuno; essendo che non può tra due date chorde, che danno il Tuono, col me-
zo del numero √ 72. porre una terza chorda mezana, che tramezi (dirò cosi) ò partisca
equalmente il Tuono in parti equali, ouero equali Interualli di tal sorte; che tanta sia
la proportione del Suono, che nasce dalla chorda graue & dalla mezana; quanta quel-
la del Suono, che nasce da questa & dall'acuta. Et che ciò sia uero, poniamo l'essem-
pio dell'Interuallo ab. della Precedente, nel quale si ritroui tra ab. & cb. collocato il
Tuono. Pigliate qual si uoglia di uoi un Compasso, & ponete tra a & c. la quantità
di una mezana chorda, secondo i Numeri trouati nella diuisione del Tuono, che hà di-
mostrato il Signor Desiderio; di maniera che diuida la proportione ab. & cb. in due
parti equali, & che tanto sia la proportione di ab. con la detta mezana; quanto quel-
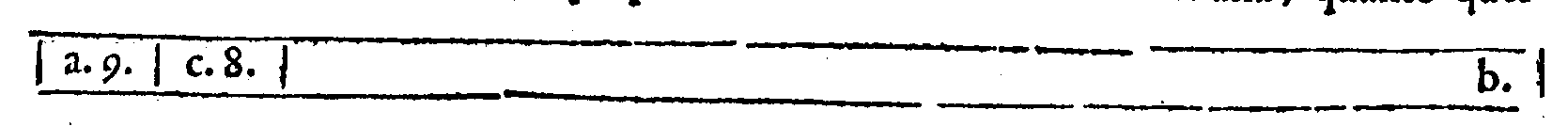
lo, che honestamente mi condannarete. Io per me non lo saprei fare; rispose M.
Adriano; Il che dissero anco gli altri. Ma il Signor Desiderio udendo questo, disse; In
page 147 uerità ch'è cosa impossibile: Et se questo non ui dà l'animo di far uoi, che pratticate le
cose della Musica; uoglio creder, che quello, ch'è à uoi impossibile, possa anco à me & ad
altri intrauenire. Però non sò che mi dire in questo fatto. Dite uoi appresso qualche cosa
M. Gioseffo, s'hauete da dire. Vi uoglio dir questo, dissi; che cō tutte le brauure, che hab-
bia fatto 'l Stifellio; nō lo pote, ne potrebbe anco fare, se ui fusse, cō questi suoi numeri cer-
ti & determinati. A questo; soggiunse M. Adriano. Che ha uoluto adūque fare quest'huo-
mo da bene? Mostrare, dissi; il suo ingegno contra alcuni, che detto haueano, che non si
poteua partire il Tuono in due parti equali con certi & determinati numeri; non hauen-
do nominato i Rationali. Per quel ch'io ueggio, disse il Viola; da queste Diuisioni fatte
à questo modo, poca utilità si puo cauar nelle cose della Musica; & però le iudico, per dir-
ui il uero liberamente, uane & inutili; & in ciò non credo offendere 'l Stifellio, ne etian-
dio altri. Sono ueramente inutili & superflue, dissi; quanto all'uso prattico; ma quanto
poi alla parte speculatiua, non ui potete appagare se non di quello, che ueduto hauete.
Allora, disse; di nuouo il Viola; Non dite più cosa alcuna, per uostra fè, di questa cosa,
& ritornate al uostro proposito. Et se non fusse, che hauete nell'Istititioni2. par.
cap. 24. &. 25. insegnato il
modo di ritrouare in due maniere le Chorde mezane; ui uorrei pregare, poi che 'l luogo
lo ricerca, che hora le doueste dimostrare; ma sarebbe superflua cotal cosa. Anzi ui uor-
rò, risposi dimostrar l'uno & l'altro modo, in queste due proposte seguenti; espedito che
mi haurò da questa. Per qual cagione? disse il Merulo; Perche quantunque habbia
dimostrato ritrouar cotali Chorde mezane, dissi; non hò però in tal maniera & cosi co-
piosamente dimostrato & prouato il tutto, ch'appresso d'alcuno non possa nascer qualche
dubio; essendo che iui hò dimostrato cotal cosa con breue modo; ma à mano à mano ui
dimostrerò tutto quello, che in questa fattura si può dimostrare. Vi ricordate quello che
io dissi il Primo giorno dimostrandoui la Nona proposta? Ce lo ricordiamo, disse M.
Adriano. Vi dissi, soggiunsi; che l'Interuallo Superparticolare non riceue ne uno, ne più
mezani termini, che lo diuida proportionalmente in due, ò più parti equali; Et per la
Prima dimanda d'hoggi; Quell'istessa proportione, che si troua da Spacio à spacio; si tro-
ua anco da Suono à suono; Ma il Tuono non nasce egli da un Superparticolare? essendo
che è contenuto dalla proportione Sesquiottaua? E' uero, rispose il buon Vecchio, & io
gli aggiunsi; Fate hora uoi la conclusione. Adunque bisogna dire, diss'egli; che 'l Tuono
non si possa partire in due parti equali & proportionali, con certo & determinato numero
rationale; quantunque si possa diuidere con numeri Sordi & irrationali; com'hauete di-
mostrato. Cosi è Messere, gli risposi; ma per il Corollario etiandio della Ventesimaquin-
ta proposta del giorno passato, habbiamo; che, Di quelle proportioni, le quali non han-
no nelle lor Radici il maggior termine, che sia Numero quadrato, & lo minore la Vnità;
le Parti delle lor diuisioni sono incognite & irrationali; Ma i termini della proportione
del Tuono, i quali sono 9. & 8. non sono sottoposti à cotal legge; quantunque il primo sia
Numero quadrato; Adunque le proportioni delle diuisioni, che si facessero del Tuono,
sarebbono incognite & irrationali. Ma l'essere à questo modo, è, che non si possino co-
me poco fà ui hò dichiarato) descriuer con numeri determinati & rationali; Adunque
il Tuono non si può diuidere in due parti equali & proportionali, cō certi & determina-
ti numeri rationali; come dice la Proposta; & come ui douea dimostrare. Ma aggiunge-
te anco questo; che 'l non si possa diuidere minormente in più de due parti. Disse allora
il Sig. Desiderio; Hauete dichiarato il tutto ottimamente & dimostrato; di maniera che
non ui resta dubio alcuno; però potrete seguitare à uostro piacere; & dimostrare in che
modo si possano ritrouar queste Chorde mezane tra gli estremi suoni d'un'Interuallo, di
modo che lo diuida in due parti equali & proportionali. Seguitai adunque in questo
modo; Volendo far questo, uerrò prima à dirui; che
page 148
PROPOSTA X.
li, & dimostrare i termini delle vere metà nelle chorde.
minati & rationali; hora la Presente dimostrerà, che tal diuisione si può fare Geo-
metricamente, senza ragione dimostratiua de numeri. Et questo ui uoglio di-
mostrare in due modi; de i quali il primo sarà, di ritrouare una Chorda sola mezana pro-
portionale, che lo partisca in due parti equali; L'altro sarà, di ritrouarne non solamen-
te una; ma più ancora, che lo diuida proportionalmente in quante parti equali sarà dibi-
sogno. Iquali modi seruiranno, non solamente alla diuisione del Tuono, ma etiandio di
qual si uoglia Interuallo. Il primo modo adunque sarà questo. Sia la chorda ab. sopra
la quale, per la Prima d'hoggi, sia accommodato il Tuono alla sua proportione; & sia ab.
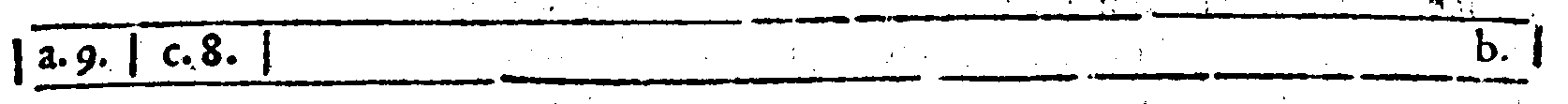
alla ab. & fe. equale alla cb. Onde sia dibisogno tra la chorda de. & la fe. che sono l'estre-
me chorde del Tuono, porre una Chorda mezana proportionale. Il perche seruendomi
della Nona proposta del Sesto de gli Elementi d'Euclide; secōdo la tradottione del Cam-
pano; ò delle Terzadecima di Theone; aggiungo dopoi, per la Quartadecima del primo
la linea eg equale alla fe. & compono tutta la dg. sopra la quale descriuo 'l Semicircolo
dhg. & sopra 'l punto e. doue la de. si coniunge con la eg. per la Vndecima del detto, tiro
la perpendicolare eh. che uada alla circonferenza dhg & descriuo le linee dh. & gh. Et
perche, per la Trentesimaprima del Terzo, l'angolo dhg. nel semicircolo è angolo retto;
& nel Triangolo dgh. dall'angolo retto alla base perpendicolarmente fù tirato la linea
eh. però per il Corollario dell'Ottaua del Sesto, eh. uiene ad esser la ricercata Linea, ò
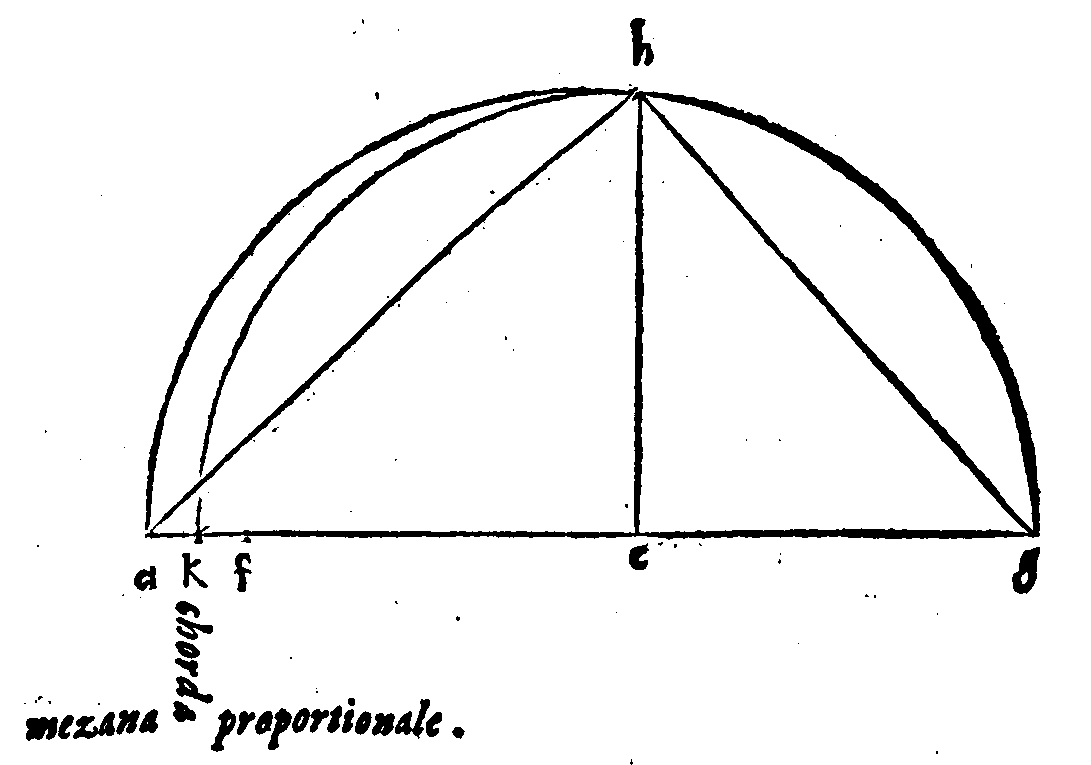
he. essere il termine della uera metà del Tuono nella chorda de. & la ri-
page 149 trouata Chorda mezana proportionale tra de. & fe. secondo 'l proposito. Et si come tan-
ta è la proportione di Spacio à spacio; come per la Prima dimanda è concesso; cosi tan-
ta è la proportione di Suono à suono. A questa maniera adunque si potrà diuidere non
solamente il Tuono; ma qualunque Interuallo minimo; ritrouando la Chorda mezana
proportionale, secondo la lunghezza delle linee, che ueranno nella figura. Haueua in
animo, disse M. Francesco, di dimandarui quel che dicono & dimostrano le da uoi alle-
gate proposte d'Euclide; onde quando ui tornasse commodo, mi fareste grande piacere
à dichiararle; per non esser molto prattico in queste cose. Son contento, dissi; perche, per
esser facili, & pigliandosi & accettandosi per uere, come dimostrate; in quattro parole ui
risoluerò il tutto. La Decimaquarta proposta del primo d'Euclide dimostra; che Se da
una retta; come sarebbe dire he. nell'essempio dato; & da un punto, che sia in essa; come
saria e. due rette non poste dalla medesima parte; come sono de. & egh. faranno gli ango
li, che sono à canto l'uno & l'altro; come sono deh. & heg. equali à due retti; quelle due
rette sarāno poste à drittura l'una cō l'altra; come sono de. & eg. & farāno una linea sola.
Son satisfatto di questa, aggiunse M. Francesco; andate all'altra. La Vndecima del Pri-
mo anco è facile, dissi; percioche dimostra in qual maniera, Da un punto segnato; come
sarebbe e. in una linea retta, come è la dg. si possa leuare una perperdicolare; come eh.
la quale faccia due angoli retti; i quali sono li già mostrati. Et accioche quando ui oc-
corresse di leuar tal linea, lo possiate far prestamente; ui voglio mostrar un modo prattico
bello & breue. Sia dg. vna linea retta, com'è quella posta nell'essempio, che ui hò dato;
& sia e il punto, dal quale faccia bisogno di leuare un'altra retta perpendicolare, la qua-
le dall'una parte & l'altra faccia due angoli retti. Segnaremo prima due punti nella li-
nea dg. che siano equidistanti dall'una parte & dall'altra dal punto e. & saranno k. & l.
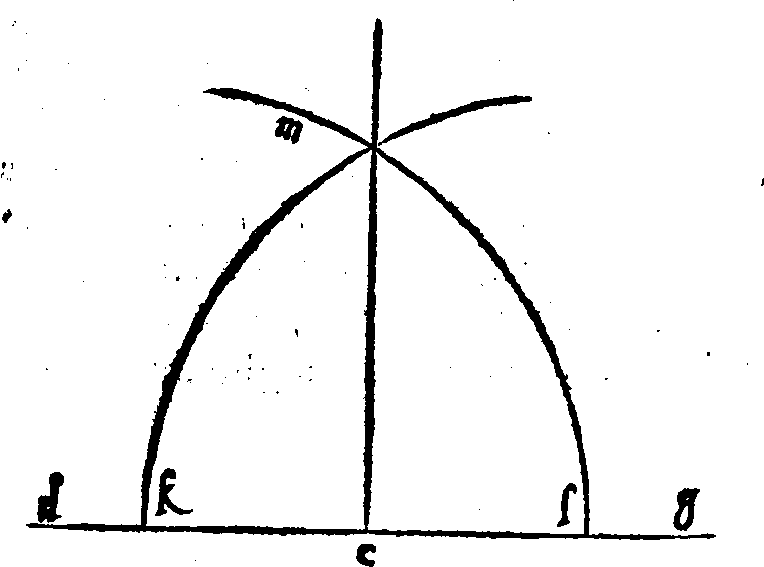
ti; come sarebbe k. & con quella apertura, che più piacerà; pur che di poco sia distante
dall'altro punto l. per maggior commodità, discriueremo la piegata linea lm. Hora con
quell'istessa apertura porremo il piede immobile nel punto l. & descriueremo la piega-
ta linea km. secondo la quantità della lm. Il che fatto, dal punto e. al punto m. doue
si coniungono lm. & km. tiraremo una linea retta giustamente, la quale sarà em. &
questa dico, che sarà la Perpendicolare ricercata. Mi hauete fatto un singolare pia-
cere, disse M. Adriano; ad insegnarci questo bel modo & facile di leuar cotal linea; per-
cioche mi verrà commodo in un certo mio proposito; & è necessario saperlo massime ad
vno, che si adoperi nelle cose delle misure. Vdito questo seguirai nella proua della De-
mostratione. La Trentesimaprima del Terzo dimostra, che Tutti gli angoli, che si fanno di
due linee rette; che sono le dh. & hg. nel Semicircolo dhg. sono retti, come è l'angolo dh
g. Questa è manifesta, disse M. Claudio; oltra l'essempio, che mostrato hauete; Ma che dice
il Corollario dell'Ottaua del Sesto? Che in ogni Triangolo rettangolo; soggiūsi subito; co-
page 150 me dgh. se dall'angolo retto dhg. alla basa dg. si condurrà una linea perpendicola-
re; come è la he. tal linea sarà mezana proportionale tra i due partimenti della detta ba-
se dc. & eg. Et simigliantemente l'uno & l'altro lato, hg. & hd. tra tutta la base dg. & la
parte della base ad esse parti conterminale. Et questo è detto; perche la linea he. diuide
il Triangolo dhg. in due triangoli minori d'un'istessa specie; che ciascheduno col mag-
giore hà un'angolo retto; & sono hed. & heg. Et la eg. si chiama conterminale al lato
gh. & la ed. al lato dh. Vedete di gratia, disse il Sig. Desiderio; che bella & sonora Har-
monia nel suo genere si ritroua tra le linee de questi Triangoli; i quali si fanno per la det-
ta perpendicolare. Gli rispose; M. Adriano; Veramente è cosa mirabile quella de i
Numeri; ma sopra ogn'altra è miracolo nella natura l'Huomo, il quale col suo diuino in-
telletto và inuestigando & ritrouando cose tanto sottili, difficili & rare. Questo è poco
Messere, gli dissi; rispetto à quello, che uede il Mathematico; per che in uerità uede tal
cosa tra i Numeri & altre Quantità, che meritamente può stimare con i Pitagorici; che
tra loro siano alcune cose diuine. Ma passiamo hormai all'altra proposta.
PROPOSTA IX.
strare i Punti delle parti nelle chorde sonore.
rare il Mesolabio; non è cosi M. Giosseffe? Cosi è, dissi; percioche senza 'l suo
mezo non vi potrei dimostrar cosa alcuna. A questo disse il Signor Deside-
rio; Parmi che sia quasi superfluo il uoler replicar quello, ch'altre fiate haue-
te dimostrato. Non giudico superfluo quello, gli risposi; che hà dibisogno d'esser ricor-
dato & dimostrato, per le Dimostrationi, che hanno da seruire à nostri ragionamenti. Tan
to più, che già v'inseguai, col mezo di quest'Istrumento, ritrouar Tra due linee date una
linea sola mezana proportionale; & hora ui uoglio dimostrar, che non solamente una, ma
due, & anco più se ne potrà porre, se mi prestarete udienza. Disse allora il buon Vecchio;
Altro non desideriamo; però seguitate pure allegramēte à dimostrar quello, che ci hauete
proposto. Cosi uoglio far Messere, risposi; ne mi uoglio smarrire à patto alcuno. Sia adūque
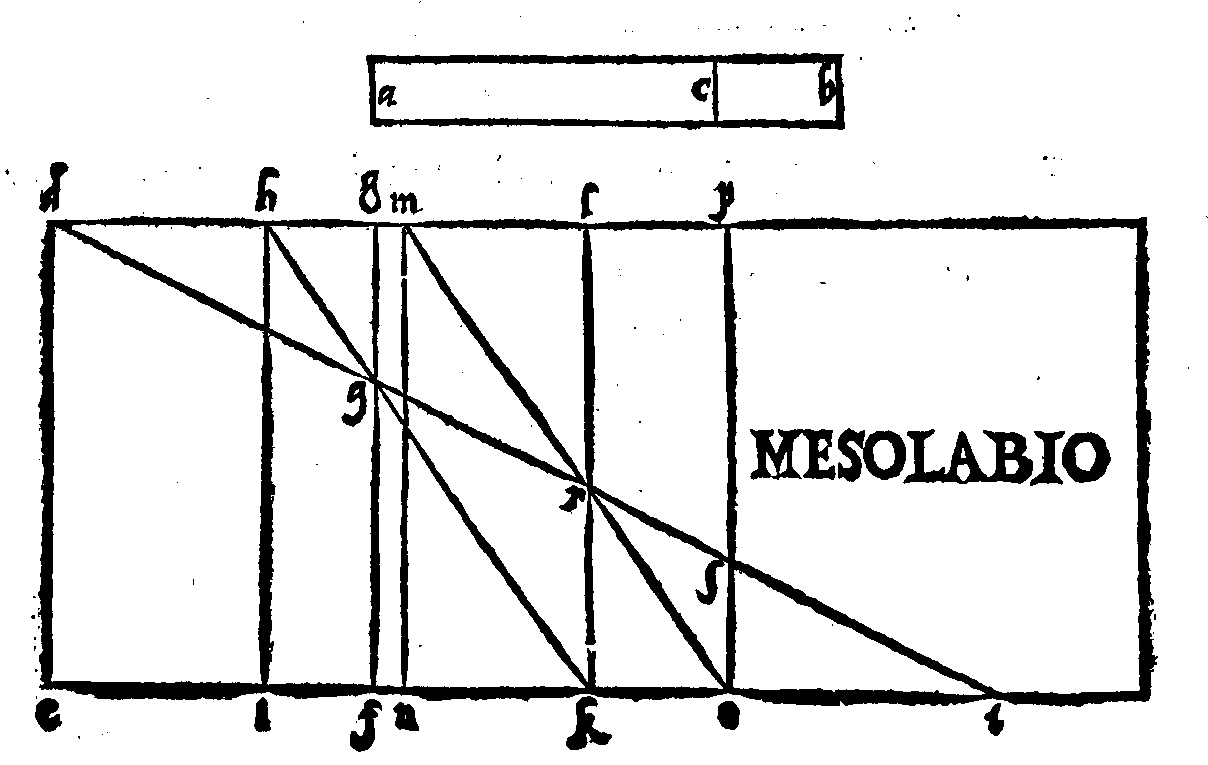
dibisogno di partirlo in tre interualli. Bisogno è, che secondo 'l modo mostrato nelle Isti-
tutioni, si ritroui tra la chorda ab. & la cb. due chorde mezane proportionali. Onde pi-
glio primieramente l'istrumento Mesolabio; & l'acconcio nel modo, che si conuiene; po-
nendo tre Paralellogrammi defg. hikl. mnop. l'uno sotto l'altro; come uedete. Di mo-
do che defg. stia sopra gli altri; & il lato de. uiene ad esser di punto equale alla quantità
della chorda proposta ab. Faccio dopoi il lato po. del terzo paralellogrammo mnop.
equale alla chorda cb. in punto s. Et accōmodo gli altri di maniera, che i loro diametri k
h. & mo. s'affrontino con i lati gf. & lk. ne i punti q & r. Onde nasce due mezane linee. q
f & rk. lequali dico essere alle de. & so. proportionali; & che tra le chorde ab. & cb. si
haueranno à collocare; percioche diuideranno l'Interuallo ab. & cb delle date chorde
in tre parti equali; secondo 'l proposito. Et che tali Linee siano proportionali, lo dimostro
in questo modo. Poniamo, che le linee causate nel Mesolabio siano de. qf. rk. so. & sia-
no q & r. i segni de gli affronti de i lati de i Paralellogrammi con li diametri. Produco le
linee ds & eo. tanto, che concorrino insieme; le quali, per la Quinta Dimanda d'Eucli-
de, concorreranno nel punto t. Onde nascerà il Triangolo dte. il quale haurà l'angolo e
dt. minore dell'angolo det. & per la Vndecima definitione, è detto Acuto; & anco de. il
quale, per l'Ottaua, si chiama Retto. Ma perche inanti che si mouessero i Paralellogram-
mi, gli angoli def. hik. & mno. de i Paralellogrammi, & i lati loro à questi angoli op-
positi, erano equali; saranno etiandio tra loro equali gli angoli efd. ikh. & nom. co-
m'è determinato & dimostrato per la Sesta del Sesto. Et, per la Ventesimaottaua del
Primo, le Linee df. hk. & mo. saranno etiandio Paralelle. Et perche i Triangoli det.
qft. rkt. & sot. hanno l'angolo dte. commune, & ancora commune un'angolo retto; pe-
rò, per il Secondo Commun parere, & per la seconda parte della Trentesima del Pri-
mo, dico tali Triangoli esser di angoli retti. Et per la Quarta del Sesto; simigliantemen-
te per la Seconda del medesimo; hauere i lati proportionali, & essere; si come de. si con-
uiene con qf. cosi dt. con qt. Et si come rk. con so. cosi rt. con st. Dopoi, perche all'altro
lato del Triangolo dft. fù fatto hk. paralella; però, dico prima separatamente, per la
Seconda del Sesto; si come si troua dq. con qf. cosi ritrouarsi fk. con ft. Et insieme do-
poi, per la Decimaottaua del Quinto; si come dt. conuiene con qt. cosi ft. conuiene con
kt. Et perche il lato qf. del Triangolo qtf. è fatto paralello di rk. però, per l'istesse Pro-
poste, si come conuiene ft. con kt. cosi conuiene qt. con rt. Et per la Vndecima del Quin
to; cosi conuengono dt. con qt. Et di nuouo, per l'istesse Proposte; si come insieme con
uengono qt. con rt. cosi conuengono rt. con st. Onde queste quattro Linee dt. qt. rt. &
st. dico esser proportionali. Ma habbiamo dimostrato, che si come si trouano dt. con
qt. cosi conuenirsi qf. con rk. Simigliantemente, quella conuenienza, che si troua esser
tra rt. & st. essere etiandio tra r. k. & so. adunque, per la Vndecima del Quinto, queste
linee de. qf. rk. & so. saranno proportionali; & tra de. & so saranno ritrouate Due linee
mezane qf. & rk. le quali sono proportionali; come ui douea dimostrare. E' adunque
il proposto Interuallo ab. & cb. diuiso in tre parti equali; com'hauete potuto uedere; &
& come ui douea dimostrare. Finito ch'io hebbi, disse allora il Signor Desiderio; Tanto
bene hauete dimostrato questa proposta, ch'è impossibile, che possa essere altramente.
Ma cotal dimostratione, non hauete trattato come Musico; ma come Geometra. E' ue-
ro; risposi; & non è inconueniente; percioche applico poi questa dimostratione al propo-
sito; come hauete veduto. Disse dopò questo il Viola; Nelle Precedenti hauete di-
chiarato sopra la Figura tutte le proposte, c'hauete allegato, d'Euclide, con le quali di-
mostrato hauete 'l uostro proposito; però se 'l non ui rincrescie fatelo (di gratia) anco in
questa. E' giusta dimanda; risposi; però son all'ordine; se ben le cose andaranno un poco
in lungo. Lasciate però, soggiunse egli; la Sesta del Sesto; percioche è manifesta da quel-
lo, che detto hauete, & dichiarateci la Ventesimaottaua del Primo; & cosi uerete ad es-
page 152 sere vn poco più breue. Allora dissi; Questa proposta dice; Se vna retta linea; come sa-
rebbe nella Figura la quale hò fatto; la dt. verrà sopra due rette, come sono gf. & lk. &
l'angolo di fuori causato da quella, come dqf. sarà equale all'angolo opposto di dentro;
come qrk. ouer che i due angoli di dentro; come sarebbono fqr. & qrk. da vna medesi-
ma parte saranno equali à due angoli retti; quelle due linee saranno equidistanti. Soggiūse
il Merulo; Il secondo commun parere è manifesto. E vero, risposi; & dice, che Se à co-
se equali, come sono dsoe; qsof. & rsok. s'aggiungerà cose equali; come sto. di modo
che ne venga dte. qtf. & rtk. tutte le somme saranno equali. Dichiarateci adunque se-
guitò il Merulo; la Seconda parte della Trentesimaseconda del Primo con l'essempio. Al
quale satisfeci in questo modo. Questa dice; che Tutti tre gli angoli d'un Triangolo di
dentro, come sono gli angoli d. t. & e. del Triangolo dte. è necessario, che siano equali à
due retti angoli, i quali sono kos. & sot. Vi entra vna gran fattura, disse M. Adriano; à di-
mostrar queste Linee proportionali; poi che bisogna passar per il mezo di tāte cose. Ma di-
teci la Quarta, la Seconda del Secondo. Anzi vi uoglio mostrar quello, che dimostra &
cōclude l'una & l'altra, risposi; & incominciando prima dalla Secōda, questa propone; che
Se una linea retta, come è la gf. sarà posta paralella ad'un lato d'alcun triangolo; come de.
del Triangolo dte. segarà proportionatamente i lati di esso Triangolo, che sono dt. & et.
Et se, per il cōtrario, i lati d'un triangolo saranno segati da una linea retta proportionata-
mēte; ꝗlla retta linea sarà all'altro lato del Triangolo paralella. Dimostra dopoi la Quarta
proposta del Sesto, ch'io v'allegai; Se due triangoli, come sono det. & qft. sono insieme
d'angoli pari; che i lati, i quali sono intorno à tali angoli, sono proportionali; & quelli, che
sono sotto questi angoli, come de. et. qf. ft. & rk. kt. sono di simil ragione. Vi dichiararò
hora la Ottaua del Quinto; & credo che questa vi parerà un poco strana; percioche par,
c'habbia in se qualche contrarietà; Ma in uero è cosi, secondo ch'ella si dimostra; essendo
ch'ella dice; Tra le grandezze inequali, come sarebbe de. qf. & rk. la maggior de. hà
maggior proportione, che la minore qf. ad una medesima rk. Dice dopoi; & la medesima
rk. ha maggior proportione alla minore qf. che alla maggiore de. Si consumarebbe mol
to tempo à uolerla dimostrar di modo, che si restasse senza dubitanza alcuna; Ma tene-
tela per vera, perche è cosi in fatto. Cosi la crediamo, disse M. Adriano; Ma ui è anco da
dichiarar la Vndecima pur del Sesto. Allegandoui tal proposta, ui diedi anco gli essem-
pij, risposi; però non ui è in essa alcuna difficultà; & chi uolesse dimostrar tutte le Propo-
ste, ch'io hò addutte, non bastarebbe una giornata intiera. Troppo hauete fatto; disse M.
Francesco; anzi più di quello, che bisognaua a qualcheduno de noi, percioche queste co-
se s'accettano tutte per uere; essendo dimostrate nella Geometria. Onde tutto quello, che
è stato dimandato, non è ad altro fine, che per hauerne un poco di maggiore intelligenza.
S'hauete qualche dubitatione appresso di uoi; replicai; scopritela, inanzi ch'io passi più ol-
tra. Non ci resta cosa alcuna da dubitare; rispose M. Claudio; Ma diteci di gratia, S'io uo-
lessi diuider l'Interuallo, c'hauete dimostrato diuiso in tre parti in più ancora, che mo-
do haurò da tenere? Il modo istesso, risposi; ma bisognerebbe aggiungere ad ogni parte,
che uoi uoleste fare, oltra le tre fatte, vn Parallelogrammo; se ben fussero (dirò cosi) mil-
le, & per tal modo haurete sempre quello, che ricercarete. Ma lasciamo hormai queste
cose Geometriche da un canto, & ritorniamo alle cose proprie della Musica. Vdendo
questo il Sig. Desiderio, disse; Per vostra fè, inanti che passate più oltra, lasciatemi dir
quattro parole. Se nō è uero che 'l Tuono si possa partire in due parti equali; come fin'ho-
ra tutti siamo certi, per quello che ci hauete dimostrato; parmi che quella opinione che
hauea quel gran Musico antico Aristosseno, douesse esser da pochi abbraciata; il quale
diuideua in altra maniera il Tuono di quello, che hauete dimostrato nella Nona propo-
sta; & non si curaua, che le parti de i suoi Tuoni diuisi in Semituoni fussero l'una più ri-
stretta dell'altra, contra il Corollario della Quinta. Ma secondo che le chiamaua Semi-
tuono, uoleua che s'intendessero per la intera metà del Tuono. A questo risposi; Questa
page 153 opinione non si può cō uerità accettare ne per buona, ne per uera; percioche, come haue-
te veduto nella Sesta proposta à punto, è falsissimo dire; che Diuisa la Differenza del Tuo-
no nella chorda in due parti equali, si diuida il Tuono in due parti proportionali. Onde
la diuisione di Aristosseno era; per darui un'essempio; & porloui dauanti li occhi; acciò
più facilmente lo cōprendiate; la nominata Sesta proposta di sopra, Percioche diuiso l'In
teruallo ac. in due parti equali al. & lc. nasce due proportioni l'una Sesquidecimasettima
al. & l'altra Sesquisestadecima lc. delle quali la prima senza dubio alcuno ò minore della
seconda; come ciaschedun di uoi lo potrà conoscere, s'hauerete riguardo à i Denomina-
tori dell'una & dell'altra delle due nominate parti, ò proportioni, che chiamar le uoglia-
te. La onde quanto questa cosa sia ragioneuole; lascio far giudicio à uoi altri, che hor-
mai sete in queste cose bene istrutti. Disse allora M. Claudio; Eui alcun'altro, che hab-
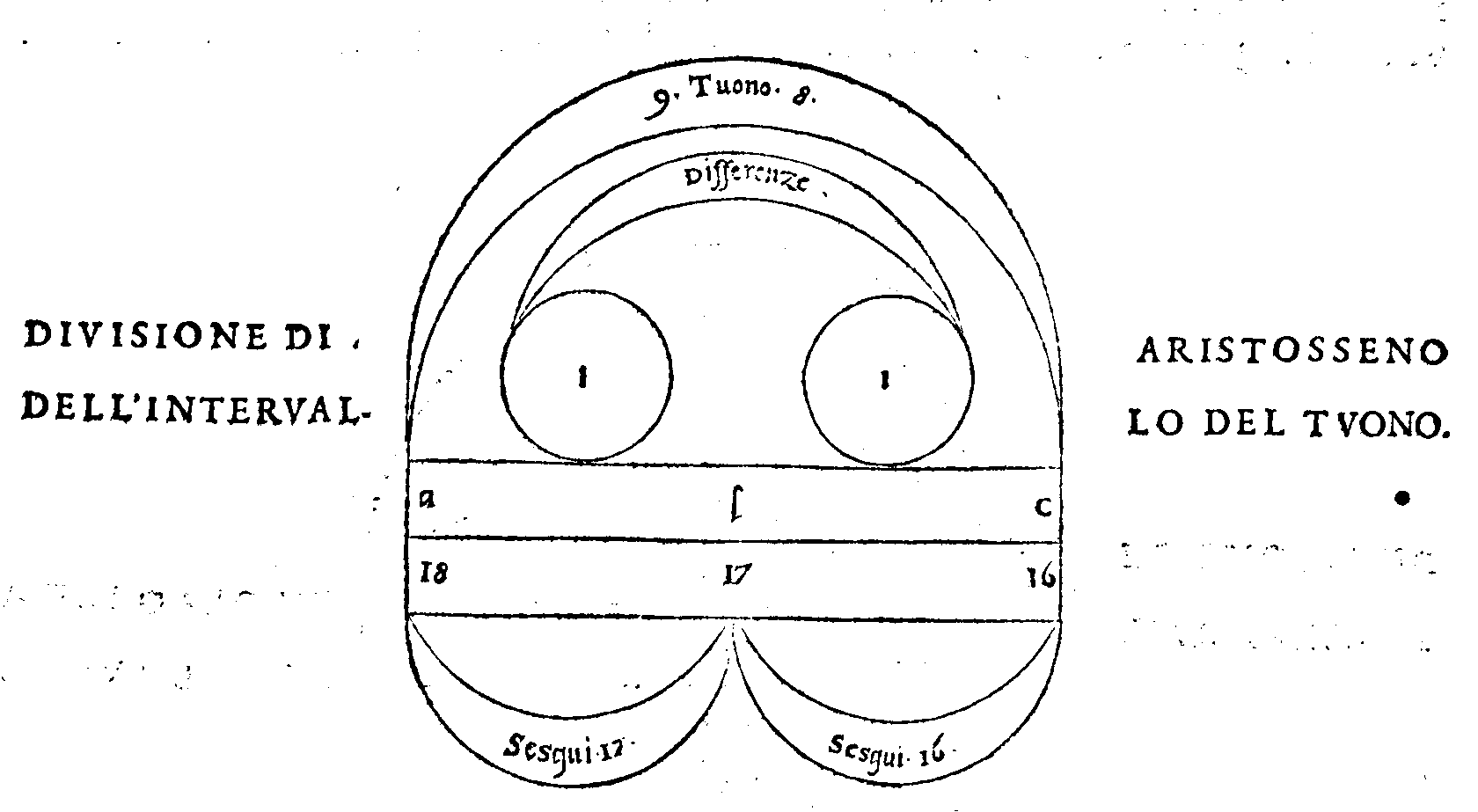
lea. Vi dico, che molti ne sono, tra i quali (lasciando gli altri per breuità) è uno Martiano
capella, ilquale ragionando nel Lib. 9. de i Generi ne i Tetrachordi, nō solamente hà diui-
so il Tuono in due parti, come faceua Aristosseno; ma in tre & anco in quattro. Et quando
lo diuideua in due, chiamaua ciascheduna di quelle parti Semituono; & quando in tre
Diesis tritemoria; ma quando lo partiua in quattro, le nominaua Diesis tetartemoria. Es-
sendo che poneua tali Diesis hora per la Terza parte, & hora per la Quarta del Tuono.
Disse M. Francesco; Che uogliono dire, per l'amor di Dio, queste parole cosi saluatiche;
Tritemoria & Tetartemoria, che nomina quest'huomo da bene di Martiano? Mi fate ri-
dere, dissi; sono parole Greche; & la prima vuol dir Terza, & la seconda Quarta parte, del-
le qual parti si cōpongono al modo suo le specie de i tre Generi, Diatonico, Chromatico,
& Enharmonico. Soggiūse allora il Sig. Desiderio; Ma che diremo dell'opinione, c'hebbe
Filolao nella diuisione medesimamente del Tuono? percioche tentò di diuiderlo per
un'altro uerso. Et parmi, se ben mi ricordo, che hauesse più del ragioneuole, che non heb-
be Aristosseno. Di gratia, se ui ricordate, disse M. Claudio; diteci, che opinione hebbe
questo grande huomo. Mi ricordo, dissi; quel, che dice BoetioMusicae. lib
3. cap. 5. in questo proposito. Pe-
rò douete sapere, che Filolao fù Filosofo pitagorico, & seguitaua molto (com'era costume
de i Pitagorici) le ragioni de i Numeri; onde pose il principio del Tuono in quel numero,
ch'è il Primo dopò il Primo pare, & questo fù il Ternario, riputato da i Pitagorici Nu-
mero perfetto; come dimostra Aristotele nel principio de i Libri del Cielo; & hauuto in
page 154 somma ueneratione. Questo in se stesso molteplicato prduce il 9. & molteplicato nel 9.
produce il 27. il quale è il secondo numero Cubo, & il termine maggiore della propor-
tione del Tuono maggiore, che accompagnato col 24. che nasce dalla molteplicatione
del Ternario nel Primo Cubo, ch'è 8. è il minor termine della proportione del Tuono
nominato, contenuto nella proportione Sesquiottaua, la quale si troua ne i suoi termini
radicali tra il nominato Primo numero Cubo, & il Nouenario, ch'è il secondo numero
de i Quadrati. Onde essendo il 27. maggiore del 24. serua l'istessa differenza del Terna-
rio; percioche esso è l'Ottaua parte di 24. al quale aggiunto esso Ternario, ritorna me-
desimamente 27 La onde questo Filosofo & Musico eccellentissimo de quei tempi di-
uise tutta questa somma in due parti à questo modo; in 14. & 13. & la maggior chiamò
Apotome, & la minore Diesis; la quale fù dopoi nominata da i Musici Semituono mino-
re. Et la differenza de queste due parti 14. & 13. ch'è la Vnità, nominò Comma, come
vedete dissegnato in questa figura. Et uolse che 'l Diesis fusse di 13. Vnità; essendo che
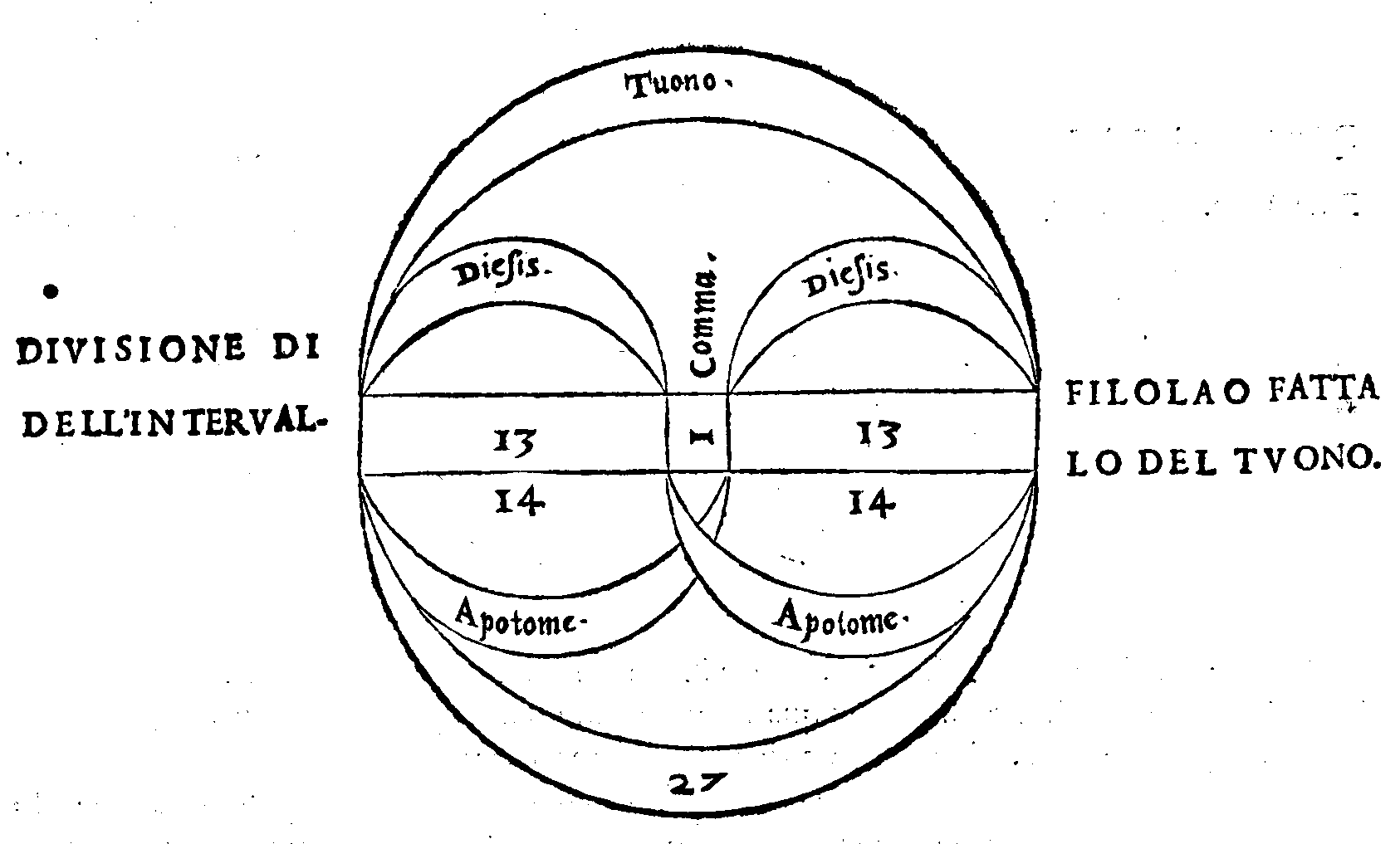
tuono de gli Antichi, & è composto della Vnità del Ternario, & del Nouenario numero.
La quale Vnità poneua come quella, che tiene il luogo del Punto; il Ternario, come
quello, che tiene il luogo della Prima linea impare; & il Nouenario, del Primo impare
Quadrato. Ma dall'ordine nato della molteplicatione del 27. ne i termini radicali del
Tuono 9 & 8. & dalla forma del Comma, che è la Differenza, che si troua tra l'Apotome
& lo Diesis; cauato questo da quello, & leuatone due Apotome dal Tuono; contenuto
nella seguente figura; potrete conoscer l'intentione di questo gran Filosofo. Nacque do-
poi che da i Musici furono riceuuti i Nomi de queste parti di maniera, che fin'hora non
si hanno cambiati. Et se ben si uede, che questa diuisione sia fatta con molta ragione, &
habbia più del verisimile, che quella fatta d'Aristosseno; tuttauia quanto ella sia com-
moda alle cose della Musica; da quello, c'hò dimostrato, & anche son per dimostrar-
ui lo potrete comprendere. Ma lasciamo hormai queste cose da un canto, & ritorniamo
page 155
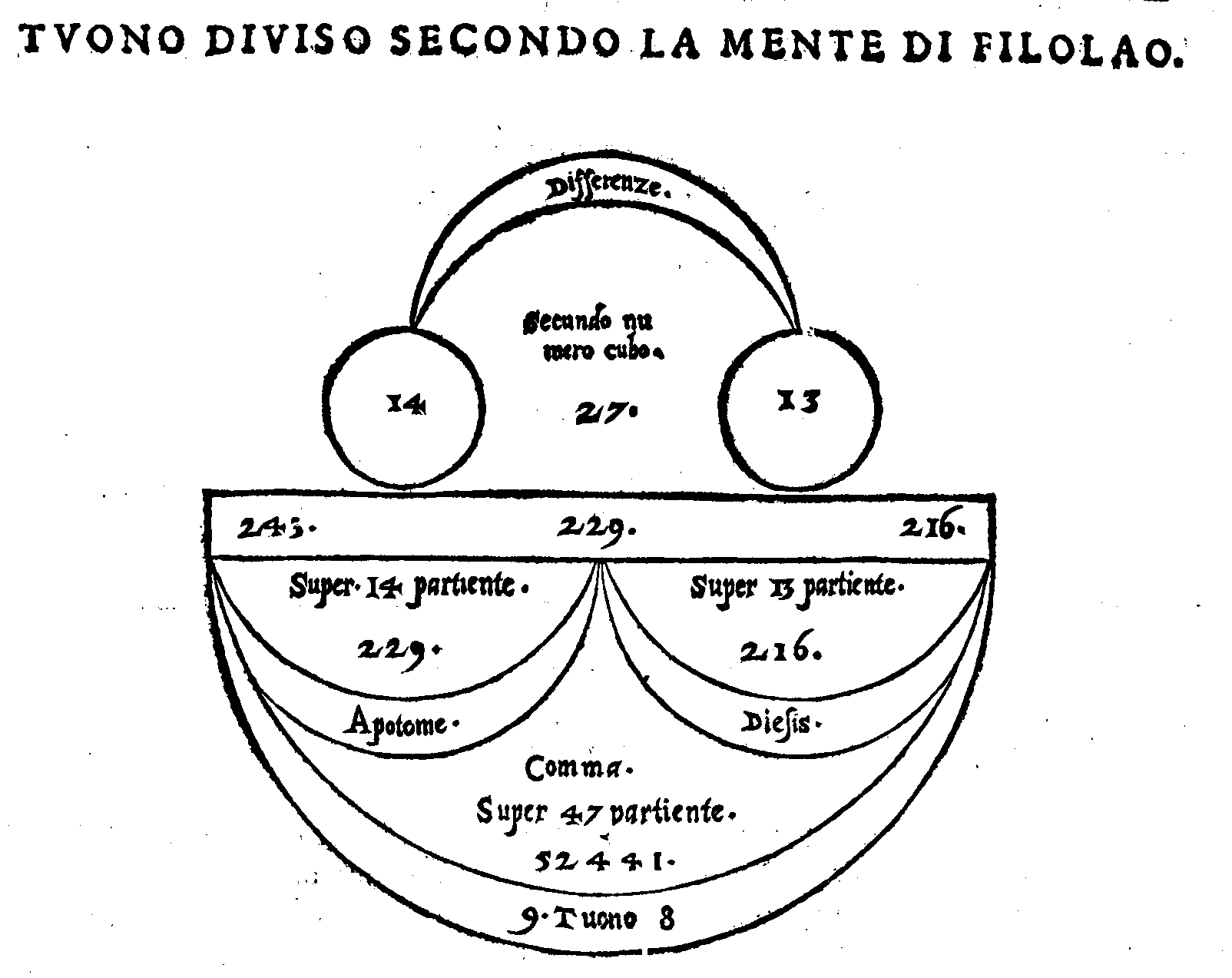
condo la diuisione, che faceua Aristosseno del Tuono)
PROPOSTA XII.
mini dell'interuallo del Tuono; & siano l & b. l'interuallo Sesquisestode-
cimo. Dico lb. esser maggiore della intiera metà di ab. Onde, per la Quin-
tadecima proposta del Primo ragionamento, ritroueremo prima la parte Aliquota
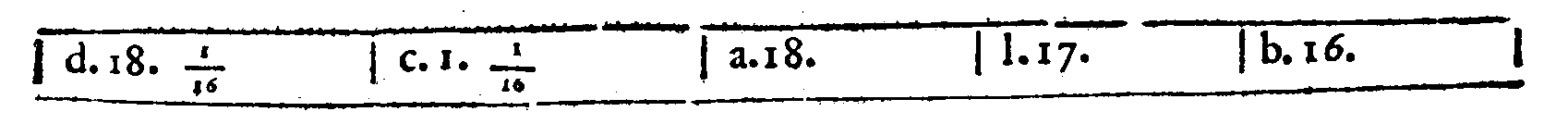
Sestadecima parte di l. la quale aggiungeremo adesso l. & ne risulterà d. & il d.
comparato allo l. per la Definitione de i Superparticolari, è Sesquisestadecima;
adunque d. comparato ad l; & l. comparato al b. sono due Sesquisestedecime congiunte;
Ma il d. comparato al b. per la Trentesimasesta del Primo, contiene maggior proportio-
ne, di quella che contiene a & b. adunque d & b. proportione raddopiata trapassa la pro-
portione a & b. ch'è quella del Tuono, ouero il suo Interuallo. Et perche, per la Quar-
tadecima dignità; Ciascheduna cosa, la quale raddopiata trapassa un'altra, è necessario,
page 156 che ella sia più della sua metà; però dico, che la Sesquidecimasesta proportione supera
la intiera metà del Tuono. Et questo è quello, che ui douea dimostrare. La onde aggiun-
geremo questo Corollario.
COROLLARIO.
sariamente supera l'intera metà del Tuono Sesquiottauo.
tione Sesquiquintadecima sia la forma del nostro Semituono maggiore. Ma se-
guitate à pagar quello (che per uostra cortesia) ui sete fatto debitore. E' cosa giu-
sta & honesta; risposi io; pero ascoltate.
PROPOSTA XIII.
l'interuallo del Tuono; & siano c. Dicesette. Ritrouo prima, per la Quintadeci-
ma proposta del Primo giorno, la parte Aliquota di a. secondo 'l c. & uiene f. il
quale aggiunto à da. nasce d. Dopoi ritrouo, per l'istessa Quintadecima la parte Aliquo-
ta di c. secondo 'l g. Denominatore della Sesquiottaua, ch'è la forma del Tuono, & ne vie-
ne h. il quale aggiunto al c. ne dà e. Dico hora a. & c. & simigliantemente d. & a. per la
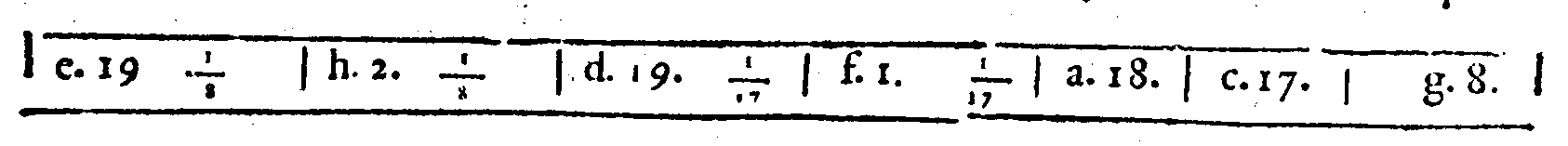
settime congiunte. Ma, per la definitione de i Superparticolari, c. ad e. uiene ad essere
Sesquiottauo; imperoche e. contiene c. & una sua ottaua parte; & per la Trentesimasesta
del Primo, maggiore è la proportione di e. al c. di quello ch'è d. ad esso c. Adunque la
Sesquidecimasettima proportione, per la Quintadecima Dignità, è minore della intera
metà del Tuono. Imperoche; Quello, che raddopiato non arriua all'intero, non può esser
per modo alcuno la sua metà. Da questo adunque ui sarà manifesto, che la Sesquide-
cimasettima proportione è minore della intera metà del Tuono maggiore. Et questo è
quello che (secondo la proposta) ui douea dimostrare. Adunque; concluse questo parlare
il Sig. Desiderio in questa maniera; per quel che si uede fin hora bisogna dire; che
PROPOSTA XIIII.
sestadecima & la Sesquidecimasettima.
mostrare; onde dico. Essendo che, per la Duodecima di questo, la Sesquisestade-
cima, è maggior della intiera metà dal Tuon maggiore; & , per la Precedente, la
page 157 Sesquidecimasettima è minore; è necessario, per la Sestadecima Dignità, che la metà di
vna cosa caschi nel mezo di due, delle quali l'vna sia maggiore & l'altra minore di essa
metà. Ma perche la Sesquidecimasesta è maggior della metà, & la Sesquidecimasetti-
ma è minore; però è necessario, che la metà del Tuono Sesquiottauo cadi tra la Sesqui-
decimasesta, & la Sesquidecimasettima proportione; come secondo la proposta dimo-
strar ui douea. Non uolete, disse qui M. Claudio, dire anco qualche cosa intorno al Tuo-
no minore? Voglio per certo, dissi; Dimostrateci, disse allora M. Adriano; tra quali pro-
portioni possa cascar simigliantemente la intiera metà di questo Tuono; accioche cono-
sciuta quella del maggiore, conosciamo etiandio quella del minore. Cosi voglio fare,
risposi; onde ui propongo questa; che
PROPOSTA XV.
diuiso in Dieci parti equali; di modo che tra ab. & cb. sia collocato il Tuono mi-
nore alla sua proportione. Et sia anco diuiso lo spacio ac. simigliantemente in
Due parti equali; di maniera che ad. sia la della chorda ab. & dc. sia la
Decimanona; & ab. uenga à contener Venti fiate la ad. & db. la contenga Dicenoue.
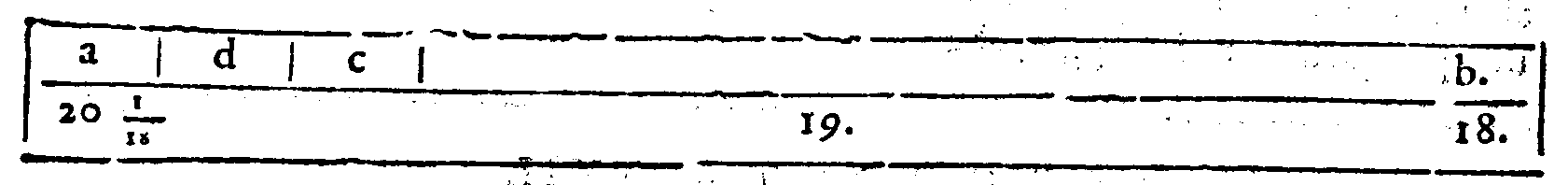
tione Sesquidecimaottaua; percioche cb. contiene Diciotto uolte dc. ouero ad. la qual
proportione dico esser maggiore della intiera metà del Tuono minore. Et perche, per la
Quintadecima del Primo, la Vnità & 1/18 è la Decimaottaua parte della somma 19. la qua-
le Vnità, & 1/18 aggiunta à tal somma, fà 20 1/18; però questo numero, per la Definitione
de i Superparticolari, con 19. è Sesquidecimaottaua. Sono adunque 20 1/18 con 19. & 19.
con 18. due Sesquidecimaottaua. Ma 20 & 1/18 comparato à 18. per la Trentesimasesta del
Primo, è maggior proportione, che non è la Sesquinona; essendo che 20. con 18. è pro-
portione Sesquinona; adunque la Sesquidecimaottaua raddoppiata sopr'auanza & su-
pera il Tuono minore, & lo suo interuallo. La onde, per la Quarta decima Dignità, la
Sesquidecimaottaua supera la intiera metà del Tuono minore; Poi che quella cosa, ch'è
raddoppiata & supera vn'altra, è necessario ch'ella sia più della metà. Onde si può ag-
giunger questo Corollario.
COROLLARIO.
sopr'auanzerà la metà intiera del Tuono minore.
che è consequente à quello che hò dimostrato; che
page 158
PROPOSTA XVI.
Sia etiandio d. per la Quintadecima del Primo nostro ragionamento, la parte
Aliquota di a. presa secondo il c. & aggiunta ad esso a. & e. per l'istessa Quintade-
cima, sia la parte Aliquota di c. presa secondo 'l 9. Denominator della Sesquinona, ag-

per l'istessa Quintadecima, simigliantemente Sesquidecimonono; però dico db. & cb. es-
ser due Sesquideciminoni congiunti. Ma, per la Definitione de i Superparticolari, e. alla
c. è Sesquinono; cioè, Tuono minore; essendo che e. contiene c. vna fiata & una sua nona
parte. Et per la Trentesimasesta del Primo ragionamento, dc. è minor proportione, di e
c. imperoche, per la Nona dignità anco, la Nona parte è maggior della Decimanona;
però concludendo dico, che la Sesquidecinanona proportione, per la Quintadecima
dignità, è minore della metà del Tuono minore. Essendo che raddoppiata non arriua
all'intiero; com'era 'l proposito di dimostrarui. Si può etiandio concludere, disse; M. Adria-
no: per quello, che io ueggio; che
PROPOSTA XVII.
proportione necessariamente.
d'hoggi la Sesquidecimaottaua è maggior della uera metà; del Tuono minore;
&, per la Prossima, la Sesquidecimanona è minore; però, per la Decimasesta
dignità, se tra 'l maggiore & lo minore del mezo d'alcuna cosa, cade esso mezo; la vera
& intiera metà del Tuono proposto caderà tra la Sesquidecimaottaua, & la Sesquideci-
manona proportione; come era 'l proposito di dimostrare. Ma poi che siamo nel ragiona-
mento de i Tuoni & delle parti loro; uoglio che vediamo hora, in qual maniera.
PROPOSTA XVIII.
Tuono maggiore alla sua proportione sopra la chorda ab. diuidendola in Noue,
parti equali; di maniera che tra ab. & cb. haueremo quel che cerchiamo; al
quale soggiungeremo il minore, diuidendo la chorda cb. per la Seconda, in Dieci parti
& haueremo il proposito tra cb. & db. Onde, per la Nona proposta di heri, il Tuono mag-
giore consiste nella proportione Sesquiottaua; &, per l'istessa proposta, il minore consta
della Sesquinona. Ma perche, per la Ventesimaottaua ancora di heri, la Diatessaron
page 159
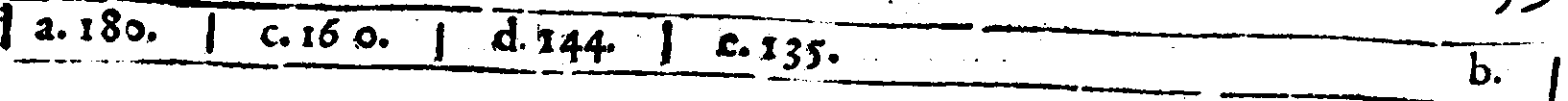
il Tuono maggiore col minore; come sue parti, per l'ultima Dignità, sono minori della
Diatessaron, come suo Tutto. La onde hauendo la Diatessaron la forma dalla Sesqui-
terza proportione; non è dubio, che ab. & db. sarà minore Interuallo del Sesquiterzo.
Diuideremo adunque ab. in Quattro parti equali, & nel principio della Terza faremo
il punto e. di maniera che eb. contenghi tre parti di essa; Onde dico, che contenendo
ab. quattro parti, & eb. contenendone due; ab. & eb. per la Quinta definitione del Pri-
mo, viene ad esser la Sesquiterza proportione. Ma la Sesquiterza proportione ab. &
eb. sopr'auanza il Tuono maggiore ab. & cb. & lo minore cb. & db. che fanno (per la
Ventesimasettima di heri) il Ditono; nella proportione db. & eb. adunque db & eb.
per la Definitione Ventesimaseconda del giorno passato, è la proportione del Semi-
tuono maggiore; ilquale (secondo 'l proposito) è maggiore, & al minore Tuono è soggiun-
to. Volendo proporre tal Semituono, disse M. Adriano; che modo si haurà da tene-
re? Poco differente; risposi. Onde porrò prima la proposta, & poi ui mostrerò il mo-
do. Et la proposta sarà questa.
PROPOSTA XIX.
chorda ab. in quattro parti equali, & farò ab. & cb. interuallo Sesquiterzo.
Et sopra c. uerso a. farò dc. equale ad una delle Noue parti di cb. di modo che
db. sia diuiso in Dieci parti. Onde (per la Definitione de i superparticolari) d
b. & cb uiene ad essere Sesquinono, & Tuono minore; percioche db. contiene cb. &
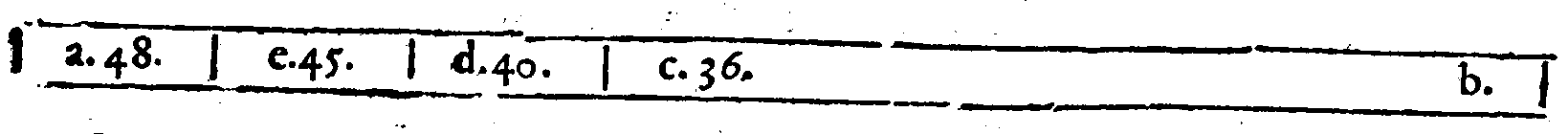
aggiungo Vna sopra il d. nel punto e. & per tal modo eb. & db. per la nominata Defi-
nitione, è Sesquiottauo, & Tuono maggior; poi che db. contiene Otto parti, & eb. Noue.
Sono adunque due Tuoni; eb. & db. maggiore; & db. & cb. minore; iquali per la Tren-
tesimasettima di heri, fanno l'interuallo del Ditono. Ma ab. & cb. Sesquiterza propor-
tione è maggior di essi due Tuoni; come si è detto altre fiate; della proportione ab. & e
b. adunque, per la Ventesmaseconda definitione di heri, ab. & eb. è l'interuallo del mag-
gior Semituono; il quale essendo posto inanzi à i due sudetti Tuoni; & preposto à quelli
nella parte graue di tutta la chorda ab. dico, che noi habbiamo hauuto il tutto secondo 'l
nostro proposito. Et questo è quello, che dimostrarui douea. Disse à questo M. Fran-
cesco. Chi uolesse porre il Semituono nominato tra l'vno & l'altro de i Tuoni nomi-
nati, che si haurebbe da fare? Bene, gli risposi; onde son per dimostrarui questa proposta,
ò conclusione; che
PROPOSTA XX.
minore.
modato la Sesquiterza tra ab. & cb. Dalla parte di a. uerso il c. faccio prima il
Tuono Sesquiottauo; diuidendo ab. in Noue parti, per la Prima di questo; &
pigliando db. per le Otto; tra ab. & db. per la Definitione, haueremo collocato il Tuo-
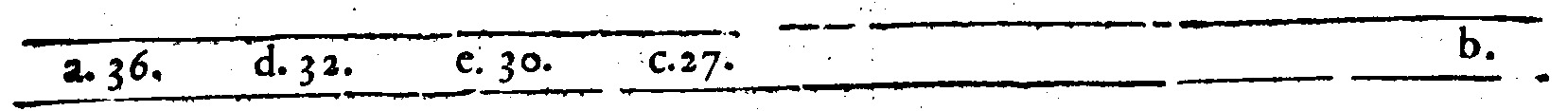
fatto nella Precedente; diuidendo cb. in Noue parti, & aggiungendoui la Decima ec.
dico, che tra eb. & cb. è contenuto il Tuono minore. Onde essendo ab. & db. Tuono
maggiore, & eb. con cb. Tuono minore, che fanno il Ditono; è manifesto, che ab. & cb.
Sesquiterza, supera tali Tuoni per la mezana proportione db. & eb. Adunque, per la
Ventesimaseconda definitione di heri, db. & eb. Semituon maggiore è collocato meza-
no tra il Tuono maggiore posto nel graue, & lo minore posto nell'acuto sopra la chorda
data. Et questo è quello, che vi douea dimostrare. Vdito questo M. Claudio, disse;
Non si poteua por nel graue; cioè, nel principio della chorda il Tuono Sesquinono?
Si poteua per certo, risposi; & tale ordine sarebbe stato più naturale; essendo che si ritro-
ua prima il Tuono maggiore nell'Ordine naturale delle Consonanze & de gli Interualli,
dopoi il minore; à i quali seguita subito il Semituono maggiore. Ma qui importa poco,
à porre primo più vno che l'altro; purche si dimostri quello, che si propone; tanto più,
che nella proposta non si troua tal differenza. Auertite però; che hauendo fin qui essa-
minato vna gran parte de quelli accidenti; che necessariamente occorre à dire intorno
al Tuono maggiore & lo minore; secondo la diuisione fatta del Tuono da Aristosseno
in due Semituoni; non sarà fuori di proposito, che vediamo quelle cose, che sono più
necessarie da sapere, intorno alla uarietà del nostro, & de i suoi Semituoni. Onde uo-
glio che sapiate; che
PROPOSTA XXI.
ab. & cb. sia Sesquisestodecimo; & cb. & db. Sesquiquintodecimo; Per la Quin-
ta proposta d'hoggi; maggior è la proportione, che si troua tra cb. & db. che non
è quella, ch'è posta tra ab. & cb. Ma cb. & db. è l'interuallo del Semituono maggiore, &
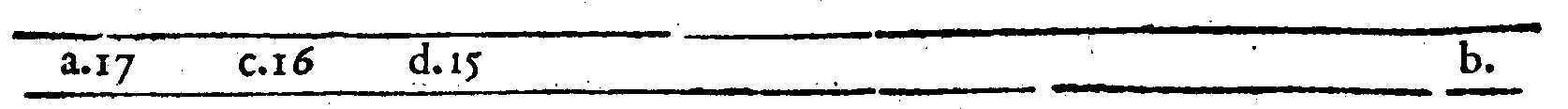
in maggior proportione, che non è la Sesquisestadecima. Di più; Siano per la Quintade-
cima proposta del giorno passato, a & b. la Sesquiquintadecima proportione, & i minimi
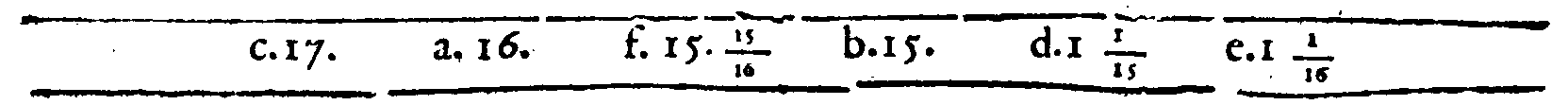
stadecima. Ritrouo prima, secondo 'l modo mostrato nelle Istitutioni,1. Par.
cap. 25. il Denominatore
della Sesquiquintadecima; ilquale uiene d. dopoi ritrouo quello della Sesquisestadeci-
ma, che viene e. Hora dico la Sesquiquintadecima ab. sopr'auanzar la Sesquisestadeci-
page 161 ma ca. Imperoche essendo il Denominator della prima, ab. maggior della seconda ca.
ne seque, per la Ottaua Dignità, ò Massima; che la ab. sia anco maggiore della ca. & per
consequente, il Semituono maggiore consista in maggior proportione, che non è la
Sesquisestadecima; come ui douea dimostrare. Si può anco dimostrar questa Propo-
sta in questo modo. Siano medesimamente a & b. i minimi termini del Semituono mag-
giore, & ca. quelli della Sesquidecimasesta. Piglio, per la Quintadecima Proposta del
Primo giorno, la Sestadecima parte di b. & l'aggiungo ad esso b. onde ne nasce f. Sarà
adunque f. al b. Sesquisestodecimo. Ma f. è minore di a. adunque, per la Trentesimasesta
del detto giorno, la proportione del Semituon maggiore consiste in maggior proportio-
ne, che non è la Sesquisestadecima. Et più oltra dico;
PROPOSTA XXII.
Sesquidecimosettimo, & db. con eb. sia Sesquiquintodecimo. Per la Quinta
Proposta del giorno presente; la proportione, che si troua tra ab. & cb. è minor
di quella, che si troua tra db. & eb. Ma tra db. & eb. ui si troua il Semituono
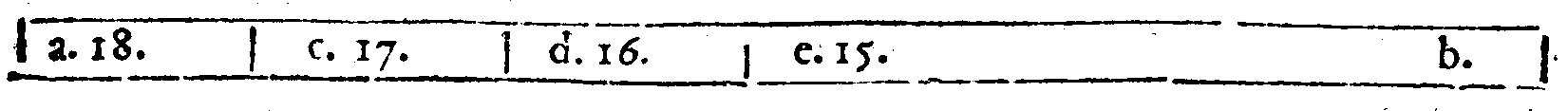
tuon maggiore consiste in maggior proportione, che non è la Sesquidecimasettima. An-
cora; Siano a & b. minimi termini della Sesquidecima settima proportione; & c. con d.
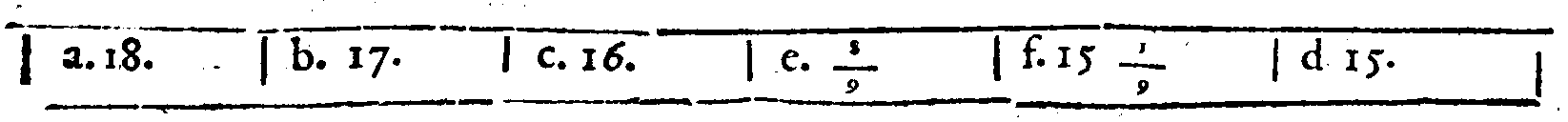
La onde piglio, per la Quintadecima del Primo, la parte di c. secondo a. & nasce e. la qua-
le cauo da esso c. & uiene f. Dico hora, che tra c. & f. si troua quella proportione istessa, ch'è
contenuta tra a & b. La onde, perche f. è maggior numero, che non è d. dico, per la Tren-
tesimasesta del Primo giorno, ch'è minore la proportione, che si troua tra e & f. che quel-
la, ch'è collocata tra c & d. Ma la c & d. è la proportione, che si troua tra c & f. che è quella,
ch'è collocata tra c & d. Ma la c & d. è la proportione del Semituono maggiore, & a con
b. è quella della Sesquidecimasettima; adunque il Semituono maggiore consiste in mag-
gior proportione, che non è la Sesquidecimasettima; come dimostrar ui douea. Onde da
queste due proposte cauaremo questo Corollario; che
COROLLARIO.
Tuono in due parti equali.
do 'l Tuono in questa maniera; dall'una parte; come nell'acuto, uiene là Sesqui-
sestadecima proportione; & dall'altra, come è nel graue, la Sesquidecimaset-
page 162 tima; delle quali ciascheduna il nostro maggior Semituono è maggiore. Et per il con-
trario, ciascheduna di esse è di essi minore; com'hò dimostrato. Seguirò anco à dimo-
strarui; che
PROPOSTA XXIII.
mi disse; Messere Gioseffo; se quella Proportione è maggiore, per l'Ottaua Di-
gnità allegata ancora nella Penultima di questo, la quale hà maggiore 'l suo De-
nominatore; & essendo contenuto il Semituono maggiore dalla proportione Sesquiquin
tadecima, della quale il Denominatore è 1 1/15. & quello della Sesquiquartadecima 1 1/14.
non è dubio, ch'essendo 1 1/14. maggiore di 1 1/15. che anco non sia maggior la proportio-
ne Sesquidecimaquarta, che non è la Sesquidecimaquinta. Et se bene à tutti noi questa
cosa è manifesta; tuttauia non mancate, vi prego, di dimostrarcela; ne habbiate riguardo
alcuno alle mie parole. Le vostre parole, risposi subito; non mi danno noia alcuna; anzi
mi diletta grandemente il conoscere, che quello ch'io dico, sia da uoi bene inteso; & che
la mia fatica non sia vana. Onde maggior'animo mi date di seguitar l'impresa incomin-
ciata, che di restare in dietro; però seguitando dico. Siano a & b. i termini radicali della
proportione del Semituono maggiore, & sia c. la parte ritrouata di b. per la Quintadeci-
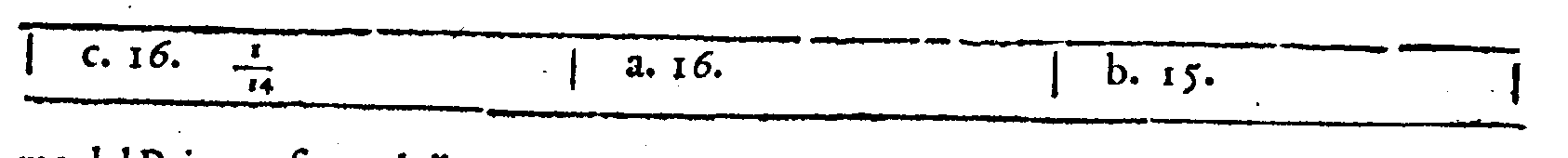
14. aggiunta al b. Dico hora, che cb. è proportione Sesquidecimaquarta. Ma c. è maggio-
re, che non è a. imperoche lo sopr'auanza di 1/14. sua parte; adunque, per la Trentesimase-
sta del Primo, è maggior la proportione, che si troua tra c & b. che quella, che è posta tra
a & b. Ma la proportione di c & b. è Sesquiquartadecima, & la a & b. è quella del Semi-
tuono maggiore; adunque la proportione Sesquiquartadecima è maggiore del maggior
Semituono; & come dimostrar vi douea. Queste due ultime dimostrationi, disse M.
Adriano; mi son molto piaciute; & ciò è auenuto, per hauer' ueduto le relationi de questi
due numeri. 16. & 16. 1/14. le quali si fanno al 15. Ma se andarete di lungo, spero di vedere
hoggi qualche cosa di bello, oltra l'altre cose, c'habbiamo ueduto. Auertite Messere, li dis-
si; che vi voglio dimostrare, auanti che andiamo più oltra; che
PROPOSTA XXIIII.
hauete dimostrato, che 'l Semituono maggiore necessariamente è maggior della
proportione Sesquidecimasesta; & in questa uolete dimostrar, che questa pro-
portione sia minore di esso. Voi la intendete; gli dissi; & però mi espedirò prestissimo.
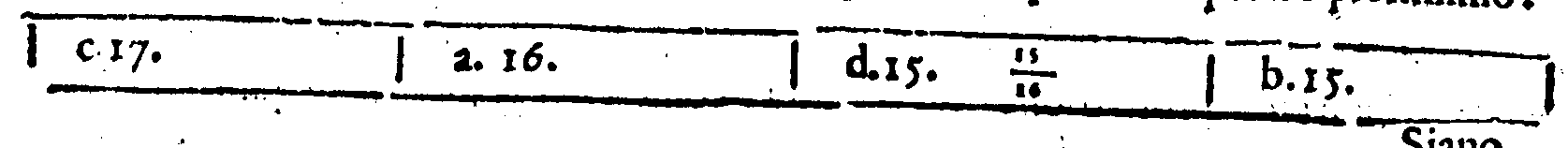
Sesquidecimasesta proportione. Dico questa proportione esser minore del Semituon
maggiore. Piglio adunque, per la Quintadecima Proposta del Primo giorno, la Sestade-
cima parte di b. la quale aggiungo ad esso b. & ne uiene d. La onde dico, che db. è propor-
tione Sesquisestadecima. Et perche a. uiene ad esser maggior Numero del numero d. pe-
rò dico, per la Trentesimasesta tante fiate allegata, la proportione db. esser minore della
ab. cioè, la Sesquisestadecima proportione, esser minore del maggior Semituono; com'e-
ra il mio proposito di dimostrarui. Aggiunse à questo M. Adriano; Questa ancora era no-
tissima da i Denominatori delle proportioni; ma molto più d'ogn'altra ragione mi piace
la Dimostratione; percioche ella fà chiaro l'oscuro. Ma per uostra fè ditemi; per qual ca-
gione hauete quasi replicato la Ventesimaprima, con questa conuersione? Risposi; Accio-
che potesse nascer questo Corollario, il quale dice à questo modo.
COROLLARIO.
decimaquarta & la Sesquisestadecima.
tadecima è maggiore del Semituono maggiore, & la Sesquidecimasesta è mino-
re; è necessario, che la sua proportione sia collecata tra l'uno & l'altra delle due
nominate; & questo non può esser, se non nella Sesquiquintadecima; percioche le due
nominate non riceuono altra proportione mezana di essa. Ma sapiate; che
PROPOSTA XXV.
maggiore era contenuto dalla proportione Super. 139. Partiente. 2048. Onde uo
lendoui dimostrare, che 'l nostro maggior Semituono è minore de il loro maggio-
re, faremo in questo modo. Siano primieramente a & b. i radicali termini del Semituono
maggiore; dopoi siano c & d. quelli dell'Apotome. Dico la proportione di ab. esser mi-

Nonaliquota di b. secondo e. Denominator della proportione cd. & uiene 1. 37/2048. cioè, f.
Aggiungo questa ad esso. & ne nasce g. il quale con b. è Super. 339. partiente. 2048. Ma
(come uedete) a. è minor numero di g. imperoche a. solamente è 16. & g. lo sopr'auanza
di 37/2048. Adunque, per la Trentesimasesta del Primo giorno, si conclude, che la proportio-
ne, la quale si troua tra a & b. è minor di quella, ch'è collocata tra g & b. Et per consequen
te, che la proportione del nostro maggior Semituono sia minore dell'Apotome; com'era
debitore di dimostrarui. Disse qui M. Claudio; La difficultà de queste dimostrationi, cre-
do che consista nel cauar le parti, & nell'aggiungerle à quel numero, al quale si vuol far la
relatione; il resto parmi che non sia molto difficile. Non è cosi M. Gioseffo? E' cosi per
page 164 certo, risposi. Et perche habbiamo (come mi pare) à sufficienza ragionato intorno al
Tuono & al Semituono maggiori; & dimostrato quello, che (secondo 'l mio parere) era
necessario di dimostrar, cōtra l'opinione d'Aristosseno; ò vogliam dire de gli Aristossenici
della diuisione del Tuono, & della quantità de i suoi Semitoni; & veduto quel che si può
tenere per uero intorno al Semituono maggiore de gli Antichi; ilquale chiamauano Απο-
τομὴ, però parmi hora, che sarà ben fatto ragionare etiandio & dimostrare insieme qual-
che cosa intorno la diuisione, che fece Filolao, laquale di sopra hò dimostrato. Percioche
se ben pare, ch'ella non sia fatta senza ragione; non è però da tenere, ch'ella sia quella,
della quale il Musico, secondo che porta la Scienza & anco la prattica, se n'habbia da ser-
uire. La onde uoglio in questo proposito, prima che io vi dimostri alcun altra cosa, di-
mostrarui (parlando sempre, quando ui nominerò il Semituono maggiore, di quello, il
quale habbiamo definito & dimostrato) alcune cose intorno lo Apotome & lo Diesis di
questo Filosofo & Musico celebratissimo; il quale Apotome nominerò Secondo; per farlo
differente da quello che di sopra si è dimostrato; Onde incominciando, dirò.
PROPOSTA XXVI.
d. termini radicali di questo Apotome, mostrati nell'ultimo essempio, che ui die-
di nella Vndecima Proposta di questo ragionamento. Dico ab. esser di maggior
proportione, che non è cd. Onde piglio, per la Quintadecima del Primo, la parte Nonali-
quota, del numero b. secondo e. Denominatore della cd. la qual uiene simigliantemen-
te ad essere e. Aggiungo adunque e al b. & ne risulta f. Non è da dubitare, che tanto sia la
proportione fb. quanta la cd. cioè, Super. 14. partiente. 229. Ma f. è minor numero, che
non è a. percioche a. è 16. & f. 15. 14/129. Adunque, per la Trentesimasesta del Primo, la
proportione ab. è maggior della proportione fb. Ma perche fb. è la dello
Apotome Secondo; & ab. quella del Semituono maggiore; però dico, Il secondo Apo-
tome esser minore del Semituono maggiore; come dimostrar ui douea. Disse hora il Sig.
Desiderio; Veramente queste cose sono degne d'essere hauute in consideratione; massi-

ch'alcune opinioni de gli Antichi Musici non siano da tenersi per buone; tuttauia non
è fuori della buona creanza; essendo che per dimostrar la uerità d'una cosa, non bisogna
hauer timore d'offendere alcuno; massimamente quando s'usano quei termini di mo-
destia, che sono conueneuoli. Ma se ben'un gran numero de quelli, che danno opera alla
Musica poco si curano di saperle; non uoglio però, che si poniamo nel numero loro però
seguitiamo il nostro ragionamento. Questo è buon pensiero dissi; però vi uoglio hora
dimostrare, che etiandio.
PROPOSTA XXVII.
quelli del Diesis, mostrati medesimamente nel fine dell'Vndecima Proposta di
hoggi. Dico, che ab. è maggior proportione di cd. Il perche ritrouo, per la poco
fà nominata Quintadecima del Primo, la parte Nonaliquota di b. secondo e. Denomi-
nator della cd. laquale uiene f. Questa aggiunta alla b. rende g. Dico hora, senza dubio
alcuno, che tanta è la gb. proportione Super. 13. partiente 216. quanta è la cd. Ma g. è
minor numero, che non è a. essendo ch'è solamente 15. 195/216. & a. è 16. Onde, per la tante fia-
te nominata Trentesimasesta del Primo, la proportione di gb. è minore, che quella di ab.
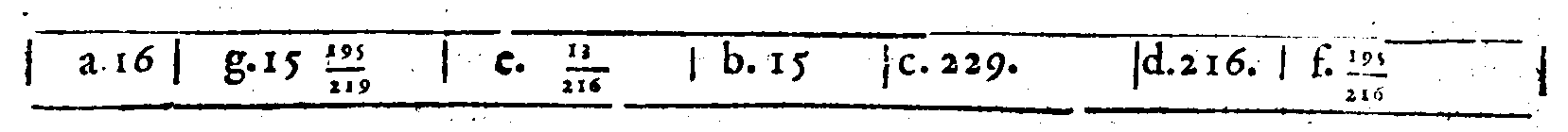
(secondo che douea dimostrarui) che 'l Diesis sia minore del maggior Semituono. Disse
qui M. Adriano; Parmi che poca sia la differenza, che si troua tra il Secondo Apotome
& lo Diesis; quando il nostro Semituono sopr'auanza l'uno & l'altro. E' uero, soggunsi;
ma uoglio che sapiate; che ne questi due Interualli fatti della diuisione del Tuono da Fi-
lolao; ne quelli fatti da Aristosseno, sono atti (aggiungendo ciascheduno da per sè à due
Tuoni Sesquiottaui, ouero al nostro Ditono) di produrre alcuna Consonanza. Et uoi
sapete che la Diatessaron senza dubio è consonanza; nondimeno pigliate qual ui piace
delle nominate parti, che sono Quattro, & aggiungetela à due Tuoni maggiori, com'hò
detto, ouero al Ditono ch'adoperiamo; ouer che trappassano la Diatessaron di poco; oue-
ramente che di poco non gli arriuano. Et accioche uoi siate certi di questo, & uediate, che
tali Interualli sono inutili nella Musica; ui uoglio dimostrar cotal cosa in quattro fiate se-
paratamēte, per ciascheduno de i nominati Interualli; le Proportioni de i quali ui mostrai
nella Decima Proposta. Auertite però, che 'l Mezo de queste dimostrationi sarà la forma
della Diatessaron, che è la Sesquiterza proportione. Onde dico, incominciando da quel-
le d'Aristosseno; che
PROPOSTA XXVIII.
ri, trappassa lo Sesquiterzo.
insieme questi Interualli, & che trappassano il Sesquiterzo, che siano dissonanti;
simigliantemente quando non arriuano; & però non mi dispiaceranno le dimo-
strationi, che hauete detto di fare. Verrò adunque, soggiunsi; senza por tempo alcun di
mezo à dimostrarui quello; che ui hò proposto. Siano, per la Prima del primo, a & b. gli
estremi termini radicali di due Interualli Sesquiottaui continuati; & sia prima à questi
separatamente aggiunto etiandio, per la Seconda, l'Interuallo Sesquidecimosettimo;
dopoi lo Sesquisestodecimo; di modo che cd. sia Interuallo composto de due Tuoni

ui, simigliantemente, & uno interuallo Sesquisestodecimo, ne i lor termini radicali. Sia
etiandio gh. l'interuallo Sesquiterzo. Dico che cd & ef. ciascheduno da per sè trappas-
sano l'Interuallo gh. Ritrouo adunque, per la Quintadecima del , la parte Nonali-
quota di h. secondo il Denominatore di cd. ilquale è p. & ne uiene k. Questo aggiunto cō
h. ci dà l. Onde dico, lh. contenere la Super. 185. partiente 544. Ma perche l. senza dubio
è maggior di g. percioche l. cōtiene il g. & di più 11/544. però dico, per la Trentesimasesta pro-
posta del Primo, che l'interuallo Sesquidecimosettimo aggiunto à due Tuoni maggiori
trappassa l'interuallo Sesquiterzo; Et questo sia detto quanto al primo. Ma quanto al se-
condo; ritrouo, per l'istessa Quintadecima, la parte di h. secondo m. Denominator della
Super. 353. partiente. 1024. La qual uiene ad essere n. che aggiunta ad h. ci dà o. Dico ho-
ra o. esser con h. simigliantemente Super. 353. partiente. 1024. Et perche o. uiene ad esser
maggiore di g. però la Super. 353. partiente. 1024. è maggiore dell'interuallo Sesquiterzo.
Il perche diremo; che l'interuallo Sesquidecimosesto aggiunto à due Tuoni Sesquiottaui
trappassa l'interuallo Sesquiterzo: & questo quanto al secondo. L'interuallo Sesquide-
cimosettimo adunque, ouer lo Sesquisestodecimo aggiunto à due Tuoni maggiori, trap-
passa il Sesquiterzo. Et questo è quello, che ui douea dimostrare. Fin qui si uede che la
Musica si puo preualer poco de i Semituoni d'Aristosseno, disse M. Claudio; percioche
quando sono aggiunti a questo modo, & trappassano il Sesquiterzo; & l'Interuallo che
danno, non è compreso tra le Proportioni contenute nelle parti del Senario; come molte
fiate hauete detto; tale Interuallo non può esser consonante. Ne anco essendo minore;
gli soggiusi, come dimostrerò hora; per il che douete sapere; che
PROPOSTA XXIX.
viene vn'Interuallo minore del Sesquiterzo.
gionamento, sia primieramēte aggiunto il Sesquidecimosettimo, & ne uenga cd.
dopoi sia aggiunto il Sesquidecimosesto, & ne risulti hp. & sia etiandio no. inter-
uallo sesquiterzo. Dico cd. & hp. ciascheduno da per se, esser maggiori di no. Primamen-
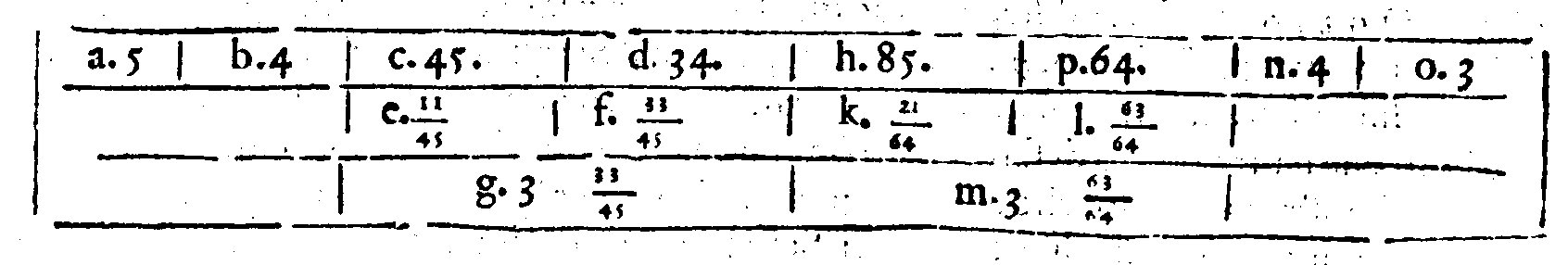
uiene f. Questa posta insieme con o. ci dà g. Onde non è da dubitare, che g. con o. con-
tenga lo Super. 11. partiente. 45. Ma perche g. è minor di n. com'è manifesto; percioche
4. è maggior di 3. 33/45. però, per la Trentesimasesta del Primo, maggior proportione è tra
n & o. che non è & o. Il perche essendo go. la quantità de due Interualli congiunti;
cioè, Super. 11. partiente. 45. & del Sesquiquarto; & no. quello del Sesquiterzo; & ri-
trouandosi questo di maggior proportione, che non è quello; seguita, ch'aggiunto l'in-
teruallo Sesquidecimosettimo al Sesquiquarto, ne uenga un'Interuallo minor di quel-
lo, ch'è lo Sesquiterzo. Et questo è quanto al primo. Quanto al secondo dico;
page 167 Ritrouo prima la parte Non aliquota di o. secondo k. denominator della Super. 21. par-
tiente. 64. & uiene l. il quale aggiungo con o. & ne nasce m. Dico hora m & o. contener l'i-
stessa proportione, che si troua tra h & p. Ma essendo m. minore di n. percioche n. è Quat-
tro vnità, & m. Tre vnità, & con 63/64 di vna appresso; & essendo n & o. Sesquiterzo, & m
con o. Interuallo composto de due Interualli insieme congiunti; cioè, Sesquisestodeci-
mo & Sesquiquarto; dico, & concludendo il tutto affirmo; che aggiunto l'interuallo Ses-
quidecimosettimo, ouer Sesquisestodecimo al Sesquiquarto; ne uien minore Interuallo
di quello, che è lo Sesquiterzo; come ui douea dimostrare. Questa conclude benissimo,
disse il Sig. Desiderio; & non ui resta cosa alcuna, che si possa dire in contrario. Però ha-
uendoui espedito di quello, c'hauete à dire intorno i Semituoni d'Aristosseno; sarà bene
che date speditione all'Apotome & al Diesis di Filolao. Cosi uoglio fare; gli risposi; però
auertite, che non solamente gli Interualli nominati aggiunti à due Sesquiottaui & al Di-
tono, non danno Consonanza alcuna; come hauete potuto comprendere; ma ne anco
questi due nominati. Et accioche me lo crediate, statemi ad ascoltare, che io ue lo uo-
glio dimostrare.
PROPOSTA XXX.
Interuallo di quel, ch'è lo Sesquiterzo.
sia aggiunto, per la Seconda del Primo giorno, la proportione del secondo Apo-
tome, la quale è la Super. 14. partiente. 229. onde ne uenga c & d. & quella del
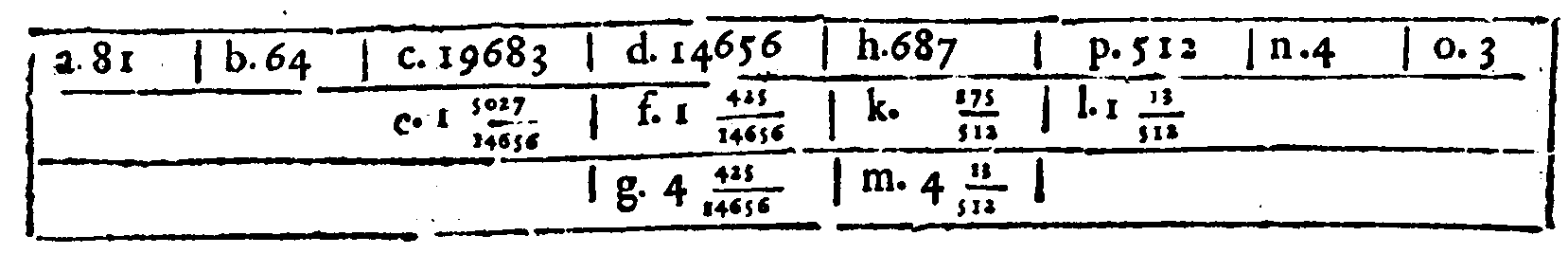
d. & anco hp separatamente l'un dall'altro, esser maggiore di n & o. Et che sia cosi lo pro-
uo. Ritrouo prima; come feci nelle Precedenti; per la Quintadecima del Primo; la parte
Nonaliquota di o. secondo e. la quale uiene f. Questa aggiungo con o. & risulta g. La on-
de go. sono due Sesquiottaui aggiunti al secondo Apotome; cioè, vna proportione Super.
5027. partiente. 14656. Ma perche g. è maggiore di n. poi che g. contiene quattro Vnità; &
425/14656. & n. ne contiene quattro solamente; però, per la Trentesimasesta del Primo,
maggior proportione è tra g & o. che non è tra n & o. La onde dico, essendo go. due
Tuoni sesquiottaui aggiunti al Secondo Apotome; che aggiunto cotale Apotome à due
Tuoni sesquiottaui, fà maggiore Interuallo di quello, ch'è lo Sesquiterzo. Et questo è
quanto all'Apotome. Ma quanto al Diesis; ritrouo di nouo la parte Non aliquota di o
secondo k. Denominator della proportione hp. la quale uiene l. Questa aggiungo con o
& ne nasce m. Onde dico m & o. essere il Diesis à due Sesquiottaui congiunto; cioè, una
Super. 175. partiente. 512. E' uero che m. è maggior di n. essendo che lo contiene una fia-
ta, & 13/512. Adunque mo. è maggior di no. Concludiamo hora & diciamo, che Aggiun-
to il Diesis à due Tuoni sesquiottaui, fanno maggiore Interuallo di quello, che non è il
Sesquiterzo; & questo è quanto al Diesis. Onde, secondo la proposta dico; che Aggiūgēdo
page 168 il secondo Apotome; ouero il Diesis à due Tuoni sesquiottaui, fanno maggiore Inter-
uallo di quello ch'è lo Sesquiterzo. Et questo è tutto quel che dimostrar ui douea. Non
è dubio, disse il Viola; che questi Interualli composti à questo modo non accordano. Et
mi marauiglio forte, che questi Filosofi & Musici tanto giudiciosi, non s'accorgessero di
cotal fatto. Voi uedete con me passa la cosa, risposi; Ma accioche non pensaste, ch'aggiun-
te queste due parti del Tuono fatte da Filolao al nostro Ditono, rendessino gli Interualli
consonanti; ascoltate quello, ch'io ui propongo à dimostrare.
PROPOSTA XXXI.
interuallo del Sesquiterzo.
sis; l'uno & l'altro de questi due aggiunto al Ditono; & siano l & m. l'interuallo
Sesquiterzo. Dico cd. & fg. etiandio, ciascheduna da per sè, esser minore,
non è lm. Piglio prima, per la Quintadecima del Primo, la parte Nonaliquo-
ta di m. secondo e. Denominator della proportione del sudetto Apotome; la quale uie-
ne p. Dopoi l'aggiungo allo m. & ne uiene k. che con m. contiene la Super. 299. partien-
te. 916. Onde dico; per la Trentesimasesta medesimamente del Primo; km. esser minore
di proportione, senza dubio alcuno, di lm. & per consequente il secondo Apotome ag-
giunto al Ditono far minore interuallo del Sesquiterzo; percioche k. infallibilmente è
minor numero di l. Et questo si è detto quanto al Primo. Ma quanto al Secondo; ritro-
uo la parte Nonaliquota primieramente di m. secondo h. Denominator della fg. cioè
della proportione del Diesis, la quale è n. & dopoi l'aggiungo ad m. & ne nasce o. il quale
con m. contiene la Super. 281. partiente, 864. ch'è la forma della proportione del Diesis
congiunto col Ditono. Ma perche l. contiene o. una fiata, & di più, 821/864 di vna sua Vnità.
Però l. è maggior di o. Onde, per la Trentesimasesta nominata, è minor la proportione,
che si troua tra o & m. che quella, la quale si scorge tra l & m. Essendo adunque o & m. la
proportione del Diesis aggiunta al Ditono, minore della proportione l & m. Sesquiter-
za; Seguita, che Accompagnato il Diesis col Ditono, fanno minore Interuallo del Ses-
quiterzo. Adunque, reassumendo tutto quello che dimostrato habbiamo, dico; Il secon-
do Apotome; ouero il Diesis accōpagnato col Ditono separatamente, fanno un'interual-
lo minore del Sesquiterzo. Et tutto questo è quello che mi douea dimostrare. Ogni co-
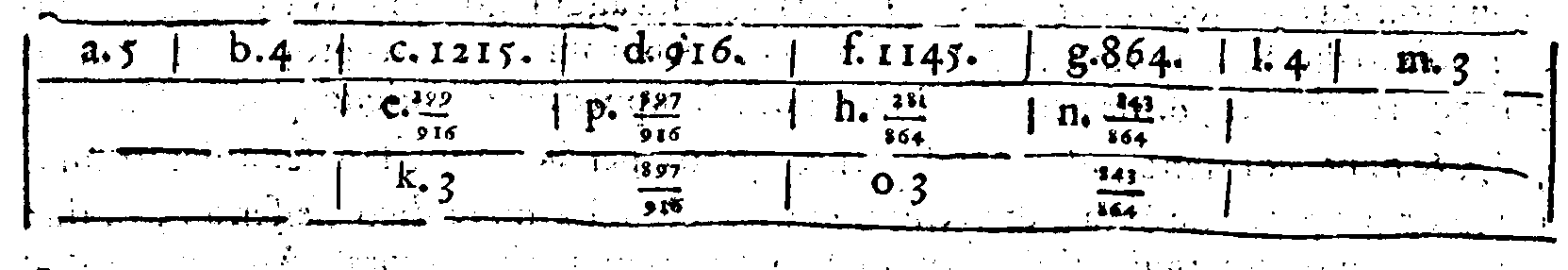
cosa anco intorno al nostro Semituono minore? Si uoglio; risposi. Et accioche non pen-
siate ch'io ui burli Mesere, statemi ad vdire.
PROPOSTA XXXII.
sua Definitione, è quell'Interuallo, per il quale il Ditono sopr'auanza il Semidi-
tono; Onde essendo il Ditono Interuallo d'un Tuono maggiore & d'un minore;
come nella Ventesimasettima proposta heri ui dimostrai; non è dubio, leuandosi da esso
Ditono il Tuono maggiore, & lo maggior Semituono, i quali sono contenuti nel Semi-
ditono; come nella Ventesimasesta di heri hauete potuto comprendere; che 'l minor Se-
mituono sia l'auanzo del Tuono minore; quando da esso si leua il maggior Semituono.
Essendo adunque cosi; Sia ab. & cb. per la Seconda d'hoggi, l'Interuallo del Tuono mi-
nore; & sia ac. la Decima parte di ab. Partisco ac. per la Terza dimanda d'hoggi, in Cin-
que parti equali, delle quali ne piglio Due nel punto d. Onde dico, che tra ab. & db. è
collocato alla sua proportione il minor Semituono; & cosi lo dimostro. Perche ac. è di-
uiso in Cinque parti; non è dubio, che tutta la chorda ab. uenga à contener Cinquanta
parti; percioche ac. è la Decima parte di ab. & Dieci molteplicato nel Cinque, rēde Cin-
quanta. Ma ab. contiene Cinquanta, & ac. ne contiene Cinque; però necessariamente
cb. ne uerrà à cōtenerne Quarantacinque. Simigliantemente; perche ad. contiene Due
parti; db. ne contiene Quarantaotto; & 48. à 45. per la Definitione de i Superparticola-
ri, si ritroua in proportione Sesquiquintadecima; percioche 48. contiene il 45. una fiata,
& 1/15 sua parte; però, per la quintadecima del passato giorno, db & cd. uiene ad essere il
Seemituono maggiore. Ma ab. & cb. è l'interuallo del Tuono minore; adunque, per il
Corollario della Decimanona proposta del Secondo; se da ab. & cb. Tuono minore le-
uaremo db. & cb. Semituon maggiore, resterà ab. & db. minor Semituono. Et cosi tra
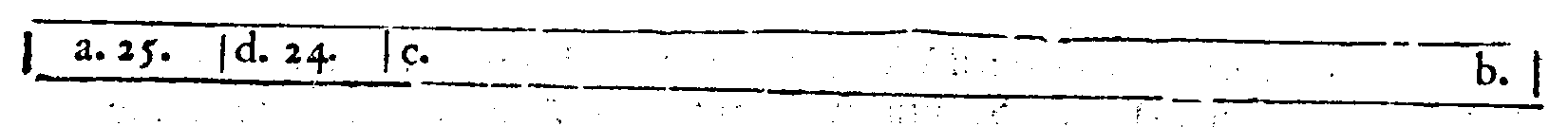
dimostrar ui douea. Si può etiandio tenere un'altro modo; come fù dimostrato nella Pri-
ma Proposta. Sia la data chorda, sopra la quale uogliamo accommodare il Semituono
minore, ab. Diuido ab. per la Terza dimanda in Venticinque parti equali per il termine
maggior della sua proportione; di maniera che db. ne contenga Ventiquattro, per il mi-
nor termine; & sia ad. Vna parte, per la sua differenza. Dico ab. & db. contenere il mi-
nor Semituono; percioche tutto lo spacio della chorda ab. contiene lo spacio db. & 1/24
sua parte, ch'è equale ad una delle Venticinque; Onde nasce la proportione Sesquiuen-
tesimaquarta, che per la Decimasettima del giorno passato, è la forma di tal Semituono.
Et perche, per la Prima dimanda, sarà l'istessa proportione del Suono di tutta la chorda
ab. al suono della db. che si ritroua tra lo spacio b. & lo db. però (secōdo che dimostrar
ui douea) il Semituono minore sopra la data chorda è collocato alla su a proportione.
Qui replicò M. Adriano, & disse; Questo stà molto bene, quando si uolesse accommoda-
re il detto Semituono sopra tal chorda nella parte graue; mà uolendolo accommodar tra
il Tuono minore nella parte acuta; come si douerà fare? Quel modo istesso quasi terret-
te, risposi io; che si è tenuto nell'accommodare il Maggiore; & è cosa facile. Ancora che
cotal modo sia facile; soggiunse il buon Vecchio; tuttauia sarete contento di dimostrar-
celo. Vi voglio satisfare per ogni modo Messere, gli dissi; onde ui propongo questa.
PROPOSTA XXXIII.
(per la Decimanona di questo) l'Interuallo del Semituono maggiore, tra ab. & c
b. Accommodo poi, per la Seconda Proposta, il Tuono minore alla sua propor-
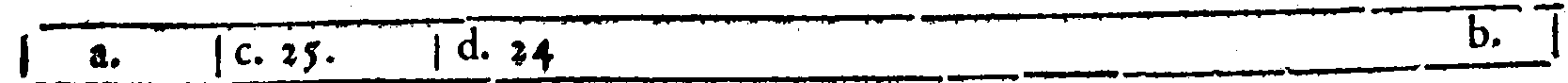
no minore soggiunto al maggiore sopra la data chorda. Et per dimostrarui questo; leuo,
per il Corollario della Decimanona del passato giorno, ab. & cb. Semituon maggiore da
ab. & db. Tuono minore; di modo che ne resti cb. & db. Et perche cb. & db. è quella
parte, per la quale il Tuono minore sopr'auanza 'l Semituon maggiore; però dico, per la
Ventesimaterza Definitione di heri, cb. & db. essere Semituono minore; come era 'l no-
stro principale intendimento; & esser soggiunto al maggiore sopra la data chorda; come
dimostrar vi douea. Ma poi che siamo à ragionar del Semituon minore, ui uoglio anco
dimostrare, che questo Interuallo è minore d'uno Super. 13. partiente. 243. ilquale è la
forma del Semituono minore del Diatonico diatono de gli Antichi; il qual è nominato
(come altroue vi hò detto) Λε͂ιμμα; Però dico.
PROPOSTA XXXIIII.
uoi ragionato sopra i Semituoni d'Aristosseno & quelli di Filolao; bisognaua
anco dir qualche cosa sopra di questa Limma; laquale hà tanto limato il ceruel-
lo à molti, che poco più di niente ui resta; ne si sanno cauar fuori de gli intrichi
di questo benedetto Interuallo; perche uogliamo pur, che s'adoperi nelle nostre compo- sitioni. Et per dire il uero, ui haueui fatto debitore di ragionarne; essendo c'hauete an-
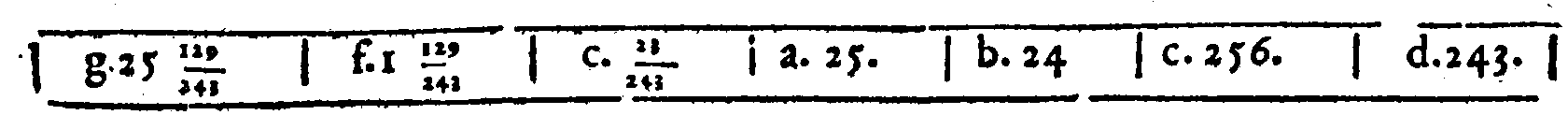
risposi; Onde auanti ch'io uada più oltra, voglio satisfare al mio debito. Siano adunque
a & b. Termini radicali della proportione del nostro minor Semituono; & siano etiandio
c & d. quelli del nominato Lemma. Dico la proportione ab. esser minore della cd. Piglio
adunque, per la Quintadecima del Primo nostro ragionamento, la parte Nonaliquota di
b. numero, secondo e. Denominator di cd. & uiene f. Questa aggiungo alla b. onde ne
rifulta g. E' cosa manifesta, che g. con b. contiene quella istessa proportione, ch'è tra c & d.
Ma g. è maggior numero, che non è a. imperoche g. è 25. &129/243. & a. è solamente 25. Adun-
que, per la Trentesimasesta del Primo, maggiore è la proportione, che si troua tra g & b.
che non è quella, la qual si troua tra a & b. & per consequente il Semituono minore hà mi-
nore Interuallo, che non hà lo Super. 13. partiente 243. ouer'il Lemma: come mi feci de-
bitore di dimostrarui. Et questo non si può negare; come anco non si potrà negare, fatta
la dimostratione; che
PROPOSTA XXXV.
pr'auanza 'l maggior Semituono.
maggior Semituono; & e. con f. quelli del minore. Molteplico prima a in c & d.
& ne uiene g & h. Dopoi molteplico b in g. & ne nasce k. Dico hora, che g & k.
contengono il nominato Tuono maggiore; & g con h. il maggior Semituono.
Percioche Ogni numero, per la Quinta dignità, molteplicato in due altri, produce una
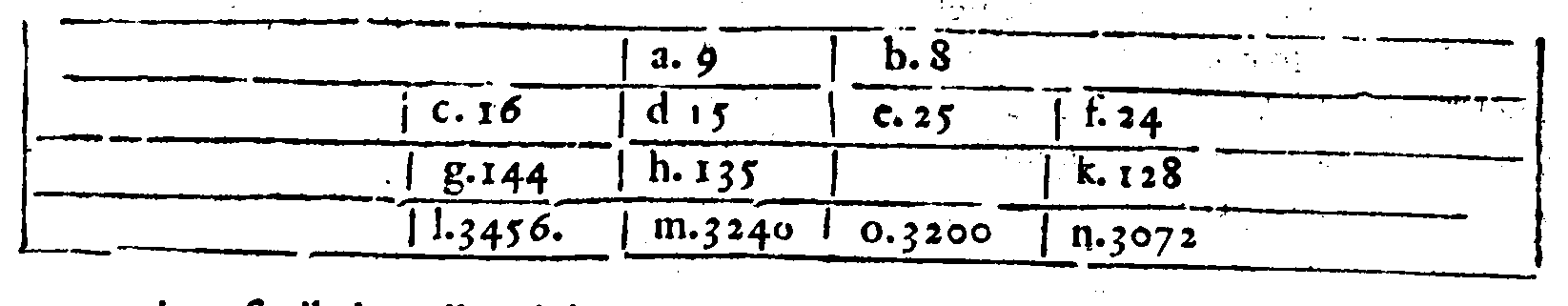
c & d. per a. ne nasce g & h. che ccntengono la proportione, ch'è tra c & d. & molteplica-
to g per b. ne uiene k. che con g. contiene la proportione contenuta tra a & b. Habbiamo
adunque tra g & h. il maggior Semituono, & tra h & k. il Tuono maggiore. Hora aggiun-
go al k. termine minore del Tuono, il Semituono minore; facendo commune esso termine
all'uno & l'altro; molteplicando prima f. in g. h & k. onde ne risulta lm. & n. i quali, per
l'istessa Quinta dignità, contengono per ordine quelle proportioni, che sono contenute
tra gh. & k. dopoi molteplico e. simigliantemente in k. & ne uiene o. il quale con k. per la
nominata Dignità, contiene il nominato Semituono minore; che si troua tra e & f. Per-
che e & f. si trouano esser molteplicati da vn'istesso numero, il quale è k. Ma perche l & n. è
Tuono maggiore, & lm. è Semituono anco maggiore; però dico, che se dal & n. Tuono
maggiore leuaremo l & m. maggior Semituono; resterà m & n. il qual dico esser maggio-
re dell'Interuallo o & n. percioche o. è minor numero, che non è m. onde, per la Trente-
simasesta del Primo, è minor la proportione, che si troua tra o & n. che non è quella, che
si troua tra m & n. Ma perche o & n. è l'interuallo del Semituon minore, & m cō n. è quel-
l'Interuallo, che sopr'auanza il Semituono maggiore per compimēto del Maggior Tuo-
no; però dico, che 'l Semituono minore hà minor proportione di quella, che hà l'Inter-
uallo, per il quale il Tuon maggiore sopr'auanza 'l maggior Semituono; come ui douea
dimostrare. Ma ascoltate un Corollario, che nasce da quel, che si è dimostrato.
COROLLARIO.
lo di maggior proportione, che non è quella del minor Semituono.
d'altra proua. Ma perche (come uedo) fin'hora hauete ragionato de quelli In-
terualli solamente, i quali sono Dissonanti; però (quando non haueste da dirci
altro sopra di essi) buona cosa sarebbe che ragionaste etiandio sopra de quelli, che sono
Consonanti. Onde mi pare, che se uolete tener l'ordine, il quale è stato da uoi fin'hora
tenuto; habbiate à ragionare intorno al Ditono & al Semiditono; come quelli, che sono
minori de gli altri. Parmi, disse anco M. Claudio; che ci resti un'altro Interuallo Messere;
del quale non è stato fin'hora in questo ragionamento d'hoggi detto cosa alcuna; onde
sarebbe bona cosa, che si hauesse anche sopra di lui à ragionar un poco; se però tal ragio-
namento torna al proposito. A questo; disse M. Francesco; Quale è questo Interuallo M.
Claudio? E' il Minimo che ci sia, rispose; & questo è il Comma. E' uero soggiunse M.
Francesco. Vdendo questo M. Adriano quasi ridendo, disse; Vedete quello che importa
page 172 l'esser picciolo, come son io; che di quattro che siamo, niuno l'hauea ueduto. Fermateui
Messere, disse io; & contentateui di esser quello che uoi sete; percioche tutti i piccioli
hanno molti auantaggi, che non hanno i grandi; i quali non uoglio stare à raccontare, per
non partirmi dal nostro proposito; & ui dee bastare, che se bene tra gli Huomini grandi
sete picciolo di statura, il uostro ualore tra i grandi & honorati ui hà posto nel numero de
quelli che essercitano la Musica nel più honorato & alto seggio. Ma questo Interuallo
cotanto picciolo non mi era molto lontano dal pensiero; percioche è necessario, per le co-
se, che ui hò da dimostrare, che anco à lui toccasse la sua parte; & è quiui à punto il suo luo
go. Ma sopra di esso non uoglio farui troppo lunga diceria; perche mi uoglio espedire in
poche parole. Et per incominciare, diremo prima; che
PROPOSTA XXXVI.
tione.
re alla sua proportione il sudetto Interuallo Musico. Accommodo prima sopra
di essa, per la Prima di questo, l'interuallo Sesquiottauo, ò Tuono maggiore ab.
& cb. alla sua proportione; dopoi, per la Seconda, accōmodo il Sesquinono, ouer Tuono
minore ab. & db. Dico hora, che tra db. & cb. il Cōma habbiamo collocato alla sua pro-
portione. Percioche, essendo ab. & cb. Tuono maggiore, & ab. & db. Tuono minore;
seguita, che l'Interuallo dc. sia quello, per il quale il Tuon maggiore sopr'auanza il mino-
re. Ma, per la Ventesimaquinta definitione del giorno inanzi; il maggior supera il mino-
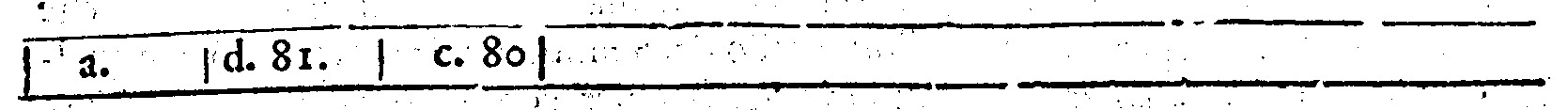
dato sopra la data chorda alla sua proportione; come era 'l mio proposito di dimostrarui.
Hauete accommodato il Comma in tal maniera, disse M. Adriano; che tra il Tuono mag-
giore & lo minore tiene la parte acuta; ma quando si uolesse accommodar di modo, che
tenesse la parte graue; che strada si hauerà da tenere? Quasi l'istessa; soggiunsi; la quale
hora ui uoglio dimostrare. Sia la chorda ab. & sopra di essa uogliamo accommoda-
re in tal maniera il Comma, che sia collocato nella parte graue; & sia ab & cb. per la
Prima di questo il Tuono maggiore accommodato a la sua proportione. Accommodo
hora il minore in questo modo. Diuido prima lo spacio cb. in noue parti equali, secon-
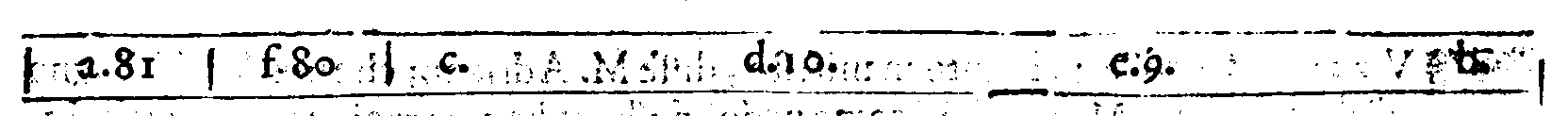
delle noue fino al punto f. di maniera; che fb. contenga Dieci parti, secondo d. termine
maggiore della proportione del Tuono minore de. Onde dico, che quella Proportione,
che si troua tra d & e. per la Quinta dimanda d'hoggi, si troua anco tra fb. & cb. Et per-
che de. tien la forma del Tuono minore; però dico; che anco fb & cb. è Tuono minore.
Ma hauendo già prouato, che fb & cb. è Tuono minore, & ab & cb. Tuono maggiore;
dico hora che l'Interuallo ab & fb. è quello, per il quale il Tuono maggiore sopr'auanza
il minore. Et perche questo Interuallo, seconda la Ventesimaquinta definitione già no-
minata, è il Comma; però dico; ab & fb. esser l'interuallo del Comma, accommodato so-
pra la data chorda nella parte graue, secondo 'l proposito; come ui douea, secondo la vo-
page 173 stra richiesta, dimostrare. Resto satisfatto benissimo; disse M. Adriano; & io gli dissi; per
dimostrarui quello, che poco fà proponeste da dimostrare & ragionare intorno al Dito-
no & lo Semiditono; percioche qui è il suo luogo; Ascoltate quello, che hora ui uo-
glio dire; che è questo; che
PROPOSTA XXXVII.
ma, per la Terza dimanda d'hoggi, ab. in sei parti equali; di modo che cb. ne
contenga cinque, & sia ac. una delle sei. Dico che ab & cb. contengo lo Semi-
ditono; & sopra la data chorda hauerlo collocato alla sua proportione. Imperoche tutto
lo spacio della chorda ab. contiene lo spacio cb. & di più una quinta parte di esso, ch'è

spacio ab è Sesquiquinto al cb. Onde, per la Prima dimanda d'hoggi, Quell'istessa pro-
portione si ritroua etiandio tra 'l suono di tutta la chorda ab. & quello della cb. Ma
essendo il Sesquiquinto la forma del Semiditono interuallo; però dico, che sopra la data
chorda ab. habbiamo, secondo 'l proposito, collocato il Semiditono tra ab & cb. come
ui douea dimostrare. Questa dimostratione, per certo facile; ne ui è da dubitar cosa al-
cuna; onde passarò all'altra; ragionando però del Semiditono qualche cosa. Sapiate
adunque; che
PROPOSTA XXXVIII.
tiene un Tuono maggiore & un minore; L'un de i quali, per la Nona proposta
medesimamente di heri, è Sesquiottauo, & l'altro Sesquinono. Ma il Sesquiotta-
uo & maggiore supera, per la Ventesimaquinta definition del giorno passato simiglian-
temente, il Sesquinono; cioè, il minore per un Comma. Adunque il Ditono è minor di
due Tuoni Sesquiottaui di un Comma. Ma perche, per la Ventesimaterza definitione
del medesimo giorno, il Ditono sopr'auanza il Semiditono per un Semituono minore;
però il Semiditono è minore del Ditono d'un Semituon minore. Et è simigliantemen-
te minor de due Tuoni sesquiottaui d'un minor Semituono & di un Comma; come dice
la Proposta. Et questo è quello, che ui douea dimostrare. Ma accioche uediate qualche
differenza del nostro Semiditono con quello, che adoperauano gli Antichi nella specie
Diatonica detta Diatona; sapiate; che
PROPOSTA XXXIX.
strarui questa, torrò questo mezo. Sia a & b. per la Duodecima definitione di
heri, la proportione Sesquiquinta, la quale è forma di questo nostro Interual-
lo; & sia c & d. la Super 5. partiente. 27. forma del loro Semiditono, com'hò
detto. Dico a & b. esser di maggior proportione, che c & d. onde, per la Quintadecima del
Primo giorno, piglio le 5/27 parti di b. che sono secōdo e. Denominator della Super 5. par-
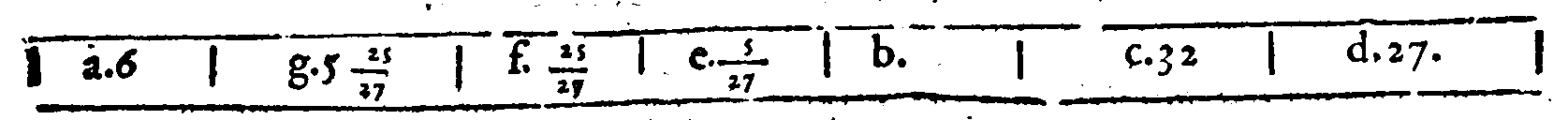
la proportione, che si troua tra c & d. Ma g. è minore di a. percioche a. lo contiene una
fiata con 2/27 parti; adunque, per la Trentesimasesta simigliantemente del Primo giorno,
a & b. è maggior di proportione, che non è g & b. ouer c & d. Et perche cd. è Super 5. par-
tiente 27. pero dico; che 'l Semiditono ab. è maggior della proportione Super 5. partien-
te 27. cioè, di cd. come dice la Proposta. Et questo è quello, che bisognaua dimostrare.
Ma sapiate oltra di questo; che
PROPOSTA XL.
to dalla proportione Sesquiquarta; però sia ab. qual si uoglia Chorda data; Fà
dibisogno, che questa sia diuisa in Cinque parti equali; come sono ac. cd. de. ef.
& fb. Onde dico ab & cb. consonare 'l Ditono. Imperoche ab. contiene cb. & di più
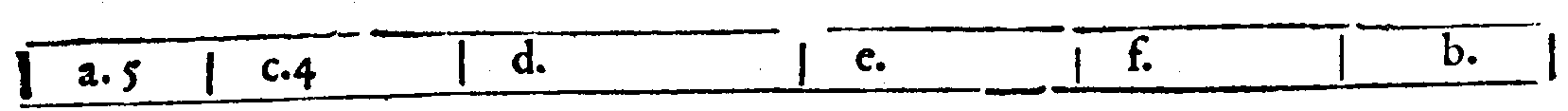
Prima dimanda di hoggi, ab & cb. consonano il Ditono. Et cosi sopra la data Chorda
ab. uiene ad esser collocato 'l Ditono alla sua proportione, secondo 'l proposito; come ui
douea dimostrare. Verrò ancora à dimostrarui; che
PROPOSTA XLI.
contiene due Tuoni, l'un maggiore & l'altro minore; & due Tuoni sesquiottaui
sono due Tuoni maggiori; Ma, per la sua Ventesimaquinta Definitione, il
Tuon maggiore sopr'auanza 'l minore per un Comma; Adunque un Tuon maggiore &
un minore sono minori de due maggiori, per un Comma; & per consequente il Ditono è
minor di due Tuoni sesquiottaui per un tale Interuallo; come, secondo la Proposta, ui do
uea dimostrare. E' ancora che questa dimostratione sia breue, facile & chiara; uoglio pe-
rò anco dimostrar questa Proposta con un'altro mezo. Sia a & b. la proportione del Di-
tono, & c con d. quella del Tuono Sesquiottauo; l'una & l'altra contenuta ne i suoi ter-
page 175
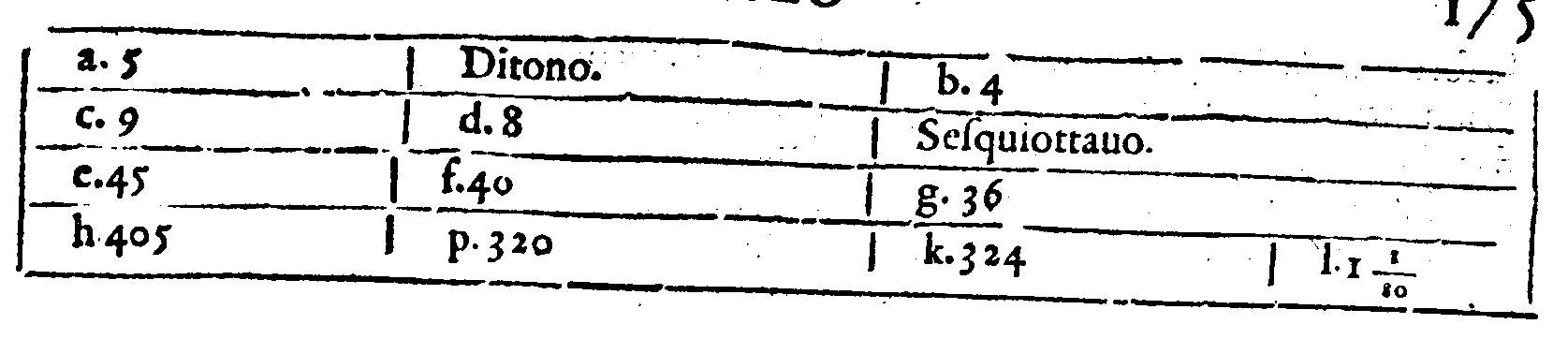
& ne nasce g. Dico hora e & f. esser l'interuallo del Tuono Sesquiottauo, percioche, per la
quinta Dignità, molteplicando qual si uoglia numero in due altri numeri; i prodotti con-
tengono quella proportione istessa, che contengono i due primi molteplicati. Onde es-
sendo molteplicati c & d. per a. senza dubio alcuno tra e & f. è quella proportione, che si
troua tra c & d. Il perche essendo cd. Sesquiottaua, etiandio ef. uiene ad essere Sesqui-
ottaua. Simigliantemente dico, che tra e & g. si troua il Ditono; essendoche molteplica-
to il c. in a & b. per l'istessa Quinta nominata, produce e & g. che contengono quella pro-
portione istessa. Di nuouo molteplico c in e. & d in f. & ne risulta h & p. i quali conten-
gono due Tuoni congiunti; cioè, cd & ef. Molteplico ancora c in g. & ne nasce k. il qua-
le con h contiene la proportione eg. perche c. molteplicato in e. & in g. produce una si-
mile alla e & g. Ma perche k. è maggior numero, che non è p. però, per la Trentesimasesta
del Primo, la proportione, che si troua tra h & p. è maggior di quella, ch'è tra h & k. Et
perche tra h & p. sono sommati insieme due Sesquiottaui; & tra h & k. si troua la propor-
tione del Ditono; però dico, che 'l Ditono è minor de due Tuoni Sesquiottaui; di quan-
to h & k. è superato da h & p. Essendo poi kp. proportione Sesquiottantesima; come si
conosce dal suo Denominatore, che è 1. & 1/10. il quale si può ritrouar nel modo, ch'io in-
segnai nell'Istitutioni;1. par. c. 25. & essendo da tal quantità, per la Ventesima proposta di heri, conte-
nuto l'interuallo del Comma; seguita, che 'l Ditono è minor de due Tuoni Sesquiottaui,
di un Comma; come dimostrarui . Ne altro ui uoglio dir sopra di cotal cosa; ma
uerò à dimostrarui; che
PROPOSTA XLII.
alle loro proportioni sopra qual si uoglia data chorda.
le tre nominate Consonanze alle loro proportioni. Diuido prima ab. in Quat-
tro parti equali; dopoi faccio cb. equale à Due, & db. equale à Tre parti. Di-
co hora, che tra ab & db. è collocata la Diatessaron, & tra db & cb. la Diapente, simi-
gliantemente tra ab. & cb. la Diapason alle loro proportioni. Et perche ab. il Tutto
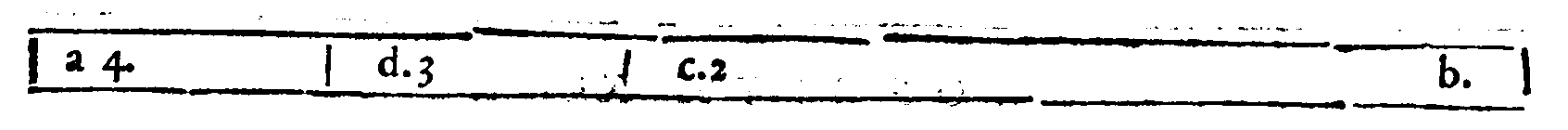
db. ch'è ad. però dico ab & db. per la Definitione, esser Sesquiterzo. Ma perche la Ses-
quiterza, per la Decima definitione del giorno passato, è la forma della Diatessa-
ron; però dico primieramente, che tra ab. & db. è collocata la Diatessaron alla sua
proportione. Simigliantemente, perche db. contiene tre parti, & cd. ne contiene due
della chorda db. Però dico db & cb. essere Sesquialtero; percioche db. contiene cd. &
la sua metà, la quale è equale à dc. Ma la Sesquialtera, per la Nona definitione di heri, è
page 176 la forma della Diapente; adunque tra db & cb. secondariamente è accommodato la
Diapente alla sua proportione. Vltimamente; perche ab. tutta la chorda contiene Due
fiate intiere cb. però dico (per la Definitione) ab & cb. essere interuallo Duplo. Ma il
Duplo, per la Definitione, è la forma della consonanza Diapason; adunque tra ab. &
cb. habbiamo collocato la Diapason alla sua proportione. Et cosi habbiamo tutto 'l
proposito; come dimostrar si douea. Dopo una lunga pausa fatta da ogn'uno, disse alla
fine Messere Adriano; Essendo accommodate queste Consonanze in cotal maniera; la
Diatessaron uiene ad esser preposta alla Diapente, & tiene il luogo graue; ma quando si
uolesse soggiungere essa Diatessaron alla Diapente; di modo che essa Diapente occu-
passe cotal luogo, & la Diatessaron l'acuto, come si farebbe? Quasi all'istesso modo, ri-
sposi; onde dico di nuouo. Sia ab. la data chorda, sopra la quale uogliamo accommodar
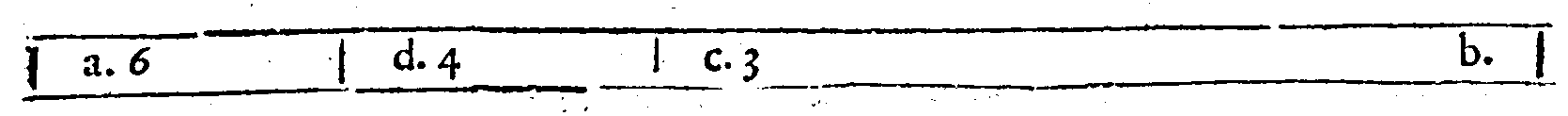
parti equali nel punto c. il che fatto, dico ab. & cb. contenere, per le ragioni addotte di
sopra; le quali non replicherò, per non esser lungo; la Diapason consonanza. Diuido
dopoi cb. in Tre parti equali, & aggiungo in punto d. Vna parte; di modo che db. ven-
ga à contener Quattro parti. Onde tutta la chorda ab. uiene ad esser diuisa in Sei par-
ti; percioche essendo cb. la metà di ab. & essendo essa cb. diuisa in tre parti; dc. vie-
ne ad essere una Sesta parte di ab. & ad. Due. La onde dico, che tra ab. & db. uie-
ne ad esser collocata la Diapente alla sua proportione, & tra db. & cb. la Diatessaron.
Percioche se ab. contiene Sei parti, db. uiene à contenerne Quattro. Ma tra quattro &
sei numeri Tra loro Composti, si troua la proportione Sesquialtera; la quale, per la Nona
definitione già detta, è la forma della Diapente; adunque tra ab. & db. habbiamo collo-
cato alla sua proportione la Diapente. Ma tra ab. è collocato la Diapason; & fe, per il
Corollario della Quarta del giorno passato, da ab. & cb. Diapason, leuaremo ab. & db.
Diapente; resterà db. & cb. Diatessaron; Onde db. & cb. senza contrasto alcuno sarà
la Diatessaron. Et per tal modo haueremo accommodato questa Consonanza insieme
con le due altre alle loro proportioni; & soggiunto essa Diatessaron alla diapente; come
in particolar mi hauete fatto la proposta, Messere. Questa dimostratione adunque è
stato fatta per mio conto, disse egli. Cosi è, risposi. Rendoui adunque gratia della fa-
tica, disse egli. Disse allora il Sig. Desiderio; Queste dimostrationi fatte in questo modo
molto piacciono; perche, oltra che hanno un non so chè d'ingegnoso, hanno anco in
sè una breuità, che diletta. Et uoi sapete, che la breuità piace à tutti. Per questo hò
voluto porle insieme, risposi; Ma poiche habbiamo espedito di dimostrare in qual ma-
niera separatamente ciascheduno Interuallo consonante s'accommodi alla sua propor-
tione; uoglio che hora uediamo in qual maniera si possano porre insieme ordinatamen-
te ne i lor proprij & naturali luoghi, secondo che tra i Numeri harmonici collocati sono.
Però auertite; che noi.
PROPOSTA XLIII.
Consonanze, & di quelle farne sensatamente l'.
cotali Consonanze secondo l'ordine, che ui hò dimostrato; incominciando dal
Semiditono, & uenire in fino alla Diapason; ma uoglio incominciar primiera-
page 177 mente da quella Consonanza, che hà la sua forma tra i numeri prima, & è più semplice
d'ogn'altra. Et questa sarà la Diapason; & dopoi uerrò alla Diapente; & à questa ag-
giungerò la Diatessaron; & di mano in mano il Ditono & ultimamente lo Semiditono; &
cosi hauerò accommodato tutte le Consonanze, delle quali fin'hora hò ragionato, alla
lor proportione. Ilche fatto, potrete udire, oltra le Consonanze nominate, la Disdia-
pason, la Diapasondiapente, la Disdiapasonditona, & la Disdiapasondiapente, essendo
che in cotal maniera acommodate, si potrà anco udire la Diapasondiatessaron, & qual si
uorrà Harmonia. Sarà ben fatto, soggiunse M. Adriano; Ma ditemi per uostra fè; per
qual cagione non hauete incominciato à far le Dimostrationi secondo quest'ordine, il
quale mi par, che sia più ragioneuole? Perche ui hò uoluto dimostrare, risposi; che i mag-
giori Interualli sono reintegrati da i minori, come da sue parti. Et se ben, come sapete;
il Tutto, il quale è sottoposto alla Qantità, è prima che le sue Parti; & si hà la cognitione
loro per la sua misura; tuttauia uolendoui mostrare in qual maniera esso Tutto da esse Par
ti uenga integrato; insiememente ui uengo à mostrar la loro ragione; però non ui mara-
uigliate. Intendo hora la cagione, soggiunse il buon Vecchio; però seguitate 'l vostro pro-
posito. La onde ripigliando il mio ragionamento, dissi. Hauendo voi inteso tutte queste
cose, dirò. Sia la chorda ab. sopra la quale uogliamo accommodare alla lor proportio-
ne tutte le Musicali consonanze, le quali fin'hora hò dimostrato. Diuido primieramente
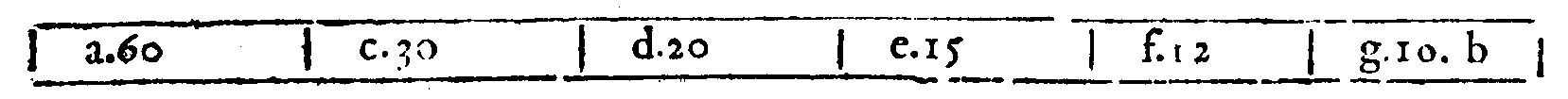
Compasso nel punto a. uenendo con l'altro uerso b. Fatto questo piglio la metà &
segno e. Diuido poi cb. in tre parti equali, & piglio la Terza parte da banda destra; on-
de segno d. Ilche fatto partisco db. in Quattro parti, & pigliando la Quarta uerso man de-
stra, segno e. Diuido ancora eb. in Cinque parti equali, & presa la Prima più propinqua
ad e. segno f. Hora partendo fb. in Sei parti, pigliando la Sesta parte, noto g. Onde dico, So-
pra la data chorda hauer collocato tutte le Cōsonanze musicali l'una dopo l'altra per or-
dine à i proprij luoghi; & anco soggiunte l'una dopo l'altra alle loro proportioni. Et che
questo sia uero, cosi lo manifesto. Non è dubio, che la chorda ab. contiene due fiate la cb.
onde, per la Definitione, uiene ad esser tra queste due chorde la proportione Dupla. Ma
essendo, per la Prima dimanda d'hoggi, tanta la proportione di Suono à suono, quanto è
quella di chorda à chorda; & essendo la Dupla forma della Diapason; necessariamente
douemo confessare, che etiandio i Suoni, i quali nascono dalle chorde ab. & cb. ren-
dino la Diapason. Disse allora M. Adriano; Chi può dubitar di questo? Alcuno, che
non hauesse giudicio; risposi io; Ma perche tra la chorda cd. diuisa in tre parti, &
la db. che ne contiene due, per la Definitione, è contenuta la proportione Sesqui-
altera; però, per la medesima Dimanda, è necessario, che cb. & db. consonino la
Diapente. Simigliantemente, perche ab. & db. si compone di ab. & cb. la quale
habbiamo detto esser Dupla & consonare la Diapason; & di cb. & db. che è propor-
tione Sesquialtera, & consonanza Diapente: però dalla Ventesimaseconda del Pri-
mo, & dalla Quarantesimaprima proposta del giorno passato, & dalla Terzadecima
definitione simigliantemente di heri, ab. & db. contengono la proportione Tripla,
& per consequente la Diapasondiapente. Oltra di questo non è dubio, essendo la
db. diuisa in quattro parti, & la eb. hauendone le tre, che tra queste due, per la De
finitione, non si troui la proportione Sesquiterza. La onde essendo cosi, com'è uera-
mente, db. & eb. uengono à dar la consonanza Diatessaron. Ma perche ab. & eb. si com-
pone della ab. & cb. & della cb. & db. & anco della db. & eb. & già hò detto la ab. &
db. esser Tripla & la Diapason diapente; però aggiungendo à questa la db. & eb. ha-
ueremo ab. & eb. che conteneranno la Quadrupla & la Disdiapason consonanza. Per-
page 178 cioche essendo cb & db. Sesquialtera & la Diapente, & db. cō eb. Sesquiterza & la Dia-
tessaron; queste poste insieme, per la Decimasettima del Primo, & per il suo Corollario, &
per la Quarta di heri; fanno la Dupla & la consonanza Diapason. La onde essendo ab &
cb. Diapason; simigliantemente cb & eb. seguita, per la Ventesimaterza del Primo, & per
l'Vltima proposta di heri; che ab & eb. sia la Consonanza Disdiapason. Fù poi diuisa eb.
in cinque parti, di maniera che fb. ne contiene quattro; onde per la Definitione, contie-
ne la Sesquiquarta, & per consequente il Ditono. Ma perche di sopra hò detto, che ab.
& eb. contengono la Disdiapason; però aggiungendole eb & fb. cioè, il Ditono; ab.
& fb. verranno à contenere la Disdiapason col Ditono; ilquale con db. & eb. Diatessa-
ron; per la Trentesimaquarta proposta di heri; farà l'Hexachordo maggiore. Perche
anco, per la sua Definitione, la Disdiapasonditona è contenuto dalla proportione Quin-
tupla; però ab & fb. contengono la nominata proportione. Habbiamo etiandio (se ui
ricordate) diuiso fb. in sei parti equali; di maniera, che tra fb. che contiene il Tutto, &
gb. che contiene Cinque parti; venimo, secondo la Definitione, hauer la proportione
Sesquiquinta; & secondo 'l Primo parer commune, ò Dignità, il Semiditono. Ma perche
ab & gb. è composta di ab. & cb. di cb. & db. di db. & eb. di eb. & fb. & di fb. & gb. &
già hò detto, che ab. & sb. contengono la Quintupla proportione, & risonano la Disdia-
pasonditona; però aggiungendole fb. & gb. uerranno ab. & gb. che conteneranno la
Disdiapasondiapente; la quale, per la sua Definitione, contiene la Sestupla proportione;
percioche essendo eb. & fb. Ditono, & fb. & gb. Semiditono; aggiunti questi due Inter-
ualli insieme, nasce, per la Trentesimaprima di heri, la Diapente; la quale aggiunta alla
Disdiapason ab. & eb. senz'alcun dubio, ne nasce la Disdiapason diapente, come hò an-
cora detto. Et cosi Sopra vna data chorda haueremo soggiunto per ordine l'una dopo
l'altra à i lor luoghi proprij tutte le Musicali consonanze, secondo 'l proposito, come ui do-
uea dimostrare. Le quali uolendo udire, si aggiungerà una, ò più chorde accordate per-
fettamente vnisone alla ab. che, secondo la Seconda dimanda d'hoggi, saranno riputate
vna chorda sola, & faranno un solo, & non diuerso suono. Onde ponendo sotto di esse
gli Hemispherij à i notati punti, i quali da Greci sono detti Α'ποψάλματα; si potrà udire
di vna in vna qual si vorrà Consonanza; & anco, essendo l'una di esse qual si uoglia da
vna mezana chorda tramezata; si potrà udir qual si uorrà Harmonia; secondo 'l proposi-
to. Et se porremo sopra ciascheduno de i segnati punti, sotto le chorde tirate sopra la
Regola harmonica un'Hemispherio; toccandole tutte insieme, udiremo un'accordo tan-
to eccellente & mirabile, che non si potrà desiderare un migliore. Questo accordo; disse
il Viola; hauete ancora commemorato nelle Istitutioni,1. Par.
cap. 15. & nel principio del Primo di que
sti nostri Ragionamenti; ond'io ne feci immediatamente la proua, dopo ch'io intesi co-
tal cosa, & ritrouai ch'era cosi in fatto, come detto hauete. Et quando si pongono quelle
Consonanze, che vanno poste nel graue, nella parte acuta del concento; & le acute nel
graue, per il contrario; per esser loro fuori de i loro luoghi naturali, danno non poco fa-
stidio à quelli, che le odono. Questo è pur troppo vero; disse il Merulo; & ne faccio ogni
giorno, quando sono 'l mio Organo la proua. Ma diteci di gratia M. Gioseffo; Quest'or-
dine de suoni, quando si volesse descriuer con Numeri; di maniera che tra loro potessimo
conoscere la proportione di qual si uolesse Interuallo; come si farebbe? Si farebbe bene,
risposi. Non vi rincresca, ei soggiunse; per cortesia d'insegnarci il modo, che lo hauere-
mo molto grato. Son contento; vdite adunque, risposi.
PROPOSTA XLIIII.
te ne i proprij luoghi alla loro proportione sopra la data chorda, secondo le diuisioni fatte
del Tutto nelle sue parti.
Proposta, le Proportioni delle diuisioni, che nascono dalla diuisione fatta della
chorda, nell'accommodar le Consonanze alle lor proportione nella Precedente,
ne i proprij Siti, ò Luoghi. Bisogna prima sapere i termini maggiori radicali de tutte le

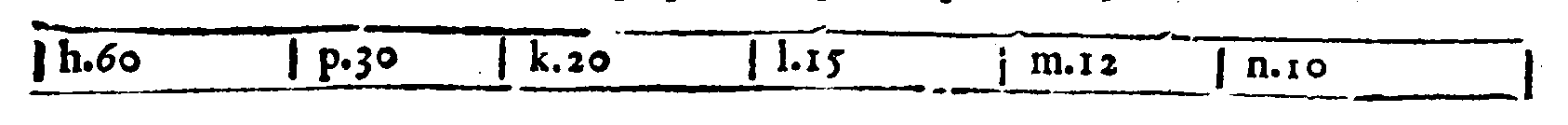
ritrouare vn Numero maggiore, che contenga le Parti denominate da tali termini; ilche
ritrouato, facil cosa sarà da fare il resto. Siano adunque 2. 3. 4. 5. 6. i termini maggiori del-
le Proportioni radicali delle già accommodate Consonanze sopra la chorda ab. come
nella Precedente. Ritrouo prima; per la Ventesima quinta del Primo giorno; un Numero
maggiore, che contenga le Parti denominate da i numeri de tali termini; al quale si possa
assegnar tutte le sue Proportioni; & tal numero è 720. che si può diuidere per ciaschedu-
no de i Cinque dati termini. Piglio prima la metà di esso, & facio c. supponendo però,
che a. sia le Parti fatte di tutta la chorda ab. della Precedente. La onde a. ad esso c. senza
dubio è Duplo. Onde, per la Definitione, ac. uiene à contenere la forma della Diapason
consonanza. Piglio dopoi la Terza parte di a. & cosi facendo d. il quale con à contiene
la Tripla; onde conseguentemente ac. è la Diapasondiapente. Ma perche fù detto, che
ac. è Duplo; però se noi leuaremo ac. Duplo da ad. Triplo; ne uerrà cd. Sesquialtero es-
sendo che, per la Ventesimaseconda del Primo, il Triplo nasce dall'aggiuntione de que-
sti due interualli Duplo & Sesquialtero insieme; onde cd. sarà, per la Definitione, la for-
ma ò proportione della Diapente. Piglio hora la Quarta parte di a. & segno e. onde a &
e. uiene Quadruplo, che è la forma della Disdiapason. Et perche habbiamo detto ac. es-
ser Duplo; per tanto leuando ac. Duplo da ae. Quadruplo; resta senza dubio ce. anco
Duplo; percioche, per la Ventesimaterza, il Quadruplo nasce dal Duplo raddoppiato. Ma
perche habbiamo detto cd. essere Sesquialtero; pero se da ce. Duplo leuaremo cd. Sesqui-
altero; senz'errore alcuno, resterà lo Sesquiterzo; percioche, per il Corollario della De-
cimasettima proposta del Primo; il Duplo è reintegrato da questi due Interualli. Onde,
per la Definitione, de. uiene ad esser la forma della Diatessaron. Fatto questo piglio anco
la Quinta parte di a. & ne risulta f. Dico af. esser la proportione Quintupla; & la forma del-
la Disdiapasonditona. Ma se noi leuaremo ae. da af. cioè, la Disdiapason dalla Disdia-
pasonditona; ne resterà, com'è manifesto, ef. Ditono; del quale, per la Definitione la
Sesquiquarta è la sua forma; adunque ef. verrà ad essere Sesquiquarto. Cauo ultima-
mente la Sesta parte di a. & uiene g. Dico hora ag. contenere la Sestupla proportione; la
quale è la forma della Disdiapasondiapente; & che fg. contiene la Sesquiquinta propor-
tione; ch'è la forma del Semiditono. Percioche se da ag. Disdiapason diapente, leuare-
mo ae. Disdiapason; senz'alcun dubio resterà eg. Diapente; ma leuando 'l Ditono della
Diapente, per certo ne resterà il Semiditono; essendo, per il Corollario della Sesta del
Secondo la Diapente reintegrata dal Ditono & dal Semiditono, come da sue parti. La
onde leuato e f. Ditono da eg. Diapente, resta fg. Semiditono. Et perche, per la Defi-
nitione, la forma del Semiditono è la Sesquiquinta proportione; però dico fg. contener
la Sesquiquinta proportione. Sono adunque con Numeri rationali, secondo 'l proposi-
to, segnate le Proportione de tutte le Consonanze, accommodate sopra la chorda data;
di maniera ch'ogni parte uiene ad esser segnata secondo la proportione, che hà al suo
Tutto; come ui douea dimostrare Ma auertite, che i numeri, ò termini, iquali conten-
gono in questo ordine le Proportioni, non sono Radicali; essendo che sono Tra lor com-
page 180 posti, & non Contraseprimi. Onde non si può dire, che tali Proportioni siano collocate
per ordine ne i lor minimi termini. Però uolendole ridurre, sarà bisogno di trouare un
Numero, il maggior che si possa ritrouare, che misuri communemente ciascheduno di es-
si; & diuider ciascun di loro per esso numero, & li prodotti, quando saranno posti per or-
dine sotto i producenti, faranno un'ordine, il quale sarà Radicale; percio che sarà conte-
nuto da Numeri Contraseprimi. La onde operando nel modo, ch'io mostrai nelle Istitu-
tioni,1. Par.
cap. 43. ritroueremo, che sarà 12. per il quale diuiso che si hauerà gli altri a. c. d. e. f. g. ne uer-
rà h. p. k l. m. n. iquali saranno, per la Nona definitione del Primo giorno, numeri Contra
seprimi, & insieme la Radice de tutte le nominate proportioni. Et per tal modo hauere-
mo 'l nostro proposito. Parmi; disse, vdendo questo, M. Adriano; s'hauete altro da dir
sopra di questo, che seguitate; Se anche nò; passate ad un'altra proposta. Ma perche ha-
uete mostrato tutte queste cose in un'Ordine naturale di Consonanze; per vostra fè, non
vi sia in dispiacere di mostrarle in vn'Ordine de Interualli, l'un dopo l'altro; che siano con
sonanti; ma che tal'Ordine sia d'altra maniera. Lo farò molto uolentieri, gli risposi; Ma
voglio prima dirui, & dimostrarui alcune cose inanzi ch'io venga à quel che mi richie-
dete; però ascoltatemi.
PROPOSTA XLV.
uandone la Diapason, gli estremi loro non fanno con la detta mezana alcuna maniera
d'Harmonia.
cettione, che si faceua della Diapason, la quale uolendola qui dimostrare, sareb-
be vn replicar l'istesso; però non starò à farui altre parole; ma , ch'io
verrò à dimostrarui il resto. Sapiate adunque; che l'Aggiungere insieme Due semplici &
simili consonanze; non vuol dir'altro, che raddoppiar qual si voglia di esse; nel modo
ch'io dimostrai nella nominata Seconda proposta. Però siano ab. cb. & db. le due sem-
plici & simili consonanze; di modo che ab. & cb. sia la prima; cb. & db. la seconda; &
siano insieme aggiunte alla cb. chorda mezana commune. Dico che gli estremi loro ab.
& db. non fanno alcuna sorte d'Harmonia. Percioche, per la Seconda proposta nomi-

consonante. Ma ab & db. è semplice Consonanza raddoppiata; adunque ab & db. non
da interuallo alcuno, che sia consonante. Et perche tutti quelli Interualli, ò Consonan-
ze, che sono diuise in due altre consonanze da una chorda mezana, & peruengono soaue-
mente all'Vdito, se non semplicemente; almeno ad un certo modo; per la Quarta & Quin
ta definitione del giorno passato; fanno l'una delle due maniere d'Harmonia; però non si
ritrouando in queste due consonanze simili, aggiunte ad vn mezano termine, cotali con-
ditioni; seguita, ch'elle non facino alcuna maniera d'Harmonia. Aggiunte adunque
insieme Due semplici & simili consonanze ad vna mezana chorda commune; cauan-
done, come si è detto, la Diapason; gli estremi loro non fanno con la detta chorda alcu-
na maniera d'Harmonia. Et questo è tutto quello, che secondo la proposta ui douea di-
mostrare. In vero, disse M. Francesco; noi vediamo questa cosa in prattica che aggiun-
ti insieme due Diapente, fanno una Nona; due Diatessaron fanno vna Settima, due Di-
toni fanno vna Quinta superflua; & due Semiditoni vna Quinta diminuta; di modo
page 181 che anco senza la dimostratione bisogna confessar, che questo sia uero. Perche se ben
ciascheduna da per sè è Consonante; tuttauia aggiunte insieme non fanno Harmonia al-
cuna; come ottimamente hauete dimostrato. Questo è tanto euidente, risposi; che non
hà dibisogno d'altro commento; però ascoltate il resto.
PROPOSTA XLVI.
nia semplicemente detta.
ritrouarsi l'Harmonia semplicemente detta per la Quarantesimaterza dimostra-
ta poco fà; cb & db. è la Diapente, db & eb. la Diatessaron, & cb & eb. La Dia-
pason; & per la Prima proposta di heri, la cb & eb. è diuisa dalla db. In Harmonica me-
diocrità; adunque tra cb. db. & eb. si ritroua la detta Mediocrità. Ma tra le Consonan-

si troua l'Harmonica semplicemente detta; adunque tra cb. db. & eb. seconda, terza, &
quarta chorda delle di sopra mostrate, si ritroua cotale Harmonia, come dimostrar ui
douea. Più oltra.
PROPOSTA XLVII.
lità, & l'Harmonia detta Ad vn certo modo.
de; & apparino 4. & 3. termini della Diatessaron; 3 & 2. quelli della Diapente;
& 4. & 2. quelli della Diapason. Perche questi termini 4. 3 2. si trouano equal-
mente l'un dall'altro differenti; però, per la Vndecima definitione del primo
giorno; tra db. eb. & gb si ritroua la proportionalità Arithmetica. Ma perche l'Harmo-
nia detta Ad vn certo modo è consonanza; per la Quinta definitione del Secondo; da
una mezana chorda diuisa in due Consonanze; non però in Harmonica proportionalità;
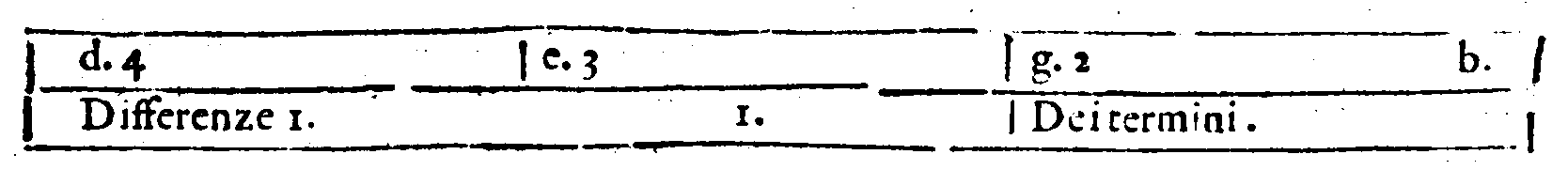
Diapente eb. & gb. le quali sono l'una & l'altra consonanti; & essendo contenute tutte
queste Consonanze tra le tre nominate chorde; dico, che tra loro anco si ritroua l'Har-
monia detta Ad vn certo modo. Tra la chorda terza, quarta, & sesta adunque delle mo-
strate di sopra; si ritroua l'Arithmetica proportionalità & l'Harmonia Ad vn certo modo
detta; come dimostrar ui douea. Questa Harmonia, disse allora il Sig. Desiderio; Può ella
Consonanze, che non siano sotto poste ad alcuna delle proportionalità? Può
veramente; risposi, & ve lo voglio dimostrare; però ascoltate.
page 182
PROPOSTA XLVIII.
certo modo detta.
terza; contenghino tra db. & fb. l'Hexachordo maggiore; tra fb. & gb. il Semi-
ditono; & tra db. & gb. la Diapason. Dico tra queste tre chorde ritrouarsi sola-
mente l'Harmonia detta ad un certo modo. Et perche la Consonanza db. & gb. è diuisa
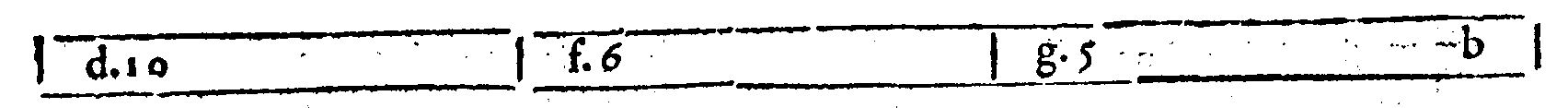
& ancora perche tra i termini delle db. fb. & gb. nō si ritroua, ne la Proportionalità har-
monica, ne la Arithmetica; però, per la Quinta definitione di heri; tra le chorde db. fb. &
gb. habbiamo solamente l'Harmonia ad un certo modo detta, come secondo la proposta
ui douea dimostrare. Il tutto stà bene; à questo disse M. Adriano; aricordateui però della
promessa. E' il douere risposi; di pagare il debito; Ascoltate adunque.
PROPOSTA XLIX.
di modo che tal chorda sia commune à ciascheduna di esse, & le potiamo vdire ad ogni no-
stro piacere.
commune à ciascheduna di esse? Al quale risposi, Percioche nella Quarantesima-
terza, che ui hò dimostrato; la chorda graue della Diapason non è commune con
alcuna della Diapente; ne la graue di questa Consonanza è commune con alcuna dell'al-
tre consonanze; & cosi di mano in mano. Ma in questa la chorda graue d'una Consonan-
za minore sarà commune con la graue della maggiore; anzi quell'istessa. Alora vdendo
questo il Sig. Desiderio, disse; Questo che detto hauete, mi ha fatto uenire in mente; se ben
è fuori di proposito; che molte fiate hò udito dir da uoi altri; che nelle uostre compositio-
ni, quando accommodate due Consonanze insieme, non nasce vn'Interuallo, che con-
tenga 'l numero delle chorde numerate delle due Consonanze; ma si bene contiene un nu
mero minore; cioè, una chorda meno; come sarebbe dire, che quando accōodate quelle
due consonanze, che chiamate Quinta & Quarta; non nasce la Nona, ma uiene la Otta-
ua; tuttauia quando aggiungiamo insieme Cinque & Quattro, nasce senza dubio Noue.
Ma l'hauer commemorato questa chorda cōmune mi ha leuato ogni dubio, che io hauea;
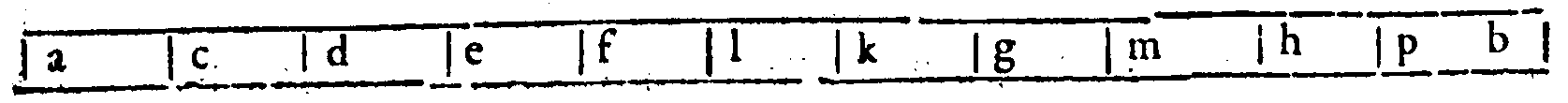
queste due quantità; dirò cosi; onde si uede, che più tosto la Musica s'auicina alla Geome-
tria, che all'Arithmetica; se bene il Musico si serue delle Ragioni & Proportioni dell'una &
dell'altra; onde, dico, che nō sarebbe incōueniēte forse, il dire che 'l suo Soggetto fusse più
tosto il Corpo sonoro proportionato, che il Numero sonoro. Cosi è, & forse ch'un giorno
spēderò un poco di tēpo intorno à questa cosa; acciò sia meglio intesa. Non sarà fuori di
proposito, disse il Sig. Desiderio, & farete piacere à molti; [[per]]cioche sarà cosa noua; e nō più
vdita. Però s'io hò interrotto il uostro parlare perdonatemi; perche 'l nō hauere esperiēza
page 183 più che tanto delle cose della Musica, mi fà dubitare cotali cose; quantunque non siano di
molto momento. Il uostro interrompermi; risposi; non è senza mio grande contento. Et il
dubitare (come hò ancora detto) non è mai senza utilità. Ma per dimostrarui quello, che
ui hò proposto, dico. Sia ab. la data chorda, nella quale vogliamo, secondo la Proposta,
accommodar tutte le Consonanze musicali alla lor proportione. Partisco prima ab. in
Sei parti equai; onde ne piglio vna, & segno c. Diuido poi di nuouo la medesima ab. in
Cinque parti, & prendendone Vna segno d. Di nuouo la partisco in Quattro parti, & si-
migliantemente ne piglio Vna & segno e. Partisco ancora ab. in tre parti al modo detto,
delle quali ne piglio Vna & segno f. Faccio hora di nuouo Due parti dell'istessa ab. & do-
ue cade la diuisione, ch'è giustamente nel mezo, segno g. Ancora diuido ab. in Tre parti
equali; & pigliandone Due segno h. Vltimamente la diuido in Quattro, & ne piglio Tre,
& segno p. Et cosi uengo ad hauer'accommodato alla lor proportione tutte le Consonan
ze, c'hanno le forme loro contenute nel Genere molteplice, ò Superparticolare. Hora per
accommodar quelle, c'hanno tal forma nel Superpartiente; diuido primieramente ab. in
cinque parti; delle quali pigliandone due, segno k. Secondariamente la diuido in otto; &
prima ne prendo tre, & segno l. dopoi ne piglio cinque, & segno m. Ilche fatto dico, che
sono accommodate per ordine tutte le Consonanze musicali alle lor proportioni; inco-
minciando dalle minori procedendo alle maggiori, sopra una chorda commune. Percio-
che, per la Trentesimasettima di questo ragionamento, ab. & cb. uiene ad esser Semidito
no; & per la Quarantesima, ab. & db. Ditono. Simigliantemente, per la Quarantesimase-
conda, ab. & eb. è la Diatessaron; & per l'istessa, ab. & fb. è la Diapente. Viene anco, per
la sua Definitione, ab. & lb. essere Hexachordo minore; essendo che ab. contiene lb. vna
fiata & tre sue ottaue parti, che sono ab. Ma ab. & kb. contengono 'l maggiore; percioche
ab. contiene kb. una fiata & due quinte parti, che sono ak. Ma, per la Quarantesimase-
conda ancora, ab & gb. contengono la Diapason, & ab. & mb. la Diapasondiatessaron;
percioche ab. contiene mb. due fiate & due sue terze parti; cioè. ae. Onde tal proportio-
ne si chiama Dupla superbipartienteterza; la qual (come nella Quarantesima proposta di
heri uedemmo) è la forma di essa Diapasondiatessaron; se ue lo ricordate. Simigliātemen-
te ab. & hb. per la Quarantesimaprima pur di heri, uiene ad esser Diapasondiapente; es-
sendo che ab. & hb. contengono la Tripla proportione, come dimostrai anco nella Qua-
rantesimaterza di questo. Vltimamente ab. & pb. contiene la Disdiapason; percioche
ab. contiene la pb. quattro fiate intiere; Onde nasce la Quadrupla proportione, la quale,
per la Definitione, è la forma di essa Disdiapason. Hora aggiungendo alla chorda ab. ti-
rata sopra la Regola harmonica un'altra chorda, accordata perfettamente unisona; & po-
nendoli sotto un'Hemispherio; accommodandolo sopra ogni punto fatto nelle diuisioni;
si vdirà sensibilmente tutte le ordinate consonanze, senza punto di errore: toccando &
percuotendo la ab. segnata con l'aggiunta. Et questo è tutto quel, che ui hò uoluto dimo-
strare, secondo che m'hauete richiesto. Ma questa Proposta fatta à uostra instanza Mes-
sere, m'hà fatto uenir uoglia di non finir cosi presto, come dissegnato hauea; percioche mi
hà ridutto alla memoria alcune cose, lequali con il suo mezo ui potrò ; & se sta-
rete à disaggio, datene la colpa à uoi stesso; perche non uoglio lasciar la cosa imperfetta;
ne uoglio hauer cagione di replicarui un'altra fiata cosa alcuna. Io per me, disse il buon
Vecchio, non starò mai à disaggio; quando uedrò di cauar frutto d'alcuna cosa. Ne io mi
potrei dolere di una cosa, disse anco il Viola; dalla quale io uenga à farne qualche guada-
gno. Siamo adunque in questo tutti d'accordo, soggiunse il Sig. Desiderio, & il Merulo;
Ma di gratia, auanti che passate più oltra, siate contento di dimostrarci, in qual maniera.
PROPOSTA .
Consonanze alle loro proportioni.
Primo ragionamento, vn Termine, ò Numero maggiore, il quale habbia tutte
quelle parti, che rappresentano i maggior termini delle Proportioni delle conso
nanze, che habbiamo collocato alle loro proportioni; il quale sarà a. & lo chiameremo a.
il quale ci rappresenterà sempre la chorda ab. della Precedente. Da questo cauo pri-
ma la Sesta parte, di maniera che resta c. ilquale è il primo numero, che con a. è Sesqui-
quinto. La onde, per la Definitione, viene ad esse la forma del Semiditono. Cauo poi
dal detto alla Quinta parte, & quel che nasce è d. ilquale con a. è Sesquiquarto; onde uie-
ne il Ditono. Di nuouo cauo da a. la sua Quarta parte, & resta e. questo con a. è Sesqui-
terzo, & contiene la forma della Diatessaron. Cauo etiandio dal medesimo a. la Terza
parte, & lo restante uiene f. che con a. è Sesquialtero, & contiene la Diapente. Piglio di
nuouo i Cinque ottaui di a. & ne nasce l. questo con a. contiene la Supertripartientequin
ta, & insieme l'Hexachordo minore. Fatto questo, ritorno à cauar da a. i Tre quinti, &
ne risulta k. che contiene con a. la Superbipartienteterza, ch'è la forma dell'Hexachordo
maggiore. Hora se dalla detta a. cauaremo la metà intiera, haueremo g. ilquale con essa a.
contenerà la Dupla, & insieme la Diapason consonanza. Ma se da essa a. leuaremo i Tre
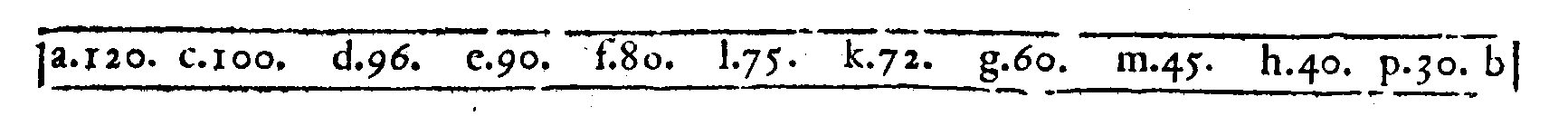
diatessaron. Se anco da a. cauaremo la Terza parte, haueremo h. il quale con a. contenerà
la Tripla, & sarà la forma della consonanza Diapason diapente. Et se ultimamente da a.
leuaremo la Quarta parte, non è dubio, che haueremo p. ilquale con essa a. contenerà la
Quadrupla, & per consequente la Disdiapason consonanza. Di modo che i numeri a. c.
d. e. f. l. k. g. m. h. p. uerranno ad essere i segni delle proportioni nate dalle Diuisioni fatte so
pra la data chorda ab. secondo che ui douea dimostrare. Et tale ordine de Numeri uerrà
esser collocato nella sua Radice; percioche sono numeri Contraseprimi. Son satisfatto;
disse il Sig. Desiderio; però seguitate à dir quello, che vi piace. Voglio dirui questo, sog-
giunsi; che
PROPOSTA LI.
differenza del Semituono minore; & dal fine del Ditono à quello della Diatessaron ui
è quella del Semituon maggiore. Il fine della Diatessaron da quello della Diapente si tro-
ua differente per il Tuono maggiore; & il fine della Diapente da quello dell'Hexachordo
minore è differente per il Semituono maggiore. Dal fine di questo Hexachordo al fine
del maggiore vi cade la differenza del minor Semituono. Et dal fine della Diapente à
quello dell'Hexachordo maggiore vi è la differenza del Tuono minore. Dal fine dell'He-
xachordo minore al fine della Diapason si troua la differenza del Ditono. Et dal fine del-
l'Hexachordo maggiore à quello dell'istessa Diapason vi è quella del Semiditono. Simi-
gliantemente il fine della Diapason da quello della Diapason diatessaron è differente per
la Diatessaron, & da quello della Diapason diatessaron à quello della Diapason diapente
casca la differenza del Tuono maggiore. Vltimamente dal fine della Diapason à quello
della Diapason diapente vi è la differenza della Diapente; & da quello della Diapason
diapente al fine della Disdiapason si troua la differenza della Diatessaron.
strare; acciò lo sapiate dalla Scienza. Perche se bene la proposta è lunga; credo
che non ui par difficile ne ui rincrescerà l'ascoltare. Siano a. c. d. e. f. k. l. g. m. h. p.
le ordinate Consonanze, segnate con i suoi numeri, per le due Precedenti. Dico dalla
cb. fine del Semiditono alla db. fine del Ditono, esserui 'l Semituono minore per differen
za; percioche, per la Penultima, ab. & cb. è Semiditono; & ab & db. ò Ditono. Leuato
adunque ab & cb. Semiditono da ab & db. Ditono, resta cb & db. il quale, per la Ven-
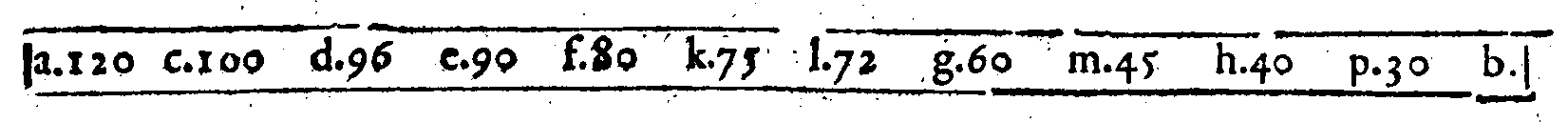
quale esso Ditono sopr'auanza il Semiditono. Et perche, per la Penultima proposta, ab.
& eb. è la Diatessaron; però cauato ab & db. Ditono di ab & eb. Diatessaron, resta db.
& eb. che, per la Ventesimaseconda definitione del giorno passato, è Semituono maggio-
re; essendo ch'è quell'Interuallo, per il quale la Diatessaron supera esso Ditono. Ma, per
la Penultima ancora, ab & f. b. risona la Diapente; onde leuato ab & eb. Diatessaron da
ab & fb. Diapente; quel che resta è Tuono maggiore. Percioche, per la sua Definitione,
è quello interuallo, per ilquale la Diapente sopr'auanza la Diatessaron. Di nuouo, per la
Penultima nominata, ab & kb. contiene l'Hexachordo minore; però se da ab & kb. He-
xachordo minore leuaremo ab & fb. Diapente; resterà fb. & kb. Semituon maggiore; es-
sendo che, per la Trentesimaquarta proposta di heri, l'Hexachordo minore si fà dall'ag-
giuntione del Semituono maggiore con la Diapente; & quello, per il suo Secondo Co-
rollario, sopr'auanza questa per tal Semituono. Ancora per la Penultima, ab & lb. fan-
no l'Hexachordo maggiore; però leuato ab & kb. Hexachordo minore da ab & lb. il
maggiore, resta kb & lb. Semituono minore; percioche, per la Trentesimaquarta nomi-
nata, essendo 'l Tuono minore quell'Interuallo, che s'aggiunge alla Diapente per l'acqui-
sto dell'Hexachordo maggiore, & il Semituono maggiore quello, che s'aggiunge mede-
simamente per l'acquisto del minore; & ritrouandosi, per la sua definitione, il Semituon
minore esser quella differenza, per la quale il Tuono minore supera il maggior Semituo-
no; ne seguita, ch'essendo kb & lb. la nominata differenza, che etiandio ella anco sia il
minor Semituono. Cosi ancora, perche ab & fb è Diapente, & ab & lb. Hexachordo
maggiore; però leuando ab & fb. Diapente da ab & lb. Hexachordo maggiore, ne resta
il Tuon minore; Percioche (com'hò detto poco fà) tal Tuono s'aggiunge alla Diapente,
& ne nasce il detto Hexachordo. Per la medesima Penultima ancora, ab & gb. è la Dia-
pason; però leuato ab & kb. Hexachordo minore dalla ab & gb. Diapason; resta kb &
gb. Ditono; percioche, se per la Trentesima di heri, la Diapason contiene tre Tuoni
maggiori, due minori, & due maggiori Semituoni; & per la Trentesima ancora, la Dia-
pente contiene due Tuoni maggiori, un minore, & un maggior Semituono; l'Hexa-
chordo minore verrà à contenere più della Diapente; per la Trentesimasesta; il Semi-
tuono maggiore, & saranno due Tuoni maggiori, un minore, & due maggiori Semi-
tuoni; i quali cauati dalla Diapason, resterà vntuono maggiore & un minore; iquali,
per la Trentesimasettima, fanno un Ditono. Il che è secondo 'l proposito. Ma se da nuo-
uo da ab & gb. Diapason si leuarà ab & lb. Hexachordo maggiore; resterà lb & gb.
Semiditono; Percioche aggiunto, per la medesima Trentesimaquarta, il Tuono mi-
nore alla Diapente, risulterà l'Hexachordo nominato; ilquale contenerà due Tuoni
maggiori, due minori & un maggior Semituono; i quali leuati dalla Diapason, reste-
rà un Tuono maggiore & un maggior Semituono; che, per la Ventesimasesta, sono con-
tenuti nel Semiditono. Onde ne uiene il proposito. Fu dimostrato etiandio, per la
Quarantesimanona d'hoggi db & mb. esser la Diapason diatessaron; però cauando ab &
gb. Diapason da ab & mb. Diapason diatessaron; ne resta gb & mb. Diatessaron; com'è
page 186 troppo manifesto, per la Quarantesima proposta del giorno passato. La Quarantesima-
nona nominata etiandio ci dimostrò ab. & hb. esser Diapasondiapente; però, chi uorrà
negare, per esser cosa chiara, leuando ab & mb. Diapasondiatessaron, che resti mb. &
hb. Tuono maggiore, non sarà egli in errore? percioche questo è noto, per il primo Co-
rollario della Trentesima del Secondo. Ma se da ab. & hb. Diapason diapente, per la
medesima Quarantesinanona; leuaremo ab. & gb. Diapason; è troppo manifesto, che
resterà gb. & hb. Diapente. Hora per finirui questa dimostratione; sapiamo, per
l'istessa Penultima di questo, che ab. & pb. la Disdiapason; però se da questa
leuaremo ab. & hb. Diapason diapente; resterà hb. & pb. Diatesaron. Imperoche
questa da se è manifesta; che leuando una Diapason da vna Diasdiapason, ne resta un'al
tra. Ma leuando una Diapente da una Diapason; per il Corollario della Quarta pro-
posta di heri, ne uiene la Diatessaron. Et cosi habbiamo il proposito di tutto quello,
che secondo la proposta dimostrar ui douea. Disse (hauendo vdito il fine) M. Adriano;
Se le cose facili possono dilettare; questa è stata una di quelle, che sommamente m'hà
piaciuto, & mi è stato gratissima; percioche con molta facilità hauete dimostrato que-
sta proposta, la qual contiene una lunga diceria. Et mi pensaua, che doueste dimostrarui
sopra un gran pezzo; Ma poi ch'io uedo, che la cosa è andato in un'altro modo; non ha-
uendoci altro che dire, sarà buono seguitar qualche altra cosa. Attendete, risposi; ch'io
ui uoglio con quella istessa facilità dimostrare; che
PROPOSTA LII.
consona il Semiditono; con quello dell'Hexachordo maggiore, la Diatessaron; col fine
della Diapason, l'Hexachordo minore; con quello della Diapason diapente, la Diapa-
son Somiditona; & col fine della Disdiapason consona la Diapason con l'Hexachordo
minore. Simigliantemente col fine dell'Hexachordo minore, & col fine della Diapa-
son diatessaron è dissonante.
importa poco; essendo che da questa si potrà hauere il modo di dimostrare una
cosa simile; incominciando da qual si uoglia Consonanza, ouer'Interuallo. Sia
adunque; al modo mostrato; di nuouo a. c. d. e. f. k. l. g. m. h. p. le già ordinate Consonanze,
per la Quarantesimanona di questo. Dico il fine del Ditono db. col fine della Diapente
fb. consonare 'l Semiditono. Imperoche, per la Quarantesimanona nominata, ab. &
db. contengono il Ditono, & ab. & fb. la Diapente. Ma perche, per la Sesta, & anco
per la Trentesimaprima proposta di heri, il Ditono & lo Semiditono fanno la Diapente;
però leuato ab. & db. Ditono da ab. & fb. Diapente, resta db. fine del Ditono, & sb.
fine della Diapente, i quali insieme consonano il Semiditono. Et perche, per la nomi-
nata Quarantesimanona, simigliantemente ab. & kb. è l'Hexachordo maggiore; però le
uato da esso il Ditono ab. & db. resta db. & kb. Diatessaron; percioche, per la Trentesi-
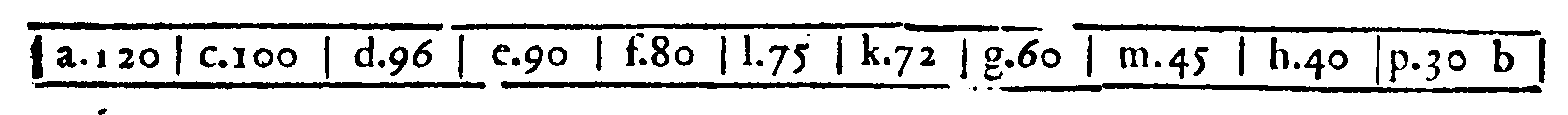
chordo sudetto. La onde leuato 'l Ditono dall'Hexachordo maggiore resta la Diatessa-
ron; & cosi tra db. & kb. risona essa Diatessaron. La Quarantesimanona anco ci dimo-
stra, che tra ab. & gb. sia la Diapason; però leuato ab. & db. Ditono da ab. & gb Dia-
pason, resta l'Hexachordo minore. Percioche la Diapason, per la Trentesimanona di
heri; contiene Tre tuoni maggiori, due minori, con due maggiori Semituoni; & per la
Ventesimasettima, il Ditono contiene un Tuono minore & un maggiore. Ma leuato
page 187 due Tuoni l'un maggiore & l'altro minore, da Tre tuoni maggiori, due minori, con due
maggiori Semituoni; restano due Tuoni maggiori, un minore & due maggiori Semituo-
ni; Ma queste (per la Trentesimasesta del Secondo) fanno l'Hexachordo minore; adunque
leuato ab. & db. Ditono da ab. & gb. Diapason; resta db. & gb. Hexachordo minore.
Di nuouo, per la medesima Quarantesimanona, ab. & hb. è la Diapasondiapente; però
leuando ab. & db. Ditono da ab. & hb. Diapason diapente, resta la Diapasonsemidito-
na. Et perche quello che sopr'auanza è db. & hb. però dico db. & hb. esser tale Interuallo;
percioche oltra la Diapason quando si leua il Ditono dalla Diapente; per il Corollario
della Trentesimaprima del Secondo; resta il Semiditono. Ma perche oltra il Semidito-
no non ui è la Diapason intiera; onde aggiunti questi due Interualli insieme, fanno la Dia-
pason semiditona; però dico, che db & hb. consonano la Diapason semiditona. Vltima-
mente fù dimostrato nella tante fiate nominata proposta, che ab. & pb. è la consonanza
Disdiapason; però se da ab. & pb. cauaremo ab. & db. ne uerrà a restar la Diapason con
l'Hexachordo minore; & questo, perche quel che resta è db. & pb. onde dico db. &
pb. esser tale Interuallo, & db. & pb. risonare la Diapason con l'Hexachordo minore.
Imperoche, come habbiamo dimostrato poco fà, leuato il Ditono dalla Diapason, sen-
z'alcun dubio resta 'l nominato Hexachordo. Essendo etiandio ab. & lb. Hexachordo mi-
nore; se noi uorremo leuar da esso il Ditono ab. & db. resterà un'Interuallo dissonante.
Percioche essendo questo Hexachordo composto (per la Trentesimaquarta del giorno
passato) d'una Diatessaron & d'un Semiditono, i quali per la Ventesimasesta & la Ven-
tesimaottaua insieme, contengono due Tuoni maggiori, un minore & due maggiori Se-
mituoni; Se da questi leuaremo il Ditono, il quale, per la Ventesimasettima, contiene un
Tuono maggiore & un minore; ne uerrà un tuono maggiore & due maggiori Semituo-
ni, i quali aggiunti insieme à patto alcuno non fanno consonanza; percioche non si ritro-
ua Interuallo che sia consonante, che contenga questi tre interualli; Oltra che la propor-
tione de gli estremi è contenuta da numeri, che non hanno luogo tra le parti del nume-
ro Senario, & l'Ottonario; come facendone proua sarà manifesto. Et perche db. & lb. è
quell'Interuallo, che resta; però dico ab. & lb. essere Interuallo dissonante. Simigliante-
mente; perche ab. & mb. è la Diapason diatessaron; però dico, che leuando ab. & db. Di-
tono da ab. & mb. Diapasondiatessaron, resta un'Interuallo dissonante. Percioche le-
uando da la Diatessaron il Ditono, resta Semituon maggiore, il quale è dissonante, & ag-
giunto alla Diapason, per quello ch'io ui dissi nella Quarantesima proposta del giorno pas-
sato, fà vn'Interuallo dissonante. Et perche db. & nb. è quel che si lascia; però dico, db. &
mb. essere Interuallo dissonante. Et cosi hauete tutto quello, che dimostrarui douea, con
tenuto nella proposta. Altro per hora non mi accade dimostrarui, che sia d'importanza.
E' ben uero, ch'io uolea farui un'altra dimostratione, quasi all'istesso modo; ma la lascia-
remo, perche l'hora è hormai tarda, & non è cosa, che sia di gran momento; accioche
qualcheduno di uoi nō stia à disaggio. Non restate per me, disse M. Adriano; di dir quel-
lo, c'hauete nell'animo; perche mi fareste dispiacer grande; essendo che questo (ui fò sa-
pere) è il mio cibo questa fiata, che mi nutrirà & mi darà vita lieta; però dite quel che
uoi uolete, & non ce lo ascondete. Risposi allora; Se bene siamo lontani dalle nostre
stanze, & uoi Messere state in casa; per questo non uoglio lasciar di darui questo conten-
to; percioche presto son per ispedirmi. Ascoltate adunque.
PROPOSTA LIII.
xachordo maggiore si modula il Ditono; & dal fine del detto Hexachordo al fine della
Diapason, il Semiditono. Cosi dal fine della Diapason à quel della Diapasondiatessaron
si modula la Diatessaron; ma dal fine della Diapason diatessaron à quel della Diapason
page 188 diapente, il Tuono maggiore. Vltimamente dal fine della Diapasondiapente alla chorda
estrema acuta della Disdiapason si modula la Diatessaron.
te ab. & kb. l'Hexachordo maggiore. Dico che cauādo ab. & eb. da ab. & kb. re
sta eb. & kb. il quale è Ditono; Percioche cōponēdosi l'Hexachordo nominato,
per il Trētesimaquarta di heri, della Diatessarō & del Ditono; nō è dubio, che leuandoli
la Diatessarō, nō resti il Ditono; percioche questo Hexachordo, per il primo suo Corolla
rio, sopr'auāza la Diatessarō per un tale interuallo. Et [[per]]che quel & che resta, è eb. & kb.
è il Ditono; però dico, che dal fine della Diatessarō à quello dell'Hexachordo maggiore
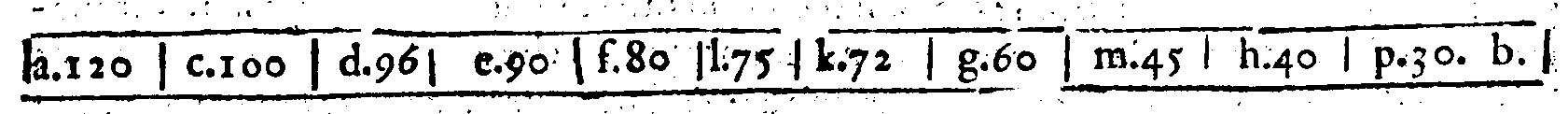
sendo ab. & gb. la Diapason, & leuando ab. & kb. da ab. & gb. resta kb. & gb. Semidito-
no; percioche se da ab. & gb. la quale per la Quarantesimanona nominata, è Diapason, le-
uaremo ab. & eb. Diatessarō; per il Corollario della Quarta del Secōdo, resterà la Diapē
te. Ma habbiamo prouato eb. & kb. esser Ditono; però leuato eb. & kb. Ditono dalla eb.
& gb. Diapēte; per il Corollario della Trēetesimaprima di heri, resta il Semiditono Et per-
che kb. & gb. è quello, che resta; però dico, che da kb. à gb. si canta il Semiditono. Hor-
mai è manifesto ab. & gb. esser Diapason, & ab. & mb. Diapasondiatessaron; onde è co-
sa assai chiara, che leuato ab. & gb. da ab. & mb. resti gb. & mb. Diatessaron, percioche
(come dimostrai heri nella Quarantesima proposta) la Diapason diatessaron si compone
della Diapason & della Diatessarō. Et perche quel che resta, è gb. & mb. però dico gb. &
mb. esser la , che si fà dal fine della Diapason al fine della Diapason diatessa-
ron: che è la Diatessaron. Essendo poi ab. & mb. Diapasondiatessaron, & ab. & hb. Dia-
pason diapēte; se 'l si leuerà ab. & mb. da ab. & hb senza dubio alcuno resterà mh. & hb.
la quale dico esser l'interuallo del Tuono maggiore; percioche essendo gb. & hb. Diapē-
te, & gb. & mb. Diatessaron; restando ab. & gb. Diapason all'uno & l'altro commune; se
da gh. & hb. si leuerà gb. & mb, per il primo Corollario della Trentesima del Secōdo, re-
sterà mb. & hb. che sarà Tuon maggiore. Però dico, che dal fine della Diapason diatessa-
ron mb. al fine della Diapason diapente hb. si canta 'l Tuono maggiore. Vltimamēte; per
quel c'habbiamo detto & dimostrato fin'hora; essendo ab. & hb. Diapason diapēte, & ab
& pb. Disdiapason; non è dubio, che leuato ab & hb. Diapason diapente da ab. & pb.
Disdiapason; non resti hb. & pb. Diatessaron. Percioche cauata gb. & hb. Diapente dalla
Diapason diapente gb. & pb. restando la Diapason ab. & gb. commune; ne uiene, per il
Corollario della Quarta del Secondo, la Diatessaron. Et perche 'l restante hb. & pb. è la
Diatessaron; però concludo, che dal fine della Diapasondiapente à quel della Disdiapa-
son si modula la Diatessaron. Et tutto questo è quello, che secondo la proposta ui hò uolu-
to dimostrare. Ma quel che fin'hora hò detto, per hoggi ui può assai ben bastare; percioche
è stato buona misura, rispetto à quel che heri fù ragionato. Et essendo hormai stanco ui
lascierò tutti con la pace di Dio; perche dopo l'hauer pigliato un poco di fresco, m'andrò
à risposare. Hauete gran ragione; disse M. Adriano; & se uolete star meco à cena tutti mi
farete sommo fauore. Vi ringratio, dissi Messere; ma ricordateui che i Storni, [[per]] andar sem-
pre in frotta, si trouano magri; non uoglio dir altro, sò che m'intendete; però restateui in
pace. Ancora noi uenimo; soggiunse M. Francesco; Cosi anco, disse il Sig. Desiderio; An-
dianci con Dio, adunque tutti. Andiamo; soggiunse M. Claudio; Messere Iddio ui dia
quello che desiderate. Et à voi tutti felicità, rispose il buon Vecchio; & cosi tutti insieme
partissemo, & andassemo uerso la nostra habitatione.
DIMOSTRATIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
RAGIONAMENTO QVARTO.
senza dubio alcuno uero; ch'Ogni huomo naturalmente desidera
sapere;Prooe. lib.
1. che se mai per alcun tempo fù Arte alcuna, la quale haues-
se hauuto i suoi Artefici priui de quelle ragioni, che seruono alla
cognitione di quel che in essa si opera; la Musica è una di quelle.
Imperoche pochi si trouano de moderni; oltra quel poco di pratti-
ca, & anco non buona, che hanno di porre insieme le Consonan-
ze; che sapiano render ragione alcuna di quello, che operano. Et credo ueramente
che questo da altro proceduto non sia, che da viltà d'animo, & dalla dapocaggine lo-
ro. Percioche hauendo egli solamente applicato il loro Studio ad un modo facile di
comporre; da quel saper conoscere & discernere le Consonanze dalle Dissonanze in
fuori; indricciati però da alcune lor Regole; benche poche; non fanno caso d'hauerne
altra cognitione. Essendo che li par cosa strana & di molta fatica, & anco piena di diffi-
cultà (com'è ueramente) il cercar la Ragione, & l'inuestigar le Cagioni dele cose. E' ben
uero, che molto caro hauerebbono saperle; quando non ui entrasse difficultà alcuna nel
uolerle acquistare. Ma non si può arriuare à tal grado senza fatica; come Hesiodo Poe-
ta Antichissimo celo dimostra; quando dice.Dies &
Opera
Lungo camino faticoso & aspero
E' quel ch'alla Virtù l'Huom può conducere;
Che giunto al sommo il resto troua ageuole.
Onde soaui frutti allor'accoglie
Del suo trauaglio; Percioche i Dei uolsero,
Che col sudor tai pregi s'acquistassero.
Ne credo, che da altro sia proceduto, ch'à i tempi nostri oltra modo sia cresciuto 'l nu-
mero de quelli, che compongono in Musica; che dalla facilità (come hò ancora detto)
che hanno di porre insieme le Consonanze, con quelle poche di Regole, le quali ado-
perano, senza hauer pensiero di saper più oltra cosa alcuna, se non che posta la tal Con-
sonanza sopra, ò sotto la tale, faccia un'accordo. Onde noi uediamo; che si come già
fù tempo, che tal numero era di maniera picciolo, che se in una delle maggiori città,
non dirò solamente d'Italia; ma etiandio d'un'altra Prouincia, se ne hauesse ritrouato
un solo, oueramente due; erano tenuti per cosa marauigliosa, & ammirati come cosa di-
page 190 una; cosi à i tempi nostri, non è città, o castello per picciolo ch'ello sia, che non sia co-
pioso di tal sorte d'huomini. Et non pur le città, ò le castella; ma si puo credere ch'al
presente, non ui sia Villa, la quale non habbia il suo Compositore; sia poi di qual si uo-
glia qualità; che poco à quelli, che non intendono, importa. Onde parmi, che la
Musica & la Poesia à i giorni nostri siano quasi arriuate ad un'istessa conditione percio-
che si come questa è copiosissima di Versificatori, & il numero de buoni & eccellenti Poe-
ti è picciolo; cosi la Musica è ripiena d'un numero quasi infinito de Compositori; tra i
quali pochi se ne ritrouano, c'habbiano nome di buono & uero Musico. Et si come
hora non si troua Canta in banco, ò Cerettano (dirò cosi) che non faccia professione
di cantar Stanze all'improuisa; cosi pochissimi sono quelli Cantori, & altri professori di
Musica, che non faciano professione di far miracoli improuisamente nel lor cantare.
Ma uolesse Iddio, che la Musica andasse di pari alla Poesia; perche si trouerebbe un
buon numero d'Huomini dotti, i quali saprebbono minutamente render ragione delle
opere loro, & non haurebbono l'ignoranza tanto, com'hanno, per amica. Questa cosa
sempre mi è grandemente spiacciuta; la onde hauendo ueduto & conosciuto già per
molti anni inanzi questo si grande abuso; per l'amore ch'io porto à questa tanto nobile
Scienza; sforzato dalla mia natural dilettatione, pigliai l'impresa, quantunque diffici-
le, di uoler uedere, s'io poteua, se non in tutto spengere, almeno leuare in una buona
parte & scacciare dalle menti de i professori di questa Scienza, l'ignoranza, & ridurli nel
dritto camino, & darli tal modo & lume, che di tutto quel ch'operassero sapessero ren-
der buona ragione; acciò non fussero al tutto ciechi, & inferiori à gli altri Artefici, i
quali dell'Arte che fanno, sanno render ragione, & buon conto, & dire il Perche d'ogni
loro operatione. La onde diedi opera di condur questo mio pensiero al desiderato fine;
doue col mezo delle Istitutioni, le quali già molti anni sono, ch'io diedi in luce, mi sfor-
zai di dar lume di tutto quel ch'io potei in questa nobil Scienza, tanto nella Prattica,
scoprendo molti belli & mirabili secreti, non ancora intesi da un gran numero de Com-
positori, quanto nella Speculatiua; dichiarando molte cose oscure & confuse, & ag-
giungendoui molti belli & noui concetti, non più d'altri (per quel ch'io hò potuto uede-
re) non solamente scritti; ma ne anco accennati. Et ueramente hò conosciuto di non mi
hauere affaticato in vano; ma di hauer molto giouato à i Professori di quest'Arte nobile;
percioche con questo mezo molti si sono ridutti in buon essere, & nella cognitione de
molte cose necessarie & importanti. Il perche hauendo io veduto le mie Fatiche non es-
sere state ingrate à i Spiriti nobili & uirtuosi; pigliai forza & ardire di passar più oltra; On-
de mi affaticai intorno le presenti Dimostrationi; accioche le cose della Musica dimostra-
tiuamente si sapessero, & per quel uerso che saper si debbono. Le quali hauendo ridot-
to nell'essere, che si ueggono; spero che non saranno se non di grande utilità à i Professo-
ri di questa Scienza; come ciascheduno, dopo che le haurà con diligenza studiate, lo
potrà uedere & conoscere. Oltra di questo; accioche non mancassi di dar quella cognitio-
ne delle cose della Musica, che per me dar si potea, formai, à guisa dell'Oratore perfetto di
Marco Tullio Cicerone, un Perfetto Musico; nel quale si può ueder tutto quello, che bi-
sogna, per uoler'esser Perfetto in questa Scienza. Et se ben sò, ch'è impossibile, ch'uno
habbia in se tutto quello, ch'al Perfetto si conuiene, & come lo descriuo; non sarà almeno
impossibile, che colui si possa chiamare ad un certo modo Perfetto; alquale mancheranno
poche cose di quelle, ch'al Perfetto conuengono. Volentieri mi son affaticato, & volen-
tieri m'affatico, ne mai mi è per rincrescer fatica alcuna; percioche quel ch'io faccio, lo
fò con dilettatione; & quel che mi hà mosso sempre & mi muoue all'operare è à laude &
gloria del sommo Iddio santo & benedetto, datore de tutte le gratie & de tutti i beni. Ne
di queste mie fatiche ricerco dal Mondo alcun premio; ma lascio la cura alla Diuina
Maestà, non solamente di questo, ma ancora del castigo contra gli Emuli & Dettratto-
ri dell'altrui buone opere, i quali mai non mancano. A' i quali protesto di non hauer
pigliato questa impresa per uoler satisfare alle uoglie loro maluaggie, & contaminate
page 191 percioche questo è vn'impossibile; ma si bene (s'io potrò) all'animo nobile & uirtuoso de
Studiosi. Et per ritornare al nostro proposito, dico ch'era già uicina l'hora destinata à
i nostri ragionamenti, quando il Viola uenne à ritrouarmi alla stanza: accioche insieme
andassimo à ritrouar M. Adriano. Onde hauendomi prima ricercato d'alcune cose sopra
il ragionamento del giorno passato; pigliassemo il camino uerso il luogo solito. Il per-
che arriuati, ritrouassimo oltra la solita compagnia molti altri Gentil'huomini; ch'era-
no uenuti per uedere M. Adriano, i quali hauendoci intratenuto per un buon pezzo di
tempo sopra i ragionamenti delle cose della Musica, & alla fine partiti; stando ogn'uno
quasi chetto; cosi incominciò il buon uecchio M. Adriano à ragionare. Sarebbe buo-
na cosa Sig. miei; che si desse principio à seguitare i nostri già principiati ragionamenti,
& si seguitasse quello, che ci resta; percioche tanto più per tempo, che parrerà à M.
Gioseffo d'hauer finito, potremmo poi discorrere sopra quello, che si uorrà, qualche
cosa. Però à uoi tocca M. Gioseffo à dar le mosse, se cosi ui è in piacere. Cosi farò adun-
que Messere; risposi; & son tenuto d'obedirui in cosa tanto honesta, come è questa. Et
uoglio che sapiate; che essendomi stato nelle cose della prattica Precettore, & datomi
una buona parte del ben'essere; come si dice; non ui tengo minore obligo (per non es-
serui; come hanno fatto molti altri, in grato) di quel ch'io tengo à quel Padre, che mi
hà generato. Ma lasciandole parole da un canto, & uenendo à i fatti; per dar principio
uoglio, che uoi sapiate, che 'l nostro ragionamento hoggi non hà da esser d'altro, se non
della Fabrica, ò Costruttione del Monochordo, per tutti tre i Generi delle Cantilene; &
de quelli accidenti, che occorrer possono in simili costruttioni. Onde per maggiore intel-
ligenza di quel che ui hò da dire, fà dibisogno, che prima habbiate la cognitione d'alcu-
ni Termini & Principij; i quali non sapendo, non ne potreste esser capaci. I quali termi-
ni con breuità ui saranno noti per le Definitioni. Et se bene alcuni di loro furono da me
dichiarati & definiti nelle Istitutioni, & che forse ui potrebbe bastare; tuttauia non
uoglio mancar di replicarueli in questo luogo; percioche potrebbe essere, che ciò non
fusse senza qualche guadagno; percioche udendoli ricordare, ui si potrebbe rappresenta-
re inanzi qualche dubio sopra essi, de i quali potrete esser da me risolti. Sarà ben fatto;
disse M. Francesco; percioche molte uolte anco nell'udir di nuouo una cosa già udita, si
uiene non senza utilità de chi ascolta ad affissarsi nella memoria, di maniera che mai più
si parte. Questo conosco io per esperienza; disse M. Adriano; che maggiormente mi
s'affissano le cose nella memoria, che da un'altro odo, che quelle, che, da me stesso stu-
diando, leggo. Cosi è ueramente; soggiunse il Sig. Desiderio; perche la viua uoce, che
intuona all'orecchie hà maggior forza di fuori, di quel che nō hà l'occhio, nelle cose della
Scienza. Questo dico; perche la maggior parte di quelle cose, che si studiano leggendo si
scorrono con l'occhio, oueramente se si leggono; si leggono di maniera, che la uoce non
si ode; la onde non gli è quella forza, che si troua nella uoce d'uno, ch'alle orecchie intuo-
ni. Però, mi piacciono ueramente tali repliche; percioche non possono esser fatte, se
non con qualche vtile. Risposi à questo & dissi; Questa è stata una delle cagioni, che
ne i passati ragionamenti, alle fiate hò replicato alcune cose, le quali hò dichiarato nelle
Istitutioni. Replicate purquanto ui piace; disse M. Adriano; & secondo che ui torna
commodo; che tutti siamo contenuti; percioche molto ben sapiamo, che non replica-
te se non quello, ch'è necessario; & per dichiarar quello, che non è da noi inteso. Allo-
ra udito questo; ripigliai il mio parlare à questo modo. Volendo adunque uenire alla di-
uisione del Monochordo; uederemo prima quello, che ello sia; & dopoi quelle cose, che
cadono per accidēte nella sua diuisione. Onde douete sapere; che se ben ui hò detto nelle
Istitutioni2. par. c. 27 che Monochordo & Regola harmonica sia una cosa istessa; hora uoglio ch'in-
tendiate per Monochordo un'altra cosa; ancora che poco differente sia; il che compren-
derete dalla sua definitione, la quale è questa.
page 192
DEFINITIONE
PRIMA.
& ogni Interuallo, secondo i gradi loro per ordine, come porta la natura di quel Genere,
nel quale si uengono ad accommodare.
possono chiamar Monochordi, secondo la sua Ethimologia; percioche questo
nome deriua da due parole Greche poste insieme; l'una delle quali è Μόνος, che
vuol dir Solo; & l'altra Χορδὴ, che significa Chorda; Onde si dice Monochordo, quasi
Istrumento d'una sola chorda. Ma quando un'Istrumento contiene più chorde, si ua-
ria il nome; percioche quando è di Quattro chorde, è chiamato Tetrachordo, ò Qua-
drichordo; & Pentachordo, quando è di Cinque; & di Sei chorde Hexachordo; & di
Sette Heptachordo; & cosi discorrendo da 'l numero delle Chorde; & per finirla, quan-
do contiene molte chorde, si chiama Polichordo. Il perche potiamo dire, che Trachor-
do sia Istrumento, che contiene quattro chorde. Ma perche nella Musica non solamen-
te si hà consideratione dell'Istrumento in quanto al predetto numero; ma etiandio in-
quanto all'ordine; percioche sono contenute sott'un Genere determinato di modulatio-
ne; però quando nominerò per l'auenire Tetrachordo, uoglio che l'intendiate secondo
la sua definitione, la quale son per mostrarui. Il simile anco dico del Pentachordo, ouer
dell'Hexachordo, & d'altri simili. Ma uediamo prima quel che sia Genere, & poi uede-
remo il resto. Dico adunque; che
DEFINITIONE II.
Quattro chorde.
Γένος δὲ ἐστι ποιὰ τεττάρων φθόγγων διαίρεσις; il Genere è vna diuisione certa di
quattro suoni. Ma perche i Generi della Melodia sono tre, Diatonico, Chro-
matico, & Enharmonico; però auanti che passiamo più oltra, uoglio che uediamo se-
paratamente quel che sia ciaschedun di loro. Volete forse ragionare, disse M. France-
sco; de tutte le Specie de cotesti Generi; com'hauete fatto nelle Istitutioni? Messere nò
risposi; perche non si uerrebbe mai al fine; Ma uoglio dimostrarui solamente quelle
Specie, che sono utili, & possono dar qualche aiuto all'Harmonie. Il perche dico; che
DEFINITIONE III.
maniera, che dal graue all'acuto si và per vn Semituono maggiore, per vn Tuono , & per vn minore; Et per il contrario; per vn Tuono minore, per un maggiore; &
per vn Maggior semituono, procedendo dall'acuto al graue.
sto Genere si possa passar cantando dalla Prima chorda alla Terza per salto; per-
cioche si fà l'interuallo del Semiditono, ò Trihemituono; ne dalla Seconda alla
Quarta; essendo che si fà quello del Ditono, senz'alcuna chorda mezana. Et dicono, che
questi Interualli non sono del Diatonico; Ma che tutte le fiate, che si cantano al modo
detto, si fanno gli altri due Generi. O bella sottilità Messere; disse ridendo M. Francesco;
Adunque tutte le uolte che noi uorremo cantare in questo Genere diatonico, bisognerà
sempre proceder per i gradi nominati nella definitione, & mai non trappassar questa leg-
ge? Ma credo, che costoro pensano, che i gradi di quest'ordine siano fatti alla quisa de
quelli delle Scale, ch'adoperano i contadini, quando uindemiano le vue, ò colgono gli
altri frutti da gli arbori; che tutte le fiate, che in esse mācasse uno de i scaglioni, ò se ne la-
sciasse uno per sorte de quelli di mezo; massimamente quando sono un poco lontani l'un
dall'altro; andarebbono à pericolo di cadere, & di fiaccarsi il collo. Ma qui non è tal peri-
colo; se ben se ne lasciasse anche due. A questo soggiunsi; Non è cosa ridicolosa (per uostra
fè) il dire, che non possiamo passare per salto da una chorda all'altra, come torna più com-
modo, & cantare il Ditono & lo Semiditono, se non mutiamo Genere; & pur questi due
Interualli si ritrouano nel Diatonico in potenza, & anco inatto? In potenza dico; per-
cioche con le proprie chorde & naturali diatoniche si può nelle compositioni formare il
Ditono & lo Semiditono tra due parti; Et in atto si ritrouano nelle modulationi di cia-
schedun numero de Quattro chorde in questo Genere. Et questo è ben ridicoloso da ve-
ro; che nelle Compositioni loro, le quali chiamano Chromatiche non vogliono le modu-
lationi del Ditono; ma solamēte quelle del Semiditono; nōdimeno tra le Parti non si ode
altro che Ditoni. Simigliātemēte nelle Cōpositioni, che dimandano Enharmoniche, fan-
no modulare il Ditono solamente, & li parrebbe commettere un grande errore, se 'l si udis-
se pure una fiata il Semiditono; tuttauia tra le Parti delle lor cantilene altro che 'l Semidi-
tono noi si sente. Quest'istessa osseruanza hanno ancora in quelle, che chiamano Diatoni
che; nelle quali non uogliono, che si canti ne il Ditono, ne meno il Semiditono; nondi-
meno tra le parti della cantilena altro non vi si sente, che questi due Interualli. Et queste
lor Compositioni fatte con tali osseruanze chiamano Diatoniche, ò Chromatiche, ouera
mente Enharmoniche semplici; Percioche quando si seruono nelle modulationi de simili
interualli, le chiamano Miste. Vedete di gratia se udiste mai le più belle & dolci chimere
di queste. Ma se gli addimandaste, se gli Antichi modulauano nel Diatonico il Ditono &
lo Semiditono, auanti che fussero ritrouati i due Generi ultimi; non sò quello, che rispon-
der vi potessero. Io non lo sò; disse di nuouo M. Francesco; ma sò ben, che dicono; che
quel Tetrachordo, il quale serue al Diatonico, non è quello, che chiamate nelle Istitutio-
ni2. par. c. 16 Diatonico syntono; ma bisogna che sia quello, che nominate Diatono. Questo è
ben peggio; risposi; che 'l Ditono di questa specie ne gli estremi non è consonante, ma si
della prima; & che accettino questo ne i loro Contrapunti, & rifiutino quel-
lo nelle lor modulationi. Ma che importa ditemi di gratia voi Messere, che quanto alla
ragione del cantare sia più l'un, che l'altro? percioche per le cose dette non ueggo, che si
habbia da hauer più rispetto al Diatono, che al Syntono, ouero à qual si uoglia altro.
Che uorranno poi dire del Ditono & Semiditono, che pongono nelle compositioni, con-
tenuti dalle proportioni, che sono le uere forme de gli interualli Ditono & Semiditono;
se 'l bisognasse por quelli, che si trouano esser del Diatono? Parmi, disse M. Adriano; che
nō sanno quel che si dicano, & che si muouino cōtra ogni ragione; tanto più, che 'l Dito-
no Enharmonico, essendo contenuto da due Tuoni sesquiottaui, non può causar ne
gli estremi (come già hauete dimostrato) consonanz'alcuna. Et la forza delle lor ragio-
ni consiste in quello, che dice Boethio nel Cap. 23. del Primo Libro della Musica. Doue
nomina il Ditono composto nel Diatonico de due Tuoni sesquiottaui, & nell'Enharmo-
nico lo chiama Incomposto. Guardate, soggiunsi, per uostra fè se sono fuori di loro stessi;
che vogliono por nelle cōpositioni quell'Interualli, che sono nel Diatono, i quali ne i loro
page 194 estremi non accordano; come hò dimostrato nella Seconda parte delle Istitutioni;Cap. 31. il che
non si può negare; & poi uogliono dire, che questo non è quello, che serue al Diatonico,
& all'Enharmonico. Ma quanto alla autorità di Boethio, ch'allegano in lor fauore, non
ne uoglio dir qui altro; percioche nel Cap. 75. della Terza parte delle Istitutioni, ne hò
ragionato à bastanza; Onde di nuouo leggendolo, potrete uedere, come costoro la inten-
dano. Però lasciamogli hormai da un canto; & ritorniamo al nostro proposito.
DEFINITIONE IIII.
ogni Quattro chorde per vn Semituono maggiore, & per vn minore, & per un Semidi-
tono, ò Trihemituono.
lo partisca in due parti. Et quel ch'io hò detto del Cantare ascendendo dal gra-
ue all'acuto, douete intendere anco per il contrario; cantando dall'acuto al gra-
ue; percioche allora si canta per un Semiditono, per un Semituono minore, & per un
maggiore. Qui disse M. Francesco; Mi ricordo c'hauete detto nelle Istitutioni,1. par. c. 32 che
questo Genere hà la Prima, la Seconda, & la Quarta chorda de i suoi Tetrachordi com-
mune con la Prima, Seconda, & Quarta del Diatonico. E' uero risposi. Et che la Terza
del Diatonico (ei soggiunse) è particolare Diatonica, ne serue ad alcun de gli altri Gene-
ri. E tcosi la Terza chromatica è particolare, ne hà da far cosa alcuna con l'altre de gli
altri Generi. Cosi è in fatto dissi. Adunque, disse egli, la differenza, che nasce tra questi
due Generi nominati, consiste in una chorda sola. La onde aggiungendola tra quelle del
Diatonico, si fà un Pentachordo. Et sono adunati insieme due Generi; cioè, il Diatoni-
co & il Chromatico; che nella Terza chorda & nella Quarta solamente di questo Penta-
chordo sono l'un dall'altro differenti. Allora dissi; La intendete; Ma sapete per qual ca-
gione gli Antichi fecero di questo Pentachordo due Generi, & non altramente? Questo
hauerei caro di sapere, aggiunse M. Francesco. Perche non considerarono, soggiunsi; altra
adunanza de suoni; se non quelli, ch'erano contenuti tra Quattro chorde; i cui estremi
fussero contenuti dalla proportione Sesquiterza; percioche uoleuano, che tali estremi
contenessero la Diatessaron, la quale era appresso loro la Prima Consonanza. Onde ue-
dendo, che tra Cinque chorde del Pentachordo si ritrouaua un'altra maniera di modula-
tione, la quale era diuersa dalla Prima; uolsero di cotal cosa mostrarne la ragione; & at-
tesero alla ragione del Tetrachordo, & non à quella del Pentachordo. Quest'istessa ra-
gione conuiene all'adunanza delle Sei chorde, contenute ne gli estremi suoni del Tetra-
chordo, per l'aggiuntione dell'Enharmonica, la quale insieme con le Cinque nominate,
fà un'Hexachordo. Vi hò inteso benissimo; però passate all'Enharmonico, se 'l ui piace,
disse M. Francesco. Ond'io proposi; che
DEFINITIONE V.
lare dal Graue all'acuto per vn Diesis, & per vn'altro, & per vn Ditono; & all'acuto
al Graue per vn Ditono & per due Diesis l'un dopo l'altro.
portione hauranno eglino? Risposi; Il primo posto nel graue è di maggior pro-
portione, che non e il secondo posto immediatamente uerso l'acuto; percioche
quello è il Semituono minore del Chromatico, il quale nell'Enharmonico è il
Diesis maggiore, & è contenuto dalla proportione Sesquiuentesima quarta; & questo, il
qual viene ad essere il Diesis minore, è contenuto dalla Supertripartiente 125. come ui
dichiarai il secondo giorno, col mezo delle loro definitioni. Ma auertite; che
DEFINITIONE VI.
dia; incominciando dalla parte graue, salendo verso l'acuta per ordine; sono.
| 1. | Προσλαμβανόμενοσ. | Cioè, | Acquistata; ouero Aggiunta. |
| 2. | Υ῾πάτη ὑπατῶν. | Principale delle principali. | |
| 3. | Παρυπάτη ὑπατῶν. | Appresso la principale delle principali. | |
| 4. | Λιχανὸσ ὑπατῶν. | Indice delle principali. | |
| 5. | Υ῾πάτη μεσῶν. | Principale delle mezane. | |
| 6. | Παρυπάτη μεσῶν. | Appresso la principale delle mezane. | |
| 7. | Λιχανὸσ μεσῶν. | Indice delle mezane. | |
| 8. | Μέση. | Mezana. | |
| 16. | Τρίτησυνημμένων. | Terza delle congiunte. | |
| 17. | Παρανήτη συνημμένων. | Penultima delle congiunte. | |
| 18. | Νήτη συνημμένων. | Vltima delle congiunte. | |
| 9. | Παραμέση. | Appresso la mezana. | |
| 10. | Τρίτη διεζευγμένων. | Terza delle separate. | |
| 11. | Παρανήτη διεζευγμένων. | Penultima delle separate. | |
| 12. | Νήτη διεζευγμένων. | Vltima delle separate. | |
| 13. | Τρίτη ὑπερβολαίων. | Terza delle acutissime. | |
| 14. | Παρανήτη ὑπερβολαίων. | Penultima delle acutissime. | |
| 15. | Νήτη ὑπερβολαίων. | Vltima delle acutissime. |
le Voci & delle Chorde, secondo che le nominano al presente i Moderni; che
l'hauete nominate secondo, che faceuano gli Antichi, con i nomi Greci? Gli ri-
sposi; Per non generar confusione di mente; Ma lo farò quando sarà al suo
tempo, Sapiate però; che
DEFINITIONE VII.
di ciascun Genere, la quale è distante per l'interuallo del Tuono dalla Hypatehypaton.
diuisione di qual si uoglia Genere, hauete posto cotal chorda nella parte Grauis-
sima, distante per tale Interuallo, com'hauete detto. Et mi ricordo etiandio il nu
mero de i Tetrachordi per ogni diuisione, i quali sono Cinque. E' uero, risposi, Ma auer-
tite, auanti che si uada più oltra; che per Il procedere il numero de Quattro chorde in
ciaschedun'ordine de questi tre Generi; com'hò detto nelle loro definitioni; intendo
page 196 Il procedere in ogni loro Tetrachordo, & non per ogni numero de Quattro chorde asso-
lutamente. Apunto io vi volea dire, soggiunse M. Claudio; che quando noi caminiamo
(parlando come prattico) da F. G. a. &
 . verso l'acuto per il numero de queste Quattro
. verso l'acuto per il numero de queste Quattro chorde; oueramente ritornando dalla.
 a. g & f. verso 'l Graue; non si ritroua quelli Inter-
a. g & f. verso 'l Graue; non si ritroua quelli Inter-ualli, c'hauete nominato; nondimeno si procede pur per il numero de Quattro chorde.
Cosi è; dissi; però accioche per l'auenire non v'ingannaste; tal Numero intenderete per
quello, che si ritroua nel Tetrachordo quale, acciò lo conosciate; lo definiremo in que-
sto modo.
DEFINITIONE VIII.
quiterza; nel quale si può modulare per tre Interualli, in vn certo & determinato modo
contenuto tra esse chorde; secondo la forma che ritiene nella diuisione del suo Genere.
è quello del Pentachordo, che si può modulare, ouer cantare secondo i
spacij contenuti nel numero de Cinque chorde. Il che si può etian dire dell'He-
xachordo, & de gli altri, i quali, per non andare in lungo, non voglio nominare.
Aggiunse à questo il Signor Desiderio; Ditemi di gratia M.Gioseffo; da che nacque, che
gli Antichi nelle dimostrationi de i Generi, maggiormente s'appoggiarono alla diuisione
del Tetrachordo, che di qualunque altro numero, ouer'ordine de chorde? Due cose (ri-
sposi) vi uoglio dir sopra di questo, con breuità. Prima; perche hebbero la Diatessaron,
la quale contiene esso Tetrachordo, per la Prima Consonanza come ui dichiarai il Pri-
mo giorno; dopoi, perche nel numero de Quattro chorde si trouano tutte le uarietà, che
possono far gli Interualli uariati della Musica, nelle Modulationi. Et questa è la uera ra-
gione; onde diuisero, ò composero i lor Monochordi, per Tetrachordi, & non per Pen-
tachordi, ouer'altri simili. Et se ben tornaua à loro questo più commodo; era anco me-
glio fatto; quantunque i nostri Latini moderni gli habbiano composti, ò diuisi per Hexa-
chordi, & non senza proposito; come dichiarai nel Cap. 48. della Seconda parte dell'Isti-
tutioni, & come ancora uederemo. Auertite oltra di questo; che
DEFINITIONE IX.
ne, contiene le chorde Hypate hypaton, Parhypate hypaton, Lychanos hypaton, &
Hypate meson; & si chiama Hypaton. Il Secondo contiene nel Secondo luogo uerso
l'acuto le Hypate meson, Parhypatemeson, Lychanos meson, & Mese; & si nomina
Meson. Il Terzo nel terzo luogo contiene Paramese, Tritediezeugmenon, Paranete
diezeugmenon, & Netediezeugmenon; & si addimanda Diezeugmenon. Il Quar-
to nell'ultimo & acuto luogo contiene Netediezeugmenon, Tritehyperboleon, Paranete
hyperboleon, & Netehyperboleon; & si chiama Hyperboleon: Il Quinto posto ap-
presso il Meson, & adesso congiunto, contiene Mese, , & Netesynemennon; & si chiama Synemennon.
Separato. Et perciò di loro porrò la definitione; accioche li conosciate, & sa-
piate discerner l'un dall'altro.
DEFINITIONE X.
rio; il principio dell'uno è fine dell'altro, che gli è appresso.
nete la chorda Hypatemeson, la quale è il fine del tetrachordo Hypaton, & è
principio del Meson. Simigliantemente la chorda Meson è principio del tetra-
chordo Synemennon, & è il fine del Meson. De qui potete comprendere, dissi; che noi
chiamiamo il Synemennon Congiunto; come hò posto nella definitione; perche si con-
giunge co 'l Meson. La qual congiuntione tanto più si fà manifesta; quanto più si uede in
quel luogo istesso, che 'l Diezeugmenon è dal detto Meson separato. Onde da tal separa-
tione acquistò il suo nome. Ma notate anco; che
DEFINITIONE XI.
melodia è lontano dall'ultima chorda acuta del Tetrachordo precedente per un Tuono; ò
per il contrario.
Separato; percioche non hà alcuna chorda commune col Meson, come hà il Sy
nemennon. Ma uoglio che sapiate di nuouo, che di tutte le chorde, c'hò nomina-
to, alcune sono Stabili, alcune Mobili, & alcune Neutrali; la onde
DEFINITIONE XII.
no ne luogo, ne nome; ma sono l'istesse;
DEFINITIONE XIII.
DEFINITIONE XIIII.
& non mutano luogo.
quello, che hoggi ui voglio ragionare. Onde nō hauendo altri Principij che que
sti da proporui; uerrò alle Dimostrationi; & questa sarà la proposta della Prima.
page 198
PROPOSTA
PRIMA.
Monochordo regolare.

MONOCHORDO REGOLARE DIATONICO.
no; del Monochordo regolare, & non assolutamente
& senz'alcuno aggiunto, del Monochordo? Per que-
sta cagione Messere, diss'io, perche con vna sola chorda tirata
sopra la Regola harmonica, andiamo inuestigando le Conso-
nanze musicali con ragione & regola. Oueramente per il re-
golato ordine de gli Interualli, che in esso si pongono ò perche
l'ordine, ch'ello contiene è regolato da quelli Tetrachordi, che
in esso si pone. La onde, hò voluto far portare hoggi quest'Istru
mento, fatto à questo modo, il quale è la nostra Regola harmo-
nica, & anco sarà il Monochordo; percioche contiene, come
voi uedete, una sol chorda; se bene alcuni uogliono, come dissi
heri, sopra la Prima Definitione; che la Regola harmonica
sia vna Listella fatta di legno, la quale habbia da vn capo al-
l'altro tirata una riga, o linea, & diuisa si ponga sotto alla
chorda. Ma questo importa poco; essendo che questo Istru-
mento contiene il tutto; non pur la Linea, che è la a & b. co-
me vedete, la quale arriua da un capo all'altro; ma etiandio
la Chorda. Et questo Istrumento mi fece fare il nostro M.
Vincenzo Colombi ottimo fabricatore d'Organi, per sua cor-
tesia. Et per dar principio; Sia la ab. Linea, ouer Chorda;
come più ui piace di dirla; sopra la quale habbiamo à dimo-
strar la compositione del Monochordo regolare Diatonico.
Auanti ogn'altra cosa, per la prima del Terzo, sopra ab. ac-
commodaremo il Tuono maggiore ab & cb. Il che fatto, per
la Quarantesimaseconda ancora, sopra cb. accommodaremo
la consonanza Diatessaron cb & db. Oltra di ciò, per la De-
cimanona, sopra cb. accommodaremo il Semituon maggio-
re cb & eb. preponendolo al Tuono maggiore eb & fb. & al
minore fb & db. di modo che 'l Tuono maggiore segua imme-
diatamente il Semituono. Onde a. sarà posta per la Proslam-
banomenos. Fatto questo, di nuouo accommodaremo la
Diatessaron alla sua proportione sopra la chorda db. & haue-
remo db & gb. Hora sopra db. accommodaremo il maggior
Semituono, preponendolo al Tuono maggiore & al minore;
come di sopra facemmo; secondo la detta Decimanona pro-
posta; & db. & hb. uerrà il Semituono; hb. & ib. il Tuo-
no maggiore; & ib. & gb. il minore. Ma sopra gb. per l'i-
stessa Prima del Terzo, accommodaremo il Tuon maggiore
db. & kb. Ilche fatto, sopra kb. accommodaremo la ter-
za fiata la Diatessaron kb. & lb. ne i cui estremi accommo-
daremo per l'ordine il Semituon maggiore kb & mb. il Tuo-
page 199 no maggiore mb. & nb. & cosi il minore nb. & lb. Vltimamente sopra lb. accommo-
daremo la Diatessaron lb. & cb. tra la quale portemo nella parte graue il maggior Se-
mituono lb. & pb. soggiungendoli il Tuono maggiore pb. & qb. qb. & ob. sarà il
Tuono minore. Et cosi in questa compositione, ò diuisione uerrà, che dopo il Tuono
collocato nella parte grauissima della chorda Proslambanomenos, seguirà tal ordine,
che immediatamente si trouerà il Semituono maggiore; dopo questo il Tuono maggio-
re; & ultimamente il minore. Fatto questo s'incomincia di nuouo quest'ordine, il quale
arriua fin'alla chorda gb. Et quest'ordine tutto, che fin qui hò mostrato, si troua etian-
dio dalla gb. sino alla ob. replicato. La onde dico, il Monochordo ab. nel Genere
diatonico esser regolarmente diuiso da c. e. f. d. h. i. g. k. m. n. l. p. q. & o. Et perche ab.
& cb. è Tuon maggiore; & cb. & db. è la Diatessaron; però dico, per il secondo Co-
rollario della Trentesima del Secondo, ab. & db. consonar la Diapente. Ma di so-
pra si è mostrato db. & gb. esser la Diatessaron; adunque, per la Quarta del Secondo,
ab. & gb. che contiene la Diapente & la Diatessaron, contiene anco la Diapason. Si-
migliantemente gb. & kb. contiene il Tuono maggiore, & kb. & lb. contiene la Dia-
tessaron; il perche gb. & lb. contiene due Tuoni maggiori, un minore & un maggior
Semituono; adunque, per la Trentesimanona del Secondo ragionamento, gb. & lb.
consonano la Diapente. Ma già hò mostrato, che ab. & gb. contiene la Diapason;
adunque per; la Quarantesima pur del Secondo, ab. & lb. contiene la Diapasondia-
pente. Ancora; perche hò dimostrato lb. & ob. esser la Diatessaron; adunque gb. & ob.
per la Quarta nominata, contiene la Diapason. Ma perche già hò mostrato, che ab. &
gb. contiene la Diapason; però dico ab. & ob. esser la consonanza Disdiapason. Oltra
di questo; perche tal'ordine procede nel numero de Quattro chorde per un Semituono
maggiore, & per un maggior Tuono, con un minore; però dico, per la Definitione; che
si è fatto la Regolare diuisione del Monochordo Diatonico; secondo che vi douea dimo-
strare. Inteso questo; M. Adriano mosse un dubio dicendo; Parmi che tra la Prima
chorda grauissima & la Quarta del detto Monochordo, non si ritroui la consonanza Dia-
tessaron nella sua proportione; ne tra la Quarta & la Ottaua quella della Diapente; da
che nasce questo? Nasce, diss'io, dalla natura di questa Specie; percioche si serue del Se-
mituon maggiore, il quale accompagnato con due Tuoni maggiori, ch'ello hà auanti &
dopo se, fà un'Interuallo maggiore, che non è la Diatessaron di un Comma; & quel del-
la Diapente d'altra tanta quantità uien minore. Questo è quello, replicò M. Adriano;
che io uolea dirui. Ma perche non hauete posto il Tuono minore immediatamente
auanti, ò dopo il Semituono, & auanti 'l maggior Tuono; che hauereste fatto acquisto
de questi due Interualli, de i quali parliamo, & non sarebbono imperfetti? Per molti
rispetti; soggiunsi; prima, per non partirmi dall'ordine tenuto da gli Antichi, i quali
in tutte le loro Diuisioni hanno collocato il Tuon maggiore nella parte più graue. Do-
poi, perche mentre ch'io hauesse acquistato (facēdo al modo che dite) queste Consonan-
ze; ne hauerei perdutto dell'altre. Oltra di questo, s'io ha uesse posto il Tuono minore
immediatamente dopo il maggior Semituono; haurei peruertito l'ordine della Natura
de gli Interualli; percioche, come dimostrai nelle Istitutioni, la Natura pone nella parte
graue quelli Interualli, che sono di maggior proportione, & quelli di minore uerso l'acu-
to; di modo che l'hauer collocato il Tuon maggiore auanti 'l Minore, è stato fatto secondo
la natura. Ilche ci commanda anco l'Arte con i suoi precetti; come quella che di essa Na-
tura è imitatrice. Mi ricordo, disse M. Claudio che già faceste fare un'Istrumento,Vide c. 11.
Lib. 4. Sup.
ple. il
quale conteneua la mostrata hora da uoi Diuisione; & lo vdì sonare accordato con le
Diapente & le Diatessaron perfette nella lor uera forma, & senza esser temperate col me-
zo della Partecipatione; nel quale simigliantemente ui era la perdita della Diatessaron
nel graue, & nell'acuto quella della Diapente. Onde per acquistar queste due conso-
nanze, & ancora molte altre appresso; li facesti raddoppiare molte chorde; tra le quali
si udiua l'Interuallo del Comma; nell'altre poi ogn'altra Cōsonanza et Interuallo, conte-
page 200 nuto era nella sua vera & natural forma. Et veramente facea vn dolce & soaue vdire;
quando non si passaua alcuni termini; percioche alle fiate bisognaua adoperar esso Com-
ma, per poter formare alcune Consonanze in alcuni luoghi; onde si udiua un non so chè
non già di tristo; ma si bene di poco buono. Et mi ricordo, che nelle Istitutioni1. Par.
cap. 40. dimo-
strate la necessità di tal raddoppiamento. Ma se 'l si potesse fare vn'Istrumento, che con-
tenesse ogn'Interuallo nella sua uera forma & naturale, senza questi aggiunti, sarebbe una
cosa molto perfetta. E' però impossibile, massimamente volendo fare acquisto di molte
Consonanze in diuersi luoghi, che siano contenute nella lor uera proportione, che si per-
derebbono. Et quantunque pare à molti cosa strana, che non si possa far ne gli Istrumen
ti arteficiali quello, che si fà con le Voci; è perche non si ricordano quello, c'hauete detto
nelle suddette Istitutioni;2. par. cap.
41. che le Voci, ò Suoni, che da naturali istrumenti procedono,
i quali non sono sottoposti ad una determinata estensione, ò determinato luogo; come so-
no le chorde de gli Istrumenti; da ogni parte piegar si possono. Et li Suoni nascono da
Istrumenti, i quali sono dall'Arte fabricati, che non si possono alterare, ne fare più gra-
ui, ò più acuti, di quel che portano le estensioni delle chorde loro;Vide cap.
4. 5. & 6.
Lib. 1. Sup ple. senza deprauatione
dell'Harmonia; ma sempre in una qualità rimangono, & ad un modo. Bisogna adunque
chettarsi, percioche l'Arte non potrà mai arriuar, doue la Natura arriua. L'Istrumento,
dissi, che m'hauete nominato, mi fece uenire in cognitione de molte cose. Et vidi l'in-
trico, che nasceua da un tale raddoppiamento & molteplicatione de tante chorde in tali
Istrumenti; Onde giudicai, che colui, il quale ritrouò prima il modo di ridurli al tem-
peramento, che hora vsiamo in essi; & chiamiamo Partecipatione, la qual non è altro,
che 'l leuare il Comma, che si troua nella Diapason C & c. tra le chorde d. & d. come si è
dimostrato nel Cap. 43. della 2. parte delle Istitutioni; disperdendolo con la sua Distribu-
tione, tra quelli Interualli tanto cōsonanti, quanto dissonanti; in ogni Diapason; senza of-
fesa notabile dell'Vdito; hora accrescendoli & hora ; habbialo poi ritroua-
to à caso, ouero studiosamente; ritrouasse una bella cosa, molto utile, & molto commo-
da à i Musici. Et perche uidi, che tal Temperamento era mezano tra 'l Diatonico diato-
no, il quale contiene nelle sue chorde le proportioni co 'l Numero etiandio delle chorde
Pitagoriche; & tra lo Syntono di Tolomeo; & compresi anco, che fin'allora non era stato
alcuno, il quale hauesse, non dirò scritto; ma pur tocco la ragione di tal Temperamento
& Partecipatione; ne mostrato di quanta quantità si vengano à minuire, ò crescere i suoi
Interualli; però mi cadè nell'animo di uoler far proua, s'io potesse arriuare à cotal cosa.
La onde dopo molte fatiche ritrouai il modo di dimostrar questo Temperamento, ò Par-
tecipatione; & ritrouai, che con ogni ragione si poteua fare, non solamente in una; ma
in tre maniere cotale temperamento. Il primo de i quali, ridotto al Numero delle chorde
del Diatonico diatono, com'anco gli altri, è molto conforme ne gli accordi al Diatonico
Syntono; per essere le proportioni, ò forme de i loro Interualli musicali non molto, ma in
vna quantità minima, tra loro differenti; & anco al sudetto Diatono; rispetto che retiene
in se l'equalità de i Tuoni, come in esso Diatono si ritroua. Et perche questa cosa è stata da
me dimostrata nelle Istitutioni;2. par. cap.
42. 43. &
44. però non uoglio in questi nostri Ragionamenti replicar
cosa alcuna. Il Secondo anco è molto simile al sudetto Diatonico diatono; percioche si
come in questa specie si ritrouano due Tuoni simili in ogni Tetrachordo; cosi anco si ri-
trouano in questo secondo temperamento. Ma si come nel primo modo le proportioni
de tutti i suoi Interualli; da quella della Diapason in fuori; sono sorde & irrationali; cosi
in questa, quelli della Diapason, del Ditono & dell'Hexachordo minore restano nella lor
naturale & uera forma; & sono rationiali, quantunque l'altre sorde & irrationali siano. Et
questo Secondo temperamento è molto all'Vdito grato; n'è anco molto difficile da fare;
come sono i due altri. Vi è poi la Terza specie, ò Terzo modo, il quale contiene in se il
Semiditono & l'Hexachordo maggiore nelle lor uere & naturali forme; ma gli altri Inter-
ualli; eccettuando sempre la Diapason; la quale non patisce mai alteratione alcuna, sen-
z'offesa dell'Vdito, vengono tutti accresciuti, ò diminuiti di quella parte di Comma, co-
page 201 me porta la natura sua. E' ben uero, che 'l Temperamento fatto
à questo terzo modo, non è cosi sonoro, come i due primi, anzi al
mio parere è un poco più languido. Onde douendoui dimostra-
re alcune cose, uoglio proporui il Secondo modo; & sopra di es-
so, per fuggir le difficultà & gli intrichi, che possono occorrere;
voglio fondare il mio ragionamento; poi che quando ui piace
potete uedere nelle Istitutioni dimostrato il Primo; Et ciò fa-
rò il giorno sequente, concedendolo Iddio; percioche hoggi nō
ui sarà tempo. Qui aggiunse M. Adriano; Hò sempre stimato di
gran lode esser degno colui, il quale tende alla facili tà delle cose;
& non al molteplicarle con molta difficultà, & senza frutto alcu-
no, & senz'alcuna necessità. Et però in questo sarete sempre lo-
dato dalle persone di giudicio. Onde laudo il uostro dissegno.
Et mi souiene hora una bella sentenza, lasciata scritta da Giusti-
niano Imperatore à Triboniano Giureconsulto in una Epistola
nel principio delle Pandete; la quale uidi, quando mi daua allo
studio delle Leggi Imperiali in Pariggi; che dice in questa manie-
ra; Colui ch'emenda vna cosa, che non sia stata fatta con sottili-
tà, è più da lodare, che colui, che la ritrouò prima. Di maniera che
da questo si può far'un'argomento; che 'l facilitar le cose difficili,
sia di maggior lode, che 'l ritrouarle intricate; come dice questo
Augustissimo Imperatore. Mentre hauete allegato un'autorità di
Giustiniano; disse il Sig. Desiderio; me n'hauete ridotto un'altra
alla memoria. Scriue questo grande Imperatore al Senato & à
tutti i popoli; Ch'è cosa più vtile figurar conuenientemente po-
che cose, che caricar sopramodo gli huomini de molte inutili. La
onde vedete quanto si debbono hauere in memoria questi ricor-
di, & quanto conto si dè far di coloro, che le cose facili fanno dif-
ficili, & propongono mille cose impertinenti & inutili. Tendia-
mo adunque, disse il Viola; alla facilità & al decoro delle cose;
del resto poi lasciamo l'impaccio ad altri. Cosi bisogna fare, dissi;
& con questo uerrò alla Seconda proposta.
PROPOSTA II.
tione del Monochordo.

MONOCHORDO REGOLARE CHROMATICO.
alla memoria alcune cose, le quali già voi sapete per la
lettione delle Istitutioni, & saranno; che in ogni Mono-
chordo regolarmente diuiso, l'Ottaua chorda (come habbiamo
veduto nella Precedente) corrisponde alla prima nel graue per
vna Diapason, & alla Quintadecima nell'acuto per una simile
consonanza, Simigliantemente douete auertire a quello, ch'io
dissi; che nella parte grauissima d'ogni compositione s'accommo-
da il Tuono, & anco s'accommoda immediatamente dopo l'Ot-
taua chorda; di maniera che tra la Seconda chorda & la Nona, si
ritroua la nominata Diapason. Douete ancora sapere, che la
Prima, Seconda, Quarta, Ottaua, Nona, Duodecima & Quin-
page 202 tadecima chorda in ogni compositione del Monochordo regolare, sono Stabili; & le chor
de, le quali cōtengono 'l Semituono maggiore del mostrato Monochordo, sono etiandio
communi al Chromatico & all'Enharmonico. Et la Terza con la Quinta; la Sesta con la
Ottaua; la Decima con la Duodecima; & la Terzadecima cō la Quintadecima contengo-
no il Ditono, & sono cōmuni con l'Enharmonico. La onde lasciando da vn canto la Quar
ta, la Settima, la Vndecima, & la Quartadecima; si potremo seruire del resto nella cōposi-
tione del Monochordo Chromatico. Et questo douete hauere in memoria; percioche
ne farà passar più breuemente quello, che ui hò da dire. Ma ascoltate il modo che si vie-
ne à porre le chorde chromatiche tra le diatoniche nominate. Sia come nella Precedente
la chorda ab. nella quale siano segnate la cb. eb. db. hb. gb. kb. mb. lb. pb. & ob. Ac-
commodo prima, per la Trentesimasettima del giorno passato, il Semiditono, ò Trihe-
mituono alla sua prpportione; preponendolo al Semituono db. & hb. diuidendo db. in
Cinque parti, & aggiungendoui la sesta in punto r. Il che fatto dico; che rb. & db. è il
Trihemituono, & eb. con rb. il minor Semituono. Percioche essendo eb. & db. Ditono,
& rb. & db. Semiditono; se da eb. & db. Ditono leuaremo rb. & db. Semiditono; il so-
pr'auanzo eb. & rb. sarà Semituono minore; il quale per la sua definitione, è quell'In-
teruallo, per il quale il Ditono sopr'auanza 'l Semiditono. Il simile haueremo accom-
modando alla gb. alla lb. alla ob. il nominato Trihemituono; che sarà sb. & gb. tb. &
lb. & ub. & ob. Et tra hb. & sb. tra mb. & tb. & tra pb. & ub. il Semituon minore. Et
perche tutto quest'ordine per ogni Quattro chorde procede per il Semituon maggiore, &
per lo minore, & per il Trihemituono; se non in quei luoghi (com'ho detto) doue è ag-
giunto il Tuono intero; che sono ab. & cb. gb. & kb. acciò la Diapason sia d'ogni parte
intiera & perfetta; però, per la Definitione del Genere, dico; che la mostrata composi-
tione è fatta regolarmente nel Genere ; secōdo che dice la proposta. Hor'ho-
ra mi era uenuto desiderio, disse M. Adriano; di dimandarui, per qual cagione non di-
mostrate l'altre specie de questi due Generi; ma subito mi son ricordato, che nelle Isti-
tutioni2. Par. cap.
31. 34. &
37. le riprouate; come quelle, che non fanno punto al proposito; & lo dimostrate con
buone & viue ragioni. Onde sarebbe pazzia in uerità, & un voler perdere il tempo, uolen-
done di esse alcuna cosa ragionare; Però non procederò più oltra; Ma ui pregherò à se-
guitare il uostro ragionamento nell'altro Genere; se non hauete à dir sopra di questo più
cosa alcuna. Altro non uoglio dire; risposi; Ma uerrò alla Terza proposta.
PROPOSTA III.
na, Decima, Duodecima, Terzadecima, & Quintadecima chorda del Diatoni-
co seruono etiandio all'Enharmonico; & che tra la Seconda & la Quinta; la
Sesta & la Ottaua; la Decima & la Duodecima; & tra la Terzadecima & la Quintade-
cima si troua il Ditono; Però bastarà solamente pigliare il mostrato Monochordo Dia-
tonico; con le nominate chorde; & tra la Seconda & la Terza; la Sesta & la Settima; la
Nona & la Decima; & tra la Duodecima & la Terzadecima porre una Chorda mezana,
che diuida questi interualli in due parti; l'una delle quali; cioè, la graue, contenga il Pri-
mo Diesis, ò Semituono minore, & l'altra contenga il Secondo posto in acuto; & per tal
modo haueremo il nostro intento. Sia adunque, come nella Prima proposta, la chorda
ab. nel sottoposto essempio, & l'altre etandio; cb. eb. db. hb. gb. kb. mb. lb. pb. & ob.
Partisco hora, per la Trentesimaterza del Terzo, ciascheduna delle chorde cb. db. kb. &
lb. in Venticinque parti, & lasciandone in ogni partimento nel Graue una parte, segno
page 203

MONOCHORDO REGOLARE ENHARMONICO.
giore contenuto tra cb. & eb. db. & hb. kb. & mb. lb & pb. uie-
ne ed esser diuiso in due Diesis; in un maggior posto nel Graue,
cb. & xb. db. & yb. kb. & zb. & lb. con & b. & in un minore po-
sto in acuto xb. & eb. yb. & hb. zb. & mb. & & b. con pb. Et che
questo sia uero, lo prouo. Se dal Semituono maggiore cb. & eb.
si leua il minore, il quale è il Diesis graue; senza dubio alcuno re-
sta xb. & eb. Et perche xb. & eb. è la differenza, per la quale il
maggior Semituono supera 'l minore; & essendo, per la Ventesi-
maquarta definitione di heri; il Diesis acuto tal differenza; però
dico xb. & eb. essere il Diesis acuto & minore di questo Genere.
Ilche si potrebbe anco dir de gli altri, d'uno in uno. Ma perche
il progresso & la modulatione di quest'ordine si fà per il numero
de Quattro chorde, per Diesis & Diesis, & per un Ditono; però,
per la Definitione, è manifesto, che tal compositione sia del Mo-
nochordo regolare Enharmonico; come proposi à douerui di-
mostrare. Fin qui le dimostrationi, ch'io hò fatto, sono state nel
costruire & fabricare, & etiandio ordinare i Monochordi di cia-
schedun Genere; ma da qui indietro ui dimostrerò in qual manie-
ra s'ordinino i Tetrachordi, i Pentachordi, gli Hexachordi, &
gli altri per ordine; infin'al numero delle Quindeci chorde; il
qual numero da Greci è chiamato Pentadecachordo. Adun que
non uolete passare oltra questo numero de chorde; per quello
ch'io ueggio; disse il Merulo. Messere nò; risposi. Et ei aggiun-
se; Per qual cagione lo fatte? Per tre cagioni, dissi; la Prima del-
le quali è, che questo numero è basteuole à seruirmi di tutto quel
ch'io uoglio dimostrarui; La Seconda; perche in questo nume-
ro è compreso tutto 'l numero delle Consonanze semplici, & an-
co delle composte; Onde hauendo cognitione di queste, si può
hauer facilmente cognitione di quelle, che trappassassero queste
d'interuallo; La Terza; perche non hauendo gli Antichi passato
cotal numero; non hò voluto anch'io trappassarlo; accioche mi
potesse seruire de i nomi delle chorde, che di sopra ui hò dichia-
rato. Et ciò hò voluto fare, non solamente per commodo mio;
ma per mostrarui & farui conoscere, che 'l nome de quei Anti-
chi Padri, Inuentori di tante & cosi belle & vtili, cose sarà sem-
pre appresso di me uenerando & riuerendo. Ne uoglio in questo
essergli ingrato; anzi dall'uso de questi Nomi uoglio che si cono-
sca, che da loro habbiamo il principio del buono & del bello;
c'habbiamo, & la cognitione & scienza uera de molte cose. Qui
non tacque il Viola; ma disse; Voi fate, come far si dee; percioche
si debbe molto hauer gratia à gli Inuentori delle cose; ancora che
la inuentione rare fiate si troua, che non sia mescolata con mol
ti errori; essendo che è cosa molto difficile il ritrouar le cose; ma
l'aggiungerui, ò leuarle alcuna cosa, si fà con poca fatica. Però
lodo, c'habbiate questa buona opinione. Si dee far per certo;
disse M. Adriano. Perche se bene i Greci non hanno ritrouato i
Principij tutti delle cose; & che quelli della Musica habbiano
hauuto origine da altri Popoli; come si può dir con uerità; tutta-
uia si hanno tanto intorno ad essa affaticati, & tanto l'hanno il-
page 204 lustrata, che si può ben dire, che ella sia stato suo parto. Ma che volete dire di nouo?
Vi voglio dire; rispose; che
PROPOSTA IIII.
chorde; & che tra Cinque chorde è contenuta da Proslambanomenos à Hypatemeson
la consonanza Diapente.
siano anco b. c. d. & e. la Seconda, Terza, Quarta, & Quinta; di modo che a. con
b. contenghino il Tuon maggiore, b. con c. il maggior Semituono; c. con d. il
Tuono maggiore, & d con e. lo miniore. Dico prima per la Settima definitione; a. esser
la grauissima chorda Proslambanomenos di quest'ordine, & dopoi b. c. d & e. essere il Pri-
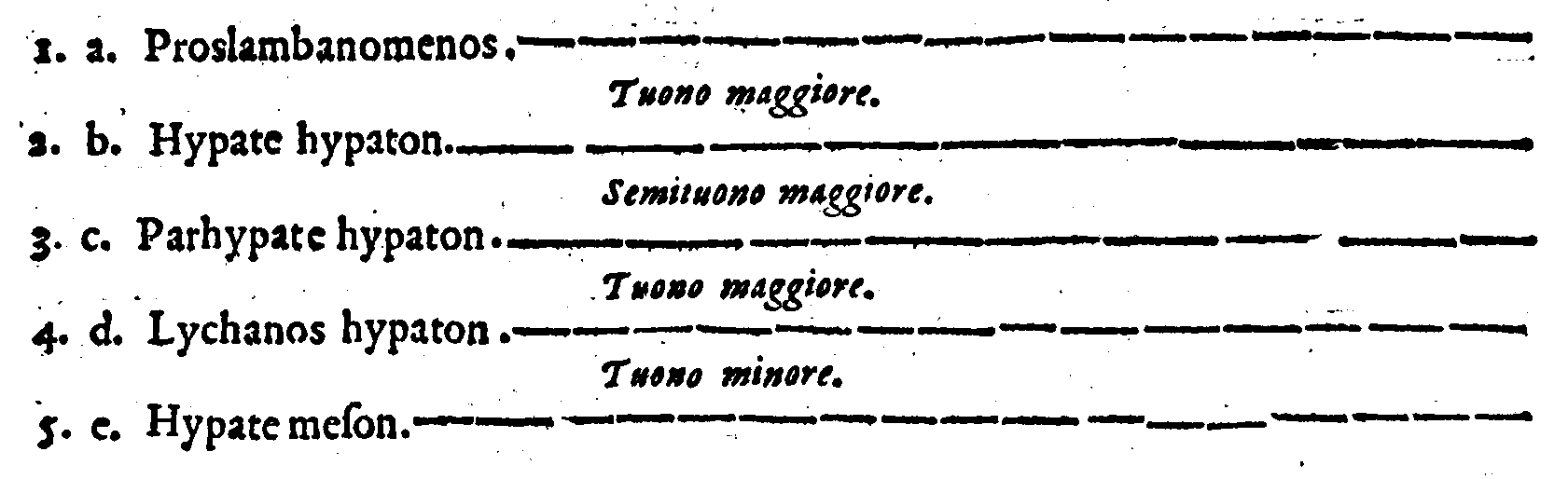
nico, & è distante dalla b. per un Tuono maggiore; essendo anco la b. grauissima delle
b. c. d & e. ne segue, per la Settima Definitione, che a. sia la Proslambanomenos. Ma per-
che ogni Tetrachordo diatonico procede dal graue all'acuto modulando per un Semi-
tuon maggiore, un Tuono maggiore, & un minore, & tale ordine si ritroua nelle sudette
chorde b. c. d & e. però dico b. c. d & e. esser Tetrachordo diatonico. La onde essendo
questo Tetrachordo il Primo & grauissimo di quest'ordine; per la Nona Definitione;
viene ad essere il Tetrachordo hypaton, & b la Hypate hypaton; c. la Parhypaton hy-
paton; d. la Lychanos hypaton; & e. la Hypate meson; chorde assignate di questo Tetra-
chordo; come ui douea dimostrare. Et perche ogni Tetrachordo, per l'Ottaua Defini-
tione, è contenuto ne i suoi estremi dalla proportione Sesquiterza, la quale è la forma
della Diatessaron; onde aggiunto ad essa il Tuono maggiore, per il Secondo Corollario
della Trentesima proposta del Secondo ragionamento, nasce la Diapente; però aggiun-
gendo la chorda a. con le b. c. d & e. haueremo tra Cinque chorde un Pentachordo, il
quale da Proslambanomenos ad Hypate meson contenerà la Diapente consonanza. Et
questo è tutto quel che secondo la proposta, ui douea dimostrare. Disse hora il Sig. Desi-
derio; Per quel ch'io ueggio, gli Antichi aggiunsero la Proslambanomenos, che con la
Hypate hypaton contiene un Tuono al primo Tetrachordo; accioche con la chorda
Mese hauessero la consonanza Diapason. Onde da tale effetto nominarono questa chor
da Acquistata. Stà bene, io la intendo; Ma per qual ragione i nostri non si contenta-
rono chorda, che anco ue n'aggiunsero un'altra? Risposi à questo. Hò detto
nelle Istitutioni,2. par. c. 18. che gli Antichi procedeuano nella Diuisione, ò costruttione de i lor
Monochordi per Tetrachordi, & non per altro numero de chorde; Onde dopo l'hauere
page 205 accopiato insieme due Tetrachordi, erano al numero de Sette chorde arriuati, le quali
ne i loro estremi faceuano Dissonanza; il perche uolendo acquistare una Consonanza,
la quale è la principale & Regina de tutte l'altre, ch'è la Diapason; aggiunsero la Proslam-
banomenos distante da Hypate hypaton per un Tuono maggiore. Ma i nostri Musici, i
quali non considerarono la diuisione, ò compositione del loro Monochordo fatta per
molti Tetrachordi; ma per Hexachordi; aggiunsero un'altra chorda sotto la Proslam-
banomenos; acciò potessero hauere un'intero Hexachordo, il quale fusse da queste sei
sillabe; Vt; Re; Mi; Fa; Sol; La, circonscritto. Percioche applicarono à ciascheduna
chorda di esso Vna, & Due, & fino à Tre (come uederemoCap. 30.
par. 2. Istit.
. Demost.
Def. 18.) delle nominate sillabe; secōdo
che fù dibisogno; facendo che l'interuallo del maggior Semituono fusse contenuto da
queste due; Mi & Fa. La onde uolendo auere il principio del primo Hexachordo, il
quale contiene il Semituono nominato tra Hypate hypaton & Parhypate hypaton; li fù
bisogno d'aggiungere cotal chorda; altramente non hauerebbono hauuto il loro intento.
Per tal ragione adunque i nostri Latini aggiunsero la Chorda sotto la Proslambanome-
nos; la quale chorda si può nominare Υ῾πὸπροσλαμβανόμενος; quando con nome greco de-
nominar la uorremo. Ma veniamo all'altra proposta.
PROPOSTA V.
all'Hypaton; & assegnar le sue Chorde; & dimostrar, che da Proslambanomenos à Me-
se ui sia l'Interualo della Diapason.
tima, & Ottaua chorda; di modo che e & h. uenga Sesquiterzo; g & h. Sesqui-
nono; & f con g. Sesquiottauo. Dico, che per la Decima Definitione del Secon-
do; e ad h. viene ad esere Diatessaron. Et perche g con h. è Tuono minore; & f con g. è
Tuono maggiore; però, per la Ventesimasettima del Secondo nostro , e

na definitione; il Tetrachordo Meson; percioche, per la Ottaua, procede per un Semi-
tuono maggiore, & per un Tuono maggiore, & per vn minore; diuiso secondo la natu-
page 206 ra del Genere diatonico. Et la chorda Hypate meson e. viene ad esser la Prima & gra-
ue di questo Tetrachordo; & l'acuta dell'Hypaton, la f. Parhypate meson, con la g. Ly-
chanos meson mezane, & h. la Mese & l'acuta. Ma perche la chorda e. uiene ad esser la
più acuta del Tetrachordo Hypaton, & la più graue del Meson; di maniera che all'uno
& all'altro è commune; però, per la Decima Definitione, dico che ciaschedun de questi
due Tetrachordi si può chiamar Congiunto; ancora che questo nome sia attribuito da
alcuni Musici al Synemennon solamente. Hauendo M. Adriano vdito questo, disse ver-
so di me; Mi hauete troncato la strada, percioche hauete proposta la Questione, & anco
in due parole l'hauete risolta. Seguitate adunque il resto. Cosi farò, risposi; Et perche,
per la Precedente, habbiamo; che a & e. Proslambanomenos & Hypate meson conso-
nano la Diapente, & nella Presente e con h. Hypate meson con Mese la Diatessaron; pe-
rò, per la Quarta proposta del Secondo, diremo; che Proslambanomenos con Mese
consonino la Diapason; come vi douea dimostrare. Et perche la cosa da se è chiara, io
non ui terrò à bada; ma uerrò à dimostrarui, che;
PROPOSTA VI.
menon, & assegnar le sue Chorde, & dimostrar nel Dodecachordo la Diapason dia-
pente.
mente aggiungo la i. Paramese, la quale con Mese contenga il Tuono sesquiot-
tauo; aggiungo dopoi le chorde k. l & m. & faccio m con i. cioè Netediezeugme-

tediezeugmenon con l. Paranete diezeugmenon Sesquinona; & questa con k. Trite
page 207 diezeugmenon Sesquiottaua. Et perche Nete diezeugmenon con Mese consonano la
Diapente, & con Paramese la Diatessaron; però, per il Primo Corollario della Tren-
tesima proposta del Secondo; h. con i. contiene l'interuallo del Tuono maggiore. Ma es-
sendo i con m. Diatessaron, & m. con l. Tuono minore; simigliantemente l. con k. Tuo-
no maggiore; dico che i. con k. per la Ventesimaottaua del Secondo, uiene ad essere Se-
mituono maggiore. Sarà adunque Paramese alla Tritediezeugmenon Semituon mag-
giore; Trite alla Paranete Tuono maggiore; & Paranete alla Nete diezeugmenon Tuo-
no minore. Onde, per la Definitione. i. k. l & m. sarà il Tetrachordo diezeugmenon, sog-
giunto nel già mostrato Ottochordo nel Genere diatonico; & Paramese, Tritediezeug-
menon, Paranete diezeugmenon, & Nete hyperboleon saranno le sue chorde. Et
questo è quanto ad una parte delle cose contenute nella proposta. Ma venendo à quello,
che resta, dico; che hauendoui dimostrato nella Precedente a & h. esser la Diapason, &
nella Presente, h & m. esser la Diapente; seguita, per la Quarantesimaprima del Secon-
do giorno, che da a. allo m. com'è da Proslambanomenos à Netediezeugmenon, del Do-
decachordo a. b. c. d. e. f. g. h. i. k l. & m. sia contenuto la Diapason diapente. Et questo è tut-
to quello, che ui douea dimostrare. Disse allora M. Adriano; Non hauete fatto mentio-
ne alcuna ancora del tetrachordo Synemennon; il quale mi par, se ben mi ricordo, c'ha-
uete detto, che si congiunge alla chorda Mese. Et per qual cagione non hauete prima
fatto mentione di lui, che del Diezeugmenon? Risposi; Per due cagioni; l'vna, per di-
mostrarui semplicemente l'ordine delle Quindeci chorde diuise ne i Tetrachordi, nelle
quali si troua tal corrispondenza in ciascheduna di quelle, che sono collocate in esse da
Mese à Nete hyperboleon, con una di quelle, che sono contenute tra Proslambanome-
nos & Mese, che fanno vdire la Diapason. L'altra è; accioche conosciate, che quantunque
il Synemennon sia con tanto bell'ordine aggiunto tra le Quindeci chorde; non è però,
ne si può chiamar naturale; ma più presto accidentaleVide Cap.
5. Lib. 5.
Supple.. Percioche la chorda Trite di que-
sto tetrachordo non hà alcuna chorda corrispondente nella parte graue per vna Dia-
pason; come hanno tutte l'altre; ne meno la chorda Nete. Per questo adunque non hò
uoluto cosi tosto aggiungerlo; ma hò aggiunto lo Diezeugmenon; onde dopo l'Hyper-
boleon aggiungerò etiandio esso al Meson; acciò habbiate il tutto con ordine, & distin-
to. V'intendo benissimo soggiunse M. Adriano; seguitate pure il uostro ragionamento.
Cosi farò, risposi; Porrò adunque la proposta in tal modo.
PROPOSTA VII.
mostrar le sue chorde; & che tra le chorde del Pentadecachordo si troua la Disdia-
pason.
no la Diapason diapente. Aggiungo à queste le chorde n. o & p. di maniera
che m & n. cioè, Netediezeugmenon & Tritehyperboleon siano in Sesquiter-
za proportione, & si possa cantar la Diatessaron; & sia p & o. Tuono minore; &
o con n. Tuono maggiore. Adunque, per la Ventesimaottaua del Secondo giorno, m
& n. sarà Semituono maggiore. E' adunque m. n. o & p. secondo 'l nostro proposito, il te-
trachordo Hyperboleon misurato nel Genere diatonico, per un Semituon maggiore, per
un Tuon maggiore, & un minore soggiunto al Diezeugmenon; del quale, secondo la
Definitione, Netediezeugmenon, Tritehyperboleon, Paranete hyperboleon, & Nete
hyperboleon sono le sue chorde. Et questo sarà quanto alla Prima parte della proposta.
Quanto poi alla Seconda; è manifesto; per la Precedente; che da h ad m. cioè, da Mefe à
Nete diezeugmenon sia la consonanza Diapente; adunque da h à p. cioè, da Mese à Ne-
page 20 tehyperboleon, che si fà della Diapente & della Diatessaron, per la Quarta proposta del
Secondo, consona la Diapason. Et perche, per la Quinta dhoggi, habbiamo dimo-

l'Vltima proposta del Secondo, da a. à p. ò da Proslambanomenos à Netehyperboleon
consonerà la Disdiapason. La onde essendo da a. fino à p. il numero de Quindeci chorde;
dico, che nel Pentadecachordo nel Genere diatonico si contiene la Disdiapason. Et que-
sto è tutto quello, ch'è contenuto nella proposta, che vi douea dimostrare. Parmi, disse
M. Claudio; che quello, che non si dimostra nel detto numero de chorde; non si dimo-
strerà anco in numero maggiore. Et quello, c'hauete detto del tetrachordo Synemen-
non, comprendo hora chiaramente esser uero; percioche doue si può aggiungere in
quest'ordine cotale Tetrachordo, se non alla chorda Mese? Ne sò uedere, doue possa
hauer la Seconda chorda di questo Tetrachordo tra le Otto graui alcuna chorda corri-
spondente, che faccia la Diapason. Onde mi pare, che queste due cose ueramente basti-
no à mostrare, che cotal Tetrachordo non sia naturale; ma (com'hauete detto) acciden-
tale. Et perche hauete dimostrato in qual maniera i nominati Tetrachordi stiano per
ordine nel mostrato Pentadecachordo; però piacciaui anco di porre in cotale ordine
quello, che resta; acciò non manchiate in cosa veruna, che si possa desiderare. Hora sarà
il tempo; risposi. Dico adunque; che
page 209
PROPOSTA VIII.
k. l. m. n. o & p. & all'Ottaua h. aggiungo q. r & s. di modo che h. & s. ò Mese & Ne-
tesynemennon siano in Sesquiterza proportione, & si possa cantar la Diatessa-
ron. Siano anco q. & r. Tritesynemennon & Paranete synemennon distanti l'una dal-
l'altra per un Tuono maggiore, & r. con s. ò Paranete synemennon con Netesynemen-

mento, h & q. Mese & Tritesynemennon sarà l'Interuallo del Semituono maggiore. On-
de, per la Decima Definitione d'hoggi. h. q. r & s. sarà il Tetrachordo synemennon; ò Cō-
giunto al Meson nel Genere diatonico; & per la Nona; Mese, Tritesynemennon, Parane-
tesynemennon, & Netesynemēnon sarāno le sue chorde. Et questo è quello, ch'io douea,
secondo la proposta, dimostrare. Ma sappiate, che per l'aggiuntione di questo Tetrachor-
do; si uēgono à giungere alle Quindeci chorde già nominate due altre chorde; onde arri-
page 210 uano al numero de Dicesette; percioche la Trite & la Nete hanno da far nulla con alcu-
na delle Quindici, come la Prima Mese, & la Terza Paranete synemennon di questo, Te-
trachordo; poi che la Prima è commune con la Quarta del Tetrachordo Meson, & l'al-
tra uiene ad esser la Tridiezeugmenon. Onde da tale aggiuntione nascono tra le chorde
di questo Tetrachordo, & quelle del Diezeugmenon alcuni interualli, che nel Diatoni-
co diatono non sono cantabili; i quali hanno dato cagione ad alcuni moderni di Filoso-
fare, & dire, che la Specie che vsiamo nel cantare & sonare non è la Naturale, ò Synto-
na di Tolomeo; ma un'altra; come uederemo presto ne i Sopplimenti nominati, piacen-
do à Dio. In efetto è pur cosi; disse il Viola; come uoi dite nelle Istitutioni,1. par. cap.
40. che se la Na-
tura nelle Voci, & l'Arte ne gli Istrumenti arteficiali con la Partecipatione non aiutasse à
disperdere alcuni Interualli; si udirebbe alle fiate in tristo effetto, quando si ad operasse-
ro. Ma benedetto sia colui, che ritrouò la Partecipatione, ò Temperamento de i nomi-
nati Istrumenti; perche è stato, & è, & sarà ancora di gran commodo nella Musica, essen-
do che leua uia tutti quelli impedimenti, ch'accascar possono. Siaui adunque in piacere,
per uostra fè, dimostrarci la ragione de quelli Interualli; che per l'aggiuntione del Tetra-
chordo synemennon sono stati diuisi in due parti. Son contento, risposi, di satisfarui, &
d'aggiungere à uostra instantia, una proposta di più di quello, ch'io hauea dissegnato di
fare; & sarà questa.
PROPOSTA IX.
Synemennon & Diezeugmenon aggiunti insieme.
nemennon; & i. k. l & m. il Diezeugmenon. Dico h. & q. contenere 'l maggior Se-
mituono; q. & i. un', ch'è maggiore del Semituono minore, contenuto
dalla proportione Super. 7. partiente. 128. tra i. & k. medesimamēte il Semituono maggio-

no minore. Percioche essendo, per la Prima proposta d'hoggi, k. & l. Tuono maggiore; &
per la Precedente; k. & s. Tuono minore; dico, che se da k. & b. leuaremo k. & s. resterà sen-
za dubio il Comma; il quale, per la sua Definitione, è quella quantità, di quanto il Tuo-
no maggiore sopr'auanza 'l minore. Simigliantemente, per la Precedente, habbiamo, che
q. & k. contengono il Tuono maggiore, & che i. & k. contengono, per la Prima di questo, il
Semituon maggiore. Onde se da q. & k. Tuono maggiore leuaremo i. & k. maggior Semi-
tuono, per il Corollario della Trentesimaquinta del Terzo ragionamento, resterà un'In-
page 211 teruallo, il quale sarà maggior di proportione, che non è il minor Semituono; & sarà q.
& i. che nel Genere diatonico non è cantabile. Et questo è quello, ch'io douea dimo-
strar delle cose contenute nella proposta; ma di questo ne ragiono più lungo nel Cap. 6.
del Lib. 4. De i Sopplimenti. Disse il Merulo; & questo uedremo piacendo à Dio; però
non sarà fuor di proposito, se dimostrasti anche il modo, che si tiene, uolendo segnar que-
ste chorde insieme con l'altre, con i suoi Numeri; acciò si uedesse la proportione, che si
troua tra l'una & l'altra; poi c'hauete detto nelle Istitutioni,2. par.
cap. 41. che i Numeri sono le Ima-
gini de i suoni. Al quale risposi; Vi uoglio anco di questo far contento M. Claudio;
Ascoltate adunque la proposta.
PROPOSTA X.
diatonico.
h. & p. corrispondono alle chorde a. b. c. d. e. f. g & h. della Prima a. & h. di manie-
ra che h. corrisponde alla a. i alla b. k alla c. l alla d. m alla e. n alla f. o alla g. & p al
la h. La onde corrispondendo ciascheduna delle chorde della Prima Diapason, alle chor-
de della Seconda, per ordine in Dupla proportione; sarà facil cosa, hauēdo ritrouato i Nu
meri delle proportioni di una, ritrouar quelli dell'altra; le quali in Dupla proportione cor
rispondino. Ma bisogno è di uedere & considerar prima, qual di esse due Diapason hab-
bia maggior difficultà in sè; & ritrouaremo, che sarà la h. & p. percioche oltra gli Interual
li, che contiene, i quali sono simili à gli Interualli contenuti nella Prima a. & h. contiene
di più, come nella Precedente habbiamo ueduto; l'Interuallo di proportione Super. 7. par
tiente. 128. maggior di quel ch'è il Semituono minore; & contiene anco l'interuallo del
Cōma. Di maniera, che se 'l si incominciasse dalla a. & h. & si ritrouassi tutti quei Numeri,
che seruono à i suoi Interualli; non però corrisponderebbono tutti al numero delle chor-
de, che tiene la h. & p. essendo che le chorde q. & r. poste nella Diapason h. & p. non hanno
alcuna chorda corrispōdente nella Diapason a. & h. che per simile interuallo corrispondi.
La onde se ben si trouassero i Numeri della seconda Diapason corrispondenti à i numeri
delle chorde della prima; restarebbono tuttauia le due nominate chorde senza numeri;
onde bisognarebbe dopoi ritrouarli, co 'l molteplicar tutti i numeri primi, che cōtenesse-
ro le proportioni de tutte le Quindeci chorde; il perche nascerebbe un'ordine de numeri
tanto più maggiori, quanto sarebbono molteplicati i primi per quella parte; che si uoles-
se pigliare d'alcun numero; come dimostra la Quintadecima del Primo nostro ragiona-
mento, per accommodare in questo ordine la proportioni, ch'accommodar si uolessero.
Però adunque per più breuità & più commodità di operare, ritrouaremo prima i Nu-
meri & le proportioni de gli Interualli contenuti nella Seconda Diapason. h. & p. & do-
poi ritrouati, con facilità si potrà, raddopiando quelli che corrispondono alle chorde
della Prima Diapason a. & h. hauere 'l proposito. Siano le chorde a. b. c. d. e. f. g. h.
q. i. k. i. l. m. n. o & p. continenti i Cinque tetrachordi, Hypaton, Meson, Diezeugme-
non, Hyperboleon, & Synemenon. Et sia tra a & h.. la Prima Diapason, & tra h
& p. la Seconda. Vedo primieramente, che Interuallo si troua tra la Prima & la Se-
conda chorda graue della seconda Diapason h & p. il quale; per la Precedente; è il
Semituon maggiore; la proportione del quale è contenuta ne i suoi termini radicali
tra 16 & 15. i quali scriuo nel Primo ordine, & sono h. & q. Vedo dopoi l'Interuallo,
che si troua tra la Seconda & la Terza chorda q. & i. & ritrouo; per la medesima prece-
dente; ch'è quello, il quale è di maggior proportione, che quello del Semituono mino-
re; la cui proportione, per il Corollario della Trentesima quinta del Terzo; è Super.
page 212

ra bisogna aggiungere tal proportione alla proportione h & q. di maniera che q. sia il
maggior termine della nominata. Ma perche q. non hà la parte Centesima trentesima-
quinta; però molteplico q. posta nel Primo ordine per 135. & ne uiene q. posto nel Secon-
do, il quale contiene cotal parte. Molteplico etiandio h. posto nel Primo ordine per 135.
& nasce h. posto nel Secondo; il quale, per la Quinta Dignità, ò Parer commune, con q.
posto medesimamente nel Secōdo; cōtiene la proportione Sesquiquintadecima & Semi-
tuono maggiore. Cauo hora, per la Quintadecima del Primo giorno; da q. la parte Non-
aliquota della nominata proportione; cioè, cauo Sette fiate la parte Centesima trentesi-
maquinta; percioche tra 135. & 128. ui è la differenza di Sette, & quel che uiene è i. il
quale con q. contiene la proportione di questo Interuallo. A questo aggiungo per ordi-
ne la proportione del Maggior semituono, ch'è contenuto tra i. & k. il che uien fatto, ca-
uando da i. la Sestadecima parte; & tra i. & k. posti nel Secondo ordine, habbiamo il pro-
posito. Et perche tra k. & r. si ritroua il Tuono minore, la proportione del quale si troua
tra 10. & 9. però cauando da m. la Decima parte; tra il prodotto, che sarà r & k. posti nel
Secondo ordine; haueremo 'l nostro intento. Ma tra r. & l. si troua il Comma di propor-
tione Sesquiottantesima; onde cauando da r. la Ottantesimaprima parte, resterà nel Se-
condo ordine l. il quale con r. contenerà la proportione del Comma nominato. Seguita
poi l'interuallo del Tuono minore, l & m. il perche se noi cauaremo dalla Decima parte; il
restante m. col detto l. contenerà la proportione del detto Tuono. Ma à questo aggiunge-
remo il Semituono maggiore; il perche cauando da m. la Sestadecima parte; ne uerrà n.
che con m. contenerà la proportione del nominato Semituono. Cauando poi da n. la No
na parte, ne uerrà o. il quale con n. contenerà la proportione del Tuono maggiore; al qua-
le uolendo aggiunger quella del minore, che segue; cauando da o. la Decima parte; il re-
stante uerrà p. & cosi tra o. & p. haueremo la proportione di questo Tuono. Et per tal mo-
do haueremo tutti i Numeri & Proportioni de gli Interualli contenuti nella seconda Dia-
pason h & p. Hora per hauer quelli della Prima a & h. raddoppiaremo i Numeri h. i. k. l. m.
n & o. & haueremo i Numeri a b. c. d. e. f & g Dico hora, che i Numeri posti nel Secondo
ordine, sono i Numeri ritrouati delle proportioni, che sono contenute tra le Dicesette
mostrate chorde, tra due Diapason. E' ben uero che tali Numeri non sono Radicali di ta-
le ordine. La onde uolendoli ridurre alla lor Radice, bisogna osseruare il modo tenuto
nelle Istitutioni;Cap. 43. primae par
tis. ritrouando vn Maggior numero, che si possa hauere; il quale numeri &
misuri ciascheduno de loro interamente; & sarà il 5. Onde ne uerrà il Terzo ordine, che;
per la Nona definitione del nostro Primo ragionamento, farà nelle sue Radici, & li troua-
ti numeri simigliantemente, secondo 'l nostro proposito. Et che questo sia uero, lo prouo.
Per le Precedenti, b con e. contiene la Diatessaron; & c. con d. è Tuono maggiore; simigliā
temēte d. con e. è Tuono minore; adunque, per la Vētesimaotta del Secondo, b. ad c. è
Semituon maggiore. Et perche a. ad h. è la Diapason, & a. con e. è la Diapente; adunque,
per la Prima & la Quarta proposta del Secondo giorno, e & h. è la Diatessaron. Ma hò già
dimostrato f & g esser Tuono maggiore, & g. con h. fare 'l Tuono minore; adunque, per l'i-
stessa Vētesimaottaua, e & f. è Semituono maggiore. Con l'istesso modo etiādio potrei di
mostrar h. & q. i & k. con m & n. esser Semituoni maggiori; & che q. & i. sia l'interuallo del
Semituono minore; & l con r. contenga il Cōma; ma perche nella Precedēte hò dimostra
to il tutto; però non uoglio hora replicarui cosa alcuna. Solamente ui uoglio dire; essendo
m. & p. Diatessaron; n & c. Tuono maggiore; & o con p. Tuono minore; che m & n. è Semi
tuono . Il perche cōcludendo dico, che a. b. c. d. e. f. g. h. i. k r. l. m. n. o & p. sono del
le nominate Diapason nel Genere Diatonico i ritrouati numeri. Imperoche il numero
di Proslābanomenos cō ꝗllo di Hypate hypaton cōtiene la proportione del Tuono mag
giore; da Hypate hypatō à Parhypate hypaton quella del Semituono maggiore; da Parhy
pate hypaton à Lychanos hypaton la forma del Tuono maggiore, & da Lychanos hypatō
ad Hypate meson quella del Tuono minore. Simigliātemente dal numero di Hypatete me-
page 214 son à quello della sua Parhypate è il Semituono maggiore; Parhypate meson alla sua Ly-
chanos il Tuono maggiore, & Lychanos meson à Mese il Tuono minore. Oltra di ciò il
numero di Mese con quello di Paramese contiene la proportione del Tuono maggiore;
quello di Paramese con quello di Trite diezeugmenon, quella del maggior Semituono; il
numero di Trite diezeugmenon con quello della sua Paranete contiene la proportione
del Tuono maggiore; & quello della Paranete diezeugmenon con quello della Nete-
diezeugmenon contiene il Tuono minore. Ma dal numero della Netediezeugmenon à
quello di Trite hyperboleon si troua la proportione del Semituon maggiore; da quello di
Trite hyperboleon à quello della sua Paranete, il Tuono maggiore; & da quello di questa
à quello della Nete hyperboleon, il Tuono minore. Di nuouo, dal numero di Mese & dal
numero di Trite synemennon è compresa la proportione del maggior Semituono; da
quello di Trite & da quello di Paranete synemennon quella del Tuono maggiore; & per
finirla hormai, da quello di Paranete synemennon alla sua Nete è contenuta la propor-
tione del Tuono minore. Ma ui uoglio replicare una parola; che dalla Trite synemen-
non & dalla Paramese habbiamo la proportione di quello Interuallo, il quale è maggior
del Semituono minore; & dal numero della Nete synemennon & da quello della Parane
te diezeugmenon habbiamo la proportione del Comma. La onde dico; che questo è tut-
to quello, che secondo la proposta ui douea dimostrare. Et s'hauete alcun dubio sopra di
questa diuisione, ò costruttione, fatteui inanti; percioche di questo Genere non ui hò da
far per hora più parola. Io per me non hò dubitanza alcuna, disse M. Adriano à M.
Francesco; onde disse à me il Sig. Desiderio; Vi diamo adunque tutti licenza, che passate
più oltra. Cosi farete; disse anco M. Claudio; ond'io seguitai; dicendo. Venendo adunque
à quello, ch'io ui uoglio dimostrare, dico; che
PROPOSTA XI.
chordo Hypaton.
se la beccano. Già molti anni credeua, che fusse cosa molto rara; Ma per quel che
fin'hora hò veduto & ueggio; parmi che coloro che intorno di esso uo-
gliano ritrouare, come fanno gli una loro Quinta essentia; cioè, una cosa, che
non conoscono. Percioche per quello, non dirò poco lume, ma assai, che hauete dato di
lui nelle Istitutioni, & per l'Istrumento, che ui fece Maestro Dominico da PesaroVide cap. 9
Lib. 6. sup-
ple. uostro
amico & eccellente nella sua Arte, à questo proposito l'Anno 1548. & mi mostraste in casa
uostra; parmi di conoscerlo, se non diffinitiuamente, almeno per negatione. Come dite
Messere, disse il Viola, per negatione? Rispose; Vi par strano, ch'io dica di conoscer cotal
cosa per negatione. Sapiate, ch'io dico Sapere per negatione; quando alcuno ha una cosa
nella sua Idea, ò Intelletto, la quale non sappia, ò non possa esplicar bene; per non hauere
alle mani quelle differenze, & quei termini cōueneuoli, che farebbono alla sua esplicatio-
ne. La onde uedēdo, ouero udēdo rapresentarsi da alcuno la cosa, che lui conosce, [[per]] quel-
la, che hà nella mente; & che ueramente conosce, che non pure è quella; ma ne anco se le
assimiglia; se ben non sà render la ragione, & dire in che maniera la cosa stia; negherà al-
meno, ch'ella sia quella, che colui afferma essere. La onde tal negatione procederà, perche
di cotal cosa non haurà ragione alcuna distinta, ma confusa; per mancarui quei termini,
che uengono ad esprimere essentialmente la cosa. Ma se per auentura se ne rapresen-
tasse alcuna, che fusse à quella simile; se ben non sarà quella, haurà però da essaminar
cotal cosa, & uedere se in sè contiene tutte quelle parti, che li parerà d'hauer quel-
la che hà nell'intelletto. Et quest'io chiamo appresso di me Conoscere per negatione.
page 215 Credete adunque; replicò M. Francesco; che quelle Canzoni, le quali compongono que-
sti nostri moderni Compositori per Chromatiche, elle siano Chromatiche? Credo che
non siano, rispose egli. Vi darebbe l'animo di dirne qualche ragione? soggiunse M.
Francesco. Si bene; rispose M. Adriano; Ditela di gratia, replicò M. Francesco di nuo-
uo. Son cōtento, disse il buon Vecchio; Prima; non mi par, ch'elle siano Chromatiche, per
questa ragione; perche gli Antichi ne i loro Tetrachordi; com'habbiamo imparato; ha-
ueano solamente Quattro chorde diatoniche, & una Chromaticha particolare, la quale
cascaua tra la Secōda & la Terza diatonica, & con la Quarta acuta faceua il Semiditono,
che chiamano Trihemituono. Et costoro non solamente adoperano cotal chorda in una
Diatessaron, ò Tetrachordo; ma ue n'aggiungono di più quante uogliono, di maniera
che nelle loro Canzoni non si uedono altro che Diesis
 , & b molli. Dopoi; non mi par,
, & b molli. Dopoi; non mi par, ch'elle siano Chromatiche; percioche le chorde antiche haueano i lor proprij nomi; come
sono Hypate, Lychanos, Trite & l'altre; nondimeno le chorde, che pongono costoro nelle
lor cantilene, non si possono denominare con alcuno de i detti nomi; oueramente con al-
tri, che siano simili à quelli. Onde è manifesto segno, che non sono, ne mai potranno esser
quello, che costoro predicano. Oltra di questo, non osseruano Modo, ò Tuono alcuno nel
loro comporre; di modo che si possa dire, questa cantilena è composta nel modo Dorio,
Ionico, ouer Frigio, ò sotto un'altro Modo; come diceuano gli Antichi; ma sono cōposte
di confusione; & con una certa mistura de cose, che offendono grandemente l' de i giudiciosi; essendo che si troua in esse poco ordine; ne si scorge modo alcuno sta-
bile di Harmonia. Queste ragioni sono buone; disse il Viola; & per dire il uero, chi vuol cō
porre una cantilena Chromaticha, bisogna che imiti in ciò gli Antichi; ne bisogna allon-
tanarsi molto dal modo loro; & bisogna etiandio osseruare i Tuoni, ò Modi, de i quali essi
Antichi erano grandi osseruatori, & faceuano gran stima; se non vuol far le cose di suo ca-
po; ma non saranno poi le cose; che loro dicono che sono. Percioche si come uolendo fa-
re una Veste, fà dibisogno che ui sia la materia & la forma atta à far cotal Veste; altramen
te non sarebbe Veste; ma un'altra cosa, & forse strana; cosi à uoler comporre vna cantile-
na Chromaticha, bisogna che ui concorrino tutte quelle cose, che fanno all'esser di cotal
cantilena.Vide cap. 9
Lib. 6. Sup-
ple. Onde quando nelle compositioni loro usano altri Interualli, che Chromatici;
secondo 'l mio parere; questo non è comporre Chromatico; ma in un modo, che non hà
ne dell'uno, ne anco dell'altro. Però parmi, che dourebbono usar solamente quelle chorde
& Interualli, che sono contenute nel Tetrachordo Chromatico, se uogliono comporre
Chromatico; come dicono; & non altre chorde straniere; come essi fanno. E' uero, rispose
M. Adriano; Et quantunque le cose, ch'io hò detto, siano basteuoli à dimostrare il contra-
rio di quello, che sentono; tuttauia aggiungerò anco quest'altra; che non è di poca impor-
tanza; che usano nel cantare alcuni Interualli tanto sgarbati, come sono Semidiatessaron,
Tritoni, Semidiapente, Diapente superflui, & anco Diapason false, con altri simili, che ap-
portano poco piacere all'udito; Nōdimeno li hanno nel numero de i buoni; se bene i buo
ni & dotti Antichi molto li schiuauano & aborriuano; percioche mai non li hebbero per
consonanti nelle Modulationi loro, & che potessero far buona harmonia; se non erano cō
tenuti nelle lor proportioni del Genere superparticolare. Disse allora M. Claudio. Vi sò
che dire, che osseruano questa legge; Voi Messere ui sete affaticato molto insieme con mol
t'altri buoni Musici più Antichi di uoi, nel ridurre la Musica ad una certa maniera, ò for-
ma, c'hauesse qualche grauità & maestà insieme; ma con costoro è stato quasi uano il uo-
stro disegno; percioche oltra che non osseruano i precetti buoni dell'Arte; insegnano anco
& essortano gli altri à guastare il buono & ben ordinato, & à far peggio che sanno. Et quā
do fanno alcuna cosa che sia fuori del buono & bello della Musica; si coprono col scudo
dell'; & dicono che sono cose fatte nel Genere Chromatico; se ben nō conosco-
no, ne sanno quel ch'ello sia. Vedete di gratia quanto siano costoro non solo degni di bia-
simo; ma etiandio di castigo. Sapiate, risposi egli;Boeth. lib.
1. c. 1. Musi
ces. che se gli Antichi Lacedemonij scaccia
rono & bādirono della sua Città quel gran Musico Timotheo inuētore del Chromaticho
page 216 (come dicono) per hauer solamente nel solito Istrumēto aggiunto una sol chorda; pensate
pure che se fussero à i tempi nostri Giudici di costoro, quel che farebbono. Son certo che li
scacciarebbono del mondo; acciò non amorbassero gli huomini con tante loro strane cose,
che fanno vdire, le quali nascono; non già da una chorda sola, che aggiungono al solito &
usato numero; ma da molte & imolte aggiunte senza verun proposito, & senza giudicio. Co
storo si possono assimigliare à quello insolentissimo & ambitiosissimo Herostrato,Io. Rauis.
Text. in Of
ficina, De
Arrogan-
tibus. &
Au. Gell.
lib. 2. c. 6.
Noct. At-
tic. ilquale
abbrusciò l'antichissimo & celebratissimo Tempio di Diana Effesina; non per odio di lei;
ma per lasciar memoria di sè à i posteri con una tanta sceleratezza; poi che poca gratia
hebbe di farlo con fatti illustri, che lui hauesse operato. Onde, costoro perche non han-
no potuto acquistar nome d'eccellenti Musici con le opere loro, ci sono affaticati & anco
s'affaticano di fare il peggio che sanno, per acquistar nome, & diuentar famosi. Ma il pen-
siero li và fallito; perche si vede, che 'l mondo tien poco conto di simili huomini.Vide Prooe
mium Lib.
1. Supple. Dissi
allora, voltatomi uerso M. Adriano; Messere, bastaui fin quì hauer ragionato di costoro;
& lasciateli andar per uostra fè; che con tutto 'l peggio che faranno; non credo che siano
mai tanto stimati ualorosi nella Musica, come sete stimato uoi & molt'altri, che non uanno
dietro à queste cose tanto strane. Però hauendo voi fatto mentione d'una sola Chorda
aggiunta da Timotheo; uerremo à dimostrar la proposta; ritrouando questa solamente;
per esser breue; la quale sarà Terza in ogni Tetrachordo; & farà la uarietà del Genere.
Ma perch'io dissi nella Seconda proposta, che la Prima, la Seconda, & la Quarta chor-
da d'ogni Tetrachordo diatonico, sono etiandio communi alla Prima, Secōda, & Quarta
d'ogni Tetrachordo chromatico; però cercaremo solamente d'accommodar la Terza tra
le nominate Diatoniche, la quale sia lontana dalla Quarta acuta d'ogni Tetrachordo per
un Semiditono, ò Trihemituono. Bisogna però auertir quello, che più fiate hò detto; che
la Proslambanomenos & la Mese siano lontane da i tetrachordi Hypaton & Diezeugme-
non per un Tuono maggiore; quella da Hypate hypaton, & questa da Paramese. Questo
ci ricordiamo; disse il Viola; hauendolo uoi detto anche per inanti. Ma perche si pone
questa chorda del Tetrachordo Chromatico lontana dalla Quarta chorda per un Semi-
ditono; se d'alcuno non è stato mai fatto mentione in simil Genere di questo interuallo?
Risposi; Anzi TolomeoHarmonic.
Lib. 1. c. 15 parlando del Genere Chromatico molle, pone questo Interual-
lo, il quale è il terzo del suo Tetrachordo, sotto la proportione Sesquiquinta. Ma la ra-
gione ui hò detto anco nelle Istitutioni,2. par.
cap. 47. & al presente son per replicarla: Percioche se
bene gli Antichi hanno segnato altri Interualli, ò proportioni al Trihemituono, che non
è quella del nostro Semiditono; tuttauia, com'hò detto ancora, parmi che inutilmen-
te s'aggiunga una chorda in qual si uoglia Istrumento; quando con un'altra non faccia
Consonanza alcuna. Et perche l'altre Chorde, che s'aggiungono, non fanno con la
Quarta de i Tetrachordi alcuna consonanza; però dico, che vanamente & senza utilità
cotali Chorde si pongono ne gli Istrumenti. La onde giudicai, & anco son di parere, che 'l
Semiditono del diatonico, posto da Tolomeo nella proportione Sesquiquinta, il quale
poco fà ui hò cōmemorato, & serue etiandio per il Trihemituono del Chromatico mol-
le, douessi esser quello, che si hauesse da noi adoperare nel Chromatico, & non altro inter-
uallo; il quale è al tutto senza consonanza. Aggiunse M. Claudio; Parmi ueramente,
c'habbiate ragione. Ne sò ueder cosa alcuna, che ui possa esser contraria. Onde inco-
minciarete à dimostrar quello, c'hauete proposto, se non hauete altro che dirci. Vdito
questo, senza por tempo di mezo, incominciai, dicendo. Siano le Chorde diatoniche a.
b. c & e. & sia a. Proslambanomenos, & b. la Prima chorda più graue dell'altre seguenti
del Tetrachordo Hypaton diatonico, c. la Seconda, & e. la Quarta. Et siano a. con b. di-
stanti per un Tuon maggiore, b & c. per il maggior Semituono, & sia b & e. la Diatessaron,
& a con e. la Diapente. Faccio hora la chorda d. con la e. in proportione Sesquiquinta;
onde, per la Duodecima Definitione del Secondo giorno; d & e. sarà Trihemituono. Et
perche, per il Primo Corollario della Trentesima, pur del detto giorno; leuato ab. Tuo-
no maggiore, da a & e. Diapente; resta b & e. Diatessaron. Simigliantemente; perche, per
page 217 la Ventesimasettima del giorno istesso; due Tuoni l'un maggiore & l'altro minore, con vn
Semituono maggiore appresso fanno la Diatessaron; & essendo bc. & cd, insieme; per la
Decimanona pur del Secondo giorno, Tuono minore; seguita; che d & e. contiene il
Tuono maggiore & il maggior Semituono, i quali, per la Ventesimasesta del Secondo fan
no il Semiditono, ò Trihemituono. Viene adunque d & e. ad essere 'l Trihemituono.

Lychanos hypaton & Hypate meson Trihemituono; com'hò dimostrato; resta che, per la
Quarta & per la Nona Definitione d'hoggi, b. c. d & e. sia Tetrachordo Chromatico & an
co il Tetrachordo Hypaton; come vi douea dimostrare; percioche è posto nel Primo &
grauissimo luogo di questo Genere, & contiene le chorde Hypate hypaton, Parhypate
hypaton; Lychanos hypaton, & Hypate meson. Et auertite à quello, ch'io hò detto sopra
la Duodecima definitione del Secondo; ch'io piglio il Semiditono, il Trisemituono, &
lo Trihemituono, per un'Interuallo istesso. E' ben uero, che 'l primo termine usiamo mag-
giormente nel Diatonico, & si troua tramezato da una chorda, & li due altri vsiamo in
questo Genere; intendendoli senz'alcuna chorda, che diuida questo Interuallo in due
parti. Auertite ancora; ch'alle chorde Chromatiche, oltra 'l nome di Lychanos, ò Pa-
ranete, le aggiungerò questo nome Chromatica; accioche dall'altre siano conosciute; il
che farò etiandio nell'Enharmonico. Mi piace, disse M. Adriano, la distintione, che fatte
ne i nomi; & anco l'aggiunto, che fatte alle chorde; percioche uerremo meglio ad inten-
dere il tutto; & schiuaremo la confusione, che nascer potrebbe. Passarò adunque all'al-
tra, risposi; & dirò.
PROPOSTA XII.
Meson.
te, le chorde f & h. & sia a & h. Dupla; di modo che consoni la Diapason; &
e con f. il Semituono maggiore. Faccio hora h & g. Sesquiquinto; di modo
che tenga il Semiditono, ouer Trihemituono. Onde f & g. uiene ad essere Semituono
minore; percioche essendo f & h. per la Quinta proposta d'hoggi; l'interuallo d'un Tuo-
mo maggiore & d'un minore; i quali, per la Ventesimasettima del Secondo nostro ragio-
namento, fanno il Ditono; Se da f & h. Ditono leuaremo g & h. Semiditono; ne uerrà
f & g. ch'è la differenza, che si troua tra l'uno & l'altro; & per la Ventesimaterza definitio-
ne del medesimo giorno; farà il Semituono minore. Habbiamo però dimostrato a & e.
esser la Consonanza Diapente; Onde se noi leuaremo da a & h. Diapason la a & e. Dia-
pente, per il Corollario della Quarta proposta del Secondo giorno; resterà e & h. Diates-
page 218 saron. Ma perche e. f. g & h. è composto de due Semituoni, l'un maggiore e & f. & l'al-
tro minore f & g, & del Trihemituono g & h. però e f. g & h. sarà; per le Definitioni

uea dimostrare, & questi due Tetrachordi Hypaton & Meson sono congiunti; ma dimo-
strero hora lo Diezeugmenon; che sarà il Separato; Statemi ad ascoltare.
PROPOSTA XIII.
Hyperboleon, à i due graui; & tra le Quindeci chorde hauer la Disdiapason.
perboleon; acciò più presto si espediamo. Siano adunque a. b. c. d. e. f. g & h. le
chorde della Precedente; & siano b. c. d & e. il Primo Tetrachordo graue; & e. f.
g & h. il Secondo. Aggiungo à questo i. k. m. n & p. chorde diatoniche; per hauer gli altri
due tetrachordi Diezeugmenon, & Hyperboleon. Ma perche il tetrachordo Diezeug-
menon; per la Vndecima definitione; è tetrachordo separato dal Meson; però tra la
chorda Mese & la Paramese casca l'interuallo del Tuono maggiore; & cosi tra Mese &
Nete diezeugmenon si troua la Diapente, & tra Mese & Nete hyperboleon ui è la Dia-
pason. Faccio hora la chorda l. distante dalla m. per un Semiditono, & anco la chorda o.
pur distante dalla p. per un simile Interuallo; come si fece nelle Precedenti delle chorde
d. con e. & g con h. & haueremo i, k. l & m. Tetrachordo Diezeugmenon; & m. n. o & p.
Tetrachordo Hyperboleon, per le ragioni istesse, che nella Precedente habbiamo usate;
ne i Tetrachordi Hypaton & Meson; diuisi secondo la natura di questo Genere. Ma
perche noi sapiamo già, che a & b. è la Diapason, & simigliantemente h & p. però a & p.
uiene ad esser Disdiapason, la quale essendo contenuta tra Quindeci chorde; è manife-
sto, che tra questo numero habbiamo collocato i due proposti Tetrachordi, & essa Dis-
diapason; secondo 'l nostro proposito. Voglio anco dimostrar; soggiunsi; il Tetrachor-
do Synemennon, accioche conosciate quanto sia stato di utile la Partecipatione, che si
page 219

leuar uia tutti i garbugli, che nascono per l'aggiuntione di questo Tetrachordo à gli altri
mostrati. Onde dico; che
PROPOSTA XIIII.
nere Chromatico.
alle quali aggiungeremo la r. Diatonica, distante dalla h per una Diatessaron.
Et faremo h & q. lontane per un Semituon maggiore, & s distante dalla r. per
vn Semiditono; & haueremo tra h. q. s & r. il proposito. Percioche essendo h
& r. Diatessaron; se da essa leuaremo h & q. Semituon maggiore; & da q & r. il Semidi-
tono; senza dubio alcuno resterà s & q. Semituon minore. Et perche la modulatione,
che si troua in queste chorde, procede per Semituono maggiore, & Semituono minore;
& per un Trihemituono; però, per la Definitione h. q. f & r. uiene ad essere il Tetrachor-
do synemennon Chromatico; perche è congiunto alla chorda h. cioè, alla Mese. Allora
page 220 disse M. Adriano; Non uorrete forse tener l'ordine, c'hauete tenuto nel Diatonico; se-
gnando ciascheduna chorda con Numeri; acciò si possa comprendere quanta pro-
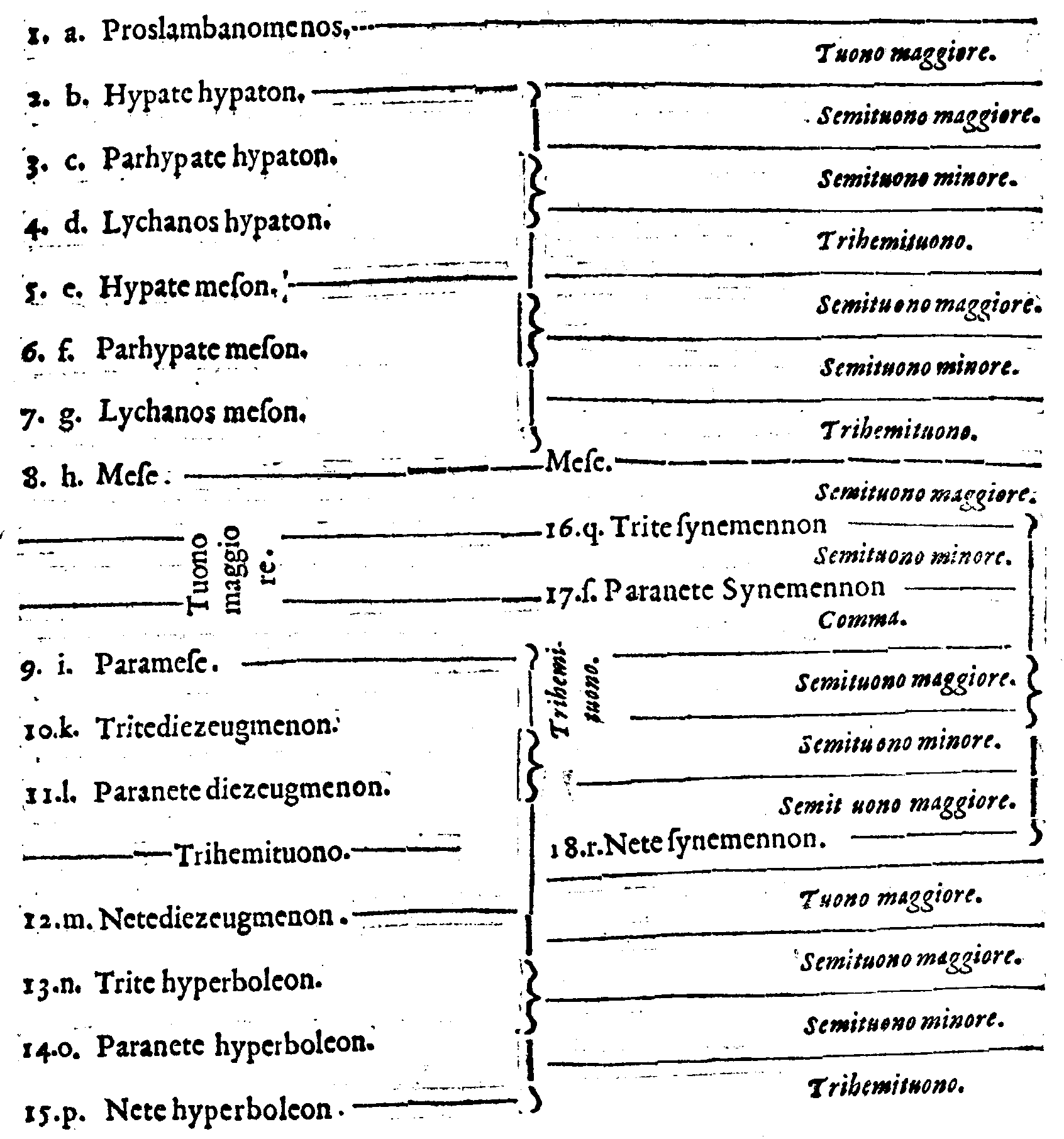
mio uolere; ui propongo questa.
PROPOSTA XV.
chromatico.
chorde diatoniche sono communi con le Chromatiche; la onde essendo com-
muni le chorde; uengono etiandio ad esser cōmuni gli Interualli loro & i Suoni. Il
perche piglieremo solamente la Prima, la Secōda, & la Quarta chorda d'ogni Tetrachor-
do diatonico con i suoi segnati numeri; & aggiungendo ad ogni Quarta uerso 'l graue i
Numeri d'una chorda distante per una Sesquiquinta; haueremo 'l proposito. Pigliaremo
adunque a. b. c. e. f. h. q. i. k. r. m. n & p. con i suoi Numeri posti nel Secondo ordine della
Decima proposta d'hoggi, & faremo d. g. r. l & o. distanti da e. h. s. m & p per una Sesqui-
quinta, la quale è la proportione, che contiene il Trihemituono; aggiungendo à ciasche-
dun di loro la sua Quinta parte, & haueremo 'l proposito. Et perche e. h. m. p & s. sono
Numeri, che hanno la Quinta parte; porò incominciando da e. posto nel secondo ordi-
ne; pigliaremo cotal parte, la quale aggiungeremo ad esso e. & ne darà d. posto medesi-
mamente nel Secondo ordine nominato, che con essa e. contenerà il Trihemituono; per-
cioche d. uerrà à contenere e. una fiata & la sua Quinta parte. La onde, per la Defini-
tione, d & e. vēgono à contener la Sesquiquinta proportione, ch'è la forma di esso Trihe-
mituono. Et per tal modo haueremo segnata la Terza chorda acuta del Tetrachordo
Hypaton con i suoi Numeri. Il che auerrà ancora quando si cauerà da c. la Ventesima-
quinta sua parte; percioche nascerà medesimamente d. il qual con esso c. contenerà la
proportione Sesquiuentesimaquarta; ò Semituon minore, che lo uogliamo dire; & tra
d & e. il nominato Trihemituono; come ui hò dimostrato. Hora aggiungendo ad
h. m. p & s. la lor Quinta parte; ouer cauandone la Ventesimaquinta da f k. n & q. ne uerrà
g l. o & r. le quali saranno le Terze chorde de gli altri Tetrachordi, segnate con i loro nu-
meri; secondo 'l proposito; come ui douea dimostrare. Ma perche quest'ordine de Nu-
meri non è contenuto nella sua Radice; percioche sono Tra loro composti; onde da al-
tro numero, che dalla Vnità; per la Decima definitione del Primo giorno; possono es-
ser numerati & diuisi; però uolendoli ridurre alla loro Radice, & numeri Contrasepri-
mi; ritrouaremo un Numero, secondo 'l modo dato nel Capitolo penultimo della prima
parte delle Istitutioni, il quale numeri & misuri ciaschedun de quelli, che sono conte-
nuti nell'ordine nominato; cioè, nel Secondo; che sarà il Ternario; Onde nascerà un
Terzo ordine, il qual per la Quinta Dignità; contenerà quell'istesse proportioni, che con-
tiene per ordine il Secondo; & tutti quelli Interualli, che sono contenuti nella costrut-
tione, ò fabrica del Monochordo del Genere Chromatico. Habbiamo adunque ritro-
uati i Numeri delle chorde del Monochordo chromatico; secondo la proposta; percio-
che a & b. è Tuono maggiore; b & c. maggior Semituono; & cd. è Semituono minore.
Et perche a. con e. contiene l'interuallo Sesquialtero; però a & e. sono i numeri della Dia-
pente; & a & b. quelli del Tuono maggiore. Se adunque da a & e. leuaremo a & b. Tuo-
no maggiore; ne resterà, per il Primo Corollario della Trentesima del Secondo, b & e.
Diatessaron. Ma b & c. con c & d. posti insieme, per la Decimanona pur del Secondo,
fanno un Tuono minore; adunque e & h. fanno la Diatessaron. Et perche a & h. uiene
ad essere la Diapason, & a con e. la Diapente; però e & h. è la Diatessaron. Ma perche
e & f è Semituono maggiore, & fg. è Semituono minore; però, per la nominata De-
cimanona; g & h. è Trihemituono. Potrei anco dimostrare, che h & i. è Tuono mag-
giore, i & k. con k. & l. due Semituoni; l'un maggiore & l'altro minore; & l con m. il Tri-
hemituono. Simigliantemente m. n & o. due Semituoni, come i due nominati; & o con
p. Trihemituono; & cosi gli altri; ma per esser questa cosa chiara, per non andar più in
lungo, farò fine à questa dimostratione; con questo parto però; che se ui occorrerà qual-
che dubio sopra di essa, lo dimandate senza rispetto alcuno. Disse à questo M. France-
sco; Ho posto mente ad una cosa; che tanto nel Genere Chromatico, quanto nel Dia-
tonico; nel Primo interuallo di ciascun Tetrachordo si uà modulando, ò cantando; come
dir uogliamo; per un Semituono maggiore, di maniera che questo Interuallo è commu-
ne à ciascuno de i due Generi nominati. Et se gli interualli de i Tetrachordi sono, co-
page 222
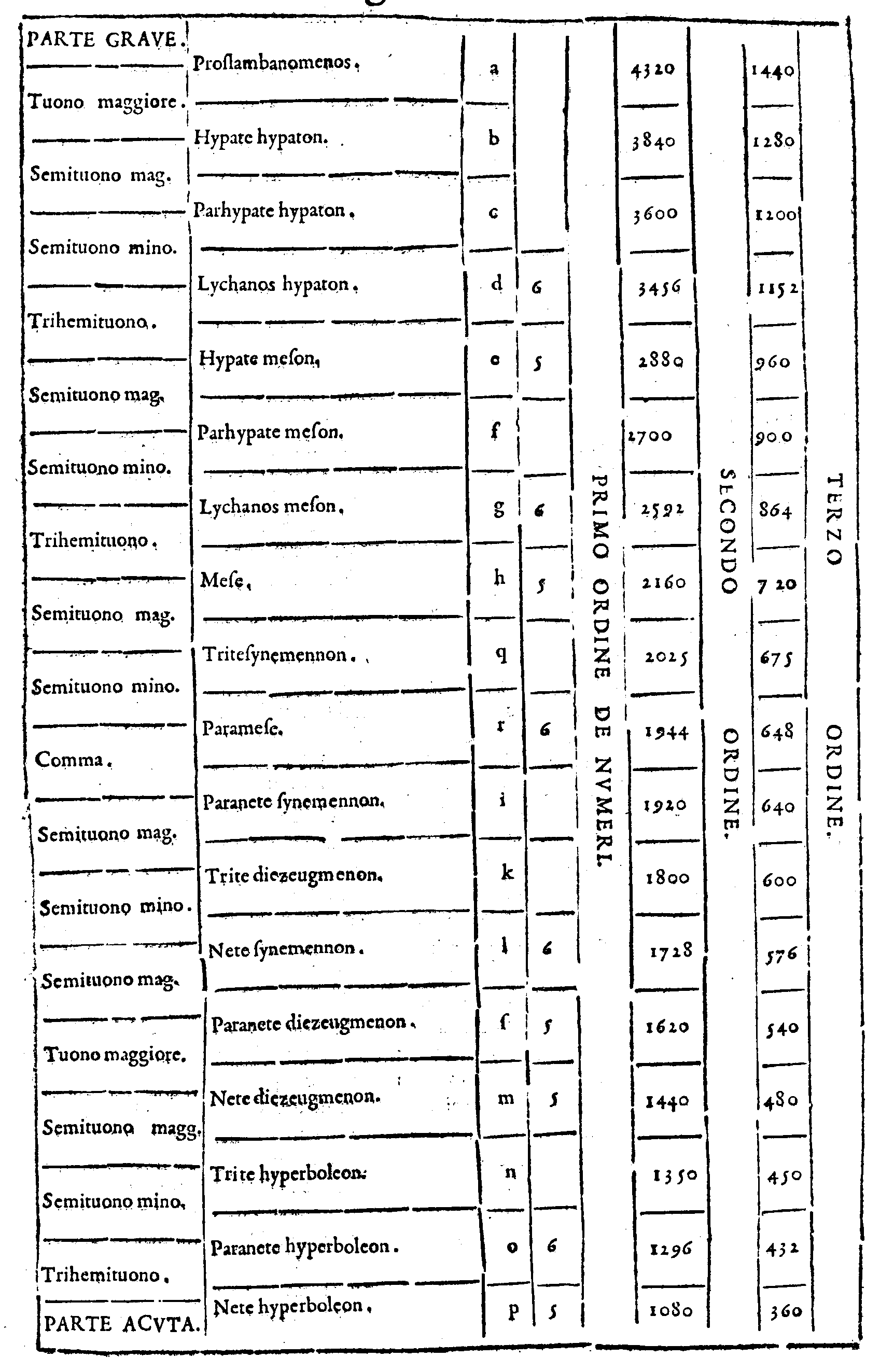
17. Elementi de i lor Generi; non è dubio alcuno, che 'l Se-
mituono maggiore sarà Elemento tanto del Diatonico genere, quanto del Chromatico;
& ciò vediamo espressamente; percioche tale Interuallo in questi due Generi è indiuisi-
bile; & s'adopera nell'uno & l'altro. Voi dite benissimo; risposi; & ciò non è inconuenien-
te, & questo auiene;
PROPOSTA XVI.
Diatonico, corrispondono alle Hypate, alle Parhypate, alla Mese, alla Paramese, alle
Trite, & alle Paranete de i modi del Chromatico.
Semituono maggiore dalla Hypate alla Parhypate; simigliantemente dalla Me-
se alla Tritesynemennon; dalla Paramese alla Tritediezeugmenon; & dalla
Nete diezeugmenon alla Trite hyperboleon; com'etiandio si troua il Tuono maggiore
dalla Mese alla Paramese; & anco dalla Proslambanomenos alla Hypate hypaton. Di
maniera che ciascun de uoi può conoscere, che nel Diatonico, & nel Chromatico, quel-
le Voci, che sono contenute in una delle nominate chorde d'un Genere; corrispondo-
no à quelle, che sono contenute in una delle nominate chorde, contenute nell'altro; &
che realmente non ui è differenza alcuna da una all'altra. Il perche nasce, che non sola-
mente ciò da uoi stessi comprendete; ma etiandio conoscete perfettamente, come buo-
ni Musici; che la Proslambanomenos, le Hypate, le Parhypate; la Mese, la Paramese, le
Trite, le Paranete, & le Nete d'uno de i nominati Generi, scambieuolmente alla Pros-
lambanomenos, alle Hypate, alle Parhypate; alla Mese, alla Paramese, alle Trite, alle
Paranete, & alle Nete dell'altro corrispondono. Questo è uero; disse M. Adriano; per-
cioche nell'uno & nell'altro de i due Generi (com'hauete detto) dalla Proslambanome-
nos alla Hypate uicina, ui è l'interuallo del Tuono maggiore, & alla Hypate meson, la
Diapente. Questo si potrebbe anco dire; soggiunse il Sig. Desiderio; che dalla Proslam-
banomenos alla Netediezeugmenon, si troua la Diapason diapente; & alla Nete hyper-
boleon la Disdiapason. Allora M. F rancesco disse; non accade che faciamo al presen-
te questi conti; percioche è pur troppo manifesto da quel, che fin'hora habbiamo uedu-
to. Ma perche hauete nominato di sopra Modi diatonici & Modi chromatici; però per
uostra fè M. Gioseffo, diteci quel che uoi intendete per questi Modi; ancora che mi pa-
re, che uoi intendiate per Modo l'interuallo, il quale si canta; come ho potuto com-
prender dall'essempio, che uoi hauete addotto del Tuono maggiore & del maggior Se-
mituono. E' uero, diss'io, che queste modulationi fatte per questi Interualli, si chiamano
Modi; ma ricordateui, che più propriamente si chiamano Modi quelle Modulationi, le
quali si cantano per più di uno interuallo; come sono le modulationi de i Ditoni & Se-
miditoni tramezati da una chorda, & quelle delle Diatessaron & delle Diapente diuise
in Tuoni & Semituoni; oueramente in altri interualli. Ma quelli, che proprijssimamen-
te (se cosi posso dire) si chiamano Modi; sono quelli, de i quali hò parlato nella Quarta
parte delle Istitutioni; & sono le forme de tutte le cantilene. Et coloro, che non co-
noscono, ò non nintendono la natura & compositione loro, & come si formano, & in
quali Chorde fanno le terminationi, ò Cadenze loro; questi mai componeranno cosa
alcuna, che stia bene. Et se pur faranno cosa, che riuscisca appresso bene; l'hauran-
no fatto à caso; percioche caminano à guisa de ciechi col bastone. Di questi al presen-
te non ne uoglio dir cosa alcuna; ma solamente dopo ch'io haurò dimostrato in qual ma-
niera le chorde di ciaschedun Genere di Melodia ne gli moderni Istrumenti si riducano
page 224 alla temperatura, col mezo della Partecipatione; uorrò dimostrare il Numero loro, il
Sito & la loro Forma. Ma sarà bene, che passiamo più oltra, & non perdiamo tempo;
dimostrandoui; che;
PROPOSTA XVII.
chordo Hypaton. Primieramente aggiungo alla chorda b. la chorda a. la qua-
le sia Proslambanomenos; Onde la faccio Sesquiottaua alla b. Hypate hypa-
ton, Prima chorda del Tetrachordo, che uogliamo dimostrare; Dopoi faccio e. Hypa-
te meson Sesquialtera con la chorda a. Sarà adunque, come fù anco ne gli altri, a & b.

nor Semituono, & d. con b. Semituono maggiore; onde c & d. per la Ventesimaquarta
definitione del Secondo ragionamento; sarà il Diesis minore. Et perche, per il Primo
Corollario della Trentesima del detto ragionamento, leuato a & b. Tuono dalla conso-
nanza Diapente a & e resta la Diatessaron b & e. però b & e. modulerà la Diatessaron.
Ma, per la Ventesimaottaua medesimamente del Secondo, la Diatessaron contiene un
Tuono maggiore, un minore, & un maggior Semituono; & bc. con cd. sono posti insie-
me un Semituono maggiore; per tanto dico, che d con e. contiene il Tuono maggiore
& lo minore insieme. E' adunque d con e. per la Ventesimasettima del Secondo, il Di-
tono. Onde essendo ancora b & c. Hypate hypaton & Parhypate hypaton Diesis mag-
giore, & c con d. Parhypate hypaton con Lychanos hypaton Diesis minore; è manife-
sto, per la Quinta, & per la Nona Definitione, che b. c. d & e. sia il Tetrachordo Hypa-
ton; Primo nel Genere enharmonico; come douea dimostrarui. Però seguitando 'l
PROPOSTA XVIII.
sis maggiore; & l'istesso e. con g. faccio Semituon maggiore. Sarà adunque
f. con g. per la Ventesimaquarta definitione del Secondo giorno, Diesis mi-
nore. Et perche (com'hò dimostrato) a & e. contiene la Diapente; però ca-
uandola da a & h. che è la Diapason; per il Corollario della Quarta proposta del detto
page 225 Ragionamento; resta la Diatessaron. Ma perche, per la Ventesimaottaua del Secondo
nominato, la Diatessaron Tuono maggiore & un minore, con un maggior
Semituono; & e con g. è Semituono maggiore; de qui nasce, che g & h. contiene il Tuo-
no maggiore col minore, Sarà adunque g & h. per la Ventesimasettima del Secondo me-

maggiore, & d'un minore, con un Ditono, per la Definitione, nel Genere Enharmoni-
co; come douea, secondo la proposta, dimostrarui. Onde passarò à dimostrar gli altri
due; se cosi ui piace. Anzi ui preghiamo; disse M. Adriano; percioche se si hanno da
soggiungere à questo modo, non ui sarà troppo difficultà; ne molta fatica. Aggiungerò
anche il Quinto, soggiunsi;
PROPOSTA XIX.
leon, & Synemennon, & nel Systema massimo collocar la Disdiapason.
re gli altri Tetrachordi. Et perche il Tetrachordo Meson è separato dal Die-
zeugmenon; però faremo i. Paramese lontana da h. Mese per un Tuono maggio-
re; & m. Netediezeugmenon per una Diapente; cosi p. Nete hyperboleon per una Dia-
pason. Onde ridurremo i k. l & m. Tetrachordo Diezeugmenon; come si ridusse l'Hy-
paton; & il Tetrachordo m. n. o & p. Hyperboleon; come fù ridotto il precedente Me-
son. Sarà adunque l'uno & l'altro accommodato nel Genere enharmonico. Ma perche a.
con h. cōtiene la Diapason; come si è detto; simigliantemente sarà h & p. Diapason adun-
que a. con p. contenerà la Disdiapason, la quale hauendo in se Quindeci chorde, ò uoci;
è manifesto, che noi habbiamo quello, che prima era 'l nostro proposito. Ma per aggiun-
gere il Synemennon; faremo q. distante dalla h. per vn Diesis maggiore; & r. lontana me-
desimamente da essa h. per un maggior Semituono; & haueremo, secondo la proposta;
come vi potrei di nuouo dimostrare; che per esser breue lo uoglio lasciare; tutto quel che
desiderauamo. Non è cosa difficile questo, c'hauete hora dimostrato, disse M. Adriano,
onde ci potiamo gentilmente contentare. Et se non gli è altra difficultà nell'assignare
& raccogliere i Numeri delle sue proportioni nelle sue chorde; sarà molto lodeuole.
page 226 Credo, disse M. Francesco; che 'l modo tenuto nell'adunare i Numeri delle chorde de
gli altri due Generi, possa etiandio seruire à questo; essendo che molte di queste chorde

la maggior difficultà sarà nell'accommodare i Numeri del Diesis minore. Non dubitate,
risposi; ch'io farò il tutto facilmente. Et che ciò sia il uero ascoltatemi. Questa sarà la
proposta, ch'io vi voglio dimostrare.
PROPOSTA XX.
ti nella lor Radice.
che i Numeri della Diapason posta nel graue, corrispondino in Doppia propor-
tione à i Numeri della Diapason posta in acuto; però ritrouando primieramen-
te quelli, che sono della Diapason acuta; per esser la cosa alquanto più difficile; sarà faci-
lissima cosa il ritrouar quelli della Diapason graue, poi che i Numeri di questa in Dupla
proportione à i numeri di quella corrispondono. Siano adunque h & q. minimi termini
del Diesis maggiore posto nel graue della Diapason h & p. al minore de i quali; cioè, al q.
faccia dibisogno d'aggiungere il Diesis minore acuto. Molteplico primieramente h &
q. posti nel Primo ordine, per il maggior termine del Diesis minore, ch'è 128. il quale,
per l'Ottaua proposta del Primo giorno, pongo per la differenza di h & q. acciò possa ha-
uer la Centesima uentesimaottaua parte; percioche q. è numero, il quale non hà in se co-
tal parte, & uiene h & q. nel Secondo ordine; i quali, per la Quinta dignità, contengo-
no l'istessa proportione, che contiene h & q. del Primo; cioè, la Sesquiuentesimaquarta.
Hora perche q. nel secondo ordine, hà in parte; però leuo da lui, per la Quinta-
decima proposta del Primo giorno, tre fiate la Centesimauentesimaottaua parte; & uiene
r. il quale con q. contiene la proportione del Diesis minore posto nell'acuto. Et perche,
per il Corollario della Trentesimaseconda del Primo nostro ragionamento; il Semituon
maggiore, ò Sesquiquintodecimo interuallo è reintegrato dalla proportione Sesquiuen-
tesimaquarta, & dalla Supertripartiente 25. ò uogliamo dire dal Diesis maggiore &
dal minore; però diremo h & r. esser'il maggior Semituono, il quale nel genere enharmo-
nico si diuide in due parti; secondo la natura & proprietà di questo Genere. Cauaremo
poi dalla r. la Quarta parte, & ne uerrà l. il quale con esso r. contenerà la Sesquiquarta, &
per consequente il Ditono. Et per tal maniera haueremo ritrouato i numeri h. q. r & s.
nel secondo ordine del Tetrachordo Synemennon. I quali Numeri non sono Radicali;
essendo che sono Tra loro composti. Onde accioche con più breuità & facilità si possà
ritrouare gli altri; ridurremo quest'ordine alla sua Radice; ritrouando un Numero, che
misuri ciascuno di essi; nel modo ch'io mostrai nel Penultimo capitolo del Primo libro
delle Istitutioni; & haueremo 8. il quale diuiderà ciascheduno de i nominati numeri,
del Secondo ordine; & haueremo h. q. r & s. nel Terzo, che saranno Contraseprimi, &
nella loro Radice. Ma per ritrou ar quelli del Diezeugmenon, uederemo se da h. del
Terzo ordine si può hauer la Nona parte; acciò possiamo aggiungere al numero h. la pro-
portione Sesquiottaua. Et perche ueramente non l'hà; però molteplicheremo h. q. r & s.
di questo ordine, per il q. & uerranno h. q. r & s. posti nel Quarto & ultimo; i quali, per la
Quinta dignità, conteneranno l'istesse proportioni, che sono contenute tra i termini del
Terzo ordine. Hora da questi Numeri haueremo il tutto; percioche se cauaremo da h. la
Nona parte, ne uerrà i. il quale con esso h. contenerà la Sesquiottaua proportione, che è
la forma del Tuono maggiore. Da i. etiandio cauaremo la Ventesimaquinta parte, & ha-
ueremo k. il quale con esso i. contenerà i numeri del Diesis maggiore. Ma per ritrouar
quelli, che contengono il minore; leuaremo tre fiate la Centesima uentesimaottaua par-
te di k. & quel che uerrà, sarà l. che contenerà con k. la proportione del nominato Die-
sis. Ma cauando da l. la Quarta parte, nascerà m. il quale con esso l. contenerà la pro-
portione del Ditono; ch'è la Sesquiquarta. Al medesimo modo cauando da m. la Ven-
tesimaquinta parte, nascerà n. che con il detto m. contenerà la proportione del Diesis
maggiore. Imperoche leuando da n. tre fiate la Centesima ventesimaottaua, ne uerrà o.
la quale con n. contenerà quella del minore. Ma se da o. leuaremo la Quinta parte, uerrà
p. che con o. contenerà la proportione Sesquiquarta, & anco il Ditono. Et per tal ma-
niera haueremo adunato insieme tutti i Numeri della Seconda diapason acuta, i quali
conteneranno tre Tetrachordi; h. q. r & s. Synemennon; i. k. l & m. Diezeugmenon; & m. n.
o & p. Hyperboleon. Ma per hauer quelli della Diapason graue; bastarà solamente rad-
dopiare h. i. k l. m. n & o. & ne uerrà a. b. c. d. e. f & g. iquali con h. conteneranno tutti quelli
della detta Diapason, diuisa in due Tetrachordi; b. c. d & e. Hypaton; & e. f. g & h. Meson.
page 228
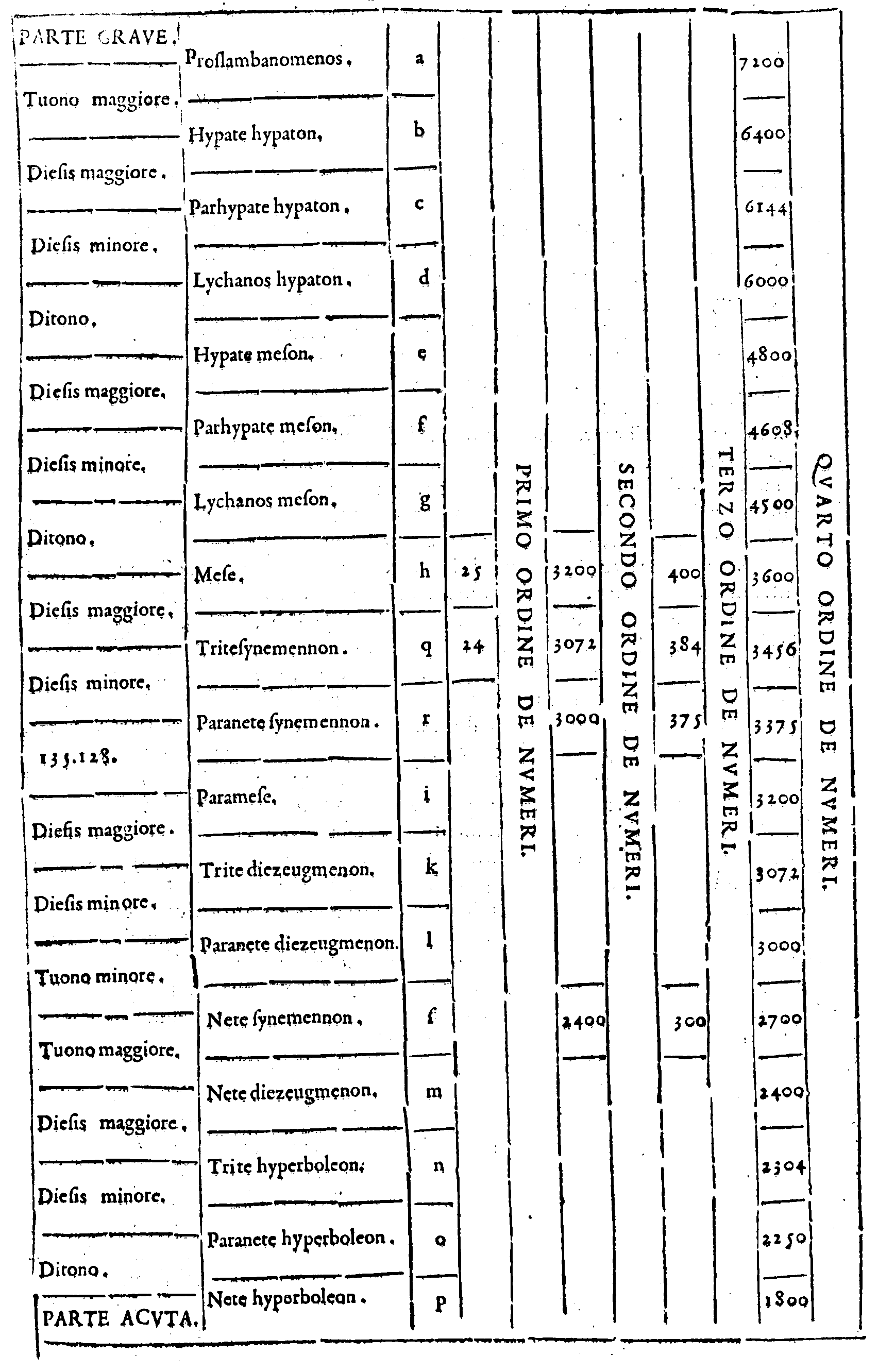
nici; secondo 'l proposito nostro; posti, per la Nona definitione del Primo giorno, nella lo-
ro Radice. Ilperche essendo a & b. Tuono maggiore, & b con c. Semituono minore,
ouer Diesis maggiore; & c con d. Diesis minore; simigliantemente, poi che a con e. uiene
Sesqiualtero, & a con e. sono i Numeri della Diapente, & a con b. numeri del Tuono mag
giore; però cauato 'l Tuono a & b. della Diapente a & e. per il primo Corollario della Tren
tesima del Secondo; resta b & e. Diatessaron, & bc. con cd. insieme; per il Corollario del-
la Trentesimaseconda del Primo giorno; fanno il Semituon maggiore. Adunque, per la
Ventesimaseconda definitione del Secondo, d con e. contengono il Ditono. Et a con h.
è la Diapason; adunque, per il Corollario della Quarta proposta del nominato Secondo,
e con h. è la Diatessaron. Et perche ef & fg. sono due Diesis; cioè, il maggiore & lo mi-
nore; però g & h. uiene ad essere il Ditono. Con questo modo istesso si potrebbe dimo-
strare h & i. esser Tuono maggiore; ik & kl. due Diesis; l & m il Ditono; & cosi gli altri
Interualli ancora; come mn. & no. due Diesis; & op. il Ditono; & anco hq & qr. esser si-
migliantemente due Diesis; & l con r essere un Ditono. Ma per non vi attediare, per
esser quello, c'hò detto, chiaro; farò fine. Hò in fatto osseruato una cosa, disse M. Adria-
no; mentre hauete fatto queste dimostrationi; & parmi di non mi hauere ingannato; &
è questa; che
PROPOSTA XXI.
tioni Enharmoniche, & leTrite vengono Paranete.
ò costruttione Diatonica, quanto nella Chromatica. Imperoche in ciaschedu-
na di queste due, da Proslambanomenos à Hypate hypaton ui casca il Tuono
maggiore: il che accade anco nella diuisione Enharmonica; Ma da Hypate hypa-
ton à Parhypate hypaton ui è l'interuallo del maggior Semituono, ilquale nell'Enhar-
monico da Hypate hypaton à Lychanos hypaton si troua. Adunque la Parhypate dia-
tonica & chromatica si muta; & nell'Enharmonico diuenta Lychanos, senza dubio alcu-
no. Il che si potrebbe anche dir de gli altri; cioè, delle Trite con le Paranete. In effetto,
soggiunse allora M. Claudio; gli Istrumenti insegnano assai più di quello, che non si crede;
percioche ui si uede in atto il tutto. & è ueramente l'essempio di tutto quello, che fabri-
cato hà con l'intelletto lo Speculatiuo. Di nuouo replicò M. Adriano; questo si può fa-
cilmente capire & comprender col senso ne gli istrumenti Musicali nominati; massima-
mente nel testame de gli Organi, Grauecembali, Arpichordi, Monochordi & altri simili;
essendo che se ne i tre generi nominati saranno le Proslambanomenos & le Hypate uni-
sone; allora conosceremo chiaramente, che la Lychanos dell'Enharmonico è unisona cō
la Parhypate de gli altri. Et potremo ancora conoscere, che le Paranete dell'Enharmo-
nico saranno unisone alle Trite del Diatonico & del Chromatico. Questo è tutto uero
Messere; risposi; ma aggiunggete etiandio à questo; che
PROPOSTA XXII.
ramese, & le Nete sono communi.
decima, con l'altre per ordine con la Decimanona di questo; lasciando da un
canto la Quintadecima; in ciascheduno de i generi nominati le Proslambanome-
nos distanti dalle Hypate hypaton per il Tuono maggiore, & dalle Hypate meson per la
Diapēte, & dalla Mese per la Diapason; simigliantemente dalle Netediezeugmenon per
la Diapason diapente, & dalle Netesynemennon per la Diapasondiatessaron; & ultima-
mente dalle Nete hyperboleon per la Disdiapason; bisogna dire, che sia uero necessaria-
mente quello, che nella Proposta habbiamo detto; Che in ciaschedun genere le Proslam-
banomenos, le Hypate, la Mese, la Paramese & le Nete siano communi. Questo non si
può negare, disse M. Adriano. Bisogno è, diss'io, che hora ui ricordate quello, ch'io ui dissi
nella Duodecima, Tertiadecima & Quartadecima definitione; che Sono alcune chorde
nelle mostrate diuisioni de questi generi, le quali sono in tutto & per tutto Stabili; alcun'al
tre, che sono in tutto Mobili; & alcune, le quali nō sono ne al tutto Mobili, ne al tutto Sta-
nili; & queste le chiamo Neutrali. Me ne ricordo; ei rispose; & Voi chiamate Stabili quel-
le; ch'in ogni diuisione hanno un'istesso interuallo & una proportione istessa con la chor-
da Proslābanomenos: & non mutano ne luogo, ne nome in qual si uoglia de i tre nomina-
ti generi. La onde le Mobili saranno quelle, s'io non m'inganno; che non haueranno tali
conditioni. Voi dite bene Messere; risposi, & non u'ingannate punto. Ma le Neutrali no-
minai nella Quartadecima definitione quelle, ch'essendo Stabili ne i due primi generi; si
mutano però nell Terzo. La onde per dimostrarui tutte quelle, che sono sottoposte ad
una di queste tre sorti, dirò in questo modo.
PROPOSTA XXIII.
ciascuna diuisione de i nominati Generi.
Paramese, & le Nete in ciaschedun genere de i tre nominati sono Communi. Et
per , che si è dimostrato, tengono gli istessi Interualli con la Proslambano-
menos; onde non mutano ne nome ne luogo; Adunque, per la Duodecima definitione
d'hoggi, la Proslambanomenos, la Hypate, la Mese, la Paramese, & le Nete sono sempli-
cemente Stabili & ferme. Ma perche si è dimostrato nella Ventesimaprima di questo, che
la Parhypate diatonica diuenta Lychanos enharmonica; simigliātemente la Trite diuen-
ta Paranete; però è manifesto, per la Terzadecima definitione, che le Lychanos & le Para
nete sono in tutto Mobili. Ditemi questo, ui prego; disse M. Frācesco; nella Decima & nel-
la Quintadecima proposta d'hoggi; se ben mi ricordo; mi è paruto uedere, che le Parhypa-
te & le Trite del Diatonico & del Chromatico insieme , & siano contenute
sotto gli istessi Numeri & Interualli con la Proslambanomenos; come adunque le potre-
mo noi chiamare Mobilo? A fè, diss'io, che mi piace M. Francesco, che dimostrate d'haue
re in memoria quello, ch'io hò detto; & che dubitate molto bene. Però à questa uostra di-
man da rispondo; che queste Chorde non chiamaremo in tutto, come l'altre facemmo,
Stabili, e Mobili; Ma si bene; per la Definitione Quartadecima data da principio di que-
sto ragionamēto; & come feci nelle Istitutioni;2. Par. Cap. 38. Ne in tutto stabili, Ne in tutto mobili. On-
de di sopra dissi, che le Stabili si chiamano semplicemente Stabili, & l'altre in tutto Mo-
bili; però le porremo nel numero de quelle, c'habbiamo nominato Neutrali. Percioche
essendo la Parhypate insieme con la Paranete communi ne i due primi generi; si muta la
prima nella Lychanos dell'Enharmonico; & la Secōda nelle Paranete, lasciando solamen-
te, ò perdendo il nome, che riteneuano ne i due nominati generi. Hora lasciamo
questo da un canto, & ueniamo à dimostrar; che
page 231

PROPOSTA XXIIII.
consonanze, fino à Nete hyperboleon, si troua Otto fiate la Diapason; prima Quattro
fiate tra le chorde Stabili; dopoi due tra le Neutrali; & oltra di questo Due tra le Mo-
bili. La Diapente si troua Sette volte; cioè, Tre nelle Stabili; Due tra le Neutrali &
Mobili; Vna tra le Neutrali; & Vna tra le Mobili. Simigliantemente Otto fiate si
troua la Diatessaron; come, Quattro fiate tra le chorde Stabili; Due nelle Neutrali; &
Due nelle Mobili.
gli risposi; La Prima chorda della Diuisione, ò Compositione, che è Proslam-
banomenos, come dice la proposta. Per qual cagione la nominate in cotal mo-
do, disse M. Claudio; Perche iui s'incomincia à formare, seguendo di mano in mano, le
page 232 Consonanze, risposi. Quando dicete, Fino à Nete hyperboleon, soggiunse M. France-
sco; intendete uoi, che si con numeri essa Nete? Messer si, risposi. Stà bene; disse egli;
seguitate adunque. Et cosi seguitai. Siano adunque le chorde a. b. c. d. e. f. g. h. i. k. l. m. n. o
& p. le quali contenghino i Quattro Tetrachordi, Hypaton, Meson, Diezeugmenon, &
Hyperboleon. Dico primieramente da a. Proslambanomenos fino à p. Nete hyperbo-
leon, contenersi Otto fiate la Diapason. Et questo, Quattro fiate nelle chorde Stabi-
li; Due nelle Neutrali; & altre Due nelle Mobili. Imperoche a. con h. per la Quinta
proposta di questo, contiene in se tre Tuoni maggiori, due minori, & due maggiori Se-
mituoni; Adunque, per la Trentesimanona del Secondo, a. con h. contiene la Diapason
consonanza. Sarà adunque a. con h. la prima Diapason. Simigliantemente; perche b.
con i. c. con k. & d. con l. ciascheduna di esse contengono i Cinque Tuoni nominati & li
due Semituoni; il che fà anco e. con m. f. con n. g. con o. & h. con p. però dico e. con m. esser
la Quinta Diapason; f. con n. la Sesta; g. con o. la Settima; & h. con p. la Ottaua; come
diciamo b. & i. esser la seconda; c. & k. laTerza; & d con l. la Quarta. Adunque da Pros-
lambanomenos a. fino alla Netehyperboleon p. sono contenute Otto Diapason; secon-
do 'l nostro proposito. Ma Proslambanomenos & Mese ci danno la Prima; la Seconda
uiene da Hypate hypaton & Paramese; & da Hypatemeson & Netediezeugmennon uie-
ne la Quinta; simigliantemente da Mese & Netehyperboleon nasce l'Ottaua; Ma la
Precedente ci hà dimostrato la Proslambanomenos, le Hypaton, la Mese, la Parame-
se, & le Nete esser chorde Stabili; adunque tra le Otto consonanze della Diapason si ri-
trouano Quattro Diapason tra le chorde Stabili. La terza poi si troua tra la Parhypate
hypaton & la Tritediezeugmenon, la Sesta tra la Parhypate meson & la Trite hyperbo-
leon; Ma la Precedente ci hà dimostrato, che le Parhypate & le Trite sono Neutrali; cioè
Ne mobili ne stabili; adunque tra Otto Diapason se ne ritrouano Due collocate tra le
chorde Neutrali. Lychanos hypaton con Paranete diezeugmenon ci danno la Quarta:
& la Settima nasce tra Lychanos meson & Paranete hyperboleon; Et perche la Prece-
dente dimostrò, che le Lychanos & le Paranete sono mobili; però tra le Otto nominate
Diapason se ne trouano Due tra le chorde Mobili, che sono la Quarta & la Settima. Se-
condariamente dico da a. Proslambanomenos à p. Netehyperboleon contenersi la Dia-
pente Sette fiate; & cosi lo prouo. Per la Trentesima del Secondo giorno, la Diapente
contiene due Tuoni maggiori, un minore & un maggior Semituono & per la Quarta
di hoggi ab. & cd. sono Due Tuoni maggiori, d & e. un Tuono minore, & b con c. il mag-
gior Semituono, adunque a & e. contiene la Diapente. Sarà adunque a & e. la Prima
Diapente. Ma perche c & g. contiene simigliantemente i due Tuoni maggiori & il mino-
re, con il Maggior semituono; il che fà anco e. con i. f con k. g con l. h con m. & k con o. però
dico c & g. esser la Seconda Diapente; e. con i. la Terza; f. con k. la Quarta; g. con l. la
Quinta; h. con m. la Sesta; & k. con o. la Settima. Ma la Prima è contenuta da a & e. da
Proslambanomenos & Hypate meson; la Terza da e & i. da Hypate meson & Paramese;
& la Sesta tra h & m. che sono Mese & Netediezeugmenon. Et già nella Precedente
habbiamo dimostrato tutte queste chorde essere Stabili; però diremo, che la Prima, la
Terza, & la Sesta Diapente sono contenute tra le chorde Stabili. La Seconda etiandio
si troua collocata tra c & g. cioè, tra Parhypate hypaton & Lychanos meson; & la Setti-
ma tra k & o. tra Trite diezeugmenon & Paranete hyperboleon; Onde, per la Preceden-
te habbiamo, le Parhypate, & le Trite esser chorde Neutrali; & le Lychanos con le Pa-
ranete esser Mobili; adunque la Seconda & la Settima Diapente si trouano collocate tra
le chorde Neutrali & le Mobili sopra nominate. Ma la Quarta Diapente si troua essere tra
f & k. cioè, tra la Parhypate meson & la Trite diezeugmenon; & la Precedente ci dimo-
stra, che ciascheduna di queste chorde è Neutrale; adunque la Quarta diapente è collo-
cata tra le Neutrali. Resta la Quinta, la quale è posta tra g & l. ò tra Lychanos me-
son & Paranete diezeugmenon; & habbiamo, per la Precedente, che queste due chor-
de sono collocate tra le Mobili; adunque la Quinta Diapente è posta tra le chorde Mo-
page 233 bili. Bisogna hora dimostrare, che da a. fino à p. ò da Proslambanomenos Nete hyper-
boleon sia contenuta Otto fiate la Diatessaron; Prima tra le chorde Stabili Quattro uolte;
dopoi Due tra le Neutrali; & Due tra le Mobili; onde dico. Nella Quarta proposta di
questo fu mostrato, che b con e. contiene il Semituono maggiore, & c con d. il Tuono me-
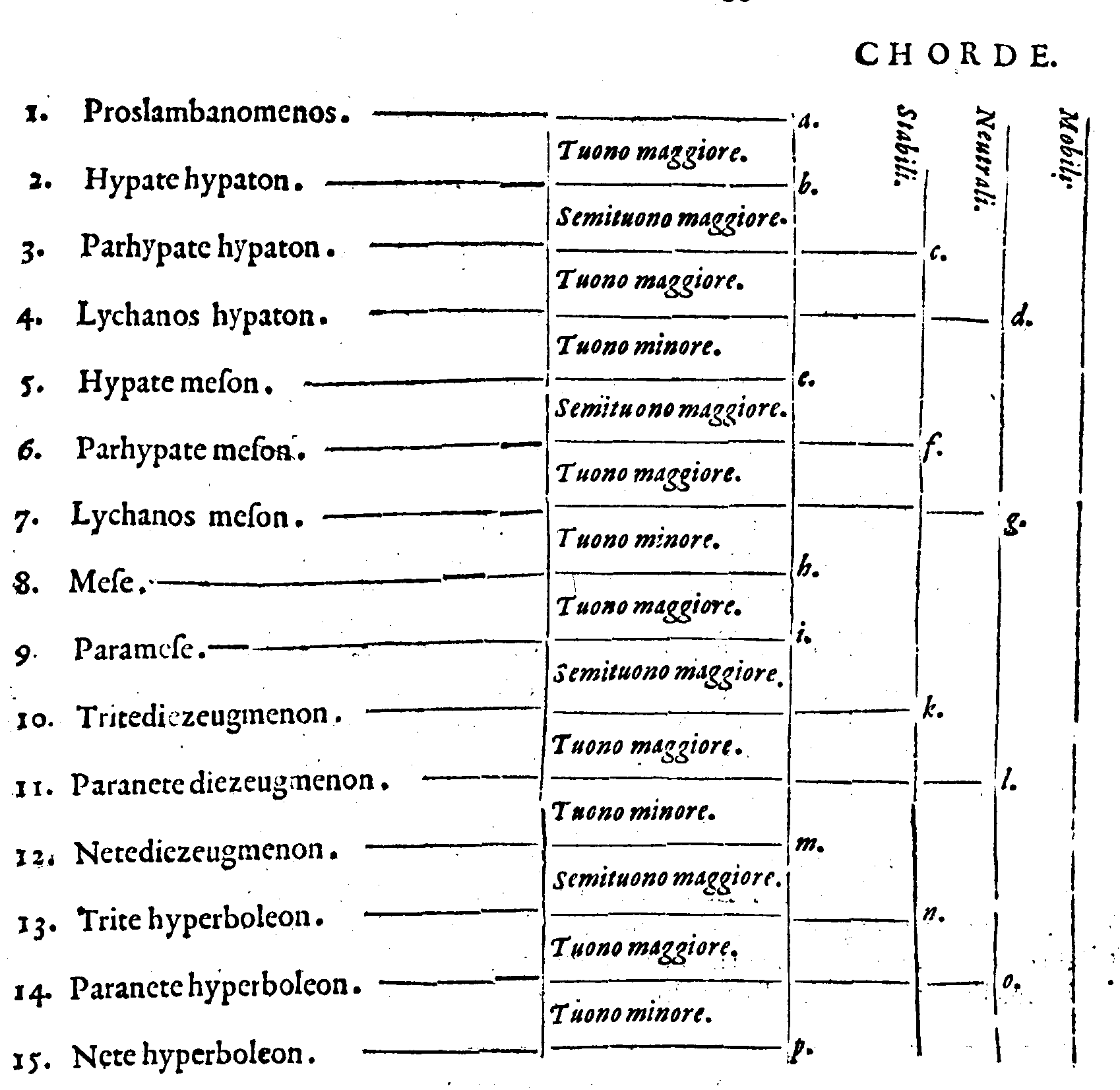
che, per la Ventesimasettima del Secondo giorno; la Diatessaron contiene tutti questi In-
terualli; però b con e. sarà la prima Diatessaron. Ma perche e & h. simigliantemente con-
tiene i Due Tuoni nominati & il maggior Semituono, il che fanno anco i. con m. & m.
con p. però dico e. & h. esser la Quarta diatessaron; i & m. la Quinta; & m con p. la Ottaua.
La onde essendo la Prima b & e. contenuta da Hypate hypaton & Hypate meson la Quar
ta e. & i. tra Hypate meson & Mese; la Quinta i & m. tra Paramese & Nete diezeugmenon;
simigliantemente la Ottaua m & p. tra Nete diezeugmenon & Nete hyperboleon. Et, per
la Precedente habbiamo, che tutte queste Chorde sono Stabili; adunque tra le Otto Dia-
tessaron contenute da Proslambanomenos à Nete hyperboleon se ne trouano Quattro
contenute tra le chorde Stabili. Hauendosi anco prouato, che c con d. & d. con e. siano
Due tuoni, il Primo maggiore & il Secondo minore; & per la Quinta di questo giorno,
hauendosi mostrato e & f. esser Semituono maggiore; confessaremo tutti, che c & f. sia
un'altra Diatessaron; & diremo, ch'ella sia la Seconda. Il che diremo ancora di k & n.
page 234 Ma perche la Prima di queste due c & f. è da Parhypate hypaton à Parhypate meson; &
la Seconda è da k ad n. ouero da Trite diezeugmenon à Trite hyperboleon, le quali sono
chorde; come si è dimostrato nella Precedente, Neutrali; però seguita, tra le otto Dia-
tessaron nominate di sopra; ritrouarsene Due nelle chorde Neutrali. Più oltra; perche
d & g. contiene un Tuono maggiore, un minore, & un maggior Semituono; il che con-
tiene anco l & o. però dico d & g. esser la Terza diatessaron; & l con o. la Settima. Ma la
Terza è contenuta tra Lychanos hypaton & Lychanos meson; & la Settima tra Paranete
diezeugmenon & Paranete hyperboleon; & già habbiamo, per la Precedente, che tut-
te queste Chorde sono Mobili; adunque tra le Otto Diatessaron contenute da Proslam-
banomenos à Nete hyperboleon si trouano due Diatessaron, collocate tra le chorde
Mobili. Et cosi habbiamo per cotal modo manifestato & dimostrato tutto quello, che
contiene la Proposta. Ditemi per uostra fè; disse hora M. Adriano; non usiamo noi
nelle Compositioni la Diatessaron posta tra Proslambanomenos & Lychanos hypaton;
ouer tra Mese & Paranete diezeugmenon, le quali danno buoni accordi? E' uero che
le usiamo, dissi. Da che nasce adunque; ei soggiunse; che tra le chorde già mostrate non
le hauete numerate? A questo risposi; Perche altro ordine si troua nelle Voci di quel
che si troua ne gli Istrumenti arteficiali; Onde in quelle, perche da ogni parte piegar si
possono, & non son stabili; si potrà sempre formare qual si uorrà Interuallo, riducen-
dolo alla sua uera & natura le forma; ma in questi non si potrà fare, se non quel tanto, quan
to patisce l'ordine contenuto nelle chorde loro, le quali dopo l'essere state tirate sotto
quelle proportioni, che si trouano in un'ordine; non si possono più alterare, senza guastare
cotal ordine. Ma perche gli Istrumenti arteficiali si possono ritrouar di due sorti; come
sono quelli, che hanno tutti i loro Interualli contenuti nella lor uera & natural forma; &
quelli che hanno gli Interualli ridotti à quella temperatura, che habbiamo nominato
Partecipatione; però dico, che se in questi si ritroueranno le Consonanze, che hauete
nominato; non si ritroueranno però ne i primi, quando non ui s'aggiungeranno altre
chorde di quelle, che si è dimostrato. Onde concludendo dico, che è uerissimo quello,
ch'io hò dimostrato; & è uero, che non si ritrouano uoi nominati Interualli tra quel-
le chorde, lequali nominato hauete. Ma non per questo seguita; che non si possino ritro-
uare ne gli Istrumenti al modo già detto temperati; & maggiormente formar con le Voci
ad ogni nostro bel piacere. Et perche sopra di questo nelle Istitutioni2. Par.
Cap. 45. hò ragionato lun-
gamente; & ne ragionarò etiandio ne i Sopplimenti;4. Supple.
cap. 11. però hauendo qualche dubio; cre-
do che leggendoli quando ui sarà commodo; potrete esser fatto chiaro. Onde con uostra
buona licenza seguiterò l'altra Proposta.
PROPOSTA XXV.
Quattro nelle Stabili, Due nelle Neutrali, & Due nelle Mobili. Oltra ciò; Tre
fiate si ritroua la Diapente nelle chorde Stabili; & la Diatessaron si troua Otto volte,
Quattro nelle Stabili, Due nelle Neutrali, & Due nelle Mobili.
per la Duodecima, e & h. Diatessaron; per la Quarta del Secondo; a & h sarà
la Diapason. Sarà adunque a & h. la Prima, & b con i. la Seconda; percioche
b & e. si troua essere Diatessaron; essendo che b & c. uiene ad essere Semituono maggio-
re; c & d. il minore, i quali; per la Decimanona del Secondo ragionamento; aggiunti
insieme fanno un Tuono minore, & d con e. il Trihemituono. Il perche essendo anco-
ra e & i. Diapente; percioche contiene e & h. Diatessaron; & h con i. Tuono maggiore; ne-
page 235 cessariamente b & i. contengono la Diapason. Et perche, per la Duodecima proposta
d'hoggi, e & h. contiene la Diatessaron; & h con i. è Tuono maggiore; simigliantemen-
te perche i & m. è la Diatessaron; però aggiunto h & i. Tuono maggiore alla Diatessaron;
per il Secondo Corollario della Trentesima proposta del Secondo; nasce la Diapente.
Onde aggiunta essa Diapente alla Diatessaron, per la Quarta proposta del Secondo gior-
no, nasce la Diapason e. & m. la quale è la Quinta. Simigliantemente; perche h & m. è
Diapente; & m con p. è Diatessaron; h & p. sarà l'ottaua Diapason. Ma perche la prima
Diapason è contenuta da Proslambanomenos & Mese, la seconda da Hypate hypaton &
Paramese; la Quinta tra Hypatemeson & Netediezeugmenon; & la ottaua tra Mese &
Netehyperboleon; le quali tutte sono; per la Ventesimaterza di questo; chorde Stabi-
li; però diremo; tra le Quindeci chorde chromatiche ritrouarsi quattro Diapason col-
locate tra le chorde Stabili. Oltra di questo; perche f & g. è Semituon minore; & g con
h. è Semiditono, ouer Trihemituono; però f & h. sarà un Ditono; essendo che; per la
Ventesimaterza Definitione del Secondo ; il Semituon minore è quell'Interual-
lo, per il quale esso Ditono sopr'auanza 'l nominato Semiditono, ouer Trihemituono.
Ma h & i. è Tuono maggiore; simigliantemente i & k. è Semituono maggiore; che, per
la Ventesimasesta proposta del Secondo nominato, fanno un Semiditono; adunque f
con k. per la Trentesima & Trentesimaprima del Secondo ancora, è Diapente. Et c con
f. è una Diatessaron, che con la Diapente; per la Quarta del Secondo; fanno una Dia-
pason; adunque da c à k. si ritroua la terza Diapason. Et all'istesso modo potremo dire
della Sesta, la quale è contenuta tra e & m. Ma perche la Terza si ritroua tra Parhypate
hypaton & Tritediezeugmenon; & la Sesta è collocata tra meson & Tritehy-
perboleon; essendo tutte queste chorde, per la Ventesimaterza di questo giorno, Neu-
trali; però dico; che tra le Quindeci chorde, che contengono otto Diapason; due ue
ne sono contenute tra le chorde Neutrali. Et perche d & g. è Diatessaron, & g con l. è
Diapente; essendo che g con h. è Semiditono, h & i. Tuono maggiore, & i con k. Semi-
tuono maggiore, il quale con k & l. Semituono minore, per la Decimanona del Secon-
do, giorno, fà un Tuono minore; però h & l. per la Ventesimasettima pur del Secondo; è
Ditono; & per la Trentesima, g con l. è Diapente; onde, per la Quarta del giorno istes-
so, d & l. uiene Diapason, la quale è la Quarta. Il simile si può dire anco di g & o. per-
cioche già habbiamo prouato g & l. esser Diapente, & l con o. com'è manifesto; uiene
una Diatessaron; adunque, per la medesima Quarta; g & o. uiene la settima Diapason.
Ma perche la prima di queste due è contenuta da Lychanos hypaton, & da Paranete
diezeugmenon; & la seconda da Lychanosmeson, & da Paranete hyperboleon, le qua-
li chorde sono, per la Ventesimaterza d'hoggi, chiamate Mobili; però tra le chorde
Mobili habbiamo due Diapason delle otto contenute tra le Quindeci chorde, che sono
la Quarta & la Settima. Adunque tra le Quindeci chorde chromatiche, otto fiate si tro-
ua la Diapason; quattro nelle Stabili; due nelle Neutrali; & due nelle Mobili. Segui-
terò anco à dimostrarui; che tra le nominate Quindeci chorde, non si troua altro che tre
fiate la Diapente; & ciò le chorde Stabili. Et perche chiaramente si uede, che b &
e. & e con h. simigliantemente i & m. uiene una Diatessaron; & a con b. & anco h con i.
un Tuono maggiore; però, per il secondo Corollario della Trentesima del Secondo
giorno; a & e. sarà la prima Diapente; e. con i. la seconda, & h con m. la terza. Percio-
che questa corrisponde in Dupla proportione con a & e. Onde lascio per breuità di dirne
altro, per esser la cosa da se stessa chiara & manifesta. Ma essendo contenuta la prima
Diapente tra Proslambanomenos & Hypatemeson, la seconda tra Hypatemeson & Pa-
ramese, & la terza tra Mese & Tritehyperboleon; le quali sono, per la Ventesimaterza
d'hoggi, tutte chorde Stabili; però si può dire, che la Diapente si troui esser tre fiate col-
locata nelle chorde Stabili; come dice la proposta. Questo stà bene; disse qui M. Fran-
cesco ; ma dimostrateci la Diatessaron quante fiate ella si troui tra le dette Quindeci chor
de. La Diatessaron, dissi, è contenuta solamente Quattro fiate tra le otto prime chorde delle
page 236 delle mostrate Quindeci, & quattro fiate nell'altre corrispondenti à coteste in Dupla
proportione. Onde quattro uolte si troua tra le Stabili, due tra le Neutrali, & due tra
le Mobili; Imperoche, per la Vndecima di questo, b & e. fanno la Diatessaron; adun-
que b & e. sarà la prima. Et perche, per l'istessa Vndecima, c & d. Semituono minore, &
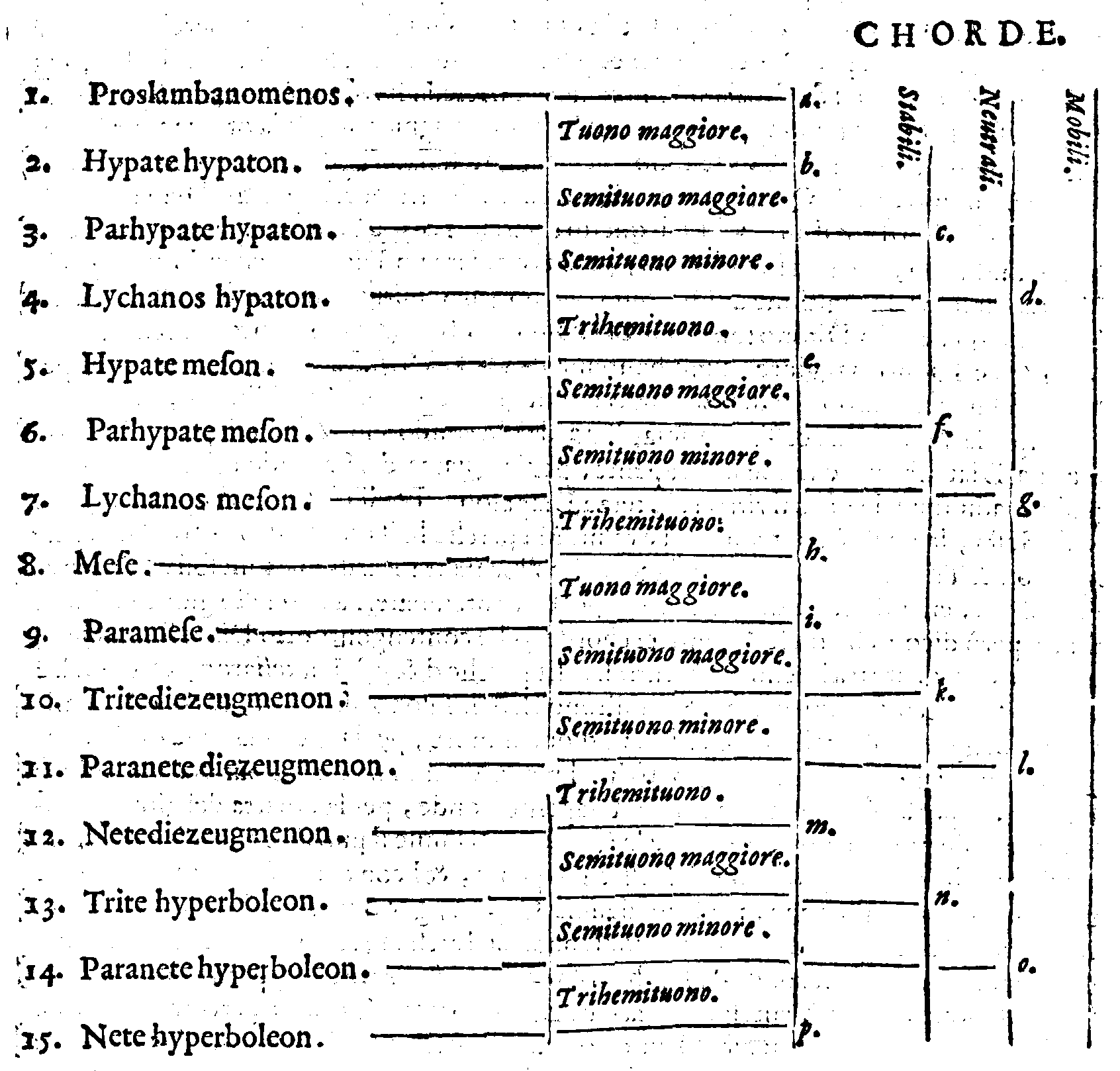
nore. Et, per la Duodecima di questo, e & f. è Semituono maggiore; adunque c & f.
sono due Tuoni; l'un maggiore & l'altro minore, con un maggior Semituono; & fan-
no, per la Ventesimasettima del Secondo, la Diatessaron. Sarà adunque c & f. la secon-
da Diatessaron. Et perche ancora, per la Duodecima proposta d'hoggi; e con f. è Tri-
hemituono; però d & g. contiene un Tuono maggiore & un minore, con un maggior Se-
mituono. E' adunque d & g. la terza Diatessaron. Ma, per l'istessa Duodecima; e &
h. contengono la Diatessaron; adunque e & h. sarà la Quarta. Et per tal modo haueremo
tra la prima Diapason a & h. quattro fiate la Diatessaron; alle quali corrispondono quat-
tro altre poste tra la Diapason h & p. come i & m. alla b & e. k & n, alla c & f. l et o. alla d &
g. et m con p. alla e et h. Et perche la prima b et e. si ritroua tra Hypate hypaton et Hypa-
te meson; la quarta e et h. tra Hypate meson et Mese; la quinta tra i et m. tra Paranete et
Netediezeugmenon; et la ottaua met p. tra Netediezeugmenon et Netehyperboleon;
essendo tutte queste chorde, per la Ventesimaterza sudetta, Stabili; seguita che queste
page 237 quattro Diatessaron siano collocate tra le chorde Stabili. Essendo poi c & f. contenuta
tra Parhypate hypaton et Parhypate meson; et k con n. collocata tra Tritediezeugmenon
et Trite hyperboleon, lequali sono chorde Neutrali; seguita, che tra le otto Diatessaron
contenute tra le Quindeci chorde chromatiche, due se ne ritrouino poste tra le chorde
Neutrali. Ancora; perche d et g. è collocata tra Lychanos hypaton et Lychanos meson;
& l con o. è posta tra Paranete diezeugmenon et Paranete hyperboleon; essendo per la
Ventesimaterza nominata; le Lychanos et le Paranete chorde Mobili; seguita, che queste
due Diatessaron siano collocate tra le chorde Mobili. Et questo è tutto quello, che se-
condo la proposta ui douea dimostrare. Vn'altra sola proposta ui uoglio proporre, et
poi far fine; & sarà questa.
PROPOSTA XXVI.
pason consonanza; tre la Diapente; & otto la Diatessaron; sotto l'istesse conditioni mo-
strate nella Precedente.
che. Dico primieramente, che tra esse si troua; come etiādio si troua tra le Diato-
niche & le chromatiche, otto fiate la Diapason; come per la Ventesimaquarta, &
per la Precedente, si è dimostrato; & ciò quattro fiate nelle Stabili; due nelle Neutrali; &
altre due nelle Mobili. Dico dopoi, che la Diapente si ritroua solamente tre fiate nelle
chorde Stabili, Percioche essēdo a & b. per la Decimasettima di questo, Tuono maggio-
re; & b con e. Diatessaron; per l'istessa; a con e. è la prima Diapente. Simigliantemente, e &
i. sarà la seconda; percioche essendo e & h. per la Decimaottaua d'hoggi, Diatessaron; & h
con i. Tuono maggiore; per il secondo Corollario della Trentesima del Secondo giorno, e
& i. sarà Diapente. Il simile si può dire di h & m. che si è detto di a & e. percioche corrispō-
dono per ogni lor chorda l'una all'altra in Dupla proportione, & un'istesso ordine. Onde
h & m è la terza Diapente. Ma perche ciascheduna di esse è compresa ne i suoi estremi da
una Hypate, ò Mese; ouer da Paramese, ò da Nete, le quali, per la Ventesimaterza di que-
sto, sono tutte chorde Stabili; però dicemo la Diapente ritrouarsi tre fiate nelle chorde
Stabili tra le Quindeci chorde proposte enharmoniche. Ma senza dubio è impossibile, che
tra a & d. & tra h & l. caschi la Diatessarō; Percioche a & b. & h con i. sono due Tuoni mag
giori, & b con c. ouero i. con k. Diesis maggiore; il qual Diesis con c & d. ouer con k & l.
Diesis minore cōtiene il Semituono maggiore. Onde mancarebbe in ciascheduna di que-
ste due Diatessaron un Tuono minore; essendo che, per la Ventesimasettima del Secondo;
la Diatessaron contiene un Tuono maggiore, & un minore, con un maggior Semituono;
& a con d. contenerebbe, per la Decimaottaua, & la Ventesimasesta pur del Secondo; un
Semiditono solamente. Questa impossibilità si troua anco tra f & i. & tra g & k. che sopr'a-
uanzono la Diatessaron; essendo che questa contiene (come hò detto) un Tuono maggio-
re, con un minore, & il minor Semituono; ma f & i. contiene un Diesis minore, un Ditono,
& un Tuono maggiore, & g con k. contiene un Ditono, un Tuono maggiore, & un Diesis
maggiore; com'è manifesto. Onde da queste in fuori; per ogni Quattro chorde continue si
troua una Diatessaron perfetta; come sono b & e. e & h. i & m. & m & p. con le lor mezane
chorde, che si trouano collocate tra le chorde Stabili. Il simile dico di c & f. & di k & n. le
quali sono comprese tra le Neutrali, & di d & g. & di l & o. che si trouano poste tra le Mo-
bili. Onde considerato & dimostrato tutte queste Diatessaron; secōdo che habbiamo fat-
to nella Precedente; habbiamo il proposito di tutto quel che nella proposta si cōtiene. Et
perdonatemi, s'io particolarmente non uengo à tutte le dimostrationi, che si potrebbono
fare in questa proposta; dimostrando ciascheduna cosa di una in una; il che faccio per al-
cuni rispetti. Prima, perche hormai son stanco di tanto ragionare; dopoi, perche ricordan-
page 238 doui le Dimostrationi fatte di sopra, il tutto ui può esser manifesto. Cōtentateui adunque,
ui prego, d'hauere hauuto da me hoggi tutto ꝗsto, che ui hò detto, & dimostrato. Vi aspet-
to di mane all'hora solita; perche ui uoglio finire di dimostrare & ragionar quello, che sarà
alla [[per]]fettione di questi nostri Ragionamenti. Et s'altro hauete che dirmi al presente; son
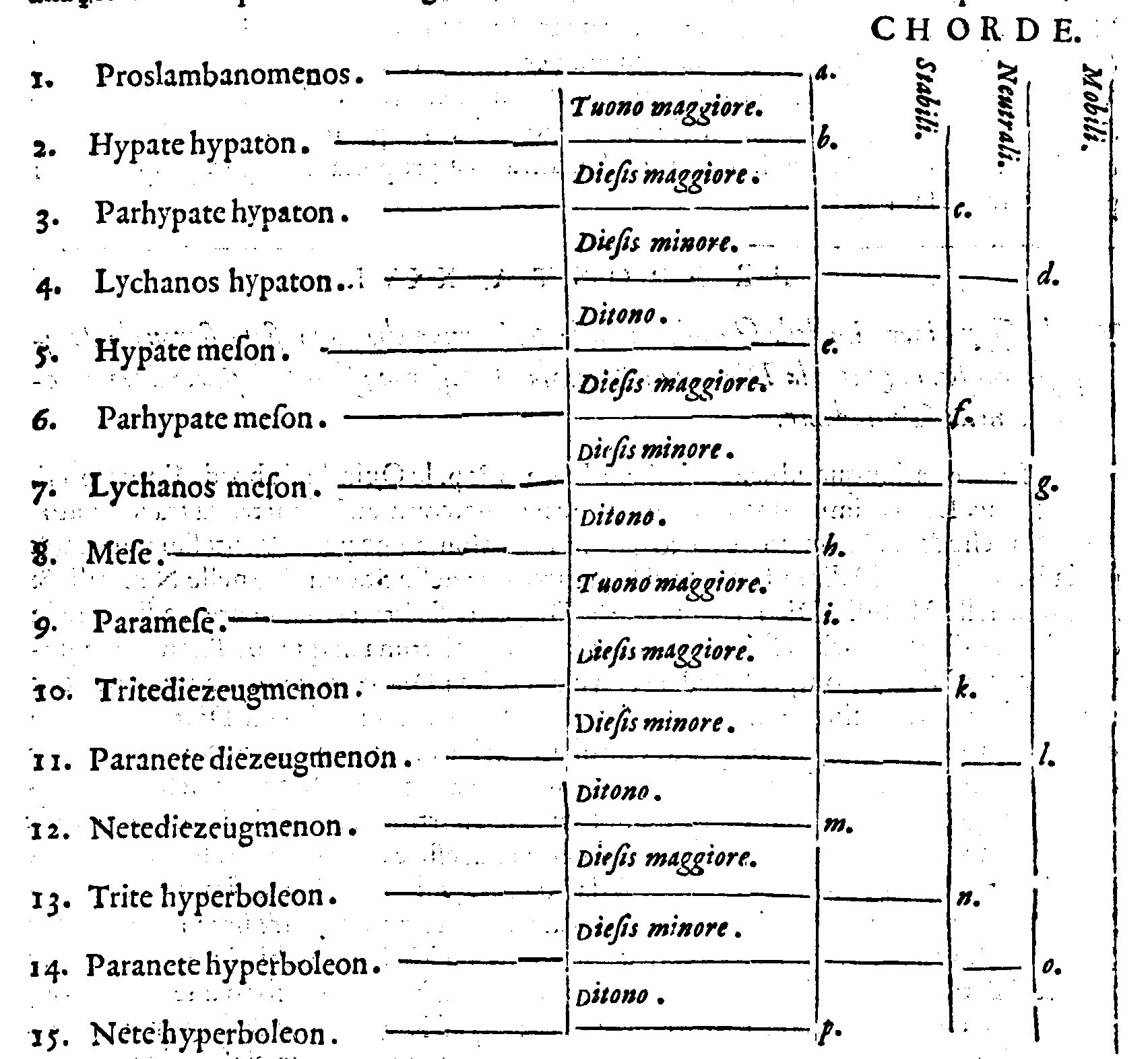
facciate fine; percioche è buon pezzo di tēpo, che uoi ragionate; ne mi resta cosa alcuna,
ch'io possa dubitare. Onde se 'l ui fusse in piacere; mi fareste un segnalato fauore à restar
tutti insieme à cena meco; & è cosa, che facilmente & senza uostro discommodo far si po-
trebbe. Io non posso per questa fiata seruirui Messere; gli dissi; perche mi resta à fare alcu-
ni seruirij, i quali uoglio hauer fatto auanti ch'io ceni. Però ui lascierò con la pace di Dio.
Et il Sig. Desiderio soggiunse; Tutti noi vi ringratiamo M. Adriano del uostro cortese &
amoreuole inuito; ne alcun di noi dissegna di restarui; perche tutti habbiamo da far qual-
che negocio inanzi cena; però restateui in pace. Cosi farò anche io, disse M. Claudio rin-
grantiandoui & lasciandoui la buona sera. Ne io agggiunse M. Francesco; posso restarci;
adunque à Dio Messere, Andateui tutti in pace; disse il buon Vecchio; & ricordateui di
ritornar dimane alla hora solita; ch'io starò ad aspettarui con gran desiderio; acciò pi-
glia vn poco di ristoro & di consolatione. Cosi faremo; rispose il Viola; la onde tutti
insieme partendosi, ciascuno andò à fare i suoi negocij.

DIMOSTRATIONI
HARMONICHE
DEL REV. M. GIOSEFFO ZARLINO
DA CHIOGGIA,
Maestro di Cappella della Serenissima Signoria
DI VENETIA:
RAGIONAMENTO QVINTO.
fero hebbe un discepolo, chiamato Ismenia; il quale hauendo fat-
to delle cose della Musica buonissmo acquisto;Val. Max.
Lib. 3. cap.
7. una fiata hauendosi
portato molto bene in cantar nel Teatro; per sua disauentura, ap-
presso il popolo (com'alle fiate intrauiene) non fù molto grato. La
onde stando mal contento, & hauendosi di ciò accorto Antigeni-
da, li disse di maniera, che tutti l'udirono; Non ti curare Ismenia
del popolo; percioche basta, che tu piaccia à me & alle Muse. Volendo dimostrare,
che bisogna far poca stima del giudicio della imperita moltitudine, la quale quasi sem-
pre non sà discernere, ne conoscer le cose buone dalle triste; essendo che la maggior
parte di essa sono Huomini di basso, uile, rozzo & abietto ingegno; dati più tosto al
uitio, che alla uirtù. Et diceua bene; percioche mi par'esser grande & abbondante
premio d'un'Arte & d'una Scienza, il conoscer prima di sapere; dopoi da huomini pe-
riti & giudiciosi esser giudicato, lodato & stimato. A' questo secondo quel gran musico
Timotheo essortaua il suo discepolo Harmonide;Lucianus
in Harmonide. à questo dico; che uolesse cercar di
piacere à quelli, che sono periti & di qualche autorità, & far poco stima del giudicio
della uolgar moltitudine. La qual cosa non solamente conuiene ad Harmonide; ma à
qualunque altro, il quale nel Teatro di questo pazzo mondo uoglia comparere. Essen-
do che faccia pur quello che uoglia di buono; che contraponendosegli l'ignoranza, ò
la malitia, & qualche fiata l'una & l'altra di queste due insieme aggiunte; sarà impossi-
bile, che non solamente possa satisfare alla plebea moltitudine; ma etiandio à quelli,
che fanno professione di sapere. Ma per applicare questa Historia al caso mio, dico; che
non hauea ancora scritto la metà di queste Dimostrationi; quando alcuni professori del-
l'Arte della Musica; ancora che poco intendenti fussero della scienza; dubitando for-
se, ch'io non hauesse à scoprir con questo mezo la loro ignoranza; come sarà in fatto;
quasi riprendendomi mi essortauano con assai parole à douer lasciar questa impresa; di-
cendo, ch'io mi potea contentar d'hauer dato in luce le Istitiutioni, le quali mi era-
no stato buon mezo d'hauermi fatto acquistare appresso il mondo buona opinione. Per-
cioche essendo opera, che tratta uarie cose, è anco diletteuole molto & di utilità non
poca à tutti quelli, che si dilettano dell'Arte di comporre Musica; & essendo le Dimo-
strationi materia difficile; per trattar de Numeri & Proportioni, iquali apportano più
tosto noia alle menti, che diletto; che non sarebbono forse tanto grate a i Professori di
page 240 quest'Arte; quanto sono state quelle; Onde meglio sarebbe, ch'io uoltassi l'animo mio
ad impiegare il tempo nel scriuere altre cose; come sono materie appartinenti allo Stu-
dio della Sacra scrittura; non sapendo eglino, che se ben'io dò opera allo studio della
Musica; per hauere il carico & l'obligo ch'io tengo con i Signori Illustrissimi; non
manco tuttauia à quello, che ciaschedun mio pari è obligato; percioche oltra il Trat-
tato della Patienza posto in luce da me già fanno molti anni; ne hò anco de gli altri;Oltra que-
sti vi so-
no anco il
Trattato
del Vero
Giorno del
la morte di
Christo; et
Della Ori-
gine de i
Frati Ca-
puccini.
Cō un Trat
tato della
Oratione,
che si fà à
Dio.
tra i quali ui è il Trattato De uera Anni forma, siue de Recta eius emendatione; che
quando saranno usciti fuori si potrà uedere, & conoscere, ch'io non cesso di affatticar-
mi in quelle cose, che possono giouare altrui & anco à me stesso. Il perche non essendo
ancora non solo uscito fuori per farmi uedere in questo Theatro, non che udire; & non
hauendomi quasi imaginato di uenirui; appresso di questa sciocca & ignorante gente;
senza udir, ne uedere cosa alcuna di quello, ch'io hauea da recitare; non solamente non
riportaua honore, ò premio delle mie lunghe fatiche; ma incominciaua a riceuerne
biasimo. Hora che pure alla fine son uscito fuori & udito da ogn'uno, che uedere & udir
mi vuole; non sò quel che si uorranno dire. Io sò troppo bene, che à questi Galli di
Esopo queste mie Dimostrationi non piaceranno; percioche saranno un gran mezo à
scoprire (come temono & hò detto anco) la loro ignoranza, & manifestare al mondo
quanto siano poco intendenti delle cose della Musica; & tanto poco, che considerando-
lo, si potranno grandemente (se haueranno uergogna alcuna della loro dapocaggine)
arroscire; percioche da esse comprenderanno, da quanta ignoranza l'intelletto loro sia
offuscato, & quanto siano meriteuoli d'esser connumerati tra i Musici. Et se per sorte
questo mio nuouo parto biasimeranno; uoglio attenermi à quello, ch'il nominato Mae-
stro disse al suo Discepolo; di piacere à tutti quelli, che sono Studiosi della buona Musica,
& desiderano di sapere i buoni fondamenti di quest'Arte; come ad uno Antigenida, &
maggiormente alle Muse; cioè, à gli huomini dotti & periti delle buone arti, dediti à i
buoni costumi; poco curandomi de quelli, che più tosto si dilettano di biasimare, che di
imitare l'altrui opere buone. Et mi basterà solamente per il premio delle fatiche; ripor-
tare, che se elle non saranno da questi nobili spiriti lodate; almeno non siano biasimate.
Ma lasciamo queste cose da un canto, & ritorniamo al nostro proposito. Dico, che il gior-
no sequente già era passato l'hora del Vespero per un gran pezzo di tempo; essendomi già
ridotto prima d'ogn'uno dal buon Vecchio M. Adriano; & hauendo molte cose discorse
soprà 'l ragionamento del passato giorno; quando il restante della nostra solita compagnia
insieme comparse; iscusandosi della loro tardanza; per essere stati insieme col Sig. Duca
à ueder la marauigliosa casa dell'Arsenale. Onde hauendo essi commemorato con gran-
de lor marauiglia infinite cose, che in quella haueano ueduto, le quali sono tutte per gli
apparecchi, che si fanno nelle guerre di Terra & di Mare; uedendo M. Adriano, che 'l tem-
po era per una buona parte, oltra il solito de gli altri giorni passato; incominciò ad essor-
tarci, che si douesse dar principio per poter finire il resto di quelle cose, che si haueano in-
cominciato à discorrere in questi nostri Ragionamenti. Il perche desideroso di satisfare
al suo uolere; incominciai cosi à dire. Per dar fine hormai questo nostro honorato tra-
tenimento Messere, & terminar quello, che io hò principiato di dimostrarui, uoglio pri-
ma, secondo la promessa, che ui hò fatto; dimostrare una Temperatura, ò Partecipatio-
ne; come più ui piace di nominarla; de gli Istrumenti arteficiali; come sono Organi,
Grauocembali, Arpichordi, Monochordi, & altri simili, che hanno il Tastame loro di
un'istessa maniera, alquanto diuersa (come già ui hò detto) da quella, ch'io dimostrai nelle
Istitutioni,2. Par.
Cap. 43.
& 44. & ridurre il numero delle Sedici chorde contenute nell'ordine Diatonico tra
i cinque Tetrachordi; mostrate il giorno passato; al numero de Quindeci; per fugir mol-
te difficultà, che potrebbono occorrere nel far le Dimostrationi. Ilche fatto, hauendo
prima aggiunto al numero delle Quindeci una chorda nel graue; & diuise hauendole in
cinque Hexachordi; per tener l'ordine, che tengono i nostri Musici moderni; uerrò poi
à ragionar con un nuouo pensiero; delle Specie della Diapason, di quelle Diapente, & di
page 241 quelle della Diatessaron. Finalmente, per concludere il nostro Ragionamento, ui di-
mostrerò una gran parte di quelle cose, che accascar possono intorno à tutti i nostri Dodi-
ci modi, ò Tuoni, che li uogliate dire; & poi farò fine à Dio piacendo. Ma auanti ch'io
uenga à ragionar cosa alcuna; uoglio, secondo l nostro solito, che sapiate alcuni Prin-
cipij, i quali essendo da uoi non saputi, non si potrebbe condurre al desiderato fine il no-
stro lauoro. Ditemi di gratia M. Gioseffo, disse il Sig. Desiderio; auanti che procediate
più oltra; che utilità apporta il saper questo Temperamento ò Partecipatione da uoi no-
minato, nelle cose della Musica? A questo uoglio che 'l nostro M. Claudio ui risponda;
dissi; accioche conosciate, che tutti coloro, che sono huomini di giudicio, & pratticano
questa sorte d'Istrumenti, conoscono l'utile grande, che si caua da essa. Però M. Claudio
satisfacete, ui prego, alla dimanda di questo Signore. Per obedire (subito rispose egli)
farò quello che ui piace, & dirò tutto quello, che mi uerrà alla memoria di questa cosa;
& dirò prima; che questa è stata una delle belle Inuentioni, che s'habbia potuto ritro-
uar nella Musica. La quale (per quello che da altri hò udito) ne da Greco, ne da La-
tino, ò Barbaro scrittore, è stata mai non solamente tocca, ma ne anco accennata.
Onde per dirui della sua utilità, dico che è tale; che col mezo di essa si può sapere in-
fallibilimente di quanta quantità ogni Interuallo, che si troua ne gli Istrumenti; che
poco fà furono nominati; sia accresciuto, ò sciemato fuori della sua uera & naturale
proportione. Et è cosa, che non solo è utile à saper la, per la perfettione della Scien-
za; ma anco è necessaria per l'Arte del fabricar con ragione cotali Istrumenti. Impero-
che gioua molto in saper la Ragione di cotal Temperamento, & forse più di quel che si
potrebbe alcuno imaginare. Essendo che nella misura de i Corpi sonori, che entrano
in cotali Istrumenti, i quali sono le Canne & le Chorde; si uede, che quando tali Cor-
pi sono regolati, & i luoghi doue si posano le Chorde sopra gli archetti; cioè, quell'In-
teruallo che contiene la chorda & l'altre cose ancora, siano fatte con misura & propor-
tione; ne segue grandissimo utile; percioche ne risulta una grande & eccellente bontà in
simili Istrumenti; quando anco si hanno ben regolato i loro corpi. Et tanta è la differen-
za di quello Interuallo, che non è proportionato, con quello ch'è fatto con proportione;
quanta è (dirò cosi) dalla luce alle tenebre. Essendo che quando le chorde sono tese so-
pra quei luoghi, che proportionati non sono; sono sproportionati anco tra loro i Suoni,
che da esse nascono; di maniera, ch'essendo l'una più lunga, ò più curta del douere & fuo-
ri di misura; nell'accordarle l'una uiene più tesa, ò più molle dell'altra; onde si ode ne i
Suoni l'uno hauer maggior uehementia, ò esser più debole dell'altro, & tra loro essere
sproportionati. Ma quando sono tali luoghi proportionati, ogni cosa torna commoda, &
il tutto stà bene. Et questo è non solamente utile nel regolar le estensioni & i luoghi doue
si posano le chorde; ma etiandio alla grandezza de i corpi delle canne de gli Organi; co-
me hò detto. Percioche con tal mezo si uengono à regolare non solamente quanto alla
lunghezza loro; ma ancora quanto à i loro diametri; come troppo ben conoscono tutti
quelli, che sono periti nell'Arte di far simili Istrumenti. Queste sono quelle cose, ch'io ui
posso dire, che mi sono uenute alla mente; ma ue ne sono molt'altre, le quali portarebbo-
no lungo tempo, se si uolessero d'una in una raccontare. Queste poche mi bastano; disse
il Sig. Desiderio; percioche da esse intendo l'utile che apporta questa cosa alla Musica.
Onde tocca à uoi hora M. Gioseffo à seguitare di dir quello, che uoi uoleuate dire. An-
cora io uoglio dimandarui una cosa aggiunse M. Francesco; auanti che procediate più
oltra. Ditela, dissi; che ui ascolto. Per qual cagione (soggiunse) non dimostrate pri-
ma le specie delle consonanze, che hauete nominato, & anco i Modi, & dopoi far la
Partecipatione, ò Temperamento, che uoi dite di fare? Molte cagioni mi muouono à far
questo; risposi; delle quali ue ne dirò solamente una, & sarà questa. Che poco mi impor-
ta, che tali dimostrationi si habbiano à far auanti, ò dopo la dimostratione del Tempera-
mento nominato; se non fusse, che si fuggono (com'hò già detto) molte difficultà; perche
dopo fatta la Partecipatione, ò temperamento; si dimostra il tutto più cōmodamente, &
page 242 con manco intrichi di quello, che si farebbe per inanzi. Quali sono questi intrichi? dis-
se M. Adriano. Il raddopiamento della chorda d. dissi; parlando secondo 'l modo nostro
prattico; com'hò dimostrato nelle Istitutioni;2. par. cap.
40. che si troua tra la chorda Netesynemen-
non & la Paranetediezeugmenon, le quali contengono l'interuallo del Comma; com'he-
ri ui dimostrai nella Ottaua, Nona & Decima proposta; per l'acquisto d'una Diapente
& di una Diatessaron, che si uengono à perdere, se non si aggiunge la Chorda Nete no-
minata, la quale fà un tale raddoppiamento, per l'aggiungimento del Tetrachordo syne-
mennon à gli altri quattro; anzi al Tetrachordo meson; & anco per la perdita de molte
Consonanze imperfette, le quali si uengono ad acquistar col mezo di tal Temperamen-
to. Onde per cotal mezo il tutto si rende facile & piano; che cosa lunga sarebbe & diffi-
cile in uoler mostrare, come s'acquistano, con l'aggiungere hora nel graue, hora nell'acu-
to l'interuallo del Comma. Soggiunse qui il buon Vecchio; Hò molto bene inteso, & mi
piace quando si leuano le difficultà nelle cose; onde resto satisfatto. Ma ditemi; Nella
Partecipatione, ò Temperamento, che sete per fare; si troueranno i Tuoni maggiori &
minori; come si trouano nelle già mostrate diuisioni de i Monochordi? Simigliantemen-
te, si troueranno quell'istessi Interualli, che hauete dimostrato nella Participatione fatta
nelle Istitutioni?2. par. cap.
43. & 44. Risposi à questo; Già hò detto heri, che questa Partecipatione, ò Tem-
peramento sarà d'un'altra maniera, & diuerso da quello; percioche haurà il Ditono &
l'Hexachordo minore contenuto nella lor uera & naturale forma; ma gli altri Interualli
saranno compresi da un'altra; percioche le lor proportioni faranno sorde & irrationali,
come uederete; e i Tuoni, quantunque non si possino con numeri certi & rationali deno-
minare nelle forme loro; saranno tuttauia equali di proportione; come si trouano equali
in proportione quelli, della Partecipatione fatta nelle Istitutioni; & quelli che seruono
al Diatonico diatono; che l'uno & l'altro di questi in ciascun Tetrachordo è di propor-
tione Sesquiottaua. Et perche i Tuoni della detta Partecipatione dimostrata nelle Isti-
tutioni, non sono differenti l'un dall'altro di proportione; ancora che sia Irrationale; & il
Ditono & l'Hexachordo minore ancora è cōtenuto insieme con qualunque altro suo In-
teruallo da proportione irrationale; però questa sarà molto differente da quella. Adun-
que, disse M. Claudio; uolete fare un nouo Temperamento, & dimostrare una noua Par-
tecipatione. Cosi uoglio fare, risposi. Et ei soggiunse; Questo mi piace assai però quan-
to più tosto incominciarete à dimostrarci questa cosa; tanto più l'haueremo cara. Et io
seguitai in questa maniera. Per ritornare adunque doue lasciai, dico; Bisogna prima che
sapiate la forma de quelli Interualli, che si accrescono, ò minuiscono; acciò non proce-
diamo senza cognitione di quel che prima dobbiamo sapere. Però uerremo alle Defi-
nitioni loro; accioche da esse possiate uenire in cotale cognitione. Ma auertite; ch'io
non uoglio diffinirui se non quelli Interualli, i quali patiscono alteratione della lor pro-
pria forma; essendo che de quelli, i quali non sono sottoposti à tal passione, & restano nel-
la lor pura essentia, già ne sete capaci. Et perche la Diapason non si può alterare accre-
scendola, ò minuendola più, ò meno della sua forma naturale, che è la Dupla proportio-
ne; senz'offesa dell'Vdito; sia in quale accordo, ò temperamento, ò partecipatione si
uoglia; simigliantemente; perche il Ditono & l'Hexachordo minore restano in questo
Temperamento nella lor uera & naturale forma & proportione; però quando nominerò
questi tre interualli; sempre li haurete da intendere in ogni luogo esser compresi nella lor
perfettione. Ma quando uorrò intendere ragionando d'alcun altro Interuallo, che sia
alterato, & fuori della sua forma; sempre gli aggiungerò una parola, con la quale ui farò
auertiti, di quale Interuallo si haurà da intendere. Incominciando adunque dalla Dia-
pente, la quale è più uicina alla forma della Diapason nella sua proportione, & è mag-
giore d'ogn'altro Interuallo semplice; sia qual si uoglia; dirò in questa maniera.
page 243
DEFINITIONE
PRIMA.
la sua uera forma, d'vna quarta parte intiera d'vn Comma.
due settime parti, ò pure una quarta parte di una cosa? Crederei, disse il Vio-
la; che fussero maggiori due settime parti, che una quarta parte. Cosi è; risposi;
percioche vna Quarta parte è minore de due settime per una Ventesimaottaua parte de
la cosa. Adunque; soggiunse il buon uecchio; la Diapente auanza in questa Partecipa-
tione, che far uolete, una Ventesimaottaua parte di un Comma; della qual lei era mi-
nore nella Participatione, fatta nelle Istitutioni; Onde è più vicina alla sua perfettione,
essendo sciema d'un quarto; che non è essendo fatta imperfetta di due settimi. E' uero
dissi. A fè, replicò M. Adriano, che mi piace questo guadagno; poi che 'l Ditono & l'
Hexachordo minore restano nella loro perfettione naturale, & la Diapente s'auicina al-
l'esser suo perfetto; ilche fà anco la Diatessaron di ragione. Questo è uero; dissi; percio-
che quel che si leua alla Diapente, si dà alla Diatessaron; & quel che s'aggiunge a quella,
da questa si leua. Et non può essere altramente; percioche restando (come u'hò detto)
la Diapason nella sua vera forma; & essendo integrata da questi due Interualli; come di-
mostrai nella Quarta proposta del nostro Secondo ragionamento; bisogna necessaria-
mente, che la cosa passi in questo modo; Che quello che si leua ad uno, si rendi all'al-
tro; accioche le cose caminino giustamente. Però diremo, che
DEFINITIONE II.
sua uera forma, d'vna quarta parte intiera d'un Comma.
tesima ottaua parte d'vn Comma, da quella ch'è posta nella Partecipatione
fatta nelle Istitutioni. Cosi stà la cosa; risposi. Soggiunse allora M. Adriano;
Questa differenza può ella causare alcun tristo effetto? Messer nò; gli risposi; percioche tal
quantita e tanto picciola, che quasi non ue lo sapreste imaginare. Di gratia ditecela,
disse il buon Vecchio. Son contento; risposi; onde soggiunsi, che il Comma à una Ot-
tantesima prima parte d'un Corpo sonoro, il quale Comma se diuiderete in sette parti
(come nella partecipatione delle Istitutioni si troua fatto) una settima parte uiene ad
essere 1/567 di tutto il nominato Corpo; percioche molteplicate queste 81 parti per il nu-
mero Settenario; fanno 567. Ma perche la differenza, ch'è tra due settimi & un quarto,
è uno Ventesimoottauo; questa differenza uiene ad esser la 1/2268 parte di cotal Corpo; es-
sendo che molteplicato 81. per 28. ne risulta 2268. Questa parte, disse il Signor Deside-
rio; ch'è la differenza già detta, è tanto picciola, ch'è quasi lontana dal senso; com'io
credo. Credete bene; gli risposi; percioche, si come il Vedere non sarebbe capace del-
l'alteratione d'un Numero tale, quando ad una tanta quantità de Scuti sen'aggiungesse,
ò leuasse uno solamente; cosi l'Vdito non potrebbe comprendere un tale accrescimento,
ò diminuione fatta in un corpo sonoro. Ne ueramente si potrebbe anco udire; quando
udir si uolesse, un'Interuallo si picciolo posto da per sè. Ma quando alcun'Interuallo si
page 244 accrescessse, ò minuisce di , una buona & purgata orecchia lo potrebbe for-
se udire. Ma uediamo quello, che segue.
DEFINITIONE III.
ramente; Perche se, per la Trentesima del Secondo giorno, la Diapente nasce
dalla congiuntione del Ditono col Semiditono; restandò 'l Ditono nella sua ue-
ra forma; bisogna ch'el Semitono sia minor di quella quantità istessa, ch'è la Diapente.
Io intendo; soggiunse il Buon Vecchio; seguitate pure. ;
DEFINITIONE IIII.
Comma.
siderio. Dissi allora, sarà questo; che
DEFINITIONE V.
quarte parti intiere del Comma.
tesimasesta Definitione del nostro Secondo ragionamento, diceste; che 'l
Comma è interuallo, per il quale il Tuono maggiore sopr'auanza il minore;
adunque il Comma è la differenza; che si troua tra 'l Tuono maggiore & lo minore. Co-
si mi pare, che sia, risposi. Adunque ei soggiunse; se uno sciema la intiera metà
del Comma, & l'altro di tanta quantità piglia accrescimento, è buon conto da far;
che in questa Partecipatione, ò Temperamento i Tuoni uengono ad esser'equali.
Et tanta uiene ad esser la proportione di uno, quanto quella dell'altro. Questo è tutto
uero; risposi; Mesere; & già ue l'hò detto due fiate. Ma sommamente mi diletta il ue-
derui; che in questa uostra età senile habbiate memoria di ricordarui cosi ben quello,
che si è dimostrato; & che sapiate cosi ben far conto delle cose della Musica; cosa uera-
mente, che non suol cosi spesso esser'in un Vecchio; & questo mi dà tanto contento,
che non mi rincrescerebbe mai di parlare in questa materia, per farui piacere. Ma an-
diamo pure auanti.
DEFINITIONE VI.
Sedici chorde diatoniche, uiene ad esser maggiore della sua natural forma, d'una quarta
parte d'un Comma.
nitione del Secondo, la Diatessaron è maggior del Ditono per il Semituono
maggiore; è necessario, ch'essendo accresciuta la Diatessaron per una tal parte;
& restando 'l Ditono nella sua uera forma, che 'l Semituono maggiore riceua un tale ac-
crescimēto; se uogliamo che 'l Ditono co 'l Semituono nominato facciano la Diatessaron.
Tutto quello, che uoi dite M. Claudio è uero; dissi; però seguiterò l'altra proposta; se
non hauete alcuna cosa da dire. Altro non hò da dire per hora, ei rispose; & io soggiun-
si subito; Io potrei à queste aggiunger le Definitioni de gli altri Interualli composti; i
quali uengono in tal Temperamento accresciuti, ouer sciemati della lor uera forma; Ma
perche questi saranno basteuoli à quel, ch'io uoglio di mostrare; però non uoglio di loro
dir cosa alcuna. Allora il Sig. Desiderio disse; Da quel c'hauete detto della Diapason,
che in ogni Partecipatione, ò Temperamento resta intiera nella sua uera forma & natu-
rale; mi date da intendere, ch'ella è Regina de gli altri Interualli; percioche non vuol
ciancie; ma vuol tutto quello, che le peruiene interamente. Però non mi faccio mara-
uiglia, s'Aristotele gran Filosofo ne i ProblemiProbl. 35.
Part. 19. chiama essa Diapason solamente, & non
altro interuallo, Consonanza perfetta. Quiesta non vuol dare, ne riceuere cosa alcuna,
oltra quello, che tiene; onde mi par, che gli altri Interualli siano miglior compagni; per-
cioche s'accordano tra loro, & si lasciano (quando si fà con destrezza) trattare, come si
vuole. ll perche si caua, che l'interuallo della Diapason sarà sempre rationale, & si po-
trà in ogni luogo, che si trouerà, descriuere con numeri rationali, & anco il Ditono con
l'Hexachordo minore di questo Temperamento; come hauete detto; ma gli altri non si
potranno descriuere con i numeri nominati; & per tal modo resteranno irrationali. Que-
sto già ui hò detto di sopra, risposi; Ma dopoi c'habbiamo definito gli Interualli, che so-
no temperati, ò partecipati; uoglio che ueniamo à definir le Specie delle Prime con-
sonanze; ma auertite prima; acciò conosciate quello di che ragiono; che
DEFINITIONE VII.
forma, secondo ciaschedun genere, de terminata ne i termini di qual si uoglia proportio-
ne, la quale faccia Consonanza.
Diapason, la Diapente & la Diatessaron, dissi. Douete però sapere, che le
specie della Diapason sono sette; quelle della Diapente sono Quattro; & quel-
le della Diatessaron sono Tre; come dimostrai nel Cap. 12. 13. & 14. del Terzo
delle Istitutioni. Di maniera che sempre si ritrouano esser le loro Specie una meno del nu
mero delle chorde, che contengono. Onde Sette sono le specie della Diapason; percio-
che otto sono le chorde, ch'ella contiene; Quattro quelle della Diapente; perche cin-
que sono le sue chorde; & Tre quelle della Diatessaron; essendo quattro il numero delle
chorde, che le danno l'essere. Onde uolendole conoscer, diremo il tutto insieme.
DEFINITIONE VIII.
settima & la ottaua acuta, contiene il Semituono maggiore. La Seconda è quella, che lo
page 246 contiene tra la seconda & la terza; & tra la sesta & la settima. La Terza è quella, che lo
contiene tra la prima & la seconda, & tra la quinta & la sesta. La Quarta è quella, che lo
contiene tra la quarta & la quinta chorda; & tra la settima & la ottaua. La Quinta è
lo contiene tra la terza & la quarta, & tra la sesta & la settima. La Sesta è quella, che
lo contiene tra la seconda & la terza, & tra la quinta & la sesta chorda. Et la Settima
è quella, che cotal Semituono contiene tra la prima & la seconda chorda, & tra la quar-
ta & la quinta; procedendo sempre dal graue all'acuto.
parlò in questo modo. Due cose hora ui uoglio dimandare M. Gioseffo; L'una
è; per qual cagione non fate distintione alcuna di Tuono maggiore & di mi-
nore in queste Specie: come hauete fatto nella Terza parte dell'Institutioni?Cap. 12. L'altra;
onde auiene, che uoi fate la Prima specie delle Diapason quella, ch'hà il Semituono
maggiore tra la terza & la quarta chorda, & anco tra la Settima & la Ottaua; & fin'hora
da tutti i Musici è stato tenuto quella esser Prima, ch'hà il detto Semituono tra la Seconda
& la Terza, & tra la Sesta & la Settima; la quale è ueramente la Seconda specie, c'hauete
definito, nel uostro ordine? Al quale risposi; Quanto alla prima dimanda M. Claudio, ui
rispondo; che hauend'io (per schiuar molte difficultà) da fondar tutto 'l mio ragionamen
to sopra la Partecipatione, ò Temperamento, ch'io uoglio dimostrare; nel quale i Tuoni
vengono equali, & non ui è tra loro alcuna differenza di maggiore & di minore; non im-
porta, ch'io ò non faccia cotale differenza; pur che la sappiate dalle mie Istitutioni, che mi
hauete allegato; tanto più, per esser tal differenza incognita al senso; quantunque dalla
Ragione sia troppo ben conosciuta; ma basta hora, che uoi conosciate la differenza del
Tuono da quella del Semituono; la quale, senz'alcun dubio, è manifesta, per la molta
differenza, che si troua tra l'uno & l'altro; & che conosciate ancora, che il detto Semituo-
no sia il maggiore, & non il minore. Ma questo Quesito ancora mi poteui fare sopra i
due Tuoni, rispetto al maggiore & al minore: onde ui si può rispondere anco quello, che
si è detto de i Semituoni; & cotal risposta può anche seruirui sopra quello, che si è dimo-
strato nella prima Partecipatione, & primo Temperamento, fatto nelle Istitutioni.2. Par.
Cap. 44. Ma
quanto alla Seconda dimanda; uoglio che sapiate; che questo ch'io fò; non lo faccio sen-
za ragione; & le cagioni che mi muouono sono molte, le quali si ridurranno finalmente in
una, & è questa; Accioche le cose della Musica siano ben regolate, & intese per quel uer-
so, ch'intender si debbono. Et accioche uoi le sapiate, vi dico la Prima essere; Che ha-
uendo dimostrato nelle Istitutioni;2. Par.
Cap. 39. che dalla Diuisione harmonicamente fatta della Dia-
pason nelle sue parti; per quanto comporta la natura della cosa; nasce un'ordine d'Inter-
ualli; nel primo de i quali, ch'è il più graue, si ritroua il Tuon maggiore; nel Secondo il
minore; & nel Terzo il maggior Semituono. Simigliantemente di nuouo nel Quarto è
collocato il Tuono maggiore; nel Quinto il minore; nel Sesto ancora il Tuono maggiore;
& nel Settimo & ultimo posto nell'acuto si troua il Maggior Semituono; chiaramente cō-
presi, che tale Diapason, diuisa secōdo la natura del Numero harmonico; era collocata tra
le nostre modern e chorde C. D. E. F. G. a.
 & c. & anco era la prima Diapason, che natu-
& c. & anco era la prima Diapason, che natu-ralmente era considerata nella Musica. Onde fui sforzato da ogni ragione à credere; che
essendo prima tra l'altre, le quali (per l'aggiunger delle chorde. Γ. A &
 . nel graue; & d. e.
. nel graue; & d. e. s. g & aa. con molt'altre nell'acuto) nascono dopo questa; ch'anco douesse tra tutte l'altre
tenere il Primo luogo; & ch'essendo in questo Genere d'ogni altra più naturale; ella do-
uesse etiandio tenere il nome di prima Specie; & che l'altre, ch'à questa succedeuano di
mano in mano, il lor luogo tenessero; secondo che per ordine erano collocate; & che ha-
uessero i lor principij nelle chorde significate & notate per le Sette prime lettere, che ui
hò mostrato. Questa adunque è stata la prima cagione, che mi hà mosso à far questo.
page 247 Voltosi allora M. Claudio uerso M. Adriano, & disse; Che ne dite uoi Messere? parmi ch'à
questo non si possa contradire per alcun modo. In uerità, rispose il buon Vecchio; che
non si puote; & parmi che M. Gioseffo habbia una gran ragione. Et per dirui il uero; non
ui era cosa nella Musica, che mi paresse più strana di questa. Percioche hauendo noi
quest'ordine de uoci Vt. Re. Mi. Fa. Sol. La. era pur contra 'l douere, che la Prima spe-
cie de tutte le Prime consonanze hauesse ad incominciar nella Seconda uoce, & non nel-
la prima di tale ordine; però sommamente hò in piacere, che M. Gioseffo uoglia ragio-
nar di questa cosa; & che sia entrato in questa buona opinione di ordinar questo disordi-
nato ordine. Messere; gli dissi allora; mi allegro molto, che à uoi piaccia questo mio pen-
siero. Onde hauendoui sempre conosciuto per Huomo d'intelletto & di giudicio; non
mi poteua capire nell'animo, che le cose fatte con ragione ui hauessero à dispiacere. Pe-
rò uoglio seguitare allegramente la Seconda cagione, la quale è quell'istessa, c'hà mosso
uoi. Perche hauendo i nostri Maggiori ridotto l'ordine delle Chorde musicali in Hexa-
chordi; & hauendoli attribuito quell'ordine de Voci, che nominato hauete; più tosto
bisognaua dar principio à queste Specie nella prima uoce Vt; che nella Re, che è la Se-
conda; accioche quando si peruiene alla Quarta specie, al modo loro; non si hauesse à ri-
tornare in dietro, & incominciar nel Quarto luogo di tale ordine dalla uoce Vt, la qua-
le, per ogni douere, dourebbe tenere il primo, & non l'ultimo luogo; come uedete fat-
ro nella loro Quarta specie de tutte le prime Consonanze. Questa adunque fù la Secon-
da cagione. Questa è cagione ragioneuole, disse il Viola. Ond'io soggiunsi; La Terza
cagione fu; che oltra quel c'hò detto, il quale è tutto fatto con ragione; uedeua, che po-
nendo per fondamento di queste Specie la Prima chorda della nominata diuisa Diapa-
son; & applicandole (per parlarui al modo prattico) le uoci Vt. Re. Mi. Fa. Sol. La; la-
sciamo star da un canto, che queste Sillabe seruino alla memoria; per ricordarsi, che la
Prima è il fondamento della Prima specie di ciascheduna delle nominate Consonanze,
& la Seconda quello della Seconda, & cosi l'altre per ordine; haueressimo etiandio in
questa Prima specie adunate tutte le Specie dell'altre Consonanze nominate, le quali or-
dinatamente hauerebbono il loro principio & fondamento nella C. prima chorda della
detta Diapason, & nella Vt. prima sillaba del nostro Hexachordo; il che tornarebbe som-
mamente bene, & meglio di quello, che hanno fatto i nostri Antichi, i quali hauendo pri-
ma collocato la Prima specie nella chorda A, & nella sillaba Re; quantunque seguitassero
poi, & il tutto li tornasse commodo; tuttauia non poterono porre le Specie della Diapen-
te in cotal modo l'una dopo l'altra; percioche la Seconda specie non poteua cadere tra
la chorda
 . & la F. Onde furono costretti ad incominciar nella chorda D. & seguitar di
. & la F. Onde furono costretti ad incominciar nella chorda D. & seguitar di mano in mano. Ma non potero già dar principio alle specie delle loro Diatessaron in co-
tal chorda; percioche la Terza specie à patto alcuno non può cascare tra la chorda F. &
la
 . essendo che (come sapete, & come lo chiamate) è un Tritono, il quale è Interuallo
. essendo che (come sapete, & come lo chiamate) è un Tritono, il quale è Interuallo dissonantissimo nella Musica. Questo è pur troppo uero; disse M. Adriano; & ueramente
ui dico, che quest'ordine è molto necessario; prima per regolare & indrizzar ben le cose
della Musica; dopoi è vtile per la memoria delle cose; com'hauete detto; però laudo mol-
to questa cosa. Et se bene ad alcuno nella prima uista questo parerà forse strano, difficile &
amaro; non dubitate, che l'uso farà facile & addolcirà il tutto. Cosi credo Messere, diss'io.
Ma la Quarta cagione, che m'ha mosso è questa; perch'io uedeua di potere accommo-
dare i nostri Modi, ò Tuoni, che sono come ui potete ricordare) Dodici; l'un dopo l'al-
tro per ordine naturale & non interrotto; come fin hora si è fatto. Essendo che accommo-
dando, ò attribuendo il Primo modo alla prima Diapason C & c. & alla prima uoce Vt;
seguendo l'altre sillabe, ò uoci, & gli altri Modi per ordine; le corde loro finali ordinata-
mente ueniuano C. D. E. F. G & a. & le Modulationi loro con bello & regolato ordine
ueniuano à finire nelle uoci Vt. Re. Mi. Fa. Sol. La; come potrete à suoi luoghi uedere. Et
le Sedici chorde. Γ. A.
 . C. D. E. F. G. a.
. C. D. E. F. G. a.  c. d. e. f. g & aa. veniuano à contenere essi
c. d. e. f. g & aa. veniuano à contenere essi Modi tutti; tanto gli Autentichi, quanto i Plagali; senz'auanzar chorda alcuna.
page 248 L'utile & il commodo adunque, che apporta quest'ordine; per quello che mi pare; mi fe-
ce entrare già molti giorni sono in questo pensiero. Questi m'inuitauano & persuade-
uano; la ragione mi daua animo & essortaua; & la natura istessa della cosa mi costringe-
ua & facea uiolenza. Il che scorgerete da quel che son per dimostrarui; di modo che se
mai per il passato in questo hebbi altro parere, & hebbi animo di seguitar i nostri Anti-
chi; non dico de Greci; hora in tutto & per tutto mi rimuouo. Molte fiate, disse M. Fran-
cesco; de questi ordini de Specie mi son forte marauigliato tra me stesso, & non sapea ri-
trouare altra ragione; se non che i Nostri maggiori hauessero cosi voluto. Ma molto mi
sono piaciute le ragioni, che hauete detto; & se bene altro non portasse meco à Ferra-
ra; porterò almeno questo, come cosa bella & noua; & ui prometto che da noi la porre-
mo in prattica con tutto 'l nostro potere. Non uoglio pero che crediate, risposi; ch'io uo-
glia esser destruttore delle cose de gli Antichi; percioche non hebbi mai tanto tristo pen-
sero; ma uoglio ben, che pensate; che lasciando le cose loro nel loro essere, le uerrò à mu-
tare solamente secondo certi accidenti; come è di ordine di Primo & di Secondo, sen-
za'alcun'altra alteratione della loro sostanza; & cercarò sempre di facilitar le cose di que-
sta Scienza. Ne ui pensate ancora, ch'io possa fare altramente; essendo che qual si uoglia
Specie di consonanza; quanto alla sua forma è sempre immutabile & inuariabile; ma
quanto poi à gli accidenti, i quali anco sono estrinsechi; come di Primo, ò Secondo; ò di
Graue, ò di Acuto; si può senz'alcuna alteratione, quanto al nome, uariare. Et uolete ue-
dere, che cosi sia; pigliate qual si uoglia Diapason, & datele nome di Prima, ò di Secon-
da; come meglio ui piace; tale accidente non haurà forza di farle uariar forma; Percio-
che se uoi le attribuisti mille & poi mille nomi, & la riportaste, ouer le deste mille luoghi
uariati; mai ella si cambierà di forma & sostanza; ma resterà sempre quella; essendo che 'l
nome di Primo, ò di Secondo nasce da pura Relatione, la quale tra gli altri accidenti è
debolissimo & estrinseco delle cose ridotte in un'ordine. Onde tale Relatione si può ad
ogni nostro piacere mutare; senza uarietà alcuna della Forma, ò della Sostanza delle co-
se. Ma se in lei si rimouerà alcun Tuono ò Semituono; trasportandolo verso l'acuto, ò
verso 'l graue; non è dubio, che tale Diapason non sarà com'ella era prima; ma cambierà
la prima forma in un'altra; come da quello ch'io mostrai nel Cap. 16. & 17. della Terza
parte delle Istititioni si può comprendere. Percioche sarà mutata nelle cose intrinseche
& essentiali. Onde per ritornare à dir qualche cosa al proposito, dico; che se alla Diapa-
son D & d. hò dato il Secondo luogo nell'ordine delle sue specie, & alla C & c. il Primo;
per questo, ne l'una, ne meno l'altra hò mutato di forma & di essentia; ma sono nel primo
loro essere. Et se i nostri Antichi attribuirono alla Diapason posta tra Proslambanome-
nos & Mese il nome di Prima specie; lo fecero, perche la Proslambanomenos era la
Prima chorda dell'ordine de i loro Suoni; la onde era 'l douere che in cotal chorda, co-
me prima d'ogni altra, dessero principio alle loro Specie; tanto più, perche non hebbe-
ro mai in consideratione, che la nominata Diapason fusse diuisa in harmonica diuisione,
ò non; come habbiamo noi; & ciò non senza proposito; Essendo che hauendo noi al lo-
ro ordine aggiunto un'altra chorda nel graue, la quale chiamate Gamma vt; & conside-
rando la detta Diapason C & c. al modo nominato diuisa; sà dibisogno, che di lei habbia-
mo altra consideratione. Disse qui il Sig. Desiderio; In uerità che è cosa ragioneuole &
lodeuole molto; che siate entrato in questo honorato pensiero, degno da essere abbrac-
ciato da ogn'uno; perche mi par uedere, c'hauerete accommodato molto gentilmente
le cose della Musica. Ond'io à questo soggiunsi; Vi voglio ancora aggiungere, oltra l'altre,
una cagione, che mi spinse à uolere tener quest'ordine; la quale hor'hora mi è souenuta;
& è questa; perche dall'ordine, che nasce da queste specie delle prime Consonanze fatto
in cotal maniera, io poteua ordinare i Modi l'un doppo l'altro, secondo la mente de gli
Antichi; percioche accommodando 'l Primo modo alla Prima nostra Diapason C & c. &
il Terzo alla D & d. & gli altri poi per ordine; ueniua ad accommodar questi tre modi à i
loro tre primi & principali; come il Primo al Dorio, il Secondo al Frigio, & il Terzo al
page 249 Lidio, i quali sono distanti l'un dall'altro per un Tuono; nel modo, che sono i modi di essi
Antichi; come ne i loro Scritti si può uedere; & massime nel Cap. 10. del 2. Lib. de gli Har-
monici di Tolomeo. E' vero quello, che dite; disse il Sig. Desiderio; & per quello, che
mi ricordo, l'hò ueduto anch'io appresso de molti Autori, tanto Greci, quanto Latini.
Vi ricordate bene; risposi; & di questo forse che ne ragionerò ne i miei Sopplimenti; se-
condo che mi uerrà l'occasione. Ma questo, per hora ui potrà bastare; per farui lasciar da
un canto le marauiglie; se pure alcuna in uoi ne hauete; & che ui potrebbono auenire in-
torno questa cosa. Io per me; disse M. Adriano; ne son fuori; perche le ragioni, c'haue-
te addotto mi costringono à confessar, che questo sia ben detto, & ben fatto. Questa co-
sa è troppo ragioneuole; soggiunse M. Claudio; & li uorrebbe assai contrarij à distrugger-
la. Che ne dite uoi M. Francesco? Questo è uero; egli rispose; ne hà contradittione alcuna;
onde piacēdoui M. Gioseffo; seguitarete il resto. Cosi uoglio fare; dissi; poi che io uedo,
che 'l mio parlare non ui torna in dispiacere. Ma ui uoglio prima dire; che se bene sopra di
questa cosa li sarebbe da dire assai; uoglio però hauer fatto fine; & se 'l ui resterà qualche
dubio intorno alla materia de i Modi, potrete (leggendo la Quarta parte delle mie Istitu-
tioni & il Sesto Libro de i miei sudetti SopplimentiCap. 3.) d'ogni dubio, che ui potesse occor-
rere, pienamente esser risolti. Passerò adunque à dirui dell'altre Specie, seguitando
questo nuouo Ordine.
DEFINITIONE IX.
il Semituon maggiore. La Seconda è quella, che lo contiene tra la seconda & la ter-
za. La Terza è quella, che lo contiene tra la prima & la seconda. Et la Quarta
quella, che lo contiene tra la quarta & l'ultima; andando sempre dal graue all'acuto.
molto facile da intendere. Però passate più inanzi. Cosi farò; gi risposi; & uer-
rò à definire le Specie della Diatessaron, in questo modo.
DEFINITIONE X.
& la quarta chorda. La Seconda è quella, che lo contiene tra la seconda & la terza.
Et la Terza è quella, che lo contiene tra la prima & la seconda; procedendo sempre dal
graue all'acuto.
mi piace che la Prima specie di ciascheduna habbia principio in un luogo istes-
so; ma in che cosa ue ne seruirete di esse? per uostra fè. Risposi à questa diman-
da; Non senza cagione le hò poste in questo luogo; & uoi sapete pure; che i Modi, ò
Tuoni moderni pigliano la forma loro, come faceuano anco gli antichi, da queste Spe-
cie; ne per altro à i tempi nostri sono l'un dall'altro differenti; se non per l'Harmonia, ò
Modulatione più tosto, che usciscono da esse. Hora u'intendo; disse ancora il Viola; Per-
che uolendo ragionar di essi; uolete che ciaschedun si conosca da esse, come da Parti prin-
cipali, che li compongono. Cosi è; risposi; Però accioche meglio intendiate quello, che ui
son per dire; uoglio definirui il Modo, ò Tuono, che lo uogliate chiamare, & dirui; che
page 250
DEFINITIONE XI.
son, modulata per quelle specie di Diapente & di Diatessaron, ch'alla sua forma sono
conueneuoli.
scriuete nelle Istitutioni.4. par. cap.
10. & 11. Tanti sono ueramente, soggiunsi. Et egli; Volete uoi
por la definitione di ciascheduno, accioche si conoscano separaramente l'un
dall'altro? Ben sapete, gli risposi; Perche è cosa molto necessaria. Ma uoglio
che sappiate; che uolēdo proceder secondo l'uso & la ragione ancora; si diuidono in due
parti; nella Prima si pongono quelli, che sono contenuti nella Diapason, diuisa in una
Diapente & in una Diatessaron; di maniera che questa tenga la parte acuta, & quella la
parte graue della diuisione, la quale si chiama (come lo dichiarai nelle Istitutioni,4. par. c. 9. & lo di-
chiararò anco) diuisa harmonicamente. Et nella seconda si pongono quelle, che sono
contenute nella Diapason diuisa medesimamente ne i due nominati Interualli, di manie-
ra, che siano in essa al contrario di quello, che sono posti & collocati i primi; cioè, che la
Diapente stia nella parte acuta, & la Diatessaron nella graue di tale Diapason. Onde da
tale diuisione si chiama diuisa arithmeticamente; Il perche diremo.
DEFINITIONE XII.
in una Diapente & in una Diatessaron, di maniera che la Diapente sia collocata nella
parte graue di essa, & la Diatessaron nell'acuta.
detto nelle Istitutioni; Onde passate all'altra definitione, quando ui piace. A'
questa aggiungeremo, dissi; che
DEFINITIONE XIII.
chorda in tal maniera è partita, che la Diatessaron occupi il luogo graue, & la Diapente
l'acuto tra essa, in tale diuistone.
mostrato hauete; imperoche la Decimasettima proposta del nostro Primo ra-
gionamento (se ben mi ricordo) dimostra; che l'interuallo Duplo nasce dalla
congiuntione de i due maggiori Superparticolari, Sesquialtero & Sesquiterzo; & la De-
cimaottaua dimostra, che aggiunti insieme questi due, costituiscono la Proportionalità
harmonica. Onde essendo l'interuallo Duplo la forma della Diapason, lo Sesquialtero,
quello della Diapente, & lo Sesquiterzo quello della Diatessaron; aggiunti insieme que-
sti due ultimi; necessariamente costituiscono questa proportionalità. Il che ne segue an-
co, quando essa Diapason è diuisa al modo detto nella Definitione nelle due nominate
parti da una chorda mezana. Cosa che niun sano di giudicio è per negare. Allora M.
page 251 Francesco; disse; Ne questa si potrà negare Messere; parlando della Diapason arithmeti-
camente diuisa come dice la Definitione; percioche, dalla Duodecima proposta del Se-
condo ragionamento, si uede dimostrato; che tra questa Arithmetica progressione 4. 3. 2.
si troua la Dupla 4 & 2. che è la forma della Diapason, diuisa dal 3. in due parti; in 4 & 3.
che è la Sesquiterza, la quale è la forma della Diatessaron; & in 3 & 2 Sesquialtera, che è
la forma della Diapente. Et perche (come si è detto più uolte) il numero maggiore di qual
si uoglia ordine di proportioni Musicali rappresenta la parte graue, ò la maggior chorda
qual si uoglia diuisione; però non si può negare, che occupando la Diatessaron colloca-
ta tra i termini 4 & 3. la parte più graue; che la Diapente posta tra 3 & 2. non tenga la par-
te più acuta nella Diapason diuisa in cotal maniera, & ch'ella non sia diuisa in Arithme-
tica proportionalità. Questo è uero, rispose M. Adriano. Et io subito soggiunsi; Ma per
uenire alla definitione de tutti quei Modi, che sono nella Prima parte delle due nomina-
te; li definiremo prima tutti insieme; dopoi definiremo tutti quelli, che sono contenuti
da numero Impare; come 'l Primo, il Terzo, il Quinto, il Settimo, il Nono, & l'Vndeci-
mo. Il che fatto definiremo quelli, che sono di numero Pari; come sono il Secondo, il
Quarto, il Sesto, l'Ottauo, il Decimo, & il Duodecimo. Onde i primi nominaremo (co-
me da i Prattici sono chiamati) Principali ouero Autentici; ma gli altri diremo Non
principali, Laterali, ouer Plagali; percioche sono posti al lato de i primi. Definiamo
adunque tutti i Primi insieme con tutti i Secondi à questo modo.
DEFINITIONE XIIII.
diuisa. Il Secondo è quello, ch'è collocato nella quinta, arithmeticamente partita. Il
Terzo è quel, ch'è posto tra la seconda, diuisa harmonicamente. Il Quarto è quello,
ch'è situato tra la sesta, diuisa etiandio arithmeticamente. Il Quinto è quello, chè po-
sto tra la Terza harmonicamente partita. Il Sesto è collocato tra la settima, ch'è diui
sa arithmeticamente. Il Settimo è quello, c'hà luogo tra la quarta specie simigliante-
mente di essa Diapason, harmonicamente partita. L'Ottauo è quel, che si trouua tra la
prima arithmeticamente tramezzata. Il Nono è quello, che tra la quinta specie pur di
essa Diapason diuisa harmonicamente si troua collocato. Il Decimo si troua tra la se-
conda arithmeticamente diuisa. L'Vndecimo è posto tra la sesta, pur diuisa harmo-
nicamente. Et lo Duodecimo è collocato tra la Terza specie diuisa secondo l'arithme-
tica progressione.
cile da intendere, che quella de i Modi; secondo l'uso de gli Antichi; percioche
non si uede di loro pur'un'essempio al mondo; & dell'altre cose si uede almeno
un poco di ritratto; come uediamo ne gli Antichi edificij, iquali appartengono alla
Scienza dell'Architettura; che se bene alcun di loro non si uede nella sua perfettione; si
troua almeno la sua pianta, dalla quale si può trarre qualche cognitione della sua forma.
Ma di quel che si troua in questa materia de i Modi; più tosto genera confusione, che
scienza. Veramente che è cosi, gli dissi; Vedete di gratia, già che sia non questo
proposito, leggendo Boethio in questa materia; che costrutto ne potete cauare, & che
distintione far potete de questi Modi l'un dall'altro, da quello ch'ei scriue? Essendo che
vuole, che facēdosi acuto tutto l'ordine dell'Hypodorio per un Tuono; restādo quelli In-
terualli istessi primi nel primo loro essere; senza lasciaruene alcuno; si generi il modo Hy-
page 252 pofrigio. Et facendo questo ordine di nuouo più acuto per vn Tuono, simigliantemente,
senza rimouere alcuno Interuallo de i primi, si faccia il modo Hypolydio; & cosi gli al-
tri di mano in mano; facendoli l'un più acuto dell'altro, ò più graue d'un Tuono, ò d'un
Semituono; senz'alteratione alcuna del primo ordine. Parmi cosa molto strana, disse
il Sig. Desiderio; che Boethio pigliasse questo errore. Allora gli risposi; Questo si fà no-
to dalle sue parole & dà gli essempij, che pone, & non si può negare. Ma non è da ma-
rauigliarsi; percioche ogn'un si può ingannar nelle cose, nelle quali non è molto pratti-
co; come forse non era Boethio; il quale fù solamente Tradottore delle cose altrui; co-
me si può conoscere da quello ch'incominciò scriuere nel Quinto Libro della Musica;
ch'è tutto di Tolomeo; tolto dal Primo de gli Harmonici. Dobbiamo bene hauere à
quest'huomo Santissimo molto obligo; percioche quanto si hà di buono tra i Latini della
Musica; l'habbiamo lui. Et che i Modi fussero distanti l'un dall'altro per un Tuono, ò
per un Semituono; in questo non u'è inganno alcuno; percioche è conforme à quel, che
scriue Tolomeo nel cap. 10. del Lib. 2 de gli Harmonici, & molti altri; iquali non starò
qui à nominarli. Onde si uede, che i nostri hanno errato à nominar Dorio quel modo,
ch'appresso loro chiamano Primo; Frigio quello, che nominano Terzo; & Lydio quel
che addimandano Quinto. Percioche il Primo è distante dal Terzo, per un Tuono;
& questo dal Quinto, per un Semituono; com'è noto à tutti quelli, ch'essercitano la Mu-
sica. La onde bisogna, uolendosi affrontar con gli Antichi ne i nomi almeno, chiamar
Dorio quello, che in questo nostro ragionamento chiamo Primo; ch'è contenuto nel-
la Prima specie della Diapason diuisa harmonicamente, la quale di sopra hò definito;
Frigio quello, che chiamo Terzo, il quale è contenuto nella Seconda specie; & Lydio
quello, ch'addimando Terzo, ch'è contenuto tra la Terza specie; essendo che cosi in-
tesi, saranno posti per ordine, secondo la mente di questi due nominati & d'altri Au-
tori celebratissimi. Et questo sarà ueramente ordine naturale; percioche ad ogni chor-
da del nostro Hexachordo, senz'interrompimento alcuno si potrà commodamente attri-
buire il fine de due Modi, l'uno Pare & l'altro Impare; di maniera che 'l Primo sarà di-
stante dal Terzo per un Tuono; questo dal Quinto per un'altro; & il Quinto dal Setti-
mo per un Semituono. Et forse non sarà detto male il dire in questo nuouo ordine, che 'l
Primo sia, ouero almeno s'assimigli al Dorio, il Terzo al Frigio, il Quinto al Lydio, il
Settimo al Mistolydio, ò Lochrese; il Nono all'Ionico, & l'Vndecimo all'Eolio; come
ordine più con forme alla mente de cotali Autori, & de molt'altri ancora. A' questo
disse il Sig. Desiderio; In uero i tre primi Modi sono lontani l'un dall'altro per un Tuono;
onde non sò uedere con che fondamento i Nostri chiamassero à punto Dorio il Primo
loro, che uerrebbe ad essere il Terzo uostro, & il Frigio il loro Terzo, che uiene à cor-
rispondere al uostro Quinto; & cosi gli altri. Ma sia come si uoglia, non bisogna atten-
dere hora à i nomi, ma alle cose. Però mi piace sommamente l'ordine, c'hauete propo-
sto di tenere; ma guardate di gratia, che non si confondiamo. Non ui sarà confusione
alcuna; risposi; quando ui terrete à memoria questo; che quando parlerò in questo ra-
gionamento de i Modi, sempre intenderò de quelli, de i quali ui son per parlare; secon-
do la proposta, che sono posti l'un dopo l'altro per ordine naturale & non interrotto. Ma
quando nominerò un de quelli, che sono contenuti nell'ordine interrotto; sempre gli
aggiungerò qualche parola, dalla quale potrete intender quello, ch'io uoglia dire. Di-
mandò qui il Sig. Desiderio; Per qual cagione detto hauete, Ordine interrotto? Al qual
risposi; Perche quelli non sono posti l'un dopo l'altro per ordine tutti immediatamente.
Ma il quinto de gli Impari, ch'è il loro Nono in ordine, è distante dal Sesto, ch'è il loro
Vndecimo per un Semiditono; onde ui cade in mezo una chorda, alla quale non è ap-
plicato Modo alcuno. Laonde hauendo egli inteso la mia risposta, aggiunse; Son satis-
fatto, & u'intendo benissimo; però seguitate quello, c'hauete à dire; onde seguitando
dissi; Quel che ui hò da dire; per poter ragionare con qualche fondamento, è; che
page 253
DEFINITIONE XV.
specie della Diapason, diuisa harmonicamente da una Chorda mezana nella modulatio-
ne d'una Diapente & d'una Diatessaron; com'è nell'ordine loro naturale il Primo, Ter-
zo, Quinto, Settimo, Nono & l'Vndecimo.
tender quello, che sia Modo con queste definitioni; il che da alcun'altro non è
stato fatto; però seguitate à dichiararci quello, che sia il Non principale, ò Pla-
gale State adunque ad udirmi, soggiunsi;
DEFINITIONE XVI.
cie della Diapason, diuisa arithmeticamente da una chorda mezana in due modulationi,
in quella della Diatessaron posta nel graue, & in quella de la Diapente posta nell'acuto;
come sono nell'ordine loro il Secondo, il Quarto, il Sesto, l'Ottauo, il Decimo, & il
Duodecimo.
diuisione harmonica & arithmetica; però queste definitioni ci sono facili. On-
de potrete passare à uostro bel piaccere à dirci qualche altra cosa. Sapiate adun-
que, seguitai; auanti che si uada più oltra; che
DEFINITIONE XVII.
è la grauissima della sua Diapente.
si denomini tutte le cose; onde meritamente scrisse Ouidio nel 3. Lib. delle
Trasfigurationi quella bella Sentenza di Solone la qual dice;
--Sed scilicet vltima semper
Expectanda dies homini est: diciꝗ beatus
Ante obitum nemo supremaꝗ funera debet.
La quale dal Petrarca breuemente nella Quarta Canzone del Lib. 1. fù esplicata in que-
sto uerso;
La vita il fin, e 'l dì loda la sera.
Onde bisogna, ch'anco i Modi habbiano una chorda, nella quale ciascheduno habbia
regolarmente à terminare, & finire; acciò si possa conoscere dal suo fine, & si possa diritta-
mente denominare. Questa adunque sarà la grauissima chorda delle loro Diapente;
soggiunsi io; Sia poi posta nella parte più graue, oueramēte nel mezo della Diapason; che
questo non fà caso; & mi piace che V. Sig. si diletti de questi due Poeti; i quali sono cop-
piosi di belle inuentioni, & belle Sentenze; come è quella, che hauete allegata. Ma per-
page 254 che le chorde de i Modi sono per tornare al proposito altramente denominate da i No-
stri, di quel che faceuano gli Antichi; però non sarà male il porre una Definitione, dalla
quale comprender si possa ciascheduna delle chorde antiche, à quale delle Moderne cor
risponda; & sarà questa.
DEFINITIONE XVIII.
do dalla grauissima; & salendo per ordine all'acutissima; i quali corrispondono à no-
mi antichi; sono questi.

Dicisette, & pure io odo alle fiate dir da uoi altri Musici; che sono alcuni Canti,
che trappassano questo numero; & arriuano al numero de Venti, & più oltra
ancora. Da che nasce adunque M. Gioseffo, che non hauete uoluto por maggior nume-
ro di esse, di quello che hauete posto? Allora gli risposi; Perche questo numero è bastan-
te à dimostrar tutto quello, ch'io uoglio dire in questo ragionamento. Essendo che com-
prende di punto tutti i Dodici modi, senz'auanzarne alcuna Et la chorda Γ. la quale è
detta da i nostri Gammaut, hò circonscritta con questo nome Hypoproslambanome-
nos; ch'è tanto, quanto s'io dicesse; Sotto proslambanomenos; accioche tutte habbia-
no le sue corrispondenti; percioche i Greci non haueano sotto la loro Proslambanome-
nos chorda alcuna. Et fù necessario, ch'ella fusse aggiunta da i Nostri; perche col suo me-
zo si uenne à fare acquisto d'un Hexachordo intiero nella parte graue di quest'ordine;
come chiaramente si vede. Ma che non si possa trappassare 'l numero delle mostrate chor-
de; colui, che lo credesse sarebbe in manifesto errore; essendo che la Prattica ci dimo-
stra 'l contrario; poi che ad ogni chorda qual si uoglia delle mostrate se ne può sempre ag-
giungere un'altra nel graue, ò nell'acuto; che corrisponda per una Diapason, & si può
circonscriuere con le medesime lettere; come si uede appresso d'alcuni, che di queste co-
se hanno lungamente scritto. Pur che; come habbiamo detto nel Cap. 13. del Secondo
delle Istitutioni; gli Interualli Naturali & gli Artificiali lo comportino. Chiaritemi; re-
plicò il Signor Desiderio; di un dubio, & poi seguitarete il uostro parlare. Da che viene,
page 255 che alle chorde, c. sol, fa, ut, & d. la, sol, re, hauete assegnato due nomi? non bastaua uno
solamente? Messer nò, risposi; percioche le due nominate chorde seruono à due Tetra-
chordi; de i quali l'uno è il Meson, & l'altro il Diezeugmenon. Intendo hora il tutto;
soggiunse egli; però seguitate. Cosi uoglio fare, dissi. Ma accioche non manchiamo in
cosa veruna, che faccia dibisogno in questo nostro negotio; definiremo questa chorda
aggiunta, & diremo.
DEFINITIONE XIX.
aggiunta alla Προσλαμβανόμενος, distante da essa per un Tuono.
no fatto gli Antichi per Tetrachordi; anzi più ragioneuolmente per Hexachor-
di; come dissi nelle Istitutioni,2. par. c. 48 i quali contengono le chorde de tutte le specie
della Diatessaron; incominciando dalla parte graue, uenendo uerso l'acuta; ò per il
contrario; & la uarietà che possono partorir le chorde de i Tetrachordi; però fù dibiso-
gno alle Quindeci chorde del Monochordo diatonico aggiuingerne un'altra grauissima;
la quale i Nostri chiamarono Gamma ut; per quella ragione, ch'io dissi nel Cap. 30. del-
la Seconda parte nominata. Et quantunque i Latini prattici habbiano chiamato i loro
Hexachordi col nome di Natura, di
 quadro, & di b molle; come nel Cap. 2. della Ter
quadro, & di b molle; come nel Cap. 2. della Terza parte dimostrai; tuttauia non uoglio partirmi al presente dall'uso & nome de gli An-
tichi; essendo che io uoglio nominare col nome de i Tetrachordi, che conteneranno nel-
se lor quattro chorde più acute di ciascheduno; secondo 'l costume de quelli, c'hanno
speculatiuamente ragionato delle cose della Musica. Onde si come cinque sono i Tetra-
chordi contenuti nel numero delle Sedici chorde del nominato Monochordo; cosi sa-
ranno etiandio cinque gli Hexachordi. Ma sapiate prima; che
DEFINITIONE XX.
maggiore nel Terzo luogo; & tra le Quattro più acute l'uno de gli antichi Tetra-
chordi; dal quale ello piglia il nome.
ello piglia il nome? Perche il nome di Hexachordo; risposi; è commune à tutti
gli ordini de Suoni, che contengono Sei chorde; ordinate però nel modo c'hò
dichiarato nella Definitione. Ma il proprio nome di cotali ordini, acquistano dal Te-
trachordo de gli Antichi, che contengono nelle più acute loro chorde: Onde al nome
d'Hexachordo; che è commune à ciascheduno de i nominati ordini, s'aggiunge Hypaton,
ò Meson; ò qualunque altro, che li fanno l'uno dall'altro differenti; almeno per il sito, se
non per altro. Ma gli Hexachordi, com'hò detto ancora, sono Cinque; Et se ben Sei so-
no le loro specie; come hò dimostrato nelle Istitutioni;3. par. cap.
20. & 21. cioè, Tre del maggiore & Tre
del minore Hexachordo; tuttauia in questa definitione, & sempre uoglio che intendia-
te, quando nominerò assolutamente Hexachordo, senz'altro aggiunto; quello, che hà
il maggior Semituono collocato tra la Terza & la Quarta chorda; incominciando come
fanno i Prattici, dalla uoce Vt, & seguendo l'altre per ordine; come poco fà nella De-
cimanona definitione hò dimostrato. Ilche incominciando dal primo; dico.
page 256
DEFINITIONE XXI.
Diatonico, & hà principio nella chorda Hypoproslambanomenos, ouer Gammaut;
seguendo Proslambanomenos, Hypate hypaton, Paripate hypaton, Lychanos hypa-
ton, & Hypate meson per ordine; il quale dal Tetrachordo hypaton, che contiene
nominato Hypaton; cioè Principale.
Tetrachordo interamente; & dalla denominatione, che hanno le sue chorde
comprendiamo tutte le specie della Diatessaron, che sono Tre; Vt. re. mi. fa;
parlando pratticamente, & intendendo tali specie; come uolete, che qui s'intendino;
Re. mi. fa. sol. & Mi. sa. sol. la. Onde mi piace questo uostro ordine; però seguitate il re-
sto. Ascoltate adunque Messere, risposi.
DEFINITIONE XXII.
do per ordine l'altre, Lychanos hypaton, Hypate meson, Parhypate meson, Lycha-
nos meson, & Mese; & è nominato Meson, è Mezano, dal Tetrachordo intero,
che contiene.
fallo. E' uero; risposi; onde uerremo al terzo, il quale facilmente si conoscerà
dalla sua definitione, che è questa.
DEFINITIONE XXIII.
& seguendo l'altre, Mese, Paramese, Tritediezeugmenon, Paranete diezeugme-
non, & Netediezeugmenon; ilquale chiamiamo Diezeugmenon; ouer Separato per
il Tetrachordo, ch'interamente contiene.
chorde del Diezeugmenon; per quel che dice la Ventesima prima definitione
proposta. Ben sapete; risposi; Ma l'altro si definirà à questo modo.
DEFINITIONE XXIIII.
do l'altre, Paranetediezeugmenon, Netediezeugmenon, Tritehyperboleon, Paranete-
hyperboleon, & Netehyperboleon; & si chiama Hyperboleon, ò vogliamo dire
Eccellente.
nominato, è detto Hyperboleon, percioche è più acuto, & è posto sopra tutti
gli altri. Cosi è soggiunsi; ma,
DEFINITIONE XXV.
do la Lychanosmeson, la Mese, la Tritesynemennon, la Paranetesynemennon, &
la Netesynemennon; & è chiamato Hexachordo synemennon, ò Congiunto.
molle; Percioche parlandoui come prattico, la uoce del Fa. è contenuta nella
Quarta chorda, la quale è circoscritta da questa lettera rotonda b; come dalla De
cimanona definitione di hoggi si può comprendere; percioche è la Decimasettima chor da posta in quell'ordine. Cosi è risposi; & Quello, poi che ui hò da dire al presente; per
poterui ragionar le cose con fondamento, sarà; che
DEFINITIONE XXVI.
portione della parte, che s'aggiunge, ouer si leua dal suo Tutto.
è alquanto oscura. E cosa honesta; risposi; Sia adunque la linea ab. diuisa in die
ci parti; di maniera che cb. ne contenga noue, & db. otto; simigliantemente
eb. ne contenga sette; & sia per essempio tra cb. & db. la proportione Sesqui
ottaua. Aggiungo ac. alla cb, onde ne nasce ab; uedete, che l'Interuallo cd. & db; è
fatto maggior di tanto, quanto è la proportione, che si troua tra ab. & cb. Et perche el-
la è Sesquinona; però cb. & db. è fatto maggior tra ab. & db. di una Sesquinona pro-
portione. Et questo è quanto all'accrescere del termine maggiore, che contiene la pro-
portione Sesquiottaua. Ma quanto al decrescere del minore, dico; che se noi lasciare-
mo da un canto la parte de della db; non è dubio, che resterà eb. Onde dico, che la pro-
portione, che si troua tra cd & db, la quale è Sesquiottaua, è fatta maggior di tanta quan
tità, quanta è quella, che si troua tra db & eb. Et perche db & eb. è Sesquisettima; però
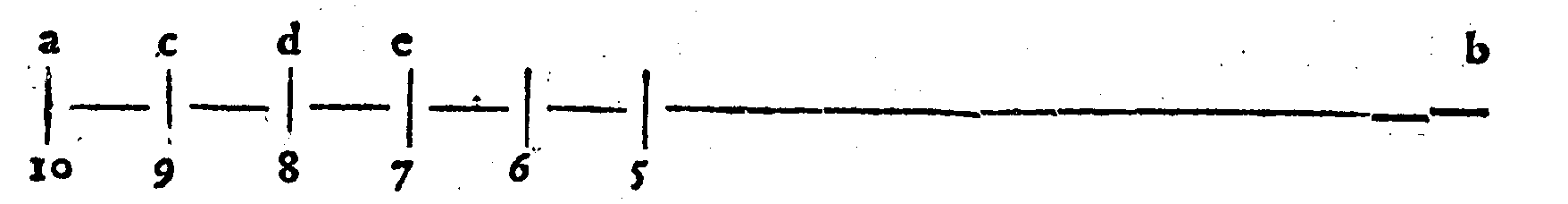
ma. Et questo sia detto quanto al farsi maggiore. Ma quanto al farsi minore; sia di nuo
uo l'interuallo ab & db. Dico se leuaremo da esso Interuallo ac; cioè, se noi faremo mino
re la ab. d tanta quantità, quanta è a c; ne resterà cb & db; & ab & db. uerrà minore
di tanta quantità, quanta è quella che si troua tra ab & cb. Simigliantemente se aggiun-
geremo cb. à db. minor termine dell'Interuallo ab; senza dubio uerrà cb; onde dire-
mo ab & db esser fatta minore di tanta proportione, quanta era quella, che si ritroua
tra cb & db. Et perche questo non è molto difficile da intendere; però passaremo all'al-
tra definitione. Venendo adunque à seguitar quello, che bisogna sapere; dico.
page 258
DEFINITIONE XXVII.
portione della chorda, che se gli aggiunge, ò leua, tanto dalla parte graue, quanto dal-
la parte acuta.
(com'io uedo) intesa la precedente, sia facil cosa d'intendere anche questi. Cosi
è ueramente risposi; ma per maggiore intelligenza la dichiararemo, in questo
modo. Sia la linea ab. sopra la quale sia accommodato l'Interuallo del Tuono maggiore
alla sua proportione tra cb & db. Se noi tra a & c. accommodaremo di nuouo il detto
Tuono, di maniera che cb. sia la sua chorda acuta & eb. la graue; non è dubio, che 'l det-
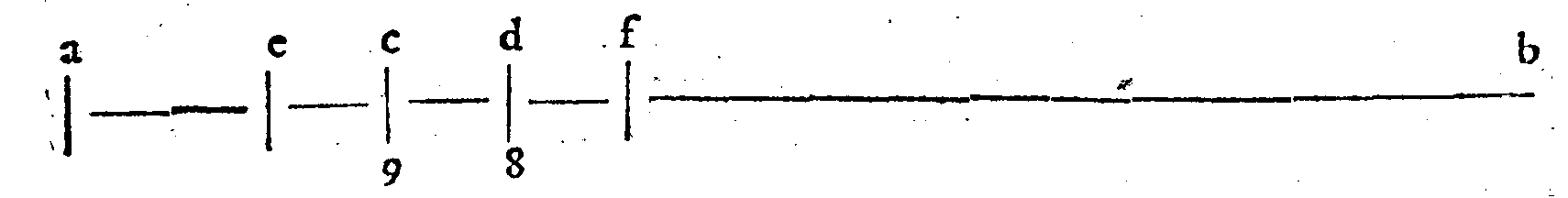
le è Sesquiottaua. Mai se sopra la chorda db. lo uorremo accommodare; di maniera che
la chorda graue sia essa db. senza dubio potremmo dire, che 'l detto Tuono farà fatto più
acuto di tanta proportione, quanta è quella, che nominato habbiamo. Et ciò sarà tra
db & fb. Percioche se cb & db. è Sesquiottaua; non è dubio, che sarà fatto più acuto
il Tuono db & fb. dello cb & db. per tale proportione. Er questo credo, che non sia du-
bioso appresso alcun di uoi; onde Voglio etiandio che sapiate; come.
DEFINITIONE XXVIII.
una irrationale, ouer dal cauar l'una dell'altra.
Voglio risposi. Et che troppo ben sapete quello, che sia quantità rationale & ir-
rationale; se ui hauete conseruato nella memoria quello, che da me udito hauete
molte fiate; & anco letto nelle Istitutioni; Però dico Messere che s'haueste dauanti (dirò
cosi). Mille fiorini; di quelli, che tenete serrati in prigione; & uenisse un'altro, che ue n'ag-
giungesse Cinquecento; non sapreste uoi la quantità, & somma de tutti quelli denari? Si
bene, disse egli. Simigliantemente soggiunsi; se da questa somma se ne leuasse Quat-
trocento; non sapreste uoi anco quella somma, che ui restarebbe dauanti? Senza du-
bio; soggiunse; percioche restarebbono Mille & cento. Vedete adunque, dissi, che sa-
pendo quel, che s'aggiunge, & quello che si leua; sapete anco l'accrescimento & il cal-
lo de i uostri fiorini? Cosi in proposito dico; che sapendo la proportione che uolete ag-
giungere, ò leuare da un'altra maggiore, ò minore di lei; conoscete anco facilmente
quello, che dall'aggiungere, ò leuar ne risulta. Et questo auiene; perche tutte queste
quantità sono rationali, & si possono con numeri descriuere. Ma non auerrà cosi, quan-
do una di esse sarà rationale & l'altra irrationale; oueramente quando l'una & l'altra ir-
rationale fusse. Percioche quello, che nascerebbe, sarebbe tutto irrationale. Et piglia-
te l'essempio de i fiorini; poi che siamo à ragionar di essi; che hauendone molti dauanti,
de i quali ne sapeste il numero; dico che se à quelli ue n'aggiungeste, ò leuaste una quan
tità; & che non sapeste quanti fussero; la quantità, che restasse, ui sarebbe anco inco-
gnita & irrationale. Io intendo hora benissimo ogni cosa disse il buon Vecchio; che det-
page 259 to m'hauete; sete però nella burla de i fiorini. Non ui burlo altramente Messere; risposi;
perche uoi non sete huomo da esser burlato. Ma ui hò dato l'essempio di esssi; perche sò,
che sapete quello che sono; per hauerne guadagnato assai col mezo del uostro ualore, &
honoratamente li hauete dispensati; dando à ciascheduno de i uostri più congiunti la par
te sua; & ue n'hauete anche saluato una buona parte; che ui farà uiuere allegramente; se
spender la uorrete. Ma lasciamo da un canto queste cose, & attendiamo à quel ch'impor
ta. Questi sono quei Principii, che ne seruiranno à tutto quello, che hoggi habbiamo da
trattare; & per daruene un poco di cappara; uoglio incominciarui à dimostrar (secon-
do la promessa) questo; che
PROPOSTA
PRIMA.
nochordo diatonico in tal temperamento, & proportione; che i Tuoni tutti saranno
equali, & da una istessa proportione contenuti; & l'Interuallo del Ditono, con quel-
lo del minore Hexachordo solamente resteranno nella lor vera & natural forma, ò
proportione; & potremo acquistar due Diapente, l'una tra la Quarta & la Ot-
taua; & l'altra tra la Vndecima & la Quintadecima chorda; & due Diatessaron,
l'una tra la prima & la quarta; & l'altra tra la ottaua & la Vndecima; & ciò
senz'offesa alcuna dell'Vdito.
veggio; non è cosi? M. Gioseffo. Cosi è risposi; Però sia, secondo la Prima pro-
posta del giorno passato, il Monochordo diatonico; il quale per la sua Vente-
simaquarta simigliantemente contenga tra il numero de Quindeci chorde; considerate
però segnate in questa maniera; hb, Kb, Cb, lb, Eb, mb, nb, ob, pb, cb, qb, eb,
rb, sb, & tb. Otto fiate la Diapason; Sette la Diapente; & otto uolte la Diatessaron. Et
uogliamo ridurre tal numero ad un temperamento, ò proportione; che acquistiamo due
Diapente; le quali tra la Quarta & la Ottaua chorda, & tra la Vndecima & la Quinta
decima; cioè, tra lb. & ob, & tra qb. & tb. non hanno luogo; & due Diatessaron, che
mancano tra la Prima & la Quarta, & tra l'Ottaua & la Vndecima chorda; cioè, tra hb.
& lb, & tra ob, & qb; lasciando il Ditono & l'Hexachordo minore nelle lor uere & na-
turali forme, ò proportioni. Accommodo prima sopra la chorda hn. l'interuallo del
Comma; per la Trentesimasesta proposta del Terzo giorno; alla sua proportione uerso
h; di maniera che nb. uenga ad essere il suo estremo acuto. Il qual Comma per la Vnde-
cima pur del detto giorno partisco in quattro parti; onde pigliandone le tre parti, più gra
ui nel punto G; per la Ventesima sesta definitione d'hoggi; uengo à far minore lInterual-
lo C. & n. di una quarta parte del detto Cōma, & accrescere l'Interuallo n. & c. di tal quan
tità. Ma perche C & n. contiene; per la Prima di heri; due Tuoni maggiori, un minore,
& un minor Semituono; però C & n; per la Trentesima del Secondo uerrà ad essere una
Diapente contenuta nella sua uera forma. Ma C & n. resta sciema & diminuta d'una
quarta parte del Comma, che è G & n. adunque, per la Prima definitione d'hoggi; la
Diapente C & n. resta diminuta della quarta parte d'un Comma, & temperata tra C &
G; secondo 'l proposito. Medesimamente; perche n & c. contiene un Tuono mag-
giore, con un minore, & un maggior Semituono; però, per la Ventesima ottaua
del Secondo ragionamento; n & c. è Diatessaron nella sua uera forma, la quale
essendo accresciuta d'una quarta parte del detto Comma, che è G & n; dico che G
page 260
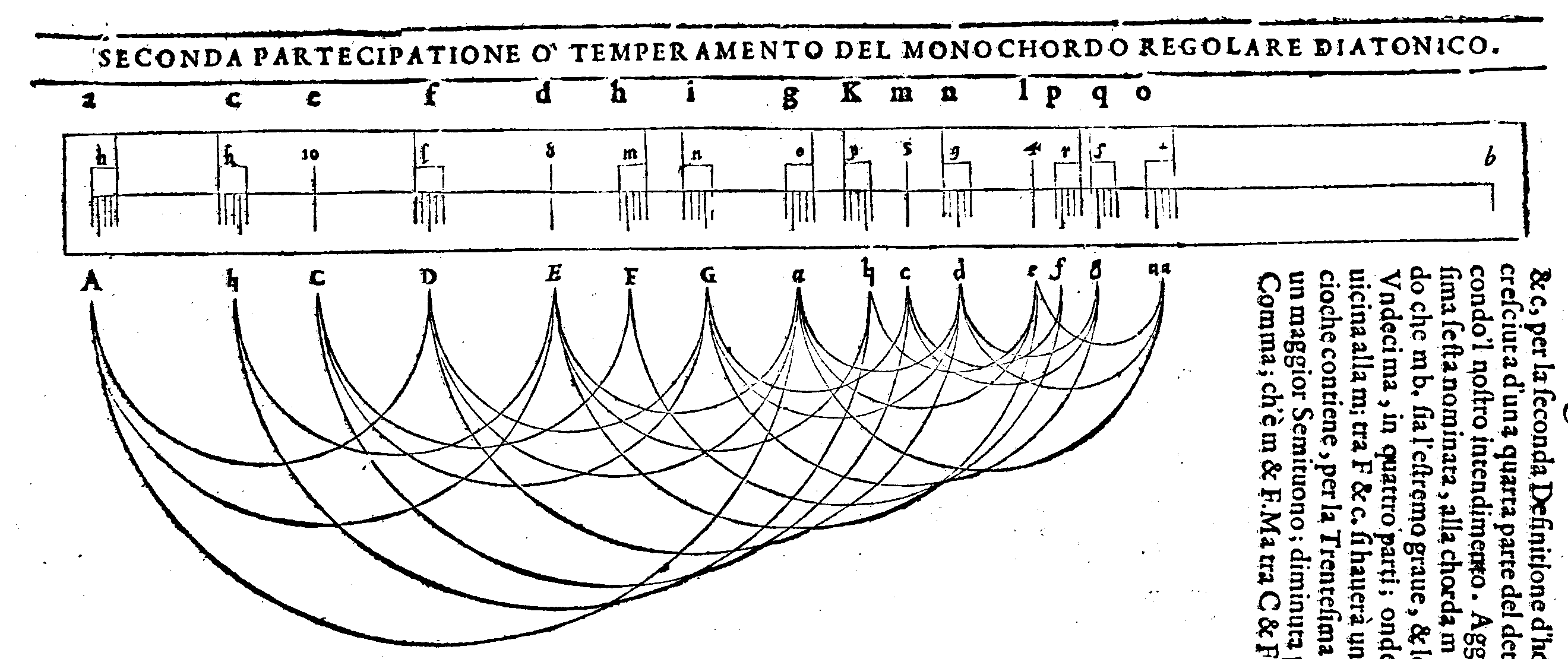
cresciuta d'una quarta parte del detto Comma; & temperata se-
condo 'l nostro intendimento. Aggiungo hora, per la Trente-
sima sesta nominata, alla chorda mb. il Comma uerso b; di mo-
do che mb. sia l'estremo graue, & lo partisco, per la nominata
Vndecima, in quattro parti; onde lasciandone una parte più
uicina alla m; tra F & c. si hauerà una Diapente temperata; Per-
cioche contiene, per la Trentesima detta di sopra; Tre tuoni, &
un maggior Semituono; diminuta però d'una quarta parte del
Comma; ch'è in & F. Ma tra C & F. haueremo una Diatessaron,
che per la detta Ventesima
ottaua; contiene due Tuoni
& un maggior Semituono;
accresciuta però della parte
m. & F. del detto Comma.
Et cosi saranno ridotte que-
ste due consonanze nel tem-
peramento loro; essendo mb.
& cb. Diapente; & Cb &
mb. Diatessaron. Onde Fb
& cb, resta imperfetta d'una
quarta parte del Comma, la
quale; per la Definitione; è
una Diapente temperata; &
Cb & Fb. uiene ad essere ac
cresciuta di tal quantità; Il
perche Cb & Fb. uiene; se-
condo la Definitione; una
Diatessaron simigliantemen-
te accresciuta di tal quantità.
Più oltra; per la quarta De-
finitione; Fb & Gb. uiene
ad essere un Tuono tempe-
rato; essendo che mb & nb.
Tuono maggiore si ritroua
diminuto de due quarte par-
ti del Comma; cioè, d'una
quarta parte mF, & d'una
quarta parte Gn; come si
può uedere. Ma perche C
& E. è Ditono; & restando
questi due termini nella loro
proportione naturale; dico
Eb & pb; per la Trentesima
del Secondo giorno; esser
Diapente; percioche con-
tiene tre Tuoni & un mag-
gior Semituono, la quale
accommodaremo al suo tem
peramento; aggiungendo,
per la Trentesima sesta del
page 261 Terzo; alla chorda pb. il Comma uerso la parte graue, & diuidendolo come gli al-
tri facemmo, in quattro parti equali; pigliando solamente le tre più graui, & trà Eb.
&
 b. haueremo temperata la Diapente, & diminuta, per la Ventesima sesta defini-
b. haueremo temperata la Diapente, & diminuta, per la Ventesima sesta defini-tione; d'una quarta parte d'un Comma, la quale è
 & p. La onde tra Gb &
& p. La onde tra Gb &  b. ha-
b. ha-ueremo anche un Ditono contenuto nella sua uera proportione; percioche ri-
trouandosi prima tra nb. & pb. nella sua uera forma; è fatto più graue; per la
Ventesima settima Definitione d'hoggi di tanta quantità, quanta è quella di Gn.
& di
 p. Et perche Eb. & on. contiene un Tuono maggiore, un minore, & un mag-
p. Et perche Eb. & on. contiene un Tuono maggiore, un minore, & un mag-gior Semituono; per tanto Eb. & ob, per la Ventesima ottaua del Secondo, è una
Diatessaron; onde per ridurla al suo temperamento aggiungeremo il Comma, alla
chorda segnata ob, uerso l'acuto, il quale diuiso al modo detto in quattro parti, &
aggiunto ad Eb. & ob. la quarta parte o & a; tra Eb & ab haueremo la Diatessaron
accresciuta d'una quarta parte del Comma, la quale sarà ridotta, secondo la sua
Definitione; al suo temperamento. Diremo ancora, per la quinta definitione, Gb.
& ab. esser un Tuono ridotto al suo temperamento; percioche essendo nb. & ob. Tuo-
no minore; uiene accresciuto tra Gb. & ab. de due quarte parti d'un Comma, che
sono Gn. & oa; com'è manifesto. Il che fà etiandio il maggiore ob. & pb; percio-
che ob. si fà più acuta in ab. d'una quarta parte del Comma, & pb. si fà più gra-
ue in
 b. per un'altra quarta parte. Onde uiene à diminuirsi dell'intiera metà d'un
b. per un'altra quarta parte. Onde uiene à diminuirsi dell'intiera metà d'un Comma. Ilperche, per la quarta definitione; esso Tuono uiene à contenersi tra ab. &
 b. fatto minore della metà di esso Comma. Ancora perche ob. & cb. contiene un Tuo
b. fatto minore della metà di esso Comma. Ancora perche ob. & cb. contiene un Tuono maggiore, & un maggior Semituono; però per la Ventesima sesta del Secondo; ob.
& cb. uiene ad esser lInteruallo del Semituono; contenuto nella sua uera forma. Et per
che tale Interuallo si fà minore d'una quarta parte del Comma o, laquale è o. & a; però,
per la terza Definitione; ab. & cb. è l'Interuallo del Semiditono, ridotto al suo tempe-
ramento. Ancora; perche pb. & cb. è Semituono maggiore; & dalla chorda
 b. è ac-
b. è ac-cresciuto d'un quarto d'un Comma, che è
 & p; però secondo la Sesta definitione da-
& p; però secondo la Sesta definitione da-ta di sopra;
 b, & cb. è l'Interuallo del Semituono maggiore accresciuto d'una quarta
b, & cb. è l'Interuallo del Semituono maggiore accresciuto d'una quarta parte del detto comma, & ridotto al suo temperamento. Il che si può anco dire del Se-
mituono Eb. & mb; il quale è accresciuto di tanta quantità del Comma m, la quale è
m. & F; come chiaramente si uede. Hora per far acquisto d'una Diapente, che non
si troua tra la chorda lb. & la ob. percioche questo Interuallo contiene solamente due
Tuoni minori, & un maggiore, con un maggior Semituono; & per la Trentesima
del Secondo, uorrebbe contenere due Tuoni maggiori, un minore, & un maggior
Semituono; onde resta diminuta d'un Comma intiero, il quale per la Ventesima
quinta definitione medesimamente del secondo giorno; è la differenza, che si troua
tra 'l Tuono maggiore & lo minore. Però aggiungo alla chorda lb. uerso 'l graue
il Comma l; onde tra il suo tutto aggiunto alla lb. & la ob; uiene la Diapente con-
tenuta nella sua uera & naturale proportione. Diuido hora il detto Comma, per
la Vndecima del Terzo, in quattro parti equali; & perche tutto l'Interuallo del
Comma l. congiunto alla chorda lb, fa con ab. una Diapente, maggiore d'una
quarta parte del Comma, che è o. & a; però lascio prima da un canto la quarta parte
più graue del detto Comma, equale alla o. & a; & ne uiene la Diapente nella sua ue-
ra forma; ma per il temperamento ne lascio dopoi un'altra quarta parte seguente; &
cosi tra Db. & ab; per la definitione; uiene la Diapente temperata, secondo 'l pro-
posito. Et di più; il Tuono maggiore, che si troua tra cb. & lb. per uirtù della chor-
da Db. si troua diminuto, & sciemo de due quarte parti; ò uogliamo dire della metà
intiera del Comma, che sono D & l. Et il minore, che si troua tra lb. & Eb, accresciu
to, secondo le loro definitioni; dell'istessa quantità. Et dico ancora, che la Diatessa-
ron, la quale si troua tra lb. & nb. nella sua uera, & natural forma, si troua accresciuta di
una quarta parte del Comma; percioche se la chorda nb. diuenta più graue d'una quarta
page 262 parte nella chorda Gb, & la chorda lb. più si estende uerso 'l graue per due quarte parti,
nella chorda Db; non è dubio, che tra Db. & Gb. si ritroui la Diatessaron accresciuta,
secondo la Ventesimasesta Definitione, della quarta parte d'un Comma. Onde per tal
modo habbiamo temperato le chorde Cb, lb, Eb, mb, nb, ob, pb, & cb, del proposto
Monochordo tra le chorde Cb, Db, Eb, Fb, Gb, ab,
 b, & cb; di maniera, che re-
b, & cb; di maniera, che re-stando 'l Ditono Cb. & Eb, & l'Hexachordo minore Eb. & cb, nelle loro proportioni
& uere forme; gli altri Interualli uengono ad esser ridotti in un temperamento tale; che
se 'l si porrà gli Hemisperij, ò scannelli sotto le temperate chorde, secondo la ragione mo
strata; si potrà vdire qual si uorrà Consonanza, che l'Vdito grandemente ne resterà con-
tento. Ma per ridur la hb. & Kb. poste nel graue insieme con l'altre à tal temperamento;
per poter'acquistare una Diatessaron, che non si troua tra la prima & la quarta chorda
hb. & lb; basterà solamente di far, che la Ab. &
 b. corrispondino con le ab. &
b. corrispondino con le ab. &  b.
b. per una Diapason, in Dupla proportione; facendo la Aa. equale alla ab; & la

 . e-
. e-quale alla
 b; Essendo che allora tanto la chorda Ab, quanto la
b; Essendo che allora tanto la chorda Ab, quanto la  b. sarà diuisa in due
b. sarà diuisa in due parti equali ne i punti a. &
 . Onde tāto sarà la proportione di Ab. & ab, & di
. Onde tāto sarà la proportione di Ab. & ab, & di  b. &
b. &  b.
b. di suono à suono, per la Prima & per la Quinta dimanda del Terzo ragionamento; quan
to di numero à numero. La onde essendo Ab. & ab; simigliantemente
 b. &
b. &  b. in
b. in proportione Dupla; per l'Ottaua definitione del Secondo; Ab. & ab; simigliantemen-
te
 b. &
b. &  b. faranno la Diapason Consonanza. Et il Tuono Ab. &
b. faranno la Diapason Consonanza. Et il Tuono Ab. &  b. sarà equale al
b. sarà equale al Tuono ab. &
 b; cosi ancora il Semituono
b; cosi ancora il Semituono  b. & Cb. sarà equale al Semitiuono
b. & Cb. sarà equale al Semitiuono  b. &
b. & cb; essendo che tanta è la proportione, che si troua tra hb. & Ab, & tra
 b. & Kb;
b. & Kb; quanta è quella, che si troua tra ob. & ab, & tra
 b. & pb. Percioche la Diapason hb.
b. & pb. Percioche la Diapason hb. & ob. per la Ventesima settima definitione d'hoggi; è fatta più acuta della quantità ob.
& ab; ch'è la quarta parte del Comma; & la Kb. & pb. più graue di tal quantità; quella
nelle chorde Ab. & ab. & questa nella
 b. &
b. &  b. Ma perche Ab. & ab. contengono la
b. Ma perche Ab. & ab. contengono la Diapason; essendo Db. & ab, Diapente; Ab. & Db. uerrà ad essere; per il Corollario
della Quarta proposta del Secondo giorno, Diatessaron. Et si come Db. & ab. è Diapen
te ridotta al suo temperamento; cosi Ab. & Db. uerrà ad essere Diatessaron, ridotta ad
una tale qualità; & per tal modo uerremo ad hauer acquistato una Diatessaron tra la Pri-
ma & la Quarta chorda, laquale non si ritrouaua in essere; & questo secondo 'l nostro pro
posito. Oltra di questo; se diuideremo la chorda Db. in due parti equali, & segnaremo
la metà in punto d; haueremo, per la Quarantesima seconda del Terzo, tra la chorda Db.
& db. la Dupla proportione; & per la Ottaua Definitione di sopra nominata; la Diapason
consonāza. Et l'Interuallo cb. & db. equale allo Cb & Db. ch'è il Tuono, & lo db. & eb.
equale allo Db. & Eb. medesimamente Tuono; restādo le chorde Eb & eb. immobili, le
quali con le Cb, & cb. cōtengono il Ditono nella sua uera & natural forma & proportio
ne. Ma per ritrouar la corrispondente per una Diapason alla Fb; diuideremo, per la Qua
rantesima secōda nominata, essa Fb. in due parti equali, & tra essa Fb, che cōtenerà due
parti, & fb, che ne cōtenerà una; haueremo la Diapason consonanza nella sua uera forma,
& il Semituono maggiore tra eb. & fb. sarà accresciuto d'una quarta parte del Cōma. Ri
trouaremo anco la corrispondente per Diapason alla Gb, diuidēdola in due parti equali,
per la nominata poco fà proposta; & pigliandone una in pūto g; tra Gb. & gb. haueremo il
proposito; & tra fb. & gb. haueremo il Tuono, ilquale sarà di equale proportione del Tuo
no Fb. & Gb. Il simile faremo della chorda ab; perche diuidēdola in due parti, & piglian
done una di essa in punto aa; tra ab. & aab. haueremo una Diapason, la quale sarà equa-
le alla Ab & ab, & sarà più acuta (per la Ventesima settima Definitione d'hoggi) della
ob. & tb, per una quarta parte d'un Comma; come è etiandio la Ab. & ab. della hb. &
ob. Ma il Tuono gb. & ab. sarà equale allo Gb & ab; percioche è accresciuto de due quar
te parti del Cōma; che sono gs. & taa; com'è accresciuto anco Gb. & ab. di Gn. & oa. Et
si come le chorde ab. & db. corrispondono alle Ab. & Db. in Dupla proportioine, & tra le
due prime si troua la Diatessaron temperata; cosi si troua anco tra l'altre due; percioche,
page 263 per la Ventesima ottaua del Secondo giorno; l'una & l'altra contiene due Tuoni & un Se
mituon maggiore. Onde habbiamo fatto acquisto de due Diatessaron; l'una Ab. & Db.
posta nel graue, & l'altra ab. & db. posta nell'acuto, le quali mancauano tra la prima &
la quarta, & tra l'ottaua & la undecima delle proposte Quindeci chorde; come dice la
proposta. Et si come Db. & ab. corrispondono alle db. & aab. medesimamente in Du
pla proportione, & tra le due prime si troua la Diapente temperata; cosi si ritroua etian-
dio tra le due seguenti. Onde habbiamo due Diapente acquistate, le quali tra la Quarta
& l'Ottaua chorda, & tra l'Vndecima & la Quintadecima delle Quindeci proposte man
cauano, l'una è tra Db. & ab; l'altra tra db. & aab; secondo 'l proposito. Ma hauendo
col Senso esperimentato, che 'l concento, che uscisse da queste chorde Ab,
 b,Cb;
b,Cb; Db, Eb, Fb, Gb, ab,
 b, cb, db, eb, fb, gb, & aab; è grato & soaue all'Vdito; però
b, cb, db, eb, fb, gb, & aab; è grato & soaue all'Vdito; però diremo; che questi Interualli tutti, ridotti à tal temperamento, siano consonanti, senz'al-
cuna contradittione. Et questo è tutto quello, che secondo la proposta, ui douea dimo-
strare. Vdito che hebbe il Signor Desiderio la conclusione, disse; Questo è stato un lun-
go tiro, & ueramente ch'è cosa bella da sapere; massimamente da uoi altri, che fate
professione delle cose della Musica. Et credo che coloro, i quali sono ignoranti di que-
sta cosa; manchino d'una gran perfettione, quelli dico, che fanno professione di fabrica-
re Istrumenti musicali; come posso comprender dalle parole poco fà dette da M. Claudio.
Cosi è ueramente; rispose egli, & niun lo potrà con uerità negare. O quanto arroganti so
no quelli soggiunse M Adriano; che sono semplici Compositori di Musica, che se ben so
no ignoranti delle cose della Scienza, uogliono non dimeno tenere in quest'Arte il prin-
cipato, & li par di essere i più dotti, & più saputi huomini del mondo. Ma leuateli da quel
poco di comporre, che fanno & con poca prattica; restano nudi, senza saper cosa ueru-
na; però è cosa buona l'imparare, acciò non s'entri nella schiera de costoro, che uiuo-
no solamente tra gli huomini, per far numero. Seguitate adunque M. Gioseffo il uostro
ragionamento; per che tutti noi ui ascoltiamo uolontieri, tanto più che uediamo, ch'ogni
tratto ci proponete di nouo qualche cosa bella & ingeguosa. Statemi adunque ad ascol-
tare, dissi; c'hauerete piacere.
PROPOSTA II.
tità, la quale non si può descriuere, ò denomimare con Numeri rationali; co-
me poco fà, sopra la 28. Def. & nelle Istitutioni1. p. c. 21. & in questi ragionamenti nel-
la Ventesima quinta proposta del Secondo hauete detto. E' cosi Messere; risposi; quan-
tunque si possa dire, la Diapente esser maggiore, ò minore d'una intera Quarta parte
d'una Sesquiottantesima proportione, ch'è la forma del Comma, & tal parte sia ad un
certo modo rationale; perche, come si è detto & dimostrato per la Nona del primo no-
stro ragionamento; l'interuallo Superparticolare, com'è il nominato, non riceue ne
uno, nè più termini mezani rationali, che lo partisca in due ò più parti proportiona-
li. La onde tornando al nostro proposito, dico; Quella quantità, per l'Vltima definitio-
ne dhoggi, si dice essere Irrationale, la quale nasce dell'aggiungere, ò leuare una ratio-
nale da una irrationale, ò per il contrario, una irrationale da una rationale. Il perche es-
sendosi leuato, ouero aggiunto nel temperamento fatto nella Precedente alle quantità
della Diapēte, della Diatessaron, del Semiditono, del Tuono, & del Semituono maggiore,
che sono tutte Rationali, una tal quantità Irrationale; seguità che tutti questi Interualli
nominati; quando sono tēperati, siano contenuti da proportioni sordi & irrationali. Impe
page 264 roche la proportione della Diapente; com'è manifesto per la Precedente; nel suo tempe
ramento resta diminuita, come dice anche la sua Definitione; d'una quarta parte del
Comma, la quale con certi & determinati numeri (per la Nona del Primo; poco fà no-
minata) non si può descriuere, ò denominare. Onde leuata cotal parte della Sesquial-
tera, ch'è la forma uera della Diapente, ch'è rationale; per l'Vltima Definitione già no-
minata; senza dubio alcuno ne uiene una proportione sorda & irrrationale. Quest'iste-
so dico della Diatessaron; percioche uiene accresciuta di tal parte. Il perche aggiunta la
quarta parte del Comma, ch'è irrationale, con la Sesquiterza, ch'è rationale, & è la
forma della detta Diatessaron; ne uiene un'Interuallo & quantità irrationale. Il medesi-
mo diciamo del Semiditono, che si fà minore d'una quarta parte, & del Tuono maggio
re, che si fà medesimamente minore delle due quarte parti, & del Minore, che di tanta
quantità piglia accrescimento; & ultimamente del Semituono maggiore, il quale s'ac-
cresce al medesimo modo d'una quarta parte del nominato Comma. Onde dico, le pro-
portioni della Diapente & della Diatessaron, quelle del Semiditono & del Tuono; con
quelle del maggior Semituono, esser Sordi & Irrationali; come, secondo la proposta,
ui douea dimostrare. Notate, però che
PROPOSTA III.
Υ῾ποπροσλαμβανόμενος.
sta Chorda col numero dell'altre? Al quale risposi; Due cose solamente, ui voglio
dire, per uostra intelligenza. La prima è, perche da questa chorda, ch'io uoglio
aggiungere; come ui hò detto ancora; hà principio il primo & grauissimo Hexachordo
Hypaton. La seconda è, perche col suo mezo uengo a collocare i Modi per ordine l'un
dopo l'altro, tra Sedeci chorde, senza mancar cosa alcuna, & senza esserui cosa alcuna
di sopr'abondante; come uederete; onde non ui essendo questa Chorda, si rompe ogni
nostro dissegno. Queste sono due cagioni importanti; soggiunse egli; però seguitate; il
che feci in questo modo. Siano adunque, secondo la prima proposta di questo, sopra la
chorda h. & b. segnate le Quindeci chorde Ab,
 b, Cb, Db, Eb, FB, GB, ab,
b, Cb, Db, Eb, FB, GB, ab,  b,
b, cb, db, eb, fb, gb, & aab; & sia Ab. la Proslambanomenos alla quale habbiamo da
proporre la Υ῾ποπροσλαμβανόμενος; ouer Gammaut. Accommodo prima, per la Prima
proposta del Terzo giorno; il Tuono maggiore alla sua proportione, sopra la chorda hb; di
maniera che Ab. uenga ad essere il suo estremo acuto. Però diuiso essa Ab. In Otto par-
ti equali, per il minor termine della Sesquiottaua, ch'è la sua proportione; & aggiungo à
queste parti la Nona nel punto l. tra lb. & Ab. habbiamo il proposito, & hauēdolo proposto
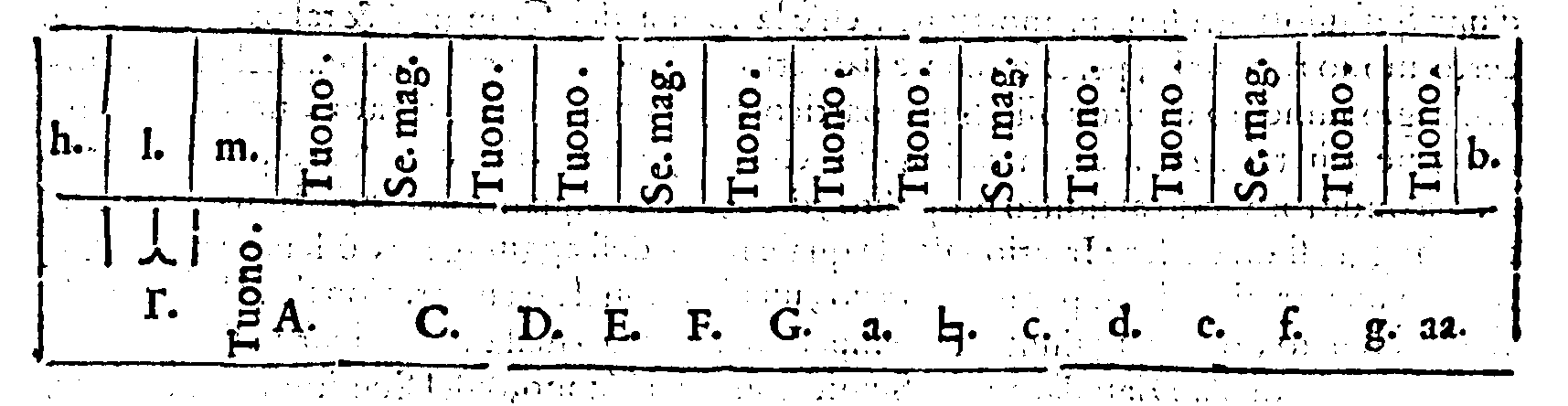
 b. Ma perche bisogna ridur questo Interuallo al temperamento de gli
b. Ma perche bisogna ridur questo Interuallo al temperamento de gli altri Tuoni; accioche la chorda graue di questo Tuono accōmodato corrispondi giusta-
page 265 mente cō la Gh. in Dupla proportione; & consoni cō essa la Diapason; però, per la Trente-
simasesta del giorno Terzo, accōmodaremo il Cōma sopra la chorda lb. il quale sarà lb.
& mb. & lo diuideremo, per la Decima del nominato Terzo giorno; in due parti equali.
Onde lasciandone la più graue & più uicina alla l. da un canto; tra Γb. Ab. haueremo
collocato il Tuono proposto alla sua proportione & lo hauaremo etia&ndio preposto al Tuo
no Ab &
 b. Ma perche lb. & Ab. è Tuono maggiore, contenuto nella sia naturale pro-
b. Ma perche lb. & Ab. è Tuono maggiore, contenuto nella sia naturale pro-portione, & dalla chorda Γb. è fatto minore della metà d'un Comma, i quale è lb. & mb.
però dico, per la sua Definitione, Γb. & Ab. essere il Tuono maggiore temperato; co-
me faceua dibisogno. Et perche Ab. per l'Ottaua definitione del Quarto; è la Pros-
lambanomenos, & la Γ. è distante da essa per un Tuono, & è posta nel graue; però di-
co, per la Decimanona Definitione d'hoggi medesimamente; Γb. esser la chorda Hy-
poproslambanomenos, preposta alla Proslambanomenos & alle Quindeci proposte
chorde; come ui douea, secondo la proposta, dimostrare. Voglio ancora dirui una
cosa, auanti che passiamo più oltra; che la nominata chorda Hypoproslambanomenos
si può aggiungere con un'altro mezo. Percioche se raddopiaremo la chorda Gb. la
quale uerrà raddopiata nel punto Γ. haueremo la chorda Γb. che per la Quarta Defini-
tione del Primo giorno; con essa Gb. contenerà la Dupla proportione; percioche Γb.
contiene Gb. due fiate di punto; Onde; per l'Ottaua Definitione del secondo ragiona-
mento; uengono à contenere la Diapason consonanza. Et perche questa contiene in sè;
per la Trentesimanona del Secondo; Cinque Tuoni & Due maggiori Semituoni, & l'In-
teruallo Ab. & Gb. contiene solamente Quattro Tuoni & li nominati due Semituoni;
per l'interuallo Γb. & Ab. uerrà à contenere il Tuono, il quale posto insieme con gli altri
Quattro & li Due Semituoni, faranno una Diapason. Essendo adunque
 b. & Ab. Tuo-
b. & Ab. Tuo-no; & essendo
 b. distante da Ab. Proslambanomenos per un Tuono; seguita, per la
b. distante da Ab. Proslambanomenos per un Tuono; seguita, per la nominata Decimanona Definitione; che la Γb. sia la Hypoproslambanomenos; come
bisognaua dimostrare. In uerità, disse M. Claudio; che non si può dir cosa alcuna in-
contrario & questo c'hauete hora dimostrato col mezo della Dupla, ò Diapason, è tan-
to manifesto; che non discordando punto dalla Definitione data; bisogna per forza con-
fessare, che tal chorda aggiunta sia la Hypoproslambanomenos, c'hauete detto; ò la
Gammaut; come da i Prattici è chiamata. Seguitate adunque il resto; se ui piace. Se-
guirò adunque à dirui; risposi; che,
PROPOSTA IIII.
Meson, Diezeugmenon, & Hyperboleon.
 . C. D. E F. G. a.
. C. D. E F. G. a.  . c. d. e. f. g & aa. Dico primie-
. c. d. e. f. g & aa. Dico primie-ramente, che tra le chorde Γ. A.
 . C. D & E. è contenuto i primo Hexachor-
. C. D & E. è contenuto i primo Hexachor-do, detto Hypaton; percioche Γ. per la Decimaottaua definitione d'hoggi; è
chorda la quale corrisponde alla Hypoproslambanomenos; alla Proslambanome-
nos;
 alla Hypate hypaton; C alla Parhypate hypaton; D alla Lychanos hypaton; &
alla Hypate hypaton; C alla Parhypate hypaton; D alla Lychanos hypaton; & E alla Hypate meson. Et perche queste Sei chorde sono collocate nel primo & grauissi-
mo luogo di quest'ordine, & hanno il loro principio nella Hypoproslambanomenos, ò
Gammaut, & contengono Quattro Tuoni & un maggior Semituono, & tra le Quattro
più acute contengono il Primo Tetrachordo, da gli Antichi detto hypaton; però per la
Definitione Ventesimaprima d'hoggi, dico Γ. A.
 . C. D & E. esser 'l primo Hexacordo,
. C. D & E. esser 'l primo Hexacordo, detto Hypaton. Dico poi; C. D. E. F. G & a. contenere il Secondo detto Meson; percio-
che C. corrisponde, per la Decimaottaua nominata definitione, alla Parhypate hypaton;
page 266 D alla Lychanos hypaton; E. alla Hypate meson; F. alla Parhypate meson; G. alla Lycha-
nosmeson; & a alla Mese. Onde essendo la Parhypate hypaton la prima chorda de que-
ste Sei, & contenendo cotal numero Quattro Tuoni & un maggior Semituono; & anco
ritrouandosi tra le Quattro più acute il Tetrachordo Meson; non è dubio alcuno, che
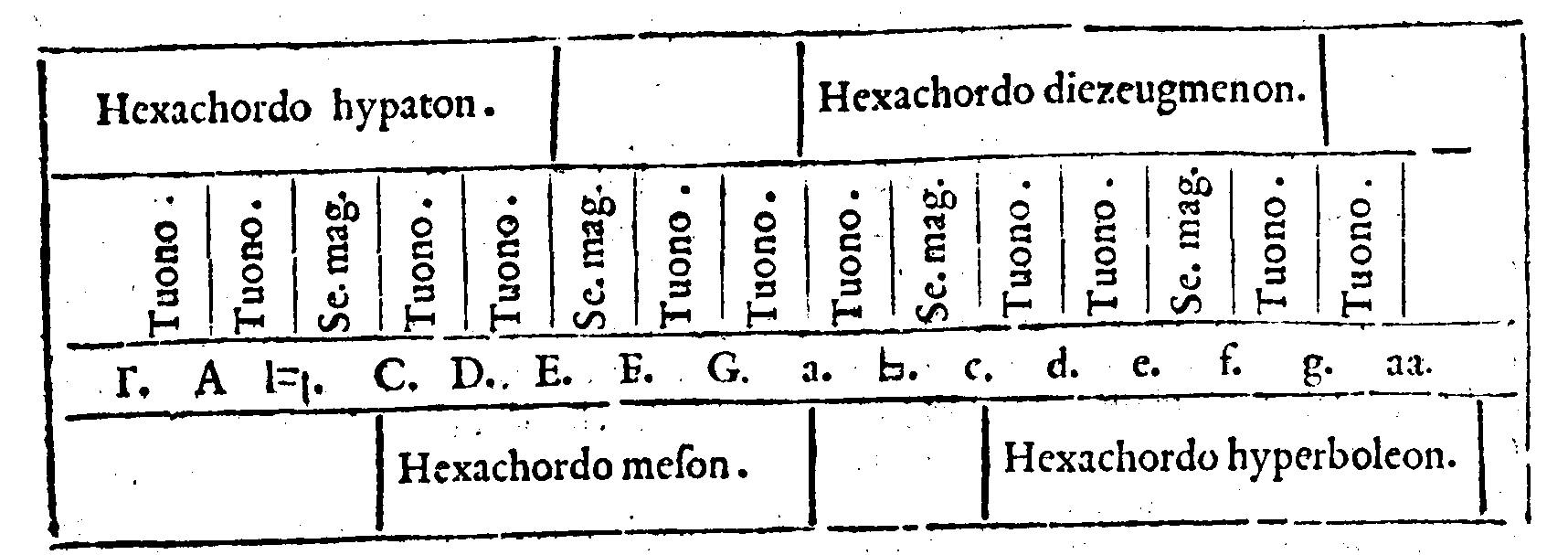
chiamato Meson. Più oltra dico; che le chorde G. a
 . c. d & e. contengono il Terzo,
. c. d & e. contengono il Terzo, nominato Diezeugmenon. Percioche G. corrisponde alla Lychanosmeson; a. alla Me-
son; &
 alla Paramese; c. alla Tritediezeugmenon; d. alla Paranete diezeugmenon; & e.
alla Paramese; c. alla Tritediezeugmenon; d. alla Paranete diezeugmenon; & e. alla Netediezeugmenon; onde hauendo etiandio queste Sei chorde il loro principio
nella chorda Lychanosmeson, & contenendo quattro Tuoni & un maggior Semituo-
no; & ritrouandosi nelle quattro più acute il terzo Tetrachordo detto Diezeugmenon;
non è da dubitare; secondo ch'insegna la Ventesimaterza definitione, che G. a.
 . c. d &
. c. d & e. sia Hexachordo Diezeugmenon & il Terzo. Finalmente dico; che 'l quarto nomi-
nato Hyperboleon si troua collocato tra le chorde c. d. e. f. g & aa. percioche queste Sei
chorde sono collocate nella più acuta parte del nominato ordine, contenuto tra Sedi-
ci chorde; & c. per la Decimaottaua definitione, corrisponde alla Tritediezeugmenon;
d. alla Paranete; e. alla Nete; f. alla Tritehyperboleon; g. alla Paranete; & a. alla Nete-
hyperboleon. Onde hauendo cotal ordine principio nella Tritediezeugmenon, & con-
tenendo simigliantemente quattro Tuoni & un maggior Semituono; per la Definitione
Ventesima & Ventesimaquarta già detta, seguita; che c. d. e. f. g & aa. sia Hexachordo, &
il Quarto & più acuto d'ogn'altro, detto Hyperboleon; percioche contien nelle sue più
acute chorde il Tetrachordo Hyperboleon. Potiamo adūque porre tra le Sedici mostra-
te chorde i quattro primi Hexachordi, Hypaton, Meson, Diezeugmennon, & Hyperbo-
leon; come ui douea, secondo che dice la proposta, dimostrare & assignare. Se i nostri
Hexachordi, disse M. Adriano, hanno à corrispondere, come fanno in effetto, à i
Tetrachordi de gli Antichi; bisogno è, che ue ne sia un'altro, che corrispondi al Sy-
nemennon; però se 'l ui è in piacere, dimostratecelo; acciò habbiamo la cosa perfet-
ta. E' il douere risposi di satisfarui Messere; essendomeui già fatto debitore però sta-
temi ad ascoltare.
PROPOSTA V.
 . C. D. E. F. G.
. C. D. E. F. G. a.
 . c. d. e. f. g & aa. sopra la notata chorda h & k. le quali; come nella Precedente;
. c. d. e. f. g & aa. sopra la notata chorda h & k. le quali; come nella Precedente; contengono i quattro primi Hexachordi, Hypaton, Meson; Diezeugmenon,
page 267 & Hyperboleon; à i quali sia dibisogno aggiungere il quinto detto Synemennon. Ac-
commodo prima sopra la chorda ak. per la Decimanona del Terzo giorno; il Semituon
maggiore alla sua proportione; onde ne uiene ak. & lk. Ma perche ak & lk. è Semituon
maggiore, & è contenuto nella sua forma naturale; però bisogna, secondo la sua Defi-
nitione; ch'ello sia maggior d'una quarta parte d'un Comma. Onde accommodo prima
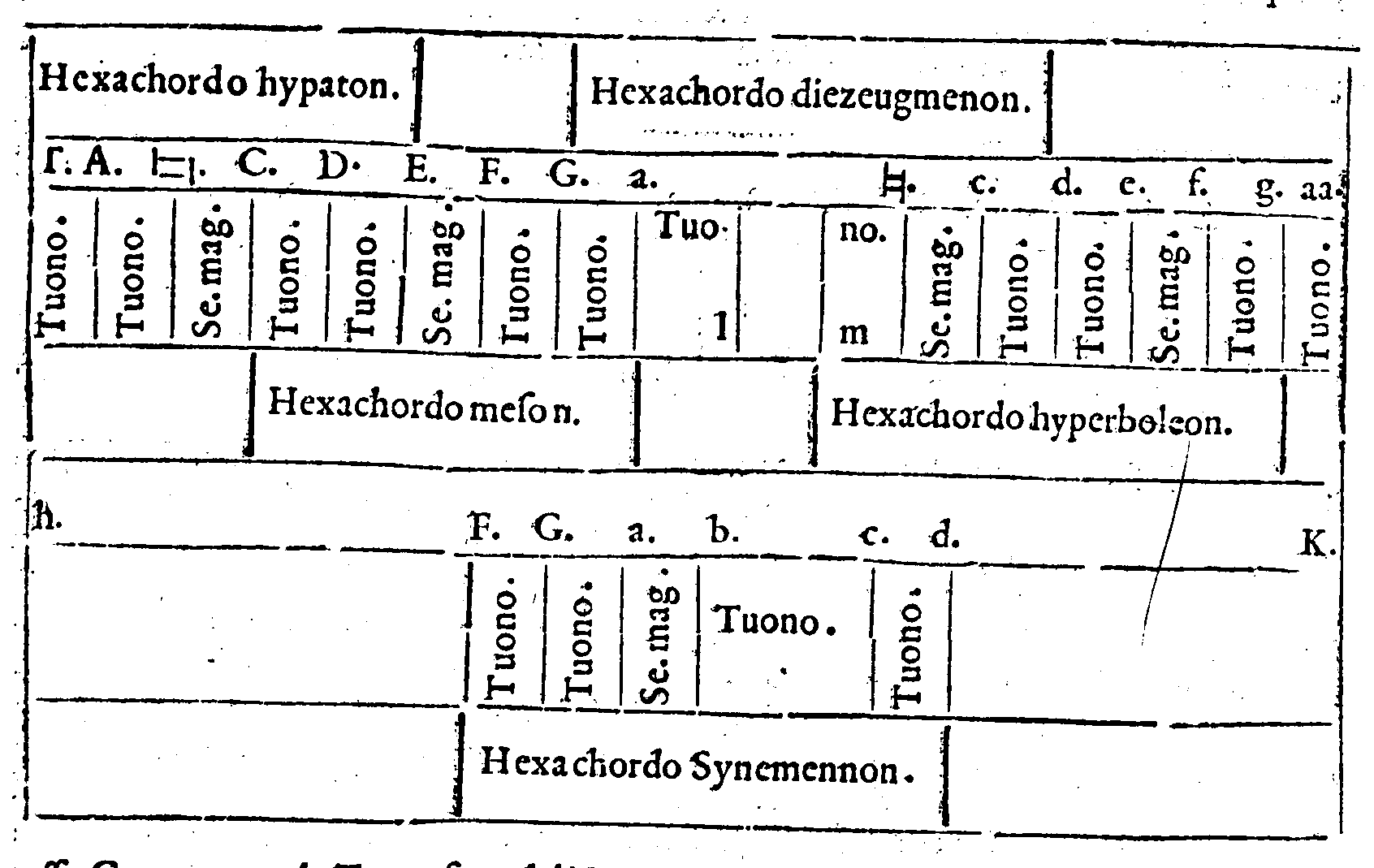
do che la chorda lk. sia l'estremo graue di questo Interuallo, & mk l'acuto; dopoi lo di-
uido, per la Vndecima simigliantemente del Terzo nominato, in quattro parti equali;
& aggiungendo lb. con al. tra ak. & bk. haueremo, per la sua Definitione, il Semituono
maggiore, accresciuto però; per la Ventesimasesta definitione d'hoggi; d'una quarta par-
te del Comma lk. & mk. & com'al senso è manifesto. Hora dico, che ritrouandosi tra
F. G. a. b. c & d. quattro Tuoni, & un maggior Semituono; come tra F. G. G a. b. c. & c d.
il Tuono; & tra ab. il nominato Semituono; dico per la Ventesima definitione F. G. a.
b. c & d. esser'Hexachordo. Et perche F. corrisponde per la Decimaottaua Definitio-
ne, alla Parhypatemeson; G. alla Lychanos, a. alla Mese, b. alla Tritesynemennon, c.
alla Paranetesynemennon, & d. alla Netesynemennon; & l'ordine de queste Sei chorde
hà principio nella Parhypate meson; & contiene anco nelle quattro più acute chorde il
tetrachordo Synemennon; però F. G. a. b. c & d. per la Ventesimaquinta Definitione, è
il Quinto, & ultimo Hexachordo nominato Synemennon. Et questo è quello, che ui
douea dimostrare. Questo Hexachordo è quello, disse M. Francesco che noi chiamia-
mo della proprietà di b molle; il Primo & il Terzo sono detti di quella di
 quadro, &
quadro, & il Secondo col Quarto della proprietà di Natura. Cosi è, risposi; Ma ascoltate quel, che
hora ui uoglio dire.
PROPOSTA VI.
Diapason si troua due fiate, due la Seconda, due la Terza, una la Quarta, due la
Quinta, due la Sesta, & una la Settima.
dimostrerò risposi, senza tardare. Siano Γ. A.
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f g &
. c. d. e. f g & aa. Dico prima, che tra esse la Prima specie della Diapason si troua Due fiate;
l'una tra C. D. E. F. G. a
 . & c. & l'altra tra F. G. a. b. c. d. e. & f. percioche per
. & c. & l'altra tra F. G. a. b. c. d. e. & f. percioche per l'Ottaua Definitione d'hoggi; quella è la Prima specie della Diapason, la quale contie-
ne tra la Terza, & la Quarta sua chorda, & tra la Settima & la Ottaua il Semituon mag-
giore. La onde ritrouandosi la E. esser la Terza chorda, & F. la Quarta della Diapason
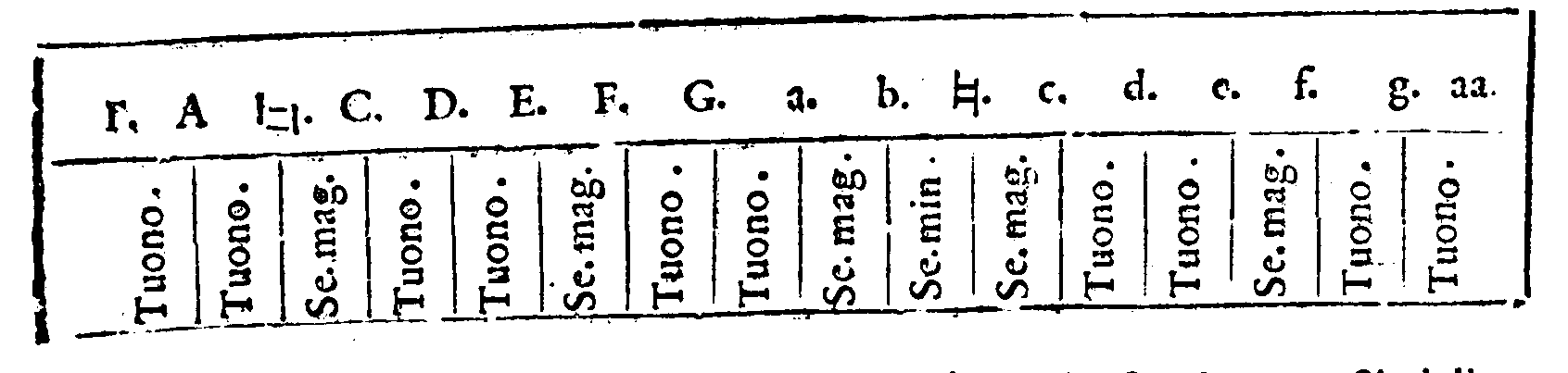
temente ritrouandosi la
 . esser la Settima chorda, & la c. la Ottaua, & contenere etian-
. esser la Settima chorda, & la c. la Ottaua, & contenere etian-dio esso Semituono; Seguita, che la Diapason C & c. con le sue mezane chorde; sia la
prima specie. Il che dico etiandio della Diapason F & f. con le sue mezane chorde; es-
sendo che tra la sua Terza chorda a. & la Quarta b. & tra la Settima e. & la Ottaua f. si ri-
troua anco il Semituono già nominato. Adunque tra le proposte Dicesette chorde si
troua due fiate la Prima specie della Diapason. Ma la Seconda specie si troua due fiate;
tra D. E. F. G. a.
 . c. & d. & tra G. a. b. c. d. e f & g. percioche tra E. & F. Seconda & Terza
. c. & d. & tra G. a. b. c. d. e f & g. percioche tra E. & F. Seconda & Terza chorda; & tra
 & c. Sesta & Settima della Diapason D & d. con l'altre mezane, & cosi
& c. Sesta & Settima della Diapason D & d. con l'altre mezane, & cosi tra la a. & b. Seconda & Terza; & tra e. & f. Sesta & Settima della Diapason G & g con
le sue mezane già mostrate; si troua il maggior Semituono. Onde, per la detta Ottaua
definitione; D & d. simigliantemente G con g. uengono ad esser due Diapason della Se-
conda specie. La Terza specie si ritroua due fiate; prima tra E. F. G. a.
 . c. d & e. dopoi
. c. d & e. dopoi tra a. b. c. d.e. f. g & aa. essendoche tra la prima E. & la seconda F & tra la quinta
 & la se-
& la se-sta c. della Diapason E & e. con le sue mezane chorde. Et cosi tra la prima chorda & la
seconda; a. & b. & tra la quinta et la sesta, che sono e. & f. della Diapason a & aa. inten-
dendouisi sempre anco le chorde mezane; si troua 'l maggior Semituono. Il perche, per
la Definitione poco fà addotta; E & e. con a & aa. sono due Diapason della Terza spe-
cie. La Quarta specie etiandio si troua una fiata solamente tra F. G a.
 . c. d. e & f. percio-
. c. d. e & f. percio-che tra la sua Quarta chorda
 . & la Quinta c. & tra la Settima e. & lOttaua f. si troua il
. & la Quinta c. & tra la Settima e. & lOttaua f. si troua il nominato Semituono maggiore. Onde, per la detta Definitione, F & f. con le sue me-
zane chorde è una Diapason della Quarta specie. La Quinta specie si troua due fiate; tra
Γ. A.
 . C. D. E. F.& G. & tra G. a.
. C. D. E. F.& G. & tra G. a.  . c. d. e. f. & g. poi che la Terza et la quarta sua
. c. d. e. f. & g. poi che la Terza et la quarta sua chorda
 . & C ouer
. & C ouer  . & c. & tra la Sesta & la Settima E & F. ouero e. & f. delle nomina-
. & c. & tra la Sesta & la Settima E & F. ouero e. & f. delle nomina-te due Diapason; si ritroua il Semituon maggiore. Onde, per listessa Ottaua Definitione
l'una & l'altra sono due Diapason contenute nella Quinta specie. Dico ancora, che la
Sesta specie della Diapason si ritroua tra 'l nominato numero di chorde due fiate; Prima,
tra A.
 . C. D. E. F. G. & a. dopoi, tra a.
. C. D. E. F. G. & a. dopoi, tra a.  . c. d. e. f. g & aa. essendo che, per la sua Definitio-
. c. d. e. f. g & aa. essendo che, per la sua Definitio-ne, tra le Seconde chorde
 . &
. &  . & le Terze C. & c. & tra le Quinte E. & e. et le Seste F.
. & le Terze C. & c. & tra le Quinte E. & e. et le Seste F. & f. delle due Diapason mostrate si troua il maggior Semituono. Però dico, esser due
Diapason della Sesta specie. Finalmente dico, che tale ordine contiene una fiata la Set-
tima specie della Diapason; tra
 C. D. E F. G. a &
C. D. E F. G. a &  percioche, per la sudetta Ottaua
percioche, per la sudetta Ottaua Definitione, quella è detta Settima specie, la quale tra la sua Prima & la Seconda chor-
da, & tra la Quarta et la Quinta contiene il Semituon maggiore. La onde, perche la
Diapason
 . &
. &  . tra la sua estrema chorda graue & l'estrema acuta, con le mezane in
. tra la sua estrema chorda graue & l'estrema acuta, con le mezane in page 269 sieme; tra
 . & C. Prima & Seconda, & tra E. & F. Quarta & Quinta chorda contiene il
. & C. Prima & Seconda, & tra E. & F. Quarta & Quinta chorda contiene il detto Semituono; però dico, la detta esser la Settima specie della Diapason. Tra le Di-
cesette chorde mostrate adunque continenti i Cinque Hexachordi; la prima specie del-
la Diapason si troua due fiate; due la Seconda; due la Terza; una la Quarta; due la Quin-
ta; due la Sesta; & una la Settima. Et questo è quello, che secondo il continente della
proposta, ui douea dimostrare. Qui disse M. Claudio; Ancora che fin'hora da i Musici
sia stato tenuto, che la Prima specie della Diapason sia contenuta tra le chorde D & d.
con le sue mezane, & cosi l'altre specie seguenti per ordine; per questo non credo, ch'ap-
presso gli Huomini intendenti u'habbia da esser confusione. Et parmi, che non sola-
mente per gli Hexachordi, che sono collocati in questo ordine de chorde; ma etiandio,
perche è cosa più naturale; come detto hauete poco fà, & anco nelle uostre Istitutioni;
che debba esser cosi. Il perche facesti palese per la diuisione harmonicamente fatta del-
la Dupla & della Diapason nelle sue parti; cosa da niun'altro per auanti pur pensata.
Però laudo molto quest'ordine. Che ne diteuoi Messere di questo? Rispose M. Adria-
no; Non posso se non laudarlo; perche anco l'ordine de i Modi, ò Tuoni sarà posto
senza interrompimento. Et se bene appresso d'alcuni parerà questa cosa essere altramen
te; ci ricordaremo, che M. Gioseffo hauendo uoluto più tosto seruire (come si uede in
fatto) alla prattica moderna, che alla speculatiua; in questo luogo egli parla secondo la
Scienza, & secondo che porta l'ordine naturale di questa cosa. Soggiunse à questo M.
Francesco; Questo importa poco appresso quelli, ch'intendono le cose della Musica; ma
ueniamo pure à quello, che segue. Per seguitare adunque l'ordine principiato, diss'io; ui
dico; che
PROPSTA VII.
si troua la Prima specie della Diapente, Cinque la Seconda; due la Terza, & due la
Quarta.
 . C. D. E. F. G. a. b
. C. D. E. F. G. a. b  . c. d. e. f. g & aa. le nominate Dicesette chorde,
. c. d. e. f. g & aa. le nominate Dicesette chorde, le quali contengono i cinque Hexachordi. Dico prima, che cinque fiate tra
loro si ritroua la prima specie della Diapente, tra C. D. E. F & G. tra F. G. a. b
& c. tra G. a.
 . c & d. tra c. d. e f & g. & tra Γ. A.
. c & d. tra c. d. e f & g. & tra Γ. A.  . C & D. percioche ritrouando-
. C & D. percioche ritrouando-si il maggior Semituono tra la Terza & la Quarta chorda di ciascheduna delle mostrate
Diapente; come tra E. & F. della Prima; tra a & b. della Seconda; tra
 & c. della Terza;
& c. della Terza; tra e & f. della Quarta, & tra
 & C. della Quinta; però dico, per la Nona Definitione,
& C. della Quinta; però dico, per la Nona Definitione, che le mostrate sono Cinque Diapente contenute nella Prima specie, tra le Dicesette
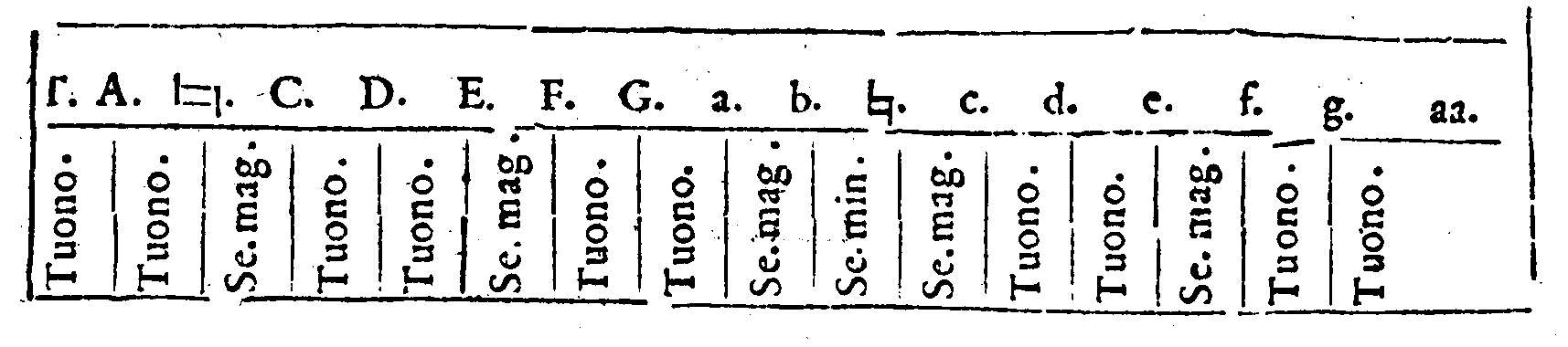
che ella si troua cinque fiate tra A.
 . C. D & E. tra D. E. F. G et a. tra a.
. C. D & E. tra D. E. F. G et a. tra a.  . c. d. e. & tra d. e. f.
. c. d. e. & tra d. e. f. g et aa. et tra G. a. b. c et d percioche ritrouandosi il nominato Semituono tra la Secōda et
a Terza chorda di ciascheduna; tra
 et C. della A & E. tra E et F. della D et a. tra
et C. della A & E. tra E et F. della D et a. tra  et c.
et c. page 270 della a & e; tra e & f. della d & g; & tra a & b. della G & d; per la sopradetta Definitione;
seguita, che le mostrate cinque Diapente siano tra le nominate chorde, & siano della se-
conda specie. Simigliantemente dico, che si troua due fiate la Terza specie della Dia-
pente; prima tra E. F. G. a. &
 ; dopoi tra a b. c. d & e; percioche tra la prima & la se-
; dopoi tra a b. c. d & e; percioche tra la prima & la se-conda loro chorda, che sono E. & F. delle Diapente E &
 ; & a. & b. della a. & e; si tro-
; & a. & b. della a. & e; si tro-ua esser collocato il maggior Semituono. Onde, per l'istessa nominata Definitione, E.
F. G a &
 ; ancora a. b. c. d & e. sono due Diapente della Terza specie, contenute tra 'l
; ancora a. b. c. d & e. sono due Diapente della Terza specie, contenute tra 'l numero delle già mostrate Dicisette chorde. Vltimamente dico, la Quarta specie con-
tenersi tra esse chorde due fiate; tra F. G. a.
 . & c; & tra b c. d. e & f; essendo che tra la
. & c; & tra b c. d. e & f; essendo che tra la quarta & la quinta loro chorde si troua esso Semituono; com'è manifesto dalle chorde
 . & c della prima, & e. con f. della seconda; Il perche, per la nominata nona Defini-
. & c della prima, & e. con f. della seconda; Il perche, per la nominata nona Defini-tione, dico; F. G. a.
 & c; simigliantemente b. c. d. & f; esser due Diapente della Quar-
& c; simigliantemente b. c. d. & f; esser due Diapente della Quar-ta specie, contenute tra le proposte chorde. Tra le dicisette Chorde, che contengono
i Cinque Hexachordi; adunque cinque fiate si troua la Prima specie della Diapente;
cinque la Seconda; due la Terza, & due la Quarta. Et questo sia tutto quello, che si
contiene nella proposta, che ui douea dimostrare. Quello, che si è detto disse M. Fran-
cesco; intorno alle Specie della Diapason, dell'ordine di prima & seconda, si potrebbe
anco dire intorno alle specie della Diapente; ma perche sarebbe un perder tempo fuora
di proposito; però giudico dal canto mio, che sia ben fatto, à proceder più oltra. Ver-
rò adunque dissi à dimostrare, che
PROPOSTA VIII.
ron, cinque la seconda, & cinque la Terza.
sue precedenti, il numero delle chorde Γ. A.
 C. D. E. F. G a. b
C. D. E. F. G a. b  . c. d. e f. g &
. c. d. e f. g & aa; & dirò prima, che tra loro si coniene cinque fiate la prima specie della Dia-
tessaron, tra Γ. A.
 & C; tra C. D. E & F tra G. a.
& C; tra C. D. E & F tra G. a.  & c. tra c. d. e & f, & tra F. G a & b;
& c. tra c. d. e & f, & tra F. G a & b; percioche tra la terza & la quarta chorda di ciascheduna si troua l'Interuallo del maggior
Semituono; come tra
 & C. della Γ & C; tra E & F. della C & F; tra
& C. della Γ & C; tra E & F. della C & F; tra  & c. della G
& c. della G & c; tra e & f. della c & f; & tra a & b. della F & b. La onde, per la Decima Definitione
d'hoggi; seguita, che ciascuna de queste Diatessaron sia contenuta nella prima specie,
& che tra le mostrate Dicisette chorde cinque fiate si contenga la Prima specie della Dia
tessaron. Dico poi, che tra loro si troua anco cinque fiate la seconda specie, tra A.
 . C
. C & D, tra D E. F & G, tra a.
 . c & d. tra d. e. f & g, & tra G. a. b & c; essendo che 'l Semi-
. c & d. tra d. e. f & g, & tra G. a. b & c; essendo che 'l Semi-tuono è contenuto tra la seconda & la terza chorda di ciascheduna, come tra
 & C.
& C. della A & D, tra E & F. della D & G; tra
 & c. della a & d, tra e f della d & g, & tra a &
& c. della a & d, tra e f della d & g, & tra a & b. della G & c. La onde, per la nominata Definitione, segue; che tutte le mostrate Dia-
tessaron siano contenute nella Seconda specie. Tra le mostrate Dicisette chorde adun-
que, cinque fiate è contenuta la Seconda specie della Diatessaron. Vltimamente dico,
che la Terza specie è contenuta tra essa Dicisette chorde cinque fiate, tra
 . C. D & E,
. C. D & E, tra E. F. G & a, tra
 . c. d & e, tra e. f. g & aa, et tra a. b. c et d, essendo che la prima et la
. c. d & e, tra e. f. g & aa, et tra a. b. c et d, essendo che la prima et la 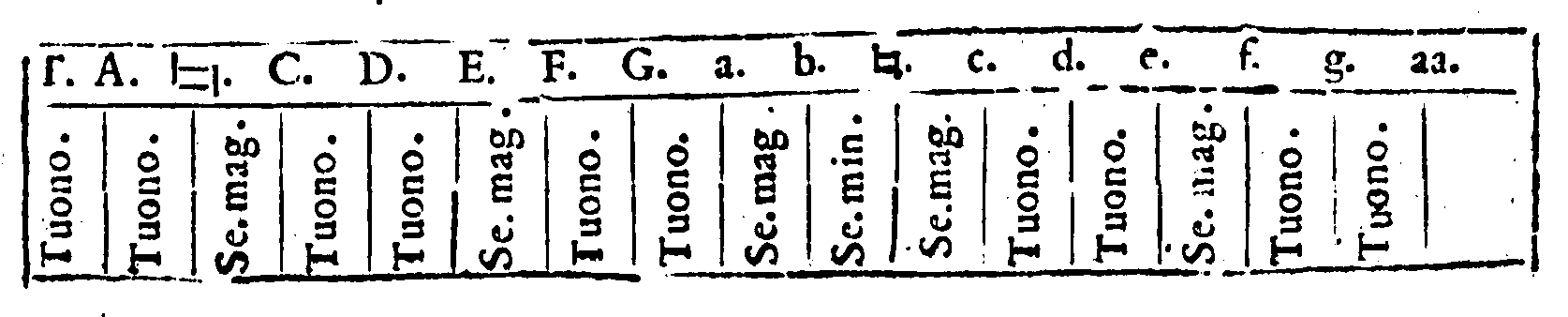
 & C. della
& C. della  & E. la E & F. della E & a. la
& E. la E & F. della E & a. la  & c. della
& c. della  & e. la e & f. del
& e. la e & f. della e & a. & la a & b. della a & d. contengono il nominato Semituono. Il perche dico, per
l'istessa Decima Definitione, tra le Dicesette chorde mostrate, contenersi cinque fiate
la Terza specie della Diatessaron. Et tutto questo è quello, che si contiene nella proposta,
& dimostrarui douea. Queste cose, disse M. Adriano; sono consequenti; imperoche se
la Diapente & la Diapason mutano il nome, ouer'ordine di Prima specie & di Seconda;
bisogno è che anco l'istesso faccia la Diatessaron, quando 'l Semituono uiene à mutar luo-
go; ma passate pure à dimostrarci qualche altra cosa; perche questo è chiaro. Ascolta-
te questa, soggiunsi.
PROPOSTA IX.
Diapente, ne tra la Settima & la Vndecima ui è quella della Diatessaron.
urò ben molto caro, che ce lo dimostriate. Et io per farui questo piacere risposi;
lo dimostrerò uolentieri. Dirò adunque; La Trentesima proposta del Secon-
do giorno dimostra, che la Diapente contiene due Tuoni maggiori & un mi-
nore, con un maggior Semituono; & ridotta al suo temperamento, per la Prima d'hog-
gi, contiene tre Tuoni equali & un Semituono maggiore; ma tra la Terza & la Settima
chorda delle nominate Dicesette, non ui sono se non due Tuoni, & due maggiori Semi-
tuoni; percioche, per la nominata Prima proposta, tra
 & C. ui si troua 'l Semituono
& C. ui si troua 'l Semituono maggiore, tra C & D. un tuono, tra D & E un'altro tuono, & tra E & F. un'altro mag-
gior Semituono; i quali Interualli posti insieme non arriuano à tre Tuoni & un Semituo-
no maggiore; Adunque tra la Terza & la Settima chorda delle proposte non si troua la
Consonanza Diapente. Soggiungo ancora et dico; che tra la Settima chorda et la Vn-
decima non si ritroua la Diatessaron; essendo che per la Ventesimaottaua proposta del
Secondo nostro ragionamento; la Diatessaron contiene un Tuono maggiore con un
minore, et un maggior Semituono; la quale, per la Prima nominata di questo, ridotta
al suo temperamento, contiene due Tuoni equali con un maggior Semituono. Ma tra
la settima et la undecima chorda si trouano tre Tuoni; percioche tra F et G. si troua 'l pri-
mo; tra G et a. il secondo; et tra a et
 . il terzo; et tre Tuoni, per la Ventesimanona del
. il terzo; et tre Tuoni, per la Ventesimanona del Secondo, sopr'auanzano la Diatessaron; adunque tra la Settima et la Vndecima chorda
delle Dicesette proposte; non si troua la Diatessaron. Et questo è quello, che ui douea
dimostrare. A fè, quasi ridendo disse M. Claudio; che mi è piaciuto questa dimostra-
tione, si per la sua breuità; com'anco per la sua facilità; onde credo che la Proposta sia
stata Theorema & non Problema; perche non si è uenuto all'atto dell'operare; però ui
prego, che senza por tempo di mezo, passate all'altra. Soggiunsi allora; Quel che haue-
te detto è uero, et per satisfarui, uoglio dimostrare in questa sequente; che
PROPOSTA X.
la possa diuidere in due parti.
che la dimostriate; accioche la sapiamo. Eccoui adunque dissi. Siano le Otto
chorde della Settima specie della Diapason
 . C. D. E. F. G. a. &
. C. D. E. F. G. a. &  . Dico che tra
. Dico che tra page 272 queste non cade alcuna chorda mezana, che la possa diuidere harmonicamente in una
Diapente nel graue, & in una Diatessaron nell'acuto. Imperoche tra
 & F. corda me
& F. corda me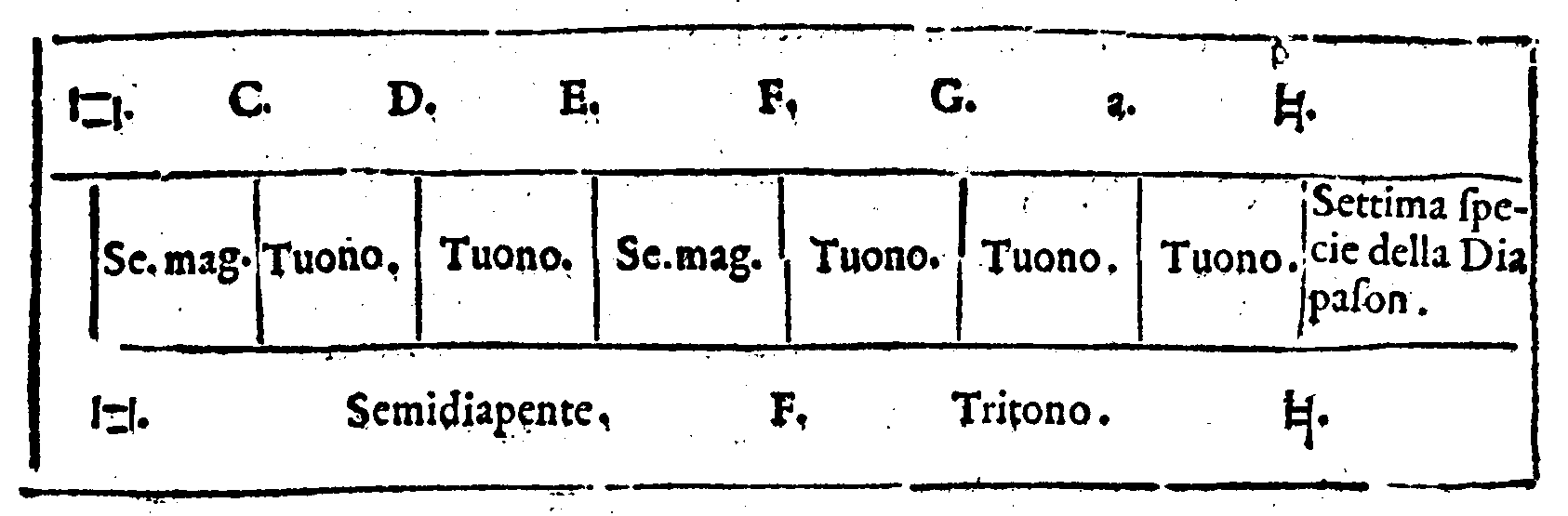
 . la Diatessaron; poiche tra
. la Diatessaron; poiche tra  & F. si tro-
& F. si tro-uano solamente due Tuoni & due maggiori Semituoni, com'è manifesto, i quali, per la
Trentesima del Secondo; non arriuano ad una Diapente. Simigliantemente, tra F &
 .
. non ui è la Diatessaron; essendo che, per la Ventesima ottaua del nominato Secondo
giorno; la Diatessaron contiene due Tuoni; l'un de i quali è maggiore & l'altro minore;
oueramente, per le Definitioni Quarta & Quinta d'hoggi; sono due Tuoni equali, & di
più un maggior Semituono; & F con
 . contiene tre Tuoni, i quali, per la Ventesima
. contiene tre Tuoni, i quali, per la Ventesima nona del nominato Secondo; sono maggiori d'una Diatessaron; adunque
 & F. non
& F. non fanno una Diapente, ne F &
 . una Diatessaron. Ma perche, per la Duodecima Defi-
. una Diatessaron. Ma perche, per la Duodecima Defi-nitione d'hoggi, la Diapason è detta essere harmonicamente diuisa, quando da una me-
zana chorda è partita in una Diapente posta nel graue & nella Diatessaron nell'acuto;
non si potendo fare tal diuisione col mezo della chorda F; però dico, che Tra la Settima
specie della Diapason non cade alcuna chorda mezana, che la partisca harmonicamen-
te in due parti; come dimostrar ui douea. Voglio ancora che sapiate, in consequenza di
quello, c'hò dimostrato; che
PROPOSTA XI.
diuise in due parti harmonicamente.
 . C. D. E. F. G. a.
. C. D. E. F. G. a.  . c. d. e. f. g & aa. Dico che sei Specie di essa, & non più, po-
. c. d. e. f. g & aa. Dico che sei Specie di essa, & non più, po-tranno essere diuise harmonicamente in due parti. Et perche, per la Duodecima
definitione d'hoggi; tal diuisione nasce da una chorda mezana, che la diuide in una Dia
pente nel graue, & in una Diatessaron nell'acuto; essendo la Diapason C & c. della prima
specie diuisa in cotal modo dalla chorda G; la D & d. della seconda dalla a; la E & e. del-
la terza specie della
 . la F & f. della quarta dalla c; la G & g. della quinta specie dalla d;
. la F & f. della quarta dalla c; la G & g. della quinta specie dalla d; & la a & aa. della Sesta dalla e; Il che si potrebbe anco dire della Γ & G; medesimamen
te della quinta specie, la quale è diuisa dalla D; & della A & a. della Sesta, che è partita
dalla E; però la mezana chorda, che partisce la Prima specie sarà G; la mezana della Se
conda sarà a; quella della Terza sarà
 ; la mezana della Quarta sarà c la mezana della
; la mezana della Quarta sarà c la mezana della Quinta sarà d; & la mezana della Sesta sarà e. Essendoche la prima, ch'è G. diuiderà la
Diapason C & c. in una Diapente C & G. posta nella parte graue, & in una Diatessaron
G & c. posta nella parte acuta; & la a. partirà la Seconda D & d. in una Diapente D & a.
nel graue, & in una Diatessaron a & d. nell'acuto. Simigliantemente
 diuiderà la Ter
diuiderà la Terpage 273
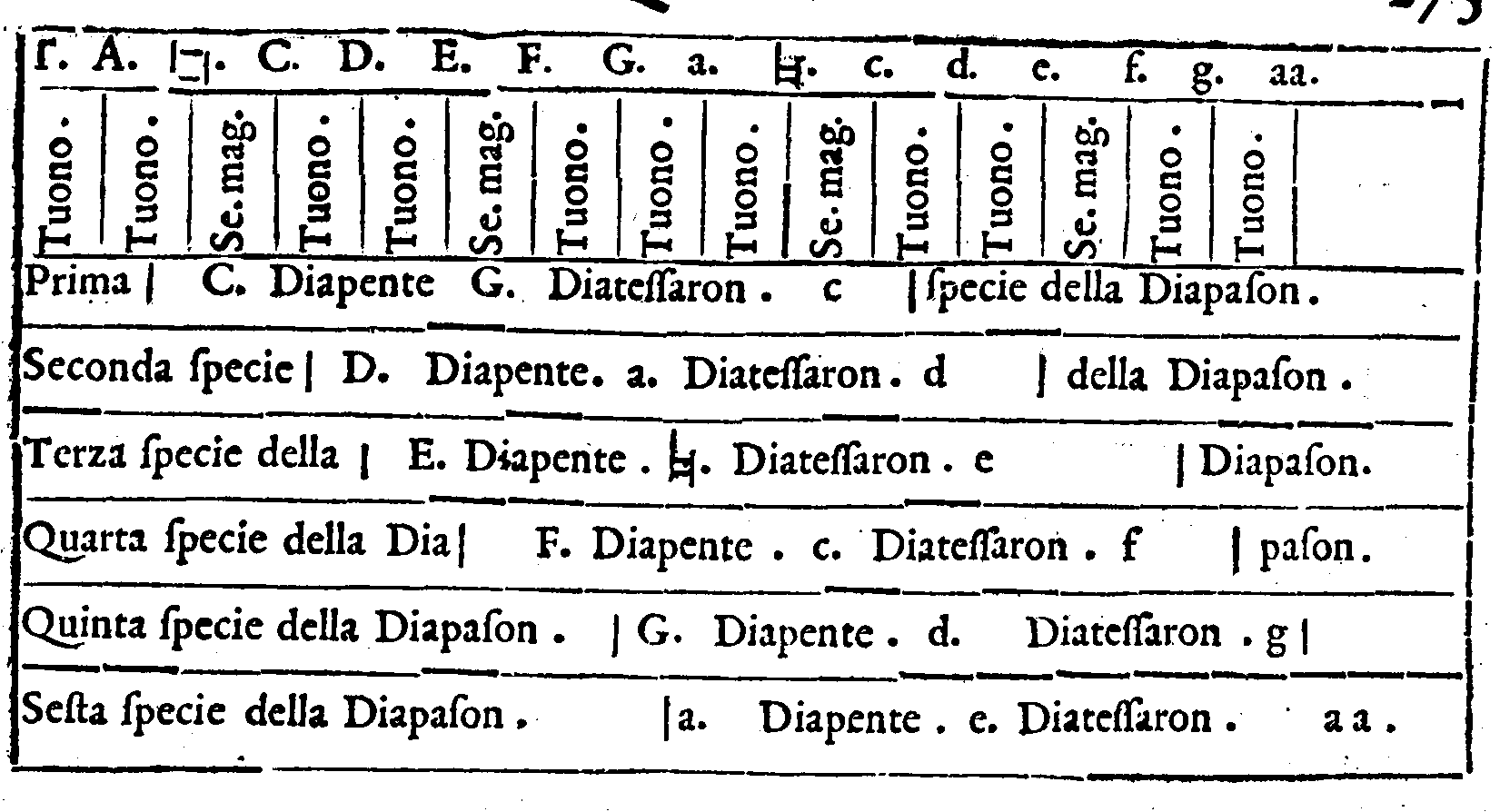
 . nel graue, & in una Diatessaron
. nel graue, & in una Diatessaron  & e. nell'acuto. Et
& e. nell'acuto. Et c. diuiderà la Quarta F & f. in una Diapente posta nel graue, che sarà F & c, & in una Dia-
tessaron posta nella parte acuta, la quale sarà c & f. Ma la d. partirà la Quinta specie G
& g. nella Diapente G & d. nel graue, & nella Diatessaron d & g. nell'acuto. Vltimamen
te la Sesta specie a & aa. sarà diuisa da e. in una Diapente a & e. posta nel graue, & in una
Diatessaron e & aa. posta nell'acuto. La onde non è dubio alcuno essendo C G, D a,
E
 , F c, G d & a e Diapente; perche, per la Trentesima del Secondo giorno, ciasche-
, F c, G d & a e Diapente; perche, per la Trentesima del Secondo giorno, ciasche-duna di esse contiene Tre tuoni & un maggior Semituono; il che dico ancora della G c,
a d,
 e, c f, d g & e aa Diatessaron, che contengono ciascheduna da per se; per la Ven-
e, c f, d g & e aa Diatessaron, che contengono ciascheduna da per se; per la Ven-tesima ottaua pur del Secondo; due Tuoni & un maggior Semituono; che le chorde me
zane, le quali partiscono le nominate Sei prime specie della Diapason, siano la G. a
 .
. c. d & e. Et perche Sei sono le specie della Diapason, com'habbiamo dimostrato, che
si possono in cotal modo diuidere; & la Settima, per la Precedente, al tutto è indiui-
sibile; però dico, che Delle Sette specie della Diapason Sei & non più, da una mezana
chorda possono esser diuise harmonicamente in due parti; come, secondo la proposta
ui douea dimostrare. Vi uoglio etiandio dimostrare; che
PROPOSTA XII.
meticamente in due parti.
le chorde F. G. a.
 . c. d. e & f. tra le quali ui è la Quarta
. c. d. e & f. tra le quali ui è la Quarta  , che la diuide in due
, che la diuide in due parti; F. G. a &
 . & in
. & in  . c. d. e & f. Ma tra F. G. a &
. c. d. e & f. Ma tra F. G. a &  ; per la Decima di questo;
; per la Decima di questo; si troua Tre tuoni; i quali sono, per la Ventesima nona del Secondo, maggiori d'una
Diatessaron; adunque F &
 . non è una Diatessaron. Simigliantemente tra
. non è una Diatessaron. Simigliantemente tra  . c. d. e & f.
. c. d. e & f. si trouano due Tuoni & due maggiori Semituoni. Ma la Diapente, per la Trentesima del
nominato Secondo giorno, contiene tre Tuoni & un maggior Semituono, adunque
 &
& f. non è Diapēte. Nō essendo adunque F
 . Diatessaron, ne
. Diatessaron, ne  f. Diapente; & essendo F & f.
f. Diapente; & essendo F & f. la Quarta specie della Diapason; nō sarà anco la
 . chorda mezana, laquale la diuida arith
. chorda mezana, laquale la diuida arithpage 274
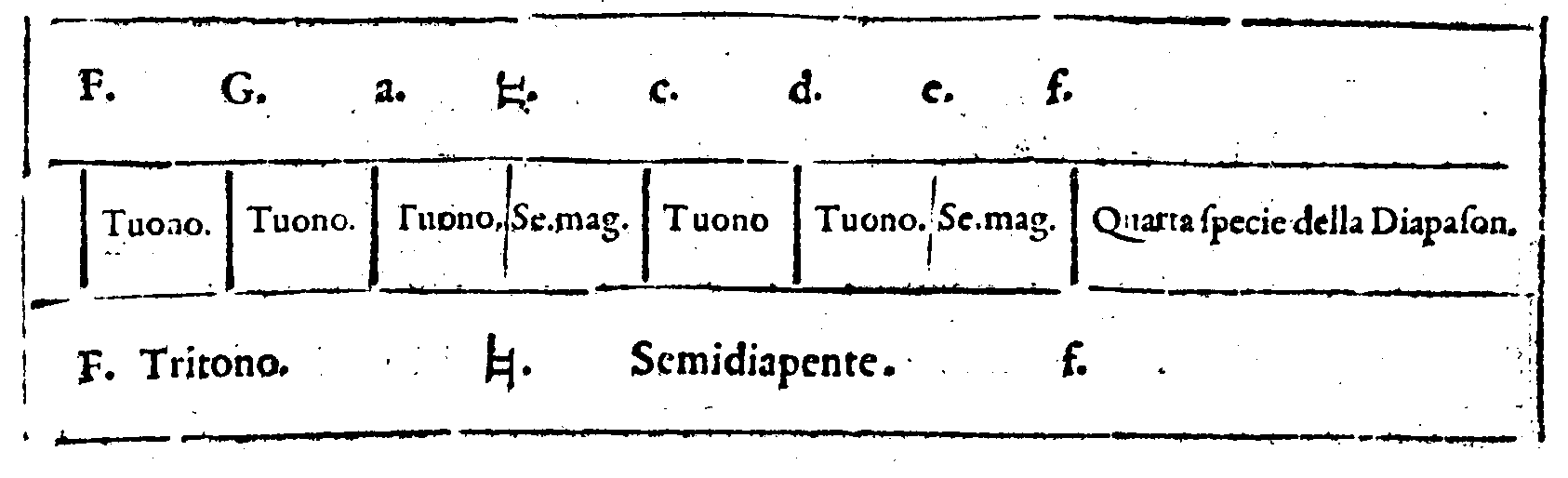
è detta esser'allora arithmeticamente diuisa; quando da una chorda mezana è partita in
vna Diatessaron, che tenga 'l luogo graue, & in una Diapente, che tenga l'acuto. Tra la
Quarta specie adunque della Diapason non si troua alcuna chorda, che la diuida arith-
meticamente in due parti; come vi douea dimostrare. Qui disse M. Adriano; Questo è
noto à tutti noi, che siamo istrutti nelle cose della prattica della Musica; però passate pure
inanzi al uostro bel piacere. Allora soggiunsi; Questa cosa senza dubio la cognosceuate
inanzi per la prattica; ma hora la sapete, col mezo della dimostratione. Oltra di questo
saperete; che questa và in consequenza.
PROPOSTA XIII.
parti arithmeticamente, non ne potrà diuidere, se non Sei specie.
arithmeticamente; quando da una mezana chorda è in tal maniera partita, che
nella parte graue sia accōmodato la Diatessaron, & nell'acuta la Diapente. Però
siano Γ. A
 . C. D. E. F. G. a.
. C. D. E. F. G. a.  . c d. e. f g & aa, le quali cōtengano le Sette specie della Dia
. c d. e. f g & aa, le quali cōtengano le Sette specie della Diapason. Dico che tra questo numero di chorde, la chorda mezana, che partisce in due parti
arithmeticamēte le Diapason, non ne potrà diuidere se non Sei specie, lequali sarāno (per
seguitare unordine continuo & non interrotto) Γ & G, ouer G & g. Quinta specie; A & a
ouero a & aa. Sesta;
 &
&  . Settima; C & c. prima; D & d. Secōda; ultimamēte E & e. Ter-
. Settima; C & c. prima; D & d. Secōda; ultimamēte E & e. Ter-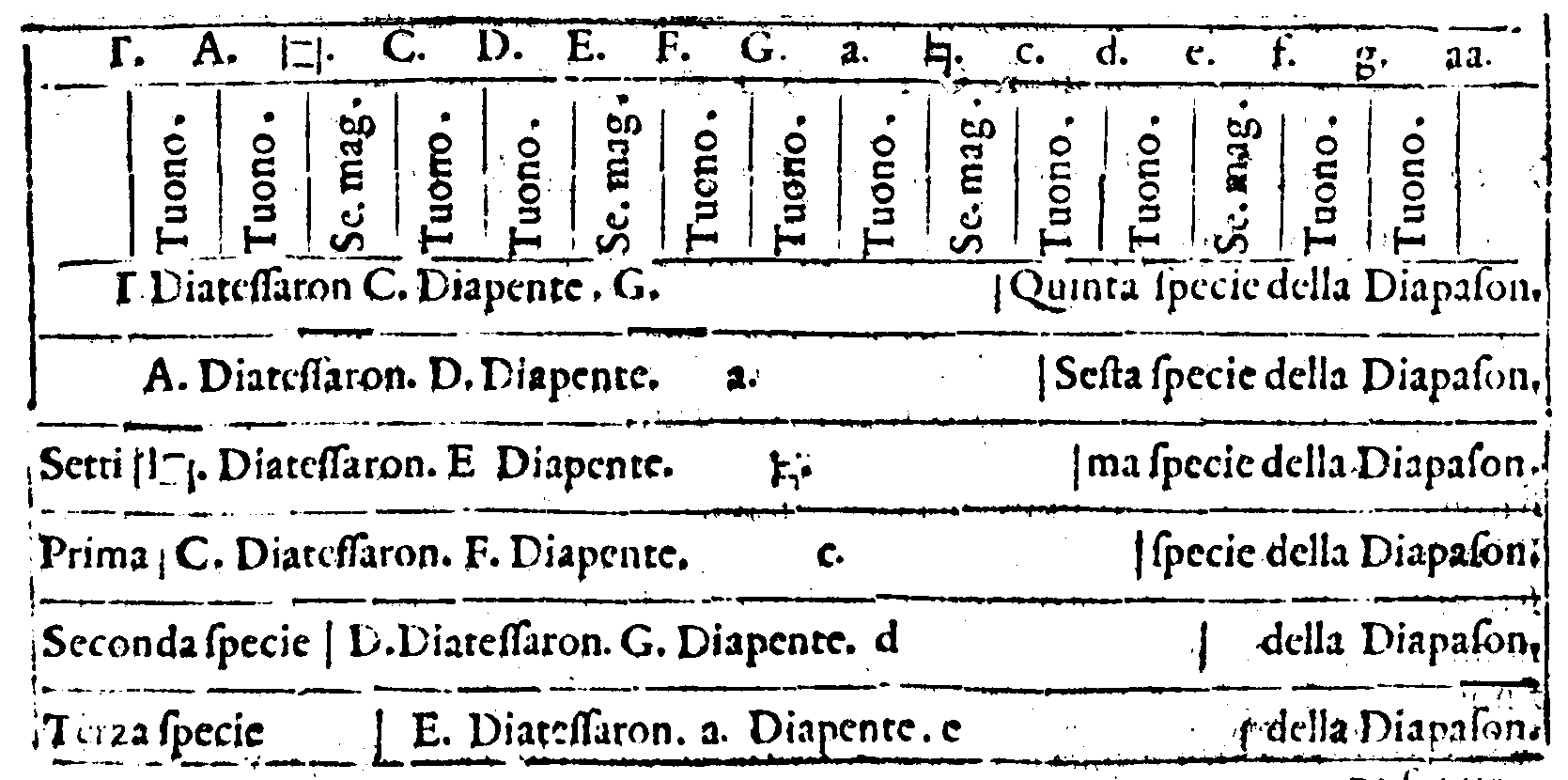
C. diuide la Γ & G. in una Diatessaron Γ & C. posta nel graue & in una Diapente C & G.
posta nell'acuto, la D. diuide la A & a. in una Diatessaron A & D, & in una Diapēte D &
a; la E. diuide la
 &
&  . in una Diatessaron
. in una Diatessaron  & E. & in una Diapente E &
& E. & in una Diapente E &  ; la F. di
; la F. diuide la C. & c. in una Diatessaron C & F. & in una Diapente F & c; la G; parte la D & d.
in una Diatessaron D & G. & in una Diapente G & d. Vltimamente la a. diuide la E & e.
in una Diatessaron E & a. & in una Diapente a & e. Onde non è da dubitare, che contenen
do ciascheduna di queste Γ & c, A & D,
 . & E, C & F, D & G, & E & a. due Tuoni & un
. & E, C & F, D & G, & E & a. due Tuoni & un maggior Semituono; elle siano, per la Ventesima ottaua del Secōdo ragionamento, tan-
te Diatessaron. Si come non è anco da dubitare delle C & G, D & a; E &
 , F & c, G &
, F & c, G & d; & a con e; per la Trentesima nona del Secondo medesimamente, che elle siano Dia-
pente; percioche contengono tre Tuoni & un maggior Semituono. Et perche Sette so-
no le specie della Diapason, & tali diuisioni non si possono fare in più di Sei; essendo
che per la Precedente, la Quarta specie non riceue cotal diuisione; però dico, che tra 'l
numero delle Sedeci chorde mostrate, la mezana chorda, che diuide in due parti arithme
ticamente la Diapason, non potrà diuidere se non Sei specie di essa; come dimostrarui
douea. Voglio ancora che sapiate; che da questo ch'io u'hò dimostrato, ne segue; che
PROPOSTA XIIII.
& Sei nonprincipali, & plagali.
che contiene in se una forma, ò qualità dharmonia; che si troua in una delle Set-
te specie della Diapason; modulata per quelle specie della Diapente & della Dia-
tessaron, che alla sua forma sono conueneuoli. Ma perche tali Specie non si possono mo
dulare se non in Dodici maniere; percioche; per la Vndecima proposta d'hoggi, la Dia
pason si troua harmonicamente diuisa in sei modi, & per la Duodecima proposta, in sei
altri modi arithmeticamente; onde tutte queste maniere ascendono al numero de Dodi-
ci; però dico, che i Modi non possono esserne più, ne meno de Dodici. Et perche; per
la Quintadecima definitione; dalla prima diuisione nascono sei Modi principali & Au-
tentici; & dalla seconda; per la Decimasesta; uengono i Sei nonprincipali & Plagali;
però sono Sei li Modi principali & Autentici, & Sei etiandio i Nonprincipali & Plagali;
come dimostrar ui douea; il che non si può negare; percioche è troppo cosa manifesta.
Però seguiterò l'altra; per non perdere il tempo; la qual sarà questa.
PROPOSTA XV.
laterali.
spiacerà, che ce la dimostrate. Cosi uoglio fare; risposi; La uera Chor-
da finale di ciascheduno de i Modi; per la Decimasettima definitione
di questo Ragionamento; è la grauissima chorda delle loro Diapen-
te; ma la grauissima della Diapente del Primo & del Secondo modo; per la Vn-
decima proposta di questo & per la Precedente è la C; quella del Terzo & del Quar-
to è la D; quella del Quinto & del Sesto è la E; quella del Settimo & dell'Otta-
page 276 uo è la F; quella del Nono & del Decimo è la G; & quella dell'Vndecimo & del Duodeci-
mo è la a; Adunque la chorda del Primo è commune con quella del Secondo; quella del
Terzo con quella del Quarto; quella del Quinto con quella del Sesto; quella del Settimo
con quella dell'Ottauo; quella del Nono con quella del Decimo; finalmente quella del-
l'Vndecimo con quella del Duodecimo. Ma tutti i Primi de i nominati Modi sono Prin-
cipali, & li Secondi sono i Collaterali; adunque le chorde finali de i Sei modi principali
sono cōuni con quelle de i Sei modi suoi collaterali; come ui douea dimostrare. A que-
sto disse M Francesco; Questa dimostratione è facile & chiara; & se non era il saper tale
conclusione per uirtù de i principij; non accascaua farla altramente. Ma ueniamo pure
ad un'altra. Allora soggiunsi; Voglio che sapiate ancora; che
PROPOSTA XVI.
cipale, ouer'Autentico; ne tra la Quarta, quella d'alcun Modo nonprincipale, ouer
plagale.
lo, ch'è contenuto tra le chorde d'una delle sette Specie della Diapason diuisa
harmonicamente da una chorda mezana nella modulatione d'una Diapente &
in una della Diatessaron. Ma per la Decima proposta; tra la Settima specie della Diapa-
son non cade tal diuisione; adunque tra la Settima specie della Diapason non cade mo-
dulatione d'alcun Modo principale, ouero Autentico. Oltra di questo; per la Decima-
sesta definitione; il Modo nonprincipale, ò plagale è quello, ch'è contenuto tra le chorde
d'una delle Sette specie della Diapason diuisa arithmeticamente da una mezana chorda
in due modulationi; in quella della Diatessaron posta nel graue; & in una della Diapen-
te posta in acuto; ma per la Duodecima proposta d'hoggi; tra la Quarta specie della Dia-
pason non ui casca chorda alcuna mezana: che la diuida arithmeticamente in due parti;
adunque tra la Quarta specie della Diapason non cade modulatione d'alcun Modo non-
principale, ouer Plagale; come, secondo tutto quello, che contiene la proposta, vi douea
dimostrare. In effetto credo, disse M. Francesco, che chi saprà ritrouare i mezi, saprà anco
ritrouare & far le dimostrationi delle cose. Però non mi marauiglio; che una cosa tanto
chiara al senso, la quale non hauea dibisogno di dimostratione, ce l'habbiate tanto chia-
ramente proposta auanti gli occhi, che se prima la sapeuamo ad un certo modo, hora
semplicemente per la sua cagione la sapiamo. Soggiunse il Sig. Desiderio, à queste pa-
role; Questo è quello, ch'è detto propriamente Sapere; come M. Gioseffo vi ragionò il
primo giorno. Ma andiamo pur di lungo. Vi fò sapere; dissi; che
PROPOSTA XVII.
diatoniche l'un dopo l'altro, nelle Sedici chorde mostrate.
 &
&  . nō
. nō cade modulatione alcuna di Modo Principale, ouero Autentico; però siano le
chorde C. D. E. F. G. a.
 . c. d. e. f. g & aa. del numero delle Sedici nominate
. c. d. e. f. g & aa. del numero delle Sedici nominate solamente. Dico, tra C. D. E. F. G. a.
 . & c. esser collocato il Primo modo & principale;
. & c. esser collocato il Primo modo & principale; page 277

MODI PRINCIPALI, ET AVTENTICI.
 . c & d. il. Terzo; tra E. F. G. a.
. c & d. il. Terzo; tra E. F. G. a.  . c. d & e. il Quinto; tra F. G. a.
. c. d & e. il Quinto; tra F. G. a.  . c.
. c. d. e & f. il Settimo; tra G. a.
 . c. d. e. f & g. il Nono; & tra a.
. c. d. e. f & g. il Nono; & tra a.  . c. d. e. f. g & aa. l'Vndeci-
. c. d. e. f. g & aa. l'Vndeci-mo. Imperoche, per la Sesta di questo, C. D. E. F. G. a.
 & c. è la Prima specie della
& c. è la Prima specie della Diapason; & per la Vndecima, tale Diapason è diuisa harmonicamente dalla chorda G.
in una Diapente C & G, & in una Diatessaron G & c; onde, per la Quartadecima & Quin
tadecima definitione, seguita; che tale Diapason contenga il primo Modo principale &
autentico. Simigliantemente; perche D. E. F. G. a. b. c & d, per la Sesta nominata; è la
seconda specie della Diapason, & per la Vndecima proposta nominata, tale Diapason
è harmonicamente diuisa dalla chorda a. in una Diapente D & a. in una Diatessaron a &
d; però, per le nominate Definitioni, tal Diapason contiene il Terzo modo principale.
Ancora; perche E. F. G. a.
 . c. d & e, è la Terza specie della Diapason, & per la Vndecima
. c. d & e, è la Terza specie della Diapason, & per la Vndecima di questo, è diuisa harmonicamente dalla
 . in due parti; cioè, in una Diapente E &
. in due parti; cioè, in una Diapente E &  , in
, in una Diatessaron
 & e; però dico E. F. G. a.
& e; però dico E. F. G. a.  . c. d & e. essere; per le dette due Definitioni,
. c. d & e. essere; per le dette due Definitioni, il Quinto modo & principale. Oltra ciò; perche; per la nominata Vndecima; F. G. a.
 . c. d. e & f. è la Quarta specie della Diapason diuisa dalla c. in una Diapente F & c, & i in
. c. d. e & f. è la Quarta specie della Diapason diuisa dalla c. in una Diapente F & c, & i in una Diatessaron c & f; però dico, per l'istesse due nominate Definitioni, tal Diapason,
contenere la modulatione del Settimo modo & principale. Dico ancora G. a.
 .
. c. d. e. f & g, contenere 'l Nono & principale; percioche essendo la Quinta specie del-
la Diapason diuisa; come dimostra l'Vndecima d'hoggi; dalla chorda d. in due
parti; cioè, in G & d. Diapente, & in d & g. Diatessaron; ne segue, per le Defi-
nitioni addotte di sopra, senza dubitar cosa alcuna, il nostro proposito. Final-
mente essendo a.
 . c. d. e. f. g & aa. la Sesta specie della Diapason, & essendo diuisa in
. c. d. e. f. g & aa. la Sesta specie della Diapason, & essendo diuisa in una Diapente a & e. harmonicamente, & in una Diatessaron e & aa. dalla chorda
page 278 e; seguita medesimamente, per le due di sopra nominate Definitioni; che nella detta Dia-
pason sia contenuta la modulatione dell'Vndecimo modo, & che esso modo sia uno delli
Autentici & principali. Et tutto questo è quello, che faceua bisogno di dimostrarui. Dis-
se allora M. Adriano; Quelli, che negano i Modi esser Dodici, sono in grand'errore; &
tal'errore si và sempre facendo più palese dalle dimostrationi. Et perche hauete dimo-
strato per ordine i Principali; però seguitarete à dimostrarci gli altri; se ben non è cosa
difficile da intendere. Qui è il suo luogo Messere; dissi; però attendete.
PROPOSTA XVIII.
l'un dopo l'altro, nelle Sedici chorde già nominate.
pason non cade modulatione alcuna di Modo non principale, ouer Plagale; Pe-
rò lasciando da un canto le chorde f. g & aa; essendo che non fanno al presente
di bisogno; siano le chorde Γ. A. C. D. E. F. G. a.
 . c. d & e. separate dal numero delle
. c. d & e. separate dal numero delle Sedici tante fiate nominate. Dico tra Γ. A. C. D. E. F & G. esser collocato il Secondo
modo non principale, ouer Plagale; tra A.
 . C. D. E. F. G & a; il Quarto; tra
. C. D. E. F. G & a; il Quarto; tra  C. D. E.
C. D. E. F. G. a &
 . il Sesto; tra C. D. E F. G. a
. il Sesto; tra C. D. E F. G. a  & c; l'Ottauo; tra D. E. F. G. a.
& c; l'Ottauo; tra D. E. F. G. a.  . c & d; il Decimo;
. c & d; il Decimo; & tra E. F. G. a.
 . c. d & e. il Duodecio. Percioche essendo Γ. A.
. c. d & e. il Duodecio. Percioche essendo Γ. A.  . C. D. E. F & G, per
. C. D. E. F & G, per la Sesta proposta d'hoggi; la Quinta specie della Diapason, & per la Terzadecima diuisa
arithmeticamente dalla chorda C. in una Diatessaron Γ & C. & in una Diapente C & G;
quella posta nel graue & questa nell'acuto; per le Definitioni Quartadecima & Decima-
sesta; tal Diapason uiene ad essere 'l Secondo modo, & Nonprincipale, ouer Plagale.
Simigliantemente; perche A.
 . C. D. E. F. G & a, per la detta proposta, è la Settima spe-
. C. D. E. F. G & a, per la detta proposta, è la Settima spe-cie della Diapason, & per la nominata Decimaterza, è diuisa arithmeticamente in una
Diatessaron A & D, & in una Diapente D & a; però dico A.
 . C. D. E. F. G & a, per le
. C. D. E. F. G & a, per le Definitioni nominate, essere 'l Quarto modo & Nonprincipale. Ancora; per la detta Se-
sta proposta
 . C. D. E. F. G. a &
. C. D. E. F. G. a &  ; è la Settima specie della Diapason diuisa, per la detta
; è la Settima specie della Diapason diuisa, per la detta Terzadecima proposta, dalla chorda E. in una Diatessaron
 & E, & in una Diapente E
& E, & in una Diapente E &
 ; però dico per la Quartadecima definitione; tal Diapason essere il Sesto modo, &
; però dico per la Quartadecima definitione; tal Diapason essere il Sesto modo, & anco essere; per la Decimasesta; uno de i Modi nonprincipali, ouer Plagali. Ma la C. D.
E. F. G. a.
 & c; per la nominata proposta, è la prima specie della Diapason diuisa in una
& c; per la nominata proposta, è la prima specie della Diapason diuisa in una Diatessaron C & F, & in una Diapente F & c. dalla chorda F; onde dico, questa Diapason
contenere l'Ottauo modo, uno de i Nonprincipali. Et perche D. E. F. G. a.
 . c & d. è la
. c & d. è la seconda specie, per la Sesta di questo, della Diapason diuisa, per la Terzadecima, in
una Diatessaron D & G, & in una Diapente G & d. dalla chorda G; però dico, per le addotte di sopra; D. E. F. G. a.
 . c & d, contenere la modulatione del Decimo
. c & d, contenere la modulatione del Decimo modo & Plagale. Vltimamente; perche E. F. G. a.
 . c. d & e; per la Sesta nominata, è la
. c. d & e; per la Sesta nominata, è la Terza specie della Diapason diuisa arithmeticamente in una Diatessaron E & a, & in
una Diapente a & e; dalla chorda a; però dico, per le due nominate di sopra Definitioni;
tale Diapason contenere il modo Duodecimo, uno de i Nonprincipali. La onde per tal
modo haurò dimostrato per ordine i Modi Nonprincipali & Plagali; come ui douea di-
mostrare. Voglio hora dimostrarui; che
page 279
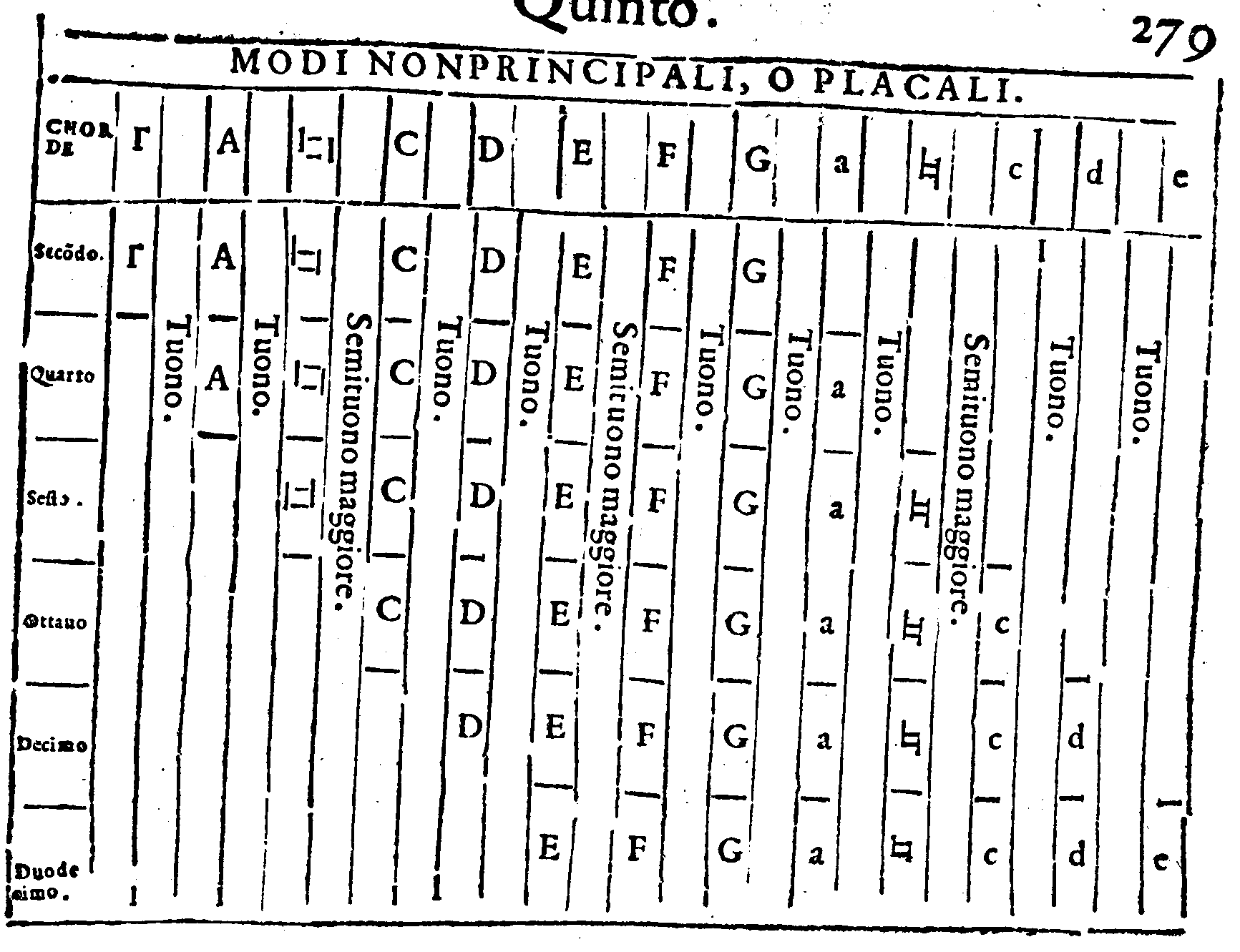
MODI NON PRINCIPALI, O PLACALI.
PROPOSTA XIX.
Quinto più acute di quelle del Terzo simigliantemente per un Tuono; quelle del
Settimo più acute di quelle del Quinto per un Semituono maggiore; quelle del No-
no più acute di quelle del Settimo per un Tuono; & quelle dell'Vndecimo ancora più
acute di quelle del Nono per un Tuono. Simigliantemente le chorde del Quarto
modo sono più acute di quelle del Secondo per un Tuono; quelle del Sesto di quel-
le del Quarto per un Tuono; quelle dell'Ottauo più acute di quelle del Sesto per
un Semituono maggiore; & quelle del Decimo sono più acute di quelle dell'Ot-
tauo per un Tuono. Ancora quelle del Duodecimo modo sono più acute di quelle
del Decimo per un Tuono.
cendo à Dio; ascoltate adunque. Non è dubio alcuno, che per la Prima pro
posta d'hoggi, la chorda D. sia più acuta della C; la E. della D; la G. dlla
F; & la a. della G, ciascheduna da per se, per un Tuono. Simigliantemente, che
la F. sia più acuta della E; & anco la C. della
 . per un Semituono maggiore. La
. per un Semituono maggiore. La onde essendo la C. chorda grauissima del Primo modo; la D. quella del Terzo; la
E. quella del Quinto; la F. quella del Settimo; la G. quella del Nono; & la a. quella
dell'Vndecimo. Ancora essendo Γ. la grauissima chorda del Secondo modo; A quel-
la del Quarto;
 . quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; &
. quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; & page 280 E quella del Duodecimo; seguendo l'altre per ordine; secondo la natura delle loro Dia-
pason; non è da dubitare, che le chorde del Terzo modo siano più acute di quelle del
Primo, quelle del Quinto più acute di quelle del Terzo, quelle del Nono più acute di
quelle del Settimo, & quelle dell'Vndecimo più acute di quelle del Nono, per un Tuo-
no. Et che quelle del Settimo siano più acute di quelle del Quinto per un Semituono
maggiore, come dice la prima parte della proposta. Et per la seconda parte dico; che,
per la Prima proposta nominata, la chorda A. è più acuta della Γ. la
 . della A. ancora
. della A. ancora la D. della C. la E. della D. per un Tuono. Et la C. della
 . più acuta per un Semituo-
. più acuta per un Semituo-no maggiore. Ma Γ. è chorda grauissima del Secondo modo; A. quella del Quarto;
 . quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; & E. quella del Duo-
. quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; & E. quella del Duo-decimo. Adunque le chorde del Quarto modo sono più acute di quelle del Secondo;
quelle del Sesto di quelle del Quarto; quelle del Decimo di quelle dell'Ottauo; & quel-
le del Duodecimo di quelle del Decimo, per un Tuono. Cosi ancora quelle dell'Otta-
uo sono ueramente più acute di quelle del Sesto per un maggior Semituono. Et questo
è tutto quello, ch'è contenuto nella seconda parte della proposta, & insieme tutto
quello, che secondo essa proposta dimostrar ui douea. Disse qui il Sig. Desiderio; Le
cose, che sono facili & note al senso, uolendole dimostrare, alle fiate rendono diffi-
cultà & lunghezza; & questa è in parte una di quelle. Ma uolendole sapere col mezo
de i Principij & dalle loro Cagioni; non si può fare altramente. Però si può andar
più oltra; poiche questa non hà dibisogno d'altra dichiaratione. E' cosi, come di-
te in fatto; risposi; & non si può fare altramente. Ascoltate adunque quello, che ui
uoglio dire.
PROPOSTA XX.
no più acute di quelle de i loro Modi non principali; & per il contrario; quelle de
i Non principali sono più graui di quelle de i loro Modi principali per una Diates-
saron.
Quinto, Settimo, Nono & Vndecimo modo sono modi Principali; & per la
Decimasesta, che 'l Secondo, Quarto, Sesto, Ottauo, Decimo & Duodeci-
mo sono Modi non principali. Ma per la Quartadecima definitione, il Pri-
mo modo è contenuto dalla Prima specie della Diapason C. D. E. F. G. a.
 & c. il Secon-
& c. il Secon-do dalla Quinta Γ. A.
 . C. D. E. F & G. il Terzo dalla Seconda specie D. E. F. G. a.
. C. D. E. F & G. il Terzo dalla Seconda specie D. E. F. G. a.  c &
c & d. il Quarto dalla Sesta A.
 . C. D. E. F. G & a. il Quinto dalla Terza E. F. G. a.
. C. D. E. F. G & a. il Quinto dalla Terza E. F. G. a.  . c. d & e.
. c. d & e. il Sesto dalla Settima
 . C. D. E F. G. a &
. C. D. E F. G. a &  . il Settimo dalla Quarta F. G. a.
. il Settimo dalla Quarta F. G. a.  . c. d. e & f.
. c. d. e & f. l'Ottauo dalla Prima C. D. E. F. G. a.
 & c. il Nono dalla Quinta G. a.
& c. il Nono dalla Quinta G. a.  . c. d. e. f & g. il De-
. c. d. e. f & g. il De-cimo dalla Seconda D. E. F. G. a.
 . c & d. l'Vndecimo dalla Sesta a.
. c & d. l'Vndecimo dalla Sesta a.  . c. d. e. f. g & aa. & lo
. c. d. e. f. g & aa. & lo Duodecimo dalla Terza E. F. G. a.
 . c. d & e. Ma la chorda più graue del Primo, ch'è C.
. c. d & e. Ma la chorda più graue del Primo, ch'è C. è più acuta della chorda più graue del Secondo, ch'è Γ. ò per il contrario, questa è più
graue di quella per una Diatessaron; quella del Terzo D. è più acuta di quella del Quarto
A. quella del Quinto E. è più acuta di quella del Sesto
 . quella del Settimo F. è più acu-
. quella del Settimo F. è più acu-ta di quella dell'Ottauo C. quella del Nono G. è più acuta di quella del Decimo D. &
quella dell'Vndecimo a. è più acuta di quella del Duodecimo E. oueramente tutte le no-
minate seconde sono più graui delle prime per una Diatessaron; adunque le chorde del-
le Modulationi de i modi Principali sono più acute di quelle de i Non principali; ouer le
chorde di questi sono più graui delle chorde de gli altri per una Diatessaron; come ui do-
uea dimostrare. Onde aggiungeremo; che
page 281
PROPOSTA XXI.
doli secondo 'l numero & gradi loro.
Ond'io; Siano dissi C. D. E. F. G. a.
 & c. le chorde della Prima specie della Dia-
& c. le chorde della Prima specie della Dia-pason nel Primo & nell'ottauo ordine; quelle della Quinta Γ. A.
 . C. D. E. F &
. C. D. E. F & G. nel Secondo; quelle della seconda D. E. F. G. a.
 . c & d. nel terzo & nel decimo; quel-
. c & d. nel terzo & nel decimo; quel-le della Sesta A.
 C. D. E. F. G & a. nel quarto, quelle della Terza E. F. G. a.
C. D. E. F. G & a. nel quarto, quelle della Terza E. F. G. a.  c. d & e. nel
c. d & e. nel quinto & duodecimo ordine; quelle della Settima
 . C. D. E. F. G. a &
. C. D. E. F. G. a &  . nel sesto; quelle
. nel sesto; quelle della Quarta F. G. a.
 . c. d. e. & f. nel Settimo; quelle della Quinta ancora G. a.
. c. d. e. & f. nel Settimo; quelle della Quinta ancora G. a.  . c. d. e. f &
. c. d. e. f & g. nel nono; simigliantemente quelle della Sesta a.
 . c. d. e. f. g & aa. nell'undecimo. Di-
. c. d. e. f. g & aa. nell'undecimo. Di-co, che i Modi principali, ouero Autentici sono ridotti & accompagnati insieme con i
Non principali, ò plagali; secondo 'l numero & i gradi loro; percioche ritrouandosi la
prima specie della Diapason nel primo ordine, & nel Secondo la Quinta; & essendo tra
la prima tramezata harmonicamente dalla chorda G. contenuto il Primo modo, & nella
Quinta mediata arithmeticamente, il Secondo; & essendo la chorda Γ. della Diapason
posta nel secondo ordine più graue della chorda C. della Diapason posta nel primo; se-
guita, che nel primo ordine sia contenuto 'l Primo modo autentico, & nel secondo ordi-
ne il Secondo modo plagale, & che dopo il Primo modo & principale habbiamo collo-
cato il Secondo non principale, & accompagnatolo al Primo, secondo 'l numero & li gra-
di dell'uno & dell'altro; perche non ha dubio alcuno; che il Secondo in ogni genere,
c'habbia ordine; non habbia da seguitare immediatamente dopo il Primo. Dopo il Se-
condo succede il Terzo; percioche, per la Decimanona di questo, il Terzo è più acuto
del Primo per un Tuono; la onde essendo la Diapason D. E. F. G. a.
 . c & d. del Terzo or-
. c & d. del Terzo or-dine più acuta di quella del primo per un Tuono; essendo che C. è lontana da D. come
più fiate hò dimostrato; per un simile Interuallo, & diuisa harmonicamente dalla chor-
da a. in una Diapente & in una Diatessaron; seguita, che essa Diapason contenga il Ter-
zo modo & autentico, collocato secondo 'l numero & grado suo dopo il Secondo & pla-
gale. A questo succede il Quarto, collocato nel Quarto ordine, per la Quartadecima
definitione, tra la Sesta specie della Diapason A.
 . C. D. E. F. g & a. arithmeticamente
. C. D. E. F. g & a. arithmeticamente diuisa; il quale è distante dal Secondo, per la Decimanona proposta di questo, per un
Tuono. Onde hauendo dimostrato la Diapason D & d. con le sue mezane chorde con-
tenere il Terzo modo; seguita, che senz'alcun mezo; secondo 'l numero & grado suo;
habbiamo collocato dopo il Terzo il Quarto modo; dopo il quale immediatamente uie-
ne il Quinto; percioche la Diapason E. F. G. a.
 . c. d & e. contenuta nel quinto ordine,
. c. d & e. contenuta nel quinto ordine, diuisa dalla chorda
 . in due parti harmonicamēte, per la Decimaquarta definitione no-
. in due parti harmonicamēte, per la Decimaquarta definitione no-minata; contiene esso Quinto modo. Et per la detta Decimanona proposta, il Quinto
modo è distante dal Terzo per un Tuono; percioche E. uiene ad essere, per l'istessa De-
cima, più acuto di D. per un tale interuallo. La onde essendo E. F. G. a.
 . c. d & e. Quin-
. c. d & e. Quin-to modo; & A.
 . C. D. E. F. G & a. Quarto; dico che 'l Quinto & principale modo è ac-
. C. D. E. F. G & a. Quarto; dico che 'l Quinto & principale modo è ac-commodato dopo il Quarto & plagale secondo che ricerca l'ordine & i gradi loro. Dopo
il Quinto segue il Sesto tra la Diapason del Sesto ordine
 . C. D. E. F. G. a &
. C. D. E. F. G. a &  . , per la nominata Definitione, contiene tramezata dalla chorda E. arithmetica-
. , per la nominata Definitione, contiene tramezata dalla chorda E. arithmetica-mente il Sesto modo. Et perche, per la Decimanona proposta, il Sesto è più acuto del
Quarto per un Tuono; essendo
 &
&  . con le sue mezane chorde Sesto modo, & E. con
. con le sue mezane chorde Sesto modo, & E. con e. con le sue mezane medesimamente Quinto; seguita, che dopo 'l Quinto sia collocato
il Sesto modo; secondo che ricerca il numero & li gradi loro. Dopo questo segue il Set-
timo; percioche nel Settimo ordine è contenuta la Diapason F. G. a.
 . c. d. e & f. la qual
. c. d. e & f. la qual page 282
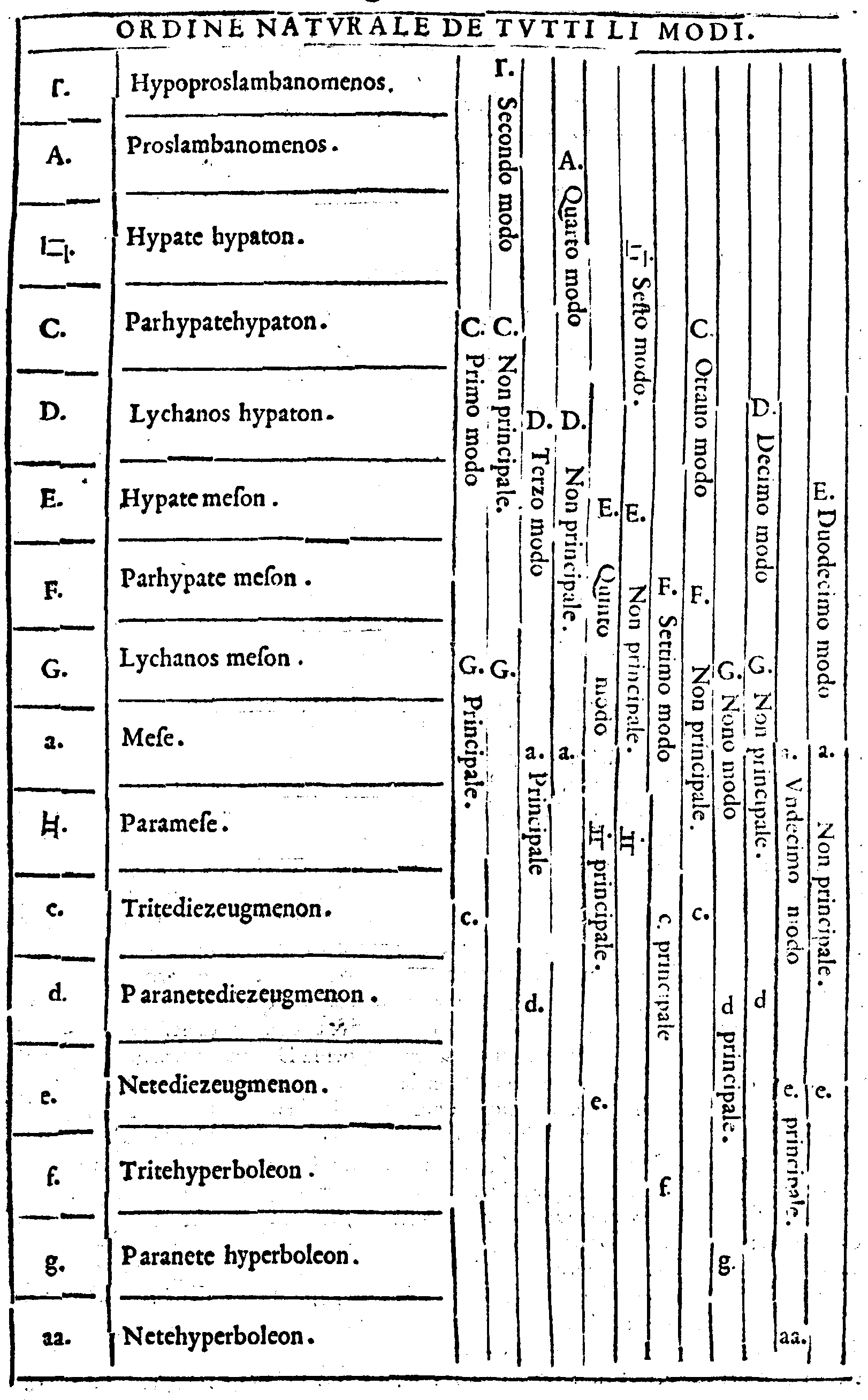
ORDINE NATVRALE DE TVTTI LI MODI.
quale, per la proposta Decimanona nominata, è distante dal Quinto per un Semituon
maggiore; percioche tra E & F. come più fiate si è dimostrato, & massimamente nella
Decimanona nominata; si troua tal distanza. La onde essendo
 &
&  . con le sue chorde
. con le sue chorde mezane Sesto modo; & F con f. medesimamente con le sue mezane il Settimo; seguita,
che secondo 'l numero & gradi loro habbiamo collocato il Settimo dopo il Sesto modo.
Viene hora l'Ottauo dopo il Settimo, il quale dico essere C. D. E. F. G a.
 & c. diuisa
& c. diuisa arithmeticamente dalla F. essendo che, secondo la Decimanona proposta nominata, è
lontano dal Sesto per un Semituono maggiore. Et perche questo segue immediatamen-
te dopo il Settimo; però dico, essere accommodato l'Ottauo dopo il Settimo mo-
do, secondo il numero & gradi loro. Dico ancora, che la Diapason G a.
 . c. d. e. f & g.
. c. d. e. f & g. contiene il Nono modo; percioche, per la Vndecima proposta, è la Quinta specie diui-
sa dalla chorda d. harmonicamente in due parti; la quale essendo più acuta della F & f.
contenuta nel Settimo luogo, per vn Tuono; seguita, che G & g. con le sue mezane
chorde contengano il Nono modo, & sia accommodato dopo l'Ottauo; come porta l'or-
dine & gradi loro. Simigliantemente dico, tra la Diapason D. E F. G. a.
 . c & d. la quale
. c & d. la quale immediatamente succede alla G & g. nel decimo ordine, esser collocato il Decimo mo-
do & nonprincipale; percioche la D & d è diuisa, secondo che habbiamo dimostrato
nella Decimaterza proposta d'hoggi, dalla chorda G. in due parti; &
per la Decimanona, è più graue della G & g. per una Diatessaron; onde per la Defini-
tione, secondo l'ordine numerale & li gradi de i Modi; il Decimo & plagale è accompa-
gnato & accommodato dopo 'l Nono, il quale è il suo principale. A questo succede l'Vn-
decimo, & è collocato tra la diapason a.
 c. d. e. f. g & aa collocata nell'ordine undecimo;
c. d. e. f. g & aa collocata nell'ordine undecimo; & perche è diuisa arithmeticamente in due parti dalla e. però uiene à contenere l'Vnde-
cimo modo; essendo chè più acuta della G & g. per un Tuono. Il perche essendo D &
d. con le sue mezane il modo Decimo; uenimo, secondo 'l proposito, hauer dimostrato,
appresso lui hauere accommodato l'Vndecimo, secondo l'ordine & gradi de i Modi. Vl-
timamente dico, che habbiamo accommodato il Duodecimo dopo l'Vndecimo tra la
Diapason E. F. G. a.
 . c. d & e. percioche è diuisa dalla chorda a. in due parti arithmetica-
. c. d & e. percioche è diuisa dalla chorda a. in due parti arithmetica-mente, & tal modo è più graue dell'Vndecimo per una Diatessaron, & del Decimo per
un Tuono. Onde per la Definitione, la Diapason E & e. con le sue chorde mezane uie-
ne à contenere il Duodecimo modo. Et perche ello succede immediatamente dopo l'Vn-
decimo, secondo l'ordine & li gradi de i modi; però dico, che dopo l'Vndecimo modo
habbiamo il Duodecimo, accommodato secondo 'l proposito. Et per tal maniera, se-
condo la proposta, habbiamo ridotto in uino per ordine i Modi principali con i Non
principali, & accompagnatoli insieme, secondo l'ordine numerale & gradi loro; come ui
douea dimostrare. Finito ch'io hebbi disse M. Adriano; Questa è stata una lunga diceria,
à approuare & dimostrare una cosa per se stessa apparente & facile; ma perche l'ordine
della Scienza porta questo; però bisogna contentarci; & io per me mi contento; per-
cioche uado sempre imparando qualche cosa di nuouo. Ma passate più oltra; s'altro
non hauete, che dirci. Cosi uanno le cose dimostrabili Messere; dissi; sè bene auanti
ch'elle si dimostrino, si toccano quasi con le mani & sono facili. Ascoltate adunque
quello, che segue.
PROPOSTA XXII.
delle Sedici chorde mostrate di sopra.
che mi par di uedere. Et io credo risposi, che non ui ingannate; però diremo.
La Prima & grauissima chorda del primo modo de i principali; il quale è più gra
ue d'ogn'altro; & la Ottaua & acutissima dell'Vndecimo, il quale è più d'ogn'altro Mo-
do acuto; come è manifesto, per la precedente; sono termini, tra i quali sono contenu-
ti gli altri Modi principali; ma per l'istessa Precedente, la chorda grauissima del Primo
modo è la C; & l'acutissima dell'Vndecimo è la aa; adunque tra la C. & la aa. sono
compresi tutti i Modi principali. Et perche dalla chorda C. alla chorda aa; computan
do queste due estreme; si ritroua il numero di Tredeci chorde, che sono le più acute de
tutte le Sedeci date di sopra nell'ordine già mostrato; però seguita, che tutti i Modi prin
cipali & Autentici sono collocati tra le Tredici più acute chorde delle Sedeci già mostra
te; come ui douea dimostrare. Et di più;
PROPOSTA XXIII.
le Tredeci più graui delle Sedeci chorde già mostrate.
che essendo la prima chorda & grauissima del Secondo modo, il quale è il primo
de i Nonprincipali; simigliantemente l'Ottaua del Duodecimo modo acutissi-
ma termini, tra i quali sono compresi i Modi nominati; come nella Ventesima prima si
è potuto uedere; & essendo per l'istessa proposta la Γ. grauissima chorda del detto Secon
do; ilquale è più graue d'ogn'altro Modo; essendo anco la chorda e. l'acutissima del Duo-
decimo, ilquale è più d'ogni altro acuto; non è dubio alcuno, che tra la chorda Γ. & la e.
non siano collocati tutti li Modi Nonprincipali. Ma perche dalla chorda Γ. fin'alla chor
da e; computando le mezane; si ritroua 'l numero di Tredeci chorde; & sono le più gra-
ui de tutte quelle, che sono contenute nell'ordine delle Sedeci già mostrate; però dico,
che tutti i Modi nonprincipali, ouer Plagali sono collocati tra 'l numero delle Tredici
più graui delle Sedeci chorde nominate; come ui douea dimostrare. A questa aggiun-
gerò; che
PROPOSTA XXIIII.
dici chorde.
gi: più d'ogn'altra graue, contiene il Secondo modo; & la a. & aa. d'ogn'altra
più acuta contiene l'Vndecimo; & l'altre mezane poi contengono gli altri modi
per ordine. Ma la chorda Γ; per la Decimaottaua & per la uentesima prima d'hoggi; è la
grauissima di ciascheduna delle Sedeci nominate; & la aa, per la Decimasettima & Ven
tesima prima simigliantemente; è la acutissima. Adunque le chorde de tutti i Modi inte
ramente abbracciano il numero delle Sedeci nominate; come ui douea dimostrare. Ol-
tra di questo ui fò sapere; per dar fine hormai à questo ragionamento, che
page 285
PROPOSTA XXV.
graue per una Diapason, oueramente si può far più acuta per una Diatessaron; ò più
graue per una Diapente.
d'hoggi. Γ. A.
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f. g & aa. le quali contenghino i cin-
. c. d. e. f. g & aa. le quali contenghino i cin-que Hexachordi; tra le quali siano Γ. A.
 . C. D. E. F & G. la Quinta specie del-
. C. D. E. F & G. la Quinta specie del-la Diapason diuisa dalla chorda C, per la Terzadecima proposta, in arithmetica diuisio-
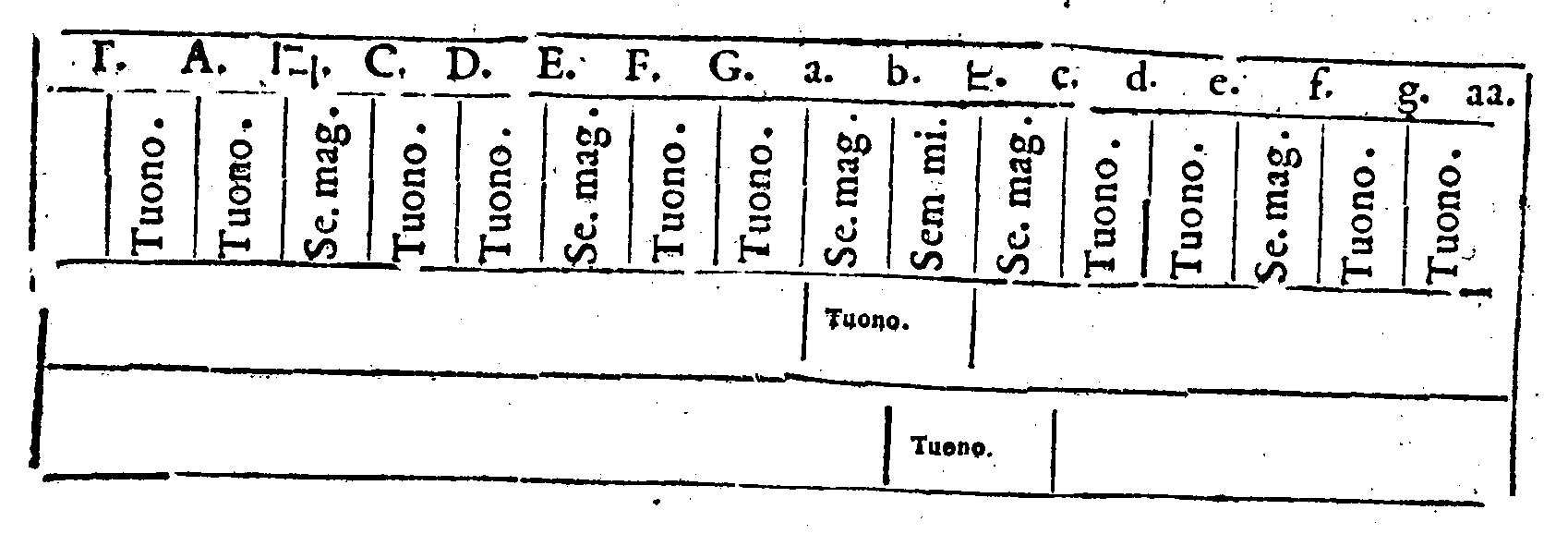
dulatione si può trasportare più uerso l'acuto per una Diapason tra le chorde G. a.
 . c. d.
. c. d. e. f & g; percioche se noi porremo la chorda c, per la chorda mezana, che diuida arithme-
ticamente questa Diapason; come fa la C, la prima Diapason in due parti; in una Dia-
tessaron G & c. posta nel graue, & in una Diapente c & g. posta in acuto; haueremo
tanto tra le chorde G. a.
 & c. di questa la modulatione della prima specie della Diates-
& c. di questa la modulatione della prima specie della Diates-saron; quanto si hà tra le chorde Γ. A.
 & C. di quella. Et tanto la modulatione della
& C. di quella. Et tanto la modulatione della prima specie della Diapente tra le chorde c. d. e. f & g. di questa seconda Diapason; quan-
to tra le chorde C. D. E. F & G. della prima; essendo che tanto in una delle dette Diates-
saron si modula dal graue all'acuto per due Tuoni & un maggior Semituono, quanto
nell'altra. Et cosi tanto si modula dal graue all'acuto per tuono, tuono, Semituono
maggiore, & tuono in una di esse Diapente; come si modula nell'altra. Onde tanto uer-
rà ad essere la Diapason Γ & G, della Quinta specie, quanto la G & g; percioche, per
la Settima dignità; Quelli Interualli si chiamano simili, che sono da simili termini & pro-
portioni contenuti. Il perche essendo i termini della prima Diapason mostrata simili à
quelli della Seconda; non è dubio, che tra loro non ui può cader differenza alcuna, se
non di graue & di acuto. Però essendo la G & g. diuisa arithmeticamente dalla c; come
è diuisa la Γ & G. dalla C; & essendo l'una & l'altra Diapason della Quinta specie; segui-
ta anco, per la Quartadecima definitione dhoggi, che tanto l'una quanto l'altra con-
tenga il Secondo modo. Ma perche la Diapason G & g. è distante dalle Diapason Γ &
G. per una Diapason intiera, & quello che si modula in questa, si può etiandio modula-
re in quella; però dico, che la modulatione del Secondo modo si può trasportare più
acuta, ouer più graue (quando la trasportatione si facesse al contrario) per una Diapason.
Et questa ragione può anco seruire à dimostrare, che la nominata Diapason Γ & G. har-
monicamente diuisa dalla chorda D. contenerà l'istesso modo, che è contenuto tra la
Diapason G & g. al medesimo modo diuisa; mutando però nella dimostratione quei ter-
mini, che sono necessarij di mutare; & questo sarà il Nono modo; come per la Vndeci-
page 286 ma proposta si è dimostrato. Et perche in questa maniera ogni Modo, sia qual si uo-
glia (come facendone proua, chiaramente si potrà uedere) si può dal graue all'acuto, &
dall'acuto al graue per una Diapason trasportare; però dico, che la modulatione di cia-
scheduno de i Dodici modi si può trasportare più acuta, ouer più graue per una Diapa-
son; come primieramente ui douea dimostrare. Ma per dimostrarui, che tali modula-
tioni si possono trasportare per una Diatessaron uerso l'acuto; oueramente per una Dia-
pente uerso 'l graue; siano le chorde C. D. E. F. G. a.
 & c, lequali contenghino la modula-
& c, lequali contenghino la modula-tione del Primo modo; essendo tali chorde diuise harmonicamente dalla chorda G; di
co, che etiandio dalla Diapason F. G. a. b. c. d. e & f. diuisa dalla chorda c. à cotal modo,
potiamo hauer l'istessa modulatione; essendo che tanto si modula nella Diapente F. G. a.
b & c. di questa Diapason per tuono, tuono, Semituono maggiore, & tuono; com'è ma
nifesto; quanto nella Diapente C. D. E. F & G. di quella. Et tanto si procede per tuono,
tuono & Semituono maggiore nella Diatessaron c. d. e & f. della Diapason F & f; quanto
nella Diatessaron G. a.
 . & c; nella Diapason C & c. Ma perche, per la Sesta proposta
. & c; nella Diapason C & c. Ma perche, per la Sesta proposta d'hoggi; tanto la Diapason C. D. E. F. G. a.
 & c. è la prima specie; quanto la F. G. a. b.
& c. è la prima specie; quanto la F. G. a. b. c. d. e & f; però, per la Quartadecima definitione di questo, dico; tanto questa contene
re il Primo modo, quanto quella. Et perche la Diapason F & f; per la Ventesima d'hog-
gi, è più acuta della C & c. d'una Diatessaron; & quella modulatione, che si troua nella
Diapason C & c, si troua anco nella F & f; però dico, che la modulatione della Diapa-
son C & c. si può trasportar per una Diatessaron più acuta nella Diapason F & f. Ma per
che tali Trasportationi si possono far commodamente per tutti i Modi col fauore dell'He
xachordo Synemennon; però dico, che la Modulatione di ciascheduno de i Dodici Mo
di si può trasportare in acuto per una Diatessaron; come secondariamente intendeua di
dimostrarui. Et che tali modulationi si possino trasportare uerso il graue per una Diapen
te; cosi lo dimostro. Sia la Diapason a.
 . c. d. e. f. g & aa; la quale diuisa harmonicamen-
. c. d. e. f. g & aa; la quale diuisa harmonicamen-te dalla chorda e. contenga la modulatione dell'Vndecino modo. Dico, che tale modu
latione si può trasporre anco uerso 'l graue nella Diapason D. E. F. G. a. b. c & d; percioche
diuisa al medesimo modo dalla Chorda a. harmonicamente in due parti, quella modula
tione istessa contenerà la Diapente D. E. F. G & a, che contenerà la a.
 . c. d & e; & per
. c. d & e; & per quell'istessi Interualli modulerà la Diatessaron e. f. g & aa, che si modulera anco la Dia-
tessaron a. b. c & d. Ma perche, per l'Ottaua definitione & per la Sesta proposta d'hoggi,
la Diapason a & aa. è della Sesta specie, & anco la D & d. è della Sesta specie, & l una &
l'altra diuisa harmonicamente contengono l'Vndecimo modo; & essendo per la Settima
& per la Ventesima prima proposta, la D & d. più graue della a & aa. per una Diapente;
però dico, che la modulatione dell'Vndecimo modo è trasportata piu graue per una Dia
pente. Ma perche à questo modo si può trasportare qual si uoglia modulatione di qual
Modo si uuole; come dalla proua manifestamente si può sempre conoscere; però dico;
che la Modulatione di ciascheduno de i Dodici modi si può fare ultimamente più graue
per una Diapente. La modulatione adunque di qual si uoglia Modo de i Dodici si può
trasportare più acuta, ouer più graue per una Diapason; Ouer si può far più acuta per
una Diatessaron; Oueramente più graue per una Diapente. Et questo è tutto quello,
che secondo la proposta, dimostrar ui douea. Noi altri Organisti disse M. Claudio; lo
sapiamo, quanto sia di utile queste trasportationi, & come si possino fare. Et se ben la
prattica c'insegna cotesta cosa, & che ueramente io la sapeua con tal mezo; non però
m'hà dispiacciuto ueder cotale dimostratione dipendere dalle dimostrationi fatte per
inanzi. Qui dopo che hebbe parlato M. Claudio, disse M. Francesco; Voi hauete hor-
mai M. Gioseffo dimostrato tante & tante cose; che mi penso, che poco più ci debba re
stare in questo fatto da dire. Onde essendo l'hora tarda, & hauendo io da fare alcuni ne-
gotii; percioche domattina à buon'hora partire uogliamo; s'altro ui resta da dire, non
perdiamo tempo ma uenimo al fine della cosa. A questo soggiunsi; Ancora che si po-
trebbe, oltra le cose dimostrate, ragionare & dimostrarne molte altre; tuttauia hauen-
page 287 do proposto (secondo 'l mio parere) quello che mi pareua esser più necessario; & toccate
tutte quelle cose, che mi hò pensato essere utili da dimostrare in questa Scienza; non uo-
glio aggiungerui altro. Ma questa proposta ui uoglio solamente aggiungere, che sarà per
la conclusione de tutti questi nostri Ragionamenti; ne i quali, se ui haurò satisfatto, ren-
dete gratie al Signore DIO benedetto datore de tutte le buone & ottime cose. Se anco
per auentura fusse auenuto (cosa che potrebbe essere) altramente, imputatene il mio po-
co sapere; percioche ui hò detto in questo fatto tutto quello, che per me dirui si potea,
senza diffimularui, ò tener celato cosa alcuna. Et se per sorte hauessi mancato nel di-
chiarirui alcuna cosa, per cagione di breuità, & non cosi compiutamente, come deside-
rauate, ui hauesse satisfatto; non dubito, che se hauerete à memoria quelle cose, lequali
hò scritto nelle Istitutioni harmoniche; & se uederete quello, ch'io hò dettato nel libro, il
quale hò intitolato IL MELOPEO, ouer MVSICO PERFETTO; & ne i SVP-
PLEMENTI MVSICALI; iquali prima à Dio piacendo mandarò in luce, con Venticin-
que Libri scritti in lingua Latina; iquali nomino De re Musica, siue De vtraque Musica;
non ne siate d'ogni dubio, che ui potrà occorrere, ottimamente istrutti; Percioche è im-
possibile di potere in una fiata esplicar perfettamente le cose. La onde essendo hormai
stanco farò fine al mio ragionare. E' molto bene il douere, disse il Sig. Desiderio. Ma se
ben mi ricordo M. Gioseffo io fui quello, che vi hà promosso à questa impresa; & si bene
& scientificamente hauete ragionato con molta copia delle cose della Musica, che oltra
l'hauermi satisfatto in particolare, in uniuersale ancora tutti noi si chiamiamo contenti.
Et io ui prometto di tenerne perpetua memoria, & di hauerui obligo perpetuo, essendo
c'hauere tocco & risolto tanto bene tutte quelle cose, le quali mi dauano noia & fastidio,
che non hò punto cosa alcuna più da dubitare. Et se uerrà tempo, nel quale ui possa di-
mostrar con fatti, quanto questo mi sia stato grato, ue lo farò uedere. Onde al presente non
posso fare altro, che ringratiarui. Io son debitore, risposi à tutti gli Animi nobili & uir-
tuosi; come è quello di V. Sig. però non uoglio che tra noi ui sia altro obligo, che di amo-
re. Percioche amando io lei, reciprocamente desidero che ella mi ami. A' questo, sog-
giunse; sarò sempre debitore. Anch'io, disse M. Claudio; ui son in questa parte debitore;
& questo debito non sò come lo potrò mai, non dico pagare; ma sciemare. Con quel-
l'istesso mezo, risposi; ch'io hò detto al Sig. Desiderio, farete atto à fare il tutto; ne uoglio,
ch'altro ui concorri; se non quello che scriue nel fine d'un suo Epigramma quel S. Ve-
scouo & martire di CHRISTO Cipriano:
Dilige pro tantis, sat mihi solus Amor.
Cosi farò, replicò M. Claudio; onde il Viola, disse; Hora siamo entrati nelle cerimonie
& nelle belle parole, & Dio il sà, quando si darà fine; però uoglio anch'io breuemente
ringratiarui M. Gioseffo della uostra cortesia. Et perche dimane à bon'hora siamo per
montare in barca tutti, & col Sig. Duca nostro ritornarsene à Ferrara; uoglio pregarui,
che doue uoi uederete, che io sia buono à sarui seruitio; che senza rispetto alcuno mi uo-
gliate commandare. Et à voi Messere dirò essortandoui, che uiuiate allegramente; pre-
gandoui di tenermi & con seruarmi nella uostra memoria. Cosi farò Messer Francesco
mio; rispose il buon Vecchio; ma basciarete, ui prego la mano à sua Eccellenza in nome
mio; & ui prego di nuouo à mantenermi uiuo nella memoria di questo Signore. Onde an-
darete al buon uiaggio. Dette adunque queste & altre parole da una parte & l'altra dolci
& amoreuoli; ciascheduno di noi partitosi, tenne quella bella strada, che lo pote facilmen-
te & presto condurre à far qualche suo particolar negocio inanti cena; Et cosi fù posto.
Di Pier Giacomo Bannadini.
Signor DIO datore di tutte le gratie.