Title: Breve introduttione di musica misurata
Author: Del Lago, Giovanni
Publication: (Venice, 1540)
Principal editor: Paloma Otaola
Edition: 2002
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht Netherlandsrata,
Venetiano: scritta al Magnifico Lorenzo Mo-
resino patricio Venetiano patron suo
honorendissimo.
 Ex prælo Brandini & Octauiani Scoti fratrum habentur excussæ.
Ex prælo Brandini & Octauiani Scoti fratrum habentur excussæ. VENETIIS. M. D. XXXX.page 2page 3
AL MAGNIFICO LORENZO MORESINO PATRICIO VENE
tiano del Magnifico Bartholomeo figliolo.
se in luce alcune cose circa la pratica del Canto misurato: ho voluto per
le sue essortationi a comune vtilitate di tutti quegli che amano tale scien
za con vna breue cōpilatione dimostrare quello che da molti e stato scrit-
to sopra tale materia: i quali per essere stati troppo lunghi sono stati te-
diosi a lettori. Vnde per l'amore il quale e & alla scienza: & a me portate: &
anchora per i beneficii receuuti dalla casa vostra: io mi sono sforzato di compiacerui
hauendo accolto sotto breuita queste mie regolette: & pero non dubito per la beniuo
lentia che per vostra humanita mi portate che le primitie delle mie lucubrationi com-
poste per vostro contento con grande allegrezza d'animo non debbiate pigliare: per-
che da queste oltra a gli altri vostri studii non picciolo ornamento conseguirete.
¶Ad Lectorem Gregorii Oldouini Carmen.
Si placet Harmonici discors concordia cantus:
Hoc breue Ioannis perlege lector opus
Δὼριον Hic, phrigiumꝗ docet, lydiumꝗ libellus:
Nec non multiplici ἰωνικὸν arte melos,
Ένθεον ἦ γλαφυρὸν, σεμνὸν, καὶ βακχικὸν ἐίδοσ
Δεικνυσι, καὶ γλυκερὴσ πᾶν γένοσ ἁρμονίησ,
Non hic ambages, non hic enigmata cernes:
Sed patulos, faciles artis amice modos,
Consona dissimili currit symphonia ductu:
Obice, nec scrupulo sit mora tarda tibi,
En breuiter, nitideꝗ monet, cognosce camænam
Multiplicem, uariam pectine, & arte grauem,
Orpheus hac syluas traxit, delphinas Arion:
Dauid & hac saulem dæmone atroce ferum,
Hac iouis exhilarant Musæ conuiuia magni.
Quum binæ cantant, pulsat Apollo chelyn,
Diuinum certe mortali Musica donum:
Qua nihil est homini gratius orbe datum,
Disce igitur studio cœlestia munera disce:
Oblectaꝗ animum nocte, dieꝗ tuum
DELLA INTRODVTTIONE DE LA
Mano secondo Guido Monacho Aretino.
sette lettere, le quali sette differentie dimostrano, & in la quale
le mutationi, & interualli delle consonantie per Γ, A, B, C, D
E, F, se comprendono. Nella mano sono uenti lettere,
cioe, Γ, A, B, C, D, E, F, G. A,
 C, D, E, F, G. A,
C, D, E, F, G. A,  C, D, E,
C, D, E, de le quali le prime sette sono dette graui, per esser le piu basse. Le altre set-
te acute. Le sei ultime sopra acute, & queste uenti lettere si diuidono ancho
ra in due parti, cioe dieci in riga, & dieci in spatio, come appar qui sotto
in essa Mano.
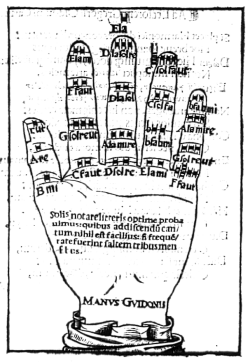
Introductorium Musices.
page 5
re. B, mi. C, fa ut. D, sol re. E, la mi. F, fa ut. G, sol re
ut. A, la mi re.
 , fa
, fa  mi. C, sol fa ut. D, la sol, re E
mi. C, sol fa ut. D, la sol, re E la mi. F, fa ut. G, sol re ut. A, la mi re.
 , fa
, fa  mi. C, sol fa.
mi. C, sol fa. D, la sol. E la. & cosi discēdendo cioe dicēdo, E, la. D, la sol. C, sol fa &c. Et sap
piate che la prima nota si comincia in riga, & la scđa in spacio, & cosi gradatim
una in riga & laltra in spacio insino alla fine, poste sopra le giūture de i diti de
la mano sinistra, cominciādo nella summita del dito grosso, & cosi [[per]] ordine [[per]]
infino alla summita del dito medio, dicendo cosi. Γ, ut ha una lettera & una
nota. Γ e la lettera, ut e la nota. Vt se canta per
 quadro graue, & se reg-
quadro graue, & se reg-ge da se medesimo, dicendo ut. A re, ha una lettera, & una nota. A e la let
tera, re, e la nota, re se canta per
 quadro graue, & si regge da lo ut, de Γ,
quadro graue, & si regge da lo ut, de Γ, ut dicendo, ut re, re ut. B, mi, ha una lettera, & una nota. B, e la lettera,
mi e la nota. mi se canta per
 quadro graue, & si regge da lo ut de Γ, ut di-
quadro graue, & si regge da lo ut de Γ, ut di-cendo, ut re mi, mi re ut. C, fa ut, ha una lettera, & due note. C, e la let-
tera, fa ut, sono le note, fa se canta per
 quadro graue, & si regge da lo ut
quadro graue, & si regge da lo ut de Γ, ut, dicendo ut re mi fa, fa mi re ut, & ut si canta per natura graue, &
si regge da se medesimo dicendo ut. D, sol re, ha una lettera & due note. D,
e la lettera sol re sono le note, sol si canta per
 quadro graue & si regge da lo
quadro graue & si regge da lo ut de Γ, ut. dicendo ut re mi fa sol, sol fa mi re ut. il re si canta per natura
graue, e si regge da lo ut, de C, fa ut, dicendo ut re, re ut. E la mi, ha una
lettera & due note. E, e la lettera, la mi sono le note, la si canta per
 quadro
quadro graue & si regge da lo ut de Γ, ut dicēdo ut re mi fa sol la, la sol fa mi re ut, il
mi si cāta [[per]] natura graue, & si regge da lo ut de C fa ut, dicēdo, ut re mi, mi re
ut. F fa ut, ha una lettera & due note. F, e la lettera & fa ut, sono le note. fa si cāta
[[per]] natura graue, & si regge da lo ut di C fa ut dicendo, ut re mi fa. fa mi re ut, &
ut si cāta [[per]]
 molle graue, & si regge da se medesimo dicēdo ut. G sol re ut ha
molle graue, & si regge da se medesimo dicēdo ut. G sol re ut ha una lettera & tre note. G e la lettera, sol re ut, sono le note. sol si cāta per natura
graue, & si regge da lo ut di C fa ut dicendo, ut re mi fa sol, sol fa mi re ut. il re
si canta per
 molle graue & si regge da lo ut de F fa ut dicendo, ut re, re ut,
molle graue & si regge da lo ut de F fa ut dicendo, ut re, re ut, & ut si canta per
 quadro acuto, & si regge da se medesimo dicendo, ut. , ha una lettera & tre note. A e la , la mi re sono le note, la si can
quadro acuto, & si regge da se medesimo dicendo, ut. , ha una lettera & tre note. A e la , la mi re sono le note, la si canta per natura graue, & si regge da lo ut de C fa ut dicendo, ut re mi fa sol la.
la sol fa mi re ut. il mi si canta per
 molle graue, & si regge da lo ut di F, fa
molle graue, & si regge da lo ut di F, fa ut dicendo ut re mi. mi re ut. il re si canta per
 quadro acuto & si regge de
quadro acuto & si regge de lo ut de G sol re ut, dicendo, ut re. re ut.
 fa
fa  mi ha due lettere & due no-
mi ha due lettere & due no-te

 sono le lettere, & fa mi le note. fa si canta per
sono le lettere, & fa mi le note. fa si canta per  molle graue, & si
molle graue, & si page 6regge da lo ut, di F fa ut dicendo, ut re mi fa. fa mi re ut. il mi si canta per

quadro acuto, & si regge da lo ut de G sol re ut, dicendo, ut re mi. mi re ut.
& cosi seguitarete questo ordine per infino alla fine. Anchora notate questa
nostra regola utilissima si circa il saper de le note quali sono in riga, ouer in
spacio, come per sapere perche le si cantino. Prima tu dei sapere che si una
lettera graue sara in riga, quella medesima in le sopr'acute sara in riga. ma
in le acute in spacio. Ma se la lettera graue sara in spacio, quella medesima
in le sopr'acute sara in spacio. & l'acuta in riga Le lettere principali sono set
te, cioe, Γ, A, B, C, D, E, F, & comenciasi da Γ greca, laquale e G latina,
& subsequenter seguitando reiterando quelle per infino alla fine, come ap-
pare nella prescritta mano. ma le lettere familiari sono tre cioe C F & G in le
quali le deduttioni hanno principio. Le deduttioni ouer ordini de la mano
sono sette. La prima ha origine ouer comincia in Γ ut. la seconda in C fa ut
la terza in F fa ut graue. la quarta in G sol re ut acuto. la quinta in C sol fa
ut. la sesta in F fa ut acuto. & la settima in G sol re ut sopr'acuto. dedu-
tione e una naturale progressione de sei sillabe cioe ut re mi fa sol la: le qua-
li in Musica se dimandino uoci. il modo & ordine di pronunciare queste sei
sillabe ouer uoci, e tale che tra la prima & la seconda cioe, ut re, se ascende
la uoce una distantia di tuono. cosi anchora da re al mi. ma da mi al fa un
interuallo di un semituono minore da la nota fa, al sol un tuono; & simil-
mente dal sol al la & cosi discendendo.
 molle, & lal-
molle, & lal-tra di
 duro, & cognoscesi a questo che ogni ut in C si canta per natura, ogni
duro, & cognoscesi a questo che ogni ut in C si canta per natura, ogni ut in F si canta per
 molle, & ogni ut in G si canta per
molle, & ogni ut in G si canta per  duro come appare
duro come appare per questo uerso el quale dice cosi
C naturam dat f,  , molle. G quoꝗ
, molle. G quoꝗ 
durum,
el C dimostra natura F  molle, el G
molle, el G  duro, & notate che quel
duro, & notate che quello che e detto che ogni ut in C si canta per natura &c. Si intende etiam deli su
diti suoi compagni, & perche ogni ut ha sotto di se, re mi fa sol la, uerbi gra
tia lo ut di C fa ut si canta per natura perche ogni ut in C si canta per natura,
seguita adonꝗ che re in D sol re. mi in E la mi. fa in F fa ut. sol in G sol re
ut. & la in A la mi re. tutti si cantino per natura, & cosi e di tutti gli altri. E
sono dui segni, uno di
 molle el quale e questo
molle el quale e questo  , e doue e posto tal segno
, e doue e posto tal segno o sia in riga, ouer in spacio se dice sempre fa. quia ubi
 ibi fa, ma non se de
ibi fa, ma non se deue cantare per
 molle se nol se uedi segnado o per necessita. L'altro se-
molle se nol se uedi segnado o per necessita. L'altro se-gno sie de
 duro, & e questo
duro, & e questo  ouer questo
ouer questo  & doue e posto tal segno
& doue e posto tal segno si dice sempre mi. Le chiaui del canto sono due principalmente, cioe una
page 7di natura graue & l'altra di
 duro acuto. La chiaue di natura
duro acuto. La chiaue di natura graue e figurata di tre note, & e posta in F fa ut, pri-
mo, a questomodo
 & la chiaue di
& la chiaue di  duro acuto e fi
duro acuto e figurata di due note, & e posta in C sol fa ut, come e qui
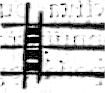 & luna da
& luna da l'altra e distante per quinta, & sempre la chiaue si pone in riga. ma antiqua-
mente nel canto ecclesiastico se usaua alla chiaue de natura la riga rossa, & a
quella de
 duro la riga gialla. Dapoi e stato aggiunto la terza chiaue, la qua
duro la riga gialla. Dapoi e stato aggiunto la terza chiaue, la quale e figurata de le preditte due note posta in C sol fa ut, con ad-
ditione del
 rotundo nel inferior spacio di sotto la linea de la
rotundo nel inferior spacio di sotto la linea de la chiaue cosi segnata.
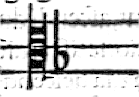 & nota che sempre doue e la chiaue li e sem
& nota che sempre doue e la chiaue li e sempre fa, saluo se per il
 rotundo ouer molle non uien impedito, perche allho
rotundo ouer molle non uien impedito, perche allhora si dice sol. ma alcuna uolta, e questo accade nel canto figurato per lascēder
suo in luogo di chiaue usiamo, questa lettera G la qual dinota G sol re ut so
pr'acuto. Anchora notate questo uerso per le mutationi el quale dice cosi,
(Vt re mi scandunt, fa sol la quoꝗ descendunt.)
cioe che ogni uolta che le necessita far mutatione da proprieta in proprieta uedi doue ui trouiate cioe in
qual luogo de la mano, & sel canto ascende bisogna dir o ut, o re, ouer mi,
& sel descende bisogna dir o fa, o , ouer la, secondo el luogo doue ui tro
ueuate. Doue e una sola nota ouer uoce, non si fa mutatione, come
e in Γ ut. in A re. in B mi. in tutti duoi
 fa
fa  mi, & in E la, perche mu-
mi, & in E la, perche mu-tatione altro non e che mutare una proprieta in un'altra, & per consequen-
te una uoce in laltra in uno medesimo suono. Anchora che le siano diuerse
di nome per esser di diuerse proprieta. Doue sono due uoci sono due mu-
tationi come e, in C fa ut. D sol re. E la mi. F fa ut. C sol fa, & D la sol. Lo
essemplo in C fa ut, fa in ut, ascendendo di
 quadro in natura ut in fa
quadro in natura ut in fa descendendo de natura in
 quadro, ma questa regola falisce in
quadro, ma questa regola falisce in  fa
fa 
mi. Anchora che in
 fa
fa  mi gli siano due proprietati, & per consequente
mi gli siano due proprietati, & per consequente due uoci non si puo pero far mutatione, perche quelle due uoci non si puo
proferire in uno medesimo suono per esser el mi distante dal fa, uno semi
tuono maggiore, & perche mutatione altro non e che mutare il nome de la
uoce, ouer de la nota in un'altro nome di nota che sia in un medesimo luo-
go, & suono, intrando de una in l'altra proprieta, ouer qualita, come diso-
pra ho detto. Doue douete sapere che quello semituono maggiore si cau-
sa per uirtu del
 molle, il quale e accidentale, perche el puo esser messo e nō
molle, il quale e accidentale, perche el puo esser messo e nō messo, & fu trouato per tre cause. Prima, per tor la durezza del tritono per
poter procedere per il modo diatonico cioe per tuono, & tuono & semituo
page 8no ouer per semituono tuono & tuono. Secondo per meglior sonorita. Ter
tio per necessita, ouer colorata musica. & cosi per esser accidentale, e non
de esser connumerato nelle sette lettere musicali, la ragione e perche el non
puo corrispondere per diapason, ouer ottaua, ne con le graui, ne con le acu
te. Con le graui il diapason e diminuto con le sopra acute le superfluo. Do
ue concludo non esser in computo, ma esser accidentale. Doue sono tre no
te, ouer uoci si fa sei mutationi, come in G sol re ut. A la mi re. C sol fa ut, &
D la sol re. lo essemplo in G sol re ut, sol in ut, ascendēdo de natura graue in
 acuto, & tal mutatione si domanda mutatione ascendente, ut in sol descen-
acuto, & tal mutatione si domanda mutatione ascendente, ut in sol descen-dēdo de
 quadro in natura, la quale si dimāda descendēte. sol in re, ascēden
quadro in natura, la quale si dimāda descendēte. sol in re, ascēdendo di natura graue in
 molle graue. re in sol, descendendo di natura in
molle graue. re in sol, descendendo di natura in 
molle, ut in re ascendendo di
 quadro in
quadro in  molle, re in ut ascendendo di
molle, re in ut ascendendo di 
molle in
 quadro & similmente procederite ne li altri luoghi. Egli e mani
quadro & similmente procederite ne li altri luoghi. Egli e manifesto per tre cagioni bisognar farsi la mutatione. Primo accio che & sopra, &
sotto ciascuno esacordo esse uoci commodulato transito, & concinna prola
tione si possino in acuto intendere, & in graue rimettere, & sbassare. Secon
do per cagion di concipere el transito di piu soaue & dolce canto. Tertio per
cagione di piu facile transito di consonanti figure, cioe diatessaron & diapen
te. Disopra ui ho detto che in G sol re ut si fanno sei mutationi. La prima
mutatione si fa quando mutamo la prima sillaba, ouer nota. In la seconda
cioe da sol in re ascendendo da natura in
 molle. La seconda si fa al contra
molle. La seconda si fa al contrario mutando la seconda sillaba in la prima cioe re in sol descendendo da

molle in natura. La terza mutatione si fa quando mutamo la prima sillaba
in la terza, cioe, sol in ut ascendendo da natura in
 quadro. La quarta si fa
quadro. La quarta si fa al contrario, ut in sol descendendo da
 quadro in natura. La quinta muta
quadro in natura. La quinta mutatione si fa quando si muta la seconda sillaba in la terza, cioe, re in ut, per
causa di ascendere da
 molle in
molle in  quadro. La sesta mutatione si fa mutan-
quadro. La sesta mutatione si fa mutan-do la terza sillaba in la secōda cioe ut in re per causa di ascendere da
 duro
duro in
 molle, & queste tali mutationi le chiamo dirette & regolare, e certamēte
molle, & queste tali mutationi le chiamo dirette & regolare, e certamēte la diretta & regolare mutatione quella la quale si oppone alla precedente &
sequente unisona mutatione, cioe quando la prima si fa per causa di ascen-
dere. La seconda di descendere. La terza di ascendere. La quarta di descen
dere. La quinta ascendere. La sesta di descendere La mutatione ascen-
dente, e, quando mutato il nome de la uoce unisona, el primo moto de la
uoce tende in acumine: ma la descendente e, quando el primo moto della
uoce remette & abassa in grauita. Dico douersi fuggire la pluralita & mol-
page 9titudine delle mutationi. quando apertamente si uedera el progresso, & or-
dine del canto cioe con una sola mutatione esser bene & congruamente dis
posto. Dico anchora oltra di questo la mutatione douersi prosequire & piu
tarda; & piu longamente in quanto el sia possibile, ne far si deue (nisi neces-
sitate cogente) cioe quando cantando si fa el transito oltra l'ordine de l'esacor
do come e quando se ascende, ouer descende per sette; ouer otto uoci, o an
chora per piu &c.
El luogo delle mutationi per  molle.
molle.
 molle in ascender re, cioe la mutation si fa in uno & l'altro, D, & in
molle in ascender re, cioe la mutation si fa in uno & l'altro, D, & in G, cioe in ascendere si deue dire re: ma la, in descendere: si fa in uno & l'al-
tro, A & in D, cioe in descendere se deue dire la come in questo essemplo.
La definitione del  molle.
molle.
 el quale serue l'uno & l'altro
el quale serue l'uno & l'altro  fa
fa  mi
mi & E la mi: in el qual luogo cioe doue e segnato sempre si dice fa.

Le chiaui
La Definitione di natura
 molle, &
molle, & il
 quadro, perche le media tra l'un' & l'altro.
quadro, perche le media tra l'un' & l'altro. Quia omne mediū de utroꝗ
participat extremo.El luogo de le mutationi per  quadro.
quadro.
 quadro in ascendere re, cioe la mutation si fa in uno & l'altro, A, &
quadro in ascendere re, cioe la mutation si fa in uno & l'altro, A, & in D, cioe in ascendere si deue dire re. ma la, in descendere si fa in l'uno &
l'altro A, & in E, cioe in descēdere douemo dire la come qui in questo essem-
page 10plo e manifesto.
La definitione di  duro.
duro.
 duro e segno quadrato come questo
duro e segno quadrato come questo  el quale serue a tutti dui
el quale serue a tutti dui  fa
fa 
mi, & transcende oltra el
 molle l'interuallo de duoi diesis & uno comma,
molle l'interuallo de duoi diesis & uno comma, in el quale deuemo dire mi, nientedimeno in la medesima proportione pos
siamo dire anchora fa.

Le chiaui
pio da le figure a questa disciplina competente e determinate con li nomi
suoi proprii. Et per esser la massima simplicissima & facilissima, pero da que
sta faro initio & essordio, & consequentemente a tutte le altre figure, & a
tutte l'altre cose congiunte & pertinente a questa misurata harmonia descen
dero allo essemplo delle figure.
sima:

 lon
longa:

 bre
breue:
 semi-
semi-breue
 mini
minima:
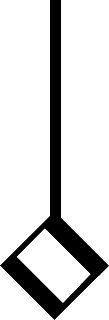 semimi
semiminima:
 : cro
: croma:
 : semi-
: semi-croma,

 Et notate che apresso li antiqui erano so
Et notate che apresso li antiqui erano solamente quatro segni principali et cinꝗ
essentiale figure, li segni erano maggior perfetto & imperfetto ut hic.

 & minor perfetto &
& minor perfetto & imperfetto, ut hic:


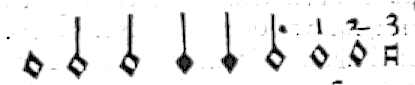
Le figure erano: Massima, lunga:
breue, semibreue, & minima. Ma
quando uoleuano celerar le figure nelli segni tagliauano tali segni, & simil
mente il negrizar de le minime celerauano le lor minime, & cosi la diuersita
page 11del figurar di esse minime, o in duplo o in quadruplo &c. Si che notate che
il tagliar de i segni non tolgono il nome a segni, ne la perfettione, ne la im
perfettione, ne anchora l', si come le figure per il negrizar cioe
le minime non mutano il nome, ma solamente prestano celerita a esse fi-
gure, come appar in la pratica. Et pero la nota minima non e diuisibile in
tre equali parti, perche la saria agente e patiente, cioe che la si poria perfice-
re & imperficere lo essemplo delle figure & pause spettante alli segni sopra-
detti.

Delli Segni.
per perfetto & imperfetto, & similmente il minore per perfetto & imper
fetto, per la qual cosa ogni segno si dimanda o maggiore o minore: o per-
fetto, ouer imperfetto. El segno si dimanda maggiore per il punto & mi-
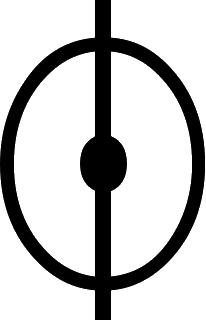
nore per non gli esser il punto: & si dimanda perfetto per il circuolo, & imper
fetto [[per]] il semicircuolo. Et notate doue e il punto nel segno alhora per il pun
to la semibreue e perfetta, cioe ual tre minime: ma doue non e punto , & cosi ual due minime. Doue e il circuolo la breue e perfetta, cioe ual
tre semibreue: doue non e circuolo imperfetta, & cosi ual due semibreue: Si
che niuna figura si puo perficere per uirtu di segni saluo che la breue & la se
mibreue: ma la massima & la lunga per uirtu di pause (come uederemo)
assumano perfettione doue douete sapere che in ciascuno segno si perfetto,
come imperfetto: & si maggior come minor per uirtu delle pause: la massi
ma & la lunga si possono perficere come al suo luogo uederemo: Ma do-
ue e il circuolo la massima ual due lunghe, la lunga due breui, ma la bre
ue per il circuolo tre semibreui & cosi la massima ual dodeci semibreui, & la
lunga sei, & doue non e circolo anchora la massima ual due lunghe, e la lun
ga due breui: ma la breue per il semicircolo ual solamente due semibreui.
si che la massima in questi tal segni uale otto semibreui & la lunga quattro.
ma anchora debbiate sapere che appresso di noi si parliamo del modo mag
giore intendiamo de la massima la quale e duplex, cioe perfetta & imperfetta
(come demostreremo) si del modo minore de la lunga: la qual anchora lei
page 12e perfetta & imperfetta. si del tempo della breue la qual e perfetta & imper-
fetta secondo la qualita de i segni, & si de la prolatione de la semibreue, & cosi
lei e perfetta, & imperfetta: figura perfetta si dimanda quella che contiene
in se tre parti propinꝗ, & imperfetta che contiene due. Parte propinqua e
quella che senza mezo alcuno uien da poi la sua maggiore, come la lunga
de la massima, la breue de la lunga, la qual breue e parte remota de la mas
sima, la semibreue de la breue la qual e parte remota de la lunga, & piu re-
mota de la massima, & la minima de la semibreue la qual e remota de la bre
ue, & piu remota de la lunga, & remotissima de la massima. Et di queste
figure, alcune sono agenti, alcune patienti, & alcune agenti & patienti. La
minima e agente, perche come indiuisibile non puo riceuere perfettione al
cuna: la massima e solamente patiente per non gli essere maggior figura di
lei: ma la patisce imperfettione. La lunga: la breue: & la semibreue sono
agenti & patienti: la ragion si e perche le possono imperficere & esser fatte im
perfette come in li luoghi suoi saranno dimostrate.
De la imperfettione delle figure.
lunga quando tre breui. La breue quando tre semibreui, & la
quando tre minime, se imperficisce da la sua minore propinqua che gli segui
ta pur che non gli sia punto di diuision ouer di redution che e quel medesi-
mo, o ueramente dapoi non si troui il suo numero compito, dapoi se gli tro
ui una figura simile, o ueramente non, se troui due parti propinque tra due
perfette senza punto di diuisione tra esse parti propinque, ouer che non si tro
ui tra due figure perfette (intendete pero simile, parti remotte, ouer piu re-
motte) & anchora remotissime equiualenti a una parte propinqua & poi
una parte propinqua, perche allhora la figura perfetta sempre restaria per-
fetta. Ma se tra due perfette simili si trouasse prima una parte propinqua, &
poi parti remotte, o piu remotte, ouer remotissime equiualenti ad una par-
te propinqua allhora quelle due perfette restariano imperfette, la qual cosa
non causa in lo essemplo contrario, perche la parte propinqua per esser l'ul
tima altera, & cosi rende il suo numero perfetto, de la qual alteratione al luo
go suo dechiareremo: ma da una sua simile non si puo far imperfetta.
Nam
similis a simili imperfici non potest, quia par in parem non habet imperium ne da una sua maggiore, ne anchora dinanzi ad una sua simile: perche la
regola dice.
Similis ante similem non potest imperfici: si che si uorrete imperficere una figura perfetta posta dinanzi ad una sua simile la farete negra, &
page 13allhora sara imperfetta, perche ogni figura perfetta per la negrezza perde
la terza parte del suo ualore. La figura perfetta si puo imperficere da la sua
minore propinqua, ouer dal suo ualore dala parte dinanzi non essendo po
sta pero dinanzi a una sua simile & etiam da la parte di dietro, & questo che
ui ho detto disopra ui sia essemplo di ciascuna figura perfetta, & sapiate che
la similitudine de le figure se intende respetto de la forma, & non del colore,
& che se una breue perfetta, poniamo fosse inanzi une breue negra la si in-
tenderia inanzi una sua simile per respetto de la forma.
Nam forma, est que
dat esse rei. Si che regolarmente ogni figura perfetta quando li seguita im-mediate la sua minore propinqua la perde la terza parte del suo ualore. Et
se la breue perfetta uien posta dinanzi a due semibreui ligate, ouer dinanzi
a due pause de semibreui poste in una medesima riga sempre la resta perfet
ta per la uirtu unita, ma se la ligatura e cosi le pause fussino disgiūte, cioe po
ste in due rige diuenteria imperfetta, el simil farete de la massima inanzi la
ligatura de le lunghe, ouer de le sue pause, & similmente de la lunga auan
ti la ligatura de breui &c Et queste tali figure si possono imperficere si dalla
parte dinanzi come di drieto, & aduertite che mai si deue imperficere alcuna
figura perfetta, & cosi le sue parti perfette incluse in essa oltra la terza parte,
& allhora questa tal figura saria imperfetta: quo ad omnes partes eius, la ra
gione e accio almeno la possi remanere in l'ultimo esser della imperfettione
cioe, se la e masssima, la resti in otto semibreui imperfette, se lunga in quat-
tro, & se breue in due.
De l'alteratione delle figure.
tione pero e da sapere che alteration altro non e che il duplicar ciascuna figu
ra del suo proprio ualor, & l'alteration si causa sempre nelle parti propinꝗ
delle figure perfette, & in la seconda ouer ultima sempre, la ragion si e, per-
che la prima ha la natura de la unita, & la seconda de la binalita. Per le qua
li nature resulta la proportion dupla, come dimostra Boetio ne l'arithmeti-
ca nel capitolo ultimo del primo libro nel qual dimostra come ogni inequa
lita ha causato & processo da la equalita, doue se trouerete poniamo
sotto el circolo ut hic:

 due semibreue tra due breui senza punto de di-
due semibreue tra due breui senza punto de di-uisione fra le ditte semibreui, ouer cinque semibreui tra due breui per esser
la semibreue parte propinqua de la breue, la seconda ouer l'ultima altera.
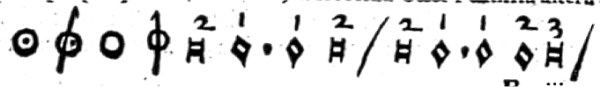
page 14
questa uia & forma potrete procedere.
Del punto in canto misurato.
ne, ouer d'alteratione per dimostrare & fare causare il numero perfetto di-
uidendo & reducendo una figura con l'altra. Il qual punto ha attribuiti que
sti nomi, & l'altro di augmentatione. Il punto di diuisione non si canta co-
me quello di augmentatione, ma diuide le figure una da l'altra & riduce una
figura con l'altra, & questo tal punto e quello che ancora se pone apresso
a ciascuna figura perfetta, el qual uien dimandato (d'alcuni) punto di per-
fettione & usiamo questo quando uogliamo che qualche figura non alteri,
ouer [[per]] dimostrar, & far qualche figura im[[per]]fetta, & far qualche figura alteri
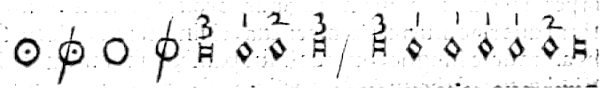
tissime habbiano uirtu de le perfette accio si causi alteratione: ut hic
 ouer quando uolemo imperficere una
ouer quando uolemo imperficere una figura perfetta quāto in se, ouer quan-
to alle sue parti, cioe de una sola, ouer
piu parti, ouer una parte perfetta, o piu parti, incluse in una figura imper-
fetta. Et cosi se aduertirete alla regola uoi potrete formar essempli assai in tut-
te le figure perfette, La uirtu di questo punto e grande, lui ha possanza di
escludere & includere, & redurre come facilmente potrete uedere & consi-
derare. El punto di si canta, & e quello che si pone appres-
so la figura imperfetta, & sempre l'augmenta la meta del suo ualore. si che ua-
le la mita de la figura a chi le appresso posto. doue se e appresso alla massi-
ma tale punto ha il ualore di una longa, si appresso una lunga una breue,
si appresso una breue, una semibreue, & cosi per ordine procedendo.
Delle pause.
to) sempre sono imperfette, ma se perficeno per uirtu di pause, donde in
ciascuno segno o sia perfetto, o imperfetto: la massima & la lunga per uir-
tu di pause possono esser fatte perfette, le quali pause sono alcune uolte indi
tiali cioe che non si numerano, ma solamente dimostrano la massima & la
lunga perfette. ouer la massima perfetta, & la lunga imperfetta, ouer la mas
page 15sima imperfetta, & la lunga perfetta: ouer la massima & la lunga imperfette.
& tali pause si poneno tra la chiaue & il segno, & alcune uolte sono indiciali, &
essentiali, cioe che nō solamēte dimostrano la [[per]]fettione de la massima & lū-
ga, ma oltra di questo si cōuien numerare, & tali pause si metteno dapoi el
segno come qui appare in questo essemplo & pausa e taciturnita di uoce mi
(surata.

Lo essemplo de le pause.
page 16
tione da minore, perche la e immobile, & cosi se due semibreui in questi segni


 sara senza punto di diuisione tra due pause de breui, ouer
sara senza punto di diuisione tra due pause de breui, ouer tra una breue, & una pausa di breue, sempre l'ultima semi
breue altera, & similmente se fosse tra due breui, ouer tra
esse pause, una pausa di semibreue, & poi una semibreue senza punto di di-
uisione, la semibreue si altera. ma se prima fosse la semibreue & poi la pau-
sa de semibreue non saria alteratione, perche la pausa (come ui ho detto) e
immobile, & questo modo osseruarete in tutte le altre pause & figure &c.

Essemplo de l'alteratione.
page 17

Essemplo del punto.
De li accidenti i quali si segnano fra le notule in processu cantus
dinotante la perfettione.
fetta si cognoscono cosi per li segni intrinseci come [[per]] li extrinseci. Li segni
extrīseci sono el circolo, & il semicircolo, & altri segni simili & si poneno in
fronte cantus & significano tempo perfetto, & imperfetto. Perfetto il circo
lo, & imperfetto el semicircolo. Ma li segni intrinseci sono li accidenti come
e il colore el qual consiste nelle notule piene come e il punto di diuisione, le
note alterate, redutte, & le pause le quali dinotino tale perfettione & altri si-
mili accidenti li quali si segnano in processu cantus, cioe tra notule canta-
bili, perche quando li antiqui segnauano li accidenti, li quali dinotauano
perfettione fra le notule cantabili in processu di ciascuna particula di qua-
lunꝗ concento, allhora non poneano in principio di tali particule altro se-
gno di perfettione come appar in questi essempi qui sotto notati.

Modus maior & minor perfectus.
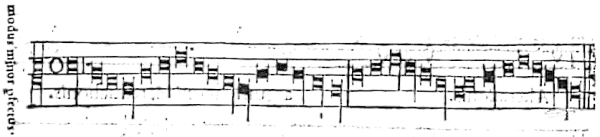
Accidentia quæ denotant tam modum maiorem [[quam]] minorem perfectum.

Accidentia quæ denotant perfectum.

Accidentia quæ denotant prolationem perfectam.
Del ualore de le notule cosi perfette, come imperfette dimostrate
per li segni, & per le pause.

Exemplum utriusꝗ modi, ac temporis perfecti, prolationisꝗ perfectæ.

Exemplum utriusꝗ modi, ac temporis perfecti prolationisꝗ imperfectæ.

Exemplū utriusꝗ modi perfecti, temporis imperfecti, [[pro]]lationisꝗ perfectæ.

Exemplū utriusꝗ modi [[per]]fecti, tēporis im[[per]]fecti [[pro]]lationisꝗ imperfectæ.

Exemplum modi maioris perfecti, minoris imperfecti temporis perfecti pro
lationisꝗ perfectæ
page 20

Exemplum modi maioris perfecti, minoris imperfecti, temporis per-
fecti, prolationisꝗ imperfectæ.

Exemplum modi maioris perfecti, minoris imperfecti, temporis im-
perfecti prolationis uero imperfectæ.

Exemplum modi maioris perfecti, minoris imperfecti, temporis ac pro
lationis .

Exemplum modi maioris imperfecti, minoris perfecti, temporis ac
prolationis perfectæ.

Exemplum modi maioris imperfecti, minoris perfecti, temporisꝗ
prolationis uero imperfectæ.
page 21

Exemplum modi maioris imperfecti, minoris perfecti, temporis im-
perfecti, prolationisꝗ perfectæ.

Exemplum modi maioris imperfecti, minoris perfecti, temporis ac
prolationis imperfectæ.

Exemplum utriusꝗ modi imperfecti, temporis ac prolationis
perfectæ.

Exemplum modi imperfecti temporis imperfecti prolatio-
nis uero imperfectæ.

Exemplum utriusꝗ modi imperfecti, temporis imperfecti, prolatio-
nis perfectæ.

Exemplum utriusꝗ modi imperfecti, ac temporis imperfecti, pro-
lationis imperfectæ.
Delli segni del tempo con prolatione.

Exemplum temporis perfecti, prolationisꝗ perfectæ.

Exemplum temporis perfecti, prolationisꝗ imperfectæ.

Exemplum temporis imperfecti, prolationisꝗ perfectæ.

Exemplum temporis imperfecti, prolationisꝗ imperfectæ.
De li segni del modo con tempo secondo li antichi.
el circolo & semicircolo con la cifra ternaria. & binaria imme-
diate poste da poi, ut hic.
 3,
3,  3,
3,  2,
2,  2, el circolo & semi-
2, el circolo & semi-circolo dimostrano il modo. Ma la cifra 3, 2, dimostra il tempo,
per tanto doue sara il circolo con la cifra ternaria ut hic,
 3, iui sara il mo-
3, iui sara il mo-do minore perfetto, & il tempo perfetto. Et doue sara il semicircolo con la ci-
fra ternaria come qui,
 3, iui sara el modo minore imperfetto, & il tempo
3, iui sara el modo minore imperfetto, & il tempo perfetto. Ma doue sara il circolo con la cifra binaria ut hic,
 2, iui sara il
2, iui sara il modo minore perfetto, & il tempo imperfetto. Et doue sara il semicircolo
page 23con la cifra binaria come qui,
 2, iui sara il modo minore imperfecto, & il
2, iui sara il modo minore imperfecto, & il tempo imperfetto come qui appar in questi essempli.

Exemplum modi minoris perfecti, ac temporis perfecti.

Exemplum modi minoris imperfecti, temporisꝗ perfecti.

Exemplum modi minoris perfecti, ac temporis imperfecti.

Exemplum modi minoris imperfecti, temporisꝗ imperfecti.
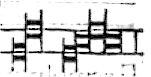
Delle ligature delle notule del canto figurato.
insiemi ligate, & e duplex, cioe ascendente, & discendente. Ascenden-
te e quando la seconda nota e piu alta de la pri-
ma. Discendente quando la seconda e piu bassa ut hic.
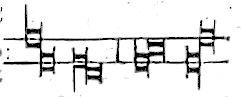
Ma sia ascendente ouer discendente, & habbia la uir-
gola, ouer coda dalla [[par]]te sinistra ascendēte sempre la prima & la secōda sono
page 24semibreui, & l'altre breui, saluo l'ultima
se la e quadra & discēda, e lūga ut hic.

Et se queste due ligature ut hic.
 & altre simili se faran-
& altre simili se faran-no sotto el segno di perfettione doue la breue sia per-
fetta come in questi segni



 . sempre la
. sempre la seconda semibreue altera. Ma se la ligatura hauera la co
da dalla parte sinistra discendente, tutte sono breui, eccet
to l'ultima se la e quadra, & discenda, allhora la
e lunga, ut hic.
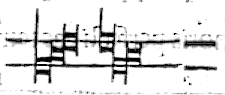
 Se la ligatura hauera la uirgola
Se la ligatura hauera la uirgola dalla [[par]]te destra, o ascendente, ouer discenden-
te, tutte sono lunghe, ut hic.
 Et notate che la lunga non se de
Et notate che la lunga non se deue poner se non in principio & in fine della ligatura, perche
oēs mediæ sunt breues, & questo se intende quando sono piu de due note insiemi ligate. Ma se la ligatura ascende senza uirgola, tutte so
no breui, eccetto l'ultima, se la e quadra & discēda, la e lungha
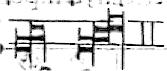
se la discendera senza coda, o sia la prima quadra, ouer obli-
qua semper la prima e lungha, tutte le altre sono breui, saluo l'ultima se la
e quadra, & discenda, perche allhora la e lungha. La massima in ligatu-
ra se cognosce per la grandez-
za della sua forma, ut hic.
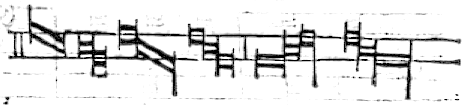
Et ꝗsto basti quāto alle ligature.
Delle proportioni.
la quale e di equalita, & inequalita. di equalita, come e
- dui a dui
2/2 - tre a tre 3/3
me e
- duo ad uno 2/1
- tre a due 3/2
- cinꝗ a duo 5/2 &
- otto a tre 8/3
portiōe di ma-
gior inequalita rationale si contiene cinꝗ parti, delle quali tre sono simplici
cioe multiplice. Superparticolare, & , & due composite mul-
tiplice superparticolare, & moltiplice , alle quali uien opposto
altre cinꝗ [[par]]ti di minor inelita le quali sortiscono quel medesimo nome cō
additiōe di questa [[pro]]positiōe sub, come e submultiplice, sub su[[per]][[par]]ticolare &c.
& in le [[pro]]portiōi di maggiore ine[[q-a]]lita sempre il maggior numero si pone di-
sopra, & il minore disotto, & ī ꝗlla de minor ine[[q-a]]lita si pone al cōtrario il mag
gior numero in ciascuna [[pro]]portiōe si dimāda dux, & il minore comes. si che
per dar principio alla dichiaratione nostra principiero dalla piu anticha &
piu nobile, per hauer assunto la sua origine dalla unita cioe dalla multiplice
page 25la qual si causa sempre quando el maggior numero contiene il minor piu
uolte precise, donde sel maggior numero conterra il minore due uolte sara
- du-
pla. 2/1 4/2 - se tre uol-
te tripla 3/1 6/2 - se quattro uol
te quadrupla 4/1 - se cinque uol
te quintupla 5/1 - si sei uolte
sestupla 6/1 12/2 - si sette uol
te settupla 7/1 - si otto
ottupla 8/1 - si noue uol
te nonupla. 9/1 - si dieci uol
te decupla, 10/1 20/2
& cosi in in
finitum, ma
sel minore sara contenuto dal
maggiore
- due uolte subdupla 1/2
- si tre uolte
subtripla. 1/3
&c. La superparticolare si e
ogni uolta chel maggior nu
mero cōtiene il minore una uolta & una parte aliquota di esso minore. Par
te aliquota e quella che piu uolte tolta rēde [[pre]]ecise il suo tutto come e tre respet
to di sei, donde se torrete due uolte tre, ui rendera precise sei. Parte non aliquo
ta, ouer aliquāta, ma cōposita di parti aliquote e quella che piu uolte tolta nō
rende il suo tutto precise come e duo respetto di cinꝗ, doue si torrete due uol
te dua, fa manco di cinꝗ. se tre uolte piu. si che e da uedere sel maggior nu
mero contiene il minore una uolta e mezza, ouer una uolta e'lla terza par-
te o la quarta, o la quinta, e cosi in infinitum, se una uolta e mezza, quel-
la habitudine, ouer proportione sara
- sesqualtera, ouer emiolia, quod idē est
3/2 6/4 - se una uolta ella ter-
za parte sesquitertia. 4/3 8/6 - se una uolta ella quar
ta parte sesquiquarta. 5/4 - se una uolta e,
una quinta par-
te sesqui
quinta. 6/5 - se una uolta e una se
sta parte . 7/6 - se una parte e una set
tima sesquisettima. 8/7 - se una parte e
una ottaua ses
quiot
taua. 9/8
& cosi in infinitum ma sel minor numero sara conte-
nuto dal maggior
- una uolta e la mita sara 2/3
- se una
uolta e
la terza parte
subsesquitertia 3/4
La superpartiente proportione si e ogni uolta chel mag-
gior numero contien il minore una uolta, & oltra, o due, o
tre, o quattro, o cinꝗ, o sei parti, e cosi in infinitū, di ditto numero, adunꝗ sel
maggior numero cōterra il minore una uolta il tutto e di piu due parti, quel
la proportione, ouer habitudine
si dimādera
- superbipartiēs tertias 5/3 10/6
- ma se una uolta e tre parti sara
supertripartiens quartas come 7/4 - se una uolta e quattro parti
superquadripartiens quintas 9/5
&c. Ma sel minor numero sara contenu
to si dimandera subsuperpartiēs tertias. 3/5
La multiplice superparticolare e ogni uolta chel maggior numero contiene
il minore piu uolte, & questo inquanto multiplice, & oltra di questo una
parte aliquota del minore, & questo inquanto superparticolare, & pero e
da uedere prima quante uolte come multiplice el maggior numero contie-
ne il minore. Da poi come superparticolare, se quella parte aliquota e la mi
page 26ta del minore, o la terza, o la quarta parte &c. Si che sel maggior numero
conterra il minore due uolte e la mitta quella proportione si dimanda
- du-
pla ses-
qualtera 5/2 10/4 - se due uolte e la terza
parte dupla sesquitertia 7/3 - se due uolte e la quar-
ta dupla sesquiquarta 9/4
& cosi
in infini
tū. ma sel maggior conterra il minore tre uolte, & la mita si dimandera tal ha
bitudine
- tripla
sesquialtera 7/2 14/4 - se tre uolte e la terza
[[par]]te tripla sesquitertia 10/3 - ma se quattro uolte e la mita
quadrupla sesqualtera co-
me
qui 9/2 - se quattro uolte e la terza
[[par]]te quadrupla sesquitertia 13/7
e cosi procederete in infinitum, & a que
sta similmente, come a l'altre uien op
posto la submultiplice su
perparticolare come saria 2/5 &c.
La multiplice superpartiēte si e ogni uolta
chel maggior numero contiene il minore piu
uolte, come multiplice, & oltra di questo due o tre o quattro o cinꝗ parti &
cosi in infinitum, e questo e inquanto superpartiente. & pero deuemo uede-
re come multiplice quante uolte il maggior contiene il minore. Donde sel
maggior numero conterra il minore due uolte, & di piu due parti d'esso mi
nore, tal proportione sara dupla
superbipartiens tertias come e 8/3
ma sel maggior numero conterra il mi-
nore due uolte & tre parti sara dupla su-
[[per]]tripartiēs
quartas 11/4
& cosi in infinitum potrete inuestigare. ma sel maggior nu-
mero conterra il minore tre uolte, & due parti sara
- tripla
tertias 11/3 - se quattro uolte, & due parti superbipartiens tertias. 14/3
& cosi con questo ordine
potrete facilmente trouare
spetie di proportioni, & similmente a questa gli e per opposition la mi-
nore come e in l'altre cioe submultiplice su[[per]]partiēte, com'e subdupla su[[per]]bi
partiēs
tertias. 3/8
& cosi anderete procedendo in questa forma. Oltra a questo e da
sapere che alcuni cōpositori nel tēpo im[[per]]fetto, ouer in la prolatio
ne im[[per]]fetta, per uirtu della [[pro]]portione sesqualtera, & de la tripla, & de la sestu
pla consequire attestano il tēpo, & la prolatione la sua [[per]]fettione, consideranti
solamente la [[per]]fettione del nūero ternario, ouer senario, ma niente attendēte
la im[[per]]fettione del nūero binario, & quaternario, io [[per]] piu ragioni con le loro
opinioni nō mi cōcordo, & primieramēte dico, che la loro cōsideratione nō
appartiene al musico, [[per]]che il musico la relatione ad aliquid .i. ad alcuna cosa
cōsidera, & non il nūero perfetto come larithmetico .i. lo abbachista. Propria
mente la consideratione, & l'officio del musico e in inuestigare, & diligen-
temente perquirere, & cercare circa l'habitudini ouer proportioni in che mo
do da esse proportioni resultino le symphonie, & se in questa pratica nostra
per relatione come parti a parti sortiscano el suo effetto, per il che, Vtrum el
page 27numero per se sia perfetto, ouero imperfetto, questa e cosa pertinente co-
me ho detto allo Arithmetico, & sua propria consideratione, & speculatio-
ne, ma il musico considerante solamente la relatione, uuole la medesima
perfettione & imperfettione competere & quadrare ad segni, & anchora
ad esse proportioni, essendo el segno quid principale & fundamēto delle re
lationi, per la qual cosa (come ho detto) le prolationi di qualunꝗ genere,
& qualitate siano, per se stesse, ne perfettione, ne imperfettione concerna-
no, se non inquanto fanno li segni perfetti, o imperfetti, ma solamente la
diminutione concernano, ouero augmentatione per relatione alle parti. Se
condariamente contra la loro opinione prendo & adduco tale argumento,
uoglion loro il numero ternario, ouer senario in esse proportioni causante
ne segni imperfetti la perfettione consistere come nella sesqualtera, tripla, &
sestupla. adunꝗ (essendo una medesima disciplina quella de li oppositi) ne
segni perfetti, medesimamente la dupla, ouero la quadrupla dimostrerano
la imperfeccione de le figure. perche il numero binario, ouer quaternario
se chiama & e feminino, diminuto, ouero imperfetto, la qual cosa e falsa per
la ragioni disopra allegate. & secondo le loro compositioni non uolendo es-
si ne segni perfetti denotare tali habitudini imperfettioni di figure. ma la di-
minutione solamente de la quantita, adunꝗ &c. Alcuni tengono questa no-
stra opinione, & la approbano, & confermano, cioe che la perfettione, &
imperfettione delle notule, ouer figure non si causa per cagione de le pro-
portioni, ma per uirtu de segni, perche le proportioni secondo ho per la relatione, come parti a parti, in questa pratica solamente la uirtu
& operation sua conseguiscono, nientedimeno, quasi nulla differentia con
cernenti tra le figure uacue, & piene di color negro dicenti la sesqualtera con
cernere le figure uacue, & la emiolia le piene essēdo quel medesimo la emio
lia, & la sesqualtera como scriue Boetio in l'Arithmetica nel primo libro al
cap. xxiiii. el [[q-a]]le dice cosi. emiolia .i. sesqualtera. Dicono āchora che la emio-
lia sortisce sem[[per]] la im[[per]]fettiōe. ma la sesqualtera no. tēgono etiādio cōsiderar-
se la sesqualtera [[per]] la plenitudine de le notule niente [[pre]]meditāti, & cōsiderāti la
diffinitiōe della [[pro]]portione, ma solamēte el numero [[per]] se attēto che nō si co-
gnoscēdo & nō si sappiādo la definitiōe nō si sa, & non si cognosce el defini-
to. [[pro]]portione e (sc[[d-hook]]o Boetio, Euclide & gli altri) habitudine adinuicē di duoi
numeri, ouer de duoi termini. Et percio dirai che tali notule di color negro
descritte equiuagliono, & conuengono alla proportione della sesqualtera,
ouero emiolia, il che quel medesimo e che tali notule presupongono per-
page 28fettione. & utrum questo sia uero, el prouo cosi ho la regola: che in tre mo
di la figura perfetta puo consequire la imperfettione, cioe per uirtu del nu-
mero, per necessita del punto, & per causa del colore. ma la imperfetta figu
ra non. la ragion di questo e, perche se la e imperfetta da se piu imperficere
non si puo, ma perdendo ogni figura perfetta la terza parte da la negrezza,
ouer da la nigredine, & in questa da quelli la dimandano emiolia, ancho-
ra questa medesima diminutione di figure sortiscono, adūꝗ tali figure, ouer
notule presuppongono perfettione. per il che essendo stabili ouer immobi-
li le pause di esse notule, perche uersano, & continuano nella quantita con
tinua, sempre adunꝗ consequentemente rimāgono perfette, & hauemo la
regola, che la pausa accidentalmente come essa figura, ne imperficere, ne
alterare si puo, la ragione e (come ho detto) perche da se la e immobile e ben
uero che le notule, le pause per consimili diminutione si considerano nel-
le proportioni iusta la loro naturale, & propria possanza, quanto alle sue
quantita. ma quanto a gli accidenti non cosi, ma altri modi, perche altri-
menti si debbono considerare le diminutioni delle proportioni, alle quali le
notule & le pause soggiacciono, che le imperfettioni delle notule, ouero le
alterationi di esse, perche le notule patiscono li accidenti la raggione, la quanti
ta (secondo dice Boetio nostro nel prohemio de larithmetica) da se e di im
mutabile sustantia. ma aggionta al corpo si permuta, come si dimostra nelle
figure musicali, adunꝗ le figure conseguiscono gli accidenti circa la imper
fettione, & alteratione, ma potrebbe dire alcuno, io ho secondo el philosopho
Frustra fit per plura, quod fieri potest per pauciora .i. che in uan si fa per piu quello, che si puo far commanco, ma essendo cosi che la sesqualtera quel
medesimo effetto, & quella medesima possanza sortir possa, come conse-
quisce essa emiolia, adunꝗ inane & uana e la dispositione de la emiolia, oue
ro la plenitudine de le notule equiualente alla habitudine della sesqualtera.
respondo, che senza causa li musici hanno instituita & ordinata questa
plenitudine di notule equipollente alla sesqualtera, (anzi diuersi effetti con
seguisce) & primo che sempre (como ho prouato) presuppone perfettione.
secondo, accio che le parole disposte alli moduli alternatamēte secondo li lo
ro affetti correspōdano, perche come appresso gli oratori tre generi, cioe tre
sorti & qualitati di dire se considerano, cioe dimostratiua, deliberatiua, & giu
diciale, & questo per la exigentia di diuersi negotii, & di diuerse facende, co
se, & operationi, cosi appresso li musici, otto modi si considerano. per il che
poco cōto far si deue di quelli compositori li quali ignorano li effetti de mo-
page 29di, & de signi & de le proportioni. Questo che e detto fin qui bastera quan
to alla cognitione delle proportioni, & alla ragione, & uso di quelle.
Seguita il contrapunto.
quanti sono i modi ouero tuoni, & quali sono autentici, & quali plaga-
li, & quali sono perfetti, & quali sono diminuti, & quali misti, & quali com
misti, & quali sono regolari, & quali sono irregolari, & in che modo si com
pongono, & i loro principii, & le sue distintioni o cadentie, & doue finisco
no cosi regolarmente, come irregolarmente, & quanto debbono ascendere
& discendere, & la sua intonatione & mediatione, & i loro effetti che proce
deno da quegli, & altre parti pertinenti a essi tuoni. Dico adunque esser ot
to i tuoni nel canto, cioe primo, secondo, terzo, quarto, quinto, sesto, set
timo, & ottauo. de quali quattro sono autentici, & quattro plagali. I tuoni
autentici sono questi, cioe primo, terzo, quinto, & settimo, & tali tuoni si
dimandano autentici, perche sopra il suo fine regolarmente possono ascen-
dere otto, noue, & alcuna uolta dieci uoci, & discendere una. Ma i tuoni
plagali sono questi, cioe secondo, quarto, sesto, & ottauo. plagali si diman
dano perche disotto dal suo fine regolarmente possono discendere quattro,
ouer cinque uoci, & ascendere cinque, ouer sei. I predetti tuoni finiscono
accompagnati a due a due, cioe primo & secondo, finiscono in D sol re. Ter
zo, & quarto, in E la mi. Quinto & sesto in F fa ut. Settimo & ottauo in
G sol re ut. & tali fini sono detti regolari. Ma il fine irregolare del primo &
del secōdo tuono, sono in G sol re ut. Del terzo, & del quarto in A la mi
re. Del quinto & del sesto in
 fa
fa  mi del settimo, & ottauo in C sol fa
mi del settimo, & ottauo in C sol fa ut. posto pero il segno del
 rotundo, ouer molle
rotundo, ouer molle  fa
fa  mi. Et que-
mi. Et que-sti tali tuoni sono detti irregolari, perche finiscono in altro luoco che nel suo
proprio, & determinato. Ma ciascun tuono puo terminare & finire
in quo-
libet loco manus, ubi species propriæ reperiri possunt. Et ciascuno de pre-detti tuoni puo esser perfetto, diminuto, superfluo: misto, commisto: re-
golare, & irregolare. I tuoni autentici perfetti sono quegli che ascendono in
fino al diapason, cioe una ottaua sopra il suo regolar fine, & se ascendono
piu si dimandano superflui, & se manco diminuti. I tuoni plagali perfetti
sono quegli che discendono una quarta sotto il suo regolare fine, & se discen
dono piu si dimandano superflui, & se manco si dimandano diminuti. Ma
page 30i tuoni misti ueramente sono quegli che participano del ascendere, & discen
dere del suo socio come e il primo con il secōdo, il terzo con il quarto. I tuoni
commisti sono quegli che participano del ascendere & discendere, & anchor
mediatione con altro tuono che non sia suo compagno com'e il primo, con
il terzo &c. I tuoni regolari sono quegli che finiscono ne luoghi suoi proprii
& determinati. I tuoni irregolari sono quegli che finiscono in altro luoco
che nel suo loco proprio. Anchora notate circa la compositione de predetti
tuoni che il primo & il secondo tuono si compongono della prima specie del
diapente, cioe, re la, & della prima specie del diatessaron, cioe, re sol, el dia
tessaron nel primo tuono e disopra del diapente, nel secondo e disotto. Il ter
zo & quarto tuono si compongono della seconda specie del diapente, cioe,
mi mi, & della seconda del diatessaron mi la, el diatessaron nel terzo tuono
e disopra del diapente, nel quarto e disotto. Il quinto & sesto tuono si com-
pongono della terza specie del diapente, cioe fa fa. & della terza del diatessa
ron, ut fa, el diatessaron nel quinto tuono e disopra del diapente, nel sesto
e disotto. Il settimo & ottauo tuono si compongono della quarta specie del
diapente, cioe ut sol, & de la prima specie del diatessaron re sol, el diatessa-
ron nel settimo tuono e disopra del diapente, nel ottauo e disotto. Tutti i tuo
ni plagali hanno medesimi diapente, & come i suoi autentici, ma
sono differenti in questo, che gli autentici hanno il diatessaron sopra il dia-
pente, & i plagali disotto, come appar qui in questo essemplo.

De principii & distintioni de tuoni.
in G sol re ut & in A la mi re acuti, & similmente le sue distintioni.
fa ut graue, similmente le sue distintioni.
page 31
ut, &
 mi, acuti, & in C sol fa ut, & similmente le sue distintioni.
mi, acuti, & in C sol fa ut, & similmente le sue distintioni. la mi, & in F fa ut, graui, & in G sol re ut, & A la mi re acuti, similmente
le sue distintioni.
in C sol fa ut: similmente le sue distintioni.
A la mi re acuta: similmente le sue distintioni.
 mi
mi acuti, in C sol fa ut, & in D la sol re: similmente le sue distintioni.
G sol re ut, in A la mi re acuti, & in C sol fa ut: similmente le sue distintioni.
Della intonatione, & mediatione de psalmi di ciascun tuono.
labe, fa sol la, gradatim & la sua mediatione fa in
 fa
fa  mi per
mi per  molle, con
molle, con queste sillabe fa mi re mi.
ut re fa. & la sua mediatione fa in F fa ut graue con queste syllabe, fa sol fa.
labe, ut re fa. ma la prima & la seconda sillaba sono ligate, & la sua media
tione fa in D la sol re, con queste sillabe, sol fa, mi fa.
sillabe, la sol la. ma la sua mediatione fa in G sol re ut acuto, con queste sil-
labe ut re, mi re.
labe fa, la re fa. ma la sua mediatiōe fa in C sol fa ut, con queste sillabe fa sol fa.
labe, fa sol la. & la sua mediatione fa in
 fa
fa  mi, per
mi, per  molle, con queste
molle, con queste sillabe, fa mi, re mi.
fa mi fa sol, & la sua mediatione fa in F fa ut acuto, cō ꝗste sillabe, fa mi re mi.
sillabe ut re fa. Ma la sua mediatione fa in C sol fa ut con queste sillabe
fa sol fa. Ma accio che ui tegniate bene a mente le intonationi delle sopra-
dette psalmodie, & le sue mediationi mettereteui a memoria i sequenti
page 32uersi, & primo per le intonationi.
Primus cum sexto fa sol la semper habeto
Tertius & octauus, ut re fa, sicꝗ secundus,
la sol la, quartus, fa la re fa, sit
tibi quintus.
Septimus fa mi fa sol sic omnes esse recordor.
Hora per le me-diationi saranno questi.
Septimus & sextus, dant fa mi re mi quoꝗ primus.
Quintus & octauus, dant
fa sol fa sicꝗ secundus.
Sol fa mi fa Ternus, ut re mi re dat tibi quartus.
Delle consonantie.
ta & sesta. De le quali due sono perfette & due imperfette. Le perfette sono
l'unisono, & la quinta. Le imperfette sono la terza, & la sesta. Ma da l'uni
sono si compongono la ottaua, la quintadecima, & la uigesima seconda.
Le quali tutte sono specie perfette. Da la quinta si compongono la duodeci-
ma, & la decimanona. Da la terza se compongono la decima, & la decima
settima. Ma de la sesta se compungono la terzadecima, & la uigesima. Le
quali tutte sono specie imperfette. Le intermedie sono le dissonantie come e
la seconda, la quarta, la settima, la nona, la undecima, & le sue simili, &
equisonanti, & esse anchora sono necessarie in la compositione de esso con
trapunto.
terza. Nientedimeno e d'auertire che l'unisono non e consonantia in actu,
sed in potentia, per essere origine & principio di ciascuna consonantia. La
tertia post se uuole la quinta. La quinta post se richiede la sesta, stante il te-
nore in una medesima sede, ouer luoco, cioe in una medesima linea, oue-
ro in uno medesimo spatio. Et la sesta, l'ottaua in diuersi luoghi, cioe una
parte in linea ascendendo immediate, cioe senza mezo, & l'altra discenden
do immediate in spatio, & cosi al contrario. & la ottaua uuole la decima,
cosi la decima, la duodecima.
sibilita lo possiamo osseruare. Perche alcune uolte andaremo, & procedere
mo da l'unisono alla quinta, & econuerso. Alcune uolte da lo unisono al
la ottaua, & econuerso. Alcune uolte anchora procederemo da la ottaua alla
terza, & econuerso. & similmente in le altre si deue osseruare la regola con
habilita & possibilita. Oltra questo aduertite, che da l'unisono insino alla ot
taua, tutte sono specie simplici. ma dalla ottaua in suso sono composite. La
decima se compone da la ottaua, & da la terza, se la sara congionta con la ter
tia maggiore, diuentera decima maggiore, se con la tertia minore, diuente
page 33ra decima minore. La ottaua ha la natura de l'unisono. La decima de la . La duodecima de la quinta. La terzadecima de la sesta, & la quintade
cima de la ottaua, & de l'unisono. La decimasettima ha lei anchora la natu
ra della terza. perche la si forma di due ottaue & una terza (come ho detto)
maggiore ouer minore. La decimanona ha la natura de la quinta, la uige
sima de la sesta. & la uigesima seconda de l'unisono, ouero ottaua. & cosi si
puote procedere in infinitum.
De la prima regola da esser osseruata in la composition del contrapunto.
cie perfetta, & che la penultima sia specie imperfetta, atta a quella specie per
fetta che li seguita. Tamen tale regola e arbitraria, quanto al principiare per
specie [[per]]fetta. Onde se uoi uorrete finire [[per]] quinta, la penultima bisogna sia ter
tia, & se uorrete finire per ottaua, bisogna che la penultima sia sesta. Non pe-
ro questa regola ut quanto al principiare, che non possi principia
re anchora per specie imperfetta, ma quanto al finire, si deue terminare per
specie perfetta, perche si finirebbe per consonātia imperfetta terrebbe le orec-
chie delli auditori sospese, perche laudito sempre aspetta con desiderio el fine
perfetto, pertanto el fine di qualunche concento debbe esser perfetto, perche
nel fine consiste la perfettione di ciascuna cosa.
re, & econuerso, la ragione e perche la perfettione se causa per la dissimili-
tudine, cioe per la uarieta de i suoni. Et pero consonantia e una certa mistu
ra de suoni graui, & acuti. La quale con suauita, & con uniformita peruiene
alle nostre orecchie, & di qui nasce, che non si puote ordinare si ascenden-
do, come discendendo immediate, due specie perfette simili, perche ogni
uolta che siamo peruenuti a qualunche specie perfetta, semo ad esso fine, &
perfettione, alla quale tende essa musica. Onde, se uolessimo procedere per
specie perfette si ascendendo, come discendendo, per tale identita resolteria
dissonātia. concio sia cosa che l'harmonia resulti per la dissimilitudine, & ua
riatione de le specie, si come la consonantia per la uarieta, & dissimilitudi-
ne dei suoni. Niente di meno questa regula alcune uolte falisce, perche al-
cune fiate e di bisogno, che tutte due le parti insieme , ouer discēda
no con specie imperfette, accio habilmente possiamo [[per]]uenire alla specie per
fetta, ascendere con specie perfette, non laudo, cioe, quando andiamo con
page 34la parte del soprano da una minore ad una maggiore, come e da la quinta
alla ottaua, ma ben dalla ottaua alla quinta: In discendendo si, la ragione
e accio perueniamo alla cadentia. Certamente discendendo li moti se tardia
no, per la qual tardita facilmente si comprende la diuersita delle specie
la quale non comprēde cosi ageuolmente in li suoni acuti, per la celerita de
i moti, immo tendono ad una similitudine di specie, massimamente quan-
do ascēdono con le parti (come ho detto) da una minor perfetta ad una mag
gior perfetta, ne anchor laudo il ascendere insieme di due parti da una im
perfetta maggiore ad una perfetta minore cō disgiontione di esse parti, come
e andare dalla decima alla ottaua. Ma al contrario si, cioe andare dalla ottaua
alla decima, la ragiōe nō si uede, ne si cognosce dalli idioti. anchora che lhab
bino dinanti a gliocchi. Ditemi andrete uoi, sel soprano ascende da C sol
fa ut ad E la mi, col tenore da A la mi re, ad E la mi, che sara da tertia a l'u-
nisono: nō potrete dire chel sia regolato & bon processo, ma ben potresti an
dare da l'unisono, ascendendo tutte due le parti, alla terza: Si che se uoi con
sidererete da l'unisono alla ottaua, & ben cōprēderete li effetti, li quali se cau
sano si in lo unisono come in la terza, in la quinta, in la sesta, & in la otta-
ua, la quale ottaua e simile & equisonante allo unisono, uoi harete simil-
mente la cognitione delli effetti de le composite: si che attendete alla grauita
la quale si ha uendicata piu tardita de moti, che acuita. Et similmente alla
acuita, la quale constituisce li moti assunti piu celeri. Doue facilmente oc-
culta le durezze, le quali per la tardita de i moti causati per la grauita si de-
prendeno, & senteno, che similmente la differentia delle specie.
dendo, come discendendo: ma dissimili si ben, stante il tenore fermo in una
medesima linea, ouero in uno medesimo spacio, oueramente che se una
parte ascende l'altra discenda, cosi anchora ascendendo tutte due le parti (co
me ui ho detto in la seconda regola) purche andiamo da una maggiore per
fetta ad una minore perfetta, la qual cosa potete anchora ordinare nel di-
scendere a fortiori, immo uoi potete nel discendere per la tardita de moti cau
sati da la grauita non solamente uenire dalla maggiore alla minore, ma etiā
dio dalla minore alla maggiore, come sempre usiamo con il tenore, & il bas
so, quando uolemo andare alla cadentia della ottaua, ordinemo la penul-
tima quinta, & l'ultima ottaua cioe disotto dal tenore, ouer canto fermo. l'ul
tima quinta supra il tenore, per non uenire con il soprano sempre in quin-
tadecima, ma alcuna uolta in ottaua, & allhora il contralto dara terza sopra
page 35il tenore. come uedemo nel componere a quattro uoci.
te, ma in diuersi moti pero, cioe che una parte ascenda, & l'altra discenda,
& econuerso. Lo essempio, io son col soprano in G sol re ut sopr'acuto. &
dico sol fa sol. perche uengo in F fa ut & ritorno in G sol re ut predetto, &
con il tenore dico per ottaua ut in G sol re ut acuto, & poi dico re ut, perche
uengo in A la mi re, & ritorno in lo antedetto G sol re ut. poi salto con il te
nore in loco del soprano, usando quelle medesime uoci, che ha usato il det
to soprano, & con il soprano discendo nel luoco del tenore, usando ancho
ra quelle medesime uoci chel detto hauea usato, doue in diuersi moti io & ordino due ottaue, una po l'altra. & questo e permesso, immo pre
sta & rende harmonia suauissima, cosi anchora con le altre potrete [[pro]]cedere.
fette simili come sono tertie, seste, decime. la ragione e, perche sonno ua
ghe, & dissimili di interuallo ouer sistema, cioe una e maggiore, la quale
e atta alla acuita, l'altra e minore, la quale e atta alla grauita, la qual cosa nō
puole accadere in le specie perfette perche le specie perfette sono immobili.
gione e, perche se uitia, & corrompe la specie, o per diminutione, o per su-
perfluita, ma ben potemo usare fa contra mi in specie imperfette, perche le rendono suauita, & dolcezza.
processo, quando queste reiterationi se causano ad uno medesimo tempo
da tutte due le parti.
ascendere, & in lo discendere per la uirtu di tutte due le parti, perche ogni co-
sa e inconsonante. questa regola ui ho limata in la seconda rego
la, & assai diffusamēte ui ho fatto cauto in tal materia. & questo ui sia quan
to appartiene a nota contra nota.
Seguita unaltra regola del contrapunto ad uidendum.
la ottaua sua equisonante, la seconda alta per la nona, la terza alta [[per]]
la decima, la quarta alta per la undecima, la quinta alta per la duo-
decima, la sesta alta per la terzadecima, la settima alta per la quartadecima,
page 36la ottaua alta per la quintadecima. Et questo si intende sopra il tenore. Ma in
fra il tenore lo unisono si piglia per la ottaua, la seconda bassa per la settima,
la terza bassa per la sesta, la quarta bassa per la quinta, la quinta bassa per la
quarta, la sesta bassa per la terza, la settima bassa per la seconda, la bassa per lo unisono. Et se questo tale modo di fare il contrapunto si di-
manda ad uidendum, perche non potete preterire la quarta linea del canto
fermo con l'occhio, & per questo e nominato da li pratici ad uidendum.
trapunto, quanto appartiene a nota contra nota, ouero punto contra punto.
L'e da uedere in che forma lo habbiamo a cōstituire diminuto, massime so
pra il canto fermo, primo con habilita, & possibilita uoi douete osseruare
regole sopraposte nel principiar del tempo, ouer della misura. poi nel
resto se ben ui accadeno dissonantie come sono seconde, quarte, & simi-
li, non importa per la celerita delle figure. Ma ben douete sapere che nessu
na figura che toglie integra misura come saria la semibreue in questi segni.
 ,
,  ,
,  ,
,  , non puote sottogiacere a dissonantia alcuna. Ma si ben le mi-
, non puote sottogiacere a dissonantia alcuna. Ma si ben le mi-nime, & altre minori, la ragione e per la tardita, per la quale la dissonantia
ne offenderia, nel segno per medium si ben. Et nel segno duplex per me-
dium una breue. Et in el segno triplex una lunga imperfecta. Et notate per
fallentia di questa regola, che una dissonātia puole stare in principio di tem
po, ouer misura, in sincopa perho. Et questo perche la nota, ouer uoce per-
cuote l'altra nel durare che fa la uoce da un moto a l'altro, El quale durare
e dal senso de laudito compreso, come taciturnita, ouer sospensione di uoce
la quale taciturnita e stata scritta dal mio don Franchino gaffurio, d'ogni
dottrina scientissimo, nel tratato suo de harmonia instrumentorum nel ca-
pi .ii. del primo libro, & quale cosi dice,
in medio enim percussionum, quæ
per sonos fiunt, quædam eueniunt taciturnitates, quibus soni abinuicem di
scernuntur. Et notate che quante uolte uoi uorrete sincopare per tertie, & se-conde, & poi uenire a l'unisono, ouer schiuarlo, cioe fingēdo uoler andare,
farete chel soprano principia per terza con il tenore con figure simili. Ma fate
chel tenore faccia una pausa di minima in integra misura. Et in la non inte-
gra uoi anchora el potete usare & la penultima sia minima del tenore & al-
hora il tenore, cioe el canto fermo sara mobile, & figurato per la diuersita de
la figuratione delle figure. Et questo modo di sincopare operiamo discendē
do tutte due le parti. Et cosi anchora ascendēdo si forma la sincopa per sesta
& settima, ma la pausa, ouer suspiro (come i uolgari la chiamano) tocca al
page 37 al cōtrario della sincopa per terza, & seconda causante, & la penulti
ma del soprano sara minima, che battera sesta con il tenore, & l'ultima dara
ottaua, uolendo andare a la cadentia propria, Et se qualche uolta la uorrete
schiuare, ui con qual parte ui parrera piu a proposito uostro, perche (come
ui ho detto) la perfettione si causa per la uarieta. & notate, che se il cāto fermo
ascendesse, ouer discendesse per quinta, & uoi fussi in quinta col soprano,
cioe col tenore su la penultima nota, non ascenderete mai con diminutione,
poniamo di semiminime, ne anchora discenderete per trouarui su la secon-
da in quinta, perche le sariano due quinte, & non uale a dire la seconda semi
minima e quarta, la terza e terza, & la quarta e seconda, & questo e per la ce-
lerita di moti, si che le tanto, quanto se uoi dicessi ut sol, ut sol, a dir ut sol, ut re
mi fa sol, ouer dire sol ut, sol fa mi re ut, & similmente aduertirete in le altre
specie [[per]]fette. Anchora notate che se noi ne ritrouiamo col cāto fermo in otta-
ua cō il soprano, poniamo, chel cāto fermo sia ī A la mi re acuto, & descēda
in G sol re ut acuto, dicēdo re ut. Il soprano principia [[per]] ottaua ī A la mi re Et
dice [[per]] una minima, & due seminime, & poi una semibreue la sol fa sol. La mi
nima e ottaua, la prīa semiminima settima, & la sc[[d-hook]]a sesta. Et poi la semibre-
ue ottaua, ch'e in G sol re ut sopracuto. Io ui dico, che per la celerita de moti
li quali se causano in quelle semiminime, uoi nō douete usarle, perche le pa
reriano due ottaue. Si che per queste regole sappiate usare le specie, si perfet-
te, come imperfette. Et quando uoi uorrete andare a la cadentia perfetta sem
pre la penultima de essere dissonantia in sincopa con la penultima la quale
de essere specie imperfetta, come ui ho diachiarato in le regole soprascritte. Si
che uolendo peruenire a la cadētia de la ottaua, fate che l'antepenultima sia
settima sincopa, & la penultima sesta. Intendete perho col canto fermo, ouer
tenore, & tal sesta bisogna sia maggiore, perche la sesta minore nō e atta a la
acuita, ma ben a la grauita. Et perho assumate una regola generale che ogni
uolta, che uoi anderete ad una specie imperfetta, & poi uorrete ascendere ad
una maggiore specie d'essa, cosi perfetta, come imperfetta, se quella specie e
minore, fatela maggiore con il segno de la sustentatione, la quale susten
tatione si dimostra con questo segno.
 La ragione e, perche ogni specie
La ragione e, perche ogni specie imperfetta (come ho dimostrato) est duplex, cioe maggiore, & minore, la
maggiore ha piu de la minore uno apotome, cioe uno semituono maggio-
re. Si che la sesta maggiore piglia piu del cōtinuo di quello, che fa la minore.
Et per cōsequente la e piu acuta, & adunꝗ piu atta alla acuita. Et la minore
non cosi per assumere manco del continuo, la e meno acuta, & per cōsequen
page 38te piu atta alla grauita. Et questa e generale a tutte le specie imperfet-
te. se uorrete finire, ouero far cadētia per quinta, farete l'antepenultima quar
ta in sincopa, & la penultima tertia. Ma se uorrete finire, ouer far cadētia per
unisono, farete l'antepenultima secōda in sincopa, & la penultima terza. Et
poi anchora potrete con la parte del soprano sincopare per quinta, & sesta
ascendendo
Regola di comporre a tre uoci.
il tenore in ottaua, sesta, quinta, ouer tertia.
decima, ottaua, sesta, ouer tertia.
quinta, ouer tertia.
ottaua ouer sesta.
quinta ouer tertia.
ottaua, quinta, ouero tertia.
Regola di comporre a quattro uoci.
re in ottaua, fanno il contralto con il basso in quinta, & se il basso con il teno-
re e in decima, fa il contralto in ottaua, intendi perho sempre con il basso.
quinta, & lo contralto in tertia con il basso.
taua, fanno il contralto con il basso in decima. Et sel basso col tenore e in se-
sta, fa il contralto in ottaua, ouer tertia.
fanno il contralto con il basso ottaua, ouer tertia. & se'l basso col tenore e in
tertia fa il contralto quinta. & se'l basso col tenore e in ottaua, fa il contralto
page 39con il basso in decima.
taua, fanno il cōtralto con il basso decima, ouero duodecima, & sel basso col
tenore e in quinta, fa il contralto ottaua, ouer decima, & sel basso col tenore
e in tertia, ouero ottaua, ouer sesta, & sempre dipoi la sesta la ottaua, & se il
basso col tenore e in quinta, disopra, fa col contralto tertia disotto.
Modo, & osseruatione di comporre qualunche concento.
drigale, o sonetto, o barzaletta, o altra canzone, prima bisogna consi-
derare nella mente, & in quella inuestigando ritrouare uno aire con
ueniente alle parole, ut cantus consonet uerbis, cioe, che conuenga alla ma-
teria, perche quante uolte, che i dotti compositori hanno da comporre una
cantilena, sogliono prima diligentemente fra se stessi considerare a che fine,
& a che proposito quella potissimamente instituiscono, & componghino,
cioe quali affetti d'animo con quella cātilena mouere debbino, cioe di qual
tuono si deue comporre, perche altri sono allegri, altri plausibili, altri graui,
& sedati, alcuni mesti, & gemibūdi, di nuouo iracūdi, altri impetuosi, cosi an-
chora le melodie de canti, perche, chi in un modo, & chi in un'altro cōmuo
uono, uariamente sono distinte da musici. Dico adunꝗ, & primo chel sopra
no di ciascun cōcento nō deue ascendere piu di sedeci uoci sopra l'ultima no
ta inferiore del tenore di ciascun tuono, si autētico come plagale, [[per]]che si ascē
desse piu, saria incōmodo al cantore. Et oltra questo eccederia il suo cōueniē
te termine. Similmente quando diminuirete le notule, farete il contrapunto
con bella diminutione, & sincope spesse uolte fugare il soprano hor con il
tenore, hor con il basso, o con altra parte. Alcuna uolta fingere di far caden-
tia, & poi nella conclusione di essa cadentia pigliare una consonantia nō pro
pinqua ad essa cadentia per accommodarsi e cosa laudabile. Et questo s'in-
tende con il soprano, o altra parte. Ma bisogna che sempre il tenore in que-
sto caso, faccia lui la cadentia, ouer distintione. Accio che sia intesa la senten-
tia delle parole cātate. Osseruerete questo nelle uostre compositioni sempre
compire il numero ternario, o binario, ouero quaternario nella penultima
nota della cadētia, cioe nō si debbe cōputare la penultima nota cō la sequen-
te, la quale include la cadentia, ouero distintione, perche la e principio di nu-
page 40mero, similmente si debbe finire il numero della penultima nota del concen-
to, e non nel l'ultima, perche la penultima include il numero precedente.
& l'ultima nota e fine del canto, & perho non si computa con altra nota. Le
cadentie ueramente sono necessarie, & non arbitrarie, come alcuni in-
consideratamente dicono, massimamente nel canto composto sopra le
parole. Et questo per distinguere le parti di la oratione, cioe far la distintio
ne del comma, & cola, & del periodo accio che sia intesa la sententia delle par
ti della oratione perfetta, si nel uerso, come nella prosa, perche la cadentia e co
me il punto, ouero una certa distintione & riposo nel canto, ouero la ca-
dentia e una terminatione di essa parte del canto come e nel contesto
dell'oratione, la media distintione & la finale, & auertite di far le caden-
tie, doue la parte dell'oratione, ouero il membro finisce, & non sempre in un
medesimo luoco, perche il luoco proprio delle cadentie e, doue finisce la sen
tentia del contesto delle parole, perche glie cosa conueniente tendere & pari
mente insieme finire la distintione, & delle parole, & delle notule. FOR-
TVNATIANVS,
distinctio est temporis, & sensus finitio. Subdistin
ctio est nec temporis, nec sensus finitio. Mora est requiem animi. Inter di-
stinctionem, & subdistinctionem, & moram, hoc interest, quod distinctio
perfectum sensum declarat, subdistinctio inferri aliquid significat. Mora re
ficit lectorem simulꝗ sensibus lumen accommodat. Oltra questo sforzate-ui di far il concento uostro che sia allegro, suaue, pieno d'armonia, dolce,
risonante, graue, & facile nel cantare, cioe di consonantie usitate, come so-
no tertie, quarte, quinte, seste, & ottaue. Ma schiuateui di porre nelle uostre
compositioni il tritono, il diapente diminuto, & il diapason superfluo, co-
si ascendenti, come discendenti, per essere interuali distonati, & difficili
a pronuntiarli, non si debbono porre ne concenti. Et cosi la settima, la no-
na, & la undecima,
ob earum difficultatē raro accedunt in usum musicū. Similmente non fate chel contrabasso del uostro concento sia incommodo,
cioe che non continuano in profundum. Et auertite di non far barbarismi
nel comporre le notule sopra le parole, cioe non ponete lo accento lungo
sopra le sillabe breui, ouer l'accento breue sopra le sillabe lunghe.
quia est
contra regulam artis grammatice. senza la quale niuno puo esser buono musico, la quale insegna pronunciare & scriuere drittamente. Schiuateui
adunque dal barbarismo, il quale secondo Isidoro e enunciatione di paro-
le corrota la lettera, ouer il suono, pertanto: osseruerete li accenti gramma-
tici, i quali hanno quantita temporale, cioe tempo lungo & breue. Benche
page 41sono pochi compositori, che osseruano li accenti nel comporre
le notule sopra le parole (de indoctis loquor). L'accēto e certa legge, &
a alzare, & abassare la sillaba di particella di oratione, & debbesi fare
causalmente nella lettera, initialmēte nella sillaba, & ditionalmēte nella ditio-
ne, & particolarmēte nella oratione. Accento si dice quasi a canti, cioe secōdo
il canto, perche si fa conoscere le sillabe nella cantilena della uoce. I greci lo
dicono prosodia, da latini anchora si chiama tuono & tenore, perche quiui il
suono cresce & finisce. I tenori delli accēti sono tre, acuto, graue, & circunfles-
so. Acuto accento e detto [[per]]che acuisce & eleua la sillaba. Graue perche depri
me & depone perche e cōtrario allo acuto il circunflesso, [[per]]che e cōposto dal-
lo acuto & del graue, perche cominciando dallo acuto finisce, nel graue, & cosi
mentre che saglie & discēde si fa circunflesso. Et lo acuto & il circunflesso so-
no simili, perche l'uno & l'altro inalza la sillaba. Il graue appare cōtrario am
beduoi, [[per]]che sempre deprime le sillabe eleuandole quegli. Le figure degli ac
centi (le quali da grāmatici si pingino [[per]] le distintioni de parole sono tre, cioe
acuto, graue, & circunflesso. Accento acuto e linea tendente dalla sinistra nel
la destra allo in su a questo modo ´ grave e linea tendente dalla destra nella
sinistra allo ingiu in questo modo ` Il circunflesso si compone di ambeduoi
in questo modo ^ Lo accento acuto si pone sopra l'ultima, penultima, & an
tepenultima sillaba. Graue si pone solamente sopra la ultima, & di raro usa-
no questi i latini. Circunflesso si pone sopra la ultima, & sopra la penultima
si troua appresso Vergilio nel sesto. Li accenti sono stati trouati o per la di-
stintione, o per la pronunciatione, o per causa di discernere la ambiguita. Cir
ca gli accenti nel uerso uulgare sono tre modi. primo, quando cade nella sil
laba antepenultima, quale rende il suono sdruccioloso, quando cade poi so-
pra l'ultima sillaba, rende il suono graue, & quādo cade sopra la penultima,
rende il suono temperato, se cadera lo accento sopra l'ultima in fine del uer-
so, & che sia d'una sillaba, si puo numerare per due sillabe, che uerria il uerso
essere di dieci sillabe, il che molto si usa. Alla formation del uerso necessaria-
mēte richiede, che gli accēti caggino sopra la quarta, o sesta, o decima sillaba,
perche ogni uolta che in altro luoco cadesse, non saria piu uerso, & che sotto
uno accēto nō stano piu che tre sillabe, & nō si pōgono gli accenti se nō sopra
le sillabe lūghe. Notate ultimamēte questa regola, che tutti i uersi uulgari di
sette sillabe sempre la penultima si tiene, & in tutti quegli di otto la terza, & la
penultima. Et in tutti quegli de undeci la sesta & la penultima, & qualche
uolta la quarta, ma rare uolte accade. Ma quādo accadesse tenere la quarta,
page 42non torrete la sesta, ma la quarta, & la penultima. E necessario, chel compo-
sitore habbia cognitione del metro, o uerso, saper che cosa e piede, & quante
sillabe puo hauere, & la qualita di quelle, cioe quali sono lunghe, & quali so
no breui, & saper scandere il uerso, & doue si fa la cesura, & la collisione. Et si
milmente sapere, doue cade la cōma, & il cola nel periodo, si nel uerso come
nella prosa. BEDA
cōma genus distinctionis, quando post duos, uel tres
pedes superest syllaba, quæ partē terminet orationis quādo uero post duos
uel tres pedes nihil remanet, colum dicitur, quæ tamen nomina apud orato-
res indifferenter ponuntur, qui integram sententiam periodon appellant.
Partem autem cola, & cōmata dicuntur, ut puta apud apostolū, sustinetis
enim, si quis uos in seruitutem redigit, colum est, si quis deuorat, colum est,
si quis accipit, colū est, si quis extollitur, & cætera usꝗ ad plenā sentētiam,
cola sunt, & cōmata. Plena autem sententia periodus est. Interpretatur autē
colū membrū, cōma incisio, periodus clausula, siue circuitus. DONATVS tres sunt posituræ, uel distinctiones, quas thesis græci uocant distinctio,
subdistinctio, media distinctio. Distinctio est, ubi finitur plena sententia, hu-
ius punctum ad summā litterā ponimus. Subdistinctio est, ubi non multū
superest de sententia, quod tamen necessario separatim mox inferendū sit.
huius punctū ad imam littera ponimus Media distinctio est, ubi fere tan
tum de sentētia superest, quantū iam diximus, quum tamen respirandū est.
huius punctum ad mediam litteram ponimus. In lectione tota sententia pe
riodus dicitur, cuius partes sunt cola, & cōmata. Il piede nel uerso e eleuatione, & positione di due, o tre, o piu sillabe compresa dallo spatio, ouer piede e
compositione di sillabe con certa osseruatione di tempi riceuente la , & la positione, le quali si dicano in greco arsis, & thesis, perche di una silla
ba, anchora che fusse lunga, non si puo fare il piede, perche si fa di due reper
cosse, non con dui tempi. perche bisogna ferire due uolte anchora due bre-
ui. La cesura nel metro e una decora terminatione di uoce notata nel mezo
de uersi. La scansione e legitima distintione, e dimēsione del metro in ciascu-
no piede. La collisione, che in greco si dice synalephe & , si fa quando
finisce alcuna dittione in uocale, ouer in m littera, & la sequēte comincia an-
chora da uocale, perche all'hora la prima uocale, ouer m con la sua uocale
si esclude. Fassi anchora nel fine del uerso, quādo finendo in uocale, o in m
littera suprabonda la sillaba, & il sequēte uerso comincia dalle uocali. Il me-
tro e una certa connessione, & ordinatione di piedi trouata alla delettatione
de gli orechi. Medesimamente il metro e una struttura, & copulatione di uo-
page 43ci finita con numero, & modo, & e il medesimo, che il uerso. Il quale per que
sto si dice cosi, che tanto lungamente si debba uoltare in fino a che rettamen
te si constituisca. Metro in greco in latino si dice dimensione, perche misuria
mo il uerso con certi piedi. I piedi cō tempi, & e differente dal rhythmo, il qua
le Fabio uuole che sia numero, che il metro ha certo, & finito spacio, il rhyth
mo ne ha fine certo, ne alcuna uarieta nel contesto. ma perche comincio per
la leuatione, & positione scorre in fine al fine. Ma BEDA interpreta il ryth
mo una modulata cōpositione, esaminata non per metrica ragione, ma per
numero de sillabe a giudicio de gli orecchi, come sono uersi di poeti uulga-
ri, & appare il rhythmo essere simile a metri, & certamēte per se senza metro
nō puo esser, perche metro e ragione con modulatione, rhythmo modula
tione senza ragione. Nondimeno el piu delle volte per certo caso trouerrai
anchora la nel rhythmo nō seruata per la moderatione dello artifi-
cio, ma per suono, & essa modulatione conducente, il quale i uulgari poeti
di necessita rusticamente, dotti fanno dottamente. Ma i greci affermano il
rhythmo essere composto di arsis & thesis, & di tempo. Il che alcuni chiama
uano uacuo. disse, questo essere tēpo diuiso in ciascuno di que-
sti che numerosamente si possono comporre. Ma secondo Nicomaco rhyth
mo e una ordinata compositione di tempi. medesimamente rhythmo uulga
re e uno certo genere di dettare. Dettare niente altro e, che una congrua & or
dinata, o decora loquutione di qualunche cosa. ma della struttura, o dissimi
le contesto non appartiene a noi definire regole o canoni a tutte le cose per-
che ad essi poeti le lor cose proprie.
diletta di sappere la pratica di canto misurato, stampate
in Vinegia del Mese di Maggio Ne l'anno
M. D. XXXX.