Title: Dimostrationi harmoniche
Author: Gioseffo Zarlino
Publication: Francesco de' Franceschi (Venezia, 1589)
Principal editor: Frans Wiering
Funder: Utrecht University Netherlands Organization for Scientific Research (NWO)
Edition: 2000
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht NetherlandsΚαὶ καμάτῳ ἀκαματῳ ἅμα εὔξησα,
Εὐνόῳ νῆν νόῳ, καὶ ὁδῳ εὐόδῳ ἐδιδαξα.

Καὶ μὴ διδόντος, ὀυδὲν ἰσχύι πόνος.IN VENETIA, MDLXXXIX. Appresso Francesco de' Franceschi Senese.page iipage iii

AL SERENISSIMO PRENCIPE DI VENETIA ALVIGI MOCENIGO
 GIOSEFFO ZARLINO DA CHIOGGIA.
GIOSEFFO ZARLINO DA CHIOGGIA.
TAVOLA DI TVTTE LE COSE NOTABILI CONTENVTE NELL'OPERA.
A
C
D
E
F
G
H
 quadro. 267. f. Contiene tutte le Specie della Diatessaron. 256. p
quadro. 267. f. Contiene tutte le Specie della Diatessaron. 256. p
I
L
M
N
O
P
Q
R
S
T
V
LETTORI STVDIOSI.
| Facciata. | Linea. | leggi. |
| 4. | 48. | senza aspettar altra. |
| 50. | che conoscessero. | |
| 12. | 16. | che cosi fusse, |
| 23. | 32. | hauete dichiarato |
| 27. | nel principio della seconda linea dell'essempio manca la lettera f. | |
| 12. | Sesquiquarta; & quella che si troua tra ac. è Dupla, come quella che si troua tra fg. | |
| 30. | 32. | bene, dissi; onde. |
| 38. | 6. | che non ui sono. |
| 39. | 1. | PROPOSTA III. |
| 48. | nell'ordine de i Molteplici. superparticolari. d.10. | |
| 93. | 2. | Messer Claudio; lasciamo |
| Facciata. | Linea. | |
| 105. | 33. | compreso da i Quattro primi che si uedono, che anco gli altri sono Quattro, |
| 213. | 11. | Semituono. |
| 135. | di sopra. | TERZO. |
| 137. | di sopra. | TERZO. |
| 137. | 28. | per la terza. |
| 139. | di sopra. | TERZO. |
| 144. | 4. | & cb. è quello |
| 146. | 14. | cifera √ la |
| 149. | 12. | & eg faranno. |
| 214. | 29. | studiano |
| 246. | 20. | ch'io non faccia. |
| 254. | 1. | (per tornar al proposito) |
| 44. | gli Istrumenti Naturali. | |
| 183. | 46. | PROPOSTA L. |
 page 1
page 1DIMOSTRATIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA: Diuise in Cinque Ragionamenti.
RAGIONAMENTO PRIMO.
DEFINITIONE PRIMA.
DEFINITIONE II.
DEFINITIONE III.
DEFINITIONE IIII.
DEFINITIONE V.
DEFINITIONE VI.
DEFINITIONE VII.
DEFINITIONE VIII.
DEFINITIONE IX.
DEFINITIONE X.
DEFINITIONE XI.

DEFINITIONE XII.
DEFINITIONE XIII.
DEFINITIONE XIIII.
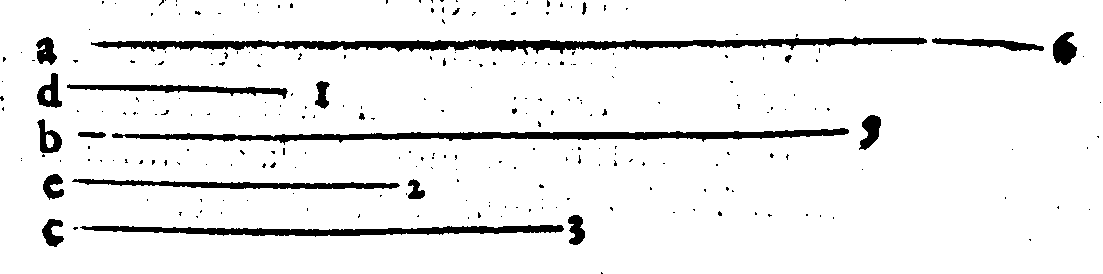
DIMANDA PRIMA.
DIMANDA II.
DIMANDA III.
DIMANDA IIII.

DIGNITA' PRIMA.
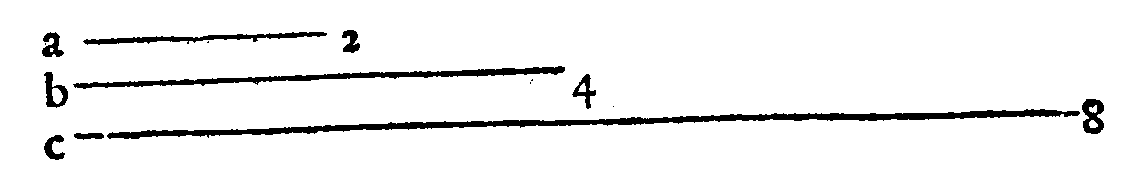
DIGNITA' II.
DIGNITA' III.
DIGNITA' IIII.
DIGNITA' V.
DIGNITA' VI.
DIGNITA' VII.
DIGNITA' VIII.
DIGNITA' IX.
DIGNITA' X.

DIGNITA' XI.
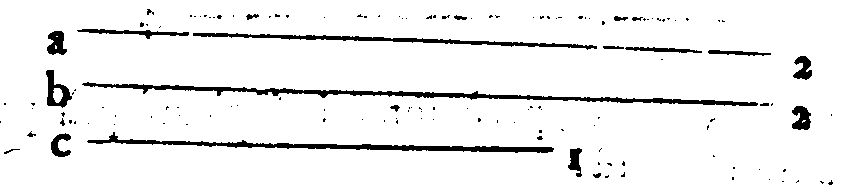
DIGNITA' XII
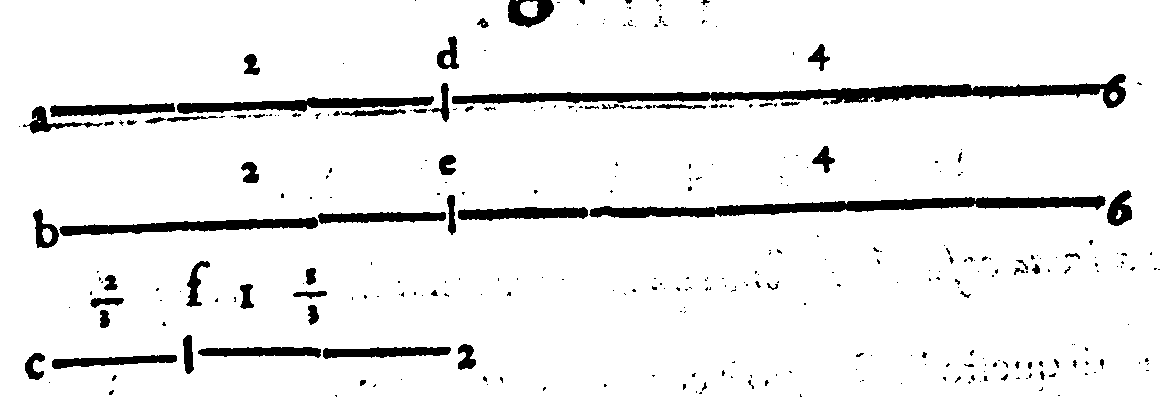
DIGNITA' XIII.
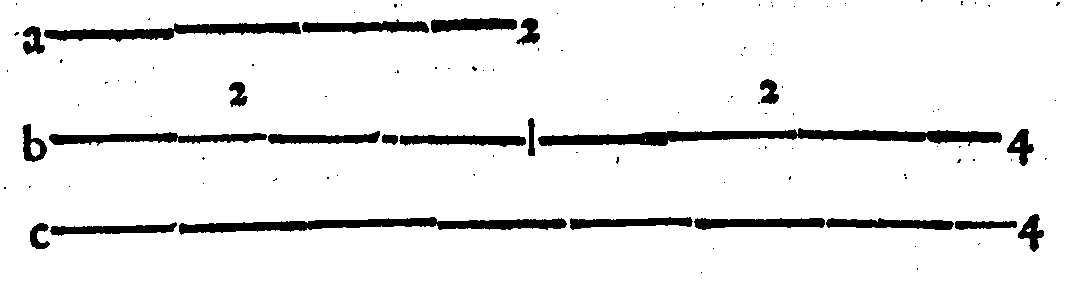
DIGNITA' XIIII.
DIGNITA' XV.

DIGNITA' XVI.

DIGNITA' XVII.
PROPOSTA PRIMA.

PROPOSTA II.

PROPOSTA III.
PROPOSTA IIII.
PROPOSTA V.
PROPOSTA VI.
PROPOSTA VII.

PROPOSTA VIII.

PROPOSTA IX.
PROPOSTA X.
PROPOSTA XI.
PROPOSTA XII.

PROPOSTA XIII.

PROPOSTA XIIII.
PROPOSTA XV.
COROLLARIO.
PROPOSTA XVI.
PROPOSTA XVII.


COROLLARIO.
PROPOSTA XVIII.
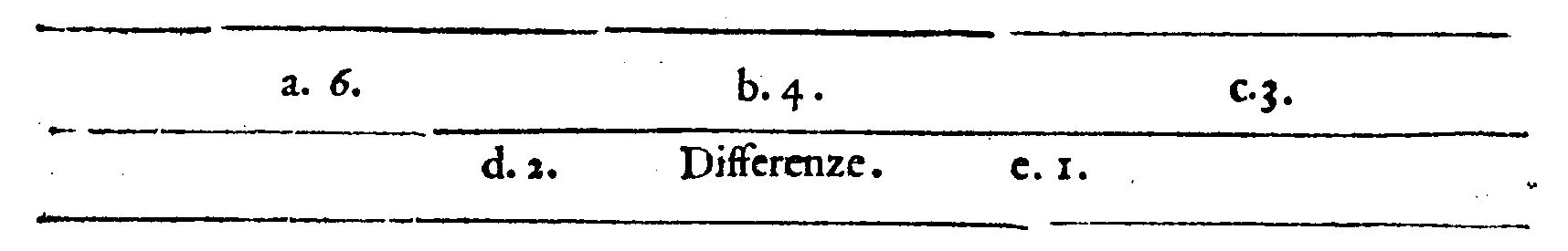
PROPOSTA XIX.
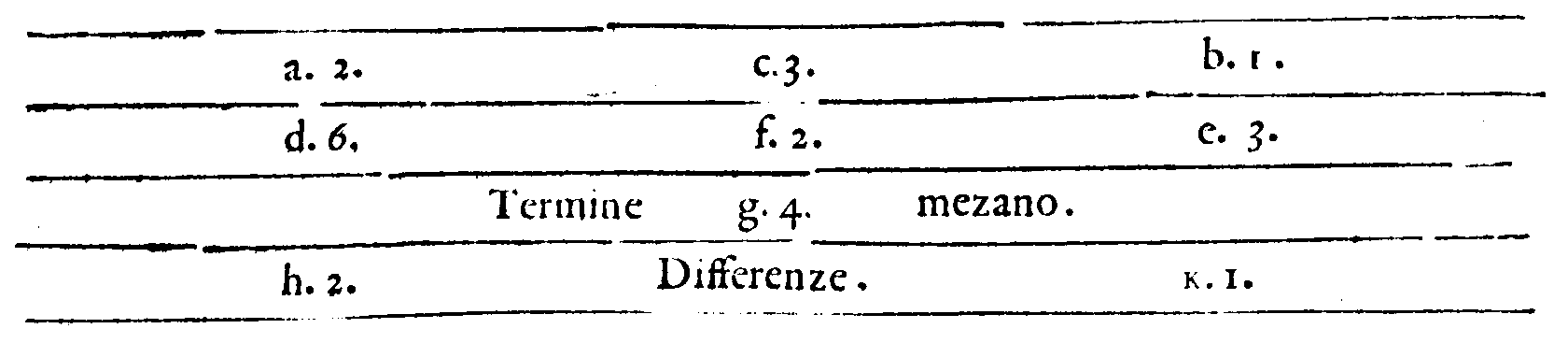

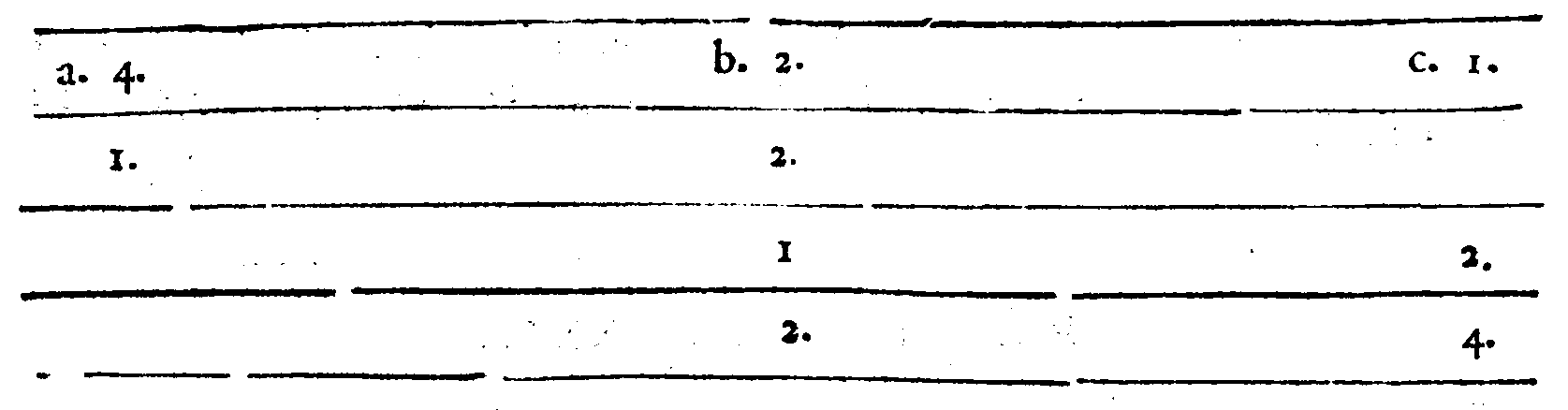
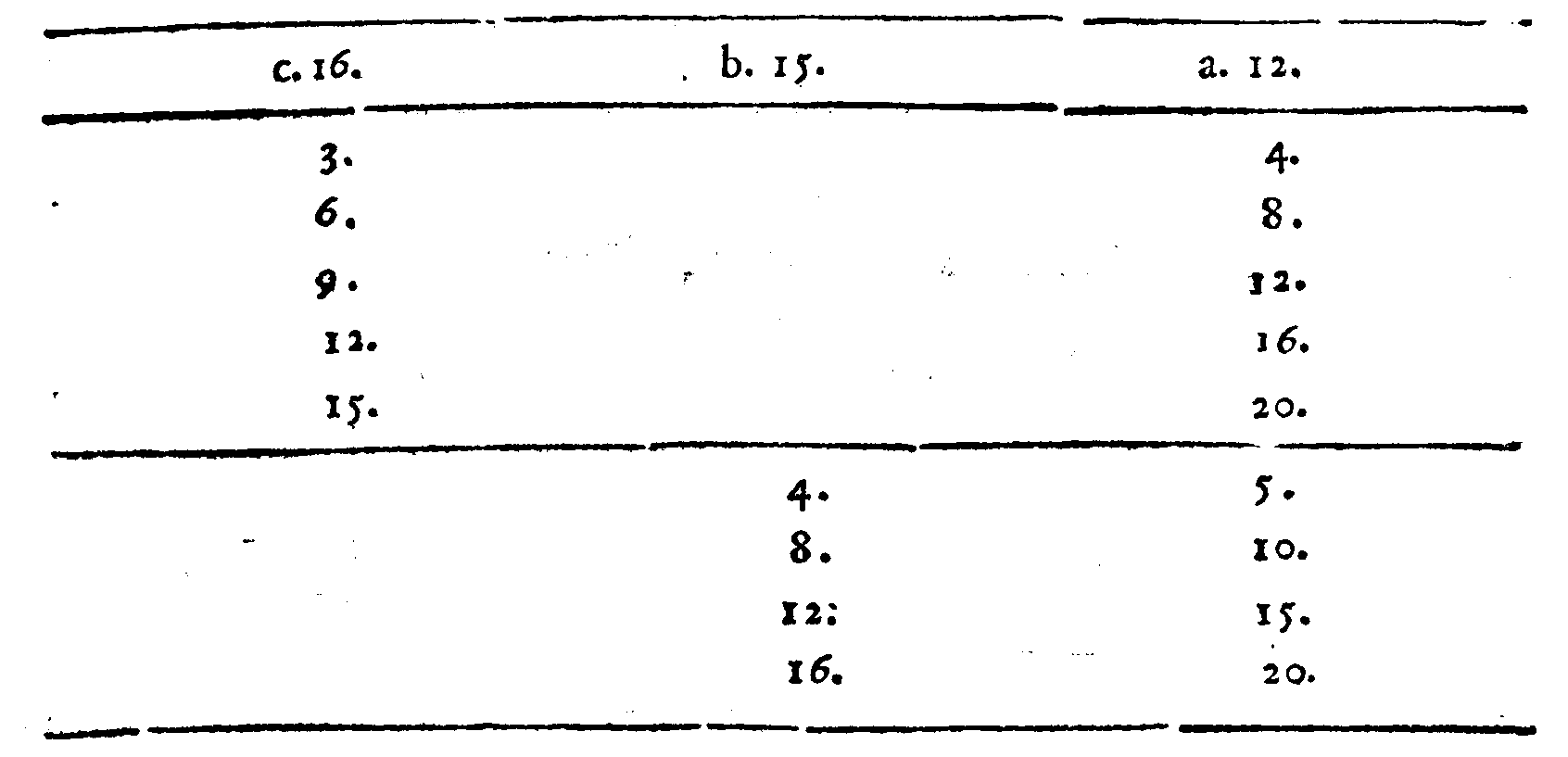
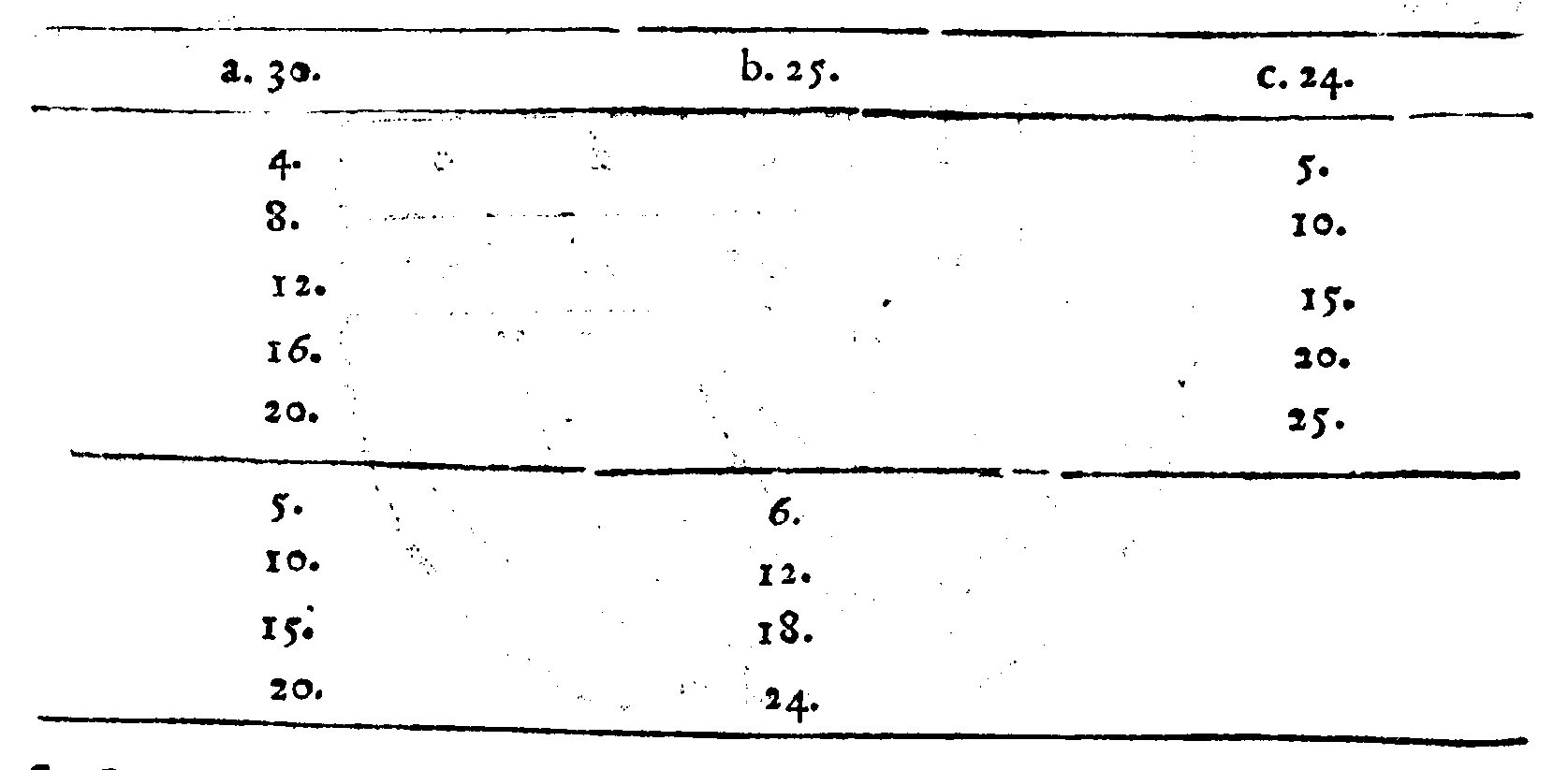
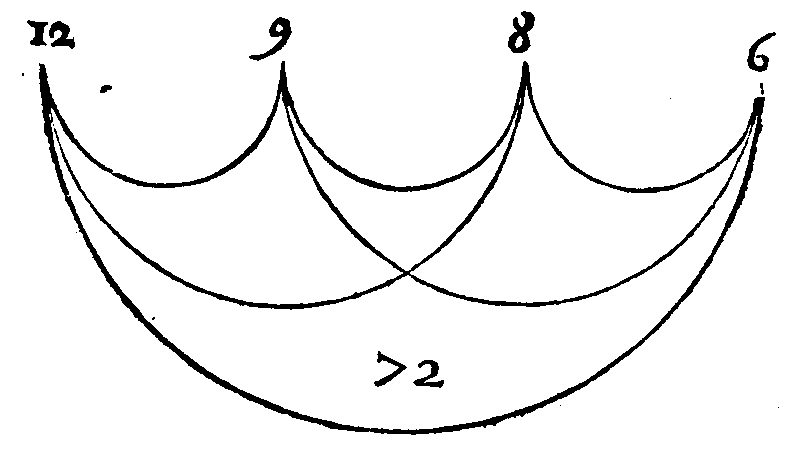
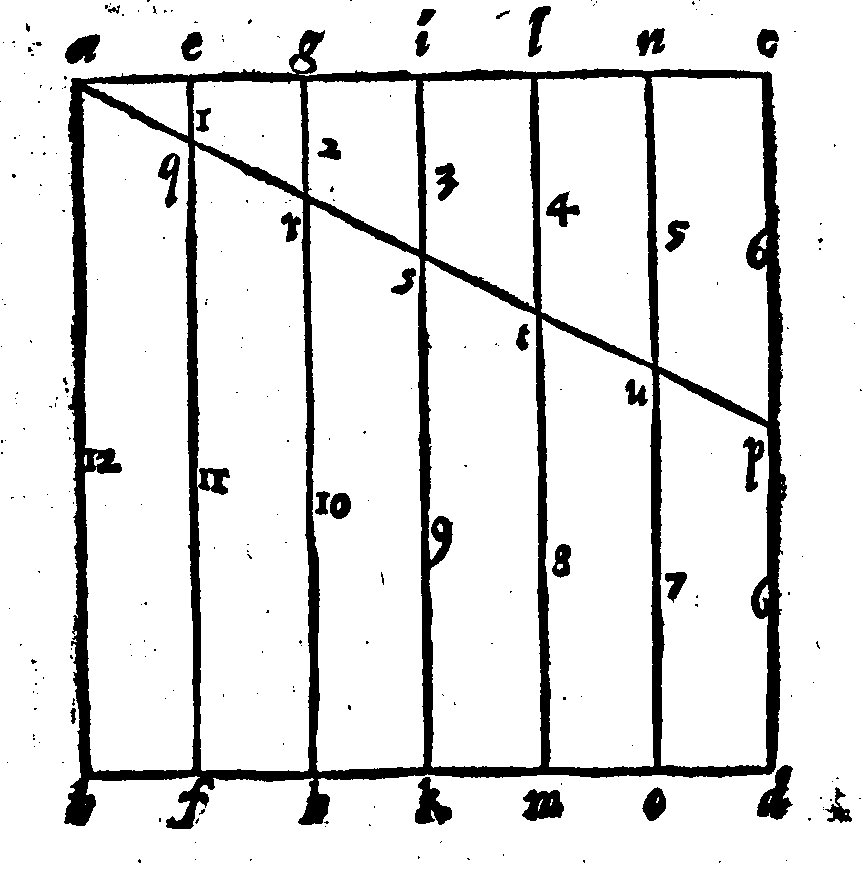
Se vorrai ritrouare tra due numeriQuesti Versi non mi dispiaceno, allora disse il Signor Desiderio; poiche le cose mathematiche per la lor natura presto si partono delle menti nostre; onde saranno cagione di far, che non cosi facilmente cotesta cosa si scompagnarà da noi; essendo che 'l Verso per sua natura non si domentica tanto facilmente, quanto auiene della Prosa; però hauendo fatto questo poco di guadagno, ui prego M. Gioseffo, à seguitare il resto. Sappiate adunque questo, dissi, essere infallibilmente uero, come ui dimostrerò, che: page 58
Dati, che un terzo sia Mezano harmonico;
Fà che tu aggiunga insieme cotai numeri;
Et quel che nascerà con quei molteplica;
Et ne uerrà due altri maggior numeri.
Fatto questo, bisogna che molteplichi
I due Dati tra loro, & che raddoppij
Il prodotto, & uerrà 'l sudetto harmonico.
S'anco delli due Dati il minor numero
Leuarai dal maggior; fà che 'l residuo
Con il minor insieme tu molteplichi;
Et quel che nasce dal maggior de i termini
Leua, e tra lor quello ch'auanza colloca,
C'hauerai lo mezano Contr'harmonico.
PROPOSTA XX.

COROLLARIO.
PROPOSTA XXI.
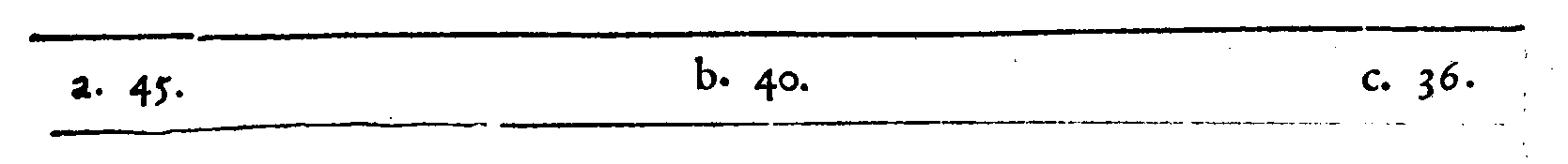
COROLLARIO.
PROPOSTA XXII.
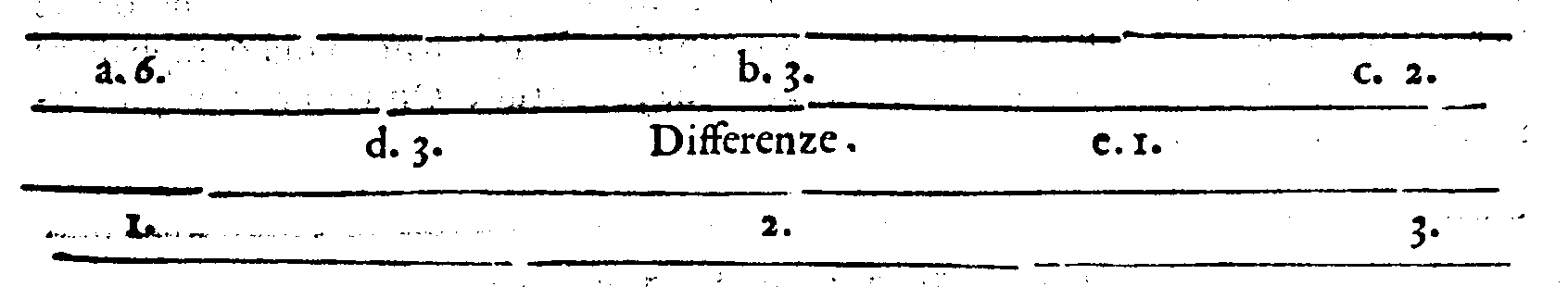
PROPOSTA XXIII.
PROPOSTA XXIIII.

PROPOSTA XXV.
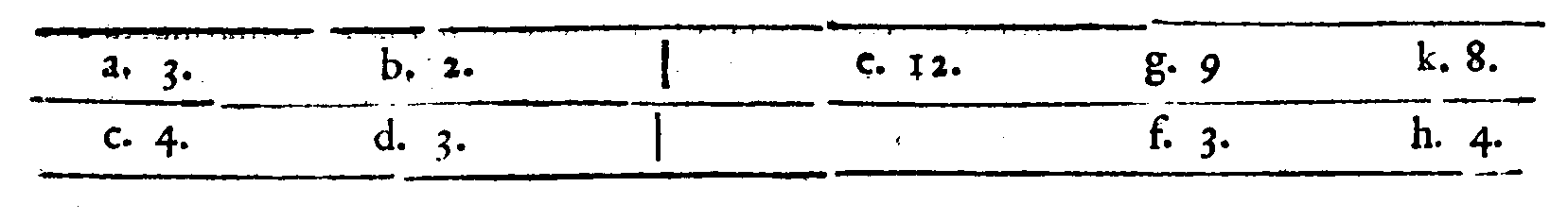
PROPOSTA XXVI.
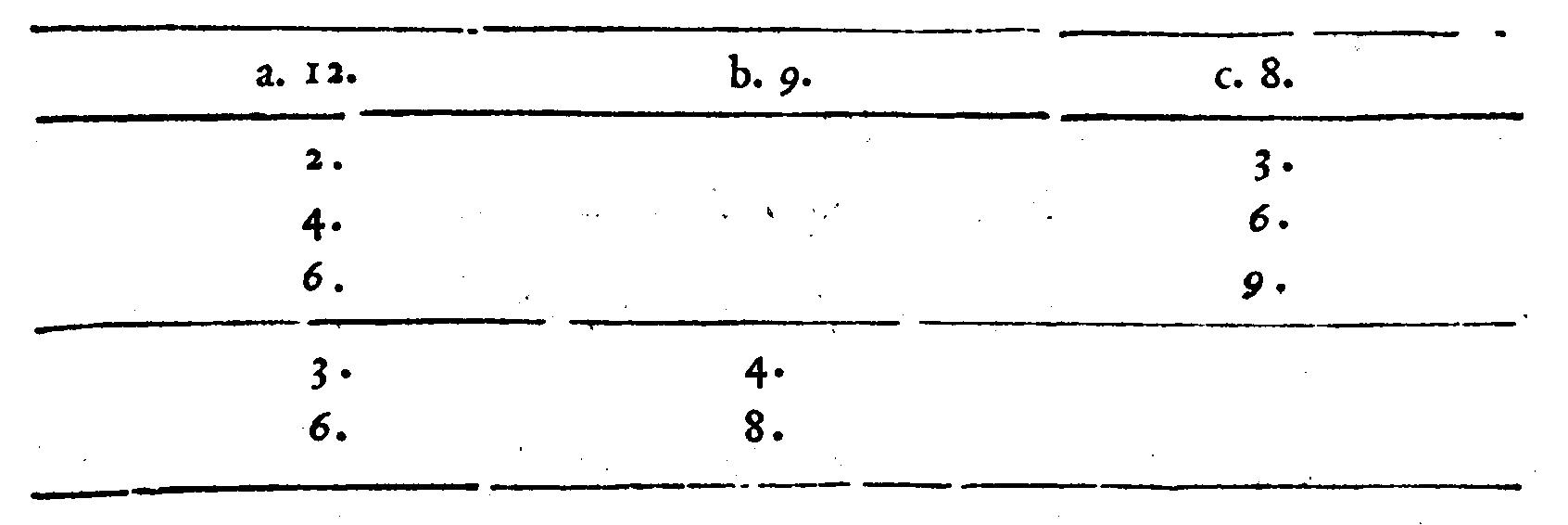
COROLLARIO.
PROPOSTA XXVII.
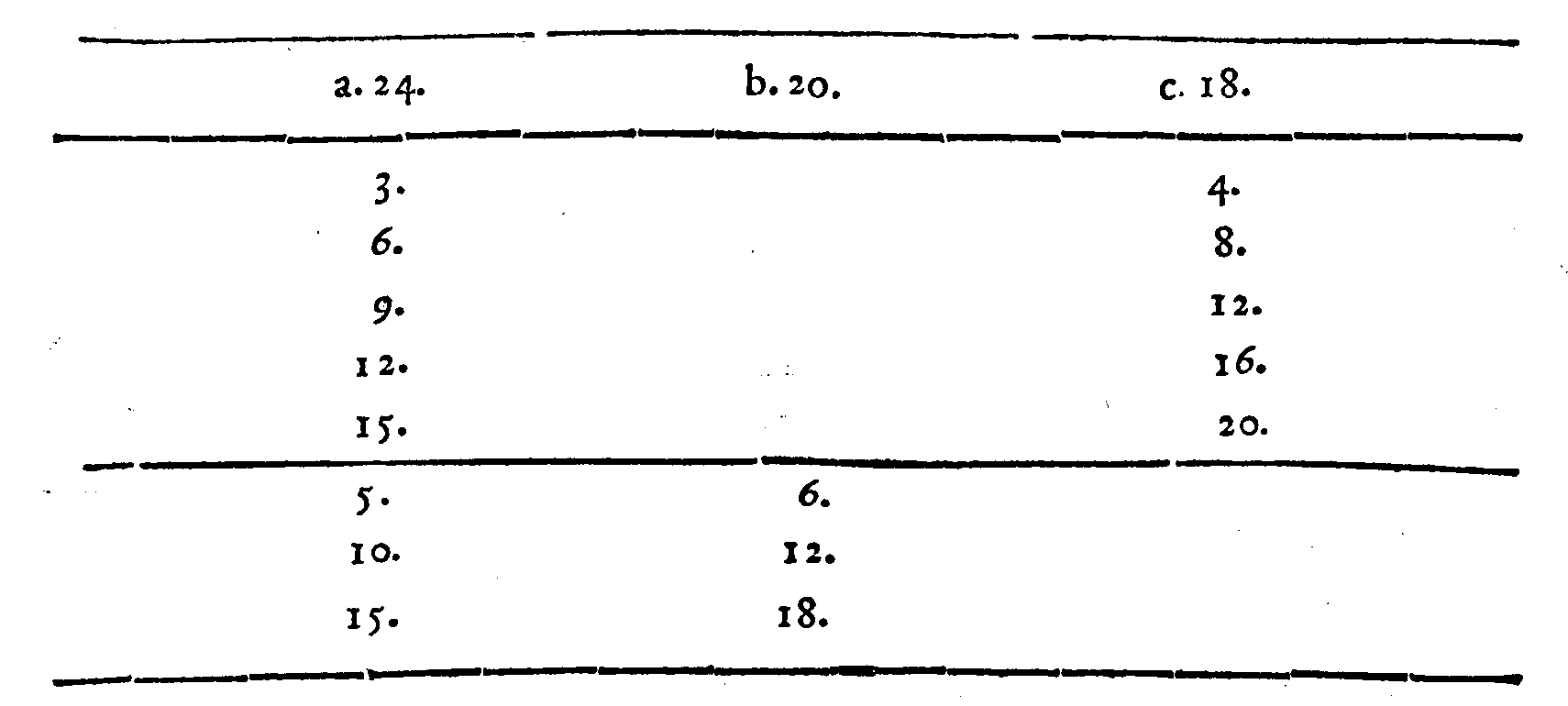
CORROLLARIO.
PROPOSTA XXVIII.
COROLLARIO.
PROPOSTA XXIX.
COROLLARIO.
PROPOSTA XXX.
PROPOSTA XXXI.

COROLLARIO.
PROPOSTA XXXII.

COROLLARIO.
PROPOSTA XXXIII.
PROPOSTA XXXIIII.

PROPOSTA XXXV.

PROPOSTA XXXVI.
PROPOSTA XXXVII.
PROPOSTA XXXVIII.
PROPOSTA XXXIX.
DIMOSTRATIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA: RAGIONAMENTO SECONDO.
Iam saliare Numae carmen, qui laudat, & illud,Veramente Messere, che uoi sete un buon scolare; dissi; perche ui hauete tenuto molto bene à memoria la lettione, ch'io già ui lessi sopra questi Versi; à proposito de quei maligni, che cantando una fiata le uostre compositioni, le biasimauano molto; lodando fuor d'ogni proposito grandemente quelle di Giosquino con parole; ma con i fatti, al lor dispetto lodauano uoi, & ueniuano à biasimare il lodato; percioche ne i conserti loro non adoperauano cosa alcuna di Giosquino, ne d'alcuna sua cosa se ne seruiuano, ma si ben delle uostre; il che ui è di somma laude. Onde ui dico, che questo Horatio è stato & è un gran Poeta. Vedete, com'egli ci pone auanti gli occhi questa mala generatione d'huomini dipingendoci la lor natura; perch'ancora lui à i suoi tempi da simil Gente inuida, maligna, & peruersa era bersagliato. Ma di gratia non parliamo più cosa alcuna di costoro; percioche non uoglio c'habbiamo da far con loro; & desidero, che ritorniamo à ragionar di quelle cose, delle quali heri incominciassemo il nostro ragionamento. Sarà ben fatto M. Gioseffo; disse il Signor Desiderio; & incominciarete da quello che ui torna più commodo. Ripigliai adunque il mio ragionamento in questo modo. Hauendoui à ragionar de quelle cose, che fanno alla cognitione delle Consonanze, & anco delle Dissonanze, & à dimostraruene molte, che accascano intorno ad esse, secondo la uerità, & come la Scienza richiede; è necessario il porui prima inanzi quei Principij, da i quali dipendono tutti i nostri Ragionamenti, & dichiararui quel ch'importino alcuni termini, & il Nome d'alcuni Interualli usati nella Scienza; ancora che della maggior parte de loro ne habbiate acquistato la cognitione, col mezo delle Istitutioni; accioche per auentura non procediamo per cose non conosciute. Et ciò non sarà senza utilità; percioche non resterò di dichiararui alcune cose, & aprirui alcuni secreti, che ui saranno di gran contentezza & giouamento. Et per non andar molto in lungo, darò principio alla definitione della Consonanza; laquale (com'altroue hò detto) è primieramente dal Musico considerata; & dopoi dirò quel che sia la Dissonanza, ch'è il suo Opposito, ò contrario; la qual'è considerata nel secondo luogo, & per accidente. Ma auanti, che passiamo più oltra, ui uoglio fare un poco di discorso, che ui sarà page 78 di grande utile, & forse non più udito in questo proposito; & tornerà bene, per poter risoluere alcune cose, che ui son per dimostrare. Attendete adunque prima, & dopoi uerremo senza por tempo di mezo, à por le Definitioni l'una dopo l'altra. Dico adunque incominciando, che la Oppositione, secondo 'l Filosofo,Prd. Trat. 3. cap. 1. si troua esser de Quattro maniere; acciò sappiate per qual cagione hò detto, che la Dissonanza è opposita ò contraria alla Consonanza; come è, Relatiua, Contraria, Priuatiua, & Contradittoria. Ma perche la prima & le due ultime non fanno al nostro proposito; però le uoglio lasciar da un canto, & dir solamente della Seconda; la quale non è altro, che la Ripugnanza de due contrarij, che non conuengono insieme in un'istesso Soggetto; ma per lor natura l'un scaccia ò destrugge l'altro. Et questi Contrarij sono de due maniere; percioche ouer che sono mediati, oueramente immediati. I primi sono quelli che riceuono alcuni mezi ne i loro estremi; come tra 'l Nero & il Bianco molti mezani colori. Onde non è necessario sempre, che l'un de i due estremi sia nel soggetto; percioche 'l Corpo può esser Rosso, ò Verde, ò di qualch'altro colore; se ben non è Nero, ò Bianco. Ma i Secondi sono quelli, che non riceuono cosa alcuna mezana dell'istesso Genere; com'è la Sanità & la Infermità; tra lequali non ui si dà mezo alcuno, secondo i Filosofi; ancora che i Medici habbiano altra opinione. Il Mezo però in questo luogo è di due sorti; prima per Participatione dell'uno & dell'altro estremo, come sono i mezani Colori & Sapori; dopoi per Negatione dell'uno & dell'altro de gli nominati estremi; & quando si troua un Soggetto, il quale non habbia estremo alcuno. Onde da quel c'hò detto potete comprendere, che essendo la Consonanza & la Dissonanza senz'alcun dubio Suono, uengono ad esser Qualità passibili; percioche da l'una & da l'altra il Senso è mutato; la onde essendo à questo modo; chiara cosa è, che si hanno à porre nel Predicamento della Qualità, & si debbono collocar come due estremi nella Seconda specie de gli Oppositi; essendo che riceuono molti mezi tra loro. Et questo è uero; percio che, si come il Corpo uisibile non è per necessità sempre bianco, ò nero; ma tallora è rosso, tallora uerde, & tallora di qualch'altro colore; ne anco il Tangibile, è sempre freddo, ò caldo; ò duro ò tenero; ma alle fiate tepido; & hora più & hora men caldo ò freddo; oueramente di qualch'altra mezana qualità; come anco il Gustabile, che non è sempre per necessità dolce, ouer'amaro; ma garbo, ò acerbo, oueramente in altro modo; cosi l'Vdibile non è sempre semplicemente Consonante, ò Dissonante; ma alle fiate partecipa d'una qualità mezana, che tiene dell'uno & dell'altro, più & meno, secondo che più s'auicina all'un de i nominati estremi. Per il che non sò ueder, ne ritrouar ragione, che mi costringa à dire & credere; che tra gli estremi Oggetti de gli altri Sensi possano cascar molti mezi, & non in quelli dell'Vdito. Però adunque diciamo, che tra la Consonanza, & la Dissonanza, che sono due estremi nella Seconda specie de gli Oppositi; ui cascano; contra l'opinione de molti; per non hauere di questa Aristotele fatto mentione alcuna; molti mezani interualli, i quali partecipano (secondo che maggiormente s'accostano più all'una, che all'altra) de questi due estremi udibili. Et questi saranno quelli (lasciando di por qualch'altra differenza tra loro, che si potrebbe fare) che nascono d'altra proportione, che da alcuna de quelle, che sono contenute nel Genere Molteplice & Superparticolare, collocate tra le parti del numero Senario. La onde diuideremo la Consonanza in due specie; delle quali la prima chiamaremo Consonanza propriamente detta, & la seconda Consonanza detta Communemente. Le quali uolendo conoscere, incominciando dalla prima; diremo.
Quod mecum ignorat, solus uult scire uideri.
Ingenijs non ille famet, plauditque sepultis:
Nostra sed impugnat; nos, nostraque liuidus odit.
DEFINITIONE PRIMA.
DEFINITIONE II.
DEFINITIONE III.
DEFINITIONE IIII.
DEFINITIONE V.
DEFINITIONE VI.
DEFINITIONE VII.
DEFINITIONE VIII.
DEFINITIONE IX.
DEFINITIONE X.
DEFINITIONE XI.
DEFINITIONE XII.
DEFINITIONE XIII.
DEFINITIONE XIIII.
DEFINITIONE XV.
DEFINITIONE XVI.
DEFINITIONE XVII.
DEFINITIONE XVIII.
DEFINITIONE. XIX.
DEFINITIONE XX.
DEFINITIONE XXI.
DEFINITIONE XXII.
DEFINITIONE XXIII.
DEFINITIONE XXIIII.
 . il quale chiamiamo Diesis, & ciò discendendo; quasi quasi, che si potrebbe, se non in tutto, almeno
in parte, tener da loro; ma non già altramente. In che modo Messere, soggiunse il Viola ; uorreste tenere con loro in questa cosa. In questo, rispose; quando la nominata Consonanza si ritrouasse esser collocata
tra una chorda Diatonica, segnata E. & una Chromatica, segnata
. il quale chiamiamo Diesis, & ciò discendendo; quasi quasi, che si potrebbe, se non in tutto, almeno
in parte, tener da loro; ma non già altramente. In che modo Messere, soggiunse il Viola ; uorreste tenere con loro in questa cosa. In questo, rispose; quando la nominata Consonanza si ritrouasse esser collocata
tra una chorda Diatonica, segnata E. & una Chromatica, segnata  . com'hò detto di sopra; perche allora non si ritrouerebbe esser semplicemente tra le chorde Diatoniche; ma tra una segnata E. Diatonica, & una signata
. com'hò detto di sopra; perche allora non si ritrouerebbe esser semplicemente tra le chorde Diatoniche; ma tra una segnata E. Diatonica, & una signata  . Chromatica; & à questo modo potrei tener dalla sua. Ma che quest'Interuallo non si troui nel Diatonico tra le chorde
. Chromatica; & à questo modo potrei tener dalla sua. Ma che quest'Interuallo non si troui nel Diatonico tra le chorde  . & d. & tra e. & g. & non si possa cantare, senza interponerui una
chorda mezana; & ch'ello non sia interuallo Diatonico, questo non li consentirò mai; percioche se 'l si canta la Diatessaron
senz'esser tramezata d'alcun'altro suono, & in un solo
Interuallo, & questa non faccia alcuna uarietà di Genere; il simile etiandio bisogna che
auenga, quando si canta il Ditono, ò lo Semiditono con un solo Interuallo; percioche non
ui sò uedere, ne ritrouar maggior ragione, c'habbia l'un più che l'altro de questi Interualli; essendo tutti consonanti. Anzi
se 'l si douesse hauer qualche rispetto ad alcun di loro;
che, come più consonanti, si potessero cantar tramezati & non tramezati, & non facessero uarietà alcuna di Genere, come forse questi potrebbono dire della Diatessaron; percioche da gli Antichi era tenuta la Prima consonanza; maggiormente dourebbe hauer questo priuilegio il Ditono & lo Semiditono; percioche tra i Moderni fin'hora la Diatessaron da molti non è posta nel numero delle Consonanze; come sono la Diapason & la Diapente; ma si bene il Ditono & lo Semiditono.
Et che questo sia uero, uedete questi due Interualli consonanti, che scambieuolmente tanto si pongono nella parte graue delle nostre compositioni l'uno sotto, ouer
sopra l'altro, quanto nell'acuto; il che non si fà della Diatessaron con la Diapente; percioche questa sempre si pone sotto la Diatessaron, & questa le stà di sopra; oueramente
costumiamo di porle sotto il Ditono, ò lo Semiditono. Io uoglio dire, disse il Merulo,
una parola Messere, & poi seguitarete. Ditemi per uostra cortesia; di che Genere fanno
costoro, che sia il Tritono, il Semidiatessaron, la Diapente superflua, la Semidiapente, &
altri simili Interualli saluatichi, i quali non sono consonanti, ch'essi pongono nelle lor
compositioni? Voleua anch'io à punto dimandarui, soggiunse il Viola; Di che Genere
li fanno. Dicono, rispose egli all'uno & l'altro; che sono di un Genere misto, questi gapage 93
lant'huomini; ma non conoscono però la sua mistura. Vdita questa Conclusione, dissi;
Horsu Messere; lasciamo hormai queste cose da un canto, & torniamo al nostro proposito, che sarà cosa più utile: & sarà la
Definitione del minimo Interuallo rationale, che si
troua nella Musica, il quale è chiamato Comma; onde diremo.
. & d. & tra e. & g. & non si possa cantare, senza interponerui una
chorda mezana; & ch'ello non sia interuallo Diatonico, questo non li consentirò mai; percioche se 'l si canta la Diatessaron
senz'esser tramezata d'alcun'altro suono, & in un solo
Interuallo, & questa non faccia alcuna uarietà di Genere; il simile etiandio bisogna che
auenga, quando si canta il Ditono, ò lo Semiditono con un solo Interuallo; percioche non
ui sò uedere, ne ritrouar maggior ragione, c'habbia l'un più che l'altro de questi Interualli; essendo tutti consonanti. Anzi
se 'l si douesse hauer qualche rispetto ad alcun di loro;
che, come più consonanti, si potessero cantar tramezati & non tramezati, & non facessero uarietà alcuna di Genere, come forse questi potrebbono dire della Diatessaron; percioche da gli Antichi era tenuta la Prima consonanza; maggiormente dourebbe hauer questo priuilegio il Ditono & lo Semiditono; percioche tra i Moderni fin'hora la Diatessaron da molti non è posta nel numero delle Consonanze; come sono la Diapason & la Diapente; ma si bene il Ditono & lo Semiditono.
Et che questo sia uero, uedete questi due Interualli consonanti, che scambieuolmente tanto si pongono nella parte graue delle nostre compositioni l'uno sotto, ouer
sopra l'altro, quanto nell'acuto; il che non si fà della Diatessaron con la Diapente; percioche questa sempre si pone sotto la Diatessaron, & questa le stà di sopra; oueramente
costumiamo di porle sotto il Ditono, ò lo Semiditono. Io uoglio dire, disse il Merulo,
una parola Messere, & poi seguitarete. Ditemi per uostra cortesia; di che Genere fanno
costoro, che sia il Tritono, il Semidiatessaron, la Diapente superflua, la Semidiapente, &
altri simili Interualli saluatichi, i quali non sono consonanti, ch'essi pongono nelle lor
compositioni? Voleua anch'io à punto dimandarui, soggiunse il Viola; Di che Genere
li fanno. Dicono, rispose egli all'uno & l'altro; che sono di un Genere misto, questi gapage 93
lant'huomini; ma non conoscono però la sua mistura. Vdita questa Conclusione, dissi;
Horsu Messere; lasciamo hormai queste cose da un canto, & torniamo al nostro proposito, che sarà cosa più utile: & sarà la
Definitione del minimo Interuallo rationale, che si
troua nella Musica, il quale è chiamato Comma; onde diremo.
DEFINITIONE XXV.
DEFINITIONE XXVI.
DEFINITIONE XXVII.
PROPOSTA PRIMA.

PROPOSTA II.

PROPOSTA III.
PROPOSTA IIII.
COLLORARIO.
PROPOSTA V.
PROPOSTA VI.

COROLLARIO.
PROPOSTA VII.
PROPOSTA VIII.
PROPOSTA IX.
PROPOSTA X.
PROPOSTA XI.

PROPOSTA XII.

PROPOSTA XIII.

PROPOSTA XIIII.

PROPOSTA XV.
PROPOSTA XVI.
PROPOSTA XVII.
PROPOSTA XVIII.
PROPOSTA XIX.

COROLLARIO.
PROPOSTA XX.
PROPOSTA XXI.

PROPOSTA XXII.
PROPOSTA XXIII.

PROPOSTA XXIIII.

PROPOSTA XXV.

COROLLARIO.
PROPOSTA XXVI.
PROPOSTA XXVII.
PROPOSTA XXVIII.
PROPOSTA XXIX.
PROPOSTA XXX.
COROLLARIO I.
COROLLARIO II.
PROPOSTA XXXI.
COROLLARIO.
PROPOSTA XXXII.
PROPOSTA XXXIII.
PROPOSTA XXXIIII.

COROLLARIO I.
COROLLARIO II.
PROPOSTA XXXV.
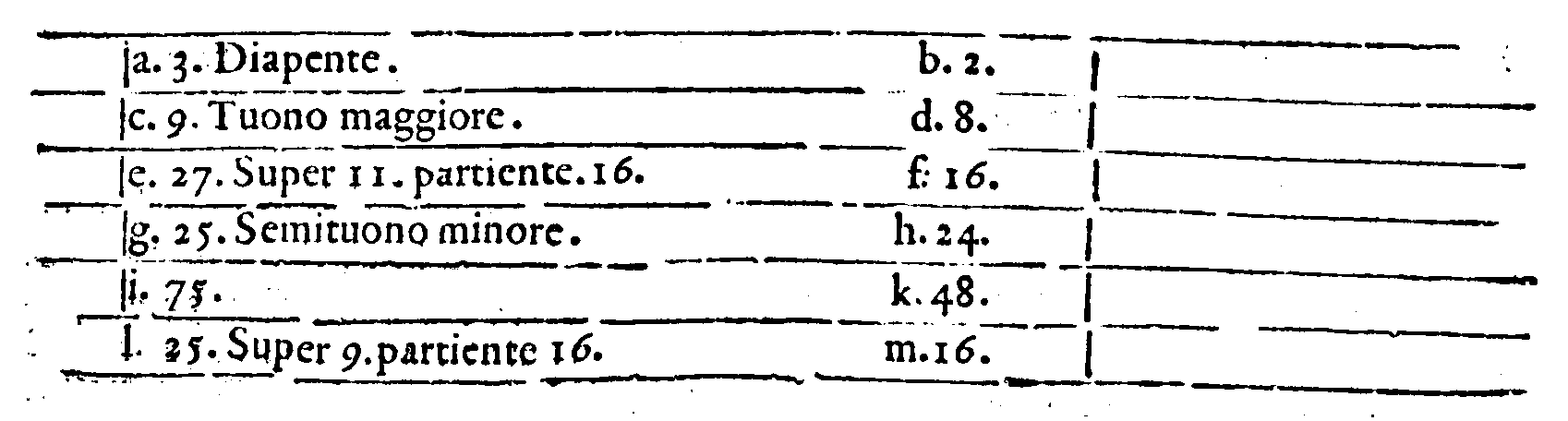
PROPOSTA XXXVI.
PROPOSTA XXXVII.
PROPOSTA XXXVIII.
PROPOSTA XXXIX.
PROPOSTA XL.
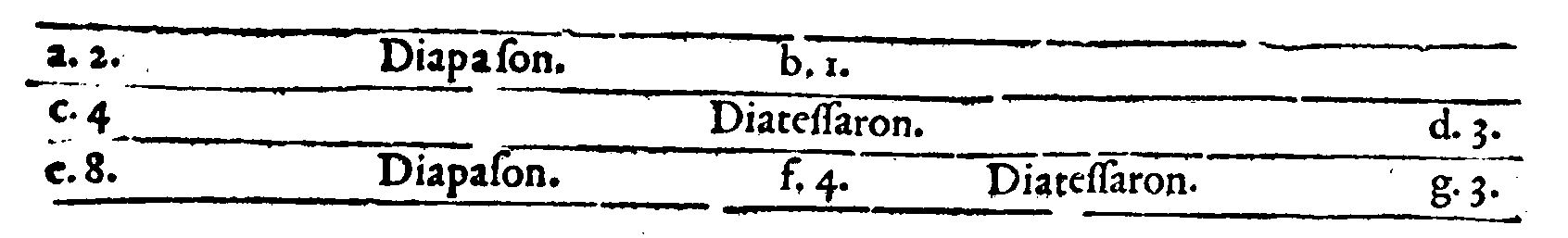
PROPOSTA XLI.
PROPOSTA XLII.
DIMOSTRATIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA: RAGIONAMENTO TERZO.
DEFINITIONE PRIMA.
DEFINITIONE II.

DIMANDA PRIMA.
DIMANDA II.
DIMANDA III.
DIMANDA IIII.
DIMANDA V.
PROPOSTA PRIMA.
PROPOSTA II.
PROPOSTA III.
PROPOSTA IIII.
PROPOSTA V.
COROLLARIO.
PROPOSTA VI.
PROPOSTA VII.
PROPOSTA VIII.
PROPOSTA IX.

PROPOSTA X.
PROPOSTA IX.
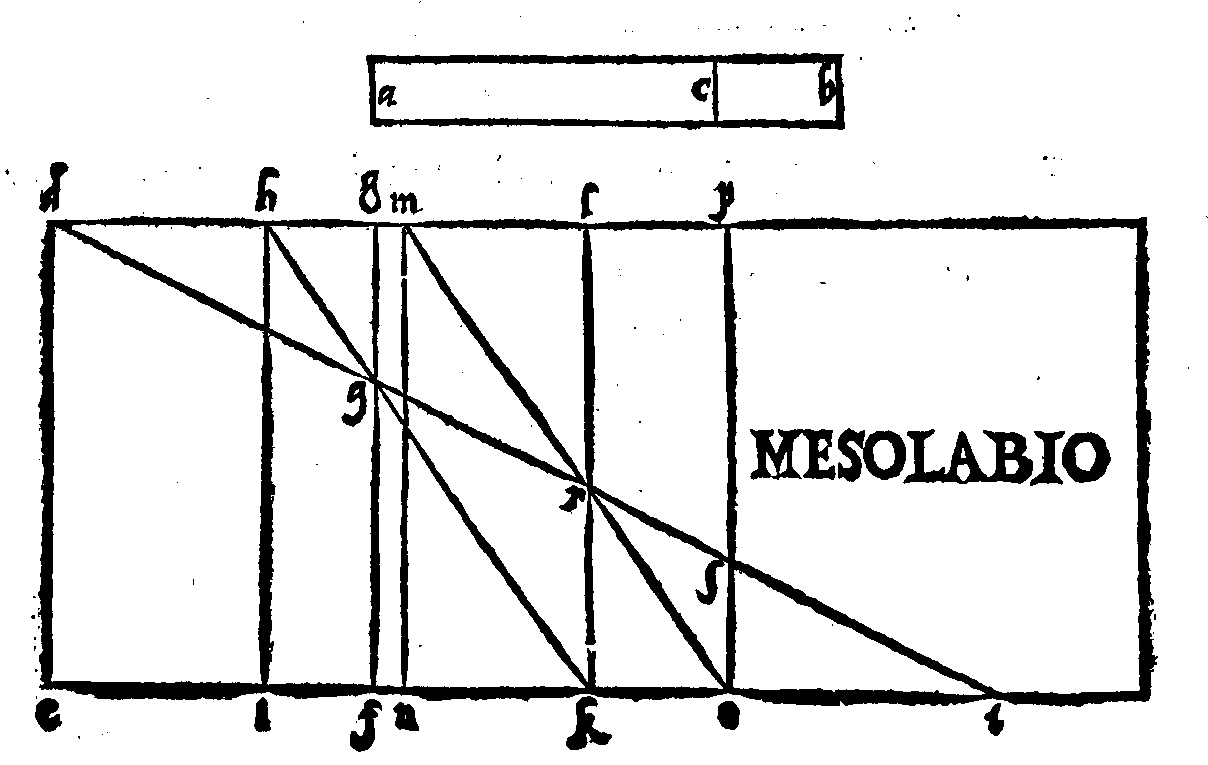
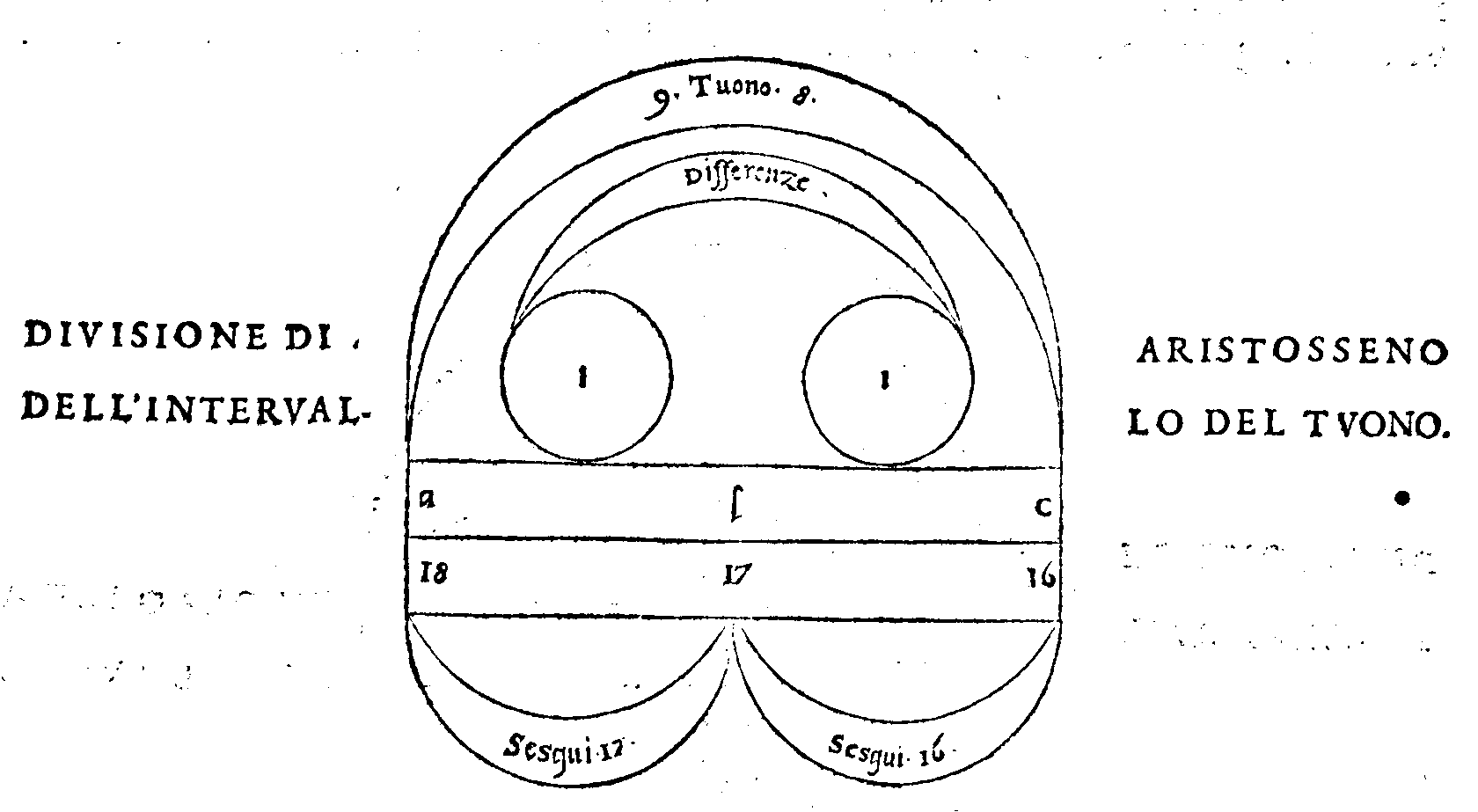
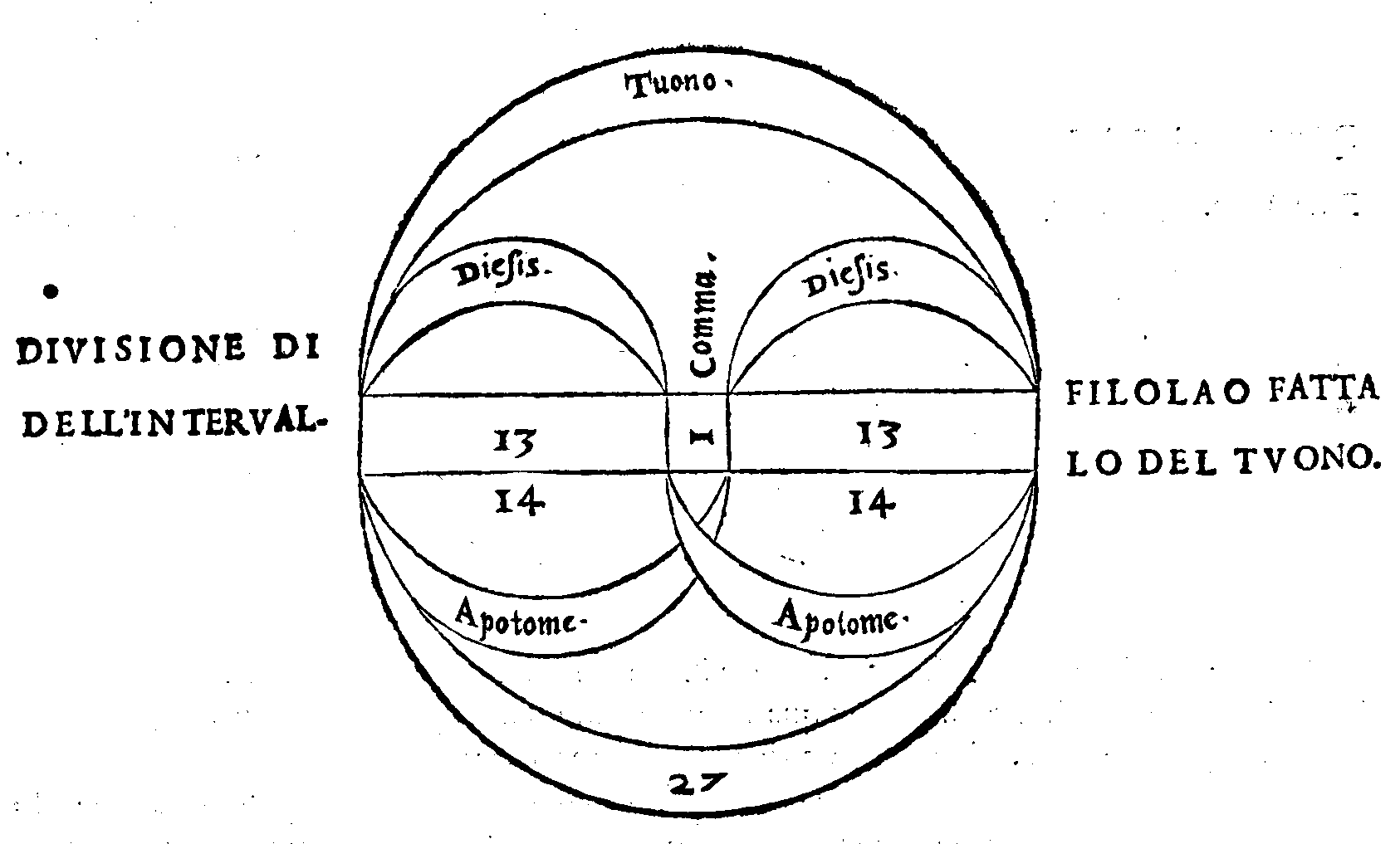
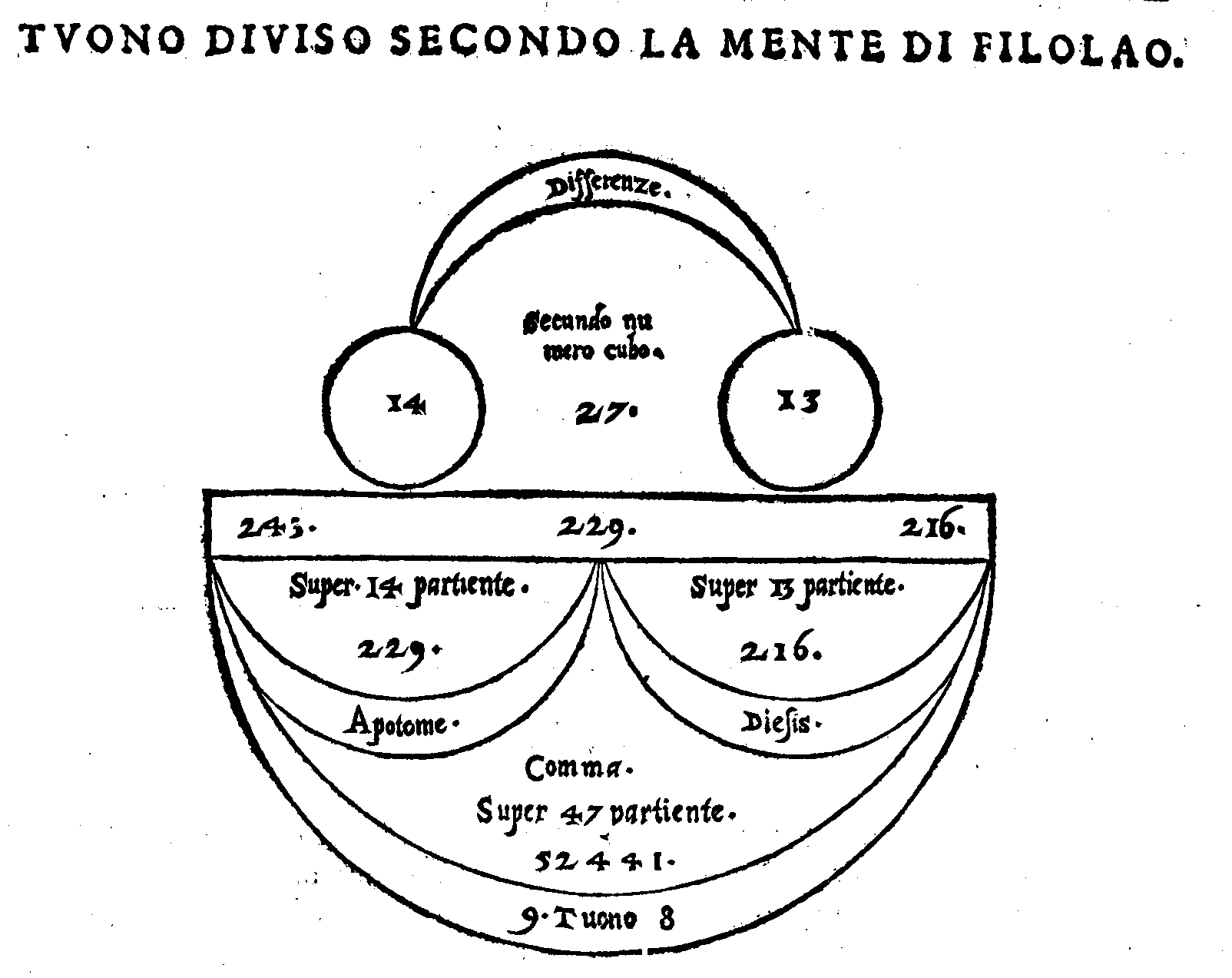
PROPOSTA XII.
COROLLARIO.
PROPOSTA XIII.
PROPOSTA XIIII.
PROPOSTA XV.
PROPOSTA XVI.

PROPOSTA XVII.
PROPOSTA XVIII.
PROPOSTA XIX.
PROPOSTA XX.
PROPOSTA XXI.
PROPOSTA XXII.
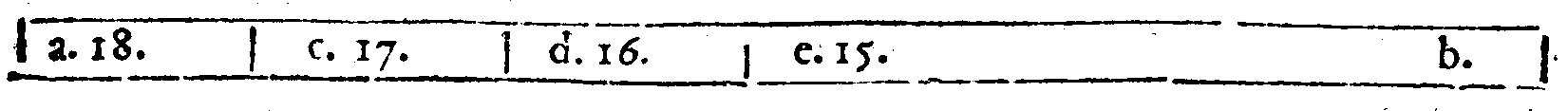
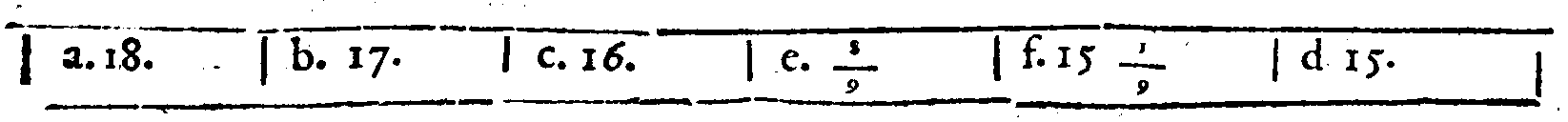
COROLLARIO.
PROPOSTA XXIII.
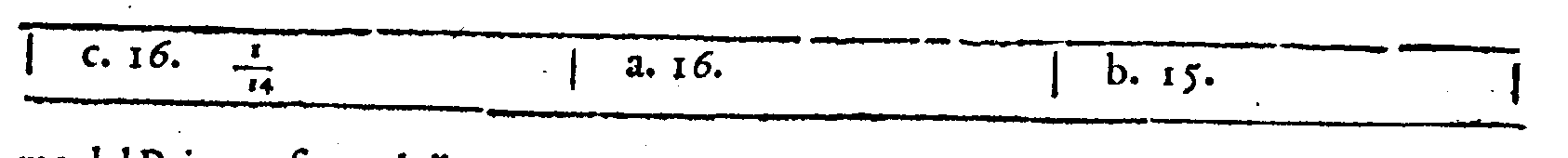
PROPOSTA XXIIII.
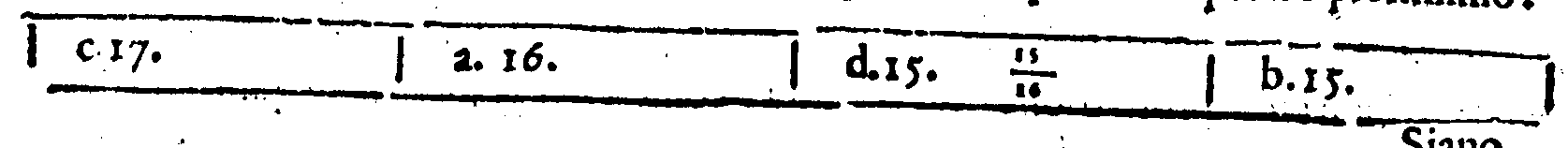
COROLLARIO.
PROPOSTA XXV.

PROPOSTA XXVI.

PROPOSTA XXVII.
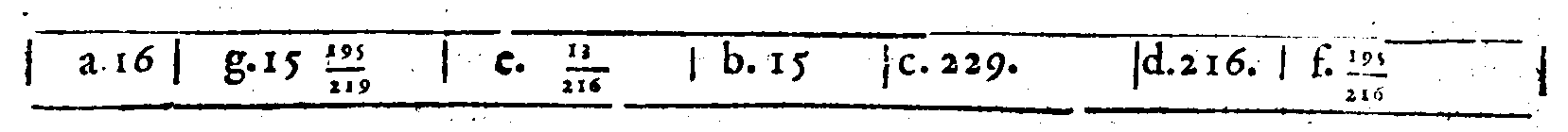
PROPOSTA XXVIII.

PROPOSTA XXIX.
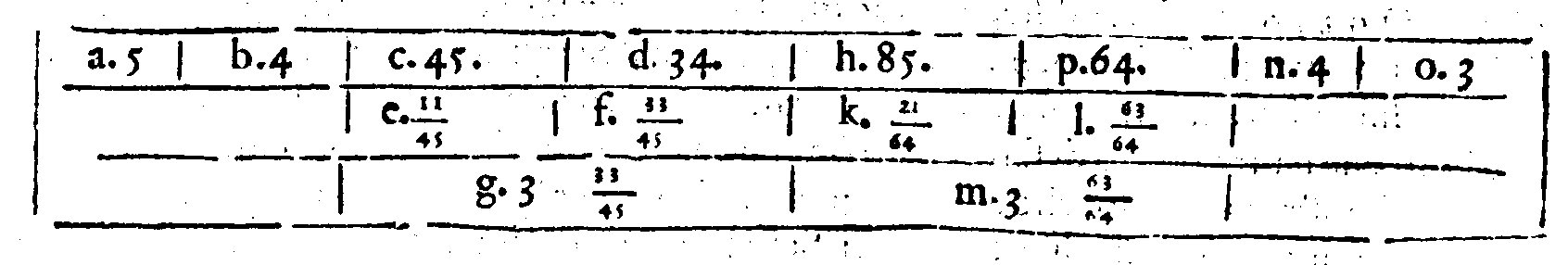
PROPOSTA XXX.
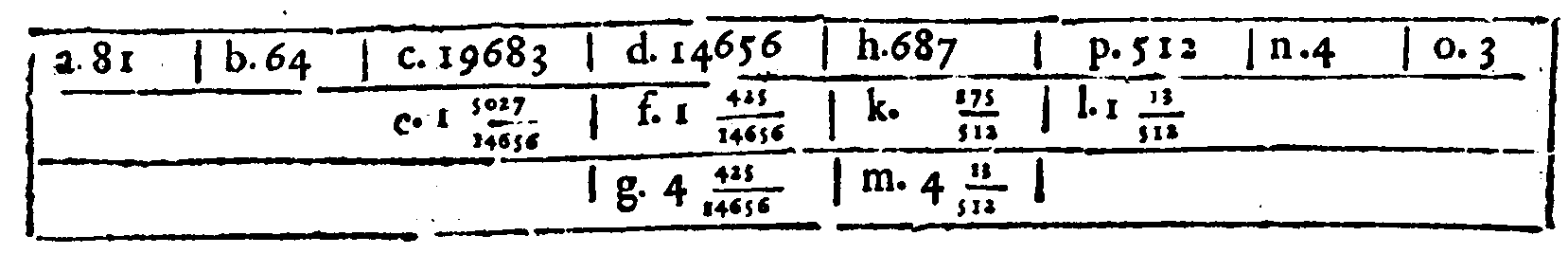
PROPOSTA XXXI.
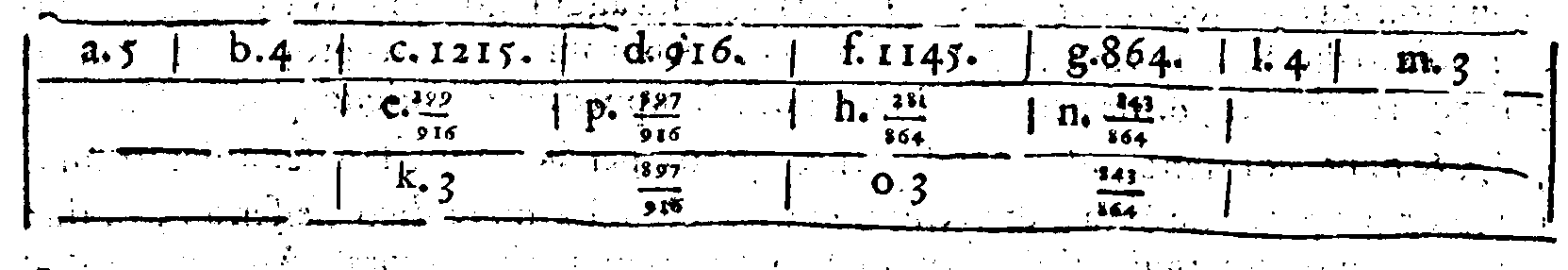
PROPOSTA XXXII.
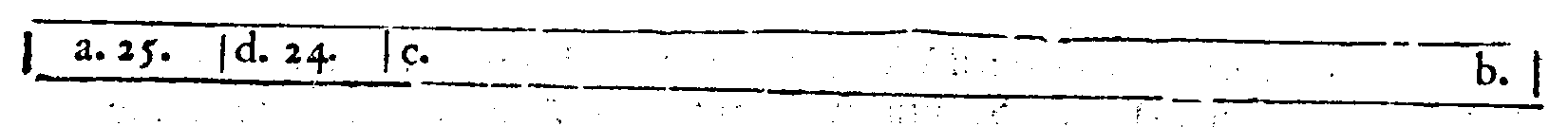
PROPOSTA XXXIII.
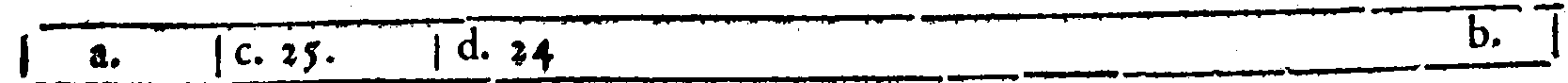
PROPOSTA XXXIIII.
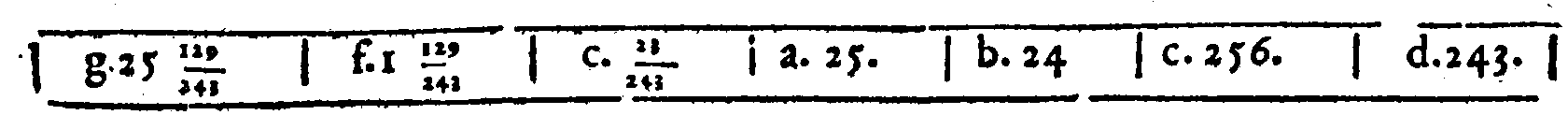
PROPOSTA XXXV.
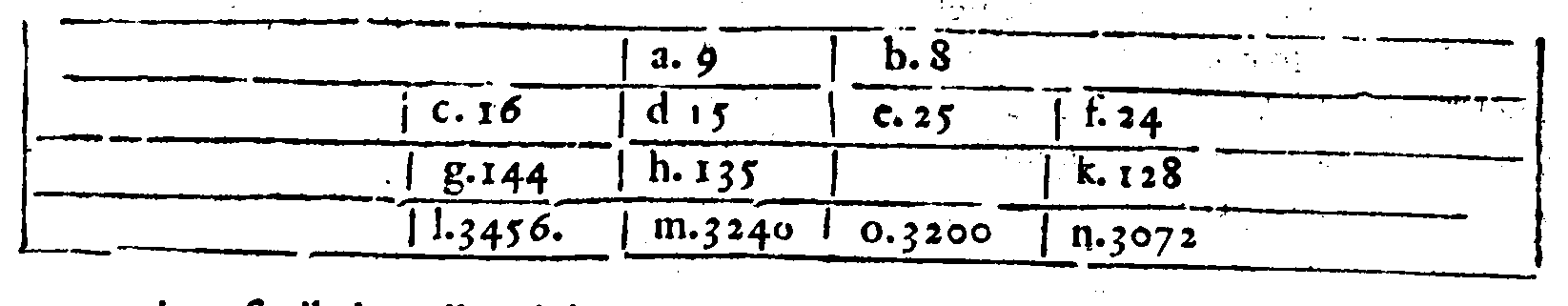
COROLLARIO.
PROPOSTA XXXVI.
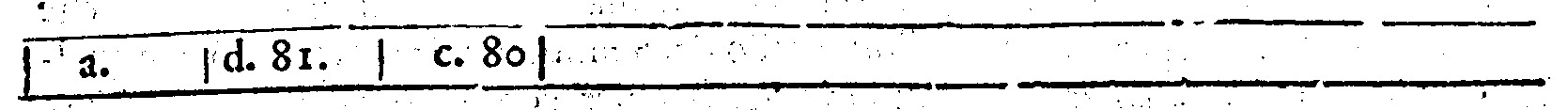
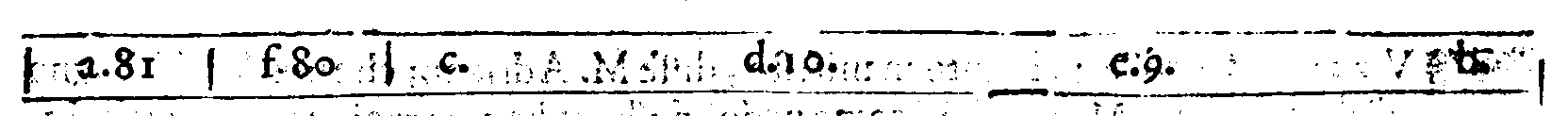
PROPOSTA XXXVII.

PROPOSTA XXXVIII.
PROPOSTA XXXIX.
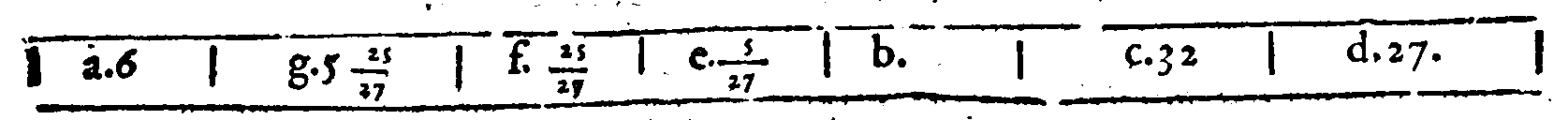
PROPOSTA XL.
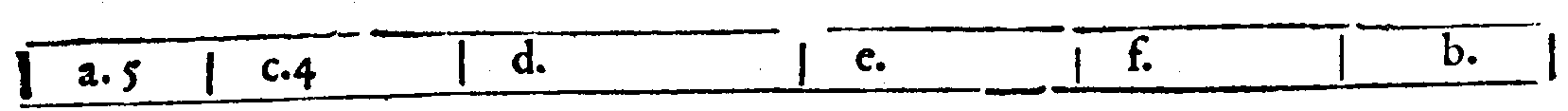
PROPOSTA XLI.
PROPOSTA XLII.
PROPOSTA XLIII.
PROPOSTA XLIIII.

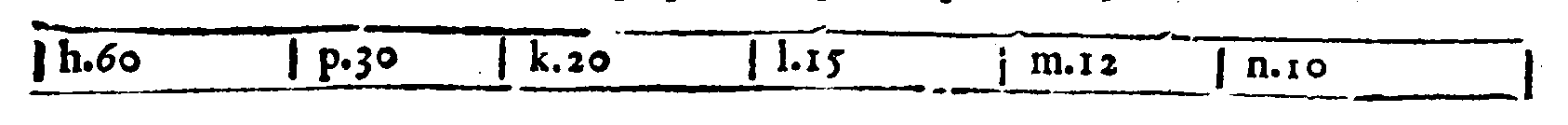
PROPOSTA XLV.

PROPOSTA XLVI.

PROPOSTA XLVII.
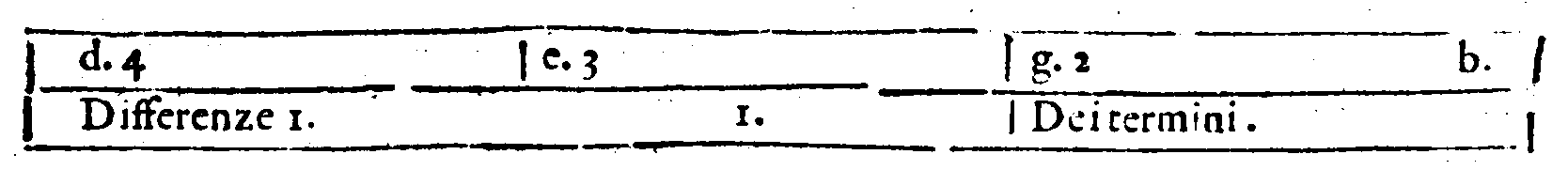
PROPOSTA XLVIII.
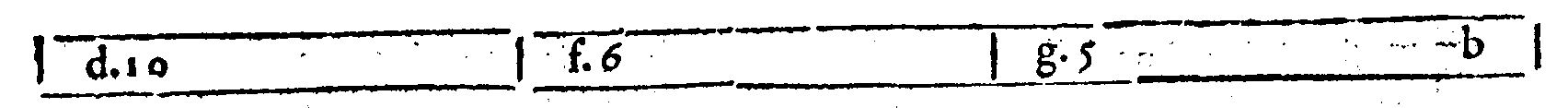
PROPOSTA XLIX.
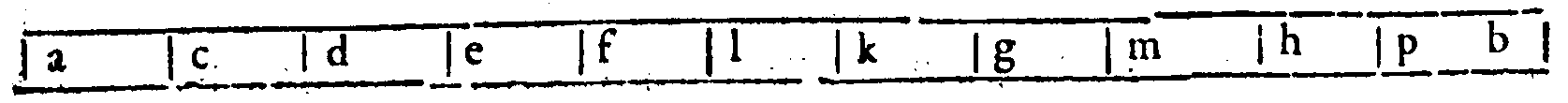
PROPOSTA L.
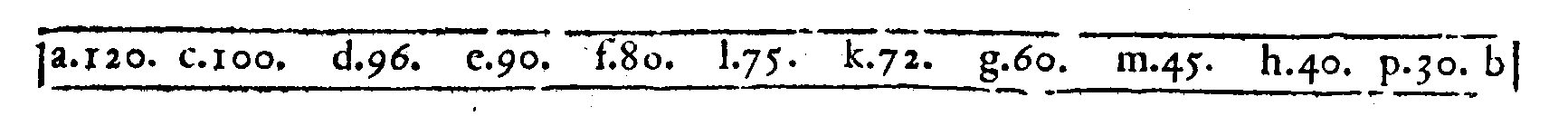
PROPOSTA LI.
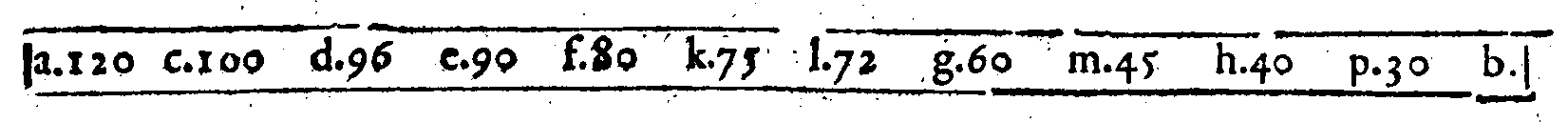
PROPOSTA LII.
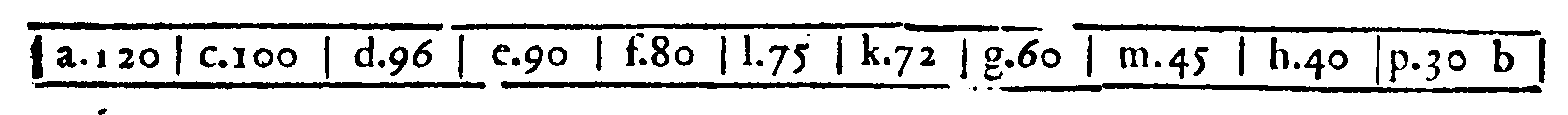
PROPOSTA LIII.
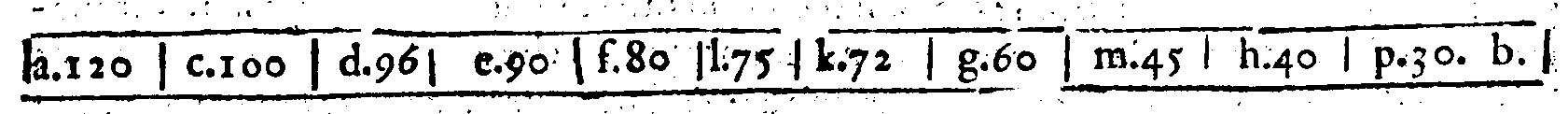
DIMOSTRATIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA: RAGIONAMENTO QVARTO.
Lungo camino faticoso & asperoNe credo, che da altro sia proceduto, ch'à i tempi nostri oltra modo sia cresciuto 'l numero de quelli, che compongono in Musica; che dalla facilità (come hò ancora detto) che hanno di porre insieme le Consonanze, con quelle poche di Regole, le quali adoperano, senza hauer pensiero di saper più oltra cosa alcuna, se non che posta la tal Consonanza sopra, ò sotto la tale, faccia un'accordo. Onde noi uediamo; che si come già fù tempo, che tal numero era di maniera picciolo, che se in una delle maggiori città, non dirò solamente d'Italia; ma etiandio d'un'altra Prouincia, se ne hauesse ritrouato un solo, oueramente due; erano tenuti per cosa marauigliosa, & ammirati come cosa dipage 190 una; cosi à i tempi nostri, non è città, o castello per picciolo ch'ello sia, che non sia copioso di tal sorte d'huomini. Et non pur le città, ò le castella; ma si puo credere ch'al presente, non ui sia Villa, la quale non habbia il suo Compositore; sia poi di qual si uoglia qualità; che poco à quelli, che non intendono, importa. Onde parmi, che la Musica & la Poesia à i giorni nostri siano quasi arriuate ad un'istessa conditione percioche si come questa è copiosissima di Versificatori, & il numero de buoni & eccellenti Poeti è picciolo; cosi la Musica è ripiena d'un numero quasi infinito de Compositori; tra i quali pochi se ne ritrouano, c'habbiano nome di buono & uero Musico. Et si come hora non si troua Canta in banco, ò Cerettano (dirò cosi) che non faccia professione di cantar Stanze all'improuisa; cosi pochissimi sono quelli Cantori, & altri professori di Musica, che non faciano professione di far miracoli improuisamente nel lor cantare. Ma uolesse Iddio, che la Musica andasse di pari alla Poesia; perche si trouerebbe un buon numero d'Huomini dotti, i quali saprebbono minutamente render ragione delle opere loro, & non haurebbono l'ignoranza tanto, com'hanno, per amica. Questa cosa sempre mi è grandemente spiacciuta; la onde hauendo ueduto & conosciuto già per molti anni inanzi questo si grande abuso; per l'amore ch'io porto à questa tanto nobile Scienza; sforzato dalla mia natural dilettatione, pigliai l'impresa, quantunque difficile, di uoler uedere, s'io poteua, se non in tutto spengere, almeno leuare in una buona parte & scacciare dalle menti de i professori di questa Scienza, l'ignoranza, & ridurli nel dritto camino, & darli tal modo & lume, che di tutto quel ch'operassero sapessero render buona ragione; acciò non fussero al tutto ciechi, & inferiori à gli altri Artefici, i quali dell'Arte che fanno, sanno render ragione, & buon conto, & dire il Perche d'ogni loro operatione. La onde diedi opera di condur questo mio pensiero al desiderato fine; doue col mezo delle Istitutioni, le quali già molti anni sono, ch'io diedi in luce, mi sforzai di dar lume di tutto quel ch'io potei in questa nobil Scienza, tanto nella Prattica, scoprendo molti belli & mirabili secreti, non ancora intesi da un gran numero de Compositori, quanto nella Speculatiua; dichiarando molte cose oscure & confuse, & aggiungendoui molti belli & noui concetti, non più d'altri (per quel ch'io hò potuto uedere) non solamente scritti; ma ne anco accennati. Et ueramente hò conosciuto di non mi hauere affaticato in vano; ma di hauer molto giouato à i Professori di quest'Arte nobile; percioche con questo mezo molti si sono ridutti in buon essere, & nella cognitione de molte cose necessarie & importanti. Il perche hauendo io veduto le mie Fatiche non essere state ingrate à i Spiriti nobili & uirtuosi; pigliai forza & ardire di passar più oltra; Onde mi affaticai intorno le presenti Dimostrationi; accioche le cose della Musica dimostratiuamente si sapessero, & per quel uerso che saper si debbono. Le quali hauendo ridotto nell'essere, che si ueggono; spero che non saranno se non di grande utilità à i Professori di questa Scienza; come ciascheduno, dopo che le haurà con diligenza studiate, lo potrà uedere & conoscere. Oltra di questo; accioche non mancassi di dar quella cognitione delle cose della Musica, che per me dar si potea, formai, à guisa dell'Oratore perfetto di Marco Tullio Cicerone, un Perfetto Musico; nel quale si può ueder tutto quello, che bisogna, per uoler'esser Perfetto in questa Scienza. Et se ben sò, ch'è impossibile, ch'uno habbia in se tutto quello, ch'al Perfetto si conuiene, & come lo descriuo; non sarà almeno impossibile, che colui si possa chiamare ad un certo modo Perfetto; alquale mancheranno poche cose di quelle, ch'al Perfetto conuengono. Volentieri mi son affaticato, & volentieri m'affatico, ne mai mi è per rincrescer fatica alcuna; percioche quel ch'io faccio, lo fò con dilettatione; & quel che mi hà mosso sempre & mi muoue all'operare è à laude & gloria del sommo Iddio santo & benedetto, datore de tutte le gratie & de tutti i beni. Ne di queste mie fatiche ricerco dal Mondo alcun premio; ma lascio la cura alla Diuina Maestà, non solamente di questo, ma ancora del castigo contra gli Emuli & Dettrattori dell'altrui buone opere, i quali mai non mancano. A' i quali protesto di non hauer pigliato questa impresa per uoler satisfare alle uoglie loro maluaggie, & contaminate page 191 percioche questo è vn'impossibile; ma si bene (s'io potrò) all'animo nobile & uirtuoso de Studiosi. Et per ritornare al nostro proposito, dico ch'era già uicina l'hora destinata à i nostri ragionamenti, quando il Viola uenne à ritrouarmi alla stanza: accioche insieme andassimo à ritrouar M. Adriano. Onde hauendomi prima ricercato d'alcune cose sopra il ragionamento del giorno passato; pigliassemo il camino uerso il luogo solito. Il perche arriuati, ritrouassimo oltra la solita compagnia molti altri Gentil'huomini; ch'erano uenuti per uedere M. Adriano, i quali hauendoci intratenuto per un buon pezzo di tempo sopra i ragionamenti delle cose della Musica, & alla fine partiti; stando ogn'uno quasi chetto; cosi incominciò il buon uecchio M. Adriano à ragionare. Sarebbe buona cosa Sig. miei; che si desse principio à seguitare i nostri già principiati ragionamenti, & si seguitasse quello, che ci resta; percioche tanto più per tempo, che parrerà à M. Gioseffo d'hauer finito, potremmo poi discorrere sopra quello, che si uorrà, qualche cosa. Però à uoi tocca M. Gioseffo à dar le mosse, se cosi ui è in piacere. Cosi farò adunque Messere; risposi; & son tenuto d'obedirui in cosa tanto honesta, come è questa. Et uoglio che sapiate; che essendomi stato nelle cose della prattica Precettore, & datomi una buona parte del ben'essere; come si dice; non ui tengo minore obligo (per non esserui; come hanno fatto molti altri, in grato) di quel ch'io tengo à quel Padre, che mi hà generato. Ma lasciandole parole da un canto, & uenendo à i fatti; per dar principio uoglio, che uoi sapiate, che 'l nostro ragionamento hoggi non hà da esser d'altro, se non della Fabrica, ò Costruttione del Monochordo, per tutti tre i Generi delle Cantilene; & de quelli accidenti, che occorrer possono in simili costruttioni. Onde per maggiore intelligenza di quel che ui hò da dire, fà dibisogno, che prima habbiate la cognitione d'alcuni Termini & Principij; i quali non sapendo, non ne potreste esser capaci. I quali termini con breuità ui saranno noti per le Definitioni. Et se bene alcuni di loro furono da me dichiarati & definiti nelle Istitutioni, & che forse ui potrebbe bastare; tuttauia non uoglio mancar di replicarueli in questo luogo; percioche potrebbe essere, che ciò non fusse senza qualche guadagno; percioche udendoli ricordare, ui si potrebbe rappresentare inanzi qualche dubio sopra essi, de i quali potrete esser da me risolti. Sarà ben fatto; disse M. Francesco; percioche molte uolte anco nell'udir di nuouo una cosa già udita, si uiene non senza utilità de chi ascolta ad affissarsi nella memoria, di maniera che mai più si parte. Questo conosco io per esperienza; disse M. Adriano; che maggiormente mi s'affissano le cose nella memoria, che da un'altro odo, che quelle, che, da me stesso studiando, leggo. Cosi è ueramente; soggiunse il Sig. Desiderio; perche la viua uoce, che intuona all'orecchie hà maggior forza di fuori, di quel che non hà l'occhio, nelle cose della Scienza. Questo dico; perche la maggior parte di quelle cose, che si studiano leggendo si scorrono con l'occhio, oueramente se si leggono; si leggono di maniera, che la uoce non si ode; la onde non gli è quella forza, che si troua nella uoce d'uno, ch'alle orecchie intuoni. Però, mi piacciono ueramente tali repliche; percioche non possono esser fatte, se non con qualche vtile. Risposi à questo & dissi; Questa è stata una delle cagioni, che ne i passati ragionamenti, alle fiate hò replicato alcune cose, le quali hò dichiarato nelle Istitutioni. Replicate purquanto ui piace; disse M. Adriano; & secondo che ui torna commodo; che tutti siamo contenuti; percioche molto ben sapiamo, che non replicate se non quello, ch'è necessario; & per dichiarar quello, che non è da noi inteso. Allora udito questo; ripigliai il mio parlare à questo modo. Volendo adunque uenire alla diuisione del Monochordo; uederemo prima quello, che ello sia; & dopoi quelle cose, che cadono per accidente nella sua diuisione. Onde douete sapere; che se ben ui hò detto nelle Istitutioni2. par. c. 27 che Monochordo & Regola harmonica sia una cosa istessa; hora uoglio ch'intendiate per Monochordo un'altra cosa; ancora che poco differente sia; il che comprenderete dalla sua definitione, la quale è questa. page 192
E' quel ch'alla Virtù l'Huom può conducere;
Che giunto al sommo il resto troua ageuole.
Onde soaui frutti allor'accoglie
Del suo trauaglio; Percioche i Dei uolsero,
Che col sudor tai pregi s'acquistassero.
DEFINITIONE PRIMA.
DEFINITIONE II.
DEFINITIONE III.
DEFINITIONE IIII.
DEFINITIONE V.
DEFINITIONE VI.
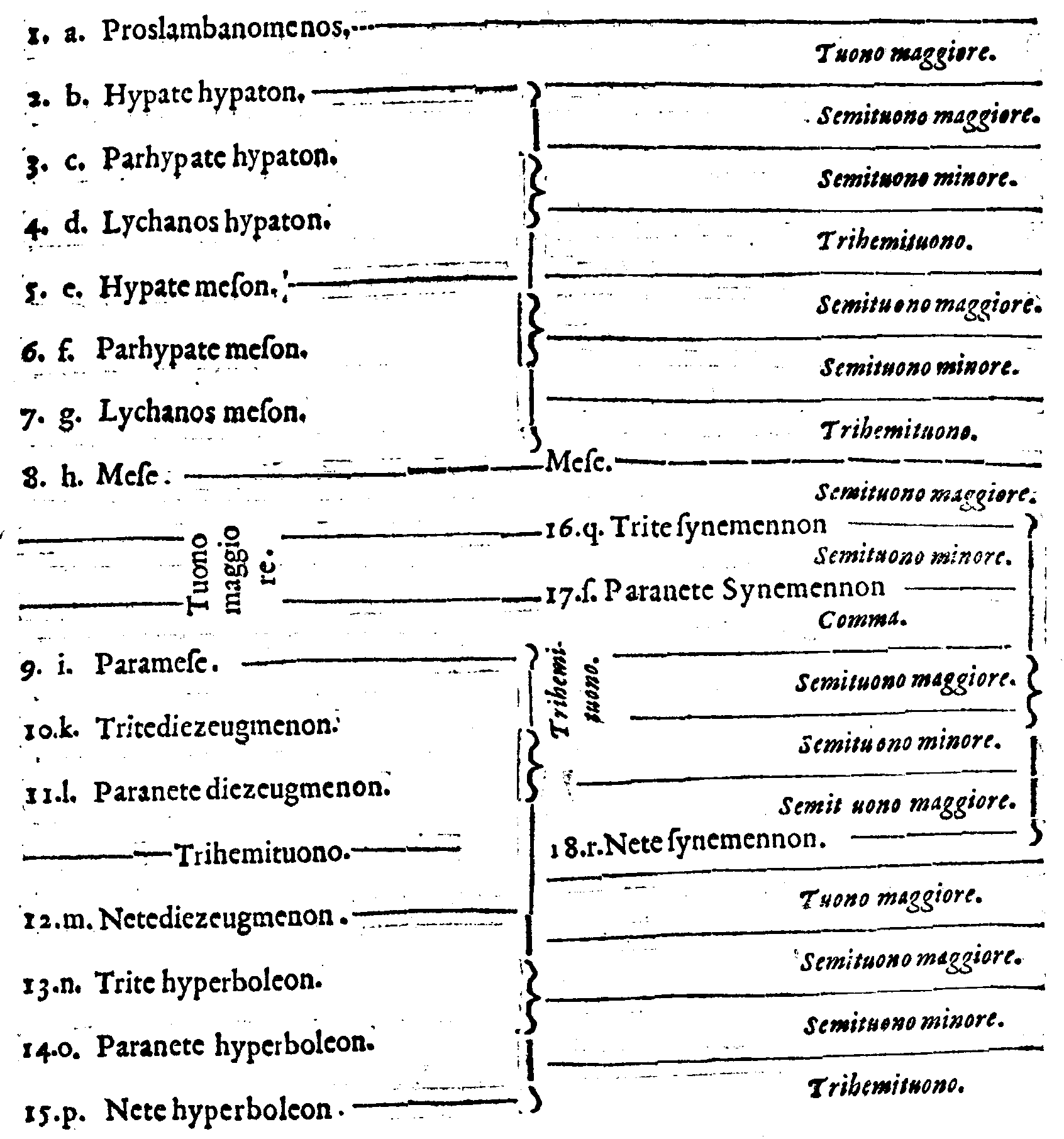
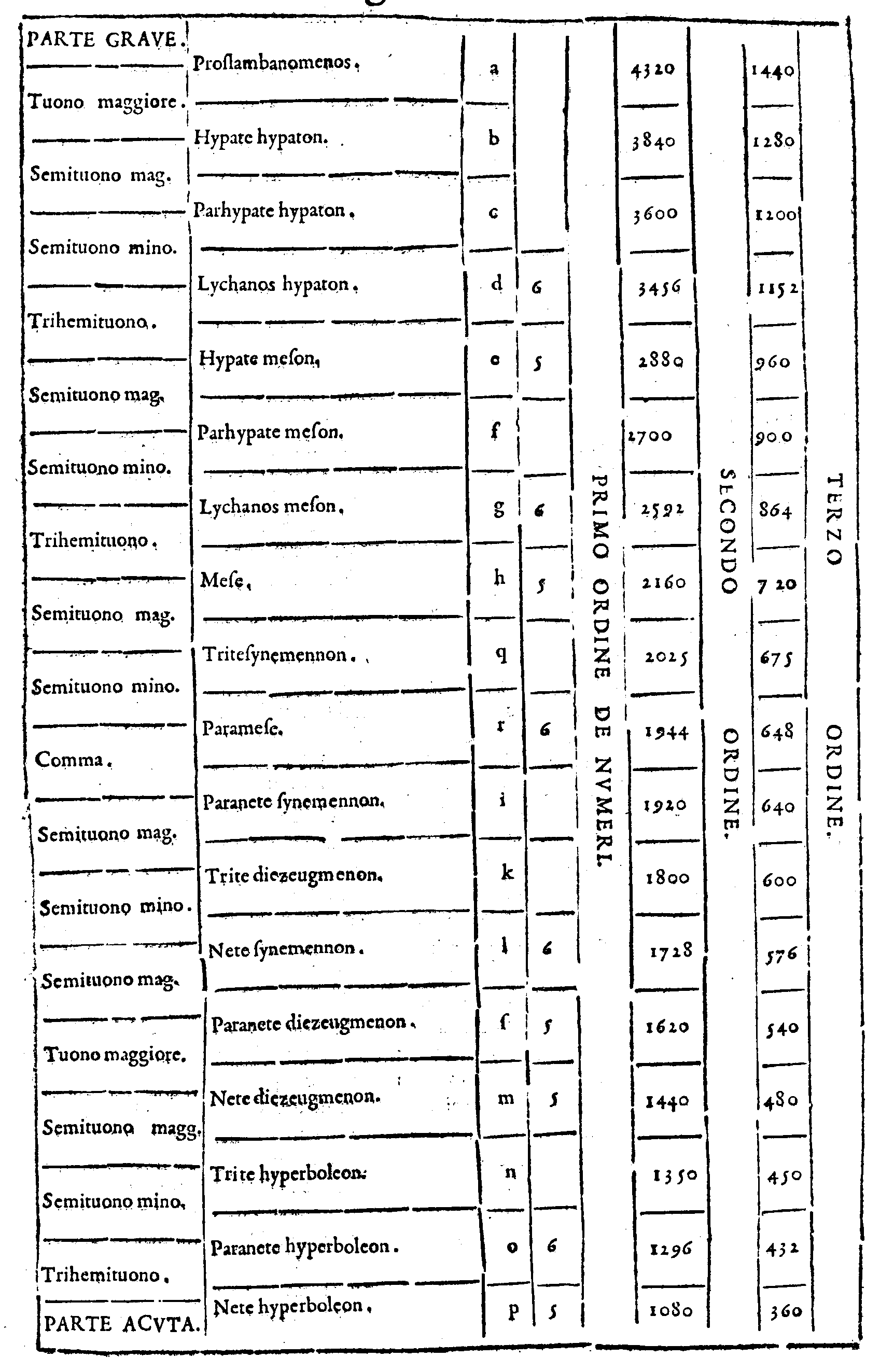
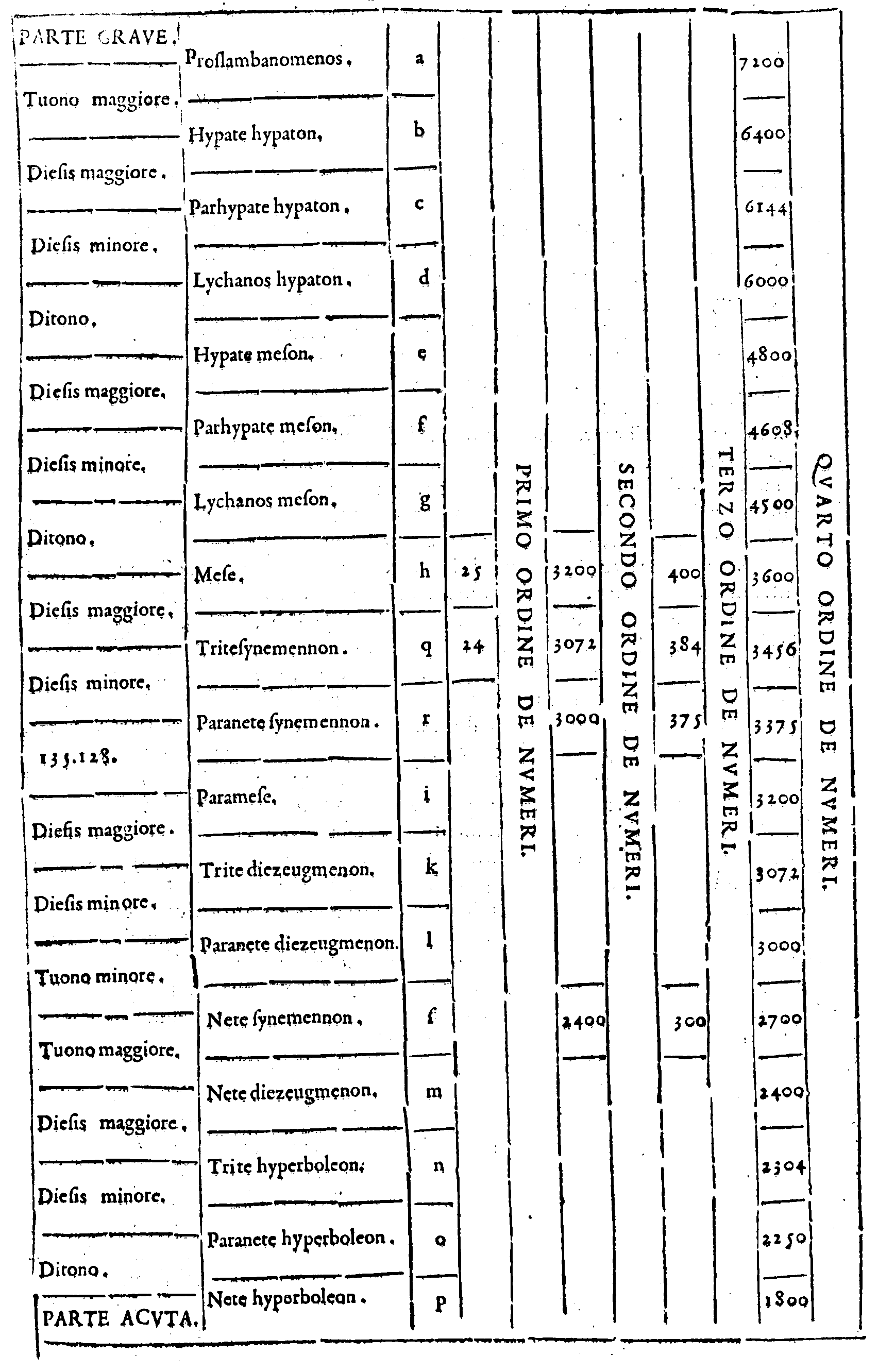
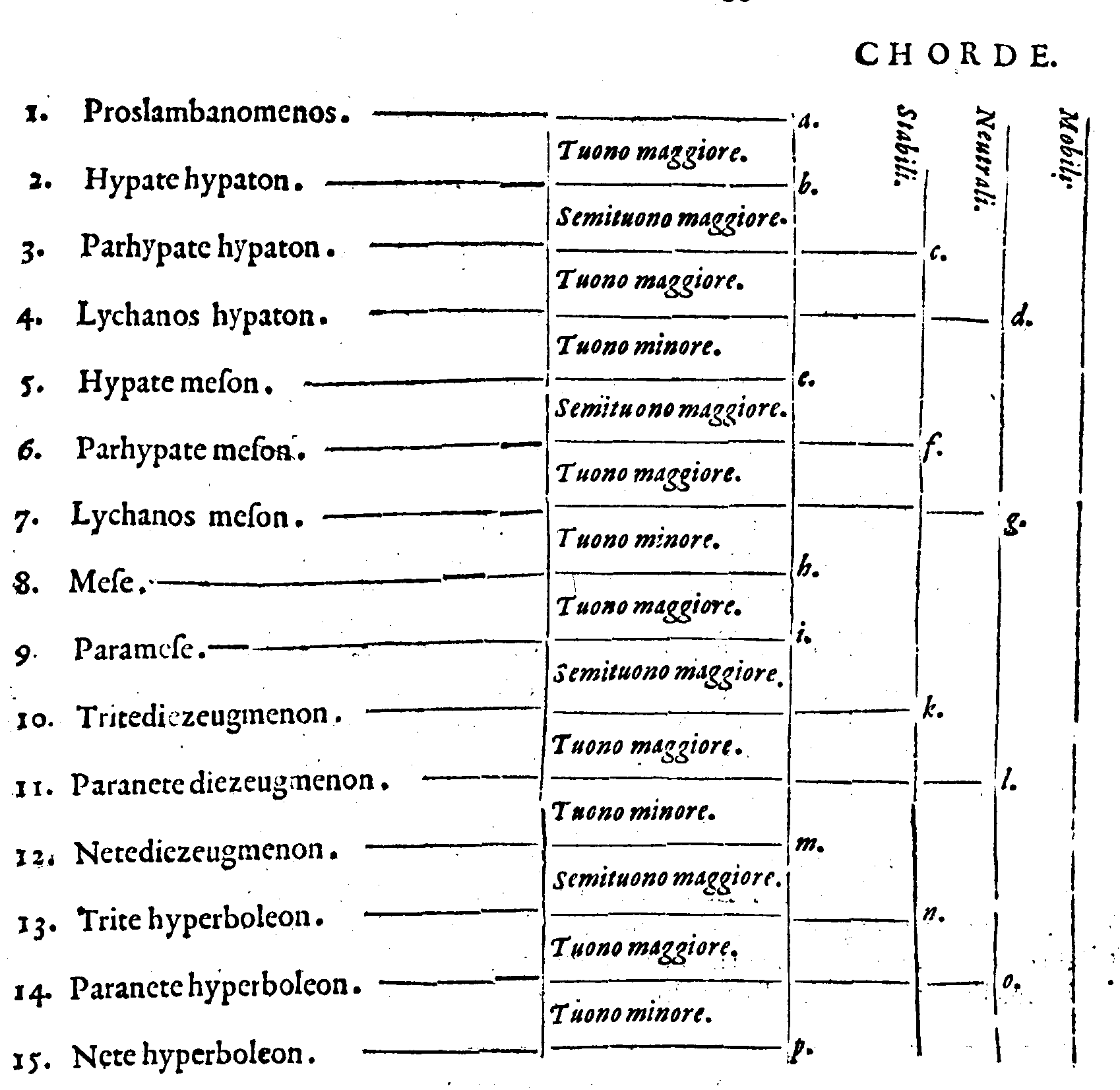
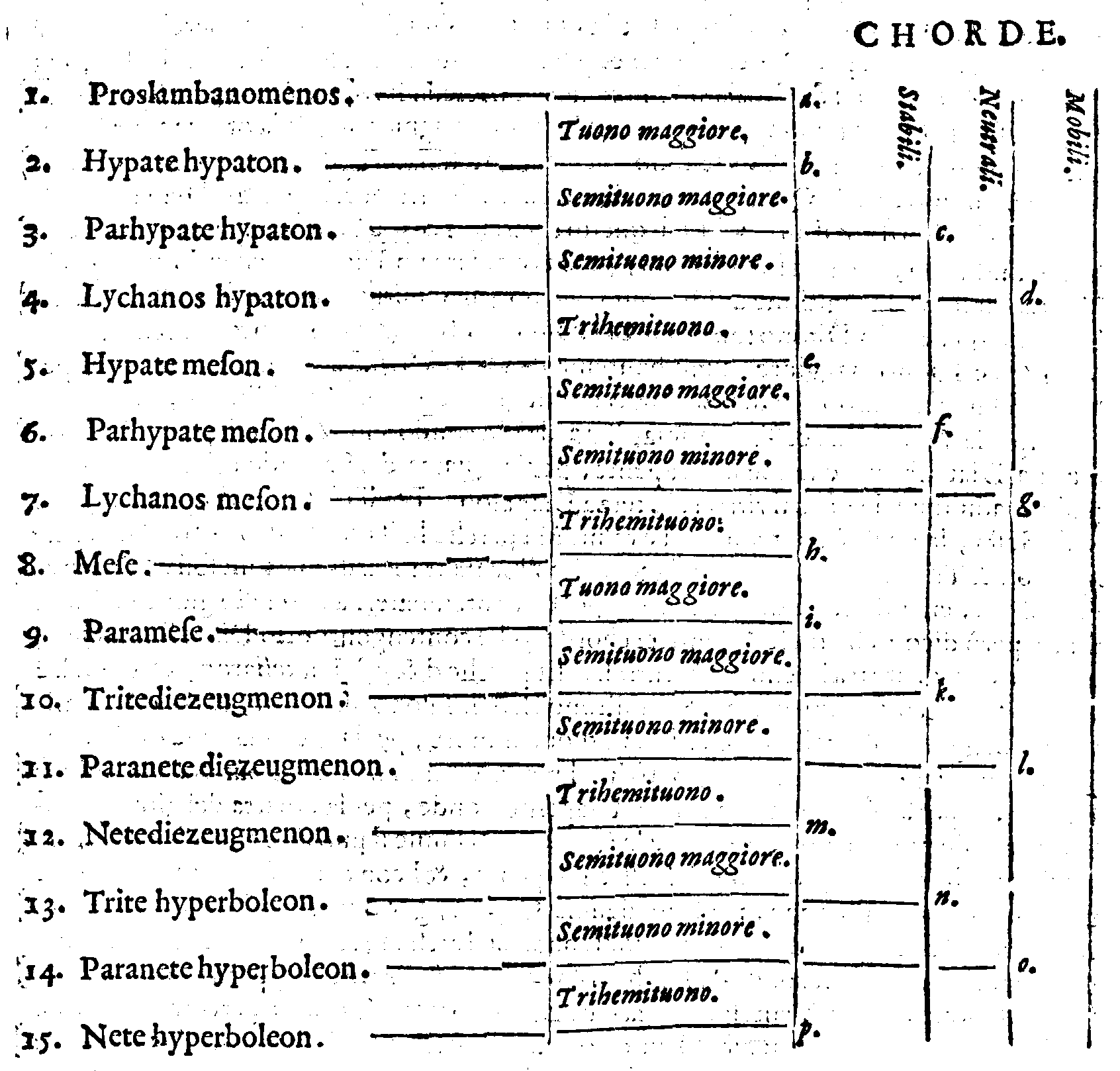
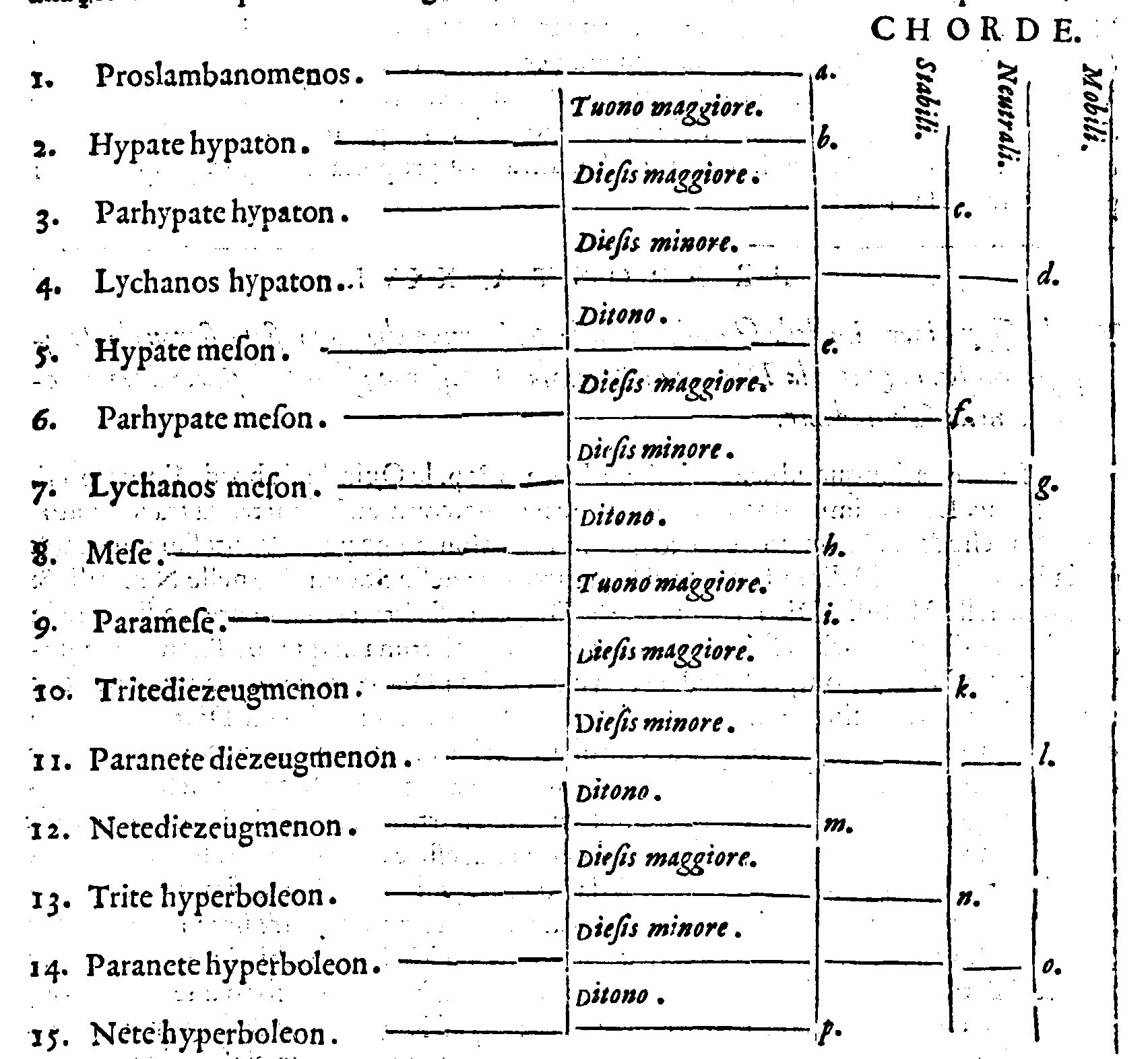
| 1. | Προσλαμβανόμενοσ. | Cioè, | Acquistata; ouero Aggiunta. |
| 2. | Υ῾πάτη ὑπατῶν. | Principale delle principali. | |
| 3. | Παρυπάτη ὑπατῶν. | Appresso la principale delle principali. | |
| 4. | Λιχανὸσ ὑπατῶν. | Indice delle principali. | |
| 5. | Υ῾πάτη μεσῶν. | Principale delle mezane. | |
| 6. | Παρυπάτη μεσῶν. | Appresso la principale delle mezane. | |
| 7. | Λιχανὸσ μεσῶν. | Indice delle mezane. | |
| 8. | Μέση. | Mezana. | |
| 16. | Τρίτησυνημμένων. | Terza delle congiunte. | |
| 17. | Παρανήτη συνημμένων. | Penultima delle congiunte. | |
| 18. | Νήτη συνημμένων. | Vltima delle congiunte. | |
| 9. | Παραμέση. | Appresso la mezana. | |
| 10. | Τρίτη διεζευγμένων. | Terza delle separate. | |
| 11. | Παρανήτη διεζευγμένων. | Penultima delle separate. | |
| 12. | Νήτη διεζευγμένων. | Vltima delle separate. | |
| 13. | Τρίτη ὑπερβολαίων. | Terza delle acutissime. | |
| 14. | Παρανήτη ὑπερβολαίων. | Penultima delle acutissime. | |
| 15. | Νήτη ὑπερβολαίων. | Vltima delle acutissime. |
DEFINITIONE VII.
 . verso l'acuto per il numero de queste Quattro
chorde; oueramente ritornando dalla.
. verso l'acuto per il numero de queste Quattro
chorde; oueramente ritornando dalla. a. g & f. verso 'l Graue; non si ritroua quelli Interualli, c'hauete nominato; nondimeno si procede pur per il numero de Quattro chorde.
Cosi è; dissi; però accioche per l'auenire non v'ingannaste; tal Numero intenderete per
quello, che si ritroua nel Tetrachordo; il quale, acciò lo conosciate; lo definiremo in questo modo.
a. g & f. verso 'l Graue; non si ritroua quelli Interualli, c'hauete nominato; nondimeno si procede pur per il numero de Quattro chorde.
Cosi è; dissi; però accioche per l'auenire non v'ingannaste; tal Numero intenderete per
quello, che si ritroua nel Tetrachordo; il quale, acciò lo conosciate; lo definiremo in questo modo.
DEFINITIONE VIII.
DEFINITIONE IX.
DEFINITIONE X.
DEFINITIONE XI.
DEFINITIONE XII.
DEFINITIONE XIII.
DEFINITIONE XIIII.
PROPOSTA PRIMA.

MONOCHORDO REGOLARE DIATONICO.
PROPOSTA II.

MONOCHORDO REGOLARE CHROMATICO.
PROPOSTA III.

MONOCHORDO REGOLARE ENHARMONICO.
PROPOSTA IIII.
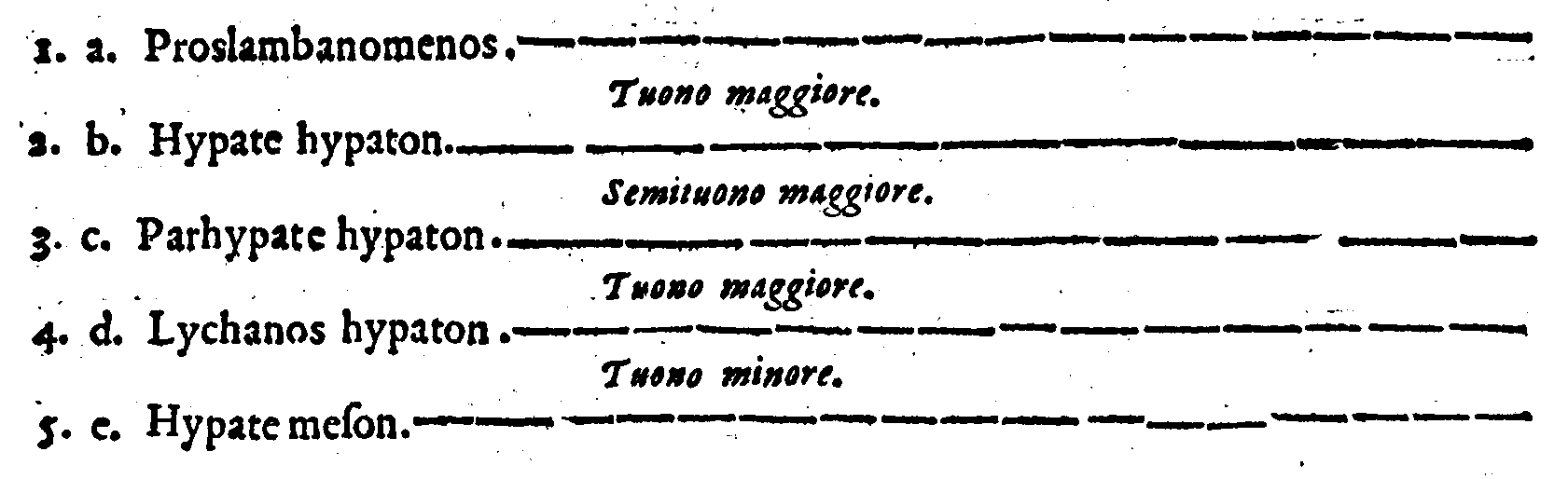
PROPOSTA V.

PROPOSTA VI.

PROPOSTA VII.

PROPOSTA VIII.

PROPOSTA IX.

PROPOSTA X.

PROPOSTA XI.
 , & b molli. Dopoi; non mi par,
ch'elle siano Chromatiche; percioche le chorde antiche haueano i lor proprij nomi; come
sono Hypate, Lychanos, Trite & l'altre; nondimeno le chorde, che pongono costoro nelle
lor cantilene, non si possono denominare con alcuno de i detti nomi; oueramente con altri, che siano simili à quelli. Onde è manifesto segno, che non sono, ne mai potranno esser
quello, che costoro predicano. Oltra di questo, non osseruano Modo, ò Tuono alcuno nel
loro comporre; di modo che si possa dire, questa cantilena è composta nel modo Dorio,
Ionico, ouer Frigio, ò sotto un'altro Modo; come diceuano gli Antichi; ma sono composte
di confusione; & con una certa mistura de cose, che offendono grandemente l'udito purgato de i giudiciosi; essendo che si troua in esse poco ordine; ne si scorge modo alcuno stabile di Harmonia. Queste ragioni sono buone; disse il Viola; & per dire il uero, chi vuol comporre una cantilena Chromaticha, bisogna che imiti in ciò gli Antichi; ne bisogna allontanarsi molto dal modo loro; & bisogna etiandio osseruare i Tuoni, ò Modi, de i quali essi
Antichi erano grandi osseruatori, & faceuano gran stima; se non vuol far le cose di suo capo; ma non saranno poi le cose; che loro dicono che sono. Percioche si come uolendo fare una Veste, fà dibisogno che ui sia la materia & la forma atta à far cotal Veste; altramente non sarebbe Veste; ma un'altra
cosa, & forse strana; cosi à uoler comporre vna cantilena Chromaticha, bisogna che ui concorrino tutte quelle cose, che fanno all'esser di cotal
cantilena.Vide cap. 9
Lib. 6. Supple. Onde quando nelle compositioni loro usano altri Interualli, che Chromatici;
secondo 'l mio parere; questo non è comporre Chromatico; ma in un modo, che non hà
ne dell'uno, ne anco dell'altro. Però parmi, che dourebbono usar solamente quelle chorde
& Interualli, che sono contenute nel Tetrachordo Chromatico, se uogliono comporre
Chromatico; come dicono; & non altre chorde straniere; come essi fanno. E' uero, rispose
M. Adriano; Et quantunque le cose, ch'io hò detto, siano basteuoli à dimostrare il contrario di quello, che sentono; tuttauia aggiungerò anco quest'altra; che non è di poca importanza; che usano nel cantare alcuni Interualli tanto sgarbati, come sono Semidiatessaron,
Tritoni, Semidiapente, Diapente superflui, & anco Diapason false, con altri simili, che apportano poco piacere all'udito; Nondimeno li hanno nel numero de i buoni; se bene i buoni & dotti Antichi molto li schiuauano & aborriuano; percioche mai non
li hebbero per
consonanti nelle Modulationi loro, & che potessero far buona harmonia; se non erano contenuti nelle lor proportioni del Genere superparticolare. Disse allora M. Claudio. Vi sò
che dire, che osseruano questa legge; Voi Messere ui sete affaticato molto insieme con molt'altri buoni Musici più Antichi
di uoi, nel ridurre la Musica ad una certa maniera, ò forma, c'hauesse qualche grauità & maestà insieme; ma con costoro è stato quasi uano il uostro disegno; percioche oltra che non osseruano i precetti buoni dell'Arte; insegnano anco
& essortano gli altri à guastare il buono & ben ordinato, & à far peggio che sanno. Et quando fanno alcuna cosa che sia fuori del buono & bello della Musica; si coprono col scudo
dell'ignoranza; & dicono che sono cose fatte nel Genere Chromatico; se ben non conoscono, ne sanno quel ch'ello sia. Vedete di gratia quanto siano costoro non solo degni di biasimo; ma etiandio di castigo. Sapiate, risposi egli;Boeth. lib.
1. c. 1. Musices. che se gli Antichi Lacedemonij scacciarono & bandirono della sua Città quel gran Musico Timotheo inuentore del Chromaticho
page 216
(come dicono) per hauer solamente nel solito Istrumento aggiunto una sol chorda; pensate
pure che se fussero à i tempi nostri Giudici di costoro, quel che farebbono. Son certo che li
scacciarebbono del mondo; acciò non amorbassero gli huomini con tante loro strane cose,
che fanno vdire, le quali nascono; non già da una chorda sola, che aggiungono al solito &
usato numero; ma da molte & imolte aggiunte senza verun proposito, & senza giudicio. Costoro si possono assimigliare à quello
insolentissimo & ambitiosissimo Herostrato,Io. Rauis.
Text. in Officina, De
Arrogantibus. &
Au. Gell.
lib. 2. c. 6.
Noct. Attic. ilquale
abbrusciò l'antichissimo & celebratissimo Tempio di Diana Effesina; non per odio di lei;
ma per lasciar memoria di sè à i posteri con una tanta sceleratezza; poi che poca gratia
hebbe di farlo con fatti illustri, che lui hauesse operato. Onde, costoro perche non hanno potuto acquistar nome d'eccellenti Musici con le opere loro, ci sono affaticati & anco
s'affaticano di fare il peggio che sanno, per acquistar nome, & diuentar famosi. Ma il pensiero li và fallito; perche si vede, che 'l mondo tien poco conto di simili huomini.Vide Prooemium Lib.
1. Supple. Dissi
allora, voltatomi uerso M. Adriano; Messere, bastaui fin quì hauer ragionato di costoro;
& lasciateli andar per uostra fè; che con tutto 'l peggio che faranno; non credo che siano
mai tanto stimati ualorosi nella Musica, come sete stimato uoi & molt'altri, che non uanno
dietro à queste cose tanto strane. Però hauendo voi fatto mentione d'una sola Chorda
aggiunta da Timotheo; uerremo à dimostrar la proposta; ritrouando questa solamente;
per esser breue; la quale sarà Terza in ogni Tetrachordo; & farà la uarietà del Genere.
Ma perch'io dissi nella Seconda proposta, che la Prima, la Seconda, & la Quarta chorda d'ogni Tetrachordo diatonico, sono etiandio communi alla Prima, Seconda, & Quarta
d'ogni Tetrachordo chromatico; però cercaremo solamente d'accommodar la Terza tra
le nominate Diatoniche, la quale sia lontana dalla Quarta acuta d'ogni Tetrachordo per
un Semiditono, ò Trihemituono. Bisogna però auertir quello, che più fiate hò detto; che
la Proslambanomenos & la Mese siano lontane da i tetrachordi Hypaton & Diezeugmenon per un Tuono maggiore; quella da Hypate hypaton, & questa da Paramese. Questo
ci ricordiamo; disse il Viola; hauendolo uoi detto anche per inanti. Ma perche si pone
questa chorda del Tetrachordo Chromatico lontana dalla Quarta chorda per un Semiditono; se d'alcuno non è stato mai fatto mentione in simil Genere di questo interuallo?
Risposi; Anzi TolomeoHarmonic.
Lib. 1. c. 15 parlando del Genere Chromatico molle, pone questo Interuallo, il quale è il terzo del suo Tetrachordo, sotto la proportione Sesquiquinta. Ma la ragione ui hò detto anco nelle Istitutioni,2. par.
cap. 47. & al presente son per replicarla: Percioche se
bene gli Antichi hanno segnato altri Interualli, ò proportioni al Trihemituono, che non
è quella del nostro Semiditono; tuttauia, com'hò detto ancora, parmi che inutilmente s'aggiunga una chorda in qual si uoglia Istrumento; quando con un'altra non faccia
Consonanza alcuna. Et perche l'altre Chorde, che s'aggiungono, non fanno con la
Quarta de i Tetrachordi alcuna consonanza; però dico, che vanamente & senza utilità
cotali Chorde si pongono ne gli Istrumenti. La onde giudicai, & anco son di parere, che 'l
Semiditono del diatonico, posto da Tolomeo nella proportione Sesquiquinta, il quale
poco fà ui hò commemorato, & serue etiandio per il Trihemituono del Chromatico molle, douessi esser quello, che si hauesse da noi adoperare nel Chromatico, & non altro interuallo; il quale è al tutto senza consonanza. Aggiunse M. Claudio; Parmi ueramente,
c'habbiate ragione. Ne sò ueder cosa alcuna, che ui possa esser contraria. Onde incominciarete à dimostrar quello, c'hauete proposto, se non hauete altro che dirci. Vdito
questo, senza por tempo di mezo, incominciai, dicendo. Siano le Chorde diatoniche a.
b. c & e. & sia a. Proslambanomenos, & b. la Prima chorda più graue dell'altre seguenti
del Tetrachordo Hypaton diatonico, c. la Seconda, & e. la Quarta. Et siano a. con b. distanti per un Tuon maggiore, b & c. per il maggior Semituono, & sia b & e. la Diatessaron,
& a con e. la Diapente. Faccio hora la chorda d. con la e. in proportione Sesquiquinta;
onde, per la Duodecima Definitione del Secondo giorno; d & e. sarà Trihemituono. Et
perche, per il Primo Corollario della Trentesima, pur del detto giorno; leuato ab. Tuono maggiore, da a & e. Diapente; resta b & e. Diatessaron. Simigliantemente; perche, per
page 217
la Ventesimasettima del giorno istesso; due Tuoni l'un maggiore & l'altro minore, con vn
Semituono maggiore appresso fanno la Diatessaron; & essendo bc. & cd, insieme; per la
Decimanona pur del Secondo giorno, Tuono minore; seguita; che d & e. contiene il
Tuono maggiore & il maggior Semituono, i quali, per la Ventesimasesta del Secondo fanno il Semiditono, ò Trihemituono. Viene adunque d & e. ad essere 'l Trihemituono.
, & b molli. Dopoi; non mi par,
ch'elle siano Chromatiche; percioche le chorde antiche haueano i lor proprij nomi; come
sono Hypate, Lychanos, Trite & l'altre; nondimeno le chorde, che pongono costoro nelle
lor cantilene, non si possono denominare con alcuno de i detti nomi; oueramente con altri, che siano simili à quelli. Onde è manifesto segno, che non sono, ne mai potranno esser
quello, che costoro predicano. Oltra di questo, non osseruano Modo, ò Tuono alcuno nel
loro comporre; di modo che si possa dire, questa cantilena è composta nel modo Dorio,
Ionico, ouer Frigio, ò sotto un'altro Modo; come diceuano gli Antichi; ma sono composte
di confusione; & con una certa mistura de cose, che offendono grandemente l'udito purgato de i giudiciosi; essendo che si troua in esse poco ordine; ne si scorge modo alcuno stabile di Harmonia. Queste ragioni sono buone; disse il Viola; & per dire il uero, chi vuol comporre una cantilena Chromaticha, bisogna che imiti in ciò gli Antichi; ne bisogna allontanarsi molto dal modo loro; & bisogna etiandio osseruare i Tuoni, ò Modi, de i quali essi
Antichi erano grandi osseruatori, & faceuano gran stima; se non vuol far le cose di suo capo; ma non saranno poi le cose; che loro dicono che sono. Percioche si come uolendo fare una Veste, fà dibisogno che ui sia la materia & la forma atta à far cotal Veste; altramente non sarebbe Veste; ma un'altra
cosa, & forse strana; cosi à uoler comporre vna cantilena Chromaticha, bisogna che ui concorrino tutte quelle cose, che fanno all'esser di cotal
cantilena.Vide cap. 9
Lib. 6. Supple. Onde quando nelle compositioni loro usano altri Interualli, che Chromatici;
secondo 'l mio parere; questo non è comporre Chromatico; ma in un modo, che non hà
ne dell'uno, ne anco dell'altro. Però parmi, che dourebbono usar solamente quelle chorde
& Interualli, che sono contenute nel Tetrachordo Chromatico, se uogliono comporre
Chromatico; come dicono; & non altre chorde straniere; come essi fanno. E' uero, rispose
M. Adriano; Et quantunque le cose, ch'io hò detto, siano basteuoli à dimostrare il contrario di quello, che sentono; tuttauia aggiungerò anco quest'altra; che non è di poca importanza; che usano nel cantare alcuni Interualli tanto sgarbati, come sono Semidiatessaron,
Tritoni, Semidiapente, Diapente superflui, & anco Diapason false, con altri simili, che apportano poco piacere all'udito; Nondimeno li hanno nel numero de i buoni; se bene i buoni & dotti Antichi molto li schiuauano & aborriuano; percioche mai non
li hebbero per
consonanti nelle Modulationi loro, & che potessero far buona harmonia; se non erano contenuti nelle lor proportioni del Genere superparticolare. Disse allora M. Claudio. Vi sò
che dire, che osseruano questa legge; Voi Messere ui sete affaticato molto insieme con molt'altri buoni Musici più Antichi
di uoi, nel ridurre la Musica ad una certa maniera, ò forma, c'hauesse qualche grauità & maestà insieme; ma con costoro è stato quasi uano il uostro disegno; percioche oltra che non osseruano i precetti buoni dell'Arte; insegnano anco
& essortano gli altri à guastare il buono & ben ordinato, & à far peggio che sanno. Et quando fanno alcuna cosa che sia fuori del buono & bello della Musica; si coprono col scudo
dell'ignoranza; & dicono che sono cose fatte nel Genere Chromatico; se ben non conoscono, ne sanno quel ch'ello sia. Vedete di gratia quanto siano costoro non solo degni di biasimo; ma etiandio di castigo. Sapiate, risposi egli;Boeth. lib.
1. c. 1. Musices. che se gli Antichi Lacedemonij scacciarono & bandirono della sua Città quel gran Musico Timotheo inuentore del Chromaticho
page 216
(come dicono) per hauer solamente nel solito Istrumento aggiunto una sol chorda; pensate
pure che se fussero à i tempi nostri Giudici di costoro, quel che farebbono. Son certo che li
scacciarebbono del mondo; acciò non amorbassero gli huomini con tante loro strane cose,
che fanno vdire, le quali nascono; non già da una chorda sola, che aggiungono al solito &
usato numero; ma da molte & imolte aggiunte senza verun proposito, & senza giudicio. Costoro si possono assimigliare à quello
insolentissimo & ambitiosissimo Herostrato,Io. Rauis.
Text. in Officina, De
Arrogantibus. &
Au. Gell.
lib. 2. c. 6.
Noct. Attic. ilquale
abbrusciò l'antichissimo & celebratissimo Tempio di Diana Effesina; non per odio di lei;
ma per lasciar memoria di sè à i posteri con una tanta sceleratezza; poi che poca gratia
hebbe di farlo con fatti illustri, che lui hauesse operato. Onde, costoro perche non hanno potuto acquistar nome d'eccellenti Musici con le opere loro, ci sono affaticati & anco
s'affaticano di fare il peggio che sanno, per acquistar nome, & diuentar famosi. Ma il pensiero li và fallito; perche si vede, che 'l mondo tien poco conto di simili huomini.Vide Prooemium Lib.
1. Supple. Dissi
allora, voltatomi uerso M. Adriano; Messere, bastaui fin quì hauer ragionato di costoro;
& lasciateli andar per uostra fè; che con tutto 'l peggio che faranno; non credo che siano
mai tanto stimati ualorosi nella Musica, come sete stimato uoi & molt'altri, che non uanno
dietro à queste cose tanto strane. Però hauendo voi fatto mentione d'una sola Chorda
aggiunta da Timotheo; uerremo à dimostrar la proposta; ritrouando questa solamente;
per esser breue; la quale sarà Terza in ogni Tetrachordo; & farà la uarietà del Genere.
Ma perch'io dissi nella Seconda proposta, che la Prima, la Seconda, & la Quarta chorda d'ogni Tetrachordo diatonico, sono etiandio communi alla Prima, Seconda, & Quarta
d'ogni Tetrachordo chromatico; però cercaremo solamente d'accommodar la Terza tra
le nominate Diatoniche, la quale sia lontana dalla Quarta acuta d'ogni Tetrachordo per
un Semiditono, ò Trihemituono. Bisogna però auertir quello, che più fiate hò detto; che
la Proslambanomenos & la Mese siano lontane da i tetrachordi Hypaton & Diezeugmenon per un Tuono maggiore; quella da Hypate hypaton, & questa da Paramese. Questo
ci ricordiamo; disse il Viola; hauendolo uoi detto anche per inanti. Ma perche si pone
questa chorda del Tetrachordo Chromatico lontana dalla Quarta chorda per un Semiditono; se d'alcuno non è stato mai fatto mentione in simil Genere di questo interuallo?
Risposi; Anzi TolomeoHarmonic.
Lib. 1. c. 15 parlando del Genere Chromatico molle, pone questo Interuallo, il quale è il terzo del suo Tetrachordo, sotto la proportione Sesquiquinta. Ma la ragione ui hò detto anco nelle Istitutioni,2. par.
cap. 47. & al presente son per replicarla: Percioche se
bene gli Antichi hanno segnato altri Interualli, ò proportioni al Trihemituono, che non
è quella del nostro Semiditono; tuttauia, com'hò detto ancora, parmi che inutilmente s'aggiunga una chorda in qual si uoglia Istrumento; quando con un'altra non faccia
Consonanza alcuna. Et perche l'altre Chorde, che s'aggiungono, non fanno con la
Quarta de i Tetrachordi alcuna consonanza; però dico, che vanamente & senza utilità
cotali Chorde si pongono ne gli Istrumenti. La onde giudicai, & anco son di parere, che 'l
Semiditono del diatonico, posto da Tolomeo nella proportione Sesquiquinta, il quale
poco fà ui hò commemorato, & serue etiandio per il Trihemituono del Chromatico molle, douessi esser quello, che si hauesse da noi adoperare nel Chromatico, & non altro interuallo; il quale è al tutto senza consonanza. Aggiunse M. Claudio; Parmi ueramente,
c'habbiate ragione. Ne sò ueder cosa alcuna, che ui possa esser contraria. Onde incominciarete à dimostrar quello, c'hauete proposto, se non hauete altro che dirci. Vdito
questo, senza por tempo di mezo, incominciai, dicendo. Siano le Chorde diatoniche a.
b. c & e. & sia a. Proslambanomenos, & b. la Prima chorda più graue dell'altre seguenti
del Tetrachordo Hypaton diatonico, c. la Seconda, & e. la Quarta. Et siano a. con b. distanti per un Tuon maggiore, b & c. per il maggior Semituono, & sia b & e. la Diatessaron,
& a con e. la Diapente. Faccio hora la chorda d. con la e. in proportione Sesquiquinta;
onde, per la Duodecima Definitione del Secondo giorno; d & e. sarà Trihemituono. Et
perche, per il Primo Corollario della Trentesima, pur del detto giorno; leuato ab. Tuono maggiore, da a & e. Diapente; resta b & e. Diatessaron. Simigliantemente; perche, per
page 217
la Ventesimasettima del giorno istesso; due Tuoni l'un maggiore & l'altro minore, con vn
Semituono maggiore appresso fanno la Diatessaron; & essendo bc. & cd, insieme; per la
Decimanona pur del Secondo giorno, Tuono minore; seguita; che d & e. contiene il
Tuono maggiore & il maggior Semituono, i quali, per la Ventesimasesta del Secondo fanno il Semiditono, ò Trihemituono. Viene adunque d & e. ad essere 'l Trihemituono.

PROPOSTA XII.

PROPOSTA XIII.

PROPOSTA XIIII.
PROPOSTA XV.
PROPOSTA XVI.
PROPOSTA XVII.

PROPOSTA XVIII.

PROPOSTA XIX.

PROPOSTA XX.
PROPOSTA XXI.
PROPOSTA XXII.
PROPOSTA XXIII.

PROPOSTA XXIIII.
PROPOSTA XXV.
PROPOSTA XXVI.

DIMOSTRATIONI HARMONICHE DEL REV. M. GIOSEFFO ZARLINO DA CHIOGGIA, Maestro di Cappella della Serenissima Signoria DI VENETIA: RAGIONAMENTO QVINTO.
DEFINITIONE PRIMA.
DEFINITIONE II.
DEFINITIONE III.
DEFINITIONE IIII.
DEFINITIONE V.
DEFINITIONE VI.
DEFINITIONE VII.
DEFINITIONE VIII.
 & c. & anco era la prima Diapason, che naturalmente era considerata nella Musica. Onde fui sforzato da ogni ragione à credere; che
essendo prima tra l'altre, le quali (per l'aggiunger delle chorde. Γ. A &
& c. & anco era la prima Diapason, che naturalmente era considerata nella Musica. Onde fui sforzato da ogni ragione à credere; che
essendo prima tra l'altre, le quali (per l'aggiunger delle chorde. Γ. A &  . nel graue; & d. e.
s. g & aa. con molt'altre nell'acuto) nascono dopo questa; ch'anco douesse tra tutte l'altre
tenere il Primo luogo; & ch'essendo in questo Genere d'ogni altra più naturale; ella douesse etiandio tenere il nome di prima Specie; & che l'altre, ch'à questa succedeuano di
mano in mano, il lor luogo tenessero; secondo che per ordine erano collocate; & che hauessero i lor principij nelle chorde significate & notate per le Sette prime lettere, che ui
hò mostrato. Questa adunque è stata la prima cagione, che mi hà mosso à far questo.
page 247
Voltosi allora M. Claudio uerso M. Adriano, & disse; Che ne dite uoi Messere? parmi ch'à
questo non si possa contradire per alcun modo. In uerità, rispose il buon Vecchio; che
non si puote; & parmi che M. Gioseffo habbia una gran ragione. Et per dirui il uero; non
ui era cosa nella Musica, che mi paresse più strana di questa. Percioche hauendo noi
quest'ordine de uoci Vt. Re. Mi. Fa. Sol. La. era pur contra 'l douere, che la Prima specie de tutte le Prime consonanze hauesse ad incominciar nella Seconda uoce, & non nella prima di tale ordine; però sommamente hò in piacere, che M. Gioseffo uoglia ragionar di questa cosa; & che sia entrato in questa buona opinione di ordinar questo disordinato ordine. Messere; gli dissi allora; mi allegro molto, che à uoi piaccia questo mio pensiero. Onde hauendoui sempre conosciuto per Huomo d'intelletto & di giudicio; non
mi poteua capire nell'animo, che le cose fatte con ragione ui hauessero à dispiacere. Però uoglio seguitare allegramente la Seconda cagione, la quale è quell'istessa, c'hà mosso
uoi. Perche hauendo i nostri Maggiori ridotto l'ordine delle Chorde musicali in Hexachordi; & hauendoli attribuito quell'ordine de Voci, che nominato hauete; più tosto
bisognaua dar principio à queste Specie nella prima uoce Vt; che nella Re, che è la Seconda; accioche quando si peruiene alla Quarta specie, al modo loro; non si hauesse à ritornare in dietro, & incominciar nel Quarto luogo di tale ordine dalla uoce Vt, la quale, per ogni douere, dourebbe tenere il primo, & non l'ultimo luogo; come uedete fatro nella loro Quarta specie de tutte le prime Consonanze. Questa adunque fù la Seconda cagione. Questa è cagione ragioneuole, disse il Viola. Ond'io soggiunsi; La Terza
cagione fu; che oltra quel c'hò detto, il quale è tutto fatto con ragione; uedeua, che ponendo per fondamento di queste Specie la Prima chorda della nominata diuisa Diapason; & applicandole (per parlarui al modo prattico) le uoci Vt. Re. Mi. Fa. Sol. La; lasciamo star da un canto, che queste Sillabe seruino alla memoria; per ricordarsi, che la
Prima è il fondamento della Prima specie di ciascheduna delle nominate Consonanze,
& la Seconda quello della Seconda, & cosi l'altre per ordine; haueressimo etiandio in
questa Prima specie adunate tutte le Specie dell'altre Consonanze nominate, le quali ordinatamente hauerebbono il loro principio & fondamento nella C. prima chorda della
detta Diapason, & nella Vt. prima sillaba del nostro Hexachordo; il che tornarebbe sommamente bene, & meglio di quello, che hanno fatto i nostri Antichi, i quali hauendo prima collocato la Prima specie nella chorda A, & nella sillaba Re; quantunque seguitassero
poi, & il tutto li tornasse commodo; tuttauia non poterono porre le Specie della Diapente in cotal modo l'una dopo l'altra; percioche la Seconda specie non poteua cadere tra
la chorda
. nel graue; & d. e.
s. g & aa. con molt'altre nell'acuto) nascono dopo questa; ch'anco douesse tra tutte l'altre
tenere il Primo luogo; & ch'essendo in questo Genere d'ogni altra più naturale; ella douesse etiandio tenere il nome di prima Specie; & che l'altre, ch'à questa succedeuano di
mano in mano, il lor luogo tenessero; secondo che per ordine erano collocate; & che hauessero i lor principij nelle chorde significate & notate per le Sette prime lettere, che ui
hò mostrato. Questa adunque è stata la prima cagione, che mi hà mosso à far questo.
page 247
Voltosi allora M. Claudio uerso M. Adriano, & disse; Che ne dite uoi Messere? parmi ch'à
questo non si possa contradire per alcun modo. In uerità, rispose il buon Vecchio; che
non si puote; & parmi che M. Gioseffo habbia una gran ragione. Et per dirui il uero; non
ui era cosa nella Musica, che mi paresse più strana di questa. Percioche hauendo noi
quest'ordine de uoci Vt. Re. Mi. Fa. Sol. La. era pur contra 'l douere, che la Prima specie de tutte le Prime consonanze hauesse ad incominciar nella Seconda uoce, & non nella prima di tale ordine; però sommamente hò in piacere, che M. Gioseffo uoglia ragionar di questa cosa; & che sia entrato in questa buona opinione di ordinar questo disordinato ordine. Messere; gli dissi allora; mi allegro molto, che à uoi piaccia questo mio pensiero. Onde hauendoui sempre conosciuto per Huomo d'intelletto & di giudicio; non
mi poteua capire nell'animo, che le cose fatte con ragione ui hauessero à dispiacere. Però uoglio seguitare allegramente la Seconda cagione, la quale è quell'istessa, c'hà mosso
uoi. Perche hauendo i nostri Maggiori ridotto l'ordine delle Chorde musicali in Hexachordi; & hauendoli attribuito quell'ordine de Voci, che nominato hauete; più tosto
bisognaua dar principio à queste Specie nella prima uoce Vt; che nella Re, che è la Seconda; accioche quando si peruiene alla Quarta specie, al modo loro; non si hauesse à ritornare in dietro, & incominciar nel Quarto luogo di tale ordine dalla uoce Vt, la quale, per ogni douere, dourebbe tenere il primo, & non l'ultimo luogo; come uedete fatro nella loro Quarta specie de tutte le prime Consonanze. Questa adunque fù la Seconda cagione. Questa è cagione ragioneuole, disse il Viola. Ond'io soggiunsi; La Terza
cagione fu; che oltra quel c'hò detto, il quale è tutto fatto con ragione; uedeua, che ponendo per fondamento di queste Specie la Prima chorda della nominata diuisa Diapason; & applicandole (per parlarui al modo prattico) le uoci Vt. Re. Mi. Fa. Sol. La; lasciamo star da un canto, che queste Sillabe seruino alla memoria; per ricordarsi, che la
Prima è il fondamento della Prima specie di ciascheduna delle nominate Consonanze,
& la Seconda quello della Seconda, & cosi l'altre per ordine; haueressimo etiandio in
questa Prima specie adunate tutte le Specie dell'altre Consonanze nominate, le quali ordinatamente hauerebbono il loro principio & fondamento nella C. prima chorda della
detta Diapason, & nella Vt. prima sillaba del nostro Hexachordo; il che tornarebbe sommamente bene, & meglio di quello, che hanno fatto i nostri Antichi, i quali hauendo prima collocato la Prima specie nella chorda A, & nella sillaba Re; quantunque seguitassero
poi, & il tutto li tornasse commodo; tuttauia non poterono porre le Specie della Diapente in cotal modo l'una dopo l'altra; percioche la Seconda specie non poteua cadere tra
la chorda  . & la F. Onde furono costretti ad incominciar nella chorda D. & seguitar di
mano in mano. Ma non potero già dar principio alle specie delle loro Diatessaron in cotal chorda; percioche la Terza specie à patto alcuno non può cascare tra la chorda F. &
la
. & la F. Onde furono costretti ad incominciar nella chorda D. & seguitar di
mano in mano. Ma non potero già dar principio alle specie delle loro Diatessaron in cotal chorda; percioche la Terza specie à patto alcuno non può cascare tra la chorda F. &
la  . essendo che (come sapete, & come lo chiamate) è un Tritono, il quale è Interuallo
dissonantissimo nella Musica. Questo è pur troppo uero; disse M. Adriano; & ueramente
ui dico, che quest'ordine è molto necessario; prima per regolare & indrizzar ben le cose
della Musica; dopoi è vtile per la memoria delle cose; com'hauete detto; però laudo molto questa cosa. Et se bene ad alcuno nella prima uista questo parerà forse strano, difficile &
amaro; non dubitate, che l'uso farà facile & addolcirà il tutto. Cosi credo Messere, diss'io.
Ma la Quarta cagione, che m'ha mosso è questa; perch'io uedeua di potere accommodare i nostri Modi, ò Tuoni, che sono come ui potete ricordare) Dodici; l'un dopo l'altro per ordine naturale & non interrotto; come fin hora si è fatto. Essendo che accommodando, ò attribuendo il Primo modo alla prima Diapason C & c. & alla prima uoce Vt;
seguendo l'altre sillabe, ò uoci, & gli altri Modi per ordine; le corde loro finali ordinatamente ueniuano C. D. E. F. G & a. & le Modulationi loro con bello & regolato ordine
ueniuano à finire nelle uoci Vt. Re. Mi. Fa. Sol. La; come potrete à suoi luoghi uedere. Et
le Sedici chorde. Γ. A.
. essendo che (come sapete, & come lo chiamate) è un Tritono, il quale è Interuallo
dissonantissimo nella Musica. Questo è pur troppo uero; disse M. Adriano; & ueramente
ui dico, che quest'ordine è molto necessario; prima per regolare & indrizzar ben le cose
della Musica; dopoi è vtile per la memoria delle cose; com'hauete detto; però laudo molto questa cosa. Et se bene ad alcuno nella prima uista questo parerà forse strano, difficile &
amaro; non dubitate, che l'uso farà facile & addolcirà il tutto. Cosi credo Messere, diss'io.
Ma la Quarta cagione, che m'ha mosso è questa; perch'io uedeua di potere accommodare i nostri Modi, ò Tuoni, che sono come ui potete ricordare) Dodici; l'un dopo l'altro per ordine naturale & non interrotto; come fin hora si è fatto. Essendo che accommodando, ò attribuendo il Primo modo alla prima Diapason C & c. & alla prima uoce Vt;
seguendo l'altre sillabe, ò uoci, & gli altri Modi per ordine; le corde loro finali ordinatamente ueniuano C. D. E. F. G & a. & le Modulationi loro con bello & regolato ordine
ueniuano à finire nelle uoci Vt. Re. Mi. Fa. Sol. La; come potrete à suoi luoghi uedere. Et
le Sedici chorde. Γ. A.  . C. D. E. F. G. a.
. C. D. E. F. G. a.  c. d. e. f. g & aa. veniuano à contenere essi
Modi tutti; tanto gli Autentichi, quanto i Plagali; senz'auanzar chorda alcuna.
page 248
L'utile & il commodo adunque, che apporta quest'ordine; per quello che mi pare; mi fece entrare già molti giorni sono in questo pensiero. Questi m'inuitauano & persuadeuano; la ragione mi daua animo & essortaua; & la natura istessa della cosa mi costringeua & facea uiolenza. Il che scorgerete da quel che son per dimostrarui; di modo che se
mai per il passato in questo hebbi altro parere, & hebbi animo di seguitar i nostri Antichi; non dico de Greci; hora in tutto & per tutto mi rimuouo. Molte fiate, disse M. Francesco; de questi ordini de Specie mi son forte marauigliato tra me stesso, & non sapea ritrouare altra ragione; se non che i Nostri maggiori hauessero cosi voluto. Ma molto mi
sono piaciute le ragioni, che hauete detto; & se bene altro non portasse meco à Ferrara; porterò almeno questo, come cosa bella & noua; & ui prometto che da noi la porremo in prattica con tutto 'l nostro potere. Non uoglio pero che crediate, risposi; ch'io uoglia esser destruttore delle cose de gli Antichi; percioche non hebbi mai tanto tristo pensero; ma uoglio ben, che pensate; che lasciando le cose loro nel loro essere, le uerrò à mutare solamente secondo certi accidenti; come è di ordine di Primo & di Secondo, senza'alcun'altra alteratione della loro sostanza; & cercarò sempre di facilitar le cose di questa Scienza. Ne ui pensate ancora, ch'io possa fare altramente; essendo che qual si uoglia
Specie di consonanza; quanto alla sua forma è sempre immutabile & inuariabile; ma
quanto poi à gli accidenti, i quali anco sono estrinsechi; come di Primo, ò Secondo; ò di
Graue, ò di Acuto; si può senz'alcuna alteratione, quanto al nome, uariare. Et uolete uedere, che cosi sia; pigliate qual si uoglia Diapason, & datele nome di Prima, ò di Seconda; come meglio ui piace; tale accidente non haurà forza di farle uariar forma; Percioche se uoi le attribuisti mille & poi mille nomi, & la riportaste, ouer le deste mille luoghi
uariati; mai ella si cambierà di forma & sostanza; ma resterà sempre quella; essendo che 'l
nome di Primo, ò di Secondo nasce da pura Relatione, la quale tra gli altri accidenti è
debolissimo & estrinseco delle cose ridotte in un'ordine. Onde tale Relatione si può ad
ogni nostro piacere mutare; senza uarietà alcuna della Forma, ò della Sostanza delle cose. Ma se in lei si rimouerà alcun Tuono ò Semituono; trasportandolo verso l'acuto, ò
verso 'l graue; non è dubio, che tale Diapason non sarà com'ella era prima; ma cambierà
la prima forma in un'altra; come da quello ch'io mostrai nel Cap. 16. & 17. della Terza
parte delle Istititioni si può comprendere. Percioche sarà mutata nelle cose intrinseche
& essentiali. Onde per ritornare à dir qualche cosa al proposito, dico; che se alla Diapason D & d. hò dato il Secondo luogo nell'ordine delle sue specie, & alla C & c. il Primo;
per questo, ne l'una, ne meno l'altra hò mutato di forma & di essentia; ma sono nel primo
loro essere. Et se i nostri Antichi attribuirono alla Diapason posta tra Proslambanomenos & Mese il nome di Prima specie; lo fecero, perche la Proslambanomenos era la
Prima chorda dell'ordine de i loro Suoni; la onde era 'l douere che in cotal chorda, come prima d'ogni altra, dessero principio alle loro Specie; tanto più, perche non hebbero mai in consideratione, che la nominata Diapason fusse diuisa in harmonica diuisione,
ò non; come habbiamo noi; & ciò non senza proposito; Essendo che hauendo noi al loro ordine aggiunto un'altra chorda nel graue, la quale chiamate Gamma vt; & considerando la detta Diapason C & c. al modo nominato diuisa; sà dibisogno, che di lei habbiamo altra consideratione. Disse qui il Sig. Desiderio; In uerità che è cosa ragioneuole &
lodeuole molto; che siate entrato in questo honorato pensiero, degno da essere abbracciato da ogn'uno; perche mi par uedere, c'hauerete accommodato molto gentilmente
le cose della Musica. Ond'io à questo soggiunsi; Vi voglio ancora aggiungere, oltra l'altre,
una cagione, che mi spinse à uolere tener quest'ordine; la quale hor'hora mi è souenuta;
& è questa; perche dall'ordine, che nasce da queste specie delle prime Consonanze fatto
in cotal maniera, io poteua ordinare i Modi l'un doppo l'altro, secondo la mente de gli
Antichi; percioche accommodando 'l Primo modo alla Prima nostra Diapason C & c. &
il Terzo alla D & d. & gli altri poi per ordine; ueniua ad accommodar questi tre modi à i
loro tre primi & principali; come il Primo al Dorio, il Secondo al Frigio, & il Terzo al
page 249
Lidio, i quali sono distanti l'un dall'altro per un Tuono; nel modo, che sono i modi di essi
Antichi; come ne i loro Scritti si può uedere; & massime nel Cap. 10. del 2. Lib. de gli Harmonici di Tolomeo. E' vero quello, che dite; disse il Sig. Desiderio; & per quello, che
mi ricordo, l'hò ueduto anch'io appresso de molti Autori, tanto Greci, quanto Latini.
Vi ricordate bene; risposi; & di questo forse che ne ragionerò ne i miei Sopplimenti; secondo che mi uerrà l'occasione. Ma questo, per hora ui potrà bastare; per farui lasciar da
un canto le marauiglie; se pure alcuna in uoi ne hauete; & che ui potrebbono auenire intorno questa cosa. Io per me; disse M. Adriano; ne son fuori; perche le ragioni, c'hauete addotto mi costringono à confessar, che questo sia ben detto, & ben fatto. Questa cosa è troppo ragioneuole; soggiunse M. Claudio; & li uorrebbe assai contrarij à distruggerla. Che ne dite uoi M. Francesco? Questo è uero; egli rispose; ne hà contradittione alcuna;
onde piacendoui M. Gioseffo; seguitarete il resto. Cosi uoglio fare; dissi; poi che io uedo,
che 'l mio parlare non ui torna in dispiacere. Ma ui uoglio prima dire; che se bene sopra di
questa cosa li sarebbe da dire assai; uoglio però hauer fatto fine; & se 'l ui resterà qualche
dubio intorno alla materia de i Modi, potrete (leggendo la Quarta parte delle mie Istitutioni & il Sesto Libro de i miei sudetti SopplimentiCap. 3.) d'ogni dubio, che ui potesse occor-
rere, pienamente esser risolti. Passerò adunque à dirui dell'altre Specie, seguitando
questo nuouo Ordine.
c. d. e. f. g & aa. veniuano à contenere essi
Modi tutti; tanto gli Autentichi, quanto i Plagali; senz'auanzar chorda alcuna.
page 248
L'utile & il commodo adunque, che apporta quest'ordine; per quello che mi pare; mi fece entrare già molti giorni sono in questo pensiero. Questi m'inuitauano & persuadeuano; la ragione mi daua animo & essortaua; & la natura istessa della cosa mi costringeua & facea uiolenza. Il che scorgerete da quel che son per dimostrarui; di modo che se
mai per il passato in questo hebbi altro parere, & hebbi animo di seguitar i nostri Antichi; non dico de Greci; hora in tutto & per tutto mi rimuouo. Molte fiate, disse M. Francesco; de questi ordini de Specie mi son forte marauigliato tra me stesso, & non sapea ritrouare altra ragione; se non che i Nostri maggiori hauessero cosi voluto. Ma molto mi
sono piaciute le ragioni, che hauete detto; & se bene altro non portasse meco à Ferrara; porterò almeno questo, come cosa bella & noua; & ui prometto che da noi la porremo in prattica con tutto 'l nostro potere. Non uoglio pero che crediate, risposi; ch'io uoglia esser destruttore delle cose de gli Antichi; percioche non hebbi mai tanto tristo pensero; ma uoglio ben, che pensate; che lasciando le cose loro nel loro essere, le uerrò à mutare solamente secondo certi accidenti; come è di ordine di Primo & di Secondo, senza'alcun'altra alteratione della loro sostanza; & cercarò sempre di facilitar le cose di questa Scienza. Ne ui pensate ancora, ch'io possa fare altramente; essendo che qual si uoglia
Specie di consonanza; quanto alla sua forma è sempre immutabile & inuariabile; ma
quanto poi à gli accidenti, i quali anco sono estrinsechi; come di Primo, ò Secondo; ò di
Graue, ò di Acuto; si può senz'alcuna alteratione, quanto al nome, uariare. Et uolete uedere, che cosi sia; pigliate qual si uoglia Diapason, & datele nome di Prima, ò di Seconda; come meglio ui piace; tale accidente non haurà forza di farle uariar forma; Percioche se uoi le attribuisti mille & poi mille nomi, & la riportaste, ouer le deste mille luoghi
uariati; mai ella si cambierà di forma & sostanza; ma resterà sempre quella; essendo che 'l
nome di Primo, ò di Secondo nasce da pura Relatione, la quale tra gli altri accidenti è
debolissimo & estrinseco delle cose ridotte in un'ordine. Onde tale Relatione si può ad
ogni nostro piacere mutare; senza uarietà alcuna della Forma, ò della Sostanza delle cose. Ma se in lei si rimouerà alcun Tuono ò Semituono; trasportandolo verso l'acuto, ò
verso 'l graue; non è dubio, che tale Diapason non sarà com'ella era prima; ma cambierà
la prima forma in un'altra; come da quello ch'io mostrai nel Cap. 16. & 17. della Terza
parte delle Istititioni si può comprendere. Percioche sarà mutata nelle cose intrinseche
& essentiali. Onde per ritornare à dir qualche cosa al proposito, dico; che se alla Diapason D & d. hò dato il Secondo luogo nell'ordine delle sue specie, & alla C & c. il Primo;
per questo, ne l'una, ne meno l'altra hò mutato di forma & di essentia; ma sono nel primo
loro essere. Et se i nostri Antichi attribuirono alla Diapason posta tra Proslambanomenos & Mese il nome di Prima specie; lo fecero, perche la Proslambanomenos era la
Prima chorda dell'ordine de i loro Suoni; la onde era 'l douere che in cotal chorda, come prima d'ogni altra, dessero principio alle loro Specie; tanto più, perche non hebbero mai in consideratione, che la nominata Diapason fusse diuisa in harmonica diuisione,
ò non; come habbiamo noi; & ciò non senza proposito; Essendo che hauendo noi al loro ordine aggiunto un'altra chorda nel graue, la quale chiamate Gamma vt; & considerando la detta Diapason C & c. al modo nominato diuisa; sà dibisogno, che di lei habbiamo altra consideratione. Disse qui il Sig. Desiderio; In uerità che è cosa ragioneuole &
lodeuole molto; che siate entrato in questo honorato pensiero, degno da essere abbracciato da ogn'uno; perche mi par uedere, c'hauerete accommodato molto gentilmente
le cose della Musica. Ond'io à questo soggiunsi; Vi voglio ancora aggiungere, oltra l'altre,
una cagione, che mi spinse à uolere tener quest'ordine; la quale hor'hora mi è souenuta;
& è questa; perche dall'ordine, che nasce da queste specie delle prime Consonanze fatto
in cotal maniera, io poteua ordinare i Modi l'un doppo l'altro, secondo la mente de gli
Antichi; percioche accommodando 'l Primo modo alla Prima nostra Diapason C & c. &
il Terzo alla D & d. & gli altri poi per ordine; ueniua ad accommodar questi tre modi à i
loro tre primi & principali; come il Primo al Dorio, il Secondo al Frigio, & il Terzo al
page 249
Lidio, i quali sono distanti l'un dall'altro per un Tuono; nel modo, che sono i modi di essi
Antichi; come ne i loro Scritti si può uedere; & massime nel Cap. 10. del 2. Lib. de gli Harmonici di Tolomeo. E' vero quello, che dite; disse il Sig. Desiderio; & per quello, che
mi ricordo, l'hò ueduto anch'io appresso de molti Autori, tanto Greci, quanto Latini.
Vi ricordate bene; risposi; & di questo forse che ne ragionerò ne i miei Sopplimenti; secondo che mi uerrà l'occasione. Ma questo, per hora ui potrà bastare; per farui lasciar da
un canto le marauiglie; se pure alcuna in uoi ne hauete; & che ui potrebbono auenire intorno questa cosa. Io per me; disse M. Adriano; ne son fuori; perche le ragioni, c'hauete addotto mi costringono à confessar, che questo sia ben detto, & ben fatto. Questa cosa è troppo ragioneuole; soggiunse M. Claudio; & li uorrebbe assai contrarij à distruggerla. Che ne dite uoi M. Francesco? Questo è uero; egli rispose; ne hà contradittione alcuna;
onde piacendoui M. Gioseffo; seguitarete il resto. Cosi uoglio fare; dissi; poi che io uedo,
che 'l mio parlare non ui torna in dispiacere. Ma ui uoglio prima dire; che se bene sopra di
questa cosa li sarebbe da dire assai; uoglio però hauer fatto fine; & se 'l ui resterà qualche
dubio intorno alla materia de i Modi, potrete (leggendo la Quarta parte delle mie Istitutioni & il Sesto Libro de i miei sudetti SopplimentiCap. 3.) d'ogni dubio, che ui potesse occor-
rere, pienamente esser risolti. Passerò adunque à dirui dell'altre Specie, seguitando
questo nuouo Ordine.
DEFINITIONE IX.
DEFINITIONE X.
DEFINITIONE XI.
DEFINITIONE XII.
DEFINITIONE XIII.
DEFINITIONE XIIII.
DEFINITIONE XV.
DEFINITIONE XVI.
DEFINITIONE XVII.
--Sed scilicet vltima semperLa quale dal Petrarca breuemente nella Quarta Canzone del Lib. 1. fù esplicata in questo uerso;
Expectanda dies homini est: dicique beatus
Ante obitum nemo supremaque funera debet.
La vita il fin, e 'l dì loda la sera.Onde bisogna, ch'anco i Modi habbiano una chorda, nella quale ciascheduno habbia regolarmente à terminare, & finire; acciò si possa conoscere dal suo fine, & si possa dirittamente denominare. Questa adunque sarà la grauissima chorda delle loro Diapente; soggiunsi io; Sia poi posta nella parte più graue, oueramente nel mezo della Diapason; che questo non fà caso; & mi piace che V. Sig. si diletti de questi due Poeti; i quali sono coppiosi di belle inuentioni, & belle Sentenze; come è quella, che hauete allegata. Ma perpage 254 che le chorde de i Modi sono per tornare al proposito altramente denominate da i Nostri, di quel che faceuano gli Antichi; però non sarà male il porre una Definitione, dalla quale comprender si possa ciascheduna delle chorde antiche, à quale delle Moderne corrisponda; & sarà questa.
DEFINITIONE XVIII.

DEFINITIONE XIX.
 quadro, & di b molle; come nel Cap. 2. della Terza parte dimostrai; tuttauia non uoglio partirmi al presente dall'uso & nome de gli Antichi; essendo che io uoglio nominare col nome de i Tetrachordi, che conteneranno nelse lor quattro chorde più acute di ciascheduno; secondo 'l costume de quelli, c'hanno
speculatiuamente ragionato delle cose della Musica. Onde si come cinque sono i Tetrachordi contenuti nel numero delle Sedici chorde del nominato Monochordo; cosi saranno etiandio cinque gli Hexachordi. Ma sapiate prima; che
quadro, & di b molle; come nel Cap. 2. della Terza parte dimostrai; tuttauia non uoglio partirmi al presente dall'uso & nome de gli Antichi; essendo che io uoglio nominare col nome de i Tetrachordi, che conteneranno nelse lor quattro chorde più acute di ciascheduno; secondo 'l costume de quelli, c'hanno
speculatiuamente ragionato delle cose della Musica. Onde si come cinque sono i Tetrachordi contenuti nel numero delle Sedici chorde del nominato Monochordo; cosi saranno etiandio cinque gli Hexachordi. Ma sapiate prima; che
DEFINITIONE XX.
DEFINITIONE XXI.
DEFINITIONE XXII.
DEFINITIONE XXIII.
DEFINITIONE XXIIII.
DEFINITIONE XXV.
DEFINITIONE XXVI.
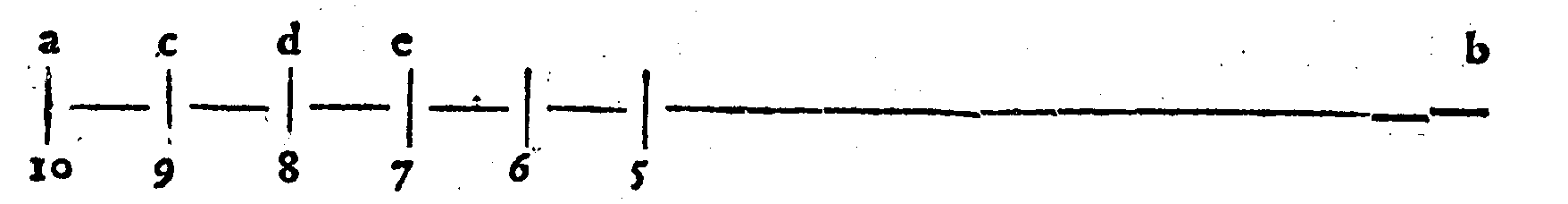
DEFINITIONE XXVII.
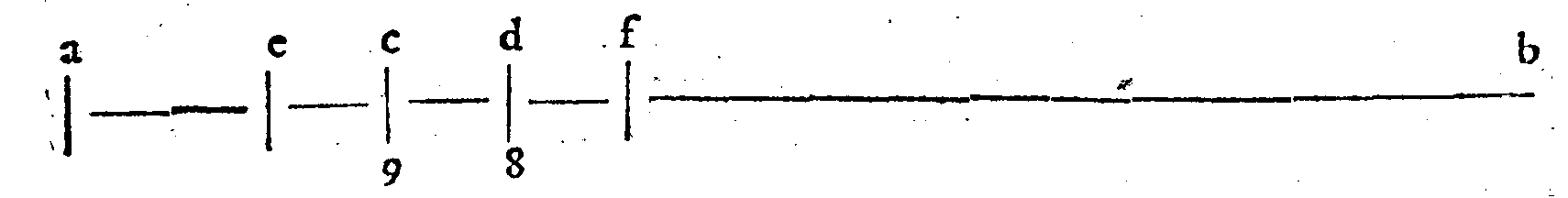
DEFINITIONE XXVIII.
PROPOSTA PRIMA.
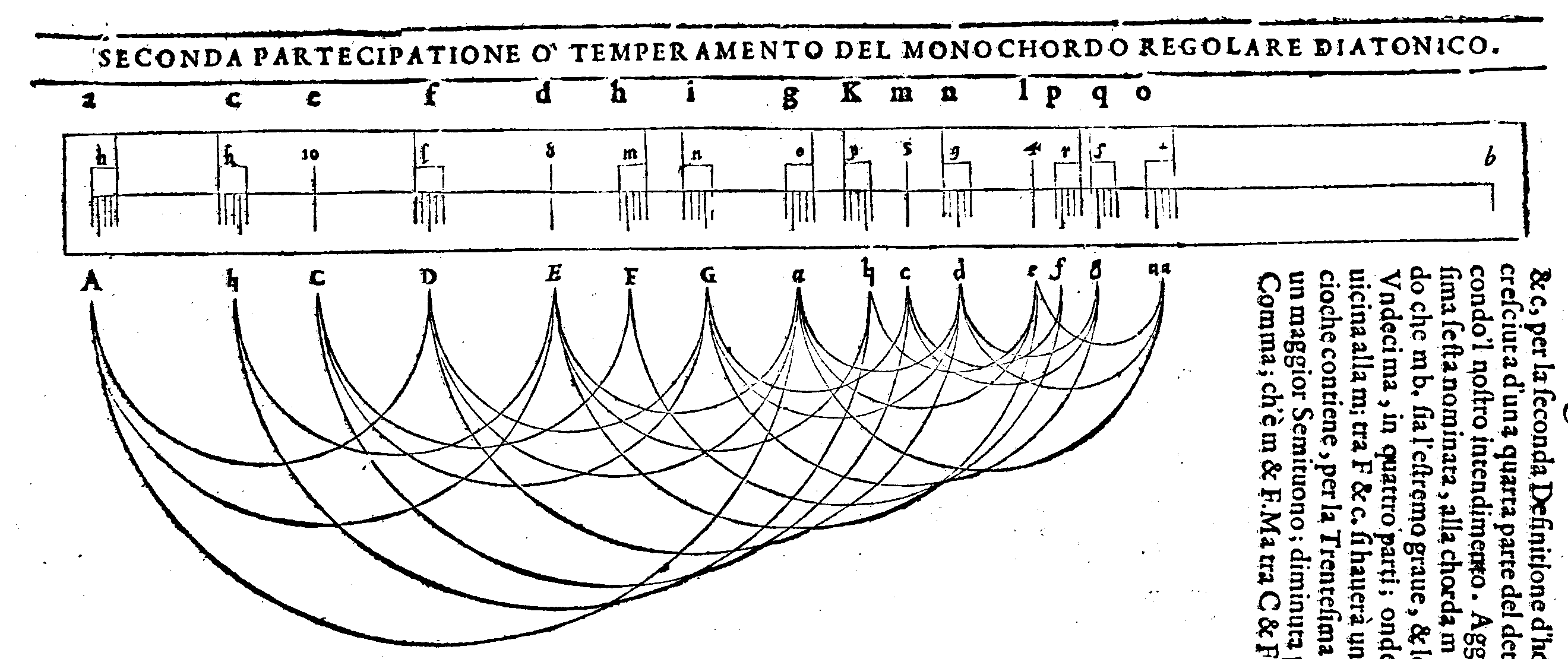
 b. haueremo temperata la Diapente, & diminuta, per la Ventesima sesta definitione; d'una quarta parte d'un Comma, la quale è
b. haueremo temperata la Diapente, & diminuta, per la Ventesima sesta definitione; d'una quarta parte d'un Comma, la quale è  & p. La onde tra Gb &
& p. La onde tra Gb &  b. haueremo anche un Ditono contenuto nella sua uera proportione; percioche ritrouandosi prima tra nb. & pb. nella sua uera forma; è fatto più graue; per la
Ventesima settima Definitione d'hoggi di tanta quantità, quanta è quella di Gn.
& di
b. haueremo anche un Ditono contenuto nella sua uera proportione; percioche ritrouandosi prima tra nb. & pb. nella sua uera forma; è fatto più graue; per la
Ventesima settima Definitione d'hoggi di tanta quantità, quanta è quella di Gn.
& di  p. Et perche Eb. & on. contiene un Tuono maggiore, un minore, & un maggior Semituono; per tanto Eb. & ob, per la Ventesima ottaua del Secondo, è una
Diatessaron; onde per ridurla al suo temperamento aggiungeremo il Comma, alla
chorda segnata ob, uerso l'acuto, il quale diuiso al modo detto in quattro parti, &
aggiunto ad Eb. & ob. la quarta parte o & a; tra Eb & ab haueremo la Diatessaron
accresciuta d'una quarta parte del Comma, la quale sarà ridotta, secondo la sua
Definitione; al suo temperamento. Diremo ancora, per la quinta definitione, Gb.
& ab. esser un Tuono ridotto al suo temperamento; percioche essendo nb. & ob. Tuono minore; uiene accresciuto tra Gb. & ab. de due quarte parti d'un Comma, che
sono Gn. & oa; com'è manifesto. Il che fà etiandio il maggiore ob. & pb; percioche ob. si fà più acuta in ab. d'una quarta parte del Comma, & pb. si fà più graue in
p. Et perche Eb. & on. contiene un Tuono maggiore, un minore, & un maggior Semituono; per tanto Eb. & ob, per la Ventesima ottaua del Secondo, è una
Diatessaron; onde per ridurla al suo temperamento aggiungeremo il Comma, alla
chorda segnata ob, uerso l'acuto, il quale diuiso al modo detto in quattro parti, &
aggiunto ad Eb. & ob. la quarta parte o & a; tra Eb & ab haueremo la Diatessaron
accresciuta d'una quarta parte del Comma, la quale sarà ridotta, secondo la sua
Definitione; al suo temperamento. Diremo ancora, per la quinta definitione, Gb.
& ab. esser un Tuono ridotto al suo temperamento; percioche essendo nb. & ob. Tuono minore; uiene accresciuto tra Gb. & ab. de due quarte parti d'un Comma, che
sono Gn. & oa; com'è manifesto. Il che fà etiandio il maggiore ob. & pb; percioche ob. si fà più acuta in ab. d'una quarta parte del Comma, & pb. si fà più graue in  b. per un'altra quarta parte. Onde uiene à diminuirsi dell'intiera metà d'un
Comma. Ilperche, per la quarta definitione; esso Tuono uiene à contenersi tra ab. &
b. per un'altra quarta parte. Onde uiene à diminuirsi dell'intiera metà d'un
Comma. Ilperche, per la quarta definitione; esso Tuono uiene à contenersi tra ab. &
 b. fatto minore della metà di esso Comma. Ancora perche ob. & cb. contiene un Tuono maggiore, & un maggior Semituono; però
per la Ventesima sesta del Secondo; ob.
& cb. uiene ad esser l'Interuallo del Semituono; contenuto nella sua uera forma. Et perche tale Interuallo si fà minore d'una
quarta parte del Comma o, laquale è o. & a; però,
per la terza Definitione; ab. & cb. è l'Interuallo del Semiditono, ridotto al suo temperamento. Ancora; perche pb. & cb. è Semituono maggiore; & dalla chorda
b. fatto minore della metà di esso Comma. Ancora perche ob. & cb. contiene un Tuono maggiore, & un maggior Semituono; però
per la Ventesima sesta del Secondo; ob.
& cb. uiene ad esser l'Interuallo del Semituono; contenuto nella sua uera forma. Et perche tale Interuallo si fà minore d'una
quarta parte del Comma o, laquale è o. & a; però,
per la terza Definitione; ab. & cb. è l'Interuallo del Semiditono, ridotto al suo temperamento. Ancora; perche pb. & cb. è Semituono maggiore; & dalla chorda  b. è accresciuto d'un quarto d'un Comma, che è
b. è accresciuto d'un quarto d'un Comma, che è  & p; però secondo la Sesta definitione data di sopra;
& p; però secondo la Sesta definitione data di sopra;  b, & cb. è l'Interuallo del Semituono maggiore accresciuto d'una quarta
parte del detto comma, & ridotto al suo temperamento. Il che si può anco dire del Semituono Eb. & mb; il quale è accresciuto di tanta quantità del Comma m, la quale è
m. & F; come chiaramente si uede. Hora per far acquisto d'una Diapente, che non
si troua tra la chorda lb. & la ob. percioche questo Interuallo contiene solamente due
Tuoni minori, & un maggiore, con un maggior Semituono; & per la Trentesima
del Secondo, uorrebbe contenere due Tuoni maggiori, un minore, & un maggior
Semituono; onde resta diminuta d'un Comma intiero, il quale per la Ventesima
quinta definitione medesimamente del secondo giorno; è la differenza, che si troua
tra 'l Tuono maggiore & lo minore. Però aggiungo alla chorda lb. uerso 'l graue
il Comma l; onde tra il suo tutto aggiunto alla lb. & la ob; uiene la Diapente contenuta nella sua uera & naturale proportione. Diuido hora il detto Comma, per
la Vndecima del Terzo, in quattro parti equali; & perche tutto l'Interuallo del
Comma l. congiunto alla chorda lb, fa con ab. una Diapente, maggiore d'una
quarta parte del Comma, che è o. & a; però lascio prima da un canto la quarta parte
più graue del detto Comma, equale alla o. & a; & ne uiene la Diapente nella sua uera forma; ma per il temperamento ne lascio dopoi un'altra quarta parte seguente; &
cosi tra Db. & ab; per la definitione; uiene la Diapente temperata, secondo 'l proposito. Et di più; il Tuono maggiore, che si troua tra cb. & lb. per uirtù della chorda Db. si troua diminuto, & sciemo de due quarte parti; ò uogliamo dire della metà
intiera del Comma, che sono D & l. Et il minore, che si troua tra lb. & Eb, accresciuto, secondo le loro definitioni; dell'istessa
quantità. Et dico ancora, che la Diatessaron, la quale si troua tra lb. & nb. nella sua uera, & natural forma, si troua accresciuta di
una quarta parte del Comma; percioche se la chorda nb. diuenta più graue d'una quarta
page 262
parte nella chorda Gb, & la chorda lb. più si estende uerso 'l graue per due quarte parti,
nella chorda Db; non è dubio, che tra Db. & Gb. si ritroui la Diatessaron accresciuta,
secondo la Ventesimasesta Definitione, della quarta parte d'un Comma. Onde per tal
modo habbiamo temperato le chorde Cb, lb, Eb, mb, nb, ob, pb, & cb, del proposto
Monochordo tra le chorde Cb, Db, Eb, Fb, Gb, ab,
b, & cb. è l'Interuallo del Semituono maggiore accresciuto d'una quarta
parte del detto comma, & ridotto al suo temperamento. Il che si può anco dire del Semituono Eb. & mb; il quale è accresciuto di tanta quantità del Comma m, la quale è
m. & F; come chiaramente si uede. Hora per far acquisto d'una Diapente, che non
si troua tra la chorda lb. & la ob. percioche questo Interuallo contiene solamente due
Tuoni minori, & un maggiore, con un maggior Semituono; & per la Trentesima
del Secondo, uorrebbe contenere due Tuoni maggiori, un minore, & un maggior
Semituono; onde resta diminuta d'un Comma intiero, il quale per la Ventesima
quinta definitione medesimamente del secondo giorno; è la differenza, che si troua
tra 'l Tuono maggiore & lo minore. Però aggiungo alla chorda lb. uerso 'l graue
il Comma l; onde tra il suo tutto aggiunto alla lb. & la ob; uiene la Diapente contenuta nella sua uera & naturale proportione. Diuido hora il detto Comma, per
la Vndecima del Terzo, in quattro parti equali; & perche tutto l'Interuallo del
Comma l. congiunto alla chorda lb, fa con ab. una Diapente, maggiore d'una
quarta parte del Comma, che è o. & a; però lascio prima da un canto la quarta parte
più graue del detto Comma, equale alla o. & a; & ne uiene la Diapente nella sua uera forma; ma per il temperamento ne lascio dopoi un'altra quarta parte seguente; &
cosi tra Db. & ab; per la definitione; uiene la Diapente temperata, secondo 'l proposito. Et di più; il Tuono maggiore, che si troua tra cb. & lb. per uirtù della chorda Db. si troua diminuto, & sciemo de due quarte parti; ò uogliamo dire della metà
intiera del Comma, che sono D & l. Et il minore, che si troua tra lb. & Eb, accresciuto, secondo le loro definitioni; dell'istessa
quantità. Et dico ancora, che la Diatessaron, la quale si troua tra lb. & nb. nella sua uera, & natural forma, si troua accresciuta di
una quarta parte del Comma; percioche se la chorda nb. diuenta più graue d'una quarta
page 262
parte nella chorda Gb, & la chorda lb. più si estende uerso 'l graue per due quarte parti,
nella chorda Db; non è dubio, che tra Db. & Gb. si ritroui la Diatessaron accresciuta,
secondo la Ventesimasesta Definitione, della quarta parte d'un Comma. Onde per tal
modo habbiamo temperato le chorde Cb, lb, Eb, mb, nb, ob, pb, & cb, del proposto
Monochordo tra le chorde Cb, Db, Eb, Fb, Gb, ab,  b, & cb; di maniera, che restando 'l Ditono Cb. & Eb, & l'Hexachordo minore Eb. & cb, nelle loro proportioni
& uere forme; gli altri Interualli uengono ad esser ridotti in un temperamento tale; che
se 'l si porrà gli Hemisperij, ò scannelli sotto le temperate chorde, secondo la ragione mostrata; si potrà vdire qual si
uorrà Consonanza, che l'Vdito grandemente ne resterà contento. Ma per ridur la hb. & Kb. poste nel graue insieme con l'altre à tal temperamento;
per poter'acquistare una Diatessaron, che non si troua tra la prima & la quarta chorda
hb. & lb; basterà solamente di far, che la Ab. &
b, & cb; di maniera, che restando 'l Ditono Cb. & Eb, & l'Hexachordo minore Eb. & cb, nelle loro proportioni
& uere forme; gli altri Interualli uengono ad esser ridotti in un temperamento tale; che
se 'l si porrà gli Hemisperij, ò scannelli sotto le temperate chorde, secondo la ragione mostrata; si potrà vdire qual si
uorrà Consonanza, che l'Vdito grandemente ne resterà contento. Ma per ridur la hb. & Kb. poste nel graue insieme con l'altre à tal temperamento;
per poter'acquistare una Diatessaron, che non si troua tra la prima & la quarta chorda
hb. & lb; basterà solamente di far, che la Ab. &  b. corrispondino con le ab. &
b. corrispondino con le ab. &  b.
per una Diapason, in Dupla proportione; facendo la Aa. equale alla ab; & la
b.
per una Diapason, in Dupla proportione; facendo la Aa. equale alla ab; & la 
 . equale alla
. equale alla  b; Essendo che allora tanto la chorda Ab, quanto la
b; Essendo che allora tanto la chorda Ab, quanto la  b. sarà diuisa in due
parti equali ne i punti a. &
b. sarà diuisa in due
parti equali ne i punti a. &  . Onde tanto sarà la proportione di Ab. & ab, & di
. Onde tanto sarà la proportione di Ab. & ab, & di  b. &
b. &  b.
di suono à suono, per la Prima & per la Quinta dimanda del Terzo ragionamento; quanto di numero à numero. La onde essendo Ab. & ab; simigliantemente
b.
di suono à suono, per la Prima & per la Quinta dimanda del Terzo ragionamento; quanto di numero à numero. La onde essendo Ab. & ab; simigliantemente  b. &
b. &  b. in
proportione Dupla; per l'Ottaua definitione del Secondo; Ab. & ab; simigliantemente
b. in
proportione Dupla; per l'Ottaua definitione del Secondo; Ab. & ab; simigliantemente  b. &
b. &  b. faranno la Diapason Consonanza. Et il Tuono Ab. &
b. faranno la Diapason Consonanza. Et il Tuono Ab. &  b. sarà equale al
Tuono ab. &
b. sarà equale al
Tuono ab. &  b; cosi ancora il Semituono
b; cosi ancora il Semituono  b. & Cb. sarà equale al Semitiuono
b. & Cb. sarà equale al Semitiuono  b. &
cb; essendo che tanta è la proportione, che si troua tra hb. & Ab, & tra
b. &
cb; essendo che tanta è la proportione, che si troua tra hb. & Ab, & tra  b. & Kb;
quanta è quella, che si troua tra ob. & ab, & tra
b. & Kb;
quanta è quella, che si troua tra ob. & ab, & tra  b. & pb. Percioche la Diapason hb.
& ob. per la Ventesima settima definitione d'hoggi; è fatta più acuta della quantità ob.
& ab; ch'è la quarta parte del Comma; & la Kb. & pb. più graue di tal quantità; quella
nelle chorde Ab. & ab. & questa nella
b. & pb. Percioche la Diapason hb.
& ob. per la Ventesima settima definitione d'hoggi; è fatta più acuta della quantità ob.
& ab; ch'è la quarta parte del Comma; & la Kb. & pb. più graue di tal quantità; quella
nelle chorde Ab. & ab. & questa nella  b. &
b. &  b. Ma perche Ab. & ab. contengono la
Diapason; essendo Db. & ab, Diapente; Ab. & Db. uerrà ad essere; per il Corollario
della Quarta proposta del Secondo giorno, Diatessaron. Et si come Db. & ab. è Diapente ridotta al suo temperamento; cosi Ab. & Db. uerrà ad essere
Diatessaron, ridotta ad
una tale qualità; & per tal modo uerremo ad hauer acquistato una Diatessaron tra la Prima & la Quarta chorda, laquale non si ritrouaua in essere; & questo secondo 'l nostro proposito. Oltra di questo; se diuideremo
la chorda Db. in due parti equali, & segnaremo
la metà in punto d; haueremo, per la Quarantesima seconda del Terzo, tra la chorda Db.
& db. la Dupla proportione; & per la Ottaua Definitione di sopra nominata; la Diapason
consonanza. Et l'Interuallo cb. & db. equale allo Cb & Db. ch'è il Tuono, & lo db. & eb.
equale allo Db. & Eb. medesimamente Tuono; restando le chorde Eb & eb. immobili, le
quali con le Cb, & cb. contengono il Ditono nella sua uera & natural forma & proportione. Ma per ritrouar la corrispondente per una Diapason alla Fb;
diuideremo, per la Quarantesima seconda nominata, essa Fb. in due parti equali, & tra essa Fb, che contenerà due
parti, & fb, che ne contenerà una; haueremo la Diapason consonanza nella sua uera forma,
& il Semituono maggiore tra eb. & fb. sarà accresciuto d'una quarta parte del Comma. Ritrouaremo anco la corrispondente per Diapason alla Gb, diuidendola in due parti equali,
per la nominata poco fà proposta; & pigliandone una in punto g; tra Gb. & gb. haueremo il
proposito; & tra fb. & gb. haueremo il Tuono, ilquale sarà di equale proportione del Tuono Fb. & Gb. Il simile faremo della
chorda ab; perche diuidendola in due parti, & pigliandone una di essa in punto aa; tra ab. & aab. haueremo una Diapason, la quale sarà equale alla Ab & ab, & sarà più acuta (per la Ventesima settima Definitione d'hoggi) della
ob. & tb, per una quarta parte d'un Comma; come è etiandio la Ab. & ab. della hb. &
ob. Ma il Tuono gb. & ab. sarà equale allo Gb & ab; percioche è accresciuto de due quarte parti del Comma; che sono gs. & taa; com'è accresciuto anco Gb. & ab. di Gn. & oa. Et
si come le chorde ab. & db. corrispondono alle Ab. & Db. in Dupla proportioine, & tra le
due prime si troua la Diatessaron temperata; cosi si troua anco tra l'altre due; percioche,
page 263
per la Ventesima ottaua del Secondo giorno; l'una & l'altra contiene due Tuoni & un Semituon maggiore. Onde habbiamo fatto acquisto de due Diatessaron;
l'una Ab. & Db.
posta nel graue, & l'altra ab. & db. posta nell'acuto, le quali mancauano tra la prima &
la quarta, & tra l'ottaua & la undecima delle proposte Quindeci chorde; come dice la
proposta. Et si come Db. & ab. corrispondono alle db. & aab. medesimamente in Dupla proportione, & tra le due prime si troua
la Diapente temperata; cosi si ritroua etiandio tra le due seguenti. Onde habbiamo due Diapente acquistate, le quali tra la Quarta
& l'Ottaua chorda, & tra l'Vndecima & la Quintadecima delle Quindeci proposte mancauano, l'una è tra Db. & ab; l'altra tra
db. & aab; secondo 'l proposito. Ma hauendo
col Senso esperimentato, che 'l concento, che uscisse da queste chorde Ab,
b. Ma perche Ab. & ab. contengono la
Diapason; essendo Db. & ab, Diapente; Ab. & Db. uerrà ad essere; per il Corollario
della Quarta proposta del Secondo giorno, Diatessaron. Et si come Db. & ab. è Diapente ridotta al suo temperamento; cosi Ab. & Db. uerrà ad essere
Diatessaron, ridotta ad
una tale qualità; & per tal modo uerremo ad hauer acquistato una Diatessaron tra la Prima & la Quarta chorda, laquale non si ritrouaua in essere; & questo secondo 'l nostro proposito. Oltra di questo; se diuideremo
la chorda Db. in due parti equali, & segnaremo
la metà in punto d; haueremo, per la Quarantesima seconda del Terzo, tra la chorda Db.
& db. la Dupla proportione; & per la Ottaua Definitione di sopra nominata; la Diapason
consonanza. Et l'Interuallo cb. & db. equale allo Cb & Db. ch'è il Tuono, & lo db. & eb.
equale allo Db. & Eb. medesimamente Tuono; restando le chorde Eb & eb. immobili, le
quali con le Cb, & cb. contengono il Ditono nella sua uera & natural forma & proportione. Ma per ritrouar la corrispondente per una Diapason alla Fb;
diuideremo, per la Quarantesima seconda nominata, essa Fb. in due parti equali, & tra essa Fb, che contenerà due
parti, & fb, che ne contenerà una; haueremo la Diapason consonanza nella sua uera forma,
& il Semituono maggiore tra eb. & fb. sarà accresciuto d'una quarta parte del Comma. Ritrouaremo anco la corrispondente per Diapason alla Gb, diuidendola in due parti equali,
per la nominata poco fà proposta; & pigliandone una in punto g; tra Gb. & gb. haueremo il
proposito; & tra fb. & gb. haueremo il Tuono, ilquale sarà di equale proportione del Tuono Fb. & Gb. Il simile faremo della
chorda ab; perche diuidendola in due parti, & pigliandone una di essa in punto aa; tra ab. & aab. haueremo una Diapason, la quale sarà equale alla Ab & ab, & sarà più acuta (per la Ventesima settima Definitione d'hoggi) della
ob. & tb, per una quarta parte d'un Comma; come è etiandio la Ab. & ab. della hb. &
ob. Ma il Tuono gb. & ab. sarà equale allo Gb & ab; percioche è accresciuto de due quarte parti del Comma; che sono gs. & taa; com'è accresciuto anco Gb. & ab. di Gn. & oa. Et
si come le chorde ab. & db. corrispondono alle Ab. & Db. in Dupla proportioine, & tra le
due prime si troua la Diatessaron temperata; cosi si troua anco tra l'altre due; percioche,
page 263
per la Ventesima ottaua del Secondo giorno; l'una & l'altra contiene due Tuoni & un Semituon maggiore. Onde habbiamo fatto acquisto de due Diatessaron;
l'una Ab. & Db.
posta nel graue, & l'altra ab. & db. posta nell'acuto, le quali mancauano tra la prima &
la quarta, & tra l'ottaua & la undecima delle proposte Quindeci chorde; come dice la
proposta. Et si come Db. & ab. corrispondono alle db. & aab. medesimamente in Dupla proportione, & tra le due prime si troua
la Diapente temperata; cosi si ritroua etiandio tra le due seguenti. Onde habbiamo due Diapente acquistate, le quali tra la Quarta
& l'Ottaua chorda, & tra l'Vndecima & la Quintadecima delle Quindeci proposte mancauano, l'una è tra Db. & ab; l'altra tra
db. & aab; secondo 'l proposito. Ma hauendo
col Senso esperimentato, che 'l concento, che uscisse da queste chorde Ab,  b,Cb;
Db, Eb, Fb, Gb, ab,
b,Cb;
Db, Eb, Fb, Gb, ab,  b, cb, db, eb, fb, gb, & aab; è grato & soaue all'Vdito; però
diremo; che questi Interualli tutti, ridotti à tal temperamento, siano consonanti, senz'alcuna contradittione. Et questo è tutto quello, che secondo la proposta, ui douea dimostrare. Vdito che hebbe il Signor Desiderio la conclusione, disse; Questo è stato un lungo tiro, & ueramente ch'è cosa bella da sapere; massimamente da uoi altri, che fate
professione delle cose della Musica. Et credo che coloro, i quali sono ignoranti di questa cosa; manchino d'una gran perfettione, quelli dico, che fanno professione di fabricare Istrumenti musicali; come posso comprender dalle parole poco fà dette da M. Claudio.
Cosi è ueramente; rispose egli, & niun lo potrà con uerità negare. O quanto arroganti sono quelli soggiunse M. Adriano; che
sono semplici Compositori di Musica, che se ben sono ignoranti delle cose della Scienza, uogliono non dimeno tenere in quest'Arte
il principato, & li par di essere i più dotti, & più saputi huomini del mondo. Ma leuateli da quel
poco di comporre, che fanno & con poca prattica; restano nudi, senza saper cosa ueruna; però è cosa buona l'imparare, acciò non s'entri nella schiera de costoro, che uiuono solamente tra gli huomini, per far numero. Seguitate adunque M. Gioseffo il uostro
ragionamento; per che tutti noi ui ascoltiamo uolontieri, tanto più che uediamo, ch'ogni
tratto ci proponete di nouo qualche cosa bella & ingeguosa. Statemi adunque ad ascoltare, dissi; c'hauerete piacere.
b, cb, db, eb, fb, gb, & aab; è grato & soaue all'Vdito; però
diremo; che questi Interualli tutti, ridotti à tal temperamento, siano consonanti, senz'alcuna contradittione. Et questo è tutto quello, che secondo la proposta, ui douea dimostrare. Vdito che hebbe il Signor Desiderio la conclusione, disse; Questo è stato un lungo tiro, & ueramente ch'è cosa bella da sapere; massimamente da uoi altri, che fate
professione delle cose della Musica. Et credo che coloro, i quali sono ignoranti di questa cosa; manchino d'una gran perfettione, quelli dico, che fanno professione di fabricare Istrumenti musicali; come posso comprender dalle parole poco fà dette da M. Claudio.
Cosi è ueramente; rispose egli, & niun lo potrà con uerità negare. O quanto arroganti sono quelli soggiunse M. Adriano; che
sono semplici Compositori di Musica, che se ben sono ignoranti delle cose della Scienza, uogliono non dimeno tenere in quest'Arte
il principato, & li par di essere i più dotti, & più saputi huomini del mondo. Ma leuateli da quel
poco di comporre, che fanno & con poca prattica; restano nudi, senza saper cosa ueruna; però è cosa buona l'imparare, acciò non s'entri nella schiera de costoro, che uiuono solamente tra gli huomini, per far numero. Seguitate adunque M. Gioseffo il uostro
ragionamento; per che tutti noi ui ascoltiamo uolontieri, tanto più che uediamo, ch'ogni
tratto ci proponete di nouo qualche cosa bella & ingeguosa. Statemi adunque ad ascoltare, dissi; c'hauerete piacere.
PROPOSTA II.
PROPOSTA III.
 b, Cb, Db, Eb, FB, GB, ab,
b, Cb, Db, Eb, FB, GB, ab,  b,
cb, db, eb, fb, gb, & aab; & sia Ab. la Proslambanomenos alla quale habbiamo da
proporre la Υ῾ποπροσλαμβανόμενος; ouer Gammaut. Accommodo prima, per la Prima
proposta del Terzo giorno; il Tuono maggiore alla sua proportione, sopra la chorda hb; di
maniera che Ab. uenga ad essere il suo estremo acuto. Però diuiso essa Ab. In Otto parti equali, per il minor termine della Sesquiottaua, ch'è la sua proportione; & aggiungo à
queste parti la Nona nel punto l. tra lb. & Ab. habbiamo il proposito, & hauendolo proposto
b,
cb, db, eb, fb, gb, & aab; & sia Ab. la Proslambanomenos alla quale habbiamo da
proporre la Υ῾ποπροσλαμβανόμενος; ouer Gammaut. Accommodo prima, per la Prima
proposta del Terzo giorno; il Tuono maggiore alla sua proportione, sopra la chorda hb; di
maniera che Ab. uenga ad essere il suo estremo acuto. Però diuiso essa Ab. In Otto parti equali, per il minor termine della Sesquiottaua, ch'è la sua proportione; & aggiungo à
queste parti la Nona nel punto l. tra lb. & Ab. habbiamo il proposito, & hauendolo proposto
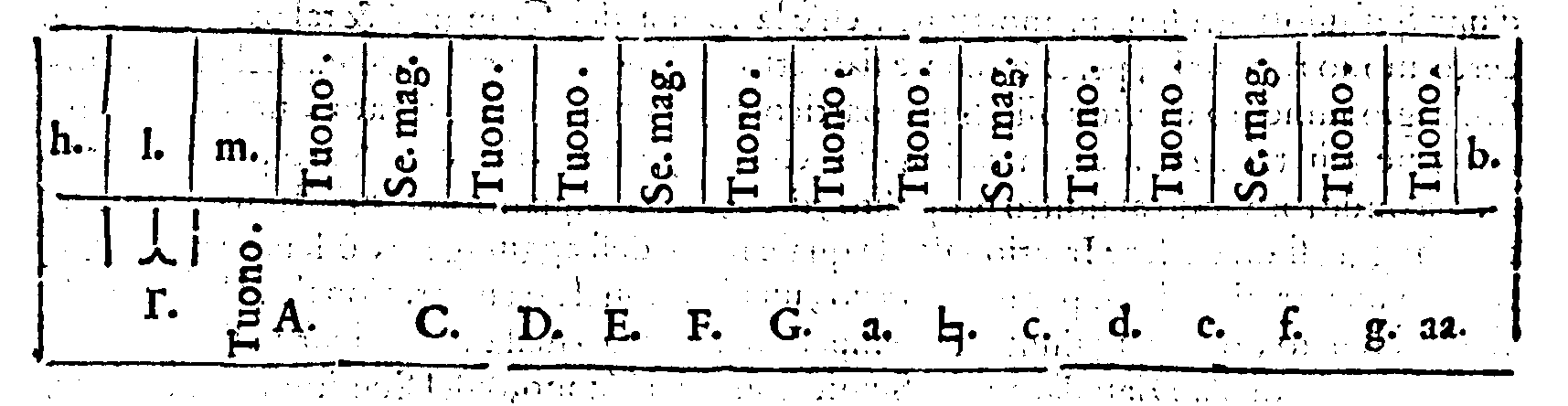
 b. Ma perche bisogna ridur questo Interuallo al temperamento de gli
altri Tuoni; accioche la chorda graue di questo Tuono accommodato corrispondi giustapage 265
mente con la Gh. in Dupla proportione; & consoni con essa la Diapason; però, per la Trentesimasesta del giorno Terzo, accommodaremo il Comma sopra la chorda lb. il quale sarà lb.
& mb. & lo diuideremo, per la Decima del nominato Terzo giorno; in due parti equali.
Onde lasciandone la più graue & più uicina alla l. da un canto; tra Γb. Ab. haueremo
collocato il Tuono proposto alla sua proportione & lo hauaremo etia&ndio preposto al Tuono Ab &
b. Ma perche bisogna ridur questo Interuallo al temperamento de gli
altri Tuoni; accioche la chorda graue di questo Tuono accommodato corrispondi giustapage 265
mente con la Gh. in Dupla proportione; & consoni con essa la Diapason; però, per la Trentesimasesta del giorno Terzo, accommodaremo il Comma sopra la chorda lb. il quale sarà lb.
& mb. & lo diuideremo, per la Decima del nominato Terzo giorno; in due parti equali.
Onde lasciandone la più graue & più uicina alla l. da un canto; tra Γb. Ab. haueremo
collocato il Tuono proposto alla sua proportione & lo hauaremo etia&ndio preposto al Tuono Ab &  b. Ma perche lb. & Ab. è Tuono maggiore, contenuto nella sia naturale proportione, & dalla chorda Γb. è fatto minore della metà d'un Comma, i quale è lb. & mb.
però dico, per la sua Definitione, Γb. & Ab. essere il Tuono maggiore temperato; come faceua dibisogno. Et perche Ab. per l'Ottaua definitione del Quarto; è la Proslambanomenos, & la Γ. è distante da essa per un Tuono, & è posta nel graue; però dico, per la Decimanona Definitione d'hoggi medesimamente; Γb. esser la chorda Hypoproslambanomenos, preposta alla Proslambanomenos & alle Quindeci proposte
chorde; come ui douea, secondo la proposta, dimostrare. Voglio ancora dirui una
cosa, auanti che passiamo più oltra; che la nominata chorda Hypoproslambanomenos
si può aggiungere con un'altro mezo. Percioche se raddopiaremo la chorda Gb. la
quale uerrà raddopiata nel punto Γ. haueremo la chorda Γb. che per la Quarta Definitione del Primo giorno; con essa Gb. contenerà la Dupla proportione; percioche Γb.
contiene Gb. due fiate di punto; Onde; per l'Ottaua Definitione del secondo ragionamento; uengono à contenere la Diapason consonanza. Et perche questa contiene in sè;
per la Trentesimanona del Secondo; Cinque Tuoni & Due maggiori Semituoni, & l'Interuallo Ab. & Gb. contiene solamente Quattro Tuoni & li nominati due Semituoni;
per l'interuallo Γb. & Ab. uerrà à contenere il Tuono, il quale posto insieme con gli altri
Quattro & li Due Semituoni, faranno una Diapason. Essendo adunque
b. Ma perche lb. & Ab. è Tuono maggiore, contenuto nella sia naturale proportione, & dalla chorda Γb. è fatto minore della metà d'un Comma, i quale è lb. & mb.
però dico, per la sua Definitione, Γb. & Ab. essere il Tuono maggiore temperato; come faceua dibisogno. Et perche Ab. per l'Ottaua definitione del Quarto; è la Proslambanomenos, & la Γ. è distante da essa per un Tuono, & è posta nel graue; però dico, per la Decimanona Definitione d'hoggi medesimamente; Γb. esser la chorda Hypoproslambanomenos, preposta alla Proslambanomenos & alle Quindeci proposte
chorde; come ui douea, secondo la proposta, dimostrare. Voglio ancora dirui una
cosa, auanti che passiamo più oltra; che la nominata chorda Hypoproslambanomenos
si può aggiungere con un'altro mezo. Percioche se raddopiaremo la chorda Gb. la
quale uerrà raddopiata nel punto Γ. haueremo la chorda Γb. che per la Quarta Definitione del Primo giorno; con essa Gb. contenerà la Dupla proportione; percioche Γb.
contiene Gb. due fiate di punto; Onde; per l'Ottaua Definitione del secondo ragionamento; uengono à contenere la Diapason consonanza. Et perche questa contiene in sè;
per la Trentesimanona del Secondo; Cinque Tuoni & Due maggiori Semituoni, & l'Interuallo Ab. & Gb. contiene solamente Quattro Tuoni & li nominati due Semituoni;
per l'interuallo Γb. & Ab. uerrà à contenere il Tuono, il quale posto insieme con gli altri
Quattro & li Due Semituoni, faranno una Diapason. Essendo adunque  b. & Ab. Tuono; & essendo
b. & Ab. Tuono; & essendo  b. distante da Ab. Proslambanomenos per un Tuono; seguita, per la
nominata Decimanona Definitione; che la Γb. sia la Hypoproslambanomenos; come
bisognaua dimostrare. In uerità, disse M. Claudio; che non si può dir cosa alcuna incontrario & questo c'hauete hora dimostrato col mezo della Dupla, ò Diapason, è tanto manifesto; che non discordando punto dalla Definitione data; bisogna per forza confessare, che tal chorda aggiunta sia la Hypoproslambanomenos, c'hauete detto; ò la
Gammaut; come da i Prattici è chiamata. Seguitate adunque il resto; se ui piace. Seguirò adunque à dirui; risposi; che,
b. distante da Ab. Proslambanomenos per un Tuono; seguita, per la
nominata Decimanona Definitione; che la Γb. sia la Hypoproslambanomenos; come
bisognaua dimostrare. In uerità, disse M. Claudio; che non si può dir cosa alcuna incontrario & questo c'hauete hora dimostrato col mezo della Dupla, ò Diapason, è tanto manifesto; che non discordando punto dalla Definitione data; bisogna per forza confessare, che tal chorda aggiunta sia la Hypoproslambanomenos, c'hauete detto; ò la
Gammaut; come da i Prattici è chiamata. Seguitate adunque il resto; se ui piace. Seguirò adunque à dirui; risposi; che,
PROPOSTA IIII.
 . C. D. E F. G. a.
. C. D. E F. G. a.  . c. d. e. f. g & aa. Dico primieramente, che tra le chorde Γ. A.
. c. d. e. f. g & aa. Dico primieramente, che tra le chorde Γ. A.  . C. D & E. è contenuto i primo Hexachordo, detto Hypaton; percioche Γ. per la Decimaottaua definitione d'hoggi; è
chorda la quale corrisponde alla Hypoproslambanomenos; alla Proslambanomenos;
. C. D & E. è contenuto i primo Hexachordo, detto Hypaton; percioche Γ. per la Decimaottaua definitione d'hoggi; è
chorda la quale corrisponde alla Hypoproslambanomenos; alla Proslambanomenos;  alla Hypate hypaton; C alla Parhypate hypaton; D alla Lychanos hypaton; &
E alla Hypate meson. Et perche queste Sei chorde sono collocate nel primo & grauissimo luogo di quest'ordine, & hanno il loro principio nella Hypoproslambanomenos, ò
Gammaut, & contengono Quattro Tuoni & un maggior Semituono, & tra le Quattro
più acute contengono il Primo Tetrachordo, da gli Antichi detto hypaton; però per la
Definitione Ventesimaprima d'hoggi, dico Γ. A.
alla Hypate hypaton; C alla Parhypate hypaton; D alla Lychanos hypaton; &
E alla Hypate meson. Et perche queste Sei chorde sono collocate nel primo & grauissimo luogo di quest'ordine, & hanno il loro principio nella Hypoproslambanomenos, ò
Gammaut, & contengono Quattro Tuoni & un maggior Semituono, & tra le Quattro
più acute contengono il Primo Tetrachordo, da gli Antichi detto hypaton; però per la
Definitione Ventesimaprima d'hoggi, dico Γ. A.  . C. D & E. esser 'l primo Hexacordo,
detto Hypaton. Dico poi; C. D. E. F. G & a. contenere il Secondo detto Meson; percioche C. corrisponde, per la Decimaottaua nominata definitione, alla Parhypate hypaton;
page 266
D alla Lychanos hypaton; E. alla Hypate meson; F. alla Parhypate meson; G. alla Lychanosmeson; & a alla Mese. Onde essendo la Parhypate hypaton la prima chorda de queste Sei, & contenendo cotal numero Quattro Tuoni & un maggior Semituono; & anco
ritrouandosi tra le Quattro più acute il Tetrachordo Meson; non è dubio alcuno, che
. C. D & E. esser 'l primo Hexacordo,
detto Hypaton. Dico poi; C. D. E. F. G & a. contenere il Secondo detto Meson; percioche C. corrisponde, per la Decimaottaua nominata definitione, alla Parhypate hypaton;
page 266
D alla Lychanos hypaton; E. alla Hypate meson; F. alla Parhypate meson; G. alla Lychanosmeson; & a alla Mese. Onde essendo la Parhypate hypaton la prima chorda de queste Sei, & contenendo cotal numero Quattro Tuoni & un maggior Semituono; & anco
ritrouandosi tra le Quattro più acute il Tetrachordo Meson; non è dubio alcuno, che
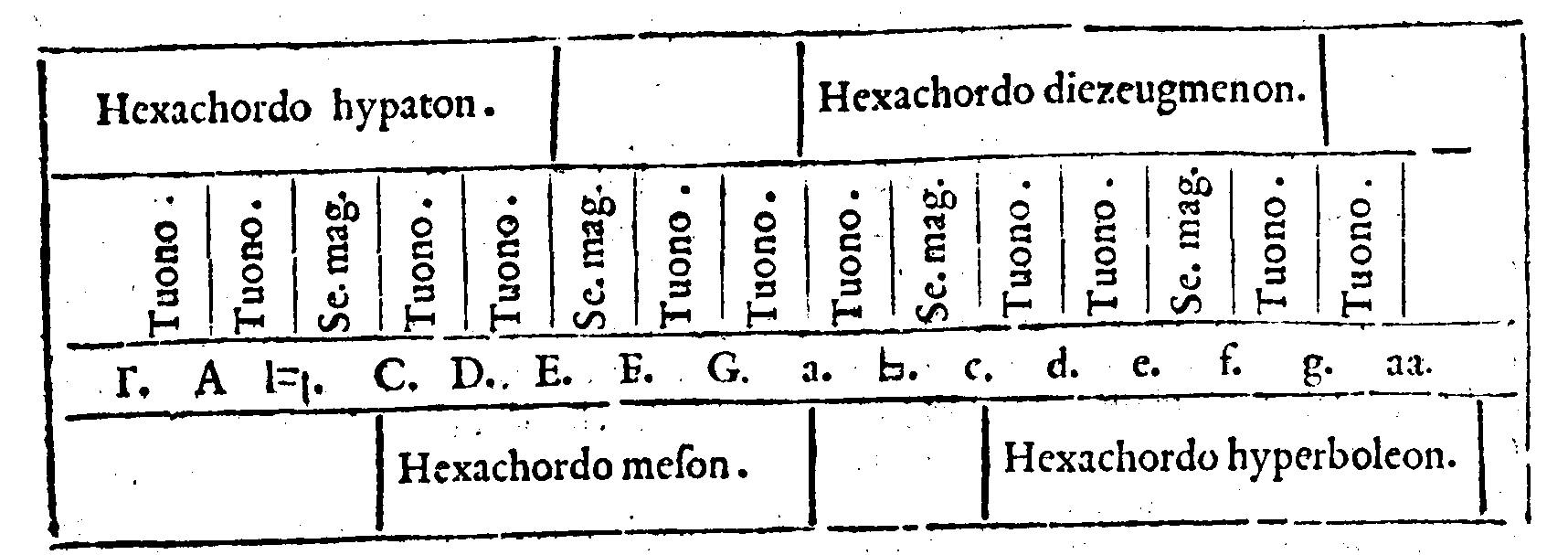
 . c. d & e. contengono il Terzo,
nominato Diezeugmenon. Percioche G. corrisponde alla Lychanosmeson; a. alla Meson; &
. c. d & e. contengono il Terzo,
nominato Diezeugmenon. Percioche G. corrisponde alla Lychanosmeson; a. alla Meson; &  alla Paramese; c. alla Tritediezeugmenon; d. alla Paranete diezeugmenon; & e.
alla Netediezeugmenon; onde hauendo etiandio queste Sei chorde il loro principio
nella chorda Lychanosmeson, & contenendo quattro Tuoni & un maggior Semituono; & ritrouandosi nelle quattro più acute il terzo Tetrachordo detto Diezeugmenon;
non è da dubitare; secondo ch'insegna la Ventesimaterza definitione, che G. a.
alla Paramese; c. alla Tritediezeugmenon; d. alla Paranete diezeugmenon; & e.
alla Netediezeugmenon; onde hauendo etiandio queste Sei chorde il loro principio
nella chorda Lychanosmeson, & contenendo quattro Tuoni & un maggior Semituono; & ritrouandosi nelle quattro più acute il terzo Tetrachordo detto Diezeugmenon;
non è da dubitare; secondo ch'insegna la Ventesimaterza definitione, che G. a.  . c. d &
e. sia Hexachordo Diezeugmenon & il Terzo. Finalmente dico; che 'l quarto nominato Hyperboleon si troua collocato tra le chorde c. d. e. f. g & aa. percioche queste Sei
chorde sono collocate nella più acuta parte del nominato ordine, contenuto tra Sedici chorde; & c. per la Decimaottaua definitione, corrisponde alla Tritediezeugmenon;
d. alla Paranete; e. alla Nete; f. alla Tritehyperboleon; g. alla Paranete; & a. alla Netehyperboleon. Onde hauendo cotal ordine principio nella Tritediezeugmenon, & contenendo simigliantemente quattro Tuoni & un maggior Semituono; per la Definitione
Ventesima & Ventesimaquarta già detta, seguita; che c. d. e. f. g & aa. sia Hexachordo, &
il Quarto & più acuto d'ogn'altro, detto Hyperboleon; percioche contien nelle sue più
acute chorde il Tetrachordo Hyperboleon. Potiamo adunque porre tra le Sedici mostrate chorde i quattro primi Hexachordi, Hypaton, Meson, Diezeugmennon, & Hyperboleon; come ui douea, secondo che dice la proposta, dimostrare & assignare. Se i nostri
Hexachordi, disse M. Adriano, hanno à corrispondere, come fanno in effetto, à i
Tetrachordi de gli Antichi; bisogno è, che ue ne sia un'altro, che corrispondi al Synemennon; però se 'l ui è in piacere, dimostratecelo; acciò habbiamo la cosa perfetta. E' il douere risposi di satisfarui Messere; essendomeui già fatto debitore però statemi ad ascoltare.
. c. d &
e. sia Hexachordo Diezeugmenon & il Terzo. Finalmente dico; che 'l quarto nominato Hyperboleon si troua collocato tra le chorde c. d. e. f. g & aa. percioche queste Sei
chorde sono collocate nella più acuta parte del nominato ordine, contenuto tra Sedici chorde; & c. per la Decimaottaua definitione, corrisponde alla Tritediezeugmenon;
d. alla Paranete; e. alla Nete; f. alla Tritehyperboleon; g. alla Paranete; & a. alla Netehyperboleon. Onde hauendo cotal ordine principio nella Tritediezeugmenon, & contenendo simigliantemente quattro Tuoni & un maggior Semituono; per la Definitione
Ventesima & Ventesimaquarta già detta, seguita; che c. d. e. f. g & aa. sia Hexachordo, &
il Quarto & più acuto d'ogn'altro, detto Hyperboleon; percioche contien nelle sue più
acute chorde il Tetrachordo Hyperboleon. Potiamo adunque porre tra le Sedici mostrate chorde i quattro primi Hexachordi, Hypaton, Meson, Diezeugmennon, & Hyperboleon; come ui douea, secondo che dice la proposta, dimostrare & assignare. Se i nostri
Hexachordi, disse M. Adriano, hanno à corrispondere, come fanno in effetto, à i
Tetrachordi de gli Antichi; bisogno è, che ue ne sia un'altro, che corrispondi al Synemennon; però se 'l ui è in piacere, dimostratecelo; acciò habbiamo la cosa perfetta. E' il douere risposi di satisfarui Messere; essendomeui già fatto debitore però statemi ad ascoltare.
PROPOSTA V.
 . C. D. E. F. G.
a.
. C. D. E. F. G.
a.  . c. d. e. f. g & aa. sopra la notata chorda h & k. le quali; come nella Precedente;
contengono i quattro primi Hexachordi, Hypaton, Meson; Diezeugmenon,
page 267
& Hyperboleon; à i quali sia dibisogno aggiungere il quinto detto Synemennon. Accommodo prima sopra la chorda ak. per la Decimanona del Terzo giorno; il Semituon
maggiore alla sua proportione; onde ne uiene ak. & lk. Ma perche ak & lk. è Semituon
maggiore, & è contenuto nella sua forma naturale; però bisogna, secondo la sua Definitione; ch'ello sia maggior d'una quarta parte d'un Comma. Onde accommodo prima
. c. d. e. f. g & aa. sopra la notata chorda h & k. le quali; come nella Precedente;
contengono i quattro primi Hexachordi, Hypaton, Meson; Diezeugmenon,
page 267
& Hyperboleon; à i quali sia dibisogno aggiungere il quinto detto Synemennon. Accommodo prima sopra la chorda ak. per la Decimanona del Terzo giorno; il Semituon
maggiore alla sua proportione; onde ne uiene ak. & lk. Ma perche ak & lk. è Semituon
maggiore, & è contenuto nella sua forma naturale; però bisogna, secondo la sua Definitione; ch'ello sia maggior d'una quarta parte d'un Comma. Onde accommodo prima
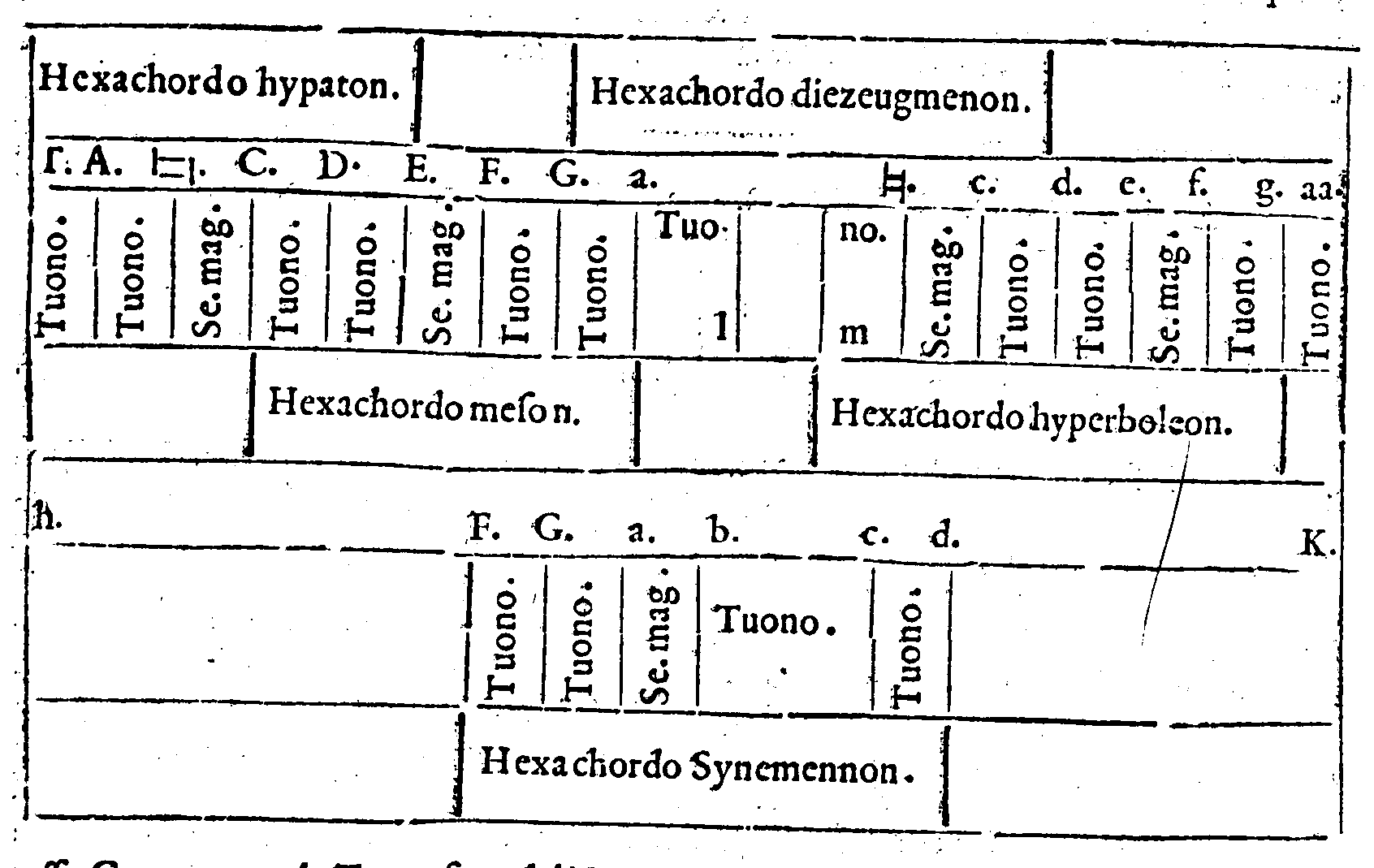
 quadro, &
il Secondo col Quarto della proprietà di Natura. Cosi è, risposi; Ma ascoltate quel, che
hora ui uoglio dire.
quadro, &
il Secondo col Quarto della proprietà di Natura. Cosi è, risposi; Ma ascoltate quel, che
hora ui uoglio dire.
PROPOSTA VI.
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f g &
aa. Dico prima, che tra esse la Prima specie della Diapason si troua Due fiate;
l'una tra C. D. E. F. G. a
. c. d. e. f g &
aa. Dico prima, che tra esse la Prima specie della Diapason si troua Due fiate;
l'una tra C. D. E. F. G. a  . & c. & l'altra tra F. G. a. b. c. d. e. & f. percioche per
l'Ottaua Definitione d'hoggi; quella è la Prima specie della Diapason, la quale contiene tra la Terza, & la Quarta sua chorda, & tra la Settima & la Ottaua il Semituon maggiore. La onde ritrouandosi la E. esser la Terza chorda, & F. la Quarta della Diapason
. & c. & l'altra tra F. G. a. b. c. d. e. & f. percioche per
l'Ottaua Definitione d'hoggi; quella è la Prima specie della Diapason, la quale contiene tra la Terza, & la Quarta sua chorda, & tra la Settima & la Ottaua il Semituon maggiore. La onde ritrouandosi la E. esser la Terza chorda, & F. la Quarta della Diapason
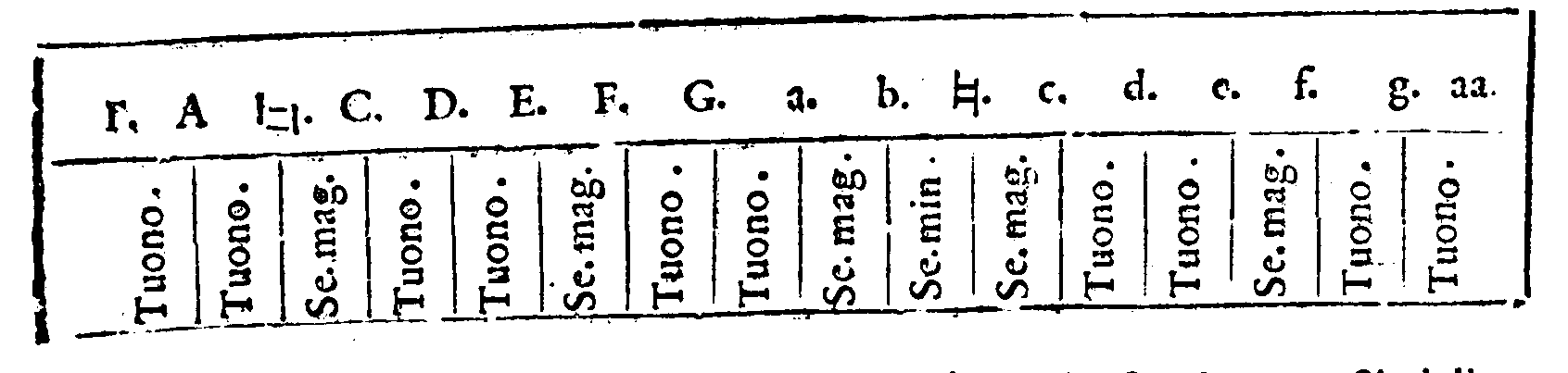
 . esser la Settima chorda, & la c. la Ottaua, & contenere etiandio esso Semituono; Seguita, che la Diapason C & c. con le sue mezane chorde; sia la
prima specie. Il che dico etiandio della Diapason F & f. con le sue mezane chorde; essendo che tra la sua Terza chorda a. & la Quarta b. & tra la Settima e. & la Ottaua f. si ritroua anco il Semituono già nominato. Adunque tra le proposte Dicesette chorde si
troua due fiate la Prima specie della Diapason. Ma la Seconda specie si troua due fiate;
tra D. E. F. G. a.
. esser la Settima chorda, & la c. la Ottaua, & contenere etiandio esso Semituono; Seguita, che la Diapason C & c. con le sue mezane chorde; sia la
prima specie. Il che dico etiandio della Diapason F & f. con le sue mezane chorde; essendo che tra la sua Terza chorda a. & la Quarta b. & tra la Settima e. & la Ottaua f. si ritroua anco il Semituono già nominato. Adunque tra le proposte Dicesette chorde si
troua due fiate la Prima specie della Diapason. Ma la Seconda specie si troua due fiate;
tra D. E. F. G. a.  . c. & d. & tra G. a. b. c. d. e f & g. percioche tra E. & F. Seconda & Terza
chorda; & tra
. c. & d. & tra G. a. b. c. d. e f & g. percioche tra E. & F. Seconda & Terza
chorda; & tra  & c. Sesta & Settima della Diapason D & d. con l'altre mezane, & cosi
tra la a. & b. Seconda & Terza; & tra e. & f. Sesta & Settima della Diapason G & g con
le sue mezane già mostrate; si troua il maggior Semituono. Onde, per la detta Ottaua
definitione; D & d. simigliantemente G con g. uengono ad esser due Diapason della Seconda specie. La Terza specie si ritroua due fiate; prima tra E. F. G. a.
& c. Sesta & Settima della Diapason D & d. con l'altre mezane, & cosi
tra la a. & b. Seconda & Terza; & tra e. & f. Sesta & Settima della Diapason G & g con
le sue mezane già mostrate; si troua il maggior Semituono. Onde, per la detta Ottaua
definitione; D & d. simigliantemente G con g. uengono ad esser due Diapason della Seconda specie. La Terza specie si ritroua due fiate; prima tra E. F. G. a.  . c. d & e. dopoi
tra a. b. c. d.e. f. g & aa. essendoche tra la prima E. & la seconda F & tra la quinta
. c. d & e. dopoi
tra a. b. c. d.e. f. g & aa. essendoche tra la prima E. & la seconda F & tra la quinta  & la sesta c. della Diapason E & e. con le sue mezane chorde. Et cosi tra la prima chorda & la
seconda; a. & b. & tra la quinta et la sesta, che sono e. & f. della Diapason a & aa. intendendouisi sempre anco le chorde mezane; si troua 'l maggior Semituono. Il perche, per
la Definitione poco fà addotta; E & e. con a & aa. sono due Diapason della Terza specie. La Quarta specie etiandio si troua una fiata solamente tra F. G a.
& la sesta c. della Diapason E & e. con le sue mezane chorde. Et cosi tra la prima chorda & la
seconda; a. & b. & tra la quinta et la sesta, che sono e. & f. della Diapason a & aa. intendendouisi sempre anco le chorde mezane; si troua 'l maggior Semituono. Il perche, per
la Definitione poco fà addotta; E & e. con a & aa. sono due Diapason della Terza specie. La Quarta specie etiandio si troua una fiata solamente tra F. G a.  . c. d. e & f. percioche tra la sua Quarta chorda
. c. d. e & f. percioche tra la sua Quarta chorda  . & la Quinta c. & tra la Settima e. & l'Ottaua f. si troua il
nominato Semituono maggiore. Onde, per la detta Definitione, F & f. con le sue mezane chorde è una Diapason della Quarta specie. La Quinta specie si troua due fiate; tra
Γ. A.
. & la Quinta c. & tra la Settima e. & l'Ottaua f. si troua il
nominato Semituono maggiore. Onde, per la detta Definitione, F & f. con le sue mezane chorde è una Diapason della Quarta specie. La Quinta specie si troua due fiate; tra
Γ. A.  . C. D. E. F.& G. & tra G. a.
. C. D. E. F.& G. & tra G. a.  . c. d. e. f. & g. poi che la Terza et la quarta sua
chorda
. c. d. e. f. & g. poi che la Terza et la quarta sua
chorda  . & C ouer
. & C ouer  . & c. & tra la Sesta & la Settima E & F. ouero e. & f. delle nominate due Diapason; si ritroua il Semituon maggiore. Onde, per l'istessa Ottaua Definitione
l'una & l'altra sono due Diapason contenute nella Quinta specie. Dico ancora, che la
Sesta specie della Diapason si ritroua tra 'l nominato numero di chorde due fiate; Prima,
tra A.
. & c. & tra la Sesta & la Settima E & F. ouero e. & f. delle nominate due Diapason; si ritroua il Semituon maggiore. Onde, per l'istessa Ottaua Definitione
l'una & l'altra sono due Diapason contenute nella Quinta specie. Dico ancora, che la
Sesta specie della Diapason si ritroua tra 'l nominato numero di chorde due fiate; Prima,
tra A.  . C. D. E. F. G. & a. dopoi, tra a.
. C. D. E. F. G. & a. dopoi, tra a.  . c. d. e. f. g & aa. essendo che, per la sua Definitione, tra le Seconde chorde
. c. d. e. f. g & aa. essendo che, per la sua Definitione, tra le Seconde chorde  . &
. &  . & le Terze C. & c. & tra le Quinte E. & e. et le Seste F.
& f. delle due Diapason mostrate si troua il maggior Semituono. Però dico, esser due
Diapason della Sesta specie. Finalmente dico, che tale ordine contiene una fiata la Settima specie della Diapason; tra
. & le Terze C. & c. & tra le Quinte E. & e. et le Seste F.
& f. delle due Diapason mostrate si troua il maggior Semituono. Però dico, esser due
Diapason della Sesta specie. Finalmente dico, che tale ordine contiene una fiata la Settima specie della Diapason; tra  C. D. E. F. G. a &
C. D. E. F. G. a &  percioche, per la sudetta Ottaua
Definitione, quella è detta Settima specie, la quale tra la sua Prima & la Seconda chorda, & tra la Quarta et la Quinta contiene il Semituon maggiore. La onde, perche la
Diapason
percioche, per la sudetta Ottaua
Definitione, quella è detta Settima specie, la quale tra la sua Prima & la Seconda chorda, & tra la Quarta et la Quinta contiene il Semituon maggiore. La onde, perche la
Diapason  . &
. &  . tra la sua estrema chorda graue & l'estrema acuta, con le mezane in
page 269
sieme; tra
. tra la sua estrema chorda graue & l'estrema acuta, con le mezane in
page 269
sieme; tra  . & C. Prima & Seconda, & tra E. & F. Quarta & Quinta chorda contiene il
detto Semituono; però dico, la detta esser la Settima specie della Diapason. Tra le Dicesette chorde mostrate adunque continenti i Cinque Hexachordi; la prima specie della Diapason si troua due fiate; due la Seconda; due la Terza; una la Quarta; due la Quinta; due la Sesta; & una la Settima. Et questo è quello, che secondo il continente della
proposta, ui douea dimostrare. Qui disse M. Claudio; Ancora che fin'hora da i Musici
sia stato tenuto, che la Prima specie della Diapason sia contenuta tra le chorde D & d.
con le sue mezane, & cosi l'altre specie seguenti per ordine; per questo non credo, ch'appresso gli Huomini intendenti u'habbia da esser confusione. Et parmi, che non solamente per gli Hexachordi, che sono collocati in questo ordine de chorde; ma etiandio,
perche è cosa più naturale; come detto hauete poco fà, & anco nelle uostre Istitutioni;
che debba esser cosi. Il perche facesti palese per la diuisione harmonicamente fatta della Dupla & della Diapason nelle sue parti; cosa da niun'altro per auanti pur pensata.
Però laudo molto quest'ordine. Che ne diteuoi Messere di questo? Rispose M. Adriano; Non posso se non laudarlo; perche anco l'ordine de i Modi, ò Tuoni sarà posto
senza interrompimento. Et se bene appresso d'alcuni parerà questa cosa essere altramente; ci ricordaremo, che M. Gioseffo
hauendo uoluto più tosto seruire (come si uede in
fatto) alla prattica moderna, che alla speculatiua; in questo luogo egli parla secondo la
Scienza, & secondo che porta l'ordine naturale di questa cosa. Soggiunse à questo M.
Francesco; Questo importa poco appresso quelli, ch'intendono le cose della Musica; ma
ueniamo pure à quello, che segue. Per seguitare adunque l'ordine principiato, diss'io; ui
dico; che
. & C. Prima & Seconda, & tra E. & F. Quarta & Quinta chorda contiene il
detto Semituono; però dico, la detta esser la Settima specie della Diapason. Tra le Dicesette chorde mostrate adunque continenti i Cinque Hexachordi; la prima specie della Diapason si troua due fiate; due la Seconda; due la Terza; una la Quarta; due la Quinta; due la Sesta; & una la Settima. Et questo è quello, che secondo il continente della
proposta, ui douea dimostrare. Qui disse M. Claudio; Ancora che fin'hora da i Musici
sia stato tenuto, che la Prima specie della Diapason sia contenuta tra le chorde D & d.
con le sue mezane, & cosi l'altre specie seguenti per ordine; per questo non credo, ch'appresso gli Huomini intendenti u'habbia da esser confusione. Et parmi, che non solamente per gli Hexachordi, che sono collocati in questo ordine de chorde; ma etiandio,
perche è cosa più naturale; come detto hauete poco fà, & anco nelle uostre Istitutioni;
che debba esser cosi. Il perche facesti palese per la diuisione harmonicamente fatta della Dupla & della Diapason nelle sue parti; cosa da niun'altro per auanti pur pensata.
Però laudo molto quest'ordine. Che ne diteuoi Messere di questo? Rispose M. Adriano; Non posso se non laudarlo; perche anco l'ordine de i Modi, ò Tuoni sarà posto
senza interrompimento. Et se bene appresso d'alcuni parerà questa cosa essere altramente; ci ricordaremo, che M. Gioseffo
hauendo uoluto più tosto seruire (come si uede in
fatto) alla prattica moderna, che alla speculatiua; in questo luogo egli parla secondo la
Scienza, & secondo che porta l'ordine naturale di questa cosa. Soggiunse à questo M.
Francesco; Questo importa poco appresso quelli, ch'intendono le cose della Musica; ma
ueniamo pure à quello, che segue. Per seguitare adunque l'ordine principiato, diss'io; ui
dico; che
PROPOSTA VII.
 . C. D. E. F. G. a. b
. C. D. E. F. G. a. b  . c. d. e. f. g & aa. le nominate Dicesette chorde,
le quali contengono i cinque Hexachordi. Dico prima, che cinque fiate tra
loro si ritroua la prima specie della Diapente, tra C. D. E. F & G. tra F. G. a. b
& c. tra G. a.
. c. d. e. f. g & aa. le nominate Dicesette chorde,
le quali contengono i cinque Hexachordi. Dico prima, che cinque fiate tra
loro si ritroua la prima specie della Diapente, tra C. D. E. F & G. tra F. G. a. b
& c. tra G. a.  . c & d. tra c. d. e f & g. & tra Γ. A.
. c & d. tra c. d. e f & g. & tra Γ. A.  . C & D. percioche ritrouandosi il maggior Semituono tra la Terza & la Quarta chorda di ciascheduna delle mostrate
Diapente; come tra E. & F. della Prima; tra a & b. della Seconda; tra
. C & D. percioche ritrouandosi il maggior Semituono tra la Terza & la Quarta chorda di ciascheduna delle mostrate
Diapente; come tra E. & F. della Prima; tra a & b. della Seconda; tra  & c. della Terza;
tra e & f. della Quarta, & tra
& c. della Terza;
tra e & f. della Quarta, & tra  & C. della Quinta; però dico, per la Nona Definitione,
che le mostrate sono Cinque Diapente contenute nella Prima specie, tra le Dicesette
& C. della Quinta; però dico, per la Nona Definitione,
che le mostrate sono Cinque Diapente contenute nella Prima specie, tra le Dicesette
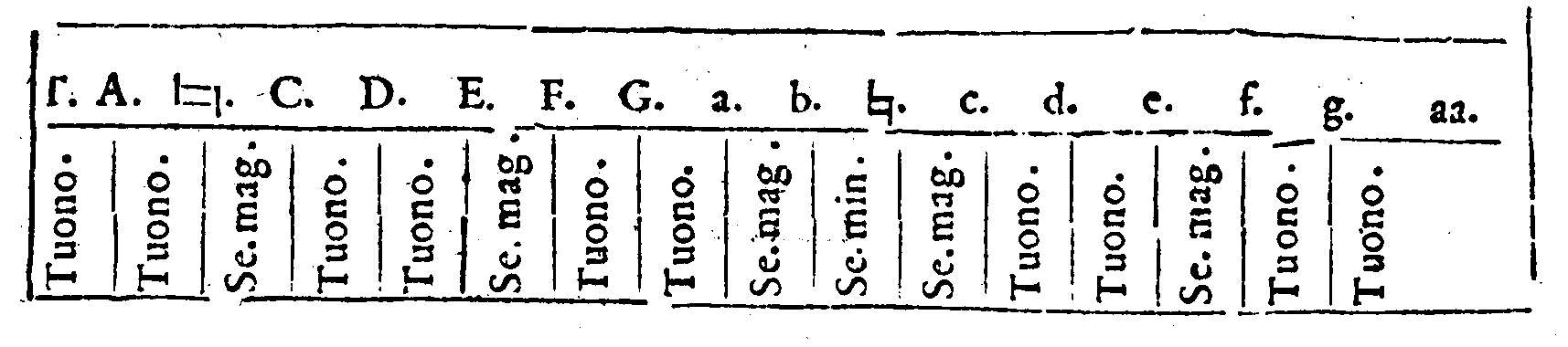
 . C. D & E. tra D. E. F. G et a. tra a.
. C. D & E. tra D. E. F. G et a. tra a.  . c. d. e. & tra d. e. f.
g et aa. et tra G. a. b. c et d percioche ritrouandosi il nominato Semituono tra la Seconda et
la Terza chorda di ciascheduna; tra
. c. d. e. & tra d. e. f.
g et aa. et tra G. a. b. c et d percioche ritrouandosi il nominato Semituono tra la Seconda et
la Terza chorda di ciascheduna; tra  et C. della A & E. tra E et F. della D et a. tra
et C. della A & E. tra E et F. della D et a. tra  et c.
page 270
della a & e; tra e & f. della d & g; & tra a & b. della G & d; per la sopradetta Definitione;
seguita, che le mostrate cinque Diapente siano tra le nominate chorde, & siano della seconda specie. Simigliantemente dico, che si troua due fiate la Terza specie della Diapente; prima tra E. F. G. a. &
et c.
page 270
della a & e; tra e & f. della d & g; & tra a & b. della G & d; per la sopradetta Definitione;
seguita, che le mostrate cinque Diapente siano tra le nominate chorde, & siano della seconda specie. Simigliantemente dico, che si troua due fiate la Terza specie della Diapente; prima tra E. F. G. a. &  ; dopoi tra a. b. c. d & e; percioche tra la prima & la seconda loro chorda, che sono E. & F. delle Diapente E &
; dopoi tra a. b. c. d & e; percioche tra la prima & la seconda loro chorda, che sono E. & F. delle Diapente E &  ; & a. & b. della a. & e; si troua esser collocato il maggior Semituono. Onde, per l'istessa nominata Definitione, E.
F. G. a &
; & a. & b. della a. & e; si troua esser collocato il maggior Semituono. Onde, per l'istessa nominata Definitione, E.
F. G. a &  ; ancora a. b. c. d & e. sono due Diapente della Terza specie, contenute tra 'l
numero delle già mostrate Dicisette chorde. Vltimamente dico, la Quarta specie contenersi tra esse chorde due fiate; tra F. G. a.
; ancora a. b. c. d & e. sono due Diapente della Terza specie, contenute tra 'l
numero delle già mostrate Dicisette chorde. Vltimamente dico, la Quarta specie contenersi tra esse chorde due fiate; tra F. G. a.  . & c; & tra b. c. d. e & f; essendo che tra la
quarta & la quinta loro chorde si troua esso Semituono; com'è manifesto dalle chorde
. & c; & tra b. c. d. e & f; essendo che tra la
quarta & la quinta loro chorde si troua esso Semituono; com'è manifesto dalle chorde
 . & c della prima, & e. con f. della seconda; Il perche, per la nominata nona Definitione, dico; F. G. a.
. & c della prima, & e. con f. della seconda; Il perche, per la nominata nona Definitione, dico; F. G. a.  & c; simigliantemente b. c. d. & f; esser due Diapente della Quarta specie, contenute tra le proposte chorde. Tra le dicisette Chorde, che contengono
i Cinque Hexachordi; adunque cinque fiate si troua la Prima specie della Diapente;
cinque la Seconda; due la Terza, & due la Quarta. Et questo sia tutto quello, che si
contiene nella proposta, che ui douea dimostrare. Quello, che si è detto disse M. Francesco; intorno alle Specie della Diapason, dell'ordine di prima & seconda, si potrebbe
anco dire intorno alle specie della Diapente; ma perche sarebbe un perder tempo fuora
di proposito; però giudico dal canto mio, che sia ben fatto, à proceder più oltra. Verrò adunque dissi à dimostrare, che
& c; simigliantemente b. c. d. & f; esser due Diapente della Quarta specie, contenute tra le proposte chorde. Tra le dicisette Chorde, che contengono
i Cinque Hexachordi; adunque cinque fiate si troua la Prima specie della Diapente;
cinque la Seconda; due la Terza, & due la Quarta. Et questo sia tutto quello, che si
contiene nella proposta, che ui douea dimostrare. Quello, che si è detto disse M. Francesco; intorno alle Specie della Diapason, dell'ordine di prima & seconda, si potrebbe
anco dire intorno alle specie della Diapente; ma perche sarebbe un perder tempo fuora
di proposito; però giudico dal canto mio, che sia ben fatto, à proceder più oltra. Verrò adunque dissi à dimostrare, che
PROPOSTA VIII.
 C. D. E. F. G a. b
C. D. E. F. G a. b  . c. d. e f. g &
aa; & dirò prima, che tra loro si contiene cinque fiate la prima specie della Diatessaron, tra Γ. A.
. c. d. e f. g &
aa; & dirò prima, che tra loro si contiene cinque fiate la prima specie della Diatessaron, tra Γ. A.  & C; tra C. D. E & F tra G. a.
& C; tra C. D. E & F tra G. a.  & c. tra c. d. e & f, & tra F. G a & b;
percioche tra la terza & la quarta chorda di ciascheduna si troua l'Interuallo del maggior
Semituono; come tra
& c. tra c. d. e & f, & tra F. G a & b;
percioche tra la terza & la quarta chorda di ciascheduna si troua l'Interuallo del maggior
Semituono; come tra  & C. della Γ & C; tra E & F. della C & F; tra
& C. della Γ & C; tra E & F. della C & F; tra  & c. della G
& c; tra e & f. della c & f; & tra a & b. della F & b. La onde, per la Decima Definitione
d'hoggi; seguita, che ciascuna de queste Diatessaron sia contenuta nella prima specie,
& che tra le mostrate Dicisette chorde cinque fiate si contenga la Prima specie della Diatessaron. Dico poi, che tra loro
si troua anco cinque fiate la seconda specie, tra A.
& c. della G
& c; tra e & f. della c & f; & tra a & b. della F & b. La onde, per la Decima Definitione
d'hoggi; seguita, che ciascuna de queste Diatessaron sia contenuta nella prima specie,
& che tra le mostrate Dicisette chorde cinque fiate si contenga la Prima specie della Diatessaron. Dico poi, che tra loro
si troua anco cinque fiate la seconda specie, tra A.  . C
& D, tra D E. F & G, tra a.
. C
& D, tra D E. F & G, tra a.  . c & d. tra d. e. f & g, & tra G. a. b & c; essendo che 'l Semituono è contenuto tra la seconda & la terza chorda di ciascheduna, come tra
. c & d. tra d. e. f & g, & tra G. a. b & c; essendo che 'l Semituono è contenuto tra la seconda & la terza chorda di ciascheduna, come tra  & C.
della A & D, tra E & F. della D & G; tra
& C.
della A & D, tra E & F. della D & G; tra  & c. della a & d, tra e f della d & g, & tra a &
b. della G & c. La onde, per la nominata Definitione, segue; che tutte le mostrate Diatessaron siano contenute nella Seconda specie. Tra le mostrate Dicisette chorde adunque, cinque fiate è contenuta la Seconda specie della Diatessaron. Vltimamente dico,
che la Terza specie è contenuta tra essa Dicisette chorde cinque fiate, tra
& c. della a & d, tra e f della d & g, & tra a &
b. della G & c. La onde, per la nominata Definitione, segue; che tutte le mostrate Diatessaron siano contenute nella Seconda specie. Tra le mostrate Dicisette chorde adunque, cinque fiate è contenuta la Seconda specie della Diatessaron. Vltimamente dico,
che la Terza specie è contenuta tra essa Dicisette chorde cinque fiate, tra  . C. D & E,
tra E. F. G & a, tra
. C. D & E,
tra E. F. G & a, tra  . c. d & e, tra e. f. g & aa, et tra a. b. c et d, essendo che la prima et la
. c. d & e, tra e. f. g & aa, et tra a. b. c et d, essendo che la prima et la
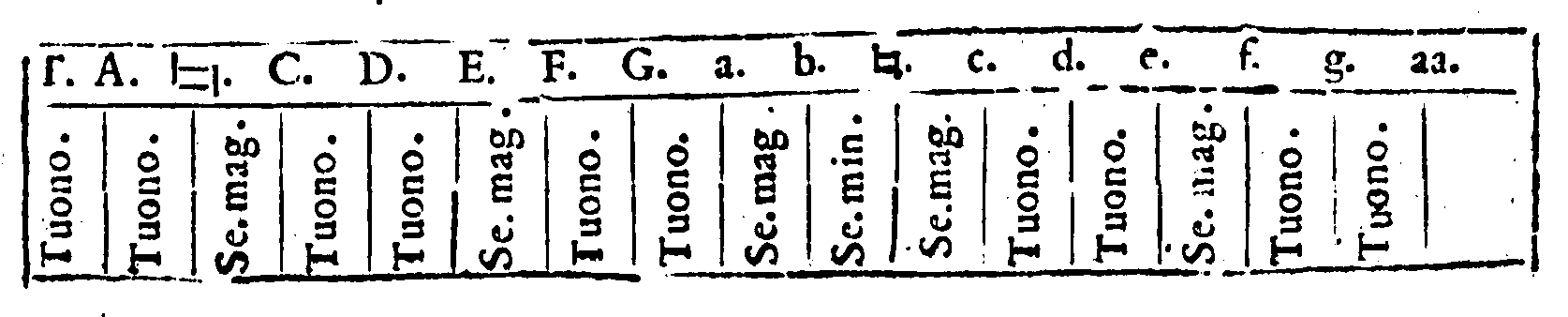
 & C. della
& C. della  & E. la E & F. della E & a. la
& E. la E & F. della E & a. la  & c. della
& c. della  & e. la e & f. della e & a. & la a & b. della a & d. contengono il nominato Semituono. Il perche dico, per
l'istessa Decima Definitione, tra le Dicesette chorde mostrate, contenersi cinque fiate
la Terza specie della Diatessaron. Et tutto questo è quello, che si contiene nella proposta,
& dimostrarui douea. Queste cose, disse M. Adriano; sono consequenti; imperoche se
la Diapente & la Diapason mutano il nome, ouer'ordine di Prima specie & di Seconda;
bisogno è che anco l'istesso faccia la Diatessaron, quando 'l Semituono uiene à mutar luogo; ma passate pure à dimostrarci qualche altra cosa; perche questo è chiaro. Ascoltate questa, soggiunsi.
& e. la e & f. della e & a. & la a & b. della a & d. contengono il nominato Semituono. Il perche dico, per
l'istessa Decima Definitione, tra le Dicesette chorde mostrate, contenersi cinque fiate
la Terza specie della Diatessaron. Et tutto questo è quello, che si contiene nella proposta,
& dimostrarui douea. Queste cose, disse M. Adriano; sono consequenti; imperoche se
la Diapente & la Diapason mutano il nome, ouer'ordine di Prima specie & di Seconda;
bisogno è che anco l'istesso faccia la Diatessaron, quando 'l Semituono uiene à mutar luogo; ma passate pure à dimostrarci qualche altra cosa; perche questo è chiaro. Ascoltate questa, soggiunsi.
PROPOSTA IX.
 & C. ui si troua 'l Semituono
maggiore, tra C & D. un tuono, tra D & E un'altro tuono, & tra E & F. un'altro maggior Semituono; i quali Interualli posti insieme non arriuano à tre Tuoni & un Semituono maggiore; Adunque tra la Terza & la Settima chorda delle proposte non si troua la
Consonanza Diapente. Soggiungo ancora et dico; che tra la Settima chorda et la Vndecima non si ritroua la Diatessaron; essendo che per la Ventesimaottaua proposta del
Secondo nostro ragionamento; la Diatessaron contiene un Tuono maggiore con un
minore, et un maggior Semituono; la quale, per la Prima nominata di questo, ridotta
al suo temperamento, contiene due Tuoni equali con un maggior Semituono. Ma tra
la settima et la undecima chorda si trouano tre Tuoni; percioche tra F et G. si troua 'l primo; tra G et a. il secondo; et tra a et
& C. ui si troua 'l Semituono
maggiore, tra C & D. un tuono, tra D & E un'altro tuono, & tra E & F. un'altro maggior Semituono; i quali Interualli posti insieme non arriuano à tre Tuoni & un Semituono maggiore; Adunque tra la Terza & la Settima chorda delle proposte non si troua la
Consonanza Diapente. Soggiungo ancora et dico; che tra la Settima chorda et la Vndecima non si ritroua la Diatessaron; essendo che per la Ventesimaottaua proposta del
Secondo nostro ragionamento; la Diatessaron contiene un Tuono maggiore con un
minore, et un maggior Semituono; la quale, per la Prima nominata di questo, ridotta
al suo temperamento, contiene due Tuoni equali con un maggior Semituono. Ma tra
la settima et la undecima chorda si trouano tre Tuoni; percioche tra F et G. si troua 'l primo; tra G et a. il secondo; et tra a et  . il terzo; et tre Tuoni, per la Ventesimanona del
Secondo, sopr'auanzano la Diatessaron; adunque tra la Settima et la Vndecima chorda
delle Dicesette proposte; non si troua la Diatessaron. Et questo è quello, che ui douea
dimostrare. A fè, quasi ridendo disse M. Claudio; che mi è piaciuto questa dimostratione, si per la sua breuità; com'anco per la sua facilità; onde credo che la Proposta sia
stata Theorema & non Problema; perche non si è uenuto all'atto dell'operare; però ui
prego, che senza por tempo di mezo, passate all'altra. Soggiunsi allora; Quel che hauete detto è uero, et per satisfarui, uoglio dimostrare in questa sequente; che
. il terzo; et tre Tuoni, per la Ventesimanona del
Secondo, sopr'auanzano la Diatessaron; adunque tra la Settima et la Vndecima chorda
delle Dicesette proposte; non si troua la Diatessaron. Et questo è quello, che ui douea
dimostrare. A fè, quasi ridendo disse M. Claudio; che mi è piaciuto questa dimostratione, si per la sua breuità; com'anco per la sua facilità; onde credo che la Proposta sia
stata Theorema & non Problema; perche non si è uenuto all'atto dell'operare; però ui
prego, che senza por tempo di mezo, passate all'altra. Soggiunsi allora; Quel che hauete detto è uero, et per satisfarui, uoglio dimostrare in questa sequente; che
PROPOSTA X.
 . C. D. E. F. G. a. &
. C. D. E. F. G. a. &  . Dico che tra
page 272
queste non cade alcuna chorda mezana, che la possa diuidere harmonicamente in una
Diapente nel graue, & in una Diatessaron nell'acuto. Imperoche tra
. Dico che tra
page 272
queste non cade alcuna chorda mezana, che la possa diuidere harmonicamente in una
Diapente nel graue, & in una Diatessaron nell'acuto. Imperoche tra  & F. corda me
& F. corda me
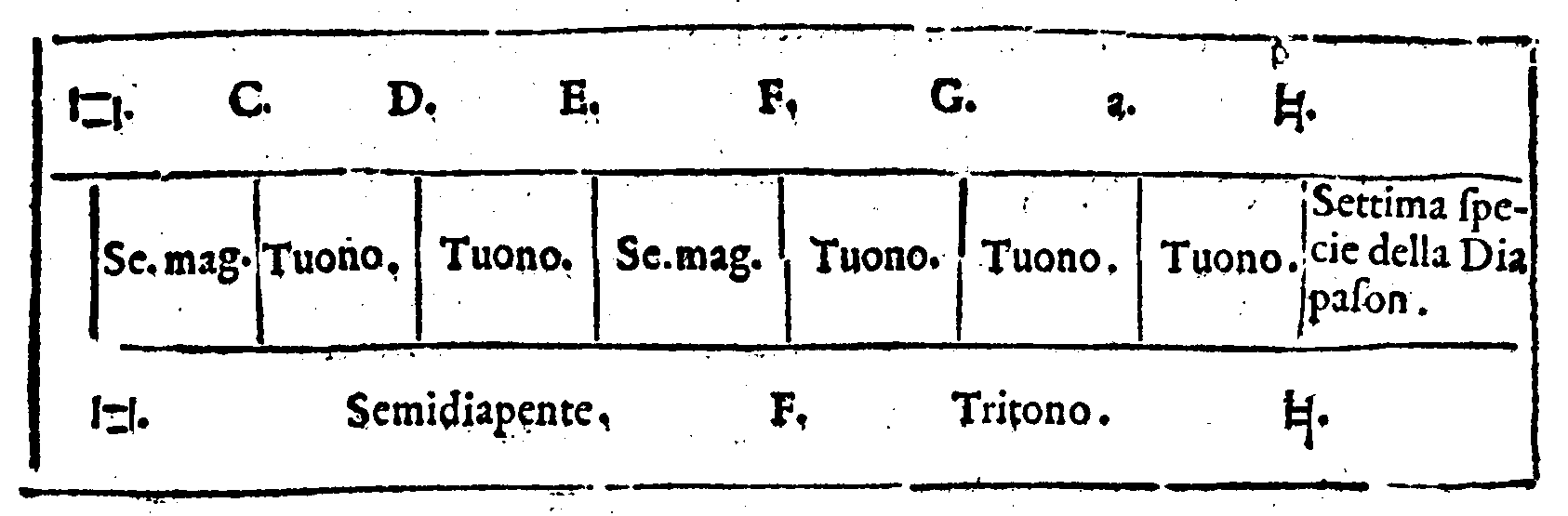
 . la Diatessaron; poiche tra
. la Diatessaron; poiche tra  & F. si trouano solamente due Tuoni & due maggiori Semituoni, com'è manifesto, i quali, per la
Trentesima del Secondo; non arriuano ad una Diapente. Simigliantemente, tra F &
& F. si trouano solamente due Tuoni & due maggiori Semituoni, com'è manifesto, i quali, per la
Trentesima del Secondo; non arriuano ad una Diapente. Simigliantemente, tra F &  .
non ui è la Diatessaron; essendo che, per la Ventesima ottaua del nominato Secondo
giorno; la Diatessaron contiene due Tuoni; l'un de i quali è maggiore & l'altro minore;
oueramente, per le Definitioni Quarta & Quinta d'hoggi; sono due Tuoni equali, & di
più un maggior Semituono; & F con
.
non ui è la Diatessaron; essendo che, per la Ventesima ottaua del nominato Secondo
giorno; la Diatessaron contiene due Tuoni; l'un de i quali è maggiore & l'altro minore;
oueramente, per le Definitioni Quarta & Quinta d'hoggi; sono due Tuoni equali, & di
più un maggior Semituono; & F con  . contiene tre Tuoni, i quali, per la Ventesima
nona del nominato Secondo; sono maggiori d'una Diatessaron; adunque
. contiene tre Tuoni, i quali, per la Ventesima
nona del nominato Secondo; sono maggiori d'una Diatessaron; adunque  & F. non
fanno una Diapente, ne F &
& F. non
fanno una Diapente, ne F &  . una Diatessaron. Ma perche, per la Duodecima Definitione d'hoggi, la Diapason è detta essere harmonicamente diuisa, quando da una mezana chorda è partita in una Diapente posta nel graue & nella Diatessaron nell'acuto;
non si potendo fare tal diuisione col mezo della chorda F; però dico, che Tra la Settima
specie della Diapason non cade alcuna chorda mezana, che la partisca harmonicamente in due parti; come dimostrar ui douea. Voglio ancora che sapiate, in consequenza di
quello, c'hò dimostrato; che
. una Diatessaron. Ma perche, per la Duodecima Definitione d'hoggi, la Diapason è detta essere harmonicamente diuisa, quando da una mezana chorda è partita in una Diapente posta nel graue & nella Diatessaron nell'acuto;
non si potendo fare tal diuisione col mezo della chorda F; però dico, che Tra la Settima
specie della Diapason non cade alcuna chorda mezana, che la partisca harmonicamente in due parti; come dimostrar ui douea. Voglio ancora che sapiate, in consequenza di
quello, c'hò dimostrato; che
PROPOSTA XI.
 . C. D. E. F. G. a.
. C. D. E. F. G. a.  . c. d. e. f. g & aa. Dico che sei Specie di essa, & non più, potranno essere diuise harmonicamente in due parti. Et perche, per la Duodecima
definitione d'hoggi; tal diuisione nasce da una chorda mezana, che la diuide in una Diapente nel graue, & in una Diatessaron nell'acuto; essendo
la Diapason C & c. della prima
specie diuisa in cotal modo dalla chorda G; la D & d. della seconda dalla a; la E & e. della terza specie della
. c. d. e. f. g & aa. Dico che sei Specie di essa, & non più, potranno essere diuise harmonicamente in due parti. Et perche, per la Duodecima
definitione d'hoggi; tal diuisione nasce da una chorda mezana, che la diuide in una Diapente nel graue, & in una Diatessaron nell'acuto; essendo
la Diapason C & c. della prima
specie diuisa in cotal modo dalla chorda G; la D & d. della seconda dalla a; la E & e. della terza specie della  . la F & f. della quarta dalla c; la G & g. della quinta specie dalla d;
& la a & aa. della Sesta dalla e; Il che si potrebbe anco dire della Γ & G; medesimamente della quinta specie, la quale è
diuisa dalla D; & della A & a. della Sesta, che è partita
dalla E; però la mezana chorda, che partisce la Prima specie sarà G; la mezana della Seconda sarà a; quella della Terza sarà
. la F & f. della quarta dalla c; la G & g. della quinta specie dalla d;
& la a & aa. della Sesta dalla e; Il che si potrebbe anco dire della Γ & G; medesimamente della quinta specie, la quale è
diuisa dalla D; & della A & a. della Sesta, che è partita
dalla E; però la mezana chorda, che partisce la Prima specie sarà G; la mezana della Seconda sarà a; quella della Terza sarà
 ; la mezana della Quarta sarà c la mezana della
Quinta sarà d; & la mezana della Sesta sarà e. Essendoche la prima, ch'è G. diuiderà la
Diapason C & c. in una Diapente C & G. posta nella parte graue, & in una Diatessaron
G & c. posta nella parte acuta; & la a. partirà la Seconda D & d. in una Diapente D & a.
nel graue, & in una Diatessaron a & d. nell'acuto. Simigliantemente
; la mezana della Quarta sarà c la mezana della
Quinta sarà d; & la mezana della Sesta sarà e. Essendoche la prima, ch'è G. diuiderà la
Diapason C & c. in una Diapente C & G. posta nella parte graue, & in una Diatessaron
G & c. posta nella parte acuta; & la a. partirà la Seconda D & d. in una Diapente D & a.
nel graue, & in una Diatessaron a & d. nell'acuto. Simigliantemente  diuiderà la Terpage 273
diuiderà la Terpage 273
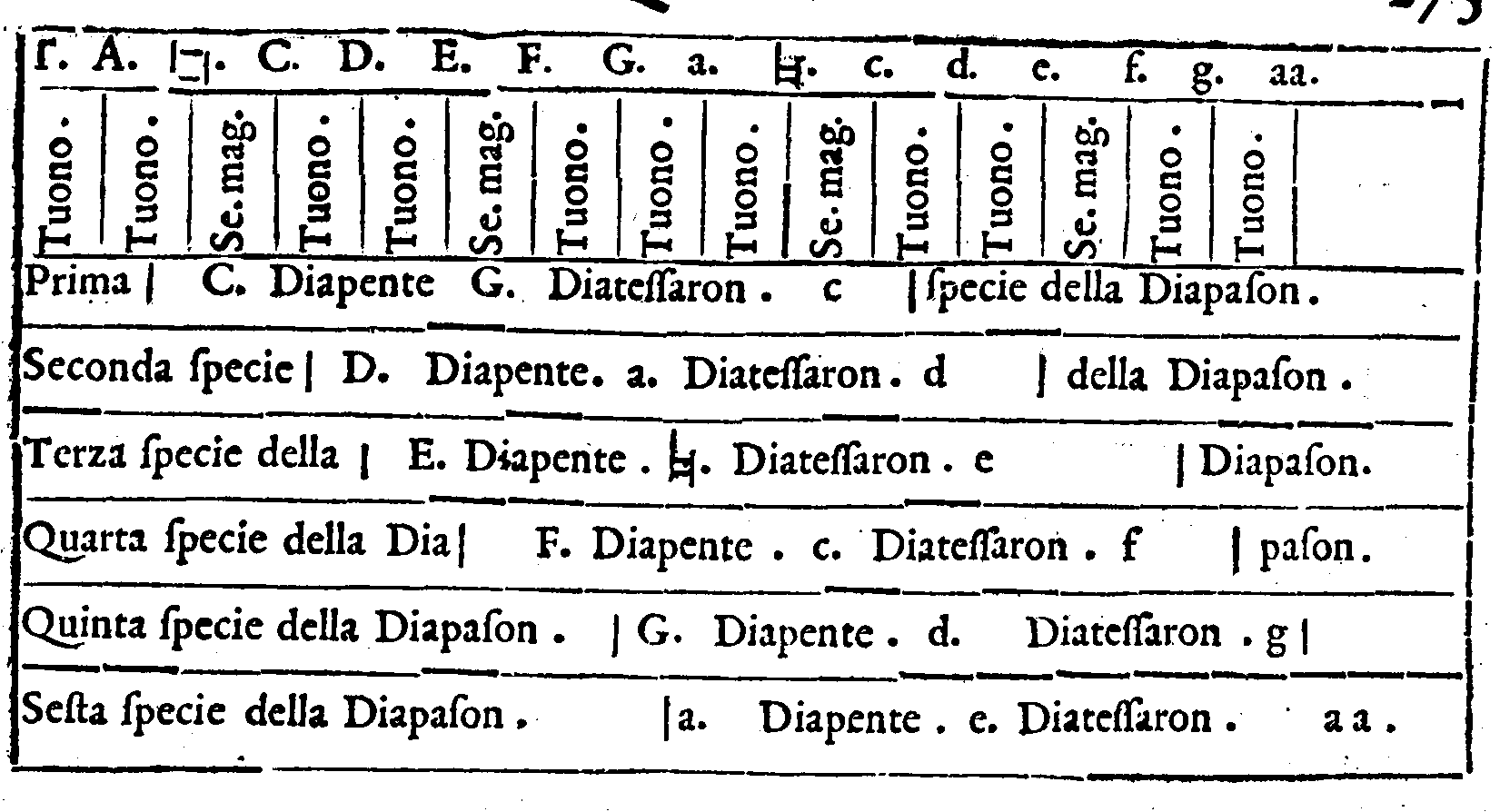
 . nel graue, & in una Diatessaron
. nel graue, & in una Diatessaron  & e. nell'acuto. Et
c. diuiderà la Quarta F & f. in una Diapente posta nel graue, che sarà F & c, & in una Diatessaron posta nella parte acuta, la quale sarà c & f. Ma la d. partirà la Quinta specie G
& g. nella Diapente G & d. nel graue, & nella Diatessaron d & g. nell'acuto. Vltimamente la Sesta specie a & aa. sarà diuisa
da e. in una Diapente a & e. posta nel graue, & in una
Diatessaron e & aa. posta nell'acuto. La onde non è dubio alcuno essendo C G, D a,
E
& e. nell'acuto. Et
c. diuiderà la Quarta F & f. in una Diapente posta nel graue, che sarà F & c, & in una Diatessaron posta nella parte acuta, la quale sarà c & f. Ma la d. partirà la Quinta specie G
& g. nella Diapente G & d. nel graue, & nella Diatessaron d & g. nell'acuto. Vltimamente la Sesta specie a & aa. sarà diuisa
da e. in una Diapente a & e. posta nel graue, & in una
Diatessaron e & aa. posta nell'acuto. La onde non è dubio alcuno essendo C G, D a,
E , F c, G d & a e Diapente; perche, per la Trentesima del Secondo giorno, ciascheduna di esse contiene Tre tuoni & un maggior Semituono; il che dico ancora della G c,
a d,
, F c, G d & a e Diapente; perche, per la Trentesima del Secondo giorno, ciascheduna di esse contiene Tre tuoni & un maggior Semituono; il che dico ancora della G c,
a d,  e, c f, d g & e aa Diatessaron, che contengono ciascheduna da per se; per la Ventesima ottaua pur del Secondo; due Tuoni & un maggior Semituono; che le chorde mezane, le quali partiscono le nominate Sei prime specie
della Diapason, siano la G. a
e, c f, d g & e aa Diatessaron, che contengono ciascheduna da per se; per la Ventesima ottaua pur del Secondo; due Tuoni & un maggior Semituono; che le chorde mezane, le quali partiscono le nominate Sei prime specie
della Diapason, siano la G. a  .
c. d & e. Et perche Sei sono le specie della Diapason, com'habbiamo dimostrato, che
si possono in cotal modo diuidere; & la Settima, per la Precedente, al tutto è indiuisibile; però dico, che Delle Sette specie della Diapason Sei & non più, da una mezana
chorda possono esser diuise harmonicamente in due parti; come, secondo la proposta
ui douea dimostrare. Vi uoglio etiandio dimostrare; che
.
c. d & e. Et perche Sei sono le specie della Diapason, com'habbiamo dimostrato, che
si possono in cotal modo diuidere; & la Settima, per la Precedente, al tutto è indiuisibile; però dico, che Delle Sette specie della Diapason Sei & non più, da una mezana
chorda possono esser diuise harmonicamente in due parti; come, secondo la proposta
ui douea dimostrare. Vi uoglio etiandio dimostrare; che
PROPOSTA XII.
 . c. d. e & f. tra le quali ui è la Quarta
. c. d. e & f. tra le quali ui è la Quarta  , che la diuide in due
parti; F. G. a &
, che la diuide in due
parti; F. G. a &  . & in
. & in  . c. d. e & f. Ma tra F. G. a &
. c. d. e & f. Ma tra F. G. a &  ; per la Decima di questo;
si troua Tre tuoni; i quali sono, per la Ventesima nona del Secondo, maggiori d'una
Diatessaron; adunque F &
; per la Decima di questo;
si troua Tre tuoni; i quali sono, per la Ventesima nona del Secondo, maggiori d'una
Diatessaron; adunque F &  . non è una Diatessaron. Simigliantemente tra
. non è una Diatessaron. Simigliantemente tra  . c. d. e & f.
si trouano due Tuoni & due maggiori Semituoni. Ma la Diapente, per la Trentesima del
nominato Secondo giorno, contiene tre Tuoni & un maggior Semituono, adunque
. c. d. e & f.
si trouano due Tuoni & due maggiori Semituoni. Ma la Diapente, per la Trentesima del
nominato Secondo giorno, contiene tre Tuoni & un maggior Semituono, adunque  &
f. non è Diapente. Non essendo adunque F
&
f. non è Diapente. Non essendo adunque F  . Diatessaron, ne
. Diatessaron, ne  f. Diapente; & essendo F & f.
la Quarta specie della Diapason; non sarà anco la
f. Diapente; & essendo F & f.
la Quarta specie della Diapason; non sarà anco la  . chorda mezana, laquale la diuida arith
page 274
. chorda mezana, laquale la diuida arith
page 274
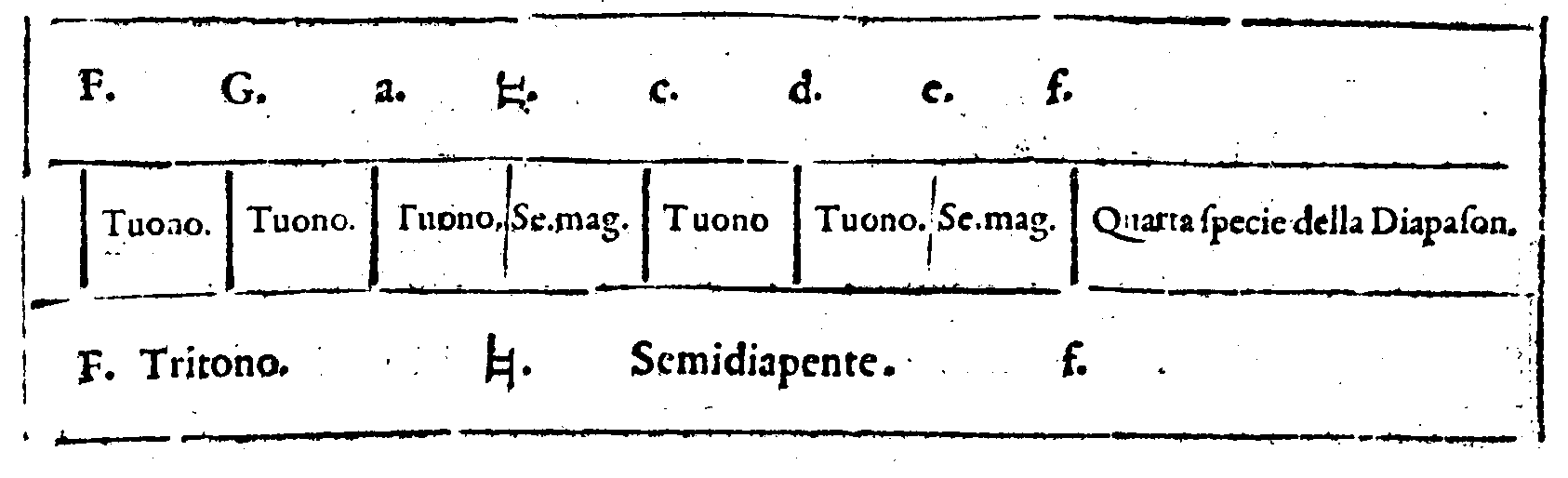
PROPOSTA XIII.
 . C. D. E. F. G. a.
. C. D. E. F. G. a.  . c d. e. f. g & aa, le quali contengano le Sette specie della Diapason. Dico che tra questo numero di chorde, la chorda mezana, che partisce in due parti
arithmeticamente le Diapason, non ne potrà diuidere se non Sei specie, lequali saranno (per
seguitare un'ordine continuo & non interrotto) Γ & G, ouer G & g. Quinta specie; A & a
ouero a & aa. Sesta;
. c d. e. f. g & aa, le quali contengano le Sette specie della Diapason. Dico che tra questo numero di chorde, la chorda mezana, che partisce in due parti
arithmeticamente le Diapason, non ne potrà diuidere se non Sei specie, lequali saranno (per
seguitare un'ordine continuo & non interrotto) Γ & G, ouer G & g. Quinta specie; A & a
ouero a & aa. Sesta;  &
&  . Settima; C & c. prima; D & d. Seconda; ultimamente E & e. Ter
. Settima; C & c. prima; D & d. Seconda; ultimamente E & e. Ter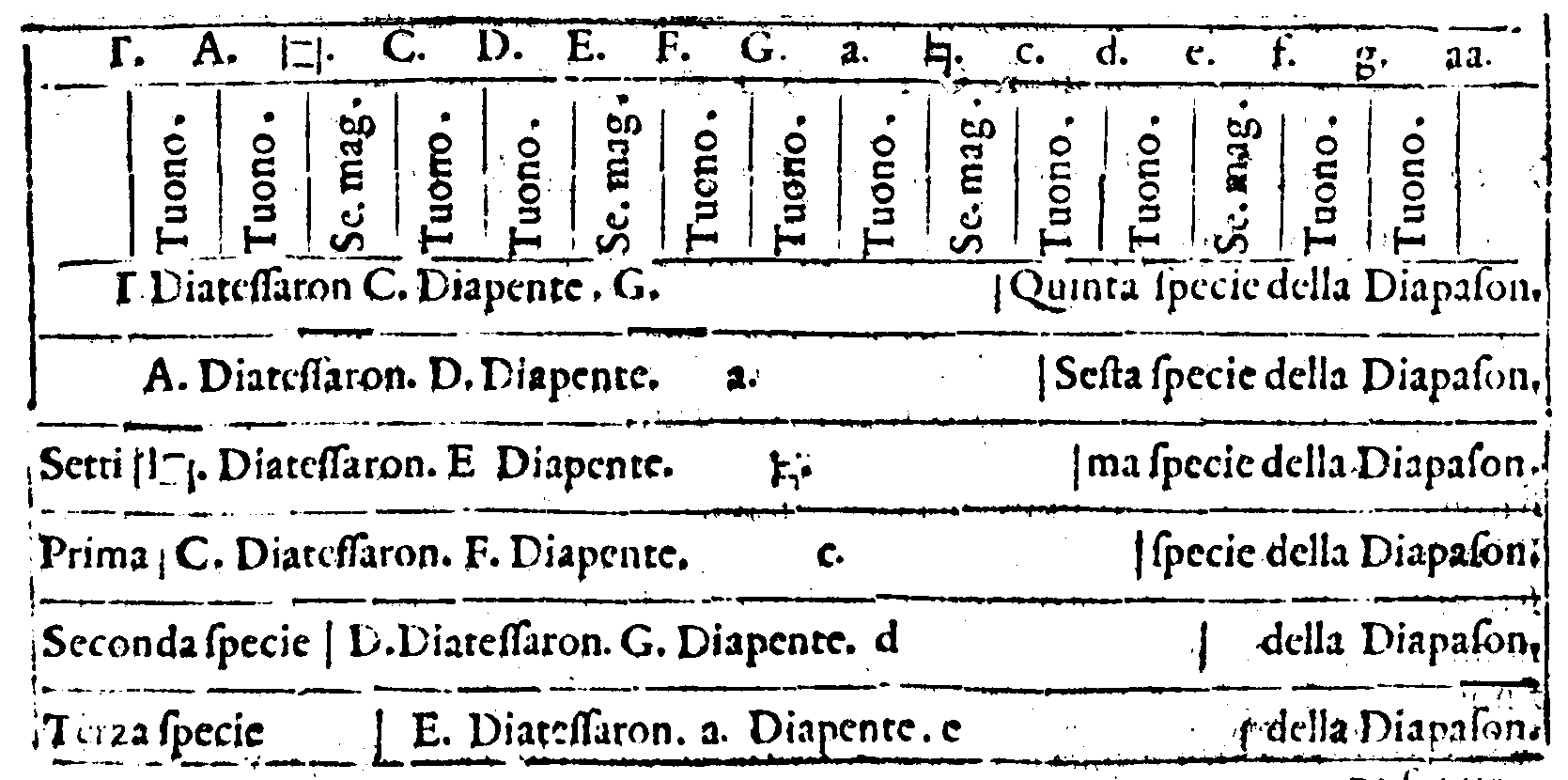
 &
&  . in una Diatessaron
. in una Diatessaron  & E. & in una Diapente E &
& E. & in una Diapente E &  ; la F. diuide la C. & c. in una Diatessaron C & F. & in una Diapente F & c; la G; parte la D & d.
in una Diatessaron D & G. & in una Diapente G & d. Vltimamente la a. diuide la E & e.
in una Diatessaron E & a. & in una Diapente a & e. Onde non è da dubitare, che contenendo ciascheduna di queste Γ & c, A &
D,
; la F. diuide la C. & c. in una Diatessaron C & F. & in una Diapente F & c; la G; parte la D & d.
in una Diatessaron D & G. & in una Diapente G & d. Vltimamente la a. diuide la E & e.
in una Diatessaron E & a. & in una Diapente a & e. Onde non è da dubitare, che contenendo ciascheduna di queste Γ & c, A &
D,  . & E, C & F, D & G, & E & a. due Tuoni & un
maggior Semituono; elle siano, per la Ventesima ottaua del Secondo ragionamento, tante Diatessaron. Si come non è anco da dubitare delle C & G, D & a; E &
. & E, C & F, D & G, & E & a. due Tuoni & un
maggior Semituono; elle siano, per la Ventesima ottaua del Secondo ragionamento, tante Diatessaron. Si come non è anco da dubitare delle C & G, D & a; E &  , F & c, G &
d; & a con e; per la Trentesima nona del Secondo medesimamente, che elle siano Diapente; percioche contengono tre Tuoni & un maggior Semituono. Et perche Sette sono le specie della Diapason, & tali diuisioni non si possono fare in più di Sei; essendo
che per la Precedente, la Quarta specie non riceue cotal diuisione; però dico, che tra 'l
numero delle Sedeci chorde mostrate, la mezana chorda, che diuide in due parti arithmeticamente la Diapason, non potrà diuidere
se non Sei specie di essa; come dimostrarui
douea. Voglio ancora che sapiate; che da questo ch'io u'hò dimostrato, ne segue; che
, F & c, G &
d; & a con e; per la Trentesima nona del Secondo medesimamente, che elle siano Diapente; percioche contengono tre Tuoni & un maggior Semituono. Et perche Sette sono le specie della Diapason, & tali diuisioni non si possono fare in più di Sei; essendo
che per la Precedente, la Quarta specie non riceue cotal diuisione; però dico, che tra 'l
numero delle Sedeci chorde mostrate, la mezana chorda, che diuide in due parti arithmeticamente la Diapason, non potrà diuidere
se non Sei specie di essa; come dimostrarui
douea. Voglio ancora che sapiate; che da questo ch'io u'hò dimostrato, ne segue; che
PROPOSTA XIIII.
PROPOSTA XV.
PROPOSTA XVI.
PROPOSTA XVII.
 &
&  . non
cade modulatione alcuna di Modo Principale, ouero Autentico; però siano le
chorde C. D. E. F. G. a.
. non
cade modulatione alcuna di Modo Principale, ouero Autentico; però siano le
chorde C. D. E. F. G. a.  . c. d. e. f. g & aa. del numero delle Sedici nominate
solamente. Dico, tra C. D. E. F. G. a.
. c. d. e. f. g & aa. del numero delle Sedici nominate
solamente. Dico, tra C. D. E. F. G. a.  . & c. esser collocato il Primo modo & principale;
page 277
. & c. esser collocato il Primo modo & principale;
page 277

MODI PRINCIPALI, ET AVTENTICI.
 . c & d. il. Terzo; tra E. F. G. a.
. c & d. il. Terzo; tra E. F. G. a.  . c. d & e. il Quinto; tra F. G. a.
. c. d & e. il Quinto; tra F. G. a.  . c.
d. e & f. il Settimo; tra G. a.
. c.
d. e & f. il Settimo; tra G. a.  . c. d. e. f & g. il Nono; & tra a.
. c. d. e. f & g. il Nono; & tra a.  . c. d. e. f. g & aa. l'Vndecimo. Imperoche, per la Sesta di questo, C. D. E. F. G. a.
. c. d. e. f. g & aa. l'Vndecimo. Imperoche, per la Sesta di questo, C. D. E. F. G. a.  & c. è la Prima specie della
Diapason; & per la Vndecima, tale Diapason è diuisa harmonicamente dalla chorda G.
in una Diapente C & G, & in una Diatessaron G & c; onde, per la Quartadecima & Quintadecima definitione, seguita; che tale Diapason contenga il primo Modo principale &
autentico. Simigliantemente; perche D. E. F. G. a. b. c & d, per la Sesta nominata; è la
seconda specie della Diapason, & per la Vndecima proposta nominata, tale Diapason
è harmonicamente diuisa dalla chorda a. in una Diapente D & a. in una Diatessaron a &
d; però, per le nominate Definitioni, tal Diapason contiene il Terzo modo principale.
Ancora; perche E. F. G. a.
& c. è la Prima specie della
Diapason; & per la Vndecima, tale Diapason è diuisa harmonicamente dalla chorda G.
in una Diapente C & G, & in una Diatessaron G & c; onde, per la Quartadecima & Quintadecima definitione, seguita; che tale Diapason contenga il primo Modo principale &
autentico. Simigliantemente; perche D. E. F. G. a. b. c & d, per la Sesta nominata; è la
seconda specie della Diapason, & per la Vndecima proposta nominata, tale Diapason
è harmonicamente diuisa dalla chorda a. in una Diapente D & a. in una Diatessaron a &
d; però, per le nominate Definitioni, tal Diapason contiene il Terzo modo principale.
Ancora; perche E. F. G. a.  . c. d & e, è la Terza specie della Diapason, & per la Vndecima
di questo, è diuisa harmonicamente dalla
. c. d & e, è la Terza specie della Diapason, & per la Vndecima
di questo, è diuisa harmonicamente dalla  . in due parti; cioè, in una Diapente E &
. in due parti; cioè, in una Diapente E &  , in
una Diatessaron
, in
una Diatessaron  & e; però dico E. F. G. a.
& e; però dico E. F. G. a.  . c. d & e. essere; per le dette due Definitioni,
il Quinto modo & principale. Oltra ciò; perche; per la nominata Vndecima; F. G. a.
. c. d & e. essere; per le dette due Definitioni,
il Quinto modo & principale. Oltra ciò; perche; per la nominata Vndecima; F. G. a.
 . c. d. e & f. è la Quarta specie della Diapason diuisa dalla c. in una Diapente F & c, & i in
una Diatessaron c & f; però dico, per l'istesse due nominate Definitioni, tal Diapason,
contenere la modulatione del Settimo modo & principale. Dico ancora G. a.
. c. d. e & f. è la Quarta specie della Diapason diuisa dalla c. in una Diapente F & c, & i in
una Diatessaron c & f; però dico, per l'istesse due nominate Definitioni, tal Diapason,
contenere la modulatione del Settimo modo & principale. Dico ancora G. a.  .
c. d. e. f & g, contenere 'l Nono & principale; percioche essendo la Quinta specie della Diapason diuisa; come dimostra l'Vndecima d'hoggi; dalla chorda d. in due
parti; cioè, in G & d. Diapente, & in d & g. Diatessaron; ne segue, per le Definitioni addotte di sopra, senza dubitar cosa alcuna, il nostro proposito. Finalmente essendo a.
.
c. d. e. f & g, contenere 'l Nono & principale; percioche essendo la Quinta specie della Diapason diuisa; come dimostra l'Vndecima d'hoggi; dalla chorda d. in due
parti; cioè, in G & d. Diapente, & in d & g. Diatessaron; ne segue, per le Definitioni addotte di sopra, senza dubitar cosa alcuna, il nostro proposito. Finalmente essendo a.  . c. d. e. f. g & aa. la Sesta specie della Diapason, & essendo diuisa in
una Diapente a & e. harmonicamente, & in una Diatessaron e & aa. dalla chorda
page 278
e; seguita medesimamente, per le due di sopra nominate Definitioni; che nella detta Diapason sia contenuta la modulatione dell'Vndecimo modo, & che esso modo sia uno delli
Autentici & principali. Et tutto questo è quello, che faceua bisogno di dimostrarui. Disse allora M. Adriano; Quelli, che negano i Modi esser Dodici, sono in grand'errore; &
tal'errore si và sempre facendo più palese dalle dimostrationi. Et perche hauete dimostrato per ordine i Principali; però seguitarete à dimostrarci gli altri; se ben non è cosa
difficile da intendere. Qui è il suo luogo Messere; dissi; però attendete.
. c. d. e. f. g & aa. la Sesta specie della Diapason, & essendo diuisa in
una Diapente a & e. harmonicamente, & in una Diatessaron e & aa. dalla chorda
page 278
e; seguita medesimamente, per le due di sopra nominate Definitioni; che nella detta Diapason sia contenuta la modulatione dell'Vndecimo modo, & che esso modo sia uno delli
Autentici & principali. Et tutto questo è quello, che faceua bisogno di dimostrarui. Disse allora M. Adriano; Quelli, che negano i Modi esser Dodici, sono in grand'errore; &
tal'errore si và sempre facendo più palese dalle dimostrationi. Et perche hauete dimostrato per ordine i Principali; però seguitarete à dimostrarci gli altri; se ben non è cosa
difficile da intendere. Qui è il suo luogo Messere; dissi; però attendete.
PROPOSTA XVIII.
 . c. d & e. separate dal numero delle
Sedici tante fiate nominate. Dico tra Γ. A. C. D. E. F & G. esser collocato il Secondo
modo non principale, ouer Plagale; tra A.
. c. d & e. separate dal numero delle
Sedici tante fiate nominate. Dico tra Γ. A. C. D. E. F & G. esser collocato il Secondo
modo non principale, ouer Plagale; tra A.  . C. D. E. F. G & a; il Quarto; tra
. C. D. E. F. G & a; il Quarto; tra  C. D. E.
F. G. a &
C. D. E.
F. G. a &  . il Sesto; tra C. D. E. F. G. a
. il Sesto; tra C. D. E. F. G. a  & c; l'Ottauo; tra D. E. F. G. a.
& c; l'Ottauo; tra D. E. F. G. a.  . c & d; il Decimo;
& tra E. F. G. a.
. c & d; il Decimo;
& tra E. F. G. a.  . c. d & e. il Duodecio. Percioche essendo Γ. A.
. c. d & e. il Duodecio. Percioche essendo Γ. A.  . C. D. E. F & G, per
la Sesta proposta d'hoggi; la Quinta specie della Diapason, & per la Terzadecima diuisa
arithmeticamente dalla chorda C. in una Diatessaron Γ & C. & in una Diapente C & G;
quella posta nel graue & questa nell'acuto; per le Definitioni Quartadecima & Decimasesta; tal Diapason uiene ad essere 'l Secondo modo, & Nonprincipale, ouer Plagale.
Simigliantemente; perche A.
. C. D. E. F & G, per
la Sesta proposta d'hoggi; la Quinta specie della Diapason, & per la Terzadecima diuisa
arithmeticamente dalla chorda C. in una Diatessaron Γ & C. & in una Diapente C & G;
quella posta nel graue & questa nell'acuto; per le Definitioni Quartadecima & Decimasesta; tal Diapason uiene ad essere 'l Secondo modo, & Nonprincipale, ouer Plagale.
Simigliantemente; perche A.  . C. D. E. F. G & a, per la detta proposta, è la Settima specie della Diapason, & per la nominata Decimaterza, è diuisa arithmeticamente in una
Diatessaron A & D, & in una Diapente D & a; però dico A.
. C. D. E. F. G & a, per la detta proposta, è la Settima specie della Diapason, & per la nominata Decimaterza, è diuisa arithmeticamente in una
Diatessaron A & D, & in una Diapente D & a; però dico A.  . C. D. E. F. G & a, per le
Definitioni nominate, essere 'l Quarto modo & Nonprincipale. Ancora; per la detta Sesta proposta
. C. D. E. F. G & a, per le
Definitioni nominate, essere 'l Quarto modo & Nonprincipale. Ancora; per la detta Sesta proposta  . C. D. E. F. G. a &
. C. D. E. F. G. a &  ; è la Settima specie della Diapason diuisa, per la detta
Terzadecima proposta, dalla chorda E. in una Diatessaron
; è la Settima specie della Diapason diuisa, per la detta
Terzadecima proposta, dalla chorda E. in una Diatessaron  & E, & in una Diapente E
&
& E, & in una Diapente E
&  ; però dico per la Quartadecima definitione; tal Diapason essere il Sesto modo, &
anco essere; per la Decimasesta; uno de i Modi nonprincipali, ouer Plagali. Ma la C. D.
E. F. G. a.
; però dico per la Quartadecima definitione; tal Diapason essere il Sesto modo, &
anco essere; per la Decimasesta; uno de i Modi nonprincipali, ouer Plagali. Ma la C. D.
E. F. G. a.  & c; per la nominata proposta, è la prima specie della Diapason diuisa in una
Diatessaron C & F, & in una Diapente F & c. dalla chorda F; onde dico, questa Diapason
contenere l'Ottauo modo, uno de i Nonprincipali. Et perche D. E. F. G. a.
& c; per la nominata proposta, è la prima specie della Diapason diuisa in una
Diatessaron C & F, & in una Diapente F & c. dalla chorda F; onde dico, questa Diapason
contenere l'Ottauo modo, uno de i Nonprincipali. Et perche D. E. F. G. a.  . c & d. è la
seconda specie, per la Sesta di questo, della Diapason diuisa, per la Terzadecima, in
una Diatessaron D & G, & in una Diapente G & d. dalla chorda G; però dico, per le Definitioni addotte di sopra; D. E. F. G. a.
. c & d. è la
seconda specie, per la Sesta di questo, della Diapason diuisa, per la Terzadecima, in
una Diatessaron D & G, & in una Diapente G & d. dalla chorda G; però dico, per le Definitioni addotte di sopra; D. E. F. G. a.  . c & d, contenere la modulatione del Decimo
modo & Plagale. Vltimamente; perche E. F. G. a.
. c & d, contenere la modulatione del Decimo
modo & Plagale. Vltimamente; perche E. F. G. a.  . c. d & e; per la Sesta nominata, è la
Terza specie della Diapason diuisa arithmeticamente in una Diatessaron E & a, & in
una Diapente a & e; dalla chorda a; però dico, per le due nominate di sopra Definitioni;
tale Diapason contenere il modo Duodecimo, uno de i Nonprincipali. La onde per tal
modo haurò dimostrato per ordine i Modi Nonprincipali & Plagali; come ui douea dimostrare. Voglio hora dimostrarui; che
page 279
. c. d & e; per la Sesta nominata, è la
Terza specie della Diapason diuisa arithmeticamente in una Diatessaron E & a, & in
una Diapente a & e; dalla chorda a; però dico, per le due nominate di sopra Definitioni;
tale Diapason contenere il modo Duodecimo, uno de i Nonprincipali. La onde per tal
modo haurò dimostrato per ordine i Modi Nonprincipali & Plagali; come ui douea dimostrare. Voglio hora dimostrarui; che
page 279
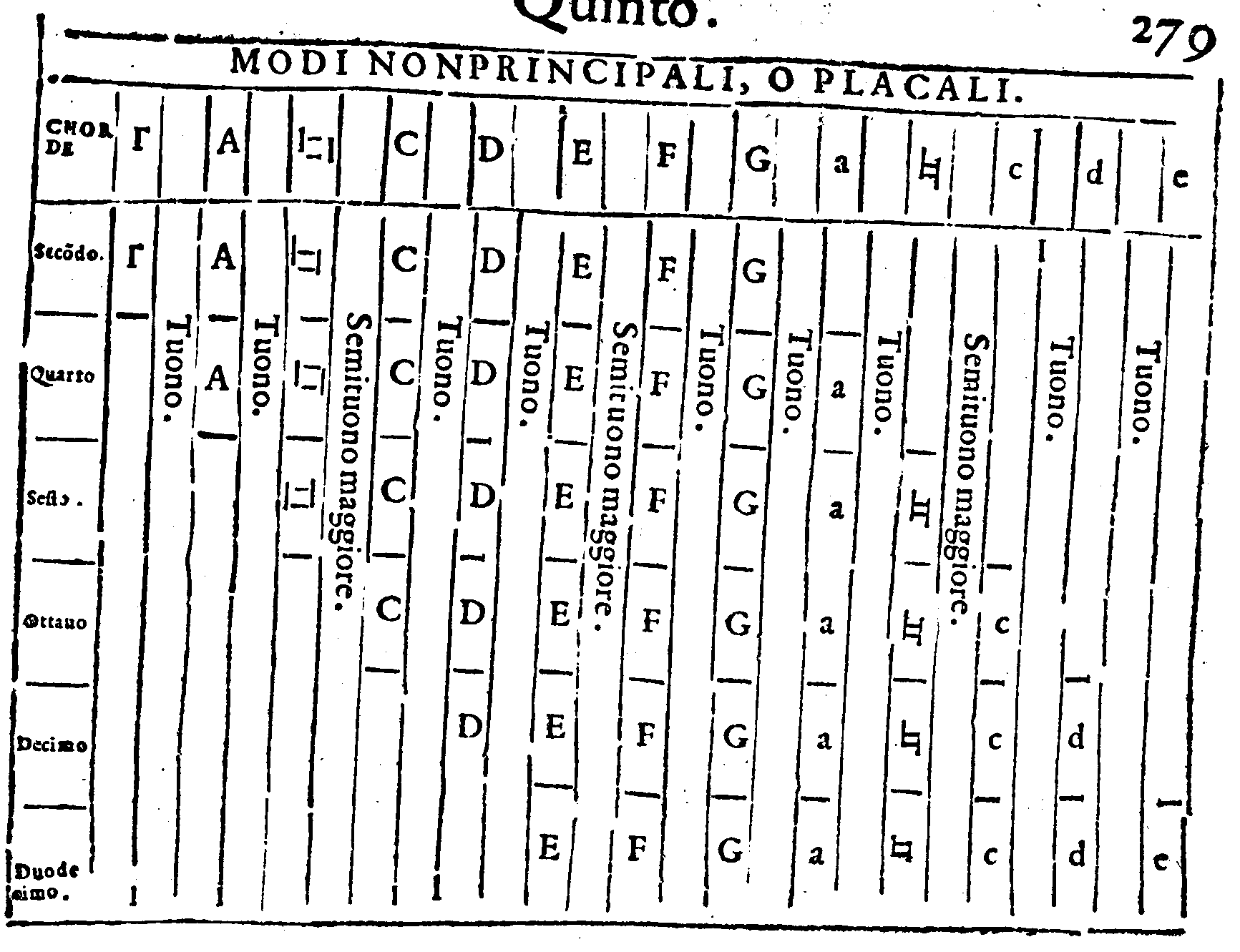
MODI NON PRINCIPALI, O PLACALI.
PROPOSTA XIX.
 . per un Semituono maggiore. La
onde essendo la C. chorda grauissima del Primo modo; la D. quella del Terzo; la
E. quella del Quinto; la F. quella del Settimo; la G. quella del Nono; & la a. quella
dell'Vndecimo. Ancora essendo Γ. la grauissima chorda del Secondo modo; A quella del Quarto;
. per un Semituono maggiore. La
onde essendo la C. chorda grauissima del Primo modo; la D. quella del Terzo; la
E. quella del Quinto; la F. quella del Settimo; la G. quella del Nono; & la a. quella
dell'Vndecimo. Ancora essendo Γ. la grauissima chorda del Secondo modo; A quella del Quarto;  . quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; &
page 280
E quella del Duodecimo; seguendo l'altre per ordine; secondo la natura delle loro Diapason; non è da dubitare, che le chorde del Terzo modo siano più acute di quelle del
Primo, quelle del Quinto più acute di quelle del Terzo, quelle del Nono più acute di
quelle del Settimo, & quelle dell'Vndecimo più acute di quelle del Nono, per un Tuono. Et che quelle del Settimo siano più acute di quelle del Quinto per un Semituono
maggiore, come dice la prima parte della proposta. Et per la seconda parte dico; che,
per la Prima proposta nominata, la chorda A. è più acuta della Γ. la
. quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; &
page 280
E quella del Duodecimo; seguendo l'altre per ordine; secondo la natura delle loro Diapason; non è da dubitare, che le chorde del Terzo modo siano più acute di quelle del
Primo, quelle del Quinto più acute di quelle del Terzo, quelle del Nono più acute di
quelle del Settimo, & quelle dell'Vndecimo più acute di quelle del Nono, per un Tuono. Et che quelle del Settimo siano più acute di quelle del Quinto per un Semituono
maggiore, come dice la prima parte della proposta. Et per la seconda parte dico; che,
per la Prima proposta nominata, la chorda A. è più acuta della Γ. la  . della A. ancora
la D. della C. la E. della D. per un Tuono. Et la C. della
. della A. ancora
la D. della C. la E. della D. per un Tuono. Et la C. della  . più acuta per un Semituono maggiore. Ma Γ. è chorda grauissima del Secondo modo; A. quella del Quarto;
. più acuta per un Semituono maggiore. Ma Γ. è chorda grauissima del Secondo modo; A. quella del Quarto;
 . quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; & E. quella del Duodecimo. Adunque le chorde del Quarto modo sono più acute di quelle del Secondo;
quelle del Sesto di quelle del Quarto; quelle del Decimo di quelle dell'Ottauo; & quelle del Duodecimo di quelle del Decimo, per un Tuono. Cosi ancora quelle dell'Ottauo sono ueramente più acute di quelle del Sesto per un maggior Semituono. Et questo
è tutto quello, ch'è contenuto nella seconda parte della proposta, & insieme tutto
quello, che secondo essa proposta dimostrar ui douea. Disse qui il Sig. Desiderio; Le
cose, che sono facili & note al senso, uolendole dimostrare, alle fiate rendono difficultà & lunghezza; & questa è in parte una di quelle. Ma uolendole sapere col mezo
de i Principij & dalle loro Cagioni; non si può fare altramente. Però si può andar
più oltra; poiche questa non hà dibisogno d'altra dichiaratione. E' cosi, come dite in fatto; risposi; & non si può fare altramente. Ascoltate adunque quello, che ui
uoglio dire.
. quella del Sesto; C. quella dell'Ottauo; D. quella del Decimo; & E. quella del Duodecimo. Adunque le chorde del Quarto modo sono più acute di quelle del Secondo;
quelle del Sesto di quelle del Quarto; quelle del Decimo di quelle dell'Ottauo; & quelle del Duodecimo di quelle del Decimo, per un Tuono. Cosi ancora quelle dell'Ottauo sono ueramente più acute di quelle del Sesto per un maggior Semituono. Et questo
è tutto quello, ch'è contenuto nella seconda parte della proposta, & insieme tutto
quello, che secondo essa proposta dimostrar ui douea. Disse qui il Sig. Desiderio; Le
cose, che sono facili & note al senso, uolendole dimostrare, alle fiate rendono difficultà & lunghezza; & questa è in parte una di quelle. Ma uolendole sapere col mezo
de i Principij & dalle loro Cagioni; non si può fare altramente. Però si può andar
più oltra; poiche questa non hà dibisogno d'altra dichiaratione. E' cosi, come dite in fatto; risposi; & non si può fare altramente. Ascoltate adunque quello, che ui
uoglio dire.
PROPOSTA XX.
 & c. il Secondo dalla Quinta Γ. A.
& c. il Secondo dalla Quinta Γ. A.  . C. D. E. F & G. il Terzo dalla Seconda specie D. E. F. G. a.
. C. D. E. F & G. il Terzo dalla Seconda specie D. E. F. G. a.  c &
d. il Quarto dalla Sesta A.
c &
d. il Quarto dalla Sesta A.  . C. D. E. F. G & a. il Quinto dalla Terza E. F. G. a.
. C. D. E. F. G & a. il Quinto dalla Terza E. F. G. a.  . c. d & e.
il Sesto dalla Settima
. c. d & e.
il Sesto dalla Settima  . C. D. E F. G. a &
. C. D. E F. G. a &  . il Settimo dalla Quarta F. G. a.
. il Settimo dalla Quarta F. G. a.  . c. d. e & f.
l'Ottauo dalla Prima C. D. E. F. G. a.
. c. d. e & f.
l'Ottauo dalla Prima C. D. E. F. G. a.  & c. il Nono dalla Quinta G. a.
& c. il Nono dalla Quinta G. a.  . c. d. e. f & g. il Decimo dalla Seconda D. E. F. G. a.
. c. d. e. f & g. il Decimo dalla Seconda D. E. F. G. a.  . c & d. l'Vndecimo dalla Sesta a.
. c & d. l'Vndecimo dalla Sesta a.  . c. d. e. f. g & aa. & lo
Duodecimo dalla Terza E. F. G. a.
. c. d. e. f. g & aa. & lo
Duodecimo dalla Terza E. F. G. a.  . c. d & e. Ma la chorda più graue del Primo, ch'è C.
è più acuta della chorda più graue del Secondo, ch'è Γ. ò per il contrario, questa è più
graue di quella per una Diatessaron; quella del Terzo D. è più acuta di quella del Quarto
A. quella del Quinto E. è più acuta di quella del Sesto
. c. d & e. Ma la chorda più graue del Primo, ch'è C.
è più acuta della chorda più graue del Secondo, ch'è Γ. ò per il contrario, questa è più
graue di quella per una Diatessaron; quella del Terzo D. è più acuta di quella del Quarto
A. quella del Quinto E. è più acuta di quella del Sesto  . quella del Settimo F. è più acuta di quella dell'Ottauo C. quella del Nono G. è più acuta di quella del Decimo D. &
quella dell'Vndecimo a. è più acuta di quella del Duodecimo E. oueramente tutte le nominate seconde sono più graui delle prime per una Diatessaron; adunque le chorde delle Modulationi de i modi Principali sono più acute di quelle de i Non principali; ouer le
chorde di questi sono più graui delle chorde de gli altri per una Diatessaron; come ui douea dimostrare. Onde aggiungeremo; che
page 281
. quella del Settimo F. è più acuta di quella dell'Ottauo C. quella del Nono G. è più acuta di quella del Decimo D. &
quella dell'Vndecimo a. è più acuta di quella del Duodecimo E. oueramente tutte le nominate seconde sono più graui delle prime per una Diatessaron; adunque le chorde delle Modulationi de i modi Principali sono più acute di quelle de i Non principali; ouer le
chorde di questi sono più graui delle chorde de gli altri per una Diatessaron; come ui douea dimostrare. Onde aggiungeremo; che
page 281
PROPOSTA XXI.
 & c. le chorde della Prima specie della Diapason nel Primo & nell'ottauo ordine; quelle della Quinta Γ. A.
& c. le chorde della Prima specie della Diapason nel Primo & nell'ottauo ordine; quelle della Quinta Γ. A.  . C. D. E. F &
G. nel Secondo; quelle della seconda D. E. F. G. a.
. C. D. E. F &
G. nel Secondo; quelle della seconda D. E. F. G. a.  . c & d. nel terzo & nel decimo; quelle della Sesta A.
. c & d. nel terzo & nel decimo; quelle della Sesta A.  C. D. E. F. G & a. nel quarto, quelle della Terza E. F. G. a.
C. D. E. F. G & a. nel quarto, quelle della Terza E. F. G. a.  c. d & e. nel
quinto & duodecimo ordine; quelle della Settima
c. d & e. nel
quinto & duodecimo ordine; quelle della Settima  . C. D. E. F. G. a &
. C. D. E. F. G. a &  . nel sesto; quelle
della Quarta F. G. a.
. nel sesto; quelle
della Quarta F. G. a.  . c. d. e. & f. nel Settimo; quelle della Quinta ancora G. a.
. c. d. e. & f. nel Settimo; quelle della Quinta ancora G. a.  . c. d. e. f &
g. nel nono; simigliantemente quelle della Sesta a.
. c. d. e. f &
g. nel nono; simigliantemente quelle della Sesta a.  . c. d. e. f. g & aa. nell'undecimo. Dico, che i Modi principali, ouero Autentici sono ridotti & accompagnati insieme con i
Non principali, ò plagali; secondo 'l numero & i gradi loro; percioche ritrouandosi la
prima specie della Diapason nel primo ordine, & nel Secondo la Quinta; & essendo tra
la prima tramezata harmonicamente dalla chorda G. contenuto il Primo modo, & nella
Quinta mediata arithmeticamente, il Secondo; & essendo la chorda Γ. della Diapason
posta nel secondo ordine più graue della chorda C. della Diapason posta nel primo; seguita, che nel primo ordine sia contenuto 'l Primo modo autentico, & nel secondo ordine il Secondo modo plagale, & che dopo il Primo modo & principale habbiamo collocato il Secondo non principale, & accompagnatolo al Primo, secondo 'l numero & li gradi dell'uno & dell'altro; perche non ha dubio alcuno; che il Secondo in ogni genere,
c'habbia ordine; non habbia da seguitare immediatamente dopo il Primo. Dopo il Secondo succede il Terzo; percioche, per la Decimanona di questo, il Terzo è più acuto
del Primo per un Tuono; la onde essendo la Diapason D. E. F. G. a.
. c. d. e. f. g & aa. nell'undecimo. Dico, che i Modi principali, ouero Autentici sono ridotti & accompagnati insieme con i
Non principali, ò plagali; secondo 'l numero & i gradi loro; percioche ritrouandosi la
prima specie della Diapason nel primo ordine, & nel Secondo la Quinta; & essendo tra
la prima tramezata harmonicamente dalla chorda G. contenuto il Primo modo, & nella
Quinta mediata arithmeticamente, il Secondo; & essendo la chorda Γ. della Diapason
posta nel secondo ordine più graue della chorda C. della Diapason posta nel primo; seguita, che nel primo ordine sia contenuto 'l Primo modo autentico, & nel secondo ordine il Secondo modo plagale, & che dopo il Primo modo & principale habbiamo collocato il Secondo non principale, & accompagnatolo al Primo, secondo 'l numero & li gradi dell'uno & dell'altro; perche non ha dubio alcuno; che il Secondo in ogni genere,
c'habbia ordine; non habbia da seguitare immediatamente dopo il Primo. Dopo il Secondo succede il Terzo; percioche, per la Decimanona di questo, il Terzo è più acuto
del Primo per un Tuono; la onde essendo la Diapason D. E. F. G. a.  . c & d. del Terzo ordine più acuta di quella del primo per un Tuono; essendo che C. è lontana da D. come
più fiate hò dimostrato; per un simile Interuallo, & diuisa harmonicamente dalla chorda a. in una Diapente & in una Diatessaron; seguita, che essa Diapason contenga il Terzo modo & autentico, collocato secondo 'l numero & grado suo dopo il Secondo & plagale. A questo succede il Quarto, collocato nel Quarto ordine, per la Quartadecima
definitione, tra la Sesta specie della Diapason A.
. c & d. del Terzo ordine più acuta di quella del primo per un Tuono; essendo che C. è lontana da D. come
più fiate hò dimostrato; per un simile Interuallo, & diuisa harmonicamente dalla chorda a. in una Diapente & in una Diatessaron; seguita, che essa Diapason contenga il Terzo modo & autentico, collocato secondo 'l numero & grado suo dopo il Secondo & plagale. A questo succede il Quarto, collocato nel Quarto ordine, per la Quartadecima
definitione, tra la Sesta specie della Diapason A.  . C. D. E. F. g & a. arithmeticamente
diuisa; il quale è distante dal Secondo, per la Decimanona proposta di questo, per un
Tuono. Onde hauendo dimostrato la Diapason D & d. con le sue mezane chorde contenere il Terzo modo; seguita, che senz'alcun mezo; secondo 'l numero & grado suo;
habbiamo collocato dopo il Terzo il Quarto modo; dopo il quale immediatamente uiene il Quinto; percioche la Diapason E. F. G. a.
. C. D. E. F. g & a. arithmeticamente
diuisa; il quale è distante dal Secondo, per la Decimanona proposta di questo, per un
Tuono. Onde hauendo dimostrato la Diapason D & d. con le sue mezane chorde contenere il Terzo modo; seguita, che senz'alcun mezo; secondo 'l numero & grado suo;
habbiamo collocato dopo il Terzo il Quarto modo; dopo il quale immediatamente uiene il Quinto; percioche la Diapason E. F. G. a.  . c. d & e. contenuta nel quinto ordine,
diuisa dalla chorda
. c. d & e. contenuta nel quinto ordine,
diuisa dalla chorda  . in due parti harmonicamente, per la Decimaquarta definitione nominata; contiene esso Quinto modo. Et per la detta Decimanona proposta, il Quinto
modo è distante dal Terzo per un Tuono; percioche E. uiene ad essere, per l'istessa Decima, più acuto di D. per un tale interuallo. La onde essendo E. F. G. a.
. in due parti harmonicamente, per la Decimaquarta definitione nominata; contiene esso Quinto modo. Et per la detta Decimanona proposta, il Quinto
modo è distante dal Terzo per un Tuono; percioche E. uiene ad essere, per l'istessa Decima, più acuto di D. per un tale interuallo. La onde essendo E. F. G. a.  . c. d & e. Quinto modo; & A.
. c. d & e. Quinto modo; & A.  . C. D. E. F. G & a. Quarto; dico che 'l Quinto & principale modo è accommodato dopo il Quarto & plagale secondo che ricerca l'ordine & i gradi loro. Dopo
il Quinto segue il Sesto tra la Diapason del Sesto ordine
. C. D. E. F. G & a. Quarto; dico che 'l Quinto & principale modo è accommodato dopo il Quarto & plagale secondo che ricerca l'ordine & i gradi loro. Dopo
il Quinto segue il Sesto tra la Diapason del Sesto ordine  . C. D. E. F. G. a &
. C. D. E. F. G. a &  . percioche, per la nominata Definitione, contiene tramezata dalla chorda E. arithmeticamente il Sesto modo. Et perche, per la Decimanona proposta, il Sesto è più acuto del
Quarto per un Tuono; essendo
. percioche, per la nominata Definitione, contiene tramezata dalla chorda E. arithmeticamente il Sesto modo. Et perche, per la Decimanona proposta, il Sesto è più acuto del
Quarto per un Tuono; essendo  &
&  . con le sue mezane chorde Sesto modo, & E. con
e. con le sue mezane medesimamente Quinto; seguita, che dopo 'l Quinto sia collocato
il Sesto modo; secondo che ricerca il numero & li gradi loro. Dopo questo segue il Settimo; percioche nel Settimo ordine è contenuta la Diapason F. G. a.
. con le sue mezane chorde Sesto modo, & E. con
e. con le sue mezane medesimamente Quinto; seguita, che dopo 'l Quinto sia collocato
il Sesto modo; secondo che ricerca il numero & li gradi loro. Dopo questo segue il Settimo; percioche nel Settimo ordine è contenuta la Diapason F. G. a.  . c. d. e & f. la qual
page 282
. c. d. e & f. la qual
page 282
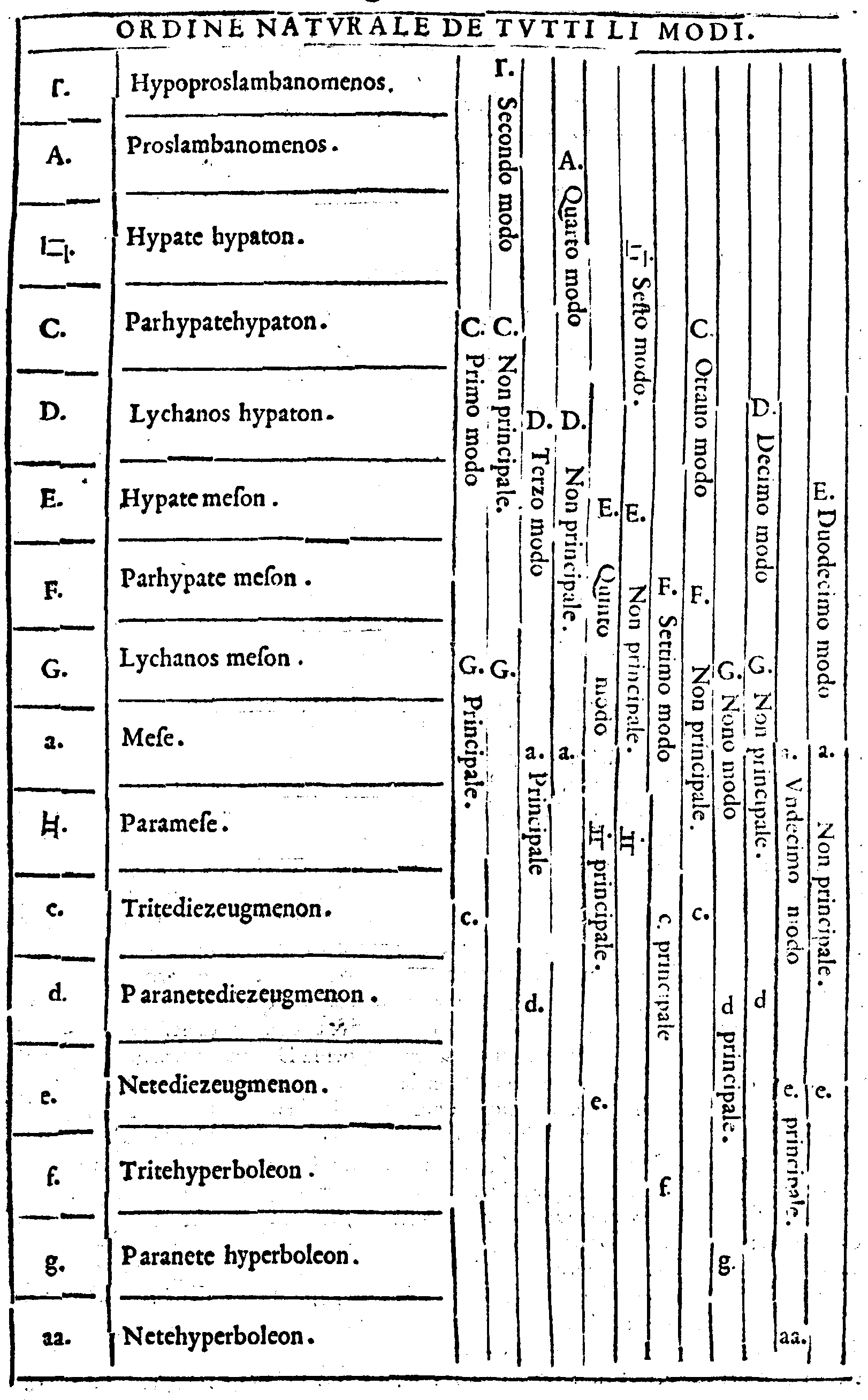
ORDINE NATVRALE DE TVTTI LI MODI.
 &
&  . con le sue chorde
mezane Sesto modo; & F con f. medesimamente con le sue mezane il Settimo; seguita,
che secondo 'l numero & gradi loro habbiamo collocato il Settimo dopo il Sesto modo.
Viene hora l'Ottauo dopo il Settimo, il quale dico essere C. D. E. F. G a.
. con le sue chorde
mezane Sesto modo; & F con f. medesimamente con le sue mezane il Settimo; seguita,
che secondo 'l numero & gradi loro habbiamo collocato il Settimo dopo il Sesto modo.
Viene hora l'Ottauo dopo il Settimo, il quale dico essere C. D. E. F. G a.  & c. diuisa
arithmeticamente dalla F. essendo che, secondo la Decimanona proposta nominata, è
lontano dal Sesto per un Semituono maggiore. Et perche questo segue immediatamente dopo il Settimo; però dico, essere accommodato l'Ottauo dopo il Settimo modo, secondo il numero & gradi loro. Dico ancora, che la Diapason G a.
& c. diuisa
arithmeticamente dalla F. essendo che, secondo la Decimanona proposta nominata, è
lontano dal Sesto per un Semituono maggiore. Et perche questo segue immediatamente dopo il Settimo; però dico, essere accommodato l'Ottauo dopo il Settimo modo, secondo il numero & gradi loro. Dico ancora, che la Diapason G a.  . c. d. e. f & g.
contiene il Nono modo; percioche, per la Vndecima proposta, è la Quinta specie diuisa dalla chorda d. harmonicamente in due parti; la quale essendo più acuta della F & f.
contenuta nel Settimo luogo, per vn Tuono; seguita, che G & g. con le sue mezane
chorde contengano il Nono modo, & sia accommodato dopo l'Ottauo; come porta l'ordine & gradi loro. Simigliantemente dico, tra la Diapason D. E F. G. a.
. c. d. e. f & g.
contiene il Nono modo; percioche, per la Vndecima proposta, è la Quinta specie diuisa dalla chorda d. harmonicamente in due parti; la quale essendo più acuta della F & f.
contenuta nel Settimo luogo, per vn Tuono; seguita, che G & g. con le sue mezane
chorde contengano il Nono modo, & sia accommodato dopo l'Ottauo; come porta l'ordine & gradi loro. Simigliantemente dico, tra la Diapason D. E F. G. a.  . c & d. la quale
immediatamente succede alla G & g. nel decimo ordine, esser collocato il Decimo modo & nonprincipale; percioche la D & d è diuisa, secondo che habbiamo dimostrato
nella Decimaterza proposta d'hoggi, dalla chorda G. arithmeticamente in due parti; &
per la Decimanona, è più graue della G & g. per una Diatessaron; onde per la Definitione, secondo l'ordine numerale & li gradi de i Modi; il Decimo & plagale è accompagnato & accommodato dopo 'l Nono, il quale è il suo principale. A questo succede l'Vndecimo, & è collocato tra la diapason a.
. c & d. la quale
immediatamente succede alla G & g. nel decimo ordine, esser collocato il Decimo modo & nonprincipale; percioche la D & d è diuisa, secondo che habbiamo dimostrato
nella Decimaterza proposta d'hoggi, dalla chorda G. arithmeticamente in due parti; &
per la Decimanona, è più graue della G & g. per una Diatessaron; onde per la Definitione, secondo l'ordine numerale & li gradi de i Modi; il Decimo & plagale è accompagnato & accommodato dopo 'l Nono, il quale è il suo principale. A questo succede l'Vndecimo, & è collocato tra la diapason a.  . c. d. e. f. g & aa collocata nell'ordine undecimo;
& perche è diuisa arithmeticamente in due parti dalla e. però uiene à contenere l'Vndecimo modo; essendo ch'è più acuta della G & g. per un Tuono. Il perche essendo D &
d. con le sue mezane il modo Decimo; uenimo, secondo 'l proposito, hauer dimostrato,
appresso lui hauere accommodato l'Vndecimo, secondo l'ordine & gradi de i Modi. Vltimamente dico, che habbiamo accommodato il Duodecimo dopo l'Vndecimo tra la
Diapason E. F. G. a.
. c. d. e. f. g & aa collocata nell'ordine undecimo;
& perche è diuisa arithmeticamente in due parti dalla e. però uiene à contenere l'Vndecimo modo; essendo ch'è più acuta della G & g. per un Tuono. Il perche essendo D &
d. con le sue mezane il modo Decimo; uenimo, secondo 'l proposito, hauer dimostrato,
appresso lui hauere accommodato l'Vndecimo, secondo l'ordine & gradi de i Modi. Vltimamente dico, che habbiamo accommodato il Duodecimo dopo l'Vndecimo tra la
Diapason E. F. G. a.  . c. d & e. percioche è diuisa dalla chorda a. in due parti arithmeticamente, & tal modo è più graue dell'Vndecimo per una Diatessaron, & del Decimo per
un Tuono. Onde per la Definitione, la Diapason E & e. con le sue chorde mezane uiene à contenere il Duodecimo modo. Et perche ello succede immediatamente dopo l'Vndecimo, secondo l'ordine & li gradi de i modi; però dico, che dopo l'Vndecimo modo
habbiamo il Duodecimo, accommodato secondo 'l proposito. Et per tal maniera, secondo la proposta, habbiamo ridotto in uino per ordine i Modi principali con i Non
principali, & accompagnatoli insieme, secondo l'ordine numerale & gradi loro; come ui
douea dimostrare. Finito ch'io hebbi disse M. Adriano; Questa è stata una lunga diceria,
à approuare & dimostrare una cosa per se stessa apparente & facile; ma perche l'ordine
della Scienza porta questo; però bisogna contentarci; & io per me mi contento; percioche uado sempre imparando qualche cosa di nuouo. Ma passate più oltra; s'altro
non hauete, che dirci. Cosi uanno le cose dimostrabili Messere; dissi; sè bene auanti
ch'elle si dimostrino, si toccano quasi con le mani & sono facili. Ascoltate adunque
quello, che segue.
. c. d & e. percioche è diuisa dalla chorda a. in due parti arithmeticamente, & tal modo è più graue dell'Vndecimo per una Diatessaron, & del Decimo per
un Tuono. Onde per la Definitione, la Diapason E & e. con le sue chorde mezane uiene à contenere il Duodecimo modo. Et perche ello succede immediatamente dopo l'Vndecimo, secondo l'ordine & li gradi de i modi; però dico, che dopo l'Vndecimo modo
habbiamo il Duodecimo, accommodato secondo 'l proposito. Et per tal maniera, secondo la proposta, habbiamo ridotto in uino per ordine i Modi principali con i Non
principali, & accompagnatoli insieme, secondo l'ordine numerale & gradi loro; come ui
douea dimostrare. Finito ch'io hebbi disse M. Adriano; Questa è stata una lunga diceria,
à approuare & dimostrare una cosa per se stessa apparente & facile; ma perche l'ordine
della Scienza porta questo; però bisogna contentarci; & io per me mi contento; percioche uado sempre imparando qualche cosa di nuouo. Ma passate più oltra; s'altro
non hauete, che dirci. Cosi uanno le cose dimostrabili Messere; dissi; sè bene auanti
ch'elle si dimostrino, si toccano quasi con le mani & sono facili. Ascoltate adunque
quello, che segue.
PROPOSTA XXII.
PROPOSTA XXIII.
PROPOSTA XXIIII.
PROPOSTA XXV.
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  . c. d. e. f. g & aa. le quali contenghino i cinque Hexachordi; tra le quali siano Γ. A.
. c. d. e. f. g & aa. le quali contenghino i cinque Hexachordi; tra le quali siano Γ. A.  . C. D. E. F & G. la Quinta specie della Diapason diuisa dalla chorda C, per la Terzadecima proposta, in arithmetica diuisio-
. C. D. E. F & G. la Quinta specie della Diapason diuisa dalla chorda C, per la Terzadecima proposta, in arithmetica diuisio-
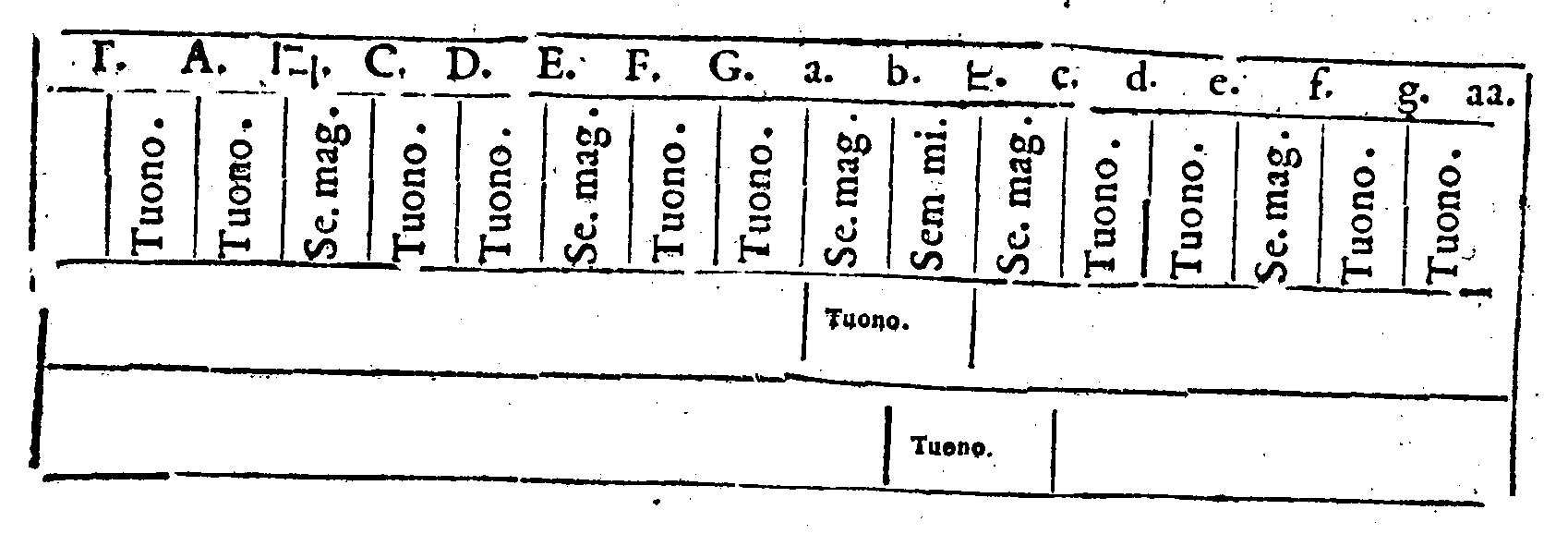
 . c. d.
e. f & g; percioche se noi porremo la chorda c, per la chorda mezana, che diuida arithmeticamente questa Diapason; come fa la C, la prima Diapason in due parti; in una Diatessaron G & c. posta nel graue, & in una Diapente c & g. posta in acuto; haueremo
tanto tra le chorde G. a.
. c. d.
e. f & g; percioche se noi porremo la chorda c, per la chorda mezana, che diuida arithmeticamente questa Diapason; come fa la C, la prima Diapason in due parti; in una Diatessaron G & c. posta nel graue, & in una Diapente c & g. posta in acuto; haueremo
tanto tra le chorde G. a.  & c. di questa la modulatione della prima specie della Diatessaron; quanto si hà tra le chorde Γ. A.
& c. di questa la modulatione della prima specie della Diatessaron; quanto si hà tra le chorde Γ. A.  & C. di quella. Et tanto la modulatione della
prima specie della Diapente tra le chorde c. d. e. f & g. di questa seconda Diapason; quanto tra le chorde C. D. E. F & G. della prima; essendo che tanto in una delle dette Diatessaron si modula dal graue all'acuto per due Tuoni & un maggior Semituono, quanto
nell'altra. Et cosi tanto si modula dal graue all'acuto per tuono, tuono, Semituono
maggiore, & tuono in una di esse Diapente; come si modula nell'altra. Onde tanto uerrà ad essere la Diapason Γ & G, della Quinta specie, quanto la G & g; percioche, per
la Settima dignità; Quelli Interualli si chiamano simili, che sono da simili termini & proportioni contenuti. Il perche essendo i termini della prima Diapason mostrata simili à
quelli della Seconda; non è dubio, che tra loro non ui può cader differenza alcuna, se
non di graue & di acuto. Però essendo la G & g. diuisa arithmeticamente dalla c; come
è diuisa la Γ & G. dalla C; & essendo l'una & l'altra Diapason della Quinta specie; seguita anco, per la Quartadecima definitione d'hoggi, che tanto l'una quanto l'altra contenga il Secondo modo. Ma perche la Diapason G & g. è distante dalle Diapason Γ &
G. per una Diapason intiera, & quello che si modula in questa, si può etiandio modulare in quella; però dico, che la modulatione del Secondo modo si può trasportare più
acuta, ouer più graue (quando la trasportatione si facesse al contrario) per una Diapason.
Et questa ragione può anco seruire à dimostrare, che la nominata Diapason Γ & G. harmonicamente diuisa dalla chorda D. contenerà l'istesso modo, che è contenuto tra la
Diapason G & g. al medesimo modo diuisa; mutando però nella dimostratione quei termini, che sono necessarij di mutare; & questo sarà il Nono modo; come per la Vndecipage 286
ma proposta si è dimostrato. Et perche in questa maniera ogni Modo, sia qual si uoglia (come facendone proua, chiaramente si potrà uedere) si può dal graue all'acuto, &
dall'acuto al graue per una Diapason trasportare; però dico, che la modulatione di ciascheduno de i Dodici modi si può trasportare più acuta, ouer più graue per una Diapason; come primieramente ui douea dimostrare. Ma per dimostrarui, che tali modulationi si possono trasportare per una Diatessaron uerso l'acuto; oueramente per una Diapente uerso 'l graue; siano le chorde C. D. E. F. G. a.
& C. di quella. Et tanto la modulatione della
prima specie della Diapente tra le chorde c. d. e. f & g. di questa seconda Diapason; quanto tra le chorde C. D. E. F & G. della prima; essendo che tanto in una delle dette Diatessaron si modula dal graue all'acuto per due Tuoni & un maggior Semituono, quanto
nell'altra. Et cosi tanto si modula dal graue all'acuto per tuono, tuono, Semituono
maggiore, & tuono in una di esse Diapente; come si modula nell'altra. Onde tanto uerrà ad essere la Diapason Γ & G, della Quinta specie, quanto la G & g; percioche, per
la Settima dignità; Quelli Interualli si chiamano simili, che sono da simili termini & proportioni contenuti. Il perche essendo i termini della prima Diapason mostrata simili à
quelli della Seconda; non è dubio, che tra loro non ui può cader differenza alcuna, se
non di graue & di acuto. Però essendo la G & g. diuisa arithmeticamente dalla c; come
è diuisa la Γ & G. dalla C; & essendo l'una & l'altra Diapason della Quinta specie; seguita anco, per la Quartadecima definitione d'hoggi, che tanto l'una quanto l'altra contenga il Secondo modo. Ma perche la Diapason G & g. è distante dalle Diapason Γ &
G. per una Diapason intiera, & quello che si modula in questa, si può etiandio modulare in quella; però dico, che la modulatione del Secondo modo si può trasportare più
acuta, ouer più graue (quando la trasportatione si facesse al contrario) per una Diapason.
Et questa ragione può anco seruire à dimostrare, che la nominata Diapason Γ & G. harmonicamente diuisa dalla chorda D. contenerà l'istesso modo, che è contenuto tra la
Diapason G & g. al medesimo modo diuisa; mutando però nella dimostratione quei termini, che sono necessarij di mutare; & questo sarà il Nono modo; come per la Vndecipage 286
ma proposta si è dimostrato. Et perche in questa maniera ogni Modo, sia qual si uoglia (come facendone proua, chiaramente si potrà uedere) si può dal graue all'acuto, &
dall'acuto al graue per una Diapason trasportare; però dico, che la modulatione di ciascheduno de i Dodici modi si può trasportare più acuta, ouer più graue per una Diapason; come primieramente ui douea dimostrare. Ma per dimostrarui, che tali modulationi si possono trasportare per una Diatessaron uerso l'acuto; oueramente per una Diapente uerso 'l graue; siano le chorde C. D. E. F. G. a.  & c, lequali contenghino la modulatione del Primo modo; essendo tali chorde diuise harmonicamente dalla chorda G; dico, che etiandio dalla Diapason F. G. a.
b. c. d. e & f. diuisa dalla chorda c. à cotal modo,
potiamo hauer l'istessa modulatione; essendo che tanto si modula nella Diapente F. G. a.
b & c. di questa Diapason per tuono, tuono, Semituono maggiore, & tuono; com'è manifesto; quanto nella Diapente C. D. E. F
& G. di quella. Et tanto si procede per tuono,
tuono & Semituono maggiore nella Diatessaron c. d. e & f. della Diapason F & f; quanto
nella Diatessaron G. a.
& c, lequali contenghino la modulatione del Primo modo; essendo tali chorde diuise harmonicamente dalla chorda G; dico, che etiandio dalla Diapason F. G. a.
b. c. d. e & f. diuisa dalla chorda c. à cotal modo,
potiamo hauer l'istessa modulatione; essendo che tanto si modula nella Diapente F. G. a.
b & c. di questa Diapason per tuono, tuono, Semituono maggiore, & tuono; com'è manifesto; quanto nella Diapente C. D. E. F
& G. di quella. Et tanto si procede per tuono,
tuono & Semituono maggiore nella Diatessaron c. d. e & f. della Diapason F & f; quanto
nella Diatessaron G. a.  . & c; nella Diapason C & c. Ma perche, per la Sesta proposta
d'hoggi; tanto la Diapason C. D. E. F. G. a.
. & c; nella Diapason C & c. Ma perche, per la Sesta proposta
d'hoggi; tanto la Diapason C. D. E. F. G. a.  & c. è la prima specie; quanto la F. G. a. b.
c. d. e & f; però, per la Quartadecima definitione di questo, dico; tanto questa contenere il Primo modo, quanto quella. Et perche la Diapason F & f; per la Ventesima d'hoggi, è più acuta della C & c. d'una Diatessaron; & quella modulatione, che si troua nella
Diapason C & c, si troua anco nella F & f; però dico, che la modulatione della Diapason C & c. si può trasportar per una Diatessaron più acuta nella Diapason F & f. Ma perche tali Trasportationi si possono
far commodamente per tutti i Modi col fauore dell'Hexachordo Synemennon; però dico, che la Modulatione di ciascheduno de i
Dodici Modi si può trasportare in acuto per una Diatessaron; come secondariamente intendeua di
dimostrarui. Et che tali modulationi si possino trasportare uerso il graue per una Diapente; cosi lo dimostro. Sia la Diapason
a.
& c. è la prima specie; quanto la F. G. a. b.
c. d. e & f; però, per la Quartadecima definitione di questo, dico; tanto questa contenere il Primo modo, quanto quella. Et perche la Diapason F & f; per la Ventesima d'hoggi, è più acuta della C & c. d'una Diatessaron; & quella modulatione, che si troua nella
Diapason C & c, si troua anco nella F & f; però dico, che la modulatione della Diapason C & c. si può trasportar per una Diatessaron più acuta nella Diapason F & f. Ma perche tali Trasportationi si possono
far commodamente per tutti i Modi col fauore dell'Hexachordo Synemennon; però dico, che la Modulatione di ciascheduno de i
Dodici Modi si può trasportare in acuto per una Diatessaron; come secondariamente intendeua di
dimostrarui. Et che tali modulationi si possino trasportare uerso il graue per una Diapente; cosi lo dimostro. Sia la Diapason
a.  . c. d. e. f. g & aa; la quale diuisa harmonicamente dalla chorda e. contenga la modulatione dell'Vndecino modo. Dico, che tale modulatione si può trasporre anco uerso 'l graue
nella Diapason D. E. F. G. a. b. c & d; percioche
diuisa al medesimo modo dalla Chorda a. harmonicamente in due parti, quella modulatione istessa contenerà la Diapente D. E.
F. G & a, che contenerà la a.
. c. d. e. f. g & aa; la quale diuisa harmonicamente dalla chorda e. contenga la modulatione dell'Vndecino modo. Dico, che tale modulatione si può trasporre anco uerso 'l graue
nella Diapason D. E. F. G. a. b. c & d; percioche
diuisa al medesimo modo dalla Chorda a. harmonicamente in due parti, quella modulatione istessa contenerà la Diapente D. E.
F. G & a, che contenerà la a.  . c. d & e; & per
quell'istessi Interualli modulerà la Diatessaron e. f. g & aa, che si modulera anco la Diatessaron a. b. c & d. Ma perche, per l'Ottaua definitione & per la Sesta proposta d'hoggi,
la Diapason a & aa. è della Sesta specie, & anco la D & d. è della Sesta specie, & l' una &
l'altra diuisa harmonicamente contengono l'Vndecimo modo; & essendo per la Settima
& per la Ventesima prima proposta, la D & d. più graue della a & aa. per una Diapente;
però dico, che la modulatione dell'Vndecimo modo è trasportata piu graue per una Diapente. Ma perche à questo modo si può
trasportare qual si uoglia modulatione di qual
Modo si uuole; come dalla proua manifestamente si può sempre conoscere; però dico;
che la Modulatione di ciascheduno de i Dodici modi si può fare ultimamente più graue
per una Diapente. La modulatione adunque di qual si uoglia Modo de i Dodici si può
trasportare più acuta, ouer più graue per una Diapason; Ouer si può far più acuta per
una Diatessaron; Oueramente più graue per una Diapente. Et questo è tutto quello,
che secondo la proposta, dimostrar ui douea. Noi altri Organisti disse M. Claudio; lo
sapiamo, quanto sia di utile queste trasportationi, & come si possino fare. Et se ben la
prattica c'insegna cotesta cosa, & che ueramente io la sapeua con tal mezo; non però
m'hà dispiacciuto ueder cotale dimostratione dipendere dalle dimostrationi fatte per
inanzi. Qui dopo che hebbe parlato M. Claudio, disse M. Francesco; Voi hauete hormai M. Gioseffo dimostrato tante & tante cose; che mi penso, che poco più ci debba restare in questo fatto da dire. Onde essendo
l'hora tarda, & hauendo io da fare alcuni negotii; percioche domattina à buon'hora partire uogliamo; s'altro ui resta da dire, non
perdiamo tempo ma uenimo al fine della cosa. A questo soggiunsi; Ancora che si potrebbe, oltra le cose dimostrate, ragionare & dimostrarne molte altre; tuttauia hauenpage 287
do proposto (secondo 'l mio parere) quello che mi pareua esser più necessario; & toccate
tutte quelle cose, che mi hò pensato essere utili da dimostrare in questa Scienza; non uoglio aggiungerui altro. Ma questa proposta ui uoglio solamente aggiungere, che sarà per
la conclusione de tutti questi nostri Ragionamenti; ne i quali, se ui haurò satisfatto, rendete gratie al Signore DIO benedetto datore de tutte le buone & ottime cose. Se anco
per auentura fusse auenuto (cosa che potrebbe essere) altramente, imputatene il mio poco sapere; percioche ui hò detto in questo fatto tutto quello, che per me dirui si potea,
senza diffimularui, ò tener celato cosa alcuna. Et se per sorte hauessi mancato nel dichiarirui alcuna cosa, per cagione di breuità, & non cosi compiutamente, come desiderauate, ui hauesse satisfatto; non dubito, che se hauerete à memoria quelle cose, lequali
hò scritto nelle Istitutioni harmoniche; & se uederete quello, ch'io hò dettato nel libro, il
quale hò intitolato IL MELOPEO, ouer MVSICO PERFETTO; & ne i SVPPLEMENTI MVSICALI; iquali prima à Dio piacendo mandarò in luce, con Venticinque Libri scritti in lingua Latina; iquali nomino De re Musica, siue De vtraque Musica;
non ne siate d'ogni dubio, che ui potrà occorrere, ottimamente istrutti; Percioche è impossibile di potere in una fiata esplicar perfettamente le cose. La onde essendo hormai
stanco farò fine al mio ragionare. E' molto bene il douere, disse il Sig. Desiderio. Ma se
ben mi ricordo M. Gioseffo io fui quello, che vi hà promosso à questa impresa; & si bene
& scientificamente hauete ragionato con molta copia delle cose della Musica, che oltra
l'hauermi satisfatto in particolare, in uniuersale ancora tutti noi si chiamiamo contenti.
Et io ui prometto di tenerne perpetua memoria, & di hauerui obligo perpetuo, essendo
c'hauere tocco & risolto tanto bene tutte quelle cose, le quali mi dauano noia & fastidio,
che non hò punto cosa alcuna più da dubitare. Et se uerrà tempo, nel quale ui possa dimostrar con fatti, quanto questo mi sia stato grato, ue lo farò uedere. Onde al presente non
posso fare altro, che ringratiarui. Io son debitore, risposi à tutti gli Animi nobili & uirtuosi; come è quello di V. Sig. però non uoglio che tra noi ui sia altro obligo, che di amore. Percioche amando io lei, reciprocamente desidero che ella mi ami. A' questo, soggiunse; sarò sempre debitore. Anch'io, disse M. Claudio; ui son in questa parte debitore;
& questo debito non sò come lo potrò mai, non dico pagare; ma sciemare. Con quell'istesso mezo, risposi; ch'io hò detto al Sig. Desiderio, farete atto à fare il tutto; ne uoglio,
ch'altro ui concorri; se non quello che scriue nel fine d'un suo Epigramma quel S. Vescouo & martire di CHRISTO Cipriano:
. c. d & e; & per
quell'istessi Interualli modulerà la Diatessaron e. f. g & aa, che si modulera anco la Diatessaron a. b. c & d. Ma perche, per l'Ottaua definitione & per la Sesta proposta d'hoggi,
la Diapason a & aa. è della Sesta specie, & anco la D & d. è della Sesta specie, & l' una &
l'altra diuisa harmonicamente contengono l'Vndecimo modo; & essendo per la Settima
& per la Ventesima prima proposta, la D & d. più graue della a & aa. per una Diapente;
però dico, che la modulatione dell'Vndecimo modo è trasportata piu graue per una Diapente. Ma perche à questo modo si può
trasportare qual si uoglia modulatione di qual
Modo si uuole; come dalla proua manifestamente si può sempre conoscere; però dico;
che la Modulatione di ciascheduno de i Dodici modi si può fare ultimamente più graue
per una Diapente. La modulatione adunque di qual si uoglia Modo de i Dodici si può
trasportare più acuta, ouer più graue per una Diapason; Ouer si può far più acuta per
una Diatessaron; Oueramente più graue per una Diapente. Et questo è tutto quello,
che secondo la proposta, dimostrar ui douea. Noi altri Organisti disse M. Claudio; lo
sapiamo, quanto sia di utile queste trasportationi, & come si possino fare. Et se ben la
prattica c'insegna cotesta cosa, & che ueramente io la sapeua con tal mezo; non però
m'hà dispiacciuto ueder cotale dimostratione dipendere dalle dimostrationi fatte per
inanzi. Qui dopo che hebbe parlato M. Claudio, disse M. Francesco; Voi hauete hormai M. Gioseffo dimostrato tante & tante cose; che mi penso, che poco più ci debba restare in questo fatto da dire. Onde essendo
l'hora tarda, & hauendo io da fare alcuni negotii; percioche domattina à buon'hora partire uogliamo; s'altro ui resta da dire, non
perdiamo tempo ma uenimo al fine della cosa. A questo soggiunsi; Ancora che si potrebbe, oltra le cose dimostrate, ragionare & dimostrarne molte altre; tuttauia hauenpage 287
do proposto (secondo 'l mio parere) quello che mi pareua esser più necessario; & toccate
tutte quelle cose, che mi hò pensato essere utili da dimostrare in questa Scienza; non uoglio aggiungerui altro. Ma questa proposta ui uoglio solamente aggiungere, che sarà per
la conclusione de tutti questi nostri Ragionamenti; ne i quali, se ui haurò satisfatto, rendete gratie al Signore DIO benedetto datore de tutte le buone & ottime cose. Se anco
per auentura fusse auenuto (cosa che potrebbe essere) altramente, imputatene il mio poco sapere; percioche ui hò detto in questo fatto tutto quello, che per me dirui si potea,
senza diffimularui, ò tener celato cosa alcuna. Et se per sorte hauessi mancato nel dichiarirui alcuna cosa, per cagione di breuità, & non cosi compiutamente, come desiderauate, ui hauesse satisfatto; non dubito, che se hauerete à memoria quelle cose, lequali
hò scritto nelle Istitutioni harmoniche; & se uederete quello, ch'io hò dettato nel libro, il
quale hò intitolato IL MELOPEO, ouer MVSICO PERFETTO; & ne i SVPPLEMENTI MVSICALI; iquali prima à Dio piacendo mandarò in luce, con Venticinque Libri scritti in lingua Latina; iquali nomino De re Musica, siue De vtraque Musica;
non ne siate d'ogni dubio, che ui potrà occorrere, ottimamente istrutti; Percioche è impossibile di potere in una fiata esplicar perfettamente le cose. La onde essendo hormai
stanco farò fine al mio ragionare. E' molto bene il douere, disse il Sig. Desiderio. Ma se
ben mi ricordo M. Gioseffo io fui quello, che vi hà promosso à questa impresa; & si bene
& scientificamente hauete ragionato con molta copia delle cose della Musica, che oltra
l'hauermi satisfatto in particolare, in uniuersale ancora tutti noi si chiamiamo contenti.
Et io ui prometto di tenerne perpetua memoria, & di hauerui obligo perpetuo, essendo
c'hauere tocco & risolto tanto bene tutte quelle cose, le quali mi dauano noia & fastidio,
che non hò punto cosa alcuna più da dubitare. Et se uerrà tempo, nel quale ui possa dimostrar con fatti, quanto questo mi sia stato grato, ue lo farò uedere. Onde al presente non
posso fare altro, che ringratiarui. Io son debitore, risposi à tutti gli Animi nobili & uirtuosi; come è quello di V. Sig. però non uoglio che tra noi ui sia altro obligo, che di amore. Percioche amando io lei, reciprocamente desidero che ella mi ami. A' questo, soggiunse; sarò sempre debitore. Anch'io, disse M. Claudio; ui son in questa parte debitore;
& questo debito non sò come lo potrò mai, non dico pagare; ma sciemare. Con quell'istesso mezo, risposi; ch'io hò detto al Sig. Desiderio, farete atto à fare il tutto; ne uoglio,
ch'altro ui concorri; se non quello che scriue nel fine d'un suo Epigramma quel S. Vescouo & martire di CHRISTO Cipriano:
Dilige pro tantis, sat mihi solus Amor.Cosi farò, replicò M. Claudio; onde il Viola, disse; Hora siamo entrati nelle cerimonie & nelle belle parole, & Dio il sà, quando si darà fine; però uoglio anch'io breuemente ringratiarui M. Gioseffo della uostra cortesia. Et perche dimane à bon'hora siamo per montare in barca tutti, & col Sig. Duca nostro ritornarsene à Ferrara; uoglio pregarui, che doue uoi uederete, che io sia buono à sarui seruitio; che senza rispetto alcuno mi uogliate commandare. Et à voi Messere dirò essortandoui, che uiuiate allegramente; pregandoui di tenermi & con seruarmi nella uostra memoria. Cosi farò Messer Francesco mio; rispose il buon Vecchio; ma basciarete, ui prego la mano à sua Eccellenza in nome mio; & ui prego di nuouo à mantenermi uiuo nella memoria di questo Signore. Onde andarete al buon uiaggio. Dette adunque queste & altre parole da una parte & l'altra dolci & amoreuoli; ciascheduno di noi partitosi, tenne quella bella strada, che lo pote facilmente & presto condurre à far qualche suo particolar negocio inanti cena; Et cosi fù posto. Di Pier Giacomo Bannadini.

