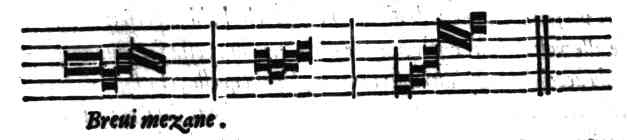Title: Le istitutioni harmoniche
Author: Gioseffo Zarlino
Publication: (Venezia, 1558)
Gioseffo Zarlino, Le istitutioni harmoniche, Venice, 1558. Copy Koninklijke Bibliotheek, The Hague Gioseffo Zarlino, Le istitutioni harmoniche, Venice, 1558. Copy Koninklijke Bibliotheek, The HaguePrincipal editor: Frans Wiering
Funder: Utrecht University Netherlands Organization for Scientific Research (NWO)
Edition: 2000
Department of Information and Computing Sciences Utrecht University P.O. Box 80.089 3508 TB Utrecht NetherlandsΚαὶ μὴ διδόντος, ὀυδὲν ἰσχύει πόνος.

Il Priuilegio della Illustrissima Signoria di Venetia
1557 Die 16 Octobris in Rogatis.Iosephus Tramezinus Duc. Not.
ALLO ILLVSTRISSIMO ET REVERENDISS. SIGNORE, IL SIG.OR VINCENZO DIEDO PATRIARCA DI VENETIA.
Di V.S. Illustr. & Reuerendiss.ma Seruitore affettionatissimo Gioseffo Zarlino.
page vTAVOLA DI TVTTE LE MATERIE PRINCIPALI che sono contenute nell'Opera.
| IL Proemio | Facciata 1 | |
| Della origine, & certezza della Musica | Cap. 1. | fac. 3 |
| Delle laudi della Musica | Cap. 2. | 4 |
| A che fine la Musica si debba imparare | Cap. 3. | 8 |
| Dell'vtile, che si hà della Musica, & dello studio, che vi douemo porre, & in qual modo vsarla | Cap. 4. | 8 |
| Quello che sia Musica in vniuersale, & della sua diuisione | Cap. 5. | 10 |
| Della Musica mondana | Cap. 6. | 12 |
| Della Musica humana | Cap. 7. | 16 |
| Della Musica piana & misurata, o vogliono dire Canto fermo, & figurato | Cap. 8. | 18 |
| Della Musica Rhithmica, & della Metrica | Cap. 9. | 19 |
| Quello che sia Musica in particolare, & perche sia cosi detta | Cap. 10. | 19 |
| Diuisione della Musica in Speculatina, & in Prattica; per laquale si pone la differenza tra'l Musico, & il Cantore | Cap. 11. | 20 |
| Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità è numero | Cap. 12. | 21 |
| Delle varie specie de Numeri | Cap. 13. | 22 |
| Che dal numero Senario si comprendeno molte cose della Natura, & dell'Arte | Cap. 14. | 23 |
| Delle Propietà del numero Senario, & delle sue parti; & come in esse si ritroua ogni consonanza musicale | Cap. 15. | 25 |
| Quel che sia Consonanza semplice, e Composta; & che nel Senario si ritrouino le forme di tutte le semplici consonanze; & onde habbia origine l'Essachordo minore | Cap. 16. | 27 |
| Della Quantità continoua, & della discreta | Cap. 17. | 28 |
| Del Soggetto della Musica | Cap. 18. | 28 |
| Quello che sia Numero sonoro | Cap. 19. | 29 |
| Per qual cagione la Musica sia detta subalternata all'Arithmetica, & mezana tra la mathematica, & la naturale | Cap. 20. | 30 |
| Quel che sia Proportione, & della sua diuisione | Cap. 21. | 31 |
| In quanti Modi si compara l'vna quantità all'altra | Cap. 22. | 32 |
| Quel che sia Parte aliquota, & non aliquota | Cap. 23. | 33 |
| Della produttione del genere Moltiplice | Cap. 24. | 33 |
| Quel che sia Denominatore, & in qual modo si ritroui; & come di due proposte proportioni si possa conoscere la maggiore, o la minore | Cap. 25. | 34 |
| Come nasca il genere Superparticolare | Cap. 26. | 36 |
| Della produttione del genere Superpatiente | Cap. 27. | 36 |
| Del genere Moltiplice superparticolare | Cap. 28. | 37 |
| Della produttione del quinto & vltimo genere, detto Moltiplice superpartiente | Cap. 29. | 38 |
| Della natura & propietà de i sopranominati generi | Cap. 30. | 39 |
| Del Moltiplicar delle Proportioni | Cap. 31. | 41 |
| Il secondo modo di moltiplicar le Proportioni | Cap. 32. | 43 |
| Del Sommare le Proportioni | Cap. 33. | 43 |
| Del Sottrare le Proportioni | Cap. 34. | 44 |
| Del Partire, o Diuidere le proportioni, & quello che sia Proportionalità | Cap. 35. | 45 |
| Della Proportionalità, o Diuisione arithmetica | Cap. 36. | 46 |
| Della Diuisione, o Proportionalità geometrica | Cap. 37. | 47page vi |
| In qual modo si possa cauare la Radice quadrata da i Numeri | cap. 38. | 49 |
| Della diuisione, ouero Proportionalità harmonica | cap. 39. | 50 |
| Consideratione sopra quello, che si è detto intorno alle Proportioni, & Proportionalità | cap. 40. | 51 |
| Che il Numero non è cagione propinqua, & intrinseca delle Proportioni musicali, ne meno delle Consonanze | cap. 41. | 54 |
| Della inuentione delle Radici delle proportioni | cap. 42. | 55 |
| In che modo si possa ritrouar la Radice di più proportioni moltiplicate insieme | cap. 43. | 56 |
| Della Proua di ciascuna delle sopramostrate operationi | cap. 44. | 57 |
| QVANTO la Musica sia stata da principio semplice, rozza, & pouera di consonanze | cap. 1. | fac. 58 |
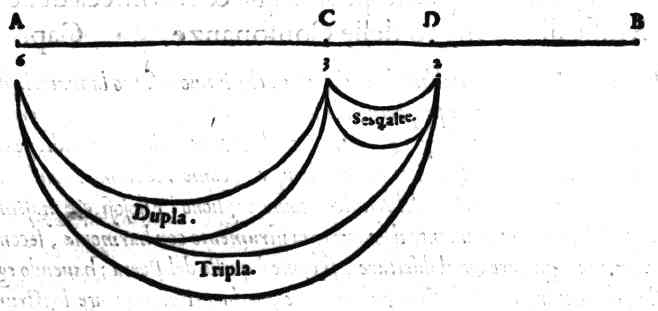
| Per qual cagione gli antichi nelle loro harmonie non vsassero le consonanze imperfette, & Pithagora vietasse il passare oltra la Quadrupla | cap. 2. | 60 |
| Dubbio sopra la inuentione di Pithagora | cap. 3. | 61 |
| Della Musica antica | cap. 4. | 62 |
| Le materie che recitauano gli antichi nelle loro canzoni, & di alcune leggi musicali | cap. 5. | 65 |
| Quali siano stati gli antichi Musici | cap. 6. | 67 |
| Quali cose nella Musica habbiano possanza da indurre l'huomo in diuerse passioni | cap. 7. | 70 |
| In qual modo la Melodia, & il Numero possino muouer l'animo, disponendolo a varij affetti; & indur nell'huomo varij costumi | cap. 8. | 73 |
| In qual genere di Melodia siano stati operati li sopranarrati effetti | cap. 9. | 75 |
| Delli Suoni, & delle Voci, & in qual modo naschino | cap. 10. | 77 |
| Da che nascono i suoni graui, & da che gli acuti | cap. 11. | 78 |
| Quel che sia Consonanza, Dissonanza, Harmonia, & Melodia | cap. 12. | 79 |
| Diuisione delle Voci | cap. 13. | 80 |
| Quel che sia Canto, & Modulatione; & in quanti modi si può cantare | cap. 14. | 81 |
| Quel che sia Interuallo, & delle sue specie | cap. 15. | 81 |
| Quel che sia Genere; et di tre generi di Melodia, o cantilena appresso gli antichi; et delle loro specie | cap. 16. | 82 |
| Per qual cagione ciascuno de gli Interualli contenuto ne i mostrati Tetrachordi sia detto Incomposto. | cap. 17. | 86 |
| In qual Modo si possa accommodare alla sua proportione qual si voglia consonanza, ouero interuallo | cap. 18. | 86 |
| Vn'altro modo di accommodare le consonanze alla loro proportione | cap. 19. | 88 |
| In qual modo si possa vdire qual si voglia consonanza accommodata alla sua proportione | cap. 20. | 89 |
| Del Moltiplicar le consonanze | cap. 21. | 90 |
| Del secondo modo di moltiplicar le consonanze | cap. 22. | 91 |
| In qual modo si diuida rationalmente qualunque si voglia consonanza, ouero interuallo | cap. 23. | 93 |
| In qual modo si possa diuidere qual si voglia interuallo musicale in due parti equali | cap. 24. | 93 |
| Vn'altro modo di diuidere qual si voglia consonanza, ouero interuallo musicale in due, ouero in più parti equali | cap. 25. | 94 |
| In qual modo la Consonanza si faccia diuisibile | cap.26. | 96 |
| Quel che sia Monochordo; & perche sia cosi chiamato | cap. 27. | 97 |
| Della Diuisione, ouero Ordinatione del Monochordo della prima specie del genere diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi fu l'inuentore di questo Genere, & del suo ordine | cap. 28. | 97 |
| Che gli Antichi attribuirono alcune chorde de i loro istrumenti alle Sphere celesti | cap. 29. | 101 |
| In che Modo le predette Sedici chorde siano state da i Latini denominate | cap. 30. | 103 |
| Consideratione sopra la mostrata Diuisione, ouero Ordinatione; & sopra le altre specie del genere Diatonico poste da Tolomeo | cap. 31. | 105page vii |
| Del genere Chromatico; & chi sia stato il suo inuentore; & in qual maniera lo potesse trouare | cap. 32. | 108 |
| Diuisione del monochordo Chromatico | cap. 33. | 111 |
| Consideratione sopra la mostrata diuisione, & sopra alcune altre specie di questo genere, ritrouate da Tolomeo | cap. 34. | 113 |
| Chi sia stato l'inuentore del genere Enharmonico | cap. 35. | 114 |
| Diuisione, o compositione del monochordo Enharmonico | cap. 36. | 115 |
| Consideratione sopra la mostrata particione, ouero compositione; & sopra quella specie di questo genere, che ritrouò Tolomeo | cap. 37. | 117 |
| Della compositione del Monochordo Diatonico diatono, inspessato dalle chorde Chromatiche, & dalle Enharmoniche | cap. 38. | 118 |
| Che'l Diatonico sintono di Tolomeo sia quello, che hà il suo essere naturalmente da i numeri harmonici | cap. 39. | 120 |
| Della diuisione del Monochordo Diatonico sintono, fatta secondo la natura de i numeri sonori | cap. 40. | 123 |
| Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle specie Diatoniche mostrate | cap. 41. | 125 |
| Quel, che si dee osseruare nel temperare, ouero accordare gli Interualli di ciascuno istrumento arteficiale moderno, riducendo il numero delle chorde del Diatonico sintono a quello del Diatono; & che tali interualli non siano naturali: ma si bene accidentali | cap. 42. | 126 |
| Dimostratione dalla quale si può comprendere, che la sopramostrata Partecipatione, o Distributione sia ragioneuolmente fatta; & che per altro modo non si possa fare | cap. 43. | 128 |
| Della compositione del Monochordo diatonico equalmente temperato, & ridutto al numero delle chorde Pithagorice | cap. 44. | 131 |
| Se nelle Canzoni seguitiamo cantando gli interualli produtti da i veri, & sonori numeri, ouero li mostrati; & della solutione di alcuni altri dubbij | cap. 45. | 135 |
| Della inspessatione del Monochordo Diatonico, dalle chorde del genere Chromatico | cap. 46. | 137 |
| In che maniera possiamo inspessare il detto Monochordo con le chorde Enharmoniche | cap. 47. | 139 |
| Che è più ragioneuole dire, che gli interualli minori naschino dalli maggiori; che dire, che i maggiori si componghino delli minori; & che meglio è ordinato l'Essachordo moderno, che il Tetrachordo antico | cap. 48. | 142 |
| Che ciascuno delli Generi nominati, si può dire Genere, & Specie; & che ciascun'altra diuisione, ouero ordinatione de suoni sia vana, & inutile | cap. 49. | 143 |
| Per qual cagione le Consonanze hanno maggiormente la loro origine dalle Proportioni di maggiore inequalità, che da quelle di minore | cap. 50. | 144 |
| Dubbio sopra quello, che si è detto | cap. 51. | 146 |
| QVEL che sia Contrapunto, & perche sia cosi nominato | cap. 1. | fac. 147 |
| Della inuentione delle Chiaui, & delle Figure cantabili | cap. 2. | 148 |
| De gli Elementi, che compongono il Contrapunto | cap. 3. | 149 |
| Diuisione delle sopramostrate specie | cap. 4. | 151 |
| Se la Quarta è consonanza; & donde auiene, che li Musici non l'habbiano vsata, se non nelle compositioni di più voci | cap. 5. | 152 |
| Diuisione delle consonanze nelle Perfette, & nelle Imperfette | cap. 6. | 153 |
| Che la Quarta, & la Quinta sono mezane tra le consonanze perfette, & le imperfette | cap. 7. | 154 |
| Quali consonanze siano più piene, & quali più vaghe | cap. 8. | 155 |
| Della differenza che si troua tra le consonanze Imperfette | cap. 9. | 155page viii |
| Della propietà, o natura delle consonanze Imperfette | cap. 10. | 156 |
| Ragionamento particolare intorno all'Vnisono | cap. 11. | 157 |
| Della Prima consonanza; cioè della Diapason, ouero Ottaua | cap. 12. | 158 |
| Della Diapente, ouer Quinta | cap. 13. | 159 |
| Della Diatessaron, ouer Quarta | cap. 14. | 160 |
| Del Ditono, ouer Terza maggiore | cap. 15. | 161 |
| Del Semiditono, ouer Terza minore | cap. 16. | 162 |
| Dell'vtile, che apportano nella Musica gli Interualli dissonanti | cap. 17. | 162 |
| Del Tuono maggiore, & del Minore | cap. 18. | 163 |
| Del Semituono maggiore, & del Minore | cap. 19. | 164 |
| Dello Essachordo maggiore, ouero Sesta maggiore | cap. 20. | 165 |
| Dello Essachordo minore, ouer Sesta minore | cap. 21. | 166 |
| Della Diapente col Ditono; ouero della Settima maggiore | cap. 22. | 166 |
| Della Diapente col Semiditono, ouero della Settima minore | cap. 23. | 167 |
| In qual maniera naturalmente, o per accidente, tali interualli da i Prattici alle volte si ponghino superflui, o diminuti | cap. 24. | 168 |
De gli effetti che fanno questi segni  . .  . & . &  |
cap. 25. | 170 |
| Quel che si ricerca in ogni Compositione, & prima del Soggetto | cap. 26. | 171 |
| Che le Compositioni si debbeno comporre primieramente di Consonanze, & dipoi per accidente di Dissonanze | cap. 27. | 172 |
| Che si debbe dar principio alle compositioni per vna delle consonanze perfette | cap. 28. | 173 |
| Che non si dè porre due Consonanze, contenute sotto vna istessa proportione, l'vna dopo l'altra ascendendo, ouero discendendo senza alcun mezo | cap. 29. | 176 |
| Quando le parti della cantilena hanno tra loro Harmonica relatione; & in qual modo potemo vsare la Semidiapente, & il Tritono nelle compositioni | cap. 30. | 179 |
| Che rispetto si dè hauere a gli Interualli relati nelle compositioni di più voci | cap. 31. | 181 |
| In qual Maniera due, o più Consonanze perfette, ouero imperfette, contenute sotto vna istessa forma, si possino porre immediatamente l'vna dopo l'altra | cap. 32. | 182 |
| Che due, o più Consonanze perfette, ouero imperfette, contenute sotto diuerse forme, poste immediatamente l'vna dopo l'altra si concedeno | cap. 33. | 183 |
| Che dopo la Consonanza perfetta stà bene il porre la imperfetta: ouero per il contrario | cap. 34. | 183 |
| Che le parti della Cantilena debbeno procedere per mouimenti contrarij | cap. 35. | 184 |
| In qual maniera le parti della Cantilena possino insieme ascendere, o discendere | cap. 36. | 184 |
| Che si debbe schiuare, più che si può, li Mouimenti separati; & similmente le Distanze, che possono accascare tra le parti della cantilena | cap. 37. | 187 |
| In qual maniera si debba procedere da vna Consonanza all'altra | cap. 38. | 187 |
| In qual maniera si debba terminare ciascuna cantilena | cap. 39. | 191 |
| Il modo, che si dè tenere nel far li Contrapunti semplici a due voci, chiamati a Nota contra Nota | cap. 40. | 191 |
| Che nelli Contrapunti si dè schiuare gli Vnisoni, più che si puote; & che non si dè molto di lungo frequentare le Ottaue | cap. 41. | 194 |
| Delli Contrapunti diminuiti a due voci; & in qual modo si possino vsare le Dissonanze | cap. 42. | 195 |
| Il modo, che hà da tenere il Compositore nel fare li contrapunti sopra vna Parte, o Soggetto diminuito | cap. 43. | 200 |
| Che non e necessario, che la parte del Soggetto, & quella del Contrapunto incomincino insieme | cap. 44. | 202 |
| Che le Modulationi debbeno essere ben regolate, & quel che dè osseruare il Cantante nel cantare | cap. 45. | 203 |
| Che non si dè continouare molto di lungo nel graue, o nell'acuto nelle modulationi | cap. 46. | 205 |
| Che'l porre vna Dissonanza, ouero vna Pausa di minima tra due Consonanze perfette di vna istessa specie, che ascendino insieme, o discendino, non fà, che tali consonanze non siano replicate. | cap. 47. | 205page ix |
| Della Battuta | cap. 48. | 207 |
| Della Sincopa | cap. 49. | 209 |
| Delle Pause | cap. 50. | 211 |
| Delle Fughe, o Consequenze, ouero Reditte, che dire le vogliamo | cap. 51. | 212 |
| Delle Imitationi; & quello, che elle siano | cap. 52. | 217 |
| Della Cadenza; quello che ella sia; delle sue specie; & del suo vso | cap. 53. | 221 |
| Il modo di fuggir le Cadenze; & quello, che si hà da osseruare, quando il Soggetto farà il mouimento di due, o più gradi | cap. 54. | 226 |
| Quando è lecito di vsare in vna parte della Cantilena due, o più volte vn passaggio, & quando non | cap. 55. | 227 |
| Delli Contrapunti doppij, & quello che siano | cap. 56. | 229 |
| Quel che dè osseruare il Contrapuntista oltra le Regole date; & di alcune licenze, che può pigliare | cap. 57. | 234 |
| Il modo, che si hà da tenere nel comporre le cantilene a più di due voci; & del nome delle parti | cap. 58. | 238 |
| Delle cantilene, che si compongono a Tre voci; & di quello, che si dè osseruare nel comporle | cap. 59. | 242 |
| In qual maniera la Quarta si possa porre nelle compositioni | cap. 60. | 245 |
| Regole in commune | cap. 61. | 246 |
| Delle varie sorti di contrapunti; & prima di quelli, che si chiamano Doppij | cap. 62. | 251 |
| Delli contrapunti a Tre voci, che si fanno con qualche obligo | cap. 63. | 256 |
| Quel che si dè osseruare, quando si volesse fare vna Terza parte alla sproueduta sopra due altre proposte | cap. 64. | 258 |
| Quel che bisogna osseruare intorno le compositioni di quattro, o di più vòci | cap. 65. | 260 |
| Alcuni auertimenti intorno le compositioni, che si fanno a più di Tre voci | cap. 66. | 263 |
| Del Tempo, del Modo, & della Prolatione; & in che quantità si debbino finire, o numerare le Cantilene | cap. 67. | 268 |
| Della perfettione delle Figure cantabili | cap. 68. | 270 |
| Della imperfettione delle Figure cantabili | cap. 69. | 273 |
| Del Punto; delle sue specie; & della suoi effetti | cap. 70. | 274 |
| Dell'Vtile, che apportano li mostrati Accidenti nelle buone harmonie | cap. 75. | 277 |
| Delle Chorde communi, & delle Particolari delle cantilene Diatoniche, Chromatiche, & Enharmoniche | cap. 72. | 280 |
| Se li Due vltimi Generi si possono vsare semplici nelle lor chorde naturali, senza adoperare le chorde particolari delli Generi mostrati | cap. 73. | 281 |
| Che la Musica si può vsare in due maniere; & che le cantilene, che compongono alcuni de i moderni, non sono di alcuno delli nominati Generi | cap. 74. | 282 |
| Che'l Diatonico può procedere nelle sue modulationi per gli interualli di Terza maggiore, o di minore; & che ciò non faccia variatione alcuna di genere | cap. 75. | 283 |
| Che oue non si ode nelle compositione alcuna varietà di Harmonia, iui non può essere varietà alcuna di Genere | cap. 76. | 285 |
| Dell'vtile, che apportano li predetti due Generi; & in qual maniera si possino vsare, che faccino buoni effetti | cap. 77. | 285 |
| Per qual cagione le Compositioni, che compongono alcuni moderni per Chromatiche, facciano tristi effetti | cap. 78. | 287 |
| Delle cose, che concorreuano anticamente nella compositione de i Generi | cap. 79. | 289 |
| Opinioni delli Chromatisti ributtate | cap. 80. | 290 |
| QVELLO, che sia Modo | cap. 1. | fac. 293 |
| Che li Modi sono stati nominati da molti diuersamente; & per qual cagione | cap. 2. | 298 |
| Del Nome, & del Numero delli Modi | cap. 3. | 299 |
| De gli Inuentori delli Modi | cap. 4. | 300 |
| Della Natura, o Propietà delli Modi | cap. 5. | 301 |
| Dell'Ordine de i Modi | cap. 6. | 304 |
| Che l'Hipermistolidio di Tolomeo non è quello, che noi chiamiamo Ottauo modo | cap. 7. | 306 |
| In qual maniera gli Antichi segnauano le chorde de i loro Modi | cap. 8. | 307 |
| In qual maniera s'intenda la Diapason essere harmonicamente, ouero arithmeticamente mediata | cap. 9. | 308 |
| Che li Modi moderni sono necessariamente Dodici; & in qual maniera si dimostri | cap. 10. | 309 |
| Altro modo da dimostrare il numero delli Dodici Modi | cap. 11. | 311 |
| Diuisione delli Modi in Autentichi, & Plagali | cap. 12. | 313 |
| Delle Chorde finali di ciascun Modo; & quanto possa ascendere, o discendere di sopra, & di sotto le nominate chorde | cap. 13. | 314 |
| Delli Modi communi, & delli Misti | cap. 14. | 315 |
| Altra diuisione delli Modi; & di quello, che si hà da osseruare in ciascuno, nel comporre le cantilene | cap. 15. | 315 |
| Se col leuare da alcuna cantilena il Tetrachordo Diezeugmenon; ponendo il Synemennon in suo luogo, restando gli altri immobili; vn Modo si possa mutare nell'altro | cap. 16. | 317 |
| Della Trasportatione delli Modi | cap. 17. | 319 |
| Ragionamento particolare intorno al Primo modo; della sua Natura; delli suoi Principij; & delle sue Cadenze | cap. 18. | 320 |
| Del Secondo Modo | cap. 19. | 322 |
| Del Terzo modo | cap. 20. | 323 |
| Del Quarto modo | cap. 21. | 324 |
| Del Quinto modo | cap. 22. | 325 |
| Del Sesto Modo | cap. 23. | 326 |
| Del Settimo modo | cap. 24. | 327 |
| Del Ottauo modo | cap. 25. | 328 |
| Del Nono modo | cap. 26. | 329 |
| Del Decimo modo | cap. 27. | 332 |
| Dell'Vndecimo modo | cap. 28. | 333 |
| Del Duodecimo modo | cap. 29. | 334 |
| Quello, che dè osseruare il Compositore componendo; & in qual maniera si habbia da far giuditio delli Modi | cap. 30. | 336 |
| Del modo, che si hà da tenere, nell'accommodar le parti della cantilena; & delle estremità loro; & quanto le chorde estreme acute di ciascuna di quelle, che sono poste nell'acuto, possino esser lontane dalla estrema chorda, posta nel graue del Concento | cap. 31. | 337 |
| In qual maniera le Harmonie si accommodino alle soggette Parole | cap. 32. | 339 |
| Il modo, che si hà da tenere, nel porre le Figure cantabili sotto le Parole | cap. 33. | 340 |
| Delle Legature | cap. 34. | 342 |
| Quel, che debbe hauere ciascuno, che desidera di venire a qualche perfettione nella Musica | cap. 35. | 343 |
| Della fallacia de i Sentimenti; & che'l giuditio non si dè fare solamente col loro mezo: ma si dè accompagnarli la ragione | cap. 36. | 344 |
A I LETTORI.
| 4. | 23. | Leggi, si fa |
| 6. | 20. | l'inuitano |
| 9. | 5. | in lui, & che di essa |
| 12. | 25. | precor |
| 14. | poni 8. nella figura sopra la parola Terra | |
| 25. | tra i numeri 6 & 4 della figura, leggi Diapente | |
| 26. | 7. | auerrebbe |
| 30. | 14 | li corpi sonori sono |
| 33. | 15. | seguendo in infinito |
| 50. | 1. | dico che primieramente |
| 53. | 27. | tra questi: |
| 58. | 7. | & delle |
| 68. | 32. | ἀρχώμεθ' |
| 83. | 44. | dall'acuto al |
| 88. | 4. | alla loro |
| 88. | 18. | contenerebbe tre parti |
| 101. | 28. | che'l |
| 111. | 16. | volse |
| 119. | 10. | Nete synemennon. |
| linea 14. | Paramese. | |
| lin. 15. | Paranete synemen. diat. | |
| 120. | 23. | banda sinistra |
| 126. | 37. | di vna settima parte |
| 133. | 9. | questa con la aa |
| 136. | 35. | ritornano |
| 138. | 31. | di vna parte del |
| 142. | 47. | vedere, i quali sono le parti delle Quantità sonore; come altroue hauemo veduto |
| 160. | bisogna porre la chiaue di C nella quarta riga del Secondo essempio nella parte graue | |
| 166. | 11. | cap. 15. della |
| 166. | poni la chiaue nella quarta riga nel secondo essempio della parte graue | |
| 166. | 34. | cap. 15. della |
| 167, | volta il libro, & leggi il Secondo essempio alla rouescia, & starà bene | |
| 167. | 19. | cap. 15. della |
| 181. | 13. | chiamiamo |
| 190. | 30. | allora la parte acuta cascherà |
| 192. | 31. | non è aiutato |
| 193. | 17. | a i loro luoghi |
| 205. | 26. | non siano |
| 206. | 16. | Semiminime con la Minima auanti: ouero la Minima col punto, & le due chrome seguenti, non sono |
| 207. | 26. | dell'altro, poteua nascere qualche disordine; ordinarono |
| 218. | il Consequente vuole hauere la chiaue nella terza riga | |
| 229. | 10. | graue, & la graue acuta |
| 230. | la parte graue della Replica si canta tutta per b molle | |
| 248. | 20. | diletto apporti |
| 250. | tra la 14, & la 15 nota dell'Alto, manca vna Semibreue nella Quarta riga. | |
| 252. | 3. | che le loro specie |
| 267. | 6. | Soggetto; però il medesimo |
| 269. | 14. | nella Quarta parte |
| 271. | 3. | poiche possono fare perfetto, & imperfetto: & non |
| 281. | nell'ordine Chromatico, la cifera  vuol essere posta dritta nel spacio, oue è posto il vuol essere posta dritta nel spacio, oue è posto il  . .
|
|
| 284. | 1. | si come non vale a dire, Questo è animale rationale, adunque è Huomo:percioche questa differenza Rationale è commune a noi & alli Dei; come vuol Porfirio: ma si bene vale a dire. |
| lin. 2. | la differenza propia è quella | |
| 285. | 22 | non nelle compositioni Chromatiche moderne, che chiamano semplici, lassarò |
| 303. | 1. | perturbatione; cosi quelli, che odeno li Filosofi, non tutti si parteno attoniti, & impiagati: ma solamente quelli, ne i quali si ritroua vn certo incitamento alla Filosofia. |
| 314. | 28. | F; quella del Settimo, & dell'Ottauo la G. |
| 318. | 18. | habbia possanza di |
| 322. | 4. | è Modo religioso, & diuoto. |
LA PRIMA PARTE Delle istitutioni harmoniche DI M. GIOSEFFO ZARLINO DA CHIOGGIA.
Proemio.
DELLA ORIGINE ET certezza della Musica. CAPITOLO PRIMO
Delle laudi della Musica.Cap. 2.
Et longum formose vale, vale (inquit) Iola,facendo dal pianto, & da sospiri quasi interrompere il verso, fa proferir lunga quella sillaba, che prima hauea posta breue. Dipoi volendo mostrare quanto sia veloce il Tempo, lo dimostra col verso composto di molti Datili, che sono piedi atti alla velocità, & a mostrar vn tale effetto, dicendo;
Sed fugit interea fugit irreparabile tempus.Lassarò hora di dire, come volendo mostrare li Cartaginesi sempre nemici & contrarij a Romani, nel descriuere il sito di Cartagine, pospose a bello studio quella parola, che andaua preposta, & disse;
Italiam contra.Et volendo dimostrare con quanto silentio la città de Ilio fusse da Greci assalita, lo mostra con vn verso composto di molti Spondei, li quali sono piedi per sua natura atti alla tardità, & alle cose deboli & ociose, dicendo;
Inuadunt vrbem somno, vinoque sepultam;& infiniti altri, che troppo lungo sarebbe il raccontargli in questo luogo, de i quali l'opera è piena. Basterà hora per vltima conclusione dire, che la poesia sarebbe senza leggiadria alcuna, se dalle parole harmonicamente poste non gli fusse data. Oltra di ciò lascerò da parte dire, quanta simiglianza & vnione con essa habbiano l'Arithmetica, & la Geometria; & dirò solamente, che se l'Architettore non hauesse cognitione della Musica; come ben lo dimostra Vitruuio, non saprebbe con ragione fare il temperamento delle machine, & nelli Theatri collocare li uasi, & dispor bene & musicalmente gli edificij. L'Astronomia medesimamente, se non fusse aiutata dalli fondamenti harmonici, non saprebbe gl'influssi buoni & rei. Anzi dirò più, se l'Astronomo non sapesse la concordanza delli sette pianeti, & quando l'uno con l'altro si congiunga, ouero l'vno all'altro si opponga, non predirebbe mai le cose future. La Filosofia ancora, la quale hà per suo propio il discorrere con ragione le cose produtte dalla natura, & possibili a prodursi, non confessa ella dal primo motore dependere ogni cosa, & esser ordinata con si mirabil ordine, che ne risulta nell'vniuerso vna tacita harmonia? Ecco, che primieramente le cose graui tengono il luogo basso, le leggieri il soprano, & quelle di men peso, secondo la loro natura, posseggono il luogo di mezo. Et più oltra procedendo, i Filosofi affermano, che i Cieli riuolgendosi fanno harmonia; la quale se bene non vdimo, questo può auenire o per la loro veloce reuolutione, o per la troppo distanza, ouero per altra cagione a noi occulta. La Medicina da questa non può stare lontana: imperoche se'l medico non hà cognitione della Musica, come sapra egli nelli suoi medicamenti proportionare le cose calide con le frigide, secondo li loro gradi? & come potrà hauere ottima cognitione de i polsi? liquali il dottissimo Herofilo dispose secondo l'ordine delli numeri musici. Et per salire più alto, la Theologia nostra ponendo nel cielo gli spiriti angelici, diuide quelli in nuoue Chori & tre Hierarchie, come scriue Dionisio Areopagita. Queste sono di continuo presenti al conpage 6spetto della Diuina maestà, & non cessano di cantare Santo, Santo, Santo, Signore Iddio de gli esserciti, come è critto in Esaia. Et non solo questi, ma li quattro Animali ancora, i quali nel libro delle sue Reuelationi sono descritti da San Giouanni, stanno auanti il trono d'Iddio, & cantano l'istesso canto. Stanno poi li ventiquattro vecchi inanzi all'Agnello immaculato, & con suono di Cetere & altissime voci cantano all'altissimo Iddio vn nuouo canto, ilquale è cantato ancora dalle voci de Citaristi citarizanti nelle cetere loro auanti li quattro animali et ventiquattro vecchi. Di queste et altre quasi infinite cose al proposito nostro n'è piena la diuina Scrittura, lequali per breuità trappassaremo, bastando solamente dire per suprema laude della Musica, che senza far mentione alcuna d'altra scienza, ella, secondo la testimonianza de sacri libri, sola si troua nel Paradiso, et è quiui nobilissimamente essercitata. Et si come nella celeste corte, che chiesa triumfante vien detta, cosi nella nostra terrena, che Militante si chiama, non con altro, che con la Musica, si lauda et ringratia il Creatore. Ma lasciamo hormai da parte le cose superiori, et ritorniamo a quelle che sono dalla natura produtte per ornamento del mondo, che ogni cosa vederemo piena di musici concenti. Il Mare primamente hà le Sirene, le quali, se è lecito dar fede a gli scrittori, a nauiganti vdire si fanno di tal sorte, che vinti molte volte dall'harmonia loro, & soprapresi dal sonno, perdeno quello, che sopra ogn'altra cosa è carissimo a tutti gli animali. Nell'Aria & nella Terra insieme sono gli vccelli, che anchora essi co i loro concenti dilettano et ricreano non pur gli animi lassi & pieni di noiosi pensieri, ma li corpi ancora; percioche il viandante molte volte stanco per il lungo viaggio, ricrea l'animo, riposa il corpo, & si dimentica elle passate fatiche per la soaue harmonia de boscarecci canti de gli vccelli di tante varie sorti, che sarebbe impossibile poterle raccontare. Li Fiumi & li Fonti medesimamente dalla natura fabricati soglion dare grato piacere a chiunque ad essi vicino si ritroua; & l'inuitano bene spesso per ricrearsi ad accompagnare il suo rustico canto co i loro strepitosi concenti. Tutte queste cose il Dottissimo Virgilio espresse con poche parole, quando disse, che al canto di Sileno, non solo li Fauni, & le altre fiere, ma le dure Quercie ancora, ballauano; saltando quelli, & queste spesso mouendosi con numerosi mouimenti; dinotandoci, che non pure le cose sensibili; ma ancora quelle, che mancano del senso, sono quasi prese & vinte dalli concenti musicali; & fansi di dure & aspre, mansuete & piaceuoli. Ma se tanta harmonia si troua nelle cose celesti & terrestri: ouero per dir meglio, se'l mondo dal Creatore fu composto pieno di tanta harmonia, perche douemo credere l'Huomo esserne priuo? Et se l'Anima del Mondo (come vogliono alcuni) non è altro che Harmonia, potrà esser che l'Anima nostra non sia in noi cagione d'ogni harmonia, & che col corpo non sia harmonicamente congiunta? massimamente hauendo Iddio creato l'huomo alla similitudine del Mondo maggiore, detto da Greci κόσμος, cioè ornamento, ouero ornato; & essendo fatto a quella similitudine di minor quantità, a differenza di quello vien chiamato μικρόκοσμος, cioè piccol mondo: certo che non e cosa ragioneuole. Onde Aristotele volendo mostrar il musicale componimento dell'huomo molto ben disse, la parte vegetatiua alla sensitiua, & questa alla intellettiua hauer la medesima conuenienza, che hà la figura di tre lati a quella di quattro. Certa cosa è adunque, che non si ritroua alcuna cosa buona, che non habbia musicale dispositione; & la Musica veramente, oltra che rallegra l'animo, riduce anche l'huomo alla contemplatione delle cose celesti; & hà tal proprietà, che ogni cosa a cui si aggiunge fa perfetta; & quegli huomini sono veramente felici & beati, che sono dottati di essa, come afferma il Santo Profeta dicendo, Beato è quel popolo, che sa la giubilatione. Per la quale autorità, Hilario Vescouo Pittauiense dottore catholico, esponendo il Salmo 65. Si mosse a dire, che la Musica è necessaria all'huomo Christiano; Conciosia che nella scienza di essa si ritroua la beatitudine. Onde per questo ho ardimento di dire, che quelli, che non hanno cognitione di questa scienza, sono da esser connumerati tra gl'ignoranti. Anticamente, come dice Isidoro, non era meno vergogna il non sapere la Musica, che le lettere: pero non e marauiglia, se Hesiodo poeta famosissimo, & antichissimo, come narra Pausania, fu escluso dal certame, come colui, che non hauea mai imparato a sonare la Cetera, ne col suono di quella accompagnare il canto. Cosi ancora Temistocle, come narra Tullio, rifiutando di sonare la Lira nel conuito, fu men dotto, & men sauio riputato. Il contrario leggemo, che furno in gran pregio appresso gli antichi Lino, & Orfeo, amendue figliuoli delli Dei: percioche col loro soaue canto (come si dice) non solamente addolciuano gli animi humani: ma le fiere, & gli vcelli ancora; & quello, che è più marauiglioso da dire, moueano le pietre da i propij luoghi, & a i fiumi riteneuano il corso. Et questo istesso il Dotto Horatio attribuisce ad Anfione dicendo. page 7
Dictus & Amphion Thebanae conditor arcisDa i quali per auentura imparorno li Pithagorici, che con musici suoni inteneriuano gli animi feroci; & Asclepiade medesimamente, che molte volte per questa via racchetò la discordia nata nel popolo, & col suono della Tromba restituì l'vdito a i sordi. Parimente Damone Pithagorico ridusse col canto a temperata & honesta vita alcuni gioueni dediti al vino & alla lussuria. Et però ben dissero coloro, che affermauano la Musica esser vna certa legge & regola di modestia. Et dico che Theophrasto ritrouò alcuni Modi musicali da racchetare gli spiriti perturbati. Però meritamente, & sapientemente Diogene Cinico beffaua li Musici de suoi tempi, li quali hauendo le chorde delle loro cetere concordi, haueano l'animo incomposto & discorde, essendo abbandonato dall'harmonia de costumi. Et se douemo prestar fede alla historia, ci debbe parer quasi nulla quello, ch'habbiamo detto: percioche molto maggior cosa è l'hauere virtù di sanar gl'infermi, che di coreggere la vita di sfrenati gioueni, come ancora leggemo di Senocrate, il quale col suono de gli organi ridusse li pazzi alla pristina sanità; & di Talete di Candia, che col suono della Cetera scacciò la pestilenza. Et noi vedemo hoggidi, che per via della Musica si oprano cose marauigliose: imperoche tanta è la forza de i suoni & de i balli contra il veleno delle Tarantole, che in breuissimo tempo risana coloro, che da esse sono stati morsi: come si vede ogni giorno per esperienza nella Puglia paese abondantissimo de tali animali. Ma senza più testimonij profani, non hauemo noi nelle Sacre lettere, che il profeta Dauid racchetaua lo spirito maligno di Saul col suono della sua Cetera? Et per questo credo io, che esso regio Profeta ordinasse, che nel Tempio d'Iddio si vsassero li canti & gli harmonici suoni, conoscendo che erano atti a rallegrare gli spiriti, & a ridur gli huomini alla contemplatione delle cose celesti. Li Profeti ancora, (come dice Ambrosio sopra'l Salmo 118.) volendo profetizare dimandauano, ch'vno perito del suono si mettesse a sonare; accioche inuitati da quella dolcezza gli fusse infusa la gratia spirituale. Però Eliseo non volse profetizare al Re d'Israele quel, che douesse fare per l'acquisto delle acque, accioche gli esserciti non morissero di sete; se prima non gli fu menato al suo conspetto vn Musico, il quale cantasse; & cantando egli fu dello Spirito diuino inspirato, & predisse il tutto. Ma passiamo più oltra: percioche non mancano gli essempij. Timotheo (si come insieme con molti altri narra il Gran Basilio) con la Musica incitaua il Re Alessandro al combattere; & quello medesimo essendo incitato riuocaua. Narra Aristotele nel libro della natura de gli animali, che li Cerui per il canto de cacciatori sono presi, & della Sampogna pastorale, & del canto ancora molto si dilettano; il che conferma Plinio nella sua naturale historia. Et per non mi distendere più sopra di questo, solamente dirò di conoscere alcuni i quali hanno veduto de i Cerui, che fermando il lor corso se ne stauano attenti ad ascoltare il suono della Lira, & del Leuto; & medesimamente si vede ogni giorno gli vccelli vinti & ingannati dall'harmonia, il più delle volte restare presi dall'vccellatore. Narra etiandio Plinio, che la Musica campò Arione dalla morte, che precipitandosi nel mare, fu portato dal Delfino nel lito di Tenaro isola. Ma lasciamo stare hormai molti altri essempi, che potremmo addurre, & diciamo vn poco del buon Socrate maestro di Platone, che gia vecchio & pieno di sapienza volse imparare a sonar la cetera, & il vecchio Chirone tra le prime arti che insegnasse ad Achille nella tenera età, fu la Musica; & volse, che le sanguinolenti sue mani, prima che s'imbrattassero del sangue Troiano, sonassero la Cetera. Platone & Aristotele non comportano, che l'huomo bene istituito sia senza Musica: anzi persuadono con molte ragioni tale scienza douersi imparare; & mostrano la forza della Musica esser in noi grandissima; & perciò uogliono, che dalla fanciullezza vi si dia opera: conciosia che è sofficiente a indurre in noi vn nuouo habito & buono, & vn costume tale, che ne guida & conduce alla virtù, & rende l'animo più capace di felicità; & il seuerissimo Licurgo Re de Lacedemonij tra le sue seuerissime leggi lodò, & sommamente approuò la Musica; percioche molto ben conosceua, che all'huomo era necessaria molto, & di giouamento grandissimo nelle cose della guerra; di modo che i loro esserciti (come narra Valerio) non vsauano di andar mai a combattere, se prima non erano ben riscaldati & inanimati dal suono de Pifferi. Osseruasi ancora tal costume alli tempi nostri; percioche di due esserciti l'uno non assalirebbe l'inimico, se non inuitato dal suono delle Trombe & de Tamburi, ouero da alcun'altra sorte de musicali istrumenti. Et benche, oltra li narrati, non manchino infiniti altri essempi, dalli quali si potrebbe maggiormente conoscere la dignità, & eccellenza della Musica; nondimeno, per non andar più in lungo, gli lassaremo, essendo a bastanza quello, che fin hora si è ragionato. page 8
Saxa mouere sono testudinis, & prece blanda
Ducere quo vellet;
A che fine la Musica si debba imparare.Cap. 3.
Dell'vtile che si ha della Musica & dello studio che vi douemo porre, & in quanto modo vsarla.Cap. 4.
Eneruant animos citharae, cantusque lyraeque,Ne di altro sanno ragionare che di tali cose; ne altro che dishoneste parole dalla loro sporca bocca si sentono vscire. Per il contrario poi, sono alcuni, li quali per tale studio no solo molli & effeminati: ma importuni, dispiaceuoli, superbi, pertinaci, & inhumani diuentano; di modo che vedendosi ad vn certo termine arriuati, stimandosi sopra d'ogn'altro eccellenti, si gloriano, si essaltano, si lodano, & vituperando gli altri, per parere essi pieni di sapienza & di giudicio, stanno con la maggior riputatione & superbia del mondo: ne mai se non con grande istantia di prieghi, & con laudi molto maggiori che a loro non conuengono, si possono ridurre a mostrare vn poco del loro sapere. Per la qual cosa di tutti questi Tigelij si verifica il detto di Horatio, il quale dice;
Et vox, & numeris brachia mota suis.
Omnibus hoc vitium est cantoribus, inter amicos,A tali faceua dibisogno, che li lor padri più presto hauessero fatto insegnare qualch'altro mestiero, quantunque vile, che forse non sarebbeno caduti in tali errori, et harebbeno acquistate megliori creanze. Tutto questo hò voluto dire, accioche quelli, che dell'arte della Musica vogliono fare professione, s'innamorino della scienza, & diano opera allo studio della speculatiua: percioche non dubito, che congiungendo insieme queste cose, non habbiano da diuentare virtuosi, honesti, & costumati: et in tal modo verranno ad imitare gli antichi; li quali (come si è detto) accompagnauano la Musica con la Ginnastica: percioche cosi ella sarà potente di ridurre ciascuno nella diritta via de i buoni costumi. Ne alcuno debbe credere, che quello ch'io hò detto dell'arte della Musica, l'habbia detto, ne per vituperarlo, ne coloro che in tal maniera si essercitano; cosa che giamai non mi è caduto nell'animo: ma più tosto l'hò detto, accioche congiunta in tal modo, & ad altre honoreuoli scienze piene di seuerità, la difendiamo dalli vagabondi & otiosi ruffianesmi de bagatellieri, & la riponiamo nel suo vero luogo; si che ella non habbia da seruire a coloro che sono dediti solamente alle voluttà: masia per vso delli studiosi delle buone scienze, & di coloro che seguitano le uirtù, costumatamente & ciuilmente viuendo.
Vt nunquàm inducant animum cantare rogati,
Iniussi nunquàm desistant.
Quello che sia la Musica in vniuersale, & della sua Diuisione.Cap. 5.
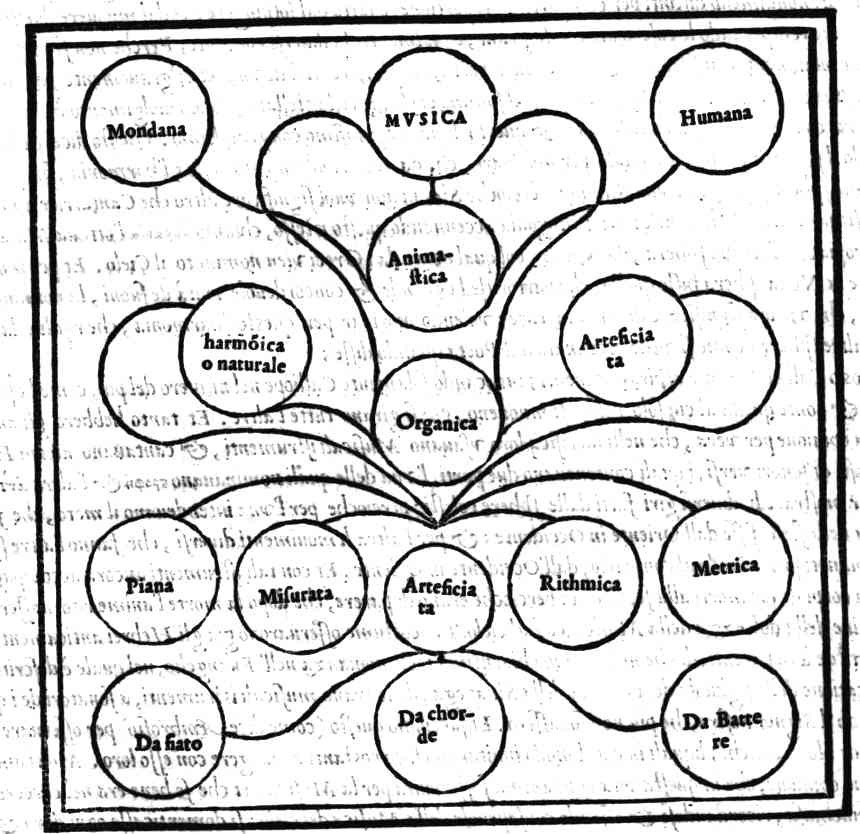
Della Musica mondana.Cap. 6.
Vos o Calliope precor aspirate canenti;inuocando solamente Calliope nel numero del più, come la principale, & come quella al cui solo volere si muoueno, & si girano tutte l'altre. Et tanto hebbero gli antichi questa opinione per vera, che nelli sacrificij loro vsauano Musicali istrumenti, & cantauano alcuni Hinni composti di sonori versi, i quali conteneuano due parti, l'vna delle quali nominauano στροφή & l'altra ἀντιστροφή; per mostrare li diuersi giri fatti dalle sphere celesti: percioche per l'vna intendeuano il moto, che fa la sphera delle stelle fisse dall'Oriente in Occidente; & per l'altra li mouimenti diuersi, che fanno l'altre sphere de pianeti procedendo al contrario, dall'Occidente in Oriente. Et con tali istrumenti ancora accompagnauano li corpi de lor morti alla sepoltura: percioche erano di parere, che dopo la morte l'anime ritornassero alla origine della dolcezza della Musica, cioè al cielo. Tal costume osseruarono gia gli Hebrei anticamente nella morte de loro parenti, di che ne hauemo chiarissima testimonianza nell'Euangelio, nel quale è descritta la risuscitatione della figliuola del prencipe della Sinagoga, doue erano musicali istrumenti, a sonatori de i quali comandò il Signor nostro, che più non sonassero. Et faceuano questo (come dice Ambrosio) per osseruare l'vsanza de i loro antichi; liquali in cotal modo inuitauano li circostanti a piangere con esso loro. Molti ancora haueano opinione, che in questa vita ogni anima fusse vinta per la Musica; et che se bene era nel carcere corporeo rinchiusa, ricordandosi & essendo consapeuole della Musica del cielo; si domenticasse ogni dura & noiosa fatica. Ma se ciò ne paresse strano, hauemo dell'harmonia del cielo il testimonio delle Sacre lettere, doue il Signore parla a Giobbe dicendo; Chi narrerà le ragioni o voci de Cieli? Et chi farà dormire il loro concento? Et se mi fusse dimandato; onde proceda, che tanto grande & si dolce suono non sia vdito da noi; altro non saprei rispondere, che quello, che dice Cicerone nel luogo di sopra allegato; Che gli orecchi nostri ripieni di tanta harmonia sono sordi; si come per essempio auiene a gli habitatori di quei luoghi doue il Nilo da monti altissimi precipita, detti Catadupa; i quali per la grandezza del rimbombo mancano del senso dell'vdito. Ouero che si come l'occhio nostro non può fissare lo sguardo nella luce del Sole, restando da i suoi raggi vinta la nostra luce; cosi gli orecchi nostri non possono capire la dolcezza dell'harmonia celeste, per l'eccellenza et grandezza sua. Ma ogni ragione ne persuade a credere almeno, che il mondo sia composto con harmonia; page 13si perche (come vuol Platone) l'anima di esso è harmonia; si anche perche li cieli sono girati intorno dalle loro intelligenze con harmonia: come si comprende da i loro riuolgimenti; liquali sono l'uno dell'altro proportionatamente più tardi, o più veloci. Si conosce anchora tale harmonia dalle distanze delle sphere celesti: percioche sono distanti tra loro (come piace a molti) in harmonica proportione; laquale, benche non venga misurata dal senso, è nondimeno misurata dalla ragione: imperoche li Pithagorici (come dimostra Plinio) misurando la distanza de cieli, & li loro interualli, poneuano dalla Terra alla prima Sphera lunare essere lo spatio di 12600 stadij; & questo diceuano essere l'interuallo del tuono; auegna che questo (secondo il mio parere) sia fuori d'ogni ragione: conciosia che non può essere, che quelle cose le quali per lor natura sono immobili, si come è la Terra, siano atte a generare l'harmonia; hauendo li suoni (come vuol Boetio) il loro principio dal mouimento. Dipoi andauano ponendo dalla sphera della Luna a quella di Mercurio l'interuallo d'un Semituono maggiore; & da Mercurio a Venere quello del minore; e da Venere al Sole il Tuono, & il minor semituono; & questa diceuano esser distante dalla terra per tre tuoni, & vno semituono; il qual spatio è nominato Diapente. Et dalla Luna al Sole poneuano la distanza di due tuoni, & vno semituono; li quali costituiscono lo spatio della Diatessaron. Ritornando poi al principiato ordine, dissero, il Sole esser lontano da Marte per la medesima distanza, che è la Luna dalla terra; & da Marte a Gioue essere l'interuallo del semituono minore; & da questo a Saturno lo spatio del semituono maggiore: dal quale per fino all'vltimo cielo, oue sono li segni celesti, posero lo spatio del minor semituono. Per la qual cosa dall'vltimo cielo alla sphera del Sole si comprende esser lo spatio, o interuallo della Diatessaron; & dalla terra all'vltimo cielo lo spatio di cinque tuoni, & due minori semituoni, cioè la Diapason. Chi vorrà poi essaminare li cieli nelle sue parti, secondo che con gran diligenza hà fatto Tolomeo, ritrouerà (comparate insieme le dodici parti del Zodiaco, nelle quali sono li dodici segni celesti) le consonanze musicali, cioè la Diatessaron, la Diapente, la Diapason, & le altre per ordine; et nelli motti fatti verso l'Oriente & l'Occidente potrà conoscere esser collocati li suoni grauissimi; & in quelli, che si fanno nel mezo del cielo gli acutissimi. Nelle altitudini poi ritrouerà il Diatonico, il Chromatico, & l'Enharmonico genere. Similmente nelle latitudini li Tropi, o Modi, che vogliamo nominarli; & nelle faccie della Luna, secondo gli varij aspetti col Sole, esser le congiuntioni delli Tetrachordi. Ma non solo dalle predette cose si può conoscere cotale harmonia; ma dalli varij aspetti de i sette Pianeti ancora; dalla natura, & dalla positione, o sito loro. Da gli aspetti, si come dal Trino, dal Quadrato, dal Sestile, dalle congiuntioni, & dalle oppositioni; li quali fanno nelle cose inferiori, secondo i loro influssi buoni, & rei, vna tale & tanta diuersità di harmonia di cose, che è impossibile di poterla esplicare. Dalla natura poi, conciosia che essendone alcuno (come vogliono gli Astrologi) di natura trista & maligna; da quelli, che buoni & benigni sono, in tal modo vengono ad esser temperati; che ne risulta poi tale harmonia; che apporta gran commodo & vtile a mortali. Et questa si comprende ancora dal Sito, ouero dalla Positione loro; conciosia che sono tra loro in tal modo collocati, quasi nel modo che sono collocate le virtù tra gli vitij. Onde si come questi, che sono estremi, si riducono ad vn'habito virtuoso, per via di vno mezo conueniente; cosi quelli pianeti, che sono di natura maligni, si riducono alla temperanza per via di vn'altro pianeta posto nel mezo loro, che sia di natura benigna. Però si vede, che essendo Saturno & Marte posti nel luogo soprano di natura maligni, cotal malignità da Gioue posto tra l'vno & l'altro, & dal Sole posto sotto di Marte con vna certa harmonia è temperata; si che non lassano operare a i loro influssi cattiui nelle cose inferiori quel maligno effetto, che potrebbeno operare non vi essendo tale interpositione. Et hanno i loro influssi si gran possanza sopra li corpi inferiori, che mentre li due primi nominati pianeti si ritrouano hauere il dominio dell'anno; allora si disciolge l'harmonia de i quattro Elementi: percioche si corrompe l'aria de tal maniera, che genera nel mondo pestilenza vniuersale. Vogliono ancora, che i due luminari maggiori, che sono il Sole & la Luna, facino corrispondente harmonia di beniuolenza tra gli huomini, quando nel nascimento dell'vno quello si ritroua essere in Sagittario, & questa nel Montone; & nel nascimento dell'altro il Sole sia nel Montone, & la Luna nel Sagittario. Simil harmonia dicono ancora farsi, quando nel loro nascimento hanno hauuto vn medesimo segno, ouero di simile natura, ouero vn medesimo pianeta, o di natura simile in ascendente: ouero che due benigni pianeti col medesimo aspetto habbiano riguardato l'angolo dell'oriente. Questo istesso dicono auenire, quando Venere si ritroua nella medesima casa della loro natiuità, o nel medesimo grado. Hauendo adunque hauuto riguardo a tutte le sopradette opinioni, & essendo (si come affermarono alcuni) il page 14Mondo l'organo d'Iddio, nella dichiaratione della Musica mondana hò detto, che è harmonia, la quale, si scorge tra quelle cose, che si veggono, & conoscono nel cielo. Et soggiunsi, che anche nel legamento de gli Elementi si comprende: conciosiache essendo stati creati dal grande Architettore Iddio (si come creò ancora tutte l'altre cose) in Numero, in Peso, & in Misura, da ciascuna di queste tre cose si può comprendere tale harmonia; & prima dal Numero, medianti le qualità passibili, che sono quattro & non più, cioè la Siccità, la Frigidità, la Humidità, & la Calidità, che si ritrouano in essi: conciosiache a ciascuno di loro principalmente vna di esse qualità è appropiata; si come la siccità alla terra, la frigidità all'acqua, l'humidità all'aria, & la calidità al fuoco; Ancora che la siccità secondariamente si attribuisca al fuoco, la calidità all'aria, l'humidità all'acqua, & la frigidità alla terra; per le quali non ostante, che tra loro essi elementi siano contrarij, restano nondimeno in vno mezano elemento, secondo vna qualità concordi & vniti: essendo che ad ogn'vno di loro (come hauemo veduto) due ne sono appropiate, per mezo delle quali mirabilmente insieme si congiungono, & in tal modo; che si come due numeri Quadrati conuengono in vno mezano numero proportionato, cosi due di essi elementi in vno mezano si congiungono. Conciosia che al modo che il Quaternario, & Nouenario numeri quadrati si conuengono nel Senario, il quale supera il Quaternario di quella quantità, che esso è superato dal Nouenario; in tal modo il Fuoco & l'Acqua, che sono in due qualità contrarij, in vno mezano elemento si congiungono: Impero che essendo il Fuoco per sua natura caldo & secco, & l'Acqua fredda & humida, nell'Aria calda & humida mirabilmente con grande proportione s'accompagnano; il quale se bene dall'Acqua per il calido si scompagna, seco poi per l'humido si vnisce. Et se l'humido dell'Acqua ripugna al secco della Terra, il frigido non resta però d'vnirli insieme. Di modo che sono con tanto marauiglioso ordine insieme vniti, che tra essi non si ritroua più disparità, che si ritroui tra due mezani numeri proportionati, collocati nel mezo di due numeri Cubi; come nel sottoposto essempio si può chiaramente vedere.
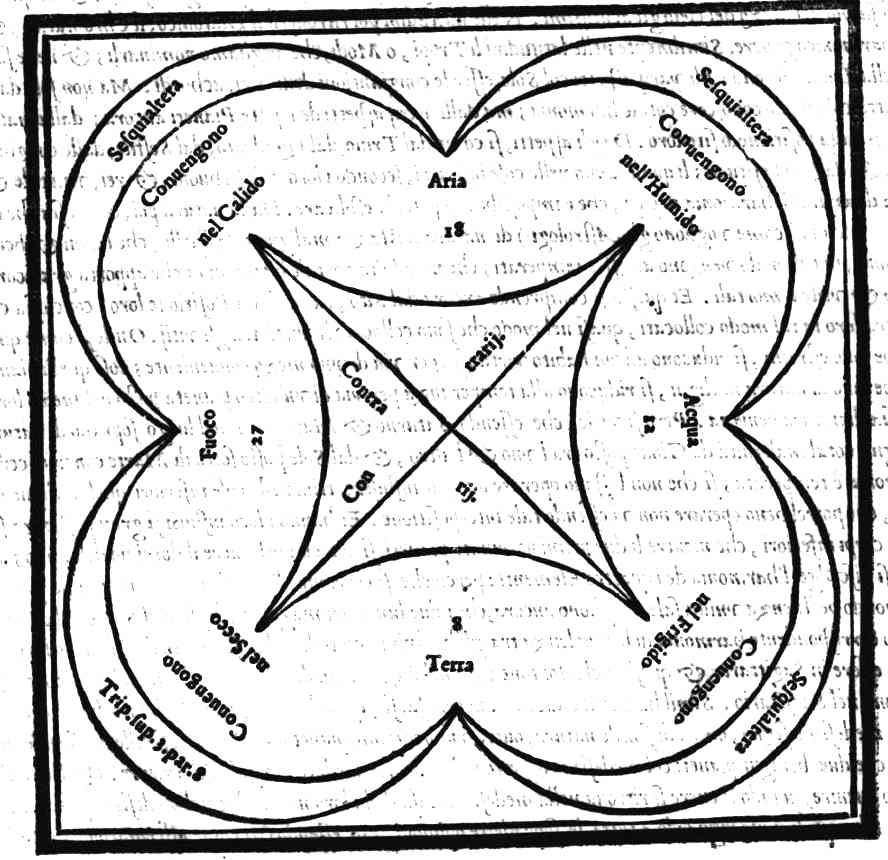
Tu numeris elementa ligas, vt frigora flammisEt in vn'altro luogo;
Arida conueniant liquidis, ne purior ignis
Euolet, aut mersas deducant pondera terras.
Tu triplicis mediam naturae cuncta mouentem
Connectens animam, per consona membra resoluis.
Haec concordia temperat aequisMa chi vorrà dal peso loro comprendere ancora la Mondana harmonia la potrà conoscere: percioche essendo l'vno dell'altro più graue, o più leggiero, sono di tal modo insieme concatennati & legati, che con vna certa harmonia la circonferenza di ciascuno proportionatamente è lontana dal centro del Mondo. Noi vedemo che quelli, che sono per lor natura graui, sono tirati all'insù da quelli, che sono per loro natura leggieri; & li graui tirano all'ingiù li leggieri in tal maniera, che niuno di loro va fuori del suo propio luogo. Et in tal guisa stanno insieme sempre vniti & serrati, che tra loro non si troua per alcun tempo, quantunque breue, in alcuna parte il Vacuo; il quale la Natura grandemente abhorisce. Et sono poi in tal Modo collocati, che la Terra, la quale per sua natura è semplicemente graue, & il Fuoco, che è semplicemente leggiero, sono quelli, che posseggono gli vltimi luoghi. La Terra tien l'infimo luogo: percioche ogni graue tende al basso; & il Fuoco stà nel supremo: conciosia che ogni cosa leggiera tende a tal luogo. Ma perche li mezi ritengono la natura de i loro estremi, però hà ordinato bene il Creatore, che essendo l'Acqua & l'Aria, secondo vn certo rispetto graui & leggieri, douessero tenere il luogo mezano, l'Acqua accompagnandosi alla Terra come più graue; & l'Aria al Fuoco, come piu leggero; accioche ciascuno si accompagnasse a quello, che era di natura a lui piu simile. Il qual ordine & legamento leggiadramente Ouidio espresse dicendo.
Elementa modis, vt pugnantia
Vicibus cedant humida siccis
Iungantque fidem frigora flammis.
Pendulus ignis surgat in altum,
Terraeque graues pondere sidant.
Ignea conuexi vis, & sine pondere coeliMa se più sotilmente ancora vorremo essaminare la cosa, ritrouaremo l'harmonia mondana nella loro misura & quantità, mediante la trammutatione delle parti, che fa dall'vno nell'altro, si come mostra il Filosofo: conciosiache cosi si trammuta vna parte di terra in acqua, & vna parte di acqua in aria, come si trammuta vna parte di aria in fuoco. Et cosi come si trammuta vna parte di fuoco in aria, & vna parte di aria in acqua, cosi si trammuta vna parte di acqua in terra: essendo che trammutandosi la terra in acqua, si viene a far tale trammutatione in proportione Decupla. Di modo che quando si trammuta vn pugno di terra in acqua, si genera (come dicono i Filosofi) dieci pugni di acqua; & quando si trammuta tale acqua in aria, viene a fare cento pugni di aria. per la qual cosa trammutandosi tutto questo in fuoco, viene a multiplicare in mille pugni di fuoco. Cosi per il contrario, mille pugni di fuoco si conuerteno in cento di aria, & questi in dieci di acqua, & dieci di acqua in vno di terra; & questo auiene dalla rarità & spessezza, che si ritroua più in vno, che in vn'altro elemento: Percioche quanto piu s'auicinano al cielo, & sono lontani dal centro del mondo, tanto più sono rari; & quanto più s'auicinano a questo, & si allontanano da quello, tanto più sono spessi.Onde quando da questo si volesse giudicare la loro misura, si potrebbe dire, che la quantità del fuoco fusse in proportione Decupla con quella dell'aria; et quella dell'aria, con quella dell'acqua medesimamente in proportione decupla; & cosi la quantità dell'acqua con tutta la quantità della terra nella medesima proportione. Et si potrebbe anche dire (poi che gli Elementi sono corpi d'vno istesso genere, & il tutto con le parti conuiene in vna istessa natura, et in vna ragione istessa) che la proportione, che si ritroua tra la quantità della sphera del fuoco, & tutta la massa della terra, sia quella, che si ritroua tra il numero Millenario & l'vnitade. A questo modo adunque, dal mouimento, dalle page 16distanze, & dalle parti del cielo; & similmente da gli aspetti, dalla natura, & dal sito de i sette pianetti; & dal numero etiandio, dal peso, & dalla misura de i quattro elementi, venimo alla cognitione dell'harmonia Mondana. Conciosia che la concordanza & l'harmonia loro partorisca l'harmonia de i tempi, che si conosce prima ne gli Anni, per la mutatione della Primauera nella State; & di questa nell'Autunno: similMente dell'Autunno nel Verno; & del Verno nella Primauera. Et dipoi nelli Mesi per il crescere & sciemare regolatamente, che fa la Luna; & finalmente ne i Giorni per il cambieuole apparir della luce, et delle tenebre; dalla quale harmonia nasce la diuersità di fiori, & di frutti: Percioche, si come afferma Platone, quando il caldo col freddo, & il secco con l'humido proportionatamente s'vniscono; dall'harmonia di queste qualità ne risulta l'anno a ciascun viuente vtilissimo, pieno di varie sorti di fiori odoriferi, & di frutti ottimi; ne alcun'altra sorte di piante, o di animali viene a patire offesa. Si come all'opposito auiene, che dalla discordanza & distemperamento loro si generano pestilenza, sterilità, infirmità, & ogni cosa a gli huomini, alle bestie, & alle piante nociua. Et veramente la Natura hà seguito vn bello & ottimo ordine, facendo che quel che il Verno ristringe & rinchiude, Primauera lo apra, & mandi fuori; & quel che la State secca, l'Autunno finalmente maturi. Di maniera che si vede l'vn tempo all'altro porgere aiuto; & di quattro tempi harmonicamente disposti farsi vn corpo solo. Questa tale harmonia ben fu conosciuta da Mercurio, et da Terpandro; conciosia che l'vno hauendo ritrouata la Lira, oueramente la Cetera, pose in essa quattro chorde ad imitatione della Musica mondana (come dice Boetio & Macrobio) la quale si scorge ne i quattro Elementi, ouero nella varietà de i quattro tempi dell'anno; & l'altro la ordinò con sette chorde alla similitudine de i sette Pianeti. Fu poi il numero delle quattro chorde nominato Quadrichordo, ouer Tetrachordo, che tanto vuol dire, quanto di quattro chorde. Et quello di sette Eptachordo, che vuol dire di sette chorde. Ma il primo fu da i Musici di maniera riceuuto & abbracciato, che le quindeci chorde comprese nel Sistema massimo, furno accresciute secondo il numero delle chorde del predetto Tetrachordo, anchora che si ritrouino distanti l'una dall'altra sotto diuerse proportioni. Et questo basti quanto alla dichiaratione della Musica mondana.
Emicuit, summaque locum sibi legit in arce.
Proximus est aer illi leuitate locoque.
Densior his tellus elementaque grandia traxit,
Et praessa est grauitate sui. circunfluus humor
Vltima possedit, solidumque coercuit orbem.
Della Musica humana.Cap. 7.
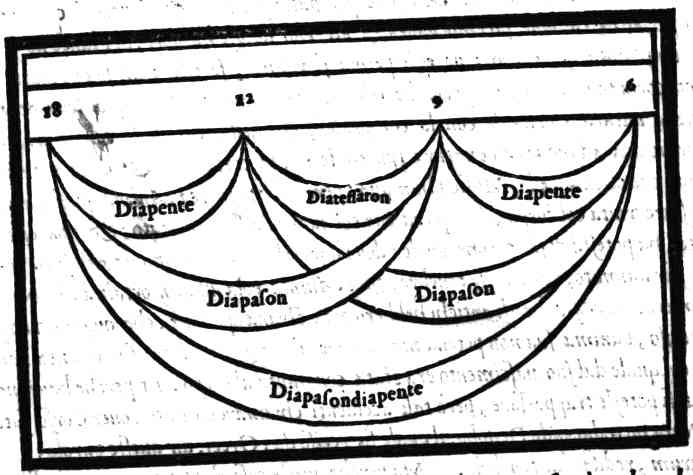
Explebo numerum, reddarque tenebris.Ma perche queste cose s'appartengono più alli ragionamenti della Filosofia, che a quelli della Musica, lascierò di parlarne più oltra, contentandomi di hauerne detto queste poche, & dimostrato la varietà della Musica animastica; della quale, come di quella, che nulla o poco fa al nostro proposito, non ne farò più mentione.
Della Musica piana, & misurata; o vogliamo dire Canto fermo, & figurato.Cap. 8.
Della Musica Rithmica, & della Metrica.Cap. 9.
Quello che sia Musica in particolare, & perche sia cosi detta.Cap. 10
Pan primus calamos cera coniungere pluresEt quantunque queste opinioni siano buone, tuttauia quello che a me par più ragioneuole, et più mi piace è l'opinione di Platone, che ella sia nominata dalle Muse, alle quali (come dice Agostino) è conceduto vna certa onnipotenza di cantare: & vogliono li Poeti, che siano figliuole di Gioue & di Memoria; & dicono bene: percioche se l'huomo non ritiene li suoni & gli interualli delle voci musicali nella memoria, non fa profitto alcuno; & questo auiene: perche non si possono a via alcuna scriuere: tanto più, che ogni scienza, & ogni disciplina (come vuole Quintiliano) consiste nella memoria: conciosia che in vano ci è insegnato, quando quello che noi ascoltiamo dalle menti nostre si parte. Et perche habbiamo detto la Musica essere scienza speculatiua, però auanti che più oltra passiamo, vederemo (hauendo consideratione del fine) come anche la possiamo dimandare Prattica.
Instituit.
Diuisione della Musica in Speculatiua & in Prattica; per la quale si pone la differenza tra il Musico & il Cantore.Cap. 11.
Quanto sia necessario il Numero nelle cose; & che cosa sia Numero; & se l'Vnità è numero.Cap. 12.
Delle varie specie de NumeriCap. 13.
Che dal numero Senario si comprendeno molte cose della natura & dell'arte.Cap. 14.
Delle Proprietà del numero Senario, & delle sue parti; & come in esse si ritroua ogni consonanza musicale.Cap. 15.
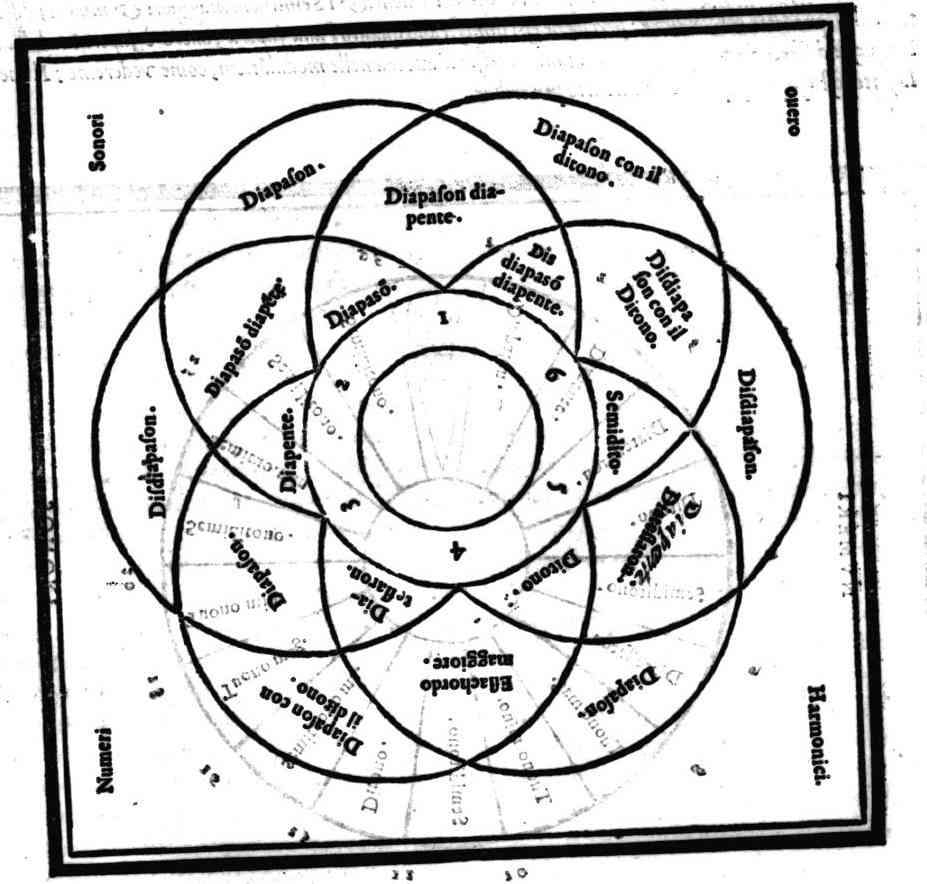
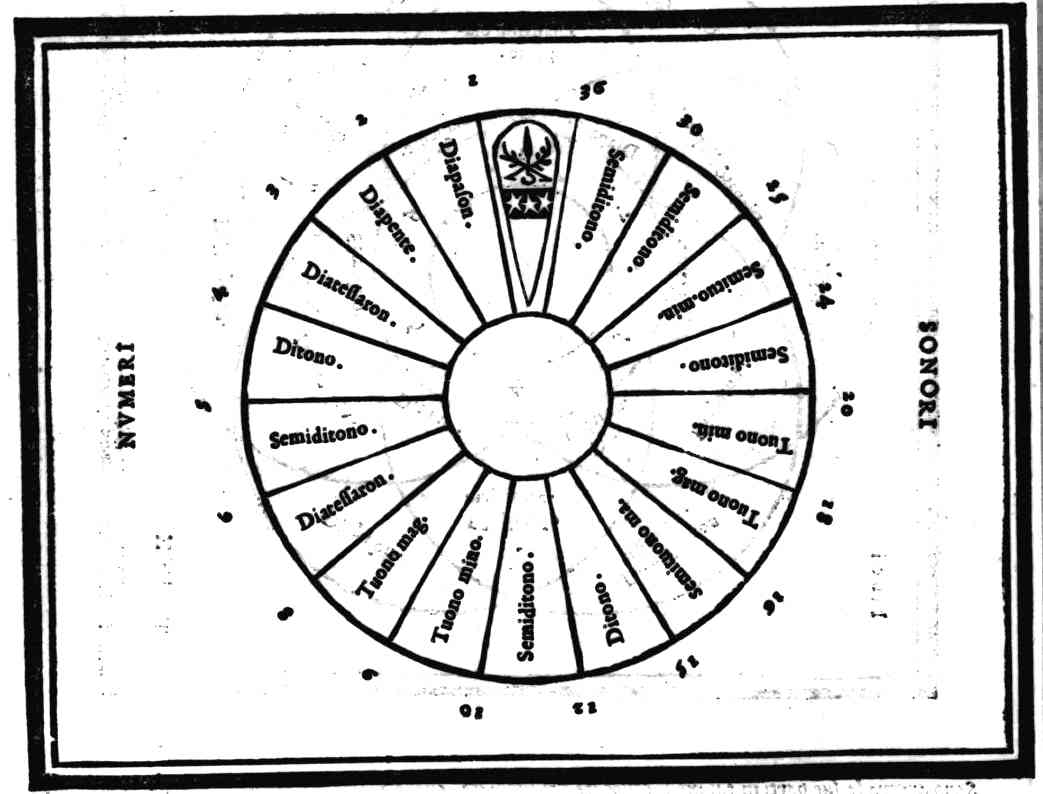
Quel che sia Consonanze semplice, e Composta; & che nel Senario si ritrouano le forme di tutte le semplici consonanze; & onde habbia origine l'Essachordo minore.Cap. 16.
Della quantità continoua & della discreta.Cap. 17.
Del soggetto della Musica.Cap. 18.
Quello che sia Numero sonoro.Cap. 19.
Per qual cagione la Musica sia detta subalternata all'Arithmetica, & mezana tra la mathematica, & la naturale.Cap. 20.
Quel che sia Proportione, & della sua diuisione.Cap. 21.
In quanti modi si compara l'vna Quantità all'altra.Cap. 22.
Quel che sia parte aliquota, & non aliquota.Cap. 23.
Della produttione del genere Moltiplice.Cap. 24.
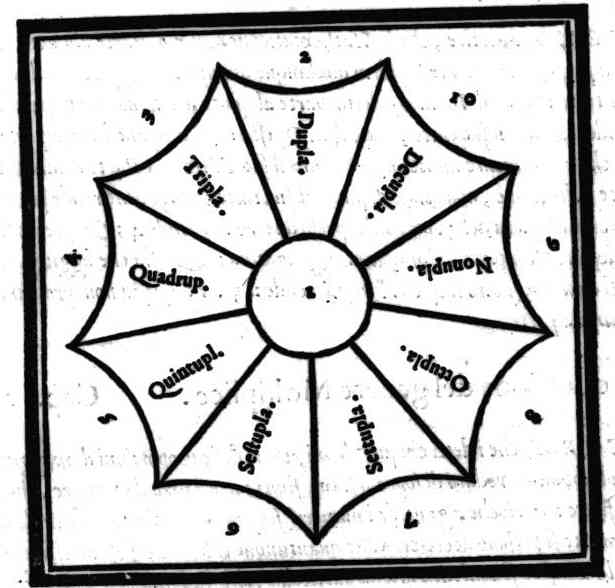
Quel che sia Denominatore, & in qual modo si troui; & come di due proposte proportioni si possa conoscere la maggiore, o la minore.Cap. 25.
Come nasca il genere Superparticolare.Cap. 26.
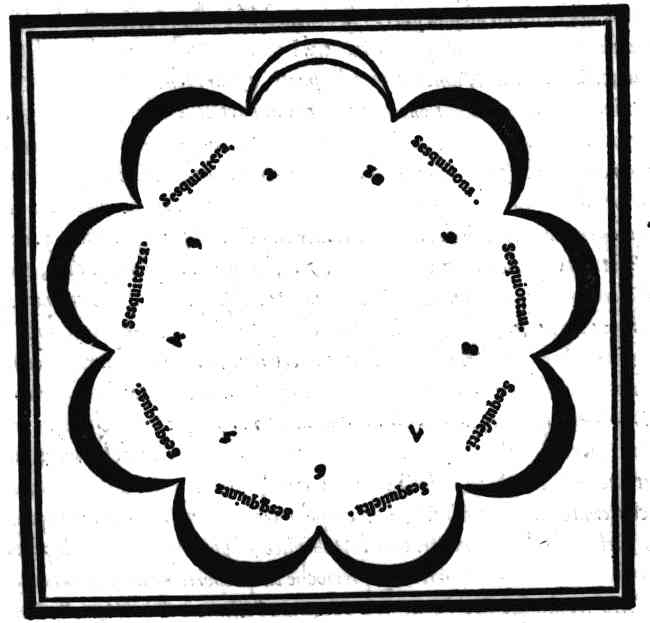
Della produttione del genere Superpartiente.Cap. 27.
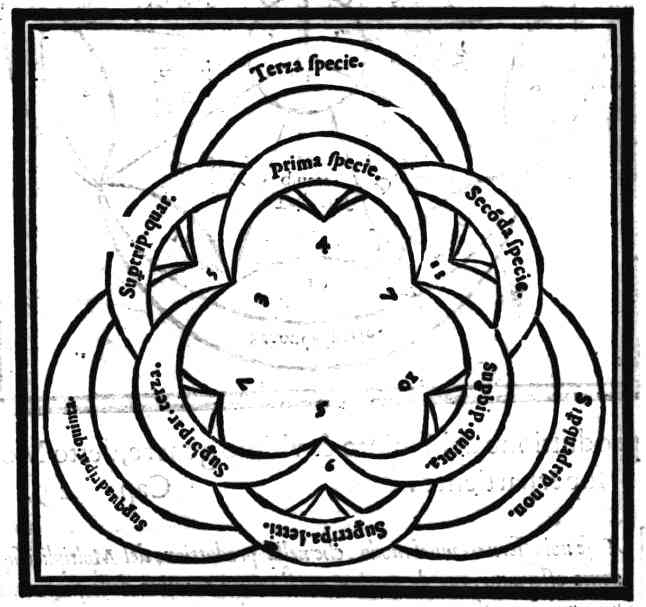
Del genere Moltiplice superparticolareCap. 28.
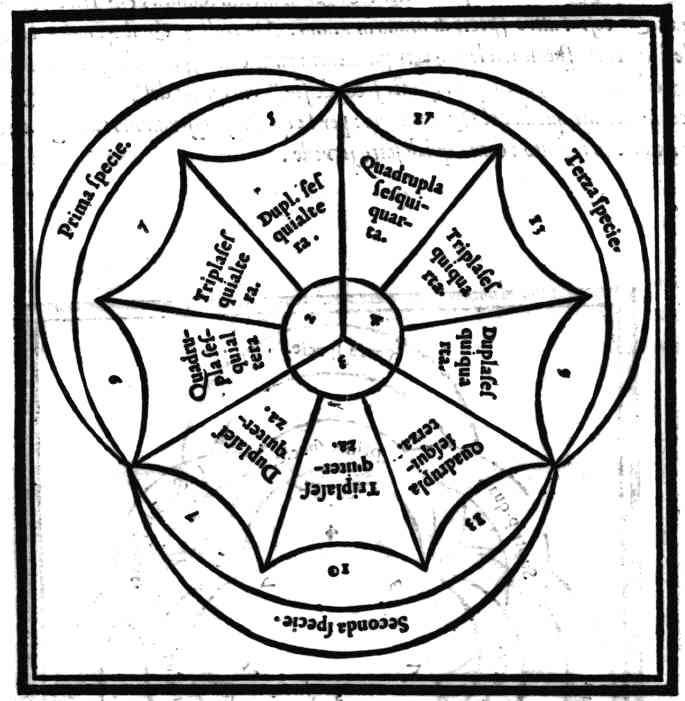
Della produttione del Quinto & vltimo genere, detto Moltiplice superpartiente.Cap. 29.
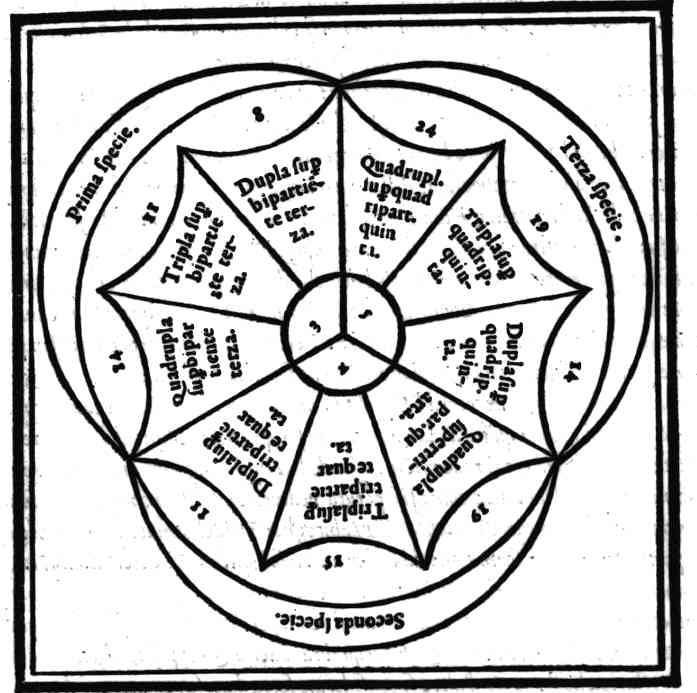
Della natura & proprietà de i nominati Generi.Cap. 30.

Del Moltiplicar delle proportioni.Cap. 31.
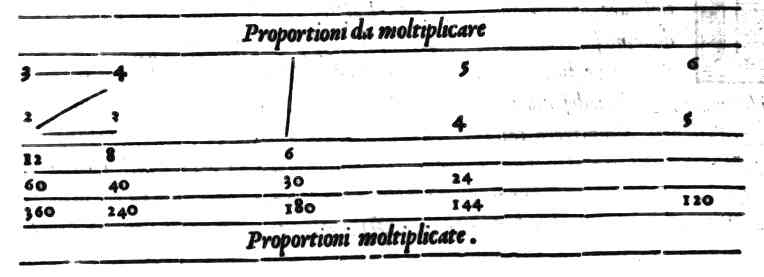
Il Secondo modo di moltiplicar le proportioni.Cap. 32.

Del Sommare le proportioni.Cap. 33.
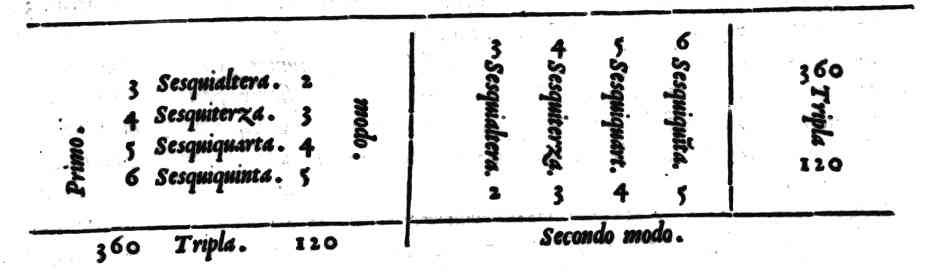
Del Sottrar le proportioni.Cap. 34.

Del Partire, o Diuidere le proportione; & quello che sia Proportionalità.Cap. 35.

Della Proportionalità, o Diuisione arithmetica.Cap. 36.

Della Diuisione, o Proportionalità Geometrica.Cap. 37.
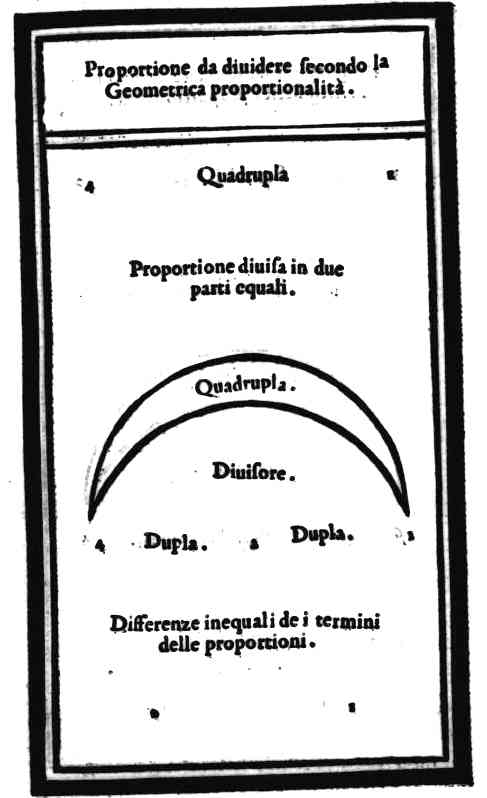
![Proportioni da diuidere secondo la
Geometrica proportionalità.
3Sesquialtera2
Proportione diuisa irrationalmen-
te in due parti equali.
Sesquialtera.
Diuisore.
3[[mus.Resp]]. 6.2](../../zarins58/ill/137-2.jpg)
In qual modo si possa cauare la Radice quadrata da i numeri.Cap. 38.

Della Diuisione, ouero Proportionalità harmonica.Cap. 39.

Consideratione sopra quello che si è detto intorno alle Proportioni & Proportionalità.Cap. 40.
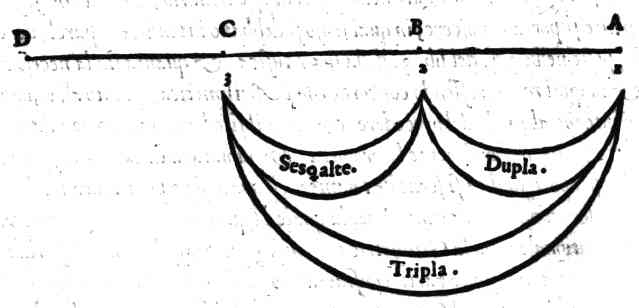
Che il Numero non è cagione propinqua & intrinseca delle Proportioni Musicali, ne meno delle Consonanze.Cap. 41.
Della inuentione delle Radici delle proportioni.Cap. 42.
In che modo si possa ritrouar la Radice di più proportioni moltiplicate insieme.Cap. 43.

Della Proua di ciascuna delle mostrate operationi.Cap. 44.
LA SECONDA PARTE Delle Istitutioni harmoniche DI M. GIOSEFFO ZARLINO DA CHIOGGIA.
Quanto la Musica sia stata da principio semplice, rozza, & pouera di consonanze.Cap. 1.
Tibia non, vt nunc, oricalcho vincta, tubaequeAl quale dipoi Hiagne Frigio a quei tempi dotto nella Musica, che fu padre & maestro di Marsia, vi aggiunse li fori, & incominciò a sonar quello con variati suoni, & fu il primo, che fece sonar due Pifferi con vn sol fiato, & che sonò tale istrumento con la destra & con la sinistra mano; cioè che mescolò il suono graue con l'acuto, con destri fori & sinistri. Vsarono etiandio gli antichi da principio la Cetera, o la Lira con tre chorde, ouer con quattro solamente, della quale fu inuentore Mercurio (come vuol Boetio) & erano in quella ordinate di modo, che la prima con la seconda, & la terza con la quarta conteneuano la Diatessaron; & la prima con la terza, & la seconda con la quarta, la Diapente: & di nuouo la seconda con la terza il Tuono, & la prima con la quarta la Diapason; Et insino al tempo di Orfeo fu seruato cotale ordine, il quale fu dipoi accresciuto in varij istrumenti; et prima Chorebo di Lidia vi aggiunse la quinta chorda; dipoi dal sopranominato Hiagne vi fu aggiunta la sesta; ma la settima aggiunse Terpandro Lesbio. Et questo numero di chorde veramente (come dice Clemente Alessandrino) era contenuto nell'antica Lira, o Cetra; dipoi da Licaone Samio fu aggiunta la ottaua; ancora che Plinio attribuisca la inuentione di tal chorda a Simonide, & della nona a Timotheo; & Boetio voglia, che questa chorda sia stata aggiunta da Profrasto Periota, la decima da Estiacho Colofonio, & la vndecima da esso Timotheo: Ma sia come si voglia, Suida attribuisce l'aggiuntione della Decima & della Vndepage 59cima chorda a Timotheo Lirico. Et certo è che da molti altri ve ne furno aggiunte tante, che crebbero al numero de Quindici. Aggiunsero dipoi a queste la sestadecima chorda, ne più oltra passorno, & si contentarono di tal numero; & le collocorno nell'ordine, che più oltra dimostraremo, diuidendole per Tuoni & Semituoni in cinque Tetrachordi: osseruando le ragioni delle proportioni Pithagoriche, ritrouate ne i martelli da Pithagora, nel modo che nella prima Parte hò mostrato; le quali conteneuano quelle istesse, che si ritrouauano tra le chorde della sopradetta Cetera, o Lira ritrouata da Mercurio; & che nel sottoposto essempio si veg
Aemula, ed tenuis, simplexque foramine pauco
Adspirare, & adesse choris erat vtilis;
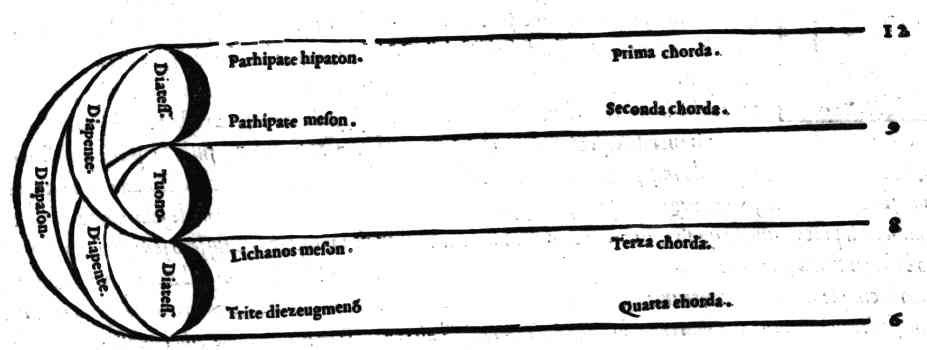
Per qual cagione gli antichi nelle loro Harmonie non vsassero le consonanze imperfette, & Pithagora vietasse il passare oltra la Quadrupla.Cap. 2.
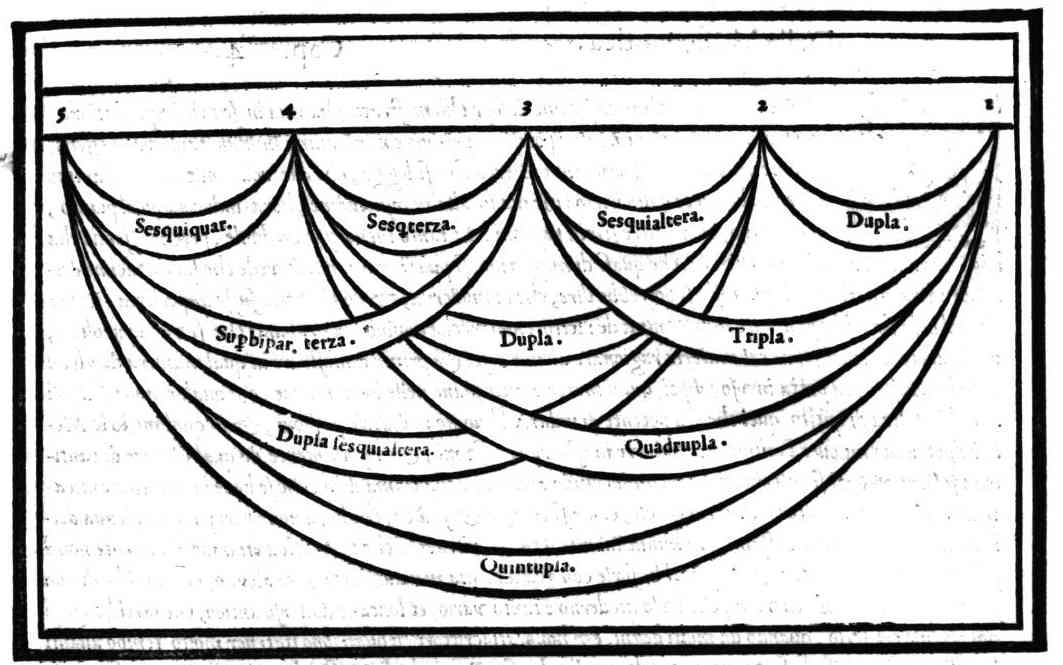
Dubbio sopra l'inuentione di Pithagora.Cap. 3.
Della Musica antica.Cap. 4.
Si plausoris eges aulaea manentis, & vsqueEt era vsanza (come afferma il Filosofo) che li Poeti istessi recitassero le Tragedie & le Comedie, che page 63haueano composte, & le cantauano. Onde, come narra Titoliuio, vno chiamato Liuio, hauendo fatto vna Fauola in versi, ordinata col suo argomento, egli stesso la recitaua; dipoi non potendo più dire: percioche la voce gli era mancata, pregò che li fusse perdonato; & pose vn fanciullo a cantarla, il quale hauendosi portato bene, fu introdutta vna vsanza, che cotali cose fussero cantate dagl'Istrioni; Et di questo ne tocca vna parola Horatio dicendo nella sua dell'Arte Poetica;
Sessuri, donec cantor, vos plaudite dicat.
Ignotum Tragicae genus inuenisse camoenaeIo credo anco, che gli Oratori orassero al popolo al suono di qualche istrumento, ancora che al parer mio tale vsanza durasse poco tempo: imperoche Cicerone nella Oratione, che fece in fauor di P. Sestio, la quale si ritroua imperfetta, ne tocca vna parola; Et anche nel fine del lib. 3. dell'Oratore, parlando di Gaio Gracco, lo dimostra, benche questo paia alquanto strano ad Aulo Gellio: Ma Plutarco modestamente recita tal cosa, & dice; Che essendo Gaio Gracco huomo vehemente nel dire, spesse volte era trasportato dall'ira, di modo che veniua alle villanie, & vituperij; & cosi egli soleua turbare la sua oratione: Onde conoscendo tal cosa, s'imaginò di rimediarui, col fare, che vn seruo dotto nella Musica nominato Licino li stesse dopo nel pulpito, & che mentre lo vdiua in asprirsi & ritirarsi fuori della sua voce, con vno istrumento lo auertiua, & gli faceua achetare cotal vehementia. Et di ciò non ci douemo marauigliare, poi che l'arte Oratoria hà hauuto principio (come vuole Strabone) dalla poesia, & li Poeti orauano al popolo cantando versi al suono della Cetera, o Lira, & lo tirauano a fare il lor volere; il che ben lo dimostra anco l'Ariosto dicendo;
Dicitur, & plaustris vexisse poemata Thespis,
Quae canerent, agerentque peruncti fecibus ora.
Cantauano anco gli antichi al suono del Piffero, recitando diuerse canzoni composte in versi; & questo faceuano alle volte, quando due erano insieme, l'vno de i quali sapesse cantare, & l'altro sonare; come accennò il Poeta, quando introdusse Menalca dire a Mopso pastore queste parole;Li scrittori indi fer l'indotta plebe
Creder, che al suon delle soaui cetre
L'vn Troia, & l'altro edificasse Thebe.E hauesson fatto scendere le pietre
Da gli alti monti, & Orpheo tratto al canto.
Tigri, e Leon, dalle spelunche tetre.
Tu calamos inflare leueis, ego dicere versus:Percioche l'vno era perito sonatore di Piffero, & l'altro cantaua ottimamente. Era anco appresso gli antichi vsanza di saltare & di ballare, mentre che il Musico al suono della Lira, o Cetera, ouer di alcuno altro istrumento recitaua alcuna cosa; come si vede appresso di Homero nella Odissea, che cantando Demodoco al suono della Cetera, li Greci saltauano & ballauano. Et similmente Virgilio, nel lib. 1. dell'Eneida, imitandolo dice, che cantando Ioppa al suono della Cetera,
Ingeminant plausu Tyrij, Troesque sequuntur;Et in vn'altro luogo piu chiaramente manifesta tal cosa dicendo;
Pars pedibus plaudunt Choreas, & carmina dicunt.Similmente Horatio (auegna che non faccia mentione alcuna, che si cantasse) dice;
Sic priscae motumque & luxuriam addidit arti Tibicen.Di questo si potrebbeno hauere infiniti essempij, i quali hora per breuità io lasso; poi che le Ode di Pindaro di ciò fanno indubitata fede: conciosia che essendo diuise in tre parti, delle quali la prima è chiamata στροφή. ἀντιστροφή. la seconda, & la terza ἐπωδός, & sono comprese sotto i versi lirici; gli antichi le cantauano al suono della Lira, o della Cetera; & ballauano, o saltauano in tal maniera, che quando li saltatori si volgeuano dalla parte destra verso la sinistra, cantauano la prima parte; & quando andauano dalla sinistra alla destra cantauano la seconda; & veniuano a riposarsi quando cantauano la terza; La qual maniera di ballare, o saltare dura fino al dì d'hoggi appresso li Candioti & quelli, che habitano nell'isola di Cipro. Gli antichi adunque vsauano la Musica nella maniera, che habbiamo detto, accompagnando la voce ad un solo istrumento; & se alle volte vsauano più sorti d'istrumenti, vi accompagnauano la voce, si come tra genti barbare al presente ancora si costuma in alcune parti, & massimamente del Leuante, come da huomini degni di fede più volte hò vdito dire. Ma li due primi modi, (come fanno fede le historie) erano grandemente in vso. Vsarono gli antichi ne i loro esserciti varie sorti d'istrumenti: imperoche i Thoscani vsarono la page 64Tromba della quale essi furono gli inuentori, come vogliono alcuni; gli Arcadi la Sampogna; i Siciliani alcuni istrumenti, i quali nominauano πύκτιδας; li Candioti la Lira; i Lacedemonij il Piffero; quelli di Thracia il Corno: gli Egittij il Timpano; & gli Arabi il Cembalo. Li Romani si seruirno nelle loro comedie di alcune sorti di Pifferi, i quali chiamauano Destri & Sinistri; da i quali gli Spettatori poteuano comprendere sotto qual genere si contenessero le Comedie, che doueuano recitare: Imperoche quando la Comedia conteneua in se materia, o soggetto seuero & graue, si vdiua il concento graue de i Pifferi sinistri; quando poi era giocoso & festeuole, il concento che nasceua da i Pifferi destri era acuto; & se era mista, le cantilene musicali erano temperate dell'vna & dell'altra sorte di concento. Et tali cantilene non erano fatte dal Poeta, che hauea composto la Comedia, ma da vn perito nell'arte della Musica; si come nel principio di ciascuna Comedia di Terentio si può vedere. Et erano variate del Modo, o Tuono, che vogliamo dire; & le faceuano vdire auanti che cominciassero a rappresentar la Comedia, accioche la materia compresa in essa (come hò detto) si potesse sapere auanti da gli Spettatori. Nondimeno a i nostri tempi ancora sono incognite cotali sorti di Pifferi: ancorache, Seruio nel lib. 9. dell'Eneide di Virgilio, sopra quel verso O uere Phrygiae, mostri che erano di due sorti, delle quali l'vna nomina Pifferi Serani, & l'altra Frigij: Li primi erano Pari; & cosi li chiama: percioche haueuano le loro cauerne pari, & equali; li secondi Impari: conciosia che le cauerne loro erano inequali. Adduce dipoi Seruio l'autorità di Marco Varrone, volendo dichiarar quali siano Pifferi destri, & sinistri dicendo; che la Tibia frigia destra hà vn sol foro, la sinistra ne hà due, de quali l'vno hà il suono acuto, & l'altro graue; Ma queste parole sono differenti da quelle, che sono poste nel lib. 1. al cap. 2. delle cose della Villa; doue egli dice, che l'vna sorte di Pifferi sonaua i modi di vno istesso Verso in voce acuta, & l'altra nella graue: Onde seguendo più a basso, dalle sue parole si può comprendere, che'l sinistro man daua fuori il suono graue, & il destro lo acuto. Et questo si può confermare con l'autorità di Plinio, il quale parlando de i Calami acquatici dice, Che si soleuano tagliare in tempo conueniente circa la stella Arturo, fino alla età di Antigene sonatore di Piffero, vsandosi ancora la Musica semplice a quei tempi; & cosi preparati dopo alcuni anni incominciauano ad esser buoni; & anche allora bisognaua addoperarli molto spesso, & quasi insegnar loro sonare: percioche le linguelle se veniuano a toccare l'vna con l'altra; il che era molto più vtile per mostrare i costumi ne i Theatri: Ma dipoi che soprauene la varietà, et la lasciuia de i canti, incominciorno a tagliarli auanti il Solsticio, & il terzo anno erano buone; conciosia che haueano le linguelle loro più aperte, & più atte a variare i suoni, le quali hoggidi ancora cosi sono. Ma allora era opinione, che si accordassero insieme quelli, che erano d'vna medesima canna; & quella parte ch'era vicina alla radice conuenirsi al Piffero sinistro, & quella che era vicina alla cima al destro. Questo dice Plinio, & parmi esser ben detto: imperoche quelli, che sono vicini alla radice, sono necessariamente più grossi di quelli, che sono più verso la cima: onde ogni giorno si vede per esperienza, che essendo il corpo loro più grande, & più largo, rende anco il suono più graue: come il contrario si scorge in quelli, che sono più miniuti, & più ristretti. Il che ancora si vede, & ode ne gli istrumenti, che chiamano Organi, le canne de i quali quanto sono più larghe, tanto rendeno i suoni più graui; & le più minute i più acuti. Ma a questo che si è detto, pare che sia contrario vno Autore incerto di quello Epigramma Greco, che incomincia τὸν σοφὸν ἐν κιθάρῃ: percioche chiama la chorda graue δεξιτλρὴν ὑπάτην, cioè destra Hipate, & l'acuta λαιὴν νήτην, cioè sinistra Nete: Ma questo importa poco: conciosia che considerata bene la cosa, torna commodo all'vno, & all'altro modo; essendo che le parti d'ogni istrumento si possono considerare, & denominare in due modi; prima, in quanto a noi; dipoi in quanto ad esso istrumento: In quanto a noi, la parte dell'istrumento posta dalla mano destra è detta Destra, & rende i suoni acuti, come ne gli Organi, Monochordi, & altri istrumenti simili si vede; & quella, che è posta dalla sinistra è detta Sinistra, & rende i suoni graui: Ma inquanto all'istrumento, quella che è destra a noi, ad esso è sinistra; & per il contrario, quella che è a lui destra, a noi è sinistra, come si può vedere in due, i quali insieme giuocassero a lottare, che la parte destra dell'vno è sinistra all'altro, & la sinistra destra. Non è adunque inconueniente, se l'vno nomina quella parte destra, la quale l'altro chiama sinistra, essendo tali parti diuersamente secondo alcune loro opinioni considerate. In questo modo adunque da gli antichi era posta in vso la Musica, il qual modo quanto sia differente dall'vso moderno, ciascuno da se lo potrà sempre vedere; si come etiandio potrà vedere altroue, quanto era differente il loro concento dal moderno. Ma quali materie recitassero nelle lor cantilene, quel che si contiene nel seguente capitolo ce lo fara manifesto. page 65
Le materie che recitauano gli antichi nelle loro canzoni, & di alcune leggi musicali.Cap. 5.
Musa dedit fidibus diuos, puerosque deorum,Et, si come dimostra Platone nel Protagora, gli antichi insegnauano tutte queste materie a i loro giouani; accioche le hauessero a cantare al suono della Lira, ouer della Cetera. Onde Homero scriue di Achille;
Et pugilem victorem, & equum certamine primum,
Et iuuenum curas, & libera vina referre.
ἄειδε δ´ἁρα κλέα ἀνδρῶν.cioè Ma le lodi de gli huomini cantaua; al suono della Cetera. Et di Demodoco dice; Che cantaua le gloriose imprese de gli huomini, la contentione di Vlisse con Achille, la fauola di Venere & di Marte, & il Cauallo Troiano. Femio anche nella Odissea si escusa con Vlisse dicendo: Che cantaua alli Dei, & a gli huom ini: Onde è da pensare, che non cantasse se non cose graui, & seuere; hauendo gia cantato il lugubre & funebre ritorno de i Greci nella loro patria. Et se bene cantò l'adulterio di Marte & di Venere, non lo fece perche lodassi tal sceleratezza; ma per rimuouere (come dice Atheneo) li Pheaci dalle dishoneste loro volutà, et piaceri. In cotal modo ancora appresso di Virgilio;
Cithara crinitus IopasEt Creteo amico alle Muse medesimamente,
Personat aurata, docuit quae maximus Atlas.
Hic canit errantem Lunam, Solisque labores:
Vnde hominum genus & pecudes, vnde imber & ignes:
Arcturum, pluuiasque Hyadas, geminosque Triones:
Quid tantum Oceano properent se tingere Soles
Hyberni, vel quae tardis mora noctibus obstet.
Semper equos, atque arma virûm, pugnasque canebat.Nerone etiandio, appresso di Suetonio nella vita di questo scelerato Imperatore, canta al suono della Cetera la fauola di Niobe; & cantò molte altre Tragedie mascherato, come Canace parturiente, Oreste vcciditore della madre, Edippo fatto cieco, & Hercole furioso. Et Luciano dice, che gli Argomenti, et le materie delle cantilene appresso gli antichi, erano quelle cose, cominciando dal principio del mondo, che erano successe fino a i tempi di Cleopatra regina di Egitto. Le quali, mi pare page 66(secondo che lui racconta) che siano quasi tutte quelle cose, che scriue Ouidio nelle sue Trasformationi; et a cotal canto ballauano. Tutte queste cose recitauano sotto vna determinata Harmonia, con determinati Rithmi et Versi, & Percussioni; ancora che fussero variati in ogni maniera di cantilena. Et cosi con tai numeri, percussioni, modi, & concenti; et con la voce humana, esprimeuano materie conueneuoli et buoni costumi. Nominarono poi tali determinationi Leggi: imperoche altro non è Legge nella Musica, che vn modo di cantare, ilqual contiene in se vn determinato concento & vn determinato Rithmo, & Metro. Et furono cosi chiamate: percioche non era lecito ad alcuno di mutare, ouero innouare in esse alcuna cosa, si nelle harmonie, come etiandio ne i Rithmi, & Metri; ancora che siano alcuni, che dicano, che si chiamauano Leggi: imperoche auanti che si scriuessero le Leggi ciuili, si cantauano tal Leggi in versi al suono della Lira, o Cetera, accioche i popoli più facilmente ritenessero nella memoria quello, che douessero osseruare. Ma sia come si voglia, erano le Leggi di tre sorti: imperoche alcune erano dette Citharistice, che si cantauano alla Cetera, o Lira; & alcune Tibiarie, le quali si cantauano al suono de i Pifferi. La terza sorte poi si chiamauano Communi & si cantauano al suono dell'vna & dell'altra sorte de gli istrumenti nominati. Et benche tal Leggi fussero molte; nondimeno ciascuna hauea il suo nome acquistato, o dalli popoli, che le vsauano; o dalli Rithmi & Metri, ouero dalli Modi; da gli Inuentori; o da i loro amatori, oueramente da gli argomenti. Dalli popoli fu nominata l'Eolia & la Beotia; da i Rithmi & Metri la Orthia & la Trochea; dalli Modi l'Acuta & la Tetraedia; da gli amatori & inuentori la Terpandria & la Hieracia; & da gli argomenti il Certame Pithico & il Currule. Queste leggi (come vuol Plutarco) furno publicate da Terpandro; il quale hauendo prima diuiso le Citharistice, pose nome alle lor parti. Le leggi Tibiarie hebbero molti nomi, che si lassano per non andare in lungo; i quali (secondo che si dice) ritrouò Cleone ad imitatione di Terpandro. La legge Orthia apparteneua a Pallade, & conteneua in se materie di guerra; Et era vna specie di modulatione nella Musica, la quale Aulo Gellio nomina Verso orthio; forse detto in tal modo dalli suoi numeri, i quali sono veloci, & sonori: conciosia che li Greci nominan ὅρθιος quello, che noi chiamiamo Sonoro; ancora che molti lo interpretano per il Canto appartenente ad vn Campo, ouero ad vno Essercito d'huomini d'arme. Era la Trochea vn segno, che dauano gli antichi a i soldati col canto, o suono della Tromba; & i Lacedemonij vsauano ne i loro esserciti il canto della legge Castoria, per accender l'animo de i soldati a prender l'arme contra gli inimici; & tal legge era composta sotto vn Rithmo detto Embaterio.La Currule s'acquistò il nome dalla materia, che conteneua in se, cioè dall'argumento, nel quale si narraua il modo, che Hettore figliuolo del Re Priamo fu strascinato con le carrette a torno le mura Troiane. Di queste Leggi hò voluto far vn poco di dichiaratione; accioche si possa vedere, che erano composte di verso numeroso, accommodate a commouere, & generare ne gli animi diuerse passioni. Non sarà etiandio fuori di proposito, che veggiamo in qual maniera li Musici anticamente recitassero alcuna delle predette Leggi al suono del Piffero cantando; accioche possiamo comprendere, in qual modo poteuano recitar l'altre; & questa sarà il Certame Pithico, del quale fa mentione Horatio, dimostrando le qualità del Musico, che hauea da recitarlo dicendo;
Abstinuit Venere, & Vino, qui Pythia cantatLequali troppo bene conobbe Nerone (come si legge in Suetonio) che si asteneua dalli pomi, vsaua il vomito & li christeri, per purgarsi bene il petto; accioche hauesse recitando nella Scena la voce chiara & netta. L'Argomento adunque di tal legge era la Battaglia di Apolline col serpente Pithone, il quale dà il nome alla fauola; & il nome di tutta la cantilena era Delona; & forse fu cosi nominata: percioche Apollo nacque nella isola di Delo. Era questa legge (si come mostra Giulio Polluce) diuisa in cinque parti, delle quali la prima nominauano Rudimento, ouero Esploratione; la seconda Prouocatione; Iambico la terza; la quarta Spondeo; Et la quinta & vltima Ouatione, o Saltatione. La rapresentatione (come hò detto) era il modo della pugna di Aollo col Dragone, & nella prima parte si recitaua, in qual modo Apollo inuestigaua, & contemplaua il luogo, se era atto alla pugna, ouer non: Nella seconda si dichiaraua il modo, che teneua a prouocare il Serpente alla battaglia: Nella terza il combattimento; & questa parte conteneua vn modo di cantare al suono del Piffero, chiamato ὀδοντισμός: conciosia che il serpente batteua li denti nel saettarlo: Nella quarta si raccontaua la vittoria di Apollo; et nella vltima si dichiaraua, come Apollo faceua festa con balli et salti, per la riceuuta vittoria. Non sarebbe gran marauiglia, se gli antichi hauessero saltato, et ballato, quando si recitaua cotal legge: percioche vsauano anco di saltare, & ballare nelle loro Tragedie, & Comedie; & a ciascuna di esse haueano accommodato il suo propio modo: page 67conciosia che (come mostra Atheneo) haueano ritrouato vna specie di saltatione detta Emmelia, & alla Comedia vna detta Cordace. Era ancora appresso di loro vna specie di Saltatione satirica, la quale chiamorno σίκιννις, & fu istituita da Bacco, dopo che hebbe domata l'India. Questa era vna delle Leggi tibiarie, nella quale i Rithmi, i Moduli, i Costumi, & le Harmonie si mutauano, secondo che la materia ricercaua. Haueano etiandio la saltatione detta Carpea, la quale lassarò di raccontare: percioche è posta da Atheneo tanto chiaramente, che ogn'vno leggendola potrà conoscere quello, che ella fusse, & in qual maniera la vsassero; & da queste due, cioè dal Certame Pithico, & dalla Saltatione carpea, si potrà scorgere, in qual modo gli antichi recitassero l'altre Leggi. Potemo hora vedere da quello, che si è detto, che la Musica hauea più parti, cioè l'Harmonia, il Rithmo, il Metro, & lo Istrumento, dal quale questa parte si diceua Organica. Eraui etiandio la Poesia, & la Saltatione; & queste parti alle uolte concorreuano tutte in una compositione, & tallora la maggior parte di esse. Ne era lecito (come altre uolte hò detto) di mutare, ouero innouare alcuna cosa, che di tal mutatione l'inuentore non ne hauesse a riportare la punitione. Et durò lungo tempo tal costume, la onde conseruandosi la Musica in cotale essere, si conseruò anche la sua riputatione; ridutta dipoi a poco a poco nel stato, nel quale hoggidi la ueggiamo, hauendosi dato i popoli alla crapula, & alla lussuria, poco curandosi di tal cosa, presero i Musici maggior licenza, & con molte altre cose insieme, perdero essi & la Musica la sua antica grauità & riputatione; il che si vede detto da Horatio, quando dice;
Tibicen, didicit prius extimuitque magistrum;
Postquàm coepit agros extendere victor, & vrbemEt più oltra seguita dicendo quello, che di sopra hò commemorato; cioè
Latior amplecti muros, vinoque diurno
Placari genius festis impune diebus,
Accessit numerisque, modisque licentia maior:
Sic priscae motumque & luxuriam addidit artiEt dipoi segue etiandio dicendo,
Tibicen.
Sic etiam fidibus voces creuere seueris.Onde è da notare, che Horatio nomina le antiche chorde seuere: percioche (come hò detto) gli antichi al suono di quelle recitauano se non cose seuere, & graui. In tal modo adunque gli antichi Musici, nella età che la Musica più fioriua, & era in maggior prezzo & riputatione, recitauano le narrate materie nelle lor cantilene. Ma quali cose, & in qual modo da i moderni siano recitate; & quali siano state lassate da vn canto, ogn'vno che hà cognitione della Musica, da se lo potrà giudicare, amp; vedere.
Quali siano stati gli antichi Musici.Cap. 6.
Ne forte pudoriPercioche dice prima sonatore della Lira, come quello (come vogliono alcuni) che fu l'inuentore di essa; poi lo chiama Poeta col nome di Cantore. Lassarò di raccontare, quali fussero Orfeo & Arione: percioche è manifesto, che costoro non solo furno Musici, ma celebratissimi Poeti ancora. Hesiodo etiandio fu posto tra i Musici, ancora che non vsasse mai di accompagnare il canto col suono della Lira: percioche vsaua vna verga di lauro, con la quale percotendo l'aria (come narra Pausania) faceua vn certo suono, al quale era solito cantare li suoi poemi; la onde gli antichi li fecero vna statua con la Cetera sopra le ginocchia, & la posero tra quelle di Thamira, Arione, Sacada, & di altri nobilissimi & eccellentissimi Musici, per non priuarlo di cotale honore. Pindaro similmente fu Musico & Poeta, si come dalle sue opere si può comprendere, & da quello etiandio che fece il magno Alessandro: imperoche quando fece ispianare & ruinare Thebe, fece scriuere (come dice Dione Chrisostomo) sopra la sua casa queste parole; πινδάρου τοῦ μουσοποιοῦ τὴν στέγην μὴ καίετε; che vogliono dire, Non abbrusciate la casa di Pindaro musico. Et per non andare più in lungo, il Santissimo Dauid Re di Hierusalem & gran Profeta da Basilio magno è chiamato non solamente Musico, ma Poeta anco di sacre cantilene; & dal dottissimo Hieronimo vien chiamato Simonide, Pindaro, Alceo, Flacco, Catulo, & Sereno: percioche scrisse con stile elegante i sacri Salmi in verso lirico, alla guisa di Horatio, & delli nominati: Et si può credere, che più volte li cantasse al suono della Cetera, nel modo che cantaua, quando iscacciaua il maligno spirito di Saul. Onde non è dubbio, che essendo stato Poeta, non si debba anco nominare Musico: conciosia che la Scrittura santa lo chiama in più luoghi Psaltes, che vuol dire Cantore, o Sonatore; & il suo diuino Poema nomina Psalterio. Et di questo è testimonio Origene nella Homilia 18. del cap. 24. del libro de i Numeri, dicendo; Che diremo noi della Musica? della quale il sapientissimo Dauid ne hauea ogni scienza, & hauea raccolto la disciplina di tutta la Melodia et delli Rithmi, accioche da tutte queste cose potesse ritrouar suoni, con li quali potesse mitigare sonando il Re turbato & molesta to dal spirito maligno. Il simile dice Agostino nel lib. 17. al capitolo 4. del libro della Città di Dio, come iui si puo vedere. Ogni ragione adunque ne persuade a credere, che i Poeti antichi cantassero lor stessi li suoi poemi; & che hauessero congiunto la Musica con la Poesia: Percioche se fusse stato altramente, non hauerebbeno vsato tanto spesso nelle loro compositioni questa voce Cantare, come fece Homero; il quale diede principio alla Illiade in cotal modo;
Sit tibi musa lirae solers, & cantor Apollo:
Μῆνιν ἄειδε θεὰ.cioè Canta Dea l'ira; & Hesiodo, che incominciò la Theogonia in questa maniera;
Μουσάων ἑλικωνιάδων ἀρχώμεθ'ἀείδειν;che vuol dire, Le Muse di Elicona incominciamo Cantare: A i quali aggiungeremo il prencipe de i Poeti latini Virgilio, il quale incominciò in cotal modo la sua Georgica;
Quid faciat laetas segetes, quo sydere terramEt alla sua Eneide pose vn tal principio;
Vetere Mecoenas, vlmisque adiungere vites
Conueniat, quae cura boum, qui cultus habendo
Sit pecori atque apibus quanta experientia parcis
Hinc canere incipiam;
Arma, virumque cano.Cosi anche Ouidio incomincia li Fasti con questi uersi;
Tempora cum causis Latium digesta per annum,Onde il `archa imitando tutti costoro diede principio ad vna sua canzone in questa maniera;
Lapsaque sub terras, ortaque signa canam.
Nel dolce tempo della prima etade.Et il moderno Ariosto, perseguire tal costume, incominciò ancor lui il suo elegante poema in questo modo;
Che nascer vide, & ancor quasi in herba,
La fera voglia, che per mio mal crebbe.
Perche cantando il duol si disacerba,
Canterò com'io vissi in libertade;
Le donne, i caualier, l'arme, gli amori,page 69Ma doue vo io più vagando, se Terentio poeta comico dimostrandoci la Poesia & la Musica esser congiunte, & quasi vna istessa cosa, la nominò Studio musicale. Non è adunque marauiglia, se i Musici & li Poeti erano anticamente riputati essere vna cosa istessa. Et se bene il Poeta è chiamato alle volte con questa voce latina Vates, che si conuiene etiandio all'Indouino, non è fuori di proposito: conciosia che l'vno & l'altro (secondo il parer di Platone) sono mossi & agitati da vna istessa diuinità, o diuina alienatione di mente, & da vno istesso furore. Onde Homero nomina il Musico αὐτοδίδακτος: percioche canta non per humana istitutione, ma inspirato dalli Dei, il che si scorge dalle parole che soggiunge, le quali dicono;
Le cortesie, l'audaci imprese io canto.
θεὸς δέμοι ἐν θρεσὶν οἵμας.cioè Percioche Dio mi produsse in la mente Ogni mia cantilena. Però adunque molti Poeti gentili hanno alcuna volta predetto cose, che haueano da venire; come si vede, che Virgilio, secondo la opinione di Agostino Dottor Santo, non conoscendo il nostro Redentore ne per lume naturale, ne per viua fede, cantò sotto'l nome di vn'altro il suo nascimento, quando disse;
παντοίας ἐνέφυσεν;
Vltima cumaei venit iam carminis aetas:Ancora che il diuino Hieronimo scriuendo a Paulino sia di altro parere: Conciosia che Virgilio si mosse a cantare queste cose, inuitato da gli Oracoli della Sibilla Cumana; si come cantò poco più oltra la liberatione del peccato originale in cotal modo;
Magnus ab integrò, seclorum nascitur ordo.
Iam redit & virgo, redeunt Saturnia regna.
Iam noua progenies coelo demittitur alto;
Te duce si qua manent sceleris vestigia nostriEt, che colui, che hauea da nascere sarebbe Dio & Huomo, seguendo più a basso;
Irrita, perpetuo soluent formidine terras:
Ille Deûm vitam accipiet, diuisque videbitEt che il Serpente nimico della humana natura douea perdere il regno, & douea rimanere in noi alcuna cosa, per rispetto del peccato originale, dicendo;
Permixtos heroas, & ipse videbitur illis:
Occidet & Serpens, & fallax herba veneni.&Ouidio ancor lui nelle sue trasformationi chiaramente mostrò la venuta del Figliuolo di Dio in carne, con queste parole;
Pauca tamen suberunt priscae vestigia fraudis.
Summo delabor Olympo,Et delli miracoli che fece, poco più abasso disse.
Et deus humana lustro sub imagine terras:
Signa dedi venisse Deum.Pose etiandio le parole, che dissero quelli, che lo crucifissero, cioè se era figliuol di Dio, che si liberasse da quella, & disse;
Experiar Deus hic discrimine aperto,Lucano ancora cantò quello, che auerrebbe auanti il futuro vniuersale & finale Giudicio con tali parole;
An sit mortalis, nec erit dubitabile verum.
Sic cum compage solutaHauendo medesimamente Ouidio cantato tal cosa con queste parole; page 70
Saecula tot mundi suprema coegerit hora,
Antiquum repetens iterum Chaos, omnia mistis
Sidera sideribus concurrent, ignea pontum
Astra petent, tellus extendere littora nolet,
Excutientque fretum: fratrique contraria Phaebe
Ibit, & obliquum bigas agitare per orbem
Indignata, diem poscet sibi, totaque discors
Machina diuulsi turbabit faedera mundi.
In se magna ruunt:
Esse quoque infatis reminiscitur, affore tempusDi coteste cose sono molti essempij: ma lassandoli da un canto verremo a quelli de i Sacri libri, & ritroueremo l'autorità del Santissimo Apostolo Paulo, il quale scriuendo a Tito, adducendo vna sentenza di Epimenide poeta, lo chiama Profeta, dicendo; Ι῎διος τῶν αὐτῶν προφήτης; che vuol dire, Propio Profeta di costoro, cioè de i Candioti. Douendosi adunque chiamare allora il Musico, & il Poeta, o l'Indouino per vn nome commune, era conueniente ancora, che il nome di Sapiente li conuenisse: Percioche (come ne fa auertiti Platone) al vero Musico s'appartiene sapere & hauer cognitione di tutte le scienze, & cosi al Poeta, secondo il parere di Strabone; la onde meritò da gli antichi esser chiamato solo Sapiente: conciosia che a quei tempi le città della Grecia faceuano imparare a lor figliuoli la Poesia, non solo per cagione di piacere, ma per cagione di casta moderatione. Onde li Musici, che insegnauano la Poesia, il Canto & li Modi, che si sonauano con la Lira, o Cetera & col Piffero, fecero professione, & si attribuirono tal virtù, di esser non solo correttori & & emendatori di costumi, ma si fecero etiandio chiamare maestri; la qual cosa conferma Homero con queste parole;
Quo mare, quo tellus, correptaque regia coeli
Ardeat, & mundi moles operosa laboret.
Πὰρ γὰρ ἔην καὶ ἀειδὸς ἀνὴρ, ᾥ πόλλ´ἐπετελλενche vogliono dire;
Α'τρείδης τροίην δὲ κιὼν εἴρυσθαι ἄκοιτιν;
Hauea presso di se vn Cantore, al qualeMeritamente adunque gli antichi riputauano i Musici, li Poeti, ouero Indouini, & li Sapienti essere vna medesima cosa.
Atride andando a Troia impose molto,
Che douessi seruar casta la moglie.
Quali cose nella Musica habbiano possanza da indurre l'huomo in diuerse passioni.Cap. 7.
Giunto Alessandro alla famosa tombaSi ricerca adunque vn Soggetto tale: conciosia che senza esso (come ancora hò detto) nulla o poco si vederebbe. Et benche in simili mouimenti fatti per la Musica, vi concorrino le nominate cose; nondimeno page 72il preggio & l'honore si dà al composto delle tre prime, che si chiama Melodia: Percioche se bene l'Harmonia sola hà vna certa possanza di dispor l'animo, & di farlo allegro, o mesto; et che dal Numero posto in atto le siano raddoppiate le forze; non sono però potenti queste due cose poste insieme, di generare alcuna passione estrinseca in alcun sogetto, al modo detto: conciosia che tal possanza acquistano dalla Oratione, che esprime alcuni costumi. Et che questo sia vero lo potemo vedere: percioche Alessandro non fu mosso dall'harmonia solamente; ne meno dall'harmonia accompanato col numero: ma si bene, (come vuole Suida, Euthimio, & altri ancora) dalla legge Orthia di sopra commemorata, & dal Modo Frigio: Dal qual modo, & forse anco da tal Legge, il nominato giouane Taurominitano ebbrio (come narra Boetio) fu sospinto, quando uolse abbrusciar la casa di quel suo riuale, nella quale era nascosa vna meretrice; la onde Pithagora conoscendo tal cosa, comandò al Musico, che mutasse il Modo, & cantasse il Spondeo, col quale placò l'ira del giouine, & lo ridusse al primo stato. Arione etiandio Musico, & inuentore del Dithirambo (secondo l'opinione di Herodoto, & di Dione Chrisostomo) prese ardire di precipitarsi nel mare, hauendo (per mio parere) cercato di comporsi prima col mezo di tal legge (come pone Gellio) vno animo intrepido & virile, per poter fare cotal cosa senza alcun timore. Hora potemo vedere, che tali & cosi fatti mouimenti sono stati fatti, non per virtù delle prime parti della Melodia; ma si bene dal tutto, cioè dalla Melodia istessa, la quale hà gran forza in noi, per virtù della terza parte, cioè delle parole, che concorreno alla sua compositione: Percioche il Parlare da se senza l'harmonia & il numero hà gran forza di commuouer l'animo: conciosia che se noi haueremo riguardo a cotal cosa, vederemo che alcune fiate quando vdimo leggere, o raccontare alcuna Fauola, ouero Historia, siamo costretti ridere, o piangere; & alcune volte ci induce all'ira, & alla colera; & alle volte di mesti ne fa diuentare allegri; & cosi per il contrario. Il Parlare adunque ne induce alla furia, & ne placa; ne fa esser crudeli, & ne addolcisce. Quante volte è accaduto, che leggendosi semplicemente alcuna pietosa Historia o Nouella, gli ascoltanti non siano stati presi da compassione in tal modo, che al suo dispetto doppo alcuni sospiri, li sia stato dibisogno accompagnarli le lagrime? Dall'altra parte, quante fiate e auenuto, che leggendosi, o narrandosi alcuna Facetia, o Burla, alcuni non siano quasi scoppiati dalle risa? Et non è marauiglia: percioche il più delle volte se'l si rappresenta a noi alcuna cosa degna di comiseratione, l'animo è commosso & indutto a piangere. Et se vdimo cosa, la quale habbia del feroce & del crudele, l'animo declina, et si piega in quella parte. Et di cio (oltra che è manifesto) è testimonio Platone, quando dice; Che qualunque volta alcun de noi vdimo Homero, ouero alcuno altro Poeta tragico, che imiti alcun de gli Heroi alitto per il dolore gridar fortemente, & pianger la sua fortuna con modi flebili, percuotendosi il petto con pugni; ad vn certo modo si dilettiamo, & hauendo vna certa inchinatione a coteste cose, seguimo quelle, & insieme siamo presi da tal passioni, & lodiamo quello come buon Poeta, il qual grandemente commuoua l'animo nostro. Questo ancora più espressamente conferma Aristotele dicendo; Ancora si vede, che gli huomini vdendo le imitationi, hanno compassione a quei casi, quantunque siano senza numero & senza melodia. Ma se'l parlare (come hauemo veduto) hà possanza di muouer gli animi, & di piegarli in diuerse parti, & ciò senza l'Harmonia & senza il Numero, maggiormente hauerà forza, quando sarà congiunto co i Numeri, & co i Suoni musicali, & con le Voci. Et tal possanza si fa chiaramente manifesta per il suo contrario: percioche si vede, che quelle parole muoueno men l'animo, le quali sono proferte senza melodia & proportione, che quelle, che sono proferte con debiti modi. Però gran forza hà da se stesso il Parlare, ma molto più hà forza, quando è congiunto all'harmonia, per la simiglianza che hà questa con noi, & alla potenza dell'Vdito: Conciosia che niuna cosa è tanto congiunta con le nostre menti (come dice Tullio) che li Numeri & le Voci, per le quali si commouemo, infiammamo, plachiamo, & rendemo languidi. Non è questo gran marauiglia (dice egli) che i sassi, le solitudini, le spelunche, & gli antri rispondeno alle voci? & le bestie crudeli & feroci spesse volte sono dal canto fatte mansuete; & da esso sono fermate? Ne ci douemo di ciò marauigliare: conciosia che se'l vedere vna historia, o fauola dipinta solamente ne muoue a compassione tallora, tallora ne induce a ridere, & tallora ne sospinge alla colera; maggiormente questo puo fare il parlare, il quale meglio esprime le cose, che non fa alcun pittore quantunque eccellente col suo pennello. Onde si legge di vno, il quale risguardò vna imagine pinta, & fu sospinto a piangere; Et di Enea, che entrato nel tempio fabricato da Didone nella nuoua Carthagine;
Del fero Achille, sospirando disse,
O fortunato, che si chiara tromba
Hauesti, che di te si alto scrisse.
Videt Iliacas ex ordine pugnas,Et di Porcia figliuola di Catone Vticense si legge ancora, che hauendo veduto vna certa Tauola di pittura, pianse amaramente. Et benche la Pittura habbia forza di commouer l'animo, nondimeno maggior forza hebbe la viua voce di Demodoco Musico & sonatore di Cetera, il quale riducendo in memoria Vlisse, dipingendoli le cose passate, come se li fussero state presenti, lo costrinse a piangere; dal quale effetto (come dice Homero, & Aristotele) fu subito conosciuto dal Re Alcinoo.Ma non pure allora accascauano coteste cose: ma etiandio a i nostri tempi si vede accascare il medesimo tra molte genti Barbare: imperoche raccontandosi da i lor Musici co certi versi al suono di vno istrumento i fatti di alcuno; secondo le materie che recitano, quelli che ascoltano cambiano il volto, facendolo per il riso sereno, & tallora per le lagrime oscuro; & per tal modo sono presi da diuerse passioni. Si può adunque concludere, che dalla Melodia, & principalmente dalla Oratione, nella quale si contenga alcuna historia, o fauola, ouero altra cosa simile, che esprima imitationi, & costumi, siano stati, & ancora si possino porre in atto cotali effetti; & l'Harmonia, & il Numero esser cose, le quali dispongono l'animo; pur che'l Soggetto sia sempre preparato, & disposto; senza il quale in vano ogni Musico sempre si affaticarebbe.
Bellaque iam fama totum vulgata per orbem, page 73
Atridas, Priamumque , & saeuum ambobus Achillem.
Constitit: & lacrymans, Quis iam locus (inquit) Achate,
Quae regio in terris nostri non plena laboris?
En Priamus: sunt hîc etiam sua premia laudi:
Sunt lacrymae rerum: & mentem mortalia tangunt.
Solue metus: feret haec aliquam tibi fama salutem.
Sic ait: atque animum pictura pascit inani.>
Multa gemens, largoque humectat flumine vultum;
In qual modo la Melodia, & il Numero possino muouer l'animo, disponendolo a varij affetti; & indur nell'huomo varij costumi.Cap. 8.
Proprio rabies armauit Iambo.Dalle quali cose si può comprendere, in qual modo la Melodia, & le sue parti possino con vna certa dispositione, diuersamente mutar le passioni, & costumi dell'animo. Ma perche ho detto di sopra, che ogn'vno naturalmente più si diletta di quella harmonia, la quale è più simile, conueniente, & proportionata alla sua natura, o complessione; & secondo che è disposto; però è da notare, ch'io dissi Secondo che è disposto, et hora dico, che la Melodia può mutar li costumi dell'animo: percioche indubitatamente (secondo la dottrina del Filosofo) le Virtù morali, et li Vitij non nascono con esso noi: ma si generano per molti habiti buoni, o tristi frequentati, nel modo che vno per sonare, o scriuere spesse fiate male, diuenta tristo Sonatore, o Scrittore: Ouer per il contrario, essercitandosi spesse volte bene, diuenta buono & eccellente. Similmente nelle virtù morali, colui che spesso essercita la Iniustitia per tal modo diuenta Iniusto; & colui che essercita la Iustitia diuenta Iusto, nel modo che colui, che si vsa a temere i pericoli diuenta timido, & non li stimando diuiene audace. Di maniera che, quali sono le operationi, tali sono gli habiti; Et dalle buone sono li buoni, & dalle triste li tristi nascono.Essendo adunque le Harmonie, & li Numeri simili alle passioni dell'animo, come afferma Aristotele, potemo dire, che lo assuefarsi alle Harmonie, & alli Numeri non sia altro, che vno assuefarsi, & disporsi a diuerse passioni, & diuersi habiti morali, & costumi dell'animo: Percioche quelli che odono le Harmonie, & li Numeri, si sentono trammutare secondo la dispositione dell'animo, alcuna volta nell'amore; alcuna volta nell'ira; & alcuna volta nell'audacia; Il che da altro non auiene (come hò detto) che dalla simiglianza, che si troua tra le sopradette passioni con le harmonie. Et questo si vede: conciosia che vno, il quale hauerà più volte vdito vna sorte di Harmonia, o di Numeri, si dilettarà maggiormente, per hauersi già assuefatto in quella. Douemo però auertire, per maggiore intelligenza di quello, che si è detto; che il Numero quantunque si piglia (come nella Prima parte vedemmo) per la moltitudine composta di più vnità, & per l'Aria (dirò cosi) di alcuna canzone; come intese il Poeta quando disse;
Numeros memini, si verba tenerem;Et in molti altri modi; nondimeno in questo luogo non è altro, che vna certa misura di tempo breue, o lungo, nel quale si scorge la proportione, o misura di due mouimenti, o piu insieme comparati, secondo vna cambieuole ragione di tempo di essi mouimenti; & si scorge ne i piedi del Metro, & del Verso, che si compongono di più Numeri, con vn certo ordine, o spacio determinato. Ma il Metro, et il Verso è vna certa compositione, & ordine de piedi, ritrouata per dilettar l'vdito: Oueramente è vn'ordine, & compositione di più voci, finita con Numero, & modo. Potrei hora dire la differenza, che si ritroua tra il Metro, et il Verso: ma per breuità la voglio passare: imperoche coloro, che desiderassino di saperla, leggendo il cap. 2. del Terzo lib. della Musica di Agostino, potrano d'ogni suo desiderio esser satisfatti. page 75Solamente si hauerà da auertire, che il Rithmo è differente dal Metro, & dal Verso in questo; che il Metro, & il Verso contengono in se vn certo spacio determinato; & il Rithmo è più vniuersale, & hà li suoi spacij liberi, & non determinati. Onde è come il Genere, & il Metro, & il Verso sono meno vniuersali, & sono come la Specie: percioche da quello si hà la quantità, o la materia; & da questi la qualità, o la forma. Alcuni altri dicono, che'l Metro & il Verso è ragione con modulatione; & il Rithmo modulatione senza ragione. Ma questo sia detto a bastanza intorno a tal cosa.
In qual genere di Melodia siano stati operati li narrati effetti.Cap. 9.
Delli Suoni & delle Voci, & in qual modo naschino.Cap. 10.
Da che nascono i suoni graui, & da che gli acuti.Cap. 11.
Quel che sia Consonanza, Dissonanza, Harmonia, & Melodia.Cap. 12.
Diuisione delle Voci.Cap. 13.
Quel che sia Canto, & Modulatione; & in quanti modi si può cantare.Cap. 14.
Vt reduces illi ludunt stridentibus alis,Et questo vltimo modo non fa al nostro proposito, ma li due primi: percioche in essi si comprende ogni Harmonia, & ogni Melodia. Ma la Modulatione è vn mouimento fatto da vn suono all'altro per diuersi interualli, il quale si ritroua in ogni sorte di Harmonia, & di Melodia; & la vsiamo in due modi: prima quando si mouemo da vn suono all'altro senza variatione di tempo, con diuersi interualli, no facendo alcuna Propia harmonia, procedendo equalmente da vno interuallo all'altro per il medesimo tempo; come si fa ne i Canti fermi; Et questa è detta Modulatione impropiamente: perche contiene solamente vn proceder semplice, senza alcuna consonanza; dal quale effetto si vede, che tal modulatione hà ragion de imperfettione: essendo che manca a se stessa del debito fine. Ma l'altro modo è detta propiamente, quando per il suo mezo peruenimo all'vso dell'Harmonia, & della Melodia, come al suo propio fine; si come facemo nel Canto figurato; nel quale cantiamo non solo con semplici suoni, & semplici eleuationi, & abbassamenti de voci, ma si muouemo anco da uno interuallo all'altro con veloci, & tardi mouimenti, secondo il tempo mostrato nelle sue figure cantabili. Onde toccando allora varie consonanze, dal nostro cantare è formata ogni sorte di harmonia, & di melodia, la quale non può nascere se non con l'aiuto delle consonanze; ancorache possiamo hauer la modulatione senza l'harmonia propia, et senza alcuna consonanza, et senza la melodia. Potemo nondimeno hauer la modulatione in tre modi; prima quando noi cantiamo nominatamente ciascuna chorda, o suono col nome di vna di queste sei sillabe, Vt, Re, Mi, Fa, Sol, La, secondo il modo ritrouato da Guidone Aretino, come vederemo al suo luogo; il qual modo li Prattici chiamano Solfizare, & non si può far se non con la voce. Dipoi quando noi proferimo solamente il suono, o la voce, & gli interualli descritti, come fanno gli istrumenti artificiali. Ma l'vltimo modo è, quando noi applichiamo le parole alle figure cantabili, il quale è propio del Cantore: percioche da questa maniera di cantare nasce la Melodia come hauemo veduto.
Et coetu cinxêre polum, Cantusque dedêre:
Quel che sia Interuallo, & delle sue specie.Cap. 15.
Quel che sia Genere; & di tre Generi di Melodia, o Cantilena appresso gli antichi; & delle sue specie.Cap. 16.

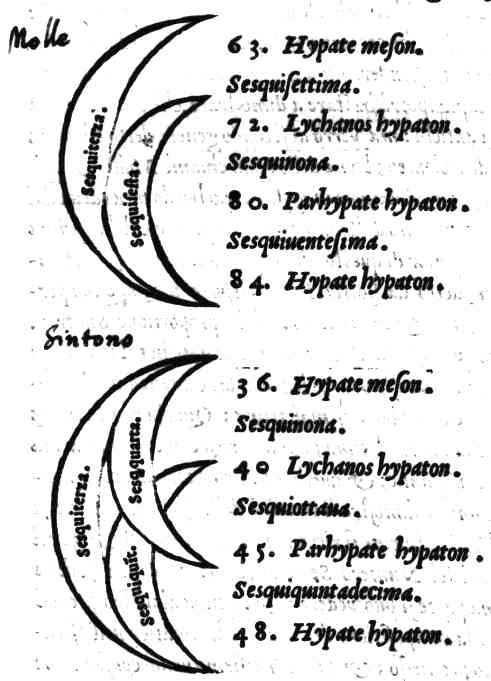





Per qual cagione ciascun de gli Interualli contenuto ne i mostrati Tetrachordi sia detto Incomposto.Cap. 17.
In qual Modo si possa accommodare alla sua proportione qual si voglia consonanza, ouero Interuallo.Cap. 18.
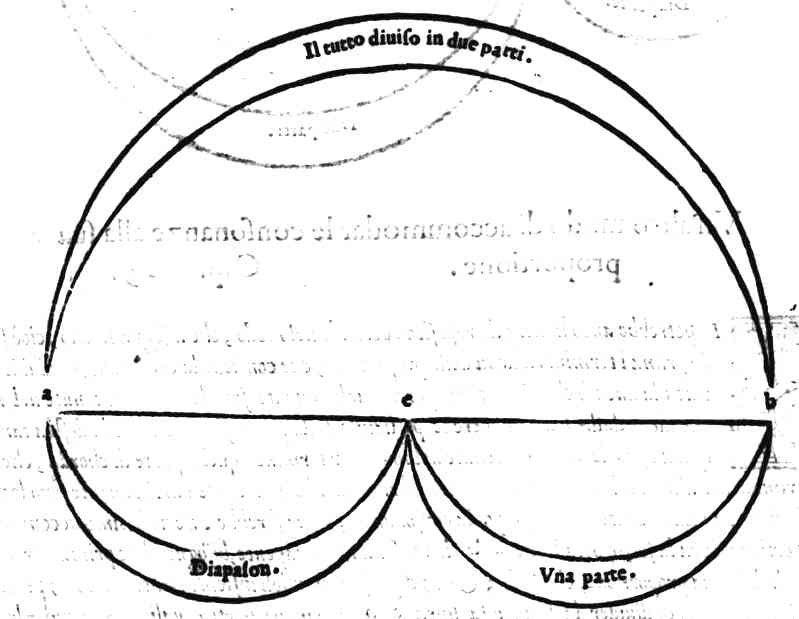
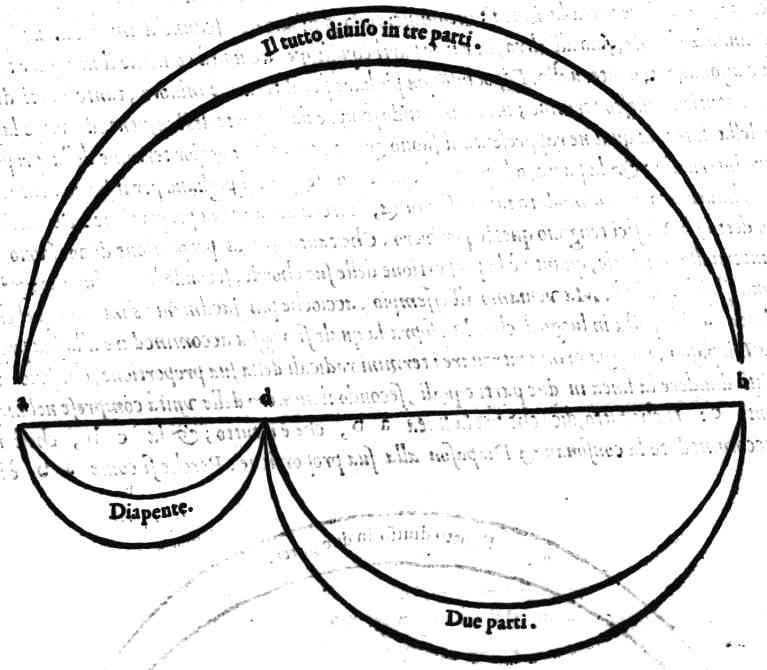
Vn'altro modo di accommodar le consonanze alla loro proportione.Cap. 19.
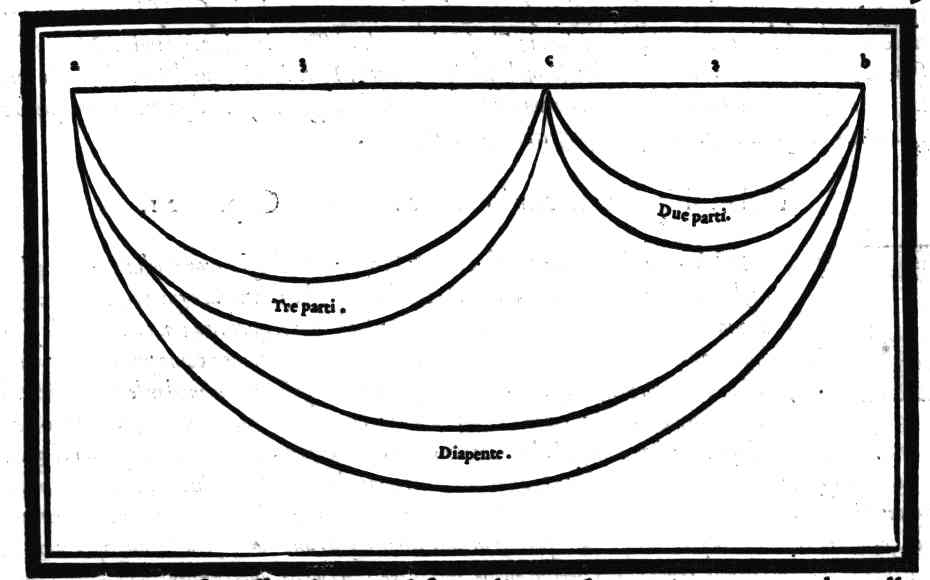
In qual modo si possa vdire qual si voglia consonanza accommodata alla sua proportione.Cap. 20.
 modo fabicati, ouero in altra maniera, purche siano secondo le qualità, che hò descritto. Ordinate poi le cose in tal guisa;
se noi pigliaremo uno di questi scannelli, et lo porremo sotto qual
si voglia delle tirate chorde, di maniera che tal chorda si posi sopra il scannello in punto c, posto nello essempio del cap. 18; se'l si percuoterà la chorda c b posta dalla parte destra con qualche altra chorda senza
scannello (percioche in tal parte sempre porrò li suoni acuti, si per rispetto delli termini delle sue proportioni,
come etiandio perche ne gli istrumenti si ritrouano da questa parte) tra il suono di questa, che sarà a b; et
il suono della c b, si vdirà la Diapason consonanza. Ma se noi segnaremo con vno de i scannelli mobili una
terza chorda in punto d, come si vede nel secondo essempio nel luogo nominato, percuotendo questa insieme
con vna delle non segnate, cioè d b con a b; da i suoni nati da queste due chorde si farà la consonanza
Diapente. Similmente se noi percuoteremo insieme le chorde a b & c b, con la d b, vdiremo la
Diapason tramezata dalla d b, & diuisa in proportionalità harmonica in vna Diapente a b &
d b; & in vna Diatessaron d b & c b; le quali (come altre volte hò detto) insieme aggiunte fanno la consonanza Diapason.Oltra
di questo, se vorremo vdire la già accommodata Diapente nel capitolo precedente, bastarà solamente porre vno delli scannelli mobili in punto c: percioche percuotendo dalla parte destra, & dalla sinistra le chorde a c & c b: si potrà udire senza dubbio tal consonanza:
Conciosia che in questa diuisione è sofficiente vna sola chorda: è ben vero, che questo modo è più difficile, che
il primo; Et nel primo mostrato modo fanno dibisogno più di vna chorda, come hauemo veduto, & è mopage 90do più facile; & si può vdire non solo ogni consonanza semplice, contenuta da due suoni solamente; ma qualunque etiandio,
che sia tramezata da più suoni; Che sarebbe molto difficile da vdire, quando il Musico si volesse seruire di vna chorda sola, seguendo il secondo modo mostrato. Essendo adunque il Secondo modo meno
vtile, & più faticoso del primo, lo lassarò da vn canto, & seguirò in ogni diuisione il primo, come quello che
hà da condurre ogni mia fatica a quella perfettione, ch'io desidero.
modo fabicati, ouero in altra maniera, purche siano secondo le qualità, che hò descritto. Ordinate poi le cose in tal guisa;
se noi pigliaremo uno di questi scannelli, et lo porremo sotto qual
si voglia delle tirate chorde, di maniera che tal chorda si posi sopra il scannello in punto c, posto nello essempio del cap. 18; se'l si percuoterà la chorda c b posta dalla parte destra con qualche altra chorda senza
scannello (percioche in tal parte sempre porrò li suoni acuti, si per rispetto delli termini delle sue proportioni,
come etiandio perche ne gli istrumenti si ritrouano da questa parte) tra il suono di questa, che sarà a b; et
il suono della c b, si vdirà la Diapason consonanza. Ma se noi segnaremo con vno de i scannelli mobili una
terza chorda in punto d, come si vede nel secondo essempio nel luogo nominato, percuotendo questa insieme
con vna delle non segnate, cioè d b con a b; da i suoni nati da queste due chorde si farà la consonanza
Diapente. Similmente se noi percuoteremo insieme le chorde a b & c b, con la d b, vdiremo la
Diapason tramezata dalla d b, & diuisa in proportionalità harmonica in vna Diapente a b &
d b; & in vna Diatessaron d b & c b; le quali (come altre volte hò detto) insieme aggiunte fanno la consonanza Diapason.Oltra
di questo, se vorremo vdire la già accommodata Diapente nel capitolo precedente, bastarà solamente porre vno delli scannelli mobili in punto c: percioche percuotendo dalla parte destra, & dalla sinistra le chorde a c & c b: si potrà udire senza dubbio tal consonanza:
Conciosia che in questa diuisione è sofficiente vna sola chorda: è ben vero, che questo modo è più difficile, che
il primo; Et nel primo mostrato modo fanno dibisogno più di vna chorda, come hauemo veduto, & è mopage 90do più facile; & si può vdire non solo ogni consonanza semplice, contenuta da due suoni solamente; ma qualunque etiandio,
che sia tramezata da più suoni; Che sarebbe molto difficile da vdire, quando il Musico si volesse seruire di vna chorda sola, seguendo il secondo modo mostrato. Essendo adunque il Secondo modo meno
vtile, & più faticoso del primo, lo lassarò da vn canto, & seguirò in ogni diuisione il primo, come quello che
hà da condurre ogni mia fatica a quella perfettione, ch'io desidero.
Del Moltiplicar le consonanze.Cap. 21.
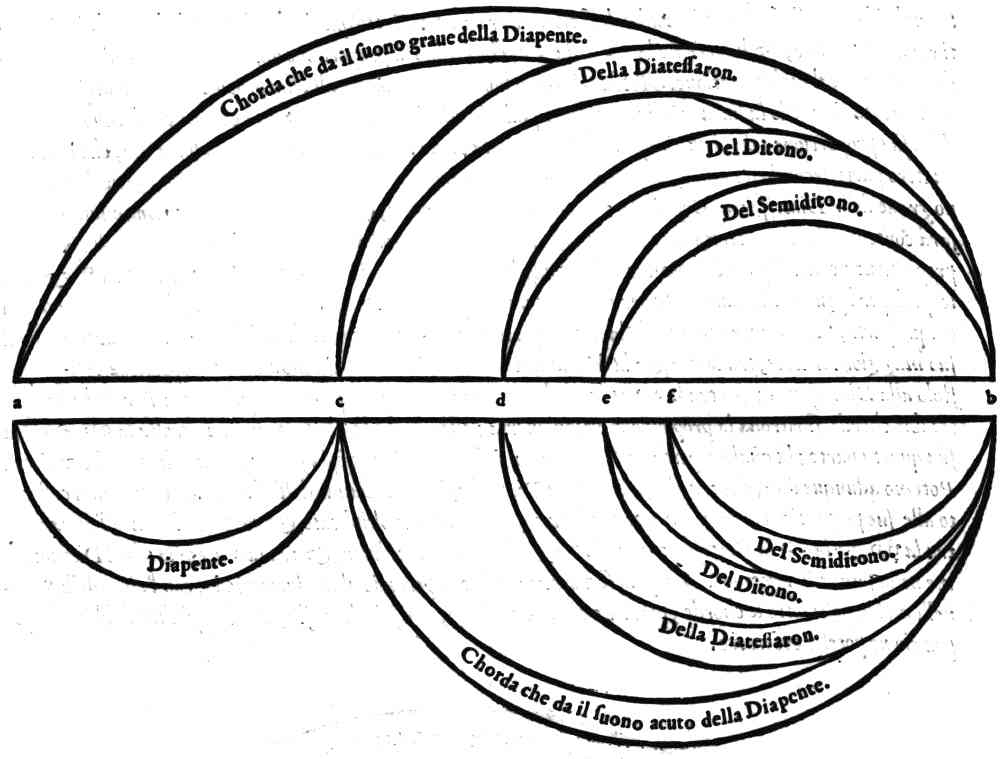
Del secondo modo di moltiplicar le consonanze.Cap. 22.
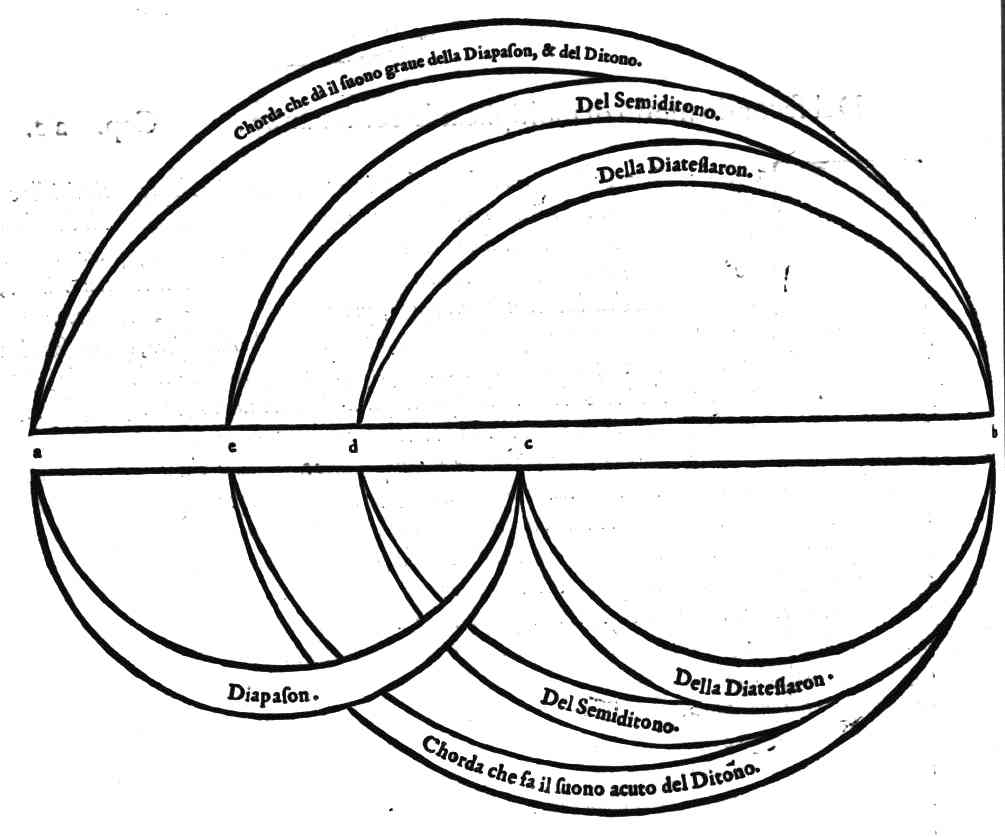
In qual modo si diuida rationalmente qualunque si voglia consonanza, ouero interuallo.Cap. 23.
In qual modo si possa diuidere qual si voglia interuallo Musicale in due parti equali.Cap. 24.
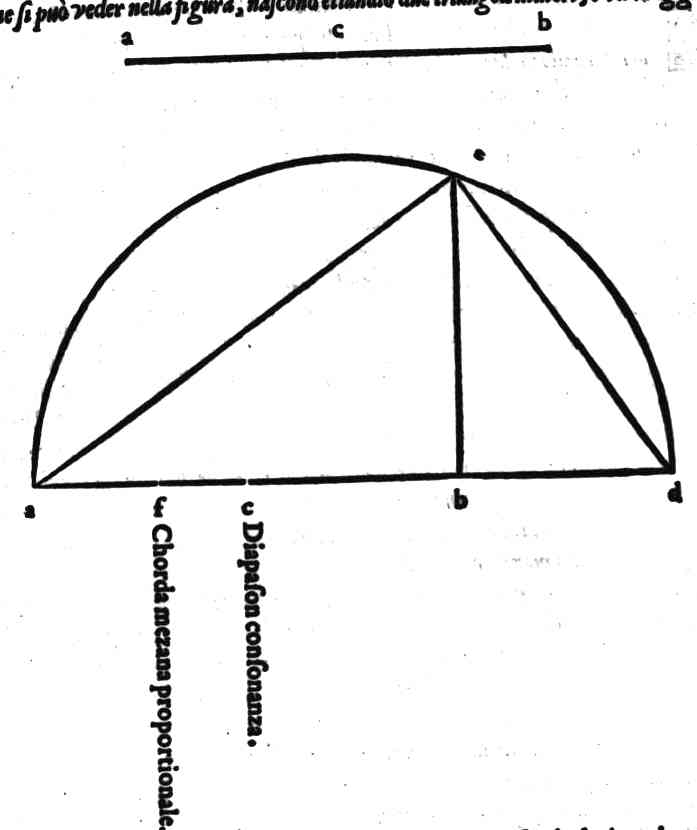
Vn'altro modo di diuider qual si voglia Consonanza, ouero Interuallo musicale in due, ouero in più parti equali.Cap. 25.
 equali, come qui si vede. Porremo dipoi li Quadrati nel detto canale l'vn
dopo l'altro in tal modo; che'l primo senza diametro sia nella parte sinistra, & resti immobile; dipoi gli altri, che hanno li diametri, cioè il secondo, & il terzo per ordine a banda destra, di
maniera che'l lato destro dell'uno sia posto sopra il sinistro dell'altro; & cosi haueremo fatto il detto
Istrumento: Il quale sarà d e f g: & sia h i k l il primo quadrato immobile senza diametro; il secondo n o p q, il cui diametro
sia
n q; & il terzo sia r s t u; del quale r u sia il diametro. Poniamo hora che si habbia da ritrouare vna chorda mezana proportionale, la
qual diuida in due parti equali la consonanza Diapason, cotenuta dalla proportion Dupla, tra le due sottoposte chorde, o linee a b & c b; &
siano queste equali alla a b, et alla c b poste nel capitolo precedente. Faremo primieramente il lato destro del primo quadrato, cioè l k equale alla
a b in punto m, & sarà l m; dipoi pigliaremo il secondo quadrato,
& lo spingeremo sotto'l primo tanto, che'l suo diametro n q seghi il lato k l del primo quadrato inpunto m; & cosi il primo, & il secondo
quadrato resteranno immobili. Faremo poi il lato destro del terzo quadrato, cioè u t equale alla c b in punto x; & posto vn fillo sottilissimo
in punto m, che sarà la m x del sottoposto essempio, lo distenderemo tanto, che passi per il punto x. Spingeremo hora il terzo
quadrato tanto sotto'l secondo, che'l lato p q venghi ad esser segato dal diametro
r u, & dal detto fillo in vn punto, che sarà y; & quella parte del lato destro del secondo quadrato, la
qual resterà sotto'l fillo, che è la q y sarà la ricercata linea, o chorda proportionale; come nella figura si
vede. Et questo è manifesto per la demostratione precedente: imperoche la linea mezana proportionale
q y ritroua ta nel Mesolabio tra la a b & la c b è equale alla b e ritrouata nel capitolo precedente. Questo si potrebbe prouare, se'l si descriuesse in vna superficie piana tutte le linee fatte nel Mesolabio, allungando primieramente
per la Seconda dimanda del primo di Euclide, la linea m x in punto z: percioche
allora haueressimo tre Triangoli continenti vno angolo retto, cioè l m z: q t z: et u x z: da i quali si
dimostrarebbe per gli Principij & Demostrationi di Euclide, il tutto esser vero; si come per il Secondo parer commune, & per il nono: per la 28, & per la Seconda parte della 32. del primo: per la seconda, per la
quarta, & per la sesta del Sesto; & per la vndecima del Quinto; le quali lasso: percioche nelle nostre Demostrationi harmoniche hò cotal cosa diffusamente trattato. Bastarami adunque solamente dire, che volendo ritrouar più linee mezane, o chorde proportionali; cioè volendo diuidere in più parti qual si voglia Interuallo
Musicale, bisogna vsare il mostrato modo. Bisogna però auertire, che per ogni linea, o chorda che si vorrà
aggiungere oltra la ritrouata, sarà dibisogno di aggiungere etiandio vn altro Paralellogrammo, o Quadrato col suo diametro, fatto di maniera, & di grandezza, come sono li primi; facendo poi, che i lati destri di
ogni Quadrato venghino ad esser segnati in vn punto istesso da i diametri, & dal fillo al mostrato modo. page 96
equali, come qui si vede. Porremo dipoi li Quadrati nel detto canale l'vn
dopo l'altro in tal modo; che'l primo senza diametro sia nella parte sinistra, & resti immobile; dipoi gli altri, che hanno li diametri, cioè il secondo, & il terzo per ordine a banda destra, di
maniera che'l lato destro dell'uno sia posto sopra il sinistro dell'altro; & cosi haueremo fatto il detto
Istrumento: Il quale sarà d e f g: & sia h i k l il primo quadrato immobile senza diametro; il secondo n o p q, il cui diametro
sia
n q; & il terzo sia r s t u; del quale r u sia il diametro. Poniamo hora che si habbia da ritrouare vna chorda mezana proportionale, la
qual diuida in due parti equali la consonanza Diapason, cotenuta dalla proportion Dupla, tra le due sottoposte chorde, o linee a b & c b; &
siano queste equali alla a b, et alla c b poste nel capitolo precedente. Faremo primieramente il lato destro del primo quadrato, cioè l k equale alla
a b in punto m, & sarà l m; dipoi pigliaremo il secondo quadrato,
& lo spingeremo sotto'l primo tanto, che'l suo diametro n q seghi il lato k l del primo quadrato inpunto m; & cosi il primo, & il secondo
quadrato resteranno immobili. Faremo poi il lato destro del terzo quadrato, cioè u t equale alla c b in punto x; & posto vn fillo sottilissimo
in punto m, che sarà la m x del sottoposto essempio, lo distenderemo tanto, che passi per il punto x. Spingeremo hora il terzo
quadrato tanto sotto'l secondo, che'l lato p q venghi ad esser segato dal diametro
r u, & dal detto fillo in vn punto, che sarà y; & quella parte del lato destro del secondo quadrato, la
qual resterà sotto'l fillo, che è la q y sarà la ricercata linea, o chorda proportionale; come nella figura si
vede. Et questo è manifesto per la demostratione precedente: imperoche la linea mezana proportionale
q y ritroua ta nel Mesolabio tra la a b & la c b è equale alla b e ritrouata nel capitolo precedente. Questo si potrebbe prouare, se'l si descriuesse in vna superficie piana tutte le linee fatte nel Mesolabio, allungando primieramente
per la Seconda dimanda del primo di Euclide, la linea m x in punto z: percioche
allora haueressimo tre Triangoli continenti vno angolo retto, cioè l m z: q t z: et u x z: da i quali si
dimostrarebbe per gli Principij & Demostrationi di Euclide, il tutto esser vero; si come per il Secondo parer commune, & per il nono: per la 28, & per la Seconda parte della 32. del primo: per la seconda, per la
quarta, & per la sesta del Sesto; & per la vndecima del Quinto; le quali lasso: percioche nelle nostre Demostrationi harmoniche hò cotal cosa diffusamente trattato. Bastarami adunque solamente dire, che volendo ritrouar più linee mezane, o chorde proportionali; cioè volendo diuidere in più parti qual si voglia Interuallo
Musicale, bisogna vsare il mostrato modo. Bisogna però auertire, che per ogni linea, o chorda che si vorrà
aggiungere oltra la ritrouata, sarà dibisogno di aggiungere etiandio vn altro Paralellogrammo, o Quadrato col suo diametro, fatto di maniera, & di grandezza, come sono li primi; facendo poi, che i lati destri di
ogni Quadrato venghino ad esser segnati in vn punto istesso da i diametri, & dal fillo al mostrato modo. page 96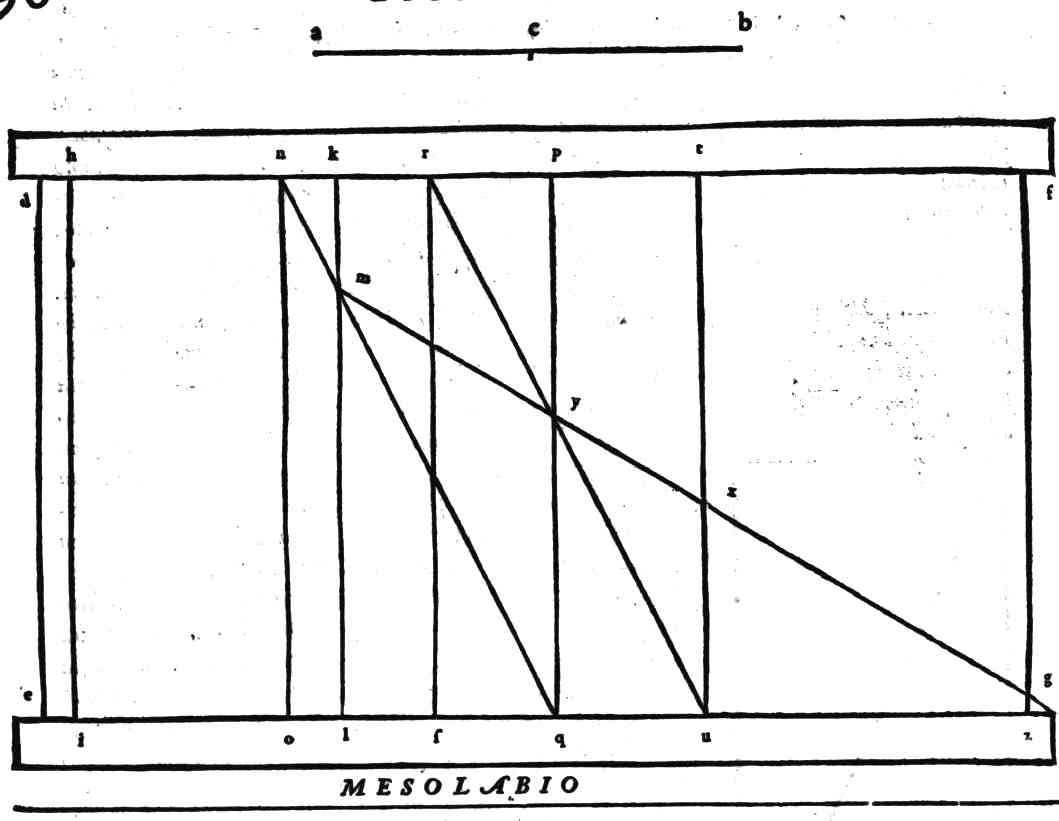
In qual modo la Consonanza si faccia diuisibile.Cap. 26.
Quel che sia Monochordo, & perche sia cosi chiamato. Cap. 27.
Della Diuisione, ouero Ordinatione del Monochordo della prima specie del genere diatonico, detta Diatonico diatono; del nome di ciascuna chorda; & chi fu l'Inuentore di questo Genere, & del suo ordine.Cap. 28.
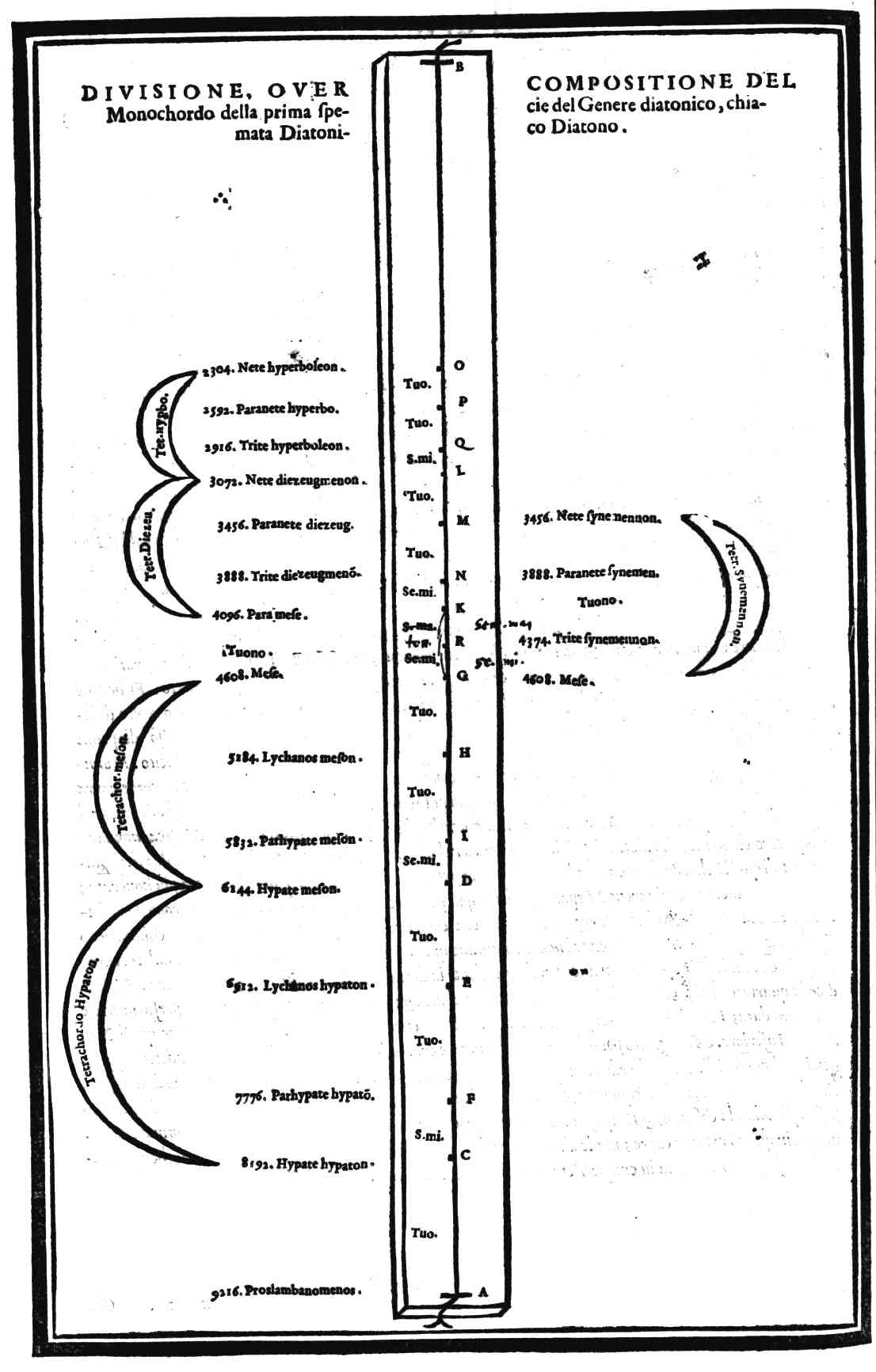
Che gli Antichi attribuirono alcune chorde de i loro istrumenti alle Sphere celesti.Cap. 29.
Insonuere poli, longeque auditus ab altoE ben vero, che quello, che dice, si puo accommodare a qual si voglia delle due narrate opinioni: Percioche se noi vorremo attribuire la tardità del mouimento annuale alla Sphera di Saturno, veramente il suo mouimento è più tardo d'ogn'altra Sphera, come mostra Platone nello Epinomide: conciosia che fa la sua reuolutione in trenta anni; & questo sarà in fauor di quelli, che tengono, che li corpi maggiori facino il suono più graue. Ma se la tardanza si attribuirà al mouimento diurno; sarà in fauor di quelli, che fauoriscono la prima opinione, & bisognerà intendere il contrario: conciosia che non gli è dubbio alcuno, come si vede col senso, che'l mouimento della Sphera della Luna non sia più tardo d'ogn'altro, quando dall'Oriente si muoue all'Occidente. Ma sia pure più tardo, o più veloce, come si voglia, che questo importa poco a noi; però lassaremo della tardità, o velocità loro la cura a gli Astronomi. Dell'altra fattione si ritrouano molti: Imperoche Dione historico raccontando la cagione, perche li Giorni siano stati denominati dal nome delle Sphere celesti, & non siano numerati secondo l'ordine loro, incomincia rendere tal ragione secondo l'opinione de gli Egittij dalla Sphera di Saturno, venendo a quella del Sole, ponendo l'vna & l'altra per gli estremi della consonanza Diatessaron, lassando le due mezane, cioè quella di Gioue, & quella di Marte; Dipoi da quella del Sole và a quella della Luna, & forma vn'altra Diatessaron; similmente da questa a quella di Marte; & da Marte a Mercurio ne fa due altre; di modo che lassando sempre le due mezane Sphere, rende la ragion di tal Problema, ritornando sempre circolarmente alla prima Sphera: Onde si vede, che incominciando dalla Sphera di Saturno, & venendo a quella del Sole; & da questa à quella della Luna, pone la prima come quella, che fa il suono graue; & venendo verso le altre Sphere, le pone come quelle, che fanno li suoni acuti: Imperoche è costume della maggior parte di coloro, che trattano della Musica, di por prima il graue nelle loro ragioni, come cosa più ragioneuole, & dipoi lo acuto. Ne debbe parer strano, se Dione ritorna dalla Sphera della Luna a quella di Marte, facendo vn'ordine rouescio, procedendo dall'acuto al graue, contrario di quello che hauea mostrato prima: percioche a lui basta solamente con tal mezo dimostrar la ragione di cotal cosa; anchora che questa ragion non sia molto sufficiente a fauorir tale opinione. Euui etiandio l'opinione de gli Antichi, che pone Plinio nella sua Historia naturale, primieramente dell'Harmonia celeste, dipoi dell'ordine; onde dice, che la Sphera di Saturno fa il tuono Dorio, quella di Gioue il Frigio, & le altre per ordine altri Tuoni. Onde non è dubbio, che essendo il Dorio tenuto dalla maggior parte de i Musici più graue del Frigio, la Sphera di Saturno non sia quella, che faccia il suopage 102no graue. Oltra di questo (lassando molti altri da parte) ui è Boetio, il quale, quasi recitando l'altrui opinione, attribuisce la chorda Hypate a Saturno, che è d'ogn'altra grauissima; dipoi più abasso attribiuisce alla medesima sphera (secondo la prima opinione medesimamente da lui recitata) il suono acuto, & li graui per ordine, attribuendo il grauissimo al globo lunare. Da queste differenze nacque, che i Filosofi, per voler mostrare in atto quella harmonia, che per ragioni conosceuano esser nelle sphere celesti, attribuirono a ciascuna (si come erano di diuersi pareri del sito de i suoni graui, & acuti) diuerse chorde de i loro istrumenti, variatamente ordinate: Imperoche quelli, che fauoriuano la prima opinione, attribuirono alla sphera della Luna, Pianeta a noi più vicino, la chorda Proslambanomenos, perche fa il suono più graue di qualunque altra; a quella di Mercurio la Hypate hypaton; & all'altre sphere l'altre chorde per ordine, secondo che sono poste nella figura mostrata disopra. Ma quelli, che haueano contraria opinione; attribuirono la chord Hypate meson alla sphera di Saturno; perche si pensauano, che facesse il suono più graue d'ogn'altra sphera; la Parhypate a Gioue; Lychanos a Marte; & Mese al Sole; & cosi all'altre attribuirono altre chorde, secondo il mostrato ordine. Et si come furono di vario parere intorno a quello, che hò detto; cosi anco furono differenti nel porre le chorde a i loro istrumenti: Imperoche quelli, che hebbero opinione, che Saturno facesse il suono acuto, et la Luna il graue
Concentus, mixtumque melos, pars ocyus acta
Clarius, & cantu longè resonabat acuto,
Tarda ibat grauiore sonò.
![Diapa-son
Diapte. Diapt.
Diatessar.
Diatessa.
Mese. Vrania. [Heaven]
tuo. Lychanos meson. . [Saturn]
tuo. Parhypate mes. . [Jupiter]
sem. Hypate meson. . [Mars]
tuo. Lychanos hypa. . [Sun]
tuo. Parhypate hypa. . [Venus]
sem. Hypate hypat. . [Mercury]
tuo. Proslbanomenos . [Moon]
Diapa-son
Diapte. Diapte.
Diatessa.
Diatess.
Netesynemnon. .
tuo. Paranetesynem.
tuo. Tritesynemn.
sem. Mese.
tuo. Lychanos mes.
tuo. Parhypat. meson.
sem. Hypate meson.
tuo. Lychanos hypa.](../../zarins58/ill/229-1.jpg)
In che modo le predette Sedici chorde siano state da i Latini denominate.Cap. 30.
Vt queant laxis Resonare fibris Mira gestorum Famuli tuorum, Solue polliuti Labij reatum Sancte Iohannes;& li concatennò con tale artificio, & in tal maniera; che ciascuno contiene tutte le specie della Diatessaron, le quali sono tre, come vederemo nella Terza parte; accommodando il Semituono, circoscritto da queste due sillabe mezane Mi, & Fa nel mezo di ciascuno. Ma aggiunse primieramente alla chorda Proslambanomenos nella parte graue vna chorda, distante per vn Tuono, & la segnò con vna lettera greca maiuscola in questo modo Γ, & le altre poi con lettere latine; per dinotarci, che la Musica (come vogliono alcuni) fu ritrouata primamente da i Greci, & posta in vso, & che al presente da i Latini è honoreuolmente posseduta, abbracciata, & accresciuta. Et alla predetta lettera aggiunse la prima delle sei sillabe; cioè Vt in questo modo Γ, ut, che vuol dire Gamma, ut; et cosi nominò la chorda aggiunta di tal nome, & è la prima chorda della sua ordinatione. Chiamò poi Proslambanomenos de i Greci A re, ponendo insieme la prima lettera latina, & la seconda sillaba delle mostrate; & fu la seconda chorda del suo Introduttorio. La terza poi, cioè la seconda greca, detta Hypate hypaton, nominò
 , mi; ponendo insieme la seconda lettera latina, & la terza sillaba seguente; & pose tal lettera quadrata, differente dalla
, mi; ponendo insieme la seconda lettera latina, & la terza sillaba seguente; & pose tal lettera quadrata, differente dalla  rotonda, per dinotarci la differenzaa de i Semituoni, che fanno queste due chorde: conciosiache non sono in vno istesso luogo, quantunque siano congiunte quasi in vna istessa lettera; come altroue vderemo. Nominò dipoi la quarta C, fa ut, & il resto per ordine fino a Nete hyperboleon, applicandoli vna delle prime lettere latine, cioè A,
rotonda, per dinotarci la differenzaa de i Semituoni, che fanno queste due chorde: conciosiache non sono in vno istesso luogo, quantunque siano congiunte quasi in vna istessa lettera; come altroue vderemo. Nominò dipoi la quarta C, fa ut, & il resto per ordine fino a Nete hyperboleon, applicandoli vna delle prime lettere latine, cioè A,  , ouer
, ouer  , C, D, E, F, G, descriuendole nel primo ordine maiuscole, nel secondo
picciole, & nel terzo raddo piate; come nell'Introduttorio si vedeno.Ma sopra Nete hyperboleon aggiunse altre cinque chorde nel terzo ordine, cioè
, C, D, E, F, G, descriuendole nel primo ordine maiuscole, nel secondo
picciole, & nel terzo raddo piate; come nell'Introduttorio si vedeno.Ma sopra Nete hyperboleon aggiunse altre cinque chorde nel terzo ordine, cioè 
 fa,
fa, 
 mi; cc, sol fa; dd, la sol, et ee, la; et
fece questo per finire gli vltimi due Essachordi, de i quali l'vno hà principio in f, & l'altro in g; & per
tal modo le chorde Grece acquistarono altra denominatione. Fu tenuto tale ordine da Guidone (com'io credo) forse non senza
consideratione, applicando cotali sillabe alle chorde sonore, moltiplicate per il numero Settenario: perche comprese, che nel
Senario si conteneua la diuersità de i Tetrachordi, & che nel Settenario erano Sette suoni, o voci, l'vna dall'altra per natural diuisione al tutto variate & differenti; come si può page 104
mi; cc, sol fa; dd, la sol, et ee, la; et
fece questo per finire gli vltimi due Essachordi, de i quali l'vno hà principio in f, & l'altro in g; & per
tal modo le chorde Grece acquistarono altra denominatione. Fu tenuto tale ordine da Guidone (com'io credo) forse non senza
consideratione, applicando cotali sillabe alle chorde sonore, moltiplicate per il numero Settenario: perche comprese, che nel
Senario si conteneua la diuersità de i Tetrachordi, & che nel Settenario erano Sette suoni, o voci, l'vna dall'altra per natural diuisione al tutto variate & differenti; come si può page 104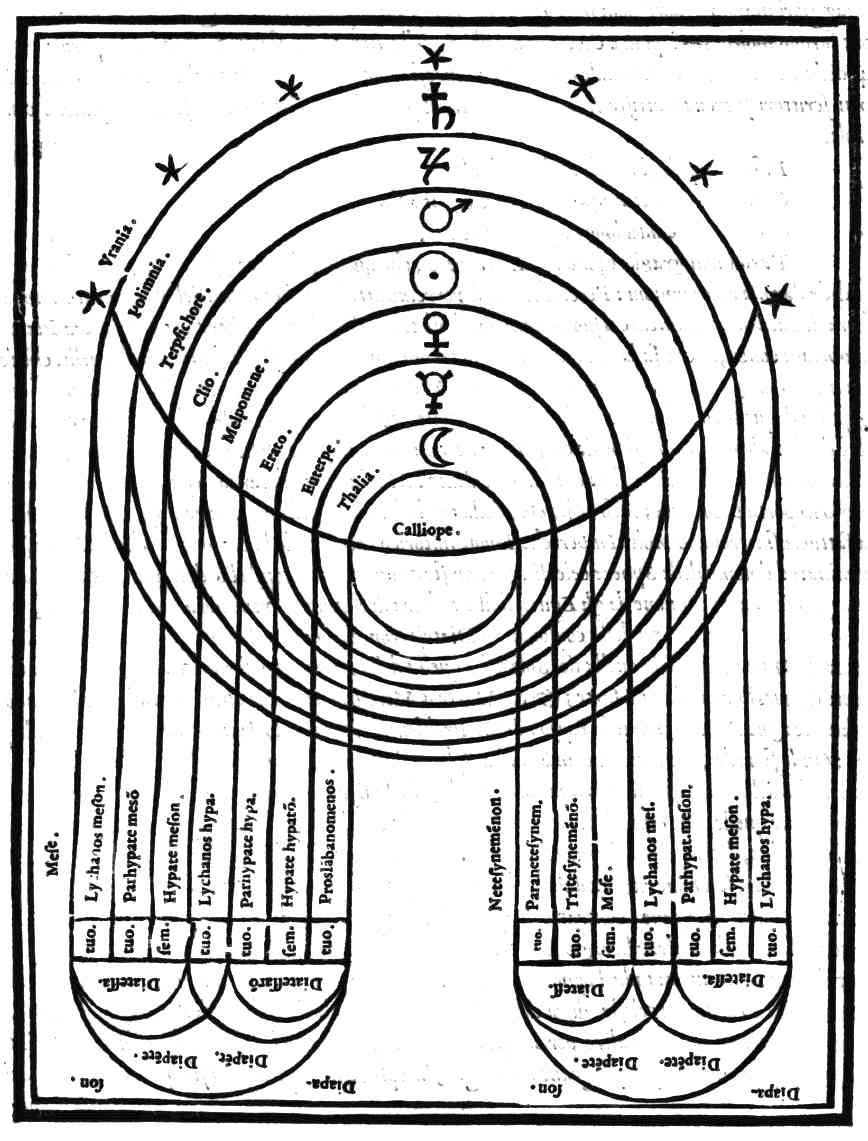
Ε'πτὰ δὲ συμφώνους ὀίων ἐτανύσσατο χορδάς.cioè
Ma Sette chorde fatte di budellaCosi Horatio parlando allo istesso Mercurio, commemorò tali chorde con queste parole.
Di pecore distese, che tra loro
Erano consonanti.
Tuque testudo resonare septemEt se bene Teocrito pone, che la Sampogna di Menalca pastore facesse Nuoue suoni differenti, quando disse; Σύριγγ' ἅν ἐπόησαν καλὰν ἐγὼ ἐννεάφωνον, che vuol dire,
Callida neruis.
Questa bella Sampogna, la qual feciCredo io, che questo habbia fatto: perche (come è manifesto, & lo afferma Giouanni Grammatico) Teocrito scrisse nella lingua Dorica le sue poesie, le quali cantandosi alla Cetera, ouer Lira, si cantauano nel Modo Dorio, che procedeua (secondo che vederemo nella Quarta parte) dal graue all'acuto, o per il contrario, per un tal numero di chorde. Ma Virgilio suo imitatore accordandosi page 105con Homero, nella Bucolica espresse il numero di Sette chorde solamente dicendo;
Di Nuoue suoni;
Est mihi disparibus septem compacta cicutisEt nel libro Sesto della Eneida toccò tal numero dicendo;
Fistula.
Nec non threicius Vates, & longa cum veste sacerdos,Similmente Ouidio nel secondo libro delle Trasformationi disse;
Obloquitur numeris septem discrimina vocum.
Dispar septenis fistula cannis.Et però con giudicio (come hò detto) esse lettere da Guidone furono replicate, & non variate: perche conobbe, che l'Ottaua chorda era simile di voce alla prima, la Nona alla seconda, la Decima alla terza, & le altre per ordine. E vero, che non mancano quelli, che per le auttorità addute de i Poeti vogliono intendere le Sette consonanze diuerse, contenute nella Diapason, che sono l'Vnisono, il Semiditono, il Ditono, la Diapente, l'Essachordo minore, il maggiore, & essa Diapason; Et altri anco, che intendeno il simigliante, lassando fuori l'Vnisono, perche non è consonanza propiamente detta (come vederemo al suo luogo) ponendoui la Diatessaron; Le quali opinioni non sarebbeno da spezzare, quando fussero secondo la mente di tali autori, & non fussero lontane dalla verità: Imperoche seguendo i Poeti indubitatamente la opinione di Pithagora, di Platone, di Aristotele, & di altri eccellentissimi Musici & Filosofi più antichi; non si può dire, che mai hauessero alcuna opinione, di porre il Semiditono, il Ditono, & li due Essachordi nel numero delle consonanze, per le ragioni dette di sopra nel cap. 10. Ma se alcuno dicesse, che nella Diapason si ritrouano non solo Sette suoni, o voci differenti; ma di più ancora, come si può vedere ne gli istrumenti artificiali; il che arguisce contra quello, che di sopra hò detto: Si risponderebbe, che è vero, che tra la Diapason si ritrouano molti suoni differenti, oltra li Sette nominati: ma tali suoni non sono ordinati secondo la natura del genere Diatonico; ne meno sono cauati per alcuna diuisione dalla Proportionalità harmonica.
Consideratione sopra la mostrata Diuisione, ouero Ordinatione, & sopra l'altre specie del genere Diatonico poste da Tolomeo.Cap. 31.
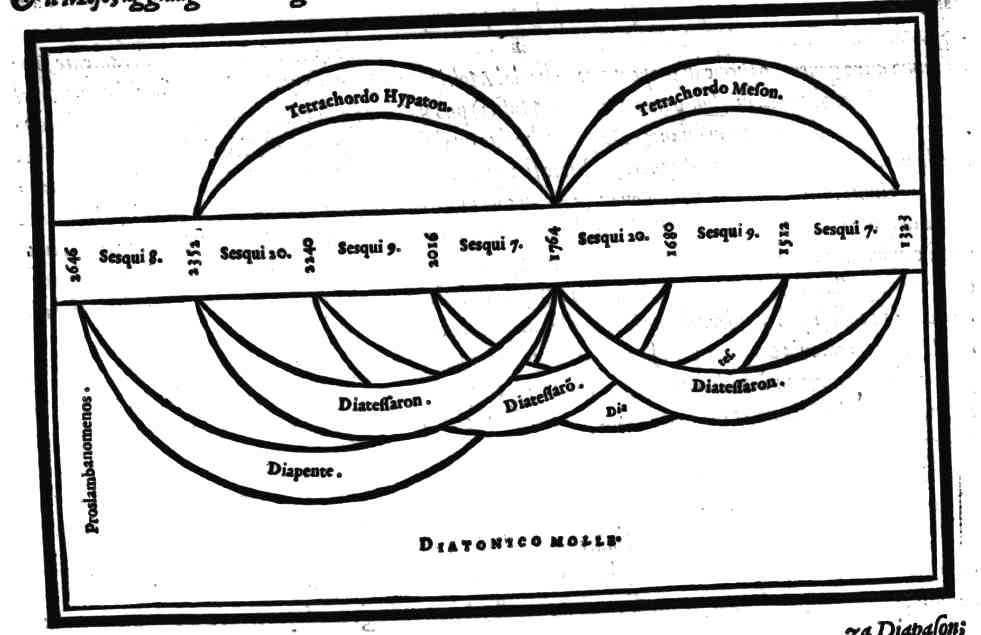
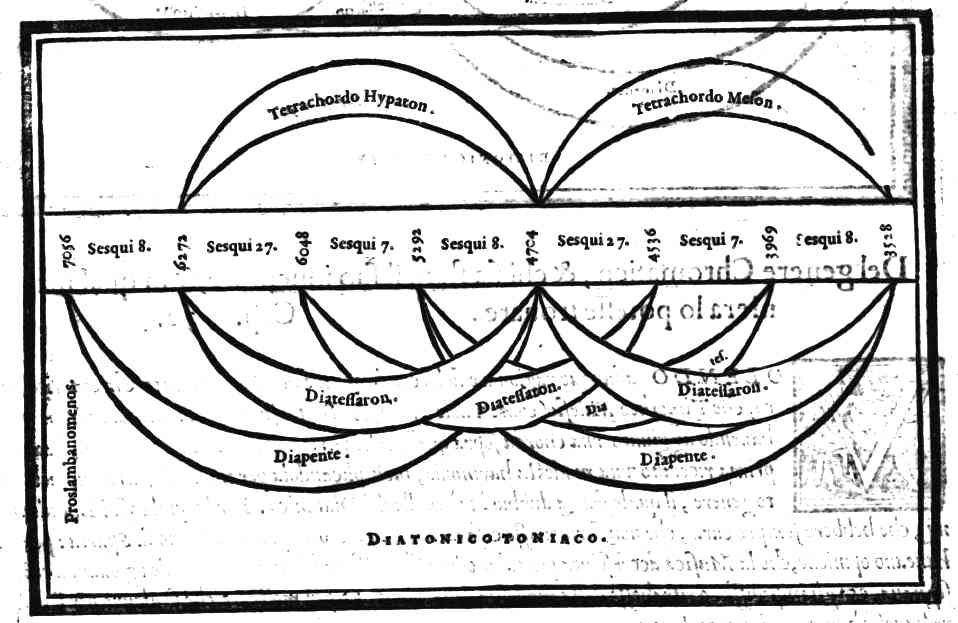
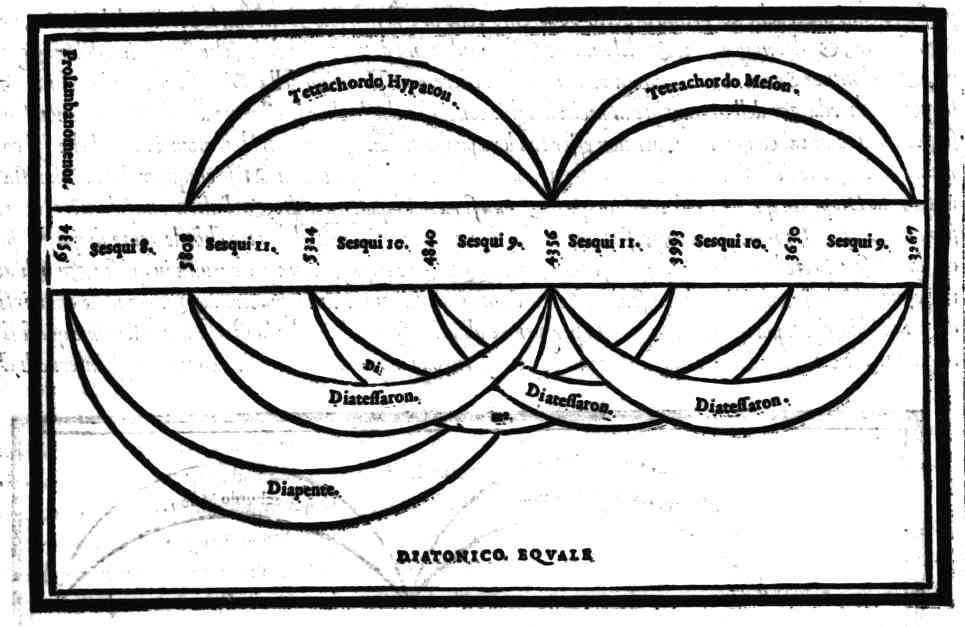
Del genere Chromatico, & chi sia stato il suo inuentore, & in qual maniera lo potesse trouare.Cap. 32.

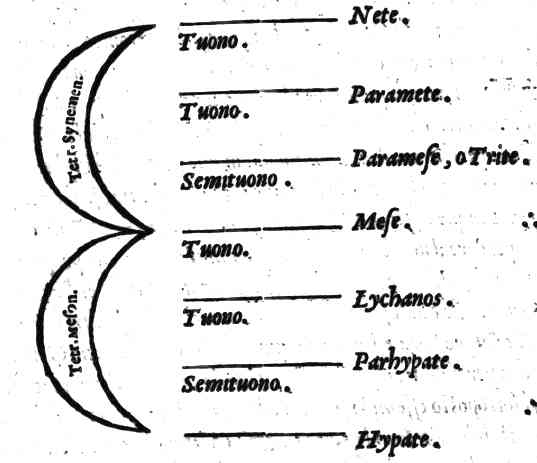

Diuisione del Monochordo Chromatico.Cap. 33.
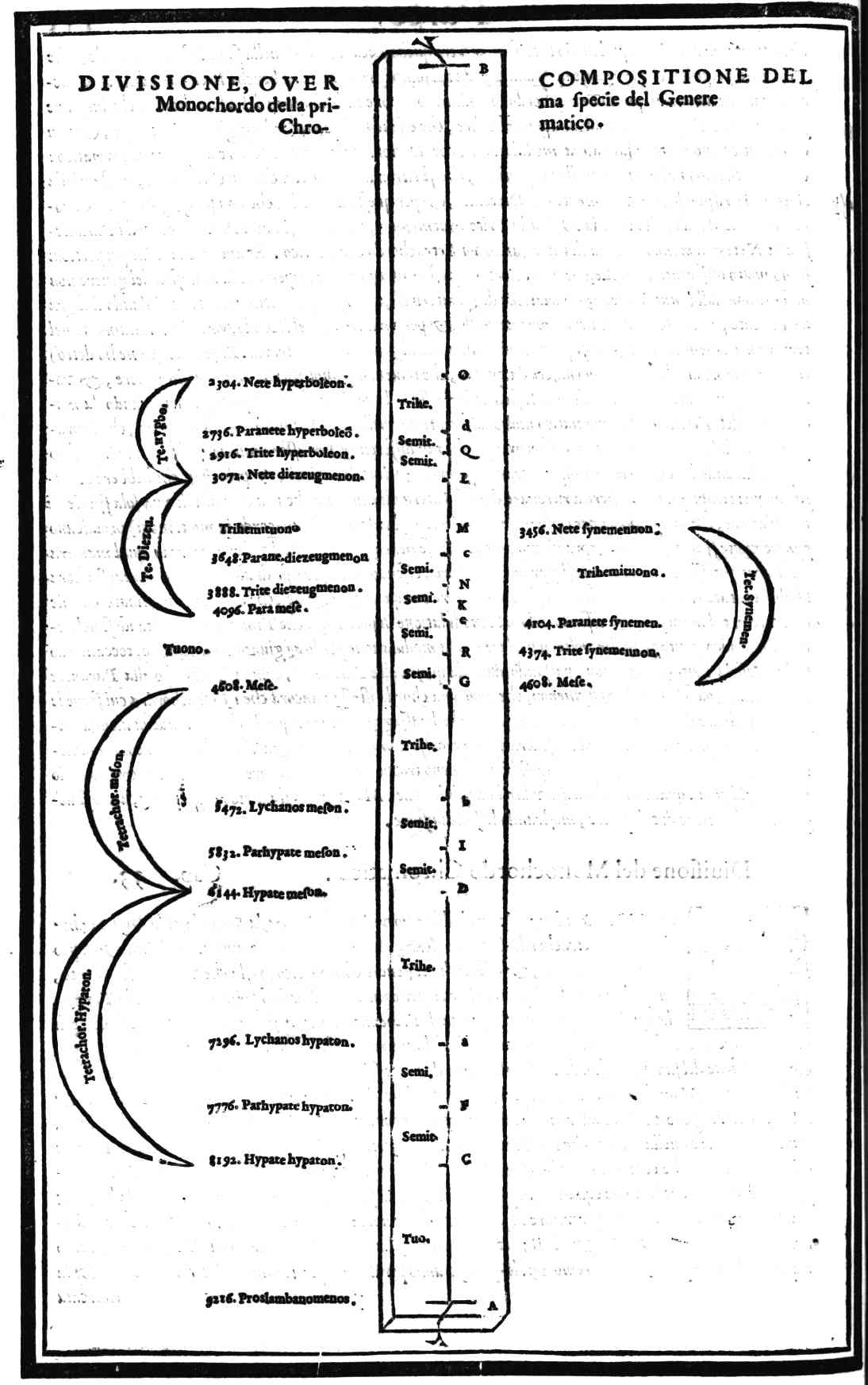
Consideratione sopra la mostrata diuisione, & sopra alcune altre specie di questo genere, ritrouate da Tolomeo.Cap. 34.
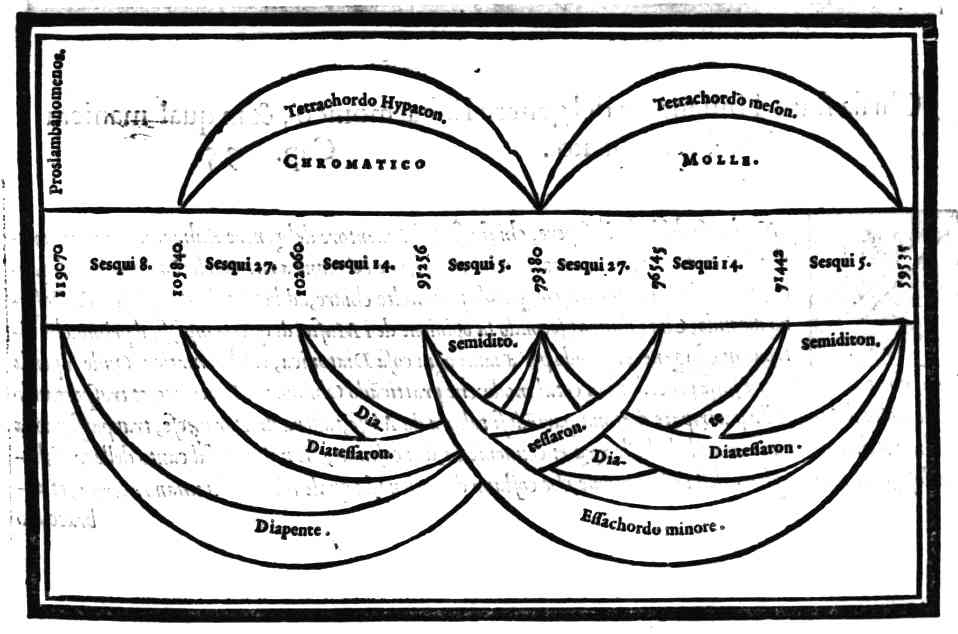
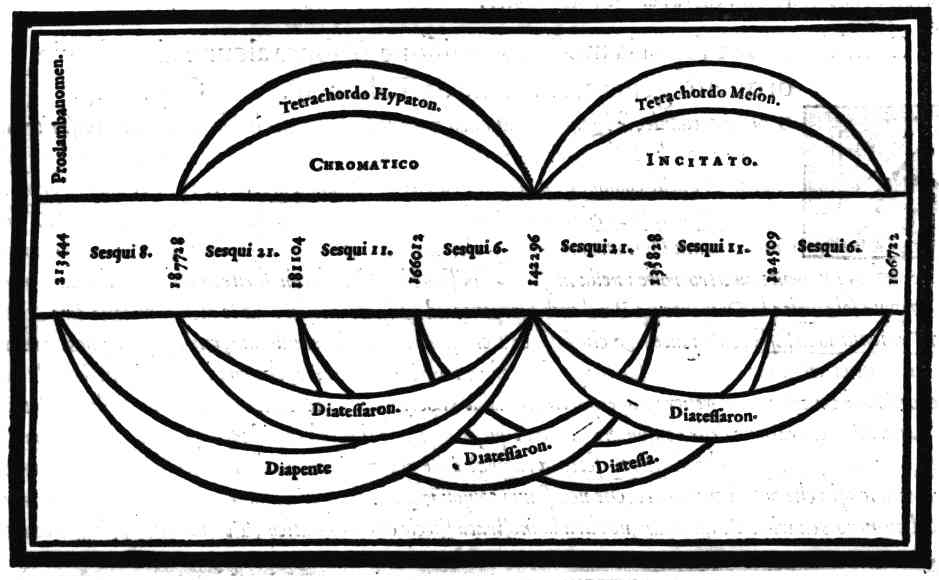
Chi sia stato l'Inuentore del genere Enharmonico, & in qual maniera l'habbia ritrouato.Cap. 35.
Della Diuisione, o Compositione del Monochordo Enharmonico.Cap. 36.
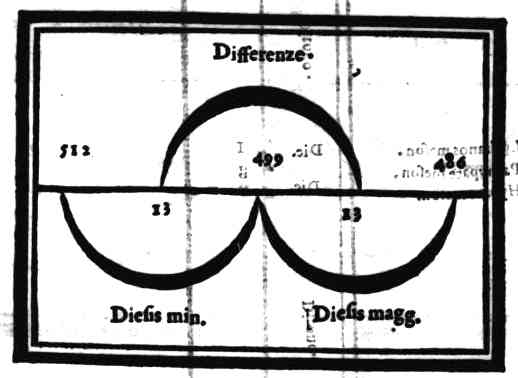
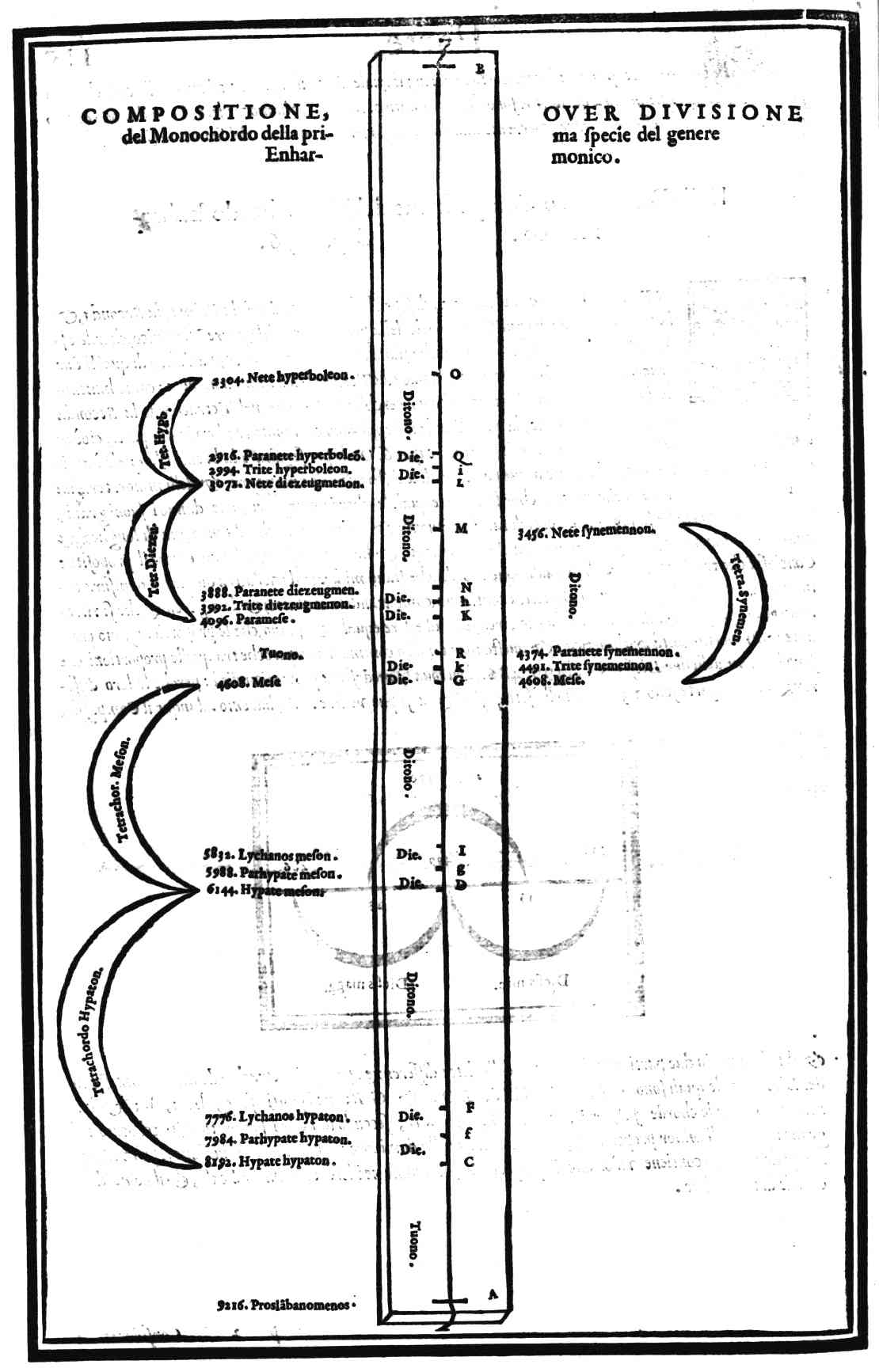
Consideratione sopra la mostrata particione, ouero compositione, & sopra quella specie di questo genere, che ritrouò Tolomeo.Cap. 37.
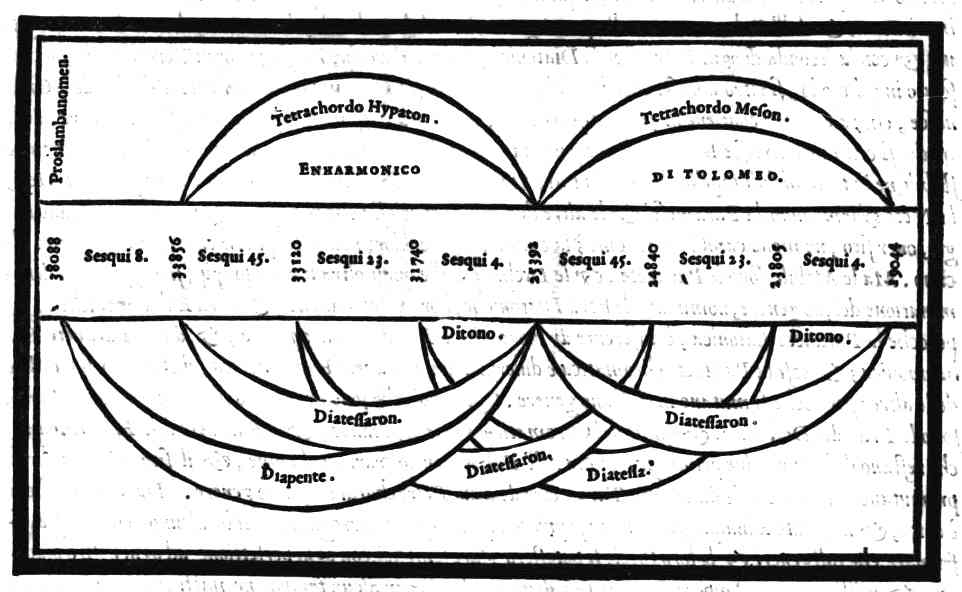
Della compositione del Monochordo Diatonico diatono, inspessato dalle chorde Chromatiche, & dalle Enharmoniche.Cap. 38.

Che'l Diatonico sintono di Tolomeo sia quello, che hà il suo essere naturalmente da i Numeri harmonici.Cap. 39.
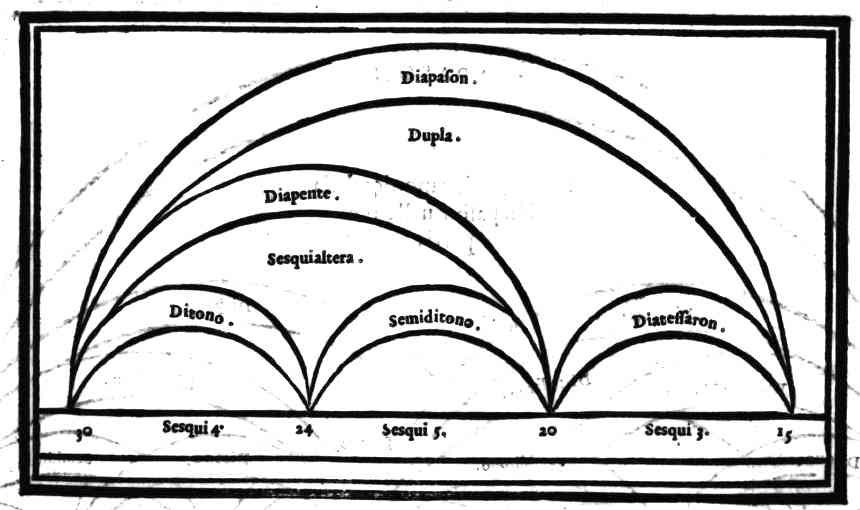
 .
& c. Et questa diuisione è fatta con ogni debito modo: conciosia che se in questa maniera diuideremo secondo la proportionalità harmonica la proportione Sesquialtera, ne verrà due proportioni, cioè la Sesquiquarta, et
la Sesquiquinta. La onde diuidendo la maggiore, nascerà la Sesquiottaua, & la Sesquinona; delle quali gli interualli sono detti Tuoni; & la maggior parte della Diapente da essi prende il nome, perche si chiama Ditono, cioè di due Tuoni; & la minor si nomina Semiditono: percioche non ariua alla quantità del Ditono. Et veramente la natura non hà operato questo in uano: essendo che la Diatessaron è superata dalla Diapente per li
Tuono maggiore, & il Semiditono è superato dalla Diatessaron per il minore. Et se bene l'interuallo della
Sesquiquintadecima proportione non nasce per uia di alcuna diuisione harmonica, fu nondimeno da Tolomeo page 122
.
& c. Et questa diuisione è fatta con ogni debito modo: conciosia che se in questa maniera diuideremo secondo la proportionalità harmonica la proportione Sesquialtera, ne verrà due proportioni, cioè la Sesquiquarta, et
la Sesquiquinta. La onde diuidendo la maggiore, nascerà la Sesquiottaua, & la Sesquinona; delle quali gli interualli sono detti Tuoni; & la maggior parte della Diapente da essi prende il nome, perche si chiama Ditono, cioè di due Tuoni; & la minor si nomina Semiditono: percioche non ariua alla quantità del Ditono. Et veramente la natura non hà operato questo in uano: essendo che la Diatessaron è superata dalla Diapente per li
Tuono maggiore, & il Semiditono è superato dalla Diatessaron per il minore. Et se bene l'interuallo della
Sesquiquintadecima proportione non nasce per uia di alcuna diuisione harmonica, fu nondimeno da Tolomeo page 122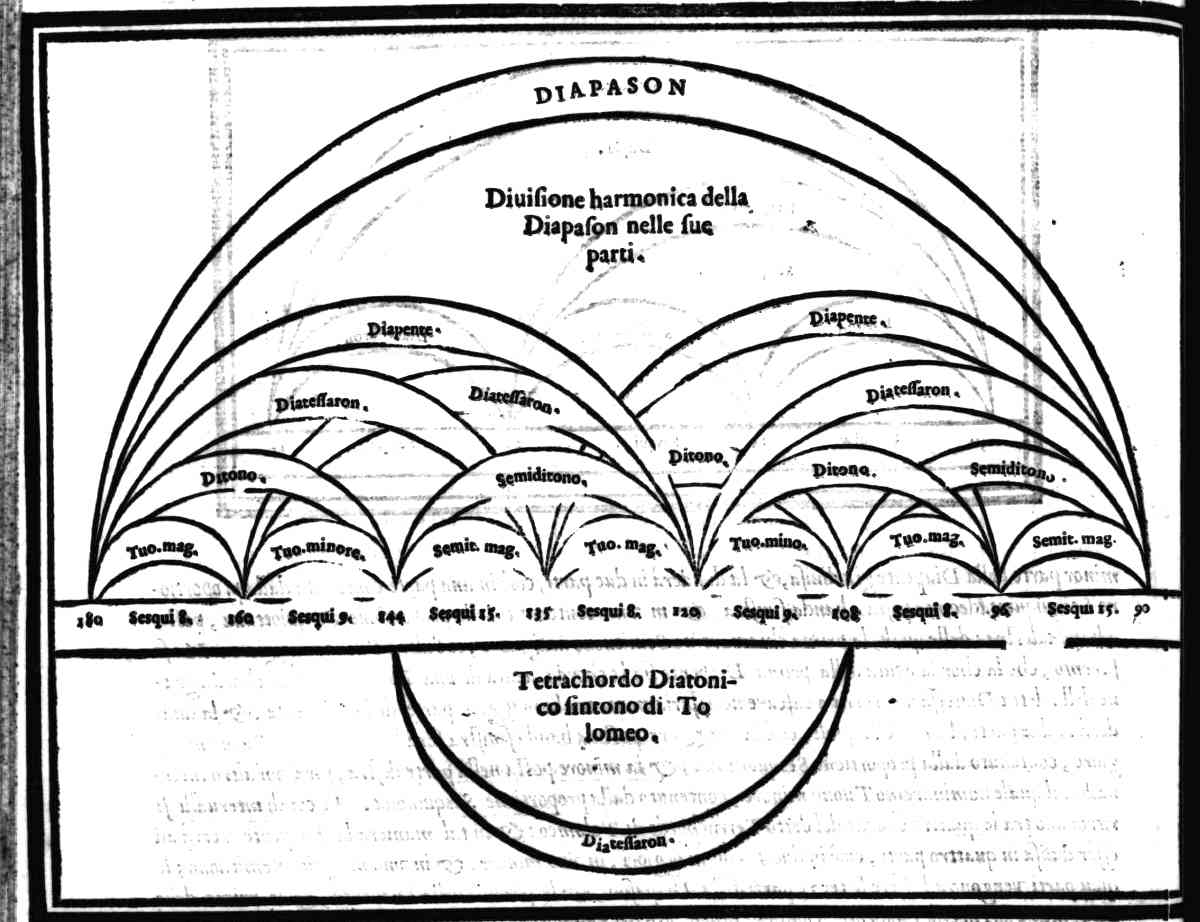
Della diuisione del Monochordo Diatonico sintono fatta secondo la natura de i numeri sonori.Cap. 40.

Che ne gli Istrumenti arteficiali moderni non si adopera alcuna delle specie Diatoniche mostrate.Cap. 41.
 &
&  , in fuori; che sia compreso nella sua vera, & natural forma, ouero proportione: Percioche
il numero delle lor chorde non può dare gli interualli, che si ritrouano nel Diatonico sintono; ne meno comprendeno quelli del Diatonico diatono mostrato: perche in esso si ritrouano il Ditono, & il Semiditono (come habbia mo veduto) che sono interualli dissonanti; & tra quelle di questi istrumenti sono consonanti; si
come ciascuno potrà vdire; quantunque siano fuori della loro vera, & natural forma. Et è cosi in fatto:
percioche tutti quelli interualli, che si ritrouano in detti istrumenti, cauandone li due nominati, sono temperati da i Musici, nello accordare detti istrumenti, in tal maniera; che ritrouandosi fuori delle loro forme, o
proportioni vere, sono ridutti in tal temperamento, con lo accrescerli, o diminuirli, secondo il proposito, di
vna certa quantità, nel modo che più oltra vederemo, che l'Vdito se ne contenta. Et tale temperamento li
Moderni chiamano Participatione, della quale fin hora non so, che da alcun'altro sia stato ragionato, o mostrato cosa alcuna. Et vogliono alcuni, che sia stato fatta, o ritrouata, per ridurre il numero delle chorde del
monochordo Diatonico sintono mostrato, al numero delle chorde Pithagorice, contenute nel Diatono; accioche tra loro fussero collocate tutte le consonanze, tanto perfette, quanto imperfette, le quali sono necessarie
alla generatione della perfetta Harmonia; & accioche il Sonatore sonando fusse più libero; & l'harmonia,
che vscisse da tali istrumenti si potesse vdire con maggior satisfattione dell'Vdito, che non si hauerebbe fatto, quando si hauesse voluto stare nel numero delle chorde del Diatonico sintono: percioche sarebbe stato dibisogno di vsare spesse volte l'interuallo del Coma, aggiungendolo, o leuandolo da alcuni interualli, per fare
acquisto di molte consonanze; massimamente volendo passare dal graue all'acuto: o per il contrario da una
consonanza all'altra: Il che non solamente difficultà al Sonatore; ma etiandio poco diletto a gli ascoltanti
hauerebbe apportato: perche in cotal caso si hauerebbe vdito vn non so che di tristo, che hauerbbe fatto non
poco fastidio. Et quantunque dichino anco, che tale Temperamento, o Participatione, sia stata ritrouata
studiosamente, accioche per essa in cotali istrumenti si venisse ad imitar la Natura, la qual si dee imitare in
tutte le cose, più che si puote: perche si come nel genere Diatonico si può procedere naturalmente con le voci
(come è manifesto) per gli suoi interualli, dal graue all'acuto, & per il contrario; senza incommodo alcuno; cosi anche in tali istrumenti si potesse passare dall'acuto al graue, o per il contrario senza alcuno impedimento, & senza alcuna offesa del Sentimento: Tuttauia credo veramente, che tal Temperamento, o Participatione sia stata introdutta a caso, & non studiosamente. Et ciò mi muoue a credere: perche non è dubbio, che ne il Ditono, ne il Semiditono, ne li due Essachordi, & altri interualli molti, i quali hora a noi sono
consonanti; non furono mai da alcuno de gli Antichi (come da i loro scritti si può comprendere) riceuuti nel
numero delle consonanze: ne anco veramente le vsarono per consonanti, nel modo che le vsiamo noi; massimamente hauendo loro sempre vsato il numero delle chorde Pithagorice; si come dalle chorde, che sono collocate in molti antichi istrumenti si può comprendere. La onde è credibile, che alcuno perito nella Musica
dopo vn certo spacio di tempo, a caso prima, & di poi fatto molte esperienze, nell'istesso istrumento le ridu<page 126
cesse a tal temperamento, sotto le proportioni, o forme, le quali hora vsiamo: non però sotto alcuna di quelle,
che di sopra in molte diuisioni hò mostrato: percioche sarebbe stato impossibile, di osseruare il Numero delle
chorde, l'Ordine de gli interualli, & le Forme, o Proportioni mostrate: ma si bene sotto quelle, ch'io sono
per mostrare.
, in fuori; che sia compreso nella sua vera, & natural forma, ouero proportione: Percioche
il numero delle lor chorde non può dare gli interualli, che si ritrouano nel Diatonico sintono; ne meno comprendeno quelli del Diatonico diatono mostrato: perche in esso si ritrouano il Ditono, & il Semiditono (come habbia mo veduto) che sono interualli dissonanti; & tra quelle di questi istrumenti sono consonanti; si
come ciascuno potrà vdire; quantunque siano fuori della loro vera, & natural forma. Et è cosi in fatto:
percioche tutti quelli interualli, che si ritrouano in detti istrumenti, cauandone li due nominati, sono temperati da i Musici, nello accordare detti istrumenti, in tal maniera; che ritrouandosi fuori delle loro forme, o
proportioni vere, sono ridutti in tal temperamento, con lo accrescerli, o diminuirli, secondo il proposito, di
vna certa quantità, nel modo che più oltra vederemo, che l'Vdito se ne contenta. Et tale temperamento li
Moderni chiamano Participatione, della quale fin hora non so, che da alcun'altro sia stato ragionato, o mostrato cosa alcuna. Et vogliono alcuni, che sia stato fatta, o ritrouata, per ridurre il numero delle chorde del
monochordo Diatonico sintono mostrato, al numero delle chorde Pithagorice, contenute nel Diatono; accioche tra loro fussero collocate tutte le consonanze, tanto perfette, quanto imperfette, le quali sono necessarie
alla generatione della perfetta Harmonia; & accioche il Sonatore sonando fusse più libero; & l'harmonia,
che vscisse da tali istrumenti si potesse vdire con maggior satisfattione dell'Vdito, che non si hauerebbe fatto, quando si hauesse voluto stare nel numero delle chorde del Diatonico sintono: percioche sarebbe stato dibisogno di vsare spesse volte l'interuallo del Coma, aggiungendolo, o leuandolo da alcuni interualli, per fare
acquisto di molte consonanze; massimamente volendo passare dal graue all'acuto: o per il contrario da una
consonanza all'altra: Il che non solamente difficultà al Sonatore; ma etiandio poco diletto a gli ascoltanti
hauerebbe apportato: perche in cotal caso si hauerebbe vdito vn non so che di tristo, che hauerbbe fatto non
poco fastidio. Et quantunque dichino anco, che tale Temperamento, o Participatione, sia stata ritrouata
studiosamente, accioche per essa in cotali istrumenti si venisse ad imitar la Natura, la qual si dee imitare in
tutte le cose, più che si puote: perche si come nel genere Diatonico si può procedere naturalmente con le voci
(come è manifesto) per gli suoi interualli, dal graue all'acuto, & per il contrario; senza incommodo alcuno; cosi anche in tali istrumenti si potesse passare dall'acuto al graue, o per il contrario senza alcuno impedimento, & senza alcuna offesa del Sentimento: Tuttauia credo veramente, che tal Temperamento, o Participatione sia stata introdutta a caso, & non studiosamente. Et ciò mi muoue a credere: perche non è dubbio, che ne il Ditono, ne il Semiditono, ne li due Essachordi, & altri interualli molti, i quali hora a noi sono
consonanti; non furono mai da alcuno de gli Antichi (come da i loro scritti si può comprendere) riceuuti nel
numero delle consonanze: ne anco veramente le vsarono per consonanti, nel modo che le vsiamo noi; massimamente hauendo loro sempre vsato il numero delle chorde Pithagorice; si come dalle chorde, che sono collocate in molti antichi istrumenti si può comprendere. La onde è credibile, che alcuno perito nella Musica
dopo vn certo spacio di tempo, a caso prima, & di poi fatto molte esperienze, nell'istesso istrumento le ridu<page 126
cesse a tal temperamento, sotto le proportioni, o forme, le quali hora vsiamo: non però sotto alcuna di quelle,
che di sopra in molte diuisioni hò mostrato: percioche sarebbe stato impossibile, di osseruare il Numero delle
chorde, l'Ordine de gli interualli, & le Forme, o Proportioni mostrate: ma si bene sotto quelle, ch'io sono
per mostrare.
Quel che si dee osseruare nel temperare, ouero accordare gli Interualli di ciascuno Istrumento arteficiale moderno, riducendo il numero delle chorde del Diatonico sintono a quello del Diatono; & che tali interualli non siano naturali, ma si bene accidentali.Cap. 42.
Dimostratione dalla quale si può comprendere, che la mostrata Participatione, o Distributione sia ragioneuolmente fatta; & che per altro modo non si possa fare.Cap. 43.
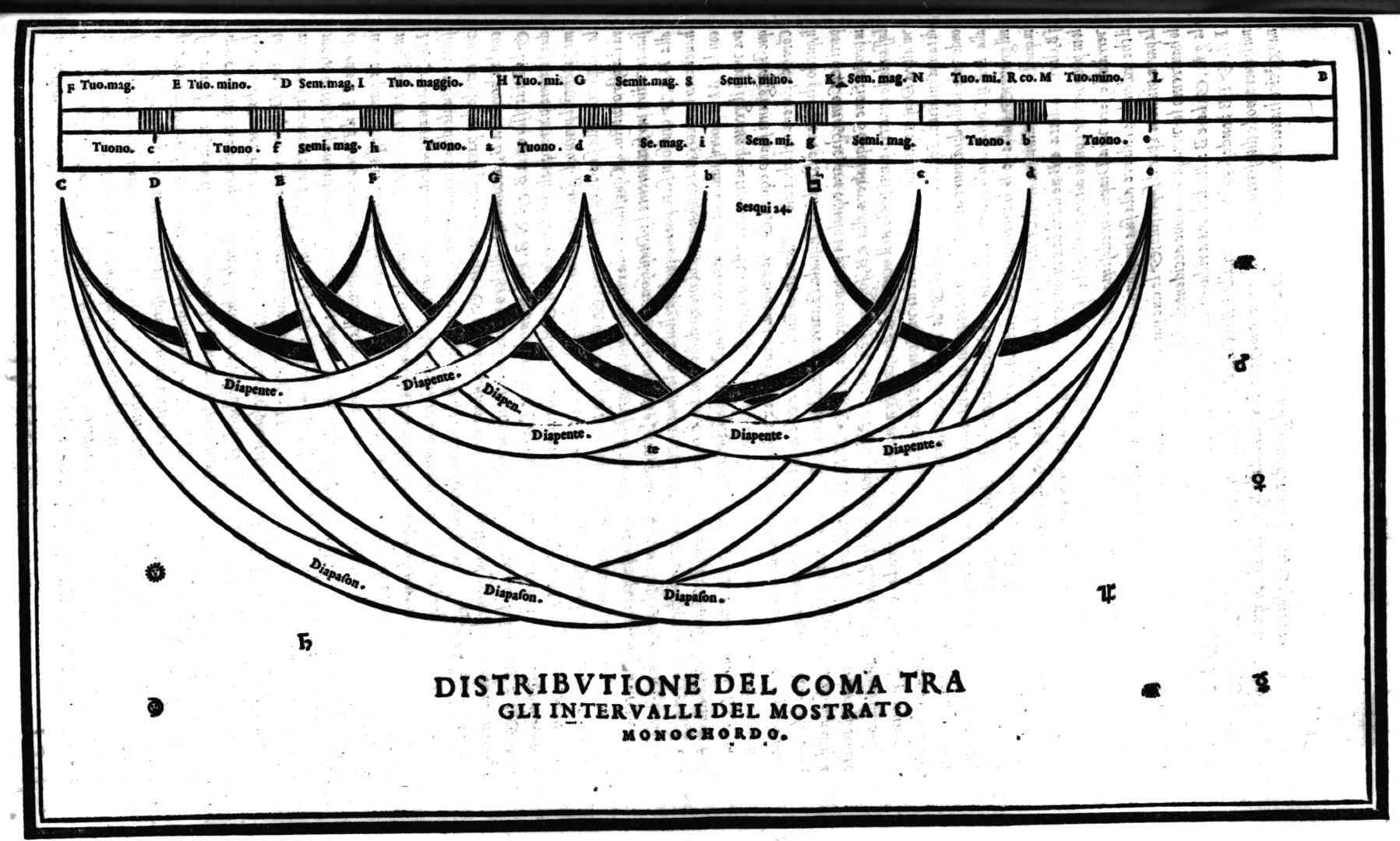
Della Compositione del Monochordo diatonico equalmente temperato, &lb> ridutto al numero delle chorde Pithagorice.Cap. 44.
 , minore di quattro parte di vno Coma. Soggiungeremo immediatamente il Semituono maggiore, contenuto dalla proportione Sesquiquintadecima;
il quale aggiunto al Tuono maggiore fa il Semiditono, contenuto dalla proportione Sesquiquinta, come hò
detto più volte. Et perche il Semituono piglia aumento di tre settime parti del Coma, & il Tuono discresce
quattro; però cauando le tre dalle quattro, ne restarà vna, che sarà quella parte, della quale il Semiditono si
viene a minuire, secondo che di sopra si è detto. Pigliaremo adunque solamente vna parte del Coma a b, &
c b, che sarà la più vicina alla c, & la metteremo insieme con la c b: diuidendo poi questo Tutto in sei
parti equali, & pigliando le cinque, che sarà in punto f, tra la diuisa, & la f b, haueremo collocato il Semiditono alla sua
naturale proportione; & tra la c b, & la f b haueremo il diminuto di vna settima parte del Coma, per le ragioni già dette,
& nella sua forma accidentale. In tal maniera adunque haueremo vna
terza chorda, la quale segnaremo con la lettera C, & sarà la seconda del primo Tetrachordo, che con la
, minore di quattro parte di vno Coma. Soggiungeremo immediatamente il Semituono maggiore, contenuto dalla proportione Sesquiquintadecima;
il quale aggiunto al Tuono maggiore fa il Semiditono, contenuto dalla proportione Sesquiquinta, come hò
detto più volte. Et perche il Semituono piglia aumento di tre settime parti del Coma, & il Tuono discresce
quattro; però cauando le tre dalle quattro, ne restarà vna, che sarà quella parte, della quale il Semiditono si
viene a minuire, secondo che di sopra si è detto. Pigliaremo adunque solamente vna parte del Coma a b, &
c b, che sarà la più vicina alla c, & la metteremo insieme con la c b: diuidendo poi questo Tutto in sei
parti equali, & pigliando le cinque, che sarà in punto f, tra la diuisa, & la f b, haueremo collocato il Semiditono alla sua
naturale proportione; & tra la c b, & la f b haueremo il diminuto di vna settima parte del Coma, per le ragioni già dette,
& nella sua forma accidentale. In tal maniera adunque haueremo vna
terza chorda, la quale segnaremo con la lettera C, & sarà la seconda del primo Tetrachordo, che con la
 contenerà il Semituono maggiore, accresciuto di tre settime parti. Aggiungeremo poi a questo immediatamente il Tuono, accioche la prima chorda con la quarta habbia la consonanza Diatessaron. Et tal
Tuono sarà il primo del primo Tetrachordo posto nel graue. Ma perche tal consonanza contiene il Tuono
maggiore, il minore, & il maggior Semituono; hauendo collocato per auanti il Tuono maggiore tra la prima, & la seconda chorda; fa dibisogno, che noi habbiamo il minore; & però procederemo in tal modo, accommodando prima la detta consonanza alla sua proportione, lassando da vn canto le due prime parti del
Coma c b, & d b, poste appresso la c; & pigliando solamente le cinque, diuideremo tutta la linea fina
in punto b in quattro parti equali, per il maggior termine della Sesquiterza proportione, che è la vera forma di essa Diatessaron, & pigliando tre parti in punto g, haueremo prima tra la diuisa, & la g b, la
Diatessaron nella sua vera forma; & dipoi la accresciuta di due parti del Coma tra la c b, & la g b:
Conciosia che se le aggiunge quelle due parti, che prima che si diuidesse tal linea, furono lassate da vn canto. Et
perche tra'l Tutto diuiso, & la g b, si ritroua la proportione Sesquiterza; se per l'aggiuntione di alcuna
parte si viene a crescere alcuna proportione di quella quantità, che se le aggiunge; è manifesto (per quello che
si è detto di sopra) che hauendosi aggiunto due settime parti delle mostrate alla chorda graue della proportiopage 133ne Sesquiterza; & rimanendo la acuta nel suo primo essere, tal proportione sia fatta maggiore di tanta
quantità, quanta era quella, che è stato aggiunto. Ma perche tra la chorda c b, & la e b hauemo il Tuono
maggiore diminuto, et tra la e b, et la f b il Semituono maggiore accresciuto; però tra la f b, & la g b
haueremo il Tuono minore, il quale verrà per la integratione della Diatessaron accresciuta di due parti del
Coma, come la ragione sempre ne farà vedere. Haueremo adunque la chorda D, che con la C contiene
il Tuono minore, accresciuto di tre parti del Coma; il qual Tuono in questo luogo solamente, & nelle sue
chorde corrispondenti in proportione Dupla, segue immediatamente dopo il Semituono maggiore, procedendo dal graue all'acuto. Onde mi penso, che da altro non possa nascere la difficultà, che si troua nello accordare, o temperar bene ne i moderni Istrumenti la chorda G con la d, & questa con la aa, se non perche le chorde D, et d, de i detti istrumenti pigliano il luogo del Coma, onde ne segueno due Tuoni minori immediatamente l'vno dopo l'altro, tra le chorde C, & D, &
tra le D, & E; & cosi tra quelle, che
corrispondeno con queste in Dupla proportione. Et per seguir quello, che hauemo incominciato, aggiungeremo alla chorda D vn'altra chorda, la quale con essa lei dalla parte acuta contenghi il Tuono minore, il
quale viene ad essere il Secondo del primo Tetrachordo; & faremo che questa chorda aggiunta con la A
contenerà la Diapente: ma prima è dibisogno, che sappiamo la sua proportione, la quale è la diminutione di
due settime parti di vn Coma. Pigliaremo adunque le due parti più propinque alla c, poste tra a, & c,
& le accompagneremo con tutta la c b, & cosi diuideremo questo Tutto in tre parti equali, secondo il
maggior termine continente la proportione della Diapente; Dipoi pigliate le due per il minore, che sarà la
h b, tra questa, & la diuisa haueremo collocato alla sua vera proportione la Diapente; & la diminuta,
secondo le ragioni altre volte addute, sarà tra la c b, & la h b; & per tal via haueremo la chorda E,
che con la D contenerà il sopradetto Tuono, accresciuto di quelle parti, che fanno dibisogno; & sarà la Vltima chorda acuta
del primo Tetrachordo, & la Prima graue del secondo. Et per ritrouare la Seconda, la
quale sia distante per vn Semituono maggiore dalla E, & per vno Essachordo minore dalla A; fa dibisogno di sapere primamente la ragione della sua proportione, la quale è, come hauemo veduto, che'l detto
Essachordo si aumenta di vna settima parte del Coma, come si accresce etiandio il maggiore. Per il che prenderemo la linea
c b diminuta di vna settima parte del Coma c b, & d b, & diuideremo il restante in
otto parti equali: conciosia che 8 è il termine maggiore della proportione dello Essachordo; pigliando dipoi
cinque parti solamente, che saranno per il termine minore in punto i, haueremo tra il Tutto della diuisa,
& la i b, che sarà. la chorda F, il detto Essachordo, collocato nella sua uera proportione; & tra la c b,
& la i b lo accresciuto di tal parte. Aggiungeremo hora a questa sesta chorda, la setttima, la quale sarà da
lei distante per vn Tuono maggiore: ma bisogna sapere primieramente, che proportione habbia con la prima,
& di quanta quantità questo interuallo, che si nomina Eptachordo minore, si accresca, o diminuisca; & ritrouaremo, che la sua vera proportione è la Superquadripartientequinta, & che si accresce di quattro delle
sopradette parti: Conciosia che di quelle parti, che si diminuisce quello interuallo, che si aggiunge oltra la
settima chorda, per venire alla ottaua, di quelle medesime si accresce lo Eptachordo, che le è posto auanti. Et
di quanto tale interuallo si fa maggiore, di tanto si diminuisce lo Eptachordo. Et perche quello interuallo, che
resta per andare alla Diapason, è il Tuono maggiore, il quale si diminuisce di quattro settime parti del Coma; però si accresce il detto Eptachordo di tante parti. Il medesimo anco si osserua nello accommodare le altre chorde, hauendo sempre riguardo a quello interuallo, che segue immediatamente quello, che si vuole accommodare. Pigliaremo adunque la linea c b diminuta delle quattro parti più vicine alla c, che saranno quelle, che sono poste tra c & d, & cosi la diuideremo in noue parti equali; & pigliando cinque parti in punto k, tra la diuisa, & la k b, haueremo accommodato il detto Eptachordo alla sua vera proportione; & tra la c b, & la k b, lo haueremo accresciuto di quattro parti del Coma; & la chorda G
verrà ad esser la settima di tale ordine, & la terza del secondo Tetrachordo. A queste aggiungeremo la
ottaua chorda, la quale con la prima contenerà la consonanza Diapason, diuidendo solamente la d b in due
parti equali: percioche tal consonanza resta nella sua perfettione, cioè nella proportione Dupla, & nel punto l haueremo la chorda a secondo il proposito; & tra le chorde A,
contenerà il Semituono maggiore, accresciuto di tre settime parti. Aggiungeremo poi a questo immediatamente il Tuono, accioche la prima chorda con la quarta habbia la consonanza Diatessaron. Et tal
Tuono sarà il primo del primo Tetrachordo posto nel graue. Ma perche tal consonanza contiene il Tuono
maggiore, il minore, & il maggior Semituono; hauendo collocato per auanti il Tuono maggiore tra la prima, & la seconda chorda; fa dibisogno, che noi habbiamo il minore; & però procederemo in tal modo, accommodando prima la detta consonanza alla sua proportione, lassando da vn canto le due prime parti del
Coma c b, & d b, poste appresso la c; & pigliando solamente le cinque, diuideremo tutta la linea fina
in punto b in quattro parti equali, per il maggior termine della Sesquiterza proportione, che è la vera forma di essa Diatessaron, & pigliando tre parti in punto g, haueremo prima tra la diuisa, & la g b, la
Diatessaron nella sua vera forma; & dipoi la accresciuta di due parti del Coma tra la c b, & la g b:
Conciosia che se le aggiunge quelle due parti, che prima che si diuidesse tal linea, furono lassate da vn canto. Et
perche tra'l Tutto diuiso, & la g b, si ritroua la proportione Sesquiterza; se per l'aggiuntione di alcuna
parte si viene a crescere alcuna proportione di quella quantità, che se le aggiunge; è manifesto (per quello che
si è detto di sopra) che hauendosi aggiunto due settime parti delle mostrate alla chorda graue della proportiopage 133ne Sesquiterza; & rimanendo la acuta nel suo primo essere, tal proportione sia fatta maggiore di tanta
quantità, quanta era quella, che è stato aggiunto. Ma perche tra la chorda c b, & la e b hauemo il Tuono
maggiore diminuto, et tra la e b, et la f b il Semituono maggiore accresciuto; però tra la f b, & la g b
haueremo il Tuono minore, il quale verrà per la integratione della Diatessaron accresciuta di due parti del
Coma, come la ragione sempre ne farà vedere. Haueremo adunque la chorda D, che con la C contiene
il Tuono minore, accresciuto di tre parti del Coma; il qual Tuono in questo luogo solamente, & nelle sue
chorde corrispondenti in proportione Dupla, segue immediatamente dopo il Semituono maggiore, procedendo dal graue all'acuto. Onde mi penso, che da altro non possa nascere la difficultà, che si troua nello accordare, o temperar bene ne i moderni Istrumenti la chorda G con la d, & questa con la aa, se non perche le chorde D, et d, de i detti istrumenti pigliano il luogo del Coma, onde ne segueno due Tuoni minori immediatamente l'vno dopo l'altro, tra le chorde C, & D, &
tra le D, & E; & cosi tra quelle, che
corrispondeno con queste in Dupla proportione. Et per seguir quello, che hauemo incominciato, aggiungeremo alla chorda D vn'altra chorda, la quale con essa lei dalla parte acuta contenghi il Tuono minore, il
quale viene ad essere il Secondo del primo Tetrachordo; & faremo che questa chorda aggiunta con la A
contenerà la Diapente: ma prima è dibisogno, che sappiamo la sua proportione, la quale è la diminutione di
due settime parti di vn Coma. Pigliaremo adunque le due parti più propinque alla c, poste tra a, & c,
& le accompagneremo con tutta la c b, & cosi diuideremo questo Tutto in tre parti equali, secondo il
maggior termine continente la proportione della Diapente; Dipoi pigliate le due per il minore, che sarà la
h b, tra questa, & la diuisa haueremo collocato alla sua vera proportione la Diapente; & la diminuta,
secondo le ragioni altre volte addute, sarà tra la c b, & la h b; & per tal via haueremo la chorda E,
che con la D contenerà il sopradetto Tuono, accresciuto di quelle parti, che fanno dibisogno; & sarà la Vltima chorda acuta
del primo Tetrachordo, & la Prima graue del secondo. Et per ritrouare la Seconda, la
quale sia distante per vn Semituono maggiore dalla E, & per vno Essachordo minore dalla A; fa dibisogno di sapere primamente la ragione della sua proportione, la quale è, come hauemo veduto, che'l detto
Essachordo si aumenta di vna settima parte del Coma, come si accresce etiandio il maggiore. Per il che prenderemo la linea
c b diminuta di vna settima parte del Coma c b, & d b, & diuideremo il restante in
otto parti equali: conciosia che 8 è il termine maggiore della proportione dello Essachordo; pigliando dipoi
cinque parti solamente, che saranno per il termine minore in punto i, haueremo tra il Tutto della diuisa,
& la i b, che sarà. la chorda F, il detto Essachordo, collocato nella sua uera proportione; & tra la c b,
& la i b lo accresciuto di tal parte. Aggiungeremo hora a questa sesta chorda, la setttima, la quale sarà da
lei distante per vn Tuono maggiore: ma bisogna sapere primieramente, che proportione habbia con la prima,
& di quanta quantità questo interuallo, che si nomina Eptachordo minore, si accresca, o diminuisca; & ritrouaremo, che la sua vera proportione è la Superquadripartientequinta, & che si accresce di quattro delle
sopradette parti: Conciosia che di quelle parti, che si diminuisce quello interuallo, che si aggiunge oltra la
settima chorda, per venire alla ottaua, di quelle medesime si accresce lo Eptachordo, che le è posto auanti. Et
di quanto tale interuallo si fa maggiore, di tanto si diminuisce lo Eptachordo. Et perche quello interuallo, che
resta per andare alla Diapason, è il Tuono maggiore, il quale si diminuisce di quattro settime parti del Coma; però si accresce il detto Eptachordo di tante parti. Il medesimo anco si osserua nello accommodare le altre chorde, hauendo sempre riguardo a quello interuallo, che segue immediatamente quello, che si vuole accommodare. Pigliaremo adunque la linea c b diminuta delle quattro parti più vicine alla c, che saranno quelle, che sono poste tra c & d, & cosi la diuideremo in noue parti equali; & pigliando cinque parti in punto k, tra la diuisa, & la k b, haueremo accommodato il detto Eptachordo alla sua vera proportione; & tra la c b, & la k b, lo haueremo accresciuto di quattro parti del Coma; & la chorda G
verrà ad esser la settima di tale ordine, & la terza del secondo Tetrachordo. A queste aggiungeremo la
ottaua chorda, la quale con la prima contenerà la consonanza Diapason, diuidendo solamente la d b in due
parti equali: percioche tal consonanza resta nella sua perfettione, cioè nella proportione Dupla, & nel punto l haueremo la chorda a secondo il proposito; & tra le chorde A,  . C. D. E. F. G. & a,
haueremo la Diapason tramezata da sei chorde, & diuisa in sette interualli, ciascuno de i quali è accresciuto,
ouero diminuto secondo la proportione, che se gli appartiene, nel modo che si è mostrato. Et perche diuidendo in due parti equali qualunque chorda si vuole, se le può ritrouare la corrispondente per vna Diapason, copage break
. C. D. E. F. G. & a,
haueremo la Diapason tramezata da sei chorde, & diuisa in sette interualli, ciascuno de i quali è accresciuto,
ouero diminuto secondo la proportione, che se gli appartiene, nel modo che si è mostrato. Et perche diuidendo in due parti equali qualunque chorda si vuole, se le può ritrouare la corrispondente per vna Diapason, copage break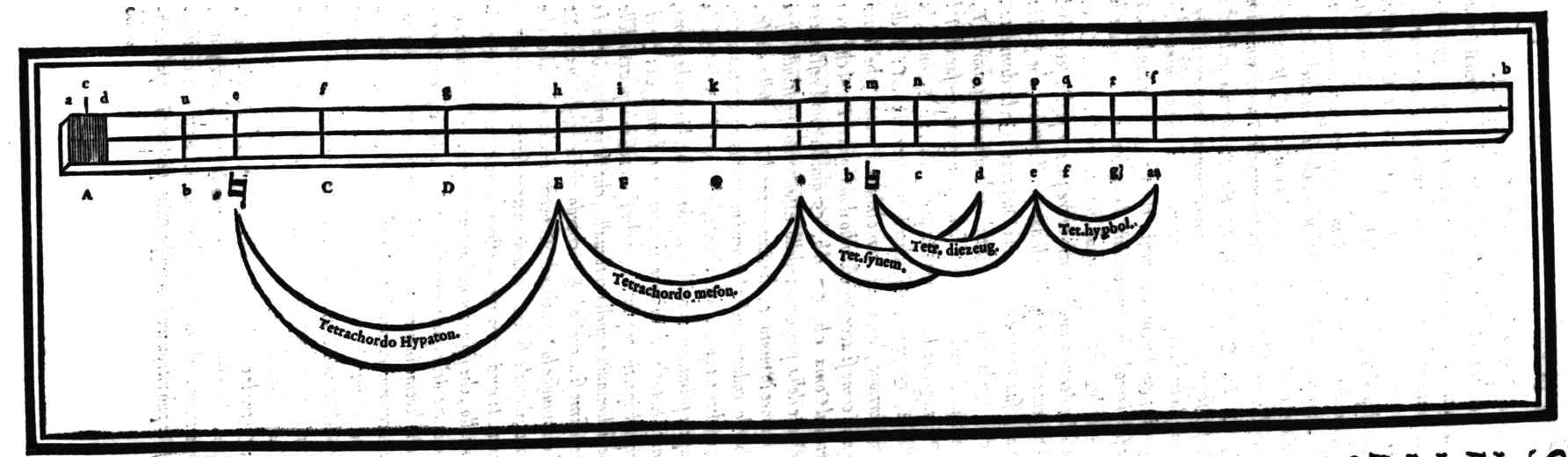
 . C. D. E. F. G. a. b.
. C. D. E. F. G. a. b.  .
c. d. e. f. g. & aa. come nella figura si
può vedere. Con questo mezo adunque potremo hauere senza molta fatica, & senza alcuno
errore la via, & il modo di comporre il Monochordo temperato ne i suoi interualli, & accommodato al numero delle chorde pithagorice; nel
quale potremo accommodare quante chorde vorremo, accrescendo, o diminuendo li suoi internalli,
con la proportione di ciascuno, secondo il modo ch'io
hò mostrato di sopra. page 135
.
c. d. e. f. g. & aa. come nella figura si
può vedere. Con questo mezo adunque potremo hauere senza molta fatica, & senza alcuno
errore la via, & il modo di comporre il Monochordo temperato ne i suoi interualli, & accommodato al numero delle chorde pithagorice; nel
quale potremo accommodare quante chorde vorremo, accrescendo, o diminuendo li suoi internalli,
con la proportione di ciascuno, secondo il modo ch'io
hò mostrato di sopra. page 135
Se nelle Canzoni seguitiamo cantando gli interualli produtti da i veri, & sonori numeri, ouero li mostrati; & della solutione di alcuni altri dubbij.Cap. 45.
Della Inspessatione del mostrato Monochordo diatonico, dalle chorde del genere Chromatico.Cap. 46.
 , viene ad esser diuiso dalla chorda b in due parti; cioè
in vn Semituono maggiore, & in vno minore; per il che a caso nasce un nuouo Tetrachordo, tra le chorde
a. b.
, viene ad esser diuiso dalla chorda b in due parti; cioè
in vn Semituono maggiore, & in vno minore; per il che a caso nasce un nuouo Tetrachordo, tra le chorde
a. b.  . & d: imperoche tra la, & la b si ritroua il Semituono maggiore; tra la b, & la
. & d: imperoche tra la, & la b si ritroua il Semituono maggiore; tra la b, & la  il Semituono minore; et tra la
il Semituono minore; et tra la  , & la d il Trihemituono; come nelle sottoposte quattro chorde si può vedere.
, & la d il Trihemituono; come nelle sottoposte quattro chorde si può vedere.

 & la
& la  il Semituono minore, che non si vsa nelle modulationi diatoniche, ne anco nelle Enharmoniche; et
tra la chorda
il Semituono minore, che non si vsa nelle modulationi diatoniche, ne anco nelle Enharmoniche; et
tra la chorda  & la d, hà il Trihemituono incomposto, che nel diatonico è composto, il quale è contenuto dalla proportione Sesquiquinta; si come è contenuto quello interuallo, che è posto nella parte acuta del Chromatico molle
di Tolomeo; come si può conoscere riducendo le quattro mostrate chorde nelle loro propie forme,
che sono contenute tra gli harmonici numeri; come nel cap. 15. della Prima parte, nelle chorde del primo Tetrachordo detto Hypaton, si come nella sottoposta figura si può chiaramente vedere.
& la d, hà il Trihemituono incomposto, che nel diatonico è composto, il quale è contenuto dalla proportione Sesquiquinta; si come è contenuto quello interuallo, che è posto nella parte acuta del Chromatico molle
di Tolomeo; come si può conoscere riducendo le quattro mostrate chorde nelle loro propie forme,
che sono contenute tra gli harmonici numeri; come nel cap. 15. della Prima parte, nelle chorde del primo Tetrachordo detto Hypaton, si come nella sottoposta figura si può chiaramente vedere.

 rotunda di Guidone, la quale chiamano
rotunda di Guidone, la quale chiamano  molle; & cosi tutte
quelle, che sono consonanti con questa, tanto nel graue, quanto nell'acuto, per vna Diapason, oueramente per vna
Diapente, o per vna Diatessaron; L'altre poi notarono con questo segno
molle; & cosi tutte
quelle, che sono consonanti con questa, tanto nel graue, quanto nell'acuto, per vna Diapason, oueramente per vna
Diapente, o per vna Diatessaron; L'altre poi notarono con questo segno  , il quale nominano Diesis; forse
hauendo la opinione di Filolao, il quale (come recita Boetio) diceua, che quel Spacio, per il quale la Sesquiterza
è maggiore di due Tuoni; si chiamaua Diesis; il qual spatio alcuni Moderni chiamano Semituono minore:
perche il più delle volte si pone, per fare l'interuallo del Semituono, come altroue vederemo. Et quando voleuano che tal Semituono si cantasse in alcun luogo delle lor cantilene, & saliuano dal graue all'acuto, poneuano il b: ma quando discendeuano dall'acuto nel graue, poneuano il
, il quale nominano Diesis; forse
hauendo la opinione di Filolao, il quale (come recita Boetio) diceua, che quel Spacio, per il quale la Sesquiterza
è maggiore di due Tuoni; si chiamaua Diesis; il qual spatio alcuni Moderni chiamano Semituono minore:
perche il più delle volte si pone, per fare l'interuallo del Semituono, come altroue vederemo. Et quando voleuano che tal Semituono si cantasse in alcun luogo delle lor cantilene, & saliuano dal graue all'acuto, poneuano il b: ma quando discendeuano dall'acuto nel graue, poneuano il  , il che fanno anco li più Moderni, quando salendo, & discendendo, col mezo di tali segni, o chorde, vogliono porre il Tuono. Credo che questo segno
, il che fanno anco li più Moderni, quando salendo, & discendendo, col mezo di tali segni, o chorde, vogliono porre il Tuono. Credo che questo segno  fusse introdutto da alcuni, che si sognarono, che il Tuono fusse, o si componesse di noue Coma; ouer che si potesse diuidere almeno in tante parti: percioche voleuano, che il Semituono maggiore fusse di cinque Coma, et
il minore di quattro; & per questo, quando procedeuano dalle chorde diatoniche alle chromatiche, nel modo
ch'io hò detto; per lo spatio di vn Semituono poneuano tal segno, per dinotarci questo interuallo: perche hebbero opinione
(come hanno anche molti de i Moderni) che tale interuallo fusse il Semituono minore, & fusse di
quattro Coma; onde segnauano il spacio con quattro virgolette incrociate, che sono le quattro poste in tal segno: conciosia che seguiuano l'ordine delle chorde, il numero, & le proportioni Pithagorice, mostrate di sopra. Ma quanto costoro si ingannino, facilmente si può comprendere da quello, che detto, & veduto hauemo
di sopra, & da quello, che dice Boetio nel cap. 15. del Terzo libro della Musica, mostrando che il Tuono di
proportione Sesquiottaua è maggiore di otto, & minore di noue Coma. Et nel cap. 14. dice, che'l Semituono
minore è maggiore di tre Coma, & minore di quattro. Però adunque se'l Tuono è maggior di otto, & minor di noue Coma, & non si può hauere certezza alcuna della sua quantità; parmi certamente grande arroganza, il volere affermare determinatamente vna cosa, che la Scienza pone in dubbio, & indeterminata.
Onde se questo interuallo non si può denominare con vna quantità determinata, minormente si potranno denominar quelli, che sono minori; come sono il Semituono maggiore, & il minore, & gli altri simili.
fusse introdutto da alcuni, che si sognarono, che il Tuono fusse, o si componesse di noue Coma; ouer che si potesse diuidere almeno in tante parti: percioche voleuano, che il Semituono maggiore fusse di cinque Coma, et
il minore di quattro; & per questo, quando procedeuano dalle chorde diatoniche alle chromatiche, nel modo
ch'io hò detto; per lo spatio di vn Semituono poneuano tal segno, per dinotarci questo interuallo: perche hebbero opinione
(come hanno anche molti de i Moderni) che tale interuallo fusse il Semituono minore, & fusse di
quattro Coma; onde segnauano il spacio con quattro virgolette incrociate, che sono le quattro poste in tal segno: conciosia che seguiuano l'ordine delle chorde, il numero, & le proportioni Pithagorice, mostrate di sopra. Ma quanto costoro si ingannino, facilmente si può comprendere da quello, che detto, & veduto hauemo
di sopra, & da quello, che dice Boetio nel cap. 15. del Terzo libro della Musica, mostrando che il Tuono di
proportione Sesquiottaua è maggiore di otto, & minore di noue Coma. Et nel cap. 14. dice, che'l Semituono
minore è maggiore di tre Coma, & minore di quattro. Però adunque se'l Tuono è maggior di otto, & minor di noue Coma, & non si può hauere certezza alcuna della sua quantità; parmi certamente grande arroganza, il volere affermare determinatamente vna cosa, che la Scienza pone in dubbio, & indeterminata.
Onde se questo interuallo non si può denominare con vna quantità determinata, minormente si potranno denominar quelli, che sono minori; come sono il Semituono maggiore, & il minore, & gli altri simili.
In che maniera possiamo inspessare il detto Monochordo con le chorde Enharmoniche.Cap. 47.
![Diatessaron.
Semit. maggiore.
Diesis.
Diesis.
Ditono
300. a. Mese.
Sesquiquarta.
375. F. Lychanos meson.
Supertripartiente 125.
384. [[mus.hsharp]]. Parhypate meson.
Sesquiuentesimaquarta.
400. E. Hypate meson.](../../zarins58/ill/247-1.jpg)

Che è più ragioneuole dire, che gli Interualli minori naschino dalli maggiori; che dire, che i maggiori si componghino de i minori; & che meglio è ordinato l'Essachordo moderno, che il Tetrachordo antico.Cap. 48.
Che ciascuno delli Generi nominati, si può dire Genere, & Specie; &lb> che ciascuna altra diuisione, ouero ordinatione de Suoni sia vana, & inutile.Cap. 49.
Per qual cagione le Consonanze hanno maggiormente la loro origine dalle Proportioni di maggiore inequalità, che da quelle di minore.Cap. 50.
Dubbio sopra quel che si è detto.Cap. 51.
LA TERZA PARTE Delle Istitutioni harmoniche DI M. GIOSEFFO ZARLINO DA CHIOGGIA,
Quel che sia Contrapunto, & perche sia cosi nominato. Capitolo primo.
Della inuentione delle Chiaui, & delle Figure cantabili.Cap. 2.
 ritondo, ouer molle, che lo vagliam dire: Ma quando haueua principio dalla lettera G, voleua che si
cantasse per quella del
ritondo, ouer molle, che lo vagliam dire: Ma quando haueua principio dalla lettera G, voleua che si
cantasse per quella del  quadrato, ouer duro; & disse che la Propietà era vna Deriuatione di più voci, o
suoni da vno istesso principio; ouero che era vna Deduttione singulare, o particolare di ciascuno ordinato Essachordo. La onde bisogna sapere, che Guidone congiunse ogni Deduttione con vno delli Tetrachordi greci,
aggiungendo a ciascun Tetrachordo due chorde di più dalla parte graue, come è quella dell'Vt, & quella del
Re: percioche ogni Tetrachordo hà principio nella chorda del Mi; come nella Seconda parte fu commemorato: di maniera che ogni
Essachordo contiene ciascuna specie della Diatessaron, che sono Tre; come vederemo al suo luogo. La sede poi, ouero il luogo delle voci, o suoni, il quale i Musici nominano Chorde, nominò
Chiaui; le quali sono distinte l'vna dall'altra per linee equidistanti, & parallele; intendendoui però i spacij
di mezo; abenche le Voci, o Suoni non siano equalmente distanti l'vna dall'altra. Onde collocò la prima
chiaue, la quale nominò Gamma, vt; nella linea, ouer riga; & A, re; che è la seconda nel spatio. Similmente collocò,
quadrato, ouer duro; & disse che la Propietà era vna Deriuatione di più voci, o
suoni da vno istesso principio; ouero che era vna Deduttione singulare, o particolare di ciascuno ordinato Essachordo. La onde bisogna sapere, che Guidone congiunse ogni Deduttione con vno delli Tetrachordi greci,
aggiungendo a ciascun Tetrachordo due chorde di più dalla parte graue, come è quella dell'Vt, & quella del
Re: percioche ogni Tetrachordo hà principio nella chorda del Mi; come nella Seconda parte fu commemorato: di maniera che ogni
Essachordo contiene ciascuna specie della Diatessaron, che sono Tre; come vederemo al suo luogo. La sede poi, ouero il luogo delle voci, o suoni, il quale i Musici nominano Chorde, nominò
Chiaui; le quali sono distinte l'vna dall'altra per linee equidistanti, & parallele; intendendoui però i spacij
di mezo; abenche le Voci, o Suoni non siano equalmente distanti l'vna dall'altra. Onde collocò la prima
chiaue, la quale nominò Gamma, vt; nella linea, ouer riga; & A, re; che è la seconda nel spatio. Similmente collocò,  , mi, in riga: & C, fa ut in spacio, & di mano in mano collocò etiandio in tal maniera le altre; come si vedeno per ordine nello Introduttorio nominato di sopra, segnando ciascuna con la sua propia lettera.
Ma perche alle volte tal cosa poteua generar confusione, i più moderni, forse ricordandosi, che
in vano si fa alcuna cosa col mezo di più cose, che si può fare con poche, & bene; ritrouarono alcune Cifere;
per le quali i Cantori si hauessero à reggere, accioche hauendone lassate alcune altre, per quelle solamente hauessero cognitione
di ogni modulatione, & di ogni cantilena; & da quelle hauessero notitia de i Spacij, ouero Interualli di Tuono, di Semituono, & de gli altri ancora. Le quali Cifere si chiamarono sempre Chiaui; stando in questa similitudine, che si come per la Chiaue si apre l'vscio, & si entra in casa, & iui si vede quello, che si troua entro; Cosi per tali Cifere si apre la modulatione, & si conosce ciascuno delli nominati interualli. Intrauerrebbe bene il contrario, quando fusse rimossa: percio che all'ora ogni cosa si empirebbe
di confusione; si come ogn'vno si può imaginare. Nominarono poi quelle Chiaue con li nomi, che sono notate
nel sottoposto essempio, le quali, benche tall'ora alcune di esse siano poste sopra vna medesima delle cinque
mostrate righe, sono nondimeno distanti tra loro per cinque lettere, cioè per vna Diapente. Ritrouarono page 149
, mi, in riga: & C, fa ut in spacio, & di mano in mano collocò etiandio in tal maniera le altre; come si vedeno per ordine nello Introduttorio nominato di sopra, segnando ciascuna con la sua propia lettera.
Ma perche alle volte tal cosa poteua generar confusione, i più moderni, forse ricordandosi, che
in vano si fa alcuna cosa col mezo di più cose, che si può fare con poche, & bene; ritrouarono alcune Cifere;
per le quali i Cantori si hauessero à reggere, accioche hauendone lassate alcune altre, per quelle solamente hauessero cognitione
di ogni modulatione, & di ogni cantilena; & da quelle hauessero notitia de i Spacij, ouero Interualli di Tuono, di Semituono, & de gli altri ancora. Le quali Cifere si chiamarono sempre Chiaui; stando in questa similitudine, che si come per la Chiaue si apre l'vscio, & si entra in casa, & iui si vede quello, che si troua entro; Cosi per tali Cifere si apre la modulatione, & si conosce ciascuno delli nominati interualli. Intrauerrebbe bene il contrario, quando fusse rimossa: percio che all'ora ogni cosa si empirebbe
di confusione; si come ogn'vno si può imaginare. Nominarono poi quelle Chiaue con li nomi, che sono notate
nel sottoposto essempio, le quali, benche tall'ora alcune di esse siano poste sopra vna medesima delle cinque
mostrate righe, sono nondimeno distanti tra loro per cinque lettere, cioè per vna Diapente. Ritrouarono page 149

 quadrati,
quadrati,  rotondi, Diesis, Pause, Legature, Prese, Coronate, Ritornelli & mille altri, che possono accascare; delli quali vna buona
parte ne adoperano anco li moderni; nondimeno io non intendo parlare, se non di quelli, che faranno al proposito, & secondo che torneranno commodi: Imperoche principalmente intendo di trattar quelle cose, che sono necessarie, & cadeno sotto
il sentimento dall'vdito, il cui oggetto è veramente il Suono; lassando (per quanto potrò) da parte quelle,
che a tal sentimento sono strane, & forastiere.
rotondi, Diesis, Pause, Legature, Prese, Coronate, Ritornelli & mille altri, che possono accascare; delli quali vna buona
parte ne adoperano anco li moderni; nondimeno io non intendo parlare, se non di quelli, che faranno al proposito, & secondo che torneranno commodi: Imperoche principalmente intendo di trattar quelle cose, che sono necessarie, & cadeno sotto
il sentimento dall'vdito, il cui oggetto è veramente il Suono; lassando (per quanto potrò) da parte quelle,
che a tal sentimento sono strane, & forastiere.
De gli Elementi, che compongono il Contrapunto.Cap. 3.

Diuisione delle mostrate Specie.Cap. 4.
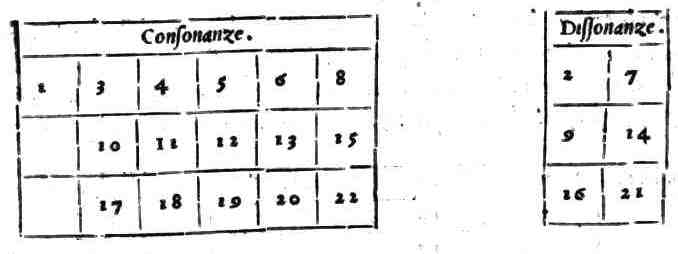
Se la Quarta è consonanza; & donde auiene, che li Musici non l'habbiano usata, se non nelle compositioni di più uoci. Capitolo. 5.
Diuisione delle consonanze nelle Perfette, & nelle Imperfette.Cap. 6.

Che la Quarta, & la Quinta sono mezane tra le consonanze perfette, & le imperfette.Cap. 7.
Quali consonanze siano più piene, & quali più vaghe.Cap. 8.
Della Differenza, che si troua tra le consonanze Imperfette.Cap. 9.
| Consonanze imperfette Maggiori. | Consonanze imperfette Minori. |
| Ditono, o Terza maggiore. | Semiditono, o Terza minore. |
| Essachordo, o Sesta maggiore. | Essachordo, o Sesta minore. |
| Et le replicate. | Et le replicate. |
Della propietà, o natura delle consonanze Imperfette.Cap. 10.
Ragionamento particolare intorno all'Vnisono.Cap. 11.
 Il medesimo potremo anco dire, quando due, o più parti di tal canzone si ritroueranno essere in vna medesima chorda; come sono le due sottoposte. page 158
Il medesimo potremo anco dire, quando due, o più parti di tal canzone si ritroueranno essere in vna medesima chorda; come sono le due sottoposte. page 158
Della Prima consonanza, cioè della Diapason, ouero Ottaua.Cap. 12.
 &
&  , tal Semituono si ritroua
nel primo, & nel quarto luogo; & cosi di mano in mano, secondo l'ordine delle mostrate sette lettere. Onde
essendo in tal maniera mediata, dicono i Musici, che la Diapason è vna compositione di otto suoni, diatonicamente, & secondo la natura del numero sonoro accommodati, & ordinati in essa; dalli quali la nominarono etiandio Ottaua; & contengono in se cinque Tuoni, cioè tre maggiori, due minori, & due Semituoni
maggiori; come ne i sottoposti essempij si veggono.
, tal Semituono si ritroua
nel primo, & nel quarto luogo; & cosi di mano in mano, secondo l'ordine delle mostrate sette lettere. Onde
essendo in tal maniera mediata, dicono i Musici, che la Diapason è vna compositione di otto suoni, diatonicamente, & secondo la natura del numero sonoro accommodati, & ordinati in essa; dalli quali la nominarono etiandio Ottaua; & contengono in se cinque Tuoni, cioè tre maggiori, due minori, & due Semituoni
maggiori; come ne i sottoposti essempij si veggono.
 Quando adunque nelle compositioni ritrouaremo due parti; l'vna distante dall'altra per vn
simile interuallo, di modo che la graue occupi il luogo graue, & la acuta il luogo acuto di
qual si voglia dell'vna delle specie de i mostrati essempi; allora diremo, che tal parti saranno distanti tra loro per vna ottaua; come in questo essempio si vedeno.
Quando adunque nelle compositioni ritrouaremo due parti; l'vna distante dall'altra per vn
simile interuallo, di modo che la graue occupi il luogo graue, & la acuta il luogo acuto di
qual si voglia dell'vna delle specie de i mostrati essempi; allora diremo, che tal parti saranno distanti tra loro per vna ottaua; come in questo essempio si vedeno.

Della Diapente, ouero Quinta.Cap. 13.
 Et ciascuna di loro contiene in se cinque voci, o suoni, & quattro interualli; che hanno tra loro due Tuoni
maggiori, vno minore, & vn Semituono maggiore; Et per questa cagione, dal numero delle chorde, che contiene è detta Quinta da i Prattici: Ma li Greci la chiamarono Diapente, con queste due parole, διὰ, che significa Per; & πέντε,
che vuol dir Cinque; quasi volendo dire Consonanza, che procede per cinque voci, o suoni. Quando adunque saranno due parti lontane l'vna dall'altra di maniera, che l'vna tenghi la parte graue
di ciascuna delle dette specie; & l'altra l'acuta: allora diremo, che saranno lontane l'vna dall'altra per vna
Diapente, o per vna Quinta: come qui si vedeno.Et quantunque io habbia posto gli essempij della Diapason
Et ciascuna di loro contiene in se cinque voci, o suoni, & quattro interualli; che hanno tra loro due Tuoni
maggiori, vno minore, & vn Semituono maggiore; Et per questa cagione, dal numero delle chorde, che contiene è detta Quinta da i Prattici: Ma li Greci la chiamarono Diapente, con queste due parole, διὰ, che significa Per; & πέντε,
che vuol dir Cinque; quasi volendo dire Consonanza, che procede per cinque voci, o suoni. Quando adunque saranno due parti lontane l'vna dall'altra di maniera, che l'vna tenghi la parte graue
di ciascuna delle dette specie; & l'altra l'acuta: allora diremo, che saranno lontane l'vna dall'altra per vna
Diapente, o per vna Quinta: come qui si vedeno.Et quantunque io habbia posto gli essempij della Diapason
 nel cap. precedente nelle chorde graui; non si possono pero por quelli della Diapente
l'vno dopo l'altro, come si è fatto quelli della Diapason, senza alcuno interrompimento dell'ordine: conciosia che se io li hauessi posto nelle chorde A.
nel cap. precedente nelle chorde graui; non si possono pero por quelli della Diapente
l'vno dopo l'altro, come si è fatto quelli della Diapason, senza alcuno interrompimento dell'ordine: conciosia che se io li hauessi posto nelle chorde A.  . C &
D: ancora che la prima, la terza, & la quarta chorda hauessero date le specie della
Diapente perfette; nondimeno la seconda non l'hauerebbe potuto dare: percioche dalla chorda
. C &
D: ancora che la prima, la terza, & la quarta chorda hauessero date le specie della
Diapente perfette; nondimeno la seconda non l'hauerebbe potuto dare: percioche dalla chorda  alla chorda F si ritroua la Diapente diminuta di vn Semituono;
come è manifesto a ciascuno, che è perito nella Musica; ancora che Boetio non si guardasse da tal cosa, quando nel cap. 13. del Quarto libro della Musica, pose la seconda
specie di questa consonanza tra le chorde Hypate hypaton, & parhypate meson,
che è vna Quinta diminuta, & contiene due Tuoni, & due Semituoni. Ma credo
io, che non si curasse di porre essatamente il vero della cosa, pur che mostrasse con lo essempio delle chorde
quello, che volea intendere.
alla chorda F si ritroua la Diapente diminuta di vn Semituono;
come è manifesto a ciascuno, che è perito nella Musica; ancora che Boetio non si guardasse da tal cosa, quando nel cap. 13. del Quarto libro della Musica, pose la seconda
specie di questa consonanza tra le chorde Hypate hypaton, & parhypate meson,
che è vna Quinta diminuta, & contiene due Tuoni, & due Semituoni. Ma credo
io, che non si curasse di porre essatamente il vero della cosa, pur che mostrasse con lo essempio delle chorde
quello, che volea intendere.
Della Diatessaron, ouer Quarta.Cap. 14.
 Questa (come hò detto altroue) da i Greci è chiamata prima Sinfonia, ouero (come la nomina Filone Giudeo) prima Harmonia;
Et Boetio la dimanda Minima consonanza: La onde si vede, che non hebbero il
Ditono, ne il Semiditono per consonanze. La chiamarono etiandio Diatessaron dal numero delle chorde, o
voci, che in se contiene: percioche ogni Diatessaron procede al modo mostrato per quattro voci: Imperoche
è detta da Διὰ, che vuol dire Per, & da τέσσαρα, che vuol dir Quattro, cioè Consonanza di quattro voci, o
Questa (come hò detto altroue) da i Greci è chiamata prima Sinfonia, ouero (come la nomina Filone Giudeo) prima Harmonia;
Et Boetio la dimanda Minima consonanza: La onde si vede, che non hebbero il
Ditono, ne il Semiditono per consonanze. La chiamarono etiandio Diatessaron dal numero delle chorde, o
voci, che in se contiene: percioche ogni Diatessaron procede al modo mostrato per quattro voci: Imperoche
è detta da Διὰ, che vuol dire Per, & da τέσσαρα, che vuol dir Quattro, cioè Consonanza di quattro voci, o
 suoni; dal qual numero i nostri Moderni la chiamarono Quarta. Quando adunque vorremo far due parti nelle nostre compositioni, le quali siano tra loro distanti per vna Diatessaron, porremo in vna delle chorde estreme di uno delli sopraposti essempi la voce graue, & nell'altro l'acuta, come si vede nello essempio. Il perche ritrouandosi anco nelle cantilene
due parti accommodate l'vna con l'altra in cotal modo; potremo dire,
che l'vna sia distante dall'altra per vna Diatessaron, oueramente per
una Quarta.
suoni; dal qual numero i nostri Moderni la chiamarono Quarta. Quando adunque vorremo far due parti nelle nostre compositioni, le quali siano tra loro distanti per vna Diatessaron, porremo in vna delle chorde estreme di uno delli sopraposti essempi la voce graue, & nell'altro l'acuta, come si vede nello essempio. Il perche ritrouandosi anco nelle cantilene
due parti accommodate l'vna con l'altra in cotal modo; potremo dire,
che l'vna sia distante dall'altra per vna Diatessaron, oueramente per
una Quarta.
Del Ditono, ouer Terza maggiore.Cap. 15.
 Et tal differenza nasce dalla varietà delli suoi interualli: conciosia che nel primo interuallo della prima specie si ritroua il Tuono maggiore, & nel secondo il minore; & nella seconda specie si ritroua il contrario, cioè
il minore nel primo, et nel secondo il maggiore. Diremo adunque, che allora le parti de i Contrapunti sono distanti page 162
Et tal differenza nasce dalla varietà delli suoi interualli: conciosia che nel primo interuallo della prima specie si ritroua il Tuono maggiore, & nel secondo il minore; & nella seconda specie si ritroua il contrario, cioè
il minore nel primo, et nel secondo il maggiore. Diremo adunque, che allora le parti de i Contrapunti sono distanti page 162 l'vna dall'altra per vn Ditono, quando l'vna di esse si ritroua in alcuna delle chorde estreme graui delli mostrati essempi, & l'altra nelle estreme acute; come nello essempio si vede.Questa consonanza è detta
Ditono: perche contiene in se due Tuoni;
quantunque li Prattici la dimandino Terza maggiore, perche è diuisa in due interualli, contenuti da tre chorde, delle quali le estreme sono più distanti di quello, che
sono le estreme del Semiditono, per vn Semituono minore; come a mano a mano
vederemo.
l'vna dall'altra per vn Ditono, quando l'vna di esse si ritroua in alcuna delle chorde estreme graui delli mostrati essempi, & l'altra nelle estreme acute; come nello essempio si vede.Questa consonanza è detta
Ditono: perche contiene in se due Tuoni;
quantunque li Prattici la dimandino Terza maggiore, perche è diuisa in due interualli, contenuti da tre chorde, delle quali le estreme sono più distanti di quello, che
sono le estreme del Semiditono, per vn Semituono minore; come a mano a mano
vederemo.
Del Semiditono, ouero Terza minore.Cap. 16.
 Ma considerandola senza alcun mezano suono, cioè nelli suoi estremi solamente, è di vna sola specie: conciosia che (come si è detto dell'altre consonanze) le chorde estreme di vno posto nel graue, & quelle di uno
posto nell'acuto, sono contenute da vna istessa proportione. Dicono li Prattici, che quando le parti delle lor
compositioni sono distanti l'vna dall'altra, di maniera, che l'vna parte occupi qualunque chorda si uoglia graue, & l'altra
occupi qualunque chorda acuta di vno, de gli essempi mostrati disopra, che sono lontane per vn
Semiditono, ouer Terza minore; come sono le due sottoposte.Questo interuallo è chiamato Semiditono,
Ma considerandola senza alcun mezano suono, cioè nelli suoi estremi solamente, è di vna sola specie: conciosia che (come si è detto dell'altre consonanze) le chorde estreme di vno posto nel graue, & quelle di uno
posto nell'acuto, sono contenute da vna istessa proportione. Dicono li Prattici, che quando le parti delle lor
compositioni sono distanti l'vna dall'altra, di maniera, che l'vna parte occupi qualunque chorda si uoglia graue, & l'altra
occupi qualunque chorda acuta di vno, de gli essempi mostrati disopra, che sono lontane per vn
Semiditono, ouer Terza minore; come sono le due sottoposte.Questo interuallo è chiamato Semiditono,
 non gia da Semis parola latina, che vuol dir Mezo, come se fusse mezo
Ditono apunto; ma si bene da Semus: percioche (come vuole Boetio)
in tal maniera si chiama quella cosa, che non ariua al mezo intero: Onde si dice Semituono quello interuallo, che non è lo intero mezo del Tuono: ma è Tuono imperfetto. Si dice adunque il Semiditono, Ditono imperfetto: conciosia che è diminuto di vn Semituono minore,
contenuto dalla
proportione Sesquiuentesima quarta. Lo nominano anco Terza, dal numero delle chorde, & le aggiungono Minore: percioche li suoi estremi
sono più ristretti, & di minor proportione, che non sono quelli del Ditono.
Ma questo sia detto a bastanza intorno a quelli interualli, che veramente
sono consonanti.
non gia da Semis parola latina, che vuol dir Mezo, come se fusse mezo
Ditono apunto; ma si bene da Semus: percioche (come vuole Boetio)
in tal maniera si chiama quella cosa, che non ariua al mezo intero: Onde si dice Semituono quello interuallo, che non è lo intero mezo del Tuono: ma è Tuono imperfetto. Si dice adunque il Semiditono, Ditono imperfetto: conciosia che è diminuto di vn Semituono minore,
contenuto dalla
proportione Sesquiuentesima quarta. Lo nominano anco Terza, dal numero delle chorde, & le aggiungono Minore: percioche li suoi estremi
sono più ristretti, & di minor proportione, che non sono quelli del Ditono.
Ma questo sia detto a bastanza intorno a quelli interualli, che veramente
sono consonanti.
Dell'vtile che apportano nella Musica gli Interualli dissonanti.Cap. 17.
Del Tuono maggiore, & del minore.Cap. 18.
 ; & a,
; & a,  senza alcun mezo; come qui si vede.Ma il minore segue sem
senza alcun mezo; come qui si vede.Ma il minore segue sem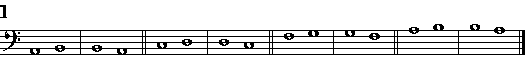 pre il maggiore verso l'acuto, &
tiene sempre lo interuallo, che è
il terzo di ciascun Tetrachordo
nella parte acuta; come nello essempio si uede.Hauemo adunque nel genere Diatonico due specie di Tuono, cioè il Tuono maggiore, &
pre il maggiore verso l'acuto, &
tiene sempre lo interuallo, che è
il terzo di ciascun Tetrachordo
nella parte acuta; come nello essempio si uede.Hauemo adunque nel genere Diatonico due specie di Tuono, cioè il Tuono maggiore, &
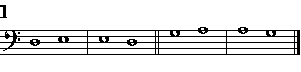 il minore: però quando noi ritrouaremo due parti nelli contrapunti,
che saranno distanti l'una dall'altra per vno di questi interualli, diremo, che quelle sono lontane per vn Tuono maggiore, ouer minore;
oueramente diremo, che siano distanti per vna Seconda maggiore:
conciosia che cosi è nominato da i Prattici tale interuallo, a differenza della minore, che è il Semituono maggiore: & è cosi chiamata dal numero delle sue chorde, le quali
il minore: però quando noi ritrouaremo due parti nelli contrapunti,
che saranno distanti l'una dall'altra per vno di questi interualli, diremo, che quelle sono lontane per vn Tuono maggiore, ouer minore;
oueramente diremo, che siano distanti per vna Seconda maggiore:
conciosia che cosi è nominato da i Prattici tale interuallo, a differenza della minore, che è il Semituono maggiore: & è cosi chiamata dal numero delle sue chorde, le quali
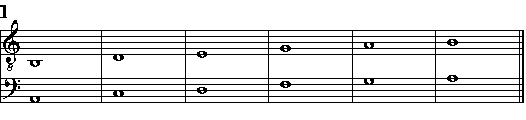 contengono questi interualli, che sono diatonici; come nello essempio posto di sopra si veggono.
contengono questi interualli, che sono diatonici; come nello essempio posto di sopra si veggono.
del Semituono maggiore, & del minore.Cap. 19.
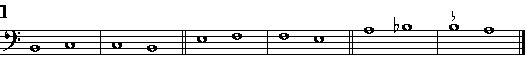 de poste in questo essempio: Guidone pose il Semituono nel mezo di ciascun Essachordo, come
in luogo più degno, & più honorato; nel quale
(come si dice) consiste la Virtù: conciosia che
la eccellenza, & nobilità sua è tale, che senza
lui ogni cantilena sarebbe aspra, & insoportabile da vdire: ne si potrebbe hauere alcuna harmonia, che fusse perfetta, senza il suo mezo. Questo è detto Maggiore, a differenza del Minore, che si ritroua in acuto
de poste in questo essempio: Guidone pose il Semituono nel mezo di ciascun Essachordo, come
in luogo più degno, & più honorato; nel quale
(come si dice) consiste la Virtù: conciosia che
la eccellenza, & nobilità sua è tale, che senza
lui ogni cantilena sarebbe aspra, & insoportabile da vdire: ne si potrebbe hauere alcuna harmonia, che fusse perfetta, senza il suo mezo. Questo è detto Maggiore, a differenza del Minore, che si ritroua in acuto
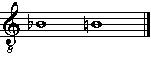 ascendendo, tra le chorde
ascendendo, tra le chorde  &
&  : o per il contrario, il quale non si adopera nel genere Diatonico, & è il sottoposto.Quando adunque l'vna delle parti delle
nostre
Canzoni sarà lontana dall'altra per vno delli gradi acuti de i mostrati essempi, & l'altra per vno delli graui; allora diremo, che quelle sono distanti per un Semituono magpage 165
: o per il contrario, il quale non si adopera nel genere Diatonico, & è il sottoposto.Quando adunque l'vna delle parti delle
nostre
Canzoni sarà lontana dall'altra per vno delli gradi acuti de i mostrati essempi, & l'altra per vno delli graui; allora diremo, che quelle sono distanti per un Semituono magpage 165 giore, ouer per una Seconda maggiore; come nell'essempio si uede. Fù chiamato Semituono, per le ragioni, ch'io dissi parlando nel cap. 16. del Semiditono, da quella voce
Semus, che vuol dir Sciemo, & Imperfetto: percioche il Tuono non è mai diminuto,
ouer fatto imperfetto della sua meza parte intera; come la esperienza lo dimostra: essendo che niuna proportione (come hò
detto più volte) si possa diuidere in due parti equali.
Ma questo sia detto a bastanza intorno gli interualli diatonici, contenuti dalle proportioni Moltiplici, & dalle Superparticolari.
giore, ouer per una Seconda maggiore; come nell'essempio si uede. Fù chiamato Semituono, per le ragioni, ch'io dissi parlando nel cap. 16. del Semiditono, da quella voce
Semus, che vuol dir Sciemo, & Imperfetto: percioche il Tuono non è mai diminuto,
ouer fatto imperfetto della sua meza parte intera; come la esperienza lo dimostra: essendo che niuna proportione (come hò
detto più volte) si possa diuidere in due parti equali.
Ma questo sia detto a bastanza intorno gli interualli diatonici, contenuti dalle proportioni Moltiplici, & dalle Superparticolari.
Dello Essachordo maggiore, ouero Sesta maggiore.Cap. 20.
 Li Musici chiamano questo interuallo Essachordo, per il numero delle chorde, che contiene, che sono Sei: Percioche appresso de i Greci tanto vuol dire Ε῞ξ, quanto significa Sei appresso di noi; & similmente tanto uuol
dire Χορδὴ appresso di loro, quanto Chorda appresso di noi. Onde è detto Interuallo, che contiene Sei chorde;
ouero Consonanza di sei uoci: percioche è compreso da tal numero di chorde. La onde li Prattici lo chiamano
Li Musici chiamano questo interuallo Essachordo, per il numero delle chorde, che contiene, che sono Sei: Percioche appresso de i Greci tanto vuol dire Ε῞ξ, quanto significa Sei appresso di noi; & similmente tanto uuol
dire Χορδὴ appresso di loro, quanto Chorda appresso di noi. Onde è detto Interuallo, che contiene Sei chorde;
ouero Consonanza di sei uoci: percioche è compreso da tal numero di chorde. La onde li Prattici lo chiamano
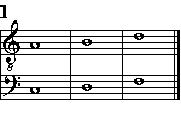 Sesta maggiore, a differenza della minore, la quale è compresa da minor proportione; & dicono, che la Sesta maggiore, ouero
il maggiore Essachordo è
vna compositione di sei voci, ouersuoni, che contiene quattro Tuoni, & vn
Semituono maggiore. Quando adunque saranno due parti nelli nostri contrapunti, distanti l'vna dall'altra per il graue, & per l'acuto, secondo la ragione de gli estremi di alcuno delli sopraposti essempi; allora diremo, che tal parti seranno distanti l'vna dall'altra per vno Essachordo, ouer Sesta maggiore; come qui in essempio si uede. page 166
Sesta maggiore, a differenza della minore, la quale è compresa da minor proportione; & dicono, che la Sesta maggiore, ouero
il maggiore Essachordo è
vna compositione di sei voci, ouersuoni, che contiene quattro Tuoni, & vn
Semituono maggiore. Quando adunque saranno due parti nelli nostri contrapunti, distanti l'vna dall'altra per il graue, & per l'acuto, secondo la ragione de gli estremi di alcuno delli sopraposti essempi; allora diremo, che tal parti seranno distanti l'vna dall'altra per vno Essachordo, ouer Sesta maggiore; come qui in essempio si uede. page 166Dello Essachordo monore, ouero Sesta minore.Cap. 21.
 Ma quando fusse considerato nelli suoi estremi solamente, senza esser tramezato da alcuna chorda mezana;
si trouerebbe di lui vna sola specie, per le ragioni dette de gli altri interualli. Et ancora che non si possa chiamare assolutamente Semplice: percioche li suoi termini radicali sono tramezati dal numero Senario in cotal
modo 5. 6. 8; come si può uedere tra li numeri harmonici, posti nel cap. 15. della Prima parte; onde lo potemo chiamar composto della Diatessaron, & del Semiditono; Tuttauia per le ragioni dette dello Essachordo maggiore, lo chiamaremo anco lui Semplice ad vn certo modo. Quando adunque due parti delli no
Ma quando fusse considerato nelli suoi estremi solamente, senza esser tramezato da alcuna chorda mezana;
si trouerebbe di lui vna sola specie, per le ragioni dette de gli altri interualli. Et ancora che non si possa chiamare assolutamente Semplice: percioche li suoi termini radicali sono tramezati dal numero Senario in cotal
modo 5. 6. 8; come si può uedere tra li numeri harmonici, posti nel cap. 15. della Prima parte; onde lo potemo chiamar composto della Diatessaron, & del Semiditono; Tuttauia per le ragioni dette dello Essachordo maggiore, lo chiamaremo anco lui Semplice ad vn certo modo. Quando adunque due parti delli no stri contrapunti saranno distanti l'vna dall'altra per il graue, & per lo acuto, secondo la ragione delle chorde estreme di alcuno delli mostrati essempij, allora potremo dire, che saranno distanti per vno Essachordo, o Sesta minore; come qui in essempio si ritroua. Questo etiandio si chiama Essachordo per le ragioni dette dello Essachordo maggiore, la onde
a sua differenza gli aggiunsero, Minore: & tanto l'uno, quanto l'altro non erano connumerati da gli Antichi tra
le consonanze: conciosiache le loro estreme chorde sono tirate sotto le ragioni delle proportioni predette, le quali si ritrouano
esser connumerate tra quelle del genere Superpartiente. Ma perche li Musici moderni le pongono in cotale ordine;
& per che sono composte (se cosi le vogliam considerare) della Diatessaron, &
del Ditono, ouer Semiditono; che poste insieme, non possono essere se non consonanti, quando sono collocati a
i loro luoghi propij; però hò voluto far di loro particolar mentione, & mostrar le loro specie. Onde facendo
hora fine di ragionar più di quelli interualli, le cui proportioni sono comprese nel genere Moltiplice, & nel
Superparticolare; & di quelli, che hanno le lor forme nel genere Superpartiente, & sono accettati da ciascuno Musico per consonanti;
verrò a ragionar di quelli, che hanno le lor forme in questo genere istesso, & sono al tutto Dissonanti.
stri contrapunti saranno distanti l'vna dall'altra per il graue, & per lo acuto, secondo la ragione delle chorde estreme di alcuno delli mostrati essempij, allora potremo dire, che saranno distanti per vno Essachordo, o Sesta minore; come qui in essempio si ritroua. Questo etiandio si chiama Essachordo per le ragioni dette dello Essachordo maggiore, la onde
a sua differenza gli aggiunsero, Minore: & tanto l'uno, quanto l'altro non erano connumerati da gli Antichi tra
le consonanze: conciosiache le loro estreme chorde sono tirate sotto le ragioni delle proportioni predette, le quali si ritrouano
esser connumerate tra quelle del genere Superpartiente. Ma perche li Musici moderni le pongono in cotale ordine;
& per che sono composte (se cosi le vogliam considerare) della Diatessaron, &
del Ditono, ouer Semiditono; che poste insieme, non possono essere se non consonanti, quando sono collocati a
i loro luoghi propij; però hò voluto far di loro particolar mentione, & mostrar le loro specie. Onde facendo
hora fine di ragionar più di quelli interualli, le cui proportioni sono comprese nel genere Moltiplice, & nel
Superparticolare; & di quelli, che hanno le lor forme nel genere Superpartiente, & sono accettati da ciascuno Musico per consonanti;
verrò a ragionar di quelli, che hanno le lor forme in questo genere istesso, & sono al tutto Dissonanti.
Del Diapente col Ditono; ouero della Settima maggiore.Capo. 22.
 Li Prattici lo nominano Settima de numero delle voci, o de i suoni, che sono contenuti in esso; & lo chia
Li Prattici lo nominano Settima de numero delle voci, o de i suoni, che sono contenuti in esso; & lo chia mano anco Eptachordo, da Ε῾πτὰ, che significa Sette, & da Χορδὴ, che vuol dire Chorda; & a differenza del minore gli aggiungono questa particella Maggiore. Diremo etiandio di esso quello, che si è detto de gli altri interualli; che tutte le
volte, che si ritrouerà in alcuna cantilena due parti, che siano poste, l'una nelle
chorde graui delli mostrati essempi, & l'altra nell'acuta; che tali parti saranno distanti l'vna dall'altra per vna Settima maggiore, oueramente per vno Eptachordo maggiore; come sono queste due parti di questo essempio.
mano anco Eptachordo, da Ε῾πτὰ, che significa Sette, & da Χορδὴ, che vuol dire Chorda; & a differenza del minore gli aggiungono questa particella Maggiore. Diremo etiandio di esso quello, che si è detto de gli altri interualli; che tutte le
volte, che si ritrouerà in alcuna cantilena due parti, che siano poste, l'una nelle
chorde graui delli mostrati essempi, & l'altra nell'acuta; che tali parti saranno distanti l'vna dall'altra per vna Settima maggiore, oueramente per vno Eptachordo maggiore; come sono queste due parti di questo essempio.
Della Diapente col Semiditono, ouer Settima minore.Cap. 23
 Dal numero delle chorde i Prattici lo chiamarono Settima; è ben vero che vi aggiunsero questa parola Minore, per farlo differente dal maggiore. Lo nominarono etiandio Eptachordo minore, da quelle due parole
greche poste di sopra nel capitolo precedente. Quando adunque saranno due parti distanti l'vna dall'altra, come sono le chorde estreme delli sopraposti essempi, allora diremo, che sono lontani per vna Settima minore:
cone sono le sottoposte. Qui porrò fine al ragionare delle Consonanze, & de gli altri Interualli semplici; lassando
Dal numero delle chorde i Prattici lo chiamarono Settima; è ben vero che vi aggiunsero questa parola Minore, per farlo differente dal maggiore. Lo nominarono etiandio Eptachordo minore, da quelle due parole
greche poste di sopra nel capitolo precedente. Quando adunque saranno due parti distanti l'vna dall'altra, come sono le chorde estreme delli sopraposti essempi, allora diremo, che sono lontani per vna Settima minore:
cone sono le sottoposte. Qui porrò fine al ragionare delle Consonanze, & de gli altri Interualli semplici; lassando
 etiandio, per più breuità, di ragionare delli Composti: conciosia
che ogn'altro qual si uoglia, che sia maggior della Diapason, si
considera composto di lei, & di vna sua parte; & non sarà molto difficile, quando si vorrà sapere la loro ragione, la quale sempre
potremo hauere, quando noi aggiungeremo sopra la Diapason quell'altro interuallo, che le vorremo porre appresso, sommando insieme i termini radicali, che contengono ta li interualli. Dirò ben
questo, che gli estremi suoni della Diapasondiapente, ouer Duodecima, sono contenuti dalla proportione Tripla; quelli della Disdiapason, ouer Quintadecima, dalla Quadrupla; quelli della Disdiapason col
Ditono, ouer Decimasettima, dalla Quintupla; & quelli della Disdiapasondiapente, ouer Decimanona, dalla Sestupla: ma gli altri si potranno inuestigar facilmente con la ragione.
etiandio, per più breuità, di ragionare delli Composti: conciosia
che ogn'altro qual si uoglia, che sia maggior della Diapason, si
considera composto di lei, & di vna sua parte; & non sarà molto difficile, quando si vorrà sapere la loro ragione, la quale sempre
potremo hauere, quando noi aggiungeremo sopra la Diapason quell'altro interuallo, che le vorremo porre appresso, sommando insieme i termini radicali, che contengono ta li interualli. Dirò ben
questo, che gli estremi suoni della Diapasondiapente, ouer Duodecima, sono contenuti dalla proportione Tripla; quelli della Disdiapason, ouer Quintadecima, dalla Quadrupla; quelli della Disdiapason col
Ditono, ouer Decimasettima, dalla Quintupla; & quelli della Disdiapasondiapente, ouer Decimanona, dalla Sestupla: ma gli altri si potranno inuestigar facilmente con la ragione.
In qual maniera naturalmente, o per accidente tali interualli da i Prattici alle volte si ponghino superflui, o diminuti.Cap. 24.
 ad F, collocata tra cinque chorde, è senza dubbio alcuno
diminuta di vn Semituono minore: percioche in luogo di tre Tuoni, & di vno Semituono maggiore, contiene due Tuoni, & due Semituoni; & è ne li suoi estremi dissonante: perche è contenuta dalla proportione
Super 19 partiente 45, che non hà luogo tra i numeri harmonici; & perciò la chiamano Semidiapente, &
Quinta imperfetta, ouer diminuta. Il medesimo potemo dir della Quarta contenuta nel numero di quattro
chorde, tra F &
ad F, collocata tra cinque chorde, è senza dubbio alcuno
diminuta di vn Semituono minore: percioche in luogo di tre Tuoni, & di vno Semituono maggiore, contiene due Tuoni, & due Semituoni; & è ne li suoi estremi dissonante: perche è contenuta dalla proportione
Super 19 partiente 45, che non hà luogo tra i numeri harmonici; & perciò la chiamano Semidiapente, &
Quinta imperfetta, ouer diminuta. Il medesimo potemo dir della Quarta contenuta nel numero di quattro
chorde, tra F &  , che per ritrouarsi in lei tre Tuoni, è chiamata Tritono; & è superflua di vn Semituono minore. La onde non essendo le sue chorde estreme contenute sotto le proportioni de gli harmonici numeri: percioche la sua forma è contenuta dalla Super 13 partiente 32, è sopramodo dissonante; & sono li sottoposti interualli. Questo errore non solamente può accascare nella Quinta, et nella Quarta: ma etiandio nella page 169
, che per ritrouarsi in lei tre Tuoni, è chiamata Tritono; & è superflua di vn Semituono minore. La onde non essendo le sue chorde estreme contenute sotto le proportioni de gli harmonici numeri: percioche la sua forma è contenuta dalla Super 13 partiente 32, è sopramodo dissonante; & sono li sottoposti interualli. Questo errore non solamente può accascare nella Quinta, et nella Quarta: ma etiandio nella page 169 Ottaua: percioche se'l si hauerà riguardo al numero delle chorde solamente, che si ritrouano tra la chorda
Ottaua: percioche se'l si hauerà riguardo al numero delle chorde solamente, che si ritrouano tra la chorda  & la
& la  , diremo che tale Ottaua sia senza alcun dubbio diminuta di un Semituono minore: essendo che è
contenuta nelle sue estreme chorde dalla proportione Super 13 partiente 25; onde è dissonante quanto si può
dire; & si vede posta tra le chorde diatoniche del sottoposto essempio, et si può anco nominare Semidiapason.
, diremo che tale Ottaua sia senza alcun dubbio diminuta di un Semituono minore: essendo che è
contenuta nelle sue estreme chorde dalla proportione Super 13 partiente 25; onde è dissonante quanto si può
dire; & si vede posta tra le chorde diatoniche del sottoposto essempio, et si può anco nominare Semidiapason.
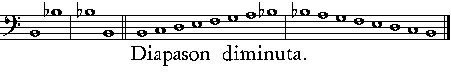 Simili errori si possono ancora commettere tra le chorde diatoniche, & le chromatiche: percioche se noi porremo la chorda
Simili errori si possono ancora commettere tra le chorde diatoniche, & le chromatiche: percioche se noi porremo la chorda  posta in acuto, tra la c & la d, per l'uno de gli estremi della Ottaua; & la chorda C
posta nel graue per l'altro estremo; haueremo vna Ottaua dissonantissima, contenuta dalla proportione Dupla sesquiduodecima, & sarà vna Diapason superflua di vn Semituono minore. Onde se di nuouo pigliaremo
la detta chorda
posta in acuto, tra la c & la d, per l'uno de gli estremi della Ottaua; & la chorda C
posta nel graue per l'altro estremo; haueremo vna Ottaua dissonantissima, contenuta dalla proportione Dupla sesquiduodecima, & sarà vna Diapason superflua di vn Semituono minore. Onde se di nuouo pigliaremo
la detta chorda  con la F, haueremo una Quinta dissonante, contenuta dalla proportione Super 9 partiente 16, detta Diapente superflua. La medesima chorda ancora accompagnata alla G ne darà il Tritono: che contiene tre Tuoni; come nel sotto posto essempio si vede.
con la F, haueremo una Quinta dissonante, contenuta dalla proportione Super 9 partiente 16, detta Diapente superflua. La medesima chorda ancora accompagnata alla G ne darà il Tritono: che contiene tre Tuoni; come nel sotto posto essempio si vede.
 Tutti questi interualli si potranno diminuire della istessa quantità, quando pigliaremo la chorda chromatica
Tutti questi interualli si potranno diminuire della istessa quantità, quando pigliaremo la chorda chromatica
 posta nel graue, tra la C & la D, in luogo della C, & faremo la ottaua
posta nel graue, tra la C & la D, in luogo della C, & faremo la ottaua  & c: percioche allora tale Ottaua sarà minuita di vn Semituono minore, & contenuta dalla proportione Super 23 partiente 25, che è minor della Dupla, la onde si chiama Semidiapason. Similmente tal chorda accompagnata con
la G ne darà vna Semidiapente, contenuta dalla Super 11 partiente 25; & accompagnata con la F ne
darà la Semidiatessaron, compresa sotto la forma della proportione Super 21 partiente 75, la quale insieme con le altre sono contenute nel sotto posto essempio, & sono al tutto dissonanti.
& c: percioche allora tale Ottaua sarà minuita di vn Semituono minore, & contenuta dalla proportione Super 23 partiente 25, che è minor della Dupla, la onde si chiama Semidiapason. Similmente tal chorda accompagnata con
la G ne darà vna Semidiapente, contenuta dalla Super 11 partiente 25; & accompagnata con la F ne
darà la Semidiatessaron, compresa sotto la forma della proportione Super 21 partiente 75, la quale insieme con le altre sono contenute nel sotto posto essempio, & sono al tutto dissonanti.
 Questi, & tutti gli altri interualli mostrati disopra sono dissonantissimi, & non si debbeno porre ne i Contrapunti: perche generarebbeno fastidio all'vdito. Onde non senza giuditio, i Musici prattici più periti diedero
vna Regola, per chiuar questi errori, Che non si douesse mai porre la voce del Mi contra quella del Fa, nelle
consonanze perfette; come più oltra vederemo. Si debbe però auertire, che alle volte si pone la Semidiapente ne i Contrapunti in luogo della Diapente; similmente il Tritono in luogo della Diatessaron, che fanno buopage 170ni effetti: ma in qual maniera si habbiano a porre, lo dimostrerò più oltra. Quando adunque ritrouaremo due
parti, l'una delle quali nell'acuto tenghi il luogo di alcuna delle chorde estreme, di alcuno delli mostrati essempi; & l'altra tenghi il luogo di alcuna posta nel graue; allora diremo, che saranno distanti l'vna dall'altra
Questi, & tutti gli altri interualli mostrati disopra sono dissonantissimi, & non si debbeno porre ne i Contrapunti: perche generarebbeno fastidio all'vdito. Onde non senza giuditio, i Musici prattici più periti diedero
vna Regola, per chiuar questi errori, Che non si douesse mai porre la voce del Mi contra quella del Fa, nelle
consonanze perfette; come più oltra vederemo. Si debbe però auertire, che alle volte si pone la Semidiapente ne i Contrapunti in luogo della Diapente; similmente il Tritono in luogo della Diatessaron, che fanno buopage 170ni effetti: ma in qual maniera si habbiano a porre, lo dimostrerò più oltra. Quando adunque ritrouaremo due
parti, l'una delle quali nell'acuto tenghi il luogo di alcuna delle chorde estreme, di alcuno delli mostrati essempi; & l'altra tenghi il luogo di alcuna posta nel graue; allora diremo, che saranno distanti l'vna dall'altra
 per uno delli detti interualli; come qui
si vede. Qui si hauerebbe potuto porre molti altri essempi, & mostrar
più in lungo in quante maniere tali interualli si accrescono, & minuiscono,
col mezo delle chorde chromatiche:
ma per non andare in lungo, gli hò voluti lassare. Similmente si hauerebbe
potuto mostrare in qual modo, per uia
delle istesse chorde chromatiche, il Ditono diuenti Semiditono; & il Semiditono Ditono: ma perche cambiandosi in tal maniera,
non fanno alcuno interuallo dissonante; però hò voluto etiandio lassar da parte tal ragionamento; accioche io possa dichiarare, & mostrar
gli effetti, che fanno questi tre segni; cioè il
per uno delli detti interualli; come qui
si vede. Qui si hauerebbe potuto porre molti altri essempi, & mostrar
più in lungo in quante maniere tali interualli si accrescono, & minuiscono,
col mezo delle chorde chromatiche:
ma per non andare in lungo, gli hò voluti lassare. Similmente si hauerebbe
potuto mostrare in qual modo, per uia
delle istesse chorde chromatiche, il Ditono diuenti Semiditono; & il Semiditono Ditono: ma perche cambiandosi in tal maniera,
non fanno alcuno interuallo dissonante; però hò voluto etiandio lassar da parte tal ragionamento; accioche io possa dichiarare, & mostrar
gli effetti, che fanno questi tre segni; cioè il  quadrato, il
quadrato, il  molle, & il
molle, & il  Diesis.
Diesis.
De gli effetti che fanno questi segni.  .
.  .
.  .Cap. 25.
.Cap. 25.
 , & il
, & il  , che si veggono nel sottoposto essempio: percioche la voce, o chor
, che si veggono nel sottoposto essempio: percioche la voce, o chor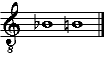 da segnata col
da segnata col  , è più acuta di quella, che è segnata col
, è più acuta di quella, che è segnata col  . La onde Guidone
Aretino, per non confondere li Cantori, pose nel suo Introduttorio le due lettere, o cifere mostrate differenti, & non variò il luogo; & volse, che per l'vna di
esse si intendesse la chorda Tritesynemennon, & per l'altra la chorda Paramese.
Vedendo dipoi li Musici questa differenza, ordinarono due sorti di cantilena, l'vna delle quali chiamarono di Natura, & di
. La onde Guidone
Aretino, per non confondere li Cantori, pose nel suo Introduttorio le due lettere, o cifere mostrate differenti, & non variò il luogo; & volse, che per l'vna di
esse si intendesse la chorda Tritesynemennon, & per l'altra la chorda Paramese.
Vedendo dipoi li Musici questa differenza, ordinarono due sorti di cantilena, l'vna delle quali chiamarono di Natura, & di  quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, & per quelle del Tetrachordo Diezeugmenon; & non si pone nel principio delle parti della cantilena alcuna delle mostrate cifere. L'altra nominarono di Natura, & di
quadrato; & è quella, che procede per le chorde del Tetrachordo Meson, & per quelle del Tetrachordo Diezeugmenon; & non si pone nel principio delle parti della cantilena alcuna delle mostrate cifere. L'altra nominarono di Natura, & di  molle; & questo quando
le parti toccano le chorde del Tetrachordo Synemennon, & quelle del Tetrachordo Meson; lassando da un
canto quelle, che sono del Tetrachordo Diezeugmenon; & in questa sorte di canzone si pone nel principio
delle parti della cantilena la cifera, ouer segno del
molle; & questo quando
le parti toccano le chorde del Tetrachordo Synemennon, & quelle del Tetrachordo Meson; lassando da un
canto quelle, che sono del Tetrachordo Diezeugmenon; & in questa sorte di canzone si pone nel principio
delle parti della cantilena la cifera, ouer segno del  molle, auanti i segni del Tempo. Et se bene nelle cantilene, che procedeno per il Tetrachordo Meson, & per il Diezeugmenon, non si pone la cifera del
molle, auanti i segni del Tempo. Et se bene nelle cantilene, che procedeno per il Tetrachordo Meson, & per il Diezeugmenon, non si pone la cifera del  ; nondimeno ue la intendeno: et tal cifera si ritroua ne i Libri ecclesiastici, cioè ne i Canti fermi molto spesso, se bene
ne i Canti figurati sia stata, et è anco poco vsata: percioche i Moderni quando vogliono porre alle volte la chorda Paramese in luogo della Tritesynemennon, pongono la cifera
; nondimeno ue la intendeno: et tal cifera si ritroua ne i Libri ecclesiastici, cioè ne i Canti fermi molto spesso, se bene
ne i Canti figurati sia stata, et è anco poco vsata: percioche i Moderni quando vogliono porre alle volte la chorda Paramese in luogo della Tritesynemennon, pongono la cifera  in luogo del
in luogo del  ; ancora che tal cosa si faccia contra ogni douere: conciosiache si douerebbe vsare la propia cifera della cosa, che vogliono intendere, et non vn'altro
segno forestiero: quantunque questo importi poco: percioche hormai ogn'vn conosce, qual chorda si hà da vsare in luogo
della Tritesynemennon, quando pongono la cifera del
; ancora che tal cosa si faccia contra ogni douere: conciosiache si douerebbe vsare la propia cifera della cosa, che vogliono intendere, et non vn'altro
segno forestiero: quantunque questo importi poco: percioche hormai ogn'vn conosce, qual chorda si hà da vsare in luogo
della Tritesynemennon, quando pongono la cifera del  : Ma in vero io lodarei molto, che si vsasse il segno propio.
Per tornare adunque a gli effetti, che fanno cotali Cifere dico, che leuano, ouer aggiungono il Semituono minore: Impage 171peroche se noi vorremo essaminare con diligenza il primo delli due sottoposti essempi, ritrouaremo, che dalla
prima figura alla seconda, vi è lo interuallo del Tuono; Onde se tra loro porremo il segno del
: Ma in vero io lodarei molto, che si vsasse il segno propio.
Per tornare adunque a gli effetti, che fanno cotali Cifere dico, che leuano, ouer aggiungono il Semituono minore: Impage 171peroche se noi vorremo essaminare con diligenza il primo delli due sottoposti essempi, ritrouaremo, che dalla
prima figura alla seconda, vi è lo interuallo del Tuono; Onde se tra loro porremo il segno del  , come si ve
, come si ve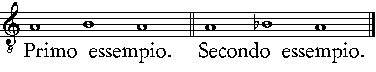 de nel secondo essempio; non è dubbio, che verremo a leuare dalla
parte acuta del detto Tuono il Semituono minore; & tra le figure del secondo essempio, si ritrouerà il Semituono maggiore: perche dalla diuisione del Tuono, fatta per la chorda Tritesynemennon, nasce il Semituono maggiore, & il minore; come altroue
si è detto. Similmente il
de nel secondo essempio; non è dubbio, che verremo a leuare dalla
parte acuta del detto Tuono il Semituono minore; & tra le figure del secondo essempio, si ritrouerà il Semituono maggiore: perche dalla diuisione del Tuono, fatta per la chorda Tritesynemennon, nasce il Semituono maggiore, & il minore; come altroue
si è detto. Similmente il  fà vn tale effetto, nel secondo delli
sottoposti essempi: perche si come tra le figure del primo si ritroua il Tuono, cosi posta la chorda
fà vn tale effetto, nel secondo delli
sottoposti essempi: perche si come tra le figure del primo si ritroua il Tuono, cosi posta la chorda  in luo
in luo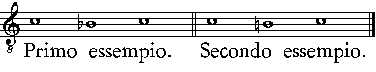 go della
go della  , è rimosso dalla parte graue il minore, & resta il maggior Semituono.Tale effetto farà anco il
, è rimosso dalla parte graue il minore, & resta il maggior Semituono.Tale effetto farà anco il  :
percioche si come tra le figure del primo essempio delli due
sottoposti, si scorge il Tuono; cosi tra quelle del secondo è
posto il Semituono maggiore. Et tutto questo si è detto per
la diminutione dello interuallo del Tuono, col mezo delle
mostrate cifere, o chorde, leuandoli il Semituono minore: Ma se noi vorremo accrescere lo interuallo del Se
:
percioche si come tra le figure del primo essempio delli due
sottoposti, si scorge il Tuono; cosi tra quelle del secondo è
posto il Semituono maggiore. Et tutto questo si è detto per
la diminutione dello interuallo del Tuono, col mezo delle
mostrate cifere, o chorde, leuandoli il Semituono minore: Ma se noi vorremo accrescere lo interuallo del Se mituono maggiore, con lo aggiungerli il minore, si potrà far lo istesso con le predette cifere, o chorde; come nelli sottoposti essempi si vede.
mituono maggiore, con lo aggiungerli il minore, si potrà far lo istesso con le predette cifere, o chorde; come nelli sottoposti essempi si vede.
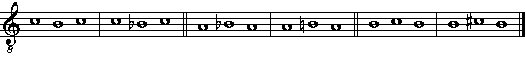 Douemo però auertire, accioche le parti della cantilena riuscischino più facili, & più ageuoli da cantare;
che quando si vorrà porre la chorda del
Douemo però auertire, accioche le parti della cantilena riuscischino più facili, & più ageuoli da cantare;
che quando si vorrà porre la chorda del  , che la figura cantabile, la quale è posta auanti quella, che si vuol
segnare con tal segno, proceda dal graue all'acuto; & quando si vorrà porre il
, che la figura cantabile, la quale è posta auanti quella, che si vuol
segnare con tal segno, proceda dal graue all'acuto; & quando si vorrà porre il  , ouero il
, ouero il  , fare, che procedino al contrario, cioe dall'acuto al graue; & questo: perche (come hò detto) le parti sono più facili da
cantare, & tali interualli sono più ageuoli da proferire, come la esperienza lo dimostra; Ancora che non sarebbe grande errore, quando si facesse altramente.
, fare, che procedino al contrario, cioe dall'acuto al graue; & questo: perche (come hò detto) le parti sono più facili da
cantare, & tali interualli sono più ageuoli da proferire, come la esperienza lo dimostra; Ancora che non sarebbe grande errore, quando si facesse altramente.
Quel che si ricerca in ogni compositione, & prima del Soggetto.Cap. 26.
Aut prodesse volunt, aut delectare poetae:hà nel suo Poema per soggetto la Historia, ouero la Fauola, la quale, o sia stata ritrouata da lui, ouero se l'habbia pigliata da altrui: l'adorna, & polisse in tal maniera con varij costumi, come più gli aggrada, non lassando da parte alcuna cosa, che sia degna, & lodeuole, per dilettar l'animo de gli vditori; che hà poi del magnifico, & marauiglioso; cosi il Musico, oltra che è mosso dallo istesso fine, cioè di giouare, & di dilettare gli animi de gli ascoltanti con gli accenti harmonici, hà il Soggetto, sopra il quale è fondata la sua cantilena, laquale adorna con varie modulationi, & varie harmonie, di modo che porge grato piacere a gli ascoltanti. La Seconda è, che sia composta principalmente di consonanze, dipoi habbia in sè per accidente molte dissonanze, collocate in essa con debiti modi, secondo le Regole, le quali più abasso voglio mostrare. La terza è, che le parti della cantilena procedino bene, cioè che le modulationi procedino per veri, & legittimi interualli, che nascono da i numeri sonori; accioche per il mezo loro acquistiamo l'vso delle buone harmonie. La Quarta conditione, che si ricerca, è, che le modulationi, & il concento sia variato: percioche da altro non nasce l'harmonia, che dalla diuersità delle modulationi, & dalla diuersità delle consonanze, messe insieme con variatione. La Quinta è, che la cantilena sia ordinata sotto vna prescritta, & determinata Harmonia, o Modo, o Tuono, che vogliam dire; & che non sia disordinata: Et la Sesta, & vltima (oltra l'altre, che si potrebbeno aggiungere) è, che l'harmonia, che si contiene in essa, sia talmente accommodata alla Oratione, cioè alle Parole, che nelle materie allegre, l'harmonia non sia flebile; & per il contrario, nelle flebili, l'harmonia non sia allegra. Onde accioche del tutto si habbia perfetta cognitione, verrò à ragionare di tutte queste cose separatamente, secondo che mi verranno al proposito, & secondo il bisogno. Incominciando adunque dalla Prima dico, che il Soggetto di ogni compositione musicale si chiama quella parte, sopra laquale il Compositore caua la inuentione di far le altre parti della cantilena, siano quante si vogliano. Et tal Soggetto può essere in molti modi: prima può essere inuentione propia, cioè, che il Compositore l'hauerà ritrouato col suo ingegno; dipoi può essere, che l'habbia pigliato dalle altrui compositioni, accommodandolo alla sua cantilena, & adornandolo con varie parti, & varie modulationi, come più gli aggrada, secondo la grandezza del suo ingegno. Et tal Soggetto si può ritrouare di più sorte: percioche può essere vn Tenore, ouero altra parte di qualunque cantilena di Canto fermo, ouero di Canto figurato; ouero potranno esser due, o più parti, che l'vna seguiti l'altra in Fuga, o Consequenza, ouero a qualunque altro modo: essendo che li varij modi di tali Soggetti sono infiniti. Ritrouato adunque che hauerà il Compositore il Soggetto, farà poi le altre parti, nel modo che più oltra vederemo; Il che fatto tal maniera di comporre si chiamerà, secondo li Prattici, Far contrapunto. Ma quando non hauerà ritrouato prima il Soggetto; quella parte, che sarà primieramente messa in atto; ouer quella con la quale il Compositore darà principio alla sua cantilena, sia qual si voglia, & incomincia a qual modo più li piace; o sia graue, oueramente acuta, o mezana; sempre sarà il Soggetto, sopra il quale poi accommodarà le altre in Fuga, o Consequenza, ouero ad altro modo, come più li piacerà di fare; accommodando le harmonie alle parole, secondo che ricerca la materia contenuta in esse. Ma quando il Compositore andrà cauando il Soggetto dalle parti della cantilena, cioè quando cauerà vna parte dall'altra, & andrà cauando il Soggetto per tal maniera, & facendo insieme la compositione, come uederemo altroue; quella particella, che lui cauerà fuori delle altre, sopra laquale dipoi componerà le parti della sua compositione, si chiamerà sempre il Soggetto. Et tal modo di comporre li Prattici dimandano Comporre di fantasia: ancorache si possa etiandio nominare Contrapuntizare, o Far contraponto, come si vuole.
Aut simul et iucunda, et idonea dicere vitae;
Che le Compositioni si debbeno comporre primieramente di Consonanze, & dipoi per accidente di Dissonanze.Cap. 27.
Che si debbe dar principio alle compositioni per vna delle Consonanze perfette.Cap. 28.
 Il medesimo douemo osseruare ne i Principij delli Contrapunti, o Compositioni, quando si ponesse nel principio della parte del Soggetto alcuna Pausa; come intrauiene quando si piglia vn Tenore di qualche Canzone,
o Madrigale, o di altra cantilena, per comporli sopra le altre parti: percioche allora le parti, che si aggiungono, si debbeno incominciare al modo mostrato, osseruando quello, che intorno ciò è stato detto; come si vede ne i sottoposti essempi, delli quali il Sogggetto è composto nel Quarto modo. page 175
Il medesimo douemo osseruare ne i Principij delli Contrapunti, o Compositioni, quando si ponesse nel principio della parte del Soggetto alcuna Pausa; come intrauiene quando si piglia vn Tenore di qualche Canzone,
o Madrigale, o di altra cantilena, per comporli sopra le altre parti: percioche allora le parti, che si aggiungono, si debbeno incominciare al modo mostrato, osseruando quello, che intorno ciò è stato detto; come si vede ne i sottoposti essempi, delli quali il Sogggetto è composto nel Quarto modo. page 175 Si debbe etiandio auertire (il che è cosa di non poca importanza) di ordinare nelle Compositioni, & ne i Contrapunti a più voci in tal maniera le parti, che i loro principij corrispondino tra loro, & habbiano relatione
per vna delle consonanze perfette, ouero imperfette; di modo che volendole cantare, nel pigliar le voci delle parti, non si oda alcuna dissonanza. Et questo, percioche non solo porge fastidio a quelli, che vogliono cantare: ma alle
volte è cagione di farli errare più facilmente, pigliando vna voce per vn'altra; massimamente quando non sono molto sicuri. E ben vero, che è lecito porre nel graue il principio di due parti, che siano
distanti l'vna dall'altra per vna Quarta, senza esserui alcun'altra parte più graue, alle quali le altre parti
corrispondino per Ottaua; massimamente ne i Modi placali, ouero Impari, che li vogliamo dire; quando le
parti della cantilena incominciano a cantare sopra le chorde principali de i loro Modi, ne i quali è composta: Conciosiache volendo torre questa libertà al Compositore, di poter porre due parti in tal maniera, non è cosa honesta; massimamente potendolo fare a due voci; & sarebbe farlo Soggeto, & obligato
ad vna cosa fuori di ogni proposito: essendo che lo incominciare in tal modo è stato posto in vso da molti Prattici periti; si come da Iosquino, da Motone, & da altri ancora antichi, & moderni Musici; & di ciò potemo hauere lo essempio nel Motetto che fece Adriano a cinque voci Laus tibi sacra rubens; Lassandone infiniti altri de moderni, & antichi compositori. Tal licenza presi io anche in quelli tre motetti, Osculetur me
osculis oris sui; Ego rosa Saron; & Capite nobis vulpes paruulas; i quali già composi a cinque voci; come
ogn'vno potrà vedere; & saranno essempio alle cose, che di sopra sono state dette. Questo adunque si concede a tutti li Compositori: ma non è però da lodare, che due parti siano distanti ne i loro principij dalla parte
del Soggetto, o nel graue, o nello acuto, l'vna per vna Quarta, & l'altra per vna Quinta: percioche allora queste parti verrebbeno ad esser distanti l'vna dall'altra per vna Seconda, & nel pigliar le voci farebbeno dissonanza, & potrebbe essere, che l'una di esse parti facesse il suo principio sopra vna chorda, che non sarebbe del Modo,
sopra'l quale è fondata la compositione, o cantilena. Et quantunque tale auertimento sia buono, tuttauia non è necessario,
quando il Soggetto principale della compositione fusse composto con tale arteficio, che l'vna parte cantasse sopra l'altra in Fuga, o Consequenza, di modo che due di loro cantassero sopra
la parte principale del Soggetto, nell'acuto, ouer nel graue, l'vna distante dall'altra per vna Quinta, ouero
per vna Quarta: oueramente che l'vna fusse distante dal Soggetto per vna Quarta, et l'altra per vna Quinta, o per altro interuallo;
Si come si puo vedere nel motetto Pater de celis deus, che fece P. della Rue a sei
voci, & nel motetto Virgo prudentissima, che gia composi à sei voci, nel quale tre parti cantano in fuga, o
consequenza, due verso l'acuto, & vna verso il graue per gli istessi interualli; & nel pigliar le voci si ode
vn tal incommodo. Ma si debbe auertire, che io chiamo quella la parte del Soggetto, sopra la quale sono accommodate le altre parti in consequenza, & è la principale, & la guida di tutte le altre. Io non dico quella, che prima di ogn'altra incomincia a cantare; ma quella dico, che osserua, & mantiene il Modo sopra
laquale sono accommodate le altre distanti l'vna dall'altra per qual si voglia interuallo; Come si potrà vedere nella Oratione dominicale Pater noster, & nella Salutatione angelica Aue maria, ch'io per il passato
composi a sette voci; doue il principale Soggetto di quelle tre parti, che cantano in fuga, non è quella parte
che è prima al incominciare a cantare; ma si bene la seconda. In simili casi adunque sarà lecito porre in vna page 176compositione molte parti tra loro discordanti ne i loro principij, massimamente non volendo, ne potendo veramente discommo dare l'artificioso Soggetto, che facendolo sarebbe pazzia: ma ne gli altri non si debbe
(per mio consiglio) dare tale incommodità alli cantanti.
Si debbe etiandio auertire (il che è cosa di non poca importanza) di ordinare nelle Compositioni, & ne i Contrapunti a più voci in tal maniera le parti, che i loro principij corrispondino tra loro, & habbiano relatione
per vna delle consonanze perfette, ouero imperfette; di modo che volendole cantare, nel pigliar le voci delle parti, non si oda alcuna dissonanza. Et questo, percioche non solo porge fastidio a quelli, che vogliono cantare: ma alle
volte è cagione di farli errare più facilmente, pigliando vna voce per vn'altra; massimamente quando non sono molto sicuri. E ben vero, che è lecito porre nel graue il principio di due parti, che siano
distanti l'vna dall'altra per vna Quarta, senza esserui alcun'altra parte più graue, alle quali le altre parti
corrispondino per Ottaua; massimamente ne i Modi placali, ouero Impari, che li vogliamo dire; quando le
parti della cantilena incominciano a cantare sopra le chorde principali de i loro Modi, ne i quali è composta: Conciosiache volendo torre questa libertà al Compositore, di poter porre due parti in tal maniera, non è cosa honesta; massimamente potendolo fare a due voci; & sarebbe farlo Soggeto, & obligato
ad vna cosa fuori di ogni proposito: essendo che lo incominciare in tal modo è stato posto in vso da molti Prattici periti; si come da Iosquino, da Motone, & da altri ancora antichi, & moderni Musici; & di ciò potemo hauere lo essempio nel Motetto che fece Adriano a cinque voci Laus tibi sacra rubens; Lassandone infiniti altri de moderni, & antichi compositori. Tal licenza presi io anche in quelli tre motetti, Osculetur me
osculis oris sui; Ego rosa Saron; & Capite nobis vulpes paruulas; i quali già composi a cinque voci; come
ogn'vno potrà vedere; & saranno essempio alle cose, che di sopra sono state dette. Questo adunque si concede a tutti li Compositori: ma non è però da lodare, che due parti siano distanti ne i loro principij dalla parte
del Soggetto, o nel graue, o nello acuto, l'vna per vna Quarta, & l'altra per vna Quinta: percioche allora queste parti verrebbeno ad esser distanti l'vna dall'altra per vna Seconda, & nel pigliar le voci farebbeno dissonanza, & potrebbe essere, che l'una di esse parti facesse il suo principio sopra vna chorda, che non sarebbe del Modo,
sopra'l quale è fondata la compositione, o cantilena. Et quantunque tale auertimento sia buono, tuttauia non è necessario,
quando il Soggetto principale della compositione fusse composto con tale arteficio, che l'vna parte cantasse sopra l'altra in Fuga, o Consequenza, di modo che due di loro cantassero sopra
la parte principale del Soggetto, nell'acuto, ouer nel graue, l'vna distante dall'altra per vna Quinta, ouero
per vna Quarta: oueramente che l'vna fusse distante dal Soggetto per vna Quarta, et l'altra per vna Quinta, o per altro interuallo;
Si come si puo vedere nel motetto Pater de celis deus, che fece P. della Rue a sei
voci, & nel motetto Virgo prudentissima, che gia composi à sei voci, nel quale tre parti cantano in fuga, o
consequenza, due verso l'acuto, & vna verso il graue per gli istessi interualli; & nel pigliar le voci si ode
vn tal incommodo. Ma si debbe auertire, che io chiamo quella la parte del Soggetto, sopra la quale sono accommodate le altre parti in consequenza, & è la principale, & la guida di tutte le altre. Io non dico quella, che prima di ogn'altra incomincia a cantare; ma quella dico, che osserua, & mantiene il Modo sopra
laquale sono accommodate le altre distanti l'vna dall'altra per qual si voglia interuallo; Come si potrà vedere nella Oratione dominicale Pater noster, & nella Salutatione angelica Aue maria, ch'io per il passato
composi a sette voci; doue il principale Soggetto di quelle tre parti, che cantano in fuga, non è quella parte
che è prima al incominciare a cantare; ma si bene la seconda. In simili casi adunque sarà lecito porre in vna page 176compositione molte parti tra loro discordanti ne i loro principij, massimamente non volendo, ne potendo veramente discommo dare l'artificioso Soggetto, che facendolo sarebbe pazzia: ma ne gli altri non si debbe
(per mio consiglio) dare tale incommodità alli cantanti.
Che non si debbe porre due Consonanze, contenuto sotto vna istessa proportione, l'vna dopo l'altra ascendendo, ouero discendendo senza alcun mezo.Cap. 29.
 conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra loro diuerse, discordanti, & contrarie;
& non da quelle, che in ogni cosa si conuengono. La onde se da tal varietà nasce l'Harmonia, sarà dibisogno, che nella Musica,
non solo le parti della cantilena siano distanti l'vna dall'altra per il
graue, & per lo acuto: ma etiandio che le loro modulationi siano differenti ne i mouimenti: & che contenghino varie consonanze, contenute da diuerse proportioni. Et tanto più potremo allora giudicare che sia harmoniosa quella
cantilena, quanto più si ritrouerà nella compositione delle sue parti diuerse distanze tra l'vna,
et l'altra, per il graue, & per lo acuto; diuersi mouimenti, & diuerse proportioni. Videro forse gli Antichi
che le Consonanze poste insieme in altra maniera, di quella, ch'io hò detto (ancorache fussero alle volte varie
ne i loro estremi per il graue, & per lo acuto) erano simili nel procedere, & simili di forma nelle loro proportioni: però conoscendo, che tale simiglianza non generaua alcuna varietà di concento, & giudicando (come era il vero) che
la perfetta harmonia consistesse nella varietà, non tanto delli Siti, o Distanze delle parti della cantilena, quanto nella varietà de i Mouimenti, delle Modulationi, & delle Proportioni; giudicarono, che il porre due Consonanze l'vna dopo l'altra, simili di proportione, variauano se non il luogo di graue in
acuto: o per il contrario, senza fare alcuna buona harmonia, ancora che i loro estremi fussero variati l'vno
dall'altro: Però non volsero, che due, o più Consonanze perfette, contenute da vna istessa proportione, ascendenti insieme, o discendenti le parti, si potessero porre nelle compositioni l'vna dopo l'altra, senza alcuno altro mezano interuallo. Et massimamente vietarono gli Vnisoni, i quali non hanno alcuno estremo ne i suoni,
ne sono differenti di sito, ne sono distanti tra loro, ne fanno variatione alcuna nel procedere, & sono simili
in tutto, & per tutto; Ne si ritroua in loro cantando differenza alcuna di graue, o di acuto; non cadendo
tra l'vno, & l'altro suono, alcuno interuallo: percioche le voci di vna parte si ritrouano in quello istesso luogo, che si
ritrouano le voci dell'altra; come nello essempio posto disopra, & nella definitione posta al cap. 11
dell'Vnisono, si può vedere: Ne anco si ritroua diuersità alcuna di modulatione: percioche per quelli istessi
interualli canta vna parte, per li quali procede l'altra. Il medesimo si potrebbe etiandio dire di due, o più Ottaue; se non fusse, che i loro estremi sono differenti l'vno dall'altro per il graue, & per lo acuto; cosa che porge all'vdito
alquanto più diletto, di quello, che non fanno gli Vnisoni; per esser la Ottaua ne i suoi estremi alquanto varia. L 'istesso si può dire di due, o più Quinte; che per il procedere che fanno per gradi, & per proportioni simili, alcuni de gli Antichi hebbero opinione, che più presto ne vscisse ad vn certo modo dissonanza, page 177che harmonia, o consonanza: Onde hebbero per vero, che qualunque volta si perueniua ad vna Consonanza perfetta, si fusse venuto al fine, & alla perfettione, alla quale tende la Musica; la qual perfettione, non
volsero, che si replicasse molte volte, per non generare sacietà all'vdito. Questo bello, & vtile auertimento conferma esser vero, & buono le operationi della stupenda Natura, la quale nel produrre in essere gli Indiuidui
di ciascuna specie; mai li produce di maniera, che si assimiglino in tutto l'uno all'altro; ma si bene variati,
per qualche differenza; la qual differenza, o varietà molto piacere porge alli nostri sentimenti. Debbe adunque ogni Compositore
imitare vn tale, & tanto bello ordine: percioche sarà riputato tanto migliore, quanto
le sue operationi si assimiglieranno a quelle della Natura. A tale osseruanza ne inuitano i Numeri, & le
Proportioni: percioche tra loro non si ritroua nell'ordine naturale due proportioni l'vna immediatamente dopo l'altra, che
siano simili; si come è vn progresso simile, 1. 1. 1. oueramente 2. 2. 2. & altri simiglianti, che sarebbeno le forme di due Vnisoni; ne meno vn tal progresso 1. 2. 4. 8. il quale non è Harmonico, ma Geometrico, nel quale si contengono le forme di tre Ottaue continoue: ne meno si ritroua un tale
ordine 4. 6. 9. che contiene le forme di due Quinte continouate. Non douemo adunque per alcun modo
porre due Vnisoni l'vno dopo l'altro immediatamente, ne due Ottaue, ne due Quinte; poi che naturalmente
la cagione delle consonanze, che è il Numero harmonico, non contiene nel suo progresso, ouero ordine naturale due proportioni simili, l'vna dopo l'altra, senza alcun mezo; come nel cap. 15. della Prima parte si può
vedere: Percioche se bene queste consonanze, quando fussero poste in tal maniera, non facessero euidentemente alcuna dissonanza tra le parti; tuttauia farebbeno vdire un non sò che di tristo, che dispiacerebbe. Per tante ragioni
adunque non douemo a patto alcuno far contra questa Regola; cioè non douemo porre le Consonanze l'vna dopo l'altra, al modo mostrato disopra: ma douemo cercare di variar sempre li Suoni, le Consonanze,
li Mouimenti, & gli Interualli; & per tal modo, dalla varietà di queste cose, verremo a fare vna buona,
& perfetta harmonia. Et non douemo hauer riguardo, che alcuni habbiano voluto fare il contrario, più
presto per presuntione, che per ragione alcuna, che loro habbiano hauuto; come vedemo nelle loro compositioni: Conciosia che non douemo imitar coloro, che fanno sfacciatamente contra li buoni costumi, &
buoni precetti di vn'Arte, & di vna Scienza, senza renderne ragione alcuna; ma douemo imitar quelli,
che sono stati osseruatori de i buoni precetti, & accostarsi a loro, & abbracciarli come buoni maestri; lassando sempre il
tristo, & pigliando il buono. Onde si come il vedere vna Pittura, che sia dipinta con varij colori, maggiormente diletta l'Occhio, di quello che non farebbe se fusse dipinta con vn solo colore; cosi l'Vdito
maggiormente si diletta, & piglia piacere delle Consonanze, & delle Modulationi variate, poste dal diligentissimo Compositore nelle sue compositioni, che delle semplici, & non variate. Questo adunque volsero che si
osseruasse i Musici Antichi più diligenti, alli quali siamo molto debitori; & aggiungeremo a questo, che per
le ragioni gia dette, non si debbe anco porre due, o più Imperfette consonanze l'vna dopo l'altra, senza alcun
mezo; come sono due Terze maggiori, due minori, due Seste maggiori anco, & due minori; come qui in es
conciosiache molto ben sapeuano, che l'Harmonia non può nascere, se non da cose tra loro diuerse, discordanti, & contrarie;
& non da quelle, che in ogni cosa si conuengono. La onde se da tal varietà nasce l'Harmonia, sarà dibisogno, che nella Musica,
non solo le parti della cantilena siano distanti l'vna dall'altra per il
graue, & per lo acuto: ma etiandio che le loro modulationi siano differenti ne i mouimenti: & che contenghino varie consonanze, contenute da diuerse proportioni. Et tanto più potremo allora giudicare che sia harmoniosa quella
cantilena, quanto più si ritrouerà nella compositione delle sue parti diuerse distanze tra l'vna,
et l'altra, per il graue, & per lo acuto; diuersi mouimenti, & diuerse proportioni. Videro forse gli Antichi
che le Consonanze poste insieme in altra maniera, di quella, ch'io hò detto (ancorache fussero alle volte varie
ne i loro estremi per il graue, & per lo acuto) erano simili nel procedere, & simili di forma nelle loro proportioni: però conoscendo, che tale simiglianza non generaua alcuna varietà di concento, & giudicando (come era il vero) che
la perfetta harmonia consistesse nella varietà, non tanto delli Siti, o Distanze delle parti della cantilena, quanto nella varietà de i Mouimenti, delle Modulationi, & delle Proportioni; giudicarono, che il porre due Consonanze l'vna dopo l'altra, simili di proportione, variauano se non il luogo di graue in
acuto: o per il contrario, senza fare alcuna buona harmonia, ancora che i loro estremi fussero variati l'vno
dall'altro: Però non volsero, che due, o più Consonanze perfette, contenute da vna istessa proportione, ascendenti insieme, o discendenti le parti, si potessero porre nelle compositioni l'vna dopo l'altra, senza alcuno altro mezano interuallo. Et massimamente vietarono gli Vnisoni, i quali non hanno alcuno estremo ne i suoni,
ne sono differenti di sito, ne sono distanti tra loro, ne fanno variatione alcuna nel procedere, & sono simili
in tutto, & per tutto; Ne si ritroua in loro cantando differenza alcuna di graue, o di acuto; non cadendo
tra l'vno, & l'altro suono, alcuno interuallo: percioche le voci di vna parte si ritrouano in quello istesso luogo, che si
ritrouano le voci dell'altra; come nello essempio posto disopra, & nella definitione posta al cap. 11
dell'Vnisono, si può vedere: Ne anco si ritroua diuersità alcuna di modulatione: percioche per quelli istessi
interualli canta vna parte, per li quali procede l'altra. Il medesimo si potrebbe etiandio dire di due, o più Ottaue; se non fusse, che i loro estremi sono differenti l'vno dall'altro per il graue, & per lo acuto; cosa che porge all'vdito
alquanto più diletto, di quello, che non fanno gli Vnisoni; per esser la Ottaua ne i suoi estremi alquanto varia. L 'istesso si può dire di due, o più Quinte; che per il procedere che fanno per gradi, & per proportioni simili, alcuni de gli Antichi hebbero opinione, che più presto ne vscisse ad vn certo modo dissonanza, page 177che harmonia, o consonanza: Onde hebbero per vero, che qualunque volta si perueniua ad vna Consonanza perfetta, si fusse venuto al fine, & alla perfettione, alla quale tende la Musica; la qual perfettione, non
volsero, che si replicasse molte volte, per non generare sacietà all'vdito. Questo bello, & vtile auertimento conferma esser vero, & buono le operationi della stupenda Natura, la quale nel produrre in essere gli Indiuidui
di ciascuna specie; mai li produce di maniera, che si assimiglino in tutto l'uno all'altro; ma si bene variati,
per qualche differenza; la qual differenza, o varietà molto piacere porge alli nostri sentimenti. Debbe adunque ogni Compositore
imitare vn tale, & tanto bello ordine: percioche sarà riputato tanto migliore, quanto
le sue operationi si assimiglieranno a quelle della Natura. A tale osseruanza ne inuitano i Numeri, & le
Proportioni: percioche tra loro non si ritroua nell'ordine naturale due proportioni l'vna immediatamente dopo l'altra, che
siano simili; si come è vn progresso simile, 1. 1. 1. oueramente 2. 2. 2. & altri simiglianti, che sarebbeno le forme di due Vnisoni; ne meno vn tal progresso 1. 2. 4. 8. il quale non è Harmonico, ma Geometrico, nel quale si contengono le forme di tre Ottaue continoue: ne meno si ritroua un tale
ordine 4. 6. 9. che contiene le forme di due Quinte continouate. Non douemo adunque per alcun modo
porre due Vnisoni l'vno dopo l'altro immediatamente, ne due Ottaue, ne due Quinte; poi che naturalmente
la cagione delle consonanze, che è il Numero harmonico, non contiene nel suo progresso, ouero ordine naturale due proportioni simili, l'vna dopo l'altra, senza alcun mezo; come nel cap. 15. della Prima parte si può
vedere: Percioche se bene queste consonanze, quando fussero poste in tal maniera, non facessero euidentemente alcuna dissonanza tra le parti; tuttauia farebbeno vdire un non sò che di tristo, che dispiacerebbe. Per tante ragioni
adunque non douemo a patto alcuno far contra questa Regola; cioè non douemo porre le Consonanze l'vna dopo l'altra, al modo mostrato disopra: ma douemo cercare di variar sempre li Suoni, le Consonanze,
li Mouimenti, & gli Interualli; & per tal modo, dalla varietà di queste cose, verremo a fare vna buona,
& perfetta harmonia. Et non douemo hauer riguardo, che alcuni habbiano voluto fare il contrario, più
presto per presuntione, che per ragione alcuna, che loro habbiano hauuto; come vedemo nelle loro compositioni: Conciosia che non douemo imitar coloro, che fanno sfacciatamente contra li buoni costumi, &
buoni precetti di vn'Arte, & di vna Scienza, senza renderne ragione alcuna; ma douemo imitar quelli,
che sono stati osseruatori de i buoni precetti, & accostarsi a loro, & abbracciarli come buoni maestri; lassando sempre il
tristo, & pigliando il buono. Onde si come il vedere vna Pittura, che sia dipinta con varij colori, maggiormente diletta l'Occhio, di quello che non farebbe se fusse dipinta con vn solo colore; cosi l'Vdito
maggiormente si diletta, & piglia piacere delle Consonanze, & delle Modulationi variate, poste dal diligentissimo Compositore nelle sue compositioni, che delle semplici, & non variate. Questo adunque volsero che si
osseruasse i Musici Antichi più diligenti, alli quali siamo molto debitori; & aggiungeremo a questo, che per
le ragioni gia dette, non si debbe anco porre due, o più Imperfette consonanze l'vna dopo l'altra, senza alcun
mezo; come sono due Terze maggiori, due minori, due Seste maggiori anco, & due minori; come qui in es sempio si veggono. Conciosiache non solo si fà contra quello, che hò detto delle Perfette; ma il loro procedere si fa vdire alquanto aspro, per non hauere nella modulatione delle parti, da parte alcuna lo interuallo del
Semituono maggiore, nel quale consiste tutto il buono della Musica; percioche senza lui ogni modulatione,
& ogni harmonia è dura, aspra, & quasi inconsonante. Et ciò nasce anco: conciosiache tra le parti, ouero
tra le voci delle due Terze maggiori, & delle due Seste minori non si troua la Relatione harmonica, si come
più oltra vederemo. La onde douemo sommamente auertire, che in ogni progresso, ouero modulatione, che
fanno le parti cantando insieme, almeno vna di quelle si muoua, o faccia l'interuallo del Semituono maggiore, potendolo fare, accioche la modulatione, & l'harmonia che nasce dalli mouimenti, che fanno
insieme le parti della cantilena, siano più diletteuoli & più soaui. La qual cosa si hauerà facilmenpage 178te, quando le Consonanze si porranno l'vna dopo l'altra, che siano diuerse di specie; come dopo la Terza, o
la Sesta maggiore, si porrà la Minore; o per il contrario; Et quando dopo la Terza maggiore, si porrà la Sesta minore; ouero dopo questa, si porrà quella; & dopo la Terza minore, la Sesta maggiore: Similmente dopo la Sesta maggiore, la Terza minore. Ne vi è maggior ragione, che più ne vieti il porre due Perfette, che
due Imperfette consonanze immediatamente, l'vna dopo l'altra: percioche se bene le prime sono consonanze
Perfette, tuttauia ciascuna delle Imperfette si ritroua esser perfetta nella sua proportione. Et si come non si
può dire con verità, che vno Huomo sia più Huomo di vn'altro; cosi non si può dire, che vna Terza
maggiore, ouero vna minore, & cosi l'vna, o l'altra delle due Seste posta nel graue, sia maggiore, o minore
di vn'altra posta nell'acuto; o per il contrario: di modo che, si come è vietato il porre due Consonanze perfette di vna istessa specie l'vna dopo l'altra, cosi maggiormente non douemo porre due imperfette di vna istessa proportione: conciosiache non sono tanto consonanti, quanto sono le perfette. E' ben vero, che due Terze minori poste l'vna
dopo l'altra ascendenti insieme, ouero descendenti per vn grado, il qual grado chiamaremo
Mouimento congiunto, ouero Continouato; similmente due Seste maggiori, si potranno sopportare: percioche, se bene nelle loro modulationi non si ode cantare il Semituono maggiore, & le Terze siano per loro natura alquanto meste, & le Seste alquanto dure; quella poca differenza, che si troua ne i mouimenti, che fanno le parti, viene
a fare alquanto di varietà: conciosia che la parte graue sempre ascende, o discende per vn
Tuono minore, & l'acuta per vno maggiore: o per il contrario; & fa un non sò che di buono all'vdito; tanto più, quanto che
le voci delle parti sono lontane tra loro in harmonica relatione. Ma quando le parti si mouessero per più di vn grado, tal mouimento nominaremo Senza congiuntione, ouero Mouimento separato; &
allora per niun modo porremo due, o più simili l'vna dopo l'altra: percioche, oltra il non osseruare le conditioni toccate disopra, le voci delle parti non sarebbeno distanti l'vna dall'altra in harmonica relatione; come
qui sotto si veggono.
sempio si veggono. Conciosiache non solo si fà contra quello, che hò detto delle Perfette; ma il loro procedere si fa vdire alquanto aspro, per non hauere nella modulatione delle parti, da parte alcuna lo interuallo del
Semituono maggiore, nel quale consiste tutto il buono della Musica; percioche senza lui ogni modulatione,
& ogni harmonia è dura, aspra, & quasi inconsonante. Et ciò nasce anco: conciosiache tra le parti, ouero
tra le voci delle due Terze maggiori, & delle due Seste minori non si troua la Relatione harmonica, si come
più oltra vederemo. La onde douemo sommamente auertire, che in ogni progresso, ouero modulatione, che
fanno le parti cantando insieme, almeno vna di quelle si muoua, o faccia l'interuallo del Semituono maggiore, potendolo fare, accioche la modulatione, & l'harmonia che nasce dalli mouimenti, che fanno
insieme le parti della cantilena, siano più diletteuoli & più soaui. La qual cosa si hauerà facilmenpage 178te, quando le Consonanze si porranno l'vna dopo l'altra, che siano diuerse di specie; come dopo la Terza, o
la Sesta maggiore, si porrà la Minore; o per il contrario; Et quando dopo la Terza maggiore, si porrà la Sesta minore; ouero dopo questa, si porrà quella; & dopo la Terza minore, la Sesta maggiore: Similmente dopo la Sesta maggiore, la Terza minore. Ne vi è maggior ragione, che più ne vieti il porre due Perfette, che
due Imperfette consonanze immediatamente, l'vna dopo l'altra: percioche se bene le prime sono consonanze
Perfette, tuttauia ciascuna delle Imperfette si ritroua esser perfetta nella sua proportione. Et si come non si
può dire con verità, che vno Huomo sia più Huomo di vn'altro; cosi non si può dire, che vna Terza
maggiore, ouero vna minore, & cosi l'vna, o l'altra delle due Seste posta nel graue, sia maggiore, o minore
di vn'altra posta nell'acuto; o per il contrario: di modo che, si come è vietato il porre due Consonanze perfette di vna istessa specie l'vna dopo l'altra, cosi maggiormente non douemo porre due imperfette di vna istessa proportione: conciosiache non sono tanto consonanti, quanto sono le perfette. E' ben vero, che due Terze minori poste l'vna
dopo l'altra ascendenti insieme, ouero descendenti per vn grado, il qual grado chiamaremo
Mouimento congiunto, ouero Continouato; similmente due Seste maggiori, si potranno sopportare: percioche, se bene nelle loro modulationi non si ode cantare il Semituono maggiore, & le Terze siano per loro natura alquanto meste, & le Seste alquanto dure; quella poca differenza, che si troua ne i mouimenti, che fanno le parti, viene
a fare alquanto di varietà: conciosia che la parte graue sempre ascende, o discende per vn
Tuono minore, & l'acuta per vno maggiore: o per il contrario; & fa un non sò che di buono all'vdito; tanto più, quanto che
le voci delle parti sono lontane tra loro in harmonica relatione. Ma quando le parti si mouessero per più di vn grado, tal mouimento nominaremo Senza congiuntione, ouero Mouimento separato; &
allora per niun modo porremo due, o più simili l'vna dopo l'altra: percioche, oltra il non osseruare le conditioni toccate disopra, le voci delle parti non sarebbeno distanti l'vna dall'altra in harmonica relatione; come
qui sotto si veggono.
 Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre due Terze, o due Seste
l'vna dopo l'altra, osseruaremo di porre primieramente la maggiore, & dipoi la minore, o per il contrario;
pongansi poi in qual maniera si voglino, o con Mouimenti congiunti, o con Mouimenti separati: percioche
ogni cosa tornerà bene. Ma si debbe auertire, che quando si porrà la Terza dopo la Sesta, oueramente la Sesta dopo la Terza, di fare, che l'vna sia maggiore, & l'altra minore; & ciò faremo quando ciascuna delle
parti farà il mouimento nel graue, ouero nell'acuto. Ma quando l'una di esse non facesse alcuno mouimento,
allora tal regola non si potrà osseruare, senza partirsi dalle regole, che più oltra daremo, che saranno per il
bene essere della cantilena: conciosiache allora dopo la Terza maggiore sarà dibisogno darli la Sesta maggiore, & dopo la
minore la Sesta minore: ouero per il contrario; come nel sottoposto essempio si vede.
Per schiuare adunque gli errori, che possono occorrere, quando sarà dibisogno porre due Terze, o due Seste
l'vna dopo l'altra, osseruaremo di porre primieramente la maggiore, & dipoi la minore, o per il contrario;
pongansi poi in qual maniera si voglino, o con Mouimenti congiunti, o con Mouimenti separati: percioche
ogni cosa tornerà bene. Ma si debbe auertire, che quando si porrà la Terza dopo la Sesta, oueramente la Sesta dopo la Terza, di fare, che l'vna sia maggiore, & l'altra minore; & ciò faremo quando ciascuna delle
parti farà il mouimento nel graue, ouero nell'acuto. Ma quando l'una di esse non facesse alcuno mouimento,
allora tal regola non si potrà osseruare, senza partirsi dalle regole, che più oltra daremo, che saranno per il
bene essere della cantilena: conciosiache allora dopo la Terza maggiore sarà dibisogno darli la Sesta maggiore, & dopo la
minore la Sesta minore: ouero per il contrario; come nel sottoposto essempio si vede.
 Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette, nel modo ch'io hò mostrato, che non si douerebbe anco porre due Quarte in qual si voglia compositione, come fanno alcuni in alcune particelle
delle loro canzoni, che chiamano Falso bordone: conciosia che, senza dubbio alcuno, la Quarta
(come si è detto altroue) è consonanza perfetta: Ma di questo ne ragionerò forse, quando mostrerò il modo
di comporre a più voci.
Aggiungeremo etiandio, che non essendo lecito porre due Perfette, ne due Imperfette, nel modo ch'io hò mostrato, che non si douerebbe anco porre due Quarte in qual si voglia compositione, come fanno alcuni in alcune particelle
delle loro canzoni, che chiamano Falso bordone: conciosia che, senza dubbio alcuno, la Quarta
(come si è detto altroue) è consonanza perfetta: Ma di questo ne ragionerò forse, quando mostrerò il modo
di comporre a più voci.
Quando le parti della cantilena hanno tra loro Harmonica relatione, & in qual modo potemo vsare la Semidiapente, & il Tritono nelle compositioni.Cap. 30.
 Tra le quali si ritroua la Diapason superflua, la Semidiapason, la Semidiapente, & il Tritono, per relatione delle figure di una parte, alle figure dell'altra. Onde accioche le nostre compositioni siano purgate da ogni
errore, & accioche siano corrette, cercaremo di fuggire tale relatione; massimamente quando componeremo a due voci: percioche genera alle purgate orecchie alquanto di fastidio: conciosia che simili interualli non si ritrouano esser collocati tra i numeri sonori, et non si cantano in alcuno genere, sia qual si uoglia; ancora che alcuni
habbiano hauuto contraria opinione: ma sia come si voglia, sono molto difficili da cantare, et fanno tristo effetto.
Et molto mi merauiglio di costoro, che non si habbiano punto schiuato, di far cantare in alcuna delle parti delle lor
cantilene alcuno di questi interualli; ne mi sò imaginare, per qual ragione l'habbiano fatto. Et ancorache sia minormale,
il ritrouarlo per relatione tra due parti, & tra due modulationi, che vdirlo nella modulatione di alcuna parte; tuttauia quel male istesso, che si ode in una parte, si ritroua diuiso tra due, et è quella istessa offesa dell'vdito: Percioche nulla, o poco rileua l'essere offeso di vno istesso colpo più da vno, che da molti,
quando il male non è
minore. Questi interualli adunque, che nel modulare non si ammettono, si debbeno schiuare di porli nelle cantilene di
maniera, che si odino per relationi tra le parti; la qual cosa verrà fatta, quando le parti si potranno mutar fra
loro con interualli harmonici proportionati, contenuti nel genere diatonico; cioè quando da vna voce della parpage 180te graue, si potrà ascendere alla seguente della parte acuta per vn spatio legittimo, & cantabile: & cosi per
il contrario. Il che si potrà fare, quando tra le parti di qual si voglia compositione, tra due voci al detto modo, non si vdirà la relatione de i detti interualli, che non si possono, se non con grande discommodo, mutare;
come ne i sottoposti essempi tutti si veggono mutati.
Tra le quali si ritroua la Diapason superflua, la Semidiapason, la Semidiapente, & il Tritono, per relatione delle figure di una parte, alle figure dell'altra. Onde accioche le nostre compositioni siano purgate da ogni
errore, & accioche siano corrette, cercaremo di fuggire tale relatione; massimamente quando componeremo a due voci: percioche genera alle purgate orecchie alquanto di fastidio: conciosia che simili interualli non si ritrouano esser collocati tra i numeri sonori, et non si cantano in alcuno genere, sia qual si uoglia; ancora che alcuni
habbiano hauuto contraria opinione: ma sia come si voglia, sono molto difficili da cantare, et fanno tristo effetto.
Et molto mi merauiglio di costoro, che non si habbiano punto schiuato, di far cantare in alcuna delle parti delle lor
cantilene alcuno di questi interualli; ne mi sò imaginare, per qual ragione l'habbiano fatto. Et ancorache sia minormale,
il ritrouarlo per relatione tra due parti, & tra due modulationi, che vdirlo nella modulatione di alcuna parte; tuttauia quel male istesso, che si ode in una parte, si ritroua diuiso tra due, et è quella istessa offesa dell'vdito: Percioche nulla, o poco rileua l'essere offeso di vno istesso colpo più da vno, che da molti,
quando il male non è
minore. Questi interualli adunque, che nel modulare non si ammettono, si debbeno schiuare di porli nelle cantilene di
maniera, che si odino per relationi tra le parti; la qual cosa verrà fatta, quando le parti si potranno mutar fra
loro con interualli harmonici proportionati, contenuti nel genere diatonico; cioè quando da vna voce della parpage 180te graue, si potrà ascendere alla seguente della parte acuta per vn spatio legittimo, & cantabile: & cosi per
il contrario. Il che si potrà fare, quando tra le parti di qual si voglia compositione, tra due voci al detto modo, non si vdirà la relatione de i detti interualli, che non si possono, se non con grande discommodo, mutare;
come ne i sottoposti essempi tutti si veggono mutati.
 Tutte le volte adunque che le parti della compositione, o cantilena non si potranno mutar l'vna nell'altra,
dalla qual mutatione ne naschi il procedere per veri interualli legittimi cantabili, tal compositione si debbe fuggire; massimamente se noi desideriamo di hauere vna corretta compositione, & purgata
da ogni errore. E
ben vero, che nelle compositioni di più voci molte volte è impossibile di poterli schiuare, & di non incorrere
in simili intrichi: percioche accade alle volte, che il Compositore componerà sopra alcun Soggetto, che lo inuiterà spesse
volte a far contra questo precetto; onde astretto dalla necessità lo lassarà scorrere; si come quando lui vedesse, che le parti della compositione non si potessero cantare accommodatamente, ouero quando
volesse accommodare una Fuga, o Consequenza; si come altroue vederemo: Ma quando la necessità ne
astringesse, douemo almeno hauer riguardo, che tale diffetto si commetta nelle chorde diatoniche, & in quelle, che sono propie
& naturali del Modo, & non tra quelle, che sono accidentali, cioè tra quelle, che nel mezo delle cantilene si segnano con questi segni
Tutte le volte adunque che le parti della compositione, o cantilena non si potranno mutar l'vna nell'altra,
dalla qual mutatione ne naschi il procedere per veri interualli legittimi cantabili, tal compositione si debbe fuggire; massimamente se noi desideriamo di hauere vna corretta compositione, & purgata
da ogni errore. E
ben vero, che nelle compositioni di più voci molte volte è impossibile di poterli schiuare, & di non incorrere
in simili intrichi: percioche accade alle volte, che il Compositore componerà sopra alcun Soggetto, che lo inuiterà spesse
volte a far contra questo precetto; onde astretto dalla necessità lo lassarà scorrere; si come quando lui vedesse, che le parti della compositione non si potessero cantare accommodatamente, ouero quando
volesse accommodare una Fuga, o Consequenza; si come altroue vederemo: Ma quando la necessità ne
astringesse, douemo almeno hauer riguardo, che tale diffetto si commetta nelle chorde diatoniche, & in quelle, che sono propie
& naturali del Modo, & non tra quelle, che sono accidentali, cioè tra quelle, che nel mezo delle cantilene si segnano con questi segni  ,
,  , &
, &  : percioche allora non generano tanto tristo
effetto. Si debbe però notare, ch'io chiamo errori naturali quelli, che nascono nel modo mostrato di sopra nel
primo essempio; & quelli dico nascere per accidente, quando tra le vere chorde di alcun Modo se ne pone
vn'altra, che non è di quello ordine, & da tal chorda nasce vn tal disordine; come per essempio può accascare nel Terzo Modo, del quale molte fiate la mezana chorda, cioè la
: percioche allora non generano tanto tristo
effetto. Si debbe però notare, ch'io chiamo errori naturali quelli, che nascono nel modo mostrato di sopra nel
primo essempio; & quelli dico nascere per accidente, quando tra le vere chorde di alcun Modo se ne pone
vn'altra, che non è di quello ordine, & da tal chorda nasce vn tal disordine; come per essempio può accascare nel Terzo Modo, del quale molte fiate la mezana chorda, cioè la  è lassata da vn canto, & in suo
è lassata da vn canto, & in suo
 luogo si pone la
luogo si pone la  per accidente. Onde tra questa & la precedente, o la seguente nasce uno delli
mostrati disordini; come qui si vede. Et tanto
più è senza soauità, quanto che la chorda
per accidente. Onde tra questa & la precedente, o la seguente nasce uno delli
mostrati disordini; come qui si vede. Et tanto
più è senza soauità, quanto che la chorda  , che
è la chorda principale del Terzo modo, è rimossa
dal suo propio luogo, & posto la chorda
, che
è la chorda principale del Terzo modo, è rimossa
dal suo propio luogo, & posto la chorda  , la
quale è accidentale. Et benche per le ragioni dette non si possa vsare tali interualli, accommodati
in cotal maniera nelle cantilene; nondimeno potremo vsare alle volte la Semidiapente in vna istessa percus
, la
quale è accidentale. Et benche per le ragioni dette non si possa vsare tali interualli, accommodati
in cotal maniera nelle cantilene; nondimeno potremo vsare alle volte la Semidiapente in vna istessa percus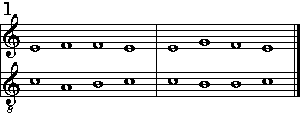 sione; & ciò faremo, quando immediatamente
da esse verremo al Ditono; come nello essempio
vedemo: Percioche le parti si possono mutar tra
loro senza alcun discommodo; come nello essempio di sotto si vede. Et questo si osserua da i migliori Musici moderni, come è stato etiandio osseruato per il passato da alcuni delli più antichi.
Ne solamente sarà lecito vsare la Semidiapente:
ma il Tritono anche alle volte, si come vederemo al suo luogo. Si debbe però auertire, che quelle parti, che
sione; & ciò faremo, quando immediatamente
da esse verremo al Ditono; come nello essempio
vedemo: Percioche le parti si possono mutar tra
loro senza alcun discommodo; come nello essempio di sotto si vede. Et questo si osserua da i migliori Musici moderni, come è stato etiandio osseruato per il passato da alcuni delli più antichi.
Ne solamente sarà lecito vsare la Semidiapente:
ma il Tritono anche alle volte, si come vederemo al suo luogo. Si debbe però auertire, che quelle parti, che
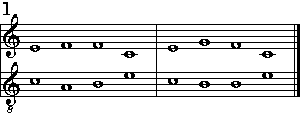 haueranno la Semidiapente, ouero il Tritono,
debbino hauere primieramente auanti la Diapente senza alcun mezo, vna consonanza, sia poi
perfetta, ouero imperfetta, che questo non fa cosa page 181
alcuna: percioche dalla consonanza precedente,
& dalla seguente, la detta Semidiapente viene
a temperarsi di maniera, che non fa tristo effetto, anzi buono; come si proua con la esperienza.
haueranno la Semidiapente, ouero il Tritono,
debbino hauere primieramente auanti la Diapente senza alcun mezo, vna consonanza, sia poi
perfetta, ouero imperfetta, che questo non fa cosa page 181
alcuna: percioche dalla consonanza precedente,
& dalla seguente, la detta Semidiapente viene
a temperarsi di maniera, che non fa tristo effetto, anzi buono; come si proua con la esperienza.
Che rispetto si de hauere a gli Interualli relati nelle compositioni di più voci.Cap. 31.
 , &
il
, &
il  : oueramente quando concorresse vn solo di questi segni solamente, non ci douemo per niente schiuare:
percioche essendo due mediationi harmoniche, fanno buono effetto, come è manifesto: ancora che non siano variate. Et di ciò alcuno non si debbe marauigliare: percioche quando vorrà con diligenza essaminare le consonanze poste in cotali ordini, ritrouerà, che quell'ordine, che è Arithmetico, ouer si assimiglia alla proportionalità Arithmetica; si lontana vn poco dalla perfettione dell'harmonia: conciosia che le sue parti uengono ad esser
collocate fuori de i lor luoghi naturali. Per il contrario ritrouerà, che l'harmonia che nasce dalla diuisione Harmonica,
ouero a quella si assimiglia, consonerà perfettamente: perche le parti di tal diuisione saranno collocate,
& ordinate secondo i propij gradi di tal proportionalità; & secondo l'ordine, che tengono i Numeri sonori nel
loro ordine naturale; come si può vedere nel cap. 15. della Prima parte. Et questo sia detto à bastanza per hora: percioche forse vn'altra fiata, per maggiore intelligenza di questo ch'io hò detto, ne toccherò vna parola.
: oueramente quando concorresse vn solo di questi segni solamente, non ci douemo per niente schiuare:
percioche essendo due mediationi harmoniche, fanno buono effetto, come è manifesto: ancora che non siano variate. Et di ciò alcuno non si debbe marauigliare: percioche quando vorrà con diligenza essaminare le consonanze poste in cotali ordini, ritrouerà, che quell'ordine, che è Arithmetico, ouer si assimiglia alla proportionalità Arithmetica; si lontana vn poco dalla perfettione dell'harmonia: conciosia che le sue parti uengono ad esser
collocate fuori de i lor luoghi naturali. Per il contrario ritrouerà, che l'harmonia che nasce dalla diuisione Harmonica,
ouero a quella si assimiglia, consonerà perfettamente: perche le parti di tal diuisione saranno collocate,
& ordinate secondo i propij gradi di tal proportionalità; & secondo l'ordine, che tengono i Numeri sonori nel
loro ordine naturale; come si può vedere nel cap. 15. della Prima parte. Et questo sia detto à bastanza per hora: percioche forse vn'altra fiata, per maggiore intelligenza di questo ch'io hò detto, ne toccherò vna parola.
In qual maniera due, o piu Consonanze perfette, ouero imperfette contenute sotto vna istessa forma, si possino porre immediatamente l'vna dopo l'altra.Cap. 32.
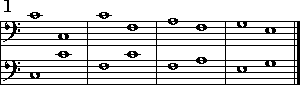 il contrario; come qui si vede.Percioche nel
mutare, o cambiare tali chorde tra loro, la consonanza non si trasporta dall'acuto al graue, ouero
dal graue all'acuto: ma resta nelle sue prime chorde, non mutando ne luogo, ne suoni; la onde non si ode
alcuna varietà di graue, o di acuto. Non si vdendo adunque tal variatione, non si può dire, che siano due consonanze contenute da vna istessa forma, poste l'vna dopo l'altra, nel modo che si intende di sopra: ma si bene vna sola consonanza replicata nelle istesse chorde;
come è manifesto al senso. Et quantunque le parti si mutino tra loro, ascendendo & discendendo, & che l'una pigli il luogo dell'altra, & le loro
modulationi siano variate, per li mouimenti contrarij che fanno; non sono però variati i loro suoni; ancora
che si potesse vdire qualche varietà, quando la parte che era nel graue, si vdisse più nello acuto, & quella che
era nell'acuto, più si vdisse quando fusse nel graue. Ma tal cosa non farebbe assolutamente varietà alcuna secondo il proposito, ma si bene ad vn certo modo; come si può comprendere dal sottoposto essempio, che quando
le parti non mutassero luogo, necessariamente le modulationi di ciascuna verebbeno ad essere vnisone. page 183
il contrario; come qui si vede.Percioche nel
mutare, o cambiare tali chorde tra loro, la consonanza non si trasporta dall'acuto al graue, ouero
dal graue all'acuto: ma resta nelle sue prime chorde, non mutando ne luogo, ne suoni; la onde non si ode
alcuna varietà di graue, o di acuto. Non si vdendo adunque tal variatione, non si può dire, che siano due consonanze contenute da vna istessa forma, poste l'vna dopo l'altra, nel modo che si intende di sopra: ma si bene vna sola consonanza replicata nelle istesse chorde;
come è manifesto al senso. Et quantunque le parti si mutino tra loro, ascendendo & discendendo, & che l'una pigli il luogo dell'altra, & le loro
modulationi siano variate, per li mouimenti contrarij che fanno; non sono però variati i loro suoni; ancora
che si potesse vdire qualche varietà, quando la parte che era nel graue, si vdisse più nello acuto, & quella che
era nell'acuto, più si vdisse quando fusse nel graue. Ma tal cosa non farebbe assolutamente varietà alcuna secondo il proposito, ma si bene ad vn certo modo; come si può comprendere dal sottoposto essempio, che quando
le parti non mutassero luogo, necessariamente le modulationi di ciascuna verebbeno ad essere vnisone. page 183
Che due o più Consonanze perfette, ouero imperfette contenute sotto, diuerse forme, poste l'una immediatamente dopo l'altra si concedeno.Cap. 33.
 Osseruando però, che le parti procedino nelle loro modulationi per interualli cantabili, & con bel procedere;
accioche ne risulti buona, & diletteuole harmonia.
Osseruando però, che le parti procedino nelle loro modulationi per interualli cantabili, & con bel procedere;
accioche ne risulti buona, & diletteuole harmonia.
Che dopo la Consonanza perfetta stà bene il porre la imperfetta: ouero per il contrario.Cap. 34.
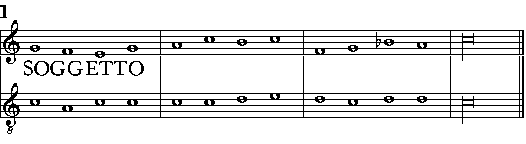 Imperoche da tal varietà non potrà nascere se non buona, vaga, diletteuole, & perfetta harmonia. Osseruando sempre (come ho detto ancora) che le parti della cantilena siano cantabili, cioè che cantino bene, accioche
dalla compositione di tante cose poste bene insieme, habbiamo l'vso delle perfette harmonie.
Imperoche da tal varietà non potrà nascere se non buona, vaga, diletteuole, & perfetta harmonia. Osseruando sempre (come ho detto ancora) che le parti della cantilena siano cantabili, cioè che cantino bene, accioche
dalla compositione di tante cose poste bene insieme, habbiamo l'vso delle perfette harmonie.
Che le parti della Cantilena debbeno procedere per mouimenti contrarij.Cap. 35.
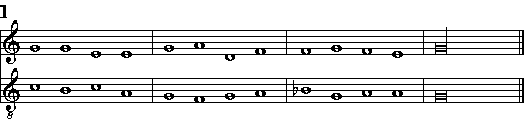
In qual maniera le parti della Cantilena possino insieme ascendere, o discendere.Cap. 36.
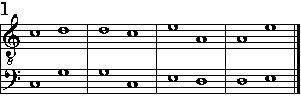 E' ben vero, che è molto più lodeuole, quando le parti discendeno insieme nel graue: percioche allora necessariamente i Mouimenti loro si fanno tardi; & tanto più è lodeuole quanto più sono graui; perche per la tardità si comprende facilmente la diuersità delle specie: Il che non cosi facilmente si comprende ne i suoni acuti,
nati dalla velocità delli mouimenti: conciosiache tendeno quasi ad vna simiglianza di specie; massimamente quando le parti ascendeno insieme dalla Perfetta minore alla Perfetta maggiore. Ma perche queste cose
non sono hoggidi considerate dalli Prattici: perche pongono tali passaggi ne i loro contrapunti senza alcuno
auertimento; però dico solamente, che non si debbeno vsare spesse fiate nelli contrapunti a due voci:
conciosia che dal sentimento sono maggiormente compresi, di quello che sarebbeno, se tali mouimenti si
ritrouassero in una cantilena à più voci: percioche allora la diuersità de i mouimenti, che farebbeno
le parti tra loro, & la moltitudine, non lassarebbeno udire ne questi, ne altri simili mouimenti. Ne anco
è cosa lodeuole, che si oda ne i contrapunti due parti, che ascendino insieme da una consonanza maggiore,
che sia di specie Imperfetta, ad una minore, che sia Perfetta, & facino i loro mouimenti separati, cioè per
più di vno grado; oueramente due parti che ascendino, o discendino insieme per detti mouimenti, da vna consonanza contenuta da vna proportione maggiore, sia perfetta, ouero imperfetta, ad vna che segue, che sia
perfetta; come dalla Terza all'Vnisono, & dalla Decima alla Ottaua: percioche sempre darà qualche noia
alle purgate orecchie. Ne anco torna bene il porre la Sesta auanti la Quinta, quando le parti ascendino, o discendino insieme; ancora che l'una si muoui con mouimento congiunto, & l'altra con mouimento separato;
come nel sotto posto essempio si può comprendere.
E' ben vero, che è molto più lodeuole, quando le parti discendeno insieme nel graue: percioche allora necessariamente i Mouimenti loro si fanno tardi; & tanto più è lodeuole quanto più sono graui; perche per la tardità si comprende facilmente la diuersità delle specie: Il che non cosi facilmente si comprende ne i suoni acuti,
nati dalla velocità delli mouimenti: conciosiache tendeno quasi ad vna simiglianza di specie; massimamente quando le parti ascendeno insieme dalla Perfetta minore alla Perfetta maggiore. Ma perche queste cose
non sono hoggidi considerate dalli Prattici: perche pongono tali passaggi ne i loro contrapunti senza alcuno
auertimento; però dico solamente, che non si debbeno vsare spesse fiate nelli contrapunti a due voci:
conciosia che dal sentimento sono maggiormente compresi, di quello che sarebbeno, se tali mouimenti si
ritrouassero in una cantilena à più voci: percioche allora la diuersità de i mouimenti, che farebbeno
le parti tra loro, & la moltitudine, non lassarebbeno udire ne questi, ne altri simili mouimenti. Ne anco
è cosa lodeuole, che si oda ne i contrapunti due parti, che ascendino insieme da una consonanza maggiore,
che sia di specie Imperfetta, ad una minore, che sia Perfetta, & facino i loro mouimenti separati, cioè per
più di vno grado; oueramente due parti che ascendino, o discendino insieme per detti mouimenti, da vna consonanza contenuta da vna proportione maggiore, sia perfetta, ouero imperfetta, ad vna che segue, che sia
perfetta; come dalla Terza all'Vnisono, & dalla Decima alla Ottaua: percioche sempre darà qualche noia
alle purgate orecchie. Ne anco torna bene il porre la Sesta auanti la Quinta, quando le parti ascendino, o discendino insieme; ancora che l'una si muoui con mouimento congiunto, & l'altra con mouimento separato;
come nel sotto posto essempio si può comprendere.
 Ma quanto siano grati questi mouimenti all'vdito, la esperienza maestra delle cose, per via del senso, ce lo
manifesta: percioche la natura odia le cose senza proportione, & senza misura; & si diletta di quelle,
che hanno tra loro conuenienza. Per il contrario adunque sarà lecito, il porre vna consonanza maggiore, che
sia imperfetta, auanti vna minore, che sia perfetta; quando le parti ascenderanno; delle quali l'vna, cioè l'acuta ascendi per mouimento congiunto, & la graue per mouimento separato. Stà anche bene, che da vna consonanza imperfetta minore si vada ad vna perfetta maggiore, ascendendo la parte graue per mouimento congiunto, & l'acuta per
mouimento separato; ouero ascendendo l'acuta per mouimento congiunto, & la graue page 186per mouimento separato. Si concede etiandio, che dalla Consonanza imperfetta, che sia minore di proportione della seguente, si vadi alla Ottaua, quando insieme ascendeno, ouer discendeno le parti; pur che vna di esse faccia il Mouimento congiunto, & tal mouimento sia di vn Semituono maggiore; Si come nello
essempio sottoposto si vede.
Ma quanto siano grati questi mouimenti all'vdito, la esperienza maestra delle cose, per via del senso, ce lo
manifesta: percioche la natura odia le cose senza proportione, & senza misura; & si diletta di quelle,
che hanno tra loro conuenienza. Per il contrario adunque sarà lecito, il porre vna consonanza maggiore, che
sia imperfetta, auanti vna minore, che sia perfetta; quando le parti ascenderanno; delle quali l'vna, cioè l'acuta ascendi per mouimento congiunto, & la graue per mouimento separato. Stà anche bene, che da vna consonanza imperfetta minore si vada ad vna perfetta maggiore, ascendendo la parte graue per mouimento congiunto, & l'acuta per
mouimento separato; ouero ascendendo l'acuta per mouimento congiunto, & la graue page 186per mouimento separato. Si concede etiandio, che dalla Consonanza imperfetta, che sia minore di proportione della seguente, si vadi alla Ottaua, quando insieme ascendeno, ouer discendeno le parti; pur che vna di esse faccia il Mouimento congiunto, & tal mouimento sia di vn Semituono maggiore; Si come nello
essempio sottoposto si vede.
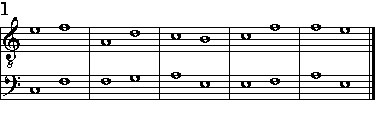 E' concesso etiandio il venire dalla Consonanza perfetta alla imperfetta, quando le parti ascendeno, ouer discendeno insieme; pur che l'vna di esse faccia il Mouimento congiunto, & la Consonanza imperfetta sia di
maggior proportione della perfetta. E' lecito etiandio porre due consonanze l'vna dopo l'altra, che faccino
tra due parti il mouimento separato; pur che l'una di esse si muoua per vno Semiditono; come qui si vede.
E' concesso etiandio il venire dalla Consonanza perfetta alla imperfetta, quando le parti ascendeno, ouer discendeno insieme; pur che l'vna di esse faccia il Mouimento congiunto, & la Consonanza imperfetta sia di
maggior proportione della perfetta. E' lecito etiandio porre due consonanze l'vna dopo l'altra, che faccino
tra due parti il mouimento separato; pur che l'una di esse si muoua per vno Semiditono; come qui si vede.
 Si può ancora con mouimenti separati porre due parti nelli Contrapunti, che insieme ascendino, o discendino, quando la parte acuta discende per vna Terza, & la graue per vna Quinta, & si viene dalla Terza alla Quinta; ouero per il contrario, si ascende dalla Quinta alla Terza; & l'vna delle parti, cioè la graue ascende per vna Quinta, & l'acuta per vna Terza. E' ben vero, che quando vna di loro facesse il moto per vn Ditono, massimamente discendendo, che tali mouimenti si potranno schiuare: percioche il procedere in cotal modo
è alquanto aspro; come la esperienza ce lo manifesta.Ma lo ascendere dalla Quinta al
Si può ancora con mouimenti separati porre due parti nelli Contrapunti, che insieme ascendino, o discendino, quando la parte acuta discende per vna Terza, & la graue per vna Quinta, & si viene dalla Terza alla Quinta; ouero per il contrario, si ascende dalla Quinta alla Terza; & l'vna delle parti, cioè la graue ascende per vna Quinta, & l'acuta per vna Terza. E' ben vero, che quando vna di loro facesse il moto per vn Ditono, massimamente discendendo, che tali mouimenti si potranno schiuare: percioche il procedere in cotal modo
è alquanto aspro; come la esperienza ce lo manifesta.Ma lo ascendere dalla Quinta al
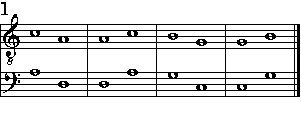 Ditono, si concede; percioche le parti procedeno per alcuni mouimenti, i quali non solamente sono soportabili; ma
anco molto dilettano: essendo che sono molto sonori: et questo percioche procedeno verso l'acuto, onde si generano
li Mouimenti veloci, da i quali sono ascose le durezze, che per la tardità delli mouimenti si manifestano, quando
vano verso il graue. Lungo sarebbe, il voler porre uno essempio particolare di tutti li mouimenti, & passaggi,
che possono far le parti delli Contrapunti; et di uno in vno volerne assignare la ragione particolare: ma di ciò sia
detto a sufficienza: percioche da quello, che si è detto, si può hauere vn modo, o Regola generale di conopage 187scere i buoni passaggi dalli tristi; la qual cognitione non sarà molto difficile da acquistare a tutti coloro, che
si voranno essercitare nella osseruanza delle nostre Regole.
Ditono, si concede; percioche le parti procedeno per alcuni mouimenti, i quali non solamente sono soportabili; ma
anco molto dilettano: essendo che sono molto sonori: et questo percioche procedeno verso l'acuto, onde si generano
li Mouimenti veloci, da i quali sono ascose le durezze, che per la tardità delli mouimenti si manifestano, quando
vano verso il graue. Lungo sarebbe, il voler porre uno essempio particolare di tutti li mouimenti, & passaggi,
che possono far le parti delli Contrapunti; et di uno in vno volerne assignare la ragione particolare: ma di ciò sia
detto a sufficienza: percioche da quello, che si è detto, si può hauere vn modo, o Regola generale di conopage 187scere i buoni passaggi dalli tristi; la qual cognitione non sarà molto difficile da acquistare a tutti coloro, che
si voranno essercitare nella osseruanza delle nostre Regole.
Che si debbe schiuare più che si può li Mouimenti separati, & similmente le Distanze, che possono accascare tra le parti della cantilena.Capitolo 37.
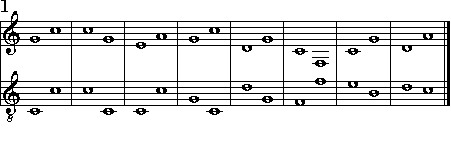 Conciosia che tali distanze, oltra che sono più difficili da cantare (essendo che non cosi facilmente si possono formare le voci, & proportionare gli interualli, & le consonanze in quelle modulationi, che procedeno in cotal
modo, come quelle, che si cantano l'vna per Mouimento congiunto, & l'altra per Mouimento separato) generano etiandio alcuni effetti, che alle volte all'vdito non sono molto grati. Onde è da notare, che li Mouimenti quanto più sono vniti, cioè non molto lontani; come sono quelli, che si moueno per vn grado, sono senza dubbio più cantabili, & con maggior diletto fanno vdire l'harmonia, che nasce da loro tra le parti, che
quelli, che sono separati; & ciò nasce: per che quanto più sono congiunti, tanto più sono naturali: essendo
che allora si procede naturalmente, quando si và dall'vno estremo all'altro di alcuna cosa, per li debiti mezi. Di maniera che molto è da lodare, & da commendare tale vicinità; come quella, che si accosta più alla
natura. Il che molto lodò anco Agostino nel cap. 10. del 2. lib. della Musica dicendo; che La vicinità delle parti, tanto era più degna di essere approuata, quanto era più vicina alla equalità; ancora che
lui ragionasse in
altro proposito. Et quantunque queste distanze da sè non siano dissonanti, generano nondimeno (come hò
detto) vn non sò che di tristo all'vdito, che non si può vdire con diletto. Schiuaremo adunque queste distanze, accioche li nostri contrapunti siano grati, dolci, sonori, harmoniosi, & pieni di ogni buona melodia.
Conciosia che tali distanze, oltra che sono più difficili da cantare (essendo che non cosi facilmente si possono formare le voci, & proportionare gli interualli, & le consonanze in quelle modulationi, che procedeno in cotal
modo, come quelle, che si cantano l'vna per Mouimento congiunto, & l'altra per Mouimento separato) generano etiandio alcuni effetti, che alle volte all'vdito non sono molto grati. Onde è da notare, che li Mouimenti quanto più sono vniti, cioè non molto lontani; come sono quelli, che si moueno per vn grado, sono senza dubbio più cantabili, & con maggior diletto fanno vdire l'harmonia, che nasce da loro tra le parti, che
quelli, che sono separati; & ciò nasce: per che quanto più sono congiunti, tanto più sono naturali: essendo
che allora si procede naturalmente, quando si và dall'vno estremo all'altro di alcuna cosa, per li debiti mezi. Di maniera che molto è da lodare, & da commendare tale vicinità; come quella, che si accosta più alla
natura. Il che molto lodò anco Agostino nel cap. 10. del 2. lib. della Musica dicendo; che La vicinità delle parti, tanto era più degna di essere approuata, quanto era più vicina alla equalità; ancora che
lui ragionasse in
altro proposito. Et quantunque queste distanze da sè non siano dissonanti, generano nondimeno (come hò
detto) vn non sò che di tristo all'vdito, che non si può vdire con diletto. Schiuaremo adunque queste distanze, accioche li nostri contrapunti siano grati, dolci, sonori, harmoniosi, & pieni di ogni buona melodia.
In qual maniera si debba procedere da vna Consonanza ad vn'altra.Cap. 38.
 Quando poi si va alla consonanza Imperfetta con la Perfetta, allora non è necessario hauere questa consideratione, pur che si osserui, che li mouimenti, che fanno le parti, siano regolati, secondo il modo mostrato
di sopra. Io dico dalla Perfetta alla Imperfetta per questa ragione: percioche ciascuna cosa desidera naturalmente la sua perfettione, alla quale desidera di peruenire più presto, & col migliore, & più breue modo, che puote; la qual perfettione, in questo genere, si attribuisce alle Consonanze perfette. La onde ciascuna cosa facilmente (come ad ogn'vno è manifesto) dalla perfettione può passare alla imperfettione; ma non
per il contrario: percioche è cosa più facile fare vna cosa, che non è distruggerla, & rouinarla. Di modo che quando si operasse altramente di quello che hò detto, sarebbe vno operare contra l'ordine, & contra
la natura delle cose: Conciosia che le Imperfette tanto più participano della perfettione, quanto più si
accostano alla loro vicina Perfetta; & si rendeno etiandio all'udito tanto più dolci, & più soaui. Mi potrebbe hora alcuno dire; Se la Sesta maggiore è piu vicina alla Quinta, che non è alla Ottaua; come è
manifesto; per qual cagione la douemo maggiormente porre auanti la Ottaua, che auanti la Quinta; poi che page 189douemo andare dalla Consonanza Imperfetta alla Perfetta con la più vicina? Dico, che quantunque la Sesta maggiore sia più vicina alla Quinta, che alla Ottaua; per questo non è vero, che la Minore non sia più vicina alla Quinta
della Maggiore. Onde douemo sapere, che essendo tra le Perfette, la Ottaua maggior della
Quinta; & tra le Seste la maggiore di maggior quantità, che non è la minore; douemo accompagnare la maggiore delle Perfette con la maggiore delle Imperfette; per quel simbolo (dirò cosi) o consenso, che è tra loro:
percioche facil cosa è di passare da vna cosa ad vn'altra, & senza molta fatica; quando tra loro si ritroua simile consenso. Onde douemo andare alla Quinta con la Sesta minore: percioche hà tal consentimento con lei,
& a lei è piu vicina. Similmente andaremo alla Ottaua con la maggiore: conciosia che con lei hà tale consenso, & è a lei piu propinqua. Ne sò veder ragione alcuna, che dimostri, che ad vna cosa, alla quale se habbia
solamente vn rispetto, se le conuenga due cose diuerse, & quasi contrarie; Et parmi, che vsandole ad altro modo, sarebbe fare,
come fà quel Medico, che Galeno chiama Empirico, che con vna istessa medicina
vuol curare diuerse egritudini, non facendo caso alcuno, che il male procedi più da humor calido, che da frigido: conciosia che non conosce l'humore peccante. Alla Ottaua veramente si conuiene la Sesta maggiore, &
non la minore; & questa si accompagna ottimamente con la Quinta; come si può prouare con ragione, con
autorità, & con lo essempio. Et primieramente si proua con ragione, come hò mostrato di sopra; & anco, perche se noi haueremo riguardo al Numero harmonico, dal quale hà la sua forma ogni Consonanza musicale,
ritrouaremo, che la Sesta maggiore hà la sua forma dalla proportione Superbipartienteterza, contenuta (come altroue hò detto) tra questi termini 5 & 3, che sono la radice di tal proportione. Onde se noi procederemo più oltra nell'ordine naturale de i numeri sopradetti; ritrouaremo, che dopo'l 5 senza alcun mezo
succede il 6, che col 5 contiene la forma della Terza minore; la quale se noi accompagnaremo con la detta Sesta, haueremo a punto la Ottaua. Per laqual cosa se noi porremo il 3, che habbia due relationi, cioè al
5 & al 6. procedendo per ordine naturale in questo modo. 6. 5. 3. quasi nella maniera, che procedeno due parti, delle quali l'vna vadi dall'acuto al graue, & l'altra non si muoui: Oueramente se noi porremo lo istesso ordine tra 10. 6. 5. quasi nel modo, che procedeno due parti, delle quali l'vna si parti dal
graue, & vada verso l'acuto, procedendo per vn Semiditono, & peruiene alla Ottaua; & l'altra non si muoui medesimamente; vederemo
quanto sia necessaria la osseruatione della predetta Regola. Questa osseruanza
ritrouaremo etiandio in tale ordine, tra il 15 & il 9, che contengono la forma della Sesta maggiore,
fuori delli suoi termini radicali: perche, si come due parti, l'vna delle quali ascendi per vn Tuono maggiore,
& l'altra per vn maggiore Semituono discendi, vengono alla Ottaua con mirabil modo, cosi ponendo lo 8
sopra il 9, & aggiungendo il 16 sotto'l 15, ritrouaremo la forma della Diapason fuori delli suoi termini radicali tra il 16
et l'8, in questo ordine naturale 16. 15. 9. 8. Et si come non si ritroua in vn tale ordine, che dalla
forma della Sesta maggiore si possa venire alla forma della Quinta, se non con l'aiuto del Tuono; cosi mai si potrà procedere dalla Sesta minore alla Quinta, se non con l'aiuto del Semituono; Si come si può comprendere da questi
quattro termini 50. 45. 30. 27. tra i quali commodamente si ritroua la forma della Quinta tra
45. & 30, & quella del Tuono minore da ogni parte; Et tra questi 24. 16. 15. 10. la forma
del Semituono maggiore nel luogo di mezo; & quella della Quinta da ogni parte tra 24 & 16, &
tra 15 & 10; a guisa di vna parte, che proceda dal graue all'acuto, o per il contrario; & l'altra posta nel
graue, o nell'acuto non faccia mouimento alcuno; E questi termini non si potranno ritrouare in altra maniera
nell'ordine naturale de i detti Numeri harmonici, se non con grande difficultà, & non saranno posti nell'ordine naturale: ma si bene accidentale. Et quelle ragioni, ch'io hò detto della Sesta maggiore con la Ottaua, si
possono applicare alla minore con la Quinta, & alle altre Consonanze ancora, lequali lasso per breuità. Ecci
vn'altra ragione ancora, per dimostrare cotal cosa, che di due Consonanze Imperfette proposte, siano qual si
vogliano, pur che siano denominate da vno istesso numero di chorde, sempre la maggiore è più atta a pigliare
accrescimento nel graue, o nell'acuto, che la minore; laquale hà natura di restringersi, & farsi anco minore:
conciosia che la maggiore hà piu del continouo, che non hà la minore. La onde auiene, che desiderando, &
appetendo ogni cosa simile naturalmente il suo simile, la Sesta maggiore, per hauer più perfettione della minore, maggiormente desidera di auicinarsi alla Ottaua, la quale per sua natura è più perfetta della Quinta;
anzi è d'ogn'altra perfettissima; come altre volte hò detto; & la Sesta minore, come meno perfetta, da qual
parte si voglia, sia graue, o acuta, appetisce quella, che è piu conforme alla sua natura, che è la Quinta. Questa
istessa osseruanza si conferma con la autorità di Franchino Gaffuro, ilquale vuole, che il propio della Sesta page 190maggiore sia, di venire alla Ottaua; & il propio della Minore sia, di auicinarsi alla Quinta. Essendo adunque
tale la natura di queste consonanze, bisogna dire, che sempre habbiano tal natura, & inclinatione; & che
quando si pongono altramente nelle compositioni, si ponghino contra la natura loro. Onde se quelle cose, che
si pongono contra la lor natura in opera, non possono far buono effetto: percioche sono ritirate dal propio lor
fine; potremo dire, che qualunque volta tali Consonanze si porranno ne i Contrapunti contra la loro natura,
che non potranno apportare all'vdito cosa, che molto diletti. Potemo hora vedere cotal cosa esser vera con la
esperienza in mano, & venire allo essempio promesso: conciosia che migliore effetto fanno poste ne i Contrapunti al modo mostrato di sopra, che in altra maniera. La onde la Natura, laquale hà iurisditione in ogni cosa, hà fatto, che non pur quelli, che sono periti nella Musica, ma gli Idioti, & li Contadini ancora, i quali cantano a loro modo, senza alcuna ragione, vsano di andare dalla Sesta maggiore alla Ottaua, come sono insegnati naturalmente; ilche si ode maggiormente nelle Cadenze, che in ogn'altra parte delle lor Canzoni; come è
manifesto a ciascuno perito nella Musica. Et forse, che il detto Franchino da questo prese ardir di dire, che
lo andare dalla Sesta maggiore alla Ottaua, si douea osseruare solamente nelle Cadenze: percioche in esse si
fanno le terminationi delle cantilene: ma al mio giuditio parmi (come si può comprendere) dalle sue parole poste di sopra, che ciò non sia detto con ragione, se vorremo attendere alla Natura dell'vna, & dell'altra. Non
sarà adunque lecito volendo osseruare cotal Regola, di passare dalla Sesta maggiore alla Quinta, ne anco dalla minore alla Ottaua; senza deprauatione della natura delle predette consonanze. Onde bisogna auertire,
accioche con facilità si osserui questa Regola, che qualunque volta si vorrà procedere dalla consonanza Imperfetta alla Perfetta; di fare, che almeno vna delle parti si muoua con alcuno mouimento, nel quale sia il Semituono maggiore, tacito, ouero espresso. Et per conseguire tal cosa giouerà molto l'vso delle chorde Chromatiche, & delle Enharmoniche, adoperandole nel modo, che altroue son per dimostrare. Ma perche, si come non
torna sempre commodo al Compositore di passar dalla Sesta maggiore alla Ottaua, ne dalla Minore alla
Quinta; cosi non torna alle volte commodo di procedere dalla Terza minore all'Vnisono, nel modo ch'io hò
mostrato di sopra: per tanto accioche ogn'vno sappia, in qual modo habbia da procedere in simil casi, porrò il
sottoposto essempio, nel quale potrà vedere, in quanti modi si potrà passare dall'vna, o l'altra Sesta: & cosi
dalla Terza maggiore, & dalla minore, & altre simili ad vn'altra consonanza.
Quando poi si va alla consonanza Imperfetta con la Perfetta, allora non è necessario hauere questa consideratione, pur che si osserui, che li mouimenti, che fanno le parti, siano regolati, secondo il modo mostrato
di sopra. Io dico dalla Perfetta alla Imperfetta per questa ragione: percioche ciascuna cosa desidera naturalmente la sua perfettione, alla quale desidera di peruenire più presto, & col migliore, & più breue modo, che puote; la qual perfettione, in questo genere, si attribuisce alle Consonanze perfette. La onde ciascuna cosa facilmente (come ad ogn'vno è manifesto) dalla perfettione può passare alla imperfettione; ma non
per il contrario: percioche è cosa più facile fare vna cosa, che non è distruggerla, & rouinarla. Di modo che quando si operasse altramente di quello che hò detto, sarebbe vno operare contra l'ordine, & contra
la natura delle cose: Conciosia che le Imperfette tanto più participano della perfettione, quanto più si
accostano alla loro vicina Perfetta; & si rendeno etiandio all'udito tanto più dolci, & più soaui. Mi potrebbe hora alcuno dire; Se la Sesta maggiore è piu vicina alla Quinta, che non è alla Ottaua; come è
manifesto; per qual cagione la douemo maggiormente porre auanti la Ottaua, che auanti la Quinta; poi che page 189douemo andare dalla Consonanza Imperfetta alla Perfetta con la più vicina? Dico, che quantunque la Sesta maggiore sia più vicina alla Quinta, che alla Ottaua; per questo non è vero, che la Minore non sia più vicina alla Quinta
della Maggiore. Onde douemo sapere, che essendo tra le Perfette, la Ottaua maggior della
Quinta; & tra le Seste la maggiore di maggior quantità, che non è la minore; douemo accompagnare la maggiore delle Perfette con la maggiore delle Imperfette; per quel simbolo (dirò cosi) o consenso, che è tra loro:
percioche facil cosa è di passare da vna cosa ad vn'altra, & senza molta fatica; quando tra loro si ritroua simile consenso. Onde douemo andare alla Quinta con la Sesta minore: percioche hà tal consentimento con lei,
& a lei è piu vicina. Similmente andaremo alla Ottaua con la maggiore: conciosia che con lei hà tale consenso, & è a lei piu propinqua. Ne sò veder ragione alcuna, che dimostri, che ad vna cosa, alla quale se habbia
solamente vn rispetto, se le conuenga due cose diuerse, & quasi contrarie; Et parmi, che vsandole ad altro modo, sarebbe fare,
come fà quel Medico, che Galeno chiama Empirico, che con vna istessa medicina
vuol curare diuerse egritudini, non facendo caso alcuno, che il male procedi più da humor calido, che da frigido: conciosia che non conosce l'humore peccante. Alla Ottaua veramente si conuiene la Sesta maggiore, &
non la minore; & questa si accompagna ottimamente con la Quinta; come si può prouare con ragione, con
autorità, & con lo essempio. Et primieramente si proua con ragione, come hò mostrato di sopra; & anco, perche se noi haueremo riguardo al Numero harmonico, dal quale hà la sua forma ogni Consonanza musicale,
ritrouaremo, che la Sesta maggiore hà la sua forma dalla proportione Superbipartienteterza, contenuta (come altroue hò detto) tra questi termini 5 & 3, che sono la radice di tal proportione. Onde se noi procederemo più oltra nell'ordine naturale de i numeri sopradetti; ritrouaremo, che dopo'l 5 senza alcun mezo
succede il 6, che col 5 contiene la forma della Terza minore; la quale se noi accompagnaremo con la detta Sesta, haueremo a punto la Ottaua. Per laqual cosa se noi porremo il 3, che habbia due relationi, cioè al
5 & al 6. procedendo per ordine naturale in questo modo. 6. 5. 3. quasi nella maniera, che procedeno due parti, delle quali l'vna vadi dall'acuto al graue, & l'altra non si muoui: Oueramente se noi porremo lo istesso ordine tra 10. 6. 5. quasi nel modo, che procedeno due parti, delle quali l'vna si parti dal
graue, & vada verso l'acuto, procedendo per vn Semiditono, & peruiene alla Ottaua; & l'altra non si muoui medesimamente; vederemo
quanto sia necessaria la osseruatione della predetta Regola. Questa osseruanza
ritrouaremo etiandio in tale ordine, tra il 15 & il 9, che contengono la forma della Sesta maggiore,
fuori delli suoi termini radicali: perche, si come due parti, l'vna delle quali ascendi per vn Tuono maggiore,
& l'altra per vn maggiore Semituono discendi, vengono alla Ottaua con mirabil modo, cosi ponendo lo 8
sopra il 9, & aggiungendo il 16 sotto'l 15, ritrouaremo la forma della Diapason fuori delli suoi termini radicali tra il 16
et l'8, in questo ordine naturale 16. 15. 9. 8. Et si come non si ritroua in vn tale ordine, che dalla
forma della Sesta maggiore si possa venire alla forma della Quinta, se non con l'aiuto del Tuono; cosi mai si potrà procedere dalla Sesta minore alla Quinta, se non con l'aiuto del Semituono; Si come si può comprendere da questi
quattro termini 50. 45. 30. 27. tra i quali commodamente si ritroua la forma della Quinta tra
45. & 30, & quella del Tuono minore da ogni parte; Et tra questi 24. 16. 15. 10. la forma
del Semituono maggiore nel luogo di mezo; & quella della Quinta da ogni parte tra 24 & 16, &
tra 15 & 10; a guisa di vna parte, che proceda dal graue all'acuto, o per il contrario; & l'altra posta nel
graue, o nell'acuto non faccia mouimento alcuno; E questi termini non si potranno ritrouare in altra maniera
nell'ordine naturale de i detti Numeri harmonici, se non con grande difficultà, & non saranno posti nell'ordine naturale: ma si bene accidentale. Et quelle ragioni, ch'io hò detto della Sesta maggiore con la Ottaua, si
possono applicare alla minore con la Quinta, & alle altre Consonanze ancora, lequali lasso per breuità. Ecci
vn'altra ragione ancora, per dimostrare cotal cosa, che di due Consonanze Imperfette proposte, siano qual si
vogliano, pur che siano denominate da vno istesso numero di chorde, sempre la maggiore è più atta a pigliare
accrescimento nel graue, o nell'acuto, che la minore; laquale hà natura di restringersi, & farsi anco minore:
conciosia che la maggiore hà piu del continouo, che non hà la minore. La onde auiene, che desiderando, &
appetendo ogni cosa simile naturalmente il suo simile, la Sesta maggiore, per hauer più perfettione della minore, maggiormente desidera di auicinarsi alla Ottaua, la quale per sua natura è più perfetta della Quinta;
anzi è d'ogn'altra perfettissima; come altre volte hò detto; & la Sesta minore, come meno perfetta, da qual
parte si voglia, sia graue, o acuta, appetisce quella, che è piu conforme alla sua natura, che è la Quinta. Questa
istessa osseruanza si conferma con la autorità di Franchino Gaffuro, ilquale vuole, che il propio della Sesta page 190maggiore sia, di venire alla Ottaua; & il propio della Minore sia, di auicinarsi alla Quinta. Essendo adunque
tale la natura di queste consonanze, bisogna dire, che sempre habbiano tal natura, & inclinatione; & che
quando si pongono altramente nelle compositioni, si ponghino contra la natura loro. Onde se quelle cose, che
si pongono contra la lor natura in opera, non possono far buono effetto: percioche sono ritirate dal propio lor
fine; potremo dire, che qualunque volta tali Consonanze si porranno ne i Contrapunti contra la loro natura,
che non potranno apportare all'vdito cosa, che molto diletti. Potemo hora vedere cotal cosa esser vera con la
esperienza in mano, & venire allo essempio promesso: conciosia che migliore effetto fanno poste ne i Contrapunti al modo mostrato di sopra, che in altra maniera. La onde la Natura, laquale hà iurisditione in ogni cosa, hà fatto, che non pur quelli, che sono periti nella Musica, ma gli Idioti, & li Contadini ancora, i quali cantano a loro modo, senza alcuna ragione, vsano di andare dalla Sesta maggiore alla Ottaua, come sono insegnati naturalmente; ilche si ode maggiormente nelle Cadenze, che in ogn'altra parte delle lor Canzoni; come è
manifesto a ciascuno perito nella Musica. Et forse, che il detto Franchino da questo prese ardir di dire, che
lo andare dalla Sesta maggiore alla Ottaua, si douea osseruare solamente nelle Cadenze: percioche in esse si
fanno le terminationi delle cantilene: ma al mio giuditio parmi (come si può comprendere) dalle sue parole poste di sopra, che ciò non sia detto con ragione, se vorremo attendere alla Natura dell'vna, & dell'altra. Non
sarà adunque lecito volendo osseruare cotal Regola, di passare dalla Sesta maggiore alla Quinta, ne anco dalla minore alla Ottaua; senza deprauatione della natura delle predette consonanze. Onde bisogna auertire,
accioche con facilità si osserui questa Regola, che qualunque volta si vorrà procedere dalla consonanza Imperfetta alla Perfetta; di fare, che almeno vna delle parti si muoua con alcuno mouimento, nel quale sia il Semituono maggiore, tacito, ouero espresso. Et per conseguire tal cosa giouerà molto l'vso delle chorde Chromatiche, & delle Enharmoniche, adoperandole nel modo, che altroue son per dimostrare. Ma perche, si come non
torna sempre commodo al Compositore di passar dalla Sesta maggiore alla Ottaua, ne dalla Minore alla
Quinta; cosi non torna alle volte commodo di procedere dalla Terza minore all'Vnisono, nel modo ch'io hò
mostrato di sopra: per tanto accioche ogn'vno sappia, in qual modo habbia da procedere in simil casi, porrò il
sottoposto essempio, nel quale potrà vedere, in quanti modi si potrà passare dall'vna, o l'altra Sesta: & cosi
dalla Terza maggiore, & dalla minore, & altre simili ad vn'altra consonanza.
 Questo è vltimamente da notare, che quello, che si è detto delle Consonanze semplici, si debbe anco intendere delle Replicate. Similmente si debbe auertire, che quando due parti della cantilena discenderanno insieme;
Questo è vltimamente da notare, che quello, che si è detto delle Consonanze semplici, si debbe anco intendere delle Replicate. Similmente si debbe auertire, che quando due parti della cantilena discenderanno insieme;
 et dalla Sesta maggiore verranno alla Terza, che sia
Maggiore; allora la parte acuta cascherà meglio, & farà megliore
effetto, che se cascasse sopra la Minore; ancora che l'uno, & l'altro modo sia buono: Percioche cascherà senza dubbio alcuno, sopra vna consonanza, che più si
auicina alla perfettione, che non fa la Terza minore;
si come si potrà vdire, & essaminare in questi due
essempi, posti qui da canto. page 191
et dalla Sesta maggiore verranno alla Terza, che sia
Maggiore; allora la parte acuta cascherà meglio, & farà megliore
effetto, che se cascasse sopra la Minore; ancora che l'uno, & l'altro modo sia buono: Percioche cascherà senza dubbio alcuno, sopra vna consonanza, che più si
auicina alla perfettione, che non fa la Terza minore;
si come si potrà vdire, & essaminare in questi due
essempi, posti qui da canto. page 191In qual maniera si debba terminare ciascuna Cantilena.Cap. 39.
Il modo che si debbe tenere nel fare li Contrapunti semplici a due voci, chiamati a Nota contra nota.Cap. 40.
Ordinis haec virtus erit, & Venus, aut ego fallor,Laqual Regola molto bene sapeua il dottissimo Virgilio; come si può comprendere; che hauendo preso vn Soggetto determinato, che era di scriuere la Rouina, & lo Incendio di Troia, & la Nauigatione di Enea; incominciò primieramente dalla Nauigatione, interrompendo l'ordine; nondimeno la Nauigatione fù dopo: Ma comprese, che con maggiore arteficio, & con maggior maestà sarebbe riuscito il suo Poema, se hauesse fatto recitare la historia per ordine da Enea, alla presentia di Didone, come fece, prendendo la occasione dalla fortuna che hebbe, riducendolo in Carthagine. Cosi sogliono fare i Poeti, & non solo i Poeti, ma anco li Pittori: percioche la Pittura non è altro, che vna poesia muta; i quali accommodano le historie, o fauole, come meglio li tornano in proposito. Onde hauendosi proposto alcuna volta di dipingere una historia, o fauola, accommoda le figure, & le accompagna insieme, secondo che pare a lui, che stiano meglio, & che faccino megliori effetti; ne fà caso alcuno di porre vna figura più in vn mopage 193do, che in vno altro; cioè che più stia in piedi, ouero a sedere in vna maniera, che in vn'altra; pur che faccia buono effetto, & osserui l'ordine della historia, o fauola, che vuol dipingere; il che si vede, che infiniti Pittori haueranno dipinto vna cosa istessa in infinite maniere; si come più volte hò veduto la historia di Lucretia moglie di Bruto; quella di Horatio, il quale combattè contra Toscani sopra il ponte; & molte altre: nondimeno tutti haueranno hauuto vno istesso fine, cioè di rapresentare le dette historie. Et non solamente questo si vede fatto da diuersi Pittori, in vno istesso soggetto: ma etiandio da vn solo, il quale dipingerà vna cosa istessa in diuersi modi. Cosi debbe adunque fare etiandio il Musico; cioè cercare di variar sempre il suo Contrapunto sopra vn Soggetto: & potendo fare molti passaggi, eleggerà quello, che sarà il migliore, & che li tornerà più in proposito; cioè quelli, che faranno il suo Contrapunto più sonoro, & meglio ordinato; & lasserà da vn canto gli altri. Però adunque quando gli occorrerà di poter fare vn passaggio; come sarebbe dire vna Cadenza, & non tornerà cosi al proposito, la debbe riseruare ad vn'altro luogo con miglior commodo. Et ciò farà, quando la Clausula, ouero il Periodo nelle parole, ouero Oratione non sarà terminato: Conciosia che debbe sempre aspettare, che ciascuno di questi sia finito; & similmente auertire, che sia il luogo propio, cioè che'l Modo, sopra il quale è fondata la cantilena, lo ricerchi. Tutte queste cose debbe osseruare colui, ilquale desidera di introdursi bene nell'arte del Contrapunto: ma sopra ogn'altra cosa debbe con ogni studio essercitarsi primieramente molti giorni in tal sorte di compositione; accioche con più facilità possa venire dipoi all'uso del Contrapunto diminuito, nel quale potrà vsare molte altre cose; come vederemo a i loro luoghi. Ma accioche si habbia qualche intelligenza di tutto quello, che hò detto, porrò qui sotto alcuni Contrapunti di nota contra nota variati, composti sopra il Soggetto nominato, hora nell'acuto, & hora nel graue; i quali essaminati, si potranno dipoi facilmente intendere quelle cose, che mostrerò altroue; & si potra operare con minori fatica.
Vt iam nunc dicat: iam nunc debentia dici
Pleraque differat, & praesens in tempus omittat.
 Ciascuno debbe essere auertito, che'l fare del Contrapunto di nota contra nota, pare, & è veramente alquanto più difficile di quello, che non è, il fare il diminuito; & questo procede; perche non gli è quella libertà, che
si ritroua nel diminuito: essendo che nel primo è dibisogno, che ogni Nota, ò Figura cantabile habbia vna consonanza solamente,
& nel secondo se ne ponghino molte, mescolate con molte dissonanze, secondo l'arbitrio,
& il buon giuditio del Compositore. Onde nel primo modo non si può cosi bene, & a suo volere ordinar le parti, che siano senza
salti, & facili da cantare; massimamente quando sopra vno istesso Soggetto si volesse
comporre molti Contrapunti, che fussero in ogni parte variati. Ne per questo alcuno si debbe attristare: conciosia che quantunque da questa radice si gusti alquanto di amaritudine; dopo non molto tempo si gode de i frutti, page 194che da essa nascono, che sono dolci, soaui, & saporosi: essendo che la Virtù (come affermano li Sauij) consiste intorno al difficile, & non intorno alla cosa facile.
Ciascuno debbe essere auertito, che'l fare del Contrapunto di nota contra nota, pare, & è veramente alquanto più difficile di quello, che non è, il fare il diminuito; & questo procede; perche non gli è quella libertà, che
si ritroua nel diminuito: essendo che nel primo è dibisogno, che ogni Nota, ò Figura cantabile habbia vna consonanza solamente,
& nel secondo se ne ponghino molte, mescolate con molte dissonanze, secondo l'arbitrio,
& il buon giuditio del Compositore. Onde nel primo modo non si può cosi bene, & a suo volere ordinar le parti, che siano senza
salti, & facili da cantare; massimamente quando sopra vno istesso Soggetto si volesse
comporre molti Contrapunti, che fussero in ogni parte variati. Ne per questo alcuno si debbe attristare: conciosia che quantunque da questa radice si gusti alquanto di amaritudine; dopo non molto tempo si gode de i frutti, page 194che da essa nascono, che sono dolci, soaui, & saporosi: essendo che la Virtù (come affermano li Sauij) consiste intorno al difficile, & non intorno alla cosa facile.
Che nelli Contrapunti si debbe schiuare gli Vnisoni, più che si puote, & che non si debbe molto di lungo frequentare le Ottaue.Cap. 41.
O fortunatam natam me consule Romam;per il raddoppiamento della sillaba Natam, & per la terminatione del verso nella sillaba Mam, che porgono all'vdito poco piacere; & nel principio di quella Epistola, che scriue Cicerone a Lentulo Proconsule; Ego omni officio; che in tre parole si legge quattro volte la litera O, & in altri luoghi quasi infiniti, onde si ode alcuna cosa di tristo, che le orecchie purgate non possono vdire; Sarebbe veramente il Musico degno di riprensione, quando comportasse vn simile disordine nelli suoi componimenti: conciosiache se tutti costoro di commun parere hanno con leggi vniuersali concluso, che non è lecito, ne in Prosa, ne in Verso (saluo se non fusse posto cotal cosa arteficiosamente, per mostrar qualche effetto) porre questi modi strani di parlare; maggiormente il Musico debbe bandire dalle sue compositioni ogni tristo suono, & qualunque altra cosa, che possa offendere l'vdito. Debbe adunque il Musico auertire, di non commettere simili cose nelle sue cantilene: ma debbe regolare in tal maniera li suoi concenti, che in loro si odi ogni cosa di buono. Et veramente allora il Contrapunto non sarebbe cosi ben purgato, quando si vdisse in lui simili disordini molto spesso, et senza alcun proposito. Il che auerebbe allora, quando facesse vdire molti Vnisoni, o molte Ottaue l' vna dopo l'altra, che fussero tramezate solamente da vn'altra consonanza; massimamente quando fussero poste sopra vna chorda istessa; ancora che procedesseno le parti con mouimenti separati; Le quali consonanze, quando fussero collocate in cotal maniera, dal sottoposto essempio si potrà conoscere quanto sarebbeno grate a ciascuno di sano giuditio.
 page 195Io non dico però che non si debbino adoperare; ma dico, che non si debbono vsare troppo spesso: percioche quando occorresse, che'l Compositore non potesse accommodare vna buona, & commoda modulatione, cioè un bello, & elegante procedere;
con vn bello, & leggiadro cantare, le debbe per ogni modo vsare, tramezate però
da alcune altre consonanze; & debbe più presto porre sempre la Ottaua, che l'Vnisono; quando li tornerà
commodo: percioche questo (come hauemo veduto) non è per alcun modo Consonanza: ma si bene la Ottaua.
page 195Io non dico però che non si debbino adoperare; ma dico, che non si debbono vsare troppo spesso: percioche quando occorresse, che'l Compositore non potesse accommodare vna buona, & commoda modulatione, cioè un bello, & elegante procedere;
con vn bello, & leggiadro cantare, le debbe per ogni modo vsare, tramezate però
da alcune altre consonanze; & debbe più presto porre sempre la Ottaua, che l'Vnisono; quando li tornerà
commodo: percioche questo (come hauemo veduto) non è per alcun modo Consonanza: ma si bene la Ottaua.
Delli Contrapunti diminuiti a due voci, & in qual modo si possino vsar le Dissonanze.Cap. 42

 nel leuare della Battuta, nel Contrapunto diminuito: percioche poste in tal maniera hanno molta gratia;come la esperienza ce lo manifesta. Ma quando il Soggetto fusse diminuito, cioè vna parte di Canto figurato;
allora le figure del Contrapunto si possono fare equali alle sue figure; pur che procedino in tal modo insieme,
che se bene è diminuito, il Contrapunto habbia in se qualche leggiadria; & tal volta procedi con figure di alquanto più valore, che quelle, che sono contenute nel Soggetto: percioche fa dibisogno, ch e si oda almeno vna
parte, che faccia mouimento, si nel battere, come anco nel leuar la Battuta. Quando adunque tra molte Minime se ne ritrouasse alcuna, che non procedesse per mouimento congiunto; non sarà mai lecito, che ella sia dissonante; anzi l'vna, & l'altra di due figure, che faranno tal mouimento, si debbeno porre consonanti:
Conciosia che se bene la Dissonanza è posta nella seconda minima, nel mouimento congiunto; tal mouimento,
& quel poco di velocità, che si ritroua nel proferir simili figure, non lassano vdire cosa alcuna, che dispiaccia. Ma non è gia cosi nelli Mouimenti separati: percioche per tal separatione la Dissonanza si fa tanto manifesta; che apena
si può tolerare; come è manifesto a tutti coloro, che hanno giuditio di tal cosa.
nel leuare della Battuta, nel Contrapunto diminuito: percioche poste in tal maniera hanno molta gratia;come la esperienza ce lo manifesta. Ma quando il Soggetto fusse diminuito, cioè vna parte di Canto figurato;
allora le figure del Contrapunto si possono fare equali alle sue figure; pur che procedino in tal modo insieme,
che se bene è diminuito, il Contrapunto habbia in se qualche leggiadria; & tal volta procedi con figure di alquanto più valore, che quelle, che sono contenute nel Soggetto: percioche fa dibisogno, ch e si oda almeno vna
parte, che faccia mouimento, si nel battere, come anco nel leuar la Battuta. Quando adunque tra molte Minime se ne ritrouasse alcuna, che non procedesse per mouimento congiunto; non sarà mai lecito, che ella sia dissonante; anzi l'vna, & l'altra di due figure, che faranno tal mouimento, si debbeno porre consonanti:
Conciosia che se bene la Dissonanza è posta nella seconda minima, nel mouimento congiunto; tal mouimento,
& quel poco di velocità, che si ritroua nel proferir simili figure, non lassano vdire cosa alcuna, che dispiaccia. Ma non è gia cosi nelli Mouimenti separati: percioche per tal separatione la Dissonanza si fa tanto manifesta; che apena
si può tolerare; come è manifesto a tutti coloro, che hanno giuditio di tal cosa.

 page 197
Si potrà nondimeno porre la Prima parte della battuta, che sia disonante; quando sarà la seconda minima di
vna Semibreue sincopata del Contrapunto; percioche la prima parte di tal figura, sarà posta senza dubbio nel
leuar la battuta, & la seconda nel battere; & tal Dissonanza si potrà sopportare: percioche nel cantare la Semibreue sincopata, si tien salda la voce, & si ode quasi vna sospensione, o taciturnità, che si troua nel mezo
della percussione, dalla quale nascono i suoni, & per essa si discerneno l'vn dall'altro, & consiste nel tempo;
onde l'Vdito quasi non la sente: percioche da lei non è mosso, di maniera, che la possa comprendere pienamente: per non esser da lei percosso, & per la debolezza del mouimento, che si scorge in essa: perche manca della
percussione, che lo muoue: la onde la Voce allora nel perseuerare della Sincopa perde quella viuacità, che hauea nella prima percussione; di modo che fatta debole, et essendo percossa sopra la seconda parte della sincopa,
nella quale è nascosta la Dissonanza, da vn mouimento più gagliardo di vn'altra voce forte, che si muoue da
vn luogo all'altro con più gagliardo mouimento, tal Dissonanza a pena si ode; essendo anco, che prestamente
se ne passa. Et se pure il Senso è da qualche parte offeso; è dipoi ragguagliato per tal maniera dalla Consonanza, che succede senza alcun mezo; che non solamente tal Dissonanza non li dispiace; ma grandemente in lei
si compiace: perche con maggior dolcezza, & maggior soauità li fà vdire tal Consonanza. Et questo forse
auiene, perche Ogni contrario maggiormente si scopre, & si fà al sentimento più noto, per la comparatione
del suo Opposto. Ma no si debbe giamai porre la Prima parte della Semibreue, che sia dissonante; sia poi sincopata, o non sincopata; & si debbe auertire per ogni modo due cose; la prima, che Dopo la dissonanza segua
vna consonanza a lei piu vicina; la seconda, chel Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, & esser congiunto: & non ascendere. Onde potrà essere vtile questa Regola, che Quando la
Dissonanza sarà posta nella seconda parte della Semibreue sincopata, laquale sarà vna Seconda; allora dopo
lei accommodaremo ottimamente la Terza, che le è più vicina. Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Settima poi se le accompagnerà la Sesta: percioche le è più vicina. Similmente si potrebbe dire delle Replicate; si come della Nona, alla quale si accompagna la Decima;
& della Vndecima, dietro laquale similmente si debbe porre la Decima; come si può vedere.
page 197
Si potrà nondimeno porre la Prima parte della battuta, che sia disonante; quando sarà la seconda minima di
vna Semibreue sincopata del Contrapunto; percioche la prima parte di tal figura, sarà posta senza dubbio nel
leuar la battuta, & la seconda nel battere; & tal Dissonanza si potrà sopportare: percioche nel cantare la Semibreue sincopata, si tien salda la voce, & si ode quasi vna sospensione, o taciturnità, che si troua nel mezo
della percussione, dalla quale nascono i suoni, & per essa si discerneno l'vn dall'altro, & consiste nel tempo;
onde l'Vdito quasi non la sente: percioche da lei non è mosso, di maniera, che la possa comprendere pienamente: per non esser da lei percosso, & per la debolezza del mouimento, che si scorge in essa: perche manca della
percussione, che lo muoue: la onde la Voce allora nel perseuerare della Sincopa perde quella viuacità, che hauea nella prima percussione; di modo che fatta debole, et essendo percossa sopra la seconda parte della sincopa,
nella quale è nascosta la Dissonanza, da vn mouimento più gagliardo di vn'altra voce forte, che si muoue da
vn luogo all'altro con più gagliardo mouimento, tal Dissonanza a pena si ode; essendo anco, che prestamente
se ne passa. Et se pure il Senso è da qualche parte offeso; è dipoi ragguagliato per tal maniera dalla Consonanza, che succede senza alcun mezo; che non solamente tal Dissonanza non li dispiace; ma grandemente in lei
si compiace: perche con maggior dolcezza, & maggior soauità li fà vdire tal Consonanza. Et questo forse
auiene, perche Ogni contrario maggiormente si scopre, & si fà al sentimento più noto, per la comparatione
del suo Opposto. Ma no si debbe giamai porre la Prima parte della Semibreue, che sia dissonante; sia poi sincopata, o non sincopata; & si debbe auertire per ogni modo due cose; la prima, che Dopo la dissonanza segua
vna consonanza a lei piu vicina; la seconda, chel Mouimento, ilquale farà la parte della sincopa, debba sempre discendere, & esser congiunto: & non ascendere. Onde potrà essere vtile questa Regola, che Quando la
Dissonanza sarà posta nella seconda parte della Semibreue sincopata, laquale sarà vna Seconda; allora dopo
lei accommodaremo ottimamente la Terza, che le è più vicina. Cosi ancora quando in essa Sincopa sarà posta la Quarta, si farà il medesimo. Alla Settima poi se le accompagnerà la Sesta: percioche le è più vicina. Similmente si potrebbe dire delle Replicate; si come della Nona, alla quale si accompagna la Decima;
& della Vndecima, dietro laquale similmente si debbe porre la Decima; come si può vedere.

 Si potrà anco alle volte (come costumano di fare li buoni Musici, non senza suo grande commodo) dalla Seconda sincopata per venire all'Vnisono; & ciò quando le parti saranno ordinate in tal maniera, che l'vna
faccia il mouimento di Tuono, & l'altra di Semituono, che siano mouimenti congiunti. Vsaremo etiandio page 198
Si potrà anco alle volte (come costumano di fare li buoni Musici, non senza suo grande commodo) dalla Seconda sincopata per venire all'Vnisono; & ciò quando le parti saranno ordinate in tal maniera, che l'vna
faccia il mouimento di Tuono, & l'altra di Semituono, che siano mouimenti congiunti. Vsaremo etiandio page 198 la Quarta sincopata, dopo laquale segua senza alcun mezo la Semidiapente, & dopo
questa immediatamente succeda la Terza
maggiore: Percioche la Semidiapente è posta in tal maniera, che fà buono effetto: essendo che tra le parti non si ode alcuna trista relatione. Ma non è cosi sopportabile la Quinta,
quando casca il Tritono per relatione, secondo
il modo mostrato disopra; come si può vdire nelli due sottoposti essempi. Sogliono ancora li Prattici vsare di
porre la Nona, quando dopo essa si viene alla Ottaua per contrarij Mouimenti, & l'vna delle parti ascenda
la Quarta sincopata, dopo laquale segua senza alcun mezo la Semidiapente, & dopo
questa immediatamente succeda la Terza
maggiore: Percioche la Semidiapente è posta in tal maniera, che fà buono effetto: essendo che tra le parti non si ode alcuna trista relatione. Ma non è cosi sopportabile la Quinta,
quando casca il Tritono per relatione, secondo
il modo mostrato disopra; come si può vdire nelli due sottoposti essempi. Sogliono ancora li Prattici vsare di
porre la Nona, quando dopo essa si viene alla Ottaua per contrarij Mouimenti, & l'vna delle parti ascenda
 per Quarta, o discenda per Quinta, & l'altra discenda per Mouimento congiunto; come
qui si vede. Si debbe però osseruare, che
quella figura, laqual segue la Dissonanza, &
discende, senza esser tramezata da altra figura; non sia legata ad vn'altra Consonanza,
cioè che non faccia vn'altra sincopa, che sia
tutta consonante: ma che di due cose sia l'vna;
ouero che tal figura discenda, o pure ascenda
per Mouimento congiunto, o separato; o che ella sia legata ad vn'altra figura, che sia simigliantemente dissonante, & che tra loro facciano vn'altra Sincopa. Io hò detto legata ad vn'altra figura: percioche
per Quarta, o discenda per Quinta, & l'altra discenda per Mouimento congiunto; come
qui si vede. Si debbe però osseruare, che
quella figura, laqual segue la Dissonanza, &
discende, senza esser tramezata da altra figura; non sia legata ad vn'altra Consonanza,
cioè che non faccia vn'altra sincopa, che sia
tutta consonante: ma che di due cose sia l'vna;
ouero che tal figura discenda, o pure ascenda
per Mouimento congiunto, o separato; o che ella sia legata ad vn'altra figura, che sia simigliantemente dissonante, & che tra loro facciano vn'altra Sincopa. Io hò detto legata ad vn'altra figura: percioche
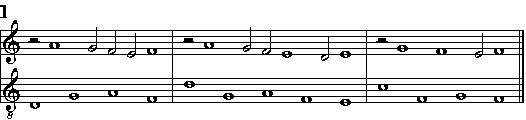 quando si risolue la sincopa di Semibreue, nella quale sia la Dissonanza, allora seguita la Minima, senza alcuna mezana figura; laquale dico allora esser legata, quando dopo la Dissonanza segue vn'altra Semibreue
sincopata, ouero vna Minima col punto. La onde dico, che al primo modo la Minima è legata ad vn'altra
Minima; & al secondo modo la Minima è legata alla Semiminima, che è il Punto. Quelle adunque, che nelle
cantilene si concedeno sono le sottoposte. Quelle veramente, che li buoni Compositori non vsano, sono quel
quando si risolue la sincopa di Semibreue, nella quale sia la Dissonanza, allora seguita la Minima, senza alcuna mezana figura; laquale dico allora esser legata, quando dopo la Dissonanza segue vn'altra Semibreue
sincopata, ouero vna Minima col punto. La onde dico, che al primo modo la Minima è legata ad vn'altra
Minima; & al secondo modo la Minima è legata alla Semiminima, che è il Punto. Quelle adunque, che nelle
cantilene si concedeno sono le sottoposte. Quelle veramente, che li buoni Compositori non vsano, sono quel le, che seguitano: imperoche quando non si osserua in loro la sopradata Regola, la figura, che segue la
Dissonanza, non fà bene il suo officio, & quello, che debitamente a lei s'appartiene. Onde la Dissonanza si risolue con vn modo freddo (dirò cosi) conciosia che non ragguaglia pienamente l'Vdito di
quello, che forse per auanti in qualche modo fù offeso dalla Dissonanza; come nelli sottoposti essempi si
potrà vdire. Et perche gli Antichi Prattici hanno vsato, & li Moderni ancora vsano, di porre alle volte confusamente ne i loro Contrapunti nel luogo della Consonanza, hora la prima, & hora la seconda page 199
le, che seguitano: imperoche quando non si osserua in loro la sopradata Regola, la figura, che segue la
Dissonanza, non fà bene il suo officio, & quello, che debitamente a lei s'appartiene. Onde la Dissonanza si risolue con vn modo freddo (dirò cosi) conciosia che non ragguaglia pienamente l'Vdito di
quello, che forse per auanti in qualche modo fù offeso dalla Dissonanza; come nelli sottoposti essempi si
potrà vdire. Et perche gli Antichi Prattici hanno vsato, & li Moderni ancora vsano, di porre alle volte confusamente ne i loro Contrapunti nel luogo della Consonanza, hora la prima, & hora la seconda page 199 Semiminima, che segueno la Minima battuta, ouero la Semibreue col punto, o senza il punto sincopata,
quando il loro procedere si fà per Mouimenti congiunti verso la perte graue; però accioche non si generi confusione nell'animo
del Compositore, determinaremo hora, quale delle due Semiminime, si habbia da porre, che
sia consonante. Onde dico, che per ogni modo si debbe porre la seconda, & non la prima: percioche questo è
stato vsato communemente non solamente da i buoni, & dotti Musici; ma dagli altri ancora, quantunque la
prima caschi sopra il leuar la battuta; cioè nella seconda parte; perche veramente vn simil procedere non è
altro, che vna sopportabile diminutione di due Minime distanti l'vna dall'altra per vna Terza, fatta per cagione di far cantar bene le parti, o per la commodità di commodar le harmonie alle parole, lequali nascono
dalla pronuntia delle figure, o note della cantilena. La onde poste in tal maniera sono sopportabili, & passano bene: percioche la tardità, & dimora della prima figura, o nota precedente; et la velocità della Semiminima seguente, della quale il tempo, & il suono, o la voce insieme passano presto, fanno, che la Dissonanza, che
è posta sopra la detta Semiminima, non è facilmente compresa dall'Vdito; & però dalli Musici non è posta
in alcuna consideratione; Et se pure è compresa immediatamente la nota seguente, che è consonante, pienamente acconcia il tutto. Quando adunque dopo la Minima, o Semibreue col punto, o senza il punto, seguiranno due Semiminime, poste l'vna dopo l'altra al modo detto disopra, porremo sempre la seconda, che sia
consonante; ancora che la prima sia dissonante: Ma quando saranno più di due potremmo fare altramente,
cioè potremmo porre la prima consonante, & le altre poi, si come è stato detto disopra; ancora che in alcuni
casi la detta prima Semiminima, che si pone dissonante, si possa porre consonante; massimamente quando
dalla Ottaua si verrà alla Quinta, o per il contrario, procedendo per contrarij mouimenti, nelli Contrapunti
diminuiti; come si potrà vedere. Tutto questo ho detto, per leuare dall'animo del Compositore la confusione:
perche non è il douere, che in questa Scienza, laquale ordina, & dà regola ad ogn'altra: caschi nella parte de i
Suoni, cosa veruna, che sia disordinata; massimamente non essendo il douere, che l'vna, & l'altra delle nominate Semiminime siano poste da vna parte de i Musici in vno passaggio istesso ad vn modo, & da vn'altra
parte ad vn'altro. Se adunque ne occorrerà di fare per ornamento, o per necessità simili passaggi; auertiremo di porle secondo il modo determinato, & nella maniera, che si veggono nello essempio posto qui disotto.
Semiminima, che segueno la Minima battuta, ouero la Semibreue col punto, o senza il punto sincopata,
quando il loro procedere si fà per Mouimenti congiunti verso la perte graue; però accioche non si generi confusione nell'animo
del Compositore, determinaremo hora, quale delle due Semiminime, si habbia da porre, che
sia consonante. Onde dico, che per ogni modo si debbe porre la seconda, & non la prima: percioche questo è
stato vsato communemente non solamente da i buoni, & dotti Musici; ma dagli altri ancora, quantunque la
prima caschi sopra il leuar la battuta; cioè nella seconda parte; perche veramente vn simil procedere non è
altro, che vna sopportabile diminutione di due Minime distanti l'vna dall'altra per vna Terza, fatta per cagione di far cantar bene le parti, o per la commodità di commodar le harmonie alle parole, lequali nascono
dalla pronuntia delle figure, o note della cantilena. La onde poste in tal maniera sono sopportabili, & passano bene: percioche la tardità, & dimora della prima figura, o nota precedente; et la velocità della Semiminima seguente, della quale il tempo, & il suono, o la voce insieme passano presto, fanno, che la Dissonanza, che
è posta sopra la detta Semiminima, non è facilmente compresa dall'Vdito; & però dalli Musici non è posta
in alcuna consideratione; Et se pure è compresa immediatamente la nota seguente, che è consonante, pienamente acconcia il tutto. Quando adunque dopo la Minima, o Semibreue col punto, o senza il punto, seguiranno due Semiminime, poste l'vna dopo l'altra al modo detto disopra, porremo sempre la seconda, che sia
consonante; ancora che la prima sia dissonante: Ma quando saranno più di due potremmo fare altramente,
cioè potremmo porre la prima consonante, & le altre poi, si come è stato detto disopra; ancora che in alcuni
casi la detta prima Semiminima, che si pone dissonante, si possa porre consonante; massimamente quando
dalla Ottaua si verrà alla Quinta, o per il contrario, procedendo per contrarij mouimenti, nelli Contrapunti
diminuiti; come si potrà vedere. Tutto questo ho detto, per leuare dall'animo del Compositore la confusione:
perche non è il douere, che in questa Scienza, laquale ordina, & dà regola ad ogn'altra: caschi nella parte de i
Suoni, cosa veruna, che sia disordinata; massimamente non essendo il douere, che l'vna, & l'altra delle nominate Semiminime siano poste da vna parte de i Musici in vno passaggio istesso ad vn modo, & da vn'altra
parte ad vn'altro. Se adunque ne occorrerà di fare per ornamento, o per necessità simili passaggi; auertiremo di porle secondo il modo determinato, & nella maniera, che si veggono nello essempio posto qui disotto.

 page 200
page 200Il modo che hà da tenere il Compositore nel fare li Contrapunti sopra vna Parte, o Soggetto diminuito.Cap. 43.
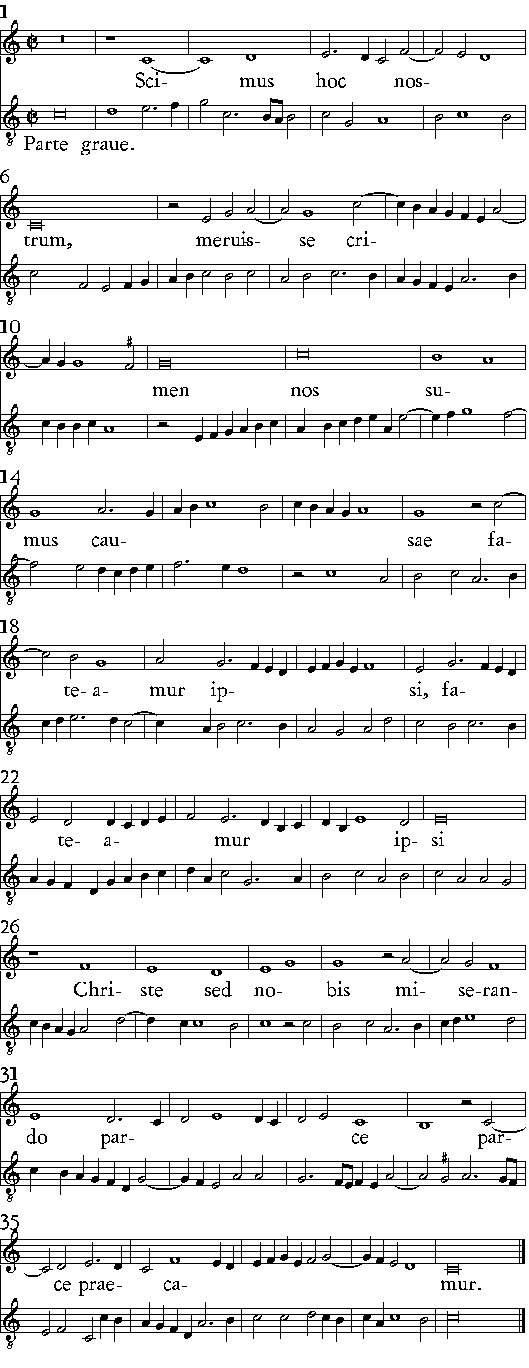
 page 202
page 202Che non è necessario, che la parte del Soggetto, & quella del Contrapunto incomincino insieme.Cap. 44.
Che le Modulationi debbeno esser ben regolate, & quel che debbe osseruare il Cantore nel cantare.Cap. 45.
Che non si debbe continouare molto di lungo nel graue, o nell'acuto nelle modulationi.Cap. 46.
Che'l porre vna Dissonanza, ouero vna Pausa di minima tra due Consonanze perfette di vna istessa specie, che insieme ascendino, o discendino, non fa, che tali consonanze non siano replicate.Cap. 47.
 Sogliono anco alle volte li Compositori in una particella della compositione, dopo la Ottaua posta sopra una figura di Semibreue, che discenda, & habbia sopra, o sotto di se vna Minima, porre immediatamente due Semiminime, lequali discendino per mouimenti congiunti, & senza altro mezo dipoi la figura seguente ascendi,
& venghi alla Ottaua. Simigliantemente sogliono, dopo vna figura di Semiminima, posta in Ottaua sopra vna Minima, che discendi, porre vn'altra Semiminima, laquale faccia il mouimento separato, & venghi medesimamente alla Ottaua: & non solo ciò fanno: ma etiandio pongono in luogo delle semiminime la
minima col punto, con due chrome seguenti, & altre cose simili; come qui si vede.
Sogliono anco alle volte li Compositori in una particella della compositione, dopo la Ottaua posta sopra una figura di Semibreue, che discenda, & habbia sopra, o sotto di se vna Minima, porre immediatamente due Semiminime, lequali discendino per mouimenti congiunti, & senza altro mezo dipoi la figura seguente ascendi,
& venghi alla Ottaua. Simigliantemente sogliono, dopo vna figura di Semiminima, posta in Ottaua sopra vna Minima, che discendi, porre vn'altra Semiminima, laquale faccia il mouimento separato, & venghi medesimamente alla Ottaua: & non solo ciò fanno: ma etiandio pongono in luogo delle semiminime la
minima col punto, con due chrome seguenti, & altre cose simili; come qui si vede.
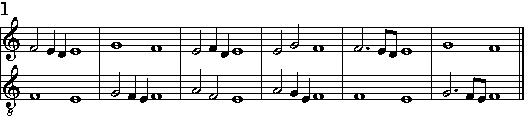 Et auegna che non si possa dire con verità, che siano due Ottaue poste l'vna dopo l'altra, senza alcun mezo:
percioche si ritroua vn'altra consonanza posta tra loro, che è la Sesta, ouer la Decima; nondimeno non si
debbeno vsare, per due ragioni: La prima delle quali fù detta disopra nel cap. 42; & la seconda è, che per la
mutatione veloce, che fa la Sesta, o la Decima poste tra loro; ouero per il veloce mouimento, che fanno, quasi non
si ode; tanto più, che nelle due semiminime, che segueno la minima, ouero la Semibreue sincopata, la prima
è posta nel numero delle Dissonanze, & la seconda nel numero delle Consonanze. Onde maggiormente tali
Ottaue si odeno, & si viene a fare contra quello, che si è determinato disopra nel cap. 41. che non si douesseno vsare molto spesso accommodate nel Contrapunto in cotal maniera. Et per dire il vero, li passaggi, che
fanno le due Semiminime con la Minima auanti: ouero la Minima col punto, & le due chrome seguenti, non sono altro, che la
Diminutione del mouimento congiunto, che fanno insieme due
Semibreui. A cotesti anco si aggiunge, che non de vsare quel passaggio, che fanno due parti ascendendo, o
discendendo insieme, l'vna per mouimenti congiunti di Quinta, procedendo per quattro semiminime, & l'alpage 207tra per mouimento separato, ascendendo per semibreui senza alcuna diminutione; & le consonanze, che cascano nel battere sono
due Quinte; come nello essempio si vede: percioche se bene sono tramezate dalla Ter
Et auegna che non si possa dire con verità, che siano due Ottaue poste l'vna dopo l'altra, senza alcun mezo:
percioche si ritroua vn'altra consonanza posta tra loro, che è la Sesta, ouer la Decima; nondimeno non si
debbeno vsare, per due ragioni: La prima delle quali fù detta disopra nel cap. 42; & la seconda è, che per la
mutatione veloce, che fa la Sesta, o la Decima poste tra loro; ouero per il veloce mouimento, che fanno, quasi non
si ode; tanto più, che nelle due semiminime, che segueno la minima, ouero la Semibreue sincopata, la prima
è posta nel numero delle Dissonanze, & la seconda nel numero delle Consonanze. Onde maggiormente tali
Ottaue si odeno, & si viene a fare contra quello, che si è determinato disopra nel cap. 41. che non si douesseno vsare molto spesso accommodate nel Contrapunto in cotal maniera. Et per dire il vero, li passaggi, che
fanno le due Semiminime con la Minima auanti: ouero la Minima col punto, & le due chrome seguenti, non sono altro, che la
Diminutione del mouimento congiunto, che fanno insieme due
Semibreui. A cotesti anco si aggiunge, che non de vsare quel passaggio, che fanno due parti ascendendo, o
discendendo insieme, l'vna per mouimenti congiunti di Quinta, procedendo per quattro semiminime, & l'alpage 207tra per mouimento separato, ascendendo per semibreui senza alcuna diminutione; & le consonanze, che cascano nel battere sono
due Quinte; come nello essempio si vede: percioche se bene sono tramezate dalla Ter za, non hanno però gratia alcuna. E' ben vero, che
questi passaggi sono più sopportabili delli primi: ma non
sono però lodeuoli: percioche nel cantar la parte diminuita, si ode la Terza posta tra due Quinte nella terza semiminima, la quale è consonante; & è percossa
nella seconda parte della Battuta. Et tanto più si possono sopportare, quanto che le Quinte tramezate in cotal maniera, non sono cosi facilmente comprese dall'vdito: perche non sono semplici, come è la Ottaua: & li mouimenti, che fanno le parti, che contengono le Semibreui, non sono congiunti, come sono quelli altri, ch'io hò mostrato di sopra. Ma perche alcuni cantano tali passaggi per diminuire il mouimento separato di Quinta, che fanno alle volte le parti; però dico, che si debbeno fuggire
per ogni modo. Et se pure ad alcuni paresse di vsare non solamente questi, ma gli altri ancora
mostrati di sopra; non debbe però vsarli molto spesso: percioche quando non vi fussero altre ragioni, vi sono
almeno queste; che si uiene a far contra quella Regola, che dice, Che douemo procedere da vna consonanza
all'altra per mouimenti contrarij; & contra quella, che ne auertisce, Che noi faciamo muouere le parti insieme, quando ascendeno, o discendeno, l'una di esse almeno per mouimenti congiunti; che douerebbeno ritrouarsi
in quelle parti, che si muoueno per mouimenti separati, & contengono le Semibreui; & nondimeno non lo
fanno; come si può chiaramente vedere.
za, non hanno però gratia alcuna. E' ben vero, che
questi passaggi sono più sopportabili delli primi: ma non
sono però lodeuoli: percioche nel cantar la parte diminuita, si ode la Terza posta tra due Quinte nella terza semiminima, la quale è consonante; & è percossa
nella seconda parte della Battuta. Et tanto più si possono sopportare, quanto che le Quinte tramezate in cotal maniera, non sono cosi facilmente comprese dall'vdito: perche non sono semplici, come è la Ottaua: & li mouimenti, che fanno le parti, che contengono le Semibreui, non sono congiunti, come sono quelli altri, ch'io hò mostrato di sopra. Ma perche alcuni cantano tali passaggi per diminuire il mouimento separato di Quinta, che fanno alle volte le parti; però dico, che si debbeno fuggire
per ogni modo. Et se pure ad alcuni paresse di vsare non solamente questi, ma gli altri ancora
mostrati di sopra; non debbe però vsarli molto spesso: percioche quando non vi fussero altre ragioni, vi sono
almeno queste; che si uiene a far contra quella Regola, che dice, Che douemo procedere da vna consonanza
all'altra per mouimenti contrarij; & contra quella, che ne auertisce, Che noi faciamo muouere le parti insieme, quando ascendeno, o discendeno, l'una di esse almeno per mouimenti congiunti; che douerebbeno ritrouarsi
in quelle parti, che si muoueno per mouimenti separati, & contengono le Semibreui; & nondimeno non lo
fanno; come si può chiaramente vedere.
Della Battuta.Cap. 48.

 , ouero con questi
, ouero con questi

 ; & quando intendeuano la Inequale, le signauano con questi
; & quando intendeuano la Inequale, le signauano con questi 
 , oueramente con
questi
, oueramente con
questi 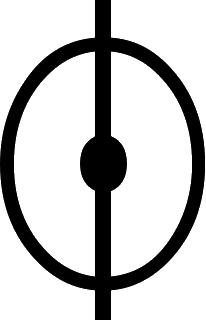
 . Et se alle volte non voleuano segnare la Battuta inequale con questi, poneuano la cifra del Ternario sopra quella del Binario
in cotal modo 3/2, accompagnandole non senza ragione: percioche si possono considerare in quattro maniere; Prima, quando sono poste nel principio di tutte
le parti della cantilena; & allora si vsa la Battuta inequale; Seconda, quando sono poste medesimamente nel principio; ma
non in tutte le parti: onde ciascuna parte si viene a regolare sotto la Battuta equale; Terza, quando sono poste nel mezo della cantilena in ciascuna parte, & si vsa medesimamente la
Battuta inequale; Et quarta, quando sono poste nel mezo di alcuna parte solamente, & le parti si uengono a
regolare similmente dalla Battuta equale. Onde cotali Cifre possono significare due cose; prima (come è opinione de i Moderni) che hauendo rispetto al Segno del tempo, si uiene a porre la Misura inequale contra la
Equale, cioè tre Tempi lunghi, ò breui contra due; Dipoi, significano, che nella Battuta intera sono contenuti Tre tempi lunghi, o breui, che siano; de i quali due si pongono nella Positione, & uno nella Leuatione; massimamente quando non ui concorreno altre cifre numerali, che dinotino alcuna proportione nelle figure, o note della
cantilena: come gia faceuano alcuni Musici: conciosiache intesa la Battuta in questa maniera, leua molte difficultà, che possono occorre alli Compositori, & alli Cantori anco. Potemo hora uedere da
quello che si è detto, che la Battuta non è altro, che un Segno fatto dal Musico equalmente, ouero inequalmente, secondo alcuna proportione, con la positione, & con la leuatione della mano a simiglianza del Polso
humano. Essendo adunque la Battuta di due sorti; come hauemo ueduto, tanto il Musico quanto il Poeta potranno in esse accommodare la Misura del tempo di ciascun piede del Verso. Imperoche nella Equale po tranno accommodare il Pirrhichio, che è vn piede composto di due sillabe breui, le quali i Poeti sogliono segnare con
tali cifre ˘ ˘; onde li Musici sogliono segnare i loro tempi, che sono due tempi breui con due figure equali;
come sono queste
. Et se alle volte non voleuano segnare la Battuta inequale con questi, poneuano la cifra del Ternario sopra quella del Binario
in cotal modo 3/2, accompagnandole non senza ragione: percioche si possono considerare in quattro maniere; Prima, quando sono poste nel principio di tutte
le parti della cantilena; & allora si vsa la Battuta inequale; Seconda, quando sono poste medesimamente nel principio; ma
non in tutte le parti: onde ciascuna parte si viene a regolare sotto la Battuta equale; Terza, quando sono poste nel mezo della cantilena in ciascuna parte, & si vsa medesimamente la
Battuta inequale; Et quarta, quando sono poste nel mezo di alcuna parte solamente, & le parti si uengono a
regolare similmente dalla Battuta equale. Onde cotali Cifre possono significare due cose; prima (come è opinione de i Moderni) che hauendo rispetto al Segno del tempo, si uiene a porre la Misura inequale contra la
Equale, cioè tre Tempi lunghi, ò breui contra due; Dipoi, significano, che nella Battuta intera sono contenuti Tre tempi lunghi, o breui, che siano; de i quali due si pongono nella Positione, & uno nella Leuatione; massimamente quando non ui concorreno altre cifre numerali, che dinotino alcuna proportione nelle figure, o note della
cantilena: come gia faceuano alcuni Musici: conciosiache intesa la Battuta in questa maniera, leua molte difficultà, che possono occorre alli Compositori, & alli Cantori anco. Potemo hora uedere da
quello che si è detto, che la Battuta non è altro, che un Segno fatto dal Musico equalmente, ouero inequalmente, secondo alcuna proportione, con la positione, & con la leuatione della mano a simiglianza del Polso
humano. Essendo adunque la Battuta di due sorti; come hauemo ueduto, tanto il Musico quanto il Poeta potranno in esse accommodare la Misura del tempo di ciascun piede del Verso. Imperoche nella Equale po tranno accommodare il Pirrhichio, che è vn piede composto di due sillabe breui, le quali i Poeti sogliono segnare con
tali cifre ˘ ˘; onde li Musici sogliono segnare i loro tempi, che sono due tempi breui con due figure equali;
come sono queste 
 , ouero altre simili: conciosia che'l Poeta considera sola mente la Sillaba se è Lunga,
la qual segna con questa cifra ¯; ouero si è Breue, la quale nota con questa'altra ˘; & il Musico
considera il Tempo lungo, o breue, & lo segna con una delle otto figure cantabili, come meglio li torna commodo. Potranno anco accommodare lo Spondeo, che segnano con queste due ¯ ¯, che dinotano
due sillabe lunghe, ouero con queste
, ouero altre simili: conciosia che'l Poeta considera sola mente la Sillaba se è Lunga,
la qual segna con questa cifra ¯; ouero si è Breue, la quale nota con questa'altra ˘; & il Musico
considera il Tempo lungo, o breue, & lo segna con una delle otto figure cantabili, come meglio li torna commodo. Potranno anco accommodare lo Spondeo, che segnano con queste due ¯ ¯, che dinotano
due sillabe lunghe, ouero con queste 
 , che significano due tempi lunghi, de i quali è composto. Potranno similmente accommodare il Dattilo, il quale contiene una sillaba lunga, & due breui, in cotal
modo ¯ ˘ ˘; ouero contiene un tempo lungo, & due breui, in questa maniera
, che significano due tempi lunghi, de i quali è composto. Potranno similmente accommodare il Dattilo, il quale contiene una sillaba lunga, & due breui, in cotal
modo ¯ ˘ ˘; ouero contiene un tempo lungo, & due breui, in questa maniera 
 Similmente potranno accommodare lo Anapesto in questo modo ˘ ˘ ¯, oueramente page 209
Similmente potranno accommodare lo Anapesto in questo modo ˘ ˘ ¯, oueramente page 209
 : perche contiene due sillabe breui, & vna lunga; ouero due tempi breui, & vno lungo; &
in tal guisa lo Proceleumatico ˘ ˘ ˘ ˘ ouero
: perche contiene due sillabe breui, & vna lunga; ouero due tempi breui, & vno lungo; &
in tal guisa lo Proceleumatico ˘ ˘ ˘ ˘ ouero 
 : conciosia che tutti questi piedi sono contenuti sono vna proportione equale; come è noto a tutti gli intelligenti. Sotto la Inequale poi si può accommodare lo Iambo a questo modo ˘ ¯, oueramente
: conciosia che tutti questi piedi sono contenuti sono vna proportione equale; come è noto a tutti gli intelligenti. Sotto la Inequale poi si può accommodare lo Iambo a questo modo ˘ ¯, oueramente
 , o pure in questa guisa
, o pure in questa guisa 
 : percioche è composto di vna sillaba breue, & di vna lunga, ouero di vn tempo breue, & di vno lungo. Cosi anco si potrà accommodare il Trocheo
in questa maniera ¯ ˘, &
: percioche è composto di vna sillaba breue, & di vna lunga, ouero di vn tempo breue, & di vno lungo. Cosi anco si potrà accommodare il Trocheo
in questa maniera ¯ ˘, & 
 : ouero
: ouero 
 : perche contiene vna sillaba lunga,
& vna breue; che contengono vn tempo lungo, & vno tempo breue. In cotal modo si
potrà accommodare lo Tribracho ˘ ˘ ˘, &
: perche contiene vna sillaba lunga,
& vna breue; che contengono vn tempo lungo, & vno tempo breue. In cotal modo si
potrà accommodare lo Tribracho ˘ ˘ ˘, & 
 cosi lo Ionico maggiore, lo minore, il Choriambo, lo Antispasto, & molti altri piedi, hora sotto l'vna, & hora
sotto l'altra Battuta. Ma perche è costume delli Musici, di porre il più delle volte nella Battuta
equale vna Breue imperfetta, la quale contenghi due Tempi lunghi; & nella inequale vna Breue perfetta,
che contenghi tre Tempi; però ci contaremo al presente di queste due: percioche ciascun'altra Battuta, che
si potesse imaginare, si potrà sempre riurre a queste; la prima delle quali si potrà veramente chiamare battuta Spondaica, & la seconda Trochaica. Et se alcuno prendesse di ciò marauiglia, legga il nostro Boetio
nel proemio della Musica, oue ritrouerà, che Pithagora volendo ritrahere quel giouine Taurominitano dalla furia alla quiete, comandò che'l Musico douesse cantare lo Spondeo, il quale veramente si vdiua, si come etiandio si ode a i nostri giorni ne i Balli, che dimandano Passo e mezo, & in quelli, che chiamano Padouane; si come etiandio in quelli, che nominano Balletti, vdimo la battuta del Trocheo. Douemo oltra di
ciò auertire, accioche alcuno non si marauigli, che essendo necessario, che ogni Compositione incominci, &
finisca ancora nella Positione della mano, cioè nel principio della Battuta; però di sopra hò detto, che lo Iambo si può accommodare sotto la Battuta inequale; pur che la cantilena venghi a terminare secondo il costume
de i Musici moderni. Ma questo sia detto a bastanza intorno alla Battuta.
cosi lo Ionico maggiore, lo minore, il Choriambo, lo Antispasto, & molti altri piedi, hora sotto l'vna, & hora
sotto l'altra Battuta. Ma perche è costume delli Musici, di porre il più delle volte nella Battuta
equale vna Breue imperfetta, la quale contenghi due Tempi lunghi; & nella inequale vna Breue perfetta,
che contenghi tre Tempi; però ci contaremo al presente di queste due: percioche ciascun'altra Battuta, che
si potesse imaginare, si potrà sempre riurre a queste; la prima delle quali si potrà veramente chiamare battuta Spondaica, & la seconda Trochaica. Et se alcuno prendesse di ciò marauiglia, legga il nostro Boetio
nel proemio della Musica, oue ritrouerà, che Pithagora volendo ritrahere quel giouine Taurominitano dalla furia alla quiete, comandò che'l Musico douesse cantare lo Spondeo, il quale veramente si vdiua, si come etiandio si ode a i nostri giorni ne i Balli, che dimandano Passo e mezo, & in quelli, che chiamano Padouane; si come etiandio in quelli, che nominano Balletti, vdimo la battuta del Trocheo. Douemo oltra di
ciò auertire, accioche alcuno non si marauigli, che essendo necessario, che ogni Compositione incominci, &
finisca ancora nella Positione della mano, cioè nel principio della Battuta; però di sopra hò detto, che lo Iambo si può accommodare sotto la Battuta inequale; pur che la cantilena venghi a terminare secondo il costume
de i Musici moderni. Ma questo sia detto a bastanza intorno alla Battuta.
Della Sincopa.Cap. 49.
 intero, ouero tagliato
intero, ouero tagliato  , che si termina per il numero Ternario; ma etiandio nello
imperfetto, che s'intende per il mezo circolo intero
, che si termina per il numero Ternario; ma etiandio nello
imperfetto, che s'intende per il mezo circolo intero  , o tagliato
, o tagliato  , terminato nel numero Binario:
percioche il Tempo (come vederemo al suo luogo) appresso il Musico è di due sorti. Onde quella figura, o nota si chiama Sincopata, ouero si dice, che fa la Sincopa, quando incomincia nella leuatione della
battuta, & è sotto posta anco alla positione; ne mai può cascare, come porta la sua natura, sotto la positione, fino a tanto, che non ritroui vna figura minore, ouero altre figure, che siano equale a questa di valore,
con le quali si accompagni, & ritorni, oue la battuta hebbe principio. Per il che è da notare (per dare uno
essempio) che il propio della Semibreue è di cascare, & di essere insieme cantata nel Tempo perfetto, &
nello imperfetto anco nel principio della battuta, cioè sotto questi due segni
, terminato nel numero Binario:
percioche il Tempo (come vederemo al suo luogo) appresso il Musico è di due sorti. Onde quella figura, o nota si chiama Sincopata, ouero si dice, che fa la Sincopa, quando incomincia nella leuatione della
battuta, & è sotto posta anco alla positione; ne mai può cascare, come porta la sua natura, sotto la positione, fino a tanto, che non ritroui vna figura minore, ouero altre figure, che siano equale a questa di valore,
con le quali si accompagni, & ritorni, oue la battuta hebbe principio. Per il che è da notare (per dare uno
essempio) che il propio della Semibreue è di cascare, & di essere insieme cantata nel Tempo perfetto, &
nello imperfetto anco nel principio della battuta, cioè sotto questi due segni  &
&  . & la Breue sotto
quest'altro
. & la Breue sotto
quest'altro  : Ma se auiene, che l'vna, o l'altra si canti, o proferisca nel leuare della battuta, tal figura, o
nota è detta Sincopa, ouer Sincopata; come nelli due essempi posti qui di sotto si uede. page 210
: Ma se auiene, che l'vna, o l'altra si canti, o proferisca nel leuare della battuta, tal figura, o
nota è detta Sincopa, ouer Sincopata; come nelli due essempi posti qui di sotto si uede. page 210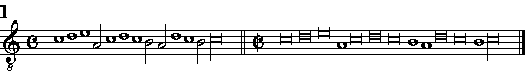 Si può etiandio chiamar Sincopata quella Minima, che hà appresso di se il punto, ne i primi segni, quando è
posta nel leuare della battuta; & cosi la Semibreue col punto, sotto l'altro segno; come qui sotto si vedeno;
Si può etiandio chiamar Sincopata quella Minima, che hà appresso di se il punto, ne i primi segni, quando è
posta nel leuare della battuta; & cosi la Semibreue col punto, sotto l'altro segno; come qui sotto si vedeno;
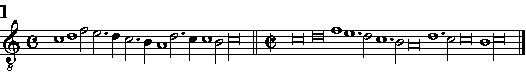 ancora che si possa veramente dire, che non siano Sincope, se non impropiamente. E ben vero, che la Semibreue si chiama sincopata, sotto qual segno si voglia, che dimostri il Tempo perfetto, o imperfetto, quando
vien posta dalli Compositori ne i loro contrapunti al detto modo. La Sincopa adunque si fa da vna figura, o
nota, che le vadi auanti, la qual sia di valore della metà della figura sincopata: Oueramente si fa, quando
se le pone auanti due, o più figure, che siano equiualenti a tal metà. Sono anco tali figure sincopate alle uolte dalle Pause, che si pongono a loro inanti, & tali Pause sono di valore della meza parte delle figure sincopate: come qui si veggono.
ancora che si possa veramente dire, che non siano Sincope, se non impropiamente. E ben vero, che la Semibreue si chiama sincopata, sotto qual segno si voglia, che dimostri il Tempo perfetto, o imperfetto, quando
vien posta dalli Compositori ne i loro contrapunti al detto modo. La Sincopa adunque si fa da vna figura, o
nota, che le vadi auanti, la qual sia di valore della metà della figura sincopata: Oueramente si fa, quando
se le pone auanti due, o più figure, che siano equiualenti a tal metà. Sono anco tali figure sincopate alle uolte dalle Pause, che si pongono a loro inanti, & tali Pause sono di valore della meza parte delle figure sincopate: come qui si veggono.
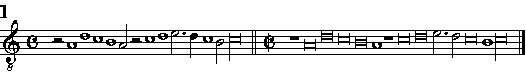 Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne sta bene il sincopare le Pause, siano
poste sotto qual segno si voglia, o perfetto, ouero imperfetto che sia il Tempo; si come sono le sotto poste:
Et benche la Sincopa si faccia nelle figure mostrate; non è però lecito, ne sta bene il sincopare le Pause, siano
poste sotto qual segno si voglia, o perfetto, ouero imperfetto che sia il Tempo; si come sono le sotto poste:
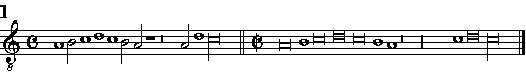 Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il principio di ciascuna, sotto i lor segni propij, come mostrerò altroue; & genera anco incommodo alli Cantori, i quali confidandosi spesse volte nella loro integrità, non pensando che'l Tempo sia in loro variato, senza tenerne memoria,
& conto alcuno, pongono la Battuta nel loro principio, & per tal maniera ingannati, vengono necessariamente ad errare cantando. Questi incommodi adunque si debbeno per ogni modo schiuare: percioche non furono mai sopportati dalli buoni, & discreti Musici; come si può vedere nelle compositioni di Ocheghen, di Iosquino, di Motone, & di altri più Antichi di loro; pur che non siano state guaste da alcuno ignorante scrittore. Per la qual cosa, quando occorrerà di porre le Pause di breue, o di semibreue,
& non cascheranno nel principio della battuta, & del loro Tempo, allora si debbeno ridurre alla Battuta,
& sotto il Tempo; si come nel sottoposto essempio si vede, il che dalli buoni Musici è stato sempre osseruato.
Conciosia che si rompe la Misura, & il Tempo, che naturalmente casca sopra il principio di ciascuna, sotto i lor segni propij, come mostrerò altroue; & genera anco incommodo alli Cantori, i quali confidandosi spesse volte nella loro integrità, non pensando che'l Tempo sia in loro variato, senza tenerne memoria,
& conto alcuno, pongono la Battuta nel loro principio, & per tal maniera ingannati, vengono necessariamente ad errare cantando. Questi incommodi adunque si debbeno per ogni modo schiuare: percioche non furono mai sopportati dalli buoni, & discreti Musici; come si può vedere nelle compositioni di Ocheghen, di Iosquino, di Motone, & di altri più Antichi di loro; pur che non siano state guaste da alcuno ignorante scrittore. Per la qual cosa, quando occorrerà di porre le Pause di breue, o di semibreue,
& non cascheranno nel principio della battuta, & del loro Tempo, allora si debbeno ridurre alla Battuta,
& sotto il Tempo; si come nel sottoposto essempio si vede, il che dalli buoni Musici è stato sempre osseruato.
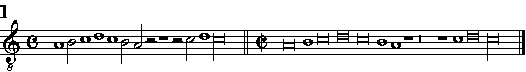 page 211
page 211Delle Pause.Cap. 50.

Quod caret alterna requie, durabile non est:ritrouarono il rimedio opportuno; La onde si può dir con verità della Pausa quello, che segue;
Haec reparat vires, fessaque membra leuat.Furono poi ritrouate le Pause per ornamento: percioche col mezo loro, le parti si possono porre l'vna dopo l'altra in fuga, o consequenza; come vederemo; il qual modo fa la cantilena non solo arteficiosa, ma etiandio diletteuole: conciosia che'l cantare di continouo, che fanno le parti della cantilena insieme, genera noia non solamente alli cantori; ma anche a gli ascoltanti induce sacietà: Et lo far tacere le parti alcune volte con qualche proposito, cioè facendone cantare hora due, hora tre, hora quattro, & tallora (essendo la compositione a più voci) tutte insieme, massimamente nel fine; conciosia che è necessario, che tutte le parti insieme cantino, & insieme finiscano; fa, che le compositioni per tal varietà riusciscono più vaghe, & più diletteuoli. Onde ritrouarono vn segno, che rappresentasse questa taciturnità, o silentio, & lo vsarono per la cosa significata, & lo nominarono Pausa. La quale, dal suo vfficio dissero essere vn certo intralasciamento arteficioso di voce. Et bene dissero arteficioso intralasciamento, volendone auertire, che non douessimo porre le Pause nelle cantilene fuori di proposito, & senza arteficio; ma collocarle di maniera, che si vedesse, che la necessità, & l'arteficio lo richiedeua. Imperoche si come è vitiosa cosa ad alcuno, che parli sempre, & non sappia por fine, ò meta al suo parlare; cosi è cosa vitiosa al Musico, che non sappia a tempo, & luogo dar riposo alle parti della sua compositione. Di modo che; si come non è senza virtù il saper ragionare, & tacere con proposito; cosi ancora non è senza virtù, che'l Musico sappia far tacere, & cantare le parti della sua cantilena a tempo, & luogo. Ma si debbe auertire, che doue accascasse di porre più Pause, le quali eccedessino il valore di quella della Lunga, allora questa si debbe raddoppiare; si come auerebbe, quando si volesse segnar la Pausa della Massima: Ma quando si volesse raddoppiare le Pause, che rappresentano essa Massima, ouer porle appresso altre pause minori, allora si potrà porre quelle, che si aggiungono sopra le altre linee; si come in questo essempio posto qui di sotto si veggono. page 212
 Sono state uarie opinioni di questo nome Pausa: percioche alcuni hanno hauuto parere, che Pausa sia stata
detta da Παύομαι parola greca, che significa Cessare, Posarsi, o Lassare. Altri hanno voluto, che sia cosi
chiamata dal Batter delle mani, che da i latini è detto Plauso: conciosiache è misurata dalla positione, &
dalla leuatione della battuta, la quale si conosce dal segno formato dalla mano; si come di sopra habbiamo ueduto. Et forse, che non fu detta da principio ne all'uno, ne all'altro modo delli due nominati; ma più presto
(come pare ad alcuni) da Posa parola francese, che significa Posata. Onde si suol dire Vna pausa, due pause, & le altre; cioè una posata, due posate, & cosi il resto. Ma sia detta da che si uoglia, questo importa
poco; purche si sappia, che quando il compositore pone le Pause nella cantilena, vuole, che iui il cantore taccia per tanto
spacio di tempo, quanto significa il valor delle Pause. Gli Ecclesiastici etiandio pongono le Pause ne i loro canti, non gia per ornamento, ma per necessità: perche è impossibile di poter peruenire al fine di
cotali cantilene, senza pigliare alcun riposo; La onde di cio aueduti, ritrouarono vn segno, dal quale ciascuno cantore è auertito, che ariuando a quello, si habbia da fermare, & pigliare Spirito. Per il che da vn tale effetto lo chiamarono πνεῦμα, che vuol dir Spirito. Posero etiandio cotal segno, accioche ogn'vno de i cantori concordeuolmente si hauesse da fermare, onde lo dimandarono νεῦμα, che vuol dir Cenno, & Consenso. E' ben vero, che non pongono tali Pause nel modo, che si pongono le altre mostrate di sopra: percioche
le pongono di maniera, che cingono, & abbracciano tutte le linee della cantilena; tallora ponendole semplilici, & tallora raddoppiate; come qui si veggono. Et si debbe per ogni modo osseruar quello, che gia mol
Sono state uarie opinioni di questo nome Pausa: percioche alcuni hanno hauuto parere, che Pausa sia stata
detta da Παύομαι parola greca, che significa Cessare, Posarsi, o Lassare. Altri hanno voluto, che sia cosi
chiamata dal Batter delle mani, che da i latini è detto Plauso: conciosiache è misurata dalla positione, &
dalla leuatione della battuta, la quale si conosce dal segno formato dalla mano; si come di sopra habbiamo ueduto. Et forse, che non fu detta da principio ne all'uno, ne all'altro modo delli due nominati; ma più presto
(come pare ad alcuni) da Posa parola francese, che significa Posata. Onde si suol dire Vna pausa, due pause, & le altre; cioè una posata, due posate, & cosi il resto. Ma sia detta da che si uoglia, questo importa
poco; purche si sappia, che quando il compositore pone le Pause nella cantilena, vuole, che iui il cantore taccia per tanto
spacio di tempo, quanto significa il valor delle Pause. Gli Ecclesiastici etiandio pongono le Pause ne i loro canti, non gia per ornamento, ma per necessità: perche è impossibile di poter peruenire al fine di
cotali cantilene, senza pigliare alcun riposo; La onde di cio aueduti, ritrouarono vn segno, dal quale ciascuno cantore è auertito, che ariuando a quello, si habbia da fermare, & pigliare Spirito. Per il che da vn tale effetto lo chiamarono πνεῦμα, che vuol dir Spirito. Posero etiandio cotal segno, accioche ogn'vno de i cantori concordeuolmente si hauesse da fermare, onde lo dimandarono νεῦμα, che vuol dir Cenno, & Consenso. E' ben vero, che non pongono tali Pause nel modo, che si pongono le altre mostrate di sopra: percioche
le pongono di maniera, che cingono, & abbracciano tutte le linee della cantilena; tallora ponendole semplilici, & tallora raddoppiate; come qui si veggono. Et si debbe per ogni modo osseruar quello, che gia mol ti de gli Antichi hanno osseruato; cioè di non porre tali Pause,
se non nel fine delle Clausule, o punti della Oratione, sopra la quale è composta la cantilena, & simigliantemente nel fine
di ogni
Periodo. Il che fa dibisogno, che li Compositori etiandio auertiscano; accioche li Membri della oratione siano diuisi, & la sentenza delle parole si oda, & intenda interamente: percioche facendo in cotal modo, allor si potrà dire, che
le Pause siano state poste nelle parti della cantilena con qualche proposito, & non a caso. Ne si debbeno porre per alcun modo, auanti che sia finita la sentenza, cioè nel mezo della Clausula: conciosia che colui, che le
ponesse a cotal modo, dimostrarebbe veramente essere vna pecora, vn goffo, & vno ignorante. Però adunque il Musico si sforzerà di non cascare in simili errori; accioche non dia alli dotti mala opinione di se, il che
molto si debbe prezzare, & preporre ad ogn'altra cosa.
ti de gli Antichi hanno osseruato; cioè di non porre tali Pause,
se non nel fine delle Clausule, o punti della Oratione, sopra la quale è composta la cantilena, & simigliantemente nel fine
di ogni
Periodo. Il che fa dibisogno, che li Compositori etiandio auertiscano; accioche li Membri della oratione siano diuisi, & la sentenza delle parole si oda, & intenda interamente: percioche facendo in cotal modo, allor si potrà dire, che
le Pause siano state poste nelle parti della cantilena con qualche proposito, & non a caso. Ne si debbeno porre per alcun modo, auanti che sia finita la sentenza, cioè nel mezo della Clausula: conciosia che colui, che le
ponesse a cotal modo, dimostrarebbe veramente essere vna pecora, vn goffo, & vno ignorante. Però adunque il Musico si sforzerà di non cascare in simili errori; accioche non dia alli dotti mala opinione di se, il che
molto si debbe prezzare, & preporre ad ogn'altra cosa.
Delle Fughe, o Consequenze, ouer Reditte, che dir le vogliamo.Cap. 51.

 page 214rado la Fughe cosi vicine, & vnite; & si allontaneremo alquanto da quelle Consequenze, che sono tanto
communi; & cercaremo con ogni nostro potere di fare delle Fughe, che siano più noue: Conciosia che
quando faremo la Guida, & il Consequente alquanto distanti l'vno dall'altro, per tre Pause di Minima,
ouero per cinque, o per altre simili; verremo senza dubbio, a far qualche noua variatione. Io non dico gia,
che le Consequenze distanti per vna Pausa di Minima, o di Semibreue non si debbino vsare: ma dico, che
non si debbeno vsar molto spesso; per non cascare in quelle Fughe, che sono tanto communi, che non si ritroua libro, nel quale non siano molte, & molte volte replicate; lequali lasso di mostrare, per non esser tedioso,
& per non offendere alcuno. Ma accioche si caui qualche frutto da quello, ch'io hò detto, hò posto prima di sopra lo essempio di quelle, che si nominano Sciolte, le quali si fanno sopra li canti fermi, à loro imitatione: percioche delle Sciolte, che si trouano tra due parti diminuite, se ne potrà hauere due accommodati essempi, posti
di sopra nel Cap. 43. Nelle Fughe poi, che si chiamano Legate, si hauerà da osseruar questo, che siano poste
l'vna con l'altra in Consequenza all'Vnisono, ouero alla Quarta, oueramente alla Quinta, o pure alla Ottaua;
incominciando da qual parte si voglia, sia la graue, ouero la acuta, che questo importa poco. Et quella parte,
che si incomincierà a comporre prima, sarà la Guida; & quella che si componerà dipoi con le istesse figure, &
ogn'altro accidente, sarà il Consequente. La onde finito che sarà il tutto; come qui si vede, si piglierà la par
page 214rado la Fughe cosi vicine, & vnite; & si allontaneremo alquanto da quelle Consequenze, che sono tanto
communi; & cercaremo con ogni nostro potere di fare delle Fughe, che siano più noue: Conciosia che
quando faremo la Guida, & il Consequente alquanto distanti l'vno dall'altro, per tre Pause di Minima,
ouero per cinque, o per altre simili; verremo senza dubbio, a far qualche noua variatione. Io non dico gia,
che le Consequenze distanti per vna Pausa di Minima, o di Semibreue non si debbino vsare: ma dico, che
non si debbeno vsar molto spesso; per non cascare in quelle Fughe, che sono tanto communi, che non si ritroua libro, nel quale non siano molte, & molte volte replicate; lequali lasso di mostrare, per non esser tedioso,
& per non offendere alcuno. Ma accioche si caui qualche frutto da quello, ch'io hò detto, hò posto prima di sopra lo essempio di quelle, che si nominano Sciolte, le quali si fanno sopra li canti fermi, à loro imitatione: percioche delle Sciolte, che si trouano tra due parti diminuite, se ne potrà hauere due accommodati essempi, posti
di sopra nel Cap. 43. Nelle Fughe poi, che si chiamano Legate, si hauerà da osseruar questo, che siano poste
l'vna con l'altra in Consequenza all'Vnisono, ouero alla Quarta, oueramente alla Quinta, o pure alla Ottaua;
incominciando da qual parte si voglia, sia la graue, ouero la acuta, che questo importa poco. Et quella parte,
che si incomincierà a comporre prima, sarà la Guida; & quella che si componerà dipoi con le istesse figure, &
ogn'altro accidente, sarà il Consequente. La onde finito che sarà il tutto; come qui si vede, si piglierà la par te, che incomincia a cantare, cioè la Guida, & si scriuerà di lungo; & doue il Consequente hà da incominciare a cantare, cioè sopra la figura posta nella guida, si porrà vn segno tale, [[mus.sigcon]] ilqual vien detto dai Musici
Presa; Et nel fine, oue hà da fermarsi, si segna la parte della Guida col detto segno, ouer con questo [[mus.ferm]], ponendolo sopra la figura finale, oue si hà da fermare il Consequente; & tal segno chiamano Coronata. Fatto questo, per dar notitia, in qual maniera si habbiano a cantare le parti, si pone vna Regola
sopra la parte della Guida, laquale essendo chiamata da i Greci Κανών, alcuni Musici poco intelligenti nominano Canon quello, che douerebbeno dire Fuga, o Consequenza, ouer Reditta; laqual Regola si scriue in
questo modo; Fuga, o Consequenza alla Diapason: & se'l Consequente è più acuto della Guida, si aggiunge
in acuto; aggiungendoui oltra di ciò il Tempo, che hà da aspettare la parte del Consequente, auanti che incomincia a cantare, ancora che sia segnato il luogo col segno [[mus.sigcon]]; La onde si scriue.
te, che incomincia a cantare, cioè la Guida, & si scriuerà di lungo; & doue il Consequente hà da incominciare a cantare, cioè sopra la figura posta nella guida, si porrà vn segno tale, [[mus.sigcon]] ilqual vien detto dai Musici
Presa; Et nel fine, oue hà da fermarsi, si segna la parte della Guida col detto segno, ouer con questo [[mus.ferm]], ponendolo sopra la figura finale, oue si hà da fermare il Consequente; & tal segno chiamano Coronata. Fatto questo, per dar notitia, in qual maniera si habbiano a cantare le parti, si pone vna Regola
sopra la parte della Guida, laquale essendo chiamata da i Greci Κανών, alcuni Musici poco intelligenti nominano Canon quello, che douerebbeno dire Fuga, o Consequenza, ouer Reditta; laqual Regola si scriue in
questo modo; Fuga, o Consequenza alla Diapason: & se'l Consequente è più acuto della Guida, si aggiunge
in acuto; aggiungendoui oltra di ciò il Tempo, che hà da aspettare la parte del Consequente, auanti che incomincia a cantare, ancora che sia segnato il luogo col segno [[mus.sigcon]]; La onde si scriue.
 Ma se'l Consequente cantasse nel graue, in luogo di dire Acuta, si porrebbe Graue. Et se la Consequenza fusse fatta per vna Quarta, allora si direbbe In Diatessaron; & se cantasse per una Quinta, si direbbe in Diapente; & se per lo Vnisono, si direbbe all'Vnisono, oueramente nello istesso suono, o voce istessa. Lungo sarebbe il voler racco tare tutte le Fughe, o Consequenze di vna in vna; & il voler dare vno essempio particolare: ma perche di queste ne sono i libri pieni, però lassarò di ragionarne più oltra, rimettendo il resto al
buon giuditio del Compositore; che vedendo, & essaminando gli essempi sopra dati, saranno guida, & lume
di ritrouar cose assai maggiori. Non voglio però restare di dire, che si troua etiandio vn'altra sorte di Consequenza, o Fuga, la quale si fa per gli istessi interualli, per mouimenti contrarij, detta Fuga, o Consequenza per ἅρσιν, & θέσιν, cioè per leuatione, & abbassamento di voce, il qual modo è vsato da i buoni Prattici;
& nel comporla si procede a quello istesso modo, col quale si procede nelle altre. Sono nondimeno due le sue specie, cioè Legate, & Sciolte. Le Legate potremo conoscere, quando haueremo piena cognitione delle precedenti;
il simile anco auerrà delle Sciolte. Ma perche, considerato quello, che di sopra hò detto, con facilita si può
fare, o comporre le Sciolte, lassandole da vn canto, verrò a mostrar le Legate, che sono alquanto più difficili,
et porrò solamente alcuni essempi, da i quali si potrà conoscere, & comprendere quello, che si dè osseruare,
quando si vorrà comporre in tal maniera. Se noi adunque ordinaremo in tal maniera la Guida col Consequente, che procedino l'vno contra l'altro per contrarij mouimenti, osseruando di porre quelli istessi interualli
di Tuoni, di Semituoni, & gli altri in vna parte, che si pone nell'altra, non è dubbio, che queste parti si potranno ordinare in diuerse maniere: Percioche si potrà porre il Consequente sopra la Guida distante per lo
spatio del Semitono, aspettando due Tempi interi di Breue imperfetta, cioè dimorando allo incominciare per
spatio di vna Pausa di Lunga, & cosi haueremo il sottoposto essempio; Ouero si potra porre l'vna delle par
Ma se'l Consequente cantasse nel graue, in luogo di dire Acuta, si porrebbe Graue. Et se la Consequenza fusse fatta per vna Quarta, allora si direbbe In Diatessaron; & se cantasse per una Quinta, si direbbe in Diapente; & se per lo Vnisono, si direbbe all'Vnisono, oueramente nello istesso suono, o voce istessa. Lungo sarebbe il voler racco tare tutte le Fughe, o Consequenze di vna in vna; & il voler dare vno essempio particolare: ma perche di queste ne sono i libri pieni, però lassarò di ragionarne più oltra, rimettendo il resto al
buon giuditio del Compositore; che vedendo, & essaminando gli essempi sopra dati, saranno guida, & lume
di ritrouar cose assai maggiori. Non voglio però restare di dire, che si troua etiandio vn'altra sorte di Consequenza, o Fuga, la quale si fa per gli istessi interualli, per mouimenti contrarij, detta Fuga, o Consequenza per ἅρσιν, & θέσιν, cioè per leuatione, & abbassamento di voce, il qual modo è vsato da i buoni Prattici;
& nel comporla si procede a quello istesso modo, col quale si procede nelle altre. Sono nondimeno due le sue specie, cioè Legate, & Sciolte. Le Legate potremo conoscere, quando haueremo piena cognitione delle precedenti;
il simile anco auerrà delle Sciolte. Ma perche, considerato quello, che di sopra hò detto, con facilita si può
fare, o comporre le Sciolte, lassandole da vn canto, verrò a mostrar le Legate, che sono alquanto più difficili,
et porrò solamente alcuni essempi, da i quali si potrà conoscere, & comprendere quello, che si dè osseruare,
quando si vorrà comporre in tal maniera. Se noi adunque ordinaremo in tal maniera la Guida col Consequente, che procedino l'vno contra l'altro per contrarij mouimenti, osseruando di porre quelli istessi interualli
di Tuoni, di Semituoni, & gli altri in vna parte, che si pone nell'altra, non è dubbio, che queste parti si potranno ordinare in diuerse maniere: Percioche si potrà porre il Consequente sopra la Guida distante per lo
spatio del Semitono, aspettando due Tempi interi di Breue imperfetta, cioè dimorando allo incominciare per
spatio di vna Pausa di Lunga, & cosi haueremo il sottoposto essempio; Ouero si potra porre l'vna delle par ti, cioè il Consequente lontano dalla Guida per vna Settima, & haueremo la sottoposta cantilena, nella quale
il Consequente seguirà la Guida per due Tempi di Breue imperfetta, cioè dopo vna Pausa di Lunga. page 216
ti, cioè il Consequente lontano dalla Guida per vna Settima, & haueremo la sottoposta cantilena, nella quale
il Consequente seguirà la Guida per due Tempi di Breue imperfetta, cioè dopo vna Pausa di Lunga. page 216 Volendo poi scriuere in lungo cotali essempi, o cantilene, si potranno ordinare di maniera, che li Consequenti
potranno hauer le loro chiaui, che li dimostreranno, per quali chorde haueranno a procedere nel cantare, si come hà la Guida. Le quali chiaui si porranno sempre auanti quella, che serue alla Guida, & tra queste, &
quelle si porranno le Pause, che'l Consequente hauerà da fare, auanti che incominci a cantare; ancora che la
Regola posta sopra di loro gli insegni, in qual maniera si habbia da procedere; si come nelli due sottoposti
essempi si vede.
Volendo poi scriuere in lungo cotali essempi, o cantilene, si potranno ordinare di maniera, che li Consequenti
potranno hauer le loro chiaui, che li dimostreranno, per quali chorde haueranno a procedere nel cantare, si come hà la Guida. Le quali chiaui si porranno sempre auanti quella, che serue alla Guida, & tra queste, &
quelle si porranno le Pause, che'l Consequente hauerà da fare, auanti che incominci a cantare; ancora che la
Regola posta sopra di loro gli insegni, in qual maniera si habbia da procedere; si come nelli due sottoposti
essempi si vede.

 page 217Vederemo poi al suo luogo, quel che importi vn tempo, due tempi, & più ancora: conciosia che allora mostrarò etiandio, quante figure in esso si ponghino, & a qual figura il Tempo si attribuisca. Si debbe oltra di
ciò auertire, che queste maniere di Consequenza non sono per alcun modo da sprezzare, anzi si debbeno abbracciare; percioche oltra che sono belle, eleganti, & ingegnose; hanno anco vn certo non sò che di grandezza: essendo che vn tal modo di comporre non è cosi commune, come sono gli altri modi. Però adunque, chi
si vorrà essercitare nel comporre in simili maniere, non è dubbio, che in breue tempo diuenterà vn buon Musico. Et quello che hò detto nelle Consequenze legate, voglio che si intenda anco delle Slegate, o Sciolte, che si
compongono senza obligo alcuno. Ne si debbe alcuno imaginare, hauendo io solamente posto li mostrati essempi, che siano solamente tutte le maniere delle Fughe, & che non se ne possa fare alcun'altra, per altra maniera; si come porre più, o meno tempi; & che la Guida non si possa porre nell'acuto, & il Consequente nel
graue: conciosia che sono quasi infiniti li modi, & lungo sarebbe il raccontarli di vno in vno; ma hò posto
solamente quelli, accioche siano vn lume, & vna guida a ciascuno, che vorrà sottoentrare a questa bella, ingegnosa, & honoreuol fatica.
page 217Vederemo poi al suo luogo, quel che importi vn tempo, due tempi, & più ancora: conciosia che allora mostrarò etiandio, quante figure in esso si ponghino, & a qual figura il Tempo si attribuisca. Si debbe oltra di
ciò auertire, che queste maniere di Consequenza non sono per alcun modo da sprezzare, anzi si debbeno abbracciare; percioche oltra che sono belle, eleganti, & ingegnose; hanno anco vn certo non sò che di grandezza: essendo che vn tal modo di comporre non è cosi commune, come sono gli altri modi. Però adunque, chi
si vorrà essercitare nel comporre in simili maniere, non è dubbio, che in breue tempo diuenterà vn buon Musico. Et quello che hò detto nelle Consequenze legate, voglio che si intenda anco delle Slegate, o Sciolte, che si
compongono senza obligo alcuno. Ne si debbe alcuno imaginare, hauendo io solamente posto li mostrati essempi, che siano solamente tutte le maniere delle Fughe, & che non se ne possa fare alcun'altra, per altra maniera; si come porre più, o meno tempi; & che la Guida non si possa porre nell'acuto, & il Consequente nel
graue: conciosia che sono quasi infiniti li modi, & lungo sarebbe il raccontarli di vno in vno; ma hò posto
solamente quelli, accioche siano vn lume, & vna guida a ciascuno, che vorrà sottoentrare a questa bella, ingegnosa, & honoreuol fatica.
Delle Imitationi, & quel che elle siano.Cap. 52.
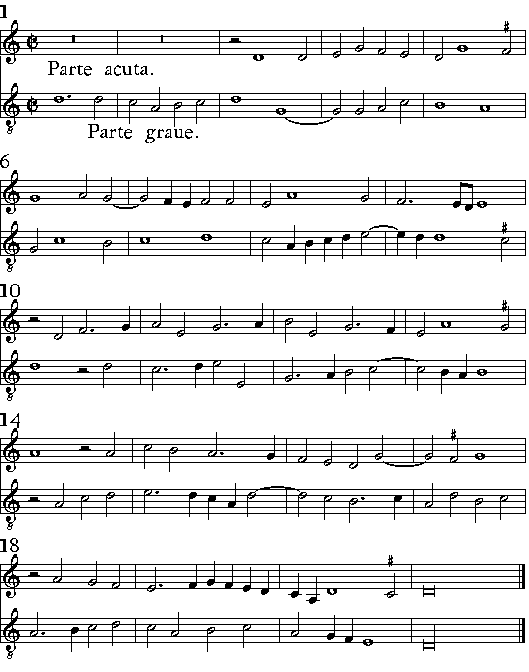 tioni adunque, che si fanno per contrarij mouimenti, hanno al medesimo modo, che hanno le Fughe, le Guida, & il Consequente: Onde si vsa anco nel scriuere in lungo la Guida gli istessi modi, che furono vsati nelle page 218Fughe, cioè porre le lor Prese, & le Coronate, come hò mostrato. Ma il Canone, o Regola di queste si scriue
in cotal guisa. Si canta alla Seconda, ouero alla Terza, o pur ad altre simili, acuta, ouer graue, pausando due
tempi, o più, o meno. & se le parti procedeno per mouimenti contrarij, si aggiunge questa particella, Per mouimenti contrarij.
Si debbe dipoi auertire, che nelle Sciolte si può cauare il Consequente dalla Guida, parte
per imitatione, & parte in consequenza. Cosi parte in mouimenti simili, & parte in mouimenti contrarij;
dilche sarebbe troppo lungo, se'l si volesse dar notitia particolare di ogni cosa minima. Hora ciascuno sarà
auertito per sempre, di ordinare in tal maniera le parti della sua compositione, massimamente nelle Fughe, &
Imitationi legate, che procedeno per mouimenti contrarij, che si possino cantare senza discommodo. Et per dare di ciò qualche
lume, hò posto di sopra lo essempio particolare delle Imitationi sciolte; accioche da esso si possa
trar frutto di quello, ch'io hò detto di sopra; ilche mostrato, verrò poi a gli essempi delle Imitationi legate.
La Imitatione legata si potrà conoscer da questo, che hauerà la Guida, & il Consequente, che l'vno seguiterà
l'altro; non per gli istessi interualli: ma si bene per quelli istessi mouimenti, ouer gradi; come nell'essempio posto
qui sotto si vede. Et questa si conosce esser manifestamente vna Imitatione, & non Fuga: percioche il Con
tioni adunque, che si fanno per contrarij mouimenti, hanno al medesimo modo, che hanno le Fughe, le Guida, & il Consequente: Onde si vsa anco nel scriuere in lungo la Guida gli istessi modi, che furono vsati nelle page 218Fughe, cioè porre le lor Prese, & le Coronate, come hò mostrato. Ma il Canone, o Regola di queste si scriue
in cotal guisa. Si canta alla Seconda, ouero alla Terza, o pur ad altre simili, acuta, ouer graue, pausando due
tempi, o più, o meno. & se le parti procedeno per mouimenti contrarij, si aggiunge questa particella, Per mouimenti contrarij.
Si debbe dipoi auertire, che nelle Sciolte si può cauare il Consequente dalla Guida, parte
per imitatione, & parte in consequenza. Cosi parte in mouimenti simili, & parte in mouimenti contrarij;
dilche sarebbe troppo lungo, se'l si volesse dar notitia particolare di ogni cosa minima. Hora ciascuno sarà
auertito per sempre, di ordinare in tal maniera le parti della sua compositione, massimamente nelle Fughe, &
Imitationi legate, che procedeno per mouimenti contrarij, che si possino cantare senza discommodo. Et per dare di ciò qualche
lume, hò posto di sopra lo essempio particolare delle Imitationi sciolte; accioche da esso si possa
trar frutto di quello, ch'io hò detto di sopra; ilche mostrato, verrò poi a gli essempi delle Imitationi legate.
La Imitatione legata si potrà conoscer da questo, che hauerà la Guida, & il Consequente, che l'vno seguiterà
l'altro; non per gli istessi interualli: ma si bene per quelli istessi mouimenti, ouer gradi; come nell'essempio posto
qui sotto si vede. Et questa si conosce esser manifestamente vna Imitatione, & non Fuga: percioche il Con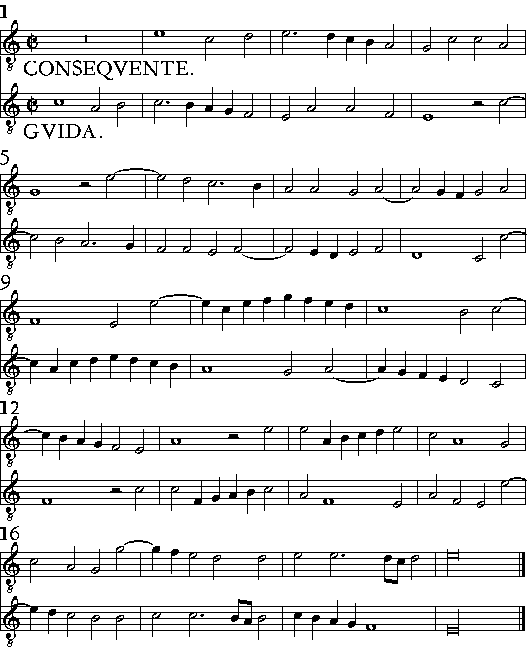 sequente canta per vn Ditono più acuto della Guida. Et ancora che l'vno, & l'altro procedino per gli istessi
gradi; non procedeno però per gli istessi interualli; come hò detto. Volendo adunque ridurre tale Imitatione in
vna parte sola, la disponeremo al sottoposto modo; ponendole di sopra la Regola, che insegnerà quello, che si
hauerà da tenere nel cantarla, in questa maniera.
sequente canta per vn Ditono più acuto della Guida. Et ancora che l'vno, & l'altro procedino per gli istessi
gradi; non procedeno però per gli istessi interualli; come hò detto. Volendo adunque ridurre tale Imitatione in
vna parte sola, la disponeremo al sottoposto modo; ponendole di sopra la Regola, che insegnerà quello, che si
hauerà da tenere nel cantarla, in questa maniera.
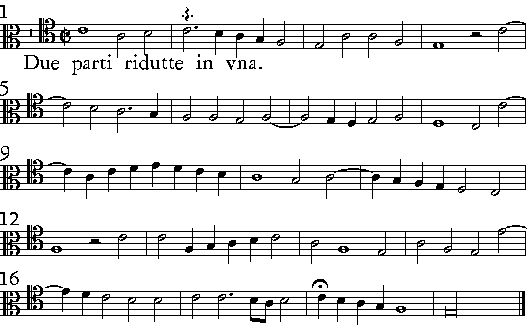 Ma in quelle Imitationi, che procedeno per mouimenti contrarij, si tiene altro modo, come nello essempio posto qui sotto si può vedere.
Ma in quelle Imitationi, che procedeno per mouimenti contrarij, si tiene altro modo, come nello essempio posto qui sotto si può vedere.
 Et acciò si vegga in qual maniera per l'auenire si habbia da procedere, quando si vorrà porre insieme la
Guida, & il Consequente, scriuerò tale Imitatione in lungo, col suo Canone, o Regola in cotal modo.
Et acciò si vegga in qual maniera per l'auenire si habbia da procedere, quando si vorrà porre insieme la
Guida, & il Consequente, scriuerò tale Imitatione in lungo, col suo Canone, o Regola in cotal modo.
 Si ritroua etiandio vna sorte di compositione simile, laqual contiene la Guida, & il Consequente, parte in
Fuga, & parte in Imitatione; come qui si vede. page 220
Si ritroua etiandio vna sorte di compositione simile, laqual contiene la Guida, & il Consequente, parte in
Fuga, & parte in Imitatione; come qui si vede. page 220 La quale si suol ridurre sopra vna parte sola, col suo Canone, o Regola in questo modo.
La quale si suol ridurre sopra vna parte sola, col suo Canone, o Regola in questo modo.
 Imperoche communemente è detta Fuga; & si vsa molto spesso nelle compositioni a più voci, come si può
vedere in molte cantilene. Et in vero non è da sprezzare, anzi da porla spesse volte in vso: percioche fà la
compositione ingegnosa, & fà anco buonissimo effetto. Ma si debbe sapere, che nelle Fughe, & nelle Imitationi, che si trouano nelle compositioni a più voci, Legate, o Sciolte che siano, si possono porre le Quarte, &
fare molti altri passaggi, che ritornano bene: percioche le altre parti sono di grande aiuto al Compositore,
ancora che nelle compositioni di due voci le Quarte non si ponghino: perche non fanno buono effetto. Però
sarà bisogno, che il Compositore stia auertito, che non cadesse in qualche errore. Ma questo sia detto a sufficienza intorno alle Fughe, & alle Imitationi; percioche di alcune di quelle, che si pongono nelle compositioni a più voci, ragionaremo altroue. page 221
Imperoche communemente è detta Fuga; & si vsa molto spesso nelle compositioni a più voci, come si può
vedere in molte cantilene. Et in vero non è da sprezzare, anzi da porla spesse volte in vso: percioche fà la
compositione ingegnosa, & fà anco buonissimo effetto. Ma si debbe sapere, che nelle Fughe, & nelle Imitationi, che si trouano nelle compositioni a più voci, Legate, o Sciolte che siano, si possono porre le Quarte, &
fare molti altri passaggi, che ritornano bene: percioche le altre parti sono di grande aiuto al Compositore,
ancora che nelle compositioni di due voci le Quarte non si ponghino: perche non fanno buono effetto. Però
sarà bisogno, che il Compositore stia auertito, che non cadesse in qualche errore. Ma questo sia detto a sufficienza intorno alle Fughe, & alle Imitationi; percioche di alcune di quelle, che si pongono nelle compositioni a più voci, ragionaremo altroue. page 221Della Cadenza, quello che ella sia, delle sue specie, & del suo vso.Cap. 53.
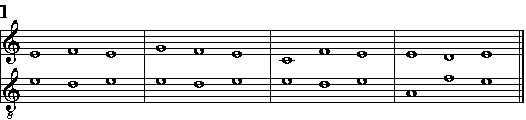 page 222Le Diminuite terminate per l'Vnisono sono quelle, che contengono vn simil procedere; ma si fanno con diuerse figure, tra le quali si ritroua la Sincopa, della quale la sua seconda parte; che è quella, che è percossa
dalla Battuta, si troua dissonante, cioè vna Seconda. Onde dopo essa immediatamente seguendo la Terza minore, si viene a finire nell'Vnisono.
page 222Le Diminuite terminate per l'Vnisono sono quelle, che contengono vn simil procedere; ma si fanno con diuerse figure, tra le quali si ritroua la Sincopa, della quale la sua seconda parte; che è quella, che è percossa
dalla Battuta, si troua dissonante, cioè vna Seconda. Onde dopo essa immediatamente seguendo la Terza minore, si viene a finire nell'Vnisono.
 Et perche li Prattici sogliono il più delle volte diminuire quella parte della Cadenza, che
contiene la Sincopa, per potere, secondo che
li torna commodo, accommodar le harmonie
alle Parole; però auanti ch'io vada più oltra,
voglio porre tali Diminutioni, che si veggano, & saranno le sotto poste, le quali ne potranno apportare molto commodo; come vederemo nella
Et perche li Prattici sogliono il più delle volte diminuire quella parte della Cadenza, che
contiene la Sincopa, per potere, secondo che
li torna commodo, accommodar le harmonie
alle Parole; però auanti ch'io vada più oltra,
voglio porre tali Diminutioni, che si veggano, & saranno le sotto poste, le quali ne potranno apportare molto commodo; come vederemo nella
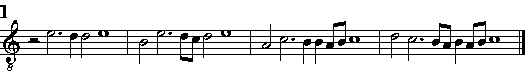 Quarta parte. Qui debbe ciascuno Compositore auertire, acciò non pigliasse qualche errore, che quantunque le
Cadenze siano poste solamente ne i mostrati luoghi; nondimeno si possono fare anco in qualunque altro luogo, oue
torna più commodo, pur che si osserui la Regola data di sopra nel cap. 38. di andare dalla Consonanza imperfetta alla Perfetta con la più vicina. La onde fa dibisogno, che nelle penultime figure di queste Cadenze
sia la Terza minore; la qual sempre si vdirà, quando faranno il mouimento all'Vnisono di maniera, che l'vna discendi per mouimento congiunto del Tuono, & l'altra con un simile mouimento di Semituono maggiore, o per il contrario. Et ciò si potrà sempre fare in ciascun luogo, senza porre il segno della chorda chromatica, per fare dell'interuallo del Tuono un Semituono: Imperoche in quella parte, che tra la penultima figura, & la ultima si troua il mouimento, che ascende, sempre si intende essere collocato il Semituono; pur che
l'altra parte non discenda per simile interuallo: conciosiache allora il Semituono non si potrebbe porre da due
parti, cioè nella parte graue, & nella acuta: perche si udirebbe uno interuallo minore di un Semiditono, che
sarebbe dissonante. Ma la Natura hà prouisto in simil cosa: percioche non solamente li periti della Musica:
ma anco li contadini, che cantano senza alcuna arte, procedeno per l'interuallo del Semituono. Et queste sono dette Cadenze propiamente; ancora che quando le lor prime figure ritrouassero distanti l'una dall'altra
per Quinta, & le seconde per un Semiditono, & le ultime finissero per l'Vnsono; come sono le sottoposte,
non farebbeno, che non si potessero chiamare Cadenze: quantunque si potesse dire, che si chiamassero Caden
Quarta parte. Qui debbe ciascuno Compositore auertire, acciò non pigliasse qualche errore, che quantunque le
Cadenze siano poste solamente ne i mostrati luoghi; nondimeno si possono fare anco in qualunque altro luogo, oue
torna più commodo, pur che si osserui la Regola data di sopra nel cap. 38. di andare dalla Consonanza imperfetta alla Perfetta con la più vicina. La onde fa dibisogno, che nelle penultime figure di queste Cadenze
sia la Terza minore; la qual sempre si vdirà, quando faranno il mouimento all'Vnisono di maniera, che l'vna discendi per mouimento congiunto del Tuono, & l'altra con un simile mouimento di Semituono maggiore, o per il contrario. Et ciò si potrà sempre fare in ciascun luogo, senza porre il segno della chorda chromatica, per fare dell'interuallo del Tuono un Semituono: Imperoche in quella parte, che tra la penultima figura, & la ultima si troua il mouimento, che ascende, sempre si intende essere collocato il Semituono; pur che
l'altra parte non discenda per simile interuallo: conciosiache allora il Semituono non si potrebbe porre da due
parti, cioè nella parte graue, & nella acuta: perche si udirebbe uno interuallo minore di un Semiditono, che
sarebbe dissonante. Ma la Natura hà prouisto in simil cosa: percioche non solamente li periti della Musica:
ma anco li contadini, che cantano senza alcuna arte, procedeno per l'interuallo del Semituono. Et queste sono dette Cadenze propiamente; ancora che quando le lor prime figure ritrouassero distanti l'una dall'altra
per Quinta, & le seconde per un Semiditono, & le ultime finissero per l'Vnsono; come sono le sottoposte,
non farebbeno, che non si potessero chiamare Cadenze: quantunque si potesse dire, che si chiamassero Caden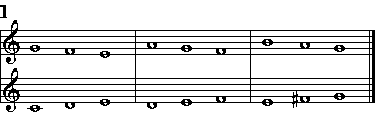 ze impropiamente. La Cadenza terminata per Ottaua è di tal sorte, che le sue figure uogliono essere ordinate in cotal modo; che la prima, la seconda, & la terza figura della parte acuta; & la prima, la seconda,
& la terza della parte graue si muouino con mouimenti contrarij, & congiunti, l'vna parte contra l'altra; et
le seconde figure delle parti siano distanti l'vna dall'altra per vna Sesta maggiore, & le vltime per vna Ottaua. Et quantunque potesse essere alcuna differenza di page 223mouimenti tra le prime, & le seconde figure: percioche facendo le figure della parte acuta i loro mouimenti
sempre congiunti, quelle della parte graue alcune volte potranno procedere per mouimenti separati, discendendo alcuna volta insieme; tuttauia, siano accommodate in qual maniera si vogliono, le seconde figure della
Cadenza si porranno sempre distanti l'vna dall'altra, per l'interuallo di Sesta maggiore, & le vltime finiranno in Ottaua. Et ciò sempre tornerà bene, quando vna parte farà il mouimento del Semituono, o nel graue, oueramente nell'acuto; & l'altra quello del Tuono, cosi in queste come in ogn'altra sorte di Cadenza, sia
semplice, o diminuita. E ben vero che le Cadenze diminuite hanno la Sincopa, nella quale si ode la Settima
sopra la sua seconda parte, cioè nel battere: Ma la Cadenza semplice è tutta consonante: percioche le sue figure sono tra
loro equali; si come ne i sotto posti essempi si può vedere.
ze impropiamente. La Cadenza terminata per Ottaua è di tal sorte, che le sue figure uogliono essere ordinate in cotal modo; che la prima, la seconda, & la terza figura della parte acuta; & la prima, la seconda,
& la terza della parte graue si muouino con mouimenti contrarij, & congiunti, l'vna parte contra l'altra; et
le seconde figure delle parti siano distanti l'vna dall'altra per vna Sesta maggiore, & le vltime per vna Ottaua. Et quantunque potesse essere alcuna differenza di page 223mouimenti tra le prime, & le seconde figure: percioche facendo le figure della parte acuta i loro mouimenti
sempre congiunti, quelle della parte graue alcune volte potranno procedere per mouimenti separati, discendendo alcuna volta insieme; tuttauia, siano accommodate in qual maniera si vogliono, le seconde figure della
Cadenza si porranno sempre distanti l'vna dall'altra, per l'interuallo di Sesta maggiore, & le vltime finiranno in Ottaua. Et ciò sempre tornerà bene, quando vna parte farà il mouimento del Semituono, o nel graue, oueramente nell'acuto; & l'altra quello del Tuono, cosi in queste come in ogn'altra sorte di Cadenza, sia
semplice, o diminuita. E ben vero che le Cadenze diminuite hanno la Sincopa, nella quale si ode la Settima
sopra la sua seconda parte, cioè nel battere: Ma la Cadenza semplice è tutta consonante: percioche le sue figure sono tra
loro equali; si come ne i sotto posti essempi si può vedere.
 Si può etiandio vedere, in qual maniera spesse volte si può cambiar le parti
della Cadenza tra loro, & porre quel passaggio, che fa la parte posta nel
graue, nella parte acuta; & per il contrario, quel che fa la parte acuta,
porlo nella parte graue, che corrispondino per vna Ottaua: percioche tali
mutationi sono molto commode alli Compositori. Oltra queste due sorti di
Cadenza, ve n'è vn'altra terminata per Ottaua, ouero per Vnisono, la qual
si fa, quando si pone le seconde figure della parte graue, & quelle della parte acuta distanti tra loro per vn Ditono, facendo
discendere la parte graue per mouimento di Quinta, ouero
ascendere per quello di Quarta; & ascendere la parte acuta per mouimento congiunto; come si vede.
Si può etiandio vedere, in qual maniera spesse volte si può cambiar le parti
della Cadenza tra loro, & porre quel passaggio, che fa la parte posta nel
graue, nella parte acuta; & per il contrario, quel che fa la parte acuta,
porlo nella parte graue, che corrispondino per vna Ottaua: percioche tali
mutationi sono molto commode alli Compositori. Oltra queste due sorti di
Cadenza, ve n'è vn'altra terminata per Ottaua, ouero per Vnisono, la qual
si fa, quando si pone le seconde figure della parte graue, & quelle della parte acuta distanti tra loro per vn Ditono, facendo
discendere la parte graue per mouimento di Quinta, ouero
ascendere per quello di Quarta; & ascendere la parte acuta per mouimento congiunto; come si vede.
 page 224
Et sono queste Cadenze di due sorti medesimamente; cioè, Semplici & Diminuite; come si può vedere. Quelle che sono Semplici,
hanno le figure simili; & le Diminuite hanno le figure diuerse; & tra loro si ritroua
la Sincopa, che hà nella sua seconda parte la Quarta, dopo la quale segue immediatamente la Terza maggiore; come hò mostrato. Ma perche queste Cadenze non si vsano molto di lungo nelle compositioni di due
voci: conciosia che lo ascendere per li mostrati mouimenti separati, & lo discendere anco è propio della parte grauissima di alcuna compositione composta a più voci, nella quale si vsano; però si guardaremo di porle troppo spesso; & quando le uorremo porre, sempre le porremo nel mezo, & non nel fine della cantilena; & quando la necessità a ciò fare ne astringesse; cioè quando volessimo porre le parti della compositione in Consequenza, ouero nella Imitatione; secondo li modi mostrati di sopra; & quando non si potesse hauere per
altra via vn passaggio commodo al cantare, & vna grata modulatione. E ben vero, che questo voglio
che più tosto sia conseglio, che precetto: percioche quando si ponessero anco nel principio, & nel fine non sarebbe grande errore. Oltra di questo si troua la Cadenza terminata per Quinta, ouero per Terza, o per altra consonanza, la quale è detta Cadenza impropiamente; & è contenuta similmente da vn numero simile di figure; & è ordinata in tal modo, che essendo le seconde figure dell'vna, & dell'altra parte distanti
per vna Terza, le vltime vengono a cascare in vna delle nominate consonanze; & questo quando la parte
acuta fa il mouimento congiunto ascendendo. Et è di due sorti, cioè Semplice, & Diminuita; ciascuna delle quali hormai per tanti essempi dati di sopra, credo che sia da ogn'uno conosciuta: La onde bastarà dire solamente, che nella Diminuita si ode la Quarta nella seconda parte della Sincopa, & non altra dissonanza; si
come si può vdire in ciascuna che si troua nelli sotto posti essempi.
page 224
Et sono queste Cadenze di due sorti medesimamente; cioè, Semplici & Diminuite; come si può vedere. Quelle che sono Semplici,
hanno le figure simili; & le Diminuite hanno le figure diuerse; & tra loro si ritroua
la Sincopa, che hà nella sua seconda parte la Quarta, dopo la quale segue immediatamente la Terza maggiore; come hò mostrato. Ma perche queste Cadenze non si vsano molto di lungo nelle compositioni di due
voci: conciosia che lo ascendere per li mostrati mouimenti separati, & lo discendere anco è propio della parte grauissima di alcuna compositione composta a più voci, nella quale si vsano; però si guardaremo di porle troppo spesso; & quando le uorremo porre, sempre le porremo nel mezo, & non nel fine della cantilena; & quando la necessità a ciò fare ne astringesse; cioè quando volessimo porre le parti della compositione in Consequenza, ouero nella Imitatione; secondo li modi mostrati di sopra; & quando non si potesse hauere per
altra via vn passaggio commodo al cantare, & vna grata modulatione. E ben vero, che questo voglio
che più tosto sia conseglio, che precetto: percioche quando si ponessero anco nel principio, & nel fine non sarebbe grande errore. Oltra di questo si troua la Cadenza terminata per Quinta, ouero per Terza, o per altra consonanza, la quale è detta Cadenza impropiamente; & è contenuta similmente da vn numero simile di figure; & è ordinata in tal modo, che essendo le seconde figure dell'vna, & dell'altra parte distanti
per vna Terza, le vltime vengono a cascare in vna delle nominate consonanze; & questo quando la parte
acuta fa il mouimento congiunto ascendendo. Et è di due sorti, cioè Semplice, & Diminuita; ciascuna delle quali hormai per tanti essempi dati di sopra, credo che sia da ogn'uno conosciuta: La onde bastarà dire solamente, che nella Diminuita si ode la Quarta nella seconda parte della Sincopa, & non altra dissonanza; si
come si può vdire in ciascuna che si troua nelli sotto posti essempi.
 Ne in queste (quando si fanno a due voci) è necessario, che sempre si odi in vna parte il mouimento del Semituono maggiore, o graue, ouero acuta che ella sia: percioche si vdirebbe alle uolte tra le parti la relatione, che non sarebbe harmonica; si come nel cap. 30. ho dichiarato. Sarebbe cosa molto tediosa, se io volesse dare vno essempio particolare di ogni Cadenza propia, & non propia: conciosia che sono quasi infinite;
onde è dibisogno, che'l Contrapuntista s'ingegni di ritrouarne sempre di nuoue, inuestigando di continouo nuoue maniere; &
si guardi di non commettere errore. Et accioche lui possa vedere in qual modo le Cadenze si
possino per diuersi modi ordinare, & in qual maniera si possino vsare, per non andare in lungo, porrò molti
essempi, da i quali si potrà scorgere quello, che si hauerà da fare nella inuentione delle altre. page 225
Ne in queste (quando si fanno a due voci) è necessario, che sempre si odi in vna parte il mouimento del Semituono maggiore, o graue, ouero acuta che ella sia: percioche si vdirebbe alle uolte tra le parti la relatione, che non sarebbe harmonica; si come nel cap. 30. ho dichiarato. Sarebbe cosa molto tediosa, se io volesse dare vno essempio particolare di ogni Cadenza propia, & non propia: conciosia che sono quasi infinite;
onde è dibisogno, che'l Contrapuntista s'ingegni di ritrouarne sempre di nuoue, inuestigando di continouo nuoue maniere; &
si guardi di non commettere errore. Et accioche lui possa vedere in qual modo le Cadenze si
possino per diuersi modi ordinare, & in qual maniera si possino vsare, per non andare in lungo, porrò molti
essempi, da i quali si potrà scorgere quello, che si hauerà da fare nella inuentione delle altre. page 225 Non voglio etiandio restar di dire, che li Prattici sogliono vsare alle volte nelle Cadenze, & in altri luoghi
etiandio, in vece della Semibreue sincopata, la Semibreue col punto, posto dissonante; vsando poi quelle circostanze, che
conuengono alla Cadenza, & alla Sincopa posta in cotal modo. Et benche cotal cosa sia tollerata, nondimeno non sodisfà a pieno il sentimento. La onde essortarei il compositore a non fare simil passaggi molto spesso
nelle sue compositioni, ancora che siano in vso: percioche (secondo'l mio giuditio) parmi, che
non siano da esser poste nel numero delle Cadenze; massimamente non osseruando tutto quello, che ricerca
la Cadenza; si come ogn'vno potrà giudicare, dopo che hauerà vditi, & essaminati li sottoposti essempi.
Non voglio etiandio restar di dire, che li Prattici sogliono vsare alle volte nelle Cadenze, & in altri luoghi
etiandio, in vece della Semibreue sincopata, la Semibreue col punto, posto dissonante; vsando poi quelle circostanze, che
conuengono alla Cadenza, & alla Sincopa posta in cotal modo. Et benche cotal cosa sia tollerata, nondimeno non sodisfà a pieno il sentimento. La onde essortarei il compositore a non fare simil passaggi molto spesso
nelle sue compositioni, ancora che siano in vso: percioche (secondo'l mio giuditio) parmi, che
non siano da esser poste nel numero delle Cadenze; massimamente non osseruando tutto quello, che ricerca
la Cadenza; si come ogn'vno potrà giudicare, dopo che hauerà vditi, & essaminati li sottoposti essempi.
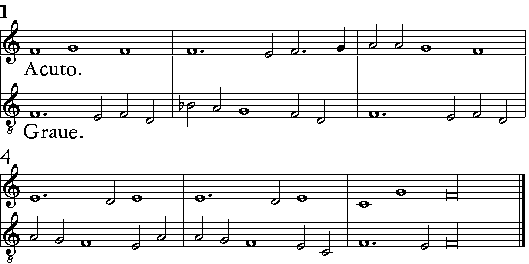 Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfettione delle parti di tutto il concento; come anco, accioche per il suo mezo si hauesse a finire la sentenza perfetta delle parole; è honesto, che volendola terminare per esse, che si finisca per vna delle consonanze perfettissime, cioè per la Ottaua, o almeno per l'Vnisono; accioche il Perfetto proportionatamente si venga a finire col Perfetto. Ma
quando si vorrà fare alcuna distintione mezana dell'harmonia, & delle parole insieme, le quali non habbiano finita perfettamente la loro sentenza; potremo vsar quelle Cadenze, che finiscono per Terza, per
Quinta, per Sesta, o per altre simili consonanze: perche il finire a cotesto modo, non è fine di Cadenza perfetta: ma si chiama
fuggir la Cadenza; si come hora la chiamano i Musici. Et fu buono il ritrouare, che le Cadenze finissero anco in tal maniera:
conciosia che alle volte accasca al Compositore, che venendoli alle mani vn bel passaggio, nel quale si accommodarebbe ottimamente la Cadenza, & non hauendo fatto fine al
Periodo nelle parole; non essendo honesto, che habbiano a finire in essa; cerca di fuggirla, non solamente al
modo mostrato: ma nella maniera ch'io mostrerò nel seguente capitolo. Et se bene da quello, che hò detto,
si possa concludere, che qualunque volta alcuna Cadenza non finirà nella Ottaua, ouer nell'Vnisono, si possa
chiamare Imperfetta: perche si fugge il fine perfetto; tuttauia perche il fuggir la Cadenza si fa in molti altri modi, voglio che vediamo hora in qual guisa la si possa fuggire, & il modo che si potrà tenere, quando
vna parte del Contrapunto farà il mouimento separato; cioè quando si muouerà di due, o più gradi; come
accade molte volte nelle compositioni. page 226
Il perche concludendo hormai dico, che se le Cadenze furono ritrouate, si per la perfettione delle parti di tutto il concento; come anco, accioche per il suo mezo si hauesse a finire la sentenza perfetta delle parole; è honesto, che volendola terminare per esse, che si finisca per vna delle consonanze perfettissime, cioè per la Ottaua, o almeno per l'Vnisono; accioche il Perfetto proportionatamente si venga a finire col Perfetto. Ma
quando si vorrà fare alcuna distintione mezana dell'harmonia, & delle parole insieme, le quali non habbiano finita perfettamente la loro sentenza; potremo vsar quelle Cadenze, che finiscono per Terza, per
Quinta, per Sesta, o per altre simili consonanze: perche il finire a cotesto modo, non è fine di Cadenza perfetta: ma si chiama
fuggir la Cadenza; si come hora la chiamano i Musici. Et fu buono il ritrouare, che le Cadenze finissero anco in tal maniera:
conciosia che alle volte accasca al Compositore, che venendoli alle mani vn bel passaggio, nel quale si accommodarebbe ottimamente la Cadenza, & non hauendo fatto fine al
Periodo nelle parole; non essendo honesto, che habbiano a finire in essa; cerca di fuggirla, non solamente al
modo mostrato: ma nella maniera ch'io mostrerò nel seguente capitolo. Et se bene da quello, che hò detto,
si possa concludere, che qualunque volta alcuna Cadenza non finirà nella Ottaua, ouer nell'Vnisono, si possa
chiamare Imperfetta: perche si fugge il fine perfetto; tuttauia perche il fuggir la Cadenza si fa in molti altri modi, voglio che vediamo hora in qual guisa la si possa fuggire, & il modo che si potrà tenere, quando
vna parte del Contrapunto farà il mouimento separato; cioè quando si muouerà di due, o più gradi; come
accade molte volte nelle compositioni. page 226Il modo di fuggir le Cadenze; & quello, che si hà da osseruare, quando il Soggetto farà il mouimento di due, o più gradi.Cap. 54.
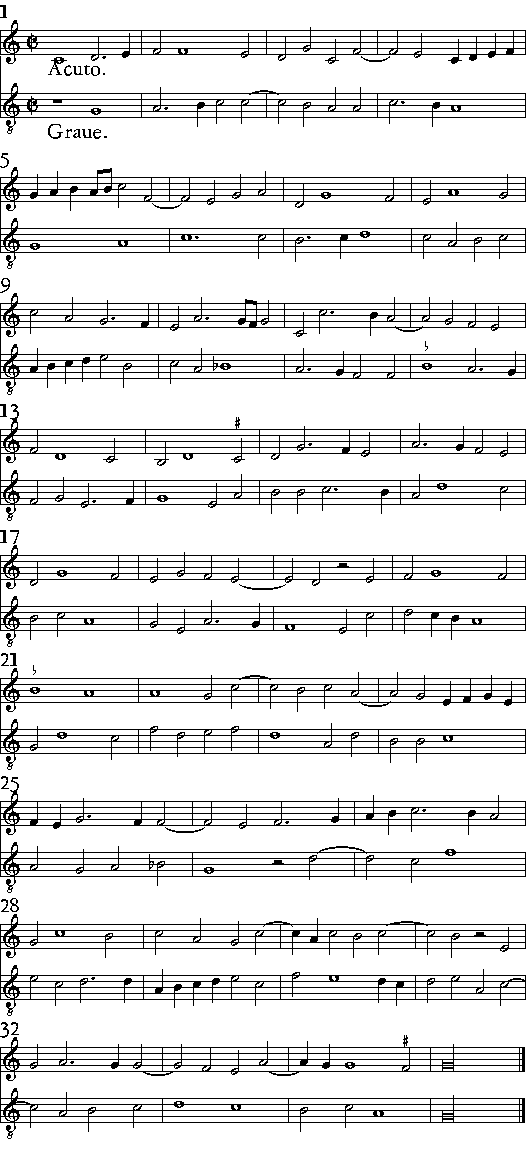 page 227
page 227Quando è lecito di vsare in vna parte della Cantilena due, o più volte vn passaggio, & quando non.Cap. 55.
 Hò detto, che non si debbe vsar molte volte vn passaggio, intendendo del Contrapunto replicato nelle istesse consonanze, ne gli istessi mouimenti, & nelle istesse chorde: percioche non solo è lecito, ma è molto lodeuole il replicar quante volte si vuole, o puote vna modulatione istessa, & vno istesso passaggio, pur che'l
Contrapunto sia sempre differente, & variato: essendo che tali repliche hanno vn non so che di ingegnoso;
la onde ogn'vno si de sforzare di far tali repliche, qualunque volta gli occorrerà di poterle fare, che stiano
bene, senza esserli alcuno errore: percioche sarà riputato da gli intelligenti huomo di pellegrino ingegno, &
abondante di inuentione. Hò detto, che si de sforzare: percioche non è obligato il Contrapuntista di maniera, che non possa mutare, & cambiar simili passaggi secondo'l suo volere: essendo che replicati in cotal modo, non si potrebbeno
vsar troppo di lungo, se non con grande discommodo delle parti; cioè con sinistre
modulationi. Ma quando non accaderanno cotali inconuenienti, si potranno replicare: percioche fanno buono effetto; si come nelli sottoposti essempi si può vdire.
Hò detto, che non si debbe vsar molte volte vn passaggio, intendendo del Contrapunto replicato nelle istesse consonanze, ne gli istessi mouimenti, & nelle istesse chorde: percioche non solo è lecito, ma è molto lodeuole il replicar quante volte si vuole, o puote vna modulatione istessa, & vno istesso passaggio, pur che'l
Contrapunto sia sempre differente, & variato: essendo che tali repliche hanno vn non so che di ingegnoso;
la onde ogn'vno si de sforzare di far tali repliche, qualunque volta gli occorrerà di poterle fare, che stiano
bene, senza esserli alcuno errore: percioche sarà riputato da gli intelligenti huomo di pellegrino ingegno, &
abondante di inuentione. Hò detto, che si de sforzare: percioche non è obligato il Contrapuntista di maniera, che non possa mutare, & cambiar simili passaggi secondo'l suo volere: essendo che replicati in cotal modo, non si potrebbeno
vsar troppo di lungo, se non con grande discommodo delle parti; cioè con sinistre
modulationi. Ma quando non accaderanno cotali inconuenienti, si potranno replicare: percioche fanno buono effetto; si come nelli sottoposti essempi si può vdire.
 page 228
page 228 Et perche alle uolte li Musici si sogliono obligare di fare il contrapunto, usando sempre un passaggio, uariando però il concento; il qual modo è detto Far contrapunto con obligo; & tali repliche, o passaggi si chiamano Pertinacie; però quando alcuno si uorrà obligare ad una cosa simile, piglierà un Thema, o passaggio,
& incomincierà a fare il contrapunto sopra il proposto Soggetto. Ma perche questa maniera di far contrapunto è molto difficile; però il Contrapuntista potrà prendere alcune licenze; come sarebbe di usare alle uolte
alcune modulationi, che non fussero cosi ageuoli al cantare, si come vorebbe il douere, che fussero, quando il
contrapunto si ponesse in iscritto, & fusse senza obligo alcuno. Et potrà vsar quelle figure, che più gli torneranno commode, variando il concento, vsando hora le Breui, hora le Semibreui, hora le Minime, & le
altre figure; Le quali potrà porre hora sincopate, & hora senza la sincopa; a ciò possa satisfare all'obligo.
Debbe nondimeno sempre hauer l'occhio alla osseruanza di quello, che è stato detto di sopra, & mostrato;
& di schiuare quanto potrà gli errori; accioche il suo contrapunto non sia piu tosto biasimato, che lodato:
Percioche quella cosa, che si fa bene nel difficile, è molto più da lodare, che non è quella, che è fatta bene senza alcuna difficultà. Adunque accioche si habbia di tal cosa piena cognitione, porrò due essempi, da i quali si
potrà conoscere quello, che si potrà fare ne gli altri simili;
Et perche alle uolte li Musici si sogliono obligare di fare il contrapunto, usando sempre un passaggio, uariando però il concento; il qual modo è detto Far contrapunto con obligo; & tali repliche, o passaggi si chiamano Pertinacie; però quando alcuno si uorrà obligare ad una cosa simile, piglierà un Thema, o passaggio,
& incomincierà a fare il contrapunto sopra il proposto Soggetto. Ma perche questa maniera di far contrapunto è molto difficile; però il Contrapuntista potrà prendere alcune licenze; come sarebbe di usare alle uolte
alcune modulationi, che non fussero cosi ageuoli al cantare, si come vorebbe il douere, che fussero, quando il
contrapunto si ponesse in iscritto, & fusse senza obligo alcuno. Et potrà vsar quelle figure, che più gli torneranno commode, variando il concento, vsando hora le Breui, hora le Semibreui, hora le Minime, & le
altre figure; Le quali potrà porre hora sincopate, & hora senza la sincopa; a ciò possa satisfare all'obligo.
Debbe nondimeno sempre hauer l'occhio alla osseruanza di quello, che è stato detto di sopra, & mostrato;
& di schiuare quanto potrà gli errori; accioche il suo contrapunto non sia piu tosto biasimato, che lodato:
Percioche quella cosa, che si fa bene nel difficile, è molto più da lodare, che non è quella, che è fatta bene senza alcuna difficultà. Adunque accioche si habbia di tal cosa piena cognitione, porrò due essempi, da i quali si
potrà conoscere quello, che si potrà fare ne gli altri simili;
 page 229
page 229
Delli Contrapunti doppij, & quello che siano.Cap. 56.
 te graue per vna Ottaua, & la graue acuta per vna Duodecima; procedendo per gli istessi mouimenti, &
per li medesimi interualli; come qui si vede in essempio. Dal quale si potrà comprendere che'l suo Contra
te graue per vna Ottaua, & la graue acuta per vna Duodecima; procedendo per gli istessi mouimenti, &
per li medesimi interualli; come qui si vede in essempio. Dal quale si potrà comprendere che'l suo Contra punto è molto variato da quello del Principale, & che molto è differente il suo concento; Et questo si chiama
Contrapunto doppio alla Duodecima. Si potrebbe etiandio porre la parte acuta nel graue distante per vna Otpage 231taua, & la graue nell'acuto distante per vna Duodecima: Ma perche non da variatione alcuna di concento
differente da quello, che si vdiua nella Replica, non lo porrò altramente; acciò non si venga a moltiplicar le
cose senza proposito. Volendo dipoi comporre quello, che tiene il secondo luogo nella prima maniera; cioè quello, che nella Replica procede per gli istessi mouimenti: ma per interualli differenti da quelli, che sono nel Principale;
osseruaremo di non porre per alcun modo nel Principale due consonanze simili; come sono due Terze, o due Seste, o simili altre, l'vna dopo l'altra senza alcun mezo; ancora che l'vna fusse maggiore, &
l'altra minore; Et di porre le Sincope, che siano in tutte le lor parti consonanti. Io dissi, che non si pone due
Seste: percioche in questi, & in altri simili Contrapunti, la Sesta si può vsare, che fa buono effetto; Et si può
far che la parte graue pigli il luogo della acuta, & questa quella del graue; come torna più commodo; con
questa conditione però, che quando saranno poste in tal maniera, l'vna non sia lontana dall'altra per più di
vna Terza: essendo che restando ciascuna nelli suoi termini, allora si potranno porre distanti l'una dall'altra
per vna Duodecima. E ben vero, che si potrebbe passar più oltra: ma quando si passasse non bisogna porre
per alcun modo la Terzadecima: perche tornarebbe molto discommoda. Non passaremo adunque la Duodecima, & osseruaremo le Regole date, & faremo, che le parti della cantilena cantino commodamente,
con mouimenti congiunti, più che sia possibile: percioche quelli di Quarta, & di Quinta, possono in alcuni
luoghi della Replica generare qualche discommodo. Il che osseruato, potremo hauere vn Contrapunto purgato da ogni errore simile a questo.
punto è molto variato da quello del Principale, & che molto è differente il suo concento; Et questo si chiama
Contrapunto doppio alla Duodecima. Si potrebbe etiandio porre la parte acuta nel graue distante per vna Otpage 231taua, & la graue nell'acuto distante per vna Duodecima: Ma perche non da variatione alcuna di concento
differente da quello, che si vdiua nella Replica, non lo porrò altramente; acciò non si venga a moltiplicar le
cose senza proposito. Volendo dipoi comporre quello, che tiene il secondo luogo nella prima maniera; cioè quello, che nella Replica procede per gli istessi mouimenti: ma per interualli differenti da quelli, che sono nel Principale;
osseruaremo di non porre per alcun modo nel Principale due consonanze simili; come sono due Terze, o due Seste, o simili altre, l'vna dopo l'altra senza alcun mezo; ancora che l'vna fusse maggiore, &
l'altra minore; Et di porre le Sincope, che siano in tutte le lor parti consonanti. Io dissi, che non si pone due
Seste: percioche in questi, & in altri simili Contrapunti, la Sesta si può vsare, che fa buono effetto; Et si può
far che la parte graue pigli il luogo della acuta, & questa quella del graue; come torna più commodo; con
questa conditione però, che quando saranno poste in tal maniera, l'vna non sia lontana dall'altra per più di
vna Terza: essendo che restando ciascuna nelli suoi termini, allora si potranno porre distanti l'una dall'altra
per vna Duodecima. E ben vero, che si potrebbe passar più oltra: ma quando si passasse non bisogna porre
per alcun modo la Terzadecima: perche tornarebbe molto discommoda. Non passaremo adunque la Duodecima, & osseruaremo le Regole date, & faremo, che le parti della cantilena cantino commodamente,
con mouimenti congiunti, più che sia possibile: percioche quelli di Quarta, & di Quinta, possono in alcuni
luoghi della Replica generare qualche discommodo. Il che osseruato, potremo hauere vn Contrapunto purgato da ogni errore simile a questo.
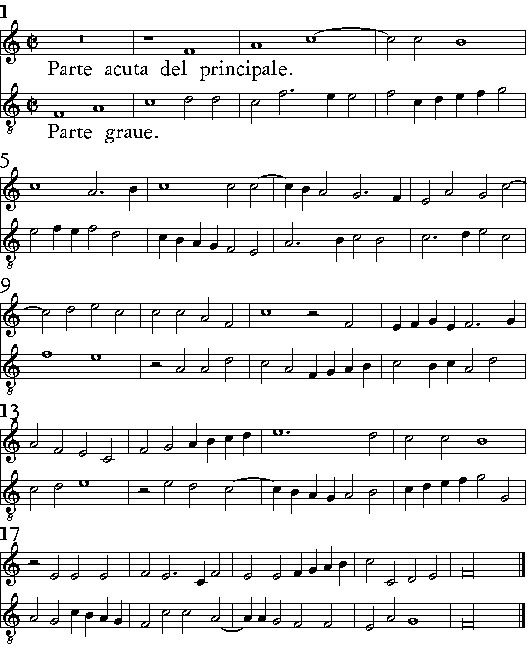 Haueremo poi la Replica, quando faremo la parte graue più acuta per vna Ottaua, & l'acuta più graue
per vna Decima. Et questo si chiamarà Contrapunto doppio alla Decima, che si contiene in queste due parti
poste qui di sotto. Si potrebbe etiandio far graue per vna Ottaua la parte acuta, & la graue acuta per
vna Decima; & più mi piacerebbe: perche si vdirebbe il Modo mantenuto maggiormente nelli suoi termini,
& anco altra harmonia: ma il Contrapunto non tornarebbe cosi bene osseruato, come quello, che si vede nella
Replica. Et si potrebbeno questi Contrapunti cantare etiandio a Tre voci, facendo cantare sopra la parte graue
del Principale vn'altra parte distante per vna Decima; & nella Replica sotto l'acuta, distante per vna Decimasettima. E ben vero che'l Contrapunto non verria ad esser cosi bene espurgato da molti errori, come sarebbe il douere. Ma perche il fare questa sorte di Contrapunto è molto difficile, volendolo far, che venghi nella Replica senza errore; però voglio porre alcune Regole generali, delle quali la prima sarà (lassando molte
altre cose alla discrettione, & al buon giuditio del Compositore) che non si de por mai la Terza dopo l'Vnisono, ne la Terza medesimamente, ouer la Decima dopo la Ottaua, quando le parti della cantilena discenderanno insieme. Osseruaremo anco, che quando le parti ascenderanno, di non por dopo la Quinta la Sesta; ne page 232
Haueremo poi la Replica, quando faremo la parte graue più acuta per vna Ottaua, & l'acuta più graue
per vna Decima. Et questo si chiamarà Contrapunto doppio alla Decima, che si contiene in queste due parti
poste qui di sotto. Si potrebbe etiandio far graue per vna Ottaua la parte acuta, & la graue acuta per
vna Decima; & più mi piacerebbe: perche si vdirebbe il Modo mantenuto maggiormente nelli suoi termini,
& anco altra harmonia: ma il Contrapunto non tornarebbe cosi bene osseruato, come quello, che si vede nella
Replica. Et si potrebbeno questi Contrapunti cantare etiandio a Tre voci, facendo cantare sopra la parte graue
del Principale vn'altra parte distante per vna Decima; & nella Replica sotto l'acuta, distante per vna Decimasettima. E ben vero che'l Contrapunto non verria ad esser cosi bene espurgato da molti errori, come sarebbe il douere. Ma perche il fare questa sorte di Contrapunto è molto difficile, volendolo far, che venghi nella Replica senza errore; però voglio porre alcune Regole generali, delle quali la prima sarà (lassando molte
altre cose alla discrettione, & al buon giuditio del Compositore) che non si de por mai la Terza dopo l'Vnisono, ne la Terza medesimamente, ouer la Decima dopo la Ottaua, quando le parti della cantilena discenderanno insieme. Osseruaremo anco, che quando le parti ascenderanno, di non por dopo la Quinta la Sesta; ne page 232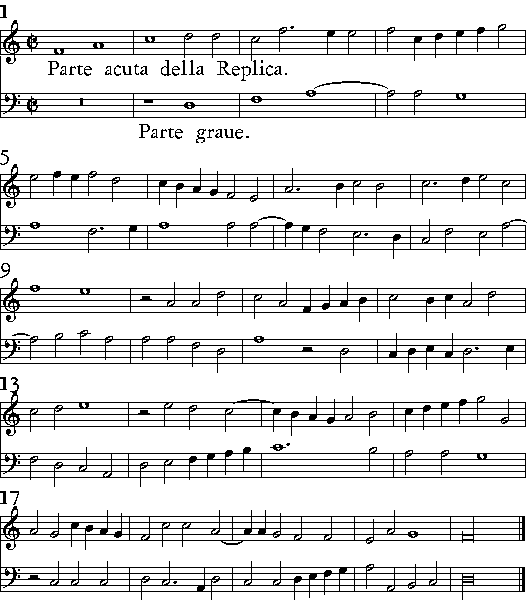 meno la Decima dopo la Duodecima; massimamente quando la parte acuta non procederà per mouimento
congiunto, il quale è alquanto più tolerabile del separato. Similmente si auertirà, di non procedere dalla Ottaua alla Decima minore, se non quando la parte acuta farà il mouimento di Tuono, & la graue quello del Semituono; ne meno dalla Terza, o dalla Quinta alla Decima minore, per contrarij mouimenti. Schiuaremo
il porre la parte acuta, che si muoua dalla Quinta alla Terza maggiore; quando la graue non farà mouimento alcuno. Cosi quando la parte acuta non farà mouimento, & la graue si muouerà, procedendo dalla Quinta alla Terza minore,
ouer dalla Duodecima alla Decima minore: Imperoche la Replica non verrebbe ad
essere osseruata, secondo le Regole date. In questa maniera di Contrapunto ogni Decima, che si pone nel
Principale, diuenta Ottaua nella Replica; & ogni Terza ritorna Quintadecima. Ma debbe il Contrapuntista comporre insieme il Principale, & la Replica; & cosi il tutto verrà ad esser senza errore. Nel secondo
modo, oue la Replica và modulando per mouimenti contrarij a quelli, che sono contenuti nel Principale, osseruando nelle sue parti gli istessi interualli; fà dibisogno, che esso Principale habbia le Sincope (se ne hauerà alcuna) che siano tutte consonanti; siano poste poi a qual modo si voglia: percioche se hauessero alcuna dissonanza, non verrebbeno a far buoni effetti nella Replica. Qui si potrà vsare (facendo bisogno) la Sesta nel principale: ma bisogna auertire, di non porre la Decima, dopo la quale seguiti la Ottaua; ne la Terza auanti
l'Vnisono, quando le parti ascendeno insieme; si come nel sottoposto esempio si è osseruato.
meno la Decima dopo la Duodecima; massimamente quando la parte acuta non procederà per mouimento
congiunto, il quale è alquanto più tolerabile del separato. Similmente si auertirà, di non procedere dalla Ottaua alla Decima minore, se non quando la parte acuta farà il mouimento di Tuono, & la graue quello del Semituono; ne meno dalla Terza, o dalla Quinta alla Decima minore, per contrarij mouimenti. Schiuaremo
il porre la parte acuta, che si muoua dalla Quinta alla Terza maggiore; quando la graue non farà mouimento alcuno. Cosi quando la parte acuta non farà mouimento, & la graue si muouerà, procedendo dalla Quinta alla Terza minore,
ouer dalla Duodecima alla Decima minore: Imperoche la Replica non verrebbe ad
essere osseruata, secondo le Regole date. In questa maniera di Contrapunto ogni Decima, che si pone nel
Principale, diuenta Ottaua nella Replica; & ogni Terza ritorna Quintadecima. Ma debbe il Contrapuntista comporre insieme il Principale, & la Replica; & cosi il tutto verrà ad esser senza errore. Nel secondo
modo, oue la Replica và modulando per mouimenti contrarij a quelli, che sono contenuti nel Principale, osseruando nelle sue parti gli istessi interualli; fà dibisogno, che esso Principale habbia le Sincope (se ne hauerà alcuna) che siano tutte consonanti; siano poste poi a qual modo si voglia: percioche se hauessero alcuna dissonanza, non verrebbeno a far buoni effetti nella Replica. Qui si potrà vsare (facendo bisogno) la Sesta nel principale: ma bisogna auertire, di non porre la Decima, dopo la quale seguiti la Ottaua; ne la Terza auanti
l'Vnisono, quando le parti ascendeno insieme; si come nel sottoposto esempio si è osseruato.
 Haueremo la Replica, ponendo graue la parte acuta, & la acuta graue; questa distante dalle parti principali per vna Settima, & quella per vna Nona; come qui si vede.
Haueremo la Replica, ponendo graue la parte acuta, & la acuta graue; questa distante dalle parti principali per vna Settima, & quella per vna Nona; come qui si vede.
 Componendo in cotal maniera, le parti della compositione si possono porre nel Principale distanti l'vna dall'altra per qual
si voglia interuallo; se bene ariuassero alla Quintadecima: perche nella Replica tornano bene: ma
non si debbe porre le parti molto lontane l'vna dall'altra. Hò voluto dare questi pochi essempi, accioche essaminati, il diligente Compositore possa ritrouare col suo intelletto altre nuoue, & belle inuentioni. La onde
voglio etiandio auertire vna cosa; che se noi osseruaremo tutte quelle Regole, che ne toglie, il potere vsare alcuna cosa nelli Contrapunti mostrati di sopra; potremo comporre vn Contrapunto di tal sorte, che si potrà
cantare a ciascuno delli modi mostrati, con grande variatione di harmonia; come nelli sottoposti si potrà
vedere, & vdire.
Componendo in cotal maniera, le parti della compositione si possono porre nel Principale distanti l'vna dall'altra per qual
si voglia interuallo; se bene ariuassero alla Quintadecima: perche nella Replica tornano bene: ma
non si debbe porre le parti molto lontane l'vna dall'altra. Hò voluto dare questi pochi essempi, accioche essaminati, il diligente Compositore possa ritrouare col suo intelletto altre nuoue, & belle inuentioni. La onde
voglio etiandio auertire vna cosa; che se noi osseruaremo tutte quelle Regole, che ne toglie, il potere vsare alcuna cosa nelli Contrapunti mostrati di sopra; potremo comporre vn Contrapunto di tal sorte, che si potrà
cantare a ciascuno delli modi mostrati, con grande variatione di harmonia; come nelli sottoposti si potrà
vedere, & vdire.

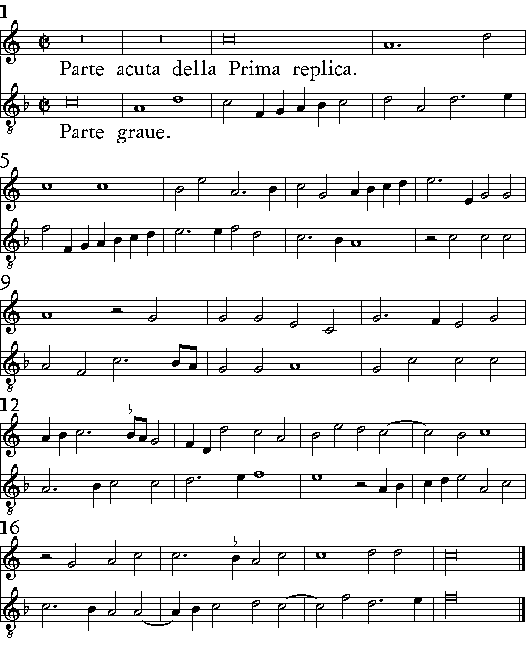 page 234
page 234
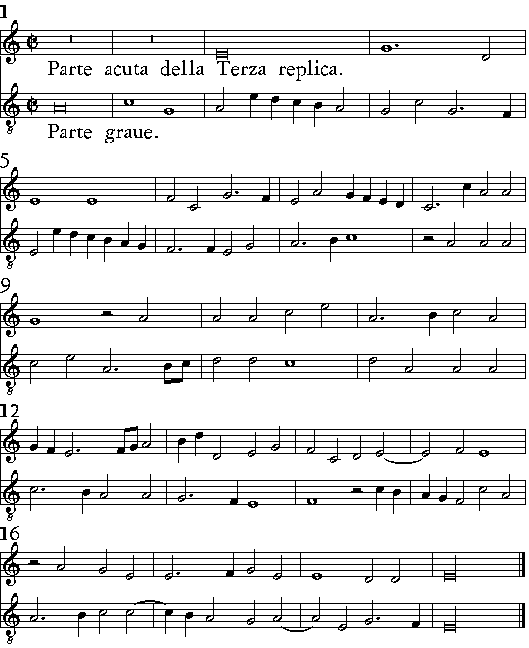 Non voglio tacere anco questo, per mostrar l'arteficio grande di questo Contrapunto; che se noi aggiungeremo
alla parte graue del Principale, & della prima, & della terza Replica, vna parte acuta distante per vna Decima; similmente
se alla parte acuta della seconda Replica aggiungeremo vn'altra parte graue distante per
vna Decima settima; oueramente se porremo la parte graue più acuta per vna Ottaua, et aggiungeremo vna
parte più graue della acuta per vna Decima, ciascuno da per sè si potrà cantare a tre voci. E ben vero, che le
parti aggiunte non verranno con la osseruanza delle Regole date di sopra. Ma di questo sia detto a sufficienza.
Non voglio tacere anco questo, per mostrar l'arteficio grande di questo Contrapunto; che se noi aggiungeremo
alla parte graue del Principale, & della prima, & della terza Replica, vna parte acuta distante per vna Decima; similmente
se alla parte acuta della seconda Replica aggiungeremo vn'altra parte graue distante per
vna Decima settima; oueramente se porremo la parte graue più acuta per vna Ottaua, et aggiungeremo vna
parte più graue della acuta per vna Decima, ciascuno da per sè si potrà cantare a tre voci. E ben vero, che le
parti aggiunte non verranno con la osseruanza delle Regole date di sopra. Ma di questo sia detto a sufficienza.
Quel che de osseruare il Contrapuntista oltra le Regole date, & di alcune licenze, che può pigliare.Cap. 57.
 cope sono sopportate; quanto maggiormente si de tollerare la Sesta, che non
solamente non è dissonante: ma appresso
di ogn'vno è riceuuta per consonante?
Potrebbe forse qui alcun dire, che con
questa licenza istessa, & con lo istesso
modo si potrebbe anco peruenire dalla
Sesta minore alla Ottaua. Rispondo,
che questo si farebbe contra ogni douere: Imperoche quantunque la Maggiore habbia natura di peruenire alla Ottaua, come alla sua propinqua; è
nondimeno più vicina alla Quinta, che non è la Minore alla Ottaua. La onde si vede, che douendosi (come è il
cope sono sopportate; quanto maggiormente si de tollerare la Sesta, che non
solamente non è dissonante: ma appresso
di ogn'vno è riceuuta per consonante?
Potrebbe forse qui alcun dire, che con
questa licenza istessa, & con lo istesso
modo si potrebbe anco peruenire dalla
Sesta minore alla Ottaua. Rispondo,
che questo si farebbe contra ogni douere: Imperoche quantunque la Maggiore habbia natura di peruenire alla Ottaua, come alla sua propinqua; è
nondimeno più vicina alla Quinta, che non è la Minore alla Ottaua. La onde si vede, che douendosi (come è il
 douere) andar dalla Consonanza imperfetta alla perfetta con la più uicina;
stando in questa licenza; la Sesta maggiore conuiene più alla Quinta, che la
minore alla Ottaua. Non gli è adunque
ragione alcuna, che ne scusi, o diffendi,
quando si volesse commettere vn tal
disordine. Potrà etiandio dalla Sesta
minore andare alla Ottaua con una fipage 236gura di Semiminima; perche la Quarta Semiminima, che si parte dalla Terza co'l mouimento congiunto, si
può sempre pigliar per non buona; si come nel Cap. 42. fu detto. Onde se vna Seconda, ouero vna Settima,
o qualunque altra dissonanza posta in cotal modo si sopporta, quanto maggiormente si può tollerare una Sesta posta in cotal maniera? Et tanto più è da tollerare, quanto spesse fiate dalli Cantori periti, non potendo
il loro vdito sentire alcun discommodo in alcuna cosa quantunque minima, è fatta maggiore. Ma veramen
douere) andar dalla Consonanza imperfetta alla perfetta con la più uicina;
stando in questa licenza; la Sesta maggiore conuiene più alla Quinta, che la
minore alla Ottaua. Non gli è adunque
ragione alcuna, che ne scusi, o diffendi,
quando si volesse commettere vn tal
disordine. Potrà etiandio dalla Sesta
minore andare alla Ottaua con una fipage 236gura di Semiminima; perche la Quarta Semiminima, che si parte dalla Terza co'l mouimento congiunto, si
può sempre pigliar per non buona; si come nel Cap. 42. fu detto. Onde se vna Seconda, ouero vna Settima,
o qualunque altra dissonanza posta in cotal modo si sopporta, quanto maggiormente si può tollerare una Sesta posta in cotal maniera? Et tanto più è da tollerare, quanto spesse fiate dalli Cantori periti, non potendo
il loro vdito sentire alcun discommodo in alcuna cosa quantunque minima, è fatta maggiore. Ma veramen te questi passagi non sono altro, che
la diminutione di quelli, che sono posti
qui da canto; Ne per questo non si toglie
ad alcuno, che non possa aggiungere
a suo bel piacere a tal Semiminima posta ne i primi essempi, ilsegno
te questi passagi non sono altro, che
la diminutione di quelli, che sono posti
qui da canto; Ne per questo non si toglie
ad alcuno, che non possa aggiungere
a suo bel piacere a tal Semiminima posta ne i primi essempi, ilsegno  . &
far la Sesta maggiore, per virtù della
chorda Chromatica; et cosi quella del
. &
far la Sesta maggiore, per virtù della
chorda Chromatica; et cosi quella del
 , secondo che occorrer puote nel fare
li Contrapunti: & se bene tal chorde non si segnassero, non si debbe attribuire al Compositore, che lo habbia
fatto per errore, massimamente in cotali cose minime. Potrà similmente vsare alle volte: ma non spesso,
vna modulatione di vna Semidiapente, quando tornarà commodo nello accommodar la modulatione alle parole, & procederà per le chorde diatoniche naturali del Modo, sopra ilquale è fondata la cantilena; come qui si
, secondo che occorrer puote nel fare
li Contrapunti: & se bene tal chorde non si segnassero, non si debbe attribuire al Compositore, che lo habbia
fatto per errore, massimamente in cotali cose minime. Potrà similmente vsare alle volte: ma non spesso,
vna modulatione di vna Semidiapente, quando tornarà commodo nello accommodar la modulatione alle parole, & procederà per le chorde diatoniche naturali del Modo, sopra ilquale è fondata la cantilena; come qui si
 vede. Ma quando vi entrasse alcuna
delle chorde chromatiche (quantunque
si ponesse per lo acquisto di alcuna consonanza) non si debbe vsare: Conciosia
che tali chorde non furono ritrouate a
destruttione delle buone harmonie, &
delli buoni costumi musicali: ma si bene alla loro costruttione, & al loro bene essere. Non sarà adunque lecito di
vsare alcun passaggio, che sia simile ad vno di questi posti qui in essempio: Percioche le chorde chromatiche
vede. Ma quando vi entrasse alcuna
delle chorde chromatiche (quantunque
si ponesse per lo acquisto di alcuna consonanza) non si debbe vsare: Conciosia
che tali chorde non furono ritrouate a
destruttione delle buone harmonie, &
delli buoni costumi musicali: ma si bene alla loro costruttione, & al loro bene essere. Non sarà adunque lecito di
vsare alcun passaggio, che sia simile ad vno di questi posti qui in essempio: Percioche le chorde chromatiche
 haueranno sempre nella modulatione
vna chorda diatonica corrispondente
per vna Semidiapente, ouero per vn
Tritono, o Semitritono, secondo la compositione; liquali sono Interualli, o Modulationi senza harmonia. Li sarà anco permesso di potere vsare alle volte
le chorde chromatiche, quando vorrà
procedere da vna Sesta, fatta maggiore per virtù di tal chorde, alla Decima, o Terza maggiore, col mouimento di Quarta, o
di Quinta; per potere
da quelle peruenire alla Ottaua, oueramente all'Vnisono; come qui si vede; Et ciò per due ragioni, l'vna delle
haueranno sempre nella modulatione
vna chorda diatonica corrispondente
per vna Semidiapente, ouero per vn
Tritono, o Semitritono, secondo la compositione; liquali sono Interualli, o Modulationi senza harmonia. Li sarà anco permesso di potere vsare alle volte
le chorde chromatiche, quando vorrà
procedere da vna Sesta, fatta maggiore per virtù di tal chorde, alla Decima, o Terza maggiore, col mouimento di Quarta, o
di Quinta; per potere
da quelle peruenire alla Ottaua, oueramente all'Vnisono; come qui si vede; Et ciò per due ragioni, l'vna delle
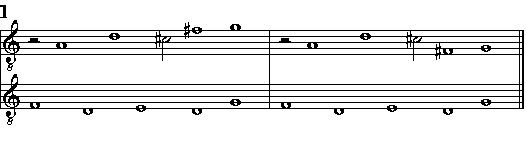 quali è; perche il procedere è Diatonico nelle chorde chromatiche; L'altra
perche li mouimenti, che fanno le parti, procedeno per gli interualli harmonici, & sono anco regolati secondo li
precetti mostrati di sopra. Queste
chorde si debbeno segnar col segno
quali è; perche il procedere è Diatonico nelle chorde chromatiche; L'altra
perche li mouimenti, che fanno le parti, procedeno per gli interualli harmonici, & sono anco regolati secondo li
precetti mostrati di sopra. Queste
chorde si debbeno segnar col segno  per molti rispetti; et massimamente per
li poco accorti Cantori; acciò non commettessino alle volte qualche errore, ponendo vna chorda in luogo di un'altra; cioè la Diatonica in luogo della Chromatica,
& si odi la dissonanza. page 237E' ben vero, che nelle modulationi si trouano alcuni interualli, come sono quelli di Quarta, di Quinta, & di
Ottaua, ne i quali il Cantore dè porre la chorda chromatica, ancora che non sia stata segnata dal Compositore; accioche la modulatione delle parti sia drittamente ordinata. Ne il Compositore la debbe porre: perche
è superfluo: essendo che non si dè cantare veramente se non quelli interualli, che sono harmonici; come qui si
vede. Ne debbe fare come fanno alcuni, i quali fuori di ogni proposito, & senza alcuna vtilita, o neces
per molti rispetti; et massimamente per
li poco accorti Cantori; acciò non commettessino alle volte qualche errore, ponendo vna chorda in luogo di un'altra; cioè la Diatonica in luogo della Chromatica,
& si odi la dissonanza. page 237E' ben vero, che nelle modulationi si trouano alcuni interualli, come sono quelli di Quarta, di Quinta, & di
Ottaua, ne i quali il Cantore dè porre la chorda chromatica, ancora che non sia stata segnata dal Compositore; accioche la modulatione delle parti sia drittamente ordinata. Ne il Compositore la debbe porre: perche
è superfluo: essendo che non si dè cantare veramente se non quelli interualli, che sono harmonici; come qui si
vede. Ne debbe fare come fanno alcuni, i quali fuori di ogni proposito, & senza alcuna vtilita, o neces sità, danno principio alle lor cantilene sopra alcune chorde, che veramente non sono naturali de i Modi; &
mescolano le chorde chromatiche con le diatoniche di maniera, che non solamente nel principio; ma nel mezo, & nel fine anco, non si vede altro che
sità, danno principio alle lor cantilene sopra alcune chorde, che veramente non sono naturali de i Modi; &
mescolano le chorde chromatiche con le diatoniche di maniera, che non solamente nel principio; ma nel mezo, & nel fine anco, non si vede altro che  Diesis, &
Diesis, &  molli; la qual cosa, quando la compositione
la ricercasse, sarebbe da sopportare. Però sarà auertito il Compositore, di astenerse, più che puote da simil cosa, se non fusse costretto dalle parole, ouer da altra cosa, che accade nella cantilena: conciosia che per il lungo continouare in essi, la cantilena viene a mutare il Modo, entrando di vno nell'altro; come è vitio particolare di qualcheduno.
Et sopra'l tutto si dè guardare, da porre tali chorde nel principio senza proposito; come fanno alcuni, che non solamente segnano la seconda figura della modulatione col segno
molli; la qual cosa, quando la compositione
la ricercasse, sarebbe da sopportare. Però sarà auertito il Compositore, di astenerse, più che puote da simil cosa, se non fusse costretto dalle parole, ouer da altra cosa, che accade nella cantilena: conciosia che per il lungo continouare in essi, la cantilena viene a mutare il Modo, entrando di vno nell'altro; come è vitio particolare di qualcheduno.
Et sopra'l tutto si dè guardare, da porre tali chorde nel principio senza proposito; come fanno alcuni, che non solamente segnano la seconda figura della modulatione col segno  Chromatico;
ma segnano etiandio la prima, & fanno, che spesse volte, credendosi di dar principio ad vna modulatione
del primo Modo (per dare vno essempio) non si accorgendo incominciano vna cantilena del Settimo; come
Chromatico;
ma segnano etiandio la prima, & fanno, che spesse volte, credendosi di dar principio ad vna modulatione
del primo Modo (per dare vno essempio) non si accorgendo incominciano vna cantilena del Settimo; come
 si può vedere nello essempio posto qui da
canto. Auertisca etiandio il Compositore, che si pone alle volte tra la chorda g,
& la a a vn'altra chorda, segnata col
segno commune chromatico
si può vedere nello essempio posto qui da
canto. Auertisca etiandio il Compositore, che si pone alle volte tra la chorda g,
& la a a vn'altra chorda, segnata col
segno commune chromatico  ; onde nascono alcune modulationi, che non si possono veramente chiamar Diatoniche semplicemente, ne Chromatiche: percioche
tanto nell'acuto quanto nel graue, non si
possono accommodare tra le chorde naturali diatoniche ad vna modulatione, che sia diatonica; come sono le
sequenti: Conciosia che essendo il primo interuallo, che fanno le tre prime figure il Semituono maggiore,
; onde nascono alcune modulationi, che non si possono veramente chiamar Diatoniche semplicemente, ne Chromatiche: percioche
tanto nell'acuto quanto nel graue, non si
possono accommodare tra le chorde naturali diatoniche ad vna modulatione, che sia diatonica; come sono le
sequenti: Conciosia che essendo il primo interuallo, che fanno le tre prime figure il Semituono maggiore,
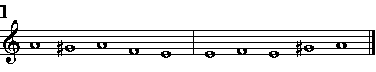 & quello che fanno la terza, & la quarta il Ditono; & medesimamente è il Semituono maggiore quello, che è contenuto tra le due vltime; Se noi discorreremo
tutte le chorde diatoniche, & anche le
chromatiche insieme, non ritrouaremo, ne verso il graue, ne verso l'acuto, di potere accommodar questi interualli, senza l'aiuto di vn'altra chorda forestiera, la qual segnaremo con questo segno, [[mus.hsharp]] col quale si segna
ogni seconda chorda di ogni Tetrachordo Enharmonico. Et questa chorda non si potrà chiamare Diatonica:
perche non hà luogo tra le chorde diatoniche; ne anco chromatica: conciosia che per il suo mezo da parte alcuna non si puo hauere il Trihemituono; ne meno la potremo nominare Enharmonica: essendo che non diuide
il Semituono maggiore in due Diesis; il che è ufficio della vera chorda Enharmonica; come si può vedere in
ciascuna diuisione fatta nella Seconda parte. Et benche tal chorda si possa chiamare Diatonica: perche si troua in una compositione
diatonica, & fa il Semituono, che è diatonico; tuttauia è nominata impropiamente:
essendo che allora sarà detta veramente Diatonica, o Chromatica, oueramente Enharmonica; quando sarà
posta in luogo, oue potrà in vno delli detti generi fare il suo vfficio: ma non giamai altramente; come auiene di quella, che è posta nel quarto luogo del Quarto essempio posto qui di sotto. Et se bene tal chorda posta in cotal maniera non è Diatonica, non si debbe restare di vsarla, poi che in questi, & altri simili passaggi, non fa alcun tristo effetto; & torna molto al proposito alle volte al Compositore. Et perche si ritrouano
infinite cantilene Diatoniche, le quali sono piene di questi, & altri simili passaggi, & non sono considerati page 238
& quello che fanno la terza, & la quarta il Ditono; & medesimamente è il Semituono maggiore quello, che è contenuto tra le due vltime; Se noi discorreremo
tutte le chorde diatoniche, & anche le
chromatiche insieme, non ritrouaremo, ne verso il graue, ne verso l'acuto, di potere accommodar questi interualli, senza l'aiuto di vn'altra chorda forestiera, la qual segnaremo con questo segno, [[mus.hsharp]] col quale si segna
ogni seconda chorda di ogni Tetrachordo Enharmonico. Et questa chorda non si potrà chiamare Diatonica:
perche non hà luogo tra le chorde diatoniche; ne anco chromatica: conciosia che per il suo mezo da parte alcuna non si puo hauere il Trihemituono; ne meno la potremo nominare Enharmonica: essendo che non diuide
il Semituono maggiore in due Diesis; il che è ufficio della vera chorda Enharmonica; come si può vedere in
ciascuna diuisione fatta nella Seconda parte. Et benche tal chorda si possa chiamare Diatonica: perche si troua in una compositione
diatonica, & fa il Semituono, che è diatonico; tuttauia è nominata impropiamente:
essendo che allora sarà detta veramente Diatonica, o Chromatica, oueramente Enharmonica; quando sarà
posta in luogo, oue potrà in vno delli detti generi fare il suo vfficio: ma non giamai altramente; come auiene di quella, che è posta nel quarto luogo del Quarto essempio posto qui di sotto. Et se bene tal chorda posta in cotal maniera non è Diatonica, non si debbe restare di vsarla, poi che in questi, & altri simili passaggi, non fa alcun tristo effetto; & torna molto al proposito alle volte al Compositore. Et perche si ritrouano
infinite cantilene Diatoniche, le quali sono piene di questi, & altri simili passaggi, & non sono considerati page 238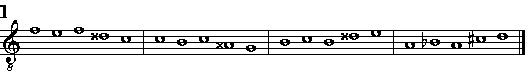 dalli Prattici; però ne hò voluto fare commemoratione, & rimettere cotal cosa al sano giudicio de i buoni,
& eccellenti Compositori; acciò vedino, in qual maniera si debbino vsare. Rimetto etiandio molte altre cose,
delle quali non voglio tacere questa; che non è il douere, che si ponghi la Semibreue sincopata, in modo, che
dopo le seguiti immediatamente la Minima dissonante col mouimento congiunto; conciosia che si farebbe contra quello, che si
conuiene alla natura della Sincopa tutta consonante; la quale non riceue dopo se alcuna dissonanza: ma si bene la consonanza. Però quando vorremo porre tal Minima dissonante, porremo sempre
la battuta sopra la Semibreue, ponendoli appresso il punto, il quale dè esser sempre consonante; & venga poi
la Minima a qual modo si voglia, o consonante, o dissonante; pur che procedi con mouimenti congiunti, come qui si uede. Debbe oltra di questo auertire, che tutte le volte, che vorrà fare il Contrapunto alquanto
dalli Prattici; però ne hò voluto fare commemoratione, & rimettere cotal cosa al sano giudicio de i buoni,
& eccellenti Compositori; acciò vedino, in qual maniera si debbino vsare. Rimetto etiandio molte altre cose,
delle quali non voglio tacere questa; che non è il douere, che si ponghi la Semibreue sincopata, in modo, che
dopo le seguiti immediatamente la Minima dissonante col mouimento congiunto; conciosia che si farebbe contra quello, che si
conuiene alla natura della Sincopa tutta consonante; la quale non riceue dopo se alcuna dissonanza: ma si bene la consonanza. Però quando vorremo porre tal Minima dissonante, porremo sempre
la battuta sopra la Semibreue, ponendoli appresso il punto, il quale dè esser sempre consonante; & venga poi
la Minima a qual modo si voglia, o consonante, o dissonante; pur che procedi con mouimenti congiunti, come qui si uede. Debbe oltra di questo auertire, che tutte le volte, che vorrà fare il Contrapunto alquanto
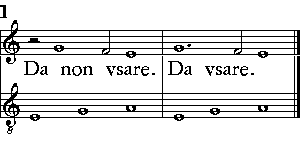 languido, o mesto; simigliantemente dolce, o soaue, debbe procedere anco per mouimenti dolci, & soaui; come
sono quelli, che procedeno per il Semituono, per il Semiditono, & per altri simili; vsando le Consonanze imperfette minori, che sono il Semiditono, l'Essachordo minore, & le altre Replicate; le quali consonanze per sua
natura sono (come hò detto nel cap. 10.) atte a tali cose. Per il contrario, volendolo fare allegro, vsarà il mouimento del Tuono, quello del Ditono, & di altri simili, con li suoi interualli. Et volendolo fare, che qualche
volta habbia dell'aspro potrà vsare le Maggiori, che sono il Ditono, l'Essachordo maggiore, & le Replicate, nelle parti graui della cantilena. Et tanto più sarà aspro, quanto maggiormente hauerà in se il detto
Essachordo, nelle figure di alquanto valore, nella parte graue del concento. E' cosa difficile veramente il volere insegnare particolarmente, in qual maniera, & a che tempo si habbiano da vsar tal cose: ma perche questo ch'io hò detto
potrà molto giouare, quando si vorrà alle uolte vsare cotali maniere; però bastarà questo per
hora: percioche forse vn'altra volta ne dirò più diffusamente.
languido, o mesto; simigliantemente dolce, o soaue, debbe procedere anco per mouimenti dolci, & soaui; come
sono quelli, che procedeno per il Semituono, per il Semiditono, & per altri simili; vsando le Consonanze imperfette minori, che sono il Semiditono, l'Essachordo minore, & le altre Replicate; le quali consonanze per sua
natura sono (come hò detto nel cap. 10.) atte a tali cose. Per il contrario, volendolo fare allegro, vsarà il mouimento del Tuono, quello del Ditono, & di altri simili, con li suoi interualli. Et volendolo fare, che qualche
volta habbia dell'aspro potrà vsare le Maggiori, che sono il Ditono, l'Essachordo maggiore, & le Replicate, nelle parti graui della cantilena. Et tanto più sarà aspro, quanto maggiormente hauerà in se il detto
Essachordo, nelle figure di alquanto valore, nella parte graue del concento. E' cosa difficile veramente il volere insegnare particolarmente, in qual maniera, & a che tempo si habbiano da vsar tal cose: ma perche questo ch'io hò detto
potrà molto giouare, quando si vorrà alle uolte vsare cotali maniere; però bastarà questo per
hora: percioche forse vn'altra volta ne dirò più diffusamente.
Il modo che si hà da tenere nel comporre le Cantilene a più di due voci; & del nome delle parti.Cap. 58.
Plus ascoltantum Sopranus captat orecchias.I quali hò voluto porre, accioche il Compositore ricordandoseli, possa sapere quello, che haurà da fare, componendo coteste parti. Queste sono adunque le parti principali, & Elementali di ogni compositione perfetta; delle quali, ancora che l'Alto sia l'ultimo page 240a comporsi: percioche composte l'altre parti, viene a supplire, & a far perfetta l'harmonia, che tra loro non si potea far perfetta; nondimeno non è legge fatale, che'l si habbia da porre sempre vltimo nella compositione; si come etiandio non è cosa alcuna, che ne astringa, a compor prima l'vna, che l'altra parte della compositione. Si debbe però auertire, che quando li Musici vogliono comporre alcuna cantilena a Tre voci, il più delle volte lassano fuori il Contralto, ouero il Soprano, & pigliano l'altre parti. Et se vogliono procedere oltra le Quattro nominate, non ui aggiungono alcuna parte noua; ma le vengono a raddoppiare, ponendo due Soprani, o due Alti, o due Tenori, & cosi due Bassi; & hanno il loro proposito. Qualunque volta adunque che si vorrà comporre alcuno concento sopra vn Soggetto ritrouato; o sia Canto fermo, o figurato; ouero se'l si vorrà comporre alcuna Canzone, Madrigale, ouer Motteto, & faccia dibisogno, che'l Compositore sia l'inuentore del Soggetto, debbe prima auertire, di qual Modo sia il Soggetto; oueramente sopra qual Modo vorrà comporre la sua cantilena, acciò conosca le chorde, sopra le quali si habbiano da far le Cadenze, per poter comporre il concento in tal maniera, che'l fine non sia dissonante dal mezo, & dal principio. La onde considerate queste cose, si potrà incominciare, da qual parte tornerà più commoda; incominciando però sempre in vna chorda, la quale sia regolare del Modo, sopra il quale si habbia da fondare la cantilena, osseruando quello, che in molte regole poste di sopra si contiene. Ma perche li Musici costumano di dar principio alle loro Compositioni il più delle volte per il Tenore; & dipoi pongono il Soprano, alquale aggiungono il Basso, & vltimamente l'Alto; hauendo io di sopra mostrato molti essempi, contenuti tra queste due parti; cioè tra'l Soprano, & il Tenore; però non accade, se non porre la sottoposta Tauola, nella quale si potrà comprendere senza molta fatica tutti gli accordi, che potranno fare le parti aggiunte insieme alle due nominate, siano quanti si vogliono. Et hò tenuto tale ordine, di porre primieramente gli accordi, che danno insieme il Soprano col Tenore, di poi quanto potrà essere il Basso lontano dal Tenore nella parte graue; accioche il tutto si accordi; & cosi stante le nominate parti, quello che fa dibisogno, che sia l'Alto sopra'l Basso, accioche l'harmonia venghi ad esser perfetta. Ma si debbe auertire, che si trouerà alle volte nell'Alto più di vno accordo; onde tali accordi potranno seruire non solamente ad esso Alto; ma etiandio alle altre parti, che si aggiungessero alla cantilena, oltra le quattro nominate. Ne si trouerà il Contralto posto con le altre parti in Vnisono, ne in Ottaua, se non in quattro luoghi: percioche quando le altre parti haueranno tra loro la Quinta, & la Terza, ouero le Replicate, allora le aggiunte a queste, siano quante si vogliano, necessariamente verranno ad essere con vna delle tre nominate in Ottaua, ouero in Vnisono. Ma accioche si habbia piena intelligenza di quello, che si è detto porrò vno essempio. Poniamo che nella compositione il Soprano sia posto Vnisono col Tenore; cioè sopra vna chorda istessa: dico che volendo aggiunger la Terza parte a queste due, sarà dibisogno di porre il Basso distante per vna di queste consonanze, cioè Terza, o Quinta, o Sesta, ouero Ottaua, o per qualunque altra (come si vede nella Tauola) sotto 'l Tenore. Onde essendo il Basso lontano per vna Terza; l'Alto potrà esser distante dal Basso nell'acuto per vna Quinta, o per vna Sesta; & le altre parti (se fussero più di Quattro) potranno essere Vnisone, ouer distanti per vna Ottaua da l'vna di queste quattro. Ma se'l Basso fusse distante dal Tenore nel graue per vna Quinta, l'Alto si potrà porre sopra'l Basso distante per vna Terza, ouer per vna Decima; & le altre parti, che si aggiungessero sarebbeno Vnisone, ouero lontane da l'vna di queste quattro per vna Ottaua. Et se'l Basso fusse anco distante per vna Sesta, riguardando nel Terzo essempio della Tauola, si trouerà quello, che potrà essere il Contralto; il che si potrà etiandio vedere delle altre per ordine, si come sono poste ordinatamente; come si può veder chiaramente qui di sotto, & distintamente per ordine. page 241
Sed Tenor est vocum rector, vel Guida Tonorum.
Altus Apollineum carmen depingit & ornat.
Bassus alit voces, ingrassat, fundat, & auget.
| DELL'VNISONO. |
|
| DELLA TERZA. |
|
| DELLA QVARTA. |
|
| DELLA QVINTA. |
|
| DELLA SESTA. |
|
| DELLA OTTAVA. |
|
Delle Cantilene, che si compongono a Tre voci, & di quello che si dè osseruare nel comporle.Cap. 59.
 page 243Ma si debbe auertire, che quando le parti del Contrapunto daranno principio alla cantilena, di incominciare
sopra quella chorda, che incomincia la prima figura del Canto fermo; come porta il douere; imitandolo più
che si possa; ponendo le parti del Contrapunto tra loro in Consequenza: & se bene si porranno etiandio col
Canto fermo non sarà male. E' ben vero, che a porle a questo secondo modo, non è noua maniera, ne inuention noua: perche non si può far cosa alcuna, che non sia stato fatta le migliaia di volte. Ma dirò bene, che'l
primo modo, se non sarà cosa noua, almeno sarà appresso di noua, & poco vsata. Si potrà etiandio, con grandissimo commodo (il che è anco lodeuole) porre in Consequenza le parti tra loro; non con quell'ordine istesso,
& dispositione, come si vsa nelle Fughe legate: ma con vn'ordine interrotto; ponendo parte delle figure ascendenti, & parte discendenti; & porre solamente il numero delle figure, che siano di vno istesso valore; ponendo
tallora vna Imitatione di figure al contrario, cioè porre la Guida, o Principale, che procedi per vn numero di
figure ascendenti, & il Consequente, che con l'istesso numero discendi; come dal sotto posto essempio si può com
page 243Ma si debbe auertire, che quando le parti del Contrapunto daranno principio alla cantilena, di incominciare
sopra quella chorda, che incomincia la prima figura del Canto fermo; come porta il douere; imitandolo più
che si possa; ponendo le parti del Contrapunto tra loro in Consequenza: & se bene si porranno etiandio col
Canto fermo non sarà male. E' ben vero, che a porle a questo secondo modo, non è noua maniera, ne inuention noua: perche non si può far cosa alcuna, che non sia stato fatta le migliaia di volte. Ma dirò bene, che'l
primo modo, se non sarà cosa noua, almeno sarà appresso di noua, & poco vsata. Si potrà etiandio, con grandissimo commodo (il che è anco lodeuole) porre in Consequenza le parti tra loro; non con quell'ordine istesso,
& dispositione, come si vsa nelle Fughe legate: ma con vn'ordine interrotto; ponendo parte delle figure ascendenti, & parte discendenti; & porre solamente il numero delle figure, che siano di vno istesso valore; ponendo
tallora vna Imitatione di figure al contrario, cioè porre la Guida, o Principale, che procedi per vn numero di
figure ascendenti, & il Consequente, che con l'istesso numero discendi; come dal sotto posto essempio si può com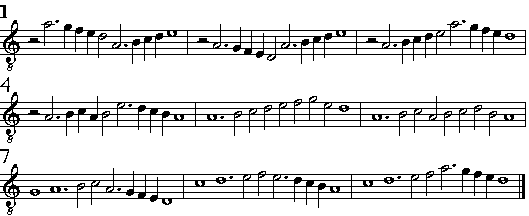 prendere; nel quale hò voluto porre vna parte
sola per due cagioni: Prima: perche non mancano le dotte compositioni di molti eccellenti Musici, che sono piene di queste cose, dalle quali si potrà comprendere il modo, che si hauerà
da tenere nella compositione dell'altre cantilene; Dipoi, per non accrescere il volume con tanti essempi; essendo che da questa sola parte si potrà comprendere quello, ch'io hò voluto dire, & in qual maniera si potrà procedere, cauando l'inuentione di vna parte dal proceder dell'altra, per
potere impire il Contrapunto di belle fantasie, & leggiadri inuentioni. Ma si debbe auertire, che quantunque il Basso (come hò detto altroue) possa alle volte tenere il luogo del Tenore, & cosi l'vna delle altre parti
quello dell'altra; nondimeno si dè fare, che'l Basso finisca sempre sopra la chorda regolare, & finale del Modo, sopra'l quale è composta la cantilena; & cosi le altre parti a i loro luoghi propij: percioche da tal chorda
haueremo a giudicare il Modo. Et se bene il Tenore venisse a finire in altra chorda, che nella finale, questo non sarebbe di molta importanza; pur che habbia proceduto nella sua modulatione secondo la natura del
Modo della cantilena; Il che si debbe anche intendere di ciascuna delle altre parti. Oltra di questo è da auertire, che quella compositione si può chiamare Perfetta, la quale in ogni mutatione di chorda, tanto verso il graue, quanto verso l'acuto, sempre si odeno tutte quelle Consonanze, che fanno varietà di suono ne i
loro estremi. Et quella è veramente Harmonia perfetta, che in essa si ode tal consonanze: Ma li Suoni, o
Consonanze, che possono fare diuersità al sentimento sono due, cioè la Quinta, & la Terza, ouer le Replicate dell'vna, & dell'altra: percioche i loro estremi non hanno tra loro alcuna simiglianza, come hanno
quelli della Ottaua; ne gli estremi dell'vna si assimigliano a gli estremi dell'altra: essendo che gli estremi della Quinta
non muoueno l'vdito nella maniera, che fanno quelli della Terza; ne per il contrario: Onde aggiunto il Ditono al Semiditono, generano la Quinta, la quale è nelli suoi estremi contenuta da suoni molto variati da quelli, che si odeno ne gli estremi del Ditono, o del Semiditono: perche gli estremi del Ditono sono anco molto differenti da quelli del Semiditono. Et ciò non si ritroua nella Ottaua: imperoche li suoi estremi
hanno tal simiglianza, che paiono vn solo suono; & si assimigliano di maniera all'Vnisono, che aggiungendole qual Consonanza si voglia, par che sia congiunto (come etiandio hò detto altroue) quasi ad vn solo
suono. Ritrouandosi adunque la varietà solamente tra gli estremi della Quinta, & quelli della Terza; &
componendosi l'Harmonia di cose, che tra loro sono diuerse; douemo per ogni modo (accioche habbiamo perfetta cotale harmonia) cercare con ogni nostro potere, di fare vdire nelle nostre Compositioni queste due Consonanze, più che sia possibile, ouero le loro Replicate. E' ben vero, che molte volte li Prattici pongono la page 244Sesta in luogo della Quinta, & è ben fatto: Masi debbe auertire, che quando si porrà in vna delle parti la
detta Sesta sopra il Basso, di non porre alcun'altra parte, che sia distante per vna Quinta sopra di esso: percioche queste
due parti verrebbeno ad esser distanti tra loro per vn Tuono, ouero per vn Semituono; di maniera
che si vdirebbe la dissonanza. Io ho detto, che douemo fare ogni nostro potere, di por sempre queste due Consonanze nelle compositioni: conciosia che sempre non si possono porre; massimamente nelle compositioni di
Tre voci: perche in luogo di vna di loro si pone spesso la Ottaua, per non guastare il bello, elegante, & facil
cantare, che fanno le parti: la onde volendo osseruare di por sempre cotali Consonanze in simili compositioni, sarebbe quasi impossibile: Ma nelle Compositioni di Quattro voci, sarebbe più errore lassarne vna delle
due nominate, che in quelle, che si compongono a Tre voci: conciosia che oue non si può osseruare cotal Regola con tre parti,
la Quarta parte ce lo permette. Et tanto maggiormente siamo obligati alla osseruanza di tal
Legge, quanto più cresce il numero delle parti. Gran vergogna è veramente di alcuni, che non solo fanno pouere le loro compositioni
di Quattro voci, di vna delle dette consonanze: ma fanno anco peggio, che pongono
le parti in tal maniera, che sono tra loro Vnisone, ouer lontane l'vna dall'altra, per vna Ottaua solamente:
onde si ode l'harmonia molto smembrata, & pouera: percioche le parti sono distanti l'vna dall'altra per simili Ottaue, che si chiamano Raddoppiate. Ma questo sarebbe di poco momento, quando non si ritrouasse l'istesso errore nelle compositioni di Cinque, di Sei, di Sette, et di più voci; nelle quali sono alcuni luoghi smembrati, & poueri in tal maniera; che si odeno con poca satisfattione dell'vdito. Però il Contrapuntista si debbe guardare da commettere tali mancamenti, degni veramente di correttione; & debbe sapere, che tali errori si commetteno non solamente nelle figure, che si proferiscono nel battere, o nel leuare della battuta: ma
anche in ogni figura cantabile, che si pone nel numero delle consonanze. Osseruarà adunque il Compositore
questo, accioche la sua cantilena venghi ad esser sonora & piena; & accioche contenghi in se ogni perfettione di harmonia. Ma non per questo si dè intendere, che lui debba osseruare tal legge dal principio della compositione infino
al fine: imperoche si dè anco auertire in ogni cantilena, di dar qualche riposo alle parti; &
di non farle cantare sempre insieme: ma di far che se ne odi hora due, hora tre, hora quattro, secondo'l numero che saranno, & tallora tutte insieme, & massimamente nel fine: percioche tal variatione verrà a
portar seco commodo al compositore & al cantore, bellezza alla cantilena, & diletto & piacere all'vdito:
prendere; nel quale hò voluto porre vna parte
sola per due cagioni: Prima: perche non mancano le dotte compositioni di molti eccellenti Musici, che sono piene di queste cose, dalle quali si potrà comprendere il modo, che si hauerà
da tenere nella compositione dell'altre cantilene; Dipoi, per non accrescere il volume con tanti essempi; essendo che da questa sola parte si potrà comprendere quello, ch'io hò voluto dire, & in qual maniera si potrà procedere, cauando l'inuentione di vna parte dal proceder dell'altra, per
potere impire il Contrapunto di belle fantasie, & leggiadri inuentioni. Ma si debbe auertire, che quantunque il Basso (come hò detto altroue) possa alle volte tenere il luogo del Tenore, & cosi l'vna delle altre parti
quello dell'altra; nondimeno si dè fare, che'l Basso finisca sempre sopra la chorda regolare, & finale del Modo, sopra'l quale è composta la cantilena; & cosi le altre parti a i loro luoghi propij: percioche da tal chorda
haueremo a giudicare il Modo. Et se bene il Tenore venisse a finire in altra chorda, che nella finale, questo non sarebbe di molta importanza; pur che habbia proceduto nella sua modulatione secondo la natura del
Modo della cantilena; Il che si debbe anche intendere di ciascuna delle altre parti. Oltra di questo è da auertire, che quella compositione si può chiamare Perfetta, la quale in ogni mutatione di chorda, tanto verso il graue, quanto verso l'acuto, sempre si odeno tutte quelle Consonanze, che fanno varietà di suono ne i
loro estremi. Et quella è veramente Harmonia perfetta, che in essa si ode tal consonanze: Ma li Suoni, o
Consonanze, che possono fare diuersità al sentimento sono due, cioè la Quinta, & la Terza, ouer le Replicate dell'vna, & dell'altra: percioche i loro estremi non hanno tra loro alcuna simiglianza, come hanno
quelli della Ottaua; ne gli estremi dell'vna si assimigliano a gli estremi dell'altra: essendo che gli estremi della Quinta
non muoueno l'vdito nella maniera, che fanno quelli della Terza; ne per il contrario: Onde aggiunto il Ditono al Semiditono, generano la Quinta, la quale è nelli suoi estremi contenuta da suoni molto variati da quelli, che si odeno ne gli estremi del Ditono, o del Semiditono: perche gli estremi del Ditono sono anco molto differenti da quelli del Semiditono. Et ciò non si ritroua nella Ottaua: imperoche li suoi estremi
hanno tal simiglianza, che paiono vn solo suono; & si assimigliano di maniera all'Vnisono, che aggiungendole qual Consonanza si voglia, par che sia congiunto (come etiandio hò detto altroue) quasi ad vn solo
suono. Ritrouandosi adunque la varietà solamente tra gli estremi della Quinta, & quelli della Terza; &
componendosi l'Harmonia di cose, che tra loro sono diuerse; douemo per ogni modo (accioche habbiamo perfetta cotale harmonia) cercare con ogni nostro potere, di fare vdire nelle nostre Compositioni queste due Consonanze, più che sia possibile, ouero le loro Replicate. E' ben vero, che molte volte li Prattici pongono la page 244Sesta in luogo della Quinta, & è ben fatto: Masi debbe auertire, che quando si porrà in vna delle parti la
detta Sesta sopra il Basso, di non porre alcun'altra parte, che sia distante per vna Quinta sopra di esso: percioche queste
due parti verrebbeno ad esser distanti tra loro per vn Tuono, ouero per vn Semituono; di maniera
che si vdirebbe la dissonanza. Io ho detto, che douemo fare ogni nostro potere, di por sempre queste due Consonanze nelle compositioni: conciosia che sempre non si possono porre; massimamente nelle compositioni di
Tre voci: perche in luogo di vna di loro si pone spesso la Ottaua, per non guastare il bello, elegante, & facil
cantare, che fanno le parti: la onde volendo osseruare di por sempre cotali Consonanze in simili compositioni, sarebbe quasi impossibile: Ma nelle Compositioni di Quattro voci, sarebbe più errore lassarne vna delle
due nominate, che in quelle, che si compongono a Tre voci: conciosia che oue non si può osseruare cotal Regola con tre parti,
la Quarta parte ce lo permette. Et tanto maggiormente siamo obligati alla osseruanza di tal
Legge, quanto più cresce il numero delle parti. Gran vergogna è veramente di alcuni, che non solo fanno pouere le loro compositioni
di Quattro voci, di vna delle dette consonanze: ma fanno anco peggio, che pongono
le parti in tal maniera, che sono tra loro Vnisone, ouer lontane l'vna dall'altra, per vna Ottaua solamente:
onde si ode l'harmonia molto smembrata, & pouera: percioche le parti sono distanti l'vna dall'altra per simili Ottaue, che si chiamano Raddoppiate. Ma questo sarebbe di poco momento, quando non si ritrouasse l'istesso errore nelle compositioni di Cinque, di Sei, di Sette, et di più voci; nelle quali sono alcuni luoghi smembrati, & poueri in tal maniera; che si odeno con poca satisfattione dell'vdito. Però il Contrapuntista si debbe guardare da commettere tali mancamenti, degni veramente di correttione; & debbe sapere, che tali errori si commetteno non solamente nelle figure, che si proferiscono nel battere, o nel leuare della battuta: ma
anche in ogni figura cantabile, che si pone nel numero delle consonanze. Osseruarà adunque il Compositore
questo, accioche la sua cantilena venghi ad esser sonora & piena; & accioche contenghi in se ogni perfettione di harmonia. Ma non per questo si dè intendere, che lui debba osseruare tal legge dal principio della compositione infino
al fine: imperoche si dè anco auertire in ogni cantilena, di dar qualche riposo alle parti; &
di non farle cantare sempre insieme: ma di far che se ne odi hora due, hora tre, hora quattro, secondo'l numero che saranno, & tallora tutte insieme, & massimamente nel fine: percioche tal variatione verrà a
portar seco commodo al compositore & al cantore, bellezza alla cantilena, & diletto & piacere all'vdito:
 page 245La onde facendo in tal modo, è impossibile di osseruare sempre cotal legge; massimamente: perche facendo cantare alle volte
poche parti, per uolere acquistare le sopradette consonanze, si potrebbe procedere per alcuni
mouimenti tanto discommodi, che sarebbeno cagione di rouinare ogni buona & sonora compositione. Crescendo poi il numero delle parti, & non osseruando quello, che si è detto, verrà a mostrare, quanto sia stato buono
imitatore della Natura, laquale (quando non è deprauata) riduce tutte le cose alla loro perfettione. Oltra di questo si debbe sapere, che hauendo accommodato tre parti di qualunque compositione, lequali tra loro contenghino le gia dette consonanze, ouero la Sesta in luogo della Quinta, tutte le altre parti, che si aggiungessero a queste, verrebbeno ad esser necessariamente Vnisone, ouero in Ottaua con vna delle tre nominate; siano poi quante
si voglino le aggiunte; si come di sopra nello essempio in molti luoghi si può comprendere. Però il Compositore potrà accommodarle alla cantilena, come meglio li tornera commodo. E ben vero, che più tosto si debbe
eleggere la Ottaua, che l'Vnisono; percioche (come dicemmo altre volte) non è consonanza.
page 245La onde facendo in tal modo, è impossibile di osseruare sempre cotal legge; massimamente: perche facendo cantare alle volte
poche parti, per uolere acquistare le sopradette consonanze, si potrebbe procedere per alcuni
mouimenti tanto discommodi, che sarebbeno cagione di rouinare ogni buona & sonora compositione. Crescendo poi il numero delle parti, & non osseruando quello, che si è detto, verrà a mostrare, quanto sia stato buono
imitatore della Natura, laquale (quando non è deprauata) riduce tutte le cose alla loro perfettione. Oltra di questo si debbe sapere, che hauendo accommodato tre parti di qualunque compositione, lequali tra loro contenghino le gia dette consonanze, ouero la Sesta in luogo della Quinta, tutte le altre parti, che si aggiungessero a queste, verrebbeno ad esser necessariamente Vnisone, ouero in Ottaua con vna delle tre nominate; siano poi quante
si voglino le aggiunte; si come di sopra nello essempio in molti luoghi si può comprendere. Però il Compositore potrà accommodarle alla cantilena, come meglio li tornera commodo. E ben vero, che più tosto si debbe
eleggere la Ottaua, che l'Vnisono; percioche (come dicemmo altre volte) non è consonanza.
In qual maniera la Quarta si possa porre nelle compositioni.Cap. 60.
 cuno da se stesso con la esperienza potrà conoscere dalli sottoposti essempi
sensatamente, & euidentemente comprendere delli due accompagnamenti, qual sia veramente il buono. Quando poi si accompagna
la Quarta con
la Terza posta in acuto, ciò si può fare simigliantemente in due modi: percioche; oueramente se le aggiunge la Terza maggiore, ouero se le accompagna la minore. Quando è accompagnata con la maggiore fà buono effetto. Ma quando è accompagnata con la minore, fà quasi dissonanza. Et
ciò non è senza cagione: percioche, oltra che si potrà comprendere dalli due
essempi posti qui di sotto, quando le voci, o li suoni saranno ridutti in atto;
l'ordine naturale de i Numeri harmonici ce lo dimostra; nel quale ritrouandosi la proportione della Diatessaron tra questi ter mini 4 & 3;
come si può vedere nel detto luogo; segue senza alcuno mezo la proporpage 246tione del Ditono, posta tra 5 & 4. Ma in cotale ordine non si troua, che dopo la proportione, o forma della Quarta segua immediatamente procedendo nel detto ordine la forma della Terza minore; come ogn'vno
può vedere. Per questo adunque auiene, che quelle Consonanze, che sono fuori de i loro luoghi naturali, &
cuno da se stesso con la esperienza potrà conoscere dalli sottoposti essempi
sensatamente, & euidentemente comprendere delli due accompagnamenti, qual sia veramente il buono. Quando poi si accompagna
la Quarta con
la Terza posta in acuto, ciò si può fare simigliantemente in due modi: percioche; oueramente se le aggiunge la Terza maggiore, ouero se le accompagna la minore. Quando è accompagnata con la maggiore fà buono effetto. Ma quando è accompagnata con la minore, fà quasi dissonanza. Et
ciò non è senza cagione: percioche, oltra che si potrà comprendere dalli due
essempi posti qui di sotto, quando le voci, o li suoni saranno ridutti in atto;
l'ordine naturale de i Numeri harmonici ce lo dimostra; nel quale ritrouandosi la proportione della Diatessaron tra questi ter mini 4 & 3;
come si può vedere nel detto luogo; segue senza alcuno mezo la proporpage 246tione del Ditono, posta tra 5 & 4. Ma in cotale ordine non si troua, che dopo la proportione, o forma della Quarta segua immediatamente procedendo nel detto ordine la forma della Terza minore; come ogn'vno
può vedere. Per questo adunque auiene, che quelle Consonanze, che sono fuori de i loro luoghi naturali, &
 non sono ordinate, secondo che hanno le lor forme tra i numeri harmonici,
senza alcun dubbio fanno qualche dissonanza: Onde dico, che la Quarta
accompagnata con la Terza minore posta nel graue, si potrà sempre vsare; & quella etiandio, che hauerà la Terza maggiore nello acuto: percioche non potranno fare se non buoni effetti. Ma quando hauerà la Terza
maggiore nel graue, ouer la minore nello acuto, sempre si vdirà qualche
effetto tristo. Ne ciò debbe parer strano ad alcuno: conciosia che quello
che intrauiene al Vedere intorno alla cosa visibile, intrauiene anco all'
Vdito intorno alla cosa vdibile. Onde si come è strana cosa da vedere in
vno edificio alcuna parte posta nel luogo di vn'altra; come sarebbe dire li
Fondamenti nel luogo del Tetto; & nel luogo delle Porte le Finestre, &
ogni cosa posta al contrario fuori delli suoi naturali luoghi, & senza alcuna proportione; cosi è cosa strana da vdire vna
massa di suoni, o consonanze poste insieme senza proportione, & fuori de i loro luoghi naturali. Si ritrouerà etiandio, volendo
inuestigare più oltra, che la Quarta, laquale hà nell'acuto il Ditono, è più grata all'vdito di quella, che l'hà nel graue;
si come etiandio è più grata quella, che hà il Semiditono nella parte graue, di quella che l'hà nella acuta; &
che di queste due compositioni, quella Quartà, che sarà accompagnata con la Terza minore nel graue farà
migliore effetto di ciascun'altro accompagnamento; come si potrà comprendere da questi essempi. Percioche
non sono ordinate, secondo che hanno le lor forme tra i numeri harmonici,
senza alcun dubbio fanno qualche dissonanza: Onde dico, che la Quarta
accompagnata con la Terza minore posta nel graue, si potrà sempre vsare; & quella etiandio, che hauerà la Terza maggiore nello acuto: percioche non potranno fare se non buoni effetti. Ma quando hauerà la Terza
maggiore nel graue, ouer la minore nello acuto, sempre si vdirà qualche
effetto tristo. Ne ciò debbe parer strano ad alcuno: conciosia che quello
che intrauiene al Vedere intorno alla cosa visibile, intrauiene anco all'
Vdito intorno alla cosa vdibile. Onde si come è strana cosa da vedere in
vno edificio alcuna parte posta nel luogo di vn'altra; come sarebbe dire li
Fondamenti nel luogo del Tetto; & nel luogo delle Porte le Finestre, &
ogni cosa posta al contrario fuori delli suoi naturali luoghi, & senza alcuna proportione; cosi è cosa strana da vdire vna
massa di suoni, o consonanze poste insieme senza proportione, & fuori de i loro luoghi naturali. Si ritrouerà etiandio, volendo
inuestigare più oltra, che la Quarta, laquale hà nell'acuto il Ditono, è più grata all'vdito di quella, che l'hà nel graue;
si come etiandio è più grata quella, che hà il Semiditono nella parte graue, di quella che l'hà nella acuta; &
che di queste due compositioni, quella Quartà, che sarà accompagnata con la Terza minore nel graue farà
migliore effetto di ciascun'altro accompagnamento; come si potrà comprendere da questi essempi. Percioche
 quantunque le Seste, che contengono gli estremi di queste parti poste insieme, non siano l'vn dall'altro differenti nella proportione, & non facino variatione de suoni & di consonanze; nondimeno la
varietà delle chorde,
che riceueno nel loro mezo, è cagione, che l'vno accompagnamento si vdirà megliore dell'altro; & di far la differenza tra due accompagnamenti,
che siano buoni, dal buono al migliore. Veramente tanta è la possanza
delle consonanze, quando sono poste ne i loro propij luoghi naturali, che
non solamente quelle, che sono tramezate in cotal maniera secondo la natura de gli harmonici numeri, sono più grate all'vdito di quelle, che sono
poste al contrario: ma anche fanno più allegra, & più sonora ogni compositione, nella quale sono poste. Questo adunque ricoglieremo da quel, che si
è detto, che le Quarte si potranno porre ottimamente nelle compositioni,
quando saranno collocate in tal maniera, che sotto di loro nel graue habbiano la Quinta, ouer la Terzà; come hò mostrato di sopra; & etiandio si potrà porre alle volte con la Terza
nell'acuto, massimamente quando sarà la maggiore; ancora che questo dalla vniuersità de i Musici prattici
fin hora sia stata poco considerata: Percioche se l'accompagnamento della Quarta con la Terza maggiore
posta nel graue, che non è veramente molto consonante è sopportata; non sò veder ragione, perche non si dè
sopportare l'accompagnamento della Terza maggiore posta nell'acuto: essendo che veramente questo accompagnamento è migliore,
si come la esperienza ce lo farà sempre vedere.
quantunque le Seste, che contengono gli estremi di queste parti poste insieme, non siano l'vn dall'altro differenti nella proportione, & non facino variatione de suoni & di consonanze; nondimeno la
varietà delle chorde,
che riceueno nel loro mezo, è cagione, che l'vno accompagnamento si vdirà megliore dell'altro; & di far la differenza tra due accompagnamenti,
che siano buoni, dal buono al migliore. Veramente tanta è la possanza
delle consonanze, quando sono poste ne i loro propij luoghi naturali, che
non solamente quelle, che sono tramezate in cotal maniera secondo la natura de gli harmonici numeri, sono più grate all'vdito di quelle, che sono
poste al contrario: ma anche fanno più allegra, & più sonora ogni compositione, nella quale sono poste. Questo adunque ricoglieremo da quel, che si
è detto, che le Quarte si potranno porre ottimamente nelle compositioni,
quando saranno collocate in tal maniera, che sotto di loro nel graue habbiano la Quinta, ouer la Terzà; come hò mostrato di sopra; & etiandio si potrà porre alle volte con la Terza
nell'acuto, massimamente quando sarà la maggiore; ancora che questo dalla vniuersità de i Musici prattici
fin hora sia stata poco considerata: Percioche se l'accompagnamento della Quarta con la Terza maggiore
posta nel graue, che non è veramente molto consonante è sopportata; non sò veder ragione, perche non si dè
sopportare l'accompagnamento della Terza maggiore posta nell'acuto: essendo che veramente questo accompagnamento è migliore,
si come la esperienza ce lo farà sempre vedere.
Regole in commune.Cap. 61.
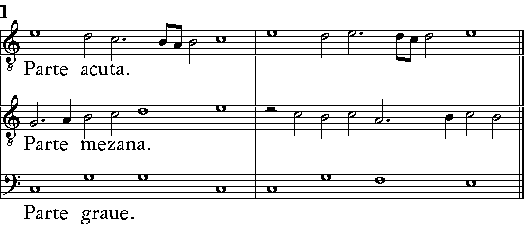 potrebbe nascere alle volte tra le parti della
cantilena; come nel secondo essempio si può
comprendere. Si potrà anco vsar la Vndecima; come più a basso si vede; laqual si
compone della Ottaua, & della Quarta; poi
che Tolomeo nel Capitolo Quinto del Primo libro della Harmonica, & Boetio nel
Cap. 10. del libro Primo della Musica la pongono tra le consonanze: Di modo che da
questi essempi si potrà conoscere la lor natura, & quanto possino esser grate all'vdito;
ancora che ne potrebbe bastare l'vso de i
Moderni, & de gli Antichi compositori, i quali molte volte l'hanno accompagnata in tal maniera. Vsano
potrebbe nascere alle volte tra le parti della
cantilena; come nel secondo essempio si può
comprendere. Si potrà anco vsar la Vndecima; come più a basso si vede; laqual si
compone della Ottaua, & della Quarta; poi
che Tolomeo nel Capitolo Quinto del Primo libro della Harmonica, & Boetio nel
Cap. 10. del libro Primo della Musica la pongono tra le consonanze: Di modo che da
questi essempi si potrà conoscere la lor natura, & quanto possino esser grate all'vdito;
ancora che ne potrebbe bastare l'vso de i
Moderni, & de gli Antichi compositori, i quali molte volte l'hanno accompagnata in tal maniera. Vsano
 alcuni di porre la parte acuta con la mezana distante per vna Quarta; & questa con la graue per vna Terza; di maniera che'l Basso viene ad esser lontano dal Soprano per vna Sesta, tramezata dalla Terza, o maggiore, o minore.
Onde essendo le parti composte in tal maniera, sogliono farle ascendere, o discendere insieme
più gradi; & tal modo di procedere chiamano Falso bordone. Ma in verità, ancora che tal maniera sia molto in vso, et che con
difficultà grande si potesse leuare; dico, che non è lodeuole: Imperoche, oltra che la Quarta è consonanza perfetta; come
altroue hò mostrato; & che non douemo far contra la Regola data nel Cap.
29; genera alle uolte tra le parti alcune relationi, che non sono harmoniche: La onde poco diletto apportano
all'vdito; si come ciascuno col mezo dello essempio posto qui di sotto potrà conoscere. L'errore di cotal cosa
alcuni di porre la parte acuta con la mezana distante per vna Quarta; & questa con la graue per vna Terza; di maniera che'l Basso viene ad esser lontano dal Soprano per vna Sesta, tramezata dalla Terza, o maggiore, o minore.
Onde essendo le parti composte in tal maniera, sogliono farle ascendere, o discendere insieme
più gradi; & tal modo di procedere chiamano Falso bordone. Ma in verità, ancora che tal maniera sia molto in vso, et che con
difficultà grande si potesse leuare; dico, che non è lodeuole: Imperoche, oltra che la Quarta è consonanza perfetta; come
altroue hò mostrato; & che non douemo far contra la Regola data nel Cap.
29; genera alle uolte tra le parti alcune relationi, che non sono harmoniche: La onde poco diletto apportano
all'vdito; si come ciascuno col mezo dello essempio posto qui di sotto potrà conoscere. L'errore di cotal cosa
 si manifesta da questo; percioche se noi vorremo porre le Terze a i loro luoghi naturali, oue si debbono ragioneuolmente porre, ouero sopra la Ottaua almeno; si potrà conoscere con quanta ragione si potrà fare vna cosa
simile: conciosia che; si come nel mostrato essempio si vdiuano molte Quarte; cosi nel sottoposto potremo vdire altretante Quinte. Io sò bene, che appresso di molti più varranno le autorità di alcuni, che si habbiano
si manifesta da questo; percioche se noi vorremo porre le Terze a i loro luoghi naturali, oue si debbono ragioneuolmente porre, ouero sopra la Ottaua almeno; si potrà conoscere con quanta ragione si potrà fare vna cosa
simile: conciosia che; si come nel mostrato essempio si vdiuano molte Quarte; cosi nel sottoposto potremo vdire altretante Quinte. Io sò bene, che appresso di molti più varranno le autorità di alcuni, che si habbiano
 vsurpata cotal licenza, che le ragioni addutte di sopra: ma facino pure il peggio, che sanno, con dire questa cosa
è stata vsata da molti, che poco mi curo, poi che non sono, ne vogliono esser capaci di ragione. Et benche la
Terza sia consonanza, & si possa porre in qual luogo torna commodo; tuttauia il suo vero luogo non è nel
graue; ma nell'acuto, sopra la Disdiapason, ouero Quintadecima: Imperoche naturalmente la Ottaua posta
nel graue, non può esser tramezata da altro suono: ma vuole esser posta semplice, senza alcuna mediatione; si
come ne mostrano li numeri harmonici, posti nel Ca. 15. della Prima parte; tra i quali, si vede la prima Dupla
contenuta nel Senario tra 2 & 1, che è la sua forma, laquale non è mediata da alcun termine mezano;
ma si bene la seconda posta tra 4 & 2, laquale è diuisa dal 3 in vna Sesquialtera, che si troua tra 3 &
2, & in vna Sesquiterza, che si troua tra 4 & 3, che sono le forme della Diapente, & della Diatessaron consonanze. Onde la Sesquialtera nella detta seconda Diapason resta non diuisa, & intera: ma oltra la
Quadrupla, che è la forma della Disdiapason, si troua diuisa in due parti; cioè in vna Sesquiquarta, che è la forpage 248ma vera del Ditono, & in vna Sesquiquinta, che è la forma del Semiditono; delle quali, l'vna è collocata tra
5 & 4, & l'altra tra 6 & 5. Si vede adunque, che la prima Ottaua è collocata naturalmente
tra i Numeri sonori senza alcun'altro numero mezano; & che la Quinta le succede senza alcun mezo; dipoi
segue la quarta; & da queste due parti maggiori si compone la seconda Diapason, onde nasce la Disdiapason,
cioè la Quintadecima. Dopo queste viene il Ditono, & immediatamente dopo lui segue il Semiditono: di
maniera che, se tali consonanze fussero poste nelli Contrapunti (se ciò si potesse far sempre commodamente)
a i loro luoghi propij & naturali; non è dubbio, che nascerebbe vn concento tanto harmonioso, quanto l'huomo
si potesse imaginare. Et di ciò potemo vedere la esperienza sempre ne gli istrumenti arteficiali, massimamente
nell'Organo, oue poste le consonanze nominate per ordine l'vna dopo l'altra, secondo che hò mostrato; non si
può dire il buono effetto che fanno. Ma se per caso la prima Ottaua si pone tramezata nel graue dalla Quinta; allora il concento si fà alquanto tristo; et se tal Quinta si diuidesse in due Terze, non si potrebbe apena vdire
tal composto; massimamente se la Terza minore tenesse il luogo della maggiore, cioè se ella fusse posta nel graue. E' nondimeno sopportabile
la prima Ottaua tramezata in proportionalità harmonica per la Quinta; &
quando sopra di essa si pone la Terza, non fà tristo effetto; ancora che cotali consonanze non siano poste a i loro luoghi propij; & ciò intrauiene: percioche tengono il luogo mezano nello istrumento, oue si contiene tale ordine. Si debbe adunque porre la Terza immediatamente dopo la Quintadecima, o almeno dopo la Ottaua in
ordine; & debbe esser la maggiore; accio che'l concento sia più allegro, & più pieno: ma se'l si abbatterà, che
ella sia la minore; come infinite volte suole accascare, allora il concento sarà più mesto. Queste cose veramente
sono poco considerate da i Prattici: percioche senza alcun riguardo pongono la Quinta tra le chorde graui, &
anco la Terza, come torna a loro più commodo; laqual cosa quanto diletto apporti all'vdito, lassarò considerare
a coloro, che hanno giuditio. Onde voglio dir questo solamente, che douendosi porre la Terza nella compositione, è meglio
porla sempre sopra la Ottaua, che tra essa; voglio inferire, che migliore effetto farà sempre la Decima, che la Terza. Et quantunque si potrebbe dire, che meglio sarebbe anco, porre la Quinta sopra la Ottaua
posta nel graue della cantilena; come cosa più propinqua, secondo la natura de i Numeri harmonici; che la
Terza, come più lontana; tuttauia pongasi a qual modo si voglia, tornarà sempre bene. Ma quanto migliore
effetto faccia la Decima che la Terza; da questi due essempi, ciascuno che hà giuditio lo potrà conoscere.
vsurpata cotal licenza, che le ragioni addutte di sopra: ma facino pure il peggio, che sanno, con dire questa cosa
è stata vsata da molti, che poco mi curo, poi che non sono, ne vogliono esser capaci di ragione. Et benche la
Terza sia consonanza, & si possa porre in qual luogo torna commodo; tuttauia il suo vero luogo non è nel
graue; ma nell'acuto, sopra la Disdiapason, ouero Quintadecima: Imperoche naturalmente la Ottaua posta
nel graue, non può esser tramezata da altro suono: ma vuole esser posta semplice, senza alcuna mediatione; si
come ne mostrano li numeri harmonici, posti nel Ca. 15. della Prima parte; tra i quali, si vede la prima Dupla
contenuta nel Senario tra 2 & 1, che è la sua forma, laquale non è mediata da alcun termine mezano;
ma si bene la seconda posta tra 4 & 2, laquale è diuisa dal 3 in vna Sesquialtera, che si troua tra 3 &
2, & in vna Sesquiterza, che si troua tra 4 & 3, che sono le forme della Diapente, & della Diatessaron consonanze. Onde la Sesquialtera nella detta seconda Diapason resta non diuisa, & intera: ma oltra la
Quadrupla, che è la forma della Disdiapason, si troua diuisa in due parti; cioè in vna Sesquiquarta, che è la forpage 248ma vera del Ditono, & in vna Sesquiquinta, che è la forma del Semiditono; delle quali, l'vna è collocata tra
5 & 4, & l'altra tra 6 & 5. Si vede adunque, che la prima Ottaua è collocata naturalmente
tra i Numeri sonori senza alcun'altro numero mezano; & che la Quinta le succede senza alcun mezo; dipoi
segue la quarta; & da queste due parti maggiori si compone la seconda Diapason, onde nasce la Disdiapason,
cioè la Quintadecima. Dopo queste viene il Ditono, & immediatamente dopo lui segue il Semiditono: di
maniera che, se tali consonanze fussero poste nelli Contrapunti (se ciò si potesse far sempre commodamente)
a i loro luoghi propij & naturali; non è dubbio, che nascerebbe vn concento tanto harmonioso, quanto l'huomo
si potesse imaginare. Et di ciò potemo vedere la esperienza sempre ne gli istrumenti arteficiali, massimamente
nell'Organo, oue poste le consonanze nominate per ordine l'vna dopo l'altra, secondo che hò mostrato; non si
può dire il buono effetto che fanno. Ma se per caso la prima Ottaua si pone tramezata nel graue dalla Quinta; allora il concento si fà alquanto tristo; et se tal Quinta si diuidesse in due Terze, non si potrebbe apena vdire
tal composto; massimamente se la Terza minore tenesse il luogo della maggiore, cioè se ella fusse posta nel graue. E' nondimeno sopportabile
la prima Ottaua tramezata in proportionalità harmonica per la Quinta; &
quando sopra di essa si pone la Terza, non fà tristo effetto; ancora che cotali consonanze non siano poste a i loro luoghi propij; & ciò intrauiene: percioche tengono il luogo mezano nello istrumento, oue si contiene tale ordine. Si debbe adunque porre la Terza immediatamente dopo la Quintadecima, o almeno dopo la Ottaua in
ordine; & debbe esser la maggiore; accio che'l concento sia più allegro, & più pieno: ma se'l si abbatterà, che
ella sia la minore; come infinite volte suole accascare, allora il concento sarà più mesto. Queste cose veramente
sono poco considerate da i Prattici: percioche senza alcun riguardo pongono la Quinta tra le chorde graui, &
anco la Terza, come torna a loro più commodo; laqual cosa quanto diletto apporti all'vdito, lassarò considerare
a coloro, che hanno giuditio. Onde voglio dir questo solamente, che douendosi porre la Terza nella compositione, è meglio
porla sempre sopra la Ottaua, che tra essa; voglio inferire, che migliore effetto farà sempre la Decima, che la Terza. Et quantunque si potrebbe dire, che meglio sarebbe anco, porre la Quinta sopra la Ottaua
posta nel graue della cantilena; come cosa più propinqua, secondo la natura de i Numeri harmonici; che la
Terza, come più lontana; tuttauia pongasi a qual modo si voglia, tornarà sempre bene. Ma quanto migliore
effetto faccia la Decima che la Terza; da questi due essempi, ciascuno che hà giuditio lo potrà conoscere.
 Ma si debbe auertire, che in vno essempio, cioè nel primo si contiene il Tritono, & nel secondo la Semidiapente; liquali tanto più sono sopportabili, quanto che dopo sè hanno l'vno la Terza, & l'altro la Decima maggiori, che fanno relatione harmonica con le voci, che contengono il Tritono, ouer la Semidiapente. Et se bene gli
interualli, che sono nelle seconde figure delli mostrati essempi, sono veramente dissonanti; tuttauia sono in tal
maniera collocati, che per il loro procedere, secondo l'ordine mostrato nelle Regole, se ne passano di maniera, che
l'vdito se ne contenta. Si debbe oltra di ciò auertire, che quando dissi di sopra, che la prima Ottaua si pone senza
alcun mezo, potemo intendere tale Ottaua esser quella, laquale incomincia nella chorda più graue del Basso
della cantilena, salendo di mano in mano all'acuto fino alla Ottaua chorda; et per la seconda si può intender
quella, che incomincia dalla chorda estrema acuta di tale Ottaua, & và fino alla Quintadecima. Pongono i
Prattici alle volte il Tritono tra due parti, ilquale casca sopra la seconda parte di alcuna Semibreue sincopata, posta nel graue in cotal maniera; Ilquale si ode nella relatione delle parti: ma non è percossa l'vna delle par
Ma si debbe auertire, che in vno essempio, cioè nel primo si contiene il Tritono, & nel secondo la Semidiapente; liquali tanto più sono sopportabili, quanto che dopo sè hanno l'vno la Terza, & l'altro la Decima maggiori, che fanno relatione harmonica con le voci, che contengono il Tritono, ouer la Semidiapente. Et se bene gli
interualli, che sono nelle seconde figure delli mostrati essempi, sono veramente dissonanti; tuttauia sono in tal
maniera collocati, che per il loro procedere, secondo l'ordine mostrato nelle Regole, se ne passano di maniera, che
l'vdito se ne contenta. Si debbe oltra di ciò auertire, che quando dissi di sopra, che la prima Ottaua si pone senza
alcun mezo, potemo intendere tale Ottaua esser quella, laquale incomincia nella chorda più graue del Basso
della cantilena, salendo di mano in mano all'acuto fino alla Ottaua chorda; et per la seconda si può intender
quella, che incomincia dalla chorda estrema acuta di tale Ottaua, & và fino alla Quintadecima. Pongono i
Prattici alle volte il Tritono tra due parti, ilquale casca sopra la seconda parte di alcuna Semibreue sincopata, posta nel graue in cotal maniera; Ilquale si ode nella relatione delle parti: ma non è percossa l'vna delle par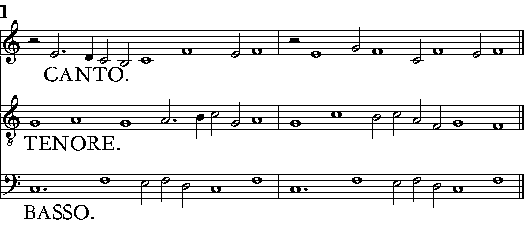 ti acute con la parte graue da tale interuallo. Et perche le parti procedeno in cotal modo, & sono concatenate tra loro di maniera,
che senza partirsi dalla osseruanza delle repage 249gole date, fanno buono effetto; Però queste parti porgono all'vdito grato, & soaue piacere: percioche quel poco di dissonanza,
che si ode nel Tritono, & nella Semidiapente, se ne passa presto, & aggiunge soauità alla
consonanza seguente, più di quello, che si vdirebbe, se non vi fusse: essendo che di due oppositi, l'vno si conosce
maggiormente per la comparatione, che si fa con l'altro. Frequentano i moderni molto spesso tali passaggi,
onde parendoli la cosa riuscibile pongono alle volte la parte graue sincopata in tal maniera, che la seconda parte della Sincopa
contiene col Tenore la Seconda, & il Tenore col Soprano hora la Terza, hora la Quarta, et
ti acute con la parte graue da tale interuallo. Et perche le parti procedeno in cotal modo, & sono concatenate tra loro di maniera,
che senza partirsi dalla osseruanza delle repage 249gole date, fanno buono effetto; Però queste parti porgono all'vdito grato, & soaue piacere: percioche quel poco di dissonanza,
che si ode nel Tritono, & nella Semidiapente, se ne passa presto, & aggiunge soauità alla
consonanza seguente, più di quello, che si vdirebbe, se non vi fusse: essendo che di due oppositi, l'vno si conosce
maggiormente per la comparatione, che si fa con l'altro. Frequentano i moderni molto spesso tali passaggi,
onde parendoli la cosa riuscibile pongono alle volte la parte graue sincopata in tal maniera, che la seconda parte della Sincopa
contiene col Tenore la Seconda, & il Tenore col Soprano hora la Terza, hora la Quarta, et
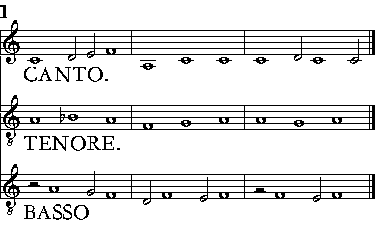 tallora la Quinta, come qui si vede.Ma quello, che contiene la Quarta, senza dubbio è men buono de gli altri: percioche si ode tale interuallo senza alcuno accompagnamento. Oltra
di questo si dè auertire, che alle volte si potrà passare dalla Sesta minore alla Ottaua, quando le parti saranno collocate in tal maniera, che'l Basso col Tenore procedino
ordinatamente secondo l'ordine, & il modo dato nelle Regole vniuersali; & il canto procedi per Decima sopra'l Basso; come qui si vede.Si potrà anche dalla Terza maggiore passare all'Vnisono, quando il So
tallora la Quinta, come qui si vede.Ma quello, che contiene la Quarta, senza dubbio è men buono de gli altri: percioche si ode tale interuallo senza alcuno accompagnamento. Oltra
di questo si dè auertire, che alle volte si potrà passare dalla Sesta minore alla Ottaua, quando le parti saranno collocate in tal maniera, che'l Basso col Tenore procedino
ordinatamente secondo l'ordine, & il modo dato nelle Regole vniuersali; & il canto procedi per Decima sopra'l Basso; come qui si vede.Si potrà anche dalla Terza maggiore passare all'Vnisono, quando il So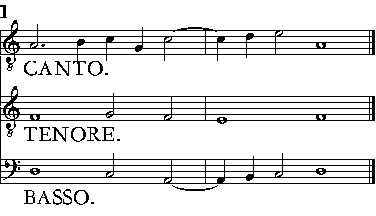 prano procederà dall'acuto al graue col mouimento del Ditono; & il Basso col Soprano sarà ordinato secondo i precetti dati di sopra; stando il Tenore senza mutar luogo; come si vede; Percioche essendo le parti estreme, che sono più delle altre comprese dal senso, ben regolate; se alle volte verrà qualche cosa nell'altre parti, che
non sia cosi ben regolata, si potrà sopportare. La onde si concede al compositore, che possa pigliare
alle volte qualche licenza fuori della Regola data di sopra nel Cap. 38. Gli sarà etiandio lecito di passare dalla Terza minore, per contrarij mouimenti all'Ottaua; quando le parti saranno ordinate in tal maniera, che
quella, che si trouerà lontana per simile consonanza, & dipoi passarà alla Ottaua, habbia nel graue la Terza maggiore, di maniera che la parte acuta sia lontana dalla graue per vna Quinta; come qui si vede.
prano procederà dall'acuto al graue col mouimento del Ditono; & il Basso col Soprano sarà ordinato secondo i precetti dati di sopra; stando il Tenore senza mutar luogo; come si vede; Percioche essendo le parti estreme, che sono più delle altre comprese dal senso, ben regolate; se alle volte verrà qualche cosa nell'altre parti, che
non sia cosi ben regolata, si potrà sopportare. La onde si concede al compositore, che possa pigliare
alle volte qualche licenza fuori della Regola data di sopra nel Cap. 38. Gli sarà etiandio lecito di passare dalla Terza minore, per contrarij mouimenti all'Ottaua; quando le parti saranno ordinate in tal maniera, che
quella, che si trouerà lontana per simile consonanza, & dipoi passarà alla Ottaua, habbia nel graue la Terza maggiore, di maniera che la parte acuta sia lontana dalla graue per vna Quinta; come qui si vede.
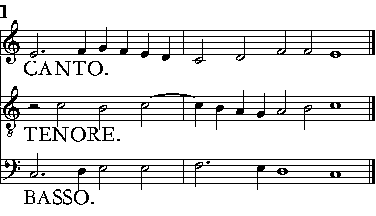 Anzi sarà necessario, che le parti stiano in cotal modo: perche se si ponessero altramente, facendo quella Terza, che è minore,
maggiore col segno
Anzi sarà necessario, che le parti stiano in cotal modo: perche se si ponessero altramente, facendo quella Terza, che è minore,
maggiore col segno  , accioche (secondo le date Regole) dalla imperfetta più propinqua
si peruenghi alla perfetta; non si potrebbe far tal cosa per alcun modo, senza grande offesa dell'vdito: conciosia che si verrebbe a fare vna Quinta, che hauerebbe due Terze maggiori: Ma ciò sia detto per sempre,
che l'obligo stà nelle cose possibili, & non nelle impossibili; al quale niuno è obligato. Douemo oltra di questo
osseruare, che nelle Cadenze principali della cantilena, le parti siano ordinate, & accommodate in tal maniera, che la seconda parte della figura sincopata, la qual si pone dissonante, sia sempre con la parte graue distante per vna Quarta; oueramente per vna Vndecima; & con l'altra sia sempre lontana per vna Seconda, o per vna Settima; il che si debbe osseruare etiandio in ogni figura sincopata, nella quale sia la dissonanza;
si come si vede in questi essempi, da i quali si potrà comprendere il modo, che si hauerà da tenere in altre simili,
quando accascheranno. Ma se vorremo aggiungere la Quarta parte a queste, sempre ella si porrà in Ottaua
dell'vna delle due, che sono distanti tra loro per Quinta, o per Duodecima; accommodandola hora in vn luogo, & hora in vn'altro, secondo che tornerà meglio. page 250
, accioche (secondo le date Regole) dalla imperfetta più propinqua
si peruenghi alla perfetta; non si potrebbe far tal cosa per alcun modo, senza grande offesa dell'vdito: conciosia che si verrebbe a fare vna Quinta, che hauerebbe due Terze maggiori: Ma ciò sia detto per sempre,
che l'obligo stà nelle cose possibili, & non nelle impossibili; al quale niuno è obligato. Douemo oltra di questo
osseruare, che nelle Cadenze principali della cantilena, le parti siano ordinate, & accommodate in tal maniera, che la seconda parte della figura sincopata, la qual si pone dissonante, sia sempre con la parte graue distante per vna Quarta; oueramente per vna Vndecima; & con l'altra sia sempre lontana per vna Seconda, o per vna Settima; il che si debbe osseruare etiandio in ogni figura sincopata, nella quale sia la dissonanza;
si come si vede in questi essempi, da i quali si potrà comprendere il modo, che si hauerà da tenere in altre simili,
quando accascheranno. Ma se vorremo aggiungere la Quarta parte a queste, sempre ella si porrà in Ottaua
dell'vna delle due, che sono distanti tra loro per Quinta, o per Duodecima; accommodandola hora in vn luogo, & hora in vn'altro, secondo che tornerà meglio. page 250 Et perche la Cadenza si può fare in molte maniere con varietà delle parti; però voglio por qui molti essempi
accommodati a Quattro voci, i quali potranno etiandio seruire alle compositioni di Tre voci, ouero se li potrà
aggiungere altre parti, quando fusse bisogno; accioche io non habbia da replicare più cosa alcuna in questa
materia. Ma non voglio restar di dire, che si conosce per esperienza, che quella Cadenza non ha gratia al
Et perche la Cadenza si può fare in molte maniere con varietà delle parti; però voglio por qui molti essempi
accommodati a Quattro voci, i quali potranno etiandio seruire alle compositioni di Tre voci, ouero se li potrà
aggiungere altre parti, quando fusse bisogno; accioche io non habbia da replicare più cosa alcuna in questa
materia. Ma non voglio restar di dire, che si conosce per esperienza, che quella Cadenza non ha gratia al cuna, o leggiadria in sè, laqual sia senza la Dissonanza, che si troua nelle mostrate; massimamente quando le parti procedeno insieme per le istesse figure; ancora che siano sincopate, ouero non sincopate, che si proferiscono nel leuare, o nel battere della battuta; come sono queste. page 251
cuna, o leggiadria in sè, laqual sia senza la Dissonanza, che si troua nelle mostrate; massimamente quando le parti procedeno insieme per le istesse figure; ancora che siano sincopate, ouero non sincopate, che si proferiscono nel leuare, o nel battere della battuta; come sono queste. page 251 Però il Contrapuntista si guardarà di vsarle; & debbe schiuare al tutto, di fare che alcuna parte della cantilena non faccia la Cadenza, quando l'altre parti fussero ordinate in vn modo, che qualunque altra delle più
graui facesse la Quinta con la figura mezana della cadenza posta nell'acuto, facendo il mouimento congiunto del Semituono, quando tale figura si potrà segnare con la cifra
Però il Contrapuntista si guardarà di vsarle; & debbe schiuare al tutto, di fare che alcuna parte della cantilena non faccia la Cadenza, quando l'altre parti fussero ordinate in vn modo, che qualunque altra delle più
graui facesse la Quinta con la figura mezana della cadenza posta nell'acuto, facendo il mouimento congiunto del Semituono, quando tale figura si potrà segnare con la cifra  Chromatica: percioche (come ho detto altroue) proferendosi tal parte della cadenza naturalmente col Semituono, sarebbe cosa difficile, che'l cantore potesse hauere in tal caso riguardo, di non proferirla con quel modo, che si proferisce naturalmente. Onde
verrebbe poi a commettere errore, & a porre vna dissonanza in luogo della consonanza; cioè verrebbe a
porre la Diapente superflua in luogo della vera; come qui si vede.
Chromatica: percioche (come ho detto altroue) proferendosi tal parte della cadenza naturalmente col Semituono, sarebbe cosa difficile, che'l cantore potesse hauere in tal caso riguardo, di non proferirla con quel modo, che si proferisce naturalmente. Onde
verrebbe poi a commettere errore, & a porre vna dissonanza in luogo della consonanza; cioè verrebbe a
porre la Diapente superflua in luogo della vera; come qui si vede.
 Accascherà anco vn simile errore, quando le parti a Tre voci saranno ordinate in tal maniera, che essendo
il Tenore sopra il Basso lontano per una Terza, discendendo per mouimento separato di Quarta sotto'l
Basso vna Terza, ascendendo il Basso per mouimento congiunto di vn Tuono; & ritornando dipoi ciascuno
alli suoi primi luoghi; il Soprano farà la Cadenza distante dalla parte graue per una Quinta verso l'acuto;
come in questo essempio si vede.Seguirebbe anco vn'altro errore, qualunque volta che si volesse sonare
Accascherà anco vn simile errore, quando le parti a Tre voci saranno ordinate in tal maniera, che essendo
il Tenore sopra il Basso lontano per una Terza, discendendo per mouimento separato di Quarta sotto'l
Basso vna Terza, ascendendo il Basso per mouimento congiunto di vn Tuono; & ritornando dipoi ciascuno
alli suoi primi luoghi; il Soprano farà la Cadenza distante dalla parte graue per una Quinta verso l'acuto;
come in questo essempio si vede.Seguirebbe anco vn'altro errore, qualunque volta che si volesse sonare
 queste tre parti sopra vno istrumento, perche si vdirebbe senza
alcun dubbio tre Quinte. La onde li Compositori debbono auertire a cotal cosa, & non fare che
le parti mutino luogo tra loro in questa maniera: percioche tale inconueniente apportarebbe all'vdito cosa, che
non molto li piacerebbe; ancora che nel cantare le parti non si possino udire tali Quinte. Et perche da molti Prattici questo non è molto auertito; però hò voluto toccarne vna parola.
Hauendo fin hora a bastanza ragionato
intorno alle cose necessarie a simili compositioni, lassarò le altre cose, che possono accascare, & non sono di molto
momento, al giuditio del Compositore: Imperoche col mezo delle Regole date, potrà quando gli occorrerà alcun dubbio, quantunque fusse di molta importanza, darne perfetta risolutione. Lassando adunque di parlare
più intorno a cotal materia, verrò a ragionare delli Contrapunti, che si compongono a Tre voci, che si chiamano Doppij, & di quelli, che si fanno con qualche obligo.
queste tre parti sopra vno istrumento, perche si vdirebbe senza
alcun dubbio tre Quinte. La onde li Compositori debbono auertire a cotal cosa, & non fare che
le parti mutino luogo tra loro in questa maniera: percioche tale inconueniente apportarebbe all'vdito cosa, che
non molto li piacerebbe; ancora che nel cantare le parti non si possino udire tali Quinte. Et perche da molti Prattici questo non è molto auertito; però hò voluto toccarne vna parola.
Hauendo fin hora a bastanza ragionato
intorno alle cose necessarie a simili compositioni, lassarò le altre cose, che possono accascare, & non sono di molto
momento, al giuditio del Compositore: Imperoche col mezo delle Regole date, potrà quando gli occorrerà alcun dubbio, quantunque fusse di molta importanza, darne perfetta risolutione. Lassando adunque di parlare
più intorno a cotal materia, verrò a ragionare delli Contrapunti, che si compongono a Tre voci, che si chiamano Doppij, & di quelli, che si fanno con qualche obligo.
Delle varie sorti di Contrapunti, & prima di quelli, che si chiamano Doppij.Cap. 62.
 osseruasse, di non por mai il Basso nel Principale con le altre parti distante per vna Sesta; ancora che le altre due si possino porre. Similmente non si dè por mai il Basso col Tenore in Terza, dopo la quale seguiti la
Quinta: Ne il Basso col Soprano in Decima, dopo la quale venghi la Duodecima, quando le parti insieme
discendeno: percioche la Duodecima, che si pone nel Principale tra'l Basso, & il Soprano; nella Replica
viene Vnisono tra'l Tenore, & il Soprano; & la Quinta simigliantemente viene Ottaua. Potemo hora vedere, che in simil sorte
di contrapunto, o compositione, nel Principale non si può fare la Sincopa di Settima:
conciosia che non si può risoluere con la Sesta; Ne si può far Decima, & poi Quinta, procedendo per mouimenti contrarij. Ma quando il Basso sarà in Ottaua col Tenore, allora il Soprano potrà esser sotto'l Tenore vna Terza; & similmente quando l'vno dall'altro saranno distanti per vna Decima; il che non si concede in altro modo. Il Tenore potrà similmente discendere sotto'l Basso, per qualunque interuallo si uoglia:
ma bisogna auertire, che non passi la Sesta: percioche le parti vengono ad esser distanti l'vna dall'altra per
lungo spacio. Si potrebbe anco porre il Soprano sotto'l Basso, quando fusse dibisogno: ma non bisognarebbe
passare la Quinta: percioche le parti poste in cotal modo, nella Replica vengono molto lontane l'vna dall'altra. Si potrà anco vsar la Settima posta nel Soprano nella sincopa; quando si porrà il Basso sopra'l Tenore
lontano per vna Quinta. Medesimamente si potrà vsarla nel Basso: ma non altramente, se non quando sarà posto sopra'l Tenore. Molte altre cose sarebbe dibisogno di mostrare, che si hanno da osseruare, per hauere il modo facile da comporre; le quali, per non andare in lungo, & per non esser molto necessarie, si lassano. Et veramente mi ho mosso a lassarle per questa cagione, che desiderando alcuno di voler fare cosa ottima, è dibisgno, che faccia insieme il Principale, & la Replica; & cosi potrà vedere tutti gli incommodi,
che potranno occorrere. Vltimamente è dibisogno sapere, che se'l si componerà il Principale secondo l'osseruanza delle Regole nostre mostrate di sopra; la Replica similmente verrà ad essere osseruata; & se'l si farà
altramente, ne seguirà il contrario. Et ciò sia detto a bastanza intorno la Prima sorte del Contrapunto doppio a tre voci,
la cui Replica procede con simili mouimenti contenuti nel Principale.La Seconda sorte è
quella, della quale la Replica procede per mouimenti contrarij a quelli, che si trouano nelle parti del Principale; come ne i sotto posti essempi si può vedere.Ma la Replica non potrebbe mai tornar bene, se non si
osseruasse alcune cose; come sarebbe dire; far che tutte le parti delle Sincope, che si pongono nel Principale
siano consonanti; & non por mai il Tenore distante dal Soprano per vna Quarta. Queste cose si debbeno
principalmente per ogni modo osseruare; l'altre poi, che potrebbeno accascare non saranno difficili; quando
osseruasse, di non por mai il Basso nel Principale con le altre parti distante per vna Sesta; ancora che le altre due si possino porre. Similmente non si dè por mai il Basso col Tenore in Terza, dopo la quale seguiti la
Quinta: Ne il Basso col Soprano in Decima, dopo la quale venghi la Duodecima, quando le parti insieme
discendeno: percioche la Duodecima, che si pone nel Principale tra'l Basso, & il Soprano; nella Replica
viene Vnisono tra'l Tenore, & il Soprano; & la Quinta simigliantemente viene Ottaua. Potemo hora vedere, che in simil sorte
di contrapunto, o compositione, nel Principale non si può fare la Sincopa di Settima:
conciosia che non si può risoluere con la Sesta; Ne si può far Decima, & poi Quinta, procedendo per mouimenti contrarij. Ma quando il Basso sarà in Ottaua col Tenore, allora il Soprano potrà esser sotto'l Tenore vna Terza; & similmente quando l'vno dall'altro saranno distanti per vna Decima; il che non si concede in altro modo. Il Tenore potrà similmente discendere sotto'l Basso, per qualunque interuallo si uoglia:
ma bisogna auertire, che non passi la Sesta: percioche le parti vengono ad esser distanti l'vna dall'altra per
lungo spacio. Si potrebbe anco porre il Soprano sotto'l Basso, quando fusse dibisogno: ma non bisognarebbe
passare la Quinta: percioche le parti poste in cotal modo, nella Replica vengono molto lontane l'vna dall'altra. Si potrà anco vsar la Settima posta nel Soprano nella sincopa; quando si porrà il Basso sopra'l Tenore
lontano per vna Quinta. Medesimamente si potrà vsarla nel Basso: ma non altramente, se non quando sarà posto sopra'l Tenore. Molte altre cose sarebbe dibisogno di mostrare, che si hanno da osseruare, per hauere il modo facile da comporre; le quali, per non andare in lungo, & per non esser molto necessarie, si lassano. Et veramente mi ho mosso a lassarle per questa cagione, che desiderando alcuno di voler fare cosa ottima, è dibisgno, che faccia insieme il Principale, & la Replica; & cosi potrà vedere tutti gli incommodi,
che potranno occorrere. Vltimamente è dibisogno sapere, che se'l si componerà il Principale secondo l'osseruanza delle Regole nostre mostrate di sopra; la Replica similmente verrà ad essere osseruata; & se'l si farà
altramente, ne seguirà il contrario. Et ciò sia detto a bastanza intorno la Prima sorte del Contrapunto doppio a tre voci,
la cui Replica procede con simili mouimenti contenuti nel Principale.La Seconda sorte è
quella, della quale la Replica procede per mouimenti contrarij a quelli, che si trouano nelle parti del Principale; come ne i sotto posti essempi si può vedere.Ma la Replica non potrebbe mai tornar bene, se non si
osseruasse alcune cose; come sarebbe dire; far che tutte le parti delle Sincope, che si pongono nel Principale
siano consonanti; & non por mai il Tenore distante dal Soprano per vna Quarta. Queste cose si debbeno
principalmente per ogni modo osseruare; l'altre poi, che potrebbeno accascare non saranno difficili; quando
 page 254
page 254 si componerà la Replica insieme col Principale. In simil sorte di Contrapunto si potranno vsar le Seste, &
porre le parti lontane l'vna dall'altra, per quale interuallo si vorrà; il Tenore potrà pigliare il luogo del Basso; & il Soprano quello del Tenore, & quello del Basso anco. Et per hauer la Replica, si porrà il Basso del
Principale nel luogo del Soprano, più acuto per vna Sesta; il Soprano nel luogo del Basso, più graue per vna
Decima; & il Tenore, più graue per vn Tuono; facendo, che le parti procedino per contrarij mouimenti di
quelli, che si trouano nel Principale; & haueremo l'harmonia differente; si come varij, & differenti sono
li siti dell'vno, & dell'altro, & li mouimenti. Et se noi osseruaremo nella compositione del Principale le Regole, che in molti luoghi sono state dichiarate; non è dubbio, che la Replica (se non in tutto, almeno in molte parti) verrà ad essere osseruata. Si potrà anche comporre vn'altra specie di simile Contrapunto doppio,
che participarà dell'vna, & dell'altra sorte di questi Contrapunti; quando si osseruarà tutte quelle Regole,
che si osseruano nella loro compositione, le quali Regole sono negatiue; cioè vietano il fare alcuna cosa. Il che
fatto haueremo poi vn Contrapunto, che potrà hauere la Replica simile a quella del Primo, & del Secondo
modo mostrati; come qui si può vedere.
si componerà la Replica insieme col Principale. In simil sorte di Contrapunto si potranno vsar le Seste, &
porre le parti lontane l'vna dall'altra, per quale interuallo si vorrà; il Tenore potrà pigliare il luogo del Basso; & il Soprano quello del Tenore, & quello del Basso anco. Et per hauer la Replica, si porrà il Basso del
Principale nel luogo del Soprano, più acuto per vna Sesta; il Soprano nel luogo del Basso, più graue per vna
Decima; & il Tenore, più graue per vn Tuono; facendo, che le parti procedino per contrarij mouimenti di
quelli, che si trouano nel Principale; & haueremo l'harmonia differente; si come varij, & differenti sono
li siti dell'vno, & dell'altro, & li mouimenti. Et se noi osseruaremo nella compositione del Principale le Regole, che in molti luoghi sono state dichiarate; non è dubbio, che la Replica (se non in tutto, almeno in molte parti) verrà ad essere osseruata. Si potrà anche comporre vn'altra specie di simile Contrapunto doppio,
che participarà dell'vna, & dell'altra sorte di questi Contrapunti; quando si osseruarà tutte quelle Regole,
che si osseruano nella loro compositione, le quali Regole sono negatiue; cioè vietano il fare alcuna cosa. Il che
fatto haueremo poi vn Contrapunto, che potrà hauere la Replica simile a quella del Primo, & del Secondo
modo mostrati; come qui si può vedere.


 page 255La Terza specie del detto Contrapunto si fa, quando si compone il Principale di maniera, che dipoi il Basso
resta nelle sue chorde principali, senza alcuna mutatione; & il Soprano diuenta nella Replica il Basso, trasportato per una Duodecima più graue; & il Tenore per vna Quinta, nel modo che qui si vede.
page 255La Terza specie del detto Contrapunto si fa, quando si compone il Principale di maniera, che dipoi il Basso
resta nelle sue chorde principali, senza alcuna mutatione; & il Soprano diuenta nella Replica il Basso, trasportato per una Duodecima più graue; & il Tenore per vna Quinta, nel modo che qui si vede.

 E' ben vero, che questo modo è più difficile di ciascuno delli mostrati; onde volendolo fare, acciò la Replica
torni bene, bisogna osseruare molte cose, & prima: Quando'l Tenore canterà col Basso a due voci; non bisogna, che le parti siano distanti l'vna dall'altra per Ottaua, ne per Sesta; massimamente quando'l Tenore si
porrà sopra'l Basso: Ma quando si porrà sotto'l Basso, non si dè porre distante dal Basso, ne per Terza, ne per
Quinta: ma si bene per Sesta, o per Ottaua, & per Quinta ancora; con questa conditione però, che tal Quinta si troui nella seconda parte della sincopa, dopo la quale senza alcun mezo ne venga la Sesta:
Percioche
quando queste due parti si pongono a i loro luoghi propij, non possono esser distanti l'vna dall'altra per maggior spacio, che di quello della Quinta; & tal Quinta nella Replica viene a far l'Vnisono. Non si fa etiandio la sincopa della Settima; ma solamente quella di Seconda, o di Quarta. Simigliantemente, quando'l Soprano, & il Basso canteranno soli, bisogna auertir di non fare, che'l Soprano passi sotto'l Basso; ne si debbe
porre la sincopa di Settima; benche quella di Seconda, & di Quarta si possa vsare ottimamente nel Soprano: ne si debbe porre queste parti lontane l'vna dall'altra per vna Sesta, ne vogliono esser più distanti di una
Duodecima. Non si fa la Terza, & dipoi la Quinta; ouero non si fa la Decima, & dipoi la Duodecima,
quando le parti discendeno. Quando poi il Tenore, & il Soprano canteranno insieme, non si dè far la Quinta, se non quando'l Tenore farà la Sincopa, nella seconda parte della quale tal Quinta sia contenuta, & dopo lei bisogna che seguiti senza alcun mezo la Sesta; & dopo questa la Terza, ouero vn'altra Sesta. Non
si fa Sesta, & dipoi Ottaua, quando le parti discendeno: ma si pone la Sesta ad vn'altro modo, che venghi bene. Il Soprano può discendere sotto'l Tenore fino alla ottaua voce, quando torna commodo; Et
quando si vorrà porre la sincopa di Quarta nell'vna, & nell'altra di queste due parti, tornerà molto bene.
Bisogna auertire di non dimorare lungo tempo sopra la Terza: percioche nella Replica viene col Basso
la Sesta; Ne douemo anco fermare le parti sopra la Ottaua: conciosia che torna Vnisono. Tutte queste cose si debbeno osseruare, accioche si possa peruenire con qualche facilità al fine desiderato. Et perche osseruando queste Regole, sarà facile il comporre questi Contrapunti a Tre uoci: tanto più, che si dè comporre in un
tempo il Principale, & la Replica; accioche'l Compositore possa vedere gli incommodi, che possono occorrere in tali compositioni. Però si dè auertire per vltima conclusione, che quantunque il Principale si purgasse page 256da ogni errore, che si potesse commettere contra le date Regole vniuersali; è impossibile, che la Replica in
tutto possa venire osseruata. Questi pochi essempi hò voluto porre, da i quali ciascuno potrà vedere il modo,
che hauerà da tenere volendone comporre de gli altri.
E' ben vero, che questo modo è più difficile di ciascuno delli mostrati; onde volendolo fare, acciò la Replica
torni bene, bisogna osseruare molte cose, & prima: Quando'l Tenore canterà col Basso a due voci; non bisogna, che le parti siano distanti l'vna dall'altra per Ottaua, ne per Sesta; massimamente quando'l Tenore si
porrà sopra'l Basso: Ma quando si porrà sotto'l Basso, non si dè porre distante dal Basso, ne per Terza, ne per
Quinta: ma si bene per Sesta, o per Ottaua, & per Quinta ancora; con questa conditione però, che tal Quinta si troui nella seconda parte della sincopa, dopo la quale senza alcun mezo ne venga la Sesta:
Percioche
quando queste due parti si pongono a i loro luoghi propij, non possono esser distanti l'vna dall'altra per maggior spacio, che di quello della Quinta; & tal Quinta nella Replica viene a far l'Vnisono. Non si fa etiandio la sincopa della Settima; ma solamente quella di Seconda, o di Quarta. Simigliantemente, quando'l Soprano, & il Basso canteranno soli, bisogna auertir di non fare, che'l Soprano passi sotto'l Basso; ne si debbe
porre la sincopa di Settima; benche quella di Seconda, & di Quarta si possa vsare ottimamente nel Soprano: ne si debbe porre queste parti lontane l'vna dall'altra per vna Sesta, ne vogliono esser più distanti di una
Duodecima. Non si fa la Terza, & dipoi la Quinta; ouero non si fa la Decima, & dipoi la Duodecima,
quando le parti discendeno. Quando poi il Tenore, & il Soprano canteranno insieme, non si dè far la Quinta, se non quando'l Tenore farà la Sincopa, nella seconda parte della quale tal Quinta sia contenuta, & dopo lei bisogna che seguiti senza alcun mezo la Sesta; & dopo questa la Terza, ouero vn'altra Sesta. Non
si fa Sesta, & dipoi Ottaua, quando le parti discendeno: ma si pone la Sesta ad vn'altro modo, che venghi bene. Il Soprano può discendere sotto'l Tenore fino alla ottaua voce, quando torna commodo; Et
quando si vorrà porre la sincopa di Quarta nell'vna, & nell'altra di queste due parti, tornerà molto bene.
Bisogna auertire di non dimorare lungo tempo sopra la Terza: percioche nella Replica viene col Basso
la Sesta; Ne douemo anco fermare le parti sopra la Ottaua: conciosia che torna Vnisono. Tutte queste cose si debbeno osseruare, accioche si possa peruenire con qualche facilità al fine desiderato. Et perche osseruando queste Regole, sarà facile il comporre questi Contrapunti a Tre uoci: tanto più, che si dè comporre in un
tempo il Principale, & la Replica; accioche'l Compositore possa vedere gli incommodi, che possono occorrere in tali compositioni. Però si dè auertire per vltima conclusione, che quantunque il Principale si purgasse page 256da ogni errore, che si potesse commettere contra le date Regole vniuersali; è impossibile, che la Replica in
tutto possa venire osseruata. Questi pochi essempi hò voluto porre, da i quali ciascuno potrà vedere il modo,
che hauerà da tenere volendone comporre de gli altri.
Delli Contrapunti a Tre voci, che si fanno con qualche obligo.Cap. 63.

 page 257Il Secondo modo è quando due parti del Contrapunto si seguitano, distanti l'vna dall'altra per Quinta, dopo vna Pausa di Minima. Et questo medesimamente si può fare in due maniere: Percioche, ouero la Guida
sarà la parte acuta delle due parti del Contrapunto, & la graue il Consequente: oueramente per il contrario, che la Guida sarà la graue, & il Consequente la acuta. Bisogna però auertire, che'l propio dell'uno, &
dell'altro modo è, di modulare, o cantare (che uogliam dire) per salti, o mouimenti di Ottaua, di Sesta,
& di Terza; & rarissime volte auiene, che si possa cantare per quelli di Quinta. Et quando procederanno per molti gradi congiunti, il propio del primo modo è, che la Guida proceda dall'acuto al graue; & nel
secondo modo per il contrario, cioè dal graue all'acuto; si come nell'vno, & l'altro di questi due essempi
si può vedere.
page 257Il Secondo modo è quando due parti del Contrapunto si seguitano, distanti l'vna dall'altra per Quinta, dopo vna Pausa di Minima. Et questo medesimamente si può fare in due maniere: Percioche, ouero la Guida
sarà la parte acuta delle due parti del Contrapunto, & la graue il Consequente: oueramente per il contrario, che la Guida sarà la graue, & il Consequente la acuta. Bisogna però auertire, che'l propio dell'uno, &
dell'altro modo è, di modulare, o cantare (che uogliam dire) per salti, o mouimenti di Ottaua, di Sesta,
& di Terza; & rarissime volte auiene, che si possa cantare per quelli di Quinta. Et quando procederanno per molti gradi congiunti, il propio del primo modo è, che la Guida proceda dall'acuto al graue; & nel
secondo modo per il contrario, cioè dal graue all'acuto; si come nell'vno, & l'altro di questi due essempi
si può vedere.

 Et bisogna che'l Contrapuntista mentre farà il contrapunto a ciascuno delli mostrati modi; faccialo scriuendo, oueramente alla sproueduta, habbia sempre riguardo a quello, che può fare il Consequente; acciò non
commetta errore. Queste cose adunque si debbeno osseruare principalmente in simili contrapunti: perche se
bene occorresse alcun'altra osseruanza, sarebbe di poco momento. Ma si dè sapere, che è impossibile in tutte queste sorti di Contrapunti doppij, & fatti con simili oblighi, di osseruar pienamente le Regole date di
sopra; massimamente quando cotali oblighi crescono: essendo che non si può osseruare la bellezza, & il decoro
del Contrapunto, si in quanto alla modulatione, quanto ancora intorno la inuentione, & il modo di porre le page 258consonanze: percioche è leuata la libertà al Compositore, che hauea nel comporre gli altri senza alcun obligo: & questo dico, accioche il diligente osseruatore de i nostri Precetti, vedendo alcune cose, che non sono
cosi ben corrette, non si marauigli: perche non hò posto qui cotali Compositioni, accioche lungamente, &
per sempre si habbiano da vsare; ma si bene alle volte, quando li tornerà in proposito; per mostrar la viuacità del suo ingegno, & la prontezza del suo intelletto con alcuni, che ad altro non attendeno, che a simil
cose, & poi nel resto si ritrouano essere nudi. Sono queste maniere veramente molto ingegnose, ancora che
si oda alle volte qualche cosa, che sia strana da udire: Ma è buono sapere tutte le cose (se fusse possibile) massimamente le necessarie, & le vtili in ciascuna Arte, & in ciascuna Scienza; & non solo queste, che sono buone; ma le altre ancora, quantunque siano triste; L'vne per mettere in opera, l'altre poi per sapersi
guardare, & seruirsene di esse a tempo, & luogo conueniente. Et se alle volte hò mostrato delle cose, che
non tornano cosi bene, hò voluto in cio imitare il Filosofo, il quale, hauendo mostrato il buono della Logica,
& della Filosofia, & mostrato il vero modo di argumentare; dopo l'hauer scritto molte cose nell'vna, &
nell'altra facultà; scrisse etiandio i Libri de i Silogismi fallaci, o Soffistici, i quali chiamò Elenchi; non perche si hauessero da vsare: ma accioche (accadendo) ogn'vno si sapesse guardare da gli intrichi de i Soffisti,
che vogliono esser tenuti dotti, ancora che non siano. Buona cosa è veramente, & ottima il sapere cotali
Contrapunti, & vsarli quando torna commodo: ma il frequentarli non lodo molto: conciosia che non si può
fare, che essendo il Contrapuntista obligato alla osseruanza di tante cose, il Contrapunto venga ad essere in
tal maniera elegante, & sonoro, che porga grato piacere all'Vdito.
Et bisogna che'l Contrapuntista mentre farà il contrapunto a ciascuno delli mostrati modi; faccialo scriuendo, oueramente alla sproueduta, habbia sempre riguardo a quello, che può fare il Consequente; acciò non
commetta errore. Queste cose adunque si debbeno osseruare principalmente in simili contrapunti: perche se
bene occorresse alcun'altra osseruanza, sarebbe di poco momento. Ma si dè sapere, che è impossibile in tutte queste sorti di Contrapunti doppij, & fatti con simili oblighi, di osseruar pienamente le Regole date di
sopra; massimamente quando cotali oblighi crescono: essendo che non si può osseruare la bellezza, & il decoro
del Contrapunto, si in quanto alla modulatione, quanto ancora intorno la inuentione, & il modo di porre le page 258consonanze: percioche è leuata la libertà al Compositore, che hauea nel comporre gli altri senza alcun obligo: & questo dico, accioche il diligente osseruatore de i nostri Precetti, vedendo alcune cose, che non sono
cosi ben corrette, non si marauigli: perche non hò posto qui cotali Compositioni, accioche lungamente, &
per sempre si habbiano da vsare; ma si bene alle volte, quando li tornerà in proposito; per mostrar la viuacità del suo ingegno, & la prontezza del suo intelletto con alcuni, che ad altro non attendeno, che a simil
cose, & poi nel resto si ritrouano essere nudi. Sono queste maniere veramente molto ingegnose, ancora che
si oda alle volte qualche cosa, che sia strana da udire: Ma è buono sapere tutte le cose (se fusse possibile) massimamente le necessarie, & le vtili in ciascuna Arte, & in ciascuna Scienza; & non solo queste, che sono buone; ma le altre ancora, quantunque siano triste; L'vne per mettere in opera, l'altre poi per sapersi
guardare, & seruirsene di esse a tempo, & luogo conueniente. Et se alle volte hò mostrato delle cose, che
non tornano cosi bene, hò voluto in cio imitare il Filosofo, il quale, hauendo mostrato il buono della Logica,
& della Filosofia, & mostrato il vero modo di argumentare; dopo l'hauer scritto molte cose nell'vna, &
nell'altra facultà; scrisse etiandio i Libri de i Silogismi fallaci, o Soffistici, i quali chiamò Elenchi; non perche si hauessero da vsare: ma accioche (accadendo) ogn'vno si sapesse guardare da gli intrichi de i Soffisti,
che vogliono esser tenuti dotti, ancora che non siano. Buona cosa è veramente, & ottima il sapere cotali
Contrapunti, & vsarli quando torna commodo: ma il frequentarli non lodo molto: conciosia che non si può
fare, che essendo il Contrapuntista obligato alla osseruanza di tante cose, il Contrapunto venga ad essere in
tal maniera elegante, & sonoro, che porga grato piacere all'Vdito.
Quel che si dè osseruare, quando si volesse far vna Terza parte alla sproueduta sopra due altre proposte.Cap. 64.

 page 260Hauendo adunque il Contrapuntista tal riguardo, potrà ottimamente accommodare il suo Contrapunto, in
quella maniera, che li parerà meglio, & li tornerà più commodo; tanto volendo aggiungere vna parte acuta sopra la parte graue delle due proposte; quanto volendo fare sotto di esse vna parte graue. E' ben vero,
che'l porre alle volte la parte, che si aggiunge distante per vna Decima, ouero per vna Terza dall'vna delle due, torna molto commodo: Ma bisogna auertire, che quando le proposte fussero per vna Terza lontane
l'vna dall'altra, & quella che si aggiunge cantasse per vna Decima; tra la aggiunta, & l'una delle due;
che sarebbe la graue, quando la parte si aggiungesse nell'acuto; ouero sarebbe l'acuta, quando l'aggiunta fusse più graue; sempre si vdirebbe la Ottaua; & cosi dico, quando fussero distanti per vna Decima, & la aggiunta cantasse per vna Terza; Onde se le due proposte hauessero molte Terze, o Decime l'vna dopo l'altra; come si sogliono porre alle volte, si vdirebbeno con l'aggiunto tante Ottaue, senza mezo alcuno; quante
erano le Terze, o le Decime contenute tra le parti; & per tal maniera si verrebbe a fare errore. Però è cosa buona, anzi necessaria il vedere il Contrapunto delle due proposte, per potere schiuare gli errori, che potessero occorrere: percioche quando si facesse altramente, sarebbe impossibile di far cosa buona; se almeno non
si hauesse alla memoria ciascuna delle parti. Et perche può occorrere di accommodare, ouero aggiungere
tal parte in due maniere, cioè ad alcune cantilene, che non saranno composte secondo gli auertimenti, o Regole date: & medesimamente
ad alcune, che saranno ordinate secondo li modi mostrati di sopra; però il Contrapuntista non sarà obligato cosi strettamente di osseruare li Precetti dati di sopra, nel fare la Terza parte,
sopra quelle, che saranno composte senza li mostrati auertimenti; ancora che sarà sempre lo deuole, quando
si potrà fare, che tal parte aggiunta sia posta con quelle conditioni, che si ricerca in ciascuna buona compositione. Ma quando la Cantilena sarà composta regolatamente, debbe per ogni modo stare nella osseruanza de
i mostrati precetti, più che puote: percioche è il douere. Ma accioche si possa comprendere il modo, che si dè
tenere in vn tal negotio, hò voluto aggiungere due Terze parti, variate l'vna dall'altra: aggiunte, dico, ad
vna compositione a due voci di Iosquino, che si troua nel Motetto Benedicta es coelorum regina, a sei voci;
le quali, di poi che saranno state vedute, & essaminate, si potrà vedere il modo, che si hauerà a tenere volendo aggiungere
tal parte in alcun' altra compositione composta a Due voci. Ma si debbe auertire, che le parti aggiunte, alcune volte procedeno per alcuni mouimenti alquanto lontani; & questo è sopportabile; per la
difficultà, che si troua nell'accommodar tal parte alla modulatione continoua della cantilena: essendo che, altro è il comporre
insieme tutte le parti, & altro è aggiungere a due parti la Terza; che è cosa molto difficile, & da huomo consumato nella Musica; & cosa molto lodeuole, quando si aggiunge, che stia bene.
page 260Hauendo adunque il Contrapuntista tal riguardo, potrà ottimamente accommodare il suo Contrapunto, in
quella maniera, che li parerà meglio, & li tornerà più commodo; tanto volendo aggiungere vna parte acuta sopra la parte graue delle due proposte; quanto volendo fare sotto di esse vna parte graue. E' ben vero,
che'l porre alle volte la parte, che si aggiunge distante per vna Decima, ouero per vna Terza dall'vna delle due, torna molto commodo: Ma bisogna auertire, che quando le proposte fussero per vna Terza lontane
l'vna dall'altra, & quella che si aggiunge cantasse per vna Decima; tra la aggiunta, & l'una delle due;
che sarebbe la graue, quando la parte si aggiungesse nell'acuto; ouero sarebbe l'acuta, quando l'aggiunta fusse più graue; sempre si vdirebbe la Ottaua; & cosi dico, quando fussero distanti per vna Decima, & la aggiunta cantasse per vna Terza; Onde se le due proposte hauessero molte Terze, o Decime l'vna dopo l'altra; come si sogliono porre alle volte, si vdirebbeno con l'aggiunto tante Ottaue, senza mezo alcuno; quante
erano le Terze, o le Decime contenute tra le parti; & per tal maniera si verrebbe a fare errore. Però è cosa buona, anzi necessaria il vedere il Contrapunto delle due proposte, per potere schiuare gli errori, che potessero occorrere: percioche quando si facesse altramente, sarebbe impossibile di far cosa buona; se almeno non
si hauesse alla memoria ciascuna delle parti. Et perche può occorrere di accommodare, ouero aggiungere
tal parte in due maniere, cioè ad alcune cantilene, che non saranno composte secondo gli auertimenti, o Regole date: & medesimamente
ad alcune, che saranno ordinate secondo li modi mostrati di sopra; però il Contrapuntista non sarà obligato cosi strettamente di osseruare li Precetti dati di sopra, nel fare la Terza parte,
sopra quelle, che saranno composte senza li mostrati auertimenti; ancora che sarà sempre lo deuole, quando
si potrà fare, che tal parte aggiunta sia posta con quelle conditioni, che si ricerca in ciascuna buona compositione. Ma quando la Cantilena sarà composta regolatamente, debbe per ogni modo stare nella osseruanza de
i mostrati precetti, più che puote: percioche è il douere. Ma accioche si possa comprendere il modo, che si dè
tenere in vn tal negotio, hò voluto aggiungere due Terze parti, variate l'vna dall'altra: aggiunte, dico, ad
vna compositione a due voci di Iosquino, che si troua nel Motetto Benedicta es coelorum regina, a sei voci;
le quali, di poi che saranno state vedute, & essaminate, si potrà vedere il modo, che si hauerà a tenere volendo aggiungere
tal parte in alcun' altra compositione composta a Due voci. Ma si debbe auertire, che le parti aggiunte, alcune volte procedeno per alcuni mouimenti alquanto lontani; & questo è sopportabile; per la
difficultà, che si troua nell'accommodar tal parte alla modulatione continoua della cantilena: essendo che, altro è il comporre
insieme tutte le parti, & altro è aggiungere a due parti la Terza; che è cosa molto difficile, & da huomo consumato nella Musica; & cosa molto lodeuole, quando si aggiunge, che stia bene.
Quel che bisogna osseruare intorno le Compositioni di Quattro, o di più voci.Cap. 65.
Quo semel imbuta recens, seruabit odoremEt se la Speculatiua senza la Prattica (come altre volte hò detto) val poco; atteso che la Musica non consiste solamente nella Speculatiua; cosi questa senza la prima è veramente imperfetta. Et questo è manifesto: conciosia che hauendo voluto alcuni Theorici trattare alcune cose della Musica; per non hauere hauuto buona cognitione della Prattica, hanno detto mille chiachiere, & commesso mille errori. Simigliantemente alcuni, che si hanno voluto gouernare con la sola Prattica, senza conoscere alcuna ragione, hanno fatto nelle loro compositioni mille, & mille pazze, senza punto auedersene di cosa alcuna. Ma per ritornare al nostro proposito dico, che volendo dar principio alle Compositioni nominate di sopra; primieramente si ritrouarà il Soggetto; dipoi ritrouato, si potrà incominciare il Contrapunto da quella parte, che tornarà più commodo. La onde poniamo, che si volesse dar principio alla cantilena con la parte del Bassoo; subito il Compositore potrà conoscere il luogo del Contralto, del Soprano, & quello del Tenore. Cosi ancora volendo dar principio per qualunque altra parte; si come per il Tenore, o per il Basso; saprà i luoghi dell'altre parti per ordine, reggendosi secondo'l modo mostrato di sopra nella Tauola; osseruando anche quelle Regole, che disopra in molti luoghi hò mostrato, quando fu ragionato intorno il modo di comporre a Due, & a Tre voci. Per la qual cosa osseruando il tutto, potrà hauere il desiderato fine, & acquistarsi honore; al quale spesse fiate ne conseguita grande vtile ancora. Ma accioche si vegga il modo, che si hauerà da tenere, & il procedere in simili compositioni; ancora che siano infiniti gli essempi a Quattro voci, composti da molti compositori eccellenti; porrò solamente due compositioni sopra il Canto fermo, dalle quali, poi che si haueranno essaminate, si potrà hauere qualche lume, per potere seguire più oltra di bene in meglio, et porsi a maggiori imprese; et comporre altre cantilene di fantasia; come sono Motetti, Madrigali, & altre belle Canzoni; preparandosi il Soggetto, o pigliando alcuno altro Canto fermo, ouero qualunque altra parte, come parerà meglio al Compostore.
Testa diu.
 page 262
page 262 Et benche in ogni compositione perfetta quattro parti solamente siano basteuoli, si come il Soprano, l'Alto, il
Tenore, & il Basso; tuttauia quando si vorrà passare più oltra, & hauer maggior numero de parti, bastarà
solamente raddoppiare (come hò detto altroue) vna delle Quattro nominate; & cotal parte aggiunta si chiamerà medesimamente
Soprano, o Tenore, ouero Alto, o Basso; secondo la parte, che si hauerà doppiata; aggiungendoli Secondo, o Terzo secondo'l numero di quelle parti, che si troueranno in tale cantilena. Et si fanno
le chorde estreme della parte aggiunta, equali a quelle della parte, che viene raddoppiata; ancora che non sarebbe errore, quando non fussero equali, & le chorde della parte aggiunta si estendessero più verso'l graue, o
verso l'acuto, che quelle della raddoppiata; cioè della parte principale. Si debbe però auertire, che alle volte si page 263costuma di comporre la cantilena senza il Soprano; nel luogo del quale si pone vn Contr'alto, alquanto più acuto del principale
per vna Terza più, o meno, che importa poco. Il medesimo si fà, lassando il Soprano, & l'Alto; componendo con tre Tenori,
& vn Basso; oueramente con tre Bassi, & vno Tenore; & alle volte con quattro Bassi, & ad altro modo anco, si come torna più commodo; ilqual modo di comporre si chiama a Voci mutate, ouero a Voci pari. Si compone anche con due Soprani, & vn Contr'alto, ouero vn Tenore, & il Basso;
alle volte con tre Soprani, & vn Basso; & alle volte con quattro Soprani, tanto a quattro voci, quanto a cinque, & più oltra; sempre aggiungendo quelle parti, che fanno dibisogno; come si vede ogni giorno nelle moderne compositioni. Ma questa maniera di comporre; ancora che le parti si venghino a moltiplicare, & accommodare altramente
di quello, che si fà nelle a tre: non fà varietà alcuna di concento; cioè non partorisce variatione di accordi, oltra quelli, che nel Cap. 58. di sopra hò mostrato. E ben vero, che si troua tal differenza
tra le prime, & queste seconde compositioni; che essendo in quelle il campo più largo; cioè più lontana la parte
graue dalla parte acuta di tutto il concento; in questo il luogo è più ristretto: percioche gli estremi delle parti
graui, & delle acute insieme si conchiudono assai commodamente tra Quindeci chorde al più, & meno anco, secondo che fà dibisogno; & in quelle si conchiudono in Venti; come nella Quarta parte vederemo.
Et benche in ogni compositione perfetta quattro parti solamente siano basteuoli, si come il Soprano, l'Alto, il
Tenore, & il Basso; tuttauia quando si vorrà passare più oltra, & hauer maggior numero de parti, bastarà
solamente raddoppiare (come hò detto altroue) vna delle Quattro nominate; & cotal parte aggiunta si chiamerà medesimamente
Soprano, o Tenore, ouero Alto, o Basso; secondo la parte, che si hauerà doppiata; aggiungendoli Secondo, o Terzo secondo'l numero di quelle parti, che si troueranno in tale cantilena. Et si fanno
le chorde estreme della parte aggiunta, equali a quelle della parte, che viene raddoppiata; ancora che non sarebbe errore, quando non fussero equali, & le chorde della parte aggiunta si estendessero più verso'l graue, o
verso l'acuto, che quelle della raddoppiata; cioè della parte principale. Si debbe però auertire, che alle volte si page 263costuma di comporre la cantilena senza il Soprano; nel luogo del quale si pone vn Contr'alto, alquanto più acuto del principale
per vna Terza più, o meno, che importa poco. Il medesimo si fà, lassando il Soprano, & l'Alto; componendo con tre Tenori,
& vn Basso; oueramente con tre Bassi, & vno Tenore; & alle volte con quattro Bassi, & ad altro modo anco, si come torna più commodo; ilqual modo di comporre si chiama a Voci mutate, ouero a Voci pari. Si compone anche con due Soprani, & vn Contr'alto, ouero vn Tenore, & il Basso;
alle volte con tre Soprani, & vn Basso; & alle volte con quattro Soprani, tanto a quattro voci, quanto a cinque, & più oltra; sempre aggiungendo quelle parti, che fanno dibisogno; come si vede ogni giorno nelle moderne compositioni. Ma questa maniera di comporre; ancora che le parti si venghino a moltiplicare, & accommodare altramente
di quello, che si fà nelle a tre: non fà varietà alcuna di concento; cioè non partorisce variatione di accordi, oltra quelli, che nel Cap. 58. di sopra hò mostrato. E ben vero, che si troua tal differenza
tra le prime, & queste seconde compositioni; che essendo in quelle il campo più largo; cioè più lontana la parte
graue dalla parte acuta di tutto il concento; in questo il luogo è più ristretto: percioche gli estremi delle parti
graui, & delle acute insieme si conchiudono assai commodamente tra Quindeci chorde al più, & meno anco, secondo che fà dibisogno; & in quelle si conchiudono in Venti; come nella Quarta parte vederemo.
Alcuni auertimenti intorno le Compositioni, che si fanno a più di Tre voci.Cap. 66.
 Et perche accaderà alle volte, di comporre sopra le parole, le quali ricercano la harmonia alquanto dura, &
aspra; acciò si venga con gli effetti ad imitare il Soggetto contenuto nella Oratione; però quando bisognarà
vsar simili durezze, allora si potranno porre le Seste, nelle quali siano le figure di alquanto valore; come de
Breui, & di Semibreui mescolate; oueramente si porranno le Dissonanze tra loro, che siano ordinate secondo
le Regole, & modi mostrati di sopra; & si hauerà il proposito; si come auerrebbe ponendo la Quarta, ouer
la Vndecima nella Sincopa; come nelli sottoposti essempi si può vedere.Accascherà alle volte, che nella
prima, o nella seconda parte della Battuta si troueranno due parti sopra vna medesima chorda; ouero si trouaranno in vn tempo esser lontane l'vna dall'altra per vna Ottaua; dico, che se bene tali parti ascendessero, o
discendessero dipoi per vn sol grado, & per più gradi ancora, & toccassero vna istessa chorda: ouero se si ripage 264
Et perche accaderà alle volte, di comporre sopra le parole, le quali ricercano la harmonia alquanto dura, &
aspra; acciò si venga con gli effetti ad imitare il Soggetto contenuto nella Oratione; però quando bisognarà
vsar simili durezze, allora si potranno porre le Seste, nelle quali siano le figure di alquanto valore; come de
Breui, & di Semibreui mescolate; oueramente si porranno le Dissonanze tra loro, che siano ordinate secondo
le Regole, & modi mostrati di sopra; & si hauerà il proposito; si come auerrebbe ponendo la Quarta, ouer
la Vndecima nella Sincopa; come nelli sottoposti essempi si può vedere.Accascherà alle volte, che nella
prima, o nella seconda parte della Battuta si troueranno due parti sopra vna medesima chorda; ouero si trouaranno in vn tempo esser lontane l'vna dall'altra per vna Ottaua; dico, che se bene tali parti ascendessero, o
discendessero dipoi per vn sol grado, & per più gradi ancora, & toccassero vna istessa chorda: ouero se si ripage 264 trouassero medesimamente distanti per vna Ottaua; pur che ascendino, o discendino l'vna dopo l'altra; &
che quella, che sarà la prima a toccare la seconda chorda, non aspetti l'altra parte, ma subito muti luogo;
hauendo la seconda fatto primieramente vna Pausa, che sia del valore della figura posta sopra la secon da chorda: se bene l'vna, & l'altra di queste due parti toccassero tal chorda; mai si potrà con verità dire, che tra
loro siano fatti due Vnisoni, ouer due Ottaue. Et se bene hò gia detto nel Cap. 47. che la Pausa, o la
Dissonanza posta tra due consonanze perfette, non è atta a far variatione alcuna di concento; dico hora, che
iui mostrai le Figure, che fanno il Contrapunto, esser poste in altra maniera, di quello, che sono poste in simili Contrapunti: Percioche veramente allora si fanno due Vnisoni, o due Ottaue; quando le parti ascendeno, o
discendeno insieme senza esser tramezate da alcuna Pausa: ouero quando dopo la Pausa, l'vna delle parti casca sopra l'altra, senza alcun mezo. Quando adunque si interpone le Pause, & l'vna parte fugge, auanti, che
l'altra arriui alla gia toccata chorda; non si intendeno, ne sono, ne si potrà mai dire per alcun modo, che siano
poste contra alcuna delle date Regole; come qui sotto in essempio si vede.Il perche quando si porranno in
trouassero medesimamente distanti per vna Ottaua; pur che ascendino, o discendino l'vna dopo l'altra; &
che quella, che sarà la prima a toccare la seconda chorda, non aspetti l'altra parte, ma subito muti luogo;
hauendo la seconda fatto primieramente vna Pausa, che sia del valore della figura posta sopra la secon da chorda: se bene l'vna, & l'altra di queste due parti toccassero tal chorda; mai si potrà con verità dire, che tra
loro siano fatti due Vnisoni, ouer due Ottaue. Et se bene hò gia detto nel Cap. 47. che la Pausa, o la
Dissonanza posta tra due consonanze perfette, non è atta a far variatione alcuna di concento; dico hora, che
iui mostrai le Figure, che fanno il Contrapunto, esser poste in altra maniera, di quello, che sono poste in simili Contrapunti: Percioche veramente allora si fanno due Vnisoni, o due Ottaue; quando le parti ascendeno, o
discendeno insieme senza esser tramezate da alcuna Pausa: ouero quando dopo la Pausa, l'vna delle parti casca sopra l'altra, senza alcun mezo. Quando adunque si interpone le Pause, & l'vna parte fugge, auanti, che
l'altra arriui alla gia toccata chorda; non si intendeno, ne sono, ne si potrà mai dire per alcun modo, che siano
poste contra alcuna delle date Regole; come qui sotto in essempio si vede.Il perche quando si porranno in
 tal maniera, si potranno sempre vsare in ciascuna compositione; sia di Quattro, di Cinque, o di qual'altro numero si voglia de voci. Di questi, et di altri simili casi, che potranno occorrere, ciascuno potrà hauere da quello, che si è detto piena resolutione: La onde non mi estenderò più oltra, per non perdere il tempo. Qualunque
volta etiandio occorrerà di voler comporre alcuna Cantilena a Cinque, ouero a Sei, oueramente à più voci; si
potrà osseruar quello, che da molti Musici celebratissimi è stato osseruato: Conciosia che pigliauano alle volte
per Soggetto vn Tenore di Canto fermo, & dipoi lo accommodauano con varie figure, come li tornaua più
commodo; et fondauano la Compositione sopra tal Tenore, & faceuano cantare le parti a quel modo, che li
tornauano meglio; di maniera, che facessero buona harmonia; vsando di porle in Fuga l'vna con l'altra; ouer
di fare, che l'vna imitasse l'altra, nel modo, che hò mostrato di sopra. Ilche si può vedere, volendo di ciò qualche essempio, in più Motetti gia composti da Adriano, si come in quello, che incomincia Nil postquam sacrum,
a Sei voci; & in quelli Victor io salue; et Inclite sforciadum, composti a Cinque voci; & in molti altri fatti da
altri Compositori. Pigliauano anco vn Tenore di canto fermo, sopra ilquale accommodauano (come fanno
etiandio al di d'hoggi) due, o Tre parti in Consequenza; & dipoi sopra di quelle faceuano l'altre; & di ciò si
può hauer l'essempio ne i Motetti Verbum supernum; sopra il canto di O salutaris hostia; & in quello, che incomincia Praeter rerum seriem, composti da Adriano a Sette voci; & in quello di Iachetto a Sei voci, che incomincia Descendi in ortum meum; oltra che si ritrouerà nella medesima maniera composti il motetto Miserere mei Deus, miserere mei, sopra l'Antifona Ne reminiscaris Domine; & la Oratione dominicale Pater
noster, con la Salutatione angelica Aue Maria; i quali gia composi l'vno a Sei, & gli altri a Sette voci.
Debbe però auertire il Compositore, che in quelle Fughe, lequali si fanno sopra tali Tenori, le parti possono esser
tra loro distanti per vna Terza, per vna Quarta, per vna Quinta, per vna Sesta, & altre simili Consonanze:
ma di raro si pone la Quarta, dopo laquale segua immediatamente la Sesta: o per il contrario. Similmente rare page 265volte si pongono due Seste: percioche sono difficili da accompagnare con le altre parti. Tali Consequenze si
sogliono, & si debbono veramente comporre prima, che si componghino le altre parti: ma bisogna hauer sempre riguardo nel comporle, in qual maniera le parti, che si hanno da aggiungere, si possino accommodare nella cantilena; accioche non si habbia doppia fatica nel comporre tutto'l corpo della Compositione, quando venisse alcuna cosa di sinistro in tali Consequenze. Et se nell'aggiungere le altre parti, si trouasse qualche discommodo; ouero, che per mutare le parti del Canto fermo posto in tali Consequenze, facesse migliore effetto;
allora non dè il Compositore perdonare a fatica; ma debbe mutare opinione, aggiungendo, o leuando alle dette parti quello, che farà dibisogno. Ilche sarà facile, quando le parti saranno state ben ordinate da principio. Ma si dè auertire, che le parti, che cantano in Fuga, non si possono sempre ordinare in tal maniera,
che'l Consequente canti tutto quello, che canta la Guida; onde è necessario, che seguendo la Guida il cantare
in fino al fine, il Consequente si venga a fermar poco lontano; si come si può vedere in molte cantilene composte a tal guisa; & massimamente in quelli Motetti. Veni sancte Spiritus di Adriano composti a Sei voci; & O beatum pontificem, che gia composi imitando il canto fermo, a Cinque voci. Si debbe vsare
etiandio tal discrettione nell'accommodar le parti; che quella, che canta nel suo luogo propio il Canto fermo;
dopo l'hauer cantato tutto quello, che fà dibisogno, o sia Canto fermo, ouero Imitatione; quello, che cantasse
più oltra, di quello, che dè cantare il Consequente, sia almeno quasi replicato. Il Consequente poi debbe essere ordinato in tal modo, che canti, & finisca tutto il Canto fermo, & non fuori del suo ordine. Di questi si
potrà hauere molti essempi accommodati, come sarebbe il Motetto, Salue regina misericordiae; & quello,
che incomincia, Litigabant Iudaei, sopra il canto fermo, Comedite pinguia, i quali gia molti anni composi a
Sei voci. Si potra anco pigliare vn Canto fermo, & ordinare sopra di lui molte parti; ponendone due, o più
l'vna all'altra in Fuga continoua, o legata, come vogliamo dire; come fece Iachetto nel motetto Murus tuus; & Adriano nel motetto Salue sancta parens a Sei voci. Potremo simigliantemente pigliare alcun Tenore, ordinandolo con vn'altra parte in Fuga in tal maniera; che volendo replicare le parti, facino
vna seconda parte, di modo, che quella che prima fù la Guida diuenti il Consequente; & similmente
quella, che era il Consequente diuenti la Guida. Di questa maniera si trouano molte compositioni, tra lequali è il motetto di Adriano, Venator lepores, sopra'l Canto fermo, Argentum, & aurum non est mihi; &
il motetto In principio Deus antequàm terram faceret, sopra quel canto fermo, Omnis sapientia, ilquale gia
composi da cantare a Sei voci, si come si canta etiandio il sopra detto. Vsano etiandio alle volte li Prattici,
imitando due, o più Tenori diuersi di varij canti ecclesiastici, comporre alcune cantilene a più voci, di maniera, che l'vna delle parti venghi ad imitar l'vno, & l'altra l'altro; come fece Iosquino, ilquale in cotal
maniera in vna compositione di Sei voci ne imitò Quattro, cioè Alma redemptoris mater. Aue regina
coelorum. Inuiolata, integra, & casta. & Regina coeli; si come fece anche Gomberto in vna Cantilena
a Quattro voci, che incomincia Salue regina. Alma redemptoris. Inuiolata. Aue regina coelorum, imitandone molti, come iui si può vedere; Ilche potrà etiandio fare ciascuno, imitandone diuersi altri: percioche veramente cotal cosa è molto lodeuole; per essere ingegnosa. Si potrà anco pigliare due Tenori di canto fermo, & accommodarli, come torna meglio alla cantilena, & sopra di essi comporre le altre parti; come fece Costanzo Festa nel motetto Exaltabo te Domine a Sei Voci, che accommodo l'Antifona Cum iucunditatem, & il primo verso del Cantico di Zacaria, Benedictus Dominus Deus Israel. Potremo etiandio
(come hanno fatto de gli altri) porre due parti della cantilena, lassando da parte il canto fermo, in Consequenza; oueramente porle legate insieme con la Imitatione; dilche si può hauere l'essempio nel motetto
Ecce tu pulchra es, ilquale gia composi a Cinque voci. Si potrebbe anche comporre le Cantilene facendo
le parti raddoppiate, cioè ponendo le parti a due, a due in Consequenza, ouero nella Imitatione; come fece
Motone nel motetto Nesciens mater; & Gomberto nel motetto Inuiolata, integra, & casta; l'vno, &
l'altro composto a Otto voci; & Adriano il nominato motetto Salue sancta parens, & la canzone Sur
l'herbe brunette, che l'vno, & l'altra si cantano a Sei voci. Oltra di questo si potrà comporre a Quattro,
a Cinque, & a più voci in mille modi (dirò cosi) ponendo le parti hora in Consequenza, hora nella Imitatione; oue si ritrouerà esser tanti li Consequenti, quante saranno le Guide; come si può vedere in quel motetto di Adriano, Sancta, & imaculata virginitas; & in vna sua canzone Petite camusete, a Quattro voci. Sarà anco lodeuole il comporre Quattro parti sopra vna, ponendone alcune in Fuga, & alcune nella
Imitatione; come fece P. della Rue nella messa O salutaris hostia; & Adriano anche, con molta legpage 266giadria, nella messa Mente tota; delle quali l'vna, & l'altra si troua a Quattro voci. Infiniti sono li modi del
comporre in simili maniere; & difficile anzi impossibile sarebbe, il voler raccontare di vna in vna le dispositioni delle parti, & del'ordine tenuto: Ma per non esser lungo farò fine; massimamente perche ogni giorno si veggono molte altre compositioni, composte dallo Eccellentissimo Adriano Vuillaert, lequali, oltra che
sono piene di mille belle, & leggiadri inuentioni; sono anche dottamente, & elegantemente composte. Infinite altre etiandio ue ne sono, composte da altri Eccellentissimi Musici; delle quali molte se ne ritrouano in
vn libretto, ilquale gia fù stampato in Vinegia da Andrea antico in ottauo foglio; lequali vedute, potranno
esser di grande aiuto per ritrouare altre simili inuentioni: percioche da quelle, si hauerà vn tal lume, che ciascuno dipoi si potrà porre a maggiori, & a più difficili imprese, & honoreuoli. Non mancarebbeno veramente oltra di queste
mille leggiadre inuentioni, che si potrebbeno fare; come sarebbe il voler comporre Tre parti
sopra vn Tenore di canto fermo in questa maniera; che due si seguitino per mouimenti contrarij; & l'altra
sia composta secondo il volere del Compositore; come qui in essempio si veggono.
tal maniera, si potranno sempre vsare in ciascuna compositione; sia di Quattro, di Cinque, o di qual'altro numero si voglia de voci. Di questi, et di altri simili casi, che potranno occorrere, ciascuno potrà hauere da quello, che si è detto piena resolutione: La onde non mi estenderò più oltra, per non perdere il tempo. Qualunque
volta etiandio occorrerà di voler comporre alcuna Cantilena a Cinque, ouero a Sei, oueramente à più voci; si
potrà osseruar quello, che da molti Musici celebratissimi è stato osseruato: Conciosia che pigliauano alle volte
per Soggetto vn Tenore di Canto fermo, & dipoi lo accommodauano con varie figure, come li tornaua più
commodo; et fondauano la Compositione sopra tal Tenore, & faceuano cantare le parti a quel modo, che li
tornauano meglio; di maniera, che facessero buona harmonia; vsando di porle in Fuga l'vna con l'altra; ouer
di fare, che l'vna imitasse l'altra, nel modo, che hò mostrato di sopra. Ilche si può vedere, volendo di ciò qualche essempio, in più Motetti gia composti da Adriano, si come in quello, che incomincia Nil postquam sacrum,
a Sei voci; & in quelli Victor io salue; et Inclite sforciadum, composti a Cinque voci; & in molti altri fatti da
altri Compositori. Pigliauano anco vn Tenore di canto fermo, sopra ilquale accommodauano (come fanno
etiandio al di d'hoggi) due, o Tre parti in Consequenza; & dipoi sopra di quelle faceuano l'altre; & di ciò si
può hauer l'essempio ne i Motetti Verbum supernum; sopra il canto di O salutaris hostia; & in quello, che incomincia Praeter rerum seriem, composti da Adriano a Sette voci; & in quello di Iachetto a Sei voci, che incomincia Descendi in ortum meum; oltra che si ritrouerà nella medesima maniera composti il motetto Miserere mei Deus, miserere mei, sopra l'Antifona Ne reminiscaris Domine; & la Oratione dominicale Pater
noster, con la Salutatione angelica Aue Maria; i quali gia composi l'vno a Sei, & gli altri a Sette voci.
Debbe però auertire il Compositore, che in quelle Fughe, lequali si fanno sopra tali Tenori, le parti possono esser
tra loro distanti per vna Terza, per vna Quarta, per vna Quinta, per vna Sesta, & altre simili Consonanze:
ma di raro si pone la Quarta, dopo laquale segua immediatamente la Sesta: o per il contrario. Similmente rare page 265volte si pongono due Seste: percioche sono difficili da accompagnare con le altre parti. Tali Consequenze si
sogliono, & si debbono veramente comporre prima, che si componghino le altre parti: ma bisogna hauer sempre riguardo nel comporle, in qual maniera le parti, che si hanno da aggiungere, si possino accommodare nella cantilena; accioche non si habbia doppia fatica nel comporre tutto'l corpo della Compositione, quando venisse alcuna cosa di sinistro in tali Consequenze. Et se nell'aggiungere le altre parti, si trouasse qualche discommodo; ouero, che per mutare le parti del Canto fermo posto in tali Consequenze, facesse migliore effetto;
allora non dè il Compositore perdonare a fatica; ma debbe mutare opinione, aggiungendo, o leuando alle dette parti quello, che farà dibisogno. Ilche sarà facile, quando le parti saranno state ben ordinate da principio. Ma si dè auertire, che le parti, che cantano in Fuga, non si possono sempre ordinare in tal maniera,
che'l Consequente canti tutto quello, che canta la Guida; onde è necessario, che seguendo la Guida il cantare
in fino al fine, il Consequente si venga a fermar poco lontano; si come si può vedere in molte cantilene composte a tal guisa; & massimamente in quelli Motetti. Veni sancte Spiritus di Adriano composti a Sei voci; & O beatum pontificem, che gia composi imitando il canto fermo, a Cinque voci. Si debbe vsare
etiandio tal discrettione nell'accommodar le parti; che quella, che canta nel suo luogo propio il Canto fermo;
dopo l'hauer cantato tutto quello, che fà dibisogno, o sia Canto fermo, ouero Imitatione; quello, che cantasse
più oltra, di quello, che dè cantare il Consequente, sia almeno quasi replicato. Il Consequente poi debbe essere ordinato in tal modo, che canti, & finisca tutto il Canto fermo, & non fuori del suo ordine. Di questi si
potrà hauere molti essempi accommodati, come sarebbe il Motetto, Salue regina misericordiae; & quello,
che incomincia, Litigabant Iudaei, sopra il canto fermo, Comedite pinguia, i quali gia molti anni composi a
Sei voci. Si potra anco pigliare vn Canto fermo, & ordinare sopra di lui molte parti; ponendone due, o più
l'vna all'altra in Fuga continoua, o legata, come vogliamo dire; come fece Iachetto nel motetto Murus tuus; & Adriano nel motetto Salue sancta parens a Sei voci. Potremo simigliantemente pigliare alcun Tenore, ordinandolo con vn'altra parte in Fuga in tal maniera; che volendo replicare le parti, facino
vna seconda parte, di modo, che quella che prima fù la Guida diuenti il Consequente; & similmente
quella, che era il Consequente diuenti la Guida. Di questa maniera si trouano molte compositioni, tra lequali è il motetto di Adriano, Venator lepores, sopra'l Canto fermo, Argentum, & aurum non est mihi; &
il motetto In principio Deus antequàm terram faceret, sopra quel canto fermo, Omnis sapientia, ilquale gia
composi da cantare a Sei voci, si come si canta etiandio il sopra detto. Vsano etiandio alle volte li Prattici,
imitando due, o più Tenori diuersi di varij canti ecclesiastici, comporre alcune cantilene a più voci, di maniera, che l'vna delle parti venghi ad imitar l'vno, & l'altra l'altro; come fece Iosquino, ilquale in cotal
maniera in vna compositione di Sei voci ne imitò Quattro, cioè Alma redemptoris mater. Aue regina
coelorum. Inuiolata, integra, & casta. & Regina coeli; si come fece anche Gomberto in vna Cantilena
a Quattro voci, che incomincia Salue regina. Alma redemptoris. Inuiolata. Aue regina coelorum, imitandone molti, come iui si può vedere; Ilche potrà etiandio fare ciascuno, imitandone diuersi altri: percioche veramente cotal cosa è molto lodeuole; per essere ingegnosa. Si potrà anco pigliare due Tenori di canto fermo, & accommodarli, come torna meglio alla cantilena, & sopra di essi comporre le altre parti; come fece Costanzo Festa nel motetto Exaltabo te Domine a Sei Voci, che accommodo l'Antifona Cum iucunditatem, & il primo verso del Cantico di Zacaria, Benedictus Dominus Deus Israel. Potremo etiandio
(come hanno fatto de gli altri) porre due parti della cantilena, lassando da parte il canto fermo, in Consequenza; oueramente porle legate insieme con la Imitatione; dilche si può hauere l'essempio nel motetto
Ecce tu pulchra es, ilquale gia composi a Cinque voci. Si potrebbe anche comporre le Cantilene facendo
le parti raddoppiate, cioè ponendo le parti a due, a due in Consequenza, ouero nella Imitatione; come fece
Motone nel motetto Nesciens mater; & Gomberto nel motetto Inuiolata, integra, & casta; l'vno, &
l'altro composto a Otto voci; & Adriano il nominato motetto Salue sancta parens, & la canzone Sur
l'herbe brunette, che l'vno, & l'altra si cantano a Sei voci. Oltra di questo si potrà comporre a Quattro,
a Cinque, & a più voci in mille modi (dirò cosi) ponendo le parti hora in Consequenza, hora nella Imitatione; oue si ritrouerà esser tanti li Consequenti, quante saranno le Guide; come si può vedere in quel motetto di Adriano, Sancta, & imaculata virginitas; & in vna sua canzone Petite camusete, a Quattro voci. Sarà anco lodeuole il comporre Quattro parti sopra vna, ponendone alcune in Fuga, & alcune nella
Imitatione; come fece P. della Rue nella messa O salutaris hostia; & Adriano anche, con molta legpage 266giadria, nella messa Mente tota; delle quali l'vna, & l'altra si troua a Quattro voci. Infiniti sono li modi del
comporre in simili maniere; & difficile anzi impossibile sarebbe, il voler raccontare di vna in vna le dispositioni delle parti, & del'ordine tenuto: Ma per non esser lungo farò fine; massimamente perche ogni giorno si veggono molte altre compositioni, composte dallo Eccellentissimo Adriano Vuillaert, lequali, oltra che
sono piene di mille belle, & leggiadri inuentioni; sono anche dottamente, & elegantemente composte. Infinite altre etiandio ue ne sono, composte da altri Eccellentissimi Musici; delle quali molte se ne ritrouano in
vn libretto, ilquale gia fù stampato in Vinegia da Andrea antico in ottauo foglio; lequali vedute, potranno
esser di grande aiuto per ritrouare altre simili inuentioni: percioche da quelle, si hauerà vn tal lume, che ciascuno dipoi si potrà porre a maggiori, & a più difficili imprese, & honoreuoli. Non mancarebbeno veramente oltra di queste
mille leggiadre inuentioni, che si potrebbeno fare; come sarebbe il voler comporre Tre parti
sopra vn Tenore di canto fermo in questa maniera; che due si seguitino per mouimenti contrarij; & l'altra
sia composta secondo il volere del Compositore; come qui in essempio si veggono.
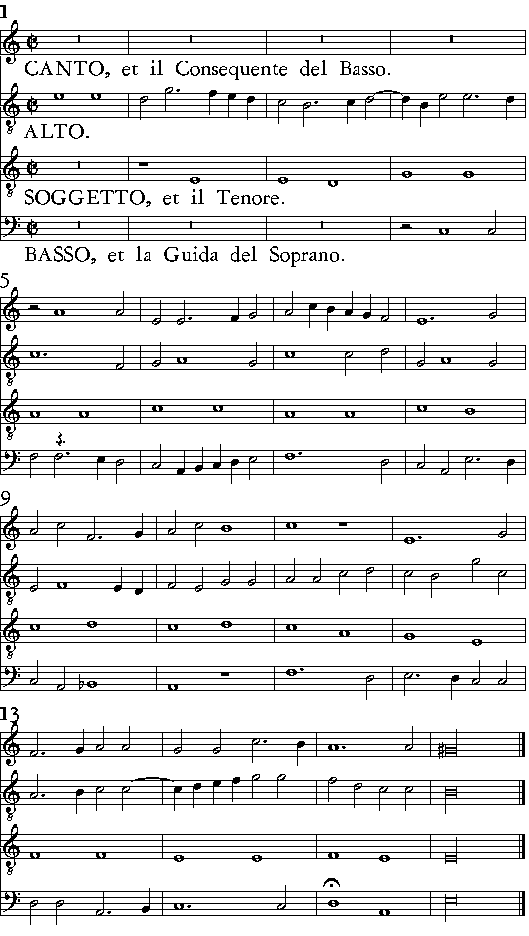 Et comporre etiandio Quattro parti in tal maniera, che'l Soprano co'l Basso; & il Contralto co'l Tenore cantino in Consequenza
per contrarij mouimenti; come nell'essempio posto qui di sotto si vede. Ma si debbe
auertire, di non porre mai l'Alto col Soprano, che facino Quarta; percioche l'altre parti non tornarebbeno bene. page 267
Et comporre etiandio Quattro parti in tal maniera, che'l Soprano co'l Basso; & il Contralto co'l Tenore cantino in Consequenza
per contrarij mouimenti; come nell'essempio posto qui di sotto si vede. Ma si debbe
auertire, di non porre mai l'Alto col Soprano, che facino Quarta; percioche l'altre parti non tornarebbeno bene. page 267 Quattro parti simili compose etiandio l'Eccellentissimo Adriano di maniera, che quando si è arriuato al fine, di nuouo si può incominciare dal principio, & ritornare quante fiate si vuole; come dimostrano li Ritornelli posti nel fine di ciascuna; delle quali ne porrò vn poco di essempio solamente, per non accrescere il volume, et
sarà il sotto posto; accioche da esso si possa comprendere, quello che sia il resto.
Quattro parti simili compose etiandio l'Eccellentissimo Adriano di maniera, che quando si è arriuato al fine, di nuouo si può incominciare dal principio, & ritornare quante fiate si vuole; come dimostrano li Ritornelli posti nel fine di ciascuna; delle quali ne porrò vn poco di essempio solamente, per non accrescere il volume, et
sarà il sotto posto; accioche da esso si possa comprendere, quello che sia il resto.
 Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osserua, di non comporre
alcuna Messa, se non sopra qualche Soggetto; però il medesimo si farà etiandio per l'auenire. Ma bisogna sapere,
che tal Soggetto può essere fatto dal Compositore, come fece Iosquino il Tenore di La, sol, fa, re, mi; & il Tenore della Messa Hercules Dux Ferrariae, cauato dalle vocali di queste parole, sopra lequali compose due
Messe a Quattro voci, che sono degne di essere vdite; Oueramente tal Soggetto lo piglia da altri: percioche si piglia alcun Tenore di Canto fermo; come fece il medesimo Iosquino, quando fece la Messa di
Pange lingua; quella di Gaudeamus, & quella di Aue maris stella; & Brumello quella de i Defunti, tutte a
Quattro voci: percioche molto si dilettauano, di comporre sopra li canti fermi; sopra i quali se ne vedeno
infinite altre, che sarebbe impossibile a numerarle. Quando adunque vorremo comporre alcuna Messa, ritrouaremo prima il Soggetto, sia Canto fermo, o qualche Motetto, come si vsa; oueramente altro simile; &
dipoi cercaremo di accommodarlo a diuersi modi; ritrouando noue inuentioni, & belle fantasie; imitando gli
Antichi, pigliando l'essempio da quella Messa, che fece P. Molù, ilquale la compose in tal maniera, che si può
cāantare cōon le Pause, et senza, et torna molto bene; et da quella, che fece Occheghen, ilquale fu maestro di Iosquino, page 268la quale compose di maniera, che si poteua cantare per qualunque Tempo, o prolatione si voleua, che faceua
buono effetto. Accaderà alle uolte di comporre alcuni Salmi in vna maniera, che si chiama a Choro spezzato, i quali spesse volte si sogliono cantare in Vinegia nelli Vesperi, & altre hore delle feste solenni; & sono ordinati, & diuisi in due Chori, ouer in tre; ne i quali cantano Quattro voci; & li Chori si cantano hora vno, hora l'altro a vicenda; & alcune volte (secondo il proposito) tutti insieme; massimamente nel fine: il che stà molto bene. Et perche cotali Chori si pongono alquanto lontani l'vn dall'altro; però auertirà il
Compositore (acciò non si odi dissonanza in alcuno di loro tra le parti) di fare in tal maniera la compositione; che ogni Choro sia consonante; cioè che le parti di un Choro siano ordinate in tal modo, quanto fussero composte a Quattro voci semplici, senza considerare gli altri Chori; hauendo però riguardo nel porre le parti, che
tra loro insiememente accordino, & non vi sia alcuna dissonanza: Percioche composti li Chori in cotal maniera, ciascuno da per sè si potrà cantare separato, che non si vdirà cosa alcuna, che offendi l'vdito. Questo
auertimento non è da sprezzare: percioche è di grande commodo; & fu ritrouato dall' Eccellentissimo Adriano. Et benche si rendi alquanto difficile, non si debbe però schiuare la fatica: percioche è cosa molto lodeuole, & virtuosa; & tale difficultà si farà alquanto più facile, quando si hauerà essaminato le dotte compositioni di esso Adriano; come sono quelli Salmi, Confitebor tibi domine in toto corde meo in consilio iustorum:
Laudate pueri dominum: Lauda Ierusalem dominum: Deprofundis: Memento domine Dauid, & molti
altri; tra i quali è il Cantico della Beata Vergine, Magnificat anima mea Dominum, il quale composi gia
molti anni a tre Chori. Queste compositioni vedute, & essaminate, saranno di gran giouamento a tutti coloro, che si dilettaranno di comporre in tal maniera: Conciosia che ritrouerà, che li Bassi de i chori si pongono tra loro sempre Vnisoni, ouero in Ottaua; ancora che alcune volte si ponghino in Terza: ma non si pongono in Quinta: percioche torna molto incommodo; & oltra la difficultà che nasce, è impossibile di far cosa,
che torni bene, secondo il proposito. Et questa osseruanza viene ad essere molto commoda alli Compositori:
percioche lieua a loro la difficultà di far cantare le parte delli Chori, che tra loro non si ritroua dissonanza.
Hora per concludere questo raggionamento, dico, che hauendo il Compositore intese tutte queste cose, dè auertire anco di terminare
il numero delle figure di ciascuna sua compositione, secondo che ricercano il Tempo, il
Modo, & la Prolatione; sotto i quali accidenti componerà la cantilena. Et perche simili accidenti erano gia
in grande consideratione, & anco appresso di alcuni sono in vso; però accioche ciascuno habbia cognitione di
simil cose, verrò a raggionare di loro alcune cose più bisognose; lassando quelle, che sono superstitiose, & che
fanno poco al proposito; & incomincierò dal Tempo, come da quello, che è (secondo'l mio parere) più vniuersale, & primo di ogn'altro accidente.
Et perche da gli antichi Musici si è osseruato, & anco al presente da i Moderni si osserua, di non comporre
alcuna Messa, se non sopra qualche Soggetto; però il medesimo si farà etiandio per l'auenire. Ma bisogna sapere,
che tal Soggetto può essere fatto dal Compositore, come fece Iosquino il Tenore di La, sol, fa, re, mi; & il Tenore della Messa Hercules Dux Ferrariae, cauato dalle vocali di queste parole, sopra lequali compose due
Messe a Quattro voci, che sono degne di essere vdite; Oueramente tal Soggetto lo piglia da altri: percioche si piglia alcun Tenore di Canto fermo; come fece il medesimo Iosquino, quando fece la Messa di
Pange lingua; quella di Gaudeamus, & quella di Aue maris stella; & Brumello quella de i Defunti, tutte a
Quattro voci: percioche molto si dilettauano, di comporre sopra li canti fermi; sopra i quali se ne vedeno
infinite altre, che sarebbe impossibile a numerarle. Quando adunque vorremo comporre alcuna Messa, ritrouaremo prima il Soggetto, sia Canto fermo, o qualche Motetto, come si vsa; oueramente altro simile; &
dipoi cercaremo di accommodarlo a diuersi modi; ritrouando noue inuentioni, & belle fantasie; imitando gli
Antichi, pigliando l'essempio da quella Messa, che fece P. Molù, ilquale la compose in tal maniera, che si può
cāantare cōon le Pause, et senza, et torna molto bene; et da quella, che fece Occheghen, ilquale fu maestro di Iosquino, page 268la quale compose di maniera, che si poteua cantare per qualunque Tempo, o prolatione si voleua, che faceua
buono effetto. Accaderà alle uolte di comporre alcuni Salmi in vna maniera, che si chiama a Choro spezzato, i quali spesse volte si sogliono cantare in Vinegia nelli Vesperi, & altre hore delle feste solenni; & sono ordinati, & diuisi in due Chori, ouer in tre; ne i quali cantano Quattro voci; & li Chori si cantano hora vno, hora l'altro a vicenda; & alcune volte (secondo il proposito) tutti insieme; massimamente nel fine: il che stà molto bene. Et perche cotali Chori si pongono alquanto lontani l'vn dall'altro; però auertirà il
Compositore (acciò non si odi dissonanza in alcuno di loro tra le parti) di fare in tal maniera la compositione; che ogni Choro sia consonante; cioè che le parti di un Choro siano ordinate in tal modo, quanto fussero composte a Quattro voci semplici, senza considerare gli altri Chori; hauendo però riguardo nel porre le parti, che
tra loro insiememente accordino, & non vi sia alcuna dissonanza: Percioche composti li Chori in cotal maniera, ciascuno da per sè si potrà cantare separato, che non si vdirà cosa alcuna, che offendi l'vdito. Questo
auertimento non è da sprezzare: percioche è di grande commodo; & fu ritrouato dall' Eccellentissimo Adriano. Et benche si rendi alquanto difficile, non si debbe però schiuare la fatica: percioche è cosa molto lodeuole, & virtuosa; & tale difficultà si farà alquanto più facile, quando si hauerà essaminato le dotte compositioni di esso Adriano; come sono quelli Salmi, Confitebor tibi domine in toto corde meo in consilio iustorum:
Laudate pueri dominum: Lauda Ierusalem dominum: Deprofundis: Memento domine Dauid, & molti
altri; tra i quali è il Cantico della Beata Vergine, Magnificat anima mea Dominum, il quale composi gia
molti anni a tre Chori. Queste compositioni vedute, & essaminate, saranno di gran giouamento a tutti coloro, che si dilettaranno di comporre in tal maniera: Conciosia che ritrouerà, che li Bassi de i chori si pongono tra loro sempre Vnisoni, ouero in Ottaua; ancora che alcune volte si ponghino in Terza: ma non si pongono in Quinta: percioche torna molto incommodo; & oltra la difficultà che nasce, è impossibile di far cosa,
che torni bene, secondo il proposito. Et questa osseruanza viene ad essere molto commoda alli Compositori:
percioche lieua a loro la difficultà di far cantare le parte delli Chori, che tra loro non si ritroua dissonanza.
Hora per concludere questo raggionamento, dico, che hauendo il Compositore intese tutte queste cose, dè auertire anco di terminare
il numero delle figure di ciascuna sua compositione, secondo che ricercano il Tempo, il
Modo, & la Prolatione; sotto i quali accidenti componerà la cantilena. Et perche simili accidenti erano gia
in grande consideratione, & anco appresso di alcuni sono in vso; però accioche ciascuno habbia cognitione di
simil cose, verrò a raggionare di loro alcune cose più bisognose; lassando quelle, che sono superstitiose, & che
fanno poco al proposito; & incomincierò dal Tempo, come da quello, che è (secondo'l mio parere) più vniuersale, & primo di ogn'altro accidente.
Del Tempo, del Modo, & della Prolatione; Et in che quantità si debbino finire, o numerare le Cantilene.Cap. 67.
 , per il quale si denota, che la Breue in
tutta la cantilena è perfetta, cioè si pone in luogo di tre Semibreui; o per il contrario tre Semibreui in luogo
di vna Breue: Ma lo Imperfetto si troua, quando nel detto principio è posto il Semicircolo
, per il quale si denota, che la Breue in
tutta la cantilena è perfetta, cioè si pone in luogo di tre Semibreui; o per il contrario tre Semibreui in luogo
di vna Breue: Ma lo Imperfetto si troua, quando nel detto principio è posto il Semicircolo  , in luogo del
circolo; per il quale si comprende, che la Breue si pone imperfetta; cioè in luogo di due Semibreui, o per il contrario, due Semibreui in luogo di vna Breue. Quando adunque si componerà alcuna cantilena sotto'l segno
del Tempo perfetto, inteso per il Circolo, che dinota il numero Ternario; secondo alcuni rispetti, detto numero Perfetto;
si numerarà quella a Breui perfette; cioè a tre Semibreui per ogni Tempo: Ma quando si componerà sotto'l segno dell'Imperfetto, dinotato per il Semicircolo; si numerarà a Breui imperfette; cioè a due
Semibreui per ogni Tempo: essendo che in questo si considera il numero Binario, chiamato da alcuni numero Imperfetto. Bisogna
però auertire, che l'vltima Figura, o Nota d'ogni cantilena non si pone in tal numero: conciosia che essendo finale in essa si termina il concento, & il Tempo: & ciascuno di questi terminano
sopra quella figura; nella quale hebbero principio, che è la prima Semibreue. Il Modo (lassando da parte
quello, del quale si ragiona nella Quarta parte) gli Antichi diceuano, essere vna Quantità di Lunghe, o di
Breui, considerata nella Massima, o nella Lunga, secondo la diuisione binaria, o ternaria: percioche lo diuisero in due parti; cioè in Maggiore, & in Minore; & ciascuno di questi considerauano Perfetto, oueramente Imperfetto. Intendeuano il Maggiore, quando poneuano due Pause di Lunga, ouer tre insieme, le quali
, in luogo del
circolo; per il quale si comprende, che la Breue si pone imperfetta; cioè in luogo di due Semibreui, o per il contrario, due Semibreui in luogo di vna Breue. Quando adunque si componerà alcuna cantilena sotto'l segno
del Tempo perfetto, inteso per il Circolo, che dinota il numero Ternario; secondo alcuni rispetti, detto numero Perfetto;
si numerarà quella a Breui perfette; cioè a tre Semibreui per ogni Tempo: Ma quando si componerà sotto'l segno dell'Imperfetto, dinotato per il Semicircolo; si numerarà a Breui imperfette; cioè a due
Semibreui per ogni Tempo: essendo che in questo si considera il numero Binario, chiamato da alcuni numero Imperfetto. Bisogna
però auertire, che l'vltima Figura, o Nota d'ogni cantilena non si pone in tal numero: conciosia che essendo finale in essa si termina il concento, & il Tempo: & ciascuno di questi terminano
sopra quella figura; nella quale hebbero principio, che è la prima Semibreue. Il Modo (lassando da parte
quello, del quale si ragiona nella Quarta parte) gli Antichi diceuano, essere vna Quantità di Lunghe, o di
Breui, considerata nella Massima, o nella Lunga, secondo la diuisione binaria, o ternaria: percioche lo diuisero in due parti; cioè in Maggiore, & in Minore; & ciascuno di questi considerauano Perfetto, oueramente Imperfetto. Intendeuano il Maggiore, quando poneuano due Pause di Lunga, ouer tre insieme, le quali
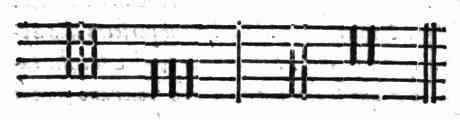 pigliassero due, ouer tre spatij; & tre, o quattro linee
delle cinque gia mostrate, come qui si vede: Ma il Minore considerauano, quando poneuano vna sola Pausa,
che abbracciasse tre, ouer quattro delle predette linee.
Il Modo perfetto maggiore intendeuano, quando poneuano tre delle mostrate pause insieme; & l'Imperfetto maggiore, quando erano solamente due. Ma per lo
pigliassero due, ouer tre spatij; & tre, o quattro linee
delle cinque gia mostrate, come qui si vede: Ma il Minore considerauano, quando poneuano vna sola Pausa,
che abbracciasse tre, ouer quattro delle predette linee.
Il Modo perfetto maggiore intendeuano, quando poneuano tre delle mostrate pause insieme; & l'Imperfetto maggiore, quando erano solamente due. Ma per lo
 Perfetto minore pigliano quello, che hauea vna pausa, che abbracciaua
quattro linee, & tre delli sopra nominati spatij: & il Minore imperfetto,
quando la detta pausa posta in tal maniera abbracciaua solamente tre linee,
& due spatij: Di maniera, che nel Modo maggior perfetto faceuano valere
la Massima tre Lunghe, & nell'Imperfetto due. Similmente nel Modo minor perfetto faceuano valere la Lunga tre Breui, & nell'Imperfetto due. La onde quando componeuano,
ordinauano in tal maniera le loro cantilene; che nel Modo maggior perfetto numerauano di tre Lunghe in
tre Lunghe; o perfette, ouero imperfette, che fussero; & sotto'l Modo maggiore imperfetto, di due Lunghe
in due Lunghe. Simigliantemente nel Modo minor perfetto numerauano di tre Breui in tre Breui, & nell'Imperfetto di due in due. Onde si può vedere, che quando il Compositore componesse sotto alcuno di questi
Modi, & non numerasse la cantilena secondo il detto numero al modo detto; si potrebbe veramente dire,
che costui fusse poco considerato; & che non hauesse alcuna cognitione di tal cosa. Poneuano gli Antichi le
nominate Pause in due maniere: imperoche ne poneuano alcune auanti i segni del Tempo, & alcune dopo.
Le prime chiamauano Inditiali solamente: percioche non si numerauano nella compositione: ma erano poste in
cotal luogo per dimostrar solamente il Modo, o maggiore, o minore che si fusse, sotto'l quale era composta la
cantilena. Le seconde nominauano Indiciali, & Essentiali: conciosia che non solo seruiuano a dimostrare il
Modo, se fusse maggiore, o minore: ma seruiuano etiandio alla cantilena; come nel sottoposto essempio si
può comprendere.
Perfetto minore pigliano quello, che hauea vna pausa, che abbracciaua
quattro linee, & tre delli sopra nominati spatij: & il Minore imperfetto,
quando la detta pausa posta in tal maniera abbracciaua solamente tre linee,
& due spatij: Di maniera, che nel Modo maggior perfetto faceuano valere
la Massima tre Lunghe, & nell'Imperfetto due. Similmente nel Modo minor perfetto faceuano valere la Lunga tre Breui, & nell'Imperfetto due. La onde quando componeuano,
ordinauano in tal maniera le loro cantilene; che nel Modo maggior perfetto numerauano di tre Lunghe in
tre Lunghe; o perfette, ouero imperfette, che fussero; & sotto'l Modo maggiore imperfetto, di due Lunghe
in due Lunghe. Simigliantemente nel Modo minor perfetto numerauano di tre Breui in tre Breui, & nell'Imperfetto di due in due. Onde si può vedere, che quando il Compositore componesse sotto alcuno di questi
Modi, & non numerasse la cantilena secondo il detto numero al modo detto; si potrebbe veramente dire,
che costui fusse poco considerato; & che non hauesse alcuna cognitione di tal cosa. Poneuano gli Antichi le
nominate Pause in due maniere: imperoche ne poneuano alcune auanti i segni del Tempo, & alcune dopo.
Le prime chiamauano Inditiali solamente: percioche non si numerauano nella compositione: ma erano poste in
cotal luogo per dimostrar solamente il Modo, o maggiore, o minore che si fusse, sotto'l quale era composta la
cantilena. Le seconde nominauano Indiciali, & Essentiali: conciosia che non solo seruiuano a dimostrare il
Modo, se fusse maggiore, o minore: ma seruiuano etiandio alla cantilena; come nel sottoposto essempio si
può comprendere.
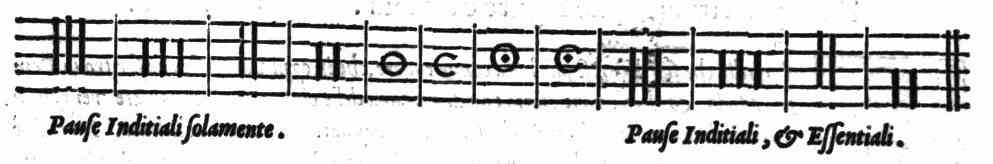

 & la Imperfetta, quando erano posti senza li punti; & faceuano valere
la Semibreue tre Minime sotto li due primi puntati, et sotto quelli, che non erano puntati due. Numerauano poi le cantilene
in questa maniera; che quelle che erano poste sotto la Prolation perfetta, procedeuano, & erano numerate di tre Minime in tre Minime; & quelle, che erano composte sotto la Imperfetta, di due in due; & numerauano la cantilena a Lunghe, ouero a Breui, oueramente a Semibreui: percioche ciascuna Lunga, o Breue, o Semibreue può esser perfetta, ouero imperfetta. Et perche spesse volte si aggiungeuano insieme questi due gradi, cio è il Perfetto & lo Imperfetto; però auertiuano in tale congiuntione:
che se'l Modo maggiore era congiunto col minore, & l'vno, & l'altro fussero stati Perfetti: allora numerauano la cantilena di tre Lunghe in tre Lunghe perfette. Ma se'l Modo fusse stato Minor perfetto, la numerauano con tre Lunghe
imperfette. Et con simili consideratione procedeuano ne gli altri gradi; si come nel
Tempo, & nella Prolatione, perfetti, & imperfetti. Potemo hora vedere, che per li segni, cioè per il Circolo, & per lo Semicircolo haueano la cognitione del Tempo perfetto, o uero imperfetto: per le Pause haueano cognitione del Modo, maggiore, o minore; perfetto, ouero imperfetto, che'l si fusse; & per li segni del Tempo puntati, o non puntati la Prolatione perfetta, ouero imperfetta: di maniera che potemo etiandio vedere,
che attribuirono il Modo maggior perfetto alla Massima di valore di tre lunghe; & a quella di valor di due
il Modo maggiore imperfetto: Similmente alla Lunga di valor di tre Breui attribuirono il Modo minor perfetto, & a quella di
valor di due il Modo minore imperfetto. Il Tempo perfetto attribuirono alla Breue di
valore di tre Semibreui, & l'imperfetto a quella, che val due. Diedero anco la Prolatione perfetta alla Semibreue di valor di tre Minime: ma la imperfetta diedero a quella di due. Soleuano anco gli Antichi tagliare li segni del Tempo in tal maniera,
& la Imperfetta, quando erano posti senza li punti; & faceuano valere
la Semibreue tre Minime sotto li due primi puntati, et sotto quelli, che non erano puntati due. Numerauano poi le cantilene
in questa maniera; che quelle che erano poste sotto la Prolation perfetta, procedeuano, & erano numerate di tre Minime in tre Minime; & quelle, che erano composte sotto la Imperfetta, di due in due; & numerauano la cantilena a Lunghe, ouero a Breui, oueramente a Semibreui: percioche ciascuna Lunga, o Breue, o Semibreue può esser perfetta, ouero imperfetta. Et perche spesse volte si aggiungeuano insieme questi due gradi, cio è il Perfetto & lo Imperfetto; però auertiuano in tale congiuntione:
che se'l Modo maggiore era congiunto col minore, & l'vno, & l'altro fussero stati Perfetti: allora numerauano la cantilena di tre Lunghe in tre Lunghe perfette. Ma se'l Modo fusse stato Minor perfetto, la numerauano con tre Lunghe
imperfette. Et con simili consideratione procedeuano ne gli altri gradi; si come nel
Tempo, & nella Prolatione, perfetti, & imperfetti. Potemo hora vedere, che per li segni, cioè per il Circolo, & per lo Semicircolo haueano la cognitione del Tempo perfetto, o uero imperfetto: per le Pause haueano cognitione del Modo, maggiore, o minore; perfetto, ouero imperfetto, che'l si fusse; & per li segni del Tempo puntati, o non puntati la Prolatione perfetta, ouero imperfetta: di maniera che potemo etiandio vedere,
che attribuirono il Modo maggior perfetto alla Massima di valore di tre lunghe; & a quella di valor di due
il Modo maggiore imperfetto: Similmente alla Lunga di valor di tre Breui attribuirono il Modo minor perfetto, & a quella di
valor di due il Modo minore imperfetto. Il Tempo perfetto attribuirono alla Breue di
valore di tre Semibreui, & l'imperfetto a quella, che val due. Diedero anco la Prolatione perfetta alla Semibreue di valor di tre Minime: ma la imperfetta diedero a quella di due. Soleuano anco gli Antichi tagliare li segni del Tempo in tal maniera, 


 & questo faceuano, quando voleuano, che le
figure sottoposte alla perfettione, & allaimperfettione, et anche all'Alteratione nel Tempo perfetto, & nello imperfetto, fussero più veloci. Le quali figure (come vederemo) sono cinque Massima, Lunga, Breue, Semibreue,
& Minima. E ben uero, che faceuano le Minime nere,
per farle veloci, di maniera che ne per il tagliare li segni, ne per il far nere le dette figure, leuauano a loro il
nome: ma lo riteneuano tanto, quanto che tali segni fussero stati interi. Ne per il tagliare de i detti segni si
leuaua la imperfettione, o la perfettione, ne meno l'Alteratione; ma tanto erano sottoposte a tali accidenti,
& passioni, quanto essi segni fussero stati interi. Al presente hauemo altra ragione della Minima nera, essendo che (come hò mostrato altroue) è chiamata Semiminima, la qual si diuide in due Chrome, & la Chroma in due Semichrome.
Haueano etiandio sotto'l segno del Tempo perfetto tagliato doppia consideratione
nel numerare componendo le cantilene: percioche numerauano a tre a tre, & anco a due a due, cioè di due
Breue perfette in due; oueramente di tre Semibreui in tre: di maniera che'l numerare delle Semibreui finiua
nel numero Senario: conciosia che se misurauano altramente non ritrouauano nelle lor cantilene la misura della Breue. Il che parimente cercaremo anche noi di osseruare, non solo nel Tempo perfetto: ma anco nell'Imperfetto tagliato; procedendo di due Breui imperfette in due; acciò la cantilena finisca nel numero Quaternario. Che diremo
hora di alcuni Compositori moderni, i quali non solamente non osseruano la misura del numero Senario, o Quaternario nelle lor cantilene: ma di più non osseruano il numero Ternario nel Tempo perfetto, ne meno nell'Imperfetto
il Binario; siano tagliati, o non tagliati; il che veramente è a loro vna gran
vergogna: conciosia che vengono a rompere il Tempo, & la misura, delle quali cose gli Antichi furono osseruatori molto diligenti; & per tal maniera guastano, & confondeno ogni cosa.
& questo faceuano, quando voleuano, che le
figure sottoposte alla perfettione, & allaimperfettione, et anche all'Alteratione nel Tempo perfetto, & nello imperfetto, fussero più veloci. Le quali figure (come vederemo) sono cinque Massima, Lunga, Breue, Semibreue,
& Minima. E ben uero, che faceuano le Minime nere,
per farle veloci, di maniera che ne per il tagliare li segni, ne per il far nere le dette figure, leuauano a loro il
nome: ma lo riteneuano tanto, quanto che tali segni fussero stati interi. Ne per il tagliare de i detti segni si
leuaua la imperfettione, o la perfettione, ne meno l'Alteratione; ma tanto erano sottoposte a tali accidenti,
& passioni, quanto essi segni fussero stati interi. Al presente hauemo altra ragione della Minima nera, essendo che (come hò mostrato altroue) è chiamata Semiminima, la qual si diuide in due Chrome, & la Chroma in due Semichrome.
Haueano etiandio sotto'l segno del Tempo perfetto tagliato doppia consideratione
nel numerare componendo le cantilene: percioche numerauano a tre a tre, & anco a due a due, cioè di due
Breue perfette in due; oueramente di tre Semibreui in tre: di maniera che'l numerare delle Semibreui finiua
nel numero Senario: conciosia che se misurauano altramente non ritrouauano nelle lor cantilene la misura della Breue. Il che parimente cercaremo anche noi di osseruare, non solo nel Tempo perfetto: ma anco nell'Imperfetto tagliato; procedendo di due Breui imperfette in due; acciò la cantilena finisca nel numero Quaternario. Che diremo
hora di alcuni Compositori moderni, i quali non solamente non osseruano la misura del numero Senario, o Quaternario nelle lor cantilene: ma di più non osseruano il numero Ternario nel Tempo perfetto, ne meno nell'Imperfetto
il Binario; siano tagliati, o non tagliati; il che veramente è a loro vna gran
vergogna: conciosia che vengono a rompere il Tempo, & la misura, delle quali cose gli Antichi furono osseruatori molto diligenti; & per tal maniera guastano, & confondeno ogni cosa.
Della perfettione delle Figure cantabili.Cap. 68.
 La Massima etiandio posta auanti vna Legatura di valor di due lunghe; & la lunga auanti quella di due
breui; & la breue auanti quella di due semibreui, ouer due pause di semibreue poste sopra vna linea istessa,
sempre saranno perfette: essendo che tali Legature, o Pause poste in cotal maniera hanno virtù di vnità: il
che auiene anco nella Semibreue, quando è posta auanti due pause di minima poste all'istesso modo. Ma se
tali Pause fussero separate, tal Regola non hauerebbe luogo. Et se alcuno volesse dire, che la Figura posta
auanti la Legatura non può esser perfetta; adduca che ragione si voglia, si potrà rispondere; che se la Breue è perfetta, quando è posta auanti due pause di semibreue, poste sopra vna istessa linea, sotto'l segno del Tempo perfetto;
maggiormente de esser perfetta auanti la Legatura; poi che le Pause non dinotano altro, che priuatione di suono, o di voce;
& la Legatura lo pone in essere; come qui si vede. page 272
La Massima etiandio posta auanti vna Legatura di valor di due lunghe; & la lunga auanti quella di due
breui; & la breue auanti quella di due semibreui, ouer due pause di semibreue poste sopra vna linea istessa,
sempre saranno perfette: essendo che tali Legature, o Pause poste in cotal maniera hanno virtù di vnità: il
che auiene anco nella Semibreue, quando è posta auanti due pause di minima poste all'istesso modo. Ma se
tali Pause fussero separate, tal Regola non hauerebbe luogo. Et se alcuno volesse dire, che la Figura posta
auanti la Legatura non può esser perfetta; adduca che ragione si voglia, si potrà rispondere; che se la Breue è perfetta, quando è posta auanti due pause di semibreue, poste sopra vna istessa linea, sotto'l segno del Tempo perfetto;
maggiormente de esser perfetta auanti la Legatura; poi che le Pause non dinotano altro, che priuatione di suono, o di voce;
& la Legatura lo pone in essere; come qui si vede. page 272 Alle volte alcuna delle mostrate figure sarà perfetta, quando dopo se haurà il Punto di perfettione; si come la Massima nel Modo maggior perfetto; la Lunga nel Modo minor perfetto; la Breue nel Tempo perfetto; & la Semibreue nella Prolation perfetta; come qui in essempio si vede.Quando saranno collocate
Alle volte alcuna delle mostrate figure sarà perfetta, quando dopo se haurà il Punto di perfettione; si come la Massima nel Modo maggior perfetto; la Lunga nel Modo minor perfetto; la Breue nel Tempo perfetto; & la Semibreue nella Prolation perfetta; come qui in essempio si vede.Quando saranno collocate
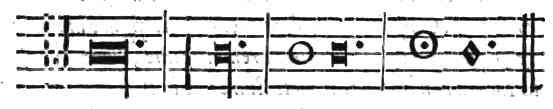 tra due figure maggiori due, o tre minori propinque; la prima maggiore sempre sarà perfetta. Si come per essempio nel Modo maggior
perfetto due, o tre Lunghe poste tra due Massime fanno, che la prima Massima sia perfetta; nel Modo minor perfetto due, o tre Breui poste tra due Lunghe fanno, che la prima Lunga sia perfetta.
Questo istesso fanno due, o tre Semibreui poste tra due Breui nel Tempo perfetto; & nella Prolation maggiore due, o tre Minime poste tra due Semibreui: percioche la prima Breue, et la prima Semibreue diuentano
perfette. L'istesso faranno le Figure, & le Pause insieme di vno istesso valore nella istessa maniera collocate: ma si de auertire, che quando si porrà tra due maggiori vna sola minore, & la sua Pausa; si porrà primieramente la Pausa, & dipoi la Figura: Ma quando si porrà due Figure minori, & vna Pausa, allora la
Pausa si potrà porre in qual luogo tornerà più commodo; si come nel sottoposto essempio si può vedere.
tra due figure maggiori due, o tre minori propinque; la prima maggiore sempre sarà perfetta. Si come per essempio nel Modo maggior
perfetto due, o tre Lunghe poste tra due Massime fanno, che la prima Massima sia perfetta; nel Modo minor perfetto due, o tre Breui poste tra due Lunghe fanno, che la prima Lunga sia perfetta.
Questo istesso fanno due, o tre Semibreui poste tra due Breui nel Tempo perfetto; & nella Prolation maggiore due, o tre Minime poste tra due Semibreui: percioche la prima Breue, et la prima Semibreue diuentano
perfette. L'istesso faranno le Figure, & le Pause insieme di vno istesso valore nella istessa maniera collocate: ma si de auertire, che quando si porrà tra due maggiori vna sola minore, & la sua Pausa; si porrà primieramente la Pausa, & dipoi la Figura: Ma quando si porrà due Figure minori, & vna Pausa, allora la
Pausa si potrà porre in qual luogo tornerà più commodo; si come nel sottoposto essempio si può vedere.
 Quando nel Tempo perfetto tra due Breui si porrà cinque, o sei Semibreui, allora la prima Breue sarà perfetta, & l'vltima
delle cinque Semibreui alterata; cioè raddoppiata. Ma la prima Breue posta auanti le
sei Semibreui sarà sempre perfetta, senza alteratione di alcuna delle Semibreui: percioche le sei Semibreui
Quando nel Tempo perfetto tra due Breui si porrà cinque, o sei Semibreui, allora la prima Breue sarà perfetta, & l'vltima
delle cinque Semibreui alterata; cioè raddoppiata. Ma la prima Breue posta auanti le
sei Semibreui sarà sempre perfetta, senza alteratione di alcuna delle Semibreui: percioche le sei Semibreui
 sono poste per due Tempi interi;
come qui si vedeno.Ma per
qual cagione le mostrate Pause
si ponghino più in vn luogo, che
in vn'altro, da quello che dirò altroue, facilmente si potrà comprendere. Et benche io habbia in questo vltimo essempio posto
solamente la
Breue nel Tempo perfetto: si può intendere tutto quello, che hò detto etiandio della Massima, & della Lunpage 273ga nel modo maggiore, & minore perfetti; & della Semibreue nella Prolatione: Imperoche non si troua
ragione, che maggiormente ne costringa a far perfetta più l'vna che l'altra; massimamente essendo accommodate a i loro luoghi, & sotto li segni loro proportionatamente.
sono poste per due Tempi interi;
come qui si vedeno.Ma per
qual cagione le mostrate Pause
si ponghino più in vn luogo, che
in vn'altro, da quello che dirò altroue, facilmente si potrà comprendere. Et benche io habbia in questo vltimo essempio posto
solamente la
Breue nel Tempo perfetto: si può intendere tutto quello, che hò detto etiandio della Massima, & della Lunpage 273ga nel modo maggiore, & minore perfetti; & della Semibreue nella Prolatione: Imperoche non si troua
ragione, che maggiormente ne costringa a far perfetta più l'vna che l'altra; massimamente essendo accommodate a i loro luoghi, & sotto li segni loro proportionatamente.
Della Imperfettione delle Figure cantabili.Cap. 69.
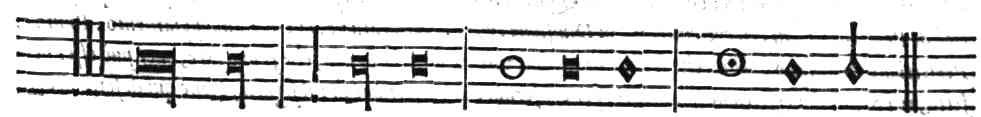 page 274Il medesimo anco può accascare nelle gia dette Figure, quando dopo esse immediatamente segue alcuna Pausa di valore della lor parte propinqua:Similmente il Colore è cagione di tale imperfettione; & tali im
page 274Il medesimo anco può accascare nelle gia dette Figure, quando dopo esse immediatamente segue alcuna Pausa di valore della lor parte propinqua:Similmente il Colore è cagione di tale imperfettione; & tali im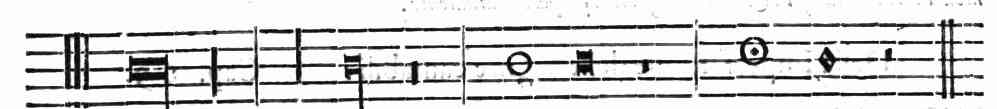 perfettioni si chiamano Dalla parte dopo: imperoche Dalla parte inanti si faranno cotali imperfettioni, quan
perfettioni si chiamano Dalla parte dopo: imperoche Dalla parte inanti si faranno cotali imperfettioni, quan do le Figure saranno poste al contrario; si come quando le Pause, o le Figure minori saranno poste inanti le
maggiori. Tali Figure saranno etiandio imperfette tanto dalla parte dopo, quanto dalla parte inanti; cioè
dalla seguente, & dalla antecedente, per il Punto; quando tra due figure maggiori saranno poste due figure minori propinque; tra le quali sia il Punto; come qui si uede:
do le Figure saranno poste al contrario; si come quando le Pause, o le Figure minori saranno poste inanti le
maggiori. Tali Figure saranno etiandio imperfette tanto dalla parte dopo, quanto dalla parte inanti; cioè
dalla seguente, & dalla antecedente, per il Punto; quando tra due figure maggiori saranno poste due figure minori propinque; tra le quali sia il Punto; come qui si uede:
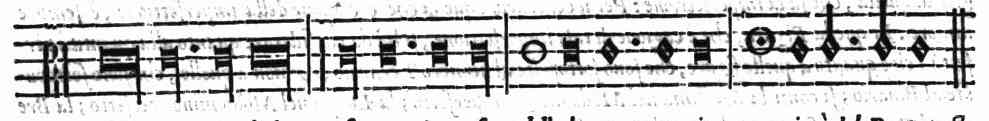 Imperoche la prima, & l'ultima resteranno imperfette della lor parte propinqua per uirtù del Punto posto
tra le minori, che si chiama di Diuisione; come più oltra uederemo. Saranno etiandio imperfette tali Figure,
quando tra due maggiori, dalla parte sinistra sarà collocato una figura, che le sia parte propinqua; alla quale senza alcun mezo succeda una Pausa di tanto ualore; come qui si uede. In molte altre maniere le Figu
Imperoche la prima, & l'ultima resteranno imperfette della lor parte propinqua per uirtù del Punto posto
tra le minori, che si chiama di Diuisione; come più oltra uederemo. Saranno etiandio imperfette tali Figure,
quando tra due maggiori, dalla parte sinistra sarà collocato una figura, che le sia parte propinqua; alla quale senza alcun mezo succeda una Pausa di tanto ualore; come qui si uede. In molte altre maniere le Figu re si fanno anco imperfette quanto al loro Tutto: ma perche sono modi alquanto superstitiosi, bastarà solamente quello, che hò detto intorno alla imperfettione delle figure cantabili quanto al Tutto; cioè quanto alla
parte propinqua: Imperoche quanto all'imperfettione delle altre loro parti, dopo che si hauerà considerato
tutto quello, ch'io hò detto di sopra, ritrouaremo, che tale imperfettione si fa, quando saranno fatte imperfette di vna quantità minore delle mostrate; siano poi imperfette dalla parte inanti, ouer dalla parte dopo;
o pur dall'vna, & l'altra delle nominate. Ma vediamo quello, che sia il Punto nella Musica, & di quante sorti si troui.
re si fanno anco imperfette quanto al loro Tutto: ma perche sono modi alquanto superstitiosi, bastarà solamente quello, che hò detto intorno alla imperfettione delle figure cantabili quanto al Tutto; cioè quanto alla
parte propinqua: Imperoche quanto all'imperfettione delle altre loro parti, dopo che si hauerà considerato
tutto quello, ch'io hò detto di sopra, ritrouaremo, che tale imperfettione si fa, quando saranno fatte imperfette di vna quantità minore delle mostrate; siano poi imperfette dalla parte inanti, ouer dalla parte dopo;
o pur dall'vna, & l'altra delle nominate. Ma vediamo quello, che sia il Punto nella Musica, & di quante sorti si troui.
Del Punto, delle sue specie, & delli suoi effetti.Cap. 70.
 Quello di Accrescimento è quel, che si pone senza alcun mezo dopo la figura, la quale non può esser, ne si
può fare perfetta per alcun modo; si come ciascuna figura posta ne i Segni di imperfettione; & ne i Segni
della perfettione a quelle, che sono di minor valore della Semibreue; come qui si veggono.
Quello di Accrescimento è quel, che si pone senza alcun mezo dopo la figura, la quale non può esser, ne si
può fare perfetta per alcun modo; si come ciascuna figura posta ne i Segni di imperfettione; & ne i Segni
della perfettione a quelle, che sono di minor valore della Semibreue; come qui si veggono.
 Onde si dè auertire, che li Punti nominati si scriueno (come hò mostrato) nel mezo del lato destro della figura, tanto perfetta, quanto imperfetta; & fanno maggiore la figura imperfetta di tanta quantità, quanta è la metà di tal figura; cioè quanta è la metà del suo Tutto; si come per essempio nella Lunga, che val
quattro Semibreui; che aggiuntole il Punto varrà sei: ma quando si aggiunge a quelle, che si possono far
perfette, sempre il Punto val la Terza parte della figura perfetta, alla quale si pone appresso; & vale la
metà della figura imperfetta. Per il che si uede la differenza, che è tra il Punto di Perfettione, & quello di
Accrescimento; che l'vno si pone solamente appresso quelle figure, che si possono far perfette, sotto i Segni
della loro perfettione; & l'altro si pone a quelle, che non si possono far perfette. Et tali Punti tanto operano nelle figure legate, quanto nelle sciolte. Il Punto di diuisione è quello, che si pone tra due figure simili
minori, & propinque poste tra due maggiori, ne i Segni della perfettione; il cui vfficio è di diuidere, & di
fare imperfetta l'una, & l'altra delle figure maggiori; si come la prima dalla parte dopo; & l'altra dalla
parte inanti. Et si scriue sopra tale figure nel mezo di loro; & tal Punto non si canta. Di maniera che in
quanto separa l'vna figura dall'altra delle due minori, & le accompagna con le maggiori, è chiamato di
Diuisione: Ma in quanto fa la imperfettione nelle maggiori, si può nominare anco Punto di Imperfettione: percioche (con ogni douere) sempre si dè porre nel fine del Tempo passato, & nel principio di quello,
che è presente. Et si pone etiandio tra la Pausa, che tiene il primo luogo, & vna Figura, che tenghi il secondo, le quali siano di vno istesso valore; come nel sottoposto essempio si vede.
Onde si dè auertire, che li Punti nominati si scriueno (come hò mostrato) nel mezo del lato destro della figura, tanto perfetta, quanto imperfetta; & fanno maggiore la figura imperfetta di tanta quantità, quanta è la metà di tal figura; cioè quanta è la metà del suo Tutto; si come per essempio nella Lunga, che val
quattro Semibreui; che aggiuntole il Punto varrà sei: ma quando si aggiunge a quelle, che si possono far
perfette, sempre il Punto val la Terza parte della figura perfetta, alla quale si pone appresso; & vale la
metà della figura imperfetta. Per il che si uede la differenza, che è tra il Punto di Perfettione, & quello di
Accrescimento; che l'vno si pone solamente appresso quelle figure, che si possono far perfette, sotto i Segni
della loro perfettione; & l'altro si pone a quelle, che non si possono far perfette. Et tali Punti tanto operano nelle figure legate, quanto nelle sciolte. Il Punto di diuisione è quello, che si pone tra due figure simili
minori, & propinque poste tra due maggiori, ne i Segni della perfettione; il cui vfficio è di diuidere, & di
fare imperfetta l'una, & l'altra delle figure maggiori; si come la prima dalla parte dopo; & l'altra dalla
parte inanti. Et si scriue sopra tale figure nel mezo di loro; & tal Punto non si canta. Di maniera che in
quanto separa l'vna figura dall'altra delle due minori, & le accompagna con le maggiori, è chiamato di
Diuisione: Ma in quanto fa la imperfettione nelle maggiori, si può nominare anco Punto di Imperfettione: percioche (con ogni douere) sempre si dè porre nel fine del Tempo passato, & nel principio di quello,
che è presente. Et si pone etiandio tra la Pausa, che tiene il primo luogo, & vna Figura, che tenghi il secondo, le quali siano di vno istesso valore; come nel sottoposto essempio si vede.
 Il Punto di Alteratione è quello, che si pone auanti due
figure minori poste auanti vna maggiore propinqua;
il cui vfficio è di raddoppiare la seconda figura minore, che si pone dopo lui, & è posta inanti la maggiore;
accioche tra queste due minori si veda il Tempo perfetto. Et si debbe osseruare, di porre tal Punto in tal
maniera, che sia nel fine del Tempo procedente, & nel principio del seguente, come hanno osseruato i dotti Musici Antichi; & tal punto (come anco quello di Diuisione) non si canta. Ne altro vuol dire Alteratione, che Raddoppiamento, che si fa nelle parti propinque delle Note, o figure, che si cantano; le quali si possono far perfette sotto i loro segni; Et questo sempre (come hò detto) nella seconda figura, che si pone dopo lui: perche hauendo la prima ragione di Vnità, & la seconda ragione di Binario, è il douere che'l
Binario sia posto dopo tale Vnità; onde tal Punto si pone in questo modo.
Il Punto di Alteratione è quello, che si pone auanti due
figure minori poste auanti vna maggiore propinqua;
il cui vfficio è di raddoppiare la seconda figura minore, che si pone dopo lui, & è posta inanti la maggiore;
accioche tra queste due minori si veda il Tempo perfetto. Et si debbe osseruare, di porre tal Punto in tal
maniera, che sia nel fine del Tempo procedente, & nel principio del seguente, come hanno osseruato i dotti Musici Antichi; & tal punto (come anco quello di Diuisione) non si canta. Ne altro vuol dire Alteratione, che Raddoppiamento, che si fa nelle parti propinque delle Note, o figure, che si cantano; le quali si possono far perfette sotto i loro segni; Et questo sempre (come hò detto) nella seconda figura, che si pone dopo lui: perche hauendo la prima ragione di Vnità, & la seconda ragione di Binario, è il douere che'l
Binario sia posto dopo tale Vnità; onde tal Punto si pone in questo modo.
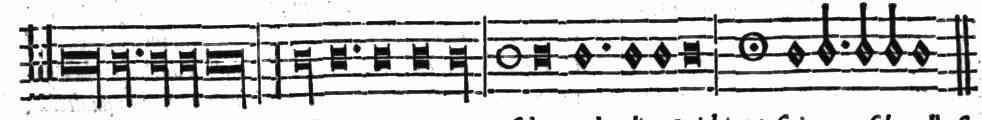 Ma tale Alteratione, o Raddoppiamento era considerato da gli Antichi Musici, non solo nelle figure poste in tal maniera: ma etiandio in molti altri modi; si come era quando poneuano due figure page 276minori, parti propinque, tra due maggiori, sotto i loro Segni. Onde poneuano la prima maggiore perfetta, &
la seconda minore raddoppiata, ouero alterata; come qui si vede.Il medesimo faceuano, quando poneua
Ma tale Alteratione, o Raddoppiamento era considerato da gli Antichi Musici, non solo nelle figure poste in tal maniera: ma etiandio in molti altri modi; si come era quando poneuano due figure page 276minori, parti propinque, tra due maggiori, sotto i loro Segni. Onde poneuano la prima maggiore perfetta, &
la seconda minore raddoppiata, ouero alterata; come qui si vede.Il medesimo faceuano, quando poneua no queste minori tra due Pause di valore delle due figure maggiori: percioche raddoppiauano similmente la
seconda minore; come nel sottoposto essempio si può vedere. Faceuano alterare, o raddoppiare etiandio la se
no queste minori tra due Pause di valore delle due figure maggiori: percioche raddoppiauano similmente la
seconda minore; come nel sottoposto essempio si può vedere. Faceuano alterare, o raddoppiare etiandio la se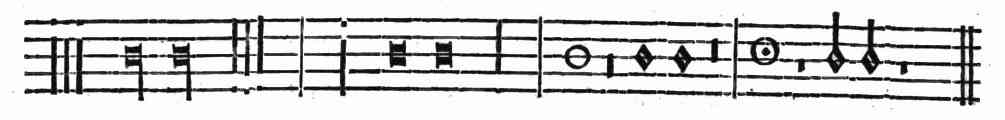 conda figura minore, quando poneuano primieramente la maggiore, & dipoi due figure minori propinque, et
vna Pausa di valore della maggiore; come qui si vede. Similmente intendeuano tale raddoppiamento,
conda figura minore, quando poneuano primieramente la maggiore, & dipoi due figure minori propinque, et
vna Pausa di valore della maggiore; come qui si vede. Similmente intendeuano tale raddoppiamento,
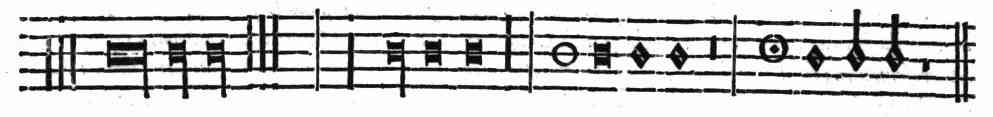 quando poneuano tra due maggiori vna Pausa di valore della minore propinqua a banda sinistra, & alla
parte destra poneuano tale minore; come qui si vede. Si debbe però auertire, che le figure alterabili sono
quando poneuano tra due maggiori vna Pausa di valore della minore propinqua a banda sinistra, & alla
parte destra poneuano tale minore; come qui si vede. Si debbe però auertire, che le figure alterabili sono
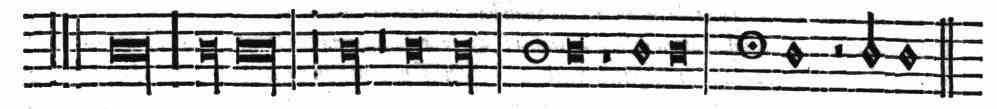 Quattro (per quanto si è potuto vedere) cioè la Lunga, la Breue, la Semibreue, & la Minima: Ma la Massima, per non essere parte propinqua di alcun'altra figura, non si può alterare. Similmente la Minima è fine di tale alteratione: essendo che non si può diuidere in due parti equali: percioche se fusse altramente, sarebbe non solamente agente: ma anco patiente. Onde casca l'Alteratione sopra quelle figure, che sono parti propinque delle maggiori; Ne mai alcuna Pausa è sottoposta alla Alteratione; Et tale Alteratione si ritroua
solamente ne i Segni di perfettione; & si fà, per il diffetto di vna figura, che manca al compimento del numero Ternario.
Le due figure minori etiandio poste tra le due maggiori, possono essere collocate in tal maniera,
che in luogo della prima si può porre la sua Pausa; ma non mai la seconda, come hauemo veduto: percioche
sempre si raddoppia la Seconda figura, tanto nelle figure legate, quanto nelle sciolte, & non mai la prima. Ma
la Negrezza, ouero il Colore, & spesse volte il Punto di diuisione, scaccia tale Alteratione, come hò mostrato. Si debbe oltra di ciò auertire, che la Perfettione delle figure si può considerare in tre maniere; Prima per
virtù delle Pause: dipoi per virtù del Segno; si come del Circolo, ouero del Semicircolo: Vltimamente per
virtù del Punto posto tra esso circolo, ouer semicircolo. Però la Massima, & la Lunga sempre saranno perfette per virtù delle Pause, siano sottoposte a qual segno si vogliano; La Breue si fà perfetta per virtù del Circolo; & la Semibreue per virtù del Segno puntato. Onde si debbe notare, che Niuna figura è perfetta per
virtù del segno, se non la Breue, & la Semibreue: L'altre poi, che sono la Massima, & la Lunga sono perfette (come si è detto) per virtù delle Pause.Oltra di ciò si debbe auertire, che tali accidenti si considerano, non solamente in quelle cantilene, che sono contenute sotto li Modi, Tempi, & Prolationi mostrate: ma
Quattro (per quanto si è potuto vedere) cioè la Lunga, la Breue, la Semibreue, & la Minima: Ma la Massima, per non essere parte propinqua di alcun'altra figura, non si può alterare. Similmente la Minima è fine di tale alteratione: essendo che non si può diuidere in due parti equali: percioche se fusse altramente, sarebbe non solamente agente: ma anco patiente. Onde casca l'Alteratione sopra quelle figure, che sono parti propinque delle maggiori; Ne mai alcuna Pausa è sottoposta alla Alteratione; Et tale Alteratione si ritroua
solamente ne i Segni di perfettione; & si fà, per il diffetto di vna figura, che manca al compimento del numero Ternario.
Le due figure minori etiandio poste tra le due maggiori, possono essere collocate in tal maniera,
che in luogo della prima si può porre la sua Pausa; ma non mai la seconda, come hauemo veduto: percioche
sempre si raddoppia la Seconda figura, tanto nelle figure legate, quanto nelle sciolte, & non mai la prima. Ma
la Negrezza, ouero il Colore, & spesse volte il Punto di diuisione, scaccia tale Alteratione, come hò mostrato. Si debbe oltra di ciò auertire, che la Perfettione delle figure si può considerare in tre maniere; Prima per
virtù delle Pause: dipoi per virtù del Segno; si come del Circolo, ouero del Semicircolo: Vltimamente per
virtù del Punto posto tra esso circolo, ouer semicircolo. Però la Massima, & la Lunga sempre saranno perfette per virtù delle Pause, siano sottoposte a qual segno si vogliano; La Breue si fà perfetta per virtù del Circolo; & la Semibreue per virtù del Segno puntato. Onde si debbe notare, che Niuna figura è perfetta per
virtù del segno, se non la Breue, & la Semibreue: L'altre poi, che sono la Massima, & la Lunga sono perfette (come si è detto) per virtù delle Pause.Oltra di ciò si debbe auertire, che tali accidenti si considerano, non solamente in quelle cantilene, che sono contenute sotto li Modi, Tempi, & Prolationi mostrate: ma


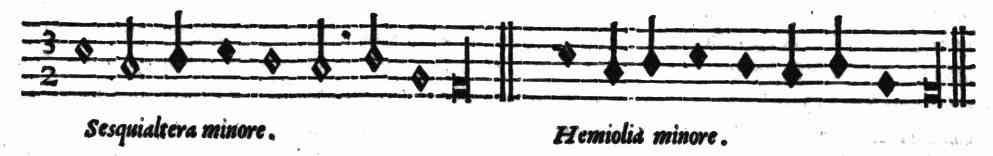
 Haueano oltra di questi gli Antichi nelle loro compositioni molti altri accidenti, & Cifere di più maniere:
ma perche poco più si vsano, & non sono di vtile alcuno alle buone, & sonore harmonie; però lassaremo il ragionar più in lungo di simil cose, a coloro, che sono otiosi, & che si dilettano di simili Cifere più di quello, che facemo noi.
Haueano oltra di questi gli Antichi nelle loro compositioni molti altri accidenti, & Cifere di più maniere:
ma perche poco più si vsano, & non sono di vtile alcuno alle buone, & sonore harmonie; però lassaremo il ragionar più in lungo di simil cose, a coloro, che sono otiosi, & che si dilettano di simili Cifere più di quello, che facemo noi.
Dell'Vtile che apportano li mostrati Accidenti nelle buone harmonie.Cap. 71.
Delle Chorde communi, & delle Particolari delle cantilene Diatoniche, Chromatiche, & Enharmoniche.Cap. 72.
 &
le communi saranno senza. Et se bene le chorde
&
le communi saranno senza. Et se bene le chorde  , &
, &  fanno in questo genere il Tetrachordo Synemennon, non saranno però particolari, ma communi a ciascuno genere: perche tal Tetrachordo si congiunge
alli quattro primi per accidente, come hò detto. Il terzo ordine poi contenerà quelle chorde, che serueno all'Enharmonico, nel quale ritrouaremo le chorde particolari di questo genere, che saranno segnate con questo
segno [[mus.hsharp]], a differenza di quelle, che sono particolari, & anco communi de gli altri due generi; come si può
vedere ne i sotto posti ordini.Onde le chorde particolari di questi generi saranno queste: Primieramente
la Terza chorda di ogni Tetrachordo del primo ordine, procedendo dal graue all'acuto sarà particolare diatonica: Dipoi la Terza d'ogni Tetrachordo posto nel secondo ordine segnata con questo segno
fanno in questo genere il Tetrachordo Synemennon, non saranno però particolari, ma communi a ciascuno genere: perche tal Tetrachordo si congiunge
alli quattro primi per accidente, come hò detto. Il terzo ordine poi contenerà quelle chorde, che serueno all'Enharmonico, nel quale ritrouaremo le chorde particolari di questo genere, che saranno segnate con questo
segno [[mus.hsharp]], a differenza di quelle, che sono particolari, & anco communi de gli altri due generi; come si può
vedere ne i sotto posti ordini.Onde le chorde particolari di questi generi saranno queste: Primieramente
la Terza chorda di ogni Tetrachordo del primo ordine, procedendo dal graue all'acuto sarà particolare diatonica: Dipoi la Terza d'ogni Tetrachordo posto nel secondo ordine segnata con questo segno  sarà particopage 281
sarà particopage 281

 lare Chromatica: Ma ogni Seconda chorda di ogni Tetrachordo del Terzo ordine segnata con tal cifera [[mus.hsharp]]
sarà particolare Enharmonica; L'altre poi, che non saranno segnate con alcuni di questi caratteri, saranno communi a ciascuno delli nominati Generi. Et se bene tali ordini sono ristretti in poche chorde, tuttauia si potranno
far maggiori, secondo che tornarà commodo; si come fin hora nelle cose della Prattica è stato fatto dalli Compositori; come si può vedere nelle loro cantilene. Ne alcuno dè prender marauiglia, ch'io habbia posto in vso
cotal segno [[mus.hsharp]], forse non più vsato per auanti: percioche non hò ritrouato segno più commodo, che sia stato posto in vso da alcuno, col mezo del quale potessi mostrare la chorda Enharmonica, & lo Interuallo, fuori che questo. Ma se è lecito alli Filosofi (come vuole Aristotele ne i Predicamenti) di fingere, o di comporre nuoui Nomi, per manifestare i loro concetti; perche non è anco lecito al Musico, di ritrouare nuoui segni,
per manifestar quelle cose, che fanno al proposito delle harmonie? tanto più, che (come è noto ad ogni studioso)
la Musica è parte della Filosofia.
lare Chromatica: Ma ogni Seconda chorda di ogni Tetrachordo del Terzo ordine segnata con tal cifera [[mus.hsharp]]
sarà particolare Enharmonica; L'altre poi, che non saranno segnate con alcuni di questi caratteri, saranno communi a ciascuno delli nominati Generi. Et se bene tali ordini sono ristretti in poche chorde, tuttauia si potranno
far maggiori, secondo che tornarà commodo; si come fin hora nelle cose della Prattica è stato fatto dalli Compositori; come si può vedere nelle loro cantilene. Ne alcuno dè prender marauiglia, ch'io habbia posto in vso
cotal segno [[mus.hsharp]], forse non più vsato per auanti: percioche non hò ritrouato segno più commodo, che sia stato posto in vso da alcuno, col mezo del quale potessi mostrare la chorda Enharmonica, & lo Interuallo, fuori che questo. Ma se è lecito alli Filosofi (come vuole Aristotele ne i Predicamenti) di fingere, o di comporre nuoui Nomi, per manifestare i loro concetti; perche non è anco lecito al Musico, di ritrouare nuoui segni,
per manifestar quelle cose, che fanno al proposito delle harmonie? tanto più, che (come è noto ad ogni studioso)
la Musica è parte della Filosofia.
Se li Due vltimi Generi si possono vsare semplici nelle lor chorde naturali, senza adoperare le chorde particolari delli Generi mostrati.Cap. 73.
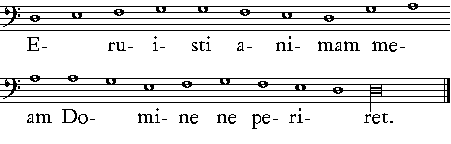 page 282che saranno le contenute nel sotto posto Tenore; ogn'uno, che hauerà giuditio potrà conoscere, ciò
essere impossibile: Conciosiache quando non si vorremo partire dalle sue chorde essentiali, contenute nel
page 282che saranno le contenute nel sotto posto Tenore; ogn'uno, che hauerà giuditio potrà conoscere, ciò
essere impossibile: Conciosiache quando non si vorremo partire dalle sue chorde essentiali, contenute nel
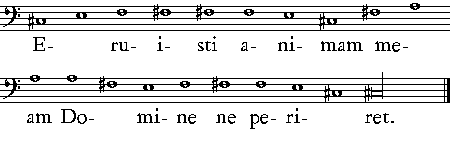 Secondo ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri generi; ritrouaremo, che
molte chorde di questo Tenore, non potranno hauere quelli accompagnamenti perfetti, che ricerca ogni perfetta compositione. La onde senza alcun dubbio potremo comprendere, che in tal genere non si potra comporre perfettamente
alcuna cantilena; si come alcuni si hanno sognato: Oltra che ritrouaremo etiandio alcune modulationi molto strane, li cui
interualli saranno molto lontani dalle forme, che sono contenute nel Numero sonoro. Ma lasciamo questo: percioche credo che sia manifesto a tutti quelli, che hanno intelligenza dell'Arte,
et passiamo all'Enharmonico, che noi vederemo quanto poco sapienti siano stati quelli, che hanno detto, che si
può comporre in questo genere qual si voglia cantilena, non si partendo dalle sue chorde propie, & naturali,
senza hauere aiuto alcuno dalle chorde particolari de gli altri generi: percioche riducendo il mostrato Tenore
nelle chorde Enharmoniche in questa maniera; se non si vorrà passare fuori delle chorde mostrate nel Terzo
Secondo ordine mostrato, & astenersi di por mano alle chorde particolari de gli altri generi; ritrouaremo, che
molte chorde di questo Tenore, non potranno hauere quelli accompagnamenti perfetti, che ricerca ogni perfetta compositione. La onde senza alcun dubbio potremo comprendere, che in tal genere non si potra comporre perfettamente
alcuna cantilena; si come alcuni si hanno sognato: Oltra che ritrouaremo etiandio alcune modulationi molto strane, li cui
interualli saranno molto lontani dalle forme, che sono contenute nel Numero sonoro. Ma lasciamo questo: percioche credo che sia manifesto a tutti quelli, che hanno intelligenza dell'Arte,
et passiamo all'Enharmonico, che noi vederemo quanto poco sapienti siano stati quelli, che hanno detto, che si
può comporre in questo genere qual si voglia cantilena, non si partendo dalle sue chorde propie, & naturali,
senza hauere aiuto alcuno dalle chorde particolari de gli altri generi: percioche riducendo il mostrato Tenore
nelle chorde Enharmoniche in questa maniera; se non si vorrà passare fuori delle chorde mostrate nel Terzo
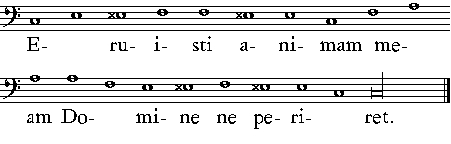 ordine; ritrouaremo molte figure, che non si potranno accompagnare in modo, che dipoi accompagnate si odi
l'harmonia perfetta, come ricercano le buone, sonore, & perfette compositioni; Anzi ritrouaremo molte
chorde, che non potranno hauere quelle consonanze, che si desiderano: Et se pur l'haueranno in alcuni luoghi,
sarà necessario, che le parti cantino in tal maniera, che rendino ingrato, & insoaue suono alle orecchie de gli
ascoltanti; come la esperienza sempre ce lo farà vedere. Potemo adunque concludere, che è impossibile di
potere vsare semplicemente, & da per se questi due generi vltimi, di maniera, che vi sia l'harmonia perfetta,
senza l'vso delle chorde particolari di alcun'altro genere.
ordine; ritrouaremo molte figure, che non si potranno accompagnare in modo, che dipoi accompagnate si odi
l'harmonia perfetta, come ricercano le buone, sonore, & perfette compositioni; Anzi ritrouaremo molte
chorde, che non potranno hauere quelle consonanze, che si desiderano: Et se pur l'haueranno in alcuni luoghi,
sarà necessario, che le parti cantino in tal maniera, che rendino ingrato, & insoaue suono alle orecchie de gli
ascoltanti; come la esperienza sempre ce lo farà vedere. Potemo adunque concludere, che è impossibile di
potere vsare semplicemente, & da per se questi due generi vltimi, di maniera, che vi sia l'harmonia perfetta,
senza l'vso delle chorde particolari di alcun'altro genere.
Che la Musica si può vsare in due maniere, & che le cantilene, che compongono alcuni de i moderni, non sono di alcuno delli nominati Generi.Cap. 74
Che'l Diatonico può procedere nelle sue modulationi per gli interualli di terza Maggiore, o di minore, & che ciò non faccia varatione alcuna di genere.Cap. 75.
Che doue si ode nelle compositioni alcuna varietà di Harmonia, iui non può essere varietà alcuna di Genere.Cap. 76.
Dell'vtile che apportano li predetti due Generi, & in qual maniera si possino vsare, che facino buoni effetti.Cap. 77.
CitharoedusEt non si marauigli alcuno, ch'io habbia detto, che si vsino le chorde delli generi, & si proceda secondo li modi mostrati di sopra: Imperoche vsiamo veramente le chorde di questi generi, ma non il genere; cioè vsiamo le Parti, ma non il Tutto: essendo che (come più oltra vederemo) l'vso intero del genere non può far buono effetto; ma si bene l'uso delle Parti; cioè delle chorde segnate con questi segni accidentali
Ridetur, chorda quisemper oberrat eadem.
 .
.  . &
. &  . & anche con questo [[mus.hsharp]].
vsandole nel modo, che di sopra hò mostrato. Et se alle volte ritrouaremo alcuna cantilena, libera al tutto da
queste cifere, potremo dire (come è il vero) che proceda per le chorde diatoniche solamente: ma quando ne
ritrouaremo alcuna, che habbia in se simili caratteri
. & anche con questo [[mus.hsharp]].
vsandole nel modo, che di sopra hò mostrato. Et se alle volte ritrouaremo alcuna cantilena, libera al tutto da
queste cifere, potremo dire (come è il vero) che proceda per le chorde diatoniche solamente: ma quando ne
ritrouaremo alcuna, che habbia in se simili caratteri  &
&  ; allora diremo, che procede per le chorde
Chromatiche, mescolate con le Diatoniche. Et se ne ritrouaremo alcuna, la quale hauesse alcuna chorda,
che non si ritroui connumerata tra le Diatoniche, ne tra le Chromatiche; la potremo nominare Enharmonica; pur che tal chorda si possa segnare col segno della chorda Enharmonica, che è questo [[mus.hsharp]]; & possa diuidere il Semituono maggiore in due parti: Imperoche tal chorda verrà ad essere vna di quelle, che si ritrouano
nel terzo ordine mostrato di sopra; & potremmo dire, che tal cantilena proceda per le chorde di ciascuno
delli tre nominati generi. Ma si debbe auertire, che tal mistione si può fare in più maniere, secondo il volere
de i Compositori, o delli Sonatori; trasportando li Modi più nel graue, ouer nell'acuto fuori delle lor chorde
naturali; contenuti nelle chorde del genere Diatonico; & la compositione (come dicono) si canta per Musica finta. La Prima delle quali è (lassando da parte quelli, che non sono cosi in vso) quando le cantilene procedeno per le chorde segnate col
; allora diremo, che procede per le chorde
Chromatiche, mescolate con le Diatoniche. Et se ne ritrouaremo alcuna, la quale hauesse alcuna chorda,
che non si ritroui connumerata tra le Diatoniche, ne tra le Chromatiche; la potremo nominare Enharmonica; pur che tal chorda si possa segnare col segno della chorda Enharmonica, che è questo [[mus.hsharp]]; & possa diuidere il Semituono maggiore in due parti: Imperoche tal chorda verrà ad essere vna di quelle, che si ritrouano
nel terzo ordine mostrato di sopra; & potremmo dire, che tal cantilena proceda per le chorde di ciascuno
delli tre nominati generi. Ma si debbe auertire, che tal mistione si può fare in più maniere, secondo il volere
de i Compositori, o delli Sonatori; trasportando li Modi più nel graue, ouer nell'acuto fuori delle lor chorde
naturali; contenuti nelle chorde del genere Diatonico; & la compositione (come dicono) si canta per Musica finta. La Prima delle quali è (lassando da parte quelli, che non sono cosi in vso) quando le cantilene procedeno per le chorde segnate col  tondo dal loro principio; trasportate verso il graue per un Tuono; si come è il Motetto Verbum iniquum, & dolosum di Morale Spagnolo a cinque voci, & il bellissimo, & arteficioso motetto Aspice Domine di Adriano a sei voci. La Seconda maniera è quella, nella quale si procede per le chorde segnate dal principio della cantilena col segno
tondo dal loro principio; trasportate verso il graue per un Tuono; si come è il Motetto Verbum iniquum, & dolosum di Morale Spagnolo a cinque voci, & il bellissimo, & arteficioso motetto Aspice Domine di Adriano a sei voci. La Seconda maniera è quella, nella quale si procede per le chorde segnate dal principio della cantilena col segno  ; & si trasporta il Modo per vn Tuono
verso l'acuto. Et nell'vna, & l'altra sorte di queste cantilene alle volte si tocca le chorde enharmoniche,
per potere hauer le consonanze imperfette maggiori, & le minori secondo il proposito; a benche si tocchino di raro: di modo che per tal maniera venimo ad vsare li due generi detti; che fanno mirabilissimi effetti.
Non dico gia (come anco hò detto) che vsiamo tutto il genere: ma si bene alcuna parte del genere, cioè alcune chorde; accommodandole al genere Diatonico, & procedendo, secondo la natura di questo genere, per
Tuoni, & Semituoni maggiori; come a ciascuno è manifesto. page 287
; & si trasporta il Modo per vn Tuono
verso l'acuto. Et nell'vna, & l'altra sorte di queste cantilene alle volte si tocca le chorde enharmoniche,
per potere hauer le consonanze imperfette maggiori, & le minori secondo il proposito; a benche si tocchino di raro: di modo che per tal maniera venimo ad vsare li due generi detti; che fanno mirabilissimi effetti.
Non dico gia (come anco hò detto) che vsiamo tutto il genere: ma si bene alcuna parte del genere, cioè alcune chorde; accommodandole al genere Diatonico, & procedendo, secondo la natura di questo genere, per
Tuoni, & Semituoni maggiori; come a ciascuno è manifesto. page 287Per qual cagione le Compositioni, che compongono alcuni Moderni per Chromatiche, facciano tristi effetti. Capitolo 78.
Delle cose che concorreuano nella compositione de i Generi.Cap. 79.
Vt gratas inter mensas Symphonia discors.Si ritroua etiandio vn'altra sorte di Istrumento lungo intorno vn braccio, il cui nome si chiama in Vinegia Altobasso, & è quadrato, & vacuo; sopra il quale sono tese alquante chorde, accordate tra loro per vna delle nominate consonanze; & si vsa in questa maniera: che mentre il Sonatore di questo istrumento sott'vn certo numero, o tempo percuote con vna mano le sue chorde con vna bachetta, con l'altra suona vn flauto, & fa vdire vn'aria di cantilena atto a suo modo. Et non solamente si trouano cotali istrumenti da chorde: ma etiandio si troua tra quelli da fiato vno istrumento, che in Thoscana si chiama Cornamusa; nel quale gia si soleua vdire due, o tre suoni continoui accordati insieme consonanti, che nasceuano da due, o tre Pifferi graui; ancora che al presente se ne odi solamente vno, & dipoi si ode vn'aria di cantilena, che si fa da vn piffero acuto, che se bene non accorda col concento di tali pifferi in ogni parte, almeno si accorda nel fine, & in alcune cadenze; come si fa etiandio in ciascuno delli nominati istrumenti. Questo istesso si ritroua etiandio nelle Trombe, che si vsano ne gli esserciti, & nelle armate di mare: percioche mentre molte di loro sonano con vn suono continouo, alcune altre fanno vdire il suono loro variato secondo il proposito; facendo hora il segno di combattere, & hora ricogliendo in vno lo essercito: Onde mi penso, che quelli Pifferi, che gli Antichi chiamauano Destri, & Sinistri, i quali vsauano (come altre volte hò detto) nelle Comedie, fussero accordati in tal maniera. Gli Organi Antichi etiandio a tal maniera si accostauano: percioche non erano fatti, come sono fatti li moderni: & di ciò me ne hà fatto fede il rarissimo fabricatore di simili istrumenti Maestro Vincenzo Colombi da Casal maggiore, il quale (secondo che mi disse in Vinegia) ritrouando si gia molti anni in Piamonte appresso Turino, ne ritrouò uno molto antico, che era senza canne, & tutto marcio; & hauea vn Tastame di tal maniera, che dalla parte sinistra, cioè nel graue, hauea li Tasti tanto larghi, che per mano grande, che fusse stato, a pena poteua arriuare il Quinto tasto; et cotale Tastame, tanto più, che si andaua verso la banda destra, cioè nell'acuto, tanto più si faceua minore. Et (per quello che lui vide) tiene per fermo, che si douea anco accordare in altra maniera di quello, che si accordano i nostri Moderni. Si ritrouano etiandio molti altri istrumenti si da chorde, come da fiato, fatti, che si sonano in tal modo; li quali per non esser lungo li lasso. Erano adunque composti li Generi di Harmonia, di Numero, & di Oratione; ne intrauano nelle Compositioni loro tutte le sorti di Versi, o Piedi: ma questo, o quello; cioe un terminato numero: & per tal maniera li Musici Antichi essercitauano la Musica ne i loro generi; ne ciò era a loro difficile, ne anco impossibile: perche poteuano, vsandola in cotal modo, fare vdire quale interuallo voleuano nelle lor cantilene, che non poteua generare fastidio di maniera, che non si potesse tollerare: conciosia che non vsauano li Contrapunti, che vsiamo nelle nostre compositioni; anzi vsauano vn semplice modo di harmonia, come si è potuto vedere.
Opinioni delli Chromatisti ributtate.Cap. 80.
LA QVARTA ET VLTIMA PARTE Delle Istitutioni harmoniche DI M. GIOSEFFO ZARLINO DA CHIOGGIA.
Quello che sia Modo.Cap. 1.
Est modus in rebus, sunt certi denique fines;Imperoche tal mediocrità, o moderatione non è altro, che vna certa maniera, ouero ordine terminato, & fermo nel procedere, per ilquale la cosa si conserua nel suo essere, per virtù della proportione, che in essa si ritroua; che non solo ne diletta, ma etiandio molto giouamento ne apporta. De qui viene, che se per caso, ouero a studio tal'ordine si allontana da tal proportione, non si può dire quanto offendi; & quanto il sentimento abhorisca questo tal'ordine. Hauendo adunque li Musici, & li Poeti antichi considerato tal cosa: perche gli vni, & gli altri erano vna cosa istessa (come hò detto altroue) chiamarono le loro compositioni Modi; nelle quali sotto varie materie, per via del Parlare esprimeuano, accompagnate l'vna all'altra con proportione, diuersi Numeri, o Metri, & diuerse Harmonie. Onde nacque dipoi, che posero tre Generi de Modi, non hauendo consideratione al Suono, ouero all'Harmonia, che nasceua: ma solamente alle altre parti aggiunte insieme; l'vno de i quali chiamarono Dithirambico, l'altro Tragico, & il terzo Nomico; de i quali le lor spetie furno molte; si come Epithalamij, Comici, Encomiastici, & altri simili. Considerando dipoi le Harmonie da per sè, che vsciuano da tali congiungimenti, perche riteneuano in loro vna certa, propia, & terminata forma, le nominarono simigliantemente Modi; aggiungendoli Dorio, o Frigio, ouero altro nome, secondo il nome de i popoli, che furno inuentori di quella harmonia, ouero da quelli, che page 294più si dilettauano di quella specie di harmonia, che di vn'altra: Imperoche l'harmonia Doria fù denominata dalli Doriensi, che furono li suoi inuentori; la Frigia dalli popoli, che habitauano la Frigia; & la Lidia da quelli di Lidia, & cosi le altre per ordine. E' ben vero, che hauendo ciascuna di esse in sè alcuna cosa propia nel suo canto: & essendo accompagnata con diuersi Numeri; chiamarono alcune di esse graui, & seuere; alcune baccanti, & furiose; alcune honeste, & religiose, & alcune altre nominarono lasciue, & bellicose. Onde per questo rispetto hebbero grande auertimento nell'accompagnare cotali Harmonie alli Numeri; et questo insieme con proposito a materie conuenienti, lequali esprimeuano nella Oratione, o Parlare, secondo la lor natura. Hauendo poi consideratione a tutte queste cose, nominauano le loro compositioni, secondo la natura del composto, come sarebbe a dire, Modi flebili, i quali sono le Elegie: Imperoche contengono materie meste, & flebili; ilche si può vedere espressamente in quelli due volumi (oltra gli altri quasi infiniti, che sono di altri autori) i quali scrisse Ouidio, dopo che fù mandato in essilio da Augusto; & da quello anco, che scriue nella Epistola di Saffo a phaon, volendo mostrare, che le cose amatorie sono materie flebili, & che conuengono alla Elegia, dicendo;
Quos vltra citraque nequit consistere rectum:
Forsitan & quare mea sint alterna requirisFece Horatio mentione di questi Modi, dicendo;
Carmina, cùm lyricis sim magis apta modis.
Flendus amor meus est. Elegeia flebile carmen.
Non facit ad lacrymas barbitos vlla meos.
Tu semper vrges flebilibus modisEt anco Boetio nel libro. 3. della Consolatione Filosfica;
Mysten ademptum.
Quondam funera coniugisSicome li commemorò etiandio Cicerone nelle Tuscolane, quando (facendo insieme mentione de gli humili, & depressi) disse. Haec cum praessis & flebilibus modis, qui totis theatris moestitiam inferant, concinuntur. Et in vn'altro luogo, facendo mentione delli tardi; Solet idem Roscius dicere, se quo plus aetatis sibi accederet, eo tardiores tibicinis modos, & cantus remissiores esse facturum. Altre nominarono Modi lamenteuoli, come si può vedere appresso di Apuleio, quando dice. Et sonus Tibiae Zigiae mutatur in quaerulum Lydij modum. Alcune poi chiamarono Modi dolci; come ne mostra l'istesso Horatio in vn'altro luogo, quando dice;
Vates thraicius gemens,
Postquàm flebilibus modis,
Syluas currere, mobiles
Amnes stare coegerat;
Me nunc Tressa Chloe regit,Et Seneca anco;
Dulces docta modos, &
Citharae sciens.
Sacrifica dulces tibia effundat modos.Nominarono etiandio alcuni altri Modi mesti; come si può vedere dalla autorità di Boetio;
Carmina qui quondam studio florente peregi,Et alcune Modi impudici, i quali commemora Quintiliano dicendo. Apertius tamen profitendum puto, non hanc a me praecipi, quae nunc in scenis effoeminata, & impudicis modis fracta. Altre chiamarono Modi rudi, o grossi, ilche dimostra Ouidio;
Flebilis heu moestos cogor inire modos;
Dumque, rudem praebente modum tibicine Tusco,Et altre Modi discordanti; & de questi ne fà mentione Statio;
Lydius aequatam ter pede pulsat humum;
Discordesque modos, & singultantia verbaVltimamente (lassandone molti altri per breuità) chiamarono in vniuersale alcune compositioni Modi lirici, si come dall'autorità di Ouidio commemorata di sopra si può comprendere. Tali materie non si esprimeuano con la voce solamente: ma se le accompagnaua l'Harmonia, che nasceua da alcuno istrumento, fusse stato poi Cetera, o Lira, oueramente Piffero, o di qualunque altra sorte. Si trouaua nondimeno grande differenza tra questi Modi: essendo che li popoli di questa prouintia vsauano vna maniera di Versi, & vno Istrumento; & quelli di quella vsauano vn'altro Istrumento, & vn'altra maniera. Et non erano differenti solamente in questi: ma nelle Harmonie ancora: Imperoche vna sorte di harmonia vsaua vn popolo, & vn'altro vn'altra; di maniera che erano anco differenti ne i Numeri, i quali si ritrouauano ne i Versi. De qui nacque dopoi, che li Modi erano denominati da quelli popoli (come di sopra hò detto) che più si page 295dilettauano di quella maniera, ouero erano stati gli inuentori. La onde da questo si può comprendere, che se vn popolo, come quello di Frigia, vdiua alcuna maniera forestiera, diceua, quello essere Modo di quella prouincia, oue più si vsaua, oueramente oue era stato ritrouato: di maniera, che chiamauano il Modo Eolio da i popoli della Eolia suoi inuentori, che era contenuto in vn certo Hinno, composto nel Modo lirico sotto alcuni Numeri: conciosia che questi popoli si dilettarono molto della Lira, o Cetera, che secondo l'opinione di alcuni (laqual reputo falsa) a quei tempi erano vna cosa istessa; al suono della quale cantauano il nominato Hinno. Tale istrumento vsauano similmente li Doriensi, anchora che forse cantassero altra maniera di Versi, & vsassero l'Harmonia molto differente; delche ne fà fede Pindaro, quando nomina simile istrumento, Δωρίαν φόρμιγγα, cioè Dorica cetera; Et Horatio,
Molior.
Sonantem mistum tibijs carmen lyra,Onde si può vedere da quella parola Barbarum, che intende per il modo Frigio, che anco i popoli della Frigia vsauano li Pifferi. Et cotal Modo veramente soleuano sonare con simili istrumenti, come potrei mostrare con molti essempi, i quali lasso per breuità; bastando solamente vno di Virgilio, ilquale dice in tal maniera.
Hac Dorium, illis Barbarum.
O vere phrigiae (neque enim phryges) ite per altaEt vno di Ouidio,
Dyndima, vbi assuetis biforem dat tibia cantum;
Tibia dat phrygios, vt dedit ante modos;Da i quali si può comprendere, esser vero quello, che hò detto. Con questo istrumento similmente quei popoli, che habitauano la Lidia, faceuano le loro harmonie, & di ciò è testimonio Horatio dicendo;
Virtute functos more patrum duces,Et Pindaro, ilquale, auanti di lui, supplicando Gioue per Psaumido Camarineo, vincitore ne i giuochi Olimpici, dice; Io vengo a te supplicheuole o Gioue Λυδίοις αὐλο͂ις, cioè con Pifferi Lidij. Non manca per dimostrar questo etiandio il testimonio di Apuleio, con l'autorità addutta di sopra, & di molti altri: ma questi bastino. Da questo adunque potemo comprendere, che li Modi anticamente consisteuano nelle Harmonie, & nelli Numeri espressi da vna sorte di istrumento; & che la diuersità loro era posta nella variatione delle Harmonie, nella diuersità de i Numeri, & nella maniera dello esprimere, cioè dello Istrumento. Et se bene alcuni popoli conueniuano con alcuni altri nelle Harmonie, ouero ne gli Istrumenti; erano poi differenti nelli Numeri; Et se in questi erano concordi, discordauano poi nelle Harmonie, & ne gli Istrumenti. Di maniera che se in vna cosa, ouero in due erano conformi, variauano poi nel resto. Questo istesso vedemo etiandio hoggidi in diuerse nationi: imperoche lo Italiano vsa il Numero, cioè il Verso di piedi, o sillabe commune col Francese, & col Spagnolo; come è quello di Vndici sillabe; nondimeno quando si odeno cantare l'vno, & l'altro, si scorge vn'Harmonia differente, & altra maniera nel procedere: Conciosiache altramenta canta lo Italiano, di quello che fà il Francese, & in altra maniera canta lo Spagnolo, di quel che fà lo Tedesco; lassando di dire delle nationi barbare de infideli, come è manifesto. Vsa lo Italiano, & anco il Francese grandemente il Leuto, & lo Spagnolo vsa il Ceterone; ancora che varia poco dal Leuto; & altri popoli vsano il Piffero. Nelli Numeri, o Versi poi, quanta differenza sia tra i popoli, & quanto vn popolo habbia differente maniera dall'altro, da questo si può conoscere (incominciando da questo capo) che se bene fuori della Italia in alcuna parte non si vsa il Verso legato, o sciolto di Vndici sillabe, fatto alla simiglianza dell'Endecasillabo latino; tuttauia nella Italia, nella Franza, & nella Spagna molto si vsa. Et quello, che in Italia si chiama Rima, credo che sia detto da questa parola greca ρυθμός, che significa (come altroue hò detto) Numero, o Consonanza: percioche da quelle corrispondenze, & legature, che si trouauano nel fine de i Versi, lequali chiamano Cadenze, nasce la Consonanza, ouero Harmonia, che si troua in essi. Vsano gli Italiani cotali Cadenze, non tanto in quella maniera de Versi, che si trouano nelle Ottaue rime, o Stanze, nelli Sonetti, ne i Capitoli, & altri simili, che dimandano Interi; quanto nelle Canzoni ancora, & Madrigali; oue si pone molte sorti de Versi; si come sono quelli di Sette sillabe, et altri simili, che chiamano Versi rotti, come è manifesto: Imperoche nella Italia, madre de i buoni, & rari intelletti, si vsa varie maniere di comporre; si come si può comprendere dalle nominate Ottaue rime, o Stanze, che dir le vogliamo, da i Terzetti, dalle Sestine, dalli Sonetti, & dalli Capitoli, ne i quali si adoperano vna sola maniera di Versi, che sono gli Interi. Et nelle Canzoni, & ne i page 296Madrigali con altri simili, ne i quali si pongono varie sorti di Numeri ad imitatione delle Ode di Horatio; a benche li Numeri Horatiani siano senza le commemorate Cadenze, & gli Italiani siano per esse Cadenze al detto modo legati; si come nelle dotte, & leggiadre Canzoni del Petrarca, & di molti altri eccellentissimi huomini si può vedere; delle quali, tengo io per certo, che li dotti spiriti Italiani siano stati gli inuentori: Conciosia che non mi ricordo hauer mai trouato appresso di alcuno altro Poeta, ne Greco, ne Latino vn simil modo di comporre, con tali Cadenze; con tutto che il dottissimo Horatio habbia cantato assaissime Ode in molte maniere. E' ben vero, che li Poeti latini (ancora che non molto spesso) hanno vsato simili Cadenze, o Corrispondenze nelle mezane sillabe, & nelle vltime di alcuni loro Versi, i quali chiamano Canini; come in ciascuno di questi hà fatto il Poeta;
Lydis remisto carmine tibijs,
Troiamque , & Anchisen, & alma
Progeniem Veneris canemus;
Ad terram misêre, aut ignibus aegra dedêre.Et Ouidio anche in questo hà osseruato cotal legge.
Cornua vellatarum obuertimus antennarum.
Illum indignanti similem; similemque minanti.
Tum caput orantis nequicquàm, & multa precantis.
Ora citatorum dextra contorsit equorum;
Vim licet appelles, & culpam nomine veles;& in molti altri, che non si metteno, per non crescere il volume. Onde il Petrarca (com'io credo) imitando tal maniera di comporre, le pose in vn'altro modo, accordando il fine del Verso precedente, col mezo del seguendo in cotal guisa:
Mai non vò più cantar com'io soleua:Et cosi il restante di tal Canzone. Ilche osseruò etiandio nella Canzone, che incomincia Vergine bella. Ma quando bene si ritrouasse tra i Greci, o tra i Latini Poeti vna tal maniera di comporre, con simili Cadenze, questo poco importarebbe essendo che tanto si potrebbe gloriare il primo inuentore di vna tal maniera di comporre Italiano, se bene hauesse pigliato la inuentione da alcun Poeta Greco, o Latino, quanto si gloriaua Horatio di esser stato il primo, che ritrouasse il modo di comporre in latino i Versi lirici, alla guisa de i Greci; come si può comprendere dalle sue parole, quando dice;
Ch'altri non m'intendeua: onde hebbi scorno.
E puossi in bel soggiorno esser molesto;
Dicar, quà violens obstrepit Aufidus,Delche si può etiandio gloriare il Tolomei, di esser stato il primo, che habbia espresso il Verso Heroico, & lo Essametro, & lo Pentametro nelle Italiane muse. Vogliono alcuni, che'l Dottissimo Dante Aligheri poeta Fiorentino fusse il primo inuentore delli Terzetti, & il Boccaccio della Ottaua rima: per ilche quando a tali maniere di comporre si volesse dare vn nome particolare, volendole denominare dalla regione, nella quale furono ritrouate: l'vna, & l'altra maniera si chiamarebbe (come ne inuita Horatio con l'autorità posta di sopra) Modi Italiani: O volendole denominar dalla patria, si chiamarebbeno Modi Thoscani. Ma se si volessero denominare da i propij inuentori, la prima maniera si nominarebbe (dirò cosi) Modo Dantesco, et la seconda maniera Modo Boccacciano; si come le Leggi citharistice, & le Tibiali (come hauemo veduto nella Seconda parte) furono denominate parte dalli Popoli, & parte da gli Inuentori. Et se bene nella Italia si troua non solo vna maniera de Versi, ma anco più maniere particolari; come hò mostrato; tuttauia li Greci a i nostri giorni, oltra l'altre loro maniere hanno il Verso di Quindici sillabe; come sono questi, che sono di Constantino Mannasì grande filosofo.
Et qua pauper aquae Daunus agrestium
Regnator populorum, ex humili potens
Princeps Aeolium carmen ad Italos
Deduxisse modos.
Ο῾ το͂υ θεο͂υ παντέλειος, καὶ παντοκτίστωρ λόγος,& vogliono dire. La Parola di Dio in tutto perfetta; & colui, che fabricò tutte le cose del Mondo, da principio fabricò il Cielo senza stelle; de i quali versi tutto il suo Essameron è pieno; & li cantano sotto vn Modo particolare, secondo'l costume loro; ilche non si vsa nella Italia. Perilche (lassando di dire de gli altri popoli) da questi due potemo vedere la differenza, che poteua esser de i Numeri, & delle Harmonie nelli Modi de quei popoli, nel tempo, che nella Grecia la Musica era in fiore: Percioche si come vedemo questi due popoli a i nostri tempi hauere vna maniera particolare di Verso; & vna maniera particolare di cantare; il simile, douemo creder, che fusse anticamente tra quei popoli. Et ancora che a i nostri giorni alcuni popoli di natione diuersa conuenghino insieme nel Numero, o nelli Piedi del Verso, & nella maniera della compositione delle lor canzoni; tuttauia sono poi differenti intorno la maniera page 297del cantare. Et non solamente si troua tra diuerse nationi tali differenze: ma anco in vna istessa natione, & in vna istessa patria; come si può vedere nella Italia: percioche in vna maniera si cantano le Canzoni, che si chiamano Villote ne i luoghi vicini a Vinegia, & in vn'altra maniera nella Thoscana, & nel Reame di Napoli; si come era anco appresso gli Antichi: percioche se bene i Popoli della Doria, & quelli della Eolia vsauano vna istessa qualità, o sorte di Verso, & vno istesso Istrumento; le Harmonie loro poi erano in qualche parte differenti. De qui si può comprendere adunque la diuersità de i nomi nelli Modi; che si come in alcun Modo si trouaua il Numero, lo Istrumento, & l'Harmonia differente da vn'altro Modo; cosi anco nacque la diuersità delli nomi. La onde credo, che il Modo Dorio fusse differente dallo Eolio; si come il Frigio era diuerso dal Lidio; & ciò non solamente nelle Harmonie: ma etiandio nelli Numeri; come si può comprendere da i varij effetti, che nasceuano dall'vno, & dall'altro; come al suo luogo vederemo. Però adunque quando leggemo di Filosseno; che hauendo tentato di fare il poema Dithirambico nel modo Dorico, & non lo puote mai condurre al desiderato fine: percioche dalla natura del Modo fù tirato di nuouo nell'harmonia Frigia, conueneuole a tal Poema; non douemo prendere ammiratione: essendo che li suoi Piedi, & il suo Numero è più veloce d'ogn'altro Poema; Et per il contrario i Numeri del modo Dorico più tardi, & più rimessi. Perilche essendo altri Numeri nella Dorica, & altri nella Frigia harmonia (come si è detto) era impossibile, che Filosseno potesse far cosa alcuna, che fusse buona; si come anco sarebbe impossibile, quando sotto li Numeri di vn Verso Saffico, che si compone del Trocheo, del Spondeo, del Dattilo, & nel fine di due Trochei; ouero di vn Trocheo, & vno Spondeo; come sono questi due Horatiani,
Τὸν ὀυρανὸν τὸν ἄναστρον παρήγαγεν ἀρχῆθεν;
Mercuri facunde nepos Atlantis:&
Persicos odi puer apparatus;si volesse cantare, o tirare in verso Heroico, che si compone di sei piedi diuersamente con Dattili, & Spondei; come si può comprendere in ciascuno delli due Virgiliani:
Sed fugit interea, fugit irreparabile tempus.&
Parcere subiectis, & debellare superbos.Tutto questo discorso hò voluto fare, forse più lungo di quello, che bisognaua, non ad altro fine, se non accioche più facilmente si comprenda quello, che era Modo nella Musica. Onde potemo veramente dire, che il Modo anticamente era una certa, & determinata forma di Melodia, fatta con ragione, & con arteficio, contenuta sotto vn determinato, & proportionato ordine de Numeri, & di Harmonia, accommodati alla materia contenuta nell'Oratione. Et benche i Musici moderni non considerino nelle lor cantilene se non vn certo ordine di cantare, & vna certa specie di harmonia, lassando da parte il considerare il Numero, o Metro determinato: percioche dicono, che questo appartiene alli Poeti, massimamente essendo hora la Musica a i nostri tempi separata dalla Poesia; tuttauia considerano cotale ordine inquanto è contenuto tra vna delle Sette gia mostrate specie della Diapason, harmonicamente, ouero arithmeticamente mediata; come più oltra vederemo; tra lequali si troua vna certa maniera di cantare in una, che in vn'altra è variata. Et tale ordine di cantare con diuersa maniera, ouero aria dimandano Modo; & alcuni lo chiamano Tropo; & alcuni Tuono. Ne di ciò douemo prender marauiglia, poi che Τρόπος è parola greca, che significa Modo, o Ragione, dalla quale vogliono, che siano cosi detti. Et se fussero anco nominati da Τροπή, che vuol dire Conuersione, o Mutatione, staria medesimamente bene; essendo che l'vno si conuerte, & muta nell'altro; come vederemo. Lo nominano etiandio Tuono, & ciò non è mal detto: percioche per il Tuono (come mostra Euclide nel suo Introduttorio) si può intendere Quattro cose: Primieramente quello, che i Greci chiamano φθόγγοσ, che significa ogni Suono, o Voce inarticolata, laquale non si estende ne verso il graue, ne verso l'acuto: Secondariamente, l'vno di quelli due interualli, mostrati nel Cap. 18. della Terza parte; Dipoi vna forte, & sonora voce; si come quando dicemo; Francesco hà vn buon tuono, sonoro, & gagliardo; cioè vna buona, sonora, & gagliarda voce. Vltimamente si può intender quello, che hauemo nominato di sopra; si come quando si dice, il Tuono Dorio, il Frigio, & gli altri; cioè il Modo Dorio, il Frigio, & li seguenti per ordine, Et perche questo nome Tuono si estende in più cose, come hauemo veduto; però io per schiuare la Equiuocatione, più che hò potuto, hò voluto nominarli Modi, & non Tuoni. Volendo adunque dichiarare quello, che sia Modo, diremo con Boetio, che Modo è vna certa costitutione in tutti gli ordini de voci, differente per il graue, & per l'acuto; & tale Costitutione è come vn corpo pieno di modulatione, laquale hà l'essere dalla congiuntione delle Consonanze; si come è la Diapason, la Diapasondiapente, ouero la Disdiapason. Di maniera che da Proslambanomenos a Mese viene ad essere vna costitutione, connumerando le chorde, o voci mezane; Cosi ancora da Mese a Nete hyperboleon, intendendoui sempre li suoi mezani suoni. Ma page 298perche queste costitutioni sono veramente le varie specie della Diapason, che si trouano dall'vna lettera all'altra; come nel Cap. 12. della Terza parte habbiamo veduto, numerando le lor chorde mezane; però diremo, che'l Modo è vna certa forma, o qualità di harmonia, che si troua in ciascuna delle nominate Sette specie della Diapason, lequali tramezate harmonicamente, secondo che si considerano hora, ne danno sette Modi principali, & autentichi; dalli quali poi nascono li suoi collaterali, per la diuisione arithmetica, che si chiamano (come vederemo) Plagali, ouero Placali.
Che li Modi sono stati nominati da molti diuersamente, & per qual cagione.Cap. 2.
Del Nome, & del Numero delli Modi. Cap. 3.
De gli Inuentori delli Modi.Cap. 4.
Non tu in triuijs indocte solebasOue si vede, che non faceuano vn tale vfficio con molti istrumenti: ma con vn piffero solo; del quale (come vuole Apuleio) Iagne Frigio, che fu padre di quel Marsia, che fu punito grauemente da Apollo della sua arroganza, fu l'inuentore. Questo istesso faceuano etiandio col Zuffolo, del quale (come vogliono alcuni, & massimamente Virgilio) Pan dio de pastori fu l'inuentore, perche; come dice egli,
Stridenti miserum stipula disperdere carmen?
Pan primus calamos caera coniungere pluresMa le melodie Dorie, secondo l'istesso Clemente, del qual parere fu anche Plinio, furono ritrouate da Thamira, che fu di Thracia. Le Frigie, la Mista lidia, & la Mista frigia (come vuole il nominato Clemente) furono ritrouate dal sopradetto Marsia, che fu di Frigia; quantunque alcuni uoglino, che Saffo Lesbia poetessa antica fusse l'inuentrice delle Miste lidie; & altri attribuischino tale inuentione a Thersandro; & altri ad vn Trombetta chiamato Pithoclide: Ma Plutarco, pigliando il testimonio di vno Lisia, vuole, che Lamprocla di Athene fusse l'inuentore de tali Melodie; & alcuni vogliono, che Damone Pithagorico fusse l'inuentore dell'Hipofrigio, & Polimnestre dell'Hipolidio. De gli altri Modi non hò ritrouato gli inuentori: ma quando l'autorità di Aristotele posta nel lib. 2. della Metafisica valesse in questo proposito, si potrebbe dire, che Timotheo fusse stato l'inuentore del resto; ancora che Frinide musico perfetto de quei tempi fusse stato auanti lui: percioche (come dice) se non fusse stato Timotheo non haueressimo molte melodie. Ma inuerità parmi, che siano più antiche di Timotheo; si come leggendo molti autori, & essaminandoli intorno al tempo, si può vedere. Quale di loro fusse il primo ritrouato, questo è, non dirò difficilissimo, anzi impossibile da sapere; ancora che alcuni voglino, che'l Lidio fusse'l primo Modo ritrouato; alla quale opinione se potressimo accostare, quando l'ordine delli Modi posti da Platone, da Plinio, da Martiano, & da molti altri, fusse posto, secondo che l'vno fu ritrouato prima dell'altro: Ma veramente è debile argomento: percioche potressimo dire l'istesso di qualunque altro Modo, che fusse posto primo in qualunque altro ordine; si come del Frigio, che è posto da Luciano primo in ordine; & dell'Eolio, che è posto da Apuleio nel primo luogo. Lassaremo hora di ragionar più di cotali cose, & verremo a dire della loro natura: percioche della propietà de i Modi moderni vn'altra fiata ne parlaremo.
Instituit.
Della Natura, o propietà delli Modi.Cap. 5
Inter quas curam Clymene narrabat inanemPer tali effetti adunque gli Antichi attribuirono le narrate propietà al modo Dorico; & ad esso applicauano materie seuere, graui, & piene di sapienza. Et quando da queste si partiuano, & passauano a cose piaceuoli, liete, & leggieri, vsauano il modo Frigio; essendo che li suoi numeri erano più veloci de i numeri di qualunque altro Modo, & la sua harmonia più acuta di quella del Dorio; Onde da questo, credo io, che sia venuto quel Prouerbio, che si dice, Dal Dorio al Frigio; che si può accommodare, quando da vn ragionamento di cose altissime, & graui, si passa ad vno, che contenga cose leggieri, basse, non molto ingegnose, et simigliantemente cose liete, et festeuoli, & anche non molto honeste. Clemente Alessandrino, seguitando la opinione di Aristosseno, vuole, che il Genere Enharmonico conuenghi grandemente alle Harmonie Doriche; come genere ornato, & elegante; & alle Frigie il Diatonico, come più vehemente, & acuto. Fù gia tanto in veneratione il Dorio, che niuno altro, da questo & il Frigio in fuori, fu approuato, & admesso dalli due sapientissimi Filosofi Platone, & Aristotele: percioche conosceuano l'vtile grande, che apportauano ad vna bene istituita Republica; istimando gli altri di poco vtile, & di poco valore. Onde volsero, che li fanciulli dalla loro tenera età fussero istrutti nella Musica. Voleuano etiandio gli Antichi, che l'Hipodorio hauesse natura in tutto diuersa da quella del Dorio: imperoche si come il Dorio disponeua ad vna certa costanza virile, & alla modestia; cosi l'Hipodorio per la grauità delli suoi mouimenti inducesse vna certa pigritia, & quiete. La onde (si come raccontano Tolomeo, & Quintiliano) li Pithagorici haueuano cotale vsanza, che soleuano col mezo dell'Hipodorio tra il giorno, & quando andauano a dormire, mitigare le fatiche, & le cure dell'animo del giorno passato; & nella notte suegliati dal sonno, col Dorio ridursi alli lassati studij. Atheneo (come altroue hò anco detto) si pensò, che questo fusse l'Eolio, & gli attribui, che inducesse ne gli animi vn certo gonfiamento, & fasto; per esser di natura alquanto molle. Attribuirono anco gli Antichi al Frigio; come ci manifesta Plutarco, natura di accender l'animo, & di infiammarlo alla ira, & alla colera; & di prouocare alla libidine, & alla lussuria: percioche lo istimarono Modo alquanto vehemente, & furioso; & anco di natura seuerissimo, & crudele; & che rendesse l'huomo attonito. La onde (secondo'l mio parere) Luciano toccò molto bene la sua natura con queste parole: Si come (quelli dice egli) i quali odono il piffero Frigio, non tutti impaciscono: ma solo tutti quelli, i quali sono tocchi da Rhea; & questi hauendo vdito il Verso, si ricordano del primo affetto, o passiopage 303ne prima, & etiam della prima perturbatione; cosi quelli, che odeno li Filosofi, non tutti si parteno attoniti, & impiagati: ma solamente quelli, ne i quali si ritroua vn certo incitamento alla Filosofia. Similmente Ouidio la accennò in questi due versi, dicendo;
Vulcani, Martisque dolos, & dulcia furta.
Attonitusque seces, vt quos Cybeleia materAristotele lo accenna Bacchico, cioè furioso, & baccante; & Luciano lo chiama furioso, o impetuoso: ancora che Apuleio lo nomini Religioso. Questo Modo (come habbiamo veduto) si sonaua anticamente col Piffero; ilquale è istrumento molto incitatiuo: per il che (come dicono alcuni) col mezo del suono de i Pifferi, li Spartani inuitauano li soldati al combattere; & (come narra Valerio) costretti dalle seuerissime leggi di Licurgo, osseruauano di non andare mai con lo essercito a combattere, se prima non erano bene inanemiti, & riscaldati dal suono de i detti istrumenti, con la misura del piede Anapesto; il qualsi compone di tre tempi, cioè di due breui, & di vno lungo. La onde dalli due primi, i quali fanno la battuta più spessa, & più veloce comprendeuano, di hauer da assalire l'inimico con grande empito; & dal lungo, di hauere a fermarsi, & resistere animosamente, quando non l'haueano rotto nel primo assalto. Il che faceuano anco li Romani, come narra Tulio, i quali non pure col suono della Tromba: ma col canto accompagnato a cotal suono, soleuano incitare gli animi de i soldati a combattere virilmente. Et ciò ne mostra anco Virgilio, parlando di Miseno,
Incitat, ad Phrygios vilia membra modos.
. . . . quo non praestantior alter,Imperoche gli Italiani vsarono la Tromba, che fu inuentione de i popoli Tirrheni, come vuole Diodoro; & Plinio vuole; che l'inuentore fusse vno nominato Piseo, pur Tirrheno. Di questa inuentione Virgilio ne tocca vna parola, quando dice. Tyrrhenusque tubae mugire per aethera clangor. Ma Gioseffo nel Primo libro delle Antichità giudaiche vuole, che l'inuentore sia stato Mose; & Homero dice, che fu Dirceo, alcuni altri Tirteo, & alcuni Maleto, col suono della quale, che era aspro, veloce, gagliardo, & forte (come si può comprendere dalle parole di Ennio poeta antico, il quale esprimendo la natura di questo istrumento disse;
Aere ciere viros, Martemque accendere cantu.
At tuba terribili sonitu taratantara dixit)proferiuano il modo Frigio. Inuitati adunque al combattere con grande vehementia dal suono del detto istrumento, erano dalla tardità del suono, cioè dalla tardità del mouimento, & dalla grauità del Modo inuitati a lassare di combattere. Il grande Alessandro anco col mezo di vn Piffero (come narra Suida) fu inuitato da Timotheo a pigliar l'arme, recitando la legge Orthia nel modo Frigio. Similmente vn giouine Taurominitano (come recita Ammonio, & Boetio, & si come molte volte hò commemorato) fu da questo Modo riscaldato. Per il che voleuano gli Antichi, che le materie, che trattauano di guerra, & fussero minaccieuoli, & spauentose, si accommodassero a cotal Modo; & che l'Hipofrigio moderasse, & sottrahesse la natura terribile, & concitata del Frigio. Onde dicono alcuni, che si come li Spartani, & li Candioti inanemiuano i soldati al combattere col modo Frigio; cosi li reuocauano dalla pugna con l'Hipofrigio al suono delli Pifferi. Vogliono anco, che Alessandro fusse riuocato dalla battaglia da Timotheo col mezo di questo Modo, recitato al suono della Cetera; & che'l giouine Taurominitano commemorato col mezo di questo Modo, & col canto del Spondeo fusse placato. Vuole Cassiodoro, che'l Frigio habbia natura di eccitare al combattere, & di infiammare gli huomini al furore; & che'l Lidio sia remedio contra le fatiche dell'animo, & similmente contra quelle del corpo. Ma alcuni vogliono, che'l Lidio sia atto alle cose lamenteuoli, & piene di pianto; per partirsi dalla modestia del Dorio, in quanto è più acuto, & dalla seuerità del Frigio. Sotto questo Modo, Olimpo (come narra Plutarco) al suono del piffero nella Sepoltura di Pithone cantò gli Epicedij; che sono alcuni versi, che si cantauano auanti il Sepolchro di alcun morto: Imperoche anticamente era vsanza di far cantare al suono del Piffero, o di altro istrumento nella morte de i parenti, o de gli amici più cari; dal qual canto erano indutti a piangere li circostanti la loro morte; & ciò faceuano fare ad vna femina vestita in habito lugubre; come anco si osserua al presente in alcune città, massimamente nella Dalmatia, nella morte di alcuno huomo honorato. Tale vsanza commemorò Statio Papinio, dicendo;
Cum signum luctus cornu graue mugit aduncoOnde si vede, che tali harmonie erano fatte nel modo Frigio, ouero nel Lidio; si come dalla autorità di Apuleio addutta di sopra si può vedere. Alcuni hanno chiamato il Lidio, dà gli effetti, horribile, tristo, & lamenteuole; & Luciano lo nomina furioso, ouero impetuoso; è ben vero, che Platone pone tre sorti di harmonie Lidie, cioè Miste, Acute, & Semplici, senza porui alcuno aggiunto. page 304Hanno hauuto opinione alcuni, che l'Hipolidio habbia natura differente, & contraria a quella del Lidio; & che contenga in se vna certa soauità naturale, & dolcezza abondante; che riempa gli animi de gli ascoltanti di allegrezza, & di giocundità, mista con soauità; & che sia lontano al tutto dalla lasciuia, & da ogni vitio; Percio lo accommodarono a materie mansuete, accostumate, graui, & continenti in se cose profunde, speculatiue, & diuine; come sono quelle, che trattano della gloria di Dio, della felicità eterna; & quelle, che sono atte ad impetrare la Diuina gratia. Et volsero similmente, che'l Mistolidio hauesse natura di incitar l'animo, & di rimetterlo. Apuleio dimanda l'Eolio semplice; & Cassiodoro vuole, che habbia possanza di far tranquillo, & sereno l'animo oppresso da diuerse passioni; & che, dopo scacciate tali passioni, habbia possanza di indurre il sonno: natura, & propietà veramente molto conforme a quella dell'Hipodorio. Onde non è da marauigliarsi, se Atheneo, adducendo l'autorità di Eraclide di Ponto, fu di parere, che l'Eolio fusse l'Hipodorio; o per il contrario. Vogliono alcuni, che allo Eolio si possino accommodare materie allegre, dolci, soaui, & seuere; essendo che (come dicono) hà in se vna grata seuerità mescolata con vna certa allegrezza, & soauità oltra modo; & sono di parere, che sia molto atto alle modulationi de i Versi lirici, come Modo aperto, & terso. Ma se è vero quello, che si pensò Eraclide, sarebbe a tutte queste cose contrario molto: percioche hauerebbe diuersa natura; come di sopra hò mostrato. Apuleio chiama lo Iastio, ouero Ionico (che tanto vale) vario; & Luciano lo nomina allegro; per essere (secondo il parere di alcuni) molto atto alle danze, & a i balli. La onde nacque, che lo dimandarono lasciuo; & li popoli, inuentori di tal Modo, che furono gli Atheniesi, popoli della Ionia, amatori di cose allegre, & gioconde; & molto studiosi della eloquenza, chiamarono Vani, & leggieri. Cassiodoro vuole, che habbia natura di acuire l'intelletto a quelli, che non sono molto eleuati; & di indurre vn certo desiderio delle cose celesti in coloro, li quali sono grauati da vn certo desiderio terrestre, & humano. Queste cose dicono intorno alla natura delli Modi; la onde si scorge vna grande varietà nelli Scrittori, volendo alcuni vna cosa, & alcuni vn'altra. Il perche mi penso, che tal varietà poteua nascere dalla varietà de i costumi di vna prouincia; che essendo dopo molto tempo variati, variassero ancora li Modi; & che vna parte de i scrittori parlasse di quelli Modi, che perseuerauano di essere nella loro prima, & pura semplicità; & l'altra parte parlasse di quelli, che gia haueano perso la loro prima natura; Come per cagione di essempio diremo del Dorio, che essendo prima honesto, graue, & seuero; per la variatione de i costumi fusse variato anche lui, & applicato dipoi alle cose della guerra. Et per questo non ci douemo marauigliare: percioche se dalla varieta delle harmonie nasce la variatione de i costumi; come altroue si è detto; non è inconueniente anco, che dalla variatione de i costumi si venga alla varietà delle Harmonie, & delli Modi. Poteua anco nascere dalla poca intelligenza, che haueano li Scrittori di quei tempi, intorno a cotal cosa; come suole accascare etiandio a i tempi nostri, che alcuni si porranno a scriuere alcune cose, che non intendeno: ma si rimetteno al giuditio, & alla opinione di vn'altro, il quale alle volte ne sa men di lui; & cosi molte volte pigliano vna cosa per vn'altra, & attribuiscono a tal cosa alcune propietà, che considerandola per il dritto, è da tal propietà tanto lontana, & diuersa, quanto è lontano, & diuerso il Cielo dalla Terra. Et molte volte vedemo, che pigliano vna cosa per vn'altra; come si può vedere in quello, che scriue Dione Chrisostomo di Alessandro Magno ne i Commentarij del Regno, essempio addutto da molti; oue dice, che fu costretto da Timotheo a pigliar l'arme col mezo del Modo Dorio; tuttauia è solo di questo parere, per quello ch'io hò potuto comprendere: Imperoche il Magno Basilio, & molti altri auanti lui, vuole; che fusse costretto a fare vn simile atto dal modo Frigio. Ma di questo sia detto a bastanza; imperoche è dibisogno, che si venghi a ragionare intorno all'ordine loro.
Tibia, cui teneros suetum producere manes,
Lege Phrygum mesta.
Dell'Ordine de i Modi.Cap. 6.
 &
&  il Quarto. Vltimamente tra la C & c: ouero tra la c & cc, che è la Terza specie accommodano l'Vndecimo, & il Sesto modo; come più abasso vederemo. Et sono al numero di Dodici, non solamente appresso gli Ecclesiastici; ma anco
appresso li Compositori prattici; ancora che da molti non siano considerati in tanto numero; de
i quali io intendo ragionare particolarmente, & mostrare in qual maniera al presente si vsi ciascuno di loro.
il Quarto. Vltimamente tra la C & c: ouero tra la c & cc, che è la Terza specie accommodano l'Vndecimo, & il Sesto modo; come più abasso vederemo. Et sono al numero di Dodici, non solamente appresso gli Ecclesiastici; ma anco
appresso li Compositori prattici; ancora che da molti non siano considerati in tanto numero; de
i quali io intendo ragionare particolarmente, & mostrare in qual maniera al presente si vsi ciascuno di loro.
Che l'Hipermistolidio di Tolomeo non è quello, che noi chiamiamo l'Ottauo modo.Cap. 7.
In qual maniera gli Antichi segnauano le chorde de i loro Modi.Cap. 8.
Verùm opere in longo fas est obrepere somnum.percioche potrà essere ottima escusatione a questo grauissimo autore, & etiandio a ciascun'altro, che scriue molto di lungo.
In qual maniera s'intenda la Diapason essere harmonicamente, ouero arithmeticamente mediata.Cap. 9.

Che li Modi moderni sono necessariamente Dodici, & in qual maniera si dimostri.Cap. 10.
 ; & le aggiungeremo nell'acuto la Seconda della Diatessaron, posta tra
; & le aggiungeremo nell'acuto la Seconda della Diatessaron, posta tra  & e; haueremo quello,
che nominiamo Terzo modo, contenuto tra la Quinta specie della Diapason E & e. Et se alla detta Diapente aggiungeremo nel graue la Nominata Diatessaron, collocata tra le chorde E &
& e; haueremo quello,
che nominiamo Terzo modo, contenuto tra la Quinta specie della Diapason E & e. Et se alla detta Diapente aggiungeremo nel graue la Nominata Diatessaron, collocata tra le chorde E &  ; haueremo la Seconda specie della Diapason
; haueremo la Seconda specie della Diapason  &
&  , laquale ne darà vn Modo diuerso dalli tre primi, che sarà quello, che
noi dimandiamo Quarto. Pigliaremo hora la Terza specie della Diapente, collocata tra F & c, & le aggiungeremo nell'acuto la Terza della Diatessaron, posta tra c & f; & haueremo tra la Sesta specie della
Diapason F & f, quello, che noi dimandiamo Quinto modo. Se piglieremo hora la istessa Diapente, & le
aggiungeremo nel graue la Diatessaron F & C, haueremo la Terza specie della Diapason, & insieme
quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei vnioni, o congiuntioni; cioè quelle della
Prima specie della Diapente con la Prima della Diatessaron, tanto nel graue, quanto nell'acuto; et quelle della Seconda di ciascuna similmente nel graue, & nell'acuto; Cosi quelle della Terza specie fatte hora nel graue, hora nell'acuto; & per tal via haueremo Sei modi. Resta hora di accompagnare la Quarta specie della Diapente con la Prima della Diatessaron, che si può accompagnare commodamente. Onde è d'auertire,
che tutte le specie della Diatessaron si possono di nuouo accommodare, & accompagnare con la Diapente in
tre maniere: percioche la Prima specie si può accompagnare con la Quarta specie della Diapente; la Seconda con la Prima; & la Terza con la Quarta specie di essa Diapente: ne tali specie si possono congiungere
insieme commodamente in altra maniera; come è manifesto a ciascuno, che sia nella Musica essercitato mediocremente. Pigliando adunque la Quarta specie della Diapente posta tra G & d, le accompagneremo
la Prima della Diatessaron d & g; & tra le chorde G & g estreme della Settima specie della Diapason con le sue mezane, haueremo il Modo, che chiamano Settimo. Ilperche se di nuouo pigliaremo la Diatessaron, posta tra G & D; & la accompagnaremo nel graue con la Diapente, haueremo tra la Diapason d & D, Quarta specie il modo chiamato Ottauo. Aggiungeremo hora la Seconda specie della Diatessaron posta tra e & aa alla Prima della Diapente, collocata tra a & e dalla parte acuta, ilche fatto, tra la Prima specie della Diapason a & aa haueremo vn'altro Modo; ilquale per esser da gli otto Modi mostrati differente,
lo nominaremo Nono modo. Dalla parte graue poi di tale Diapente congiungeremo la
istessa Diatessaron tra a & E, & haueremo tra la Quinta specie della Diapason e & E quello, che drittamente chiamiamo Decimo modo. Vltimamente se noi accompagnaremo la Terza specie della Diatessaron posta tra g & cc, dalla parte acuta, con la Quarta della Diapente posta tra c & g nella Terza specie della Diapason c
& cc, haueremo il Modo, che si chiama Vndecimo: Imperoche se accompagnaremo le dette specie per il contrario, ponendo la Diatessaron nella parte graue tra le chorde c & G, haueremo l'vltimo Modo, detto il Duodecimo, contenuto nella Settima specie della Diapason g & G; come
qui in essempio si vede.
, laquale ne darà vn Modo diuerso dalli tre primi, che sarà quello, che
noi dimandiamo Quarto. Pigliaremo hora la Terza specie della Diapente, collocata tra F & c, & le aggiungeremo nell'acuto la Terza della Diatessaron, posta tra c & f; & haueremo tra la Sesta specie della
Diapason F & f, quello, che noi dimandiamo Quinto modo. Se piglieremo hora la istessa Diapente, & le
aggiungeremo nel graue la Diatessaron F & C, haueremo la Terza specie della Diapason, & insieme
quel Modo, che nominiamo Sesto. Et per tal maniera haueremo Sei vnioni, o congiuntioni; cioè quelle della
Prima specie della Diapente con la Prima della Diatessaron, tanto nel graue, quanto nell'acuto; et quelle della Seconda di ciascuna similmente nel graue, & nell'acuto; Cosi quelle della Terza specie fatte hora nel graue, hora nell'acuto; & per tal via haueremo Sei modi. Resta hora di accompagnare la Quarta specie della Diapente con la Prima della Diatessaron, che si può accompagnare commodamente. Onde è d'auertire,
che tutte le specie della Diatessaron si possono di nuouo accommodare, & accompagnare con la Diapente in
tre maniere: percioche la Prima specie si può accompagnare con la Quarta specie della Diapente; la Seconda con la Prima; & la Terza con la Quarta specie di essa Diapente: ne tali specie si possono congiungere
insieme commodamente in altra maniera; come è manifesto a ciascuno, che sia nella Musica essercitato mediocremente. Pigliando adunque la Quarta specie della Diapente posta tra G & d, le accompagneremo
la Prima della Diatessaron d & g; & tra le chorde G & g estreme della Settima specie della Diapason con le sue mezane, haueremo il Modo, che chiamano Settimo. Ilperche se di nuouo pigliaremo la Diatessaron, posta tra G & D; & la accompagnaremo nel graue con la Diapente, haueremo tra la Diapason d & D, Quarta specie il modo chiamato Ottauo. Aggiungeremo hora la Seconda specie della Diatessaron posta tra e & aa alla Prima della Diapente, collocata tra a & e dalla parte acuta, ilche fatto, tra la Prima specie della Diapason a & aa haueremo vn'altro Modo; ilquale per esser da gli otto Modi mostrati differente,
lo nominaremo Nono modo. Dalla parte graue poi di tale Diapente congiungeremo la
istessa Diatessaron tra a & E, & haueremo tra la Quinta specie della Diapason e & E quello, che drittamente chiamiamo Decimo modo. Vltimamente se noi accompagnaremo la Terza specie della Diatessaron posta tra g & cc, dalla parte acuta, con la Quarta della Diapente posta tra c & g nella Terza specie della Diapason c
& cc, haueremo il Modo, che si chiama Vndecimo: Imperoche se accompagnaremo le dette specie per il contrario, ponendo la Diatessaron nella parte graue tra le chorde c & G, haueremo l'vltimo Modo, detto il Duodecimo, contenuto nella Settima specie della Diapason g & G; come
qui in essempio si vede.
 Et per tal maniera haueremo ne più, ne meno
di Dodici Modi: imperoche cotali specie non si possono accompagnare in altra maniera l'vna con l'altra, se non con grande incommodo; come è manifesto a ciascuno, che habbia giuditio. page 311
Et per tal maniera haueremo ne più, ne meno
di Dodici Modi: imperoche cotali specie non si possono accompagnare in altra maniera l'vna con l'altra, se non con grande incommodo; come è manifesto a ciascuno, che habbia giuditio. page 311Altro modo da dimostrare il Numero delli Dodici Modi.Cap. 11.
 ; haueremo la Diapente E
; haueremo la Diapente E  Seconda specie, &
la Seconda della Diatessaron
Seconda specie, &
la Seconda della Diatessaron  & e, lequali aggiunte insieme al mostrato modo ne danno il Terzo. Ma
pigliando la Sesta specie F & f, & diuidendola in tal maniera con la chorda c, haueremo il Quinto modo, ilquale medesimamente
nasce dalla congiuntione della Terza specie della Diapente, & della Terza della
Diatessaron, che sono F & c, & c & f, come si è detto. Presa dipoi la Settima specie della Diapason,
contenuta tra G & g, & diuisa harmonicamente con la chorda d, haueremo la Quarta specie della Diapente G & d, aggiunta alla Prima specie della Diatessaron d & g, & il Settimo modo. Dipoi pigliata la Prima specie della Diapason collocata tra a & aa, diuisa harmonicamente dalla chorda e, haueremo la Prima specie della Diapente a & e, & la Seconda della Diatessaron e & aa, che insieme aggiunte ne danno il Nono modo. Lassaremo hora da parte la Seconda specie della Diapason posta tra
& e, lequali aggiunte insieme al mostrato modo ne danno il Terzo. Ma
pigliando la Sesta specie F & f, & diuidendola in tal maniera con la chorda c, haueremo il Quinto modo, ilquale medesimamente
nasce dalla congiuntione della Terza specie della Diapente, & della Terza della
Diatessaron, che sono F & c, & c & f, come si è detto. Presa dipoi la Settima specie della Diapason,
contenuta tra G & g, & diuisa harmonicamente con la chorda d, haueremo la Quarta specie della Diapente G & d, aggiunta alla Prima specie della Diatessaron d & g, & il Settimo modo. Dipoi pigliata la Prima specie della Diapason collocata tra a & aa, diuisa harmonicamente dalla chorda e, haueremo la Prima specie della Diapente a & e, & la Seconda della Diatessaron e & aa, che insieme aggiunte ne danno il Nono modo. Lassaremo hora da parte la Seconda specie della Diapason posta tra  &
& 
 ,
percioche non si può mediare harmonicamente, & pigliaremo la Terza c & cc, & la diuideremo al sopradetto modo con la chorda g, dalla quale diuisione nascerà la Quarta specie della Diapente c & g, & la
Terza della Diatessaron g & cc, & l'Vndecimo modo; come qui sotto si vede.
,
percioche non si può mediare harmonicamente, & pigliaremo la Terza c & cc, & la diuideremo al sopradetto modo con la chorda g, dalla quale diuisione nascerà la Quarta specie della Diapente c & g, & la
Terza della Diatessaron g & cc, & l'Vndecimo modo; come qui sotto si vede.
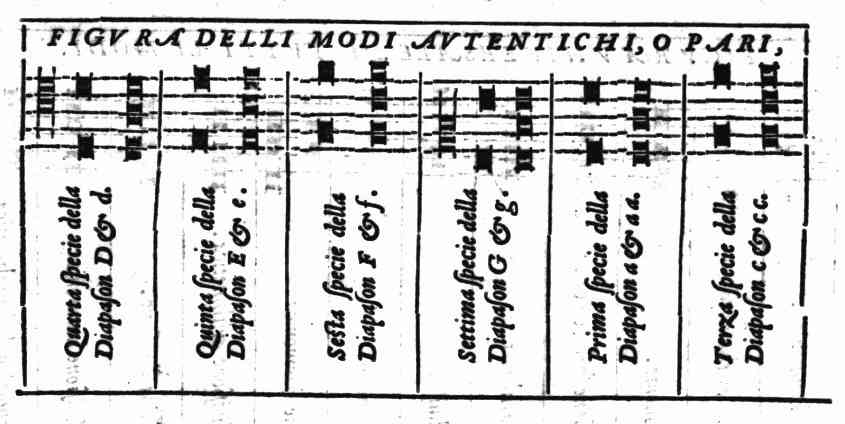
 &
&  , & la diuideremo al mostrato modo con la chorda E, & haueremo tra E &
, & la diuideremo al mostrato modo con la chorda E, & haueremo tra E &  la Seconda specie della Diatessaron;
& tra
la Seconda specie della Diatessaron;
& tra  & E la Seconda della Diapente, lequali vnite insieme ne daranno medesimamente il Quarto modo. page 312La Terza specie della Diapason c & C, diuisa per la chorda F, ne darà il Sesto modo: percioche la Terza
specie della Diatessaron F & C, posta nel graue, si vnisce con la Terza della Diapente c et F, posta in acuto. Ma se pigliaremo
la Diapason d & D, Quarta specie, diuisa dalla chorda G arithmeticamente, haueremo l'Ottauo modo: percioche G & D, Prima specie della Diatessaron, si congiunge con la Quarta della Diapente nel graue. Hora prenderemo la Quinta specie della Diapason e & E, & la diuideremo al modo mostrato con la chorda a,
& haueremo la Seconda della Diatessaron a & E, & la Prima della Diapente
e & a, che costituiscono il Decimo modo. Pigliando vltimamente la Diapason g & G, Settima specie
(lassando la f & F: perche non si può diuidere in tal maniera) se noi la diuideremo con la chorda c, haueremo il Duodecimo modo: percioche per tal diuisione nascerà la Terza specie della Diatessaron c & G, nella
parte graue, vnita alla Quarta specie della Diapente g & c; come qui sotto si può vedere.
& E la Seconda della Diapente, lequali vnite insieme ne daranno medesimamente il Quarto modo. page 312La Terza specie della Diapason c & C, diuisa per la chorda F, ne darà il Sesto modo: percioche la Terza
specie della Diatessaron F & C, posta nel graue, si vnisce con la Terza della Diapente c et F, posta in acuto. Ma se pigliaremo
la Diapason d & D, Quarta specie, diuisa dalla chorda G arithmeticamente, haueremo l'Ottauo modo: percioche G & D, Prima specie della Diatessaron, si congiunge con la Quarta della Diapente nel graue. Hora prenderemo la Quinta specie della Diapason e & E, & la diuideremo al modo mostrato con la chorda a,
& haueremo la Seconda della Diatessaron a & E, & la Prima della Diapente
e & a, che costituiscono il Decimo modo. Pigliando vltimamente la Diapason g & G, Settima specie
(lassando la f & F: perche non si può diuidere in tal maniera) se noi la diuideremo con la chorda c, haueremo il Duodecimo modo: percioche per tal diuisione nascerà la Terza specie della Diatessaron c & G, nella
parte graue, vnita alla Quarta specie della Diapente g & c; come qui sotto si può vedere.
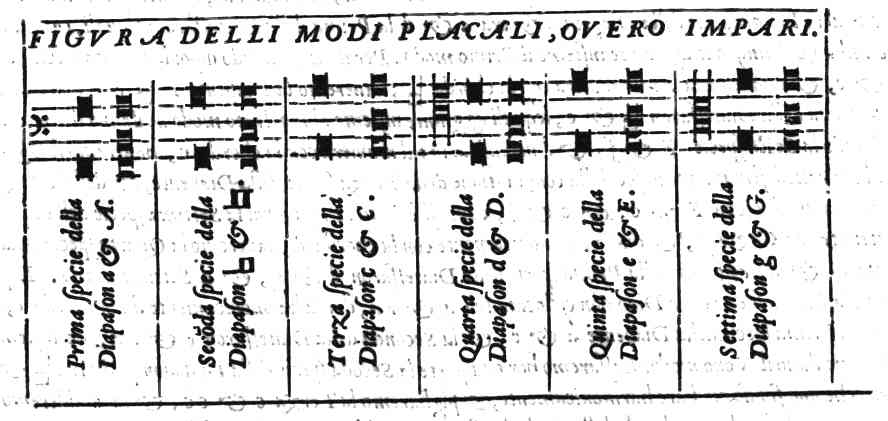
 &
&  non si possa diuidere harmoni
non si possa diuidere harmoni
 & F, & il Tritono F &
& F, & il Tritono F &  nella parte
acuta, quando fusse tramezata dalla chorda F: ne meno la Sesta specie F & f arithmeticamente; essendo
che si vdirebbe nel graue tra la chorda
nella parte
acuta, quando fusse tramezata dalla chorda F: ne meno la Sesta specie F & f arithmeticamente; essendo
che si vdirebbe nel graue tra la chorda  & F il Tritono, quando fusse diuisa dalla
& F il Tritono, quando fusse diuisa dalla  , & dalla parte acuta la Semidiapente f &
, & dalla parte acuta la Semidiapente f &  ; tuttauia sono stati alcuni, che oltra li Dodici mostrati, le hanno attribuito altri
Modi, si come alla prima diuisione il Terzodecimo, & alla seconda il Quartodecimo: ma veramente non possono essere più di Dodici; si come hauemo mostrato, i quali sono notati per ordine
nella figura di sopra.
; tuttauia sono stati alcuni, che oltra li Dodici mostrati, le hanno attribuito altri
Modi, si come alla prima diuisione il Terzodecimo, & alla seconda il Quartodecimo: ma veramente non possono essere più di Dodici; si come hauemo mostrato, i quali sono notati per ordine
nella figura di sopra.
Diuisione delli Modi in Autentici, & Plagali.Cap. 12.
Delle Chorde finali di ciascun Modo, & quanto si possa ascendere, o discendere di sopra, & di sotto le nominate chorde.Cap. 13.
 Et non solamente hanno le chorde finali communi: ma hanno etiandio i luoghi delle Cadenze; come
vederemo. Ma si debbe notare, che li Modi, quando sono perfetti, toccano le Otto chorde della loro Diapason:
è ben vero, che si troua questa differenza tra gli Autentichi, & li Plagali; che questi ascendeno solamente alla Quinta chorda sopra il loro fine, & discendeno alla Quarta: ma quelli toccano la Ottaua chorda acuta solamente; & alle volte discendeno sotto la loro Diapason per vn Tuono, o per vn Semituono; & li Plagali simigliantemente ascendeno sopra la loro Diapente per vn Tuono, ouero per vn Semituouo; come si vede in molti canti Ecclesiastici.
Di maniera che l'Autenti cosi troua tra Otto chorde tramezate harmonicamente; &
lo Plagale tra Otto arithmeticamente diuise; nel modo che si può vedere di sopra ne gli essempi. Estendendosi
adunque li Modi di sopra, & di sotto il loro fine a cotal modo, si possono chiamare Perfetti. Perilche l'Introito; che si canta nella Messa della quarta Domenica dell'Aduento, Rorate coeli desuper, si chiamarà Primo
modo perfetto; & quello, che si canta nella Messa della Ottaua della Natiuità del Signore, Vultum tuum deprecabuntur, si potrà dimandare Secondo modo perfetto. Ma quando li Plagali nel graue passassero più oltra,
ouero gli Autentichi nell'acuto; cotali Modi si potranno nominare (come li nomina Franchino Gaffuro) Superflui; si come si chiamarebbeno Imperfetti, o Diminuti, quando non arriuassero alla loro Ottaua chorda acupage 315ta, ouero alla Prima graue delle loro Diapason. Delli primi hauemo vno essempio nell'Introito Iustus es Domine del Primo modo, che si canta nella Messa della Domenica Decima settima dopo la solennità delle Pentecoste: Delli secondi sono quasi infiniti gli essempi, tra i quali si ritroua l'Introito Puer natus est nobis del Settimo modo,
che si canta alla Terza messa il Sacrosanto giorno della Natiuità del Figliuolo di Dio. Si debbe hora auertire per sempre, che quello ch'io ragiono intorno alli Modi del Canto fermo, intendo anco, che sia detto
intorno le parti delli Modi del Canto figurato; se bene io non pongo di loro gli essempi: percioche voglio, che cotale ragionamento sia commune all'vno, & all'altro. Ma perche hò detto di sopra, che ogni cosa si debbe denominare dal fine,
come da cosa più nobile; però da esso, cioè da ogni chorda finale haueremo da giudicare ciascuno Modo; di maniera, che quello, che terminerà nella chorda D, & salirà alla chorda d, dimandaremo Primo
modo perfetto, & quando non arriuasse (come hò mostrato) lo nominaremo Imperfetto; & quello che finirà
nella istessa D, & ascenderà alla chorda a, discendendo anco alla A, chiamaremo medesimamente Secondo
modo perfetto; & simigliantemente Imperfetto, quando non vi arriuasse. Similmente l'uno, et l'altro si addimandarebbe Superfluo, o Abondante, quando'l Primo passasse la Ottaua chorda sopra il suo fine, & il Secondo
la Quarta sotto di esso. Et ciò dico, quando finissero nelle lor chorde propie finali, & tenessero la loro forma
propia: percioche se finissero nelle loro chorde, che si chiamano Confinali, ouero in altre chorde, & tal forma
non si comprendesse essere in loro; allora haueremo da fare altro giuditio; si come altroue sono per dimostrare.
Et non solamente hanno le chorde finali communi: ma hanno etiandio i luoghi delle Cadenze; come
vederemo. Ma si debbe notare, che li Modi, quando sono perfetti, toccano le Otto chorde della loro Diapason:
è ben vero, che si troua questa differenza tra gli Autentichi, & li Plagali; che questi ascendeno solamente alla Quinta chorda sopra il loro fine, & discendeno alla Quarta: ma quelli toccano la Ottaua chorda acuta solamente; & alle volte discendeno sotto la loro Diapason per vn Tuono, o per vn Semituono; & li Plagali simigliantemente ascendeno sopra la loro Diapente per vn Tuono, ouero per vn Semituouo; come si vede in molti canti Ecclesiastici.
Di maniera che l'Autenti cosi troua tra Otto chorde tramezate harmonicamente; &
lo Plagale tra Otto arithmeticamente diuise; nel modo che si può vedere di sopra ne gli essempi. Estendendosi
adunque li Modi di sopra, & di sotto il loro fine a cotal modo, si possono chiamare Perfetti. Perilche l'Introito; che si canta nella Messa della quarta Domenica dell'Aduento, Rorate coeli desuper, si chiamarà Primo
modo perfetto; & quello, che si canta nella Messa della Ottaua della Natiuità del Signore, Vultum tuum deprecabuntur, si potrà dimandare Secondo modo perfetto. Ma quando li Plagali nel graue passassero più oltra,
ouero gli Autentichi nell'acuto; cotali Modi si potranno nominare (come li nomina Franchino Gaffuro) Superflui; si come si chiamarebbeno Imperfetti, o Diminuti, quando non arriuassero alla loro Ottaua chorda acupage 315ta, ouero alla Prima graue delle loro Diapason. Delli primi hauemo vno essempio nell'Introito Iustus es Domine del Primo modo, che si canta nella Messa della Domenica Decima settima dopo la solennità delle Pentecoste: Delli secondi sono quasi infiniti gli essempi, tra i quali si ritroua l'Introito Puer natus est nobis del Settimo modo,
che si canta alla Terza messa il Sacrosanto giorno della Natiuità del Figliuolo di Dio. Si debbe hora auertire per sempre, che quello ch'io ragiono intorno alli Modi del Canto fermo, intendo anco, che sia detto
intorno le parti delli Modi del Canto figurato; se bene io non pongo di loro gli essempi: percioche voglio, che cotale ragionamento sia commune all'vno, & all'altro. Ma perche hò detto di sopra, che ogni cosa si debbe denominare dal fine,
come da cosa più nobile; però da esso, cioè da ogni chorda finale haueremo da giudicare ciascuno Modo; di maniera, che quello, che terminerà nella chorda D, & salirà alla chorda d, dimandaremo Primo
modo perfetto, & quando non arriuasse (come hò mostrato) lo nominaremo Imperfetto; & quello che finirà
nella istessa D, & ascenderà alla chorda a, discendendo anco alla A, chiamaremo medesimamente Secondo
modo perfetto; & simigliantemente Imperfetto, quando non vi arriuasse. Similmente l'uno, et l'altro si addimandarebbe Superfluo, o Abondante, quando'l Primo passasse la Ottaua chorda sopra il suo fine, & il Secondo
la Quarta sotto di esso. Et ciò dico, quando finissero nelle lor chorde propie finali, & tenessero la loro forma
propia: percioche se finissero nelle loro chorde, che si chiamano Confinali, ouero in altre chorde, & tal forma
non si comprendesse essere in loro; allora haueremo da fare altro giuditio; si come altroue sono per dimostrare.
Delli Modi communi, & delli Misti.Cap. 14.
Altra diuisione delli Modi; & di quello, che si hà da osseruare in ciascuno, nel comporre le cantilene.Cap. 15.
Se col leuare da alcuna cantilena il Tetrachordo Diezeugmenon, ponendo il Synemennon in suo luogo, restando gli altri immobili, vn Modo si possa mutare nell'altro. Capitolo 16.
 , cioè la Trite synemennon incidentalmente una, o due fiate, tra la Mese, & la Paramese; Et
cosi potemo dire, che'l leuare il Tetrachordo Diezeugmenon, il cui principio hauemo nella chorda
, cioè la Trite synemennon incidentalmente una, o due fiate, tra la Mese, & la Paramese; Et
cosi potemo dire, che'l leuare il Tetrachordo Diezeugmenon, il cui principio hauemo nella chorda  , cioè
in Paramese; & il porre il Synemennon, che hà il suo principio nella chorda a, cioè il porre la
, cioè
in Paramese; & il porre il Synemennon, che hà il suo principio nella chorda a, cioè il porre la  sopradetta, non hà forza di trasmutare vn Modo nell'altro; & che tal Tetrachordo posto nella cantilena non sia
naturale, ma accidentale; & in questo caso dicono bene: Ma il secondo modo si fa, quando per tutta la cantilena, cioè in ciascuna parte, in luogo del Tetrachordo Diezeugmenon, vsiamo il Synemennon; & in luogo di cantar la detta cantilena per la propietà del
sopradetta, non hà forza di trasmutare vn Modo nell'altro; & che tal Tetrachordo posto nella cantilena non sia
naturale, ma accidentale; & in questo caso dicono bene: Ma il secondo modo si fa, quando per tutta la cantilena, cioè in ciascuna parte, in luogo del Tetrachordo Diezeugmenon, vsiamo il Synemennon; & in luogo di cantar la detta cantilena per la propietà del  quadrato, la cantiamo per quella del
quadrato, la cantiamo per quella del  molle; La
onde essendo posto in cotal maniera, non dicono bene: percioche questo Tetrachordo non è posto accidentalmente nella cantilena: ma è naturale; & il Modo si chiama Trasportato, come più a basso vederemo; &
cotale Tetrachordo hà possanza di trasmutare vn Modo nell'altro. Et che ciò sia vero, facilmente potrepage 318mo conoscere con vno accommodato essempio. Poniamo il sottoposto Tenore del Settimo modo, contenuto
nelle sue chorde naturali; cioè nelli suoi propij, & naturali luoghi, tra la Settima specie della Diapason.
molle; La
onde essendo posto in cotal maniera, non dicono bene: percioche questo Tetrachordo non è posto accidentalmente nella cantilena: ma è naturale; & il Modo si chiama Trasportato, come più a basso vederemo; &
cotale Tetrachordo hà possanza di trasmutare vn Modo nell'altro. Et che ciò sia vero, facilmente potrepage 318mo conoscere con vno accommodato essempio. Poniamo il sottoposto Tenore del Settimo modo, contenuto
nelle sue chorde naturali; cioè nelli suoi propij, & naturali luoghi, tra la Settima specie della Diapason.
 Dico, che se in tal Tenore, ouero in vn'altro simile si mutasse la chorda
Dico, che se in tal Tenore, ouero in vn'altro simile si mutasse la chorda  solamente vna, o due volte
nella
solamente vna, o due volte
nella  ; questo non farebbe, che tal Modo si trasmutasse, se non in quella particella, oue fusse posto; &
non hauerebbe possanza di fare, che tal Modo non fusse anche Settimo: Imperoche se bene tal chorda posta
in cotal modo è necessaria, per potere regolare la modulatione; tuttauia essendo accidentale, non muta la forma del Modo di
maniera, che non si habbia da conoscere per Settimo; come da questo essempio si può vedere.
; questo non farebbe, che tal Modo si trasmutasse, se non in quella particella, oue fusse posto; &
non hauerebbe possanza di fare, che tal Modo non fusse anche Settimo: Imperoche se bene tal chorda posta
in cotal modo è necessaria, per potere regolare la modulatione; tuttauia essendo accidentale, non muta la forma del Modo di
maniera, che non si habbia da conoscere per Settimo; come da questo essempio si può vedere.
 Ma se noi porremo nel principio de tali Tenori il segno
Ma se noi porremo nel principio de tali Tenori il segno  , il quale dimostra, che per tutta la cantilena douemo procedere per le chorde del Tetrachordo synemennon, dico che allora tal chorda sarà naturale, & non
accidentale; & hauerà possanza di mutare il Settimo modo nel Primo: percioche varia la specie della Diapente, che era Quarta
per inanti tra G & d; et pone in essere la Prima tra le istesse chorde; come qui si vede.
, il quale dimostra, che per tutta la cantilena douemo procedere per le chorde del Tetrachordo synemennon, dico che allora tal chorda sarà naturale, & non
accidentale; & hauerà possanza di mutare il Settimo modo nel Primo: percioche varia la specie della Diapente, che era Quarta
per inanti tra G & d; et pone in essere la Prima tra le istesse chorde; come qui si vede.
 E' ben vero, che il Modo non si troua nelle sue chorde naturali: percioche è trasportato, per vna Diatessaron
più acuta; Il perche quando si volesse porre al suo luogo, si ritrouarebbe collocato in cotal maniera.
E' ben vero, che il Modo non si troua nelle sue chorde naturali: percioche è trasportato, per vna Diatessaron
più acuta; Il perche quando si volesse porre al suo luogo, si ritrouarebbe collocato in cotal maniera.
 Non è adunque vero assolutamente, che'l porre il Tetrachordo Synemennon in vna cantilena in luogo del
Diezeugmenon, non habbia forza, di mutare quel Modo, in cui si pone, in vn'altro: ma è ben vero, quando
è posto secondo il modo mostrato. Diremo adunque, che se per la varietà del Tetrachordo, segue la variatione della Diapason; & dalla varietà della Diapason la varietà del Modo; procedendo dal primo all'vltimo diremo, che tal Tetrachordo posto al secondo mostrato modo, habbia possanza di mutare vn Modo nell'altro. In
questa maniera variò il Modo Gioan Motone nella Messa, che compose sopra l'Antifona Argentum, & aurum non est mihi, la quale è del Settimo modo; nondimeno trasportando il Tetrachordo, ouero mutandolo
la fece dell'Vndecimo. Concluderemo adunque, che qualunque volta porremo in vna cantilena la chorda
Non è adunque vero assolutamente, che'l porre il Tetrachordo Synemennon in vna cantilena in luogo del
Diezeugmenon, non habbia forza, di mutare quel Modo, in cui si pone, in vn'altro: ma è ben vero, quando
è posto secondo il modo mostrato. Diremo adunque, che se per la varietà del Tetrachordo, segue la variatione della Diapason; & dalla varietà della Diapason la varietà del Modo; procedendo dal primo all'vltimo diremo, che tal Tetrachordo posto al secondo mostrato modo, habbia possanza di mutare vn Modo nell'altro. In
questa maniera variò il Modo Gioan Motone nella Messa, che compose sopra l'Antifona Argentum, & aurum non est mihi, la quale è del Settimo modo; nondimeno trasportando il Tetrachordo, ouero mutandolo
la fece dell'Vndecimo. Concluderemo adunque, che qualunque volta porremo in vna cantilena la chorda  in luogo della
in luogo della  , che tal chorda farà sempre variare il Modo; & cosi per il contrario, ponendo la
, che tal chorda farà sempre variare il Modo; & cosi per il contrario, ponendo la  in
luogo della
in
luogo della  , come ne mostra l'esperienza. page 319
, come ne mostra l'esperienza. page 319Della Trasportatione delli Modi.Cap. 17.
 in luogo della
in luogo della  ; ouero per dir meglio, per la
trasportatione del Semituono, si possa variare vn Modo nell'altro; & di Primo farlo diuentare Settimo; & di Settimo Primo:
non è dubbio, che qualunque Modo, sia Primo,
Secondo, Terzo, Quarto, ouero alcuno de gli altri, col fauore di alcuna chorda, che muti vna Diapason nell'altra, potremo trasportare qualunque Modo verremo verso l'acuto, o verso il graue, a
nostro bel piacere. Il che quanto alle volte possa tornar commodo, lassarò giudicare a ciascuno, che habbia
giuditio: percioche tali Trasportationi sono vtili, & sommamente necessarie anco ad ogni perito Organista,
che serue alle Musiche choriste; & ad altri Sonatori similmente, che sonano altre sorti di istrumenti, per accommodare il suono di quelli alle Voci, le quali alle volte non possono ascendere, o discendere tanto, quanto
ricercano i luoghi propij delli Modi, accommodati sopra i detti istrumenti. Et tali Trasportationi sono hora
in vso appresso i Musici moderni; come furono anche appresso gli Antichi, Ocheghen, & il suo discepolo Iosquino, & infiniti altri; come nelle loro compositioni si può vedere. Quando adunque accascarà, che per necessità, o per qualunque altro accidente, farà dibisogno di trasportare il Modo, contenuto in alcuna cantilena;
sopra ogn'altra cosa bisognarà auertire, di accommodarlo in tal maniera, & in tal luogo, che si possa ascendendo, & discendendo, hauere tutte quelle chorde, che sono necessarie alla costitutione di tal Modo; cioè che
diano li Tuoni, & li Semituoni necessarij al suo essere essentiale. Et ciò debbeno sommamente osseruare li
Compositori, quando vorranno comporre tali cantilene, per sonare sopra qualche istrumento: Imperoche quando le vorranno comporre per cantare solamente, non
sarebbe grande errore, quando segnassero alcune chorde con alcuno segno accidentale, che non si ritrouassero sopra lo istrumento; massimamente sopra il Clauocembalo; come sono l'Enharmoniche, le quali si trouano in pochi istrumenti arteficiali. Et questo hò detto:
percioche la voce si può fare acuta, & graue; ouero si può vsare in qualunque altra maniera, secondo il voler del cantore, che non si può fare cosi liberamente con tali istrumenti. Hora per mostrare in qual maniera
commodamente si possa trasportare qual si voglia cantilena fuori delle sue chorde naturali, non pigliaremo
altro essempio, che il Terzo, & il Quarto posto nel Capitolo precedente: percioche ne potranno ottimamente
mostrare in qual maniera ogni cantilena, che procede per la chorda
; ouero per dir meglio, per la
trasportatione del Semituono, si possa variare vn Modo nell'altro; & di Primo farlo diuentare Settimo; & di Settimo Primo:
non è dubbio, che qualunque Modo, sia Primo,
Secondo, Terzo, Quarto, ouero alcuno de gli altri, col fauore di alcuna chorda, che muti vna Diapason nell'altra, potremo trasportare qualunque Modo verremo verso l'acuto, o verso il graue, a
nostro bel piacere. Il che quanto alle volte possa tornar commodo, lassarò giudicare a ciascuno, che habbia
giuditio: percioche tali Trasportationi sono vtili, & sommamente necessarie anco ad ogni perito Organista,
che serue alle Musiche choriste; & ad altri Sonatori similmente, che sonano altre sorti di istrumenti, per accommodare il suono di quelli alle Voci, le quali alle volte non possono ascendere, o discendere tanto, quanto
ricercano i luoghi propij delli Modi, accommodati sopra i detti istrumenti. Et tali Trasportationi sono hora
in vso appresso i Musici moderni; come furono anche appresso gli Antichi, Ocheghen, & il suo discepolo Iosquino, & infiniti altri; come nelle loro compositioni si può vedere. Quando adunque accascarà, che per necessità, o per qualunque altro accidente, farà dibisogno di trasportare il Modo, contenuto in alcuna cantilena;
sopra ogn'altra cosa bisognarà auertire, di accommodarlo in tal maniera, & in tal luogo, che si possa ascendendo, & discendendo, hauere tutte quelle chorde, che sono necessarie alla costitutione di tal Modo; cioè che
diano li Tuoni, & li Semituoni necessarij al suo essere essentiale. Et ciò debbeno sommamente osseruare li
Compositori, quando vorranno comporre tali cantilene, per sonare sopra qualche istrumento: Imperoche quando le vorranno comporre per cantare solamente, non
sarebbe grande errore, quando segnassero alcune chorde con alcuno segno accidentale, che non si ritrouassero sopra lo istrumento; massimamente sopra il Clauocembalo; come sono l'Enharmoniche, le quali si trouano in pochi istrumenti arteficiali. Et questo hò detto:
percioche la voce si può fare acuta, & graue; ouero si può vsare in qualunque altra maniera, secondo il voler del cantore, che non si può fare cosi liberamente con tali istrumenti. Hora per mostrare in qual maniera
commodamente si possa trasportare qual si voglia cantilena fuori delle sue chorde naturali, non pigliaremo
altro essempio, che il Terzo, & il Quarto posto nel Capitolo precedente: percioche ne potranno ottimamente
mostrare in qual maniera ogni cantilena, che procede per la chorda  , si possa trasportare per vna Diatessaron in acuto, con l'aiuto della chorda
, si possa trasportare per vna Diatessaron in acuto, con l'aiuto della chorda  ; ouero per il contrario, quando il canto procedesse per la chorda
; ouero per il contrario, quando il canto procedesse per la chorda  , in qual maniera si potesse trasporre nel graue commodamente per vn simile interuallo, con l'aiuto
della
, in qual maniera si potesse trasporre nel graue commodamente per vn simile interuallo, con l'aiuto
della  . Ma perche alle volte li Musici, non gia per necessità: ma più presto per burla, & per capriccio; o forse per volere intricare il ceruello (dirò cosi) alli Cantanti, sogliono trasportare li Modi più verso
l'acuto, ouero verso il graue per vn Tuono, o per altro interuallo; adoperando non solamente le chorde Chromatiche: ma anco le Enarmoniche; per potere commodamente, quando gli fa dibisogno, trasportare a i loro
luoghi li Tuoni, & li Semituoni, secondo la propia forma del Modo; però uoglio mostrare in qual modo si
soglino trasportare. Et benche li Musici soglino vsare di trasportare li Modi in più maniere; tuttauia porrò
qui due Trasportationi solamente più vsate, fatte nel Primo modo; dalle quali potrà ogn'uno comprendere il
modo, che hauerà da tenere nell'altre; & saranno le sottoposte; l'vna delle quali si fa con l'aiuto delle chorde
segnate col
. Ma perche alle volte li Musici, non gia per necessità: ma più presto per burla, & per capriccio; o forse per volere intricare il ceruello (dirò cosi) alli Cantanti, sogliono trasportare li Modi più verso
l'acuto, ouero verso il graue per vn Tuono, o per altro interuallo; adoperando non solamente le chorde Chromatiche: ma anco le Enarmoniche; per potere commodamente, quando gli fa dibisogno, trasportare a i loro
luoghi li Tuoni, & li Semituoni, secondo la propia forma del Modo; però uoglio mostrare in qual modo si
soglino trasportare. Et benche li Musici soglino vsare di trasportare li Modi in più maniere; tuttauia porrò
qui due Trasportationi solamente più vsate, fatte nel Primo modo; dalle quali potrà ogn'uno comprendere il
modo, che hauerà da tenere nell'altre; & saranno le sottoposte; l'vna delle quali si fa con l'aiuto delle chorde
segnate col  ; & l'altra con l'aiuto di quelle, che sono segnate col
; & l'altra con l'aiuto di quelle, che sono segnate col  . Bisogna auertire, che li Moderni
. Bisogna auertire, che li Moderni

 page 320chiamano queste Trasportationi Modi trasposti per Musica finta, la quale (secondo che la dichiarano) dicono essere vna Trasportatione di figure (intendendo però di tutto l'ordine, che si troua in ciascun Modo) dalla
loro propia sede in vn'altra. Lasso hora giudicare ad ogn'vno perito nella Musica, quanto potrà essere vtile tale cognitione ad ogni Organista non cosi bene istrutto nella Musica: conciosia che dalli mostrati essempi potrà vedere, & conoscere quello, che hauerà a fare, quando gli accascarà di trasportare alcuna cantilena, quando seruirà alle Capelle, oue si cantano varie cantilene appartinenti alli chori, non solo nelle Messe,
& nelli Vesperi; ma anche nell'altre Hore, tanto diurne, quanto notturne. Ma questo si debbe sapere sopra
ogn'altra cosa; che quantunque io habbia posto gli essempi solamente del Primo modo, che tali Trasportationi si possono fare nell'altre cantilene de gli altri Modi; il che hò lassato di mostrare per volere esser breue.
page 320chiamano queste Trasportationi Modi trasposti per Musica finta, la quale (secondo che la dichiarano) dicono essere vna Trasportatione di figure (intendendo però di tutto l'ordine, che si troua in ciascun Modo) dalla
loro propia sede in vn'altra. Lasso hora giudicare ad ogn'vno perito nella Musica, quanto potrà essere vtile tale cognitione ad ogni Organista non cosi bene istrutto nella Musica: conciosia che dalli mostrati essempi potrà vedere, & conoscere quello, che hauerà a fare, quando gli accascarà di trasportare alcuna cantilena, quando seruirà alle Capelle, oue si cantano varie cantilene appartinenti alli chori, non solo nelle Messe,
& nelli Vesperi; ma anche nell'altre Hore, tanto diurne, quanto notturne. Ma questo si debbe sapere sopra
ogn'altra cosa; che quantunque io habbia posto gli essempi solamente del Primo modo, che tali Trasportationi si possono fare nell'altre cantilene de gli altri Modi; il che hò lassato di mostrare per volere esser breue.
Ragionamento particolare intorno al Primo modo, della sua Natura, delli suoi Principij, & delle sue Cadenze.Cap. 18.
 Si debbe però auertire, che le Cadenze delle Salmodie si fanno sempre, doue casca il termine della mediatione della loro Intonatione: la onde le Cadenze della mediatione, ò mezano punto della Salmodia del Primo,
del Quarto, & del Sesto modo si faranno in a; quelle del Secondo in F; quelle del Terzo, del Quinto,
& dell'Ottauo in c; & quelle del Settimo in e: imperoche tali mediationi, o punti mezani terminano
iui; come si può vedere nel Recanetto, nel Thoscanello, & in molti altri libri, che contengono simili Salmodie, ouero Intonationi, che le vogliam dire. Le finale poi si fanno sempre nel luogo, che ciascuno verso di tali Salmodie,
ouero di ciascun Salmo si fanno finire. Douemo etiandio sempre osseruare, di far le Cadenze
principalmente nel Tenore: conciosia che questa parte è la guida principale delli Modi, ne i quali si compone
la cantilena; & da essa debbe il Compositore pigliare la inuentione dell'altre parti: Ma tali Cadenze si fanno nelle altre
parti della Cantilena, quando tornano bene. Questo Modo col Nono hà strettissima parentella:
percioche li Musici compongono nel suo luogo propio le loro cantilene del Nono modo, fuori delle sue chorde
naturali, trasportandolo nell'acuto per vna Diatessaron, ouero nel graue per vna Diapente; lassando la chorpage 322da
Si debbe però auertire, che le Cadenze delle Salmodie si fanno sempre, doue casca il termine della mediatione della loro Intonatione: la onde le Cadenze della mediatione, ò mezano punto della Salmodia del Primo,
del Quarto, & del Sesto modo si faranno in a; quelle del Secondo in F; quelle del Terzo, del Quinto,
& dell'Ottauo in c; & quelle del Settimo in e: imperoche tali mediationi, o punti mezani terminano
iui; come si può vedere nel Recanetto, nel Thoscanello, & in molti altri libri, che contengono simili Salmodie, ouero Intonationi, che le vogliam dire. Le finale poi si fanno sempre nel luogo, che ciascuno verso di tali Salmodie,
ouero di ciascun Salmo si fanno finire. Douemo etiandio sempre osseruare, di far le Cadenze
principalmente nel Tenore: conciosia che questa parte è la guida principale delli Modi, ne i quali si compone
la cantilena; & da essa debbe il Compositore pigliare la inuentione dell'altre parti: Ma tali Cadenze si fanno nelle altre
parti della Cantilena, quando tornano bene. Questo Modo col Nono hà strettissima parentella:
percioche li Musici compongono nel suo luogo propio le loro cantilene del Nono modo, fuori delle sue chorde
naturali, trasportandolo nell'acuto per vna Diatessaron, ouero nel graue per vna Diapente; lassando la chorpage 322da  , & ponendoui la
, & ponendoui la  ; come fece Morale Spagnuolo nel motetto Sancta, & immaculata virginitas, a quattro voci. Et perche il Primo modo hà vn certo mezano effetto tra il mesto, & lo allegro; per cagione del Semiditono, che si ode nel concento sopra le chorde estreme della Diapente, & della Diatessaron;
non hauendo altramente il Ditono dalla parte graue; per sua natura è Modo religioso, & diuoto. Però potremo ad esso
accommodare ottimamente quelle parole, le quali saranno piene di grauità, & che trattaranno di cose alte,
& sententiose; accioche l'harmonia si conuenghi con la materia, che in esse si contiene.
; come fece Morale Spagnuolo nel motetto Sancta, & immaculata virginitas, a quattro voci. Et perche il Primo modo hà vn certo mezano effetto tra il mesto, & lo allegro; per cagione del Semiditono, che si ode nel concento sopra le chorde estreme della Diapente, & della Diatessaron;
non hauendo altramente il Ditono dalla parte graue; per sua natura è Modo religioso, & diuoto. Però potremo ad esso
accommodare ottimamente quelle parole, le quali saranno piene di grauità, & che trattaranno di cose alte,
& sententiose; accioche l'harmonia si conuenghi con la materia, che in esse si contiene.
Del Secondo Modo.Cap. 19.
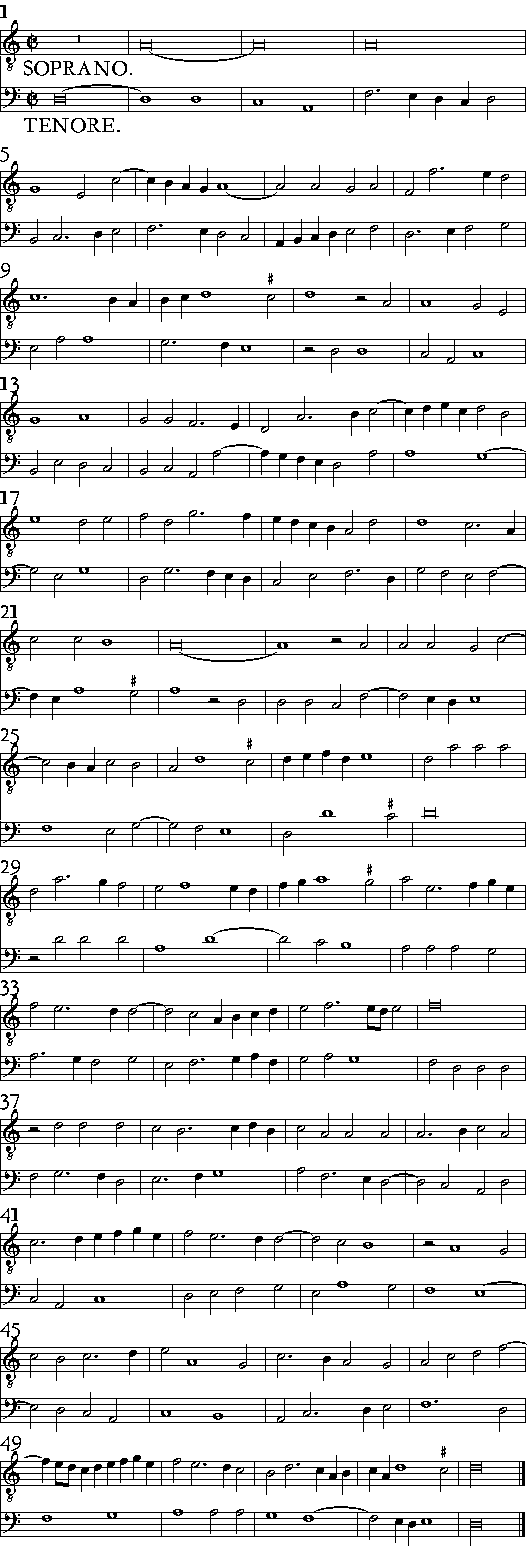 page 323no; & dicono, che è Modo atto alle parole, che rapresentano pianto, mestitia, solicitudine, cattiuità, calamità, & ogni generatione di miseria; & si troua molto in vso ne i loro canti; & le sue Cadenze principali, & regolari (per essere questo Modo dal Primo poco differente: percioche l'vno & l'altro si compongono
delle istesse specie) si pongono nelle chorde nominate di sopra, chesono a, F, D, & A; che si vedeno
nello essempio: l'altre poi, che si pongono ne i altri luoghi sono tutte Irregolari. Dicono li Prattici, che questo Modo si compone della Prima specie della Diapente a & D posta nell'acuto, & della Prima della Diatessaron D & A posta
nel graue; & lo chiamano Collaterale, ouer Plagale del Primo modo. Si trouano molte compositioni del Secondo modo, composte da molti Antichi, & da Moderni Musici; tra le
quali è il motetto, Praeter rerum seriem, composto a sei voci da Iosquino; & da Adriano a Sette voci; col
madrigale, Che fai alma, similmente a sette voci; il motetto Auertatur obsecro domine, & il madrigale,
Oue ch'i posi gli occhi; l'vno & l'altro a sei voci, con molti altri. Composi anche io in tal Modo la Oratione Dominicale, Pater noster; con la Salutatione angelica, Aue maria, a sette voci; & li motetti, Ego rosa
Saron, & Capite nobis vulpes paruulas a cinque voci. Si trouano etiandio molte altre compositioni fatte da
diuersi compositori, le quali per essere quasi infinite si lassano. Questo Modo rare volte si troua nelli Canti figurati nelle sue chorde propie: ma il più delle uolte si ritroua trasportato per vna Quarta; come si può vedere nelli Motetti nominati; & questo: percioche si può trasporre; come anco si può trasporre il Primo modo,
con l'aiuto della chorda Trite synemennon, verso l'acuto. Et si come il Primo col Nono hà molta conuenienza, cosi questo l'hà veramente col Decimo.
page 323no; & dicono, che è Modo atto alle parole, che rapresentano pianto, mestitia, solicitudine, cattiuità, calamità, & ogni generatione di miseria; & si troua molto in vso ne i loro canti; & le sue Cadenze principali, & regolari (per essere questo Modo dal Primo poco differente: percioche l'vno & l'altro si compongono
delle istesse specie) si pongono nelle chorde nominate di sopra, chesono a, F, D, & A; che si vedeno
nello essempio: l'altre poi, che si pongono ne i altri luoghi sono tutte Irregolari. Dicono li Prattici, che questo Modo si compone della Prima specie della Diapente a & D posta nell'acuto, & della Prima della Diatessaron D & A posta
nel graue; & lo chiamano Collaterale, ouer Plagale del Primo modo. Si trouano molte compositioni del Secondo modo, composte da molti Antichi, & da Moderni Musici; tra le
quali è il motetto, Praeter rerum seriem, composto a sei voci da Iosquino; & da Adriano a Sette voci; col
madrigale, Che fai alma, similmente a sette voci; il motetto Auertatur obsecro domine, & il madrigale,
Oue ch'i posi gli occhi; l'vno & l'altro a sei voci, con molti altri. Composi anche io in tal Modo la Oratione Dominicale, Pater noster; con la Salutatione angelica, Aue maria, a sette voci; & li motetti, Ego rosa
Saron, & Capite nobis vulpes paruulas a cinque voci. Si trouano etiandio molte altre compositioni fatte da
diuersi compositori, le quali per essere quasi infinite si lassano. Questo Modo rare volte si troua nelli Canti figurati nelle sue chorde propie: ma il più delle uolte si ritroua trasportato per vna Quarta; come si può vedere nelli Motetti nominati; & questo: percioche si può trasporre; come anco si può trasporre il Primo modo,
con l'aiuto della chorda Trite synemennon, verso l'acuto. Et si come il Primo col Nono hà molta conuenienza, cosi questo l'hà veramente col Decimo.
Del Terzo Modo.Cap. 20.
 ; ouero dalla vnione della Seconda specie della Diapente E &
; ouero dalla vnione della Seconda specie della Diapente E &
 , posta nel graue, con la Seconda della Diatessaron
, posta nel graue, con la Seconda della Diatessaron  & e, posta nell'acuto. Questo Modo hà la sua chorda finale E commune col Quarto modo; & gli Ecclesiastici hanno di questo Modo infinite cantilene, come ne i loro libri si può vedere. Le sue Cadenze
& e, posta nell'acuto. Questo Modo hà la sua chorda finale E commune col Quarto modo; & gli Ecclesiastici hanno di questo Modo infinite cantilene, come ne i loro libri si può vedere. Le sue Cadenze
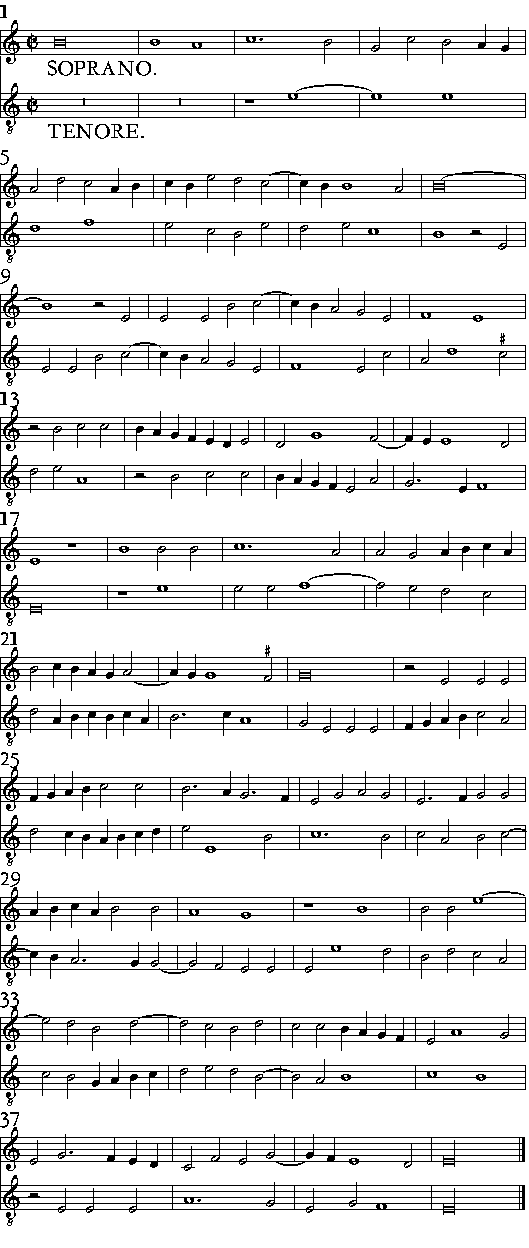 page 324principali si fanno nelle chorde de i suoi principij regolari, i quali sono le chorde mostrate E, G,
page 324principali si fanno nelle chorde de i suoi principij regolari, i quali sono le chorde mostrate E, G,  , &
e; che sono le estreme della sua Diapente, & della sua Diatessaron, & la mezana della Diapente; le altre poi, che sono Irregolari, si possono fare sopra l'altre chorde: Ma perche conosciuto le Regolari, facilmente
si può conoscere le Irregolari; però daremo vno essempio delle prime, acciò veniamo in cognitione delle seconde. Si debbe però auertire, che tanto in questo, quanto nel Quarto, nel Settimo, & nell'Ottauo modo,
regolarmente si fanno le cadenze nella chorda
, &
e; che sono le estreme della sua Diapente, & della sua Diatessaron, & la mezana della Diapente; le altre poi, che sono Irregolari, si possono fare sopra l'altre chorde: Ma perche conosciuto le Regolari, facilmente
si può conoscere le Irregolari; però daremo vno essempio delle prime, acciò veniamo in cognitione delle seconde. Si debbe però auertire, che tanto in questo, quanto nel Quarto, nel Settimo, & nell'Ottauo modo,
regolarmente si fanno le cadenze nella chorda  : ma perche tal chorda non hà corrispondenza alcuna per
Quinta nell'acuto, ne per Quarta nel graue; però è alquanto dura: ma tal durezza si sopporta nelle cantilene composte a più di due voci: percioche si tiene tal'ordine, che fanno buono effetto; come si può vedere tra
le Cadenze poste nel Cap. 61. della Terza parte. Molte compositioni si trouano composte sotto questo Modo, tra le quali è il motetto, O Maria mater Christi a quattro voci di Isac; & li motetti di Adriano, Te Deum
patrem; Huc me sydereo; & Haec est domus domini, composti a sette voci: & il Madrigale, I mi riuolgo indietro, composto da Adriano medesimamente a cinque voci: alli quali aggiungeremo, Ferculum fecit
sibi rex Salomon, il quale gia composi insieme con molti altri di tal Modo simigliantemente a cinque voci.
Se questo Modo non si mescolasse col Nono, & si vdisse semplice, hauerebbe la sua harmonia alquanto dura: ma perche è temperata dalla Diapente del Nono, & dalla Cadenza, che si fa in a, che in esso grandemente si vsa; però alcuni hanno hauuto parere, che habbia natura di commouere al pianto; la onde gli accommodarono volentieri quelle parole, che sono lagrimeuoli, & piene di lamenti. Hà grande conuenienza col detto Nono: percioche hanno la Seconda specie della Diatessaron commune tra loro; & spesse volte
i Musici moderni lo trasportano fuori delle sue chorde naturali per vna Diatessaron più acuta, con l'aiuto del
la chorda
: ma perche tal chorda non hà corrispondenza alcuna per
Quinta nell'acuto, ne per Quarta nel graue; però è alquanto dura: ma tal durezza si sopporta nelle cantilene composte a più di due voci: percioche si tiene tal'ordine, che fanno buono effetto; come si può vedere tra
le Cadenze poste nel Cap. 61. della Terza parte. Molte compositioni si trouano composte sotto questo Modo, tra le quali è il motetto, O Maria mater Christi a quattro voci di Isac; & li motetti di Adriano, Te Deum
patrem; Huc me sydereo; & Haec est domus domini, composti a sette voci: & il Madrigale, I mi riuolgo indietro, composto da Adriano medesimamente a cinque voci: alli quali aggiungeremo, Ferculum fecit
sibi rex Salomon, il quale gia composi insieme con molti altri di tal Modo simigliantemente a cinque voci.
Se questo Modo non si mescolasse col Nono, & si vdisse semplice, hauerebbe la sua harmonia alquanto dura: ma perche è temperata dalla Diapente del Nono, & dalla Cadenza, che si fa in a, che in esso grandemente si vsa; però alcuni hanno hauuto parere, che habbia natura di commouere al pianto; la onde gli accommodarono volentieri quelle parole, che sono lagrimeuoli, & piene di lamenti. Hà grande conuenienza col detto Nono: percioche hanno la Seconda specie della Diatessaron commune tra loro; & spesse volte
i Musici moderni lo trasportano fuori delle sue chorde naturali per vna Diatessaron più acuta, con l'aiuto del
la chorda  ; ancora che'l più delle volte si ritroui collocato nel suo propio, & natural luogo.
; ancora che'l più delle volte si ritroui collocato nel suo propio, & natural luogo.
Del Quarto Modo.Cap. 21.
 &
&
 , mediata dalla sua chorda finale E arithmeticamente. Questo (come dicono li
Prattici) si compone della Seconda specie della Diapente
, mediata dalla sua chorda finale E arithmeticamente. Questo (come dicono li
Prattici) si compone della Seconda specie della Diapente  & E, posta in acuto; &
della Seconda della Diatessaron E &
& E, posta in acuto; &
della Seconda della Diatessaron E &  , congiunta alla Diapente dalla parte graue. Questo medesimamente, secondo la loro opinione, si accommoda marauigliosamente
a parole, o materie lamenteuoli, che contengono tristezza, ouero lamentatione supplicheuole; come sono materie amorose, & quelle, che significano otio, quiete, tranquillità, adulatione, fraude, & detrattione; il perche dallo effetto alcuni lo chiamarono Modo adulatorio. Questo è alquanto più mesto del suo principale, massimamente quando procede per mouimenti contrarij, cioè dall'acuto al graue, con mouimenti tardi. Credo
io, che se'l si vsasse semplicemente, senza mescolarui la Diapente, & la Cadenza posta in a, che serue al
Decimo modo; che hauerebbe alquanto più del virile, di quello, che non hà cosi mescolato: ma accompagnato in tal maniera, si vsa grandemente, di modo che si trouano molte cantilene composte sotto questo
Modo, tra le quali si troua il motetto, Deprofundis clamaui ad te Domine a quattro voci di Iosquino; &
il motetto, Peccata mea Domine, col Madrigale, Rompi dell'empio cor'il duro scoglio di Adriano, l'vno, &
l'altro composti a sei voci; & il madrigale, Laura mia sacra composto a cinque voci. Composi ancora io
molte cantilene, tra le quali si troua a sei voci il motetto, Miserere mei Deus miserere mei, & vna Messa, senza vsar le osseruanze mostrate nella Terza parte; & ciò feci, non per altro, se non per mostrare, che ciascuno il quale
vorrà comporre senza partirsi dalle date Regole, potrà etiandio comporre facilmente senza queste
osseruanze, & assai meglio di quello, che fanno alcuni, che non le sanno, quando lo vorrà fare. Si trouano di
questo Modo quasi infinite cantilene ecclesiastiche, nelle quali rarissime volte (anzi s'io dicesse mai, non errarei) si vede
toccar la chorda
, congiunta alla Diapente dalla parte graue. Questo medesimamente, secondo la loro opinione, si accommoda marauigliosamente
a parole, o materie lamenteuoli, che contengono tristezza, ouero lamentatione supplicheuole; come sono materie amorose, & quelle, che significano otio, quiete, tranquillità, adulatione, fraude, & detrattione; il perche dallo effetto alcuni lo chiamarono Modo adulatorio. Questo è alquanto più mesto del suo principale, massimamente quando procede per mouimenti contrarij, cioè dall'acuto al graue, con mouimenti tardi. Credo
io, che se'l si vsasse semplicemente, senza mescolarui la Diapente, & la Cadenza posta in a, che serue al
Decimo modo; che hauerebbe alquanto più del virile, di quello, che non hà cosi mescolato: ma accompagnato in tal maniera, si vsa grandemente, di modo che si trouano molte cantilene composte sotto questo
Modo, tra le quali si troua il motetto, Deprofundis clamaui ad te Domine a quattro voci di Iosquino; &
il motetto, Peccata mea Domine, col Madrigale, Rompi dell'empio cor'il duro scoglio di Adriano, l'vno, &
l'altro composti a sei voci; & il madrigale, Laura mia sacra composto a cinque voci. Composi ancora io
molte cantilene, tra le quali si troua a sei voci il motetto, Miserere mei Deus miserere mei, & vna Messa, senza vsar le osseruanze mostrate nella Terza parte; & ciò feci, non per altro, se non per mostrare, che ciascuno il quale
vorrà comporre senza partirsi dalle date Regole, potrà etiandio comporre facilmente senza queste
osseruanze, & assai meglio di quello, che fanno alcuni, che non le sanno, quando lo vorrà fare. Si trouano di
questo Modo quasi infinite cantilene ecclesiastiche, nelle quali rarissime volte (anzi s'io dicesse mai, non errarei) si vede
toccar la chorda  . Bene è vero, che passa nell'acuto alla chorda c, di maniera che quando'l
Semituono douerebbere vdirsi nel graue, si ode nell'acuto; & cosi gli estremi di cotal Modo vengono ad essere le chorde c & C. Li suoi Principij irregolari appresso gli Ecclesiasticisi trouano in molti luoghi: ma
li regolari sono nelle chorde
. Bene è vero, che passa nell'acuto alla chorda c, di maniera che quando'l
Semituono douerebbere vdirsi nel graue, si ode nell'acuto; & cosi gli estremi di cotal Modo vengono ad essere le chorde c & C. Li suoi Principij irregolari appresso gli Ecclesiasticisi trouano in molti luoghi: ma
li regolari sono nelle chorde  , E, G &
, E, G &  solamente; si come si trouano anco le sue Cadenze regolari,
che sono le sottoposte; ancora che molte siano le Irregolari. Il più delle volte li Prattici lo trasportano per
vna Diatessaron nell'acuto, ponendo la chorda
solamente; si come si trouano anco le sue Cadenze regolari,
che sono le sottoposte; ancora che molte siano le Irregolari. Il più delle volte li Prattici lo trasportano per
vna Diatessaron nell'acuto, ponendo la chorda  in luogo della
in luogo della  , come si può vedere in infinite cantilene; il che fanno etiandio (come hò detto) ne gli altri Modi. page 325
, come si può vedere in infinite cantilene; il che fanno etiandio (come hò detto) ne gli altri Modi. page 325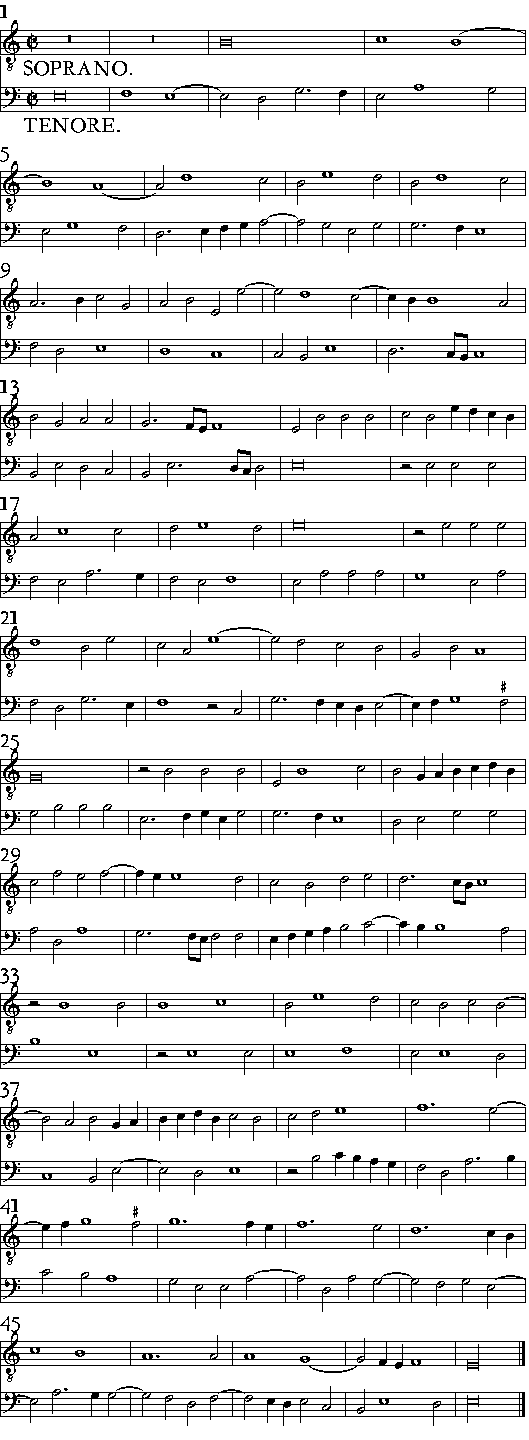
Del Quinto Modo.Cap. 22.
 che non mi soccorreno alla memoria. Questo si può trasportare per vna Diapente nel graue, con l'aiuto
della chorda
che non mi soccorreno alla memoria. Questo si può trasportare per vna Diapente nel graue, con l'aiuto
della chorda  , lassando la
, lassando la  ; si come de gli altri si è fatto nell'acuto, & la sua chorda finale verrà ad essere
la
; si come de gli altri si è fatto nell'acuto, & la sua chorda finale verrà ad essere
la  ; come ciascuno potrà vedere.
; come ciascuno potrà vedere.
Del Sesto Modo.Cap. 23.
 duto composte in questo Modo: ma al presente mi soccorreno alla memoria solamente queste; Vn motetto di
Motone a quattro voci, Ecce Maria genuit nobis Saluatorem, & vn Salmo a due chori spezzati di Adriano a otto voci, Inconuertendo Dominus captiuitatem Syon. Questo etiandio si può trasportare nell'acuto
per vna Quarta, con l'aiuto della chorda
duto composte in questo Modo: ma al presente mi soccorreno alla memoria solamente queste; Vn motetto di
Motone a quattro voci, Ecce Maria genuit nobis Saluatorem, & vn Salmo a due chori spezzati di Adriano a otto voci, Inconuertendo Dominus captiuitatem Syon. Questo etiandio si può trasportare nell'acuto
per vna Quarta, con l'aiuto della chorda  , come si trasportano gli altri; ilche quanto sia facile, ciascuno
lo potrà conoscere dalle due nominate cantilene.
, come si trasportano gli altri; ilche quanto sia facile, ciascuno
lo potrà conoscere dalle due nominate cantilene.
Del Settimo Modo.Cap. 24.
 , d & g; come qui si veggono. page 328
, d & g; come qui si veggono. page 328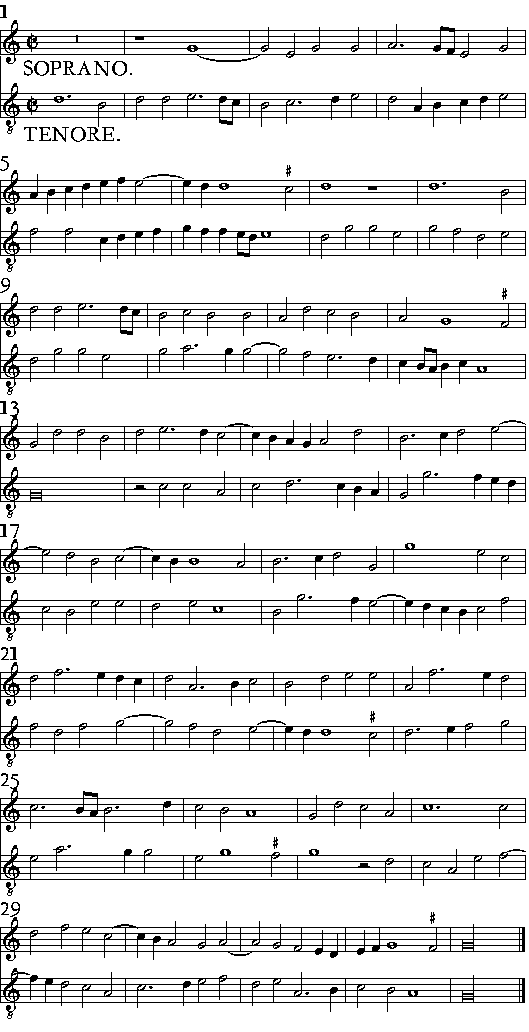 Ma le Irregolari si pongono sopra le altre. Molte cantilene si trouano composte dalli Musici di questo Modo, tra le quali sono Pater peccaui, & I piansi hor canto di Adriano a sei voci. Questo Modo è molto in vso
appresso gli Ecclesiastici; & nelle cantilene de gli altri Musici si troua il più delle volte nelle sue chorde naturali; ma
molte volte con l'aiuto della chorda
Ma le Irregolari si pongono sopra le altre. Molte cantilene si trouano composte dalli Musici di questo Modo, tra le quali sono Pater peccaui, & I piansi hor canto di Adriano a sei voci. Questo Modo è molto in vso
appresso gli Ecclesiastici; & nelle cantilene de gli altri Musici si troua il più delle volte nelle sue chorde naturali; ma
molte volte con l'aiuto della chorda  è trasportato nel graue per vna Diapente, senza alcuno incommodo.
è trasportato nel graue per vna Diapente, senza alcuno incommodo.
Dell'Ottauo Modo.Cap. 25.
 ,
G & D: ma gli Irregolari si trouano nelle altre chorde; & le sue Cadenze regolari si pongono simigliantemente nelle mostrate quattro chorde, si come nel sottoposto essempio si può vedere. page 329
,
G & D: ma gli Irregolari si trouano nelle altre chorde; & le sue Cadenze regolari si pongono simigliantemente nelle mostrate quattro chorde, si come nel sottoposto essempio si può vedere. page 329 Ma le Irregolari si pongono sopra l'altre chorde. Appresso gli altri Musici si trouano molte compositioni, tra lequali si trouano li motetti Benedicta es coelorum regina di Iosquino, & Audite insulae a
sei voci; Verbum supernum prodiens, il madrigale Liete, & pensose, accompagnate, & sole Donne,
tutti di Adriano a sette voci; & molti altri quasi infiniti. Questo Modo si può trasportare come gli
altri fuori delle sue chorde naturali, ponendolo in acuto per vna Diatessaron, con l'aiuto della chorda
Ma le Irregolari si pongono sopra l'altre chorde. Appresso gli altri Musici si trouano molte compositioni, tra lequali si trouano li motetti Benedicta es coelorum regina di Iosquino, & Audite insulae a
sei voci; Verbum supernum prodiens, il madrigale Liete, & pensose, accompagnate, & sole Donne,
tutti di Adriano a sette voci; & molti altri quasi infiniti. Questo Modo si può trasportare come gli
altri fuori delle sue chorde naturali, ponendolo in acuto per vna Diatessaron, con l'aiuto della chorda  :
imperoche altramente sarebbe impossibile.
:
imperoche altramente sarebbe impossibile.
Del Nono modo.Cap. 26.
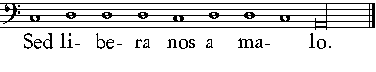 ti. Si troua ancho di questo Modo il Simbolo Niceno,
Credo in vnum Deum, ilquale hà principio per la sua
Intonatione nella chorda D, & viene à terminare
(come si vede ne i corretti essemplari) nella chorda A
medesimamente, & non nella
ti. Si troua ancho di questo Modo il Simbolo Niceno,
Credo in vnum Deum, ilquale hà principio per la sua
Intonatione nella chorda D, & viene à terminare
(come si vede ne i corretti essemplari) nella chorda A
medesimamente, & non nella  , ouero nella E trasportato per vna Diatessaron nell'acuto con l'aiuto della chorda
, ouero nella E trasportato per vna Diatessaron nell'acuto con l'aiuto della chorda  , come fanno; ilqual canto trasportato douerebbe finire nella chorda D, come è il douere: ma
, come fanno; ilqual canto trasportato douerebbe finire nella chorda D, come è il douere: ma
 è stato guasto, &
scorretto per la ignoranza de i scrittori;
come intrauiene anche nelle altre cose
di maggiore importanza. Et non solamente li fini delli mostrati canti si ritrouano fuori della loro propia, &
natural chorda; ma de gli altri ancora, che si trouano in tal maniera guasti, & corrotti, che sarebbe cosa
troppo lunga da mostrare, quando si volesse dare di ciascuno vno essempio particolare. Ma quanto sia facile
il trasmutare ne i Canti ecclesiastici vn Modo nell'altro, variando solamente la chorda finale, ouero trasportandolo dall'acuto al graue, ouero dal graue all'acuto, senza alcuno aiuto della chorda
è stato guasto, &
scorretto per la ignoranza de i scrittori;
come intrauiene anche nelle altre cose
di maggiore importanza. Et non solamente li fini delli mostrati canti si ritrouano fuori della loro propia, &
natural chorda; ma de gli altri ancora, che si trouano in tal maniera guasti, & corrotti, che sarebbe cosa
troppo lunga da mostrare, quando si volesse dare di ciascuno vno essempio particolare. Ma quanto sia facile
il trasmutare ne i Canti ecclesiastici vn Modo nell'altro, variando solamente la chorda finale, ouero trasportandolo dall'acuto al graue, ouero dal graue all'acuto, senza alcuno aiuto della chorda  , questo è facile da
vedere, da tutti coloro, che sono prattici nella Musica; se'l si vorrà essaminare minutamente le loro modulationi, & il loro procedere; laqual cosa non sarebbe molto difficile da mostrare, quando intorno a ciò si volesse perdere vn poco di tempo. In questo Modo si ritroua composta l'Antifona Aue Maria gratia plena, laquale ne i libri antichi si troua terminata tra le sue chorde naturali in cotal modo; che nelli moderni si troua
, questo è facile da
vedere, da tutti coloro, che sono prattici nella Musica; se'l si vorrà essaminare minutamente le loro modulationi, & il loro procedere; laqual cosa non sarebbe molto difficile da mostrare, quando intorno a ciò si volesse perdere vn poco di tempo. In questo Modo si ritroua composta l'Antifona Aue Maria gratia plena, laquale ne i libri antichi si troua terminata tra le sue chorde naturali in cotal modo; che nelli moderni si troua
 scritta più graue per vna Diapente. Et che
ciò sia vero, da questo potemo comprendere, che P. della Rue compose la Messa a
quattro voci sopra questa Antifona nelle
chorde uere, & essentiali di tal Modo; nel
quale si troua etiandio composto l'Introito Gaudeamus omnes in Domino. Ne alcuno prenda di questo marauiglia; massimamente vedendo, che la Salmodia del Salmo, che segue è del Primo modo: percioche (come hò detto ancora) non è inconueniente, che ciascuno de i Quattro vltimi Modi si possa ridurre alla Intonatione di alcuna delle
Otto nominate Salmodie. Et se la chorda
scritta più graue per vna Diapente. Et che
ciò sia vero, da questo potemo comprendere, che P. della Rue compose la Messa a
quattro voci sopra questa Antifona nelle
chorde uere, & essentiali di tal Modo; nel
quale si troua etiandio composto l'Introito Gaudeamus omnes in Domino. Ne alcuno prenda di questo marauiglia; massimamente vedendo, che la Salmodia del Salmo, che segue è del Primo modo: percioche (come hò detto ancora) non è inconueniente, che ciascuno de i Quattro vltimi Modi si possa ridurre alla Intonatione di alcuna delle
Otto nominate Salmodie. Et se la chorda  posta in luogo della
posta in luogo della  hà possanza di mutare vn Modo nell'altro; page 331non è dubbio, che ritrouandosi il detto Introito collocato nella Quarta specie della Diapason, & cantandosi
per la propietà di
hà possanza di mutare vn Modo nell'altro; page 331non è dubbio, che ritrouandosi il detto Introito collocato nella Quarta specie della Diapason, & cantandosi
per la propietà di  molle, non sia anco del Nono modo; come essaminando il tutto, & quello, che hò detto
di sopra nel Cap. 16. manifestamente si può vedere. Ma quando si volesse ridurre nelle sue vere chorde naturali, trasportandolo nell'acuto per vna Diapente, si trouerebbe collocato tra la Prima specie della Diapason a & aa; si come fece il Dotto Iosquino, che componendo a quattro voci la Messa sopra questo Introi-
to, la ritirò nelle sue chorde naturali; come si può vedere. La onde mi souiene hora, che alcuni non hanno detto male, quando giudicarono, che la Intonatione del Salmo, In exitu Israel de Aegypto, posta qui di sotto,
molle, non sia anco del Nono modo; come essaminando il tutto, & quello, che hò detto
di sopra nel Cap. 16. manifestamente si può vedere. Ma quando si volesse ridurre nelle sue vere chorde naturali, trasportandolo nell'acuto per vna Diapente, si trouerebbe collocato tra la Prima specie della Diapason a & aa; si come fece il Dotto Iosquino, che componendo a quattro voci la Messa sopra questo Introi-
to, la ritirò nelle sue chorde naturali; come si può vedere. La onde mi souiene hora, che alcuni non hanno detto male, quando giudicarono, che la Intonatione del Salmo, In exitu Israel de Aegypto, posta qui di sotto,
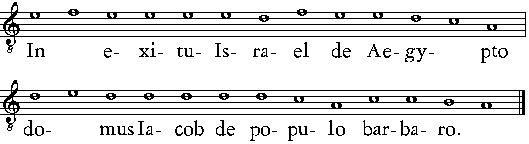 fusse del Nono modo: percio che vogliono, che la Antifona, Nos qui viuimus benedicimus Dominum, sia
stata guasta, & trasportata fuori del suo luogo, da alcuno scrittore, che habbia voluto mostrarsi più saggio
de gli altri; si come hanno fatto anche dell'altre. Questo Modo hà, come hanno gli altri Modi, li suoi Principij, & le sue Cadenze regolari, & irregolari. Li Regolari sono quelli, che si pongono nelle chorde A,
C, E & a, si come etiandio le Cadenze, che si vedeno in questo essempio.
fusse del Nono modo: percio che vogliono, che la Antifona, Nos qui viuimus benedicimus Dominum, sia
stata guasta, & trasportata fuori del suo luogo, da alcuno scrittore, che habbia voluto mostrarsi più saggio
de gli altri; si come hanno fatto anche dell'altre. Questo Modo hà, come hanno gli altri Modi, li suoi Principij, & le sue Cadenze regolari, & irregolari. Li Regolari sono quelli, che si pongono nelle chorde A,
C, E & a, si come etiandio le Cadenze, che si vedeno in questo essempio.
 page 332Ma li Principij, & similmente le Cadenze irregolari si pongono nell'altre chorde. Trouansi in questo Modo composte varie cantilene, tra le quali è il motetto, Spem in alium nunquàm habui di Giachetto, & Sancta, & immaculata virginitas di Morale Spagnuolo, l'uno & l'altro composto a quattro voci, & le due nominate Messe. Composi gia anche io sotto questo
Modo il motetto, Si bona suscepimus de manu Domini, il
madrigale, I vò piangendo il mio passato tempo, a cinque voci, & altre cose etiandio, le quali non nomino.
Ma questo Modo si può trasportare per vna Diapente nel graue, con l'aiuto della chorda
page 332Ma li Principij, & similmente le Cadenze irregolari si pongono nell'altre chorde. Trouansi in questo Modo composte varie cantilene, tra le quali è il motetto, Spem in alium nunquàm habui di Giachetto, & Sancta, & immaculata virginitas di Morale Spagnuolo, l'uno & l'altro composto a quattro voci, & le due nominate Messe. Composi gia anche io sotto questo
Modo il motetto, Si bona suscepimus de manu Domini, il
madrigale, I vò piangendo il mio passato tempo, a cinque voci, & altre cose etiandio, le quali non nomino.
Ma questo Modo si può trasportare per vna Diapente nel graue, con l'aiuto della chorda  , come si trasporta etiandio gli altri.
, come si trasporta etiandio gli altri.
Del Decimo Modo.Cap. 27.
 , senza laquale poco si farebbe, che fusse buono. page 333
, senza laquale poco si farebbe, che fusse buono. page 333
Dell'Vndecimo modo.Cap. 28.
 in
luogo dellla
in
luogo dellla  , hanno mutato nell'Vndecimo; indutti dalla sua soauità, & dalla sua bellezza. Li suoi
Principij si pongono regolarmente nelle chorde C, E, G & c, & cosi anche le sue Cadenze. Et li
suoi Principij, & Cadenze irregolari si pongono sopra le altre chorde. Li Musici hanno composte in questo Modo molte cantilene, tra le quali è, Stabat mater dolorosa di Iosquino a cinque voci; O salutaris hostia,
Alma redemptoris mater, Pien d'vn vago pensier di Adriano; & Descendi in ortum meum di Giachetto, tutti composti a sei voci. Cosi ancora il motetto, Audi filia, & vide di Gomberto, con Ego veni in
hortum meum, il quale gia molti anni composi, che sono a cinque voci; & infiniti altri, che lungo sarebbe
il numerarli. Questo Modo si trasporta fuori delle sue chorde naturali per vna Diatessaron nell'acuto; ouero per vna Diapente nel graue, con l'aiuto della chorda
, hanno mutato nell'Vndecimo; indutti dalla sua soauità, & dalla sua bellezza. Li suoi
Principij si pongono regolarmente nelle chorde C, E, G & c, & cosi anche le sue Cadenze. Et li
suoi Principij, & Cadenze irregolari si pongono sopra le altre chorde. Li Musici hanno composte in questo Modo molte cantilene, tra le quali è, Stabat mater dolorosa di Iosquino a cinque voci; O salutaris hostia,
Alma redemptoris mater, Pien d'vn vago pensier di Adriano; & Descendi in ortum meum di Giachetto, tutti composti a sei voci. Cosi ancora il motetto, Audi filia, & vide di Gomberto, con Ego veni in
hortum meum, il quale gia molti anni composi, che sono a cinque voci; & infiniti altri, che lungo sarebbe
il numerarli. Questo Modo si trasporta fuori delle sue chorde naturali per vna Diatessaron nell'acuto; ouero per vna Diapente nel graue, con l'aiuto della chorda  ; passando per le chorde del Tetrachordo synemennon. page 334
; passando per le chorde del Tetrachordo synemennon. page 334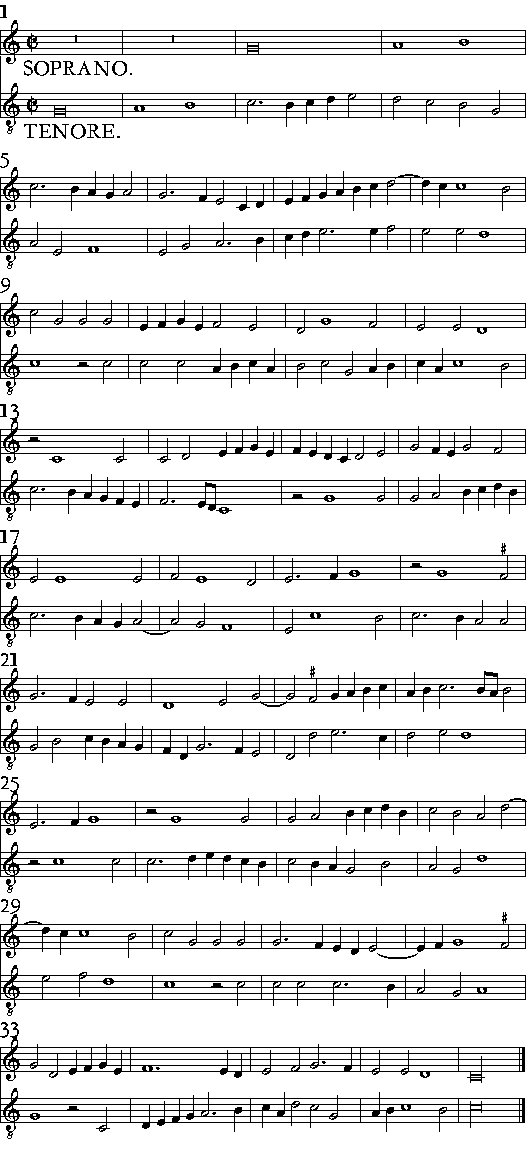
Del Duodecimo Modo.Cap. 29.
 , hanno fatto la maggior parte delle loro cantilene, che erano del Sesto modo, del modo Duodecimo; & hanno anche composto li più moderni noue cantilene in questo Modo; tra le quali si troua l'Antifona Aue regina coelorum, & molte altre. Questo Modo,
è atto alle cose amatorie, che contengono cose lamenteuoli: perche è nelli Canti fermi Modo lamenteuole, &
hà alquanto di mestitia, secondo il loro parere; tuttauia ciascuno compositore, che desidera di fare alcuna cantilena, che sia allegra, non si sa partire da lui. Li suoi Principij regolari si pongono insieme con le sue regolari Cadenze, come nello essempio si vede, nelle chorde g, e, c & G; Li Principij, & Cadenze irregolari poi si pongono sopra l'altre chorde. Si trouano di questo Modo innumerabili cantilene composte da molti Musici prattici, tra le quali è il motetto, Inuiolata integra, & casta es Maria di Iosquino a cinque, & di
Adriano a sette voci; il motetto Mittit ad virginem a sei, & li madrigali, Quando nascesti Amor a sette
voci, I vidi in terra angelici costumi a sei voci, & Quando fra l'altre donne a cinque voci, tutti composti da
Adriano; A questi si aggiunge il motetto, di Giachetto a cinque voci, Decantabat populus, & li motetti page 335
, hanno fatto la maggior parte delle loro cantilene, che erano del Sesto modo, del modo Duodecimo; & hanno anche composto li più moderni noue cantilene in questo Modo; tra le quali si troua l'Antifona Aue regina coelorum, & molte altre. Questo Modo,
è atto alle cose amatorie, che contengono cose lamenteuoli: perche è nelli Canti fermi Modo lamenteuole, &
hà alquanto di mestitia, secondo il loro parere; tuttauia ciascuno compositore, che desidera di fare alcuna cantilena, che sia allegra, non si sa partire da lui. Li suoi Principij regolari si pongono insieme con le sue regolari Cadenze, come nello essempio si vede, nelle chorde g, e, c & G; Li Principij, & Cadenze irregolari poi si pongono sopra l'altre chorde. Si trouano di questo Modo innumerabili cantilene composte da molti Musici prattici, tra le quali è il motetto, Inuiolata integra, & casta es Maria di Iosquino a cinque, & di
Adriano a sette voci; il motetto Mittit ad virginem a sei, & li madrigali, Quando nascesti Amor a sette
voci, I vidi in terra angelici costumi a sei voci, & Quando fra l'altre donne a cinque voci, tutti composti da
Adriano; A questi si aggiunge il motetto, di Giachetto a cinque voci, Decantabat populus, & li motetti page 335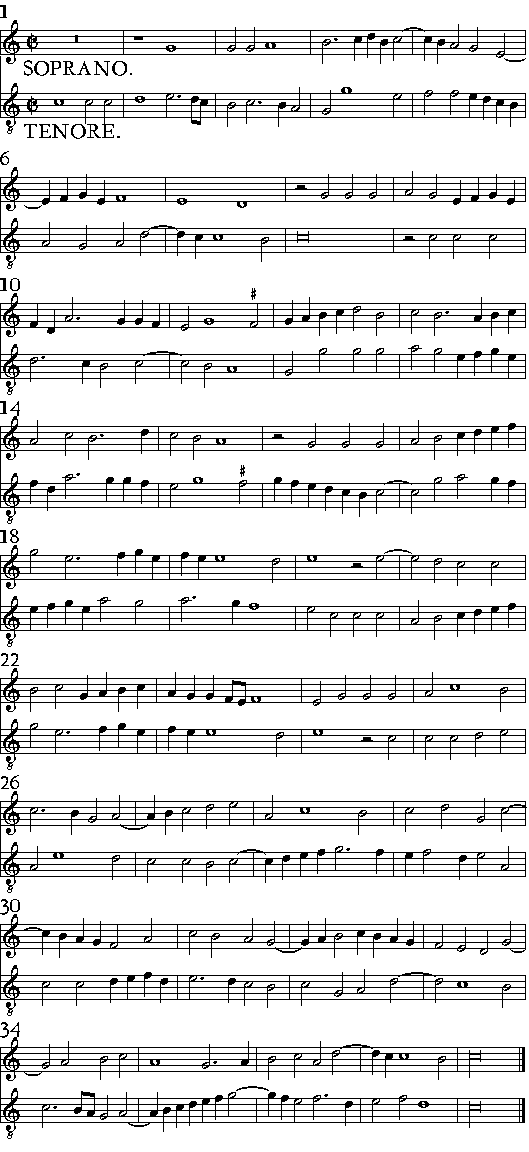 Nemo venit ad me a cinque uoci, & O quàm gloriosum est regnum, i quali gia molto tempo composi l'uno
a cinque, & l'altro a sei uoci, & molti altri. Et benche le chorde naturali di questo Modo siano le mostrate di sopra; tuttauia li Musici, con l'aiuto della chorda
Nemo venit ad me a cinque uoci, & O quàm gloriosum est regnum, i quali gia molto tempo composi l'uno
a cinque, & l'altro a sei uoci, & molti altri. Et benche le chorde naturali di questo Modo siano le mostrate di sopra; tuttauia li Musici, con l'aiuto della chorda  , lo trasportano per vna Diatessaron nel graue.
Ma tutto questo sia detto a sufficienza intorno la Natura, & la Propietà delli Modi, & intorno l'uso, li
Principij, & le Cadenze di ciascuno: imperoche fa dibisogno, che noi mostriamo primieramente quello, che
si hà da osseruare nel comporre, & nel far giuditio di loro; dipoi in qual maniera ciascuna parte delle nostre
cantilene si debba accommodare in essi; & quanto ciascuna possa ascendere, & discendere; accioche si ponga il termine de i loro estremi, & si schiui ogni confusione. page 336
, lo trasportano per vna Diatessaron nel graue.
Ma tutto questo sia detto a sufficienza intorno la Natura, & la Propietà delli Modi, & intorno l'uso, li
Principij, & le Cadenze di ciascuno: imperoche fa dibisogno, che noi mostriamo primieramente quello, che
si hà da osseruare nel comporre, & nel far giuditio di loro; dipoi in qual maniera ciascuna parte delle nostre
cantilene si debba accommodare in essi; & quanto ciascuna possa ascendere, & discendere; accioche si ponga il termine de i loro estremi, & si schiui ogni confusione. page 336Quello, che de osseruare il Compositore componendo, & in qual maniera si habbia da far giuditio delli Modi. Capitolo 30.
 , posta nel graue,
hanno la Seconda della Diatessaron E & a; & in luogo della Seconda della Diatessaron
, posta nel graue,
hanno la Seconda della Diatessaron E & a; & in luogo della Seconda della Diatessaron  & e, si
troua la Prima specie della Diapente a & e, posta nell'acuto; Di maniera che se ben le dette specie sono
contenute sotto vna istessa Diapason, che è la E & e; nondimeno si troua nell'vno Modo tramezata harmonicamente, & tiene la forma del Terzo modo; & nell'altro arithmeticamente, & tiene la forma
del Decimo: La onde vdendosi tali specie tante, & tante volte replicate, non solamente la maggior parte della
compositione viene a non hauere parte alcuna del Terzo: ma tutta la cantilena viene ad esser composta sotto'l Decimo modo. Et che ciò sia il vero, da questo si può comprendere, che se noi aggiungeremo queste due
specie insieme, cioè la Diatessaron E & a, & la Diapente a & e, collocando questa nell'acuto, &
quella nel graue; non è dubbio, che haueremo la forma del Decimo modo, contenuto tra la Quinta specie della Diapason arithmeticamente mediata. Di maniera che quella compositione, che noi giudichiamo esser del
Terzo modo, non viene ad hauer cosa alcuna, per la quale possiamo far giuditio, che sia di tal Modo, se non
il fine: percioche finisce nella chorda E. Però adunque se bene la chorda finale del Modo è quella, dalla quale (come dal fine) douemo far giuditio della cantilena, & non auanti; come alcuni vogliono: essendo che
ogni cosa drittamente si giudica dal fine; non douemo però intendere, che per tal chorda semplicemente noi possiamo venire in cognitione del Modo, sopra il quale è fondata la cantilena: percioche non si dè credere, che da
lei si debba fare il giuditio: ma che noi debbiamo aspettare tanto, che la cantilena sia condotta al
fine; & iui giudicare secondo il dritto: conciosia che allora la cantilena è perfetta, & hà la sua vera forma,
dalla quale si prende la occasione di fare tal giuditio. Ma si dè notare, che da due cose si può pigliare simile
occasione: prima dalla forma di tutta la cantilena; dipoi dal suo fine, cioè dalla sua chorda finale. La onde
essendo la forma quella, che dà l'essere alla cosa; giudicarei, che fusse ragioneuole, che non dalla chorda finale
semplicemente; come hanno voluto alcuni: ma dalla forma tutta contenuta nella cantilena, si hauesse da fare tal giuditio. Onde dico, che se io hauessi da giudicare alcuna cantilena da tal forma, cioè dal procedere, come è il douere; non hauerei per inconueniente, che il Modo principale potesse finire nella chorda mezana della sua Diapason harmonicamente tramezata; & cosi il Modo collaterale nelle estreme della sua Diapason
arithmeticamente diuisa; lassando da un canto la chorda finale. Il che quanto gentilmente si possa fare, si
può comprendere dal motetto, Si bona suscepimus de manu Domini a cinque voci, composto da Verdeloto,
& dal madrigale, O inuidia nemica di virtute di Adriano composto medesimamente a cinque voci; li quali
da vn capo all'altro, l'vno hà il procedere del Nono modo, & l'altro hà il procedere del Secondo; tuttauia non
finiscono nella loro vera chorda finale: ma nella mezana. Et questo ch'io dico del Terzo, & del Decimo modo, si potrebbe anche
mostrare ne gli altri, i quali per breuità lasso da vn canto. Per la qual cosa non è da marauigliarsi, se molte volte non
si ode alcuna differenza tra vn Modo, che finisca nella chorda E; & tra un'
altro, che termini nella a; poi che nella maniera, che si è detto, si compongono misti: Ma se si componessero
semplici senza alcuna mistione; non è dubbio, che si vdirebbe grande varietà di harmonia tra l'vno, & l'altro. Quando adunque haueremo da far giuditio di qualunque si voglia cantilena, noi haueremo da considerarla
bene dal principio al fine; & vedere sotto qual forma ella si troua esser composta; se sotto la forma del Primo, o del Secondo, o di qualunque altro Modo; hauendo riguardo alle Cadenze, le quali danno gran lume in
tale cosa; & dipoi far giuditio, in qual Modo ella sia composta; ancora che non hauesse il suo fine nella sua
propia chorda finale: ma si bene nella mezana, ouero in qualunque altra, che tornasse al proposito. Et se noi page 337vsaremo una tal maniera di finire, non sarà fatto fuori di proposito: essendo che gli Ecclesiastici anco hanno
vsato vn tal modo nelle loro cantilene; come si può vedere ne i κύριε ἐλέησον, i quali chiamano di Doppio
minore, ouero de gli Apostoli; la cui forma (come è manifesto) è del Primo modo; nondimeno l'ultimo di
essi finisce nella chorda a, la quale chiamano Confinale, & è la mezana della Diapason D & d, continente la forma del Primo modo; oltra che si troua l'Offertorio, che si canta nella Messa della Quarta feria
della Dominica terza di Quadragesima, Domine fac meum secundum misericordiam tuam, contenuto tra
le sue chorde estreme F & e. Et due cantilene; la prima delle quali è, Tollite hostias, contenuta tra le nominate chorde estreme, che si canta fatta la Communione della Messa della Dominica Decima ottaua dopo
la Pentecoste; la seconda è, Per signum Crucis, che si canta ne i giorni solenni della Inuentione, & della Essaltatione di Santa Croce; & è contenuta tra le chorde estreme F & g: le quali cantilene tengono in se
la forma del Settimo modo: percioche in esse si troua la modulatione della sua Diapente G & d; & della sua Diatessaron d & g: & finiscono nella chorda
& e, si
troua la Prima specie della Diapente a & e, posta nell'acuto; Di maniera che se ben le dette specie sono
contenute sotto vna istessa Diapason, che è la E & e; nondimeno si troua nell'vno Modo tramezata harmonicamente, & tiene la forma del Terzo modo; & nell'altro arithmeticamente, & tiene la forma
del Decimo: La onde vdendosi tali specie tante, & tante volte replicate, non solamente la maggior parte della
compositione viene a non hauere parte alcuna del Terzo: ma tutta la cantilena viene ad esser composta sotto'l Decimo modo. Et che ciò sia il vero, da questo si può comprendere, che se noi aggiungeremo queste due
specie insieme, cioè la Diatessaron E & a, & la Diapente a & e, collocando questa nell'acuto, &
quella nel graue; non è dubbio, che haueremo la forma del Decimo modo, contenuto tra la Quinta specie della Diapason arithmeticamente mediata. Di maniera che quella compositione, che noi giudichiamo esser del
Terzo modo, non viene ad hauer cosa alcuna, per la quale possiamo far giuditio, che sia di tal Modo, se non
il fine: percioche finisce nella chorda E. Però adunque se bene la chorda finale del Modo è quella, dalla quale (come dal fine) douemo far giuditio della cantilena, & non auanti; come alcuni vogliono: essendo che
ogni cosa drittamente si giudica dal fine; non douemo però intendere, che per tal chorda semplicemente noi possiamo venire in cognitione del Modo, sopra il quale è fondata la cantilena: percioche non si dè credere, che da
lei si debba fare il giuditio: ma che noi debbiamo aspettare tanto, che la cantilena sia condotta al
fine; & iui giudicare secondo il dritto: conciosia che allora la cantilena è perfetta, & hà la sua vera forma,
dalla quale si prende la occasione di fare tal giuditio. Ma si dè notare, che da due cose si può pigliare simile
occasione: prima dalla forma di tutta la cantilena; dipoi dal suo fine, cioè dalla sua chorda finale. La onde
essendo la forma quella, che dà l'essere alla cosa; giudicarei, che fusse ragioneuole, che non dalla chorda finale
semplicemente; come hanno voluto alcuni: ma dalla forma tutta contenuta nella cantilena, si hauesse da fare tal giuditio. Onde dico, che se io hauessi da giudicare alcuna cantilena da tal forma, cioè dal procedere, come è il douere; non hauerei per inconueniente, che il Modo principale potesse finire nella chorda mezana della sua Diapason harmonicamente tramezata; & cosi il Modo collaterale nelle estreme della sua Diapason
arithmeticamente diuisa; lassando da un canto la chorda finale. Il che quanto gentilmente si possa fare, si
può comprendere dal motetto, Si bona suscepimus de manu Domini a cinque voci, composto da Verdeloto,
& dal madrigale, O inuidia nemica di virtute di Adriano composto medesimamente a cinque voci; li quali
da vn capo all'altro, l'vno hà il procedere del Nono modo, & l'altro hà il procedere del Secondo; tuttauia non
finiscono nella loro vera chorda finale: ma nella mezana. Et questo ch'io dico del Terzo, & del Decimo modo, si potrebbe anche
mostrare ne gli altri, i quali per breuità lasso da vn canto. Per la qual cosa non è da marauigliarsi, se molte volte non
si ode alcuna differenza tra vn Modo, che finisca nella chorda E; & tra un'
altro, che termini nella a; poi che nella maniera, che si è detto, si compongono misti: Ma se si componessero
semplici senza alcuna mistione; non è dubbio, che si vdirebbe grande varietà di harmonia tra l'vno, & l'altro. Quando adunque haueremo da far giuditio di qualunque si voglia cantilena, noi haueremo da considerarla
bene dal principio al fine; & vedere sotto qual forma ella si troua esser composta; se sotto la forma del Primo, o del Secondo, o di qualunque altro Modo; hauendo riguardo alle Cadenze, le quali danno gran lume in
tale cosa; & dipoi far giuditio, in qual Modo ella sia composta; ancora che non hauesse il suo fine nella sua
propia chorda finale: ma si bene nella mezana, ouero in qualunque altra, che tornasse al proposito. Et se noi page 337vsaremo una tal maniera di finire, non sarà fatto fuori di proposito: essendo che gli Ecclesiastici anco hanno
vsato vn tal modo nelle loro cantilene; come si può vedere ne i κύριε ἐλέησον, i quali chiamano di Doppio
minore, ouero de gli Apostoli; la cui forma (come è manifesto) è del Primo modo; nondimeno l'ultimo di
essi finisce nella chorda a, la quale chiamano Confinale, & è la mezana della Diapason D & d, continente la forma del Primo modo; oltra che si troua l'Offertorio, che si canta nella Messa della Quarta feria
della Dominica terza di Quadragesima, Domine fac meum secundum misericordiam tuam, contenuto tra
le sue chorde estreme F & e. Et due cantilene; la prima delle quali è, Tollite hostias, contenuta tra le nominate chorde estreme, che si canta fatta la Communione della Messa della Dominica Decima ottaua dopo
la Pentecoste; la seconda è, Per signum Crucis, che si canta ne i giorni solenni della Inuentione, & della Essaltatione di Santa Croce; & è contenuta tra le chorde estreme F & g: le quali cantilene tengono in se
la forma del Settimo modo: percioche in esse si troua la modulatione della sua Diapente G & d; & della sua Diatessaron d & g: & finiscono nella chorda  , la quale è la mezana della detta Diapente. E
ben vero, che alcuni moderni attribuiscono tali canti al Quartodecimo modo; come dicono: ma di questo lassarò far giuditio ad ogn'uno, che habbia intelletto. Tali canti, in alcuni de i libri moderni, si trouano trasportati nel
graue per una Diapente, senza l'aiuto della chorda
, la quale è la mezana della detta Diapente. E
ben vero, che alcuni moderni attribuiscono tali canti al Quartodecimo modo; come dicono: ma di questo lassarò far giuditio ad ogn'uno, che habbia intelletto. Tali canti, in alcuni de i libri moderni, si trouano trasportati nel
graue per una Diapente, senza l'aiuto della chorda  , fuora delle loro chorde naturali; sia stata la
ignoranza, ouero dapocaggine delli scrittori; o pure la presuntione di alcuni altri poco intendenti: ma nelli
buoni, & corretti essemplari, de i quali ne hò fin hora uno appresso di me antico scritto a mano, che si può ancora vedere, & essaminare; si trouano tra le chorde nominate di sopra. Ma si dè auertire, ch'io nomino la
forma del Modo, la Ottaua diuisa nella Quinta, & nella Quarta; & anco queste due parti, che nascono dalla diuisione harmonica,
& arithmetica, che si odeno replicate molte fiate ne i propij Modi. Quando adunque
haueremo da comporre, potremo sapere da quello, che si è detto, il modo, che haueremo da tenere, nel
far cantare le parti della cantilena; & nel porre le Cadenze a i luoghi conuenienti, per la distintione
delle parole. Et simigliantemente potremo sapere quello, che haueremo da fare nel giudicare ogn'altra compositione, sia poi in qual maniera si voglia composta, tanto nel Canto fermo, quanto nel
Canto figurato.
, fuora delle loro chorde naturali; sia stata la
ignoranza, ouero dapocaggine delli scrittori; o pure la presuntione di alcuni altri poco intendenti: ma nelli
buoni, & corretti essemplari, de i quali ne hò fin hora uno appresso di me antico scritto a mano, che si può ancora vedere, & essaminare; si trouano tra le chorde nominate di sopra. Ma si dè auertire, ch'io nomino la
forma del Modo, la Ottaua diuisa nella Quinta, & nella Quarta; & anco queste due parti, che nascono dalla diuisione harmonica,
& arithmetica, che si odeno replicate molte fiate ne i propij Modi. Quando adunque
haueremo da comporre, potremo sapere da quello, che si è detto, il modo, che haueremo da tenere, nel
far cantare le parti della cantilena; & nel porre le Cadenze a i luoghi conuenienti, per la distintione
delle parole. Et simigliantemente potremo sapere quello, che haueremo da fare nel giudicare ogn'altra compositione, sia poi in qual maniera si voglia composta, tanto nel Canto fermo, quanto nel
Canto figurato.
Del modo, che si hà da tenere, nell'accommodar le parti della cantilena; & delle estremità loro; & quanto le chorde estreme acute di ciascuna di quelle, che sono poste nell'acuto, possino esser lontane dalla estrema chorda posta nel graue del concento. Cap. 31.
 . & nella Seconda parte dia principio sopra la chorda
. & nella Seconda parte dia principio sopra la chorda  :
o per il contrario. Sarà adunque auertito il Compositore di tal cosa, accioche la sua compositione sia purgata
da ogni errore, & da ogni discommodo; & lui sia riputato buono, & perfetto Musico.
:
o per il contrario. Sarà adunque auertito il Compositore di tal cosa, accioche la sua compositione sia purgata
da ogni errore, & da ogni discommodo; & lui sia riputato buono, & perfetto Musico.
In qual maniera le Harmonie si accommodino alle soggette Parole.Cap. 32.
Versibus exponi Tragicis res Comica non vult:Percioche si come non è lecito tra i Poeti comporre vna Comedia con versi Tragici; cosi non sarà lecito al Musico di accompagnare queste due cose, cioè l'Harmonia, & le Parole insieme, fuori di proposito. Non sarà adunque conueniente, che in una materia allegra vsiamo l'Harmonia mesta, & i Numeri graui; ne doue si tratta materie funebri, & piene di lagrime, è lecito vsare vn'Harmonia allegra, & Numeri leggieri, o veloci, che li vogliamo dire. Per il contrario bisogna vsare le harmonie allegre, & li numeri veloci nelle materie allegre; & nelle materie meste le harmonie meste, & li numeri graui; accioche ogni cosa sia fatta con proportione. Il che penso, che ciascuno lo saprà fare ottimamente, quando hauerà riguardo a quello, che hò scritto nella Terza parte, & considerato la natura del Modo, sopra'l quale vorrà comporre la cantilena. Et debbe auertire di accompagnare in tal maniera ogni parola, che doue ella dinoti asprezza, durezza, crudeltà, amaritudine, & altre cose simili, l'harmonia sia simile a lei, cioè alquanto dura, & aspra; di maniera però, che non offendi. Simigliantemente quando alcuna delle parole dimostrarà pianto, dolore, cordoglio, sospiri, lagrime, & altre cose simili; che l'harmonia sia piena di mestitia. Il che farà ottimamente, volendo esprimere li primi effetti, quando vsarà di porre le parti della cantilena, che procedino per alcuni mouimenti senza il Semituono, come sono quelli del Tuono, & quelli del Ditono, facendo vdire la Sesta, ouero la Terzadecima maggiore, che per loro natura sono alquanto aspre, sopra la chorda più graue del concento; accompagnandole anco con la sincopa di Quarta, o con quella della Vndecima sopra tal parte, con mouimenti alquanto tardi, tra i quali si potrà vsare etiandio la sincopa della Settima. Ma quando vorrà esprimere li secondi effetti, allora vsarà (secondo l'osseruanza delle Regole date) li mouimenti, che procedeno per il Semituono: & per quelli del Semiditono, & gli altri simili; vsando spesso le Seste, ouero le Terzedecime minori sopra la chorda più graue della cantilena, che sono per natura loro dolci, et soaui; massimamente quando sono accompagnate con i debiti modi, & con discrettione, & giuditio. Ma si debbe auertire, che la cagione di esprimere simili effetti non si attribuisce solamente alle predette consonanze poste in tal maniera: ma si attribuisce etiandio alli Mouimenti, che fanno cantando le parti; li quali mouimenti sono di due sorti, cioè Naturali, et Accidentali. Li Naturali sono quelli, che si fanno tra le chorde naturali della cantilena, oue non intrauiene alcun segno, o chorda accidentale; et questi mouimenti hanno più del virile, che quelli, che si fanno col mezo delle page 340chorde accidentali, segnate con tali segni, i quali sono veramente accidentali, & hanno alquanto del languido; da i quali nasce similmente vna sorte di interualli, chiamati Accidentali: ma dalli primi nascono quelli interualli, che si chiamano Naturali. La onde douemo notare, che li primi mouimenti fanno la cantilena alquanto piùsonora, & virile; & li secondi più dolce, & alquanto più languida. Per il che li primi potranno seruire ad esprimere li primi effetti; & li secondi mouimenti potranno seruire a gli altri; di maniera che accompagnando gli interualli delle maggiori, & delle minori consonanze, con li mouimenti naturali, & accidentali, che fanno le parti, con qualche giuditio; si verrà ad imitare le parole con la bene intesa harmonia. Quanto poi alla osseruanza de i Numeri, considerata primieramente la materia contenuta nella Oratione; se sarà allegra, si dè procedere con mouimenti gagliardi, & veloci; cioè con figure, che portano seco velocità di tempo; come sono le Minime, & le Semiminime: Ma quando la materia sarà flebile, si dè procedere con mouimenti tardi, et lenti; come ne hà insegnato Adriano ad esprimere l'uno, & l'altro modo in più cantilene, tra le quali si troua queste, I vidi in terra angeli costumi; Aspro core e seluaggio; Oue ch'i posi gli occhi; tutte composte a sei voci; & Quando fra l'altre donne; Giunto m'ha Amor, a cinque voci; & infiniti altri, con infiniti motetti, li quali non nomino, per non andare in lungo. Et questo non solamente si de osseruare intorno li Numeri, ancora che gli Antichi intendessero tal cosa in vn'altra maniera, di quello, che fanno li Moderni; come si vede chiaramente in molti luoghi appresso di Platone: ma etiandio douemo osseruare, di accommodare in tal maniera le parole della Oratione alle figure cantabili, con tali Numeri, che non si oda alcun Barbarismo; si come quando si fà proferire nel canto vna sillaba longa, che si douerebbe far proferir breue: o per il contrario vna breue, che si douerebbe far proferir longa; come in infinite cantilene si ode ogni giorno; il che veramente è cosa vergognosa. Ne si ritroua questo vitio solamente nelli Canti figurati; ma anco nelli Canti fermi, si come è manifesto a tutti coloro, che hanno giuditio: Conciosia che pochi sono quelli, che non siano pieni di simili barbarismi; & che in essi infinite volte non si odi proferire le penultime sillabe di queste parole Dominus, Angelus, Filius, Miraculum, Gloria, & molte altre, che passano presto, con longhezza di tempo; il che sarebbe cosa molto lodeuole, & tanto facile da correggere, che mutandoli poco poco, si accommodarebbe la cantilena; ne per questo mutarebbe la sua prima forma: essendo che consiste solamente nella Legatura di molte figure, o note, che si pongono sotto le dette sillabe breui, che senza alcun proposito le fanno lunghe; quando sarebbe sofficiente vna sola figura. Si debbe similmente auertire, di non separare alcuna parte della Oratione l'vna dall'altra con Pause, come fanno alcuni poco intelligenti, fino a tanto, che non sia finita la sua Clausula, ouero alcuna sua parte; di maniera che'l sentimento delle parole sia perfetto; & di non far la Cadenza; massimamente l'vna delle principali; o di non porre le Pause maggiori di quelle della minima, se non è finito il Periodo, o la sentenza perfetta della Oratione; & quella di minima nelli punti mezani: percioche veramente è cosa vitiosa; la quale quanto sia osseruata da alcuni Prattici poco aueduti, ciascuno, che vorrà por mente a tal cosa, lo potrà con facilità vedere, & conoscere. Debbe adunque il Compositore in cose simili aprir gli occhi, & non li tenere chiusi: percioche è di molta importanza; accioche non sia riputato ignorante di una cosa tanto necessaria; & debbe auertire di porre la Pausa di minima, o di semiminima, si come li torna commodo, in capo delli mezani punti della Oratione: percioche seruiranno per li Coma: ma in capo delli Periodi debbe porre quanta quantità di pause, li tornerà commodo: percioche mi pare, che poste in cotal maniera, si potrà ottimamente discernere li membri del Periodo l'vno dall'altro; & vdire senza incommodo alcuno il sentimento perfetto delle parole.
Il modo, che si hà da tenere, nel porre le Figure cantabili sotto le Parole.Cap. 33.
Delle Legature.Cap. 34.